Prerpints.org logo

Submitted:

06 March 2023

Posted:

06 March 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Microlens arrays (MLAs) which are increasingly popular micro-optical elements in compact integrated optical systems were fabricated by femtosecond direct laser write (fs-DLW) technique in the low-shrinkage SZ2080TM photoresist. High fidelity definition of 3D surfaces on IR transparent CaF2 substrates allowed to achieve ∼ 50% transmittance at chemical fingerprinting spectral region 2-5 μm wavelengths since MLAs were only ∼ 10 μm high corresponding to the numerical aperture of 0.3 (the lens height is comparable with the IR wavelength). To combine diffractive and refractive capabilities in miniaturised optical setup, a graphene oxide (GO) grating acting as a linear polariser was also fabricated by fs-DLW by ablation of a 1 μm-thick GO thin film. Such an ultra-thin GO polariser can be integrated with the fabricated MLA to add dispersion control at the focal plane. Pairs of MLAs and GO polarisers were characterised throughout visible-IR spectral window and numerical modeling was used to simulate their performance. Good match between experimental results of MLA focusing and simulations was achieved.
Keywords: 
laser polymerisation pgaphene oxide polariser
;  
microlens array
Subject: 
Physical Sciences  -   Optics and Photonics

1. Introduction

Microlens arrays (MLAs) are widely used micro-optical elements in integrated optical systems for specific applications such as laser beam homogenisation [1,2], wavefront sensors [3,4], integrated optofluidic microchips [5,6], photoelectric devices [7,8], artificial compound eyes [9,10], and 3D light field imaging [11,12]. The focal length of MLA and image quality is dependent on the precision of its 3D surface definition, roughness and lens material. Therefore, how to precisely manufacture MLAs has always been a hot topic in academia and industry. Although a variety of fabrication strategies and processes have been proposed, such as surface-tension-effect-assisted technologies [13,14,15], ultra-high precision machining (UPM) [16,17] and photolithography [18,19], those methods are still limited by their own challenges. For example, the surface-tension-effect-assisted approach is simple and low-cost, which is suitable for mass production, but it is difficult to precisely control the surface geometry of the MLAs, which is indirectly affected by temperature, pressure, wettability and processing time. The UPM technologies can produce the MLAs with high-accuracy, whereas they require complex processes and are time-consuming. Lithography, as the core technology in the fabrication of integrated circuits, is a process for 2D manufacturing so there is no direct control of the required third-axis for the 3D surface morphology of the MLAs. In this study, the fs-DLW technique has been utilised as a 3D lithography tool to precisely fabricate the MLAs with the low-shrinkage SZ2080 TM photoresist [20]. The process of the 3D lithography via tight focusing of high-repetition femtosecond pulses is illustrated in Figure 1(a). Based on such an ultra-high precision (sub-wavelength) and flexible direct polymerisation, the radius of curvature of the fabricated microlens identical to the design can be achieved.
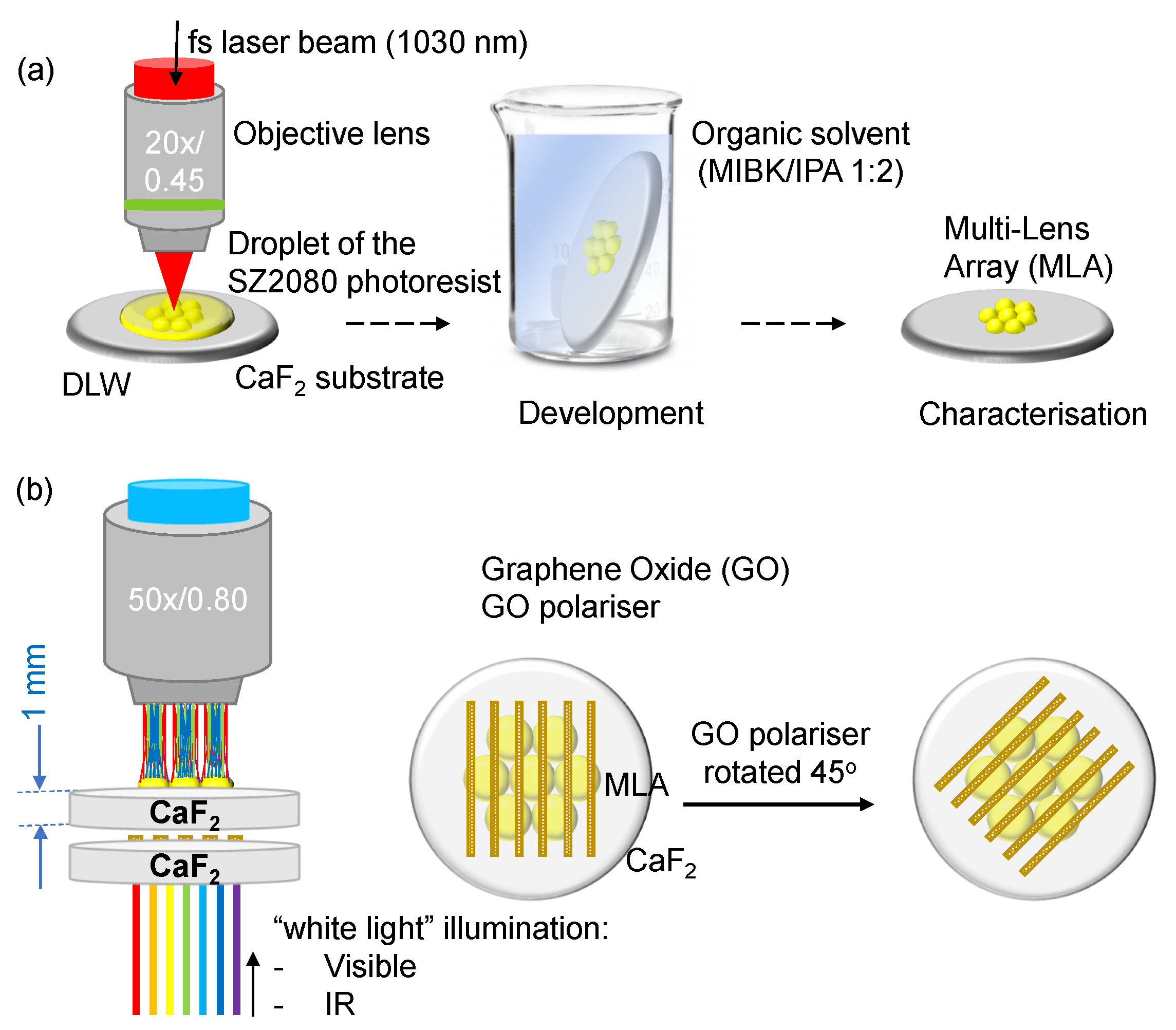
Preprints 69458 g001
Figure 1. (a) Manufacturing steps in 3D DLW lithography. Pinpoint (maskless and selective) photopolymerisation by tightly focused femtosecond pulsed laser beam. fs-DLW was carried out from the resist side due to thick 1 mm CaF2 substrate. Removal of unexposed volume by development in organic solvent (placing the sample with an angle to promote a cleaner development). Revelation of the fabricated MLA. (b) Optical characterisation of micro-optical elements (lenses/arrays and GO polarisers) at visible and IR spectral ranges; optical elements were made on IR transparent CaF2 substrate.
Figure 1. (a) Manufacturing steps in 3D DLW lithography. Pinpoint (maskless and selective) photopolymerisation by tightly focused femtosecond pulsed laser beam. fs-DLW was carried out from the resist side due to thick 1 mm CaF2 substrate. Removal of unexposed volume by development in organic solvent (placing the sample with an angle to promote a cleaner development). Revelation of the fabricated MLA. (b) Optical characterisation of micro-optical elements (lenses/arrays and GO polarisers) at visible and IR spectral ranges; optical elements were made on IR transparent CaF2 substrate.
Preprints 69458 g001
Functionality of MLAs as refractive optical elements can be enriched when combined with diffractive elements such as prism or grating. In this study, we used 2D graphene oxide (GO) grating as a polariser. Laser ablation of 2-4 μ m grooves with duty cycle ∼ 0.5 can define gratings functional at comparable IR wavelengths. This further requires an assessment of GO-polarisers and MLA lens performance at the infrared (IR) spectral region.
Here, the GO grating polariser was fabricated by ablating periodic air grooves in a 1 μ m GO thin film. Its polarisation performance in the IR region have been both experimentally and theoretically demonstrated with a Fourier transform infrared (FTIR) spectrometer and finite-difference time-domain method (FDTD; Lumerical, Ansys), respectively. Additionally, a formula fitting method was adopted and mathematically demonstrated to determine the contributions resulting from absorbance and retardance to the experimentally measured IR transmittance spectra. Such an ultrathin 2D polariser can be integrated with the fabricated MLA for polarisation and dispersion control in the IR region. They also achieve an angular tuning of dispersion in the visible range. To investigate the optical performance of the MLA and GO polariser throughout the visible-to-IR region, both of them were fabricated on CaF2 substrates rather than glass to minimise absorption.

2. Samples and Methods

2.1. Materials

Commercial hybrid organic-inorganic Zr-containing negative photopolymer SZ2080TM [20] (FORTH, Greece) was used for photopolymerisation by direct laser writing (DLW). SZ2080TM has outstanding structuring capabilities: a low shrinkage and superior mechanical robustness of the fabricated objects [21]. This photoresist consists of 20% of silica with zirconia and 80% of polymer-forming methacryl-oxypropyl-trimethoxy-silane (MAPTMS, Polysciences Inc.) with methacrylic acid (MAA, Sigma-Aldrich) both having photo-polymerisable methacrylate moieties [22] with 1 wt.% Michler’s ketone (4,4’ bis(dimethyl amino) benzophenone, referred to as Bis) as the photoinitiator. The reason why Bis was chosen as the photoinitiator is its strong nonlinear absorption at the used 1030 nm irradiation and high irradiation intensity. With Bis, the 3D polymerisation window is wide and this is beneficial for efficient fabrication of large surface and volume structures (partly at the expense of reduced resolution) [23]. Detailed description of photoresist preparation is given in Ref. [22]. Samples were prepared by drop-casting on a 1 mm-thick calcium fluoride (CaF2 IR window 10×10×1 mm (CAFP10-10-1)) substrate with subsequent annealing at 100 ° C for 15 minutes in a vacuum oven without a post-exposure bake. A vacuum oven was used to promote evaporation of the organic solvent and water out of the photoresist. By using this vacuum prebake method, volatile molecules inside the sol-gel prepolymer can be fully evaporated, thus ensuring that the prepolymer acquires a uniform hard gel form for the following laser fabrication of the 3D micro-optical structures.
The photopolymerised samples were developed for 20 minutes in a chemical bath of methylisobutylketone/isopropanol (MIBK/IPA) 1:2 developer (Nippon Kayaku) organic solvent solution after the DLW fabrication process to remove nonpolymerised material and leave the self-standing 3D structures attached to the surface of the CaF2 substrate. The sample was placed with an inclination in the glass beaker during the development. Such a method can promote the removal of unexposed photoresist volume and lead to a cleaner micro-structure standing on the substrate. The sample was later left to dry at room temperature in ambient conditions prior to further examination.
The high-quality graphene oxide (GO) solution was synthesised by the chemical reduction of graphite via a modified Hummers Method [24]. Subsequently, homogenous GO thin films with controllable thicknesses were prepared by using a vacuum filtration technique employing a polyethersulfone (PES) membrane filter with diameter of 47 mm and pore size of 0.1 μ m (Sterlitech). The thicknesses of the GO films can be controlled by monitoring the volume of the GO suspension [25]. To generate a 1- μ m-thick GO thin film, 1.5 mL GO solution with concentration of 2 mg mL−1 was mixed with 25∼30 mL deionized (DI) water. Prior to the filtration processing, the GO suspension was treated by ultrasonication for 15 minutes with a Branson Sonifier to homogenise the GO solution. Then, the GO solution was poured into the filtration equipment with the PES membrane filter. Under vacuum conditions, water in GO solution can be gradually filtrated away, thus leaving a comparatively dried GO film on the PES substrate. Finally, the 1- μ m-thick GO film was peeled off from the PES substrate and transferred onto the CaF2 substrate in the methanol/DI-water solution with the concentration of 80 % ∼ 90 % . The concentration of the organic solvent is dependent on the thickness of the GO film, and thinner film needs diluted solution.

2.2. Femtosecond direct laser writing

Femtosecond (fs-)laser microfabrication [23,26,27,28,29] setup based on Pharos (Light Conversion) laser was integrated with scanning Aerotech xy-stages and SCA software control of laser radiation and scanning conditions (Workshop of Photonics). The diameter d and height l of a single photopolymerised volume pixel (voxel) was controlled by modifying the output laser power, stage scanning speed, and focusing objective lens. In this work, the output power of the regenerative amplifier of 200 mW, the central wavelength of λ = 1030 nm, pulse duration of t p = 230 fs and repetition rate of f r e p = 200 kHz were used for both MLA and GO polariser fabrication by polymerisation and ablation, respectively.
For the MLA fabrication via direct laser polymerisation, an optical microscope objective lens (Olympus MPlanFL N 20×) with numerical aperture N A = 0.45 was utilised to focus the laser beam into the SZ2080TM photoresist (Figure 2). In order to improve the fabrication efficiency for MLA, only the outer shells of the MLA were formed with a stage scanning speed of v s = 0.1 mm/s and pulse density of 1×106 pulse/mm. The pulse-to-pulse separation is v s / f r e p = 0.5 nm. The interiors of the micro-lenses were fully polymerised by using a post-treatment with UV light for 5∼10 minutes after the development. The polymerised enclosure shells with sufficient mechanical strength can avoid the leakage of the unexposed regions inside the MLAs during the development processing, thus protecting the surface morphology. The outer shell was polymerised by writing several concentric rings from bottom to top to form a plano-convex microlens based on the designed radius of curvature. To ensure the shell was mechanically strong enough, the linespacing between two adjacent concentric rings should be less than the lateral spot diameter of the polymerised voxel.
Exposure conditions for 3D polymerisation. The spot diameter of the 20× N A = 0.45 objective lens was ⊘ = 1.22 λ / N A ≈ 2.8 μ m and the designed diameter of a single microlens in the MLA was 60 μ m. Therefore, 60 concentric rings with adjacent linespacing of 0.5 μ m were written to form a microlens with a laser fluence of F p = 0.16 J/cm2/pulse or 0.7 TW/cm2/pulse (on the sample). The exposure dose per pulse (calculated as a linear exposure) is D p = F p × t p = 36.8 × 10 − 15 J/cm2. The accumulated dose over the dwell time ⊘ / v s during which the laser beam is passing across the focal diameter ⊘ is D Σ = D p × N p ≈ 206 pJ/cm2, where number of pulses N p = ( ⊘ / v s ) / f r e p = 5.6 × 10 3 . The typical linear exposure dose of photo-lithography resists (negative and positive tone) used for a UV lamp or laser exposure is 0.1 J/cm2 for a high-contrast definition of patterns and a high-rate of development R D ≈ 100 nm/s [30]. Apparently a strong nonlinear contribution is required to deposit a comparable 0.1 J/cm2 exposure dose via the nonlinear absorption for 3D polymerisation [31]. The first nonlinear contribution, the two-photon absorption (TPA), is defined by the coefficient β = σ ( 2 ) N T P A E h ν [cm/W] with N T P A [cm−3] being the number density of TPA-absorbing molecules, E h ν = h ν [J] is the photon energy and σ ( 2 ) [cm4s/molecule] is the TPA cross section measured also in Goeppert-Mayer units 1 GM = 10 − 50 cm4s/molecule. The β and σ ( 2 ) are not usually provided by vendors of photo-resists/resins and are seldom measured. Apparently, β ≈ 20 cm/TW is required for TPA polymerisation [32]. This corresponds to σ ( 2 ) = 129 GM considering a 0.1% molecular density of photo-initiator in the host polymer matrix N h o s t = ρ N A / M h o s t [cm−3] for typical resist mass density ρ = 1.2 g/cm3 and molar mass M h o s t ≈ 234 g/mol [33]; N A is the Avogadro number. At typical I p ≈ 1 TW/cm2 intensities used in 3D polymerisation, β I ≈ 20 cm−1, which is not a large absorption contribution via TPA. The strong absorption is defined by α d > 1 , where d is the length of absorption; e.g., for d = 1 μ m, α = 10 4 cm−1. Moreover, estimates of σ ( 2 ) ≈ 1 − 10 GM are more realistic [34] also considering a spectrally narrow resonant TPA band [35]. The actual contributions to a cumulative absorption coefficient α c ≡ α + β I , along the axial depth of focus ∼ 2 z R , requires knowledge of the fast changing permittivity ε = ( n + i κ ) 2 , which defines a larger absorbance due to augmented κ , which is increasing via generation of free photo-excited carriers α = 4 π κ / λ [36,37,38].
Exposure conditions for GO ablation. For the fabrication of GO polariser, the laser beam was focused through a high numerical aperture (M Plan Apo HR 100×) objective lens of N A = 0.9 into the d = 1 μ m GO thin film to fabricate the grating structures with a stage scanning speed of 0.04 mm/s and pulse density of 5×106 pulse/mm (Figure 3). The patterned grating with a periodicity of P = 4 μ m generated a linear GO polariser with total area of 300×300 μ m2. The focal diameter was ⊘ = 1.22 λ / N A ≈ 1.4 μ m and typical pulse energies were E p = 80 nJ. The number density of pulses per diameter is N p ≡ ⊘ / ( v s / f r e p ) = 2.8 × 10 3 . The ablation groove was approximately 2 − μ m-wide and the duty cycle was 0.5 (for period P = 4 μ m) to maximise the form birefringence of the grating/polariser pattern (Figure 3).

2.3. Structural and optical characterisation

The initial structural characterisation was made using an optical microscope (Nikon ECLIPSE LV100NPol) to confirm the survival from the development of the MLA and to observe the grating structures of the GO polariser. Additionally, the optical microscope was utilised to characterise the focal spots of the MLA in the transmission mode. The 3D focal spots and longitudinal intensity distribution of the focal spots were mapped through stepping the microscope along z − axis by 1 μ m with subsequent MATLAB programming assistance.
3D optical profiler (Bruker ContourGT InMotion) was used to characterise the surface morphology and cross-sectional profile of the fabricated MLA and GO polariser.
Scanning electron microscopy (SEM) was used for structural characterisation of MLA processed by laser radiation (Raith 150TWO electron beam writer was used in a field-emission SEM mode).
Infrared (IR) transmittance spectrum of the GO polariser was measured by using the microscope Fourier transform infrared (FTIR) spectrometer (Bruker V70) from 1 μ m to 10 μ m. An FTIR condenser was used in the microscope FTIR spectrometer to focus the broadband IR radiations on the sample in the free space. Metallic linear grid polarisers were used for polariser-analyser setup to reveal polarisation response of the GO polarisers.
Preprints 69458 g002
Figure 2. (a) Optical microscopy image (transmission) of the fabricated MLA. Polymerisation of the outer shell was carried out by concentric fs-DLW from larger-to-smaller diameters. (b) Top and 45 ° tilted view SEM images of the fabricated MLA; the diameter of the microlenslet is 60 ± 0.3 μ m. (c) 3D topographic view ( 50 × ) of the fabricated MLA. (d) Height profile and coresponding circle curve; inset: 3D topographic view ( 115 × ). The entire height of the structure is comprised of 12 μ m pedestal and 10 μ m lens. The min-max roughness near the center of the lens was 90 ± 10 nm which was < λ / 10 for IR wavelengths.
Figure 2. (a) Optical microscopy image (transmission) of the fabricated MLA. Polymerisation of the outer shell was carried out by concentric fs-DLW from larger-to-smaller diameters. (b) Top and 45 ° tilted view SEM images of the fabricated MLA; the diameter of the microlenslet is 60 ± 0.3 μ m. (c) 3D topographic view ( 50 × ) of the fabricated MLA. (d) Height profile and coresponding circle curve; inset: 3D topographic view ( 115 × ). The entire height of the structure is comprised of 12 μ m pedestal and 10 μ m lens. The min-max roughness near the center of the lens was 90 ± 10 nm which was < λ / 10 for IR wavelengths.
Preprints 69458 g002
Preprints 69458 g003
Figure 3. (a) Schematics of the GO polariser. Optical microscopy image (transmission mode) of the fabricated GO polariser 300 × 300 μ m (over the footprint of MLA) and an optical profile trace (single pixel) across the grating. (b,c) Form birefringence modeling of the GO grating; see text for discussion. (b) The ordinary and extra-ordinary optical constants of a thick drop-cast GO layer determined by a multiple-location analysis of spatially resolved data obtained by spectroscopic ellipsometry [39]. (c) The ordinary and extra-ordinary complex refractive indices, as well as the birefringence Δ n = n e − n o of the GO grating structure, calculated by substituting the ordinary, extra-ordinary and complex refractive indices n ˜ = n + i κ of GO layer from (b) into the standard form-birefringence formulas given by Eqn. 4. Inset shows Δ n vs. f ′ dependence at different wavelengths λ ; the volume fraction f ′ = 1 corresponds to homogeneous GO film.
Figure 3. (a) Schematics of the GO polariser. Optical microscopy image (transmission mode) of the fabricated GO polariser 300 × 300 μ m (over the footprint of MLA) and an optical profile trace (single pixel) across the grating. (b,c) Form birefringence modeling of the GO grating; see text for discussion. (b) The ordinary and extra-ordinary optical constants of a thick drop-cast GO layer determined by a multiple-location analysis of spatially resolved data obtained by spectroscopic ellipsometry [39]. (c) The ordinary and extra-ordinary complex refractive indices, as well as the birefringence Δ n = n e − n o of the GO grating structure, calculated by substituting the ordinary, extra-ordinary and complex refractive indices n ˜ = n + i κ of GO layer from (b) into the standard form-birefringence formulas given by Eqn. 4. Inset shows Δ n vs. f ′ dependence at different wavelengths λ ; the volume fraction f ′ = 1 corresponds to homogeneous GO film.
Preprints 69458 g003

2.4. Numerical modeling

Numerical modeling of transmittance spectra of the GO grating polariser in IR region were simulated using finite-difference time-domain (FDTD; Lumerical, Ansys). For the FDTD model of the GO polariser, the optical constants of GO materials were obtained from RefractiveIndex.INFO database [40]. The GO polariser was defined by a unit cell consisting of one GO ribbon and an air groove with the periodic boundary condition. The plane wave light source with TE or TM polarisation was placed on top of the GO polariser (3 μ m away) in a normal incident direction. A transmission monitor was placed at the bottom of the GO polariser (5 μ m away) perpendicular to the normal incident direction.
The light distribution in the focal region was simulated by MATLAB program based on the Rayleigh-Sommerfeld (RS) diffraction integral [41]. Compared with Fresnel diffraction integral, the RS diffraction theory provides more accurate predictions of light diffraction, because it does not assume the paraxial approximation [42]. The E-field in the focal plane U 2 ( r 2 , θ 2 ) can be calculated with the RS diffraction integral as expressed Eqn. 1 [41]:
U 2 ( r 2 , θ 2 , z ) = − i λ ∫ ∫ U 1 ′ ( r 1 , θ 1 ) · e i k r r · cos ( n , r ) d r 1 d θ 1 ,
where λ is the incident light wavelength, k = 2 π λ is the wave vector, z is the distance between the diffraction plane and observation plane (which equals the focal length f for focusing), ( r 1 , θ 1 ) and ( r 2 , θ 2 ) are the polar coordinates in the diffraction plane (the plane immediately behind the microlens) and observation plane (the focal plane), respectively; r = ( z 2 + ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 = ( z 2 + r 1 2 + r 2 2 − 2 r 1 r 2 c o s ( θ 1 − θ 2 ) , n denotes the unit vector normal towards the observe plane, and r represents the unit vector of r direction from point ( r 1 , θ 1 ) to point ( r 2 , θ 2 ) , U 1 ′ ( r 1 , θ 1 ) is the E-field immediately behind the microlens. The incident wave U 1 ( r 1 , θ 1 ) is diffracted by the microlens through phase modulation, and the E-field modified by the microlens U 1 ′ ( r 1 , θ 1 ) can be expressed by Eqn. 2 [41]:
U 1 ′ ( r 1 , θ 1 ) = U 1 ( r 1 , θ 1 ) t ( r 1 , θ 1 ) e − i k · Φ ( r 1 , θ 1 ) ,
where t ( r 1 , θ 1 ) is the transmission coefficient (which is 1 when there is no amplitude modulation), and Φ ( r 1 , θ 1 ) = ( r 1 , θ 1 ) 2 + f 2 − f is the phase modulation provided by the microlens. Finally, the light intensity on the focal plane can be calculated, which is the square of the E-field I = U 2 2 ( r 2 , θ 2 ) . The lateral and axial intensity distributions were calculated for the visible spectrum; see Sec. Appendix B for the RS modeling of axial intensity distribution at IR 1-10 μ m wavelengths.

3. Results and discussion

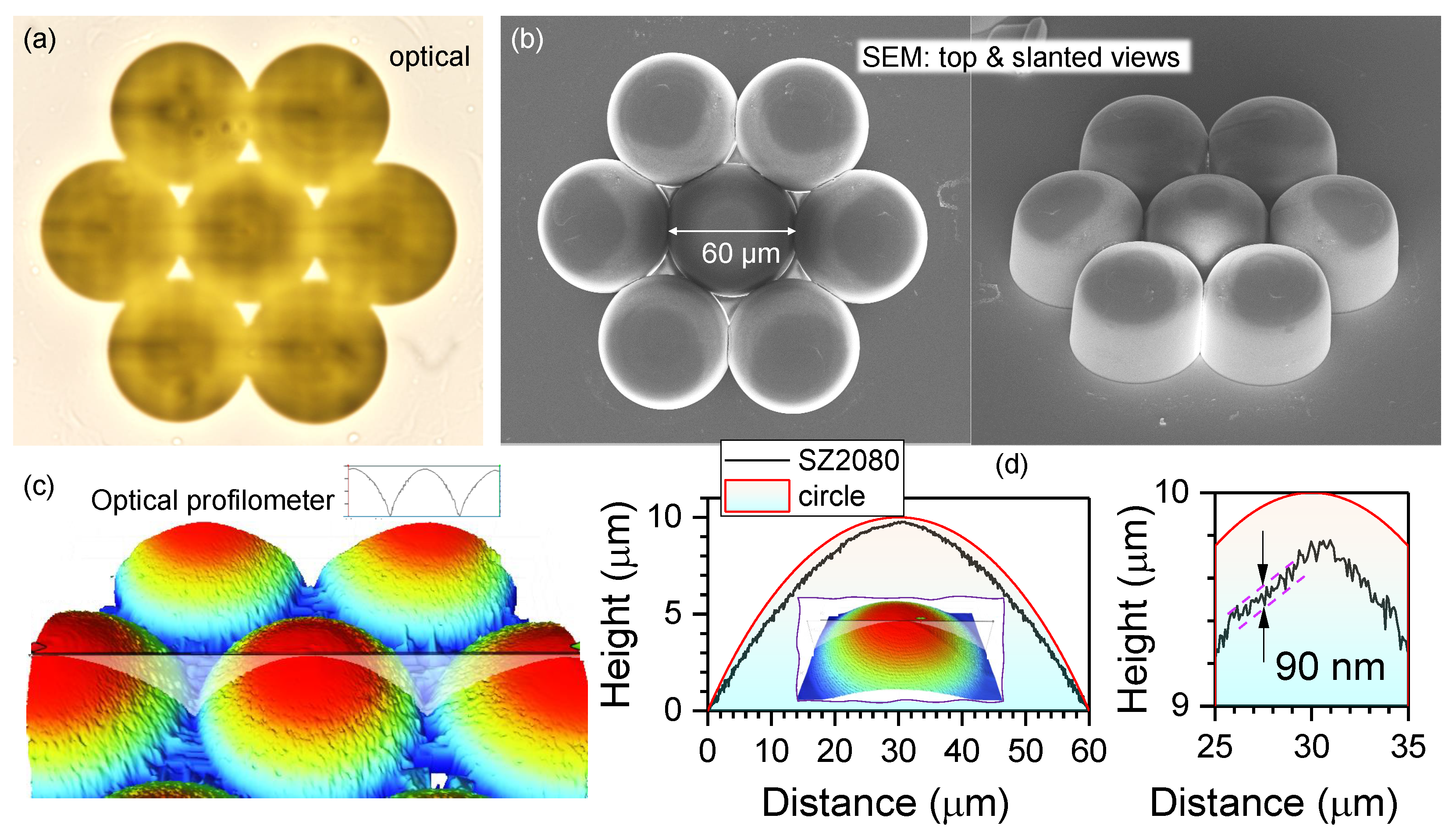
3.1. Structural characterisation of MLA

Figure 2(a) is the optical microscopy image of the fabricated MLA. The designed MLA consists of seven, closely-packed, microlenses to maximise its spatial filling ratio, which can reduce the light information loss resulting from the spacing among the microlenses. The designed diameter of each microlens is 60 μ m with a focal length of 100 μ m. According to the lensmaker’s equation with thin lens approximation [43], the radius of the curvature was calculated to be 50.4 μ m:
1 f = ( n − 1 ) 1 R 1 − 1 R 2 ,
where n s z 2080 ≈ 1.504 , and 1 R 2 ≈ 0 owing to the plano-convex design of microlenses. Based on Pythagorean theorem [44], the maximum height of the microlens was also calculated to be 9.9 μ m.
To further characterise the dimensions and surface profile of the fabricated MLA, SEM and optical profiler have been utilised. The diameter of the fabricated MLA was measured with SEM, as shown in Figure 2(b), which illustrates that the diameter of the fabricated microlens matches well with the designed value of 60 μ m. The slanted view SEM image also clearly shows the well-defined MLA that was fabricated with the 3D DLW lithography technique. The 3D topographic view ( 50 × magnification) of the fabricated MLA is shown in Figure 2(c). To accurately measure the surface profile and the maximum height of the fabricated microlens with the optical profiler, a superimposed pedestal disk has also been fabricated together with a microlens (inset in Figure 6(a)), and the radius of the pedestal disk is equal to the diameter of the microlens D d i s k = 120 μ m. The microlens and the pedestal disk both were starting at the same Z-position (height), thus polymerising a flat base platform with microlens effectively protruding out of the platform. The height of the protrusions then could be measured with the optical profiler, which should ideally be the designed height, 9.9 μ m × n S Z 2080 tall. Therefore, the expected height of the fabricated microlens can be achieved as illustrated in Figure 2(d). Measured pedestal height is expected to be equal to half the objective depth of focus, the Rayleigh length z R = π r 2 / λ ≈ 6 μ m, where r is the waist (radius) at the focus when written with focus exactly at the resist/substrate interface. Furthermore, the surface profile of the fabricated microlens showed only subwavelength surface roughness of 90 nm (min-max), which is smaller than the required roughness of < λ / 10 for demanding optical applications at the IR wavelengths. This prevents the undesired diffraction or scattering for good optical performance. It is noteworthy that polymerisation of MLAs had no observable polymerised modulation features due to interference caused by the back-reflected light [45]. This is due to a closely matching refractive indices of CaF2 and SZ2080TM.
Preprints 69458 g004
Figure 4. (a) Experimental measurements and simulations based on the model given by Eqn. 1 of the focal (xy-plane) and axial (yz-plane) cross-sections of the focal region intensity distribution for MLA at 633 nm wavelength. Cropped insets show confocally stacked intensity at the foci. (b) Sketch of lens (to scale) and the axial intensity distribution. 3D intensity was confocally mapped through stepping microscope imaging along z − axis by 1 μ m and MATLAB programming code was used to stack them for cross sectional views. The color bars represent the normalised intensity.
Figure 4. (a) Experimental measurements and simulations based on the model given by Eqn. 1 of the focal (xy-plane) and axial (yz-plane) cross-sections of the focal region intensity distribution for MLA at 633 nm wavelength. Cropped insets show confocally stacked intensity at the foci. (b) Sketch of lens (to scale) and the axial intensity distribution. 3D intensity was confocally mapped through stepping microscope imaging along z − axis by 1 μ m and MATLAB programming code was used to stack them for cross sectional views. The color bars represent the normalised intensity.
Preprints 69458 g004

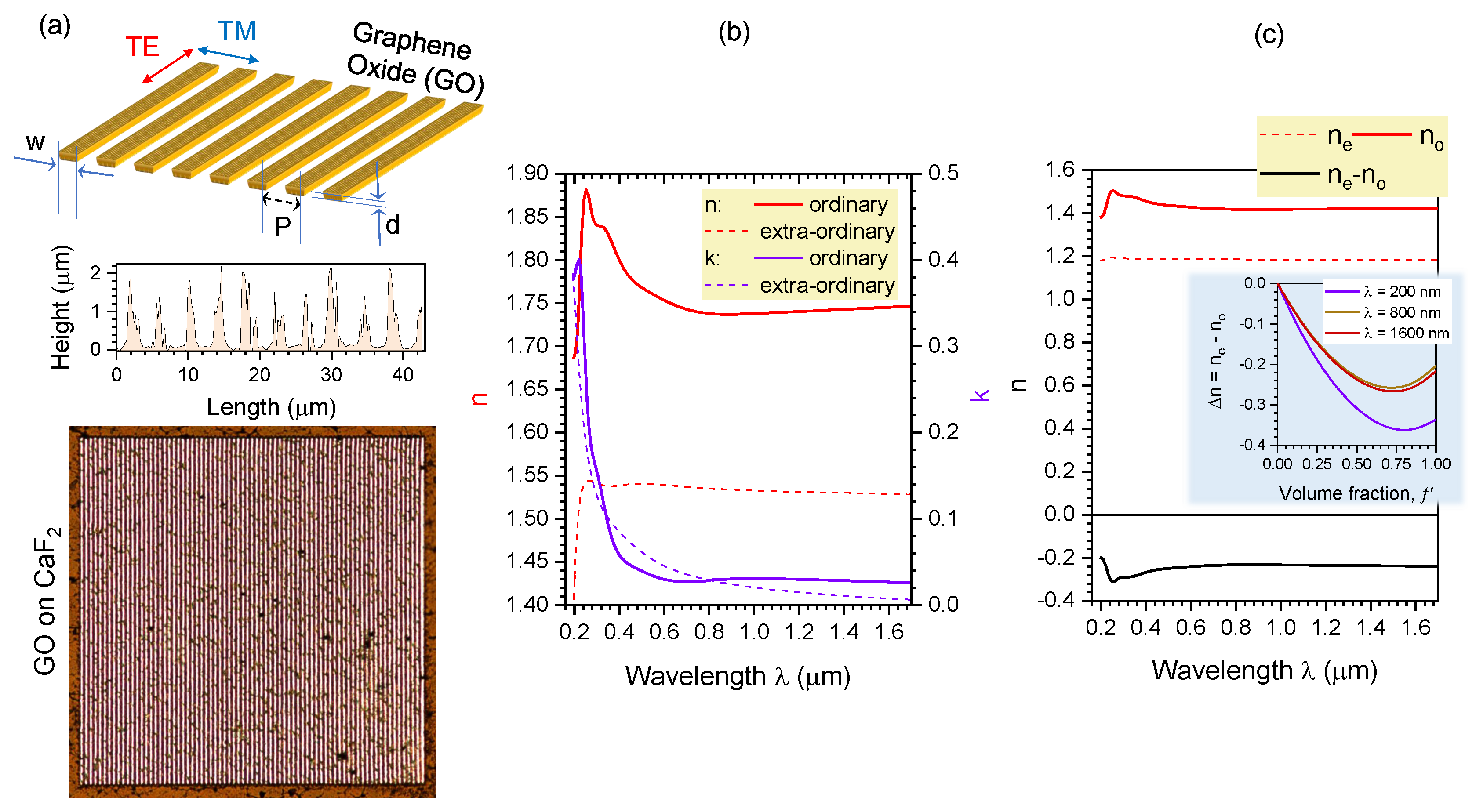
3.2. Structural characterisation of the GO polariser

The GO grating polariser was defined by the period P, width of GO ribbon w and thickness of the GO film d (Figure 3(a)). Unpolarised light incident on the GO grating as TE polarisation with electric E-field parallel to the GO grating can be coupled into a guided mode of the waveguide resulting from the guided-mode resonance [46,47,48,49], whereas its TM polarisation with E-field perpendicular to the GO grating behaves almost the same as when there is no grating. As a result, the GO grating polariser has the capability to split the two orthogonally oriented polarisations, which can couple the TE polarisation, whereas allowing the TM polarisation to pass through. Based on the geometrical configuration of the designed GO polariser with P = 4 μ m, w = 2 μ m, and d = 1 μ m, the GO grating was fabricated with the DLW technique by using fs-pulses to ablate air grooves into the GO thin film. Figure 3(a) displays the optical microscopy image of the fabricated GO polariser; the sharp edges of the GO grating reveal a good quality of fabrication with the femtosecond DLW technique. To further characterise the structures of the fabricated GO polariser, its surface morphology was measured with the 3D optical profiler (Figure 3(a)). The cross-sectional surface profile along the white line (Figure 3(a)) illustrates that the periodicity, GO ribbon width, and GO film thickness of the well-defined GO grating were close to the designed values of 4 μ m, 2 μ m, and 1 μ m, respectively. The form birefringence Δ n = n e − n o defined by the ordinary and extraordinary refractive indices n o , e of the GO grating [39] is discussed separately below and is shown for the fabricated case in Figure 3(b,c).

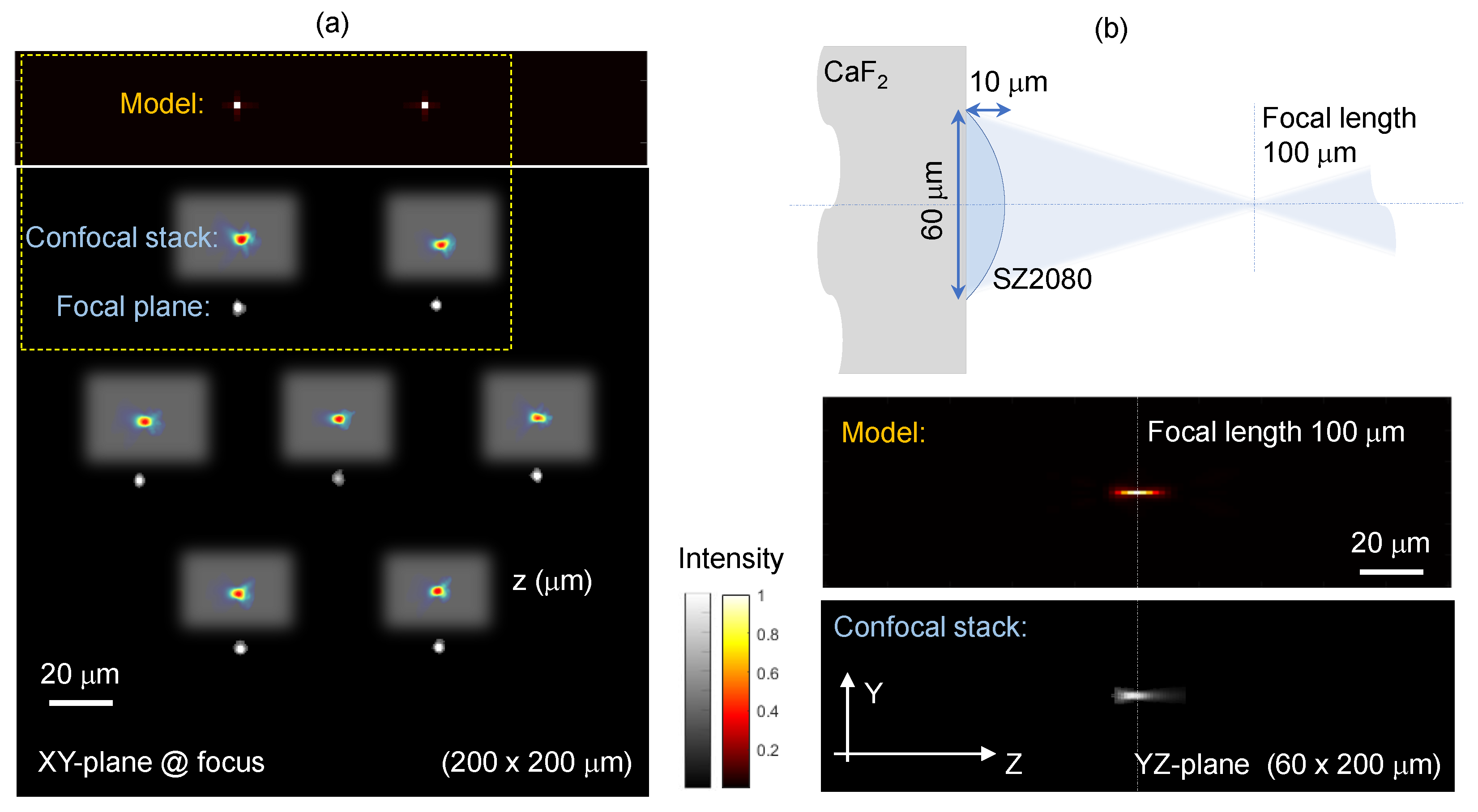
3.3. MLA focal spots characterisation

The focusing of the MLA was characterised by using the optical microscope in transmission mode with a white light condensor at the bottom of the optical microscope. The cross-sectional focusing intensity distribution of the MLA was captured by an 50× N A = 0.8 objective lens onto a CCD camera (Figure 4). For comparison, the corresponding theoretically simulated intensity distribution of the focal spots in the x y -plane is displayed, which was calculated based on the RS diffraction integral (Eqn. 1) with MATLAB code. The RS theory does not assume the paraxial approximation, thus providing more accurate predictions. All intensity values in Figure 4 have been normalised to their peak value. It is clear that the experimental measurements present a good agreement with the theoretical calculations. Moreover, the 3D focal spots of the MLA can be mapped by scanning the microscope with a step of 1 μ m along the z − axis and stacked for 3D cross sections using a home-made MATLAB code. Good focusing of the fabricated MLA was achieved in the lateral x y and axial y z planes of the microlens as well as MLA. The theoretical calculation for the axial intensity distribution was also simulated with RS diffraction integral and showed a good agreement in terms of the depth of focus ∼ 100 μ m. This demonstrates that the fabricated MLA are well-matching the design with focal spot diameter ∼ 2 μ m (at intensity maximum 1 / e 2 -level) and the depth-of-focus (or double of Rayleigh length) ∼ 13 μ m (at the full width half maximum FWHM of the axial intensity) profile at visible wavelengths modeled using λ = 633 nm. The f-number of the D = 60 μ m lens with focal length f = 100 μ m is f # = f / D = 1.67 , corresponding to the numerical aperture N A = 1 / ( 2 f # ) ≈ 0.3 .
Preprints 69458 g005
Figure 5. Optical microscopy imaging at visible spectral range under white light condenser illumination. (a) MLA and the GO-polariser are fixed together and azimuthally rotated θ -angle in respect to the aligned polariser-analyser (high transmittance mode). (b) MLA is fixed and GO-polariser is θ -rotated around the optical axis with aligned polariser - analyser. (c) Dispersion of RGB-colors at the focal region measured by the optical microscope; the color indicates the distances between the dispersed RGB colors and the center of the focal spot. Substrates for MLA and GO-polariser were 1-mm-thick CaF2. The N A of the imaging lens (Nikon Microscope TU Plan Fluor, 50 × ) was 0.80.
Figure 5. Optical microscopy imaging at visible spectral range under white light condenser illumination. (a) MLA and the GO-polariser are fixed together and azimuthally rotated θ -angle in respect to the aligned polariser-analyser (high transmittance mode). (b) MLA is fixed and GO-polariser is θ -rotated around the optical axis with aligned polariser - analyser. (c) Dispersion of RGB-colors at the focal region measured by the optical microscope; the color indicates the distances between the dispersed RGB colors and the center of the focal spot. Substrates for MLA and GO-polariser were 1-mm-thick CaF2. The N A of the imaging lens (Nikon Microscope TU Plan Fluor, 50 × ) was 0.80.
Preprints 69458 g005

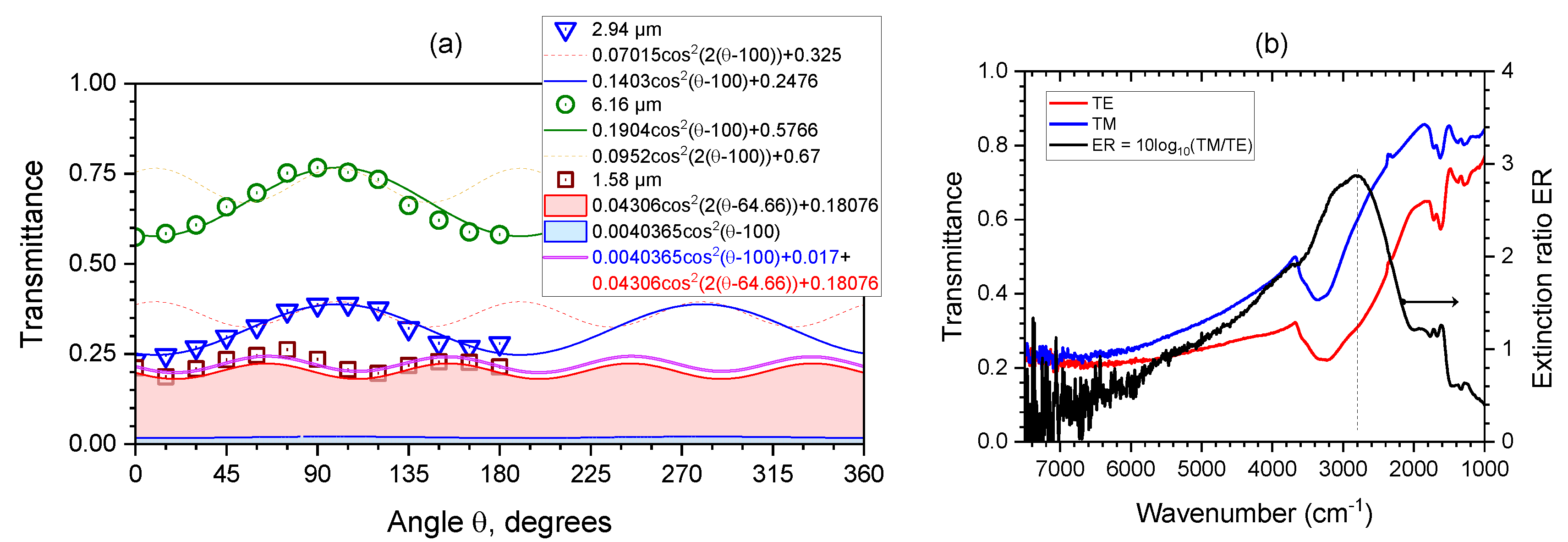
3.4. Form birefringence of GO

The GO grating polariser has contributions to polarisation in transmittance T (and reflectance R) from real and imaginary parts of the refractive index ( n + i κ ) . Namely, absorption as well as birefringence Δ n affect optical T and R polarisation dependence.
The GO grating is a form birefringent structure with the extra-ordinary n e (along the optical axis) and ordinary n o refractive indices through the adjacent regions of air grooves and GO ribbons with (sub-)wavelength widths. Those widths define the volume fraction f ′ = w Λ in a grating structure [50]:
n e = n 1 2 n 2 e 2 ( 1 − f ′ ) n 2 e 2 + f ′ n 1 2 ; n o = ( 1 − f ′ ) n 1 2 + f ′ n 2 o 2 ,
where n 1 is the refractive index of air, n 2 e and n 2 o are the extra-ordinary and ordinary complex refractive indices of GO, respectively, w is the width of one GO ribbon (2 μ m) and Λ is the period of the GO grating (4 μ m). A multiple-location analysis of experimentally measured optical constants of GO with spectroscopic ellipsometry has been reported to precisely determine the anisotropic optical constants of GO [39]. The determined extra-ordinary and ordinary refractive indices n and extinction coefficients κ of GO are plotted in Figure 3(b), which were used to derive the ordinary n 2 o and extra-ordinary n 2 e complex refractive indices of GO n ˜ = n + i κ . Therefore, the extra-ordinary n e and ordinary n o refractive indices formed by the GO grating can be calculated, then the magnitude of their difference is quantified to obtain the birefringence Δ n = n e − n o , as shown in Figure 3(c).

3.5. Angular dispersion tuning

The GO polariser also works as a diffraction grating to linearly disperse polychromatic light into its constituent wavelengths (colors), which is arisen from the wavefront division and interference of the incident radiation from the periodic GO grating structures. Diffraction gratings are indispensable and fundamental optical elements in applications for measuring atomic spectra in both laboratory instruments and telescopes. The MLAs are used to perform observations and imaging in the microscopic range. When these two optical elements are integrated, they enable imaging of microscopic areas while simultaneously providing a spectral analysis capability. The dispersed light with different wavelengths can be focused into different positions by the MLA. For flexibility of test, the GO grating and MLA were made as two separate components and assembled together for possibble azimuthal rotation along the optical axis. Such an assembly provides flexibility for orientation of the angular dispersion (Figure 5).
The optical layout of the angular dispersion-tunable assembly is displayed in Figure 1(a), where the MLA with a CaF2 substrate (thickness of 1 mm) was stacked on the GO grating polariser which has also been fabricared on a CaF2 substrate. The collimated polychromatic light from a white LED was dispersed by the GO grating polariser then focused by the MLA and captured by an optical microscope (Nikon TU Plan Fluor 50× N A = 0.80 ). The dispersion distribution at the focal region is demonstrated in Figure 5, where the colorful marks (red/green/blue) illustrate the distances between the dispersed rainbows and the focal spots. Such a dispersion distribution exhibited highly centrosymmetric property. It is worthy of note, that the dispersion distribution (distance of the rainbow from the focal spot) is dependent on the gap between the GO grating polariser and the MLA (here, it was 1 mm caused by the thickness of the CaF2 substrate). Therefore, a dynamic tuning of the dispersion distribution can be achieved by increasing or decreasing the spacing between the GO grating and the MLA. Moreover, as the GO grating polariser was separated from the MLA, it was flexible to rotate the GO grating polariser, as demonstrated in Figure 5, which can lead to angular positioning of dispersion-rainbows shown in Figure 5. Only few angles were selected for the cases of the entire assembly (a) or only GO polariser rotated at θ -angles. The dispersion rainbow-patterns were angular positioned and are caused by the orientation of the GO polariser. The spatial separation of red to blue colors of ∼ 4 μ m at the focal plane was achieved with the used setup. It is 2-3 times larger than the focal spot of 2 μ m. There was an apparent asymmetry in RGB color dispersion dependent on location of individual lenslet. That asymmetry was same irrespective of the all-assembly rotation or only the GO-polariser, (a) vs. (b). This implies that the collection power of the imaging lens (of the microscope used), as well as the MLA with the pedestal, caused some colors out of the collection angle. This type of measurement could be useful for metrological characterisation of the MLA. Inspection of homogenity in lens polymerisation can also be tested if unintended grid-like pattern is formed, as shown in Sec. Appendix A.

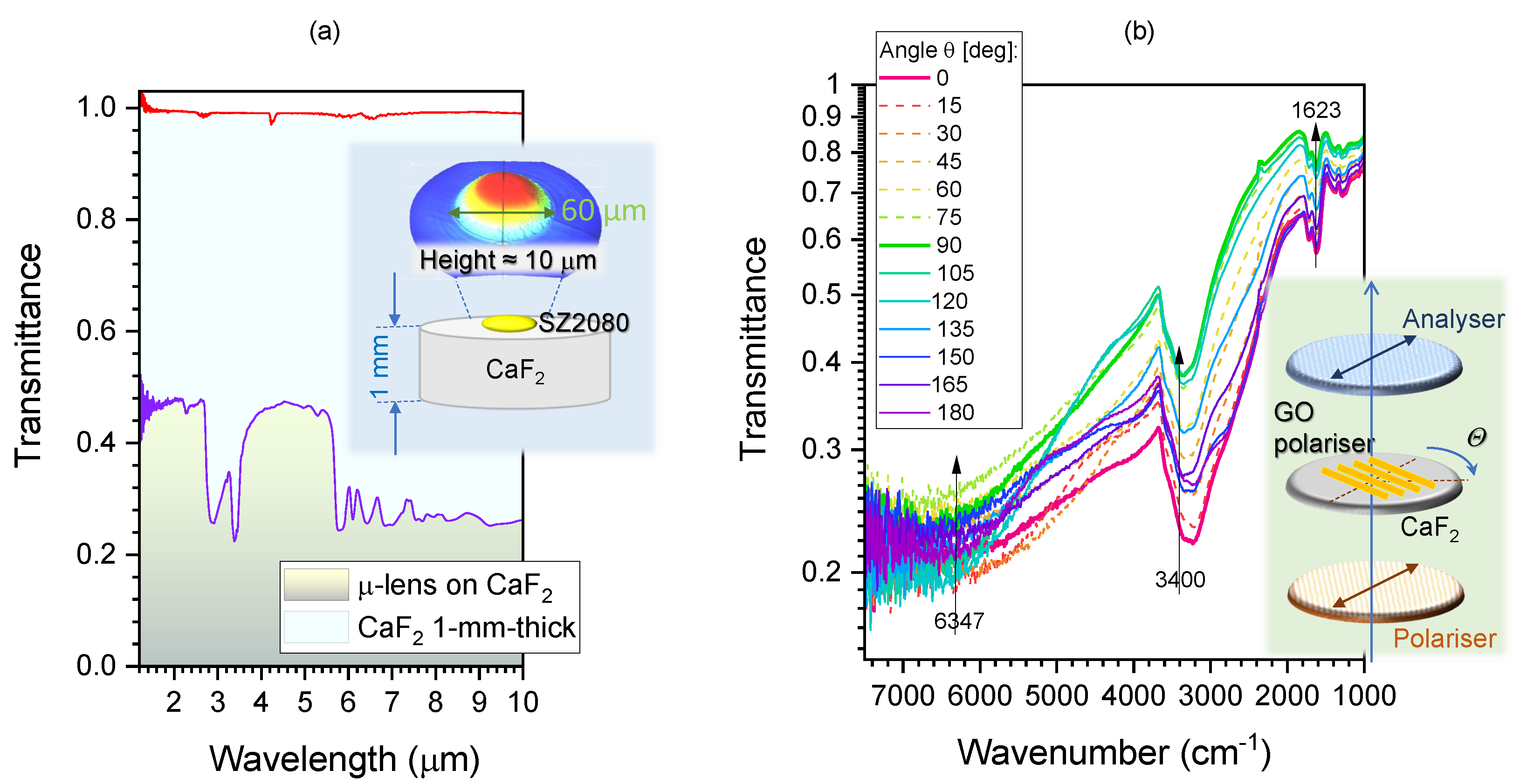
3.6. FTIR characterisation of MLA and GO polariser

The MLA and GO gratings fabricated and characterised in previous sections for visible spectral range can be also useful for IR spectral fingerprinting region 1-10 μ m especially due to less restrictive demand of spatial resolution. Interestingly, the axial extent of MLA and GO films are close to ( 0.1 − 1 ) λ range for the IR domain. Here, we characterised the same optical elements for longer wavelengths (Figure 6). Transmittance of the ∼ 10 μ m SZ2080TM MLA was close to 50% up to 6 μ m and T ≈ 0.3 for longer wavelengths up to 10 μ m (Figure 6(a)). Polymer absorption bands from the SZ2080TM resist are present; however, they would be compensated via normalisation in spectroscopic applications. Focusing performance at IR wavelengths for the N A = 0.3 micro-lens was calculated by Eqn. 1 and is shown in Sec. Appendix B.
Preprints 69458 g006
Figure 6. (a) IR transmittance spectra of the fabricated GO polariser measured by the microscope FTIR spectrometer with parallel polariser and analyser. (b) Transmittance and their fitted formulas of the contributions from absorbance and retardance at 1.58 μ m, 2.94 μ m, and 6.16 μ m, as marked in the transmittance spectra. Note that T is plotted on logarithmic scale to better reveal small changes. At 3530 c m − 1 and 1080 c m − 1 the C-OH vibrations are present [51].
Figure 6. (a) IR transmittance spectra of the fabricated GO polariser measured by the microscope FTIR spectrometer with parallel polariser and analyser. (b) Transmittance and their fitted formulas of the contributions from absorbance and retardance at 1.58 μ m, 2.94 μ m, and 6.16 μ m, as marked in the transmittance spectra. Note that T is plotted on logarithmic scale to better reveal small changes. At 3530 c m − 1 and 1080 c m − 1 the C-OH vibrations are present [51].
Preprints 69458 g006
The real n and imaginary κ parts of the complex refractive index, n ˜ = n + i κ , as well as corresponding anisotropies Δ n and Δ κ , define the optical response of materials through an anisotropic phase delay (retardance) resulting from birefringence and an amplitude change caused by absorbance (and its polarisation dependence linked to the material and geometrical size/shape of the sample/object). Birefringence Δ n defines the retardance by Δ n × d λ , where d is the sample thickness. A generic expression of combined Malus and Beer–Lambert laws has been introduced and demonstrated to exactly fit the additive contributions resulting from retardance and absorbance to transmittance through a pair of aligned polariser and analyser (setup is acting in high transmittance, oppositely to the cross-polarised arrangement with no transmittance) [52]. This setup allows to determine absorption losses as well as birefringence contribution together. The principle to separate the two contributions is due to their different angular dependence.
Here, we used the fitting formula to retrieve the two contributions resulting from retardance and absorbance to the transmittance as expressed below:
T θ = a κ cos 2 ( θ − b κ ) + o κ + a n cos 2 2 ( θ − b n ) + o n ≡ A b s + R e t + o t o t a l ,
where a κ and a n are the amplitudes related to absorbance ( A b s ) and retardance ( R e t ) contributions, b κ and b n are the orientation dependent angles (which can be different for the two anisotropies), o κ and o n are their corresponding offsets. Equation 5 indicates that the retardance caused by birefringence ∼ Δ n has twice faster angular dependence on azimuthal rotation (around the optical axis) to the absorbance ( ∼ κ ) when measured in a parallel- (same for the crossed-) polarisers setup. The θ -dependence is key to separate the two contributions via the fitting method.
To investigate the absorbance and retardance contributions in the fabricated GO polariser, the transmittance spectra T θ of the GO polariser was measured by the microscope FTIR spectrometer with parallel polariser and analyser, as shown in the inset of Figure 6(b). To avoid the absorption effects resulting from the substrate, both MLA and GO polariser were fabricated on CaF2 (cubic structure) rather than glass substrate, which was due to its IR transparent and isotropic (no birefringence) properties. The measured IR transmittance spectra T θ of CaF2 substrate is close to 100% (Figure 6(a)). During the measurement, the GO polariser was rotated by a step of θ = 15 ∘ from 0 ° to 180 ° to investigate changes in T by the fit using Eqn. 5. On the absorption bands (at 2.94 μ m and 6.16 μ m; the corresponding wavenumbers ν ˜ = 3400 and 1623 cm−1), the maximum contribution is from the absorbance A, while for the flat spectral range without distinct absorbance bands and at the telecom spectral window at ∼ 1.58 μ m ( ν ˜ = 6347 cm−1), the retardance contribution caused by birefringence is recognisable. To determine the exact contributions their formulas have been fitted with a MATLAB program and the best fits are summarised in Figure 7. The markers for the bands at 2.94 μ m and 6.16 μ m show the experimental measurements of the transmittance T θ ( ν ˜ ) showing dominance of the absorption (see the line best fit) by: T θ = 0.1403 cos 2 ( θ − 100 ∘ ) + 0.2476 and 0.1904 cos 2 ( θ − 100 ∘ ) + 0.5766 , respectively. The maximum of absorbance is at the orientation angle b n = 100 ∘ .
According to Eqn. 5, the phase change to form birefringence (retardance) has twice faster angular dependence to the absorbance.Therefore, the expected retardance contribution formulas at 2.94 μ m and 6.16 μ m can also be expressed (here the orientation dependent angle b n = 100 ∘ has been assumed). The dashed-lines shown in Figure 7 illustrate that their contributions are not present; they are plotted by 0.07015 cos 2 2 ( θ − 100 ∘ ) + 0.325 and 0.0952 cos 2 2 ( θ − 100 ∘ ) + 0.67 .
Preprints 69458 g007
Figure 7. (a) IR transmittance spectra of the fabricated GO polariser measured by the microscope FTIR spectrometer with parallel polariser and analyser. Transmittance was fitted considering contributions from absorbance and retardance at the 1.58 μ m, 2.94 μ m, and 6.16 μ m bands as marked in the transmittance spectra Figure 6(b). The best fit formulas are shown as retrieved from MATLAB best fit routine without rounding. See text for details. (b) Experimentally determined spectrum of the extinction ratio E R of GO polariser with period P = 4 μ m, thickness of GO d = 1 μ m and width of gratting ribbon w = 2 μ m (see Figure 8 for a family of the parameter study).
Figure 7. (a) IR transmittance spectra of the fabricated GO polariser measured by the microscope FTIR spectrometer with parallel polariser and analyser. Transmittance was fitted considering contributions from absorbance and retardance at the 1.58 μ m, 2.94 μ m, and 6.16 μ m bands as marked in the transmittance spectra Figure 6(b). The best fit formulas are shown as retrieved from MATLAB best fit routine without rounding. See text for details. (b) Experimentally determined spectrum of the extinction ratio E R of GO polariser with period P = 4 μ m, thickness of GO d = 1 μ m and width of gratting ribbon w = 2 μ m (see Figure 8 for a family of the parameter study).
Preprints 69458 g007
In contrast, for the flat spectral range that is out of the absorption band, the retardance contribution is present. The experimentally measured T at 1.58 μ m and the fit are plotted by 0.0471 cos 2 ( 1.9143 θ − 126 . 8 ∘ ) + 0.1979 . The fitted angular varying speed was 1.9143 θ which is close to expected 2 θ dependence for the pure birefringent waveplate. In addition, a contribution from absorbance ( θ − 100 ∘ ) at 1.58 μ m is expected. The proportion of contribution from retardance and absorbance could be fitted with 91.43% and 8.57%, respectively. Therefore, their amplitudes and offsets as well as the phase change of retardance 2 ( θ − b n ) can be correspondingly calculated. The contributions from retardance and absorbance have been plotted by color-filled areas in Figure 7. The fits are: 0.04306 cos 2 2 ( θ − 64 . 66 ∘ ) + 0.18076 and 0.0040365 cos 2 ( θ − 100 ∘ ) + 0.017 . The sum of the two is plotted as the final fit formula (see legend in Figure 7). Therefore, the contribution formulas of the retardance and absorbance resulting from the GO grating polariser can be fitted with the proposed method. It is worthy of note that the form birefringence originates from the geometry of the grating defined by its depth and duty cycle as discussed above. The retardance R e t = Δ n × d λ calculated from the form birefringence of GO is R e t ≈ 0.11 at 2.94 μ m with GO thickness d = 1 μ m.
Preprints 69458 g008
Figure 8. Numerical parameters P , w , d for the study of the GO grating properties by FDTD. (a) FDTD model. (b) Index ( n , κ ) of GO used in modeling (Lumerical database). (c) IR transmittance spectra from 3 μ m to 8 μ m of GO gratings with different parameters: (top-row) width w = 1 μ m and film thickness d = 1 μ m; while the grating period P changes 3, 4, and 5 μ m, respectively; (middle-row) P = 4 μ m, d = 1 μ m while w is 1, 2, and 3 μ m; (bottom-row) P = 4 μ m, w = 1 μ m while d is 0.5, 1, and 2 μ m, respectively.
Figure 8. Numerical parameters P , w , d for the study of the GO grating properties by FDTD. (a) FDTD model. (b) Index ( n , κ ) of GO used in modeling (Lumerical database). (c) IR transmittance spectra from 3 μ m to 8 μ m of GO gratings with different parameters: (top-row) width w = 1 μ m and film thickness d = 1 μ m; while the grating period P changes 3, 4, and 5 μ m, respectively; (middle-row) P = 4 μ m, d = 1 μ m while w is 1, 2, and 3 μ m; (bottom-row) P = 4 μ m, w = 1 μ m while d is 0.5, 1, and 2 μ m, respectively.
Preprints 69458 g008
The extinction ratio E R = 10 lg ( T E / T M ) of the GO polariser at IR wavelengths was experimentally determined (Figure 7(b)) and reached ∼ 3 at ν ˜ ∼ 3000 cm−1. This makes it sensitive for OH-bands (water) present in a wide range of organic and inorganic materials and composites and also shows hydration levels of biomaterials and food [53,54,55]. In the GO family of materials, it can also show intercalated water. The degree of polarisation D o P = T m a x − T m i n T m a x + T m i n = 0.27 at the maximum of extinction ratio E R at 2800 cm−1 (Figure 7(b)), at which the extinction ratio ρ E = T m i n T m a x = 0.5 and the extinction performance of the GO-grating as a linear polarizer, expressed as ( 1 / ρ E : 1 ) , is 2:1.

3.7. FDTD modeling of GO polariser for IR region

In terms of the phase matching condition for the guided-mode resonance [46,48], the working wavelength of the GO polariser is determined by the period P:
λ g = P · ( n e f f − n a i r · sin ϕ ) ,
where λ g is the guided-mode resonance wavelength, n e f f is the effective refractive index of the guided-mode resonance depending on the duty cycle of GO grating, n a i r = 1 is the refractive index of air, and ϕ is the angle of incidence; ϕ = 0 ∘ is the normal incidence. To investigate the performance of the GO polariser with different geometrical parameters in IR region, the numerical modeling was simulated with the finite-difference time-domain (FDTD, Lumerical, Ansys) method from 3 μ m to 10 μ m wavelengths. The GO polariser was modeled as one GO ribbon and adjacent air groove with the periodic boundary condition (Figure 8).
Figure 8 displays the main results of parameter studies as the simulated IR transmittance spectra of the GO polariser with different geometrical parameters P, w and d under both TE and TM polarisations incident and the difference between them The difference indicates the polarisation efficiency of the GO polariser, which also can be considered as a filter. Figure 8 reveals that the working wavelength is dependent on the period P of the GO grating, which is conformed to the guided-mode resonance, as expressed in Eqn. 6. The effect of the duty cycle of GO grating to the performance of the polariser is shown with period P and GO thickness d constant at 4 μ m and 1 μ m, respectively. It is clear that the smaller the duty cycle of the GO grating (the thinner the GO ribbon), the higher the modulation of transmittance T of the GO polariser. The influence of the GO film thickness d is as follows: the thicker GO film can increase the absorption of the TE polarisation but also increases the TM absorption. Therefore, to select the appropriate thickness of the GO film can effectively optimise the polarisation selectivity of the GO polariser. Hence, the performance of the GO polariser is dependent on its geometrical parameters, the working wavelength is determined by the period of the GO grating and the polarisation selectivity can be optimised by tuning the duty cycle and thickness of the grating.
Additionally, the IR transmittance spectrum of the SZ2080TM MLA on a 1 mm thick CaF2 substrate has been measured. The polymerised SZ2080TM material has the relatively higher transmittance from 3.5 μ m to 5.5 μ m. Therefore, the proposed GO polariser with flexible working wavelengths can be integrated with the fabricated MLA to achieve integrated polarisation control, and it can also serve as a selective filter working together with another plain TM polariser.

4. Conclusions and outlook

The fs-DLW technique was utilised as a 3D lithography tool to precisely fabricate the MLA in the low-shrinkage SZ2080TM photoresist. The surface morphology of the fabricated microlenses was following the design with high fidelity at the high irradiance ∼ 0.7 TW/cm2/pulse writing conditions. Compared with lengthy raster-scanning of the entire volume of the MLA, only the shell of the MLA was formed by the fs-DLW, whereas the inside volume was fully polymerised by a post-fabrication UV exposure. This sequence significantly speeds up fabrication of the MLA with prospectives for large-scale production. The experimentally measured intensity distribution of the focal spots of the MLA at visible wavelengths showed a good agreement with the theoretical calculation based on the Rayleigh–Sommerfeld (RS) diffraction integral.
Additionally, a GO grating polariser was also fabricated with the fs-DLW technique in a 1- μ m-thick GO thin film, which can provide linear polarisation in the infrared (IR) region. A formula-fitting method has also been mathematically demonstrated to determine the contributions resulting from absorbance and retardance (caused by birefringence) in the experimentally measured IR transmittance spectrum. The polarisation performance of the GO polariser is dependent on its geometrical parameters including the period, duty cycle and thickness. The GO polariser can be integrated with the fabricated MLA for polarisation control in the IR region (working wavelength of the GO polariser), and the integrated components have demonstrated a dynamic tuning of dispersion in the visible range. Future studies are required in GO gratings to harness strong anisotropy of IR absorption along the edges of the reduced GO where absorption can increase up to two orders of magnitude due to coupling between IR vibrations and free charges [51]. High refractive index of GO at IR wavelengths could be used for sensors with reflection geometries based on surface wave generation [56] as well as on ponderomotive interactions between GO and nanoparticles [57].

Author Contributions

Conceptualization, H.M. and S.J.; methodology, H.M, T.K., SH.N, D.S.; mumerical modeling, H.M.; validation, H.M., SH.N., T.K., D.G.; formal analysis, H.M., M.R., J.M., D.G., M.M., V.L., D.M.; investigation, H.M., T.V., V.L., D.M., D.S.; data curation, D.M., P.R.S., D.R., Y.N.; writing—original draft preparation, H.M. and S.J.; writing—review and editing, all the authors; visualization, H.M. and S.J.; supervision, SH.N., S.J.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by ARC Linkage LP190100505 project. M.M. was funded from EU Horizon 2020, Research and Innovation program LASERLAB-EUROPE JRA Project No. 871124. J.M. and M.R. were funded by JSPS KAKENHI Grant No. 22H02137 and JST CREST Grant No. JPMJCR19I3. M.R. was funded by JSPS KAKENHI Grant No. 22K14200.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Data can be made available upon a reasonable request.

Acknowledgments

We are grateful to Workshop of Photonics Ltd., Lithuania for fs-laser fabrication setup acquired via a technology transfer project in 2012.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Critical exposure parameters

Preprints 69458 g0a1
Figure A1. Optical images of microlenses polymerised at different scanning speeds, line spacings between neighboring lines and linear pulse densities. Polymerisation of the outer shell was carried out by concentric fs-DLW from larger-to-smaller diameters. The top-row microlenses were made at the same pulse density of 10 5 /mm. The MLA was written at 0.1 mm/s scan speed, line spacing of 0.5 μ m (hatching) and pulse density of 10 6 /mm (pulse-to-pulse separation on the sample was 0.5 nm); see text for discussion.
Figure A1. Optical images of microlenses polymerised at different scanning speeds, line spacings between neighboring lines and linear pulse densities. Polymerisation of the outer shell was carried out by concentric fs-DLW from larger-to-smaller diameters. The top-row microlenses were made at the same pulse density of 10 5 /mm. The MLA was written at 0.1 mm/s scan speed, line spacing of 0.5 μ m (hatching) and pulse density of 10 6 /mm (pulse-to-pulse separation on the sample was 0.5 nm); see text for discussion.
Preprints 69458 g0a1
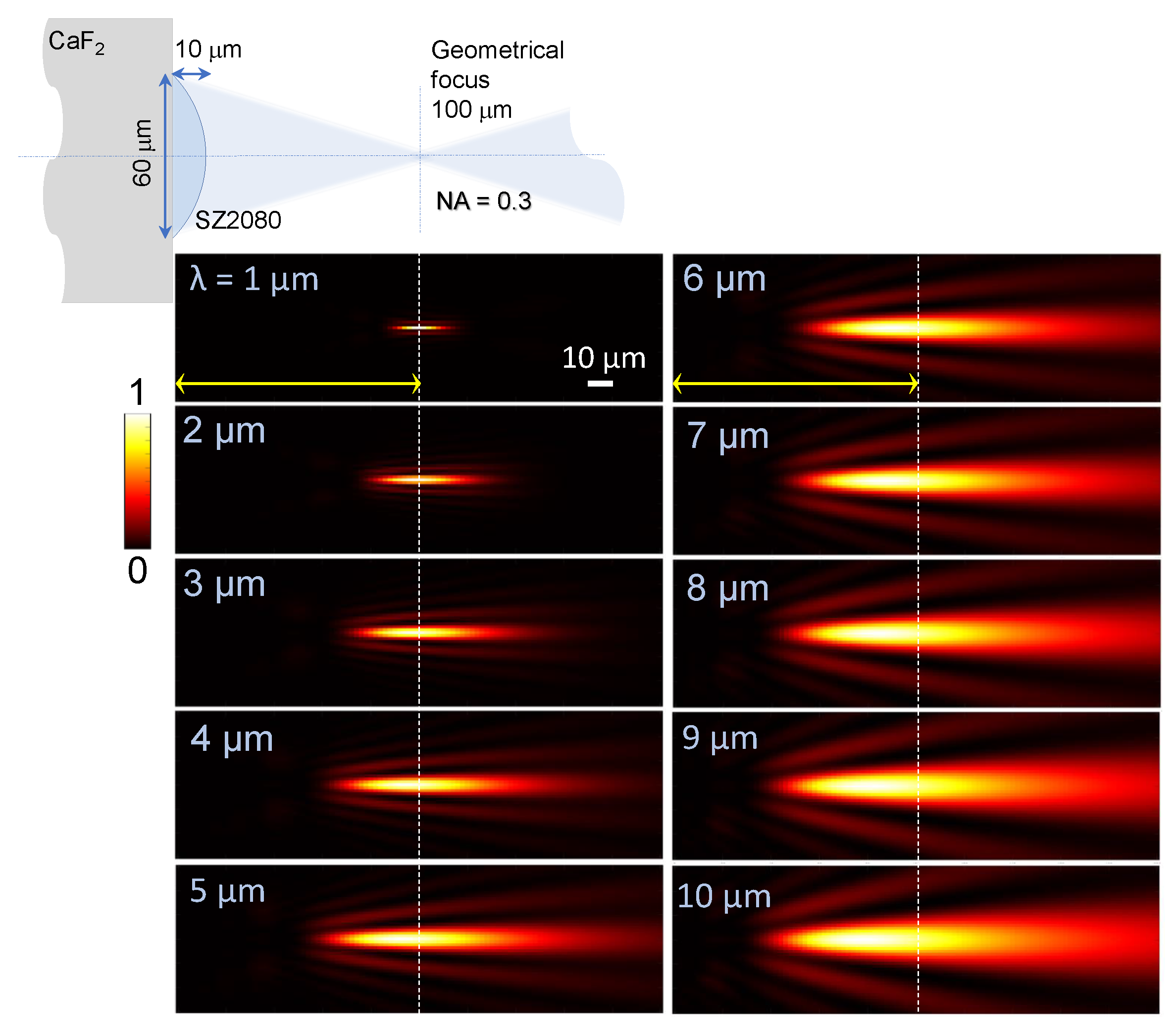
Preprints 69458 g0a2
Figure A2. The Rayleigh-Sommerfeld (RS) diffraction integral Eqn. 1 calculation of the axial lintensity distribution (normalised) at different wavelengths λ for the fixed refractive index n S Z 2080 = 1.504 . Simulations for visible 633 nm wavelength using the same approach is shown in Figure 4.
Figure A2. The Rayleigh-Sommerfeld (RS) diffraction integral Eqn. 1 calculation of the axial lintensity distribution (normalised) at different wavelengths λ for the fixed refractive index n S Z 2080 = 1.504 . Simulations for visible 633 nm wavelength using the same approach is shown in Figure 4.
Preprints 69458 g0a2
Pulse density per linear scan was an important parameter to achieve good surface quality and match with the designed 3D surface profile. Figure A1 illustrates the influence of scan speed, linear pulse density and line spacing (hatching) of the polymerised microlenses, which were defined by the shell polymerisation followed by development and UV exposure. At some set of those scan conditions, a very distinct square pattern was emerging in the polymerised lens shell (Figure A1). 3D optical profile revealed that the pattern observed in transmission using an optical microscope was also present on the surface of the lens (Figure A1) due to nonuniform polymerisation. When pulse density was the largest, 10 6 pulses per millimeter, the most uniform microlenses and MLA were fabricated and used in this study.
To explain such irregularities in the structures, it must be considered that, for the 3D polymerisation, stages were used to scan the beam in the lateral x y -plane. The periodic pattern seen in Figure A1 exactly corresponds to the stages’ nominal relative incremental encoder step of 20 μ m, and its orientation is strictly along the x y -directions. The node positions are absolute (will occur at the same absolute coordinates) and are invariant to the scan algorithm. The used controller has a servo update rate of 8 kHz and can accept and process a quadrature encoder channel frequency on the scale of at least 16 MHz (see "Npaq" specifications in [58]). The controller can interpolate the 20 μ m relative encoder signal to achieve nanoscale resolution feedback by a division factor of x65536. In these experiments, the factor was set to x20000, giving a minimum incremental step of 1 nm. A scan speed of 0.1 mm/s results in an interpolated encoder signal of 0.1 MHz. This frequency is far below MHz scale nominal limitations of the controller. As the patterns appear at lower processing speeds and continuous firing (no pulse control) modes, they cannot be explained by incorrect operation of the stages and their control hardware. One can only deduce that the subtle changes in velocity at the encoder’s physical increment edges produce a dose variation that is well apparent for the 3D polymerisation process. This effect is reproducible in similar systems. One might speculate that this effect might appear in different degrees everywhere, where incremental encoders are used in closed-loop high-speed scan operation modes.
Continuous laser writing by scanning requires equally smooth stage motion and position control. When polymerisation is made using combined stage and Galvano-scanners, this issue is less apparent and 3D polymerisation becomes not limited by one write field and stitching errors [59]. In this particular case of 3D MLA fabrication, we used the largest pulse density which delivered a good optical performance of the fabricated lenses. Precautions were taken to eliminate other stage-related issues of mechanical nature, such as initiation of large amplitude circular scan before actual polymerisation, temperature stability in the class 1000 cleanroom was ± 0 . 5 ∘ C. Observed Pharos laser regenerative amplifier power fluctuations were ± 20 mW i.e. within 0.2 % of its full range.

Appendix B. NA = 0.3 lens focusing at IR 1 − 10 μm wavelengths

Figure A2 show axial intensity distribution calculated by the Rayleigh-Sommerfeld (RS) diffraction integral Eqn. 1 for the SZ2080TM plano-convex lens of 10 μ m height and D = 60 μ m diameter corresponding to the numerical aperture of N A = 0.3 . The refractive index of SZ2080TM was kept constant at n s z 2080 = 1.504 for all the wavelengths for comparison. The refractive index defines position of the focus in ray optical expression of the focal length 1 f = n S Z 2080 − 1 R with R being the radius of surface curvature of the front surface of a spherical lens (focus is in air, hence n = 1 ). Departure from the f = 100 μ m focal position defined by the ray optics is discernible due to the wave nature of light focused with a lens which has thickness comparable with the wavelength. Such different 3D light localisation becomes important in IR broadband sources, e.g., synchrotron or thermal radiation where CaF2 substrates are widely used for optics and sample holders. Different axial position of intensity maximum at different λ (longer wavelengths are focused closer to the lens) is a signature of spherical aberration.
The lateral cross section of the focal spot scales with the wavelength, as usually estimated from the Airy disk diameter of plane wave focusing ⊘ = 1.22 λ / N A .

References

  1. Zimmermann, M.; Lindlein, N.; Voelkel, R.; Weible, K.J. Microlens laser beam homogenizer: from theory to application. Laser Beam Shaping VIII. SPIE, 2007, Vol. 6663, pp. 9–21.
  2. Liang, Y.; Zhu, T.; Xi, M.; Abbasi, H.N.; Fu, J.; Su, R.; Song, Z.; Wang, H.; Wang, K. Fabrication of a diamond concave microlens array for laser beam homogenization. Optics & Laser Technology 2021, 136, 106738. [Google Scholar] [CrossRef]
  3. Lin, V.; Wei, H.C.; Hsieh, H.T.; Hsieh, J.L.; Su, G.D. Design and fabrication of long-focal-length microlens arrays for Shack–Hartmann wavefront sensors. Micro & Nano Letters 2011, 6, 523–526. [Google Scholar] [CrossRef]
  4. Zhang, L.; Zhou, W.; Naples, N.J.; Allen, Y.Y. Fabrication of an infrared Shack–Hartmann sensor by combining high-speed single-point diamond milling and precision compression molding processes. Applied optics 2018, 57, 3598–3605. [Google Scholar] [CrossRef] [PubMed]
  5. Wu, D.; Xu, J.; Niu, L.G.; Wu, S.Z.; Midorikawa, K.; Sugioka, K. In-channel integration of designable microoptical devices using flat scaffold-supported femtosecond-laser microfabrication for coupling-free optofluidic cell counting. Light: Science & Applications 2015, 4, e228–e228. [Google Scholar] [CrossRef]
  6. Park, H.S.; Hoskinson, R.; Abdollahi, H.; Stoeber, B. Compact near-eye display system using a superlens-based microlens array magnifier. Optics Express 2015, 23, 30618–30633. [Google Scholar] [CrossRef] [PubMed]
  7. Zhu, T.F.; Liu, Z.; Liu, Z.; Li, F.; Zhang, M.; Wang, W.; Wen, F.; Wang, J.; Bu, R.; Zhang, J.; et al. Fabrication of monolithic diamond photodetector with microlenses. Optics Express 2017, 25, 31586–31594. [Google Scholar] [CrossRef]
  8. Qu, Y.; Kim, J.; Coburn, C.; Forrest, S.R. Efficient, nonintrusive outcoupling in organic light emitting devices using embedded microlens arrays. ACS photonics 2018, 5, 2453–2458. [Google Scholar] [CrossRef]
  9. Duparré, J.; Dannberg, P.; Schreiber, P.; Bräuer, A.; Tünnermann, A. Artificial apposition compound eye fabricated by micro-optics technology. Applied optics 2004, 43, 4303–4310. [Google Scholar] [CrossRef] [PubMed]
  10. Chen, F.; Liu, H.; Yang, Q.; Wang, X.; Hou, C.; Bian, H.; Liang, W.; Si, J.; Hou, X. Maskless fabrication of concave microlens arrays on silica glasses by a femtosecond-laser-enhanced local wet etching method. Optics express 2010, 18, 20334–20343. [Google Scholar] [CrossRef]
  11. Liu, W.; Ma, D.; Li, Z.; Cheng, H.; Choi, D.Y.; Tian, J.; Chen, S. Aberration-corrected three-dimensional positioning with a single-shot metalens array. Optica 2020, 7, 1706–1713. [Google Scholar] [CrossRef]
  12. Yuan, W.; Li, L.H.; Lee, W.B.; Chan, C.Y. Fabrication of microlens array and its application: a review. Chinese Journal of Mechanical Engineering 2018, 31, 1–9. [Google Scholar] [CrossRef]
  13. Syms, R.R.; Yeatman, E.M.; Bright, V.M.; Whitesides, G.M. Surface tension-powered self-assembly of microstructures-the state-of-the-art. Journal of Microelectromechanical systems 2003, 12, 387–417. [Google Scholar] [CrossRef]
  14. Yang, H.; Chao, C.K.; Wei, M.K.; Lin, C.P. High fill-factor microlens array mold insert fabrication using a thermal reflow process. Journal of micromechanics and microengineering 2004, 14, 1197. [Google Scholar] [CrossRef]
  15. Moore, S.; Gomez, J.; Lek, D.; You, B.H.; Kim, N.; Song, I.H. Experimental study of polymer microlens fabrication using partial-filling hot embossing technique. Microelectronic Engineering 2016, 162, 57–62. [Google Scholar] [CrossRef]
  16. Zhang, X.; Fang, F.; Yu, L.; Jiang, L.; Guo, Y. Slow slide servo turning of compound eye lens. Optical Engineering 2013, 52, 023401. [Google Scholar] [CrossRef]
  17. Hong, G.S.; San Wong, Y.; others. Profile error compensation in fast tool servo diamond turning of micro-structured surfaces. International Journal of Machine Tools and Manufacture 2012, 52, 13–23. [Google Scholar] [CrossRef]
  18. Kley, E.B.; Possner, T.; Göring, R. Realization of micro-optic and integrated optic components by electron-beam-lithographic surface profiling and ion exchange in glass. International Journal of Optoelectronics 1993, 8, 513–513. [Google Scholar]
  19. Fujita, T.; Nishihara, H.; Koyama, J. Fabrication of micro lenses using electron-beam lithography. Optics letters 1981, 6, 613–615. [Google Scholar] [CrossRef]
  20. Ovsianikov, A.; Viertl, J.; Chichkov, B.; Oubaha, M.; MacCraith, B.; Sakellari, I.; Giakoumaki, A.; Gray, D.; Vamvakaki, M.; Farsari, M.; others. Ultra-low shrinkage hybrid photosensitive material for two-photon polymerization microfabrication. ACS nano 2008, 2, 2257–2262. [Google Scholar] [CrossRef]
  21. Merkininkaitė, G.; Aleksandravičius, E.; Malinauskas, M.; Gailevičius, D.; Šakirzanovas, S. Laser additive manufacturing of Si/ZrO2 tunable crystalline phase 3D nanostructures. Opto-electronic advances 2022, 5, 1–11. [Google Scholar] [CrossRef]
  22. Ovsianikov, A.; Gaidukeviciute, A.; Chichkov, B.; Oubaha, M.; MacCraith, B.; Sakellari, I.; Giakoumaki, A.; Gray, D.; Vamvakaki, M.; Farsari, M.; others. Two-photon polymerization of hybrid sol-gel materials for photonics applications. Laser Chemistry 2008, 2008. [Google Scholar] [CrossRef]
  23. Malinauskas, M.; Žukauskas, A.; Purlys, V.; Belazaras, K.; Momot, A.; Paipulas, D.; Gadonas, R.; Piskarskas, A.; Gilbergs, H.; Gaidukevičiūtė, A.; others. Femtosecond laser polymerization of hybrid/integrated micro-optical elements and their characterization. Journal of Optics 2010, 12, 124010. [Google Scholar] [CrossRef]
  24. Qiu, L.; Liu, J.Z.; Chang, S.L.; Wu, Y.; Li, D. Biomimetic superelastic graphene-based cellular monoliths. Nature communications 2012, 3, 1–7. [Google Scholar] [CrossRef]
  25. Bose, S.; Drzal, L.T. Role of thickness and intercalated water in the facile reduction of graphene oxide employing camera flash. Nanotechnology 2014, 25, 075702. [Google Scholar] [CrossRef] [PubMed]
  26. Sun, H.B.; Kawata, S. Two-photon photopolymerization and 3D lithographic microfabrication. NMR• 3D Analysis• Photopolymerization 2004, pp. 169–273.
  27. Seet, K.K.; Mizeikis, V.; Juodkazis, S.; Misawa, H. Three-Dimensional Horizontal Circular Spirals Photonic Crystals with stop gaps below 1μm. Appl. Phys. Lett. 2006, 88, 221101. [Google Scholar] [CrossRef]
  28. Kondo, T.; Juodkazis, S.; Mizeikis, V.; Matsuo, S.; Misawa, H. Fabrication of three-dimensional periodic microstructures in photoresist SU-8 by phase-controlled holographic lithography. New J. Phys. 2006, 8, 250. [Google Scholar] [CrossRef]
  29. Juodkazis, S.; Matsuo, S.; Misawa, H.; Mizeikis, V.; Marcinkevicius, A.; Sun, H.B.; Tokuda, Y.; Takahashi, M.; Yoko, T.; Nishii, J. Application of femtosecond laser pulses for microfabrication of transparent media. Appl. Surf. Sci. 2002, 197-198, 705–709. [Google Scholar] [CrossRef]
  30. Mack, C. Optical lithography; field guides, SPIE, 2006.
  31. Skliutas, E.; Lebedevaite, M.; Kabouraki, E.; Baldacchini, T.; Ostrauskaite, J.; Vamvakaki, M.; Farsari, M.; Juodkazis, S.; Malinauskas, M. Polymerization mechanisms initiated by spatio-temporally confined light. Nanophotonics 2021, 10, 1211–1242. [Google Scholar] [CrossRef]
  32. Nishiyama, H.; Hirata, Y. Femtosecond Laser Nonlinear Lithography. In Lithography; Wang, M., Ed.; IntechOpen: Rijeka, 2010; chapter 4. [Google Scholar] [CrossRef]
  33. Malinauskas, M.; Žukauskas, A.; Bičkauskaitė, G.; Gadonas, R.; Juodkazis, S. Mechanisms of three-dimensional structuring of photo-polymers by tightly focussed femtosecond laser pulses. Opt. Express 2010, 18, 10209–10221. [Google Scholar] [CrossRef]
  34. Fischer, J.; Mueller, J.; Kaschke, J.; Wolf, T.; Unterreiner, A.N.; Wegener, M. Three-dimensional multi-photon direct laser writing with variable repetition rate. Optics Express 2013, 21, 26244–26260. [Google Scholar] [CrossRef]
  35. Murazawa, N.; Juodkazis, S.; Misawa, H.; Kamada, K. Two-photon excitation of dye-doped liquid crystal by a cw-laser irradiation. Mol. Cryst. Liq. Cryst. 2008, 489, 310–319. [Google Scholar] [CrossRef]
  36. Gamaly, E.G.; Rode, A.V. Ultrafast re-structuring of the electronic landscape of transparent dielectrics: new material states (Die-Met). Appl. Phys. A 2018, 124, 1–11. [Google Scholar] [CrossRef]
  37. Ng, S.; Juodkazis, S. Nanoscale plasmonic printing (in Ultrafast Laser Nanostructuring: the Pursuit of Extreme Scales; Eds. R Stoian and J Bonse); Springer Series in Optical Science, 2023; Vol. 239, p. Chapter 25.
  38. Samsonas, D.; Skliutas, E.; Čiburys, A.; Kontenis, L.; Gailevičius, D.; Berzinš, J.; Narbutis, D.; Jukna, V.; Vengris, M.; Juodkazis, S.; Malinauskas, M. 3D nanopolymerization and damage threshold dependence on laser wavelength and pulse duration. Nanophotonics 2023. [Google Scholar] [CrossRef]
  39. Schöche, S.; Hong, N.; Khorasaninejad, M.; Ambrosio, A.; Orabona, E.; Maddalena, P.; Capasso, F. Optical properties of graphene oxide and reduced graphene oxide determined by spectroscopic ellipsometry. Applied Surface Science 2017, 421, 778–782. [Google Scholar] [CrossRef]
  40. El-Sayed, M.A.; Ermolaev, G.A.; Voronin, K.V.; Romanov, R.I.; Tselikov, G.I.; Yakubovsky, D.I.; Doroshina, N.V.; Nemtsov, A.B.; Solovey, V.R.; Voronov, A.A.; others. Optical constants of chemical vapor deposited graphene for photonic applications. Nanomaterials 2021, 11, 1230. [Google Scholar] [CrossRef] [PubMed]
  41. Gu, M. Advanced optical imaging theory; Vol. 75, Springer Science & Business Media, 2000.
  42. Wei, S.; Cao, G.; Lin, H.; Mu, H.; Liu, W.; Yuan, X.; Somekh, M.; Jia, B. High tolerance detour-phase graphene-oxide flat lens. Photonics Research 2021, 9, 2454–2463. [Google Scholar] [CrossRef]
  43. Hecht, E. Optics 2nd edition. Optics 2nd edition by Eugene Hecht Reading 1987.
  44. Sally, J.D. Roots to research: a vertical development of mathematical problems; Vol. 48, American Mathematical Soc., 2007.
  45. Kondo, T.; Matsuo, S.; Juodkazis, S.; Mizeikis, V.; Misawa, H. Multiphoton fabrication of periodic structures by multibeam interference of femtosecond pulses. Appl. Phys. Lett. 2003, 82, 2758–2760. [Google Scholar] [CrossRef]
  46. Fan, S.; Joannopoulos, J.D. Analysis of guided resonances in photonic crystal slabs. Physical Review B 2002, 65, 235112. [Google Scholar] [CrossRef]
  47. Lousse, V.; Suh, W.; Kilic, O.; Kim, S.; Solgaard, O.; Fan, S. Angular and polarization properties of a photonic crystal slab mirror. Optics express 2004, 12, 1575–1582. [Google Scholar] [CrossRef]
  48. Hermannsson, P.G.; Vannahme, C.; Smith, C.L.; Kristensen, A. Absolute analytical prediction of photonic crystal guided mode resonance wavelengths. Applied Physics Letters 2014, 105, 071103. [Google Scholar] [CrossRef]
  49. Hermannsson, P.G.; Sørensen, K.T.; Vannahme, C.; Smith, C.L.; Klein, J.J.; Russew, M.M.; Grützner, G.; Kristensen, A. All-polymer photonic crystal slab sensor. Optics Express 2015, 23, 16529–16539. [Google Scholar] [CrossRef] [PubMed]
  50. Gailevičius, D.; Ryu, M.; Honda, R.; Lundgaard, S.; Suzuki, T.; Maksimovic, J.; Hu, J.; Linklater, D.P.; Ivanova, E.P.; Katkus, T.; others. Tilted black-Si: 0.45 form-birefringence from sub-wavelength needles. Optics express 2020, 28, 16012–16026. [Google Scholar] [CrossRef] [PubMed]
  51. Acik, M.; Lee, G.; Mattevi, C.; Chhowalla, M.; Cho, K.; Chaba, Y.J. Unusual infrared-absorption mechanism in thermally reduced graphene oxide. Nature Materials 2010, 9, 840–845. [Google Scholar] [CrossRef] [PubMed]
  52. Ryu, M.; Honda, R.; Balčytis, A.; Vongsvivut, J.; Tobin, M.J.; Juodkazis, S.; Morikawa, J. Hyperspectral mapping of anisotropy. Nanoscale Horizons 2019, 4, 1443–1449. [Google Scholar] [CrossRef]
  53. Gordon, S.; Mohamed, A.; Harry-O’Kuru, R.; Imam, S. A chemometric method for correcting Fourier transform infrared spectra of biomaterials for interference from water in KBr discs. Applied spectroscopy 2010, 64, 448–457. [Google Scholar] [CrossRef] [PubMed]
  54. Vu, T.; Ha, T.; Tran, T.; Thuy, T.; Le, T.; Ngan, H.; Nguyen, T.; Hoa Bui, P.; Quynh, N.; Essayem, N. A new green approach for the reduction of graphene oxide nanosheets using caffeine. Bull. Materials Science 2015, 38, 667–671. [Google Scholar]
  55. Noda, I. Recent advancement in the field of two-dimensional correlation spectroscopy. J. Molecular Structure 2008, 883, 2–26. [Google Scholar] [CrossRef]
  56. Demydenko, Y.; Juodkazis, S.; Lozovski, V. Composite Au-on-SiC nanorods for sensing. J. Opt. Soc. Am. B 2014, 31, 2893–2900. [Google Scholar] [CrossRef]
  57. Lozovski, V.; Lysenko, V.; Rusinchuk, N. Ponderomotive forces in the system of two nanoparticles. Scientific Reports 2022, 12, 17768. [Google Scholar] [CrossRef]
  58. Aerotech Npaq Hardware Manual. Available online: https://www.aerotech.com/wp-content/uploads/2020/09/Npaq.pdf (accessed on 26 January 2023).
  59. Jonušauskas, L.; Gailevičius, D.; Rekštytė, S.; Baldacchini, T.; Juodkazis, S.; Malinauskas, M. Mesoscale laser 3D printing. Optics Express 2019, 27, 15205–15221. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

306

Views

120

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated