Accuracy-Enhanced Single-Camera Three-Dimensional Digital Image Correlation Based on Four-View Imaging

Preprint

Article

Accuracy-Enhanced Single-Camera Three-Dimensional Digital Image Correlation Based on Four-View Imaging

Altmetrics

Downloads

215

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 March 2023

Posted:

08 March 2023

You are already at the latest version

Alerts

Abstract

Owing to the advantages of cost-effectiveness, compactness, and the avoidance of complicated camera synchronization, single-camera three-dimensional (3D) digital image correlation (DIC) techniques have gained increasing attention for deformation measurement of materials and structures. In the traditional single-camera 3D-DIC system, the left and right view images can be recorded by a single camera using a diffraction grating, a bi-prism or a set of planar mirrors. To further improve the measurement accuracy of single-camera 3D-DIC, this paper introduces a single-camera four-view imaging technique by installing a pyramidal prism in front of the camera. The 3D reconstruction of the measured points before and after deformation is realized with eight governing equations induced by four views, and the strong geometric constraints of four views can help to improve the measurement accuracy. A static experiment, a rigid body translation experiment and a four-point bending experiment show that the proposed single-camera 3D-DIC method can achieve higher measurement accuracy than the dual-view single-camera 3D-DIC techniques and has advantages in reducing both random error and systematic error.

Keywords:

Subject: Engineering - Other

1. Introduction

Three-dimensional (3D) digital image correlation (DIC) is now a standard technique for the determination of the mechanical properties of materials and structures [1,2]. In terms of the number of cameras used, the current 3D-DIC can be divided into traditional dual-camera 3D-DIC [1], single-camera 3D-DIC [3], and multi-camera 3D-DIC [4]. Owing to the advantages of cost-effectiveness, compactness and the avoidance of complicated camera synchronization, single-camera three-dimensional (3D) digital image correlation (DIC) techniques have attracted increasing attention for deformation measurement. Pankow et al. developed a single-lens 3D-DIC system using a single camera and a series of mirrors and they applied the system for high-speed out-of-plane displacement measurements [5]. Genovese et al. presented a single-camera pseudo-stereo system using a bi-prism in front of the camera lens to split the scene into two equivalent lateral stereo views in the two halves of the sensor [6,7]. Xia et al. developed a diffraction-assisted image correlation for 3D displacement measurement using a single camera and 2D-DIC algorithm [8,9]. The color separation-based single-camera 3D-DIC using the 3CCD color camera or an industrial color CCD camera has also been developed [10,11]. In these single-camera 3D-DIC techniques, left and right-view images of the sample can be obtained directly with a single camera. After the camera calibration, temporal matching and stereo matching, the morphological information and 3D displacement of the specimens can be measured using a single camera. At present, the single-camera 3D-DIC techniques have been used in many applications, including vibration modal measurement [12], impact deformation measurement [13], video extensometer measurement [14], internal deformation measurement of pipelines [15] and single-event-camera based 3D trajectory measurement [16].

The single-camera 3D-DIC systems reported so far all use the two views for stereo imaging, namely the left view and the right view. Compared to the two-view imaging technique, the four-view imaging technique has been proven to improve the accuracy of 3D reconstruction [17,18]. In the traditional four-view imaging-based stereo vision system, four cameras are used to capture images from four different views [17]. The use of multiple cameras has the problem of high cost and complicated camera synchronization. It will be an effective way to improve the measurement accuracy without increasing the cost by combining the single-camera 3D-DIC technique with the four-view imaging technique.

In this work, a single-camera four-view 3D-DIC technique is proposed for high-accuracy, full-field deformation measurement to further enhance the measurement accuracy. By installing a pyramidal prism in front of the camera, the four different view images of the specimen can be easily obtained. The 3D reconstruction of the full-field object points before and after deformation is realized with eight governing equations induced by these four views, and the strong constraints of four views can help to improve the measurement accuracy. This paper focuses on improving the measurement accuracy of single-camera 3D-DIC for full-field displacement and strain measurement. Compared to the video extensometer [18], full-field deformation measurement has a very broad application prospect in the field of experimental mechanics.

The rest of the paper is organized as follows. The principles of the four-view imaging technique are described and the governing equations for four-view 3D reconstruction are given in Section 2. In Section 3, to validate the effectiveness and accuracy of the proposed single-camera four-view 3D-DIC method, a static experiment, a rigid body translation experiment and a four-point bending experiment are conducted and the measurement results are analyzed and compared to the three-view and dual-view measurements. Conclusions are drawn in Section 4.

2. Methodology

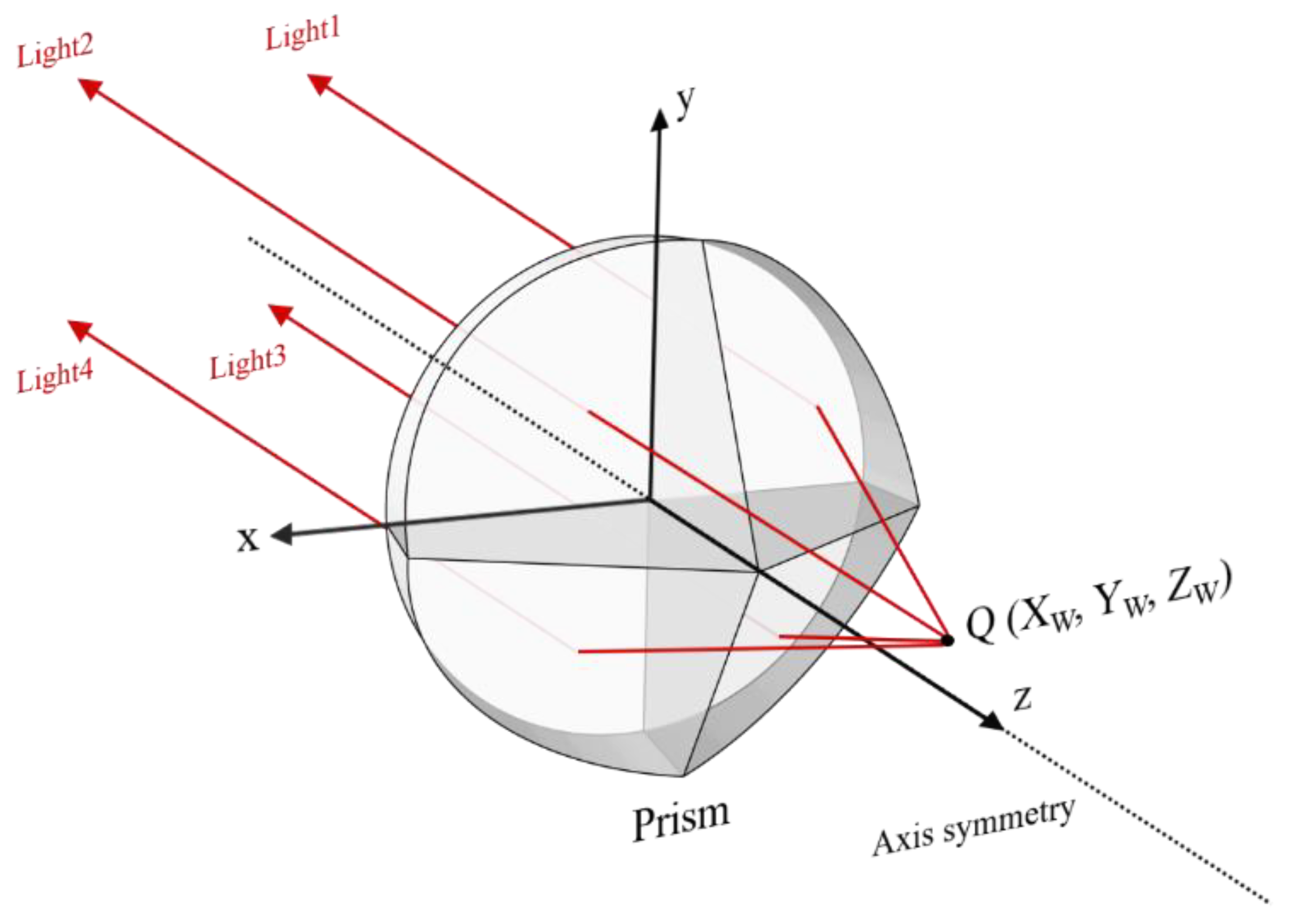
Figure 1 shows the basic schematic diagram of pyramidal prism imaging path. Through the refraction imaging of the pyramidal prism, the image of four views of the specimen can be obtained. If a camera is placed behind the pyramidal prism, the speckle image of the specimen from four views can be recorded for the single-camera 3D-DIC measurement, as shown in Figure 2.

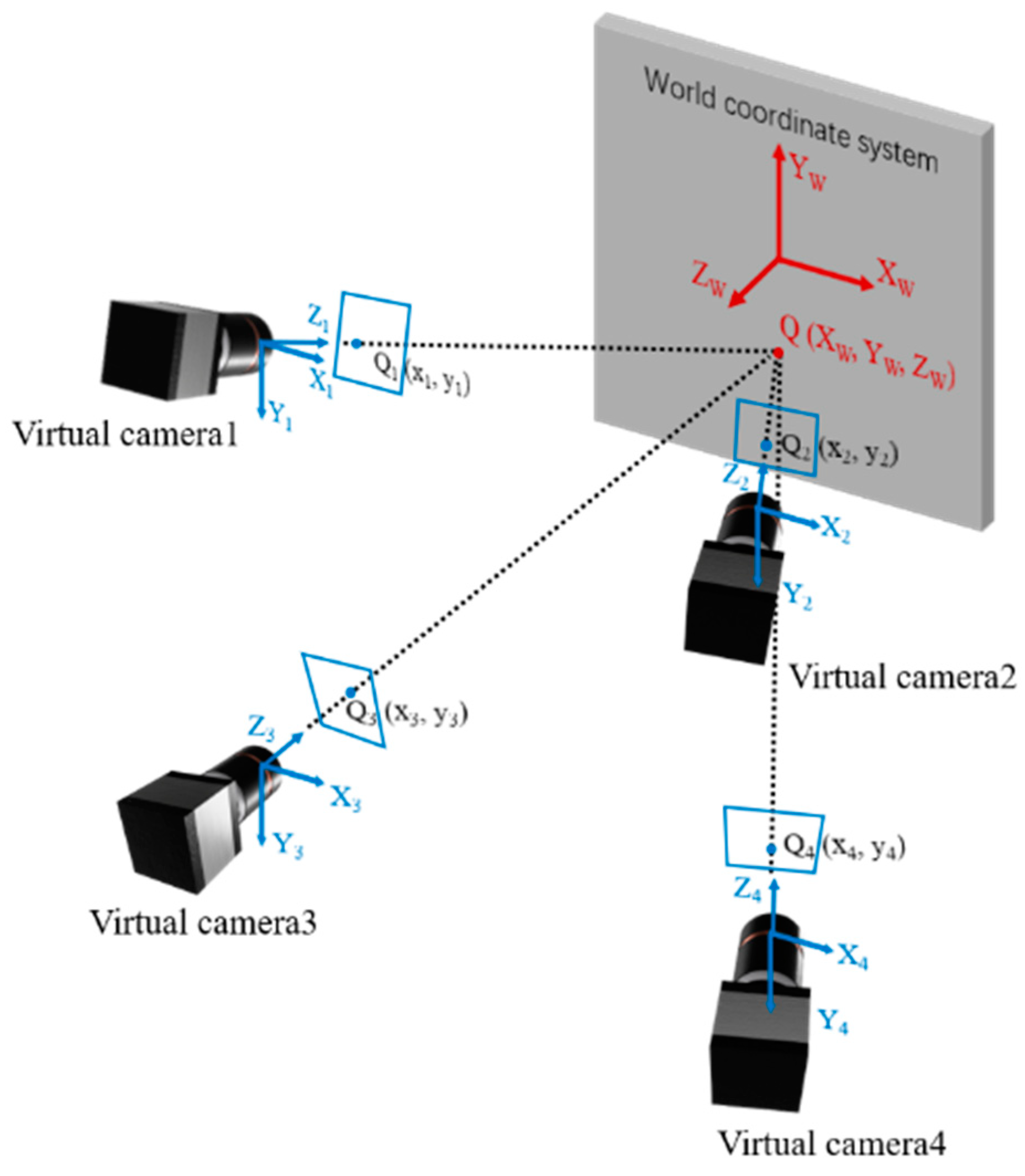
Figure 3 shows the schematic diagram of the four-view stereo vision, the four virtual cameras represent shots from different views. The point

Q

is the object point to be measured and the points

Q_{1}

Q_{2}

Q_{3}

and

Q_{4}

are the image points projected onto the image from four different views. With lens distortion removal through the distortion parameters obtained from the four-view calibration, the projection equation can be written as follows,

\{\begin{array}{l} x^{i} = f_{x} \frac{r_{11}^{i} X_{W} + r_{12}^{i} Y_{W} + r_{13}^{i} Z_{W} + t_{x}^{i}}{r_{31}^{i} X_{W} + r_{32}^{i} Y_{W} + r_{33}^{i} Z_{W} + t_{z}^{i}} + f_{s} \frac{r_{21}^{i} X_{W} + r_{22}^{i} Y_{W} + r_{23}^{i} Z_{W} + t_{y}^{i}}{r_{31}^{i} X_{W} + r_{32}^{i} Y_{W} + r_{33}^{i} Z_{W} + t_{z}^{i}} + c_{x}^{i} \\ y^{i} = f_{y} \frac{r_{21}^{i} X_{W} + r_{22}^{i} Y_{W} + r_{23}^{i} Z_{W} + t_{y}^{i}}{r_{31}^{i} X_{W} + r_{32}^{i} Y_{W} + r_{33}^{i} Z_{W} + t_{z}^{i}} + c_{y}^{i} \end{array}, i = 1, 2, 3, 4;

(1)

where

(\begin{matrix} X_{W} & Y_{W} & Z_{W} \end{matrix})

is the world coordinates of point

Q

(x^{i}, y^{i}), i = 1, 2, 3, 4

are the image coordinates of points

Q_{1}

Q_{2}

Q_{3}

and

Q_{4}

(c_{x}, c_{y}, f_{x}, f_{y}, f_{s})

are the intrinsic parameters of the single camera,

{[t_{x}, t_{y}, t_{z}]}^{T}

is the translation vector and

r_{11}

r_{33}

are the rotation matrix parameters which can be transformed from rotation vector by Rodrigues transformation, which represents the rotation matrix from upper left view coordinate system to the i-th view coordinate system, the superscripts

i

denote the i-th view.

According to Equation (1), the 3D coordinates of the object point can be solved by the least square method and the solving equation is as follows,

\begin{matrix} [\begin{matrix} x^{i} r_{31}^{i} - c_{x} r_{31}^{i} - f_{s} r_{21}^{i} - f_{x} r_{11}^{i} & x^{i} r_{32}^{i} - c_{x} r_{32}^{i} - f_{s} r_{22}^{i} - f_{x} r_{12}^{i} & x^{i} r_{33}^{i} - c_{x} r_{33}^{i} - f_{s} r_{23}^{i} - f_{x} r_{13}^{i} \\ y^{i} r_{31}^{i} - c_{y} r_{31}^{i} - f_{y} r_{21}^{i} & y^{i} r_{32}^{i} - c_{y} r_{32}^{i} - f_{y} r_{22}^{i} & y^{i} r_{33}^{i} - c_{y} r_{33}^{i} - f_{y} r_{23}^{i} \end{matrix}] [\begin{matrix} X_{W} \\ Y_{W} \\ Z_{W} \end{matrix}] \\ = [\begin{matrix} f_{x} t_{x}^{i} + f_{s} t_{y}^{i} + c_{x} t_{z}^{i} - x^{i} t_{z}^{i} \\ f_{y} t_{y}^{i} + c_{y} t_{z}^{i} - y^{i} t_{z}^{i} \end{matrix}], i = 1, 2, 3, 4 \end{matrix}

(2)

It can be seen from Equation (2) that a total of eight equations can be used to solve the three unknowns of 3D coordinates of the object point. Compared to the traditional dual-view single-camera 3D-DIC, there are two more ray geometric constraints. The four equations brought by the two ray geometric constraints can reduce the uncertainty of 3D reconstruction [14].

To calibrate the four-view single-camera 3D-DIC, the intrinsic parameters, and the extrinsic parameters between the second, third and fourth views with the first view should be obtained. These parameters can be calibrated through a planar calibration method, utilizing calibration images from all four views. An example of calibration images is shown in Figure 4.

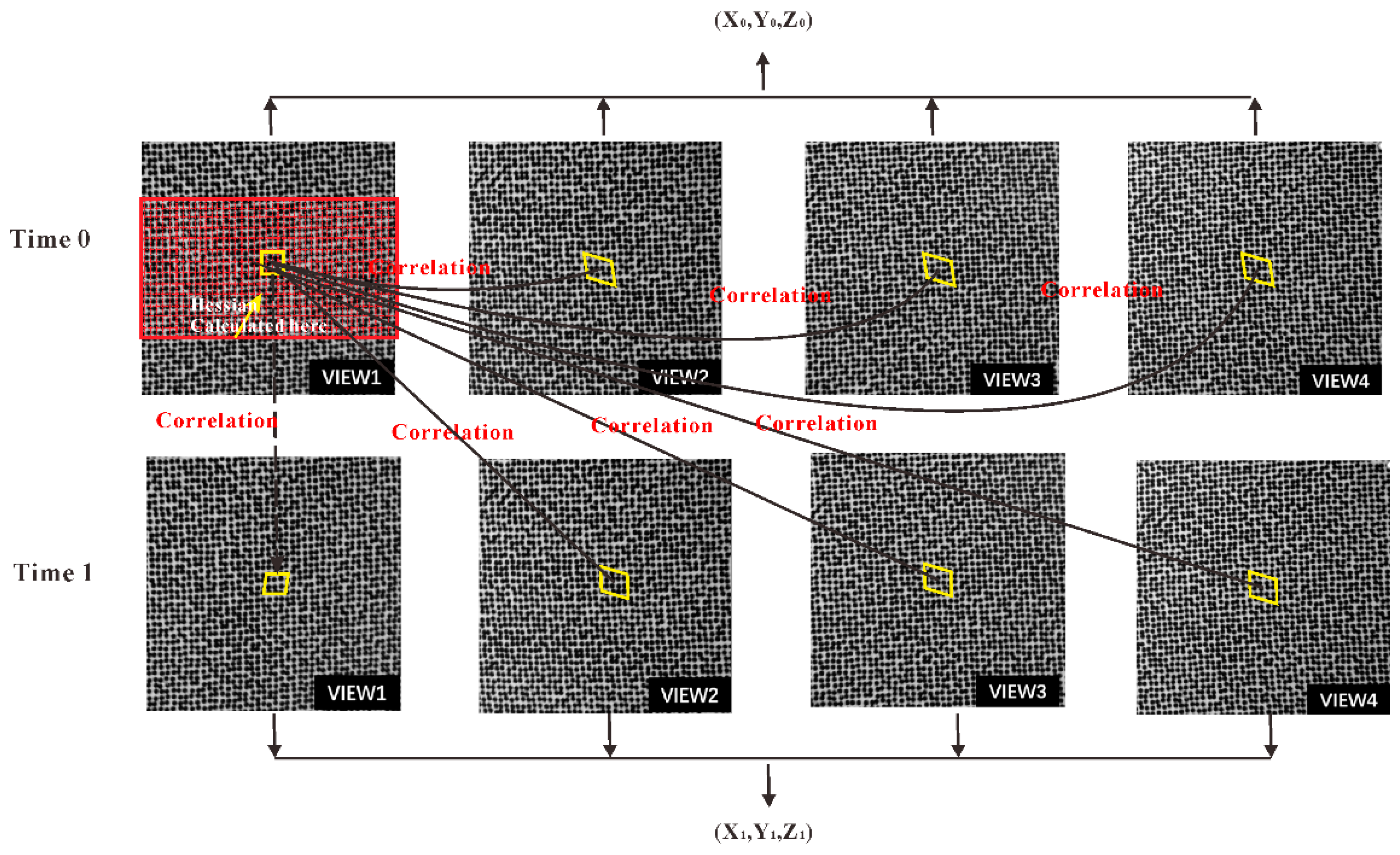
After camera calibration, the morphologic information of the object can be obtained by 3D reconstruction of the full-field data points, as shown in Figure 5. Then the 3D displacements can be calculated with the 3D coordinates of the same point before and after deformation. Based on the reconstructed 3D shape and the calculated 3D displacement, the local surface strains can be computed. Once the initial topology of the specimen has been measured, the normal direction of each point in the initial topology can be defined. Using a lease-square plane to fit the data array around each point, the local surface of each point can be defined. According to the local surface and X direction of the Lagrange world coordinate system after the 3D reconstruction, the local coordinate system can be defined. Then, all three components of displacements for each point on the surface are projected to the local Cartesian coordinate system and the strain can be calculated using least-square method.

3. Experimental Results

To validate the effectiveness and accuracy of the proposed single-camera four-view 3D-DIC, a static experiment, a rigid body translation experiment and a four-point bending experiment are conducted respectively. In the static experiment and the translation experiment, the displacement accuracy in both in-plane and out-of-plane directions is verified. In the four-point bending experiment, the strain field is measured and compared to the strain gauge technique.

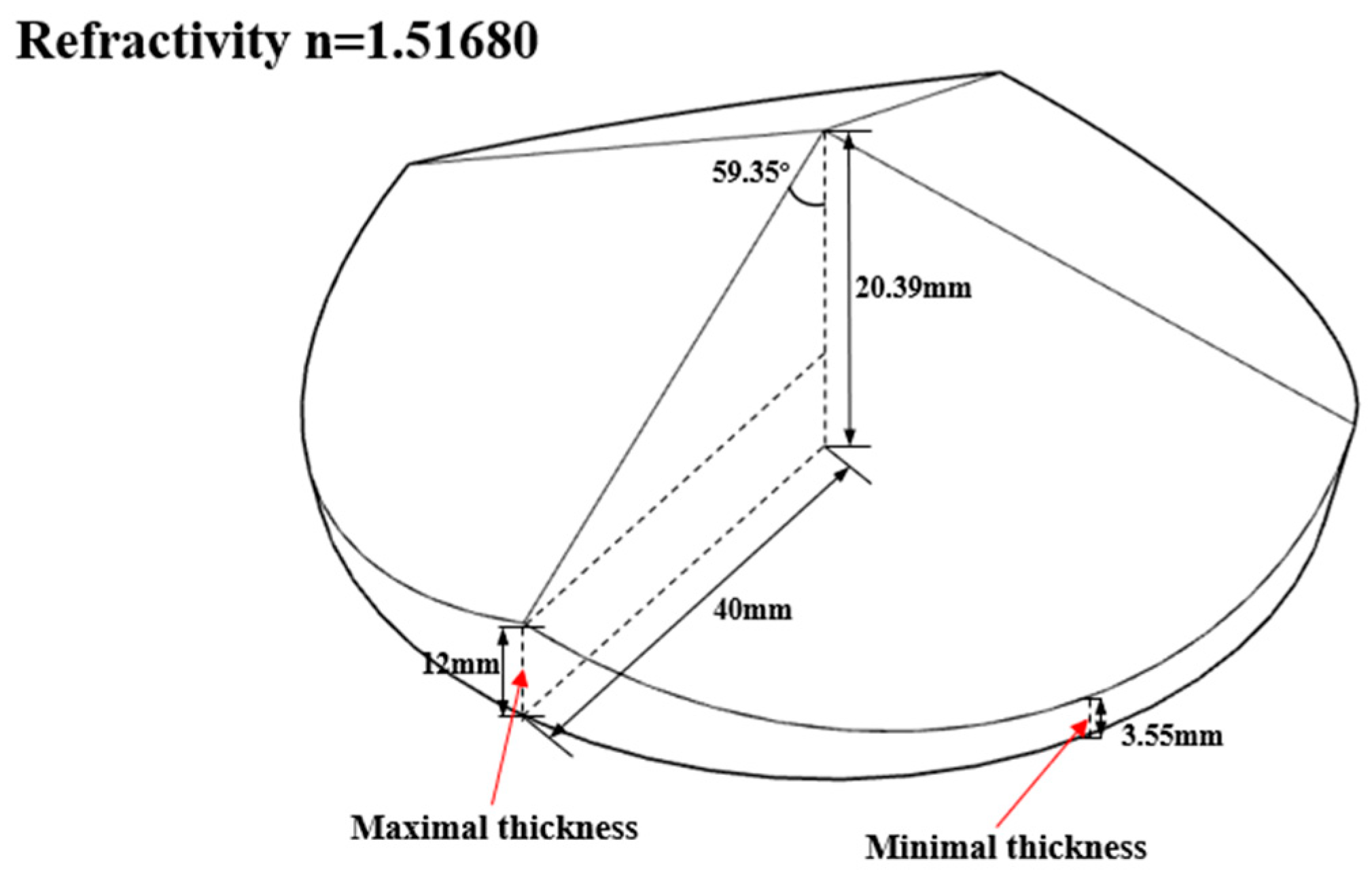
As shown in Figure 6, a single-camera four-view 3D-DIC system consisting of a single camera and a pyramidal prism is mounted on the slide rail (Daheng Optics, GCM-72) on a heavy tripod (FOBA, ASLAI). The geometry of the pyramidal prism is shown in Figure 7 and the distance between the pyramidal prism and lens is 105 mm. The detailed system configuration is listed in Table 1 and the extrinsic parameters between the first view and other views are shown in Table 2.

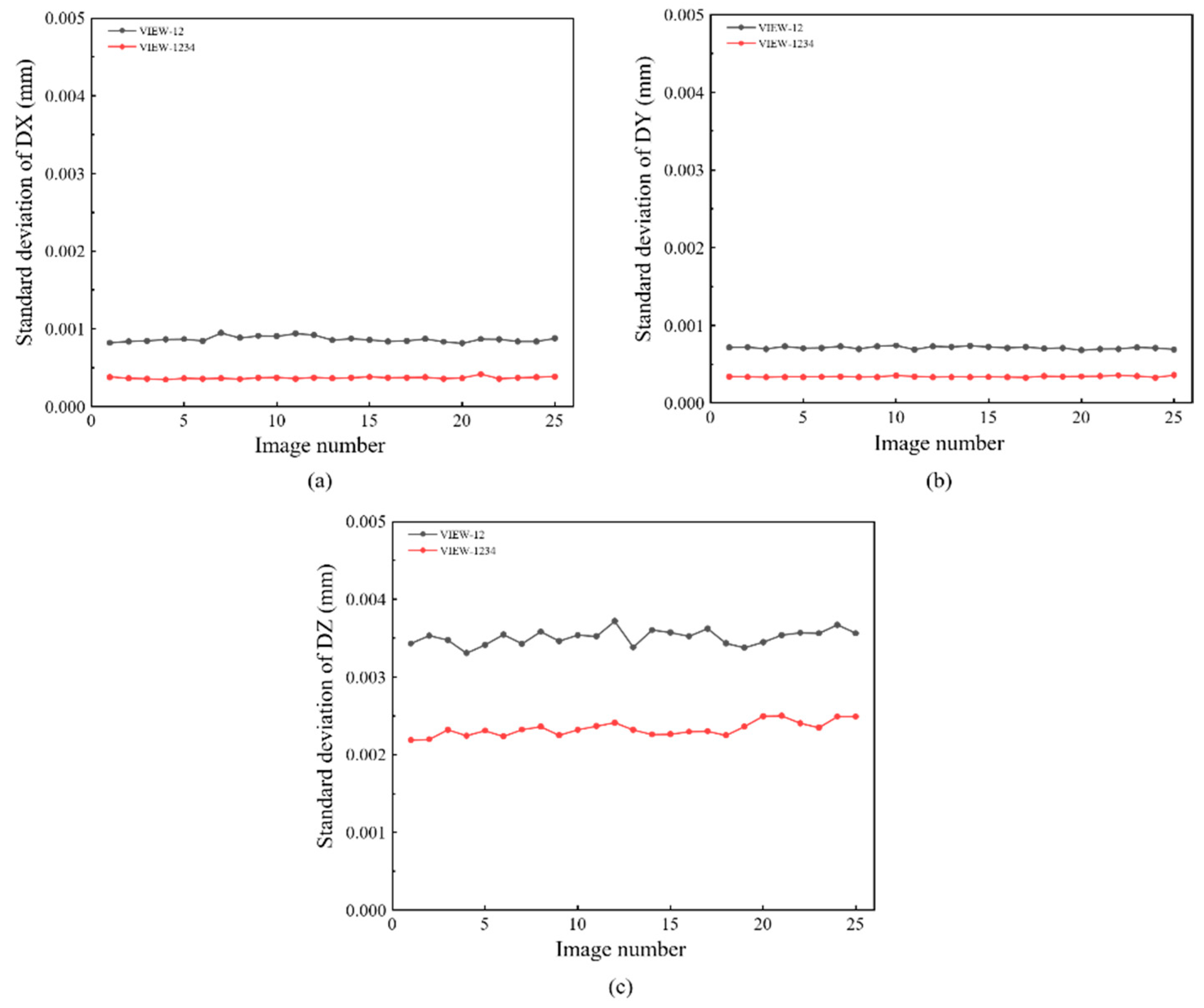
The static experiment configuration is shown in Figure 6a. Artificial speckles are generated on the surface of the specimen in Figure 6b. The working distance between the specimen and the prism is 200 mm. 25 images are captured by the single four-view camera system and calculated by DIC. In detail, VIEW 1 and VIEW 2 are used to construct a conventional two-view DIC, and all four views are combined to provide a four-view DIC measurement. The standard deviation error of displacement for different directions (DX, DY, and DZ) are shown in Figure 8, respectively. It is noticed that four-view DIC shows a distinct improvement in the random error. Compared to the two-view measurement, the in-plane displacement random error of the four-view measurement is reduced by 0.0004mm. For out-of-plane displacement random error, it is reduced from 0.0035mm to 0.002mm. It can be noticed that the random error is obviously reduced by the strong geometric constraints of four views.

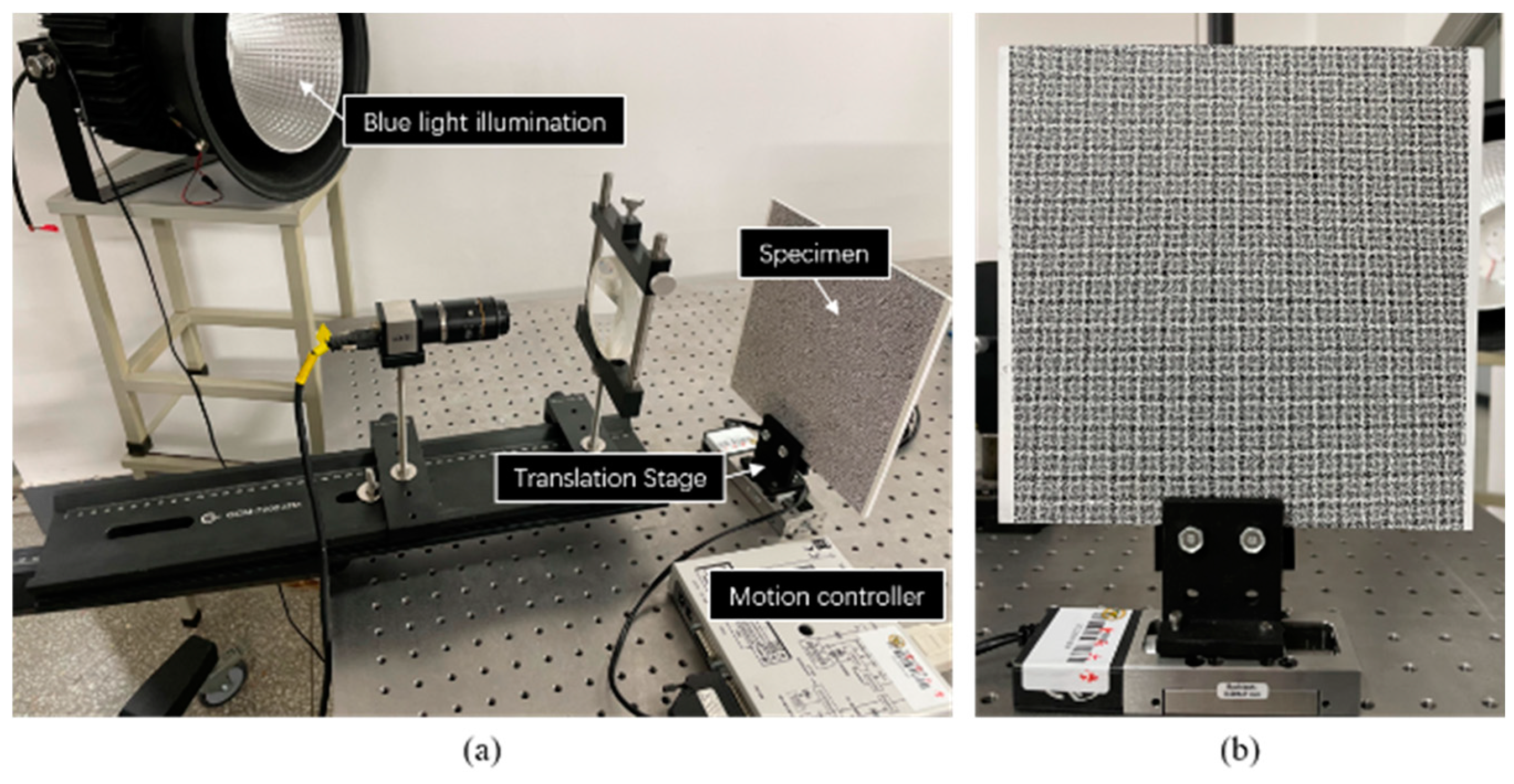
The translation experiment configuration is shown in Figure 9a. A translation stage (Newport, MFA-CC) controlled by a motion controller (Newport, SMC100) drives the specimen to move in a set direction. The specimen and the translation stage are in Figure 9b. Speckle patterns on the specimen are generated by applying the water transfer printing (WTF) technique [19], and the diameter of each speckle is 1 mm. In the experiment, the translation stage moves 0.5 mm for each step with a total of eight steps. Under each translation, 20 images are captured averagely to reduce the influence of environmental disturbances. In this experiment, the dual-view, three-view and four-view single-camera 3D-DIC are used to calculate the displacement field.

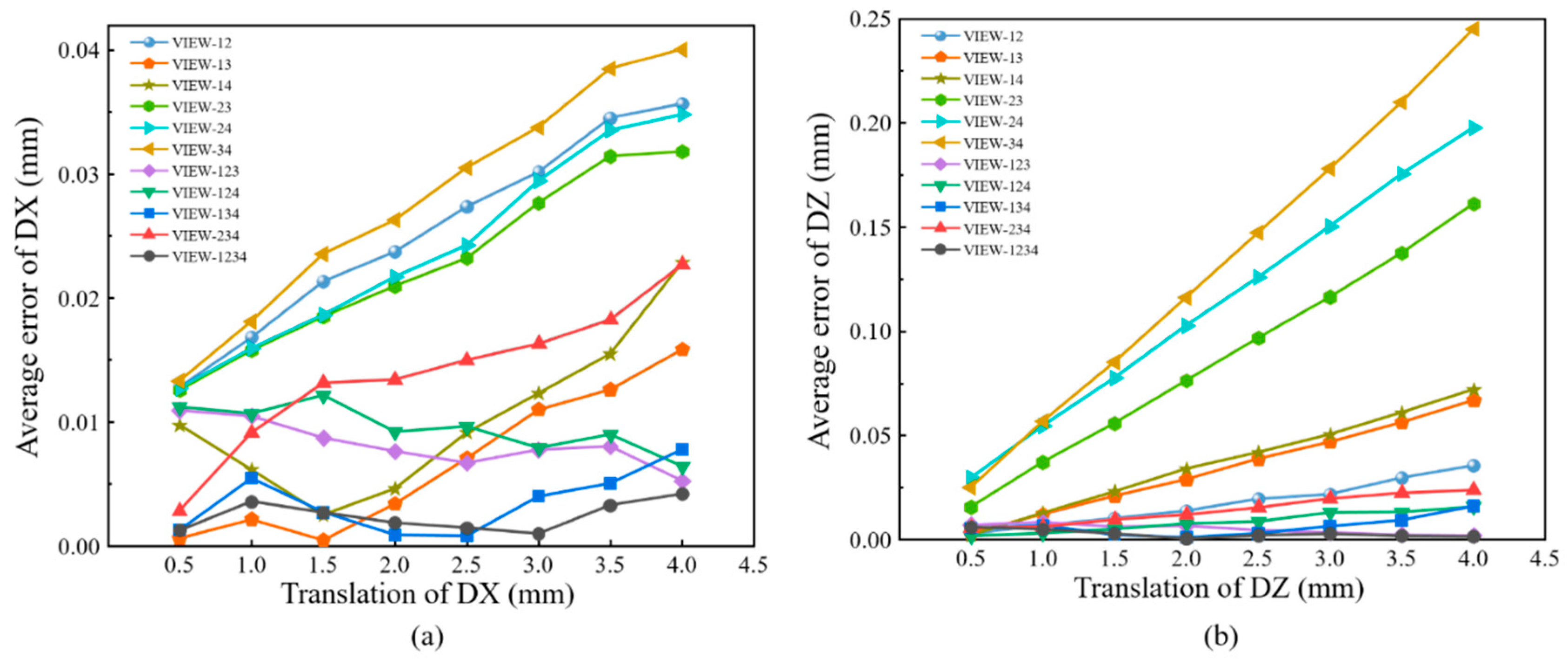
For comparisons, full-field displacements of each translation are averaged to calculate the absolute bias error, as shown in Figure 10. It can be seen in Figure 10a that the error of in-plane displacement based on four-view 3D-DIC is the smallest. For four-view 3D-DIC, the average error of all translations is about 0.002 mm, and the error keeps relatively stable. While the results of three-view 3D-DIC show a lower accuracy, the average error is about 0.01 mm. For the dual-view 3D-DIC, the VIEW14 has the smallest systematic error and the absolute bias error can reach 0.02 mm. For out-of-plane displacement, four-view 3D-DIC also achieves the highest accuracy and the average error is about 0.003 mm. For the three-view and dual-view 3D-DIC, the error rises to 0.009 mm and 0.07 mm, respectively. The translation experiment effectively proves the high accuracy and robustness of the single-camera four-view 3D-DIC. Actually, compared to the two-view system, almost an order of magnitude reduction of displacement error in the four-view system is mainly due to inaccurate calibrations. It can be seen in Figure 10 that there is a noticeable increase in error with the increasing translation of DX and DZ in two- and three-view systems. However, the error in the four-view system keeps relatively stable. The impact of calibration on the different view systems will be further analyzed in our future work.

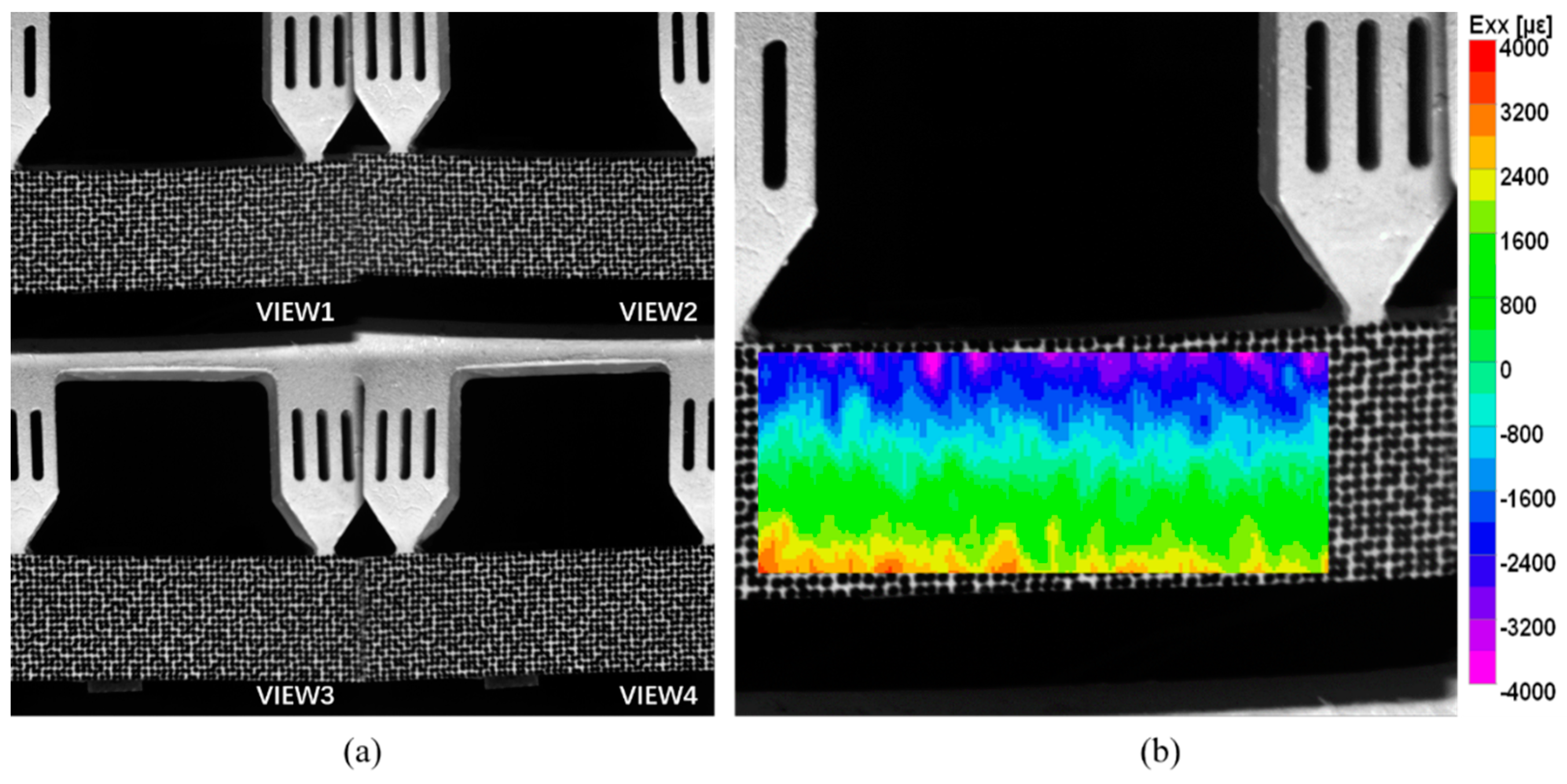
Figure 11a shows the setup of the four-point bending experiment, and the specimen is shown in Figure 11b. The four-point bending beam is 150 mm long and 20 mm wide. Speckle patterns are also made by WTP technique, and the speckle diameter is 0.8 mm. The strain gauges are attached to the middle edges of the beam to provide the reference truth of strain. The world coordinate system after 3D reconstruction is transformed to the front surface of the specimen, and the X and Y directions coincide with the horizontal and vertical directions of the beam respectively. Therefore, since the size of the gauges is known, the frontal region corresponding to the strain gauge grid area can be selected precisely for comparison. The specimen is loaded under 10 different load levels. Under each load, 20 images are captured averagely to reduce the influence of environmental disturbances. The four-view speckle image is shown in Figure 12a. Then, the dual-view, three-view and four-view single-camera 3D-DIC are used to calculate the strain field. The strain field in the pure bending section by the four-view 3D-DIC is presented in Figure 12b. The direction of the strain component Exx is the horizontal direction of the specimen. Due to the presence of subsets in the displacement and strain calculations, half of the subset size close to the upper and lower boundary of the specimen cannot be calculated. It should be noticed that although the strain gauges are placed at the specimen edge, there is still some distance between the grid and the specimen edge. The strain achieved by the strain instrument is actually the average strain in the central grid of the strain gauge. As a result, the strain of the frontal region corresponding to the strain gauge grid can be fully measured.

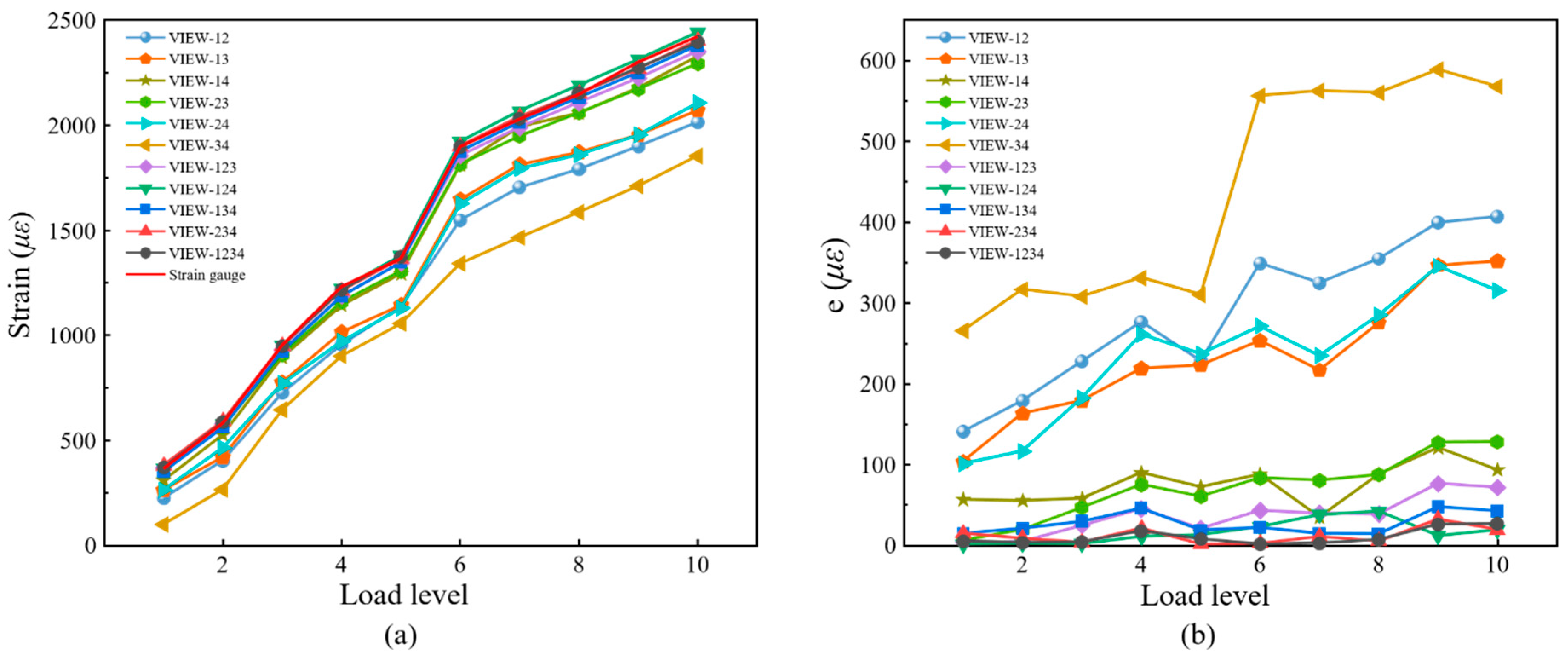
For comparison, the average strain of the speckle region corresponding to the strain gauge is extracted. The strain attained by 3D-DIC and the strain gauge is shown in Figure 13a, and the absolute errors between 3D-DIC and strain gauge are shown in Figure 13b. It can be seen in Figure 13 that the four-view 3D-DIC always achieves the highest accuracy of strain (error below 20 με) and the error keeps relatively stable under different loads. This solidly reveals the precision and stability of the single-camera four-view 3D-DIC system. In Figure 13b, the strain error of three-view 3D-DIC is about 50 με, while the dual-view 3D-DIC lead to a bigger error. In the dual-view 3D-DIC, VIEW14 has the smallest systematic error and the absolute error can even achieve 100 με. The four-point bending experiment effectively proves the high accuracy and robustness of the single-camera four-view 3D-DIC.

4. Discussion and Conclusions

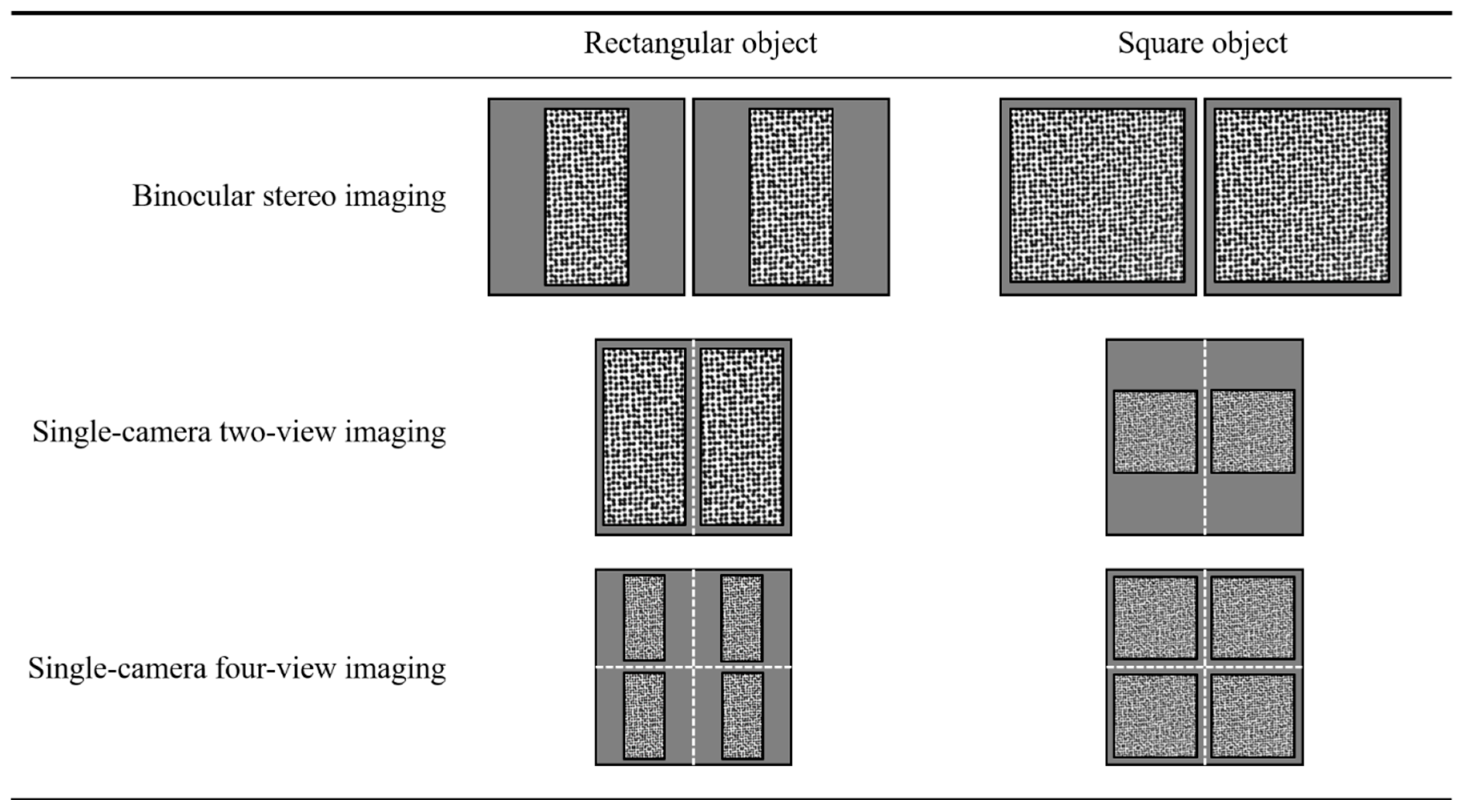
Compared to traditional binocular stereo systems, the pseudo stereo image captured by single-camera 3D-DIC techniques typically suffers considerable resolution reduction. To demonstrate clearly, a resolution comparison of binocular stereo imaging, traditional single-camera 3D-DIC based on two-view imaging, and the proposed accuracy-enhanced single-camera 3D-DIC based on four-view imaging is shown in Figure 14. When the measured objects are rectangular, the traditional two-view imaging shows the same resolution compared with the binocular system, while the four-view system suffers resolution loss. In this case, the four-view system improves the measurement accuracy, but the reduction in resolution reduces it, which is a contradiction. When the object comes to a square, the two-view and four-view systems both show reduced resolution. However, there is no resolution difference between the proposed four-view system and the conventional two-view system when measuring square objects. Actually, we aim to compare the proposed method with the two-view single-camera 3D-DIC techniques, not the traditional binocular stereo systems. It can be noticed that the proposed four-view system enjoys the advantages of higher accuracy and no resolution loss when measuring square objects. Resolution reduction is one of the inherent drawbacks of single-camera 3D-DIC techniques, and the central region with the best image quality of lens and camera sensor is underutilized. Despite these drawbacks, single-camera 3D-DIC techniques have gained increasing attention for deformation measurement due to their outstanding advantages of cost-effectiveness, compactness, and avoidance of complicated camera synchronization.

In summary, an accuracy-enhanced single-camera 3D-DIC technique is proposed based on four-view imaging. By installing a pyramidal prism in front of the camera, the speckle image of four different views of the specimen can be obtained. The basic principles and system configuration are described in detail. Both the rigid body translation experiment and four-point bending experiment show that the proposed single-camera 3D-DIC method can achieve higher measurement accuracy than the dual-view single-camera 3D-DIC and the three-view single-camera 3D-DIC techniques. In the four-point bending experiment, the absolute strain errors of the proposed four-view single-camera 3D-DIC are less than 20 με. Although the proposed single-camera 3D-DIC method has some limitations such as the decreased field of view and increased computation cost, the application of the single-camera 3D-DIC will still be greatly expanded with the improvement of their accuracy.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (under grants 12272093 and 11902074).

References

P. F. Luo, Y. J. Chao, M. A. Sutton and W. H. Petters, “Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision,” Exp. Mech. 33, 123-132 (1993). [CrossRef]
M. A. Sutton, J.J. Orteu and H. Schreier, Image Correlation for Shape, Motion and Deformation Measurements (Springer, 2009).
B. Pan, L. Yu and Q. Zhang, “Review of single-camera stereo-digital image correlation techniques for full-field 3D shape and deformation measurement,” Sci. China Technol. Sci. 61, 2–20 (2018). [CrossRef]
J. J. Orteu, F. Bugarin, J. Harvent, L. Robert, V. Velay, “Multiple-camera instrumentation of a single point incremental forming process pilot for shape and 3D displacement measurements: methodology and results,” Exp. Mech. 51 625-639 (2011). [CrossRef]
M. Pankow, B. Justusson, A. M. Waas, “Three-dimensional digital image correlation technique using single high-speed camera for measuring large out-of-plane displacements at high framing rates,” Appl. Opt. 49, 3418-3427 (2010). [CrossRef]
K. Genovese, L. Casaletto, J. A. Rayas, V. Flores, A. Martinez, “Stereo-Digital Image Correlation (DIC) measurements with a single camera using a biprism,” Opt. Lasers Eng. 51, 278-285 (2013). [CrossRef]
L. Wu, J. Zhu, H. Xie and M. Zhou, “Single-lens 3D digital image correlation system based on a bilateral telecentric lens and a bi-prism: validation and application,” Appl. Opt. 54, 7842-7850 (2015). [CrossRef]
S. Xia, A. Gdoutou, G. Ravichandran, “Diffraction assisted image correlation: a novel method for measuring three-dimensional deformation using two-dimensional digital image correlation,” Exp. Mech. 53, 755-765 (2013). [CrossRef]
B. Pan and Q. Wang, “Single-camera microscopic stereo digital image correlation using a diffraction grating,” Opt. Express 21, 25056-25068 (2013). [CrossRef]
L. Yu and B. Pan, “Color stereo-digital image correlation method using a single 3CCD color camera,” Exp. Mech. 57, 649-657 (2017). [CrossRef]
J. Li, X. Dan, W. Xu, Y. Wang, G. Yang and L. Yang, “3D digital image correlation using single color camera pseudo-stereo system,” Opt. Laser Technol. 95, 1-7 (2017). [CrossRef]
L. Yu and B. Pan, “Single-camera high-speed stereo-digital image correlation for full-field vibration measurement,” Mech. Syst. Signal. Pr. 94, 374-383 (2017). [CrossRef]
B. Pan, L. Yu, Y. Yang, W. Song and L. Guo, “Full-field transient 3D deformation measurement of 3D braided composite panels during ballistic impact using single-camera high-speed stereo-digital image correlation,” Compos. Struct. 157, 25-32 (2016). [CrossRef]
X. Shao, M. M. Eisa, Z. Chen, S. Dong and X. He, “Self-calibration single-lens 3D video extensometer for high-accuracy and real-time strain measurement,” Opt. Express 24, 30124-30138 (2016). [CrossRef]
T. Yuan, X. Dai, X. Shao, Z. Zu, X. Cheng, F. Yang and X. He, “Dual-biprism-based digital image correlation for defect detection of pipelines,” Opt. Eng. 58, 014107 (2019). [CrossRef]
Z. Gao, Y. Su and Q. Zhang, “Single-event-camera-based 3D trajectory measurement method for high-speed moving targets,” Chin. Opt. Lett. 20, 061101 (2022). [CrossRef]
C. Zhu, X. Shao, C. Liu, and X. He, “Accuracy analysis of an orthogonally arranged four-camera 3D digital image correlation system,” Appl. Opt. 58, 6535-6544 (2019). [CrossRef]
K. Wu, J. Qu, X. Shao and X. He, “Biaxial three-dimensional video extensometer based on single-camera four-view imaging,” Acta Optica Sinica, 42, 1315001 (2022). [CrossRef]
Z. Chen, C. Quan, F. Zhu and X. He, “A method to transfer speckle patterns for digital image correlation,” Meas. Sci. Technol. 26, 095201 (2015). [CrossRef]

Figure 1. Basic schematic diagram of pyramidal prism imaging path.

Figure 2. Speckle image of the specimen from four views.

Figure 3. Schematic diagram of the four-view stereo vision.

Figure 4. Calibration image of a chessboard calibrator from four views.

Figure 5. Four-view stereo vision matching and reconstruction.

Figure 6. Static experiment for: (a) experiment setup; (b) specimen.

Figure 7. The geometry of the pyramidal prism.

Figure 8. Results and comparisons of standard deviation in the static experiment for different directions: (a) DX; (b) DY; (c) DZ.

Figure 9. Translation experiment for: (a) experiment setup; (b) specimen and translation stage.

Figure 10. Results and comparisons in the rigid body translation experiment: (a) absolute error of in-plane displacement; (b) absolute error of out-of-plane displacement.

Figure 11. Four-point bending experiment: (a) experiment setup; (b) specimen; (c) strain gauge.

Figure 12. (a) Speckle image of the four-point bending beam from four views in the experiment; (b) full-field strain

ε_{x x}

of the pure bending section.

Figure 12. (a) Speckle image of the four-point bending beam from four views in the experiment; (b) full-field strain

ε_{x x}

of the pure bending section.

Figure 13. Results and comparisons in the four-point bending experiment: (a) measured strain; (b) absolute error.

Figure 14. Resolution comparison of binocular stereo imaging, single-camera two-view and four-view imaging for rectangular and square objects.

Table 1. System parameters for the proposed.

Camera	IDS, Ueye CP3370
Resolution / Pixel size	2048 × 2048 pixels / 5.5 μm
Lens	Kowa, 25 mm
Working distance	200 mm
Field of view	100mm
Subset / Step	27 × 27 pixels / 5 pixels
Illumination / Wavelength	Single narrowband blue light / 450 nm

Table 2. Extrinsic parameters between the first view with other views.

External parameters	View1-2	View1-3	View1-4
Rotation-X	0.137913°	15.7652°	15.7373°
Rotation -Y	-15.5342°	0.65436°	-15.8864°
Rotation -Z	3.61357°	0.991174°	0.168583°
Translation-X	-55.2659mm	2.8509mm	-57.034mm
Translation -Y	-3.21009mm	-57.1524mm	-57.1517mm
Translation -Z	-6.98087mm	-1.74234mm	-6.12167mm

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Accuracy-Enhanced Single-Camera Three-Dimensional Digital Image Correlation Based on Four-View Imaging

Abstract

1. Introduction

2. Methodology

3. Experimental Results

4. Discussion and Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe