Prerpints.org logo
Preprint
Article

Applying Linear Forms of Pseudo-Second-Order Kinetic Model for Feasibly Identifying Errors in the Initial Periods of Time-Dependent Adsorption Datasets

Altmetrics

Downloads

274

Views

107

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (799.63KB )

This version is not peer-reviewed

Submitted:

09 March 2023

Posted:

09 March 2023

You are already at the latest version

Alerts
Abstract
Initial periods of adsorption kinetics play an important role in estimating the initial adsorption rate and rate constant of adsorption process. Several adsorption processes rapidly occur, and the experimental data of adsorption kinetics under the initial periods can contain potential errors. The pseudo-second-order (PSO) kinetic model has been popularly applied in the field of adsorption. The use of the nonlinear optimization method to obtain the parameters of the PSO model can minimize error functions during modelling compared to the linear method. However, the nonlinear method has limitations in that it cannot directly recognize potential errors in the experimental points of time-dependent adsorption, especially under the initial periods. In this study, for the first time, the different linear types (Types 1–6) of the PSO model are applied to discover the error points under the initial periods. The result indicated that the fitting method using its linear equations (Types 2–5) is really helpful for identifying the error (doubtful) experimental points from the initial periods of adsorption kinetics. The imprecise points lead to low adjusted R2 (adj-R2), high reduced χ2 (red-χ2), and high Bayesian information criterion (BIC) values. After removing those points, the experimental data were adequately fitted with the PSO model. statistical analyses demonstrated that the nonlinear method must be used for modelling the PSO model because its red-χ2 and BIC were lower than the linear method. Type 1 has been extensively applied in the literature because of its very high adj-R2 (0.9999) and its excellent fitting to experimental points. However, its application should be limited because the potential errors from experimental points were not identified by this type. For comparison, the other kinetic models (i.e., pseudo-first-order, pseudo-nth-order, Avrami, and Elovich) are applied. The modelling result using the nonlinear forms of those models indicated that the fault experimental points from the initial periods were not detected.
Keywords: 
Subject: Chemistry and Materials Science  -   Chemical Engineering

1. Introduction

Adsorption is a combination process (adsorption and desorption occur simultaneously) [1]. Adsorption kinetic is commonly conducted under batch experiments [2]. Some adsorption processes occur very fast. Guo et al. [3] found that the adsorption process of Cd2+ ions onto biosorbent (derived from maize straw modified with succinic anhydride) rapidly occurred under the first period of adsorption kinetics, with approximately 70.0%–96.6% of total Cd2+ ion solutions (Co = 100, 300, and 500 mg/L at pH = 5.8) being removed within 1 min. Zbair et al. [4] reported that the adsorption process of bisphenol A or diuron by Argan nutshells-based hydrochar reached a fast equilibrium within 4 min of contact. An analogous result is reported by many scholars who invested in the adsorption of Cd2+ ions onto orange peels-derived biochar [5] and rhodamine B dye onto white sugar-based activated carbon [6]. Therefore, some authors [3,5,6] took a very short time (1 min, 2 min, etc.) instead of a longer one (i.e., starting from 10 min) [7].
Clearly, the initial periods of time-dependent adsorption datasets play an important role in establishing the adsorption rate constant and initial rate of adsorption kinetics. Hubbe et al. [8] called they are “early” data points. However, some potential errors or technical mistakes can occur if samples are uncarefully taken and analysed under a very short time (i.e., 1 min, 2 min, etc.). Adsorption process often includes two phases: solid (material or adsorbent) and liquid. The liquid phase often contains solute (or adsorbate) and solvent (commonly water). In general, after withdrawing small fractions from the mixture of solid and liquid at an interval time, the liquid phase is separated from the mixture by filtration or centrifugal method. A dilution step is additionally required if necessary. The available sites in a material can continue to adsorb adsorbate molecules in the withdrawn fractions if the separation process is delayed or not done instantly. As a result, the concentrations of adsorbate (Ct) at given times decrease, and the amount of adsorbate adsorbed by an adsorbent at times (qt) increases. This means that the values qt at the initial periods might be higher than those expected if researchers do not conduct experiments carefully. They can be defined as the error points in datasets and affect the results of modelling adsorption on kinetics. It might be hard to verify those doubtful results by existing techniques and this is a current limitation in this field.
In the study of kinetic adsorption, two reaction common models that are used to model time-dependent experiment data of the adsorption process are the pseudo-first-order (PFO) model and pseudo-second-order (PSO) model [9,10,11]. Lima et al. [2] concluded in their review that the PSO model describes most experimental data better than the PFO model. Some authors [12,13] indicated that the PSO model was initially established by Blanchard and co-workers [14] to describe the time-dependent process of heavy metal adsorption by clinoptilolite. However, other authors [8] found that Coleman and co-workers [15] early proposed a similar model. Its differential equation is commonly expressed as Equation 1 [12]. After taking integration by applying the boundary conditions (qt = 0 at t = 0, and qt = qt at t = t), the nonlinear form of the PSO model is obtained as Equation 2 [16].
d q t d t = k 2 ( q e ( 2 ) − q t ) 2
q t = q e ( 2 ) 2 k 2 t 1 + q e ( 2 ) k 2 t
q t = C o – C t m × V
where k2 [kg/(mol×min)] the rate constant of this model; qe(2) and qt (mol/kg) that are the amounts of pollutant in solution adsorbed by material at equilibrium and any time t (min) are obtained from Equation 3; Co and Ct (mol/L) are the concentration of pollutant at beginning and any time t (min); m (kg) is the dry mass of material; and V (L) is the volume of pollutant used in the study of adsorption kinetic.
Six types of linear forms of the PSO model are found in the literature [12,17,18,19] Although Type 5 and Type 6 have been reported elsewhere [17,19] they are not commonly applied in the literature compared to Type 1. This Type 1 that might be first introduced by Ho and McKay [20] has been intensively applied in the literature because the R2 or r2 value obtained from this type is very close 1 [2,12].
t q t = ( 1 q e ( 2 ) ) t + 1 k 2 q e ( 2 ) 2                                           ( Type   1 ;   the   plot   of   t / q t   v s .   t )
1 q t = ( 1 k 2 q e ( 2 ) 2 ) 1 t + 1 q e ( 2 )                                           ( Type   2 ;   the   plot   of   1 / q t   v s .   1 / t )
q t = – 1 k 2 q e ( 2 ) q t t + q e ( 2 )                                           ( Type   3 ;   the   plot   of   q t   v s .   q t / t )
q t t = – ( k 2 q e ( 2 ) ) q t + k 2 q e ( 2 ) 2                                           ( Type   4 ;   the   plot   of   q t / t   v s .   q t )
1 t = k 2 q e ( 2 ) 2 1 q t – k 2 q e ( 2 )                                           ( Type   5 ;   the   plot   of   1 / t   v s .   1 / q t )
1 q e ( 2 ) – q t = k 2 t + 1 q e ( 2 )                                           ( Type   6 ;   the   plot   of   1 / q e – q t   v s .   t )
For comparison, several statistical analyses were applied along with the determination coefficient (R2; Equation 10) and adjusted determination coefficient (adj-R2; Equation 11). They include chi-squared (χ2; Equation 12), reduced chi-square (red-χ2; Equation 13), and Bayesian information criterion (BIC; Equation 14) [2,12,16] A model with higher adj-R2 value and lower red-χ2 indicates a better fitting than the others. Because of the difference among the parameters of the models used, the magnitude (or the absolute value) of ΔBIC (BIC of model 1 – BIC of model 2) is used for selecting the best fitting model [2,16].
R 2 = ∑ ( y e x p − y e x p − m e a n ) 2 − ∑ ( y e x p − y m o d e l ) 2 ∑ ( y e x p − y e x p − m e a n ) 2 = 1 − ∑ ( y e x p − y m o d e l ) 2 ∑ ( y e x p − y e x p − m e a n ) 2
a d j - R 2 = 1 − ( 1 − R 2 ) × ( N − 1 D O F )
r e d - χ 2 = ∑ ( y e x p − y m o d e l ) 2 D O F
B I C = N × l n ( ∑ ( y e x p − y m o d e l ) 2 N ) + P   l n ( N )
where yexp is qt (mol/kg) obtained from experiments; yexp-mean is an average of yexp values used for modelling; ymodel is qt calculated based on the PSO model; N is the number of experimental points; P is the number of parameters of the PSO model (P = 2); and DOF is the degrees of freedom.
Although the nonlinear optimization method is often suggested to model the adsorption kinetic model because it can minimize error functions [1,2,12,16]. However, this method cannot provide information on potential errors in adsorption kinetic datasets. This study aimed to evaluate whether it is feasible to apply the linear forms of pseudo-second-order kinetic model for feasibly identifying errors in the initial periods of kinetic adsorption. This hypothesis is introduced for the first time. The kinetic adsorption data were also fitted to some common models: pseudo-first-order, pseudo-nth-order, Avrami, and Elovich ones. Commercial activated carbon and paracetamol (PRC) were used as target adsorbent and adsorbate.

2. Experimental Conditions and Procedures

The adsorption process of paracetamol (PRC, purchased from Sigma-Aldrich) using commercial activated carbon (CAC) was carried out. The surface area and total pore volume of CAC were 1275 m2/g and 0.670 cm3/g. The experiment of kinetics adsorption was conducted in triplicate, and the result of qt was averaged. The adsorption condition was maintained at 25 °C, pH 7.0, and initial PRC (3.45 mmol/L). The solutions (1.0 M NaOH and 1.0 M HCl) were used to adjust the pH of PRC solution before and during the adsorption process. A primary test indicated that the adsorption capacity of PRC onto CAC was not depenent on pH solutions from 2.0 to 9.0 (data not showed).
Approximate 1.0-gram of CAC was added to an Erlenmeyer flask containing 1 L of PRC solution (3.45 mmol/L and pH 7.0). The mixture of the solid/liquid was shaken at 150 rpm and 30 °C. The contact time range for studying adsorption kinetic was 1, 5, 15, 30, 45, 60, 90, 120, 180, 240, 300, 360, 720, 1440, 2880, and 4320 min (n = 16). After the desirable time, the solid/liquid mixture was separated using 0.45 μm filter paper. The concentration of PRC in solution was detected by a high-performance liquid chromatography (HPLC; Dionex 3000 Thermo, Sunnyvale, California, USA) coupled with a photo-diode array. The qt value was calculated based on the mass balance equation (Equation 3). The blank samples (without the presence of CAC in the PRC solution) were conducted simultaneously.

3. Pseudo-Second-Order Model

Two regions (kinetic and equilibrium) are observed in Figure 1a. The first region plays an important region in adsorption kinetic because information on adsorption rate and relevant rate constant is often identified at this region. The second region is plateau points . The PSO and PFO models often tend to fit the adsorption kinetic dataset when the second region (considering specific cases: qt values are nearly identical at this region) presents in the kinetic curve (the plot of qt vs. t) [2].
The result of modelling (using the nonlinear method) is shown in Figure 1a. Its adj-R2 value was only 0.8645, suggesting that the adsorption process was not well described by the PSO model. Clearly, the application of the nonlinear method did not provide where the experimental points of time-dependent adsorption are errors.
The results (n = 16; full raw experimental data) of modelling (using the linear method) are provided in Figure 2a,c (for Type 1 and 2), Figure 3a,c (for Type 3 and 4), and Figure 4a,c (for Type 5 and 6). Clearly, Type 1 was not helpful for recognizing errors in the experimental points. This is reflected through a very high adj-R2 value of 0.9999 (Table 1). A similar conclusion was obtained for Type 6. In contrast, the fault experimental points (denoted as Point 1 and Point 2 in the corresponding figures) were well identified by the others (Types 2, 3, 4, and 5). This is because their R2 values only ranged from 0.4571 to 0.5627 (Table 1).
Table 1. Parameters of the pseudo-second-order model obtained from the nonlinear form and its six linear forms.
Table 1. Parameters of the pseudo-second-order model obtained from the nonlinear form and its six linear forms.
Result of modelling Result of re-modelling
Full raw data (n = 16)* Manipulated data (n = 14)** Revisited data (n = 16)***
k2 qe(2) adj-R2 χ2 BIC k2 qe(2) adj-R2 χ2 BIC k2 qe(2) adj-R2 χ2 BIC
1. Nonlinear form
0.2034 1.419 0.8645 2.2E-02 –61.6 0.0635 1.501 0.9972 4.2E-04 –113.3 0.0635 1.501 0.9985 3.65E-04 –131.0
2. Linear forms
Type 1 0.0711 1.504 0.9999 3.1E-02 –52.1 0.0624 1.504 0.9999 4.6E-04 –104.4 0.0625 1.504 0.9999 4.0E-04 –121.9
Type 2 0.856 1.309 0.5627 3.4E-02 –50.8 0.0701 1.489 0.9793 6.0E-04 –100.8 0.0633 1.504 0.9999 4.0E-04 –121.9
Type 3 0.746 1.348 0.4571 3.1E-02 –52.3 0.0673 1.495 0.9731 6.0E-04 –100.8 0.0641 1.500 0.9953 3.9E-04 –122.1
Type 4 0.3498 1.418 0.4571 2.6E-02 –55.2 0.0656 1.498 0.9731 6.0E-04 –100.8 0.0638 1.501 0.9953 3.9E-04 –122.1
Type 5 0.4543 1.382 0.5627 2.6E-02 –54.8 0.0684 1.492 0.9793 6.0E-04 –100.8 0.0632 1.505 0.9999 4.0E-04 –121.7
Type 6 0.0804 0.703 0.9109 6.3E-01 –3.60 0.0804 0.672 0.9053 6.3E-04 –92.9 0.0805 0.750 0.9173 5.1E-01 –6.938
Note: *Case 1: results obtained from the raw datasets, **Case 2: results obtained after removing the outlets (the Points 1 and 2; qt = 0.741 and 0.789 mol/kg); and Case 3:**results obtained after using the new points 1 (qt = 0.131 mol/kg; Table 3) and 2 (0.484 mol/kg; Table 3) estimating from the PSO model (k2 = 0.0635 and qe(2) = 1.501); the unit of qe (mol/kg) and k2 [kg/(mol×min)]; qe,exp (1.495 ± 0.0061 mol/kg) obtained from the experiment.
Table 2. Parameters of some models obtained based on the three cases: full raw data, manipulated data, and revisited data.
Table 2. Parameters of some models obtained based on the three cases: full raw data, manipulated data, and revisited data.
Unit Result of modeling (using the nonlinear method)
Full raw data
(n = 16)*		 Manipulated data
(n = 14)**		 Revisited data
(n = 16)***
qe,exp mol/kg ~1.495 ~1.495 ~1.495
1. Pseudo-second-order (PSO) model
qe(2) mol/kg 1.419 1.501 1.501
k2 kg/(mol×min) 0.2034 0.0635 0.0635
adj-R2 0.8645 0.9972 0.9985
red-χ2 — 2.16E-02 4.20E-04 3.65E-4
BIC — –61.6 –113.3 –131.1
2. Pseudo-first-order (PFO) model
qe(1) mol/kg 1.368 1.436 1.428
k1 1/min 0.1792 0.0512 0.0576
adj-R2 — 0.7506 0.9597 0.9710
red-χ2 — 3.98E-02 6.09E-03 6.86E-03
BIC — –51.3 –85.6 –81.16
3. Elovichmodel
α mol/(kg×min) 126.1 1364 2.913
α mg/(g×min) 19,073 206,235 440.4
β kg/mol 9.299 11.11 6.335
adj-R2 — 0.9435 0.9480 0.8700
red-χ2 — 9.03E-03 7.75E-03 3.08E-02
BIC — –76.5 –81.5 –55.6
4. Avramimodel
qe(AV) mol/kg 1.536 1.496 1.472
kAV 1/min 0.0973 0.0618 0.0510
nAV — 0.2913 0.4571 0.6312
adj-R2 — 0.9801 0.9995 0.9935
red-χ2 — 3.17E-03 7.35E-05 1.54E-03
BIC — –95.4 –162.1 –107.7
5. PNO model
qe(PNO) mol/kg 1.933 1.522 1.515
kPNO kgm–1/(min×molm–1) 0.0268 0.0659 0.0631
m — 7.299 2.247 2.134
adj-R2 — 0.9605 0.9979 0.9986
red-χ2 — 6.31E-03 3.21E-04 3.25E-4
BIC — –83.8 –137.0 –134.1
Note: *Case 1: results obtained from the raw datasets; **Case 2: results obtained after removing the outlets (the Points 1 and 2; qt = 0.741 and 0.789 mol/kg) from the raw datasets; and **Case 3: results obtained after removing the Points 1–2 and submitting the new Point 1 (qt = 0.131 mol/kg; Table 3) and Point 2 (0.484 mol/kg; Table 3) estimating from the PSO model (k2 = 0.0635 and qe(2) = 1.501) into the raw datasets.
Table 3. Comparison on the result estimation of qt values at the initial periods obtained by different kinetic models and qt(exp) from the experiment.
Table 3. Comparison on the result estimation of qt values at the initial periods obtained by different kinetic models and qt(exp) from the experiment.
Time
(min)		 qt(exp) qt values estimated based on the models Difference (%) between qt(exp) and qt(model)
PFO PSO PNO Elovich Avrami PFO PSO PNO Elovich Avrami
1
(Point 1) 		0.741 0.072 0.131 0.151 0.866 0.042 164.7 140.0 132.4 –15.7 178.7
5
(Point 2) 		0.789 0.324 0.484 0.525 1.011 0.197 83.4 47.8 40.2 –24.7 120.0
15 0.933 0.770 0.883 0.905 1.110 0.517 19.1 5.43 3.03 –17.40 57.4
30 1.090 1.127 1.112 1.114 1.173 0.855 –3.290 –1.965 –2.129 –7.258 24.2
45 1.188 1.293 1.217 1.211 1.209 1.076 –8.446 –2.441 –1.928 –1.770 9.846
60 1.247 1.369 1.278 1.268 1.235 1.221 –9.327 –2.389 –1.635 1.005 2.116
Preprints 69586 g002
Figure 2. The linear forms (Type 1 and Type 2) of the pseudo-second-order model (a) before and (b) after data manipulated.
Figure 2. The linear forms (Type 1 and Type 2) of the pseudo-second-order model (a) before and (b) after data manipulated.
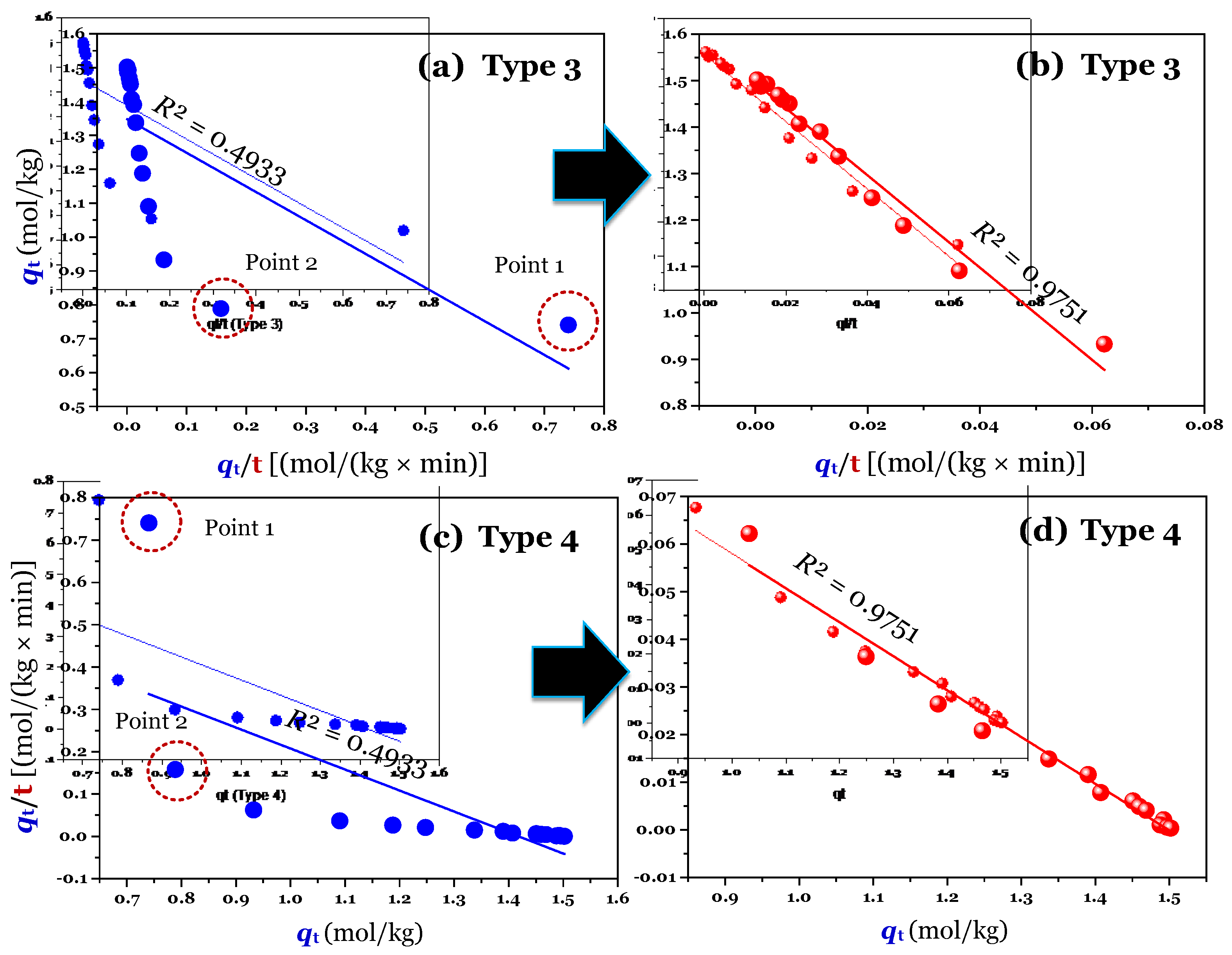
Preprints 69586 g002
Preprints 69586 g003
Figure 3. The linear forms (Type 3 and Type 4) of the pseudo-second-order model (a) before and (b) after data manipulated.
Figure 3. The linear forms (Type 3 and Type 4) of the pseudo-second-order model (a) before and (b) after data manipulated.
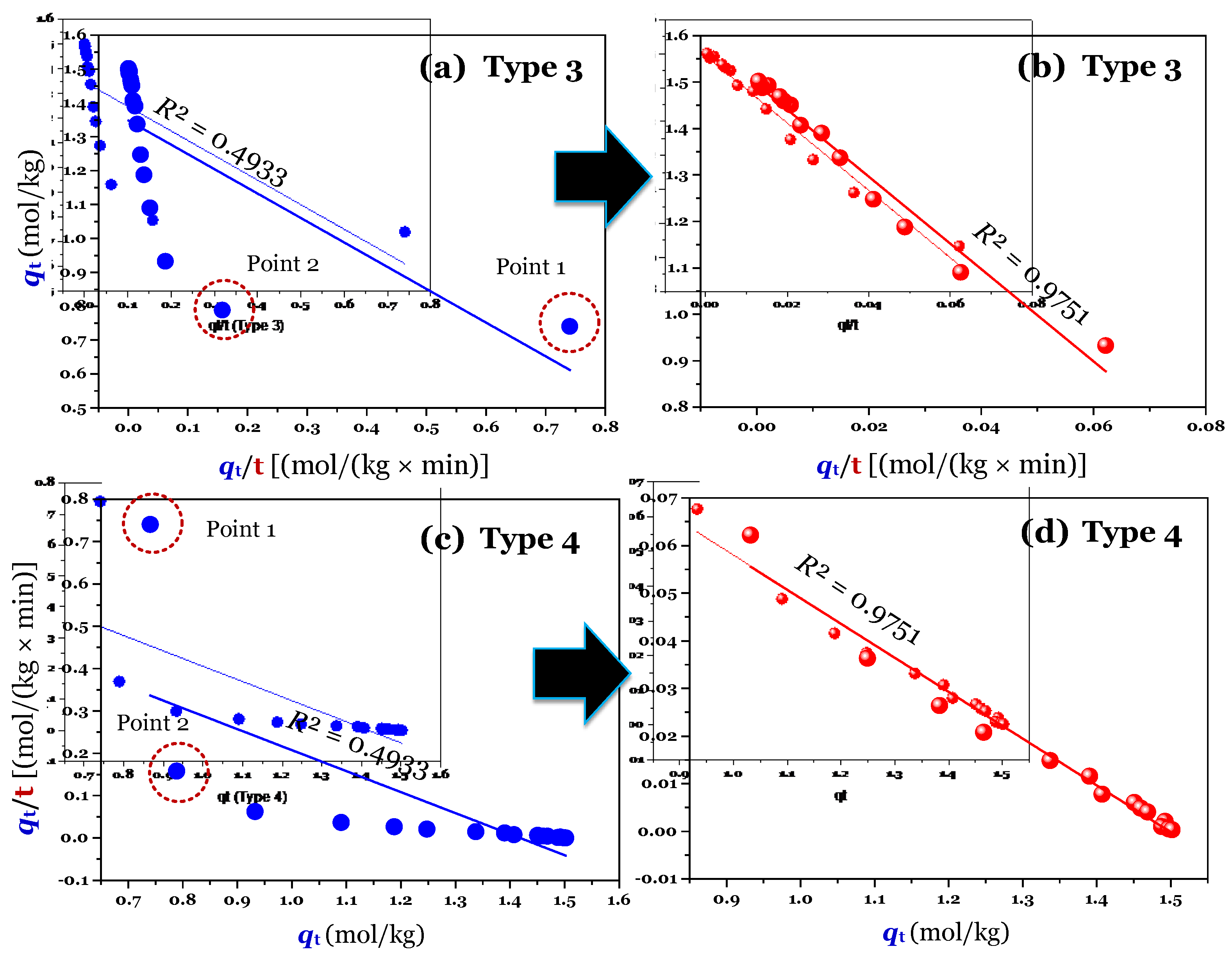
Preprints 69586 g003
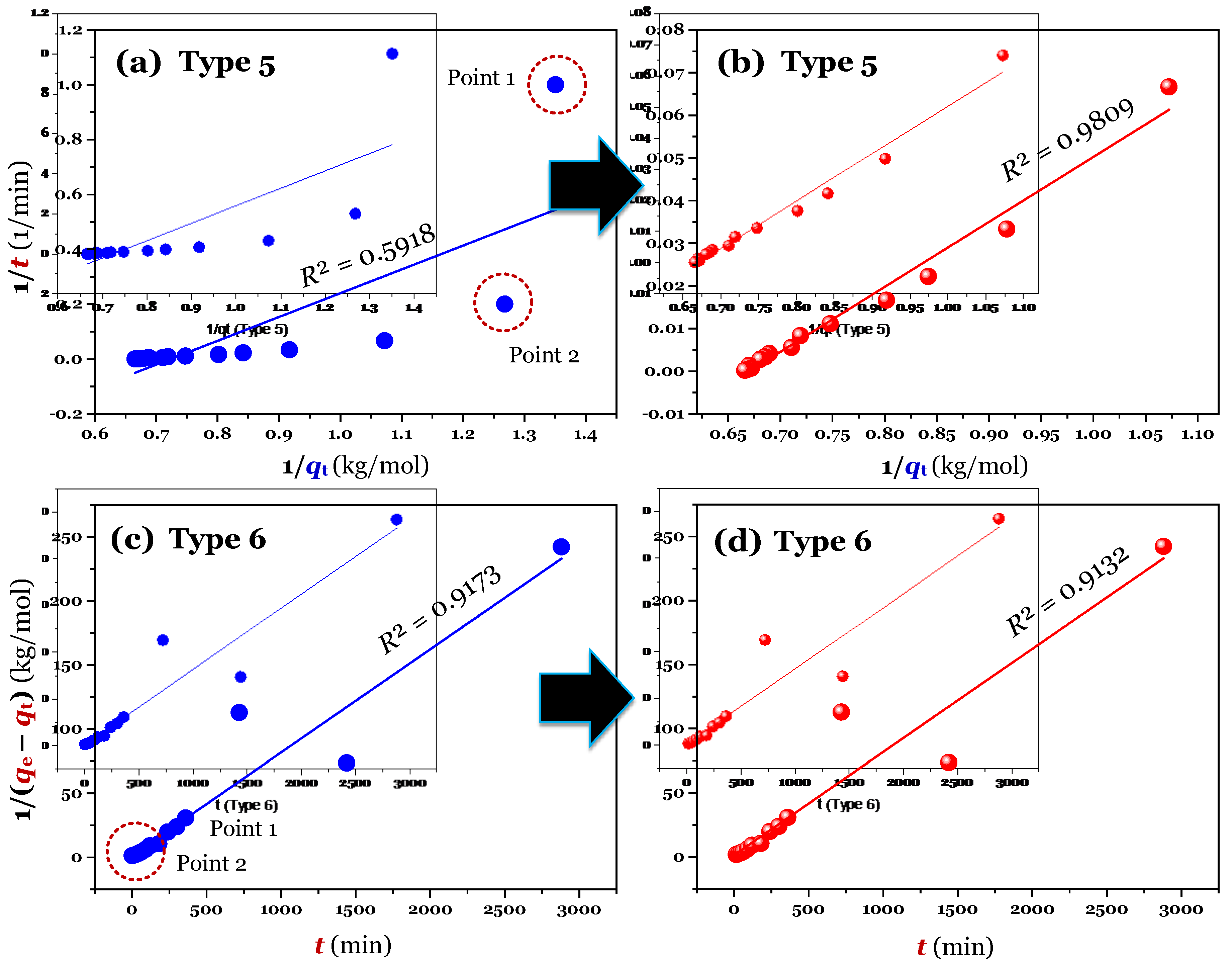
Preprints 69586 g004
Figure 4. The linear forms (Type 5 and Type 6) of the pseudo-second-order model (a) before and (b) after data manipulated.
Figure 4. The linear forms (Type 5 and Type 6) of the pseudo-second-order model (a) before and (b) after data manipulated.
Preprints 69586 g004
Considering Point 1 and Point 2 in all figures as potential errors, a manipulation was done by removing Point 1 and Point 2 from the experimental data. As expected, after manipulating (n = 14), the experimental data of time-dependent adsorption was adequately described by the PSO model, with the adj-R2 values being 0.9972 (for the nonlinear method), 0.9731–0.9793 (for the linear form of Type 2–5; Table 1). Figure 1b shows that the experimental data (after removing the point 1 and point 2 in Figure 1a) were well described by the nonlinear form of the PSO model (adj-R2 = 0.9972). Although the evaluation of regular residuals can be used to identify the potential errors within a dataset [11], it is not helpful for many cases. For example, Figure 1c shows that the outlier identification is only visible for the point 1.
Notably, the application of the linear form of Type 1 can lead to mis-conclusions. This is because its adj-R2 values did not change before (adj-R2 = 0.9999) and after manipulating (0.9999; Table 1). The difference between the k2 [0.0711 kg/(mol×min)] value of full data and the k2 value [0.0624 kg/(mol×min)] of manipulated data obtained from Type 1 was only 13% (Table 1). However, the difference was remarkable for Type 2 (170%), Type 3 (167%), Type 4 (137%), and Type 5 (148%). A similar percentage of the high difference was reported for the case of using the nonlinear method (105%). The result suggested that the use of the linear form (Type 1) of the PSO model can achieve a very high adj-R2 value and well describe the experimental data (Figure S1). However, it is very hard to verify whether the parameters of the PSO model are highly believable and accurate. In the literature, some authors have analysed the problems of the linear form of Type 1 [2,21]. They found that although the R2 value of Type 1 is very high (even reaching 1), it is a spurious correlation [2,21].
For comparing the fitting between the nonlinear and linear methods, the statistical analyses (red-χ2 and BIC were applied. The results (Table 1) demonstrated that the values of red-χ2 and BIC obtained from the nonlinear method were lower than those from the linear method. Therefore, the utilization of the nonlinear method can minimize some error functions during the modelling process. A similar conclusion has been reported by some scholars [2,18,19].
It can be concluded that the application of the linear method for calculating the parameters of the PSO model was not highly recommended compared to the nonlinear method. However, the linear method (Type 2, Type 3, Type 4, and Type 5) is very helpful to identify errors in the experimental points (outliers). The use of Type 1 of the linear form of the PSO model should be taken cautiously. This is because it is very hard to identify experimental points and verify the feasibility of the parameters obtained (especially the k2 value).

4. Other Common Adsorption Kinetic Models

A question is whether other adsorption kinetic models are helpful to identify errors in the experimental points of time-dependent adsorption. Therefore, it is necessary to use other models for modelling the experimental data. Apart from the PSO model, several models have been used for modelling the time-dependent data of adsorption data. They include the two- and three-parameter models [8,22,23] The pseudo-first-order model [24] and Elovich kinetic model [25] are expressed as Equation 14 and Equation 15, respectively [12]. The three-parameters ones are the pseudo-nth-order model (herein called the PNO model) (Equation 16) [22,23] [also known as general-order kinetic model (Equation 17) [16] and the Avrami-fractional-order model (Equation 18) [26]. More detailed information on those models has been reported in some documents [16].
q t = q e ( 1 ) 1 − exp ⁡ ( − k 1 t )
q t = 1 β l n ⁡ ( 1 + α β t )
q t = q e ( PNO ) − q e ( PNO ) 1 + m − 1 q e ( PNO ) m − 1 k P N O t 1 m − 1
q t = q e ( PNO ) 1 − 1 1 + m − 1 q e ( PNO ) m − 1 k PNO t 1 m − 1
q t = q e ( A V ) 1 − exp ⁡ ( − k A V t ) n A V
where qt (mol/kg) is defined in Equation 2; k1 (1/min), kPNO [kgm–1/(min×molm–1)], and kAV (1/min) are the adsorption rate constant of the PFO, PNO, and Avrami models, respectively; qe(1), qe(PNO), and qe(AV) are the adsorption capacity of CAC towards paracetamol at equilibrium (mol/kg) estimated by the PFO, PNO, and Avrami models, respectively; m and nAV are the exponent of the PNO and Avrami models; α [mol/(kg×min)] and β (kg/mol) are the initial rate and the desorption constant of adsorption kinetics of the Elovich model.
In general, the PFO and PSO models are frequently used in the literature. Unlike the PSO model, the linear form of the PFO model (Equation 19 or 20) indicates two un-known parameters that are qe(1) and k1. The parameter qe(1) must be supposed before applying the linear method. However, it is not easy to select qe(1) appropriately. If qe(1) is lower than (or equal to) qt, the result of calculating ln(qe(1) – qt) is an error (#NUM!). By selecting qe(1) slightly higher than the highest value of qt, the result of fitting the linear method is provided in Figure S2. Clearly, the errors in the experimental datasets of time-dependent adsorption (i.e., the points 1 and 2) were not detected through the linear fitting of the PFO model (Figure S2).
ln ⁡ ( q e ( 1 ) − q t ) = − k 1 t + ln ⁡ ( q e ( 1 ) )
log ⁡ ( q e ( 1 ) − q t ) = − k 1 2.303 t + log ⁡ ( q e ( 1 ) )
For the three-parameters models, the application of the linear method for computing the parameters is not suitable. Therefore, the non-linear optimization method is applied for calculating the parameters of those kinetic models using full data (n = 16; Figure 1a) and manipulated data (n = 14; Figure 1b). Furthermore, to obtain a fair comparison between two- and three-parameters models, the BIC statistics was used to assess the best-fitting model [2].
The result of modelling is provided in Figure S3 and Table 2. For the full data (n = 16), the fitting model followed the order of the Avrami model (BIC = –95.4) > PNO model (–83.8) > Elovich model (–76.5) > PSO (–61.6) > PFO (–51.3). Notably, some models indicated a doubtful result. For example, the m of the PNO was 7.299; this means that the overall order of the adsorption process was up to 7 (an impossible result for the adsorption kinetics). However, the results (Figure S3 and Table 2) do not indicate what the experimental points of time-dependent adsorption are errors. The conclusion is consistent with the previous finding in Section 2.
Furthermore, the points 1 and 2 in Figure 1a are assumed as outliers (errors). After removing them from the raw data, the result of modelling (based on Figure 1b; n = 14) indicates that the fitting model was in the following order: the Avrami model (BIC = –162.1) > PNO model (–137.0) > PSO model (–113.3) > PFO model (–85.6) > Elovich model (–81.5). The three-parameter models (i.e., the Avrami and PNO models) indicated the best description for the current experimental data compared to the two-parameters ones. The overall order of the adsorption kinetics (obtained based on the PNO model; m = 2.247) was close to 2 (feasibly considering it as the PSO model).

5. Re-Modelling Using the Points 1 and 2 Estimated from the PSO Model

After removing two outliers, the results of modelling (n = 14) are listed in Table 2. Using the parameters of the models, the values qt at 1 min (Point 1) and 5 min (Point 2) are estimated. The results (Table 3) indicated a remarkable difference between qt value obtained from the experiment (qt(exp)) and qt value estimated from the model (qt(model)). Taking the case of PSO model as a typical example, the values qt(exp) at 1 min and 5 min (0.741 and 0.789 mol/kg) are overwhelming higher than those obtained from the PSO model (0.131 and 0.484 mol/kg, respectively). The differences between qt(exp) and qt(model) are 140% for Point 1 and 47.8% for Point 2 (Table 3). The result confirms again they (Points 1 and 2) were errors and outliers.
The qt values for Point 1 (0.131 mol/kg) and Point 2 (0.484 mol/kg) are estimated by the PSO model. After submitting those estimated points into the datasets, the results of re-modelling are provided in Figure S4 and Table 2 (revisited data). The fitting model followed the decreasing order: the PNO model (BIC = –134.1) > PSO model (–131.1) > Avrami model (–107.7) > PFO model (–81.16) > Elovich model (–55.6). The results indicated that the Elovich and Avrami models can be considered empirical equations used for physically fitting the experiential data of time-dependence adsorption. Especially, the initial rate α of the Elovich model (Table 2) indicated a remarkable change such as 19,073 mg/(g×min) for the full raw data (n = 16), 206,235 mg/(g×min) for the manipulated data (n = 14), and 440.4 mg/(g×min) for the manipulated data (n = 16). The exponent nAV of the Avrami model that does not provide information on the overall order of the adsorption process only servers an empirically adjusted parameter. Unlike those models, the PNO model (especially its exponent m) is helpful for initially checking whether the datasets are feasible or not. The overall order of the adsorption process (m) was 2.134 which is close to the second order.
Because the linear forms of the PSO model are helpful for identifying the outlets from the initial period of the databases, it is necessary to re-verify this conclusion. After submitting the two estimated points into [the point 1 (qt = 0.131 mol/kg) and point 2 (0.484 mol/kg)] the datasets, the results of re-modelling using six linear forms of the PSO model are provided in Figure S5 and Table 1. As expected, the errors (the points 1 and 2) in experimental datasets are not observed in Types 1–5, suggesting that the application of the linear form (i.e., Types 1–5) of the PSO model can help to identify those potential errors in the initial adsorption period.
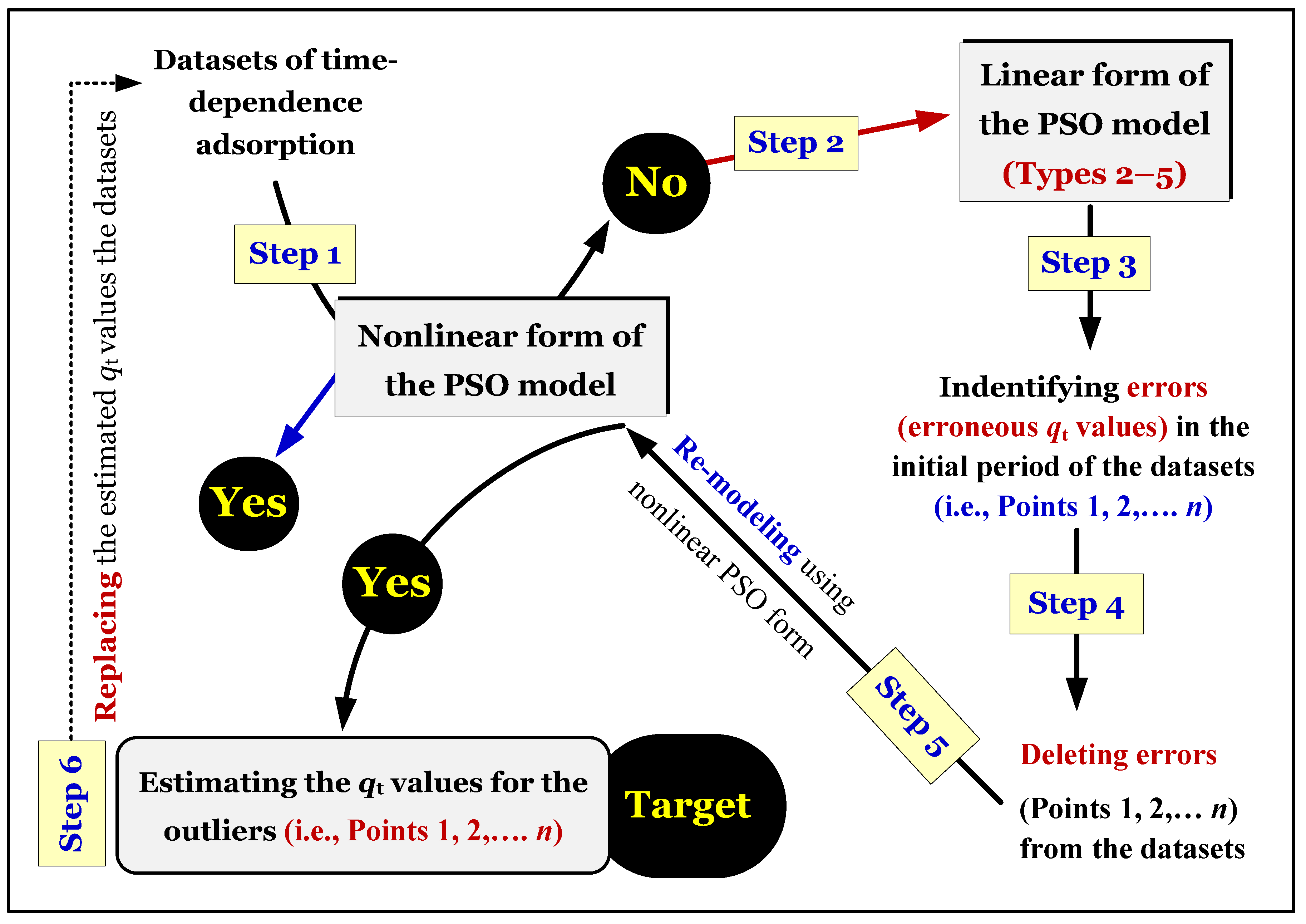
In contrast, Type 1 of the PSO model well fitted the experimental datasets (adj-R2 = 0.9999) when considering three cases: full raw data (n = 16), manipulated data (n = 14), and manipulated data (n = 16) in Table 1; therefore, it is impossible to verify whether there are errors in the datasets or not. Type 6 should be not used because it must first estimate the unknown qe value as in the case of the linear form of the PFO model. Figure 5 provides a brief summary of the validation and re-verification processes of time-dependent adsorption data. Adsorption kinetic curves (qt vs. t) must indicate an equilibrium region (as showed in Figure 5).
Notably, the conclusions of this work might be feasible for some normal adsorption processes. Although other contributions (n–π interaction, hydrogen bonding formation, and π–π interaction) existed in the adsorption process of organic pollutants (i.e. PRC), pore filling have been identified as a primary mechanism of PRC into CAC [27] and other porous carbonaceous materials (such as spherical and non-spherial biochars [28]). Those mechanisms were acknowledged as physical adsorption because low magnitudes of standard adsorption enthalpy change (ΔH° = 6.36–24.1 kJ/mol) [27,28]. Therefore, the process for validation and re-verification of time-dependent adsorption data (Figure 5) needs to be applied.
In contrast, the adsorption process of heavy metals (i.e., Cd) onto some CaCO3-enriched materials occurred very fast at the first period of adsorption. The primary adsorption was surface precipitation such as Cd(CO3) and/or (Cd,Ca)CO3 [5,29]. This mechanism was known as non-activated chemisorption that often occurs very rapidly and has low activation energy [29,30]. It might be not necessary to recheck the initial periods of time-dependent adsorption datasets. This is because it is nature of non-activated chemisorption [3,30].

6. Conclusions

Applying the non-linear optimization method for modelling the time-dependent experimental data is recommended. However, this non-linear method does not provide relevant information on potential outliers. This method should be only applied after the outliers were identified and removed. Results showed that the utilization of the linear forms (Types 2–5) of the PSO model) was appropriate for identifying errors in the experimental points (at the initial adsorption period) of time-dependent adsorption. This conclusion is valid when the plot of qt vs. t indicated two regions: kinetics and equilibrium (equilibrium is an plateau region).
Type 1 was well physically fitted to full raw experimental data, manipulated data (adj-R2 = 0.9999; n = 14), and revisited data (adj-R2 = 0.9999; n = 16). However, it (adj-R2 or r2) has been denoted as a spurious correlation in some cases. The application of Type 1 for calculating the parameters (qe(2) and k2) should be avoided because it is hard to validate the accuracy of those parameters. For Type 6, the qe value must be firstly estimated (a similar case of the linear form of the PFO model); therefore, its parameters obtained did not bring a high accuracy.
The PNO model can give some general information on doubts in the datasets. For example, its exponent m (7.299) is very high when considering the full raw data, but suitable when considering the manipulated data (m = 2.247) and the revisited data (m = 2.134 that can be called the overall order of the adsorption process). However, this model did not provide where the outlets are located in the datasets.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1. Physical fitting lines of the experimental data of kinetic adsorption by the linear form (Type 1) of the PSO model; Figure S2. The linear plot of PFO model obtained by considering the full data (n = 16) and the manipulated data (n = 14); Figure S3. Adsorption kinetic of paracetamol by commercial activated carbon fitted by various adsorption kinetic models; Figure S4. Re-modelling adsorption kinetics after submitting the Point 1 (qt = 0.131 mol/kg) and Point 2 (0.484 mol/kg) estimated from the PSO model to the datasets (Note: the modelling results for the case of the revisited data are provided in Table 2); Figure S5. Re-modelling results using the six linear forms of the PSO model after submitting the Point 1 (0.131 mol/kg) and Point 2 (0.484 mol/kg) estimated from the PSO model to the datasets six (Note: the modelling results for the case of the revisited data are provided in Table 1).

Funding

None

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Azizian, S. Kinetic models of sorption: a theoretical analysis. J. Colloid Interface Sci. 2004, 276, (1), 47-52. [CrossRef]
  2. Lima, E. C.; Sher, F.; Guleria, A.; Saeb, M. R.; Anastopoulos, I.; Tran, H. N.; Hosseini-Bandegharaei, A. Is one performing the treatment data of adsorption kinetics correctly? J. Environ. Chem. Eng. 2020, 104813.
  3. Guo, H.; Zhang, S.; Kou, Z.; Zhai, S.; Ma, W.; Yang, Y. Removal of cadmium(II) from aqueous solutions by chemically modified maize straw. Carbohydr. Polym. 2015, 115, 177-185. [CrossRef]
  4. Zbair, M.; Bottlinger, M.; Ainassaari, K.; Ojala, S.; Stein, O.; Keiski, R. L.; Bensitel, M.; Brahmi, R. Hydrothermal Carbonization of Argan Nut Shell: Functional Mesoporous Carbon with Excellent Performance in the Adsorption of Bisphenol A and Diuron. Waste and Biomass Valorization 2020, 11(4), 1565-1584. [CrossRef]
  5. Tran, H. N.; You, S.-J.; Chao, H.-P. Effect of pyrolysis temperatures and times on the adsorption of cadmium onto orange peel derived biochar. Waste Manag. Res. 2016, 34(2), 129-138. [CrossRef]
  6. Xiao, W.; Garba, Z. N.; Sun, S.; Lawan, I.; Wang, L.; Lin, M.; Yuan, Z. Preparation and evaluation of an effective activated carbon from white sugar for the adsorption of rhodamine B dye. J. Clean. Prod. 2020, 253, 119989. [CrossRef]
  7. Georgin, J.; da Boit Martinello, K.; Franco, D. S. P.; Netto, M. S.; Piccilli, D. G. A.; Foletto, E. L.; Silva, L. F. O.; Dotto, G. L. Efficient removal of naproxen from aqueous solution by highly porous activated carbon produced from Grapetree (Plinia cauliflora) fruit peels. J. Environ. Chem. Eng. 2021, 9(6), 106820. [CrossRef]
  8. Hubbe, M. A.; Azizian, S.; Douven, S. Implications of apparent pseudo-second-order adsorption kinetics onto cellulosic materials: a review. BioResources 2019, 14(3), 7582-7626.
  9. Guo, X.; Wang, J. A general kinetic model for adsorption: Theoretical analysis and modeling. J. Mol. Liq. 2019, 288, 111100. [CrossRef]
  10. Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. J. Hazard. Mater. 2020, 390, 122156. [CrossRef]
  11. Revellame, E. D.; Fortela, D. L.; Sharp, W.; Hernandez, R.; Zappi, M. E. Adsorption kinetic modeling using pseudo-first order and pseudo-second order rate laws: A review. Clean. Eng. Technol. 2020, 1, 100032. [CrossRef]
  12. Tran, H. N.; You, S.-J.; Hosseini-Bandegharaei, A.; Chao, H.-P. Mistakes and inconsistencies regarding adsorption of contaminants from aqueous solutions: A critical review. Water Res. 2017, 120, 88-116. [CrossRef]
  13. Kumar, K. V. A note on the comments by Dr. Y.S. Ho on “Remediation of soil contaminated with the heavy metal (Cd2+)”. J. Hazard. Mater. 2006, 136, (3), 993-994.
  14. Blanchard, G.; Maunaye, M.; Martin, G. Removal of heavy metals from waters by means of natural zeolites. Water Res. 1984, 18(12), 1501–1507. [CrossRef]
  15. Coleman, N. T.; McClung, A. C.; Moore, D. P.. Formation Constants for Cu(II)-Peat Complexes. Science 1956, 123, (3191), 330-331. [CrossRef]
  16. Lima, É. C.; Dehghani, M. H.; Guleria, A.; Sher, F.; Karri, R. R.; Dotto, G. L.; Tran, H. N. Chapter 3 - Adsorption: Fundamental aspects and applications of adsorption for effluent treatment. In Green Technologies for the Defluoridation of Water, Hadi Dehghani, M.; Karri, R.; Lima, E., Eds. Elsevier: 2021; pp 41-88.
  17. Hamdaoui, O.; Saoudi, F.; Chiha, M.; Naffrechoux, E. Sorption of malachite green by a novel sorbent, dead leaves of plane tree: Equilibrium and kinetic modeling. Chem. Eng. J. 2008, 143(1), 73-84. [CrossRef]
  18. Kumar, K. V. Linear and non-linear regression analysis for the sorption kinetics of methylene blue onto activated carbon. J. Hazard. Mater. 2006, 137(3), 1538-1544. [CrossRef]
  19. Lin, J.; Wang, L. Comparison between linear and non-linear forms of pseudo-first-order and pseudo-second-order adsorption kinetic models for the removal of methylene blue by activated carbon. Front Environ Sci Eng. 2009, 3(3), 320-324. [CrossRef]
  20. Ho, Y. S.; McKay, G. Sorption of dye from aqueous solution by peat. Chem. Eng. J. 1998, 70(2), 115-124.
  21. Xiao, Y.; Azaiez, J.; Hill, J. M. Erroneous Application of Pseudo-Second-Order Adsorption Kinetics Model: Ignored Assumptions and Spurious Correlations. Ind. Eng. Chem. Res. 2018, 57(7), 2705-2709. [CrossRef]
  22. Tseng, R.-L.; Wu, P.-H.; Wu, F.-C.; Juang, R.-S. A convenient method to determine kinetic parameters of adsorption processes by nonlinear regression of pseudo-nth-order equation. Chem. Eng. J. 2014, 237, 153-161. [CrossRef]
  23. Hu, Q.; Zhang, Z. Prediction of half-life for adsorption kinetics in a batch reactor. Environ. Sci. Pollut. Res. 2020, 27(35), 43865-43869. [CrossRef]
  24. Lagergren, S. K. About the theory of so-called adsorption of soluble substances. Sven. Vetenskapsakad. Handingarl 1898, 24, 1-39.
  25. Roginsky, S.; Zeldovich, Y. B. The catalytic oxidation of carbon monoxide on manganese dioxide. Acta Phys. Chem. 1934, 1, 554.
  26. Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7 (12), 1103-1112. [CrossRef]
  27. Nguyen, D.T., Tran, H.N., Juang, R.-S., Dat, N.D., Tomul, F., Ivanets, A., Woo, S.H., Hosseini-Bandegharaei, A., Nguyen, V.P. and Chao, H.-P. Adsorption process and mechanism of acetaminophen onto commercial activated carbon. J. Envi. Chem. Eng. 2020, 8(6), 104408. [CrossRef]
  28. Tran, H.N., Tomul, F., Thi Hoang Ha, N., Nguyen, D.T., Lima, E.C., Le, G.T., Chang, C.-T., Masindi, V. and Woo, S.H. Innovative spherical biochar for pharmaceutical removal from water: Insight into adsorption mechanism. J. Haz. Mater. 2020, 394, 122255. [CrossRef]
  29. Van, H.T., Nguyen, L.H., Nguyen, V.D., Nguyen, X.H., Nguyen, T.H., Nguyen, T.V., Vigneswaran, S., Rinklebe, J. and Tran, H.N. Characteristics and mechanisms of cadmium adsorption onto biogenic aragonite shells-derived biosorbent: Batch and column studies. J. Environ. Man. 2019, 241, 535-548. [CrossRef]
  30. Bai, J., Fan, F., Wu, X., Tian, W., Zhao, L., Yin, X., Fan, F., Li, Z., Tian, L., Wang, Y., Qin, Z. and Guo, J. Equilibrium, kinetic and thermodynamic studies of uranium biosorption by calcium alginate beads. J. Environ. Radioact. 2013. 126, 226-231. [CrossRef]
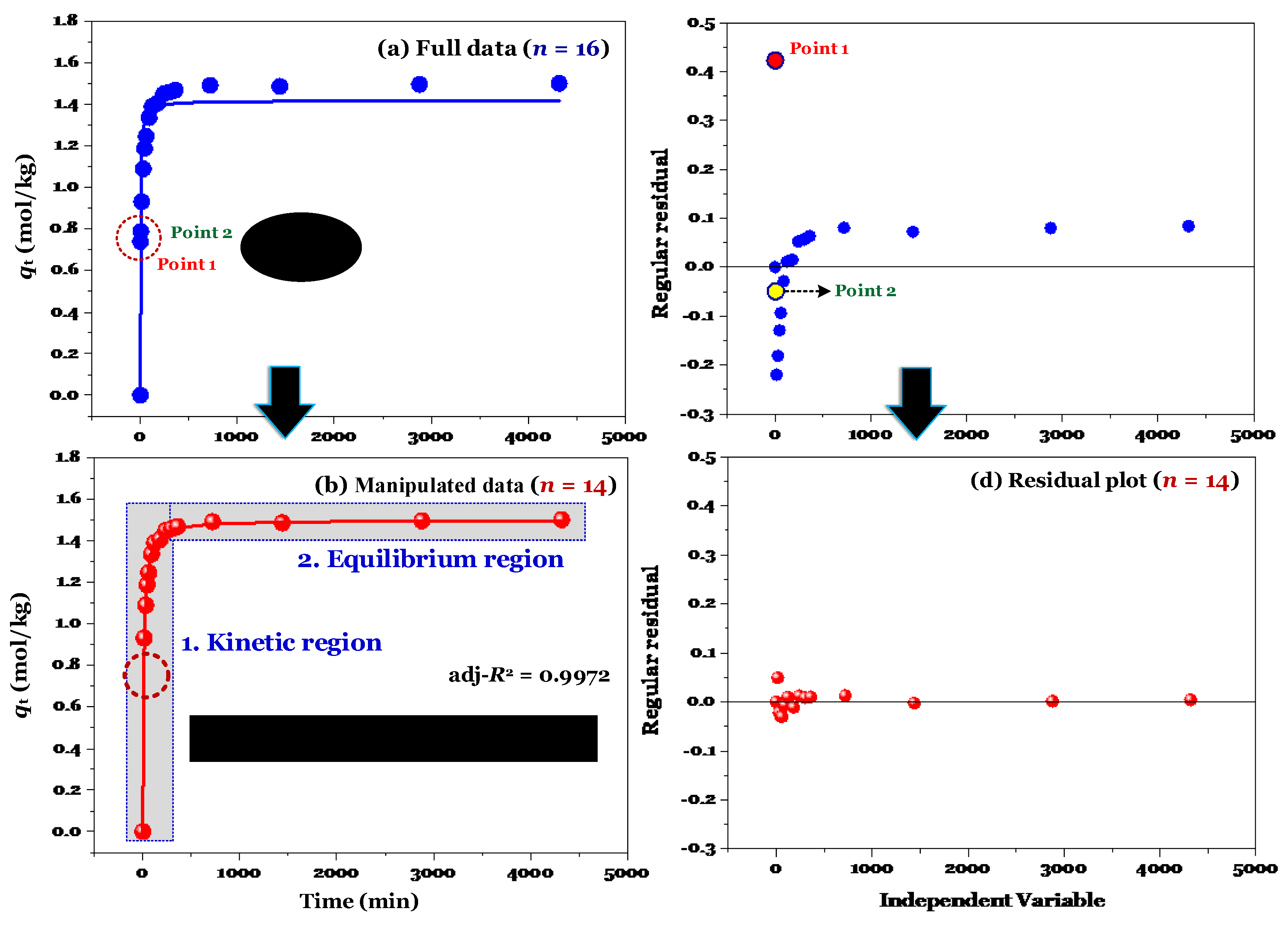
Preprints 69586 g001
Figure 1. Adsorption kinetic of paracetamol by commercial activated carbon fitted by the PSO model.
Figure 1. Adsorption kinetic of paracetamol by commercial activated carbon fitted by the PSO model.
Preprints 69586 g001
Preprints 69586 g005
Figure 5. Processes for validation and re-verification of time-dependent adsorption data (Note: adsorption kinetic curves (qt vs. t) must indicate two regions: kinetic and equilibrium; equilibrium is a plateau region).
Figure 5. Processes for validation and re-verification of time-dependent adsorption data (Note: adsorption kinetic curves (qt vs. t) must indicate two regions: kinetic and equilibrium; equilibrium is a plateau region).
Preprints 69586 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated