Prerpints.org logo
Preprint
Article

Spatial Prediction of Landslide using Hybrid Multi-Criteria Decision-Making Methods: A Case Study, Saqqez-Marivan Mountain Road

Altmetrics

Downloads

245

Views

83

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 March 2023

Posted:

15 March 2023

You are already at the latest version

Alerts
Abstract
Landslides around the main roads in the mountains not only cause fatal events but also cause ecosystem damage, including land degradation. This study aims to map the susceptibility of the landslides around the Saqqez-Marivan main rod of Kurdistan province, Iran, using ensemble Fuzzy logic with Analytic Network Process (Fuzzy Logic-ANP; FLANP), and with TOPSIS (Fuzzy Logic-TOPSIS; FLTOPSIS). A total of 100 landslides were first recognized by field surveys and then they were randomly divided into a 70% dataset (70 locations) and a 30% dataset (30 locations), respectively, for training and validating the methods. Eleven landslide conditioning factors, including slope, aspect, elevation, lithology, land use, distance to fault, distance to a river, distance to road, soil type, curvature, and precipitation were used. The performance of the methods was checked by the areas under the receiver operating curve (AUCROC). Results concluded that the prediction accuracy based on validating datasets were, respectively, 0.882 and 0.918 for FLANP and FLTOPSIS methods. Our findings demonstrated that although both models were known as promising techniques, the FLTOPSIS method had a better capacity for predicting the susceptibility of landslides in the studied area. Therefore, the susceptibility map developed by the FLTOPSIS method can be used for the proper management of areas with high landslide potential and also for managers and planners during the implementation of land allocation and development projects, especially in mountainous areas.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geography

1. Introduction

Road networks give access to nearly every area of the country, hence increasing the need for a well-established and resilient road network infrastructure. They are a significant component of critical infrastructure systems that are frequently exposed to natural and man-made hazards due to their wide spatial distribution [1]. Typically, the failures in policy planning during the rapid expansion of road networks in emerging nations are attributed to an underestimation of economic changes, fast expansion, future expansion, and uncertainties in regions with dynamic topography [2], Furthermore, unanticipated climate change can cause natural disasters such as landslides and earthquakes, which cause instability and have damaging cascading effects on the road network system [3]. Regional roads are a vital component of the infrastructure, and any disruptions caused by landslides can be disastrous for traffic [4]. In order to limit the threat posed by landslides to roadways, it is crucial to appropriately describe the risk of slope collapse at different scales, at different times, and in varied spatial locations. Nonetheless, insufficient investments were made to reduce the impact of landslides on the road system. In order to protect people's life and property, prevent ecosystem damages and also prevent waste of capital and resources, identifying areas more prone to landslides around communication roads in mountainous areas through landslide susceptibility map (LSM) with visual understanding appropriate is necessary.
To the best of knowledge from the literature review, studies on the LSM around the road networks follow the two different methodologies. One tradition focuses on assessing the immediate or indirect socio-economic effects of disruptions and makes fewer attempts to assess their likelihood [5]. The second tradition integrates GIS and geological modeling with a greater focus on landslide severity assessments without quantifying the impacts of network interruptions. In a susceptibility analysis, it is essential to simultaneously consider the probability of landslide occurrences and the consequences of network disruptions in order to provide useful guidance for the preparation and response phases of landslide disasters. Current studies of landslide risk to roads focus primarily on both the likelihood of landslides and their effects on roads, and the joint effect is frequently used to describe the impact of landslides on roads [6]. Pantelidis [7]offers a comprehensive analysis of landslide susceptibility assessment systems for highways, discussing both quantitative and qualitative approaches (We refer to methods that evaluate risk using numerical scores as "semi-quantitative."). The Federal Highway Administration (FHWA) of the United States suggested [8] a landslide susceptibility evaluation that was later changed by Budetta [9] to measure the risk of landslides along highways. The pure quantitative risk assessment (QRA) includes the hazard assessment in terms of the likelihood of failure or occurrence of an event of a certain scale multiplied by its effects [10], which semi-quantitative methods do not address. While landslide susceptibility and hazard have already been studied widely over the last two decades, using heuristic, statistical-probabilistic, or deterministic strategies (e.g., Pregnolato et al. [11] and Chamorro et al. [12]), little work has been done, for various reasons, on the spatial assessment of landslide susceptibility and on the evaluation of the value of the factors at risk [13]. Optical images were used in several landslide susceptibility mapping studies for landslide inventory, vegetation indices, and land use/land cover knowledge discovery [14,15].
Several techniques are used in MCDM, including min-max, max-min, ELECTRE, PROMETHEE, TOPSIS, fuzzy TOPSIS, compromise programming, analytic hierarchy process (AHP), fuzzy AHP, data envelopment analysis, and goal programming, that can be used to compare and rank multiple options before choosing the best-fit option. Fuzzy decision-making strategies have been drawing increasing interest among these methods for the answers to location problems that involve data that is ambiguous, partial, or has linguistic factors [16].
Multiple criterion decision-making (MCDM) is a common methodology that uses the TOPSIS method [17], which has been extensively used in the literature [18,19,20,21]. Similar to how it has been used in many other research areas, ANP has been used to predict landslides [22], floods [23], forest fires [24], Land subsidence [25], and earthquakes [26].
Risk assessment and mapping have been done in many different ways around the world, using both qualitative and quantitative methods. Analytical Network Process (ANP) and landslide susceptibility assessment factors are among the most popular and effective qualitative methods and tools [27,28]. On the other hand, multivariate and bivariate analyses are usually quantitative [29].
The most important geo-environmental factors that make landslides more likely to occur are rock type, structural discontinuity, slope gradient, relative relief, aspect, soil depth and its properties, land use and land cover, groundwater, and hydrologic conditions [30,31]. In addition to factors such as distance to faults and lineaments and distance to rivers, construction activities, especially roads, are significant contributors to the occurrence of landslides [32,33]. Numerous researchers have proposed different strategies for landslide susceptibility mapping (LSM) by considering landslide triggering and precipitating factors. According to He et al. [34], geometric factors such as elevation, aspect, and slope are among the most significant factors. Also, hydrological factors are considered, such as the topographic wetness index (TWI), the sediment transport index (STI), and the distance from rivers exacerbate and trigger the landslides. Geological and environmental factors (such as lithology and land use) and soil textures [35] also contribute to more accurate landslide detection. Numerous studies have been conducted to identify the causes of landslides. Saleem et al. [36] examined how DEM derivatives (including slope and aspect) affected risk assessment and mapping of landslide susceptibility. In order to estimate landslide areas, Zhu et al., (2022) used 14 conditioning criteria (such as lithology, slope, distance to a river, NDVI, and total surface radiation). Zhang et al. [37] used 12 conditioning parameters and ensemble learning approaches to determine landslide susceptibility. Due to the heterogeneity of the Earth's surface, it is difficult to adopt a unique strategy and identify the causes responsible for the landslide. Some scientific organizations and institutes have established recommendations for the LSM intending to use common nomenclature and guide analysts [38]. However, the applied approaches differ from area to area and even within the same area [39].
Considering the literature review, although TOPSIS and ANP have been broadly developed and used in a wide range of real-world problems, especially in priority of the alternatives such as sustainable development, environment, and renewable energy sources, there are rarely studies regarding ensemble Fuzzy logic with MCDM approaches such as TOPSIS and ANP in landslide susceptibility mapping. Consequently, the primary goals of this study are to (1) identify the most important factors affecting landslides in the studied area; (2) develop Fuzzy-ANP and Fuzzy-TOPSIS methods for identifying the areas with different potential for landslide occurrence; and (3) prepare a landslide susceptibility map for the Saqqez-Marivan road of Kurdistan province, Iran, with high prediction accuracy.

2. Data acquisition and preparation

2.1. Study area characteristics

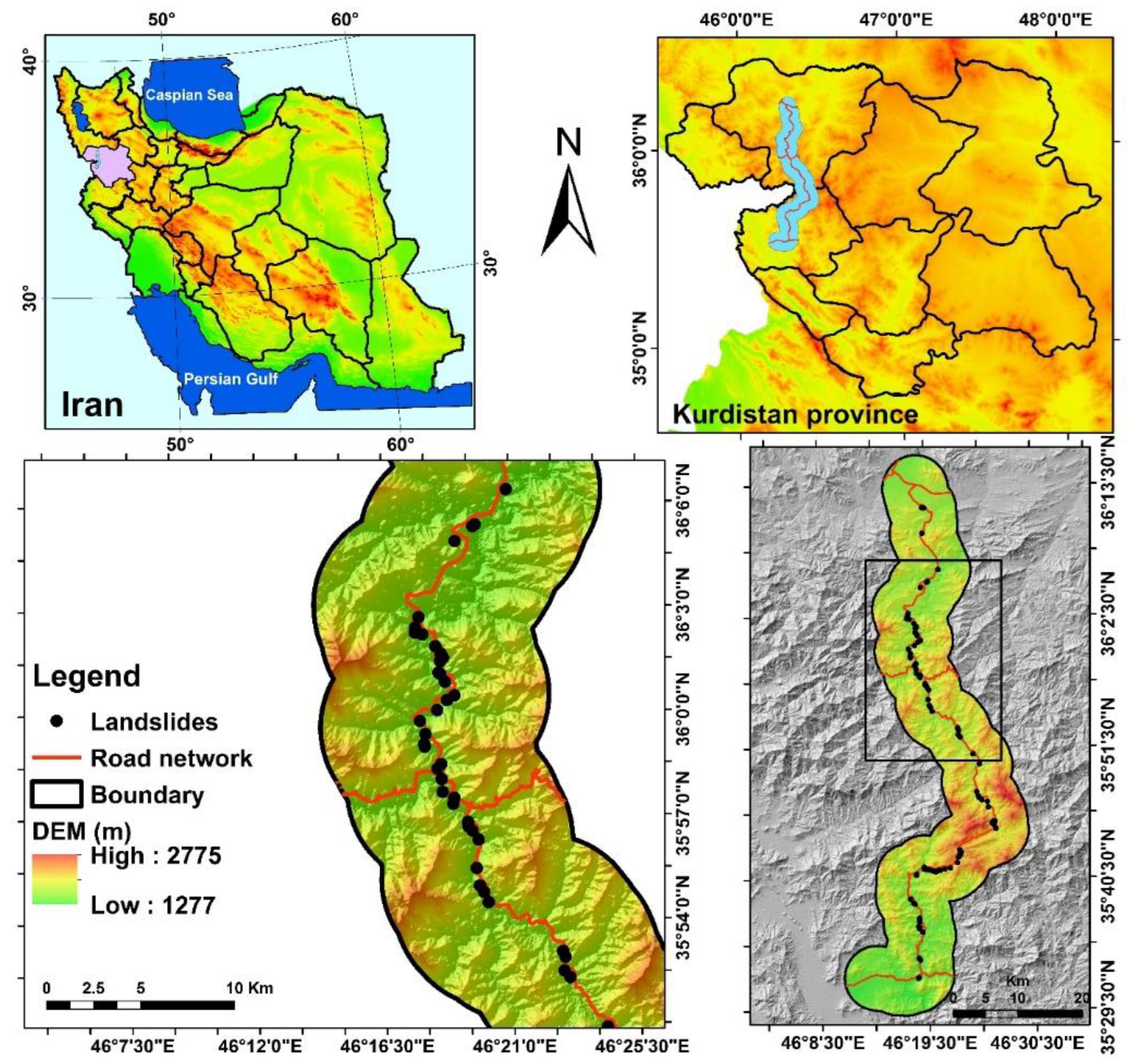
The case study is part of the communication route from Saqqez to Marivan and is located in Kurdistan province. The case study has a total of approximately 1100 km2. And it lies between the longitudes of 46˚ 10ʹ 34ʹʹ to 46˚ 29ʹ 33ʹ, east longitude and 35˚ 29ʹ 7ʹʹ to 36˚ 15ʹ 36ʹʹ north latitude (Figure 1). The Saqqez - Marivan road has been a strategic and important road due to the connection between western Iran and Iraq and having trade relations with the Kurdistan region. The length of this route is 126 km, which has winding passes and important and steep passages, so that in winter due to snow and rain there is a possibility of dangers such as landslides and avalanches. Figure 2 shows different types of landslides which have occurred in the study area.

2. Materials and Methods

2.1. Landslide conditioning factors (LCFs)

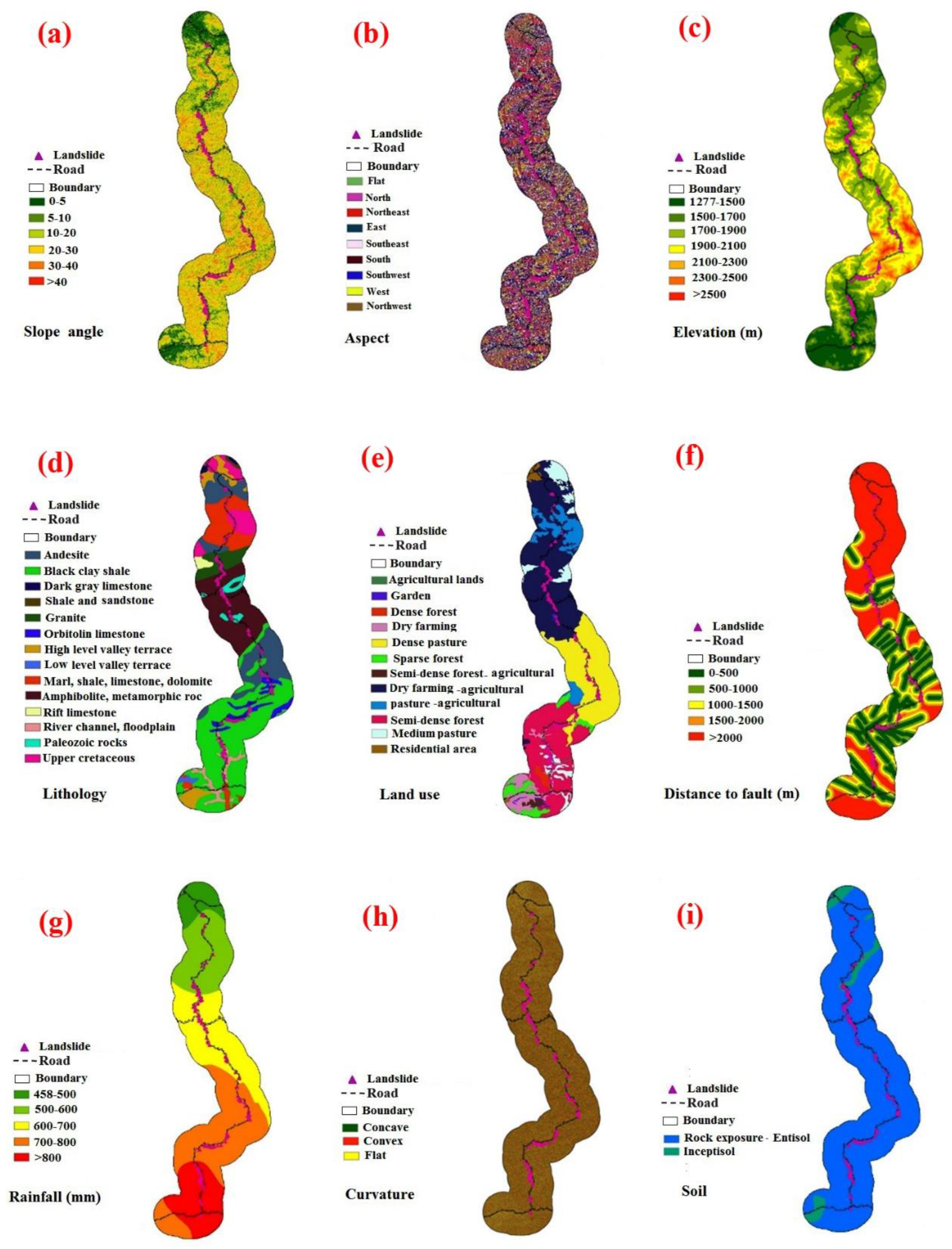
Identifying and mapping an acceptable collection of conditioning factors connected to landslide episodes requires prior knowledge of the principal landslide contributors [40]. In general, the number of landslide conditioning factors considered varies from several to dozens [41]. Based on prior studies and the features of landslide development in the study area, eleven elements were selected under five categories in order to identify the important conditioning factors of landslide susceptibility. They are slope, aspect, elevation, lithology, land use, distance to fault, distance to a river, distance to road, soil type, curvature, and rainfall. It is important to note that the classification of the layers was based on regional characteristics and the expert’s opinions. Landslide conditioning factors are reported for each factor class in the study area. First, a digital elevation model (DEM) with a resolution of 12.5m ×12.5m was prepared from the ALOS PALSAR satellite and from the site (https://vertex.daac.asf.alaska.edu/#).
In the following, a slope map was prepared using DEM in ArcGIS software and then it was classified into 6 classes (Figure 3a). The aspect layer was extracted from DEM in ArcGIS software and it was prepared and classified into 9 classes (Figure 3b). The elevation of the sea level map was obtained from DEM in Arc GIS 10.7 software in 7 classes (Figure 3c). The lithology map was then retrieved from the geological map with a scale of 1:100,000 and then it was classified into 14 classes (Figure 3d). Land use/cover map prepared from the interpretation of Landsat 7 ETM+ satellite images obtained in 2017 in 12 classes (Figure 3e). Faults map of the studied area was obtained from the geological map with a scale of 1:100,000 and the distance to the fault map was classified into 5 classes (Figure 3f). Using the kriging method, the rainfall was mapped and then divided into five classes using 20 years of data (from 1996 to 2016) from the rain gauge stations both inside and outside of the studied area (Figure 3g). In landslide modeling, the curvature is widely used as one of the most important conditioning factors (Oh and Lee 2011). The DEM 12.5m was used to make the curvature map, which was then categorized into three classes: concave, convex, and flat (no curvature) (Figure 3h). The soil layer of the region in two classes was referenced from the Map of Kurdistan province's land resources and capabilities with a scale of 1: 250,000 (Figure 3i). 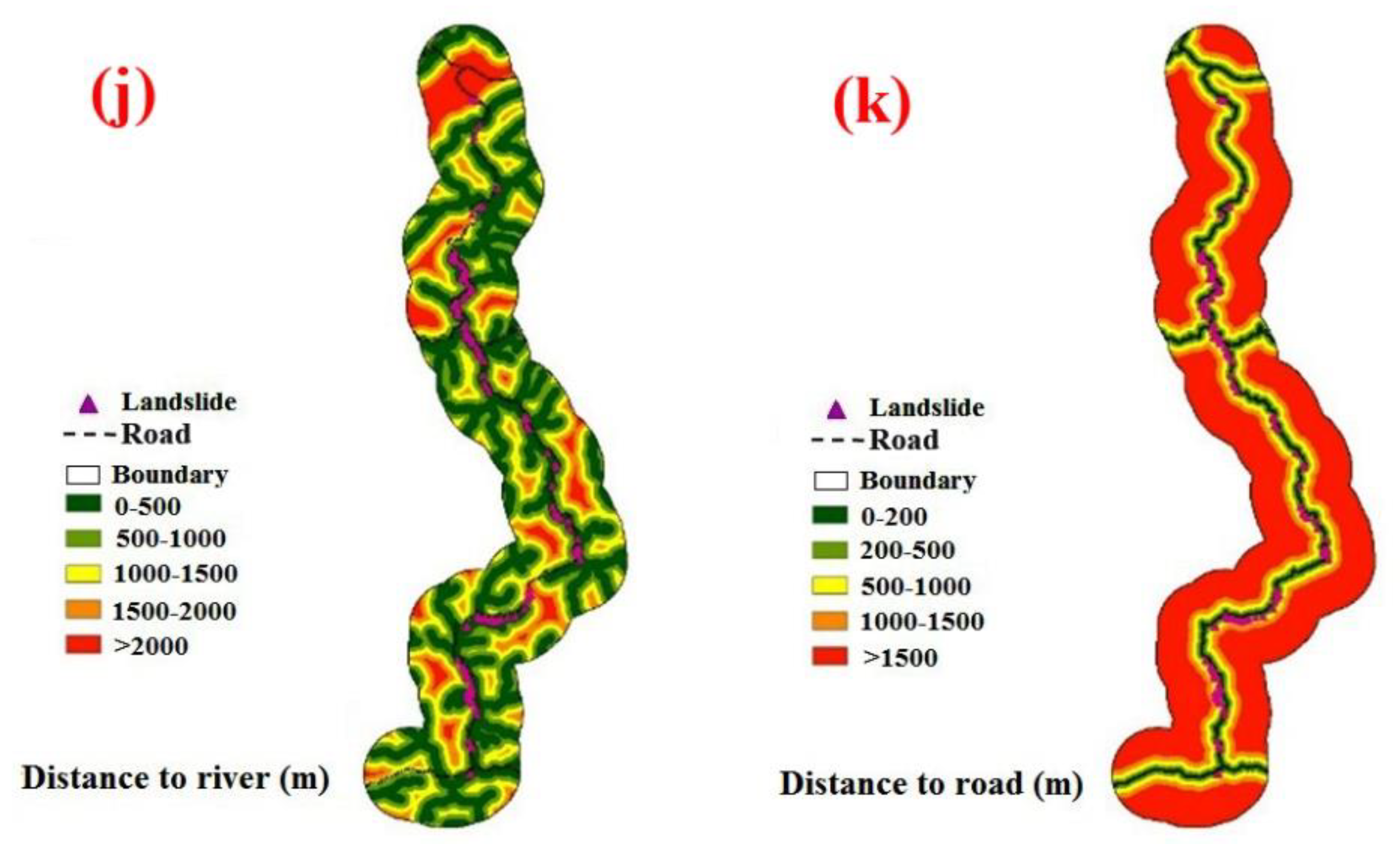River networks were extracted from the DEM 12.5m and then the distance to the river map was classified into five classes (Figure 3j). The excavation of roads in hilly areas causes slope instability and landslides [42]. The road network was obtained from the 1:50,000 scale topographic map. A distance to a road map with five categories was then created (Figure 3k).

2.2. Landslide Inventory Map (LIM)

Essentially, two datasets are required to create a landslide susceptibility map. The first dataset contains a map of the landslide inventory. The second dataset relates directly to factors that affect landslide occurrence. Landslide inventories are required for model training and validation in landslide susceptibility assessments. Inventories of landslides can be gathered using field surveys, news and government report detailing previous landslide events, and remote sensing data analysis [43]. Kavzoglu et al., 2014; Kilicoglu, 2021 [44,45] and Akinci et al. [46]used GNSS-based field surveys, high-resolution satellite images, Google Earth images, previous projects, and reports, atlases, and other sources to find the location of previous landslides. Consequently, the evidence gathered from prior landslides is referred to as an inventory map, and consists mainly of the locations of existing landslides. Obtaining knowledge about prior landslides is a critical component of landslide susceptibility assessment. Initially, a landslide inventory map with 100 landslide locations was created using Google Earth images and field surveys, among other sources. These landslides are classified into training (70%; 70 landsides) and validating (30%; 30 Landslides) for model building and validation, respectively. It is worth mentioning that there is no guideline or standard to classify the number of landslides in the training and validating datasets. We presented some references or some combinations in Table 1.
Preprints 69722 g003aPreprints 69722 g003b
Figure 3. The thematic map of landslide conditioning factors; (a) slope degree, (b) aspect, (c) elevation, (d) lithology, (e) land use, (f) distance to fault, (g) rainfall, (h) curvature, (i) soil, (j) distance to river (k) distance to road.
Figure 3. The thematic map of landslide conditioning factors; (a) slope degree, (b) aspect, (c) elevation, (d) lithology, (e) land use, (f) distance to fault, (g) rainfall, (h) curvature, (i) soil, (j) distance to river (k) distance to road.
Preprints 69722 g003aPreprints 69722 g003b

2.3. Multi-Criteria Decision-Making Methods in LSM

2.3.1. Fuzzy TOPSIS algorithm

The MCDM technique known as TOPSIS was created by Hwang and Yoon [60] and is predicated on the idea of "relative closeness to an ideal solution" [61]. In other words, the main goal is to select an optimal solution from a range of options that should be as close as feasible to the positive ideal solution (PIS) and as far as possible from the negative ideal solution (NIS) [61,62,63,64]. In this method, the weights for each predetermined criterion are defined, the scores are computed, normalised, and then the geometric distance of each alternative to the PIS and NIS is obtained [65,66].
The TOPSIS technique procedure typically involves the following steps:
Weights and decision matrices in the fuzzy TOPSIS method are defined as fuzzy numbers, and it is ranked similarly to the classic TOPSIS method according to the distance from the positive and negative values with equations (1).
D = X ~ 11 X ~ 12 X ~ 1 n X ~ 21 X ~ 22 X ~ 2 n X ~ m 1 X ~ m 2 X ~ m n                          
When using triangular fuzzy numbers, X ~ i j = ( a i j ,   b i j ,   c i j ) The function of the option (i=1,2,…,m) is in relation to the criterion (j = (1,2,…, n).
Using triangular fuzzy numbers, each component W j (standard weight) is represented by the equation (2).
W = w ~ i ,   … , w ~ j   , … . , w ~ r
If the fuzzy numbers are triangular, these equations are applied: to calculate the scales of the unmeasured decision matrix for the positive and negative criteria:
Γ ~ i j = a i j c j + , b i j c j +   , c i j c j +
Γ ~ i j = a j − c i j , a j − b i j   , a j − a i j
Which is in these relations ( c j + = m a x c i j ) and ( a j − = m i n a i j ).
Consequently, the scale-less fuzzy decision matrix (R) is derived as follows:
R ~ = r ~ 11 r ~ 1 j r ~ 1 n r ~ i 1 r ~ i j r ~ i n r ~ m 1 r ~ m j r ~ m n
where n denotes the number of criteria and m the number of options If the fuzzy numbers are triangular, equations 6 and 7 specify the requirements for the positive and negative features:
V ~ i j = r ~ i j . W ~ j = a i j c j + , b i j c j + , c i j c j + . W j 1 , W j 2 , W j 3 = a i j c j + . W j 1 , b i j c j + . W j 2 , c i j c j + . W j 3
V ~ i j = r ~ i j . W ~ j = a j − c i j , a j − b i j   , a j − a i j   . W j 1 , W j 2 , W j 3 = a j − c i j . W j 1 , a j − b i j   . W j 1 , a j − a i j . W j 1  
Equation (8) calculates the positive ideal solution matrix, while equation (9) determines the negative ideal solution matrix.
A + = V ~ 1 + , V ~ 2 +   ,   … . ,   V ~ n +
A − = V ~ 1 − , V ~ 2 −   ,   … . ,   V ~ n −
Where V ~ i +   the best is the value I of all the options and V ~ i − the worst value of criterion I of all the options.
The selections in A+ and A- represent options that are vastly superior and inferior, respectively [67].
The following equations can be used to determine the distance of each option from the positive and negative ideal solutions, respectively:
Distance from each option to the neutral and positive solutions that are optimal
Equation (10) can be used to express the distance between alternatives i and A with a positive ideal solution:
S i + = ∑ j = 1 n d ( V ~ i j , V ~ j + )   i = 1,2 , … , m                
The distance between alternative i A with the negative ideal solution can be formulated with equation (11):
S i − = ∑ j = 1 n d ( V ~ i j , V ~ j − )   i = 1,2 , … , m
d (.,.) is the distance between two fuzzy numbers that if (a1, b1, c1) and (a2, b2, c2) are two triangular fuzzy numbers, that can be formulated with equation (12):
d M ~ 1 , M ~ 2 = 1 3 ( a 1 − a 2 ) 2 +   ( b 1 − b 2 ) 2 +   ( c 1 − c 2 ) 2    
It should be noted that d ( V ~ i j , V ~ j + ) and d ( V ~ i j , V ~ j − ) are definite numbers.
The preference value for each alternative (i, V) is calculated using the following equation (13) [68]:
C i + = S i − S i + + S i − ; i = 1,2 … m
The alternatives are ranked with respect to the C i + in decreasing order [67].

2.3.2. Fuzzy analytical network process model (Fuzzy ANP)

The analytic hierarchy process (AHP) is not thought to be as comprehensive or precise as ANP [69]. However, in fact, there may be dependencies among the criteria. In AHP, it is assumed that there is no direct interaction between the criteria and that each criterion is independent in a one-way hierarchy [70]. ANP organizes decision criteria into a network of clusters and nodes in order to circumvent these limitations of AHP [71,72]. ANP is a relatively straightforward method for estimating individual decision-making model criteria. In this study, the ANP was used to calculate the final weights by following the steps below [73]:

A: Building ANP models and structuring problems

A problem should be clearly presented and divided into logical systems. As a result, based on the decision maker's judgment, a framework that represents the network can be specified using appropriate processes.

Step B: Pairwise comparisons

ANP defines the problem in terms of clusters and the decision components housed within them at various degrees of abstraction, much like AHP. For instance, the study's first cluster is its goal (for example, developing a vulnerability index), followed by the second cluster's dimensions or criteria (which include topography, geological, climate, and biology components), and the third cluster's indicators (containing the twenty selected indicators). The control criterion is used to compare how important the pairs of choice components within each cluster are. Additionally, interdependencies between cluster indicators are examined pairwise. Consequently, as suggested by Feizizadeh et al. [74], Relative significance is assessed on a scale from 1 to 9, with the lower bound denoting equal relevance and the higher bound denoting excessive significance. The eigenvector can be used to describe the measure of an element's influence on other elements. This evaluation is based on the relative weights of two indicators—a matrix row component and a matrix column component [26]. For the purpose of reverse comparison, a mutual value was established to highlight the importance of the element as it relates to the (jth) element. Similar to AHP, the comparison matrix gives pairwise comparison values, and the local priority vector is derived from the eigenvector using the following formula:
A . W = λ max . W
Matrix A is a pairwise comparison matrix with the largest eigenvalue denoted by W, which represents the eigenvector. A consistency matrix A's eigenvector X can be calculated using
( A − λ max I ) Χ = 0
The λ m a x value is an essential ANP verification criterion. This metric acts as a reference index for analyzing the estimated vector by calculating the consistency ration ( C R ) .
C I = ( λ max − n ) n − 1
The consistency of the pair-wise matrix is assessed using the consistency index (CI). The accepted consistency value (CR) must be less than 0.1.
C R = C I R I
RI indicates the average consistency index for reciprocal matrices of similar order containing any random entries. C R ≤ 0.1 , the estimated value is considered acceptable; otherwise, a new comparison matrix is continuously sought until this measure's acceptable range is not achieved.

Phase C: Calculating the Super Matrix

The super matrix's calculation, which is divided into clusters and their constituent elements, is aided by pair-wise comparison. The following describes the N-cluster supermatrix:
Preprints 69722 i001
The number of items in each kth cluster is m k , where C k represents the kth cluster and ( k = 1 , 2... n ) [26].

Step D: Selection

The goals of this step are used to analyse each signal and choose the best one for the final judgment. The selection criteria are based on the alternative weights that were acquired from the constructed supermatrix.
For the ANP model's mapping of landslide susceptibility assessment, there are three steps to the final weight calculation method:
  • Step 1: Objective (LSM). In this step, the subject model and structure are created using 11 factors including slope, aspect, elevation, lithology, land use, distance to fault, distance to a river, distance to road, curvature, and rainfall. These factors are classified into four clusters: topography (elevation, slope, curvature, and aspect), geology (soil type, distance to fault and lithology), anthropogenic (land use and distance to road), and climate (rainfall, distance to river).
  • Step 2: Construct binary comparison matrices and derive priority vectors. This step is similar to the analytical hierarchy process (AHP) in that the importance or priority of criteria or sub-criteria is determined within the range of 1–9 by the control criterion and by experts. In this stage, the final weights of the factors (clusters) are found by multiplying the relative weights of the factors in the matrix from the second stage. This creates a matrix of pairwise comparisons of the 11 research criteria (once looking at the lack of communication and again at the relationships), using even comparisons and fuzzy numbers.
  • Step 3: Determining the final weight of the criterion and sub-criterion. Before the final stage of determining the general weight of the criteria, by multiplying the matrices obtained from the fifth step together, the final weight of each criterion is finally determined. After determining the weights of the classes of each criterion by the ANP method, using fuzzy membership functions, run the model was performed in ArcGIS software. The weighing of criteria and sub-criteria was done by Super Decision software.

2.4. Validation of the methods

The precision or dependability of the landslide susceptibility maps is particularly significant for landslide susceptibility or hazard mapping investigations [75]. On the basis of standard methods, such as the receiver operating characteristics (ROC) curve, the model's performance should be assessed [15,76]. The area under the ROC curve (AUCROC) is plotted based on the sensitivity (true positive rate) and specificity (false negative rate) [77]. The AUCROC ranges between 0 and 1 in which 0.5 is the threshold and the higher the AUCROC is, the higher the performance (training dataset) and prediction accuracy (validation dataset) of the methods will be [78].

4. Results and analysis

4.1. Model building and comparison

In this study, fuzzy TOPSIS and fuzzy ANP were applied to derive the sub-criteria weights. In fuzzy ANP, after constructing the network and pairwise comparisons of internal and external factors and dependencies, Super Decision software provides three large matrices. By combining target comparison matrices, criteria, and sub-criteria, a large weightless matrix is formed. Finally, in order for a large weightless matrix to be a large weighted matrix, the large weightless matrix must be multiplied by a clustered matrix.
The final weight of each criterion in the Fuzzy ANP method is presented in Table 2. As can be seen, the criteria of distance to road, rainfall, and soil have the highest predictive capability for the landslide model while curvature, land use, and lithology have the lowest affecting on landslide occurrence in the study area. Moreover, in the fuzzy TOPSIS model results show that distance to the road has the highest predictive capability in landslide modeling and then rainfall and distance to the fault, respectively, are the most important factors. However, lithology and land use have the lowest importance on landslide occurrences. Table 3 shows the final obtained weights of the two methods (Fuzzy ANP and Fuzzy TOPSIS).

4.2. Developing landslide susceptibility mapping

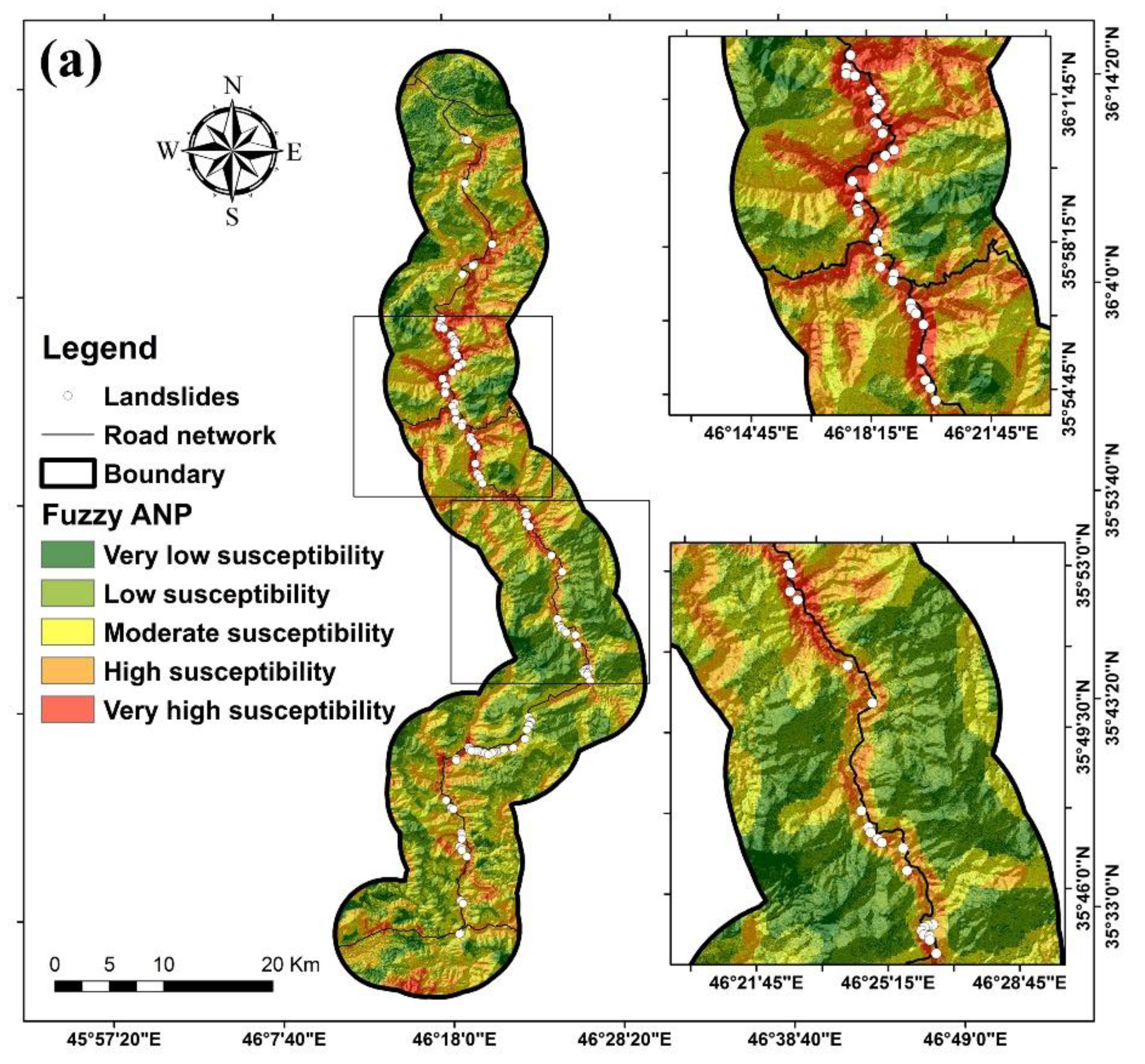
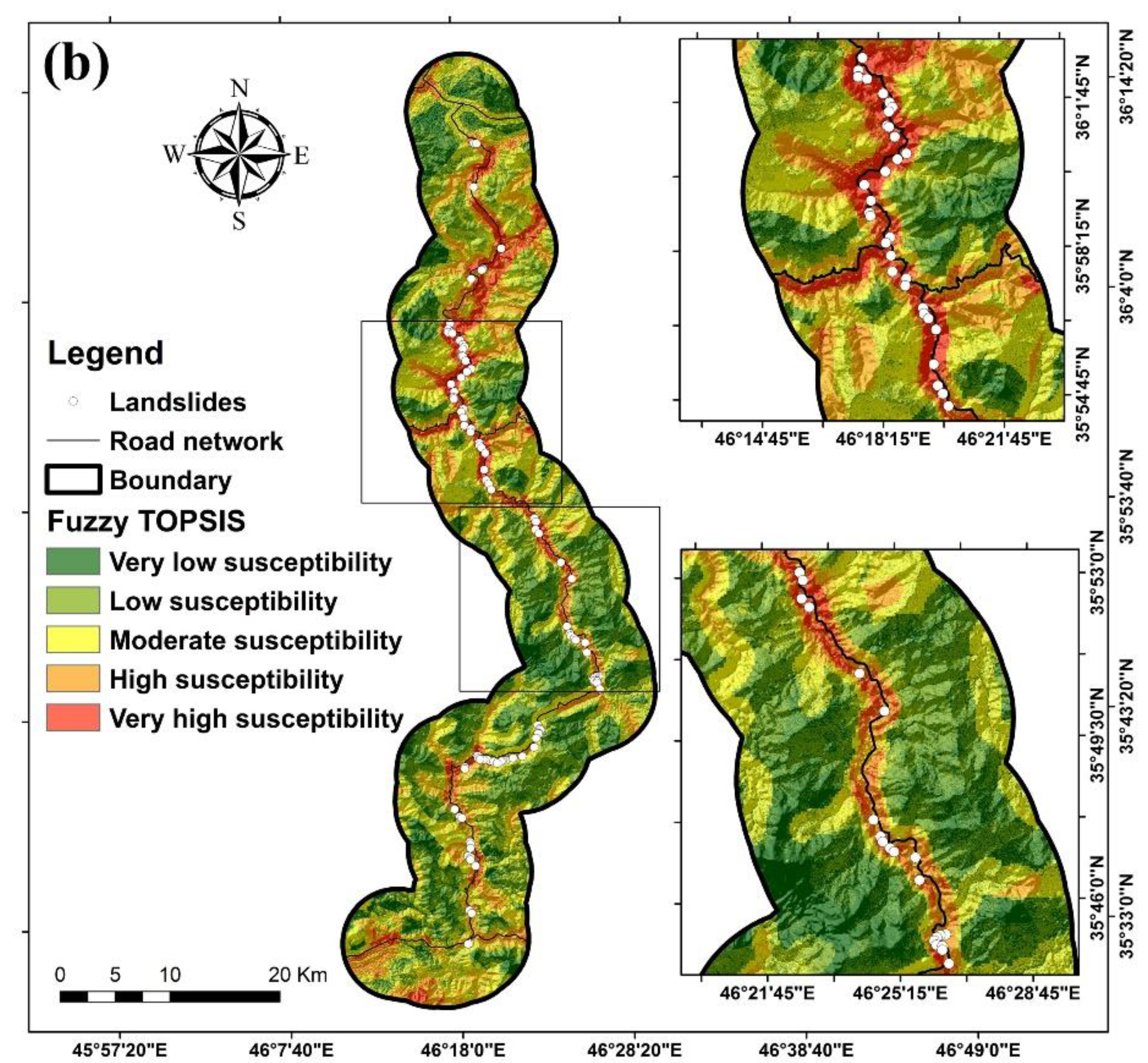
We produced and mapped landslide susceptibility based on the obtained weights of the two methods (fuzzy ANP and fuzzy TOPSIS) in Arc GIS 10.7. the weights were assigned to the sub-criteria and criteria and the landslide susceptibility maps were generated. We divided the two maps into five susceptibility categories: very low, low, moderate, high, and very high (Figure 4). Observing these figures shows an almost similar pattern in the distribution of different susceptibilities around the roads because the distance to the road was known to be the most important factor in the occurrence of landslides. Moreover, it can be said that the roads located in the northern part of the region are more susceptible to the occurrence than the southern parts of the region (Figure 4).
Preprints 69722 g004aPreprints 69722 g004b
Figure 4. Landslide susceptibility maps of the models (a) Fuzzy ANP (b) Fuzzy TOPSIS.
Figure 4. Landslide susceptibility maps of the models (a) Fuzzy ANP (b) Fuzzy TOPSIS.
Preprints 69722 g004aPreprints 69722 g004b
Table 3 displays the percentages of each class's area and the percentage of landsides in each class for both methods. It can be seen that in the Fuzzy ANP method, the low susceptibility class has the largest area (30.78%), followed by the moderate susceptibility class (28.37%), the high susceptibility class (19.29%), and the very susceptibility low (15.04%) and very high (6.51%). Moreover, the table reveals that the percentage of landslides from very low (0 %) to very high (51%) susceptibility classes decreased. In the fuzzy TOPSIS method, the percentages for the very low, low, moderate, high, and very high susceptibility classes are 19.33%, 29.52%, 27.91%, 16.98%, and 6.27%, respectively. However, the percentage of landslides is 0% for very low susceptibility calls, follows by low susceptibility (2%), moderate susceptibility (6%), high susceptibility (33%), and very high susceptibility (59%).
Table 3. Distribution of landslides in the study area's predicted landslide-prone zone, based on Fuzzy ANP and Fuzzy TOPSIS.
Table 3. Distribution of landslides in the study area's predicted landslide-prone zone, based on Fuzzy ANP and Fuzzy TOPSIS.
Fuzzy ANP Fuzzy TOPSIS
Landslide classes Class area (%Pixels) Landslide
(%Pixels) 		Class area (%Pixels) Landslide
(%Pixels)
Very low susceptibility 15.04 0 19.33 0
Low susceptibility 30.78 5 29.52 2
Moderate susceptibility 28.37 9 27.91 6
High susceptibility 19.29 35 16.98 33
Very high susceptibility 6.51 51 6.27 59
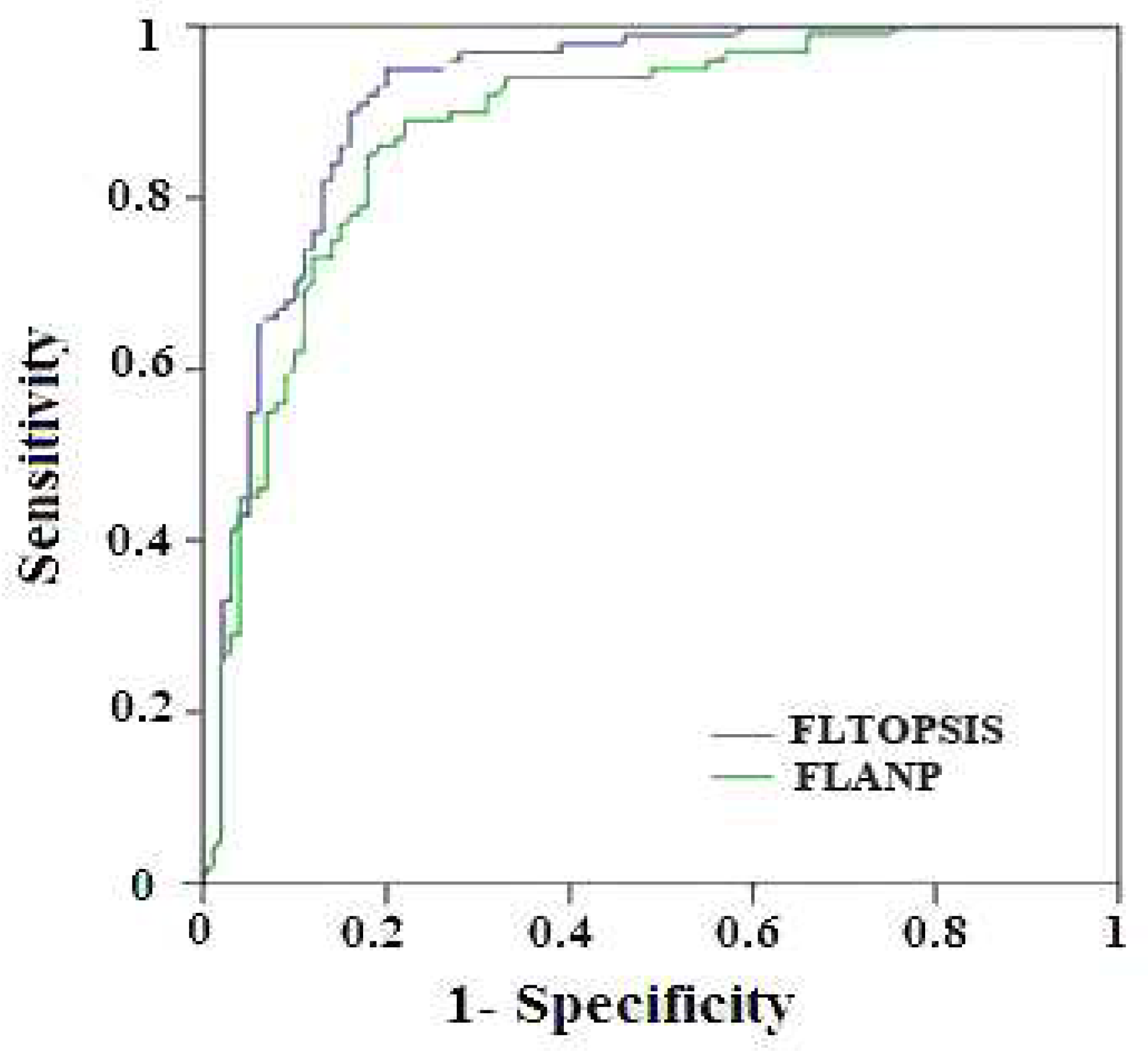
In order to validate the produced landslide susceptibility map, the area under the ROC curve (AUCROC) based on the validation dataset for the fuzzy TOPSIS method was found to be 0.918%, and for fuzzy ANP, it was found to be 0.89%. In addition, the results of the fuzzy TOPSIS method indicate that it is more precise than the fuzzy ANP method for producing a map of landslide susceptibility in the study area. These findings are shown in Table 4 and Figure 5.

Discussion

As natural hazards such as landslides are varied regarding magnitude and severity, they have significant financial and human losses. Predicting this event with the existing tools seems necessary because it is very useful for policymakers, stockholders, and land allocation projects before, during, and after the event [79]. Governments employ the basic and straightforward process of "landslide susceptibility mapping" (LSM) to develop landslide control policies [80]. The LSM can reduce losses and injuries by identifying and classifying locations that are prone to landslides [81]. The study of multidimensional occurrences like landslides has greatly benefited from the use of geographic information systems (GIS) and remote sensing techniques (RS). This has been made possible by the extraction of LCFs for landslide analysis, such as slope, distance to road, etc. [82].
Saqqez-Marivan communication main road in Kurdistan province, Iran, with a length of 126 km is one of the busiest communications roads due to its geographical location and great importance in transportation, especially access to the two border crossings between Iran and Iraq. This road has a large number of mass movements, including rock falls and landslides every year. In this study, for assessing and mapping the landslide susceptibility, the following predisposing factors were selected and mapped that including Slope, Aspect, elevation, lithology, land use, distance to fault, distance to a river, distance to road, soil type, curvature, and rainfall. Our findings indicated that based on the fuzzy ANP model the elevation of 2100 m-2300 m had the highest impact while class 1700 m- 1900 m had the lowest impact on landslide occurrence. Moreover, based on fuzzy TOPSIS the class of 1500 m-1700 m had the highest impact and the class 2100 m – 2300 m had the lowest impact on landslide incidence. Furthermore, the findings concluded that based on both models, the class of slope angle 30-40 degrees was more susceptible to landslide occurrence while the slopes lower than 5 degrees were the least susceptible to a landslide incidence.
This finding that shows the median slope is more prone to landsliding also can be validated and proved by Huang et al. [83] who reported that too high and too low slopes are not prone to landslides. Distance to rivers is one of the most important factors that control slope instability. This is because the shear stress of water flow is much more than the shear strength of soil banks and beds. In the study area, distances lower than 100 m from the rivers had the highest frequency of landslides. While the last class of distance from the river (> 2000 m) had the least impact on the landslide’s occurrence. It indicates that the lower the distance from the rivers, the higher the susceptibility to a landslide incidence. Pourghasemi et al. [84] declared and reported that with decreasing distance from the rivers, the probability of landslide occurrence is increased.
Another important factor is curvature, which is the rate of change of slope angle or aspect in a specific direction (i.e., topographic convergence or divergence). Based on both models, the class of concave slopes had the highest impact on landslide occurrence; however, flat slopes have the least effect on landslide occurrence. The obtained result also is in good agreement with Asmare [85] who claimed that concave and flat slope forms are respectively the most and lowest susceptibility to landsliding. Evaluation of the distance to the fault showed that class 1500 m -2000 m had the highest impact on landslide occurrence while the distance more than 3000 m from the faults has the least effect on landslide occurrence. Pourghasemi et al. [84] declared that landslides at a distance of 1501 and 2000 m from a fault had a higher probability of a landslide occurrence.
Also based on both models, the highest frequency of landslides was observed on the Entisols while Inceptisols has the least effect on landslides occurrence. Both Entisols and Inceptisols are young soils with mainly weak or incipient development [86] Entisols have covered most of the region and since they are young, immature, and undeveloped, and also human factors such as the improper construction of roads on these soils have manifested themselves and these soils are highly susceptible to landslides in the study area.
Land use survey shows that based on the fuzzy ANP model the class of the pasture and based on fuzzy TOPSIS the class of the semi-dense forest had the highest effect on landslides occurrence. In contrast, farming land and agricultural land classes have the least effect on landslide occurrence. The rainfall map shows that the class 700 mm - 800 mm had the highest frequency of landslide in the study area while the class 485 mm - 500 mm had the least effect on landslide occurrence. With increasing rainfall, the probability of landslide occurrence is increased. In other words, rainfall erodes and washed the topsoil of the slope surface and destroys the completeness between soil mass and rock and consequently decreasing the shear strength of the rock and soil mass increases the probability of landslide occurrence [83].
The underlying geology is one of the most significant factors for landslides. Based on the fuzzy ANP model dark gray shale formation and based on fuzzy TOPSIS the Low-level valley terrace had the highest effect on landslides occurrence while based on the fuzzy ANP model Orbit Olin limestone formation and based on fuzzy TOPSIS the Upper Cretaceous formation had the least effect to landslide occurrence. Rosly et al. [87] concluded that the areas that have been covered by shale interbedded with sandstone are more prone to landslide occurrence. In fact, shale has a high amount of clay and is classified as highly plastic soil with increasing pore water pressure from rainfall, the amount of infiltration and consequently matric suction are decreased and finally, the shear strength of the soil is diminished and landslide would be occurred [87].
We discussed and showed that FLTOPSIS mathematical method outperformed the FLANP methods in landslide susceptibility assessment. As TOPSIS is an easily understandable and programmable calculation technique, it is more popular that has been wieldy used by researchers in some fields of study. In fact, it can account simultaneously for various criteria with different units [88]. In other words, FLTOPSIS well afford the weak points of fuzzy logic including normalization and compatibility between the weights [89]. Additionally, TOPSIS due to lake of ability to solve uncertainty and ambiguity in judgment operation has attempted to combine MCDMs with other methods such as the Fuzzy theory [90].
The ANP method is simple, realistic, flexible, time-consuming, and cost-effective in use and it could create transparency and responsibility in decision procedure [91]. Balougn et al. [92] claimed that the ANP cannot well model comparison judgments because of uncertainty in the human preference model. Moreover, its applicability by combining with Fuzzy logic, FLANN, has been reported by Alilou et al.[93]in the evaluation of watershed health. The first limitation of this study is related to the FLTOPSIS method which is not applicable to solving hierarchical issues because a hierarchical system is not considered in this method. Another limitation is to complete the questionaries by expert’s knowledge to find the reliable and reasonable weights in ANP’s method.

5. Conclusion

We ensembled the Fuzzy logic with MCDM approaches such as TOPSIS, FLTOPSIS, and ANP, FLANP, in landslide susceptibility mapping around the Saqqez-Marivan mountain road, Kurdistan, Iran. were used to analyze landslide susceptibility assessment using these hybrid MCDM methods. We constructed a database constituted of eleven conditioning factors and a landslide inventory map by a combination of 70% (70 points) of the total observed landslides to generate landslide susceptibility maps and the remaining 30% (30 points) for validation of the methods. The maps were then classified into five susceptibility classes: very high, high, moderate, low, and very low. We highlighted the most important achievements and findings in this research below:
The three most important factors influencing the occurrence of landslides were, respectively, the distance to the road, rainfall, and the type of soil.
Our methodology scheme concluded that the FLTOPSIS method (AUC = 0.918) was superior to the FLANP (AUC = 0.882) in predicting landslides in the study area. We believe that FLTOPSIS could more solve uncertainty and ambiguity in judgment operation than FLANP.
The FLTOPSIS method, which rarely has been used in landslide susceptibility assessment, can be used as a promising and innovative, and potentially useful technique that to create a landslide susceptibility map in other landslide-prone areas.
The findings of this research can be utilized by the local government in order to manage appropriately, organize systematically, and plan development within the susceptible areas to landslides.
We suggest combining the Fuzzy logic with other MCDMs methods such as ELECTRE, ELECTRE, and VIKORE in the future and comparing the obtained results to achieve a highly reasonable and reliable landslide susceptibility map.

Author Contributions

Contributed equally to the work, H.S., R.T., M.A., S.M.B., M.H., A.S., E.H.A., I.D.W., and S.S.C; collected field data and conducted the landslide susceptibility analysis, H.S., R.T., M.A., M.H., A.S, and I.D.W; wrote the manuscript, S.M.B., E.H. A., and S. S.C provided critical comments in planning this paper and edited the manuscript. All the authors discussed the results and edited the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

research was funded by the University of Kurdistan, Iran, based on two grants number 01-9-19724-4469 and 01-9-22595.

Acknowledgments

The authors thank the University of Kurdistan, Iran, and Universiti Teknologi Malaysia (UTM) for preparing this international collaboration for the scientific sharing experience.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mukherjee, M.; Abhinay, K.; Rahman, M.; Yangdhen, S.; Sen, S.; Adhikari, B.R.; Nianthi, R.; Sachdev, S.; Shaw, R. Extent and evaluation of critical infrastructure, the status of resilience and its future dimensions in South Asia. Prog. Disaster Sci. 2023, 17. [CrossRef]
  2. 2. Alamgir, M.; Campbell, M.J.; Sloan, S.; Goosem, M.; Clements, G.R.; Mahmoud, M.I.; Laurance, W.F. Economic, Socio-Political and Environmental Risks of Road Development in the Tropics. Curr. Biol. 2017, 27, R1130–R1140. [CrossRef]
  3. Kanwar, N.; Kuniyal, J.C. Vulnerability assessment of forest ecosystems focusing on climate change, hazards and anthropogenic pressures in the cold desert of Kinnaur district, northwestern Indian Himalaya. J. Earth Syst. Sci. 2022, 131, 1–16. [CrossRef]
  4. Gecchele, G.; Ceccato, R.; Gastaldi, M. Road Network Vulnerability Analysis: Case Study Considering Travel Demand and Accessibility Changes. J. Transp. Eng. Part A: Syst. 2019, 145. [CrossRef]
  5. Xu, Y.; George, D.L.; Kim, J.; Lu, Z.; Riley, M.; Griffin, T.; de la Fuente, J. Landslide monitoring and runout hazard assessment by integrating multi-source remote sensing and numerical models: an application to the Gold Basin landslide complex, northern Washington. Landslides 2020, 18, 1131–1141. [CrossRef]
  6. Liu, Q.; Tang, A.; Huang, D.; Huang, Z.; Zhang, B.; Xu, X. Total probabilistic measure for the potential risk of regional roads exposed to landslides. Reliab. Eng. Syst. Saf. 2022, 228. [CrossRef]
  7. Pantelidis, L. A critical review of highway slope instability risk assessment systems. Bull. Eng. Geol. Environ. 2010, 70, 395–400. [CrossRef]
  8. Pierson, L.A.; Van Vickle, R. Rockfall hazard rating system: participant's manual; United States. Federal Highway Administration: 1993.
  9. Budetta, P. Assessment of rockfall risk along roads. Natural Hazards and Earth System Sciences 2004, 4, 71-81.
  10. Mavrouli, O.; Corominas, J.; Ibarbia, I.; Alonso, N.; Jugo, I.; Ruiz, J.; Luzuriaga, S.; Navarro, J.A. Integrated risk assessment due to slope instabilities in the roadway network of Gipuzkoa, Basque Country. Nat. Hazards Earth Syst. Sci. 2019, 19, 399–419. [CrossRef]
  11. Pregnolato, M.; Ford, A.; Wilkinson, S.M.; Dawson, R.J. The impact of flooding on road transport: A depth-disruption function. Transp. Res. Part D: Transp. Environ. 2017, 55, 67–81. [CrossRef]
  12. Chamorro, A.; Echaveguren, T.; Allen, E.; Contreras, M.; Cartes, P.; Contreras, M.; Jimenez, G.; Pattillo, C.; De Solminihac, H.; Vargas, J.; et al. Risk Management System for Road Networks Exposed to Natural Hazards. Lifelines 2022. pp. 166–177.
  13. Mattsson, L.-G.; Jenelius, E. Vulnerability and resilience of transport systems – A discussion of recent research. Transp. Res. Part A: Policy Pr. 2015, 81, 16–34. [CrossRef]
  14. Ghorbanzadeh, O.; Gholamnia, K.; Ghamisi, P. The application of ResU-net and OBIA for landslide detection from multi-temporal sentinel-2 images. Big Earth Data 2022, 1-26.
  15. Shahabi, H.; Hashim, M. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [CrossRef]
  16. Park, C.-J.; Kim, S.-Y.; Nguyen, M.V. Fuzzy TOPSIS Application to Rank Determinants of Employee Retention in Construction Companies: South Korean Case. Sustainability 2021, 13, 5787. [CrossRef]
  17. Wang, Y.-M.; Elhag, T.M. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst. Appl. 2006, 31, 309–319. [CrossRef]
  18. Olson, D.L. Comparison of weights in TOPSIS models. Mathematical and Computer Modelling 2004, 40, 721-727.
  19. Abo-Sinna, M.A.; Amer, A.H. Extensions of TOPSIS for multi-objective large-scale nonlinear programming problems. Appl. Math. Comput. 2005, 162, 243–256. [CrossRef]
  20. Cheng, S.; Chan, C.; Huang, G. An integrated multi-criteria decision analysis and inexact mixed integer linear programming approach for solid waste management. Eng. Appl. Artif. Intell. 2003, 16, 543–554. [CrossRef]
  21. Opricovic, S.; Tzeng, G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [CrossRef]
  22. Pham, Q.B.; Achour, Y.; Ali, S.A.; Parvin, F.; Vojtek, M.; Vojteková, J.; Al-Ansari, N.; Achu, A.L.; Costache, R.; Khedher, K.M.; et al. A comparison among fuzzy multi-criteria decision making, bivariate, multivariate and machine learning models in landslide susceptibility mapping. Geomatics, Nat. Hazards Risk 2021, 12, 1741–1777. [CrossRef]
  23. Dano, U.L.; Balogun, A.-L.; Matori, A.-N.; Yusouf, K.W.; Abubakar, I.R.; Mohamed, M.A.S.; Aina, Y.A.; Pradhan, B. Flood Susceptibility Mapping Using GIS-Based Analytic Network Process: A Case Study of Perlis, Malaysia. Water 2019, 11, 615. [CrossRef]
  24. Gheshlaghi, H.A.; Feizizadeh, B.; Blaschke, T. GIS-based forest fire risk mapping using the analytical network process and fuzzy logic. J. Environ. Plan. Manag. 2019, 63, 481–499. [CrossRef]
  25. Zeraatkar, Z.; Siuki, A.K.; Shahidi, A. Delineation of the Areas with Potential Land Subsidence Using the Analytic Network Process (Case Study: Birjand Aquifer, Iran). Geogr. Nat. Resour. 2021, 42, 290–295. [CrossRef]
  26. Alizadeh, M.; Ngah, I.; Hashim, M.; Pradhan, B.; Pour, A.B. A Hybrid Analytic Network Process and Artificial Neural Network (ANP-ANN) Model for Urban Earthquake Vulnerability Assessment. Remote. Sens. 2018, 10, 975. [CrossRef]
  27. Swetha, T.V.; Gopinath, G. Landslides susceptibility assessment by analytical network process: a case study for Kuttiyadi river basin (Western Ghats, southern India). SN Appl. Sci. 2020, 2, 1–12. [CrossRef]
  28. Neaupane, K.; Piantanakulchai, M. Analytic network process model for landslide hazard zonation. Eng. Geol. 2006, 85, 281–294. [CrossRef]
  29. Kavzoglu, T.; Sahin, E.K.; Colkesen, I. An assessment of multivariate and bivariate approaches in landslide susceptibility mapping: a case study of Duzkoy district. Nat. Hazards 2014, 76, 471–496. [CrossRef]
  30. El-Rashidy, R.A.; Grant-Muller, S.M. An assessment method for highway network vulnerability. J. Transp. Geogr. 2014, 34, 34–43. [CrossRef]
  31. Shano, L.; Raghuvanshi, T.K.; Meten, M. Landslide susceptibility evaluation and hazard zonation techniques – a review. Geoenvironmental Disasters 2020, 7, 1–19. [CrossRef]
  32. Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. CATENA 2012, 96, 28–40. [CrossRef]
  33. Pradhan, B.; Mansor, S.; Pirasteh, S.; Buchroithner, M.F. Landslide hazard and risk analyses at a landslide prone catchment area using statistical based geospatial model. Int. J. Remote. Sens. 2011, 32, 4075–4087. [CrossRef]
  34. 34. He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y. Landslide spatial modelling using novel bivariate statistical based Naïve Bayes, RBF Classifier, and RBF Network machine learning algorithms. Science of the total environment 2019, 663, 1-15.
  35. Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. CATENA 2019, 186, 104249. [CrossRef]
  36. Saleem, N.; Huq, M.E.; Twumasi, N.Y.D.; Javed, A.; Sajjad, A. Parameters Derived from and/or Used with Digital Elevation Models (DEMs) for Landslide Susceptibility Mapping and Landslide Risk Assessment: A Review. ISPRS Int. J. Geo Inf. 2019, 8, 545. [CrossRef]
  37. Zhang, W.; Li, H.; Han, L.; Chen, L.; Wang, L. Slope stability prediction using ensemble learning techniques: A case study in Yunyang County, Chongqing, China. J. Rock Mech. Geotech. Eng. 2022, 14, 1089–1099. [CrossRef]
  38. Cordeira, J.M.; Stock, J.; Dettinger, M.D.; Young, A.M.; Kalansky, J.F.; Ralph, F.M. A 142-Year Climatology of Northern California Landslides and Atmospheric Rivers. Bull. Am. Meteorol. Soc. 2019, 100, 1499–1509. [CrossRef]
  39. Mavrouli, O.; Corominas, J. Vulnerability of simple reinforced concrete buildings to damage by rockfalls. Landslides 2010, 7, 169–180. [CrossRef]
  40. Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [CrossRef]
  41. Devara, M.; Tiwari, A.; Dwivedi, R. Landslide susceptibility mapping using MT-InSAR and AHP enabled GIS-based multi-criteria decision analysis. Geomatics, Natural Hazards and Risk 2021, 12, 675-693.
  42. Asadi, M.; Mokhtari, L.G.; Shirzadi, A.; Shahabi, H.; Bahrami, S. A comparison study on the quantitative statistical methods for spatial prediction of shallow landslides (case study: Yozidar-Degaga Route in Kurdistan Province, Iran). Environ. Earth Sci. 2022, 81, 1–21. [CrossRef]
  43. Shen, H.; Huang, F.; Fan, X.; Shahabi, H.; Shirzadi, A.; Wang, D.; Peng, C.; Zhao, X.; Chen, W. Improving the performance of artificial intelligence models using the rotation forest technique for landslide susceptibility mapping. Int. J. Environ. Sci. Technol. 2022, 20, 11239–11254. [CrossRef]
  44. Kilicoglu, C. Investigation of the effects of approaches used in the production of training and validation data sets on the accuracy of landslide susceptibility mapping models: Samsun (Turkey) example. Arab. J. Geosci. 2021, 14, 1–18. [CrossRef]
  45. Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2013, 11, 425–439. [CrossRef]
  46. Akinci, H.; Kilicoglu, C.; Dogan, S. Random Forest-Based Landslide Susceptibility Mapping in Coastal Regions of Artvin, Turkey. ISPRS Int. J. Geo-Information 2020, 9, 553. [CrossRef]
  47. Pham, B.T.; Bui, D.T.; Dholakia, M.B.; Prakash, I.; Pham, H.V. A Comparative Study of Least Square Support Vector Machines and Multiclass Alternating Decision Trees for Spatial Prediction of Rainfall-Induced Landslides in a Tropical Cyclones Area. Geotech. Geol. Eng. 2016, 34, 1807–1824. [CrossRef]
  48. Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: a case study in northern Iran. Environ. Earth Sci. 2017, 76, 1–16. [CrossRef]
  49. Saha, S.; Roy, J.; Pradhan, B.; Hembram, T.K. Hybrid ensemble machine learning approaches for landslide susceptibility mapping using different sampling ratios at East Sikkim Himalayan, India. Adv. Space Res. 2021, 68, 2819–2840. [CrossRef]
  50. Shirzadi, A.; Solaimani, K.; Roshan, M.H.; Kavian, A.; Chapi, K.; Shahabi, H.; Keesstra, S.; Ahmad, B.B.; Bui, D.T. Uncertainties of prediction accuracy in shallow landslide modeling: Sample size and raster resolution. CATENA 2019, 178, 172–188. [CrossRef]
  51. Kornejady, A.; Ownegh, M.; Rahmati, O.; Bahremand, A. Landslide susceptibility assessment using three bivariate models considering the new topo-hydrological factor: HAND. Geocarto Int. 2017, 33, 1155–1185. [CrossRef]
  52. Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [CrossRef]
  53. Gautam, P.; Kubota, T.; Sapkota, L.M.; Shinohara, Y. Landslide susceptibility mapping with GIS in high mountain area of Nepal: a comparison of four methods. Environ. Earth Sci. 2021, 80, 1–18. [CrossRef]
  54. Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [CrossRef]
  55. Su, Q.; Zhang, J.; Zhao, S.; Wang, L.; Liu, J.; Guo, J. Comparative Assessment of Three Nonlinear Approaches for Landslide Susceptibility Mapping in a Coal Mine Area. ISPRS Int. J. Geo-Information 2017, 6, 228. [CrossRef]
  56. Moosavi, V.; Niazi, Y. Development of hybrid wavelet packet-statistical models (WP-SM) for landslide susceptibility mapping. Landslides 2015, 13, 97–114. [CrossRef]
  57. Jiao, Y.; Zhao, D.; Ding, Y.; Liu, Y.; Xu, Q.; Qiu, Y.; Liu, C.; Liu, Z.; Zha, Z.; Li, R. Performance evaluation for four GIS-based models purposed to predict and map landslide susceptibility: A case study at a World Heritage site in Southwest China. CATENA 2019, 183, 104221. [CrossRef]
  58. Kim, J.-C.; Lee, S.; Jung, H.-S.; Lee, S. Landslide susceptibility mapping using random forest and boosted tree models in Pyeong-Chang, Korea. Geocarto international 2018, 33, 1000-1015.
  59. Park, I.; Lee, S. Spatial prediction of landslide susceptibility using a decision tree approach: a case study of the Pyeongchang area, Korea. Int. J. Remote. Sens. 2014, 35, 6089–6112. [CrossRef]
  60. Hwang, C.-L.; Yoon, K.; Hwang, C.-L.; Yoon, K. Methods for multiple attribute decision making. Multiple attribute decision making: methods and applications a state-of-the-art survey 1981, 58-191.
  61. Gupta, S.; Soni, U.; Kumar, G. Green supplier selection using multi-criterion decision making under fuzzy environment: A case study in automotive industry. Comput. Ind. Eng. 2019, 136, 663–680. [CrossRef]
  62. Taherdoost, H.; Brard, A. Analyzing the Process of Supplier Selection Criteria and Methods. Procedia Manuf. 2019, 32, 1024–1034. [CrossRef]
  63. Yu, C.; Shao, Y.; Wang, K.; Zhang, L. A group decision making sustainable supplier selection approach using extended TOPSIS under interval-valued Pythagorean fuzzy environment. Expert Syst. Appl. 2018, 121, 1–17. [CrossRef]
  64. Zulqarnain, R.M.; Xin, X.L.; Siddique, I.; Khan, W.A.; Yousif, M.A. TOPSIS Method Based on Correlation Coefficient under Pythagorean Fuzzy Soft Environment and Its Application towards Green Supply Chain Management. Sustainability 2021, 13, 1642. [CrossRef]
  65. Sahin, B.; Yip, T.L.; Tseng, P.-H.; Kabak, M.; Soylu, A. An Application of a Fuzzy TOPSIS Multi-Criteria Decision Analysis Algorithm for Dry Bulk Carrier Selection. Information 2020, 11, 251. [CrossRef]
  66. Haddad, A.N.; da Costa, B.B.F.; de Andrade, L.S.; Hammad, A.; Soares, C.A.P. Application of Fuzzy-TOPSIS Method in Supporting Supplier Selection with Focus on HSE Criteria: A Case Study in the Oil and Gas Industry. Infrastructures 2021, 6, 105. [CrossRef]
  67. Chen, C.-T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [CrossRef]
  68. Wei, G.-W. GRA method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting. Knowl.-Based Syst. 2010, 23, 243–247. [CrossRef]
  69. Saaty, T.L. Decisions with the Analytic Network Process (ANP). University of Pittsburgh (USA), ISAHP 1996, 96.
  70. Leung, L.C.; Lam, K.C.; Cao, D. Implementing the balanced scorecard using the analytic hierarchy process & the analytic network process. J. Oper. Res. Soc. 2006, 57, 682–691. [CrossRef]
  71. Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [CrossRef]
  72. Youssef, A.M.; Pradhan, B.; Sefry, S.A. Flash flood susceptibility assessment in Jeddah city (Kingdom of Saudi Arabia) using bivariate and multivariate statistical models. Environ. Earth Sci. 2015, 75, 1–16. [CrossRef]
  73. Cheng, E.W.; Li, H. Application of ANP in process models: An example of strategic partnering. J. Affect. Disord. 2007, 42, 278–287. [CrossRef]
  74. Feizizadeh, B.; Jankowski, P.; Blaschke, T. A GIS based spatially-explicit sensitivity and uncertainty analysis approach for multi-criteria decision analysis. Comput. Geosci. 2014, 64, 81–95. [CrossRef]
  75. Soeters, R.; Van Westen, C. Slope instability recognition, analysis and zonation. Landslides: investigation and mitigation 1996, 247, 129-177.
  76. Lucchese, L.V.; de Oliveira, G.G.; Pedrollo, O.C. Mamdani fuzzy inference systems and artificial neural networks for landslide susceptibility mapping. Nat. Hazards 2021, 106, 2381–2405. [CrossRef]
  77. Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [CrossRef]
  78. Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total. Environ. 2018, 644, 1006–1018. [CrossRef]
  79. Tsakiris, G. Practical application of risk and hazard concepts in proactive planning. European Water 2007, 19, 47-56.
  80. Cao, Y.; Yin, K.; Alexander, D.E.; Zhou, C. Using an extreme learning machine to predict the displacement of step-like landslides in relation to controlling factors. Landslides 2015, 13, 725–736. [CrossRef]
  81. Ahmed, B. Landslide susceptibility mapping using multi-criteria evaluation techniques in Chittagong Metropolitan Area, Bangladesh. Landslides 2014, 12, 1077–1095. [CrossRef]
  82. Chowdhuri, I.; Pal, S.C.; Saha, A.; Chakrabortty, R.; Roy, P. Mapping of earthquake hotspot and coldspot zones for identifying potential landslide hotspot areas in the Himalayan region. Bull. Eng. Geol. Environ. 2022, 81, 1–23. [CrossRef]
  83. Huang, W.; Ding, M.; Li, Z.; Yu, J.; Ge, D.; Liu, Q.; Yang, J. Landslide susceptibility mapping and dynamic response along the Sichuan-Tibet transportation corridor using deep learning algorithms. CATENA 2023, 222. [CrossRef]
  84. Pourghasemi, H.R.; Jirandeh, A.G.; Pradhan, B.; Xu, C.; Gokceoglu, C. Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran. J. Earth Syst. Sci. 2013, 122, 349–369. [CrossRef]
  85. Asmare, D. Application and validation of AHP and FR methods for landslide susceptibility mapping around choke mountain, northwestern ethiopia. Sci. Afr. 2023, 19. [CrossRef]
  86. Antisari, L.V.; Trenti, W.; Buscaroli, A.; Falsone, G.; Vianello, G.; De Feudis, M. Pedodiversity and Organic Matter Stock of Soils Developed on Sandstone Formations in the Northern Apennines (Italy). Land 2022, 12, 79. [CrossRef]
  87. Rosly, M.H.; Mohamad, H.M.; Bolong, N.; Harith, N.S.H. An Overview: Relationship of Geological Condition and Rainfall with Landslide Events at East Malaysia. Trends Sci. 2022, 19, 3464–3464. [CrossRef]
  88. Ekmekçioğlu, M.; Kaya, T.; Kahraman, C. Fuzzy multicriteria disposal method and site selection for municipal solid waste. Waste Manag. 2010, 30, 1729–1736. [CrossRef]
  89. Chu, T.-C. Selecting plant location via a fuzzy TOPSIS approach. The International Journal of Advanced Manufacturing Technology 2002, 20, 859-864.
  90. Salih, M.M.; Zaidan, B.; Zaidan, A.; Ahmed, M.A. Survey on fuzzy TOPSIS state-of-the-art between 2007 and 2017. Comput. Oper. Res. 2018, 104, 207–227. [CrossRef]
  91. Kaur, P.; Mahanti, N. A fuzzy ANP-based approach for selecting ERP vendors. International Journal of Soft Computing 2008, 3, 24-32.
  92. Balogun, A.-L.; Sheng, T.Y.; Sallehuddin, M.H.; Aina, Y.A.; Dano, U.L.; Pradhan, B.; Yekeen, S.; Tella, A. Assessment of data mining, multi-criteria decision making and fuzzy-computing techniques for spatial flood susceptibility mapping: a comparative study. Geocarto Int. 2022, 37, 12989–13015. [CrossRef]
  93. Alilou, H.; Rahmati, O.; Singh, V.P.; Choubin, B.; Pradhan, B.; Keesstra, S.; Ghiasi, S.S.; Sadeghi, S.H. Evaluation of watershed health using Fuzzy-ANP approach considering geo-environmental and topo-hydrological criteria. J. Environ. Manag. 2018, 232, 22–36. [CrossRef]
Preprints 69722 g001
Figure 1. Location of landslides in the study area and Iran.
Figure 1. Location of landslides in the study area and Iran.
Preprints 69722 g001
Preprints 69722 g002
Figure 2. Photos showing different types of landslides observed in the study area.
Figure 2. Photos showing different types of landslides observed in the study area.
Preprints 69722 g002
Preprints 69722 g005
Figure 5. ROC curve of the methods using the validation dataset.
Figure 5. ROC curve of the methods using the validation dataset.
Preprints 69722 g005
Table 1. Different combinations of training and validating datasets in landslide susceptibility assessment.
Table 1. Different combinations of training and validating datasets in landslide susceptibility assessment.
Ratio (Percentage) References
70:30 [47,48,49,50,51,52]
80:20 [53,54,55]
75:25 [56,57]
50:50 [58,59]
Table 2. The performance of the methods based on Fuzzy ANP and Fuzzy TOPSIS.
Table 2. The performance of the methods based on Fuzzy ANP and Fuzzy TOPSIS.
Model Fuzzy ANP Fuzzy TOPSIS
Criteria The weight Final Rank Distance to positive ideal Distance to negative ideal Relative proximity to the ideal solution Rank
Distance to river 0.095 5 0.232 0.108 0.317 8
Distance to road 0.141 1 0.108 0.235 0.675 1
Land use 0.080 9 0.343 0.105 0.295 10
Lithology 0.028 11 0.355 0.111 0.283 11
Rainfall 0.108 3 0.117 0.185 0.598 2
Slope 0.089 7 0.201 0.108 0.343 6
Soil 0.112 2 0.151 0.110 0.423 4
curvature 0.060 10 0.343 0.111 0.303 9
Aspect 0.095 6 0.189 0.091 0.337 7
Distance to fault 0.104 4 0.145 0.149 0.502 3
Elevation 0.088 8 0.168 0.112 0.385 5
Table 4. AUCROC values of the models using the validation dataset.
Table 4. AUCROC values of the models using the validation dataset.
Row models Validating dataset
1 Fuzzy TOPSIS 0.918
2 Fuzzy ANP 0.882
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated