Preprint
Article
On Surface Waves Generated By Extra-Tropical Cyclones. Part II: Simulations
Altmetrics
Downloads
143
Views
123
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
14 March 2023
Posted:
15 March 2023
You are already at the latest version
Alerts
Abstract
In a previous companion study, satellite data were used to describe peculiar characteristics of ocean surface wave fields, generated by two extra-tropical cyclones (ETCs) rapidly propagating in the North Atlantic. Based on a 2D parametric wave model, further details are now provided to analyse and interpret the spatio-temporal evolution of ETC very intense generated waves. Significant wave height and wavelength values are shown to reach extreme values, 18 m and 500 m, respectively. Resulting energetic swell systems waves then radiate in the whole eastern part of North Atlantic, and more particularly in the Norwegian sea region. Moving to higher latitudes, wind forcing characteristics of ETCs evolve, with the shape of the wind field changing from quasi-cyclonic to "air jets/Icelandic lows". In this paper, the resulting swell generation and propagation, after the deformation of an individual ETC, are studied, as well. Confirmed with comparisons with multi-satellite observations, the application of the parametric-2D wave-ray model is demonstrated to provide robust and highly detailed information on wave generation under very complex wind regime changes.
Keywords:
Subject: Environmental and Earth Sciences - Oceanography
1. Introduction
While structure of extra-tropical cyclones (ETCs) varies significantly compared to tropical cyclones (TCs), typically exhibiting cold and warm fronts, the different storm regions have been reported to provide similar conditions to explain varying directional wave developments [1,2]. In the North Atlantic, [3] reported significant wave heights larger than 20m. Extreme wave heights have then further been found to appear in the region of ETCs where wind and wave directions align with the motion direction of the ETC [4]. In addition, the region of strongest wave growth has also been observed to vary during different development stages of ETCs [2]. In the North Pacific, [5] revealed the rear left region of the ETC to be comprised of swell and wind sea propagating in different directions. [6] showed the amplitude and period of intense swell events, reaching the coastlines, to be dependent on all ETC parameters, such as, its motion, size, lifetime, and wind speeds. [6] further revealed that the storm’s movement and its peak wind speed compress the wave energy to a small area, which then appears as a swell source location in the open ocean.
These swell fronts, generated by intense storms, dominate the sea state impact harbor safety, coastal flooding, and beach erosion [7,8,9,10,11]. Swell events are generally considered as long-crested linear wave systems, capable to propagate across the entire ocean basins [12,13,14]. Nowadays, swell waves are routinely observed by Synthetic Aperture Radar (SAR) images [15,16] and Real Aperture Radar measurements [17,18].
Moreover, spectral wave models, like WAVEWATCHIII [19], WAM [20], SWAN [21] generally successfully forecast wave fields under extreme wind conditions [22]. However, due to their sensitivities on the accuracy of the wind forcing field, spatial resolution and time step [23,24,25,26,27,28,29], poor predictions on arrival time and magnitude of swell waves generated by extreme wind events are still reported [30].
For waves generated by rapidly evolving wind systems, relatively more simple 2D parametric models can be better applicable [31,32]. Parametric models aim at describing a limited number of sea state parameters, such as energy, spectral peak frequency, and direction. Equations predicting the evolution of these parameters are derived from the basic equations of conservation of wave spectral density and momentum. The main principle is that the sources of energy and momentum must be specified to reproduce the classical 1D similarity fetch laws [33], derived for spatially homogeneous winds. More recently, such a 2D parametric wave model has been developed to rapidly characterize wave developments under spatio-temporal varying hurricane winds [34,35,36,37]. Modification of this 2D model includes the dependence of the drag coefficient on wind speed and atmospheric stratification, and effect of low air temperature on the air density [38]. This 2D wave model thus provides a simple, fast, easy-to-use, and acceptably accurate tool to rapidly estimate wave parameters under very complex spatio-temporal varying wind fields.
Already discussed in the companion paper [39] (hereinafter referred as PART I), wind fields inside ETC cases selected for this study are certainly very highly variable in both time ans space. This suggests to apply and test the simulation procedure suggested in [38] to simulate surface wave characteristics induced by ETCs, and the resulting swell systems.
In this second part of the study "On Surface Waves Generated By Extra-Tropical Cyclones", we first, Section 2.1, briefly recall the selected ETC cases and space-borne data, already reported in PART I. In Section 2.2, the 2D parametric model, simulation procedure, and the different types of model outputs are shortly described. The overall comparisons and validation of model based parameters with space-borne measurements are presented in Section 2.3. The analysis of main characteristics of ETC induced waves with cross-sections of significant wave heights (SWH) inside the storm area are presented in the Section 3. The resulting swell propagation properties, in different sides of the North Atlantic basin, are discussed in Section 4, comparing results from the 2D wave model and CFOSAT-SWIM satellite measurements. In Section 5, the analysis is performed using in situ measurements. The conclusion section summarizes the different results.
2. Materials and Methods
2.1. ETCs and Satellite Data
This paper is the second part of the study dedicated to the investigation of surface waves generated by two Extra-tropical cyclones (ETCs) in the North Atlantic using multi-satellite data. Unlike the PART I, numerical simulations are performed using a 2D parametric wave model [34,38].
The two selected ETCs traveled over the North Atlantic in the period from February 11th to February 15th. The hourly fields of wind velocity at a height of 10 meters above the sea surface are taken from the National Centers for Environmental Prediction Climate Forecast System version 2 [40] (hereinafter NCEP/CFSv2), and used to identify and trace the evolution of the selected ETCs. The first ETC (ETC#1) appeared on February 11th 2020, in the west of the basin at 48°N, and then moved east until it reached the coast of Ireland on the morning of 13-Feb-2020. The second ETC (ETC#2) originated in about the same area, but slightly later, at noon 12-Feb-2020. Unlike ETC#1, it moved to the northeast, and when it reached 60°N at noon on 14-Feb-2020, lost its initial shape, turning into an “air jet” along the southeast coast of Greenland (follow the wind fields in Animation 1 and Animation 2).
Data on significant wave heights (SWH/Hs) of surface waves were obtained from measurements by satellite altimeters Sentinel-3A, Sentinel-3B, AltiKa, CryoSat-2 and JASON-3. In addition, more wave data, namely, SWH, spectral peak parameters, and wave spectra, were obtained from the China-France Ocean Satellite for Surface Wave Investigation and Monitoring (CFOSAT-SWIM). In total, 130 altimeter tracks and 37 CFOSAT-SWIM tracks were collected over the study area during the life span of both ETCs (see Figure 3 and Figure 4 in PART I where coverage of the study area by satellite data is shown).
2.2. Model Tool
In the PART I, the satellite measurements of surface waves in the storm area of ETCs were analyzed using classical self-similar laws of wave growth within the extended fetch/duration framework. Although, applicability of these simplified laws are limited to spatially uniform and steady wind conditions, they are reported to be capable to reproduce the time evolution of maximal values of SWH and wavelength in the storm area during ETC lifespan.
In the present study, the 2D parametric wave-ray model (hereinafter 2D model) developed in [34] and modified in [38], is adapted to simulate the generation and evolution of surface waves under wind field, rapidly varying in both 2D space and time. By construction, this 2D model reproduces the classical laws of wave growth/duration under uniform and steady wind conditions. With the use of space-borne data, this 2D model can be considered as a very convenient tool to perform investigations to understand and characterize the space-time distribution of waves generated by ETC.
Description of the 2D model, its equations, and the simulation procedure are given in [34,35,36,38]. Here, we solely provide a short summary. The model equations are written in the characteristic form which describes evolution of wave energy, e (Equation (1)), spectral peak frequency (correspondingly,- peak wavenumber, , and the peak group velocity, , Equation (2)), and direction, (Equation (3)), of the wave trains along their trajectories given as in Equation (4)
In these equations: is a dimensionless energy source, representing wind energy input minus wave breaking dissipation; is the rate of energy change due to the ray convergence/divergence; is a source driving the low-frequency downshift of the spectral peak frequency due to non-linear wave interactions; is source of the spectral peak direction change due to change in the wind direction ; is the mean group velocity, averaged over wave spectrum of the wave train linked to as ; is a unit wavenumebr vector; is wave train coordinate, and subscript i takes the values .
To run the model, the hourly wind fields at 10 m above the sea surface, taken from NCEP/CSFv2 database, are used. In the present study, the ice mask in the northern part of the basin is applied. This mask is based on daily ice concentration data provided by the Bremen University, where the ice concentration of 20% is considered as the ice edge.
Model simulations were performed following the procedure described in [38]. First, wave-trains started from () spatial grid nod on each () time interval which coincide with hourly maps of NCEP/CSFv2 with resolution of . In results, families of wave-trains formed a 3D space–time volume of wave parameters, which traveled over the North Atlantic during the studying time period. In order to describe time evolution of spatial fields of wave parameters, all the trains which fit into the given space-time cell by size of were selected. All the trains caught in given space-time cell represent different wave systems (wind waves and/or swell). The parameters of each wave system, such as energy, wavelength, and direction, can strongly differ from other ones. Example of the histogram of distribution of such wave-trains parameters is given in Figure 7 and Figure 10.
There are two options to deal further with these histograms. First option follows [35] where wave-train with maximal wavelength (or optionally with maximal significant wave height) is only chosen and treated as the primary (dominant) wave system, while other trains falling into the given cell are not taken into account. The other option, suggested in [38], aimed at separating waves into several wave systems as primary - , secondary - , tertiary -, .... Correspondingly, in each spatial grid cell the total energy, , is defined as the sum of energy of all wave systems, and corresponding SWH as . The mean wavelength, and direction in each of the cell are then defined as the quantities weighted over the energy of the different wave systems (See Equation (12) in [38]).
The hourly maps of wind field, modeled SWH, , wavelength of primary wave system and its direction during the 11–15 February 2020, are illustrated in the animations Animation 1. The animation Animation 2, represents evolution of the same wind fields but fields of waves parameters weighted over different wave system: , and . In the general, wave parameters related to the primary wave system and combination of wave systems are very similar, suggesting the governing role of the primary wave system in the final formation of wave field generated by ETC.
2.3. Validation of Model Tool
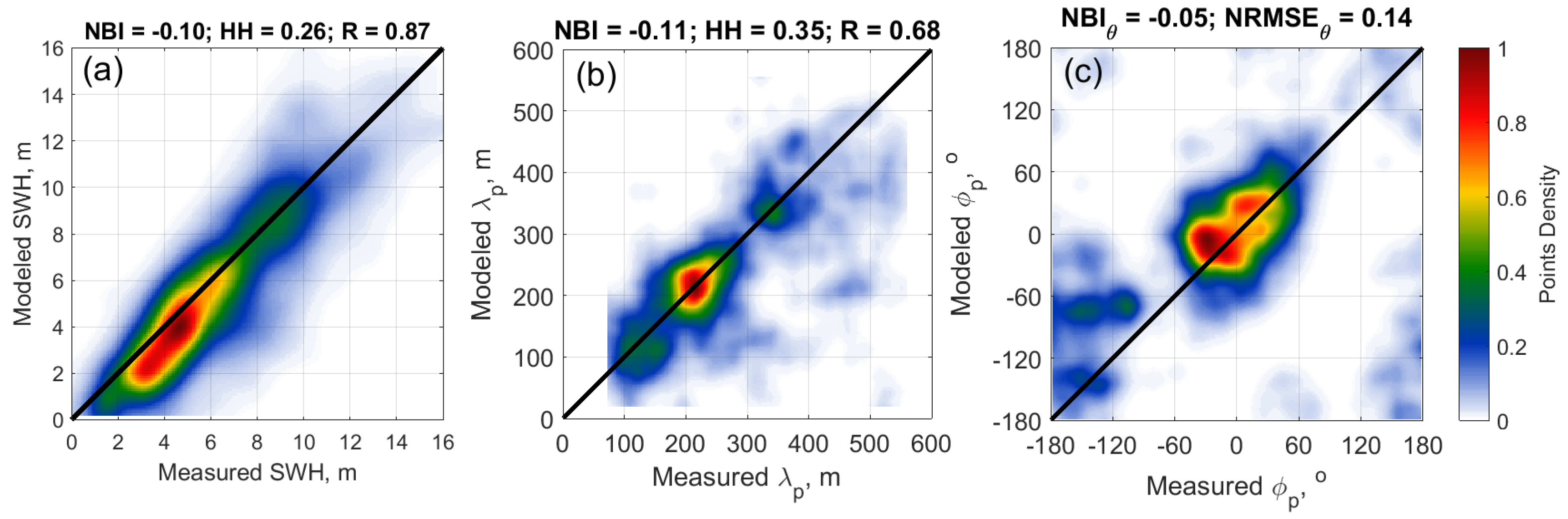
Before representing the detailed results on the characteristics of waves generated by ETCs, it is worthy to demonstrate that the model is close to available observations. To that end, we compared the simulation results of the 2D model with measurements from all altimeter and CFOSAT-SWIM tracks covering the North Atlantic during the studying period. In total, 130 altimeter tracks and 37 CFOSAT-SWIM tracks were used to perform this comparison (see Figure 2 and Figure 3 in PART I). Figure 1 demonstrates the scatter plots of “observed-vs-modeled” SWH () for all tracks crossing the North Atlantic during the lifespan of ETC#1 and ETC#2. The vs comparison, Figure 1a, demonstrates that the combination of different wave systems, suggested in [38] (see their section 4.1 step#3), quantitatively reproduces the with a normalized bias and normalized root mean square error . Due to the negative NBI value, the model apparently underestimates the measured SWHs. However, R value show that the model provides an overall good accuracy in reproducing wave heights under highly temporal-spatial changing wind fields.
Similar comparison are performed for the spectral peak wavelength and direction, available from SWIM measurement, Figure 3b,c. According to high points density, shown on the scatter-plot of Figure 3b, modeled and measured are well consistent. The NBI shows that the model underestimates the measurements by about 11%. Scatter-plot, Figure 3c, shows excellent agreements between the modeled and measured peak directions.
3. Wave Development within ETC Stormy Area
The hourly maps of SWH, , peak wavelength, and direction for the primary wave system generated by ETCs during the 11–15 February 2020, are illustrated in the animations Animation 1. The other animation Animation 2, represents the hourly maps of SWH, , mean wavelength and mean direction of the wave fields resulting from the full combination of primary-, secondary-, and tertiary-wave systems.
To gain deeper insight of characteristics of wind wave generation by ETCs, the 6-hourly fields of the surface wave parameters within the storm area are shown Figure 2 and Figure 3, for ETC#1 and ETC#2, respectively. The columns in Figure 2 and Figure 3 from left to right show: wind field, , , wave-minus-wind direction difference () and local inverse wave age (). All these fields are presented in moving orthogonal coordinate system with the origin tied to the ETC eye, defined by the minimum of the surface pressure.
3.1. Waves under ETC#1
Modeling the wind wave development starts at the origin of the low pressure area, ending (after eight hours) with the formation of ETC#1 and ETC#2 (see e.g Figure 1 from PART I). This allows to follow the space-time wave development under the ETCs from the very beginning. At the initial stage of ETC#1 evolution, as it moves to the east and acquires a completely cyclonic form, areas with continuous growth of SWH and wavelength are clearly obtained in the right sector of the ETC (Figure 2). After careful inspection of the inverse wave age maps, Figure 2, one may find that the development of wind waves begins at the front boundary of the storm area. Since developing waves are slow compared to the ETC translation velocity, they move backward relative to the moving ETC in the course of their development. In the first half of ETC#1 lifespan, fully developed waves () with direction aligned to the wind direction () can be locally found in the mid of the right sector. In the second half of its lifespan, the area of fully developed waves is shifted to the rear-right sector. Second and third columns in Figure 2 exhibit clear time growth in SWH and wavelength of waves generated in the storm area. This fact corresponds to the satellite observations of linear growth of wave energy in the storm area reported in PART I.
From the maps describing wavelength and direction characteristics, a wave system with in front of the ETC#1’s forward sector can be easily recognized. The wave direction for this system largely differs from the wind direction. The associated SWHs are much lower than the ETC generated wave ones. This wave system is not related to ETC#1, and was probably generated prior to ETC#1. Animations Animation 1 and animation 2 illustrate origin of this wave system and its evolution.
Figure 2.
6-hour fields of the wind velocity and the model wave parameters in a moving orthogonal coordinate system with the origin at the eye of ETC#1. Columns from left to right: wind velocity, significant wave height (), wavelength () and wave direction (), wave-wind directions difference (), and local inverse wave age (). The red arrow in the centre of each map indicates the movement direction of ETC#1. Circle radii start at 200m in 200m increment.
Figure 2.
6-hour fields of the wind velocity and the model wave parameters in a moving orthogonal coordinate system with the origin at the eye of ETC#1. Columns from left to right: wind velocity, significant wave height (), wavelength () and wave direction (), wave-wind directions difference (), and local inverse wave age (). The red arrow in the centre of each map indicates the movement direction of ETC#1. Circle radii start at 200m in 200m increment.
3.2. Waves under ETC#2
The simulation for ETC#2 generated waves is also considered from the first hours of its formation and illustrated Figure 3. The movement direction of ETC#2, shown by red arrows, is changing from 30°, to 110°, between initial hours and last hours of its life, respectively.
As discussed in PART I, both ETC#1 and ETC#2 are fast-moving atmospheric systems in a sense that their translation velocities are larger than the group velocity of generated wind waves. As a result, the generation of wind waves begins when the front boundary of the storm appears at a given location in the ocean. Then, in the process of their development, the generated waves move backward relative to the ETC, reaching their maximum development at the rear boundary of the storm, and, finally, leave the ETC in the form of swell systems. These peculiar wave developments are clearly exhibited in Figure 3. From the inverse wave age maps shown in the last column, the youngest waves (the largest values of ) are first located along the frontal boundary of the storm. The inverse wave age then gradually decreases towards the storm core, where the developing waves are propagating. Second, similar to the satellite observations (see PART I), the largest value of SWH and wavelength of generated waves are observed in the right and the rear-right sector. This fact suggests that, in the right sector, waves stay under wind forcing for more time than in other sectors. Waves become fully developed, running out of the storm region as swell systems. This finding coincides with the results of self-similar analyses of SWH measurements, discussed in PART I, which confirms efficiency of the extended fetch/duration mechanism when wind and developing waves directions coincide with the ETC movement direction.
At the last stage of the ETC#2 lifetime, the SWH and wavelength reach 17 m and 500 m, respectively. It corresponds to phenomenal sea conditions, defined by the World Meteorological Organization (WMO) as having a significant wave height larger than 14 m. A remarkable point is that at the final stage of ETC#2 lifespan, the waves with and in the rear-left sector occupy a radial range of km. This indicates the creation of a huge wave front which can cause a very dangerous situation for marine navigation. Another interesting feature shown Figure 3 is the presence of ETC#1 swell after its lifespan. In the up-right corner of wind fields, before 13-Feb-2020 15:00:00, we see the tail of ETC#1. However, swell waves generated by ETC#1, remain in the basin until 14-Feb-2020 09:00:00.
Figure 3.
The same as Figure 2, but for ETC#2.
Figure 3.
The same as Figure 2, but for ETC#2.
3.3. Model vs. Observations
Fields of wave parameters and discussion of their characteristics, presented in Section 3.1 and Section 3.2, are based on the outputs of the 2D model. Figure 1, shown in Section 2.3, already demonstrates a "general" validity, over all data covering the North Atlantic during the studying period. In this section, more specific satellite sensor tracks, crossing the storm area of ETC#2, are used . Both types of model outputs are considered, namely: SWH of primary waves system (), and SWH of mixed seas .
Cross sections of and , as a function of latitudes along the altimeter tracks crossing ETC#2, are shown Figure 4, together with observed SWH, . In Figure 4, the geographical location of the tracks is superimposed on the map with wind speed contours and colored map of . The altimeter tracks cover various parts of the ETC#2, Figure 4. Comparing the , and profiles, a rather good overall consistency is found between model simulations and observations. However, some differences can be notified, e.g., model underestimation of SWH highest values around 15m on 13:00:00 and 23:00:00. On the other hand, after careful inspection, these underestimations, at least on 23:00:00, are related to spatial shift of maximal model values of SWH from the altimeter track. Notice, the model values of and in the storm area of ETC, are almost the same, but a bit different outside, where the existence of the mixed seas is likely plausible.
Figure 4.
The model vs the measurements. First and third rows: altimeter tracks superimposed on maps of wind speed (contour lines) and model SWH, (color) ETC#2 . Second and fourth rows: cross section of (black curves), (blue curves), and (red curves) along the altimeter tracks as a function of latitude.
Figure 4.
The model vs the measurements. First and third rows: altimeter tracks superimposed on maps of wind speed (contour lines) and model SWH, (color) ETC#2 . Second and fourth rows: cross section of (black curves), (blue curves), and (red curves) along the altimeter tracks as a function of latitude.

4. Evolution of Swell after the ETC Lifespan
On 14-Feb-202 around 09:00:00, the ETC#2 stopped moving to the northwest, changed direction and ceased to exist. Instead, a strong wind jet formed along Greenland at a speed of about 35 ms−1. This wind jet triggered the generation of a new wind wave system developing along the coast of Greenland, which further radiated into the "open ocean" from Cape Farewell, Figure 5. At the same time, after ETC#2 ceasing, the wind waves which were generated in its storm area continued to evolve as a system of swell waves, traveling northeast, Figure 5. Both these wave systems, - swell emitting from Cape Farewell, and swell traveling northeast from ETC#2, are indicated by arrows in Figure 5. The two systems represent the main subject of investigation in this section, using the spectral information from SWIM off-nadir measurements, the altimeters observations, and the model outputs.
Figure 5.
6-hour fields of the wind velocity and the model wave parameters in geographical coordinates after cessation of ETC#2. Columns from left to right: wind velocity, significant wave height (), wavelength () and wave direction (), and local inverse wave age (). Two white arrows indicate two swell fronts considered in the text.
Figure 5.
6-hour fields of the wind velocity and the model wave parameters in geographical coordinates after cessation of ETC#2. Columns from left to right: wind velocity, significant wave height (), wavelength () and wave direction (), and local inverse wave age (). Two white arrows indicate two swell fronts considered in the text.

4.1. Evolution of the Northeastward Swell
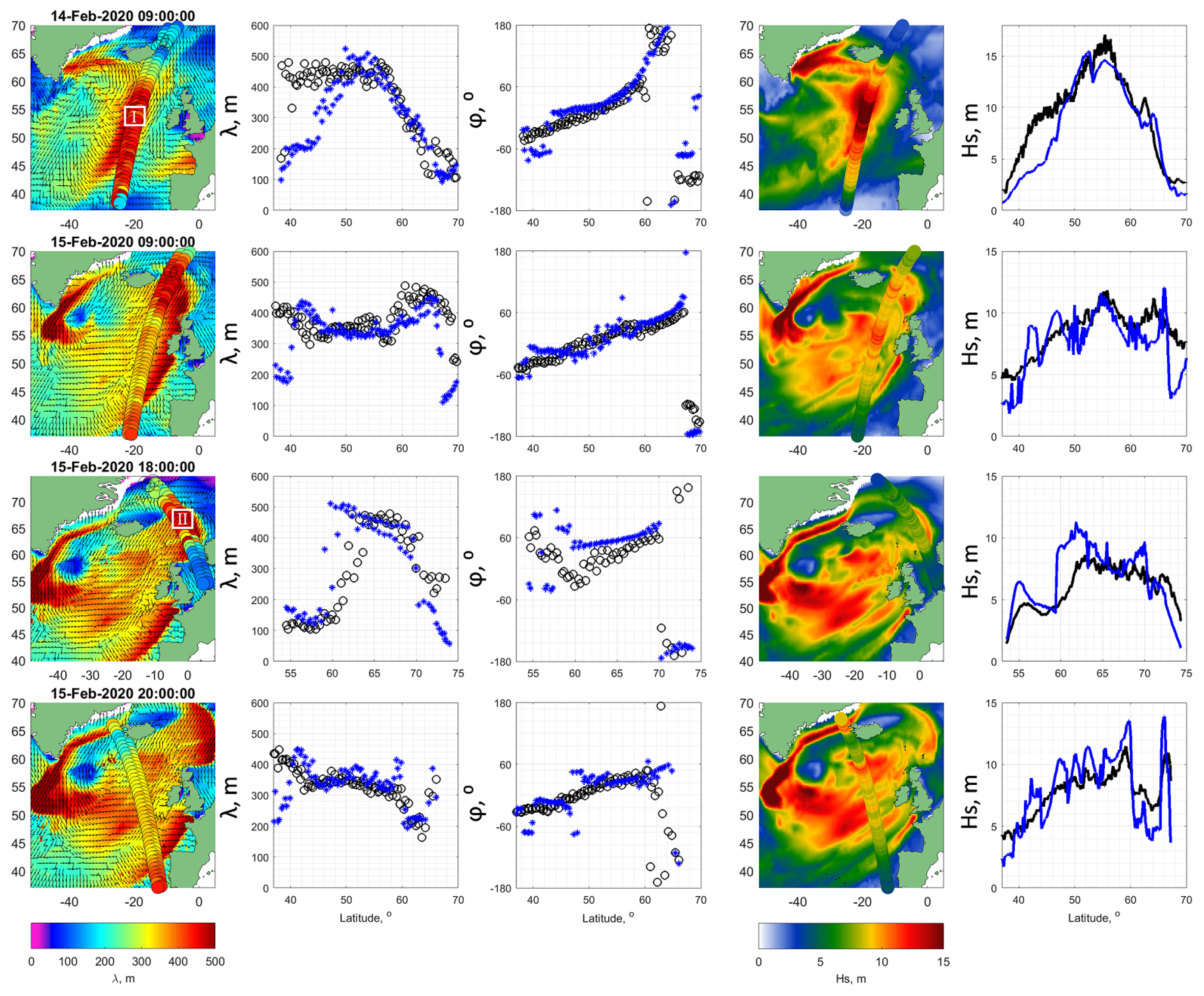
Referring to the last row of Figure 3 and first row of Figure 5, a front of waves is observed on 14-Feb-2020 morning, with m, m, and . These waves occupy a very large area in the rear-right sector of ETC#2. Travelling eastward, this wave front can reach the Celtic Sea and subarctic seas, such as the Norwegian Sea. On Figure 6 the spatio-temporal evolution of this front is illustrated at times, when the SWIM tracks crosses part of the front. First row of Figure 6 is associated with the final moments of ETC#2 life, shown in the last 2 rows of Figure 3. The SWIM tracks are superimposed on the synchronous field of SWH and wavelength obtained from the 2D model.
Going forward in time (from up to down rows of Figure 5 and Figure 6), the east–northeastward propagation of this wave front is easily recognizable. The measurements of , and also confirm this front propagation. Based on simulations and measurements, following Figure 6, the spatio-temporal evolution of swell in the eastern side of the North Atlantic Ocean is thus found to influence the European coasts and subarctic seas for a long time after the disappearance of ETC#2. On the maps, Figure 6, the maximal SWH levels decrease from about 17m on 14-FebT09 to 8m on 15-FebT20, following energy dissipation, while the maximal wavelength is > 450 m.
Figure 6.
Spatio-temporal evolution of waves, after disappearance of ETCs, when the CFOSAT-SWIM tracks cross eastward moving swell front. Columns from left to right: Geographical location of SWIM tracks superimposed on color-maps of modeled , where the arrows show ; cross section of (black circles) and (blue asteroids); cross section of (black circles) and (blue asteroids); SWIM nadir tracks superimposed on color-maps of modeled ; cross section of (black curves) and modeled (blue curves).
Figure 6.
Spatio-temporal evolution of waves, after disappearance of ETCs, when the CFOSAT-SWIM tracks cross eastward moving swell front. Columns from left to right: Geographical location of SWIM tracks superimposed on color-maps of modeled , where the arrows show ; cross section of (black circles) and (blue asteroids); cross section of (black circles) and (blue asteroids); SWIM nadir tracks superimposed on color-maps of modeled ; cross section of (black curves) and modeled (blue curves).
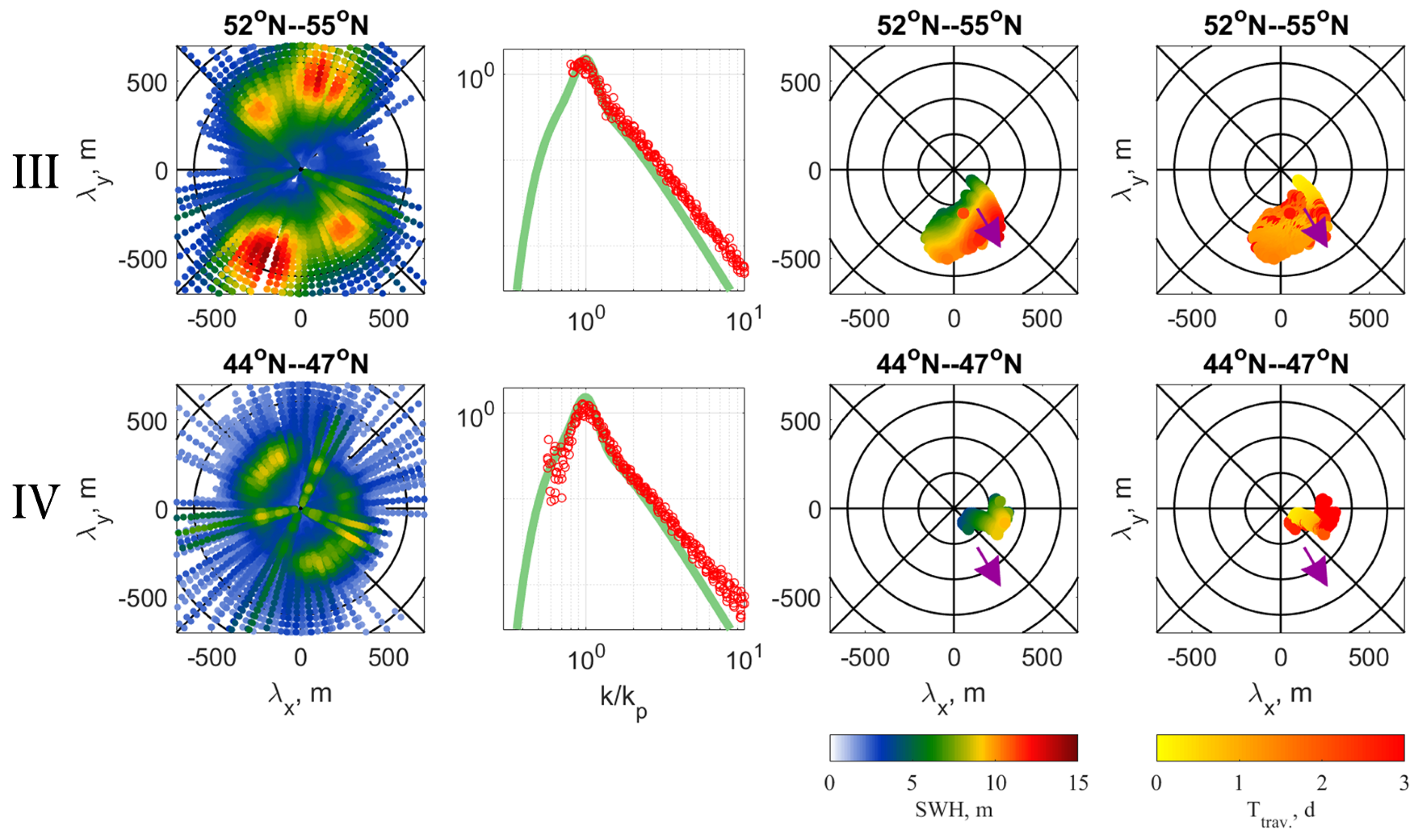
The 2D wavenumber spectra derived from SWIM data in the area of wind waves (box I in Figure 6) and in the area of swell front (box II in Figure 6) are shown Figure 7. The SWIM wave spectra are available from the IFREMER database (ftp.ifremer.fr/ifremer/cersat/projects/iwwoc). The second columns of Figure 7 display the omnidirectional spectra , scaled by , i.e. , as a function of , where e is the energy (integral of S over k) and spectral peak wavenumber. Green lines show the JONSWAP [41] spectra with the similar scaling. Measured spectrum for the the wind waves is very similar to the empirical JONSWAP one, except for some differences in the slope of the spectral tail. In the swell front area, combination of dominant swell system and much shorted wind waves can be revealed. The presence of wind waves noticeably changes the omnidirectional spectrum due to the addition of energy in the tail of the spectrum, at frequencies above the peak frequency of the wind waves. Nevertheless, shape of the scaled total spectrum (where swell dominates) is again surprisingly close to the JONSWAP spectrum. This observation is similar to what was reported by [42] and [43] under hurricane conditions, - shape of the dominant wave spectra, regardless of whether they are wind waves or swells, is very close to the shape of the JONSWAP spectrum.
Histograms of the model energy distributions of wave-trains over wavelength and directions shown in the third column, serve as a good proxy of 2D spectra. Comparing the first and third column in Figure 7, model spectral distributions of wave-trains are indeed found consistent with 2D spectra. Travel time histogram (last column) gives an idea of the history of wave packets (wind driven and swell) forming a wave pattern at a given time and at a given point.
Figure 7.
2D directional wave spectra derived from SWIM inside the boxes I and II indicated in Figure 6 (left columns). The second column: Scaled omnidirectional spectra, , (red circles) as a function of compared to scaled JONSWAP spectra (green curves). The third and fourth columns are model histograms of SWH and travel time distributions over wavelength and directions, purple arrow indicates wind direction.
Figure 7.
2D directional wave spectra derived from SWIM inside the boxes I and II indicated in Figure 6 (left columns). The second column: Scaled omnidirectional spectra, , (red circles) as a function of compared to scaled JONSWAP spectra (green curves). The third and fourth columns are model histograms of SWH and travel time distributions over wavelength and directions, purple arrow indicates wind direction.
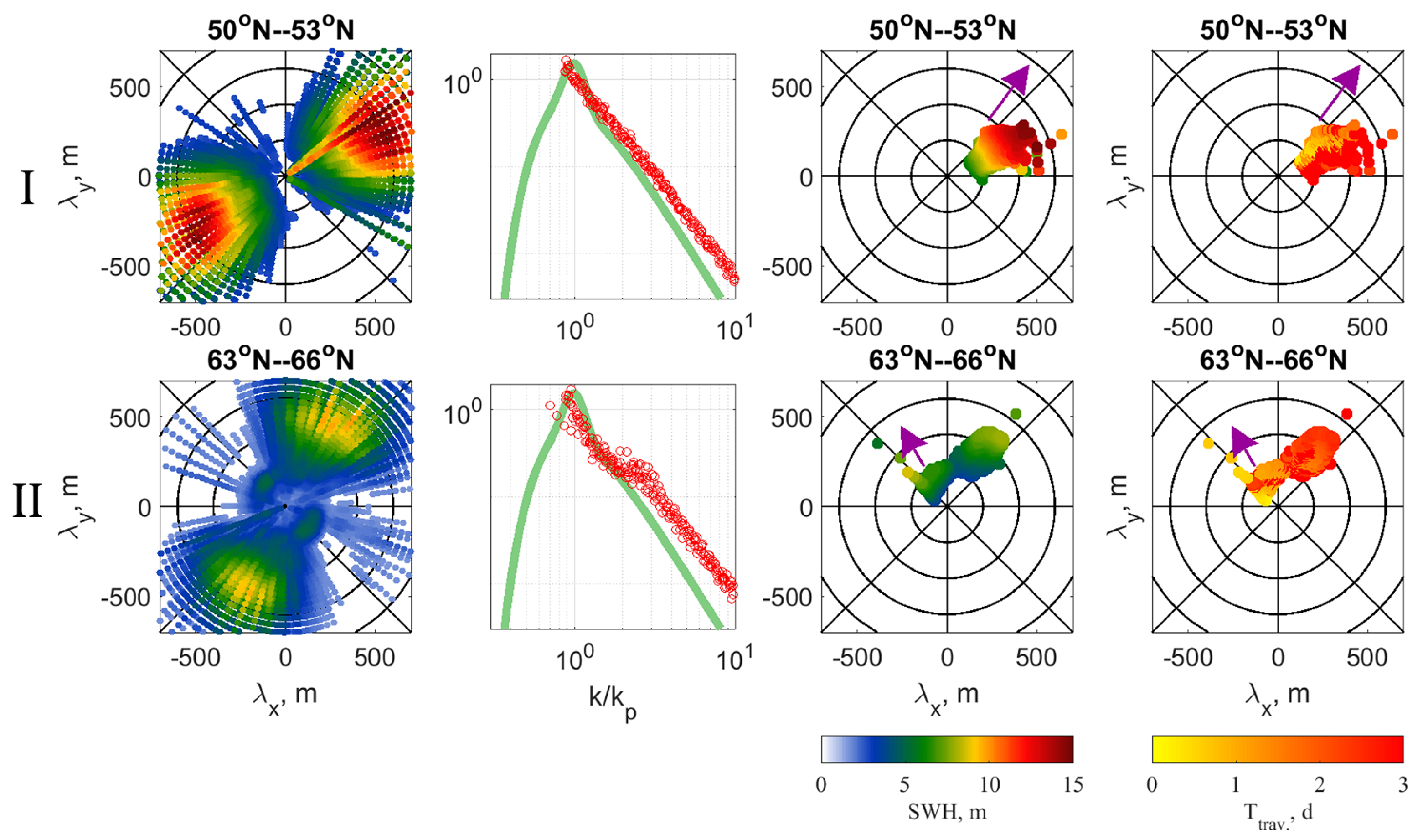
Figure 8 shows time evolution of the peak wavelength (SWIM data) and energy collected from all the altimeter tracks crossing the swell front traveling northeastward. The time countdown starts from 14-Feb-2020 9:00:00 - the end of the life of the ETC#2. Although the wavelength measurements by SWIM are very limited, they nevertheless demonstrate expected stationary behavior or slow growth, as predicted by the 2D model. In contrast, the energy of the swell at the front, measured by altimeters, decreases rather quickly. After 40 hours of travel (which is equivalent to a distance of about 2000 km), the energy drops by about 4 times. This observed energy decay is consistent with model simulations of the total wave energy, co-located with altimeter measurements (open circles), with maximal values at the part of swell front which moves east-north.
Red line in Figure 8 shows swell energy attenuation due to divergence of wave-rays which reads:
where is the initial value of cross-ray gradient of swell direction. Relationship (5) represents a straightforward solution of Equation (1), for which the effect of the energy source on swell evolution is ignored, with the swell wavelength kept constant. Full solution for swell energy and wavelength evolution due to effect of dissipation, non-linear waves interactions and wave-rays convergence/divergence can be found in [36,37]. Here we consider only the effect of wave-ray divergence, which seems to be the governing mechanism. Initial value of cross-ray gradient in Equation (5) can be evaluated as with the radius of the swell front curvature. The red curve shown Figure 8 corresponds to , which is about the radius of ETC#2. Observed attenuation of swell energy, , is remarkably faster than that predicted by effect of the swell energy dissipation [34]: , by non-linear wave-wave interactions [44]: , and that reported by [12] due to interaction of swell with the airflow.
Figure 8.
(a) Time evolution of swell energy: red circles are altimeter measurements, open circles are the model values at the point of the measurements, black curve shows maximal values of the model energy at the front. (b) Time evolution of swell wavelength: red point are SWIM measurements, black curve is the model.
Figure 8.
(a) Time evolution of swell energy: red circles are altimeter measurements, open circles are the model values at the point of the measurements, black curve shows maximal values of the model energy at the front. (b) Time evolution of swell wavelength: red point are SWIM measurements, black curve is the model.

4.2. Southward Swell
According to the wind fields, Figure 5, a strong wind jet formed along Greenland at a speed of about 35 ms−1. This wind jet results from the deformation of the frontal part of ETC#2. It provides a fetch length of about more than 1200 km for wave development for more than 12 hours. The waves, which were developing in the frontal part of the ETC#2, getting fully developed, reach phenomenal SWH and wavelength of 18 m and 600 m, respectively, and consequently further propagate as swell. Although, the wind field in the basin became quite complex, this wave front further radiated into the "open ocean" from Cape Farewell, clearly visible in Figure 5.
Some fragments illustrating the development of the wave system along the Greenland coast, leading to the formation of the radiated swell, are captured with SWIM measurements, shown in Figure 9. Model simulations of , and are consistent with these measurements, suggesting the model capability to realistically reproduce the wave development and swell evolution. Referring to Figure 5 and Figure 9, the swell front associated with and originated on 14-Feb-2020 21:00 at latitude of 56°N. The swell front then further moves southward achieving to 48°N on 15-Feb-2020 21:00 (see inverse wave age and wavelength plots on the fore-said dates on Figure 9).
A synthetic aperture radar (SAR) image in HH-polarization from Sentinel-1B acquired over Cape Farewell on 14-Feb-2020 evening, when the swell front is reaching the open ocean, is shown Figure 10a. To derive distributions of wavelength/direction of waves over this SAR scene, we apply Fast Fourier Transform (FFT) to each of the image boxes with size of pixels (Figure 10b,d), which were spread over the whole SAR image, to obtain a 2D wavenumber () image spectra; two examples are demonstrated in (Figure 10c,e). Spectral level of the SAR image can potentially be converted to the wave elevation spectrum, but this procedure is not straightforward, and we leave this issue out of the scope of this paper. Instead, focusing on wave kinematics, we consider only the SAR detected wavelength and direction. In order to remove ambiguity, we used wave direction from 2D model outputs.
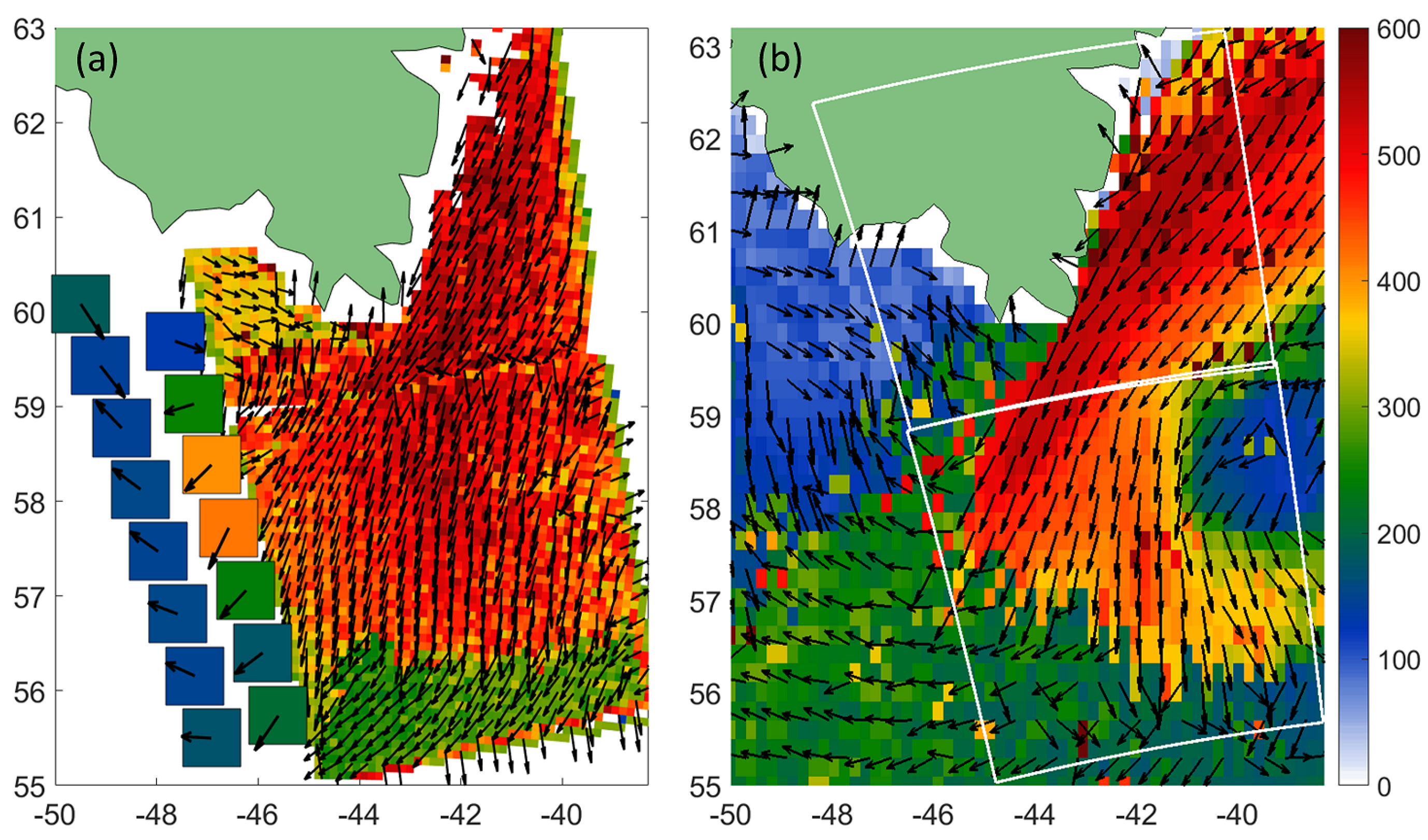
The resulting field of wavenumber vectors derived from the SAR image is shown in Figure 11a. This field exhibits spectacular swell front moving southward over which the wavelength rapidly changes from 500m to 250 m. In addition, the existence of the western boundary of the swell is confirmed by synchronous SWIM measurements shown in the same figure. Besides, SWIM measurements a day later, see Figure 9 bottom row, revealed the similar rapid drop of the spectral peak wavelength and SWH over this swell front, however already shifted southward. Model field of the swell front, Figure 11, is consistent, in general, with the measurements, providing similar change of wavelengths over the front and its location. However, the existence of an area filled with "shorter" waves in the eastern part of the model scene (coinciding with the low-wind speed area) is not confirmed by the measurements.
Figure 9.
The same as Figure 6, but when the CFOSAT-SWIM tracks cross southward radiating swell front.
Figure 9.
The same as Figure 6, but when the CFOSAT-SWIM tracks cross southward radiating swell front.
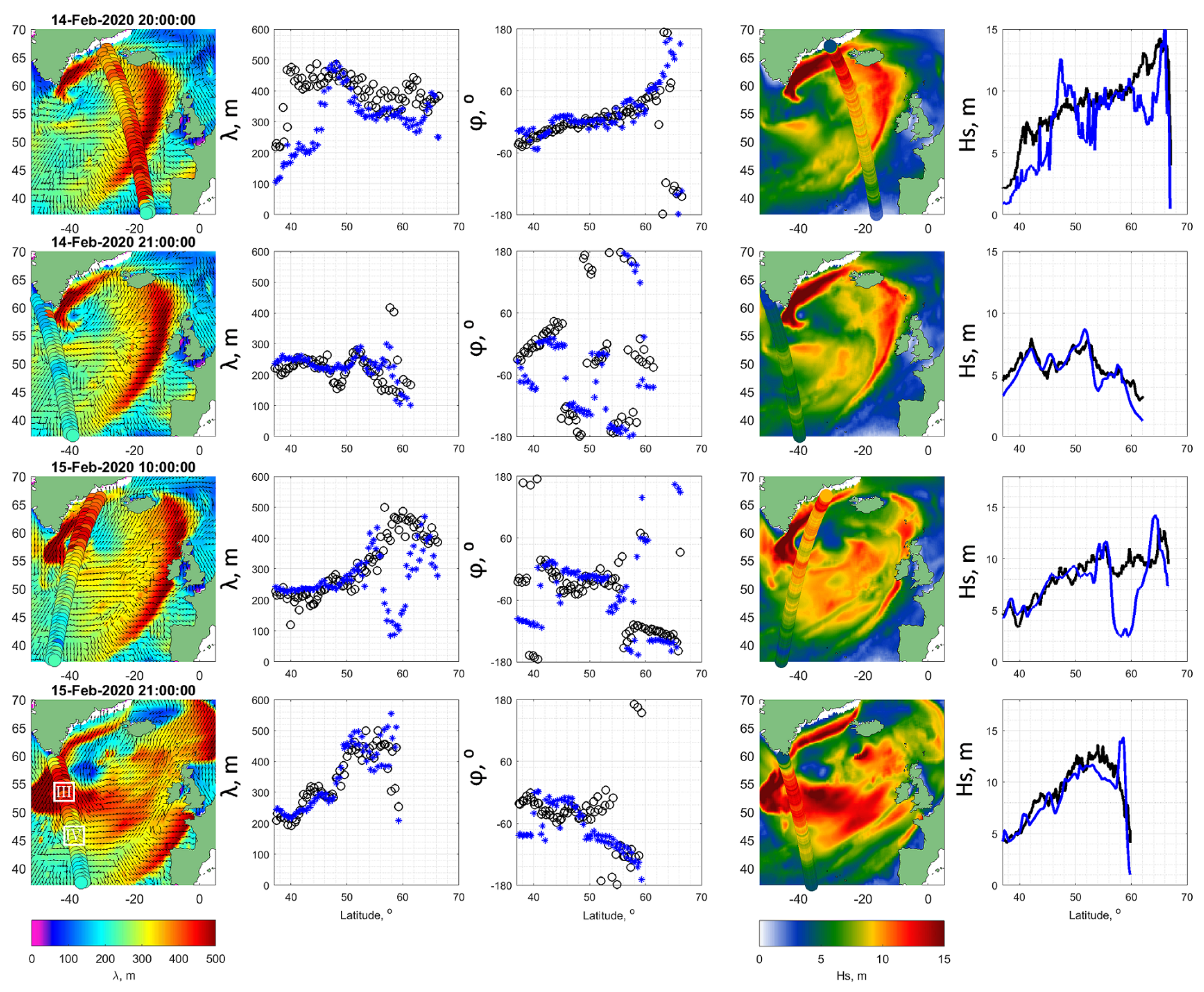
Figure 10.
(a) Sentinel-1B Synthetic Aperture Radar (SAR) image on HH polarization on 14-Feb-2020 evening of the south of Greenland. (b,d) zoom on SAR image for areas indicated by red and blue boxes in (a). (c,e) are the SAR image wavenumber (, ) spectra of (b,d) zooms.
Figure 10.
(a) Sentinel-1B Synthetic Aperture Radar (SAR) image on HH polarization on 14-Feb-2020 evening of the south of Greenland. (b,d) zoom on SAR image for areas indicated by red and blue boxes in (a). (c,e) are the SAR image wavenumber (, ) spectra of (b,d) zooms.
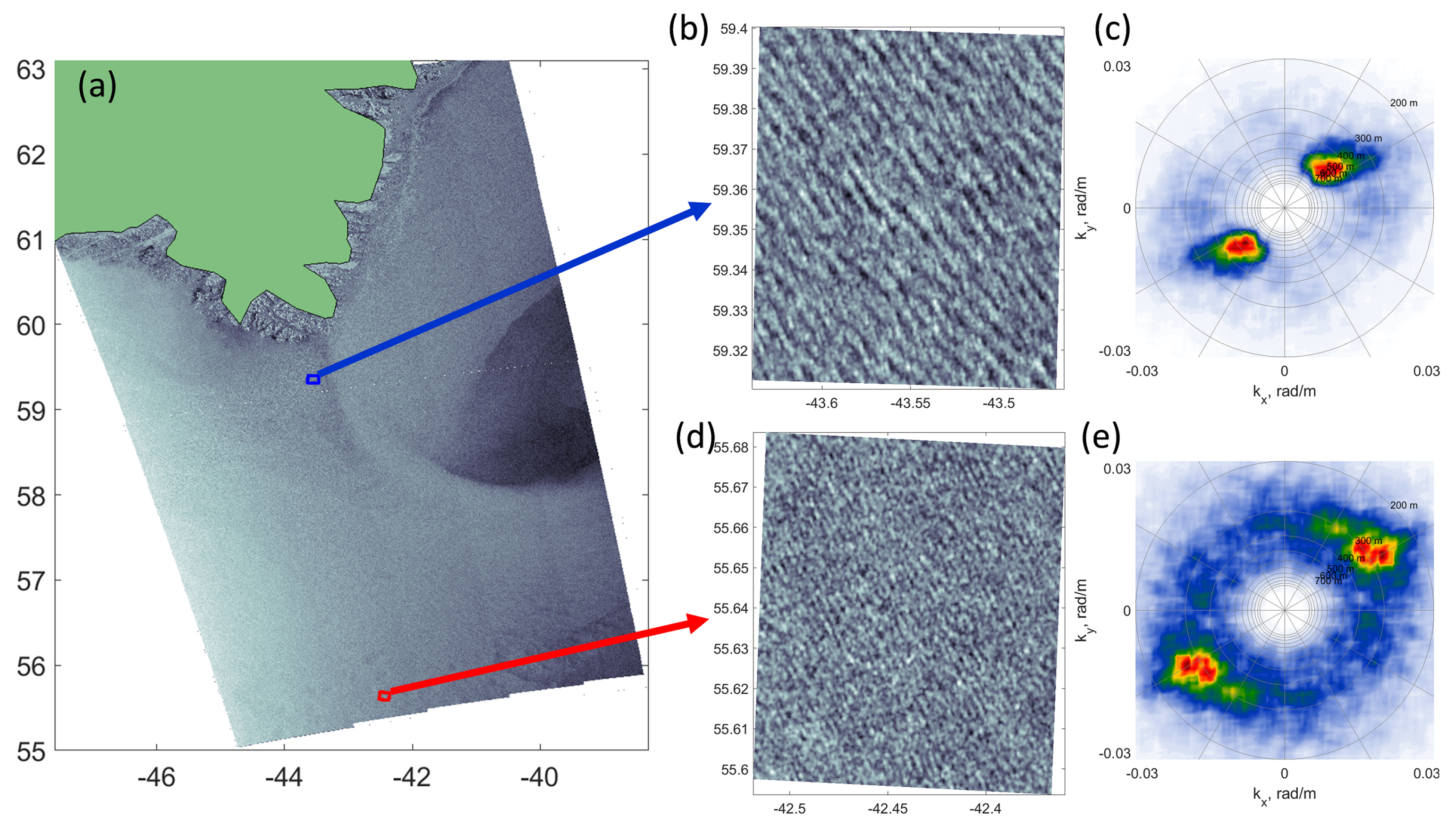
Figure 11.
(a) Spatial distributions of dominant wavelengths and directions derived from the SAR image shown in Figure 11a, with the SWIM off-nadir measurements of and . (b) The model fields of wavelength and directions of primary wave system; white lines indicate contour of SAR image.
Figure 11.
(a) Spatial distributions of dominant wavelengths and directions derived from the SAR image shown in Figure 11a, with the SWIM off-nadir measurements of and . (b) The model fields of wavelength and directions of primary wave system; white lines indicate contour of SAR image.
SWIM derived 2D wavenumber spectra on different side of the swell front (box III and box IV in Figure 9) are shown Figure 12. Spectrum inside the swell area displays the superposition of dominant swell system and system of shorter wind waves. Spectrum outside the swell front exhibits a wave system of remarkably shorter waves (as compared with swell in box III) with a wide angular spread. Similar to the case with east-north swell, the scaled omnidirectional spectra, , on different sides of the swell front are very similar and well consistent with the shape of the scaled JONSWAP spectrum, again confirming the experimental finding by [42,43] for waves in hurricanes. The histograms of distribution of the model energy of wave-trains over wavelength and directions shown in the third column, are also well consistent with 2D SWIM spectra. The travel time histogram (last column) gives the history of wave packets (wind driven and swell) forming a wave pattern at a given time and at a given point.
5. In Situ Data
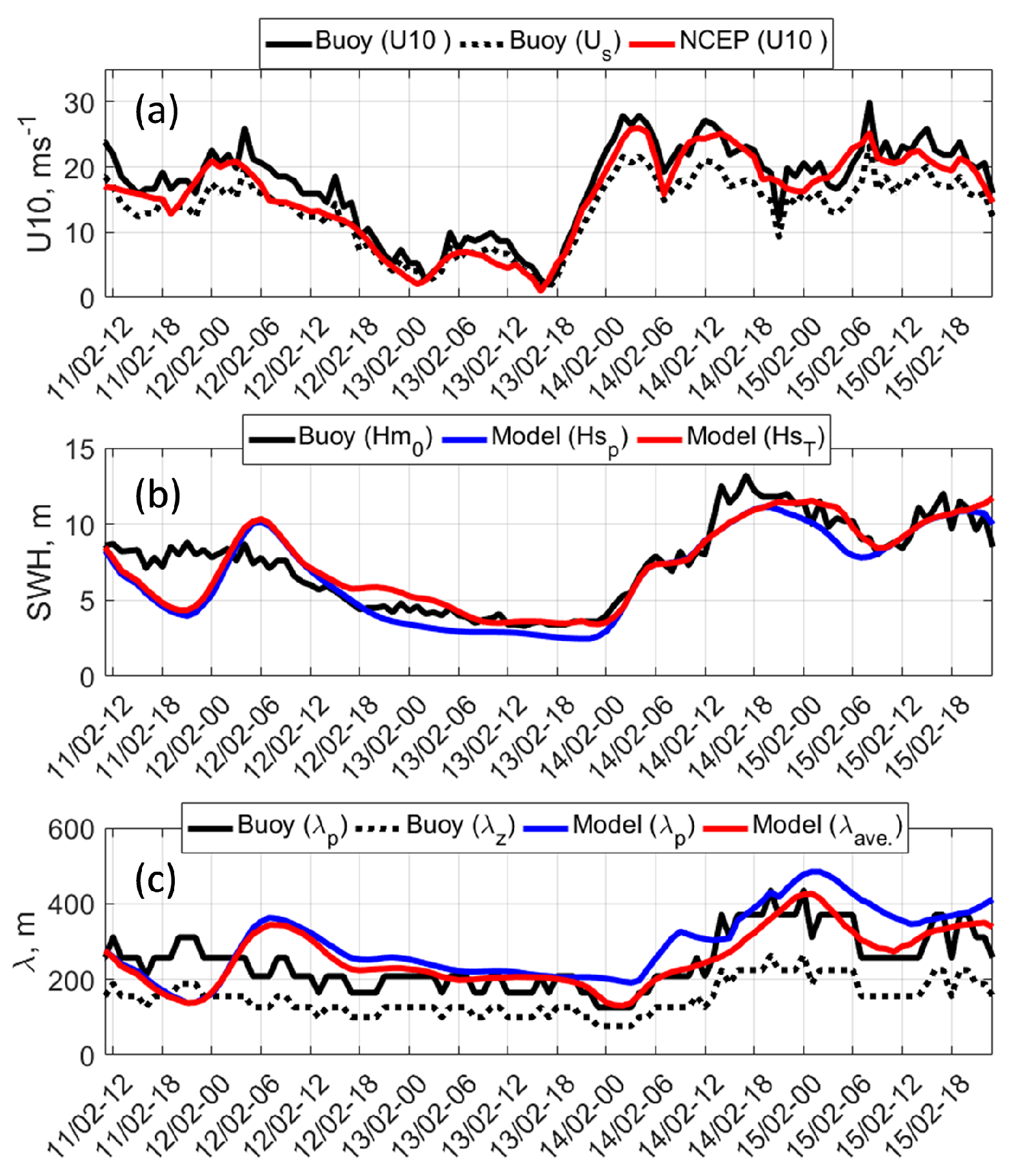
In situ buoy measurements complement the description of waves generated by ETCs, to perform additional validation of the proposed model. The hourly time series of wind speed at height 1m, significant wave height (SWH), and wave period (equal to average zero crossing period) measurements taken from the buoy "NO TS MO 6400045" located between Iceland and Ireland, on 11.4°W and 59.1°N for the period from 11-FebT12 to 15-FebT23, 2020 are shown in Figure 13. Note, to be consistent with SWIM data, we further use instead of which is calculated using the dispersion relation: . Very this quantity is shown in Figure 13 instead of . For additional comparison, the NCEP/CFSv2 10-m wind speed and model SWH and wave frequency (wavelength via the dispersion relation) at the buoy location are also plotted.
To compare in situ measurements with model estimates, the measured average zero crossing period of wave, (or equivalent frequency ), is converted to the spectral peak period (frequency, ). Following [45], is expressed through the spectral moments as:
where the is the moment of the wave elevation spectrum . As found, the shape of the observed wave spectra is very similar to the JONSAWAP spectrum [46], see Figure 7 and Figure 10. In this case, the link between and can be found by substituting the JONSWAP spectrum in (6), leading to: . Following this, an estimate of the spectral peak wavelength based on the buoy measurements of wave period (frequency ) is: .
Due to its location, the buoy should record the passage of ETC#2 generated waves from the North Atlantic to the subarctic seas, - similar to what follows from the model simulations in Animation 3. Following Figure 13a, a wind speed ms−1 was recorder on 14-FebT03 and 14-FebT12, that according to Animation 3 corresponded to the passage of the right section of ETC#2 through the buoy location. Going back in time from 14-FebT03, the wind speed increase began on 13-FebT16. However, the increase for SWH and wavelength occurred about 8 hours later. As the Animation 3 shows, the growth of SWH and on 14-FebT00 is associated with the swell front radiating out from the ETC#2, which resulted in maximal values observed between 14-FebT18 and 15-FebT06. According to the evolution of wave characteristics from 14-FebT00 to 15-FebT12, one may find that the swells produced by ETC#2 took 36 hours to pass the location of the buoy. Nevertheless, the high wind related to the ETC#2 passed the buoy location earlier (during 13-FebT18 and 14-FebT20) and in shorter time.
Buoy measurements of wave parameters thus well support satellite data and further confirm the model validity. The synergistic use of multi-sensor satellite and in situ measurements of wave parameters and modelling can thus provide a very detailed and consistent description of the wave field generated by fast moving cyclones both in the inner storm area and for radiating swell system to the far zone after the ETC passage and disparition.
Figure 13.
(a) Wind speed, (b) significant wave height, (c) wavelength at location of buoy "NO TS MO 6400045". The designation of the lines is given in the legends to the plots. Buoy-wavelength, , is derived from the measured wave period using the dispersion relation, and buoy-peak-wavelength is . Wind speed on 10-m height is derived from the measured wind speed (1-m height) using the logarithmic wind profile with . The animation, which shows the waves passing the buoy location can be found in Animation 3.
Figure 13.
(a) Wind speed, (b) significant wave height, (c) wavelength at location of buoy "NO TS MO 6400045". The designation of the lines is given in the legends to the plots. Buoy-wavelength, , is derived from the measured wave period using the dispersion relation, and buoy-peak-wavelength is . Wind speed on 10-m height is derived from the measured wind speed (1-m height) using the logarithmic wind profile with . The animation, which shows the waves passing the buoy location can be found in Animation 3.
6. Conclusions
With these two companion papers, we thoroughly investigated main characteristics of phenomenal sea state generated by fast-moving ETCs in the North Atlantic. We demonstrate that a suite of data from different sources —a combination that may not be typical in forecasting environments—can give a remarkably coherent characterization of an extreme storm event and associated wave fields. The present study indeed combine multi-satellite and in situ observations, with simplified 1D and 2D parametric models which conceptually follow self-similarity principles to quantify wave developments.
Simulations were performed to describe the spatio-temporal evolution of surface wave fields in the North Atlantic, spanning 7 days from 9 00:00 UTC to 15 23:00 UTC, February, 2020. In total, 130 altimeters tracks crossed the computational domain during this period. Rather high level of correlation between model and measured SWH (correlation coefficient is about 0.87) are found, justifying the use of the proposed simplified model framework to describe wave properties generated by ETCs.
The selected ETCs were fast-moving storms, for which the resonance (synchronism) between group velocities of generated waves and the ETC translation velocity was impossible. Satellite observations and model simulations confirms that the ETC storm areas are indeed filled with wind developing waves, with wave generation starting when the front-boundary of the storm crosses a given location in the ocean.
In the course of their development, wind waves move backward relative to the storm, and grow in time under the strong wind forcing. Waves then attain maximal development (maximal values of SWH up to 18m and wavelength up to 500m) in the rear-right ETC sectors. Spatial distributions of observed and simulated wave fields in the inner storm area of ETC are thus remarkably different from those generally associated to a TC, where waves are usually enhanced in the right-front sector.
The fast-moving nature of the ETCs further leads to the formation of swell systems, generated from the rear-right sector and trailing behind the ETC. At the precise time the ETC#2 ceases, the swell SWH and its wavelength attained abnormal phenomenal values of 17m and 450m, respectively. This swell front then propagated over the eastern part of the North Atlantic and the Norwegian sea. Satellite observations of the evolution of this swell front (during 40 hours or at a distance of about 2000 km) confirmed that the swell wavelength remained practically unchanged, while the swell SWH attenuated gradually with the distance. Waves thus closely follow principles of geometrical optics, with a constant wave period along geodesics, when following a wave packet at the group speed ([14,16]. Yet, close to their source point, initially steep swell systems rapidly attenuate. Observed estimates of the swell energy attenuation are found proportional to the inverse travel distance. Such a decay remarkably exceeds model estimates predicted by the wave energy dissipation and/or non-linear wave-wave interactions mechanisms. This non-linear behavior may possibly be postulated to trace the transition from a laminar to a turbulent air-side boundary layer ([12]. However, in the present study, observed attenuation of swell energy appear more consistently explained by the effect of wave-ray divergence caused by the initial curvature of the swell front [47].
Another spectacular wave field feature related to ETC#2 (more precisely when it ceases), is the generation of abnormally high waves in the Greenland coastal region. These waves are caused by the ETC#2 transformation to become an along coastal wind jet. This jet occurred as a part of a newly formed Icelandic lows, following the end of ETC#2. According to the satellite observations and model results, sea state parameters in this local high-wind-speed region also reached very high values: SWH of 18m and wavelength of about 600m.
At the southern tip of Greenland (Cape Farewell), these huge waves turned into a swell system that moved southward to the open ocean. Satellite measurements and model simulations captured the swell front and its southward motion, also displaying large wavelength changes over the swell front, i.e. from 600m to 250m.
We are certainly encouraged by these results reporting our ability to both model and observe extreme wave events. The proposed analysis framework shall now provide an improved understanding of spatio-temporal storm characteristics for extra-tropical swell systems, and may not only help to identify biases in swell forecast models, but also help improve air-sea fluxes, and upper-ocean mixing estimations.
Funding
The core support for this work was provided by the Russian Science Foundation through Project No. 21-47-00038. The support of the Ministry of Science and Education of the Russian Federation under State Assignment No. FNNN-2021-0004 at MHI RAS and State Assignment No. 0763-2020-0005 at RSHU is gratefully acknowledged. We also acknowledge the ESA MAXSS Project 4000132954/20/I-NB.
Data Availability Statement
The data supporting reported results are extracted as following: Sentinel-3A and B https://finder.creodias.eu; AltiKa and JASON-3 and SWIM l2 products https://aviso-data-center.cnes.fr; CryoSat-2 ftp://science-pds.cryosat.esa.int; SWIM l2s products ftp://ftp.ifremer.fr/ifremer/cersat/projects/iwwoc; NCEP/CFSv2 https://rda.ucar.edu/datasets/ds094.1/dataaccess; Sentinel-1B SAR images https://sentinel.esa.int/web/sentinel/user-guides/sentinel-1-sar; observations at buoy "NO TS MO 6400045" https://data.marine.copernicus.eu/products; ice consentrarion https://seaice.uni-bremen.de/. The model results are presented on Animation 1 and Animation 2.
Acknowledgments
CFOSAT-SWIM measurements were provided by IFREMER Wind and Wave operational Center (IWWOC), co-funded by CNES and IFREMER. NCEP/CFSv2 data provided by the OAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at NCEP/CFSv2 website.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1D 2D 3D | One, two and three Dimensional |
| SWH | Significant Wave Height |
| Hs | Height of Significant Wave |
| ETC | Extra-Tropical Cyclone |
| CFOSAT | Chinese-French Oceanographic Satellite |
| SWIM | Surface Wave Exploration and Monitoring |
| NCEP | National Centers for Environmental Prediction |
| CFSv2 | Climate Forecast System Version 2 |
| IFREMER | Institut Français de Recherche pour l’Exploitation de la Mer, |
| French Research Institute for Exploitation of the Sea | |
| JONSWAP | Joint North Sea Wave Project |
| SAR | Synthetic Aperture Radar |
| FFT | Fast Fourier Transformation |
| NBI | Normalized Bias |
References
- Hewson, T.D.; Neu, U. Cyclones, windstorms and the IMILAST project. Tellus A: Dynamic Meteorology and Oceanography 2015, 67, 27128. [CrossRef]
- Ponce de León, S.; Bettencourt, J. Composite analysis of North Atlantic extra-tropical cyclone waves from satellite altimetry observations. Advances in Space Research 2021, 68, 762–772. [CrossRef]
- Hanafin, J.A.; Quilfen, Y.; Ardhuin, F.; Sienkiewicz, J.; Queffeulou, P.; Obrebski, M.; Chapron, B.; Reul, N.; Collard, F.; Corman, D.; de Azevedo, E.B.; Vandemark, D.; Stutzmann, E. Phenomenal Sea States and Swell from a North Atlantic Storm in February 2011: A Comprehensive Analysis. Bulletin of the American Meteorological Society 2012, 93, 1825–1832. [CrossRef]
- de León, S.P.; Soares, C.G. Extreme wave parameters under North Atlantic extratropical cyclones. Ocean Modelling 2014, 81, 78–88. [CrossRef]
- Kita, Y.; Waseda, T.; Webb, A. Development of waves under explosive cyclones in the Northwestern Pacific. Ocean Dynamics 2018, 68, 1403–1418. [CrossRef]
- Hell, M.C.; Ayet, A.; Chapron, B. Swell Generation Under Extra-Tropical Storms. Journal of Geophysical Research: Oceans 2021, 126. [CrossRef]
- Enríquez, A.R.; Marcos, M.; Álvarez-Ellacuría, A.; Orfila, A.; Gomis, D. Changes in beach shoreline due to sea level rise and waves under climate change scenarios: application to the Balearic Islands (western Mediterranean). Natural Hazards and Earth System Sciences 2017, 17, 1075–1089. [CrossRef]
- Ferreira, Ó. Storm groups versus extreme single storms: predicted erosion and management consequences. Journal of Coastal Research 2005, pp. 221–227.
- Hunt, I.A. Design of Sea-Walls and Breakwaters. Transactions of the American Society of Civil Engineers 1961, 126, 542–570. [CrossRef]
- Morison, M.L.; Imberger, J. Water-Level Oscillations in Esperance Harbour. Journal of Waterway, Port, Coastal, and Ocean Engineering 1992, 118, 352–367. [CrossRef]
- Russell, P.E. Mechanisms for beach erosion during storms. Continental Shelf Research 1993, 13, 1243–1265. [CrossRef]
- Ardhuin, F.; Chapron, B.; Collard, F. Observation of swell dissipation across oceans. Geophysical Research Letters 2009, 36. [CrossRef]
- Munk, W.; Snodgrass, F. Measurements of southern swell at Guadalupe Island. Deep Sea Research (1953) 1957, 4, 272–286. [CrossRef]
- Snodgrass, F.E.; Hasselmann, K.F.; Miller, G.R.; Munk, W.H.; Powers, W.H.; Deacon, G.E.R. Propagation of ocean swell across the Pacific. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 1966, 259, 431–497, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.1966.0022]. [CrossRef]
- Chapron, B.; Johnsen, H.; Garello, R. Wave and wind retrieval from sar images of the ocean. Annales Des Télécommunications 2001, 56, 682–699. [CrossRef]
- Collard, F.; Ardhuin, F.; Chapron, B. Monitoring and analysis of ocean swell fields from space: New methods for routine observations. Journal of Geophysical Research: Oceans 2009, 114, [https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/2008JC005215]. [CrossRef]
- Hauser, D.; Tourain, C.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; et al. New Observations From the SWIM Radar On-Board CFOSAT: Instrument Validation and Ocean Wave Measurement Assessment. IEEE Transactions on Geoscience and Remote Sensing 2021, 59, 5–26. [CrossRef]
- Aouf, L.; Wang, J.; Hauser, D.; Chapron, B.; Tourain, C. On the Assimilation of Wide Swath Significant Wave Height and Directional Wave Observations in Wave Model : Perspective for Operational Use. IGARSS 2022 - 2022 IEEE International Geoscience and Remote Sensing Symposium, 2022, pp. 6772–6774. [CrossRef]
- Tolman, H.L.; others. User manual and system documentation of WAVEWATCH III TM version 3.14. Technical note, MMAB Contribution 2009, 276.
- Group, T.W. The WAM Model—A Third Generation Ocean Wave Prediction Model. Journal of Physical Oceanography 1988, 18, 1775–1810. [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. Journal of Geophysical Research: Oceans 1999, 104, 7649–7666. [CrossRef]
- Kalourazi, M.Y.; Siadatmousavi, S.M.; Yeganeh-Bakhtiary, A.; Jose, F. WAVEWATCH-III source terms evaluation for optimizing hurricane wave modeling: A case study of Hurricane Ivan. Oceanologia 2021, 63, 194–213. [CrossRef]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press, 1994. [CrossRef]
- Durrant, T.H.; Greenslade, D.J.; Simmonds, I. The effect of statistical wind corrections on global wave forecasts. Ocean Modelling 2013, 70, 116–131. [CrossRef]
- Feng, H.; Vandemark, D.; Quilfen, Y.; Chapron, B.; Beckley, B. Assessment of wind-forcing impact on a global wind-wave model using the TOPEX altimeter. Ocean Engineering 2006, 33, 1431–1461. [CrossRef]
- Janssen, P.A.; Bidlot, J.R. Progress in Operational Wave Forecasting. Procedia IUTAM 2018, 26, 14–29. [CrossRef]
- Ponce, S.; Ocampo-Torres, F.J. Sensitivity of a wave model to wind variability. Journal of Geophysical Research: Oceans 1998, 103, 3179–3201. [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Modelling 2014, 75, 65–83. [CrossRef]
- Abdolali, A.; Roland, A.; van der Westhuysen, A.; Meixner, J.; Chawla, A.; Hesser, T.J.; Smith, J.M.; Sikiric, M.D. Large-scale hurricane modeling using domain decomposition parallelization and implicit scheme implemented in WAVEWATCH III wave model. Coastal Engineering 2020, 157, 103656. [CrossRef]
- Babanin, A.V.; Rogers, W.E.; de Camargo, R.; Doble, M.; Durrant, T.; Filchuk, K.; Ewans, K.; Hemer, M.; Janssen, T.; Kelly-Gerreyn, B.; et al. Waves and Swells in High Wind and Extreme Fetches, Measurements in the Southern Ocean. Frontiers in Marine Science 2019, 6. [CrossRef]
- Hasselmann, K.; Sell, W.; Ross, D.B.; Müller, P. A Parametric Wave Prediction Model. Journal of Physical Oceanography 1976, 6, 200–228. [CrossRef]
- Gunther, H.; Rosenthal, W.; Weare, T.J.; Worthington, B.A.; Hasselmann, K.; Ewing, J.A. A hybrid parametrical wave prediction model. Journal of Geophysical Research 1979, 84, 5727. [CrossRef]
- Kitaigorodskii, S. Application of the theory of similarity to the analysis of wind-generated wave motion as a stochastic process. Izv., Geophys. Ser. Acad. Sci., USSR 1962, 1, 105–117.
- Kudryavtsev, V.; Yurovskaya, M.; Chapron, B. 2D Parametric Model for Surface Wave Development Under Varying Wind Field in Space and Time. Journal of Geophysical Research: Oceans 2021, 126. [CrossRef]
- Kudryavtsev, V.; Yurovskaya, M.; Chapron, B. Self-Similarity of Surface Wave Developments Under Tropical Cyclones. Journal of Geophysical Research: Oceans 2021, 126. [CrossRef]
- Yurovskaya, M.; Kudryavtsev, V.; Mironov, A.; Mouche, A.; Collard, F.; Chapron, B. Surface Wave Developments under Tropical Cyclone Goni (2020): Multi-Satellite Observations and Parametric Model Comparisons. Remote Sensing 2022, 14, 2032. [CrossRef]
- Yurovskaya, M.; Kudryavtsev, V.; Chapron, B. A self-similar description of the wave fields generated by tropical cyclones. Ocean Modelling 2023, 183, 102184. [CrossRef]
- Kudryavtsev, V.; Cheshm Siyahi, V.; Yurovskaya, M.; Chapron, B. On Surface Waves in Arctic Seas. Boundary-Layer Meteorology 2022. [CrossRef]
- Cheshm Siyahi, V.; Kudryavtsev, V.; Yurovskaya, M.; Collard, F.; Chapron, B. On Surface Waves Generated By Extra-Tropical Cyclones. Part I: Multi-Satellite Measurements. Remote Sens. 2023.
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. NCEP Climate Forecast System Version 2 (CFSv2) Selected Hourly Time-Series Products, 2011. [CrossRef]
- Donelan, M.A.; Hamilton, J.; Hui, W.H.; Stewart, R.W. Directional spectra of wind-generated ocean waves. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 1985, 315, 509–562, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.1985.0054]. [CrossRef]
- Young, I.R. Directional spectra of hurricane wind waves. Journal of Geophysical Research 2006, 111. [CrossRef]
- Le Merle, E.; Hauser, D.; Yang, C. Wave Field Properties in Tropical Cyclones From the Spectral Observation of the CFOSAT/SWIM Spaceborne Instrument. Journal of Geophysical Research: Oceans 2023, 128. [CrossRef]
- Badulin, S.I.; Zakharov, V.E. Ocean swell within the kinetic equation for water waves. Nonlinear Processes in Geophysics 2017, 24, 237–253. [CrossRef]
- Cartwright, D.E.; Longuet-Higgins, M.S. The statistical distribution of the maxima of a random function. Proceedings of the royal society of london. series a. mathematical and physical sciences 1956, 237, 212–232.
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.; Gienapp, A.; Hasselmann, D.; Kruseman, P.; others. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft zur Deutschen Hydrographischen Zeitschrift, Reihe A 1973.
- Delpey, M.T.; Ardhuin, F.; Collard, F.; Chapron, B. Space-time structure of long ocean swell fields. Journal of Geophysical Research: Oceans 2010, 115, [https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/2009JC005885]. [CrossRef]
Figure 1.
Comparison of measured and modeled vs (a), (b) and (c) with normalized bias (NBI), normalized root-mean-square error (HH) and correlation coefficient (R).
Figure 1.
Comparison of measured and modeled vs (a), (b) and (c) with normalized bias (NBI), normalized root-mean-square error (HH) and correlation coefficient (R).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated