Prerpints.org logo
Preprint
Article

On Surface Waves Generated By Extra-Tropical Cyclones. Part I: Multi-Satellite Measurements

Altmetrics

Downloads

130

Views

65

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 March 2023

Posted:

15 March 2023

You are already at the latest version

Alerts
Abstract
Surface waves generated by Extra-Tropical Cyclones (ETCs) can significantly affect shipping, fishing, offshore oil and gas production and other marine activities. This paper presents results of satellite-data-based investigation of wind waves generated by two North Atlantic ETCs. These ETCs were fast-moving systems, inhibiting resonance (synchronism) between the group velocity of the generated waves and the ETC translation velocity. For these cases, the wave generation begins when the front-boundary of the storm appears at a given ocean location point. Since developing waves are slow, they move backward relative to the storm, grow in time, and then leave the ETC stormy area through the rear sector. Multi-satellite observations confirm such a paradigm, and reveal that the storm regions is filled up with young developing wind waves which are most developed in the rear-right sector. As observed, the energy of these waves was growing in time during the ETC life span. It is demonstrated that the extended-fetch concept (inherent for Tropical Cyclones) does not apply for ETC. Instead, by analogy, the concept of extended-duration wave growth concept is more relevant. Satellite observations well confirm the validity of duration-laws for waves generated by ETCs, and demonstrate that extended-fetch regime for observing waves can only asymptotically be achieved, - at time intervals exceeding the lifespan of considered ETCs.
Keywords: 
Subject: Environmental and Earth Sciences  -   Oceanography

1. Introduction

In the North Atlantic, there are more than 10 extra-tropical cyclones (ETCs) every year with hurricane-force winds (e.g., [1]). ETCs and the ocean surface waves they generate can then significantly affect shipping, fishing, offshore oil and gas production and other marine activities. Estimating the probability of occurrence of high surface waves is one of the most important factors to be considered in the design of offshore and onshore infra-structures. Caused by these storm events, wave heights can become catastrophically high, with heights exceeding 20 m [1,2,3]. As argued in [4,5,6], the highest waves on the planet Earth are generally found in the northeast Atlantic, making this region particularly interesting for investigation of extreme waves and conditions of their generation.
ETCs are synoptic scale atmospheric system in the mid-latitudes that have a basin-wide impact on the weather and climate of the North Atlantic. The North Atlantic Ocean is regularly traversed by ETCs and winter low pressure systems originated in the Western part of the basin that can potentially generate dangerous extreme sea states [7,8,9]. The region where these extreme sea states occur is linked to the tracks of the low pressure systems in the North Atlantic basin. The variability of this storm tracks presents a primary dipole pattern, with centres in the extreme northeastern Atlantic and west of Portugal. A strong north-eastward extension of the storm tracks causes strong maritime flow, giving rise to mild European winters [10]. Indeed, in the North Atlantic, very high waves are to be found in the storm track region of the basin [11,12] and the west coast of Europe is regularly exposed to huge swells generated by the North Atlantic cyclones that cross the basin from west to east, with significant socio-economic consequences and increased coastal vulnerability [13,14].
In the absence of in situ measurements, satellite observations are the most robust and reliable sources for monitoring and forecasting of extreme wind/wave, taking advantage of their availability, regularity, bandwidth, and improved spatial resolution. Nowadays, large multi-mission databases of surface wind and significant wave height (SWH) from altimetry are available to study ocean wind, wave properties and climate [15]. Although satellite altimetry suffers from incomplete temporal and spatial coverage, the amount of available data from successive satellite passes enables the calculation of wind and SWH distributions and allows estimating climatological fields, trends, and extreme values prediction [4,16]. In addition to existing satellite capabilities for monitoring extreme events, the CFOSAT (Chinese-French Oceanographic Satellite) mission, launched in 2018, can now simultaneously provide the ocean surface wind field and 2D spectral wave distributions. CFOSAT does carries SCAT, a Ku-band wind field scatterometer, and a unique SWIM (Surface Wave Investigation and Monitoring) Real Aperture Scanning Radar System designed for directional detection of ocean surface waves [17,18].
Wave fields generated by moving atmospheric systems (tropical cyclones (TC), ETCs and polar lows (PL)) have a number of unique features that make them very different from waves generated by stationary wind fields. In general, these features originate from the fact that wave generation permanently occurs under a moving wind field. As a result, developing waves under moving storm with a given spatial scale of wind field (i.e., cyclone radius), stay under wind forcing for a longer time than in a stationary one and thus, become more developed (higher). When the evolving group velocity of the developing waves starts to match the translation velocity of the storm, the waves remain under the wind forcing for an “infinitely” long time. Resulting wave heights and wavelengths can thus take on anomalous values, significantly exceeding the expected values prescribed by the given wind speed and the size of the storm area. This phenomenon is called extended (effective) fetch or group velocity resonance. It is inherent for the waves generated by moving TC [19,20,21,22,23,24,25,26] and PL [27,28,29]. The importance of this mechanism for the waves generated by ETCs was argued in [30] and also found in numerical simulations using WAM [31] and WW3 [32] models. Satellite observations of SWHs generated by ETC over the global ocean also revealed a clear dependence with wind speed and translation velocity of ETCs [33].
The goal of this paper is to present a detailed description of the sea state features in the storm area of two cyclones traveling over the North Atlantic. This investigation is motivated by the present-day enhanced satellite coverage offered by multiple altimeter and CFOSAT-SWIM measurements. For the data analysis, we apply a classical approach based on the theory of self-similarity of wave development, supplemented by the extended fetch/duration concept (see e.g., [24,25,29] and references cited therein). This approach is now commonly used to describe the waves generated by TC and PL, and is extended here for ETC cases.
The paper is organized as the following.
  • Description on two ETCs in North Atlantic selected for present study is represented in Section 2.1.
  • Section 2.2 introduced the satellite data used for investigation of surface waves generated by ETCs.
  • Description of profiles of SWHs and the spectral peak parameters (wavelength, direction and steepness) across the storm area of ETCs presented in Section 3.1.
  • Spatial distributions of the surface wave parameters inside the ETCs storm area and their evolution in time are analyzed in Section 3.2 and Section 3.3) respectively.
  • Interpretation of satellite measurements of waves inside the ETC storm area within the frame of extended fetch and duration of wave growth is given in Section 4.
  • Section 5 provides summary of the results.

2. Materials and Methods

In this section, we introduce two Extra-tropical cyclones (ETCs) traveling over the North Atlantic in the period from February 11th to February 15th, 2020, and satellite measurements of surface waves generated by these ETCs.
Data on significant wave heights (SWH) of surface waves were obtained from measurements by satellite altimeters Sentinel-3A, Sentinel-3B, AltiKa, CryoSat-2 and JASON-3. In addition, more wave data, namely, SWH, spectral peak parameters, and wave spectra, were obtained from China-France Ocean Satellite for Surface Wave Investigation and Monitoring (CFOSAT-SWIM).
The hourly fields of wind velocity at a height of 10 meters above the sea surface and the surface pressure taken from the National Centers for Environmental Prediction Climate Forecast System version 2 [34] (hereinafter NCEP/CFSv2), were used to identify and trace the selected ETCs and to analyze the surface wave field. The links to publicly archived datasets are available in the Table 1.

2.1. Extra-tropical Cyclone Case

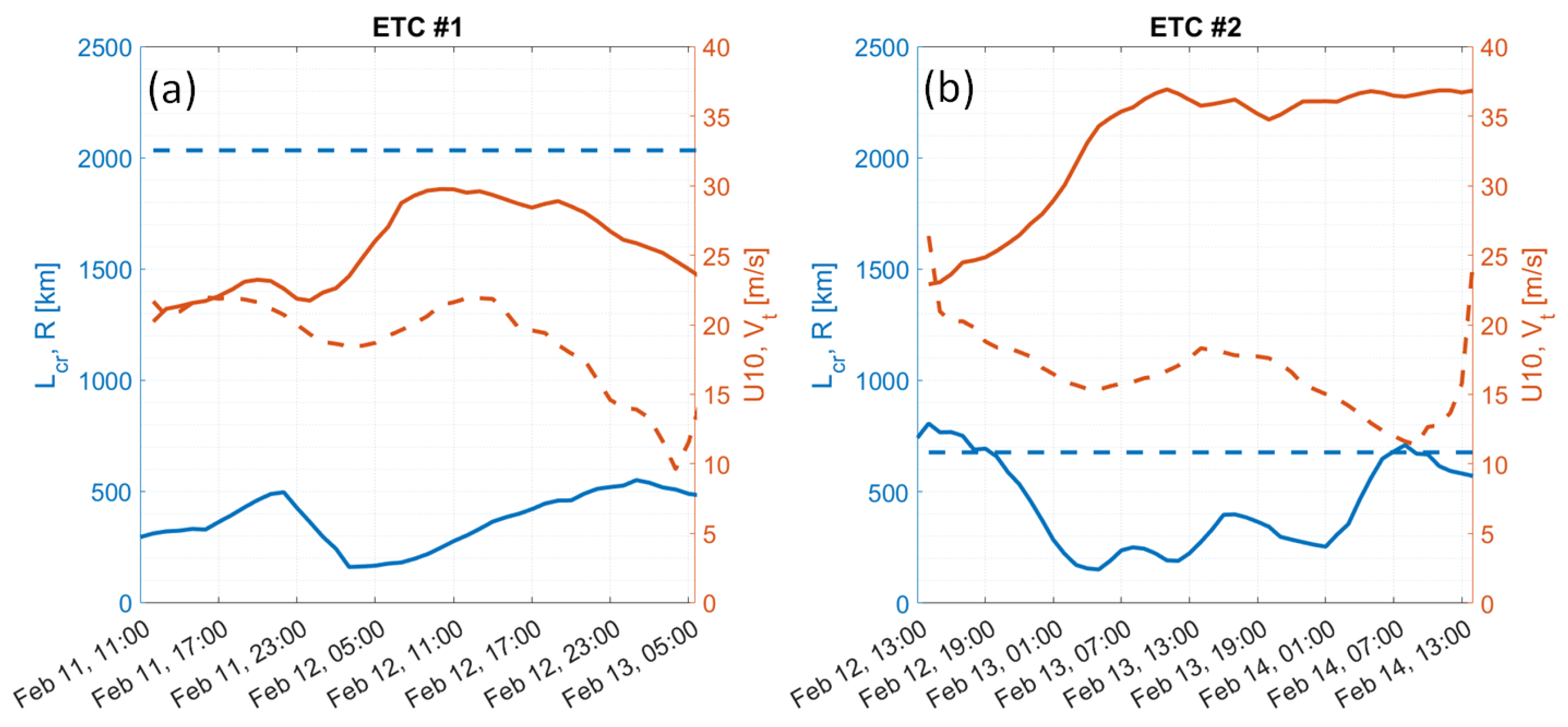
Based on the NCEP/CFSv2 hourly wind fields and surface pressure maps, two ETCs were identified moving simultaneously over the North Atlantic between February 11th , 2020 and February 15th , 2020, Figure 1 The first ETC (ETC#1) appeared on the morning of February 11th 2020, in the west of the basin at 48 degrees north latitude, and then moved east until it reached the coast of Ireland on the morning of 13-Feb-2020. The second ETC (ETC#2) also appeared in the west of the basin at 46N, but a little later, at noon 12-Feb-2020. Unlike the ETC#1, its movement was directed to the northeast, and when it reached 60 degrees north latitude at noon on 14-Feb-2020, ETC#2 lost shape and turned into an “air stream” along the southeast coast of Greenland and, in eventually, continued to exist as the Icelandic low, Figure 1.
Coordinates of the minimum surface pressure were used to derive the centre of ETCs, their trajectories, and then the translation velocities. The maximal value of wind speed in the vicinity of the ETC center, u m , and the distance from the location of u m to the center, R m , called by analogy with Tropical Cyclones (TC) the maximum wind speed radius, are considered as the main ETC parameters, characterizing its evolution. The ETC storm area is thus defined as the inner area around the ETC center where wind speed exceed a given (threshold) value, which was empirically chosen as m a x ( 0.45 u m , 12 m s − 1 ) .
The time evolution of u m , R m , and V t , for ETC#1 and ETC#2 are shown in Figure 2a,b, respectively. The ETC#1 moves with average translation velocity, V ¯ t , equal to 19 ms−1. At the initial stage of the ETC#1 evolution, u m and R m are 20 ms−1 and 300 km, respectively. The largest values of u m and R m during its life span are ∼ 31 ms−1 and 500 km, respectively, Figure 2a. The ETC#2 moves, with V ¯ t , equal to 17 ms−1. The maximum values of u m and R m during its life span are ∼ 40 ms−1 and 700 km, Figure 2b.

2.2. Measurements of Wave Parameters

2.2.1. Significant Wave Height

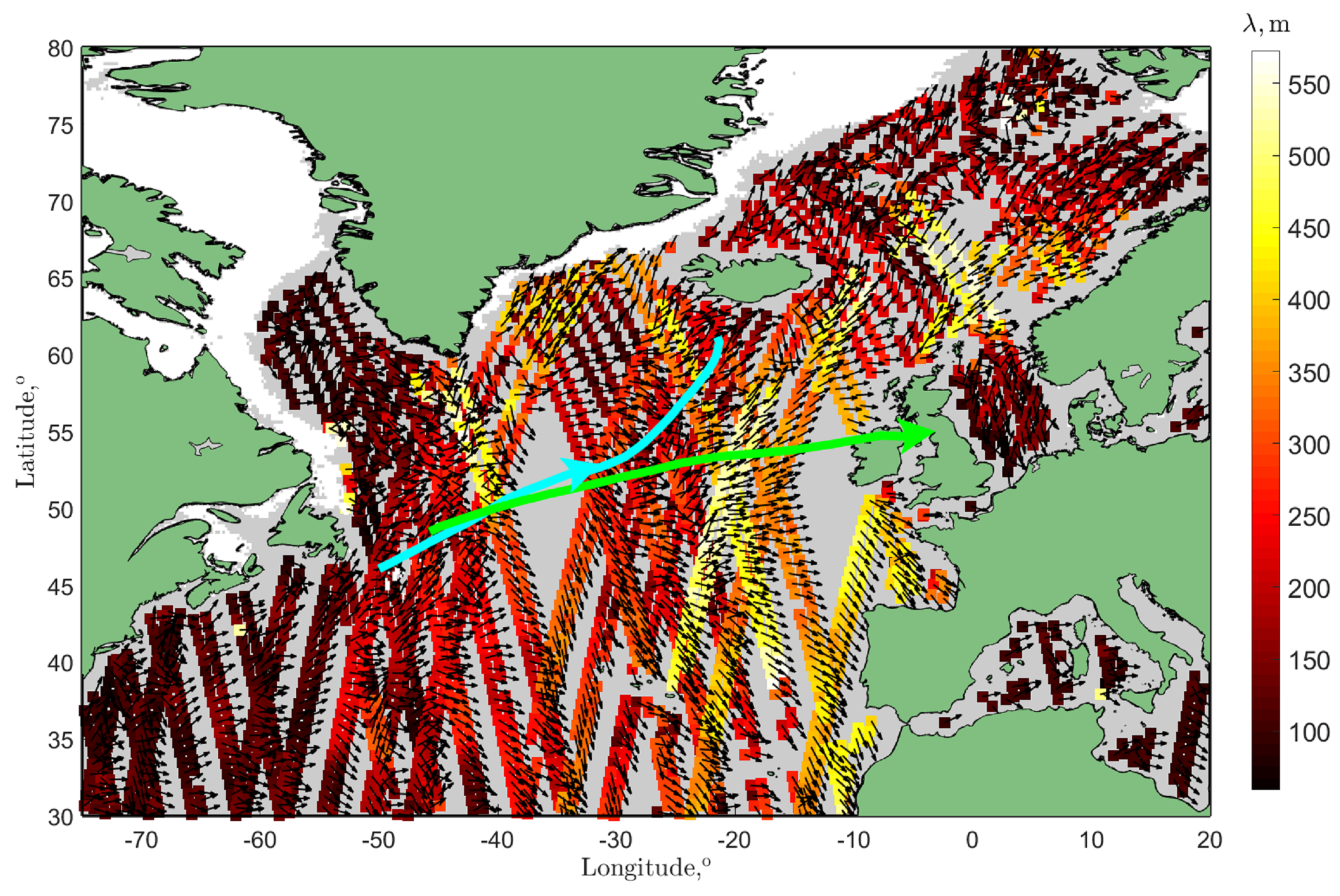
The measurements of significant wave height, SWH, products from different satellites shown in Figure 3. The SWH data, used in this study, includes level 2 altimeter 1 Hz observations of Sentinel-3A, Sentinel-3B, Jason-3, CryoSat-2, AltiKa and nadir nsec products of CFOSAT-SWIM, illustrated in Figure 3, with trajectories of ETCs. To show the SWH values, the land/ice mask and data quality flags are applied. Referring to Figure 3 one may find that the highest waves with SWH > 10 m are observed around the ETCs tracks crossing the northern Atlantic Ocean. To analyse the SWH of waves generated by ETCs in more details, the altimeter tracks which cross the storm areas of each of ETCs were selected and presented in Figure 5 and Figure 6.

2.2.2. Wave Spectrum Measurements from CFOSAT-SWIM

SWIM (Surface Waves Investigation and Monitoring) instrument is carried by the China-France Oceanography Satellite (CFOSAT). SWIM is a Ku-band radar with nadir and near-nadir scanning beam geometry designed to measure the spectral properties of surface ocean waves [17]. Here, we use level 2 products processed by CNES and IFREMER: SWH, spectral peak wavelength, λ p and wave direction, φ p , with 180 ambiguity.
The SWIM nadir measurements of SWH are already shown in Figure 3 in combination with other altimeters observations. The SWIM estimations of λ p and φ p are shown in Figure 4. To eliminate the 180 ambiguity of the SWIM wave direction, the wave directions were checked and corrected according to the corresponding wind directions, so that the wave direction is true when it is in the same quadrant with local wind directions. Otherwise, the wave direction should be corrected by adding or subtracting 180 [35].
Although CFOSAT-SWIM l2 products, processed by CNES, give a wealth of information on the peak parameters, analysing the wave spectrum using the l2s products processed by IFREMER is inevitable. The directional wave spectra are reconstructed from scanning radar measurements obtained with rotating beams directed at mean incidence angles of 0(nadir), 2, 4, 6, 8, and 10. In this study, we used observation from the angle of incidences 6, 8, and 10.

3. Features of Waves in Storm Area

The moving nature of cyclones leads to specific and important features of the generated wave fields. Specifically, waves generated in the right sector (where the wind is aligned with the cyclone heading) may stay under wind forcing for a longer period than in the left sector where the wind is opposite to the cyclone’s heading. Wind waves in the right sector are thus often more developed than in the left one (as well as in comparison with a stationary cyclone), and hence are higher and have longer wavelength [19,20,21,22,23,27,28].
Differences between waves generated in the right sector compared to those generated in the left one or in the case of a stationary cyclone, then depend on the relationship between the maximum wind speed, u m , its radius, R m and velocity of cyclone movement, V t . These parameters are combined in a critical length scale L c r
L ¯ c r = c c r u m 2 g u m 2 V t 1 / q
where c c r is a constant, q is fetch-law exponent for the peak frequency, which following [24] are set here as: c c r = 6.46 × 10 3 and q = − 1 / 4 .
The critical fetch L c r is the distance traveled by a developing train of waves from its point of origin to the point, where its group velocity reaches the value V t [23]. L c r thus helps divide all cyclones on two types: slow moving if R m / L c r > 1 and fast moving if R m / L c r < 1 . In the former case, wind waves developing in the right sector can “outrun” the storm to become swell systems propagating ahead of the cyclone. In the latter case, the developing waves move backward relative to the cyclone and leave the storm zone through the rear sector, becoming trailing swell systems. A more detailed description of waves generated by different types of cyclones can be found in [24].
For the considering ETCs, an estimation of critical fetch, L c r , can be achieved using the mean values of V t and u m which are: u ¯ m = 26 m/s and V ¯ t = 19 m/s for ETC#1 , and u ¯ m = 34 m/s and V ¯ t = 16.5 m/s for ETC#2. The average values of critical fetch are L ¯ c r ∼ 2000 km and L ¯ c r ∼ 670 km for ETC#1 and#2, respectively (Figure 2). Comparing L ¯ c r with R m one may conclude that both ETC can be classified as fast-moving cyclones. In this case we anticipate that storm area in both ETC should be filled with developing wind waves. Following [23,24], generation of these waves starts once the front boundary of the fast moving storm appears at a given point. Since these developing waves are slow, they move backward relative to the traveling storm. These waves then attain a maximal development at the rear boundary of the storm, and then leave it, propagating behind as swell systems.

3.1. Profiles of Wave Parameters Across ETCs

3.1.1. SWH

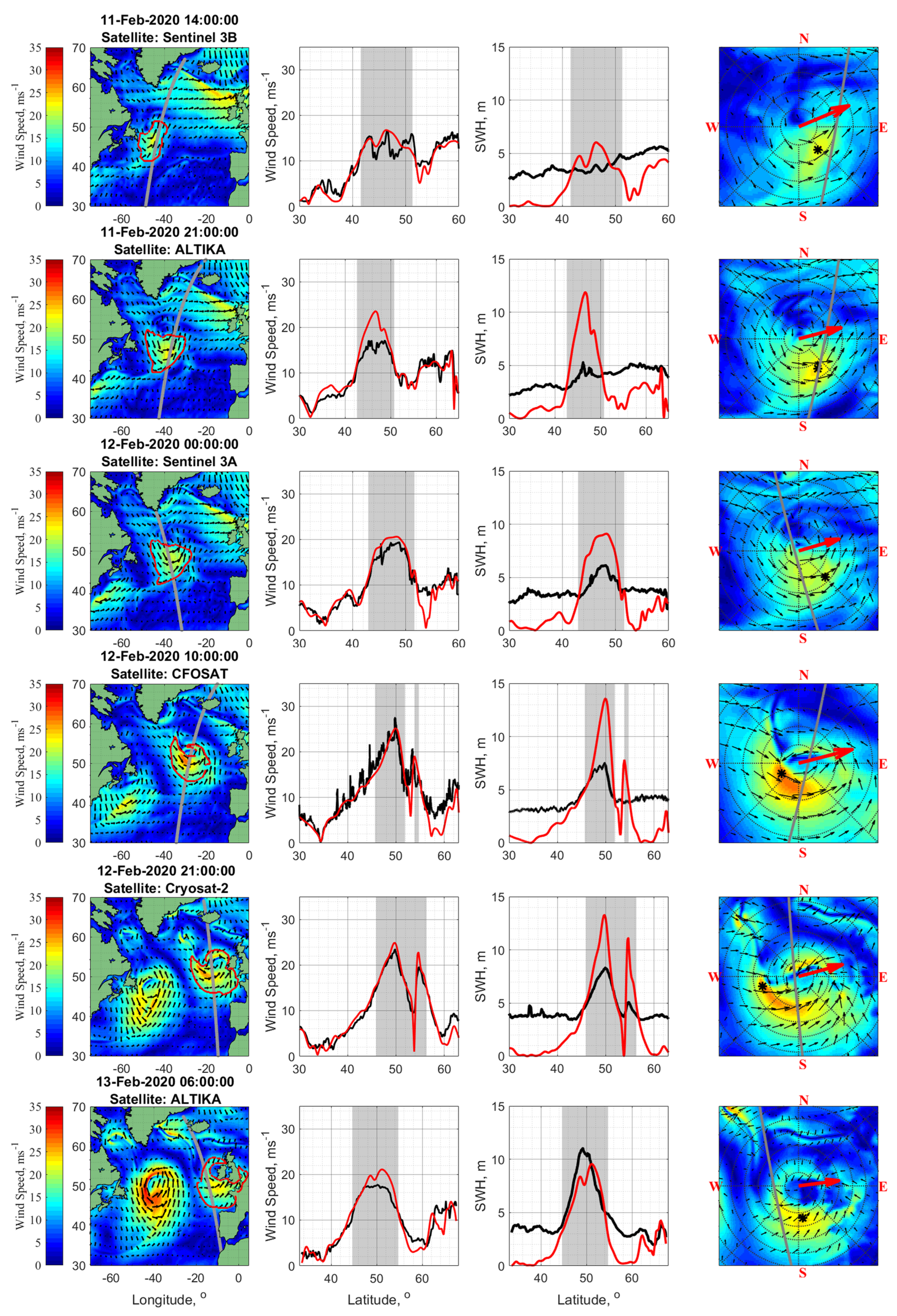
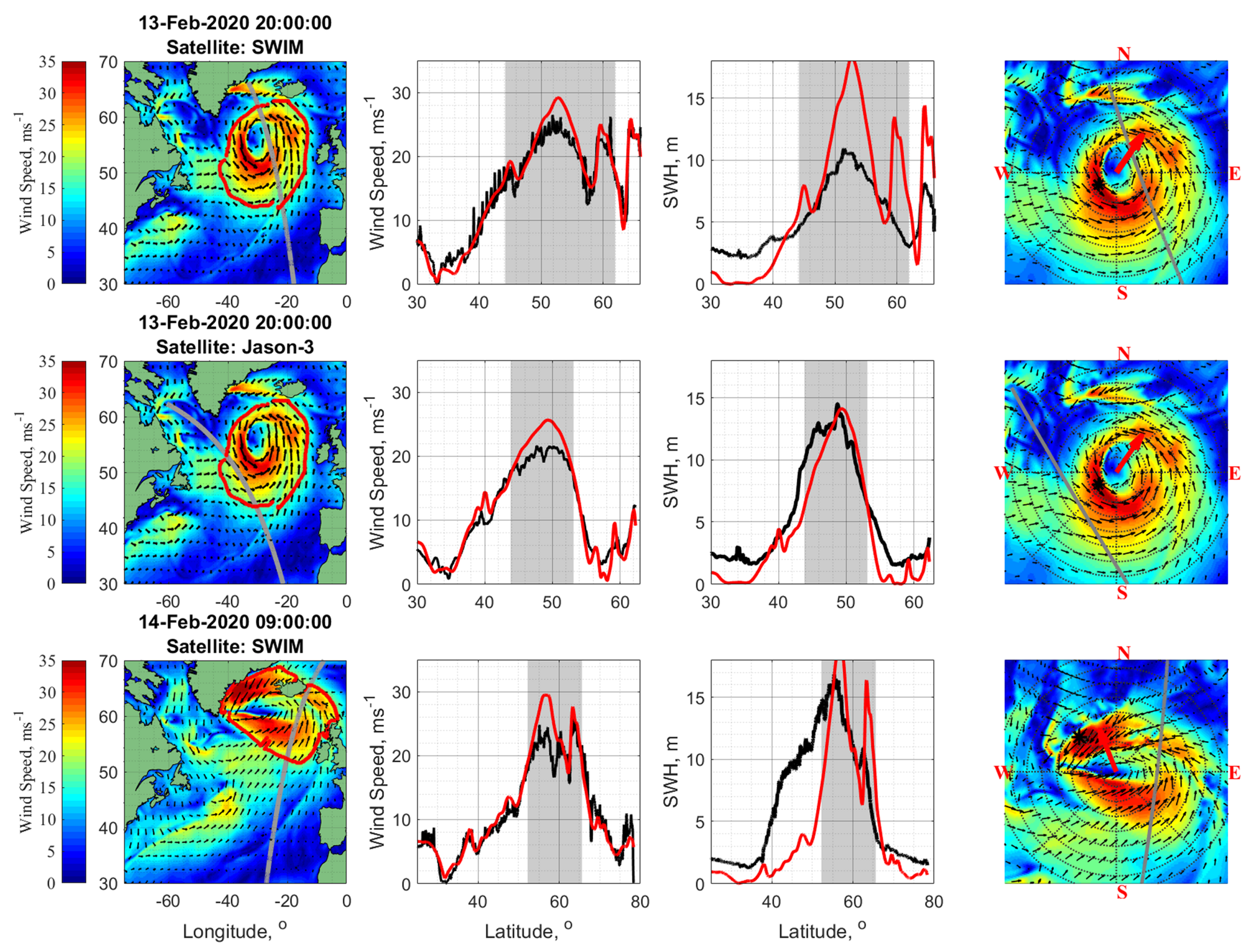
Among 130 altimeter tracks crossing the North Atlantic in the period February 2020, 11th to 15th, 14 and 26 tracks crossed the storms ETC#1 and ETC#2, respectively. Some of these tracks are displayed in Figure 5 for ETC#1 and Figure 6 for ETC#2, together with corresponding profiles of altimeter-derived wind speed and SWH (black lines), and cross-section profiles of the NCEP/CFSv2 wind speed and SWH of fully developed seas, H s = 0.21 u 2 / g , [36] along the selected altimeter tracks. Vertical shaded areas in columns 2 and 3 indicate the parts of the tracks exactly crossing the ETCs’ storm area, indicated on the wind fields, left column, by a red contour.
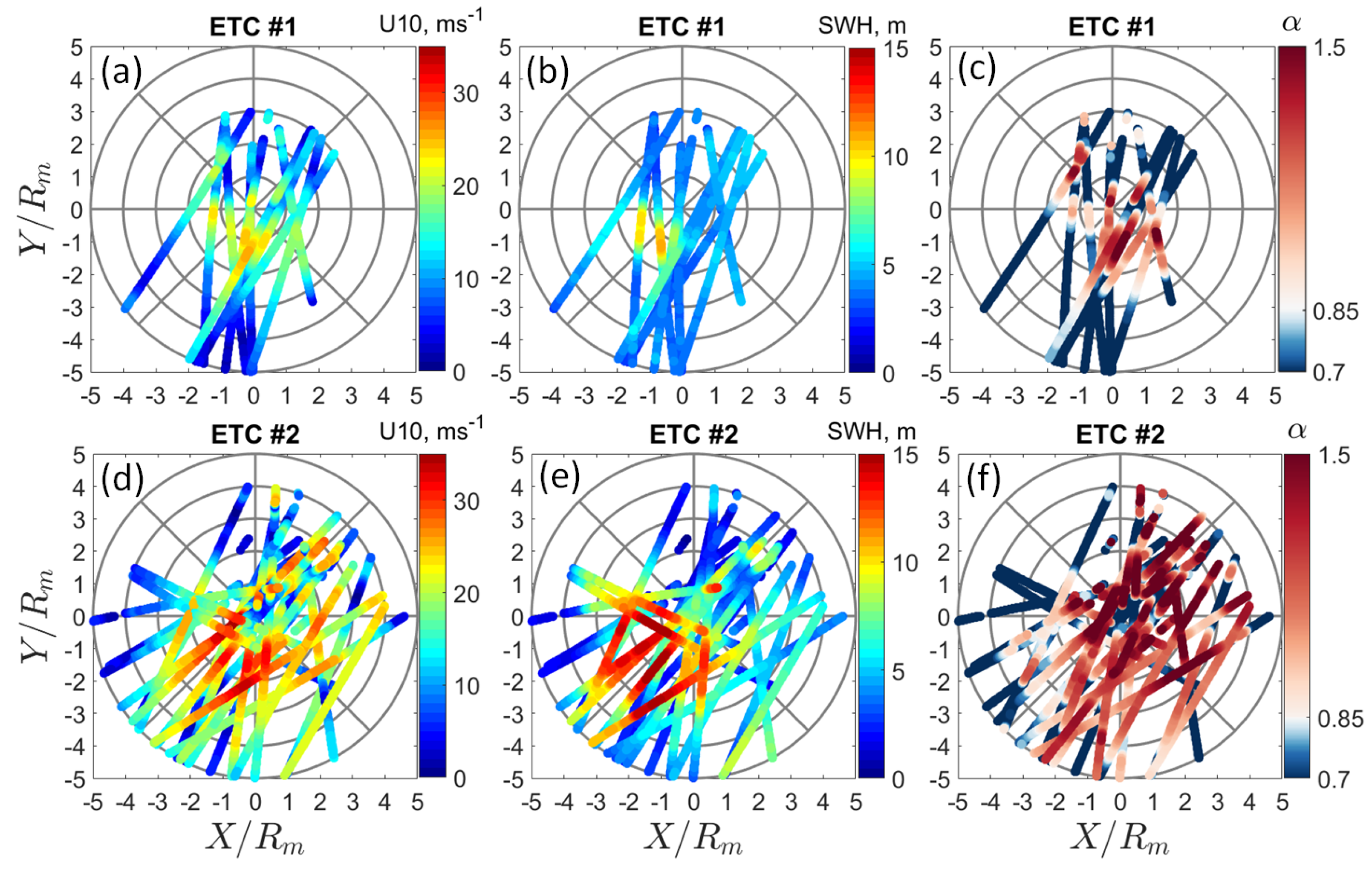
Referring to Figure 5 and Figure 6, wind fields in the ETCs are showing strong radial-azimuth asymmetry: strong winds in the right and rear sectors cover larger area than in the front and left sectors. The wind speed estimates on the tracks crossing the ETC eye is also larger in the right sector than in the left. The difference of u m between these sectors does not exceed 10 ms−1. On the other hand, the difference for the maximum SWH values between the same sectors is much larger and exceeds the values that could be expected from observed wind speed difference. In some cases, e.g., tracks of CryoSat-2 and Sentinel-3A in Figure 5 on 13-Feb, 21:00 and 23:00, the difference of SWH maxima between the right and the left sectors is about 10 m.
A zoom of the ETCs’ storm area (shown in the left column within the red curves) is presented in the last column of Figure 6 and Figure 5 in the orthogonal coordinates systems. The radius of gray circles in these plots changes from 200 km with the 200 km increment. The location of u m is displayed by a black asterisk. After careful inspection of the wind speed and SWH profiles, Figure 5 and Figure 6, the maximum SWH is found, for most cases, behind (upwind) the position of the maximum wind speed.
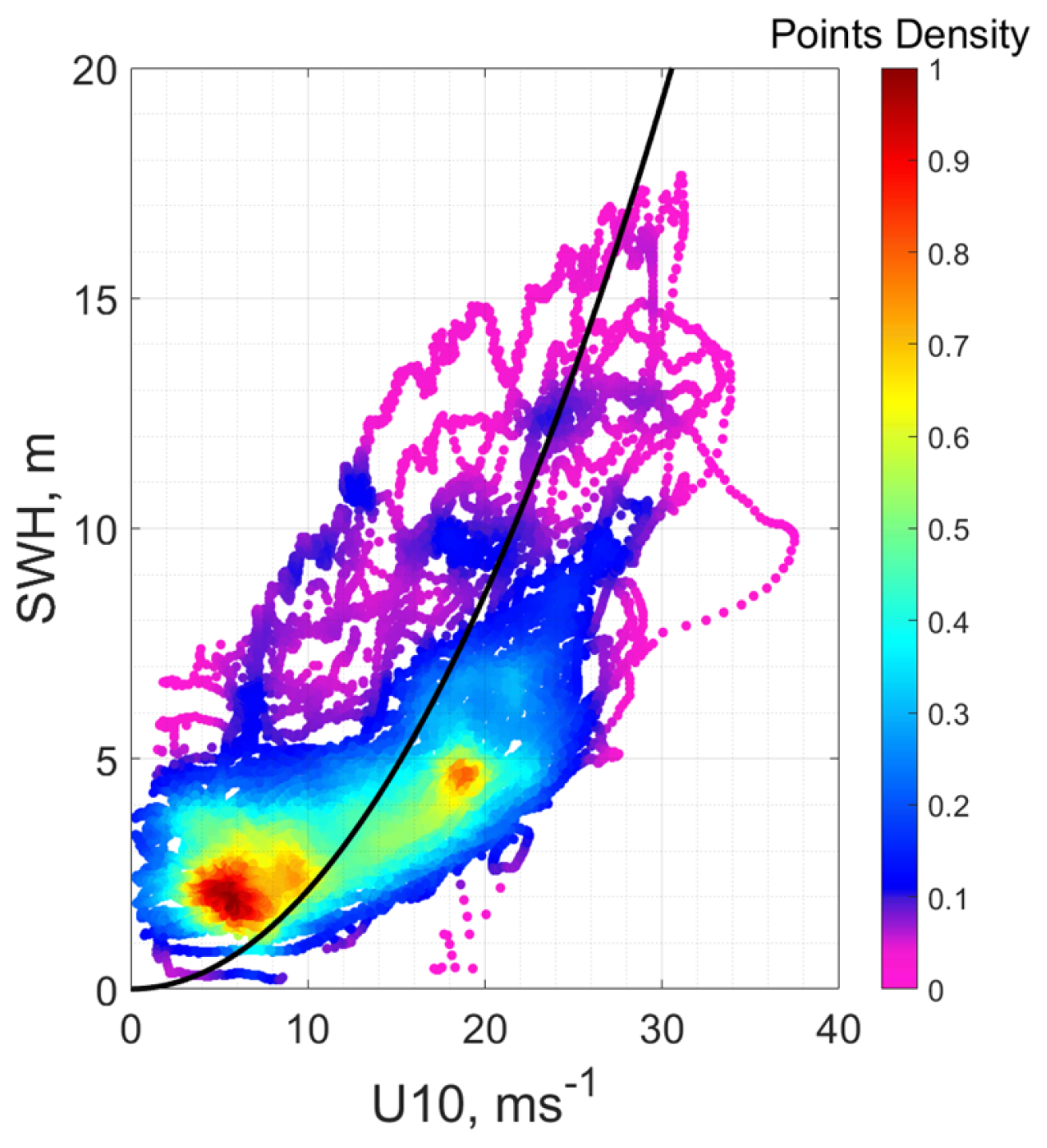
To help separate the measured SWH according to the type of surface waves including developing wind waves, mature wind waves and swell, a “threshold” SWH is introduced as
H s f d = 0.21 u 2 / g ,
which corresponds to the SWH of fully developed waves [36]. Consequently, observed waves with SWH H s < H s f d can be considered as developing waves, and waves with SWH H s > H s f d - as swell. The NCEP/CFSv2 wind speed is further used as the reference one to calculate H s f d .
Comparison of the measured SWH with H s f d , Figure 5 and Figure 6, indicates that observed waves in the inner storm area can be classified as developing and mature wind waves, and waves outside the storm area can be interpreted as swell. All the data shown in Figure 5 and Figure 6, are presented in Figure 7 as a scatter plot “SWH vs wind speed”. The measured SWHs below the “threshold” line from (2) represent wind waves developing under local wind forcing, and SWHs above—represent swell which travel outside the storm area.

3.1.2. Spectral Peak Parameters

During the period of 11–15 of February 2020, about 30 CFOSAT-SWIM tracks crossed the North Atlantic, shown in Figure 4. However, only 3 and 4 tracks perfectly crossed the storm area of ETC#1 and ETC#2, respectively. Some of those tracks are shown in Figure 5, for ETC#1 and Figure 6, for ETC#2, together with corresponding profiles of wind speed and SWH. Hereafter, we solely analyse the parameters of spectral peak, - wavelength and direction.
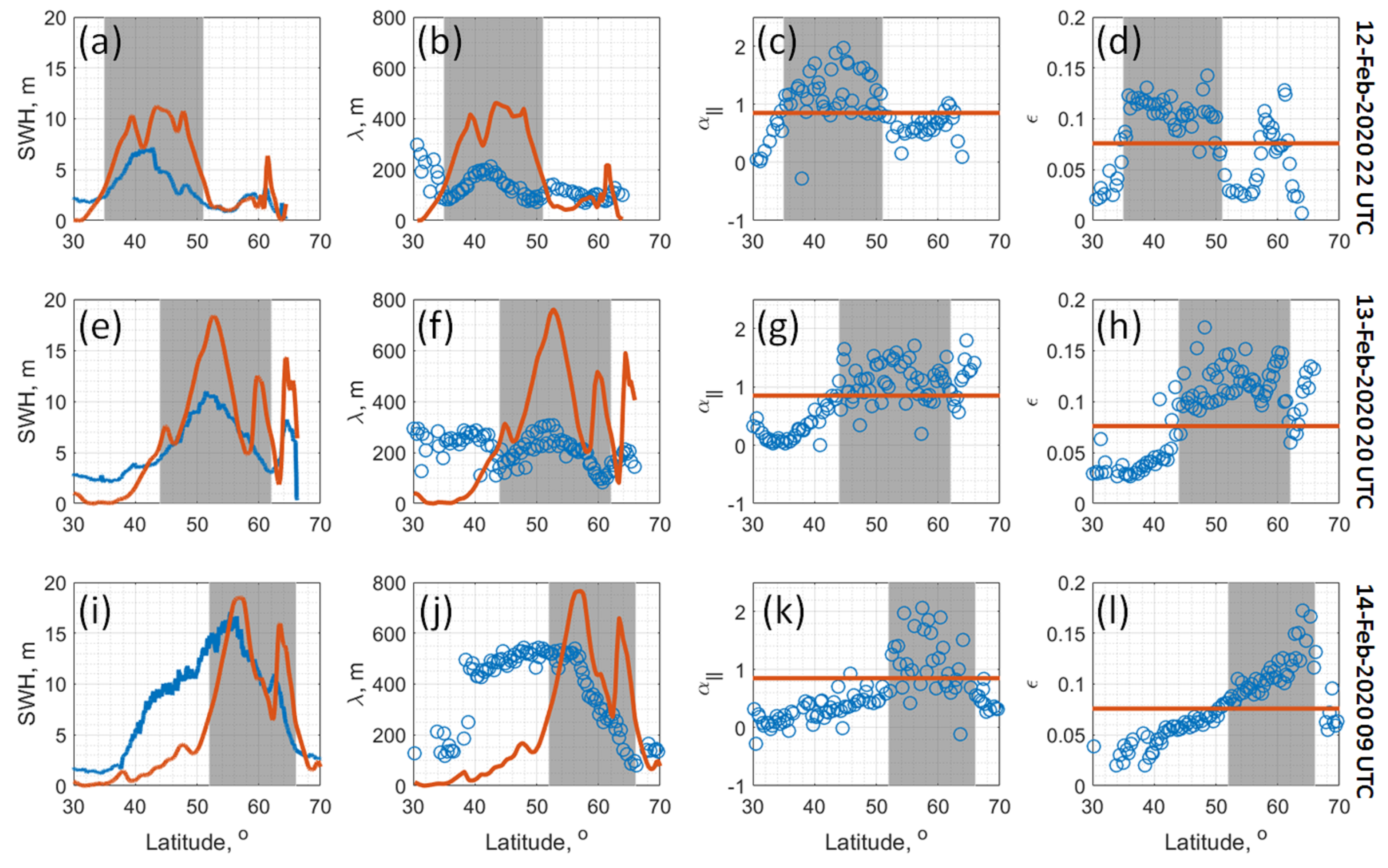
The measured along-track SWIM nadir SWH, off-nadir wavelength of spectral peak, λ p , and wave significant steepness, ϵ = k p H s / 2 , for cases on 12-FebT22, 13-FebT20, and 14-FebT09 are presented in Figure 8 (blue points). The satellite nadir track for these cases are shown on the maps of 2nd, 8th and 10th rows, Figure 6. The orange lines in each panel of Figure 8, show SWH, H s f d = 0.21 u 10 2 / g , wavelength, λ p = ( 2 π / 0.85 ) u 10 2 / g , and significant steepness, ϵ p = k p H s / 2 = 0.076 , for fully developed waves. These estimates are used as reference values to discriminate between wind seas and swells. Observed waves are classified as wind waves (resp. swell) if their measured SWH and wavelength are less (resp. larger) than these reference values. For the significant steepness, the situation is reversed, i.e., the larger values are attributed to wind waves and the smallest to swell. Such a separation based on threshold reference values appears surprisingly well consistent with direct estimates of local inverse wave age, α | | = ( u / c p ) cos ( φ p − φ w ) , shown Figure 8 , where c p = g λ p / 2 π is the peak phase velocity, φ w and φ p , the directions of the local wind and the spectral peak, respectively.
A remarkable feature, Figure 8, is that locations of wind driven waves and swell detected by different instruments (nadir altimeters and radar SWIM) for different wave parameters (SWH, λ p , ϵ p , φ p ) are very consistent. It suggests that the inner storm area of fast moving ETC is dominated by developing waves. Although this statement sounds trivial, it is an important feature of the wave field in fast moving cyclones. In case of slowly moving cyclones with parameters satisfying condition R m / L c r > 1 , the primary wave system represented by developing wind waves, occupies a limited area in the front-right sector, and in the rest of the area the primary wave system is represented by swell (see [24] and their Figure 10 for illustration).

3.2. Spatial Distributions in the ETC Storm Area

To have a better understanding of wind waves under these ETCs, the along-track distributions of wind speed and SWH are displayed Figure 9, in a rectangular coordinate system with the origin tied to the eye of ETC moving in x-direction. Figure 9a and Figure 9d confirm that the wind is stronger in the rear-right sectors of both ETCs. This is consistent with [37] who analysed wind speed fields in ETCs to reveal systematic asymmetries with maximum wind speed in the rear-right quadrant.
Spatial distributions of SWH, Figs. Figure 9b and Figure 9e, exhibits higher values in the rear-right quadrant at radial distance about 1 < r / R m < 3 . In our case, the largest surface waves approximately coincide with the area of higher wind speeds. On the one hand, relative SWH enhancements in the same quadrant have been reported by [2] and [38] using numerical simulations. This is consistent with predictions of self-similarity theory of wave development in moving storms based on the extended fetch concept [20,22,24]. This mechanism suggests that in the right sector, where wind direction coincides with ETC heading, developing waves stay under wind forcing for a longer time. Wave energy can then accumulate compared to other sectors or to stationary storm with the same u m and R m .
It is then tempting to quantify waves generated by ETCs in terms of inverse wave age. One of the fundamental results of the similarity theory for the wave growth by [39], is the proportionality of the dimensionless energy, e ˜ = e g 2 / u 10 4 , to the inverse wave age, α = u 10 / c p (which is equal to dimensionless peak frequency), to some certain power, e.g., to a power of “-3”: e ˜ ∝ α − 3 [40]. Using the definition e = H s 2 / 16 , the relationship between inverse wave age and SWH reads:
α = 0.85 H ˜ s f d H ˜ s 2 / 3 ,
where H s f d and 0.85 are SWH and inverse wave age corresponding to fully developed seas, respectively.
The inverse wave age maps, Figure 9c,f, show that the inverse wave age estimate in the right sector and partly in the left one, is α > 0.85 . This suggests that waves in the inner storm area (inside r / R m ≤ 4 for ETC#2 and r / R m ≤ 2 for ETC#1) are developed mature wind waves. It is likely because the analyzed ETCs are fast moving systems, with their R m smaller than the critical fetch L c r estimate, see Figure 2. In this case, waves start to develop in the forward sector, at the time the storm area appears at a given point in the ocean. The group velocity of the waves is then less than the ETC translation velocity, and the developing wind waves move backward relative to the ETC. Waves finally radiate out of the storm area through its rear boundary. This is what can be seen in Figure 9, in reasonable agreement with the simulations of waves generation under fast moving cyclones, [24] (see their Figure 10d,h).

3.3. SWH Time Evoloution

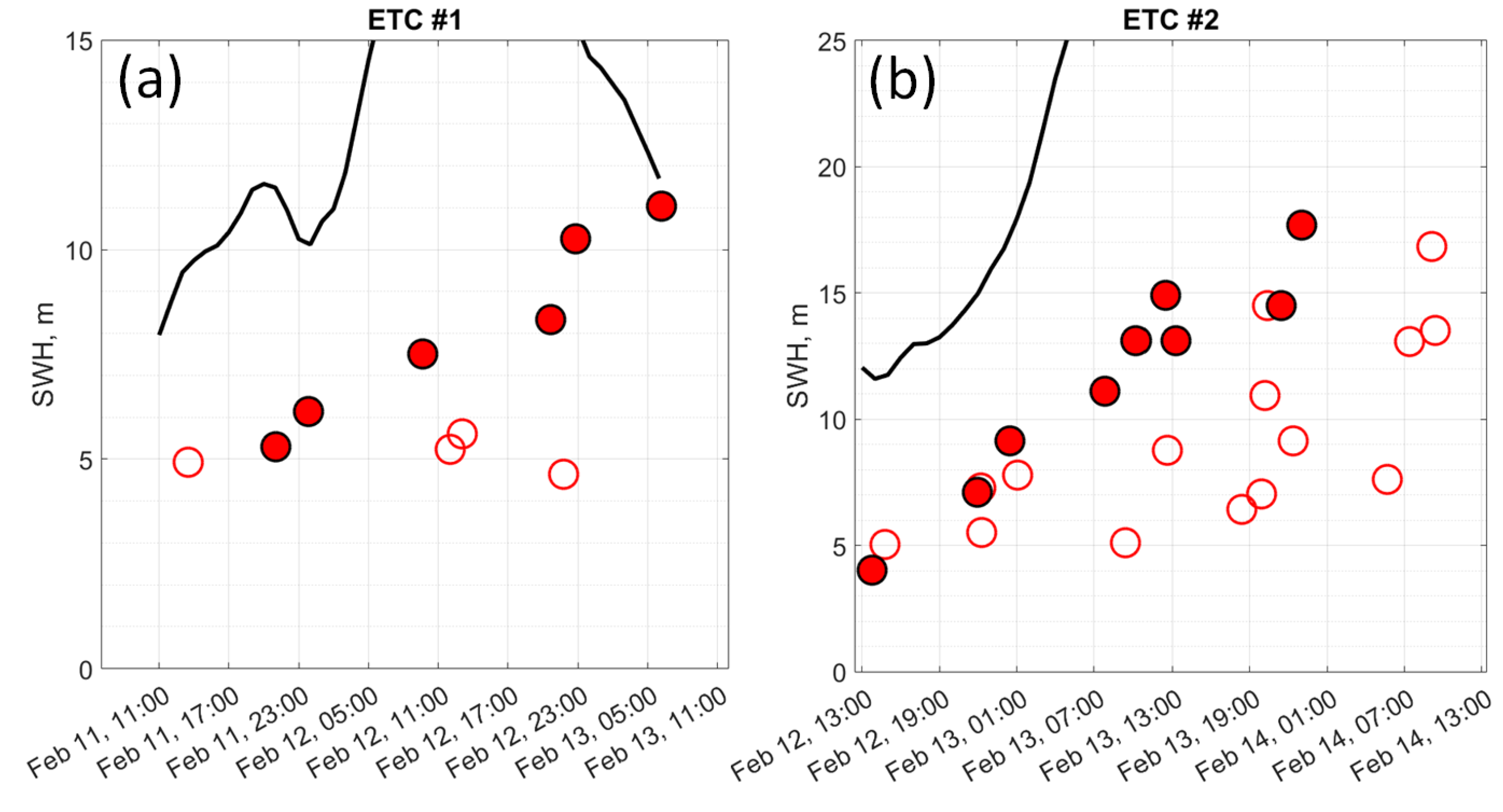
3.3.1. Data

Figure 10a,b display the time evolution of the maximal values of SWHs on each of the altimeter tracks shown before, Figure 9c,d. The highest waves, maximal SWHs, are again divided into developing wind waves, whose local inverse wave age is α > 0.85 , and swell, α < 0.85 . Distinctive characteristics are indicated in Figure 10a,b by the filled and open red circles, correspondingly. Fully developed wave heights, H s f d = 0.21 u m 2 / g , [36] calculated for the maximal local wind speed are also presented in Figure 10a,b. Hereinafter, only wind waves are considered.
Wind wave SWH for the ETC#1 (Figure 10a) demonstrate a gradual increase. By the end of the ETC life, the level of fully developed waves is almost reached. Yet, this is mainly due to a decrease in wind speed. For ETC#2, the SWH trend is more pronounced. However, the observed SWHs are still well below the fully developed level (black curve in Figure 10b).

4. Discussion

To qualify and quantify waves generated by ETCs, it is first tempting to consider the extended fetch concept, successfully applied to describe the waves generated by TCs [19,20,21,22,24,27]. This approach suggests that classical self-similar laws of wave growth by [39],
ω ˜ p ≡ α = c α x ˜ q , e ˜ = c e x ˜ p ,
can also be applied, with the wind fetch, x ˜ = x g / u 2 , more properly defined to take into account TC moving nature. Such a fetch is termed as an effective or an extended fetch [19,20,21,27]. In Equation (4), α is the inverse wave age, equal to the dimensionless spectral peak frequency, e ˜ = e g 2 / u 4 is dimensionless energy, p and q are the fetch-law exponents, and c α and c e are the constants. Examples on application of self-similar laws for description of waves in moving cyclones (either in radial and in the azimuthal directions) can be found in [24,26].
Following [24] (see their Equation (18)), the effective (extended) fetch, X ˜ e = x g / u m 2 , to determine these quantities using (...) in case of the moving storm, can be parameterized in self-similar variables as:
X ˜ e = 1.1 R ˜ m [ l e + m e ( R ˜ m / L ˜ c r m ) n e ] 1 / p , X ˜ λ = 1.8 R ˜ m [ l λ + m λ ( R ˜ m / L ˜ c r m ) n λ ] − 1 / 2 q
where [ l e , m e , n e ] and [ l λ , m λ , n λ ] are the constants, which depend on the type of storm. For slow-moving storms, L ˜ c r / R ˜ m ≥ 1 , these constants are [1, 3.84, -0.4] and [1, 1.37, -0.38] for energy and wavelength, respectively. For fast-moving storms, L ˜ c r / R ˜ m < 1 , these constants are correspondingly changed to [0, 2.92, 0.53] and [0, 1.67, 0.31].
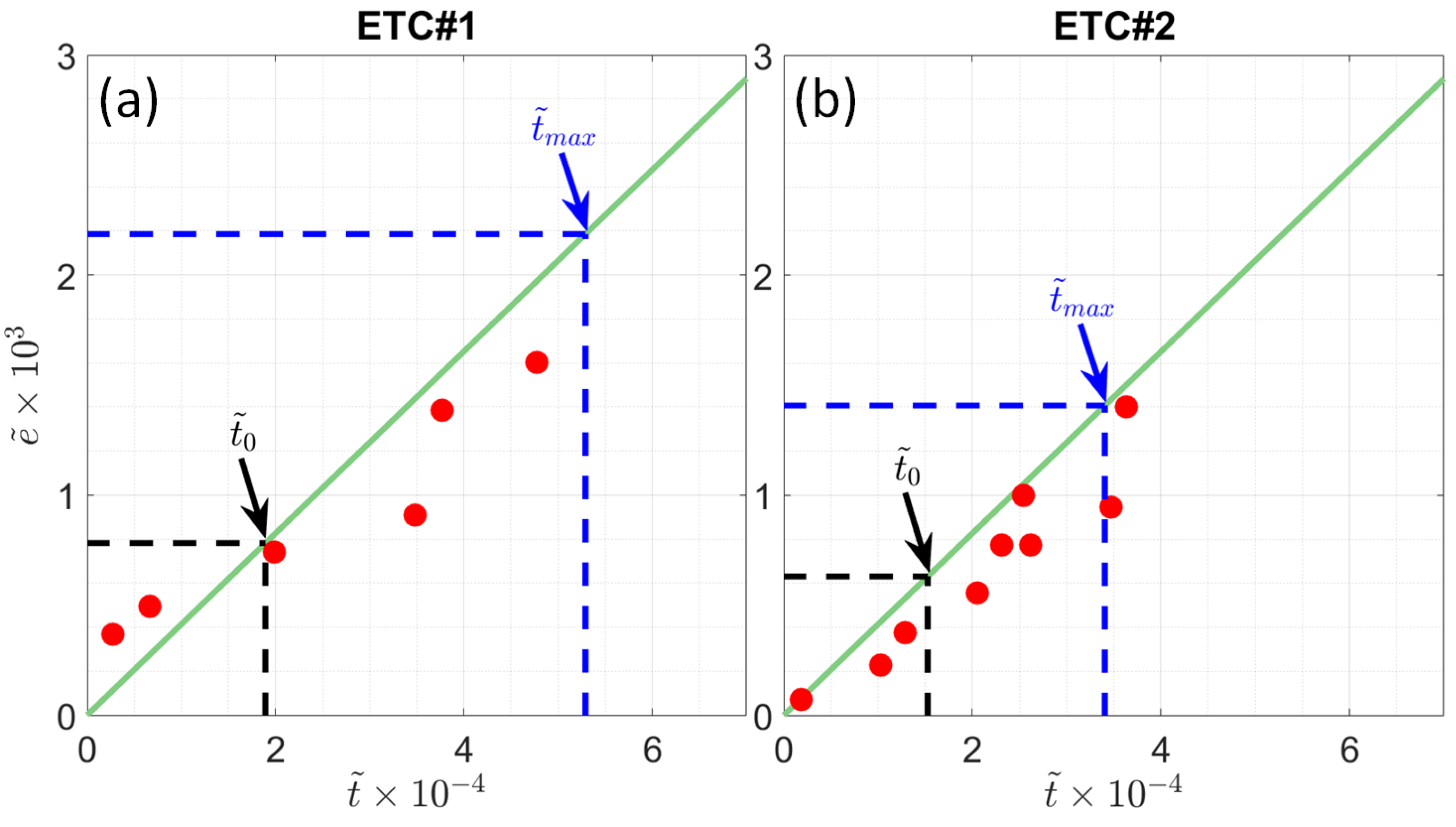
From Figure 11, the waves, generated by ETCs , exhibit clear development in time. The waves suggesting have likely not reached the steady state predicted by (5) with (1). Until reaching the steady solutions (5), the wave development must then obey duration-laws, which in the framework of the classical self-similarity theory are:
ω p u / g = c α t t g / u q t , e g 2 / u 4 = c e t t g / u p t ,
where q t and p t are duration law exponents, linked to the fetch law constants as: q t = q / ( 1 + q ) and p t = p / ( 1 + q ) . The constants α t and c e t are also linked to the corresponding fetch-law constants (see e.g., Eq.3 from [24]). Following [24], we adopt the Toba’s fetch laws [40] with exponents p = − 1 / 4 and p = 3 / 4 , which lead to duration laws exponent in (6) equal to: q t = − 1 / 3 and p t = 1 .
The wave development in time will continue until the wave parameters reach the steady solutions (4) with (5). The required time interval, t m a x , can be defined from the combination of duration laws (6) and the steady state values, (4) with (5), to give:
t λ m a x = t 0 l λ + m λ R m / L c r n λ − 1 / 2 q t , t e m a x = t 0 l e + m e R m / L c r n e 1 / p t ,
where t 0 is the timescale of wave development for a stationary storm, expressed through its radius as:
t 0 g / u m = c α / c α t 1 / q t R m q / q t .
The dimensionless energy estimates, e ˜ = e g 2 / u m 4 (where e = H s 2 / 16 , as a function of dimensionless time, t ˜ = t g / u m , where the mean maximal wind speed, u ¯ m , during the life span of each of ETCs is used for scaling, are shown in Figure 11a,b. The initial epochs of wave development, the date 11-Feb-2020 19:00:00 for ETC#1 and date 12-Feb-2020 12:00:00 for ETC#2 are chosen to best fit the observations. Duration laws (6), also shown on the same figure, exhibit an overall good agreement with the observations. Correlation coefficient of e ˜ obtained from observations and Equation (6) is ∼ 0.95 for both ETCs.
Two key time-scales, namely, time intervals required to reach the steady state in stationary ETC, t ˜ 0 = t 0 g / u m defined by (8), and in moving ETC, t ˜ m a x = t e m a x g / u m defined by (7), are shown in Figure 11a,b.
To estimate t 0 , we used the values of R m and u m averaged over the lifespan of each ETC: u ¯ m = 26 ms−1 and R ¯ m = 350 km for ETC#1, and u ¯ m = 34 ms−1 and R ¯ m = 450 km for ETC#2. These values give t 0 ≈ 14 h and t 0 ≈ 15 h for ETC#1 and ETC#2 , respectively. On the other hand, to estimate t e m a x we used the values of R m , u m and V t at the latest stage of the lifespan of ETCs, extracted from the Figure 2 as [ u m = 24 ms−1; R m = 480 km; V t = 13 ms−1], and [ u m = 36.5 ms−1; R m = 500 km; V t = 18 ms−1], for ETC#1 and ETC#2 respectively. It gives t e m a x ≈ 39 h and t e m a x ≈ 33 h for ETC#1 and ETC#2, respectively. Referring to Figure 11a,b, we may find that neither wind waves developing under ETC#1 nor under ETC#2 are capable to attain the energy level predicted by the extended fetch relationship. Thus, wind wave development in storm area of fast moving ETC can be better be considered to obey the classical duration laws. The effect of the fast moving nature of the ETC on the growth of waves is to increase the residence time of waves under wind forcing. The longer this time, the more developed and higher the waves. This phenomenon, by analogy with extended fetch, can be called extended duration, similar to what have been observed for waves generated by Polar Lows [29].

5. Conclusions

Using multi-satellite measurements, this paper presents results of an investigation of the main characteristics of wind wave field generated by fast-moving ETCs in the North Atlantic. The two considered ETCs were fast-moving cyclones, in the sense that resonance (synchronism) between the group velocity of the generated waves and the ETC translation velocity is impossible. In this case, wave generation begins when the front-boundary of the storm area crosses a given location in the ocean. Since the group velocity of the waves is always less than the ETC translation velocity, the developing waves move backward relative to the ETC, grow in time, and then leave the storm area through its rear sector. Multi-satellite observations confirm such a paradigm, and confirm that the main storm area is filled with young developing wind waves. The most developed waves are then found in the rear-right sector of moving ETC. Moreover, the energy of these waves were observed to grow with time during the ETC life span. In this context, observed wave fields in ETC are remarkably different from those generally associated to a TC. For these cases, waves are usually enhanced in the right-front sector and demonstrate quasi-stationarity. As a consequence, the extended-fetch approach, commonly used to describe waves under TC, is not applicable for ETC. Instead, the concept of extended-duration is more relevant, similar to what have been already found in PLs [29]. In this case, the moving nature of the ETC increases the residence time of waves under wind forcing. Satellite observations confirm the validity of duration-laws for waves generated by the ETC, and demonstrate that extended-fetch regime for observing waves can only be asymptotically achieved, - at time intervals exceeding the lifespan of considered ETCs.
More detailed description of the surface wave field characteristics generated by ETC based on the use of parametric model simulations and satellite observations will be discussed in the companion paper PART II [41].

Funding

The core support for this work was provided by the Russian Science Foundation through Project No. 21-47-00038. The support of the Ministry of Science and Education of the Russian Federation under State Assignment No. FNNN-2021-0004 at MHI RAS and State Assignment No. 0763-2020-0005 at RSHU is gratefully acknowledged. We also acknowledge the ESA MAXSS Project 4000132954/20/I-NB

Data Availability Statement

The data supporting reported results are extracted from the links available in the Table 1

Acknowledgments

CFOSAT-SWIM measurements were provided by IFREMER Wind and Wave operational Center (IWWOC), co-funded by CNES and IFREMER. NCEP/CFSv2 data provided by the OAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at NCEP/CFSv2 website.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SWH Significant Wave Height
Hs Height of Significant Wave
MSLP Mean Sea Level Pressure
ETC Extra-Tropical Cyclone
fd Fully developed
CFOSAT Chinese-French Oceanographic Satellite
SWIM Surface Wave Exploration and Monitoring
UTC Coordinated Universal Time
NCEP National Centers for Environmental Prediction
CFSv2 Climate Forecast System Version 2
IFREMER Institut Français de Recherche pour l’Exploitation de la Mer,
French Research Institute for Exploitation of the Sea
CNES Initialism of Centre National d’Études Spatiales, the French space agency

References

  1. Hanafin, J.A.; Quilfen, Y.; Ardhuin, F.; Sienkiewicz, J.; Queffeulou, P.; Obrebski, M.; Chapron, B.; Reul, N.; Collard, F.; Corman, D.; de Azevedo, E.B.; Vandemark, D.; Stutzmann, E. Phenomenal Sea States and Swell from a North Atlantic Storm in February 2011: A Comprehensive Analysis. Bulletin of the American Meteorological Society 2012, 93, 1825–1832. [Google Scholar] [CrossRef]
  2. Ponce de León, S.; Guedes Soares, C. Extreme wave parameters under North Atlantic extratropical cyclones. Ocean Modelling 2014, 81, 78–88. [Google Scholar] [CrossRef]
  3. Waseda, T.; Sasmal, K.; Kodaira, T.; Kita, Y.; Miratsu, R.; Zhu, T.; Fukui, T. Modeled and satellite-derived extreme wave height statistics in the North Atlantic Ocean reaching 20 m 2021. [CrossRef]
  4. Alves, J.H.G.; Young, I.R. On estimating extreme wave heights using combined Geosat, Topex/Poseidon and ERS-1 altimeter data. Applied Ocean Research 2003, 25, 167–186. [Google Scholar] [CrossRef]
  5. Caires, S.; Sterl, A. 100-Year Return Value Estimates for Ocean Wind Speed and Significant Wave Height from the ERA-40 Data. Journal of Climate 2005, 18, 1032–1048. [Google Scholar] [CrossRef]
  6. Semedo, A.; Sušelj, K.; Rutgersson, A.; Sterl, A. A Global View on the Wind Sea and Swell Climate and Variability from ERA-40. Journal of Climate 2011, 24, 1461–1479. [Google Scholar] [CrossRef]
  7. Shimura, T.; Mori, N.; Mase, H. Ocean Waves and Teleconnection Patterns in the Northern Hemisphere. Journal of Climate 2013, 26, 8654–8670. [Google Scholar] [CrossRef]
  8. Ponce de León, S.; Guedes Soares, C. Hindcast of extreme sea states in North Atlantic extratropical storms. Ocean Dynamics 2014, 65, 241–254. [Google Scholar] [CrossRef]
  9. Ponce de León, S.; Bettencourt, J.H.; Brennan, J.; Dias, F. Evolution of the Extreme Wave Region in the North Atlantic Using a 23 Year Hindcast. Volume 3: Structures, Safety and Reliability. American Society of Mechanical Engineers, 2015. [CrossRef]
  10. Rogers, J.C. North Atlantic Storm Track Variability and Its Association to the North Atlantic Oscillation and Climate Variability of Northern Europe. Journal of Climate 1997, 10, 1635–1647. [Google Scholar] [CrossRef]
  11. Takbash, A.; Young, I.R.; Breivik. Global Wind Speed and Wave Height Extremes Derived from Long-Duration Satellite Records. Journal of Climate 2018, 32, 109–126. [Google Scholar] [CrossRef]
  12. Young, I. Seasonal variability of the global ocean wind and wave climate. International Journal of Climatology 1999, 19, 931–950. [Google Scholar] [CrossRef]
  13. Lozano, I.; Devoy, R.; May, W.; Andersen, U. Storminess and vulnerability along the Atlantic coastlines of Europe: analysis of storm records and of a greenhouse gases induced climate scenario. Marine Geology 2004, 210, 205–225. [Google Scholar] [CrossRef]
  14. Pinto, J.G.; Gómara, I.; Masato, G.; Dacre, H.F.; Woollings, T.; Caballero, R. Large-scale dynamics associated with clustering of extratropical cyclones affecting Western Europe. J. Geophys. Res. 2014, 119, 13–704. [Google Scholar] [CrossRef]
  15. Young, I.; Donelan, M. On the determination of global ocean wind and wave climate from satellite observations. Remote Sensing of Environment 2018, 215, 228–241. [Google Scholar] [CrossRef]
  16. Izaguirre, C.; Méndez, F.J.; Menéndez, M.; Losada, I.J. Global extreme wave height variability based on satellite data. Geophysical Research Letters 2011, 38, n. [Google Scholar] [CrossRef]
  17. Hauser, D.; Tourain, C.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; Gouillon, F.; Gressani, V.; Grouazel, A.; Guitton, G.; Husson, R.; Mironov, A.; Mouche, A.; Ollivier, A.; Oruba, L.; Piras, F.; Suquet, R.R.; Schippers, P.; Tison, C.; Tran, N. New Observations From the SWIM Radar On-Board CFOSAT: Instrument Validation and Ocean Wave Measurement Assessment. IEEE Transactions on Geoscience and Remote Sensing 2021, 59, 5–26. [Google Scholar] [CrossRef]
  18. Aouf, L.; Hauser, D.; Chapron, B.; Toffoli, A.; Tourain, C.; Peureux, C. New Directional Wave Satellite Observations: Towards Improved Wave Forecasts and Climate Description in Southern Ocean. Geophysical Research Letters 2021, 48. [Google Scholar] [CrossRef]
  19. King, D.; Shemdin, O. RADAR OBSERVATIONS OF HURRICANE WAVE DIRECTIONS. Coastal Engineering Proceedings 1978, 1, 10. [Google Scholar] [CrossRef]
  20. Bowyer, P.J.; MacAfee, A.W. The Theory of Trapped-Fetch Waves with Tropical Cyclones—An Operational Perspective. Weather and Forecasting 2005, 20, 229–244. [Google Scholar] [CrossRef]
  21. Young, I.R. Parametric Hurricane Wave Prediction Model. Journal of Waterway, Port, Coastal, and Ocean Engineering 1988, 114, 637–652. [Google Scholar] [CrossRef]
  22. Young, I.; Vinoth, J. An “extended fetch” model for the spatial distribution of tropical cyclone wind–waves as observed by altimeter. Ocean Engineering 2013, 70, 14–24. [Google Scholar] [CrossRef]
  23. Kudryavtsev, V.; Golubkin, P.; Chapron, B. A simplified wave enhancement criterion for moving extreme events. Journal of Geophysical Research: Oceans 2015, 120, 7538–7558. [Google Scholar] [CrossRef]
  24. Kudryavtsev, V.; Yurovskaya, M.; Chapron, B. Self-Similarity of Surface Wave Developments Under Tropical Cyclones. Journal of Geophysical Research: Oceans 2021, 126. [Google Scholar] [CrossRef]
  25. Yurovskaya, M.; Kudryavtsev, V.; Mironov, A.; Mouche, A.; Collard, F.; Chapron, B. Surface Wave Developments under Tropical Cyclone Goni (2020): Multi-Satellite Observations and Parametric Model Comparisons. Remote Sensing 2022, 14, 2032. [Google Scholar] [CrossRef]
  26. Yurovskaya, M.; Kudryavtsev, V.; Chapron, B. A self-similar description of the wave fields generated by tropical cyclones. Ocean Modelling 2023, 183, 102184. [Google Scholar] [CrossRef]
  27. Dysthe, K.B.; Harbitz, A. Big waves from polar lows? Tellus A: Dynamic Meteorology and Oceanography 1987, 39, 500. [Google Scholar] [CrossRef]
  28. Orimolade, A.P.; Furevik, B.R.; Noer, G.; Gudmestad, O.T.; Samelson, R.M. Waves in polar lows. Journal of Geophysical Research: Oceans 2016, 121, 6470–6481. [Google Scholar] [CrossRef]
  29. Kudryavtsev, V.; Cheshm Siyahi, V.; Yurovskaya, M.; Chapron, B. On Surface Waves in Arctic Seas. Boundary-Layer Meteorology. [CrossRef]
  30. Hell, M.C.; Ayet, A.; Chapron, B. Swell Generation Under Extra-Tropical Storms. Journal of Geophysical Research: Oceans 2021, 126. [Google Scholar] [CrossRef]
  31. Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press, 1994. [CrossRef]
  32. Tolman, H.L.; others. User manual and system documentation of WAVEWATCH III TM version 3.14. Technical note, MMAB Contribution 2009, 276. [Google Scholar]
  33. Lodise, J.; Merrifield, S.; Collins, C.; Rogowski, P.; Behrens, J.; Terrill, E. Global Climatology of Extratropical Cyclones From a New Tracking Approach and Associated Wave Heights From Satellite Radar Altimeter. Journal of Geophysical Research: Oceans 2022, 127. [Google Scholar] [CrossRef]
  34. Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; Ek, M.; Meng, J.; Yang, R.; Mendez, M.P.; Van Den Dool, H.; Zhang, Q.; Wang, W.; Chen, M.; Becker, E. NCEP Climate Forecast System Version 2 (CFSv2) Selected Hourly Time-Series Products, 2011. [CrossRef]
  35. Le Merle, E.; Hauser, D.; Peureux, C.; Aouf, L.; Schippers, P.; Dufour, C.; Dalphinet, A. Directional and Frequency Spread of Surface Ocean Waves From SWIM Measurements. Journal of Geophysical Research: Oceans 2021, 126. [Google Scholar] [CrossRef]
  36. Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. Journal of Geophysical Research 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
  37. Rudeva, I.; Gulev, S.K. Composite Analysis of North Atlantic Extratropical Cyclones in NCEP–NCAR Reanalysis Data. Monthly Weather Review 2011, 139, 1419–1446. [Google Scholar] [CrossRef]
  38. Kita, Y.; Waseda, T.; Webb, A. Development of waves under explosive cyclones in the Northwestern Pacific. Ocean Dynamics 2018, 68, 1403–1418. [Google Scholar] [CrossRef]
  39. Kitaigorodskii. Applications of the theory of similarity to the analysis of wind-generated wave motion as a stochastic process. Deep Sea Research and Oceanographic Abstracts 1962, 9, 398. [Google Scholar] [CrossRef]
  40. Toba, Y. Local balance in the air-sea boundary processes. Journal of Oceanography 1972, 28, 109–120. [Google Scholar] [CrossRef]
  41. Cheshm Siyahi, V.; Kudryavtsev, V.; Yurovskaya, M.; Collard, F.; Chapron, B. On Surface Waves Generated By Extra-Tropical Cyclones. Part II: Simulations. Remote Sens. 2023. [Google Scholar] [CrossRef]
Preprints 69804 g001
Figure 1. MSLP maps with wind speed contours
Figure 1. MSLP maps with wind speed contours
Preprints 69804 g001
Preprints 69804 g002
Figure 2. Time evolution of ETC#1 (left) and ETC#2 parameters: (red thick line) maximum wind speed, u m ; (red dashed line) translation velocity, V t ; (blue thick line) radius of maximum wind speed, R m ; (blue dashed line) critical fetch, L ¯ c r from (1).
Figure 2. Time evolution of ETC#1 (left) and ETC#2 parameters: (red thick line) maximum wind speed, u m ; (red dashed line) translation velocity, V t ; (blue thick line) radius of maximum wind speed, R m ; (blue dashed line) critical fetch, L ¯ c r from (1).
Preprints 69804 g002
Preprints 69804 g003
Figure 3. Altimetry tracks passing through the Northern Atlantic during the period of 11-Feb-2020 00:00 UTC – 16-Feb-2020 00:00 UTC, after applying ice and land masks. The black line shows the trajectory of the ETC#1 and the gray line ETC#2. Colour of the altimeter tracks indicates measured SWH in metres
Figure 3. Altimetry tracks passing through the Northern Atlantic during the period of 11-Feb-2020 00:00 UTC – 16-Feb-2020 00:00 UTC, after applying ice and land masks. The black line shows the trajectory of the ETC#1 and the gray line ETC#2. Colour of the altimeter tracks indicates measured SWH in metres
Preprints 69804 g003
Preprints 69804 g004
Figure 4. Measured λ p (colored boxes) and φ p after eliminating 180 ambiguity (black arrows) in “wave boxes” on two sides of the CFOSAT-SWIM track in Northern Atlantic during the period of 11-Feb-2020 00:00 UTC —16-Feb-2020 00:00 UTC, after applying ice and land masks.
Figure 4. Measured λ p (colored boxes) and φ p after eliminating 180 ambiguity (black arrows) in “wave boxes” on two sides of the CFOSAT-SWIM track in Northern Atlantic during the period of 11-Feb-2020 00:00 UTC —16-Feb-2020 00:00 UTC, after applying ice and land masks.
Preprints 69804 g004
Preprints 69804 g005
Figure 5. Wind speed and SWH along the AltiKa, CryoSat-2, Sentinel-3 and CFOSAT-SWIM nadir tracks at the different moments of ETC#1 lifetime. Columns from left to right, (1st column): NCEP/CFSv2 wind field and position of the track; (2nd column): along-track wind speed from (black line) measurements and (red lines) NCEP/CFSv2; (3rd column): profile of measured SWH (black line) and SWH of fully-developed waves for local wind speed (red line); (4th column): zoom on the ETC#1 storm (inner) area (shown in first column by red contour). The red arrows in the 4th column indicate ETC’s direction, and the radius of dashed circles changes from 200 km with 200 km interval. Vertical shaded areas in columns 2 and 3 indicate the parts of the tracks that fell into the ETC’s storm area, shown in 1st column by red contour. The position of u m is indicated by black asterisk
Figure 5. Wind speed and SWH along the AltiKa, CryoSat-2, Sentinel-3 and CFOSAT-SWIM nadir tracks at the different moments of ETC#1 lifetime. Columns from left to right, (1st column): NCEP/CFSv2 wind field and position of the track; (2nd column): along-track wind speed from (black line) measurements and (red lines) NCEP/CFSv2; (3rd column): profile of measured SWH (black line) and SWH of fully-developed waves for local wind speed (red line); (4th column): zoom on the ETC#1 storm (inner) area (shown in first column by red contour). The red arrows in the 4th column indicate ETC’s direction, and the radius of dashed circles changes from 200 km with 200 km interval. Vertical shaded areas in columns 2 and 3 indicate the parts of the tracks that fell into the ETC’s storm area, shown in 1st column by red contour. The position of u m is indicated by black asterisk
Preprints 69804 g005
Preprints 69804 g006aPreprints 69804 g006b
Figure 6. The same as in Figure 5, but for ETC#2 and altimeters AltiKa, CryoSat-2, Sentinel-3, Jason-3, and CFOSAT-SWIM nadir tracks.
Figure 6. The same as in Figure 5, but for ETC#2 and altimeters AltiKa, CryoSat-2, Sentinel-3, Jason-3, and CFOSAT-SWIM nadir tracks.
Preprints 69804 g006aPreprints 69804 g006b
Preprints 69804 g007
Figure 7. Two-dimensional scatter plot of significant wave height SWH as a function of wind speed, coloured with points density.
Figure 7. Two-dimensional scatter plot of significant wave height SWH as a function of wind speed, coloured with points density.
Preprints 69804 g007
Preprints 69804 g008
Figure 8. Along-track profile of (a, d, and g) SWHs, H s ; (b, e, and h) spectral peak wavelength, λ p , and (c, f, and i) wave steepens, ϵ = k p H s / 2 with k p = 2 π / λ p . Blue circles and curves are the measurements and the orange curves represent the values associated with fully developed waves. The average time of the SWIM passage over the North Atlantic Ocean is written in the right side of each row. The SWIM nadir tracks can be found in 2nd, 8th and 10th rows of Figure 6.
Figure 8. Along-track profile of (a, d, and g) SWHs, H s ; (b, e, and h) spectral peak wavelength, λ p , and (c, f, and i) wave steepens, ϵ = k p H s / 2 with k p = 2 π / λ p . Blue circles and curves are the measurements and the orange curves represent the values associated with fully developed waves. The average time of the SWIM passage over the North Atlantic Ocean is written in the right side of each row. The SWIM nadir tracks can be found in 2nd, 8th and 10th rows of Figure 6.
Preprints 69804 g008
Preprints 69804 g009
Figure 9. Along-track wind speed, SWH and α inside the cyclone in a coordinate system associated with the coordinates of ETCs considering their heading aligned in x-direction, respectively, illustrated in (a–c) for ETC#1 and (d–f) for ETC#2.
Figure 9. Along-track wind speed, SWH and α inside the cyclone in a coordinate system associated with the coordinates of ETCs considering their heading aligned in x-direction, respectively, illustrated in (a–c) for ETC#1 and (d–f) for ETC#2.
Preprints 69804 g009
Preprints 69804 g010
Figure 10. Time evolution of maximum SWH values for ETC#1 (a) ETC#2 (b). The filled red circles are related to SWH of wind waves ( α > 0.85 ), and the open red circles - to SWH of swell. The black curves show SWH of fully developed waves calculated for local u m .
Figure 10. Time evolution of maximum SWH values for ETC#1 (a) ETC#2 (b). The filled red circles are related to SWH of wind waves ( α > 0.85 ), and the open red circles - to SWH of swell. The black curves show SWH of fully developed waves calculated for local u m .
Preprints 69804 g010
Preprints 69804 g011
Figure 11. Dimensionless energy, e ˜ , versus dimensionless time, t ˜ , for ETC#1 (a) and ETC#2 (b): red circles are observations, and green lines are duration laws (6). Dashed-black and dashed-blue lines indicate the dimensionless time interval t 0 and t m a x defined by (7) and (8), and corresponding dimensionless energy predicted by duration laws (6).
Figure 11. Dimensionless energy, e ˜ , versus dimensionless time, t ˜ , for ETC#1 (a) and ETC#2 (b): red circles are observations, and green lines are duration laws (6). Dashed-black and dashed-blue lines indicate the dimensionless time interval t 0 and t m a x defined by (7) and (8), and corresponding dimensionless energy predicted by duration laws (6).
Preprints 69804 g011
Table 1. Links to the datasets used in this study.
Table 1. Links to the datasets used in this study.
DATASET LINK
Sentinel-3 finder.creodias.eu
AltiKa aviso-data-center.cnes.fr
CryoSat-2 science-pds.cryosat.esa.int
JASON-3 aviso-data-center.cnes.fr
IFREMER l2s SWIM products ftp.ifremer.fr/ifremer/cersat/projects/iwwoc
CNES l2 SWIM products aviso-data-center.cnes.fr
NCEP/CFSv2 rda.ucar.edu/datasets/ds094.1/dataaccess
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated