Preprint
Article
Apex Method: A New Scalable Iterative Method for Linear Programming
Altmetrics
Downloads
219
Views
43
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
13 March 2023
Posted:
16 March 2023
Read the latest preprint version here
Alerts
Abstract
The article presents a new scalable iterative method for linear programming called the “apex method”. The key feature of this method is constructing a path close to optimal on the surface of the feasible region from a certain starting point to the exact solution of linear programming problem. The optimal path refers to a path of minimum length according to the Euclidean metric. The apex method is based on the predictor-corrector framework and proceeds in two stages: quest (predictor) and target (corrector). The quest stage calculates a rough initial approximation of linear programming problem. The target stage refines the initial approximation with a given precision. The main operation used in the apex method is an operation that calculates the pseudoprojection, which is a generalization of the metric projection to a convex closed set. This operation is used both in the quest stage and in the target stage. A parallel algorithm using a Fejér mapping to compute the pseudoprojection is presented. An analytical estimation of the parallelism degree of this algorithm is obtained. Also, an algorithm implementing the target stage is given. The convergence of this algorithm is proven. An experimental study of the scalability of the apex method on a cluster computing system is described. The results of applying the apex method to solve problems from the Netlib-LP repository are presented.
Keywords:
Subject: Computer Science and Mathematics - Computational Mathematics
1. Introduction
This article is an expanded and revised version of the conference paper [1]. The following motivation encouraged us to delve into this subject. The rapid development of big data storage and processing technologies [2,3] has led to the emergence of optimization mathematical models in the form of multidimensional linear programming (LP) problems [4]. Such LP problems arise in industry, economics, logistics, statistics, quantum physics and other fields [5,6,7]. An important class of LP applications are non-stationary problems related to optimization in dynamic environments [8]. For a non-stationary LP problem, the objective function and/or constraints change over the computational process. Examples of non-stationary problems are the following: decision support in high-frequency trading [9,10], hydro-gas-dynamics problems [11], optimal control of technological processes [12,13,14], transportation [15,16,17], scheduling [18,19].
One of the standard approaches to solving non-stationary optimization problems is to consider each change as the appearance of a new optimization problem that needs to be solved from scratch [8]. However, this approach is often impractical because solving a problem from scratch without reusing information from the past can take too much time. Thus, it is desirable to have an optimization algorithm capable of continuously adapting the solution to the changing environment, reusing information obtained in the past. This approach is applicable for real-time processes if the algorithm tracks the trajectory of the moving optimal point fast enough. In the case of large-scale LP problems, the last requirement necessitates the development of scalable methods and parallel algorithms of LP.
Until now, one of the most common ways to solve the LP problem was a class of algorithms proposed and developed by Danzig based on the simplex method [20]. The simplex method was found to be efficient for solving a large class of LP problems. In particular, the simplex method easily takes advantage of any hyper-sparsity in a LP problem [21]. However, the simplex method has some fundamental features that limit its use for the solution of large LP problems. First, in certain cases, the simplex method has to iterate through all the vertices of the simplex, which corresponds to exponential time complexity [22,23,24]. Second, in most cases, the simplex method successfully solves LP problems containing up to 50,000 variables. However, a loss of precision is observed when the simplex method is used for solving large LP problems [25]. Such a loss of precision cannot be compensated even by applying such computational intensive procedures as “affine scaling” or “iterative refinement” [26]. Third, in the general case, the sequential nature of simplex method makes it difficult to parallelize on multiprocessor systems with distributed memory [27]. Numerous attempts have been made to make a scalable parallel implementation of the simplex method, but all of them were unsuccessful [28]. In all cases, the scalability boundary was from 16 to 32 processor nodes (see, for example, [29]). Khachiyan proved [30], using a variant of the ellipsoid method (proposed in the 1970’s by Shor [31] and Yudin and Nemirovskii [32]), that LP problems can be solved in polynomial time. However, attempts to apply this approach in practice were unsuccessful, since in the vast majority of cases, the ellipsoid method demonstrated much worse efficiency compared to the simplex method. Later, Karmarkar [33] proposed a polynomial-time interior-point algorithm, which can be used in practice. This algorithm generated the whole field of modern interior-point methods [34], which are able to solve large-scale LP problems with millions of variables and millions of equations [35,36,37,38,39]. Moreover, these methods are self-correcting, and therefore provide high precision of calculations. A general lack of interior-point methods is the need to find some feasible point satisfying all the constraints of the LP problem before starting calculations. Finding such an interior point can be reduced to solving an additional LP problem [40]. Another method for finding an interior point is the pseudo-projection method [41], which uses Fejér mappings [42]. One more significant disadvantage of the interior-point method is its poor scalability on multiprocessor systems with distributed memory. There are several successful parallel implementations of the interior-point method for particular cases (see, for example, [43]), but, in the general case, an efficient parallel implementation on multiprocessor systems could not be built. In accordance with this, the development and research of new approaches to solving multidimensional non-stationary LP problems in real time is an urgent direction.
One of the most promising approaches to solving complex problems in real time is the use of neural network models [44]. Artificial neural networks (ANN) are a powerful universal tool that is applicable to solving problems in almost all areas. The most popular neural network model is the feedforward neural network. Training and operation of such networks can be implemented very efficiently on GPUs [45]. An important property of a feedforward neural network is that the time to solve a problem is a known constant that does not depend on the problem parameters. This feature is necessary for real-time mode. Pioneering work on the use of neural networks to solve LP problems is the article by Tank and Hopfield [46]. The article describes a two-layer recurrent neural network. The number of neurons in the first layer is the number of variables of the LP problem. The number of neurons in the second layer coincides with the number of constraints of the LP problem. The first and second layers are fully connected. The weights and biases are uniquely determined by the coefficients and the right-hand sides of the linear inequalities defining the constraints, and the coefficients of the linear objective function. Thus, this network does not require training. The state of the neural network is described by the differential equation , where is an energy function of a special type. Initially, an arbitrary point of the feasible region is fed to the input of the neural network. Then, the signal of the second layer is recursively fed to the first layer. Such process leads to convergence to a stable state in which the output remains constant. This state corresponds to the minimum of the energy function, and the output signal is a solution to the LP problem. The Tank and Hopfield approach has been expanded and improved in numerous works (see, for example, [47,48,49,50,51]). The main disadvantage of this approach is the unpredictable number of work cycles of the neural network. Therefore, a recurrent network based on an energy function cannot be used to solve large-scale LP problems in real time.
In the recent paper [52], a n-dimensional mathematical model for visualizing LP problems was proposed. This model makes it possible to use feedforward neural networks, including convolutional networks [53], to solve multidimensional LP problems, the feasible region of which is a bounded non-empty set. However, there are practically no works in scientific periodicals devoted to the use of convolutional neural networks for solving LP problems [54]. The reason is that convolutional neural networks focus on image processing, but there are no methods for constructing training datasets based on a visual representation of the multidimensional LP problems.
This article describes a new scalable iterative method for solving multidimensional LP problems. This method called “apex method”. The apex method allows you to generate training datasets for the development of feedforward neural networks capable of finding a solution to a multidimensional LP problem based on its visual representation. The apex method is based on the predictor-corrector framework. At the prediction step, a point belonging to the feasible region of the LP problem is calculated. The corrector step calculates a sequence of points converging to the exact solution of the LP problem. The rest of the paper is organized as follows. Section 2 provides a review of iterative projection-type methods and algorithms for solving linear feasibility problems and LP problems. Section 3 includes a theoretical basis of the apex method. Section 4 presents a formal description of apex method. Section 4.1 considers the implementation of the pseudoprojection operation in the form of sequential and parallel algorithms and provides an analytical estimation of the scalability of parallel implementation. Section 4.2 describes the quest stage. Section 4.3 describes the target stage. Section 5 presents an information about the software implementation of the apex method and describes the results of large-scale computational experiments on a cluster computing system. Section 6 discusses the issues related to the main contribution of this article, the advantages and disadvantages of the proposed approach, possible applications and some other aspects of using the apex method. Finally, in Section 7, we present our conclusions and comment on possible further studies of the apex method.
2. Related Work
This section provides an overview of works devoted to iterative projection-type methods used to solve linear feasibility and LP problems. The linear feasibility problem can be stated as follows. Consider the system of linear inequalities in matrix form
where , and . To avoid triviality, we assume that . The linear feasibility problem consists of finding a point satisfying matrix inequality system (1). We assume from now on that such a point exists.
Projection-type methods rely on the following geometric interpretation of the linear feasibility problem. Let be a vector formed by the elements of the ith row of the matrix A. Then, the matrix inequality is represented as a system of inequalities
Here and further on, stands for the dot product of vectors. We assume from now on that
for all . For each inequality , define the closed half space
and its bounding hyperplane
For any point , the orthogonal projection of point x onto the hyperplane can be calculated by the equation
Here and below, denotes the Euclidean norm. Let us define
We assume that , i.e. the solution of system (1) exists. In this case, M is a convex closed polytope in the space . In geometric interpretation, the linear feasibility problem consists of finding a point .
The forefathers of the iterative projection-type methods for solving linear feasibility problems are Kaczmarz and Cimmino. In [55] (English translation in [56]), Kaczmarz presented a sequential projections method for solving a consistent system of linear equations
His method, starting from an arbitrary point , calculates the following sequence of point groups:
for Here, is the orthogonal projection onto hyperplane defined by equation (6). This sequence converges to the solution of system (8). Geometrically, the method can be interpreted as follows. The initial point is projected orthogonally onto hyperplane . The projection is the point , which now is thrown onto . The resulting point is then thrown onto and gives the point , etc. As a result, we obtain the last point from the first point group. The second point group is constructed in the same way, starting from the point . The process is repeated for
Cimmino proposed in [57] (English description in [58]) a simultaneous projection method for the same problem. This method uses the following orthogonal reflection operation
which calculates the point symmetric to the point x with respect to the hyperplane . For the current approximation , the Cimmino method simultaneously calculates reflections with respect to all hyperplanes , and then a convex combination of these reflections is used to form the next approximation:
where , . When , equation (11) is transformed into the following equation:
Agmon [59] and Motzkin and Schoenberg [60] generalized the projection method from equations to inequalities. To solve problem (1), they introduce the relaxed projection
where . It is obvious that . To calculate the next approximation, relaxed projection method uses the following equation:
where
Informally, the next approximation is a relaxed projection of the previous approximation with respect to the furthest hyperplane bounding the half-space not containing . Agmon in [59] showed that sequence converges, as , to a point on the boundary of M.
Censor and Elfving, in [61], generalized the Cimmino method to the case of linear inequalities. They consider the relaxed projection onto the half-space defined as follows:
that gives the equation
Here, , and , . In [62], De Pierro proposed an approach to convergence proof for this method, which differs from the approach of Censor and Elfving. De Piero’s approach is also acceptable for the case when the underlying system of linear inequalities is infeasible. In this case, for , sequence (17) converges to the point that is the minimum of the function , i.e., it is a weighted (with the weights ) least squares solution of system (1).
The Cimmino-like methods allow efficient parallelization, since orthogonal projections (reflections) can be calculated simultaneously and independently. The article [63] investigates the efficiency of parallelization of the Cimmino-like method on Xeon Phi manycore processors. In [64], the scalability of the Cimmino method for multiprocessor systems with distributed memory is evaluated. The applicability of the Cimmino-like method for solving non-stationary systems of linear inequalities on computing clusters is considered in [65].
As a recent work, we can mention article [66], which extends the Agmon-Motzkin-Schoenberg relaxation method for the case of semi-infinite inequality systems. The authors consider the system with an infinite number of inequalities in the finite-dimensional Euclidean space :
where I is an arbitrary infinite index set. The main idea of the method is as follows. Let the hyperplane be the biggest violation with respect to x. Let be an arbitrary initial point. If the current iteration is not a solution of system (18), then let be the orthogonal projection of onto a hyperplane () near the biggest violation . If system (18) is consistent, then the sequence generated by the described method converges to the solution of this system.
Solving systems of linear inequalities is closely related to LP problems, so projection-type methods can be effectively used to solve this class of problems. The equivalence of the linear feasibility problem and the LP problem is based on the primal-dual LP problem. Consider the primal LP problem in the matrix form:
where , , , and . Here and below, stands for the dot product of vectors. Let us construct the dual problem with respect to problem (19):
where . The following primal-dual equality holds:
In [67,68], Eremin proposed the following method based on the primal-dual approach. Let the inequality system
define the feasible region of primal problem (19). This system is obtained by adding to the system the vector inequality . In this case, , and . Let stand the ith row of the matrix . For each inequality , define the closed half space
and its bounding hyperplane
Let stand the orthogonal projection of point x onto the hyperplane :
Let us define the projection onto the half-space :
This projection has the following two properties:
Define as follows:
In the same way, define the feasible region of dual problem (20) as follows:
where , , and . Denote
and define as follows:
Now, define as follows:
which is corresponding to equation (21). Here, stands for the concatenation of vectors.
Finally, define as follows:
If the feasible region of the primal problem is a bounded and nonempty set, then the sequence
converges to the point , where is the solution of primal problem (19), and is the solution of dual problem (20).
Article [69] proposes a method for solving non-degenerate LP problems based on calculating the orthogonal projection of some special point, independent of the main part of data describing the LP problem, onto a problem-dependent cone generated by the constraint inequalities. Actually, this method solves a symmetric positive definite system of linear equations of a special kind. The author demonstrates a finite algorithm of active-set family that is capable of calculating orthogonal projections for problems with up to thousands of rows and columns. The main drawback of this method is a significant increasing the dimension of the primary problem.
In article [70], Censor proposes the linear superiorization (LinSup) method as a tool for solving LP problems. The LinSup method does not guarantee finding the minimum point of the LP problem, but it directs the linear feasibility-seeking algorithm that it uses toward a point with a decreasing value of the objective function. This process is not identical with that employed by LP solvers but it is a possible alternative to the Simplex method for problems of huge size. The basic idea of LinSup is to add an extra term, called perturbation term, to the iterative equation of the projection method. The perturbation term steers the feasibility-seeking algorithm toward reduced the objective function values. In the case of LP problem (19), the objective function is , and LinSup adds as a perturbation term to iterative equation (17):
Here, is a perturbation parameter.
Article [52] proposes a mathematical model for the visual representation of multidimensional LP problems. To visualize a feasible LP problem, an objective hyperplane is introduced, the normal to which is the gradient of the objective function . In the case of seeking the maximum, the objective hyperplane is positioned in such a way that the value of the objective function at all its points is greater then the value of the objective function at all points of the convex polytope M, which is the feasible region of the LP problem. For any point , the objective projection onto M is defined as follows:
Here, denotes the orthogonal projection onto . On the objective hyperplane , a rectangular lattice of points is constructed, where K is the number of lattice points in one dimension. Each point is mapped to the real number . This mapping generates a matrix of dimension , which is an image of the LP problem. This approach opens up the possibility of using feed-forward artificial neural networks, including convolutional neural networks, to solve multidimensional LP problems. One of the main obstacles to the implementation of this approach is the problem of generating a training set. The literature review shows that there is no suitable method capable of constructing such a training set compatible with the described approach. In the next sections, we present such a method.
3. Theoretical Basis
In this section we present a theoretical basis used to construct the apex method. Consider the LP problem in the following form:
where , , , , and . We assume that the constraint is also included in the system in the form of the following inequalities:
Let stand for the set of row indices in matrix A:
Let be a vector formed by the elements of the ith row of the matrix A, and for all . We denote by the closed half space defined by the inequality , and by the hyperplane bounding :
Definition 1.
The half-space is called dominant with respect to the vector c, or briefly c-dominant, if
The geometric meaning of this definition is that a ray outgoing from a point belonging to a half-space in the direction of vector c belongs to this half-space.
Definition 2.
The half-space is called recessive with respect to the vector c, or briefly c-recessive, if it is not c-dominant, i.e.,
The following proposition provides the necessary and sufficient condition for the c-recessivity of the half-space.
Proposition 1.
Let a half-space be defined by the following equation:
Then, the necessary and sufficient condition for the c-recessivity of the half-space is
Proof.
Let us prove the necessity first. Let condition (43) hold. Denote
Substituting the right-hand side of equation (46) instead of , we obtain
Since , it follows
Thus, the necessity is proved.
Let us prove the sufficiency by contradiction. Assume that (45) holds, and is not c-recessive, i.e.,
Substituting the right-hand side of equation (46) instead of , we obtain
Since , it follows
But this contradicts (45). □
Denote
i.e., stands for the unit vector parallel to vector c.
Proposition 2.
Let the half-space be c-recessive. Then, for any point and any number , the point
does not belong to the half-space , i.e.
Proof.
The half-space is c-recessive, therefore, according to Proposition 1, the following inequality holds:
Taking (58) into account, we have
Since , by virtue of (60), the inequality holds. It follows that , i.e. . □
Define
i.e., is the set of indices for which the half-space is c-recessive. We assume from now on that
Corollary 1.
Let an arbitrary feasible point of LP problem (38) be given:
Then, for any positive number , the point
does not belong to any c-recessive half-space , i.e.,
Proof.
From (65), we obtain
Hence,
for any . Fix any , and define
where . Taking into account (70), it follows that . Using (66) and (71), we obtain
According to Proposition 2, it follows that , i.e., the point z defined by (66) does not belong to the half-space for any . □
The following proposition specifies the region containing a solution of LP problem (38).
Proposition 3.
Let be a solution of LP problem (38). Then, there is an index such that
i.e., there is a c-recessive half-space such that its bounding hyperplane includes .
Proof.
Denote by the set of indices for which the half-space is c-dominant:
Define the ray Y as follows:
By Definition 1, we have
i.e., the ray Y belongs to the all c-dominant half-spaces. By virtue of Definition 2,
Taking into account (76), it means that
i.e., the intersection of the ray Y and any hyperplane bounding the c-recessive half-space is a single point . Let
i.e., is the nearest hyperplane to the point for . Denote by the intersection of the ray Y and the hyperplane :
According to (81),
i.e., the point belongs to the all c-recessive half-spaces. By (78), it follows that
i.e., belongs to the feasible region of LP problem (38). Let
Then, in virtue of (77),
Since is a solution of LP problem (38), the following condition holds:
Comparing this with (84), we obtain that
Definition 3.
Let be a convex closed set. A single-valued mapping is called M-Fejér mapping [67], if
and
Proposition 4.
Let . If is a continuous M-Fejér mapping and
is the iterative process generated by this mapping, then
Proof.
The convergence follows directly from Theorem 6.2 and Corollary 6.3 in [67]. □
Let stand for the orthogonal projection of point x onto hyperplane :
The next proposition provides a continuous M-Fejér mapping, which will be used in the apex method.
Proposition 5.
Let be the convex closed set representing the feasible region of LP problem (38):
For any point , let us define
i.e., is the set of indices for which the half-space does not contain the point x. Then, the single-valued mapping defined by the equation
is a continuous M-Fejér mapping.
Proof.
Obviously, the mapping is continuous. Let us prove that condition (90) holds. Our proof is based on a general scheme presented in [67]. Let , and . It follows that
By virtue of the equation (94), the following inequalities holds
for all . According to Lemma 3.13 in [67], the following inequality holds for all :
It follows that
Hence,
□
Definition 4.
The correctness of this definition is ensured by propositions 4 and 5.
4. Description of Apex Method
In this section, we describe a new scalable iterative method for solving LP problem (38), called the “apex method”. The apex method is based on the predictor-corrector framework and proceeds in two stages: quest (predictor) and target (corrector). The quest stage calculates a rough initial approximation of LP problem (38). The target stage refines the initial approximation with a given precision. The main operation used in the apex method is an operation that calculates a pseudoprojection according to Definition 4. This operation is used both in the quest stage and in the target stage. In the next section, we describe and investigate a parallel algorithm for calculating a pseudoprojection.
4.1. Algorithm for Calculating Pseudoprojection
In this section, we consider the implementation of the pseudoprojection operation in the form of sequential and parallel algorithms. The pseudoprojection operation
maps an arbitrary point to a point belonging to the feasible polytope M, which is the feasible region of LP problem (38). The calculation of is organized as an iterative process using equation (95). A sequential implementation of this process is presented by Algorithm 1.

Let us give brief comments on this implementation. The main iterative process of constructing a sequence of Fejér’s approximations is represented by the repeat/until loop implemented in steps 4–20. The steps 5–10 calculate the set of indices of half-spaces violated by the point presenting the current approximation. In steps 14–18, the next approximation is calculated by equation (95). The process terminates when the distance between adjacent approximations becomes less than , where is a small positive parameter. Computational experiments (see [1,71]) show that, in the case of large LP problems, the calculation of a pseudoprojection is a process with high computational complexity. Therefore, we developed a parallel implementation of Algorithm 1, presented by Algorithm 2.

Algorithm 2 is based on the BSF parallel computation model [72] designed for a cluster computing system. The BSF model uses the master/worker paradigm and requires the representation of the algorithm in the form of operations on lists using higher-order functions Map and Reduce. In Algorithm 2, we use the list of ordinal numbers of constraints of LP problem (38) as the second parameter of the higher-order function Map. As the first parameter of the higher-order function Map, we use the parameterized function
defined as follows:
Thus, the higher-order function transforms the list of constraint numbers into a list of pairs . Here, is the orthogonal projection of the point x onto the hyperplane in the case , and the zero vector otherwise; is the indicator that x violates the half-space ():
Denote . Define a binary associative operation
which is the first parameter of the higher-order function Reduce, as follows:
The higher-order function folds the list into the single pair by sequentially applying the operation ⊕ to all elements of the list:
where
In Algorithm 2, a parallel execution of work is organized according to the master/worker scheme. The parallel algorithm includes processes: one master process and L worker processes. The master manages the computations, distributes the work among the workers, gathers the results back from them and summarizes all the results to obtain the final result. For the sake of simplicity, it is assumed that the number of constraints m of LP problem (38) is a multiple of the number of workers L. In Step 1, the master reads the space dimension n and the staring point . Step 3 of the master assigns zero to the iteration counter k. Steps 4–14 implement the main repeat/until loop calculating the pseudoprojection. In Step 5, master broadcasts the current approximation to all workers. Step 9 of the master gathers partial results from all workers. In Step 9, the master folds the partial results into the pair , which is used to calculate the next approximation in Step 10. Step 11 of the master increases the iteration counter k by 1. In Step 12, the master calculates the criterion for stopping the iterative process and assigns the result to the Boolean variable . In Step 13, master broadcasts the value of the Boolean variable to all workers. In Step 14, the repeat/until loop ends if the Boolean variable takes the value . Step 15 of the master outputs the last approximation as a result of the pseudoprojection. Step 16 terminates the master process.
All workers execute the same program codes, but with different data. In Step 1, the lth worker reads problem data. In steps 2–3, the lth worker defines its own sublist for processing. For convenience, we number the constraints starting from zero. The sublists of different workers do not overlap, and their concatenation represents the entire list to be processed:
The repeat/until loop of the lth worker corresponds to the repeat/until loop of the master (steps 4–14). In Step 5, the lth worker receives the current approximation from the master. Step 6 of the lth worker executes the higher-order function , which applies the parameterized function defined by (101) to all elements of the sublist , resulting in the sublist . Step 7 of the lth worker executes the higher-order function , which applies the operation ⊕ defined by (103) to all elements of the list , resulting in the pair . In Step 8, the lth worker sends its resulting pair to the master. In Step 13, the lth worker receives a value of the Boolean variable from the master. If then worker process is terminated. Otherwise, the repeat/until loop continues its work. The exchange operators Bcast, Gather, RecvFromMaster, and SendToMaster provide synchronization of the master and workers processes.
Let us estimate the scalability boundary of the described pseudoprojection parallel algorithm, using the cost metrics of BSF model [72]. Here, the scalability boundary refers to the number of worker processes at which the maximum speedup is achieved. The cost metric of the BSF model includes the following parameters.
- m : length of the list ;
- D : latency (time taken by the master to send one byte message to a single worker);
- : time taken by the master to send the current approximation to a single worker and receive the pair from it (including latency);
- : time taken by a single worker to process the higher-order function Map for the entire list ;
- : time taken by computing the binary operation ⊕.
According to Equation (14) from [72], the scalability boundary of a parallel algorithm can be estimated as follows:
Let us calculate the time parameters in equation (108). To do this, we introduce the following notation for one iteration of the repeat/until loop implemented in steps 4–14 of Algorithm 2:
- : quantity of numbers sent from the master to the lth worker and back within one iteration;
- : quantity of arithmetic and comparison operations required to compute the function defined by equations (101);
- : quantity of arithmetic and comparison operations required to compute the binary operation ⊕ .
In Step 5, the master sends to the lth worker one vector of dimension n. Then, in Step 8, the master receives a pair consisting of a vector of dimension n and a single number from the lth worker. In addition, in Step 13, the master sends a single Boolean value to the lth worker. Hence,
According to (103), the following equations holds for :
Let us denote by the execution time of one arithmetic or comparison operation, and by the time of sending a single real number from one process to another (excluding latency). Then, using (109), (110) and (111), we obtain
Recall that the parameter D denotes the latency. Substituting the right-hand sides of these equations into (108), we have
where n is the space dimension, m is the number of constraints. For large values of n and m, this is equivalent to
This estimation suggests that Algorithm 2 is limited-scalable, and the scalability depends on the number of constraints m.
4.2. Quest Stage
The quest stage of the apex method plays the role of a predictor and includes the following steps.
- Calculate a feasible point .
- Calculate the apex point z.
- Calculate the point that is the pseudoprojection of the apex point z onto the feasible polytope M.
The feasible point , in Step 1, can be calculated by the following equation:
where is the operation of pseudoprojection onto the feasible polytope M (see Definition 4).
Step 2 calculates the apex point z by the following equation:
where defined by equation (63) is the set of indices for which the half-space is c-recessive, and is a positive parameter. Corollary 1 guarantees that the point z chosen according to equation (117) does not belong to any c-recessive half-space . This choice is based on the intuition that the pseudoprojection from such a point will not be very far from the exact solution of the LP problem. The interpretation of this intuition comes from Proposition 3, which states that the solution of the LP problem (38) lies on some hyperplane bounding the c-recessive half-space . The parameter can significantly affect the proximity of the point to the exact solution. The optimal value of can be obtained by seeking the maximum of the objective function using the successive dichotomy method.
Step 3 calculates the initial approximation for the target stage by the following equation:
Numerous computational experiments show that the process of calculating the pseudoprojection by Definition 4 starting from an exterior point always converges to a point on the boundary of the feasible polytope M. However, at the moment, we do not have a rigorous proof of this fact.
4.3. Target Stage
The target stage of the apex method plays the role of a corrector and calculates a sequence of points
that has the following properties for all :
Here, stands for the set of boundary points of the feasible polytope M. Condition (120) means that all points of sequence (119) lie on the boundary of the polytope M. Condition (121) states that the value of the objective function at each next point of sequence (119) is greater than at the previous one. According to condition (122), sequence (119) converges to the exact solution of LP problem (38). An implementation of the Target stage is presented in Algorithm 3.

Let us give brief comments on the steps of Algorithm 3. Step 1 reads the initial approximation constructed at the quest stage. Step 2 assigns zero to the iteration counter k. Step 3 adds the vector to and assigns the result to v. Here, is a unit vector parallel to c, is a positive parameter. The parameter must be small enough to ensure that . Recall that denotes the set of boundary points of the feasible polytope M. Step 4 calculates the pseudoprojection and assigns the result to w. Steps 5–19 implement the main loop. This loop is processed while the condition
holds. Here, is a small positive parameter. Step 6 introduces the point u moving along the surface of the polytope M from the point to the next approximation . Step 7 calculates the vector d, which defines the direction of movement of the point u. The loop in steps 8–14 moves the point u along the surface of the polytope M in this direction as far as possible. To achieve this, the vector d is successively divided in half each time the next step moves u beyond the boundary of the polytope M. The movement stops when the length of the vector d becomes less than . Here, is a small positive parameter. Step 15 sets the next approximation using the value of u. Step 16 increases the iteration counter k by 1. Steps 17 and 18 calculate new points v and w for the next iteration of the main loop. Step 20 outputs as the final approximation of the exact solution of LP problem (38). Schematically, the work of Algorithm 3 is shown in Figure 1.
The following proposition guarantees the convergence of Algorithm 3.
Proposition 6.
Let the feasible polytope M of LP problem (38) be a closed bounded set, and . Then, the sequence generated by Algorithm 3 terminates in the finite number of iteration , and
Proof.
The case when is trivial. Let or . First, we show that for any the following inequality holds:
Indeed, inequality (123) implies
According to Step 7 in Algorithm 3, it follows that
Without loss of generality, we can assume that . Then, according to steps 8-15, we obtain
where . Taking into account inequality (123) and Step 7 of Algorithm 3, it follows
Now, we show that . Assume the opposite, i.e. Algorithm 3 generates the infinite sequence of points. In this case, we obtain the monotonically increasing numerical sequence
Since the feasible polytope M is bounded, sequence (129) is bounded from above. According to the monotone convergence theorem, a monotonically increasing numerical sequence bounded from above converges to its supremum. This means that there exists such that
It follows
that is equivalent to
Thus, we obtain a contradiction with the stopping criterion (123) used in Step 5 of Algorithm 3. □
The notion of pseudoprojection is a generalization of the notion of metric projection, which can be defined as follows [67].
Definition 5.
Let Q be a closed convex set in , and . The metric projection of the point onto the set Q is defined by the equation
For the metric projection, the following proposition similar to Proposition 6 for the pseudoprojection holds.
Proposition 7.
The sequence generated by Algorithm 3 with the metric projection instead of the pseudoprojection terminates in the finite number of iteration , and
Proof.
The proof follows the same scheme as the proof of Proposition 6. □
The following proposition states that Algorithm 3 with metric projection converges to the exact solution of LP problem.
Proposition 8.
Let the pseudoprojection be replaced by the metric projection in Algorithm 3. Then, Algorithm 3 converges to the exact solution of LP problem (38).
Proof.
Let stand for the terminal point of the sequence generated by Algorithm 3 with the metric projection . This point exists according to Proposition 7. Assume the opposite, i.e., . This is equivalent to
Let designate the open n-ball of radius and center v, where
According to (135), it follows that
Let
This is equivalent to
It is easy to see that the following inequality holds:
In case of using the pseudoprojection in Algorithm 3, the convergence to the exact solution is based on the intuition that with . However, a rigorous proof of this fact is beyond the scope of this article.
5. Implementation and Computational Experiments
We implemented a parallel version of the apex method in C++ using the BSF-skeleton [73], which is based on the BSF parallel computation model [72]. The BSF-skeleton encapsulates all aspects related to the parallelization of a program using the MPI library. The source code of this implementation is freely available at https://github.com/leonid-sokolinsky/Apex-method. Using this program, we investigated the scalability of the apex method. The computational experiments were conducted on the “Tornado SUSU” computing cluster [74], whose specifications are shown in Table 1.
As test problems, we used random synthetic LP problems generated by the program FRaGenLP [75]. A verification of solutions obtained by the apex method was performed using the program VaLiPro [76]. We conducted a series of computational experiments in which we investigated the dependence of speedup on the number of processor nodes used. Here, the speedup is defined as the ratio of the time required by parallel algorithm using one master node and one worker node to solve a problem to the time required by parallel algorithm using one master node and L worker nodes to solve the same problem:
The computations were performed with the following dimensions: , and . The number of inequalities was , and , respectively. The results of computational experiments are presented in Figure 2.
These experiments showed that the scalability boundary of the parallel apex algorithm depends significantly on the size of the LP problem. At , the scalability boundary was approximately 55 processor nodes. For the problem of dimension , this boundary increased to 80 nodes, and for the problem of dimension , it was close to 100 nodes. Further increasing the problem size caused the compiler error: “insufficient memory”. It should be noted that the computations were performed in the double precision floating-point format occupying 64 bits in computer memory. An attempt to use the single-precision floating-point format occupying 32 bits failed because the apex algorithm stopped to converge. The experiments have also shown that the parameter used in equation (117) to calculate the apex point z at the quest stage has a negligible effect on the total time of solving the problem when this parameter has large values (more then ). If the apex point is not far enough away from the polytope, then its pseudo-projection can be an interior point of some polytope face. If the apex point is taken far enough away from the polytope (the value was used in the experiments), then the pseudo-projection always fell into one of the polytope vertices. Also, we would like to note that, in the case of synthetic LP problems generated by the program FRaGenLP, all computed points in the sequence were vertices of the polytope. The computational experiment showed that more than 99% of the time spent for solving the LP problem by the apex method was taken by the calculation of pseudoprojections (Step 18 of Algorithm 3). At that, the calculation of one approximation for a problem of dimension on 100 processor nodes took 44 minutes.
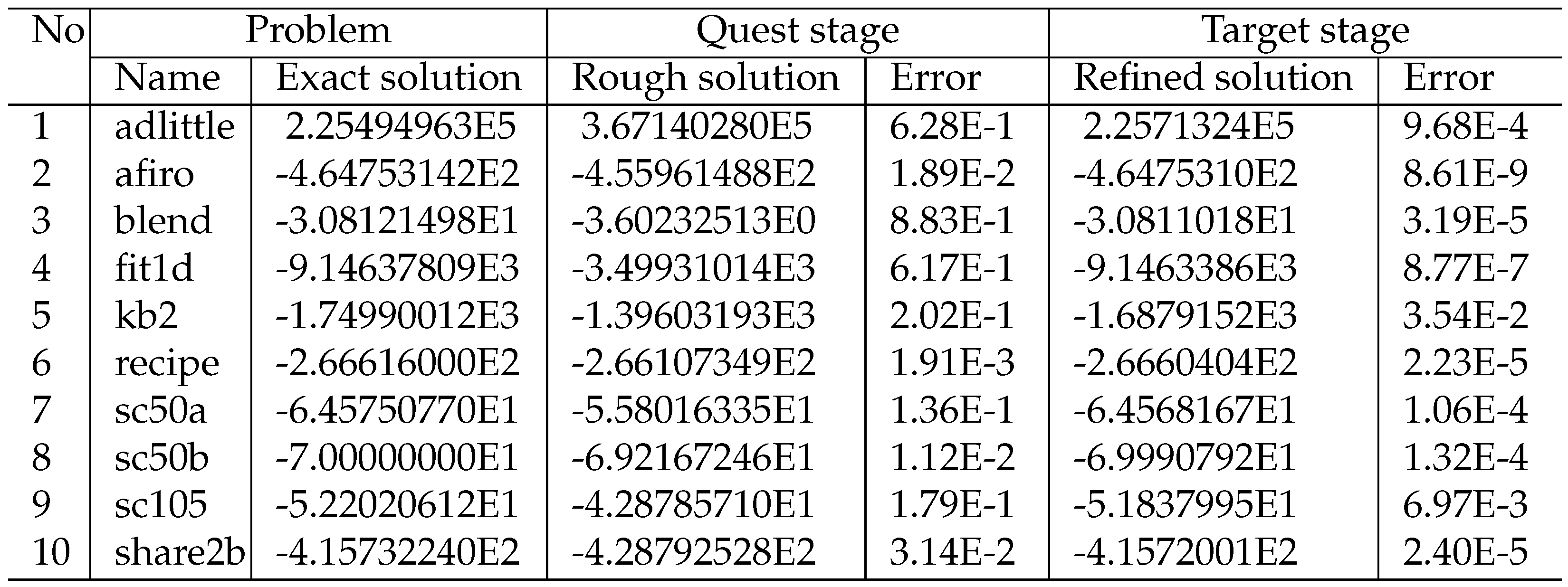
We also tested the apex method on a subset of LP problems from the Netlib-LP repository [77] available at https://netlib.org/lp/data. The Netlib suite of linear optimization problems includes many real world applications like stochastic forestry problems, oil refinery problems, flap settings of aircraft, pilot models, audit staff scheduling, truss structure problems, airline schedule planning, industrial production and allocation models, image restoration problems, and multisector economic planning problems. It contains problems ranging in size from 32 variables and 27 constraints up to 15695 variables and 16675 constraints [78]. The exact solutions (optimal values of objective functions) of all problems were obtained from paper [79]. The results are presented in Table 2.
These experiments showed that the relative error of the rough solution calculated at the quest stage was less than or equal to 0.2, excluding the adlittle, blend, and fit1d problems. The relative error of the refined solution calculated at the target stage was less than , excluding the kb2 and sc105, for which the error was and , respectively. The runtime varied from a few seconds for afiro to tens of hours for blend. One of the main parameters affecting the convergence rate of the apex method was the parameter used in Step 12 of the parallel Algorithm 2 calculating the pseudoprojection. All runs are available on https://github.com/leonid-sokolinsky/Apex-method/tree/master/Runs.
6. Discussion
In this section of the article, we will discuss some issues related to the scientific contribution and applicability of the apex method in practice and give answers to the following questions.
- What is the scientific contribution of this article?
- What is the practical significance of the apex method?
- What is our confidence that the apex method always converges to the exact solution of LP problem?
- How can we speed up the convergence of the Algorithm 1 calculating a pseudoprojection on the feasible polytope M?
The main scientific contribution of this article is that it presents the apex method that allows, for the first time, as far as we know, to construct a path close to optimal on the surface of feasible polytope from a certain starting point to the exact solution of LP problem. Here, the optimal path refers to a path of minimum length according to the Euclidean metric. By intuition, moving in the direction of the greatest increase in the value of the objective function will give us the shortest path to the point of maximum of the objective function on the surface of the feasible polytope. We intend to present a formal proof of this fact in a future work.
The practical significance of the apex method is based on the issue of applying feed-forward neural networks, including convolutional neural networks, to solve LP problems. In recent paper [52], a method of visual representation of n-dimensional LP problems was proposed. This method constructs an image of the feasible polytope M in the form of a matrix I of dimension using rasterization technique. A vector antiparallel to the gradient vector of the objective function is used as the view ray. Each pixel value in I is proportional to the value of the objective function at the corresponding point on the surface of a feasible polytope M. Such an image makes it possible to use a feedforward neural network to construct the optimal path on the surface of the feasible polytope to the solution of the LP problem. Actually, the feedforward neural network can directly calculate the vector d in Algorithm 3, making the calculation of pseudoprojection redundant. The advantage of this approach is that the feed-forward neural network works in real time, which is important for robotics. We are not aware of other methods that solves LP problems in real time. However, applying a feedforward neural network to solve LP problems involves the task of preparing a training dataset. The apex method provides the possibility to construct such a training dataset.
Proposition 6 states that Algorithm 3 converges to some point on the surface of the feasible polytope M in a finite number of steps, but leaves open the question whether the terminal point will be a solution to the LP problem. According to Proposition 8, the answer to this question is positive if, in Algorithm 3, the pseudoprojection is replaced by the metric projection. However, there are no methods for constructing the metric projection for an arbitrary bounded convex polytope. Therefore, we are forced to use the pseudoprojection. Numerous experiments show that the apex method converges to the solution of the LP problem, but this fact requires a formal proof. We plan to make such a proof in our future work.
The main drawback of the apex method is the slow rate of convergence to the solution of the LP problem. The LP problem, which takes several seconds to find the optimal solution by standard linear programming solvers, may take several hours to solve by the apex method. Computational experiments demonstrated that more than 99% of the time spent for solving the LP problem by the apex method was taken by the calculation of pseudoprojections. Therefore, the issue of speeding up the process of calculating the pseudoprojection is urgent. In the apex method, the pseudoprojection is calculated by Algorithm 1, which belongs to the class of projection-type methods discussed in detail in Section 2. In the case of closed bounded polytope , the projection-type methods have a low linear rate of convergence:
where is some constant, and is a parameter that depends on the angles between the half-spaces corresponding to the faces of the polytope M [80]. This means that the distance between adjacent approximations decreases at each iteration by a constant factor less than 1. For small angles, the convergence rate can decrease to values close to zero. This fundamental limitation of the projection-type methods cannot be overcome. However, we can reduce the number of half-spaces used to compute the pseudoprojection. According to Proposition 3, the solution of LP problem (38) belongs to some c-recessive half-space. Hence, in Algorithm 1 calculating the pseudoprojection, we can take into account only the c-recessive hyperplanes. On average, this reduces the number of half-spaces by two times. Another way to reduce the pseudoprojection calculation time is to parallelize Algorithm 1, as was done in Algorithm 2. However, the degree of parallelism in this case will be limited by the theoretical estimation (115).
7. Conclusion
In this paper, we proposed a new scalable iterative method for linear programming called the “apex method”. The key feature of this method is constructing a path close to optimal on the surface of the feasible region from a certain starting point to the exact solution of linear programming problem. The optimal path refers to a path of minimum length according to the Euclidean metric. The main practical contribution of the apex method is that it opens the possibility of using feedforward neural networks to solve multidimensional LP problems.
The paper presents a theoretical basis used to construct the apex method. The half-spaces generated by the constraints of the LP problem are considered. These half-spaces form the feasible polytope M, which is a closed bounded set. These half-spaces are divided into two groups with respect to the gradient c of the linear objective function: c-dominant and c-recessive. The necessary and sufficient condition for the c-recessivity is obtained. It is proved that the solution of the LP problem lies on the boundary of a c-recessive half-space. The equation defining the apex point not belonging to any c-recessive half-space is derived. The apex point is used to calculate the initial approximation on the surface of the feasible polytope M. The apex method constructs a path close to optimal on the surface of the feasible polytope M from this initial approximation to the solution of the LP problem. To do this, it uses a parallel algorithm constructing the pseudoprojection, which is a generalization of the notion of metric projection. For this parallel algorithm an analytical estimation of the scalability bound is obtained. This estimation says that the scalability boundary of the parallel algorithm of calculating the pseudoprojection on a cluster computing system does not exceed processor nodes, where m is the number of constrains of the linear programming problem. The algorithm constructing a path close to optimal on the surface of the feasible polytope, from the initial approximation to the exact solution of linear programming problem, is described. The convergence of this algorithm is proven.
The parallel version of the apex method is implemented in C++ using the BSF-skeleton based on the BSF parallel computation model. Large-scale computational experiments were conducted to investigate the scalability of the apex method on a cluster computing system. These experiments show that, for a synthetic scalable linear programming problem with a dimension of and a constraint number of , the scalability boundary of the apex methods is close to 100 processor nodes. At the same time, these experiments showed that more than 99% of the time spent for solving the LP problem by the apex method was taken by the calculation of pseudoprojections.
In addition, the apex method was used to solve 10 problems from the Netlib-LP repository. These experiments showed that the relative error varied from to . The runtime ranged from a few seconds for to tens of hours. The main parameter affecting the convergence rate of the apex method was the precision of calculating the pseudoprojection.
Our future research directions on this subject are as following. We plan to develop a new method for calculating the pseudoprojection onto the feasible polytope of the LP problem. The basic idea is to reduce the number of half-spaces used in one iteration. At the same time, the number of these half-spaces should remain large enough to enable the efficient parallelization. The new method should outperform Algorithm 2 in terms of convergence rate. We will also need to prove that the new method converges to a point that lies on the boundary of the feasible region. In addition, we plan to investigate the usefulness of utilizing the linear superiorization technique [70] in the apex method.
Author Contributions
All authors contributed equally to the main text. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by RSF (project No. 23-21-00356).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sokolinsky, L.B.; Sokolinskaya, I.M. Scalable Method for Linear Optimization of Industrial Processes. In Proceedings of the Proceedings - 2020 Global Smart Industry Conference, GloSIC 2020. IEEE, 2020, pp. 20–26. Article number 9267854. [CrossRef]
- Jagadish, H.V.; Gehrke, J.; Labrinidis, A.; Papakonstantinou, Y.; Patel, J.M.; Ramakrishnan, R.; Shahabi, C. Big data and its technical challenges. Communications of the ACM 2014, 57, 86–94. [CrossRef]
- Hartung, T. Making Big Sense From Big Data. Frontiers in Big Data 2018, 1, 5. [CrossRef]
- Sokolinskaya, I.; Sokolinsky, L.B. On the Solution of Linear Programming Problems in the Age of Big Data. In Proceedings of the Parallel Computational Technologies. PCT 2017. Communications in Computer and Information Science, vol. 753.; Sokolinsky, L.; Zymbler, M., Eds.; Springer: Cham, 2017; pp. 86–100. [CrossRef]
- Chung, W. Applying large-scale linear programming in business analytics. In Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM). IEEE, 2015, pp. 1860–1864. [CrossRef]
- Gondzio, J.; Gruca, J.A.; Hall, J.A.J.; Laskowski, W.; Zukowski, M. Solving large-scale optimization problems related to Bell’s Theorem. Journal of Computational and Applied Mathematics 2014, 263, 392–404. [CrossRef]
- Sodhi, M.S. LP modeling for asset-liability management: A survey of choices and simplifications. Operations Research 2005, 53, 181–196. [CrossRef]
- Branke, J. Optimization in Dynamic Environments. In Evolutionary Optimization in Dynamic Environments. Genetic Algorithms and Evolutionary Computation, vol. 3; Springer: Boston, MA, 2002; pp. 13–29. [CrossRef]
- Brogaard, J.; Hendershott, T.; Riordan, R. High-Frequency Trading and Price Discovery. Review of Financial Studies 2014, 27, 2267–2306. [CrossRef]
- Deng, S.; Huang, X.; Wang, J.; Qin, Z.; Fu, Z.; Wang, A.; Yang, T. A Decision Support System for Trading in Apple Futures Market Using Predictions Fusion. IEEE Access 2021, 9, 1271–1285. [CrossRef]
- Seregin, G. Lecture notes on regularity theory for the Navier-Stokes equations; World Scientific Publishing Company: Singapore, 2014; p. 268. [CrossRef]
- Demin, D.A. Synthesis of optimal control of technological processes based on a multialternative parametric description of the final state. Eastern-European Journal of Enterprise Technologies 2017, 3, 51–63. [CrossRef]
- Kazarinov, L.S.; Shnayder, D.A.; Kolesnikova, O.V. Heat load control in steam boilers. In Proceedings of the 2017 International Conference on Industrial Engineering, Applications and Manufacturing, ICIEAM 2017 - Proceedings. IEEE, 2017. [CrossRef]
- Zagoskina, E.V.; Barbasova, T.A.; Shnaider, D.A. Intelligent Control System of Blast-furnace Melting Efficiency. In Proceedings of the SIBIRCON 2019 - International Multi-Conference on Engineering, Computer and Information Sciences, Proceedings. IEEE, 2019, pp. 710–713. [CrossRef]
- Fleming, J.; Yan, X.; Allison, C.; Stanton, N.; Lot, R. Real-time predictive eco-driving assistance considering road geometry and long-range radar measurements. IET Intelligent Transport Systems 2021, 15, 573–583. [CrossRef]
- Scholl, M.; Minnerup, K.; Reiter, C.; Bernhardt, B.; Weisbrodt, E.; Newiger, S. Optimization of a thermal management system for battery electric vehicles. In Proceedings of the 14th International Conference on Ecological Vehicles and Renewable Energies, EVER 2019. IEEE, 2019. [CrossRef]
- Meisel, S. Dynamic Vehicle Routing. In Anticipatory Optimization for Dynamic Decision Making. Operations Research/Computer Science Interfaces Series, vol. 51; Springer: New York, NY, 2011; pp. 77–96. [CrossRef]
- Cheng, A.M.K. Real-Time Scheduling and Schedulability Analysis. In Real-Time Systems: Scheduling, Analysis, and Verification; John Wiley and Sons, 2002; pp. 41–85. [CrossRef]
- Kopetz, H. Real-Time Scheduling. In Real-Time Systems. Real-Time Systems Series; Springer: Boston, MA, 2011; pp. 239–258. [CrossRef]
- Dantzig, G.B. Linear programming and extensions; Princeton university press: Princeton, N.J., 1998; p. 656.
- Hall, J.; McKinnon, K. Hyper-sparsity in the revised simplex method and how to exploit it. Computational Optimization and Applications 2005, 32, 259–283. [CrossRef]
- Klee, V.; Minty, G. How good is the simplex algorithm? In Proceedings of the Inequalities - III. Proceedings of the Third Symposium on Inequalities Held at the University of California, Los Angeles, Sept. 1-9, 1969; Shisha, O., Ed.; Academic Press: New York-London, 1972; pp. 159–175.
- Jeroslow, R. The simplex algorithm with the pivot rule of maximizing criterion improvement. Discrete Mathematics 1973, 4, 367–377. [CrossRef]
- Zadeh, N. A bad network problem for the simplex method and other minimum cost flow algorithms. Mathematical Programming 1973, 5, 255–266. [CrossRef]
- Bartels, R.; Stoer, J.; Zenger, C. A Realization of the Simplex Method Based on Triangular Decompositions. In Handbook for Automatic Computation. Volume II: Linear Algebra; Springer: Berlin, Heidelberg, 1971; pp. 152–190. [CrossRef]
- Tolla, P. A Survey of Some Linear Programming Methods. In Concepts of Combinatorial Optimization, 2 ed.; Paschos, V.T., Ed.; John Wiley and Sons: Hoboken, NJ, USA, 2014; chapter 7, pp. 157–188. [CrossRef]
- Hall, J. Towards a practical parallelisation of the simplex method. Computational Management Science 2010, 7, 139–170. [CrossRef]
- Mamalis, B.; Pantziou, G. Advances in the Parallelization of the Simplex Method. In Algorithms, Probability, Networks, and Games. Lecture Notes in Computer Science, vol. 9295; Zaroliagis, C.; Pantziou, G.; Kontogiannis, S., Eds.; Springer: Cham, 2015; pp. 281–307. [CrossRef]
- Lubin, M.; Hall, J.A.J.; Petra, C.G.; Anitescu, M. Parallel distributed-memory simplex for large-scale stochastic LP problems. Computational Optimization and Applications 2013, 55, 571–596. [CrossRef]
- Khachiyan, L. Polynomial algorithms in linear programming. USSR Computational Mathematics and Mathematical Physics 1980, 20, 53–72. [CrossRef]
- Shor, N.Z. Cut-off method with space extension in convex programming problems. Cybernetics and Systems Analysis 1977, 13, 94–96. [CrossRef]
- Nesterov, Y.; Nemirovskii, A. Interior-Point Polynomial Algorithms in Convex Programming; Society for Industrial and Applied Mathematics, 1994; pp. ix + 396. [CrossRef]
- Karmarkar, N. A new polynomial-time algorithm for linear programming. Combinatorica 1984, 4, 373–395. [CrossRef]
- Gondzio, J. Interior point methods 25 years later. European Journal of Operational Research 2012, 218, 587–601. [CrossRef]
- Fathi-Hafshejani, S.; Mansouri, H.; Reza Peyghami, M.; Chen, S. Primal–dual interior-point method for linear optimization based on a kernel function with trigonometric growth term. Optimization 2018, 67, 1605–1630. [CrossRef]
- Asadi, S.; Mansouri, H. A Mehrotra type predictor-corrector interior-point algorithm for linear programming. Numerical Algebra, Control and Optimization 2019, 9, 147–156. [CrossRef]
- Yuan, Y. Implementation tricks of interior-point methods for large-scale linear programs. In Proceedings of the Proc. SPIE, vol. 8285. International Conference on Graphic and Image Processing (ICGIP 2011). International Society for Optics and Photonics, 2011. [CrossRef]
- Kheirfam, B.; Haghighi, M. A full-Newton step infeasible interior-point method for linear optimization based on a trigonometric kernel function. Optimization 2016, 65, 841–857. [CrossRef]
- Xu, Y.; Zhang, L.; Zhang, J. A full-modified-newton step infeasible interior-point algorithm for linear optimization. Journal of Industrial and Management Optimization 2016, 12, 103–116. [CrossRef]
- Roos, C.; Terlaky, T.; Vial, J.P. Interior Point Methods for Linear Optimization; Springer: New York, 2005; p. 500. [CrossRef]
- Sokolinskaya, I. Parallel Method of Pseudoprojection for Linear Inequalities. In Parallel Computational Technologies. PCT 2018. Communications in Computer and Information Science, vol. 910; Sokolinsky, L.; Zymbler, M., Eds.; Springer: Cham, 2018; pp. 216–231. [CrossRef]
- Eremin, I.I. Methods of Fejer’s approximations in convex programming. Mathematical Notes of the Academy of Sciences of the USSR 1968, 3, 139–149. [CrossRef]
- Gondzio, J.; Grothey, A. Direct Solution of Linear Systems of Size 109 Arising in Optimization with Interior Point Methods. In Proceedings of the Parallel Processing and Applied Mathematics. PPAM 2005. Lecture Notes in Computer Science, vol. 3911; Wyrzykowski, R.; Dongarra, J.; Meyer, N.; Wasniewski, J., Eds.; Springer: Berlin, Heidelberg, 2006; Vol. 3911 LNCS, pp. 513–525. [CrossRef]
- Prieto, A.; Prieto, B.; Ortigosa, E.M.; Ros, E.; Pelayo, F.; Ortega, J.; Rojas, I. Neural networks: An overview of early research, current frameworks and new challenges. Neurocomputing 2016, 214, 242–268. [CrossRef]
- Raina, R.; Madhavan, A.; Ng, A.Y. Large-scale deep unsupervised learning using graphics processors. In Proceedings of the Proceedings of the 26th Annual International Conference on Machine Learning (ICML ’09); ACM Press: New York, NY, USA, 2009; pp. 873–880. [CrossRef]
- Tank, D.W.; Hopfield, J.J. Simple `neural’ optimization networks: An A/D converter, signal decision circuit, and a linear programming circuit. IEEE transactions on circuits and systems 1986, CAS-33, 533–541. [CrossRef]
- Kennedy, M.P.; Chua, L.O. Unifying the Tank and Hopfield Linear Programming Circuit and the Canonical Nonlinear Programming Circuit of Chua and Lin. IEEE Transactions on Circuits and Systems 1987, 34, 210–214. [CrossRef]
- Rodriguez-Vazquez, A.; Dominguez-Castro, R.; Rueda, A.; Huertas, J.L.; Sanchez-Sinencio, E. Nonlinear Switched-Capacitor “Neural” Networks for Optimization Problems. IEEE Transactions on Circuits and Systems 1990, 37, 384–398. [CrossRef]
- Zak, S.H.; Upatising, V. Solving Linear Programming Problems with Neural Networks: A Comparative Study. IEEE Transactions on Neural Networks 1995, 6, 94–104. [CrossRef]
- Malek, A.; Yari, A. Primal–dual solution for the linear programming problems using neural networks. Applied Mathematics and Computation 2005, 167, 198–211. [CrossRef]
- Liu, X.; Zhou, M. A one-layer recurrent neural network for non-smooth convex optimization subject to linear inequality constraints. Chaos, Solitons and Fractals 2016, 87, 39–46. [CrossRef]
- Olkhovsky, N.; Sokolinsky, L. Visualizing Multidimensional Linear Programming Problems. In Proceedings of the Parallel Computational Technologies. PCT 2022. Communications in Computer and Information Science, vol. 1618; Sokolinsky, L.; Zymbler, M., Eds.; Springer: Cham, 2022; pp. 172–196. [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [CrossRef]
- Lachhwani, K. Application of Neural Network Models for Mathematical Programming Problems: A State of Art Review. Archives of Computational Methods in Engineering 2020, 27, 171–182. [CrossRef]
- Kaczmarz, S. Angenherte Auflsung von Systemen linearer Gleichungen. Bulletin International de l’Acadmie Polonaise des Sciences et des Lettres. Classe des Sciences Mathmatiques et Naturelles. Srie A, Sciences Mathmatiques 1937, 35, 355–357.
- Kaczmarz, S. Approximate solution of systems of linear equations. International Journal of Control 1993, 57, 1269–1271. [CrossRef]
- Cimmino, G. Calcolo approssimato per le soluzioni dei sistemi di equazioni lineari. La Ricerca Scientifica, XVI, Series II, Anno IX, 1 1938, pp. 326–333.
- Gastinel, N. Linear Numerical Analysis; Academic Press: New York, 1971; pp. ix+341.
- Agmon, S. The relaxation method for linear inequalities. Canadian Journal of Mathematics 1954, 6, 382–392. [CrossRef]
- Motzkin, T.S.; Schoenberg, I.J. The relaxation method for linear inequalities. Canadian Journal of Mathematics 1954, 6, 393–404. [CrossRef]
- Censor, Y.; Elfving, T. New methods for linear inequalities. Linear Algebra and its Applications 1982, 42, 199–211. [CrossRef]
- De Pierro, A.R.; Iusem, A.N. A simultaneous projections method for linear inequalities. Linear Algebra and its Applications 1985, 64, 243–253. [CrossRef]
- Sokolinskaya, I.; Sokolinsky, L. Revised Pursuit Algorithm for Solving Non-stationary Linear Programming Problems on Modern Computing Clusters with Manycore Accelerators. In Supercomputing. RuSCDays 2016. Communications in Computer and Information Science; Voevodin, V.; Sobolev, S., Eds.; Springer: Cham, 2016; Vol. 687, pp. 212–223. [CrossRef]
- Sokolinskaya, I.M.; Sokolinsky, L.B. Scalability Evaluation of Cimmino Algorithm for Solving Linear Inequality Systems on Multiprocessors with Distributed Memory. Supercomputing Frontiers and Innovations 2018, 5, 11–22. [CrossRef]
- Sokolinsky, L.B.; Sokolinskaya, I.M. Scalable parallel algorithm for solving non-stationary systems of linear inequalities. Lobachevskii Journal of Mathematics 2020, 41, 1571–1580. [CrossRef]
- Gonzalez-Gutierrez, E.; Todorov, M.I. A relaxation method for solving systems with infinitely many linear inequalities. Optimization Letters 2012, 6, 291–298. [CrossRef]
- Vasin, V.V.; Eremin, I.I. Operators and Iterative Processes of Fejer Type. Theory and Applications; Inverse and III-Posed Problems Series, Walter de Gruyter: Berlin, New York, 2009; p. 155. [CrossRef]
- Eremin, I.I.; Popov, L.D. Fejer processes in theory and practice: Recent results. Russian Mathematics 2009, 53, 36–55. [CrossRef]
- Nurminski, E.A. Single-projection procedure for linear optimization. Journal of Global Optimization 2016, 66, 95–110. [CrossRef]
- Censor, Y. Can linear superiorization be useful for linear optimization problems? Inverse Problems 2017, 33, 044006. [CrossRef]
- Gould, N.I. How good are projection methods for convex feasibility problems? Computational Optimization and Applications 2008, 40, 1–12. [CrossRef]
- Sokolinsky, L.B. BSF: A parallel computation model for scalability estimation of iterative numerical algorithms on cluster computing systems. Journal of Parallel and Distributed Computing 2021, 149, 193–206. [CrossRef]
- Sokolinsky, L.B. BSF-skeleton: A Template for Parallelization of Iterative Numerical Algorithms on Cluster Computing Systems. MethodsX 2021, 8, Article number 101437. [CrossRef]
- Dolganina, N.; Ivanova, E.; Bilenko, R.; Rekachinsky, A. HPC Resources of South Ural State University. In Proceedings of the Parallel Computational Technologies. PCT 2022. Communications in Computer and Information Science, vol. 1618; Sokolinsky, L.; Zymbler, M., Eds.; Springer: Cham, 2022; pp. 43–55. [CrossRef]
- Sokolinsky, L.B.; Sokolinskaya, I.M. FRaGenLP: A Generator of Random Linear Programming Problems for Cluster Computing Systems. In Proceedings of the Parallel Computational Technologies. PCT 2021. Communications in Computer and Information Science, vol. 1437; Sokolinsky, L.; Zymbler, M., Eds.; Springer: Cham, 2021; pp. 164–177. [CrossRef]
- Sokolinsky, L.B.; Sokolinskaya, I.M. VaLiPro: Linear Programming Validator for Cluster Computing Systems. Supercomputing Frontiers and Innovations 2021, 8, 51–61. [CrossRef]
- Gay, D.M. Electronic mail distribution of linear programming test problems. Mathematical Programming Society COAL Bulletin 1985, pp. 10–12.
- Keil, C.; Jansson, C. Computational experience with rigorous error bounds for the netlib linear programming library. Reliable Computing 2006, 12, 303–321. [CrossRef]
- Koch, T. The final NETLIB-LP results. Operations Research Letters 2004, 32, 138–142. [CrossRef]
- Deutsch, F.; Hundal, H. The rate of convergence for the cyclic projections algorithm I: Angles between convex sets. Journal of Approximation Theory 2006, 142, 36–55. [CrossRef]
Figure 1.
At each iteration of the main loop, Algorithm 3 performs the following steps. First, the algorithm constructs the vector from the point and obtains the point v. Second, the pseudoprojection of the point v gives the point w. Then, the direction vector d is calculated as a difference between the vectors w and . Finally, the point u moves from the point in the direction d along the surface of the polytope M as far as possible. As a result, we obtain the next approximation .
Figure 1.
At each iteration of the main loop, Algorithm 3 performs the following steps. First, the algorithm constructs the vector from the point and obtains the point v. Second, the pseudoprojection of the point v gives the point w. Then, the direction vector d is calculated as a difference between the vectors w and . Finally, the point u moves from the point in the direction d along the surface of the polytope M as far as possible. As a result, we obtain the next approximation .
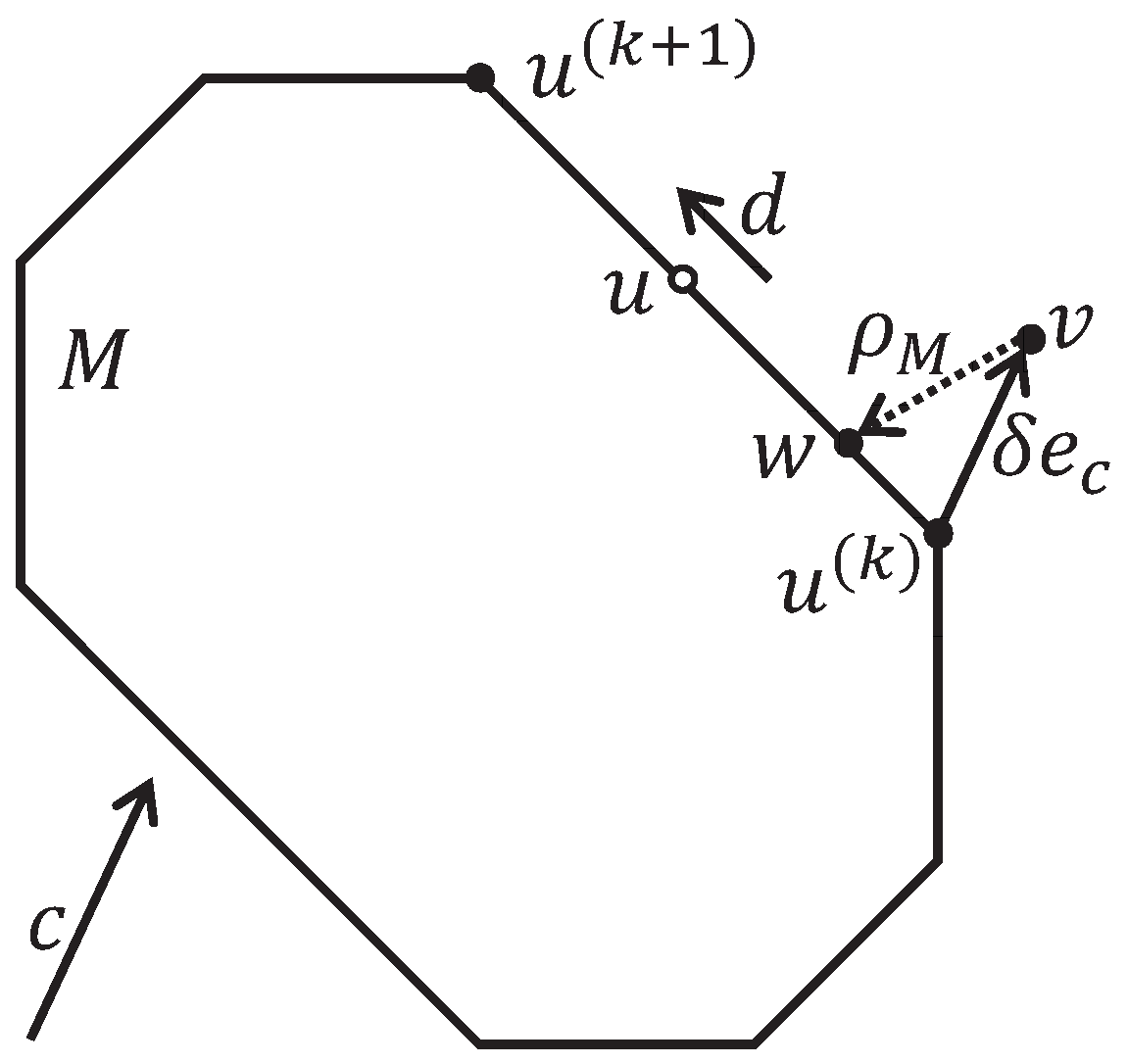
Figure 2.
The curves demonstrate the dependence of speedup on the number of processor nodes used by the parallel apex algorithm. Speedup is the ratio of the time required by parallel algorithm using one master node and one worker node to solve a problem to the time required by parallel algorithm using one master node and L worker nodes to solve the same problem. Experiments show that the scalability of the parallel apex algorithm depends significantly on the dimension n of the LP problem.
Figure 2.
The curves demonstrate the dependence of speedup on the number of processor nodes used by the parallel apex algorithm. Speedup is the ratio of the time required by parallel algorithm using one master node and one worker node to solve a problem to the time required by parallel algorithm using one master node and L worker nodes to solve the same problem. Experiments show that the scalability of the parallel apex algorithm depends significantly on the dimension n of the LP problem.
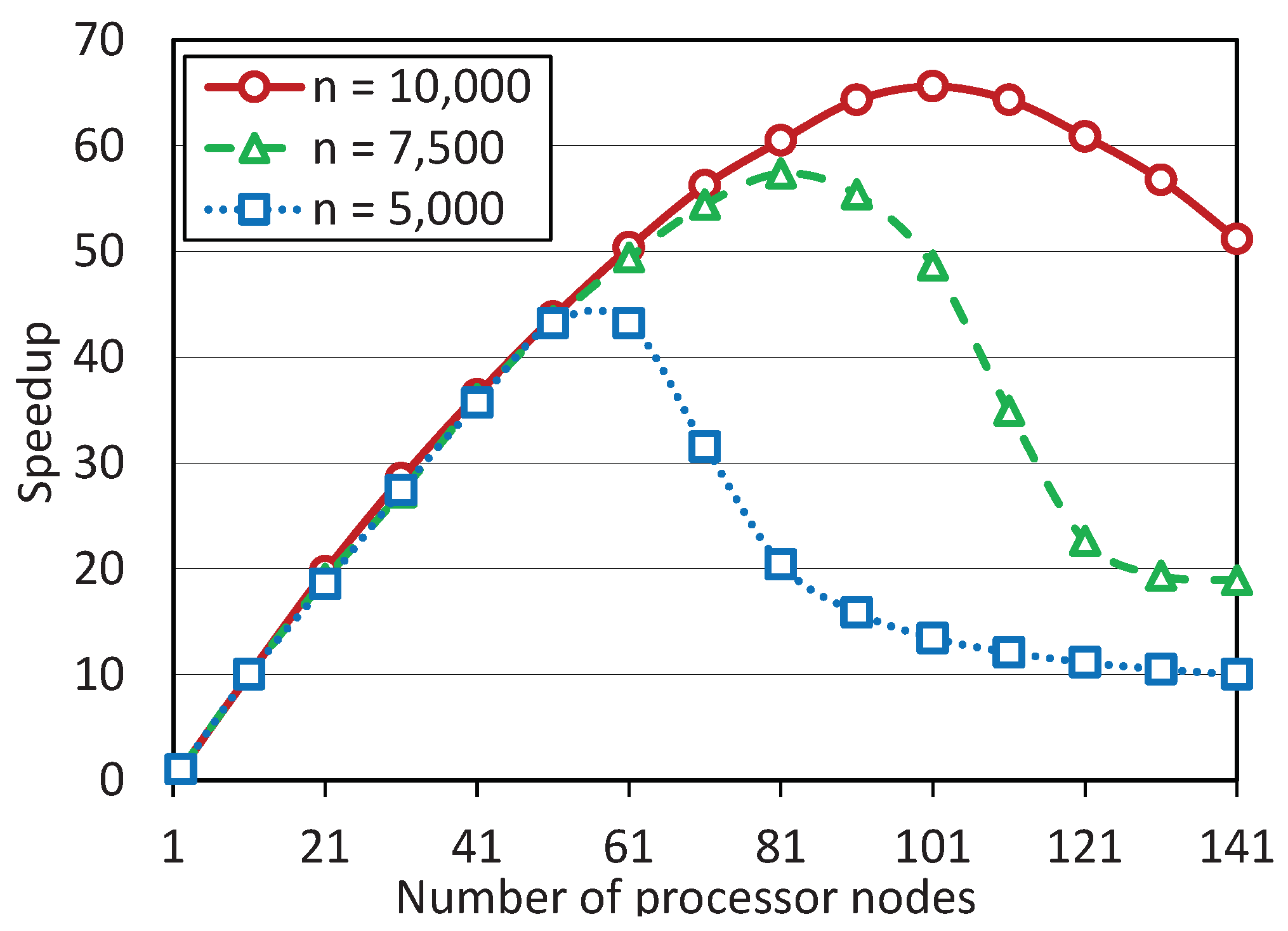
Table 1.
Specifications of the “Tornado SUSU” computing cluster.
 |
Table 2.
Applying the apex method to the Netlib-LP problems.
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







