A 3-Layer PSN for Image Encryption Utilizing Fractional-Order Chen Hyperchaotic Map and Cryptographically-Secure PRNGs

Preprint

Article

A 3-Layer PSN for Image Encryption Utilizing Fractional-Order Chen Hyperchaotic Map and Cryptographically-Secure PRNGs

Altmetrics

Downloads

186

Views

Comments

A peer-reviewed article of this preprint also exists.

Wassim Alexan^*

,Nader Alexan,Mohamed Gabr

Wassim Alexan^*

,Nader Alexan,Mohamed Gabr

This version is not peer-reviewed

Submitted:

15 March 2023

Posted:

16 March 2023

You are already at the latest version

Alerts

Abstract

Image encryption is increasingly becoming an important area of research in information security and network communications, as digital images are widely used in various applications and are vulnerable to various types of attacks. In this research work, a color image cryptosystem that is based on a 3-layer permutation-substitution network (PSN) is proposed. For every layer, an encryption key and an S-box are generated and utilized. Those are based on a four-dimensional (4D) dynamical Chen system of a fractional-order, the Mersenne Twister, OpenSLL, Rule 30 Cellular Automata and Intel’s MKL. The sequential application of Shannon’s ideas of diffusion and confusion for 3 times guarantees a total distortion of any input plain image, resulting in a totally encrypted one. Apart from the excellent and comparable performance to counterpart algorithms from the literature, showcasing resistance to visual, statistical, entropy, differential, known plaintext and brute-force attacks, the proposed image cryptosystem provides an exceptionally superior performance in 2 aspects: a vast key space of 2^1658 and an average encryption rate of 3.34 Mbps. Furthermore, the proposed image cryptosystem is shown to successfully pass all the tests of the NIST SP 800 suite.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The growing use of digital imaging technology and the increasing importance of online data storage and transmission have made research on image encryption both timely and necessary. In turn, this has also lead to increased demands for image encryption algorithms in various aspects of life, including: a) Increased use of digital imaging technology and applications [1,2]. With the widespread use of digital cameras, smartphones, and other imaging devices, the amount of sensitive and personal information stored in digital images has increased dramatically. This has made image encryption an important area of research; b) Growth of online data storage and transmission [3]. The increasing use of online data storage and transmission has made it easier for unauthorized parties to access confidential image data. This has made encryption an essential tool for protecting image data in transit and in storage; c) Threats to privacy and security [4]. As more sensitive and confidential information is stored in digital images, the risk of unauthorized access, theft, and tampering has increased. Image encryption is needed to protect against these threats; and d) Advancements in computing power [5]. As computing power continues to increase, attackers are able to use more sophisticated cryptanalysis methods to break encryption algorithms. This has made it important for researchers to continuously research and propose novel security measures for sensitive data.

While some researchers have focused their efforts into advancing cryptographic algorithms [6,7,8,9], others have dedicated their efforts towards the field of steganography [10,11]. Moreover, the literature shows a third group that combines the use of cryptography with steganography for added security [12,13,14]. Such efforts were realized because traditional data encryption algorithms such as DES [15], 3DES [16] and AES [17,18] were found to be no longer best-suited for image encryption. This is due to a number of reasons such as: a) The large size of image data, which increases the computational cost and time required for encryption and decryption; b) Different properties of image data such as redundancy, pixel-correlation, and structure, which can affect the security of traditional encryption techniques; c) Lack of adaptability, since traditional encryption techniques are not well suited to handle the unique challenges posed by image data, such as the need to preserve image quality and the requirement for real-time encryption in certain applications; and d) Vulnerability to attacks, because some traditional encryption techniques, such as DES, have already been shown to be prone to cryptanalysis [19]. To that end, scientists and engineers have been making use of various mathematical constructs and ideas inspired by nature to design secure and robust image encryption algorithms. Recent literature shows the employment of cellular automata (CA) [20,21,22], DNA coding [8,23,24,25], electric circuits [26,27], as well as heavy reliance on dynamical functions of chaotic behavior [6,28,29,30,31,32]. The following paragraph highlights the utilization of various such ideas in the development of pseudo-random number generators (PRNGs) to build encryption keys and substitution boxes (S-boxes).

The development and deployment of PRNGs comprise the majority of cryptography research efforts. This is because a randomly distributed bit-stream benefits both key generation and S-box design [33]. Numerous examples in the literature illustrate the usage of PRNGs in image cryptosystems. The researchers in [34], for instance, employ the Lucas sequence to construct an S-box for their proposed image cryptosystem. The authors of [35] produce encryption keys using the Rossler chaotic system and a Recaman’s sequence. Likewise, the authors of [36] construct PRNGs as encryption keys utilizing the Fibonacci sequence, a chaotic tan function, and a Bessel function. The researchers in [37] investigate elliptic curves and use them to create a PRNG, which they then combine with the Arnold map to encrypt images. Rule 30 CA generates a PRNG and is utilized as an encryption key in [20]. In [38], a Field Programmable Gate Array (FPGA) implementation of a PRNG utilizing a memristive Hopfield neural network with a specific activation gradient is proposed. The Mersenne Twister is deployed by the researchers in [7] as one of the encryption keys in a multi-stage cryptosystem. An S-box is designed and utilized as the core stage in a 3-stage image cryptosystem in [8], where the Lorenz system is numerically solved and its solution is used to generate a PRNG, which is then employed to generate the S-box. In another multi-stage image cryptosystem, the authors of [39] employ a discretized version of the chaotic sine map to create an S-box and the hyperchaotic Lu system as a PRNG. On the other hand, so far the literature on image encryption does not feature image cryptosystems where the PRNGs offered by Intel’s Math Kernel Library (MKL) or OpenSSL are employed. Intel’s MKL is a library of optimized mathematical functions, including a high-quality PRNG [40]. It is specifically optimized for use on Intel hardware, and can provide faster performance compared to other libraries. While OpenSSL is an open-source cryptography library that provides various cryptographic functions, including a random number generator [41].

The literature clearly shows that chaos theory has been extensively studied and applied to image cryptosystems. This is due to the diversity of desirable traits exhibited by dynamical functions of chaotic behavior. These traits include periodicity, pseudo-randomness, sensitivity to initial values, and ergodicity [42]. Broadly, these functions are categorized as either low-dimensional (LD) or high-dimensional (HD), with each class having a set of exclusive advantages [6]. LD chaotic functions dramatically simplify software and hardware implementations, but their use in image cryptosystems could in some cases be insufficiently secure. In contrast, HD chaotic functions, despite being more complex and needing more computational resources and circuitry, are capable of offering exceptionally high levels of security. Furthermore, upon studying hyperchaotic functions, a wide number of control parameters are readily apparent [43]. This implies that their use in image cryptosystems results in a significantly wider key space, which reduces the likelihood of brute-force attacks ever succeeding [8]. Attempting to solve hyperchaotic systems at a fractional-order permits a further expansion of the number of control variables and, consequently, realizing an even wider key space.

Recently, the image processing community has developed an interest in chaotic fractional-order dynamical systems [44]. Specifically, their applications in image cryptosystems have gained traction due to their superior performance compared to their integer-order counterparts [45,46,47,48,49]. The authors of [45] propose a secure image cryptosystem that employs smoothed sliding modes state observers for fractional-order chaotic systems. In [46], an image cryptosystem with a very large key space is proposed using a fractional-order four-dimensional (4D) Chen hyperchaotic map in conjunction with a Fibonacci Q-matrix. An efficient image cryptosystem is proposed in [47], where various fractional-order systems are utilized in an alternating fashion. In [48], a fractional-order logistic map is proposed by the authors for the implementation of an image cryptosystem, where its performance is then compared to that attained by a conventional logistic map. The authors of [49] present a technique for image encryption that use the solutions of chaotic fractional-order fuzzy cellular neural networks. However, it is easily observable that the use of fractional-order chaotic and hyperchaotic functions in image encryption makes for a rather new trend in the literature, with only a few articles mentioning such an application.

The previous paragraphs aimed at describing the need for research on image cryptosystems, the reliance of scholars on PRNGs to generate encryption keys and robust S-boxes, as well as the emerging utilization of hyperchaotic functions of fractional-order in this field of research. While the literature shows the prevalence of image cryptosystems that involve the use of multiple stages, in most cases these are limited to only 3 stages that comprise a total of a permutation-substitution-permutation (as in [7,8,9,20,34]). In the rare case of employing more stages, execution times are not reported [46]. This is because of the increases in complexity and the need for longer execution times that result from adding further encryption stages. To make use of multiple permutation-substitution networks (PSNs), while maintaining low complexity and short execution times, this research work proposes and achieves the following:

A highly efficient 3-layer PSN, where in each layer an encryption key is generated and utilized by XORing it with the image data, then an S-box is generated and applied to the resulting image. This effectively allows for bit-diffusion and bit-confusion, satisfying Shannon’s theory for secure communications [50].
In the first layer, a fractional-order hyperchaotic Chen map is employed for key generation, while a Mersenne Twister PRNG is utilized for S-box design and application.
In the second layer, a Mersenne Twister PRNG is employed for key generation, while an OpenSSL PRNG is utilized for S-box design and application.
In the third layer, Rule 30 CA is employed for key generation, while an Intel’s MKL PRNG is utilized for S-box design and application.
By utilizing a dynamical system with hyperchaotic behavior, as well as selecting 3 S-boxes with specific criteria, a very large key space of $2^{1658}$ , is achieved. Thus, fending off brute-force attacks.
By optimizing the code efficiency, a superior encryption rate is achieved by the proposed image cryptosystem, with an average encryption rate of $3.34$ Mbps.

This paper is organized as follows. Section 2 outlines the various mathematical constructs and PRNGs utilized in the proposed image cryptosystem, as well as the design and selection criteria for the S-boxes in use. Section 3 describes the proposed image cryptosystem in detail, along with algorithms and flow charts. Section 4 reports the attained numerical results, as well as presents a comparative study with counterpart algorithms from the literature. Finally, Section 5 draws the conclusions of this research work and suggests plausible future research directions that could be further pursued.

2. Preliminary Mathematical Constructs

This section presents the various mathematical constructs that are employed in the proposed image cryptosystem for PRNG generation and S-box design. Next, a key-establishment protocol is proposed, based on the performance evaluation metrics of the S-boxes.

2.1. The Fractional-Order Hyperchaotic Chen System

The fractional-order 4D Chen system [51,52] is a differential system which falls under the hyperchaotic systems category. Hyperchaotic systems are systems of functions which are able to produce more than one positive Lyapunov exponent. In turn, this promotes the capability of producing more robust pseudo-random number sequences. Moreover, many control variables are involved in the Chen system due to being a 4D system of equations, which is beneficial for increasing the key space of the proposed image cryptosystem as a whole. Furthermore, the adopted Chen system in this work provides a good balance between high ergodicity, an improved distribution in phase space, as well as a tolerable computation complexity, as opposed to the Lorenz system [20] with its comparatively poor ergodicity, or the hyperchaotic memristor circuit which possesses transcendental nonlinearities but is highly complex in software implementations [53].

The Chen system is mathematically described as follows:

D^{α_{1}} x = a (y - x) + u,

(1)

D^{α_{2}} y = γ x - x z + c y,

(2)

D^{α_{3}} z = x y - b z,

(3)

and

D^{α_{4}} u = y z + d u .

(4)

In (1)–(4), 13 control variables are utilized to specify the system. The first 4 variables constitute the initial values for x, y, z, and u, (or

x_{0}

y_{0}

z_{0}

, and

u_{0}

), which are the initial point in the 4D space. The second 5 variables, a, b, c, d, and

γ

, are the scale factors for the 4 equations. The last 4 variables,

α 1

α 2

α 3

, and

α 4

are the fractional differential orders.

To visually illustrate the hyperchaotic behavior of the fractional-order 4D Chen system, Figure 1 displays example plots for the system. For demonstration purposes, the figure shows the solution of the regular system, nevertheless, in application, the system is further solved in fractional-order. Further analysis of the system’s hyperchaotic behavior can be carried out through examining its bifurcation plots against various parameters, as illustrated in Figure 2 and Figure 3, for b and c, respectively. Moreover, the 4 Lyapunov characteristic exponents (LCEs), which give the rate of exponential divergence from perturbed initial conditions, are plotted in Figure 4.

2.2. The Mersenne Twister

The Mersenne Twister (MT) is a deterministic, high-quality PRNG algorithm. It was first introduced in 1997 by Makoto Matsumoto and Takuji Nishimura and is named after the French mathematician Marin Mersenne, who studied prime numbers [54]. The MT is considered to be one of the most advanced and widely-used PRNG algorithms, and it is used in a variety of applications, including simulations, games and cryptography. The MT generates random numbers by using a linear feedback shift register (LFSR), which is a simple mechanism for generating a sequence of binary numbers. The algorithm uses a specific mathematical formula to determine the next number in the sequence, based on the current state of the LFSR and a constant seed value. The seed value is used to initialize the state of the LFSR, and it determines the entire sequence of numbers generated by the algorithm. The MT has several properties that make it an attractive choice for random number generation:

High-quality random numbers: The MT produces high-quality random numbers that are evenly distributed across the range of possible values. This makes it well-suited for use in simulations, games, and other applications where randomness is important [55].
Large period: The MT has a very large period of $2^{19937} - 1$ , which means that the sequence of numbers generated by the algorithm is very long before it begins to repeat. This makes it useful for applications that require a large number of random numbers [54].
Fast generation: The MT is designed to be fast and efficient, and it can generate random numbers quickly, even on low-end hardware [56].
Easy to implement: The MT is easy to implement in a variety of programming languages and software (for example, MS Excel^®, Mathworks Matlab^® and Wolfram Mathematica^®), which makes it accessible to a wide range of developers [57].

2.3. OpenSSL

OpenSSL is an open-source cryptography library that provides a wide range of cryptographic functions, including PRNG. The PRNG functionality in OpenSSL is designed to provide fast and reliable generation of high-quality random numbers for use in a variety of applications, including simulations, games, and cryptography. OpenSSL provides several different PRNG algorithms, including the Fortuna PRNG [58], which is a well-known and widely-used PRNG. It also provides support for other PRNG algorithms, such as the Dual-EC-DRBG PRNG, which is designed for use in cryptographic applications. One of the key benefits of using OpenSSL for PRNG is its robustness and security. Moreover, it is a widely-used cryptography library that has undergone extensive security and performance testing, which makes it well-suited for use in security-sensitive applications, such as cryptography [59]. Additionally, the OpenSSL community is highly active and provides regular updates to the library, which helps to ensure that the PRNG algorithms in OpenSSL remain secure and reliable over time. OpenSSL also provides a comprehensive set of tools for controlling and configuring the PRNG, including the ability to set the seed value, specify the range of values to be generated, and control the distribution of the random numbers. This makes it easy to use OpenSSL for PRNG in a variety of applications and to tailor it to the specific needs of each application.

2.3.1. Rule 30 Cellular Automata

Rule 30 is a one-dimensional (1D) binary CA, a type of CA that uses a grid of cells to generate patterns based on a set of simple rules. Each cell in the grid can be in one of 2 states, either "on" or "off", and the state of each cell is determined based on the states of its neighbors according to the rule set. In the case of Rule 30, the rule set is simple: the state of a cell in the next generation is determined based on the states of its 2 neighbors in the current generation. Specifically, if the center cell is "off" and its 2 neighbors are both "on", the center cell will be "on" in the next generation. If the center cell is "on" and its 2 neighbors are either both "on" or both "off", the center cell will be "off" in the next generation. The behavior of Rule 30 can be visualized as a pattern of "on" and "off" cells that evolves over time, with each generation representing a new step in the evolution of the pattern. Figure 5 provides a graphical view of Rule 30 CA. Despite its simple rule set, Rule 30 exhibits a complex and seemingly random behavior, with patterns that can be difficult to predict. Figure 6 demonstrates the application of Rule 30 to generate the first 10 steps, while Figure 7 demonstrates the application of Rule 30 to generate the first 100 steps.

Rule 30 has been the subject of extensive study by mathematicians and computer scientists, who have been fascinated by its complex behavior and the seemingly random patterns it generates. It has also been used in a variety of practical applications, including cryptography, as the seemingly random patterns generated by Rule 30 can be used as the basis for secure encryption algorithms.

For the sake of the proposed image cryptosystem, however, we are only interested in the simplest nontrivial CA in which a cell’s neighborhood is defined as the nearby cells on each side of it. Thus, any given cell, along with its 2 neighbors, would create a neighborhood of 3 cells, yielding

2^{3} = 8

different patterns (as illustrated in Figure 5). More specifically, class 3 behavior is exhibited by rule 30 CA [20]. This indicates that simple input patterns result in chaotic and unpredictable outputs. Rule 30 CA mathematically determines the subsequent state of every given cell as

s_{i} (t + 1) = s_{i - 1} (t) \oplus (s_{i} (t) + s_{i + 1} (t)),

(5)

such that ⊕ and + on the RHS of (5) are the XOR and OR logical operators, respectively. A PRNG is extracted from Rule 30 CA by examining the middle column of Figure 6 and converting every black cell into a 1 and every white cell into a 0. This means that the first 10 bits are

{1, 1, 0, 1, 1, 1, 0, 0, 1, 1}

. In this work, we follow the technique proposed earlier in [34] to augment a seed in the generation procedure of the Rule 30 CA based PRNG.

2.3.2. Intel’s Math Kernel Library

Intel’s Math Kernel Library (MKL) is a numerical library that provides a variety of mathematical functions and algorithms, including PRNG. The PRNG functionality in Intel MKL is designed to provide fast and reliable generation of high-quality random numbers for use in a variety of applications, including simulations, games, and cryptography. Intel’s MKL provides several different PRNG algorithms, including a parallel PRNG, which is designed to generate random numbers in a parallel fashion across multiple processing cores [60]. One of the key benefits of using Intel’s MKL for PRNG is its performance. Intel’s MKL is optimized for Intel processors and can significantly improve the performance of random number generation compared to other PRNG algorithms. This makes it well-suited for applications that require large amounts of random numbers, such as Monte Carlo simulations or cryptography. Additionally, Intel’s MKL provides a comprehensive set of tools for controlling and configuring the PRNG, including the ability to set the seed value, specify the range of values to be generated, and control the distribution of the random numbers. This makes it easy to use Intel’s MKL for PRNG in a variety of applications, and to tailor it to the specific needs of each application.

2.3.3. S-Box Design

For the proposed image cryptosystem, a number of S-boxes are designed and employed to carry out data confusion. This is carried out in a number of steps, as follows:

Assume having a pseudo-randomly generated bit-stream $b_{P R N G}$ of a sufficiently long length $L_{P R N G}$ .
Divide $b_{P R N G}$ into N shorter bit-streams $b_{P R N G_{i}}$ , $i \in [1, N]$ , of length $L_{P R N G} / N$ each.
Partition every bit-stream $b_{P R N G_{i}}$ into groups of 8 bits each.
Convert every group of 8 bits into a decimal number. This results in a list having elements $e_{j} \in [0, 255]$ .
Eliminate duplicates, such that the list only has 256 unique elements spanning $[0, 255]$ . In case the size of the resulting list is less than 256, this list is discarded.
Repeat the above steps for the other $N - 1$ bit-streams, obtaining a maximum of N S-boxes.
For the (possibly) N S-boxes, assume having a set of target performance metrics, each S-box is evaluated using the same performance evaluation metrics, and the selected S-box is the one closer (in performance values) to the target metrics.

This procedure is provided as an algorithm in Algorithm 2.

2.3.4. Key Establishment Protocol

Since the image cryptosystem that is proposed in this research work adopts symmetric-key cryptography, it is essential for both the transmitting and receiving parties to have the same sets of keys. While the first set of keys includes those that are used as seed values for the various aforementioned PRNGs, as in the vast majority of image encryption literature, these must be pre-shared over a secure channel prior to the exchange of any sensitive data (i.e. the encrypted images). However, the second set of keys, which relates to the generation and design of S-boxes, will not take on the traditional form. These will actually be based on pre-shared specific values of S-box performance metrics.

In Section 2.3.3, having an arbitrary PRNG bit-stream, it was shown how N S-boxes could be obtained. For any S-box, a number of performance evaluation metrics may be computed and utilized to assess its cryptographic properties and strength. Those metrics are described in Section 4.13 and their ideal values are provided in Table 19. In this research work, we propose that the communicating parties would agree on a specific set of values for the performance evaluation metrics of the S-boxes to be utilized. This means that receiver will generate N S-boxes, compute their metrics, then select the S-box with identical performance evaluation metrics to those pre-shared by the transmitter. Implementing such a protocol has a number of implications, as follows:

It vastly increases the key space of the image cryptosystem, since every S-box in use has 5 metrics. In the proposed image cryptosystem, 3 S-boxes are employed. This leads to the introduction of $3 \times 5 = 15$ new variables as part of the key, and thus a giant leap in resistivity to brute-force attacks.
Using a single arbitrary PRNG bit-stream of sufficiently long length $L_{P R N G}$ , many S-boxes can be generated and applied. Their use can be varied for subsequent transmissions, thus increasing the complexity of any cryptanalysis efforts.
However, instead of generating a number of S-boxes and only selecting that with the best-performing set of metrics, near-optimum S-boxes would be employed. Nevertheless, this limitation is superseded by the fact that each of the utilized S-boxes is only a single component of a larger PSN. Thus, the performance of the PSN, as a whole, is what really matters.

3. Proposed Image Cryptosystem

Section 3.1 outlines the encryption process, while Section 3.2 outlines the decryption process. This is followed by the algorithms utilized in each of them, outlined in Section 3.3.

3.1. The Encryption Process

The proposed image cryptosystem can be outlined in a number of steps, as follows.

A plain RGB image I of dimensions $M \times N$ is selected and its pixels are converted into a 1D bit-stream of plaintext data bits d, having length $L_{d}$ .

PSN Layer 1: Chen encryption key and Mersenne Twister S-box.

(a)

The hyperchaotic Chen system of fractional-order is solved and an encryption key

k_{C h e n}

is generated from its solution, using Algorithm 1. The length

L_{d}

of this key is given by

L_{d} = M \times N \times 3 \times 8 .

(6)

(b)

A permutation process is applied, where the plaintext data bits d are XORed with the first encryption key

k_{C h e n}

, as follows:

d_{1} = d \oplus k_{C h e n} .

(7)

(c)

The bit-stream

d_{1}

is reshaped back into an image

I_{11}

(d)

Algorithm 2 is applied to the Mersenne Twister PRNG, obtaining a Mersenne Twister based S-box

S_{M T}

, such as that displayed in Table 1.

Table 1. Proposed Mersenne Twister based S-box.

4	90	209	152	178	35	92	10	240	204	181	97	187	165	116	131
252	146	44	144	180	130	223	40	24	234	76	32	201	21	150	46
33	137	83	158	27	41	248	237	119	18	109	2	227	84	170	160
251	48	222	163	211	113	172	166	62	96	118	207	37	31	107	224
102	179	226	74	112	254	205	218	5	122	60	12	200	164	81	23
13	230	190	127	34	65	169	183	54	129	1	70	236	136	245	186
85	15	132	239	58	225	123	120	221	185	125	95	124	154	195	88
202	143	232	8	219	173	145	140	208	101	79	39	247	135	194	250
20	216	26	233	87	71	55	22	241	126	238	59	244	52	121	30
49	0	214	42	210	182	196	38	53	171	45	235	82	231	242	104
7	156	168	80	77	191	111	177	6	100	57	155	117	161	217	189
103	68	203	148	66	228	43	99	229	91	134	105	128	14	93	192
157	162	138	29	47	3	212	115	50	106	213	253	246	63	151	176
75	110	147	61	9	159	72	25	193	94	16	51	167	36	206	198
139	174	188	133	220	108	17	11	215	73	64	255	141	89	69	142
67	78	175	56	184	249	28	19	98	86	199	243	149	114	197	153

(e)

A pixel value substitution process is applied on image

I_{11}

, using

S_{M T}

, and obtaining image

I_{12}

, as follows:

I_{12} = S_{M T} (I_{11}) .

(8)

(f)

The pixels of the encrypted image

I_{12}

are converted into a 1D bit-stream

d_{12}

PSN Layer 2: Mersenne Twister encryption key and OpenSSL S-box.

(a)

A Mersenne Twister based encryption key

k_{M T}

is generated, having length

L_{d}

(b)

A permutation process is applied, where the bits of the encrypted image

d_{12}

are XORed with the second encryption key

k_{M T}

, as follows:

d_{21} = d_{12} \oplus k_{M T} .

(9)

(c)

The encrypted data bits

d_{21}

are reshaped back into an image

I_{21}

(d)

Algorithm 2 is applied to the OpenSSL PRNG, obtaining an OpenSSL based S-box

S_{O p e n S S L}

, such as that displayed in Table 2.

Table 2. Proposed OpenSSL based S-box.

73	202	161	243	4	252	40	165	168	36	74	253	169	21	238	34
8	29	232	66	111	102	210	71	195	247	32	164	82	58	196	151
62	59	166	112	244	49	193	241	240	200	39	91	228	48	47	137
220	204	50	146	178	245	30	100	117	221	35	107	206	194	149	182
16	52	88	122	205	109	224	67	68	186	158	172	80	86	0	144
118	65	72	199	94	108	251	9	150	99	45	27	159	104	185	249
246	63	17	188	212	95	218	56	152	96	209	44	132	89	76	11
175	113	174	57	128	234	26	79	61	190	2	98	142	207	69	14
123	37	53	18	87	31	124	147	231	84	19	83	145	133	85	106
120	198	46	239	177	155	230	235	43	201	20	78	28	135	163	23
3	125	127	121	139	116	254	171	13	77	7	140	176	170	250	119
208	131	25	225	115	153	75	101	219	237	217	216	10	187	215	189
92	55	38	191	248	143	192	227	197	41	97	70	54	141	12	24
5	33	236	81	22	154	51	130	233	64	60	203	103	15	148	90
181	157	6	138	129	134	126	229	114	242	184	160	42	226	183	222
105	1	110	213	180	223	93	136	179	255	156	167	211	162	214	173

(e)

A pixel value substitution process is applied on image

I_{21}

, using

S_{O p e n S S L}

, and obtaining image

I_{22}

, as follows:

I_{22} = S_{O p e n S S L} (I_{21}) .

(10)

(f)

The pixels of the encrypted image

I_{22}

are converted into a 1D bit-stream

d_{22}

PSN Layer 3: Rule 30 CA encryption key and Intel’s MKL S-box.

(a)

A Rule 30 CA based encryption key

k_{C A}

is generated, having length

L_{d}

(b)

A permutation process is applied, where the bits of the encrypted image

d_{22}

are XORed with the third encryption key

k_{C A}

, as follows:

d_{3} = d_{22} \oplus k_{C A} .

(11)

(c)

The encrypted data bits

d_{3}

are reshaped back into an image

I_{31}

(d)

Algorithm 2 is applied to Intel’s MKL PRNG, obtaining an Intel’s MKL based S-box

S_{M K L}

, such as that displayed in Table 3.

Table 3. Proposed Intel’s MKL based S-box.

137	9	202	234	125	23	241	219	250	77	132	47	99	44	208	230
100	91	238	149	213	117	56	135	185	10	63	174	78	227	43	61
178	119	183	104	81	19	52	186	72	32	248	48	193	115	133	28
8	4	155	206	172	175	192	187	36	235	200	136	199	191	170	247
55	180	130	83	45	64	159	215	39	240	211	58	102	62	224	232
214	12	251	65	90	46	201	217	145	162	116	212	141	50	189	143
166	198	128	177	74	84	22	103	226	233	209	105	131	29	150	154
184	237	156	176	228	147	153	53	142	89	20	26	38	148	169	182
67	239	35	146	194	165	210	71	97	76	107	220	171	158	11	27
41	101	244	225	88	190	113	110	204	229	112	111	161	98	252	164
16	236	195	24	120	106	114	205	68	96	163	138	129	14	157	18
231	3	0	242	152	243	95	173	75	34	121	221	245	188	2	216
66	123	181	109	167	31	49	54	6	17	7	51	179	249	118	108
255	30	15	33	60	73	139	79	168	93	223	82	87	1	69	197
218	140	253	5	42	92	207	124	196	57	85	203	127	151	160	25
21	222	246	126	86	134	144	80	37	40	94	13	59	70	122	254

(e)

A pixel value substitution process is applied on image

I_{31}

, using

S_{M K L}

, and obtaining the final encrypted image

I_{32}

, as follows:

I_{32} = S_{M K L} (I_{31}) .

(12)

Figure 8 displays a flow chart for the encryption process comprising the 3 PSN layers.

3.2. The Decryption Process

The decryption process takes the form of the inverse of that of the encryption process. It can be outlined in a number of steps, as follows, applying each of the PSN layers in a reverse order.

Starting with the final encrypted image $I_{32}$ of dimensions $M \times N$ .
PSN Layer 3: Intel MKL’s S-box and Rule 30 CA encryption key.

(a)

A reverse pixel value substitution process is applied on image $I_{32}$ , using $S_{M K L}^{- 1}$ , and obtaining image $I_{31}$ , as follows:

$I_{31} = S_{M K L}^{- 1} (I_{33}) .$

(13)

(b)

The pixels of the encrypted image $I_{31}$ are converted into a 1D bit-stream $d_{3}$ .

(c)

A reverse permutation process is applied, where the data bits $d_{3}$ are XORed with the third encryption key $k_{C A}$ , as follows:

$d_{22} = d_{3} \oplus k_{C A} .$

(14)

(d)

The encrypted data bits $d_{22}$ are reshaped back into an image $I_{22}$ .
PSN Layer 2: OpenSSL S-box and Mersenne Twister encryption key.

(a)

A reverse pixel value substitution process is applied on image $I_{22}$ , using $S_{O p e n S S L}^{- 1}$ , and obtaining image $I_{21}$ , as follows:

$I_{21} = S_{O p e n S S L}^{- 1} (I_{22}) .$

(15)

(b)

The pixels of the encrypted image $I_{21}$ are converted into a 1D bit-stream $d_{2}$ .

(c)

A reverse permutation process is applied, where the data bits $d_{2}$ are XORed with the second encryption key $k_{M T}$ , as follows:

$d_{12} = d_{2} \oplus k_{M T} .$

(16)

(d)

The encrypted data bits $d_{12}$ are reshaped back into an image $I_{12}$ .
PSN Layer 1: Mersenne Twister S-box and Chen hyperchaotic fractional-order encryption key.

(a)

A reverse pixel value substitution process is applied on image $I_{12}$ , using $S_{M T}^{- 1}$ and obtaining image $I_{11}$ , as follows:

$I_{11} = S_{M T}^{- 1} (I_{12}) .$

(17)

(b)

The pixels of the encrypted image $I_{11}$ are converted into a 1D bit-stream $d_{1}$ .

(c)

A reverse permutation process is applied, where the encrypted data bits $d_{1}$ are XORed with the first encryption key $k_{C h e n}$ , as follows:

$d = d_{1} \oplus k_{C h e n} .$

(18)

(d)

The plaintext data bits d are reshaped back into a plain RGB image I.

Figure 9 displays a flow chart for the decryption process comprising the 3 PSN layers in a reverse order.

3.3. Utilized Algorithms

Algorithm 1 describes the generation of a PRNG from a chaotic system. Algorithm 2 describes the generation of an S-box given a pseudo-random bit-stream generated using one of the 3 proposed PRNGs earlier suggested in Section 2. As discussed in Section 2.3.3, given a sufficiently long bit-stream, a number of S-box trials, and a set of target performance metrics, Algorithm 2 aims at finding an S-box that is as close as possible to the provided performance metric values. It may seem counter-intuitive to provide a set of less-than-optimal performance metric values to such an algorithm, however, a near-optimal S-box can be considered as sufficient for a sub-routine in a large-scale image cryptosystem, in addition to reducing the predictability factor (as a cryptanalyst would assume that an optimal S-box must be applied).

Algorithm 1:Generate a PRNG bit-stream given a chaotic system S of k dimensions, and the number of needed bits n

Solve S for the size of $\frac{n}{k} + 1$ generating the set of lists ${L_{1}, L_{2}, . . ., L_{k}}$
Flatten the set of lists into one list $L = {L_{1} [1], L_{2} [1], . . ., L_{k} [1], L_{1} [2], L_{2} [2], . . ., L_{k} [2], . . .}$
If $| L | > n$ , drop the last $| L | - n$ elements from L
$λ = M e d i a n (L)$
Return $L_{b i t s} | L_{b i t s} [i] = \{\begin{matrix} 1, & if L [i] > λ \\ 0, & otherwise \end{matrix}$

Algorithm 2:Generate an S-box given a bit-stream

b_{P R N G}

, the number of S-box trials n, and target performance metric values

M = {N L, S A C, B I C, L A P, D A P}

$S_{b i t s} = {b_{P R N G_{1}}, b_{P R N G_{2}}, . . ., b_{P R N G_{n}}} | ⋃_{i = 1}^{n} (b_{P R N G_{i}}) = b_{P R N G}$
$S_{S b o x} =$ []
For each $S_{j} \in S_{b i t s}$ :

(a)

$W_{j} = P a r t i t i o n (S_{j}, 8)$ , creating a list of lists of bits of dimensions $L \times 8$

(b)

$Z_{j} = ⋃_{i = 1}^{L} (T o D e c i m a l (W_{j_{i}}))$

(c)

$S b o x_{j} = R e m o v e D u p l i c a t e s (Z_{j})$

(d)

Evaluate $S b o x_{j}$ creating $M_{j} = {N L_{j}, S A C_{j}, B I C_{j}, L A P_{j}, D A P_{j}}$

(e)

$A p p e n d ({S b o x_{j}, M_{j}}, S_{S b o x})$
$S b o x_{r e s} = S_{s b o x_{(1, 1)}}$
$S b o x_{D i f f} = M a g n i t u d e (M - S_{s b o x_{(1, 2)}})$
For each ${S b o x_{j}, M_{j}} \in S_{s b o x}$ :
(a)

$S b o x_{D i f f_{j}} = M a g n i t u d e (M - M_{j})$

(b)
If $(S b o x_{D i f f_{j}} < S b o x_{D i f f})$ :
$S b o x_{D i f f} = S b o x_{D i f f_{j}}$

$S b o x_{r e s} = S b o x_{j}$
Return $S b o x_{r e s}$

4. Numerical Results and Performance Evaluation

This section aims at conducting a full performance evaluation analysis of the proposed image cryptosystem, as well as at carrying out a comparative study with counterpart image encryption algorithms from the literature. The conducted analyses will test the proposed image cryptosystem’s ability at fending off attacks of various natures. Those include visual, statistical, entropy, differential as well as brute-force attacks. It will further measure how wide its key space is, how fast it carries out image encryption and decryption, and whether it can successfully pass all the tests in the National Institute of Standards and Technology (NIST) test suite. The proposed image cryptosystem and its testing are implemented in the Wolfram language, utilizing Wolfram Mathematica^® v.13.2. This is carried out on a machine with the following specifications: 2.9 GHz 6-Core Intel^® Core^TM i9 and 32 GB of 2400 MHz DDR4 RAM, running on a macOS Catalina v.10.15.7.

A number of commonly utilized images from the image processing community are employed. Those include: Lena, Mandrill, Peppers, Sailboat, House, House2 and Tree, all of dimensions

256 \times 256

, unless otherwise specified. The conducted tests are:

Visual and Histogram Analyses (Section 4.1).
Mean Squared Error (Section 4.2).
Peak Signal to Noise Ratio (Section 4.3).
Mean Absolute Error (Section 4.4).
Information Entropy (Section 4.5).
Fourier Transformation Analysis (Section 4.6).
Correlation Coefficient Analysis (Section 4.7).
Differential Attack Analysis (Section 4.8).
The National Institute of Standards and Technology Analysis (Section 4.9).
Key Space Analysis (Section 4.10).
Histogram Dependency Tests (Section 4.11)
Execution Time Analysis (Section 4.12).
S-Box Performance Analysis (Section 4.13).
Various Cryptanalyses and Noise Attacks (Section 4.14).

4.1. Visual and Histogram Analyses

The simplest performance evaluation of an image cryptosystem may be easily conducted by examining a plain image and its encrypted version employing the human visual system (HVS). Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 (including sub-figures) showcase a number of plain images and their encrypted versions, as obtained through the application of the proposed image cryptosystem. It is clear that no visual cues can be attained from the encrypted images as to what their plain versions could be. Furthermore, by incorporating a statistical measure, the histograms of the plain images and their encrypted versions, which are provided in the same set of figures, also showcase excellent performance. While the histograms of every plain image clearly depicts unique statistical characteristics, those of encrypted images show an almost uniform distribution, which cannot be traced back to any specific plain image. This signifies the ability of the proposed image cryptosystem to fend off attacks of statistical nature.

4.2. Mean Squared Error

The mean squared error (MSE) between 2 images is a widely used performance evaluation metric for image encryption algorithms. It is a measure of the difference between a plain image and its encrypted version. The purpose of any image cryptosystem is to scramble the image data in such a way that it becomes extremely difficult for an unauthorized third-party to access the original plain image. To evaluate the effectiveness of an image cryptosystem, it is thus necessary to compare the encrypted image with the plain image and measure the difference between them. The MSE is one of the most common methods of achieving this. It is basically a scalar value that measures the average of the squared difference between the pixel values of 2 images. The smaller the MSE value, the more similar the 2 images are. In image encryption, the goal is to encrypt the image in such a way that the encrypted image is as different from the original image as possible, while still being able to decrypt it back to its original form. A high MSE value between a plain image and its encrypted version indicates that the encryption process has been successful. The MSE is calculated as follows: Given 2 images I and

I^{'}

with the same dimensions

M \times N

, the MSE is calculated by summing the squared difference between each corresponding pixel in the 2 images, and then dividing by the total number of pixels in the image. Mathematically, it is expressed as:

M S E = \frac{\sum_{i = 0}^{M - 1} \sum_{j = 0}^{N - 1} {(I_{(i, j)} - I_{(i, j)}^{'})}^{2}}{M \times N} .

(19)

Table 4 displays the computed MSE values for various images, as well as how these values compare to other image cryptosystems from the literature. It is clear that a comparable performance is attained.

It is typical practice to report MSE and Peak Signal to Noise Ratio (PSNR) values together upon assessing image cryptosystems. This is usually carried out since the computation of PSNR is based on the value of MSE. Nevertheless, the authors of [61] only provide PSNR values, without reporting MSE values. This is the reason behind Table 4 showing columns of N/A under the heading of [61].

4.3. Peak Signal to Noise Ratio

The peak signal-to-noise ratio (PSNR) is based on the MSE discussed in Section 4.2. It aims to connect the error margin (represented by the MSE) to the peak value of a given signal. In this research work, the peak signal value is determined as the highest pixel intensity in an image

I_{m a x} = 255

. Therefore, for a given image I, the PSNR is mathematically expressed as:

P S N R = 10 log (\frac{I_{m a x}^{2}}{M S E}) .

(20)

As shown in (20), the PSNR is inversely proportional to the MSE, thus, achieving a minimal value is ideal. Table 5 displays the computed PSNR values for the proposed image cryptosystem, as well as those reported in the literature by counterpart algorithms. It is clear that the achieved PSNR values are comparable to the state-of-the-art.

4.4. Mean Absolute Error

The mean absolute error (MAE) between a plain image and its encrypted version refers to the average difference between the intensity values of corresponding pixels in the 2 images. It represents the average magnitude of the differences between the original and encrypted pixels, and is a measure of the quality of the encryption process in terms of preserving the visual information of the original image. The higher the MAE, the further different the encrypted image is to the original plain image in terms of pixel intensity values, and the better the image cryptosystem is at distorting the original plain image information. It is represented mathematically as:

M A E = \frac{\sum_{i = 0}^{M - 1} \sum_{j = 0}^{N - 1} | I_{(i, j)} - I_{(i, j)}^{'} |}{M \times N},

(21)

where I and

I^{'}

are 2 images. Table 6 displays the computed MAE values for the proposed image cryptosystem in comparison to counterpart algorithms from the literature. It is clear that the achieved MAE values are comparable to the state-of-the-art.

4.5. Information Entropy

In the realm of grayscale images, Shannon’s information entropy is used to quantify the randomness of an image’s gray pixel value distribution. According to Shannon’s theory, the formula for calculating information entropy is:

H (m) = \sum_{i = 1}^{M} p (m_{i}) {log}_{2} \frac{1}{p (m_{i})},

(22)

where

p (m i)

is the probability of occurrence of symbol m while M is the total number of bits for each symbol. In relation to images, as a grayscale image has 256 distinct values

[0 - 255]

and

2^{8}

potential permutations, the entropy value of an encrypted image approaches a maximum of 8. Consequently, information entropy can be used to measure the unpredictability of encrypted images. In Table 7, the entropy values computed for the proposed image cryptosystem, as well as counterpart algorithms from the literature, are displayed. It is clear that the entropy values computed for the various images are extremely close to the ideal value of 8, indicating that the proposed image cryptosystem is resistant to entropy attacks. Moreover, the disparities in the information entropy values for the state-of-the-art are demonstrated to be insignificant.

4.6. Fourier Transformation Analysis

The Discrete Fourier Transform (DFT) is a mathematical technique that transforms a discrete signal into its equivalent frequency representation. In the context of image encryption, DFT can be used as a tool for analyzing the frequency content of an image. In order to transform an image from the spatial domain to the frequency domain, the following expression mathematically describes the application of DFT:

F (k, l) = \sum_{i = 0}^{N - 1} \sum_{j = 0}^{N - 1} f (i, j) e^{- i 2 π (\frac{k i}{N} + \frac{l i}{N})},

(23)

such that

f (a, b)

is the spatial domain representation of the image, where the exponential term is the basis function corresponding to each point

F (k, l)

in the Fourier space. When applied to a plain image, the DFT separates the image into its constituent frequencies, which can be visualized as peaks in the frequency spectrum. This representation is useful for analyzing the image structure, as certain patterns and features can be identified by the presence of specific frequencies. On the other hand, when applied to an encrypted image, the result is a transformed representation of the encrypted data. However, this transformed representation typically does not provide any useful information about the original image. The encrypted data has been altered in a way that makes it difficult to extract any meaningful information, even after transforming it. The aim of any image cryptosystem is to render an image content unintelligible, and DFT can help confirm this by showing that the transformed representation of the encrypted image is not representative of the original data. Subfigures (b) and (e) of Figure 15 display the DFT as applied to the plain Tree image and its encrypted version, respectively. Unlike the various special features, such as edges and corners which result in the plus-sign-shape of the DFT of the plain image, the DFT of its encrypted version is distorted and lacks any such features.

4.7. Correlation Coefficient Analysis

This assessment approach evaluates the consistency of a single image. The objective of such an evaluation metric is to assess the cohesiveness of pixels in close proximity. This means that the aim here is to calculate the proportion of uniform regions relative to edge transitions. As a result, a rather high correlation coefficient (i.e. co-occurrence) value is anticipated in the case of plain images, which consist of more regions than edges (in terms of pixel count). Alternatively, as substantial distortion is desired in encrypted images, a lower correlation coefficient is anticipated. The following set of equations mathematically describe how the pixel cross-correlation coefficient

ρ

is computed:

ρ (x, y) = \frac{c o v (x, y)}{\sqrt{σ (x)} \sqrt{σ (y)}},

(24)

where,

c o v (x, y) = \frac{1}{N} \sum_{i = 1}^{N} (x_{i} - μ (x)) (y_{i} - μ (y)),

(25)

σ (x) = \frac{1}{N} \sum_{i = 1}^{N} {(x_{i} - μ (x))}^{2},

(26)

and

μ (x) = \frac{1}{N} \sum_{i = 1}^{N} (x_{i}) .

(27)

Classically, this metric is computed for 3 directions: horizontal, vertical and diagonal, where an image with a strong pixel cross-correlation would typically yield a value close to 1. On the other hand, for a well-encrypted image, its pixel cross-correlation would typically yield a value close to 0. Such values are well-exemplified in Table 8, where pixel correlation coefficients are computed and displayed for various plain images and their encrypted versions, each in 3 directions. Moreover, Table 9 and Table 10 provide numerical comparisons of pixel correlation coefficients with counterpart algorithms from the literature of the Lena image, both in RGB format and for each of the separate color channels.

In addition to the numerical analysis offered by computing (24)–(27), the co-occurrence matrix can be shown to visualize directional covariance. In the case of images with natural visual characteristics (more pixels indicating homogeneous regions than transitional borders), values of high similarity tend to coexist with a higher probability, leading to a predominantly linear distribution of magnitudes within the matrix. With contrast, in a heavily deformed (encrypted) image, a more uniform distribution of values is anticipated. To visually illustrate this, Figure 16 provides 2D plots of the pixel co-occurrence matrices for the plain and encrypted Tree image in 3 directions. Clearly, sub-figures (a), (b) and (c) are diagonal in nature, reflecting strong pixel correlation in the plain image, unlike sub-figures (d), (e) and (f) which reflect a rather uniform distribution, signifying random pixel values. Not surprisingly, the same pixel correlation behavior is noticed for each of the separate color channels of the Tree image, which are illustrated in Figure 17, Figure 18 and Figure 19. Moreover, a similar 3D plot of the same metric is illustrated in Figure 15, where sub-figures (c) and (f) provide pixel correlation for the plain and encrypted Tree images, respectively.

4.8. Differential Attack Analysis

This section evaluates the quality of image cryptosystems based on the direct difference between plain and encrypted images. In other words, the input plain image is compared directly with the encrypted image on a pixel-by-pixel or mean-average basis. This evaluation is performed in order to generate a percentage indicating the change in color intensities (per pixel or as a mean average) resulting from the encryption procedure. Due to the fact that the absence of resemblance between comparable pixels in both images is promoted, this evaluation must be performed pixel-by-pixel. In addition, a more global perspective of the cumulative pixel change rates between images (given as mean averages) is analyzed, indicating the existence of general color intensity similarities between these images. The literature suggests 2 tests to satisfy these requirements, the number of pixel change ratio (NPCR) for pixel-by-pixel comparison and the unified averaged change intensity (UACI) for the evaluation of the mean average difference.

The NPCR represents the percentage evaluation of the number of changed pixels. Such a difference among pixels is carried out with a strict equality perspective. Given 2 images

I_{1}

and

I_{2}

(of dimensions

M \times N

), the difference per pixel

D (x, y)

(where x and y are the coordinates of the pixel) is calculated as:

D (x, y) = \{\begin{matrix} 0 & I_{1} (x, y) = I_{2} (x, y) \\ 1 & O t h e r w i s e \end{matrix}| x \in [1, M] & y \in [1, N] .

(28)

Thus, the NPCR is mathematically expressed as:

N P C R = \frac{\sum_{x = 1}^{M} \sum_{y = 1}^{N} D (x, y)}{M \times N} \times 100 .

(29)

This means that a higher percentage reflects a larger difference between the 2 images. As a large difference is sought, the literature suggests that

99 %

is the target NPCR value for a well-encrypted image.

Utilizing a different assessment lens, the UACI attempts to assess the difference between 2 images in terms of their mean averages. The UACI is mathematically expressed as:

U A C I = \frac{1}{M \times N} \sum_{x = 1}^{M} \sum_{y = 1}^{N} \frac{| I_{1} (x, y) - I_{2} (x, y) |}{255} \times 100 .

(30)

The literature considers a target percentage of about

33 %

to reflect a well-encrypted image (with respect to the color range

[0, 255]

33 %

is approximated to 85 steps of difference in intensity.)

For the proposed image cryptosystem, Table 11 displays the computed NPCR and UACI values for various images, with average values corresponding to

99.6119 %

and

31.4563 %

, respectively, indicating very good NPCR and UACI performance. Furthermore, Table 12 presents a comparison with the literature, for the 3 separate color channels, for various images. A comparable performance is shown. Finally, Table 13, provides another comparison with the literature, for the RGB Lena image. Also here, a comparable performance is attained.

4.9. The National Institute of Standards and Technology Analysis

The National Institute of Standards and Technology (NIST) Special Publication (SP) 800 series provides guidelines, standards, and best practices for various aspects of information security, including image encryption [70]. The NIST SP 800 series is widely recognized as a leading source of information security guidance and is widely used by organizations in the public and private sectors. In relation to image encryption, NIST SP 800-60 provides guidelines for the selection and use of image encryption algorithms. The publication provides a framework for evaluating and comparing different encryption algorithms based on factors such as security, performance, and implementation complexity. The guidelines in SP 800-60 are intended to help organizations choose the most appropriate encryption algorithm for their specific needs, and to ensure the security and privacy of encrypted images. Moreover, the NIST SP 800-63-3 provides guidelines for the secure use of biometric images, such as fingerprints, iris scans, and facial recognition data. These guidelines cover various aspects of biometric image security, including the secure storage, transmission, and use of biometric images. Furthermore, those specific guidelines in SP 800-63-3 are intended to help organizations protect the confidentiality, integrity, and availability of biometric images, while also addressing privacy concerns. This make it of paramount importance to include a NIST analysis as part of the performance evaluation of any image cryptosystem. The NIST analysis suite of tests assesses a bit-stream for randomness through various tests. For such a bit-stream to successfully pass all the tests, it needs to score a

p -

value of at least

0.01

in all of them. Upon carrying out a NIST analysis on encrypted bit-streams resultant from the proposed image cryptosystem, we realize that it does indeed pass all NIST tests successfully. An example illustrates this in Table 14, where all values do indeed pass the

0.01

threshold for randomness.

4.10. Key Space Analysis

A key space analysis is performed to determine the number of distinct keys that can be employed during the encryption process. In the proposed image cryptosystem, it is assumed that the transmitter and receiver pre-share the secret keys via a secure channel. Moreover, the literature provides useful key-establishment protocols, as in [71]. For the proposed image cryptosystem, the Chen hyperchaotic map provides 13 variables, while each of the encryption keys provides a single variable as a seed, as well as the variables related to the S-box evaluation metrics, which are

5 \times 3 = 15

. This means that there is a total of

13 + 3 + 15 = 31

variables affecting the key space. With the largest machine precision being

10^{- 16}

, the key space is calculated to be

10^{31 \times 16} = 10^{496} \approx 2^{1658}

. It is clear that the achieved key space is much larger than the previously considered safe threshold of

2^{100}

[72]. This signifies that the proposed image cryptosystem is fully resistant against brute-force attacks. Table 15 carries out a comparison of key spaces of various image cryptosystems from the literature and displays how the proposed one fares amongst them, showcasing its superior performance in that regard.

4.11. Histogram Dependency Tests

In this testing category, the histograms of the plain and encrypted images are compared. Given 2 histograms, the comparisons performed are targeted at evaluating the level of the linear dependency between both of them. For the 5 evaluations carried out [77], the better the encryption performed, the less the correlation between the 2 histograms, and thus, the lower the dependency value computed. Accordingly, computing the dependency coefficient as a value in the range

[- 1, 1]

, it is favored to be as close to 0 as possible, since 1 and

- 1

both reflect a strong dependency in magnitude (aside form the direction presented by the sign). Out of many dependency evaluation techniques, in this research work, there are 5 tests carried out: Blomqvist

β

, Goodman-Kruskal

γ

, Kendall

τ

, Spearman

ρ

, and Pearson correlation r [78].

Blomqvist $β$ evaluates the correlation between 2 histograms X and Y, with their medians $\bar{x}$ and $\bar{y}$ respectively. It is mathematically expressed as:

$β = {(X - \bar{x}) (Y - \bar{y}) > 0} - {(X - \bar{x}) (Y - \bar{y}) < 0} .$

(31)

With respect to the median as a reference point, pairs of elements across the 2 histograms are either on the same side of the median (creating a linear correlation), or not (breaking the linear correlation).
Goodman-Kruskal $γ$ measure of monotonic association is computed in a pairwise manner, which demands converting the 2 histograms into one set of pairs. Comparing 2 pairs, they are either in line with the correlation ( $n_{c}$ ), or opposing it ( $n_{d}$ ). Goodman-Kruskal correlation is mathematically expressed as:

$γ = \frac{n_{c} - n_{d}}{n_{c} + n_{d}} .$

(32)
Kendall $τ$ evaluates correlation based on sample sizes, $n_{c}$ , $n_{d}$ and n. It is mathematically expressed as:

$τ = \frac{n_{c} - n_{d}}{\frac{n (n - 1)}{2}} .$

(33)
Spearman rank correlation $ρ$ test relates the position of an element in its sorted histogram, with respect to the mean rank value. It is mathematically expressed as:

$ρ = \frac{\sum (R_{i x} - {\bar{R}}_{x}) (R_{i y} - {\bar{R}}_{y})}{\sqrt{\sum {(R_{i x} - {\bar{R}}_{x})}^{2} \sum {(R_{i y} - {\bar{R}}_{y})}^{2}}},$

(34)

where x and y are the 2 evaluated variables, $R_{i l}$ is the rank of element i in list l, and ${\bar{R}}_{l}$ is the mean of ranks of l.
Pearson correlation r relates elements in the histograms directly to their mean averages. It is mathematically expressed as:

$r = \frac{\sum (X_{i} - \bar{X}) (Y_{i} - \bar{Y})}{\sqrt{\sum {(X_{i} - \bar{X})}^{2} \sum {(Y_{i} - \bar{Y})}^{2}}},$

(35)

where $\bar{X}$ and $\bar{Y}$ are the means of the histograms X and Y, respectively.

Table 16 presents the results of the 5 tests on various images. As all scores are close to 0, dependency is shown to be minimal, showcasing the excellent pixel dispersion quality of the proposed image cryptosystem.

4.12. Execution Time Analysis

An image cryptosystem’s execution time, in terms of encryption and decryption times, is a crucial performance evaluation metric. This is because: a) It reflects the efficiency of running an algorithm and its ability to handle large-scale image encryption and decryption; b) It reflects how well an image cryptosystems handles resource constraints, where the algorithm is expected to run on mobile and hand-held devices with low processing power; c) It reflects the possibility (or its lack) of scalability, which is important as some algorithms exhibit superior performance for small images, but weaken as the image size grows; and d) It allows for a comparison with state-of-the-art algorithms, as part of the trade-off between security performance and implementation complexity.

Table 17 displays the execution times for various square dimensions of the House image. For an image of dimensions

256 \times 256

, a very short time of less than half a second is reported. It is also clear that there is a linear increase in time with increases in image dimensions. Moreover, Table 18 carries out an execution time comparison with counterpart algorithms from the literature. It is clear that the proposed cryptosystem exhibits superior performance in that regard. It is worth mentioning here that execution times are not solely dependent on the complexity of an image cryptosystem. Other factors that directly influence execution times include the available processing power and random access memory (RAM), as well as the programming language or software of choice, and finally, the operating system. Traditionally, whenever execution times are reported in the literature, information is provided regarding the machine’s processor, RAM and the software upon which the image cryptosystem is implemented. Absence of such information, as in [76] is rather unusual. The proposed image cryptosystem, as well as the algorithms provided in [8,20,32] are implemented in the Wolfram language, utilizing Wolfram Mathematica^®, while the algorithms provided in [61,76,79,80] adopt Mathworks Matlab ^®. The average encryption rate of the proposed image cryptosystem is

3.34

Mbps.

4.13. S-Box Performance Analysis

With practically infinite possibilities to choose from when selecting an S-box for an image cryptosystem, performance evaluation metrics must be employed to gauge their performance and make an informed decision on which S-box would exhibit the best confusion properties. The literature offers 5 tests to achieve that. These metrics are as follows:

Nonlinearity [81] represents the measure of the effect of changing 1 bit in the input on the output (optimal value of 120, with most commonly achieved of 112).
Linear approximation probability (LAP) [82] calculates the bias for a given S-box (optimal value of 0.0625).
Differential approximation probability (DAP) [83] is a technique that examines the impact of specific variations (other than the bit level) in inputs and their effect on the confused output (optimal value of 0.0156).
Bit independence criterion (BIC) [84] evaluates repeatability in patterns in the confused output (optimal value of 112).
Strict avalanche criterion (SAC) [84] calculates the rate of change in the confused output with respect to the change in the input on a bit-by-bit level (optimal value of 0.5).

Table 19 displays the results of computing those 5 metrics for the proposed S-boxes (displayed earlier in Table 1, Table 2 and Table 3), alongside the ideal value for each metric. It is clear that the OpenSLL S-box provides the best performance, with closest proximity to the set of ideal values. Furthermore, Table 20 displays a comparison among the proposed S-boxes and a number of S-boxes utilized as part of counterpart algorithms from the literature. It is clear that a comparable performance is indeed achieved. It is worth noting here that the main advantage of opting to use those 3 proposed S-boxes is the increase in the number of variables of the key space by 15, as explained earlier in Section 2.3.4. While near-optimal S-box performance evaluation metrics were indeed pursued, other important S-box design criteria (e.g. aiming to avoid short ring cycles and fixed points [85,86]) were not considered in this research work.

4.14. Various Cryptanalyses and Noise Attacks

Table 21 provides a brief description of various forms of cryptanalyses that could be utilized to attack an image cryptosystem. However, due to the proposed image cryptosystem making use of a 3-layered SPN, none of the attacks in Table 21 would be effective against it.

A considerable portion of an encrypted image is lost during transmission in an occlusion attack. Using the same set of keys, the decryption process attempts to retrieve the original plain image from the encrypted image. Thus, some of the restored image’s information may be lost. Nonetheless, it may maintain the majority of visual information necessary to reconstruct the original image. The effect of an occlusion attack on the encrypted image created by the proposed image cryptosystem is depicted in Figure 20. Transmission causes the loss of one-fourth of the cipher picture. Yet, the decryption technique can recover some of the visual information from the image, which is sufficient to comprehend the visual content of the original plain image and identify it as the House image. As would be expected, in Figure 20, it is clear that increasing the fraction of the occlusion results in a decrypted image of a worse condition.

In a noise attack, portions of the pixel values of the encrypted images are altered during transmission owing to channel deteriorating effects. Figure 21 depicts the effect of a noise attack in which a salt-and-pepper noise is applied to encrypted images resulting from the proposed cryptosystem. When the noisy encrypted images are decrypted, the resulting images seem to retain the visual information of the original image. Thus, the cryptosystem is resistant to salt-and-pepper noise attacks. Figure 22 represents the same scenario recreated for the case of a Gaussian noise attack. In both of Figure 21 and Figure 22, it is observed that for the salt-and-pepper noise attack, with increased fraction of the image, as well as for the Gaussian noise attack, with increased standard deviation, the decrypted image, while still identifiable as the House image, is in a worse condition.

5. Conclusions and Future Works

This research work aimed at proposing a novel image cryptosystem that makes use of a 3-layer permutation-substitution network (PSN). For every layer, an encryption key and an S-box were generated and utilized. Design ideas for the encryption keys and S-boxes were pooled from the 4D dynamical Chen system of a fractional-order, the Mersenne Twister, OpenSLL, Rule 30 Cellular Automata and finally, Intel’s MKL. The employment of the hyperchaotic Chen map and the 3 PRNGs allowed for the introduction of a large number of variables, which have lead to the vast expansion of the key space to

2^{1658}

. This is indeed one of the differentiating advantages of the proposed image cryptosystem over its counterpart algorithms from the literature. Another such advantage is its superior efficiency, encrypting images at an average rate of

3.34

Mbps. Moreover, the attained security level of the proposed image cryptosystem is shown to be rather high, not only in quantitative terms, as exhibited by the comparable and sometimes superior performance evaluation metrics in relation to the state-of-the-art, but also from a qualitative aspect. Quantitatively, the proposed image cryptosystem showcases average computed values for some key performance metrics as follows. MSE of

9610.65

, PSNR of

8.33256

dB, MAE of

80.2136

, information entropy of

7.99711

, NPCR of

99.6119

, and UACI of

31.4563

. Qualitatively, upon examining many of the counterpart algorithms from the literature, it is easy to realize that they implement a one-and-a-half PSN (i.e a permutation, a substitution, and a final permutation), unlike the proposed image cryptosystem which implements 3 times a permutation-substitution sequence, while maintaining excellent code efficiency. Furthermore, inspection of the encrypted images by the HVS provides no information as to what the original plain image could be. Various cryptanalyses and noise attacks were also shown to be futile in breaking the proposed cryptosystem.

Future research could take on more than one direction. First, while the adopted idea of incorporating the S-box performance evaluation metrics as part of the encryption key itself has much improved the key space, this has inadvertently lead to the utilization of sub-optimal S-boxes. Nevertheless, the performance of the proposed image cryptosystem was not affected by this, due to the application of the 3-layer PSN. Still, further improvements could have been attained, had better-performing S-boxes been chosen. Second, some instances in the literature have indicated that while the Mersenne Twister provides an excellent PRNG performance in general, however, in strict relation to cryptography applications, other PRNGs could potentially offer improved performance [91]. Once again, this might not have affected the performance of the proposed image cryptosystem due to the application of the 3-layer PSN. In that regard, future works could attempt to replace the Mersenne Twister with other PRNGs of higher cryptographic performance and check for any noticeable overall improvement in the image cryptosystem.

Author Contributions

Conceptualization, W.A. and N. A.; methodology, M.G. and W.A.; software, W. A., N.A. and M.G.; validation, W.A; writing—original draft preparation, W.A. and M.G.; writing—review and editing, W.A.; visualization, W.A.; supervision, W.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

CA	Cellular Automata
DNA	Deoxyribonucleic acid
FPGA	Field Programmable Gate Arrays
HVS	Human Visual System
LFSR	Linear Feedback Shift Register
MAE	Maximum absolute error
MSE	Mean Square Error
NIST	National Institute of Standards and Technology
NPCR	Number of Pixel Changing Ratio
PRNG	Pseudo-Random Number Generation
PSN	Permutation-Substitution Network
PSNR	Peak Signal-to-Noise Ratio
S-box	Substitution box
UACI	Unified Averaged Change Intensity

References

Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sensing 2020, 12, 2659. [Google Scholar] [CrossRef]
Wang, C.; Fan, W.; Zhang, Z.; Wen, Y.; Xiong, L.; Chen, X. Advanced nanotechnology leading the way to multimodal imaging-guided precision surgical therapy. Advanced Materials 2019, 31, 1904329. [Google Scholar] [CrossRef] [PubMed]
Abd El-Latif, A.A.; Abd-El-Atty, B.; Mazurczyk, W.; Fung, C.; Venegas-Andraca, S.E. Secure data encryption based on quantum walks for 5G Internet of Things scenario. IEEE Transactions on Network and Service Management 2020, 17, 118–131. [Google Scholar] [CrossRef]
Kagan, D.; Alpert, G.F.; Fire, M. Zooming into video conferencing privacy and security threats. arXiv 2020, arXiv:2007.01059 2020. [Google Scholar]
Gyongyosi, L.; Imre, S. A survey on quantum computing technology. Computer Science Review 2019, 31, 51–71. [Google Scholar] [CrossRef]
Elkandoz, M.T.; Alexan, W. Image encryption based on a combination of multiple chaotic maps. Multimedia Tools and Applications 2022, pp. 1–22. [CrossRef]
Gabr, M.; Alexan, W.; Moussa, K.; Maged, B.; Mezar, A. Multi-Stage RGB Image Encryption. 2022 International Telecommunications Conference (ITC-Egypt). IEEE, 2022, pp. 1–6.
Gabr, M.; Younis, H.; Ibrahim, M.; Alajmy, S.; Khalid, I.; Azab, E.; Elias, R.; Alexan, W. Application of DNA Coding, the Lorenz Differential Equations and a Variation of the Logistic Map in a Multi-Stage Cryptosystem. Symmetry 2022, 14, 2559. [Google Scholar] [CrossRef]
Gabr, M.; Hussein, H.H.; Alexan, W. A Combination of Decimal-and Bit-Level Secure Multimedia Transmission. 2022 Workshop on Microwave Theory and Techniques in Wireless Communications (MTTW). IEEE, 2022, pp. 177–182.
Farrag, S.; Alexan, W. Secure 3d data hiding technique based on a mesh traversal algorithm. Multimedia Tools and Applications 2020, 79, 29289–29303. [Google Scholar] [CrossRef]
Alexan, W.; Elkhateeb, A.; Mamdouh, E.; Al-Seba’Ey, F.; Amr, Z.; Khalil, H. Utilization of corner filters, aes and lsb steganography for secure message transmission. 2021 International Conference on Microelectronics (ICM). IEEE, 2021, pp. 29–33.
Alexan, W.; Ashraf, A.; Mamdouh, E.; Mohamed, S.; Moustafa, M. Iomt security: Sha3-512, aes-256, rsa and lsb steganography. 2021 8th NAFOSTED Conference on Information and Computer Science (NICS). IEEE, 2021, pp. 177–181.
Yasser, S.; Hesham, A.; Hassan, M.; Alexan, W. Aes-secured bit-cycling steganography in sliced 3d images. 2020 International Conference on Innovative Trends in Communication and Computer Engineering (ITCE). IEEE, 2020, pp. 227–231.
Alexan, W.; Mamdouh, E.; ElBeltagy, M.; Hassan, F.; Edward, P. Image Feature-Based Watermarking. 2022 International Telecommunications Conference (ITC-Egypt), 2022, pp. 1–6. [CrossRef]
Coppersmith, D. The Data Encryption Standard (DES) and its strength against attacks. IBM journal of research and development 1994, 38, 243–250. [Google Scholar] [CrossRef]
Adam, N.; Mashaly, M.; Alexan, W. A 3des double–layer based message security scheme. 2019 2nd International Conference on Computer Applications & Information Security (ICCAIS). IEEE, 2019, pp. 1–5.
Daemen, J.; Rijmen, V. The design of Rijndael; Vol. 2, Springer, 2002.
Moussa, Y.; Alexan, W. Message security through aes and lsb embedding in edge detected pixels of 3d images. 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES). IEEE, 2020, pp. 224–229.
Vaudenay, S. An experiment on DES statistical cryptanalysis. Proceedings of the 3rd ACM Conference on Computer and Communications Security, 1996, pp. 139–147.
Alexan, W.; ElBeltagy, M.; Aboshousha, A. RGB Image Encryption through Cellular Automata, S-Box and the Lorenz System. Symmetry 2022, 14. [Google Scholar] [CrossRef]
Jiao, K.; Ye, G.; Mei, Q. Image Encryption Scheme Based on Quantum Logistic Map and Cellular Automata. 2021 IEEE 6th International Conference on Computer and Communication Systems (ICCCS), 2021, pp. 375–379. [CrossRef]
Ben Slimane, N.; Aouf, N.; Bouallegue, K.; Machhout, M. Hash Key-Based Image Cryptosystem Using Chaotic Maps and Cellular Automata. 2018 15th International Multi-Conference on Systems, Signals Devices (SSD), 2018, pp. 190–194. [CrossRef]
S, V.; Pujar, A.; Ankith.; Kedlaya, H.; Shahapur, V.S. Implementation of DNA cryptography based on dynamic DNA sequence table using cloud computing. International Journal of Engineering Research & Technology 2019, 7.
UbaidurRahman, N.H.; Balamurugan, C.; Mariappan, R. A Novel String Matrix Data Structure for DNA Encoding Algorithm. Procedia Computer Science 2015, 46, 820–832. Proceedings of the International Conference on Information and Communication Technologies, ICICT 2014, 3–5 December 2014 at Bolgatty Palace & Island Resort, Kochi, India. [CrossRef]
Iliyasu, M.A.; Abisoye, O.A.; Bashir, S.A.; Ojeniyi, J.A. A Review of DNA Cryptograhic Approaches. 2020 IEEE 2nd International Conference on Cyberspac (CYBER NIGERIA). IEEE, 2021, pp. 66–72.
Sambas, A.; Vaidyanathan, S.; Tlelo-Cuautle, E.; Abd-El-Atty, B.; El-Latif, A.A.A.; Guillén-Fernández, O.; Sukono.; Hidayat, Y.; Gundara, G. A 3-D Multi-Stable System With a Peanut-Shaped Equilibrium Curve: Circuit Design, FPGA Realization, and an Application to Image Encryption. IEEE Access 2020, 8, 137116–137132. [CrossRef]
Chen, J.J.; Yan, D.W.; Duan, S.K.; Wang, L.D. Memristor-based hyper-chaotic circuit for image encryption. Chinese Physics B 2020, 29, 110504. [Google Scholar] [CrossRef]
Liu, X.; Tong, X.; Wang, Z.; Zhang, M. Efficient high nonlinearity S-box generating algorithm based on third-order nonlinear digital filter. Chaos, Solitons & Fractals 2021, 150, 111109. [Google Scholar]
Alexan, W.; ElBeltagy, M.; Aboshousha, A. Image Encryption Through Lucas Sequence, S-Box and Chaos Theory. 2021 8th NAFOSTED Conference on Information and Computer Science (NICS). IEEE, 2021, pp. 77–83.
Khan, M.; Masood, F. A novel chaotic image encryption technique based on multiple discrete dynamical maps. Multimedia Tools and Applications 2019, 78, 26203–26222. [Google Scholar] [CrossRef]
Younas, I.; Khan, M. A new efficient digital image encryption based on inverse left almost semi group and Lorenz chaotic system. Entropy 2018, 20, 913. [Google Scholar] [CrossRef] [PubMed]
Alexan, W.; Elkandoz, M.; Mashaly, M.; Azab, E.; Aboshousha, A. Color Image Encryption Through Chaos and KAA Map. IEEE Access 2023. [Google Scholar] [CrossRef]
Alexan, W.; ElBeltagy, M.; Aboshousha, A. Rgb image encryption through cellular automata, s-box and the lorenz system. Symmetry 2022, 14, 443. [Google Scholar] [CrossRef]
Gabr, M.; Alexan, W.; Moussa, K. Image Encryption Through CA, Chaos and Lucas Sequence Based S-box. 2022 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA). IEEE, 2022, pp. 34–39.
ElBeltagy, M.; Alexan, W.; Elkhamry, A.; Moustafa, M.; Hussein, H.H. Image Encryption Through Rössler System, PRNG S-box and Recamán’s Sequence. 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC), 2022, pp. 0716–0722. [CrossRef]
Hussein, H.H.; Alexan, W.; ElBeltagy, M.; Aboshousha, A. Visual Data Security Incorporating Fibonacci Sequence, S-box, and Chaos Theory. 2022 International Conference on Smart Systems and Power Management (IC2SPM), 2022, pp. 85–90. [CrossRef]
AbdElHaleem, S.H.; Abd-El-Hafiz, S.K.; Radwan, A.G. A generalized framework for elliptic curves based PRNG and its utilization in image encryption. Scientific Reports 2022, 12, 13278. [Google Scholar] [CrossRef]
Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Du, S. FPGA implementation and image encryption application of a new PRNG based on a memristive Hopfield neural network with a special activation gradient. Chinese Physics B 2022, 31, 020505. [Google Scholar] [CrossRef]
Idrees, B.; Zafar, S.; Rashid, T.; Gao, W. Image encryption algorithm using S-box and dynamic Hénon bit level permutation. Multimedia Tools and Applications 2020, 79, 6135–6162. [Google Scholar] [CrossRef]
Pereira, A.; Proenca, A. PRNG-Broker: A High-Performance Broker to Supply Parallel Streams of Pseudorandom Numbers for Large-Scale Simulations. Advances in Parallel & Distributed Processing, and Applications: Proceedings from PDPTA’20, CSC’20, MSV’20, and GCC’20. Springer, 2021, pp. 167–183.
Viega, J.; Messier, M.; Chandra, P. Network security with openSSL: cryptography for secure communications; " O’Reilly Media, Inc.", 2002.
Hosny, K.M. Multimedia security using chaotic maps: principles and methodologies; Vol. 884, Springer Nature, 2020.
Kumari, M.; Gupta, S. Performance comparison between Chaos and quantum-chaos based image encryption techniques. Multimedia Tools and Applications 2021, 80, 33213–33255. [Google Scholar] [CrossRef] [PubMed]
Tavazoei, M.S. Fractional order chaotic systems: history, achievements, applications, and future challenges. The European Physical Journal Special Topics 2020, 229, 887–904. [Google Scholar] [CrossRef]
Montesinos-García, J.J.; Martinez-Guerra, R. Colour image encryption via fractional chaotic state estimation. IET Image Processing 2018, 12, 1913–1920. [Google Scholar] [CrossRef]
Hosny, K.M.; Kamal, S.T.; Darwish, M.M. Novel encryption for color images using fractional-order hyperchaotic system. Journal of Ambient Intelligence and Humanized Computing 2022, 13, 973–988. [Google Scholar] [CrossRef] [PubMed]
Hou, J.; Xi, R.; Liu, P.; Liu, T. The switching fractional order chaotic system and its application to image encryption. IEEE/CAA Journal of Automatica Sinica 2016, 4, 381–388. [Google Scholar] [CrossRef]
Bai, Y.R.; Baleanu, D.; Wu, G.C. A novel shuffling technique based on fractional chaotic maps. Optik 2018, 168, 553–562. [Google Scholar] [CrossRef]
Mani, P.; Rajan, R.; Shanmugam, L.; Joo, Y.H. Adaptive control for fractional order induced chaotic fuzzy cellular neural networks and its application to image encryption. Information Sciences 2019, 491, 74–89. [Google Scholar] [CrossRef]
Shannon, C.E. Communication theory of secrecy systems. The Bell system technical journal 1949, 28, 656–715. [Google Scholar] [CrossRef]
Hegazi, A.; Matouk, A. Dynamical behaviors and synchronization in the fractional order hyperchaotic Chen system. Applied Mathematics Letters 2011, 24, 1938–1944. [Google Scholar] [CrossRef]
Yan, Z. Controlling hyperchaos in the new hyperchaotic Chen system. Applied Mathematics and Computation 2005, 168, 1239–1250. [Google Scholar] [CrossRef]
Mohamed, S.M.; Sayed, W.S.; Madian, A.H.; Radwan, A.G.; Said, L.A. An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics 2023, 12, 1219. [Google Scholar] [CrossRef]
Matsumoto, M.; Nishimura, T. Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Transactions on Modeling and Computer Simulation (TOMACS) 1998, 8, 3–30. [Google Scholar] [CrossRef]
L’ecuyer, P.; Simard, R. TestU01: AC library for empirical testing of random number generators. ACM Transactions on Mathematical Software (TOMS) 2007, 33, 1–40. [Google Scholar] [CrossRef]
Route, M. Radio-flaring ultracool dwarf population synthesis. The Astrophysical Journal 2017, 845, 66. [Google Scholar] [CrossRef]
Mélard, G. On the accuracy of statistical procedures in Microsoft Excel 2010. Computational statistics 2014, 29, 1095–1128. [Google Scholar] [CrossRef]
McEvoy, R.; Curran, J.; Cotter, P.; Murphy, C. Fortuna: cryptographically secure pseudo-random number generation in software and hardware. 2006 IET Irish Signals and Systems Conference. IET, 2006, pp. 457–462.
Bello, L. DSA-1571-1 openssl–predictable random number generator. Debian security advisory 2008. [Google Scholar]
Wang, E.; Zhang, Q.; Shen, B.; Zhang, G.; Lu, X.; Wu, Q.; Wang, Y.; Wang, E.; Zhang, Q.; Shen, B.; others. Intel math kernel library. High-Performance Computing on the Intel® Xeon Phi™: How to Fully Exploit MIC Architectures 2014, pp. 167–188.
Iqbal, N.; Naqvi, R.A.; Atif, M.; Khan, M.A.; Hanif, M.; Abbas, S.; Hussain, D. On the Image Encryption Algorithm Based on the Chaotic System, DNA Encoding, and Castle. IEEE Access 2021, 9, 118253–118270. [Google Scholar] [CrossRef]
Khan, M.; Shah, T. An efficient chaotic image encryption scheme. Neural Computing and Applications 2015, 26, 1137–1148. [Google Scholar] [CrossRef]
Liu, H.; Zhao, B.; Huang, L. Quantum image encryption scheme using Arnold transform and S-box scrambling. Entropy 2019, 21, 343. [Google Scholar] [CrossRef]
Wang, Y.; Wu, C.; Kang, S.; Wang, Q.; Mikulovich, V. Multi-channel chaotic encryption algorithm for color image based on DNA coding. Multimedia Tools and Applications 2020, pp. 1–26.
Zhang, Y.Q.; He, Y.; Li, P.; Wang, X.Y. A new color image encryption scheme based on 2DNLCML system and genetic operations. Optics and Lasers in Engineering 2020, 128, 106040. [Google Scholar] [CrossRef]
Jithin, K.; Sankar, S. Colour image encryption algorithm combining, Arnold map, DNA sequence operation, and a Mandelbrot set. Journal of Information Security and Applications 2020, 50, 102428. [Google Scholar] [CrossRef]
Rehman, A.U.; Firdous, A.; Iqbal, S.; Abbas, Z.; Shahid, M.M.A.; Wang, H.; Ullah, F. A Color Image Encryption Algorithm Based on One Time Key, Chaos Theory, and Concept of Rotor Machine. IEEE Access 2020, 8, 172275–172295. [Google Scholar] [CrossRef]
Slimane, N.B.; Aouf, N.; Bouallegue, K.; Machhout, M. A novel chaotic image cryptosystem based on DNA sequence operations and single neuron model. Multimedia Tools and Applications 2018, 77, 30993–31019. [Google Scholar] [CrossRef]
Paul, L.; Gracias, C.; Desai, A.; Thanikaiselvan, V.; Suba Shanthini, S.; Rengarajan, A. A novel colour image encryption scheme using dynamic DNA coding, chaotic maps, and SHA-2. Multimedia Tools and Applications 2022, pp. 1–22.
Stine, K.; Kissel, R.; Barker, W.; Lee, A.; Fahlsing, J. Guide for mapping types of information and information systems to security categories: appendices. Technical report, National Institute of Standards and Technology, 2008.
ur Rehman, A.; Liao, X.; Ashraf, R.; Ullah, S.; Wang, H. A color image encryption technique using exclusive-OR with DNA complementary rules based on chaos theory and SHA-2. Optik 2018, 159, 348–367. [Google Scholar] [CrossRef]
Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. International journal of bifurcation and chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
Yang, B.; Liao, X. A new color image encryption scheme based on logistic map over the finite field ZN. Multimedia Tools and Applications 2018, 77, 21803–21821. [Google Scholar] [CrossRef]
Gao, H.; Wang, X. Chaotic Image Encryption Algorithm Based on Zigzag Transform With Bidirectional Crossover From Random Position. IEEE Access 2021, 9, 105627–105640. [Google Scholar] [CrossRef]
Ge, B.; Chen, X.; Chen, G.; Shen, Z. Secure and Fast Image Encryption Algorithm Using Hyper-Chaos-Based Key Generator and Vector Operation. IEEE Access 2021, 9, 137635–137654. [Google Scholar] [CrossRef]
Hu, X.; Wei, L.; Chen, W.; Chen, Q.; Guo, Y. Color image encryption algorithm based on dynamic chaos and matrix convolution. IEEE Access 2020, 8, 12452–12466. [Google Scholar] [CrossRef]
Asuero, A.G.; Sayago, A.; González, A. The correlation coefficient: An overview. Critical reviews in analytical chemistry 2006, 36, 41–59. [Google Scholar] [CrossRef]
Temizhan, E.; Mirtagioglu, H.; Mendes, M.; others. Which Correlation Coefficient Should Be Used for Investigating Relations between Quantitative Variables? American Academic Scientific Research Journal for Engineering, Technology, and Sciences 2022, 85, 265–277.
Gong, L.; Qiu, K.; Deng, C.; Zhou, N. An image compression and encryption algorithm based on chaotic system and compressive sensing. Optics & Laser Technology 2019, 115, 257–267. [Google Scholar]
Zhang, X.; Wang, L.; Wang, Y.; Niu, Y.; Li, Y. An image encryption algorithm based on hyperchaotic system and variable-step Josephus problem. International Journal of Optics 2020, 2020. [Google Scholar] [CrossRef]
Meier, W.; Staffelbach, O. Nonlinearity criteria for cryptographic functions. Workshop on the Theory and Application of of Cryptographic Techniques. Springer, 1989, pp. 549–562.
Hong, S.; Lee, S.; Lim, J.; Sung, J.; Cheon, D.; Cho, I. Provable security against differential and linear cryptanalysis for the SPN structure. International Workshop on Fast Software Encryption. Springer, 2000, pp. 273–283.
Biham, E.; Shamir, A. Differential cryptanalysis of DES-like cryptosystems. Journal of CRYPTOLOGY 1991, 4, 3–72. [Google Scholar] [CrossRef]
Webster, A.; Tavares, S.E. On the design of S-boxes. Conference on the theory and application of cryptographic techniques. Springer, 1985, pp. 523–534.
Liu, H.; Kadir, A.; Xu, C. Cryptanalysis and constructing S-box based on chaotic map and backtracking. Applied Mathematics and Computation 2020, 376, 125153. [Google Scholar] [CrossRef]
Si, Y.; Liu, H.; Chen, Y. Constructing keyed strong S-Box using an enhanced quadratic map. International Journal of Bifurcation and Chaos 2021, 31, 2150146. [Google Scholar] [CrossRef]
Zahid, A.H.; Arshad, M.J.; Ahmad, M. A novel construction of efficient substitution-boxes using cubic fractional transformation. Entropy 2019, 21, 245. [Google Scholar] [CrossRef] [PubMed]
Aboytes-González, J.; Murguía, J.; Mejía-Carlos, M.; González-Aguilar, H.; Ramírez-Torres, M. Design of a strong S-box based on a matrix approach. Nonlinear Dynamics 2018, 94, 2003–2012. [Google Scholar] [CrossRef]
Hayat, U.; Azam, N.A.; Asif, M. A method of generating 8× 8 substitution boxes based on elliptic curves. Wireless Personal Communications 2018, 101, 439–451. [Google Scholar] [CrossRef]
Siddiqui, N.; Yousaf, F.; Murtaza, F.; Ehatisham-ul Haq, M.; Ashraf, M.U.; Alghamdi, A.M.; Alfakeeh, A.S. A highly nonlinear substitution-box (S-box) design using action of modular group on a projective line over a finite field. PLOS one 2020, 15, e0241890. [Google Scholar] [CrossRef] [PubMed]
O’Neill, M.E. PCG: A Family of Simple Fast Space-Efficient Statistically Good Algorithms for Random Number Generation. Technical Report HMC-CS-2014-0905, Harvey Mudd College, Claremont, CA, 2014.

Figure 1. 3D plots utilizing various axes for the fractional order 4D Chen system. Values used are

{x, y, z, u} = 0.3

a = 35

b = 3

c = 12

γ = 28

d = 0.5

, and

α = 0.97

(since the system is calculated in the 4D space, initial values are needed for the 4 axes. But for visualization purposes, a single axis is ignored in each plot).

Figure 1. 3D plots utilizing various axes for the fractional order 4D Chen system. Values used are

{x, y, z, u} = 0.3

a = 35

b = 3

c = 12

γ = 28

d = 0.5

, and

α = 0.97

(since the system is calculated in the 4D space, initial values are needed for the 4 axes. But for visualization purposes, a single axis is ignored in each plot).

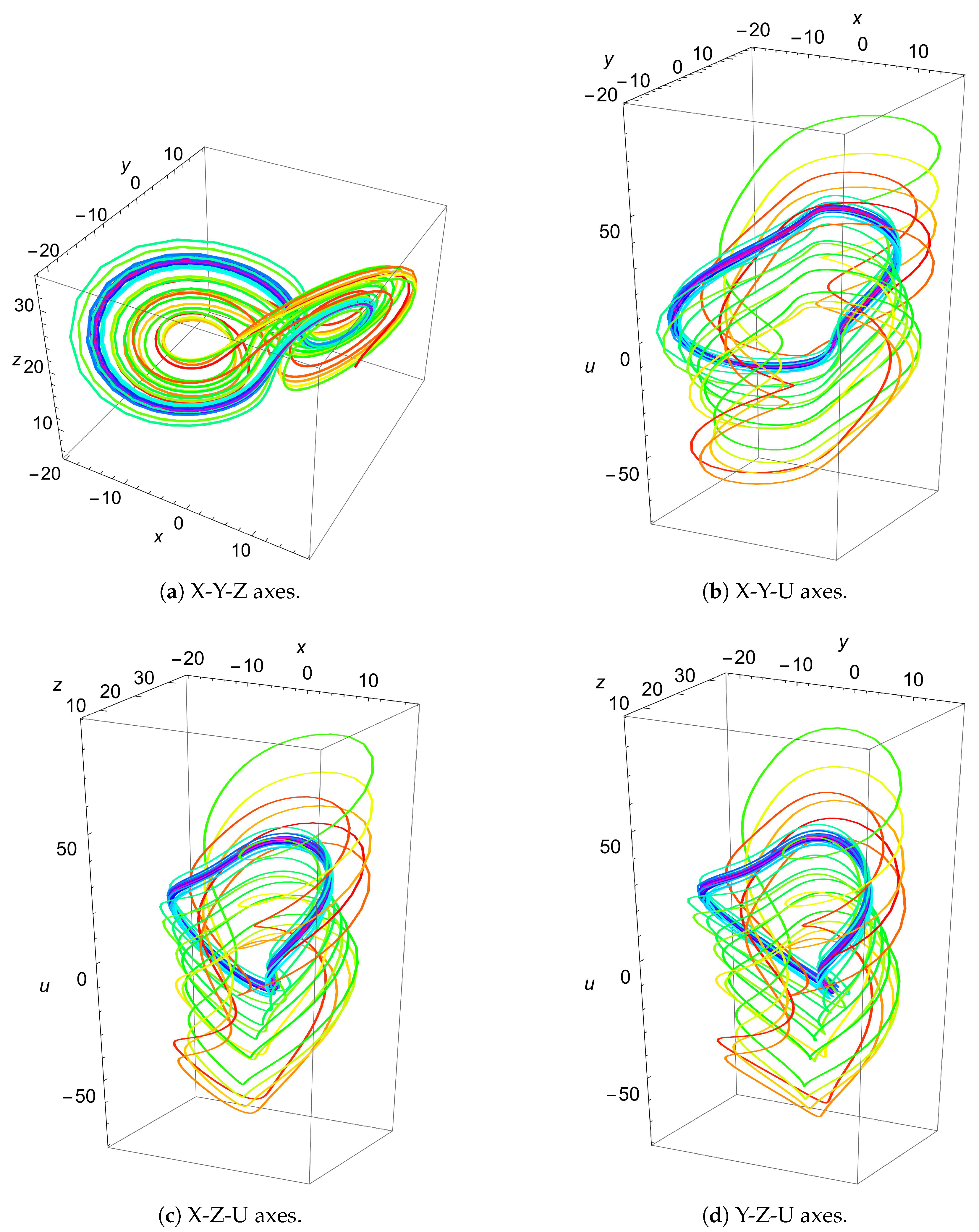
Figure 2. Bifurcation plots of the fractional order 4D Chen system for

x, y, z

and u against b.

Figure 2. Bifurcation plots of the fractional order 4D Chen system for

x, y, z

and u against b.

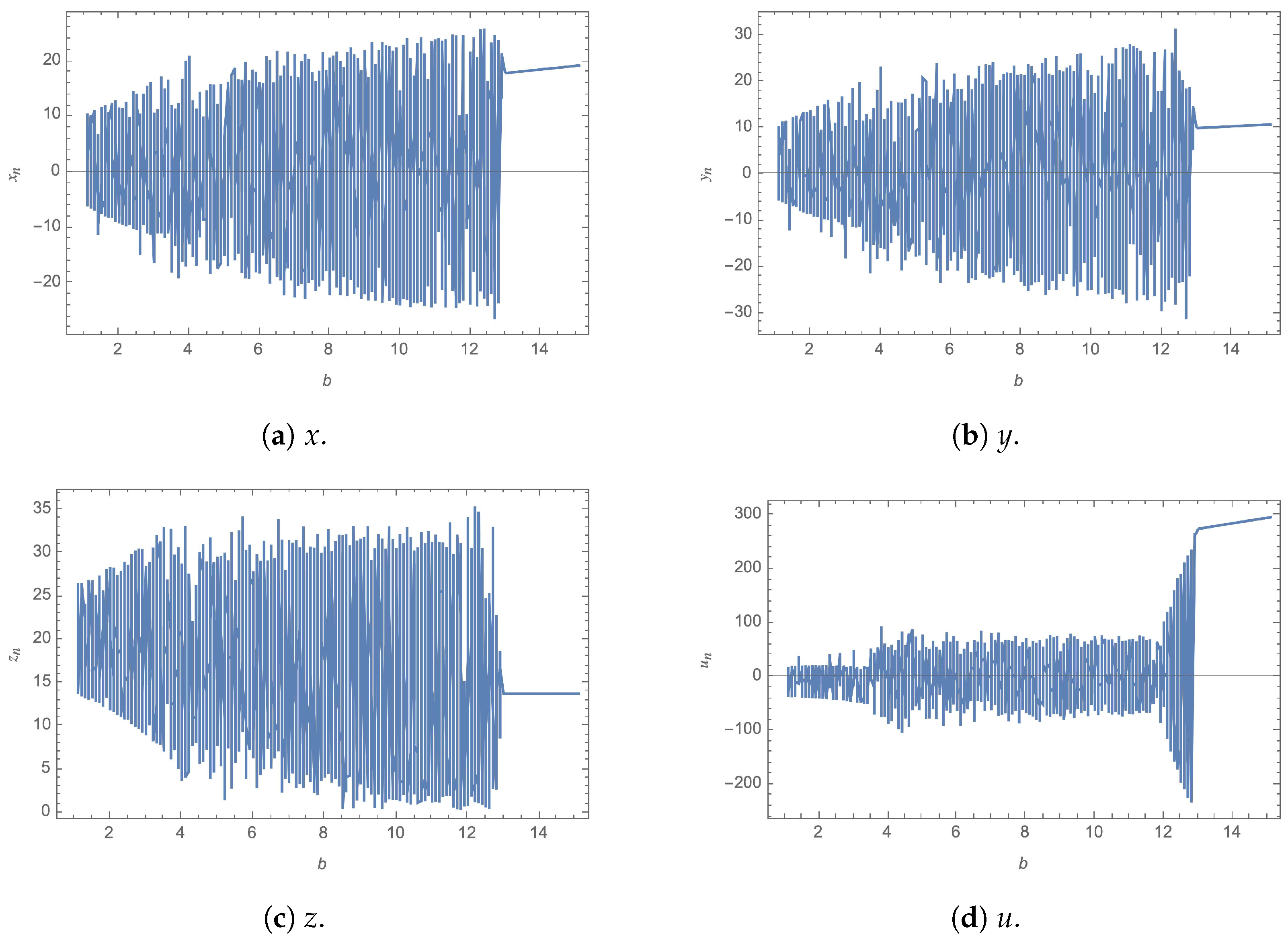
Figure 3. Bifurcation plots of the fractional order 4D Chen system for

x, y, z

and u against c.

Figure 3. Bifurcation plots of the fractional order 4D Chen system for

x, y, z

and u against c.

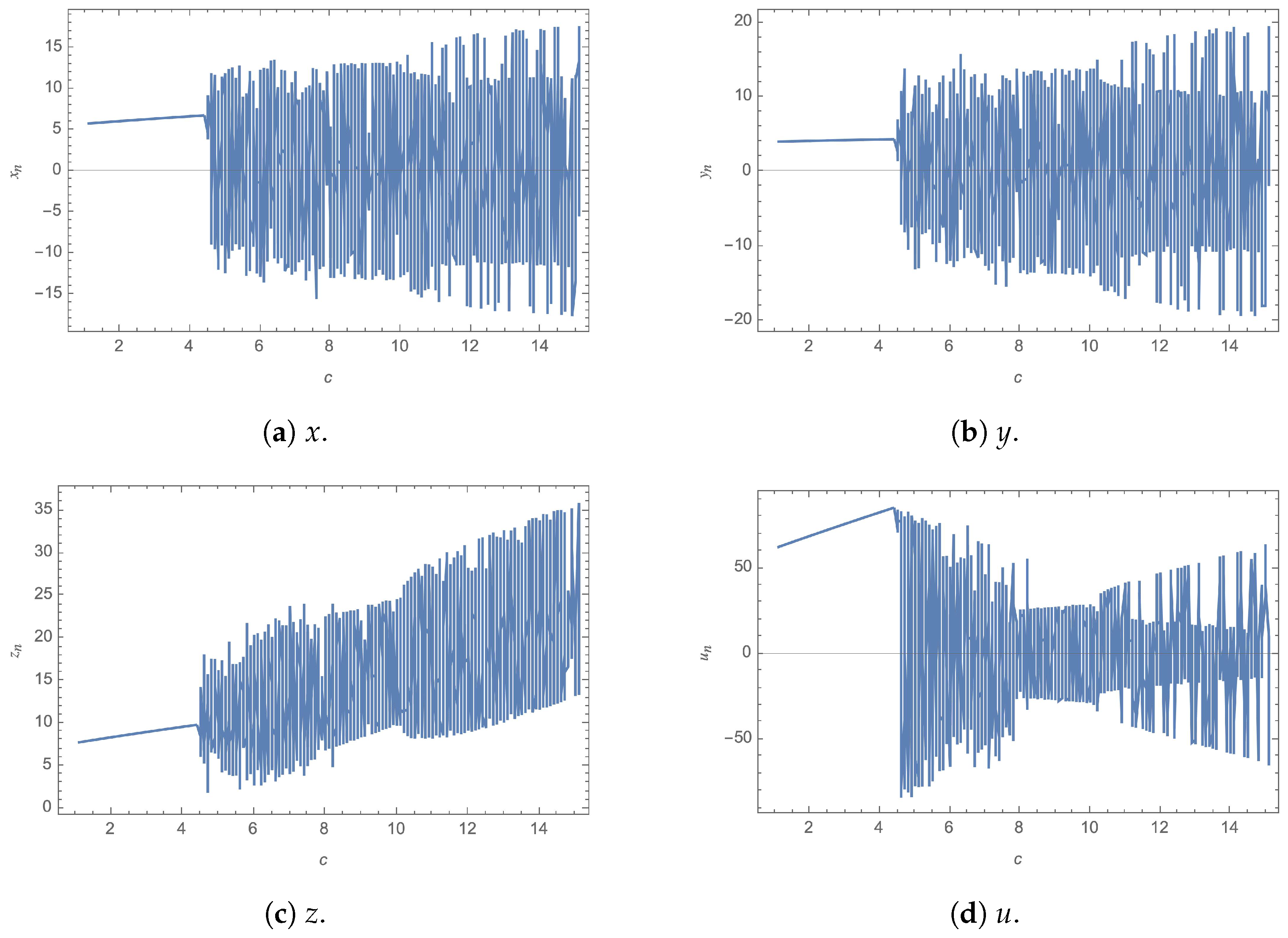
Figure 4. A plot of the 4 Lyapunov characteristic exponents of the fractional order 4D Chen system.

Figure 5. Present state and next state for center cell of Rule 30 CA.

Figure 6. A plot of the first 10 steps of Rule 30 CA.

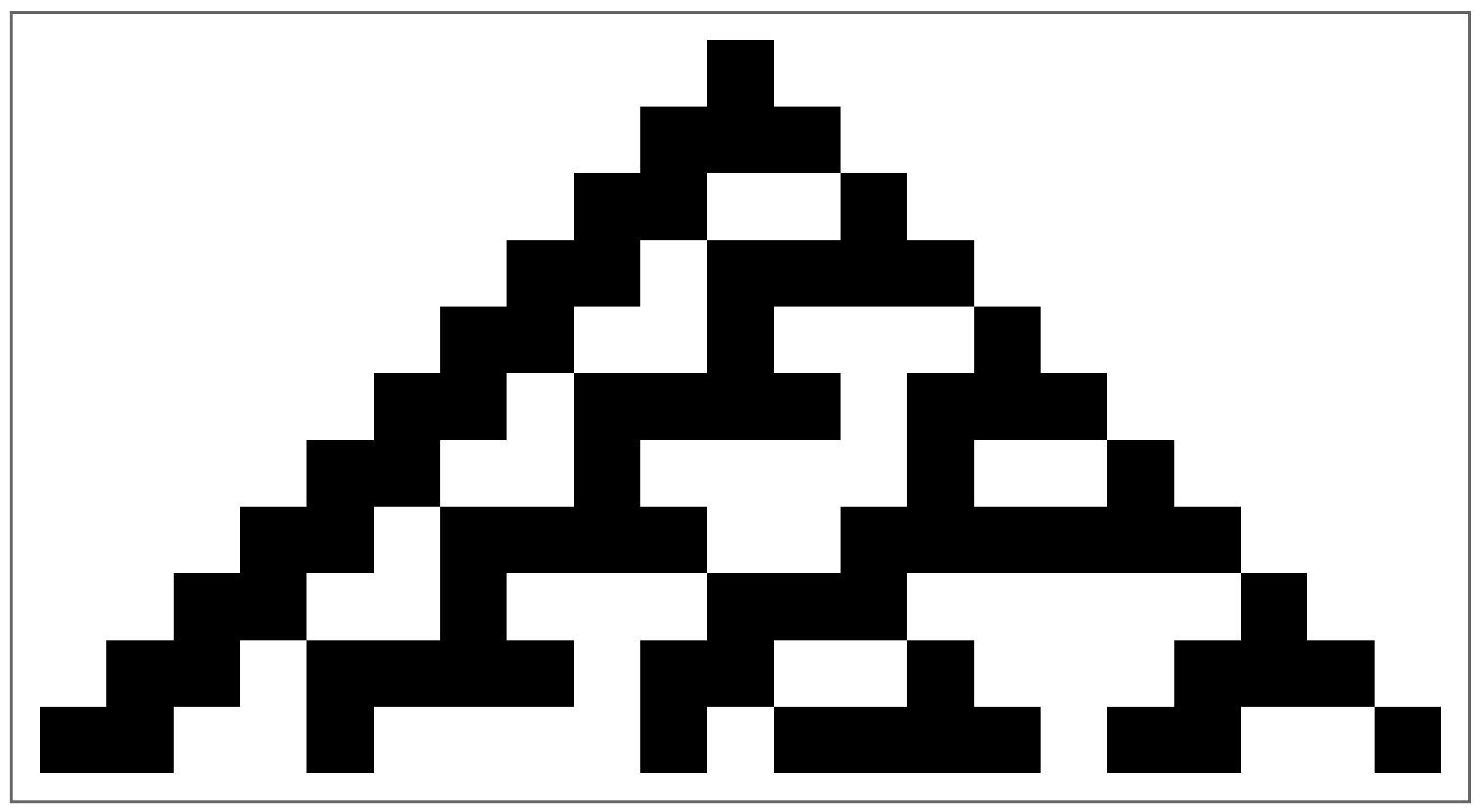
Figure 7. A plot of the first 100 steps of Rule 30 CA.

Figure 8. Flow chart of the encryption process of the proposed image cryptosystem.

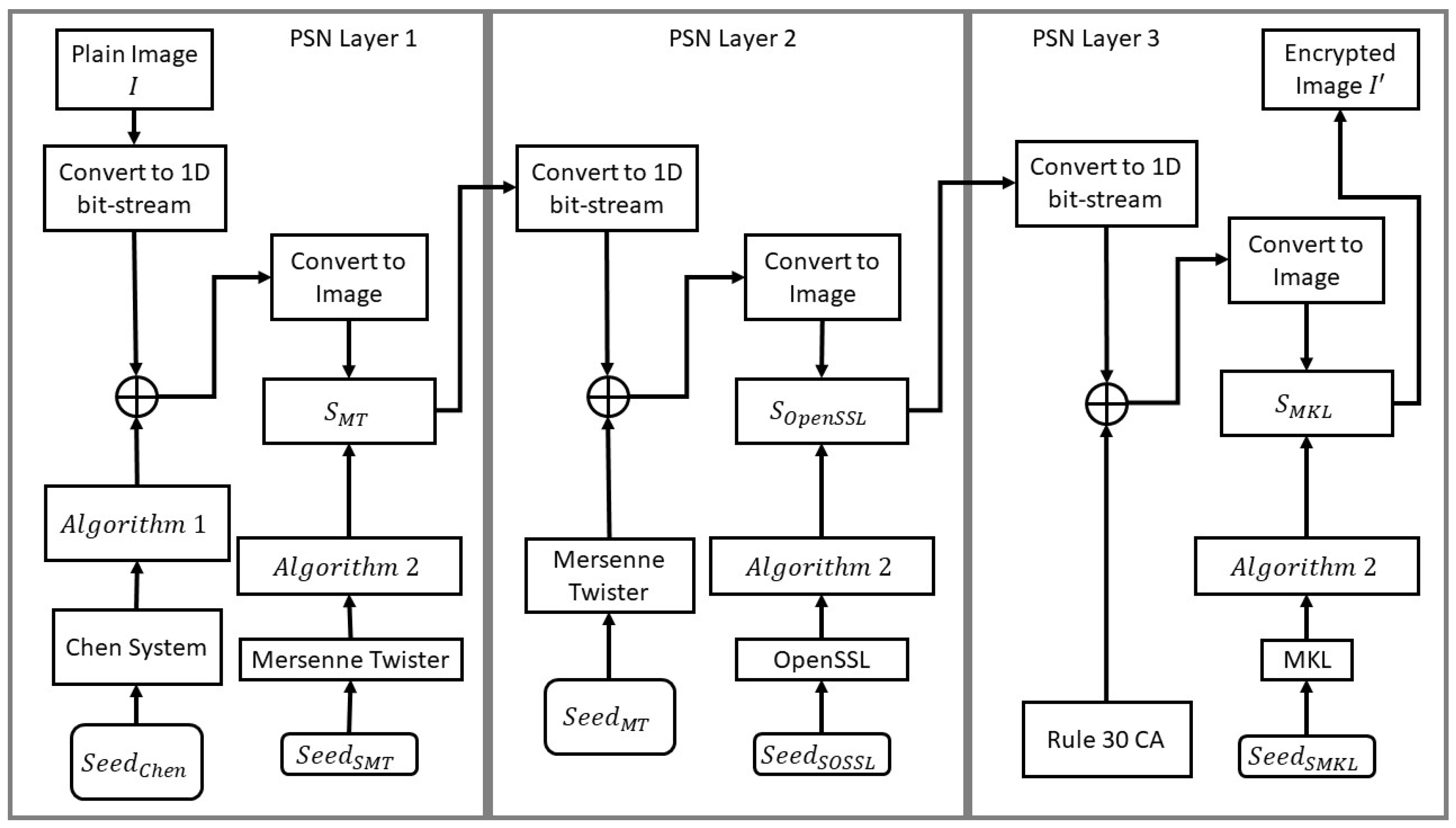
Figure 9. Flow chart of the decryption process of the proposed image cryptosystem.

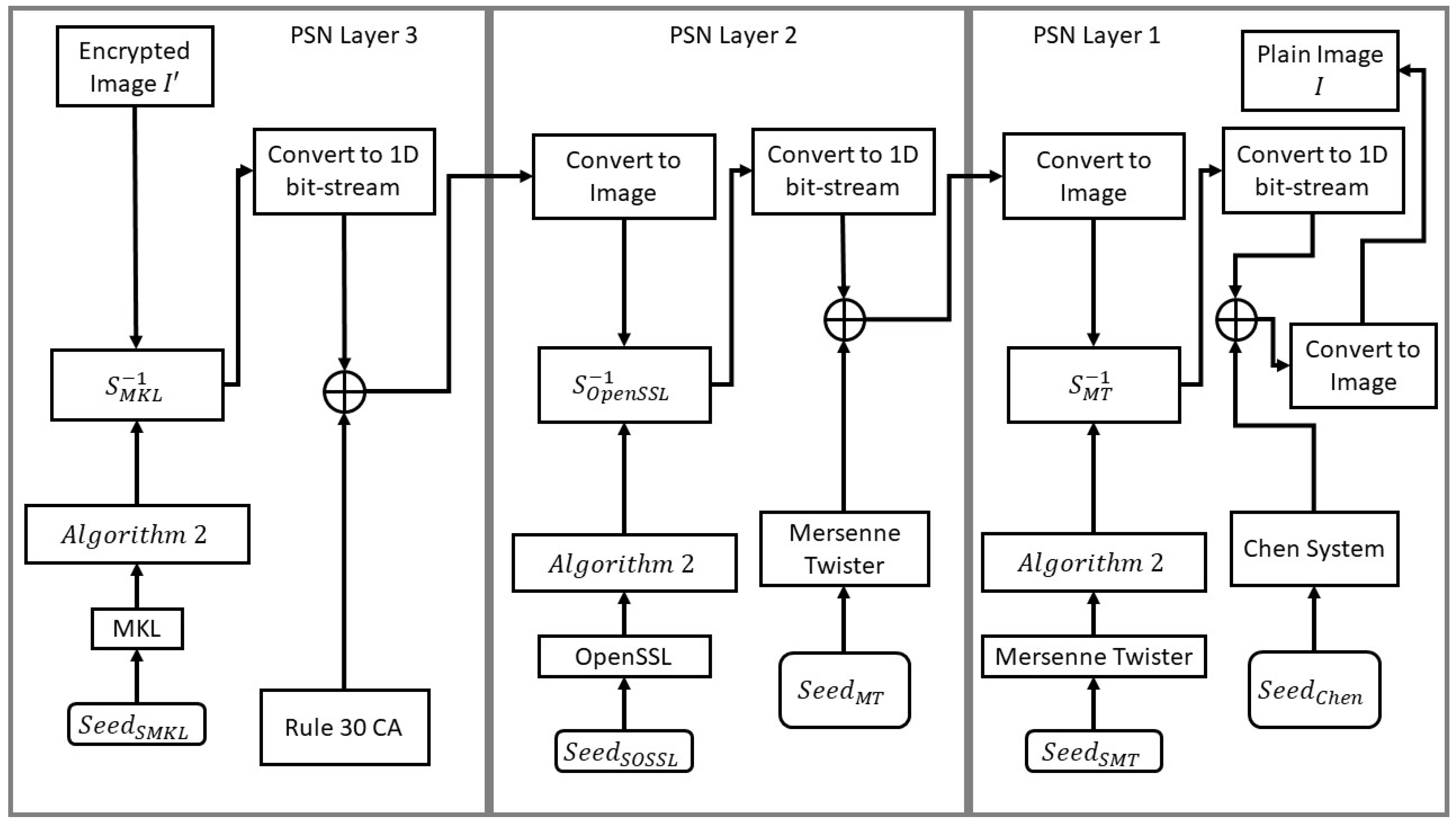
Figure 10. Mandrill image and histogram comparison pre- and post-encryption.

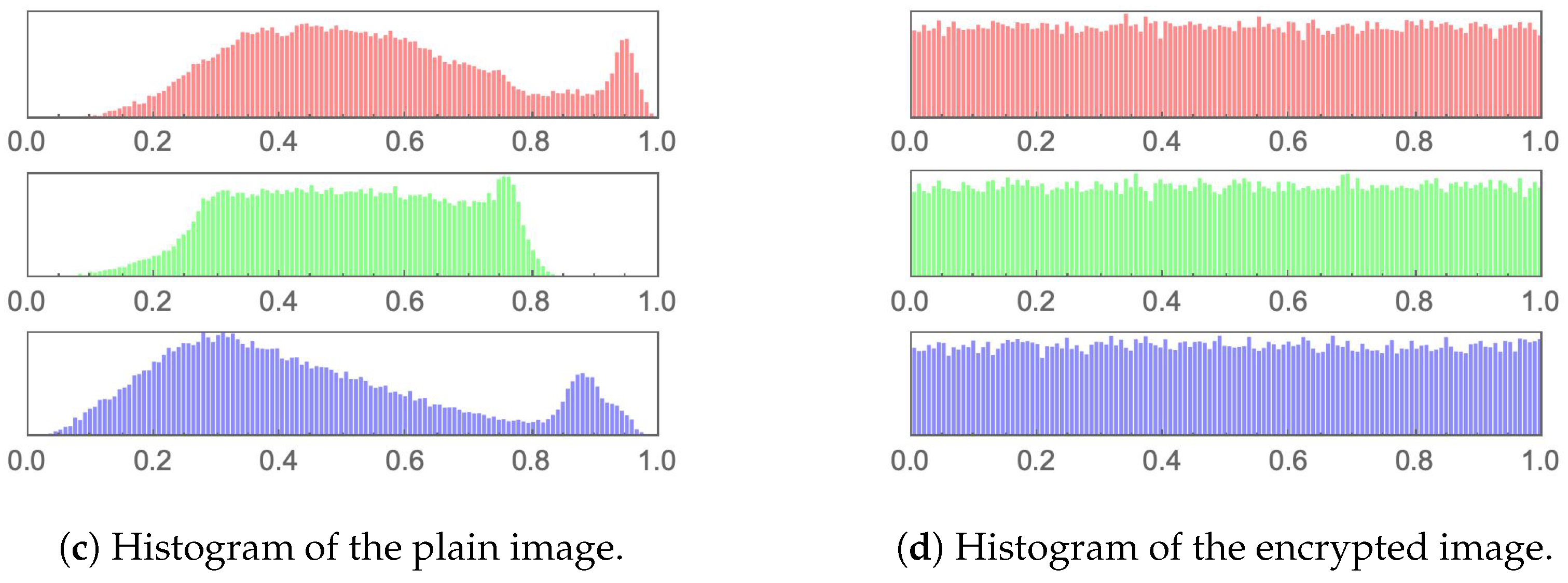
Figure 11. Sailboat image and histogram comparison pre- and post-encryption.

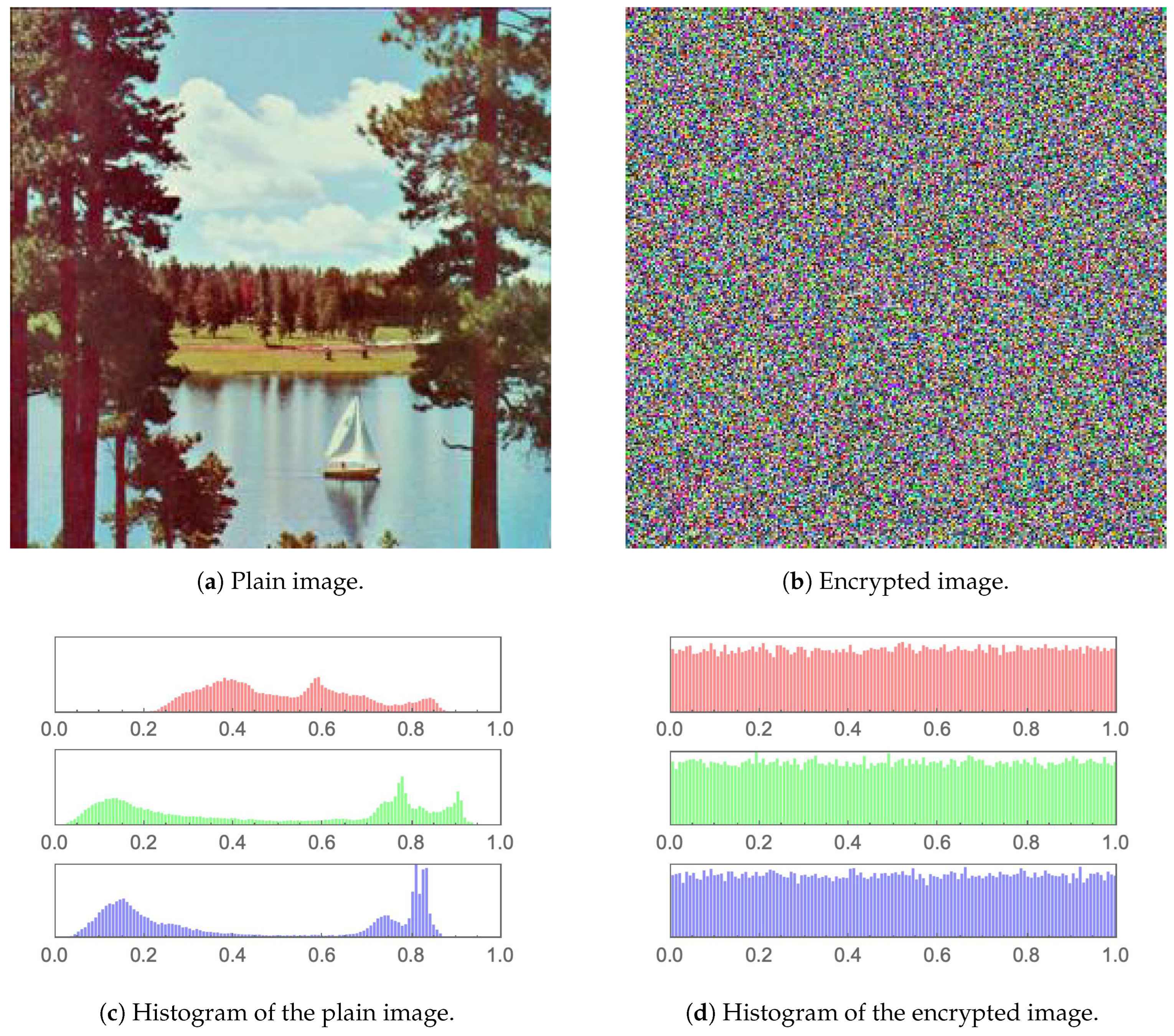
Figure 12. Peppers image and histogram comparison pre- and post-encryption.

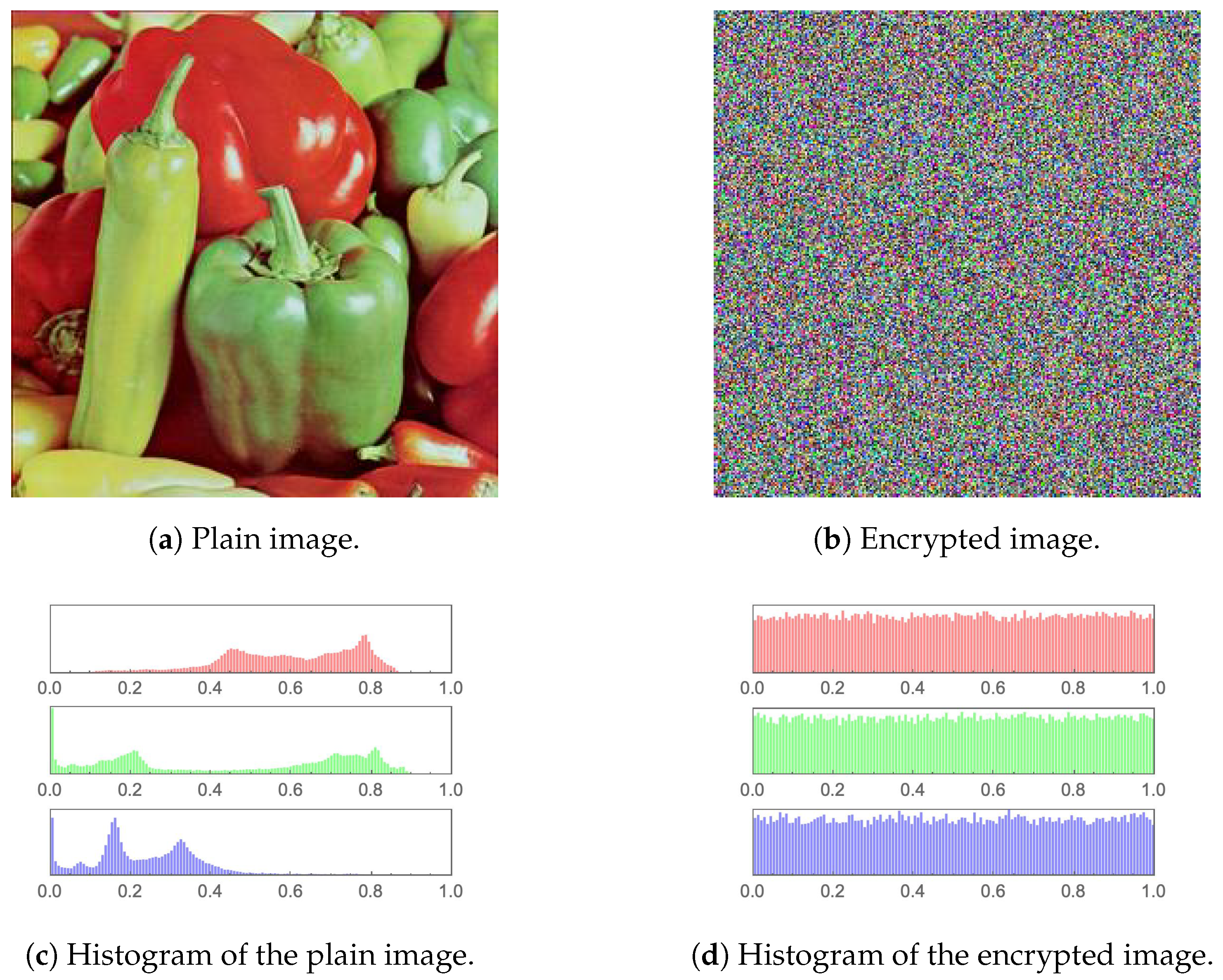
Figure 13. House image and histogram comparison pre- and post-encryption.

Figure 14. House2 image and histogram comparison pre- and post-encryption.

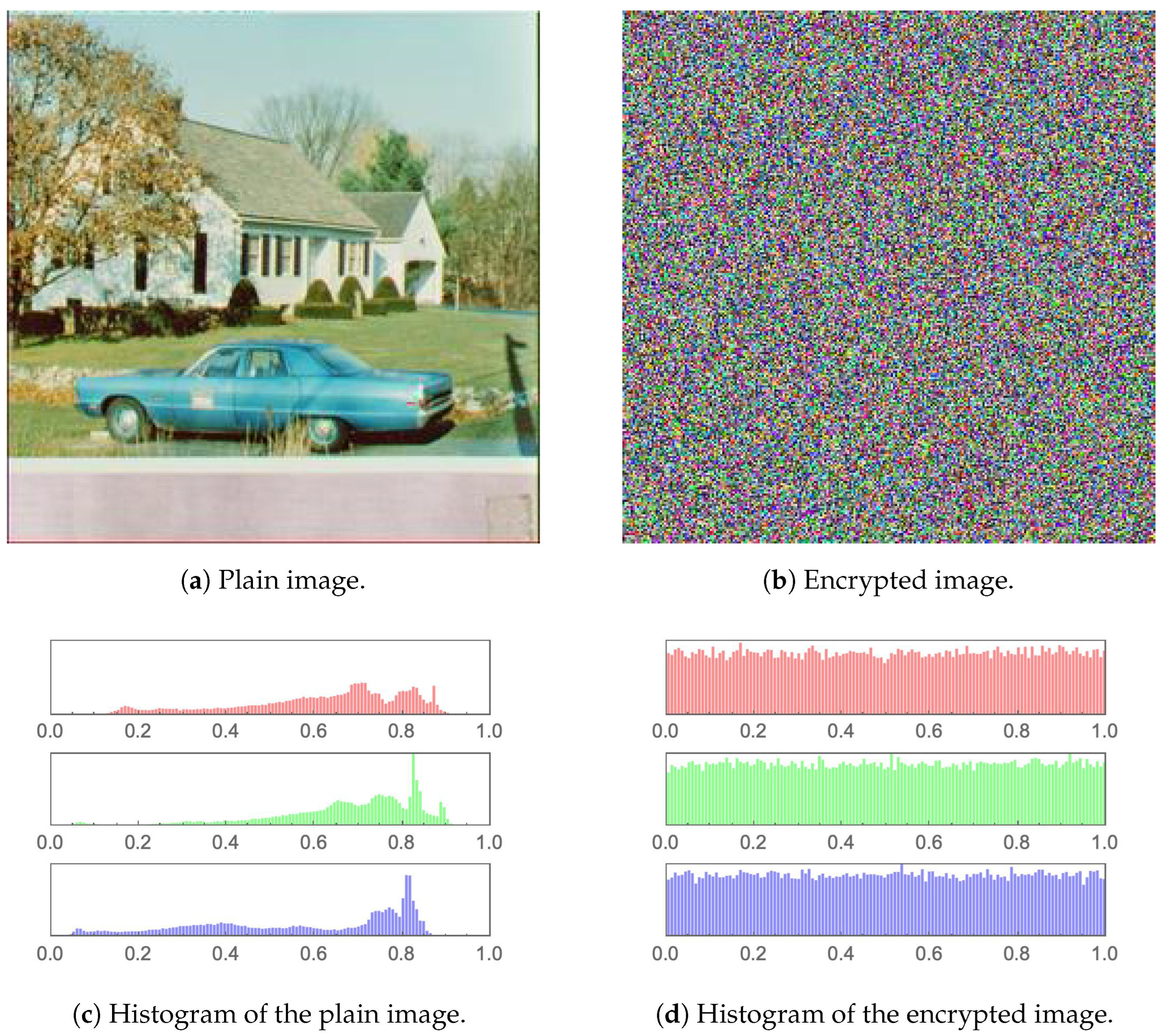
Figure 15. Tree image alongside its Fourier transformation and 3D plot of its co-occurrence matrix pre- and post-encryption.

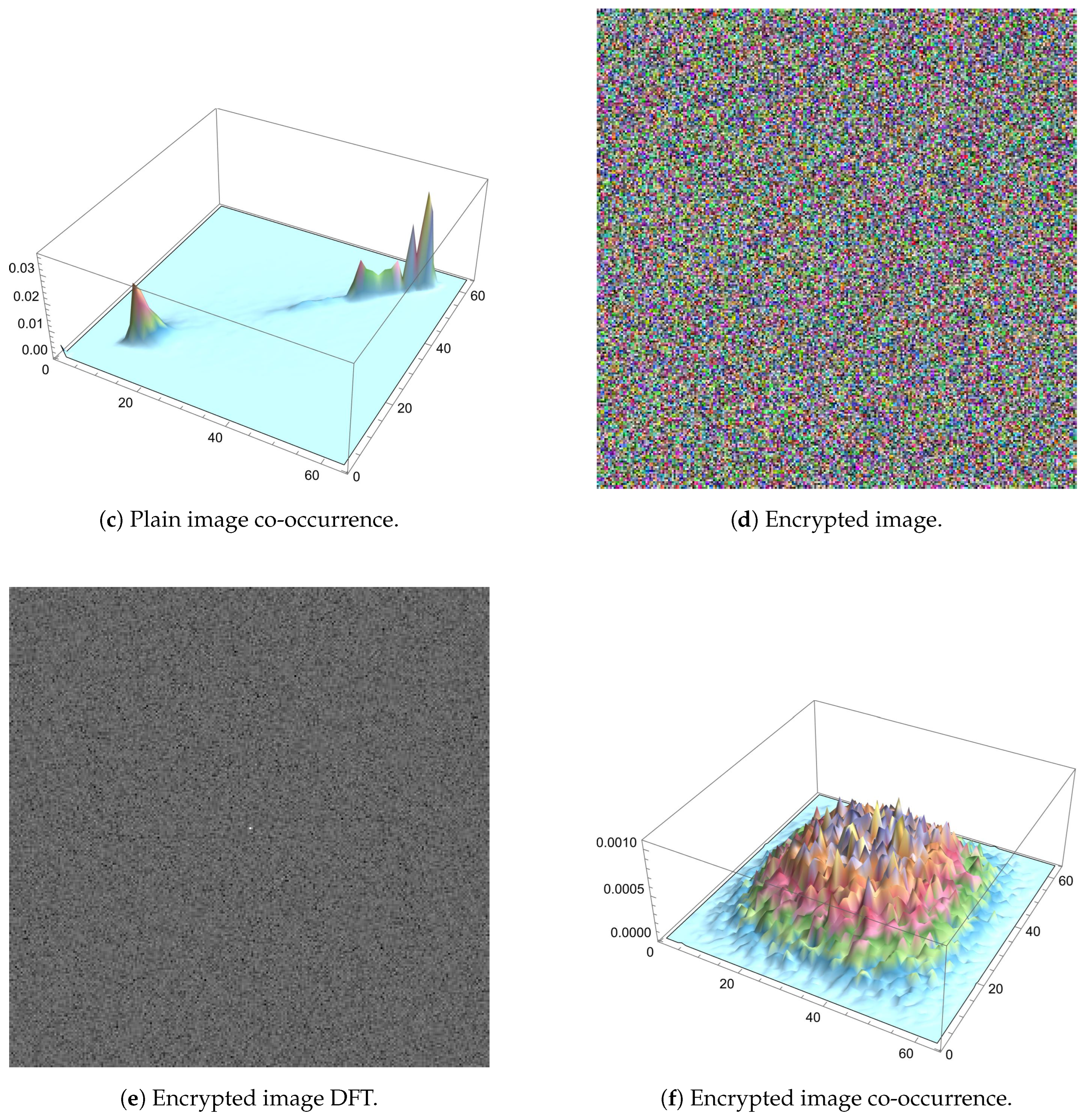
Figure 16. 2D plot of co-occurrence matrices of the Tree image pre- and post-encryption.

Figure 17. 2D plot of co-occurrence matrices of the red channel of the Tree image pre- and post-encryption.

Figure 18. 2D plot of co-occurrence matrices of the green channel of the Tree image pre- and post-encryption.

Figure 19. 2D plot of co-occurrence matrices of the blue channel of the Tree image pre- and post-encryption.

Figure 20. Various occlusion attacks on encrypted images {(a),(b),(c)}, and their corresponding decrypted versions {(d),(e),(f)}.

Figure 21. Various salt-and-pepper noise attacks to a fraction f of the encrypted images {(a),(b),(c)}, and their corresponding decrypted versions {(d),(e),(f)}.

Figure 22. Various zero-mean Gaussian noise attacks with standard deviation

σ

on the encrypted images {(a),(b),(c)}, and their corresponding decrypted versions {(d),(e),(f)}.

Figure 22. Various zero-mean Gaussian noise attacks with standard deviation

σ

on the encrypted images {(a),(b),(c)}, and their corresponding decrypted versions {(d),(e),(f)}.

Table 4. Comparison of MSE values with the literature.

Image	Proposed	[8]	[29]	[30]	[31]	[33]	[61]
Lena	$8912.4$	$9112.1$	$8926.96$	$10869.73$	$4859.03$	$8888.88$	N/A
Mandrill	$8320.41$	$8573.38$	$8290.84$	$10930.33$	$6399.05$	$8295.21$	N/A
Peppers	$10065.4$	$10298.7$	$10045.1$	N/A	$7274.44$	$10092.3$	N/A
House	$8395.53$	$8427.04$	$8351.64$	N/A	N/A	N/A	N/A
House2	$9142.54$	$9374.65$	N/A	N/A	N/A	N/A	N/A
Girl	$12104.2$	$12450.9$	N/A	N/A	N/A	N/A	N/A
Sailboat	$10071.9$	N/A	N/A	N/A	N/A	N/A	N/A
Tree	$9873.24$	N/A	N/A	N/A	N/A	N/A	N/A
Average	$9610.65$	$9706.13$	$8903.64$	10900	$6177.51$	$9092.13$	N/A

Table 5. Comparison of PSNR values, in dB, with the literature.

Image	Proposed	[8]	[29]	[30]	[31]	[33]	[61]
Lena	$8.63086$	$8.53462$	$8.6237$	$7.7677$	$11.3$	$8.64233$	$8.5674$
Mandrill	$8.92936$	$8.79929$	$8.9448$	$7.7447$	$10.10$	$8.94253$	$10.0322$
Peppers	$8.10248$	$8.00296$	$8.11128$	N/A	$9.55$	N/A	N/A
House	$8.89032$	$8.87405$	$8.91309$	N/A	N/A	N/A	N/A
House2	$8.52013$	$8.41125$	N/A	N/A	N/A	N/A	N/A
Girl	$7.30144$	$7.17879$	N/A	N/A	N/A	N/A	N/A
Sailboat	$8.0997$	N/A	N/A	N/A	N/A	N/A	N/A
Tree	$8.18621$	N/A	N/A	N/A	N/A	N/A	N/A
Average	$8.33256$	$8.30016$	$8.64822$	$7.7562$	$10.3167$	$8.79243$	$9.2998$

Table 6. Comparison of MAE values with the literature.

Image	Proposed	[8]	[33]	[30]	[62]	[61]
Lena	$77.4877$	$78.3564$	$77.3752$	87	$77.35$	$77.96$
Peppers	$81.9832$	$82.3273$	$81.7740$	N/A	$74.71$	N/A
Mandrill	$75.1632$	$81.913$	$75.1659$	92	$73.91$	$67.85$
House	$75.4983$	N/A	N/A	N/A	N/A	N/A
House 2	$78.3327$	N/A	N/A	N/A	N/A	N/A
Girl	$89.9807$	N/A	N/A	N/A	N/A	N/A
Sailboat	$82.1003$	N/A	N/A	N/A	N/A	N/A
Tree	$81.1623$	N/A	N/A	N/A	N/A	N/A
Average	$80.2136$	$80.8656$	$78.105$	$89.5$	$75.3233$	$72.905$

Table 7. Comparison of information entropy values with the literature.

Image	Proposed	[8]	[29]	[30]	[63]	[31]	[33]	[61]
Lena	$7.99887$	$7.9856$	$7.999$	$7.999$	$7.997$	$7.996$	$7.997$	$7.9972$
Mandrill	$7.99866$	$7.9905$	$7.999$	$7.999$	$7.999$	N/A	$7.996$	$7.9969$
Peppers	$7.99834$	$7.9951$	$7.999$	$7.9991$	N/A	$7.997$	$7.9969$	N/A
House	$7.99729$	$7.9577$	$7.999$	N/A	N/A	N/A	N/A	N/A
House2	$7.99848$	$7.9847$	N/A	N/A	N/A	N/A	N/A	N/A
Girl	$7.99477$	$7.9789$	N/A	N/A	N/A	N/A	N/A	N/A
Sailboat	$7.99875$	N/A	N/A	N/A	N/A	N/A	N/A	N/A
Tree	$7.99713$	N/A	N/A	N/A	N/A	N/A	N/A	N/A
Average	$7.99711$	$7.98208$	$7.999$	$7.999$	$7.99903$	$7.9965$	$7.99663$	$7.99705$

Table 8. Correlation coefficients of plain and encrypted images.

Plain image				Encrypted image
Correlation coefficient				Correlation coefficient
Image	Horizontal	Diagonal	Vertical	Horizontal	Diagonal	Vertical
Lena	$0.938611$	$0.913175$	$0.96833$	$0.0064113$	$- 0.0015143$	$0.000568333$
Peppers	$0.959422$	$0.930426$	$0.966795$	$- 0.00834328$	$- 0.00327485$	$0.00222402$
Mandrill	$0.848778$	$0.750624$	$0.79088$	$- 0.00007897$	$0.00157688$	$- 0.00200228$

Table 9. Comparison of correlation coefficient values with the literature, for plain and encrypted Lena images.

Scheme	Horizontal	Diagonal	Vertical
Proposed	$0.0064113$	$- 0.0015143$	$0.000568333$
[8]	$0.003265$	$- 0.00413$	$0.002451$
[30]	$0.0054$	$0.0054$	$0.0016$
[33]	$0.002287$	$- 0.00132$	$- 0.00160$
[61]	$- 0.0061$	$- 0.0018$	$0.0067$
[64]	$0.000199$	$0.003705$	$- 0.000924$

Table 10. Comparison of correlation coefficient values with the literature, in 3 directions, for plain and encrypted Lena images, computed for each color channel separately.

Channel	Direction	Plain image	Encrypted image	[65]	[66]	[67]	[33]
Red	Horizontal	$0.952474$	$0.00771152$	$0.001365$	$0.0021$	$0.9568$	$- 0.00364$
	Diagonal	$0.928029$	$- 0.003263$	$0.000232$	$- 0.0026$	$0.0075$	$0.00016$
	Vertical	$0.975913$	$0.00199022$	$0.004776$	$0.0018$	$- 0.0376$	$0.000697$
Green	Horizontal	$0.935628$	$- 0.000053$	$0.003294$	$- 0.0006$	$0.0020$	$0.000118$
	Diagonal	$0.910534$	$0.0026447$	$0.004807$	$0.0001$	$- 0.0046$	$0.00177$
	Vertical	$0.966647$	$- 0.003507$	$- 0.000579$	$0.0004$	$- 0.0013$	$- 0.0011$
Blue	Horizontal	$0.917439$	$- 0.000962$	$0.002060$	$- 0.005$	$0.0071$	$- 0.00164$
	Diagonal	$0.888482$	$- 0.004093$	$- 0.004043$	$- 0.0104$	$- 0.0009$	$- 0.00523$
	Vertical	$0.947961$	$0.00259674$	$0.000194$	$0.001$	$- 0.0423$	$0.006041$

Table 11. NPCR and UACI of various images.

Metric	Image	Result
NPCR	Lena	$99.5855$
	Peppers	$99.6435$
	Mandrill	$99.6023$
	House	$99.5972$
	House2	$99.6241$
	Girl	$99.6546$
	Sailboat	$99.6048$
	Tree	$99.5829$
	Average	$99.6119$
UACI	Lena	$30.3873$
	Peppers	$32.1503$
	Mandrill	$29.4757$
	House	$29.607$ 2
	House2	$30.7187$
	Girl	$35.2865$
	Sailboat	$32.1962$
	Tree	$31.8284$
	Average	$31.4563$

Table 12. Comparison of NPCR and UACI values computed for various images’ color channels.

Metric	Image	Color Channel	Proposed	[33]	[68]
NPCR	Lena	Red	$99.5712$	$99.6109$	$99.6355$
		Green	$99.5758$	$99.6109$	$99.6256$
		Blue	$99.6094$	$99.6375$	$99.6159$
	Peppers	Red	$99.6338$	$99.6032$	$99.6307$
		Green	$99.6338$	$99.6032$	$99.6250$
		Blue	$99.6628$	$99.3750$	$99.6213$
	Mandrill	Red	$99.5911$	$99.5880$	$99.6102$
		Green	$99.5865$	$99.5880$	$99.6134$
		Blue	$99.6292$	$99.5880$	$99.6057$
UACI	Lena	Red	$33.1056$	$33.4158$	$33.4657$
		Green	$30.5178$	$30.3902$	$33.4552$
		Blue	$27.5385$	$33.2420$	$33.4550$
	Peppers	Red	$28.8353$	$33.3459$	$33.4832$
		Green	$33.8409$	$33.4702$	$33.4904$
		Blue	$33.7746$	$33.4357$	$33.4619$
	Mandrill	Red	$29.5137$	$33.4273$	$33.5002$
		Green	$28.0464$	$33.4635$	$33.4711$
		Blue	$30.8671$	$33.7951$	$33.4951$

Table 13. Comparison of NPCR and UACI values of the Lena image.

Scheme	NPCR	UACI
Proposed	99.5855	30.3873
[30]	$99.52$	$26.793$
[33]	$99.63$	$30.3432$
[32]	$99.625$	$30.5681$
[61]	$99.61$	$33.516$
[69]	$99.63$	$33.48$

Table 14. NIST analysis on Lena encrypted image.

Test name	Value	Remarks
Frequency	$0.677248$	Success
Block Frequency	$0.478516$	Success
Run	$0.667837$	Success
Longest run of ones	$0.136182$	Success
Rank	$0.743617$	Success
Spectral FFT	$0.522490$	Success
Non overlapping	$0.202310$	Success
Overlapping	$0.590476$	Success
Universal	$0.775967$	Success
Linear complexity	$0.688046$	Success
Serial	$0.950997$	Success
Approximate Entropy	$0.094460$	Success
Cumulative sum (forward)	$0.704199$	Success
Cumulative sum (reverse)	$0.363251$	Success

Table 15. Key space values comparison.

Algorithm	Key space
Proposed	$10^{496} \approx 2^{1658}$
[8]	$2^{372}$
[32]	$2^{478}$
[61]	$2^{604}$
[64]	$2^{187}$
[71]	$2^{312}$
[73]	$2^{256}$
[74]	$2^{256}$
[75]	$2^{345}$
[76]	$2^{219}$

Table 16. Histogram dependency tests for various images.

Image	Color	$β$ (31)	$γ$ (32)	$τ$ (33)	$ρ$ (34)	r (35)
Lena	Red	$- 0.110694$	$- 0.0347993$	$- 0.0337626$	$- 0.0481434$	$- 0.0132834$
	Green	$- 0.0158119$	$0.0215872$	$0.0213466$	$0.0354592$	$0.0373801$
	Blue	$- 0.0514905$	$- 0.0646801$	$- 0.0608846$	$- 0.0878873$	$- 0.0543499$
	Combined	$0.015625$	$- 0.0276274$	$- 0.0274928$	$- 0.0420548$	$- 0.0527299$
Peppers	Red	$0.0553381$	$0.0327303$	$0.0320445$	$0.0441645$	$0.0552461$
	Green	$- 0.00793776$	$0.00618093$	$0.0061233$	$0.00892123$	$0.0309788$
	Blue	$- 0.0316267$	$- 0.0302744$	$- 0.0298716$	$- 0.047874$	$0.0160251$
	Combined	$- 0.0472456$	$- 0.0437633$	$- 0.0435566$	$- 0.0676501$	$- 0.0410837$
Mandrill	Red	$0.0198853$	$0.0565044$	$0.0558669$	$0.0816251$	$0.0595621$
	Green	$0.046875$	$0.00948634$	$0.00932192$	$0.0154712$	$- 0.0016778$
	Blue	$0.0825168$	$0.0616492$	$0.0611381$	$0.0939456$	$0.0924138$
	Combined	$0.046875$	$0.0745872$	$0.0742411$	$0.110141$	$0.0934929$
House	Red	$0.110243$	$0.0104633$	$0.0102083$	$0.0137227$	$0.129594$
	Green	$0.0156864$	$- 0.0230578$	$- 0.0228953$	$- 0.0316539$	$- 0.127908$
	Blue	$0.0433977$	$0.0520028$	$0.0499645$	$0.0761799$	$- 0.0458134$
	Combined	$0.03125$	$0.0195387$	$0.0194504$	$0.0282111$	$0.0149416$
House2	Red	$- 0.0594233$	$- 0.00223601$	$- 0.00220542$	$- 0.00585658$	$0.0241044$
	Green	$- 0.0828449$	$- 0.00492304$	$- 0.00488175$	$- 0.00884184$	$0.0531022$
	Blue	$0.0079207$	$- 0.0105576$	$- 0.0103937$	$- 0.0162964$	$0.00611405$
	Combined	$0.043395$	$0.0143268$	$0.0142559$	$0.0229318$	$0.0314425$
Girl	Red	$0.0866627$	$0.0242129$	$0.0204944$	$0.025068$	$- 0.0205761$
	Green	$0.0474911$	$0.0689793$	$0.0573322$	$0.077706$	$0.104362$
	Blue	$0.030644$	$0.054669$	$0.0443616$	$0.0605645$	$0.0420095$
	Combined	$0.03125$	$0.0340795$	$0.0326326$	$0.0450366$	$0.0657316$
Sailboat	Red	$0.0158114$	$0.00693224$	$0.00666217$	$0.0118382$	$- 0.0119124$
	Green	$- 0.039685$	$- 0.0265376$	$- 0.0262888$	$- 0.0422393$	$- 0.0116989$
	Blue	$0.0714466$	$0.040201$	$0.0397032$	$0.0554966$	$0.00863334$
	Combined	$- 0.0435716$	$- 0.054667$	$- 0.0544031$	$- 0.0806747$	$- 0.0740552$
Tree	Red	$0.0960611$	$0.034327$	$0.0336832$	$0.0463177$	$0.00928989$
	Green	$0.0591786$	$0.0368575$	$0.036362$	$0.0540911$	$0.0376557$
	Blue	$0.046875$	$0.045737$	$0.0441452$	$0.0640862$	$0.019782$
	Combined	0	$0.0226485$	$0.022537$	$0.034886$	$- 0.0006252$

Table 17. Encryption time, decryption time, and their added values for the proposed image cryptosystem, for the House image at various dimensions.

Image Dimensions	$t_{E n c}$ [s]	$t_{D e c}$ [s]	$t_{A d d}$ [s]
$64 \times 64$	$0.028884$	$0.026181$	$0.055065$
$128 \times 128$	$0.107976$	$0.116058$	$0.232116$
$256 \times 256$	$0.426243$	$0.463615$	$0.889858$
$512 \times 512$	$1.88184$	$1.64237$	$3.52422$
$1024 \times 1024$	$7.66508$	$6.70321$	$15.3302$

Table 18. A comparison of the encryption time for various algorithms from the literature for a Lena image with dimensions

256 \times 256

Table 18. A comparison of the encryption time for various algorithms from the literature for a Lena image with dimensions

256 \times 256

Algorithm	$t_{E n c}$ [s]	Machine specifications (CPU and RAM)
Proposed	$0.426243$	2.9 GHz Intel^® Core^TM i9, 32 GB
[8]	$1.42545$	2.9 GHz Intel^® Core^TM i9, 32 GB
[20]	$2.582389$	2.9 GHz Intel^® Core^TM i9, 32 GB
[32]	$2.750966$	3.4 GHz Intel^®
[61]	$2.7236$	2.7 GHz Intel^® Core^TM i7, 8 GB
[76]	$3.45$	N/A
[79]	$1.1168$	3.4 GHz Intel^® Core^TM i7, 8 GB
[80]	$1.112$	3.4 GHz Intel^® Core^TM i3, 4 GB

Table 19. Performance evaluation of the proposed S-boxes (displayed in Table 1, Table 2 and Table 3).

Metric	Optimal	MT	OpenSSL	Intel’s MKL
Nonlinearity	112	108	108	108
SAC	$0.5$	$0.503662$	$0.499023$	$0.499268$
BIC	112	92	112	104
LAP	$0.0625$	$0.140625$	$0.0625$	$0.09375$
DAP	$0.0156$	$0.015625$	$0.015625$	$0.015625$

Table 20. Comparison among the proposed S-boxes and those provided in the literature.

S-box	NL	SAC	BIC	LAP	DAP
Proposed, MT	108	$0.503662$	92	$0.140625$	$0.015625$
Proposed, OpenSSL	108	$0.499023$	112	$0.0625$	$0.015625$
Proposed, Intel’s MKL	108	$0.499268$	104	$0.09375$	$0.015625$
AES [17]	112	$0.5058$	112	$0.0625$	$0.0156$
Khan et al. [30]	111	$0.5036$	110	$0.0781$	$0.0234$
Zahid et al. [87]	107	$0.497$	$103.5$	$0.1560$	$0.0390$
Aboytes et al. [88]	112	$0.4998$	112	$0.0625$	$0.0156$
Hayat et al. [89]	100	$0.5007$	$104.1$	$0.0390$	$0.1250$
Nasir et al. (S4) [90]	112	$0.5$	112	$0.0625$	$0.0156$

Table 21. Description of various types of attacks.

Attack	Needed information by cryptanalyst
Ciphertext only	1. Cryptosystem
Ciphertext only	2. Encrypted image to be decoded
Known plaintext	1. Cryptosystem
	2. Encrypted image to be decoded
	3. Plain image and corresponding encrypted image with the encryption key
Chosen ciphertext	1. Cryptosystem
	2. Encrypted image to be decoded
	3. Reported encrypted image chosen by cryptanalyst alongside its corresponding plain image generated with the cryptosystem and decryption key
Chosen plaintext	1. Cryptosystem
	2. Encrypted image to be decoded
	3. Reported plain image chosen by cryptanalyst alongside its corresponding encrypted image generated with the cryptosystem and encryption key

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

4	90	209	152	178	35	92	10	240	204	181	97	187	165	116	131
252	146	44	144	180	130	223	40	24	234	76	32	201	21	150	46
33	137	83	158	27	41	248	237	119	18	109	2	227	84	170	160
251	48	222	163	211	113	172	166	62	96	118	207	37	31	107	224
102	179	226	74	112	254	205	218	5	122	60	12	200	164	81	23
13	230	190	127	34	65	169	183	54	129	1	70	236	136	245	186
85	15	132	239	58	225	123	120	221	185	125	95	124	154	195	88
202	143	232	8	219	173	145	140	208	101	79	39	247	135	194	250
20	216	26	233	87	71	55	22	241	126	238	59	244	52	121	30
49	0	214	42	210	182	196	38	53	171	45	235	82	231	242	104
7	156	168	80	77	191	111	177	6	100	57	155	117	161	217	189
103	68	203	148	66	228	43	99	229	91	134	105	128	14	93	192
157	162	138	29	47	3	212	115	50	106	213	253	246	63	151	176
75	110	147	61	9	159	72	25	193	94	16	51	167	36	206	198
139	174	188	133	220	108	17	11	215	73	64	255	141	89	69	142
67	78	175	56	184	249	28	19	98	86	199	243	149	114	197	153

73	202	161	243	4	252	40	165	168	36	74	253	169	21	238	34
8	29	232	66	111	102	210	71	195	247	32	164	82	58	196	151
62	59	166	112	244	49	193	241	240	200	39	91	228	48	47	137
220	204	50	146	178	245	30	100	117	221	35	107	206	194	149	182
16	52	88	122	205	109	224	67	68	186	158	172	80	86	0	144
118	65	72	199	94	108	251	9	150	99	45	27	159	104	185	249
246	63	17	188	212	95	218	56	152	96	209	44	132	89	76	11
175	113	174	57	128	234	26	79	61	190	2	98	142	207	69	14
123	37	53	18	87	31	124	147	231	84	19	83	145	133	85	106
120	198	46	239	177	155	230	235	43	201	20	78	28	135	163	23
3	125	127	121	139	116	254	171	13	77	7	140	176	170	250	119
208	131	25	225	115	153	75	101	219	237	217	216	10	187	215	189
92	55	38	191	248	143	192	227	197	41	97	70	54	141	12	24
5	33	236	81	22	154	51	130	233	64	60	203	103	15	148	90
181	157	6	138	129	134	126	229	114	242	184	160	42	226	183	222
105	1	110	213	180	223	93	136	179	255	156	167	211	162	214	173

137	9	202	234	125	23	241	219	250	77	132	47	99	44	208	230
100	91	238	149	213	117	56	135	185	10	63	174	78	227	43	61
178	119	183	104	81	19	52	186	72	32	248	48	193	115	133	28
8	4	155	206	172	175	192	187	36	235	200	136	199	191	170	247
55	180	130	83	45	64	159	215	39	240	211	58	102	62	224	232
214	12	251	65	90	46	201	217	145	162	116	212	141	50	189	143
166	198	128	177	74	84	22	103	226	233	209	105	131	29	150	154
184	237	156	176	228	147	153	53	142	89	20	26	38	148	169	182
67	239	35	146	194	165	210	71	97	76	107	220	171	158	11	27
41	101	244	225	88	190	113	110	204	229	112	111	161	98	252	164
16	236	195	24	120	106	114	205	68	96	163	138	129	14	157	18
231	3	0	242	152	243	95	173	75	34	121	221	245	188	2	216
66	123	181	109	167	31	49	54	6	17	7	51	179	249	118	108
255	30	15	33	60	73	139	79	168	93	223	82	87	1	69	197
218	140	253	5	42	92	207	124	196	57	85	203	127	151	160	25
21	222	246	126	86	134	144	80	37	40	94	13	59	70	122	254

4	90	209	152	178	35	92	10	240	204	181	97	187	165	116	131
252	146	44	144	180	130	223	40	24	234	76	32	201	21	150	46
33	137	83	158	27	41	248	237	119	18	109	2	227	84	170	160
251	48	222	163	211	113	172	166	62	96	118	207	37	31	107	224
102	179	226	74	112	254	205	218	5	122	60	12	200	164	81	23
13	230	190	127	34	65	169	183	54	129	1	70	236	136	245	186
85	15	132	239	58	225	123	120	221	185	125	95	124	154	195	88
202	143	232	8	219	173	145	140	208	101	79	39	247	135	194	250
20	216	26	233	87	71	55	22	241	126	238	59	244	52	121	30
49	0	214	42	210	182	196	38	53	171	45	235	82	231	242	104
7	156	168	80	77	191	111	177	6	100	57	155	117	161	217	189
103	68	203	148	66	228	43	99	229	91	134	105	128	14	93	192
157	162	138	29	47	3	212	115	50	106	213	253	246	63	151	176
75	110	147	61	9	159	72	25	193	94	16	51	167	36	206	198
139	174	188	133	220	108	17	11	215	73	64	255	141	89	69	142
67	78	175	56	184	249	28	19	98	86	199	243	149	114	197	153

73	202	161	243	4	252	40	165	168	36	74	253	169	21	238	34
8	29	232	66	111	102	210	71	195	247	32	164	82	58	196	151
62	59	166	112	244	49	193	241	240	200	39	91	228	48	47	137
220	204	50	146	178	245	30	100	117	221	35	107	206	194	149	182
16	52	88	122	205	109	224	67	68	186	158	172	80	86	0	144
118	65	72	199	94	108	251	9	150	99	45	27	159	104	185	249
246	63	17	188	212	95	218	56	152	96	209	44	132	89	76	11
175	113	174	57	128	234	26	79	61	190	2	98	142	207	69	14
123	37	53	18	87	31	124	147	231	84	19	83	145	133	85	106
120	198	46	239	177	155	230	235	43	201	20	78	28	135	163	23
3	125	127	121	139	116	254	171	13	77	7	140	176	170	250	119
208	131	25	225	115	153	75	101	219	237	217	216	10	187	215	189
92	55	38	191	248	143	192	227	197	41	97	70	54	141	12	24
5	33	236	81	22	154	51	130	233	64	60	203	103	15	148	90
181	157	6	138	129	134	126	229	114	242	184	160	42	226	183	222
105	1	110	213	180	223	93	136	179	255	156	167	211	162	214	173

137	9	202	234	125	23	241	219	250	77	132	47	99	44	208	230
100	91	238	149	213	117	56	135	185	10	63	174	78	227	43	61
178	119	183	104	81	19	52	186	72	32	248	48	193	115	133	28
8	4	155	206	172	175	192	187	36	235	200	136	199	191	170	247
55	180	130	83	45	64	159	215	39	240	211	58	102	62	224	232
214	12	251	65	90	46	201	217	145	162	116	212	141	50	189	143
166	198	128	177	74	84	22	103	226	233	209	105	131	29	150	154
184	237	156	176	228	147	153	53	142	89	20	26	38	148	169	182
67	239	35	146	194	165	210	71	97	76	107	220	171	158	11	27
41	101	244	225	88	190	113	110	204	229	112	111	161	98	252	164
16	236	195	24	120	106	114	205	68	96	163	138	129	14	157	18
231	3	0	242	152	243	95	173	75	34	121	221	245	188	2	216
66	123	181	109	167	31	49	54	6	17	7	51	179	249	118	108
255	30	15	33	60	73	139	79	168	93	223	82	87	1	69	197
218	140	253	5	42	92	207	124	196	57	85	203	127	151	160	25
21	222	246	126	86	134	144	80	37	40	94	13	59	70	122	254

A 3-Layer PSN for Image Encryption Utilizing Fractional-Order Chen Hyperchaotic Map and Cryptographically-Secure PRNGs

Abstract

1. Introduction

2. Preliminary Mathematical Constructs

2.1. The Fractional-Order Hyperchaotic Chen System

2.2. The Mersenne Twister

2.3. OpenSSL

2.3.1. Rule 30 Cellular Automata

2.3.2. Intel’s Math Kernel Library

2.3.3. S-Box Design

2.3.4. Key Establishment Protocol

3. Proposed Image Cryptosystem

3.1. The Encryption Process

3.2. The Decryption Process

3.3. Utilized Algorithms

4. Numerical Results and Performance Evaluation

4.1. Visual and Histogram Analyses

4.2. Mean Squared Error

4.3. Peak Signal to Noise Ratio

4.4. Mean Absolute Error

4.5. Information Entropy

4.6. Fourier Transformation Analysis

4.7. Correlation Coefficient Analysis

4.8. Differential Attack Analysis

4.9. The National Institute of Standards and Technology Analysis

4.10. Key Space Analysis

4.11. Histogram Dependency Tests

4.12. Execution Time Analysis

4.13. S-Box Performance Analysis

4.14. Various Cryptanalyses and Noise Attacks

5. Conclusions and Future Works

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

4	90	209	152	178	35	92	10	240	204	181	97	187	165	116	131
252	146	44	144	180	130	223	40	24	234	76	32	201	21	150	46
33	137	83	158	27	41	248	237	119	18	109	2	227	84	170	160
251	48	222	163	211	113	172	166	62	96	118	207	37	31	107	224
102	179	226	74	112	254	205	218	5	122	60	12	200	164	81	23
13	230	190	127	34	65	169	183	54	129	1	70	236	136	245	186
85	15	132	239	58	225	123	120	221	185	125	95	124	154	195	88
202	143	232	8	219	173	145	140	208	101	79	39	247	135	194	250
20	216	26	233	87	71	55	22	241	126	238	59	244	52	121	30
49	0	214	42	210	182	196	38	53	171	45	235	82	231	242	104
7	156	168	80	77	191	111	177	6	100	57	155	117	161	217	189
103	68	203	148	66	228	43	99	229	91	134	105	128	14	93	192
157	162	138	29	47	3	212	115	50	106	213	253	246	63	151	176
75	110	147	61	9	159	72	25	193	94	16	51	167	36	206	198
139	174	188	133	220	108	17	11	215	73	64	255	141	89	69	142
67	78	175	56	184	249	28	19	98	86	199	243	149	114	197	153

73	202	161	243	4	252	40	165	168	36	74	253	169	21	238	34
8	29	232	66	111	102	210	71	195	247	32	164	82	58	196	151
62	59	166	112	244	49	193	241	240	200	39	91	228	48	47	137
220	204	50	146	178	245	30	100	117	221	35	107	206	194	149	182
16	52	88	122	205	109	224	67	68	186	158	172	80	86	0	144
118	65	72	199	94	108	251	9	150	99	45	27	159	104	185	249
246	63	17	188	212	95	218	56	152	96	209	44	132	89	76	11
175	113	174	57	128	234	26	79	61	190	2	98	142	207	69	14
123	37	53	18	87	31	124	147	231	84	19	83	145	133	85	106
120	198	46	239	177	155	230	235	43	201	20	78	28	135	163	23
3	125	127	121	139	116	254	171	13	77	7	140	176	170	250	119
208	131	25	225	115	153	75	101	219	237	217	216	10	187	215	189
92	55	38	191	248	143	192	227	197	41	97	70	54	141	12	24
5	33	236	81	22	154	51	130	233	64	60	203	103	15	148	90
181	157	6	138	129	134	126	229	114	242	184	160	42	226	183	222
105	1	110	213	180	223	93	136	179	255	156	167	211	162	214	173

137	9	202	234	125	23	241	219	250	77	132	47	99	44	208	230
100	91	238	149	213	117	56	135	185	10	63	174	78	227	43	61
178	119	183	104	81	19	52	186	72	32	248	48	193	115	133	28
8	4	155	206	172	175	192	187	36	235	200	136	199	191	170	247
55	180	130	83	45	64	159	215	39	240	211	58	102	62	224	232
214	12	251	65	90	46	201	217	145	162	116	212	141	50	189	143
166	198	128	177	74	84	22	103	226	233	209	105	131	29	150	154
184	237	156	176	228	147	153	53	142	89	20	26	38	148	169	182
67	239	35	146	194	165	210	71	97	76	107	220	171	158	11	27
41	101	244	225	88	190	113	110	204	229	112	111	161	98	252	164
16	236	195	24	120	106	114	205	68	96	163	138	129	14	157	18
231	3	0	242	152	243	95	173	75	34	121	221	245	188	2	216
66	123	181	109	167	31	49	54	6	17	7	51	179	249	118	108
255	30	15	33	60	73	139	79	168	93	223	82	87	1	69	197
218	140	253	5	42	92	207	124	196	57	85	203	127	151	160	25
21	222	246	126	86	134	144	80	37	40	94	13	59	70	122	254