Submitted:
13 March 2023
Posted:
17 March 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
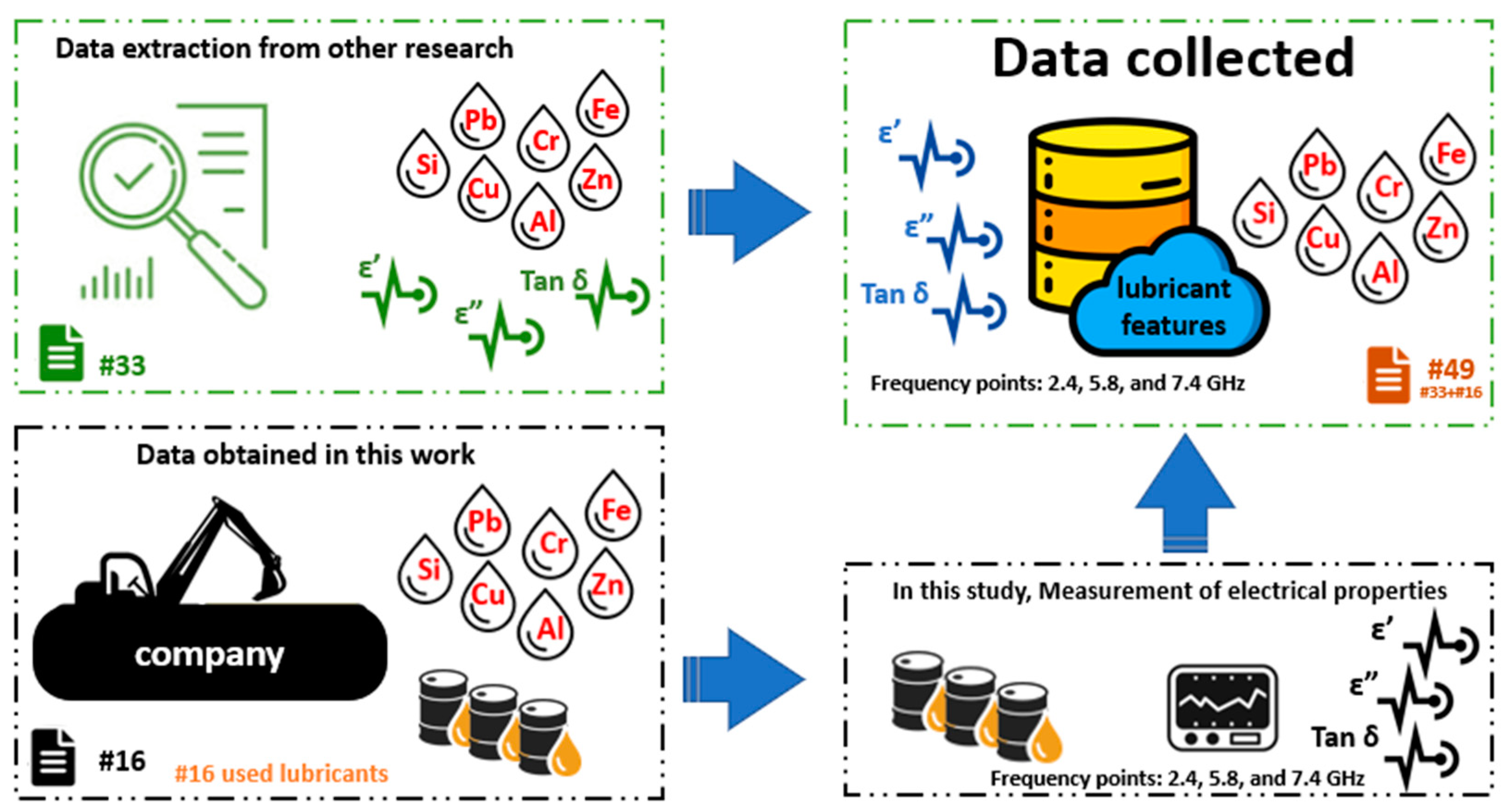
2.1. Data Set
2.1.1. Extracted Datasets
2.1.2. Experimental Datasets
2.2. Soft Computing Methods
2.2.1. Fundamentals and Theories
2.2.2. Application
2.3. Performance Criteria
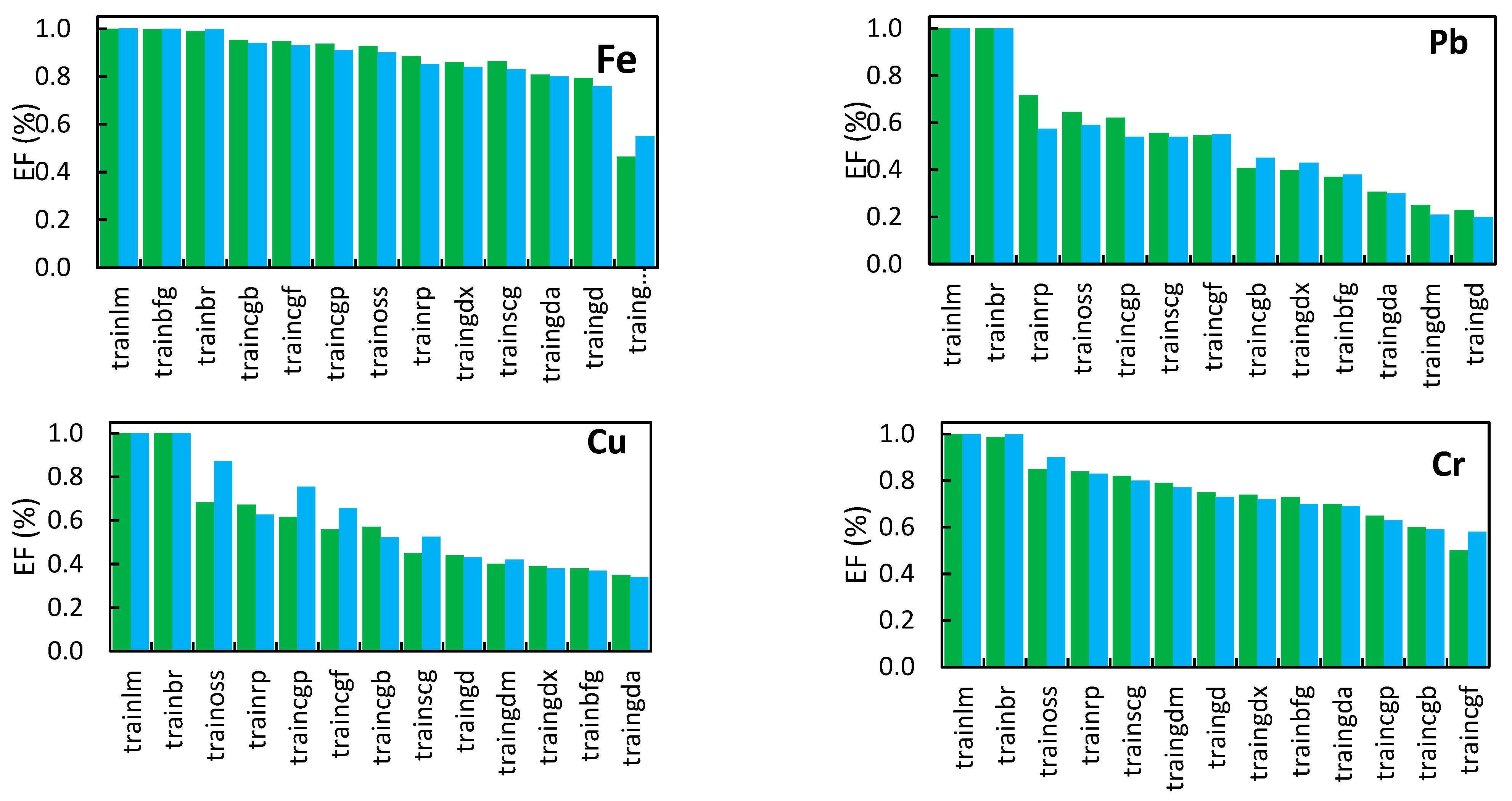
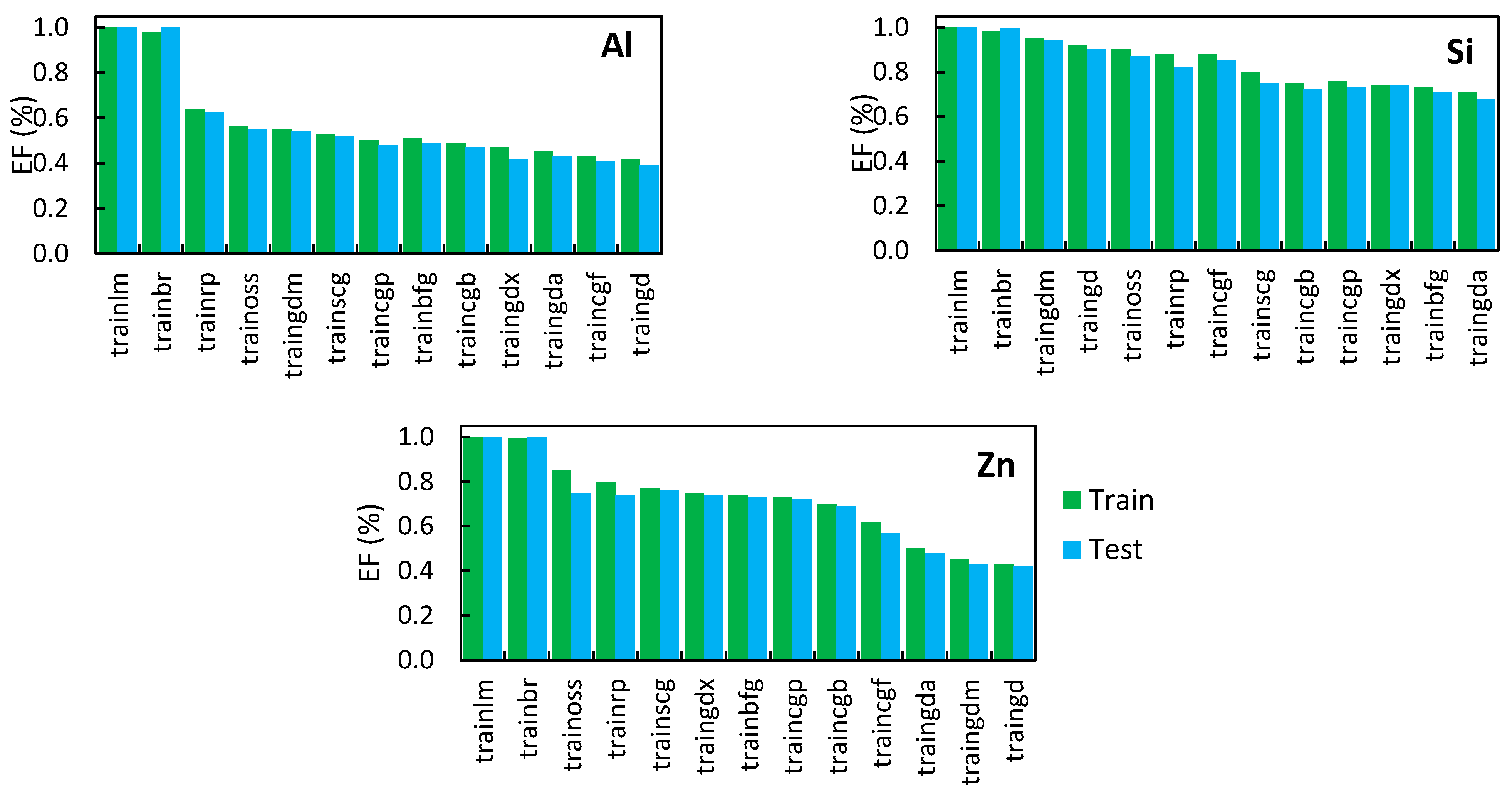
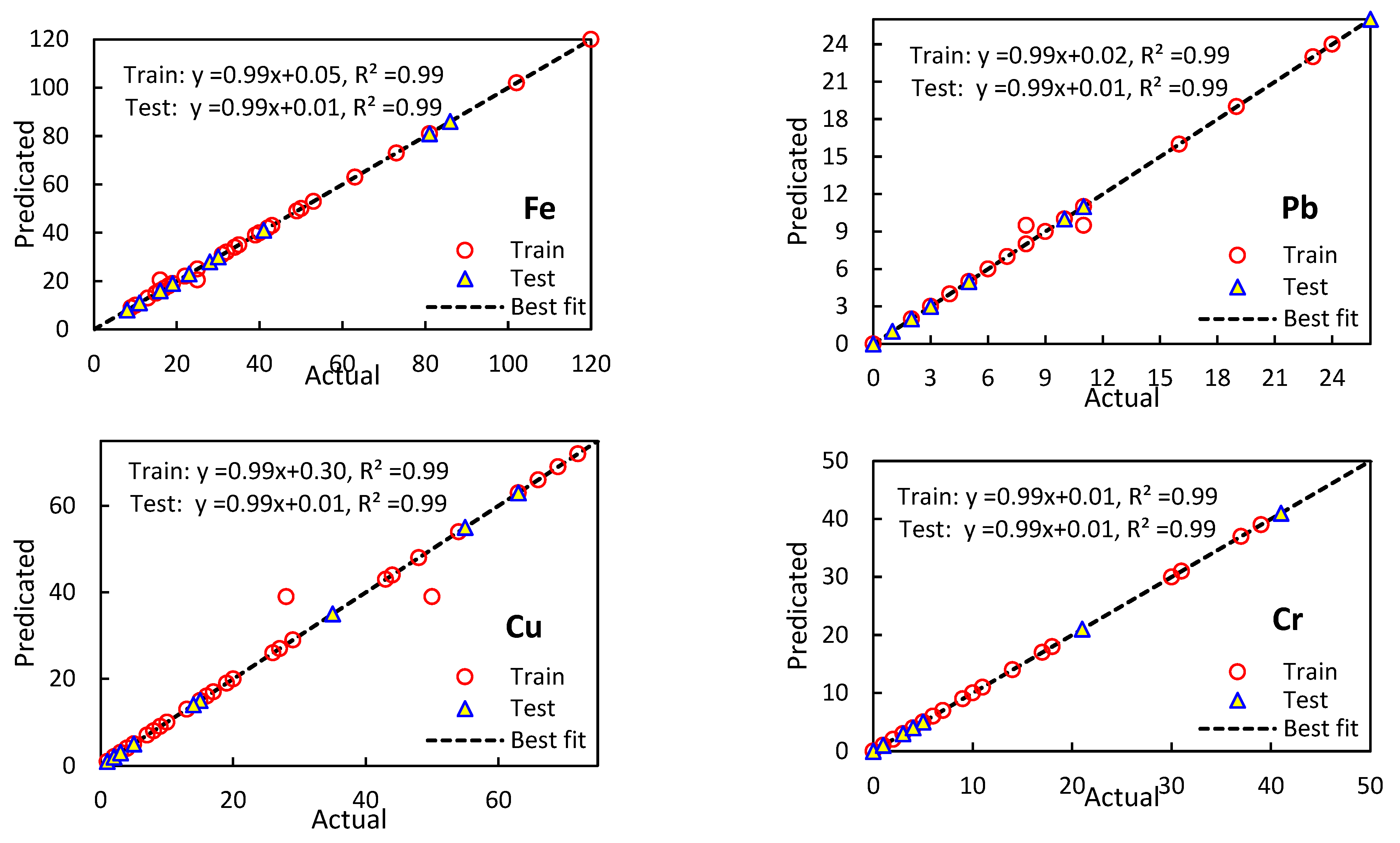
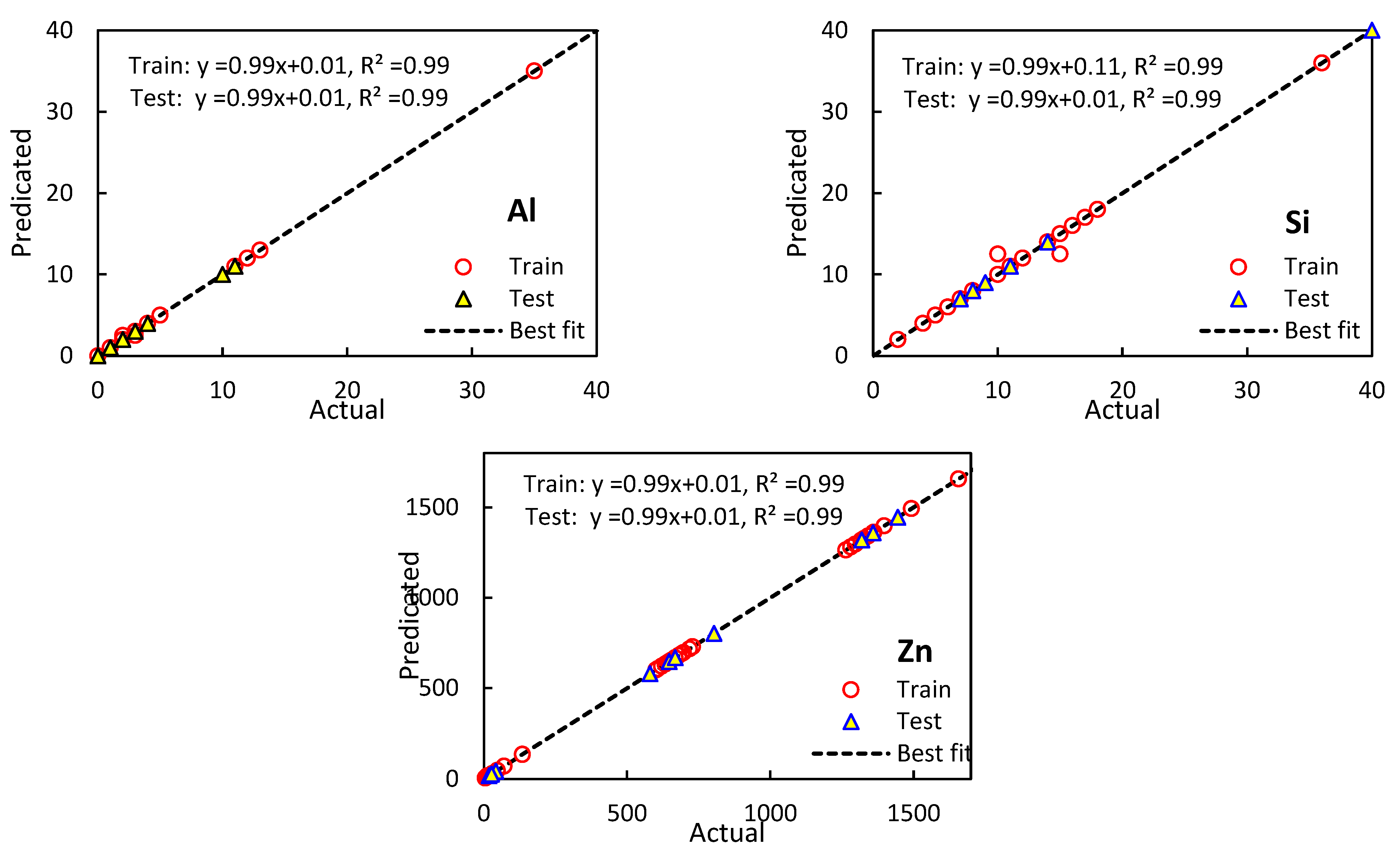
3. Results and Discussion
3.1. Preliminary Statistical Analysis
3.2. Performance Evaluation of Models
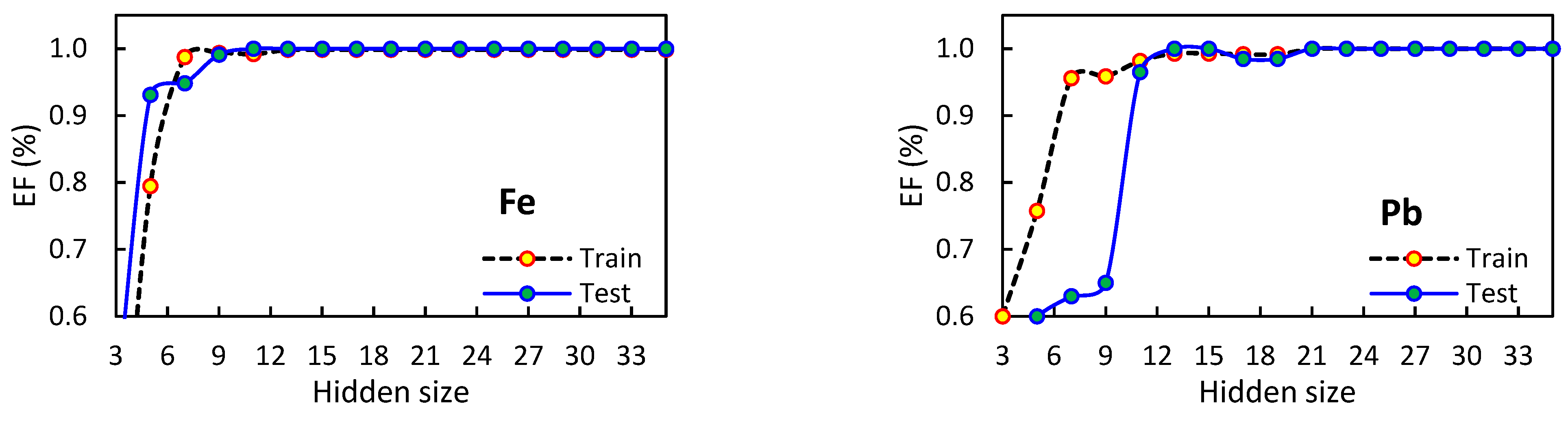
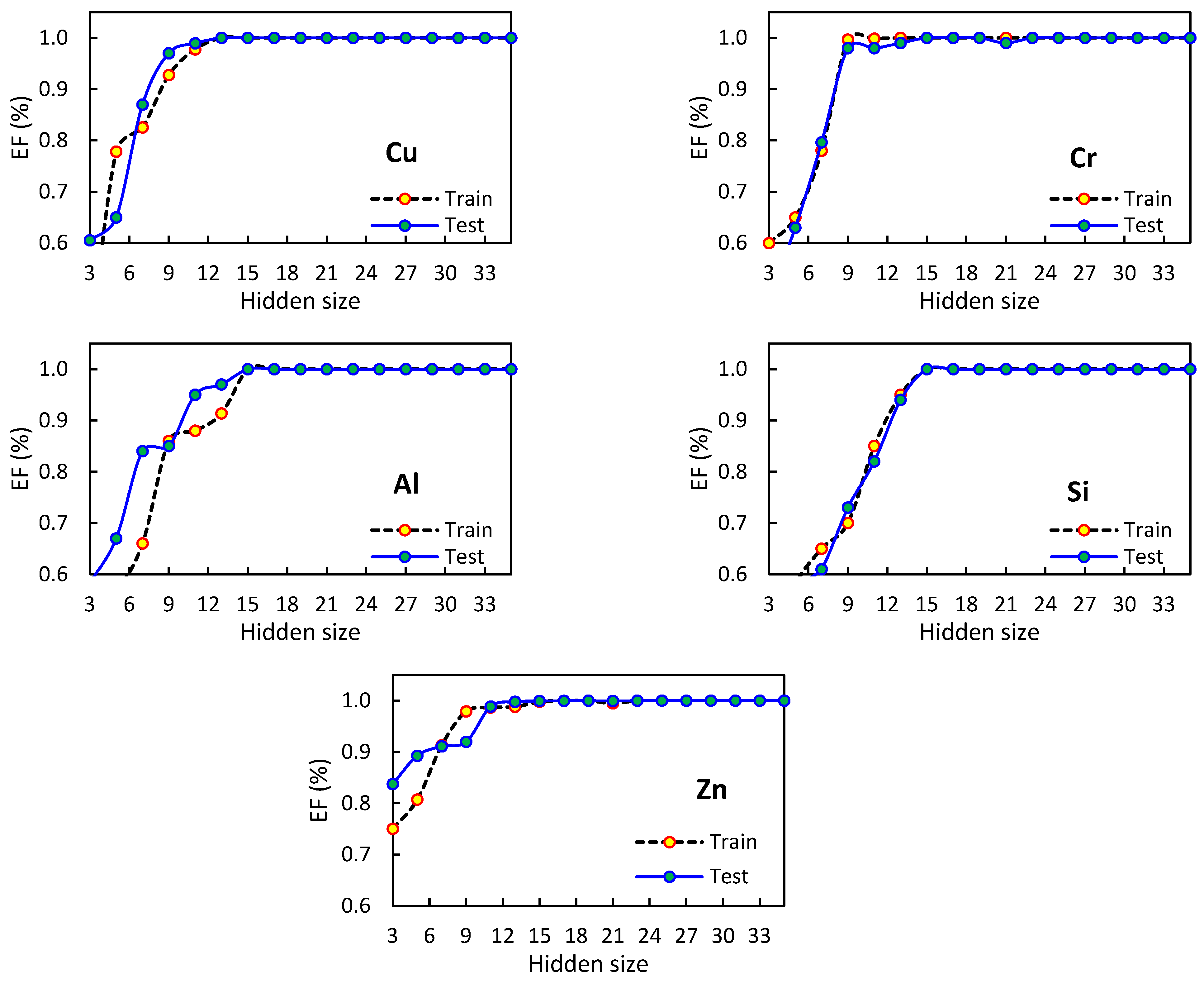
3.2.1. Adjusting RBF Parameters
3.2.2. Sensitivity Analysis
4. Conclusion
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network | MLP | Multilayer perceptron |
| ANFIS | Adaptive neuro-fuzzy inference system | MLR | Multiple Linear Regression |
| FL | Fuzzy logic | RFE | Recursive feature elimination |
| GPR | Gaussian process regression | RBF | Radial basic function |
| IAS | Infrared absorption spectroscopy | RMSE | Root means square error |
| IS | Impedance spectroscopy | SVM | Support vector machine |
| KNN | K-nearest neighbor | TDPQ | Time depending on the particle quantifier |
| MAPE | Mean absolute percentage error | VNA | Vector Network Analyzer |
References
- Vališ, D.; Gajewski, J.; Žák, L. Potential for using the ANN-FIS meta-model approach to assess levels of particulate contamination in oil used in mechanical systems. Tribol. Int. 2019, 135, 324–334. [Google Scholar] [CrossRef]
- Upadhyay, R. Microscopic technique to determine various wear modes of used engine oil. J. Microsc. Ultrastruct. 2013, 1, 111–114. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R. Complexity as a Measure for Machine Health Evaluation. IEEE Trans. Instrum. Meas. 2004, 53, 1327–1334. [Google Scholar] [CrossRef]
- Qiang, L., et al. Research on a Method for the Determination of Iron in Lubricating Oil. in 1st International Conference on Mechanical Engineering and Material Science (MEMS 2012). 2012. Atlantis Press.
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Zadhoush, M.; Nadooshan, A.A.; Afrand, M.; Ghafori, H. Constructal optimization of longitudinal and latitudinal rectangular fins used for cooling a plate under free convection by the intersection of asymptotes method. Int. J. Heat Mass Transf. 2017, 112, 441–453. [Google Scholar] [CrossRef]
- Kumbár, V.; Dostál, P. Oils degradation in agricultural machinery. Acta Universitatis Agriculturae et Silviculturae Mendelianae Brunensis 2013, 61, 1297–1303. [Google Scholar] [CrossRef]
- Alemayehu, B.; Kota, A.; Neidhard-Doll, A.; Chodavarapu, V.; Subramanyam, G. Cloud-connected real-time oil condition monitoring of utility transformers using impedance spectroscopy. Instrum. Sci. Technol. 2021, 49, 509–520. [Google Scholar] [CrossRef]
- Lazakis, I.; Raptodimos, Y.; Varelas, T. Predicting ship machinery system condition through analytical reliability tools and artificial neural networks. Ocean Eng. 2018, 152, 404–415. [Google Scholar] [CrossRef]
- Altıntaş, O.; Aksoy, M.; Ünal, E.; Akgöl, O.; Karaaslan, M. Artificial neural network approach for locomotive maintenance by monitoring dielectric properties of engine lubricant. Measurement 2019, 145, 678–686. [Google Scholar] [CrossRef]
- Pourramezan, M.-R.; Rohani, A.; Siavash, N.K.; Zarein, M. Evaluation of lubricant condition and engine health based on soft computing methods. Neural Comput. Appl. 2021, 34, 5465–5477. [Google Scholar] [CrossRef]
- Craft, J. Development of Interdigitated Electrode Sensors for Monitoring the Dielectric Properties of Lubricant Oils. 2010.
- Raadnui, S.; Kleesuwan, S. Low-cost condition monitoring sensor for used oil analysis. Wear 2005, 259, 1502–1506. [Google Scholar] [CrossRef]
- Grimmig, R.; Lindner, S.; Gillemot, P.; Winkler, M.; Witzleben, S. Analyses of used engine oils via atomic spectroscopy – Influence of sample pre-treatment and machine learning for engine type classification and lifetime assessment. Talanta 2021, 232, 122431. [Google Scholar] [CrossRef] [PubMed]
- Macin, V.; Tormos, B.; Sala, A.; Ramirez, J. Fuzzy logic-based expert system for diesel engine oil analysis diagnosis. Insight-Non-Destructive Testing and Condition Monitoring 2006, 48, 462–469. [Google Scholar] [CrossRef]
- Aghilinategh, N.; Nankali, S.; Babaei, M. Applying capacitance/inductance measurements for characterizing oil debris and pH. Indian J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef]
- Król, A.; Gocman, K.; Giemza, B. Neural networks as a tool to characterise oil state after porous bearings prolonged tests. Mater. Sci. 2015, 21, 466–472. [Google Scholar] [CrossRef]
- Li, L., et al. An identification and prediction model of wear-out fault based on oil monitoring data using PSO-SVM method. in 2017 Annual Reliability and Maintainability Symposium (RAMS). 2017. IEEE.
- RodRigues, J.; Costa, I.; Farinha, J.; Mendes, M.; Margalho, L. Predicting motor oil condition using artificial neural networks and principal component analysis. Eksploat. i Niezawodn. 2020, 22, 440–448. [Google Scholar] [CrossRef]
- Barsoukov, E. and J.R. Macdonald, Impedance spectroscopy theory, experiment, and. Applications, 2nd ed.(Hoboken, NJ: John Wiley &Sons, Inc., 2005), 2005.
- Heidari, P.; Rezaei, M.; Rohani, A. Soft computing-based approach on prediction promising pistachio seedling base on leaf characteristics. Sci. Hortic. 2020, 274, 109647. [Google Scholar] [CrossRef]
- Rezaei, M.; Rohani, A.; Heidari, P.; Lawson, S. Using soft computing and leaf dimensions to determine sex in immature Pistacia vera genotypes. Measurement 2021, 174, 108988. [Google Scholar] [CrossRef]
- Blanco, A.; Pino-Mejías, R.; Lara, J.; Rayo, S. Credit scoring models for the microfinance industry using neural networks: Evidence from Peru. Expert Syst. Appl. 2013, 40, 356–364. [Google Scholar] [CrossRef]
- Borghi, P.H.; Zakordonets, O.; Teixeira, J.P. A COVID-19 time series forecasting model based on MLP ANN. Procedia Comput. Sci. 2021, 181, 940–947. [Google Scholar] [CrossRef]
- Bazrafshan, O.; Ehteram, M.; Latif, S.D.; Huang, Y.F.; Teo, F.Y.; Ahmed, A.N.; El-Shafie, A. Predicting crop yields using a new robust Bayesian averaging model based on multiple hybrid ANFIS and MLP models. Ain Shams Eng. J. 2022, 13, 101724. [Google Scholar] [CrossRef]
- Sada, S.; Ikpeseni, S. Evaluation of ANN and ANFIS modeling ability in the prediction of AISI 1050 steel machining performance. Heliyon 2021, 7, e06136. [Google Scholar] [CrossRef] [PubMed]
- Vasileva-Stojanovska, T.; Vasileva, M.; Malinovski, T.; Trajkovik, V. An ANFIS model of quality of experience prediction in education. Appl. Soft Comput. 2015, 34, 129–138. [Google Scholar] [CrossRef]
- Stojčić, M.; Stjepanović, A.; Stjepanović, Đ. ANFIS model for the prediction of generated electricity of photovoltaic modules. Decis. Mak. Appl. Manag. Eng. 2019, 2, 35–48. [Google Scholar] [CrossRef]
- Chen, Y. and Y. Zhao. Face recognition using DCT and hierarchical RBF model. in International Conference on Intelligent Data Engineering and Automated Learning. 2006. Springer.
- Park, J.-W.; Venayagamoorthy, G.; Harley, R. MLP/RBF neural-networks-based online global model identification of synchronous generator. IEEE Trans. Ind. Electron. 2005, 52, 1685–1695. [Google Scholar] [CrossRef]
- Soleymani, S.A.; Goudarzi, S.; Anisi, M.H.; Hassan, W.H.; Idris, M.Y.I.; Shamshirband, S.; Noor, N.M.; Ahmedy, I. A novel method to water level prediction using RBF and FFA. Water Resour. Manag. 2016, 30, 3265–3283. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Gholami, R.; Ridha, S. Application of supervised machine learning paradigms in the prediction of petroleum reservoir properties: Comparative analysis of ANN and SVM models. J. Pet. Sci. Eng. 2020, 200, 108182. [Google Scholar] [CrossRef]
- Li, X.; Lord, D.; Zhang, Y.; Xie, Y. Predicting motor vehicle crashes using support vector machine models. Accid. Anal. Prev. 2008, 40, 1611–1618. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Zadeh, H.A.; Isazadeh, M.; Terzi, O. A comparative study of artificial neural network (MLP, RBF) and support vector machine models for river flow prediction. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Cui, H.; Chen, Q. Comparison of the ability of ARIMA, WNN and SVM models for drought forecasting in the Sanjiang Plain, China. Nat. Resour. Res. 2020, 29, 1447–1464. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Huang, C.-C.; Van Roy, A.F. Predicting project success in construction using an evolutionary Gaussian process inference model. J. Civ. Eng. Manag. 2013, 19 (Suppl. 1), S202–S211. [Google Scholar] [CrossRef]
- Ghanizadeh, A.R.; Heidarabadizadeh, N.; Heravi, F. Gaussian process regression (Gpr) for auto-estimation of resilient modulus of stabilized base materials. Journal of Soft Computing in Civil Engineering 2021, 5, 80–94. [Google Scholar]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Quinonero-Candela, J.; Rasmussen, C.E. A unifying view of sparse approximate Gaussian process regression. The Journal of Machine Learning Research 2005, 6, 1939–1959. [Google Scholar]
- Arvanitidis, A.I.; Bargiotas, D.; Daskalopulu, A.; Kontogiannis, D.; Panapakidis, I.P.; Tsoukalas, L.H. Clustering Informed MLP Models for Fast and Accurate Short-Term Load Forecasting. Energies 2022, 15, 1295. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Fu, D.; Shi, X.; Tang, B.; Qi, H. Snowmelt-driven streamflow prediction using machine learning techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1734. [Google Scholar] [CrossRef]
- Okwu, M.; Adetunji, O. A comparative study of artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) models in distribution system with nondeterministic inputs. Int. J. Eng. Bus. Manag. 2018, 10. [Google Scholar] [CrossRef]
- Slama, S., A. Errachdi, and M. Benrejeb. Model reference adaptive control for MIMO nonlinear systems using RBF neural networks. in 2018 international conference on advanced systems and electric technologies (IC_ASET). 2018. IEEE.
- Tabari, H.; Kisi, O.; Ezani, A.; Talaee, P.H. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444-445, 78–89. [Google Scholar] [CrossRef]
- Taki, M.; Ajabshirchi, Y.; Ranjbar, S.F.; Rohani, A.; Matloobi, M. Modeling and experimental validation of heat transfer and energy consumption in an innovative greenhouse structure. Inf. Process. Agric. 2016, 3, 157–174. [Google Scholar] [CrossRef]

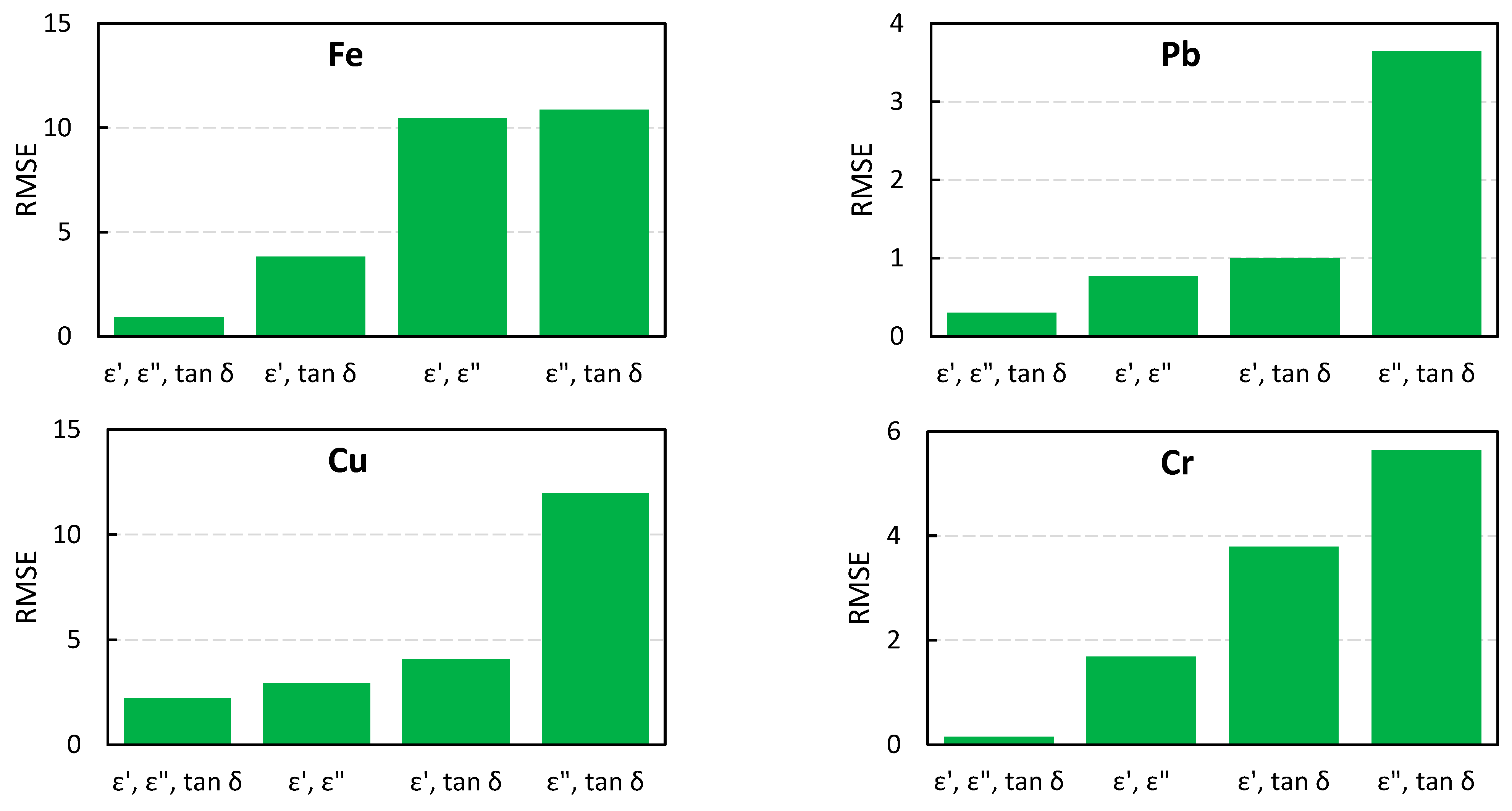
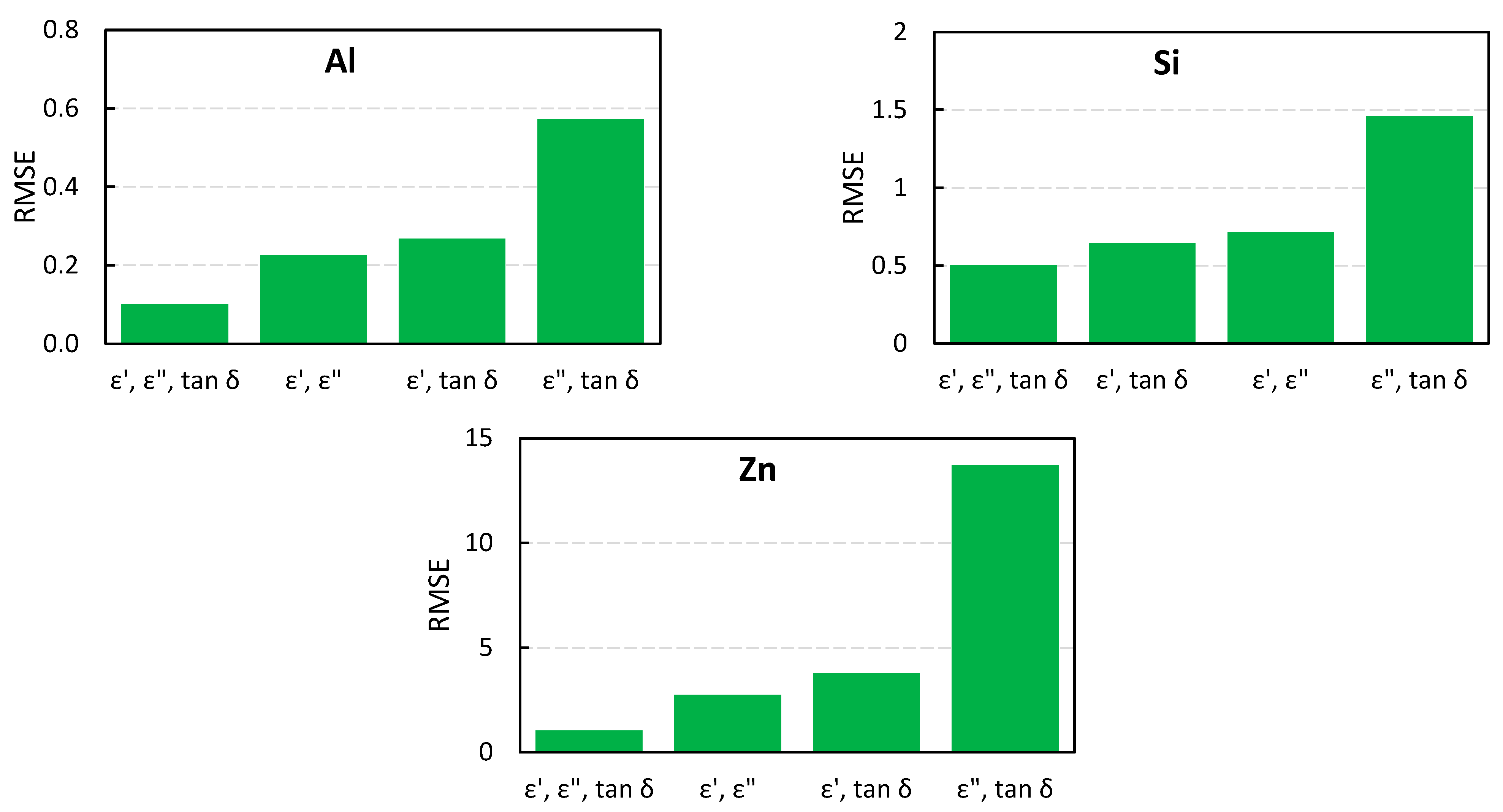
| Sample No. | Fe | Pb | Cu | Cr | Al | Si | Zn |
|---|---|---|---|---|---|---|---|
| 1 | 11.05 | 2.83 | 0.98 | 1.26 | 3.62 | 8.79 | 1319 |
| 2 | 9.94 | 0 | 0.97 | 0.46 | 1.61 | 17.77 | 1362 |
| 3 | 30.25 | 0 | 1.64 | 5.33 | 10.18 | 9.23 | 1359 |
| 4 | 81.17 | 0 | 2.59 | 7.46 | 34.59 | 36.21 | 1493 |
| 5 | 13.19 | 1.8 | 0.59 | 1.8 | 1.09 | 7.14 | 1281 |
| 6 | 24.65 | 0 | 1.25 | 1.55 | 5.05 | 9.89 | 1398 |
| 7 | 9.24 | 0 | 0.92 | 0.11 | 1 | 6.11 | 1362 |
| 8 | 15.46 | 0 | 1.75 | 0 | 0.38 | 4.01 | 1360 |
| 9 | 39 | 4.42 | 7.78 | 6.52 | 10.93 | 16.29 | 1297 |
| 10 | 39.76 | 3.2 | 1.4 | 2.2 | 3.77 | 15.44 | 1657 |
| 11 | 34.69 | 0.18 | 1.23 | 7.2 | 13.45 | 16.55 | 1264 |
| 12 | 39.67 | 3.91 | 2.31 | 6.48 | 12.45 | 16.33 | 1342 |
| 13 | 86.06 | 1.17 | 2.76 | 3.69 | 10.95 | 40.05 | 1445 |
| 14 | 21.73 | 3.22 | 7.23 | 0.91 | 5.31 | 7.27 | 1317 |
| 15 | 8.17 | 1.79 | 3.23 | 0.04 | 0 | 7.22 | 803 |
| 16 | 49.75 | 3.51 | 4.11 | 4.15 | 5.07 | 13.65 | 1327 |
| Sample No. | 2.40 GHz | 5.80 GHz | 7.40 GHz | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | ε′ | ε″ | tan δ | |
| 1 | 2.62 | 0.15 | 0.058 | 2.94 | 0.13 | 0.044 | 2.55 | 0.23 | 0.090 |
| 2 | 2.68 | 0.12 | 0.045 | 2.99 | 0.10 | 0.033 | 2.60 | 0.18 | 0.069 |
| 3 | 2.45 | 0.09 | 0.037 | 2.79 | 0.07 | 0.025 | 2.40 | 0.17 | 0.071 |
| 4 | 2.55 | 0.05 | 0.020 | 2.86 | 0.05 | 0.017 | 2.47 | 0.12 | 0.049 |
| 5 | 2.60 | 0.13 | 0.051 | 2.91 | 0.12 | 0.041 | 2.52 | 0.21 | 0.083 |
| 6 | 2.58 | 0.13 | 0.051 | 2.90 | 0.11 | 0.038 | 2.50 | 0.20 | 0.080 |
| 7 | 2.60 | 0.17 | 0.066 | 2.93 | 0.14 | 0.048 | 2.52 | 0.26 | 0.103 |
| 8 | 2.54 | 0.20 | 0.079 | 2.85 | 0.19 | 0.067 | 2.43 | 0.30 | 0.123 |
| 9 | 2.53 | 0.08 | 0.032 | 2.83 | 0.06 | 0.021 | 2.45 | 0.15 | 0.061 |
| 10 | 2.52 | 0.06 | 0.025 | 2.81 | 0.05 | 0.018 | 2.43 | 0.13 | 0.053 |
| 11 | 2.55 | 0.09 | 0.036 | 2.88 | 0.07 | 0.024 | 2.50 | 0.14 | 0.056 |
| 12 | 2.50 | 0.07 | 0.029 | 2.79 | 0.05 | 0.018 | 2.42 | 0.14 | 0.058 |
| 13 | 2.41 | 0.05 | 0.021 | 2.70 | 0.04 | 0.015 | 2.34 | 0.10 | 0.043 |
| 14 | 2.66 | 0.11 | 0.042 | 2.97 | 0.10 | 0.034 | 2.58 | 0.16 | 0.062 |
| 15 | 2.60 | 0.13 | 0.051 | 2.93 | 0.12 | 0.041 | 2.53 | 0.21 | 0.083 |
| 16 | 2.50 | 0.07 | 0.029 | 2.81 | 0.06 | 0.021 | 2.42 | 0.13 | 0.054 |
| Var. 1 | Var. 2 | Corr. | Var. 1 | Var. 2 | Corr. | Var. 1 | Var. 2 | Corr. | Var. 1 | Var. 2 | Corr. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe | ε′ | -0.13ns | Cu | ε′ | 0.45** | Al | ε′ | -0.23 *** | Zn | ε′ | -0.54** |
| ε″ | -0.20*** | ε″ | 0.53** | ε″ | -0.49** | ε″ | -0.77** | ||||
| tan δ | -0.22*** | tan δ | 0.53** | tan δ | -0.56** | tan δ | -0.79** | ||||
| Pb | ε′ | 0.41** | Cr | ε′ | 0.45** | Si | ε′ | -0.14 ns | |||
| ε″ | 0.48** | ε″ | 0.45** | ε″ | -0.42** | ||||||
| tan δ | 0.48** | tan δ | 0.41** | tan δ | -0.50** |
| Frequency | 2.4 GHz | 5.80 GHz | 7.40 GHz | |||||||||||||
| ML model | RBF | MLP | ANFIS | GPR | SVM | RBF | MLP | ANFIS | GPR | SVM | RBF | MLP | ANFIS | GPR | SVM | |
| Fe | RMSE | 2.4 | 11.0 | 2.4 | 16.8 | 23.4 | 1.4 | 23.9 | 1.5 | 19.7 | 17.3 | 0.9 | 15.5 | 0.9 | 14.3 | 16.5 |
| MAPE | 3.7 | 33.8 | 3.8 | 48.5 | 51.9 | 2.8 | 69.5 | 2.6 | 34.5 | 43.5 | 0.9 | 47.3 | 1.1 | 40.3 | 36.2 | |
| Pb | RMSE | 1.4 | 5.4 | 2.2 | 3.8 | 15.6 | 1.0 | 4.9 | 1.0 | 5.3 | 6.5 | 0.3 | 3.3 | 0.3 | 5.5 | 7.5 |
| MAPE | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| Cu | RMSE | 4.4 | 22.4 | 5.0 | 16.4 | 19.0 | 3.9 | 18.7 | 3.9 | 18.6 | 53.2 | 2.2 | 13.2 | 2.2 | 18.5 | 21.3 |
| MAPE | 10.3 | 70.0 | 10.2 | 70.7 | 68.3 | 7.9 | 40.3 | 9.3 | 93.4 | 87.2 | 1.3 | 11.0 | 2.4 | 96.8 | 72.3 | |
| Cr | RMSE | 4.0 | 13.3 | 4.3 | 12.7 | 15.7 | 3.9 | 13.2 | 8.1 | 12.7 | 15.5 | 0.2 | 13.2 | 3.5 | 11.3 | 16.2 |
| MAPE | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| Al | RMSE | 0.7 | 0.7 | 0.8 | 0.7 | 0.9 | 0.2 | 0.7 | 0.3 | 0.7 | 3.5 | 0.1 | 0.7 | 0.1 | 0.7 | 0.9 |
| MAPE | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| Si | RMSE | 0.7 | 3.4 | 2.2 | 2.5 | 4.3 | 0.6 | 2.9 | 0.8 | 3.1 | 3.5 | 0.4 | 2.2 | 0.5 | 2.9 | 3.3 |
| MAPE | 4.3 | 38.4 | 8.9 | 28.1 | 48.2 | 1.7 | 28.2 | 1.9 | 33.0 | 36.1 | 0.7 | 25.7 | 1.1 | 24.4 | 34.2 | |
| Zn | RMSE | 10.3 | 20.7 | 80.3 | 29.2 | 39.1 | 6.5 | 41.9 | 53.8 | 28.0 | 28.3 | 1.0 | 6.7 | 2.2 | 28.6 | 35.3 |
| MAPE | 16.4 | 32.0 | 70.7 | 35.3 | 48.3 | 9.0 | 80.9 | 74.9 | 75.2 | 65.4 | 1.4 | 25.4 | 2.3 | 73.1 | 65.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





