Prerpints.org logo
Preprint
Article

Multiscale Entropy Algorithms to Analyze Complexity and Variability of Trunk Accelerations Time Series in Subjects with Parkinson’s Disease

Altmetrics

Downloads

178

Views

70

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (212.36KB )

Submitted:

16 March 2023

Posted:

17 March 2023

You are already at the latest version

Alerts
Abstract
The aim of this study was to assess the ability of multiscale sample entropy (MSE), refined composite multiscale entropy (RCMSE), and complexity index (CI) to characterize gait complexity through trunk acceleration patterns in subjects with Parkinson's disease (swPD) and healthy subjects, regardless of age or gait speed. The trunk acceleration patterns of 51 swPD and 50 HS were acquired using a lumbar-mounted magneto-inertial measurement unit during their walking. MSE, RCMSE, and CI were calculated on 2000 data points, using scale factors (τ) 1-6. Differences between swPD and HS were calculated at each τ, and the area under the receiver operating characteristics, optimal cutoff points, post-test probabilities, and diagnostic odds ratios were calculated. MSE in the antero-posterior direction at τ 4 and τ 5, and MSE in the ML direction at τ 4 outperformed the other entropy measures in terms of discriminative ability and characterized the gait of swPD with 79%, 82%, and 78% probabilities, respectively, and correlated with the motor disability, pelvic kinematics, and stance phase. Using a time series of 2000 data points, a scale factor of 4 or 5 in the MSE procedure can be considered as a marker of gait variability and complexity in swPD.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Subjects with Parkinson’s disease (swPD) experience progressively invalidating gait impairment [1], which affects their quality of life and increases their risk of falling [1,2,3,4].
Because of the effects of dopamine depletion on motor control [5], swPD are characterized by increased gait variability [6,7,8], which can result in a number of gait abnormalities, including shuffling gait and reduced step length [9,10,11]. Altered trunk behavior showed to characterize gait impairment [12,13,14,15,16,17,18,19,20] and to represent a responsive outcome for medications and rehabilitation in swPD [19,20,21,22,23,24]. Wearable sensors, such as magneto-inertial measurement units (MIMUs), have shown to provide trunk acceleration-derived gait indexes that can accurately characterize gait abnormalities, falls risk, and gait variability in swPD [14,25,26], as well as responsive measures to quantify the effectiveness of rehabilitation [27].
When retrieved from trunk accelerations, the coefficient of variation (CV), a commonly used statistical measure that quantifies the variability of spatio-temporal gait parameters [14,28,29,30,31], may present some limitations in assessing gait variability in swPD, such as a high dependency on gait speed, limited ability to provide information on the underlying patterns and short-term changes in gait variability [10,14,32], and lack of identification of gait variability at earlier stages of the disease [33]. Moreover, CV is dependent on the identification of gait cycles, which is a possible source of error due to irregular acceleration signals or difficulties in the identifications of acceleration peaks, particularly in neurodegenerative diseases [34,35,36,37].
To overcome these shortcomings, researchers have proposed adopting nonlinear entropy measures, which assess gait variability by providing a measure of the complexity and regularity of a time series, regardless of step detection [38,39,40,41].
Entropy quantifies the probability of the next state of the system based on what is known about the current state of a time series [42,43]. When the probability is high, the following system states provide little new information, resulting in low entropy values. When the probability is low, the subsequent data points in the system provide a greater amount of new information, resulting in high entropy values, indicating greater gait irregularity or complexity of the gait pattern. Several methods for calculating entropy have been proposed [43,44,45,46]. Among them, sample entropy (SampEn) [45] – based methods have been described as valid tools for assessing gait regularity in healthy subjects and pathological conditions [42,47,48], including trunk acceleration-derived gait signals from swPD [49]. Multiscale entropy (MSE) and refined composite multiscale entropy (RCMSE) have been shown to be the most appropriate entropy measures for assessing the repeatability of gait signals, particularly when analyzing shorter time series [43,46], such as those generated by ambulatory gait trials, where they limit the risk of noisy and unstable entropy estimates [45,50,51,52].
MSE is an extension of SampEn that computes SampEn at different scales by segmenting the original time series into different length windows through a coarse – graining procedure [53,54,55,56,57,58]. When MSE was applied to trunk accelerations, it revealed differences between treadmill and overground walking in older but not younger individuals [59], as well as a progressive decrease in trunk acceleration complexity from childhood to adulthood during natural walking [60]. RCMSE has been proposed to overcome the probability of undefined entropy of MSE [61] by calculating the entropies of each coarse – grained time series into a composite multiscale algorithm with a scale factor [61]. Recently, another method of entropy calculations, the complexity index (CI) has been introduced to assess gait complexity of swPD across a pre-determined range of scale factors [62,63,64]. However, its ability to characterize the gait of swPD, compared to healthy subjects, has never been investigated.
Notably, when calculating MSE and RCMSE, researchers should consider which combination of signal embedding, tolerance radius, scale factor and length of data best fit with their type of data and study objectives [42]. A 2000 data points length of data (N) has been described as the acceptable trade-off between instability of the results and drift into the data, and a value of 2 and 0.2 times the standard deviation as the most popular signal embedding (m) and tolerance radius (r) values, respectively. However, the choice of number of scales, commonly referred to as τ, differs across the studies analyzing MSE and RCMSE [42,43]. Because it may significantly affect sample entropy calculations, the optimal τ related to N to identify complexity and irregularity should be identified for each pathological condition [40,65].
Furthermore, when assessing the discriminative ability of entropy measures, the effects of age [39] and gait speed [66], which can overrepresent the differences between pathological and healthy gait [67], should be considered.
Therefore, the aims of this study were: i) to identify the best τ in MSE or RCMSE procedure, or the ability of CI, to characterize the complexity and variability of trunk acceleration patterns of swPD during gait, compared with healthy subjects (HS), regardless of age and gait speed; ii) to assess the ability of MSE and RCMSE calculated using the identified optimal τ, and CI to characterize fallers within swPD; iii) to assess the ability of MSE and RCMSE as calculated through the identified optimal τ, and CI to differentiate swPD according to their disability stages; iv) identify correlations between MSE and RCMSE at the optimal τ, and CI, with clinical features and spatio-temporal and kinematic gait parameters in swPD.
We hypothesized that MSE and/or RCMSE at a single τ, or CI, could characterize trunk irregularity in swPD, regardless of age and gait speed, and that could reflect clinical status and kinematic gait abnormalities.

2. Materials and Methods

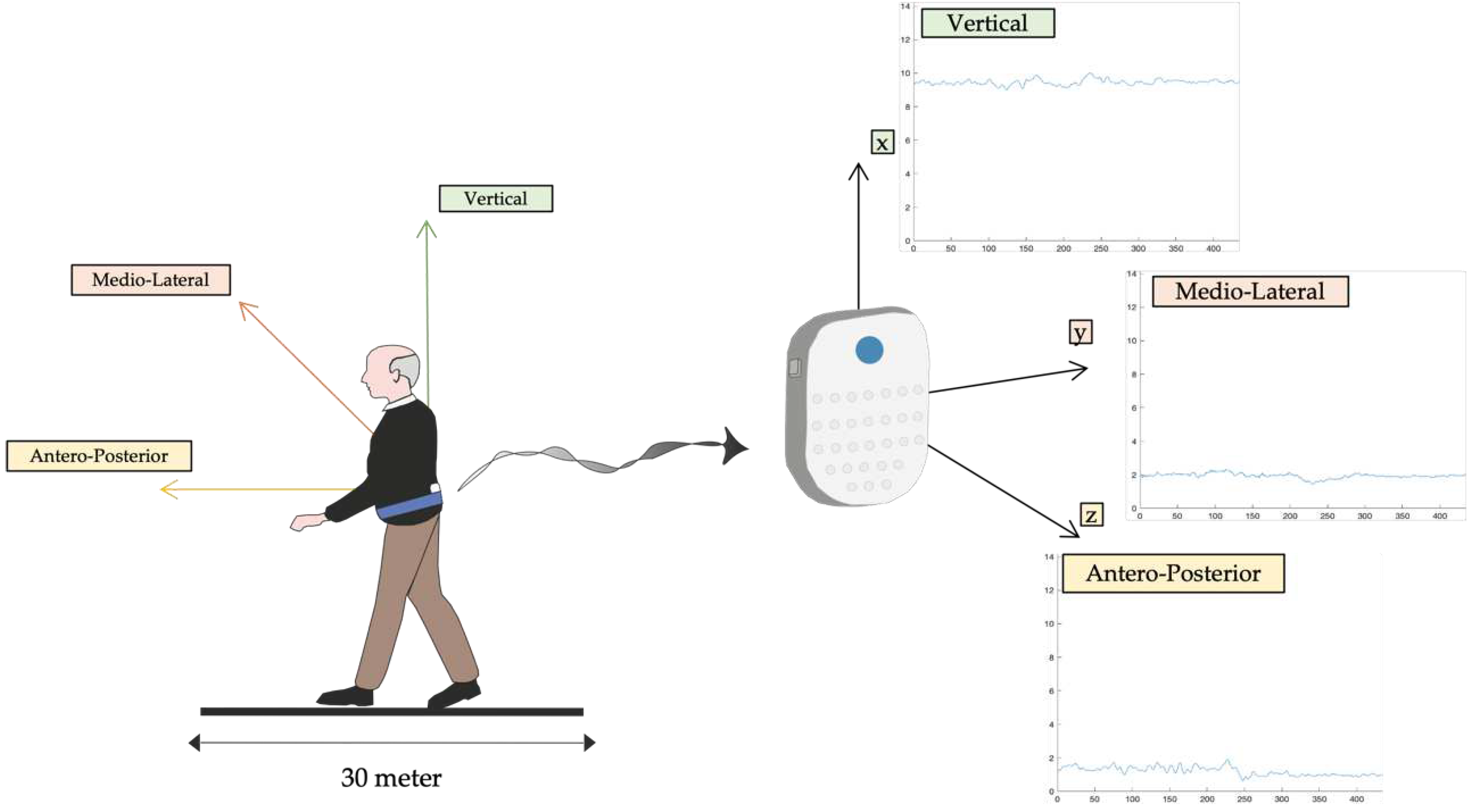
2.1. Subjects

Gait data from 51 swPD, acquired at “ICOT”, Latina, Italy, and at “IRCSS Casimiro Mondino”, Pavia Italy, were included in the study. SwPD were included according to the following inclusion criteria: (i) idiopathic PD diagnosis based on UK bank criteria [68]; (ii) Hoehn and Yahr (HY) scale classification 1-3 [69]; (iii) ability to walk unassisted for at least 30 meters along a laboratory corridor without presenting freezing of gait; (iv) a stable and accustomed drug dosage for at least 2 weeks prior to the gait assessment. Subjects with congnitive deficits as defined by Mini-Mentale State Examination score < 26 [70,71], moderate – to – severe depression, as defined by Back Depression Inventory scores > 17 [72,73], orthopedic or other diseases influencing gait behavior, such as other neurological conditions, clinically defined osteoarthritis, joint replacements, as well as subjects reporting hip or knee joint pain, limited hip range of motion, or anatomic alteration s of the joints, were excluded [74,75,76]. Gait data from 50 age and gait speed – matched healthy subjects (HS) were included for comparison. To match pwPD and HS, a 1:1 optimal matching procedure using the propensity score difference method was conducted [77]. Each HS was asked to repeat the gait task twice while walking at both their self-selected speed and a slower directed speed in order to reduce the effect of gait speed on the other speed-dependent gait parameters and to gather the largest sample size for speed-matched comparisons [19,78]. Age and gait speed were used as covariates in logistic regression analysis to calculate the propensity scores [79,80,81]. Table 1 summarizes the clinical characteristics of the included subjects.
All participants gave their informed consent in accordance with the Helsinki Declaration, and the study was approved by the local ethics committee (CE Lazio2 protocol n.° 0053667/2021).

2.2. Procedures

Data weres collected using an inertial sensor (BTS GWALK, BTS, Milan, Italy) positioned at L5 via a unique ergonomic belt. The "Walk +" protocol of the G-STUDIO software (BTS, Milan, Italy) was used to detect the linear acceleration patterns of the trunk during gait in the anterior-posterior (AP), medio-lateral (ML), and vertical (V) directions, as well as spatio-temporal parameters and pelvic kinematics, at a sampling rate of 100Hz. A triaxial accelerometer and gyroscope (16 bit / axis) as well as a triaxial magnetometer are included in the sensor (13 bit). Spatio-temporal characteristics of the included sample are described in Table 1. Because sample entropy algorithms are sensistive to concatenation of gait trials [82], to collect the largest number of consecutive data points, subjects were asked to walk through a 30-meter long pathway at their own pace (Figure 1).
Because this study focused on natural locomotion, participants were allowed to choose their desired speed without interfering with their rhythm or receiving external sensory information. HS were also requested to walk at a slower pace to increase the sample size for the matching procedure. The multiscale entropy techniques were calculated using the MATLAB software (MATLAB R2022a 7.4.0, MathWorks, Natick, MA, USA).

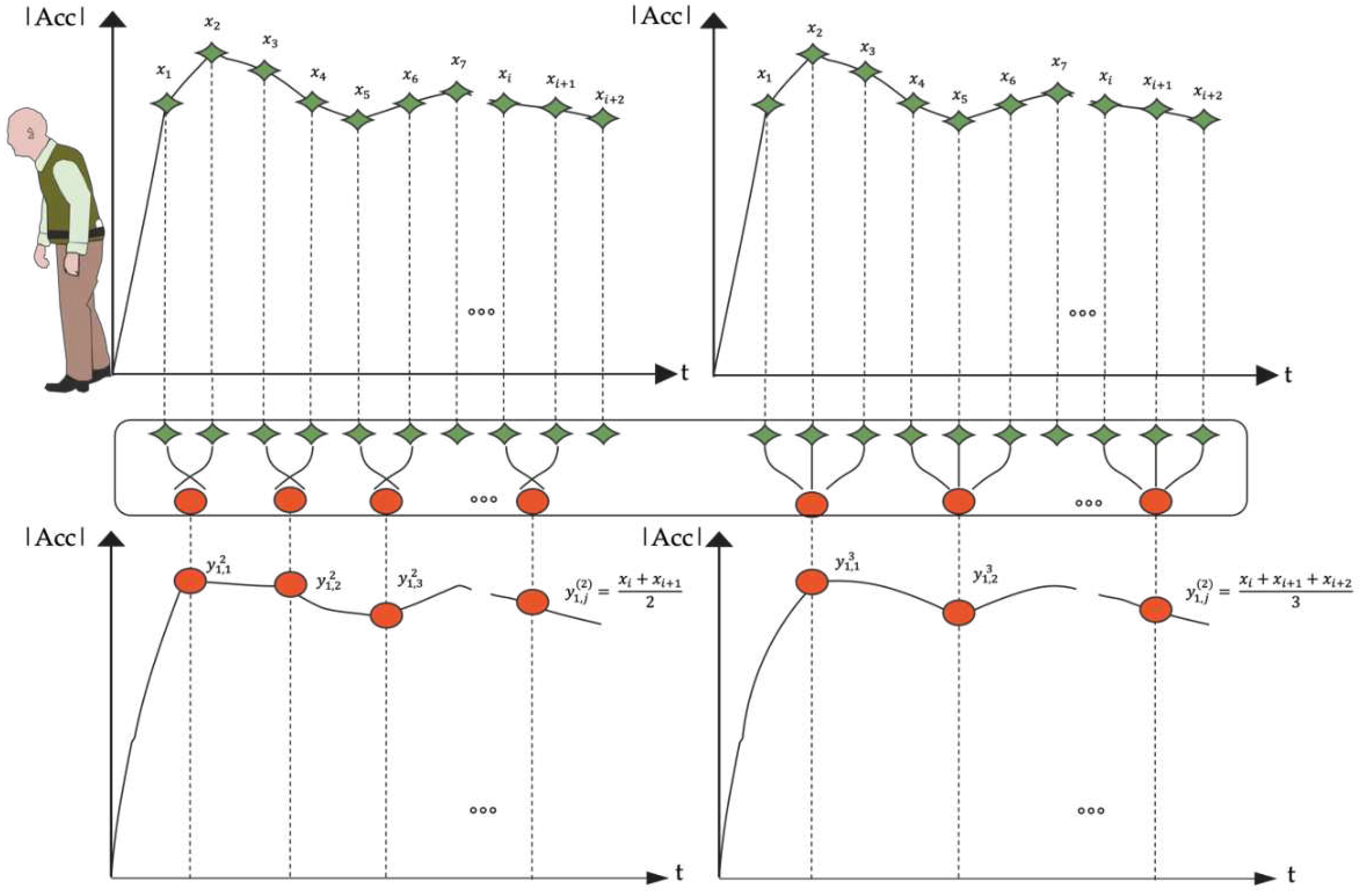
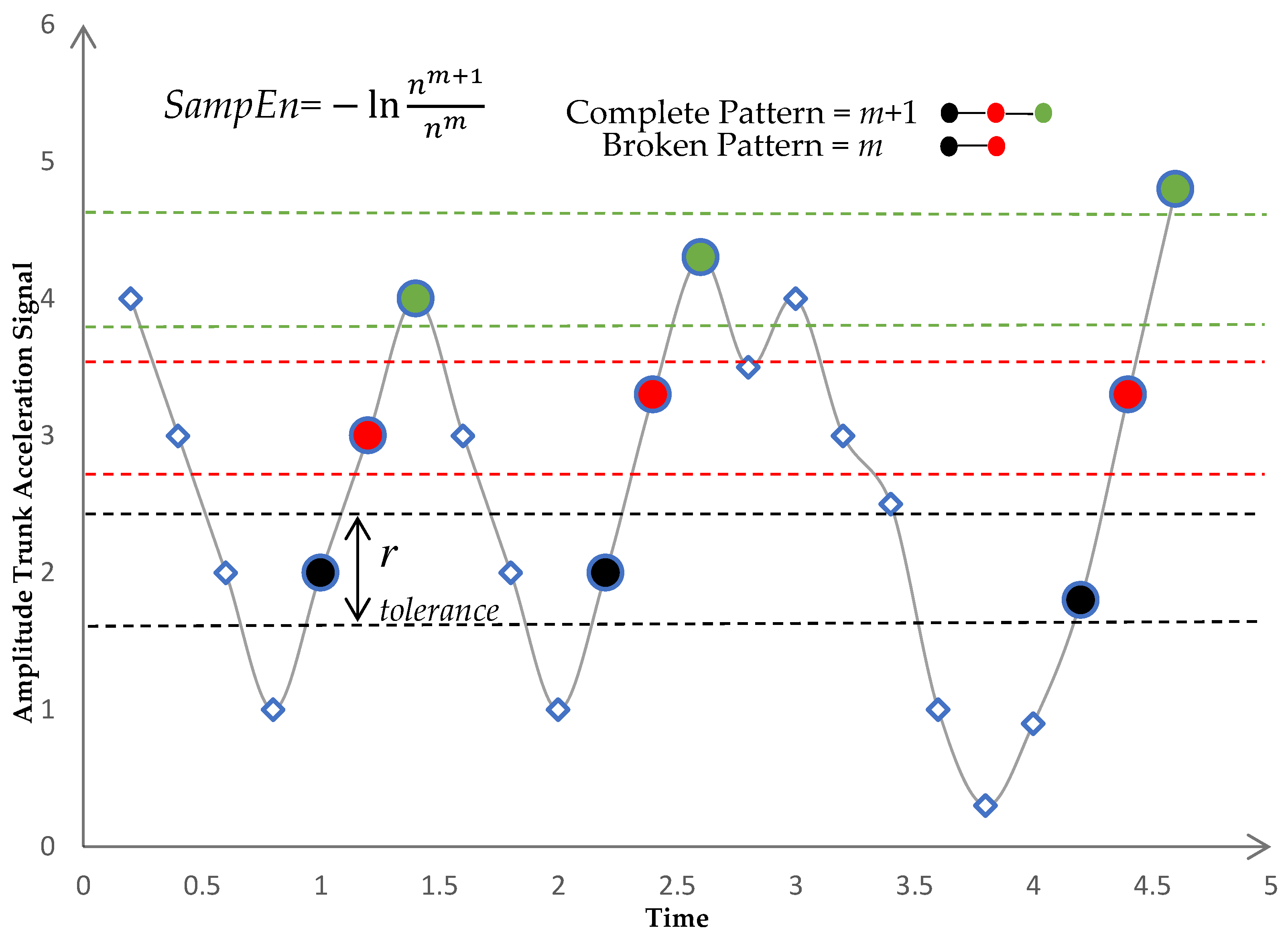
2.3. Entropy Algorithms

The MSE calculation consisted of two procedures: i) a coarse-graining procedure for obtaining representations of the original time series on various time scales (Figure 2); and ii) the SampEn procedure for quantifying the coarse-grained time series' regularities [86]. The original time series was separated into non-overlapping windows of length, and the data points inside each window were averaged to generate the coarse-grained time series at a scale factor of τ. As illustrated in Figure 2, coarse-grained time series are separated by a scale factor of τ for the original time series.
SampEn was calculated as follow:
Let x = { x 1 ,     x 2 … x N } represent a time series of length N.
Using Equation (1), build model vectors of size m:
x i m = x i   x i + 1 … x i + m − 1 ,   1 ≤ i ≤ N − m
  • There will be correspondence if the distance between two vectors (xmi, xmj) is smaller than a predefined tolerance r. The distance between the two vectors was calculated using the norm of infinity:
    d i j m = x i m − x j m ∞ ,                                                             1 ≤ i ,   j ≤ N − m ,     j ≠ i
  • If d i j m was less than or equal to the predefined tolerance r, we defined (xmi, xmj) a pair of m-dimensional matched vectors. Total number of pairs of m-dimensional matched vectors, given nm.
  • We repeated steps 1–3 for m = m + 1, where nm+1 represents the total number of (m + 1) dimensional matched vector pairs as shown in Figure 3.
  • The SampEn was defined as the logarithm of the ratio of n m + 1 to n m as in Equation (3):
    S a m p E n x ,   m , r = − ln ⁡ n m + 1 n m
The k-th coarse-grained time series y k ( τ ) = y k , 1 ( τ )     y k , 2 ( τ ) …   y k , p ( τ ) of x was defined as follows:
y k , j ( τ ) = 1 τ   ∑ i = j − 1 τ + k j τ + k − 1 x i ,                                 1 ≤ j ≤ N τ ,     1 ≤ k ≤ τ
As in the conventional MSE algorithm proposed by Costa et al. [46]., the MSE at a scale factor of τ was defined as the SampEn of the first coarse-grained time series as in Equation (5):
M S E x ,   τ ,   m , r = S a m p E n y 1 τ ,   m , r  

2.3.1. Refined Composite Multiscale Entropy (RCMSE)

To calculate RCMSE, the SampEns of all coarse-grained time series were calculated in the CMSE algorithm at a scale factor of τ, and the CMSE value was defined as the mean of τ SampEns:
C M S E x , τ , m , r = 1 τ ∑ k = 1 τ S a m p E n y k τ , m , r = 1 τ ∑ k = 1 τ ( − l n n k , τ m + 1 n k , τ m )
where n k , τ m represents the total number of m-dimensional matched vector pairs and is constructed from the k-th coarse grained time series at a scale factor of τ .
The logarithms of the ratio of n k , τ m + 1 to n k , τ m for all τ coarse-grained series are investigated first in the CMSE algorithm, and the average of these logarithms is then determined as the entropy value. When one of the values of n k , τ m + 1 to n k , τ m is 0, the CMSE value is undefined. The likelihood of inducing undefined entropy is higher when the CMSE is used to examine a short time series than when the MSE is used. Because of this flaw, the CMSE algorithm's short time series analysis applications are limited. To overcome this issue, Wu et al introduced the RCMSE method [61]. The RCMSE algorithm was calculated according to following steps:
1)
To obtain coarse-grained time series on different time scales, we utilized the coarse-graining process indicated in Equation (4).
2)
For all τ coarse-grained series, the number of matched vector pairs, n k , τ m + 1 and n k , τ m , was determined at a scale factor of τ .
3)
For 1 ≤ k ≤ τ , let n ¯ k , τ m   ( n ¯ k , τ m + 1 ) denote the mean of n k , τ m   n k , τ m + 1 . Equation (7) provides the RCMSE value at a scale factor of τ .
R C M S E x , τ , m , r = − ln ⁡ ( n ¯ k , τ m + 1 n ¯ k , τ m )
where n ¯ k , τ m + 1 = 1 τ ∑ k = 1 τ n k , τ m + 1 and n ¯ k , τ m = 1 τ ∑ k = 1 τ n k , τ m .
Eq. (7) can be written as follows:
R C M S E x , τ , m , r = − ln ⁡ n ¯ k , τ m + 1 n ¯ k , τ m − ln ⁡ 1 τ ∑ k = 1 τ n k , τ m + 1 1 τ ∑ k = 1 τ n k , τ m = − ln ⁡ ( ∑ k = 1 τ n k , τ m + 1 ∑ k = 1 τ n k , τ m )

2.3.2. Complexity Index (CI).

We also use the trapezoid rule to calculate CI by integrating the entropy values over a pre-determined range of scales [56]. This index reflects the amount of information, or entropy, in a signal over a range of time scales, as shown in Figure 4. High entropy values over a wide time scale range, and thus a high CI, indicate high complexity, and vice versa [87]. The maximum scale that can be analyzed depends on the length of the original time series [88].

2.4. Clinical Assessment

The HY disease staging system and the motor examination section of the Unified Parkinson's Disease Rating Scale (UPDRS-III) were used to determine the severity of Parkinson's disease [89] (Table 1). Clinical scales were administered by an assessor who was not aware of the gait reports. SwPD were classified as fallers (at least one fall) or non-fallers based on a self-reported history of falls in the 6 months preceding the gait assessment [90,91]. A fall was defined as an unintentional landing to the ground that was not caused by a significant intrinsic event or a dangerous situation [90,92].

2.5. Statistical Analysis

To identify entropy measures with good ability to discriminate between swPD and HS, as represented by an area under the receiver operating characteristics curve (AUC) ≥ 0.70 at a 95% significance level and 80% power under the null hypothesis of an AUC = 0.50, a minimum sample of 68 participants (34 swPD and 34 HS) was calculated.
After checking the normality of the distributions and equality of the variances through the Shapiro-Wilk and Levene’s test, respectively, a Mann-Whitney test was performed to identify significant differences between swPD and HS in entropy measures at each τ, spatio-temporal gait features, pelvic kinematics, HRs, and CV. Cohen’s d with Hedge’s correction were calculated to assess the effect size.
To identify the entropy measures that best discriminated between swPD and HS, AUCs at each τ were calculated. AUCs ≥ 0.70 were deemed to have sufficient overall discriminative ability [93]. Optimal cutoff points (OCPs) were calculated as the entropy values that maximized the sum of sensitivity and specificity. To investigate the likelihood of being correctly classified by a given combination of entropy measure and τ at the OCP, positive and negative likelihood ratios (LR+ and LR-, respectively) were calculated and transformed into positive and negative post-test probabilities (PTP+ and PTP-, respectively) through a Fagan’s nomogram [94]. Diagnostic odds ratios (DORs) were also calculated to assess the diagnostic performances [95]. The combinations of entropy measures and τ with the highest DOR and PTPs were considered as the best entropy measures to characterize gait complexity in swPD.
The ability of the identified entropy measures to discriminate between fallers and non fallers was assessed through a Mann-Whitney test.
The ability of the identified entropy measures to discriminate across the disability levels, Kruskal-Wallis test with Dunn’s post – hoc analysis and Holm’s correction was performed using the HY stage and the UPDRS III thresholds as between – subjects factors. UPDRS III scores < 32, ≥ 32, and ≥ 58 were considered as reflecting mild, moderate, and severe motor disease, respectively [96].
To assess the correlations between the identified entropy measures and the clinical features of swPD, spatio-temporal gait characteristics, pelvic kinematics, and the other trunk-acceleration-derived gait indexes that characterize swPD [12,14], a partial correlation analysis excluding the effects of age and gait speed was conducted.
Statistical analyses were carried out using the IBM SPSS ver. 27, NCSS 2022, and JASP vers. 0.16 softwares.

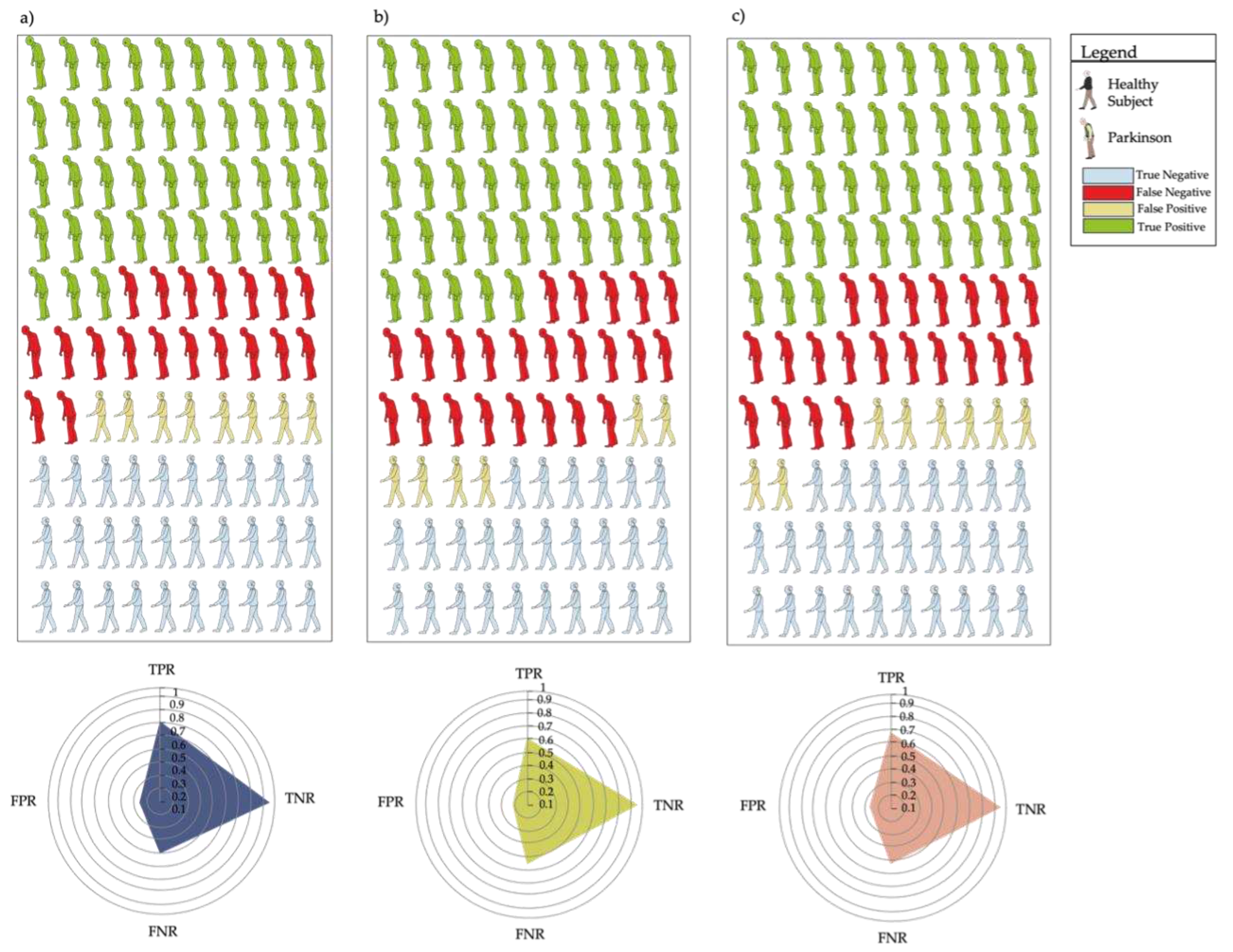
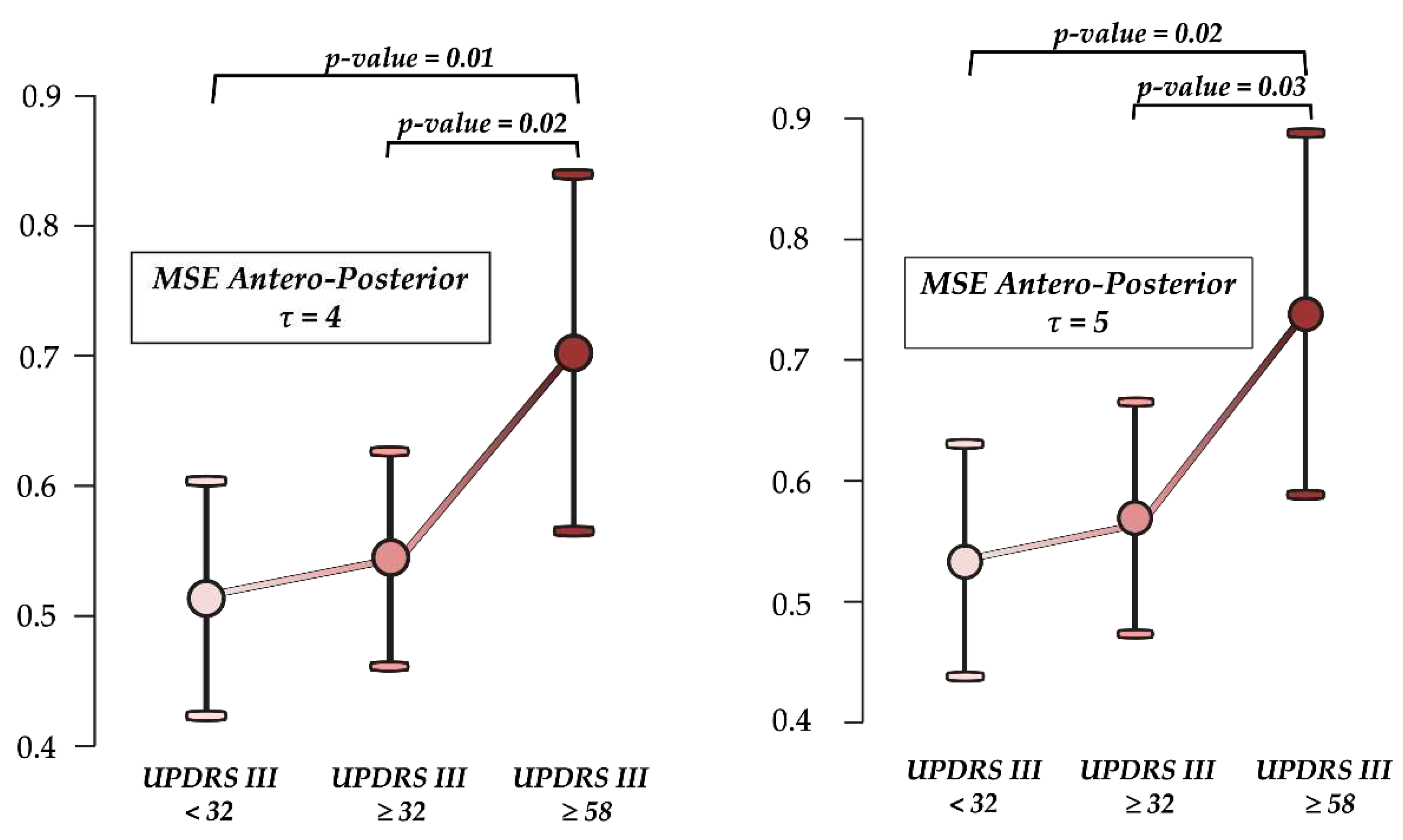
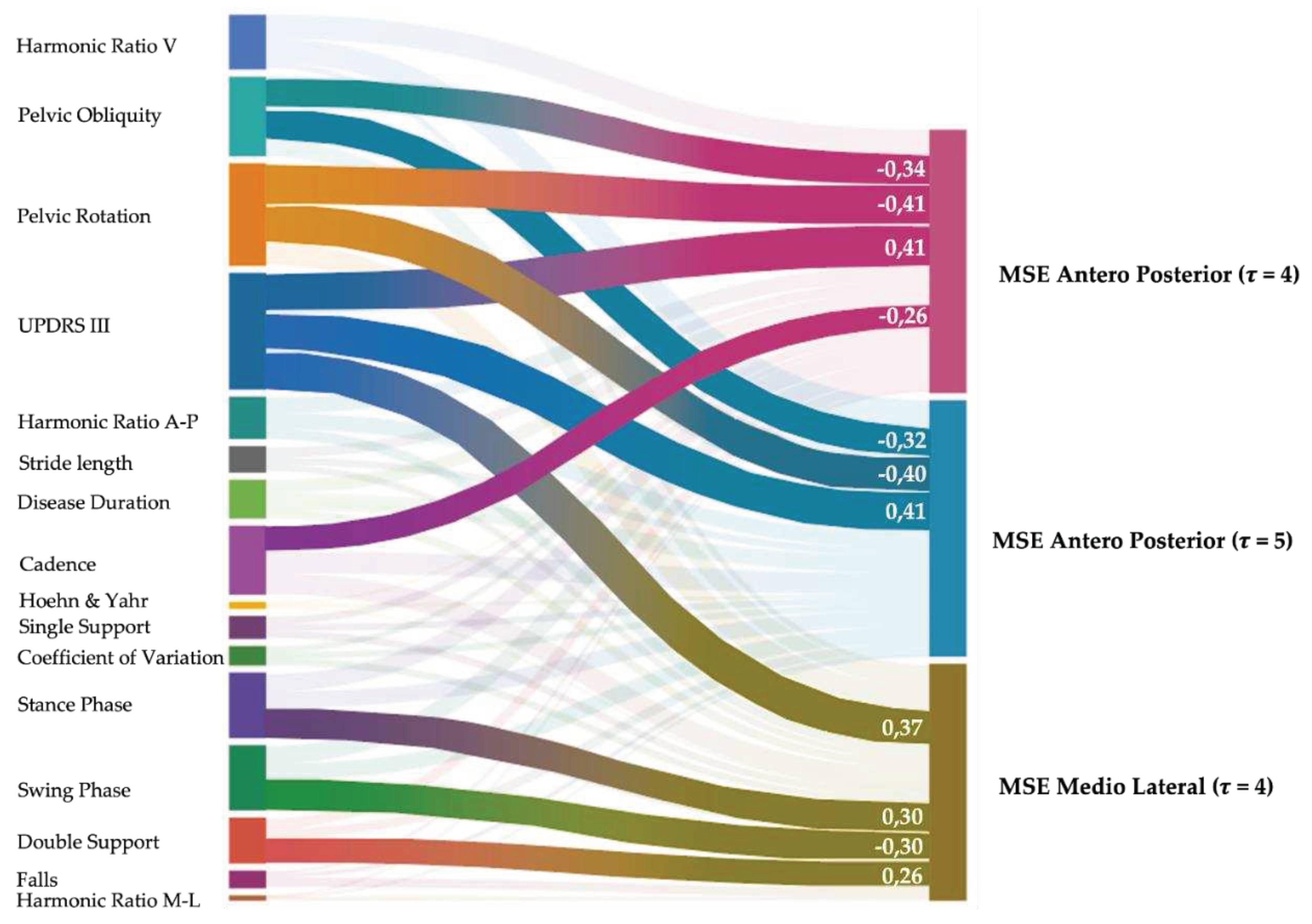
3. Results

Significant differences between swPD and HS were found in all combinations of entropy measures and τ (Table 2), and in stride length, pelvic obliquity, pelvic rotation, HRs and CV (Table 1), regardless of age and gait speed.
MSE in the AP direction at τ 4 (MSEAP τ4) and τ 5 (MSEAP τ5), and MSE in the ML direction at τ 4 (MSEML τ4), revealed the best ability to characterize the gait of swPD, compared with HS (Table 3). Particularly, MSEAP τ4 values ≥ 0.53, MSEAP τ5 values ≥ 0.60, and MSEML τ4 values ≥ 0.59 characterized swPD with 79%, 82%, and 78% probabilities, respectively, and the highest DORs (Table 3, Figure 5).
No differences between swPD fallers and non-fallers in MSEAP τ4 (p = 0.281), MSEAP τ5 (p = 0.377), and MSEML τ4 (p = 0.966) were found.
MSEAP τ4 (H2 = 7.07, p = 0.03) and MSEAP τ5 (H2= 6.50, p = 0.04) differentiated between swPD according to UPDRS III. Post – hoc analysis revealed significant differences in MSEAP τ4 and MSEAP τ5 between mildly and moderately impaired, and severely impaired swPD (Figure 6). MSEML τ4 did not differentiate across UPDRS III scores (H2 = 3.69, p = 0.16). No significant differences in age (H2 = 1.20, p = 0.55) and gait speed (H2 = 0.04, p = 0.98) were found across the UPDRS III thresholds. No differences across the HY stages in MSEAP τ4 (H2= 0.090, p = 0.956), MSEAP τ5 (H2 = 0.105, p = 0.949), and MSEML τ4 (H2 = 0.357, p = 0.836) were found.
Regardless of age and gait speed, MSEAP τ4, MSEAP τ5, and MSEML τ4 positively correlated with UPDRS III. MSEAP τ4 and MSEAP τ5 negatively correlated with pelvic obliquity and pelvic rotation. MSEAP τ4 negatively correlated with cadence. MSEML τ4 positively correlated with the stance and double support phases, and negatively correlated with the swing phase (Figure 7).

4. Discussion

The main objective of this study was to assess the ability of trunk acceleration derived MSE, RCMSE, and CI to characterize swPD gait variability as an expression of the complexity of trunk acceleration signals calculated across a range of τ 1 - 6, regardless of age and gait speed.
We found that swPD showed higher entropy values than age and gait speed matched HS for all the tested scale factors, and that MSE in the AP direction at τ 4 and τ 5, and MSE in the ML direction at τ 4, characterized the gait behavior of swPD with 79%, 82%, and 78% probabilities, respectively, and the best diagnostic performances, as expressed by DORs. These findings are consistent with previous research, which reported higher entropy values in swPD, indicating lower gait regularity than HS [49,56], and a disruption of trunk accelerations [14] due to the greater number of adjustments required to overcome the increasing instability caused by impaired sensorimotor integration [41]. Conversely, a previous study reported lower entropy values in swPD than healthy controls [97]. Aside from a different method of entropy calculation, this contradictory result may be explained primarily by differences in the healthy control group, which was significantly younger and walked faster than swPD in Kamath's study compared to our sample. Gait entropy measures are strongly related to age, with younger people exhibiting greater complexity than older people [98,99]. To avoid misrepresenting differences in gait complexity through entropy measures, the ages of the compared groups should be comparable. In this way, because we matched swPD and HS based on age in this study, we reported differences between the groups that are not dependent on age. Furthermore, nonlinear gait indexes are correlated with gait speed [43,58,100], which is known to be reduced and affects most of the spatio-temporal and kinematic gait parameters, potentially overrepresenting the differences between neurotypical and pathological gait [66]. Although we calculated entropy measures directly from trunk acceleration patterns, avoiding the need for step detection, which is a controversial issue in MIMUs- based gait analysis of subjects with neurological conditions [34], we also matched swPD and HS for gait speed. Therefore, our findings allow us to consider MSE in the antero-posterior and medio – lateral directions as age and speed -independent biomarker of gait complexity in swPD.
In this study, MSE in the AP direction as calculated at τ 4 and τ 5, and MSE in the ML direction at τ 4, outperformed the other scaling configurations in terms of discriminative ability. Riva, et al., previously found that τ 2 represented the best scale factor to identify clinically meaningful gait irregularity through trunk acceleration - derived MSE in older adults [34]. In this way, our findings suggest that higher scaling factors are required to highlight gait irregularities that are caused by Parkinson's disease rather than aging. In our study, however, MSEAP τ4, MSEAP τ5, and MSEML τ4 were unable to distinguish between fallers and non-fallers. This finding represents yet another distinction in the calculation of MSE between healthy older adults, where MSE is higher in fallers, and swPD, where the increase of gait irregularity appears to be a direct expression of the clinical features, regardless of fall history. Indeed, we found that MSE values correlated with motor disability, as assessed by UPDRS III, and that MSE in the AP direction was significantly higher in subjects with greater motor impairment. However, we found no differences in entropy values across disease stages as calculated by HY, confirming that gait irregularity in swPD is most likely due to motor symptoms, rather than the longitudinal progression of the disease [49,101], as further reinforced by the lack of correlation with disease duration. Moreover, we found that higher MSE values in the AP direction correlated with lower ranges of movement of the pelvis in the frontal and transverse plane, regardless of age and gait speed. Pelvic rigidity and trunk rotation reduction have been consistently described as characterizing features of swPD [13,19,21,102]. Because we directly calculate entropy measures from lower trunk acceleration, we can argue that abnormalities in MSE in the AP direction reflect the irregularity of trunk behavior in swPD due to pelvic rigidity, as an expression of the disruption of trunk acceleration patterns [103]. MSE in the ML direction correlated with stance, swing, and double support phases, which are temporal gait parameters that reflect gait stability in swPD [104,105,106]. In this way, we might hypothesize that MSEML τ4 represents a marker of inefficiency of the compensatory strategy to antero – posterior irregularity [58], resulting in increased medio lateral irregularity. However, because no significant differences were found in temporal gait features between swPD and HS at matched gait speed (Table 1), we cannot ascertain that this mechanism is characteristic of swPD rather than a consequence of the reduced gait speed. As a result, MSEAP τ4, MSEAP τ5, and MSEML τ4, characterize the irregularity of trunk accelerations during gait, and correlate with the motor symptoms of swPD and reduced pelvic kinematics. The lack of correlation with other trunk acceleration-derived gait indexes that have previously been shown to characterize the gait abnormalities of swPD [14], such as HR and CV, supports the hypothesis of entropy as a measure of gait irregularity that reflects a different aspect of gait variability than the CV [34]. However, because of the relatively high false positive rates (Figure 5), MSEAP τ4, MSEAP τ5, and MSEML τ4, while providing insights into the gait behavior of swPD, cannot be considered as gait biomarkers alone, requiring additional research into the integration with other gait and clinical features.
To our knowledge, this is the first application of RCMSE on trunk acceleration derived gait data from swPD. Although significant differences between swPD and HS were found in RCMSE at all scale factors, none of them achieved sufficient discriminative ability to be considered accurate biomarkers of gait irregularity in swPD in this study. Refined algorithms are used on data series with high frequency oscillations. In the field of gait analysis, RCMSE appears to fit better with less predictable signals [86,107], such as electromyographic, than with pre-filtered trunk acceleration patterns at natural steady - state locomotion, which are rather regular and repetitive in time and amplitudes. Analyzing more unstable gait conditions in swPD, such as gait initation, freezing, as well as real-world data, could provide additional insights into RCMSE. In this way, MSE was sufficient for the signal typology that we examined.
In this study, we also assessed CIs. As RCMSE, although significant differences between swPD and HS were found, their discriminative ability was not sufficient to be considered as markers of gait irregularity in swPD. Previous studies have reported increased CI in swPD after rehabilitation [62] or deep brain stimulation [63], indicating that the increase in complexity represents improvements in ability to overcome obstacles during gait [62]. In contrast, Ahmadi et al. reported higher CI values during the over imposed dual task gait condition when compared to natural locomotion [64]. Given the differences in sensor localization and the lack of healthy control groups in the aforementioned studies, a comparison with our results is difficult. In this study, we discovered that lower scale factors, regardless of age or gait speed, were unable to characterize swPD when compared to HS. As a result, the inclusion of non-discriminant entropy values in the CI calculation may have resulted in an underrepresentation of gait irregularity in swPD.
This study presents several limitations. First, in this study we fixed length of 2000 data points, m = 2 and r = 0.2 times the standard deviation because these parameters are the most used to calculate entropy measures in gait samples. Therefore, our results can be only interpreted based on the aforementioned parameters. To test the relative consistency of our calculations, different combinations of m and r should be tested [45,108]. Another limitation of this study is the retrospective self-reported history of falls, which could have led to recall bias. Furthermore, we only assessed swPD during the ON phase of the medication. Because differences in entropy measures as measured by shank – mounted MIMUs between ON and OFF phases have been reported in swPD, further studies investigating the ability of trunk acceleration – derived MSE indices to assess the effectiveness of medications are needed.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure 1: Triaxial trunk acceleration, Figure 2: Coarse graining procedure, Figure 3: Sample entropy calculation, Figure 4: Complexity Index, Figure 5: Confusion Matrices, Figure 6: Ability to differentiate across the motor disability levels., Figure 7: Partial Correlation Analysis; Table S1: Clinical and spatio-temporal gait characteristics of the included subjects. Table S2: Differences in Entropy measures between swPD and HS. Table S3: Discriminative ability of the entropy measures.

Author Contributions

Conceptualization, S.F.C., D.T. and M.S.; methodology, S.F.C., D.T., M.S.; software, S.F.C. and D.T.; validation, C.T. and M.S.; formal analysis, S.F.C, D.T., C.C. and M.S.; investigation, C.C., A.R., G.S., C.A., F.B., F.B.; resources, R.D.I., C.T. and M.S.; data curation, S.F.C., D.T. and C.A.; writing—original draft preparation, S.F.C. and D.T.; writing—review and editing, G.C., R.D.I., C.T. and M.S.; visualization, D.T.; supervision, G.C., C.T. and M.S.. All authors have read and agreed to the published version of the manuscript.

Funding

The research presented in this article was carried out as part of the SOPHIA project, which has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement No. 871237.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of CE LAZIO2 (protocol code 0053667/2021).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data presented in this study are available on request from the corresponding author and stored in a password-protected PC located in the Department of Surgical Sciences and Biotechnologies, University of Rome Sapienza.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mirelman, A.; Bonato, P.; Camicioli, R.; Ellis, T.D.; Giladi, N.; Hamilton, J.L.; Hass, C.J.; Hausdorff, J.M.; Pelosin, E.; Almeida, Q.J. Gait Impairments in Parkinson’s Disease. Lancet. Neurol. 2019, 18, 697–708. [Google Scholar] [CrossRef] [PubMed]
  2. Fasano, A.; Canning, C.G.; Hausdorff, J.M.; Lord, S.; Rochester, L. Falls in Parkinson’s Disease: A Complex and Evolving Picture. Mov. Disord. 2017, 32, 1524–1536. [Google Scholar] [CrossRef]
  3. Bouça-Machado, R.; Jalles, C.; Guerreiro, D.; Pona-Ferreira, F.; Branco, Di.; Guerreiro, T.; Matias, R.; Ferreira, J.J. Gait Kinematic Parameters in Parkinson’s Disease: A Systematic Review. J. Parkinsons. Dis. 2020, 10, 843–853. [Google Scholar] [CrossRef] [PubMed]
  4. Allen, N.E.; Canning, C.G.; Almeida, L.R.S.; Bloem, B.R.; Keus, S.H.J.; Löfgren, N.; Nieuwboer, A.; Verheyden, G.S.A.F.; Yamato, T.P.; Sherrington, C. Interventions for Preventing Falls in Parkinson’s Disease. Cochrane database Syst. Rev. 2022, 6. [Google Scholar] [CrossRef] [PubMed]
  5. Blandini, F.; Nappi, G.; Tassorelli, C.; Martignoni, E. Functional Changes of the Basal Ganglia Circuitry in Parkinson’s Disease. Prog. Neurobiol. 2000, 62, 63–88. [Google Scholar] [CrossRef] [PubMed]
  6. Ma, L.; Mi, T.M.; Jia, Q.; Han, C.; Chhetri, J.K.; Chan, P. Gait Variability Is Sensitive to Detect Parkinson’s Disease Patients at High Fall Risk. Int. J. Neurosci. 2022, 132, 888–893. [Google Scholar] [CrossRef] [PubMed]
  7. Hausdorff, J.M. Gait Dynamics in Parkinson’s Disease: Common and Distinct Behavior among Stride Length, Gait Variability, and Fractal-like Scaling. Chaos 2009, 19. [Google Scholar] [CrossRef]
  8. Bryant, M.S.; Rintala, D.H.; Hou, J.G.; Collins, R.L.; Protas, E.J. Gait Variability in Parkinson’s Disease: Levodopa and Walking Direction. Acta Neurol. Scand. 2016, 134, 83–86. [Google Scholar] [CrossRef] [PubMed]
  9. Hausdorff, J.M.; Cudkowicz, M.E.; Firtion, R.; Wei, J.Y.; Goldberger, A.L. Gait Variability and Basal Ganglia Disorders: Stride-to-Stride Variations of Gait Cycle Timing in Parkinson’s Disease and Huntington’s Disease. Mov. Disord. 1998, 13, 428–437. [Google Scholar] [CrossRef] [PubMed]
  10. Plotnik, M.; Giladi, N.; Hausdorff, J.M. A New Measure for Quantifying the Bilateral Coordination of Human Gait: Effects of Aging and Parkinson’s Disease. Exp. brain Res. 2007, 181, 561–570. [Google Scholar] [CrossRef]
  11. Kroneberg, D.; Elshehabi, M.; Meyer, A.C.; Otte, K.; Doss, S.; Paul, F.; Nussbaum, S.; Berg, D.; Kühn, A.A.; Maetzler, W.; et al. Less Is More - Estimation of the Number of Strides Required to Assess Gait Variability in Spatially Confined Settings. Front. Aging Neurosci. 2019, 11, 435. [Google Scholar] [CrossRef]
  12. Trabassi, D.; Serrao, M.; Varrecchia, T.; Ranavolo, A.; Coppola, G.; De Icco, R.; Tassorelli, C.; Castiglia, S.F. Machine Learning Approach to Support the Detection of Parkinson’s Disease in IMU-Based Gait Analysis. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
  13. Varrecchia, T.; Castiglia, S.F.; Ranavolo, A.; Conte, C.; Tatarelli, A.; Coppola, G.; Di Lorenzo, C.; Draicchio, F.; Pierelli, F.; Serrao, M. An Artificial Neural Network Approach to Detect Presence and Severity of Parkinson’s Disease via Gait Parameters. PLoS One 2021, 16. [Google Scholar] [CrossRef]
  14. Castiglia, S.F.; Tatarelli, A.; Trabassi, D.; De Icco, R.; Grillo, V.; Ranavolo, A.; Varrecchia, T.; Magnifica, F.; Di Lenola, D.; Coppola, G.; et al. Ability of a Set of Trunk Inertial Indexes of Gait to Identify Gait Instability and Recurrent Fallers in Parkinson’s Disease. Sensors 2021, 21. [Google Scholar] [CrossRef]
  15. Serrao, M.; Chini, G.; Bergantino, M.; Sarnari, D.; Casali, C.; Conte, C.; Ranavolo, A.; Marcotulli, C.; Rinaldi, M.; Coppola, G.; et al. Identification of Specific Gait Patterns in Patients with Cerebellar Ataxia, Spastic Paraplegia, and Parkinson’s Disease: A Non-Hierarchical Cluster Analysis. Hum. Mov. Sci. 2018, 57, 267–279. [Google Scholar] [CrossRef] [PubMed]
  16. Gandolfi, M.; Tinazzi, M.; Magrinelli, F.; Busselli, G.; Dimitrova, E.; Polo, N.; Manganotti, P.; Fasano, A.; Smania, N.; Geroin, C. Four-Week Trunk-Specific Exercise Program Decreases Forward Trunk Flexion in Parkinson’s Disease: A Single-Blinded, Randomized Controlled Trial. Parkinsonism Relat. Disord. 2019, 64, 268–274. [Google Scholar] [CrossRef] [PubMed]
  17. Safarpour, D.; Dale, M.L.; Shah, V. V.; Talman, L.; Carlson-Kuhta, P.; Horak, F.B.; Mancini, M. Surrogates for Rigidity and PIGD MDS-UPDRS Subscores Using Wearable Sensors. Gait Posture 2022, 91, 186–191. [Google Scholar] [CrossRef] [PubMed]
  18. Borzì, L.; Mazzetta, I.; Zampogna, A.; Suppa, A.; Irrera, F.; Olmo, G. Predicting Axial Impairment in Parkinson’s Disease through a Single Inertial Sensor. Sensors (Basel). 2022, 22. [Google Scholar] [CrossRef] [PubMed]
  19. Serrao, M.; Chini, G.; Caramanico, G.; Bartolo, M.; Castiglia, S.F.; Ranavolo, A.; Conte, C.; Venditto, T.; Coppola, G.; Di Lorenzo, C.; et al. Prediction of Responsiveness of Gait Variables to Rehabilitation Training in Parkinson’s Disease. Front. Neurol. 2019, 10. [Google Scholar] [CrossRef]
  20. Serrao, M.; Ranavolo, A.; Conte, C.; Davassi, C.; Mari, S.; Fasano, A.; Chini, G.; Coppola, G.; Draicchio, F.; Pierelli, F. Effect of 24-h Continuous Rotigotine Treatment on Stationary and Non-Stationary Locomotion in de Novo Patients with Parkinson Disease in an Open-Label Uncontrolled Study. J. Neurol. 2015, 262, 2539–2547. [Google Scholar] [CrossRef]
  21. Serrao, M.; Pierelli, F.; Sinibaldi, E.; Chini, G.; Castiglia, S.F.; Priori, M.; Gimma, D.; Sellitto, G.; Ranavolo, A.; Conte, C.; et al. Progressive Modular Rebalancing System and Visual Cueing for Gait Rehabilitation in Parkinson’s Disease: A Pilot, Randomized, Controlled Trial With Crossover. Front. Neurol. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
  22. Castiglia, S.F.; Trabassi, D.; De Icco, R.; Tatarelli, A.; Avenali, M.; Corrado, M.; Grillo, V.; Coppola, G.; Denaro, A.; Tassorelli, C.; et al. Harmonic Ratio Is the Most Responsive Trunk-Acceleration Derived Gait Index to Rehabilitation in People with Parkinson’s Disease at Moderate Disease Stages. Gait Posture 2022, 97, 152–158. [Google Scholar] [CrossRef] [PubMed]
  23. Putortì, A.; Corrado, M.; Avenali, M.; Martinelli, D.; Allena, M.; Cristina, S.; Grillo, V.; Martinis, L.; Tamburin, S.; Serrao, M.; et al. The Effects of Intensive Neurorehabilitation on Sequence Effect in Parkinson’s Disease Patients With and Without Freezing of Gait. Front. Neurol. 2021, 12. [Google Scholar] [CrossRef] [PubMed]
  24. Bartolo, M.; Serrao, M.; Tassorelli, C.; Don, R.; Ranavolo, A.; Draicchio, F.; Pacchetti, C.; Buscone, S.; Perrotta, A.; Furnari, A.; et al. Four-Week Trunk-Specific Rehabilitation Treatment Improves Lateral Trunk Flexion in Parkinson’s Disease. Mov. Disord. 2010, 25, 325–331. [Google Scholar] [CrossRef]
  25. Castiglia, S.F.; Trabassi, D.; Tatarelli, A.; Ranavolo, A.; Varrecchia, T.; Fiori, L.; Di Lenola, D.; Cioffi, E.; Raju, M.; Coppola, G.; et al. Identification of Gait Unbalance and Fallers Among Subjects with Cerebellar Ataxia by a Set of Trunk Acceleration-Derived Indices of Gait. Cerebellum 2022. [Google Scholar] [CrossRef]
  26. Brognara, L.; Palumbo, P.; Grimm, B.; Palmerini, L. Assessing Gait in Parkinson’s Disease Using Wearable Motion Sensors: A Systematic Review. Dis. (Basel, Switzerland) 2019, 7, 18. [Google Scholar] [CrossRef]
  27. Hubble, R.P.; Naughton, G.; Silburn, P.A.; Cole, M.H. Trunk Exercises Improve Gait Symmetry in Parkinson Disease: A Blind Phase II Randomized Controlled Trial. Am. J. Phys. Med. Rehabil. 2018, 97, 151–159. [Google Scholar] [CrossRef]
  28. Caliandro, P.; Conte, C.; Iacovelli, C.; Tatarelli, A.; Castiglia, S.F.; Reale, G.; Serrao, M. Exploring Risk of Falls and Dynamic Unbalance in Cerebellar Ataxia by Inertial Sensor Assessment. Sensors (Basel). 2019, 19. [Google Scholar] [CrossRef] [PubMed]
  29. Fujiwara, S.; Sato, S.; Sugawara, A.; Nishikawa, Y.; Koji, T.; Nishimura, Y.; Ogasawara, K. The Coefficient of Variation of Step Time Can Overestimate Gait Abnormality: Test-Retest Reliability of Gait-Related Parameters Obtained with a Tri-Axial Accelerometer in Healthy Subjects. Sensors (Basel). 2020, 20. [Google Scholar] [CrossRef]
  30. Tamburini, P.; Storm, F.; Buckley, C.; Bisi, M.C.; Stagni, R.; Mazzà, C. Moving from Laboratory to Real Life Conditions: Influence on the Assessment of Variability and Stability of Gait. Gait Posture 2018, 59, 248–252. [Google Scholar] [CrossRef]
  31. Lord, S.; Baker, K.; Nieuwboer, A.; Burn, D.; Rochester, L. Gait Variability in Parkinson’s Disease: An Indicator of Non-Dopaminergic Contributors to Gait Dysfunction? J. Neurol. 2011, 258, 566–572. [Google Scholar] [CrossRef]
  32. Del Din, S.; Galna, B.; Godfrey, A.; Bekkers, E.M.J.; Pelosin, E.; Nieuwhof, F.; Mirelman, A.; Hausdorff, J.M.; Rochester, L. Analysis of Free-Living Gait in Older Adults With and Without Parkinson’s Disease and With and Without a History of Falls: Identifying Generic and Disease-Specific Characteristics. Journals Gerontol. Ser. A 2019, 74, 500–506. [Google Scholar] [CrossRef] [PubMed]
  33. Bovonsunthonchai, S.; Vachalathiti, R.; Pisarnpong, A.; Khobhun, F.; Hiengkaew, V. Spatiotemporal Gait Parameters for Patients with Parkinson’s Disease Compared with Normal Individuals. Physiother. Res. Int. 2014, 19, 158–165. [Google Scholar] [CrossRef] [PubMed]
  34. Riva, F.; Toebes, M.J.P.; Pijnappels, M.; Stagni, R.; van Dieën, J.H. Estimating Fall Risk with Inertial Sensors Using Gait Stability Measures That Do Not Require Step Detection. Gait Posture 2013, 38, 170–174. [Google Scholar] [CrossRef] [PubMed]
  35. Trojaniello, D.; Ravaschio, A.; Hausdorff, J.M.; Cereatti, A. Comparative Assessment of Different Methods for the Estimation of Gait Temporal Parameters Using a Single Inertial Sensor: Application to Elderly, Post-Stroke, Parkinson’s Disease and Huntington’s Disease Subjects. Gait Posture 2015, 42, 310–316. [Google Scholar] [CrossRef] [PubMed]
  36. López, A.M.; Álvarez, D.; González, R.C.; Álvarez, J.C. Validity of Four Gait Models to Estimate Walked Distance from Vertical COG Acceleration. J. Appl. Biomech. 2008, 24, 360–367. [Google Scholar] [CrossRef] [PubMed]
  37. González, R.C.; López, A.M.; Rodriguez-Uría, J.; Álvarez, D.; Alvarez, J.C. Real-Time Gait Event Detection for Normal Subjects from Lower Trunk Accelerations. Gait Posture 2010, 31, 322–325. [Google Scholar] [CrossRef] [PubMed]
  38. Riva, F.; Grimpampi, E.; Mazzà, C.; Stagni, R. Are Gait Variability and Stability Measures Influenced by Directional Changes? Biomed. Eng. Online 2014, 13, 1–11. [Google Scholar] [CrossRef]
  39. Bisi, M.C.; Stagni, R. Complexity of Human Gait Pattern at Different Ages Assessed Using Multiscale Entropy: From Development to Decline. Gait Posture 2016, 47, 37–42. [Google Scholar] [CrossRef]
  40. Amirpourabasi, A.; Lamb, S.E.; Chow, J.Y.; Williams, G.K.R. Nonlinear Dynamic Measures of Walking in Healthy Older Adults: A Systematic Scoping Review. Sensors (Basel). 2022, 22. [Google Scholar] [CrossRef]
  41. Dingwell, J.B.; Cusumano, J.P. Nonlinear Time Series Analysis of Normal and Pathological Human Walking. Chaos 2000, 10, 848–863. [Google Scholar] [CrossRef]
  42. Yentes, J.M.; Raffalt, P.C. Entropy Analysis in Gait Research – Methodological and Recommendations. Ann. Biomed. Eng. 2021, 49, 979. [Google Scholar] [CrossRef] [PubMed]
  43. Raffalt, P.C.; Denton, W.; Yentes, J.M. On the Choice of Multiscale Entropy Algorithm for Quantification of Complexity in Gait Data. Comput. Biol. Med. 2018, 103, 93–100. [Google Scholar] [CrossRef] [PubMed]
  44. Pincus, S.M. Approximate Entropy as a Measure of System Complexity. Proc. Natl. Acad. Sci. 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
  45. Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278. [Google Scholar] [CrossRef] [PubMed]
  46. Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
  47. Leverick, G.; Szturm, T.; Wu, C.Q. Using Entropy Measures to Characterize Human Locomotion. J. Biomech. Eng. 2014, 136. [Google Scholar] [CrossRef] [PubMed]
  48. Bisi, M.C.; Riva, F.; Stagni, R. Measures of Gait Stability: Performance on Adults and Toddlers at the Beginning of Independent Walking. J. Neuroeng. Rehabil. 2014, 11, 1–9. [Google Scholar] [CrossRef]
  49. Coates, L.; Shi, J.; Rochester, L.; Din, S. Del; Pantall, A. Entropy of Real-World Gait in Parkinson’s Disease Determined from Wearable Sensors as a Digital Marker of Altered Ambulatory Behavior. Sensors (Basel). 2020, 20. [Google Scholar] [CrossRef]
  50. Montesinos, L.; Castaldo, R.; Pecchia, L. On the Use of Approximate Entropy and Sample Entropy with Centre of Pressure Time-Series. J. Neuroeng. Rehabil. 2018, 15. [Google Scholar] [CrossRef]
  51. Aboy, M.; Cuesta-Frau, D.; Austin, D.; Micó-Tormos, P. Characterization of Sample Entropy in the Context of Biomedical Signal Analysis. Annu. Int. Conf. IEEE Eng. Med. Biol. - Proc. 2007, 5942–5945. [Google Scholar] [CrossRef] [PubMed]
  52. Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The Appropriate Use of Approximate Entropy and Sample Entropy with Short Data Sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef]
  53. Costa, M.; Peng, C.-K.; Goldberger, A.L.; Hausdorr, J.M. Multiscale Entropy Analysis of Human Gait Dynamics. Physica A 2003, 330, 53–60. [Google Scholar] [CrossRef] [PubMed]
  54. Thuraisingham, R.A.; Gottwald, G.A. On Multiscale Entropy Analysis for Physiological Data. Phys. A Stat. Mech. its Appl. 2006, 366, 323–332. [Google Scholar] [CrossRef]
  55. Peng, C.K.; Costa, M.; Goldberger, A.L. ADAPTIVE DATA ANALYSIS OF COMPLEX FLUCTUATIONS IN PHYSIOLOGIC TIME SERIES. Adv. Adapt. Data Anal. 2009, 1, 61–70. [Google Scholar] [CrossRef] [PubMed]
  56. Hsieh, Y.L.; Abbod, M.F. Gait Analyses of Parkinson’s Disease Patients Using Multiscale Entropy. Electron 2021, 10, 2604. [Google Scholar] [CrossRef]
  57. Bizovska, L.; Svoboda, Z.; Vuillerme, N.; Janura, M. Multiscale and Shannon Entropies during Gait as Fall Risk Predictors-A Prospective Study. Gait Posture 2017, 52, 5–10. [Google Scholar] [CrossRef] [PubMed]
  58. Bisi, M.C.; Di Marco, R.; Ragona, F.; Darra, F.; Vecchi, M.; Masiero, S.; Del Felice, A.; Stagni, R. Quantitative Characterization of Motor Control during Gait in Dravet Syndrome Using Wearable Sensors: A Preliminary Study. Sensors 2022, 22. [Google Scholar] [CrossRef]
  59. Bizovska, L.; Svoboda, Z.; Kubonova, E.; Vuillerme, N.; Hirjakova, Z.; Janura, M. The Differences between Overground and Treadmill Walking in Nonlinear, Entropy-Based and Frequency Variables Derived from Accelerometers in Young and Older Women - Preliminary Report. Acta Bioeng. Biomech. 2018, 20, 93–100. [Google Scholar] [CrossRef]
  60. Riva, F.; Bisi, M.C.; Stagni, R. Gait Variability and Stability Measures: Minimum Number of Strides and within-Session Reliability. Comput. Biol. Med. 2014, 50, 9–13. [Google Scholar] [CrossRef]
  61. Wu, S. De; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of Complex Time Series Using Refined Composite Multiscale Entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
  62. Combs-Miller, S.A.; Dugan, E.L.; Beachy, A.; Derby, B.B.; Hosinski, A.L.; Robbins, K. Physiological Complexity of Gait between Regular and Non-Exercisers with Parkinson’s Disease. Clin. Biomech. (Bristol, Avon) 2019, 68, 23–28. [Google Scholar] [CrossRef] [PubMed]
  63. Powell, D.W.; Blackmore, S.E.; Puppa, M.; Lester, D.; Murray, N.G.; Reed-Jones, R.J.; Xia, R.P. Deep Brain Stimulation Enhances Movement Complexity during Gait in Individuals with Parkinson’s Disease. Neurosci. Lett. 2020, 728. [Google Scholar] [CrossRef] [PubMed]
  64. Ahmadi, S.; Siragy, T.; Nantel, J. Regularity of Kinematic Data between Single and Dual-Task Treadmill Walking in People with Parkinson’s Disease. J. Neuroeng. Rehabil. 2021, 18. [Google Scholar] [CrossRef] [PubMed]
  65. Ahmadi, S.; Sepehri, N.; Wu, C.; Szturm, T. Sample Entropy of Human Gait Center of Pressure Displacement: A Systematic Methodological Analysis. Entropy (Basel). 2018, 20. [Google Scholar] [CrossRef]
  66. Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. Effects of Walking Speed on Gait Biomechanics in Healthy Participants: A Systematic Review and Meta-Analysis. Syst. Rev. 2019, 8. [Google Scholar] [CrossRef] [PubMed]
  67. Kubota, K.J.; Chen, J.A.; Little, M.A. Machine Learning for Large-Scale Wearable Sensor Data in Parkinson’s Disease: Concepts, Promises, Pitfalls, and Futures. Mov. Disord. 2016, 31, 1314–1326. [Google Scholar] [CrossRef]
  68. Hughes, A.J.; Daniel, S.E.; Kilford, L.; Lees, A.J. Accuracy of Clinical Diagnosis of Idiopathic Parkinson’s Disease: A Clinico-Pathological Study of 100 Cases. J. Neurol. Neurosurg. Psychiatry 1992, 55, 181–184. [Google Scholar] [CrossRef]
  69. Hoehn, M.M.; Yahr, M.D. Parkinsonism: Onset, Progression and Mortality. Neurology 1967, 17, 427–442. [Google Scholar] [CrossRef]
  70. Folstein, M.F.; Folstein, S.E.; McHugh, P.R. “Mini-Mental State”. A Practical Method for Grading the Cognitive State of Patients for the Clinician. J. Psychiatr. Res. 1975, 12, 189–198. [Google Scholar] [CrossRef]
  71. Perneczky, R.; Wagenpfeil, S.; Komossa, K.; Grimmer, T.; Diehl, J.; Kurz, A. Mapping Scores onto Stages: Mini-Mental State Examination and Clinical Dementia Rating. Am. J. Geriatr. Psychiatry 2006, 14, 139–144. [Google Scholar] [CrossRef] [PubMed]
  72. Beck, A.T.; Ward, C.H.; Mendelson, M.; Mock, J.; Erbaugh, J. An Inventory for Measuring Depression. Arch. Gen. Psychiatry 1961, 4, 561–571. [Google Scholar] [CrossRef] [PubMed]
  73. Goodarzi, Z.; Mrklas, K.J.; Roberts, D.J.; Jette, N.; Pringsheim, T.; Holroyd-Leduc, J. Detecting Depression in Parkinson Disease: A Systematic Review and Meta-Analysis. Neurology 2016, 87, 426–437. [Google Scholar] [CrossRef] [PubMed]
  74. Altman, R.; Alarcón, G.; Appelrouth, D.; Bloch, D.; Borenstein, D.; Brandt, K.; Brown, C.; Cooke, T.D.; Daniel, W.; Feldman, D.; et al. The American College of Rheumatology Criteria for the Classification and Reporting of Osteoarthritis of the Hip. Arthritis Rheum. 1991, 34, 505–514. [Google Scholar] [CrossRef]
  75. Fitzgerald, G.K.; Hinman, R.S.; Zeni, J.; Risberg, M.A.; Snyder-Mackler, L.; Bennell, K.L. OARSI Clinical Trials Recommendations: Design and Conduct of Clinical Trials of Rehabilitation Interventions for Osteoarthritis. Osteoarthr. Cartil. 2015, 23, 803–814. [Google Scholar] [CrossRef] [PubMed]
  76. Damen, J.; Van Rijn, R.M.; Emans, P.J.; Hilberdink, W.K.H.A.; Wesseling, J.; Oei, E.H.G.; Bierma-Zeinstra, S.M.A. Prevalence and Development of Hip and Knee Osteoarthritis According to American College of Rheumatology Criteria in the CHECK Cohort. Arthritis Res. Ther. 2019, 21. [Google Scholar] [CrossRef] [PubMed]
  77. Yao, X.I.; Wang, X.; Speicher, P.J.; Hwang, E.S.; Cheng, P.; Harpole, D.H.; Berry, M.F.; Schrag, D.; Pang, H.H. Reporting and Guidelines in Propensity Score Analysis: A Systematic Review of Cancer and Cancer Surgical Studies. J. Natl. Cancer Inst. 2017, 109. [Google Scholar] [CrossRef] [PubMed]
  78. Peterson, D.S.; Mancini, M.; Fino, P.C.; Horak, F.; Smulders, K. Speeding Up Gait in Parkinson’s Disease. J. Parkinsons. Dis. 2020, 10, 245–253. [Google Scholar] [CrossRef] [PubMed]
  79. Huijben, B.; van Schooten, K.S.; van Dieën, J.H.; Pijnappels, M. The Effect of Walking Speed on Quality of Gait in Older Adults. Gait Posture 2018, 65, 112–116. [Google Scholar] [CrossRef]
  80. Hagoort, I.; Vuillerme, N.; Hortobágyi, T.; Lamoth, C.J. Outcome-Dependent Effects of Walking Speed and Age on Quantitative and Qualitative Gait Measures. Gait Posture 2022, 93, 39–46. [Google Scholar] [CrossRef]
  81. Lindemann, U. Spatiotemporal Gait Analysis of Older Persons in Clinical Practice and Research : Which Parameters Are Relevant? Z. Gerontol. Geriatr. 2020, 53, 171–178. [Google Scholar] [CrossRef] [PubMed]
  82. Orter, S.; Ravi, D.K.; Singh, N.B.; Vogl, F.; Taylor, W.R.; Ignasiak, N.K. A Method to Concatenate Multiple Short Time Series for Evaluating Dynamic Behaviour during Walking. PLoS One 2019, 14, e0218594. [Google Scholar] [CrossRef] [PubMed]
  83. Pincus, S.M.; Huang, W.-M. Approximate Entropy: Statistical Properties and Applications. Commun. Stat. - Theory Methods 1992, 21, 3061–3077. [Google Scholar] [CrossRef]
  84. Sarlabous, L.; Torres, A.; Fiz, J.A.; Gea, J.; Martínez-Llorens, J.M.; Morera, J.; Jané, R. Interpretation of the Approximate Entropy Using Fixed Tolerance Values as a Measure of Amplitude Variations in Biomedical Signals. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. IEEE Eng. Med. Biol. Soc. Annu. Int. Conf. 2010, 2010, 5967–5970. [Google Scholar] [CrossRef] [PubMed]
  85. Govindan, R.B.; Wilson, J.D.; Eswaran, H.; Lowery, C.L.; Preißl, H. Revisiting Sample Entropy Analysis. Phys. A Stat. Mech. its Appl. 2007, 376, 158–164. [Google Scholar] [CrossRef]
  86. Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
  87. Kang, H.G.; Dingwell, J.B. Differential Changes with Age in Multiscale Entropy of Electromyography Signals from Leg Muscles during Treadmill Walking. PLoS One 2016, 11, e0162034. [Google Scholar] [CrossRef] [PubMed]
  88. Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale Entropy Analysis of Biological Signals. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 2005, 71. [Google Scholar] [CrossRef]
  89. Goetz, C.G.; Tilley, B.C.; Shaftman, S.R.; Stebbins, G.T.; Fahn, S.; Martinez-Martin, P.; Poewe, W.; Sampaio, C.; Stern, M.B.; Dodel, R.; et al. Movement Disorder Society-Sponsored Revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Scale Presentation and Clinimetric Testing Results. Mov. Disord. 2008, 23, 2129–2170. [Google Scholar] [CrossRef] [PubMed]
  90. Vitorio, R.; Mancini, M.; Carlson-Kuhta, P.; Horak, F.B.; Shah, V. V. Should We Use Both Clinical and Mobility Measures to Identify Fallers in Parkinson’s Disease? Parkinsonism Relat. Disord. 2023, 106. [Google Scholar] [CrossRef]
  91. Paul, S.S.; Allen, N.E.; Sherrington, C.; Heller, G.; Fung, V.S.C.; Close, J.C.T.; Lord, S.R.; Canning, C.G. Risk Factors for Frequent Falls in People with Parkinson’s Disease. J. Parkinsons. Dis. 2014, 4, 699–703. [Google Scholar] [CrossRef] [PubMed]
  92. Kerr, G.K.; Worringham, C.J.; Cole, M.H.; Lacherez, P.F.; Wood, J.M.; Silburn, P.A. Predictors of Future Falls in Parkinson Disease. Neurology 2010, 75, 116–124. [Google Scholar] [CrossRef] [PubMed]
  93. Carter, J. V.; Pan, J.; Rai, S.N.; Galandiuk, S. ROC-Ing along: Evaluation and Interpretation of Receiver Operating Characteristic Curves. Surgery 2016, 159, 1638–1645. [Google Scholar] [CrossRef] [PubMed]
  94. Kallner, A. Bayes’ Theorem, the ROC Diagram and Reference Values: Definition and Use in Clinical Diagnosis. Biochem. medica 2018, 28. [Google Scholar] [CrossRef] [PubMed]
  95. Glas, A.S.; Lijmer, J.G.; Prins, M.H.; Bonsel, G.J.; Bossuyt, P.M.M. The Diagnostic Odds Ratio: A Single Indicator of Test Performance. J. Clin. Epidemiol. 2003, 56, 1129–1135. [Google Scholar] [CrossRef]
  96. Martínez-Martín, P.; Rodríguez-Blázquez, C.; Alvarez, M.; Arakaki, T.; Arillo, V.C.; Chaná, P.; Fernández, W.; Garretto, N.; Martínez-Castrillo, J.C.; Rodríguez-Violante, M.; et al. Parkinson’s Disease Severity Levels and MDS-Unified Parkinson’s Disease Rating Scale. Park. Relat. Disord. 2015, 21, 50–54. [Google Scholar] [CrossRef]
  97. Kamath, C. A Novel Perspective to Assessment of Neurodegenerative Disorder Gait. Sci. Postprint 2015, 1. [Google Scholar] [CrossRef]
  98. Bisi, M.C.; Tamburini, P.; Stagni, R. A “Fingerprint” of Locomotor Maturation: Motor Development Descriptors, Reference Development Bands and Data-Set. Gait Posture 2019, 68, 232–237. [Google Scholar] [CrossRef] [PubMed]
  99. Bisi, M.C.; Stagni, R. Changes of Human Movement Complexity during Maturation: Quantitative Assessment Using Multiscale Entropy. Comput. Methods Biomech. Biomed. Engin. 2018, 21, 325–331. [Google Scholar] [CrossRef]
  100. Craig, J.J.; Bruetsch, A.P.; Huisinga, J.M. Coordination of Trunk and Foot Acceleration during Gait Is Affected by Walking Velocity and Fall History in Elderly Adults. Aging Clin. Exp. Res. 2019, 31, 943–950. [Google Scholar] [CrossRef]
  101. Pantall, A.; Del Din, S.; Rochester, L. Longitudinal Changes over Thirty-Six Months in Postural Control Dynamics and Cognitive Function in People with Parkinson’s Disease. Gait Posture 2018, 62, 468–474. [Google Scholar] [CrossRef] [PubMed]
  102. Creaby, M.W.; Cole, M.H. Gait Characteristics and Falls in Parkinson’s Disease: A Systematic Review and Meta-Analysis. Parkinsonism Relat. Disord. 2018, 57, 1–8. [Google Scholar] [CrossRef] [PubMed]
  103. Latt, M.D.; Menz, H.B.; Fung, V.S.; Lord, S.R. Acceleration Patterns of the Head and Pelvis During Gait in Older People With Parkinson’s Disease: A Comparison of Fallers and Nonfallers. Journals Gerontol. Ser. A 2009, 64A, 700–706. [Google Scholar] [CrossRef] [PubMed]
  104. Schlachetzki, J.C.M.; Barth, J.; Marxreiter, F.; Gossler, J.; Kohl, Z.; Reinfelder, S.; Gassner, H.; Aminian, K.; Eskofier, B.M.; Winkler, J.; et al. Wearable Sensors Objectively Measure Gait Parameters in Parkinson’s Disease. PLoS One 2017, 12, e0183989. [Google Scholar] [CrossRef] [PubMed]
  105. Lee, M.; Youm, C.; Noh, B.; Park, H.; Cheon, S.M. Gait Characteristics under Imposed Challenge Speed Conditions in Patients with Parkinson’s Disease During Overground Walking. Sensors (Basel). 2020, 20. [Google Scholar] [CrossRef] [PubMed]
  106. Hamacher, D.; Singh, N.B.; Van Dieën, J.H.; Heller, M.O.; Taylor, W.R. Kinematic Measures for Assessing Gait Stability in Elderly Individuals: A Systematic Review. J. R. Soc. Interface 2011, 8, 1682–1698. [Google Scholar] [CrossRef]
  107. Valencia, J.F.; Porta, A.; Vallverdú, M.; Clarià, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Multiscale Sample Entropy in Heart Rate Variability of Aortic Stenosis Patients 2008, 2000–2003.
  108. Yentes, J.M.; Denton, W.; McCamley, J.; Raffalt, P.C.; Schmid, K.K. Effect of Parameter Selection on Entropy Calculation for Long Walking Trials. Gait Posture 2018, 60, 128. [Google Scholar] [CrossRef]
Preprints 69873 g001
Figure 1. Triaxial trunk acceleration. Triaxial trunk acceleration extrapolated by L5 inertial sensor after subjects were asked to walk barefoot down a 30-meter-long corridor at a self-selected speed.
Figure 1. Triaxial trunk acceleration. Triaxial trunk acceleration extrapolated by L5 inertial sensor after subjects were asked to walk barefoot down a 30-meter-long corridor at a self-selected speed.
Preprints 69873 g001
Preprints 69873 g002
Figure 2. Coarse Graining Procedure. Given a time series { x 1 ,   x 2 … x i + 2 }, we first create coarse-grained time series by averaging a growing number of data points in non-overlapping windows. Schematic illustration of the coarse-graining procedure in Multiscale Sample Entropy for scale τ = 2 in a) and for scale τ = 3 in b); data length of the trunk acceleration time series reduced respectively to N 2   and N 3 .
Figure 2. Coarse Graining Procedure. Given a time series { x 1 ,   x 2 … x i + 2 }, we first create coarse-grained time series by averaging a growing number of data points in non-overlapping windows. Schematic illustration of the coarse-graining procedure in Multiscale Sample Entropy for scale τ = 2 in a) and for scale τ = 3 in b); data length of the trunk acceleration time series reduced respectively to N 2   and N 3 .
Preprints 69873 g002
Preprints 69873 g003
Figure 3. Sample Entropy calculation. For each pattern of m points in trunk acceleration signal, places in other parts of the signal where the template is seen are identified within tolerance r. Sample Entropy is calculated as the negative natural of the conditional probability that the pattern of m+1 points will match if that the pattern of m points did match. After the signal matched the first two parts of the pattern m, this is the probability that pattern match will complete, m+1. The number of m matches are compared to the number of complete pattern (m+1) matches.
Figure 3. Sample Entropy calculation. For each pattern of m points in trunk acceleration signal, places in other parts of the signal where the template is seen are identified within tolerance r. Sample Entropy is calculated as the negative natural of the conditional probability that the pattern of m+1 points will match if that the pattern of m points did match. After the signal matched the first two parts of the pattern m, this is the probability that pattern match will complete, m+1. The number of m matches are compared to the number of complete pattern (m+1) matches.
Preprints 69873 g003
Preprints 69873 g004
Figure 4. Complexity Index. Multiscale Entropy plot of the triaxial trunk acceleration signal evaluated for all scale factors τ; the complexity index was determined for the Antero-Posterior direction of a healthy subject by calculating the area under the curve given by the multiscale Entropy values.
Figure 4. Complexity Index. Multiscale Entropy plot of the triaxial trunk acceleration signal evaluated for all scale factors τ; the complexity index was determined for the Antero-Posterior direction of a healthy subject by calculating the area under the curve given by the multiscale Entropy values.
Preprints 69873 g004
Preprints 69873 g005
Figure 5. Confusion matrices. Confusion matrices of multiscale entropy in the AP direction at τ 4 (a), and τ 5 (b), and in the medio – lateral direction at τ 4 (c). Radar plots represent the true positive (TPR), true negative (TNR), false positive (FPR) and false negative (FNR) rates at each optimal cutoff point.
Figure 5. Confusion matrices. Confusion matrices of multiscale entropy in the AP direction at τ 4 (a), and τ 5 (b), and in the medio – lateral direction at τ 4 (c). Radar plots represent the true positive (TPR), true negative (TNR), false positive (FPR) and false negative (FNR) rates at each optimal cutoff point.
Preprints 69873 g005
Preprints 69873 g006
Figure 6. Ability to differentiate across the motor disability levels. Differences in multiscale entropy (MSE) at scale factor τ 4 and τ 5 in the antero – posterior direction according to motor disability as assessed by the motor section Unified Parkinson’s Disease Rating Scale (UPDRS III). P- values represent significant differences at Dunn’s pot-hoc analysis with Holm’s correction after Kruskal – Wallis’s procedure.
Figure 6. Ability to differentiate across the motor disability levels. Differences in multiscale entropy (MSE) at scale factor τ 4 and τ 5 in the antero – posterior direction according to motor disability as assessed by the motor section Unified Parkinson’s Disease Rating Scale (UPDRS III). P- values represent significant differences at Dunn’s pot-hoc analysis with Holm’s correction after Kruskal – Wallis’s procedure.
Preprints 69873 g006
Preprints 69873 g007
Figure 7. Partial correlation analysis. Partial Spearman’s correlation analysis excluding the effects of age and gait speed between clinical features, spatio – temporal and kinematic gait characteristics, trunk acceleration derived harmonic ratios, stride length coefficient of variation, and multiscale entropy measures. Highlighted connecting lines represent significant correlations, and their width represents the strength of the correlation, which is also reported numerically. Link: https://app.flourish.studio/visualisation/12786560/edit.
Figure 7. Partial correlation analysis. Partial Spearman’s correlation analysis excluding the effects of age and gait speed between clinical features, spatio – temporal and kinematic gait characteristics, trunk acceleration derived harmonic ratios, stride length coefficient of variation, and multiscale entropy measures. Highlighted connecting lines represent significant correlations, and their width represents the strength of the correlation, which is also reported numerically. Link: https://app.flourish.studio/visualisation/12786560/edit.
Preprints 69873 g007
Table 1. Clinical and spatio-temporal gait characteristics of the included subjects.
Table 1. Clinical and spatio-temporal gait characteristics of the included subjects.
swPD HS p
Age [mean(SD)] 71.15 (5.12) 69.14 (4.80) 0.06
Gender [n (%)] F 15 (29.41) 27 (54) 0.01
M 36 (70.58) 23 (46)
Disease duration [mean(SD)] 8.04 (4.70)
HY [n (%)] 1 10 (19.60)
2 17 (33.33)
3 24 (47.05)
UPDRS III [mean(SD)] 41.41 (18.22)
UPDRS III < 32 [n (%)] 16 (31.27)
UPDRS III ≥ 32 [n (%)] 22 (43.13)
UPDRS III ≥ 58 [n (%)] 13 (25.49)
History of falls (n° of falls in the previous 6 months) [mean (SD)] 1.35 (3.28)
Gait speed (m/s) [mean (SD)] 1.08 (0.25) 1.09 (0.25) 0.91
Stance phase (% gait cycle) [mean (SD)] 60.82 (2.27) 61.41 (3.42) 0.31
Swing phase (% gait cycle) [mean (SD)] 39.18 (2.27) 38.59 (3.42) 0.31
Single support (% gait cycle) [mean (SD)] 39.24 (2.92) 37.93 (5.29) 0.13
Double support (% gait cycle) 10.88 (2.33) 11.90 (4.92) 0.19
Cadence (steps/min) [mean (SD)] 103.37 (20.44) 101.35 (14.06) 0.60
Stride length (m) [mean (SD)] 0.94 (0.21) 1.22 (0.22) < 0.00
Pelvic tilt (°) [mean (SD)] 3.33 (1.55) 3.01 (1.13) 0.25
Pelvic obliquity (°) [mean (SD)] 3.87 (2.16) 5.38 (2.70) 0.01
Pelvic rotation (°) [mean (SD)] 5.49 (3.29) 6.68 (3.90) 0.02
HR AP [mean (SD)] 1.66 (0.26) 2.32 (0.64) < 0.00
HR ML [mean (SD)] 1.62 (0.25) 2.23 (0.59) < 0.00
HR V [mean (SD)] 1.68 (0.28) 2.41 (0.76) < 0.00
stride length CV % [mean (SD)] 39.26 (19.44) 26.69 (13.76) 0.00
swPD, subjects with Parkinson’s disease; HS, age and speed-matched healthy subjects; p, significance level at 95% confidence interval in Mann-Whitney procedure; HY, Hoehn and Yahr disease stage classification; UPDRS III, motor section of the Unified Parkinson’s Disease Rating Scale; HR, Harmonic Ratio; AP, antero-posterior direction of the acceleration signal; ML medio-lateral direction of the acceleration signal; V vertical direction of the acceleration signal; CV, coefficient of variation.
Table 2. Differences in entropy measures between swPD and HS.
Table 2. Differences in entropy measures between swPD and HS.
Entropy measure Direction τ swPD [mean (SD)] HS [mean (SD)] p Cohen's d
MSE AP τ 1 0.35 (0.10) 0.30 (0.06) 0.00 0.66
τ 2 0.45 (0.15) 0.38 (0.09) 0.00 0.61
τ 3 0.52 (0.17) 0.42 (0.12) < 0.00 0.68
τ 4 0.56 (0.20) 0.44 (0.14) < 0.00 0.74
τ 5 0.59 (0.22) 0.45 (0.15) < 0.00 0.71
τ 6 0.60 (0.23) 0.46 (0.16) < 0.00 0.72
ML τ 1 0.38 (0.14) 0.32 (0.09) 0.01 0.56
τ 2 0.48 (0.20) 0.38 (0.12) 0.00 0.62
τ 3 0.55 (0.25) 0.42 (0.15) 0.00 0.64
τ 4 0.60 (0.29) 0.44 (0.17) 0.00 0.66
τ 5 0.64 (0.33) 0.46 (0.18) 0.00 0.66
τ 6 0.65 (0.34) 0.48 (0.20) 0.01 0.59
V τ 1 0.33 (0.10) 0.28 (0.09) 0.00 0.54
τ 2 0.43 (0.15) 0.34 (0.12) < 0.00 0.66
τ 3 0.49 (0.19) 0.38 (0.14) < 0.00 0.68
τ 4 0.52 (0.22) 0.38 (0.16) < 0.00 0.73
τ 5 0.54 (0.24) 0.40 (0.16) 0.00 0.69
τ 6 0.55 (0.25) 0.40 (0.17) 0.00 0.70
RCMSE AP τ 1 0.31 (0.09) 0.26 (0.07) 0.01 0.63
τ 2 0.38 (0.12) 0.32 (0.09) 0.02 0.55
τ 3 0.42 (0.14) 0.34 (0.10) 0.01 0.60
τ 4 0.44 (0.17) 0.35 (0.11) 0.00 0.64
τ 5 0.46 (0.18) 0.36 (0.12) 0.00 0.63
τ 6 0.47 (0.20) 0.37 (0.12) 0.00 0.62
ML τ 1 0.31 (0.11) 0.27 (0.08) 0.01 0.49
τ 2 0.38 (0.16) 0.31 (0.11) 0.01 0.53
τ 3 0.43 (0.20) 0.33 (0.13) 0.01 0.53
τ 4 0.45 (0.24) 0.35 (0.14) 0.01 0.54
τ 5 0.48 (0.27) 0.37 (0.14) 0.01 0.52
τ 6 0.50 (0.30) 0.38 (0.15) 0.02 0.50
V τ 1 0.28 (0.09) 0.24 (0.08) 0.00 0.52
τ 2 0.35 (0.13) 0.28 (0.11) 0.01 0.58
τ 3 0.38 (0.17) 0.29 (0.13) 0.00 0.62
τ 4 0.40 (0.19) 0.30 (0.13) 0.01 0.63
τ 5 0.41 (0.20) 0.31 (0.14) 0.01 0.61
τ 6 0.42 (0.21) 0.31 (0.14) 0.01 0.60
CI MSE AP 2.59 (0.89) 2.06 (0.59) < 0.00 0.71
ML 2.78 (1.29) 2.10 (0.75) 0.00 0.64
V 2.42 (0.96) 1.84 (0.69) < 0.00 0.70
CI RCMSE AP 2.08 (0.75) 1.69 (0.49) 0.01 0.63
ML 2.14 (1.07) 1.68 (0.62) 0.01 0.53
V 1.90 (0.82) 1.45 (0.06) 0.01 0.61
swPD, subjects with Parkinson’s disease; HS, age and gait speed – matched healthy subjects; p, significance level at 95% CI in Mann – Whitney procedure; MSE, multiscale sample entropy; RCMSE, refined composite multiscale entropy; CI, complexity index; AP, antero-posterior direction of the acceleration signal; ML, medio-lateral direction of the acceleration signal; V, vertical direction of the acceleration signal.
Table 3. Discriminative ability of the entropy measures.
Table 3. Discriminative ability of the entropy measures.
Entropy measure Direction τ AUC (95% CI) OCP LR+ LR- PTP+ PTP- DOR
MSE AP τ 1 0.69 (0.58 - 0.79) ≥ 0.39 2.55 0.72 71 41 3.54
τ 2 0.68 (0.56 - 0.77) ≥ 0.42 2.04 0.54 66 34 3.78
τ 3 0.70 (0.59 - 0.79) ≥ 0.49 3.16 0.48 75 32 6.58
τ 4 0.71 (0.59 -0.80) ≥ 0.53 3.93 0.45 79 30 8.73
τ 5 0.70 (0.58 - 0.79) ≥ 0.60 4.59 0.53 82 34 8.66
τ 6 0.70 (0.59 - 0.79) ≥ 0.63 3.78 0.57 78 35 6.63
ML τ 1 0.67 (0.55 - 0.77) ≥ 0.40 3.28 0.52 76 33 6.31
τ 2 0.69 (0.57 - 0.78) ≥ 0.46 2.87 0.49 73 32 5.86
τ 3 0.69 (0.56 - 0.78) ≥ 0.52 3.16 0.48 75 32 6.58
τ 4 0.69 (0.57 - 0.79) ≥ 0.59 3.69 0.51 78 33 7.24
τ 5 0.69 (0.57 - 0.78) ≥ 0.63 3.44 0.55 77 35 6.25
τ 6 0.67 (0.55 - 0.76) ≥ 0.62 2.35 0.55 69 35 4.27
V τ 1 0.70 (0.58 - 0.79) ≥ 0.33 2.18 0.56 68 35 3.89
τ 2 0.71 (0.59 - 0.79) ≥ 0.36 1.89 0.39 64 27 4.85
τ 3 0.70 (0.58 - 0.79) ≥ 0.39 1.94 0.36 65 26 5.39
τ 4 0.71 (0.59 - 0.79) ≥ 0.42 2.09 0.37 67 26 5.65
τ 5 0.70 (0.58 - 0.79) ≥ 0.42 2.09 0.37 67 26 5.65
τ 6 0.69 (0.58 - 0.78) ≥ 0.41 1.93 0.41 65 28 4.71
RCMSE AP τ 1 0.66 (0.54 - 0.76) ≥ 0.35 2.6 0.66 71 39 3.94
τ 2 0.65 (0.53 - 0.74) ≥ 0.33 1.81 0.57 63 35 3.18
τ 3 0.66 (0.55 - 0.76) ≥ 0.39 1.85 0.62 64 37 2.98
τ 4 0.67 (0.55 - 0.76) ≥ 0.36 1.87 0.54 65 35 3.46
τ 5 0.68 (0.56 - 0.77) ≥ 0.38 1.77 0.56 63 35 3.16
τ 6 0.67 (0.56 - 0.77) ≥ 0.38 1.72 0.59 63 37 2.92
ML τ 1 0.67 (0.55 - 0.77) ≥ 0.26 2.09 0.32 67 24 6.53
τ 2 0.67 (0.55 - 0.76) ≥ 0.33 2.55 0.43 71 30 5.93
τ 3 0.67 (0.55 - 0.76) ≥ 0.36 2.17 0.48 68 32 4.52
τ 4 0.67 (0.55 - 0.76) ≥ 0.39 2.24 0.49 69 32 4.57
τ 5 0.66 (0.54 - 0.76) ≥ 0.39 2.17 0.48 68 32 4.52
τ 6 0.65 (0.53 - 0.75) ≥ 0.42 2.11 0.55 67 35 3.84
V τ 1 0.68 (0.56 - 0.77) ≥ 0.27 2.1 0.51 67 33 4.12
τ 2 0.67 (0.56 - 0.77) ≥ 0.30 2.1 0.55 67 35 3.82
τ 3 0.68 (0.56 - 0.77) ≥ 0.31 2.04 0.54 67 35 3.78
τ 4 0.67 (0.55 - 0.76) ≥ 0.32 2.04 0.54 67 35 3.78
τ 5 0.67 (0.55 - 0.76) ≥ 0.32 1.87 0.54 65 35 3.46
τ 6 0.67 (0.55 - 0.76) ≥ 0.34 1.92 0.55 65 35 3.49
CI MSE AP 0.71 (0.59 - 0.80) ≥ 1.91 1.94 0.36 66 26 5.39
ML 0.69 (0.57 - 0.78) ≥ 2.25 2.24 0.49 69 32 4.57
V 0.71 (0.59 - 0.80) ≥ 1.63 1.67 0.51 62 33 3.27
CI RCMSE AP 0.67 (0.55 - 0.76) ≥ 2.12 2.31 0.65 69 39 3.55
ML 0.67 (0.55 - 0.76) ≥ 1.71 2.09 0.42 67 29 4.98
V 0.67 (0.56 - 0.77) ≥ 1.50 2.04 0.49 67 32 4.16
AUC, area under the receiver operating characteristics curve; OCP, optimal cutoff point; LR+, positive likelihood ratio; LR-, negative likelihood ratio; PTP+, positive post-test probability; PTP-, negative post-test probability; DOR, diagnostic odds ratio; MSE, multiscale sample entropy; RCMSE, refined composite multiscale entropy; CI, complexity index; AP, antero-posterior direction of the acceleration signal; ML, medio-lateral direction of the acceleration signal; V, vertical direction of the acceleration signal.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated