On the Cosmic Evolution of the Quantum Vacuum Using Two Variable G Models and Winterberg's Thesis

Christopher Pilot

doi:10.20944/preprints202303.0338.v1

Submitted:

17 March 2023

Posted:

20 March 2023

You are already at the latest version

Abstract

We work within a Winterberg framework where space, i.e., the vacuum, consists of a two component superfluid/super-solid made up of a vast assembly (sea) of positive and negative mass Planck particles, called planckions. These material particles interact indirectly, and have very strong restoring forces keeping them a finite distance apart from each other within their respective species. Because of their mass compensating effect, the vacuum appears massless, charge-less, without pressure, net energy density or entropy. In addition, we consider two variable models, where, , is Newton’s constant, and, , increases with an increase in cosmological time. We argue that there are at least two competing models for the quantum vacuum within such a framework. The first follows a strict extension of Winterberg’s model. This leads to nonsensible results, if increases, going back in cosmological time, as the length scale inherent in such a model will not scale properly. The second model introduces a different length scale, which does scale properly, but keeps the mass of the Planck particle as, the Planck mass. Moreover we establish a connection between ordinary matter, dark matter, and dark energy, where all three mass densities within the Friedman equation must be interpreted as residual vacuum energies, which only surface, once aggregate matter has formed, at relatively low temperatures. The symmetry of the vacuum will be shown to be broken, because of the different scaling laws, beginning with the formation of elementary particles. Much like waves on an ocean where positive and negative planckion mass densities effectively cancel each other out and form a zero vacuum energy density/ zero vacuum pressure surface, these positive mass densities are very small perturbations (anomalies) about the mean. This greatly alleviates, i.e., minimizes the cosmological constant problem, a long standing problem associated with the vacuum.

Keywords:

Winterberg model

;

Planck particles

;

positive and negative mass Planck particles

;

planckions

;

quantum vacuum

;

space as a superfluid/ supersolid

;

extended models for space

;

cosmological constant

;

Higgs field as a composite particle

;

Higgs boson

;

inherent length scale for the vacuum

;

dark energy

;

cosmological scaling behavior for the quantum vacuum

;

variable G models

;

extended gravity

;

Newton’s constant as an order parameter

;

high energy behavior for the vacuum

Subject:

Biology and Life Sciences - Horticulture

I Introduction

There are at least two competing models for the vacuum energy density, or, equivalently, vacuum pressure, based on the Winterberg Model. This model is explained at length in references, [1,2,3,4,5,6,7], and further references therein. The first is within a strict Winterberg interpretation where the Planck length,

l_{P l} \equiv {(ħ G / c^{3})}^{1 / 2}

, is considered to be the fundamental length scale to be associated with space. This is also, according to Winterberg, the nearest neighbor distance of separation between positive mass Planck particles, and negative mass ones, as well. The second model for the vacuum is a modified version [8,9,10], where the inherent length scale is,

L .

This has the same interpretation as above, but now at much larger distances for the graininess of space. In the present epoch,

L_{0} = 5.03 E - 19 m e t e r s

, and its value was derived using box quantization, and considering transitions between excited energy states for both the positive, and independently, the negative mass Planck particles. This length scale ties in nicely to the

C M B

temperature, and also, with the Higgs mass, which the former fundamental length,

l_{P l}

, in the Winterberg model, does not.

The first length scale,

l_{P l}

, leads to incredibly high number densities for each planckion species, positive, and negative, of the order,

l_{P l}^{- 3} = 2.37 E 104 p a r t i c l e s / m^{3}

, in the present epoch. The individual volumes, occupied by these particles, are thus correspondingly small. The second length scale, used in vacuum energy density model two, is much larger. Here,

L_{0} = 5.03 E - 19 m e t e r s

, and thus, the number density for both species is relatively small,

L_{0}^{- 3} = 7.86 E 54 p a r t i c l e s / m^{3}

. The subscript,

“ 0 ”

, will denote quantities defined in the present epoch, where the redshift,

Z = 0

. The individual planckion volumes are now much larger than the customary Planck volume.

Another intriguing aspect associated with this new fundamental length scale,

L

, for space, was that a connection could be made with the Higgs field [9,10]. If

“ L ”

is considered a coherence length, then it has an effective scattering mass associated with it, defined as,

M \equiv ħ / (L c)

. Its present day value is,

M_{0} \equiv ħ / (L_{0} c) = 6.99 E - 25 k g = 392.9 G e V / c^{2}

. This is very close to the Higgs mass,

125.35 G e V / c^{2}

. This has led this author to try to establish a connection between the two concepts. The result are references, [9,10]. The Higgs is treated as a composite particle, consisting of one positive with one negative Planck particle, held together by very strong superfluid forces. The individual species are compelled to rub shoulders with one another, as they both occupy the same space, and by virtue of position (potential energy), their wave functions are forced to overlap. In the current epoch, the Higgs coherence length is roughly,

3.13 t i m e s

that of the individual Planck wave functions. The Planck particles do not interact directly, as demonstrated by Winterberg.

We also showed [9,10] that the vacuum potential energy associated with the composite Higgs field equals,

U_{H P E} = M c^{2} (\bar{n_{+}} - \bar{n_{-}}) / n_{L} = ħ c L^{2} (\bar{n_{+}} - \bar{n_{-}})

. The subscript,

H P E

, stands for Higgs potential energy, and,

n_{L} \equiv L^{- 3}

, is the number density for both positive and negative mass Planck particles. The,

\bar{n_{\pm}}

, are the energy-weighted, number density averages for positive/negative mass Planck particles, within a region of space. The +/- Planck particles can have different populations within their excited energy states. If space is devoid of ordinary matter, dark matter, and dark energy, then we have a perfectly balanced vacuum, where only Planck particles and radiation are present, and in thermal equilibrium with one another. Under such conditions,

\bar{n_{+}} = \bar{n_{-}}

, and space does not have an inherent mass density or pressure associated with it. It is also massless, charge-less, and without entropy.

If, on the other hand,

\bar{n_{+}} ≷ \bar{n_{-}}

, then the vacuum is not perfectly balanced, and the rest mass of the Higgs is either increased or decreased by this amount. A nontrivial vacuum energy density, or equivalently, a non-trivial vacuum pressure, in the amount,

u_{v a c u u m} = p_{v a c u u m} = u_{H P E} = p_{H P E} = M c^{2} (\bar{n_{+}} - \bar{n_{-}})

, results. See references, [9,10]. Ordinary matter, dark matter, and dark energy, are thus considered to be residual artifacts of the quantum vacuum, small perturbations, manifesting themselves, at relatively low

C M B

temperatures, below,

1 T e V

[11,12,13,14]. According to Winterberg, elementary particles are quasi-particle excitations, upon this sea of positive and negative Planck particles. The Planck particles, in turn, interact with the

C M B

photons. The elementary particles manifest themselves in a series of steps (freeze out), as the universe cools. Going even further, dark matter and dark energy are thought to result as a consequence of ordinary matter aggregating. See in this regard, references, [10,15,16], where inherent use of the Winterberg planckion hypothesis has been made.

The question naturally arises as to how these two fundamental lengths,

l_{P l}

, and,

L

, scale upon an expansion of the universe. Do they scale realistically, as the

C M B

temperature increases, going back in cosmological time? We will find that,

l_{P l}

, does not behave as it should, which is to decrease with increasing

C M B

temperatures. The derivation of,

L

, on the other hand, explicitly invokes the

C M B

temperature, and lends itself naturally to a correct scaling behavior, as we shall see. Another plus is that it is quite conservative in its scaling, given the many orders of magnitude difference, in

C M B

temperature.

To prove this, we will subject both quantum vacuum density models, one based on,

l_{P l}

, and the other relying on,

L

, to two cosmologically time-varying

G

models, where,

G = G (Z)

, is Newton’s constant. Since the cosmic scale parameter,

“ a ”

, is related to both

C M B

temperature,

T

, and redshift,

Z

, we could just as well write,

G = G (a) = G (T) = G (Z)

, since,

a = T_{0} / T = {(1 + Z)}^{- 1}

. The,

T_{0},

is the current epoch

C M B

temperature,

T_{0} = 2.726 d e g r e e s K e l v i n .

Newton’s constant,

G

, is assumed to depend solely on the

C M B

radiation temperature, which permeates space. As a matter of fact, we consider

G^{- 1}

to be a fundamental property of the vacuum, an order parameter, which vanishes at sufficiently high temperatures [17,18,19], much like magnetization in a paramagnet. If we did not allow

G

to vary with cosmological time, then there would be no mechanism for the Planck length,

l_{P l}

, to scale.

Our two, very distinct, one-parameter models for,

G^{- 1} = G^{- 1} (a)

, which we call gravitational models,

A

, and

B

, are relatively simple functions, which mimic order parameter behavior. At low temperatures, they both approach a saturation value, and at very high temperature, both

G^{- 1}

functions increase as,

T^{- 1}

. Both models, even though functionally very different, indicate almost the same inception temperature for,

G^{- 1}

, between,

6 - 7 E 21 d e g r e e s K e l v i n

. Before that point in time, gravity, as we know it, ceased to exist. We should point out that Winterberg never entertained a variable gravitational constant. As such, his length scale,

l_{P l} \equiv {(ħ G / c^{3})}^{1 / 2}

, never varied. His fundamental length could also not scale as the universe expanded (cooled down). To make our point, however, we will proceed with the “what if” scenario, and show how his model would differ fundamentally from ours, had he allowed for such an interpretation.

We believe that, at some point,

G^{- 1}

ceases to exist. This would have important ramifications, including the fact, that then, the masses for the positive and negative Planck particles would also disappear. Remember that by definition,

m_{P l} \equiv {(ħ c / G)}^{1 / 2} = \pm ∣ m_{p l} ∣

. Thus, if,

G^{- 1}

, vanishes, then so would our masses for the positive and negative mass planckions. The inception temperature for

must be interpreted, in our view, as the freeze-out temperature for positive and negative mass planckions.

The outline of the paper is as follows. In section II, the two competing vacuum energy density models are compared. In section III, our two variable

G^{- 1}

models,

A

and,

B

, are introduced. In section IV, we focus on gravitational model,

A

. Here we show that Winterberg’s scaling model does not make physical sense if

G

is allowed to increase going back in cosmological time. Our modified version, however, based on a new length determination, which measures the graininess of space, will scale appropriately upon expansion of the universe. Two tables will be constructed, Table 1 and Table 2, which charts the evolution of the universe, where both vacuum energy density models are considered. A remarkable feature will surface, namely that in no other epoch, other than at the inception temperature for,

G^{- 1}

, do we have a match between the

C M B

radiation density, and our Planck particle energy density. In other words, both energy densities equal each other, in that particular epoch. This is to be expected at the time of Planck particle “freeze-out”. Both energy density calculations are entirely independent of each other. One is based on a gravitational model, and the other is based on radiation, two different concepts.

In section V, we will focus on gravitational model,

B,

for a variable,

G^{- 1}

. Again we consider both vacuum energy density models, that of Winterberg, and a modified version, developed by this author. We construct new tables for both vacuum energy density models, Table 3 and Table 4, which charts the evolution of the vacuum upon expansion. Here again, we will obtain qualitatively similar results. And we obtain the spectacular result, that only close to the inception temperature for,

G^{- 1}

, i.e., at,

T = T^{*}

, do we have a near perfect match between the

C M B

radiation energy density, and the Planck vacuum energy density. There is no a-prior reason to assume this, as the two concepts are seemingly unrelated, and independent of one another. This lends credence, and support, for our

G^{- 1}

models, and, equally important, their respective parametrizations, in terms of temperature.

In section VI, we focus on ordinary matter, dark matter, and dark energy. We will make a case for why these should be treated as residual energy densities, perturbations within the vacuum, in effect, which only surface at much lower

C M B

temperatures, once the planckion vacuum symmetry has been broken. The amount of symmetry breaking is truly insignificant given the vast assembly (ocean) of Planck particles, which are present. And finally, in section VII, we present our summary, and conclusions.

II Two Competing Vacuum Energy Density Models

In this section we compare the two competing vacuum energy density models. The first is due to Winterberg, if he were to assume a variable,

G

, which increases as one goes back in time. The second is a modification based a new interpretation for vacuum energy, referenced in [8,9,10]. The latter defines a new fundamental length scale for the vacuum, which we denote by,

L

, versus, Winterberg’s,

l_{P l}

.

If Winterberg is correct, then,

l_{P l} \equiv {(ħ G / c^{3})}^{1 / 2}

, would define the intrinsic length scale for the vacuum, and measure the graininess of space. In previous epochs, as

G

increases, this definition would then imply that,

l_{P l}

, also increases. This makes no sense, as space should contract, going back in time. The volume occupied by the individual Planck particles,

l_{P l}^{3}

would also increase, going back in time, and the number density,

n_{P l} = l_{P l}^{- 3}

, would therefore, decrease. This is not what we would expect. As

Z

increases, the Planck particle number density should increase, and the planckion volume should decrease.

In the current epoch, and only in this epoch, we obtain the values,

l_{P l, 0} \equiv {(ħ G_{0} / c^{3})}^{1 / 2} = 1.62 E - 35 m e t e r s

(2−1a)

l_{P l, 0}^{3} = 4.22 E - 105 m^{3}

(2−1b)

n_{P l, 0} = l_{P l, 0}^{- 3} = 2.37 E 104

(2−1c)

These are the customary values, and quite dramatic, given their orders of magnitude.

As far as the planckion energy density is concerned, for the positive and negative mass Planck particles, we would find,

ρ_{p l a n c k i o n s} = ρ_{\pm} = \pm ∣ m_{P l} ∣ / l_{P l}^{3}

(2−2)

The Planck mass is defined by,

m_{P l} \equiv \pm {(ħ c / G)}^{1 / 2} = \pm ∣ m_{P l} ∣

(2−3)

In the present epoch, we thus obtain,

ρ_{p l a n c k i o n s, 0} = \pm ∣ m_{P l, 0} ∣ / l_{P l, 0}^{3} = \pm 5.16 E 96 k g / m^{3}

(2−4)

m_{P l, 0} \equiv \pm {(ħ c / G_{0})}^{1 / 2} = \pm 2.18 E - 8 k g

(2−5)

Because of the mass compensating effect between the

\pm

mass planckions, we expect for the undisturbed vacuum, the following net mass density

〈 ρ_{p l a n c k i o n s} 〉 = 〈 ρ_{+} 〉 + 〈 ρ_{-} 〉 = 0

(2−6)

The,

〈 \dots 〉

, denote an average, within a region of space. In such a balanced state for the vacuum, we expect zero net energy density, and, no net vacuum pressure.

E q u a t i o n (2 - 6)

, represents an elegant solution to the cosmological constant problem in physics, as pointed by Winterberg.

We now turn to our second fundamental length scale for the vacuum,

L

. It is determined as follows. A Planck oscillator emits and absorbs the following amount of energy, for a given frequency,

ν

, and temperature,

T

,

Δ E = h ν / 2 + h ν / [e^{(h ν / k_{B} T)} - 1]

(2−7)

The peak frequency of blackbody photon radiation is related to the temperature via the formula,

ν_{p e a k} = 2.8214 (k_{B} T / h) = 1.601 E 11 H z

(2−8)

The,

k_{B}

, is Boltzmann’s constant, and the above frequency calculation is for the current

C M B

temperature of,

T_{0} = 2.726 d e g r e e s K e l v i n

. For this

C M B

temperature,

h ν_{p e a k} = 1.061 E - 22 J o u l e s .

Substituting this into,

e q u a t i o n, (2 - 7)

, we obtain

Δ E_{p e a k} = [.5 + .0633] (1.061 E - 22) = 5.976 E - 23 J o u l e s

(2−9)

We assume that the

C M B

photons impart energy and momentum through elastic collisions to the surrounding positive and negative mass planckions. The

C M B

blackbody photons will also absorb the same amount of peak energy, when the planckions undergo transitions from higher energy states to lower levels. The blackbody photons are assumed to be in thermal equilibrium with the surrounding planckions. Thus, the most probable amount of energy emitted and absorbed by the planckions is specified by,

e q u a t i o n, (2 - 9) .

Of course, as the

C M B

temperature increases, the peak frequency will also increase, as seen by,

e q u a t i o n, (2 - 8)

. This will serve to increase the most probable amount of energy, emitted and absorbed, by the planckions through,

e q u a t i o n, (2 - 9) .

In actual fact, however, a whole spectrum (continuous distribution) of energies (frequencies) are continuously being emitted and absorbed, because there are many different transitions possible, and not just the “most probable” one. We expect that distribution to follow a blackbody spectrum. Thus the vacuum is made up of a continuum of vibrating frequencies due to the randomly, oscillating planckions. The Heisenberg uncertainty relation results, as do many of the other characteristics associated with quantum mechanics. We believe that blackbody photon bombardment of the planckions is ultimately responsible for this “Zitterbewegung”, a random, chaotic motion inherent to space, and associated with quantum mechanics. A particle, such as an electron, when placed upon such a sea of Planck particles, will inherently rock back and forth, in a random, chaotic fashion.

Now the planckions are pretty much anchored in position due to their very strong superfluid restoring forces acting upon them within their respective species. We can thus treat each individual planckion, positive or negative, as a particle trapped in a three dimensional box. Because of box quantization, the energy levels for each species are given by the well-known quantum mechanical formula,

E_{n_{x} n_{y} n_{z}} = π^{2} ħ^{2} / (2 m L^{2}) (n_{x}^{2} + n_{y}^{2} + n_{z}^{2})

(2−10)

The,

n_{x}, n_{y}, n_{z},

are quantum numbers, which can take on the values,

1, 2, 3, \dots .

The lowest energy level, or ground state, is specified by,

(n_{x}, n_{y}, n_{z}) = (1, 1, 1)

. The size of the box is,

L^{3}

, where,

L

, is the length on one side. The formula is still valid at zero temperature, and holds for both, the quantized positive, as well as the quantized negative mass, planckions. A transition between energy states or levels, positive or negative, would emit or absorb a finite amount of energy,

Δ E = E_{n_{x} n_{y} n_{z}} - E_{n_{x}^{'} n_{y}^{'} n_{z}^{'}}

(2−11)

The unprimed quantum numbers refer to the situation before, and the primed quantum numbers correspond to the situation after the transition. This is completely analogous to the situation in the Hydrogen atom, where we have the Lyman series, the Balmer series, the Paschen series, etc. Even though the energy levels are quantized (discrete), the transitions are continuous, because the quantum numbers can approach infinity.

By considering a few transitions with actual quantum numbers, such as,

211 \to 111

(positive planckion emission), or,

- 111 \to - 112

(negative planckion emission), it is easy to convince oneself that,

E_{111}

, is the most probable, i.e., the most frequent amount of energy, either emitted or absorbed. Thus, we are justified in setting,

{(Δ E)}_{p e a k} = 2 E_{111} = 3 π^{2} ħ^{2} / (m_{P l} L^{2})

(2−12)

The factor of 2 is needed because the photon energy is, on average, equally divided between the two species of planckions, positive and negative. A negative mass particle will have its energy lowered, if it transitions upwards within the quantum mechanical box.

Now, we have a value for,

{(Δ E)}_{p e a k}

. See,

e q u a t i o n, (2 - 9)

. We also know that the Planck masses have the values,

m_{P l} = \pm ∣ m_{P l} ∣ = \pm 2.176 E - 8 k g .

Thus,

e q u a t i o n, (2 - 12)

, can be used to solve for

L

. We find that, in the present epoch,

L = l_{+} (0) = l_{-} (0) = 5.03 E - 19 m e t e r s

(2−13)

This we consider to be the fundamental length scale for the vacuum (space), in the current epoch. It is also the nearest neighbor distance of separation between two positive, or two negative, Planck particles, within the two component superfluid/ super-solid.

We note that, once this distance is known, a typical number density for both the positive, and the negative, mass planckions, can be found. We calculate,

n_{+} (0) = l_{+} {(0)}^{- 3} = 7.86 E 54 m^{- 3}

(2−14a)

n_{-} (0) = l_{-} {(0)}^{- 3} = 7.86 E 54 m^{- 3}

(2−14b)

n_{0} \equiv L_{0}^{- 3} = l_{\pm} {(0)}^{- 3} = 7.86 E 54 m^{- 3}

(2−14c)

These results were derived in a previous work, reference, [8], by this author. The (0) signifies a vacuum in the undisturbed, equilibrium state. The above numerical results hold only in the present epoch, as we used,

T_{0} = 2.726 d e g r e e s K e l v i n

, as our starting point

C M B

temperature.

As mentioned, it is important to realize that as the

C M B

temperature increases, so does the peak frequency by,

e q u a t i o n, (2 - 8) .

Thus,

{(Δ E)}_{p e a k}

, increases, as does,

E_{111}

. This shows us that at higher

C M B

temperatures, the

" L "

value actually decreases, which is what we would expect for the universe going back in cosmological time.

Also very important is the realization that the Planck mass can now take on both positive and negative values, i.e.,

m_{P l} = \pm ∣ m_{P l} ∣

. If both positive and negative mass is substituted in,

e q u a t i o n, (2 - 10),

then the average of both positive with negative energy states equals,

E_{V a c u u m} = < E_{n_{x} n_{y} n_{z}} >_{+} + < E_{n_{x} n_{y} n_{z}} >_{-} = \sum_{n_{x} n_{y} n_{z}} {(E_{n_{x} n_{y} n_{z}})}_{+} / N + \sum_{n_{x} n_{y} n_{z}} {(E_{n_{x} n_{y} n_{z}})}_{-} / N = 0

(2−15)

This implies that under normal conditions (circumstances), the quantum mechanical vacuum has no net vacuum energy density, nor does it have net vacuum pressure, as the planckions are in a perfectly balanced state, in terms of numbers, and populated energy levels. The vacuum is also devoid of net mass or charge. The vacuum will appear empty, when, in fact, it is not.

A long standing problem in physics is the cosmological constant problem. If there were only one species of Planck particle, and if it had positive mass, then the mass density of the quantum mechanical vacuum would equal the absolute value of,

e q u a t i o n, (2 - 4)

. But because there are two species, one with positive, and the other with negative mass, the net energy associated with Planck particles is zero. In our version of the quantum vacuum, we would substitute,

L = 5.03 E - 19 m e t e r s

, for

l_{P l}

. Our modified version of,

e q u a t i o n, (2 - 4)

, would thus read,

ρ_{Q M} = m_{P l} / L^{3} = \pm 1.71 E 47 k g / m^{3} (p r e s e n t e p o c h)

(2−16)

In the current epoch, the value of

L

is specified by

e q u a t i o n, (2 - 13)

. And,

m_{P l}

, has the unique value,

\pm 2.176 E - 8 k g

. Upon comparison with our previous equation,

a t i o n, (2 - 2)

, this is certainly different, numerically. We will identify the energy densities associated with ordinary matter, dark matter and dark energy, in Friedman’s equation, with something else. It is not to be compared to either,

m_{P l} / L^{3}

, nor, (

∣ m_{P l} ∣ + (- ∣ m_{P l ∣} ∣) / L^{3} = 0

. Rather, it must be a residual part of,

ρ_{v a c u u m}

, left over after the vacuum symmetry is broken, at much reduced

C M B

temperatures. More on this will be said later, in section VI.

We have seen that our length scale for the quantum vacuum is directly tied in to

C M B

temperature, unlike the Planck length,

l_{P l}

. We can write,

L = L (T) = L (a) = L (Z)

, since the cosmic scale parameter,

“ a ”

, is defined as,

a \equiv T_{0} / T = {(1 + Z)}^{- 1}

. It is now time to establish the exact dependency. We start with,

e q u a t i o n s, (2 - 7), a n d, (2 - 8)

. All variables with subscript,

“ 0 ”

, denote the current epoch

(Z = 0)

. By setting up a ratio, we find that,

Δ E_{p e a k} / Δ E_{p e a k, 0} = T / T_{0} = a^{- 1}

(2−17)

Also from,

a t i o n, (2 - 12)

, it follows that,

Δ E_{p e a k} / Δ E_{p e a k, 0} = E_{111} / E_{111, 0} = (m_{P l, 0} L_{0}^{2}) / (m_{P l} L^{2}) = (l_{P l} / l_{P l, 0}) {(L_{0} / L)}^{2}

(2−18)

From the defining relations for Planck length,

l_{P l}

, and, Planck mass,

m_{P l}

, in terms of

G

, we can establish the relation,

l_{P l} = ħ / (m_{P l} c)

. That’s how we obtained the second line in,

e q u a t i o n, (2 - 18) .

We next set the right hand side of,

e q u a t i o n, (2 - 17)

, equal to the right hand side of,

e q u a t i o n, (2 - 18)

, and rearrange terms. This gives,

L / L_{0} = {(l_{P l} / l_{P l, 0})}^{1 / 2} a^{1 / 2}

(2−19)

And finally, let us use the defining relation for the Planck length,

l_{P l} \equiv {(ℏ G / c^{3})}^{1 / 2}

, to re-express,

e q u a t i o n, (2 - 19)

, as,

L / L_{0} = {(G / G_{0})}^{1 / 4} a^{1 / 2}

(2−20)

Once

G = G (a)

is specified, we can easily find the scaling behavior for,

L / L_{0}

, using this last equation. Remember that the value of,

L_{0}

, is specified by,

e q u a t i o n, (2 - 13)

. The corresponding,

l_{P l} / l_{P l, 0}

, scaling law is simpler,

l_{P l} / l_{P l, 0} = {(G / G_{0})}^{1 / 2}

(2−21)

We notice that, if,

G

does not vary cosmologically, then there is no scaling behavior for,

l_{P l}

. The new fundamental length,

L

, by contrast, would still scale.

III Two Variable $G^{- 1} (a)$ Models

We next review our two variable,

G^{- 1} = G^{- 1} (a)

, models for Newton’s constant,

G

. These are relatively simple, one-parameter, nonlinear functions, which mimic (display) order parameter behavior for,

G^{- 1}

. These functions were first introduced, and explored in reference, [17]. We wanted to explain the quintessence parameter,

w = - .98

. In the

Λ C D M

model, this parameter is set exactly equal to minus one. But after over a decade of indirect measurements,

w = - .98

, seems to be a better fit to observation [20,21,22,23]. If we assume that,

w = - .98

, then we can fix the parameters in our two

G^{- 1}

models, designated as models

A

, and

B

. Our results reduce to the

Λ C D M

model in the limit where,

w \to - 1

. Except in the early universe, there is hardly any difference between these gravitational models,

A

and,

B

, and the

Λ C D M

model. In all fairness, given the uncertainty in the measurement of,

w

, it is also not unreasonable to assume that,

w = - 1

.

The first parametrization for,

G^{- 1}

, is called model,

A

, and has the functional form,

G^{- 1} = G_{\infty}^{- 1} [1 - e^{- 4.28 a}] (M o d e l A)

(3−1)

In,

e q u a t i o n, (3 - 1),

the,

G_{\infty}^{- 1}

is the saturated value, taken in the limit where,

a \to \infty

. The

“ a ”

is the cosmic scale parameter, equal to,

a = {(1 + Z)}^{- 1} = T_{0} / T

. A plot of,

G^{- 1} / G_{0}^{- 1}

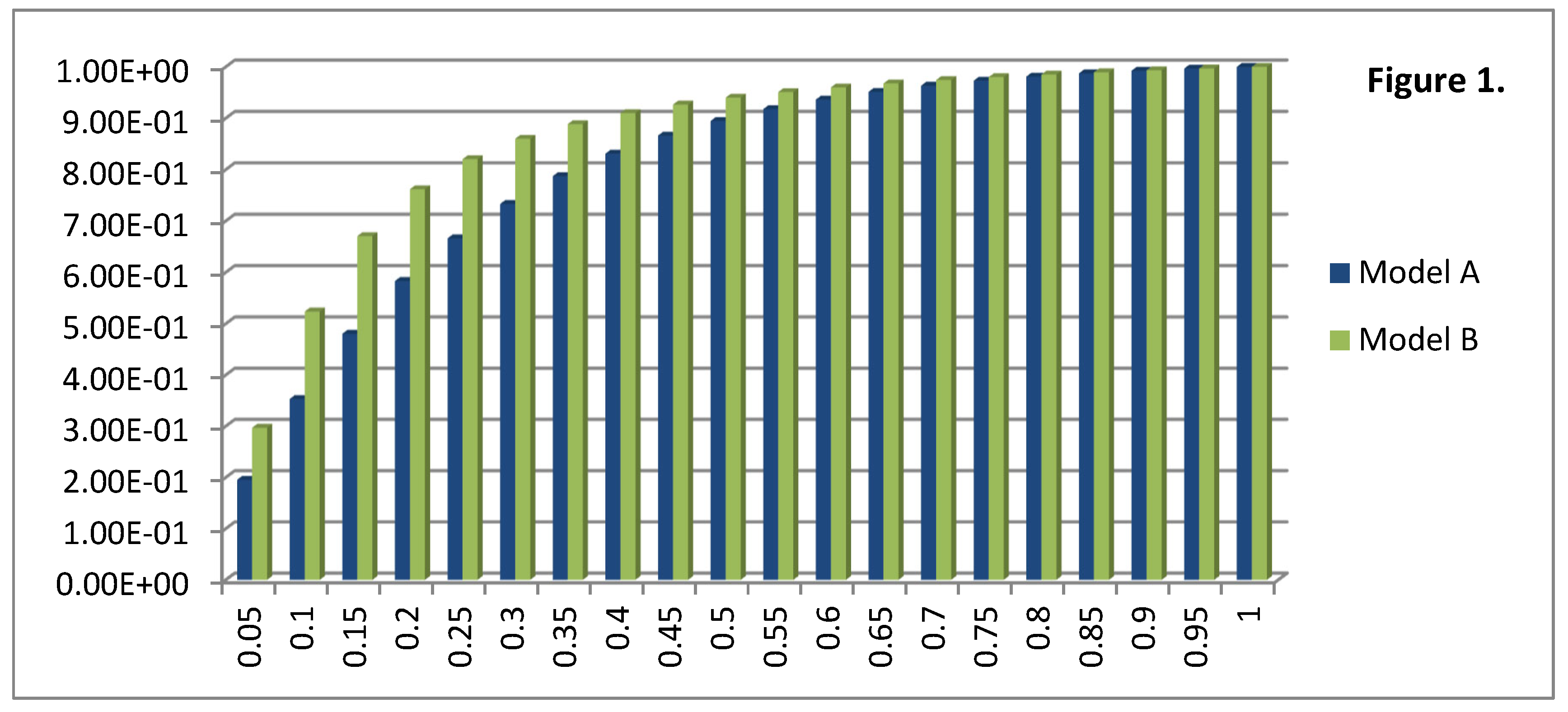
, is given by the blue histogram in, Figure 1. Notice that, in this figure, we give a ratio in terms of the present value of,

G_{0}^{- 1}

, where,

G_{0}

, is the customary value of Newton’s constant. By constructing a ratio, we factored out the constant,

G_{\infty}^{- 1}

. In the present epoch, we are close to the saturated value since it was demonstrated that,

G_{0} = 1.014 G_{\infty}

.

The second variable,

G^{- 1}

function, model,

B

, has the assumed form,

G^{- 1} = G_{\infty}^{- 1} [\coth (17.67 a) - 1 / (17.67 a)] (M o d e l B) = G_{\infty}^{- 1} * L (17.67 a)

(3−2)

This equation is proportional to the Langevin function,

L (x) = L (17.67 a)

, known from paramagnetism. Again, the,

G_{\infty}^{- 1},

is a saturation value, and with this new parametrization,

G_{0} = 1.054 G_{\infty}

. In other words we are close to saturation in the present epoch. A plot of,

G^{- 1} / G_{0}^{- 1}

, for model

B

, is given by the green histogram in, Figure 1. The two ratios,

G^{- 1} / G_{0}^{- 1}

, for models

A

and

B

, look very similar, even though the two functions, G⁻¹, are quite distinct from one another.

The parameters,

4.28

, in,

e q u a t i o n, (3 - 1),

and, 17.67, in,

e q u a t i o n, (3 - 2),

were fixed by imposing the condition that the quintessence parameter equals,

w = - .98

.

Both functions specified by,

a t i o n s, (3 - 1) a n d (3 - 2)

, mimic order parameter behavior in that they approach a saturation value (different for the two competing models), as

a \to \infty

. Moreover, both functions,

e q u a t i o n s, (3 - 1) a n d (3 - 2)

, are proportional to

T^{- 1}

, at very high

C M B

temperatures. Both indicate an inception temperature for,

G^{- 1}

, in the neighborhood of,

6 - 7 E 21 d e g r e e s K e l v i n

. For model,

A

, we found, specifically [17], that,

T^{*} = 6.19 E 21 K

, whereas for model,

B

, we obtained a very similar result,

T^{*} = 6.99 E 21 K

. Before that point in cosmological time, our premise is that gravity, as we know it, did not exist. And neither did massive planckions, by,

e q u a t i o n, (2 - 3) .

Also, the fact that both different functions give us an almost equal inception temperature leads us to suspect that there may be some inherent bias (merit) in treating inverse gravity as an order parameter.

The physical motivation behind the two functions, and their respective parametrizations, have been touched upon in reference [17], and will not be repeated here. Moreover, these two functions were also used to present a different version of inflation. For a discussion of this, we refer the reader to reference, [19].

From,

e q u a t i o n, (3 - 1)

, it should be clear that

G / G_{0} = [1 - e^{- 4.28}] / [1 - e^{- 4.28 a}] (M o d e l A)

(3−3)

The,

G_{0}

, is the current epoch value for Newton’s constant, the one we are familiar with. Similarly, using,

e q u a t i o n, (3 - 2)

, it follows that,

G / G_{0} = [c o t h (17.67) - 1 / (17.67)] / [\coth (17.67 a) - 1 / (17.67 a)] (M o d e l B)

(3−4)

Equations, (3−3) and (3−4), are all that are needed for determining the scaling behavior for our two quantum vacuum models.

IV Gravitational Model, A, Scaling for Two Planck Particle, Vacuum Energy Densities

We next look at the cosmological evolution for our two competing vacuum energy density models, presented in section II. In this section, we focus on our gravitational model,

A

, where,

G^{- 1}

, has the functional form, specified by,

e q u a t i o n, (3 - 1)

.

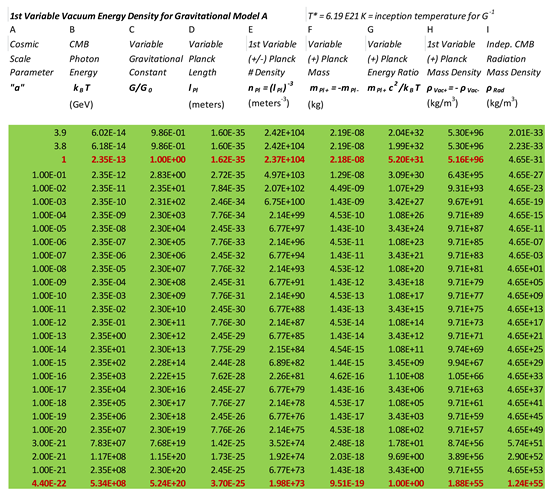
In order to structure our discussion, we will present our results in table form, Table 1 and Table 2. We proceed to illustrate how the various entries in the rows/columns are obtained. This will allow for an easy comparison with model,

B

, discussed in the next section.

Under the first column in Table 1, column “A”, we enter the cosmic scale parameter,

“ a ”

. For,

a > 1

, we are looking at future epochs, and for,

a < 1

, we are going back in cosmological time. Notice that we stop at,

a^{*} = 4.37 E - 22

, as this corresponds to our inception temperature for

G^{- 1}

. For gravitational model,

A

, the inception temperature is,

T^{*} = 6.19 E 21 d e g r e e s K e l v i n .

Column “B” gives us a typical

C M B

energy, corresponding to the entries under column “A”. We are using the formula,

E = k_{B} T

, where

k_{B}

, is Boltzmann’s constant. Notice that the energy is specified in units of billions of electron volts,

G e V = 10^{9} e V

.

Under column “C”, in Table 1, we calculate our specific values for,

G / G_{0}

. For this we use,

e q u a t i o n, (3 - 3),

where the appropriate cosmic scale parameter,

“ a ”,

is found under column “A”. This will determine the various row values. At the very highest temperature, we see that,

G^{*} \equiv G (a^{*}) = 5.273 E 20 * G_{0}

.

Columns, “D” and, “E”, in Table 1, give us the Planck length, and Planck number density, for both the positive, and the negative mass, Planck particle. We are using,

l_{P l} \equiv {(ħ G / c^{3})}^{1 / 2}

, and,

n_{P l} = l_{P l}^{- 3}

, respectively, for these calculations. The appropriate

G

value is found under column “C”. We note that, as the

C M B

temperature increases, we obtain smaller

“ a ”

values, and the fundamental length scale for the vacuum,

l_{P l}

, consequently increases. This is not what we want for a smaller sized universe, moving back in time. Also, the planckion number densities, found under column, “E”, for both the positive and negative mass Planck particle, decrease. Upon a contraction of the universe, this number should increase! In short, we believe it is a mistake to interpret,

l_{P l}

, as the fundamental length scale for space.

Column “F” gives us the absolute value of the Planck mass. We are using the formula,

∣ m_{P l} ∣ \equiv {(ħ c / G)}^{1 / 2}

, and, the relevant

G

is found under column “C”. Unless otherwise stated,

M K S

units are used throughout. For column “G”, we construct the ratio,

m_{P l} c^{2} / (k_{B} T)

. Notice that this ratio approaches unity, as the cosmic scale parameter,

“ a ”

nears,

a^{*}

, the scale parameter at

G^{- 1}

inception. We define,

a^{*} \equiv a (T^{*})

, where,

T^{*},

is our inception temperature for,

G^{- 1}

. According to this gravitational model, the temperature of inception is,

T^{*} = T_{0} / 4.40 E - 22 = 6.19 E 21 d e g r e e s K e l v i n

. This is many orders of magnitude less than the Planck temperature,

T_{P l} = 1.417 E 32 K

.

The positive planckion mass density is given under column “H”. For the negative mass Planck particle, we would take negative this value. We have used the formula,

e q u a t i o n, (2 - 2)

. Obviously, if positive is added to negative, we obtain zero net mass density. This would represent the vacuum in a perfectly balanced state. At very high energies we believe that such a state existed. The vacuum was made up exclusively of planckions, and blackbody radiation. As the universe cooled upon expansion, below energy scales of, 1 TeV, the vacuum gets broken in a series of steps, First ordinary matter appears. And then at much cooler temperatures, dark matter and dark energy make their appearance. These are, however, residual energy densities, small perturbations, upon a vast ocean of positive and negative mass planckions. We postpone discussion of this until section, VI.

Under column “I”, we consider the

C M B

blackbody radiation energy density, divided by,

c^{2}

. From the cosmic scale parameter values,

“ a ”

, listed under column, “A”, we can find the

C M B

temperature, using,

T = T_{0} / a

. Once we have the temperature, we can find the equivalent radiation mass density, utilizing the well-known formula,

ρ_{R a d .} = 4 σ T^{4} / c^{3}

(4−1)

Here,

σ

, is the Stefan-Boltzmann constant,

σ = 5.670 E - 8 (M K S u n i t s)

.

If we compare column “H” to column “I”, we will notice a remarkable coincidence. At the

G^{- 1}

inception temperature, and in no other epoch, do we have a numerical match in value, for mass density, between these two columns. The radiation mass density equals the planckion mass density, in this epoch, and no other. Of course, we do not believe that this is a coincidence. This is what is to be expected if the planckions are to freeze out of the vacuum, at this specific temperature. We emphasize that column “H” is based on a very specific gravitational order parameter model, model,

A

, for

G^{- 1}

. Column “I” on the other hand, is a property of blackbody radiation, and thus independent of gravity (column “H”). This is more than a remarkable coincidence. It lends credence, and support for our specific model for,

G^{- 1}

, and just as important, for its specific parametrization, in terms of the value,

- 4.28

, in,

e q u a t i o n, (3 - 1)

.

The above discussion has dealt with,

l_{P l}

, as the fundamental length scale for the vacuum, which defines its graininess, so to speak. This fundamental length scale is, in our view, deficient for the reasons listed above. It just does not scale correctly upon expansion of the universe. A better alternative is to introduce a new length scale,

L

. To this we now turn.

Our value for

L

was derived in section II. In particular, we consider

, (2 - 20)

, which gives the scaling behavior for,

L / L_{0}

. We notice that it depends on the scaling parameter,

“ a ”,

and,

G / G_{0}

. However, we do have a gravitational model for,

G / G_{0}

, in terms of ,

“ a ”

. It is given by,

e q u a t i o n, (3 - 3) .

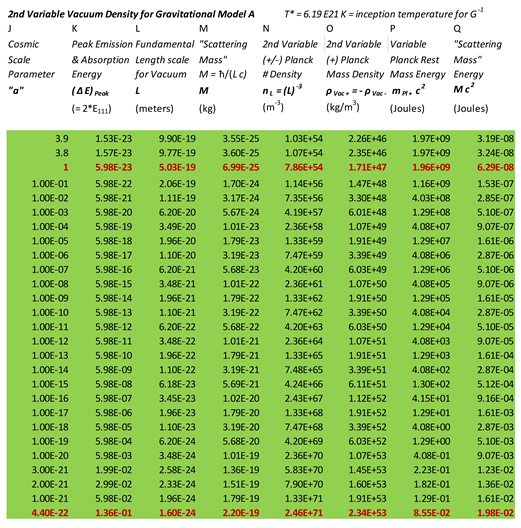
We are therefore in a position to determine the cosmic evolution of the universe, using this specific gravitational function. Let us turn to Table 2, where our alternative vacuum mass density model, will be considered.

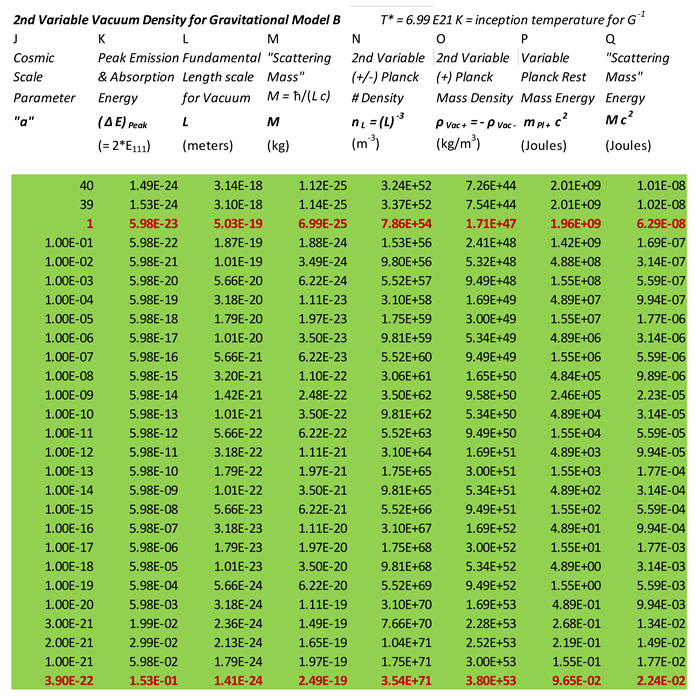
Column “J” is a repeat of column “A” from the previous table, Table 1. It lists the cosmic scale parameter,

“ a ”

. Column “K”, in Table 2, gives us,

Δ E_{p e a k}

. This is calculated from, equations, (2−7), and (2−8). We first find the new

C M B

temperature, using our entries under column “A”, remembering that,

T = T_{0} / a

. Then we employ,

e q u a t i o n, (2 - 8)

, to determine the peak frequency,

ν_{p e a k}

. This result is then entered into,

e q u a t i o n, (2 - 8)

, to find,

Δ E_{p e a k}

.

E q u a t i o n, (2 - 9)

, is valid only in the present epoch. We next calculate the new fundamental length scale for the vacuum,

L

, using,

e q u a t i o n, (2 - 12)

. This will be entered under column “L”. We have to keep in mind, however that the value of,

m_{P l}

, also changes with cosmological time. Therefore, we have to import the appropriate values from column “F”, in Table 1. It should come as no surprise that the peak energy emitted, or absorbed,

Δ E_{p e a k}

, is temperature dependent, and increases as one goes back in cosmological time. It is also not surprising that the value of

L

decreases (as it must) when we scale back to earlier epochs. This is the behavior we seek.

Column “M” in Table 2, gives us the “scattering mass” defined as,

M \equiv ħ / (L c)

. It is positive definite (unlike,

m_{P l}

), and its significance will be seen shortly. Column “N” specifies the number density for both positive and negative mass Planck particle. Here we use the simple relation,

n_{L} = L^{- 3}

, which is an extension of,

e q u a t i o n, (2 - 14 c)

, to other epochs. We notice that the “scattering mass” increases going back in cosmological time, as does the positive with negative mass, planckion number density. In the current epoch,

n_{0} = L_{0}^{- 3} = 7.86 E 54 p a r t i c l e s / m^{3}

. But at the inception temperature for,

G^{- 1}

, the planckion number density value has increased to a fantastic,

2.46 E 71 p a r t i c l e s / m^{3}

. This can be seen by referring to Table 2, column, “N”.

In column “O”, we calculate the mass density associated with the positive mass Planck particle. The negative mass Planck particle will have minus this value. The net mass density is thus zero for a vacuum in the balanced state (no perturbations). These entries are easily obtained by multiplying the appropriate entries in Column “F”, from Table 1, with those corresponding entries from column “N’, in Table 2. The result is column “O”. Needless to say, the vacuum mass densities in column “O” increase as one goes back in time. The net will always be zero, unless the vacuum symmetry is broken in some fashion. The vacuum mass density multiplied by,

c^{2}

, would give us the vacuum energy density, which according to Winterberg, is equivalent to the vacuum pressure. It is only in the unbalanced state where we would obtain a net vacuum energy density, and a net vacuum pressure.

With our second definition of vacuum energy density, we notice that we also have a match between column “O” and column “I”. The vacuum mass density has pretty much the same value as the

C M B

radiation “mass” density, but only close to the

G^{- 1}

inception temperature, and in no other epoch. This is no accident in our view. If the positive and negative planckions are to “freeze out” of the vacuum, then the Planck particle energy density should correlate with the

C M B

energy density. Again there is no a-priori reason to assume that a gravitational model should coincide with a background radiation model as these two concepts are, at first sight, totally unrelated.

Upon a more careful analysis of, columns ”O” with “I”, we note that the second to last row in column “O”, more closely matches the second to last row entry, in column “I”. One could argue, however, that the freeze-out of planckions did not happen instantaneously. In other words, it takes a certain period of time, and a specific drop in

C M B

temperature, from the start of the process, to the finish, for freeze-out to occur. As a prime example, we can point to recombination, where the process started some 150,000 years after the Big Bang, and was only completed at roughly 370,000 years after. There was a temperature drop by roughly a factor of 50 (

k_{B} T ~ 13.6 e V t o .26 e V

), from start to finish, which would be similar to the above example. While not definitive, we believe that this match is close enough for us to call it a match.

There are two remaining columns, columns, “P” and “Q”, in Table 2. Column “P” is just the vacuum mass density, column “O”, multiplied by,

c^{2}

, divided by the number density. Or, what is equivalent, it is simply the rest mass energy of the positive planckion,

∣ m_{P l} ∣ c^{2}

. This represents the energy needed within the vacuum, to dislodge one positive Planck particle, from its neighbors. A negative Planck particle would need the same amount of energy, but negative, in order to disassociate itself from particles within its species. Remember that the two species do not interact directly, but indirectly through their overlapping wave functions.

There is, however, a second rest mass energy, and that is represented by column “Q”. This is,

M c^{2}

, where, the scattering mass,

M

, is defined by the relation,

M \equiv ħ / (L c)

. This rest mass enters into the equation associated with the Higgs field, and when we have a +/- Planck particle “imbalance”. As shown in previous work [9,10], this is related to the Higgs potential energy, when we have an unbalanced vacuum, where,

(\bar{n_{+}} \neq \bar{n_{-}})

. If that is the case, then the following holds true.

U_{H P E} = M c^{2} (\bar{n_{+}} - \bar{n_{-}}) / n_{L}

(4−2)

The quantity,

M c^{2}

, is what is what is calculated under column “Q”. We take the entries in column “M”, and multiply them by,

c^{2}

, to determine these values. From,

e q u a t i o n, (4 - 2)

, we can find,

p_{H P E} = u_{H P E} = n_{L} U_{H P E}

, where,

p_{H P E}

, is the vacuum pressure, and,

u_{H P E}

, equals the net vacuum energy density, when there is a net imbalance in a region of space. The

\bar{n_{\pm}}

are the energy weighted number densities, for the positive and the negative mass Planck particles. See reference [10] for further details.

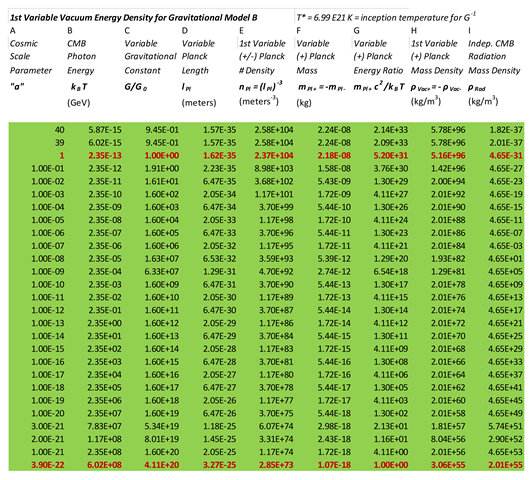
V Gravitational Model, B, Scaling for Two Planck Particle, Vacuum Energy Densities

In this section, we consider gravitational model,

B

, for,

G^{- 1}

, given by,

e q u a t i o n s, (3 - 2), a n d, (3 - 4)

. Just like in section IV we will construct two tables. Table 3 will apply for our naïve vacuum energy density model, based on scaling length,

l_{P l}

. Table 4 will hold for our alternative vacuum energy density model, where, , is the fundamental length scale for the vacuum. We believe that Table 4 represents a more sensible model. The only real difference between section IV, and this section, is our choice for,

G / G_{0}

, which is worked out under column “C” of Table 3. We will now be using, specifically,

q u a t i o n, (3 - 4)

, for its determination. Columns “A”, and “B” are the same as before.

Upon a comparison of the entries under column “C” of Table 3, with the corresponding values of those under column “C” of Table 1, we do not see much of a difference. The figure in section III, Figure 1, shows that our two

G^{- 1}

functions, are qualitatively very similar. And so, we will not expect too much of a variation going forward with our other columns, when comparing the results of this section, with those of the previous section. We have a new inception temperature for our new function,

T^{*} = 6.99 E 21 d e g r e e s K

. Previously, we had,

T^{*} = 6.19 E 21 d e g r e e s K

. Moreover, it will take longer to reach saturation with our new gravitational model,

B

. When the scale parameter,

“ a ”,

approaches,

40

, there is virtually no further change in

G^{- 1}

. We can call this the effective saturation point, i.e.,

G^{- 1} (a = 40) ≅ G_{\infty}^{- 1}

. In the previous section, we had correspondingly,

G^{- 1} (a = 3.9) ≅ G_{\infty}^{- 1}

. In general, gravitational model, , is less dramatic in its variation than model,

A

.

Figure 1.

G^{- 1} / G_{0}^{- 1} v e r s u s c o s m i c s c a l e p a r a m e t e r, a

Blue histogram refers to gravitational model,

A

Green histogram refers to gravitational model,

B

.

Figure 1.

G^{- 1} / G_{0}^{- 1} v e r s u s c o s m i c s c a l e p a r a m e t e r, a

Blue histogram refers to gravitational model,

A

Green histogram refers to gravitational model,

B

.

Because the values or entries in columns “D” through to “I” in Table 3 will not differ too much from those in the previous section, we will not comment on them further here, except to note the following. As before, the

l_{P l}

values in column “D” increase going back in cosmological time, which makes little sense. Also the entries in column ”E” for Planck particle number density go counter to what one would expect, if one goes back to previous epochs. Also note the surprising match between

ρ_{V a c +}

(column “H”) and

ρ_{R a d}

(column “I”), but only as one approaches the inception temperature for,

G^{- 1}

. In no other epoch, past or present, do we have such a convergence.

Our second table in this section is, Table 4. This holds for our alternative model, where,

L

, is the fundamental length scale to be associated with the vacuum. This table will follow the same format as Table 2, in section IV. The results will change slightly, but not appreciably. Hence the same general conclusions can be drawn. We note that there is a decrease in,

L

, as one goes back in cosmological time. And we also have an increase in +/- mass Planck number density,

n = L^{- 3}

, as the redshift,

Z

, increases. This scaling behavior is to be expected. Also the positive and negative vacuum energy densities neutralize one another, when the vacuum is in a perfectly balanced state. And so, the cosmological constant problem has been greatly reduced in scope.

We also remark that there is a match between column “I” from the previous table, Table 3, and column “O” in this table, Table 4. The values in the last three rows, of column “O” match, fairly closely, the 2^nd to last row entry in column “I”. Again, we expect that the freeze-out process for the positive and negative mass planckions to take some time. We will have a corresponding drop in temperature. Therefore, the results of column, “O” should lag, somewhat, those of column “I”. Ideally, we should start with the last row in column “I”, for the beginning of the planckion freeze out process, and finish with the second to last row, or third to last row, in column “O”. There will thus be a corresponding drop in temperature, from start to finish.

VI Possible Connection with Ordinary Matter, Dark Matter, and Dark Energy

In this section we seek to establish a connection between the vacuum energy densities introduced thus far, and ordinary matter, dark matter, and dark energy. Recently [15], we came up with a model for dark matter, and dark energy, based on ordinary matter, and a gravitational polarization model for space based on +/- mass planckions. Ordinary matter, i.e., aggregate matter, made up of atoms and molecules, can polarize the space around it at sufficiently low temperatures, and strong enough gravitational fields. The space is, of course, filled with planckions, and this can induce a slight separation between the positive and negative masses, creating gravitational dipoles or bound matter. This produces dark matter according to our thinking, where the induced gravitational field due to dipoles,

g^{(1)}

, reinforces the original gravitational field,

g^{(0)}

, due to ordinary matter. This dipole matter mass distribution is what is measured, for example, in Friedman’s equation.

Moreover, both types of masses, free, and bound dipole matter, produce gravitational fields, which contribute to their own energy density, and which we call dark energy. Thus, both dark matter and dark energy, have a common origin, and that is ordinary matter, and, assuming that space filled with planckions. Remember that the mass density parameters in Friedman’s equation are smeared values, only valid when immense distance scales , in excess of,

100 M p c

, are considered. Then, and only then, can the individual galaxies be treated much like molecules in a gas. Using Gauss’’ law at every point in the universe, it is easy to see how dark energy permeates all of space. No one location in the universe is preferred over the other, and when space is smeared, the

C M B

temperature is quite uniform. The details can be found in reference [15].

In the present epoch, based on the ordinary matter, dark matter and dark energy, percentage contributions to the critical mass density, we estimated that the gravitational susceptibility,

χ = χ_{g}

, is equal to,

χ_{0} = χ (a = 1) = .842 (p r e s e n t e p o c h)

(6−1)

This is a large amount, but then, the universe is largely cool and empty. In all epochs, the following relation must hold,

χ (a) + K (a) = 1

(6−2)

Here,

χ (a)

, is the gravitational susceptibility, and,

K (a)

is the relative gravitational permittivity. We are proceeding by analogy to electrostatics. By this equation,

K_{0} = K (a = 1) = .158

. In contrast to electrostatics, where we have,

(K - χ) = 1

, in gravistatics, we have,

(K + χ) = 1

. The former condition leads to screening, where the electrical dipole moments take away from the original field. The latter condition produces anti-screening, where the dipole gravitational field,

g^{(1)}

, will reinforce (strengthen) the original field,

g^{(0)}

.

The gravitational polarization,

\vec{P}

, in a linear approximation, equals,

\vec{P} = ε χ \vec{g} = ε \vec{g^{(1)}}

(6−3)

Here,

ε \equiv 1 / (4 π G)

, is the gravitational permittivity. The gravitational displacement field,

\vec{D}

, by analogy to electrostatics, equals.

\vec{D} = ε K \vec{g} = ε \vec{g^{(0)}}

(6−4)

And the macroscopic gravitational field,

\vec{g} = \vec{g^{(0)}} + \vec{g^{(1)}} = K \vec{g} + χ \vec{g}

(6−5)

Again,

\vec{g^{(0)}}

, is the gravitational field due to ordinary matter,

\vec{g^{(1)}}

, is the gravitational field due to dark matter, and,

\vec{g}

, is the total macroscopic field. The source terms are,

- \vec{\nabla} \cdot \vec{D} = ρ_{F} = ρ_{O r d . m a t t e r}

(6−6)

- \vec{\nabla} \cdot \vec{P} = ρ_{B} = ρ_{d a r k m a t t e r}

(6−7)

We note that by,

e q u a t i o n s, (6 - 5), (6 - 3), a n d (6 - 4),

(ε \vec{g}) = \vec{D} + \vec{P} (g r a v i s t a t i c s)

(6−8)

This equation is to be contrasted with electrostatics, where,

(ε_{0} \vec{E}) = \vec{D} - \vec{P} (e l e c t r o s t a t i c s)

(6−9)

As mentioned, the polarization of Planck particles gives the dark matter source term. See,

e q u a t i o n, (6 - 7)

.

For our purposes, we are interested in the scaling behavior for ordinary matter, dark matter, and dark energy. Within the context of our gravitational polarization model, for the mass densities in Friedman’s equation, we obtain [16],

ρ_{O M} / ρ_{O M, 0} = a^{- 3} (o r d i n a r y m a t t e r)

(6−10)

ρ_{D M} / ρ_{D M, 0} = (χ / K) (K_{0} / χ_{0}) a^{- 3} (d a r k m a t t e r)

(6−11)

ρ_{D E} / ρ_{D E, 0} = (K_{0} / K) a^{- 3} (d a r k e n e r g y)

(6−12)

In order to proceed further, we need a specific function for,

χ = χ (a)

. This we do not have. The point, however, is that these scaling laws are totally at odds with the vacuum energy density scaling laws given in the previous two sections. They look nothing like,

ρ_{V a c} / ρ_{V a c, 0} = (m_{P l} / m_{P l, 0}) {(L / L_{0})}^{- 3} = (l_{P l, 0} / l_{P l}) {(L / L_{0})}^{- 3} = {(G / G_{0})}^{- 1 / 2} {(G / G_{0})}^{- 3 / 4} a^{- 3 / 2} = {(G / G_{0})}^{- 5 / 4} a^{- 3 / 2}

(6−13)

In the third line we made use of,

e q u a t i o n s, (2 - 21), a n d (2 - 20)

. We are using the scaling laws employed in column “O”, in Table 2 and Table 4. Table 1 and Table 3, have been disqualified because the fundamental length for the vacuum,

l_{P l}

, does not scale appropriately. Because,

e q u a t i o n, (6 - 13)

, looks nothing like,

e q u a t i o n s, (6 - 10), (6 - 11) a n d (6 - 12)

, we conclude that the symmetry exemplified by these last three equations are broken. They do not have the original symmetry of the vacuum, which is,

e q u a t i o n, (6 - 13) .

As a matter of fact, the scaling laws appearing in,

e q u a t i o n s, (6 - 10), (6 - 11) a n d (6 - 12)

, do not appear to depend on,

G / G_{0}

.

Even if we consider the

Λ C D M

model, nothing would change in our conclusion. In the

Λ C D M

model, we have the conventional scaling laws for ordinary matter, dark matter, and dark energy. These are,

ρ_{O M} / ρ_{O M, 0} = a^{- 3} (o r d i n a r y m a t t e r)

(6−14)

ρ_{D M} / ρ_{D M, 0} = a^{- 3} (d a r k m a t t e r)

(6−15)

ρ_{D E} / ρ_{D E, 0} = 1 (d a r k e n e r g y)

(6−16)

Even though they are totally different from our

e q u a t i o n s, (6 - 10), (6 - 11), a n d (6 - 12),

they do not correspond to,

e q u a t i o n, (6 - 13)

. As such, adopting these equations would still imply a broken symmetry for the vacuum, if we accept a Planck particle vacuum. Notice that a Planck particle quantum vacuum scales very slightly in comparison to ordinary matter, and dark matter. The interesting feature, from our point of view, however, is its explicit dependence on,

(G / G_{0})

.

According to Winterberg, elementary particles, such as electrons, are quasi-particle excitations within the vacuum. Quite literally, they are self-sustaining and decaying vortices, with rotational symmetry, which can form within the vacuum, as the vacuum cools down. This clearly would break the lattice type symmetry inherent in our greater model for the vacuum. Dark matter and dark energy are formed from ordinary matter, once the universe has sufficiently cooled such that aggregate matter appears. Clumping is necessary. It is difficult for us to imagine how long range gravitational fields and forces can form when matter and radiation are in a plasma like state. We suspect that dark matter and dark energy can only form after recombination, i.e., for redshift values below,

Z = 1090

. Of course, this would require a major revision in current thinking. Atoms and molecules, and their clumping, are needed, from our perspective, in order for dark matter, and dark energy, to manifest themselves.

Finally, let us consider the present day contributions of ordinary matter, dark matter, and dark energy to the total mass density. The radiative component is negligible in the current epoch. We wish to compare those component values to the Planck particle vacuum energy density. According to the latest Planck collaborations [22,23], the density parameters in Friedman’s equation, assume the following values,

ρ_{O M, 0} = .049 ρ_{c r i t, 0} = .426 E - 27 k g / m^{3}

(6−17)

ρ_{D M, 0} = .260 ρ_{c r i t, 0} = 2.242 E - 27 k g / m^{3}

(6−18)

ρ_{D E, 0} = .691 ρ_{c r i t, 0} = 5.959 E - 27 k g / m^{3}

(6−19)

For the Hubble parameter, the Planck collaboration obtains, in the present epoch,

H_{0} = 67.74 k m / (s M p c)

. This would correspond to a critical mass density of,

ρ_{c r i t, 0} = 8.624 E - 27 k g / m^{3}

. The mass densities in the above equation are smeared values, valid only when immense distance scales are entertained, because only then can the individual galaxies be treated much like molecules within a fairly dilute gas.

We compare these values to,

ρ_{V a c, 0}

, which is given under column “O”, in Table 2 and Table 4. We proceed to,

a = 1

, which denotes the present epoch. The entry is found in the 3^rd row in each table. We find that,

ρ_{V a c, 0} = 1.71 E 47 k g / m^{3}

(6−20)

There is no difference between models,

A

, and

B

, if,

G = G_{0}

. Of course, according to our two component, Planck particle, superfluid/ super-solid model, there is a corresponding amount of negative Planck particle mass density. Thus, the total vacuum mass/ energy density is zero. This defines the zero net vacuum energy density and, the zero net vacuum pressure surface. If we compare the values in,

e q u a t i o n s, (6 - 17) t h r o u g h (6 - 19),

to,

e q u a t i o n, (6 - 20)

, we see that they are nothing but very minute perturbations (ripples) in this vast ocean (assembly) of a positive, with negative Planck particle mass density. This is a further indication that the mass densities, which are present in today’s universe, are residual effects, or anomalies upon a much greater whole, which is seemingly “not there”.

VII Summary and Conclusions

We introduced two competing models for a quantum vacuum, assuming that space is made up of positive and negative mass Planck particles, interacting through very strong superfluid forces. These forces act within their respective species (Winterberg model). The first model introduces the Planck length,

l_{P l}

, as the fundamental length scale for space. This is the presumed nearest neighbor distance of separation between individual positive mass planckions, as well as negative mass planckions. It also defines the graininess of the vacuum. In the present epoch, its value is,

l_{P l, 0} = 1.616 E - 35 m e t e r s

. The second vacuum model assumes a different fundamental length scale for the vacuum, which we called,

L

. This length,

L

, has the same interpretation as above, but is much larger in value. It is found using box quantization, and looking at transitions between energy states for the positive, as well as the negative, mass Planck particle. See section II. The

C M B

temperature factors in, in a critical and very direct way, in defining this new length scale,

L

. This is not the case for,

l_{P l}

. In the present epoch, the value for,

L_{0}

equals,

L_{0} = 5.030 E - 19 m e t e r s .

.

We subjected both vacuum energy density models, to a time varying gravitational constant. Only in this way, could one obtain scaling behavior for,

l_{P l}

, for an expanding universe. If the gravitational constant increases going back in cosmological time, however, the

l_{P l}

does not scale as it should, i.e., it does not get smaller, as we go back in time. The alternative length scale,

L

, however, will scale appropriately, as well as other quantities which depend on it, such as planckion number density. For these and other reasons, we focus our attention on,

L

, as the true fundamental length scale for the quantum vacuum.

Two specific functions for,

G^{- 1} = G^{- 1} (a)

, where,

G

is Newton' s constant were analyzed with respect to a specific cosmic evolution. Although these two functions were very different quantitatively, they had very similar qualitative behavior. Both displayed order parameter behavior, in that they approached a saturation value at low

C M B

temperatures. And, at very high CMB temperatures, both

G^{- 1}

functions increased as,

T^{- 1}

. Both functions had very similar inception temperatures. For gravitational model,

A

, the

G^{- 1}

formed at

C M B

temperature,

T^{*} = 6.19 E 21 d e g r e e s K .

For gravitational model,

B

, the

G^{- 1}

coalesced out of the vacuum at inception temperature,

T^{*} = 6.99 E 21 d e g r e e s K

. We consider,

G^{- 1}

, to be an inherent property of the vacuum, much like paramagnetism. When

G^{- 1}

started to form, the planckions acquired mass, positive and negative. The

C M B

temperature,

T^{*}

, is thus the freeze out temperature for Planck particles, having positive and negative mass. The rationale for these two specific gravitational functions, and their specific parametrizations, were given in another paper. Their functional form is specified in section III. See,

e q u a t i o n s, (3 - 1) a n d (3 - 2)

. Refer also to,

e q u a t i o n s, (3 - 3), w i t h (3 - 4)

. Figure 1 gives their dependency on the cosmic scale parameter.

When we used these distinct gravitational functions, we made a remarkable discovery. Using these two specific functions, with their characteristic parametrizations, we charted out a cosmic evolution for the two competing vacuum energy density models mentioned above. One was in terms of the Planck length,

l_{p l}

, whereas the other was in terms of an alternative fundamental length scale,

L

. Both competing models led to a planckion vacuum energy density, which matched the radiation energy density. This match happened only at the inception temperature for,

G^{- 1}

, and in no other epoch, past, present or future. This seems to us to be more than a coincidence. It would make sense that

G^{- 1}

froze out of the vacuum at a time when the Planck particle vacuum energy density matched the

C M B

energy density. As the

C M B

energy density decreases, the Planck particles decouple. Moreover, this match greatly supports our choice for,

G^{- 1}

, with their independent parametrizations. Remember that gravity is independent of radiation, and so, there would be no a-priori reason to assume that a correlation should even exist between the two.

The results for model,

A

, which is our first gravitational model, is summarized in Table 1 and 2. Table 1, in section IV, considers,

l_{p l}

, to be the fundamental length scale for space. This leads to unsatisfactory scaling behavior. Table 2 is better, as it rests on using

L

as the new fundamental length scale for the vacuum. A discussion of the individual columns, and entries within those columns, was presented in section IV. The results for gravitational model,

B

, was presented in section V. There, we also summarized our findings using two distinct tables, Table 3 and Table 4. The entries in Table 3 showed unsatisfactory results, as it was based on using the Planck length,

l_{p l}

, as the ultimate length scale for space. Table 4 led to better results as it was predicated on employing,

L

, as the fundamental length scale. All 4 tables scaled back to the epoch of inception for,

G^{- 1}

.

In section VI, we argued that ordinary matter, dark matter, and dark energy must be residual mass densities, remnants left over after symmetry breaking. Their scaling laws look nothing like the Planck quantum vacuum scaling laws. Even in the conventional

Λ C D M

model, no connection can be made, even if

G

is assumed to be constant. Moreover, their numerical values indicate that ordinary matter, dark matter, and dark energy, are very slight perturbations upon a much greater assembly of positive and negative mass Planck particles. It would be akin to the slightest of ripples upon a very deep and wide ocean of particles. The mass densities for the component parts, ordinary matter, dark matter, and dark energy, are nothing compared to this ocean surface of zero net vacuum mass density, and zero net vacuum pressure. See,

e q u a t i o n s, (6 - 17), t h r o u g h (6 - 20)

. Because of the mass compensating effect between the positive and negative mass planckions, the cosmological constant problem has also been greatly reduced in scope. The problem is now to find out how these perturbations came into existence, in the first place, and why.

References

Winterberg, F. (2003) Planck Mass Plasma Vacuum Conjecture, Z. Naturforsch. 58a, 231 (2003).
Winterberg, F. (2002) Planck Mass Rotons as Cold Dark Matter and Quintessence Z. Naturforsch. 57a, 202–204 (2002); received January 3, 2002.
Winterberg, F. (1995) Derivation of Quantum Mechanics from the Boltzmann Equation for the Planck Aether, International Journal of Theoretical Physics, Vol. 34, p. 2145 (1995).
Winterberg, F. (1998) - The Planck Aether Model for a Unified Theory of Elementary Particles, International Journal of Theoretical Physics 33, 1275 (1994).
Winterberg, F. (1993) - Physical Continuum and the Problem of a Finitistic Quantum Field Theory", International Journal of Theoretical Physics 32, 261(1993).
Winterberg, F. (1992) - Cosmological Implications of the Planck Aether Model for a Unified Field Theory, Z.f. Naturforsch.-Physical Sciences. 47a, 1217 (1992).
Winterberg, F. (2002) The Planck Aether Hypothesis, monograph published by the C.F. Gauss Academy of Science Press. Reno, Nevada 2002. (Copies of this work can be purchased from the C.F. Gauss Academy of Science Press, P.O. Box 18265, Reno, Nevada 89511; Price $20.00 plus shipping).
Pilot, C, (2021), Does Space Have a Gravitational Susceptibility? A Model for the Density Parameters in the Friedman Equation, Journal of High Energy Physics, Gravitation, and Cosmology (JHEPGC), Vol 7, No. 2, 478-507, Apr. 2021 https://www.researchgate.net/publication/342993272_Does_Space_Have_a_Gravitational_Susceptibility_A_Model_for_the_Density_Parameters_in_the_Friedmann_Equation , July 2020. [CrossRef]
Pilot, C, (2021), Scaling Behavior for the Susceptibility of the Vacuum, International Journal of Astronomy and Astrophysics (IJAA), Vol 11, No. 1, 11-36, March, 2021. https://www.researchgate.net/publication/342993277_Scaling_Behavior_for_the_Susceptibility_of_the_Vacuum_in_a_Polarization_Model_for_the_Cosmos , July 2020. [CrossRef]
Pilot, C, (2021), Q-Theory, A Connection between Newton’s Law ad Coulomb’s Law? , Journal of High Energy physics, Gravitation and Cosmology (JHEPGC). Vol 7, No 2, 632-660, April, 2021 https://www.researchgate.net/publication/342993436_Theory_A_Connection_between_Newton's_Law_and_Coulomb's_Law , July 2020. [CrossRef]
Pilot, C, (2021), Is the Higgs Field a Positive and Negative Mass Planckion Condensate, and Does the LHC Produce Extreme Dark Energy?, Journal of High Energy Physics, Gravitation, and Cosmology, Vol 8, No. 2, 432- 456, April 2022, https://www.researchgate.net/publication/354378610_Is_the_Higgs_Field_a_Positive_and_Negative_Mass_Planckion_Condensate_and_Does_the_LHC_Produce_Extreme_Dark_Energy? [CrossRef]
Pilot, C. (2023), A New Interpretation of the Higgs Vacuum Potential Energy Based on a Planckion Composite Model for the Higgs, submitted for publication https://www.researchgate.net/publication/369030998_A_New_Interpretation_of_the_Higgs_Vacuum_Potential_Energy_Based_on_a_Planckion_Composite_Model_for_the_Higgs. [CrossRef]
Kolb, E.W. and Turner, M.S. (1989) The Early Universe. Addison-Wesley, Reading.
Mather, J.C., et al . (1999) Calibrator Design for the COBE Far-Infrared Absolute.
Spectrophotometer (FIRAS). The Astrophysical Journal , 512, 511-520.
. [CrossRef]
Baumann, D.D. (2015) Lecture Notes on Cosmology.
http://theory.uchicago.edu/~liantaow/my-teaching/dark-matter-472/lectures.pdf.
Husdal, L. (2016) On Effective Degrees of Freedom in the Early Universe. Galaxies.
4, 78. [CrossRef]
Pilot, C, (2021), Does Space Have a Gravitational Susceptibility? A Model for the Density Parameters in the Friedman Equation, Journal of High Energy Physics, Gravitation, and Cosmology (JHEPGC), Vol 7, No. 2, 478-507, Apr. 2021 https://www.researchgate.net/publication/342993272_Does_Space_Have_a_Gravitational_Susceptibility_A_Model_for_the_Density_Parameters_in_the_Friedmann_Equation , July 2020. [CrossRef]
Pilot, C, (2021), Scaling Behavior for the Susceptibility of the Vacuum, International Journal of Astronomy and Astrophysics (IJAA), Vol 11, No. 1, 11-36, March, 2021. https://www.researchgate.net/publication/342993277_Scaling_Behavior_for_the_Susceptibility_of_the_Vacuum_in_a_Polarization_Model_for_the_Cosmos , July 2020. [CrossRef]
Pilot, C, (2018), Is Quintessence an Indication of a Time-Varying Gravitational Constant? , Journal of High Energy Physics, Gravitation and Cosmology (JHEPGC) Vol 5 No 1 (Dec, 2018) 41-81, https://arxiv.org/abs/1803.06431, https://www.scirp.org/journal/paperinformation.aspx?paperid=88999.
Pilot, C, (2019), The Age of the Universe Predicted by a Time Varying G? Journal of High Energy Physics, Gravitation and Cosmology (JHEPGC) Vol.5 No. 3 (July, 2019) 928-934 https://www.scirp.org/Journal/paperinformation.aspx?paperid=94065. [CrossRef]
Pilot, C, (2020), Inflation and Rapid Expansion in a Variable G Model, International Journal of Astronomy and Astrophysics (IJAA), Vol. 10 No.4 (Dec. 2020) 334-345 https://www.researchgate.net/publication/342988030_Inflation_and_Rapid_Expansion_in_a_Variable_G_Model_slightly_revised_version. [CrossRef]
Komatsu E., et al. [WMAP Collaboration], Astrophys. J. Suppl. 192 (2011) 18 [arXiv: 0803.0547 [astro‐ph]].The current best estimate for the quintessence parameter is, −.98 +/−.053.
Lahav, O and Liddle, A.R., Cosmological Parameters, Nov. 2015. Another value, which is quoted, is, w = −.97 +/−.05 using a compilation of CMB, SN and BAO measurements (assuming a flat universe).
Collaboration, Planck, PAR Ade, N Aghanim, C Armitage-Caplan, M Arnaud, et al., Planck 2015 results. XIII. Cosmological parameters. arXiv preprint 1502.1589v2[1 ] (https://arXiv.org/abs/1502.1589v2), 6 Feb 2015. /.
Planck Collaboration XIV, Planck 2015 results. XIV. Dark Energy and Modified.
Gravity. 2016, A&A, in press, arXiv: 1502.01590. The value quoted is, = −1.006 +/−.045 . However, this is not the most secure estimate; the tightest constraint is obtained for the Planck TT + low P + BSH combination. This gives, w > −1, and is centered about, w = −.98. See figure 28 (section 6.3) in the former publication, and figures 3a and 4a (section 5.1), in the latter publication.

Table 1. st Vacuum Energy Density Model. Assuming Gravitational Model A See text for details.

Table 2. 2nd Vacuum Energy Density Model Assuming Gravitational Model A See text for details.

Table 3. 1st Vacuum Energy Density Model Assuming Gravitational Model B See text for details.

Table 4. 2nd Vacuum Energy Density Model. Assuming Gravitational Model B. See text for details.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

On the Cosmic Evolution of the Quantum Vacuum Using Two Variable G Models and Winterberg's Thesis

Abstract

Keywords:

Subject:

I Introduction

II Two Competing Vacuum Energy Density Models

III Two Variable $G^{- 1} (a)$ Models

IV Gravitational Model, A, Scaling for Two Planck Particle, Vacuum Energy Densities

V Gravitational Model, B, Scaling for Two Planck Particle, Vacuum Energy Densities

VI Possible Connection with Ordinary Matter, Dark Matter, and Dark Energy

VII Summary and Conclusions

References

MDPI Initiatives

Important Links

Subscribe

On the Cosmic Evolution of the Quantum Vacuum Using Two Variable G Models and Winterberg's Thesis

Abstract

Keywords:

Subject:

I Introduction

II Two Competing Vacuum Energy Density Models

III Two Variable G − 1 ( a ) Models

IV Gravitational Model, A, Scaling for Two Planck Particle, Vacuum Energy Densities

V Gravitational Model, B, Scaling for Two Planck Particle, Vacuum Energy Densities

VI Possible Connection with Ordinary Matter, Dark Matter, and Dark Energy

VII Summary and Conclusions

References

MDPI Initiatives

Important Links

Subscribe

III Two Variable $G^{- 1} (a)$ Models