Channel Emulator Framework for Underwater Acoustic Communications

1. Introduction

Emerging applications like water quality monitoring [1], off-shore asset monitoring [2], bio-diversity monitoring [3], oil field exploration [4], bio-geochemical process exploration [5], and large-scale deployment of acoustic modems and their highly efficient computing and denoising capabilities [6], have driven considerable time, financial and intellectual investment from both industry and academia over the past few years towards developing feasible underwater acoustic communication (UWAC) systems. However, the complex nature of water, slow propagation speed of acoustic waves through water, limited bandwidth availability, complex noise sources and delay-Doppler effects, make it way more challenging to design and deploy a reliable UWAC system, as compared to traditional terrestrial radio systems [7,8]. The only way forward is to design dedicated signal processing algorithms and network protocols for UWAC scenario which are validated across a variety of scenarios.

Running actual sea, river or lake-experiments is both financially and logistically challenging [9]. Border security protocols of multiple nations sharing a water-body sometimes makes it almost impossible to run trials, particularly in the design stage. Therefore, it is absolutely crucial for system engineers to test their design using controllable yet realistic and comprehensive emulator platforms. Channel emulator platforms can enable designers to benchmark performances of different algorithms across a wide range of parameters, and obtain large samples of how the system performs and evolves over time via thorough empirical evaluation [10]. Once the robustness of the designed system has been synthetically validated, experimental demonstrations can be arranged for a specific environment with a much lower time, financial and logistic commitment.

Developing channel emulators for UWAC environment is extremely challenging as there is no typical underwater environment. The water characteristics vary with depth, salinity, density, geographical locations. The acoustic signal suffers from varying attenuation, absorption, delay, Doppler effects and noise effects with varying underwater characteristics, and sea-surface and sea-bottom contours [11,12]. Therefore, instead of separately characterizing each environment parameters and key affecting factors, we develop a mathematical model using the physics of the medium and acoustic signal propagation to map the interaction between the aquatic medium and the travelling signal.

Several UWAC channel modelling software and platforms have been developed over the years to realistically represent different UWAC communication scenarios. A very popular Open Source platform is BELLHOP [13] that uses beam tracing to emulate acoustic pressure fields in a particular underwater environment. Another widely used one is the Ulrick model [14] that calculates distance-related spreading loss and frequency-related absorption loss over UWAC links. Other UWA network simulators like DESERT [15], SUNSET [16], and WOSS [17] also provide researchers with valuable insights on the UWAC environments. However, there is no single unifying platform taking the flow of acoustic signal through any aquatic environment to draw insights on how the signal interacts with the environment, what changes the signal experience over time and distance, and how those changes impact the overall design of the communication system.

The primary contribution of this paper is to combine mathematical modelling of how acoustic signal travels through water and sum-of-sinusoids (SOS) [18]-based generation of channel samples in a generalized yet tractable channel emulator platform. The emulator is capable of characterizing key aspects of UWAC channel, like, signal amplitude profile, attenuation, propagation loss and delay, Doppler spread and shift, which are critical for designing signal processing techniques, networking protocols and network topology extraction. Specifically, we,

• Combine concepts of damped harmonic classical oscillators [19], Milne’s oscillator [20], and acoustic wave equations to formulate a mathematical model for propagation of acoustic signal through underwater environment.
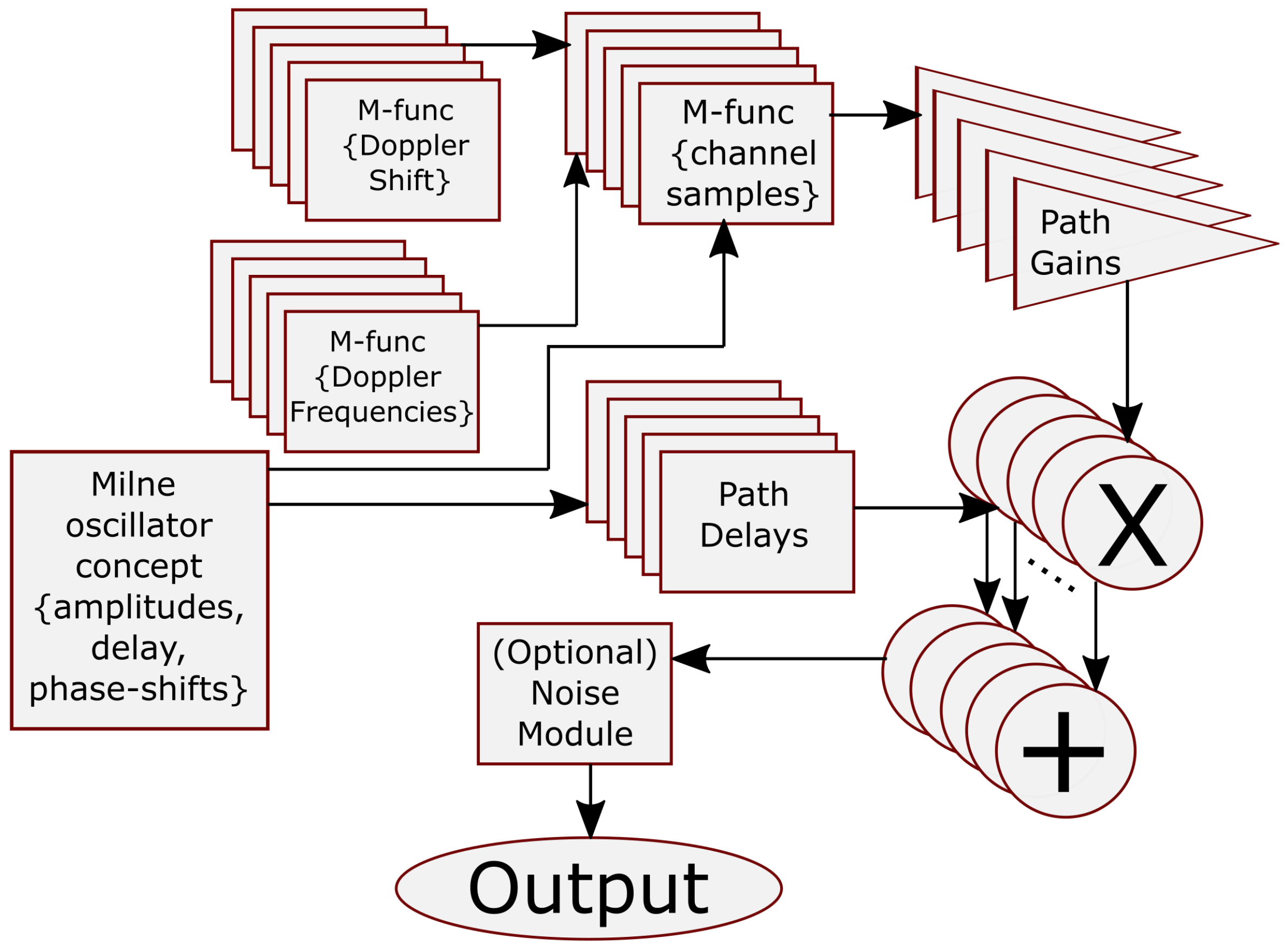
• Integrate outputs of the mathematical model with wide sense stationary uncorrelated scattering (WSSUS) and SOS-based models for synthetic generation of channel impulse response, signal amplitude and phase change profiles, and Doppler frequencies and Doppler power spectral profile.
• Develop a Simulink-based channel emulator platform that incorporates the oscillator-based mathematical model and WSSUS-based channel sample generation.
• Using the developed channel emulator platform, demonstrate i) snapshots of channel samples for different scenarios and parameters and ii) performance of two example communication systems - a) Differential M-ary Phase Shift Keying (DMPSK)- Orthogonal Frequency Division Multiplexing (OFDM) system with $1/2$-rate Turbo coding for single-transmit-single-receive scenario; b) DMPSK-OFDM system with $1/2$-rate Turbo coding for multiple-transmit-multiple-receive scenario.

2. Mathematical Modelling of Propagating Signal

2.1. Modelling the Medium

We start with the damped classical harmonic oscillator equation [19],

$$\ddot{y}+\beta \dot{y}+{\omega }^{2}y=0$$

(1)

where y is the position, $\omega$ is the operating frequency and $\beta$ is the linear damping coefficient. If varying the oscillator parameters offers modification of the classical oscillator, the harmonic oscillator equation in (1) gets modified to the parametric oscillator representation. As the travelling acoustic signal interacts with water, the water movement (medium) can be modelled using the parametric oscillator equation,

$$\ddot{x}+\beta \left(t\right)\dot{x}+{\omega }^2\left(t\right)x=0$$

(2)

where now the parameters $\beta$ and $\omega$ become functions of time, $\omega \left(t\right)>0$ and $\omega \left(t\right)\to 1$ with $t\to \pm \infty$. Using constant-time scaling, the upper limit for $\omega \left(t\right)$ is set to 1. When there is no travelling signal, $\omega =1$, i.e. the medium is an undriven oscillator state with unit frequency.

2.2. Modelling the Acoustic Signal

For signal modelling, we start with the acoustic wave equation,

$$c^2\frac{{\partial }^2\mathbf{p}}{\partial x^2}=\frac{{\partial }^2\mathbf{p}}{\partial t^2}$$

(3)

where $\mathbf{p}$ is the acoustic pressure, x is the direction of signal propagation and $c=1480$ m/s is the velocity of acoustic wave through water. In (3), $\mathbf{p}$ can be expressed as,

$$\mathbf{p}=f_1(y+ct)+f_2(y-ct)$$

(4)

with amplitude $\alpha$, wave-number k, $k=2\pi /\lambda$ and $\lambda$ is the signal wavelength. Rearranging (4),

$$y=\frac{1}{k}{cos}^{-1}\left(\frac{\mathbf{p}}{\alpha }\right)+ct$$

(5)

and inserting (5) in (2) we can obtain,

$$\begin{array}{cc}\hfill & \ddot{\mathbf{p}}\frac{{\mathbf{p}}^2}{{\alpha }^2}-\mathbf{p}{\left(\dot{\mathbf{p}}\right)}^2+\beta \left(t\right)\dot{\mathbf{p}}\frac{{\mathbf{p}}^2}{{\alpha }^2}-\beta \left(t\right)ck\mathbf{p}-{\omega }^2\left(t\right)\mathbf{p}{cos}^{-1}\left(\frac{\mathbf{p}}{\alpha }\right)-{\omega }^2\left(t\right)ctk\mathbf{p}=0.\hfill \end{array}$$

(6)

If $y=ct$ satisfies (6), we can write the so-called Milne’s equation [20] with $\mathbf{p}=\alpha$ to obtain,

$$\begin{array}{c}\hfill \ddot{\mathbf{p}}-\mathbf{p}{\left(\dot{\mathbf{p}}\right)}^2+\beta \left(t\right)\dot{\mathbf{p}}-\beta \left(t\right)ck\mathbf{p}-{\omega }^2\left(t\right)ctk\mathbf{p}=0.\end{array}$$

(7)

Here (7) is the well-known Milne’s oscillator equation. Essentially (7) represents the evolution of acoustic pressure field with time and can be solved for $\mathbf{p}$ to calculate effective receive signal strength (Milne energy), effective phase shift and time-delay experienced by the travelling signal.

2.3. Modelling the Interaction between the Medium and the Acoustic Signal

The next step is to solve for $\mathbf{p}$ using the Lagrangian of (7) for continuous media and fields with finite degrees of freedom,

$$\begin{array}{c}\hfill \mathcal{L}=\frac{1}{2}{\dot{\mathbf{p}}}^2+\frac{\beta \left(t\right)ck}{2}{\mathbf{p}}^2+\frac{\omega {\left(t\right)}^{2}ctk}{2}{\mathbf{p}}^2\end{array}$$

(8)

where $\frac{1}{2}{\dot{\mathbf{p}}}^2$ is the kinetic energy density and ($\frac{\beta \left(t\right)ck}{2}{\mathbf{p}}^2+\frac{\omega {\left(t\right)}^{2}ctk}{2}{\mathbf{p}}^2$) is the potential energy density. The next step is formulate the Hamiltonian of (8) using Euler-Lagrange concept to obtain,

$$\begin{array}{cc}\hfill \mathcal{H}(\dot{\mathbf{p}},p,t)& =\dot{\mathbf{p}}\frac{\partial \mathcal{L}}{\partial \dot{\mathbf{p}}}-\mathcal{L}=\frac{1}{2}{\dot{\mathbf{p}}}^2-\frac{\beta \left(t\right)ck}{2}{\mathbf{p}}^2-\frac{\omega {\left(t\right)}^{2}ctk}{2}{\mathbf{p}}^2.\hfill \end{array}$$

(9)

The difference between kinetic and potential energies reflected through (9) remains constant before and after the duration over which the signal exists. Consequently, the Hamiltonian, $\mathcal{H}$ can be expressed as the asymptotic Milne energy, $E_M$, rather the effective signal strength at any point between the transmit and the receive points on an UWAC link.

Here we introduce the concept of path bundles, $\mathbf{q}$, which consists the solution to the Hamiltonian in (9) bounded by $E_M\ge 1$. Physically, $\mathbf{q}$ represents the collection of transmission rays that travels along a certain direction. The corresponding Milne energy can be expressed as,

$$\begin{array}{c}\hfill E_M=\frac{1}{2}{\dot{\mathbf{q}}}^2-\frac{\beta \left(t\right)ck}{2}{\mathbf{q}}^2-\frac{\omega {\left(t\right)}^{2}ctk}{2}{\mathbf{q}}^2\end{array}$$

(10)

Solving for $\mathbf{q}$ in (10), $\mathbf{q}$ can be written as,

$$\begin{array}{c}\hfill \mathbf{q}=\sqrt{{\mathbf{q}}_{\pm }^2{cos}^2(t-\tau )+{\mathbf{q}}_{\mp }^2{sin}^2(t-\tau )}\end{array}$$

(11)

where $\mathbf{q}$ physically represents the amplitude of the acoustic ray bundles travelling through water (path bundles include both the direct ray and reflected rays that constitute the total acoustic signal), and $\tau$ is the effective time delay experienced by the travelling signal. The derivative of $\mathbf{q}$ in (11) is set to $\dot{\mathbf{q}}=0$. Putting $\dot{\mathbf{q}}=0$ back in (10),

$$\begin{array}{c}\hfill E_M=-\frac{\beta \left(t\right)ck}{2}{\mathbf{q}}^2-\frac{\omega {\left(t\right)}^{2}ctk}{2}{\mathbf{q}}^2.\end{array}$$

(12)

Equation (12) can be solved to obtain,

$$\begin{array}{cc}\hfill \mathbf{q}& =\pm ı\sqrt{2E_M/(\beta \left(t\right)ck+\omega {\left(t\right)}^{2}ctk)}\hfill \\ \hfill \mathbf{q}\left(t\right)& =\pm ı\sqrt{2E_{M}cos(2t-\tau )/(\beta \left(t\right)ck+\omega {\left(t\right)}^{2}ctk)}\hfill \end{array}$$

(13)

where $ı=\sqrt{-1}$. A demonstration of the evolution of the amplitude of the acoustic path bundles ($\mathbf{q}$) with time for varying values of the damping constant $\beta$ is presented in Figure 1. It is to be noted here that we did not vary $\beta$ as a function of time t. For our simulations, we have kept $\beta$ fixed over the time period within which the amplitude evolution of the signal path bundles is captured. The amplitude evolution of the signal paths is formulated using (12). Finally the interaction between $\mathbf{q}$ and water over time can be represented in the form of the transition matrix, ${\mathbf{M}}_{\mathbf{q}}$, where,

$$\begin{array}{c}\hfill {\mathbf{M}}_{\mathbf{q}}=\mathbf{D}\left(\begin{array}{cc}cos2\delta & {\mathbf{q}}_{-}^{2}sin2\delta \\ -{\mathbf{q}}_{+}^{2}sin2\delta & cos2\delta \end{array}\right)\mathbf{D};\mathbf{D}=\left(\begin{array}{cc}cos\tau & -sin\tau \\ sin\tau & cos\tau \end{array}\right)\end{array}$$

(14)

with $\delta$ as the effective phase shift experienced by the acoustic signal. Putting the value of $\mathbf{D}$, ${\mathbf{M}}_{\mathbf{q}}$ can be expressed as,

$$\begin{array}{c}\hfill {\mathbf{M}}_{\mathbf{q}}=\left(\begin{array}{cc}cos\tau cos\delta +{\mathbf{q}}_{-}^{2}sin\tau sin\delta & {\mathbf{q}}_{-}^{2}sin\delta cos\tau -sin\tau cos\delta \\ sin\tau cos\delta -{\mathbf{q}}_{+}^{2}sin\delta cos\tau & cos\delta cos\tau +{\mathbf{q}}_{+}^{2}sin\tau sin\delta \end{array}\right)\end{array}$$

(15)

where

$$\begin{array}{c}\hfill {\mathbf{q}}_{-}^2=\frac{2E_{M}cos(2t-\tau )}{\beta \left(t\right)ck+\omega {\left(t\right)}^{2}ctk}\end{array}$$

(16)

$$\begin{array}{c}\hfill {\mathbf{q}}_{+}^2=-\frac{2E_{M}cos(2t-\tau )}{\beta \left(t\right)ck+\omega {\left(t\right)}^{2}ctk}\end{array}$$

(17)

Using (14), (15) and (17), it is possible to generate a range of values for $\mathbf{q}$, $\delta$ and $\tau$ to represent different underwater scenarios. With the underlying mathematical model representing the flow of acoustic signal through any underwater environment formulated, the next step is to build the channel model.

2.4. Numerical Results

In Figure 2 we present the visualization of the acoustic path bundles and reflections when they are travelling through water. We simulate 3 different scenarios where the transmitter and the receiver are located at different depths, at different heights and at different distances from each other. Scenario 1 is where the receiver is at height 50m from the water-bed and is higher than the transmitter which is located at 10m from the bottom. They are 1Km from each other. Scenario 2 is where the transmitter and the receiver are at same heights of 50m from the bottom and the total water-depth is 500m. The distance between the two communicating nodes is now 2Km. Scenario 3 is where the transmitter and the receiver are separated by 5Km, and the transmitter is at a height higher than the receiver. If the transmitter is at a height lower than the receiver, numerous signal paths and reflections are experienced. With increase in depth, the echoes tend to disappear rendering only few weak direct signal paths. With increase in distance between the transmitter and the receiver, weak signal paths along with a few reflections appear.

3. Designing the UWAC Channel Emulator

Linear Time Varying (LTV) systems are primarily used to characterize UWAC channels owing to their time-varying nature and varying environmental factors affecting the flow of acoustic signal through water. When an acoustic signal travels through water, the signal gets reflected by the surface and bottom of the sea resulting in multiple delayed versions of transmission rays or path bundles. If we have Q number of distinct reflected and refracted rays (echoes) with amplitude $|{\mathbf{M}}_{\mathbf{q}}|$ ($|·|$) represents determinant of a matrix) and delays ${\tau }_{\mathbf{q}}$, then the propagation channel with multiple information paths can be mathematically represented as,

$$\begin{array}{c}\hfill \mathbf{M}(\tau ,t,f)=\sum _{q=1}^Q\left|{\mathbf{M}}_{\mathbf{q}}\right|{\gamma }_{\mathbf{q}}(f,t)\delta (\tau -{\tau }_{\mathbf{q}}\left(t\right))\end{array}$$

(18)

where ${\gamma }_{\mathbf{q}}(f,t)$ is the fading parameter characterizing small scale variations with each path bundle. If ${\gamma }_{\mathbf{q}}(f,t)$ is stationary in time, then we can use the time correlation function to derive the statistical description of ${\gamma }_{\mathbf{q}}(f,t)$,

$$\begin{array}{c}\hfill {\mathcal{R}}_{\mathbf{q}}(f,\mathrm{\Delta }t)=\mathrm{E}\left[{\gamma }_{\mathbf{q}}(f,t){\gamma }_{\mathbf{q}}^{\ast }(f,t)\right]\end{array}$$

(19)

where $\mathrm{E}[·]$ denotes the Expectation operation and ∗ denotes the complex conjugate. In this case, Fourier Transform of ${\mathcal{R}}_{\mathbf{q}}(f,\mathrm{\Delta }t)$ yields the channel Doppler spectrum,

$$\begin{array}{c}\hfill \mathcal{F}\left\{{\mathcal{R}}_{\mathbf{q}}(f,\mathrm{\Delta }t)\right\}=S_{\mathbf{q}}(f,\eta )\propto e^{{-\frac{\left|\eta \right|}{\chi }}^{\xi }}\end{array}$$

(20)

which can be approximated by the stretched exponential distribution. In (20), $\mathcal{F}\{·\}$ denotes discrete Fourier transform (DFT), $\eta$ represents Doppler frequencies, $\chi$ represents how closely the Doppler power spectrum matched to the stretched exponential function and $\xi$ denotes the stretching exponent. Time-domain auto-regressive memory process based generation of stretched exponential spectrum is neither practical nor accurate in representation. This is because, ${\mathcal{R}}_{\mathbf{q}}(f,\mathrm{\Delta }t)$ has no closed form, and its Fourier transform is no longer exponentially distributed. Instead, in our developed platform we generate random processes directly from the Doppler spectrum using the sum-of-sinusoids (SoS) model.

The delay power spectrum of the channel and its frequency correlation function can be expressed as,

$$\begin{array}{c}\hfill {\mathcal{R}}_{\mathbf{M}}\left(\tau \right)=\mathrm{E}\left[\mathbf{M}(t,\tau ){\mathbf{M}}^{\ast }(t,{\tau }^{\prime })\right]=\sum _{q=1}^Q\mathrm{E}\left[\right|{\mathbf{M}}_{\mathbf{q}}\left(t\right){|}^2]\delta (\tau -{\tau }_{\mathbf{q}}\left(t\right))\end{array}$$

(21)

and

$$\begin{array}{c}\hfill \mathrm{E}\left[\mathcal{F}\left\{\mathbf{M}(t,{\tau }^{\prime })\right\}\mathcal{F}\left\{{\mathbf{M}}^{\ast }(t,\tau )\right\}\right]=\frac{1}{2\pi }\sum _{q=1}^Q\mathrm{E}\left[\right|{\mathbf{M}}_{\mathbf{q}}\left(t\right){|}^2]e^{j2\pi (f-f^{\prime }){\tau }_{\mathbf{q}}}\end{array}$$

(22)

respectively, assuming stationarity and uncorrelatedness. The difference between the initial frequency f and the final frequency $f^{\prime }$ defines the amount of frequency correlation. Owing to the uncorrelated nature of ${\tau }_{\mathbf{q}}$, it is possible to calculate each path delay separately. We can then modify (22) in the delay domain to obtain,

$$\begin{array}{c}\hfill S(\tau ,\eta )=\mathcal{F}\left\{\sum _{q=1}^Q\mathrm{E}\left[{\mathbf{M}}_{\mathbf{q}}\left(t\right){\mathbf{M}}_{\mathbf{q}}^{\ast }(t+\mathrm{\Delta }t)\right]\delta (\tau -{\tau }_{\mathbf{q}}\left(t\right))\right\}\end{array}$$

(23)

and from (23), we can obtain $S({\tau }_{\mathbf{q}},\eta )$, the delay-domain scattering of the qth path with respect to Doppler spectrum.

Reflections due to surface, bottom, surface-bottom and surface-bottom-surface combination gives rise to different sets of reflected paths with a range of Rician K-factors. We will therefore use the SoS assumption for generating channel samples with amplitudes that are Rician-distributed. We consider the wide sense stationary uncorrelated scattering (WSSUS) assumption here and therefore we can represent channel samples ${\mathbf{M}}_q\left[i\right]={\mathbf{M}}_q\left[i{T}_s\right]$ to formulate the SoS model,

$$\begin{array}{c}\hfill \mathbf{M}\left[i\right]=\frac{1}{\sqrt{L(1+K)}}\left[\sum _{l=1}^L{e}^{j({\varphi }_l+2\pi f_dıT_S)}+\sqrt{K}{e}^{j({\varphi }_0+2\pi f_0ıT_S)}\right]\end{array}$$

(24)

with time t sampled into intervals of $T_S$, L number of path bundles for each tap, uniformly distributed random phases ${\varphi }_l$ over the interval $[0,2\pi ]$, initial phase ${\varphi }_0$ and L Doppler frequencies $f_d$ within each tap. In (24), K is the Rician K-factor depending on the ratio of signal power over the direct path to that over scattered paths and the direct line-of-sight (LoS) path acquires a Doppler frequency of $f_0$. It is evident that L sets of Doppler frequencies $f_d$ can be selected from Jake’s spectrum such that these $f_d$s, in turn, can be used to generate (24) and the probability density function (pdf) of the range of $f_d$ can be expressed as,

$$\begin{array}{c}\hfill S\left(\eta \right)=\frac{1}{2\chi }{e}^{{-\frac{\left|\eta \right|}{\chi }}^{\xi }}.\end{array}$$

(25)

From (25), the values of $f_d$ can be formulated using the inverse transform sampling lemma [21]. The inverse transform sampling lemma states that if the distribution function of input X is given by $f\left(x\right)$, the cumulative distribution function (cdf), $F\left(x\right)$ will be uniformly distributed over the range $[0,1]$. Consequently, input samples can be generated using $x=F^{-1}\left(\nu \right)$ where $\nu$ is uniformly distributed over the range $[0,1]$, where F denotes the distribution function. Using the above concept, the cdf of the Doppler frequencies $f_d$ can be expressed as,

$$\begin{array}{cc}\hfill f_d& =F^{-1}\left[{\int }_{-\infty }^{f_d}\frac{1}{2\chi }{e}^{{-\frac{\left|\eta \right|}{\chi }}^{\xi }}\mathrm{d}\eta \right]=F^{-1}\left[\frac{1}{2\chi }\mathrm{\Gamma }\left[(1/xi)-{(-f_d/\chi )}^{\xi }\right]\right]\hfill \\ \hfill & =-\chi {\left[\sum _{\mu =0}^{1/\xi -1}(\mu +1)!W\left\{\frac{1}{\mu }{\left(\frac{\mathrm{mod}(2u,1){\xi }^2}{\xi -1}\right)}^{1/\mu }\right\}\right]}^{1/\xi }\hfill \end{array}$$

(26)

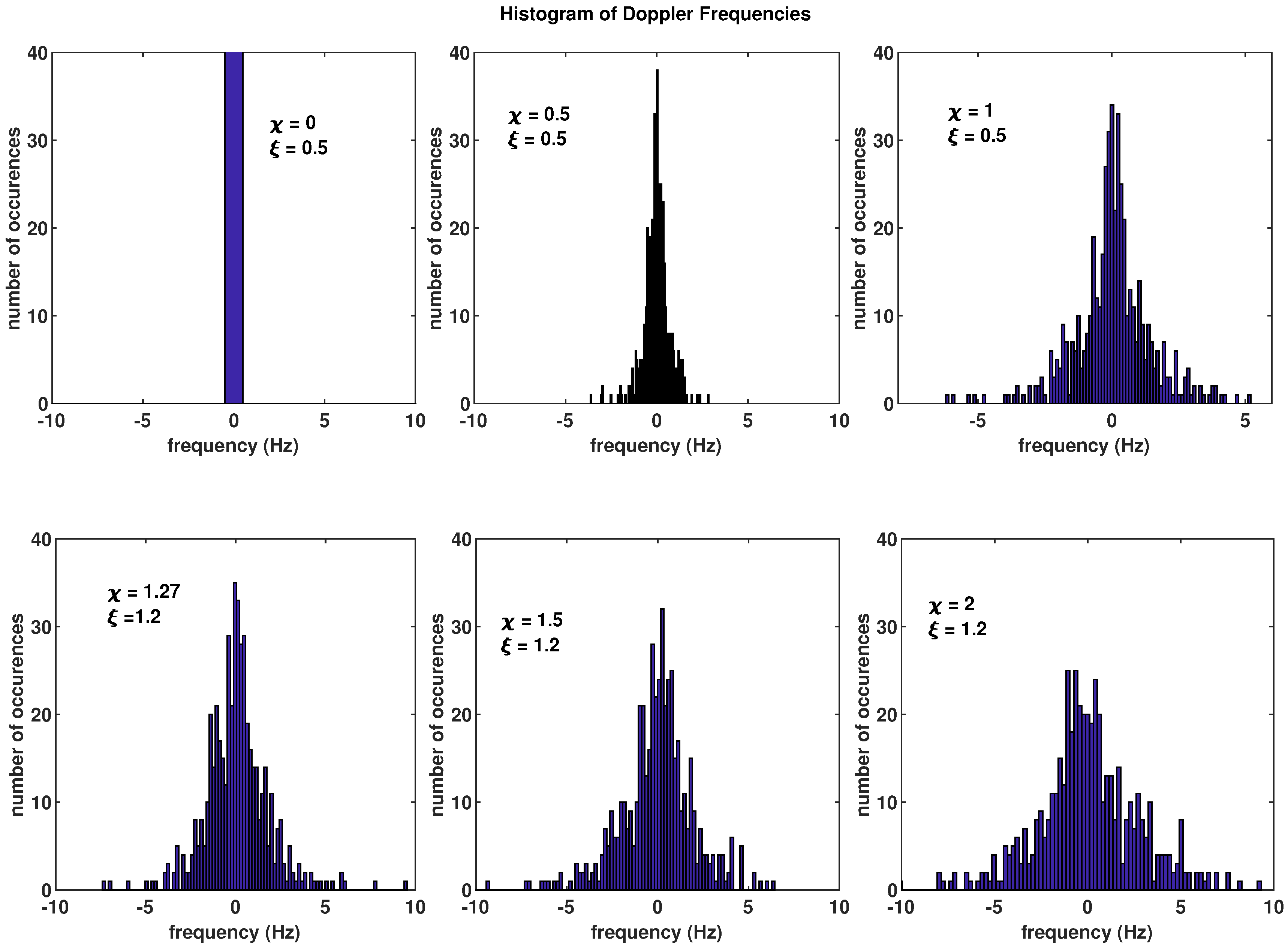
where the obtained $f_d$s are stretched exponentially distributed and mod refers to the modulo operation, W represents the Product-Log or Lambert-W function. It is worth-mentioning here that the ’modulo’ operation returns the remainder after division of $2u$ by 1 and we consider that $u=F\left(f_d\right)$. A range of histograms of the $f_d$s using (25) and (26) is plotted in Figure 3. Using the discrete frequency-selective channel model, the channel impulse response is given by,

$$\begin{array}{c}\hfill \left|\mathbf{M}\right|(t;\tau )=\sum _{q=1}^Q{E_M}_q\left(t\right)\delta (\tau -{\tau }_q\left(t\right))\end{array}$$

(27)

where ${E_M}_q\left(t\right)$ represent the fading coefficients corresponding to the originally formulated Milne energy associated with each path bundle, and $\delta$ represents the delay function quantifying the delay experienced by the qth path . The delay is represented using the $\delta$ function as we are trying to model the infinite bandwidth system. In terms of system implementation, an infinite bandwidth system needs transmit and receive filters for effective functioning.

Here, we consider a combination of pulse-shaping transmit filter with impulse response $g\left(t\right)$, the propagation channel $\left|\mathbf{M}\right|\left(t\right)$ and a matched receive filter, to represent a communication system with complex transmit samples $x_i$ and output signal $z\left(t\right)$. If $z\left(t\right)$ is sampled at intervals which are multiple of T or sampling time $T_s$, the overall communication system embodies a discrete linear time-varying filter constituted of $n=1,2,\cdots ,N$ filter taps. Therefore, such a communication system can be exemplified as a tapped delay line filter model. Towards this end, the filter taps, $h_n\left(\mu T_s\right)$, can be generated using digital filtering that has a sampling rate capable of modelling usable channel bandwidth for the channel model of (27).

These filter taps can be characterized by the following equation,

$$\begin{array}{cc}\hfill h_n\left[\mu \right]=\sum _{q=1}^Q\sqrt{\frac{|{\mathbf{M}}_q|}{L(1+K)}}& [\sum _{l=1}^{L}g(n{T}_s-{\tau }_q)e^{j({\varphi }_{l,q}+2\pi h_{l,q}(\mu T_s-{\tau }_q))}\hfill \\ \hfill & +\sqrt{K}g(n{T}_s-{\tau }_0)e^{j({\varphi }_{l,q}+2\pi h_{l,q}(\mu T_s-{\tau }_0))}]\hfill \end{array}$$

(28)

where ${\tau }_0$ is the initial delay and $|{\mathbf{M}}_q|$ are average power levels observed over Q path bundles. If we want to account for the drift velocity v between the transmit and the receive terminals in an underwater environment, (28) gets modified to,

$$\begin{array}{cc}\hfill h_n\left[\mu \right]=\sum _{q=1}^Q\sqrt{\frac{|{\mathbf{M}}_q|}{L(1+K)}}& [\sum _{l=1}^{L}g((\mu -n+a\mu )T_s-{\tau }_q)e^{j({\varphi }_{l,q}+2\pi h_{l,q}(a\mu T_s-{\tau }_q))}\hfill \\ \hfill & +\sqrt{K}g((\mu -n+a\mu )T_s-{\tau }_0)e^{j({\varphi }_{l,q}+2\pi h_{l,q}(a\mu T_s-{\tau }_0))}]\hfill \end{array}$$

(29)

where $t+vt/c=(1+a)t$, $c\sim 1500$ m/s, and a is the Mach number.

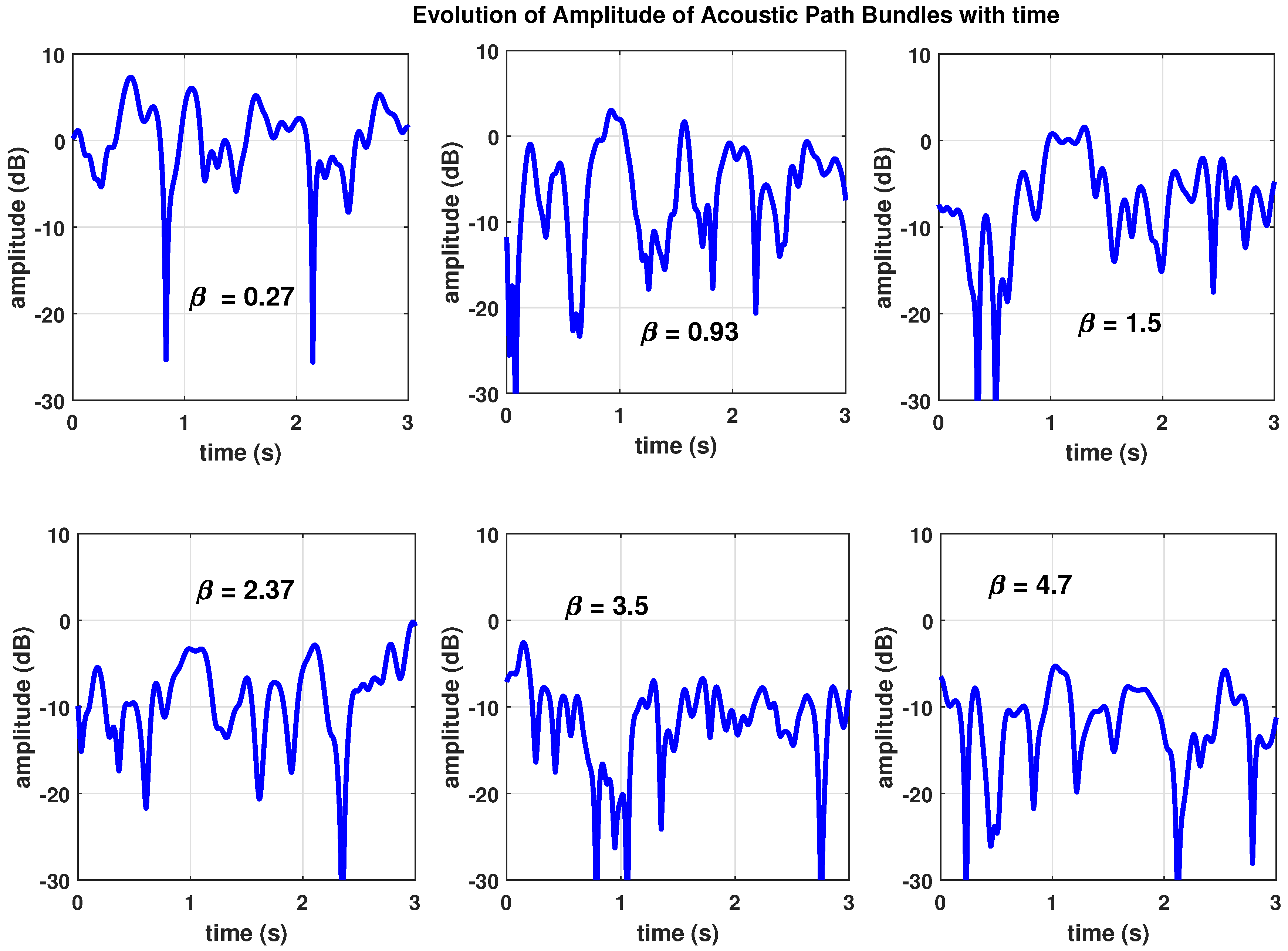
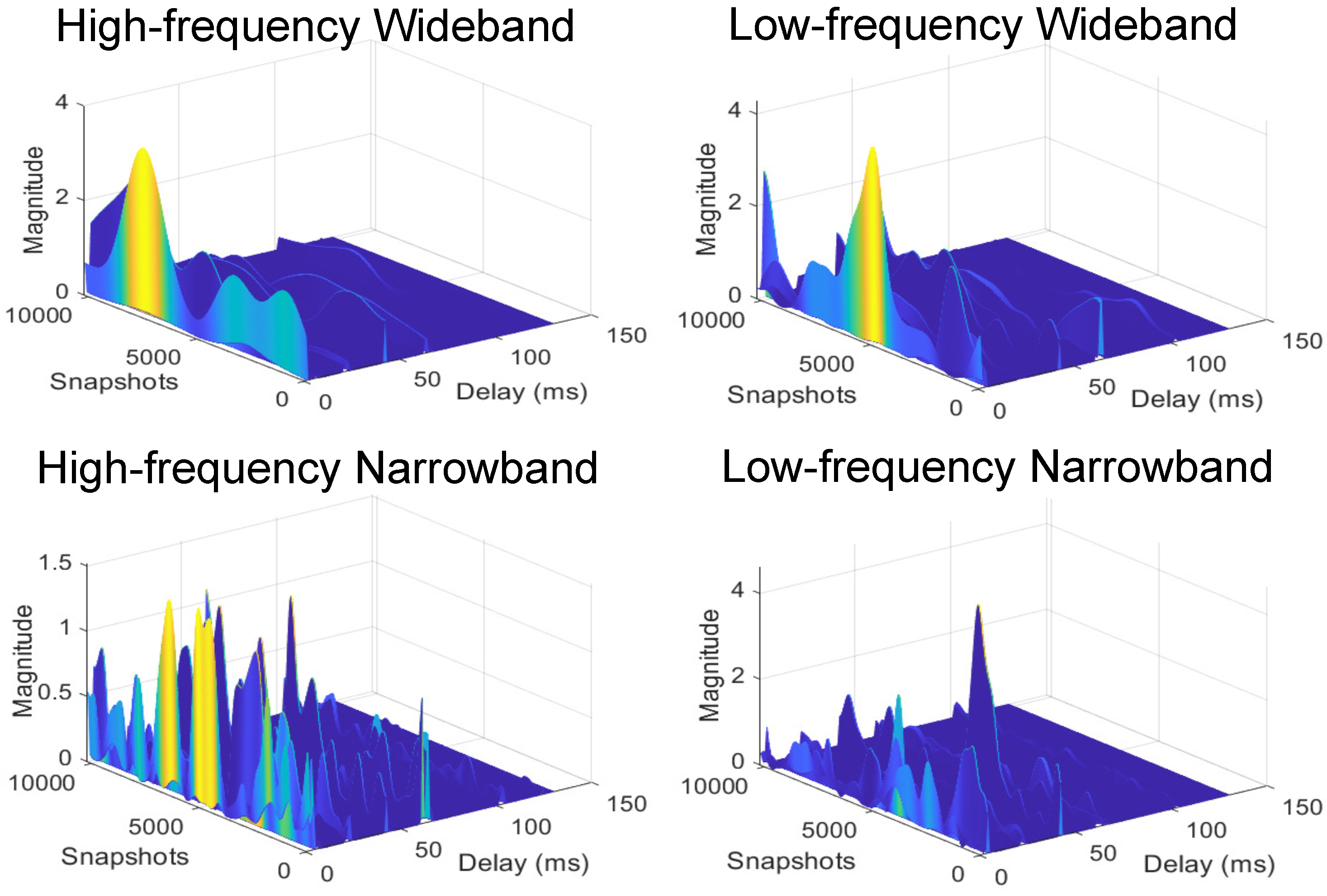
The concept of Mach number is introduced to represent the time-stretching or Doppler shift i.e., the time period t expands to $(t+vt/c)$. Now, here N is an important factor in the emulator design as it offers a trade-off between computational complexity and model stationarity. A sample set of trajectories generated over a 3-second interval and $L=1000$, $K=3$, $\xi =1.2$ is presented in Figure 4. We have also included the corresponding Doppler frequency distribution, Doppler power spectrum and temporal coherence in Figure 4. It is noted here that seldom practical measurements from trial match the WSSUS assumption for underwater propagation channels. However, in our work, we derive the amplitude of paths/echoes of travelling sound waves, delays experienced and other relevant parameters directly from the concept of physics. These concepts are directly derived from mathematical description of how acoustic waves travel through water and how water interacts and influences that flow of acoustic waves. Therefore, it is possible to identify time periods and bandwidth within which the WSSUS assumption is valid [22]. Accordingly, it is possible to determine an observation time $T_d$, over which, the auto-correlation function of $\left|\mathbf{M}\right|(t,\tau )$, ${\mathcal{R}}_{\mathbf{M}}(t,\mathrm{\Delta }\tau )$ is stationary with constant mean value. Also, we can define an observation bandwidth $B_d$, within which, the frequency auto-correlation function, ${\mathcal{R}}_{\mathbf{M}}(f,\mathrm{\Delta }t)$ is stationary.

Special Note on Measurement Campaign

We are currently in the process of collecting UWAC channel measurements in coastal and estuarine environments around Ireland and Wales as part of the project STREAMS1. In STREAM, we are deploying underwater sensors to gather valuable information on temperature, rainfall, wind, marine nutrients, oxygen content and phytoplankton abundance. However, as a part of deploying underwater sensor networks, we are also collecting propagation channel information in the underwater environment for communication among acoustic sensors using acoustic signals. This measurement campaign is ongoing at the time of writing this paper and therefore could not be reported here. In future, the model and emulator developed in this paper will be validated against the measurements collected in the STREAM project.

4. Results and Discussion

Using (29), the channel representation is implemented in Matlab Simulink to develop the channel emulator. Separated Matlab functions are used to generate programmable path amplitudes $|{\mathbf{M}}_{\mathbf{q}}|$, delays ${\tau }_{\mathbf{q}}$, phase-shifts ${\varphi }_{l,q}$, Doppler shift, Doppler frequencies. A block diagram of the Simulink platform for the channel emulator is shown in Figure 5. The Simulink platform code can be easily adapted to Register Transfer Level (RTL) code and Joint Test Action Group (JTAG) co-simulations and can be ported to the Field Programmable Gate Arrays (FPGAs) platform for hardware implementation. The emulator has further capabilities of taking in data symbols, filtering, sampling, up-converting and down-converting signals for being processed through the emulator. Example plots for channel responses over narrowband and wideband channels are provided in Figure 6.

5. Conclusions

In this paper, a novel channel model is proposed for UWAC systems to describe the underwater acoustic channel characteristics using the concepts of damped harmonic oscillators, parametric oscillators, Doppler shifts and spreads, and SOS models. Based on the proposed model, a channel emulator is developed using the Simulink platform and block-sets which can be used to generate practical UWAC links. The proposed emulator accounts for both time and delay domain variations in the channel and consequently, will be able to offer realistic prediction of the performance of different channel estimation, precoding and detection algorithms. The Simulink model developed can be easily extended to other platforms, coding techniques and co-simulations for tractable hardware implementation. If needed, details on other physical processes like pathloss, shadowing, surface motion, absorption etc. can also be included in the proposed emulator just by adding Simulink block-sets.