Preprint
Article
Applications of Semi-Structured Complex Numbers in Science and Engineering
Altmetrics
Downloads
290
Views
128
Comments
0
This version is not peer-reviewed
Submitted:
19 March 2023
Posted:
21 March 2023
You are already at the latest version
Alerts
Abstract
Recently, a paper was written to reformulate and strengthen the theory of semi-structured complex numbers H (a new number set invented to enable division by zero). Whilst the paper had profound results, the application of this number set in many areas of engineering and science has not been fully explored. Consequently, the aim of this paper was to establish the number set H as a useful mathematical tool by providing an amalgam of results arising from its application in several areas of engineering and science. In the process, this paper makes four major contributions: these are (1) determining the product of the gradients of a horizontal and vertical line; (2) developing new Euler formulas relating exponential, trigonometric and hyperbolic functions in the 3D semi-structured complex number Euclidean space; (3) establishing semi-structured complex numbers as a better extension of the complex number set than quaternions; (4) resolving singularities that may arise in engineering and science equations (because of division by zero) to develop reasonable conclusions in the absence of experimental data. These results and their applications provide a firm foundation to advance the number set H as a useful mathematical tool.
Keywords:
Subject: Engineering - Automotive Engineering
1. Introduction
1.1. Semi-Structured Complex Numbers: A Recent Development in Division by Zero
Recently there has been a range of research involving division by zero. Table 6, Appendix 1, shows sample research conducted from 2018 to 2022 on “division by zero” including using division by zero to explain cancer development on the most fundamental level.
The problem of division by zero can simply be stated as: What is where “a” is any complex number. There have been several solutions to the problem the most recent being the invention of the semi-structured complex number set [1]. The first attempt at creating this number set was riddled with issues [1], however, a second paper [2] was written to reformulate and strengthen the theory of semi-structured complex numbers and in the process produced several profound results. Table 1 shows the major results developed in paper [2].
Results 1 to Result 9 in Table 1 provide some significant foundational results for semi-structured complex numbers. Nevertheless, it is necessary to go beyond just the foundational setting and look at how this new number set can be applied in a practical setting particularly in the areas of science and engineering where real world problems are constantly being discovered and solved using mathematical tools. In this paper, several possible areas for the application of semi-structured complex numbers can be considered and examined in brief. Since semi-structured complex numbers can be represented geometrically, then the obvious starting point for establishing it as a viable mathematical tool for solving real world problems is to consider its application in trigonometry and geometry including lines, angles, and transformations such as rotations.
1.2. Semi-Structured Complex Numbers and Trigonometry
Since semi-structured complex numbers can be represented by points in a 3-dimensional Euclidean -space [2] (Result 6 in Table 1), it is only a natural progression to explore the use of semi-structured complex numbers in the area of trigonometry. Trigonometry is integral in examining the properties of real-world systems in science and engineering. For example, trigonometry is used in calculus, signal processing [3], calculating angles and forces in architecture and construction [4], various fields such as engineering, medicine, economics, architecture, space science, electronics, statistics, and pharmacology [5]. Demonstrating the use of semi-structured complex numbers in obtaining even one significant result in trigonometry would provide a solid justification for the application of these numbers in solving real-world problems.
1.3. Semi-Structured Complex Numbers and Euler’s Formula
Again from Result 6 in Table 1 semi-structured complex numbers are 3D numbers that can be represented in the real-imaginary-unstructured space (-space) as shown in Figure 1.
This space can be dividing into three planes, the real-imaginary plane (-plane), the real-unstructured plane (-plane) and the imaginary-unstructured plane (-plane) as shown in Figure 2, Figure 3 and Figure 4.
Leonhard Euler (1707–1783) developed formulas for examining complex numbers plotted on a cartesian graph [2] and established a relationship between exponential and trigonometric functions. This relationship is expressed as Euler’s formula [3] and is shown in Equation (3).
From Equation (3), is the modulus of the complex number and is the angle that the complex vector makes with the -axis along the real-imaginary plane (-plane). This angle is called the principal argument of the complex number .
According to Result 3 in Table 1 complex numbers are a subset of semi-structured complex numbers and are represented on the real-imaginary plane (-plane). This implies that perhaps some version of Euler’s Formula exists for the other two planes, the real-unstructured plane (-plane) and the imaginary-unstructured plane (-plane). If these other Euler Formulas can be derived, then this can be used as a starting point for examining the use of semi-structured complex numbers in all areas that the Euler’s formula is used in. Using semi-structured complex numbers to extend the Euler formulas would necessarily mean a greater degree of freedom in solving real world problems. Nevertheless, very little work has been done to explore this possibility.
1.4. Semi-Structured Complex Numbers, Quaternions, and Rotations
Semi-structured complex numbers are not the only number set that has been proposed to extend the complex number set. Another number set call the quaternions has been proposed and has proven to be extremely useful particularly in situations that involve 3-dimensional rotation [6]. These situations include 3D image processing [7] and robotics [6]. If semi-structured complex numbers are to be proven to be a viable extension to the complex number set and a viable mathematical tool for solving real world problems, then it should be, for the very least, as useful as quaternions.
An example of the usefulness of quaternions can be seen in their ability to represent rotations in a simplified manner. This has led to easily solving such problems as the gimbal lock problem [8].
A gimbal is a ring that is suspended so it can rotate about an axis. Gimbals are typically nested one within another to accommodate rotation about multiple axes as shown in Figure 5 (a). They appear in gyroscopes and in inertial measurement units to allow the inner gimbal’s orientation to remain fixed while the outer gimbal suspension assumes any orientation. Gimbal lock occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space as shown in Figure 5 (b)
Mathematically, gimbal rotation is usually measured by three rotational Euler angles (one for each three-dimensional axis). Gimbal lock occurs because there are some orientations of the gimbals where not every change in the rotation can be realized by a change in the Euler angles.
To solve the gimbal lock problem the modern practice is to avoid the use of Euler angles entirely. Developers of 3D computer programs, such as 3D modelling, embedded navigation systems, and video games avoid this by using quaternions to calculate the necessary rotations. For example, in the context of inertial systems, instead of using gimbals, inertial sensors are mounted directly to the body of the system and quaternions are used to derive the orientation and velocity of the body and digitally calculate the body’s rotation and acceleration. Using quaternions in rotation has proven to be very efficient as rotations can be represented using a single simple equation rather than a matrix of several rotational angles.
Therefore, if semi-structured complex numbers are to be a viable extension to the complex number set, they must not only be able to be used to solve real world problems just as well as quaternions, but they must also provide some advantage over quaternions. However, comparing the pros and cons of the two number sets has not been done in recent literature.
1.5. Semi-Structured Complex Numbers and Mathematical Singularities
In science and engineering mathematical equations are used to describe physical systems. Many mathematical equations describing physical systems have singularities. A mathematical singularity, a point at which a given mathematical object is not defined or not "well-behaved" (usually because of division by zero). For example, consider the equation where . In the past, this equation becomes a singularity because no interpretable result can be obtained from the equation at this point. Such situations limit the information that can be gained from equations at potentially critical points.
It is worth noting that, these singularities themselves are not physically real but arise from idealized assumptions made about a physical system. When a singularity happens in a mathematical solution, it means that the assumptions made in the calculations have gone as far as the available math can take it. This illustrates the fact that all singularities are artefacts of using a theory outside its range of applicability. Nevertheless, the existence of singularities in equations makes it difficult to resolve reality with mathematical descriptions. Singularities in physics usually (but not only) arise because of division by zero. It would be useful if such singularities can be resolved to agree with physical observations.
With the development of semi-structured complex numbers, it is possible to provide solutions that agree with experimental data in such situations. The application of semi-structured complex numbers can also possibly be used to provide reasonable interpretations to equations with mathematical singularities in instances where experimental data may not be available. This would provide scientists and engineers the ability to improve their solutions to problems that currently seem intractable because of these singularities. However, evidence that semi-structured complex numbers can provide such a freedom is currently not forthcoming and is worth exploring.
1.6. Major Contributions of This Paper
Given the potential importance of the unexplored uses of semi-structured complex numbers, the aim of this paper was:
To establish semi-structured complex numbers as a useful mathematical tool by providing several useful results arising from the application of this number set to different situations in the field of engineering and science.
- Based on the stated aim, this paper makes the following major contributions: In the field of trigonometry, this paper shows that semi-structured complex numbers can be used to find the product of the gradient of a horizontal and vertical line and in the process developed the following theorem: “The product of the gradient of two perpendicular lines is 1 when the lines are parallel to the coordinate axis of the Cartesian plane in which they reside and—1 otherwise”.
- This paper showed that whilst semi-structured complex numbers can be used to solve the same problems that quaternions are normally used for, semi-structured complex numbers also have several added advantages, including, being a useful tool for solving division by zero problems, being commutative (reducing the complexity of calculations when using this number set) and being able to be represented as both a three-dimensional and four-dimensional vector.
- In this paper, two new Euler formulas are developed and when combined with the original Euler formula describes the relationship between trigonometric, hyperbolic, and exponential functions for the entire semi-structured complex Euclidean xyz-space. These Euler formulas are given in Table 2.
- Semi-structured complex numbers can be used to resolve mathematical singularities in a manner that supports experimental data. The application of semi-structured complex numbers can also be used to provide reasonable interpretations to equations with mathematical singularities in instances where experimental data may not be available.
The rest of this paper is devoted to providing a detailed explanation of how the major contributions outlined were arrived at.
2. Semi-Structured Complex Numbers and Trigonometry: The Product of the Gradients of a Horizontal and Vertical Line
It is well known that the product of the gradient of two perpendicular lines is. This is stated in Theorem 1.
| Thereom1: For two perpendicular lines and with gradients and respectively, the following holds: . |
The above theorem has been proven true in all cases expect one; where one line is perfectly horizontal, and the other is perfectly vertical relative to the coordinate system in which the lines reside. First, it is important to note that the gradient of a line can be calculated using the anticlockwise angle the line forms with the -axis; that is, for a line that forms an anticlockwise angle to the -axis, the gradient of the line is given as
For a perfectly horizontal line the gradient is zero, that is and for a perfectly vertical line (a line at radians to the -axis) the gradient was formerly considered undefined; that is, . Therefore, it was previously thought to be impossible to find the product of the gradients of a vertical and horizontal line.
In this research, this issue was resolved using semi-structured complex numbers, and, in the process Theorem 1 was restated. Using semi-structured complex numbers, the product of gradient of a horizontal and vertical line can be found as follows:
| Gradient of a horizontal line is (It is noted from paper [2] that from a transformation standpoint and hence ) Gradient of a vertical line is Therefore, the product of the gradients is: (since, from paper [2], ) |
Hence the product of the gradients of a vertical and horizontal line is 1. To rewrite Theorem 1, it must first be noted that the horizontal line is parallel to the horizontal axis of the coordinate system from which the gradients are measured, and the vertical line is parallel to the vertical axis of the coordinate system from which the gradients are measured. It must also be noted that the gradient of the line is always calculated from the axis that make up the coordinate space in which the line resides. Hence with these two points, Theorem 1 can be restated as follows:
| Thereom1: The product of the gradient of two perpendicular lines is 1 when the lines are parallel to the coordinate axis of the Cartesian plane in which they reside and otherwise. |
The fact that the equation linking the gradient of perpendicular lines can be extended to lines that are parallel to the coordinate axis of the cartesian plane in which they lie is very useful in topics such as conformal mapping and other topics involving transformations from one topological space to another.
3. Deriving the Euler Formulas for Semi-Structured Complex Euclidean -Space
3.1. Euler’s Formula for the Real-Imaginary -Plane
Euler’s formula for the real-imaginary -plane is well known and establishes a relationship between exponential and trigonometric functions. Euler’s formula for the real-imaginary plane (-plane) can be written in terms of semi-structured complex numbers as shown by Equation (5).
Equation (5) can be interpreted as saying that the function is a unit semi-structured complex number that traces out the unit circle in the real-imaginary xy-plane as goes from to . Here is the angle (in radians) that a vector connecting the origin with a point on the unit circle makes with the positive real axis, measured counter-clockwise as shown in Figure 6. The derivation for Equation (5) is given in Appendix 2.
3.2. Euler’s formula for the real-unstructured -plane
The general form of a semi-structured number is represented by . The unit semi-structured complex number that parameterizes the real-unstructured -plane can be represented by Equation (6) where .
An Euler formula that expresses Equation (6) in polar coordinates can be developed for the real unstructured plane (-plane) and is given by Equation (7).
Proof of Euler’s formula for the real-unstructured plane (-plane) is given in Appendix 3. Clearly, by comparing Equation (6) and Equation (7) it can be seen that and .
Equation (7) can be interpreted as saying that the function is a unit semi-structured complex number representing a vector tracing out a unit circle in the real-unstructured plane as goes from to . Here is the angle (in radians) that a vector connecting the origin with a point on the unit circle makes with the positive real axis, measured counter-clockwise as shown in Figure 7.
3.3. Euler’s Formula for the Imaginary-Unstructured -Plane
The general form of a semi-structured number is represented by . The unit semi-structured complex number that parameterizes the imaginary-unstructured -plane can be represented by Equation (8) where .
Euler formulas can be developed for the imaginary-unstructured plane (-plane) and is given by Equation (9). Proof of Euler’s formula for the imaginary-unstructured plane (-plane) is given in Appendix 4.
There are two points to note about Equation (9). First, the Euler formula for the imaginary-unstructured -plane gives a relationship between exponentials and the hyperbolic functions. This is different from the first two Euler formulas that deal with exponentials and trigonometric functions.
Secondly, Equation (9) is a compact way of describing two different representations of Equation (8). For example, if Equation (9) is multiplied by this gives Equation (10):
Clearly, by comparing Equation (8) and Equation (10) it can be seen that and . However, Equation (9) can also be multiplied by to give Equation (11).
In this case, by comparing Equation (8) and Equation (11) it can be seen that and .
Since both Equation (10) and Equation (11) are considered legitimate representations of the semi-structured complex number in the -plane, Equation (9) is therefore considered the primary Euler formula for the -plane. Figure 8 and Figure 9 provide an interpretation for Equation (10) and Equation (11) respectively.
From Equation (5), Equation (7) and Equation (9) the Euler formulas for entire semi-structured complex Euclidean -space can be summarized as shown in Table 3.
The Euler formulas presented in Table 3 can be used to extend the range of analysis that can be done in the fields of signal processing, image processing, complex analysis, quantum mechanics and any other subject in which Euler formulas are used and division by zero needs to be solved.
4. Comparing Rotations via Quaternions and Semi-Structured Complex Numbers
Having dealt with line and angles, it is instructive to look at the use of semi-structured complex numbers in transformations such as rotations. In 3D space, according to Euler’s rotation theorem [9], any rotation or sequence of rotations of a rigid body or coordinate system about a fixed point is equivalent to a single rotation by a given angle about a fixed axis (called the Euler axis) that runs through the fixed point. The Euler axis is typically represented by a vector . Therefore, any 3D rotation can be represented as a combination of a vector and an angle . Both quaternions and semi-structured complex numbers can provide a very simple way of encoding this axis-angle representation. However, even though semi-structured complex numbers provide more advantages than quaternions, the semi-structured complex numbers method for producing rotations has not been explored. Here both methods for representing 3D rotations are presented.
4.1. Representing Axis-Angle Rotations with Quaternions
Consider a rotation of angle around an axis defined by unit vector where is given by:
Here are real numbers such that and are quaternion basis units. The unit vector can be represented by a quaternion using an extension of Euler’s formula (Equation (5)) as shown in Equation (13).
It can further be shown that the desired rotation can be applied to an ordinary vector in 3D space (here are real numbers). The vector is considered a quaternion with a real coordinate equal zero. The operation used to carry out this rotation resulting in a new rotated vector called the “conjugation operation” (which utilizes quaternion multiplication) is given by Equation (14).
An example of the use of Equation (14) is given in Appendix 5. The advantage of using quaternions is that it represents a rotation in an extremely simple manner. This is why they are normally used in rotations for graphics, accelerometers, and robotics.
1.2. Representation of Axis-Angle Rotation with Semi-Structured Complex Numbers
Semi-structured complex numbers can also be used to produce rotations. Their representation of a rotation is just as simple as that of quaternions. To rotate an ordinary vector about a rotational axis unit vector by an angle around the axis in 3D Euclidean semi-structured space, Equation (15) can be used (here are real numbers and are the semi-structured complex basis units). Equation (15) is called the Rodrigues Rotation Formula [26]. The representation and calculations are just as simple as with quaternions. An example of the use of semi-structured complex numbers to solve a rotation problem is given in Appendix 6.
Where:
Both quaternions and semi-structured complex numbers have very simple forms. This implies that semi-structured complex numbers are just as good as quaternions in producing simple calculations. However, semi-structured complex numbers have certain advantages over quaternions. The two number sets are compared in Table 4.
Clearly from Table 4, semi-structured complex numbers present some advantages over quaternions possibly establishing semi-structured complex numbers as a better extension to the complex number set.
5. Resolving Singularities in Science and Engineering Equations
5.1. Singularities in Equations Produced by Division by Zero
Singularities in science and engineering often arise because of division by zero or sometimes by raising variables to the zeroth root (that is, division by zero indices). In some cases when these situations arise simple experiments can be done to resolve these issues.
As an example, consider a simple pendulum released in zero gravity. The period (T) of the pendulum is given by Equation (16) where is the length of the pendulum and is the acceleration due to gravity.
When this gives . This results in a division by zero which makes the equation (according to standard algebra) undefined. Fortunately, several experiments [10] have been done to determine what happens to the pendulum when released in zero gravity.
It was found that the pendulum simply did not swing. This implies that in zero gravity, the pendulum had no period. That is, implies . In the absence of the experiment, Equation (16) could not be interpreted to give an answer. However, this can be done with semi-structured complex numbers, as shown below:
| Consider the equation for the period (T) of the pendulum when . From [2] . This implies: (the minus sign here can be ignored) |
(17) |
Hence using semi-structured complex numbers, implies which agrees with experimental results.
There are many other similar situations in which semi-structured complex numbers can be applied to equations to resolve division by zero to produce experimentally verifiable results. Table 5 gives examples of this.
The advantage of being able to resolve singularities in such equations is that one can confidentially resolve singularities (resulting from division by zero) in equations where experimental data is difficult or impossible to obtain. For example, consider the equation of a non-rotating blackhole shown in Equation (18).
This equation measures the distance between two events in space-time at a distance from the centre of the blackhole. This measurement is done considering the curvature of space-time produced by the blackhole given by . Semi-structured complex numbers can be used to resolve this equation when ; that is, semi-structured complex numbers can be used to determine how to measure the distance between two events at the centre of a blackhole. This is given below:
| Consider Equation (18) for distance between two events in space-time at the centre of a blackhole; that is, when . |
(19) |
Equation (19) implies that the distance between two events at the centre of a blackhole is unaffected by the curvature of space produced by the blackhole. The centre of a blackhole can be essentially treated as flat space-time (since the curvature factor disappears). This is a reasonable interpretation (produced by semi-structured complex numbers) of what happens at the centre of a blackhole in the absence of experimental data.
5.2. Singularities in Equations Produced by Raising to the Zeroth Root
Sometimes singularities may arise in science and engineering because variables may be raised to the power of . This is essentially the zeroth root of a variable. Incidentally Euler formulas shown in Table 3 can also be used to find the zeroth root of any number.
Suppose it is necessary to find the zeroth root of the semi-structured number h; that is, . By definition .Hence can be rewritten as . From standard algebra it is known that . Hence using this result and the second Euler formula shown in Table 3, this gives Equation (20).
Equation (20) can be used to find the zeroth root of a real number; that is, where (where is a real number). This is shown below.
|
Problem: Find the zeroth root of 2 and show this lies on a unit circle in the -plane. Solution: Replacing with in Equation (20) gives Equation (21). (21)The zeroth root of x = 2 is shown below: Also, zeroth root of x = 2 lie on the unit circle since . |
(21) |
Assuming that the arguments of and are in radians, Equation (21) implies that the zeroth root of a real number lies on the unit circle in the real-unstructured -plane. Additionally, because and are cyclic in nature, Equation (21) also implies that the zeroth root of a real number is not unique to that number. As a general note, if is a real number, then another real number has the same zeroth root as t (here k is some integer value). Appendix 7 provides further explanation on this point.
The ability to use semi-structured complex numbers to resolve equations with singularities (arising from division by zero or raising variables to the zeroth power) can provide scientist and engineers with outcomes that can be used to draw reasonable conclusions in the absence of experimental data. This is particularly useful in the case where such data is difficult or impossible to obtain. This is also particularly useful where innovations need to be developed.
6. Discussion
Several uses of semi-structured complex numbers have been presented in this paper to provide a very strong case of the use of these number set as a mathematical tool in science and engineering. There are many other useful cases of semi-structured complex numbers that have not been examined in this paper. It suffices at this point to emphasise that this number set can possibly extend the amount of analysis that can be done in several fields of engineering and science. It is also noteworthy that semi-structured complex numbers do present some advantages over contenting numbers set such as quaternions. This does not negate the usefulness of quaternions, but it does strengthen the need to continue to explore semi-structured complex numbers as a substantial mathematical tool.
Mathematics not only underpins engineering and science but other fields of study like economics and medicine. Consequently, the potential uses of semi-structured complex numbers in these other fields is worth examining.
7. Conclusions
The aim of this paper was to establish semi-structured complex numbers as a useful mathematical tool by providing several useful results arising from the application of this number set to different situations in the field of engineering and science. This paper made five major contributions to advance research in the topic of semi-structured complex numbers. These contributions include (1) determining the product of the gradients of a horizontal and vertical line; (2) developing new Euler formulas relating exponential, trigonometric and hyperbolic functions in the 3D semi-structured complex number Euclidean space; (3) establishing semi-structured complex numbers as a between extension of the complex number set than quaternions (4) resolving singularities that may arising in engineering and science equations that may arise because of division by zero to develop reasonable conclusions in the absence of experimental data. These contributions establish semi-structured complex numbers as a viable tool in the fields of engineering and mathematics.
Appendix
Appendix 1. Research conducted from 2018 to 2022 involving division by zero
Table 6.
Research conducted on division by zero from 2018 to 2022
| Research | Research Aim |
| [11,12,13] | Explores the application of division by zero in calculus and differentiation |
| [14] | Uses classical logic and Boolean algebra to show the problem of division by zero can be solved using today’s mathematics |
| [15] | Develops an analogue to Pappus Chain theorem with Division by Zero |
| [16] | This paper proposes that the quantum computation being performed by the cancer cell at its most fundamental level is the division by zero. This is the reason for the insane multiplication of cancer cells at its most fundamental scale. |
| [17] | Explores evidence to suggest zero does divide zero |
| [18] | Considered using division by zero to compare incomparable abstract objects taken from two distinct algebraic spaces |
| [19] | Show recent attempts to divide by zero |
| [20] | Generalize a problem involving four circles and a triangle and consider some limiting cases of the problem by division by zero. |
| [21] | Paper considers computing probabilities from zero divided by itself |
| [22,23] | Considers how division by zero is taught on an elementary level |
| [24] | Develops a method to avoid division by zero in Newton’s Method |
| [25] | This work attempts to solve division by zero using a new form of optimization called Different-level quadratic minimization (DLQM) |
Appendix 2. Derivation of Euler’s Formula for the real-imaginary xy-plane

Appendix 3. Derivation of Euler’s Formula for the real-unstructured xz-plane

Appendix 4. Derivation of Euler’s Formula for the real-unstructured -plane

Appendix 5. Example of the use of quaternions

Appendix 6: Using of semi-structured complex numbers to produce rotations with the Rodrigues Rotation Formula.

Appendix 7: The zeroth root of a real number is not unique

References
- P. Jean Paul and S. Wahid, "Unstructured and Semi-structured Complex Numbers: A Solution to Division by Zero.," Pure and Applied Mathematics Journal 2021, 10, 49–61.
- P. Jean Paul and S. Wahid, "Reformulating and Strengthening the theory of Semi-strucutred Complex Numbers," International Journal of Applied Physics and Mathematics 2022, 12, 34–58.
- . Z.-Q. Wang, K. . Z.-Q. Wang, K. Tan and D. Wang, "Deep learning based phase reconstruction for speaker separation: A trigonometric perspective," IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2019, 71–75.
- S. Husain, J. Rana and R. Pandey, "A brief description on the functions of trigonometry," ACADEMICIA: An International Multidisciplinary Research Journal 2021, 11, 115–123.
- Byju’s Future School, "The Applications of Calculus in Everyday Life (Uses & Examples)," Byju’s Future School, 2021 12 2021. [Online]. Available: https://www.byjusfutureschool.com/blog/the-application-of-calculus-in-everyday-life/#:~:text=Although%20it%20may%20not%20always,from%20the%20use%20of%20calculus.. [Accessed 28 6 2022].
- Sarabandi, S. , & Thomas, F., "A survey on the computation of quaternions from rotation matrices," Journal of Mechanisms and Robotics 2019, 11.
- Chen, Y. , Xiao, X. , & Zhou, Y., "Low-rank quaternion approximation for color image processing," IEEE Transactions on Image Processing 2019, 29, 1426–1439. [Google Scholar]
- Mansur, V. , Reddy, S., Sujatha, R., & Sujatha, R., "Deploying Complementary filter to avert gimbal lock in drones using Quaternion angles," 2020 IEEE International Conference on Computing, Power and Communication Technologies (GUCON) 2020, 751–756.
- Gothen, P. , & Guedes de Oliveira, A., "On Euler’s Rotation Theorem," The College Mathematics Journal 2022, 1–6.
- CNTV, Director, Experiment 2: demonstration of simple pendulum movement. [Film]. China: Hi China, 2013.
- S. Pinelas and S. Saitoh, "Division by Zero Calculus and Differential Equations," in Differential and Difference Equations with Applications: ICDDEA, Amadora, Portugal, 2018.
- S. Saitoh, "Introduction to the division by zero calculus," in Scientific Research Publishing, Inc, USA, 2021.
- H. Okumura, "The arbelos in Wasan geometry: Atsumi’s problem with division by zero calculus," Sangaku Journal of Mathematics 2021, 5, 32–38.
- Barukčić, "Classical logic and the division by zero," International Journal of Mathematics Trends and Technology IJMTT 2019, 65, 31–73.
- H. Okumura, "An Analogue to Pappus Chain theorem with Division by Zero," In Forum Geom 2018, 18, 409–412.
- M. P. Lobo, "Cancer: Division by Zero," Open Journal of Mathematics and Physics 2020, 2, 5.
- M. P. Lobo, "Does zero divide zero," Open Journal of Mathematics and Physics 2020, 2, 3.
- J. Czajko, "On unconventional division by zero," World Scientific News 2018, 99, 133–147.
- H. Okumura, "Is It Really Impossible To Divide By Zero," J Appl Math 2018, 27, 191–198.
- H. Okumura, "A four circle problem and division by zero," Sangaku Journal of Mathematics 2020, 4, 1–8.
- W. Mwangi, "Definite Probabilities from Division of Zero by Itself Perspective," Asian Journal of Probability and Statistics 2020, 6, 1–26.
- J. Dimmel and E. Pandiscio, "When it’s on zero, the lines become parallel: Preservice elementary teachers’ diagrammatic encounters with division by zero," The Journal of Mathematical Behavior 2020, 58, 1–27.
- F. Karakus and B. Aydin, "Elementary Mathematics Teachers’specialized Content Knowledge Related To Division By Zero," Malaysian Online Journal of Educational Sciences 2019, 7, 25–40.
- Abdulrahman, "A Method to Avoid the Division-by-Zero or Near-Zero in Newton-Raphson Method," Feburary 2022. [Online]. Available: https://www.researchgate.net/publication/358857049_A_Method_to_Avoid_the_Division-by-Zero_or_Near-Zero_in_Newton-Raphson_Method. [Accessed 28 April 2022].
- Y. Zhang, Y. Y. Zhang, Y. Ling, M. Yang and M. Mao, "Exemplar Different-Level Quadratic Minimization,," in The 2018 5th International Conference on Systems and Informatics, 2018.
- Taylor, Camillo J.; Kriegman, David J., "Minimization on the Lie Group SO(3) and Related Manifolds," 1994. [Online]. Available: https://www.cis.upenn.edu/~cjtaylor/PUBLICATIONS/pdfs/TaylorTR94b.pdf. [Accessed 24 January 2023.
Figure 1.
3-dimensional coordinate system used to graph semi-structured complex numbers.
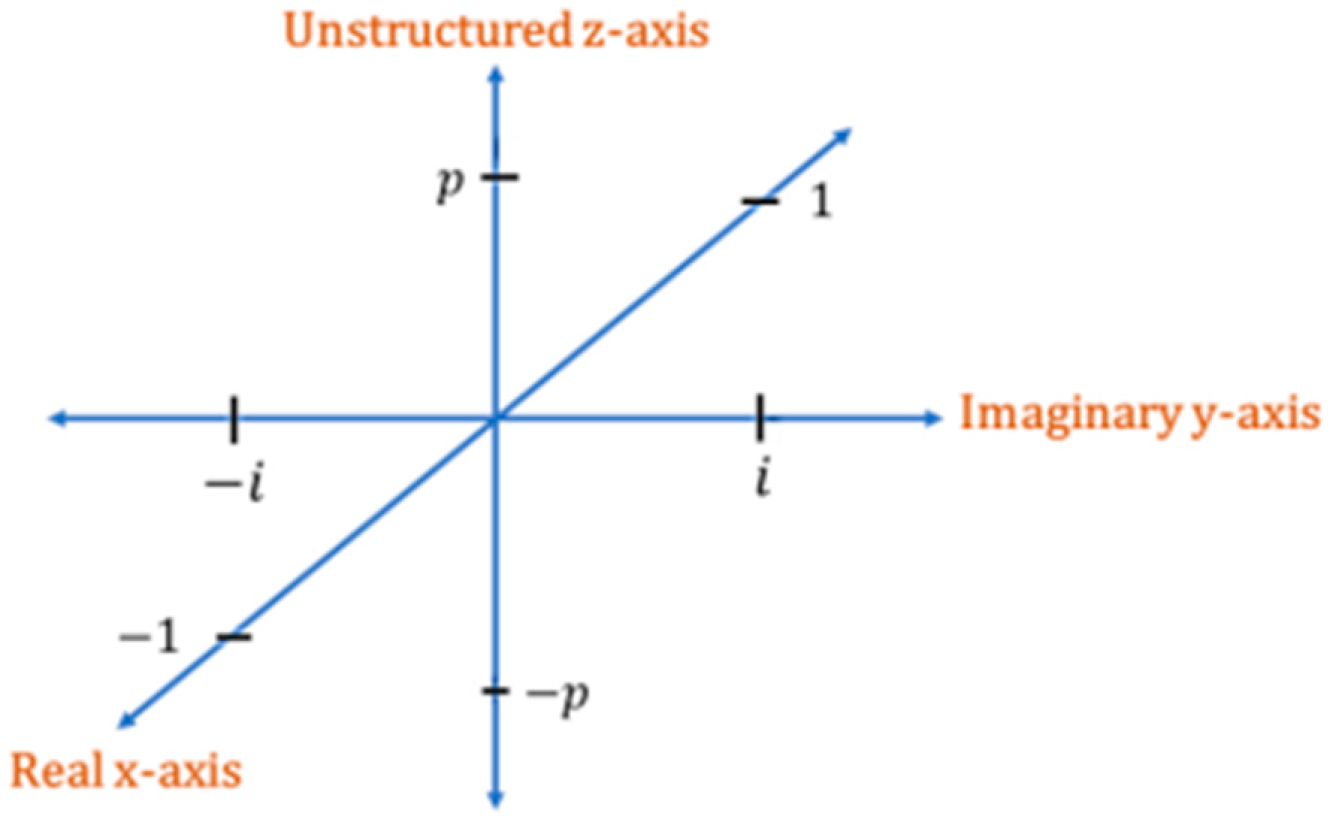
Figure 2.
A unit circle in the real-imaginary -plane
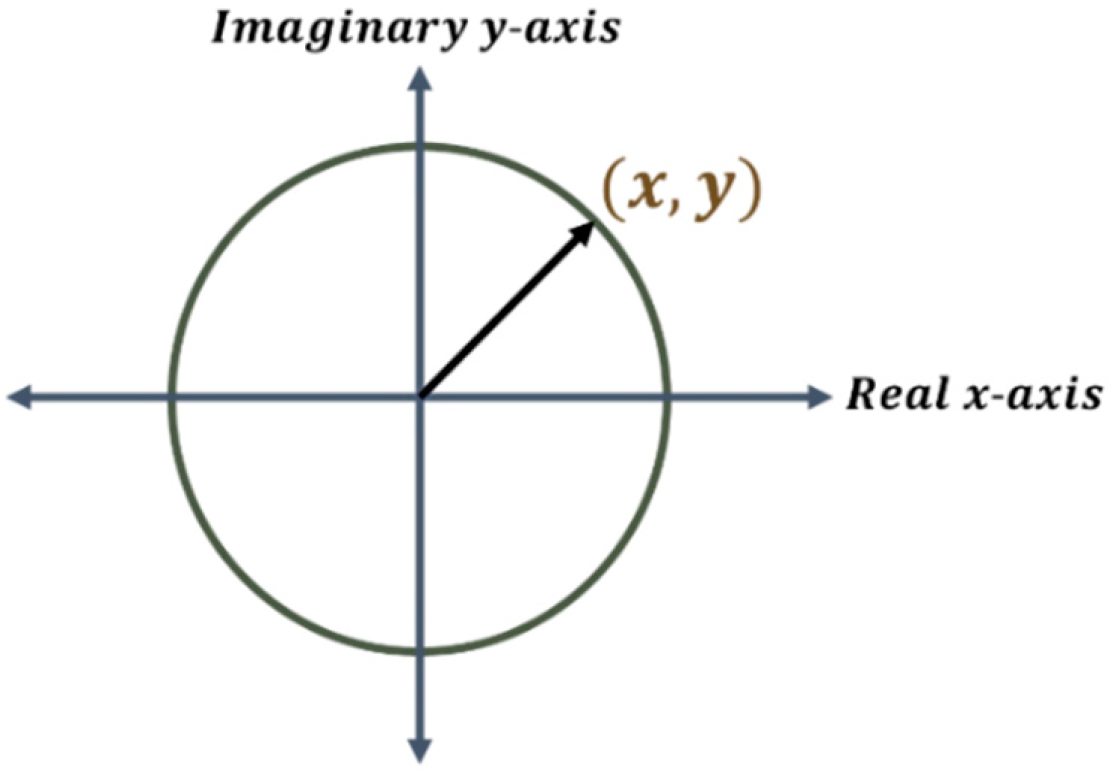
Figure 3.
A unit circle in the real-unstructured -plane
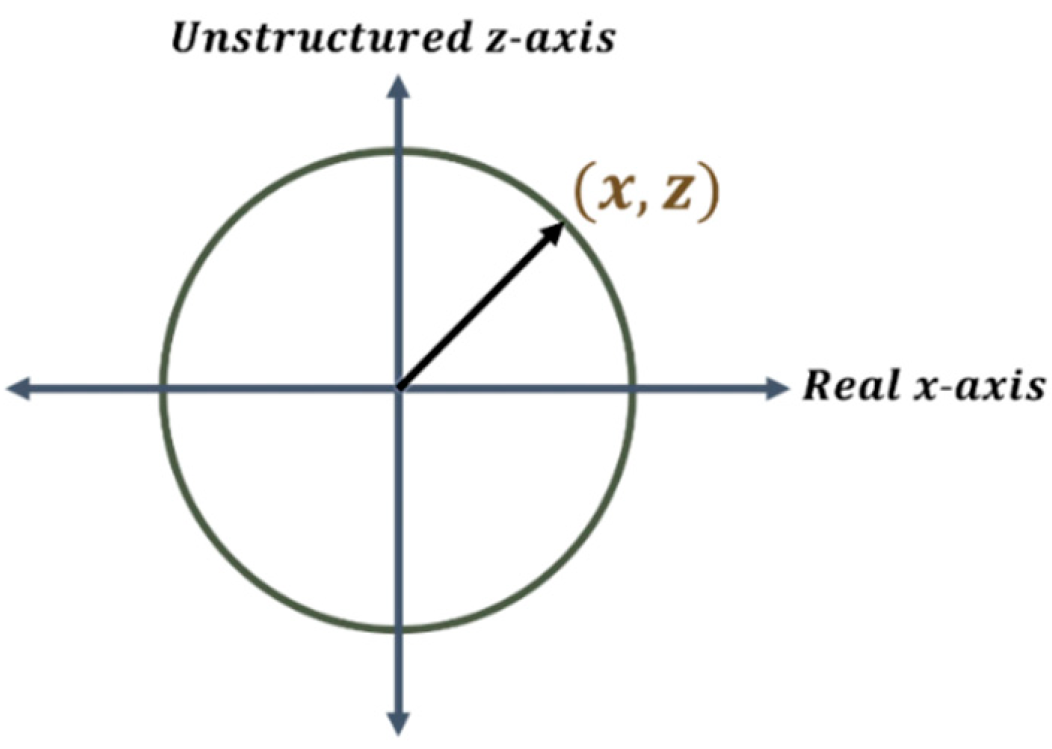
Figure 4.
A unit circle in the imaginary-unstructured -plane
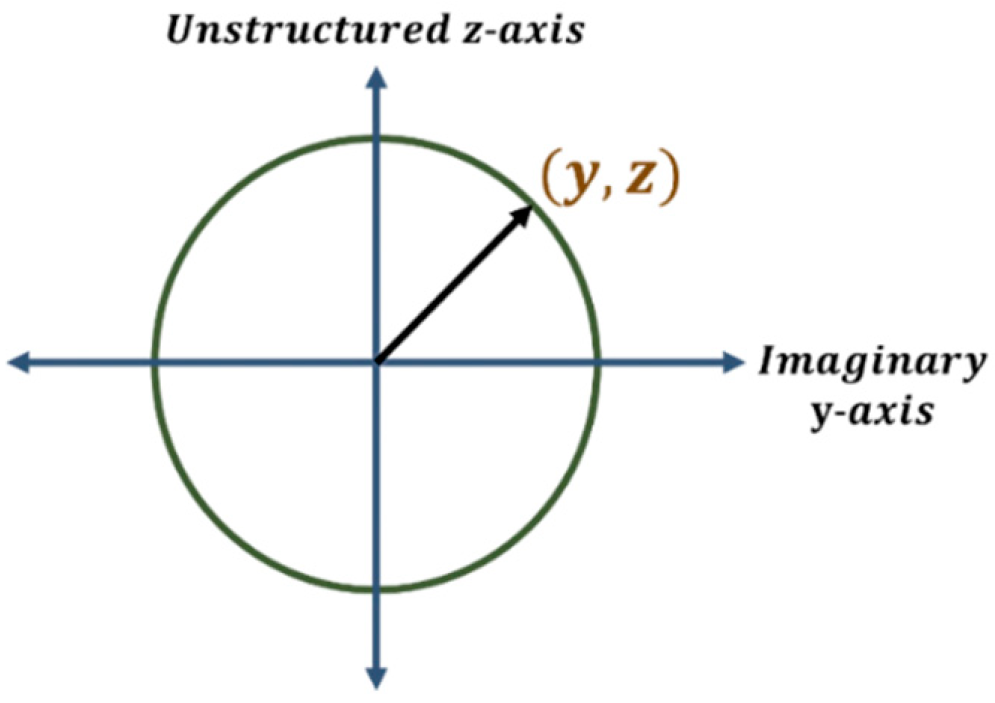
Figure 5.
An example of the gimbal lock problem. The aircraft has lost one of the degrees of freedom (b) - in this case the ability to roll. The aircraft in this case will stall.
Figure 5.
An example of the gimbal lock problem. The aircraft has lost one of the degrees of freedom (b) - in this case the ability to roll. The aircraft in this case will stall.

Figure 6.
Interpretation of Euler’s formula for real-imaginary plane.
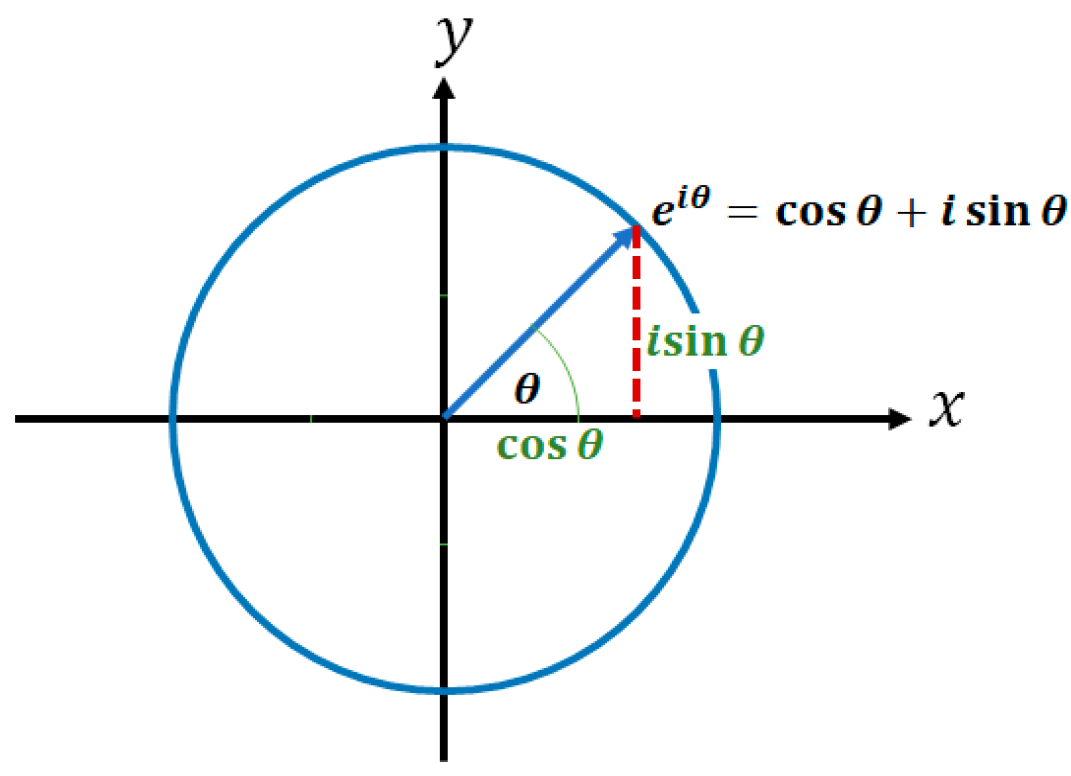
Figure 7.
Interpretation of Euler’s formula for real-unstructured -plane.
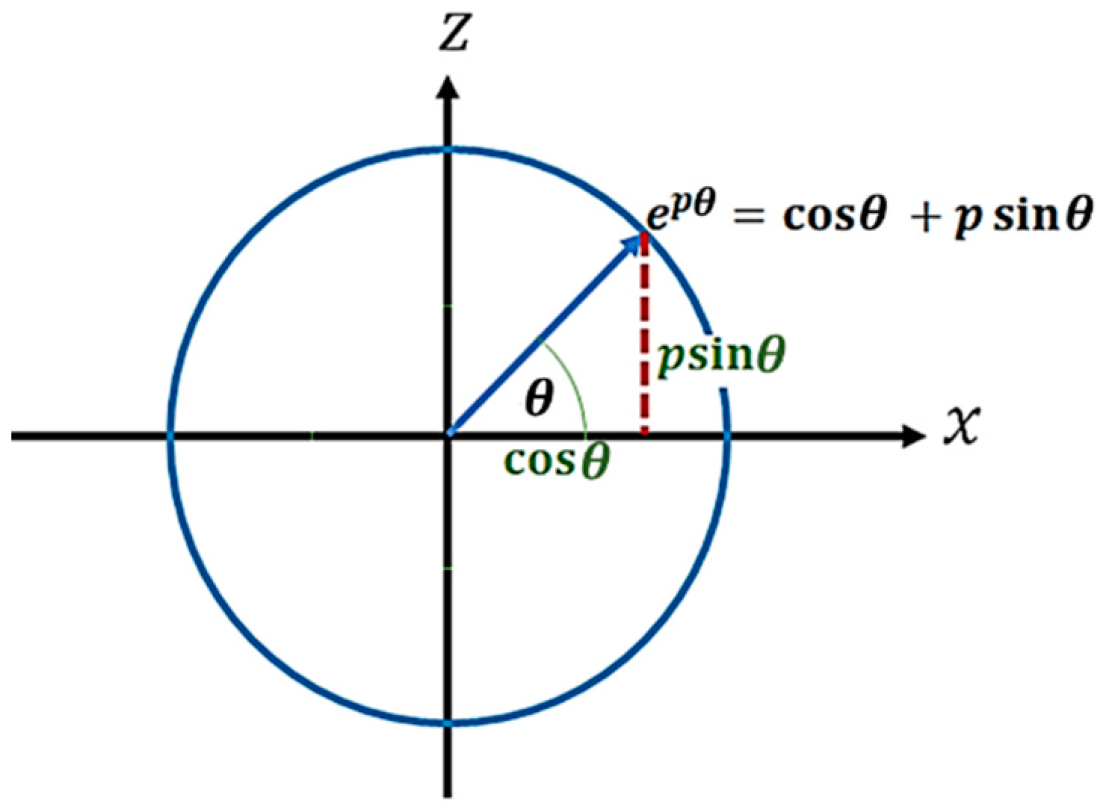
Figure 8.
Interpretation of Equation (10) for the imaginary-unstructured plane.
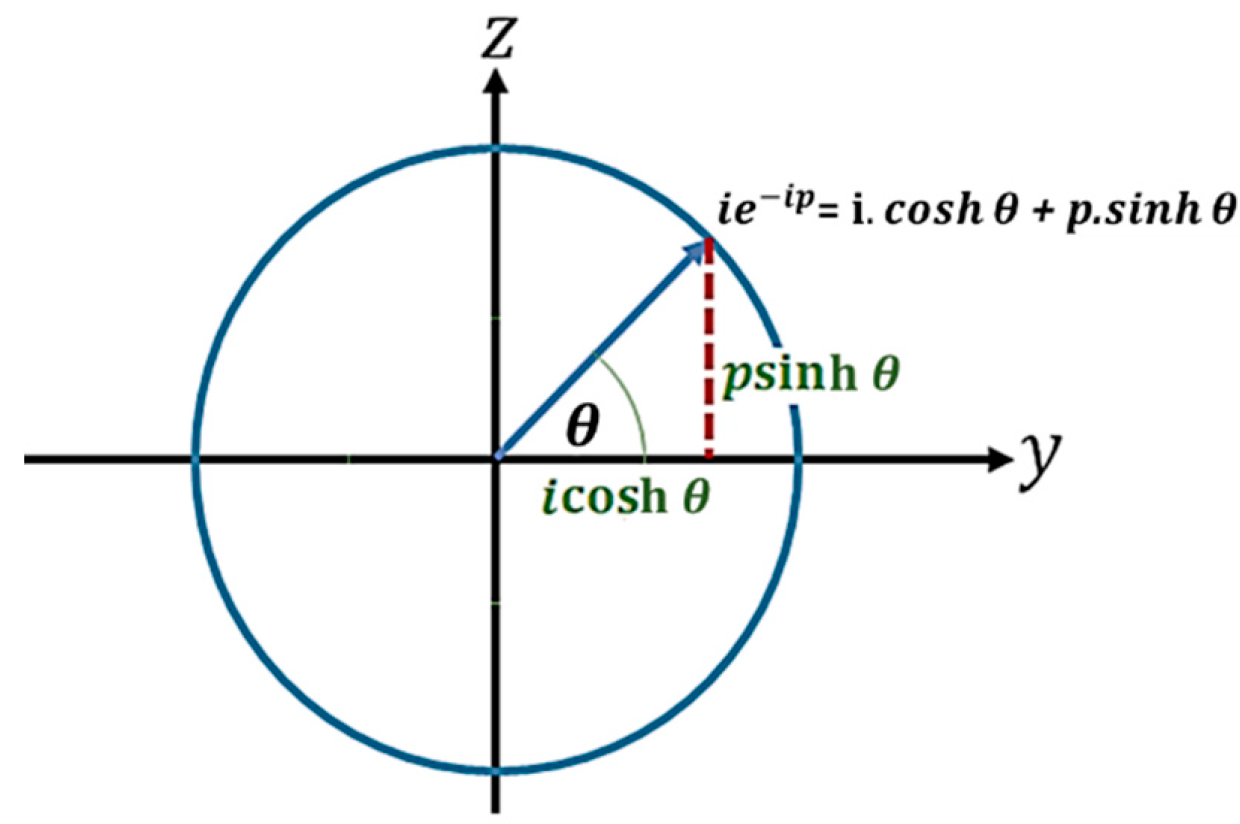
Figure 9.
Interpretation of Equation (11) for the imaginary-unstructured -plane
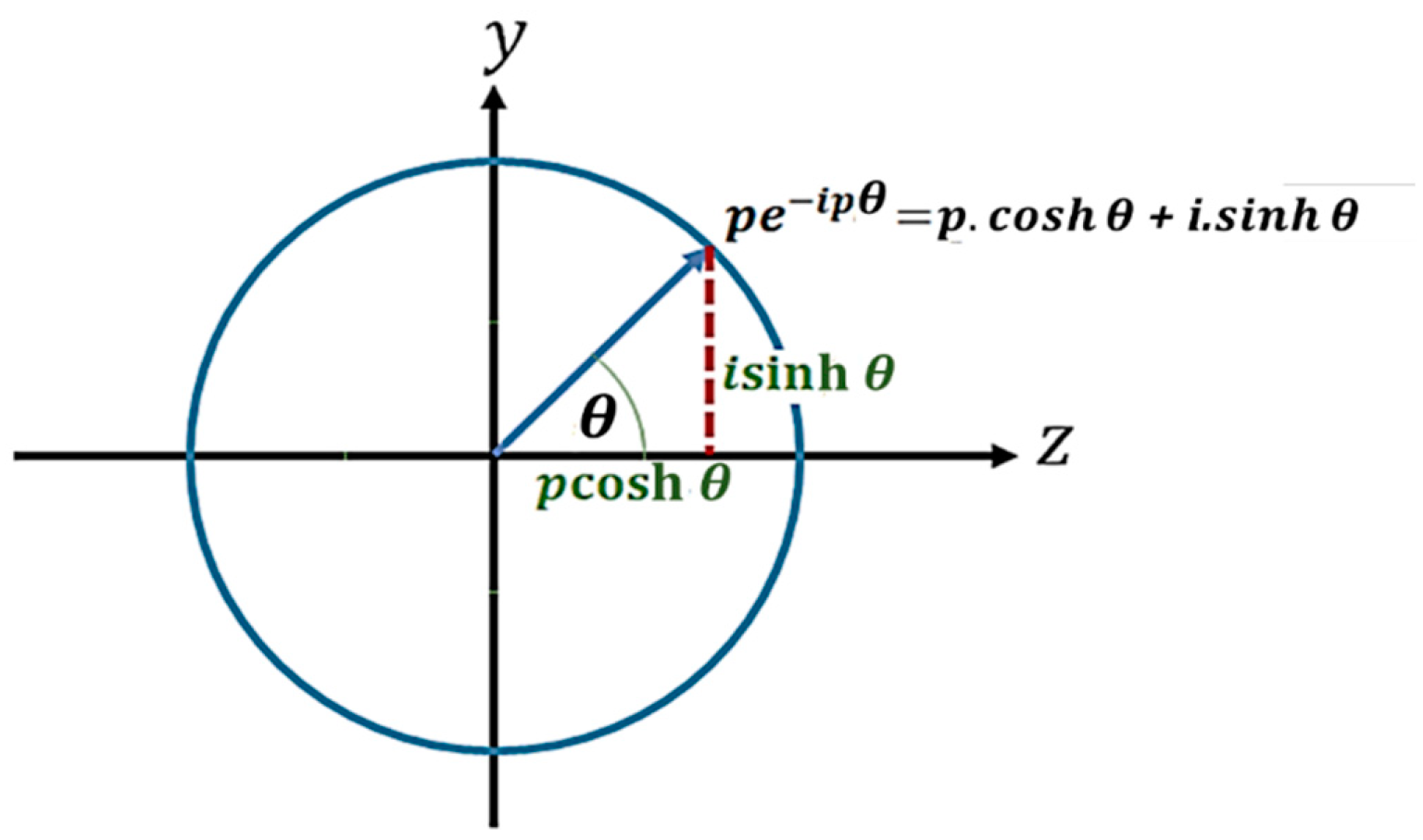
Table 1.
Major results from paper [2].
Table 1.
Major results from paper [2].
| Result 1 | Semi-structured complex number set can be defined as follows: A semi-structured complex number is a three-dimensional number of the general form that is, a linear combination of real (), imaginary () and unstructured () units whose coefficients are real numbers. The number is called semi-structured complex because it contains a structured complex part and an unstructured part . |
| Result 2 | The unstructured number was redefined as:
Integer powers of yield the following cyclic results: 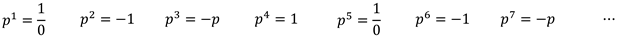
|
| Result 3 | does not belong to the set of complex numbers (that is, ), but belongs to a higher order number set called the set of semi-structured complex numbers such that the set of complex numbers is a subset of (that is, ). |
| Result 4 | The field of semi-structured complex numbers was defined, and proof was given that this field obeys the field axioms. This implies (1) the number set can easily be used in everyday algebraic expressions and can be used to solve algebraic problems, (2) the number set can be used to form more complicated structures such as vector spaces and hence solve more complex problems that may involve “division by zero”. |
| Result 5 | Semi-structured complex number set does not form an ordered field. For the objects in a field to have an order, operations such as greater than or less than can be applied to these objects. This is because in an ordered field the square of any non-zero number is greater than 0; this is not the case with semi-structured complex numbers. |
| Result 6 | Semi-structured complex numbers can be represented by points in a 3-dimensional Euclidean -space. The xyz-space consist of three perpendicular axes: the real -axis, the imaginary y-axis, and the unstructured -axis. These axes form three perpendicular planes: the real-imaginary -plane, the real-unstructured -plane, and the imaginary-unstructured -plane. |
| Result 7 | The unit was used to find a viable solution to the logarithm of zero. The logarithm of zero was found to be:
|
| Result 8 | The new definition of provided an unambiguous understanding that simply represents clockwise rotation of the vector from the positive unstructured z-axis to on the positive real x-axis along the real-unstructured -plane. Note that is any real number. |
| Result 9 | Semi-structured complex numbers has both a 3D and 4D representation in the form: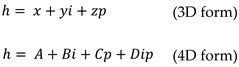 Where: are real numbered scalars and are semi-structured basis units. |
Table 2.
Euler formulas for entire semi-structured complex Euclidean
| Plain | Euler Formula |
|---|---|
| Real imaginary -plane | |
| Real unstructured -plane | |
| Imaginary unstructured -plane |
Table 3.
Euler identities for entire semi-structured complex Euclidean -space.
| Plane | Euler’s identity |
| Real imaginary -plane | |
| Real unstructured -plane | |
| Imaginary unstructured -plane |
Table 4.
Comparing quaternions and semi-structured complex numbers.
| Aspects | Quaternions | Semi-Structured Complex Numbers |
|---|---|---|
| Rotations | Calculating rotations is simple and can be done using the formula: However, quaternion multiplication rules must be followed. |
Calculating rotations is simple and can be done using the formula: This formula required only simple algebraic multiplication and addition. |
| Computation |
Non-commutative nature of quaternions makes computation tedious for complicated problems | Commutative nature of these numbers makes calculations simple even for complicated problems. |
| Division by Zero |
Cannot be used to solve problems involving division by zero | Specially designed to solve problems involving division by zero. |
| Number of dimensions used to represent number | Has only a 4D representation in the form: Where: are real numbered scalars And are quaternion basis units. |
Has both a 3D and 4D representation in the form [2]: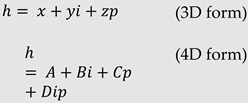 Where: are real numbered scalars and are semi-structured basis units. This enables 4D problems to be easily represented as 3D problems. |
Table 5.
Examples of semi-structured numbers used to resolve division by zero.
| Equation | Condition | Application of semi-structured complex numbers | Interpretation |
|---|---|---|---|
| The resultant gravitational force of attraction F between objects of mass and is given by: |
|
An object of mass at the center of a body of mass would experience no resultant force (since an equal force of attraction will be acting in all directions on the object of mass ). An example of this would be an object at the centre of the earth. | |
| The of a wire of length , resistivity and cross-sectional area is given by: |
|
If the wire has no cross-sectional area (that is, the wire does not exist), then it has no resistance; that is, . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





