Prerpints.org logo
Preprint
Article

A Comparison of Shell Theories for Vibration Analysis of Single-Walled Carbon Nanotubes Based on an Anisotropic Elastic Shell Model

Altmetrics

Downloads

85

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 March 2023

Posted:

22 March 2023

You are already at the latest version

Alerts
Abstract
In the present paper, the comparison is conducted between three classical shell theories as applied to the linear vibrations of single-walled carbon nanotubes (SWCNTs); specifically, the evaluation of the natural frequencies is conducted via Donnell, Sanders and Flügge shell theories. The actual discrete SWCNT is modelled by means of a continuous homogeneous cylindrical shell considering equivalent thickness and surface density. In order to take into account the intrinsic chirality of carbon nanotubes (CNTs), a molecular based anisotropic elastic shell model is considered. Simply supported boundary conditions are imposed and complex method is applied to solve the equations of motion and to obtain the natural frequencies. Comparisons with the results of molecular dynamics simulations available in literature are performed to check the accuracy of the three different shell theories, where Flügge shell theory is found to be the most accurate. Then, a parametric analysis evaluating the effect of diameter, aspect ratio and number of waves along the longitudinal and circumferential directions on the natural frequencies of SWCNTs is performed in the framework of the three different shell theories. Assuming the results of Flügge shell theory as references, it is obtained that Donnell shell theory is not accurate for relatively low longitudinal and circumferential wavenumbers, for relatively low diameters and for relatively high aspect ratios. On the other hand, it is obtained that Sanders shell theory is very accurate for all the considered geometries and wavenumbers, and therefore it can be correctly adopted instead of the more complex Flügge shell theory for the vibration modelling of SWCNTs.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

Since their discovery in 1991 in Japan in the laboratories of the NEC Corporation by Professor Sumio Iijima [1], the study of the vibrations of carbon nanotubes has represented a very demanding challenge for many researchers all over the world.
This interest in carbon nanotubes is due to their extraordinary mechanical properties, in particular very high elastic modulus and tensile strength, together with their very small diameter, which allows them to reach natural frequencies of the THz order, and therefore leads them to be applied in several high sensitivity electro-mechanical systems, such as resonators, sensors and oscillators [2,3,4,5,6].
In order to study the vibratory behaviour of carbon nanotubes, three different methods have been proposed: experimental analyses, molecular dynamics simulations and continuous models.
The experimental analyses, conducted on the basis of resonant Raman spectroscopy, allow to obtain the natural frequencies only of peculiar modes of carbon nanotubes, the so-called “radial breathing modes”, which are characterized by zero waves both longitudinal and circumferential, as undeformed axisymmetric modes [7,8,9]. In addition to this, the main limitation of experimental analyses is given by their very high technical difficulty and by the need to work with scanning or transmission electron microscopes with very high resolution (and therefore very high cost).
Molecular dynamics simulations take into account the discrete nature of carbon nanotubes by modelling the bonds and interaction forces between different carbon atoms based on the fundamental concepts of molecular mechanics [10]. These analyses allow to obtain the natural frequencies of both radial breathing modes and beam-like modes, also the latter modes being very important for carbon nanotubes which, presenting a high aspect ratio value (i.e. ratio between length and radius), have a vibratory behaviour very similar to that of a beam structure [11,12]. The main limitation of molecular dynamics simulations is given by their high computational effort in carrying out numerical analyses, especially in the presence of a large number of carbon atoms, a condition which usually occurs in carbon nanotubes, due to their peculiar high length and reduced thickness ratio (i.e. ratio between thickness and radius), which leads them to be considered as thin-walled structures.
As an alternative to the experimental analyses and numerical simulations, researchers have proposed several continuum models, mainly of beam-type or shell-type, to study carbon nanotubes by adopting the main concepts of continuum mechanics [13].
In particular, the continuous beam-type models are able to properly simulate principally the torsional vibrations of nanotubes [14], while the continuous shell-type models rightly also simulate the flexural vibrations of nanotubes, which give the highest natural frequencies, and therefore they represent more complete models [15].
In general, the main problem in the continuous modelling of carbon nanotubes is the choice of the equivalent parameters which allow to study the nanotubes, which are actually discrete structures, via continuous equivalent structures.
As regards the shell models, which as previously mentioned are the most accurate, Yakobson [16], starting from results of molecular dynamics simulations, proposed equivalent values of tensile and flexural stiffness, and therefore thickness and surface density, which allow to study carbon nanotubes as continuous isotropic homogeneous cylindrical shells.
Using these equivalent parameters, several papers have been published concerning the study of the natural frequencies of single- or multi-walled carbon nanotubes considering an isotropic elastic model based on the three most common thin shell theories, namely Donnell-Mushtari, Sanders-Koiter and Lur’ye-Flügge-Byrne [17,18,19,20,21,22,23,24,25].
Readers interested in deepening the peculiarities of these thin shell theories can find the related strain-displacement relationships and equations of motion in the fundamental monographs by Leissa [26], Yamaki [27], Amabili [28], Soedel [29] and Ventsel [30].
A very interesting comparison of shell theories for vibrations of circular cylindrical shells was carried out by Amabili [31]. From this work it can be derived that, among Donnell, Flügge and Sanders shell theories, Donnell shell theory has the lowest analytical complexity (i.e., the lowest number of terms in the expansions) and, at the same time, the lowest accuracy in modelling the vibrations of the shells; on the other hand, it is obtained that Flügge shell theory has the highest analytical complexity and, at the same time, the highest accuracy; finally, Sanders shell theory presents a relative high analytical complexity and, consequently, a relatively high accuracy. Moreover, an examination of cylindrical shell theories, specifically Donnell and Sanders shell theories, for buckling of carbon nanotubes was performed by Wang et al. [32].
However, given the intrinsically anisotropic nature of carbon nanotubes, in order to correctly study their vibratory behaviour and also to take into account the dependence of their elastic properties on chirality, it is necessary to adopt an anisotropic model.
To this aim, Chang [33,34], starting from considerations of molecular mechanics, developed a novel and very accurate anisotropic elastic shell model, capable of correctly predicting the dependence on the chirality and dimensions of the elastic properties of the material, and therefore to calculate natural frequency values very similar to those obtained via molecular dynamics simulations.
Adopting this anisotropic elastic model, linear vibrations of single-walled and multi-walled carbon nanotubes for different geometries and wave numbers were investigated on the basis of Donnell [35], Sanders [36] and Flügge [37,38] thin shell theories, separately.
To the knowledge of the Authors of this paper, a study on the linear vibrations of SWCNTs based on an anisotropic elastic shell model that compares the values obtained for the natural frequencies by applying Donnell, Sanders and Flügge thin shell theories for different geometries and wavenumbers has not yet been published in the literature. In fact, the Authors of this paper believe that it could be very useful to investigate the field of applicability and limitation of the three previously indicated classical thin shell theories, in order to identify which of them is able to provide sufficiently accurate results in the face of a relatively low computational effort.
To this aim, in the present paper, the natural frequencies of SWCNTs are obtained in the framework of Donnell, Sanders and Flügge shell theories, where the actual discrete SWCNT is modelled via a continuous homogeneous cylindrical shell considering equivalent thickness and surface density. An anisotropic elastic shell model is adopted to take into account the intrinsic chirality effects of CNTs. Simply supported boundary conditions are imposed and complex method is used to solve the dynamic equations of motion and to obtain the natural frequencies. Vibration modes with different number of longitudinal and circumferential waves are studied. SWCNTs with different geometries are analysed.
Taking the more accurate but more complex Flügge theory as a reference, the main objective of this work is to establish whether the simpler Donnell or Sanders shell theories allow to obtain sufficiently accurate natural frequencies and therefore can be adopted instead of Flügge theory to correctly model the linear vibrations of SWCNTS on the basis of an anisotropic elastic shell model.

2. Thin shell theories for SWCNTs

In the present paper, the actual discrete SWCNT of Figure 1(a) is modelled by means of an equivalent continuous elastic thin cylindrical shell, see Figures 1(b, c), with radius R , length L and thickness h . A cylindrical coordinate system ( O , x , θ , z ) is adopted, where the origin O of the reference system is located at the centre of one end of the cylindrical shell. Three displacements are present: longitudinal u ( x , θ , t ) , circumferential v ( x , θ , t ) and radial w ( x , θ , t ) , where the radial displacement w is assumed as positive outward, ( x , θ ) are the longitudinal and angular coordinates of an arbitrary point on the middle surface of the shell, z is the radial coordinate along the thickness h and t is the time.
In this paper, the natural frequencies obtained by considering three different thin shell theories are compared regarding the linear vibrations of SWCNTs with different geometries and wavenumbers. These theories are based on Love’s first approximation assumptions [26]: (i) the thickness h of the shell is small with respect to the radius of curvature R of the middle surface; (ii) the strains are small; (iii) the transverse normal stress is small; (iv) the normal to the undeformed middle surface remains straight and normal to the middle surface after the deformation, and undergoes no thickness stretching (Kirchhoff–Love kinematic hypothesis). The considered thin shell theories are: (a) Donnell-Mushtari [28], (b) Sanders-Koiter [29] and (c) Flügge–Lur’ye-Byrne [30]; for all of them, both rotary inertia and shear deformations are neglected.

2.1. Strain-displacement relationships

According to Donnell, Sanders and Flügge shell theories, the middle surface strains ( ε x , 0 , ε θ , 0 , γ x θ , 0 ) of the shell are related to the displacements ( u , v , w ) in the form [26]:
ε x , 0 = ∂ u ∂ x                     ε θ , 0 = 1 R ∂ v ∂ θ + w R                     γ x θ , 0 = ∂ v ∂ x + 1 R ∂ u ∂ θ
From equations (1) it can be observed that the middle surface strains are expressed in the same form for the three different shell theories considered.
According to Donnell, Sanders and Flügge, the middle surface changes in the curvature and torsion ( k x , k θ , k x θ ) of the shell are related to the displacements ( u , v , w ) in the form [26]:
k x = − ∂ 2 w ∂ x 2                           k θ = 1 R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w k x θ = − 2 R ∂ 2 w ∂ x ∂ θ − 1 R 2 1 2 ψ + φ ∂ u ∂ θ + 1 R 3 2 ψ + φ ∂ v ∂ x
From equations (2) it can be noted that the middle surface change in the curvature k θ and torsion k x θ are written in a different form for the three different shell theories, where parameters ( ψ = 0 , φ = 0 ) denote Donnell shell theory, parameters ( ψ = 1 , φ = 0 ) denote Sanders shell theory and parameters ( ψ = 0 , φ = 1 ) denote Flügge shell theory. Since Sanders and Flügge shell theories have more terms in the expansions (2) than Donnell shell theory, then the first two theories can be expected to be more accurate than the third in the modelling of SWCNT linear vibrations.

2.2. Strain components at an arbitrary point of the shell surface

According to Donnell, Sanders and Flügge shell theories, the strain components ( ε x , ε θ , γ x θ ) at an arbitrary point of the surface of the shell are related to the middle surface strains ( ε x , 0 , ε θ , 0 , γ x θ , 0 ) and to the changes in curvature and torsion of the middle surface ( k x , k θ , k x θ ) by the relationships [28]:
ε x = ε x , 0 + z k x                         ε θ = ε θ , 0 + z k θ                         γ x θ = γ x θ , 0 + z k x θ
where z is the distance of the considered arbitrary point of the shell from the middle surface.
Substituting equations (1-2) into equations (3) it is obtained:
ε x = ∂ u ∂ x − z ∂ 2 w ∂ x 2                         ε θ = 1 R ∂ v ∂ θ + w R + z R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w γ x θ = ∂ v ∂ x + 1 R ∂ u ∂ θ − 2 z R ∂ 2 w ∂ x ∂ θ − z R 2 1 2 ψ + φ ∂ u ∂ θ + z R 3 2 ψ + φ ∂ v ∂ x
where equations (4) relate the strain components at an arbitrary point of the shell surface ( ε x , ε θ , γ x θ ) to the displacements ( u , v , w ) .

3. Anisotropic elastic shell model

Considering the molecular based anisotropic elastic shell model developed by Chang [33,34], which includes the chirality effects characteristic of SWCNTs, the stress-strain relationships can be written as:
σ x = 1 h Y 11 ε x + Y 12 ε θ + Y 13 γ x θ σ θ = 1 h Y 21 ε x + Y 22 ε θ + Y 23 γ x θ τ x θ = 1 h Y 31 ε x + Y 32 ε θ + Y 33 γ x θ
where ( σ x , σ θ , τ x θ ) are the stress components at an arbitrary point of the shell surface and Y i j are the anisotropic surface elastic constants of an arbitrary SWCNT, which are defined as [33,34]:
Y i j = 2 3 3 K ρ G l i G l j + 2 K θ a 2 H l i H l j ,                     i , j , l = 1,2 , 3   ( s u m   o v e r l )
in which a is the carbon-carbon bond length, ( K ρ , K θ ) are force constants associated with stretching and angular distortion of the carbon-carbon bond, respectively, where these constants can be obtained from quantum (ab initio) mechanics, empirical molecular potential or fitted to experimental data, and ( G l i , G l j , H l i , H l j , ) are elements of matrices G and H , respectively, which are given in detail in Ref. [34].
Substituting equations (4) into equations (5), the following stress-displacement equations are derived:
σ x = 1 h Y 11 ∂ u ∂ x − z ∂ 2 w ∂ x 2 + Y 12 1 R ∂ v ∂ θ + w R + z R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w + Y 13 ∂ v ∂ x + 1 R ∂ u ∂ θ − 2 z R ∂ 2 w ∂ x ∂ θ − z R 2 1 2 ψ + φ ∂ u ∂ θ + z R 3 2 ψ + φ ∂ v ∂ x
σ θ = 1 h Y 21 ∂ u ∂ x − z ∂ 2 w ∂ x 2 + Y 22 1 R ∂ v ∂ θ + w R + z R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w + Y 23 ∂ v ∂ x + 1 R ∂ u ∂ θ − 2 z R ∂ 2 w ∂ x ∂ θ − z R 2 1 2 ψ + φ ∂ u ∂ θ + z R 3 2 ψ + φ ∂ v ∂ x
τ x θ = 1 h Y 31 ∂ u ∂ x − z ∂ 2 w ∂ x 2 + Y 32 1 R ∂ v ∂ θ + w R + z R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w + Y 33 ∂ v ∂ x + 1 R ∂ u ∂ θ − 2 z R ∂ 2 w ∂ x ∂ θ − z R 2 1 2 ψ + φ ∂ u ∂ θ + z R 3 2 ψ + φ ∂ v ∂ x

4. Equations of motion

The general equations of motion for an arbitrary SWCNT in terms of force ( N x , N θ , N x θ ) and moment ( M x , M θ , M x θ ) resultants are written in the form [27]:
∂ N x ∂ x + 1 R ∂ N x θ ∂ θ − 1 2 R 2 ∂ M x θ ∂ θ − ρ h ∂ 2 u ∂ t 2 = 0 1 R ∂ N θ ∂ θ + ∂ N x θ ∂ x + 3 2 R ∂ M x θ ∂ x + 1 R 2 ∂ M θ ∂ θ − ρ h ∂ 2 v ∂ t 2   = 0 ∂ 2 M x ∂ x 2 + 2 R ∂ 2 M x θ ∂ x ∂ θ + 1 R 2 ∂ 2 M θ ∂ θ 2 − N θ R −   ρ h ∂ 2 w ∂ t 2   = 0
where ρ h is the is the mass density per unit lateral area (i.e. the surface density) of SWCNT.
In the anisotropic elastic shell model, the force and moment resultants are defined based on the stress components in equations (5), in the form [37]:
N x = ∫ − h / 2 h / 2 σ x 1 + φ z R d z = Y 11 ∂ u ∂ x + Y 12 R ∂ v ∂ θ + w + Y 13 ∂ v ∂ x + 1 R ∂ u ∂ θ + φ − X 11 R ∂ 2 w ∂ x 2 − X 12 R 1 R 2 ∂ 2 w ∂ θ 2 + w R 2 + X 13 R − 2 R ∂ 2 w ∂ x ∂ θ − 1 R 2 ∂ u ∂ θ + 1 R ∂ v ∂ x
N θ = ∫ − h / 2 h / 2 σ θ d z = Y 21 ∂ u ∂ x + Y 22 R ∂ v ∂ θ + w + Y 23 ∂ v ∂ x + 1 R ∂ u ∂ θ
N x θ = ∫ − h / 2 h / 2 τ x θ 1 + φ z R d z = Y 31 ∂ u ∂ x + Y 32 R ∂ v ∂ θ + w + Y 33 ∂ v ∂ x + 1 R ∂ u ∂ θ + φ − X 31 R ∂ 2 w ∂ x 2 − X 32 R 1 R 2 ∂ 2 w ∂ θ 2 + w R 2 + X 33 R − 2 R ∂ 2 w ∂ x ∂ θ − 1 R 2 ∂ u ∂ θ + 1 R ∂ v ∂ x
M x = ∫ − h / 2 h / 2 σ x 1 + φ z R z d z = − X 11 ∂ 2 w ∂ x 2 + X 12 R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w + X 13 − 2 R ∂ 2 w ∂ x ∂ θ − 1 R 2 1 2 ψ + φ ∂ u ∂ θ + 1 R 3 2 ψ + φ ∂ v ∂ x + φ X 11 R ∂ u ∂ x + X 12 R 2 ∂ v ∂ θ + w + X 13 R ∂ v ∂ x + 1 R ∂ u ∂ θ
M θ = ∫ − h / 2 h / 2 σ θ z d z = − X 21 ∂ 2 w ∂ x 2 + X 22 R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w + X 23 − 2 R ∂ 2 w ∂ x ∂ θ − 1 R 2 1 2 ψ + φ ∂ u ∂ θ + 1 R 3 2 ψ + φ ∂ v ∂ x
M x θ = ∫ − h / 2 h / 2 τ x θ 1 + φ z R z d z = − X 31 ∂ 2 w ∂ x 2 + X 32 R 2 − ∂ 2 w ∂ θ 2 + ψ ∂ v ∂ θ − φ w + X 33 − 2 R ∂ 2 w ∂ x ∂ θ − 1 R 2 1 2 ψ + φ ∂ u ∂ θ + 1 R 3 2 ψ + φ ∂ v ∂ x + φ X 31 R ∂ u ∂ x + X 32 R 2 ∂ v ∂ θ + w + X 33 R ∂ v ∂ x + 1 R ∂ u ∂ θ
where X i j = Y i j h 2 / 12 , with i , j = 1,2 , 3 .
From equations (11-16) it is noted that the integrating functions of the circumferential force N θ and moment M θ resultants are the same for the three different shell theories. Conversely, the integrating functions of the other force and moment resultants are different, since in Flügge shell theory they also include the term ( 1 + z / R ) (in this theory the thinness assumption is delayed), whereas this term is ignored in the other two thin shell theories. On the one hand, considering this additional term within the integrating functions of the resultants certainly makes Flügge shell theory more refined (in fact, it is able of correctly modelling the vibrations of even relatively thick shells). On the other hand, this considerably increases the number of terms within the expressions of such resultants, and therefore it strongly increases the computational effort of the numerical analyses. The main goal of this paper is therefore to verify whether a less refined theory, but with lower computational effort, such as Donnell or Sanders shell theory, can give sufficiently accurate results in terms of SWCNT natural frequencies compared to those provided by Flügge shell theory, as investigated in [31] for the cylindrical shells.
By substituting the expressions of the force and moment resultants (11-16) into the dynamic equations (10), the equations of motion for the anisotropic elastic shell model are obtained, in the form:
Y 11 ∂ 2 ∂ x 2 + 2 Y 13 R − φ 3 X 13 2 R 3 ∂ 2 ∂ x ∂ θ + Y 33 R 2 + ψ − 4 φ X 33 4 R 4 ∂ 2 ∂ θ 2 u + Y 13 + φ X 13 R 2 ∂ 2 ∂ x 2 + Y 12 + Y 33 R − ψ 3 X 33 4 R 3 ∂ 2 ∂ x ∂ θ + Y 23 R 2 − ψ + φ X 23 2 R 4 ∂ 2 ∂ θ 2 v + Y 12 R − φ X 12 R 3 ∂ ∂ x + Y 23 R 2 − φ X 23 R 4 ∂ ∂ θ − φ X 11 R ∂ 3 ∂ x 3 + 1 − 6 φ X 13 2 R 2 ∂ 3 ∂ x 2 ∂ θ + 1 − 2 φ X 33 R 3 − φ X 12 R 3 ∂ 3 ∂ x ∂ θ 2 + 1 − 2 φ X 23 2 R 4 ∂ 3 ∂ θ 3 w = ρ h ∂ 2 u ∂ t 2
Y 13 + φ 3 X 13 2 R 2 ∂ 2 ∂ x 2 + Y 12 + Y 33 R − 3 ψ + 4 φ X 33 4 R 3 ∂ 2 ∂ x ∂ θ + Y 23 R 2 − X 23 2 R 4 ψ + 2 φ ∂ 2 ∂ θ 2 u + Y 33 + 9 ψ + 16 φ X 33 4 R 2 ∂ 2 ∂ x 2 + 2 Y 23 R + 6 ψ + 5 φ X 23 2 R 3 ∂ 2 ∂ x ∂ θ + Y 22 R 2 + ψ X 22 R 4 ∂ 2 ∂ θ 2 v + Y 23 R − φ X 23 R 3 ∂ ∂ x + Y 22 R 2 − φ X 22 R 4 ∂ ∂ θ − ( 3 + 2 φ ) X 13 2 R ∂ 3 ∂ x 3 − X 12 R 2 + 3 + 2 φ X 33 R 2 ∂ 3 ∂ x 2 ∂ θ − ( 7 + 2 φ ) X 23 2 R 3 ∂ 3 ∂ x ∂ θ 2 − X 22 R 4 ∂ 3 ∂ θ 3 w = ρ h ∂ 2 v ∂ t 2
− Y 12 R ∂ ∂ x − Y 23 R 2 ∂ ∂ θ + φ X 11 R ∂ 3 ∂ x 3 + − ψ + 4 φ X 13 2 R 2 ∂ 3 ∂ x 2 ∂ θ − ψ X 33 R 3 ∂ 3 ∂ x ∂ θ 2 − ψ + 2 φ X 23 2 R 4 ∂ 3 ∂ θ 3 u + − Y 23 R ∂ ∂ x − Y 22 R 2 ∂ ∂ θ + 3 ψ + 4 φ X 13 2 R ∂ 3 ∂ x 3 + ψ + φ X 12 R 2 + 3 ψ + 4 φ X 33 R 2 ∂ 3 ∂ x 2 ∂ θ + 7 ψ + 6 φ X 23 2 R 3 ∂ 3 ∂ x ∂ θ 2 + ψ X 22 R 4 ∂ 3 ∂ θ 3 v + − Y 22 R 2 − φ X 22 R 4 ∂ 2 ∂ θ 2 − X 11 ∂ 4 ∂ x 4 − 4 X 13 R ∂ 4 ∂ x 3 ∂ θ − 2 X 12 + 4 X 33 R 2 ∂ 4 ∂ x 2 ∂ θ 2 − 4 X 23 R 3 ∂ 4 ∂ x ∂ θ 3 − X 22 R 4 ∂ 4 ∂ θ 4 w = ρ h ∂ 2 w ∂ t 2

5. Solution method

In this paper, a complex method is considered to analytically solve the dynamic equations of motion (17-19) and to obtain the natural frequencies of SWCNTs. Specifically, a complex variable is used to solve the partial differential equations (17-19) by setting the real and imaginary zero.
In the present work, simply supported boundary conditions are adopted. These boundary conditions, for the complex method, impose the conditions R e v = R e w = 0 at both ends x = ( 0 ,   L ) of the SWCNT. The displacement field that satisfies these boundary conditions can be written as [38]:
u ( x , θ , t ) = U ¯ exp ⁡ i λ q x cos ⁡ s θ cos ⁡ ω t v ( x , θ , t ) = − i V ¯ exp ⁡ i λ q x sin ⁡ s θ cos ⁡ ω t w ( x , θ , t ) = − i W ¯ exp ⁡ i λ q x cos ⁡ s θ cos ⁡ ω t
where U ¯ , V ¯ , W ¯ denote the displacement amplitudes along the longitudinal u , circumferential v and radial w directions, respectively, i is the imaginary unit, λ q is the wavenumber along the longitudinal direction, with λ q = q π / L , where q is the number of longitudinal half-waves and L is the length of the SWCNT, s is the number of circumferential waves and ω is the circular frequency.
Substituting equation (20) into equations (17-19), a set of algebraic equations for the displacement amplitudes U ¯ , V ¯ , W ¯ is obtained, which can be written in the form [38]:
E ( λ q , s , ω ) 3 × 3 U ¯ V ¯ W ¯ = 0 0 0
where E is a non-symmetric matrix, whose elements are:
E 11 = Y 11 λ q 2 + 2 Y 13 R − φ 3 X 13 2 R 3 λ q s + Y 33 R 2 + ψ − 4 φ X 33 4 R 4 s 2 − ρ h ω 2
E 12 = − Y 13 + φ X 13 R 2 λ q 2 − Y 12 + Y 33 R − ψ 3 X 33 4 R 3 λ q s − Y 23 R 2 − ψ + φ X 23 2 R 4 s 2
E 13 = − Y 12 R − φ X 12 R 3 λ q − Y 23 R 2 − φ X 23 R 4 s − φ X 11 R λ q 3 + ( 1 − 6 φ ) X 13 2 R 2 λ q 2 s + ( 1 − 2 φ ) X 33 R 3 − φ X 12 R 3 λ q s 2 + 1 − 2 φ X 23 2 R 4 s 3
E 21 = − Y 13 + φ 3 X 13 2 R 2 λ q 2 − Y 12 + Y 33 R − 3 ψ + 4 φ X 33 4 R 3 λ q s − Y 23 R 2 − ψ + 2 φ X 23 2 R 4 s 2
E 22 = Y 33 + 9 ψ + 16 φ X 33 4 R 2 λ q 2 + 2 Y 23 R + 6 ψ + 5 φ X 23 2 R 3 λ q s + Y 22 R 2 + ψ X 22 R 4 s 2 − ρ h ω 2
E 23 = Y 23 R − φ X 23 R 3 λ q + Y 22 R 2 − φ X 22 R 4 s + 3 + 2 φ X 13 2 R λ q 3 + X 12 R 2 + ( 3 + 2 φ ) X 33 R 2 λ q 2 s + 7 + 2 φ X 23 2 R 3 λ q s 2 + X 22 R 4 s 3
E 31 = − Y 12 R λ q + Y 23 R 2 s − φ X 11 R λ q 3 − ψ − 4 φ X 13 2 R 2 λ q 2 s + ψ X 33 R 3 λ q s 2 − ψ + 2 φ X 23 2 R 4 s 3
E 32 = − Y 23 R λ q + Y 22 R 2 s − 3 ψ + 4 φ X 13 2 R λ q 3 + ( ψ + φ ) X 12 R 2 + ( 3 ψ + 4 φ ) X 33 R 2 λ q 2 s − ( 7 ψ + 6 φ ) X 23 2 R 3 λ q s 2 + ψ X 22 R 4 s 3
E 33 = Y 22 R 2 + X 11 λ q 4 − φ X 22 R 4 s 2 − 4 X 13 R λ q 3 s + 2 X 12 + 4 X 33 R 2 λ q 2 s 2 − 4 X 23 R 3 λ q s 3 + X 22 R 4 s 4 − ρ h ω 2
At this point it is useful to remember that, by imposing the parameters ( ψ = 0 , φ = 0 ) , we obtain the elements of matrix E for Donnell shell theory, by imposing the parameters ( ψ = 1 , φ = 0 ) we obtain the elements of matrix E for Sanders shell theory, and by imposing the parameters ( ψ = 0 , φ = 1 ) we obtain the elements of matrix E for Flügge shell theory, see expansions (2) for the middle surface change in the curvature k θ and torsion k x θ of the shell.
For the non-trivial solution, the determinant of the set of equations (21) must be equal to zero [38]:
det ⁡ E ( λ q , s , ω ) 3 × 3 = 0
Solving equation (31), we get a third-order algebraic equation in ω 2 ; this last equation provides three different eigenfrequencies for each number of waves ( q , s ) that give three different vibration modes (i.e. longitudinal, torsional and radial modes). Since the highest natural frequency corresponds to the radial vibration mode, then in the numeric results only the radial natural frequencies will be computed.

6. Numeric results

In this paper, the natural frequencies of SWCNTs are obtained in the framework of Donnell, Sanders and Flügge shell theories. An anisotropic elastic shell model is used to take into account the chirality effects of CNTs. Simply supported boundary conditions are imposed. Vibration modes with different number of waves along the longitudinal and circumferential directions are considered. SWCNTs with different values of radius R and aspect ratio L / R are investigated.
As known from the literature, two relevant open issues related to the continuous modelling of carbon nanotube vibrations are given by their intrinsic anisotropic character and their discrete configuration. To this end, it is very important to adopt parameters and models able to correctly describe the actual molecular structure of the nanotubes.
In Table 1, the values of carbon-carbon bond parameters ( a , k ρ , k θ ) and equivalent parameters ( h , ρ ) retrieved from literature are listed. In particular, parameters k ρ and k θ , which denote force constants correlated to the variance of carbon-carbon bond length a and angle θ , respectively, are adopted to express the anisotropic elastic constants of SWCNTs via the molecular mechanics based “stick-spiral model” developed by Chang [33].
Moreover, in order to study the dynamics of the actual discrete CNT via a homogeneous continuous cylindrical shell, an equivalent thickness h , which is derived from MD simulations of CNT energy, and an equivalent mass density ρ , resulting from the surface density of graphite, are considered, see Ref. [16] for more details.

6.1. Comparison of the shell theories with the results of molecular dynamics simulations

In this Section, the natural frequencies of the radial breathing mode (q = 0, s = 0) of the SWCNT of Table 1 with aspect ratio L/R = 10 obtained by considering Donnell, Sanders and Flügge shell theories are compared with the results of molecular dynamics simulations available in literature for different chirality indices (n, m), see Table 2.
Obviously, the results of molecular dynamics simulations are the most correct, since these simulations are able to correctly take into account the actual molecular structure of carbon nanotubes. However, the computational effort of molecular dynamics simulations is very high, in particular when dealing with very long and thin structures (such as carbon nanotubes), which have extremely elevated number of atoms, and therefore these results are available only for a reduced range of CNT geometries. To this end, it seems useful to investigate which shell theory is more accurate in the vibration modelling of carbon nanotubes as continuous structures.
From Table 2 it can be observed that, for all the considered chirality indices, assuming the molecular dynamics results as the reference, the percentage difference of Flügge shell theory is the lowest, while the percentage difference of Donnell shell theory is the highest, and Sanders-Koiter shell theory gives intermediate response.
These results could easily be predicted considering the strain-displacement relationships (2), in which Donnell shell theory has fewer terms than the other two (and therefore it is the least accurate theory), and considering the force and moment resultants (11-16), in which Flügge shell theory includes more terms (and therefore it is the most accurate theory).
Even if, among the three considered shell theories, Flügge is found to be the most accurate, it should be preferable not to use this shell theory, because it has a relatively high computational effort, due to the large number of terms in the expansions of force and moment resultants. This aspect is relevant not so much in the study of linear vibrations (natural frequencies) but instead in the analysis of non-linear vibrations (amplitude-frequency responses), where in the strain-displacement relationships also the non-linear terms are considered, and therefore the computational weight in solving the dynamic equations of motion would become much greater.
To this aim, it could be useful to analyse whether Donnell or Sanders shell theories are sufficiently accurate in the continuous modelling of SWCNT vibrations. Therefore, in the following, Flügge shell theory will be used as reference, and natural frequencies of simply supported SWCNTs with different geometries and wavenumbers will be computed in the framework of Donnell and Sanders thin shell theories.

6.2. Comparison of the shell theories for different SWCNT geometries and wavenumbers

In the present Section, the natural frequencies of the simply supported SWCNT of Table 1 obtained by considering Donnell, Sanders and Flügge shell theories are compared for different chirality indices (n, m), aspect ratios L/R, numbers of longitudinal half-waves q and circumferential waves s.
By taking as reference the results of Flügge shell theory (which are the closest to those obtained from molecular dynamics simulations, see Table 2), we want to investigate the fields of applicability and limitation of Donnell and Sanders shell theories.
In Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, the comparisons between Donnell and Flügge shell theories, and between Sanders and Flügge shell theories, are performed adopting increasing values of chirality indices (i.e. SWCNT radius), specifically (n = 5, m = 5) (i.e. R = 0.34 nm), (n = 10, m = 10) (i.e. R = 0.68 nm) and (n = 25, m = 25) (i.e. R = 1.70 nm), and increasing values of SWCNT aspect ratio L/R = (10,15,20).
It must be underlined that this analysis was carried out within the range commonly assumed for the radius of CNTs. In fact, it is reported that “a single-wall nanotube is defined by a cylindrical graphene sheet with a diameter of about 0.5 - 10.0 nm, though most of the observed single-wall nanotubes have diameters < 2 nm”, see Ref. [9].
As for Donnell shell theory, increasing the radius R, the percentage difference with respect to Flügge shell theory decreases for all the longitudinal wavenumbers q, where the maximum value is obtained at q = 1 and decreases with increasing q, the maximum peak corresponding to q = 1 is always located at s = 2 while the peaks corresponding to q = (2-5) move to higher circumferential wavenumbers.
On the other hand, increasing the aspect ratio L/R, the percentage difference with respect to Flügge shell theory increases for all the longitudinal wavenumbers q, where the maximum value is obtained again at q = 1 and decreases with increasing q, but now the maximum peak corresponding to q = 1 moves from s = 2 to s = 1 (lower circumferential wavenumber) while the peaks corresponding to q = (2-5) are always located at s = 2.
It should be underlined that the increase in the percentage difference at the longitudinal wavenumber q = 1 obtained by increasing the aspect ratio L/R is extremely higher than the corresponding decrease at the longitudinal wavenumber q = 1 obtained by increasing the radius R (i.e., the effect of the aspect ratio is prevalent with respect to the radius).
As for Sanders shell theory, increasing both the radius R and the aspect ratio L/R, it is always obtained that the percentage difference with respect to Flügge shell theory is relatively low for every number of longitudinal and circumferential waves (< 1%).
In particular, increasing the radius R, the maximum percentage difference moves from q = 2 to q = 1 decreasing its value (from 0.7% to 0.1%); differently, increasing the aspect ratio L/R, the maximum percentage difference moves from q = 2 to q = 5 preserving its value (0.7%).
Therefore, by considering the parametric analyses presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, it can be observed that Donnell shell theory cannot be applied for the vibration modelling of SWCNTs with relatively low radius R and relatively high aspect ratio L/R, and for the vibration modelling of modes with relatively low number of longitudinal q and circumferential s waves. However, as previously reported, the effect of the aspect ratio is prevalent with respect to the radius (and also to the wavenumbers) in providing the very high percentage difference obtained between Donnell and Flügge shell theories. This is due to the different expressions of the middle surface change in curvature k θ and torsion k x θ of the shell for the two theories, see equations (2), which present more terms in Flügge than Donnell shell theory, and in particular to the middle surface torsion, which is very sensitive to the value of aspect ratio.
Specifically, for the relatively low value of aspect ratio L/R = 10, the maximum peak of percentage difference is located at the circumferential flexure mode (q = 1, s = 2), where the effect of the middle surface change in the curvature k θ is prevalent, see Figure 2; on the other hand, for the relatively high value of aspect ratio L/R = 20, the maximum peak of percentage difference is located at the beam-like mode (q = 1, s = 1), where the effect of the middle surface torsion k x θ prevails, see Figure 10.
Conversely, by considering the parametric analyses presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, it can be observed that Sanders shell theory is able to model with very good accuracy the linear vibrations of SWCNTs for all the considered geometries and wavenumbers, and therefore it can be adopted instead of the more complex Flügge shell theory to compute the natural frequencies of SWCNTs.
This is due to the fact that, in Sanders shell theory, the effect of the aspect ratio is not present (as the equations (2) are very similar to those of Flügge shell theory), but only the effect of the radius, which is due to the insertion of additional terms of the ratio z/R in the integrating function of the force and moment resultants (11-16) of Flügge shell theory.
Since CNTs actually have a very small thickness ratio h/R (they are thin-walled structures) then the effect of these additional terms is very small and therefore the variation of the radius involves a small variation of the percentage difference between the theories (this also applies to Donnell shell theory).
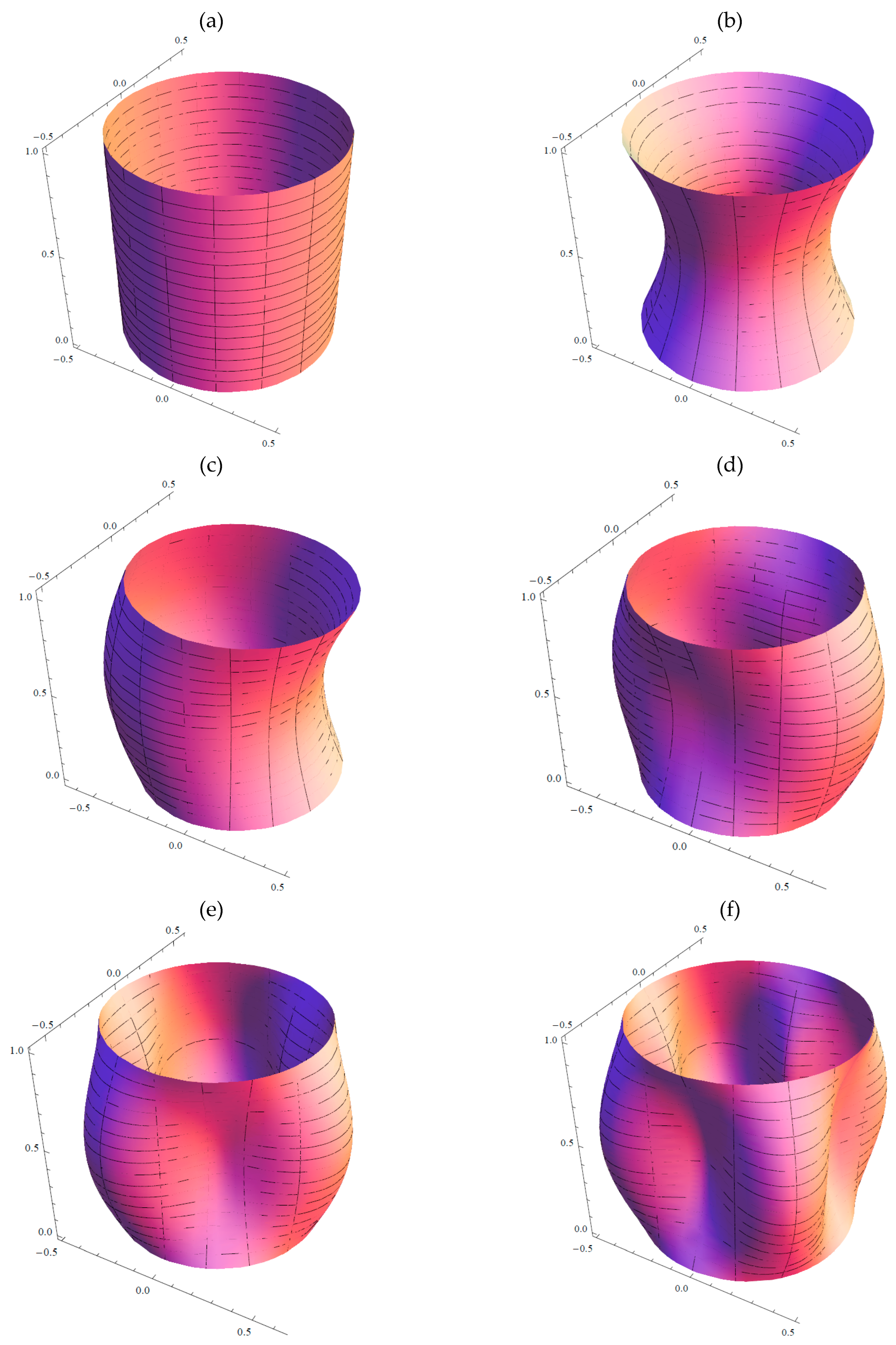
Finally, in Figure 12, six different relevant mode shapes of the simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 10 are presented. In particular, the radial breathing mode (q = 0, s = 0) corresponds to Rayleigh’s inextensional symmetrical mode (i.e. uniform vibration). Moreover, they are shown axisymmetric mode (q = 1, s = 0) (no circumferential waves), beam-like mode (q = 1, s = 1) (one circumferential wave, characteristic of structures with very long aspect ratio, such as beams) and shell-like modes (q = 1, s = 2-4) (two or more circumferential waves, characteristic of three-dimensional thin-walled structures, such as cylindrical shells). Such a graphical representation of modes could be useful for interpreting the previous results and comparisons.

7. Conclusions

In this paper, the natural frequencies of SWCNTs obtained in the framework of Donnell, Sanders and Flügge shell theories are compared. An anisotropic elastic shell model is adopted to take into account the intrinsic chirality effects of CNTs. Simply supported boundary conditions are imposed. Vibration modes with different wavenumbers along the longitudinal and circumferential directions are studied. SWCNTs with different values of radius R and aspect ratio L / R are investigated. The most important findings of the present paper are reported below.
  • By means of comparisons with results of molecular dynamic simulations reported in literature it is derived that Flügge shell theory is the most accurate one in the computation of the natural frequencies of SWCNTs and therefore it is assumed as reference.
  • Since Flügge shell theory has a very high computational effort, then it is useful to investigate whether a simpler shell theory, e.g., Donnell or Sanders shell theory, is able to model with a sufficient accuracy the linear vibrations of SWCNTs.
  • It is found that Donnell shell theory is not sufficiently accurate for relatively low longitudinal and circumferential wavenumbers, for relatively low diameters and for relatively high aspect ratios, and therefore it cannot be adopted for the vibration modelling of SWCNTs.
  • On the other hand, it is obtained that Sanders shell theory is very accurate for all the considered geometries and wavenumbers, and therefore it can be properly considered instead of the more complex Flügge shell theory for the vibration modelling of SWCNTs.
Starting from the results obtained in the present paper, the same Authors are planning to write a new paper on the effect of nonlocal elasticity and strain gradient on the linear vibrations of SWCNTs on the basis of an anisotropic elastic shell model and in the framework of Sanders-Koiter shell theory.

Author Contributions

Conceptualization: M. Strozzi and I. Elishakoff; data curation: M. Strozzi and M. Bochicchio; funding acquisition: M. Cocconcelli, R. Rubini and E. Radi; investigation: M. Strozzi and M. Bochicchio; methodology: M. Strozzi and I. Elishakoff; project administration: M. Strozzi and I. Elishakoff; supervision: M. Cocconcelli, R. Rubini and E. Radi; visualization: M. Strozzi and M. Bochicchio; writing – original draft: M. Strozzi, M. Bochicchio and I. Elishakoff; writing – review & editing: R. Rubini, M. Cocconcelli and E. Radi. All Authors have read and agreed to the published version of the manuscript.

Data Availability Statement

All data are available from the Authors.

Acknowledgments

Authors M. Strozzi, E. Radi, M. Cocconcelli and R. Rubini are grateful to the Department of Sciences and Methods for Engineering, University of Modena and Reggio Emilia, Reggio Emilia, Italy (Grant 020142_22_FRN_SOSTEGNO_RICERCA_DISMI) for the financial support of this work. The present work is dedicated to the blessed memory of Professor Leonid I. Manevitch, outstanding educator, respected teacher, admired scholar, who died, after severe illness, on 20 August 2020, at the age of 82. The great passion and enthusiasm towards scientific research that Professor Manevitch nurtured until the end of his life, in particular towards the much loved carbon nanotubes, will remain forever in the hearth of his collaborators, and will be for them a strong and always alive stimulus to progress in the knowledge of these so wonderful structures.

Conflicts of Interest

The Authors declare no conflict of interest.

References

  1. Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [CrossRef]
  2. Elishakoff, I.E.; Pentaras, D.; Dujat, K.; Versaci, C.; Muscolino, G.; et al. Carbon Nanotubes and Nanosensors. Vibration, Buckling and Ballistic Impact. John Wiley & Sons, London, UK, 2012.
  3. Jorio, A.; Dresselhaus, G.; Dresselhaus, M. Carbon Nanotubes. Advanced Topics in the Synthesis, Structure, Properties and Applications. Springer-Verlag, Berlin, Germany, 2008.
  4. Marulanda, J.M. Carbon Nanotubes. Applications on Electron Devices. InTech Open, Rijeka, Croatia, 2011.
  5. Mahar, B.; Laslau, C.; Yip, R.; Sun, Y. Development of Carbon Nanotube-Based Sensors. A Review. IEEE Sensors J. 2007, 7, 266–284. [CrossRef]
  6. Hierold, C.; Jungen, A.; Stampfer, C.; Helbling, T. Nano electromechanical sensors based on carbon nanotubes. Sens. Actuat. A 2007, 136, 51–61. [CrossRef]
  7. Rao, A.; Richter, E.; Bandow, S.; Chase, B.; Eklund, P.C.; Williams, K.; et al. Diameter-Selective Raman Scattering from Vibrational Modes in Carbon Nanotubes. Science 1997, 275, 187–191. [CrossRef] [PubMed]
  8. Bandow, S.; Asaka, S.; Saito, Y.; Rao, A.; Grigorian, L.; Richter, E.; Eklund, P.C. Effect of the Growth Temperature on the Diameter Distribution and Chirality of Single-Wall Carbon Nanotubes. Phys. Rev. Lett. 1998, 80, 3779–3782. [CrossRef]
  9. Dresselhaus, G.; Dresselhaus, M.S.; Hafner, J.H.; Hunter, M.; Jorio, A.; Lieber, C.M.; McClure, T.; Saito, R. Structural (n, m) Determination of Isolated Single-Wall Carbon Nanotubes by Resonant Raman Scattering. Phys. Rev. Lett. 2001, 86, 1118.
  10. Gupta, S.S.; Bosco, F.G.; Batra, R.C. Wall thickness and elastic moduli of single-walled carbon nanotubes from frequencies of axial, torsional and inextensional modes of vibration. Computational Materials Science 2010, 47, 1049–1059. [CrossRef]
  11. Cheng, H.C.; Liu, Y.L.; Wu, C.; Chen, W.H. On radial breathing vibration of carbon nanotubes. Comput. Methods Appl. Mech. Eng. 2010, 199, 2820–2827. [CrossRef]
  12. Duan, W.; Wang, C.; Zhang, Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J. Appl. Phys. 2007, 101, 024305. [CrossRef]
  13. Odegard, G.M.; Gates, T.S.; Nicholson, L.M.; Wise, K.E. Equivalent-Continuum Modeling of Nano-Structured Materials. Compos. Sci. Technol. 2002, 62, 1869–1880. [CrossRef]
  14. Arroyo, M.; Belytschko, T. Continuum Mechanics Modeling and Simulation of Carbon Nanotubes. Meccanica 2005, 40, 455–469. [CrossRef]
  15. Zhang, P.; Huang, Y.; Geubelle, P.H.; Hwang, K. On the continuum modeling of carbon nanotubes. Acta Mech. Sin. 2002, 18, 528–536.
  16. Yakobson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response. Phys. Rev. Lett. 1996, 76, 2511–2514. [CrossRef] [PubMed]
  17. Wang, C.; Ru, C.Q.; Mioduchowski, A. Applicability and Limitations of Simplified Elastic Shell Equations for Carbon Nanotubes. J. Appl. Mech. 2004, 71, 622–631. [CrossRef]
  18. Silvestre, N.; Wang, C.; Zhang, Y.; Xiang, Y. Sanders shell model for buckling of single-walled carbon nanotubes with small aspect ratio. Compos. Struct. 2011, 93, 1683–1691. [CrossRef]
  19. Silvestre, N. On the accuracy of shell models for torsional buckling of carbon nanotubes. Eur. J. Mech.-A/Solids 2012, 32, 103–108.
  20. Strozzi, M.; Manevitch, L.I.; Pellicano, F.; Smirnov, V.V.; Shepelev, D.S. Low-frequency linear vibrations of single-walled carbon nanotubes: Analytical and numerical models. J. Sound Vib. 2014, 333, 2936–2957. [CrossRef]
  21. Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. Nonlinear vibrations and energy exchange of single-walled carbon nanotubes. Radial breathing modes. Compos. Struct. 2018, 184, 613–632. [CrossRef]
  22. Strozzi, M.; Pellicano, F. Nonlinear Resonance Interaction between Conjugate Circumferential Flexural Modes in Single-Walled Carbon Nanotubes. Shock Vib. 2019, 2019, 3241698. [CrossRef]
  23. Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. Nonlinear normal modes, resonances and energy exchange in single-walled carbon nanotubes. Int. J. Non-Linear Mech. 2020, 120, 103398.
  24. Rizzetto, F.; Jansen, E.; Strozzi, M.; Pellicano, F. Nonlinear dynamic stability of cylindrical shells under pulsating axial loading via Finite Element analysis using numerical time integration. Thin-Walled Struct. 2019, 143, 106213.
  25. Strozzi, M. Applicability and Limitations of Ru’s Formulation for Vibration Modelling of Double-Walled Carbon Nanotubes. J. Carbon Res. 2022, 8(4), 59. [CrossRef]
  26. Leissa, A.W. Vibration of Shells. Acoustical Society of America: Columbus, Ohio, 1993.
  27. Yamaki, N. Elastic Stability of Circular Cylindrical Shells. Elsevier: Amsterdam, The Netherlands, 1984.
  28. Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates. Cambridge University Press: New York, NY, USA, 2008.
  29. Soedel, W. Vibrations of Shells and Plates, 3rd ed. Marcel Dekker: New York, NY, USA, 2004.
  30. Ventsel, E.; Krauthammer, T. Thin Plates and Shells. Theory, Analysis, and Applications. The Pennsylvania State University, Marcel Dekker: New York, NY, USA, 2001.
  31. Amabili, M. A comparison of shell theories for large-amplitude vibrations of circular cylindrical shells: Lagrangian approach. J. Sound Vib. 2003, 264, 1091–1125. [CrossRef]
  32. Wang, C.M., Tay, Z.Y., Chowdhury, A.R., Duan, W.H., Zhang, Y.Y., Silvestre, N. Examination of cylindrical shell theories for buckling of carbon nanotubes. Int. J. Struct. Stab. and Dyn. 2011, 11, 1035–1058. [CrossRef]
  33. Chang, T.; Geng, J.; Guo, X. Prediction of chirality- and size-dependent elastic properties of single-walled carbon nanotubes via a molecular mechanics model. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 2523–2540. [CrossRef]
  34. Chang, T. A molecular based anisotropic shell model for single-walled carbon nanotubes. J. Mech. Phys. Solids 2010, 58, 1422–1433. [CrossRef]
  35. Strozzi, M.; Elishakoff, I.E.; Manevitch, L.I.; Gendelman, O.V. Applicability and limitations of Donnell shell theory for vibration modelling of double-walled carbon nanotubes. Thin-Walled Structures 2022, 178, 109532.
  36. Strozzi, M.; Smirnov, V.V.; Pellicano, F.; Kovaleva, M. Nonlocal anisotropic elastic shell model for vibrations of double-walled carbon nanotubes under nonlinear van der Waals interaction forces. International Journal of Non-Linear Mechanics 2022, 146, 104172.
  37. Ghavanloo, E.; Fazelzadeh, S. Vibration characteristics of single-walled carbon nanotubes based on an anisotropic elastic shell model including chirality effect. Appl. Math. Modell. 2012, 36, 4988–5000. [CrossRef]
  38. Fazelzadeh, S.; Ghavanloo, E. Nonlocal anisotropic elastic shell model for vibrations of single-walled carbon nanotubes with arbitrary chirality. Comp. Struct. 2012, 94, 1016–1022. [CrossRef]
Preprints 70054 g001
Figure 1. Continuum modelling of a SWCNT. (a) Actual discrete SWCNT. (b) Geometry of the equivalent continuous elastic thin cylindrical shell. (c) Cross-section of the surface of the equivalent continuous shell.
Figure 1. Continuum modelling of a SWCNT. (a) Actual discrete SWCNT. (b) Geometry of the equivalent continuous elastic thin cylindrical shell. (c) Cross-section of the surface of the equivalent continuous shell.
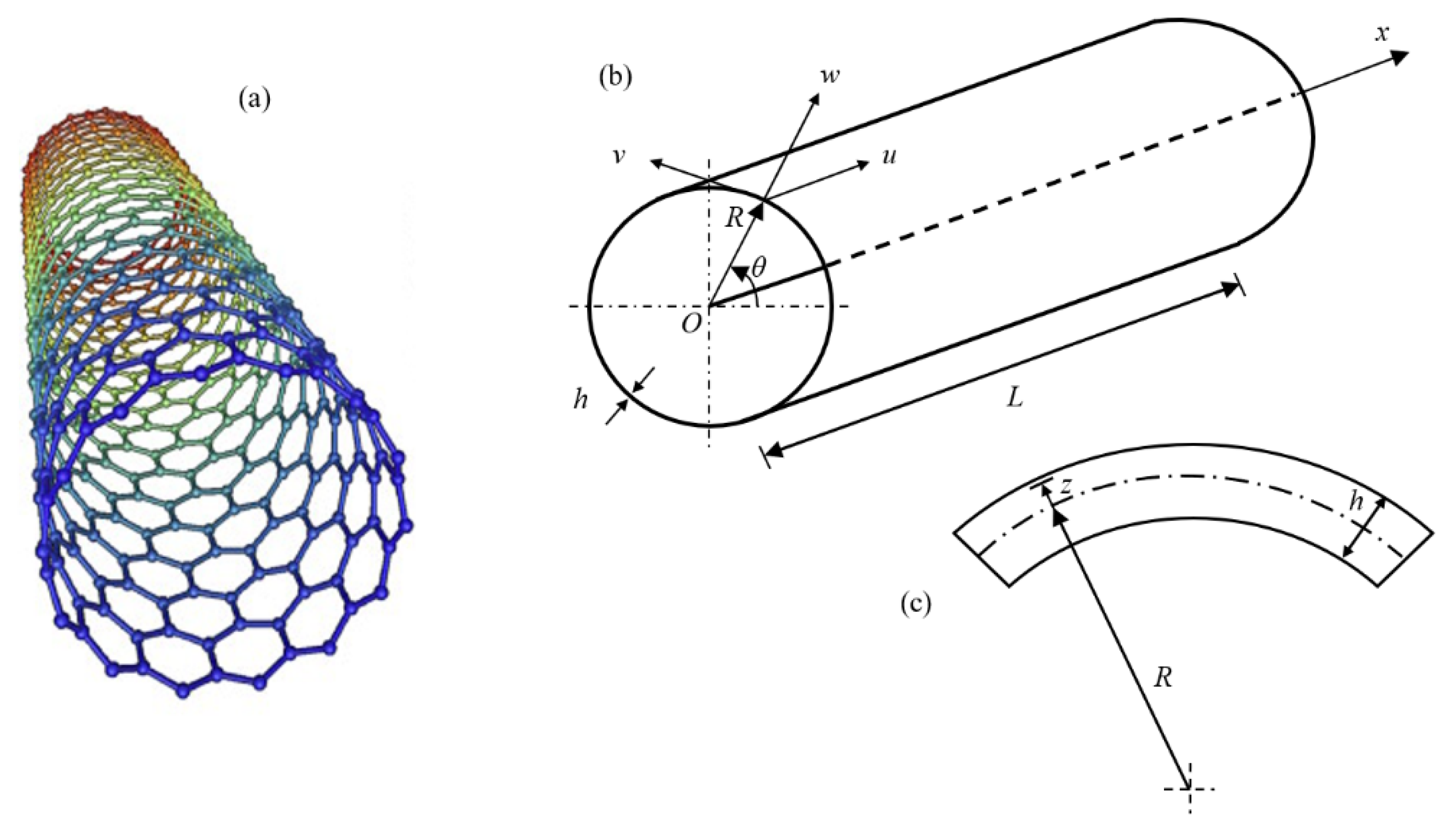
Preprints 70054 g001
Preprints 70054 g002
Figure 2. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 2. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
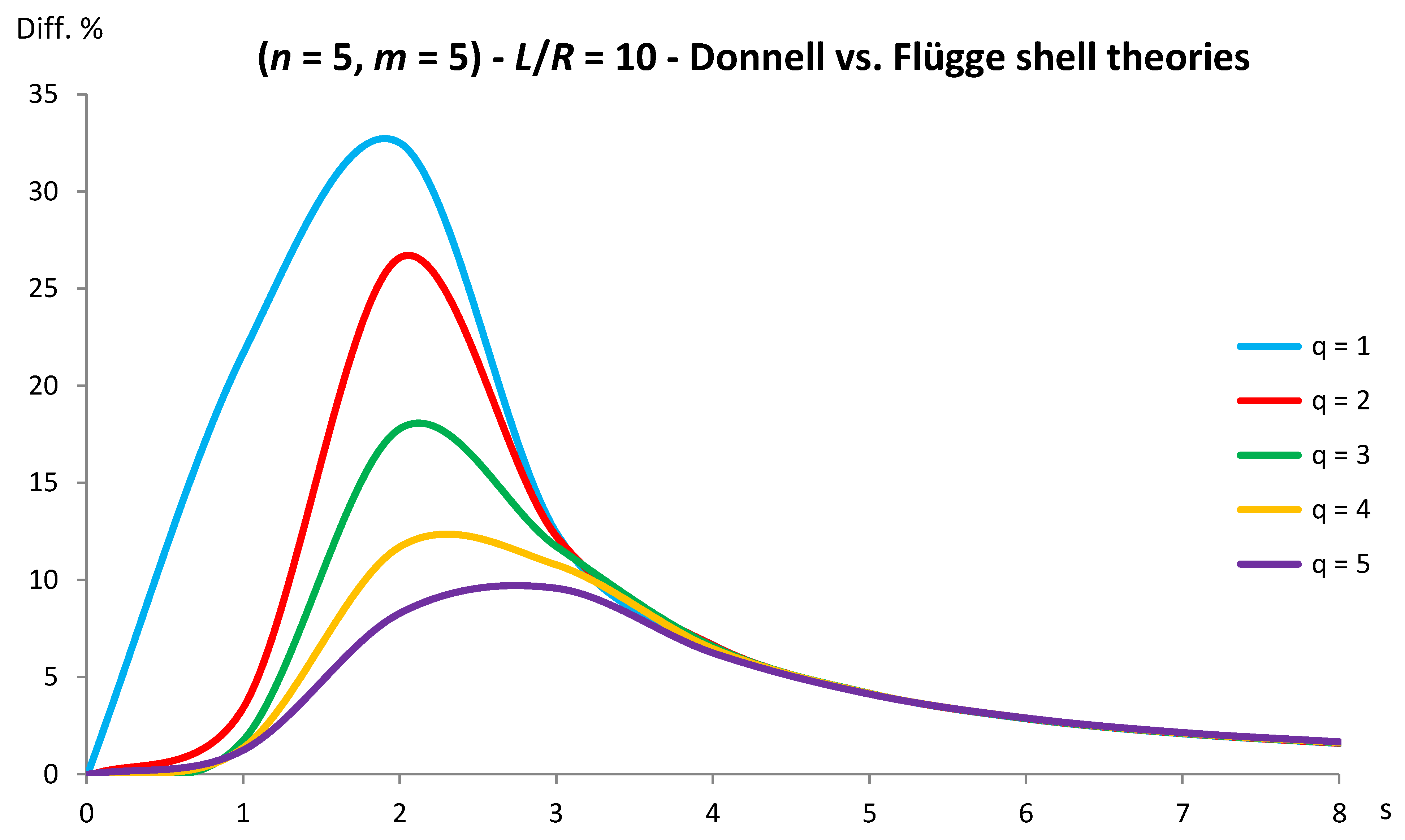
Preprints 70054 g002
Preprints 70054 g003
Figure 3. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 3. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
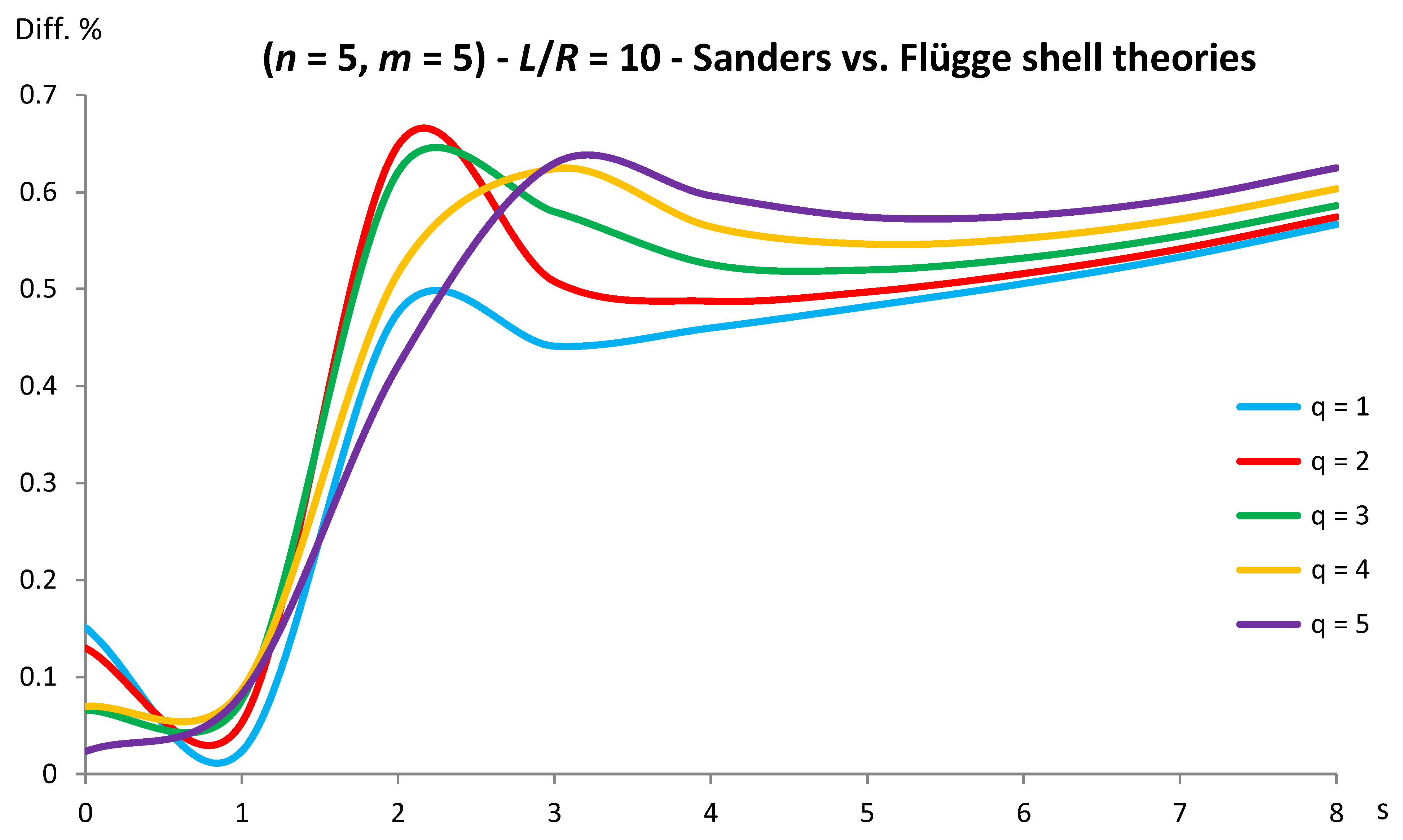
Preprints 70054 g003
Preprints 70054 g004
Figure 4. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 10, m = 10) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 4. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 10, m = 10) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g004
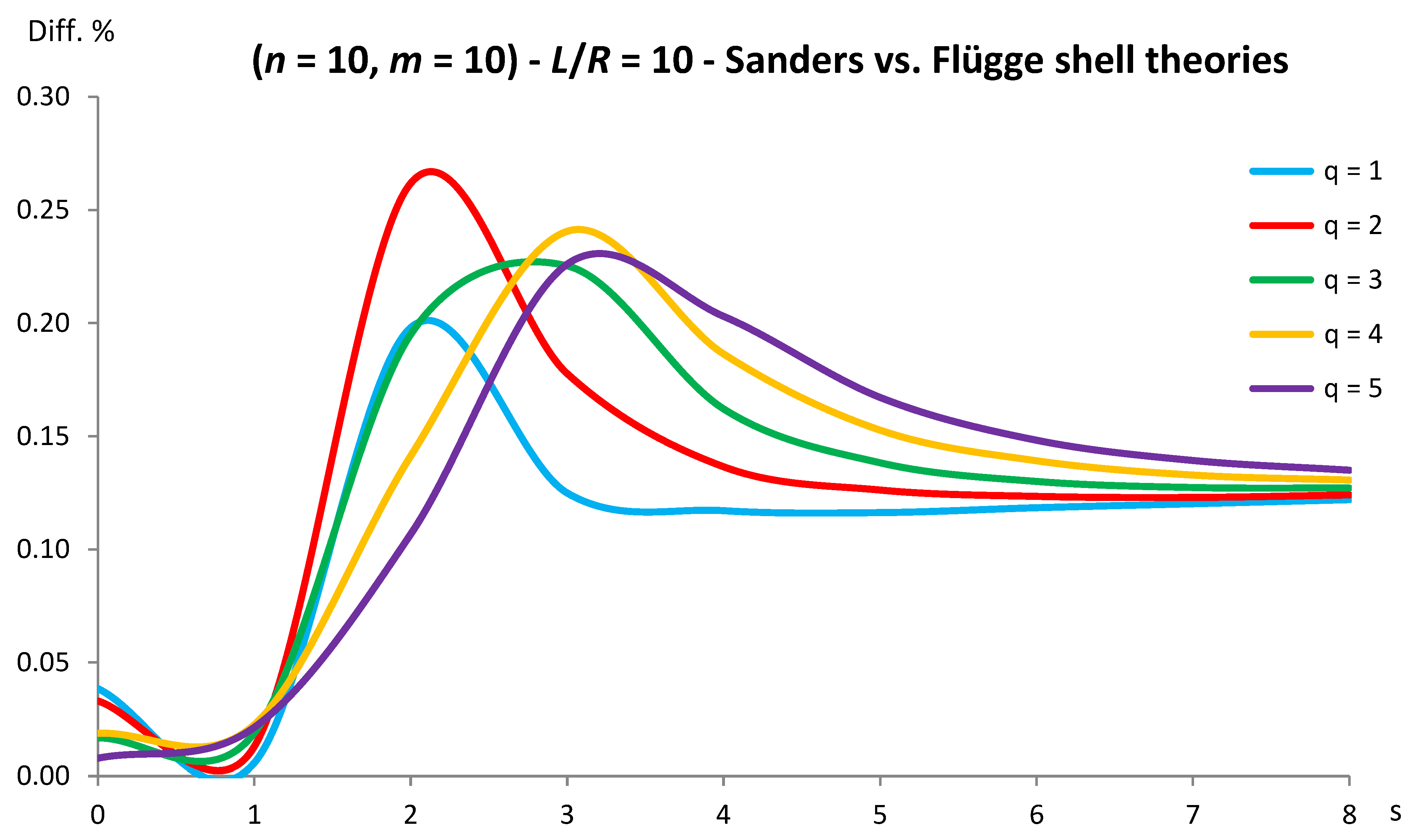
Preprints 70054 g005
Figure 5. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 10, m = 10) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 5. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 10, m = 10) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g005
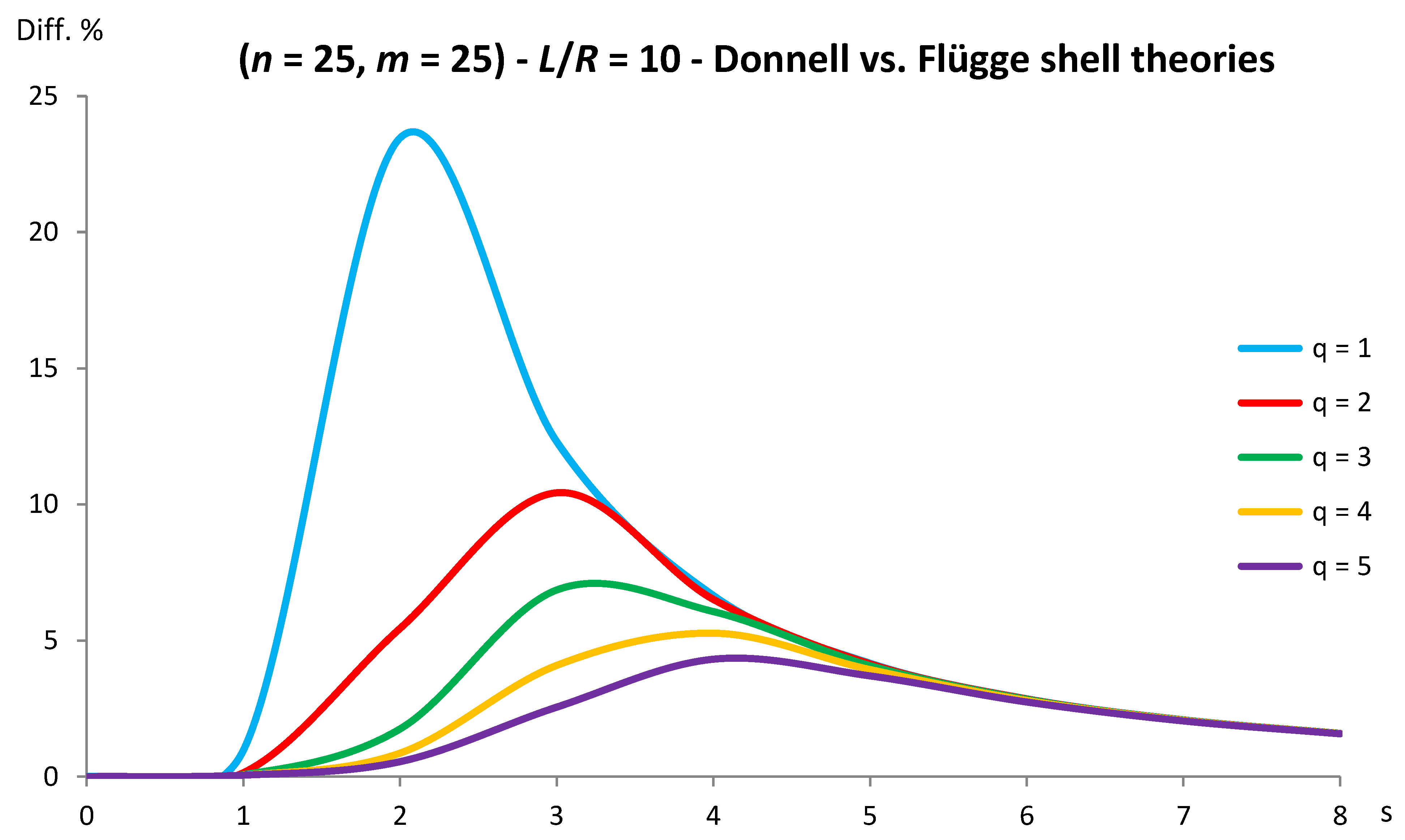
Preprints 70054 g006
Figure 6. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 25, m = 25) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 6. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 25, m = 25) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g006
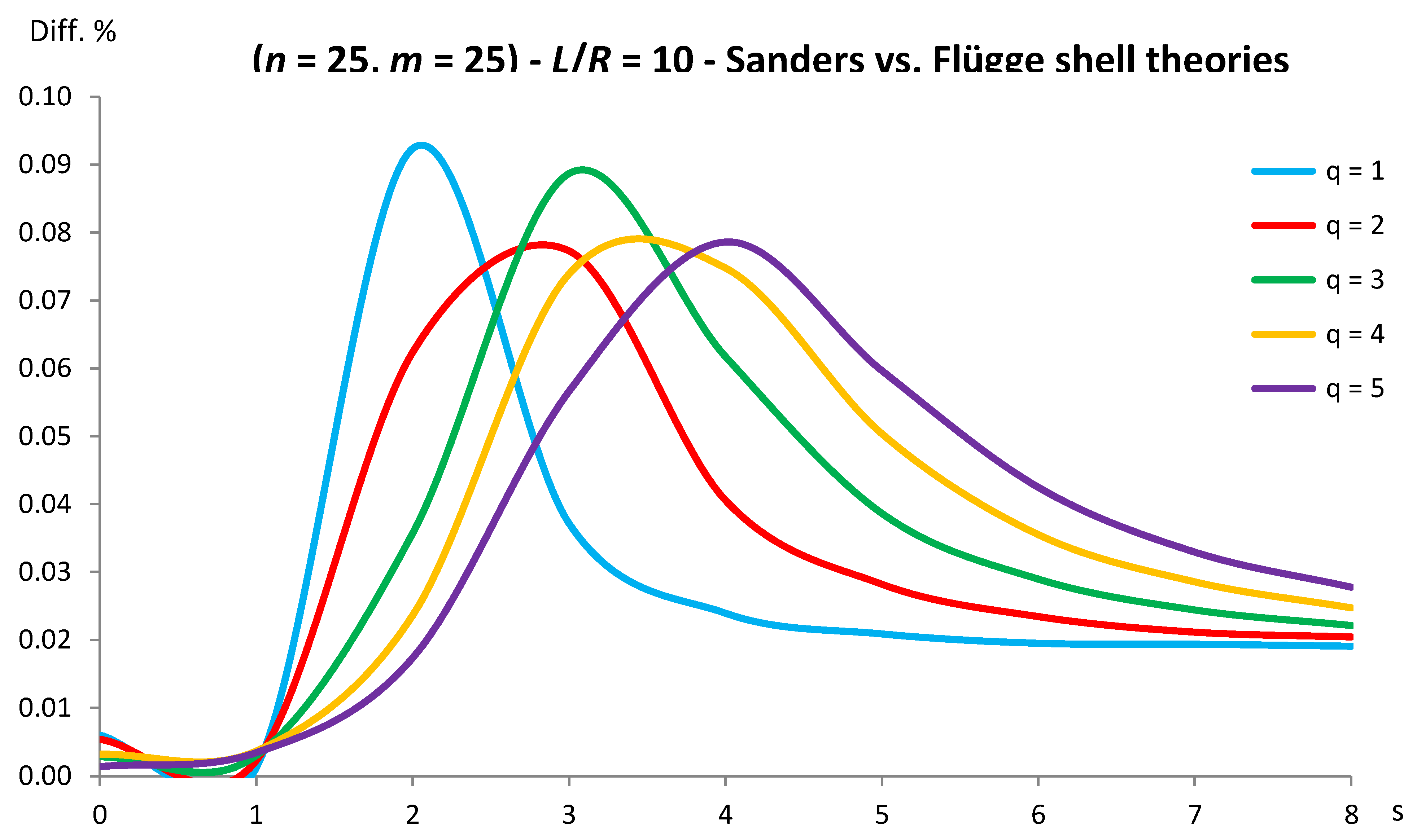
Preprints 70054 g007
Figure 7. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 25, m = 25) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 7. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 25, m = 25) and aspect ratio L/R = 10. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g007
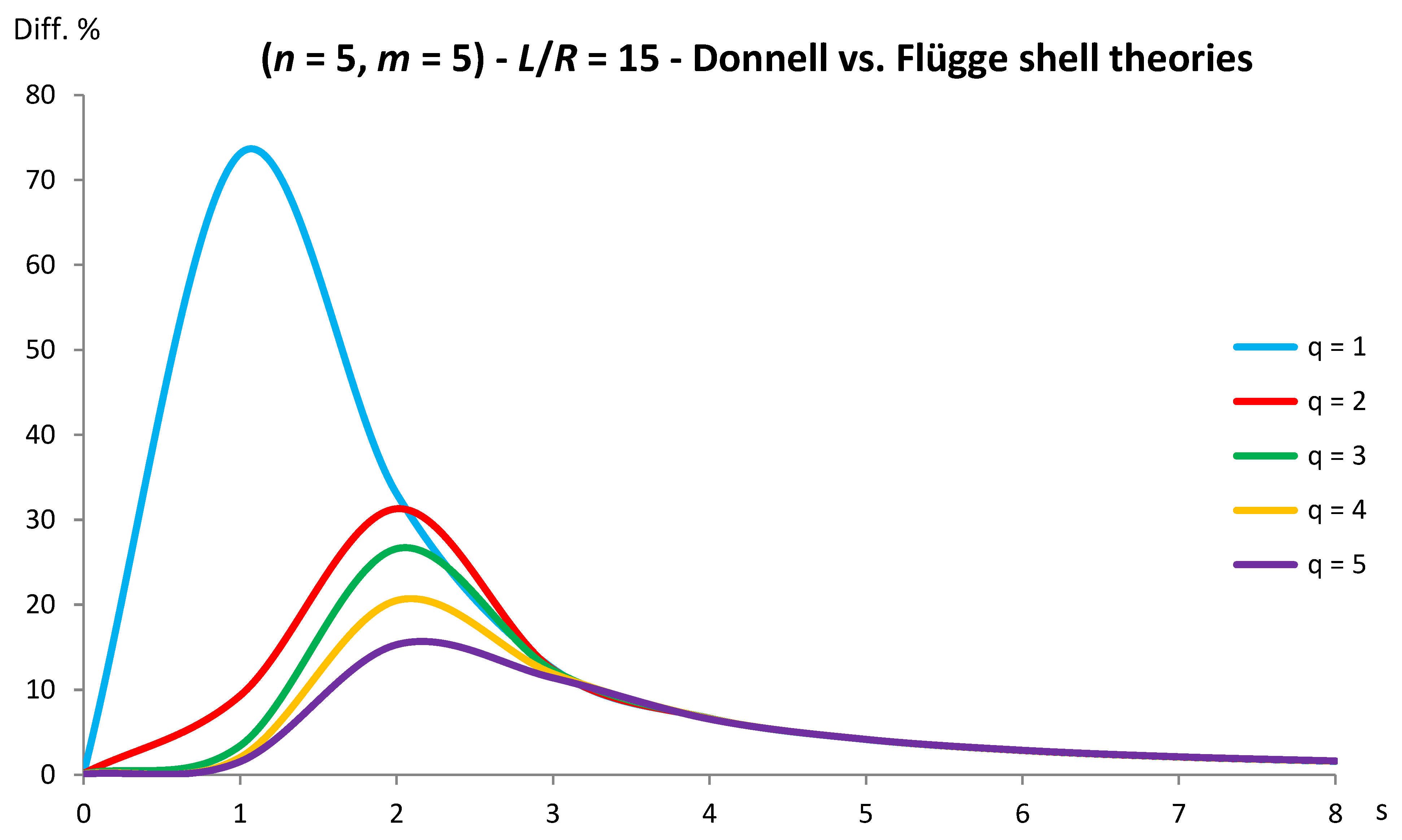
Preprints 70054 g008
Figure 8. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 15. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 8. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 15. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g008
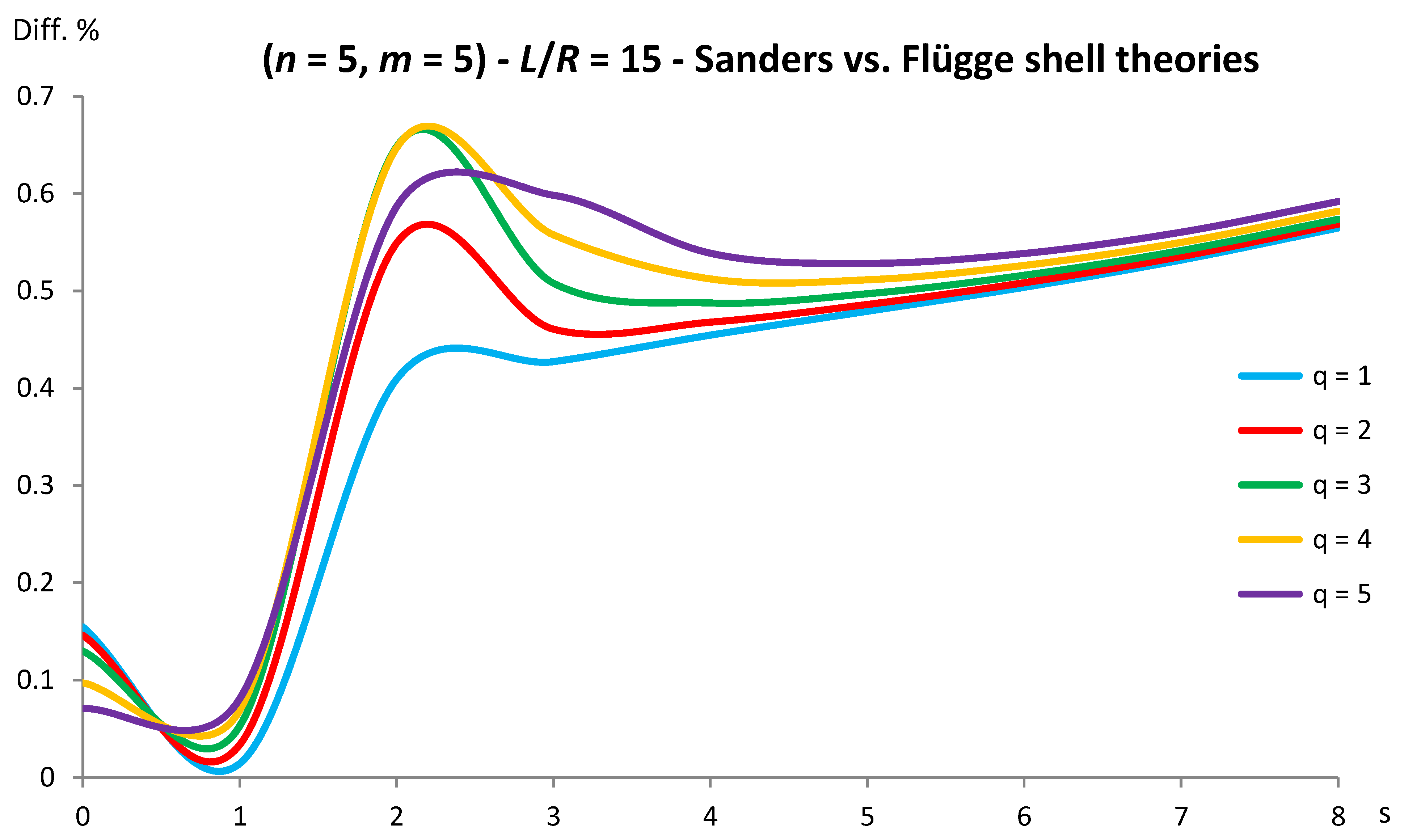
Preprints 70054 g009
Figure 9. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 15. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 9. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 15. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g009
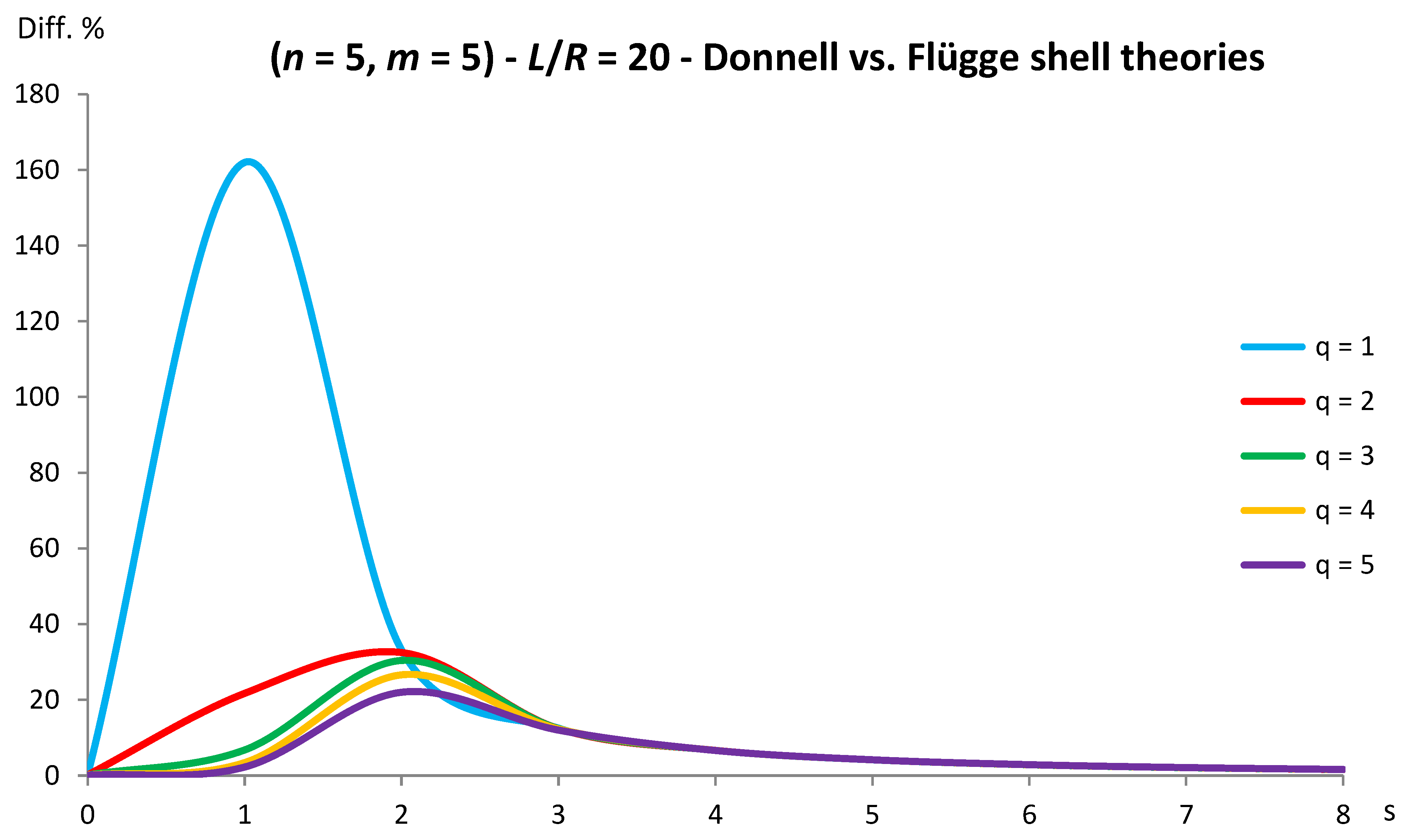
Preprints 70054 g010
Figure 10. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 20. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 10. Percentage differences between the radial natural frequencies obtained via Donnell and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 20. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g010
Preprints 70054 g011
Figure 11. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 20. Number of longitudinal half-waves q. Number of circumferential waves s.
Figure 11. Percentage differences between the radial natural frequencies obtained via Sanders and Flügge shell theories (Flügge as the reference). Anisotropic elastic shell model. Simply supported SWCNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 20. Number of longitudinal half-waves q. Number of circumferential waves s.
Preprints 70054 g011
Preprints 70054 g012
Figure 12. Mode shapes of the simply supported SWNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 10. (a) Radial breathing mode (q = 0, s = 0). (b) Axisymmetric mode (q = 1, s = 0). (c) Beam-like mode (q = 1, s = 1). (d) Shell-like mode (q = 1, s = 2). (e) Shell-like mode (q = 1, s = 3). (f) Shell-like mode (q = 1, s = 4).
Figure 12. Mode shapes of the simply supported SWNT of Table 1 with chirality indices (n = 5, m = 5) and aspect ratio L/R = 10. (a) Radial breathing mode (q = 0, s = 0). (b) Axisymmetric mode (q = 1, s = 0). (c) Beam-like mode (q = 1, s = 1). (d) Shell-like mode (q = 1, s = 2). (e) Shell-like mode (q = 1, s = 3). (f) Shell-like mode (q = 1, s = 4).
Preprints 70054 g012
Table 1. Mechanical parameters adopted in the anisotropic elastic shell model [33,16].
Table 1. Mechanical parameters adopted in the anisotropic elastic shell model [33,16].
C-C bond length a (nm) 0.142
C-C bond elongation Kρ (nN/nm) 742
C-C bond angle variance Kθ (nN·nm) 1.42
Shell thickness h (nm) 0.0665
Mass density ρ (kg/m3) 11700
Table 2. Natural frequencies of the radial breathing mode (q = 0, s = 0) of the SWCNT of Table 1 with aspect ratio L/R = 10. Comparisons between Donnell, Sanders and Flügge shell theories and molecular dynamics simulations.
Table 2. Natural frequencies of the radial breathing mode (q = 0, s = 0) of the SWCNT of Table 1 with aspect ratio L/R = 10. Comparisons between Donnell, Sanders and Flügge shell theories and molecular dynamics simulations.
Natural frequency ωRBM (cm-1) Difference (%)
Chirality
indices (n, m) 		Molecular dynamics simulations [10] Donnell shell theory Sanders shell
theory		 Flügge shell
theory
(10, 0) 290.463 2.38 1.32 0.42
(9, 6) 221.496 3.47 1.93 0.43
(8, 8) 209.008 4.05 2.25 0.51
(9, 9) 185.896 4.03 2.24 0.49
(16, 0) 181.747 3.10 1.72 0.04
(10, 10) 167.377 4.01 2.23 0.48
(11, 11) 152.207 4.00 2.22 0.47
(20, 0) 145.363 3.35 1.86 0.11
(22, 7) 110.808 3.71 2.06 0.32
(25, 10) 93.153 3.56 1.98 0.21
(30, 5) 88.750 3.51 1.95 0.16
(36, 5) 75.118 3.47 1.93 0.17
(33, 16) 67.221 3.56 1.98 0.23
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated