Zirconium nitride and carbide are important materials in the design of nuclear power plants and equipment operating under extreme conditions [1]. Uranium carbide is considered as a promising material for fuel of fast nuclear reactors due to its unique properties [2]. Actinide nitrides are of interest as the fuel of nuclear power plants, since nitrides have a higher thermal conductivity compared to actinide oxides, which reduces the thermal degradation of reactors [3]. For these nuclear materials, the problem of describing their thermal conductivity has not yet been solved. We propose a new formula that describes the change of the thermal conductivity of these materials with the temperature through a very simple dependence on atomic numbers and thermal conductivities of individual components.

Suppose we want to calculate an arbitrary physical quantity L that characterizes some physical property of an arbitrary substance with the chemical formula A_kB_lC_n... where the number of elements in the formula must be greater than one. The desired physical quantity L depends on the components of the substance and its structure. This quantity L can be the temperature of phase transition of any order and any other thermophysical quantity, mechanical, electrical, magnetic, optical and other characteristics of the substance. It can be assumed that L somehow depends on the similar physical quantities L_i of all components of the substance under consideration: L = L(L_A, L_B, L_C, ....). Since the amount of a component in a substance affects its properties, it should be concluded that chemical indexes should also be represented in the function: L = L(L_A, L_B, L_C, ...., k, l, n, …). Since the atomic number of each component ultimately determines the electronic structure of a substance, we insist that the atomic numbers of all components also be represented in a functional relationship: L = L(L_A, L_B, L_C, ...., k, l, n, …, A, B, C, …), where A is the atomic number of element A. The phase state of matter also determines L, and we assume that the state of matter should be represented by a structural parameter h: L = L(L_A, L_B, L_C, ...., k, l, n, …, A, B, C, …, h). Since the properties of a substance can change due to changes in temperature T, pressure p, radiation dose D, static electromagnetic fields (E, B), etc., the value of L changes with such changes, but we will assume that L not depends on them directly, but only through L_i and h: L(T,p,D,E,B,…) = L(L_A(T,p,D,E,B,…), L_B(T,p,D,E,B,…), L_C(T,p,D,E,B,…), ...., k, l, n, …, A, B, C, …, h(T,p,D,E,B,…)). Since the basic physical properties of a chemical element depend on a set of integers that determine the position of the element in the periodic table, and given that the crystal structure is represented through a set of rational numbers representing the space group, we insist that the structural parameter h is a rational number, although it somehow depends on the lattice parameters: h = h(a, b, c, α, β, γ)$\in$Q, where Q is a set of rational numbers.

Now suppose that L ≡ λ_ABC… is the thermal conductivity of A_kB_lC_n... and we want to find its dependence on temperature only: L(T) = L(L_A(T), L_B(T), L_C(T), ...., k, l, n, …, A, B, C, …, h(T)). We found in [4] that for oxides and silicates (ZrO₂, ZrSiO₄, (U,Zr)SiO₄, UO₂) the best agreement with experiment is given by the following formula: where the parameter h is associated with the most electronegative element, in our case with C. It has been observed that h is a constant over a certain range of temperatures. Thus, for example, for silicate (U_0.016Zr_0.984)SiO₄ at temperature range T $\in$(470, 1070] K where h = 1, the thermal conductivity is next: where atomic numbers: U = 92, Zr = 40, Si = 14, O = 8. For zircon ZrSiO₄ in the temperature range T$\in$[570, 1170] K where h = 2/3, the thermal conductivity is next: where atomic numbers are Zr = 40, Si = 14, O = 8.

We applied formula (1) to describe the thermal conductivity of carbides and nitrides and found (see the next section) that for some ceramics the structural parameter h is fixed in a certain temperature range, which makes it possible to represent the thermal conductivity of ceramics as the sum of the thermal conductivities of its components.

To assess the correctness of formula (1), relative errors were calculated in this work using the following formula: where λ_theory is the result of using formula (1) and λ_exp is taken from experimental data.

For zirconium carbide ZrC, formula (1) has the following form: where atomic numbers are Zr = 40, C = 6. The result of calculations by formula (3) and comparison with the experiment [1] is given in Table 1. The thermal conductivity of carbon in the form of bulk diamond was taken from [5], [6], where theoretical data for bulk diamond are presented, which are in good agreement with the available experimental data [7].

Table 1 shows that the parameter h decreases with increasing T. The step of changing h between 400 and 600 K is Δh = 1 at 100 K. Therefore, we can express h in terms of T in this temperature range and obtain for ${\lambda }_{ZrC}$ at T $\in$ [400, 600] K: where $a=\frac{1}{100}\left[K^{-1}\right]$. In order to fully express the thermal conductivity of a substance over the entire range of T, it is necessary to know the dependence of h on the lattice parameters as the temperature changes: h = h(a(T), b(T), c(T), α(T), β(T), γ(T))$\in$Q.

For uranium carbide UC, formula (1) has the following form: where atomic numbers are U = 92, C = 6. The result of calculations by formula (4) and comparison with the experiment [2], [9] is given in Table 2. Table 2 shows that the parameter h decreases with increasing T. The negative value of h = –1/666 at T = 800 K requires studying the function λ_UC =λ_UC(h) at fixed T, that is, at fixed λ_U and λ_C.

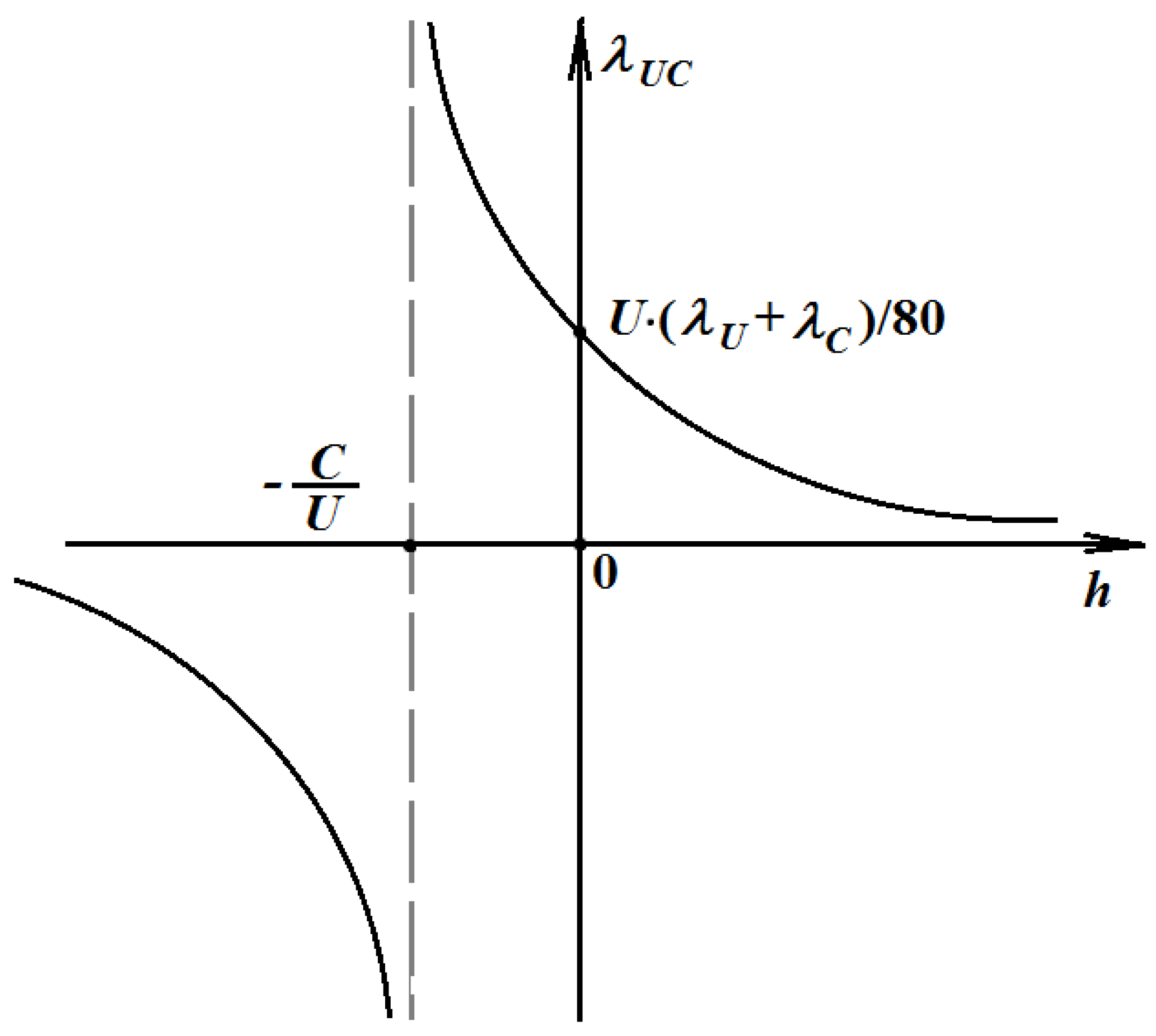
The function λ_UC =λ_UC(h) is shown in Fig.1. This is hyperbola with shifted center to the point $\left(-\frac{C}{U},0\right)$. λ_UC(h) has an essential discontinuity at $h=-\frac{C}{U}$. At h = 0,  ${\lambda }_{UC}=U\cdot ({\lambda }_U+{\lambda }_C)/80.$ The domain of positive λ_UC(h) is $h\in (-\frac{C}{U},+\infty )\subset$Q, where Q is a set of rational numbers. Only one value of h from this domain gives the physical value of λ_UC(h). The range of negative values of λ_UC(h) is not physical.

For uranium nitride UN, formula (1) has the following form: where atomic numbers are U = 92, N = 7. The result of calculations by formula (5) and comparison with the experiment [3] is given in Table 3. Table 3 shows that the parameter h is a constant at T $\in$[400, 900] K and (900, 1200] K. Therefore, we can describe λ_UN as the sum of the thermal conductivities of its components: where h = 1/10 at T $\in$ [400, 900] K and h = 1/9 at T $\in$(900, 1200] K.

For thorium nitride ThN, formula (1) has the following form: where atomic numbers are Th = 90, N = 7. The result of calculations by formula (6) and comparison with the experiment [3] is given in Table 4. Table 4 shows that the parameter h gradually increases with increasing T.

For mixed ceramics Th_xU_1-xN, where x = 0.2 and 0.5, formula (1) has the following form: where atomic numbers are Th = 90, U = 92, N = 7. The result of calculations by formula (7) and comparison with the experiment [3] is given in Table 5. Since

the influence of λ_N is negligible, since λ_N << x·λ_Th, (1–x)·λ_U over the entire temperature range, we excluded it from the calculations.

Table 5 shows that the parameter h is a constant for some temperature intervals. Therefore, we can describe, for example, ${\lambda }_{T{h}_{ 0.5 }{U}_{0.5} N}$ as the sum of the thermal conductivities of its components: where h = –10/73 at T $\in$ [400, 600] K and h = –10/71 at T $\in$(600, 1100] K.

For zirconium nitride ZrN, formula (1) has the following form: where atomic numbers are Zr = 40, N = 7. The result of calculations by formula (8) and comparison with the experiment [1] is given in Table 6. Since the influence of λ_N is negligible, since λ_N << λ_Zr over the entire temperature range, we excluded it from the calculations. Table 6 shows that the parameter h is a constant for some temperature intervals. Therefore, we can describe λ_ZrN as the sum of the thermal conductivities of its components: at T $\in$ [1070, 1370] K.

We have applied number theory to describe the thermal conductivity of carbides and nitrides of Zr, Th and U as a function of temperature. We used the same formula obtained in our previous work for oxides and silicates of Zr and U. The parameter h included in the formula (1), which is related to the crystal structure of ceramics, turned out to be constant in some temperature ranges, which made it possible to write the thermal conductivities of the ceramics in terms of the sum of the thermal conductivities of its components. Our next step is to describe the behavior of h as a function of temperature dependent lattice parameters. This will make it possible to describe the thermal conductivity of nuclear ceramics as the temperature changes in terms of the thermal conductivities of its components over the entire temperature range.