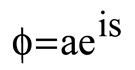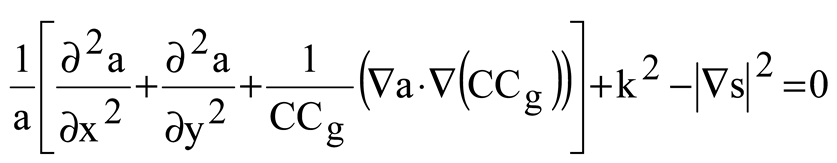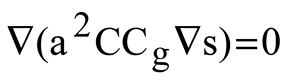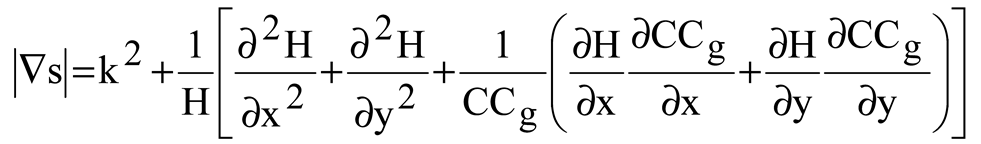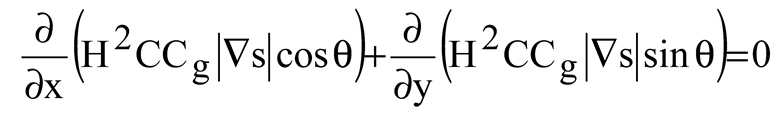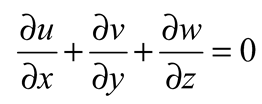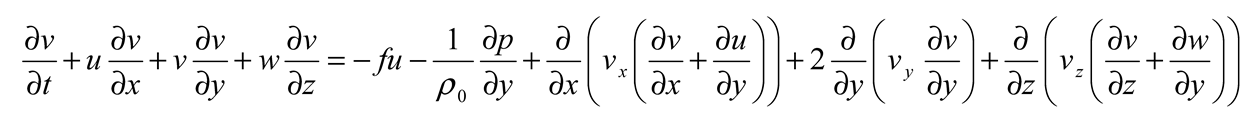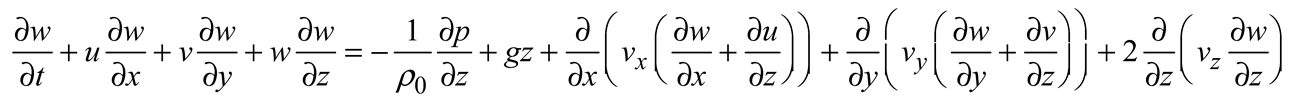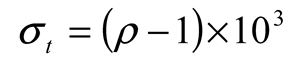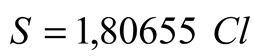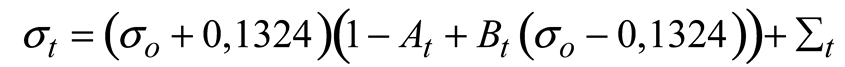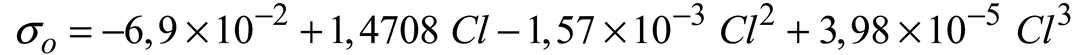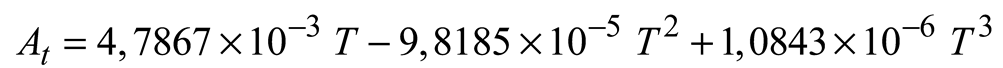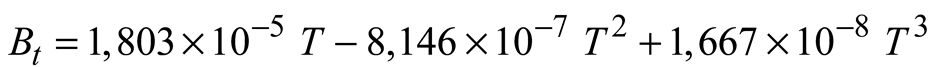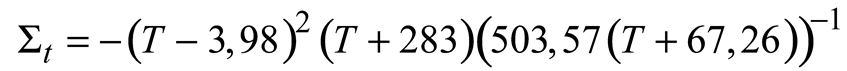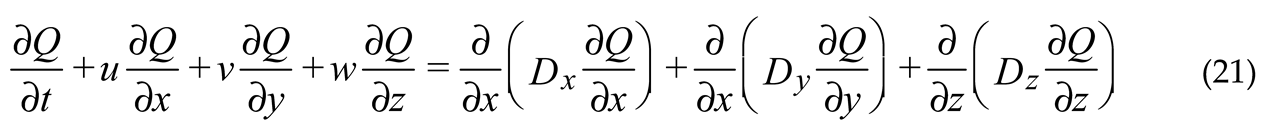1. Introduction
Coastal flow slides also referred to both retrogressive breaching and liquefaction flow slides, are geomorphological processes that involve the downslope movement and redeposition of a significant amount of material from an underwater slope of a specific steepness (Beinssen and Mastbergen, 2018). The unpredictable timing of these events, coupled with their brief lifespan and unseen initiation locations, make them difficult to observe in nature and to determine the causes and consequences of their occurrences as given in
Table 1 (Mastbergen et al., 2019). There are two categories of coastal flow slides: breaching failure and liquefaction failure. Breaching failure, also known as coastal slope failure, occurs when the slope of the beach is steep (Brothers et al., 2019a), while liquefaction failure occurs when the natural slope of beaches is mild (Mastbergen et al., 2019). The stationary suction dredger manufacturing industry in the Netherlands first discovered this failure mechanism in the 1970s. Breaching is widely recognized as a prominent failure mechanism on a worldwide scale and is considered in safety assessments.
In coastal engineering, the term "breaching" is often used to describe the retrogressive erosion and collapse of embankments, dams, and sand barriers due to overtopping (Brothers et al., 2019b). You et al. (2012) defined breaching as the slow retrogressive failure of an extremely steep subaqueous slope that exceeds the angle of repose. A comprehensive understanding of coastal processes, particularly the mechanisms that govern sediment movement, is a critical component of a coastal engineering project (Glavovic, 2014). Coastal engineers have a good understanding of the function of littoral sand drift and the kinetic energy of waves and currents that drive the process of sediment transport. However, the processes driving flow slides, particularly in the context of coastal erosion, are not well understood.
The threat to human populations, arable land, and tourist-attractive beaches near the coast has been exacerbated by recent natural hazards such as sea level rise, earthquakes, climate change, and severe weather-related floods(Butler, 2021; Sack, 2002).
As a result, many coastal protection structures, such as breakwaters and spurs, are being built in coastal areas (Dalton et al., 2008; Knight and Burningham, 2022; Smith et al., 2006; van Rijn, 2011). However, if the environmental conditions of the specific region are not considered, these structures can severely disrupt the delicate balance of the coastal morphology (Alhaddad et al., 2020; Ar Guner et al., 2011).
The construction of wave energy devices in the vicinity of the shoreline has increased in recent decades as wave energy is a renewable source (Alexander, 2022; Cloutier et al., 2017; Stoutjesdijk et al., 1995). These structures are often constructed in wave-breaking regions where wave energy is high. If the equilibrium of the slope is disrupted for any reason, such as climate change, erosion, or coastal flow slides, these structures may become ineffective (Aydoğan and Ayat, 2018; Cloutier et al., 2017; Stoutjesdijk et al., 1995; Guneroglu, 2015). Hence the movement of the seabed, coastal structures, and renewable wave energy devices can be negatively impacted (De Groot et al., 2012; Luijendijk et al., 2018; Ozkan and Mayo, 2019).
In the event of a slope failure, there are several potential impacts on the environment, such as the deterioration of water quality by increasing nitrogen and phosphorus concentrations at the surface. The reproductive habitats at the bottom of the sea could be disrupted due to slope failures caused by coastal flow slides. The global climate crisis has led to higher sea levels and more frequent storms, both of which have hastened the erosion of beaches close to human areas (Udo et al., 2012) (
Figure 1). Furthermore, the failure of the slope can render coastal protections ineffective, leading to a reduction in the width of the beach, which will have a direct impact on the coastal region and tourism industry (Kang et al., 2007).
Field and experimental studies can assist in research on how to control slope failure on the coast. Flow slides on beaches, also known as dilative slope failure, are like landslides, but in this case, the beach slope erodes with the waves in the steep areas of the shore and is carried into the sea (Ariza et al., 2008; Westoby et al., 2018; Zhang et al., 2020). This process involves the flow of a combination of water and sediment, and in certain situations, thousands of cubic meters of beach debris can be delivered into the sea within minutes(Silver and Dugan, 2020; Soldati et al., 2018; Sun and Leslie, 2020). Kang et al. (2007) employed a hybrid strategy combining the M5 model tree and Monte Carlo Simulation for the risk assessment of Coastal Flow Slides based on reliability analysis. Clare et al. (2022) utilized XBeach with Monte Carlo Simulation to develop a hybrid model for coastal sediment transport.
Efforts to reduce erosion caused by wave and storm surges have been attempted, but these measures involved either temporary solutions or have failed to consider climate change(Bricker et al., 2015; Kasmi et al., 2020; Phillips and Jones, 2006; Shahin et al., 2020). Coastal engineers recognize the importance of wave and current energy in coastal sediment transfer (Chen and Liu, 2007; Fu et al., 2019; Gong et al., 2018). However, the impact of gravitational potential energy on slope failure has not been studied, despite its critical role in the migration of vast amounts of coastal sediments (Kennedy et al., 2020; Ortega-Casanova et al., 2011; van Rhee, 2010)
The growth of population and the resultant decline in available land has led to the development of new coastal infrastructure, including airports, which can be classified as mega constructions, such as the Rize–Artvin Airport which was constructed off the coast of the Black Sea, Northeastern Turkey. Coastal slope failure or beach erosion is a widespread coastal hazard with severe outcomes, including the loss of land and property. Approximately 24% of the world's beaches are eroding at a rate of more than 0.5 m per year (Richard et al., 2020; Shimozono and Sato, 2016). An example of coastal flow slides, which happened within half an hour, is shown on the Cap Ferret coast as given in
Figure 2. Therefore, our study is focused on better understanding and mitigating the impacts of coastal slope failure.
The issue of coastal slope failure has gained significant attention in recent years due to the increasing frequency and severity of flow slides resulting from climate change. Despite this, there has been limited research on the subject, particularly regarding the mechanisms behind retrogressive breach failure. This phenomenon is characterized by the narrowing of beaches and can have severe consequences for both the tourism industry and coastal infrastructure. The challenge of coastal slope failure has far-reaching consequences for various issues such as the protection of coasts, controlling erosion, stability and control of slope failures, and the effects on the environment. This is why it is crucial to study this phenomenon and understand its underlying mechanisms.
Past studies on coastal flow slides have been limited and conducted under deterministic conditions. This study utilizes a Monte Carlo Simulation (MCS) that employs random variables to model the coastal flow slides process and assess the critical angle slope. The accuracy of the critical angle slope design is improved by incorporating hydrodynamic forces determined by the Hydrodynamic Transport and Turbulence Module. This is the first application of risk design that addresses the subject of coastal flow slide. The hydrodynamic model is coupled with Monte Carlo Simulation and Bayesian Networks for the stability assessment. Hence, the increasing frequency and severity of flow slides resulting from climate change highlight the importance of understanding the mechanisms behind coastal flow slides. This study utilizes the BN-based Monte Carlo Simulation Model to improve the accuracy of the critical angle slope design and provide insights into the consequences of this phenomenon. This research in this area enables a better understanding and addresses the challenges posed by coastal slope failure.
2. The Breach Failure Function
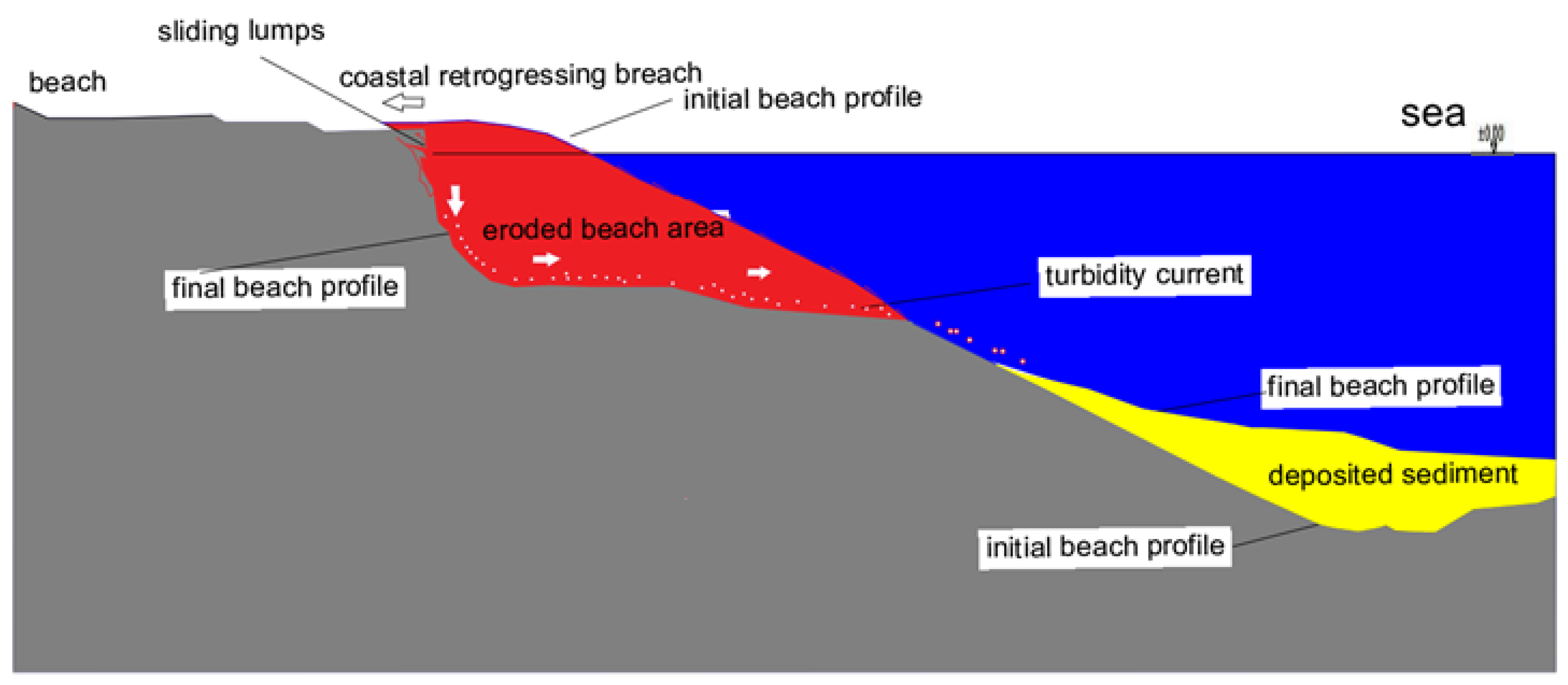
The breach can occur in the nearshore zone due to wave breaking. A typical figure of the breaching mechanism is shown in
Figure 3. Wave motion starts sediment transfer, and the transported sand accumulates in the zone of a moderate slope as shown in
Figure 3.
The sandy shorelines in the Dutch province of Zeeland were a source of concern due to their vulnerability to abrupt collapse. During a flow slide, a mixture of water and sand would roll into deeper waters, sometimes resulting in the loss of the entire dike (Remmerswaal et al., 2021). It is important to differentiate between flow slides and erosion, as they are two distinct processes.
Erosion occurs along the coastline and involves the gradual wearing of land by natural forces such as wind and water. In contrast, flow slides occur underwater and result from the shifting of bottom contour lines or depth contours, leading to the destruction of beaches. As highlighted by Ortega-Casanova et al. (2011), flow slides are characterized by the collapse of dikes and the accompanying displacement of water and sand. Sun and Leslie (2020) and Westoby et al. (2018) have emphasized the need to differentiate between flow slides and erosion, as a misidentification of the underlying process can result in inappropriate responses and management strategies. Understanding the underlying mechanisms and causes of coastal flow slides is critical for developing effective approaches to mitigating their impact and preserving coastal ecosystems and infrastructure. This research introduces a hybrid probabilistic model to enhance our understanding of these processes and help develop effective strategies for mitigating their impacts.
Figure 4 illustrates the coast of the Eastern Scheldt basin where the loosely packed sand glides start to flow for no apparent reason. The red line depicts the final pattern of the beach, while the yellow line depicts the beach's shape before the occurrence of flow slides.
3. The New Hybrid Bayesian Risk Model
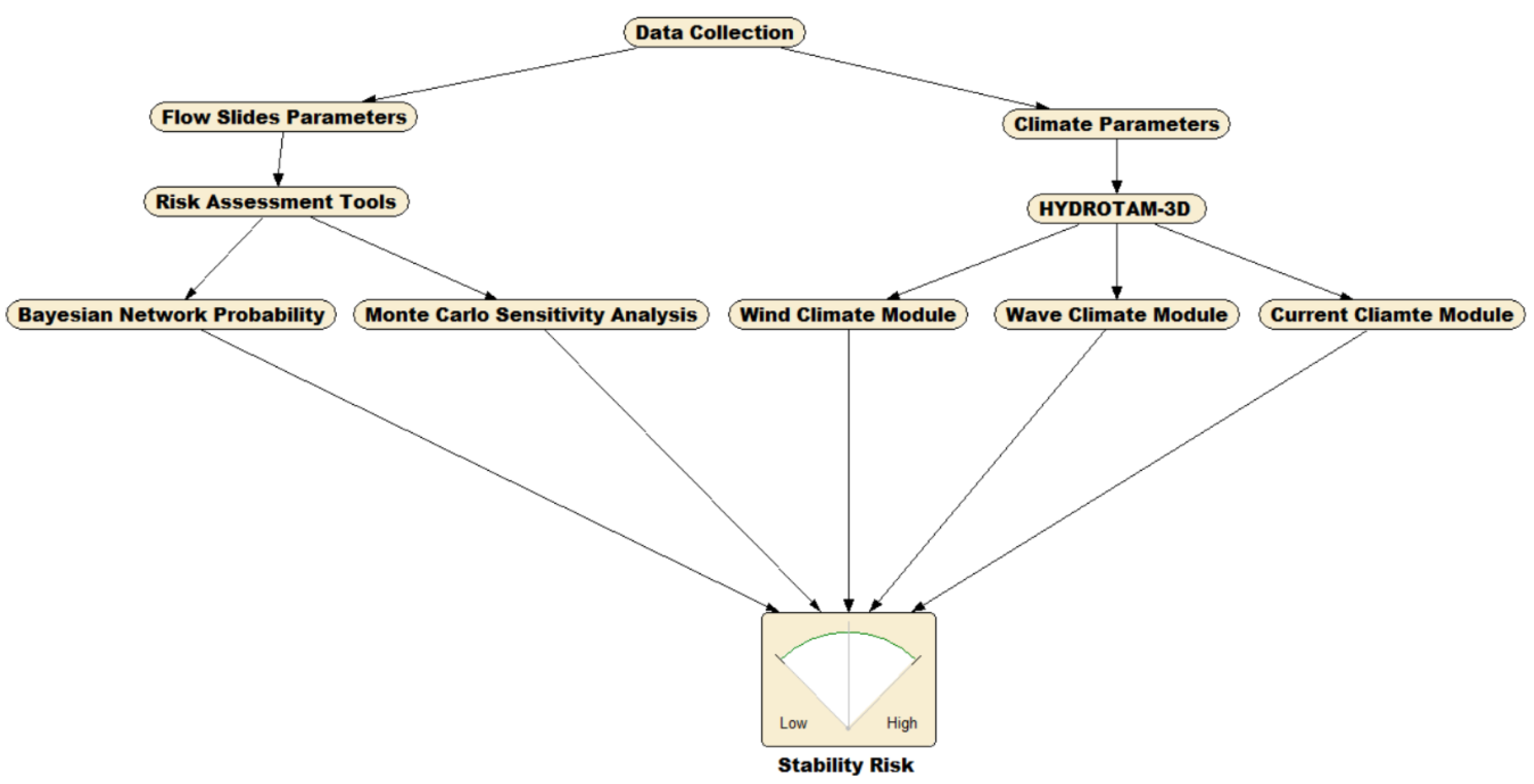
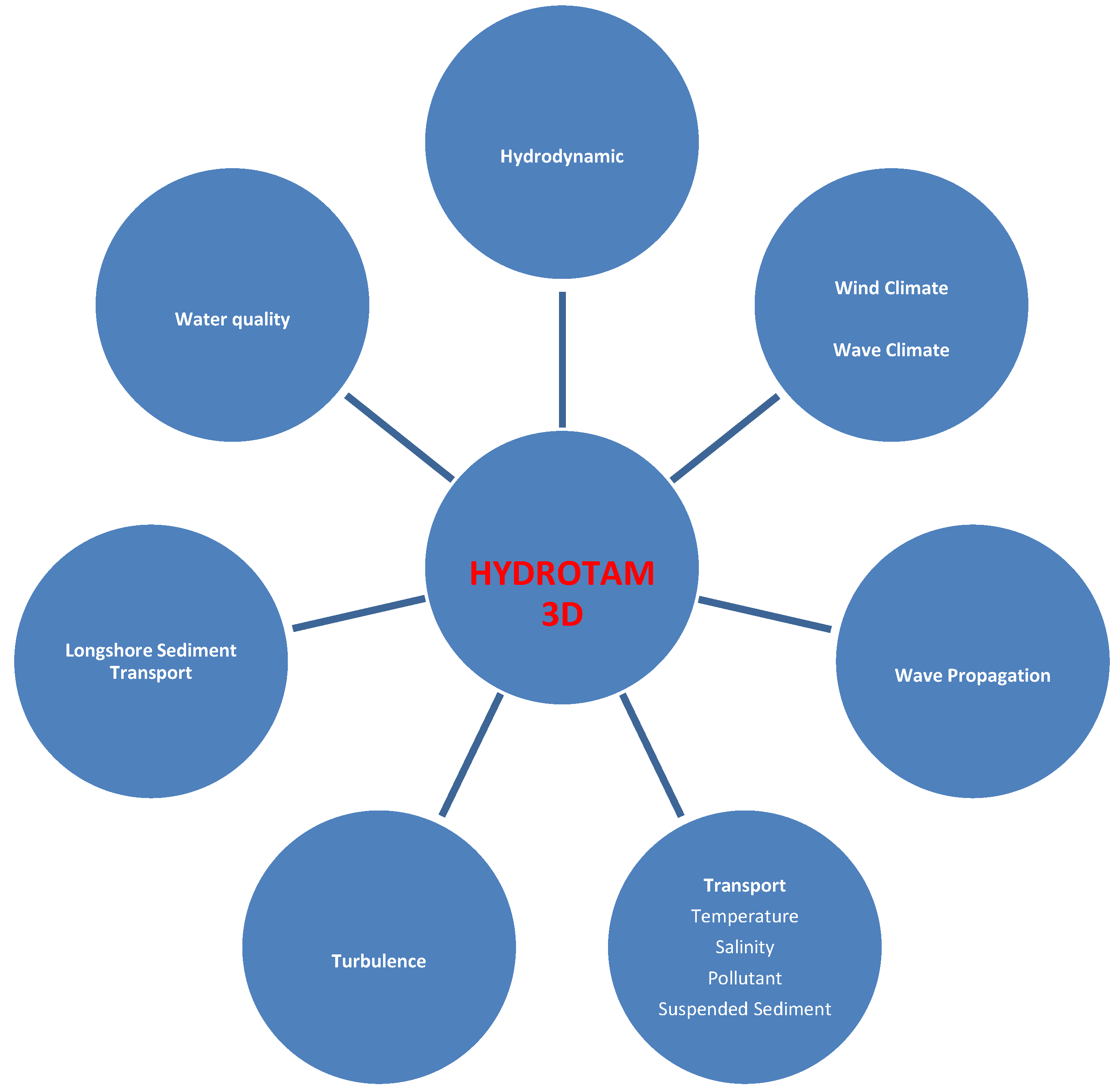
This paper presents a new Hybrid Bayesian Network Model which is integrated with the Hydrodynamic Transport and Monte Carlo Simulation (MCS) models for the risk assessment of Coastal Flow Slides. The model incorporates various modules to consider critical environmental conditions of the limit state functions, such as wind, wave, current, and sediment transport, which are modeled by using Hydrotam-3D, a simulation of the hydrodynamic transport and water quality in three dimensions. Previous research conducted by (Balas, et al. 2020, 2013, 2011, 2004), (Balas and Kucukosmanoglu 2006), (Balas and Ozhan 2003, 2002, 2000) have shown that Hydrotam-3D has proved successful for a wide range of applications in real-life scenarios around the coast of Turkey. The Hydrodynamic Transport Model is supported by Geographic Information Systems (GIS) and cloud computing, which facilitates processes such as data entry and output and remote access to all functions through a graphical user interface that is controlled by a menu structure. The model has a relational database for Turkish coastal waters that includes bathymetries of all Turkish coasts and lakes, hourly wind data since the establishment of Turkish Meteorological Stations (MS), and all measured physicochemical data at the sites.
The Hybrid Model includes six modules: Wind, wave, and current climates, sediment transport, Monte Carlo, and Bayesian network modules. The flow chart of the model procedure is demonstrated in
Figure 5.
The wind climate module conducts long-term and extreme analyses of the wind data for the specified station. Moreover, this module analyses the data using ECMWF at each 0.1-degree horizontal grid spacing by 6 hourly time frames encompassing all Turkish coastal waterways between the years 2000 and 2022. It is possible to collect annual, seasonal, and monthly wind roses, all of which give information on the directional variation of wind speeds. The highest wind speeds and the directions in which they blow are examined, and then the prevailing wind direction for the area is analyzed and calculated. The statistical analysis of the yearly maximum wind speeds is performed using the Gumbel Probability distribution, and the most appropriate line is then fitted to the wind speeds presented in this study. Extrapolation to a greater value is thus feasible.
The wave climate module gives long-term significant wave statistics, annual and seasonal wave roses, and links among wave heights and periods. In addition to this, it estimates the amplitude and duration of significant waves. To tackle the issue of coupled refraction and diffraction in the wave module, equations similar to the one that was provided by Ebersole (1985) are subjected to numerical analysis. Three equations describing the wave phase function, wave amplitude, and wave approach angle make up the mild slope equation that computes the wave field resulting from the transformation of an incident, linear wave as they propagate over irregular bottom contours. The numerical model is quite effective when it comes to modeling wave propagation across wide coastal regions that are exposed to different wave conditions from a computational standpoint (Inan and Balas, 2002). It has been selected to make use of the sophisticated velocity potential (Ebersole, 1985):
in which, a is wave amplitude, and s is the function of the wave's scalar phase. To get the following equation, substitute Equation (1) into the equation that explains the two-dimensional propagation of harmonic linear waves.
in which ∇ is horizontal gradient operator; C is wave celerity; C
g is group velocity; k is wave number respectively. They are determined by the dispersion regards. The combined equations are determined for three wave parameters, wave height H, local wave angle θ and |∇s| (Ebersole, 1985).
- 3.
The current climate module includes three-dimensional modeling of wind, tide, or density stratification-induced currents, changes in water surface elevations, and storm surges. The Hydrodynamic Turbulence Module includes a three-dimensional k-ε turbulence model for transport processes. In a Cartesian coordinate system with three dimensions, the equations that are used to regulate the system are as follows:
The continuity equation:
The momentum equations for the orthogonal horizontal directions x and y;
and in the vertical direction z;
where x and y represent the horizontal coordinates, z represents the vertical coordinate, u, v, and w are components of velocity in the x, y, and z directions at any grid place in space, and t stands for time. The viscosity coefficients in the x, y, and z directions are denoted by ν
x, ν
y, and ν
z, respectively. f: the coefficient of the Coriolis effect, (x, y, z, t): the water density at the current location, ρ
o: the density used as a reference, g: gravitational acceleration, p=pressure.
Seawater density is influenced by its salinity, temperature, and, to a lesser extent, pressure. Salinity and temperature dispersion affect its dispersal. A convention has been adopted that instead of the density ρ, a quantity σt be used. The relation between the two is:
where ρ: density in gr/cm
3. The density increases noticeably with depth due to the increased hydrostatic pressure. This compression does not affect buoyancy or stability because all water masses moved up and down are similarly compressed. Therefore, the convention has been adopted to reduce all densities to σ
t (at 1 atm pressure) and to neglect compressibility in the equations of motion. The following formulae are used to calculate σ
t as a function of salinity and temperature:
where, S: Salinity (%.), Cl= Chlorinity (gr/kg), T: Temperature (
oC).
The model includes thermohaline forcing that occurs in enclosed water bodies. Solving the three-dimensional convection-diffusion equations allows for the calculation of the fluctuations in temperature as well as salinity. Equations of three-dimensional convective diffusion are utilized to figure out the temperature, and the formula for calculating salinity is as follows:
The turbulent diffusion coefficient is denoted by the letters Dx, Dy, and Dz, which stand, in that order, for the directions x, y, and z. Q: temperature (T), salinity (S).
- 4.
The sediment transport module is interrelated with the hydrodynamic transport and turbulence modules (Balas and Ozhan, 2000; Balas and Ozhan, 2003). The Boussinesq approximation, a commonly used method that assumes that the density change is minimal in comparison to the velocity, is employed to calculate the Navier-Stokes equations in the hydrodynamic model component. To find the solution, finite elements, and finite differences are employed, combining the strengths of both techniques. The vertical plane is modeled using finite element shape functions and the horizontal plane using finite difference approximations. In a Cartesian coordinate system, the equations that regulate the system are solved implicitly.
The long-term wave environment of the region was analyzed using wind readings from meteorological stations and the European Centre for Medium-Range Weather Forecast (ECMWF) wind predictions for 30 years. Wind statistics by the hour as well as fetch lengths were used to calculate wave heights, wave durations, and wave directions. These calculations formed the basis for the wave model, which is built upon the nonlinear shallow water formulas that have vertical averaged and constant density streams.
The use of the Boussinesq approximation and the finite elements and finite differences approaches in the hydrodynamic model component offers a robust and efficient solution to the Navier-Stokes equations. The combination of wind readings and ECMWF wind predictions provides a comprehensive view of the long-term wave environment of the region. The use of the vertically averaged nonlinear shallow water equations as the foundation for the wave model ensures that the model accurately captures the physics of wave hydrodynamics. This study also demonstrates the use of advanced numerical modeling techniques and comprehensive data collection to analyze the long-term hydrodynamics of the region. The results of this study contribute to the larger body of knowledge on the modeling of fluid dynamics and wave propagation and can be used to inform decision-making in maritime and coastal engineering.
where u and v are the x- and y-directional depth-averaged current velocity components, respectively; H=h+η total water depth; h: still water depth; g: gravity acceleration; C: Chezy friction coefficient; υ: turbulent eddy viscosity coefficient; η: water surface elevation; Wave-induced forces in the directions of x and y, respectively, are denoted by the letters F
x and F
y. It can also be written F
x and F
y as (Balas, İnan and Genç, 2013):
where S
xx and S
yy are the components of the normal radiation stress that are acting, respectively, on the plane that is perpendicular to the x and y axes. The following are the sources from which radiation stress calculations are derived:
where n=Cg/C, E=ρgH
2/8 wave energy, ρ =water density, θ = incident wave angle, and H=wave height.
- 5
The Climate change module simulates the Sea Level Rise Projections for the climate change scenario of RCP8.5 for the determination of extreme design water levels of the project area. CMIP6 (Coupled Model Intercomparison Project Phase 6) is the sixth phase of the standard experimental framework for studying the output of combined atmosphere-ocean general cycle models. To determine how the project area will be affected by climate change, the CNRM-CM6-1 climate change model, which is one of the CMIP6 models, was used by the Directorate of Climate Change of Turkey to obtain the predictions (CCS, 2023). The 2041-2060 and 2081-2100 periods were modeled according to the scenario of SSP5 8.5. Initial results of the CMIP6 GCM model comparison project revealed a greater temperature increase in the 21st century than in CMIP5 models.
- 6
The Monte Carlo module presents the development of a statistical model for conducting a failure analysis of Coastal Flow slides. The module simulates the stability failure function, to provide a comprehensive understanding of the various factors that could contribute to coastal flow slides system failure. The results of the simulation deliver statistical distributions of failure probabilities, which can be used to estimate the risk associated with CRB failures under various conditions.
- 7
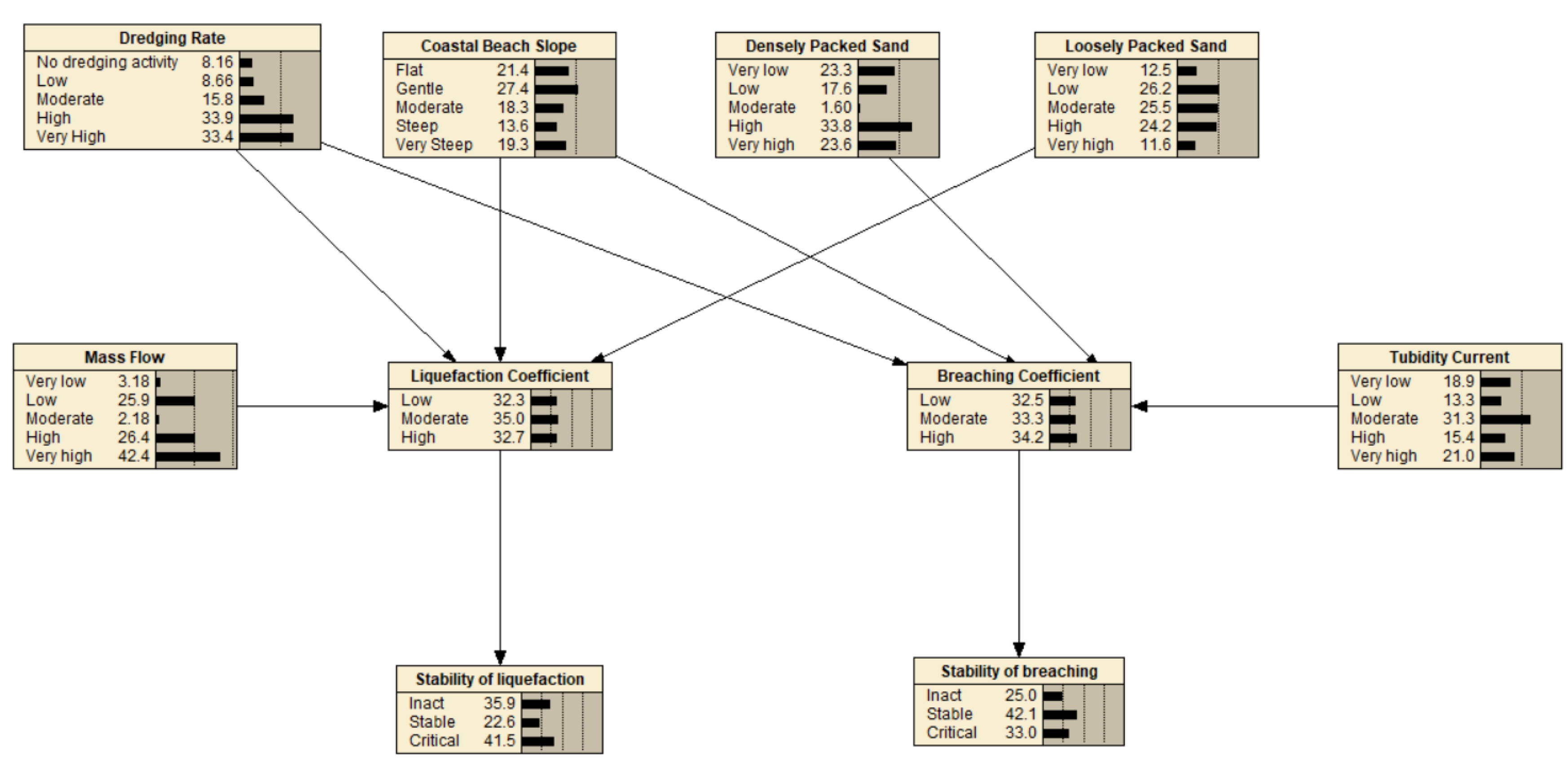
The Bayesian network module analyses the three possible conditions for the coastal flow slides: the grain size, critical angle slope, or packing type. Also, assuming that the critical angle slope may either be in the critical or non-critical state and that the packing type can either be densely packed sand or loosely packed sand. If the coastal flow slides happen, then the packing type will become loosely packed sand as the flow slide happens in loosely packed conditions. Yet, if the critical angle slope is a decisive case, this might also directly trigger the coastal flow slides to happen. When various scenarios are entered into this network that accurately captures the reality of slope failures at the site, packing tape, and coastal flow slides-use-behavior, the Bayesian Network can be used to answer a variety of pertinent questions, including such as "if the slope is critical, what are the chances it was resulted by grain size or by packing type," and "if the chance of flow slides increase, how does that affect the government or managers to budget time for recovering or mitigating the coastal flow slides effects?". In the previous era, when scientists, engineers, and economists sought out probabilistic models so that they could endeavor to forecast what was likely to take place if a different event happened, they would customarily try to represent what is known as the "joint distribution." This was done so that they could try to figure out what was probable if another occurrence happened. Since it stores one probability value for each possible combination of states, the joint probability mass table may likely grow to become large. This is because the total number of states for each node is multiplied by the total number of states in the mass table. Bayesian networks are one example of such a method. A significant amount of calculation time can be saved by using a Bayes network since it only connects the nodes in a network that are probabilistically connected by dependent relationships. It is not necessary to save every combination of solutions that may be feasible. It results in a significant reduction in the number of mass table entities required for calculation. The adaptability of Bayesian networks is a further factor that contributes to their widespread usage and success. Accurately quantifying the rate of erosion requires a comprehensive understanding of interrelated variables, such as active wall velocity, which refers to the rate at which a vertical underwater slope propagates horizontally because of coastal flow slides. This concept is critical for understanding the dynamics of sediment erosion in coastal flow slides. Therefore, the complex variety of parameters can be assessed by using the Bayesian Network. The active wall velocity is calculated by considering the balance of forces acting on a sand particle down a slope. This calculation allows for an estimation of the rate at which the underwater slope is propagating. Van Rhee (2015) described the active wall velocity by underlying its physical principles.
This research enhances the understanding of the intricacies of the erosion process by the probabilistic simulation model and improves the ability to estimate sediment erosion rates by combining with the Hydrotam-3D sediment transport module (Balas, Inan and Yilmaz, 2011):
where n
0 represents the porosity of the sand measured in situ, ρ
s represents the particle density, ρ
w represents the water density, k
l represents the permeability in the loose state,
represents the angle of the internal friction,
represents the angle of the beach slope, and n represents the relative change in porosity.
in which 𝑛
f is the largest value of porosity. The sediment particle velocity is obtained from the sediment transport model and is controlled in MCS by using Equation (10):
The critical angle slope is given in Equation (11) (van Dijk et al., 2018).
Using N various particle sizes, van Rhee (2002) defined the vertical velocity vz,j of a particle of size Dj.
where w is the vertical flow velocity obtained from the hydrodynamic model. For a uniform-sized mixture, the settling velocity w
s of a given size corresponds to the slip velocity
, which depends on the sediment concentration. The Shields parameter gives the relationship between grain size diameter and the dimensionless parameter to calculate the initiation of motion as given by Equation (13):
where
is dimensional shear stress,
is the density of the sediment,
is the density of water, and D
50 is the median particle size.
Considering the surface area dS and the control volume d
Ω, the applied horizontal and vertical momentum equations are given by:
The continuity equation for incompressible fluids is written as:
where p represents the pressure, u and w represent the horizontal and vertical flow velocities, v represents the velocity vector, and ρ is the sediment-water mixture density,
are unity vectors as obtained from the hydrodynamical model. The transport equation is given the following equation and is obtained from the sediment transport module of Hydrotam-3D.
where
denotes the particle size of the sediment, c is the sediment concentration, and
is the diffusion coefficient. The Hydrodynamic and Sediment Transport model is interrelated with the Monte Carlo Simulation and Bayesian Networks. The Monte Carlo Simulation (MCS) module is the statistical design approach to account for the uncertainty associated with the random load and resistance components of the CFS model.
Durap and Balas (2022) developed a Monte Carlo Simulation Risk Assessment Model to design natural gas pipelines. In this paper, they suggest the coupling of the hydro-morphodynamical (Hydrotam-3D) model with Monte Carlo Simulation quantify the uncertainties associated with the coastal flow slides mechanism. This paper employs the hydro-morphodynamical model with increasing degrees of resolution to speed up the Monte Carlo Simulation of the hybrid model.
4. The Durap Sensitivity Index (DSI) of CFS Failure
The authors developed the Durap Sensitivity Index (DSI) to identify the risk of CFS failure and vulnerable coastal areas to this risk. In addition, they developed a sophisticated hybrid model that allows for all possibilities of flow slides in sync with erratic variables used in this new sensitivity index of DSI.
Calculation of the DSI is determined by using the parameters listed in
Table 2, where DSI is the coastal flow slides sensitivity index of Durap. This index is calculated by using the following parameters of k
BF and k
L, where k
BF is the coefficient of breaching and k
L is the liquefaction coefficient. The breaching coefficient k
BF consists of the following variables: dredging rate, slope, packing type, and type of driving force. The liquefaction coefficient (k
L) depends only on the dredging rate, slope, densely packed slope, and mass flow as driving forces.
The calculation of CFS coefficients is given in Equation 15:
where Pi stands for the flowing variables: P1=dredging rate, P2=slope, P3=loosely packed slope, P4=densely packed slope, P5=turbidity current obtained from Hydrotam 3D, and P6=mass flow. i represents constants variables of both liquefaction and breaching that plays a paramount role in CFS.
Equation 15 is used to generate the DSI for either breaching-prone or liquefaction-sensitive zones. If the packing type is densely packed and the driving force is mass flow, then these two parameters encompass in the calculation of k
L, since they are the main reasons for the liquefaction type of failure of the slope, as given in Equation 16.
Equations 15 and 16 are used to generate the DSI for either breaching-prone or liquefaction-sensitive zones. Following that, the main risk levels are described by using the following percentages ranging from Level I: (0-25) %, Level II: (25-50) %, Level III: (50-75) %, Level IV: (75-100) %, respectively. To put it another way, a sensitivity score of Level I indicates the least amount of risk, while a sensitivity score of Level IV indicates the greatest amount of risk. Finally, the Durap Sensitivity Index (DSI) can be written in terms of coastal flow slides and liquefaction flow slides as given in Equation 17:
If the first part of the DSI equation,
, is greater than the second part, then the flow slide is dominated by breaching or vice versa. Namely,
The probabilities of liquefact ion and breaching are determined from the Monte Carlo Simulation module.
5. Application of the Hybrid Risk Model to the Osman Gazi Bridge
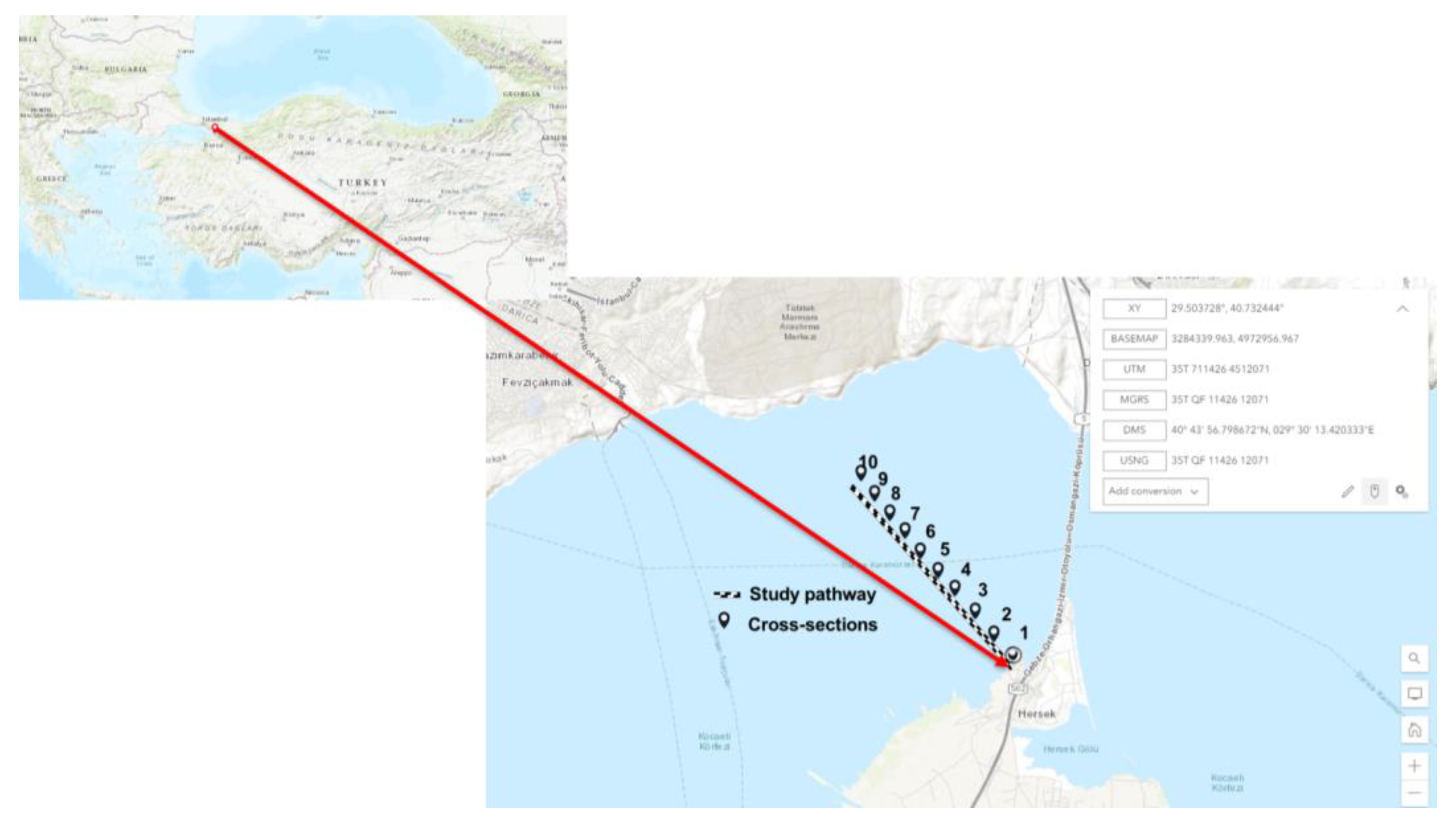
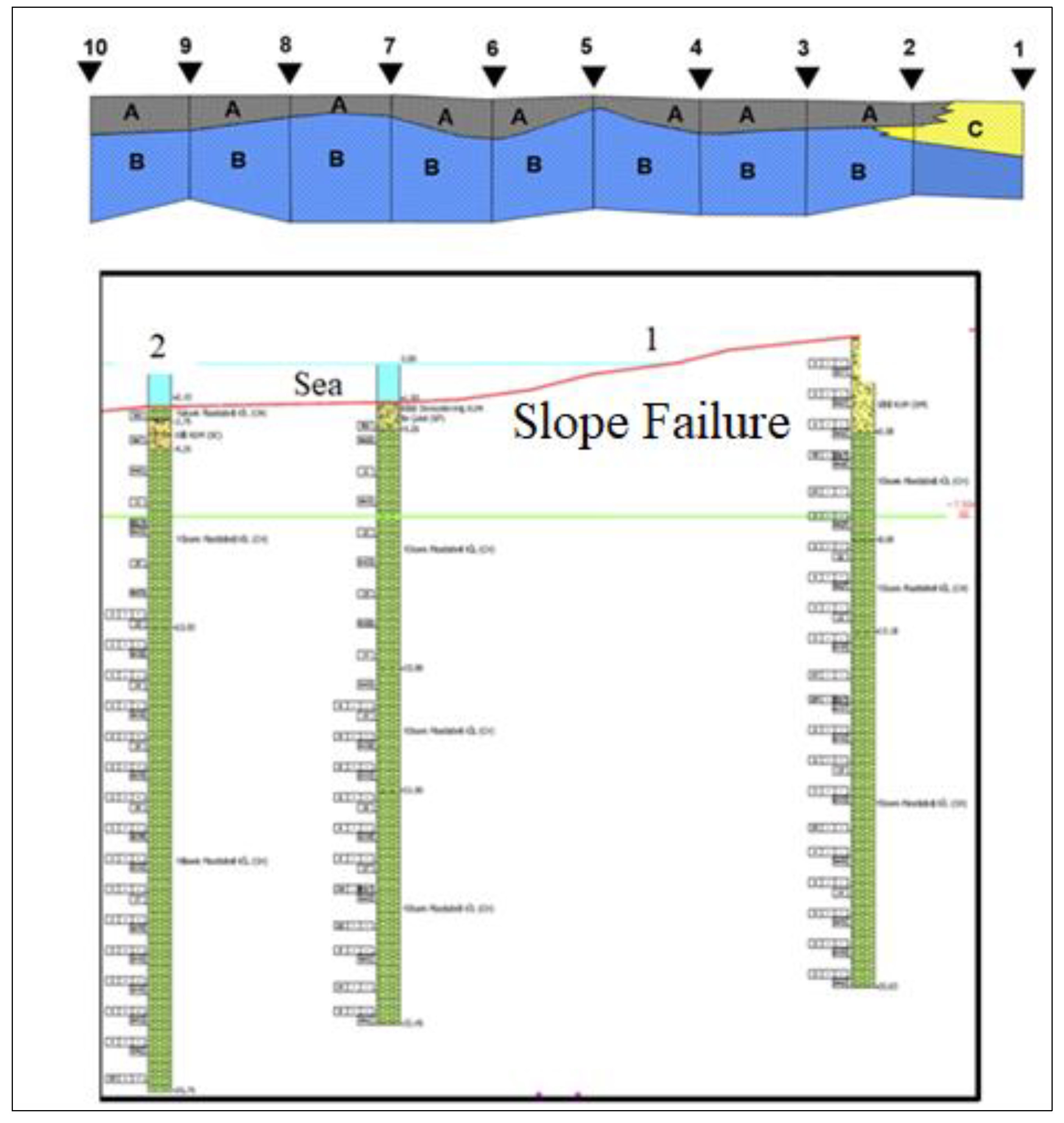
The case study focuses on the slopes in the eastern Marmara Sea of Izmit Bay near the Osman Gazi Bridge (
Figure 7), which is an earthquake area sensitive to slope failures. In the case study, the analyzed slope is illustrated in
Figure 8.
The drilling sites and bathymetric/geotechnical surveys in front of the slope are demonstrated in
Figure 8.
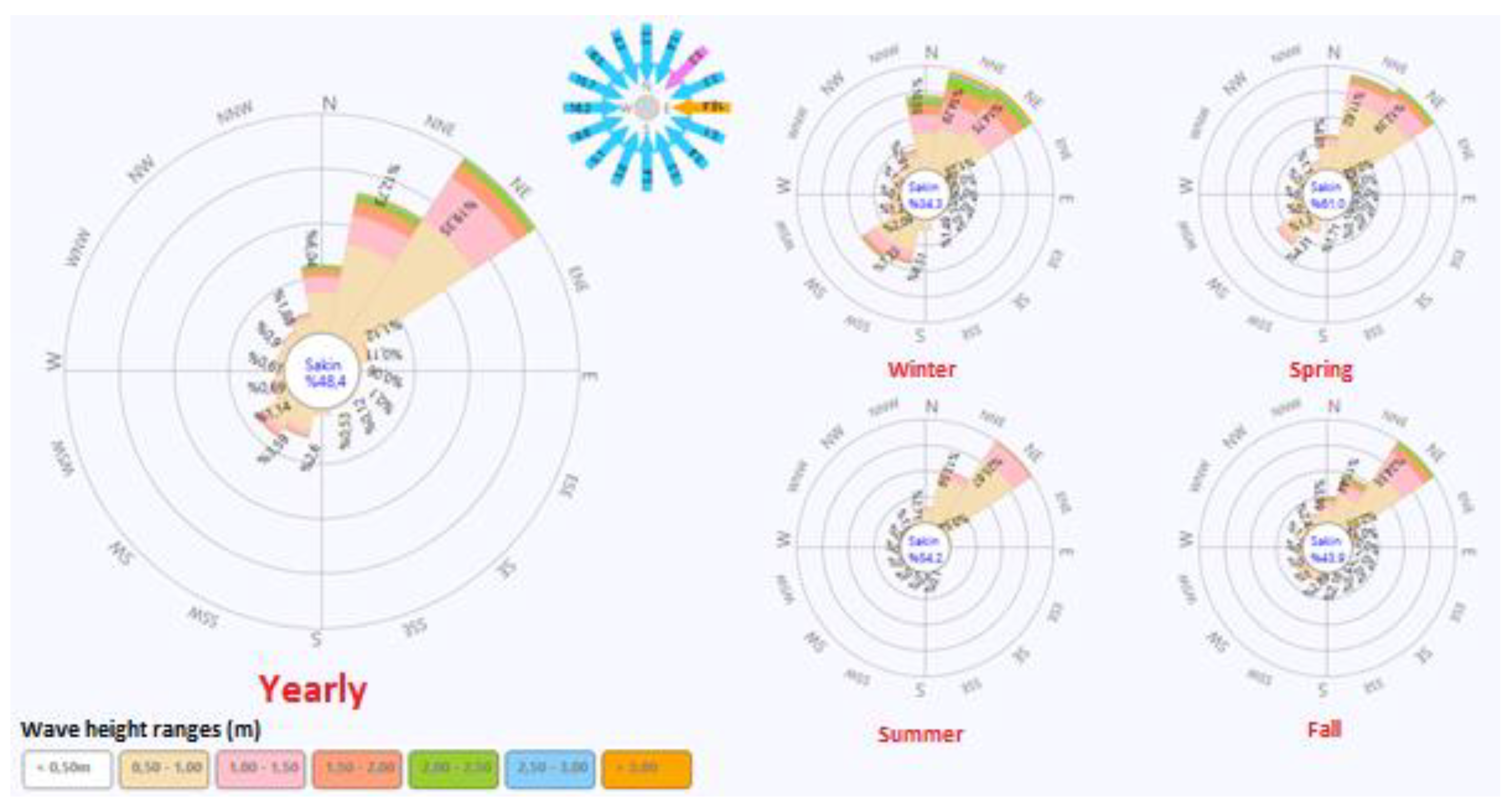
Izmit Bay, located in the Marmara Sea, is roughly 48 km in length and 1.8-9 km in width and is the narrow continuation of a two-layered current system. This research employed wind forecast data from the ECMWF Operational Archive for the location 40°75 N, 29°55 E from the years 2000 to 2020 to obtain the wave roses. The annual wave rose is shown in
Figure 9, and it was discovered that waves traveling from the north-northeast directions were the most common wave directions having a monthly average significant wave height of Hs=1.5 m during the past 20 years.
The increase in the Mean Sea Level (MSL) of Izmit Bay was determined by Climate Change module. First, the global warming scenarios and wind climate of the region were studied. Scenario analyses were made within the framework of climate change and possible disaster hazards. According to the RCP8.5 scenario; it is predicted that average temperatures will tend to increase in the Izmit Bay area at +1.5°C in the first period. It is expected that the temperature will rise to 2°C in the 2041-2070 period and above 3.5°C in the 2071-2099 period (DC, 2023). By considering this trend, the MSL increase in the future is predicted by MCS considering global warming. The MWL increase is coupled with Hydrotam 3D model, and the wind set-up, tidal effect, and wave set-up that may occur in the bay were cumulatively determined.
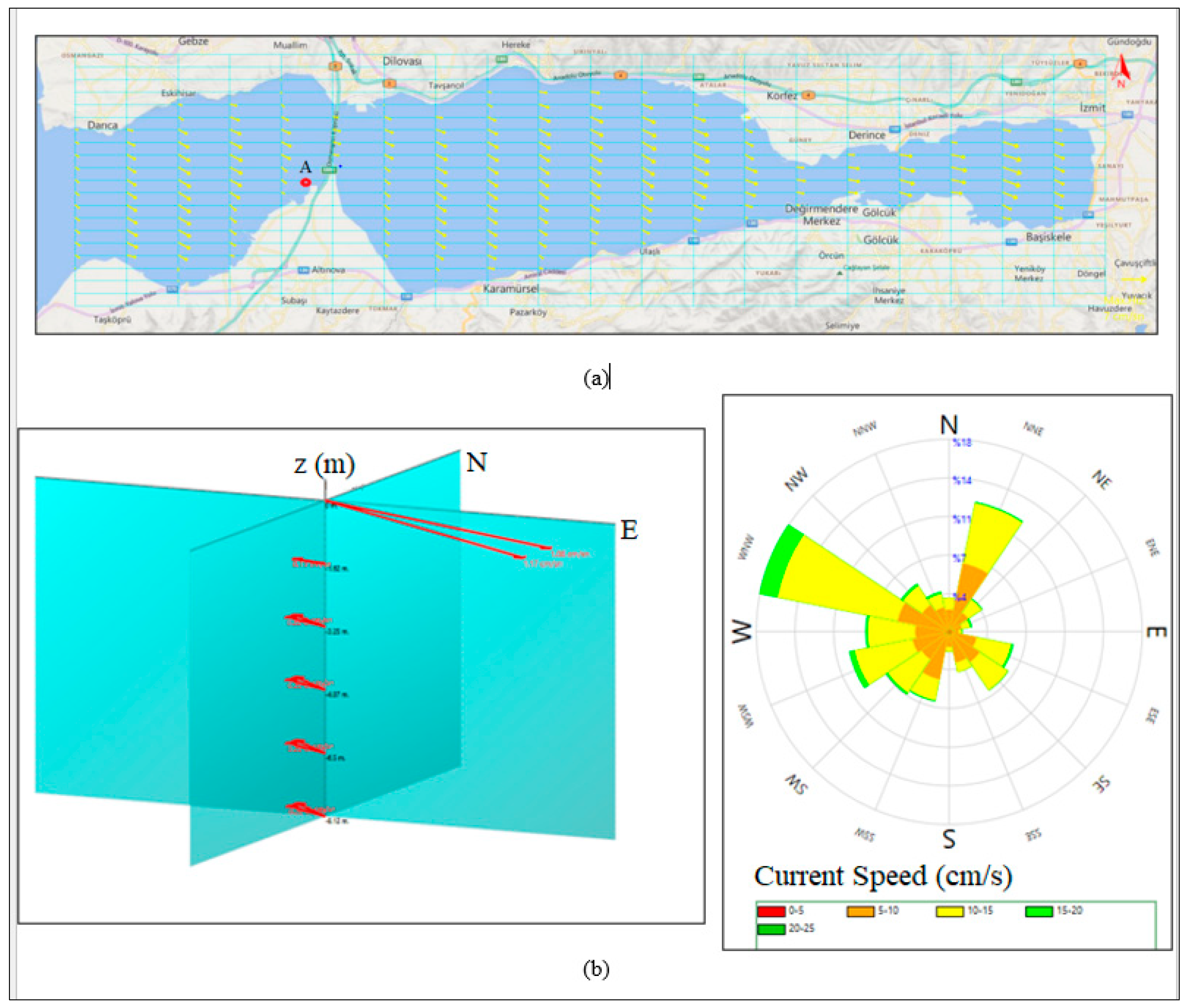
The MSL increase was predicted as 0.43 m in the next 35 years by determining the effects of the storm from the wave and wind climate modules. These modules were interrelated with MCS to estimate the water level variation of Izmit Bay. Considering the MWL change, the variations of wind and wave-generated currents are predicted by the Hydrotam 3D model. The wind and wave generated current pattern on the sea surface after one hour of hydrodynamic simulation in which the wind was blowing at 10 m/sec from the NNW direction is given in
Figure 11a. The 3D current pattern that affects the slope is given in
Figure 11b. The current rose in front of the slope at Point A is predicted as illustrated in
Figure 11 (c). The surface currents were in the NNW direction, but the rest of the water column was dominated by opposite currents. Considering the MSL increase, the average bottom current velocity was predicted as 26 cm/s which triggered the sediment motion at the bottom of the slope of medium sand. The mean particle size of the slope was found to range from 0.02 to 0.05 cm.
The critical values of active wall height were found with a range of 0,1 to 1 m. These thresholds are crucial to prevent the environmental deterioration that may be caused by the coastal flow slides. Hence considering the hydrodynamic modeling, the variations of main design parameters and probability distributions are determined and now modeled in the MCS as given in
Table 3. The characteristic fluid parameters, such as temperature and salinity, affect the fluid's density. There is a possibility that stratification will cause a change in the density of salt water, as modeled by Hydrotam 3D.
The MC simulation considers the density of the water as a random variable. Hence all the random variables are modeled in the MCS by probability distributions given in
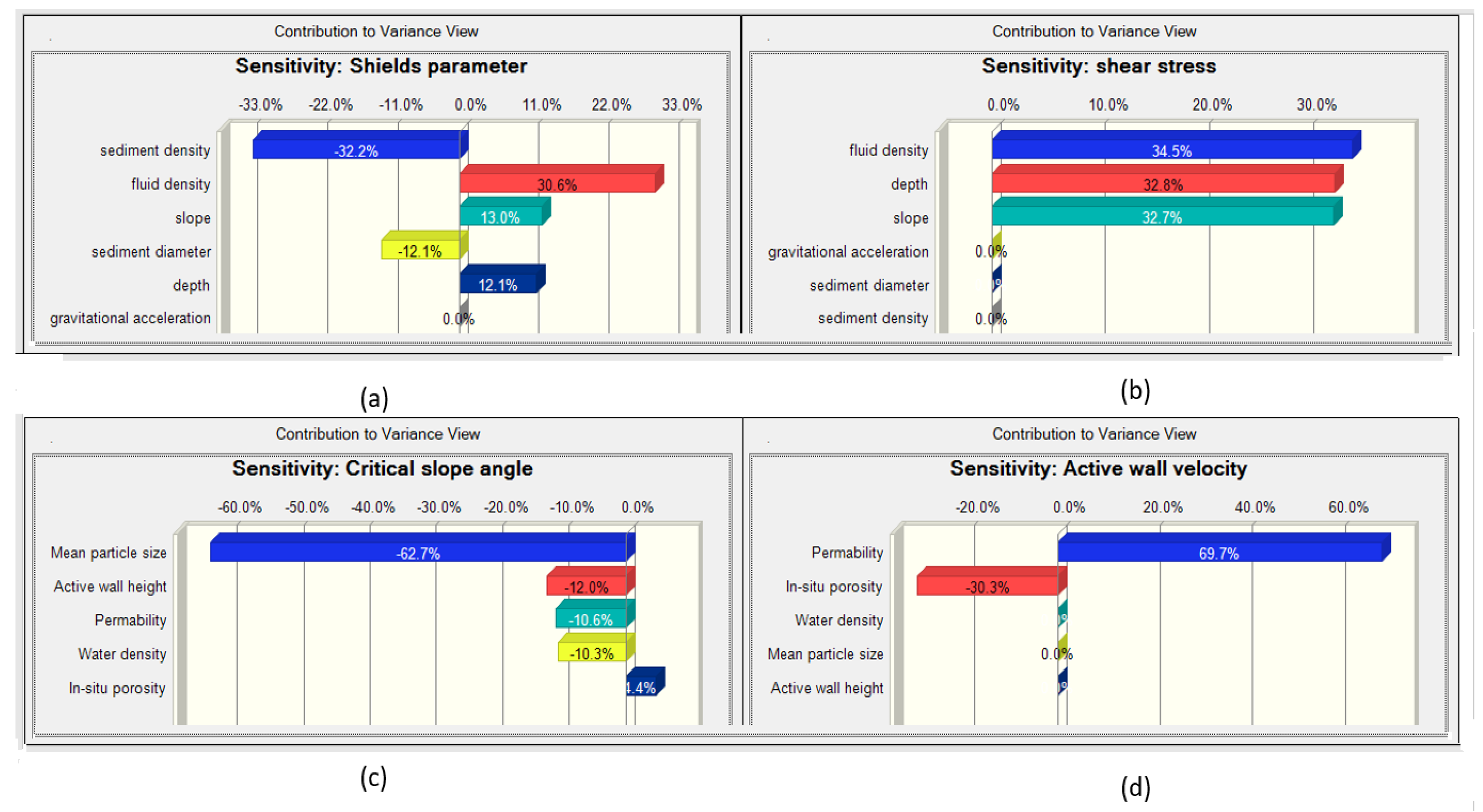
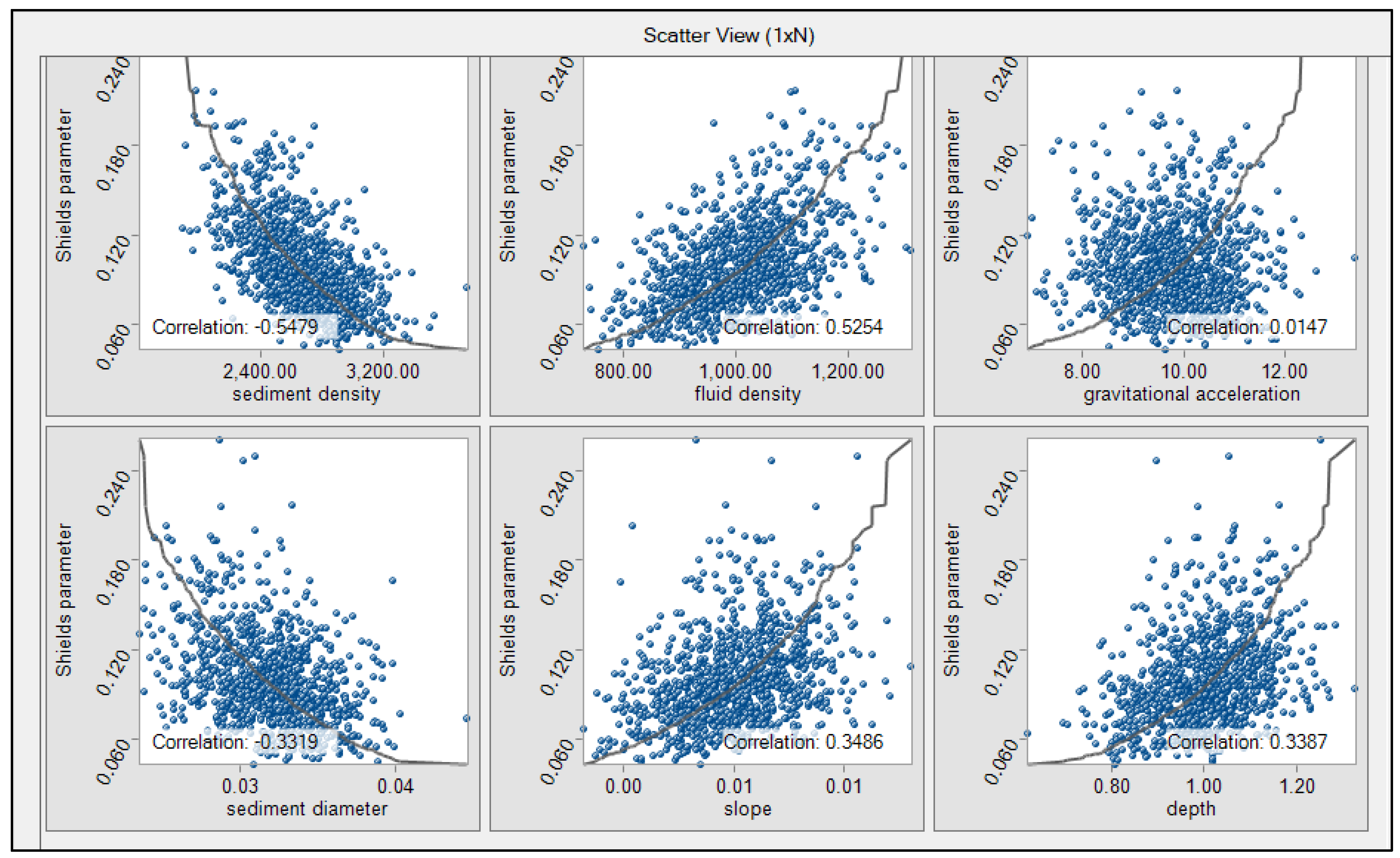
Table 3 to include their inherent variations. A sensitivity analysis of breach failure is carried out by the contribution to variance technique, and it is found that the Shields parameter is negatively impacted by both the sediment density and the sediment diameter. Although these two variables are related, the influence that sediment density has on the Shields parameter is almost three times greater than that of sediment diameter.
Figure 13 (a) shows that the Shields parameter has been influenced by sediment density -32%, fluid density +31%, slope +13%, sediment diameter -12%, and depth +12%.
The sensitivity analysis of shear stress is shown in
Figure 13 (b) and it is almost equally influenced by fluid density, depth, and slope. It is shown in
Figure 13 (c) that, the average particle size has a detrimental influence on the critical slope angle. Additionally, the slope angle is negatively affected by the active wall height, water density, and permeability. The active wall velocity rises in direct proportion to permeability as shown in
Figure 13 (d).
The mean particle sediment gained acceleration as it descended to the bottom from the eroded region as a direct result of increased wall velocity particles in flow slides. Since porosity is linked to how well-interconnected sediment particles are, it has a significant influence on slope angle. It is found from the sensitivity analysis carried out by MCS, the coastal slope stability is inherently affected by sediment/fluid characteristics and 3D wave/current interaction.
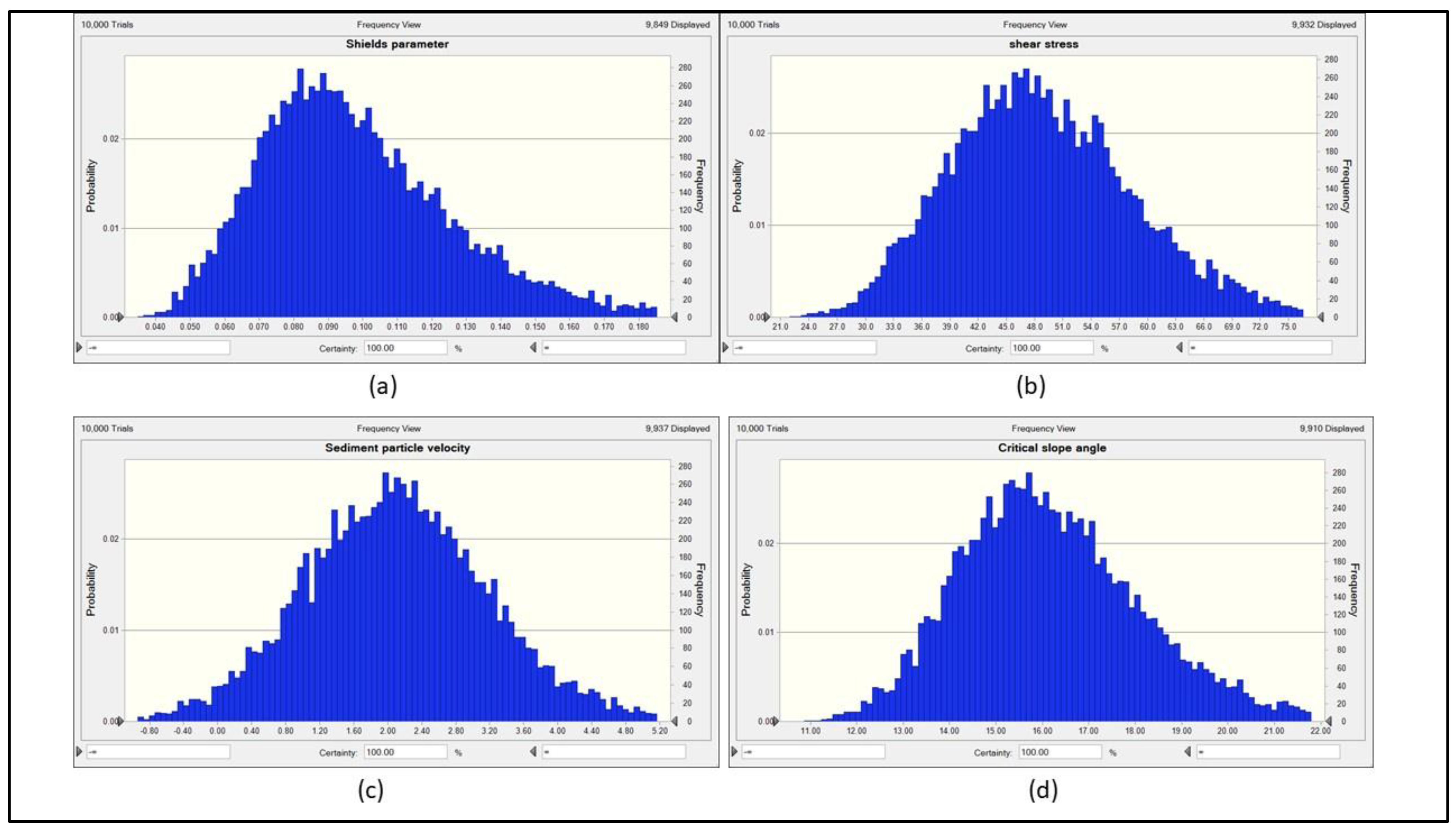
Safety analyses should be interrelated with a 3-D hydrodynamic and sediment transport model to correctly encounter the variations at the limit state. It showed the importance of the Hybrid Hydrodynamic and Sediment Transport Coupled Monte Carlo Simulation Model developed in this paper. To determine the critical angle slope by using the hybrid model, 10,000 random values are generated for each variable in the MCS. Variations of modeled parameters obtained from the Hybrid Model are given in
Figure 14 where charts display both the occurrence probability and frequency of design parameters.
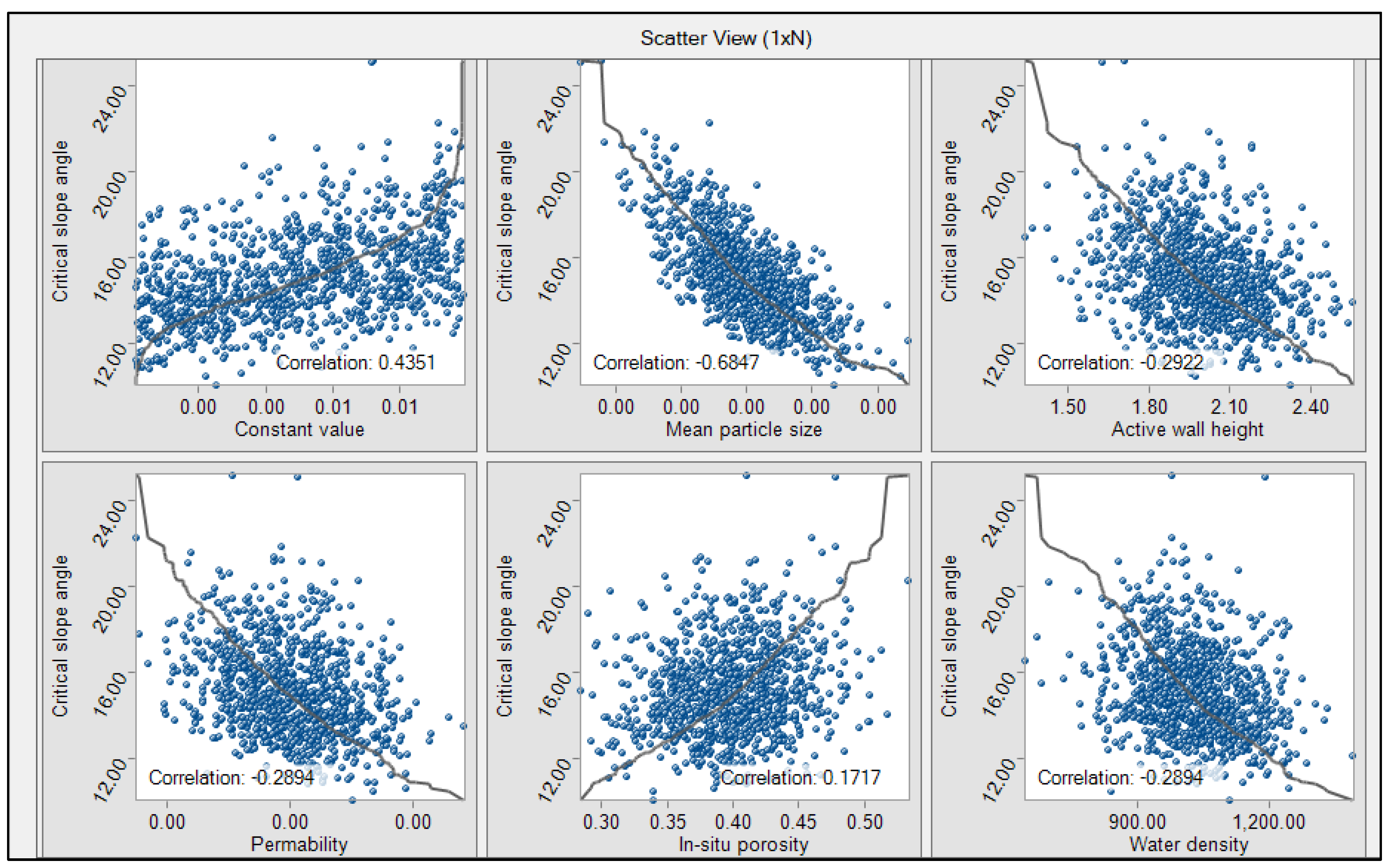
Correlations between the critical slope angle and soil/fluid parameters obtained from the Hybrid Model are shown in
Figure 15. The examination of these relations showed that they have an inherent impact on the precision of simulations of the failure phenomena. The correlation analysis is conducted to evaluate the potential risks associated with critical angle slopes, as well as to comprehend the underlying nature of relations between environmental parameters that are not taken into consideration in deterministic design. These findings suggest that sediment transport and slope failure can be influenced by various geomorphological and hydrodynamic factors and highlight the necessity for Hybrid Hydrodynamic and Sediment Transport Coupled Monte Carlo BN Simulation Model developed in this paper.
Variations of modeled parameters obtained from the Hybrid Model showed that the shear stress, sediment particle velocity, and critical slope angle follow a normal distribution with great accuracy. On the other hand, the Shields parameter conforms to a Log-normal distribution due to the asymmetry that exists within the particle size distribution. Scatter diagrams of the hybrid model were constructed to analyze the contribution of random design variables to the population. Scatter diagrams, display the dependencies and interactions between forecast and design parameters. The use of correlation coefficients allows us to determine the degree of relation between design variables.
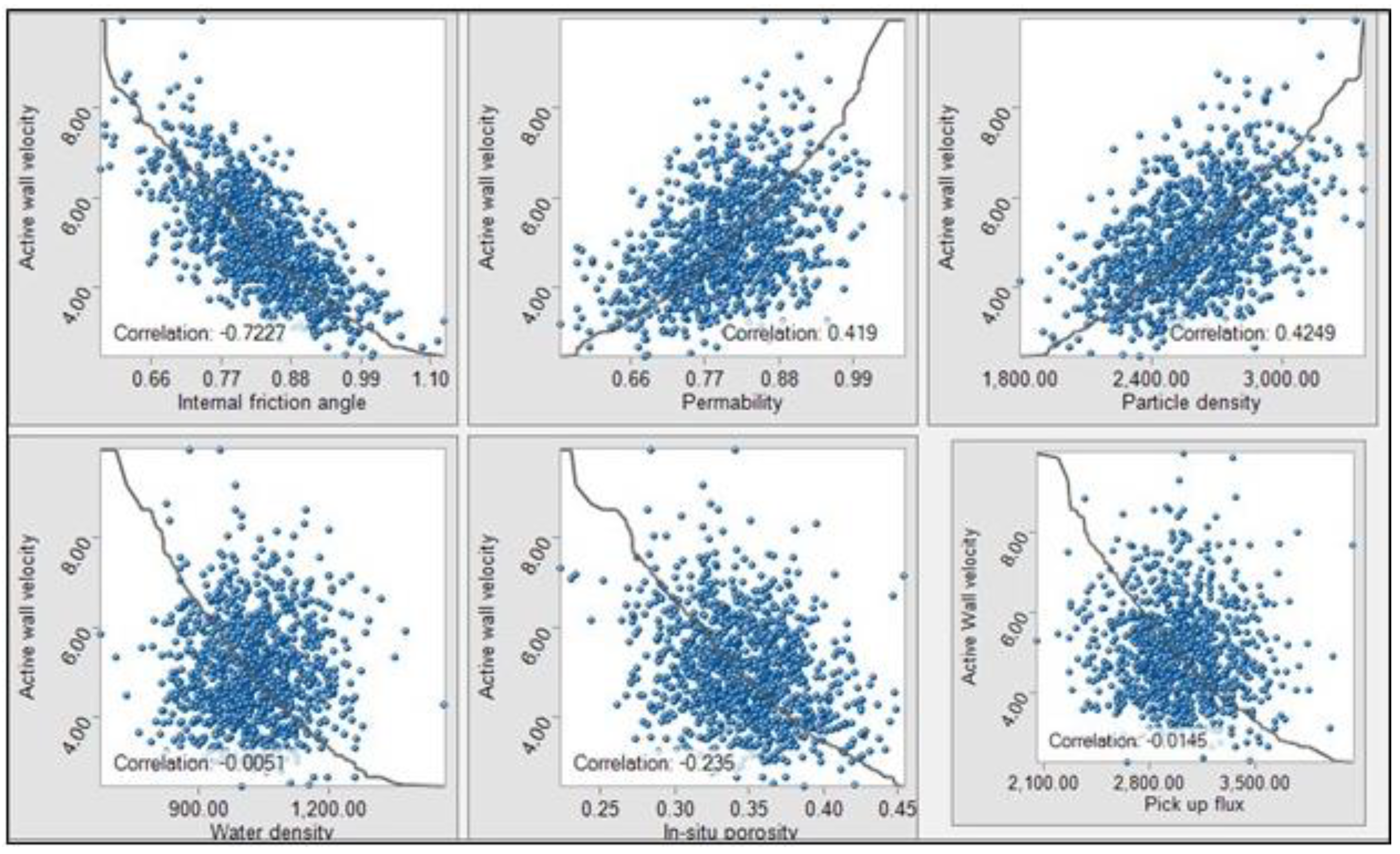
Figure 16 illustrates the relations that exist between active wall height and soil/fluid parameters of permeability, porosity, particle density, friction angle, and water density. Active wall velocity has a positive correlation with particle velocity and permeability, while it has a negative correlation with in-situ porosity, internal friction angle, water density, and pick-up flux of erosion. Hence, the hybrid model verified the velocity-permeability relations with hydraulic gradient as discussed by Prasad (2003).
The Shields parameter, which plays a crucial role in sediment transport, has been found to exhibit complex relationships with several geomorphological and hydrodynamic factors as shown in
Figure 17. In particular, the Shields parameter has a positive correlation with the density of the fluid, the gravitational acceleration, the slope, and the depth of the water.
However, this relationship is found to be negatively correlated with the density of the sediment and the diameter of the sediment particles, suggesting that increased sediment density and diameter are associated with a reduction in the Shields parameter. The study has also revealed a positive correlation between fluid density and temperature.
6. Discussions and Results
When compared to previous years, the beaches of the globe have undergone an extraordinary transformation because of climate change and human interference, and this change puts them in jeopardy. Considering coastal flow slides have the potential to devastate the surrounding region, a designer must analyze these areas to prevent construction in inappropriate spots and incurring additional costs.
Therefore, a feasibility study is required in Marine Spatial Planning (MSP) for beach conservation, where both the aesthetics and safety of the beaches will be maintained. It is anticipated that beaches will become focal points of interest, which in turn will lead to an expansion of the tourism industry. Coastal Flow Slides (CFS), which encompasses both Retrogressive Breach Failures (RBF) and Liquefaction Flow Slides (LFS), are a type of slope instability that pose a significant risk to the management practices of MSP. Despite the frequency of these failures, there exists a limited understanding of their underlying mechanisms and causes. This lack of understanding often leads to misdiagnosis, with CFS being misinterpreted as shear failures, liquefaction failures, or even simple erosion processes. The complex nature of CFS stems from its dependence on two primary factors: the characteristics of geomechanically saturated sand and the behavior of accompanying turbulent density currents. These currents can rapidly transport large volumes of suspended sand downslope, contributing to the retrogression of the breach, as modeled by the sediment transport module. Given the potentially destructive impact of flow slides, marine spatial planners and coastal engineers must possess a thorough understanding of the mechanisms driving RBF, the environmental conditions in which they may occur, the hazards posed by these failures, and the countermeasures that have been implemented successfully in different environmental conditions. This article aims to understand RBF through a case study of a specific bridge region in the Marmara Sea. The study focuses on the evaluation of the critical slope angle, a crucial factor in several environmental challenges such as beach stability, erosion, and wave energy converters. Through sensitivity analysis, the authors treat various factors as random variables with probability distributions to evaluate the critical slope angle. The results of the case study support the use of the proposed new model for assessing the threat of slope instability.
The angle of repose, also known as the critical angle of repose, is the steepest angle of decline or dipping in relation to the horizontal plane whereby a granular material may be deposited without falling over. At this particular angle, the material that is located on the slope face is dangerously close to slipping or sliding. The angle of repose can vary between 0 and 90 degrees. In this study, since the material was fine, fine sand and clay, the critical angle slope was calculated in conjunction with the particle size. The results are shown in
Figure 18.
Sensitivity analysis is a crucial step toward obtaining trustworthy results in the field of RBF studies. Given the vast number of model input parameters and the inherent uncertainty of their underlying values, sensitivity analysis allows researchers to run numerous simulations at a relatively low cost. In this study, the sensitivity analysis was performed using the combination of the Monte Carlo Simulation (MCS) and Hydrodynamic Transport and Turbulence modules, yielding computationally efficient results.
The hybrid model and the sensitivity index developed were validated by the Bayesian Network (BN) by which the relations of CFS depth, sediment density, fluid density, and porosity on vital parameters such as Shields parameters, shear stress, critical angle slope, and active wall velocity were confirmed. Simulation of coastal flow slides by the BN module is illustrated in
Figure 18. The validation of DSI was assessed by using the literature and applying the hybrid model according to the flowchart given in
Figure 19.
For this case study of Osman Gazi Bridge abutments, the sensitivity indexes of all variables are P1=1, P2=3, P3=4, and P6=5 respectively. Therefore, the liquefaction coefficient is found as 3.87 (Level IV) which is considered under high risk of liquefaction flow slide according to the level of sensitivity analysis given in
Table 2.
As a result, the case study area was deemed as an unsafe zone, and since the Hersek abutment of the Izmit Bay Osman Gazi Bridge was going to be constructed here, the soil was fortified by sheet piles of 16.00 m (
Table 4). In addition, a dry dock with an area of 22,820 m
2 and depth of -7.50 m was built in this area and 70% of the construction works of the bridge caissons were carried out in this dry dock. By using the methodology developed in this paper, the locations that are vulnerable to coastal flow slides in Turkey have been marked on the map given in
Figure 24. This study provided the template hybrid risk model and sensitivity index for evaluating areas sensitive to coastal flow slides.
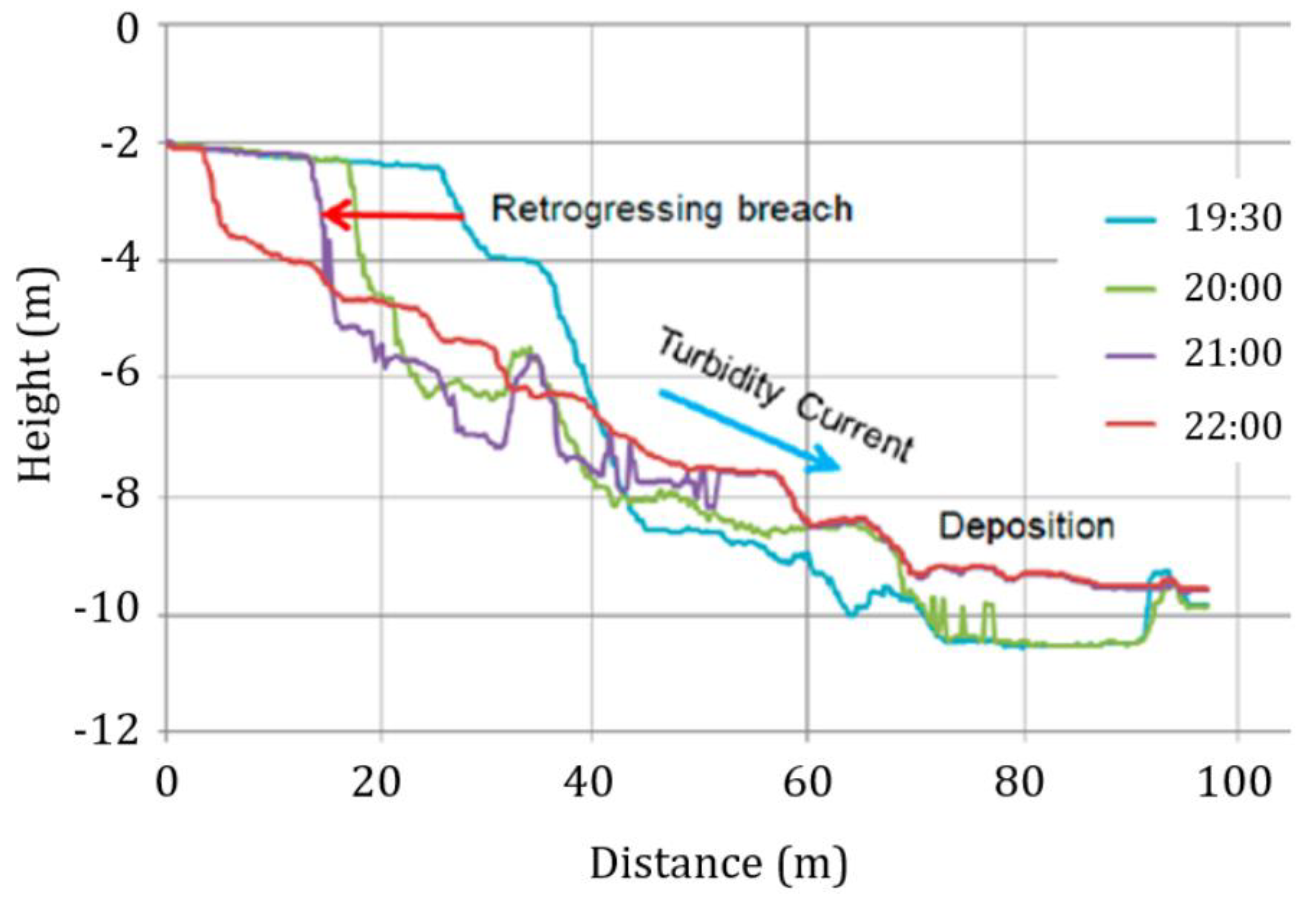
The procedure that was followed is known as the Hybrid Model, and it was used consistently all the way through the process. This was done in order to construct a BN in the simplest, most fast, and most effort-effective manner feasible. As can be seen from the BN, stability of CFS is strongly contingent on dredging rate, beach slope, packing type (densely packed sand, loosely packed sand), mass flow and turbidity current. If the turbidity current on the set of CFS is substantial enough, then it is referred to as Retrogressive Breach Failure. On the other hand, the LF will take place in accordance with the situation unless the turbidity current is commanding.
If the slope condition has a predilection towards CRBF, then the angle has to be somewhat steep, as was previously indicated in
Table 2.
Figure 20 illustrates that the angle of the beach is generally mild slope because of this reason. This indicates that the slope is not steep enough to generate CRBF; nevertheless, it is clear that the liquefaction flow sliding rate as a percentage is rather high at 41.5.
Figure 20.
Established BN in accordance with Hybrid Model.
Figure 20.
Established BN in accordance with Hybrid Model.
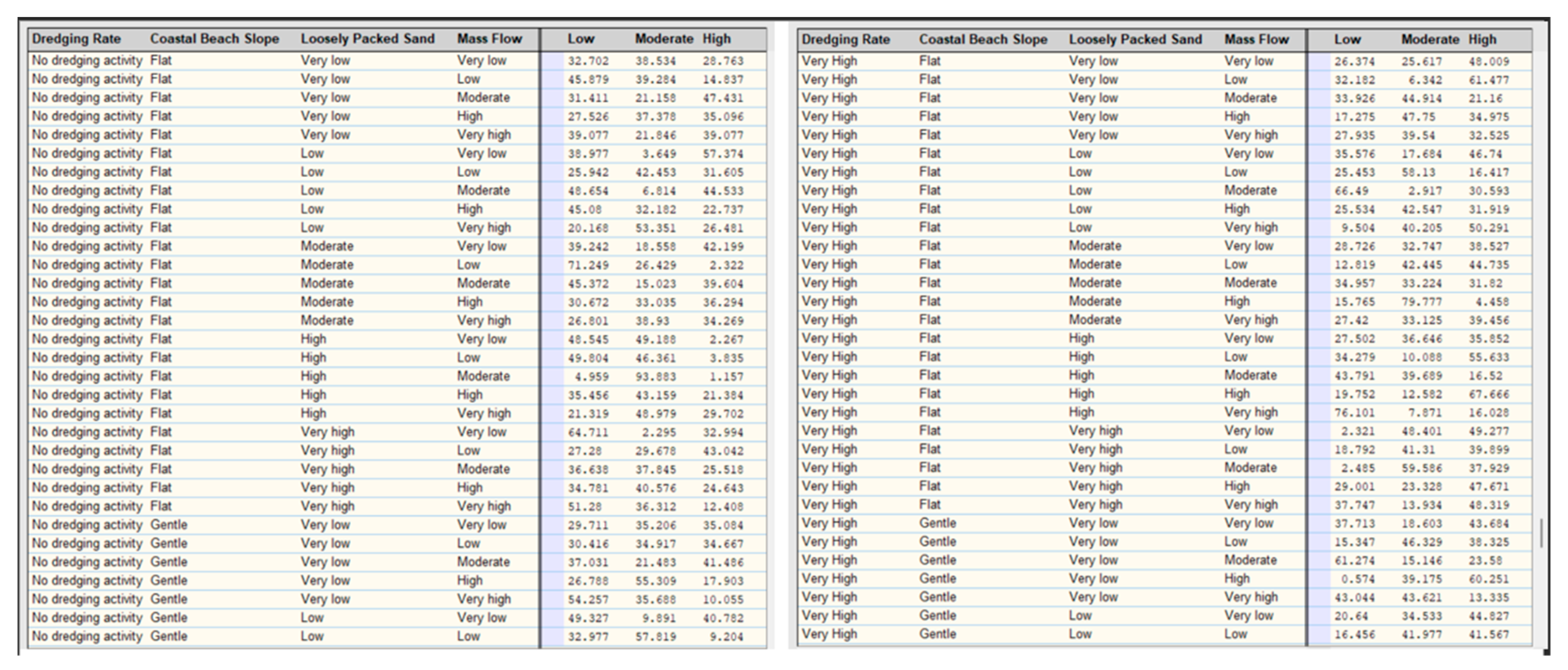
Figure 21.
Effects of parameters (Dredging rate, beach slope, loosely sand packed, mass flow) on coefficient breaching.
Figure 21.
Effects of parameters (Dredging rate, beach slope, loosely sand packed, mass flow) on coefficient breaching.
Figure 22.
Effects of parameters (Dredging rate, beach slope, loosely sand packed, mass flow) on liquefaction coefficient and their percentage.
Figure 22.
Effects of parameters (Dredging rate, beach slope, loosely sand packed, mass flow) on liquefaction coefficient and their percentage.
7. Conclusions
Coastal Flow Slides (CFS) which encompasses Retrogressive Breach Failure (RBF) and Liquefaction Flow Slide (LFS) has the potential to significantly impact the stability of coastal foreshores, structures, and hydraulic fill structures, as well as the dredging operations. Despite its importance, research on coastal flow slides has been limited in the past few decades due to the complex nature of the processes involved and the wide range of parameters associated. Previous studies on this phenomenon have relied on deterministic methods, which may not fully capture the inherent uncertainties present in the coastal flow slides process. To address this knowledge gap, this study employs a combination of the hydrodynamic sediment transport model Hydrotam-3D (Balas and Ozhan, 2000), Monte Carlo Simulation (MCS), and Bayesian Networks (BN) to estimate RBF by a new robust model. This model incorporates the Hydrodynamic Transport and Turbulence Model of Hydrotam-3D and the generation of random variables to account for the uncertainty in the RBF design.
Figure 23.
The slope was fortified by sheet piles having a length of 16.00 m for the construction of the Osman Gazi Bridge (Ince, et al., 2022).
Figure 23.
The slope was fortified by sheet piles having a length of 16.00 m for the construction of the Osman Gazi Bridge (Ince, et al., 2022).
Figure 24.
Coastal flow slides-prone regions in Turkey determined by the hybrid model.
Figure 24.
Coastal flow slides-prone regions in Turkey determined by the hybrid model.
This research enhances the understanding of the intricacies of the erosion process through the probabilistic simulation model developed and improves the ability to estimate sediment erosion rates by combining it with the Hydrotam-3D sediment transport model. This study utilizes the MCS model to improve the accuracy of the critical angle slope design and provide insights into the consequences of this phenomenon. This research enables a better understanding and addresses the challenges posed by coastal slope failure. Additionally, a sensitivity analysis of the RBF and its input parameters was conducted to gain a better understanding of their influence on the critical angle slope.
The new hybrid model uses hydrodynamic loads, obtained from the numerical model that accounts for the combined effects of waves and currents, to improve the accuracy of the critical angle slope design. The model incorporates random variables of coastal flow slides and considers the minimum and maximum values of these variables to control the simulation. It is found from the sensitivity analysis carried out by MCS, the coastal slope stability is inherently affected by sediment/fluid characteristics and wave/current interaction. Therefore, such analyses should be interrelated with a 3-D hydrodynamic sediment transport model to precisely encounter the variations at the limit state. This study provides the probabilistic sensitivity by a novel approach to evaluate RBF by combining the hydrodynamic model with Monte Carlo simulation and Bayesian Networks for the stability assessment. Hence, the use of such a hybrid model offers a robust and computationally efficient approach to evaluating the critical angle slope for RBF.
As a result, this study highlights the importance of accounting for the inherent uncertainties in the risk assessment of the coastal flow slides process and provides valuable insights into this field by developing a hybrid model.
The authors of this paper have proposed the utilization of a new hybrid model, which constitutes a novel approach to evaluating the risk sensitivity of coastal flow slides (CFS). The authors have combined the hydrodynamic model with the BN-based Monte Carlo simulation model for slope stability assessment, to produce a comprehensive evaluation of the critical angle for RBF.
As a result, the combination of the Hydrodynamic and Sediment Transport module with BN based Monte Carlo Simulation module, in conjunction with the incorporation of hydrodynamic loads and sediment properties as random variables, presented a robust and computationally efficient approach to evaluate the critical angle slope for RBF. The results of this study serve to emphasize the importance of considering inherent uncertainties in the risk assessment of the coastal flow slides process.
The hybrid model developed plays a crucial role in MSP when field observations are not feasible. The model serves as an effective design tool and can be integrated into the decision support systems of MSP. The simulation models and their applications presented in this study are valuable assets for research, particularly in the context of MSP. The Monte Carlo simulation is used as a coupled tool with the hydrodynamic and sediment transport model components.
The hybrid research model, which combines many approaches to modelling, has the greatest ability to accurately anticipate the CFS in a number of different ways when it is meticulously and strategically organized. These possible positives are:
1) An increase in overall output
2) Flexibility and the ability to enable to foresee the subject of importance are provided by a hybrid model, which in turn increases productivity.
3) It offers up additional opportunities for the individual sections to make contributions to the general topic.
References
- Alexander, D.E., 2022. On the Meaning of Impact in Disaster Risk Reduction. International Journal of Disaster Risk Science 13, 822–827. [CrossRef]
- Alhaddad, S., Labeur, R.J., Uijttewaal, W., 2020. Breaching Flow Slides and the Associated Turbidity Current. J Mar Sci Eng 8, 67. [CrossRef]
- Ar Guner, H.A., Yuksel, Y., Ozkan, E., 2011. Determination of Longshore Sediment Transport and Modelling of Shoreline Change, in: Sediment Transport. InTech. [CrossRef]
- Ariza, E., Jiménez, J.A., Sardá, R., 2008. A critical assessment of beach management on the Catalan coast. Ocean Coast Manag 51, 141–160. [CrossRef]
- Aydoğan, B., Ayat, B., 2018. Spatial variability of long-term trends of significant wave heights in the Black Sea. Applied Ocean Research 79, 20–35. [CrossRef]
- Beinssen, K., Mastbergen, D.R., 2018. Flow Slides: Understanding their geo-mechanical mechanisms, the threats they pose and how these threats can be managed Monitoring and modelling of submerged retrogressive breach flow slides View project Flow Slides: Understanding their geo-mechanical mechanisms, the threats they pose and how these threats can be managed.
- Bricker, J.D., Gibson, S., Takagi, H., Imamura, F., 2015. On the Need for Larger Manning’s Roughness Coefficients in Depth-Integrated Tsunami Inundation Models. Coastal Engineering Journal 57, 1550005-1-1550005–13. [CrossRef]
- Brothers, D.S., Andrews, B.D., Walton, M.A.L., Greene, H.G., Barrie, J.V., Miller, N.C., ten Brink, U., East, A.E., Haeussler, P.J., Kluesner, J.W., Conrad, J.E., 2019a. Slope failure and mass transport processes along the Queen Charlotte Fault, southeastern Alaska. Geological Society, London, Special Publications 477, 69–83. [CrossRef]
- Brothers, D.S., Andrews, B.D., Walton, M.A.L., Greene, H.G., Barrie, J.V., Miller, N.C., ten Brink, U., East, A.E., Haeussler, P.J., Kluesner, J.W., Conrad, J.E., 2019b. Slope failure and mass transport processes along the Queen Charlotte Fault, southeastern Alaska. Geological Society, London, Special Publications 477, 69–83. [CrossRef]
- Butler, D.R., 2021. The Anthropocene: A Special Issue. Ann Am Assoc Geogr 111, 633–637. [CrossRef]
- Chen, H. (Joanna), Liu, S.H., 2007. Slope failure characteristics and stabilization methods. Canadian Geotechnical Journal 44, 377–391. [CrossRef]
- Cloutier, C., Locat, J., Geertsema, M., Jakob, M., Schnorbus, M., 2017. Potential impacts of climate change on landslides occurrence in Canada, in: Slope Safety Preparedness for Impact of Climate Change. CRC Press, Leiden, The Netherlands : CRC Press/Balkema, [2017], pp. 71–104. [CrossRef]
- Dalton, G.J., Lockington, D.A., Baldock, T.E., 2008. Feasibility analysis of stand-alone renewable energy supply options for a large hotel. Renew Energy 33, 1475–1490. [CrossRef]
- De Groot, M.B., Lindenberg, J., Mastbergen, D.R., Van den Ham, G.A., 2012. Large scale sand liquefaction flow slide tests revisited. Amsterdam.
- Fu, B., Merritt, W.S., Croke, B.F.W., Weber, T.R., Jakeman, A.J., 2019. A review of catchment-scale water quality and erosion models and a synthesis of future prospects. Environmental Modelling & Software 114, 75–97. [CrossRef]
- Glavovic, B.C., 2014. The 2004 Manawatu Floods, New Zealand: Integrating Flood Risk Reduction and Climate Change Adaptation, in: Adapting to Climate Change. Springer Netherlands, Dordrecht, pp. 231–268. [CrossRef]
- Gong, B., Wang, S., Sloan, S.W., Sheng, D., Tang, C., 2018. Modelling Coastal Cliff Recession Based on the GIM–DDD Method. Rock Mech Rock Eng 51, 1077–1095. [CrossRef]
- Kang, J., Parker, F., Yoo, C.H., 2007. Soil-Structure Interaction and Imperfect Trench Installations for Deeply Buried Concrete Pipes. Journal of Geotechnical and Geoenvironmental Engineering 133, 277–285. [CrossRef]
- Kasmi, S., Snoussi, M., Khalfaoui, O., Aitali, R., Flayou, L., 2020. Increasing pressures, eroding beaches and climate change in Morocco. Journal of African Earth Sciences 164, 103796. [CrossRef]
- Kennedy, D.M., McSweeney, S.L., Mariani, M., Zavadil, E., 2020. The geomorphology and evolution of intermittently open and closed estuaries in large embayments in Victoria, Australia. Geomorphology 350, 106892. [CrossRef]
- Knight, J., Burningham, H., 2022. A morphological classification of coastal forelands, with examples from South Africa. Geomorphology 415, 108410. [CrossRef]
- Konrad, B., David T, N., 2015. Retrogressive Breach Failure Events at Amity Point, Australia and their Interaction with Built Defences, in: Proceedings of the 25th International Ocean and Polar Engineering Conference, ISOPE 2015. Mountain View, CA United States, pp. 1325–1330.
- Luijendijk, A., Hagenaars, G., Ranasinghe, R., Baart, F., Donchyts, G., Aarninkhof, S., 2018. The State of the World’s Beaches. Sci Rep 8, 6641. [CrossRef]
- Mastbergen, D.R., Beinssen, K., Nédélec, Y., 2019. Watching the beach steadily disappearing: The evolution of understanding of retrogressive breach failures. J Mar Sci Eng 7. [CrossRef]
- Ortega-Casanova, J., Campos, N., Fernandez-Feria, R., 2011. Experimental study on sand bed excavation by impinging swirling jets. Journal of Hydraulic Research 49, 601–610. [CrossRef]
- Ozkan, C., Mayo, T., 2019. The renewable wave energy resource in coastal regions of the Florida peninsula. Renew Energy 139, 530–537. [CrossRef]
- Phillips, M.R., Jones, A.L., 2006. Erosion and tourism infrastructure in the coastal zone: Problems, consequences and management. Tour Manag 27, 517–524. [CrossRef]
- Prasad, M., 2003. Velocity-permeability relations within hydraulic units. GEOPHYSICS 68, 108–117. [CrossRef]
- Richard, E. da C., Estrada, G.C.D., Bechtold, J., Aguiar Duarte, H., Maioli, B.G., Freitas, A.H.A., Warner, K.E., Figueiredo, L.H.M., 2020. Water and Sediment Quality in the Coastal Zone Around the Mouth of Doce River After the Fundão Tailings Dam Failure. Integr Environ Assess Manag 16, 643–654. [CrossRef]
- Sack, D., 2002. The educational value of the history of geomorphology. Geomorphology 47, 313–323. [CrossRef]
- Shahin, M.A., Jamieson, K., Cheng, L., 2020. Microbial-induced carbonate precipitation for coastal erosion mitigation of sandy slopes. Géotechnique Letters 10, 211–215. [CrossRef]
- Shimozono, T., Sato, S., 2016. Coastal vulnerability analysis during tsunami-induced levee overflow and breaching by a high-resolution flood model. Coastal Engineering 107, 116–126. [CrossRef]
- Silver, M.M.W., Dugan, B., 2020. The influence of clay content on submarine slope failure: insights from laboratory experiments and numerical models. Geological Society, London, Special Publications 500, 301–309. [CrossRef]
- Smith, T.F., Alcock, D., Thomsen, D.C., Chuenpagdee, R., 2006. Improving the Quality of Life in Coastal Areas and Future Directions for the Asia-Pacific Region. Coastal Management 34, 235–250. [CrossRef]
- Soldati, M., Barrows, T.T., Prampolini, M., Fifield, K.L., 2018. Cosmogenic exposure dating constraints for coastal landslide evolution on the Island of Malta (Mediterranean Sea). J Coast Conserv 22, 831–844. [CrossRef]
- Stoutjesdijk, T.P., de Groot, M.B., Lindenberg, J., 1995. Engineering Approach to Coastal Flow Slides, in: Coastal Engineering 1994. American Society of Civil Engineers, New York, NY, pp. 3350–3359. [CrossRef]
- Sun, Q., Leslie, S., 2020. Tsunamigenic potential of an incipient submarine slope failure in the northern South China Sea. Mar Pet Geol 112, 104111. [CrossRef]
- Udo, K., Sugawara, D., Tanaka, H., Imai, K., Mano, A., 2012. Impact of the 2011 Tohoku Earthquake and Tsunami on Beach Morphology Along the Northern Sendai Coast. Coastal Engineering Journal 54, 1250009-1-1250009–15. [CrossRef]
- van den Ham, G.A., De Groot, M.B., Mastbergen, D.R., Van den Berg, J.H., 2023. Breaching and liquefaction in subaqueous retrogressive flow slides. Canadian Geotechnical Journal 60, 72–85. [CrossRef]
- van Dijk, W.M., Mastbergen, D.R., van den Ham, G.A., Leuven, J.R.F.W., Kleinhans, M.G., 2018. Location and probability of shoal margin collapses in a sandy estuary. Earth Surf Process Landf 43, 2342–2357. [CrossRef]
- van Rhee, C., 2010. Sediment Entrainment at High Flow Velocity. Journal of Hydraulic Engineering 136, 572–582. [CrossRef]
- van Rijn, L.C., 2011. Coastal erosion and control. Ocean Coast Manag 54, 867–887. [CrossRef]
- Westoby, M.J., Lim, M., Hogg, M., Pound, M.J., Dunlop, L., Woodward, J., 2018. Cost-effective erosion monitoring of coastal cliffs. Coastal Engineering 138, 152–164. [CrossRef]
- You, Y., Flemings, P., Mohrig, D., 2012. Dynamics of dilative slope failure. Geology 40, 663–666. [CrossRef]
- Zhang, C., Zhang, M., Zhang, T., Dai, Z., Wang, L., 2020. Influence of intrusive granite dyke on rainfall-induced soil slope failure. Bulletin of Engineering Geology and the Environment 79, 5259–5276. [CrossRef]
Figure 1.
Because of CFS, portions of the 52-mile stretch of the east Yorkshire coast are vanishing far more quickly than anticipated. (The Guardian, 2020).
Figure 1.
Because of CFS, portions of the 52-mile stretch of the east Yorkshire coast are vanishing far more quickly than anticipated. (The Guardian, 2020).
Figure 2.
Field investigation in Walsoorden (Mastbergen et al., 2019).
Figure 2.
Field investigation in Walsoorden (Mastbergen et al., 2019).
Figure 3.
Coastal breaching mechanism.
Figure 3.
Coastal breaching mechanism.
Figure 4.
The flow slide occurred on the Eastern Scheldt basin's beach.
Figure 4.
The flow slide occurred on the Eastern Scheldt basin's beach.
Figure 5.
The Flow Chart of the Hybrid Bayesian Risk Model for Breach Failure.
Figure 5.
The Flow Chart of the Hybrid Bayesian Risk Model for Breach Failure.
Figure 6.
Hydrotam-3D computational module.
Figure 6.
Hydrotam-3D computational module.
Figure 7.
The case study area of the Osman Gazi Bridge Footing.
Figure 7.
The case study area of the Osman Gazi Bridge Footing.
Figure 8.
Drilling sites, bathymetric and geotechnical surveys in front of the analyzed slope in
Section 1. A: Silt and clay B: Clay C: Medium sand (STFA, 2012).
Figure 8.
Drilling sites, bathymetric and geotechnical surveys in front of the analyzed slope in
Section 1. A: Silt and clay B: Clay C: Medium sand (STFA, 2012).
Figure 9.
The Hydrotam-3D model was used to produce annual and seasonal wave roses by making use of the forecast of wind data from the ECMWF operational archive for the coordinates of 40°75 North and 29°55 East (years between 2000–2021).
Figure 9.
The Hydrotam-3D model was used to produce annual and seasonal wave roses by making use of the forecast of wind data from the ECMWF operational archive for the coordinates of 40°75 North and 29°55 East (years between 2000–2021).
Figure 10.
Projected mean sea level rise of RCP Scenarios for Turkish coasts (Word Bank, 2023).
Figure 10.
Projected mean sea level rise of RCP Scenarios for Turkish coasts (Word Bank, 2023).
Figure 11.
(a) The pattern of the currents on the surface of the water after an hour with winds coming from the north-northwest at 10 meters per second. (b) 3D current pattern (c) Current rose in front of the slope at Point A.
Figure 11.
(a) The pattern of the currents on the surface of the water after an hour with winds coming from the north-northwest at 10 meters per second. (b) 3D current pattern (c) Current rose in front of the slope at Point A.
Figure 12.
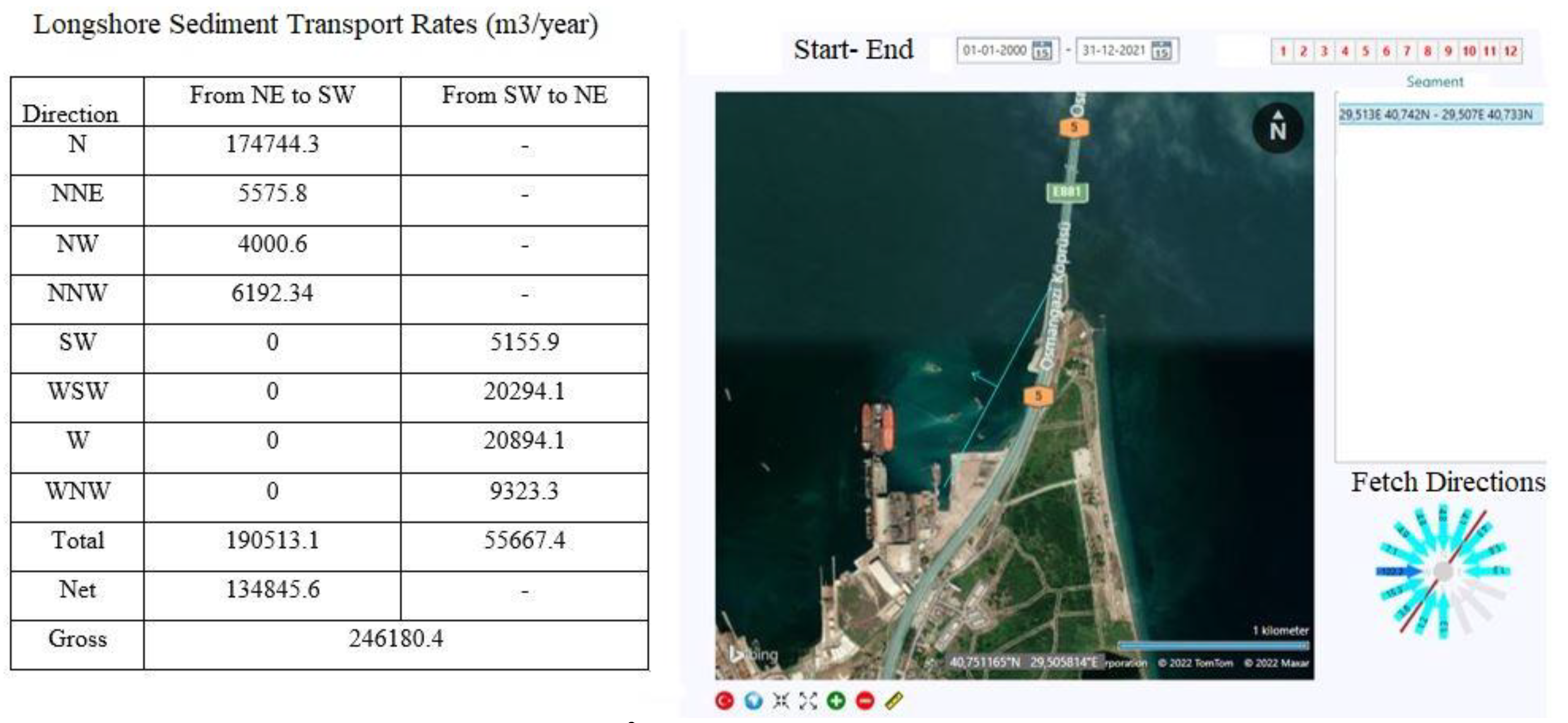
The sediment transport rates (m3/year) of the study area were obtained from the 3D hydrodynamic model.
Figure 12.
The sediment transport rates (m3/year) of the study area were obtained from the 3D hydrodynamic model.
Figure 13.
Sensitivity analysis by MCS contribution to variance technique.
Figure 13.
Sensitivity analysis by MCS contribution to variance technique.
Figure 14.
Variations of modeled parameters obtained from the Hybrid Model.
Figure 14.
Variations of modeled parameters obtained from the Hybrid Model.
Figure 15.
Correlations between the critical slope angle and soil/fluid parameters obtained from the Hybrid Model.
Figure 15.
Correlations between the critical slope angle and soil/fluid parameters obtained from the Hybrid Model.
Figure 16.
Correlations of wall velocity and soil/fluid parameters given by the Hybrid Model.
Figure 16.
Correlations of wall velocity and soil/fluid parameters given by the Hybrid Model.
Figure 17.
Correlations of the Shields and soil/fluid parameters obtained from the Hybrid Model.
Figure 17.
Correlations of the Shields and soil/fluid parameters obtained from the Hybrid Model.
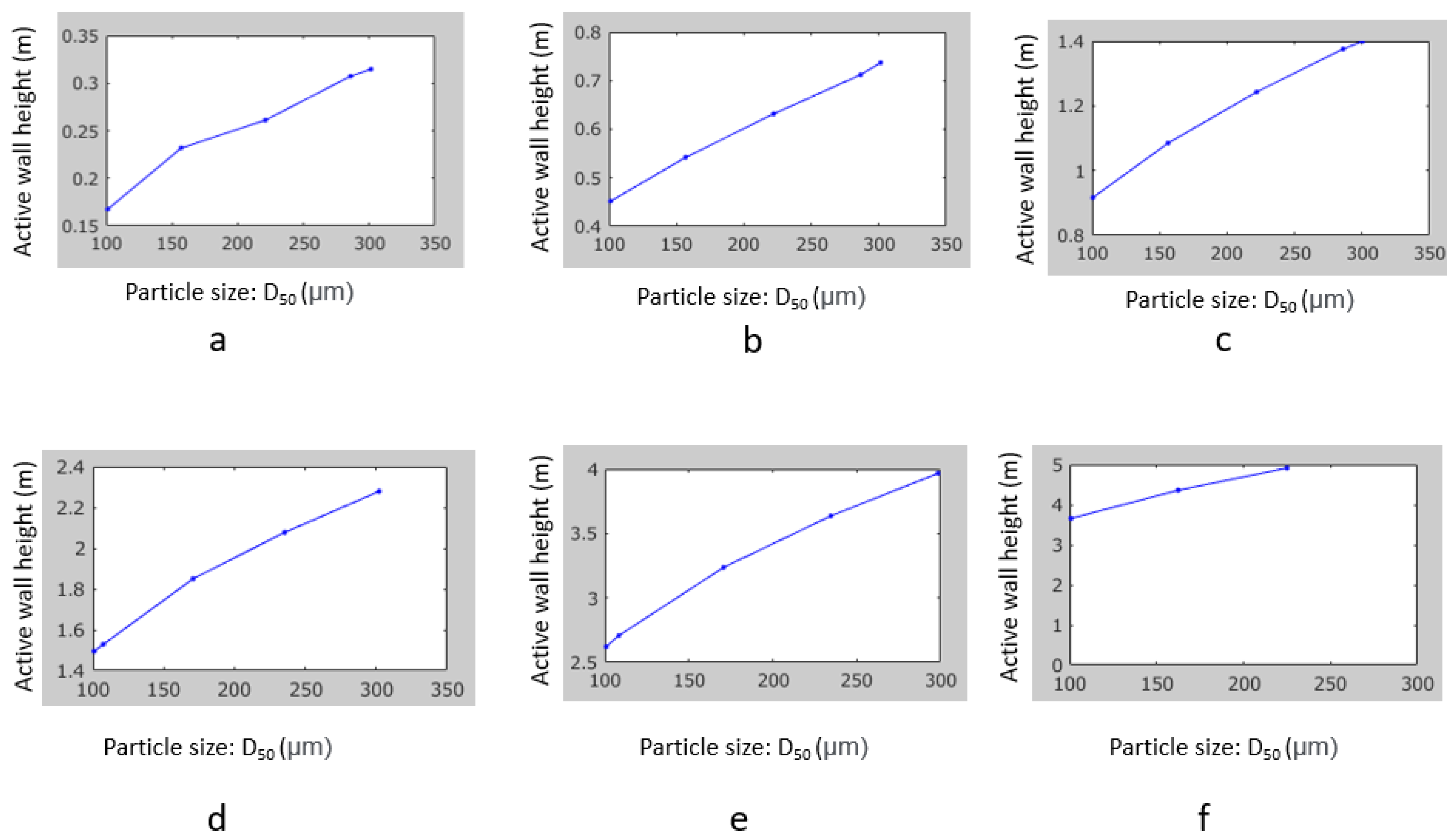
Figure 18.
Simulation of retrogressive breach failure by BN (critical angles vary a=20, b=15, c=13, d=10, e=9, and f=8 respectively. The blue lines show the critical angle slope).
Figure 18.
Simulation of retrogressive breach failure by BN (critical angles vary a=20, b=15, c=13, d=10, e=9, and f=8 respectively. The blue lines show the critical angle slope).
Figure 19.
Flowchart for the validation of the hybrid model.
Figure 19.
Flowchart for the validation of the hybrid model.
Table 1.
The global summary of events, including attributes, dates, geographic coordinates, and links (Mastbergen et al., 2019).
Table 1.
The global summary of events, including attributes, dates, geographic coordinates, and links (Mastbergen et al., 2019).
| Location |
Year and date |
Retrogression length (m) |
Generated QR Code for further information |
| Amity Point, QL, Australia |
17.8.2014 |
210 |
 |
| Inskip Point, QL, Australia |
26.9.2015 |
22 |
 |
| Jumpinpin, NSW, Australia |
24.11.2016 |
20 |
 |
| Cap Ferret, Bassin d’Arcachon, France |
8.2.2018 |
330 |
 |
| Fort Popham, MN, USA |
18.3.2011 |
. |
 |
| North Wildwood, NJ, USA |
19.9.2012 |
. |
 |
Table 2.
The CFS failure parameters of DSI.
Table 2.
The CFS failure parameters of DSI.
| DSI Parameters |
Ranking of sensitivity index |
| Very low |
Low |
Moderate |
High |
Very High |
| 1 |
2 |
3 |
4 |
5 |
| Dredging rate (P1) |
No dredging activity |
Low |
Moderate |
Higher |
Heavy |
| Slope (P2) |
Flat |
Gentle |
Moderate |
Steep |
Very steep |
| Packing type |
Loosely packed (P3) |
Very low |
Low |
Moderate |
High |
Very high |
| Densely packed (P4) |
Very low |
Low |
Moderate |
High |
Very high |
| Driving force |
Turbidity current (P5) |
Intact |
Stable |
Unstable |
High |
Very high |
| Mass Flow (P6) |
Intact |
Stable |
Unstable |
High |
Very high |
Table 3.
Probability distributions describe the fluctuations of key design parameters in the simulations.
Table 4.
Model results compared with the literature.
Table 4.
Model results compared with the literature.
| Researchers |
Focused |
DSI Parameters |
Sensitivity Ranking |
Dominant equation |
Hybrid Model Results |
| (Alhaddad et al., 2020) |
CRBF |
P1
P2
P3
P4
P5
P6 |
P1=1
P2=4
P4=4
P5=4 |
|
CRBF |
| (van den Ham et al., 2023) |
CRBF |
P1
P2
P3
P4
P5
P6 |
P1=4
P2=4
P4=4
P5=4 |
|
CRBF |
| (van den Ham et al., 2023) |
LFS |
P1
P2
P3
P4
P5
P6 |
P1=4
P2=2
P3=4
P6=4 |
|
LFS |
| (Konrad and David T, 2015) |
CRBF |
P1
P2
P3
P4
P5
P6 |
P1=1
P2=4
P4=5
P5=4 |
|
CRBF |
| (De Groot et al., 2012) |
LFS |
P1
P2
P3
P4
P5
P6 |
P1=3
P2=2
P3=4
P6=5 |
|
LFS |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).