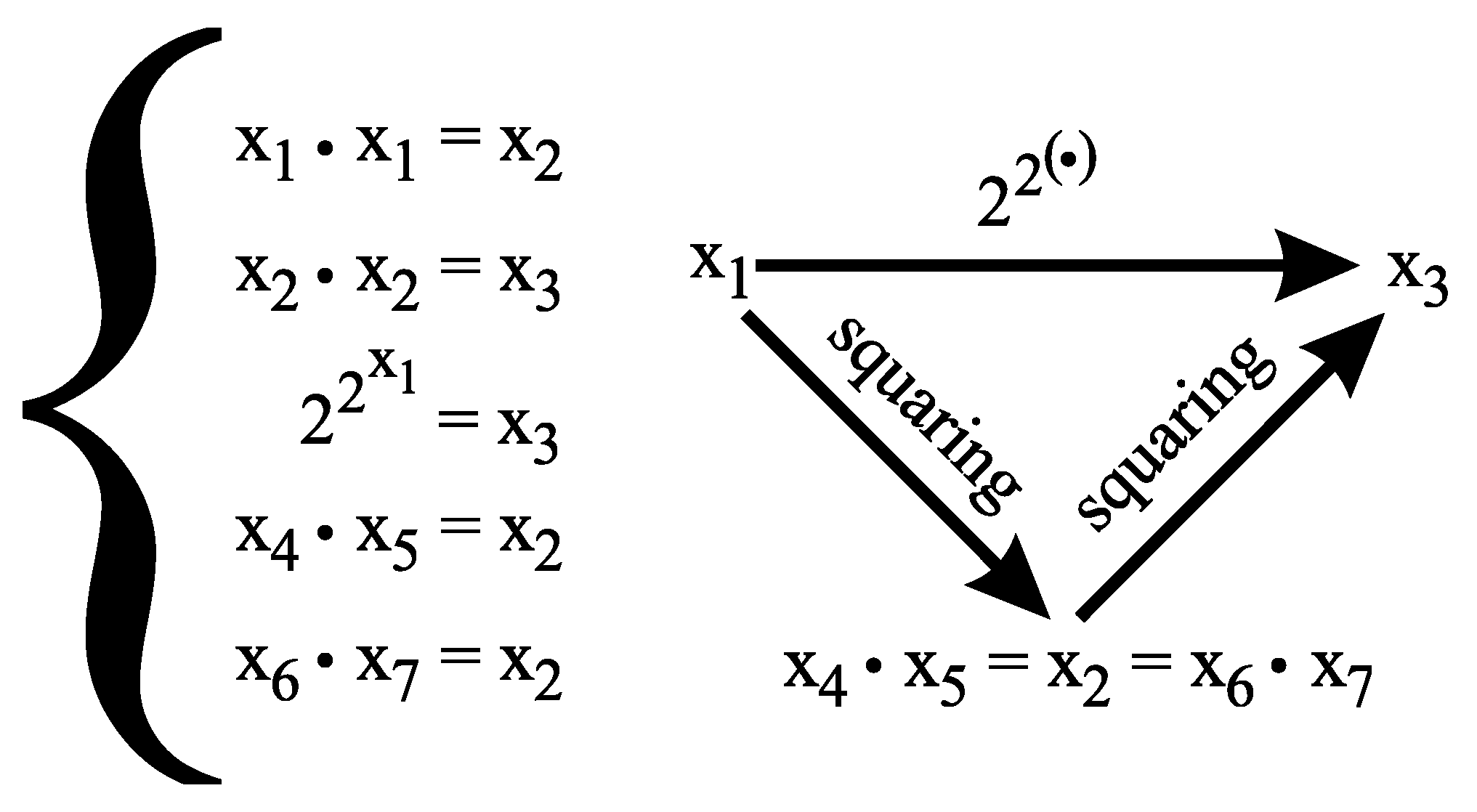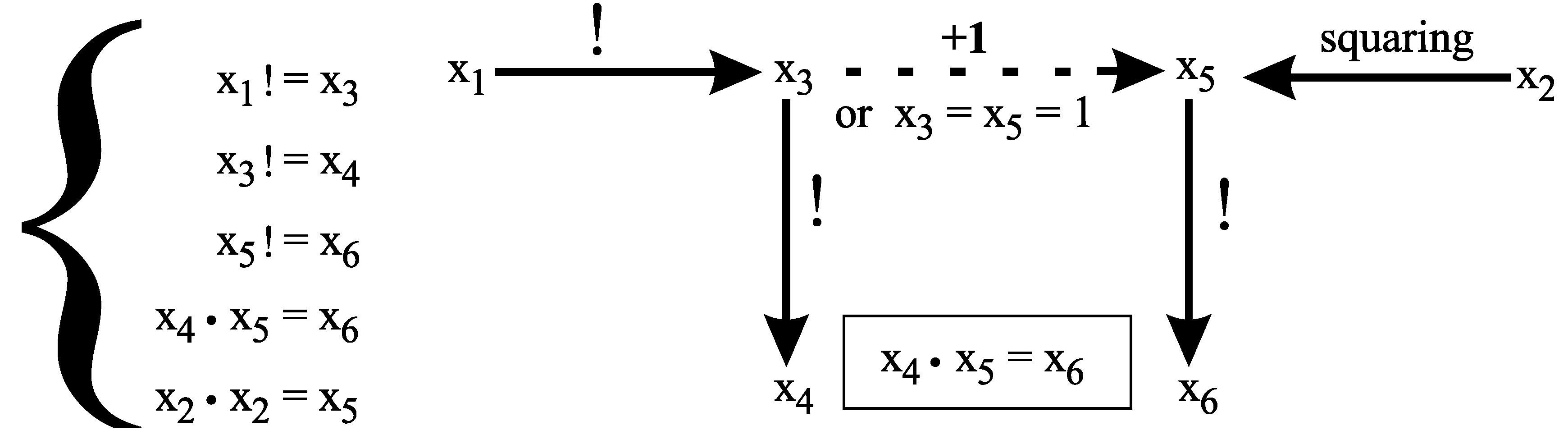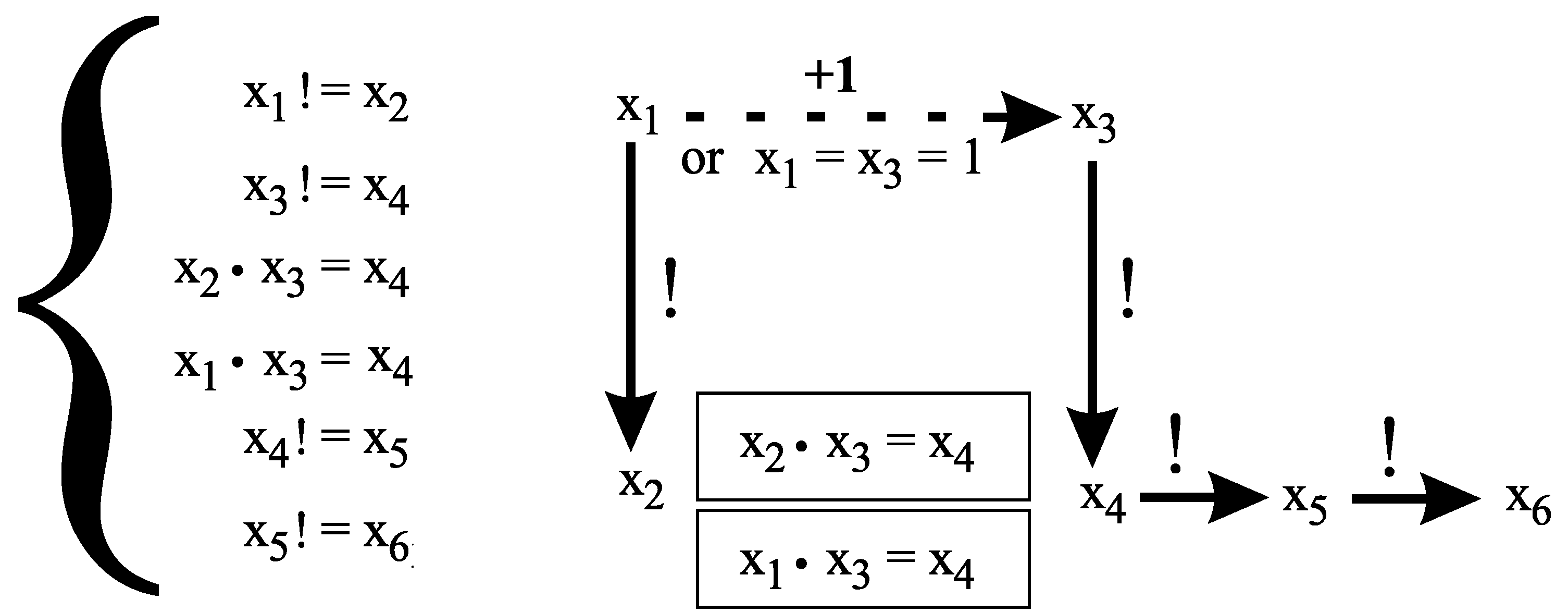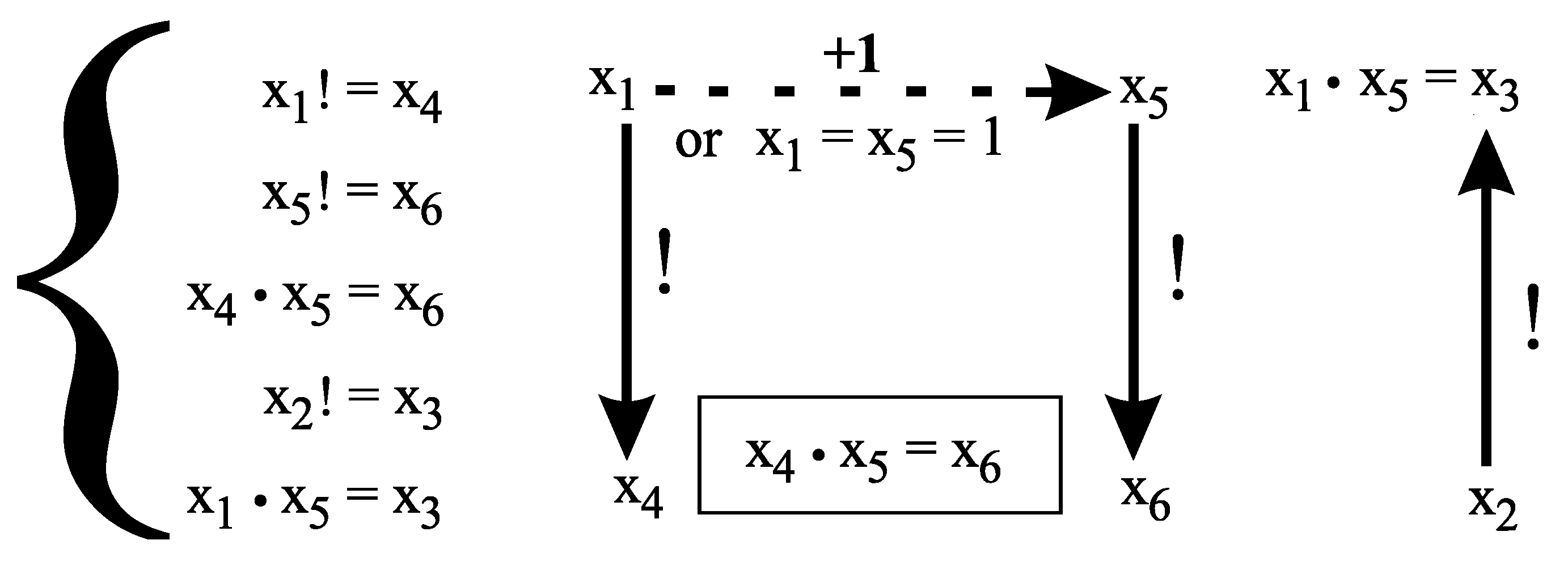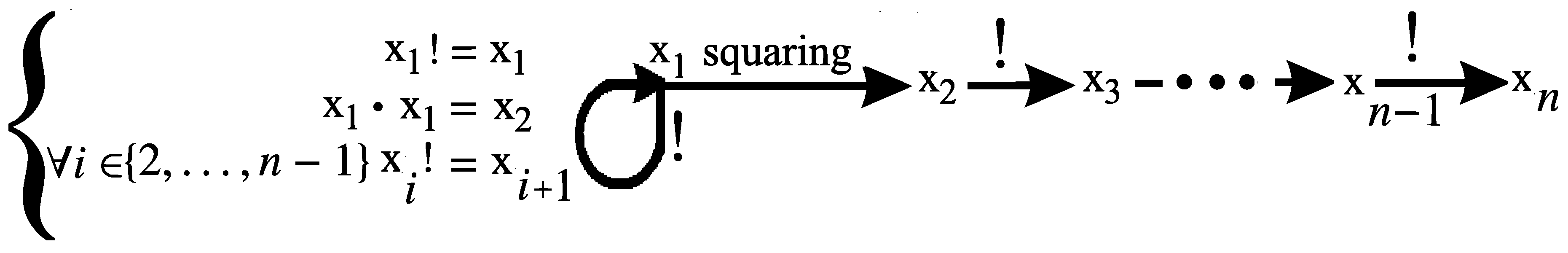A Common Approach to Three Open Problems in Number Theory

1. Composite Numbers of the Form $2^{2^n}+1$

Let $\mathcal{A}$ denote the following system of equations:

$$\left\{x_i·x_j=x_k:i,j,k\in \{1,\dots ,7\}\right\}\cup \left\{2^{2^{x_j}}=x_k:j,k\in \{1,\dots ,7\}\right\}$$

The following subsystem of $\mathcal{A}$

has exactly one solution in ${(\mathbb{N}\setminus \{0,1\})}^7$, namely $(2,4,16,2,2,2,2)$.

Hypothesis 1. 

If a system of equations $\mathcal{S}\subseteq \mathcal{A}$ has at most five equations and at most finitely many solutions in ${(\mathbb{N}\setminus \{0,1\})}^7$, then each such solution $(x_1,\dots ,x_7)$ satisfies $x_1,\dots ,x_7⩽16$.

Lemma 1.  ([7] (p. 109) ). For every non-negative integers x and y, $x+1=y$ if and only if $2^{2^x}·2^{2^x}=2^{2^y}$.

Theorem 1. 

Hypothesis 1 implies that $2^{2^{x_1}}+1$ is composite for infinitely many integers $x_1$ greater than 1.

Proof.  

Assume, on the contrary, that Hypothesis 1 holds and $2^{2^{x_1}}+1$ is composite for at most finitely many integers $x_1$ greater than 1. Then, the equation

$$x_2·x_3=2^{2^{x_1}}+1$$

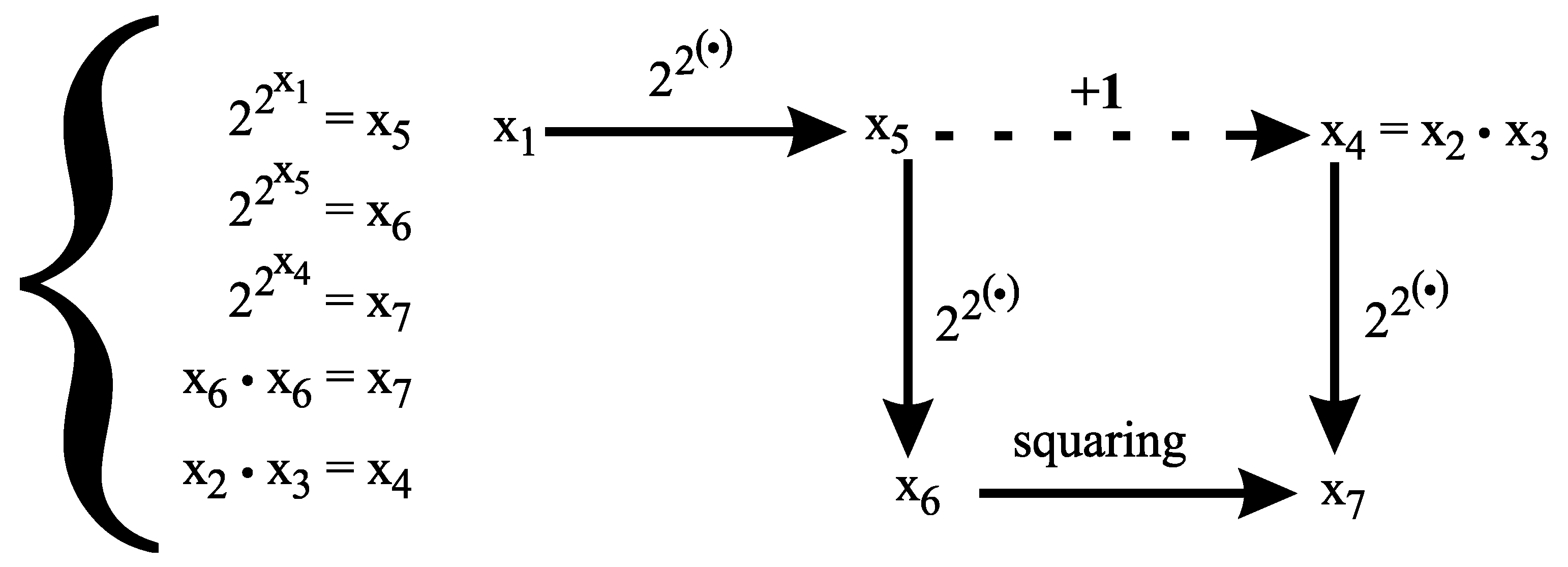
has at most finitely many solutions in ${(\mathbb{N}\setminus \{0,1\})}^3$. By Lemma 1, in positive integers greater than 1, the following subsystem of $\mathcal{A}$

has at most finitely many solutions in ${(\mathbb{N}\setminus \{0,1\})}^7$ and expresses that

$$\left\{\begin{array}{ccc}\hfill x_2·x_3& =& 2^{2^{x_1}}+1\hfill \\ \hfill x_4& =& 2^{2^{x_1}}+1\hfill \\ \hfill x_5& =& 2^{2^{x_1}}\hfill \\ \hfill x_6& =& 2^{2^{2^{2^{x_1}}}}\hfill \\ \hfill x_7& =& 2^{2^{2^{2^{x_1}}+1}}\hfill \end{array}\right.$$

Since $641·6700417=2^{2^5}+1>16$, we get a contradiction.    □

Most mathematicians believe that $2^{2^n}+1$ is composite for every integer $n⩾5$, see [2] (p. 23).    Open Problem 1.  ([3] (p. 159)). Are there infinitely many composite numbers of the form $2^{2^n}+1$?   

Primes of the form $2^{2^n}+1$ are called Fermat primes, as Fermat conjectured that every integer of the form $2^{2^n}+1$ is prime, see [3] (p. 1). Fermat remarked that $2^{2^0}+1=3$, $2^{2^1}+1=5$, $2^{2^2}+1=17$, $2^{2^3}+1=257$, and $2^{2^4}+1=65537$ are all prime, see [3] (p. 1).

   Open Problem 2.  ([3] (p. 158)). Are there infinitely many prime numbers of the form $2^{2^n}+1$?   

2. The Brocard-Ramanujan Equation $x!+1=y^2$

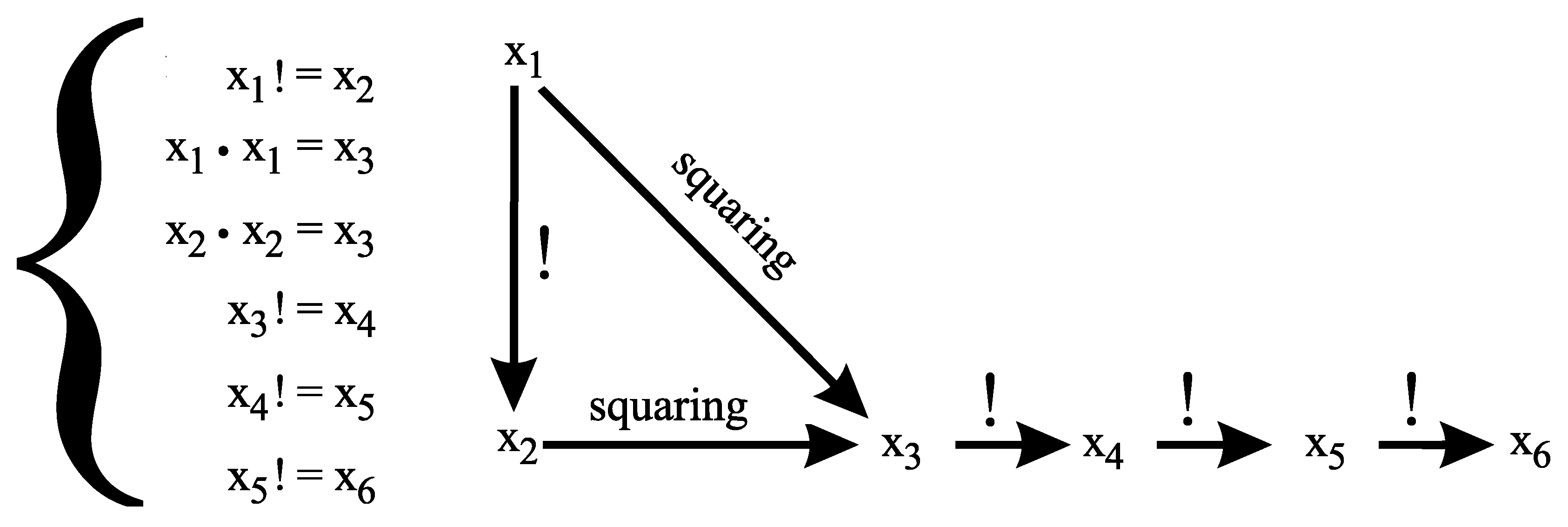
Let $\mathcal{B}$ denote the following system of equations:

$$\{x_i·x_j=x_k:i,j,k\in \{1,\dots ,6\}\}\cup \{x_j!=x_k:(j,k\in \{1,\dots ,6\})\wedge (j\ne k)\}$$

The following subsystem of $\mathcal{B}$

has exactly two solutions in positive integers, namely $(1,\dots ,1)$ and $(2,2,4,24,24!,(24!)!)$.

Hypothesis 2. 

If a system of equations $\mathcal{S}\subseteq \mathcal{B}$ has at most finitely many solutions in positive integers $x_1,\dots ,x_6$, then each such solution $(x_1,\dots ,x_6)$ satisfies $x_1,\dots ,x_6⩽(24!)!$.

Lemma 2. 

For every positive integers x and y, $x!·y=y!$ if and only if

$$(x+1=y)\vee (x=y=1)$$

Theorem 2. 

Hypothesis 2 implies that if the equation $x_1!+1=x_2^2$ has at most finitely many solutions in positive integers $x_1$ and $x_2$, then each such solution $(x_1,x_2)$ belongs to the set $\left\{\right(4,5),(5,11),(7,71\left)\right\}$.

Proof.  

The following system of equations ${\mathcal{B}}_1$

is a subsystem of $\mathcal{B}$. By Lemma 2, in positive integers, the system ${\mathcal{B}}_1$ expresses that $x_1=\dots =x_6=1$ or

$$\left\{\begin{array}{ccc}\hfill x_1!+1& =& x_2^2\hfill \\ \hfill x_3& =& x_1!\hfill \\ \hfill x_4& =& (x_1!)!\hfill \\ \hfill x_5& =& x_1!+1\hfill \\ \hfill x_6& =& (x_1!+1)!\hfill \end{array}\right.$$

If the equation $x_1!+1=x_2^2$ has at most finitely many solutions in positive integers $x_1$ and $x_2$, then ${\mathcal{B}}_1$ has at most finitely many solutions in positive integers $x_1,\dots ,x_6$ and Hypothesis 2 implies that every tuple $(x_1,\dots ,x_6)$ of positive integers that solves ${\mathcal{B}}_1$ satisfies $(x_1!+1)!=x_6⩽(24!)!$. Hence, $x_1\in \{1,\dots ,23\}$. If $x_1\in \{1,\dots ,23\}$, then $x_1!+1$ is a square only for $x_1\in \{4,5,7\}$.    □

It is conjectured that $x!+1$ is a square only for $x\in \{4,5,7\}$, see [8] (p. 297). A weak form of Szpiro’s conjecture implies that the equation $x!+1=y^2$ has only finitely many solutions in positive integers, see [6].

3. Erdös’ Equation $\mathbf{x}(\mathbf{x}+\mathbf{1})=\mathbf{y}!$

Let $\mathcal{C}$ denote the following system of equations:

$$\{x_i·x_j=x_k:(i,j,k\in \{1,\dots ,6\})\wedge (i\ne j)\}\cup \{x_j!=x_k:(j,k\in \{1,\dots ,6\})\wedge (j\ne k)\}$$

The following subsystem of $\mathcal{C}$

has exactly three solutions in positive integers, namely $(1,\dots ,1)$, $(1,1,2,2,2,2)$, and $(2,2,3,6,720,720!)$.

Hypothesis 3. 

If a system of equations $\mathcal{S}\subseteq \mathcal{C}$ has at most finitely many solutions in positive integers $x_1,\dots ,x_6$, then each such solution $(x_1,\dots ,x_6$) satisfies $x_1,\dots ,x_6⩽720!$.

Theorem 3. 

Hypothesis 3 implies that if the equation $x_1(x_1+1)=x_2!$ has at most finitely many solutions in positive integers $x_1$ and $x_2$, then each such solution $(x_1,x_2)$ belongs to the set $\left\{\right(1,2),(2,3\left)\right\}$.

Proof.  

The following system of equations ${\mathcal{C}}_1$

is a subsystem of $\mathcal{C}$. By Lemma 2, in positive integers, the system ${\mathcal{C}}_1$ expresses that $x_1=\dots =x_6=1$ or

$$\left\{\begin{array}{ccc}\hfill x_1·(x_1+1)& =& x_2!\hfill \\ \hfill x_3& =& x_1·(x_1+1)\hfill \\ \hfill x_4& =& x_1!\hfill \\ \hfill x_5& =& x_1+1\hfill \\ \hfill x_6& =& (x_1+1)!\hfill \end{array}\right.$$

If the equation $x_1(x_1+1)=x_2!$ has at most finitely many solutions in positive integers $x_1$ and $x_2$, then ${\mathcal{C}}_1$ has at most finitely many solutions in positive integers $x_1,\dots ,x_6$ and Hypothesis 3 implies that every tuple $(x_1,\dots ,x_6)$ of positive integers that solves ${\mathcal{C}}_1$ satisfies $x_2!=x_3⩽720!$. Hence, $x_2\in \{1,\dots ,720\}$. If $x_2\in \{1,\dots ,720\}$, then $x_2!$ is a product of two consecutive positive integers only for $x_2\in \{2,3\}$ because the following MuPAD program

• for x2 from 1 to 720 do
• x1:=round(sqrt(x2!+(1/4))-(1/2)):
• if x1*(x1+1)=x2! then print(x2) end_if:
• end_for:

returns 2 and 3.    □

The question of solving the equation $x(x+1)=y!$ was posed by P. Erdös, see [1]. F. Luca proved that the $abc$ conjecture implies that the equation $x(x+1)=y!$ has only finitely many solutions in positive integers, see [4].

4. There is No Hope for a Hypothesis that is Similar to Hypothesis 2 or 3 and Holds for an Arbitrary Number of Variables

Let $f\left(1\right)=2$, $f\left(2\right)=4$, and let $f(n+1)=f\left(n\right)!$ for every integer $n⩾2$. Let ${\mathcal{W}}_1$ denote the system of equations $\{x_1!=x_1$. For an integer $n⩾2$, let ${\mathcal{W}}_n$ denote the following system of equations:

For every positive integer n, the system ${\mathcal{W}}_n$ has exactly two solutions in positive integers $x_1,\dots ,x_n$, namely $(1,\dots ,1)$ and $\left(f\right(1),\dots ,f(n\left)\right)$. For a positive integer n, let ${\Psi }_n$ denote the following statement: if a system of equations

$$\mathcal{S}\subseteq \{x_i·x_j=x_k:i,j,k\in \{1,\dots ,n\}\}\cup \{x_j!=x_k:j,k\in \{1,\dots ,n\}\}$$

has at most finitely many solutions in positive integers $x_1,\dots ,x_n$, then each such solution $(x_1,\dots ,x_n)$ satisfies $x_1,\dots ,x_n⩽f\left(n\right)$.

Theorem 4. 

Every factorial Diophantine equation can be algorithmically transformed into an equivalent system of equations of the forms $x_i·x_j=x_k$ and $x_j!=x_k$. It means that this system of equations satisfies a modified version of Lemma 4 in [7].

Proof.  

It follows from Lemmas 2–5 in [7] and Lemma 2.    □

The statement $\forall n\in \mathbb{N}\setminus \left\{0\right\}{\Psi }_n$ is dubious. By Theorem 4, this statement implies that there is an algorithm which takes as input a factorial Diophantine equation and returns an integer which is greater than the solutions in positive integers, if these solutions form a finite set. This conclusion is strange because properties of factorial Diophantine equations are similar to properties of exponential Diophantine equations and a computable upper bound on non-negative integer solutions does not exist for exponential Diophantine equations with a finite number of solutions, see [5].

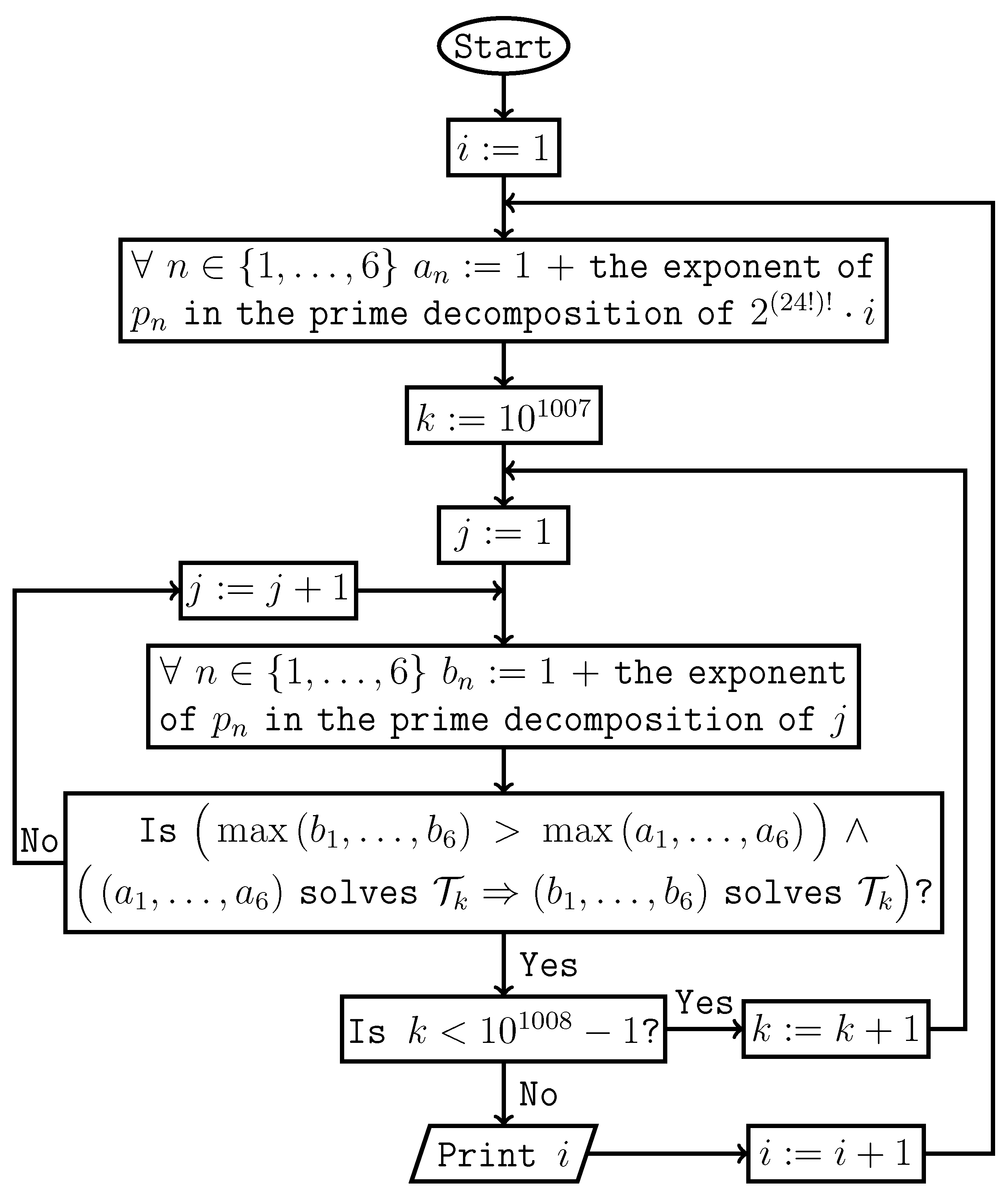
5. There are Semi-algorithms ${sem}_j$ $(j=1,2,3)$ Such that Hypothesis j Holds if and Only if ${sem}_j$ Prints Consecutive Positive Integers Starting from 1

If $k\in [{10}^{19},{10}^{20}-1]\cap \mathbb{N}$, then there are uniquely determined non-negative integers $a\left(0\right),\dots ,a\left(19\right)\in \{0,\dots ,9\}$ such that

$$\left(a\left(19\right)⩾1\right)\wedge (k=a\left(19\right)·{10}^{19}+a\left(18\right)·{10}^{18}+\dots +a\left(1\right)·{10}^1+a\left(0\right)·{10}^0)$$

Definition 4. 

For an integer $k\in [{10}^{19},{10}^{20}-1]$, ${\mathcal{S}}_k$ stands for the smallest system of equations $\mathcal{S}$ satisfying conditions(1)and(2) .

(1)If $i\in \{0,4,8,16\}$ and $a\left(i\right)\in \{0,1,2,3,4\}$, then the equation $x_{a(i+1)}·x_{a(i+2)}=x_{a(i+3)}$ belongs to $\mathcal{S}$ when it belongs to $\mathcal{A}$.

(2)If $i\in \{0,4,8,16\}$ and $a\left(i\right)\in \{5,6,7,8,9\}$, then the equation $2^{2^{x_{a(i+1)}}}=x_{a(i+2)}$ belongs to $\mathcal{S}$ when it belongs to $\mathcal{A}$.

Lemma 4. 

$\{{\mathcal{S}}_k:k\in [{10}^{19},{10}^{20}-1]\cap \mathbb{N}\}=\{\mathcal{S}:(\mathcal{S}\subseteq \mathcal{A})\wedge (\mathrm{card}\left(\mathcal{S}\right)⩽5)\}$.

Proof.  

It follows from the equality $5·4=20$.    □

For a positive integer n, let $p_n$ denote the n-th prime number.

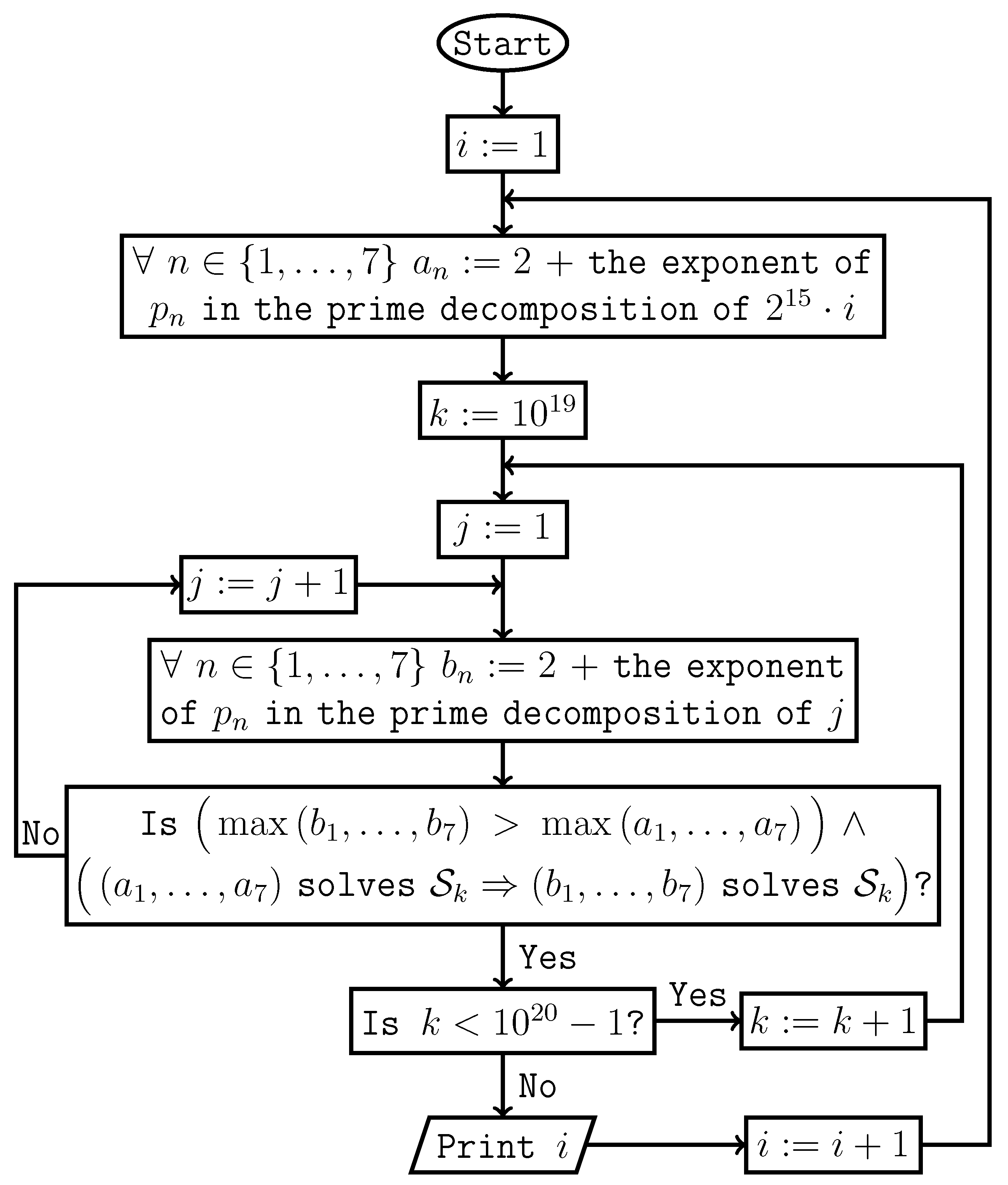
Theorem 5. 

Hypothesis 1 holds if and only if the following semi-algorithm prints consecutive positive integers starting from 1.

Proof.  

It follows from Lemma 4.    □

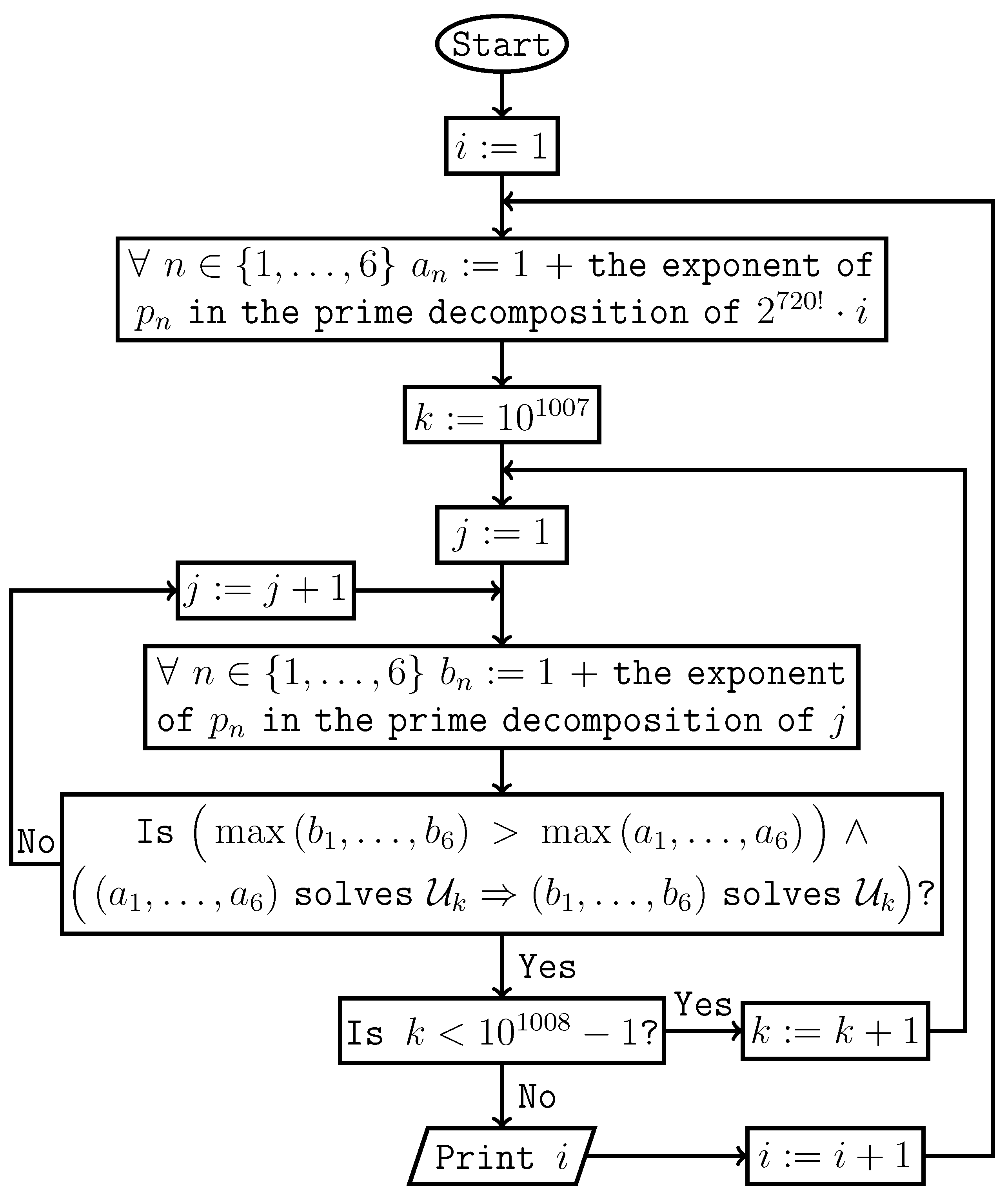
If $k\in [{10}^{1007},{10}^{1008}-1]\cap \mathbb{N}$, then there are uniquely determined non-negative integers $c\left(0\right),\dots ,c\left(1007\right)\in \{0,\dots ,9\}$ such that

$$\left(c(1007⩾1\right)\wedge \left(k=c\left(1007\right)·{10}^{1007}+c\left(1006\right)·{10}^{1006}+\dots +c\left(1\right)·{10}^1+c\left(0\right)·{10}^0\right)$$

Definition 5. 

For an integer $k\in [{10}^{1007},{10}^{1008}-1]$, ${\mathcal{T}}_k$ stands for the smallest system of equations $\mathcal{T}$ satisfying conditions(3)and(4) .

(3)If $i\in \{0,4,8,\dots ,1004\}$ and $c\left(i\right)\in \{0,1,2,3,4\}$, then the equation $x_{c(i+1)}·x_{c(i+2)}=x_{c(i+3)}$ belongs to $\mathcal{T}$ when it belongs to $\mathcal{B}$.

(4)If $i\in \{0,4,8,\dots ,1004\}$ and $c\left(i\right)\in \{5,6,7,8,9\}$, then the equation $x_{c(i+1)}!=x_{c(i+2)}$ belongs to $\mathcal{T}$ when it belongs to $\mathcal{B}$.

Lemma 5. 

$\{{\mathcal{T}}_k:k\in [{10}^{1007},{10}^{1008}-1]\cap \mathbb{N}\}=\{\mathcal{T}:\mathcal{T}\subseteq \mathcal{B}\}$.

Proof.  

It follows from the equality $(6^3+6^2)·4=1008$.    □

Definition 6. 

For an integer $k\in [{10}^{1007},{10}^{1008}-1]$, ${\mathcal{U}}_k$ stands for the smallest system of equations $\mathcal{U}$ satisfying conditions(5)and(6) .

(5)If $i\in \{0,4,8,\dots ,1004\}$ and $c\left(i\right)\in \{0,1,2,3,4\}$, then the equation $x_{c(i+1)}·x_{c(i+2)}=x_{c(i+3)}$ belongs to $\mathcal{U}$ when it belongs to $\mathcal{C}$.

(6)If $i\in \{0,4,8,\dots ,1004\}$ and $c\left(i\right)\in \{5,6,7,8,9\}$, then the equation $x_{c(i+1)}!=x_{c(i+2)}$ belongs to $\mathcal{U}$ when it belongs to $\mathcal{C}$.

Lemma 6. 

$\{{\mathcal{U}}_k:k\in [{10}^{1007},{10}^{1008}-1]\cap \mathbb{N}\}=\{\mathcal{U}:\mathcal{U}\subseteq \mathcal{C}\}$.

Proof.  

It follows from the equality $(6^3+6^2)·4=1008$. □

Theorem 6. 

Hypothesis 2 holds if and only if the following semi-algorithm prints consecutive positive integers starting from 1.

Proof.  

It follows from Lemma 5. □

Theorem 7. 

Hypothesis 3 holds if and only if the following semi-algorithm prints consecutive positive integers starting from 1.

Proof.  

It follows from Lemma 6. □