Submitted:
22 March 2023
Posted:
24 March 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- We propose a new domain aware federated distillation method named DaFKD which endows the model with different importance according to the correlation between the distillation sample and the training domain.
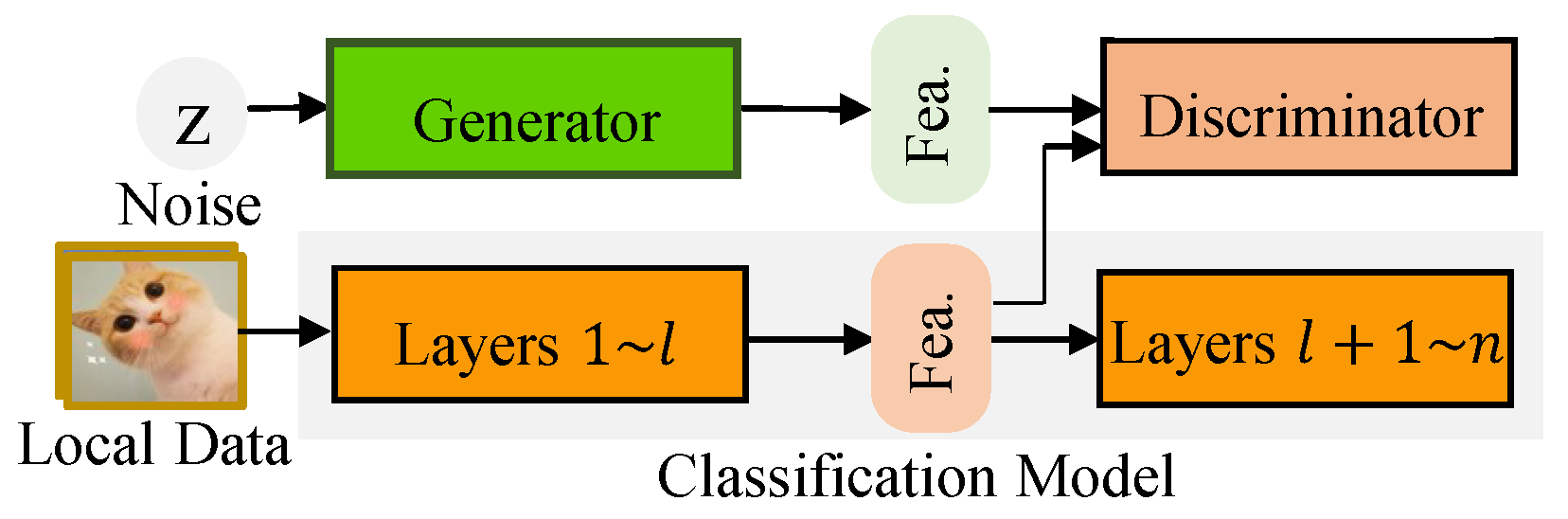
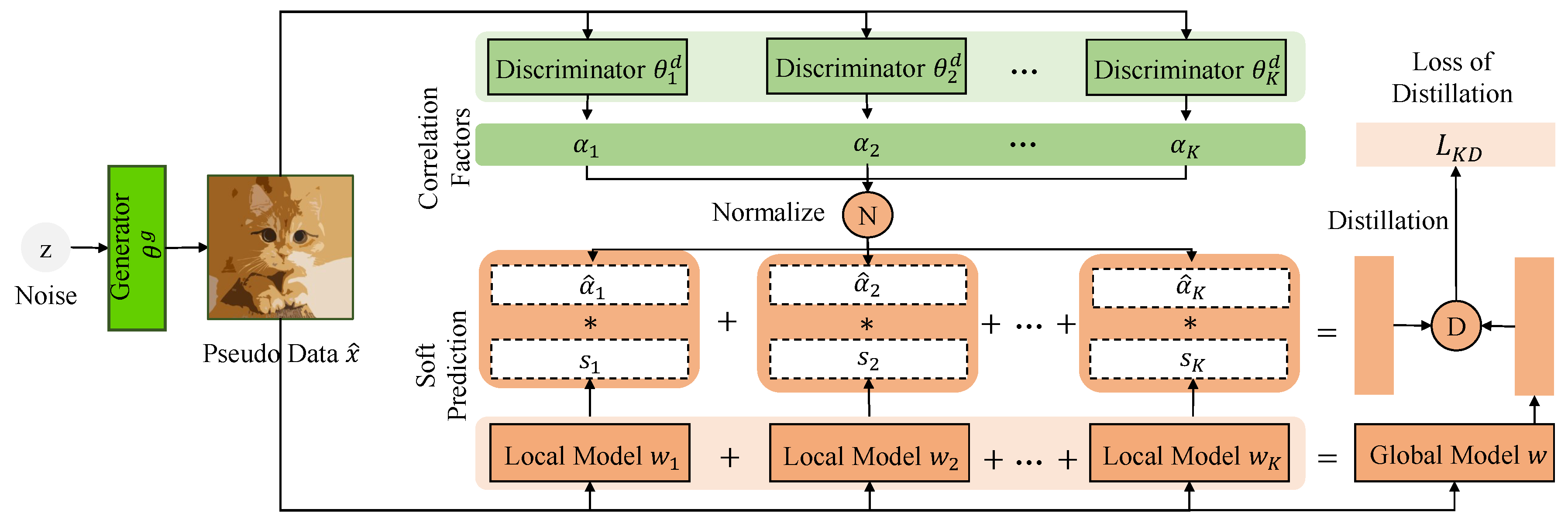
- To adaptively discern the importance of multiple local models, we propose employing the domain discriminator for each client which identifies the correlation factors. To facilitate the training of the discriminator, we further propose sharing partial parameters between the discriminator and the target classification model.
- We establish the theories for the generalization bound of the proposed method. Different from existing methods, we theoretically show that DaFKD efficiently solves the Non-IID problem where the generalization bound of DaFKD does not increases with the growth of data heterogeneity.
- We conduct extensive experiments over various datasets and settings. The results demonstrate the effectiveness of the proposed method which improves the model accuracy by up to compared to state-of-the-art methods.
2. Related Work
3. Methodology
3.1. Problem Formulation
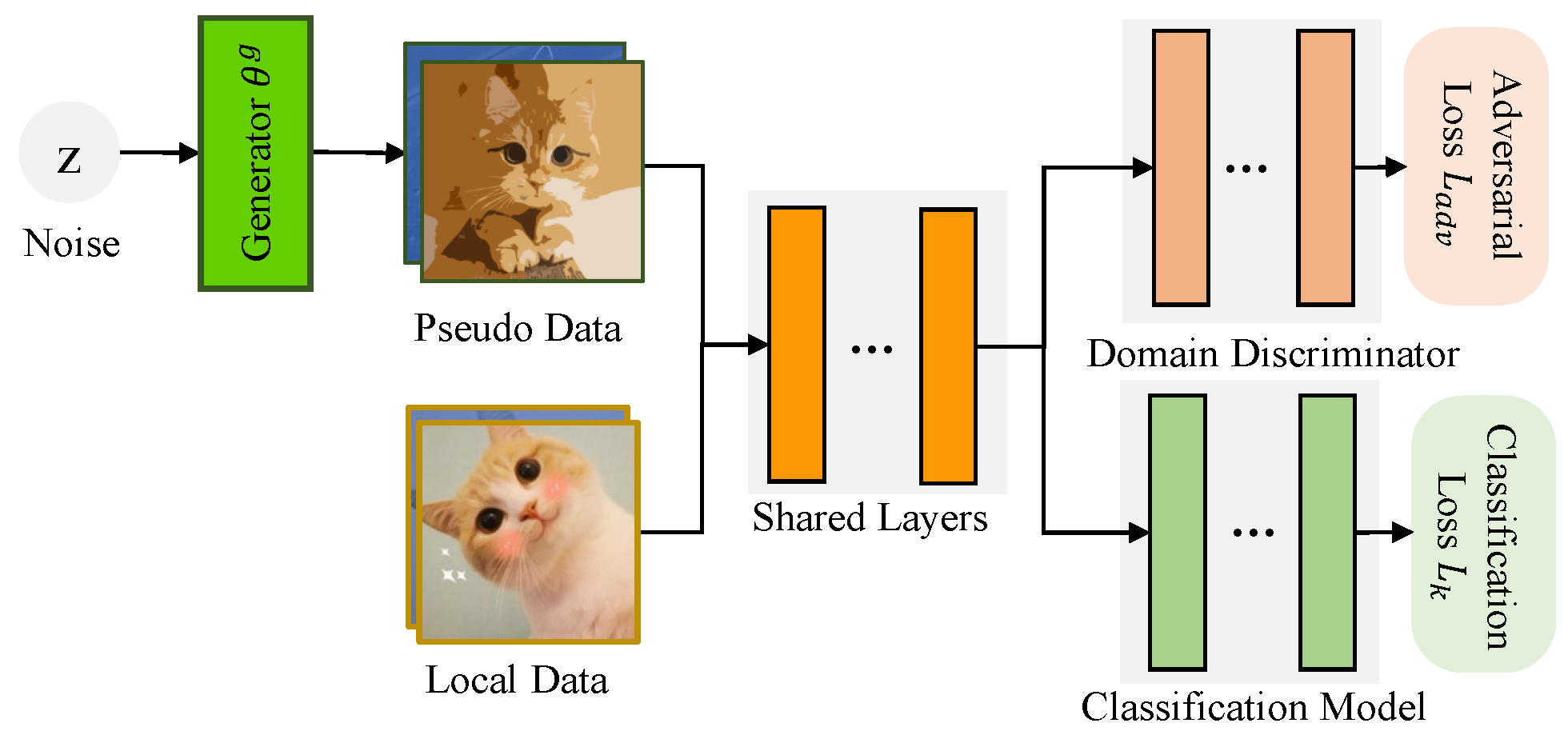
3.2. Domain Discriminator
| Algorithm 1: Workflow of DaFKD Algorithm |
 |
3.3. Domain-aware Federated Distillation
3.4. Partial Parameters Sharing
3.5. Theoretical Analysis
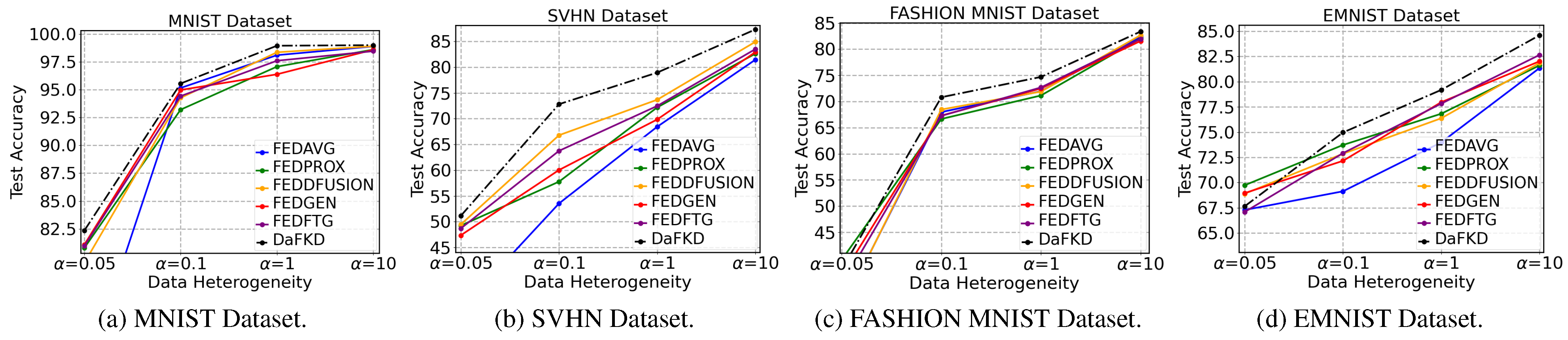
4. Experiments
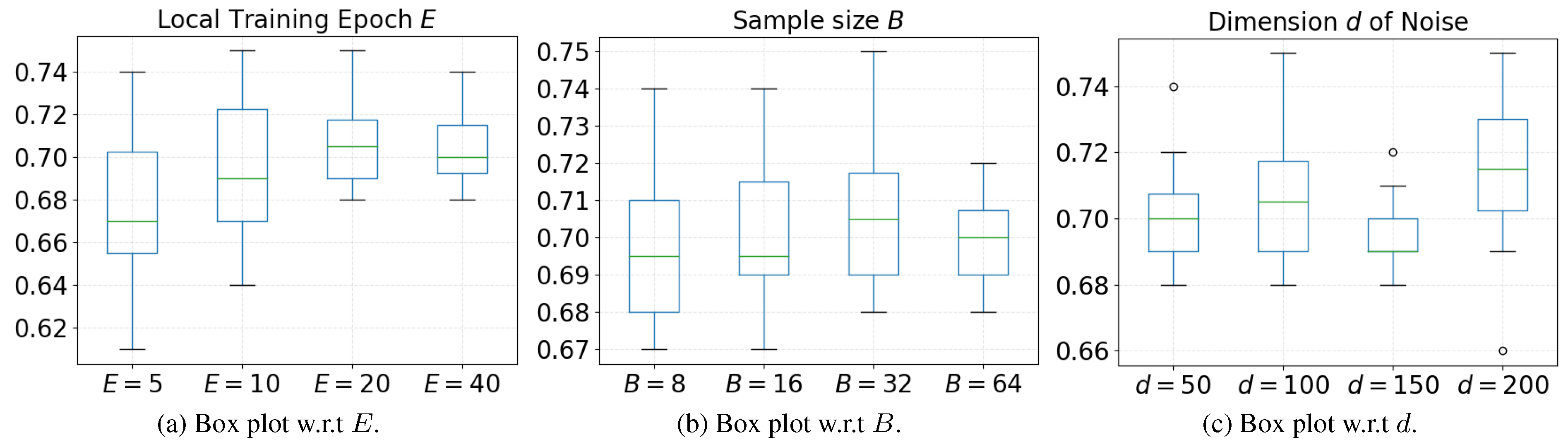
4.1. Setup
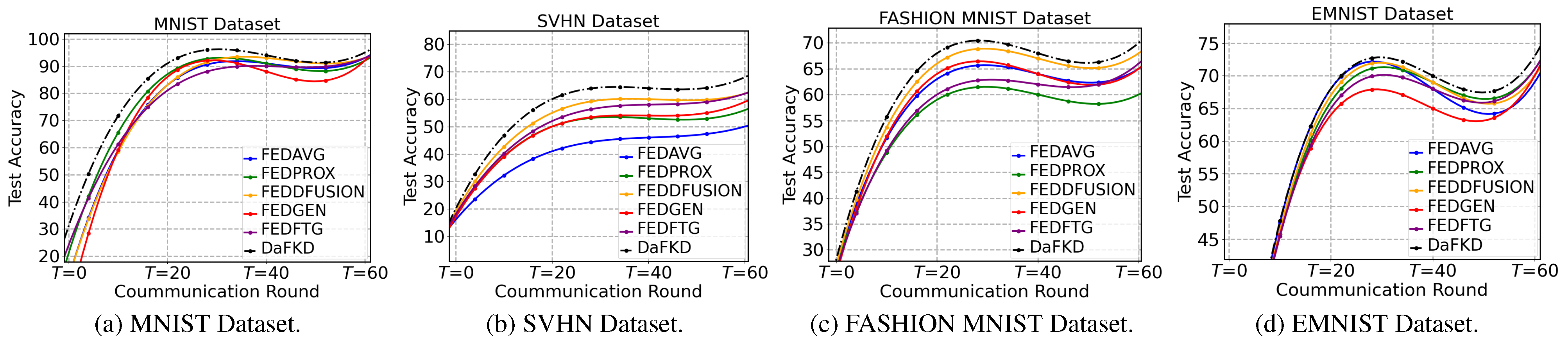
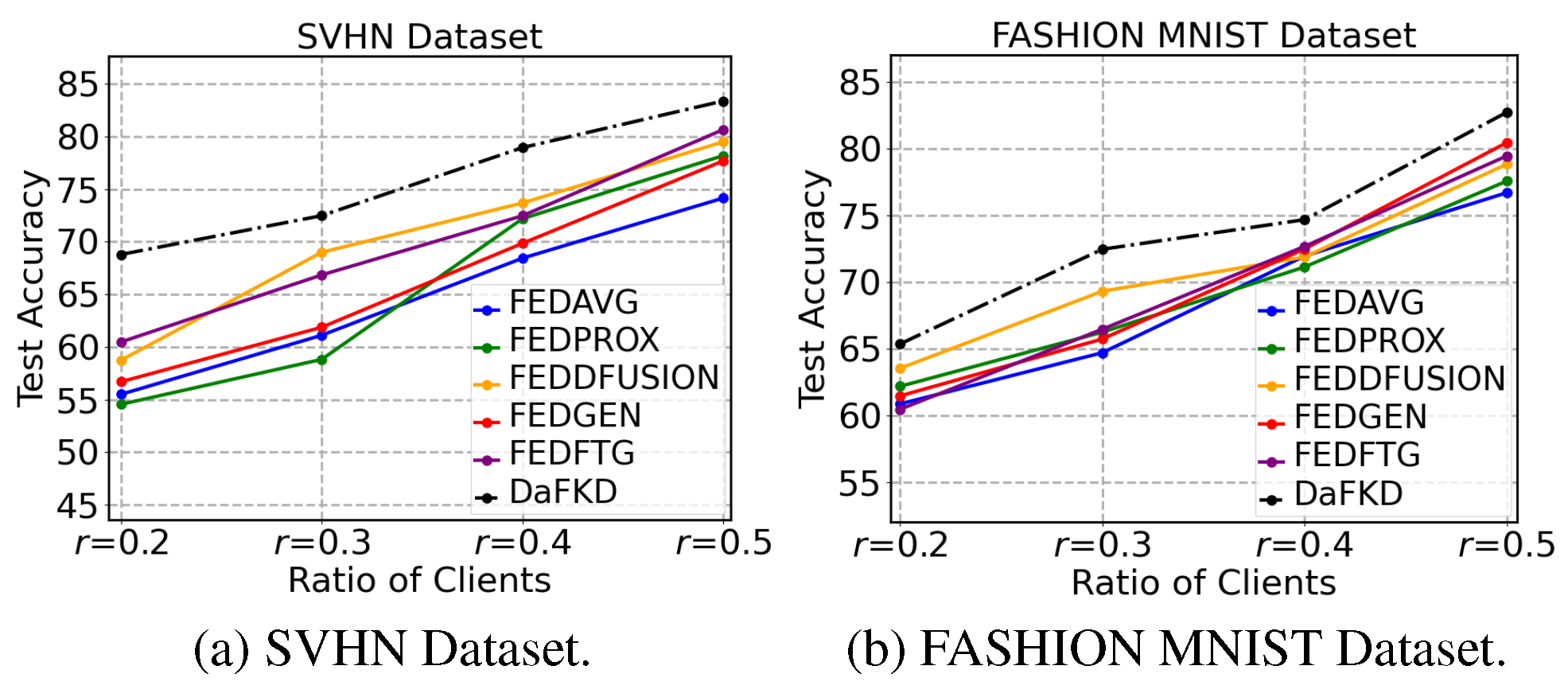
4.2. Performance Overview
5. Conclusion
A. DaFKD Without Uploading the Discriminator
B. DaFKD Without Uploading the Discriminator
C. Proof of Theorem 1
D. Proof of Theorem 2
References
- Acar, D.A.E.; Zhao, Y.; Navarro, R.M.; Mattina, M.; Whatmough, P.N.; Saligrama, V. Federated Learning Based on Dynamic Regularization. 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021.
- Ammad-ud-din, M.; Ivannikova, E.; Khan, S.A.; Oyomno, W.; Fu, Q.; Tan, K.E.; Flanagan, A. Federated Collaborative Filtering for Privacy-Preserving Personalized Recommendation System. CoRR, abs/1901.09888, 2019. [CrossRef]
- Bistritz, I.; Mann, A.; Bambos, N. Distributed Distillation for On-Device Learning. Proceedings of Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems, NeurIPS, 2020.
- Chen, H.; Chao, W. FedBE: Making Bayesian Model Ensemble Applicable to Federated Learning. 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021.
- Cho, J.H.; Hariharan, B. On the efficacy of knowledge distillation. Proceedings of 2019 IEEE/CVF International Conference on Computer Vision, ICCV, 2019, pp. 4794–4802.
- Cohen, G.; Afshar, S.; Tapson, J.; Van Schaik, A. EMNIST: Extending MNIST to handwritten letters. 2017 international joint conference on neural networks (IJCNN). IEEE, 2017, pp. 2921–2926.
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative Adversarial Nets. Advances in Neural Information Processing Systems 27: Annual Conference on Neural Information Processing Systems 2014, December 8-13 2014, Montreal, Quebec, Canada, pp. 2672–2680.
- Guo, P.; Wang, P.; Zhou, J.; Jiang, S.; Patel, V.M. Multi-Institutional Collaborations for Improving Deep Learning-Based Magnetic Resonance Image Reconstruction Using Federated Learning. IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2021, virtual, June 19-25, 2021, pp. 2423–2432.
- Guo, Q.; Wang, X.; Wu, Y.; Yu, Z.; Liang, D.; Hu, X.; Luo, P. Online knowledge distillation via collaborative learning. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR, 2020, pp. 11020–11029.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
- He, R.; Sun, S.; Yang, J.; Bai, S.; Qi, X. Knowledge Distillation as Efficient Pre-training: Faster Convergence, Higher Data-efficiency, and Better Transferability. IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, June 18-24, 2022, pp. 9151–9161.
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv preprint 2015, arXiv:1503.02531. [Google Scholar]
- Jeong, E.; Oh, S.; Kim, H.; Park, J.; Bennis, M.; Kim, S. Communication-Efficient On-Device Machine Learning: Federated Distillation and Augmentation under Non-IID Private Data. CoRR, abs/1811.11479, 2018. [CrossRef]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.J.; Stich, S.U.; Suresh, A.T. SCAFFOLD: Stochastic Controlled Averaging for Federated Learning. Proceedings of the 37th International Conference on Machine Learning, ICML 2020, 13-18 July 2020, Virtual Event, pp. 5132–5143.
- LeCun, Y.; Cortes, C.; Burges, C. MNIST handwritten digit database, 2010.
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proceedings of Machine Learning and Systems 2020, 2, 429–450. [Google Scholar]
- Li, X.; Xu, Y.; Song, S.; Li, B.; Li, Y.; Shao, Y.; Zhan, D. Federated Learning with Position-Aware Neurons. IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, June 18-24, 2022, pp. 10072–10081.
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble distillation for robust model fusion in federated learning. Advances in Neural Information Processing Systems 2020, 33, 2351–2363. [Google Scholar]
- Liu, Q.; Chen, C.; Qin, J.; Dou, Q.; Heng, P. FedDG: Federated Domain Generalization on Medical Image Segmentation via Episodic Learning in Continuous Frequency Space. IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2021, virtual, June 19-25, 2021, pp. 1013–1023.
- Lopes, R.G.; Fenu, S.; Starner, T. Data-Free Knowledge Distillation for Deep Neural Networks. CoRR, abs/1710.07535, 2017. [CrossRef]
- Malinovskiy, G.; Kovalev, D.; Gasanov, E.; Condat, L.; Richtárik, P. From Local SGD to Local Fixed-Point Methods for Federated Learning. Proceedings of the 37th International Conference on Machine Learning, ICML, 13-18 July, Virtual Event, 2020, pp. 6692–6701.
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. Artificial intelligence and statistics. PMLR, 2017, pp. 1273–1282.
- Micaelli, P.; Storkey, A.J. Zero-shot Knowledge Transfer via Adversarial Belief Matching. Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pp. 9547–9557.
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning 2011.
- Phuong, M.; Lampert, C.H. Distillation-based training for multi-exit architectures. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019, pp. 1355–1364.
- Ramaswamy, S.; Mathews, R.; Rao, K.; Beaufays, F. Federated Learning for Emoji Prediction in a Mobile Keyboard. CoRR, abs/1906.04329, 2019. [CrossRef]
- Wang, C.; Chen, X.; Wang, J.; Wang, H. ATPFL: Automatic Trajectory Prediction Model Design under Federated Learning Framework. IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR, New Orleans, LA, USA, June 18-24, 2022, pp. 6553–6562.
- Wu, G.; Gong, S. Peer Collaborative Learning for Online Knowledge Distillation. Proceedings of the AAAI Conference on Artificial Intelligence, AAAI, 2021.
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. arXiv preprint 2017, arXiv:1708.07747. [Google Scholar]
- Xie, Q.; Luong, M.T.; Hovy, E.; Le, Q.V. Self-training with noisy student improves imagenet classification. Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR, 2020, pp. 10687–10698.
- Xin, B.; Yang, W.; Geng, Y.; Chen, S.; Wang, S.; Huang, L. Private FL-GAN: Differential Privacy Synthetic Data Generation Based on Federated Learning. 2020 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP 2020, Barcelona, Spain, May 4-8, 2020, pp. 2927–2931.
- Xu, A.; Li, W.; Guo, P.; Yang, D.; Roth, H.; Hatamizadeh, A.; Zhao, C.; Xu, D.; Huang, H.; Xu, Z. Closing the Generalization Gap of Cross-silo Federated Medical Image Segmentation. IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, June 18-24, 2022, pp. 20834–20843.
- Yang, C.; Xie, L.; Qiao, S.; Yuille, A.L. Training deep neural networks in generations: A more tolerant teacher educates better students. Proceedings of the AAAI Conference on Artificial Intelligence, AAAI, 2019, Vol. 33, pp. 5628–5635.
- Yang, Z.; Li, Z.; Jiang, X.; Gong, Y.; Yuan, Z.; Zhao, D.; Yuan, C. Focal and Global Knowledge Distillation for Detectors. IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, June 18-24, 2022, pp. 4633–4642.
- Yoo, J.; Cho, M.; Kim, T.; Kang, U. Knowledge Extraction with No Observable Data. Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pp. 2701–2710.
- Zhang, L.; Luo, Y.; Bai, Y.; Du, B.; Duan, L. Federated Learning for Non-IID Data via Unified Feature Learning and Optimization Objective Alignment. IEEE/CVF International Conference on Computer Vision, ICCV, Montreal, QC, Canada, October 10-17, 2021, 2021, pp. 4400–4408.
- Zhang, L.; Shen, L.; Ding, L.; Tao, D.; Duan, L. Fine-tuning Global Model via Data-Free Knowledge Distillation for Non-IID Federated Learning. IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, June 18-24, 2022, pp. 10164–10173.
- Zhang, Y.; Xiang, T.; Hospedales, T.M.; Lu, H. Deep mutual learning. Proceedings of 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR, 2018, pp. 4320–4328.
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated Learning with Non-IID Data. CoRR, abs/1806.00582, 2018. [CrossRef]
- Zhu, Z.; Hong, J.; Zhou, J. Data-free knowledge distillation for heterogeneous federated learning. International Conference on Machine Learning. PMLR, 2021, pp. 12878–12889.
| Top-1 Test Accuracy | |||||||
|---|---|---|---|---|---|---|---|
| Dataset | Setting | FEDAVG | FEDPROX | FEDDFUSION | FEDGEN | FEDFTG | DaFKD |
| MNIST, E = 20 |
= 0.05 = 0.1 = 1 |
69.11± 1.39 95.16± 0.79 98.11± 0.14 |
80.77± 0.35 93.21± 0.55 97.08± 0.69 |
79.42± 0.57 94.27± 0.12 98.37± 0.40 |
81.06± 1.09 94.98± 0.47 96.39± 0.90 |
80.95±1.06 94.43±0.49 98.47±0.21 |
82.33±0.44 95.56±0.41 98.96±0.38 |
| SVHN, E = 20 |
= 0.05 = 0.1 = 10 |
33.01± 0.12 53.54± 0.21 81.44± 0.01 |
49.24± 0.16 57.77± 0.86 82.61± 0.34 |
49.46± 0.17 66.78± 0.33 84.91± 0.64 |
47.36± 0.42 60.03± 1.12 82.91± 0.73 |
48.69±1.87 63.75±0.11 83.49±1.32 |
51.14±0.16 72.80±0.11 87.31±0.85 |
| FASHION MNIST, E = 20 |
= 0.05 = 0.1 = 10 |
30.01± 0.54 67.97± 0.03 82.37± 0.82 |
39.71±0.23 66.65± 0.08 82.06± 0.53 |
30.08± 0.82 68.46± 0.14 82.67± 1.03 |
36.59± 0.98 67.29± 2.05 81.57± 1.96 |
34.84±0.77 67.25±0.14 81.96±1.86 |
37.85±0.24 70.81±0.21 83.37±0.06 |
| EMNIST, E = 40 |
= 0.05 = 0.1 = 10 |
67.28± 0.14 69.13± 0.23 81.35± 1.03 |
69.73± 0.17 73.72± 0.55 81.61± 0.71 |
68.89± 0.07 72.85± 0.93 81.85± 1.08 |
68.95±0.88 72.15± 2.04 82.02± 1.19 |
67.08±0.97 72.91±1.87 82.65±1.04 |
67.64±1.86 74.96±0.91 84.60±1.86 |
| Communication Round | |||||||
|---|---|---|---|---|---|---|---|
| Dataset | Accuracy | FEDAVG | FEDPROX | FEDDFUSION | FEDGEN | FEDFTG | DaFKD |
| MNIST |
= 85% = 90% |
22.67±2.33 33.33±1.00 |
18.33±3.67 40.00±3.33 |
19.67±8.33 46.33±2.33 |
21.67±2.00 39.00±3.67 |
20.67±1.33 43.67±3.67 |
19.00±2.67 38.33±1.67 |
| SVHN |
= 55% = 60% |
58.33±6.67 > 60 |
50.67±3.33 > 60 |
21.67±3.33 40.67±2.00 |
32.67±5.67 57.33±3.67 |
30.00±4.67 55.67±2.33 |
14.00±2.33 18.67±1.33 |
| FASHION MNIST |
= 60% = 65% |
21.00±1.33 35.67±3.67 |
22.67±5.67 38.33±4.00 |
20.67±3.33 34.33±0.67 |
25.00±3.33 39.67±2.67 |
27.67±4.67 43.33±6.66 |
18.67±2.33 33.67±3.00 |
| EMNIST |
= 65% = 70% |
16.33±6.33 57.66±1.33 |
18.00±3.33 44.67±2.67 |
21.33±5.67 42.67±4.67 |
23.33±1.67 50.67±2.33 |
22.67±3.67 41.33±0.67 |
20.00±3.33 40.67±4.33 |
| = 0.05 | = 0.1 | = 0.05 | = 0.1 | = 0.05 | = 0.1 | |
| MNIST | 82.33±0.44 | 95.56±0.41 | 84.67±0.92 | 95.23±0.16 | 80.57±1.67 | 94.14± 0.85 |
| SVHN | 51.14±0.16 | 72.80±0.11 | 50.78±0.03 | 74.01±1.08 | 50.33±2.08 | 72.51±0.98 |
| FASHION MNIST | 37.85±0.24 | 70.81±0.21 | 35.45±0.34 | 70.51±0.14 | 34.64±1.68 | 64.35±1.87 |
| EMNIST | 67.64±1.86 | 74.96±0.91 | 68.20±0.07 | 73.61±2.32 | 65.01±0.06 | 71.72±0.67 |
| (a) Test accuracy (%) of DaFKD with different techniques. | ||||||
| MNIST |
= 85% = 90% |
19.00±2.67 38.33±1.67 |
21.33±1.67 47.00±2.67 |
20.67±1.33 45.33±2.67 |
||
| SVHN |
= 55% = 60% |
14.00±2.33 18.67±1.33 |
22.33±2.67 35.33±5.67 |
20.67±1.33 31.00±3.67 |
||
| FASHION MNIST |
= 60% = 65% |
18.67±2.33 33.67±3.00 |
18.67±1.00 33.33±1.67 |
19.33±0.67 37.67±1.67 |
||
| EMNIST |
= 65% = 70% |
20.00±3.33 40.67±4.33 |
22.33±2.00 45.66±1.67 |
21.33±2.33 42.33±0.33 |
||
| (b) The number of communication rounds to reach the given accuracy. | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




