Prerpints.org logo
Preprint
Article

Multi-material Metamaterial Topology Optimization to Minimize the Compliance and the Constraint of Weight: Application of Non-pneumatic Tire Additive-manufactured with PLA/TPU Polymers

Altmetrics

Downloads

222

Views

136

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 March 2023

Posted:

27 March 2023

You are already at the latest version

Alerts
Abstract
Non-pneumatic tires have gained a lot of attention due to their advantages, including not having to worry about getting a flat tire. In this type of tire, metamaterial cells replace the pneumatic part of the tire. In general, metamaterials are formed by stacking cells together. These cells are obtained by various methods including topology optimization. Therefore, in this research, to achieve a metamaterial cell suitable for a non-pneumatic tire with the objective function of increasing compressive strength and bending fatigue life, optimization for three types of geometry including (1) square plane, (2) rectangular plane, and (3) entire circumference of tire and three types of material including polylactic acid (PLA), thermoplastic polyurethane (TPU) and void have been done. Optimization has been implemented by using MATLAB code in 2D mode. The cubic cell is obtained from extruding the optimized response of the square plane. From the optimized response of the rectangular plane, the cylindrical cell and from extruding the optimized response of the entire circumference of tire to the tire cross-section size, the main geometry of the tire has been calculated. Finally, to check the quality of 3D printing in producing cells and how they are connected, the optimal cell fabricated by the fused deposition modeling (FDM) method has been observed using a field-emission scanning electron microscopy (FE-SEM). The results show that in the optimization of the square plane, the sample with the minimum remaining weight constraint equal to 40% and in the optimization of the rectangular plane and the entire circumference of tire, the sample with the minimum remaining weight constraint equal to 60% was selected as the optimal sample. From checking the quality of 3D printing, it has been concluded that PLA and TPU materials are completely connected.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

As an engineering issue, optimization is basically divided into three topics: size optimization, shape optimization, and topology optimization. Optimizing the size of the variables are the dimensions of the structure such as thickness, surface and volume. Shape optimization determines the shape of structure boundaries. Topology optimization in discrete structures examines the number and optimal connection of members [1].
Then, researchers have recently realized that by taking inspiration from nature, cellular structures can be designed in such a way that they have novel characteristics [2]. In addition, with optimization methods, all types of cells with desired properties can be designed. So far, many cells have been discovered and designed, which are generally divided into four categories: foams, lattice, Triply Periodic Minimal Surfaces (TPMS) planes, and TPMS skeletons [3,4].
Metamaterials arise from the replication of cells next to each other [2,5]. Due to the complex structure of metamaterials, 3D printers are used to produce them. Among the applications of metamaterials is in car tires. Metamaterial cells replace the pneumatic part of the tire and create non-pneumatic tires. One of the advantages of these types of tires is eliminating the worry of a flat tire and lack of need for adjusting the air pressure inside the tire. These tires have been noticed due to the easy manufacturing method [6]. In addition, non-pneumatic tires are more environmentally friendly due to lower raw material usage in their production [7,8]. These tires also have other advantages such as reducing rolling resistance and thus reducing fuel consumption and emissions [6,7,9,10,11].
There have been many activities regarding non-pneumatic tires. One of the designed tires is the tweel tire. This tire has been examined from different aspects. Including, the possibility to make them with 3D printers [12], checking the mechanical behavior by a dynamic finite element model [13], checking the three-point bending properties, and simulating this test using the finite element method [14], the effects of cell thickness on vertical stiffness and maximum local stress in cells and their weight [15], noise produced by Tweel tire [16], investigation of different parameters affecting rolling resistance [17] and prediction of pressure distribution in the cell of this tire [18].
The Tweel tire was also designed for use on the moon, which led to a new structure called TweelTM. This tire has also been examined from different aspects. including modeling and simulating the dynamic interaction between tire and sand [19], the interaction of the tire shear layer with sand [20], examining different patterns to find a cell with high shear bending force bearing considering the strain energy distribution [21] and Investigating the ribbed metamaterial shear layer and selecting the shear layer with specific cell geometry with the best pressure distribution in the contact area [22].
On the other hand, the use of optimization methods for the design of metamaterial cells has been investigated. Cells have been optimized for one or more materials. Tavakli [23] has developed a multi-material optimization algorithm. Numerical results show that the proposed algorithm is very close to the discrete scheme or 0-1. Zhengtong et al. [24] have developed an optimization algorithm for a truss foundation. In this method, the optimization of the use of different materials is considered. Chen et al. [25] have developed a multi-material topology optimization algorithm for cell design by reducing stress concentration. This metamaterial cell also has the property of negative Poisson ratio.
Chung and Du [26] have developed a topology optimization framework for the design of multi-material cellular structures. This cellular structure is one of the thermal metamaterials that must be exposed to temperature changes. Mansouri et al. [27] pressed a multi-material cellular structure. The results show that the multi-material cellular structure has better compressive properties. These multi-material structures have flexibility and load-bearing characteristics. Gao et al [28] have proposed a topology fatigue optimization approach. In this method, stress, volume, and fatigue strength are considered limitations and minimum compliance is the objective function.
In another research, Gao et al. [29] have developed a design method for the design of three-material auxetic metamaterials using the isogeometric topology optimization (ITO) method. Huang and Li [30] have developed an algorithm for designing new multi-material topology optimization. Li et al. [31] have also investigated the optimization of the topology of auxetic cellular composites using the surface set method.
Nguyen et al. [32] have presented an approach for unit cell design using isogeometric analysis and parametric surface adjustment. Vogiatzis et al. [33] have proposed a surface set-based method for topology optimization of single-material and multi-material metamaterials with negative Poisson ratio (NPR). Zhang et al. [34] presented a new bi-material cell design method for chiral auxetic metamaterials. Zheng et al. [35] systematically investigate several isotropic materials concerning elastic modulus and Poisson ratio. In this research, a method of topology optimization, and optimal design of cells are used.
According to the literature, the studies for the optimization of metamaterial cells were done with:
  • different optimization methods [24,29,30,31,32,33,34],
  • different materials (one to several materials) [23,26,27,36],
  • and different objective functions and constraints [25,28].
  • Consequently, the innovation of the current research is related to:
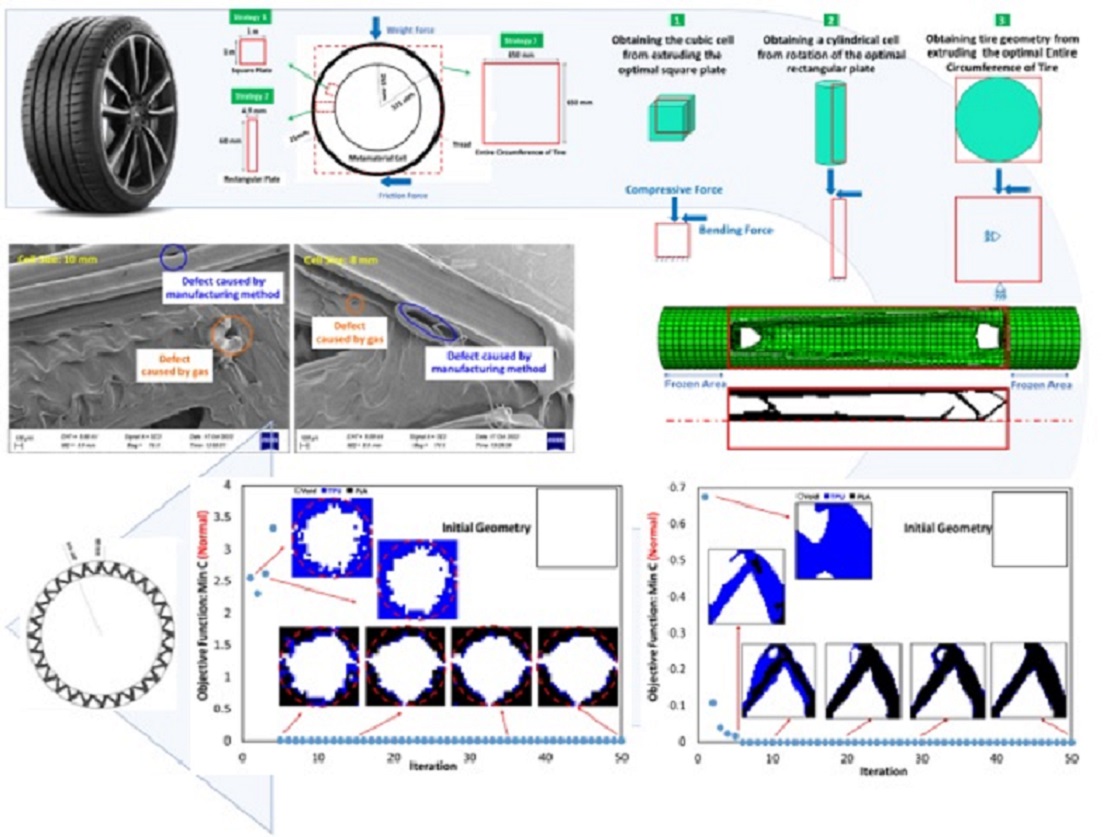
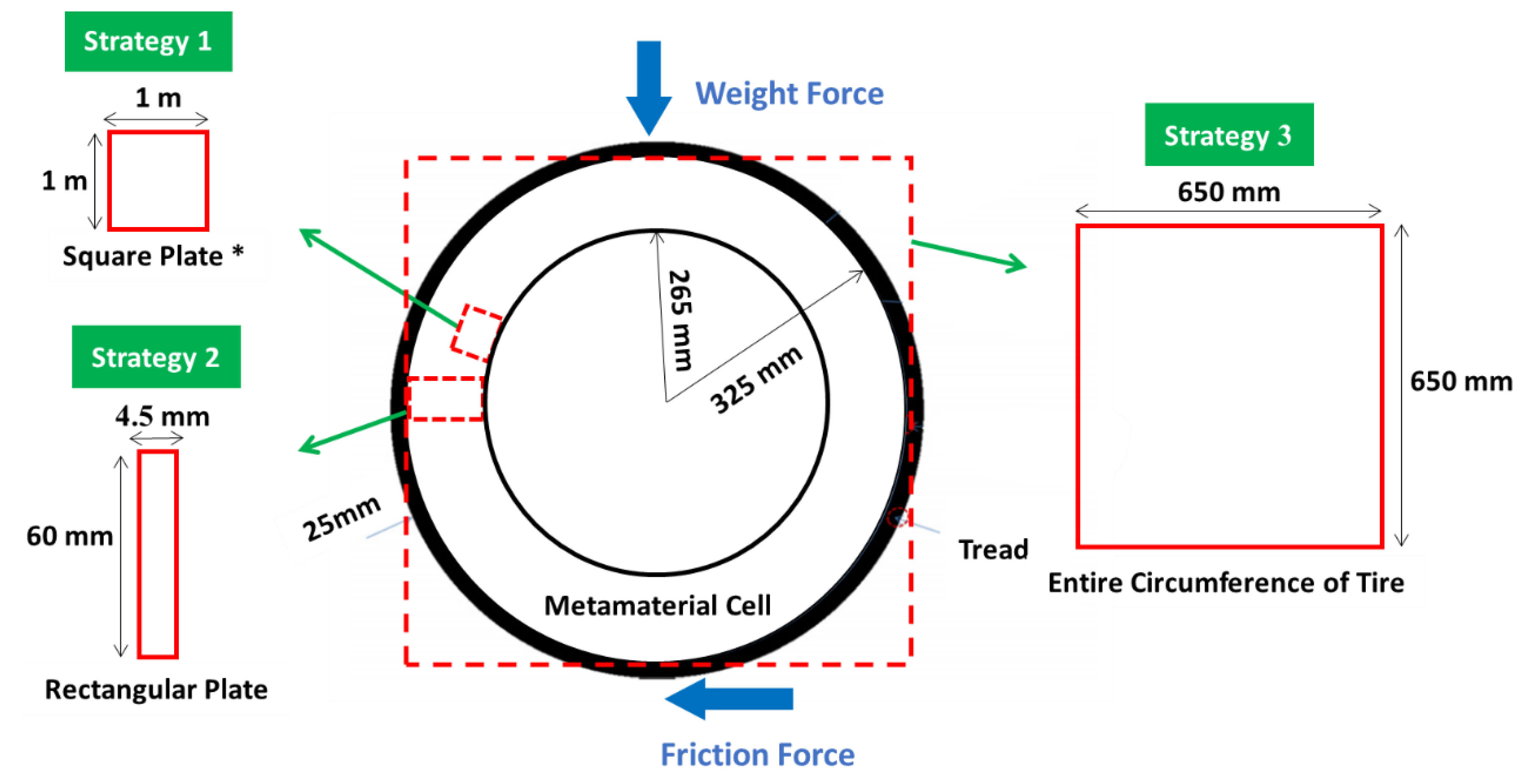
  • the optimization of the metamaterial cell with three materials and its possible application in non-pneumatic tires,
  • and the production and the examination of how to connect materials and the quality of 3D printing.

2. Materials and Methods

2.1. Samples

The main goal of this research is to design a non-pneumatic tire with an optimization method consisting of several materials. Different forces are applied to the tire. However, in this research, the compressive force caused by the weight of the car and the passengers and the bending force caused by the friction between the tire and the road was considered. In this research, it is assumed that the tire is moving in a straight road. As a result, lateral force has been omitted. In the next articles, the impact of the lateral force could also be investigated. According to this hypothesis and a review of articles, the dimensions and amount of force on the tire were selected [9,10,12,13,15,18,20,36–55]. These forces and dimensions of the tire in question are shown in Figure 1. The both compressive and bending force is selected as 1 kN. Considering that the problem is two-dimensional, concentrated load was applied.
To optimize the non-pneumatic tire, three types of solution methods have been considered. In the first case (Strategy 1), a non-pneumatic tire is obtained by optimizing a square plane and putting together the optimized response in the pneumatic part of the tire (After optimization, this cell can be used in a scaled form in the tire). In the second case (Strategy 2), a rectangular plane is considered equal to the height of the pneumatic tire section, which is obtained by putting together the optimized response in the radial direction of the non-pneumatic tire. In the third mode (Strategy 3), optimization for the entire circumference of tire is included.

2.2. Materials Specifications

In this research, to optimize and find a suitable cell to replace the pneumatic part of the tire, three types of materials including polylactic acid (PLA), thermoplastic polyurethane (TPU) and void have been used. PLA is among the harder 3D printable polymers in the market. Poisson ratio for this material is 0.36, its density is 1240 kg/m3 [56] and its melting temperature is between 180 and 230 ֯C [57]. TPU polymers show properties such as toughness, strength, and wear resistance. Poisson ratio of these materials is 0.3897, their melting temperature is 200-220 ֯C, and their density is 1200 kg/m3 [58].
In this research, the tensile properties of the materials, which have a more critical effect have been used. Tensile test samples were prepared according to ISO-527 standard at a speed of 50 mm/min and fused deposition modeling (FDM) method with repeatability of three tests and 3D printing parameters according to Table 1. The results of this test are shown in Table 2. These properties have been used in the optimization. The elastic modulus is the average of the slope of the linear region.

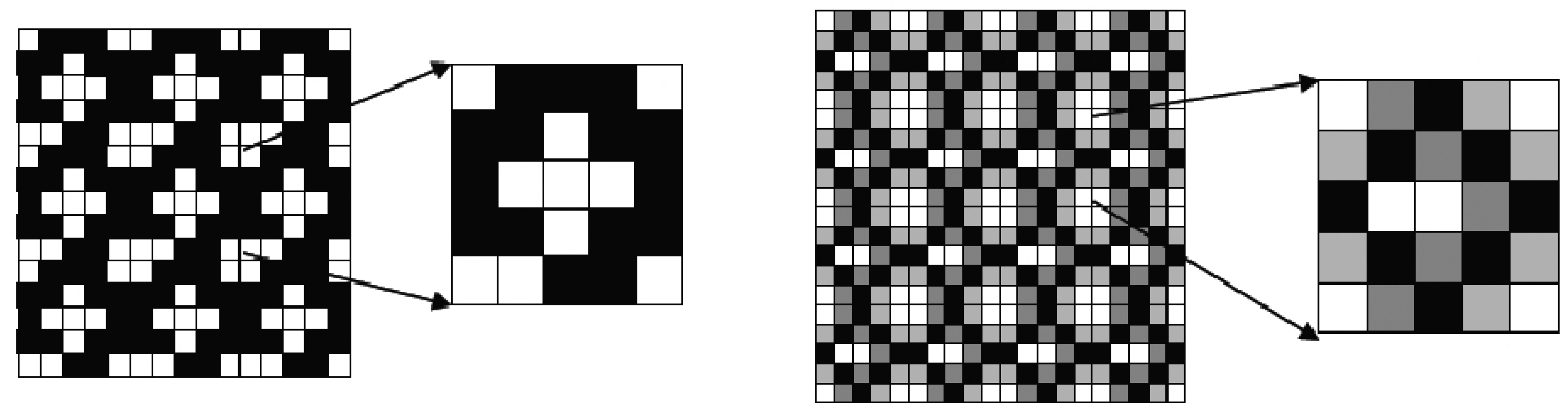
2.3. Optimization Procedures

Metamaterials can be designed by using optimization processes. In these processes, optimization is performed for one cell, then by repeating and putting this cell together, a metamaterial structure is fabricated. Topology optimization is performed based on finite element analysis and sensitivity analysis. In each step, the properties of the elements are specified. It also uses mathematical programming techniques to obtain convergence of the response. More information is provided in Appendix A [59,60,61,62,63,64,65].
To perform optimization in MATLAB software, the code written by Zuo and Saitou [66] was used. In this code, it is possible to optimize several materials in 2D mode. Therefore, the optimization of the three geometries in question is defined as shown in Figure 2. The parameters used in the optimization are also presented in Table 3.
One solution to prevent rasterization of the response is to use filters such as the neighborhood radius filter. In this filter, the color or density of each element is calculated as an average of the density of adjacent elements. The neighborhood radius is one of the optimization parameters. If there is a limitation in the construction method, a smaller neighborhood radius can be used. Moreover, if there is no limit to production, the neighborhood radius can be used more. In this case, the answer is more accurate. The neighborhood radius filter considers constructability in the optimization process. The larger radius is, the more elements are involved. As a result, more elements have the same properties. If a smaller radius is used, the boundary between the void and the solid material is clearer. However, if this radius is too small, the elements will not be grouped. Figure 3 is presented for a better understanding of this method. For the optimization, the neighborhood radius filter with the symbol of R has been used.
The used code contains two types of constraints: volume and price. However, in the present study, only the adverb of volume is used. To eliminate the effect of the price constraint, a value of 50% has been considered for this constraint. This means that both PLA and TPU materials should be used equally. The final answer should include 50% of the cheaper material and naturally 50% of the more expensive material. In addition, the normal vector related to the price of materials is defined as [1 1 1]. This means that the price of all three void, PLA and TPU, are assumed to be the same.
To optimize the square plane, a 1x1 m plane has been selected, which is subjected to a compressive and bending force of 1 kN. By extruding the optimized 2D geometry, the desired cell is calculated. This cell will be used in a scaled form in the tire. Similarly, for the optimization of the rectangular plane, a plane with dimensions of 4.5 x 60 mm has been selected, and the desired geometry will be obtained from the rotation of this plane around the axis of symmetry (see Figure 1). This plane is also subjected to a compressive and bending force of 1 kN.
Optimizing the entire circumference of tire with dimensions of 650 x 650 mm has been considered, and the desired result has been obtained by extruding its optimized response to the width of the tire section. In the design of tire, continuous contact between the tire and the road is very important for the safety of the car and its passengers. Therefore, a barrier has been considered at the point of contact between the tire and the road to prevent separation of these two. In addition, another restriction is also considered in the center of the tire to prevent the tire from sliding on the road.
In the MATLAB code used to investigate the effect of the length of the element on the optimization response, various analyses have been performed, the information of which is shown in Figure 4. According to this figure, an element size of 25 mm has been chosen.

2.4. Printing Quality

To check the quality of 3D printing in the production of parts made of PLA and TPU and to check how to connect them, the optimal cell fabricated by the FDM method has been observed using a field emission scanning electron microscopy (FESEM) (Zeiss Sigma 300 HV, Germany). A gold coating is applied on the surface of the samples prior to SEM analysis.

3. Results and Discussion

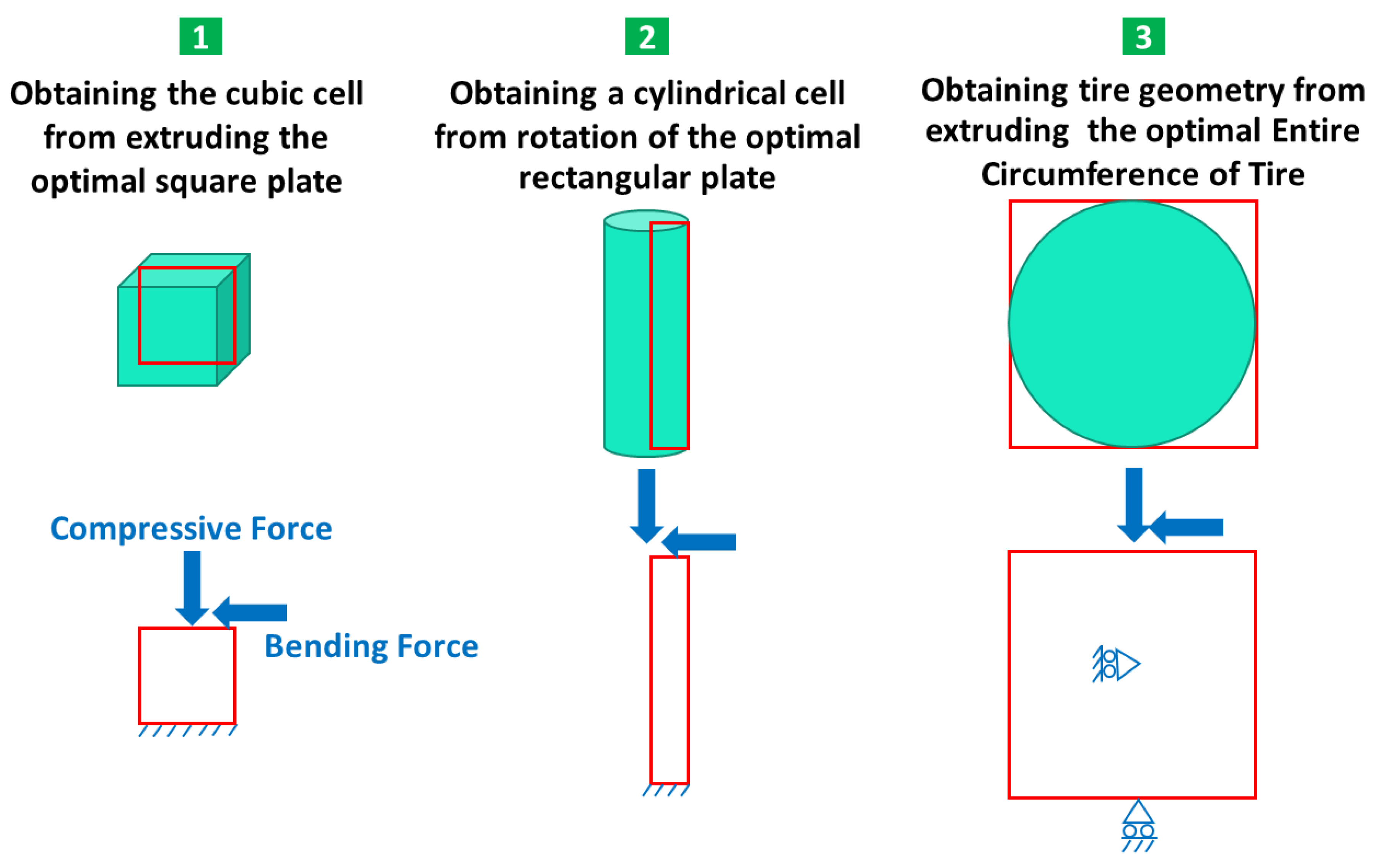
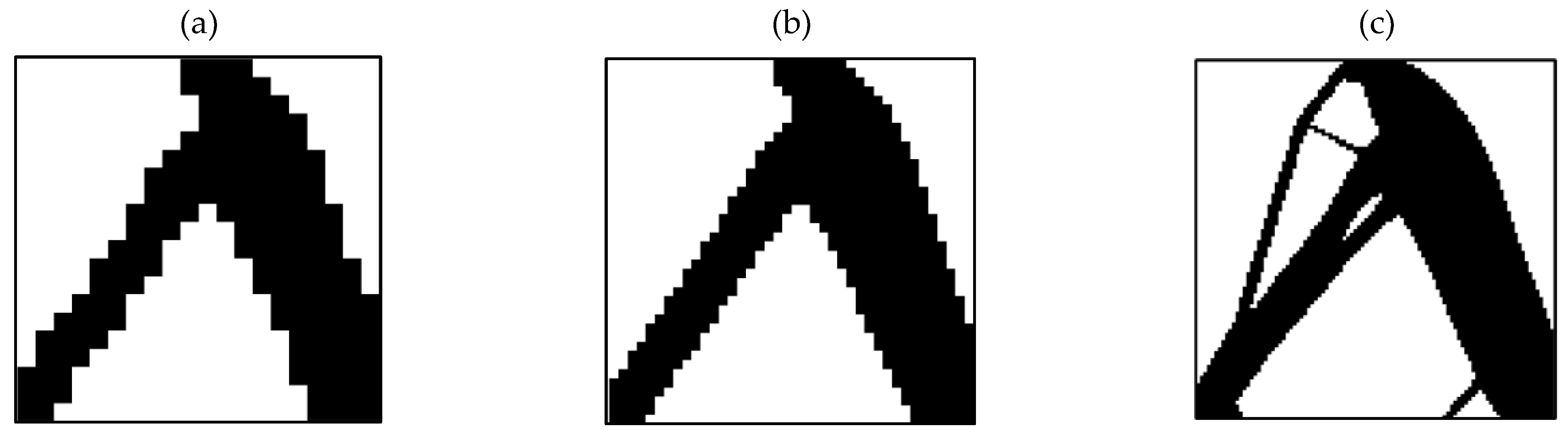
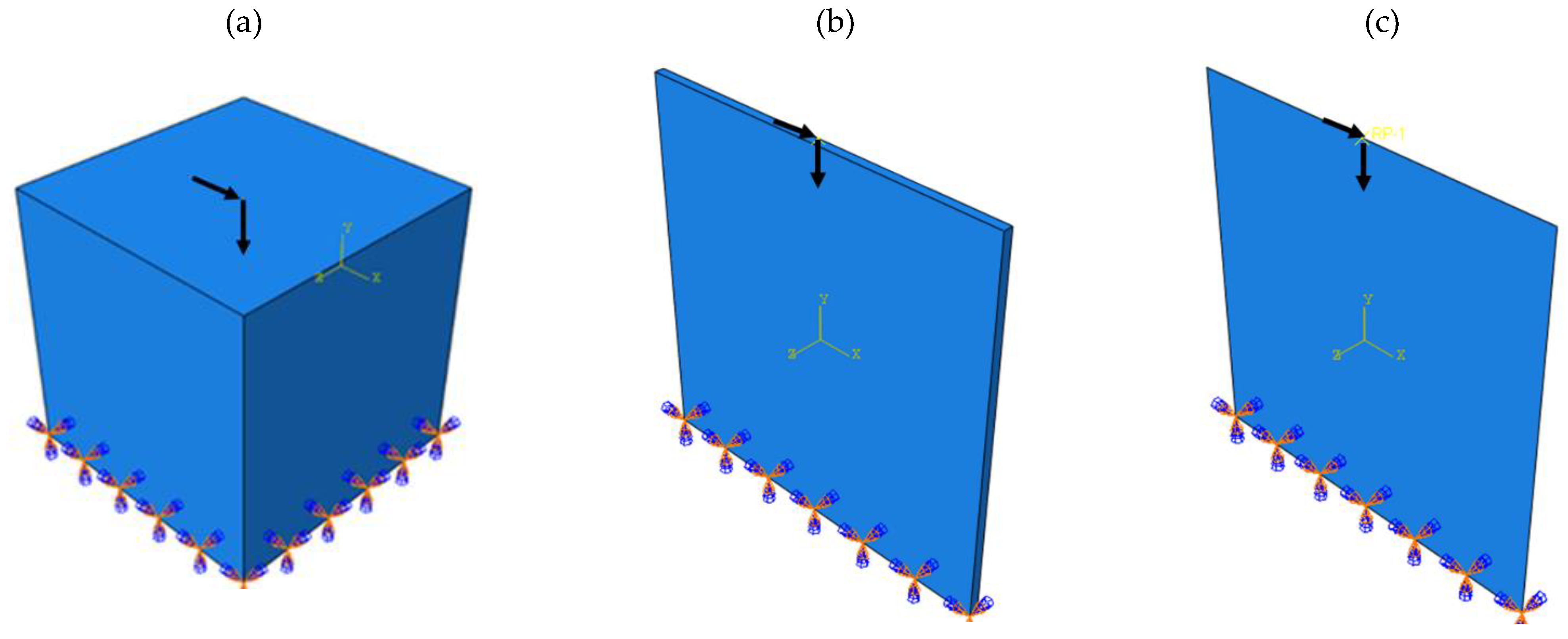
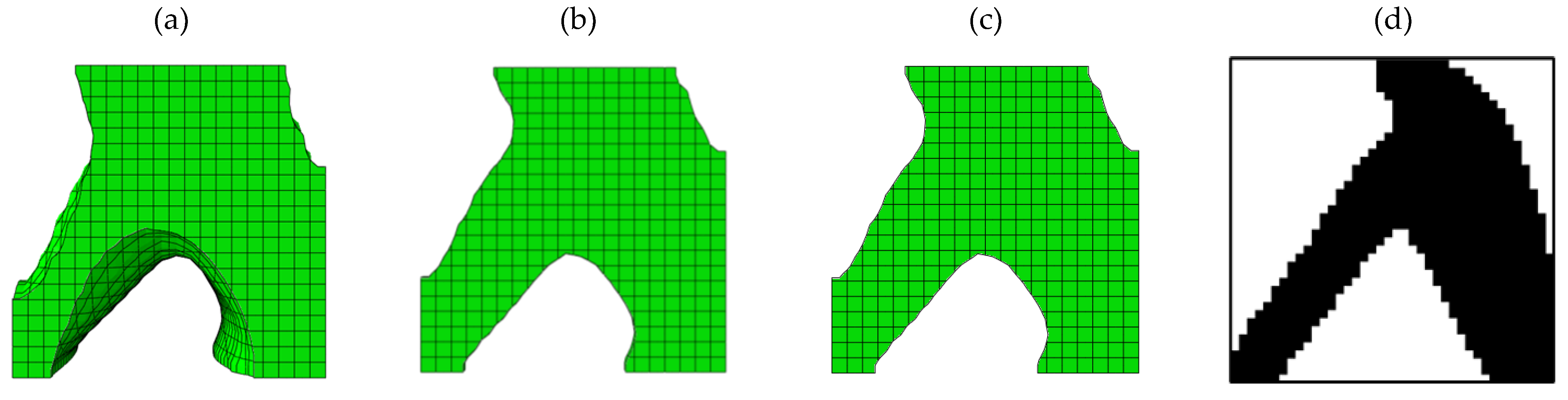
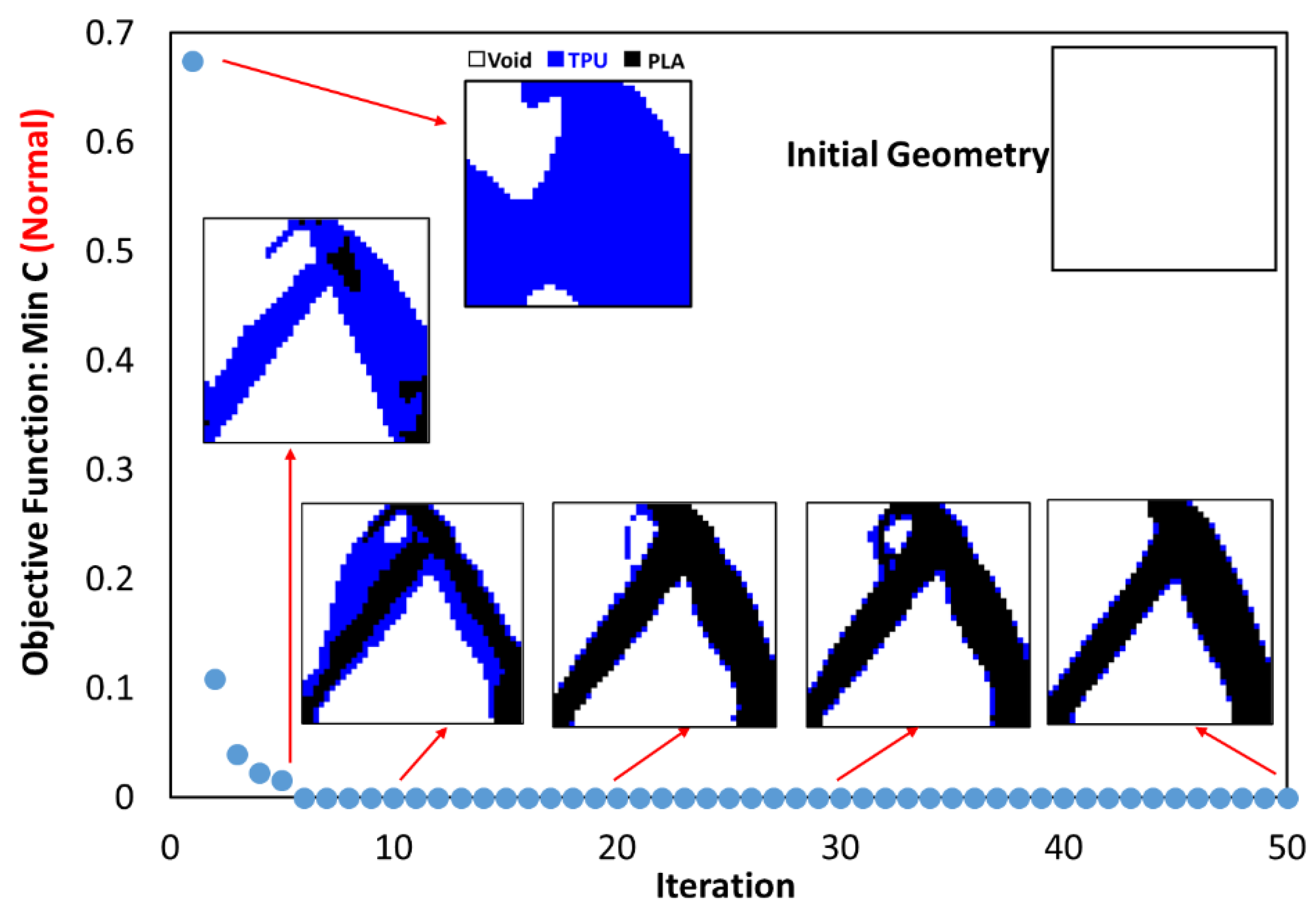
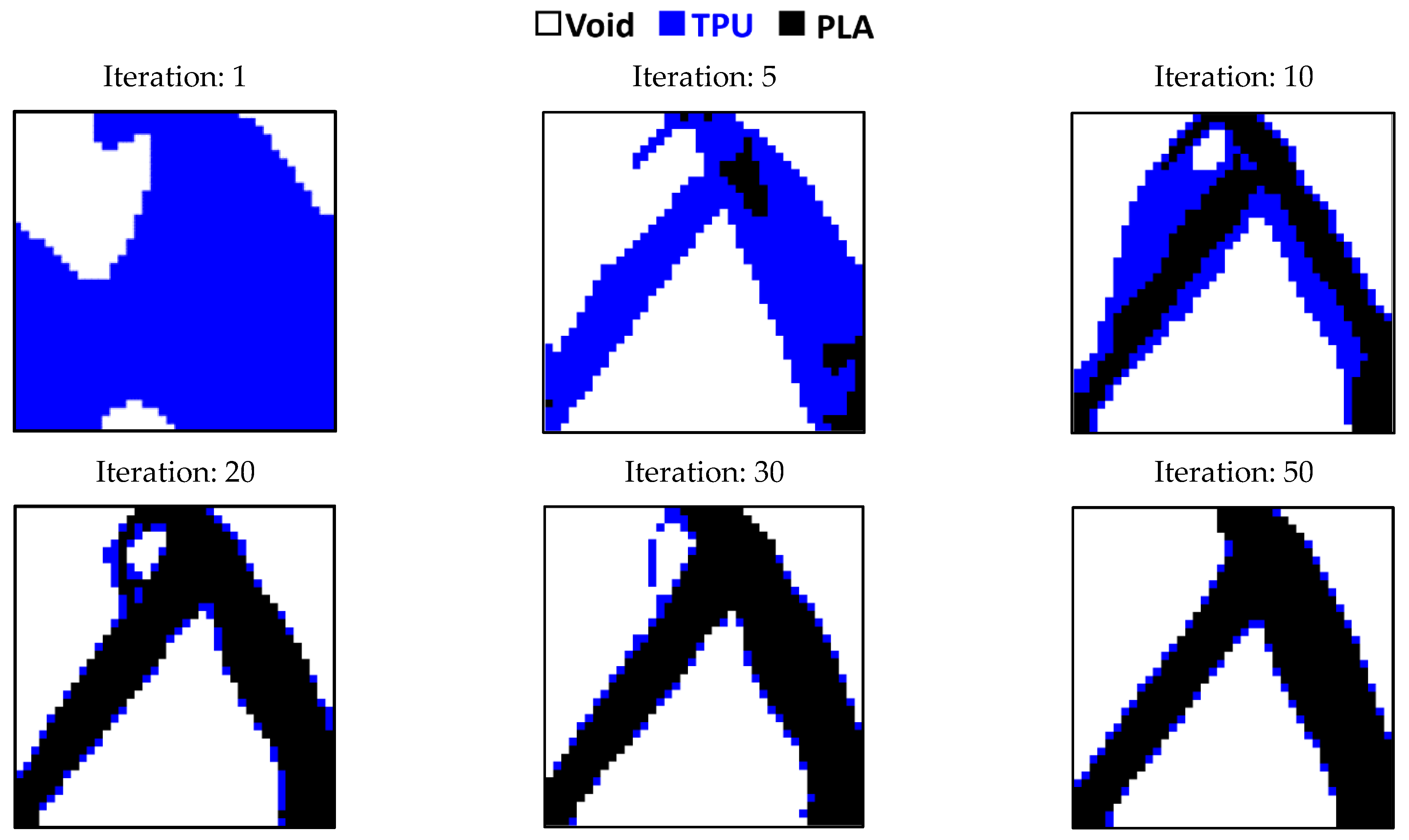
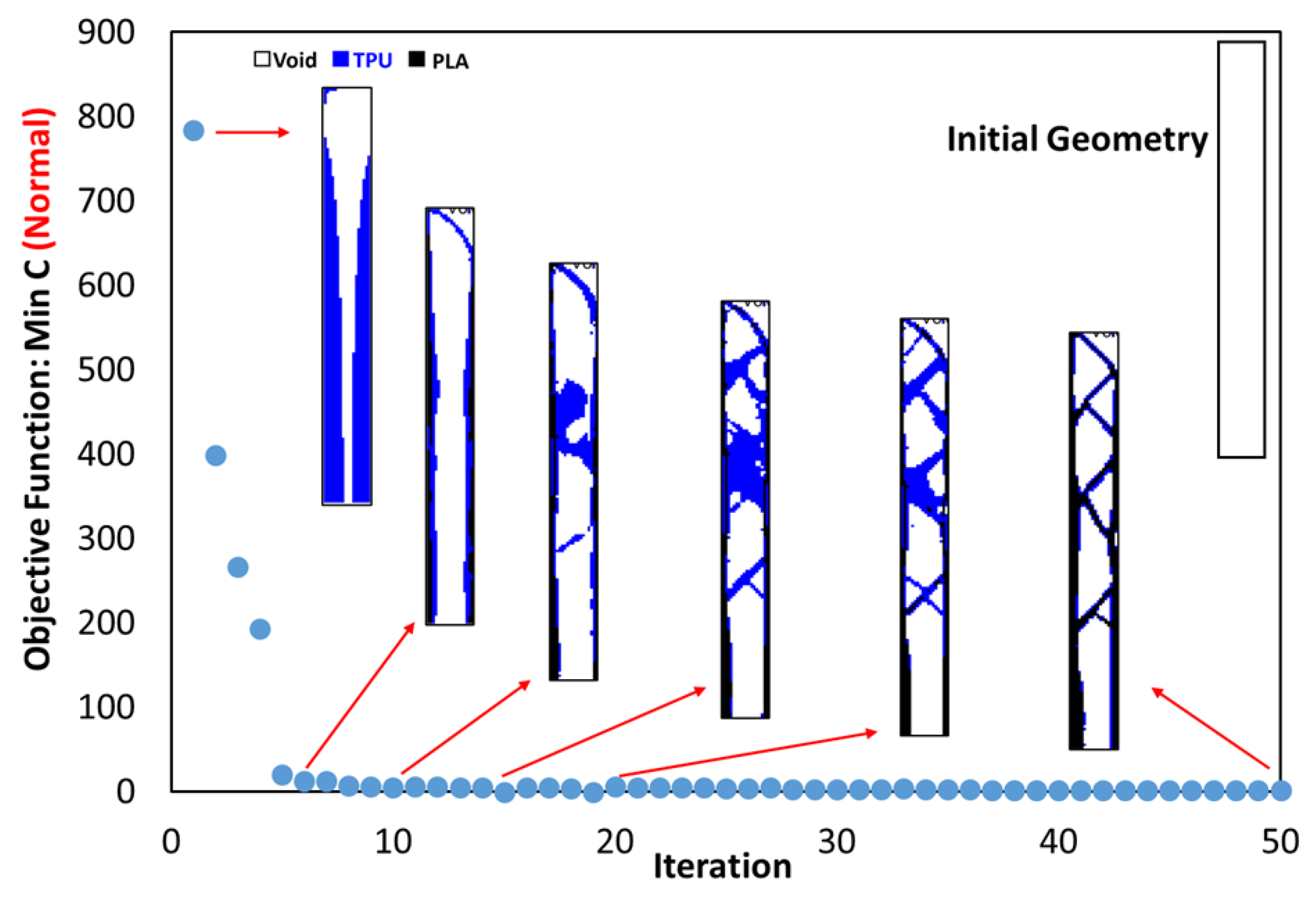
3.1. Outputs for Square Plane

A square plane with dimensions of 1x1 m with an element length of 25 mm, which is equivalent to the number of 40 elements in each direction, has been used for optimization with different volumes. Figure 5 illustrates the optimization results for various weight constraints. According to this figure, the sample with less remaining weight equal to 20% and 60% has discontinuity. This discontinuity requires support according to the selective manufacturing method (FDM), which in metamaterials is very difficult, if not impossible to separate these types of supports from the main part due to the repetition of the cell and the complexity of the part. Therefore, the sample with a remaining weight of less than 40% has been selected as the optimal sample.
This problem has been implemented in a completely similar way in ABAQUS software for both 2D and 3D modes. The problem defined in ABAQUS software is shown in Figure 6.
The answer obtained by MATLAB code compared to the optimized cell with ABAQUS software is shown in Figure 7. According to this figure, considering that the quality of the optimization results is compared with each other, the results are similar to each other to an acceptable extent. Therefore, the MATLAB code has been used in 2D mode to optimize PLA and TPU materials along with voids in the target plane. Since the sample with 40% of the original weight was selected as the optimal sample in the optimization of the square plane, the same constraint was used in this step as well.
The convergence diagram of the objective function is shown in Figure 8 and the obtained result is also shown in Figure 9. According to the results, the answer obtained can only be implemented with the help of 3D printers with two nozzles.
The answer for the optimization of a square plate consisting of PLA and TPU materials was fabricated in two scales, by the FDM 3D printer. The print parameters were considered according to Table 1. These cells are shown in Figure 10.

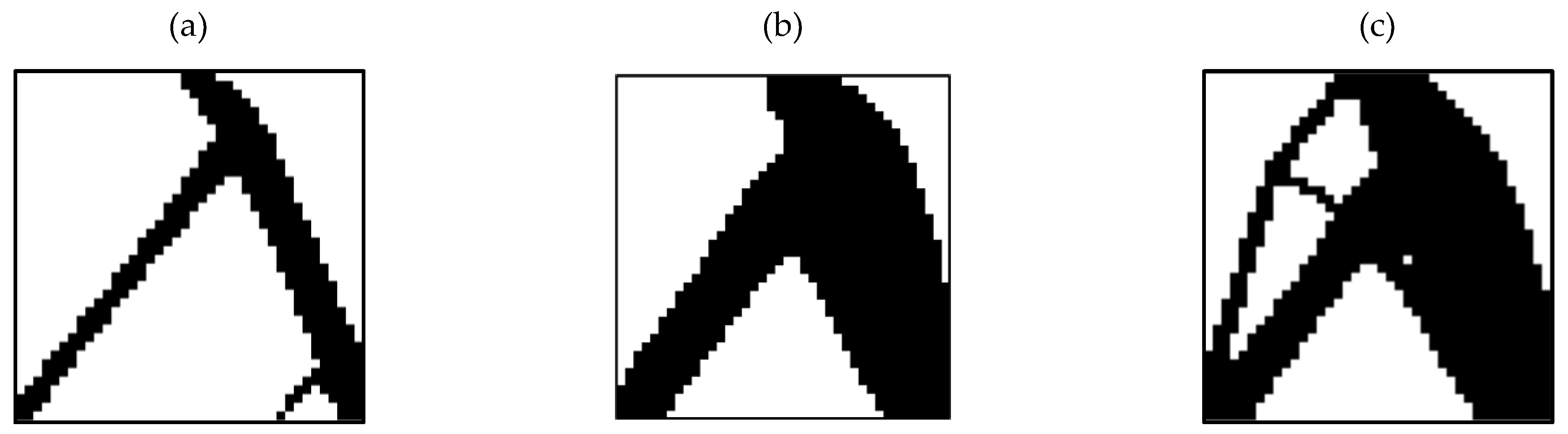
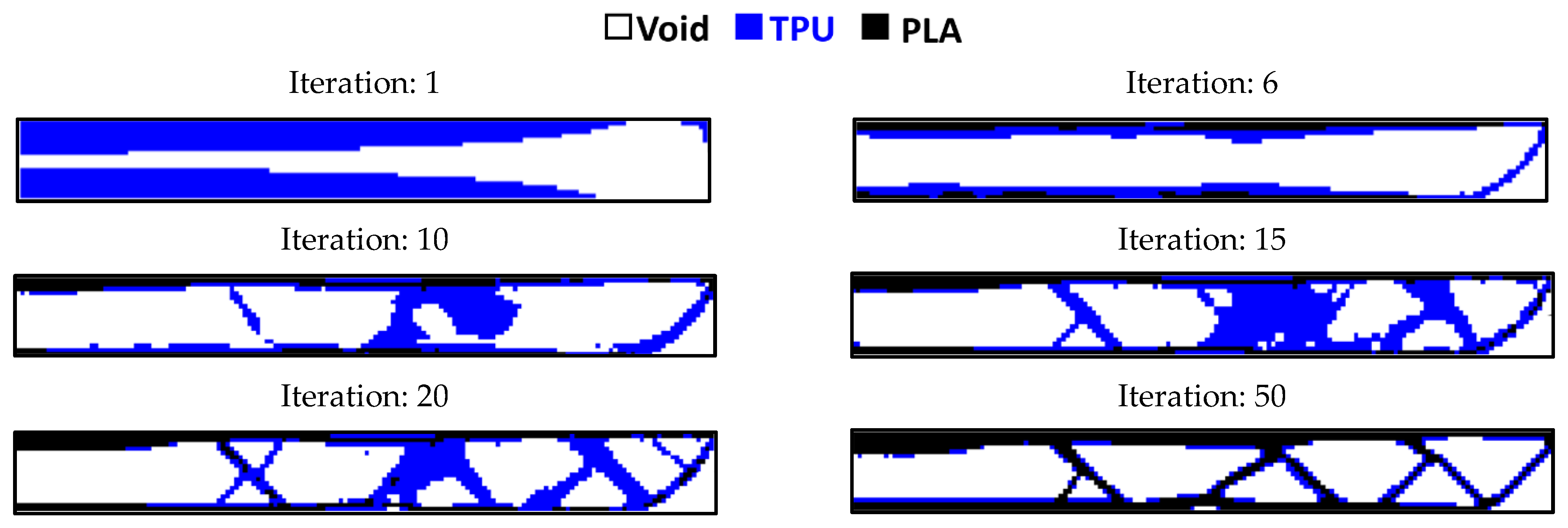
3.2. Outputs for Rectangular Plane

In optimization with MATLAB code, a rectangular plane with dimensions of 4.5x60 mm is selected. From the rotation of the optimized response, the cylindrical cell is calculated based on the axisymmetric condition. This cell is radially replaced in the tire. The friction force between the tire and the road leads to bending in this cell. These cells act like a cantilever beam. Therefore, during the movement and rotation of the tire, bending fatigue loading occurs in these cells. Therefore, this cell can be directly tested for fatigue testing. In the fatigue test, the sample is connected to the device with a screw at a distance of 1 cm from the beginning and the end. Therefore, this distance from the sample is assumed to be fixed (frozen area).
Because the length of the element is 25 mm, the dimensions of the plane in question have been analyzed in a scaled manner. 160 elements along the longitudinal axis and 18 elements along the transverse axis have been selected (scale 100 times). Figure 11 shows the results of optimization in different constraints for this plane.
According to this figure, the sample with a residual weight limit of less than 20% has a discontinuity. The sample with a remaining weight of less than 40% cannot be manufactured with the FDM 3D printer due to the creation of very thin struts. Therefore, the sample with a 60% restriction is selected as the optimal sample.
The comparison of the results of ABAQUS software and MATLAB code with the condition of remaining weight less than 60% is shown in Figure 12. This geometry is also optimized with multiple materials using the MATLAB code and, the convergence results of its objective function are shown in Figure 13 and the response in a different step of the solution is shown in Figure 14.

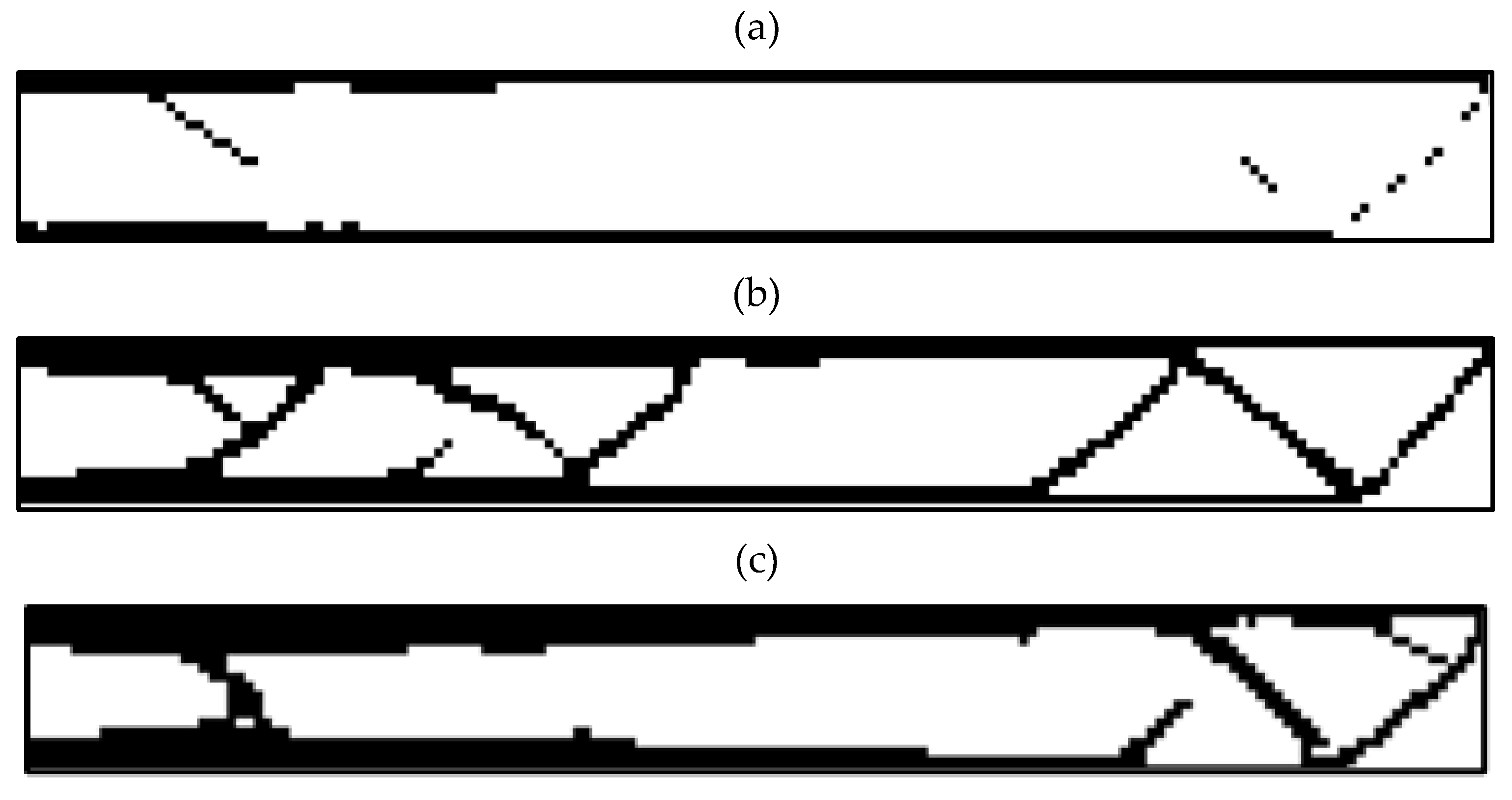
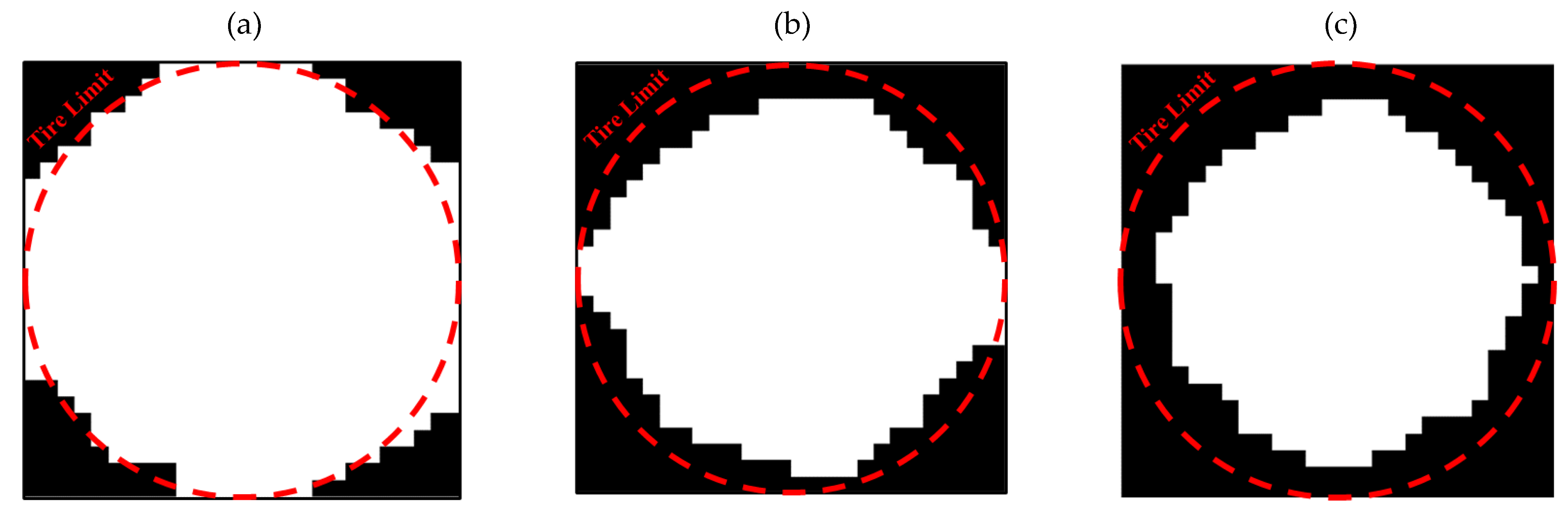
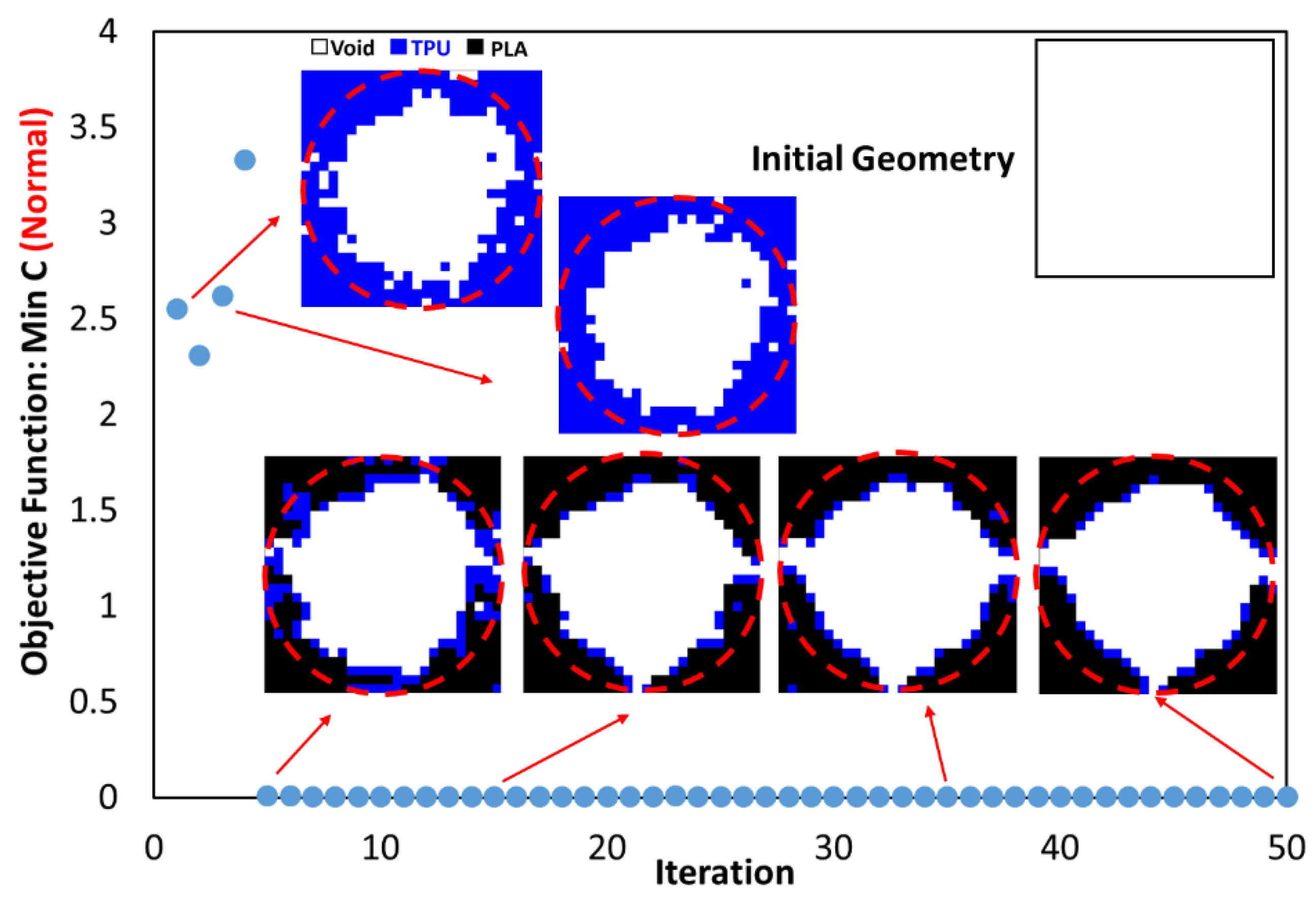
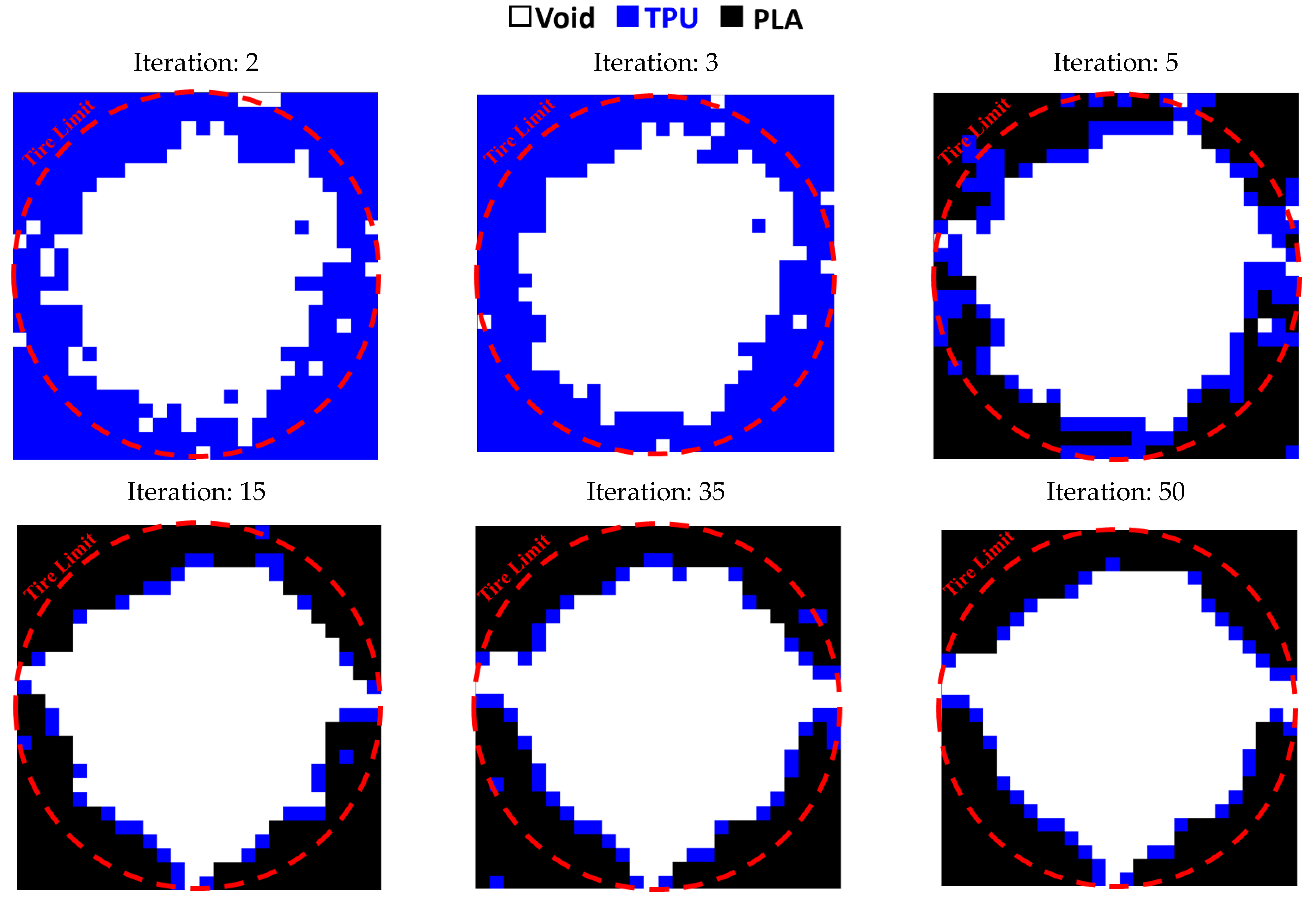
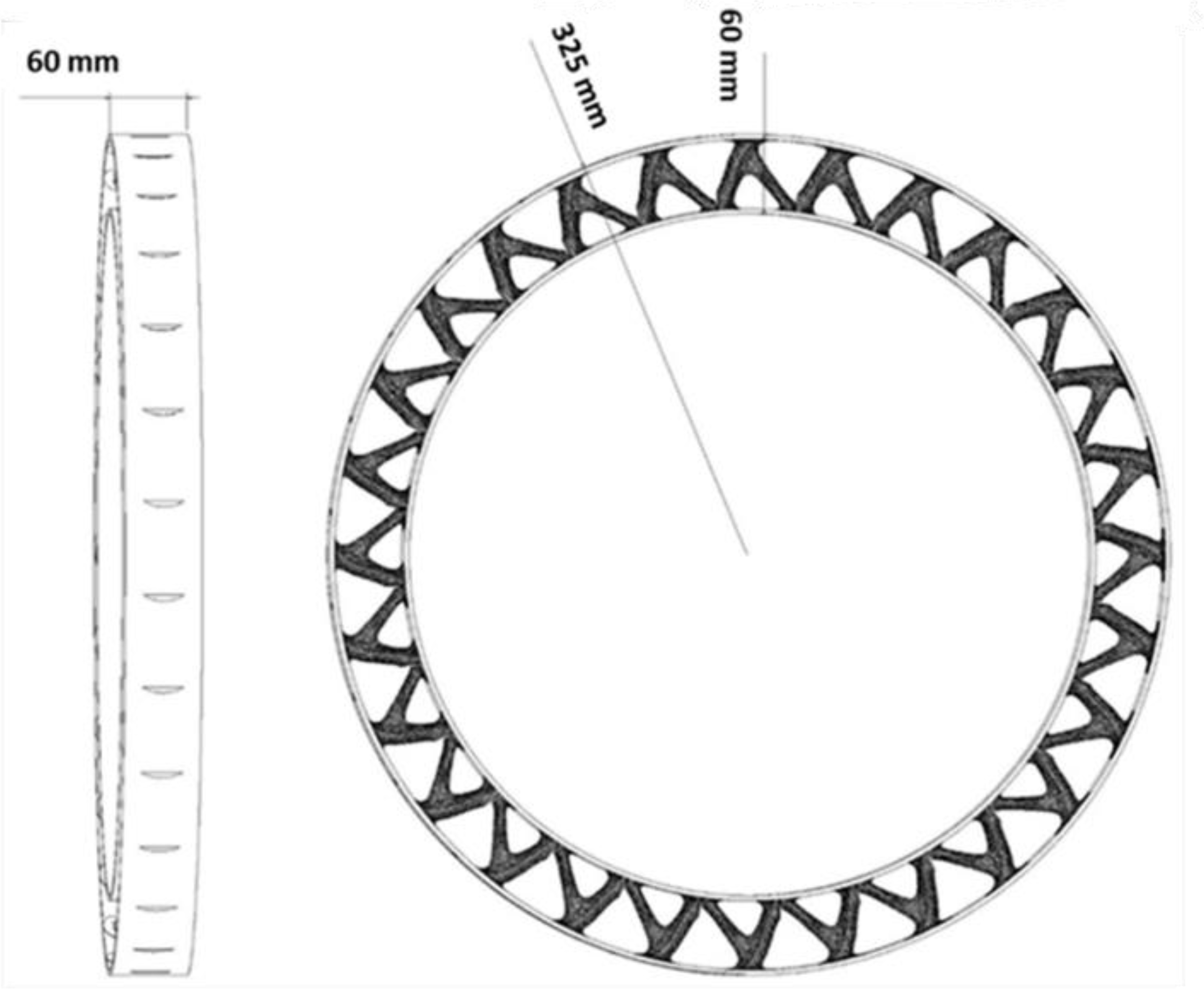
3.3. Entire Circumference of Tire

This code is also used to optimize the entire circumference of tire. For this purpose, a square plane with dimensions of 650x650 mm is subjected to compressive and bending forces of 5 kN, similar to a real tire. According to the element size, 26 elements have been selected in two directions. Figure 15 is shown the results of tire optimization with one type of material.
Due to this shape, the tire does not have continuity when weight limit of 20% and 40% are used for optimization process. Therefore, taking into account the lowest weight, the tire with 60% is selected as the optimal tire. Therefore, the same objective function and constraint have been used for the optimal distribution of PLA and TPU materials in the tire. The objective function convergence for the tire is shown in Figure 16 and the results are shown in Figure 17.
Jang et al. [67] have also performed topology optimization for tires with the objective function of compliance in terms of weight and volume constraints under pressure and tension separately. The defined supports and tire dimensions are the same for both studies. However, because the optimization of material distribution was not considered in this research, the middle part of the tire, which includes the tire core, was not considered. In other words, a hole has been included in the tire (tire inner rim) from the very beginning. In this research, three types of cells have been optimized. The value of the objective function in these cells is between 15 and 20 mm/N and the final answer is converged in the number of repetitions between 15 and 30. In the current research, the value of the target function is 12 mm/N and the final response is calculated in the number of repetitions of 5.
This code was used to optimize a rectangular plane too [66]. After optimization, this plane has become a semicircle. In addition to optimizing the distribution of two materials, they have also implemented the optimization of the distribution of three materials with voids. In the optimization of two materials along with the void, the response has converged in the number of repetitions of 20. The reason for this can be the size of the element used. In this research, the element size is 8 mm. However, in the current research, the size of the element is 25 mm. This smaller element has reduced the speed of convergence. In the code, a kind of price adverb is also included, but the effect of this adverb is not considered in the present study. In addition, 2D and 3D optimizations of a rectangular plane with 1 to 10 materials have been implemented [68]. The objective function in these optimizations is the minimum compliance and volume constraint. This plane is subjected to various forces, including tensile and bending, in a 2D state.
In the 2D plane under bending load and two materials, the objective function has converged in the number of repetitions of 10. This behavior is similar to the present work. Curved surfaces are also observed in the final response. The percentage of the final volume fraction is 35% to 60%, which is the same as the range of optimized percentages in the current research.

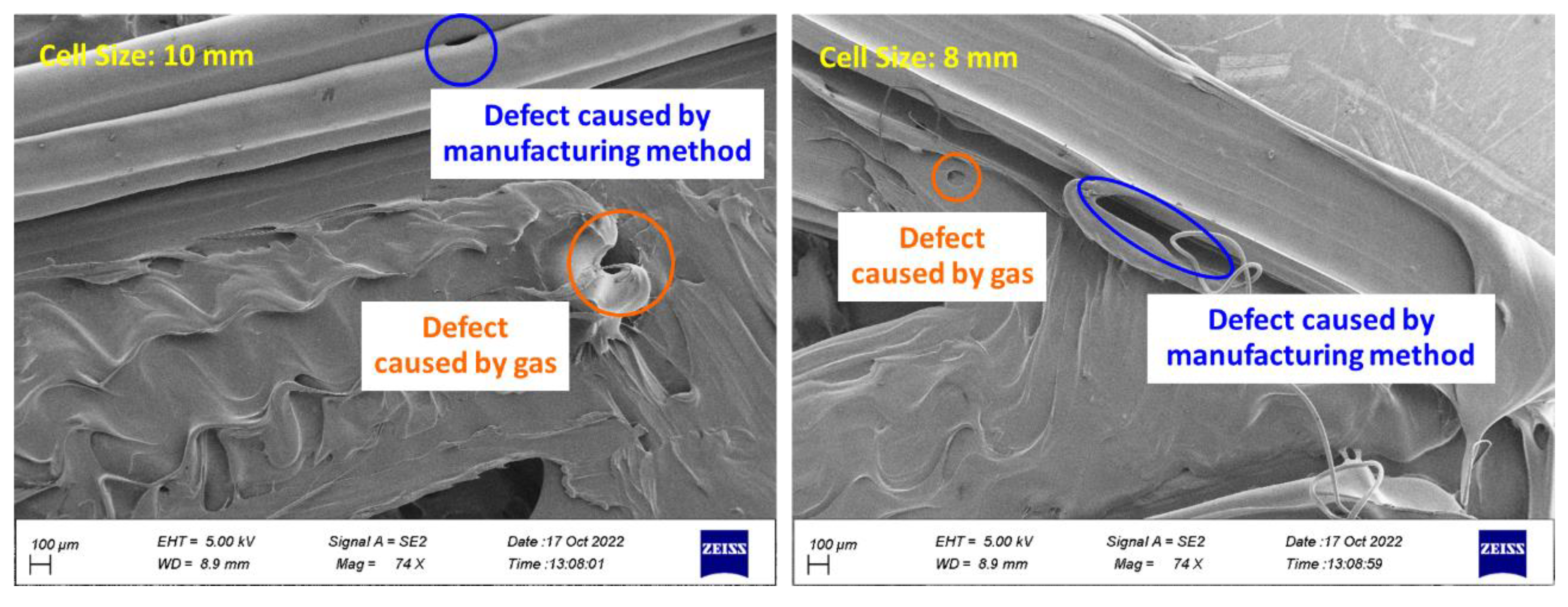
3.5. Outputs for The Quality of 3D Printing

The optimized cell of the square plane is fabricated in two sizes of 8 and 10 mm with a 3D FDM printer. Figure 18 shows the image obtained from the FE-SEM of the surface of these two cells. According to this figure, the connection between PLA and TPU material is quite clear in both scales.
Holes have been observed on the surface of the cells according to Figure 19. These holes are caused by two factors. The first factor is caused by the high temperature during 3D printing, which causes the filament to evaporate and create bubbles on the surface of the sample. These bubbles cause defect [69]. The second factor is caused by the manufacturing method. In 3D printing, parts are fabricated layer by layer. Improper connection of layers with each other causes holes in the sample. The holes caused by the manufacturing method have been observed in connecting similar layers (TPU-TPU) and connecting different layers (PLA-TPU). In other reference, the weak connection between layers in the FDM method has been observed [69,70,71].
According to Figure 20, the 3D printed cell with a size of 10 mm has better quality. In the 3D printed cell with a size of 8 mm, the PLA layers are not well connected to the TPU layer. Various factors affect the adhesion of layers of different materials. Among others, we can mention print temperature, speed and density [72,73]. However, these parameters are the same in both sizes. Therefore, it can be concluded that cell size is also effective in the adhesion of different materials in 3D printing. In another research, it was shown that the large size of the printed sample had better quality [74].
Figure 21 shows the cell placement in the tire. In the future research, the mechanical properties of this tire will be discussed. When the force is applied to this non-pneumatic tire, the adjacent cell structures will also have a strong effect on each other, which can affect the structural stress change. In the further investigations, the mechanical properties of this tire include compressive and fatigue properties will be discussed. In addition, different arrangements between the unit cell will be also studied.

4. Conclusions

In this research, to design a non-pneumatic tire, optimization has been done for three types of geometry, including a square plane, a rectangular plane, and entire circumference of tire consisting of 3 materials: PLA, TPU, and void. The objective function in this optimization is minimum compliance and weight as a constraint. The results obtained are as follows:
  • In the optimization of the square plane, the sample with the remaining weight constraint equal to 40% is selected as the optimal sample.
  • in the optimization of the rectangular plane, the sample with the remaining weight constraint equal to 60% is selected as the optimal sample.
  • In the optimization of the entire circumference of tire, the sample with a remaining weight of less than 60% has been selected as the optimal sample.
  • The objective function for all three problems in the optimal distribution of materials is convergent and acceptable.
  • PLA and TPU materials are completely connected based on FE-SEM images.

Author Contributions

Conceptualization, Mohammad Azadi; methodology, Mohammad Azadi; software, Shokouh Dezianian; validation, Mohammad Azadi; formal analysis, Shokouh Dezianian; investigation, Shokouh Dezianian and Mohammad Azadi; resources, Shokouh Dezianian and Mohammad Azadi; data curation, Shokouh Dezianian; writing—original draft preparation, Shokouh Dezianian; writing—review and editing, Mohammad Azadi; visualization, Mohammad Azadi; supervision, Mohammad Azadi; project administration, Mohammad Azadi; funding acquisition, Mohammad Azadi. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Iran National Science Foundation (INSF), grant number 4002601

Institutional Review Board Statement

Not applicable for studies not involving humans or animals.

Data Availability Statement

The data that support the findings of this study are available based on the request from the corresponding author. The experimental data are not publicly available due to restrictions and the privacy of research participants.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

Topology optimization is defined as making macroscopic changes between one or more materials. One of the materials can be considered void. In other words, in topology optimization, by defining the appropriate objective function and constraints, the material distribution in the specimen is optimized. In this method, the specimen is divided into elements and the density of the material is defined as a design variable. Then the properties of the elements are calculated. Some elements are removed and some take the properties of the material.
Figure A1 (a) shows a schematic of the solution to the problem in a discrete design. In this design each color corresponds to a material. Design variable in discrete design can be 0 or 1.
Preprints 70083 g0a1
Figure A1. The topology optimization including (a) discrete design and (b) continuous design (Note: White color is Material 1 and the black one is Material 2.) [59].
Figure A1. The topology optimization including (a) discrete design and (b) continuous design (Note: White color is Material 1 and the black one is Material 2.) [59].
Preprints 70083 g0a1
The optimization problem in the discrete design is defined according to Equation A1, as follows [59],
M i n : Ф   ( C   ( ρ ) )     s . t . :   ∑ e = 1 N v e ρ e v 0 ≤ f   : g i C   ρ < g i *     ,   i = 1 ,   … ,   M   : ρ e = 0   m a t e r i a l   1 1   m a t e r i a l   2   ,   e = 1 ,   … ,   N   : K ( ρ ) U i = F i   ,   i = 1 ,   … ,   m
In this equation, minimizing Ф is the goal of the problem, which includes C, which is a function of the variable of the problem design and is calculated according to Equation A2. C is an interpolation function that determines the properties of each element. These properties can express different physical values such as material stiffness, cost, etc. v e is volume of the element ( v 0 ) is the unit cell total volume, f is the volume fraction limit, g i C ρ is the problem limit and g i * is the limit. The relationship of K(ρ)Ui = Fi also represents the finite element analysis for loading cases.
C ρ = 1 − ρ e   C 1 + ρ e C 2  
In this equation, C2 and C1 are the material tensors of the two components. If ρ e =0, the element of the properties of the first material, and if ρ e =1, the element of the properties of the second material is taken, and thus a discrete design is obtained. This design, it brings problems such as creating a design and geometric details that are very delicate and unmanufacturable. One of the ways to solve this problem is to use geometric constraints. In addition, the use of continuous variables is also suggested. In this method, design variables include any value between 0 and 1. As a result, the discrete optimization problem becomes a continuous problem according to Figure A1 (b). This method is called the gray scheme [60].
In continuous mode, the optimization problem is defined according to equation A3 [59].
M i n : Ф   ( C   ( ρ ) )     s . t . :   ∑ e = 1 N v e ρ e v 0 ≤ f : g i C   ρ < g i *     ,   i = 1 ,   … ,   M   : 0   ≤ ρ e ≤ 1   ,   e = 1 ,   … ,   N   : K ( ρ ) U i = F i   ,   i = 1 ,   … ,   m
In this method, there is a possibility that the answers will end up in the middle values of the design variables. Therefore, to avoid this problem, different penalty plans are used. For example, it is possible to use the Solid Isotropic Material with a Penalization (SIMP) approach, where the design variable reaches the power of the penalty factor (p>1) and directs the solution toward the discrete values 0 and 1. In fact, despite continuous variables, it performs discrete solutions. In this case, the interpolator function is defined as Equation A4.
C ρ =   1 − ρ e p C 1 + ρ e p C 2
If the optimization of only one material is considered, the above relation can be replaced with Equation A5 [61].
C ( ρ ) = ρ e p C 1  
This relationship is used when one of the two materials in question is void. And if the optimization of two types of materials with the void is considered, equation A6 is used [62].
C ( ρ ) = ρ e p   1 − ρ e p C 1 + ρ e p C 2
Equation A4 can be extended to three materials [63]:
C 1,2 , 3 ρ 1 ,   ρ 2 = 1 − ρ 1 p C 1 + ( ρ 1 ) p C 2 ,   3 = 1 − ρ 1 p C 1 + ( ρ 1 ) p 1 − ρ 2 p C 2 + ρ 2 p C 3 = 1 − ρ 1 p C 1 + ( ρ 1 ) p 1 − ρ 2 p C 2 + ( ρ 1 ρ 2 ) p C 3
In recent years, another interpolator function according to Equation A8 is used, which is called the modified SIMP method. In this method, the elastic modulus of the cavity is not considered zero to avoid the singularity of the stiffness matrix. One of the advantages of this method is that the elastic modulus and the penalty number is not dependent on each other. In this regard, c m i n is the elastic modulus of the cavity [64].
  c ρ = c m i n + ρ p ( c 0 − c m i n )
If the interpolator function C is related to the stiffness of the material, it depends on the young modulus and Poisson ratio of the material. In the case that the Poisson ratio is independent of the material density and this tensor is supposed to correspond to a composite material made of empty space and the given material with real density, the bulk modulus (K) and the shear modulus (μ) of the tensor (C) should cover the Hashin-ShtrikMan range.
For two-phase materials, one phase of which is void. This range is shown in Equation A9 [61].
0   ≤ K   ≤ ρ K 0 μ 0 1 − ρ K 0 + μ 0   0   ≤ μ   ≤ ρ K 0 μ 0 1 − ρ K 0 + 2 μ 0 + K 0  
In this regard, K 0 and μ 0 are the bulk modulus and shear modulus of the material in question. In this case, Equation A10 is calculated for the elastic modulus.
0   ≤ E   ≤ ρ E 0 3 − 2 ρ  
According to Equation A5, it can be written:
0   ≤ ρ P E 0 ≤ ρ E 0 3 − 2 ρ  
Equation A11 is true if and only if p is greater than 3. However, in the SIMP model, the Poisson ratio is assumed to be independent of density. In this case, according to the definitions of young modulus and shear modulus shown in Equation A12, the Hashin-Shtrikman range is rewritten as Equation A13:
K = E 2 1 − ν   μ = E 2 1 + ν  
0   ≤ ρ P E 0 2 1 − ν     ≤ ρ E 0 4 − 2 1 + ν ρ     0   ≤ ρ P E 0 2 1 + ν     ≤ ρ E 0 2 1 − ρ 3 − ν ) + 2 ( 1 + ν )  
From the above relationship, a condition for calculating the value of p according to Equation A14 is obtained.
p   ≥ m a x ⁡ (   2 1 − ν ,   4 1 + ν )
For example, the p factor for materials with different Poisson ratios is shown in Equation A15.
i f   ν = 1 3   ,     p = 3 i f   ν = 1 2   ,     p = 4
In the 3D case, the Hashin-Shtrikman range leads to Equation A16:
p ≥ m a x ⁡ ( 15 1 − ν 7 − 5 ν     , 3 2   1 − ν 1 − 2 ν )
In this case, for example, the number p is calculated as follows:
i f   ν = 1 3   ,     p ≥ 3 i f   ν = 1 5   ,     p ≥ 2
In general, the larger the p number, the better it is to remove average densities. But the solution time increases [65]. Considering that the Poisson’s ratio for the materials used in this research is 1/3, therefore, the penalty number of 3 is also considered in the analyses carried out in this research.
In the optimization process, the impact of each design variable on the final response is important. For this reason, sensitivity analysis is performed to find out which variable has the greatest effect on the response. In sensitivity analysis, the effect of that parameter is calculated with the derivative of the desired parameter with respect to the design variable. The high importance of a parameter causes the solution to have more changes depending on the input variables.

References

  1. Li, T.; Hu, X.; Chen, Y.; Wang, L. Harnessing out-of-plane deformation to design 3D architected lattice metamaterials with tunable Poisson’s ratio. Scientific Reports 2017, 7, 1–10. [Google Scholar] [CrossRef]
  2. Askari, M.; Hutchins, D.A.; Thomas, P.J.; Astolfi, L.; Watson, R.L.; Abdi, M.; Ricci, M.; Laureti, S.; Nie, L.; Freear, S.; Wildman, R.; Tuck, C.; Clarke, M.; Woods, E.; Clare, A.T. Additive manufacturing of metamaterials: A review. Additive Manufacturing 2020, 101562. [Google Scholar] [CrossRef]
  3. Refai, K.; Brugger, C.; Montemurro, M.; Saintier, N. An experimental and numerical study of the high cycle multiaxial fatigue strength of titanium lattice structures produced by Selective Laser Melting. International Journal of Fatigue 2020, 138, 105623. [Google Scholar] [CrossRef]
  4. Benedetti, M.; du Plessis, A.; Ritchie, R.O.; Dallago, M.; Razavi, S.M.J.; Berto, F. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Materials Science and Engineering R: Reports, 1006. [Google Scholar]
  5. Jia, Z.; Liu, F.; Jiang, X.; Wang, L. Engineering lattice metamaterials for extreme property, programmability, and multifunctionality. Journal of Applied Physics 2020, 127, 150901. [Google Scholar] [CrossRef]
  6. Deptuła, A.; Osiński, P. The Optimization of Three-Involute Tooth Outline with Taking into Consideration Multi-valued Logic Trees. Proceedings of the 13th International Scientific Conference, 2017. [Google Scholar]
  7. Jafferson, J.M.; Sharma, H. Design of 3D printable airless tyres using NTopology. Materials Today: Proceedings, 1147. [Google Scholar]
  8. Sandberg, U. The Airless Tire: Will this Revolutionary Concept be the Tire of the Future? Modern Concepts in Material Science 2020, 3. [Google Scholar] [CrossRef]
  9. Jin, X.; Hou, C.; Fan, X.; Sun, Y.; Lv, J.; Lu, C. Investigation on the static and dynamic behaviors of non-pneumatic tires with honeycomb spokes. Composite Structures 2018, 187, 27–35. [Google Scholar] [CrossRef]
  10. Mazur, V.V. Experiments to Find the Rolling Resistance of Non-pneumatic Tires Car Wheels. Proceedings of the 5th International Conference on Industrial Engineering 2020, 641–648. [Google Scholar]
  11. Deziania, S.; Azadi, M. A review on metamaterial types, additive manufacturing technique and its application in automotive industry. Scientific journal of the Iranian Society of Mechanical Engineers 2021, 4, 70–80. [Google Scholar]
  12. Suvanjumrat, C.; Rugsaj, R. Study of 3D printing for forming spoke of non-pneumatic tire using finite element method. IOP Conference Series: Materials Science and Engineering, 2021; 1137, 012020. [Google Scholar]
  13. Rugsaj, R.; Suvanjumrat, C. Dynamic Finite Element Analysis of Rolling Non-Pneumatic Tire. International Journal of Automotive Technology 2021, 22, 1022. [Google Scholar] [CrossRef]
  14. Rugsaj, R.; Suvanjumrat, C. Determination of material property for non-pneumatic tire spokes by inverse method. Key Engineering Materials 2018, 777, 411–415. [Google Scholar] [CrossRef]
  15. Rugsaj, R.; Suvanjumrat, C. Proper Radial Spokes of Non-Pneumatic Tire for Vertical Load Supporting by Finite Element Analysis. International Journal of Automotive Technology 2019, 20, 801–812. [Google Scholar] [CrossRef]
  16. Ramachandran, M.; Nonlinear Finite Element Analysis of Tweel Geometric Parameter Modifications on Spoke Dynamics During High-Speed Rolling. Master of Science, Clemson University, USA, 2008.
  17. Manibaalan, C.; Keshore, B.S.; Haran, J.C. Static Analysis of Airless Tyres. International Journal of Scientific and Research Publications 2013, 3, 1–4. [Google Scholar]
  18. Zmuda, M.; Jackowski, J.; Hryciów, Z. Numerical research of selected features of the non-pneumatic tire. AIP Conference Proceedings 2019, 2078. [Google Scholar]
  19. Ma, J.; Summers, J.; Joseph, P. Dynamic impact simulation of interaction between non-pneumatic tire and sand with obstacle. SAE 2011 World Congress and Exhibition 2011, 12. [Google Scholar]
  20. Ma, J.; Summers, J.D.; Joseph, P.F. Numerical simulation of tread effects on the interaction between cellular shear band based non-pneumatic tire and sand. Proceedings of the ASME Design Engineering Technical Conference 2011, 8, 769–779. [Google Scholar]
  21. Shankar, P.; Fazelpour, M.; Summers, J.D. An energy-based design approach for a meso-structure with high shear flexure. Proceedings of the ASME Design Engineering Technical Conference 2013, 3. [Google Scholar]
  22. Ma, J.; Louis, S.; Summers, J.D.; Joseph, P.F. Numerical Investigation of Effect of Membrane on Thickness on the Performance of Cellular Shear Band Based non- pneumatic Tire. Engineering Conference, 2011; 1–11. [Google Scholar]
  23. Tavakoli, R. Multimaterial topology optimization by volume constrained Allen–Cahn system and regularized projected steepest descent method. Computer Methods in Applied Mechanics and Engineering 2014, 276, 534–565. [Google Scholar] [CrossRef]
  24. Han, Z.; Gu, Z.; Ma, X.; Chen, W. Multi material layout optimization of truss structures via an improved particle swarm optimization algorithm. Computers and Structures 2019, 222, 10–24. [Google Scholar]
  25. Chen, Y.; Ye, L.; Xu, C.; Zhang, Y.X. Multi-material topology optimization of micro-composites with reduced stress concentration for optimal functional performance. Materials & Design, 2021; 210, 110098. [Google Scholar]
  26. Chung, H.; Du, Z. Optimized Design of Multi- Material Cellular Structures by a Level-Set Method with Guyan Reduction. Journal of Mechanical Design 2021, 143, 101702. [Google Scholar] [CrossRef]
  27. Mansouri, M.R.; Montazerian, H.; Schmauder, S. 3D-printed multimaterial composites tailored for compliancy and strain recovery., Composite Structures 2018. 184, 11–17.
  28. Gao, X.; Caivano, R.; Tridello, A.; Chiandussi, G.; Ma, H.; Paolino, D.; Berto, F. Innovative formulation for topological fatigue optimisation based on material defects distribution and TopFat algorithm. International Journal of Fatigue 2021, 17, 106176. [Google Scholar] [CrossRef]
  29. Gao, J.; Wang, L.; Xiao, M.; Gao, L.; Li, P. An iso geometric approach to topological optimization design of auxetic composites with tri-material micro-architectures. Composite Structures 2021, 271, 114163. [Google Scholar] [CrossRef]
  30. Huang, X.; Li, W. A new multi-material topology optimization algorithm and selection of candidate materials. Computer Methods in Applied Mechanics and Engineering 2021, 386, 114114. [Google Scholar] [CrossRef]
  31. Li,H., Luo, Z., Gao, L., Walker, P., Topology optimization for functionally graded cellular composites with metamaterials by level sets. Computer Methods in Applied Mechanics and Engineering 2018, 328, 340–364. [CrossRef]
  32. Nguyen, C. , Zhuang, X., Chamoin, L., Zhao, X., Nguyen-Xuan, H., Rabczuk, T., Three-dimensional topology optimization of auxetic metamaterial using isogeometric analysis and model order reduction. Computer Methods in Applied Mechanics and Engineering 2020, 371, 113306. [Google Scholar] [CrossRef]
  33. Vogiatzis, P.; Chen, S.; Wang, X.; Li, T.; Wang, L. Topology Optimization of Multi-Material Negative Poisson’s Ratio Metamaterials Using a Reconciled Level Set Method. Computer-Aided Design, 2017; 83, 15–32. [Google Scholar]
  34. Huikai, Z.; Yangjun, L.; Kang, Z. Bi-material microstructural design of chiral auxetic metamaterials using topology optimization. Composite Structures 2018, 195, 232–248. [Google Scholar]
  35. Zheng, Y.; Wang, Y.; Lu, X.; Zheng, J.; Qu, J. Topology optimization for isotropic mechanical metamaterials considering material uncertainties. Mechanics of Materials 2021, 155, 103742. [Google Scholar] [CrossRef]
  36. Wei, W.; Kai, Z.; Shaoyi, B.; Lanchun, Z.; Yongzhi, W. Vibration performance analysis of vehicle with the non-pneumatic new mechanical elastic wheel in the impulse input experiment. Journal of Vibroengineering 2016, 18, 3970–3980. [Google Scholar] [CrossRef]
  37. Zhao, Y.; Du, X.; Lin, F.; Wang, Q.; Fu, H. Static stiffness characteristics of a new non-pneumatic tire with different hinge structure and distribution. Journal of Mechanical Science and Technology 2018, 32, 3057–3064. [Google Scholar] [CrossRef]
  38. Zhao, Y.Q.; Deng, Y.J.; Lin, F.; Zhu, M.M.; Xiao, Z. Transient Dynamic Characteristics of a Non-Pneumatic Mechanical Elastic Wheel Rolling Over a Ditch. International Journal of Automotive Technology 2018, 19, 499–508. [Google Scholar] [CrossRef]
  39. Deng, Y.; Zhao, Y.; Lin, F.; Xiao, Z.; Zhu, M.; Li, H. , Simulation of steady-state rolling non-pneumatic mechanical elastic wheel using finite element method. Simulation Modelling Practice and Theory 2018, 85, 60–79. [Google Scholar] [CrossRef]
  40. Du, X.; Zhao, Y.; Wang, Q.; Fu, H.; Lin, F. Grounding characteristics of a non-pneumatic mechanical elastic tire in a rolling state with a camber angle. Strojniski Vestnik/Journal of Mechanical Engineering, 2019; 65, 287–296. [Google Scholar]
  41. Du, X.; Zhao, Y.; Lin, F.; Fu, H.; Wang, Q. , Numerical and experimental investigation on the camber performance of a non-pneumatic mechanical elastic wheel. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2017, 39, 3315–3327. [Google Scholar] [CrossRef]
  42. Xiao, Z.; Zhao, Y.Q.; Lin, F.; Zhu, M.M.; Deng, Y.J. Studying the fatigue life of a non-pneumatic wheel by using finite-life design for life prediction. Journal of Mechanical Engineering 2018, 64, 56–67. [Google Scholar]
  43. Zhao, Y.Q.; Xiao, Z.; Lin, F.; Zhu, M.M.; Deng, Y.J. Influence analysis of machining and installation errors on the radial stiffness of a non-pneumatic mechanical elastic wheel. Chinese Journal of Mechanical Engineering 2018, 31, 1–9. [Google Scholar] [CrossRef]
  44. Mathew, N.J.; Sahoo, D.K.; Chakravarthy, E.M. Design and Static Analysis of Airlesstyre to Reduce Deformation. IOP Conference Series: Materials Science and Engineering, 2017; 197, 012042. [Google Scholar]
  45. Zhang, Z.; Fu, H.; Zhao, Q.; Tan, D.; Yang, K. Pattern design and performance analysis of a flexible spoke bionic non-pneumatic tire. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2021, 43, 1–11. [Google Scholar] [CrossRef]
  46. Zhang, Z.; Fu, H.; Liang, X.; Chen, X.; Tan, D. Comparative Analysis of Static and Dynamic Performance of Nonpneumatic Tire with Flexible Spoke Structure. Strojniski Vestnik/Journal of Mechanical Engineering, 2020; 66, 458–466. [Google Scholar]
  47. Wang, J.; Yang, B.; Lin, X.; Gao, L.; Liu, T.; Lu, Y.; Wang, R. Research of TPU Materials for 3D Printing Aiming at Non-Pneumatic Tires by FDM Method. Polymers 2020, 12, 2492. [Google Scholar] [CrossRef] [PubMed]
  48. Ganniari-Papageorgiou, E.; Chatzistergos, P.; Wang, X. The Influence of the Honeycomb Design Parameters on the Mechanical Behavior of Non-Pneumatic Tires. International Journal of Applied Mechanics 2020, 12, 2050024. [Google Scholar] [CrossRef]
  49. Zheng, Z.; Rakheja, S.; Sedaghati, R. Multi-axis stiffness and road contact characteristics of honeycomb wheels: A parametric analysis using Taguchi method. Composite Structures 2022, 279, 114735. [Google Scholar] [CrossRef]
  50. Fu, H.; Chen, X.; Zhao, Q.; Xiao, Z.; Liang, X. Fatigue life prediction and influencing factors analysis of mesh flexible spoke non-pneumatic tire. Advances in Mechanical Engineering 2021, 13, 1–10. [Google Scholar]
  51. Gasmi, A.; Joseph, P.F.; Rhyne, T.B.; Cron, S.M. Development of a two-dimensional model of a compliant non-pneumatic tire. International Journal of Solids and Structures 2012, 49, 1723–1740. [Google Scholar] [CrossRef]
  52. Ju, J.; Kim, D.M.; Kim, K. Flexible cellular solid spokes of a non-pneumatic tire. Composite Structures 2012, 94, 2285–2295. [Google Scholar] [CrossRef]
  53. Maharaj, Y.; James, K.A. Metamaterial topology optimization of nonpneumatic tires with stress and buckling constraints. International Journal for Numerical Methods in Engineering 2020, 121, 1410–1439. [Google Scholar] [CrossRef]
  54. Petrone, F.; Fichera, G.; Lacagnina, M. A numerical model to analyze the dynamic response of a vehicle to variations in torque transmitted by the drive-line. SAE International Journal of Passenger Cars - Mechanical Systems, 2001; 2, 1–12. [Google Scholar]
  55. Hsiao, T.; Liu, N.; Chen, S. Robust Estimation of the Friction Forces Generated by Each Tire of a Vehicle. 2011 American Control Conference 2011, 5261–5266. [Google Scholar]
  56. Torres, J.; Cotelo, J.; Karl, J.; Gordon, A.P. Mechanical property optimization of FDM PLA in shear with multiple objectives. The Minerals, Metals & Materials Society Mechanical, 2015; 67, 1183–1193. [Google Scholar]
  57. Dezianian, S. Topology optimization of the vehicle non-pneumatic tire from multi-material metamaterial with the objective of compressive strength and bending fatigue lifetime, thesis of Master of Science, Semnan university, Iran, 2022.
  58. Schollenberger, C.S.; Stewart, F.D. Thermoplastic Polyurethane Hydrolysis Stability. Journal of Elastomers and Plastics 2016, 3, 28–56. [Google Scholar]
  59. Ole Sigmund, IUTAMSymposium onModelling Nanomaterials and Nanosystems. roceedings of the IUTAM Symposium held in Aalborg 2008, 13.
  60. Panesar, A.; Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. 2019, 183, 108164.
  61. Bendsùe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Archive of Applied Mechanics 1999, 69, 635–654. [Google Scholar] [CrossRef]
  62. Sigmund, O. Design of Multiphysics actuators using topology optimization ± Part II: Two-material structures. computer method in applied mechanics and engineering 2001, 190, 6605–6627. [Google Scholar] [CrossRef]
  63. Li, D.; Yong, I. Multi-material topology optimization for practical lightweight design. Structural and Multidisciplinary Optimization 2018, 58, 1081–1094. [Google Scholar] [CrossRef]
  64. Liu, K.; Tovar, A. An efficient 3D topology optimization code written inMatlab. computer method in applied mechanics and engineering 2014, 340, 798–823. [Google Scholar]
  65. Grinde, S.; Tech, M. topology optimization for additive manufacturing using SIMP method. bachelor, general engineering, montana technology, 2018.
  66. Zuo, W.; Saitou, K. Multi-material topology optimization using ordered SIMP interpolation. Structural and Multidisciplinary Optimization 2017, 55, 477–491. [Google Scholar] [CrossRef]
  67. Jang, I.G.; Sung, Y.H.; Yoo, E.J.; Kwak, B.M. Pattern design of a non-pneumatic tyre for stiffness using topology optimization. Engineering Optimization 2012, 44, 119–131. [Google Scholar] [CrossRef]
  68. Sanders, E.D.; Aguiló, M.A.; Paulino, G.H. Multi-material continuum topology optimization with arbitrary volume and mass constraints. Computer Methods in Applied Mechanics and Engineering 2018, 340, 798–823. [Google Scholar] [CrossRef]
  69. Azadi, M.; Dadashi, A.; Dezianian, S.; Kianifar, M.; Torkaman, S.; Chiyani, M. High-cycle bending fatigue properties of additive-manufactured ABS and PLA polymers fabricated by fused deposition modeling 3D-printing. Forces in Mechanics 2021, 3, 100016. [Google Scholar] [CrossRef]
  70. Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive manufacturing of carbon fiber reinforced thermoplastic composites using fused deposition modeling. Composites Part B: Engineering, 2015; 80, 369–378. [Google Scholar]
  71. Azadi, M.; Dadashi, A.; Aghareb Parast, M.S.; Dezianian, S. A Comparative Study for High-Cycle Bending Fatigue Lifetime and Fracture Behavior of Extruded and Additive-Manufactured 3D-Printed Acrylonitrile Butadiene Styrene Polymers. Additive-Manufactured Structures, 2022; 1, 1–10. [Google Scholar]
  72. Yadav, D.; Chhabra, D.; Kumar Garg, R.; Ahlawat, A.; Phogat, A. Optimization of FDM 3D printing process parameters for multi-material using artificial neural network. Materials Today: Proceedings, 2020; 21, 1583–1591. [Google Scholar]
  73. Yin, J.; Lu, C.; Fu, J.; Huang, Y.; Zheng, Y. Interfacial bonding during multi-material fused deposition modeling (FDM) process due to inter-molecular diffusion. Materials and Design 2018, 150, 104–112. [Google Scholar] [CrossRef]
  74. Masoumi Ravandi, M.R.; Dezianian, S.; Talati Ahmad, M.; Ghoddosian, A.; Azadi, M. Compressive strength of metamaterial bones fabricated by 3D printing with different porosities in cubic cells. Materials Chemistry and Physics 2023, 299, 127515. [Google Scholar] [CrossRef]
Preprints 70083 g001
Figure 1. The dimensions of the tire plus the solution strategy.
Figure 1. The dimensions of the tire plus the solution strategy.
Preprints 70083 g001
Preprints 70083 g002
Figure 2. Problems defined in the MATLAB code.
Figure 2. Problems defined in the MATLAB code.
Preprints 70083 g002
Preprints 70083 g003
Figure 3. The radius filter to obtain a better objective.
Figure 3. The radius filter to obtain a better objective.
Preprints 70083 g003
Preprints 70083 g004
Figure 4. The effect of element size on the optimization response: (a) 50, (b) 25, and (c) 10 (mm).
Figure 4. The effect of element size on the optimization response: (a) 50, (b) 25, and (c) 10 (mm).
Preprints 70083 g004
Preprints 70083 g005
Figure 5. The response resulting from the optimization for the square plane in terms of (a) 20%, (b) 40%, and (c) 60% for the weight constraint.
Figure 5. The response resulting from the optimization for the square plane in terms of (a) 20%, (b) 40%, and (c) 60% for the weight constraint.
Preprints 70083 g005
Preprints 70083 g006
Figure 6. The problem defined in ABAQUS software: (a) 3D model, (b) 3D model with low thickness, and (c) 2D model.
Figure 6. The problem defined in ABAQUS software: (a) 3D model, (b) 3D model with low thickness, and (c) 2D model.
Preprints 70083 g006
Preprints 70083 g007
Figure 7. The comparison of the results obtained from ABAQUS software: (a) 3D model, (b) 3D model with low thickness, (c) 2D model, and (d) plus results of the MATLAB code.
Figure 7. The comparison of the results obtained from ABAQUS software: (a) 3D model, (b) 3D model with low thickness, (c) 2D model, and (d) plus results of the MATLAB code.
Preprints 70083 g007
Preprints 70083 g008
Figure 8. The convergence diagram of the objective function for optimal material distribution.
Figure 8. The convergence diagram of the objective function for optimal material distribution.
Preprints 70083 g008
Preprints 70083 g009
Figure 9. The Optimization of a square plane with multiple materials.
Figure 9. The Optimization of a square plane with multiple materials.
Preprints 70083 g009
Preprints 70083 g010
Figure 10. The bi-material metamaterial cells made by FDM 3D printer.
Figure 10. The bi-material metamaterial cells made by FDM 3D printer.
Preprints 70083 g010
Preprints 70083 g011
Figure 11. The results for the optimization of the rectangular plane in terms of (a) 20%, (b) 40%, and (c) 60% for the weight constraint.
Figure 11. The results for the optimization of the rectangular plane in terms of (a) 20%, (b) 40%, and (c) 60% for the weight constraint.
Preprints 70083 g011
Preprints 70083 g012
Figure 12. The comparison of the results obtained from ABAQUS software and MATLAB code for the rectangular plane.
Figure 12. The comparison of the results obtained from ABAQUS software and MATLAB code for the rectangular plane.
Preprints 70083 g012
Preprints 70083 g013
Figure 13. The convergence diagram of objective function for rectangular plane.
Figure 13. The convergence diagram of objective function for rectangular plane.
Preprints 70083 g013
Preprints 70083 g014
Figure 14. Optimizing the rectangular plane with multiple materials.
Figure 14. Optimizing the rectangular plane with multiple materials.
Preprints 70083 g014
Preprints 70083 g015
Figure 15. The optimized tire with one type of material: (a) 20%, (b) 40%, and (c) 60% of the weight constraint.
Figure 15. The optimized tire with one type of material: (a) 20%, (b) 40%, and (c) 60% of the weight constraint.
Preprints 70083 g015
Preprints 70083 g016
Figure 16. The convergence diagram of the objective function in tire optimization.
Figure 16. The convergence diagram of the objective function in tire optimization.
Preprints 70083 g016
Preprints 70083 g017
Figure 17. The results of the optimal distribution of materials in the tire.
Figure 17. The results of the optimal distribution of materials in the tire.
Preprints 70083 g017
Preprints 70083 g018
Figure 18. The FE-SEM image for connecting PLA/TPU materials.
Figure 18. The FE-SEM image for connecting PLA/TPU materials.
Preprints 70083 g018
Preprints 70083 g019
Figure 19. The defect fabricated on the surface of the sample during 3D printing.
Figure 19. The defect fabricated on the surface of the sample during 3D printing.
Preprints 70083 g019
Preprints 70083 g020
Figure 20. The effect of the cell size on the adhesion of two PLA/TPU layers.
Figure 20. The effect of the cell size on the adhesion of two PLA/TPU layers.
Preprints 70083 g020
Preprints 70083 g021
Figure 21. Arrangements of cells in the non-pneumatic tire.
Figure 21. Arrangements of cells in the non-pneumatic tire.
Preprints 70083 g021
Table 1. Parameters for 3D printing of PLA/TPU polymers.
Table 1. Parameters for 3D printing of PLA/TPU polymers.
Material Speed (mm/s) Nozzle temperature (°C) Infill (%) Layer height (mm) Nozzle diameter (mm) Bed temperature (°C)
PLA 20 180 100 0.2 0.2 25
TPU 20 220 100 0.2 0.2 25
Table 2. Mechanical properties of the studied materials.
Table 2. Mechanical properties of the studied materials.
Material Yield stress (MPa) Young modulus (MPa)
PLA 2.5±56.0 100.7±3089.3
TPU 1.6±4.1 0.6±12.0
Table 3. Optimization parameters.
Table 3. Optimization parameters.
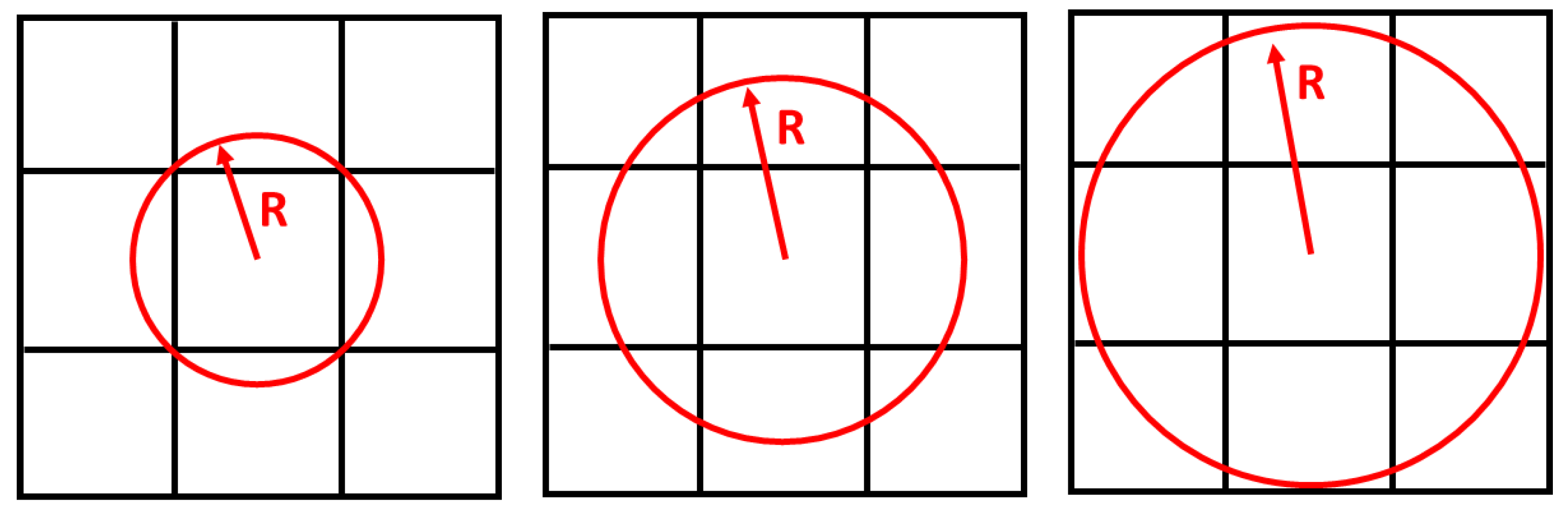
Objective Constraint R
Minimum Compliance Remaining weight for 20, 40, and 60% of the total weight 1.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated