Prerpints.org logo
Preprint
Article

Design and Development of an Intelligent Clinical Decision Support System Applied towards the Diagnosis of Suspected Obstructive Sleep Apnea Patients from the Patient’s Health Profile and Symptomatology

Altmetrics

Downloads

188

Views

96

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 March 2023

Posted:

28 March 2023

You are already at the latest version

Alerts
Abstract
Obstructive Sleep Apnea (OSA) is nowadays one of the respiratory pathologies with a higher in-cidence globally in developed countries. This situation led to an increase in the demand for medical appointments and diagnostic studies related to that condition, especially those based on poly-somnographies and cardiorespiratory polygraphies. These studies are limited in resources, causing long waiting lists with the subsequent impact on the patients’ health. Furthermore, it is necessary to mention that OSA’s symptomatology is not very specific, and it is typically present in the general population (excessive sleepiness, snore, etc.). In this regard, this paper proposes a novel intelligent clinical decision support system for the diagnosis of OSA which could be used to help medical teams, both in primary care settings and in units specialized in respiratory pathologies. The aim of the proposed system is to help discriminate the patients suspected of suffering from the pathology from those who are not. To this end, two types of information sets of heterogeneous nature are consid-ered. The first one encompasses objective data, related to the patient's health profile with infor-mation usually available in electronic health records. The second type comprises subjective data, referred to the symptomatology reported by the patient in a previous interview. To process the first group of information, a Machine Learning classification algorithm is used, Bagged Trees in this case. For processing the second information set, related with the symptomatology of the patient, a col-lection of expert systems based on fuzzy inferential systems arranged in cascade are employed. As a result, the system is able to determine two risk indicators related to the patient's risk of suffering from OSA: the Statistical Risk and the Symbolic Risk respectively. Subsequently, by interpreting both risk indicators mentioned it will be possible to determine the severity of the patients’ health, proposing a preliminary evaluation on their condition. For the initial tests of the system, a software artifact has been built using a dataset with 4,978 selected patients, suspected of suffering from OSA, from the Álvaro Cunqueiro Hospital in Vigo. The results obtained are promising, demonstrating the potential usefulness of this type of tools in medical diagnosis. Once the system has been validated with new data from clinical environments, it is considered as possible to obtain a relevant improvement in the quality of the healthcare services, and a reduction in the associated costs.
Keywords: 
Subject: Medicine and Pharmacology  -   Other

1. Introduction

Obstructive sleep apnea (OSA) is a chronic disease characterized by episodes of total or partial collapse of the upper airway during sleep, which reduces its quality causing daytime sleepiness and fatigue in those who suffer from it. In addition to these, if left untreated, OSA has a direct impact on the patient’s health as it can cause hypertension, and an increase in the risk of cardiovascular and cerebrovascular accidents, as well as being associated with the development of cognitive and metabolic disturbances [1]. In view of this problem, and with approximately one thousand million people suffering from OSA in the world [2], an effort has been made in the most developed countries to diagnose and treat patients with this pathology. The 2015 expenses associated to OSA amounted to 12.4 billion dollars in the United States of America alone [3,4]. In spite of this, it is observed that a large number of patients who suffer from this disease are not diagnosed and therefore treated [2,5], a fact that cannot be ignored due to the high health impact of OSA. In this regard, in-lab polysomnography is nowadays the reference technique used for the diagnosis of OSA [1,6,7,8,9,10]. This technique involves performing a series of physiological measurements during sleep, which after being properly interpreted and evaluated allow the characterization of a potential OSA case. The apnea-hypopnea index (AHI) is the main variable for the assessment of OSA and measures the number of apnea (complete interruption of respiratory function for at least 10 seconds [11,12]) and hypopnea (decrease of at least 30% in respiratory flow for at least 10 seconds and a microarousal or desaturation less than 4% [11,12]) events that a patient suffers in an overninght sleep study divided by the hours of total sleep [9,13]. However, despite being a widely used and recognized technique worldwide it cannot be used, at least at this time with the current technology available, to perform mass screening on the general population due to the fact that it is a very complex technique with high associated costs [1,9]. This is because it is necessary for the patient with suspected OSA to stay overnight in an accredited sleep laboratory, under the constant supervision of expert professionals. In addition, it should be noted that the number of accredited centers available with this type of equipment is limited, which means that many patients are not referred for this type of studies until they begin to present severe symptoms, after a long period of time suffering from the pathology [1]. Nevertheless, this situation is aggravated when it is observed that many of the patients who are being referred for this type of study do not really suffer from OSA, reflecting the difficulties for medical teams to discriminate between OSA patients and those who are not. All this highlights the need for standardized methods to improve the screening process, reducing in this way the number of patients who are referred to the sleep units. Thus, priority would be given to those patients in need of it, which would result in an improvement on the diagnostic process and a decrease of the associated costs.
In this context and in view of the problematic described, this work deals with the design and development of a novel intelligent clinical decision support system for the diagnosis of patients for whom OSA is suspected. To this end, the system will be based on heterogeneous patient information, both quantitative (age, body mass index, neck circumference, diagnosed conditions and prescribed treatments) and qualitative (symptoms reported by the patient in a sleep interview). From that, the intelligent system will be able to determine through the concurrent [14,15,16,17,18] use of a Machine Learning classification algorithm and a set of expert systems based on Mamdani fuzzy logic [19,20,21,22], two risk indicators associated with the risk of suffering from OSA. The first one is related to data of a more objective nature, while the second one is associated with those of a more subjective nature, also considered as the more interpretative ones. After that, both risk indicators are evaluated together allowing to determine if the patient is at risk of suffering from OSA, which would require of further confirmatory diagnostic studies.
This article is structured into five sections. The rest of Section 1 discusses the use of artificial intelligence approaches for the diagnosis of OSA. In Section 2, the conceptual description of the proposed system design is presented explaining the different involved stages as well as the information flows between them. After this, the implementation and performance of the system is explained. Section 3 shows the results obtained from the case study where the system is tested and analyzed. After that, Section 4 discusses the proposed system, and finally, Section 5 points out the conclusions and future lines of work.

1.1. Artificial Intelligence Approaches for the Diagnosis of Obstructive Sleep Apnea

In consonance with the aforementioned, and considering the complexity of the OSA diagnostic process, in recent years several approaches and tools have been developed and proposed to support the diagnostic process. In the work of Corrado Mencar et al. [23] the efficacy and applicability of Machine Learning approaches are analyzed on a dataset with 313 patients from two sleep units in North and South Italy. Both demographic data and questionnaires are used, in order to determine the degree of severity of OSA suffered by a patient. Classification approaches were employed, obtaining the best results with Support Vector Machines and Random Forest showing a maximum accuracy in the test set of 44.7%. On the other hand, regression approaches were used to determinate the apnea-hypopnea index (AHI), obtaining the best results with Support Vector Machines and linear regression with a minimum root mean squared error value of 22.17. Along this line, in the work of Lei Ming Sun et al. [24] based on the data collected from questionnaires of 110 suspected patients who performed a polysomnography in the teaching hospital in Taiwan, an approach is proposed that seeks to screen those patients with moderate-severe OSA (with an AHI ≥ 15). For this purpose, genetic algorithms were implemented obtaining a sensitivity of 81.8% and an accuracy of 88.4% for the test dataset. On the other hand, logistic regression was used showing a sensitivity of 55.6% and an accuracy of 57.2%. The authors report that the prevalence of apnea in their dataset was 77%, which is far from the real situation, so it could be that the model presents problems when it is extended to real populations. In the work by Jayroop Ramesh et al. [25] the use of Machine Learning approaches is proposed to discriminate between patients suspected of suffering from OSA from those who are not, establishing an AHI threshold value of 5. To achieve this, the Wisconsin Sleep Cohort dataset with a total of 1,479 patients (which included demographic information, physical measurements of the patient or sleep history, among other possible questions) were used. Firstly, feature selection techniques were applied to reduce the number of predictors. After that, applying optimization techniques (Bayesian Optimization and genetic algorithms) and training different models, it is observed that Support Vector Machines is the one that shows the greatest values with an accuracy of 68.06% and a sensitivity of 88.76%. In the work by Daniela Ferreira-Santos and Pedro Pereira-Rodrigues [26] the use of Bayesian network classifiers, more specifically Naïve Bayes and Tree Augmented Naïve Bayes, is proposed to help distinguishing between patients who may suffer from OSA and those who may not, in order to be able to decide which of them require the performance of a polysomnography. With this aim, using data from 194 patients two possible situations must be considered. In the first one, the models were built with 38 variables, accuracies of 67.1% and 66.9% and sensitivities of 90.0% and 81.9% are observed for the Naïve Bayes models and Tree Augmented Naïve Bayes models, respectively. The second scenario, in which only a selection of 6 variables based on a body of knowledge review is considered, shows accuracies of 70.2% and 67.5% and sensitivities of 94.1% and 90.2% for the Naïve Bayes and Tree Augmented Naïve Bayes models respectively. In the work by C. Zoroglu and S. Turkeli [27] an expert system based on a Mamdani-type fuzzy inference is proposed, which from the body mass index, the minimum blood oxygen saturation during sleep, the Mallampati score and the neck diameter are used to infer a level of AHI establishing the risk for a patient to suffer from OSA. Along the same lines, in the work by J. M. Matthews et al. [28] based on the responses to the STOP-Bang questionnaire, a fuzzy rule-based system for the screening of OSA patients is presented.
It may be appreciated that the analyzed works mostly use artificial intelligence approaches that implement learning models, thus requiring a dataset on which the algorithm can be trained. However, in the field of OSA it is not common to have public (or even private) databases available containing a considerable number of patients. Therefore, it is questionable whether these databases are meaningful and reliable, because generally the cases in them are limited and do not include different scenarios. This is the reason why the isolated use of learning-based approaches may pose a difficulty when it is desired to build robust and reliable models for clinical diagnosis.

2. Materials and Methods

2.1. Definition of the System

2.1.1. Database Usage

In order to conduct this research, a healthcare database, property of the Respiratory Sleep Disorders Unit of the Pneumology Department of the Hospital Álvaro Cunqueiro de Vigo, was used. This dataset contains information on 4,978 patients, collected between 2013 and 2022. It is important to clarify that the database includes a group of patients suspected of suffering from OSA after they have been screened by specialists, which cannot in any case be considered as general population. After performing the sleep studies and considering an AHI threshold value of 15, 3,057 patients presented a value equal or higher than 15, considered as OSA cases, while 1,921 presented a lower value and were considered as non-OSA cases. It is important to mention that an AHI value of 15 has been chosen because it allows to distinguish mild OSA cases from moderate-severe ones. Be it as it may, any other value that the medical team considers appropriate could be selected. For practical reasons, the database used can be divided into two large groups according to their nature. On the one hand, there are data showing less subjectivity such as those usually present in electronic health records. For reasons of coherence and to ease the organization of the information, it has been grouped into the categories: general data and anthropometrics (sex, age, weight, height and neck perimeter), smoking habits (smokes, does not smoke or smoked in the past, and if applicable the number of cigarettes per day and for how many years has been a smoker) and drinking habits (consumes alcohol regularly, not a consumer, or occasional consumer, and if applicable the amount of alcohol in grams consumed per day), diagnosed conditions (hypertension, resistant hypertension, ACVA, ACVA in less than a year, diabetes mellitus, ischemic heart disease, chronic obstructive pulmonary disease (COPD), home oxygen therapy, rhinitis, depression, atrial fibrillation and heart failure) as well as prescribed treatments (benzodiazepines, antidepressants, neuroleptics, antihistamines, morphics and tranquilizers/hypnotics). On the other hand, there is information that presents a greater degree of subjectivity related to the symptoms reported by the patient and collected through a sleep interview. This is summarized using the following items: hours of sleep, minutes taken to fall asleep, prolonged intra-sleep awakenings, feeling of unrefreshing sleep, daytime tiredness, morning dullness, snorer, high intensity snorer, snore related awakenings, unjustified multiple awakenings, nocturia, breathlessness awakenings and reported apneas.

2.1.2. Conceptual Design and Description of the System

Figure 1 shows the flowchart of the proposed intelligent clinical decision support system used to assist in the OSA diagnostic process. A detailed description is presented next.
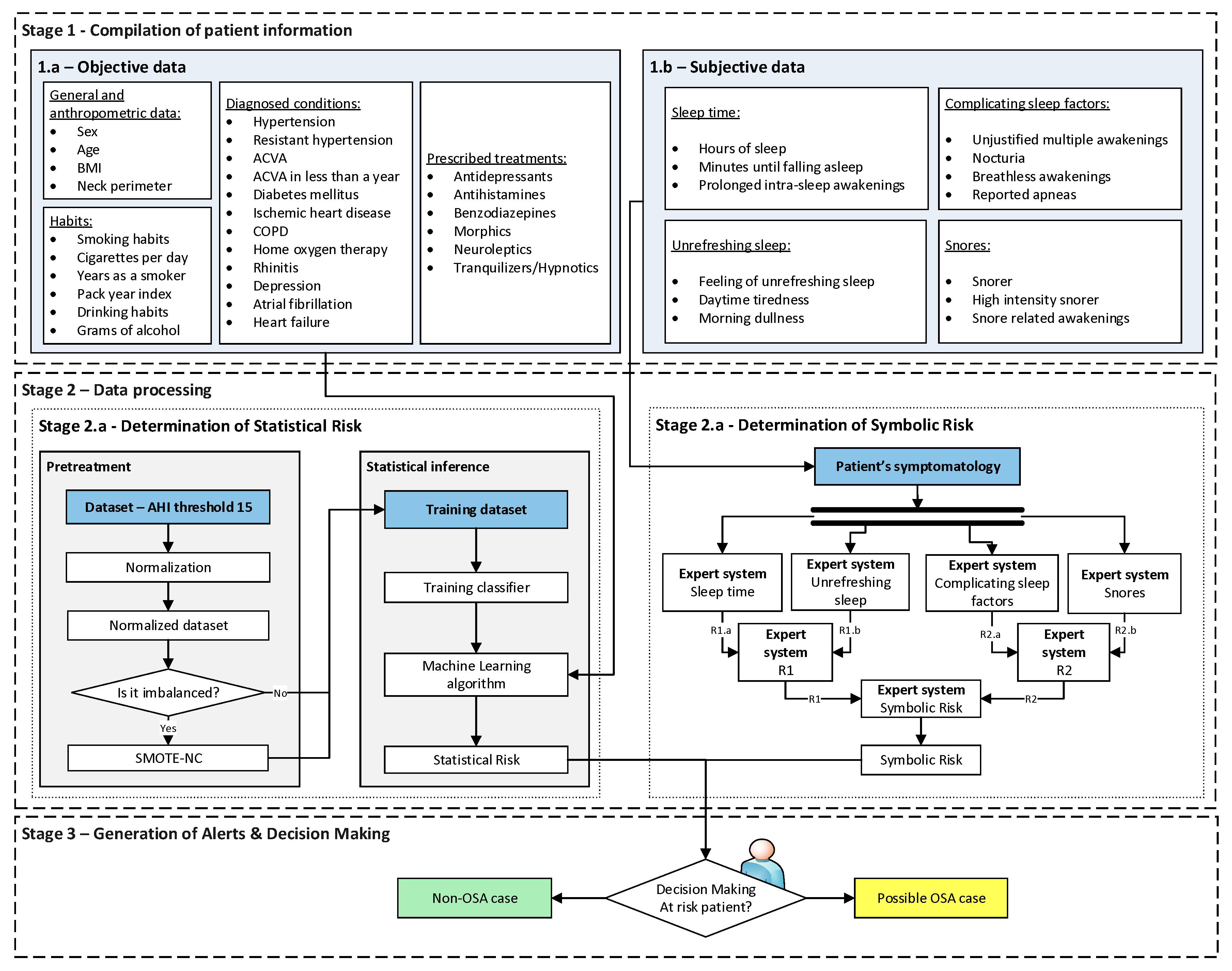
  • Stage 1: Compilation of patient information
The first stage of the proposed intelligent system is focused on the collection of the patient information, which has already been introduced in Section 2.1.1. As already mentioned, this information can be divided into two main groups depending on the nature of the information. This division is also present in the diagram through two substages which are discussed next.
  • Stage 1.a-Objective data: On the one hand, there is the more objective information, with a lower degree of subjectivity and interpretation, which is summarized in Table 1. This group has been divided into four subgroups for reasons of coherence and to facilitate the process of introducing the data into the forms. In the table, it is indicated whether each data type it is numerical or categorical.
Table 1. Summary of the objective data.
Table 1. Summary of the objective data.
Subgroup Data Data type Commentary





General and
anthropometric data		 Sex Categorical Male/Female
Age Numerical -
Weight Numerical Not provided to the algorithm but used to determine the body mass index (BMI).
Height Numerical Not provided to the algorithm but used to determine the body mass index (BMI).
Body mass index (BMI) Numerical Data derived from height and weight.
Neck perimeter Numerical -
Subgroup Data Data type Commentary





Habits		 Smoker Categorical Yes/No/No longer
Cigarettes per day Numerical Not provided to the algorithm but used to determine the pack year index.
Years as a smoker Numerical Not provided to the algorithm but used to determine the pack year index.
Pack-year index Numerical Data derived from cigarettes per day and years smoking.
Drinking habits Categorical No/Daily/Occasionally
Grams of alcohol Numerical -
Subgroup Commentary
Diagnosed
conditions		 All the comorbidities listed in Section 2.1.1 are included. Each of these fields is considered as categorical or binary, that is, either the pathology is suffered or not.
Subgroup Commentary
Prescribed
treatments		 All the drugs listed in Section 2.1.1 are included. Each of these fields is considered as categorical or binary, that is, prescribed
treatments are or are not provided.
  • Stage 1.b-Subjective data: On the other hand, there is the subjective information, more interpretative, related to the symptoms reported by the patient and collected during a sleep interview. This information is summarized in Table 2. As in the previous table, it has been decided to divide this group into four subgroups for the sake of coherence and to simplify their subsequent treatment. In the table, together with each of the data a description of its nature is also presented, depending on whether it is numerical or categorical data.
  • Stage 2: Data processing
After collecting and structuring the patient’s information, not only the more objective but also the more subjective one, it is processed. For this purpose, a Machine Learning algorithm and a series of cascaded expert systems are deployed, arranged into two substages that work concurrently [14,15,16,17,18]. Through those it is possible to determine two risk indicators, each of them associated to the groups of information previously mentioned, the Statistical Risk and the Symbolic Risk, respectively.
  • Stage 2.a–Determination of Statistical Risk: Once the most objective data has been collected, as presented in Stage 1.a, it is processed using a Machine Learning classification algorithm [29]. For the definition and configuration of the algorithm a clinical data set is used, which has already been introduced in Section 2.1.1. This data is preprocessed through normalizations and data augmentation, establishing an AHI threshold level equal to 15 for labeling the different patients according to the OSA and non-OSA classes. It is important to note that the medical team could modify this threshold if considered convenient. After this, once the model is adjusted and new patient data is available, a risk metric will be obtained as the output of the classifier, the Statistical Risk, which value will range from 0 to 100 and which can be understood as a percentage risk value of the patient actually suffering from OSA.
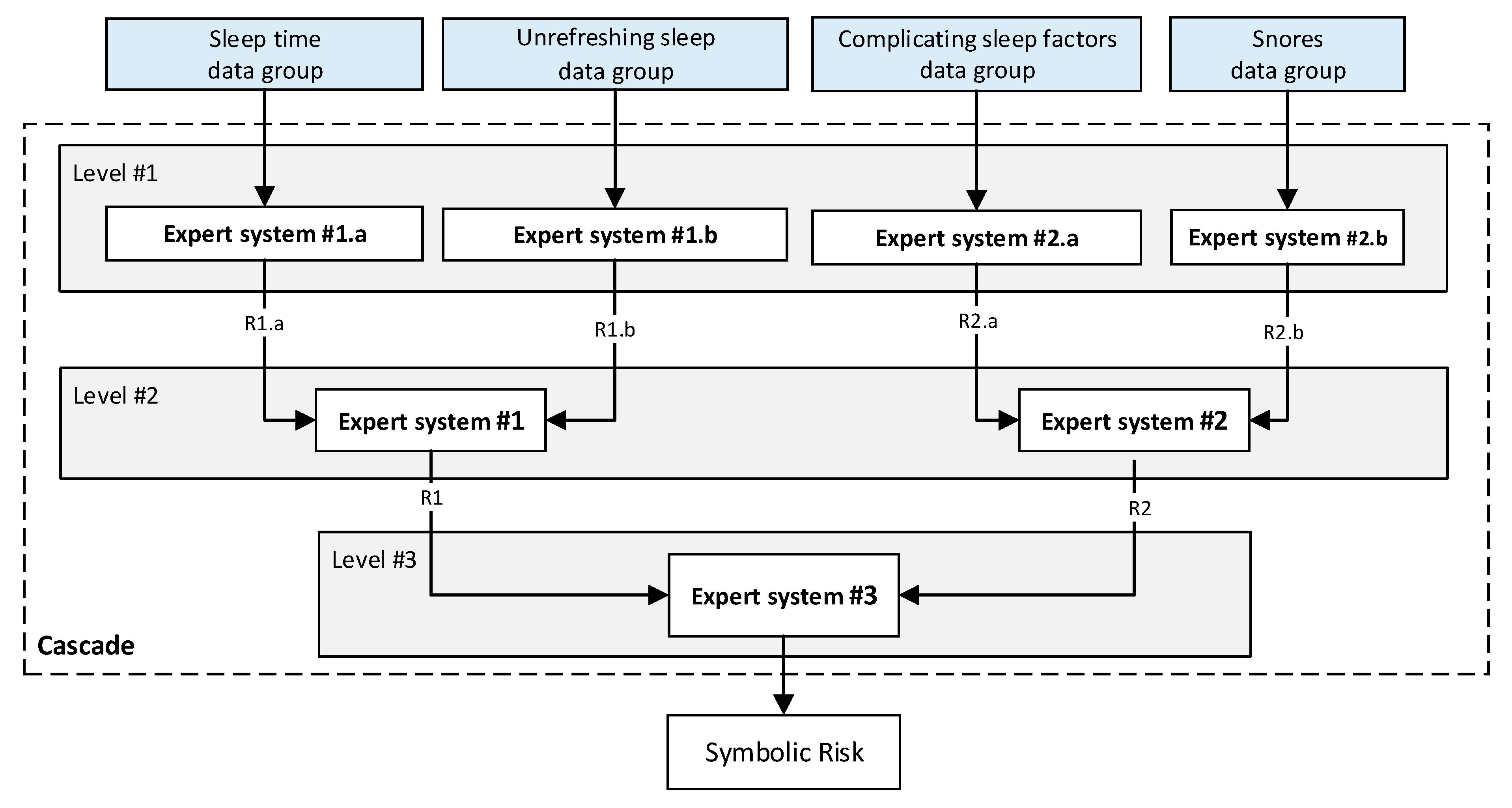
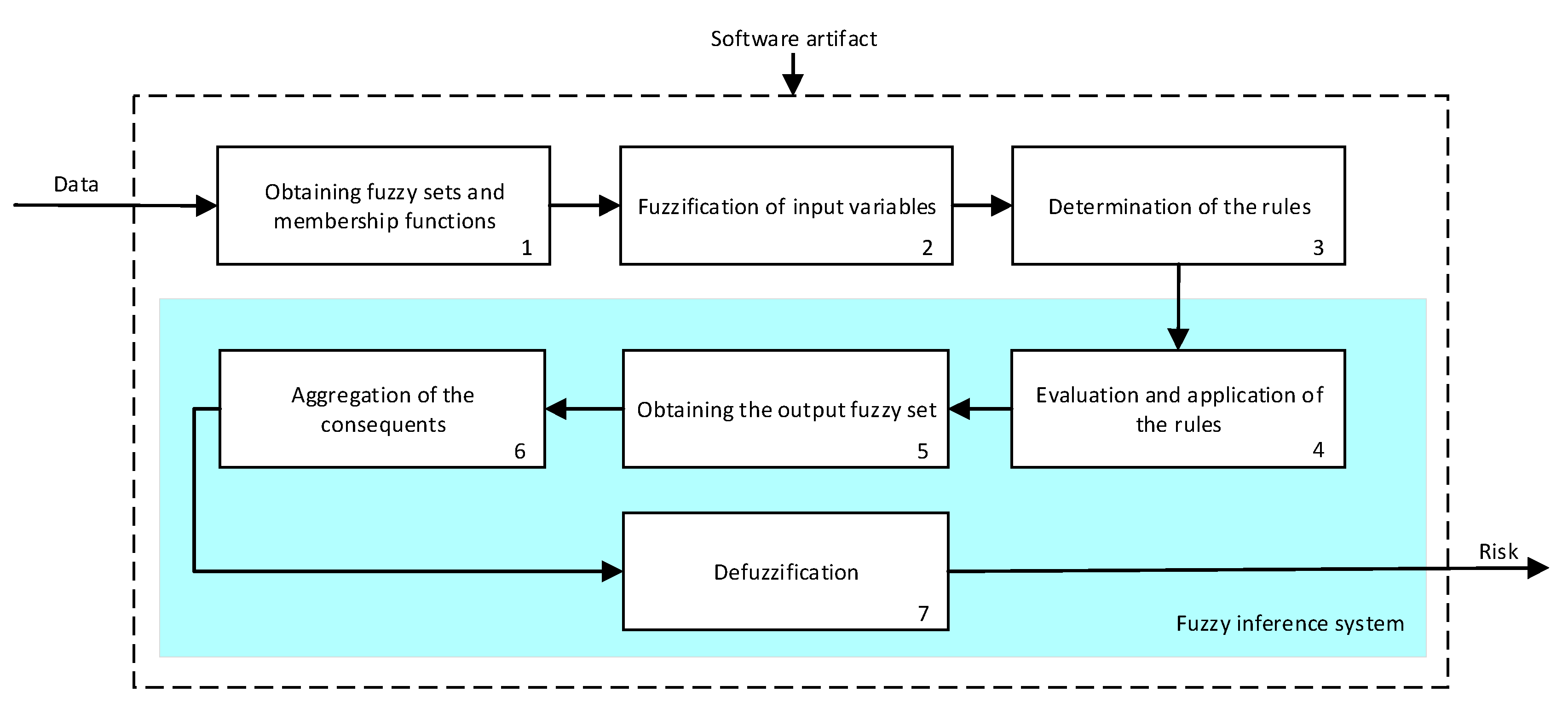
  • Stage 2.b–Determination of the Symbolic Risk: Concurrently with Stage 2.a. [14,15,16,17], in Stage 2.b the more subjective data of the patient, collected in Stage 1.b, is processed. These have been split into groups, as mentioned in Stage 1. For their processing a series of expert systems are used, all of them based on Mamdani-type fuzzy inference systems [19,20,21,22], arranged in a three-level cascade as shown in Figure 2. This is because it is intended to perform a risk assessment based on different criteria, all of which are involved in the diagnosis of OSA, which allows reducing uncertainty and creating a more accurate and suitable knowledge base. Nevertheless, since this is a multicriteria approach and aiming to obtain a global risk indicator that groups and represents them, the risks obtained as an output of the expert systems in the first level of the cascade #1.a and #1.b, #2.a and #2.b, are simultaneously fuzzified as input to expert systems #1 and #2 in the second level of the cascade. The outputs of them are also fuzzified as inputs of the expert system #3, which consists on the last level of the cascade, determining as its output a general risk indicator that contemplates the risks of the previous levels. This indicator is named Symbolic Risk, which value will range from 0 to 100, representing the risk associated with the symptoms that a patient suffers when faced with a potential OSA case. It is important to point out that the management of uncertainty in the cascade is not related to probabilities but rather to the concept of membership, which is widely known and used in the field of fuzzy logic.
  • Stage 3: Generation of Alerts & Decision Making
The risk values obtained in Stage 2, both Statistical Risk and Symbolic Risk, will be initially interpreted on an individual way on the basis of a series of threshold values that allow to establish an associated hazard level:
  • Level 1: It refers to situations in which the level of risk is low, and it seems not to indicate an OSA condition. This status will be proposed when the percentage risk to be analyzed is lower than a Limit 1 value.
  • Level 2: This refers to situations in which there is an intermediate level of risk, which does not apparently allow to distinguish whether or not it is an OSA case. This status will be proposed if the percentage risk value lies in the range [Limit 1 - Limit 2).
  • Level 3: It refers to situations in which there is a high risk level that seems to indicate the presence of an OSA condition. This status will be proposed when the percentage risk to be analyzed is higher, or equal to, the Limit 2 value.
Once this has been done, there will be two hazard levels, one of them associated with Statistical Risk and the other with Symbolic Risk, and a joint evaluation of these levels will be performed in order to establish a recommendation. For this purpose, a score will be assigned to each of the levels (a utility function is proposed that transforms the risks into numerical values, for example, if the level is 1, zero points are given; if the level is 2, one point is given; if the level is 3, two points are given) and based on these, a decision variable will be determined. The expression of this decision variable is shown in Equation 1.
Decision = Statistical_Score + Symbolic_Score
Finally, the decision variable is evaluated by considering the following thresholds:
  • Non-OSA case, do not perform diagnostic studies: This status will be proposed when the decision variable has a value lower than two.
  • Doubtful case: This status will be proposed when the decision variable equals two. The medical team should assess whether it is necessary to perform further examinations, or suggest a new medical appointment after a period of time to reconsider the patient’s condition.
  • Possible OSA case, perform diagnostic studies: This status will be proposed when the decision variable is larger than, or equal to, three.

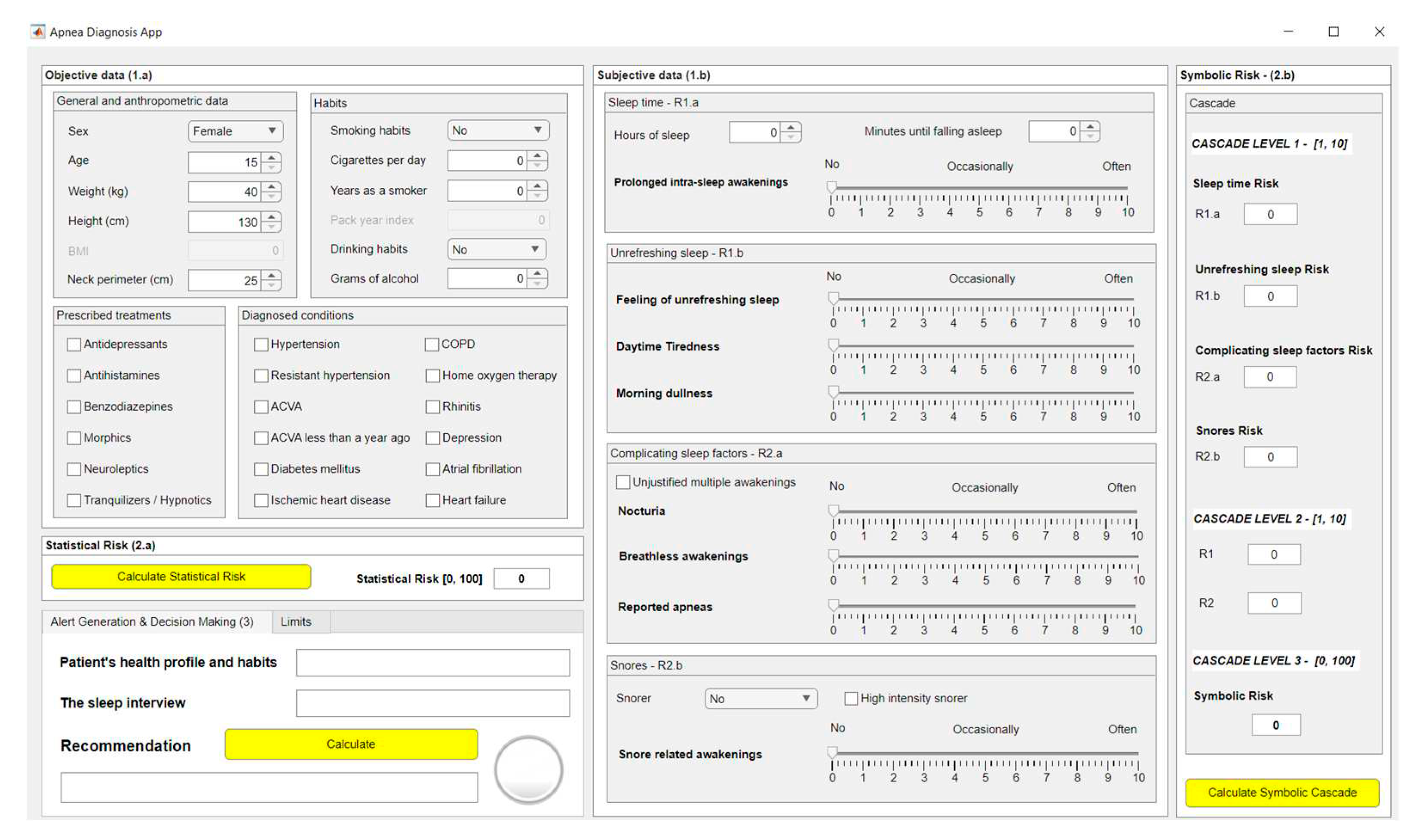
2.2. Implementation of the System

The intelligent decision support system described in Section 2.1.2 contemplates a series of stages from patient information collection, through data processing to finally generation of alerts and decision making. This section describes in detail the implementation of the intelligent system through a software artifact verifing the recommendations of Hevner et al. [30,31], which guarantees, if considered, its future integration into a hospital information system.
Such implementation has been carried out using the MATLAB© programming environment (R2021b, MathWorks©, Natick, MA, USA), making use of the App Designer module [32] for the development of the graphical user interface, the Classification Learner [33] for training the Machine Learning algorithm, and the Fuzzy Logic toolbox [34] for the implementation of fuzzy logic based engines. Furthermore, it was necessary to make an auxiliar use of Python’s (version 3.9.12) imbalanced-learn [35] library for synthetic data generation employing SMOTE-NC.
Figure 3 shows a screenshot of the graphical interface of the developed software artifact. Block (1.a) is related to the compilation and preprocessing of objective patient information, while block (1.b) is related to the subjective information. Blocks (2.a) and (2.b) are referred to the data processing, making possible to observe the Statistical Risk and the Symbolic Risk respectively. Block (3) allows to generate alerts and to visualize the system recommendations.

2.2.1. Data Acquisition

The data associated to each patient must be introduced into the application through the forms shown in Figure 3. There are two areas in it, one for the introduction of objective data (1.a) and the other for the introduction of more subjective data (1.b). It is worth emphasizing the importance associated with the task of filling the forms, since errors or omissions in them could lead to compromise the accuracy of the data, thus increasing the system’s uncertainty.

2.2.2. Data Processing

After the patient’s data have been introduced into the application, the processing is performed by the intelligent system. As previously mentioned, two blocks that act concurrently are used for this purpose [14,15,16,17,18]. The first one is based on a Machine Learning classification algorithm, while the second one is based on a series of cascaded expert systems.
The process used for the construction and definition of these blocks, as well as the determination of the associated risk metrics, are described below.
  • Classification Algorithm Based on Machine Learning
For the definition of the Machine Learning classification algorithm, the dataset presented in Section 2.1.1 was used as a starting point, more specifically the most objective data which is summarized in Table 1. As can be observed in the table, part of the data belong to the nominal or ordinal categorical data types [36,37]. Because of this, an encoding has been made using dummy encoding [42], which means that for each variable a number of auxiliary variables are created to replace it, equal to the total number of categories presented in the starting variable minus one. Moreover, it is also necessary to mention the numerical data, which were scaled from zero to one using Min-Max normalization (as shown in Equation 2). This is done because, with the help of the medical team, it has been possible to delimit for each of the cases the maximum and minimum values between which the study variables will be encompassed.
z ’ = z i − m i n ⁡ ( z ) max ⁡ z − m i n ⁡ ( z )
After that, the distribution of the class to be predicted on the dataset is analyzed. As discussed in Section 2.1.1, considering an AHI threshold value of 15, 3,057 patients present a value equal to or higher than the threshold which are labeled as apnea case. Meanwhile, 1,921 patients present a lower value than the threshold and are labeled as non-apnea case. Through the analysis of the dataset, a certain degree of imbalance is observed, which could affect the performance of the classifier. For this reason, a controlled data augmentation process is implemented as a usual approach in diagnostic environments, which tends to improve the results of binary classifiers [17,38]. A variation of the Synthetic Minority Over-Sampling Technique (SMOTE) was used for this purpose [38,39], oriented towards the processing of datasets in which numerical and categorical variables coexist, all of them already transformed into continuous variables. Data of both classes have been generated with a strategy where a number of neighbors k = 5 was selected, until there were 4,000 elements of each class.
This provides a coherent training data set that can be used for the training of Machine Learning-based classification algorithms, which makes possible to classify new patients. To this end, and in order to evaluate the different available possibilities, a series of tests have been carried out using the MATLAB© Classification Learner app. It allows the training and analysis of multiple algorithms in a massive way, establishing a k-fold cross validation [40] with k = 5. Once the analysis of the results has been done, by interpreting the validation ROC curves, the Bagged Trees algorithm stands out. It should be noted that using one algorithm or another does not constrain the system in any way and that, in the future, if it is found that other algorithms give better results, they could be replaced without causing an essential change in the system. Figure 4 shows the ROC validation curve of the Bagged Trees algorithm for the OSA class, with an AUC value close to 0.90.
At this point, the next step consists in feeding data from a new patient into the classifier and obtaining a risk indicator, called Statistical Risk. This output is associated with the percentage risk of suffering from OSA for an AHI value greater than, or equal to, the determined threshold level, 15 in this case. This risk is scaled from 0 to 100, with 0 being the minimum percentage of having an AHI greater than or equal to the threshold, and 100 being the highest one.
  • Cascade of Expert Systems
Concurrently [14,15,16,17,18] to the Machine Learning module in which the Statistical Risk was determined, in this module the Symbolic Risk is calculated. For this purpose, a cascade of expert systems is deployed, which was introduced in Section 2.1.2, using Mamdani-type fuzzy inference systems. [19,20,21,22]. As shown in Figure 2, the cascade has three levels, which are detailed below:
  • First level: at the upper level of the cascade, the processing of the four groups of information previously introduced in Stage 2.b of Section 2.1.2 is carried out (‘sleep time’ group, ‘unrefreshing sleep’ group, ‘complicating sleep factors’ group and ‘snores’ group). For this purpose, four expert systems are used to obtain a risk indicator (R1.a, R1.b, R2.a and R2.b respectively) at the output of each of them after the defuzzification process. These indicators determine the hazard level associated to suffering from OSA related to each group of data.
  • Second level: at the second level of the cascade, the data from the first level is processed using two expert systems with the aim of aggregating their outputs. This is so because of the decision to group the risks obtained in the first level of the cascade in couples (R1.a and R1.b, R2.a and R2.b) according to the degree of affinity between the starting data. As a result, two risk indicators (R1 and R2 respectively) which show the hazard associated with suffering from OSA, related to the groups of data linked to each indicator, are determined at the output of the expert systems after the defuzzification process.
  • Third level: at the third level of the cascade, the data from the second level of the cascade (R1 and R2) are processed using a single expert system. At its output, after the defuzzification process a risk indicator is obtained, the Symbolic Risk, which indicates the hazard level associated to the patient suffering from OSA according to the subjective input data.
The use of the cascade of expert systems makes possible to aggregate the information of the different levels in a progressive way. The information related to the different criteria contemplated, understood as the different groups of data involved in the evaluation of the risk of suffering from OSA, can be incorporated. In addition, the fact of using a cascade-type structure facilitates the determination of the rules of each inference system. As the number of antecedents in the expert systems is smaller, greater precision and accuracy are obtained in the elaboration of the rules.
As already mentioned, all cascade expert systems are based on Mamdani-type fuzzy inference systems [19,20,21,22]. Figure 5 shows the operation’s flow diagram for this type of inference system, which is described in detail next. First of all, the membership functions are determined for each of the variables. These make it possible to establish the degree of membership associated to a new value of a variable, with a value between zero (indicating non membership) and one (indicating absolute membership). As already mentioned, in the expert systems of the first level the input variables are those described in Table 2, while in the second and third levels of the cascade the inputs are the risks obtained after the defuzzification process of the expert systems of the immediately preceding level. As regards to the expert systems’ outputs, in this case different risk indicators associated with the initial data will be obtained. The choice of one type of function or another will depend on the characteristics of the variable to be represented. Following Ross’s recommendation [22], normal, convex and symmetrical membership functions will be used, chosing in this case between triangular and trapezoidal functions [17]. After defining the membership functions, the next step is the fuzzification of the new input values, determining a series of membership degrees associated to each of them. Once this is done, in the third stage the knowledge base of the system is established, wich is composed of a collection of declarative rules determined by the medical team. These rules are of the type ’IF … AND … THEN …’, through which it is possible to represent the knowledge of the experts by combining the different input variables and relating them to the consequents. The fourth stage then evaluates the antecedents of the rules of the Mamdani system. As in the case of study, when these connect different membership functions through the ’AND’ operator, the lowest of the membership degrees associated with each of them will be obtained. After evaluating the antecedents, in the fifth stage the next step involves obtaining the consequents by applying an implication method, in this case the ’MINIMUM’, which truncates the membership function of the consequents of each rule. These truncated consequents are subsequently aggregated in the sixth stage by applying a disjunctive approach [22] based on the use of the ’MAXIMUM’ operator, so as to achieve a graphical output equivalent to the superposition of the previously obtained consequents. This is subsequently defuzzified in the last stage by applying the centroid method [22] to determine a numerical value associated with the risk indicator at each of the risk levels.
Although the system contemplates that the variables and membership functions can be redefined based on the experience acquired during the use of the application. Table 3, Table 4, Table 5 and Table 6 below summarize the initial configuration of the expert systems of the first level of the cascade, which are used for the calculation of risks R1.a, R1.b, R2.a and R2.b respectively.
In the same way, Table 7 and Table 8 show the initial configuration of the expert systems of the second level of the cascade, which are used for the calculation of risks R1 and R2.
Finally, Table 9 shows the initial configuration of the expert system of the third level of the cascade, which is used for the calculation of the Symbolic Risk.
After the Symbolic Risk is obtained, it is rescaled in the range [0, 100] so that it can be compared to the Statistical Risk on the same scale. A higher value of the Symbolic Risk indicates a higher hazard level of suffering from OSA.

2.2.3. Generation of Alerts and Decision Making

In the case of a new patient, and after determining the couple of risk indicators, Statistical Risk and Symbolic Risk, the patient’s condition is determined, and a recommendation is proposed. As mentioned, the risk indicators will be first interpreted individually based on a series of threshold values that allow a hazard level associated with each of the risk indicators to be established. The second column of Table 10 shows a summary of the different possible cases with their correspondence to each different level.
Regarding both the Statistical Risk and the Symbolic Risk, the value of Limit 1 is proposed to be 45, and the value of Limit 2 is proposed to be 60. Nevertheless, these values may be reviewed and modified depending on the results observed during the clinical validation of the system.
After that, the hazard levels associated to each of the risk indicators will be available and their joint evaluation will be carried out in order to establish a recommendation. Before that, a score will be assigned to each of the levels as can be seen in the third column of Table 10. Once this has been done, and by adding the score associated to the risk levels, a decision variable T will be determined as shown in Equation 3.
T = Statistical_Risk_Score + Symbolic_Risk_Score
This decision variable T could be considered as part of the usefulness analysis, representing a normative tool as opposed to the descriptive measure offered by the calculated risk values. Its objective is therefore not to predict but to assist in decision making by establishing a relationship between the calculation of risks and the preferential recommendation associated to the value of T and linked by Equation 1 which, in this setting and to this end, could be considered as an utility function [41,42].
Finally, the value of the decision variable T is evaluated. Table 11 presents a summary of the different recommendations proposed according to the value of the decision variable T. Emphasis should be placed on the fact that the threshold values for the variable T can be reviewed and modified according to the results obtained.
To summarize, Table 12 shows the whole process of generation of alerts and decision making. From the individual evaluation of each of the risk indicators determining the hazard levels, to their joint evaluation determining the T variable and establishing the conclusions and recommendations. In this table, color codes have been used for the generation of alerts once the T variable has been evaluated. The green color is related to a non-OSA case, orange to a doubtful case, while red refers to a potential OSA case.

3. Results

This section presents a clinical case study of the application of the intelligent clinical decision support system proposed in this paper. The aim is to give an example on its performance and potential use in the clinical field. It is important to clarify that the intention is neither to validate the system nor to compare it with other alternatives existing in the current body of knowledge. Furthermore, previous to the presentation of the case study, it should be pointed out that the patient data analyzed in this section was not present in the dataset used for the definition and configuration of the system.

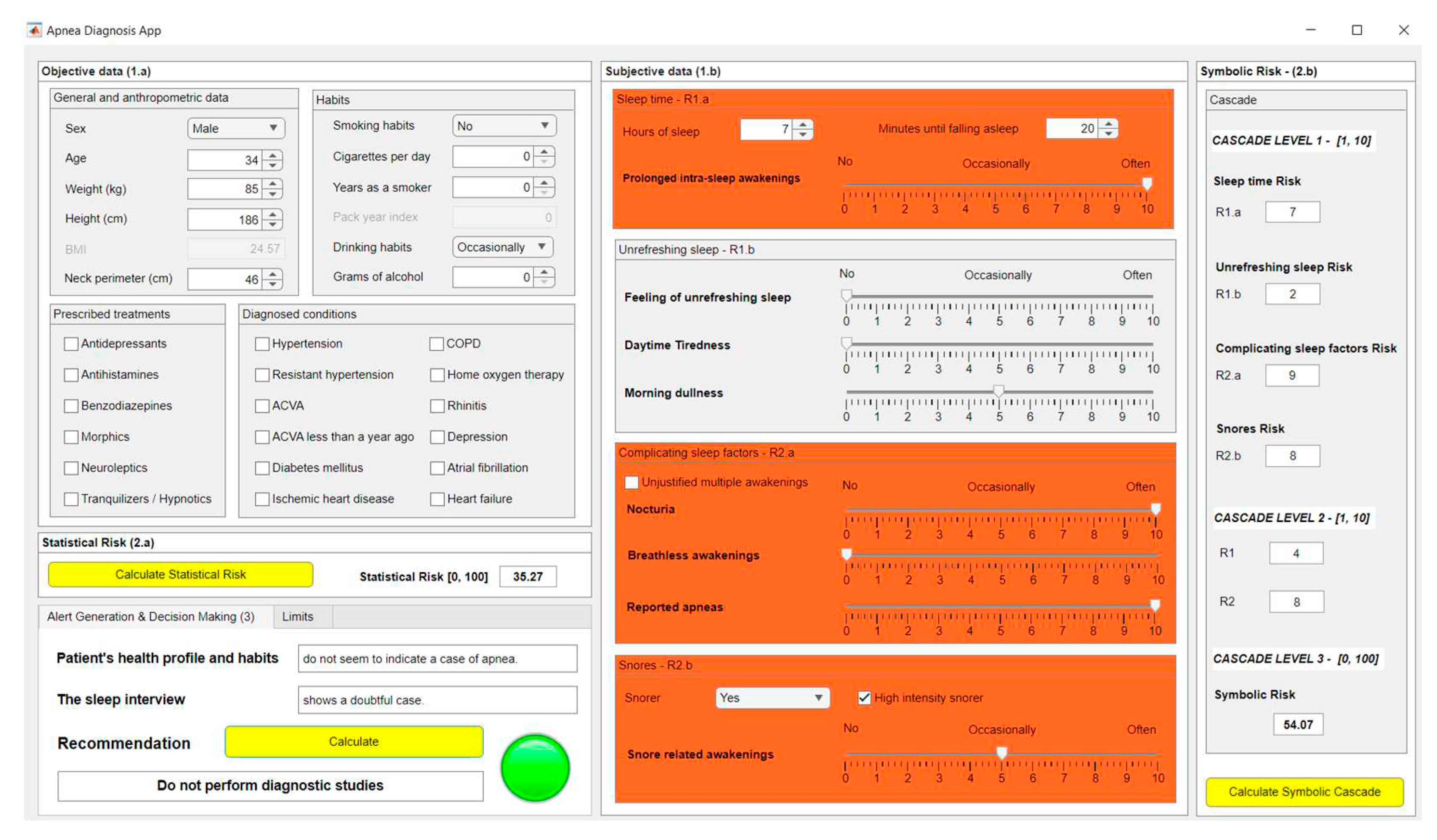
3.1. Compilation of the Patient’s Information

Table 13 shows the objective data of the patient to be analyzed, related to Stage 1.a of the proposed system. On the other hand, Table 14 presents the subjective data related to Stage 1.b of the proposed system. It is necessary to point out that this patient underwent sleep studies and presented an AHI value of 11.90. This value will be later used to evaluate the conclusions and recommendations generated by the intelligent system.
Once the data are submitted, they are introduced into the application to be processed by the intelligent clinical decision support system.

3.2. Data Processing

Subsequently, the two risk indicators previously defined in Section 2, Statistical Risk and Symbolic Risk, are determined. Figure 6 shows a screenshot of the application in which it is possible to observe the resulting risk values. In the case of Statistical Risk a percentage value of 35.27 is obtained, while in the case of the Symbolic Risk the respective value is 54.07, both of them expressed on a scale from 0 to 100.
The Symbolic Risk should be analyzed in more detail since, as mentioned in Section 2, it is the final value obtained from the cascade of expert systems. Analyzing the systems of the first level of the cascade, risk values of 7, 2, 9 and 8 were respectively obtained for risk indicators R1.a, R1.b, R2.a and R2.b, as shown in Figure 6. After that, in the second level of the cascade, risk values of 4 and 8 were obtained for risk indicators R1 and R2, respectively. These risks, R1 and R2, are used for the calculation of the Symbolic Risk at the last level of the cascade, resulting in a preliminary value of 5.407, which after being scaled from 0 to 100 presents a value of 54.07.

3.3. Generation of Alerts and Decision Making

After entering the patient’s data into the application and calculating the risk indicators associated with them, the Statistical Risk and the Symbolic Risk, that last stage is followed by their analysis and evaluation.
Both risks are first evaluated against three levels, each of them defined by two limit values. In this case, and aiming for simplicity, these limits will have the same value for both risks, but that might change if in a future time any reason justifies it. The value of Limit 1 is set to 45, while the value of Limit 2 is set to 60. A summary of the thresholds associated to the different levels, as well as their respective interpretations, are shown in Table 15.
The Statistical Risk shows a value of 26.56, which is clearly lower than Limit 1, so this indicator is in the first level corresponding to a patient who does not suffer from OSA. On the other hand, the Symbolic Risk presents a value of 54.07, higher than Limit 1 and lower than Limit 2, so it is in the second level and associated to a doubtful case.
Once the individual interpretation of the risk indicators has been carried out, which is done automatically in the application based on the established thresholds, the next step is their joint interpretation. To understand the procedure, it may be helpful to retrieve Table 12, adapting it to this case as shown in Table 16, which allows to determine the recommendation of the system through the color code in that table (green for non-OSA, orange for a doubtful case, and red for a potential OSA case).
As the interpretation in Table 16 shows, an OSA case is not considered, so it is suggested not to perform further diagnostic studies. This final interpretation is also performed automatically by the system, as can be seen in Figure 5.

3.3. Interpretation of the Results

In any case, it is interesting to make a brief analysis of the results obtained. After the interpretation of the Statistical Risk, it is apparent that this is not a case that fits the usual pattern of an OSA patient, given that the risk value is relatively low. Nevertheless, the patient presents some significant risk values in the cascade, such as R2.a and R2.b, associated with the ‘sleep complicating factors’ and ‘snores’ data groups, respectively. This may be due either to the patient not telling the truth or exaggerating their symptoms. Thus, after the joint assessment of the different levels of the cascade, the value of the Symbolic Risk obtained is average, which indicates this case would be a doubtful one.
Following the joint assessment of the indicators, it was determined that the patient did not suffer from OSA, which is feasible given that the patient had an AHI value close to 10 commonly found in mild cases. Furthermore, it should be noted that the Machine Learning classification algorithm was trained using a dataset with an AHI threshold value of 15. This was set so as to discriminate mild cases from moderate-severe ones.

4. Discussion

Nowadays, OSA has a high incidence worldwide and involves a significant detriment to the health of those who suffer from it, being remarkable the increasing demand for related medical consultations and diagnostic studies, mainly polysomnographies. These studies present a high instrumental complexity, being necessary to use large numbers of sensors, as well as to be supervised by specialized professionals during its development, in addition to the requirement of a subsequent manual analysis of the results. As a consequence of the increasing demand for this type of studies, as well as the particularities inherent to this type of tests, considerable delays are frequent for them. This entails a severe hazard to the health of the patients, together with the economic impact associated with the performance, in many cases, of tests that were not necessary. In this regard, and considering the important advances in the field of artificial intelligence, numerous and diverse approaches have been proposed in recent years for OSA diagnosis, generally based on the use of single (statistical in most cases) inferential engines.
The diagnosis of OSA is a multivariate problem in which the aim is to assess whether a patient suffers from this clinical condition on the basis of a series of variables. Other purpose may be to determine potential cause-effect relationships that exist between the different variables involved, for which it is common to use dependence, interdependence or structural approaches [43]. Nevertheless, it is also feasible to deal with this type of problem by jointly employing inferential models of a heterogeneous nature [44,45,46,47,48], both statistical and symbolic, with the common objective of representing the same reality. In this case, the diagnostic process that allows discerning between a patient who suffers from OSA and one who does not. For this purpose, in the case of the statistical inferential approaches, represented in this work through the use of the Bagged Trees algorithm, which is applied to determine the Statistical Risk, it is essential to have a representative dataset available to build the model. Meanwhile, in the case of the symbolic inferential approach particularized in this work through the use of a series of expert systems based on fuzzy logic through which it is possible to determine the Symbolic Risk, it is necessary to define the knowledge base of the different systems through a set of syllogisms. In both cases, the definition of each of the systems used contemplates a large number of variables that are not free of uncertainty. This is where the proposed intelligent system becomes important. Beyond its undeniable applicability and potential for its use in clinical settings, the capabilities of the different elements used for the determination of each of the system’s risks is evaluated, taking into account their ability to represent knowledge and manage uncertainty, are explained next.
  • Determination of Statistical Risk: as previously mentioned, a Machine Learning classification algorithm is used to determine the Statistical Risk, more specifically a Bagged Tree built on the basis of an initial dataset that has been encoded, normalized and balanced using SMOTE-NC. All this process prior to the construction of the model has been carried out with the aim of ensuring that the initial dataset used for the construction of the model is coherent and adequate. An attempt has been made to achieve a sufficient representativeness regarding the possible casuistry, as well as to aim for normality in the data distributions, in order to guarantee the subsequent obtaining of robust and reliable classifiers. As mentioned before, in this work a Bagged Trees algorithm was chosen, however, the use of one algorithm or another is not relevant because any other Machine Learning approach could provide plausible results. In any case, it should be noted that for this to be true, the datasets used in the model training and validation processes must have been obtained under similar circumstances, with common diagnostic criteria. The same circumstances should apply when it is desired to analyze data from new patients. In relation to the treatment of uncertainty, in this case it is achieved using a purely probabilistic approach.
  • Determination of the Symbolic Risk: concurrently to the calculation of the Statistical Risk, the Symbolic Risk is determined using a series of expert systems, which are perhaps the most representative models for symbolic reasoning in the field of artificial intelligence and allow diversifying and formalizing the knowledge of the specialists. In this particular case, the formalization of knowledge has been achieved through the definition of an architecture of expert systems arranged in cascade. The diversification of information is possible through the definition of a series of declarative rules in each of the expert systems that model the knowledge of events that have occurred in similar circumstances. Thus, there is a clear and undeniable dependence between the way in which the expert system performs its reasoning and who defines its knowledge base, which implies assuming a certain degree of doubt and error in the process, and therefore, the presence of uncertainty in the generation of the rules. The formalization of knowledge is an inherent characteristic of expert systems, and it is possible to do it in this case through the definition of a cascade-based architecture. This allows the gradual integration of the consequents of the previous levels, all of them considered as technical variables representing the risk of suffering from OSA. These consequents are treated, in turn, as qualitative variables when acting as antecedents of the expert systems in the next level. As discussed in the work by Casal-Guisande et al. [17], the distinction that the same variable may be treated as antecedent or consequent of a rule makes a clear difference in the very fuzziness of the variable, which is related to the uncertainty associated with its numerical representation. In addition, the cascaded expert systems architecture allows for simpler logical constructs, through which it is possible to represent knowledge. That also results in a better control and in the progressive reduction of uncertainty throughout the different stages of the cascade. It is because of all those reasons that the intelligent system, in its symbolic aspect, has capabilities to manage uncertainty.
Beyond those issues related to the architecture of the proposed intelligent system, as well as its ability to manage uncertainty, it is necessary to point out those aspects that are most beneficial from a diagnostic and practitioner’s viewpoint. Once the risks have been obtained, their analysis and interpretation provides the medical team with a metric for the hazard level derived from the patient’s risk of suffering from OSA. Such an assessment is based both on objective data related to the patient’s history and on subjective data related to the symptoms reported by the patient. This information is remarkably valuable, due to the fact that it facilitates the assessment of patients suspected of suffering from OSA. Furthermore, it could be very useful for those first medical consultations in which the patient comes to primary care, in which a general practitioner could be suspecting of a potential OSA case. This could help them to choose which cases should be referred to further specialized studies, thus reducing the overall number of referred patients, as well as focusing on those who are actually in need. This is possible thanks to the system’s ability to formalize and diversify knowledge, guiding the physician, standardizing the diagnostic process and facilitating the interpretation of data. Likewise, the system also has a great potential for its use in specialized units, being of particular interest in those cases in which specialists are faced with doubtful cases. The system enables them to discriminate between those patients who may require further diagnostic studies to confirm a potential OSA case, and those who apparently do not have that disease. In this way, the demand for sleep studies may be reduced, thus speeding up the performance of these studies while reducing waiting lists at the same time.
On a general note, and in line with what has already been mentioned, it should be pointed out that the tool presented in this article constitutes a great novelty in the field of study. Existing approaches in the current body of knowledge generally make use of single inference models, statistical in most cases, being clearly dependent on the availability of coherent and representative population healthcare databases. This could be a severe handicap for some diseases, as might be the case of OSA. Furthermore, the relevant impact of using this type of systems in the management of hospital resources, as well as their associated cost savings, should be highlighted once again.

5. Conclusions

In this article an innovative intelligent clinical decision support system has been presented. This tool allows optimizing the diagnostic process of potential OSA cases. To this end, statistical and symbolic inferential approaches are used jointly, making possible to determine two percentage risk indicators, the Statistical Risk and the Symbolic Risk, both of them associated with the risk of a patient suffering from OSA.
The proposed intelligent system has been applied in a clinical case study as a proof of concept, wich has allowed to introduce the tool, exemplifying the use of the system, highlighting both its simplicity of use and its great applicability in the field of study. Despite the aforementioned claims and the encouraging results obtained, it is worth mentioning that the proposed system is still in its early stages of development, and it is still in need of further clinical validation.
In time to come, it will be necessary to carry out tests in clinical settings to validate the results obtained and to adjust the system for its intensive use in hospital environments. Thus, it will be possible to determine its full diagnostic capabilities and the economic impact associated to its use. In addition, and from the point of view of the system’s architecture, it will still be necessary to explore new options to improve the final process of joining the risks obtained, as well as to optimize the formalization of the knowledge of the symbolic models.

Author Contributions

Conceptualization, M.C.-G. and A.C.-C.; methodology, M.C.-G. and A.C.-C.; software, M.C.-G. and L.C.-S.; investigation, M.C.-G., L.C.-S., M.M.-A., M.T.-D., J.C.-P., J.-B.B.-R., A.F.-V. and A.C.-C.; resources, M.T.-D, M.M.-A. and A.F.-V.; data curation, M.C.-G. and L.C.-S.; writing—original draft preparation, M.C.-G., L.C.-S. and A.C.-C.; writing—review and editing, J.C.-P.; supervision, M.M.-A., M.T.-D., J.C.-P., J.-B.B.-R. and A.F.-V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of Galicia (protocol code 2022/256, 02/07/2022).

Data Availability Statement

Not applicable.

Acknowledgments

M.C.-G. is grateful to Consellería de Educación, Universidade e Formación Profesional e Consellería de Economía, Emprego e Industria da Xunta de Galicia (ED481A-2020/038) for his pre-doctoral fellowship.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ramachandran, A.; Karuppiah, A. A Survey on Recent Advances in Machine Learning Based Sleep Apnea Detection Systems. Healthcare 2021, Vol. 9, Page 914 2021, 9, 914. [Google Scholar] [CrossRef]
  2. Benjafield, A. v.; Ayas, N.T.; Eastwood, P.R.; Heinzer, R.; Ip, M.S.M.; Morrell, M.J.; Nunez, C.M.; Patel, S.R.; Penzel, T.; Pépin, J.L.D.; et al. Estimation of the Global Prevalence and Burden of Obstructive Sleep Apnoea: A Literature-Based Analysis. Lancet Respir Med 2019, 7, 687–698. [Google Scholar] [CrossRef]
  3. Watson, N.F. Health Care Savings: The Economic Value of Diagnostic and Therapeutic Care for Obstructive Sleep Apnea. Journal of Clinical Sleep Medicine 2016, 12, 1075–1077. [Google Scholar] [CrossRef]
  4. Frost & Sullivan. Hidden Health Crisis Costing America Billions Underdiagnosing and Undertreating Obstructive Sleep Apnea Draining Healthcare System. American Academy of Sleep Medicine 2016. [Google Scholar]
  5. Ye, L.; Li, W.; Willis, D.G. Facilitators and Barriers to Getting Obstructive Sleep Apnea Diagnosed: Perspectives from Patients and Their Partners. Journal of Clinical Sleep Medicine 2022, 18, 835–841. [Google Scholar] [CrossRef]
  6. Douglas, N.J.; Thomas, S.; Jan, M.A. Clinical Value of Polysomnography. The Lancet 1992, 339, 347–350. [Google Scholar] [CrossRef]
  7. Rundo, J.V.; Downey, R. Polysomnography. In Handbook of Clinical Neurology; Elsevier, 2019; Vol. 160, pp. 381–392. [CrossRef]
  8. Kapur, V.K.; Auckley, D.H.; Chowdhuri, S.; Kuhlmann, D.C.; Mehra, R.; Ramar, K.; Harrod, C.G. Clinical Practice Guideline for Diagnostic Testing for Adult Obstructive Sleep Apnea: An American Academy of Sleep Medicine Clinical Practice Guideline. Journal of Clinical Sleep Medicine 2017, 13, 479–504. [Google Scholar] [CrossRef]
  9. Punjabi, N.M. The Epidemiology of Adult Obstructive Sleep Apnea. Proc Am Thorac Soc 2008, 5, 136–143. [Google Scholar] [CrossRef] [PubMed]
  10. Mostafa, S.S.; Mendonça, F.; Ravelo-García, A.G.; Morgado-Dias, F. A Systematic Review of Detecting Sleep Apnea Using Deep Learning. Sensors 2019, Vol. 19, Page 4934 2019, 19, 4934. [Google Scholar] [CrossRef] [PubMed]
  11. Prisant, L.M.; Dillard, T.A.; Blanchard, A.R. Obstructive Sleep Apnea Syndrome. The Journal of Clinical Hypertension 2006, 8, 746–750. [Google Scholar] [CrossRef] [PubMed]
  12. Koch, A.L.; Brown, R.H.; Woo, H.; Brooker, A.C.; Paulin, L.M.; Schneider, H.; Schwartz, A.R.; Diette, G.B.; Wise, R.A.; Hansel, N.N.; et al. Obstructive Sleep Apnea and Airway Dimensions in Chronic Obstructive Pulmonary Disease. Ann Am Thorac Soc 2020, 17, 116–118. [Google Scholar] [CrossRef]
  13. Pevernagie, D.A.; Gnidovec-Strazisar, B.; Grote, L.; Heinzer, R.; McNicholas, W.T.; Penzel, T.; Randerath, W.; Schiza, S.; Verbraecken, J.; Arnardottir, E.S. On the Rise and Fall of the Apnea−hypopnea Index: A Historical Review and Critical Appraisal. J Sleep Res 2020, 29, e13066. [Google Scholar] [CrossRef] [PubMed]
  14. Casal-Guisande, M.; Comesaña-Campos, A.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J.-B. Design and Development of a Methodology Based on Expert Systems, Applied to the Treatment of Pressure Ulcers. Diagnostics 2020, 10, 614. [Google Scholar] [CrossRef] [PubMed]
  15. Comesaña-Campos, A.; Casal-Guisande, M.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J.B. A Methodology Based on Expert Systems for the Early Detection and Prevention of Hypoxemic Clinical Cases. Int J Environ Res Public Health 2020, 17, 1–31. [Google Scholar] [CrossRef] [PubMed]
  16. Cerqueiro-Pequeño, J.; Comesaña-Campos, A.; Casal-Guisande, M.; Bouza-Rodríguez, J.-B. Design and Development of a New Methodology Based on Expert Systems Applied to the Prevention of Indoor Radon Gas Exposition Risks. Int J Environ Res Public Health 2020, 18, 269. [Google Scholar] [CrossRef] [PubMed]
  17. Casal-Guisande, M.; Comesaña-Campos, A.; Dutra, I.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J.-B. Design and Development of an Intelligent Clinical Decision Support System Applied to the Evaluation of Breast Cancer Risk. Journal of Personalized Medicine 2022, Vol. 12, Page 169 2022, 12, 169. [Google Scholar] [CrossRef] [PubMed]
  18. Casal-Guisande, M.; Bouza-Rodríguez, J.-B.; Cerqueiro-Pequeño, J.; Comesaña-Campos, A. Design and Conceptual Development of a Novel Hybrid Intelligent Decision Support System Applied towards the Prevention and Early Detection of Forest Fires. Forests 2023, Vol. 14, Page 172 2023, 14, 172. [Google Scholar] [CrossRef]
  19. Mamdani, E.H.; Assilian, S. An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller. Int J Man Mach Stud 1975, 7, 1–13. [Google Scholar] [CrossRef]
  20. Mamdani, E.H. Advances in the Linguistic Synthesis of Fuzzy Controllers. Int J Man Mach Stud 1976, 8, 669–678. [Google Scholar] [CrossRef]
  21. Mamdani, E.H. Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Synthesis. IEEE Transactions on Computers 1977, C–26, 1182–1191. [CrossRef]
  22. Ross, T.J. Fuzzy Logic with Engineering Applications: Third Edition; Third edit.; John Wiley & Sons, Ltd: Chichester, UK, 2010; ISBN 9781119994374.
  23. Mencar, C.; Gallo, C.; Mantero, M.; Tarsia, P.; Carpagnano, G.E.; Foschino Barbaro, M.P.; Lacedonia, D. Application of Machine Learning to Predict Obstructive Sleep Apnea Syndrome Severity. Health Informatics J 2020, 26, 298–317. [Google Scholar] [CrossRef]
  24. Sun, L.M.; Chiu, H.W.; Chuang, C.Y.; Liu, L. A Prediction Model Based on an Artificial Intelligence System for Moderate to Severe Obstructive Sleep Apnea. Sleep and Breathing 2010 15:3 2010, 15, 317–323. [Google Scholar] [CrossRef] [PubMed]
  25. Ramesh, J.; Keeran, N.; Sagahyroon, A.; Aloul, F. Towards Validating the Effectiveness of Obstructive Sleep Apnea Classification from Electronic Health Records Using Machine Learning. Healthcare 2021, Vol. 9, Page 1450 2021, 9, 1450. [Google Scholar] [CrossRef] [PubMed]
  26. Ferreira-Santos, D.; Rodrigues, P.P. A Clinical Risk Matrix for Obstructive Sleep Apnea Using Bayesian Network Approaches. Int J Data Sci Anal 2019, 8, 339–349. [Google Scholar] [CrossRef]
  27. Zoroglu, C.; Turkeli, S. Fuzzy Expert System for Severity Prediction of Obstructive Sleep Apnea Hypopnea Syndrome. The journal of cognitive systems 2017, 2. [Google Scholar]
  28. Matthews, J.M.; Kwiatkowska, M.; Matthews, L.R. A Preliminary Fuzzy Model for Screening Obstructive Sleep Apnea. Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting, IFSA/NAFIPS 2013 2013, 187–191. [CrossRef]
  29. Wasserman, L. All of Statistics : A Concise Course in Statistical Inference. In; Springer: New York, 2004; Vol. 26 ISBN 978-0-387-21736-9.
  30. Hevner, A.R.; March, S.T.; Park, J.; Ram, S. Design Science in Information Systems Research. MIS Q 2004, 28, 75–105. [Google Scholar] [CrossRef]
  31. Hevner, A.R.; Chatterjee, S. Design Research in Information Systems: Theory and Practice; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-6107-5. [Google Scholar]
  32. App Designer. Available online: https://www.mathworks.com/products/matlab/app-designer.html (accessed on 18 October 2022).
  33. Classification Learner. Available online: https://www.mathworks.com/help/stats/classificationlearner-app.html (accessed on 18 October 2022).
  34. Fuzzy Logic Toolbox - MATLAB. Available online: https://www.mathworks.com/products/fuzzy-logic.html (accessed on 1 November 2022).
  35. Imbalanced-Learn. Available online: https://imbalanced-learn.org/dev/index.html (accessed on 18 October 2022).
  36. Agresti, A. Categorical Data Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; ISBN 0471360937. [Google Scholar]
  37. Powers, D.; Xie, Y. Statistical Methods for Categorical Data Analysis; Emerald Group Publishing, 2008.
  38. Mohammed, A.J.; Hassan, M.M.; Kadir, D.H. Improving Classification Performance for a Novel Imbalanced Medical Dataset Using Smote Method. International Journal of Advanced Trends in Computer Science and Engineering 2020, 9, 3161–3172. [Google Scholar] [CrossRef]
  39. Chawla, N. v.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. Journal of Artificial Intelligence Research 2002, 16, 321–357. [Google Scholar] [CrossRef]
  40. Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. Encyclopedia of Database Systems 2009, 532–538. [Google Scholar] [CrossRef]
  41. Deborah, L. Thurston Utility Function Fundamentals. In Decision Making in Engineering Design; ASME Press: New York, USA, 2006. [Google Scholar]
  42. Sundar Krishnamurty Normative Decision Analysis in Engineering Design. In Decision Making in Engineering Design; ASME Press: New York, USA, 2006.
  43. Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis; Prentice Hall, 2009; Vol. 87; ISBN 9780138132637.
  44. Cooper, J.C.B. Artificial Neural Networks versus Multivariate Statistics: An Application from Economics. http://dx.doi.org/10.1080/02664769921927 2010, 26, 909–921. [CrossRef]
  45. Wang, C.Y.; Lee, T.F.; Fang, C.H.; Chou, J.H. Fuzzy Logic-Based Prognostic Score for Outcome Prediction in Esophageal Cancer. IEEE Trans Inf Technol Biomed 2012, 16, 1224–1230. [Google Scholar] [CrossRef]
  46. Yazdanbakhsh, O.; Dick, S. Forecasting of Multivariate Time Series via Complex Fuzzy Logic. IEEE Trans Syst Man Cybern Syst 2017, 47, 2160–2171. [Google Scholar] [CrossRef]
  47. Egrioglu, E.; Aladag, C.H.; Yolcu, U.; Uslu, V.R.; Basaran, M.A. A New Approach Based on Artificial Neural Networks for High Order Multivariate Fuzzy Time Series. Expert Syst Appl 2009, 36, 10589–10594. [Google Scholar] [CrossRef]
  48. Smithson, M. Multivariate Analysis Using ‘and’ and ‘Or. ’ Math Soc Sci 1984, 7, 231–251. [Google Scholar] [CrossRef]
Preprints 70230 g001
Figure 1. Figure 1. Flow diagram of the clinical decision support system. The different information flows between the different stages that compose the system are shown. Stage 1 is for data collection, Stage 2 is subdivided into Stage 2.a for preprocessing and statistical inference and Stage 2.b for symbolic inference and, finally, Stage 3 is for generation of alerts and decision making.
Figure 1. Figure 1. Flow diagram of the clinical decision support system. The different information flows between the different stages that compose the system are shown. Stage 1 is for data collection, Stage 2 is subdivided into Stage 2.a for preprocessing and statistical inference and Stage 2.b for symbolic inference and, finally, Stage 3 is for generation of alerts and decision making.
Preprints 70230 g001
Preprints 70230 g002
Figure 2. The cascade of expert systems in detail.
Figure 2. The cascade of expert systems in detail.
Preprints 70230 g002
Preprints 70230 g003
Figure 3. Screenshot of the application. (1.a) and (1.b) are related to the stage of collecting relevant patient’s information. (2.a) and (2.b) are referred to the stage of data processing. (3) is related to generating alerts and recommendations.
Figure 3. Screenshot of the application. (1.a) and (1.b) are related to the stage of collecting relevant patient’s information. (2.a) and (2.b) are referred to the stage of data processing. (3) is related to generating alerts and recommendations.
Preprints 70230 g003
Preprints 70230 g004
Figure 4. Validation ROC curve for the apnea class of the Bagged Trees model.
Figure 4. Validation ROC curve for the apnea class of the Bagged Trees model.
Preprints 70230 g004
Preprints 70230 g005
Figure 5. Figure 5. Functional diagram of the inference system.
Figure 5. Figure 5. Functional diagram of the inference system.
Preprints 70230 g005
Preprints 70230 g006
Figure 6. Screenshot of the application.
Figure 6. Screenshot of the application.
Preprints 70230 g006
Table 2. Summary of the subjective data.
Table 2. Summary of the subjective data.
Subgroup Data Data type Commentary


Sleep time		 Hours of sleep Numerical -
Minutes until falling
asleep		 Numerical -
Prolonged intra-sleep awakenings Categorical No/Occasionally/Often
Subgroup Data Data type Commentary

Unrefreshing sleep		 Feeling of unrefreshing sleep Categorical No/Occasionally/Often
Daytime tiredness Categorical No/Occasionally/Often
Morning dullness Categorical No/Occasionally/Often
Subgroup Data Data type Commentary

Complicating sleep factors		 Unjustified multiple awakenings Categorical Yes/No
Nocturia Categorical No/Occasionally/Often
Breathless awakenings Categorical No/Occasionally/Often
Reported apneas Categorical No/Occasionally/Often


Snores		 Snorer Categorical No/In supine position only/Yes
High intensity snorer Categorical Yes/No
Snore related
awakenings		 Categorical No/Occasionally/Often
Table 3. Initial configuration of the inference system responsible for processing the ‘sleep time’ data group.
Table 3. Initial configuration of the inference system responsible for processing the ‘sleep time’ data group.
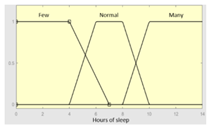
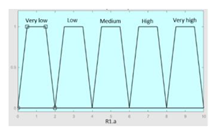
Inference system associated to the ‘sleep time’ data group
Input Data Range Output Risk Range
Hours of sleep 0–14 hours R1.a 0–10
Preprints 70230 i001 Preprints 70230 i002
Minutes until falling
asleep		 0–240 minutes Initial configuration
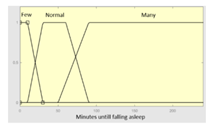Preprints 70230 i003 Fuzzy structure: Mamdani-type.
Membership function type: trapezoidal.
Defuzzification method: centroid [22].
Implication method: MIN.
Aggregation method: MAX.
Number of fuzzy rules: 46
Prolonged intra-sleep
awakenings		 0–10 Subset as an example of the 46 fuzzy rules
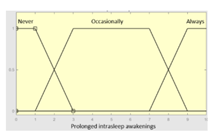Preprints 70230 i004 1. IF (Hours_of_sleep is Few) AND (Minutes_until_falling_asleep is Few) AND (Prolonged_intra-sleep_awakenings is Never) THEN (R1.a is Low).
2. IF (Hours_of_Sleep is Few) AND (Minutes_until_falling_asleep is Few) AND (Prolonged_intra-sleep_awakenings is Never) THEN (R1.a is Medium).
Graphical example of fuzzy rules 1 and 2
Preprints 70230 i005
Table 4. Initial configuration of the inference system responsible for processing the ‘unrefreshing sleep’ data group.
Table 4. Initial configuration of the inference system responsible for processing the ‘unrefreshing sleep’ data group.
Inference system associated to the ‘unrefreshing sleep’ data group
Input Data Range Output Risk Range
Feeling of
unrefreshing sleep		 0–10 R1.b 0 – 10
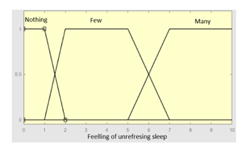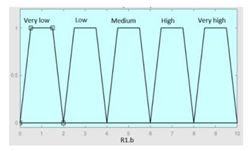Preprints 70230 i006 Preprints 70230 i007
Daytime tiredness 0–10 Initial configuration
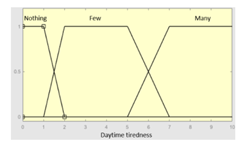Preprints 70230 i008 Fuzzy structure: Mamdani-type.
Membership function type: trapezoidal.
Defuzzification method: centroid [22].
Implication method: MIN.
Aggregation method: MAX.
Number of fuzzy rules: 45
Morning dullness 0–10 Subset as an example of the 45 fuzzy rules
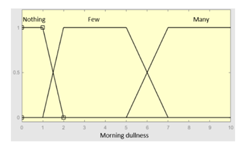Preprints 70230 i009 1. IF (Feeling_of_unrefreshing_sleep is Nothing) AND (Daytime_tiredness is Nothing) AND (Morning_dullness is Nothing) THEN (R1.b is Very_low).
2. IF (Feeling_of_unrefreshing_sleep is Nothing) AND (Daytime_tiredness is Nothing) AND (Morning_dullness is Few) THEN (R1.b is Very_low).
Graphical example of fuzzy rules 1 and 2
Preprints 70230 i010
Table 5. Initial configuration of the inference system responsible for processing the ‘complicating sleep factors’ data group.
Table 5. Initial configuration of the inference system responsible for processing the ‘complicating sleep factors’ data group.
Inference system associated to the ‘complicating sleep factors’ data group
Input Data Range Output Risk Range
Unjustified multiple awakenings 0–1 R2.a 0 – 10
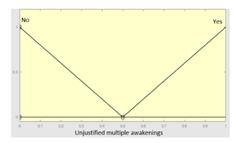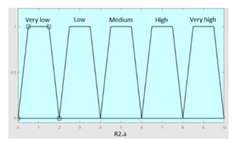Preprints 70230 i011 Preprints 70230 i012
Nocturia 0–10 Initial configuration
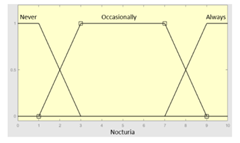Preprints 70230 i013 Fuzzy structure: Mamdani-type.
Membership function type: trapezoidal.
Defuzzification method: centroid [22].
Implication method: MIN.
Aggregation method: MAX.
Number of fuzzy rules: 78
Breathless awakenings 0–10
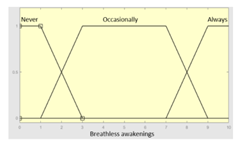Preprints 70230 i014
Reported apneas 0–10 Subset as an example of the 78 fuzzy rules
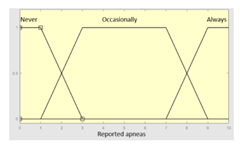Preprints 70230 i015 IF (Reported_apneas is Always) THEN (R2.a is Very_high)
IF (Unjustified_multiple_awakenings is No) AND (Nocturia is Never) AND (Beathless_awakenings is Never) AND (Reported_apneas is Never) THEN (R2.a is Very_low)
Graphical example of fuzzy rule 1
Preprints 70230 i016
Table 6. Initial configuration of the inference system responsible for processing the ‘snores’ data group.
Table 6. Initial configuration of the inference system responsible for processing the ‘snores’ data group.
Inference system associated to the ‘snores’ data group
Input Data Range Output Risk Range
Snorer 0–2 R2.b 0 – 10
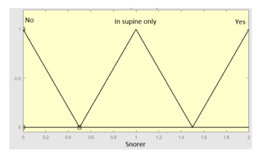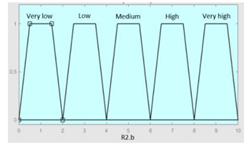Preprints 70230 i017 Preprints 70230 i018
High intensity
snorer
 0–1 Initial configuration
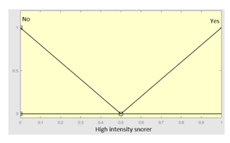Preprints 70230 i019 Fuzzy structure: Mamdani-type.
Membership function type: trapezoidal.
Defuzzification method: centroid [22].
Implication method: MIN.
Aggregation method: MAX.
Number of fuzzy rules: 30
Snore related
awakenings		 0 – 10 Subset as an example of the 30 fuzzy rules
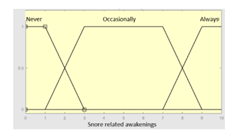Preprints 70230 i020 1. IF (Snorer is No) THEN (R2.b is Very_low)
2. IF (Snorer is In_dorsal_position_only) AND (High_intensity_snorer is No) AND (Snore_related_awakenings is Never) THEN (R2.b is Very_low)
Graphical example of fuzzy rule 1
Preprints 70230 i021
Table 7. Initial configuration of the inference system responsible of processing risks R1.a and R1.b.
Table 7. Initial configuration of the inference system responsible of processing risks R1.a and R1.b.
Inference system for the processing of risks R1.a and R1.b
Input Data Range Output Risk Range
R1.a 0–10 R1 0–10
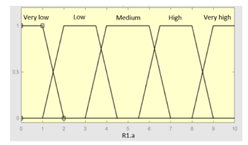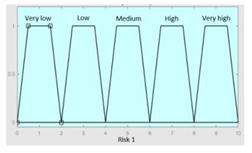Preprints 70230 i022 Preprints 70230 i023
R1.b 0–10 Initial configuration
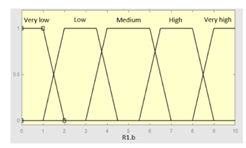Preprints 70230 i024 Fuzzy structure: Mamdani-type.
Membership function type: trapezoidal.
Defuzzification method: centroid [22].
Implication method: MIN.
Aggregation method: MAX.
Number of fuzzy rules: 49
Subset as an example of the 49 fuzzy rules
  • IF (R1.a is Very_low) AND (R1.b is Very_low) THEN (R1 is Very_low)
  • IF (R1.a is Very_low) AND (R1.b is Low) THEN (R1 is Very_low)
  • IF (R1.a is Very_low) AND (R1.b is Low) THEN (R1 is Low)
Graphical example of fuzzy rules 1, 2 and 3
Preprints 70230 i025
Table 8. Initial configuration of the inference system responsible of processing risks R2.a and R2.b.
Table 8. Initial configuration of the inference system responsible of processing risks R2.a and R2.b.
Inference system for the processing of risks R2.a and R2.b
Input Data Range Ouput Risk Range
R2.a 0–10 R2 0–10
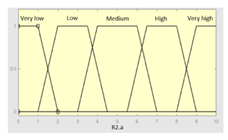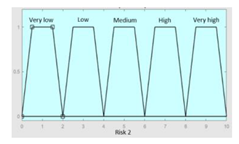Preprints 70230 i026 Preprints 70230 i027
R2.b 0–10 Initial configuration
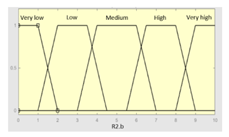Preprints 70230 i028 Fuzzy structure: Mamdani-type.
Membership function type: trapezoidal.
Defuzzification method: centroid [22].
Implication method: MIN.
Aggregation method: MAX.
Number of fuzzy rules: 57
Subset as an example of the 57 fuzzy rules
  • IF (R2.a is Very_low) AND (R2.b is Very_low) THEN (R2 is Very_low)
  • IF (R2.a is Low) AND (R2.b is Very_low) THEN (R2 is Very_low)
  • IF (R2.a is Low) AND (R2.b is Very_low) THEN (R2 is Low)
Graphical example of fuzzy rules 1, 2 and 3
Preprints 70230 i029
Table 9. Initial configuration of the inference system responsible of processing risks R1 and R2.
Table 9. Initial configuration of the inference system responsible of processing risks R1 and R2.
Inference system for the processing of risks R1 and R2
Input Data Range Output Risk Range
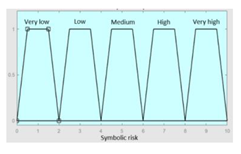
R1 0–10 Symbolic Risk 0–10
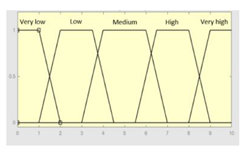Preprints 70230 i030 Preprints 70230 i031
R2 0–10 Initial configuration
Preprints 70230 i032 Fuzzy structure: Mamdani-type.
Membership function type: trapezoidal.
Defuzzification method: centroid [22].
Implication method: MIN.
Aggregation method: MAX.
Number of fuzzy rules: 57
Subset as an example of the 57 fuzzy rules
  • IF (R1 is Very_low) AND (R2 is Very_low) THEN (Symbolic_risk is Very_low)
  • IF (R1 is Very_low) AND (R2 is Low) THEN (Symbolic_risk is Very_low)
  • IF (R1 is Very_low) AND (R2 is Low) THEN (Symbolic_risk is Low)
Surface
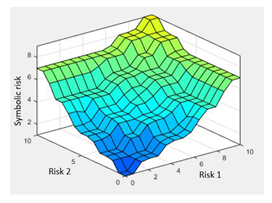Preprints 70230 i033
Table 10. Risk assessment thresholds and scores.
Table 10. Risk assessment thresholds and scores.
Level Case Score
Level 1 If Risk < Limit 1 (L1) 0
Level 2 Limit 1 (L1) ≤ Risk < Limit 2 (L2) 1
Level 3 If Risk ≥ Limit 2 (L2) 2
Table 11. Summary of recommendations.
Table 11. Summary of recommendations.
Case Recommendation
T < 2 Non-OSA case, do not perform diagnostic studies
T = 2 Doubtful case. Medical team should assess whether further tests or a new medical evaluation after a period of time is necessary to reconsider the patient’s condition.
T ≥ 3 Possible OSA case, perform diagnostic studies
Table 12. Graphical representation of the assessment process.
Table 12. Graphical representation of the assessment process.
Symbolic Risk
Statistical Risk Case Risk < L1 L1 ≤ Risk < L2 Risk ≥ L2
Case Level & Score Level 1 (0) Level 2 (1) Level 3 (2)
Risk < L1 Level 1 (0) 0+0 0+1 0+2
Level 1 ≤ Risk < L2 Level 2 (1) 1+0 1+1 1+2
Risk ≥ L2 Level 3 (2) 2+0 2+1 2+2
Table 13. Objective data of the case patient.
Table 13. Objective data of the case patient.
General and anthropometric data
Sex Male
Age 34
Weight (kg) 85
Height (cm) 186
Neck perimeter (cm) 46
Habits
Smoking habits No
Cigarettes per day -
Years smoking -
Drinking habits Occasionally
Grams of alcohol -
Diagnosed conditions -
Prescribed treatments -
Table 14. Subjective data of the case patient.
Table 14. Subjective data of the case patient.
Sleep time group
Hours of sleep 7 hours
Minutes until falling asleep 20 minutes
Prolonged intra-sleep awakenings Often
Unrefreshing sleep group
Feeling of unrefreshing sleep No
Daytime tiredness No
Morning dullness Occasionally
Complicating sleep factors group
Unjustified multiple awakenings No
Nocturia Often
Breathless awakenings No
Reported apneas Often
Snores group
Snorer Yes
High intensity snorer Yes
Snorer related awakenings Occasionally
Table 15. Thresholds for the first risk assessment of the case study.
Table 15. Thresholds for the first risk assessment of the case study.
Level Case Level interpretation
Level 1 IF Risk < 45 THEN Level 1 Non-OSA case
Level 2 IF 45 ≤ Risk < 60 THEN Level 2 Doubtful case
Level 3 IF Risk ≥ 60 THEN Level 3 Possible OSA case
Table 16. Risk assessment of the case study.
Table 16. Risk assessment of the case study.
Symbolic Risk
Statistical Risk Case Risk < 45 45 ≤ Risk < 60 Risk ≥ 60
Case Level & Score Level 1 Level 2 Level 3
Risk < 45 Level 1 - X -
45 ≤ Risk < 60 Level 2 - - -
Risk ≥ 60 Level 3 - - -
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated