Delineation of Orchard, Vineyard, and Olive Trees Based on Spectral and Phenology Metrics using Time-Series of Sentinel-2 during 2016-2021

The characteristics of the Sentinel-2 mission with a decametric resolution and frequent acquisitions allow to improve the identification of crops. The majority of the studies on crop classification using RS were targeted at herbaceous and gramineous crop classes while fewer results were obtained on woody crops which present a strong variability in management practices that make their identification difficult. Thus, this study aimed to propose a rapid, accurate, and cost-effective analytical approach for the delineation of fruit orchards (OC), vineyards (VY), and olive groves (OL) in the Mediterranean (Southern France) considering two locations. A classification based on phenology metrics (PM) de-rived from temporal Sentinel-2 time series was developed to perform the classification. The PM were computed by fitting a double logistic model on temporal profiles of vegeta-tion indices to delineate OC, VY, and a DC class gathering all remaining surfaces. The generated PM were introduced in a random forest (RF) algorithm to identify woody crops across the two sites. The method was tested on different vegetation indices, the best results being obtained with the leaf area index (LAI). To delineate OL in the DC class, the tem-poral features of the green chlorophyll vegetation index (GCVI) were found to be the most appropriated with a typical drop of the signal during the mid-season (DOY 150-250). As a final result, we obtained an overall accuracy ranging from 89-96% and Kappa of 0.86-0.95 by considering each study site and year (2016-2021), separately. This accuracy is much better than applying the RF algorithm on the LAI times series, which led to a Kappa rang-ing between 0.3 and 0.52 and demonstrates the interest of using phenological traits rather than the raw time series of the RS data. The method can be well reproduced from one year to another. Moreover, it is possible to apply the classification model of a given year to an-other, keeping good accuracy. This is an interesting feature to reduce the burden of col-lecting ground truth information. On the contrary, the use of a classification model cali-brated in one site and applied to another led to a strong degradation of the classification accuracy. Woody crop phenology is dependent on site climatic conditions as well as the cultivar and management practices that can differ from one site to another.

Keywords:

Subject: Environmental and Earth Sciences - Environmental Science

1. Introduction

Among the several hazards of climate change and global warming on natural resources, the most significant threat is its implication on the accessible availability of freshwater. Unequivocally, the agricultural sector is the highest consumer of water universally with irrigation accounting for about 70% of freshwater withdrawals [1,2,3]. Considering the constant increase in the world’s population which is a supplementary pressure on agricultural produce to meet the populace’s food demands (food security threats). Satisfying such growing food requirements is driving policymakers to escalate and bolster activities related to agriculture and consequently increasing agricultural water needs for irrigation motives. Thus, supervision of irrigation activities is crucial to buttress the execution of water management policies and to improve water use productivity [4,5]. Supervision of irrigation activities not only encompasses spatial assessments of areas under irrigation but also irrigation strategies [4,5,6,7]. To match the water requirements and resources, good organizational groundwork is required for irrigation scheduling [8]. Among the answers to good irrigation scheduling is the presentation of extensively accurate spatial mapping of areas under irrigation [9] and the characterization of crop systems with their irrigation strategies [10]. Therefore, mapping the different irrigated crops is an important issue in water management. The Mediterranean region is specifically sensitive to variations in agricultural activities and land use due to its exposure to excessive climatic threats [11]. In the past years, policymakers have been forced to regulate irrigation practices in some areas such as the Crau region due to harsh drought conditions. Around half of the region is dedicated to agriculture [12]. However, irrigation patterns and water quantity depends on crop type, for instance, permanent grasslands are mostly irrigated via flooding leading farmers to use more water than needed and that has prompted scientist to delineate fields like irrigated permanent grasslands [11,13] and field crops [14] like corn among others for accurate water requirement modelling and sharing rule policy. On the contrary, less attention has been given to the delineations of perennial woody crops such as fruit trees of orchards, vineyards, and olive groves that are common in the Mediterranean.

In recent times, various types of research were conducted on the supervision of irrigated areas using both optical and Synthetic Aperture Radar [4,7,8,10,13,15]. The metric of irrigation assessments (i.e both frequency and mapping) using SAR information depends on the changes in surface soil moisture which well corresponds with the backscattering of the radar coefficient [16]. Contrary to the SAR, the optical data were utilized mostly to delineate surfaces under irrigation using the variations in the temporal behaviors. Such variations are probably visible using vegetation indices obtained from multispectral optical satellites like normalized difference vegetation index (NDVI), and normalized difference water index (NDMI) among others [17]. However, the identification of irrigated cropping systems is an important step to better characterize the irrigation practices and the volumes of water mobilized, the knowledge of which is crucial for water resource management. Crop classification from remote sensing data is a field that has been widely studied for decades and is gaining interest with new satellite missions such as the Sentinel missions that have considerably improved temporal resolution and spectral richness. Progress in the identification of grasslands and field crops is undeniable [11,13,14]. On the other hand, the case of woody perennial crops such as fruit orchards, vineyards, or olive groves might pose more problems and progress is still possible. The difficulty comes mainly from the fact that these covers have a great diversity of development because of the age of the plantation, their density, the mode of management such as pruning, and the confusion that there can be with other plant covers (non irrigated meadows, wetlands...).

Concerning woody crops, high-resolution Landsat TM images were used to identify crop classes (olive and citrus) in Marrakech, Morocco using the temporal profile of normalized difference vegetation index (NDVI) simply by setting a threshold of maximum and minimum values of the NDVI across the season [18] leading to an overall accuracy (OA) of 83%. Peña et al. [19] classified fruit trees by comparing Landsat 8 image times series considering the full band, the normalized difference water index (NDWI), and the normalized difference vegetation index (NDVI). The best results were obtained using the full spectral information, in particular with visible and SWIRS bands (OA = 94%). while the NDVI led to the worst results. They tested the interest of dates and highlighted that the beginning (greenness) and end (senescence) of the growing cycle were the most significant phases for the separation. They obtained an OA of 94% with four dates. The interest in image acquisition during the greenness period was confirmed in [20]. In this study, it was demonstrated that up to seven types of orchards can be classified by considering all Landsat 8 spectral bands as well as a combination of bands. Recently tree fruits crop type mapping was conducted in Egypt by examing various temporal windows, spectral approaches, and several combination methods between S1 (Sentinel-1) and S2 (Sentinel-2) data inserted into RF [21]. Good accuracy was found with S2 alone while improvement was found by combining the textural S1 information with the spectral S2 observations, which led to an OA of 96%. In [22] a classification was done to delineate apple orchards, vineyards, and annual crops in Iran. Phenology was used to select the optimal dates. By combining S1, Landsat 8 images, and digital elevation model, an OA of 89% was obtained. Another recent study was conducted in Juybar, Iran where an automatic approach to map citrus orchards was implemented using S1 and S2 and the ALOS digital surface model (DSM) [23]. Without training and by considering a very large number of images (148), textural and spectral features, it was possible to separate citrus and non-citrus surface with an OA of 99.7%. The approach is a very favorable case with evergreen trees (citrus), which presents a contrast with the other surfaces. These studies have shown that good results can be obtained with perennial woody crop mapping. The quality of the results obtained came from the number of images used, the choice of the dates considered, and the complementarity between spectral indices in the optical domain and textural indices derived from SAR images. The quality of the classifications also came from the specificity of the signatures of the various covers. In this respect, the phenology makes it possible to target the dates of observation to be considered in particular during the phases of greenness and senescence. In past studies, phenology is not used directly as a classification criterion but more to determine optimal dates. The use of phenological traits may present advantages in the exploitation of time series by the fact that they are relatively independent of the dates of acquisition. This can be interesting in a situation where partial cloud cover frequent in the temperate zone, can disturb the homogeneity of the time series from one point to another in the area to be mapped. This can considerably disturb the learning algorithms.

Conventional crop phenology also termed ground phenology (GP) [24] is the particular re-occurring events of crop life traits like budburst, leaf development, senescence, flowering, and maturity [25], which is laborious to collect, time-consuming and expensive as well [24,26]. These GP observations correlate to key particular plant physiological activities that govern natural resource uptake by plants. Despite GP remaining objective and precise, its characterization over a wide-scale area remains a challenge [27]. Satellite remote sensing is capable of offering time series on vegetation development with a short revisit period, which can serve as a source of data to monitor vegetation phenology at a local and regional scale with proxies termed land surface phenology (LSP) [28]. Phenology metrics (PM) obtained from the analysis of vegetation indices time series were often used to characterize the LSP [29,30,31]. In the past, most of the studies related to crop phenology were done using medium-resolution sensors (MODIS, AVHRR) allowing frequent acquisition over the whole globe [24]. The spatiotemporal resolution was enhanced by combining those medium-resolution sensors, with high-resolution (LANDSAT) [32,33]. Most research on LSP carried out using information from these satellite sensors is faced with a drawback of mixed pixels and thus, restricted in their implementation across complex or fragmented terrains [34]. Such a drawback can be now overcome by using S2, which allows accurate supervision of crop changes [35]. PM are linked to the variation of the seasonal pattern in cropland surfaces derived from satellite observations [36]. The most common patterns are the start of the season (SOS), the peak of the growing season (POS), the end of the season corresponding to the senescence (EOS), and the length of the season (LOS) [36,37]. In other terms, in a growing year season, the major phases of phenology controlling the spectral patterns of vegetation are (i) the date of photosynthetic commencement (green-up), (ii) the date of maximum plant green leaf (maturity), (iii) the date of decline in photosynthetic activities (senescence) [38]. The mentioned PM are normally computed from the common normalized difference vegetation index (NDVI) or other popular indices for instance [37,39]. But despite that, the NDVI method can bring some drawbacks, like restricted sensitivity to vegetation photosynthetic dynamics [40] while biophysical variables like LAI (leaf area index) can improve the PM, particularly for farmlands. The use of phenology as a classifier for crop mapping has been applied in many studies. In [41] PM (SOS, EOS, LOS and the peak integral reflecting the photosynthetic activity) were derived from Modis NDVI time series using the TIMESAT algorithm [42] and used to characterize different agricultural systems (fallow, rainfed crop, irrigated crop and irrigated perennial). It was shown that the PM were able to monitor agricultural system evolution across two decades 2000-2019 with an OA ranging from 93% and 97%. In that case, irrigated perennials were evergreen orchards (citrus) which makes the distinction with annual crops easier. According to [43], they developed a phenology-based approach to delineate wheat and barley by identifying the heading date using temporal feature of the different S2 bands. Good results were obtained (OA of 76%)across three sites in Iran, and the USA (North California and Idaho). These studies, among others, have shown that the PM can be used as a classifier to map crops. The quality of the results depends very much on the specificity of the temporal signatures of the different crops to be identified and the diversity of plant cover that can be found in a given class. Moreover, the added value of using PM rather than time series of spectral and/or vegetation index data was not yet demonstrated.

In this study, we want to analyze the performance of a classification based on the use of PM as a classifier on a complex territory with a great diversity of crops and natural environments. The objective is to characterize the main classes of perennial woody crops, namely fruit orchards (OC), vineyards (VY), and olive groves (OL), which are cropping systems with different irrigation strategies. Within these classes, there is a great diversity of situations marked by the type of cover, pruning practices, or soil management in the inter-row. The study is carried out on two sites about 100 km apart but with different climatic conditions and plant cover other than the desired perennial woody crops. The challenge will be to evaluate the performance of classifications carried out with PM, to analyze the added value of using PM in comparison with approaches based on the time series of vegetation index, and to establish the genericity of a classification model from one year to another or from one site to another.

2. Materials and Methods

2.1. Study Sites

The study was conducted across two different locations in South-East France namely the Ouveze-Ventoux and the Crau area (Figure 1). These study sites are representative of the Mediterranean with a strong diversity of cropping systems including fruit orchards (cherries plums, peaches apricots), olives and vineyards.

The Ouveze-Ventoux is located at 44° 10’ N and 5° 16’ E (with the lowest and highest elevation of 230 and 630 m a.s.l) in the South France of the Provence region with a surface area of 59 km² and forest and semi-natural environments inhabiting about 57.7% [44], associated to specific bioclimatic and geomorphological surroundings. It has the typical Mediterranean climate identified by cold and moist winters and dry and hot summers. Annual precipitation is about 750 mmmm per year, annual mean temperature of 12.6°C; The number of plots on Ouveze-Ventoux is about 3500 of which OC occupied about 40% (1413), and VY occupied about 34% (1186) of the cultivated area.

The Crau is positioned between 43° 38’ N and 5 °00’ E (5m a.s.l) close to the Rhône delta in South Eastern France with a surface area of 600 km² and a typical Mediterranean climate [13]. The annual average rainfall is 600 mm (non-uniform). Potential evapotranspiration of 1100 mm and mean air temperature of 14.8 °C [11,45,46]. The soils are shallow ranging from 60-80 cm having 90% stones making water retention capacity to be very low. Soils irrigated via flooding methods have a loamy surface soil layer from the constantly deposited sediments leading to a layer depth of about 60 cm depending on the length of the irrigation period [11]. The water used for flooding irrigation contributes to more than 75% of the groundwater table which is used for irrigation of intensive orchards and market garden productions, domestic and industrial purposes to about 280,000 people around the southern part of the area [45,46]. The number of plots in Crau is about 17980 of which OC occupied about 11% (2050), VY occupied about 4% (790) and OL occupied about 5% (1050) of the cultivated area.

2.2. Ground Truth Information

The collection of ground truth data was conducted in the two study areas during the 2016-2021 period. Plot boundaries were drawn in both sites, starting from the cadastral survey and the RPG (Régistre Parcellaire Graphique), which is used for subsidy allocation to farmers. The boundaries were fine-tuned using an aerial picture to isolate homogeneously managed surfaces. The whole area was therefore segmented with 17980 and 3501 plots in the Crau and Ouveze-Ventoux areas, respectively (but 16680 and 1601 plots were used in this study due to exclusion of 20 meters from each plot boundary to avoid the effect of mixed pixels at the plot border). A subset of the controlled plot was surveyed and identified, and crop types were taken into note during field visits. In the Ouveze-Ventoux study area, a total of 234 plots (Figure 3) were identified as OC, and other classes (DC), which encompasses field crops, dry grasslands, and greenhouses. In the Crau study area, a total of 243 (out of 18058) plots were selected of which are OC, (35), (60), and DC (60) encompassing greenhouse, dry grass, forest, field crop, irrigated grassland, and wetland. Aerial photographs from IGN (the French national mapping service) and Google Earth images collected during the 2016 to 2021 period were used to understand anomalies found in vegetation time series derived from satellite, principally to assess surface heterogeneity and change in management between field visits. The number of plots in each class is given in Table 1. fields were split into two groups dedicated to the training and the validation. As there is a very few numbers of olive plots, the OL class was not considered in the Ouveze Ventoux site

2.3. Satellite Data

In our study, time-series of Sentinel-2 (S2) optical images were utilized and were obtained from both Sentinel-2A and Sentinel-2B of all dates in a given year within the 2016-2021 period considering the visible (B2, B3, and B4), the near-infrared (B8 and mid-infrared (B11 our B12) bands. We utilized the open-source service center to obtain images (https://www.theia-land.fr/, accessed on 17 May 2022), it offers cloud treatments (cloud mask) to eliminate pixels influenced by clouds (images with > 30% cloud cover), and for this obvious reason, the number of images utilized vary across study sites and years. Since Sentinel-2B satellites were functional in the time of 2017, lesser dates were obtained from the 2016-2017 year. The number of cloud-free images (with <30% cloud cover and subsequently masked) used for each year across the two study sites is reported in Table 2. An additional cloud filtering was added when creating the time series for each plot. The dates for which there was at least one pixel in the considered plot impacted by clouds were removed. This led, for a given site, to have time series with different dates from one plot to another.

2.4. Vegetation Indices and Biophysical Variables

To begin with, various vegetation indices and biophysical variables were utilized for spectral-temporal analysis which was subdivided into those highlighting greenness like the popular normalized difference vegetation index (NDVI), enhanced vegetation index (EVI), green chlorophyll vegetation index (GCVI) to those highlighting moisture like normalized difference moisture index (NDMI), land surface water index (LSWI), and finally on biophysical variables like leaf area index (LAI), fraction vegetation cover (FCOVER) and the fraction of absorbed photosynthetically active radiation (FAPAR) as summarized in Table. 3. The biophysical variables used in this study were computed with the BVNET algorithm by utilizing the B2, B3, B4, and B8 bands. The algorithm is robust and has been fused into the S2 toolbox developed by the European Space Agency, it operates on the principles of neural network calibrated (trained) on simulated spectral reflectance utilizing a radiative transfer model [47] and time series of LAI implemented across every 10-m spatial resolution. In each plot polygon across the two study sites, a buffer of 20 meters was removed to avoid the impact of mixed pixels at the plot boundary. The plot mean was computed by averaging the vegetation indices of all pixels in a given buffered polygon using the zonal statistics function in R [48] which was the values taken for the land classification.

Table 3. List of tested vegetation indices and biophysical variables.

Full Name	Index	Formula	Reference
Canopy greenness-related vegetation indices
Normalized Difference Vegetation Index	NDVI	$\frac{N I R - R E D}{N I R + R E D}$	[49]
Green Normalized Difference Vegetation Index	GNDVI	$\frac{N I R - G R E E N}{N I R + G R E E N}$	[50]
Enhanced Vegetation Index	EVI	$2.5 * \frac{N I R - R E D}{N I R + C 1 * R E D - C 2 * B L U E + L}$	[51]
Transformed Soil Adjusted Vegetation Index	TSAVI	$a * \frac{N I R - a * R E D - b}{R E D + a * (R E D + a (N I R - b) + c * (1 + a^{2})}$	[52]
Atmospherically Resistant Vegetation Index	ARVI	$\frac{N I R - (R E D - 1 * (B L U E - R E D))}{N I R + (R E D - 1 * (B L U E - R E D))}$	[53]
Green Chlorophyll Vegetation Index	GCVI	$\frac{N I R}{G R E E N} - 1$	[54]
Water-related vegetation indices
Normalized Difference Moisture Index	NDMI	$\frac{N I R - S W I R 12}{N I R + S W I R 12}$	[55]
Land Surface Water Index	LSWI	$\frac{N I R - S W I R 1}{N I R + S W I R 1}$	[56]
Biophysical variables
Leaf Area Index	LAI		[47]
Fraction Vegetation Cover	FCOVER		[47]
Fraction of Absorbed Photosynthetically Active Radiation	FAPAR		[47]

2.5. Time Series Metric Derivation for Classification

In our study, vegetation indices time series were fitted to an analytical model that represents the development of plants in relation to their phenology and uses the parameters of such relationships (PM) as a classifier used in the land classification. This is a significant variation from conventional classifiers which target directly vegetation indices or diffusion of surface reflectance. PM were generated via a double sigmoid fitting function as shown in equation 1 [57,58].

V (t) = v m i n + v a m p (\frac{1}{1 + e^{m 1 - n 1 t 1}} - \frac{1}{1 + e^{m 2 - n 2 t 2}})

(1)

Where V(t) stands for a given vegetation index at time t, vmin , and vamp are minimum (background greenness) and amplitude parameters of one year respectively, m₁, n₁, m₂, and n₂ are parameters controlling the curve shape (Figure 5). Some critical points are important to highlight as t₁ = m₁/n₁, which is the inflection point within the growth period while t₂ = m₂/n₂ corresponds to the inflection point at the end of the season during the leave senescence phase. Quantities t₁ and t₂ can be used as proxies of the start of the season (SOS) and end of the season (EOS), respectively [59]. Parameters n₁ and n₂ reflect the slope at the inflection points, t_1, and t₂.

With deciduous trees and annual crops, t₁ occurred when leaves are growing while t₂ corresponds to leave senescence. It is expected that parameters involved in equation 1 or their derivatives are specific to a given crop and thus can be used in calibration schemes. Furthermore, since t₁ is strained by the whole structure of the phenology, it is rarely impacted by noise while t₂ is more undetermined for trees since defoliation is slow which relies on water accessibility and conditions of weather [60]. The PM used in this study includes all these parameters plus the residual standard deviation (std) characterizing the difference between the fitted curves and the data. This difference might be high with vegetation development that not followed the standard shape for instance mowed grass that provide several peaks across the year. Therefore std provides good information to classify such a plot as DC.

2.6. Classification Method

Land use classification was made using a machine learning (ML) approach. Among the ML approaches, random forest (RF) is often used for land use classification.The approach is based on decision trees that can handle a lot of variables [61,62] which was the case in this study [62]. The RF method is a non-parametric ML approach that displays good results when compared to the conventional parametric approaches [43]. We optimized the performance of the RF model by tunning (automatically done) on two significant parameters namely mtry (indicates the number of predictors tested at each tree node) and ntree (displays the number of decision trees runs at each iteration), the accuracy of the classification was enhanced by tunning on the number of ntree (after starting with the default value of 500 trees) using hyperparameter tuning for each year and each site, the justification for such tunning according to the site is that each year has its specific features thus, we adopted the value that leads to the best performance of the classifier. Finally, the model output is decided by the number of a majority of votes by the classifier ensembles.

Regarding remote sensing and land surface phenology mapping, the RF classifier remains an effective approach [41] thus, for classification accuracy assessments ground truth information was equally split into two batches for each class namely calibration (50% proportional distribution from each class in the target population) and evaluation (50% from each crop class) datasets utilizing a spatial cross-validation method from the CAST package in R [63]. The aforementioned spatial cross-validation aid ensures the selected ground truth data of a similar field will be apportioned either in the calibration or evaluation dataset to keep away from over-fitting. Accuracy evaluations were done by the confusion matrix which gives the number of plots well classified on the diagonal and the number of erroneous detection between classes outside the diagonal with predicted class in column and actual class in line [64]. Accuracy metrics for the classification results include overall accuracy (OA), Kohen’s Kappa which removes the chance factor, user’s accuracy (UA), and producers’ accuracy (PA). These metrics were computed directly from classification routines or using the the CARET package in R [64] when the classification was done with different steps.

3. Results

3.1. Analysis of Temporal Profile for Orchard, Vineyard, and Olive Trees to Derive Spectral and Phenology Metrics

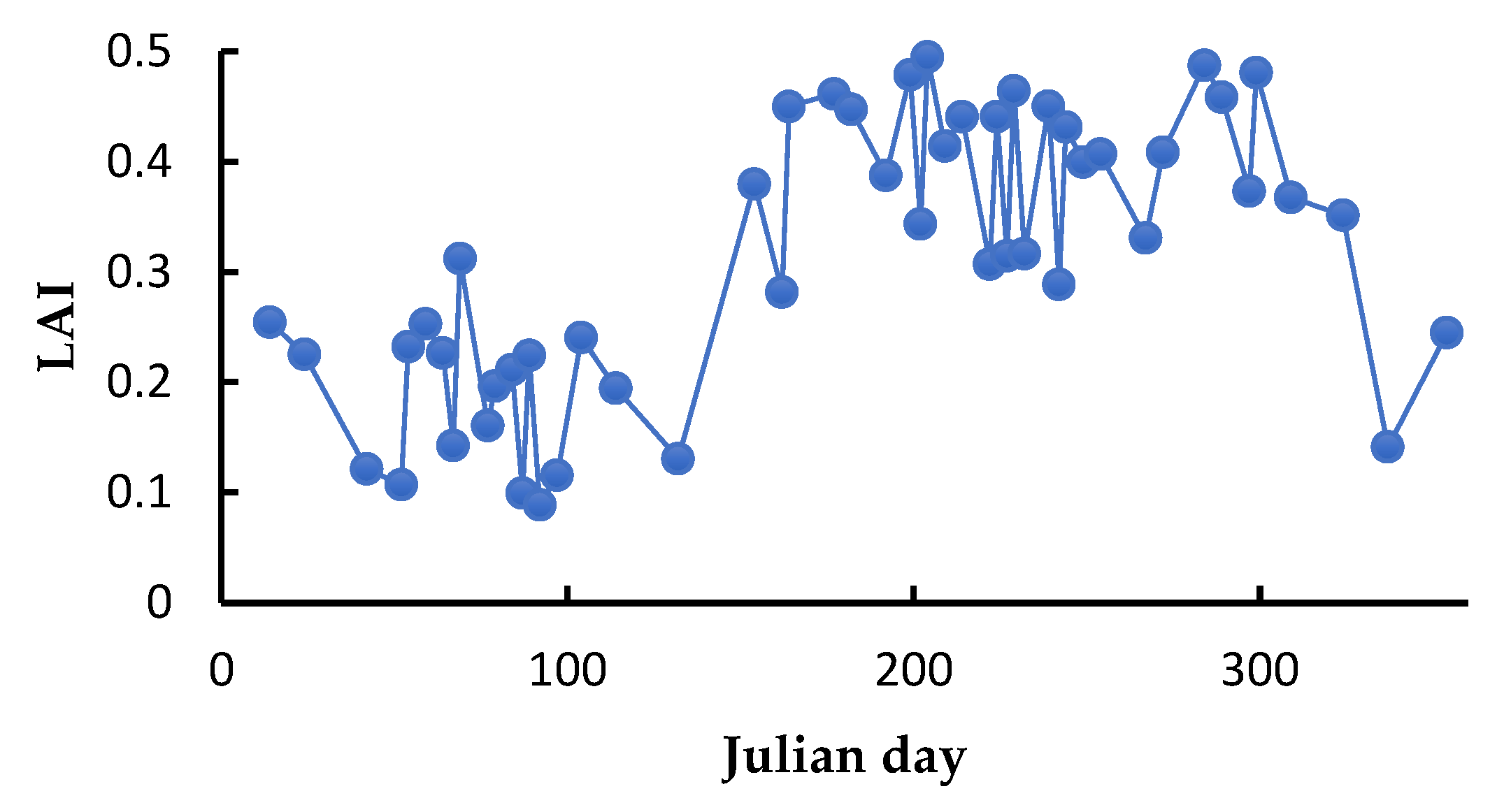
In both areas, OC and VY trees are deciduous and therefore exhibit a similar temporal pattern that is characterized by a maximum plateau in the summer. However, despite the close resemblance in the temporal patterns, there are still some significant features that can be used to separate them. For instance, OC trees mostly have SOS during 60-80 DOY and 100-120 DOY time intervals in the Crau and Ouveze-Ventoux areas, respectively. With VY, such intervals are delayed by about 30 days in both areas (Figure 4). Moreover, the growth rate with vineyards is more gradual. The differences between the areas are explained by the type of orchards and the climate, the Ouveze area being located more to the North with higher altitudes and thus lower temperature, which induces delays in phenology. The level of the plateau is variable. It depends on the age and density of the stands. However, in general, the values obtained in summer by the VY remain lower than those of the OC, except for the irrigated VY dedicated to table grapes. The LAI variations in mid-season can be variable according to the inter-row management and pruning practices. For a given field, the temporal features remain rather stable between years meaning that the classification algorithms might be applied over different years.

OL groves are observable in the Crau. The fact of having evergreen leaves leads to a very different temporal signature in comparison to that of OC and VY with variations rather governed by the soil cover. For the other surfaces (DC class), there is a great diversity of temporal signatures. For many of them, very different evolutions are observed (market gardening, irrigated meadows, dry meadows) from the previous cases, while ambiguities could appear with some surfaces such as wetlands which also show a seasonality comparable to OC plots.

3.2. Selection of Indices and Biophysical Variables Using the Proposed Method

Different vegetation indices related to canopy greenness, water, and, biophysical variables were analyzed to make the selection of the best indices and biophysical variables for the year 2021 in the Ouveze-Ventoux site. For all indices and biophysical variables, we fitted the double logistic model to infer the PM. These PMs together with statistical parameters qualifying the quality of the fit (std) were used as input in the RF algorithm to separate three classes: OC, VY, and DC. If all the considered variables representing vegetation development led to comparable results, the best results were obtained with LAI (Table 4). Moreover, using such a quantity is an advantage since it is directly comparable to field observations which facilitates its interpretation and thus the establishment of thresholds that could be useful to conduct the classification [13].

3.3. Accuracy Assessments

3.3.1. Delineation of Orchards and Vineyards in Ouveze-Ventoux Site

The classification in the Ouveze-Ventoux site was done by considering three classes namely OC, VY, and DC. The classification was made using the PM derived from the LAI temporal profiles (Table 5). Misclassified fields mainly came from confusion between VY and DC. In about half of the cases, the confusion came from young stands having a low vegetative development and thus a canopy signal which was not very clear as displayed in Figure 5. Therefore we merged young stands, presenting a maximum LAI lower than 0.5 to the DC class and replay the classification. By applying such a threshold, the classification accuracy was slightly improved (Table 6). The producer’s accuracy is revealing errors due to commission with OC class being the best with a producer’s accuracy of 0.96. To test the classification over time, the classification was done each year from 2016 to 2021 with results summarized in Table 7. The performance of the classification was slightly affected in 2017 and 2016 and the probable explanation for this might be ascribed to fewer acquisitions of S2 images since only one of the Sentinel 2 constellations was operated.

Figure 5. Temporal profile of a young VY misclassified as DC in Ouveze-Ventoux.

The classification was then applied to all fields large enough to have at least one pixel after applying a buffer of 20 meters on the plot boundary. The field distribution confirms the importance of OC and VY in the Ouveze-Ventoux area as shown in Figure 6 below.

3.3.2. Delineation of Orchards, Vineyards, and Olives in the Crau Site

On the Crau site, we find the three classes mapped on the Ouveze-ventoux site (VY, OC, and DC) to which an OL class has been added because of the high representation of olive groves. It is also worth noting the high diversity of the DC class with market gardening, steppe areas, wetlands, and field crops. First, we begin by conducting the classification considering the four classes (DC, OC, OL, VY). Results displayed in Table 8 exhibit rather weak results with particular difficulties in delineating DC and OL classes. We decided to perform the classifications in two steps. In the first step, we gathered both OL and DC in a single DC class. Then, in a second step, we delineated DC and OL. Results of the first step are reported in Table 9 showing a significant improvement with a Kappa rising from 0.69 to 0.91. Remarkably, results were also strongly improved for the VY class with user accuracy increasing from 0.28 to 0.61. Note that the OC class was very well characterized in spite of a large diversity of tree types and varieties. As for the Ouveze-Ventoux site, an analysis of the misclassified fields showed again the difficulties to identify the phenology in juvenile tree stands. A LAI threshold was therefore applied to the OC and VY by considering that all plots having a maximum LAI lower than 1 belong to the DC class. The quality of the classification continues to improve (Kappa = 0.95) but at the cost of not identifying young orchards and vineyards (Table 10).

In step 2, we distinguished the olive trees (OL) in class DC. It is necessary to identify in the time series discriminating features of the olive trees, which could then be used as classifiers. In Figure 7, we show the time series of a sample of OL plots and plots identified as DC. We conducted this comparison for two variables, the LAI used in the previous classification and the GCVI, which leads to a typical signature of olive trees with a systematic decrease of the signal in the summer period compared to earlier and later periods in the year. This signature is typical of the OC class. In order to appreciate the generality of this behavior we represented in a diagram (Figure 8) the average value of the vegetation index (VI) at the beginning of the year (between DOY 1 in 100) in abscissa and the average value in the middle of the year (between DOY 150 and 250) in ordinates. When the vegetation of the OL trees is well developed, there is a systematic decrease of the GCVI, which is all the stronger as the GCVI is high. It is also interesting to note that the area of the diagram of points covered by OC plots is specific with little coverage of DC plots, whose dispersion in the diagram reflects the diversity of vegetation cover encountered in this class. Similar results are obtained with LAI (Figure 8a) but with less specificity of olive plots and a less clear relationship between the difference in LAI over the two periods and the development of olive trees as shown by the scatter of the OC points. Concerning the behavior of the GCVI with the OL trees, the reasons for the reflectance ratio in the NIR and green band cannot be explained by the seasonality of the grass cover under the canopy. Indeed, the impact of the herbaceous cover should decrease with tree cover, which is contrary to what we observe. The reason could come from the orientation of the leaves and their spectral properties, which could be influenced by heat and summer water stress.

To carry out the classification, we calculated characteristics for each of the periods, namely the beginning of the year from DOY=1 to DOY=100 and the middle of the year from DOY=150 to DOY=250. The following characteristics were considered: the mean, the standard deviation, the slope, and the origin of the linear regression between the vegetation indices and time as well as the corresponding correlation coefficient. The classification was done with the RF method using the 12 variables thus obtained (6 per period) as classifiers. The results are given in Table 11 when using the GCVI as the vegetation indices.

When using LAI instead of the GCVI results were degraded with an OA=0.82 and a Kappa=0.70. In the misclassified plots analysis, it can be seen that the DC plots classified as OL correspond to mowed grasslands or more or less dense forests. Concerning the grasslands, it is easy to identify them because, on the periods used to calculate the characteristics of the signal, we have a strong variability of the GCVI. As far as the forests are concerned, they do not generally show the summer decrease of the GCVI. These features could not be identified by the calibration of the classification model, but can easily be taken into account by doing a post-processing. Thus, we propose to classify as DC the plots classified as OL when 1) the sum of the standard deviations of the signal obtained on each period is higher than 2, which never happens with OL trees, or 2) when the GCVI is higher than 3 and the average increases between period 1 and 2 contrary to the behavior of OL trees. Applying this post-processing we obtain an OA = 0.97 and a K= 0.94.

The final classification obtained after chaining step 1 and step 2 are displayed in Table 13, VY class being the most difficult to determine. The good results were maintained across the years (Table 14) with, however, some degradation for 2016 and 2017 years, during fewer S2 data were available. One can note little loss in accuracy in 2018, 2019 and 2020. This might be the results of the final thresholding that is specific of 2021. However they alwas remains better than the results obtained when no threshold were applied. The field distribution in the Crau site is shown in Figure 9 below after classification. The shape of the plot is often correlated the crop type, for instance small rectangular field being orchards. Some of these corresponds were classified as DC, which is mostly related to young stands or area recently converted into irrigated grasslands.

4. Discussion

4.1. Benchmark and Novelty of the Proposed Classification Approach

One of the reasons behind the scarcity of RS-based maps delineating fruit trees could be ascribed to the difficulty of differentiating several tree crop classes spectrally and temporarily to generate precise maps. For instance, the use of NDVI temporal profile of fruit trees such as grapes, mango, and banana displayed no clear distinction between the different fruit tree types [66]. The novelty in our approach was to apply the classification on plant phenological traits rather than using temporal series of images. If we obtained good results it is necessary to assess the adding value of our approach compared to existing approaches. Two benchmarks were considered :

A classification made directly on the times series of LAI without interpreting the phenology in time series. This was done using the RF method. In the Crau area, we did not consider the last step separating olive orchards from other surfaces and focused on the first step which considers the following three classes only: OC, VY, and DC.
The THEIA land use map is yearly implemented across the entire French national territory (https://www.theia-land.fr/ceslist/ces-occupationdes-sols/, accessed on 17 May 2022). It uses RF-supervised classification on all S2 dates (VIS and NIR bands) with other supplementary data like urban maps, topography, Corine Land Cover map, and ‘Registre Parcellaire Graphique ‘ (RPG) that collect yearly farmer’s declarations on subsidy collection from the European Union (EU). The number of identified classes was seventeen of which OC (tagged as 221 and 14 in 2017 and 2018 respectively) and VY (tagged as 222 and 15 in 2017 and 2018 respectively) are inclusive and in our study, the detection of orchards and vineyards were assessed. The maps were prepared at 10 m pixels of S2 and aggregated at the field level to be comparable with the results of our study.

Accuracies of the classification made on temporal series of LAI images were far below that obtained with our method with an OA ranging from 41 to 60 and a Kappa ranging from 0.31 to 0.52 across the two study sites from the 2016-2021 (Table 15) while we obtained Kappa larger than 0.80. Results from 2016-2017 had the worst performance and this might be because S2 had data acquisition limited to S2A. The difficulty of classifying directly on LAI images can be explained by the very strong diversity of situations, in particular in the DC class that might hamper the possibility to capture specific features of the crop of interest. Better results were found with the THEIA product (Table 16) which involves much more information layers that better constrained the classification. However, the use of our method led to a significant improvement.

4.2. Training Sample Size and Generality of the Proposed Approach across Years and Sites

Former studies highlighted that large data samples bolster RF classification accuracy. while in some situations, larger data samples might lower the RF classification accuracy pending on the dataset quality. In our study, we obtained good accuracy using a small training data set of 117 (out of 1601 in Ouveze-Ventoux) and 122 (out of 16680 in Crau) This corroborates the conclusions of Nguyen et al. [33] and Colditz [67] who found that datasets consisting of 0.15% to 0.35% of the study sites are sufficient to attain a precise land cover delineations. As a rule of thumb, studies related to land use/land cover should operate with restricted data because of the excessive price of organizing field data. Therefore, to reduce the ground truth collection burden, we can imagine applying the RF model determined for a given year to the other years. This idea is supported by the results displayed in Figure 10 which have shown that the main temporal patterns of the LAI times series are rather stable from one year to another. Therefore we have applied the RF model established in 2021 to the PM computed for 2016, 2017, 2018, 2019, and 2020 LAI time series. The results of the classifications thus made are given in Table 17. The results revealed that PM used for the training of the model is robust irrespective of the different years however with slightly lower accuracies with an average loss of 8% (max 14%) in OA and 0.10 (max 0.16) in kappa. Results obtained in the Crau are found to be a bit better, while the smallest time series in 2016 and less extent 2017 did not have a strong impact on the classification performance. In all cases, the accuracy remains much better than that obtained when the classification was made directly on the LAI time series and comparable to the THEIA classification.

The same exercise was done to make comparisons across sites (i.e the model of 2021 established in the Ouveze-Ventoux site to be used for Crau and vice versa). In this exercise, the performance of the model was affected (Table 17). This further corroborates the fact that each model generated is strictly adapted to a given location, the climatic and geographical variations and diversity in crop management practices across the two sites might be responsible for the decline in results performances since the model was adapted to a different location (based on their PM).

4.3. Limitations and Prospects of the Proposed Classification Approach

Despite the novelty and good performance of our proposed approach, we are faced with quite some drawbacks which are to be highlighted in this section. One of the obvious drawbacks is the inability of the approach to successfully classify young OC and VY. In general, the canopy size of young fruit trees (OC and VY) is very scanty (low) and consequently creates room for misclassification since our approach is based on the temporal dynamics of the LAI. One of the main reasons is the contribution of inter-row vegetation, which can be dominant in young stands. As a result, we can end up with an LAI signal that is no longer dominated by the plant of interest. In Figure 11, we see that the SOS is earlier with the VY plot than with the OC plot, which is contrary to the expected result. Such drawbacks are minimized by considering only OC and VY plots with sufficient development, which led us to put thresholds in our reference dataset by assimilating several young OC and VY to the DC class. To obtain an optimal result this thresholding depends on the considered area, which is probably the reflection of different cultural practices for the management of the inter-row. The determination of these thresholds is a real limitation of the method. There is therefore a strong stake to work on the separation of the contributions coming from the inter-row vegetation and the canopy of the stand of interest. A finer analysis of the spectral signature and/or a finer analysis of the temporal dynamics could contribute to a better separation of these two components and thus work on the specific signal of the crop of interest.

Another instance is the inability of the approach to accurately classify heterogeneous plots. The trees are sparse due to age differences, creating so many sources of interference most especially from soil background among others. This creates sources for interferences with the main canopy of the heterogenous orchard or vineyard fields since only the mean of all the total pixels in a given farm plot is utilized thereby creating a different form of the temporal pattern away from that of the fruit trees of interest. Such deviations from the main temporal patterns of fields used for training the model consequently lead to degraded fits by the model and lead to misclassifications when making predictions to the global extent.

Despite the highlighted drawbacks mentioned above, the prospect of PM-based delineations is encouraging for many reasons. Our analysis of data showed that we can separate three (3) crucial fruit tree types (OC, VY, and OL). PM-based classifiers were used only as input classifiers to the RF model thus the approach can be extended to profit from some spectral bands and some particular vegetation indices like enhanced bloom index (EBI) [68]) capable of separating the individual orchard (like cherry, plum, apricot, peach, nectarine, etc.) and vineyard (table and wine) classes. Despite our work using S2, we might be faced with issues of data missing (gap) in some areas due to the presence of the cloud affecting the capacity of inferring accurate PM and thus affecting the classification accuracy. Future satellite systems with better spatial and temporal resolutions can be merged with S2 or even synergy between optical and synthetic aperture radar (SAR) can be exploited.

5. Conclusions

Fruit tree delineations have been a difficult topic in crop delineation using remote sensing information. S2 has offered an encouraging avenue to build a classification strategy based on crop phenology and the temporal features of canopy development. Therefore, our study proposed a novel method to identify deciduous and evergreen fruit trees like OC, VY, and OL, by using a time series of LAI (for OC and VY) and GCVI (for OL) derived from S2 data to infer PM as classifiers used by an RF algorithm. The approach was developed in the Ouveze-Ventoux area and further implemented in another site named Crau. Both sites present deciduous fruit trees of OC and VY while OL production is significantly present in the Crau area only. The main differences are the climate with cooler and wetter climate in the Ouveze-Ventoux area and the composition of the DC class which is strongly different between sites. However, the methodology is applicable in both sites but with some adaptations to take into account the difference in phenology calendar and specific practices The obtained performances led to an overall accuracy ranging between 0.89 and 0.96 and a Kappa index ranging between 0.87 and 0.95. This is far better than the results we can obtain by applying the RF method on LAI time series (the same used to infer the phenology metrics) and significantly better than the THEIA classification which is an operational tool implemented over the France territory using multiple sources of ground information. The parsimony in ground truth is a strength of the approach which can be operated with a small database (less than 1% of the plots are required to inform classification). Moreover, as the method is independent of the satellite acquisition dates, we can apply a RF classification model obtained from one year to the other years while keeping a reasonable accuracy.

Despite the results of the proposed method displaying some degree of weakness for young stands (OC and VY) which were assimilated into the DC class. The main reason comes from the confusion between the interrow vegetation and the tree canopy. Delineation of these components would offer a margin of progress.

Author Contributions

Conceptualization, M.A.A. and A.C.; Data curation, M.A.A., F.F. and G.P.; formal analysis, M.A.A.; Methodology, M.A.A., A.C., and G.P.; Software, G.P.; Supervision A.C. and D.C.; writing-original draft, M.A.A. and A.C.; writing-review and editing, M.A.A., A.C. and D.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by Petroleum Technology Development Fund (PTDF) under the Federal Ministry of Petroleum, Nigeria, in collaboration with INRAE-EMMAH Avignon as part of a PhD research program.

Data Availability Statement

Sentinel 2 data are available at the following hyperlink: https://www. theia-land.fr/, accessed on 17 May 2022. THEIA classification data can be found at the following hyperlink: https://www.theia-land.fr/ceslist/ces-occupation-des-sols/, accessed on 17 May 2022. Inglada, Jordi, Vincent, Arthur, & Thierion, Vincent. (2018). Theia OSO Land Cover Map 2018 [Data set]. Zenodo. https://doi.org/10.5281/zenodo.3613415 (accessed on 17 May 2022). plot boundary map and evaluation data over the CRAU and OUVEZE-VENTOUX are available on request from the corresponding author.

Conflicts of Interest

We are not aware of any conflict of interest linked to this publication, and there is no significant financial aid for this work that could have influenced its outcome.

References

Kummu, M.; Guillaume, J. H. A.; de Moel, H.; Eisner, S.; Floerke, M.; Porkka, M.; Siebert, S.; Veldkamp, T. I. E.; Ward, P. J. The World’s Road to Water Scarcity: Shortage and Stress in the 20th Century and Pathways towards Sustainability. Sci Rep 2016, 6, 38495. [Google Scholar] [CrossRef]
Wada, Y.; Wisser, D.; Eisner, S.; Flörke, M.; Gerten, D.; Haddeland, I.; Hanasaki, N.; Masaki, Y.; Portmann, F. T.; Stacke, T.; Tessler, Z.; Schewe, J. Multimodel Projections and Uncertainties of Irrigation Water Demand under Climate Change. Geophysical Research Letters 2013, 40, 4626–4632. [Google Scholar] [CrossRef]
Richardson, K. J.; Lewis, K. H.; Krishnamurthy, P. K.; Kent, C.; Wiltshire, A. J.; Hanlon, H. M. Food Security Outcomes under a Changing Climate: Impacts of Mitigation and Adaptation on Vulnerability to Food Insecurity. Clim. Change 2018, 147, (1–2). [Google Scholar] [CrossRef]
Bazzi, H.; Baghdadi, N.; Ienco, D.; El Hajj, M.; Zribi, M.; Belhouchette, H.; Jose Escorihuela, M.; Demarez, V. Mapping Irrigated Areas Using Sentinel-1 Time Series in Catalonia, Spain. Remote Sens. 2019, 11, 1836. [Google Scholar] [CrossRef]
Ozdogan, M.; Gutman, G. A New Methodology to Map Irrigated Areas Using Multi-Temporal MODIS and Ancillary Data: An Application Example in the Continental US. Remote Sensing of Environment 2008, 112, 3520–3537. [Google Scholar] [CrossRef]
Xie, Y.; Lark, T. J. Mapping Annual Irrigation from Landsat Imagery and Environmental Variables across the Conterminous United States. Remote Sens. Environ. 2021, 260, 112445. [Google Scholar] [CrossRef]
Bazzi, H.; Baghdadi, N.; Amin, G.; Fayad, I.; Zribi, M.; Demarez, V.; Belhouchette, H. An Operational Framework for Mapping Irrigated Areas at Plot Scale Using Sentinel-1 and Sentinel-2 Data. Remote Sensing 2021, 13, 2584. [Google Scholar] [CrossRef]
Gao, Q.; Zribi, M.; Escorihuela, M.; Baghdadi, N.; Segui, P. Irrigation Mapping Using Sentinel-1 Time Series at Field Scale. Remote Sensing 2018, 10, 1495. [Google Scholar] [CrossRef]
Ambika, A. K.; Wardlow, B.; Mishra, V. Remotely Sensed High Resolution Irrigated Area Mapping in India for 2000 to 2015. Sci. Data 2016, 3, 160118. [Google Scholar] [CrossRef]
Massari, C.; Modanesi, S.; Dari, J.; Gruber, A.; De Lannoy, G. J. M.; Girotto, M.; Quintana-Segui, P.; Le Page, M.; Jarlan, L.; Zribi, M.; Ouaadi, N.; Vreugdenhil, M.; Zappa, L.; Dorigo, W.; Wagner, W.; Brombacher, J.; Pelgrum, H.; Jaquot, P.; Freeman, V.; Volden, E.; Prieto, D. F.; Tarpanelli, A.; Barbetta, S.; Brocca, L. A Review of Irrigation Information Retrievals from Space and Their Utility for Users. Remote Sens. 2021, 13, 4112. [Google Scholar] [CrossRef]
Courault, D.; Hadria, R.; Ruget, F.; Olioso, A.; Duchemin, B.; Hagolle, O.; Dedieu, G. Combined Use of FORMOSAT-2 Images with a Crop Model for Biomass and Water Monitoring of Permanent Grassland in Mediterranean Region. Hydrology and Earth System Sciences 2010, 14, 1731–1744. [Google Scholar] [CrossRef]
Merot, A.; Bergez, J.-E.; Capillon, A.; Wery, J. Analysing Farming Practices to Develop a Numerical, Operational Model of Farmers’ Decision-Making Processes: An Irrigated Hay Cropping System in France. Agricultural Systems 2008, 98, 108–118. [Google Scholar] [CrossRef]
Abubakar, M.; Chanzy, A.; Pouget, G.; Flamain, F.; Courault, D. Detection of Irrigated Permanent Grasslands with Sentinel-2 Based on Temporal Patterns of the Leaf Area Index (LAI). 2022. [CrossRef]
Courault, D.; Bsaibes, A.; Kpemlie, E.; Hadria, R.; Hagolle, O.; Marloie, O.; Hanocq, J.-F.; Olioso, A.; Bertrand, N.; Desfonds, V. Assessing the Potentialities of FORMOSAT-2 Data for Water and Crop Monitoring at Small Regional Scale in South-Eastern France. Sensors 2008, 8, 3460–3481. [Google Scholar] [CrossRef]
Bazzi, H.; Baghdadi, N.; Zribi, M. Comparative Analysis between Two Operational Irrigation Mapping Models over Study Sites in Mediterranean and Semi-Oceanic Regions. Water 2022, 14, 1341. [Google Scholar] [CrossRef]
Baghdadi, N.; King, C.; Chanzy, A.; Wigneron, J. P. An Empirical Calibration of the Integral Equation Model Based on SAR Data, Soil Moisture and Surface Roughness Measurement over Bare Soils. Int. J. Remote Sens. 2002, 23, 4325–4340. [Google Scholar] [CrossRef]
Pageot, Y.; Baup, F.; Inglada, J.; Baghdadi, N.; Demarez, V. Detection of Irrigated and Rainfed Crops in Temperate Areas Using Sentinel-1 and Sentinel-2 Time Series. Remote Sens. 2020, 12, 3044. [Google Scholar] [CrossRef]
Simonneaux, V.; Duchemin, B.; Helson, D.; Er-Raki, S.; Olioso, A.; Chehbouni, A. G. The Use of High-Resolution Image Time Series for Crop Classification and Evapotranspiration Estimate over an Irrigated Area in Central Morocco. Int. J. Remote Sens. 2008, 29, 95–116. [Google Scholar] [CrossRef]
Pena, M. A.; Liao, R.; Brenning, A. Using Spectrotemporal Indices to Improve the Fruit-Tree Crop Classification Accuracy. ISPRS-J. Photogramm. Remote Sens. 2017, 128, 158–169. [Google Scholar] [CrossRef]
Peña, M. A.; Brenning, A. Assessing Fruit-Tree Crop Classification from Landsat-8 Time Series for the Maipo Valley, Chile. Remote Sensing of Environment 2015, 171, 234–244. [Google Scholar] [CrossRef]
Nabil, M.; Farg, E.; Arafat, S. M.; Aboelghar, M.; Afify, N. M.; Elsharkawy, M. M. Tree-Fruits Crop Type Mapping from Sentinel-1 and Sentinel-2 Data Integration in Egypt?S New Delta Project. Remote Sens. Appl.-Soc. Environ. 2022, 27, 100776. [Google Scholar] [CrossRef]
Kordi, F.; Yousefi, H. Crop Classification Based on Phenology Information by Using Time Series of Optical and Synthetic-Aperture Radar Images. Remote Sens. Appl.-Soc. Environ. 2022, 27, 100812. [Google Scholar] [CrossRef]
Toosi, A.; Javan, F. D.; Samadzadegan, F.; Mehravar, S.; Kurban, A.; Azadi, H. Citrus Orchard Mapping in Juybar, Iran: Analysis of NDVI Time Series and Feature Fusion of Multi-Source Satellite Imageries. Ecol. Inform. 2022, 70, 101733. [Google Scholar] [CrossRef]
Misra, G.; Cawkwell, F.; Wingler, A. Status of Phenological Research Using Sentinel-2 Data: A Review. Remote Sens. 2020, 12, 2760. [Google Scholar] [CrossRef]
Zeng, L.; Wardlow, B. D.; Xiang, D.; Hu, S.; Li, D. A Review of Vegetation Phenological Metrics Extraction Using Time-Series, Multispectral Satellite Data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
Zheng, Y.; Wu, B.; Zhang, M.; Zeng, H. Crop Phenology Detection Using High Spatio-Temporal Resolution Data Fused from SPOT5 and MODIS Products. Sensors 2016, 16, 2099. [Google Scholar] [CrossRef] [PubMed]
Garrity, S. R.; Bohrer, G.; Maurer, K. D.; Mueller, K. L.; Vogel, C. S.; Curtis, P. S. A Comparison of Multiple Phenology Data Sources for Estimating Seasonal Transitions in Deciduous Forest Carbon Exchange. Agric. For. Meteorol. 2011, 151, 1741–1752. [Google Scholar] [CrossRef]
Brown, M. E.; de Beurs, K. M.; Marshall, M. Global Phenological Response to Climate Change in Crop Areas Using Satellite Remote Sensing of Vegetation, Humidity and Temperature over 26 Years. Remote Sens. Environ. 2012, 126, 174–183. [Google Scholar] [CrossRef]
Salinero-Delgado, M.; Estévez, J.; Pipia, L.; Belda, S.; Berger, K.; Paredes Gómez, V.; Verrelst, J. Monitoring Cropland Phenology on Google Earth Engine Using Gaussian Process Regression. Remote Sensing 2022, 14, 146. [Google Scholar] [CrossRef] [PubMed]
Hanes, J. M.; Liang, L.; Morisette, J. T. Land Surface Phenology. In Biophysical applications of satellite remote sensing; Springer, 2014; pp 99–125.
Henebry, G. M.; Beurs, K. M. de. Remote Sensing of Land Surface Phenology: A Prospectus. In Phenology: An integrative environmental science; Springer, 2013; pp 385–411. [CrossRef]
Frantz, D.; Stellmes, M.; Roeder, A.; Udelhoven, T.; Mader, S.; Hill, J. Improving the Spatial Resolution of Land Surface Phenology by Fusing Medium- and Coarse-Resolution Inputs. IEEE Trans. Geosci. Remote Sensing 2016, 54, 4153–4164. [Google Scholar] [CrossRef]
Nguyen, L. H.; Joshi, D. R.; Clay, D. E.; Henebry, G. M. Characterizing Land Cover/Land Use from Multiple Years of Landsat and MODIS Time Series: A Novel Approach Using Land Surface Phenology Modeling and Random Forest Classifier. Remote Sens. Environ. 2020, 238, 111017. [Google Scholar] [CrossRef]
Chen, X.; Wang, D.; Chen, J.; Wang, C.; Shen, M. The Mixed Pixel Effect in Land Surface Phenology: A Simulation Study. Remote Sens. Environ. 2018, 211, 338–344. [Google Scholar] [CrossRef]
Veloso, A.; Mermoz, S.; Bouvet, A.; Toan, T. L.; Planells, M.; Dejoux, J.-F.; Ceschia, E. Understanding the Temporal Behavior of Crops Using Sentinel-1 and Sentinel-2-like Data for Agricultural Applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
Bradley, C.; Schwartz, M.; Xiao, X. Remote Sensing Phenology: Status and Way Forward. Phenology of Ecosystem Processes—Applications in Global Change Research, 2009; 231–246. [Google Scholar]
de Beurs, K. M.; Henebry, G. M. Land Surface Phenology, Climatic Variation, and Institutional Change: Analyzing Agricultural Land Cover Change in Kazakhstan. Remote Sens. Environ. 2004, 89, 497–509. [Google Scholar] [CrossRef]
Zhang, X. Y.; Friedl, M. A.; Schaaf, C. B.; Strahler, A. H.; Hodges, J. C. F.; Gao, F.; Reed, B. C.; Huete, A. Monitoring Vegetation Phenology Using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
White, M. A.; de Beurs, K. M.; Didan, K.; Inouye, D. W.; Richardson, A. D.; Jensen, O. P.; O’Keefe, J.; Zhang, G.; Nemani, R. R.; van Leeuwen, W. J. D.; Brown, J. F.; de Wit, A.; Schaepman, M.; Lin, X.; Dettinger, M.; Bailey, A. S.; Kimball, J.; Schwartz, M. D.; Baldocchi, D. D.; Lee, J. T.; Lauenroth, W. K. Intercomparison, Interpretation, and Assessment of Spring Phenology in North America Estimated from Remote Sensing for 1982-2006. Glob. Change Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
Wang, S.; Zhang, L.; Huang, C.; Qiao, N. An NDVI-Based Vegetation Phenology Is Improved to Be More Consistent with Photosynthesis Dynamics through Applying a Light Use Efficiency Model over Boreal High-Latitude Forests. Remote Sens. 2017, 9, 695. [Google Scholar] [CrossRef]
Lebrini, Y.; Boudhar, A.; Laamrani, A.; Htitiou, A.; Lionboui, H.; Salhi, A.; Chehbouni, A.; Benabdelouahab, T. Mapping and Characterization of Phenological Changes over Various Farming Systems in an Arid and Semi-Arid Region Using Multitemporal Moderate Spatial Resolution Data. Remote Sens. 2021, 13, 578. [Google Scholar] [CrossRef]
Jönsson, P.; Eklundh, L. TIMESAT—a Program for Analyzing Time-Series of Satellite Sensor Data. Computers & Geosciences 2004, 30, 833–845. [Google Scholar] [CrossRef]
Ashourloo, D.; Nematollahi, H.; Huete, A.; Aghighi, H.; Azadbakht, M.; Shahrabi, H. S.; Goodarzdashti, S. A New Phenology-Based Method for Mapping Wheat and Barley Using Time-Series of Sentinel-2 Images. Remote Sensing of Environment 2022, 280, 113206. [Google Scholar] [CrossRef]
Tuffery, L.; Davi, H.; López-García, N.; Rigolot, E.; Jean, F.; Stenger, A.; Lefèvre, F. Adaptive Measures for Mountain Mediterranean Forest Ecosystem Services under Climate and Land Cover Change in the Mont-Ventoux Regional Nature Park, France. Reg Environ Change 2021, 21, 12. [Google Scholar] [CrossRef]
Trolard, F.; Bourrié, G.; Baillieux, A.; Buis, S.; Chanzy, A.; Clastre, P.; Closet, J.-F.; Courault, D.; Dangeard, M.-L.; Di Virgilio, N.; Dussouilliez, P.; Fleury, J.; Gasc, J.; Géniaux, G.; Jouan, R.; Keller, C.; Lecharpentier, P.; Lecroart, J.; Napoleone, C.; Mohammed, G.; Olioso, A.; Reynders, S.; Rossi, F.; Tennant, M.; de Vicente Lopez, J. The PRECOS Framework: Measuring the Impacts of the Global Changes on Soils, Water, Agriculture on Territories to Better Anticipate the Future. Journal of Environmental Management 2016, 181, 590–601. [Google Scholar] [CrossRef] [PubMed]
Séraphin, P.; Vallet-Coulomb, C.; Gonçalvès, J. Partitioning Groundwater Recharge between Rainfall Infiltration and Irrigation Return Flow Using Stable Isotopes: The Crau Aquifer. Journal of Hydrology 2016, 542, 241–253. [Google Scholar] [CrossRef]
Weiss, M.; Baret, F.; Leroy, M.; Hautecoeur, O.; Bacour, C.; Prevot, L.; Bruguier, N. Validation of Neural Net Techniques to Estimate Canopy Biophysical Variables from Remote Sensing Data. Agronomie 2002, 22, 547–553. [Google Scholar] [CrossRef]
Zonal statistics in R | GeoProfesja . 2022. Available online: http://geoprofesja.pl/en/zonal-statistics-in-r (accessed on 18 October 2022).
Rouse Jr, J. W.; Haas, R. H.; Schell, J. A.; Deering, D. W. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; 1973.
Gitelson, A. A.; Kaufman, Y. J.; Merzlyak, M. N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
Huete, A.; Didan, K.; Miura, T.; Rodriguez, E. P.; Gao, X.; Ferreira, L. G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
Baret, F.; Guyot, G.; Major, D. J. TSAVI: A Vegetation Index Which Minimizes Soil Brightness Effects On LAI And APAR Estimation. In 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium,; 1989; Vol. 3, pp 1355–1358. [CrossRef]
Kaufman, Y.; Tanre, D. Atmospherically Resistant Vegetation Index (Arvi) for Eos-Modis. IEEE Trans. Geosci. Remote Sensing 1992, 30, 261–270. [Google Scholar] [CrossRef]
Gitelson, A. A.; Keydan, G. P.; Merzlyak, M. N. Three-Band Model for Noninvasive Estimation of Chlorophyll, Carotenoids, and Anthocyanin Contents in Higher Plant Leaves. Geophysical Research Letters 2006, 33. [Google Scholar] [CrossRef]
Gao, B. A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. In Imaging Spectrometry; Descour, M. R., Mooney, J. M., Perry, D. L., Illing, L., Eds.; Spie - Int Soc Optical Engineering: Bellingham, 1995; Vol. 2480, pp. 225–236. [Google Scholar] [CrossRef]
Xiao, X. M.; Boles, S.; Liu, J. Y.; Zhuang, D. F.; Frolking, S.; Li, C. S.; Salas, W.; Moore, B. Mapping Paddy Rice Agriculture in Southern China Using Multi-Temporal MODIS Images. Remote Sens. Environ. 2005, 95, 480–492. [Google Scholar] [CrossRef]
Fisher, J. I.; Mustard, J. F. Cross-Scalar Satellite Phenology from Ground, Landsat, and MODIS Data. Remote Sens. Environ. 2007, 109, 261–273. [Google Scholar] [CrossRef]
Fisher, J. I.; Mustard, J. F.; Vadeboncoeur, M. A. Green Leaf Phenology at Landsat Resolution: Scaling from the Field to the Satellite. Remote Sens. Environ. 2006, 100, 265–279. [Google Scholar] [CrossRef]
Yang, X.; Mustard, J. F.; Tang, J.; Xu, H. Regional-Scale Phenology Modeling Based on Meteorological Records and Remote Sensing Observations. J. Geophys. Res.-Biogeosci. 2012, 117, G03029. [Google Scholar] [CrossRef]
Zhong, L.; Gong, P.; Biging, G. S. Phenology-Based Crop Classification Algorithm and Its Implications on Agricultural Water Use Assessments in California’s Central Valley. Photogramm. Eng. Remote Sens. 2012, 78, 799–813. [Google Scholar] [CrossRef]
Akbari, E.; Boloorani, A. D.; Samany, N. N.; Hamzeh, S.; Soufizadeh, S.; Pignatti, S. Crop Mapping Using Random Forest and Particle Swarm Optimization Based on Multi-Temporal Sentinel-2. Remote Sens. 2020, 12, 1449. [Google Scholar] [CrossRef]
Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving Performance of Spatio-Temporal Machine Learning Models Using Forward Feature Selection and Target-Oriented Validation. Environ. Modell. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
Jensen, J. R.; Lulla, K. Introductory Digital Image Processing: A Remote Sensing Perspective. Geocarto International 1987, 2, 65–65. [Google Scholar] [CrossRef]
Team, R. C. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. http://www. R-project. org/.
Usha, K.; Singh, B. Potential Applications of Remote Sensing in Horticulture—A Review. Scientia Horticulturae 2013, 153, 71–83. [Google Scholar] [CrossRef]
Roland Colditz, R. An Evaluation of Different Training Sample Allocation Schemes for Discrete and Continuous Land Cover Classification Using Decision Tree-Based Algorithms. Remote Sens. 2015, 7, 9655–9681. [Google Scholar] [CrossRef]
Chen, B.; Jin, Y.; Brown, P. An Enhanced Bloom Index for Quantifying Floral Phenology Using Multi-Scale Remote Sensing Observations. ISPRS Journal of Photogrammetry and Remote Sensing 2019, 156, 108–120. [Google Scholar] [CrossRef]

Figure 1. Map of France depicting the two selected study sites (Ouveze-Ventoux and Crau).

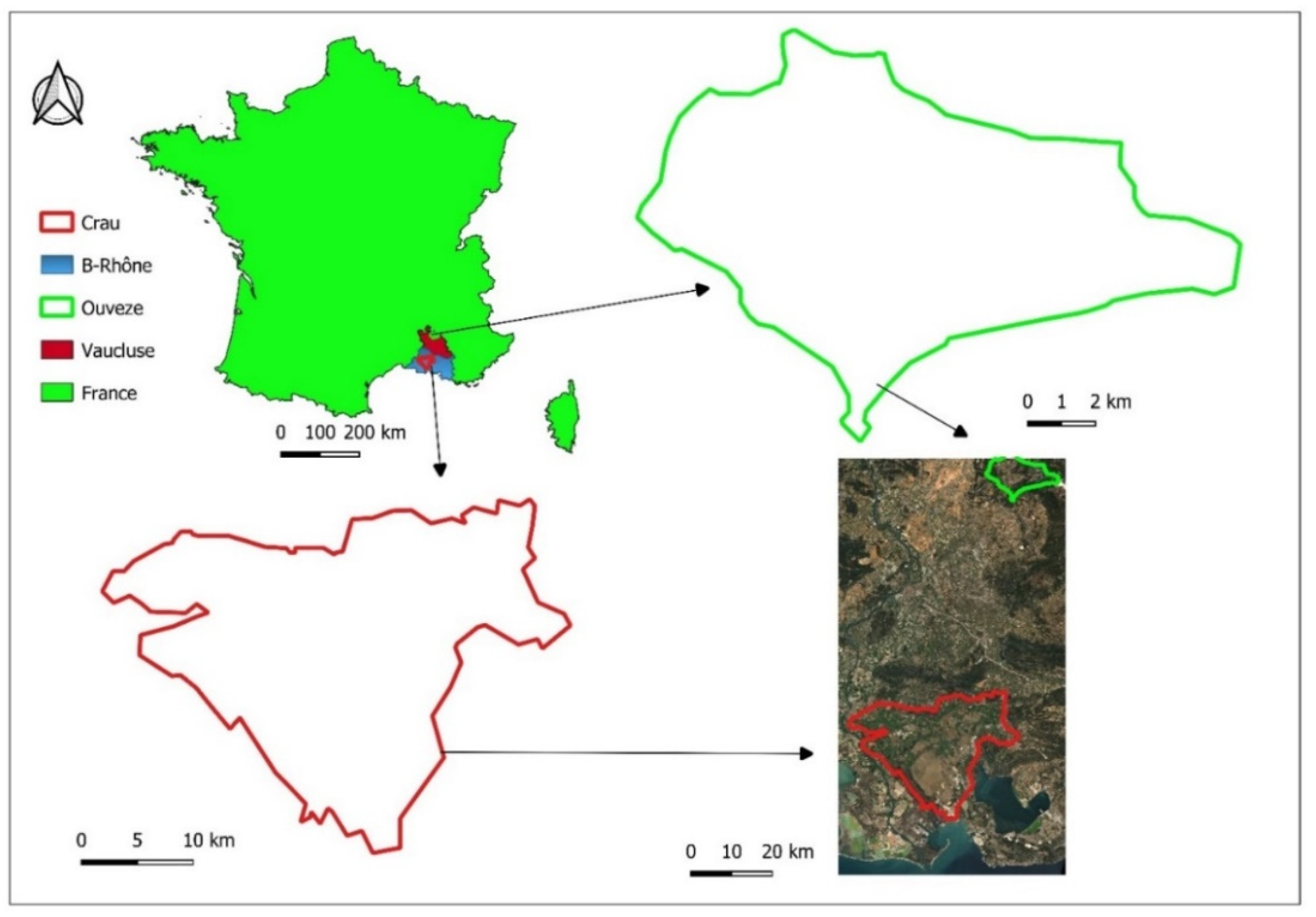
Figure 2. Map of the two study areas displaying locations of the selected ground truth plot.

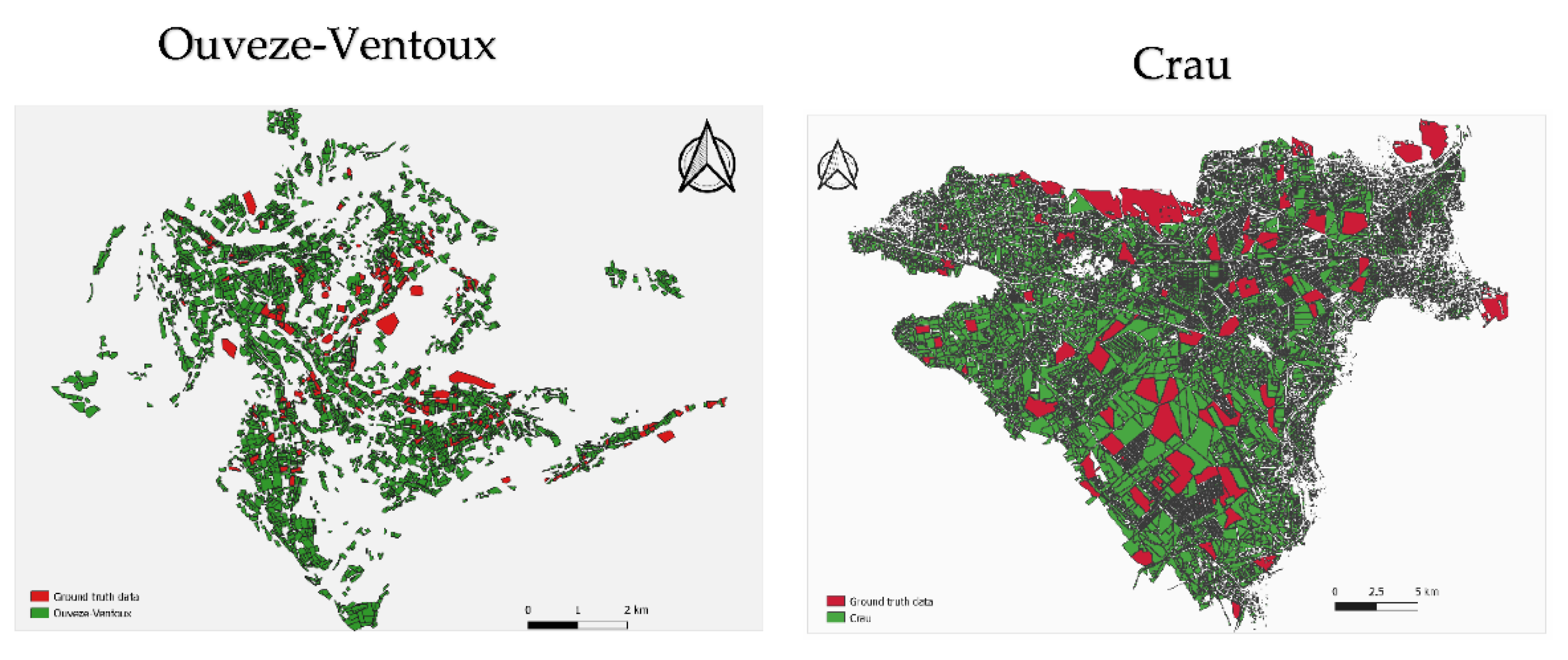
Figure 3. Double logistic fitting showing SOS and EOS.

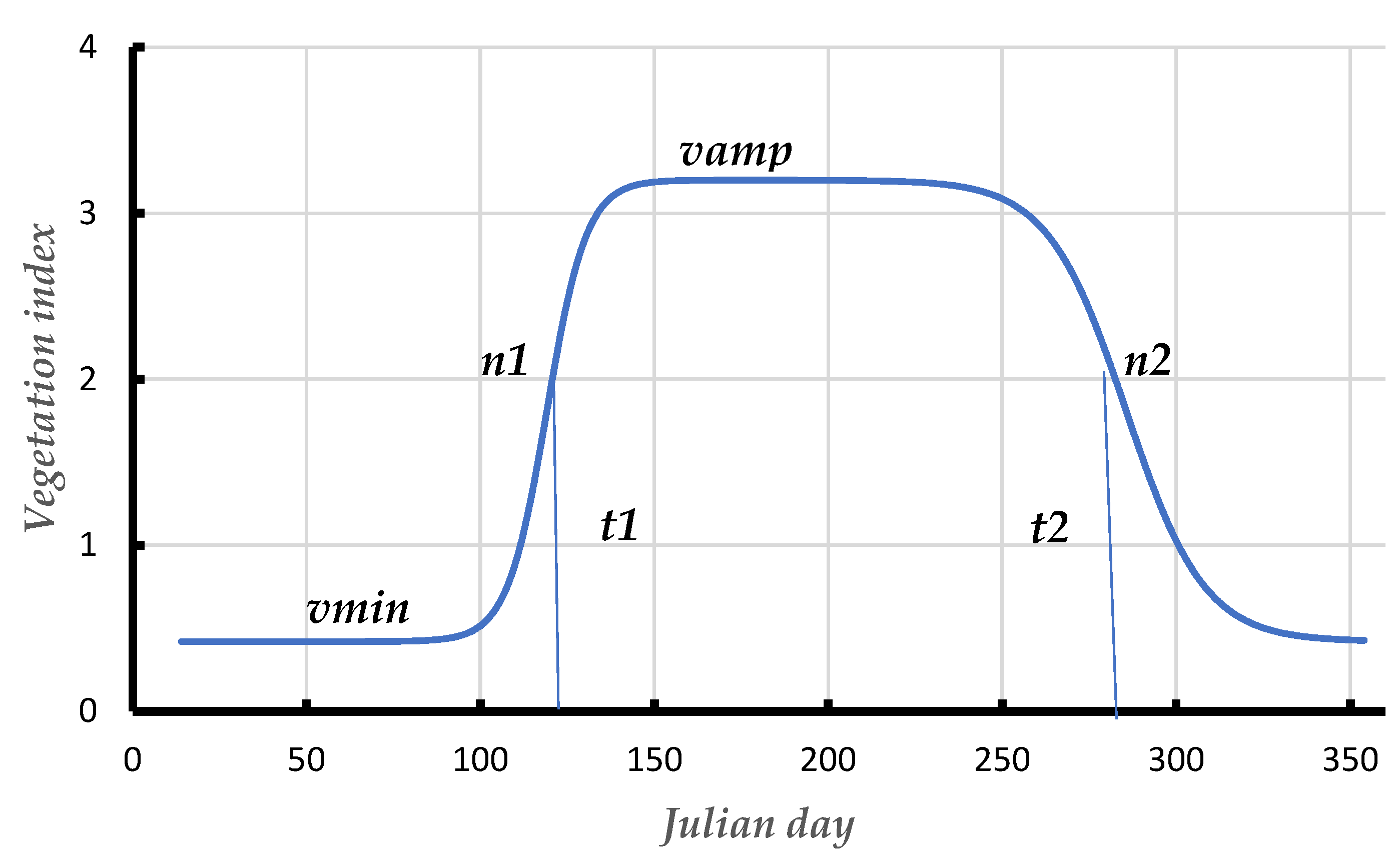
Figure 4. Temporal profile of DC (a), VY (b), OC (c) s (c) in Ouveze-Ventoux and temporal profile of DC (d), VY (e), OC (f) and OL (g) in Crau site.

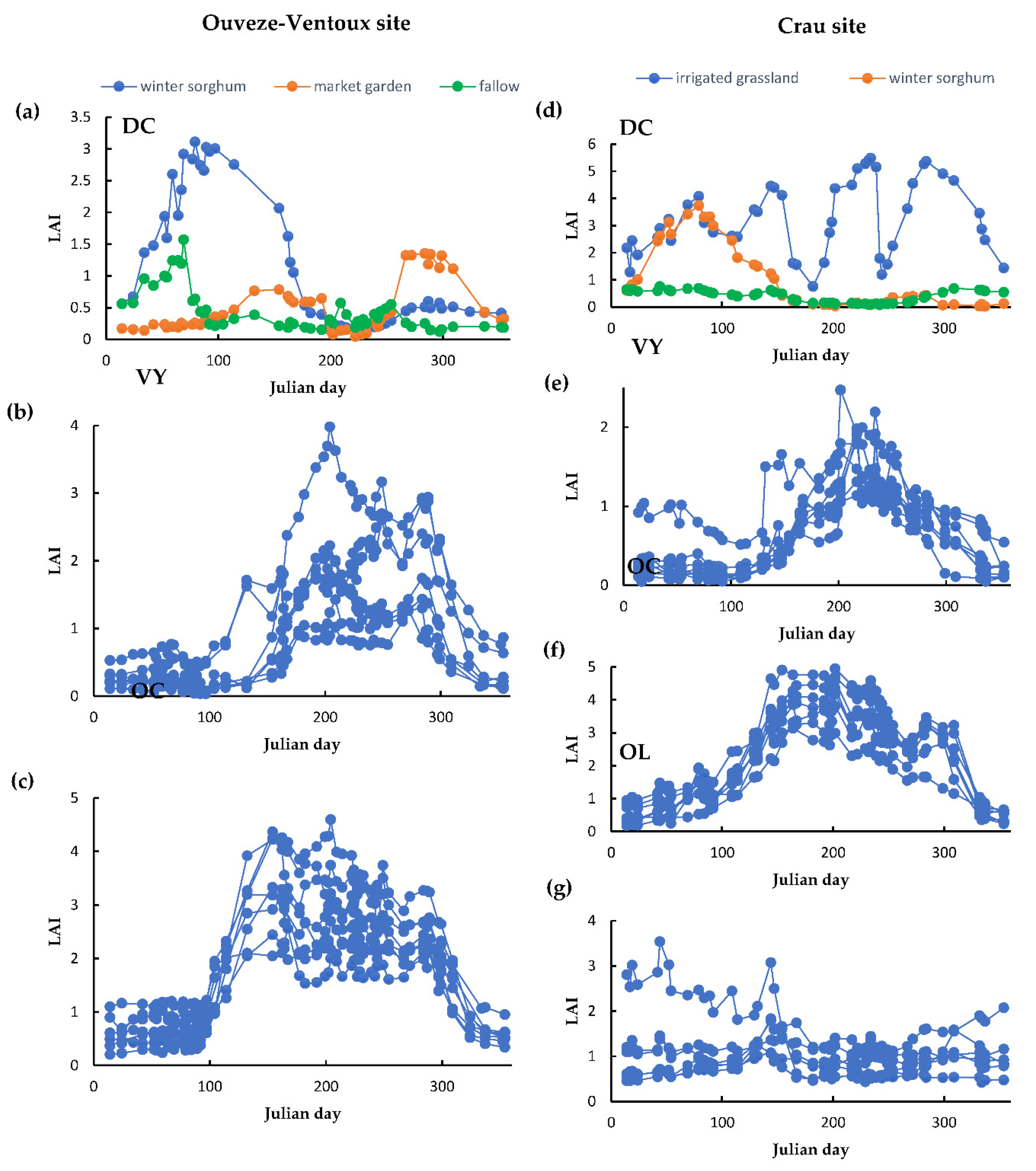
Figure 6. Spatial distribution of OC, VY, and DC classes in the Ouveze-Ventoux site for the year 2021.

Figure 7. Vegetation Indice time series observed on OL plots (red) and DC (green). In a) the vegetation indices is the LAI, in b) the vegetation indices are GCVI.

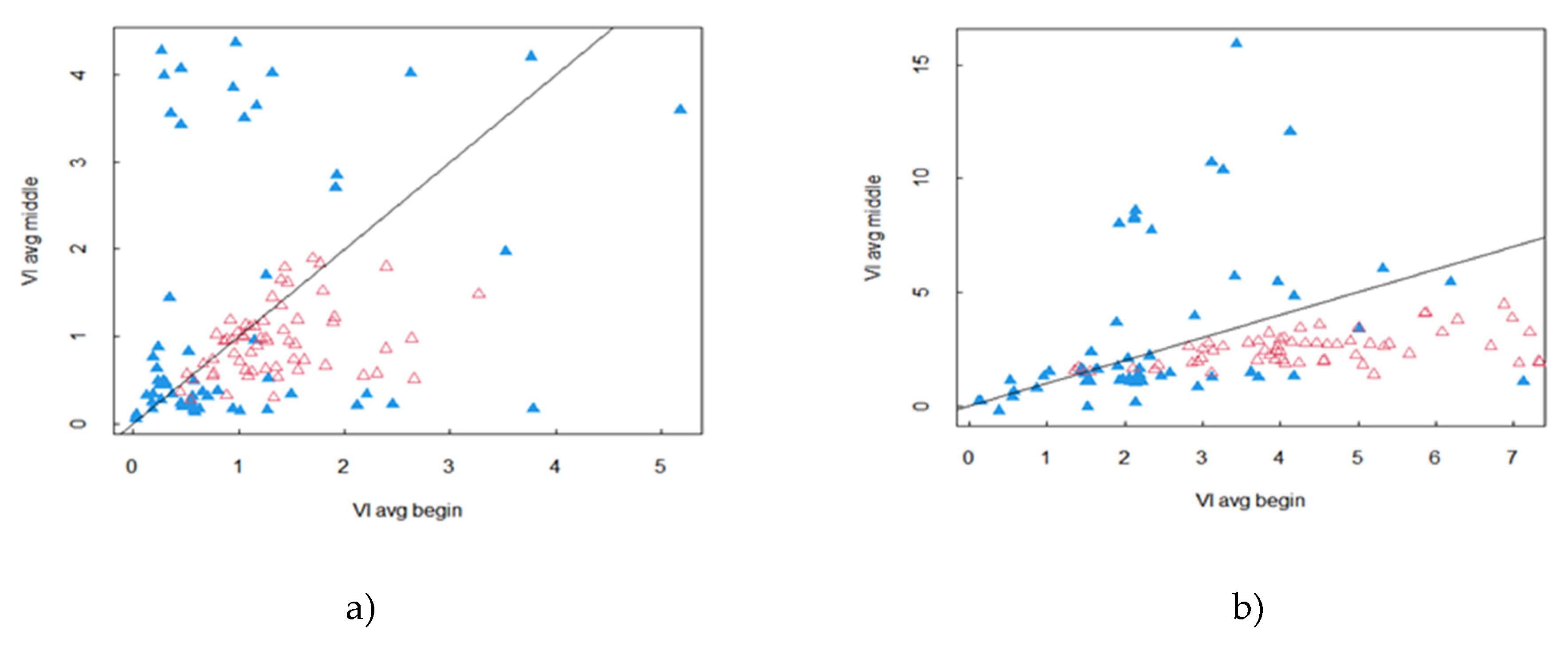
Figure 8. Average Vegetation indices during the summer period (DOY 150-250) as a function of the average vegetation indices at the beginning of the year (DOY 1-100) for olive plots (red triangle) and end DC plots (blue triangle). In a) the vegetation indices are the LAI and in b) the vegetation indices are GCVI.

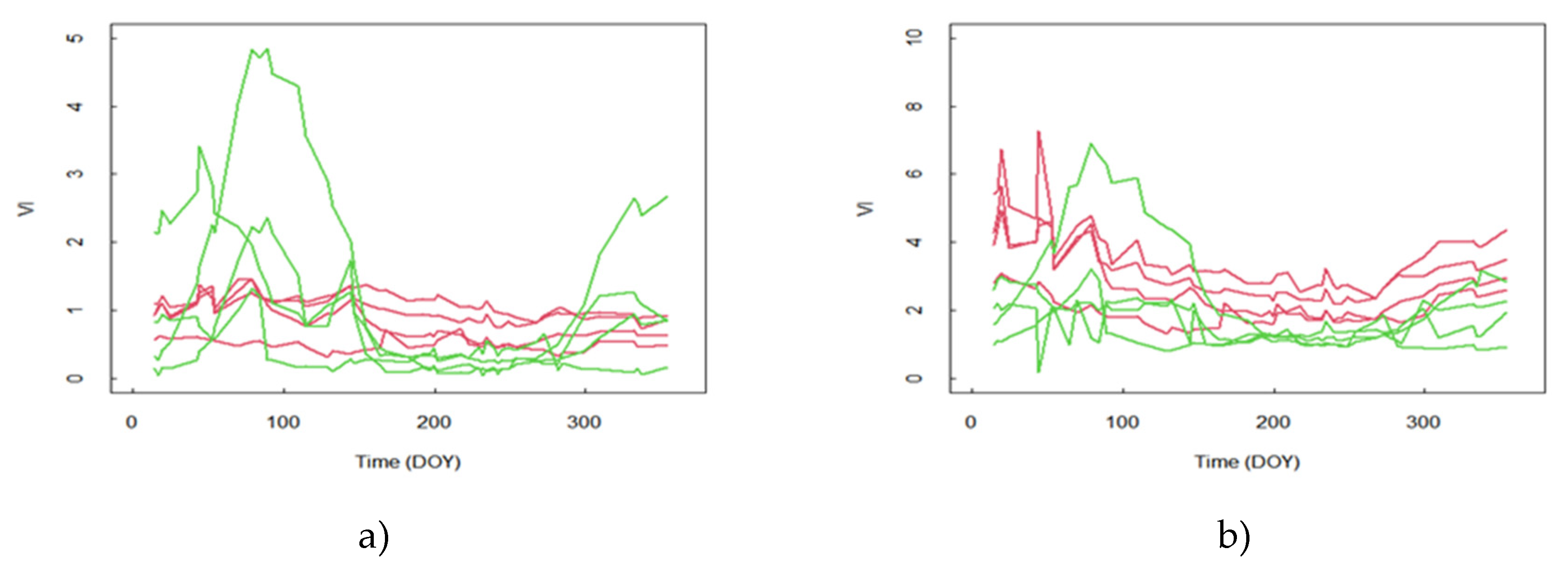
Figure 9. Spatial distribution of OC, VY, OL, and DC classes in Crau.

Figure 10. Temporal profile of OC and VY in Ouveze-Ventoux (a and b) and Crau (c and d) study areas from 2019 to 2021.

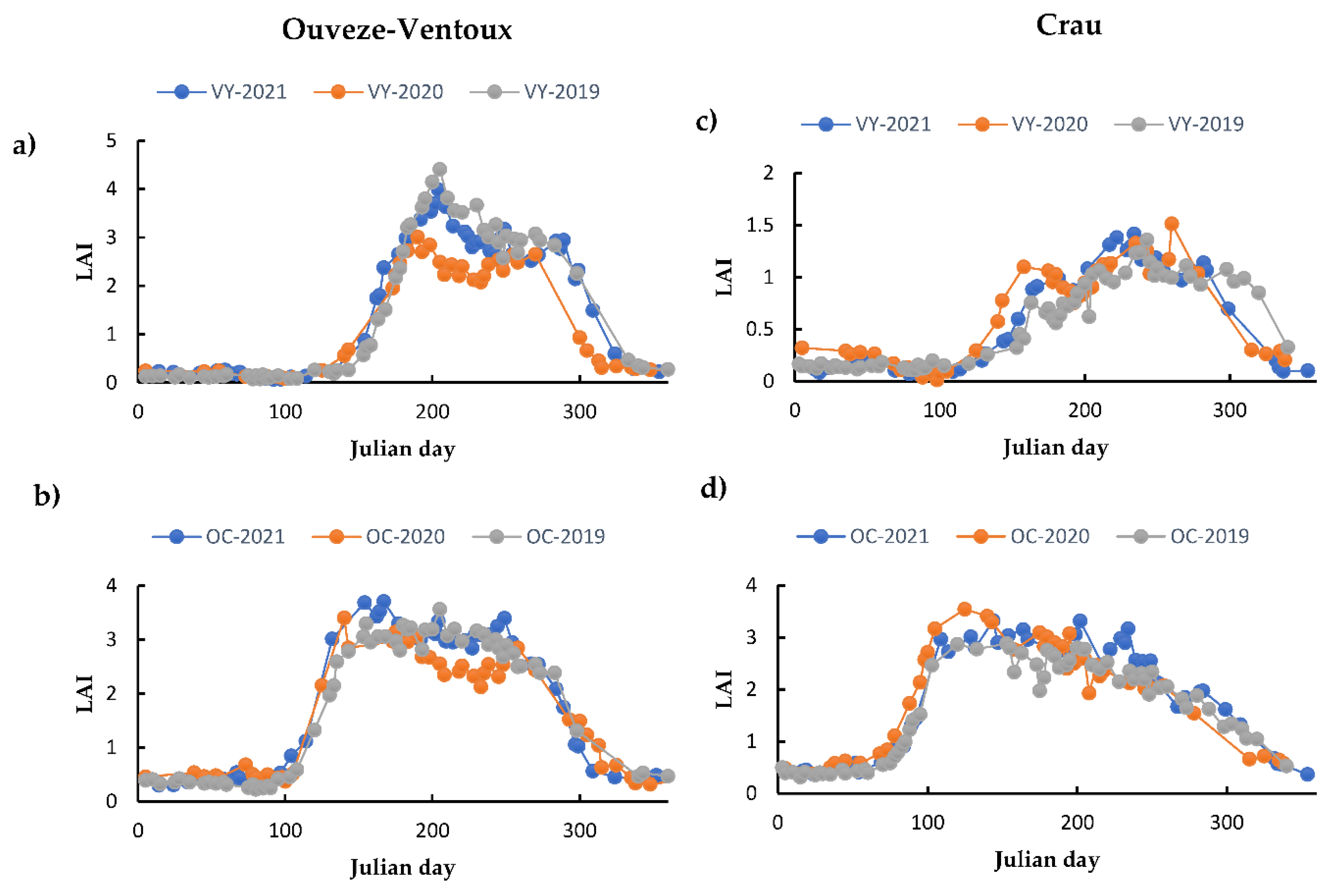
Figure 11. Temporal pattern of a young OC field and a temporal pattern of a young VY.

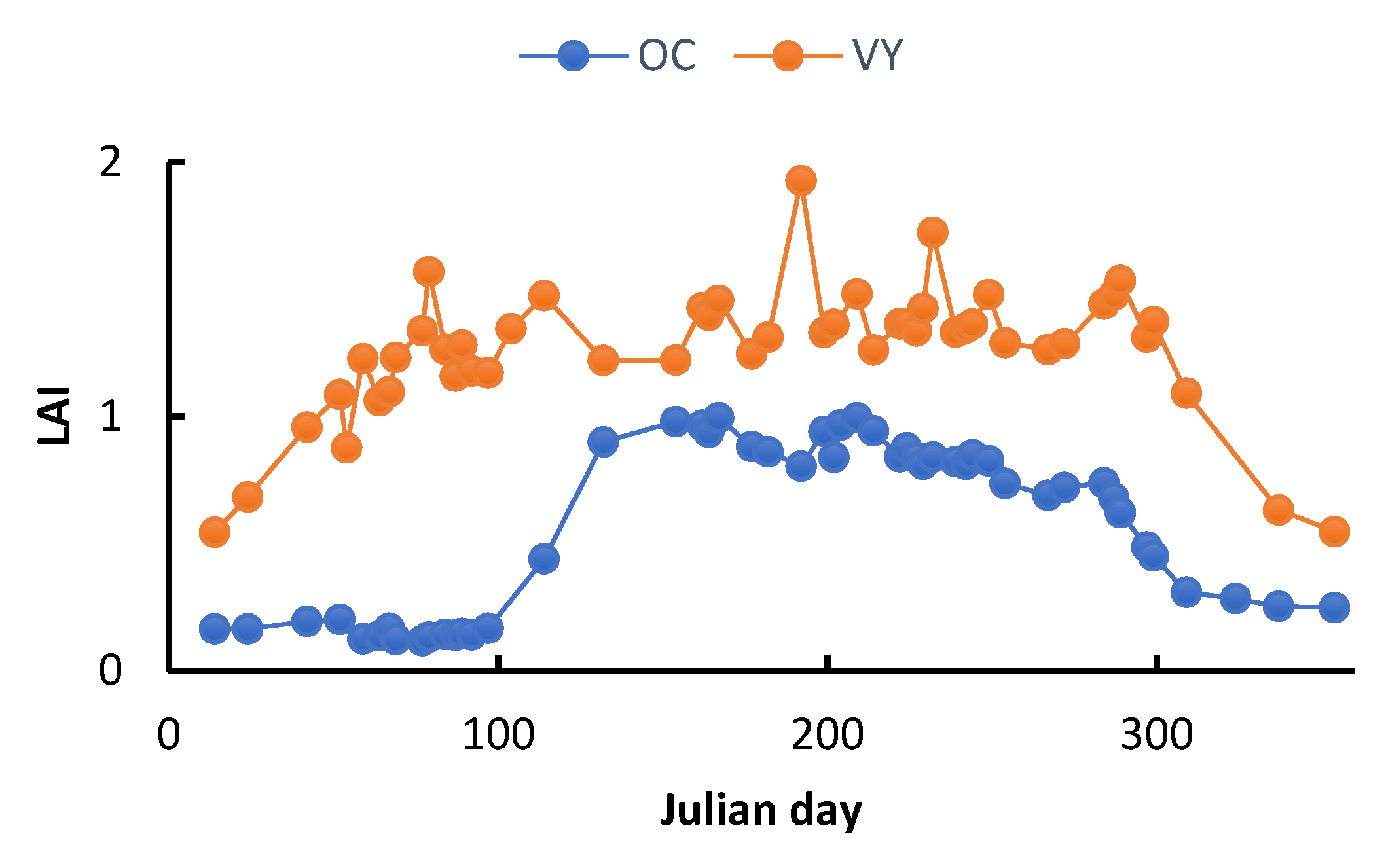
Table 1. Ground truth information of the two study sites used for model calibration and validation during 2016-2021.

Ouveze Ventoux site		Crau site
Land use	Ground data	Land use	Ground data
	(number of plots)	(number of plots)
OC	60	OC 88
VY	100	VY 35
OL	-	OL 60
DC	74	DC 60

Table 2. Number of cloud-free available images across the two study sites used for the classification.

S/N	Year	Ouveze-Ventoux	Crau
1	2016	39	43
2	2017	45	49
3	2018	52	55
4	2019	51	56
5	2020	49	52
6	2021	50	51

Table 4. Classification performance of different vegetation indices and biophysical variables in Ouveze-Ventoux for 2021.

Vegetation Indices	OA (%)	K
NDVI	82	0.71
GNDVI	80	0.70
EVI	82	0.75
TSAVI	87	0.85
ARVI	81	0.77
GCVI	73	0.70
NDMI	82	0.71
LSWI	80	0.77

Biophysical variables	OA (%)	K
LAI	92	0.89
FAPAR	90	0.88
FCOVER	87	0.85

Table 5. Confusion matrix for OC and VY classification using PM of LAI in 2021 (subscript a and p correspond to actual and predicted class, respectively).

	DC_p	OC_p	VY_p	Total	User’s accuracy
DC_a	35	0	2	37	0.94
OC_a	1	29	0	30	0.96
VY_a	5	1	44	50	0.88
Total	41	30	46	117
Producers’s accuracy	0.86	0.96	0.96
OA = 0.92 ; K = 0.89

Table 6. Confusion matrix for OC and VY classification using PM from LAI 2021 time series and applying a LAI= 0.5 for OC and VY classes (subscript a and p corresponds to actual and predicted class, respectively).

	DC_p	OC_p	VY_p	Total	User’s accuracy
DC_a	37	0	2	39	0.95
OC_a	0	30	0	30	1.00
VY_a	1	1	46	48	0.97
Total	38	31	48	117
Producers’s accuracy	0.95	0.96	0.95
OA = 0.96 ; K = 0.91

Table 7. Results of OC and VY classification in Ouveze-Ventoux from 2016-201 based on PM derived from LAI time series and applying LAI = 0.5 thresholds for OC and VY classes.

Year	Site	Accuracy assessments
		OA (%)	Kappa
2016	Ouveze-Ventoux	89	0.86
2017		90	0.89
2018		91	0.90
2019		94	0.92
2020		95	0.93
2021		96	0.91

Table 8. Confusion matrix for OC, VY, OL, and DC classification based on PM from 2021 time series (subscript a and p correspond to actual and predicted class, respectively).

	DC_p	OC_p	OL_p	VY_p	Total	User’s accuracy
DC_a	19	0	11	0	30	0.63
OC_a	0	42	0	2	44	0.95
OL_a	10	0	20	0	30	0.67
VY_a	11	2	0	5	18	0.28
Total	40	44	31	7	122
Producers’s accuracy	0.50	0.95	0.65	0.71
	OA = 0.70 ; K = 0.69

Table 9. Confusion matrix for OC and VY classification based on PM from 2021 LAI time series and after gathering OC and DC in common DC class (subscript a and p correspond to actual and predicted class, respectively).

	DC_p	OC_p	VY_p	Total	User’s accuracy
DC_a	60	0	0	60	1.00
OC_a	0	44	0	44	1.00
VY_a	6	1	11	18	0.61
Total	66	45	11	122
Producers’s accuracy	0.91	0.98	1.00
OA = 0.94 ; K = 0.91

Table 10. Same as Table 9 with an additional threshold of LAI=1 for OC and VY classes of LAI in 2021 (subscript a and p correspond to actual and predicted class, respectively).

	DC_p	OC_p	VY_p	Total	User’s accuracy
DC_a	62	0	0	62	1.00
OC_a	0	44	0	44	1.00
VY_a	3	1	12	16	0.75
Total	65	45	12	122
Producers’s accuracy	0.95	0.98	1.00
OA = 0.97 ; K = 0.95

Table 11. Confusion matrix for DC and OL classification based on a temporal feature from 2021 GCVI time series (subscript a and p correspond to actual and predicted class, respectively).

	DC_p	OL_p	Total	User’s accuracy
DC_a	25	5	30	0.87
OL_a	1	29	30	0.97
Total	26	34	60
Producers’s accuracy	0.96	0.88
OA = 0.91 ; K = 0.82

Table 12. Results of OL classification in Crau from 2016-201 using GCV.

Year	Site	Accuracy assessments
		OA (%)	Kappa
2016	Crau	90	0.86
2017		90	0.88
2018		95	0.93
2019		93	0.92
2020		94	0.91
2021		97	0.94

Table 13. Confusion matrix of DC, OC, OL and, VY classification in Crau for 2021.

	DC_p	OC_p	OL_p	VY_p	Total	User’s accuracy
DC_a	31	0	1	0	32	0.97
OC_a	0	44	0	0	44	1.00
OL_a	1	0	29	0	30	0.97
VY_a	3	1	0	12	16	0.75
Total	35	45	30	12	122
Producers’s accuracy	0.89	0.98	0.97	1.00
	OA = 0.96 ; K = 0.95

Table 14. Results of OC, VY, OL global classification accuracy in Crau from 2016-201.

Year	Site	Accuracy assessments
		OA (%)	Kappa
2016	Crau	89	0.87
2017		90	0.87
2018		92	0.90
2019		94	0.91
2020		93	0.91
2021		96	0.95

Table 15. Classification performance of the raw spectral satellite images (LAI) across the two study sites for OC and VY using RF classifier.

Year	Site	OA (%)	K
2016	Ouveze-Ventoux	43	0.30
2017		47	0.32
2018		55	0.41
2019		51	0.49
2020		55	0.51
2021		52	0.50

2016	Crau	41	0.32
2017		45	0.31
2018		49	0.41
2019		55	0.52
2020		60	0.51
2021		58	0.49

Table 16. THEIA classification performance across the two study sites for OC and VY using RF classifier and other supplementary data.

Year	Site	OA (%)	Kappa
2016	Ouveze-Ventoux	73	0.70
2017		77	0.72
2018		75	0.71
2019		78	0.75
2020		75	0.71
2021		72	0.69

2016	Crau	76	0.73
2017		75	0.69
2018		79	0.75
2019		75	0.72
2020		73	0.68
2021		78	0.75

Table 17. Classification performance using PM for classifying orchards and vineyards applying the predicted model of 2021 across years and sites.

Accuracy Assessment
	Calibrated RF model			2021 model across years
Year	Site	OA	Kappa	OA	Kappa
2016	Ouveze-Ventoux	0.89	0.86	81	0.72
2017		0.90	0.89	83	0.76
2018		0.91	0.90	82	0.79
2019		0.94	0.92	83	0.81
2020		0.95	0.93	86	0.85
2016	Crau	89	0.87	83	0.79
2017		90	0.87	82	0.78
2018		92	0.90	85	0.80
2019		94	0.91	87	0.83
2020		93	0.91	86	0.80
	Calibrated RF model			2021 model across sites
2021	Ouveze Ventoux	96	0.91	71	0.65
2021	Crau	89	0.87	60	0.51

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer