Sixteen Pairs of 4-Component Spinors for SL(4,C) and Four Types of Transformations with a Conjugate Space Which Has No Counterpart in SL(2,C)

Preprint

Article

Sixteen Pairs of 4-Component Spinors for SL(4,C) and Four Types of Transformations with a Conjugate Space Which Has No Counterpart in SL(2,C)

Altmetrics

Downloads

241

Views

206

Comments

Mehmet Ali Kuntman^*

This version is not peer-reviewed

Submitted:

23 September 2023

Posted:

25 September 2023

You are already at the latest version

Alerts

Abstract

We define a spinor-Minkowski metric for SL(4,C). It is not a trivial generalization of the SL(2,C) metric and it involves the Minkowskian one. We define 4x4 version of the Pauli matrices and eight 4-component associated generalized eigenvectors that can be regarded as undotted covariant spinors. The 4-component spinors can be grouped into four categories. Each category transforms in its own way. The outer products of pairwise combinations of 4-component spinors can be associated with 4-vectors. Including the dotted covariant, undotted and dotted contravariant forms totally we have sixteen pairs of spinors. Eight of them live in the conjugate space which has no countepart in SL(2,C).

Keywords:

Subject: Physical Sciences - Theoretical Physics

MSC: 22E43; 22E70; 53B30

1. Introduction

Let

L_{A}

be an element of SL(2,C). In an exponential form with parameters

θ

and

η

L_{A} = e x p (- \frac{i}{2} (\vec{θ} \cdot \vec{σ} + i \vec{ρ} \cdot \vec{σ}))

(1)

\vec{σ}

is the Pauli vector with

σ_{1} = σ_{x}, σ_{2} = σ_{y}, σ_{3} = σ_{z}

. The subscript

_{A}

is introduced in order to distinguish the other forms of L that will be introduced subsequently.

We rewrite

L_{A}

and its complex conjugate in the following compact forms:

L_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A} \cdot \vec{σ}), L_{A}^{*} = e x p (\frac{i}{2} {\vec{π}}_{A}^{*} \cdot {\vec{σ}}^{*})

(2)

{(π_{A})}_{i} = θ_{i} + i ρ_{i}

and

^{*}

denotes complex conjugation.

L_{A}

corresponds to the Lorentz transformation with

θ_{i}

and

ρ_{i}

being the rotation and boost parameters, respectively.

It is well known that a complex version of the

4 \times 4

Lorentz transformation matrix can be written as a matrix direct product of

L_{A}

and

L_{A}^{*}

[1,2]:

λ_{A} = L_{A} \otimes L_{A}^{*}

(3)

Let us write

L_{A}

σ

basis

L_{A} = \sum_{μ = 0}^{3} α_{μ} σ_{μ}

(4)

σ_{0}

is the

4 \times 4

identity. Explicit definitions of

α_{μ}

can be found in the Appendix. With the expansion given in Equation (4)

L_{A} \otimes L_{A}^{*} = \sum_{μ, ν = 0}^{3} α_{μ} α^{*}_{ν} (σ_{μ} \otimes σ_{ν}^{*})

(5)

We can write Equation (5) as a matrix product of two matrices by defining new basis

E_{μ} = σ_{μ} \otimes σ_{0}, {\tilde{E}}_{μ} = σ_{0} \otimes σ_{μ}^{*}

(6)

L_{A} \otimes L_{A}^{*} = W_{A} {\tilde{W}}_{A}

(7)

where

W_{A} = \sum α_{μ} E_{μ}

{\tilde{W}}_{A} = \sum α_{μ}^{*} {\tilde{E}}_{μ}

E and

\tilde{E}

basis obey the following commutation relations 1:

[E_{i}, E_{j}] = 2 i ϵ_{i j k} E_{k}, [{\tilde{E}}_{i}, {\tilde{E}}_{j}] = - 2 i ϵ_{i j k} {\tilde{E}}_{k}, [E_{i}, {\tilde{E}}_{j}] = 0

(8)

Note that in this representation

\tilde{E_{i}} \neq E_{i}^{*}

In order to obtain the familiar real

4 \times 4

matrix form of the Lorentz transformation it is enough to change the basis [3,4,5]:

Λ_{A} = A (L_{A} \otimes L_{A}^{*}) A^{- 1}

(9)

where

A = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & i & - i & 0 \\ 1 & 0 & 0 & - 1 \end{matrix}), A^{- 1} = A^{†} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 1 & - i & 0 \\ 0 & 1 & i & 0 \\ 1 & 0 & 0 & - 1 \end{matrix})

(10)

Now, it is straightforward to show that the

4 \times 4

real Lorentz transformation matrix can be written as a commutative product of two matrices one being the complex conjugate of the other [6,7,8]:

Λ_{A} = [A (L_{A} \otimes I) A^{- 1}] [A (I \otimes L_{A}^{*}) A^{- 1}] = Z_{A} Z_{A}^{*} = Z_{A}^{*} Z_{A},

(11)

Z_{A} = A (L_{A} \otimes I) A^{- 1}, Z_{A}^{*} = A (I \otimes L_{A}^{*}) A^{- 1} .

(12)

Z_{A}

and

Z_{A}^{*}

are the

4 \times 4

versions of

L_{A}

and

L_{A}^{*}

matrices. They can be expressed in terms of

Σ_{i}

matrices:

Z_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A} \cdot \vec{Σ}), Z_{A}^{*} = e x p (\frac{i}{2} {\vec{π}}_{A}^{*} \cdot {\vec{Σ}}^{*}) .

(13)

\vec{Σ} = (Σ_{1}, Σ_{2}, Σ_{3})

and

Σ_{i}

are

4 \times 4

versions of Pauli matrices [9]:

Σ_{1} = (\begin{matrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & - i \\ 0 & 0 & i & 0 \end{matrix}), Σ_{2} = (\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & i \\ 1 & 0 & 0 & 0 \\ 0 & - i & 0 & 0 \end{matrix}), Σ_{3} = (\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & - i & 0 \\ 0 & i & 0 & 0 \\ 1 & 0 & 0 & 0 \end{matrix})

(14)

By definition,

Σ_{μ} = A (σ_{μ} \otimes σ_{0}) A^{- 1}

(μ = 0, 1, 2, 3)

Σ_{0}

is the

4 \times 4

identity. Similarly, we define

\tilde{Σ}

basis as

{\tilde{Σ}}_{μ} = A (σ_{0} \otimes σ_{μ}^{*}) A^{- 1}

. But now we have an important property that

{\tilde{Σ}}_{μ} = Σ_{μ}^{*}

Σ_{μ}

basis do not form a complete set for

4 \times 4

matrices, but the set of

Σ_{μ} Σ_{ν}^{*}

does 2 .

Σ_{i}

and

Σ_{i}^{*}

matrices are traceless Hermitian and they satisfy the following commutation relations:

[Σ_{i}, Σ_{j}] = 2 i ϵ_{i j k} Σ_{k}, [Σ_{i}^{*}, Σ_{j}^{*}] = - 2 i ϵ_{i j k} Σ_{k}, [Σ_{i}, Σ_{j}^{*}] = 0

(15)

The

2 \times 2

Pauli matrices satisfy the first two relations, but the analogy breaks down because

σ_{1} = σ_{1}^{*}, σ_{2} = - σ_{2}^{*}

and

σ_{3} = σ_{3}^{*}

, hence

σ_{i}

does not commute with

σ_{j}^{*}

i \neq j

. On the other hand

Σ_{i}

commutes with

Σ_{j}^{*}

for all

i, j

From the Equation (12),

Z_{A}

can be found in terms of the elements of

L_{A}

Z_{A} = (\begin{matrix} α_{0} & α_{1} & α_{2} & α_{3} \\ α_{1} & α_{0} & - i α_{3} & i α_{2} \\ α_{2} & i α_{3} & α_{0} & - i α_{1} \\ α_{3} & - i α_{2} & i α_{1} & α_{0} \end{matrix})

(16)

where

α_{0} = \frac{1}{2} (L_{11} + L_{22})

α_{1} = \frac{1}{2} (L_{12} + L_{21})

α_{2} = \frac{i}{2} (L_{12} - L_{21})

, and

α_{3} = \frac{1}{2} (L_{11} - L_{22})

. Hence,

L_{A}

can be written in terms of

α_{μ}

L_{A} = (\begin{matrix} α_{0} + α_{3} & α_{1} - i α_{2} \\ α_{1} + i α_{2} & α_{0} - α_{3} \end{matrix})

(17)

We can write

L_{A}

and

Z_{A}

in terms of

σ_{μ}

and

Σ_{μ}

matrices:

L_{A} = α_{0} σ_{0} + α_{1} σ_{1} + α_{2} σ_{2} + α_{3} σ_{3}

(18)

Z_{A} = α_{0} Σ_{0} + α_{1} Σ_{1} + α_{2} Σ_{2} + α_{3} Σ_{3}

(19)

Or, simply

L_{A} = {(+ + + +)}_{σ}, Z_{A} = {(+ + + +)}_{Σ} .

(20)

Similarly we write

L_{A}^{*}

and

Z_{A}^{*}

in terms of

α_{μ}^{*}

L_{A}^{*} = α_{0}^{*} σ_{0}^{*} + α_{1}^{*} σ_{1}^{*} + α_{2}^{*} σ_{2}^{*} + α_{3}^{*} σ_{3}^{*} = {(+ + + +)}_{σ^{*}}^{*} = {(+ + - +)}_{σ}^{*}

(21)

Z_{A}^{*} = α_{0}^{*} Σ_{0}^{*} + α_{1}^{*} Σ_{1}^{*} + α_{2}^{*} Σ_{2}^{*} + α_{3}^{*} Σ_{3}^{*} = {(+ + + +)}_{Σ^{*}}^{*} \neq {(+ + - +)}_{Σ}^{*}

(22)

It is straightforward to show that

Z_{A}

commutes with

Z_{A}^{*}

, but

L_{A}

does not commute with

L_{A}^{*}

, in general. Actually, this property of Z matrices is more general. Let Z and Y be two matrices defined in

Σ_{μ}

and

Σ_{μ}^{*}

bases, respectively, Z and Y commute, because

Σ_{μ}

commutes with

Σ_{ν}^{*}

We also define the spinor metric g for SL(4,C) that corresponds to the spinor metric

ϵ

of SL(2,C):

g = g^{μ ν} = i η Σ_{2}^{*} = (\begin{matrix} 0 & 0 & i & 0 \\ 0 & 0 & 0 & - 1 \\ - i & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}); g^{- 1} = g_{μ ν} = g^{†} .

(23)

η

is the mostly minus Minkowski metric3.

Z_{A}

preserves the spinor metric g and the Minkowski metric

η

Z_{A}^{T} g Z_{A} = g, Z_{A}^{T} η Z_{A} = η

(24)

Since

η

is real,

Z_{A}^{T} η Z_{A} = η

directly entails

Λ^{T} η Λ = η

. In an analogy with

ϵ σ_{i} ϵ^{- 1} = - σ_{i}^{*}

, we have the following very useful relation:

g Σ_{i} g^{- 1} = - Σ_{i}^{*}

(25)

In this note it will be shown that there are eight generalized eigenvectors of

Σ_{3}^{*}

that can be interpreted as 4-component undotted covariant spinors. They can be grouped pairwise into four categories. Each category transforms in its own way. The outer products of spinor pairs can be associated with 4-vectors. When we include the dotted contravariant forms we get eight spinor pairs.

There is also a conjugate space. The dotted covariant and undotted contravariant spinor pairs live in this space. They double the number of spinor pairs, hence we have totally sixteen pairs. Due to the structural reasons there is no counterpart of this conjugate space in SL(2,C).

In the following sections we will study the first and the second categories in detail, and we will introduce the remaining ones in the subsequent sections.

2. The first and the second pairs and their transformation properties

Let

L_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A} \cdot \vec{σ})

be the

(\frac{1}{2}, 0)

representation of the Lorentz group that acts on the 2-component left-chiral spinor

ξ_{_{L}}

ξ_{_{L}} \to ξ_{_{L}}^{'} = L_{A} ξ_{_{L}} .

(26)

where

L_{A} = (\begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix})

(27)

In terms of the components

u, v

ξ_{_{L}}

u \to u^{'} = L_{11} u + L_{12} v, v \to v^{'} = L_{21} u + L_{22} v .

(28)

Let us call this transformation scheme

T_{A}

Let

{\dot{L}}_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A}^{*} \cdot \vec{σ})

be the dotted version corresponding to the

(0, \frac{1}{2})

representation of the Lorentz group.

{\dot{L}}_{A} = {(L_{A}^{- 1})}^{†}

. Let

ξ_{_{R}}

be the 2-component right-chiral spinor,

ξ_{_{R}} = ϵ ξ_{_{L}}^{*}

, where

ϵ = ϵ^{a b} = (\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}), ϵ^{- 1} = ϵ_{a b} = ϵ^{†} .

(29)

ξ_{_{R}}

transforms as

ξ_{_{R}} \to ξ_{_{R}}^{'} = {\dot{L}}_{A} ξ_{_{R}}

(30)

In terms of the components

u, v

, Equation (30) is equivalent to the scheme

T_{A}

given in Equation (28).

What happens when

L_{A}

acts on

ϵ ξ_{_{L}}

? In this case, in terms of the components

u \to u^{'} = L_{22} u - L_{21} v, v \to v^{'} = - L_{12} u + L_{11} v

(31)

Let us call this transformation scheme

T_{B}

. We can write

T_{B}

in a matrix form:

(\begin{matrix} u \\ v \end{matrix}) \to (\begin{matrix} u^{'} \\ v^{'} \end{matrix}) = (\begin{matrix} L_{22} & - L_{21} \\ - L_{12} & L_{11} \end{matrix}) (\begin{matrix} u \\ v \end{matrix})

(32)

Let us name this transformation matrix as

L_{B}

. Note that,

L_{B} = {({\dot{L}}_{A})}^{*}

, and Equation (32) is nothing but the transformation of

ξ_{_{L}}

under the action of

L_{B}

, which is a type

T_{B}

transformation.

Now, let

Z_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A} \cdot \vec{Σ})

be the

(\frac{1}{2}, 0)

representation of SL(4,C) that acts on a pair of 4-component undotted covariant spinors:

χ_{_{(1)}} \to χ_{_{(1)}}^{'} = Z_{A} χ_{_{(1)}}, χ_{_{(2)}} \to χ_{_{(2)}}^{'} = Z_{A} χ_{_{(2)}}

(33)

where

χ_{_{(1)}}

and

χ_{_{(2)}}

are the generalized eigenvectors of

Σ_{3}^{*}

χ_{_{(1)}} = \frac{1}{\sqrt{2}} (\begin{matrix} u \\ v \\ - i v \\ u \end{matrix}), χ_{_{(2)}} = \frac{1}{\sqrt{2}} (\begin{matrix} v \\ u \\ i u \\ - v \end{matrix})

(34)

Indices in the parentheses are simply labels for 4-component spinors.

We also have another pair of generalized eigenvectors for

Σ_{3}^{*}

χ_{_{(3)}} = \frac{1}{\sqrt{2}} (\begin{matrix} - v \\ u \\ - i u \\ - v \end{matrix}), χ_{_{(4)}} = \frac{1}{\sqrt{2}} (\begin{matrix} u \\ - v \\ - i v \\ - u \end{matrix})

(35)

Transformation scheme of

χ_{_{(3)}}

and

χ_{_{(4)}}

is different from that of

χ_{_{(1)}}

and

χ_{_{(2)}}

. Under the action of

Z_{A}

χ_{_{(1)}}

and

χ_{_{(2)}}

transform according to the scheme

T_{A}

, but

χ_{_{(3)}}

and

χ_{_{(4)}}

transform according to the scheme

T_{B}

. However, we may think in an alternative way: Suppose that

χ_{_{(3)}}

and

χ_{_{(3)}}

are different kind of objects with different transformation properties, such that another transformation matrix,

Z_{B}

, acts on them and under the action of

Z_{B}

they transform according to the scheme

T_{A}

χ_{_{(3)}} \to χ_{_{(3)}}^{'} = Z_{B} χ_{_{(3)}}, χ_{_{(4)}} \to χ_{_{(4)}}^{'} = Z_{B} χ_{_{(4)}} .

(36)

By definition

Z_{B} = A (L_{B} \otimes I) A^{- 1}

Z_{B} = (\begin{matrix} α_{0} & - α_{1} & α_{2} & - α_{3} \\ - α_{1} & α_{0} & i α_{3} & i α_{2} \\ α_{2} & - i α_{3} & α_{0} & i α_{1} \\ - α_{3} & - i α_{2} & - i α_{1} & α_{0} \end{matrix}) = α_{0} Σ_{0} - α_{1} Σ_{1} + α_{2} Σ_{2} - α_{3} Σ_{3} .

(37)

Or, simply

Z_{B} = {(+ - + -)}_{Σ}

(38)

Although

χ_{_{(1)}}

and

χ_{_{(2)}}

have different transformation properties than

χ_{_{(3)}}

and

χ_{_{(4)}}

, they are not completely independent:

- i Σ_{2} χ_{_{(1)}} = χ_{_{(3)}}, - i Σ_{2} χ_{_{(2)}} = χ_{_{(4)}}

(39)

where

- i Σ_{2}

corresponds to a

180^{\circ}

CCW rotation about the

x_{2}

axis in SL(4,C) 6. For more about rotations in the spinor space see Secction Section 9.

Now let

{\dot{Z}}_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A}^{*} \cdot \vec{Σ})

be the

(0, \frac{1}{2})

representation.

{\dot{Z}}_{A} = {(Z_{A}^{- 1})}^{†}

. The first pair of 4-component spinors for this representation is

{\dot{χ}}^{(1)} = \frac{1}{\sqrt{2}} (\begin{matrix} \dot{v} \\ - \dot{u} \\ i \dot{u} \\ \dot{v} \end{matrix}), {\dot{χ}}^{(2)} = \frac{1}{\sqrt{2}} (\begin{matrix} - \dot{u} \\ \dot{v} \\ i \dot{v} \\ \dot{u} \end{matrix})

(40)

These are also the generalized eigenvectors of

Σ_{3}^{*}

. Under the action of

{\dot{Z}}_{A}

{\dot{χ}}^{^{(1)}}

and

{\dot{χ}}^{^{(2)}}

transform according to the scheme

T_{A}

{\dot{χ}}^{^{(1)}} \to {\dot{χ}}^{^{{(1)}^{'}}} = {\dot{Z}}_{A} {\dot{χ}}^{^{(1)}}, {\dot{χ}}^{^{(2)}} \to {\dot{χ}}^{^{{(2)}^{'}}} = {\dot{Z}}_{A} {\dot{χ}}^{^{(2)}}

(41)

The second pair of the generalized eigenvectors of

Σ_{3}^{*}

is defined as

{\dot{χ}}^{(3)} = \frac{1}{\sqrt{2}} (\begin{matrix} \dot{u} \\ \dot{v} \\ - i \dot{v} \\ \dot{u} \end{matrix}), {\dot{χ}}^{(4)} = \frac{1}{\sqrt{2}} (\begin{matrix} \dot{v} \\ \dot{u} \\ i \dot{u} \\ - \dot{v} \end{matrix})

(42)

Under the action of

{\dot{Z}}_{A}

{\dot{χ}}^{^{(3)}}

and

{\dot{χ}}^{^{(4)}}

transform according to the scheme

T_{B}

. But, they transform according to the scheme

T_{A}

under the action of

{\dot{Z}}_{B}

{\dot{χ}}^{(3)} \to {\dot{χ}}^{{(3)}^{'}} = {\dot{Z}}_{B} {\dot{χ}}^{(3)}, {\dot{χ}}^{(4)} \to {\dot{χ}}^{{(4)}^{'}} = {\dot{Z}}_{B} {\dot{χ}}^{(4)}

(43)

where

{\dot{Z}}_{B} = {(Z_{B}^{- 1})}^{†}

by definition. We also have the following relations between them:

- i Σ_{2} {\dot{χ}}^{(1)} = {\dot{χ}}^{(3)}, - i Σ_{2} {\dot{χ}}^{(2)} = {\dot{χ}}^{(4)}

(44)

Note that

χ^{^{(a)}}

can be related to

χ_{_{(a)}}

only by the SL(4,C) metric g that involves the Minkowski metric.

χ^{(a)} = g χ_{_{(a)}}

, and its dotted version is defined as 7

{\dot{χ}}^{(a)} = {(g χ_{_{(a)}})}^{*} .

(45)

The scalar product of 4-component spinors is defined in a similar way as 2-component spinors and they are invariant under the Z transformations.

We write various forms of Z and L matrices in a compact notation to manifest the parallelism between them:

L_{A} = {(+ + + +)}_{σ} L_{B} = {(+ - + -)}_{σ} {\dot{L}}_{A} = {(+ - - -)}_{σ}^{*} {\dot{L}}_{B} = {(+ + - +)}_{σ}^{*}

(46)

Z_{A} = {(+ + + +)}_{Σ} Z_{B} = {(+ - + -)}_{Σ} {\dot{Z}}_{A} = {(+ - - -)}_{Σ}^{*} {\dot{Z}}_{B} = {(+ + - +)}_{Σ}^{*}

(47)

3. Outer products of 4-component spinors

Let us define the outer product

W_{_{L}} = ξ_{_{L}} ξ_{_{L}}^{†}

which transforms as

W_{_{L}} \to W_{_{L}}^{'} = (L_{A} ξ_{_{L}}) {(L_{A} ξ_{_{L}})}^{†} = L_{A} W_{_{L}} L_{A}^{†}

(48)

This is a type

T_{A}

transformation. Determinant of

W_{_{L}}

is zero, hence

W_{_{L}}

can be associated with a null 4-vector through the substitutions,

t = \frac{1}{2} (u \dot{u} + v \dot{v}), x = \frac{1}{2} (u \dot{v} + v \dot{u}), y = \frac{i}{2} (u \dot{v} - v \dot{u}), z = \frac{1}{2} (u \dot{u} - v \dot{v})

W_{_{L}} = (\begin{matrix} t + z & x - i y \\ x + i y & t - z \end{matrix})

(49)

We also define the outer product

W_{_{R}} = ξ_{_{R}} ξ_{_{R}}^{†}

which transforms as

W_{_{R}} \to W_{_{R}}^{'} = ({\dot{L}}_{A} ξ_{_{R}}) {({\dot{L}}_{A} ξ_{_{R}})}^{†} = {\dot{L}}_{A} W_{_{R}} {\dot{L}}_{A}^{†}

(50)

This is also a type

T_{A}

transformation. Determinant of

W_{_{R}}

is zero and

W_{_{R}}

can be associated with a null 4-vector:

W_{_{R}} = (\begin{matrix} t - z & - x + i y \\ - x - i y & t + z \end{matrix})

(51)

W_{_{R}}

can be obtained from

W_{_{L}}

by parity inversion.

We define the outer product of 4-component spinors,

W_{_{(a a)}} = χ_{_{(a)}} χ_{_{(a)}}^{†}

, which transform in a similar way as

W_{_{L}}

W_{_{(a a)}} \to W_{_{(a a)}}^{'} = (Z_{A} χ_{_{(a)}}) {(Z_{A} χ_{_{(a)}})}^{†} = Z_{A} W_{_{(a a)}} Z_{A}^{†} .

(52)

For

a = 1

and

a = 2

W_{_{(a a)}}

transforms according to the scheme

T_{A}

. Equation (52) is the main motivation behind the interpretation of

χ_{_{(a)}}

as a 4-component spinor for SL(4, C).

{\dot{W}}^{^{(a a)}} = {\dot{χ}}^{^{(a)}} {\dot{χ}}^{^{(a) †}}

transform in a similar way as

W_{_{R}}

{\dot{W}}^{^{(a a)}} \to {\dot{Z}}_{A} {\dot{W}}^{^{(a a)}} {\dot{Z}}_{A}^{†}

(53)

For

a = 1

and

a = 2

{\dot{W}}^{^{(a a)}}

transform according to the scheme

T_{A}

We also have outer products of 4-component spinors of the other kind. For

a = 3

and

a = 4

W_{_{(a a)}}

and

{\dot{W}}^{^{(a a)}}

transform according to the scheme

T_{A}

under the action of

Z_{B}

and

{\dot{Z}}_{B}

W_{_{(a a)}} \to Z_{B} W_{_{(a a)}} Z_{B}^{†}, {\dot{W}}^{^{(a a)}} \to {\dot{Z}}_{B} {\dot{W}}^{^{(a a)}} {\dot{Z}}_{B}^{†}

(54)

W_{_{(a a)}}

and

{\dot{W}}^{^{(a a)}}

are Hermitian and zero determinant matrices and they are the basic elements of the outer product forms. In the next section it will be shown that combinations of these basic elements can be associated with 4-vectors.

4. Quaternion forms and 4-vectors

In general, we can treat

t, x, y

and z as variables that do not depend on u and v. Then, we can associate the following matrices

X_{_{L}}

and

X_{_{R}}

with 4-vectors, which are not necessarily null:

W_{_{L}} \to X_{_{L}} = (\begin{matrix} t + z & x - i y \\ x + i y & t - z \end{matrix}) = t σ_{0} + x σ_{1} + y σ_{2} + z σ_{3} = {(+ + + +)}_{σ}

(55)

W_{_{R}} \to X_{_{R}} = (\begin{matrix} t - z & - x + i y \\ - x - i y & t + z \end{matrix}) = t σ_{0} - x σ_{1} - y σ_{2} - z σ_{3} = {(+ - - -)}_{σ}

(56)

det

X_{_{L}} =

det

X_{_{R}} = t^{2} - x^{2} - y^{2} - z^{2}

and in general not zero 8 .

X_{_{L}}

and

X_{_{R}}

transform as

X_{_{L}} \to X_{_{L}}^{'} = L_{A} X_{_{L}} L_{A}^{†}, X_{_{R}} \to X_{_{R}}^{'} = {\dot{L}}_{A} X_{_{R}} {\dot{L}}_{A}^{†}

(57)

In SL(4,C), in order to have a similar representation, we have to introduce the following two column objects that are pairwise combinations of 4-component spinors:

χ_{_{A}} = \frac{1}{\sqrt{2}} (\begin{matrix} u & v \\ v & u \\ - i v & i u \\ u & - v \end{matrix}), χ_{_{B}} = \frac{1}{\sqrt{2}} (\begin{matrix} - v & u \\ u & - v \\ - i u & - i v \\ v & - u \end{matrix}), {\dot{χ}}^{^{A}} = \frac{1}{\sqrt{2}} (\begin{matrix} \dot{v} & - \dot{u} \\ - \dot{u} & \dot{v} \\ i \dot{u} & i \dot{v} \\ \dot{v} & \dot{u} \end{matrix}), {\dot{χ}}^{^{B}} = \frac{1}{\sqrt{2}} (\begin{matrix} \dot{u} & \dot{v} \\ \dot{v} & \dot{u} \\ - i \dot{v} & i \dot{u} \\ \dot{u} & - \dot{v} \end{matrix})

(58)

where

χ_{_{A}} = (χ_{_{(1)}}, χ_{_{(2)}})

χ_{_{B}} = (χ_{_{(3)}}, χ_{_{(4)}})

{\dot{χ}}^{^{A}} = ({\dot{χ}}^{^{(1)}}, {\dot{χ}}^{^{(2)}})

and

{\dot{χ}}^{^{B}} = ({\dot{χ}}^{^{(3)}}, {\dot{χ}}^{^{(4)}})

Let us define an outer product of the form

W_{_{A}} = χ_{_{A}} χ_{_{A}}^{†}

, which is formally a quaternion:

W_{_{A}} = \frac{1}{2} (\begin{matrix} u \dot{u} + v \dot{v} & u \dot{v} + v \dot{u} & i u \dot{v} - i v \dot{u} & u \dot{u} - v \dot{v} \\ v \dot{u} + u \dot{v} & v \dot{v} + u \dot{u} & i v \dot{v} - i u \dot{u} & v \dot{u} - u \dot{v} \\ - i v \dot{u} + i u \dot{v} & - i v \dot{v} + i u \dot{u} & v \dot{v} + u \dot{u} & - i v \dot{u} - i u \dot{v} \\ u \dot{u} - v \dot{v} & u \dot{v} - v \dot{u} & i u \dot{v} + i v \dot{u} & u \dot{u} + v \dot{v} \end{matrix})

(59)

W_{_{A}}

can be written as a sum of two basic forms:

W_{_{A}} = W_{_{(11)}} + W_{_{(22)}}

. In its present form det

W_{_{A}} = 0

and

W_{_{A}}

corresponds to a null 4-vector, but we can associate

W_{_{A}}

with an arbitrary 4-vector in terms of the variables

t, x, y

and z:

W_{_{A}} \to Q_{_{A}} = (\begin{matrix} t & x & y & z \\ x & t & - i z & i y \\ y & i z & t & - i x \\ z & - i y & i x & t \end{matrix}) = t Σ_{0} + x Σ_{1} + y Σ_{2} + z Σ_{3} .

(60)

Q_{_{A}} = {(+ + + +)}_{Σ}

and it is the

4 \times 4

version of

X_{_{L}}

Q_{_{A}} = A (X_{_{L}} \otimes I) A^{- 1}

(61)

Similarly, we define

{\dot{W}}^{^{A}}

{\dot{W}}^{^{A}} = {\dot{χ}}^{^{A}} {\dot{χ}}^{^{A †}} = {\dot{W}}^{^{(11)}} + {\dot{W}}^{^{(22)}} = \frac{1}{2} (\begin{matrix} \dot{v} v + \dot{u} u & - \dot{v} u - \dot{u} v & - i \dot{v} u + i \dot{u} v & \dot{v} v - \dot{u} u \\ - \dot{u} v - \dot{v} u & \dot{u} u + \dot{v} v & i \dot{u} u - i \dot{v} v & - \dot{u} v + \dot{v} u \\ i \dot{u} v - i \dot{v} u & - i \dot{u} u + i \dot{v} v & \dot{u} u + \dot{v} v & i \dot{u} v + i \dot{v} u \\ \dot{v} v - \dot{u} u & - \dot{v} u + \dot{u} v & - i \dot{v} u - i \dot{u} v & \dot{v} v + \dot{u} u \end{matrix})

(62)

In terms of the variables

t, x, y

and z

{\dot{W}}^{^{A}} \to {\dot{Q}}^{^{A}} = (\begin{matrix} t & - x & - y & - z \\ - x & t & i z & - i y \\ - y & - i z & t & i x \\ - z & i y & - i x & t \end{matrix}) = t Σ_{0} - x Σ_{1} - y Σ_{2} - z Σ_{3} .

(63)

{\dot{Q}}^{^{A}} = {(+ - - -)}_{Σ}

and it is the

4 \times 4

version of

X_{_{R}}

{\dot{Q}}^{^{A}} = A (X_{_{R}} \otimes I) A^{- 1} .

(64)

{\dot{Q}}^{^{A}}

can be obtained from

Q_{_{A}}

by parity inversion and they transform as

Q_{_{A}} \to Z_{A} Q_{_{A}} Z_{A}^{†}, {\dot{Q}}^{^{A}} \to {\dot{Z}}_{A} {\dot{Q}}^{^{A}} {\dot{Z}}_{A}^{†}

(65)

These are type

T_{A}

transformations, hence these forms correspond to 4-vectors.

The outer product

W_{_{B}} = χ_{_{B}} χ_{_{B}}^{†}

is also a quaternion:

W_{_{B}} = \frac{1}{2} (\begin{matrix} v \dot{v} + u \dot{u} & - v \dot{u} - u \dot{v} & - i v \dot{u} + i u \dot{v} & v \dot{v} - u \dot{u} \\ - u \dot{v} - v \dot{u} & u \dot{u} + v \dot{v} & i u \dot{u} - i v \dot{v} & - u \dot{v} + v \dot{u} \\ i u \dot{v} - i v \dot{u} & - i u \dot{u} + i v \dot{v} & u \dot{u} + v \dot{v} & i u \dot{v} + i v \dot{u} \\ v \dot{v} - u \dot{u} & - v \dot{u} + u \dot{v} & - i v \dot{u} - i u \dot{v} & v \dot{v} + u \dot{u} \end{matrix})

(66)

In terms of variables

t, x, y

and z

W_{_{B}} \to Q_{_{B}} = (\begin{matrix} t & - x & y & - z \\ - x & t & i z & i y \\ y & - i z & t & i x \\ - z & - i y & - i x & t \end{matrix}) = t Σ_{0} - x Σ_{1} + y Σ_{2} - z Σ_{3}

(67)

In short,

Q_{_{B}} = {(+ - + -)}_{Σ}

We also write

{\dot{W}}^{^{B}}

{\dot{W}}^{^{B}} = {\dot{χ}}^{^{B}} {\dot{χ}}^{^{B †}} = \frac{1}{2} (\begin{matrix} \dot{u} u + \dot{v} v & \dot{u} v + \dot{v} u & i \dot{u} v - i \dot{v} u & \dot{u} u - \dot{v} v \\ \dot{v} u + \dot{u} v & \dot{v} v + \dot{u} u & i \dot{v} v - i \dot{u} u & \dot{v} u - \dot{u} v \\ - i \dot{v} u + i \dot{u} v & - i \dot{v} v + i \dot{u} u & \dot{v} v + \dot{u} u & - i \dot{v} u - i \dot{u} v \\ \dot{u} u - \dot{v} v & \dot{u} v - \dot{v} u & i \dot{u} v + i \dot{v} u & \dot{u} u + \dot{v} v \end{matrix})

(68)

{\dot{W}}^{^{B}} \to {\dot{Q}}^{^{B}} = (\begin{matrix} t & x & - y & z \\ x & t & - i z & - i y \\ - y & i z & t & - i x \\ z & i y & i x & t \end{matrix}) = t Σ_{0} + x Σ_{1} - y Σ_{2} + z Σ_{3} .

(69)

{\dot{Q}}^{^{B}} = {(+ + - +)}_{Σ}

and it can be obtained from

Q_{_{B}}

by parity inversion.

Q_{_{B}}

and

{\dot{Q}}^{^{B}}

are transformed by

Z_{B}

and

{\dot{Z}}_{B}

Q_{_{B}} \to Z_{B} Q_{_{B}} Z_{B}^{†}, {\dot{Q}}^{^{B}} \to {\dot{Z}}_{B} {\dot{Q}}^{^{B}} {\dot{Z}}_{B}^{†}

(70)

These transformations obey the scheme

T_{A}

also, hence

Q_{_{B}}

and

{\dot{Q}}^{^{B}}

can be associated with 4-vectors.

With our compact notation it can be shown that the form of the transformation matrix matches the form of the transformed object. For example,

Z_{A} = {(+ + + +)}_{Σ}

acts on the form

Q_{A} = {(+ + + +)}_{Σ}

Z_{B} = {(+ - + -)}_{Σ}

acts on the form

Q_{B} = {(+ - + -)}_{Σ}

{\dot{Z}}_{A} = {(+ - - -)}_{Σ}^{*}

acts on the form

{\dot{Q}}^{A} = {(+ - - -)}_{Σ}

, and

{\dot{Z}}_{B} = {(+ + - +)}_{Σ}^{*}

acts on the form

{\dot{Q}}^{B} = {(+ + - +)}_{Σ}

5. Two more pairs of spinors

There are four eigenvectors of

Σ_{3}^{*}

that constitute a complete orthonormal set of basis:

e_{1} = (\begin{matrix} 1 \\ 0 \\ 0 \\ 1 \end{matrix}), e_{2} = (\begin{matrix} 1 \\ 0 \\ 0 \\ - 1 \end{matrix}), e_{3} = (\begin{matrix} 0 \\ 1 \\ - i \\ 0 \end{matrix}), e_{4} = (\begin{matrix} 0 \\ 1 \\ i \\ 0 \end{matrix}) .

(71)

e_{1}

and

e_{3}

correspond to

+ 1

eigenvalue and

e_{2}

and

e_{4}

correspond to

- 1

eigenvalue. We obtain eight generalized eigenvectors by combining the basis corresponding to the same eigenvalue. For example, we can obtain the four generalized undotted covariant eigenvectors that we have previously studied as follows:

χ_{_{(1)}} = u e_{1} + v e_{3}, χ_{_{(2)}} = v e_{2} + u e_{4},

(72)

χ_{_{(3)}} = - v e_{1} + u e_{3}, χ_{_{(4)}} = u e_{2} - v e_{4},

(73)

We can obtain four more generalized eigenvectors of

Σ_{3}^{*}

by changing the sign or swapping u and v:

χ_{_{(5)}} = - u e_{1} + v e_{3}, χ_{_{(6)}} = v e_{2} - u e_{4},

(74)

χ_{_{(7)}} = v e_{1} + u e_{3}, χ_{_{(8)}} = u e_{2} + v e_{4},

(75)

Totally we get eight undotted covariant spinors:

χ_{_{(1)}} = (\begin{matrix} u \\ v \\ - i v \\ u \end{matrix}), χ_{_{(2)}} = (\begin{matrix} v \\ u \\ i u \\ - v \end{matrix}), χ_{_{(3)}} = (\begin{matrix} - v \\ u \\ - i u \\ - v \end{matrix}), χ_{_{(4)}} = (\begin{matrix} u \\ - v \\ - i v \\ - u \end{matrix}),

(76)

χ_{_{(5)}} = (\begin{matrix} - u \\ v \\ - i v \\ - u \end{matrix}), χ_{_{(6)}} = (\begin{matrix} v \\ - u \\ - i u \\ - v \end{matrix}), χ_{_{(7)}} = (\begin{matrix} v \\ u \\ - i u \\ v \end{matrix}), χ_{_{(8)}} = (\begin{matrix} u \\ v \\ i v \\ - u \end{matrix}) .

(77)

We can group

χ_{_{(a)}}

(

a = 1, 2, \dots 8

) pairwise:

P_{_{A}} = {χ_{_{(1)}}, χ_{_{(2)}}}, P_{_{B}} = {χ_{_{(3)}}, χ_{_{(4)}}}, P_{_{C}} = {χ_{_{(5)}}, χ_{_{(6)}}}, P_{_{D}} = {χ_{_{(7)}}, χ_{_{(8)}}},

(78)

We already know that

P_{A}

transforms with

Z_{A}

and

P_{B}

transforms with

Z_{B}

. Following the same procedure that we have applied in the previous sections we can show that

P_{C}

and

P_{D}

transform with

Z_{C}

and

Z_{D}

respectively:

Z_{C} = A (L_{C} \otimes I) A^{- 1}, Z_{D} = A (L_{D} \otimes I) A^{- 1},

(79)

where

L_{C} = (\begin{matrix} L_{11} & - L_{12} \\ - L_{21} & L_{22} \end{matrix}) = (\begin{matrix} α_{0} + α_{3} & - α_{1} + i α_{2} \\ - α_{1} - i α_{2} & α_{0} - α_{3} \end{matrix}) = {(+ - - +)}_{σ}

(80)

L_{D} = (\begin{matrix} L_{22} & L_{21} \\ L_{12} & L_{11} \end{matrix}) = (\begin{matrix} α_{0} - α_{3} & α_{1} + i α_{2} \\ α_{1} - i α_{2} & α_{0} + α_{3} \end{matrix}) = {(+ + - -)}_{σ}

(81)

{\dot{L}}_{C} = {(+ + + -)}_{σ}^{*} = L_{D}^{*}

(82)

{\dot{L}}_{D} = {(+ - + +)}_{σ}^{*} = L_{C}^{*}

(83)

The corresponding SL(4,C) matrices are

Z_{C} = (\begin{matrix} α_{0} & - α_{1} & - α_{2} & α_{3} \\ - α_{1} & α_{0} & - i α_{3} & - i α_{2} \\ - α_{2} & i α_{3} & α_{0} & i α_{1} \\ α_{3} & i α_{2} & - i α_{1} & α_{0} \end{matrix}) = {(+ - - +)}_{Σ}

(84)

Z_{D} = (\begin{matrix} α_{0} & α_{1} & - α_{2} & - α_{3} \\ α_{1} & α_{0} & i α_{3} & - i α_{2} \\ - α_{2} & - i α_{3} & α_{0} & - i α_{1} \\ - α_{3} & i α_{2} & i α_{1} & α_{0} \end{matrix}) = {(+ + - -)}_{Σ}

(85)

There are also the dotted versions:

{\dot{Z}}_{C} = (\begin{matrix} α_{0}^{*} & α_{1}^{*} & α_{2}^{*} & - α_{3}^{*} \\ α_{1}^{*} & α_{0}^{*} & i α_{3}^{*} & i α_{2}^{*} \\ α_{2}^{*} & - i α_{3}^{*} & α_{0}^{*} & - i α_{1}^{*} \\ - α_{3}^{*} & - i α_{2}^{*} & i α_{1}^{*} & α_{0}^{*} \end{matrix}) = {(+ + + -)}_{Σ}^{*}

(86)

{\dot{Z}}_{D} = (\begin{matrix} α_{0}^{*} & - α_{1}^{*} & α_{2}^{*} & α_{3}^{*} \\ - α_{1}^{*} & α_{0}^{*} & - i α_{3}^{*} & i α_{2}^{*} \\ α_{2}^{*} & i α_{3}^{*} & α_{0}^{*} & i α_{1}^{*} \\ α_{3}^{*} & - i α_{2}^{*} & - i α_{1}^{*} & α_{0}^{*} \end{matrix}) = {(+ - + +)}_{Σ}^{*}

(87)

We also define eight dotted contravariat spinors

{\dot{χ}}^{^{(a)}} = {(g χ_{_{(a)}})}^{*}

(

a = 1, 2, \dots 8

) which are also the generalized eigenvectors of

Σ_{3}^{*}

{\dot{χ}}^{^{(1)}} = (\begin{matrix} \dot{v} \\ - \dot{u} \\ i \dot{u} \\ \dot{v} \end{matrix}), {\dot{χ}}^{^{(2)}} = (\begin{matrix} - \dot{u} \\ \dot{v} \\ i \dot{v} \\ \dot{u} \end{matrix}), {\dot{χ}}^{^{(3)}} = (\begin{matrix} \dot{u} \\ \dot{v} \\ - i \dot{v} \\ \dot{u} \end{matrix}), {\dot{χ}}^{^{(4)}} = (\begin{matrix} \dot{v} \\ \dot{u} \\ i \dot{u} \\ - \dot{v} \end{matrix})

(88)

{\dot{χ}}^{^{(5)}} = (\begin{matrix} \dot{v} \\ \dot{u} \\ - i \dot{u} \\ \dot{v} \end{matrix}), {\dot{χ}}^{^{(6)}} = (\begin{matrix} \dot{u} \\ \dot{v} \\ i \dot{v} \\ - \dot{u} \end{matrix}), {\dot{χ}}^{^{(7)}} = (\begin{matrix} \dot{u} \\ - \dot{v} \\ i \dot{v} \\ \dot{u} \end{matrix}), {\dot{χ}}^{^{(8)}} = (\begin{matrix} - \dot{v} \\ \dot{u} \\ i \dot{u} \\ \dot{v} \end{matrix}) .

(89)

We group them pairwise:

P^{^{A}} = {{\dot{χ}}^{^{(1)}}, {\dot{χ}}^{^{(2)}}}, P^{^{B}} = {{\dot{χ}}^{^{(3)}}, {\dot{χ}}^{^{(4)}}}, P^{^{C}} = {{\dot{χ}}^{^{(5)}}, {\dot{χ}}^{^{(6)}}}, P^{^{D}} = {{\dot{χ}}^{^{(7)}}, {\dot{χ}}^{^{(8)}}}

(90)

Each pair of the dotted contravariant spinors transform with the associated dotted Z matrix.

We define four two-column undotted covariant objects (spinor pairs):

χ_{_{A}} = (χ_{_{(1)}}, χ_{_{(2)}}), χ_{_{B}} = (χ_{_{(3)}}, χ_{_{(4)}}), χ_{_{C}} = (χ_{_{(5)}}, χ_{_{(6)}}), χ_{_{D}} = (χ_{_{(7)}}, χ_{_{(8)}})

(91)

And we define the corresponding two-column dotted contravariant spinor pairs

{\dot{χ}}^{^{A}} = ({\dot{χ}}^{^{(1)}}, {\dot{χ}}^{^{(2)}}), {\dot{χ}}^{^{B}} = ({\dot{χ}}^{^{(3)}}, {\dot{χ}}^{^{(4)}}), {\dot{χ}}^{^{C}} = ({\dot{χ}}^{^{(5)}}, {\dot{χ}}^{^{(6)}}), {\dot{χ}}^{^{D}} = ({\dot{χ}}^{^{(7)}}, {\dot{χ}}^{^{(8)}})

(92)

Finally, we construct eight outer products that can be associated with 4-vectors:

χ_{_{A}} χ_{_{A}}^{†} \to Q_{_{A}} = {(+ + + +)}_{Σ} {\dot{χ}}^{^{A}} {\dot{χ}}^{^{A †}} \to {\dot{Q}}^{^{A}} = {(+ - - -)}_{Σ}

(93)

χ_{_{B}} χ_{_{B}}^{†} \to Q_{_{B}} = {(+ - + -)}_{Σ} {\dot{χ}}^{^{B}} {\dot{χ}}^{^{B †}} \to {\dot{Q}}^{^{B}} = {(+ + - +)}_{Σ}

(94)

χ_{_{C}} χ_{_{C}}^{†} \to Q_{_{C}} = {(+ - - +)}_{Σ} {\dot{χ}}^{^{C}} {\dot{χ}}^{^{C †}} \to {\dot{Q}}^{^{C}} = {(+ + + -)}_{Σ}

(95)

χ_{_{D}} χ_{_{D}}^{†} \to Q_{_{D}} = {(+ + - -)}_{Σ} {\dot{χ}}^{^{D}} {\dot{χ}}^{^{D †}} \to {\dot{Q}}^{^{D}} = {(+ - + +)}_{Σ}

(96)

Each form transforms in its own way with the matching Z or

\dot{Z}

matrix.

6. Complex conjugated forms

There are also dotted covariant and undotted contravariant 4-component spinors which have no counterparts in SL(2,C):

{\dot{χ}}_{_{(a)}} = {(χ_{_{(a)}})}^{*}

χ^{^{(a)}} = {({\dot{χ}}^{^{(a)}})}^{*}

. They are the generalized eigenvectors of

Σ_{3}

. We group them pairwise to get eight more two-column objects (spinor pairs):

{\dot{χ}}_{_{A}} = ({\dot{χ}}_{_{(1)}}, {\dot{χ}}_{_{(2)}}), {\dot{χ}}_{_{B}} = ({\dot{χ}}_{_{(3)}}, {\dot{χ}}_{_{(4)}}), {\dot{χ}}_{_{C}} = ({\dot{χ}}_{_{(5)}}, {\dot{χ}}_{_{(6)}}), {\dot{χ}}_{_{D}} = ({\dot{χ}}_{_{(7)}}, {\dot{χ}}_{_{(8)}})

(97)

χ^{^{A}} = (χ^{^{(1)}}, χ^{^{(2)}}), χ^{^{B}} = (χ^{^{(3)}}, χ^{^{(4)}}), χ^{^{C}} = (χ^{^{(5)}}, χ^{^{(6)}}), χ^{^{D}} = (χ^{^{(7)}}, χ^{^{(8)}})

(98)

All conjugated pairs live in the conjugate space and their outer products, that can be associated with 4-vectors, also live in the conjugate space:

Q_{_{A}} = {(+ + + +)}_{Σ} \overset{c . c .}{\to} {\dot{Q}}_{_{A}} = {(+ + + +)}_{Σ^{*}} = {\dot{χ}}_{_{A}} {\dot{χ}}_{_{A}}^{†}

(99)

Q_{_{B}} = {(+ - + -)}_{Σ} \overset{c . c .}{\to} {\dot{Q}}_{_{B}} = {(+ - + -)}_{Σ^{*}} = {\dot{χ}}_{_{B}} {\dot{χ}}_{_{B}}^{†}

(100)

Q_{_{C}} = {(+ - - +)}_{Σ} \overset{c . c .}{\to} {\dot{Q}}_{_{C}} = {(+ - - +)}_{Σ^{*}} = {\dot{χ}}_{_{C}} {\dot{χ}}_{_{C}}^{†}

(101)

Q_{_{D}} = {(+ + - -)}_{Σ} \overset{c . c .}{\to} {\dot{Q}}_{_{D}} = {(+ + - -)}_{Σ^{*}} = {\dot{χ}}_{_{D}} {\dot{χ}}_{_{D}}^{†}

(102)

{\dot{Q}}^{^{A}} = {(+ - - -)}_{Σ} \overset{c . c .}{\to} Q^{^{A}} = {(+ - - -)}_{Σ^{*}} = χ^{^{A}} χ^{^{A †}}

(103)

{\dot{Q}}^{^{B}} = {(+ + - +)}_{Σ} \overset{c . c .}{\to} Q^{^{B}} = {(+ + - +)}_{Σ^{*}} = χ^{^{B}} χ^{^{B †}}

(104)

{\dot{Q}}^{^{C}} = {(+ + + -)}_{Σ} \overset{c . c .}{\to} Q^{^{C}} = {(+ + + -)}_{Σ^{*}} = χ^{^{C}} χ^{^{C †}}

(105)

{\dot{Q}}^{^{D}} = {(+ - + +)}_{Σ} \overset{c . c .}{\to} Q^{^{D}} = {(+ - + +)}_{Σ^{*}} = χ^{^{D}} χ^{^{D †}}

(106)

The space of conjugate quaternions is spanned by

Σ_{μ}^{*}

and it has no counterpart in SL(2, C). Dotted lower indexed and undotted upper indexed forms transform with

Z_{X}^{*}

and with

{({\dot{Z}}_{X})}^{*}

matrices respectively (

X = A, B, C, D

), and all transformations obey the scheme

T_{A}

4-vector scalar product can be defined by using the conjugate forms in two equivalent ways. Let

Q

and

P

be two 4-vectors and let

Q_{_{X}}

and

P_{_{X}}

be the corresponding quaternions :

Q \cdot P = \frac{1}{4} Tr (Q_{_{X}}^{T} P^{^{X}})

(107)

Or, noting that

P^{^{X}} = g P_{_{X}} g^{- 1}

, we can also write

Q \cdot P = \frac{1}{4} (Q_{μ \dot{ν}} P^{μ \dot{ν}})

(108)

where now indices refer to the components and the summation convention is implied 9 10.

7. Four types of transformations for SL(2,C)

We can suggest a similar formalism for SL(2,C). Let

ξ_{_{A}}, ξ_{_{B}}, ξ_{_{C}}

and

ξ_{_{D}}

be covariant spinors:

ξ_{_{A}} = (\begin{matrix} u \\ v \end{matrix}), ξ_{_{B}} = (\begin{matrix} v \\ - u \end{matrix}), ξ_{_{C}} = (\begin{matrix} u \\ - v \end{matrix}), ξ_{_{D}} = (\begin{matrix} v \\ u \end{matrix})

(109)

and let

ξ^{^{A}}, ξ^{^{B}}, ξ^{^{C}}

and

ξ^{^{D}}

be contravariant spinors:

ξ^{^{A}} = (\begin{matrix} v \\ - u \end{matrix}), ξ^{^{B}} = (\begin{matrix} - u \\ - v \end{matrix}), ξ^{^{C}} = (\begin{matrix} - v \\ - u \end{matrix}), ξ_{_{D}} = (\begin{matrix} u \\ - v \end{matrix})

(110)

where

ξ^{^{A}} = ξ_{_{B}}, ξ^{^{B}} = - ξ_{_{A}}, ξ^{^{C}} = - ξ_{_{D}}, ξ^{^{D}} = ξ_{_{C}}

(111)

This proliferation is necessary for the symmetry in Figure 1.

We have the following transformation properties:

ξ_{_{A}} \to ξ_{_{A}}^{'} = L_{_{A}} ξ_{_{A}}, ξ_{_{B}} \to ξ_{_{B}}^{'} = L_{_{B}} ξ_{_{B}}, ξ_{_{C}} \to ξ_{_{C}}^{'} = L_{_{C}} ξ_{_{C}}, ξ_{_{D}} \to ξ_{_{D}}^{'} = L_{_{D}} ξ_{_{D}}

(112)

{\dot{ξ}}^{A} \to {\dot{ξ^{'}}}^{A} = {\dot{L}}_{A} {\dot{ξ}}^{A}, {\dot{ξ}}^{B} \to {\dot{ξ^{'}}}^{B} = {\dot{L}}_{B} {\dot{ξ}}^{B}, {\dot{ξ}}^{C} \to {\dot{ξ^{'}}}^{C} = {\dot{L}}_{C} {\dot{ξ}}^{C}, {\dot{ξ}}^{D} \to {\dot{ξ^{'}}}^{D} = {\dot{L}}_{D} {\dot{ξ}}^{D}

(113)

{\dot{L}}_{A} = L_{B}^{*}, {\dot{L}}_{B} = L_{A}^{*}, {\dot{L}}_{C} = L_{D}^{*}, {\dot{L}}_{D} = L_{C}^{*}

(114)

All transformations obey the scheme

T_{A}

We have the following outer products:

ξ_{_{A}} ξ_{_{A}}^{†} \to X_{_{A}} = {(+ + + +)}_{σ} ξ_{_{B}} ξ_{_{B}}^{†} \to X_{_{B}} = {(+ - + -)}_{σ}

(115)

ξ_{_{C}} ξ_{_{C}}^{†} \to X_{_{C}} = {(+ - - +)}_{σ} ξ_{_{D}} ξ_{_{D}}^{†} \to X_{_{D}} = {(+ + - -)}_{σ}

(116)

{\dot{ξ}}^{^{A}} {\dot{ξ}}^{^{A †}} \to {\dot{X}}^{^{A}} = {(+ - - -)}_{σ} {\dot{ξ}}^{^{B}} {\dot{ξ}}^{^{B †}} \to {\dot{X}}^{^{B}} = {(+ + - +)}_{σ}

(117)

{\dot{ξ}}^{^{C}} {\dot{ξ}}^{^{C †}} \to {\dot{X}}^{^{C}} = {(+ + + -)}_{σ} {\dot{ξ}}^{^{D}} {\dot{ξ}}^{^{D †}} \to {\dot{X}}^{^{D}} = {(+ - + +)}_{σ}

(118)

It is worth noting that complex conjugating these forms does not yield anything new. In order to emphasize the difference with 4-component spinor pairs let us define the following sets:

ξ = {ξ_{_{A}}, ξ_{_{B}}, ξ_{_{C}}, ξ_{_{D}}, {\dot{ξ}}^{^{A}}, {\dot{ξ}}^{^{B}}, {\dot{ξ}}^{^{C}}, {\dot{ξ}}^{^{D}}}, ξ^{*} = {{\dot{ξ}}_{_{A}}, {\dot{ξ}}_{_{B}}, {\dot{ξ}}_{_{C}}, {\dot{ξ}}_{_{D}}, ξ^{^{A}}, ξ^{^{B}}, ξ^{^{C}}, ξ^{^{D}}},

(119)

The outer products of the elements of the set

ξ

generate all forms of X matrices that are based on

σ

matrices,

X_{σ} = {{(+ + + +)}_{σ}, {(+ + + -)}_{σ}, {(+ + - +)}_{σ}, {(+ + - -)}_{σ}, {(+ - + +)}_{σ}, {(+ - + -)}_{σ}, {(+ - - +)}_{σ}, {(+ - - -)}_{σ}}

. These are the matrices given in Eqations (115)-(118). Similarly, the elements of the set

ξ^{*}

generate all forms of X matrices that are based on

σ^{*}

matrices,

X_{σ^{*}} = {{(+ + + +)}_{σ^{*}}, {(+ + + -)}_{σ^{*}}, {(+ + - +)}_{σ^{*}}, {(+ + - -)}_{σ^{*}}, {(+ - + +)}_{σ^{*}}, {(+ - + -)}_{σ^{*}}, {(+ - - +)}_{σ^{*}}, {(+ - - -)}_{σ^{*}}}

. But, the set

X_{σ}

is equal to the set

X_{σ^{*}}

11.

Likewise, we define two sets for 4-component spinor pairs

χ = {χ_{_{A}}, χ_{_{B}}, χ_{_{C}}, χ_{_{D}}, {\dot{χ}}^{^{A}}, {\dot{χ}}^{^{B}}, {\dot{χ}}^{^{C}}, {\dot{χ}}^{^{D}}}, χ^{*} = {{\dot{χ}}_{_{A}}, {\dot{χ}}_{_{B}}, {\dot{χ}}_{_{C}}, {\dot{χ}}_{_{D}}, χ^{^{A}}, χ^{^{B}}, χ^{^{C}}, χ^{^{D}}},

(120)

The outer products of the elements of the set

χ

generate all forms of Q matrices that are based on

Σ

matrices,

Q_{Σ} = {{(+ + + +)}_{Σ}, {(+ + + -)}_{Σ}, {(+ + - +)}_{Σ}, {(+ + - -)}_{Σ}, {(+ - + +)}_{Σ}, {(+ - + -)}_{Σ}, {(+ - - +)}_{Σ}, {(+ - - -)}_{Σ}}

. These are the matrices given in Eqations (93)-(96). Similarly, the elements of the set

χ^{*}

generate all forms of Q matrices that are based on

Σ^{*}

matrices,

Q_{Σ^{*}} = {{(+ + + +)}_{Σ^{*}}, {(+ + + -)}_{Σ^{*}}, {(+ + - +)}_{Σ^{*}}, {(+ + - -)}_{Σ^{*}}, {(+ - + +)}_{Σ^{*}}, {(+ - + -)}_{Σ^{*}}, {(+ - - +)}_{Σ^{*}}, {(+ - - -)}_{Σ^{*}}}

. Now, the set

Q_{Σ}

is completely distinct from the set

Q_{Σ^{*}}

8. Conjugate spaces in diagonal basis

It is possible to diagonalize

Σ_{3}

and

Σ_{3}^{*}

simultaneously. Actually, in E and

\tilde{E}

basis both

E_{3}

and

{\tilde{E}}_{3}

were already diagonal. Hence we can construct a similar 4-component spinor formalism by simply changing bases back to E and

\tilde{E}

E_{i} = A^{- 1} Σ_{i} A, {\tilde{E}}_{i} = A^{- 1} Σ_{i}^{*} A

(121)

where

A = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & i & - i & 0 \\ 1 & 0 & 0 & - 1 \end{matrix}), A^{- 1} = A^{†}

(122)

Then we have

E_{1} = (\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}), E_{2} = (\begin{matrix} 0 & 0 & - i & 0 \\ 0 & 0 & 0 & - i \\ i & 0 & 0 & 0 \\ 0 & i & 0 & 0 \end{matrix}), E_{3} = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & - 1 \end{matrix})

(123)

{\tilde{E}}_{1} = (\begin{matrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{matrix}), {\tilde{E}}_{2} = (\begin{matrix} 0 & i & 0 & 0 \\ - i & 0 & 0 & 0 \\ 0 & 0 & 0 & i \\ 0 & 0 & - i & 0 \end{matrix}), {\tilde{E}}_{3} = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & - 1 \end{matrix})

(124)

These are the definitions that were given in Equation (6). Note that

{\tilde{E}}_{i} \neq E_{i}^{*}

The new bases obey the same commutation relations as the old bases. 4-component spinor pairs in the new basis

φ

can be obtained by the transformation

φ = A^{- 1} χ

φ_{_{A}} = (\begin{matrix} u & 0 \\ 0 & u \\ v & 0 \\ 0 & v \end{matrix}), φ_{_{B}} = (\begin{matrix} - v & 0 \\ 0 & - v \\ u & 0 \\ 0 & u \end{matrix}), φ_{_{C}} = (\begin{matrix} - u & 0 \\ 0 & - u \\ v & 0 \\ 0 & v \end{matrix}), φ_{_{D}} = (\begin{matrix} v & 0 \\ 0 & v \\ u & 0 \\ 0 & u \end{matrix})

(125)

New spinor metric for this subspace is

g_{_{E}} = A^{T} g_{_{Σ}} A = (\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ - 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \end{matrix}); g_{_{Σ}} = g^{a b} = (\begin{matrix} 0 & 0 & i & 0 \\ 0 & 0 & 0 & - 1 \\ - i & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix})

(126)

Hence we obtain the following dotted contravariant spinor pairs:

{\dot{φ}}^{A} = (\begin{matrix} \dot{v} & 0 \\ 0 & \dot{v} \\ - \dot{u} & 0 \\ 0 & - \dot{u} \end{matrix}), {\dot{φ}}^{B} = (\begin{matrix} \dot{u} & 0 \\ 0 & \dot{u} \\ \dot{v} & 0 \\ 0 & \dot{v} \end{matrix}), {\dot{φ}}^{C} = (\begin{matrix} \dot{v} & 0 \\ 0 & \dot{v} \\ \dot{u} & 0 \\ 0 & \dot{u} \end{matrix}), {\dot{φ}}^{D} = (\begin{matrix} \dot{u} & 0 \\ 0 & \dot{u} \\ - \dot{v} & 0 \\ 0 & - \dot{v} \end{matrix})

(127)

Here we have

φ^{A} = - φ_{_{B}}

φ^{B} = φ_{_{A}}

φ^{C} = φ_{_{D}}

and

φ^{D} = - φ_{_{C}}

. These relations are equivalent to the ones that given Equation (111). If this were the whole story we would have to conclude that the new representation is equivalent to SL(2,C), but there is another subspace with its own spinor metric that is based on

\tilde{E}

. The spinor pairs associated with this second subspace can be obtained as

\dot{\tilde{φ}} = A^{- 1} \dot{χ}

{\dot{\tilde{φ}}}_{_{A}} = (\begin{matrix} \dot{u} & 0 \\ \dot{v} & 0 \\ 0 & \dot{u} \\ 0 & \dot{v} \end{matrix}), {\dot{\tilde{φ}}}_{_{B}} = (\begin{matrix} - \dot{v} & 0 \\ \dot{u} & 0 \\ 0 & - \dot{v} \\ 0 & \dot{u} \end{matrix}), {\dot{\tilde{φ}}}_{_{C}} = (\begin{matrix} - \dot{u} & 0 \\ \dot{v} & 0 \\ 0 & - \dot{u} \\ 0 & \dot{v} \end{matrix}), {\dot{\tilde{φ}}}_{_{D}} = (\begin{matrix} \dot{v} & 0 \\ \dot{u} & 0 \\ 0 & \dot{v} \\ 0 & \dot{u} \end{matrix})

(128)

The spinor metric for this subspace is 12

g_{_{\tilde{E}}} = A^{T} g_{_{Σ^{*}}} A = (\begin{matrix} 0 & 1 & 0 & 0 \\ - 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 0 \end{matrix})

(129)

Hence we obtain the associated contravariant forms as follows: 13

{\tilde{φ}}^{A} = (\begin{matrix} v & 0 \\ - u & 0 \\ 0 & v \\ 0 & - u \end{matrix}), {\tilde{φ}}^{B} = (\begin{matrix} u & 0 \\ v & 0 \\ 0 & u \\ 0 & v \end{matrix}), {\tilde{φ}}^{C} = (\begin{matrix} v & 0 \\ u & 0 \\ 0 & v \\ 0 & u \end{matrix}), {\tilde{φ}}^{D} = (\begin{matrix} u & 0 \\ - v & 0 \\ 0 & u \\ 0 & - v \end{matrix})

(130)

It may be useful to write the bases for the spinor pairs in both representations. Let

S

be the space of 4-component two column spinor pairs. The subspaces

S_{Σ}

and

S_{\tilde{Σ}}

associated with

Σ

and

\tilde{Σ}

are spanned by

e_{_{Σ}}^{1} = (\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & i \\ 1 & 0 \end{matrix}), e_{_{Σ}}^{2} = (\begin{matrix} 0 & 1 \\ 1 & 0 \\ - i & 0 \\ 0 & - 1 \end{matrix}); e_{_{\tilde{Σ}}}^{1} = (\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & - i \\ 1 & 0 \end{matrix}), e_{_{\tilde{Σ}}}^{2} = (\begin{matrix} 0 & 1 \\ 1 & 0 \\ i & 0 \\ 0 & - 1 \end{matrix})

(131)

Here we use the property

\tilde{Σ} = Σ^{*}

. On the other hand, The subspaces

S_{E}

and

S_{\tilde{E}}

associated with E and

\tilde{E}

are spanned by

e_{_{E}}^{1} = (\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \end{matrix}), e_{_{E}}^{2} = (\begin{matrix} 0 & 0 \\ 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{matrix}); e_{_{\tilde{E}}}^{1} = (\begin{matrix} 1 & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & 0 \end{matrix}), e_{_{\tilde{E}}}^{2} = (\begin{matrix} 0 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{matrix})

(132)

Note that none of the bases for spinor pairs that given in Eqations (131) and (132) can be written as a linear combination of the others.

In the new basis the transformation matrix

W_{A}

that corresponds to

Z_{A}

takes the form

W_{A} = (\begin{matrix} α_{0} + α_{3} & 0 & α_{1} - i α_{2} & 0 \\ 0 & α_{0} + α_{3} & 0 & α_{1} - i α_{2} \\ α_{1} + i α_{2} & 0 & α_{0} - α_{3} \\ 0 & α_{1} + i α_{2} & 0 & α_{0} - α_{3} \end{matrix}) = α_{0} E_{0} + α_{1} E_{1} + α_{2} E_{2} + α_{3} E_{3}

(133)

In short,

W_{A} = {(+ + + +)}_{E}

and

W_{A}

preserves the spinor metric

g_{_{E}}

W_{A}^{T} g_{_{E}} W_{A} = g_{_{E}}

(134)

Similarly,

{\tilde{W}}_{A}

corresponds to

Z_{A}^{*}

{\tilde{W}}_{A} = (\begin{matrix} α_{0}^{*} + α_{3}^{*} & α_{1}^{*} + i α_{2}^{*} & 0 & 0 \\ α_{1}^{*} - i α_{2}^{*} & α_{0}^{*} - α_{3}^{*} & 0 & 0 \\ 0 & 0 & α_{0}^{*} + α_{3}^{*} & α_{1}^{*} + i α_{2}^{*} \\ 0 & 0 & α_{1}^{*} - i α_{2}^{*} & α_{0}^{*} - α_{3}^{*} \end{matrix}) = α_{0}^{*} {\tilde{E}}_{0} + α_{1}^{*} {\tilde{E}}_{1} + α_{2}^{*} {\tilde{E}}_{2} + α_{3}^{*} {\tilde{E}}_{3}

(135)

In short,

{\tilde{W}}_{A} = {(+ + + +)}_{\tilde{E}}^{*}

and

{\tilde{W}}_{A}

preserves the metric

g_{_{\tilde{E}}}

{\tilde{W}}_{A}^{T} g_{_{\tilde{E}}} {\tilde{W}}_{A} = g_{_{\tilde{E}}}

(136)

W_{A}

transforms the associated outer product

P_{A} = φ_{A} φ_{A}^{†}

P_{A} = (\begin{matrix} t + z & 0 & x - i y & 0 \\ 0 & t + z & 0 & x - i y \\ x + i y & 0 & t - z & 0 \\ 0 & x + i y & 0 & t - z \end{matrix}) = t E_{0} + x E_{1} + y E_{2} + z E_{3} = {(+ + + +)}_{E}

(137)

{\tilde{W}}_{A}

transforms the associated outer product

{\dot{\tilde{P}}}_{A} = {\dot{\tilde{φ}}}_{A} {\dot{\tilde{φ}}}_{A}^{†}

{\dot{\tilde{P}}}_{A} = (\begin{matrix} t + z & x + i y & 0 & 0 \\ x - i y & t - z \\ 0 & 0 & t + z & x + i y \\ 0 & 0 & x - i y & t - z \end{matrix}) = t {\tilde{E}}_{0} + x {\tilde{E}}_{1} + y {\tilde{E}}_{2} + z {\tilde{E}}_{3} = {(+ + + +)}_{\tilde{E}}

(138)

We can also write the

4 \times 4

Lorentz transformation matrix

λ_{A}

in terms of

L_{i j}

by using the relations

α_{0} + α_{3} = L_{11}

α_{1} - i α_{2} = L_{12}

α_{1} + i α_{2} = L_{21}

and

α_{0} - α_{3} = L_{22}

λ_{A} = W_{A} {\tilde{W}}_{A} = (\begin{matrix} L_{11} L_{11}^{*} & L_{11} L_{12}^{*} & L_{12} L_{11}^{*} & L_{12} L_{12}^{*} \\ L_{11} L_{21}^{*} & L_{11} L_{22}^{*} & L_{12} L_{21}^{*} & L_{12} L_{22}^{*} \\ L_{21} L_{11}^{*} & L_{21} L_{12}^{*} & L_{22} L_{11}^{*} & L_{22} L_{12}^{*} \\ L_{21} L_{21}^{*} & L_{21} L_{22}^{*} & L_{22} L_{21}^{*} & L_{22} L_{22}^{*} \end{matrix}) = L_{A} \otimes L_{A}^{*}

(139)

Everything looks nice and simple in the diagonal basis. But now

λ_{A}

does not transform the simple and familiar form of the contravariant real 4-vector

V_{A}^{μ} = {(t, x, y, z)}^{T}

, instead, it acts on the complex 4-vector

V_{A}^{μ} = A^{- 1} V_{A}^{μ}

V_{A}^{μ} = (\begin{matrix} t + z \\ x - i y \\ x + i y \\ t - z \end{matrix})

(140)

Hence the Lorentz transformation of a 4-vector in the diagonal basis reads as follows:

V_{A}^{μ} \to V^{'} μ_{A} = λ_{A} V_{A}^{μ}

(141)

Furthermore, the Minkowski metric in the diagonal representation takes the form

η_{_{E}} = η_{\tilde{E}} = (\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 0 \\ 0 & - 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{matrix})

(142)

It can be shown that both

W_{A}

and

{\tilde{W}}_{A}

preserve

η_{_{E}}

9. Rotations in spinor space

U (α) = cos (α / 2) - i \hat{n} \cdot \vec{σ} sin (α / 2)

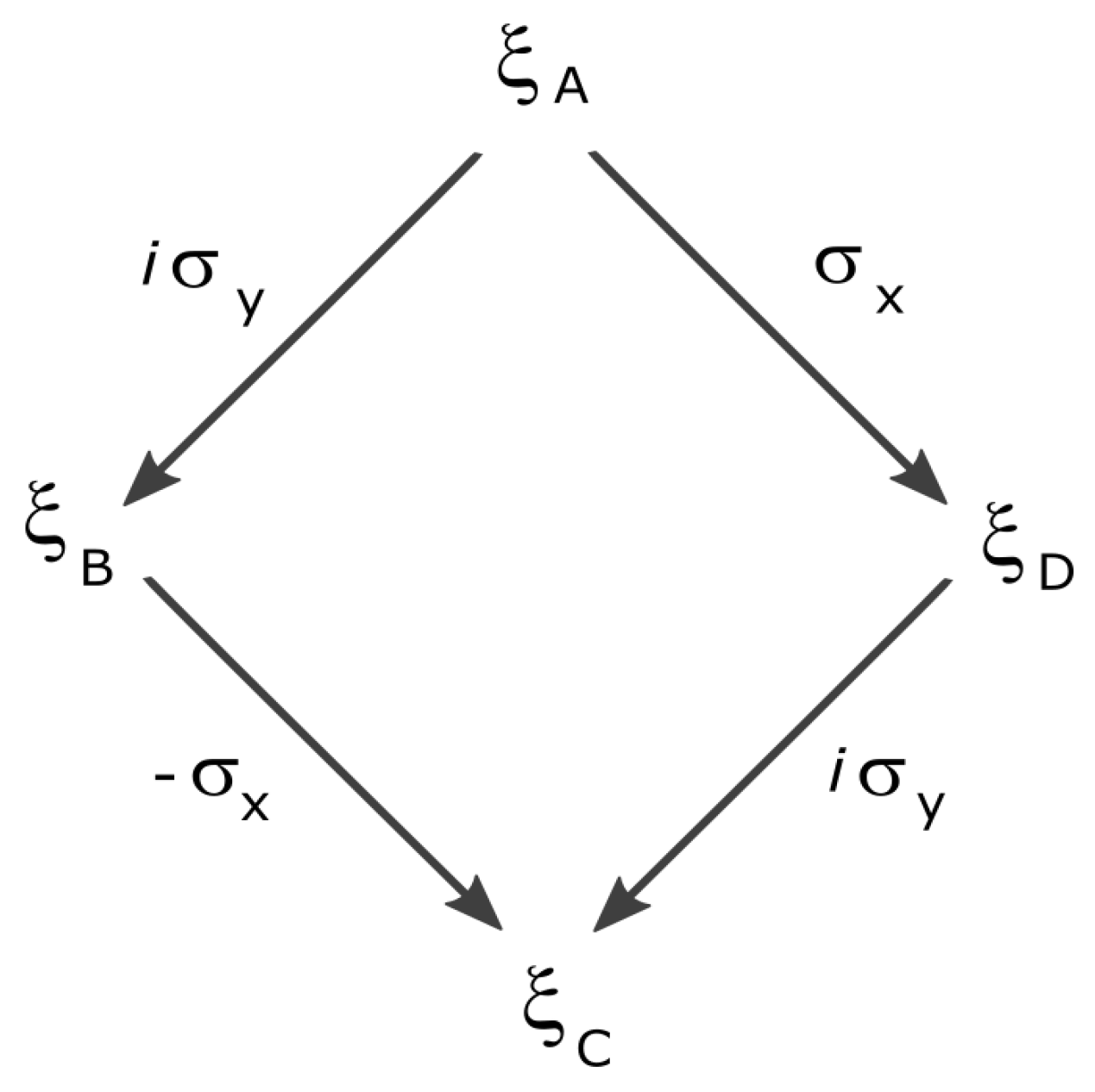
represents a CCW rotation about

\hat{n} = (n_{x}, n_{y}, n_{z})

by an angle

α

. If

α = 180^{\circ}

U (180^{\circ}) = - i \hat{n} \cdot \vec{σ}

. For example,

- i σ_{x}

represents a

180^{\circ}

CCW rotation about the x axis. When we apply this rotation on

ξ_{_{A}}

we get

- i σ_{x} ξ_{_{A}} = - i ξ_{_{D}}

, i.e. a

180^{\circ}

rotation about the x axis transforms

ξ_{_{A}}

into

ξ_{_{D}}

apart from a global phase

- i

. Some of these transformations are shown in Figure 2. The relations that are not shown can be found by successive application of rotations, such as

ξ_{_{A}} \to ξ_{_{C}} = ξ_{_{A}} \to ξ_{_{B}} \to ξ_{_{C}}

(- σ_{x}) (i σ_{y}) ξ_{_{A}} = σ_{z} ξ_{_{A}} = ξ_{_{C}}, or - i σ_{z} ξ_{_{A}} = - i ξ_{_{c}}

(143)

Likewise,

ξ_{_{B}} \to ξ_{_{D}} = ξ_{_{B}} \to ξ_{_{C}} \to ξ_{_{D}}

(- i σ_{y}) (- σ_{x}) ξ_{_{B}} = σ_{z} ξ_{_{B}} = ξ_{_{D}}, or - i σ_{z} ξ_{_{B}} = - i ξ_{_{D}}

(144)

Here we used the property that a rotation in the opposite direction is induced by the Hermitian adjoint of the forward one.

In order to visualize the orientations of different types of spinors in the spinor space the flagpole picture may be helpful [23]. Space components of a 4-vector associated with a spinor is given by

x_{i} = ξ^{†} σ_{i} ξ

(145)

For

ξ = ξ_{_{A}}

ξ_{_{A}}^{†} σ_{x} ξ_{_{A}} = x

ξ_{_{A}}^{†} σ_{y} ξ_{_{A}} = y

ξ_{_{A}}^{†} σ_{z} ξ_{_{A}} = z

, therefore the orientation of the flagpole associated with

ξ_{_{A}}

can be marked as

(+ + +)

. On the other hand, For

ξ = ξ_{_{B}}

ξ_{_{B}}^{†} σ_{x} ξ_{_{B}} = - x

ξ_{_{B}}^{†} σ_{y} ξ_{_{B}} = y

ξ_{_{B}}^{†} σ_{z} ξ_{_{B}} = - z

, therefore the orientation of the flagpole associated with

ξ_{_{B}}

(- + -)

, likewise for

ξ_{_{C}}

(- - +)

and for

ξ_{_{D}}

(+ - -)

. Hence, in Figure 1, a vector pointing from the origin to the corner of the cube can be used to describe the orientation of the spinor that carries same mark.

Similar rotation schemes apply to the dotted contravariant 2-component spinors as well.

Rotations for 4-component spinor pairs is not much different. Now we have to replace

σ_{i}

Σ_{i}

. Here are some rotations for undotted covariant and dotted contravariant 4-component spinor pairs

- i Σ_{y} χ_{_{A}} = χ_{_{B}}, - i Σ_{x} χ_{_{A}} = - i χ_{_{D}}, - i Σ_{x} χ_{_{B}} = i χ_{_{C}}, - i Σ_{y} χ_{_{D}} = χ_{_{C}}

(146)

- i Σ_{y} {\dot{χ}}^{^{A}} = {\dot{χ}}^{^{B}}, - i Σ_{y} {\dot{χ}}^{^{A}} = i {\dot{χ}}^{^{D}}, - i Σ_{x} {\dot{χ}}^{^{B}} = - i {\dot{χ}}^{^{C}}, - i Σ_{y} {\dot{χ}}^{^{D}} = {\dot{χ}}^{^{C}}

(147)

The complex conjugated forms are rotated in a slightly different way. Now we have to replace

Σ_{i}

with

Σ_{i}^{*}

. For example, for dotted covariant spinor pairs

- i Σ_{y}^{*} {\dot{χ}}_{_{A}} = - {\dot{χ}}_{_{B}}, - i Σ_{x}^{*} {\dot{χ}}_{_{A}} = - i {\dot{χ}}_{_{D}}, - i Σ_{x}^{*} {\dot{χ}}_{_{B}} = i {\dot{χ}}_{_{C}}, - i Σ_{y}^{*} {\dot{χ}}_{_{D}} = - {\dot{χ}}_{_{C}}

(148)

Similar relations hold for undotted contravariant spinor pairs.

It is also possible to rotate the spinors about an axis perpendicular to their flagpole. For example, when we rotate

ξ_{_{A}}

180^{\circ}

about an axis perpendicular to the flagpole of

ξ_{_{A}}

, apart from a global phase, we get

{\dot{ξ}}^{^{A}}

. But, the perpendicular axis is not unique and the global phase depends on its choice.

10. State space and inner product of states

When a Z matrix acts on a spinor pair the result is again a spinor pair. We may regard a spinor pair as a two column state vector which fits a certain pattern 14:

| α . β 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} α & β \\ β & α \\ - i β & i α \\ α & - β \end{matrix})

(149)

where

α

and

β

are two complex parameters. Previously defined pairs that given in Equation (58) and their dotted contravariant versions obey the same pattern 15. Under the action of Z,

| α, β 〉

transforms in such a way that the pattern is preserved

Z | α . β 〉 \to | α^{'}, β^{'} 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} α^{'} & β^{'} \\ β^{'} & α^{'} \\ - i β^{'} & i α^{'} \\ α^{'} & - β^{'} \end{matrix})

(150)

Here Z can be type

A, B, C

or D. 16

Now let us consider the inner product of two state vectors

〈 α, β | γ, δ 〉 = (\begin{matrix} \dot{α} γ + \dot{β} δ & 0 \\ 0 & \dot{α} γ + \dot{β} δ \end{matrix})

(151)

Due to the specific pattern of the states the inner product always results in this form, therefore, for later convenience, we will define the inner product of two states as one half the trace of the

2 \times 2

matrix and we will simply write:

〈 α, β | γ, δ 〉 = \dot{α} γ + \dot{β} δ

(152)

This definition is equivalent to the inner product of two 2-component spinors with components

α, β

and

γ, δ

11. Observables and states

We associate

Σ_{i}

with the components of an observable

Σ

along the axes

x, y

and z:

Σ_{1} \to Σ_{x}, Σ_{2} \to Σ_{y}, Σ_{3} \to Σ_{z}

(153)

Let

\hat{n}

be a unit vector:

\hat{n} = (n_{x}, n_{y}, n_{z}) = (sin θ cos ϕ, sin θ sin ϕ, cos θ)

, and let

{\vec{Σ}}^{A} = (Σ_{x}, Σ_{y}, Σ_{z})

{\vec{Σ}}^{A}

is the observable for Type-A states. For types

B, C

and D,

{\vec{Σ}}^{B} = (- Σ_{x}, Σ_{y}, - Σ_{z})

{\vec{Σ}}^{C} = (- Σ_{x}, - Σ_{y}, Σ_{z})

{\vec{Σ}}^{D} = (Σ_{x}, - Σ_{y}, - Σ_{z})

The component of the observable

{\vec{Σ}}^{A}

along

\hat{n}

can be written as

\hat{n} \cdot {\vec{Σ}}^{A} = (\begin{matrix} 0 & n_{x} & n_{y} & n_{z} \\ n_{x} & 0 & - i n_{z} & i n_{y} \\ n_{y} & i n_{z} & 0 & - i n_{x} \\ n_{z} & - i n_{y} & i n_{x} & 0 \end{matrix}) .

(154)

This is the

4 \times 4

analog of

\hat{n} \cdot \vec{σ}

\hat{n} \cdot \vec{σ} = (\begin{matrix} n_{z} & n_{x} - i n_{y} \\ n_{x} + i n_{y} & - n_{z} \end{matrix})

(155)

In terms of

θ

and

ϕ

the eigenstates of

\hat{n} \cdot \vec{σ}

are

{| ↑}_{θ, ϕ} 〉 = (\begin{matrix} cos (\frac{θ}{2}) \\ sin (\frac{θ}{2}) e^{i ϕ} \end{matrix}) {, | ↓}_{θ, ϕ} 〉 = (\begin{matrix} - sin (\frac{θ}{2}) e^{- i ϕ} \\ cos (\frac{θ}{2}) \end{matrix})

(156)

{| ↑}_{θ, ϕ} 〉

and

{| ↓}_{θ, ϕ} 〉

states correspond to

+ 1

and

- 1

eigenvalues respectively and they constitute a complete set of basis, hence

\hat{n} \cdot \vec{σ} = {| ↑}_{θ, ϕ} {〉 〈 ↑}_{θ, ϕ} {| - | ↓}_{θ, ϕ} {〉 〈 ↓}_{θ, ϕ} | .

(157)

In SL(4,C), the eigenstates of

\hat{n} \cdot {\vec{Σ}}^{A}

turn out to be the following two column orthogonal state vectors of Type-A that correspond to the eigenvalues

+ 1

and

- 1

, respectively:

| A_{θ, ϕ}^{↑} 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} cos (\frac{θ}{2}) & sin (\frac{θ}{2}) e^{i ϕ} \\ sin (\frac{θ}{2}) e^{i ϕ} & cos (\frac{θ}{2}) \\ - i sin (\frac{θ}{2}) e^{i ϕ} & i cos (\frac{θ}{2}) \\ cos (\frac{θ}{2}) & - sin (\frac{θ}{2}) e^{i ϕ} \end{matrix}), | A_{θ, ϕ}^{↓} 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} - sin (\frac{θ}{2}) e^{- i ϕ} & cos (\frac{θ}{2}) \\ cos (\frac{θ}{2}) & - sin (\frac{θ}{2}) e^{- i ϕ} \\ - i cos (\frac{θ}{2}) & - i sin (\frac{θ}{2}) e^{- i ϕ} \\ - sin (\frac{θ}{2}) e^{- i ϕ} & - cos (\frac{θ}{2}) \end{matrix})

(158)

| A_{θ, ϕ}^{↑} 〉

and

| A_{θ, ϕ}^{↓} 〉

constitute a complete set of basis for the state space, therefore

\hat{n} \cdot {\vec{Σ}}^{A} = | A_{θ, ϕ}^{↑} 〉 〈 A_{θ, ϕ}^{↑} | - | A_{θ, ϕ}^{↓} 〉 〈 A_{θ, ϕ}^{↓} |

(159)

In a similar way we can write

\hat{n} \cdot {\vec{Σ}}^{B}

\hat{n} \cdot {\vec{Σ}}^{C}

and

\hat{n} \cdot {\vec{Σ}}^{D}

in terms of the orthogonal states vectors associated with them.

According to the definition of the inner product that given in Equation (152), the expectation value of

\hat{n} \cdot {\vec{Σ}}^{A}

in a state with a flagpole in the direction of a unit vector

\hat{m} = (sin α cos γ, sin α sin γ, cos α)

〈 α, γ | \hat{n} \cdot {\vec{Σ}}^{A} | α, γ 〉 = \hat{n} \cdot \hat{m}

(160)

Although, the state vector has four components the state space is only two dimensional 17. It may be convenient to use

| ↑ 〉

and

| ↓ 〉

as basis states by letting

θ = ϕ = 0

in Equation (158)

| ↑ 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & i \\ 1 & 0 \end{matrix}), | ↓ 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} 0 & 1 \\ 1 & 0 \\ - i & 0 \\ 0 & - 1 \end{matrix})

(161)

In these basis basic spinor pairs can be written as

| χ_{A} 〉 = u | ↑ 〉 + v | ↓ 〉, | χ_{B} 〉 = - v | ↑ 〉 + u | ↓ 〉, | χ_{C} 〉 = - u | ↑ 〉 + v | ↓ 〉, | χ_{D} 〉 = v | ↑ 〉 + u | ↓ 〉

(162)

| {\dot{χ}}^{A} 〉 = \dot{v} | ↑ 〉 - \dot{u} | ↓ 〉, | {\dot{χ}}^{B} 〉 = \dot{u} | ↑ 〉 + \dot{v} | ↓ 〉, | {\dot{χ}}^{C} 〉 = \dot{v} | ↑ 〉 + \dot{u} | ↓ 〉, | {\dot{χ}}^{D} 〉 = \dot{u} | ↑ 〉 - \dot{v} | ↓ 〉

(163)

We can write raising and lowering operators and their effect on the

| ↑ 〉

and

| ↓ 〉

states:

Σ_{+}^{A} = Σ_{x} + i Σ_{y} = (\begin{matrix} 0 & 1 & i & 0 \\ 1 & 0 & 0 & - 1 \\ i & 0 & 0 & - i \\ 0 & 1 & i & 0 \end{matrix}), Σ_{-}^{A} = Σ_{x} - i Σ_{y} = (\begin{matrix} 0 & 1 & - i & 0 \\ 1 & 0 & 0 & 1 \\ - i & 0 & 0 & - i \\ 0 & - 1 & i & 0 \end{matrix})

(164)

Σ_{+}^{A} | ↑ 〉 = 0, Σ_{+}^{A} | ↓ 〉 = | ↑ 〉, Σ_{-}^{A} | ↑ 〉 = | ↓ 〉, Σ_{-}^{A} | ↓ 〉 = 0

(165)

Similar relations can be written for Type

B, C

and D states with the associated ladder operators:

Σ_{+}^{B} = - Σ_{x} + i Σ_{y} Σ_{-}^{B} = - Σ_{x} - i Σ_{y}

(166)

Σ_{+}^{C} = - Σ_{x} - i Σ_{y} Σ_{-}^{C} = - Σ_{x} + i Σ_{y}

(167)

Σ_{+}^{D} = Σ_{x} - i Σ_{y} Σ_{-}^{D} = Σ_{x} + i Σ_{y}

(168)

12. 8-component Dirac spinor

(i γ^{μ} \partial_{μ} - m) Ψ = 0

(169)

The 4-component Dirac spinor

Ψ

is a solution to the Dirac equation given in Equation (169). But, we have already committed ourselves to the 4-component state vectors that have the specific form given in Equation (149). Therefore we seek a solution to the Dirac equation within our state space, but there does not exist a nontrivial one. In order to write a Dirac-like equation in our state space we have to go to higher dimensions 18. In the following it will be shown that this is possible with 8-component spinors.

Let us rewrite Equation (169) with

8 \times 8

G^{μ}

matrices

(i G^{μ} \partial_{μ} - m) Φ = 0

(170)

where

G^{0} = (\begin{matrix} I_{4 \times 4} & 0 \\ 0 & - I_{4 \times 4} \end{matrix}), G^{i} = (\begin{matrix} 0 & Σ_{i} \\ - Σ_{i} & 0 \end{matrix})

(171)

Clifford algebra of

G^{μ}

is the same as

γ^{μ}

{G^{μ}, G^{ν}} = 2 η^{μ ν} 1_{8 \times 8}

(172)

Let us write

Φ

in terms of spinor pairs

Φ = (\begin{matrix} Ω \\ Δ \end{matrix}), Ω = (\begin{matrix} ω_{1} & ω_{2} \\ ω_{2} & ω_{1} \\ - i ω_{2} & i ω_{1} \\ ω_{1} & - ω_{2} \end{matrix}), Δ = (\begin{matrix} δ_{1} & δ_{2} \\ δ_{2} & δ_{1} \\ - i δ_{2} & i δ_{1} \\ δ_{1} & - δ_{2} \end{matrix})

(173)

Then Equation (170) reads

(\begin{matrix} i \partial_{0} - m & 0 & 0 & 0 & 0 & i \partial_{1} & i \partial_{2} & i \partial_{3} \\ 0 & i \partial_{0} - m & 0 & 0 & i \partial_{1} & 0 & \partial_{3} & - \partial_{2} \\ 0 & 0 & i \partial_{0} - m & 0 & i \partial_{2} & - \partial_{3} & 0 & \partial_{1} \\ 0 & 0 & 0 & i \partial_{0} - m & i \partial_{3} & \partial_{2} & - \partial_{1} & 0 \\ 0 & - i \partial_{1} & - i \partial_{2} & - i \partial_{3} & - (i \partial_{0} + m) & 0 & 0 & 0 \\ - i \partial_{1} & 0 & - \partial_{3} & \partial_{2} & 0 & - (i \partial_{0} + m) & 0 & 0 \\ - i \partial_{2} & \partial_{3} & 0 & - \partial_{1} & 0 & 0 & - (i \partial_{0} + m) & 0 \\ - i \partial_{3} & - \partial_{2} & \partial_{1} & 0 & 0 & 0 & 0 & - (i \partial_{0} + m) \end{matrix}) (\begin{matrix} ω_{1} & ω_{2} \\ ω_{2} & ω_{1} \\ - i ω_{2} & i ω_{1} \\ ω_{1} & - ω_{2} \\ δ_{1} & δ_{2} \\ δ_{2} & δ_{1} \\ - i δ_{2} & i δ_{1} \\ δ_{1} & - δ_{2} \end{matrix}) = 0

(174)

Let us try a plane wave solution

ω_{i} = A_{i} e^{- i (E t - \vec{p} \cdot \vec{x})}, δ_{i} = B_{i} e^{- i (E t - \vec{p} \cdot \vec{x})}

(175)

(\begin{matrix} E - m & 0 & 0 & 0 & 0 & - p_{1} & - p_{2} & - p_{3} \\ 0 & E - m & 0 & 0 & - p_{1} & 0 & i p_{3} & - i p_{2} \\ 0 & 0 & E - m & 0 & - p_{2} & - i p_{3} & 0 & i p_{1} \\ 0 & 0 & 0 & E - m & - p_{3} & i p_{2} & - i p_{1} & 0 \\ 0 & p_{1} & p_{2} & p_{3} & - (E + m) & 0 & 0 & 0 \\ p_{1} & 0 & - i p_{3} & i p_{2} & 0 & - (E + m) & 0 & 0 \\ p_{2} & i p_{3} & 0 & - i p_{1} & 0 & 0 & - (E + m) & 0 \\ p_{3} & - i p_{2} & i p_{1} & 0 & 0 & 0 & 0 & - (E + m) \end{matrix}) (\begin{matrix} A_{1} & A_{2} \\ A_{2} & A_{1} \\ - i A_{2} & i A_{1} \\ A_{1} & - A_{2} \\ B_{1} & B_{2} \\ B_{2} & B_{1} \\ - i B_{2} & i B_{1} \\ B_{1} & - B_{2} \end{matrix}) = 0

(176)

A nontrivial solution exists only if the determinant of the coefficients vanishes

\det = {(E^{2} - \vec{p} \cdot \vec{p} - m^{2})}^{4} = 0

(177)

We have a nontrivial solution if

E^{2} = \vec{p} \cdot \vec{p} + m^{2}

Equation (176) can be written in a compact form

(\begin{matrix} E - m & - \vec{Σ} \cdot \vec{p} \\ \vec{Σ} \cdot \vec{p} & - (E + m) \end{matrix}) (\begin{matrix} A \\ B \end{matrix}) = 0

(178)

This is equivalent to Dirac’s formulation. Hence, we expect positive and negative energy solutions for a system which has a two level intrinsic property.

In general, the 8-component spinor pair

Φ

transforms as

Φ \to Φ^{'} = S Φ

(179)

Since the Clifford algebra of

G^{μ}

and

γ^{μ}

is the same, covariance of the Dirac-like equation that given in Equation (170) can be verified by showing the existence of of a matrix S that satisfies the property [24]

S^{- 1} G^{μ} S = Λ_{ν}^{μ} G^{ν}

(180)

As a special case, it is straightforward to show the existence of such a matrix S in the

8 \times 8

version of the Weyl basis

G^{0} = (\begin{matrix} 0 & - Σ_{0} \\ - Σ_{0} & 0 \end{matrix}), G^{i} = (\begin{matrix} 0 & Σ_{i} \\ - Σ_{i} & 0 \end{matrix})

(181)

In this basis we can write Equation (179) as

(\begin{matrix} Ω_{L} \\ Δ_{R} \end{matrix}) \to (\begin{matrix} Ω_{L}^{'} \\ Δ_{R}^{'} \end{matrix}) = (\begin{matrix} Z & 0 \\ 0 & \dot{Z} \end{matrix}) (\begin{matrix} Ω_{L} \\ Δ_{R} \end{matrix})

(182)

Appendix A

Appendix A.1. Various forms of Z and L matrices

Let us begin with the exponential form

Z_{A} = e^{R}

, where

R = - \frac{i}{2} \vec{π} \cdot \vec{Σ}

π_{i} = θ_{i} + i ρ_{i}

. Let

ϕ

be the complex angle defined as

ϕ = \frac{1}{2} \sqrt{π_{1}^{2} + π_{2}^{2} + π_{3}^{2}}

. Using the property

R^{2} = - ϕ^{2} I

Z_{A} = cos ϕ I - \frac{i sin ϕ}{2 ϕ} \vec{π} \cdot \vec{Σ} = (\begin{matrix} α_{0} & α_{1} & α_{2} & α_{3} \\ α_{1} & α_{0} & - i α_{3} & i α_{2} \\ α_{2} & i α_{3} & α_{0} & - i α_{1} \\ α_{3} & - i α_{2} & i α_{1} & α_{0} \end{matrix})

(183)

where

α_{0} = cos ϕ, α_{1} = - \frac{i sin ϕ}{2 ϕ} π_{1}, α_{2} = - \frac{i sin ϕ}{2 ϕ} π_{2}, α_{3} = - \frac{i sin ϕ}{2 ϕ} π_{3} .

(184)

Or in a compact form

Z_{A} = α_{0} Σ_{0} + α_{1} Σ_{1} + α_{2} Σ_{2} + α_{3} Σ_{3} = {(+ + + +)}_{Σ} .

(185)

It is easy to show that

Z_{A}^{- 1} = α_{0} Σ_{0} - α_{1} Σ_{1} - α_{2} Σ_{2} - α_{3} Σ_{3} = {(+ - - -)}_{Σ} .

(186)

and

Z_{A}^{†} = α_{0}^{*} Σ_{0} + α_{1}^{*} Σ_{1} + α_{2}^{*} Σ_{2} + α_{3}^{*} Σ_{3} = {(+ + + +)}_{Σ}^{*}

(187)

where complex conjugation is applied only to

α_{μ}

The corresponding

L_{A}

L_{A} = (\begin{matrix} α_{0} + α_{3} & α_{1} - i α_{2} \\ α_{1} + i α_{2} & α_{0} - α_{3} \end{matrix})

(188)

In terms of the Pauli matrices:

L_{A} = α_{0} σ_{0} + α_{1} σ_{1} + α_{2} σ_{2} + α_{3} σ_{3} = {(+ + + +)}_{σ} .

(189)

In order to write

Z_{B}

we first find

L_{B} = {({\dot{L}}_{A})}^{*}

, where

{\dot{L}}_{A} = {(L_{A}^{- 1})}^{†} = (\begin{matrix} α_{0}^{*} - α_{3}^{*} & - α_{1}^{*} + i α_{2}^{*} \\ - α_{1}^{*} - i α_{2}^{*} & α_{0}^{*} + α_{3}^{*} \end{matrix}) = {(+ - - -)}_{σ}^{*} .

(190)

From the definition

Z_{B} = A (L_{B} \otimes I) A^{- 1}

Z_{B} = (\begin{matrix} α_{0} & - α_{1} & α_{2} & - α_{3} \\ - α_{1} & α_{0} & i α_{3} & i α_{2} \\ α_{2} & - i α_{3} & α_{0} & i α_{1} \\ - α_{3} & - i α_{2} & - i α_{1} & α_{0} \end{matrix}) = α_{0} Σ_{0} - α_{1} Σ_{1} + α_{2} Σ_{2} - α_{3} Σ_{3} .

(191)

Or, simply

Z_{B} = {(+ - + -)}_{Σ}

(192)

We write various forms of Z and L matrices in compact forms:

L_{A} = {(+ + + +)}_{σ}, L_{B} = {(+ - + -)}_{σ}, {\dot{L}}_{A} = {(+ - - -)}_{σ}^{*}, {\dot{L}}_{B} = {(+ + - +)}_{σ}^{*} .

(193)

Z_{A} = {(+ + + +)}_{Σ}, Z_{B} = {(+ - + -)}_{Σ}, {\dot{Z}}_{A} = {(+ - - -)}_{Σ}^{*}, {\dot{Z}}_{B} = {(+ + - +)}_{Σ}^{*} .

(194)

Although, all types of Z and L matrices are in the same form, there is a very important difference between them. Because of the particular property of the Pauli matrices,

σ_{1}^{*} = σ_{1}, σ_{3}^{*} = σ_{3}

, but

σ_{2}^{*} = - σ_{2}

, we have the following relations:

L_{B} = {\dot{L}}_{A}^{*}, {\dot{L}}_{B} = L_{A}^{*} .

(195)

For example,

{\dot{L}}_{A} = {(+ - - -)}_{σ}^{*} \to {\dot{L}}_{A}^{*} = {(+ - - -)}_{σ^{*}} = {(+ - + -)}_{σ} = L_{B} .

(196)

On the other hand we do not have a similar property with

Σ

matrices, hence

Z_{B} \neq {\dot{Z}}_{A}^{*}, {\dot{Z}}_{B} \neq Z_{A}^{*} .

(197)

The structural difference between SL(2,C) and SL(4,C) becomes more apparent when we write the matrices in exponential forms. In order to do this we have to define two types of

\vec{π}

{\vec{π}}_{A} = (π_{1}, π_{2}, π_{3})

and

{\vec{π}}_{B} = (- π_{1}, π_{2}, - π_{3})

L_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A} \cdot \vec{σ}), L_{B} = e x p (- \frac{i}{2} {\vec{π}}_{B} \cdot \vec{σ}), {\dot{L}}_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A}^{*} \cdot \vec{σ}), {\dot{L}}_{B} = e x p (- \frac{i}{2} {\vec{π}}_{B}^{*} \cdot \vec{σ}) .

(198)

Z_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A} \cdot \vec{Σ}), Z_{B} = e x p (- \frac{i}{2} {\vec{π}}_{B} \cdot \vec{Σ}), {\dot{Z}}_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A}^{*} \cdot \vec{Σ}), {\dot{Z}}_{B} = e x p (- \frac{i}{2} {\vec{π}}_{B}^{*} \cdot \vec{Σ}) .

(199)

Due to the properties,

- {\vec{π}}_{B} \cdot \vec{σ} = {\vec{π}}_{A} \cdot {\vec{σ}}^{*}

and

- {\vec{π}}_{B} \cdot {\vec{σ}}^{*} = {\vec{π}}_{A} \cdot \vec{σ}

, the relations in Equation (195) hold. But we do not have similar relations with the

Σ

matrices.

Appendix A.2. The Lorentz matrix

By definition

Λ = Z Z^{*} = Z^{*} Z

(200)

where

Z = Z_{A}

Z_{A} = (\begin{matrix} α_{0} & α_{1} & α_{2} & α_{3} \\ α_{1} & α_{0} & - i α_{3} & i α_{2} \\ α_{2} & i α_{3} & α_{0} & - i α_{1} \\ α_{3} & - i α_{2} & i α_{1} & α_{0} \end{matrix})

(201)

Λ = (\begin{matrix} α_{0} α_{0}^{*} + α_{1} α_{1}^{*} & α_{0} α_{1}^{*} + α_{1} α_{0}^{*} & α_{0} α_{2}^{*} + α_{2} α_{0}^{*} & α_{0} α_{3}^{*} + α_{3} α_{0}^{*} \\ α_{2} α_{2}^{*} + α_{3} α_{3}^{*} & + i (α_{3} α_{2}^{*} - α_{2} α_{3}^{*}) & + i (α_{1} α_{3}^{*} - α_{3} α_{1}^{*}) & + i (α_{2} α_{1}^{*} - α_{1} α_{2}^{*}) \\ α_{0} α_{1}^{*} + α_{1} α_{0}^{*} & α_{0} α_{0}^{*} + α_{1} α_{1}^{*} & α_{1} α_{2}^{*} + α_{2} α_{1}^{*} & α_{1} α_{3}^{*} + α_{3} α_{1}^{*} \\ - i (α_{3} α_{2}^{*} - α_{2} α_{3}^{*}) & - α_{2} α_{2}^{*} - α_{3} α_{3}^{*} & + i (α_{0} α_{3}^{*} - α_{3} α_{0}^{*}) & + i (α_{2} α_{0}^{*} - α_{0} α_{2}^{*}) \\ α_{0} α_{2}^{*} + α_{2} α_{0}^{*} & α_{1} α_{2}^{*} + α_{2} α_{1}^{*} & α_{0} α_{0}^{*} - α_{1} α_{1}^{*} & α_{2} α_{3}^{*} + α_{3} α_{2}^{*} \\ - i (α_{1} α_{3}^{*} - α_{3} α_{1}^{*}) & - i (α_{0} α_{3}^{*} - α_{3} α_{0}^{*}) & + α_{2} α_{2}^{*} - α_{3} α_{3}^{*} & + i (α_{0} α_{1}^{*} - α_{1} α_{0}^{*}) \\ α_{0} α_{3}^{*} + α_{3} α_{0}^{*} & α_{1} α_{3}^{*} + α_{3} α_{1}^{*} & α_{2} α_{3}^{*} + α_{3} α_{2}^{*} & α_{0} α_{0}^{*} - α_{1} α_{1}^{*} \\ - i (α_{2} α_{1}^{*} - α_{1} α_{2}^{*}) & - i (α_{2} α_{0}^{*} - α_{0} α_{2}^{*}) & - i (α_{0} α_{1}^{*} - α_{1} α_{0}^{*}) & - α_{2} α_{2}^{*} + α_{3} α_{3}^{*} \end{matrix})

(202)

Appendix A.3. Geometric phase with 4-component spinors

When the polarization state of light undergoes a series of operations and returns to its original state, the final state differs in an additional overall phase factor from the original one. It was pointed out by Pancharatnam that the phase difference is not only due to the dynamical phase from the accumulated path lengths but also involves a geometric phase [32]. Berry introduced the corresponding theory for quantum mechanical state vector and re-derived the Pancharatnam’s geometric phase [33,34]. If the cyclic path consists of only great circles, additional dynamical phase will not develop, and the geometric part increases by

\pm Ω / 2

19, where

Ω

is the solid angle that the geodesic path of cyclic operations subtends on the Poincare sphere 20.

The emergence of geometric phase can be demonstrated in SL(2,C) by considering three successive Hermitian operations on a spinor. For example, let

{\hat{n}}_{1}

{\hat{n}}_{2}

and

{\hat{n}}_{3}

be three radial unit vectors at points 1, 2 and 3 on the Poincare sphere:

{\hat{n}}_{1} = (\begin{matrix} sin θ_{1} cos ϕ_{1} \\ sin θ_{1} sin ϕ_{1} \\ cos θ_{1} \end{matrix}), {\hat{n}}_{2} = (\begin{matrix} sin θ_{2} cos ϕ_{2} \\ sin θ_{2} sin ϕ_{2} \\ cos θ_{2} \end{matrix}), {\hat{n}}_{3} = (\begin{matrix} sin θ_{3} cos ϕ_{3} \\ sin θ_{3} sin ϕ_{3} \\ cos θ_{3} \end{matrix})

(203)

And let

| ξ_{_{1}} 〉

| ξ_{_{2}} 〉

and

| ξ_{_{3}} 〉

be the spinors that correspond to these radial unit vectors:

| ξ_{_{1}} 〉 = (\begin{matrix} cos (\frac{θ_{1}}{2}) \\ sin (\frac{θ_{1}}{2}) e^{i ϕ_{1}} \end{matrix}) | ξ_{_{2}} 〉 = (\begin{matrix} cos (\frac{θ_{2}}{2}) \\ sin (\frac{θ_{2}}{2}) e^{i ϕ_{2}} \end{matrix}) | ξ_{_{3}} 〉 = (\begin{matrix} cos (\frac{θ_{3}}{2}) \\ sin (\frac{θ_{3}}{2}) e^{i ϕ_{3}} \end{matrix})

(204)

We consider a closed loop

| ξ_{_{1}} 〉 \to | ξ_{_{2}} 〉 \to | ξ_{_{3}} 〉 \to | ξ_{_{1}} 〉

projection operations that starts by acting on

| ξ_{_{1}} 〉

and finally brings the state back to

| ξ_{_{1}} 〉

which may differ from the first one only by a phase angle

γ

γ = a r g (〈 ξ_{_{1}} | [| ξ_{_{1}} 〉 〈 ξ_{_{1}} |] [| ξ_{_{3}} 〉 〈 ξ_{_{3}} |] [| ξ_{_{2}} 〉 〈 ξ_{_{2}} |] | ξ_{_{1}} 〉)

(205)

For simplicity and without loss of generality when we choose

θ_{1} = ϕ_{1} = 0

γ = arctan (\frac{sin θ_{2} sin θ_{3} sin (ϕ_{2} - ϕ_{3})}{4 {cos}^{2} (θ_{2} / 2) {cos}^{2} (θ_{3} / 2) + sin θ_{2} sin θ_{3} cos (ϕ_{2} - ϕ_{3})})

(206)

This is the geometric phase and it’s magnitude is equal to

Ω / 2

. The result can be checked by calculating the area subtended by the cyclic path in terms of the angular variables. In this example, the corners of the spherical triangle are defined by the unit vectors,

{\hat{n}}_{1}

{\hat{n}}_{2}

and

{\hat{n}}_{3}

, hence, it is convenient to use the following formula in order to calculate the area of the spherical triangle [35]:

\frac{Ω}{2} = arctan [\frac{{\hat{n}}_{1} \cdot ({\hat{n}}_{2} \times {\hat{n}}_{3})}{1 + {\hat{n}}_{1} \cdot {\hat{n}}_{2} + {\hat{n}}_{2} \cdot {\hat{n}}_{3} + {\hat{n}}_{3} \cdot {\hat{n}}_{1}}]

(207)

As an example let

θ_{1} = ϕ_{1} = 0, θ_{2} = π / 2, ϕ_{2} = 0, θ_{3} = π / 2, ϕ_{3} = π / 2

. From Equation (205),

γ = - π / 2

and from Equation (207)

Ω / 2 = π / 2

. Hence,

γ = - Ω / 2

21.

Similar relations can be derived with Z matrices and 4-component spinor pairs. But, now the type of transformation is important,

Z_{X}

must act on the pair

| χ_{_{X}} 〉

, (

X = A, B, C

or D). As an example, this time, we demonstrate the emergence of the geometric phase with unitary operations (rotations) on the 4-component spinor pairs. In order to avoid the dynamical phase we consider trajectories on the great circles. Let us start with

| χ_{_{A}} 〉

at the point

θ_{1} = ϕ_{1} = 0

| χ_{_{A}} 〉 = (\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & i \\ 1 & 0 \end{matrix})

(208)

First we rotate

| χ_{_{A}} 〉

about the y-axis CCW by

90^{\circ}

. A

Z_{A}

matrix with

α_{0} = 1 / \sqrt{2}, α_{1} = 0, α_{2} = - i / \sqrt{2}, α_{3} = 0

does this job:

\frac{1}{\sqrt{2}} (\begin{matrix} 1 & 0 & - i & 0 \\ 0 & 1 & 0 & 1 \\ - i & 0 & 1 & 0 \\ 0 & - 1 & 0 & 1 \end{matrix}) \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & i \\ 1 & 0 \end{matrix}) = \frac{1}{2} (\begin{matrix} 1 & 1 \\ 1 & 1 \\ - i & i \\ 1 & - 1 \end{matrix})

(209)

Then we apply a

90^{\circ}

CCW rotation about the z-axis

\frac{1}{\sqrt{2}} (\begin{matrix} 1 & 0 & 0 & - i \\ 0 & 1 & - 1 & 0 \\ 0 & 1 & 1 & 0 \\ - i & 0 & 0 & 1 \end{matrix}) \frac{1}{2} (\begin{matrix} 1 & 1 \\ 1 & 1 \\ - i & i \\ 1 & - 1 \end{matrix}) = \frac{1}{2 \sqrt{2}} (\begin{matrix} 1 - i & 1 + i \\ 1 + i & 1 - i \\ 1 - i & 1 + i \\ 1 - i & - 1 - i \end{matrix})

(210)

Finally we rotate the state CCW about the x-axis by

90^{\circ}

\frac{1}{\sqrt{2}} (\begin{matrix} 1 & - i & 0 & 0 \\ - i & 1 & 0 & 0 \\ 0 & 0 & 1 & - 1 \\ 0 & 0 & 1 & 1 \end{matrix}) \frac{1}{2 \sqrt{2}} (\begin{matrix} 1 - i & 1 + i \\ 1 + i & 1 - i \\ 1 - i & 1 + i \\ 1 - i & - 1 - i \end{matrix}) = \frac{1}{2} (\begin{matrix} 1 - i & 0 \\ 0 & 1 - i \\ 0 & 1 + i \\ 1 - i & 0 \end{matrix}) = \frac{e^{- i π / 4}}{\sqrt{2}} (\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & i \\ 1 & 0 \end{matrix})

(211)

The final state differs from the initial one by a phase angle

γ = - π / 4

, and this is the expected geometric phase for this cyclic unitary operations on the Poincare sphere.

If we work with

| χ_{_{B}} 〉

| χ_{_{C}} 〉

| χ_{_{D}} 〉

we have to use the associated form of the Z matrix. Similar operations are also possible with dotted and undotted contravariant states by using

\dot{Z}

and

{\dot{Z}}^{*}

matrices respectively.

Appendix A.4. Coherent parallel combination of transformations and interpretation of Z as a state of the transforming medium

Up to now Z matrices were abstract mathematical operators that transform abstract mathematical objects (spinors). In a real experiment the transformation of the physical state of the system is carried out by an apparatus. For example, the polarization state of a beam of light (or a single photon) is modified as it passes through an optical medium.

The overall effect of the interaction of light with a deterministic, i.e., non-depolarizing, medium or optical element can be described by a 2×2 complex matrix J, referred to as the Jones matrix [28]. In order to obtain the Jones matrix boost and rotation parameters of the Lorentz group should be replaced by spectroscopic parameters (diattenuation and retardation) associated with various anisotropy properties of the optical medium 22. Jones matrix J differs from L of SL(2,C) by a complex constant [25], hence it is an element of GL(2,C). This complex overall factor k is due to the isotropic phase retardation (

η)

and isotropic amplitude absorption (

κ

k = e^{- i χ / 2}

, where

χ = η - i κ

. Hence, in polarization optics,

L \to k L = J

. Similarly

Z \to k Z = N

. Accordingly,

α_{μ} \to k α_{μ}

. It may be appropriate to define new parameters,

τ = k α_{0}, α = k α_{1}, β = k α_{2}, γ = k α_{3}

[18]:

N = k Z = (\begin{matrix} τ & α & β & γ \\ α & τ & - i γ & i β \\ β & i γ & τ & - i α \\ γ & - i β & i α & γ \end{matrix})

(212)

In order to obtain the optical version of the Z matrix we have to modify Equation (184). After multiplying

α_{μ}

by k, we replace

θ_{i}

and

ρ_{i}

π_{i} = θ_{i} + ρ_{i}

by birefringence and dichroism parameters:

L B

and

L B^{'}

for linear birefringence,

C B

for circular birefringence;

L D

and

L D^{'}

for linear dichroism and

C D

for circular dichroism 23. For example, the state of the medium that given by

τ = 1 / \sqrt{2}, α = 1 / \sqrt{2}, β = γ = 0

is a horizontal linear polarizer,

τ = 1 / \sqrt{2}, α = 0, β = - 1 / \sqrt{2}, γ = 0

is a linear polarizer at

135^{\circ}

τ = 1 / \sqrt{2}, α = - i / \sqrt{2}, β = γ = 0

is a quarter wave plate (vertical fast axis),

τ = 1 / \sqrt{2}, α = 0, β = 0, γ = i / \sqrt{2}

is a circular retarder (

δ = π / 2

). List of basic optical elements and their states can be found in the Appendix.

There are basically two types of light-medium interaction: serial and parallel 24. In a serial combination Jones matrices act on a 2-component spinor in succession

J_{n} \dots J_{2} J_{1} | ξ 〉 = J | ξ 〉

(213)

In a parallel process, an optical recombination takes place during the light-medium interaction. When the light beam simultaneously illuminates different parts of the medium, each part having different optical properties, the light emerging from different parts, in general with different polarizations, may recombine into a single beam. If the medium is composed of several non-depolarizing (deterministic) components, each component with a well defined Jones matrix, then the matrix associated with the coherently combined overall optical system is simply given by a linear combination of the individual matrices of the components [26,27]:

a J_{1} | ξ 〉 + b J_{2} | ξ 〉 + c J_{3} | ξ 〉 + \dots = J | ξ 〉

(214)

where

J = a J_{1} + b J_{2} + c J_{3} + \dots

(215)

Complex coefficients

a, b, c, . . .

are generally functions of space, time and frequency and they play the role of probability amplitudes of quantum mechanics 25 26. Similar relations can be written in terms of N matrices:

a N_{1} | χ 〉 + b N_{2} | χ 〉 + c N_{3} | χ 〉 + \dots = N | χ 〉

(216)

N = a N_{1} + b N_{2} + c N_{3} + \dots

(217)

The 4×4 real matrix for transforming the Stokes vector of the light is the Mueller matrix M that is directly connected with the experimental work. If the medium is deterministic, M can be obtained from N matrix as,

M = N N^{*} = N^{*} N

. As opposed to J and N, M does not contain any information about the overall phase introduced by the material medium. M differs from the Lorentz transformation matrix

Λ

by a positive real constant 27.

The resultant matrix state N in Equation (217) corresponds to the nondepolarizing Mueller matrix of the coherently combined system. Without loss of generality we may restrict our presentation to a two-term coherent parallel combination, then M can be written in terms of N matrices as follows:

M = N N^{*} = a a^{*} N_{1} N_{1}^{*} + b b^{*} N_{2} N_{2}^{*} + a b^{*} N_{1} N_{2}^{*} + b a^{*} N_{2} N_{1}^{*} .

(218)

In this expansion,

N_{1} N_{1}^{*}

and

N_{2} N_{2}^{*}

are the Mueller matrices of the nondepolarizing component systems, whereas,

N_{1} N_{2}^{*}

and

N_{2} N_{1}^{*}

are the matrices resulting from coherence that cannot be interpreted as Mueller matrices in the usual sense. Although, the combined term

a b^{*} N_{1} N_{2}^{*} + b a^{*} N_{2} N_{1}^{*}

turns out to be a real matrix, it is still not a Mueller matrix [18].

It may be more convenient to work with vectors rather than matrices to represent optical media states. The state interpretation of the transformation matrices becomes more clear in the vector representation. The vector state can be defined as the first column of the N matrix [8]:

| h 〉 = (\begin{matrix} τ \\ α \\ β \\ γ \end{matrix})

(219)

It is possible to decompose a given vector state

| h 〉

with respect to a complete basis set of component systems:

| h 〉 = a | h_{1} 〉 + b | h_{2} 〉 + c | h_{3} 〉 + d | h_{4} 〉

(220)

Here, we simply apply the ordinary vector decomposition procedure. The natural basis are

| h_{1} 〉 = (\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix}), | h_{2} 〉 = (\begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix}), | h_{3} 〉 = (\begin{matrix} 0 \\ 0 \\ 1 \\ 0 \end{matrix}), | h_{4} 〉 = (\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix})

(221)

These basis correspond respectively to free space (identity), half-wave plate (

0^{\circ}

fast axis), half-wave plate (

45^{\circ}

fast axis) and a circular retarder (

δ = π

). We may use other states as basis if we like. For example, let

| h_{1} 〉

and

| h_{2} 〉

correspond to orthonormal vector states of a linear horizontal polarizer and a linear vertical polarizer, then the following expansion of

| h 〉

will correspond to a horizontal quarter-wave plate state [18]:

| h 〉 = \frac{1 + i}{2} | h_{1} 〉 + \frac{1 - i}{2} | h_{2} 〉 .

(222)

where

c = d = 0

28 and

| h_{1} 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ 1 \\ 0 \\ 0 \end{matrix}), | h_{1} 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ - 1 \\ 0 \\ 0 \end{matrix}), | h 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ i \\ 0 \\ 0 \end{matrix}),

(223)

Therefore, at least mathematically, we can consider an ideal quarter-wave plate state as a coherent linear combination of two orthogonal linear polarizer states. In practice, this means that, if it could be possible to combine two orthogonal polarizers coherently with the associated complex coefficients as given in Equation (222), we would obtain an artificial quarter wave plate that effectively responds to the incident light just like a genuine one.

In general, we can use non-orthogonal basis to decompose a given covariance vector

| h 〉

. However, decomposition with respect to non-orthogonal basis is more involved: we have to take into account covariant and contravariant types of bases and expansion coefficients. As an example, the covariance vector of an ideal partial polarizer can be decomposed into two non-orthogonal states, one of them being the direct beam state which corresponds to the identity Mueller matrix, and the other component being a horizontal linear polarizer state, with a suitable coefficient.

There are coherent parallel combination experiments that demonstrate the state interpretation of J, N and

| h 〉

in light-nanoparticle interactions [18,19,20,21]. In a certain interval of wavelength, a nanorod oriented at an angle

θ

in the the x-y plane responds to the incident light propagating along the z axis as a linear polaizer and the associated vector state is

| h 〉 = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ cos (2 θ) \\ sin (2 θ) \\ 0 \end{matrix})

(224)

It can be mathematically shown and experimentally observed that two crossed orthogonal identical nanorods respond to the incident light as an identity (free space)[18,19]:

| h 〉 = \frac{1}{\sqrt{2}} | h_{1} 〉 + \frac{1}{\sqrt{2}} | h_{2} 〉 = \frac{1}{2} (\begin{matrix} 1 \\ 1 \\ 0 \\ 0 \end{matrix}) + \frac{1}{2} (\begin{matrix} 1 \\ - 1 \\ 0 \\ 0 \end{matrix}) = (\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix})

(225)

In this expression, for simplicity, we let the Lorentzian polarizabilities of the nanorods equal to one.

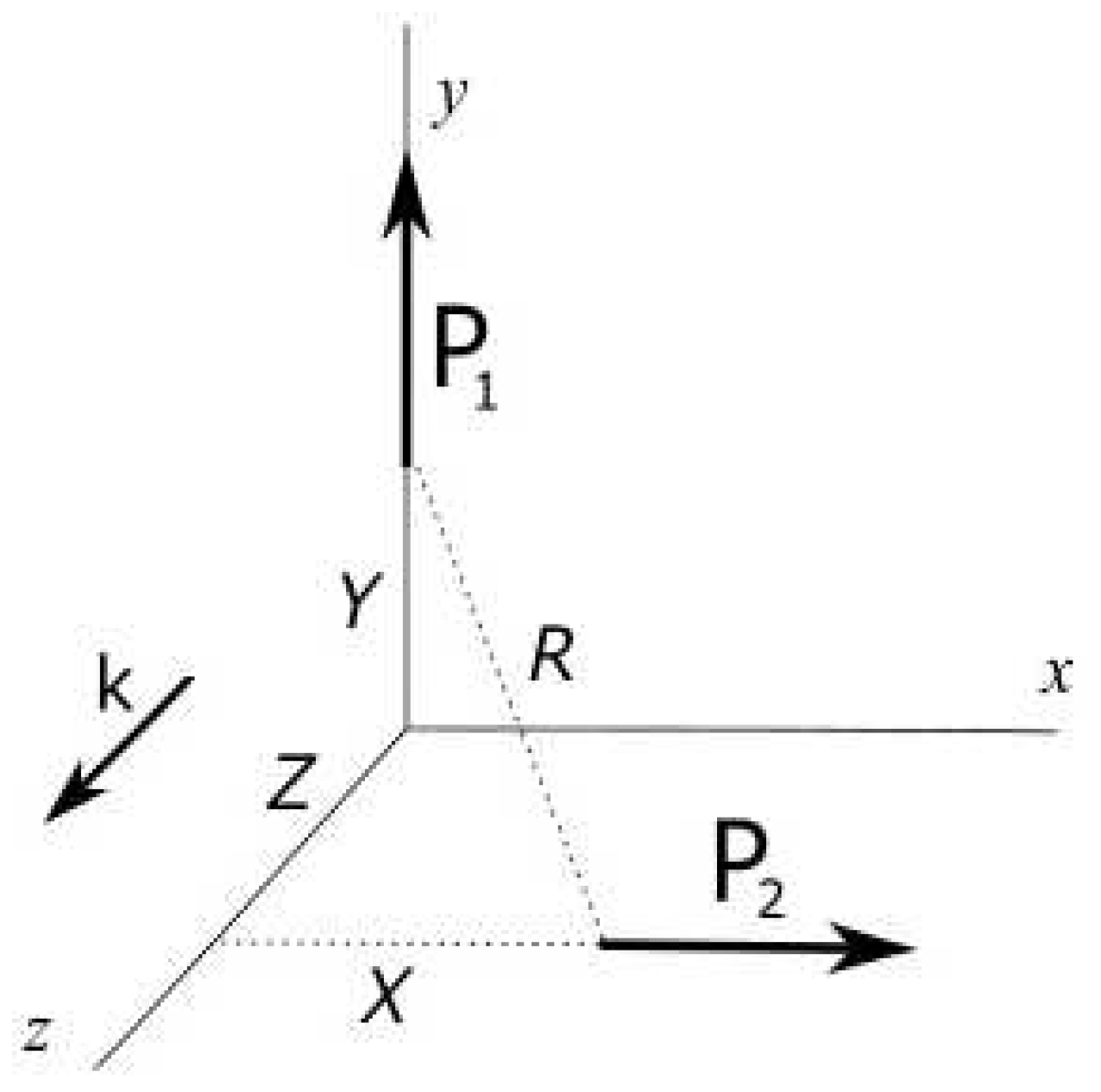
In a three dimensional arrangement, if there is a spacing between the two nanorods as depicted in Figure A1, coherently combined system manifests optical activity along the z axis due to the relative phase and mutual interaction between the nanorods. It is worth noting that, since the nonorod vector states are in the form given in Equation (224), the fourth component that corresponds to the

γ

anisotropy, which is related to the optical activity, is always zero, i.e., for non-interacting nanorods no coherent linear combination can result in a vector state with

γ \neq 0

29. For the system given in Figure A1, the emergence of optical activity can be described as a three term coherent combination of vector states, two of them associated with non-interacting nanorods and the third one being the state due the interaction:

| h 〉 = g [a | h_{1} 〉 + b | h_{2} 〉 + c_{i n t} | h_{i n t} 〉] = g [a (\begin{matrix} 1 \\ 1 \\ 0 \\ 0 \end{matrix}) + b (\begin{matrix} 1 \\ - 1 \\ 0 \\ 0 \end{matrix}) + c_{i n t} (\begin{matrix} 0 \\ 0 \\ 1 + e^{2} \\ i (1 - e^{2}) \end{matrix})]

(226)

where

e = e^{- i 2 π Z / λ}

is the phase difference due to the spacing between the nanorods along the z axis,

c_{i n t}

contains the Lorentzian polarizability and the interaction coefficient, the overall factor

g = G / (1 - Δ^{2})

, G is a function of the Lorentzian polarizability and the far field factor,

Δ

is a compound factor involving phase, polarizability and interaction coefficient [21] 30 31.

Figure A1. Optical activity in a coupled dimer.

P_{1}

and

P_{2}

are the dipoles associated with the nanorods, Light propagates along

k

Figure A1. Optical activity in a coupled dimer.

P_{1}

and

P_{2}

are the dipoles associated with the nanorods, Light propagates along

k

Appendix A.4.1. Unitary formulation of the rotation of the medium in space

J, N matrices and

| h 〉

vector are the states of the transforming medium or the optical element, therefore they are themselves subjected to transformations. Particularly, if the optical element is rotated CCW by an angle

θ

about an axis parallel to the direction of propagation of light, the state of the optical element is also rotated:

N (θ) = U (2 θ) N (0) U {(2 θ)}^{†}

(227)

U (2 θ)

is unitary

4 \times 4

matrix, element of SL(4,C):

U (2 θ) = cos (θ) - i \hat{n} \cdot \vec{Σ} sin (θ)

(228)

\hat{n}

indicates the direction of propagation of light 32. The corresponding Mueller matrix is rotated as 33

M (θ) = R (2 θ) M (0) R (- 2 θ)

(229)

If we choose the direction of the light beam along the z axis

U (2 θ) = (\begin{matrix} cos (θ) & 0 & 0 & - i sin (θ) \\ 0 & cos (θ) & - sin (θ) & 0 \\ 0 & sin (θ) & cos (θ) & 0 \\ - i sin (θ) & 0 & 0 & cos (θ) \end{matrix})

(230)

and

R (2 θ) = U (2 θ) U {(2 θ)}^{*} = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & cos (2 θ) & - sin (2 θ) & 0 \\ 0 & sin (2 θ) & cos (2 θ) & 0 \\ 0 & 0 & 0 & 1 \end{matrix})

(231)

Appendix A.5. Table for vector and matrix states of optical elements

This appendix contains a tabulated list of

| h 〉

vector states, N matrix states and their corresponding Mueller matrices M .

Optical element	$\| h 〉$	N	M
Free space	$(\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$
Half-wave plate (Ideal mirror)	$(\begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix})$	$(\begin{matrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & - i \\ 0 & 0 & i & 0 \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & - 1 \end{matrix})$
Half-wave plate 45º fast axis	$(\begin{matrix} 0 \\ 0 \\ 1 \\ 0 \end{matrix})$	$(\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & i \\ 1 & 0 & 0 & 0 \\ 0 & - i & 0 & 0 \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & - 1 \end{matrix})$
Circular retarder $(δ = π)$	$(\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix})$	$(\begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & - i & 0 \\ 0 & i & 0 & 0 \\ 1 & 0 & 0 & 0 \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$
Horizontal Linear Polarizer	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} & \frac{- i}{\sqrt{2}} \\ 0 & 0 & \frac{i}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})$
Vertical Linear Polarizer	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{- 1}{\sqrt{2}} \\ 0 \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & \frac{- 1}{\sqrt{2}} & 0 & 0 \\ \frac{- 1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} & \frac{i}{\sqrt{2}} \\ 0 & 0 & \frac{- i}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & - 1 & 0 & 0 \\ - 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})$
Linear Polarizer at 45º	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 & \frac{i}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{- i}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})$
Linear Polarizer at 135º	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{- 1}{\sqrt{2}} \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & \frac{- 1}{\sqrt{2}} & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 & \frac{- i}{\sqrt{2}} \\ \frac{- 1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{i}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 0 \\ - 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{matrix})$
Circular Polarizer (right handed)	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{2}} & \frac{- i}{\sqrt{2}} & 0 \\ 0 & \frac{i}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \end{matrix})$
Circular Polarizer (left handed)	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{- 1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & 0 & \frac{- 1}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{2}} & \frac{i}{\sqrt{2}} & 0 \\ 0 & \frac{- i}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ \frac{- 1}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ - 1 & 0 & 0 & 1 \end{matrix})$

Optical element	$\| h 〉$	N	M
QWP horizontal fast axis	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} \\ 0 \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & \frac{i}{\sqrt{2}} & 0 & 0 \\ \frac{i}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & 0 & \frac{- 1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 0 \end{matrix})$
QWP vertical fast axis	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{- i}{\sqrt{2}} \\ 0 \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & \frac{- i}{\sqrt{2}} & 0 & 0 \\ \frac{- i}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} & \frac{- 1}{\sqrt{2}} \\ 0 & 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & - 1 \\ 0 & 0 & 1 & 0 \end{matrix})$
QWP fast axis 135º	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{i}{\sqrt{2}} \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & \frac{i}{\sqrt{2}} & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 & \frac{- 1}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & - 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{matrix})$
QWP fast axis 45º	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{- i}{\sqrt{2}} \\ 0 \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & \frac{- i}{\sqrt{2}} & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{- i}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{- 1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & - 1 & 0 & 0 \end{matrix})$
Circular retarder $(δ = \frac{π}{2})$	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{i}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & 0 & \frac{i}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{- 1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ \frac{i}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$
Circular retarder $(δ = - \frac{π}{2})$	$(\begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{- i}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} \frac{1}{\sqrt{2}} & 0 & 0 & \frac{- i}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{2}} & \frac{- 1}{\sqrt{2}} & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ \frac{- i}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}} \end{matrix})$	$(\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$

References

J. Hladik, "Spinors in Physics," Springer-Verlac, New York (1996).
Başkal, S. , Kim Young S., Noz, Marilyn E, "Physics of the Lorentz Group," Morgan and Claypool Publishers, CA (2015).
Sudha and, A.V. Gopala Rao, "Polarization Elements: A Group Theoretical Study". [CrossRef]
R. Barakat, "Exponential versions of the Jones and Mueller–Jones polarization matrices," J. Opt. Soc. Am. A/Vol. 13, No. 1 (1996). [CrossRef]
R. M. A. Azzam, "Propagation of partially polarized light through anisotropic media with or without depolarization: A differential 4 × 4 matrix calculus," J. Opt. Soc. Am. 68, 1756 (1978). [CrossRef]
A. A. Bogush, V. M. Red’kov, "On unique parametrization of the linear group GL(4.C) and its subgroups by using the Dirac matrix algebra basis," arXiv:hep-th/0607054V1 (2006). [CrossRef]
E. Ovsiyuk, O. Veko, M. Neagu, V. Balan, V. Red’kov, "Some Properties of Parameters of Lorentz Matrices and Transitivity Equations," BSG Proceedings, Vol. 20, 2013, pp. 11-63.
E. Kuntman, M. A. Kuntman, and O. Arteaga, "Vector and matrix states for Mueller matrices of nondepolarizing optical media," J. Opt. Soc. Am. 2017; 34, 82–86. [CrossRef]
S.R. Cloude, “Group theory and polarization algebra”, Optik 75, 26-36 (1986).
D. Han, Y.S. Kim, M. E. Noz, "Stokes parameters as a Minkowskian four-vector,". Phys. Rev E 1997, 56. [CrossRef]
D. Han, Y. S. Kim, M. E. Noz, "Jones-matrix Formalism as a Representation of the Lorentz Group," J. Opt. Soc. Am. A, 14 (1997). [CrossRef]
W. R. Hamilton, "On a new species of imaginary quantities connected with the theory of quaternions," Proceedings of the Royal Irish Academy, 2:424–434 (1844).
Katsusada Morita, "Quaternions, Lorentz Group and the Dirac Theory," Progress of Theoretical Physics, Volume 117, Issue 3 (2007), pp 501-532. [CrossRef]
Lanlan Liu, Chonging Wu, Chao Shang, Zhengyong Li, Jian Wang, IEEE Photonics Journal ( Volume: 7, Issue: 4, Aug. 2015 ).
E. Kuntman, M. A. Kuntman, A. Canillas, and O. Arteaga, "Quaternion algebra for Stokes-Mueller formalism," J. Opt. Soc. Am. A 36, 492-497 (2019). [CrossRef]
E. Kuntman and O. Arteaga, "Decomposition of a depolarizing Mueller matrix into its nondepolarizing components by using symmetry conditions," Appl. Opt. 55 (2016). [CrossRef]
R. Ossikovski, E. Garcia-Caurel, M, Foldyna and J.J. Gil, "Application of the arbitrary decomposition to finite spot size Mueller matrix measurements," Appl. Opt. 53 (2014). [CrossRef]
E. Kuntman, M. A. Kuntman, J. Sancho-Parramon and O. Arteaga, "Formalism of optical coherence and polarization based on material media states," Phys. Rev. A 95 (2017). [CrossRef]
M. A. Kuntman, E. Kuntman, J. Sancho-Parramon and O. Arteaga, "Light scattering by coupled oriented dipoles: Decomposition of the scattering matrix," Phys. Rev B 98 (2018). [CrossRef]
O. Arteaga, R. Ossikovski, E. Kuntman, M. A. Kuntman, A. Cannilas and E. Garcia-Caurel, "Mueller matrix polarimetry on a Young’s double-slit experiment analog," Optics Letters 45 (2017). [CrossRef]
M. A. Kuntman, E. Kuntman, O. Arteaga, "Asymmetric scattering and Reciprocity in a Plasmonic Dimer," Symmetry 12 (2020). [CrossRef]
K. Kim, L. Mandel and E. Wolf, J. Opt.Soc. Am. 1987.
A. M. Steane, "An introduction to spinors,". arXiv 2013, arXiv:1312.3824v1.
J. D. Bjorken, S. D. Drell, "Relativistic Quantum Mechanics," McGraw-Hill, NY (1964).
Sudha and A., V. Gopala Rao, "Polarization Elements-A Group Theoretical Study," arxiv:physics/0007079v1 (2000).
J. J. Gil, Eur. Phys. J. Appl. Phys. 40, 1 (2007).
N. G. Parke, J. Math. Phys. 28, 131 (1949).
R. C. Jones, J. Opt. Soc. Am. 31, 488 (1941).
D. Goldstein, "Polarized Light, Revised and Expanded," Optical Science and Engineering, 2nd ed. (CRC Boca Raton, FL., 2003).
J. J. Gil and I. S. Jose, J. Opt. Soc. Am. A 30 (2013).
J. J. Gil. J. Appl. Remote Sens. 2014, 8.
S. Pancharatnam, Proc. Indian Acad. Sci 44, 247 (1956).
M. V. Berry, Proc. R. Soc. Lond. A 392, 84 (1984).
M. V. Berry, J. Mod. Opt. 34, 1401 (1987).
J. P. Gutierrez-Vega, "Pancharatnam-Berry phase of optical sysytems," Opt. Lett. 36, 1143-1145 (2011). [CrossRef]
T. van Dijk, H.F. Schouten, W. Ubachs, T.D. Visser, Optics Express 18 (2010) 10796.
José Lages, Remo Giust, Jean-Marie Vigoureux, "Geometric phase and Pancharatnam phase induced by light wave polarization," Physica E: Low-dimensional Systems and Nanostructures, Volume 59, 2014, Pages 6-14. [CrossRef]

1	This representation will be studied in detail in Section 8
2	The basis set $Σ_{μ} Σ_{ν}^{} = A (σ_{μ} \otimes σ_{ν}^{}) A^{- 1}$ is equivalent to the Dirac basis set, $σ_{μ} \otimes σ_{ν}$ .
3	We can define the spinor metric for SL(4,C) as $i η Σ_{1}^{}$ or $i η Σ_{3}^{}$ if we like. These metrics also have the same properties as g.
4	Besides $Z_{A}$ , we will subsequently define other types $Z_{B}, Z_{C}$ and $Z_{D}$ that preserve both g and $η$ . Dotted versions of all four types of transformations also preserve both g and $η$ . All types of $Z^{}$ and ${\dot{Z}}^{}$ preserve $g^{*}$ and $η$ ( $\dot{Z} = {(Z^{- 1})}^{†}$ ).
5	We may use the generalized eigenvectors of $Σ_{1}$ or $Σ_{2}$ matrices as well, but, in that case, we have to employ the other forms of the spinor metric.
6	$- i σ_{2}$ corresponds to a $180^{\circ}$ CCW rotation about the $x_{2}$ axis in SL(2,C).
7	The upper dot on a spinorial object simply means complex conjugation: ${\dot{χ}}^{^{(a)}} = {(χ^{^{(a)}})}^{}$ . But, the upper dot on an element of SL(2,C) or SL(4,C) has a particular meaning. ${\dot{L}}_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A}^{} \cdot \vec{σ}) \neq L_{A}^{}$ . Similarly, ${\dot{Z}}_{A} = e x p (- \frac{i}{2} {\vec{π}}_{A}^{} \cdot \vec{Σ}) \neq Z_{A}^{*}$ .
8	These are matrix representations of quaternions, because $- i σ_{1}, - i σ_{2}, - i σ_{3}$ matrices have the same properties as the Hamilton’s quaternion basis, $i, j, k$ : $X_{_{L}} = t σ_{0} + i x (- i σ_{1}) + i y (- i σ_{2}) + i z (- i σ_{3}) = t 1 + i x i + i y j + i z k$ , $X_{_{R}} = t 1 - i x i - i y j - i z k$ .
9	In these expressions complex conjugation is not explicit, but $P^{X} = {({\dot{P}}^{X})}^{} = {(. . . .)}_{Σ^{}}$ , i.e., $P^{X}$ is based on $Σ_{μ}^{*}$ matrices.
10	Actually, there is one more way: $Q \cdot P = \frac{1}{8} Tr (Q \dot{P} + P \dot{Q})$
11	The set $ξ$ is equal to the set $ξ^{}$ due to the relations given in Equation (111), and due to the relations $σ_{1}^{} = σ_{1}$ , $σ_{2}^{} = - σ_{2}$ , $σ_{3}^{} = σ_{3}$ , the set $X_{σ}$ is equal to the set $X_{σ^{*}}$ .
12	$g_{_{Σ^{}}} = g_{_{Σ}}^{} = g^{*}$
13	We can also obtain 16 independent spinor pairs for the diagonal basis from the eigenvectors of $E_{3}$ and ${\tilde{E}}_{3}$ by applying the procedure described in Section 5
14	$\| α . β 〉$ is an eigenvector of $Σ^{*}$
15	The pairs that obey this pattern are the generalized eigenvectors of $Σ_{3}^{*}$ . First column corresponds to the eigenvalue $+ 1$ and the second column corresponds to the eigenvalue $- 1$ .
16	Let $\| χ_{(x)} 〉$ denote a state vector of any kind and let $\| {\dot{χ}}^{(x)} 〉$ be its dotted contravariant version. These objects live in the state space and they all fit the pattern that given in Equation (149). All undotted covariant objects transform with $Z_{(x)}$ and all dotted contravariant objects transform with ${\dot{Z}}_{(x)}$ which are based on $Σ_{μ}$ . Under these transformations the pattern of the transformed object remains the same. Similar considerations also apply to the conjugated counterparts that live in the conjugate space. The only difference is that, in this case, the sign of the imaginary unit in Equation (149) is flipped and all matrix forms are now based on $Σ_{μ}^{*}$ .
17	The conjugate space is also two dimensional. Basis for the conjugate space can be obtained by simply changing the sign of the imaginary unit in Equation (161). Comjugate basis cannot be expressed as linear combinations of $\| ↑ 〉$ and $\| ↓ 〉$ basis.
18	There does not exists a fourth matrix that anticommutes with $Σ_{i}$ matrices.
19	Sign depends on the sense of the cyclic path.
20	Geometric phase can also be defined and calculated for an open loop operations on the Poincare sphere.
21	Negative sign is due to the CCW cyclic path.
22	In polarization optics, $σ_{1} = σ_{z}, σ_{2} = σ_{x}, σ_{3} = σ_{y}$ convention is usual.
23	Birefringence parameters correspond to rotations and dichroism parameters correspond to boosts.
24	We may think of more complicated combinations involving many branches with serial, parallel or mixed operations.
25	Time, space and frequency dependencies may entail depolarization effects, which was disscussed in [18,20].
26	When we interpret $J_{i}$ as the state of the component system (medium), the linear combination given in Eqations (215) may look like a superposition of states, but the elements $J_{i}$ in the sum are not representing different states of the same system, they are the states corresponding to different systems.
27	$Λ = Z Z^{} \to M = c c^{} Z Z^{} = N N^{}$ . Only the isotropic amplitude absorption survives in $c c^{*}$ .
28	In this simple example, $c = d = 0$ and the state space is two dimensional, hence we can truncate the third and fourth components of the vector states.
29	This is also true for crossed orthogonal nanorods.
30	Lorentzian polarizability and the interaction coefficient are functions of the wavelength of the incident light, hence the phenomenon of plasmonic hybridization occurs at wavelengths that make the denominator of g zero.
31	Optical activity can be observed even in a planar geometry in sideways scattering directions [21].
32	The vector state $\| h 〉$ is rotated as $\| h (θ) 〉 = R (2 θ) \| h (0) 〉$ .
33	$M (θ) = N (θ) N {(θ)}^{} = U (2 θ) N (0) U {(2 θ)}^{†} {(U (2 θ) N (0) U {(2 θ)}^{†})}^{}$ , because any complex conjugate form commutes with any Hermitian adjoint form ( $Σ_{i}^{}$ commutes with $Σ_{j}$ for all $i, j$ ), hence $M (θ) = U (2 θ) U {(2 θ)}^{} Z (0) Z {(0)}^{} {(U (2 θ) U {(2 θ)}^{})}^{†} = R (2 θ) M (0) R (- 2 θ)$ .

Figure 1. Reflections and inversions.

Σ^{*}

space is not shown.

Figure 1. Reflections and inversions.

Σ^{*}

space is not shown.

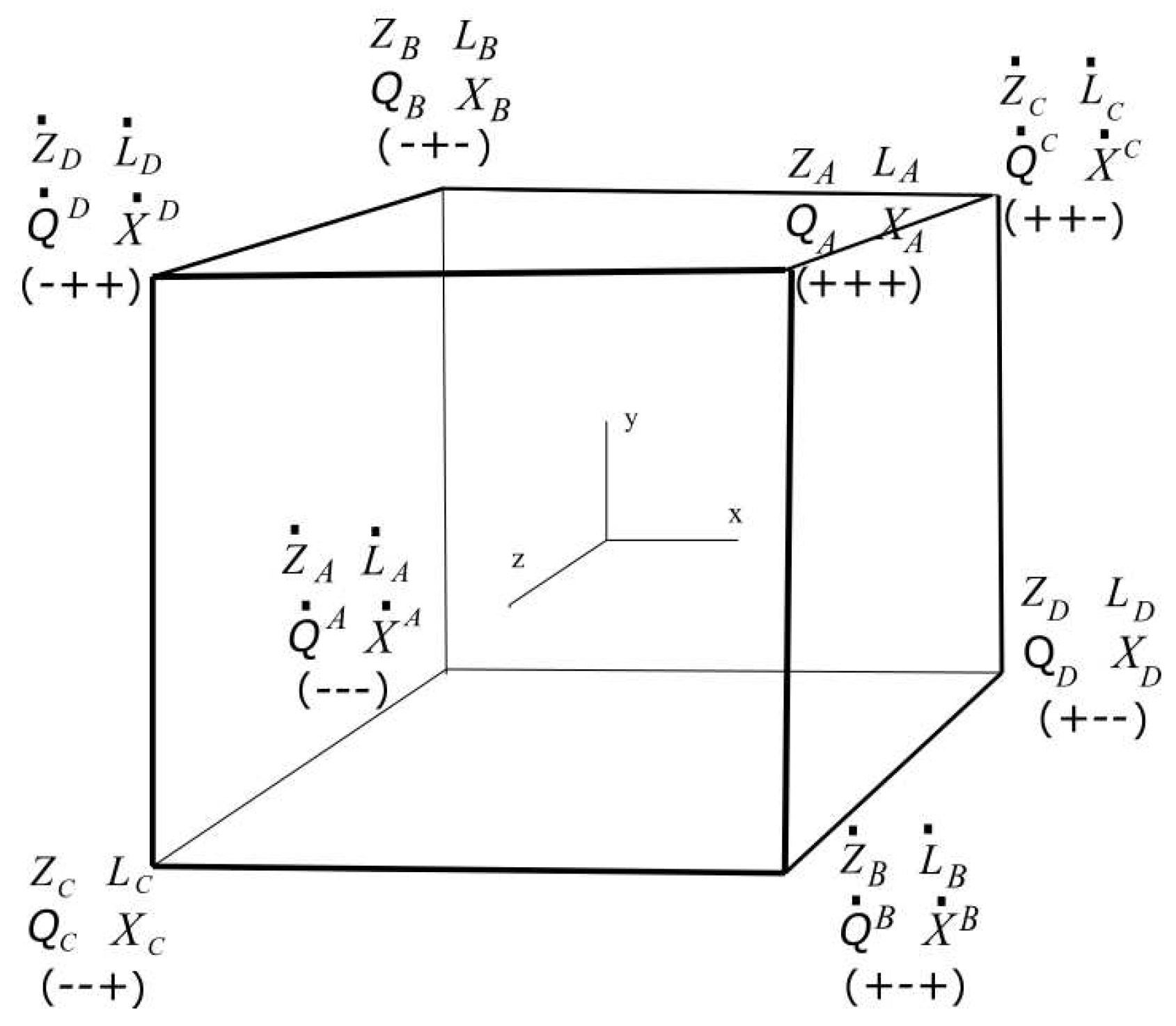
Figure 2.

180^{\circ}

rotations of spinors

Figure 2.

180^{\circ}

rotations of spinors

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Sixteen Pairs of 4-Component Spinors for SL(4,C) and Four Types of Transformations with a Conjugate Space Which Has No Counterpart in SL(2,C)

Abstract

1. Introduction

2. The first and the second pairs and their transformation properties

3. Outer products of 4-component spinors

4. Quaternion forms and 4-vectors

5. Two more pairs of spinors

6. Complex conjugated forms

7. Four types of transformations for SL(2,C)

8. Conjugate spaces in diagonal basis

9. Rotations in spinor space

10. State space and inner product of states

11. Observables and states

12. 8-component Dirac spinor

Appendix A

Appendix A.1. Various forms of Z and L matrices

Appendix A.2. The Lorentz matrix

Appendix A.3. Geometric phase with 4-component spinors

Appendix A.4. Coherent parallel combination of transformations and interpretation of Z as a state of the transforming medium

Appendix A.4.1. Unitary formulation of the rotation of the medium in space

Appendix A.5. Table for vector and matrix states of optical elements

References

MDPI Initiatives

Important Links

Subscribe