Prerpints.org logo
Preprint
Article

Constraining Neutrino Mass in Dynamical Dark Energy Cosmologies With the Logarithm Parametrization and the Oscillating Parametrization

Altmetrics

Downloads

127

Views

31

Comments

0

This version is not peer-reviewed

Submitted:

30 March 2023

Posted:

31 March 2023

You are already at the latest version

Alerts
Abstract
We constrain two dynamical dark energy models that are parametrized by the logarithm form of $w(z)=w_{0}+w_{1}\left(\frac{\ln (2+z)}{1+z}-\ln 2\right)$ and the oscillating form of $w(z)=w_{0}+w_{1}\left(\frac{\sin(1+z)}{1+z}-\sin(1)\right)$. Comparing with the Chevallier-Polarski-Linder (CPL) model, the two parametrizations for dark energy can explore the whole evolution history of the universe properly. Using the current mainstream observational data including the cosmic microwave background data and the baryon acoustic oscillation data as well as the type Ia supernovae data, we perform the $\chi^2$ statistic analysis to global fit these models, finding that the logarithm parametrization and the oscillating parametrization are almost as well as the CPL scenario in fitting these data. We make a comparison for the impacts of the dynamical dark energy on the cosmological constraints on the total mass of active neutrinos. We find that the dark energy properties could significantly change the fitting results of neutrino mass. Looser constraints on $\sum m_{\nu}$ are obtained in the logarithm and oscillating models than those derived in the CPL model. Consideration of the possible mass ordering of neutrinos reveals that the most stringent constraint on $\sum m_{\nu}$ appears in the degenerate hierarchy case.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

The fact that neutrinos have masses [1,2] has drawn significant attention from physicists. The squared mass difference between different neutrino species have been measured, i.e., Δ m 21 2 ≃ 7.5 × 10 − 5   eV 2 in solar and reactor experiments, and | Δ m 31 2 | ≃ 2.5 × 10 − 3   eV 2 in atmospheric and accelerator beam experiments [2]. The possible mass hierarchies of neutrinos are m 1 < m 2 ≪ m 3 and m 3 ≪ m 1 < m 2 , which are called the normal hierarchy (NH) and the inverted hierarchy (IH). When the mass splittings between different neutrino species are neglected, we treat the case as the degenerate hierarchy (DH) with m 1 = m 2 = m 3 .
Some famous particle physics experiments, such as tritium beta decay experiments [3,4,5,6] and neutrinoless double beta decay (0 ν β β ) experiments [7,8], have been designed to measure the absolute masses of neutrinos. Recently, the Karlsruhe Tritium Neutrino (KATRIN) experiment provided an upper limit of 1.1 eV on the neutrino-mass scale at 2 σ confidence level (C.L.) [9]. However, cosmological observations are considered to be a more promising approach to measure the total neutrino mass ∑ m ν . Massive neutrinos can leave rich imprints on the cosmic microwave background (CMB) anisotropies and the large-scale structure (LSS) formation in the evolution of the universe. Thus, the total neutrino mass ∑ m ν is likely to be measured from these available cosmological observations.
In the standard Λ cold dark matter ( Λ CDM) model with the equation-of-state parameter of dark energy w = − 1 , the Planck Collaboration gave ∑ m ν < 0.26 eV ( 2 σ ) [10] from the full Planck TT, TE, EE power spectra data, assuming the NH case with the minimal mass ∑ m ν = 0.06 eV ( 2 σ ). Adding the Planck CMB lensing data slightly tightens the constraints to ∑ m ν < 0.24 eV ( 2 σ ). When the baryon acoustic oscillations (BAO) data are considered on the basis of the Planck data, the neutrino mass constraint is significantly tightened to ∑ m ν < 0.12 eV ( 2 σ ). Further adding the type Ia supernovae (SNe) data marginally lowers the bound to ∑ m ν < 0.11 eV ( 2 σ ), which put pressure on the inverted mass hierarchy with ∑ m ν ≥ 0.10 eV.
The impacts of dynamical dark energy on the total neutrino mass have been investigated in past studies [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. In the simplest dynamical dark energy model with w = C o n s t a n t (abbreviated as wCDM model), the fitting results of ∑ m ν are ∑ m ν , NH < 0.195 eV ( 2 σ ) and ∑ m ν , IH < 0.220 eV ( 2 σ ) [33], using the full Planck TT, TE, EE power spectra data and the BAO data as well as the SNe data. From the same data combination, ∑ m ν , NH < 0.129 eV ( 2 σ ) and ∑ m ν , IH < 0.163 eV ( 2 σ ) [33] in the holographic dark energy (HDE) model [38,39,40,41,42,43,44,45]. The constraint results of ∑ m ν are different from those in the standard Λ CDM model because of impacts of dark energy properties in these cosmological models.
In addition to the wCDM model and the HDE model, the constraints on ∑ m ν are investigated in the CPL model [46,47] with w ( z ) = w 0 + w 1 z 1 + z (where w 0 and w 1 are two free parameters). Over the years, the CPL parametrization have been widely used and explored extensively. In the model, ∑ m ν , NH < 0.290 eV ( 2 σ ) and ∑ m ν , IH < 0.305 eV ( 2 σ ) [33] are obtained by using the full Planck TT, TE, EE power spectra data combined the BAO data with the SNe data. The upper limit values of ∑ m ν are larger than those in the wCDM model and the HDE model, confirming that the constraint results of ∑ m ν can be changed as the different parametrization forms of w. The CPL model has a drawback that it only explores the past expansion history, but cannot describe the future evolution. Thus the CPL parametrization does not genuinely cover the scalar field models as well as other theoretical models. Such a problem makes the fitting results of ∑ m ν untenable in the CPL model.
In this paper, we focus on two novel forms of w ( z ) , i.e., the logarithm parametrization w ( z ) = w 0 + w 1 ln ( 2 + z ) 1 + z − ln 2 and the oscillating parametrization w ( z ) = w 0 + w 1 sin ( 1 + z ) 1 + z − sin ( 1 )  [48], which are correspondingly called the Log model and the Sin model. They can inherit the advantages of the CPL model and explore the whole evolution history of the universe properly. In our present work, the constraints on ∑ m ν will be investigated in the two models. In fact, there are also some other dark energy parametrizations, such as the Jassal-Bagla-Padmanabhan parametrization [49] and the Barboza-Alcaniz parametrization [50] with the same free parameters w 0 and w 1 . They will be explored with other research motivations in our future work.
On the other hand, in order to better match the current observational result of w = − 1 , we assume the case of w 0 = − 1 in the CPL parametrization, the logarithm parametrization, and the oscillating parametrization. The forms of w ( z ) in these models are modified as w ( z ) = − 1 + w 1 z 1 + z , w ( z ) = − 1 + w 1 ln ( 2 + z ) 1 + z − ln 2 , and w ( z ) = − 1 + w 1 sin ( 1 + z ) 1 + z − sin ( 1 ) with a free parameter w 1 . We call them the MCPL model, the MLog model, and the MSin model. We also investigate the constraints on them using the same mainstream observational data.
In our work, we first constrain on the Log parametrization and the Sin parametrization by using latest mainstream observational data. Then, we investigate impacts of the dark energy properties on neutrino mass. This paper is organized as follows. In Sect. 2, we provide a brief description of the data and method used in our work. In Sect. 3, we show the constraint results of different dynamical dark energy models and discuss the physical meaning behind these results. At last, we make some important conclusions in Sect. 4.

2. Data and method

Throughout this paper, we only employ the data combination of the CMB data, the BAO data, and the SNe data, which is abbreviated as the CMB+BAO+SNe data. The usage of the data combination facilitates to make a comparison with the results derived from Refs. [10,14,33], in which this typical data combination has also been used to constrain cosmological models. For the CMB data, we use the Planck 2018 temperature and polarization power spectra data at the whole multipole ranges, together with the CMB latest lensing power spectrum data [10]. For the BAO data, we use the 6dFGS and SDSS-MGS measurements of D V / r drag  [51,52] plus the final DR12 anisotropic BAO measurements [53]. For the SNe data, we use the “Pantheon” sample [54], which contains 1048 supernovae covering the redshift range of 0.01 < z < 2.3 .
For the dynamical dark energy models with the CPL parametrization, logarithm, and oscillating parametrizations, they all have eight free parameters, i.e., the present baryons density ω b ≡ Ω b h 2 , the present cold dark matter density ω c ≡ Ω c h 2 , an approximation to the angular diameter distance of the sound horizon at the decoupling epoch θ MC , the reionization optical depth τ , the amplitude of the primordial scalar power spectrum A s at k = 0.05   Mpc − 1 , the primordial scalar spectral index n s , and the model parameters w 0 and w 1 . The priors of these parameters are shown explicitly in the Table 1. When w 0 = − 1 is fixed, there are seven free parameters in the MCPL, MLog, and MSin models.
We consider the case that ∑ m ν serves as a free parameter with different hierarchies of neutrino mass. For the NH, IH, and DH cases, the priors of ∑ m ν are [ 0.06 , 3.00 ] eV, [ 0.10 , 3.00 ] eV, and [ 0.00 , 3.00 ] eV. The neutrino mass spectrum is described as
( m 1 , m 2 , m 3 ) = ( m 1 , m 1 2 + Δ m 21 2 , m 1 2 + | Δ m 31 2 | )
with a free parameter m 1 for the NH case,
( m 1 , m 2 , m 3 ) = ( m 3 2 + | Δ m 31 2 | , m 3 2 + | Δ m 31 2 | + Δ m 21 2 , m 3 )
with a free parameter m 3 for the IH case, and
m 1 = m 2 = m 3 = m
with a free parameter m for the DH case.
In order to check the consistency between dynamical dark energy models and the CMB+BAO+SNe data, we employ the χ 2 statistic [55,56,57] to do the cosmological fits. A model with a lower value of χ 2 is more favored by the CMB+BAO+SNe data combination. Our constraint results are derived by modifying the August 2017 version of the camb Boltzmann code [58] and the July 2018 version of CosmoMC [59].

3. Results and discussions

We constrain the sum of the neutrino mass ∑ m ν in these dynamical dark energy models by using the CMB+BAO+SNe data. In the following discussion, we will present the fitting results with the ± 1 σ errors of cosmological parameters. But for the constraints on ∑ m ν , we only provide the 2 σ upper limit. Meanwhile, we also list the values of χ min 2 for different dark energy models.

3.1. Comparison of dynamical dark energy models

We constrain the models parameterized by w ( z ) = w 0 + w 1 z 1 + z , w ( z ) = w 0 + w 1 ln ( 2 + z ) 1 + z − ln 2 and w ( z ) = w 0 + w 1 sin ( 1 + z ) 1 + z − sin ( 1 ) . The fitting results are listed in Table 2. We find that the current CMB+BAO+SNe data favor the constraint results of w 0 = − 1 and w 1 = 0 in the three models. For the CPL model, we obtain Ω m = 0.3059 ± 0.0077 and H 0 = 68.37 ± 0.83 km/s/Mpc, with χ min 2 = 3821.214 . For the Log model, we have Ω m = 0.3060 ± 0.0075 and H 0 = 68.37 ± 0.81 km/s/Mpc, with χ min 2 = 3821.150 . For the Sin model, we have Ω m = 0.3056 ± 0.0077 and H 0 = 68.41 ± 0.83 km/s/Mpc, with χ min 2 = 3821.164 . The fit values of Ω m and H 0 are similar for the three models. According to the χ min 2 values, the models provide a similar fit to the CMB+BAO+SNe data.
As described in Sect. 1, when w 0 = − 1 is fixed in the above models, the form of w ( z ) is modified with a free parameter w 1 . The fitting results are also given in the last three columns of Table 2. In the MCPL model, w ( z ) = − 1 + w 1 z 1 + z . In the MLog model, w ( z ) = − 1 + w 1 ln ( 2 + z ) 1 + z − ln 2 . In the MSin model, w ( z ) = − 1 + w 1 sin ( 1 + z ) 1 + z − sin ( 1 ) . We obtain w 1 = − 0 . 12 − 0.11 + 0.13 , w 1 = 0 . 52 − 0.48 + 0.39 , and w 1 = 0 . 22 − 0.21 + 0.16 , showing a slight deviation to w 1 = 0 in the MLog model and the MSin model. This is because w 1 is intrinsically correlated with w 0 , as shown in Figure 1 ( w 1 is anticorrelated with w 0 in the CPL model, but the correlation between them is opposite in the Log model and the Sin model). When the value of w 0 is fixed to − 1 , the fitting value of w 1 will be changed to a certain extent.
Furthermore, we focus on the χ min 2 values for the three models. We obtain χ min 2 = 3821.310 in the MCPL model, χ min 2 = 3821.288 in the MLog model, and χ min 2 = 3821.290 in the MSin model. Similarly, almost identical χ min 2 values are presented in the three models. In Figure 1 and Figure 2, we also provide the one-dimensional marginalized distributions and two-dimensional contours at 1 σ and 2 σ level for these dynamical dark energy models. The fitting results of the parameter Ω m , H 0 , and σ 8 hardly change in these models despite of w ( z ) parametrized by different forms.

3.2. Constraints on neutrino masses

We investigate the constraints on total neutrino mass in these models. For the neutrino mass measurement, we consider the NH case, the IH case, and the DH case. The fitting results are listed in Table 3, Table 4 and Table 5. In the CPL+ ∑ m ν model, we obtain ∑ m ν < 0.285 eV for the NH case, ∑ m ν < 0.304 eV for the IH case, and ∑ m ν < 0.254 eV for the DH case (see Table 3). In the Log+ ∑ m ν model, we have ∑ m ν < 0.302 eV for the NH case, ∑ m ν < 0.317 eV for the IH case, and ∑ m ν < 0.282 eV for the DH case (see Table 4), showing that much looser constraints are obtained than those in the CPL+ ∑ m ν model. In the Sin+ ∑ m ν model, the constraint results become ∑ m ν < 0.327 eV for the NH case, ∑ m ν < 0.336 eV for the IH case, and ∑ m ν < 0.311 eV for the DH case (see Table 5), which are looser than those in the Log+ ∑ m ν model. All the above fitting upper limits on ∑ m ν are larger than those obtained in the standard Λ CDM model (in the Λ CDM model, the constraint results are ∑ m ν < 0.156 eV for the NH case, ∑ m ν < 0.184 eV for the IH case, and ∑ m ν < 0.121 eV for the DH case [33,60]), indicating that the dynamical dark energy with the logarithm form and the oscillating form can affect significantly the fitting value of ∑ m ν .
Considering the same neutrino mass ordering, the fitting value of ∑ m ν is smallest in the CPL model and largest in the Sin model, confirming that the fitting values of ∑ m ν can be changed by modifying the w ( z ) forms. In Figure 3, we provide two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the ∑ m ν – w 0 plane of the CPL, Log, and Sin models, considered mass hierarchy cases of NH, IH, and DH. In the three two-parametrization models, ∑ m ν is positively correlated w 0 , which ensures the same observed acoustic peak scale in the cosmological fit using the Planck data. When we compare the constraint results of ∑ m ν for the three different cases of neutrino mass orderings, we find that the smallest value of ∑ m ν is obtained in the DH case, and the largest value of ∑ m ν corresponds to the IH case, which mean that considering the mass hierarchy can also affect the fitting values of ∑ m ν .
In the CPL+ ∑ m ν model, we obtain χ min 2 = 3822.102 for the NH case, χ min 2 = 3822.516 for the IH case, and χ min 2 = 3821.168 for the DH case (see Table 3). In the Log+ ∑ m ν model, we have χ min 2 = 3822.100 for the NH case, χ min 2 = 3822.180 eV for the IH case, and χ min 2 = 3821.048 for the DH case (see Table 4). In the Sin+ ∑ m ν model, the constraint results become χ min 2 = 3822.408 for the NH case, χ min 2 = 3823.456 for the IH case, and χ min 2 = 3821.080 for the DH case (see Table 5). Obviously, the small difference of the χ min 2 values among the three mass hierarchies only stems from the different prior ranges of the patrameter ∑ m ν , which does not help to distinguish the neutrino mass orderings.
We also discuss the constraints of ∑ m ν in the MCPL model, the MLog model, and the MSin model, in which w ( z ) is parameterized with a single free parameter w 1 . In the MCPL+ ∑ m ν model, we obtain ∑ m ν < 0.250 eV for the NH case, ∑ m ν < 0.276 eV for the IH case, and ∑ m ν < 0.228 eV for the DH case (see Table 3). In the MLog+ ∑ m ν model, we have ∑ m ν < 0.268 eV for the NH case, ∑ m ν < 0.288 eV for the IH case, and ∑ m ν < 0.250 eV for the DH case (see Table 4). In the MSin+ ∑ m ν model, the constraint results become ∑ m ν < 0.298 eV for the NH case, ∑ m ν < 0.318 eV for the IH case, and ∑ m ν < 0.277 eV for the DH case (see Table 5). Not surprisingly, the constraint results of ∑ m ν are largest in the MSin model and smallest in the MCPL model.
Furthermore, comparing constraint results of ∑ m ν with those derived from the two-parametrization models, we find that the values of ∑ m ν are smaller in these one-parametrization models, indicating that a model with less parameters tends to provide a smaller fitting value of ∑ m ν . The two-dimensional marginalized contours in the ∑ m ν – w 1 plane are shown in Figure 4. We see that ∑ m ν is positively correlated with w 1 in the MCPL and MLog models, but is anti-correlated with w 1 in the MSin model. The different degeneracies between them ensure that the ratio of the sound horizon and angular diameter distance remains nearly constant.

4. Conclusions

In this paper, we constrain three dynamical dark energy models parameterized by two free parameters, w 0 and w 1 . They correspond to the CPL parametrization, the logarithm parametrization, and the oscillating parametrization. The difference from the CPL model is that the logarithm parametrization and the oscillating parametrization can overcome the future divergency problem, and successfully probe the dynamics of dark energy in all the evolution stages of the universe. We constrain these dynamical dark energy models by using current cosmological observations including the CMB data, the BAO data, and the SNe data. We find that the Log model and the Sin model behave as the same as the CPL model in the fit to the CMB+BAO+SNe data.
We investigate the constraints on the total neutrino mass ∑ m ν in these dynamical dark energy. Simultaneously, we consider the NH case, the IH case, and the DH case of three-generation neutrino mass. We confirm the fact that the different neutrino mass hierarchies can affect the constraint results of ∑ m ν significantly. The smallest fitting value of ∑ m ν is obtained in the DH case, and the largest value of ∑ m ν corresponds to the IH case. We reconfirm that the dark energy properties could indeed significantly change the fitting results of ∑ m ν . The values of ∑ m ν in the Log and Sin models are larger than those derived from the CPL model. In addition, our results does not provide more evidence for determining the neutrino mass orderings because of the similar values of χ min 2 obtained for different neutrino mass hierarchies.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 12103038 and No. 11805031) and 2022 Shaanxi University Youth Innovation Team Project (Grant No. K20220186).

References

  1. Lesgourgues, J.; Pastor, S. Massive neutrinos and cosmology. Phys. Rept. 2006, 429, 307. [Google Scholar] [CrossRef]
  2. Olive, K.A.; et al. Particle Data Group. Review of particle physics. Chin. Phys. C. 2014, 38, 090001. [Google Scholar] [CrossRef]
  3. Osipowicz, A.; et al. KATRIN: A Next generation tritium beta decay experiment with sub-eV sensitivity for the electron neutrino mass. Letter of intent. [arXiv:hep-ex/0109033 [hep-ex]]. [CrossRef]
  4. Kraus, C.; et al. Final results from phase II of the mainz neutrino mass search in tritium beta decay. Eur. Phys. J. C. 2005, 40, 447. [Google Scholar] [CrossRef]
  5. Otten, E.W.; Weinheimer, C. Limit from tritium beta decay. Rept. Prog. Phys. 2008, 71, 086201. [Google Scholar] [CrossRef]
  6. Wolf, J. KATRIN Collaboration. The KATRIN neutrino mass experiment. Nucl. Instrum. Meth. A. 2010, 623, 442. [Google Scholar] [CrossRef]
  7. Klapdor-Kleingrothaus, H.V.; Sarkar, U. Implications of observed neutrinoless double beta decay. Mod. Phys. Lett. A. 2001, 16, 2469. [Google Scholar] [CrossRef]
  8. Klapdor-Kleingrothaus, H.V.; Krivosheina, I.K.; Dietz, A.; Chkvorets, O. Search for neutrinoless double beta decay with enriched Ge-76 in Gran Sasso 1990-2003. Phys. Lett. B. 2004, 586, 198. [Google Scholar] [CrossRef]
  9. Aker, M.; et al. KATRIN. Analysis methods for the first KATRIN neutrino-mass measurement. Phys. Rev. D. 2021, 104, 012005. [Google Scholar] [CrossRef]
  10. Aghanim, N.; et al. Planck. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
  11. Zhao, M.M.; Li, Y.H.; Zhang, J.F.; Zhang, X. Constraining neutrino mass and extra relativistic degrees of freedom in dynamical dark energy models using Planck 2015 data in combination with low-redshift cosmological probes: basic extensions to ΛCDM cosmology. Mon. Not. Roy. Astron. Soc. 2017, 469, 1713. [Google Scholar] [CrossRef]
  12. Zhang, X. Impacts of dark energy on weighing neutrinos after Planck 2015. Phys. Rev. D. 2016, 93, 083011. [Google Scholar] [CrossRef]
  13. Guo, R.Y.; Zhang, J.F.; Zhang, X. Exploring neutrino mass and mass hierarchy in the scenario of vacuum energy interacting with cold dark matte. Chin. Phys. C. 2018, 42, 095103. [Google Scholar] [CrossRef]
  14. Roy Choudhury, S.; Hannestad, S. Updated results on neutrino mass and mass hierarchy from cosmology with Planck 2018 likelihoods. JCAP. 2020, 07, 037. [Google Scholar] [CrossRef]
  15. Li, H.; Zhang, X. Constraining dynamical dark energy with a divergence-free parametrization in the presence of spatial curvature and massive neutrinos. Phys. Lett. B. 2012, 713, 160. [Google Scholar] [CrossRef]
  16. Li, Y.H.; Wang, S.; Li, X.D.; Zhang, X. Holographic dark energy in a universe with spatial curvature and massive neutrinos: a full Markov Chain Monte Carlo exploration. JCAP. 2013, 1302, 033. [Google Scholar] [CrossRef]
  17. Zhang, J.F.; Li, Y.H.; Zhang, X. Cosmological constraints on neutrinos after BICEP2. Eur. Phys. J. C. 2014, 74, 2954. [Google Scholar] [CrossRef]
  18. Zhang, J.F.; Zhao, M.M.; Li, Y.H.; Zhang, X. Neutrinos in the holographic dark energy model: constraints from latest measurements of expansion history and growth of structure. JCAP. 2015, 1504, 038. [Google Scholar] [CrossRef]
  19. Geng, C.Q.; Lee, C.C.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Observational constraints on varying neutrino-mass cosmology. JCAP. 2016, 01, 049. [Google Scholar] [CrossRef]
  20. Chen, Y.; Xu, L. Galaxy clustering, CMB and supernova data constraints on ϕ CDM model with massive neutrinos. Phys. Lett. B. 2016, 752, 66–75. [Google Scholar] [CrossRef]
  21. Vagnozzi, S.; Dhawan, S.; Gerbino, M.; Freese, K.; Goobar, A.; Mena, O. Constraints on the sum of the neutrino masses in dynamical dark energy models with w(z)≥-1 are tighter than those obtained in ΛCDM. Phys. Rev. D. 2018, 98, 083501. [Google Scholar] [CrossRef]
  22. Loureiro, A.; Cuceu, A.; Abdalla, F.B.; Moraes, B.; Whiteway, L.; Mcleod, M.; Balan, S.T.; Lahav, O.; Benoit-Lévy, A.; Manera, M.; et al. On The Upper Bound of Neutrino Masses from Combined Cosmological Observations and Particle Physics Experiments. Phys. Rev. Lett. 2019, 123, 081301. [Google Scholar] [CrossRef]
  23. Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
  24. Wang, L.F.; Zhang, X.N.; Zhang, J.F.; Zhang, X. Impacts of gravitational-wave standard siren observation of the Einstein Telescope on weighing neutrinos in cosmology. Phys. Lett. B. 2018, 782, 87. [Google Scholar] [CrossRef]
  25. Wang, S.; Wang, Y.F.; Xia, D.M.; Zhang, X. Impacts of dark energy on weighing neutrinos: mass hierarchies considered. Phys. Rev. D. 2016, 94, 083519. [Google Scholar] [CrossRef]
  26. Yang, W.; Nunes, R.C.; Pan, S.; Mota, D.F. Effects of neutrino mass hierarchies on dynamical dark energy models. Phys. Rev. D. 2017, 95, 103522. [Google Scholar] [CrossRef]
  27. Huang, Q.G.; Wang, K.; Wang, S. Constraints on the neutrino mass and mass hierarchy from cosmological observations. Eur. Phys. J. C. 2016, 76, 489. [Google Scholar] [CrossRef]
  28. Sharma, R.K.; Pandey, K.L.; Das, S. Implications of an Extended Dark Energy Model with Massive Neutrinos. Astrophys. J. 2022, 934, 113. [Google Scholar] [CrossRef]
  29. Giusarma, E.; Gerbino, M.; Mena, O.; Vagnozzi, S.; Ho, S.; Freese, K. Improvement of cosmological neutrino mass bounds. Phys. Rev. D. 2016, 94, 083522. [Google Scholar] [CrossRef]
  30. Vagnozzi, S.; Giusarma, E.; Mena, O.; Freese, K.; Gerbino, M.; Ho, S.; Lattanzi, M. Unveiling ν secrets with cosmological data: neutrino masses and mass hierarchy Phys. Rev. D. 2017, 96, 123503. [Google Scholar] [CrossRef]
  31. Giusarma, E.; Vagnozzi, S.; Ho, S.; Ferraro, S.; Freese, K.; Kamen-Rubio, R.; Luk, K.B. Scale-dependent galaxy bias, CMB lensing-galaxy cross-correlation, and neutrino masses. Phys. Rev. D. 2018, 98, 123526. [Google Scholar] [CrossRef]
  32. Tanseri, I.; Hagstotz, S.; Vagnozzi, S.; Giusarma, E.; Freese, K. Updated neutrino mass constraints from galaxy clustering and CMB lensing-galaxy cross-correlation measurements. JHEAp. 2022, 36, 1–26. [Google Scholar] [CrossRef]
  33. Zhang, M.; Zhang, J.F.; Zhang, X. Impacts of dark energy on constraining neutrino mass after Planck 2018. Commun. Theor. Phys. 2020, 72, 125402. [Google Scholar] [CrossRef]
  34. Khalifeh, A.R.; Jimenez, R. Distinguishing Dark Energy models with neutrino oscillations. Phys. Dark Univ. 2021, 34, 100897. [Google Scholar] [CrossRef]
  35. Yang, N.; Jia, J.; Liu, X.; Zhang, H. Constraining Chaplygin models using diffuse supernova neutrino background. Phys. Dark Univ. 2019, 26, 100397. [Google Scholar] [CrossRef]
  36. Lee, J.; Ryum, S. Weighing the Neutrinos with the Galaxy Shape-Shape Correlations. [arXiv:2006.14477 [astro-ph.CO]]. [CrossRef]
  37. Xu, W.L.; DePorzio, N.; Muñoz, J.B.; Dvorkin, C. Ccurately Weighing Neutrinos with Cosmological Surveys. Phys. Rev. D. 2021, 103, 023503. [Google Scholar] [CrossRef]
  38. Li, M. A Model of holographic dark energy. Phys. Lett. B. 2004, 603, 1. [Google Scholar] [CrossRef]
  39. Huang, Q.G.; Li, M. The Holographic dark energy in a non-flat universe. JCAP. 2004, 08, 013. [Google Scholar] [CrossRef]
  40. Zhang, J.F.; Zhao, M.M.; `Cui, J.L.; Zhang, X. Revisiting the holographic dark energy in a non-flat universe: alternative model and cosmological parameter constraints. Eur. Phys. J. C. 2014, 74, 3178. [Google Scholar] [CrossRef]
  41. Wang, S.; Wang, Y.; Li, M. Holographic Dark Energy. Phys. Rept. 2017, 696, 1–57. [Google Scholar] [CrossRef]
  42. Wang, S.; Geng, J.J.; Hu, Y.L.; Zhang, X. Revisit of constraints on holographic dark energy: SNLS3 dataset with the effects of time-varying β and different light-curve fitters. Sci. China Phys. Mech. Astron. 2015, 58, 019801. [Google Scholar] [CrossRef]
  43. Cui, J.; Xu, Y.; Zhang, J.; Zhang, X. Strong gravitational lensing constraints on holographic dark energy. Sci. China Phys. Mech. Astron. 2015, 58, 110402. [Google Scholar] [CrossRef]
  44. He, D.Z.; Zhang, J.F.; Zhang, X. Redshift drift constraints on holographic dark energy. Sci. China Phys. Mech. Astron. 2017, 60, 039511. [Google Scholar] [CrossRef]
  45. Xu, Y.Y.; Zhang, X. Comparison of dark energy models after Planck 2015. Eur. Phys. J. C. 2016, 76, 588. [Google Scholar] [CrossRef]
  46. Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D. 2001, 10, 213–224. [Google Scholar] [CrossRef]
  47. Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef] [PubMed]
  48. Ma, J.Z.; Zhang, X. Probing the dynamics of dark energy with novel parametrizations. Phys. Lett. B. 2011, 699, 233–238. [Google Scholar] [CrossRef]
  49. Jassal, H.K.; Bagla, J.S.; Padmanabhan, T. Observational constraints on low redshift evolution of dark energy: How consistent are different observations? Phys. Rev. D. 2005, 72, 103503. [Google Scholar] [CrossRef]
  50. Barboza, E.M., Jr.; Alcaniz, J.S. A parametric model for dark energy. Phys. Lett. B. 2008, 666, 415–419. [Google Scholar] [CrossRef]
  51. Beutler, F.; et al. The 6dF galaxy survey: baryon acoustic oscillations and the local hubble constant. Mon. Not. Roy. Astron. Soc. 2011, 416, 3017. [Google Scholar] [CrossRef]
  52. Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main galaxy sample I: a 4 percent distance measure at z = 0.15. Mon. Not. Roy. Astron. Soc. 2015, 449, 835. [Google Scholar] [CrossRef]
  53. Alam, S.; et al. BOSS Collaboration. The clustering of galaxies in the completed SDSS-III baryon oscillation spectroscopic survey: cosmological analysis of the DR12 galaxy sample. Mon. Not. Roy. Astron. Soc. 2017; 470, 2617. [Google Scholar] [CrossRef]
  54. Scolnic, D.M.; et al. The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined pantheon sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
  55. Guo, R.Y.; Feng, L.; Yao, T.Y.; Chen, X.Y. Exploration of interacting dynamical dark energy model with interaction term including the equation-of-state parameter: alleviation of the H0 tension. JCAP. 2021, 12, 036. [Google Scholar] [CrossRef]
  56. Feng, L.; Guo, R.Y.; Zhang, J.F.; Zhang, X. Cosmological search for sterile neutrinos after Planck 2018. Phys. Lett. B. 2022, 827, 136940. [Google Scholar] [CrossRef]
  57. Guo, R.Y.; Zhang, J.F.; Zhang, X. Can the H0 tension be resolved in extensions to ΛCDM cosmology? JCAP. 2019, 054, 02. [Google Scholar] [CrossRef]
  58. Lewis, A.; Challinor, A.; Lasenby, A. Efficient computation of CMB anisotropies in closed FRW models. Astrophys. J. 2000, 538, 473–476. [Google Scholar] [CrossRef]
  59. Lewis, A. Efficient sampling of fast and slow cosmological parameters. Phys. Rev. D. 2013, 87, 103529. [Google Scholar] [CrossRef]
  60. Jin, S.J.; Zhu, R.Q.; Wang, L.F.; Li, H.L.; Zhang, J.F.; Zhang, X. Impacts of gravitational-wave standard siren observations from Einstein Telescope and Cosmic Explorer on weighing neutrinos in interacting dark energy models. Commun. Theor. Phys. 2022, 74, 105404. [Google Scholar] [CrossRef]
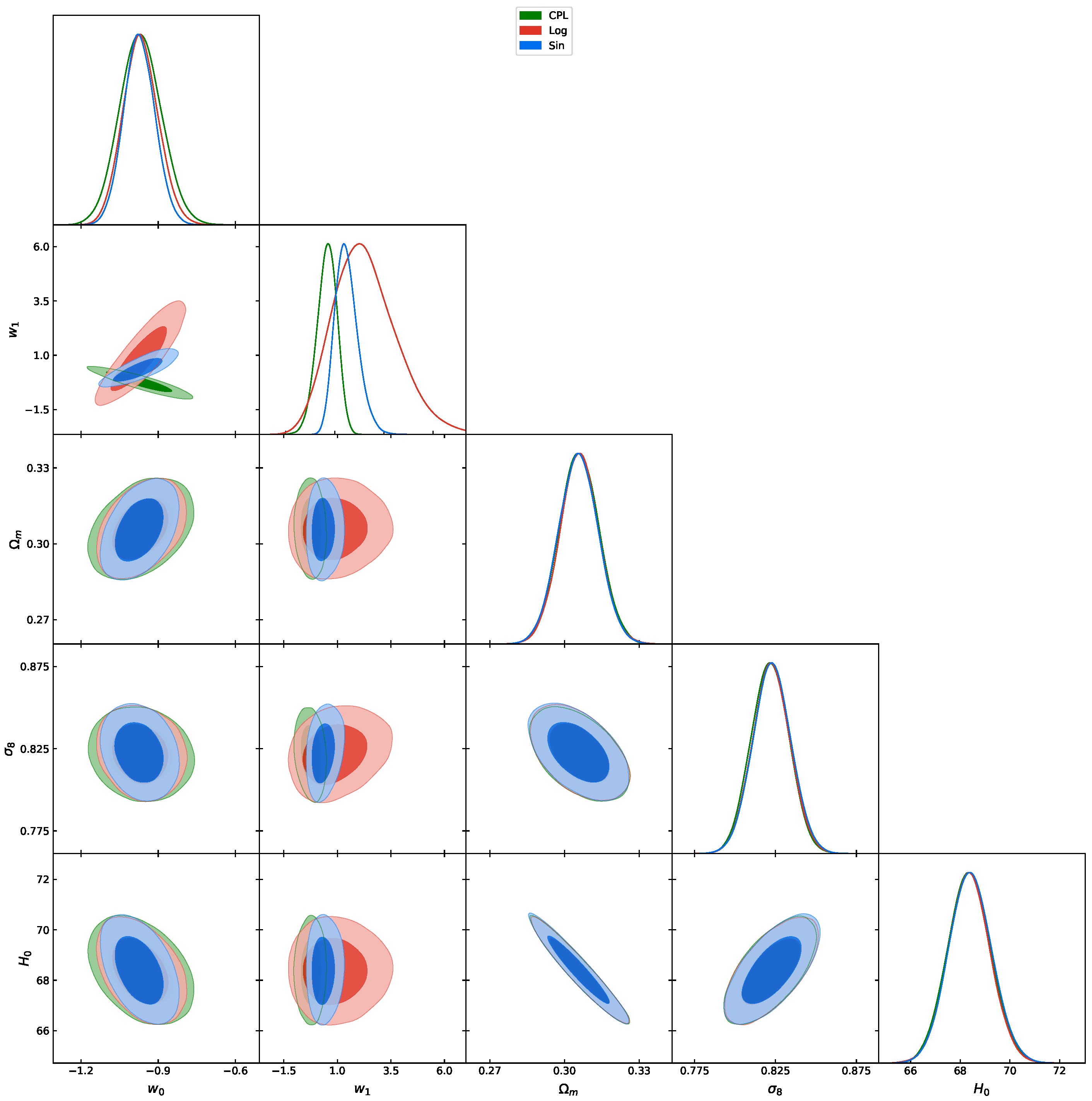
Preprints 70347 g001
Figure 1. One-dimensional marginalized distributions and two-dimensional contours at 1 σ and 2 σ level for the CPL, Log, and Sin models.
Figure 1. One-dimensional marginalized distributions and two-dimensional contours at 1 σ and 2 σ level for the CPL, Log, and Sin models.
Preprints 70347 g001
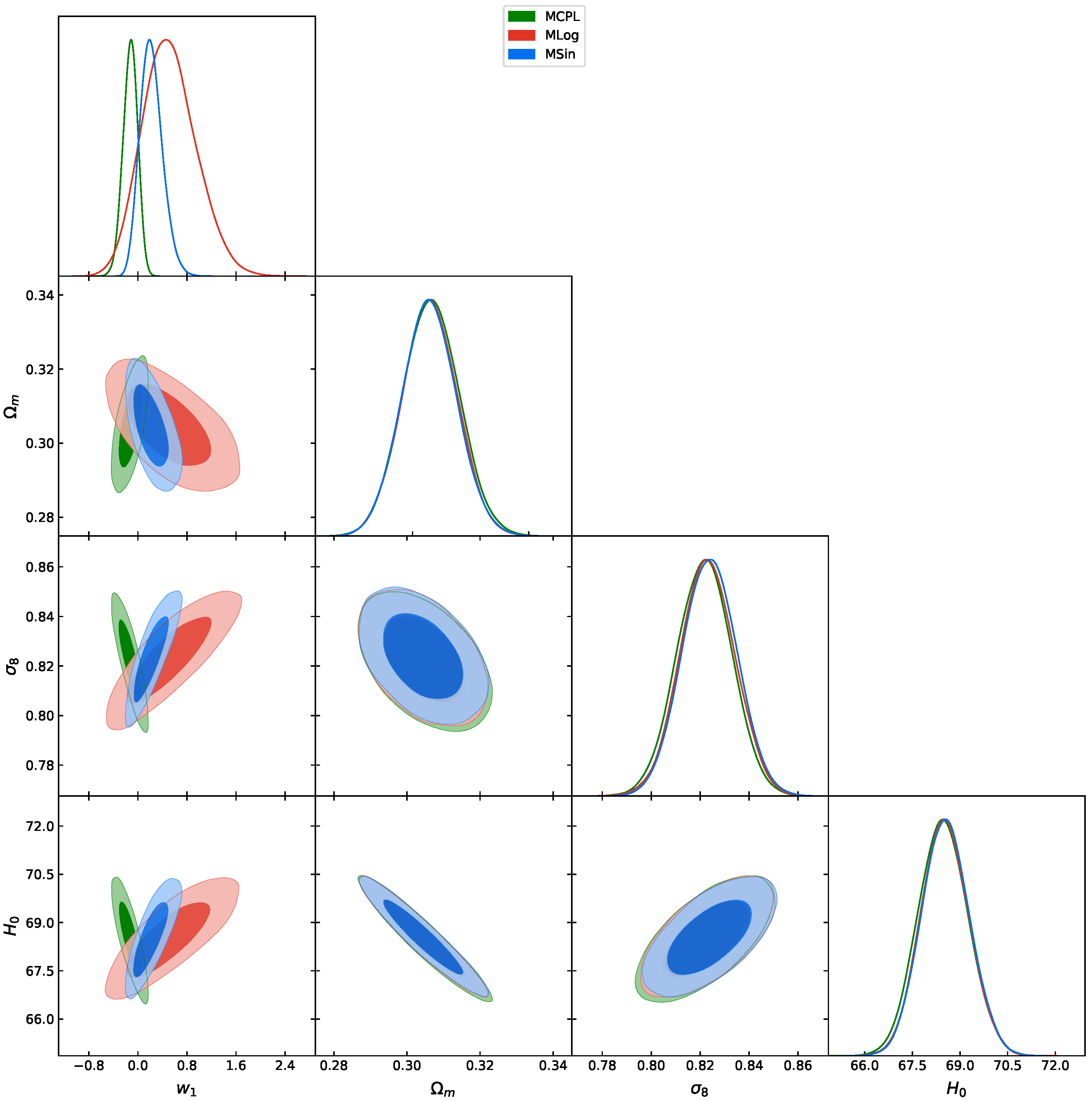
Preprints 70347 g002
Figure 2. One-dimensional marginalized distributions and two-dimensional contours at 1 σ and 2 σ level for the MCPL, MLog, and MSin models.
Figure 2. One-dimensional marginalized distributions and two-dimensional contours at 1 σ and 2 σ level for the MCPL, MLog, and MSin models.
Preprints 70347 g002
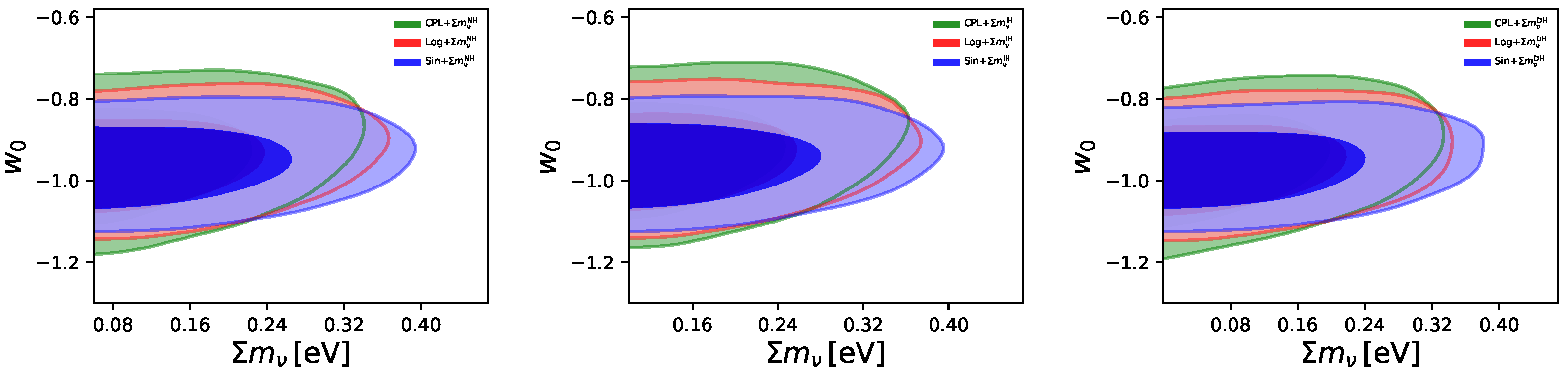
Preprints 70347 g003
Figure 3. Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the ∑ m ν – w 0 plane of the CPL, Log, and Sin models considered mass hierarchy cases of NH, IH, and DH.
Figure 3. Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the ∑ m ν – w 0 plane of the CPL, Log, and Sin models considered mass hierarchy cases of NH, IH, and DH.
Preprints 70347 g003
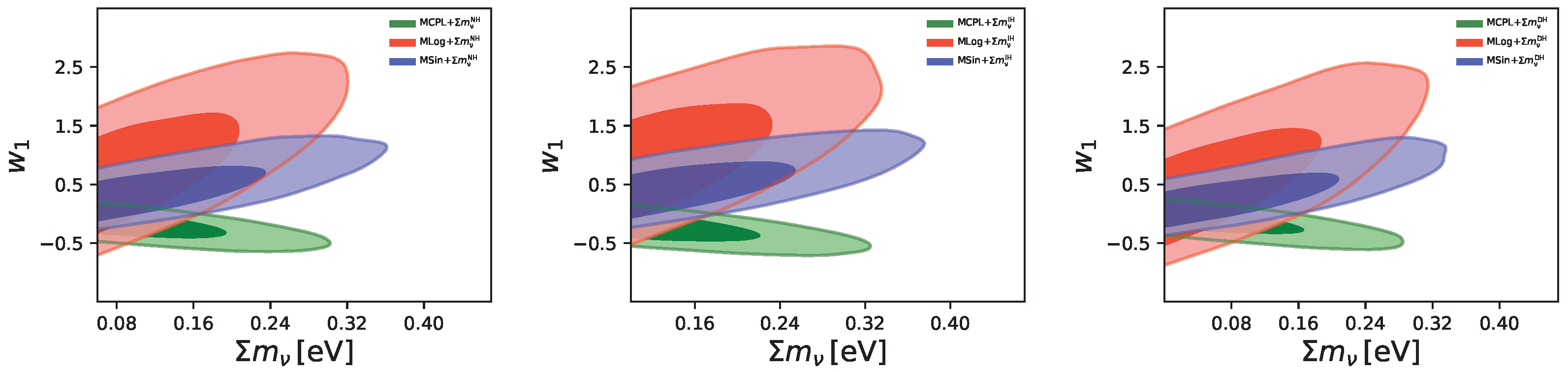
Preprints 70347 g004
Figure 4. Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the ∑ m ν – w 1 plane of the MCPL, MLog, and MSin models considered mass hierarchy cases of NH, IH, and DH.
Figure 4. Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the ∑ m ν – w 1 plane of the MCPL, MLog, and MSin models considered mass hierarchy cases of NH, IH, and DH.
Preprints 70347 g004
Table 1. Priors on the free parameters for the two-parametrization dark energy models.
Table 1. Priors on the free parameters for the two-parametrization dark energy models.
Parameter Prior
Ω b h 2 [ 0.005 , 0.100 ]
Ω c h 2 [ 0.001 , 0.990 ]
100 θ MC [ 0.5 , 10.0 ]
τ [ 0.01 , 0.80 ]
ln ( 10 10 A s ) [ 2 , 4 ]
n s [ 0.8 , 1.2 ]
w 0 [ − 3.0 , − 0.01 ]
w 1 [ − 4 , 9 ]
Table 2. The fitting values for the six dynamical dark energy models.
Table 2. The fitting values for the six dynamical dark energy models.
Parameter CPL Log Sin MCPL MLog MSin
w 0 − 0.968 ± 0.079 − 0 . 968 − 0.072 + 0.065 − 0 . 973 − 0.058 + 0.059 − 1 − 1 − 1
w 1 − 0 . 24 − 0.27 + 0.33 0 . 93 − 1.11 + 0.79 0 . 36 − 0.40 + 0.28 − 0 . 12 − 0.11 + 0.13 0 . 52 − 0.48 + 0.39 0 . 22 − 0.21 + 0.16
Ω m 0.3059 ± 0.0077 0.3060 ± 0.0075 0.3056 ± 0.0077 0 . 3048 − 0.0071 + 0.0070 0 . 3045 − 0.0068 + 0.0069 0.3044 ± 0.0068
H 0 [km/s/Mpc] 68.37 ± 0.83 68.37 ± 0.81 68.41 ± 0.83 68.47 ± 0.76 68.53 ± 0.73 68.55 ± 0.73
σ 8 0.822 ± 0.011 0.822 ± 0.011 0.823 ± 0.011 0.822 ± 0.011 0.823 ± 0.011 0.824 ± 0.011
χ min 2 3821.214 3821.150 3821.164 3821.310 3821.288 3821.290
Table 3. The fitting values for the CPL+ ∑ m ν and MCPL+ ∑ m ν models considered mass hierarchy cases of NH, IH, and DH.
Table 3. The fitting values for the CPL+ ∑ m ν and MCPL+ ∑ m ν models considered mass hierarchy cases of NH, IH, and DH.
CPL MCPL
Parameter NH IH DH NH IH DH
w 0 − 0 . 940 − 0.095 + 0.085 − 0 . 929 − 0.097 + 0.083 − 0 . 950 − 0.092 + 0.082 − 1 − 1 − 1
w 1 − 0 . 49 − 0.33 + 0.46 − 0 . 59 − 0.32 + 0.48 − 0 . 39 − 0.30 + 0.47 − 0 . 24 − 0.13 + 0.18 − 0 . 30 − 0.14 + 0.18 − 0 . 17 − 0.13 + 0.19
∑ m ν [eV] < 0.285 < 0.304 < 0.254 < 0.250 < 0.276 < 0.228
Ω m 0 . 3094 − 0.0087 + 0.0081 0 . 3103 − 0.0082 + 0.0081 0 . 3077 − 0.0090 + 0.0083 0.3069 ± 0.0073 0.3078 ± 0.0072 0 . 3058 − 0.0079 + 0.0072
H 0 [km/s/Mpc] 68.27 ± 0.82 68 . 27 − 0.81 + 0.83 68.32 ± 0.84 68.47 ± 0.76 68.49 ± 0.75 68 . 45 − 0.76 + 0.77
S 8 0.825 ± 0.012 0.823 ± 0.012 0.827 ± 0.012 0.824 ± 0.011 0.822 ± 0.011 0.826 ± 0.012
χ min 2 3822.102 3822.516 3821.168 3822.144 3823.046 3821.112
Table 4. The fitting values for the Log+ ∑ m ν and MLog+ ∑ m ν models considered mass hierarchy cases of NH, IH, and DH.
Table 4. The fitting values for the Log+ ∑ m ν and MLog+ ∑ m ν models considered mass hierarchy cases of NH, IH, and DH.
Log MLog
Parameter NH IH DH NH IH DH
w 0 − 0 . 946 − 0.080 + 0.071 − 0 . 938 − 0.081 + 0.073 − 0 . 955 − 0.079 + 0.069 − 1 − 1 − 1
w 1 1 . 90 − 1.70 + 1.00 2 . 20 − 1.70 + 1.10 1 . 52 − 1.63 + 0.95 1 . 02 − 0.78 + 0.50 1 . 21 − 0.76 + 0.51 0 . 77 − 0.80 + 0.47
∑ m ν [eV] < 0.302 < 0.317 < 0.282 < 0.268 < 0.288 < 0.250
Ω m 0.3094 ± 0.0082 0 . 3106 − 0.0082 + 0.0083 0 . 3080 − 0.0089 + 0.0081 0.3066 ± 0.0072 0.3078 ± 0.0072 0.3056 ± 0.0074
H 0 [km/s/Mpc] 68.31 ± 0.82 68 . 27 − 0.82 + 0.83 68 . 33 − 0.81 + 0.82 68.54 ± 0.74 68.52 ± 0.75 68 . 53 − 0.74 + 0.75
S 8 0.825 ± 0.012 0.823 ± 0.012 0.827 ± 0.012 0.824 ± 0.012 0.822 ± 0.011 0 . 826 − 0.012 + 0.013
χ min 2 3822.100 3822.180 3821.048 3822.458 3823.538 3821.284
Table 5. The fitting values for the Sin+ ∑ m ν and MSin+ ∑ m ν models considered mass hierarchy cases of NH, IH, and DH.
Table 5. The fitting values for the Sin+ ∑ m ν and MSin+ ∑ m ν models considered mass hierarchy cases of NH, IH, and DH.
Sin MSin
Parameter NH IH DH NH IH DH
w 0 − 0 . 956 − 0.070 + 0.063 − 0 . 952 − 0.066 + 0.065 − 0.962 ± 0.063 − 1 − 1 − 1
w 1 0 . 80 − 0.70 + 0.37 0 . 91 − 0.69 + 0.41 0 . 66 − 0.69 + 0.34 0 . 49 − 0.38 + 0.21 0 . 57 − 0.38 + 0.22 0 . 37 − 0.39 + 0.19
∑ m ν [eV] < 0.327 < 0.336 < 0.311 < 0.298 < 0.318 < 0.277
Ω m 0 . 3097 − 0.0090 + 0.0083 0 . 3106 − 0.0083 + 0.0082 0.3081 ± 0.0084 0.3069 ± 0.0072 0.3079 ± 0.0072 0.3058 ± 0.0073
H 0 [km/s/Mpc] 68 . 33 − 0.84 + 0.83 68 . 32 − 0.83 + 0.84 68.37 ± 0.82 68 . 57 − 0.73 + 0.72 68.55 ± 0.73 68 . 56 − 0.73 + 0.74
S 8 0.825 ± 0.012 0.823 ± 0.012 0.826 ± 0.012 0.824 ± 0.012 0.822 ± 0.012 0.826 ± 0.012
χ min 2 3822.408 3823.456 3821.080 3822.876 3823.574 3821.224
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated