Theoretical Explanation and Experimental Design of the Origin of Earth's Magnetic Field, Stellar Magnetic Field, and Neutron Star Magnetic Field

Preprint

Article

Theoretical Explanation and Experimental Design of the Origin of Earth's Magnetic Field, Stellar Magnetic Field, and Neutron Star Magnetic Field

Altmetrics

Downloads

129

Views

124

Comments

Sheng Qin^*

This version is not peer-reviewed

Submitted:

01 April 2023

Posted:

03 April 2023

You are already at the latest version

Alerts

Abstract

There is currently no unified explanation for the origin of Earth's magnetic field, planetary magnetic fields, stellar magnetic fields, and neutron star magnetic fields, and most importantly, none of these theories have been experimentally verified. This paper is based on a new unified theory of mechanics and its derived applications, which may provide a better explanation for the origin of magnetic fields in celestial bodies and can be experimentally tested to better answer the observed phenomena: (1) the greater the mass of the celestial body, the stronger the magnetic field; (2) the faster the rotation speed of the celestial body, the stronger the magnetic field; (3) the higher the density of the celestial body, the stronger the magnetic field produced.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

There is currently no unified explanation for the origin of Earth’s magnetic field, and no explanation has been experimentally verified. For example, Gubbins and Sreenivasan proposed the “geodynamo” theory in 2001, which is widely regarded as one of the best models for explaining the origin of Earth’s magnetic field [2]. Olson and Amit’s 2019 study found that the structure and chemical composition of Earth’s core have an important influence on the generation and evolution of Earth’s magnetic field [3]. Roberts’ 2018 study conducted numerical simulations and theoretical analyses of the evolution of Earth’s magnetic field, further deepening our understanding of the origin and evolution of Earth’s magnetic field [4].

Similarly, the explanation for the origin of neutron star magnetic fields is complex and controversial. There are several theories, including the Magnetic Field Residual Theory, the Baryonic Coupling Theory, and the Superconducting Theory, but no theory has fully explained the origin of neutron star magnetic fields. Future research will require more theoretical exploration and experimental verification.

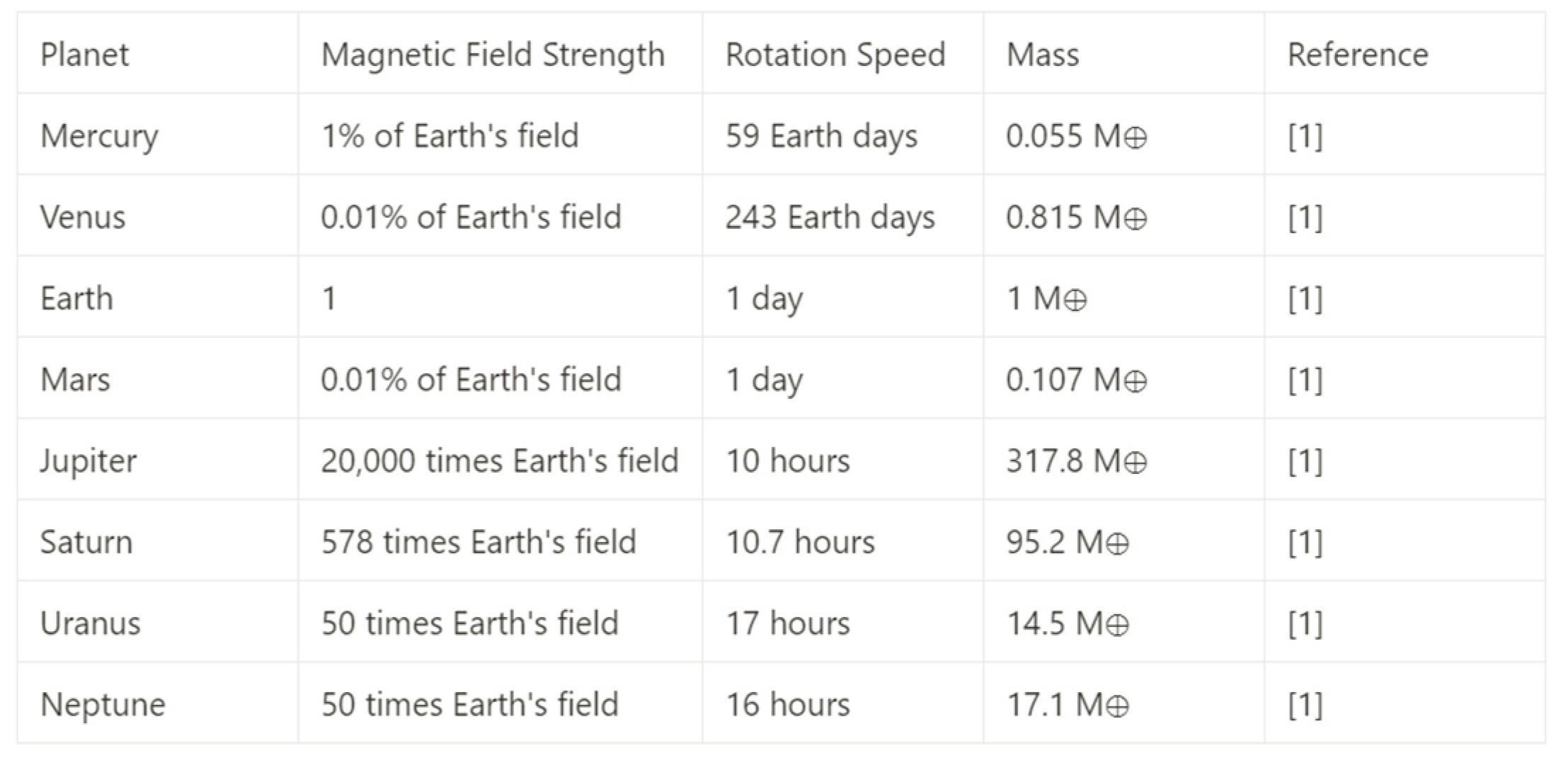
However, in our past research, we have observed the following patterns, as shown in Figure 1:

(1): The greater the mass of a celestial body, the stronger its magnetic field;
(2): For celestial bodies of equal mass, the smaller the radius, the stronger the magnetic field (neutron stars are the most typical example [8,9,10]);
(3): The faster the rotation speed of an object, the stronger its magnetic field.

Figure 1. Planetary magnetic field strength.

2. Theoretical Analysis of Celestial Magnetic Field Origin

According to our “Unified Theory of Forces”, all fields originate from “energy loss

E_{m i s s i n g}

” [11]. We have speculated that if the radius of equilibrium distance between electrons and protons is less than

r

, there will be a repulsive force between them. If external pressure causes them to be closer than

r

, the external force F will do work, which will eventually be converted into the energy of the “field” between protons and electrons, forming a new “energy loss

E_{m i s s i n g}

” state. Under this energy loss state, it will be equivalent to the generation of an “electric field” and exhibit the characteristics of an electric field.

However, as we stated in the “Unified Theory of Forces”, we cannot determine whether the repulsive force between electrons and protons when the distance is less than

r

strictly follows the inverse square law. If it does strictly follow this law, a critical value of the external force F will be required, and because any object has a large number of electrons and protons, our experiments will almost be impossible to conduct. However, we have observed that the ionization energy of the outer electrons of various atoms is different, and the size of the atoms is also different. Therefore, we have speculated in our “Unified Theory of Forces” that the energy loss state of the outer electrons of the atom may not be evenly distributed. In this case, it may be possible to generate this energy field

ε

under the action of a large enough external force F, which can achieve an equivalent motion effect of an electric field.

The principle behind this theory is shown in the following Figure 2:

Assuming the equilibrium distance between electrons and protons is

r

, if the distance between them is reduced by

d

under the action of external force F, the external force F will do work and convert into the potential energy

ε

between electrons and protons. According to our theory, this potential energy

ε

is actually equivalent to the electric field of positive or negative charge and should have equivalent motion effects of a field.

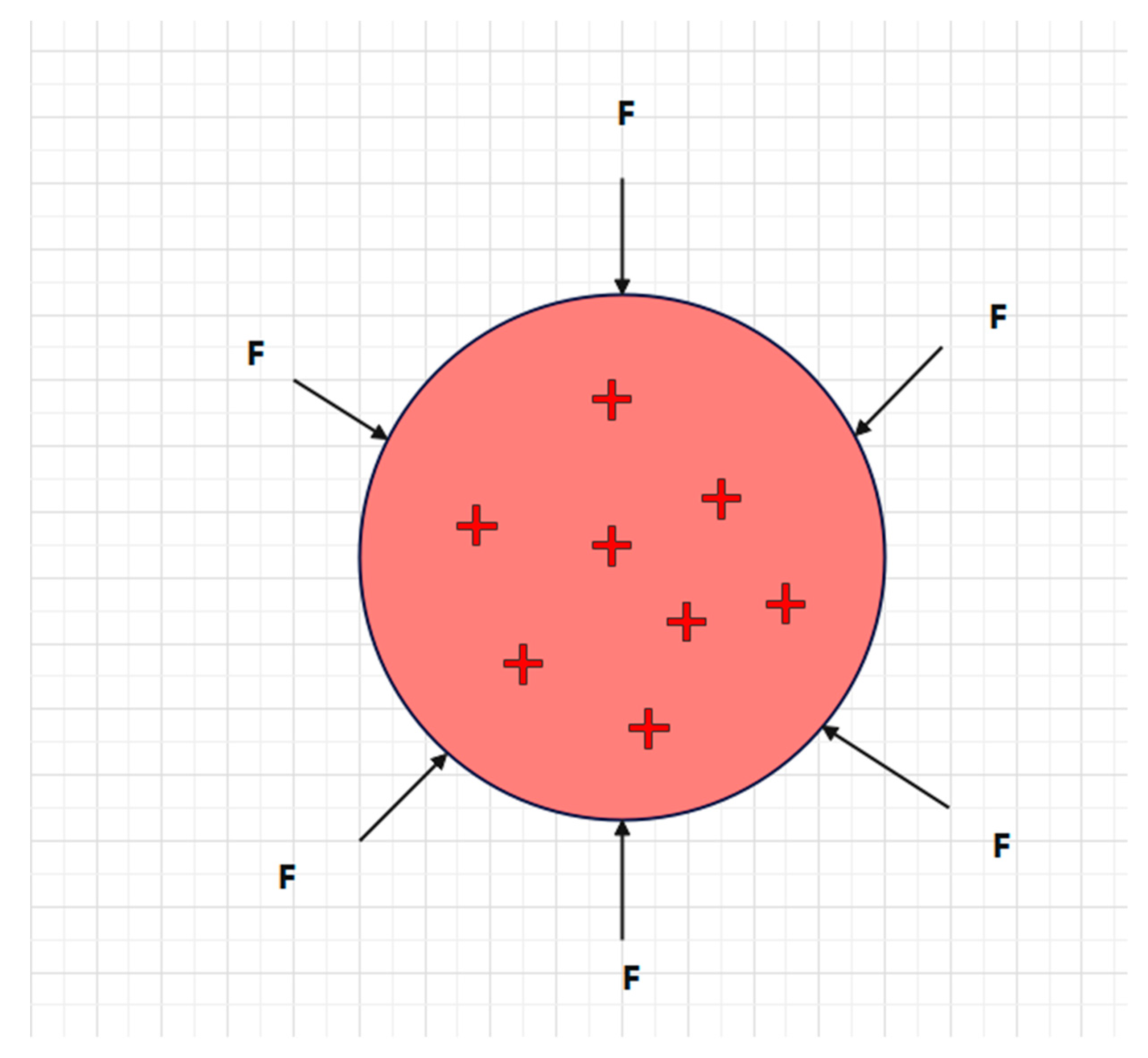
Taking a liquid sphere A as an example, as shown in Figure 3, we assume that the sphere is filled with liquid, and under the action of a uniform external force F, a uniform potential energy field

ε

is generated between atoms. In theory, this is equivalent to an electric field inside liquid sphere A (the electric field carries a positive or negative charge, but the sign of this potential energy field is currently uncertain and may show opposite sign characteristics under compression and stretching). Therefore, when liquid sphere A rotates, an equivalent effect of a magnetic field is generated.

We know that a charged metal sphere generates a magnetic field when it rotates, which indicates that a charged field does not produce radiation effects when it moves at low speeds, unlike a charged particle moving at high speeds. Similarly, when the speed is not fast enough or the field strength is not strong enough, the potential energy field

ε

generated above will not directly radiate energy during rotation, but may exist in the form of a magnetic field, which compensates for the energy loss E missing of the field

ε

during motion.

The calculation of the magnetic field strength generated by the rotation of liquid sphere A is similar to that of a charged metal sphere. The energy loss per unit volume is equivalent to the electric field energy per unit area of a charged metal sphere. According to the Biot-Savart Law:

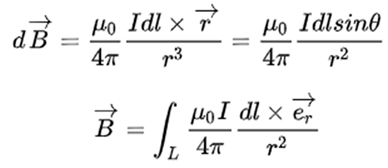
We obtain the following conclusions:

(1): The faster the rotation speed v of liquid sphere A, the larger the equivalent electric current I, and the stronger the induced magnetic field;
(2): The greater the external force F beyond the critical pressure, the stronger the equivalent potential energy field ε generated inside sphere A, which is equivalent to a larger amount of charge per unit volume, and the stronger the induced magnetic field.

Of course, we cannot determine whether the rotation of liquid sphere A under high pressure will necessarily produce a magnetic field. We are only guessing that this potential energy field ε may generate a magnetic field effect based on the characteristics observed in Earth, stars, and neutron stars.

Since the pressure generated by celestial bodies is derived from gravitational force, under the assumption that their density

ρ

remains constant, the formula for the pressure per unit area

P

at point

S

on the surface of the celestial body is as follows:

Figure 4. Formula for internal pressure of celestial bodies [12].

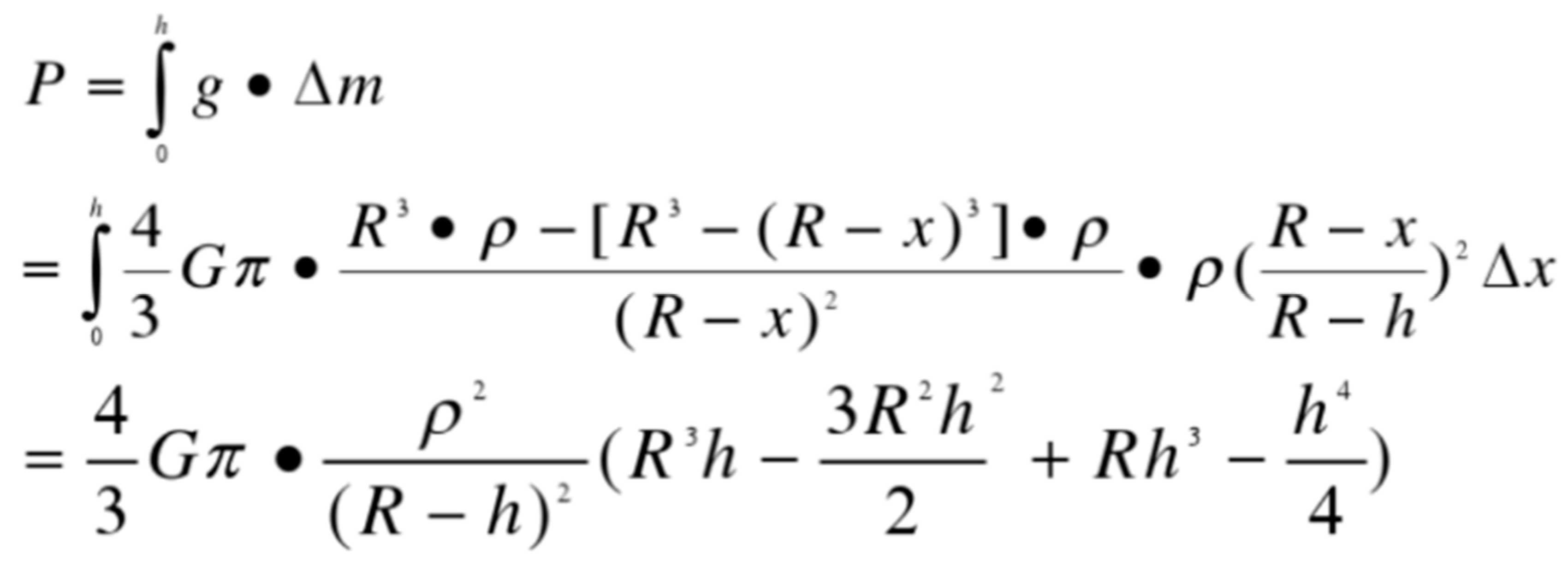
where

h

is the distance between point S and the surface of the celestial body, R is the radius of the celestial body, and P is the pressure per unit area at point S. We can easily draw the following conclusions:

(1): Under the same density ρ, the greater the mass of the celestial body, the greater the pressure P at the same distance from the center of the celestial body, and the stronger the induced potential energy field ε;
(2): The faster the rotation speed v of the celestial body, the larger the equivalent electric current I, and the stronger the induced magnetic field;
(3): Under the same mass, the greater the density ρ, the smaller the radius R, and the greater the pressure P at the same distance from the center of the celestial body, and the stronger the induced potential energy field ε.

Therefore, we can explain the following phenomena well using the above theories:

(1): The larger the mass of a celestial body, the stronger the pressure generated inside it under the same composition of matter, and therefore the potential energy field ε will be larger. The magnetic field generated under the same rotation speed will be stronger.
(2): Under the same mass and rotation speed, the smaller the radius of the celestial body, the greater the pressure it generates, resulting in a higher potential energy field ε, and therefore the magnetic field intensity produced will also be higher, just like a neutron star. However, it should be noted that we currently do not know the boundary conditions of the external force F required to generate the potential energy field ε in the matter of which neutron stars and ordinary atoms are composed.
(3): Under the same mass and radius of the celestial body, if the composition of the matter is the same, the faster the rotation speed, the stronger the magnetic field generated.

The above conclusions may explain the difference in magnetic field strength among planets in the solar system very well:

We predict that if the celestial body’s center is solid, it will affect the strength of the potential energy field

ε

that the celestial body can produce under the same pressure, thereby affecting the strength of the celestial body’s magnetic field. At the same time, the potential energy field strength

ε

produced by different materials under the same pressure should also be different. Therefore, the distribution of the material that makes up the celestial body will ultimately affect the magnetic field strength in various parts of the celestial body.

Experimental design:

To verify the above theory, we can conduct real experiments. We have the following suggestions:

(1): It is recommended to use liquid substances. Gaseous substances are more likely to convert external force F into particle kinetic energy during compression; when solid substances are compressed, it is difficult to control the influence of the intermediate gap, and cooling from liquid to solid often releases heat, which affects the potential energy.
(2): It is recommended to conduct the experiment at a low and constant temperature, which can avoid the influence of atomic kinetic energy as much as possible, and ensure that the work done by external force F is truly converted into the potential energy ε generated.
(3): It is recommended to use particles with larger atomic nuclei for the experiment, which can more easily convert external force F into potential energy, and the theoretical requirements for force F are correspondingly reduced.

The above experiments may be difficult because we must be able to ensure that there is enough force F to compress the material, and at the same time, we must also ensure that this force F truly does work on the material and is converted into the potential energy effect.

3. Experimental Design and Conclusions that Can be Drawn

We can use the above liquid sphere to conduct the above experiment and ensure that the radius of the material atoms is large enough, and the temperature is as low as possible to ensure that the external force F is converted into the potential energy

ε

under huge pressure. At this time, when we rotate the high-pressure liquid sphere quickly, a magnetic field equivalent to the magnetic field can theoretically be generated around it, and the strength of the magnetic field can be detected to verify the above theory.

Through experiments, the following two theories can be tested:

(1): The true origin of the magnetic field of the Earth, stars, and neutron stars;
(2): Verify the correctness of the “unified theory of forces”.

References

NASA. (2021). Solar System Exploration: Planets. Retrieved from https://solarsystem.nasa.gov/planets/.
Gubbins, D., & Sreenivasan, B. (2001). The geodynamo: a unique window on the deep Earth. Proceedings of the National Academy of Sciences, 98(7), 3695-3697.
Olson, P., & Amit, H. (2019). Earth’s core and the geodynamo. Nature, 570(7762), 45-56.
Roberts, P. H. (2018). Geodynamo theory and simulations. Annual Review of Earth and Planetary Sciences, 46, 523-552.
Reisenegger, A. (2001). The Origin of Pulsar Magnetism. Astrophysics and Space Science Library, 267, 171-180.
Thompson, C., & Duncan, R. C. (1993). Neutron Star Magnetic Fields and Pulsations. The Astrophysical Journal, 408, 194-217.
Lai, D. (2001). Neutron Star Magnetism: From Birth to Death. Reviews of Modern Physics, 73(1), 629-661.
Lattimer, J. M., & Prakash, M. (2016). The physics of neutron stars. Physics Reports, 621, 127-164.
Reisenegger, A. (2001). The Origin of Pulsar Magnetism. Astrophysics and Space Science Library, 267, 171-180.
Thompson, C., & Duncan, R. C. (1993). Neutron Star Magnetic Fields and Pulsations. The Astrophysical Journal, 408, 194-217.
Qin S (2022) Unified Theory of Gravity, Electromagnetic Force, Strong and Weak Forces and their Applications: Theoretical Explanation for Dark Matter. J Phys Chem Biophys. 12:335.
https://wenku.baidu.com/view/939fc309581b6bd97f19ea73.html?_wkts_=1680266938185&bdQuery=%E5%AF%86%E5%BA%A6%E5%9D%87%E5%8C%80%E7%9A%84%E7%90%83%E5%86%85%E9%83%A8%E5%8E%8B%E5%8A%9B.

Figure 2. Principle of energy field ε under pressure.

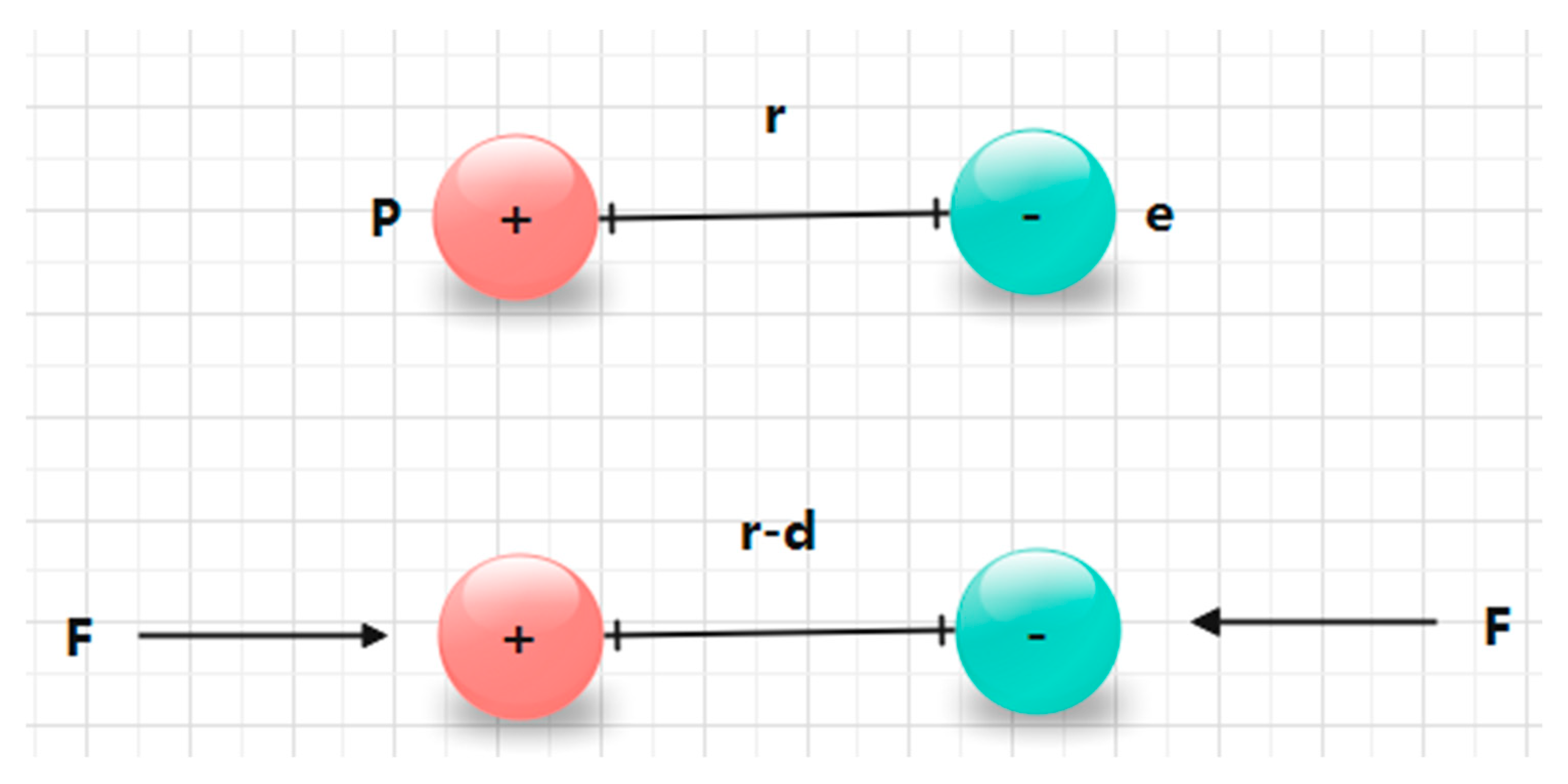
Figure 3. Principle of celestial magnetic field generation.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.