Prerpints.org logo
Preprint
Article

Predicting 6000m Performance Time in Junior Rowers using a 500m Indoor Rowing Test

Altmetrics

Downloads

312

Views

118

Comments

0

Submitted:

02 April 2023

Posted:

04 April 2023

You are already at the latest version

Alerts
Abstract
The present study aimed to develop a mathematical model to estimate the performance of an indoor rowing event of 6000m through an 500 m all out test in junior athletes. We selected141 subjects from the Brazilian rowing confederation database (15.9 ± 1.0 years), subsequently randomised the sample to the development (~70%) and cross-validation (~30%) groups of the mathematical model. Performance data for 500m and 6000m were collected (there was a 48h washout between one test and anoth-er).Subsequently, the mathematical model: Time(min) 6000m = { [( Time(s) 500-m * 6) * 2] / 60} + 1.3, was developed by arithmetic modeling using machine learning and Regression analysis, being tested by intraclass correlation coefficient (ICC), Concordance correlation coefficient (CCC), Validity (Cb ), preci-sion (ρ) and bland-Altman plotting. The prediction of the result of 6000m through the mathematical model utilizando apenas o desempenho de 500m “all-out” test showed a significant reliability in de-velopment group (r2 = 0.730, ICC = 0.753; CCC = 0.895, Cb = 0.879, ρ: 0.957, pure error: 0.2 secounds (1.0% estimative error)); and in cross-validation group (r2 = 0.710, ICC = 0.747; CCC = 0.888, Cb = 0.875, ρ: 0.903, pure error: 0.3 secounds (1.4% estimative error)). When comparing the estimated re-sults of the 6000m performance by the mathematical model with the real performance of 6000m per-formed in indoor rowing, no statistical differences were observed. In addition, the mathematical model did not present a significant proportion bias in relation to the 6000 m performance in both groups. The mathematical model for predicting 6000m performance through a 500m fast test was significant for national level junior rowing athletes.
Keywords: 
Subject: Public Health and Healthcare  -   Physical Therapy, Sports Therapy and Rehabilitation

1. Introduction

Olympic rowing requires high levels of aerobic and anaerobic power for successful performance. Therefore, male elite rowers have high oxygen consumption rates (72 ml kg-1 min-1 in men) and mean power of 469 ± 51 W [1,2,3,4,5]. In view of the above, rowers' performance is often evaluated in indoor rowing ergometer to identify changes in athletic performance [5,6]. “All-out” total test on a rowing ergometer is commonly used over a distance of 2000m, which corresponds to the actual distance used for official rowing competitions such as the Olympic Games and World Championships [7].
Maximum aerobic power can be evaluated in different tests, such as 2000 m, 6-minute all-out test and/or 7 x 2 minute incremental step test [5,6,8,9]. However, these tests are not purely aerobic, showing frequent transitions to partially anaerobic metabolism, which can cause early peripheral fatigue due to increased metabolic by-products (i.e., H+ ions) derived from the accumulation of lactic acid, resulting in decreased effort due to muscle discomfort that can occur for the long duration of these tests. Therefore, dubious information is collected about the actual physical capacity of rowers [10,11,12]. It is important to consider that performance analysis tests to evaluate cardiorespiratory capacity through maximal oxygen uptake and anaerobic threshold analysis require the use of sophisticated equipment, the need for specialists and have a relatively high financial cost, limiting factors for the wide use of these methods in routine training practices. [8,9,13].
In view of the above, tests over a distance of 6000m are also widely carried out for athlete selection and evaluation, as it is assumed that the 6000 m test in indoor rowing ergometer is a accurate alternative to estimate the aerobic fitness of rowers based on empirical information from a database collected by coaches of successful rowers in national and international events which consolidate watts production values and reference execution time of the proposed test [7]. This test is applied in the first stage of the preparatory period, which usually starts in October and aims to build a strong aerobic base through low intensity and long duration training, which occupies up to 90% of the total training time during the preparation period [7,13].
However, although regular monitoring of rowers' aerobic fitness is something very important and commonly analyzed through 6000m performance, this can present itself as a challenging task for many rowers due to its long duration and physical demands [4,14]. In addition, it is well known that prolonged high-intensity stimuli, without the necessary recovery, are associated with cases of non-functional overreaching and overtraining, which may compromise future adaptations and may be harmful to the athlete's health. [14]. Given the above, it does not seem to be feasible to routinely measure it from a 6000m indoor rowing test . Therefore, there is a need for an alternative test that can reliably and validly estimate 6000m performance from a shorter distance and thus the athlete to have a prior prediction of their performance which will contribute to plot strategies for running the suggested test, as well as mitigating the risk of overtraining [4,14,15,16].
Several approaches have been used to predict the performance of indoor rowing of 2000m with short anaerobic test [17,18,19,20,21]. Previous researchers have developed mathematical models for predicting performance in senior rowers (i.e., age >18 years) at 2000m and6000 m from the 30s, 20s, and 60s tests, respectively [17,18,19]. However, these tools did not show reproducibility in the 6000m test or other indoor rowing tests used in different categories for junior rowers (age ≤ 18 years), and using a measure of high applicability as short term tests in indoor rowing can be useful for planning the athletes' long-term development as well as their training routine without the need to apply strenuous and time-consuming tests [18,19,21].
Evaluating the performance of adolescent rowers through tests of high reliability and practical applicability becomes an essential aspect of monitoring the athlete for further planning [22,23]. As a result, coaches need reliable tests with indoor rowing ratings to delineate and assess specific sport performance [18]. Given the above, the present study aimed to develop a mathematical model to estimate performance in a 6000m indoor rowing test from performance in 500m all out test in junior athletes. We hypothesized that performance in the 500m all out test is strongly associated with performance in the 6000m test in junior rowers with somatic maturation after peak growth, and that performance in the 6,000m can be predicted with high reliability through the mathematical model using independent variable of time(s).

2. Materials and Methods

2.1. Participants

An effect size of 0.915 was used to determine the minimum sample size a priori to develop the mathematical model, referring to the linear regression result (mathematical model for peak power X peak power in indoor rowing) found in the study by Almeida-Neto et al. [24]. Thus, the G*Power® program (Verso 3.0; Berlin, Germany) was used in the “T family ” configuration. statistics for regressions ” and an α = 0.05 and a β = 0.80 considering a single variable to perform the prediction; based on this assessment, a minimum sample size of 10 subjects (t(2.0) = 2.91) was considered acceptable with an estimated sampling power of 0.90. In addition, an effect size of 0.77 was considered to calculate the “ a priori ” sample size, derived from the indoor rowing sprint performance data from the Almeida-Neto et al [24] study. Therefore, a default α value of 0.05 and a β value of 0.80 were used with the t test for comparisons of dependent means. Thus, the sample size for the present study was calculated, the sample power was 0.80 (t(11.0) = 1.79). The magnitude used for sampling power was: Unacceptable <0.70. Acceptable > 0.70 [25].
For the development of a mathematical model to predict 6000 m performance from a 500 m all out race, 141 individuals were selected from the Brazilian Rowing Confederation database [26]. The database contains information from specific rowing tests performed annually on national level athletes (tests: indoor rowing 500-m, indoor rowing 6000m and anthropometry). Therefore, we only included data from male individuals aged 14 to 17 years from the databases for the years 2013, 2016, 2017 and 2019.
Inclusion criteria from the database were: (i) the athlete had membership of a state rowing federation; (ii) information on the length of sport practice indicated that the athlete had at least one year of training experience; (iii) being aged between 14 and 16 years; and (iv) having a record of minimum training attendance of six times per week (≥60 min per training session). Exclusion criteria were: (i) having a record of presence of osteoarticular (i.e., bone tissue and joint injuries) or muscle injuries in the last six months prior to database registration; ( ii) not containing the results of all nescessary tests (indoor rowing 500-m, indoor rowing 6000m and anthropometry).
Randomization: We numbered the subjects in the database (from 1 to 141) and randomized the sample into the development (~70%) and cross-validation (~30%) groups of the mathematical model through a free online tool (https: //www.randomizer.org/).
The research was approved by the Ethics and Research with Human Beings Committee of (Blind Review ), respecting the national and international ethical principles contained in the Declaration of Helsinki. In addition, the study meets the reporting recommendations of the STROBE international checklist for observational studies [27].

2.2. Experimental design

Before all the annual tests of the Brazilian rowing confederation all the athletes performed a 10min warm up at low intensity in indoor rowing, following the specifications of the Australian Rowing Federation standardization, the tests were performed using a drag factor of 125 for junior male rowers (i.e. < 18 years), this can be consulted in a guide available on line [28]. The athletes then completed a 500m test on indoor rowing. The 6,000m test was performed after a 48 hour rest. Both distances were performed on a Concept2 indoor rowing ergometer (Model-D equipped with a PM4 and PM5 digital monitor; Morrisville , VT, USA). The tests were conducted in Brazil in a climate-controlled environment (26°C). According to the Australian Rowing Federation specifications. At the end of the tests, the results of the peak power curve in watts and test time in seconds were recorded from the equipment by a computer attached to its digital PM4 and PM5 monitor, entered into the Brazilian Rowing Confederation database.
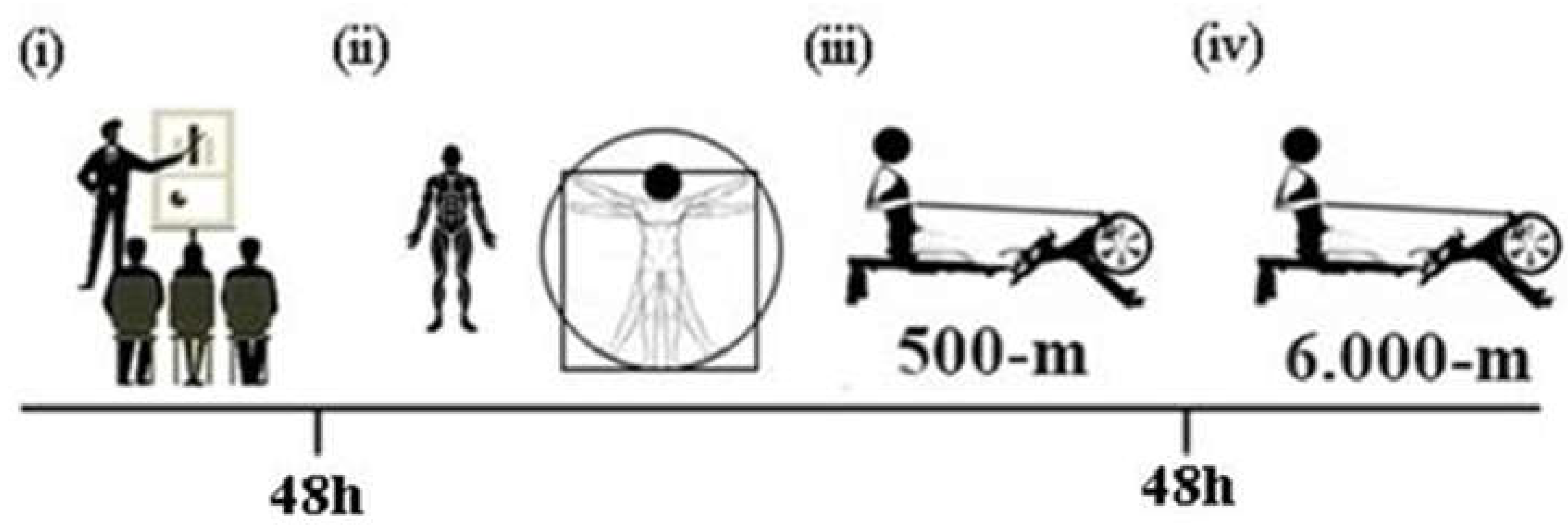
Figure 1 illustrates the procedures performed by the Brazilian Rowing Confederation during in National Rowing Evaluation [29]. The procedures were carried out in 4 moments: (i) explanation of the research procedures to the participants and their guardians; (ii) after 48 hours the anthropometric analyses occurred; (iii) after the anthropometric analyses the athletes did a 500m time trial; (iv) 48 hours after the 500m time trial the athletes did a 6000m time trial.

2.3. Procedures

2.3.1. Anthropometry

A single evaluator performed the anthropometric assessments. Standardization of procedures was based on the ISAK protocol and performed by a single experienced evaluator (International society of the Advancement of Kinanthropometry) [30]. Body mass was measured on a digital scale with a variation of 0.10 kg (FILIZOLA ® , Brazil). Standing height was assessed using a stadiometer with an accuracy of 0.01 cm (SANNY ® , Brazil).

2.5. Somatic maturation

The state of biological maturation was evaluated as biological age by obtaining the Peak Height Velocity (PHV), referred to the maturity offset; a measure of somatic maturation. Years of PHV was predicted using the mathematical model proposed by Moore et al. [31] (for boys 8-18 years, and girls 8-16 years):
Maturity shift in males = -7.999994 + [0.0036124 × (Age (years) × Height (cm))]
Participants were classified as pre-PHV (maturity compensation <-1.00 years from PHV), circum-PHV (between -1.00 and 1.00 years from PHV), and post-PHV (> 1.00 years from PHV) [31]. Categorizing the stages of maturation by means of predictive equations proved to be a valid method compared to the gold standard (hand-wrist X-ray), the details of which can be checked in the study by Almeida-Neto et al., [32]

2.6. Mathematical modeling

The present study developed a mathematical model based on the time of the 500m indoor rowing test to predict 6000m performance. In this sense, a mathematical formula was designed a priori within a theoretical model [33,34]. The theoretical model was determined by machine learning algorithms in the “R” language. he algorithms were programmed to capture mathematical expressions using the 500 m indoor rowing performance variable that could reach an output result similar to the 6000m indoor rowing. Thus, we selected the mathematical model that would theoretically provide greater reliability with the real performance of 6000m of indoor rowing. The final structure of the mathematical model developed by the present study can be found in the results section. Then, regression analyzes were performed and the theoretical model was tested through confirmatory factor analysis and the reproducibility index [35]. The open source R® software was used (version 4.0.1; Foundation for Statistical computing® , Vienna, Austria) for the mathematical modeling procedures, with a significance of p < 0.05.

2.7. Statistical analysis

The Kolmogorov-Smirnov test was applied to verify the normal distribution of the data. Descriptive analysis consisted of the mean and standard deviation, comparisons between methods (mathematical model and indoor rowing performance) were performed using Student's t-test for dependent samples (intragroup : development and cross-validation). The effect size between the differences was analyzed by Cohen's d guided by Espírito Santo & Daniel [36]: insignificant: <0.19; small: 0.20–0.49; average: 0.50–0.79; large: 0.80–1.29; very large: <1.30. We calculated the Pearson correlation coefficient (r), the coefficient of determination (r2), and the standard error of measurement to test the validity of the mathematical model in relation to the indoor rowing. The magnitude of Schober et al. [37] was used to interpret the results of the correlations as follows: insignificant: r<0.10; weak: r = 0.10-0.39; moderate: r = 0.40-0.69; strong: r = 0.70-0.89; very strong: r = 0.90-1.00. The approach proposed by Lawrence & Lin (1989) was used to analyze the correlation agreement coefficient (CCC) to verify the validity (Cb) precision (ρ), pure error and between the methods. Stepwise linear regression analysis was used to confirm the predictive power of the variables contained in the theoretical model obtained by mathematical modeling as described in the previous section.
The intraclass correlation coefficient was calculated to measure the reproducibility and reliability of the mathematical model obtained, and the magnitude used was determined by Miot [38] absence: ICC = <0; poor: ICC = 0-0.19; weak: ICC = 0.20-0.39; moderate: ICC = 0.30-0.59; substantial: ICC = 0.60-0.79; and almost complete: ICC = ≥ 0.80. Proportion bias was verified using the recommendations proposed by Bland and Altman, [39].
For the technical error of anthropometric measurements, the following magnitude was used: Acceptable ≤ 1.0% [40]. All the aforementioned analyzes were performed using MedCalc software. ® (version 12.5.0; Acacialaan , Ostend / Belgium), considering a significance of p < 0.05..

3. Results

Table 1 shows the characteristics of the sample, where there were no significant differences for chronological age, biological maturation and 500 m indoor rowing performance between the “development” and “cross-validation” groups. In addition, technical measurement errors for all anthropometric measurements were <1%.

3.1. Subsection

The 500 m indoor rowing performance in seconds showed significant correlation and predictive power for the 6000 m performance, justifying the use of the variable for the development of a mathematical model to predict the 6000 m indoor rowing performance.
The present study developed the following mathematical model to predict 6000 m performance with 500 m sprint performance in indoor rowing for young athletes.
T (min) 6-000 -m = { [( T (s) 500-m * 6) * 2] / 60} + 1.3
T (min) = time in minutes. T (s) = time in seconds
When comparing the estimated 6000m performance results by the mathematical model with the actual 6000m performance performed in indoor rowing, no statistical differences were observed (see Table 3). In addition, the mathematical model showed a significant correlation coefficient in agreement with the indoor rowing results. Similar results were observed in the cross-validation group.
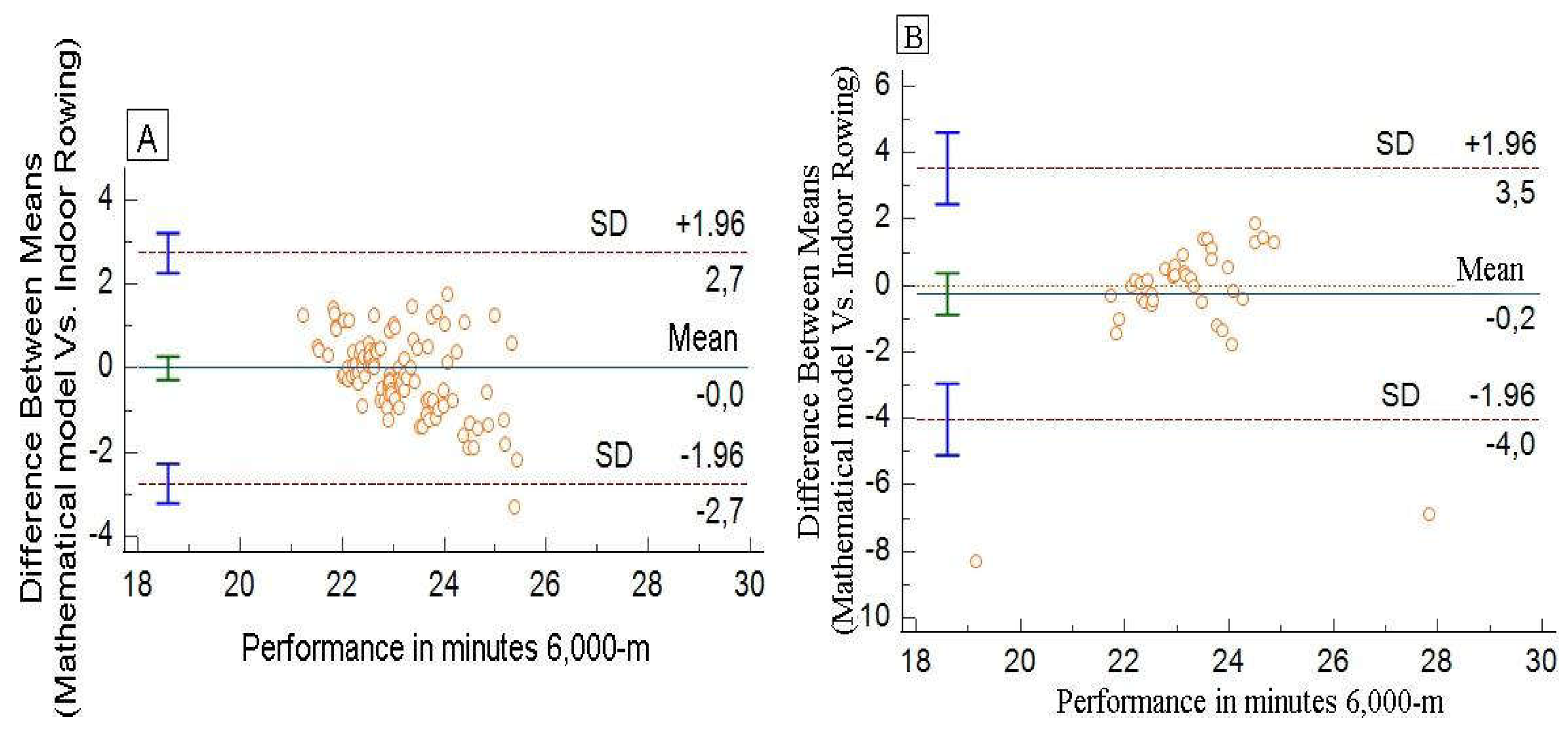
The concordance analyses performed by the Bland-Altman graph point to an adequate concordance between the mathematical model developed by the present study and indoor rowing (LOAs: -2.7; 2.7) (See Figure 2-A). Similar results were observed for the mathematical model cross-validation group (LOAs: -4.0; 3.5) (See Figure 2-B). In addition, there were no significant biases in the propensity score for any of the groups (r²<0.03; p>0.05). In addition, the model showed significant accuracy (development group - ρ: 0.957, pure error: 0.2 secounds (1.0% estimative error); Cross-validation group - ρ: 0.903, pure error: 0.3 secounds (1.4% estimative error).

4. Discussion

The present study aimed to develop a mathematical model to estimate the performance of 6000 m through a maximum test of 500 m in juvenile rowing athletes. In this sense, the main results were: (i) the mathematical model showed significant reliability and agreement to predict the performance of 6000 m from a maximum test of 500 m in development group (r2 = 0.730, ICC = 0.753; CCC = 0.895, Cb = 0.879, ρ: 0.957, pure error: 0.2 secounds (1.0% estimative error)); and in cross-validation group (r2 = 0.710, ICC = 0.747; CCC = 0.888, Cb = 0.875, ρ: 0.903, pure error: 0.3 secounds (1.4% estimative error). (ii) no statistically significant differences were found between the results obtained by the mathematical model and the results of the 6000 m indoor rowing test; (iii ) in addition, no significant bias was found in relation to the mathematical model.
The present research emphasizes that one must consider the phenomenon called biological maturation (BM) when it comes to adolescent athletes [22,23,41]. The higher the advancement of BM, the higher the efficiency of anaerobic metabolism [23,42,43]. It is emphasized that the BM may not be in sync with chronological age, and may be delayed or advanced [31]. Therefore, BM can be a potential error in junior athletes and is important to take into consideration when groups are compared. Therefore, we used BM instead of chronological age to balance the developmental group and cross-validation.
A previous study addressed the effectiveness of short distance performances in predicting 2000m rowing performance [20], which showed that short performances of 20 seconds (r=-0.952, p < 0.0001) and 60 seconds (r= - 0.930, p<0.0001) showed a strong correlation with performance in a 2000m test with prediction limits ranging from -0.12 to 0.11 m s-1 (-2.74-2.78%) . The findings of Cerasola et al, [20] corroborate with the findings of the present study (r = 0.840, p<0.001), which showed significant accuracy for the development group - ρrecision: 0.957, pure error: 0.2 secounds (1.0% estimation error) and for cross validation group - ρrecision: 0.903, pure error: 0.3 secounds (1.4% estimation error). Anaerobic performance over short distances and short duration maximal stimuli was shown to be associated with 2000m performance in indoor rowing. [17,19,20,21]. It is noteworthy that official Olympic rowing competitions take place over a 2,000 m course, and the predominant energy system in these competitions is aerobic (84%), but with constant interaction with anaerobic systems (16%), [44].
Previously, Holmes and colleagues [45], found significant associations between 3-min all - out performance maximum test with the performance of 6000m. The authors suggest that the performance of 3-min all - out maximum test can contribute to predict the performance of 6000m [45]. Corroborating these findings, the present study is a pioneer in developing a mathematical model to estimate the performance in the distance of 6000m using only the performance of 500m; not requiring laboratory variables, increasing its practical applicability during the training routine in the environment of coaches and athletes.
In another recent study, [46] was found significant associations between peak anaerobic power and 2000m indoor rowing performances (r<0.90; p<0.05). A small anaerobic power test performed on an indoor rowing machine (10 seconds with a resistance factor of 200 (N.s²/m²)) was a viable alternative to monitor the performance of the 2000m rowing [46]. Thus, the present study predicted a distance of 6000 m from a maximum sprint test of 500 m. Peak anaerobic power over short distances may indicate performance in longer runs due to the interaction between anaerobic and aerobic energy systems during rowing events [20,21].
Our findings indicated a substantial relationship between the 500m distance and the 6000m performance predicted by the equation developed in the present study (r = 0.840, p<0.001). Significant agreement was also observed between the mathematical model and 6000 m performance in both the development- and cross validation group, (development group - ρ: 0.957, pure error: 0.2 secounds (1.0% estimative error); Cross-validation group - ρ: 0.903, pure error: 0.3 secounds (1.4% estimative error). Furthermore, it should be noted that the mathematical model did not present a significant proportion bias in relation to the 6000 m performance in both groups, which suggests significant effectiveness of the mathematical model to predict the performance of 6000 m. These results corroborate previous studies that have sought to predict 2000m indoor rowing performance from short distance performance [20,21]. Akça et al, [18], employed multiple regression procedures to predict 2000 meter performance in rowers. Their equation showed a predictive power of R 2 = 0.757 and SEE = 6.37 and the variables that were used in the equation were functional anaerobic components of power, strength and anthropometric. These findings corroborate the predictive power of the equation developed in the present study, which in addition to being a pioneer for estimating 6000m performance in indoor ergometric rowing, uses only 500m performance, without requiring other variables as suggested in the study by Akça et al, [18].

5. Conclusions

The mathematical model developed to predict the performance for 6000m rowing events from a 500m indoor rowing test with maximum stimulation in male junior rowing athletes is reliable, reproducible and practical. The mathematical model can be used as monitoring tool to be used by rowing coaches in the training environment, favoring the saving of time to perform the test and avoiding the wear and tear of performing a 6000m test in junior athletes.

6. Practical application

New ways of optimizing sports performance, selection, and talent development are encouraged in rowing. Thus, the mathematical model developed in the present study is a practical and direct means for these purposes, as it uses the time in seconds of a maximum stimulus of 500 m. This new tool has demonstrated high reliability and can be used to design strategies based on the time predicted by the equation, which can be easily added to training worksheets on different devices such as computers, smartphones or tablets. It is important to note that the mathematical model developed in the present study does not invalidate the application of formal assessment at a distance of 6000 m. This test should likely remain an essential tool in the battery of tests as it considers the ability to sustain performance longer.
Furthermore, given the need for greater attention to anaerobic metabolism in Olympic rowing performance, considering the distance reduction from 2000m to 1500m at the 2028 Olympic Games in Los Angeles, resulting in a decrease in rowing competition time estimated to be approximately 90 -120 seconds, leads to an increase in the relative contribution to anaerobic metabolism of approximately 5% to 15%. Consequently, it may be necessary to adjust training periodization priorities for higher intensity interventions, especially in the period immediately preceding games [47]. The present study proposes a mathematical model to estimate the performance of 6000m from a short stimulus, with relative predominance of the anaerobic metabolism, which could be an additional tool for the improvement of the anaerobic capacity and progression of training from junior to senior (i.e. main category) during the Olympic cycle to Los Angeles.
Our tool can also be useful to mitigate the risks of overtraining and overreaching in young rowers, since prolonged high-intensity stimuli, such as the maximum test of 6000m in indoor rowing, are associated with greater cases of overtraining, which may compromise future adaptations and athlete's health.[48,49,50] Therefore, predicting the performance of athletes will be useful to reduce physical stress during the training routine.

7. Strengths of the present study

The strengths of the present study are: (i) the study design was adequate to answer the research question, presenting an evaluation model with high reliability; (ii) Gender was not a divergent factor in the current sample. Only male athletes were involved, avoiding possible interference in the presence of different genders; and (iii) the study contributes to areas of practice with high applicability for professionals, especially rowing coaches, using a protocol that is easy to apply and less physical wear and tear.

8. Limitation

Despite the relevance of the current results, the main limitation of this study is that the sample is composed only of junior athletes, and thus other categories of athletes may present different results from those found. Thus as the fact that the athletes point to an average of biological maturation in the post-PHV stage; in this way, the mathematical model cant be accurate for athletes in the pre-PHV stage and in the initial moments of the Circum-PHV stage. We suggest that future studies test the mathematical model developed by the present to predict the 6000m performance considering other categories of age, sex, and in junior athletes with pre- and circum-PHV biological maturation.

Author Contributions

Conceptualization, L.F.d.S., P.F.d.A.-N., P.M.S.D. and B.G.d.A.T.C.; methodology, L.F.d.S.; software, P.F.d.A.-N.; validation, D.G.d.M., D.B., B.M., F.J.A. and M.S.; formal analysis, B.G.d.A.T.C.J.; investigation, L.F.d.S., and P.F.d.A.-N.; resources, D.G.d.M.; data curation, P.F.d.A.-N., and S.E.R.; writing—original draft preparation, L.F.d.S., B.M., and R.B.N., writing—review and editing, B.M., D.G.d.M., P.F.d.A.-N., D.B., R.B.N., P.M.S.D., V.d.Q.,M.S., and B.G.d.A.T.C., visualization, B.M., V.d.Q., T.S.S.,F.J.A. and B.G.d.A.T.C., supervision, B.M., B.G.d.A.T.C.; project administration, B.M., P.M.S.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study was approved by the Ethics and Research Committee with Human Beings of the Federal University of Rio Grande do Norte (technical advice: 3.552.010), respecting the national and international ethical principles contained in the declaration of Helsinki.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

For your support and encouragement for the development of this academic article, we thank the Federal University of Rio Grande do Norte (UFRN), the Physical Activity and Health (AFISA) research base, the Child and Adolescent Maturation Research Group (GEPMAC). The National Council for Scientific Development (CNPQ), the Higher Education Personnel Improvement Coordination (CAPES), the Olympic rowing school, Sport Club de Natal and brazilian rowing confederation.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Nevill, A.M.; Brown, D.; Godfrey, R.; Johnson, P.J.; Romer, L.; Stewart, A.D.; Winter, E.M. Modeling Maximum Oxygen Uptake of Elite Endurance Athletes. Med. Sci. Sports Exerc. 2003, 35, 488–494. [Google Scholar] [CrossRef]
  2. Egan-Shuttler, J.D.; Edmonds, R.; Eddy, C.; O’neill, V.; Ives, S.J. Beyond Peak, a Simple Approach to Assess Rowing Power and the Impact of Training: A Technical Report. 2019, 12, 233–244.
  3. Bourdin, M.; Lacour, J.-R.; Imbert, C.; Messonnier, L.A. Factors of Rowing Ergometer Performance in High-Level Female Rowers. Int. J. Sports Med. 2017, 38, 1023–1028. [Google Scholar] [CrossRef]
  4. Mikulic, P.; Bralic, N. Elite status maintained: a 12-year physiological and performance follow-up of two Olympic champion rowers. J. Sports Sci. 2017, 36, 660–665. [Google Scholar] [CrossRef]
  5. Jensen, K.; Frydkjær, M.; Jensen, N.M.; Bannerholt, L.M.; Gam, S. A Maximal Rowing Ergometer Protocol to Predict Maximal Oxygen Uptake. Int. J. Sports Physiol. Perform. 2021, 16, 382–386. [Google Scholar] [CrossRef]
  6. Klusiewicz, A.; Borkowski, L.; Sitkowski, D.; Burkhard-Jagodzińska, K.; Szczepańska, B.; Ładyga, M. Indirect Methods of Assessing Maximal Oxygen Uptake in Rowers: Practical Implications for Evaluating Physical Fitness in a Training Cycle. J. Hum. Kinet. 2016, 50, 187–194. [Google Scholar] [CrossRef]
  7. Nolte, V. Faster Rowing. Champaign, IL: Human Kinetics.2005.
  8. Ingham, S.A.; Pringle, J.S.; Hardman, S.L.; Fudge, B.W.; Richmond, V.L. Comparison of Step-Wise and Ramp-Wise Incremental Rowing Exercise Tests and 2000-m Rowing Ergometer Performance. Int. J. Sports Physiol. Perform. 2013, 8, 123–129. [Google Scholar] [CrossRef]
  9. Vogler, A.J.; Rice, A.J.; Gore, C.J. Physiological Responses to Ergometer and On-Water Incremental Rowing Tests. Int. J. Sports Physiol. Perform. 2010, 5, 342–358. [Google Scholar] [CrossRef] [PubMed]
  10. Maciejewski, H.; Bourdin, M.; Lacour, J.; Denis, C.; Moyen, B.; Messonnier, L. Lactate accumulation in response to supramaximal exercise in rowers. Scand. J. Med. Sci. Sports 2012, 23, 585–592. [Google Scholar] [CrossRef]
  11. Martin, S.A.; Tomescu, V. ENERGY SYSTEMS EFFICIENCY INFLUENCES THE RESULTS OF 2,000 M RACE SIMULATION AMONG ELITE ROWERS. Med. Pharm. Rep. 2017, 90, 60–65. [Google Scholar] [CrossRef]
  12. Held, S.; Siebert, T.; Donath, L. Changes in mechanical power output in rowing by varying stroke rate and gearing. Eur. J. Sport Sci. 2019, 20, 357–365. [Google Scholar] [CrossRef]
  13. Treff G, Winkert K, Machus K, Steinacker JM. Computer-assisted step-by-step visualization of actual and target power allows for continuously increasing ramp tests on wind-braked rowing ergometers. Int J Sports Physiol Perform. 2018.13: 729-734. [CrossRef]
  14. Maestu, J.; Jiirimae, J.; Jiirimae, T. Monitoring of performance and training in rowing. Sport. Med. 2005, 35, 597–618. [Google Scholar] [CrossRef]
  15. Nielsen, T, Daigneault, T and Smith, M. FISA Coaching Development Program Course. Lausanne: V. 2002.3. pp.28-29.
  16. Esteve-Lanao, J.; Del Rosso, S.; Larumbe-Zabala, E.; Cardona, C.; Alcocer-Gamboa, A.; Boullosa, D.A. Predicting Recreational Runners’ Marathon Performance Time During Their Training Preparation. J. Strength Cond. Res. 2021, 35, 3218–3224. [Google Scholar] [CrossRef] [PubMed]
  17. Riechman, S.E.; Zoeller, R.F.; Balasekaran, G.; Goss, F.L.; Robertson, R.J. Prediction of 2000 m indoor rowing performance using a 30 s sprint and maximal oxygen uptake. J. Sports Sci. 2001, 20, 681–687. [Google Scholar] [CrossRef]
  18. Akça, F. Prediction of Rowing Ergometer Performance from Functional Anaerobic Power, Strength and Anthropometric Components. J. Hum. Kinet. 2014, 41, 133–142. [Google Scholar] [CrossRef]
  19. Cerasola, D.; Bellafiore, M.; Cataldo, A.; Zangla, D.; Bianco, A.; Proia, P.; Traina, M.; Palma, A.; Capranica, L. Predicting the 2000-m Rowing Ergometer Performance from Anthropometric, Maximal Oxygen Uptake and 60-s Mean Power Variables in National Level Young Rowers. J. Hum. Kinet. 2020, 75, 77–83. [Google Scholar] [CrossRef]
  20. Cerasola D, Zangla D, Grima JN, Bellafiore M, Cataldo A, Traina M, Capranica L, Maksimovic N, Drid Pand Bianco A.Can 20 and 60 s WI-Out test predict 2000 m indoor rowing performance in athletes? Front. Physiological.2022. 13:828710. doi : 10.3389/fphys.2022. 8287.
  21. da Silva, L.F.; de Almeida-Neto, P.F.; de Matos, D.G.; Riechman, S.E.; de Queiros, V.; de Jesus, J.B.; Reis, V.M.; Clemente, F.M.; Miarka, B.; Aidar, F.J.; et al. Performance Prediction Equation for 2000 m Youth Indoor Rowing Using a 100 m Maximal Test. Biology 2021, 10, 1082. [Google Scholar] [CrossRef]
  22. Mikulic, P. Maturation to elite status: a six-year physiological case study of a world champion rowing crew. Eur. J. Appl. Physiol. 2011, 111, 2363–2368. [Google Scholar] [CrossRef]
  23. Almeida-Neto PF, Silva LFD, Miarka B, De Medeiros JÁ, de Medeiros RCDSC, Teixeira RPA, Aidar FJ, Cabral BGAT, Dantas PMS. Influence of Advancing Biologial Maturation on Aerobic and Anaerobic Power and On Sport Performance of Junior Rowers: A longitudinal Study. Front Physiol. 2022, ;13:892966. Doi 10.3389/fphys.2022.892966. 17 May 3565. [CrossRef]
  24. de Almeida-Neto, P.F.; da Silva, L.F.; de Matos, D.G.; Jeffreys, I.; Cesário, T.d.M.; Neto, R.B.; Barbosa, W.d.A.; Aidar, F.J.; Dantas, P.M.S.; Cabral, B.G.d.A.T. Equation for analyzing the peak power in aquatic environment: An alternative for olympic rowing athletes. PLOS ONE 2020, 15, e0243157. [Google Scholar] [CrossRef]
  25. Sounis, E. Biostatistics; fundamental principles, statistical methodology. Application to Biological Sciences. 1971; 228-228.
  26. Remobrasil,2022. Home page. Available at:. ,: Accessed on, 27 June 2022.
  27. Strobe, Checklist Strengthening the Report of Observational Studies in Epidemiology. (2014, st). Retrieved June 20, 2020, from the STROBE Statement: https://www.strobe-statement.org/index.php?id=strobe -home. 1 September.
  28. Rowing Australia, Benchmarks, 2016 (2016,February). Retrieved February, 24, 2019, fron the Rowing Australia. Available online: https://rowingaustralia.com.au/wp-content/uploads/2019/10/2016-2020-Benchmarks-updated-10-October-2019.pdf (accessed on 24 February 2019).
  29. Rowing Brazil, 2019 season technical bulletin.(2019, January). Retrieved January, 22, 2019. Available online: https://www.remobrasil.com/boletins/boletins-tecnicos/111-temporada-2019/1532-boletim-tecnico-02-2019 (accessed on 22 January 2019).
  30. Karupaiah, T. Limited (ISAK) profiling The International Society for the Advancement of Kinanthropometry (ISAK). J. Ren. Nutr. Metab. 2018, 3, 11. [Google Scholar] [CrossRef]
  31. Moore, S.A.; Mckay, H.A.; Macdonald, H.; Nettlefold, L.; Baxter-Jones, A.D.G.; Cameron, N.; Brasher, P.M.A. Enhancing a Somatic Maturity Prediction Model. Med. Sci. Sports Exerc. 2015, 47, 1755–1764. [Google Scholar] [CrossRef]
  32. de Almeida-Neto, P.F.; de Medeiros, J.A.; Medeiros, R.M.V.; Baxter-Jones, A.; de Matos, D.G.; Aidar, F.J.; Dantas, P.M.S.; Cabral, B.G.d.A.T. Reliability of biological maturation analyses performed by equations predicting skeletal age and peak height velocity with hand and wrist X-ray results. Am. J. Hum. Biol. 2022, 34, e23775. [Google Scholar] [CrossRef]
  33. Segel, LA (Ed.). Mathematical models in molecular cell biology. 1980. CUP file.
  34. Neimark, J.I. Mathematical Models in Natural Science and Engineering; Springer Science and Business Media LLC: Dordrecht, GX, Netherlands, 2003; ISBN 3540323511. [Google Scholar]
  35. Paragios, N. , Chen, Y., & Faugeras, OD (Eds.). Manual of mathematical models in computer vision. Springer Science & Business Media.2006.
  36. Espírito Santo, H. , & Daniel, F. Calculate and Present Effect Sizes IN Scientific Works (1): Limitations of P<0.05 in the Analysis of Mean Differences of Two Groups (1): P<0.05 Limitations in the Analysis of Mean Differences of Two Groups). Portuguese Journal of Behavioral and Social Research. 2017. 1(1), 3-16.
  37. Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
  38. Miot, H.A. Análise de concordância em estudos clínicos e experimentais. J. Vasc. Bras. 2016, 15, 89–92. [Google Scholar] [CrossRef]
  39. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986 Feb 8;1(8476):307-10. [CrossRef] [PubMed]
  40. Perini, TA, Oliveira, GLD, Ornellas, JDS, Oliveira, FPD. Calculation of the technical error of intervention in anthropometry. Brazilian Journal of Sports Medicine. 2005, 11(1), 81–85. [CrossRef]
  41. Murray, A. Managing the Training Load in Adolescent Athletes. Int. J. Sports Physiol. Perform. 2017, 12, S2–42. [Google Scholar] [CrossRef]
  42. Ratel, S.; Blazevich, A.J. Are Prepubertal Children Metabolically Comparable to Well-Trained Adult Endurance Athletes? Sports Med. 2017, 47, 1477–1485. [Google Scholar] [CrossRef]
  43. Scheffler, C. , Hermanussen M. ( 2018). Growth in Childhood and Adolescence. Int. Encyclopedia. Biol. Anthropol. 2018, 1–11. [CrossRef]
  44. Mello, F.D.C.; Bertuzzi, R.C.D.M.; Grangeiro, P.M.; Franchini, E. Energy systems contributions in 2,000 m race simulation: a comparison among rowing ergometers and water. Eur. J. Appl. Physiol. 2009, 107, 615–619. [Google Scholar] [CrossRef]
  45. Holmes, C.J.; Hornikel, B.; Sullivan, K.; Fedewa, M.V. Associations between Multimodal Fitness Assessments and Rowing Ergometer Performance in Collegiate Female Athletes. Sports 2020, 8, 136. [Google Scholar] [CrossRef]
  46. Šmída, M.; Clementis, M.; Hamar, D.; Macejková, Y. Relation between Maximal Anaerobic Power Output and Tests on Rowing Ergometer. Acta Fac. Educ. Phys. Univ. Comen. 2017, 57, 68–75a. [Google Scholar] [CrossRef]
  47. Astridge, D.J.; Peeling, P.; Goods, P.S.; Girard, O.; Hewlett, J.; Rice, A.J.; Binnie, M.J. Rowing in Los Angeles: Performance Considerations for the Change to 1500 m at the 2028 Olympic Games. Int. J. Sports Physiol. Perform. 2023, 18, 104–107. [Google Scholar] [CrossRef]
  48. Steinacker, J.M.; Lormes, W.; Kellmann, M.; Liu, Y.; Reissnecker, S.; Opitz-Gress, A.; Baller, B.; Günther, K.; Petersen, K.G.; Kallus, K.W.; et al. Training of junior rowers before world championships. Effects on performance, mood state and selected hormonal and metabolic responses.. 2000, 40, 327–35. [Google Scholar]
  49. Cadegiani, F.A.; Kater, C.E. Hormonal aspects of overtraining syndrome: a systematic review. BMC Sports Sci. Med. Rehabilitation 2017, 9, 1–15. [Google Scholar] [CrossRef]
  50. Woodford, L. ‘The Dormouse’: my story as a lightweight rower with overtraining syndrome. Br. J. Sports Med. 2019, 54, 125–126. [Google Scholar] [CrossRef]
Preprints 70470 g001
Figure 1. Study design used in the present study.
Figure 1. Study design used in the present study.
Preprints 70470 g001
Preprints 70470 g002
Figure 2. Bland - Altman plot with the agreement between predicted and actual performance. - m = Meters. SD: Standard derivation. ----: 95% CI.
Figure 2. Bland - Altman plot with the agreement between predicted and actual performance. - m = Meters. SD: Standard derivation. ----: 95% CI.
Preprints 70470 g002
Table 1. Sample characterization.
Table 1. Sample characterization.
Variables Development group (n=101) Cross-validation group (n=40)
Age (years) 16.1 ± 0.7 16.2 ± 0.7
Biological maturation (PHV) 2.2 ± 0.6 2.3 ± 0.6
Height (cm) 176.7 ± 7.3 176.0 ± 6.7
Body weight (kg) 69.5 ± 9.6 67.9 ± 8.1
Body mass index (kg/m²) 22.2 ± 2.5 21.8 ± 2.2
Performance 500 m (s) 82.7 ± 5.5 83.9 ± 7.5
Peak power at 500 m (W) 393.4 ± 75.0 376.0 ± 74.7
Peak Power at 6,000-m (W) 223.0 ± 40.4 219.9 ± 30.8
PHV: Peak Height Velocity; Cm: Centimeters; Kg: Kilograms; Kg/m²: Kilogram per square meter; S: seconds; W: Watts.
Table 2. Correlation parameters and linear regression of the 500 m sprint test with the 6,000 m performance test.
Table 2. Correlation parameters and linear regression of the 500 m sprint test with the 6,000 m performance test.
Test Rowing 6,000 m
Correlation linear regression
development group
r p value r2 β IC 95% β p value
Rowing 500 m (s) 0.840* 0.001 0.705 13.6 [10.2; 17.3] 0.001
r = Pearson's product moment correlation coefficient. r² = regression determination coefficient. β = angular regression coefficient in relation to the dependent variable. - m = meters. (s): Seconds.
Table 3. Comparisons, correlation coefficient of agreement, standard error and intraclass correlation coefficient .
Table 3. Comparisons, correlation coefficient of agreement, standard error and intraclass correlation coefficient .
Method Comparation CCC Analysis
development group
Performance 6,000 m (min) p value CCC Cb r2 standard error ICC
Indoor rowing 23.09 ± 1.45 0.14
Mathematical model 23.08 ± 1.11 0.9 0.895 0.879 0.73 0.11 0.753
Cross validation group
Indoor rowing 23.30 ± 1.71 0.17
Mathematical model 23.07 ± 1.50 0.5 0.888 0.875 0.71 0.15 0.747
CCC: Agreement Correlation Coefficient; ICC: intraclass correlation coefficient; Cb : validity; (min): Minutes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated