New Applications of Action Mechanics to the Thermodynamics of Atmospheric Systems

Preprint

Article

New Applications of Action Mechanics to the Thermodynamics of Atmospheric Systems

Altmetrics

Downloads

136

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.pdf (15.12MB )

This version is not peer-reviewed

Submitted:

05 April 2023

Posted:

05 April 2023

You are already at the latest version

Alerts

Abstract

We propose that, at equilibrium, statistically equal temperatures as mechanical torques are exerted on each kind of gas phase molecules as rates of translational action [@t=ʃmvds/dt=ʃmr2ωdϕ/dt=mv2, J]. These torques result from the impulsive density of resonant quantum fields with molecules, configuring the trajectories of gas molecules while balancing molecular pressure (p=NkT) against the density of field energy (J/m3). Gibbs energy fields contain no resonant quanta at zero Kelvin, with this measure of chemical potential diminishing in magnitude as translational action of the vapor molecules and quantum field energy increases with temperature. In illustration, we show how impulsive torques from quantum fields drive the reversible thermodynamics of Carnot’s heat-work engine cycle, sustain the decreasing atmospheric temperature gradient of increasing molecular entropy with altitude, support the translational action and field energy of vortical wind flow in anticyclones, frictionally warming the Earth’s surface while recycling greenhouse infrared absorption of surface radiation, generating electrical power from air flow in wind farms and destructive power in tropical cyclones. These cases all distinguish symmetrically between a causal field of impulsive quanta (Σhν) that energizes the action of matter and the resultant vis viva of molecular mechanics (mv2). The quanta of these different fields display mean wavelengths from 10-4 m to 1012 m, with mechanical advantages many orders of magnitude greater than the corresponding translational actions, though with mean quantum frequencies (v) similar to those of radial Brownian movement for independent particles (ω). These energy fields are also thermodynamically reversible reservoirs for heat, optimizing work processes on Earth and delaying the achievement of maximum entropy production from short wave solar radiation in conversion to outgoing long wave radiation to space.

Keywords:

Subject: Environmental and Earth Sciences - Atmospheric Science and Meteorology

1. Introduction

Our primary purpose in this article is to demonstrate how quantum fields sustain the action of molecular mechanics, allowing heat to achieve work . We have analyzed this linkage with our introduction of action mechanics [1,2], recognizing action as stated by Maupertuis and Euler as the integral of momentum with respect to molecular trajectory (ʃmvds=ʃmr²ωdϕ, J.sec). In this form action has the same dimensions as the vector state of motion (dϕ=ωdt), signaling a dynamic change in spatial configuration. The action (h) of quanta at all wavelengths has the same value, a fundamental natural constant defined [3] by Planck (6.62607x10^-34 J.sec). Action of material particles is quantified as a function of radial curvature, using radial coordinates; indeed, sustained rectilinear motion other than briefly is regarded as very unusual, except for the trajectories of quanta.

We showed previously [1] that the total thermal energy required to heat all atmospheric gases from absolute zero to ambient temperatures is invariably several times their final internal energy. We regard this as a starting point for establishing the thermodynamics of independent molecules sustained in air against gravity by quantum fields of energy; these fields are required to overcome various forms of binding such as phase changes of melting from solid to liquid and liquid to vapor as well as providing impetus for kinetic energy. Effectively, the motion of the individual molecules is lubricated by the Gibbs field energy. This total heat requirement is signified by the increase in entropy that we showed [1] can be accurately calculated from the action states of each molecule’s mechanical state. We consider this extra heat requirement comprises the quantum fields sustaining the various internal degrees of freedom of Brownian action of the independent molecules of suspended gases.

We also found, to our surprise, that the more dilute a molecule in the atmosphere, the greater was the quantum field energy needed to provide its impetus; this is a conclusion that was made much earlier by Carnot in 1824 [4] in terms of the amount of calorique required in the working fluid of heat engines. These facts regarding complementary quantum fields and states of molecules have been largely neglected, given the widespread preference for a material description for molecules and their internal translational, rotational and vibrational energy; the extra motion caused by heating has been considered self-sustaining, from the principle of rectilinear inertia. Despite the widespread opinion since Clausius’ conclusion [2] that heat can disappear as work for systems of molecules that translate dynamically in a rectilinear fashion, we propose that quantum field energies are essential to sustain the torques exerted as molecular temperature; such a thermodynamic force field was originally proposed in Einstein’s theory [5] of Brownian movement.

Our recent revision of the reversible heat engine cycle showed how Carnot’s version of calorique could be seen as surrogate for the Gibbs quantum field [2]. Carnot [4] distinguished between chaleur as heat available from burning coal and calorique for heat as a property of state of the working fluid required in the cylinder of a heat engine. He recognized that the difference between the quantity of chaleur absorbed isothermally by the working fluid from a hot source such as a coal furnace (a) and the lesser amount of calorique needing to be removed at the temperature of a much colder sink (a’), allowing the cycle to return to its initial state, represented the maximum work (a – a’) possible by the heat engine. Carnot was deprived of recognition for these findings because of his early death from cholera and the neglect for 50 years of his manuscripts. To better understand his inspiration, we examined his cycle in detail, reinterpreting caloric as consisting of a field of quanta. We will show how our direct method to estimate the absolute Gibbs energy [1,2] from molecular data for gases establishes the configurational state of the working fluid, proposing that the statistical value of temperature for molecules can be understood dynamically as torque, or a common rate of exchange of action [@_t=ʃmvds/dt=ʃmr²ωdϕ/dt=mv², J] if at equilibrium.

In this article, we will describe how a novel linkage can be fashioned between quantum fields and molecules exhibiting action, using as examples a group of natural systems operating in our everyday world. To a large extent, previous observations regarding fields of quanta have not been pressed to logical conclusions, perhaps from too much reliance on partial differential equations to provide solutions to natural phenomena. Instead, we recommend a novel revision based on the integrating physical property of action [1,6], as a surrogate for molecular temperature and density. Indeed, this common property of the momentum of faster quanta matching that of material particles may also provide a unifying principle for the mechanics of many scientific disciplines.

2. Basic Theory and Methods

2.1. Complementary fields for virtual quanta and dynamics of material particles

Our investigations of quantum action fields and interactions between quanta and matter will be made across large variations in scale, bridging in part the chasm between quantum mechanics and gravity. These practical illustrations include the following topics, given as new forms of applied mechanics.

Using data from our previous action revision of the Carnot cycle [2] to examine the thermodynamics of the working fluid in expressing power from heat engines in terms of variable quantum fields. That study showed for Carnot’s cycle how the difference between the quantity of calorique obtained from a hot source and that absorbed by a colder sink gives the maximum work possible from any heat engine, while returning the engine to its initial thermodynamic state. The total energy (U) of the working fluid is not the source of the external work performed, but merely a scaffold for the variation in Gibbs quantum fields between the two distinct isothermal states that allows maximum work. A method to define the mean wavelength and frequency of the field quanta is given.

Applying action mechanics to sustain the thermal and gravitational structure of the atmosphere [7], showing how the virial theorem establishes the temperature gradient with altitude rather than adiabatic expansion. The quantum fields characteristics of increasing altitude are calculated in this article, partitioned between translational and rotational energies.

Illustrating the role of the vortical action (ΣmR²ω) of concerted molecular flow in anticyclones and cyclones as a higher degree of freedom storing thermal energy as vortical work, capable of warming the surface by turbulent friction.

Estimating the maximum potential of vortical wind power in the Earth’s atmosphere, already foreshadowed in an article now in review explaining a new method to calculate maximum power of wind turbines [8].

Explaining the destructive power of tropical cyclones derived from solar heat consumed in evaporation of seawater can also using vortical energy dependent on quantum impulses at the molecular level.

2.2. The principle of least action exemplified in the Gibbs field mechanics

We appeal to the principle of least action as justification for regarding molecular thermodynamics as action mechanics. In previous articles [1,2] we abbreviated action as having the same physical dimensions as angular momentum (mr²ω), stressing that it is a scalar function indicating change in configuration; including a spatial variation in the dimensionless property of angular motion (@=mr²ωδϕ = Jδϕ) by reference to a local couple and distant stars. Symmetry factors may also be needed to account for symmetrical pairing of particles or repeated structures. Any variation of action as the rate of change of this angle (dϕ/dt=ω) can be expressed as a variation in torque (mr²ω²).

Expressed in terms of the Lagrangian (L= T – V) for a conservative system of constant total energy (E = T + V), we can show a correspondence with action (S or @ in our terms) with respect to its integral

\int_{0}^{t} L d t

with respect to time.

S = \int_{0}^{t} (T - V) d t = \int_{0}^{t} \begin{matrix} (\frac{m r^{2} ω^{2}}{2} - (- m r^{2} ω^{2})) d t \end{matrix}

(1)

= \int_{0}^{t} {3 / 2 m r}^{2} ω^{2} d t = \int_{0}^{t} J ω d t = J \int_{0}^{t} ω d t = J \int_{0}^{t} d ϕ = J δ ϕ

(2)

Here the variation (δϕ) indicates the change in angle of ϕ in the time integrated (t). So the variation of Lagrangian for a system with constant angular momentum can be represented entirely as the variation of angular motion with respect to time. The action per unit time, or torque, is maximal where the rate of change (dϕ/dt=ω) is maximal. The minimum action per orbit must be 2πJ. Obviously, the action per radian must be stationary as J. For centres of force like molecular interactions or gravity, any deviation from an elliptical orbit will increase the pathlength of the Maupertuis action considered as

\int m v d s = \int m r ω . r d ϕ = J \int d ϕ = J δ ϕ .

Only in systems where the relative magnitude of quanta is very large will deviation of orbits as smooth curves be observable, such as for the motion of electrons..

Least action is often expressed as given in the Feynman lectures [9] in terms of a Lagrangian consisting of the difference between kinetic energy and variation in gravitational potential energy (mgh). However, this relationship can be shown as equal to Equation (3) considering that gravitational acceleration (g) is not constant with height or radius from the centre. Known to Newton, any parabolic trajectory on Earth is equivalent to a comet-like orbit to its centre, but with the fall intercepted by the Earth’s surface.

Then the following integral of the Lagrangian as action (S) in Equation (3) can be considered as applying, where r₁ and r₂ are radii to the Earth’s gravitational centre. Analogous processes are assumed to occur in many-bodied systems of molecules, with quantum fields generating the same torques and temperatures for each molecular species.

S = \int L d t = \int (\frac{{m v}^{2}}{2} - m g h) d t = \int (\frac{m v^{2}}{2} - m (r_{1} ω_{h}^{2} - r_{2} ω_{2}^{2}) r) d t

(3)

Given that the gravitational acceleration (ca. rω²) decreases with height or radius, the Lagrangian and thus the action will have the same torque-like form in Equation (3), just as in Equation (1). We claim that this theoretical account is equally valid for many-bodied molecular system in a variable microcanonical heat bath as for a gravitational system.

2.3. Mathematical basis and procedure for estimating dynamic action and quantum fields

For diatomic atmospheric gases like N₂, the complex macroscopic variables of temperature and volume or density expressing entropy (S) and heat (ST) of statistical mechanics (e.g., Hill, T.L, Statistical Mechanics, 1956) have been integrated in simplified form [1] as functions of translational action (@_t=mrv) and rotational action (@_r= Iω), including factors for symmetry (z_t, σ). This process involved a reinterpretation [1] of the partition functions for translation and rotation, shown in all textbooks on statistical mechanics.

(4)

(5)

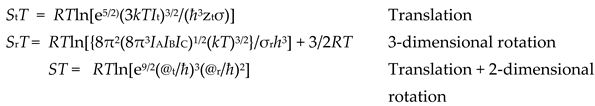
In these equations, the inversed magnitude of the Gibbs energy is given as the log_e of action ratios (@/ħ), with Planck’s reduced constant (ħ) in the denominator to measure the mean level of the quantum state. Certainly, this is classical statistical physics, but physics in a new form. The heat capacity exponential term depends on whether the volume is constant (C_v) or able to expand at atmospheric pressure (C_p). In the following analysis, molecular pressure (p) for gases is expressed as a mean value for each species by the ideal gas law, shown in Equation (6), where N is the number of molecules per unit volume (a³).

p = kT/a³ = NkT

(6)

We can observe that kT is equivalent to root mean square velocity in mv²/3, where a is the mean separation of molecules (r =a/2); each molecule is regarded as confined to its mean specific volume of a³.

We have shown by modifying Willard Gibbs statistical mechanics of extension in phase using action mechanics [1,2,6] that it is possible to estimate absolute values for action and entropy, quantum state numbers per molecule and the mean translational, rotational and vibrational quanta in the field. Equation (7) gives a formula for estimating mean molecular properties for entropic energy per mole as (ST), energy [E, C_vT, J] or enthalpy [H, C_pT, J] and Gibbs energy [-G, J], though as energy per molecule. It is easier to consider average values for molecules. In a variable-pressure volume system doing reversible mechanical work like the Carnot cycle, for estimating the internal molecular energy (e), c_pT must be replaced by c_vT with c_v equal to 3/2 for a monatomic gas like argon. No work is done against the atmosphere, with the internal field energy varying with internal pressure reversibly, with respect to the back pressure from the external work. For maximum efficiency, the whole cycle must be performed reversibly, as Carnot defined.

s_tT = c_vT + kTln[(@_{t /}ћ)³] = c_vT + kTln[(n_t)] = e - g_t

(7)

The Gibbs energy per molecule (g_t) is zero at absolute zero K and becomes progressively more negative as the temperature increases and the Gibbs field spontaneously gains quantum energy. This is consistent with the Maxwell relationship that ΔG equals ΔH – TΔS and that spontaneous reactions have negative changes in Gibbs energy, as when enetropy increases. In Equation (7), kT is equal to mv²/3, for translational kinetic energy.

In principle, the same procedure we have used previously [1,2,6] is applied throughout this article. Here, this is based on achieving a field condition where the time-integrated momentum exchange from impulses caused by the quantum field (Σhv_i/c) and the reversible momentum exchange for the material particles (Σmv_i) is equal, within the same Brownian [5] or random walk matrix. Per se, neither material particles nor quanta exchange momentum directly and particles only do so in collisions by way of the far swifter intervening quanta. In terms of the rate of action impulses, establishing the number of quanta keeping the material particles separated is effectively magnified by the factor c/v_i; so a simple comparison of the ratio of momentum (hv_i/cmv_i) or (h/λ_imv_i) will be greater by this factor than is needed for quanta in the field. This hypothesis will be tested during the various applied exercises given following.

The mean translational (or rotational) action (@_t=mrv_t) of molecules is estimated for the molecular field based on macroscopic concentration and temperature, including any effect of symmetry. The more symmetry exhibited in a mechanical system, the lower the action and the field energy needed to sustain the system [1]. To estimate action (@_t=mrv), the mean velocity is required rather than the root mean square velocity, about 1.09 times less. We have explained in detail the simple methods used in action mechanics to calculate entropy and absolute Gibbs energy based on molecular properties in a paper [6] examining thermodynamics of H₂, its lysis to hydrogen atoms at the temperature of the Sun’s surface, its formation by thermal decomposition of water above 4500 K and its reversible formation from ammonia in the Haber process near 400 K.
The mean number (n_t) for translational quantum microstates per molecule for the current mechanics is extracted by the ratio of the mean molecular action to Planck’s reduced quantum of action (n = @/ћ). For all cases examined in this article this ratio exceeds unity by a significant margin, indicating a high entropy for this degree of freedom. For this reason, these translational processes all behave classically, given the low rate of occupancy of quantum microstates.
The absolute value of the translational Gibbs energy (g_t) is then estimated as a logarithmic function of the number of quantum microstates, as we have published previously [1,2,6]. As this value becomes more negative, the field quantum energy increases, as anticipated by the second law of thermodynamics.
The mean value of virtual quanta in the field is then calculated (hv=-g_t/n_t), enabling the virtual frequency and wavelength in the field to be estimated. Peak values for translational quanta will reflect the vis viva, twice the kinetic energy for the Carnot cycle (mv² = 3kT). For other processes such as the dynamics of air molecules in wind, the vis viva involved is very low, according to wind speed, indicating a very low temperature using the 1-dimensional relationship mv² = kT.

It is assumed in this theory that no quantum entanglements or coherence between molecular quantum states operate, as would occur if kinetic temperature was too low to ensure significant occupation of quantum states. This action-based method focuses on translational dynamics of particles for reversible heat and work. Given the very small size of translational quanta at ambient temperatures, all processes dealt with here approximate classical physics.

3. Results and Discussion

3.1. Revising the Carnot cycle as a basis for a Gibbs action field

Equation (7) shows that the total heat content needed is the sum of the internal energy (c_vT ) plus the absolute energy of the field (-g_t), that becomes more positive as its quantum state increases. Removing temperature (T) in Equation (7) gives the absolute entropy per molecule of the quantum state under the current environmental conditions of temperature and pressure. Table 1 reproduces and extends data from our earlier article [2]; shown are relationships between matter and quantum fields relevant to all four stages proposed by Carnot as reversible, determining the most efficient generation of power in the heat engine cycle. The table shows that Carnot’s formal explanation of the cycle using caloric is consistent with quantum theory, with its modern surrogate shown as negative Gibbs energy (-g_t). Carnot specifically indicated that the maximum possible work was equal to the second differences of a–a’ or b’–b, where a, b’, a’ and b were primary differences between absolute Gibbs energy values that we calculated for argon and nitrogen shown in Table 1. For two working materials as ideal gases, we make the following conclusions from the heat engine cycle, considering the impulsive quantum properties of the working fluid as causal. Most formulae such as the Schrödinger wave equation estimate quanta absorbed or emitted as the difference between states, but Table 1 gives their absolute mean values. Note that these values for translational action (@_t) are corrected here for a simple programming error in reference [2], that underestimated action by a factor of 1.47.

At all four stages of the cycle, the relative action (@) of the working fluid calculated indicates its entropy state, according to Equation (7). We remind you that Gibbs energy (g_t) is always zero or negative, decreasing from minimum action near absolute zero K. Uniquely, action mechanics quantifies the Gibbs field here as mean numbers of virtual quanta needed per molecule to sustain their temperature and pressure.

Atmospheric pressure is not relevant to the enclosed Carnot cycle, so from Equation (7) all effects of changes in pressure in the cycle can be calculated as changes in Gibbs energy calculated from macroscopic temperature and pressure, given these are equivalent [2,6]. Shown in Table 1, the field of virtual quanta (Σhv) contains almost 10 times as much field energy (largely provided in melting and vaporization) as the kinetic energy of the material particles, sustaining molecular torques (mv²) and material pressures.

Each turn of the Carnot cycle shown in Table 1 is assumed to absorb kT of heat from the hot source quantized appropriately for the temperature and pressure and the same quantity kT removed at the colder sink as different quanta of lower frequency.

The pressure values shown in the table also produce the ratio of torque intensity mv²/3a³ or kT/a³ to the negative Gibbs energy (-g_t/a³) or mean density of virtual quanta held within the mean volume a³ occupied by each molecule. For argon, this energy ratio is constant for transitions in adiabatic or isentropic states with no change in heat content. Where isothermal processes at constant temperature (or torque) occur, there is a change in this ratio, as heat is added or removed.

For nitrogen, the interaction between quantum cells for translation and rotation requires that the product of the quantum densities, shown as (n_t³ x j_r²) respectively in the table, must remain constant for adiabatic processes that are isentropic exhibiting constant action.

The ratio for wavelength of virtual quanta and the material radial motion (λ/2πr; r=a/2) of about 10⁵ for the gases is indicative of the ratio between the speed of light (λν = rω) and speed of the Brownian spiral of gas molecules. This can be visualised as the frequency of the conjugate quanta being of a similar order to that of the orbital frequency of the molecules, though with the photon’s impulse cycling on a much longer radius, proportional to the ratio of speeds (c/v).

Table 1 also illustrates the correspondence for both argon (mass 40) and nitrogen (mass 28) of the ratio of the cumulative quantum impulse (nh/λ) and the dynamic impulse (Σmv=mrω) per molecule. This is a factor near 1x10^-5, the inverse of the ratio of the speed of light to that of the molecules. In calculating translational action of molecules [2] we found it necessary to make two corrections. One, a factor of 1/1.09, corrects root mean square velocity from the Maxwell distribution (3kT=mv²) to mean velocity. The second corrects action for symmetry, to avoid double counting of molecules (1/2). For cubic translation, this is an overall factor of 1/10.2297). This correction then allows the entropy calculated to match that for third law experiments in the literature. This correction factor (z_t) was initially established empirically [1], then interpreted rationally [2]. Overall, it allows the density of quanta needed to sustain the system to fall by a factor of 2.3205.

Another possible source for lack of correspondence in matching action impulses between quanta and molecules is that phase space for position and momentum can never exactly match true action space. The ideal coordinate system may not be Cartesian phase space since this separates variables (mv and r) that must be combined when quantized. A radial or polar system (r, ϕ, θ) is needed [7] but also one that recognizes that changes in position in 3-dimensions is absolutely quantized as jumps in the space of objects from one locus to another. There is no such thing as a smooth curve in nature for translation of rotation except by perception within the space of views, as explained a century ago by Jean Nicod [10].

Our algorithm obviously gives good correspondence between potential impulse rates of quantum and dynamic molecules in the field, though not exact. There is plainly an effect in the case of the nitrogen molecule an effect of rotation, responsible for about 20% of the quantum energy density. The number of quantum states for translation increases with lower temperature and pressure but that for rotation does the opposite. We continue to analyze the significance of this matter.

It is unfortunate that the text of Carnot’s monograph [4] was lost for many years after his premature death from cholera in 1832. Caloric was clearly regarded by Carnot as causal for the power (puissance motrice) of heat engines. Lord Kelvin and Clausius assumed for convenience that the heat consumed in Carnot’s cycle reappeared directly as the external work performed by the heat engine. This was despite Clausius originally speculating that heat was concerned with performing internal work of the fluid needed to support external work. Later, this process of internal work that he named the system’s ergal, suggesting this term could replace Rankine’s new definition of potential energy [2], was neglected; the heat consumed was judged to be transformed directly to external work, not that it was required internally to support the external work, as we now find [2].

We coined the term radial action to indicate the complementary relationship between maintaining the action of a particle and the action of its complementary quantum, of similar frequency. The wavelength of the quantum is always much larger than the radial motion of the particle, by orders of magnitude. However, it is relevant that impulses from particles such as quanta and molecules exert torques counted as kinetic energy proportional to their radius of action. The impulse of the quanta on their conjugate wavelength exerting torque is equal to that of the molecules on their radius (r).

3.2. Thermodynamic stabilization with altitude for atmospheric gases by quantum fields of molecules in air

Assuming that translational action of molecules in air refers to non-linear or erratically curved motion in the dimensional form mr²ω as used for calculating translational entropy in heat engines, shown in Table 1, we can derive the following relations by equating thermodynamic and gravitational pressure with altitude. In Equation (8), a represents the mean length of the side of a cube occupied by each different molecule and r, the mean radial separation, half this value. Then M is equal to Nm, the total mass of n molecules in the atmospheric column above a square with base of side a cm, of weight Nmg, assuming the value of gravity (g) is invariant in the troposphere. It is assumed that the inertial force

m r ω^{2}

provides the internal pressure on the six faces of the cube of side a, tending to equilibrate with the gravitational pressure of the atmosphere.

p = \frac{k T}{a^{3}} = \frac{m r ω^{2}}{3 a^{3}} = \frac{M g}{a^{2}}

p = \frac{N m g}{4 r^{2}} = \frac{m r ω^{2}}{24 r^{2}}

m r ω^{2} / 6 = N m g

(8)

Thus, the instantaneous gravitational force on average necessarily exerted by each molecule is one-sixth of the centrifugal or inertial force exerted in each 6-faced cell of side a by the translational motion of each molecule. The primary gravitational pressure from the weight of air is exerted only downwards and not to all six cardinal points. The thermodynamic relationship is statistical ─ according to the Maxwell-Boltzmann distribution, with the molecular velocities having values statistically varying around the root mean square velocity, characteristic of the temperature. Incidentally, the hydrostatic or isobaric requirement that the pressure is a function of density is only true for an isothermal atmosphere. In a real atmosphere, with a tropospheric temperature gradient with altitude a little more than 6.5 K per km [7], pressure also varies as a function of temperature.

We challenged the assumption that the decline in temperature with altitude is an adiabatic response to expansion of atmospheric gases as may occur in a cylinder with increasing volume. Instead, the decline in temperature with altitude indicates the operation of the virial theorem for gases of differing gravitational potential and thermal energy [7]. Changes in potential energy indicate changes in both quantum state and field as well as changes in kinetic energy. According to the virial theorem, the absorption of a quantum of gravitational energy causes a decrease in kinetic energy of the same magnitude, meaning that the increase in potential energy is twice either the decrease in the kinetic energy or the increase in the field gravitational energy. Thermal and gravitational fields are quite separate.

Action mechanics [1,2] combines the macroscopic variations in volume (Na³ = 8Nr³) or density and temperature of molecules as action (mrvδϕ), illustrated in Section 3.1. In Table 2, estimates are given for thermodynamic properties of atmospheric N₂ as translational (n_t) and rotational (j_r) molecular action. Activation of vibrational states for N₂ in the atmosphere are negligible, as shown previously [1] given the high frequency and energies involved. If required, vibrational Gibbs energy can be estimated from the statistical component of vibrational entropy together with the zero-point energy Nhν/2 of 14.115 kJ per mol. More than 75% of the energy content indicated for N₂ is required to sustain its translational Gibbs field, shown in Table 2, with resonant quanta in the range 3.8 to 2.2x10^-22 J of frequency 5.7x10¹¹ to 3.32x10¹¹ Hz and wavelengths from 523 to 904 μm. N₂ contributes almost nothing [1] to the thermal emission to space in the infrared and far infrared up to 100 μm wavelength, unlike water and other greenhouse gases.

However, both the translational and rotational fields contain large numbers of quanta, of wavelengths longer than 520 μm and 100 μm respectively. We have described in detail how these values are easily calculated and employed [1,2,6]. In our opinion, too much emphasis is placed on the calculus of the Maxwell relations in teaching thermodynamics and too little on mechanical methods of computation for real world molecules. Equation (7) has the advantage of yielding mean quantum values, with the radial action needed to provide torques sustaining the dynamic motion of the molecules indicated by the temperature (T). The use of the form ST equals H - G emphasizes the fact that entropy or its product with temperature is not a single property that stands alone but consists of the sum of the internal energy or enthalpy and a statistical field containing quantum information required for the molecular configuration of the system.

Given that the Gibbs energy defined by Equation (7) is regarded as responsible for the configuration of the molecular system as well as positions of equilibrium in chemical reactions [6] it is surprising that this field receives so little attention. In proposing its importance in the atmosphere, we need to consider more the likelihood that this energy field for translation and rotation can also contribute to radiation lost to space. Much information is collected on surface radiation from Earth by satellites, but this is usually restricted to the thermal region of vibrational infrared wavelengths of less than 100 μm wavelength than of longer microwaves or radio waves that will be released from the upper atmosphere when less caged by matter. Any such field energy losses will be continuously replenished with thermal energy from the surface, as predicted by the equipartition principle, subject to quantum restrictions at lower temperatures.

For translation and rotation of N₂ molecules, Table 2 shows estimates with altitude for entropy per mole (S), absolute Gibbs quantum state levels (n_t), the total heat energy required to reach the state (ST) and the mean value of virtual field quanta (hv). Vibrational energy for N₂ is negligible. To estimate peak wavelengths of quanta in the field energy, the virtual quantum value (hv) is divided by h to obtain frequency (v), then inverted and multiplied by the speed of light c to obtain wavelength. Thus, at the surface temperature and pressure we estimate that some 1.14833x10²⁶ quanta per mol of peak translational energy 3.809x10^-22 J support the kinetic activity of N₂ with a frequency of 5.74848x10¹¹ (574.849 GHz) with a peak frequency at a wavelength of 521.52 μm. At 12 km of altitude, the peak wavelength is almost twice as long at 901.704 μm, though there are more quanta per molecule. The table also shows absolute values for the Gibbs field energy per mol, a property that is always negative and becomes more so as spontaneous processes occur that increase the entropy.

Gibbs energy is often referred to as Gibbs free energy or chemical potential. It can be made positive in value when expressed in the usual form at atmospheric pressure as G = H – ST, but it must be appreciated that ST contains the Gibbs energy (G) and the enthalpy (H) or internal energy (E). Little attention is paid to this major reservoir of internal quantum state energy in the atmosphere with the kinetic energy and macroscopic pressure-volume work at atmospheric pressure usually given prominence.

3.3. Vortical action as high level atmospheric thermodynamics in anticyclones

Our hypothetical introduction of vortical energy [2] for a molecular field in concerted motion is estimated by a similar method to that used for the Carnot cycle (Figure 1). The translational action (@_w) of air molecules in anticyclones concerted in motion as wind velocity is estimated as mrv from a knowledge of the mass of a material particle, the radial separation r equal to a/2, where a is the radial coordinate diameter of the anticyclone (Figure 1 and Figure 2). The number of quantum levels is estimated using division by the reduced Planck’s constant of action (1.054x10^-34) (n_t = mrv/ћ), with a symmetry factor of 2 for symmetrical partners. The Gibbs vortical energy per matter cell a³ is then estimated using the logarithm of the quantum number multiplied by the appropriate torque factor. Frequency and wavelength is then easily determined. Just as in the case of the Carnot cycle, the ratio of mean quantum wavelength and that of the radius to the centre of the anticyclone is of the same magnitude as the ratio of the mean velocity of the molecule to the speed of light. The total vortical Gibbs energy is obtained from the product of number of molecules per cubic metre and the number of molecules.

Figure 1 integrates the vortical rotational energy in anticyclones and cyclones with the global Trenberth heat flow budget [11] for radiation. The Kiehl-Trenberth budget proposes that 332 W per m² of downwelling radiation is returned from the atmosphere, needed to explain the blackbody temperature of the Earth’s surface. We propose instead of net radiation from higher in a colder atmosphere to the surface that vortical action in anticyclones is generated as work processes in air, facilitated by Coriolis accelerations in each hemisphere. This work process requires significant absorption of heat radiated from the surface in greenhouse processes involving mainly water and carbon dioxide without rises in temperature. As shown in the Carnot cycle, any increase in freedom of relative translational motion of molecules increases the heat capacity of the gas phase. For anticyclones, this allows turbulent friction processes nearer the surface to release heat in the boundary layer of the lower atmosphere (v), to the extent (h=a+e+c+g=v) of about 330 watts per m² [2] as a global average, rather than by radiation from a colder atmosphere to the surface, in accordance with the second law of thermodynamics. The decreasing wind speed near the surface regarded as vorticity represents the loss of power with wind speed, warming air and causing spectral radiation proportional to temperature.

Our model for greenhouse warming in Figure 1 (g=r-o) involves the difference between black body radiation from the surface (r=aT⁴) and outgoing longwave radiation (o), with the atmosphere warmed by solar absorption by water in air (a), latent heat of evapotranspiration at the surface followed by condensation under convection (e), thermal conduction from the surface (c) and the greenhouse effect itself (r-o). The work of vortical action and energy (v) provides a mechanism for turbulent release of heat as radiation near the surface. No conflict with the second law of thermodynamics is required, solving an objection voiced by some. As shown in Table 3, a wind speed of 10 m per sec contains vortical energy of 1.47x10³ J per m³ of air in wind, many times greater than the kinetic energy, with an additional to 2.4 MJ per m³ of thermal energy required for air to be heated from 0 K to 298 K [1].

3.4. Estimation of power produced by wind turbines from vortical energy in anticyclones

In our new theory to estimate wind power based on action mechanics [8] the rate of impulsive action or torque is estimated for both windward and leeward surfaces of wind turbines. Using the difference in these torques, power can then be estimated using the angular velocity of the turbine rotors (Ω). Current blade element momentum theory estimates the potential wind power available by using the rate of kinetic energy of wind flowing through the area swept by the rotor blades, despite most of air passing through not impacting the turbine blades. By analogy to Figure 1 showing winds in anticyclones, we regard the impulsive power of the energy in air in vortical action striking turbine blades as a better model of turbine function. In Table 3, we produce radial action estimates at different speeds for a wind turbine with 83 m rotor diameter. This value is also corrected to the kinetic energy actually impacting the blades, reducing the power estimate to a fraction of that actually achieved. We therefore reject the idea that the wind power is derived from the quantity of kinetic energy of the wind, except to provide the molecular pressure sustained in turn by the field quanta.

Table 3 compares the power available from kinetic energy and from vortical potential energy for a parcel of air (per m³) located 1000 km from an anticyclone centre (Figure 1 and Figure 2). The analysis considers the wind impacting the rotor blades as well as that passing through the circle of blade rotations. Only in the latter case does the kinetic energy available to the blades exceed the radial action estimate. By comparison, the maximum vortical power estimated is more than five times greater, restricted to the blade area.

As shown in Table 4, the virtual Gibbs field contains about 70 times as much energy as the density of kinetic energy of the molecules. We conclude that this field configurational energy sustains the kinetic energy. We challenge the idea that all air passing through the circle swept by the turbines but mainly never contacting the turbine blades could have sufficient solidity to have a significant effect on power output. This defies reason. We prefer the idea that the impulsive radial action must generate torques strictly exerted on the blades. Some proposals regarding the nature of vortical energy per paired molecule are given in Table 4. Using the torque generated per molecule (kT = mv²) at 1000 km radius estimates vortical energy available almost two orders of magnitude greater than that of kinetic energy.

A feature of the action mechanics model for quantum fields is that it allows absolute values of Gibbs energy content per molecule to be calculated, rather than transitional values (δg).

For example, for wind at 10 m per sec, the mean virtual quantum (hv) has the value of 7.46018x10^-38 J with a wavelength of 2.6627x10¹² m. This wavelength is more than 10⁶ greater than the material radius. This means that the curvature of the oscillating longitudinal motion is relatively linear and the action velocity for the molecules is about 10⁶ less than the velocity of light. Differences in Gibbs energy per molecule with wind speed are easily calculated. We have proposed methods in our articles [2,6,8] to test the vortical energy field hypothesis using appropriate sensors allowing release of this energy under turbulent conditions. If confirmed, this could be an important source of regional warming and land dehydration [8], possibly raising fire risk from wind farms. We have estimated that a 100 MW windfarm could raise the temperature of air downwind by turbulent release of vortical energy up to 2 ⁰C, increasing evapotranspiration for many km distance. This prediction is recommended [8] to be tested as a matter of due diligence regarding the location of windfarms.

3.5. Power in tropical cyclones from action mechanics of heat of volatilization on the ocean surface and convective condensation of water at the eyewalls

Tropical cyclones are known to be fully energized by the heat of vaporization of water at warm ocean surfaces in low latitudes. Condensation by strong spiral convection near the eyewall releases radiant infrared energy as directly resonant quanta, from H-bonding between water molecules in the formation of water droplets [12]. Yet it is also well known that the kinetic energy of the cyclonic motion is only a small percentage of the total energy and power dissipated in the path of a cyclone’s trajectory.

Vortical action and entropy generated at the cyclone’s eye-wall near its centre provides the direct connection needed between heat of condensation and the power of the cyclone, with the kinetic pressure and torque being sustained by the impulses of the Gibbs field energy. The field energy pressure is a large multiple of the kinetic energy pressure and can sustain the torques required, at least while the cyclone continues to evaporate water from the sea surface. On land, the energy of the cyclone, no longer sustained by evaporation from the ocean, is soon dissipated by frictional turbulence releasing heat to the surface atmosphere. Such intense regional warming on land is an anecdotal feature of the aftermath of tropical cyclones.

In action mechanics, it is assumed that specific radial action (r²ω) will be approximately constant across the cyclone, given the inverse square radial distribution of radiation from convective condensation at the eyewall, generating a radially acting Gibbs energy field as mv²ln[n_v], shown in Table 5. Furthermore, considering the cyclone as simultaneously rotational and convective, conservation of angular momentum will ensure constant Σmr²ω ensuring intensified velocity (rω) nearer the eye-wall.The heat of vaporization at an estimated rate matches the vortical Gibbs energy and power generated shown in Table 5. Vortical entropic energy is directly provided by infrared radiation from condensing water in the convective eyewall of a tropical cyclone. The model shown in Figure 3 exhibits vortical action and energy as shown in Table 5. Note the 70-fold ratio of energy density in the Gibbs field compared to that of kinetic pressure, similar to that observed for wind driving turbines to develop electrical power (Table 4).

As discussed in section 3.2, the pressure equation underestimates the kinetic energy density by 50%, adjusted in Table 5. The greater the vortical energy in the field, the more negative the Gibbs energy of the molecules in the field as the potential to take up thermal energy in the system is exhausted.

This vortical version of the dynamics of a tropical cyclone may be more consistent with the rotating convective model now accepted for best explaining destructive cyclonic intensification [13]. Previous opinion [14,15] favored intensification as caused by large latent heat fluxes from the surface in the core region and that an intensive evaporation-wind feedback process (WISHE) was not needed. Vortical energy would be stored cumulatively during convective processes leading to condensation nearer the eye-wall, or walls if serried in convective configuration. The vortical inertia of the cyclone would require a continuous feed of thermal energy from evaporation and condensation of water but this can be modelled as intensifying as updraft increases, shrinking the radius and providing a higher pressure of vortical field energy nearer the eye wall, with higher wind speeds. The model data in Table 5 represent a snapshot of the process at one stage in time. Researchers in the dynamics of tropical cyclones are invited to include vortical energy in their models.

We regard the ability of action mechanics to explain the intensifying power of tropical cyclones quantitatively is a major point in favor for the vortical action and energy theory.

4. General Discussion

The scientific strategy in this article is based on results from our previous analyses of the action, entropy and Gibbs energy of the atmosphere [1] and of the Carnot cycle [2] concluding quantum fields of thermal energy sustain the internal energy and configuration of molecules. Simple methods [6] to calculate the action, entropy and Gibbs field energy from molecular properties of gases such as hydrogen, water and ammonia strengthen the value of this approach, providing new insights for catalytic transitions and equilibrium states, where Gibbs field energies for reactants and products are in balance [6]. Wherever molecules exhibit action spatially with respect to others such as by vibration, rotation or translation a field of impulsive quanta sustains a rate of molecular action as torque or kinetic energy. In this article we extended this mechanism based on relative rates of action establishing vortical torques exerted in molecular flows of atmospheric systems also requiring resonant Gibbs quantum fields sustaining this freedom of action. This innovation allows a significant expansion to the reversible heat and work capacity of the Earth’s atmosphere possibly of major significance in climate science consistent with the law of increasing entropy.

One difference between the Carnot heat engine cycle and the higher level vortical systems is its absence in the ideal Carnot cycle. The ability of a heat engine to reversibly store heat and perform external work depends entirely on the differences in the Gibbs quantum field at the extremes of temperature. The net variation in energy as kinetic work between the source and sink temperatures in the cycle is zero. Although the vortical field energy of anticyclones and cyclones expressed in the Earth’s gravitational field is also shown to provide work potential that can decrease Gibbs energy this was not predicted until we considered climate change in our work. The ability of the vortical hypothesis to provide solutions to questions regarding (i) the warming of the Earth’s surface by frictional dissipation of vortical energy in anticyclones and cyclones, rather than by downwelling radiation [18] from higher, colder air in the atmosphere, (ii) how vortical energy in anticyclones can power wind turbines by torques exerted only by the air flow impacting turbine blades [8] and (iii) how the destructive force of cyclones is directly powered by vortical action linked to energy flow from a thermal cycle of solar evaporation of tropical water with convective condensation at the eyewall solves the riddle of the negligible kinetic energy in tropical cyclones.

The Bernoulli interpretation of energy in fluids as a continuum with kinetic pressure-related energy is insufficient to explain these phenomena. The governing equations of fluid motion as formulated by Bernoulli, Laplace and others proposed no such reversible heat-work process for vortices, favoring absorption and release of heat in adiabatic processes. For streamlines as in a laminar wind flow, the Bernoulli Equation (9) relates kinetic energy (ρv²/2), the static pressure-energy P (Σmv²/3=pV) and gravitational potential energy, regarded overall in steady flow as constant.

ρv²/2 + P + ρgh = K

(9)

However, the vortical Gibbs energy we have calculated for wind (Table 3 and Table 4) provides a much larger reservoir of thermal energy as a large multiple of the kinetic energy (ρv²/2) in Equation (9); we would write the following Equation (10) as prevailing in laminar flows of anticyclones.

ρv²/2 + P + ρgh - (Σg_t) = K’

(10)

This equation might form the fundamental basis for extended solutions to the Navier-Stokes equation, taking into account the potential field energy -(Σg_t) able to be released as heat (+Q_v) in vorticity caused by frictional turbulence at surfaces (Figure 1), such as a rough landscape, wind turbines, airfoils and in the destructive dissipation of tropical cyclones on land. This process amounts to an irreversible loss of work potential as surface heat, although the charging of anticyclones in the atmosphere with radiant heat absorbed by water and other greenhouse gases such as CO₂ and CH₄ as illustrated in Figure 1 represents physicochemical work processes influenced by Coriolis effects of the Earth’s different latitudes rotating at different speeds.

Furthermore, the release of vortical Gibbs energy as heat when air masses collide, or even in flows of sea water, could cause turbulent heat release such as in catastrophic bush fire, or encourage biological production in oceanic gyres. Furthermore, some of the global warming as human population increases could be from increasing frictional resistance of the surface in new vertical cities in addition to heat island effects, or in heat released by turbulence downwind from wind farms [8].

Although the large ratio of vortical energy to kinetic energy in cyclones may seem surprising, this increased means of energy storage in air is small compared to the total energy needed to heat and sustain the translational, rotational and vibrational freedom of air molecules suspended in the Earth’s gravitational field. In 2019 we showed using action mechanics [1] that air at the Earth’s surface requires 2.4 MJ of heat per cubic metre to bring it from absolute zero to ambient surface temperatures, estimated for still air in laboratory conditions. The additional energy of 4.2x10⁵ J (0.42 MJ) per cubic metre predicted in Table 5 at the eye of a tropical cyclone is only 5% greater than the total entropic heat content. The vortical inertial energy shown in Table 3 at a wind speed of 15 m per sec needs only 3.4x10³ J of quanta per cubic metre, just over one-thousandth the energy stored in air warmed from absolute zero. From this viewpoint, storing extra energy in air as vortical energy on this scale is unsurprising. However, if experiment shows this prediction is true, it will have important consequences for climate science.

5. Conclusion

Most importantly in a debate on the quantum causation of molecular dynamics, wherever possible these proposals must all be subject to rational experimental testing, in the spirit recommended by Karl Popper’s book on conjectures and refutation [16]. Our hypothesis that very similar interaction of quantum fields with molecular mechanics may apply for a range of atmospheric systems is consistent with Ockham’s razor that multiplicity in explanations should be avoided. We have examined reviews in the literature [17,18] to find similar action approaches to link quantum fields to molecular dynamics without success. Our approach may be the only one that utilizes the integrated property of action measured with Planck’s quantum of action as a unit in place of the macroscopic properties of temperature and density for this purpose. We point to the following novel proposals that are in need of testing and we invite readers to assist in this process.

The genesis of the linkage hypothesis between quantum fields and thermodynamics presented here was provided in the 2001 treatise entitled Action in Ecosystems [10]. There, action thermodynamics was introduced for the Carnot cycle, combining separate variations in molecular density or volume and the temperature of phase space as action. We consider that using action in dynamic descriptions enables causation by quantum fields to exercise their role in achieving these molecular quantum states.

Our propositions for atmospheric science are testable, both theoretically and experimentally. Certainly, the detection of the very long wavelengths of translational quanta proposed in anticyclonic winds or tropical cyclone is challenging, though possible with very large antennae such as combining satellites in orbit or using higher frequency harmonics. However, those proposed in the Carnot cycle are in the microwave region and those for the N₂ column in the atmosphere are just an order of magnitude longer; there is an acknowledged dearth of efficient detectors for wavelengths excess to far infrared or microwaves. Careful spectral studies of such electromagnetic signals with new detectors are called for.

For the stochastic thermodynamical interactions of quantum fields with material particles in this article we have emphasised the role of torque with physical dimensions the same as vis viva, employing it as a surrogate for temperature. Thus, in the analysis of the changes in gases in the Carnot cycle where translational quanta are considered as in a 3-dimensional field, temperature was estimated from the equivalence T = mv²/3k. In the 1-dimensional fields considered as operating for cyclonic and gravitational motion we have taken kT = mv², indicating the characteristic temperature from T equal to mv²/k, although this conclusion may need further examination. For wind this indicates a torque equivalent to a surrogate temperature near zero Kelvin.

Given that the Gibbs field is related as a logarithmic function of the molecular action, the inverse symmetry factor of 1/2 makes little difference (x0.693) for the field energy of a very large numbers of possible microstates of equal probability (n), as in vortical action of cyclones or gravity. The algorithm in Equation (7) has been shown as an important relationship, enabling action mechanics to be used to estimate Gibbs fields for heat engine cycles to be extended to wind power, cyclonic motion and gravity. Since this leads to definite values for mean or maximum resonance frequencies in a field spectrum, there is a need for appropriate tests to confirm that such quanta with resonant wavelengths exist at each of these scales.

The quantum field hypothesis challenges the common opinion that heat is no more that the inertial motion of molecules. Instead, we claim to have confirmed that molecular inertia and motion is sustained by field energy, consistent with the density of activated quantum states as in Table 1. The smaller magnitude of translational quanta presents a difficulty for confirmation as there are few spectrometers capable of measuring the intensity of radiation at these long wavelengths. This gap in current technology is likely to be overcome in future.

Given the flow of solar energy through the Earth’s ecosystems (Figure 1), there is an average dissipation of 239 Watts of solar energy per square metre, a minimum rate of entropy production of 239/6000 – 239/288 or 0.790 SI entropy units per second, given the 20-fold change in the temperature of emission of outgoing longwave radiation from 6000 K on the Sun’s surface to a mean temperature of 288 K on Earth. Since we claim that work by winds is possible even for a 288 K surface emission, the temperature of outgoing emission must be colder, perhaps near 220 K, 70 K colder nearer the top of the troposphere. A whole series of heat-work processes intervenes between the initial absorption of solar energy and its emission to space, delaying the expression of maximum entropy. As vortical energy is capable of performing work as wind power, this form of negative Gibbs energy cannot be considered as contributing to entropy, unless all anticyclones on Earth are considered simultaneously.

An essential linking of the separate fields of matter and resonant quanta provides the dynamic configuration or a Gesalt for sustainability in all dynamical systems. Its proper investigation is suggested to be a very worthwhile exercise that will help reconcile our understanding of these dynamic systems. Some of the problems regarding structure in biological systems such as nucleic acids and proteins [19] as well as Monte Carlo molecular dynamics simulations [20] could be improved if the requisite Gibbs fields for all degrees of freedom could be determined.

We affirm that these quantum fields are the causative source of the inertia in dynamical systems and that the supposition that rectilinear inertia can endure unsupported by field quanta is untenable. Although the strange theory of quanta and matter explained by Richard Feynman [21] in the 1980s dealt with some of the paradoxes introduced into physics by quantum mechanics, we hope that on the scales of the phenomena examined in this article, useful new understanding can still be obtained using action mechanics for quantum theory of significance for global sustainability.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1, Carnot8/Cal program; Table S2 Entropy8/Cal; Table S3, Turbine5/Cal; Table S4, Tropcyc2/Cal; these four microcomputer programs and some data outputs are included.

Author Contributions

Conceptualization, I.K. and M.H.; methodology, I.K.; software, I.K.; validation, M.H.; data curation, I.K.; writing – original draft preparation, I.K.; review and editing, M.H. and I.K.. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data is given in the article or in Supplementary Materials.

Acknowledgments

We are grateful to our host institutions for general support.

Conflicts of Interest

The authors declare no conflict of interest.

References

Kennedy, I.R.; Geering, H.; Rose, M.; Crossan, A. A simple method to estimate entropy and free energy of atmospheric gases from their action. 2019, Entropy 21, 454-47. [CrossRef]
Kennedy, I.R.; Hodzic, M. Action and entropy in heat engines: An action revision of the Carnot cycle. 2021, Entropy 23, 860. [CrossRef]
Planck, M. The Theory of Heat Radiation. 1913, Dover Publications New York.
Carnot, S. Réflexions sur la puissance motrice du feu et sur les machines propres a developer cette puissance. Chez Bachelier, Libraire, Paris, 1824, Reprinted by M.H. Carnot in Annales scientifique de l’Ecole Normale superiere 2e Serie, 1872.
Einstein, A. On the movement of small particles suspended in a stationary liquid demanded by the molecular-kinetic theory of heat. 1905, Ann. Phys. 17, 549.
Kennedy, I.R.; Hodzic, M. Partitioning entropy with action mechanics: Predicting chemical reaction rates and gaseous equilibria of reactions of hydrogen from molecular properties. 2021, Entropy, 23, 1056. [CrossRef]
Kennedy, I.R. Computation of planetary atmospheres by action mechanics using temperature gradients consistent with the virial theorem. 2015, Int. J. Energy Environ. 9, 129-146.
Kennedy, I.R.; Hodzic, M.; Crossan, A.N.; Acharige, N.; Runcie, J. A new method for estimating maximum power from wind turbines: A fundamental Newtonian approach. 2021, arXiv:2110.15117.
Feynman, R.P. The principle of least action. The Feynman Lectures on Physics, Chapter 29, Volume II, 2010, California Institute of Technology, USA.
Kennedy, I.R. Action in Ecosystems: Biothermodyamics for Sustainability. Research Studies Press/John Wiley: 2001, Baldock, United Kingdom.
Kiehl, J.T,; Trenberth, K.E.. Earth’s annual global mean energy budget. 1997, Bull. Amer. Meteor. Soc. 78, 197-208.
Tatartchenko, V.; Liu, Y.; Chen, W.; Smirnov, P. Infrared characteristic radiation of water condensation and freezing in connection with atmospheric phenomena.: Experimental data. 2012, Earth-Sci. Rev. 114, 218-223.
Montgomery, M.T.; Smith, R.K. Paradigms for tropical cyclone intensification. 2014, Aust. Met. Ocean J., 61, 37-66. [CrossRef]
Emanuel, K.A. Some aspects of hurricane inner-core dynamics and energetics. 1997, J. Atmos. Sci., 54, 1014-1026.
Emanuel, K.A. Tropical cyclones. 2003, Anu. Rev. Earth Planet Sci., 31, 75-104.
Kennedy, I.R.; Rose, M.T.; Crossan, A.N. Improved numerical plotting of elliptical orbits using radial action coordinates -- has the symmetry of Leibniz radial theory based on inertia versus gravity been ignored? 2023, arXiv:2302.01768.
Popper, K.R. Conjectures and Refutations. The Growth of Scientific Knowledge. 1963. Routledge & Kegan Paul, London.
Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. 1990, J. Comp. Chem. 11, 663-763. [CrossRef]
Azevedo Santos, L.; Prandi, I.G.; Ramalho, T.C. Could quantum mechanical properties be reflected on classical molecular dynamics? The case of halogenated organic compounds of biological interest. 2019, Front. Chem., 7, 1-10. [CrossRef]
Koehl, P.; Levitt, M. A brighter future for protein structure prediction. Nature Struc. Biol., 6, 108-111. [CrossRef]
Bartels, C. Analyzing biased Monte Carlo and molecular dynamics simulations. 2000, Chem. Phys. Lett., 331, 446-454.
Feynman, R.P. The Strange theory of light and Matter. 1985, Princeton University Press, Princeton USA.

Figure 1. Global model for the role of vortical action in wind flows of anticyclones and cyclones, coupled to the Kiehl-Trenberth heat budget [11]. Vortical energy (v) for warming the Earth’s surface is calculated as shown or from vortical action of molecules per m³ circulating in motion around the higher pressure centre, acting as rotational winds of low curvature in the plane of the Earth’s surface.

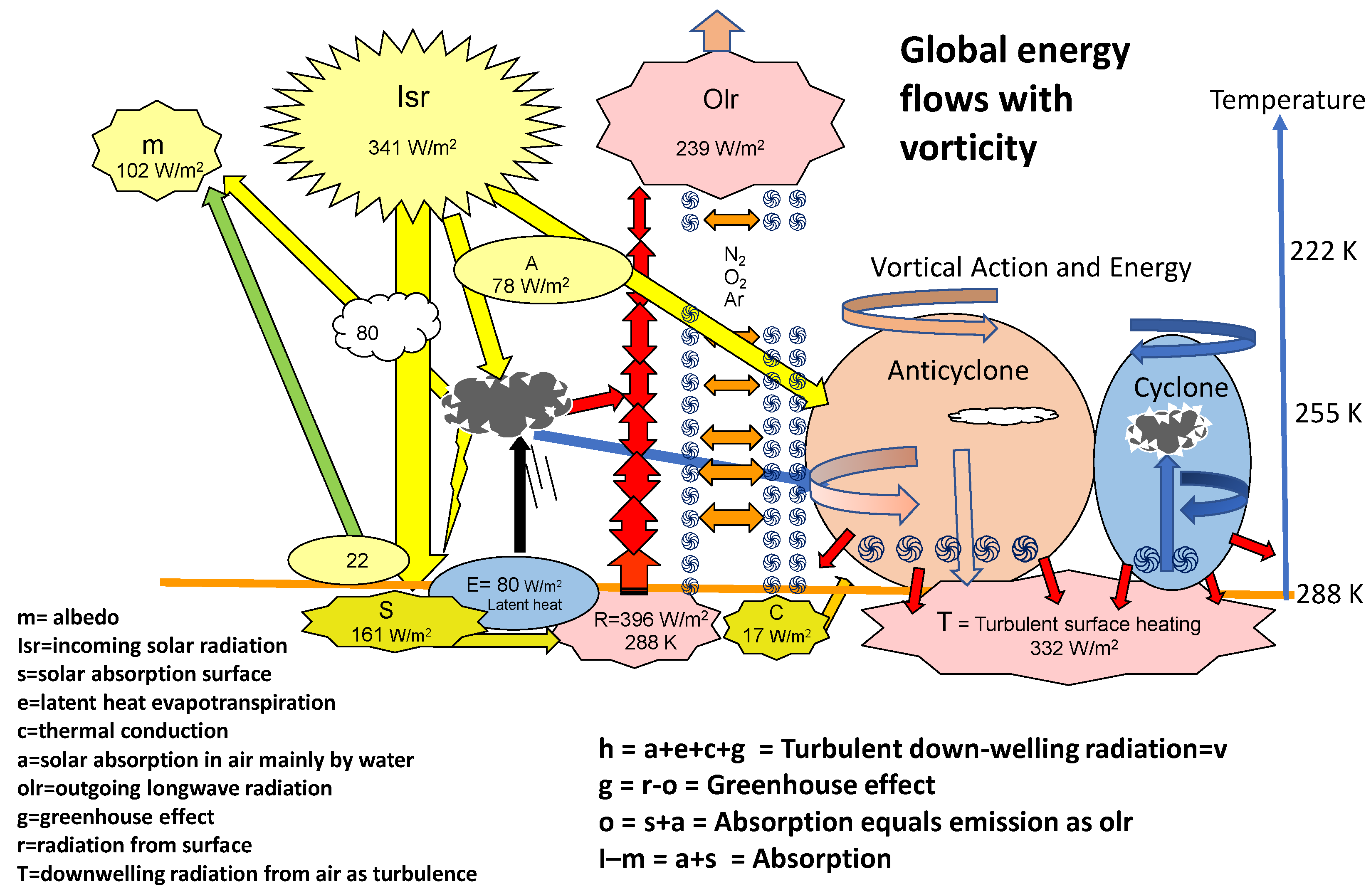
Figure 2. Vortical action (@_w) and entropy in anticyclones. Action for a cubic metre of wind molecules is computed to generate vortical Gibbs energy at r cm from the origin. The associated quantum field has a wavelength λ so that c/V is of the same order as λ/r.

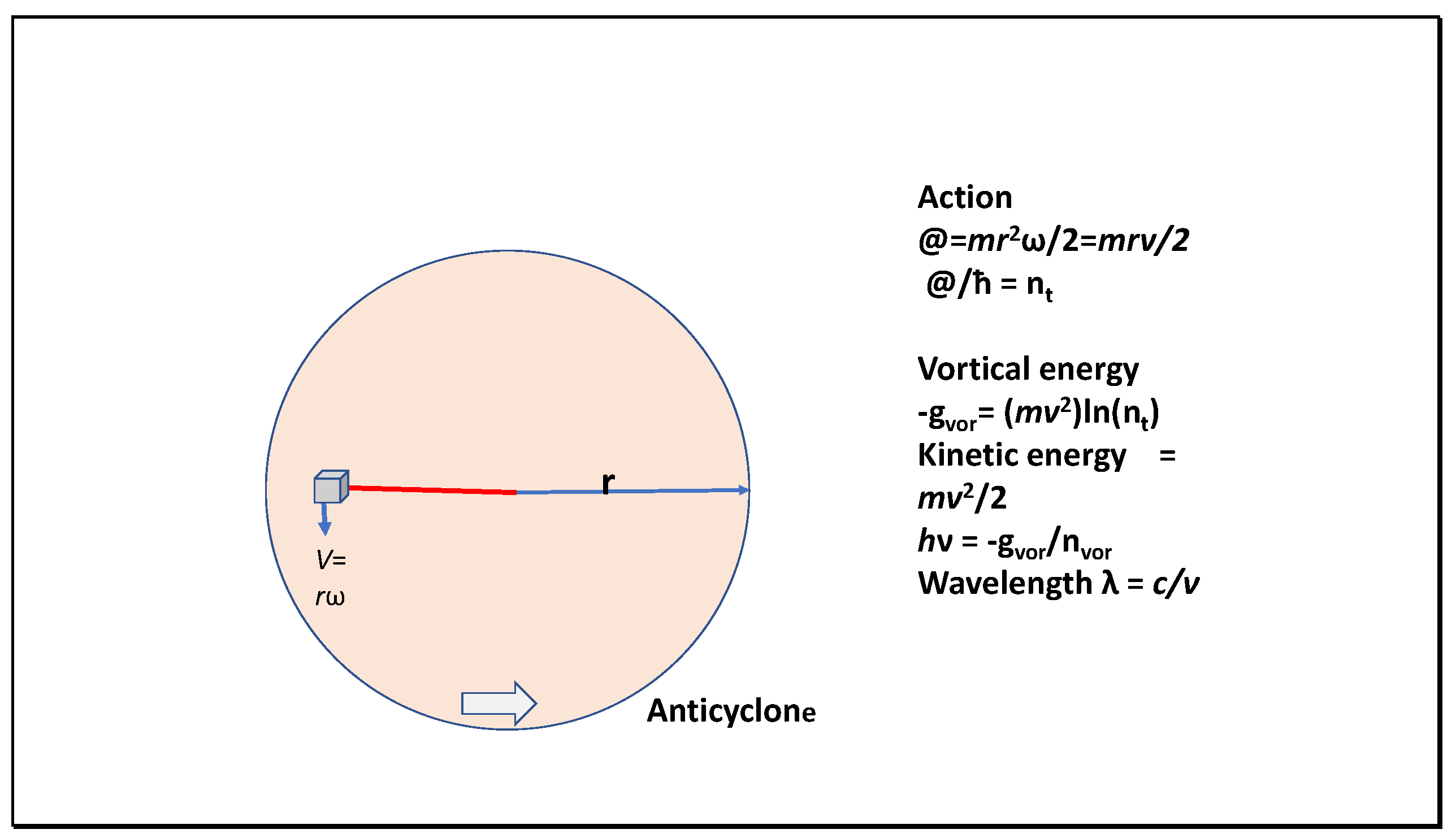
Figure 3. Profile of a tropical cyclone at 17^o S latitude showing greatest intensity to the south-west accentuated by the Coriolis effect deflecting the cyclone to the south-west. The kinetic energy pressure or torque appears minor but its intensity is maintained by the much larger Gibbs field energy.

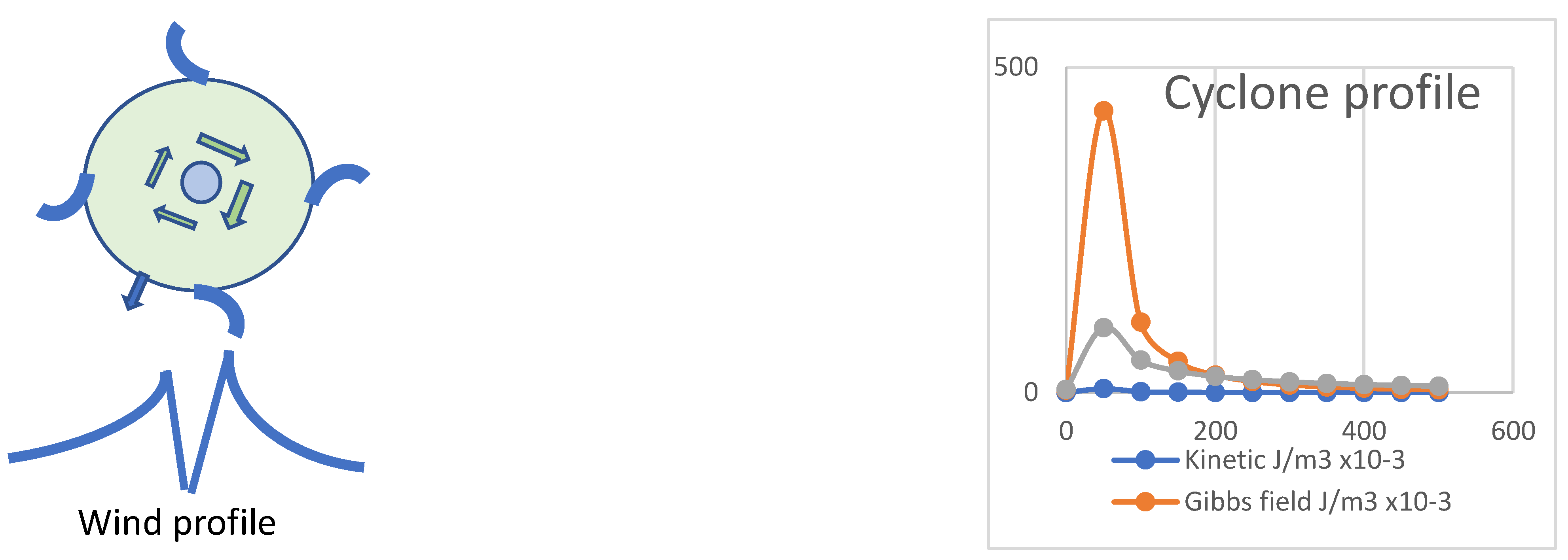
Table 1. Action thermodynamics of the Carnot cycle for working fluids of Argon and Nitrogen molecules.

Property	Stage 1	Stage 2	Stage 3	Stage 4
Kelvin temperature	640-640	640-288	288-288	288-640
Argon (Ar)	Isothermal	Isentropic	Isothermal	Isentropic
Radius (a/2 = r, m)	6.410895×10^-10	8.947125×10^-10	13.337586×10^-10	9.556798×10^-10
Pressure (kT/a³, J/m³)	4.191891 x10⁶	1.542111 x10⁶	0.2094820 x10⁶	0.5694312 x10⁶
Translational action (@_t, J.sec)	12.43697 x10^-33	17.35719 ×10^-33	17.35719 ×10^-33	12.43697 ×10^-33
Mean quantum number (n_t=@_t,/)	117.932	164.587	164.587	117.932
Negative Gibbs energy (-g_t, J)	12.6446 x10^-20 (a)	13.5282 ×10^-20 (b’)	6.0877 ×10^-20 (a’)	5.6901 ×10^-20 (b)
Mean quantum (hv, J)	1.07220 ×10^-21	0.82195 × 10⁻²¹	0.36988 × 10⁻²¹	0.48249 × 10⁻²¹
Energy density (g_t/a³, J/m³)	5.998728 ×10⁷	2.361020 ×10⁷	0.320724 ×10⁷	0.814874 ×10⁷
Quantum frequency (v, Hz)	1.61812 ×10¹²	1.24045 ×10¹²	0.55820 ×10¹²	0.72815×10¹²
Wavelength (m)	1.85272× 10^-4	2.41680 ×10^-4	5.37066 ×10^-4	4.11716 ×10^-4
λ/2πr (quanta/molecular)	4.59951 ×10⁴	4.29909 ×10⁴	6.40870 ×10⁴	6.85654 ×10⁴
Molecular frequency (ω)	9.81843x10¹¹	7.03521x10¹¹	3.16585x10¹¹	4.41829x10¹¹
Ratio (ν/ω)	1.64804	1.76321	1.76321	1.64804
Pressure ratio (g_t/kT)	14.3103	15.3103	15.3103	14.3103
nh/λmv x10^-5	1.0024 c/v=4.77x10⁵	1.0732 c/v=4.77x10⁵	1.0732 c/v=7.1x10⁵	1.0024 c/v=7.1x10⁵
Nitrogen (N₂) translational
Radius (a/2= r, m)	6.410895×10^-10	8.947125 ×10^-10	17.40496 ×10^-10	12.47120 ×10^-10
Pressure (kT/a³, J/m³)	4.191891 x10⁶	1.542111 x10⁶	0.942669 x10⁵	2.56244 x10⁵
Translational action (@_t, J.sec)	10.40552 ×10^-33	14.52207×10^-33	18.95066 ×10^-33	13.5787 ×10^-33
Mean quantum number (n_t)	98.669	137.703	179.697	128.758
Negative Gibbs energy (-g_t, J)	12.1719 × 10⁻²⁰	13.0555 × 10⁻²⁰	6.1925 × 10⁻²⁰	5.79484× 10⁻²⁰
Mean quantum (hv, J)	1.23361 × 10⁻²¹ (a)	0.94809 × 10⁻²¹ (b’)	0.34461 × 10⁻²¹ (a’)	0.45006 × 10⁻²¹ (b)
Energy density (g_t/a³, J/m³)	5.774446 x10⁷	2.278515 ×10⁷	0.146810 x10⁷	0.37345 x10⁷
Quantum frequency (v, Hz)	1.86172 x10¹²	1.43082 ×10¹²	0.52007 x10¹²	0.67921 x10¹²
Wavelength (m)	1.61030 x10^-4	2.09525 ×10^-4	5.76450 x10^-4	4.41385 x10^-4
λ/2πr (quanta/molecular)	3.99768 x10⁴	3.72712x10⁴	5.27119 x10⁴	5.04682x10⁴
Molecular frequency (ω)	11.73527x10¹¹	8.40869x10¹¹	2.89965x10¹¹	4.04678x10¹¹
Ratio (ν/ω)	1.58664	1.70159	1.79355	1.67839
Pressure ratio (g_t/kT)	13.77530	14.77530	15.57381	14.57381
nh/λmv x10^-5	1.1541 c/v= 3.99x10⁵	1.2379 c/v= 3.99x10⁵	0.8753 c/v=1.14x10⁵	0.8191 c/v=1.1x10⁵
Nitrogen rotational
Negative rotational Gibbs energy (-g_{r ,} J)	4.1575 × 10⁻²⁰ (a)	4.1575 × 10⁻²⁰ (b’)	1.5534× 10⁻²⁰ (a’)	1.5534 × 10⁻²⁰ (b)
Mean quantum number (j_r)	10.513	10.513	7.052	7.052
Mean quantum (hv, J)	3.9547×10⁻²¹	3.9547 × 10⁻²¹	2.20268 × 10⁻²¹	2.20268 × 10⁻²¹
Energy density (g_t/a³, J/m³)	1.97236 x10⁷	7.28400 ×10⁶	0.36828 x10⁶	1.00107 x10⁶
Frequency (v, Hz)	5.96831x10¹²	5.96831 ×10¹²	3.32421 x10¹²	3.32421 x10¹²
Wavelength (m)	5.02308×10^-5	5.02308×10^-5	9.01846^-5	9.01846×10^-5
λ/2πr	1.24702×10⁴	8.93525×10³	8.24669x10³	1.15092x10⁴
n_t³ x j_r²	1.0616259×10⁸	2.885798 × 10⁸	2.885798 × 10⁸	1.0616259 × 10⁷

Table 2. Tropospheric variation with altitude in molar entropy (S) and Gibbs function (G/T) for the major tropospheric gas N₂ (78.04%) in the Model 6 US standard reference atmosphere.

Alt Km	Temp K	Press Atm	S_trans J/mol/K	Mean level n_t	ST Trans. kJ/mol	Mean hν(x10^-22J) quanta	S_Rotation J/mol/K	Mean level n_r	Mean (x10^-21J) quanta hν	Total (St+Sr)T kJ /mol	Gibbs G kJ/mol
0	288.2	1.000	151.76	190.69	43.74	3.809	40.92	10.05	1.94900	55.556	-61.225
1	281.7	0.886	152.28	194.71	42.90	3.659	40.73	9.94	1.91743	54.370	-60.284
2	275.2	0.785	152.81	198.93	42.05	3.511	40.54	9.82	1.88723	53.210	-59.316
3	268.7	0.692	153.36	203.34	41.20	3.446	40.34	9.70	1.85625	52.047	-58.340
4	262.2	0.609	153.91	207.92	40.36	3.223	40.14	9.59	1.82303	50.880	-57.365
5	255.7	0.534	154.48	212.73	39.50	3.083	39.93	9.47	1.79095	49.771	-56.385
6	249.2	0.466	155.08	217.89	38.65	2.946	39.71	9.35	1.75808	48.544	-55.405
7	242.7	0.401	155.78	224.09	37.81	2.802	39.49	9.22	1.72675	47.394	-54.444
8	236.2	0.352	156.36	228.80	36.93	2.680	39.27	9.10	1.69318	46.194	-53.475
9	229.7	0.302	157.00	235.26	36.06	2.545	39.04	8.97	1.66066	45.028	-52.458
10	223.3	0.262	157.59	240.92	35.19	2.426	38.80	8.85	1.62623	43.854	-51.471
11	216.8	0.224	158.28	247.67	34.59	2.319	38.56	8.72	1.59251	42.672	-50.479
12	216.7	0.192	159.55	260.63	34.57	2.203	38.55	8.71	1.58327	42.928	-50.737

SI data were calculated [1] from molecular properties, temperature and pressure values shown using Equation (7) relating to translation and rotation only. A capable program to compute all relevant quantities in cgs units (1 Joule = 10⁷ ergs) is available from the author attached in Supplementary Materials.

Table 3. Kinetic and vortical energy impacting a wind turbine of 1.5MW power output.

Wind speed V (m/sec)	Kinetic energy/sec 83 m diam J	Kinetic energy /blade-area/sec J	Vortical pressure, J/m³	Vortical power for blade area Watts	Power estimated by radial action model Watts
					At λ=9, pitch θ=55^o
5.0	0.21670x10⁶	8.4066x10³	0.36107x10³	0.33038x10⁶	0.031168x10⁶
10.0	1.7336x10⁶	6.7253x10⁴	1.47258x10³	2.69482x10⁶	0.40541x10⁶
15.0	5.8509x10⁶	2.2698x10⁵	3.35055x10³	9.19727x10⁶	1.54381x10⁶
20.0	1.3869x10⁷	5.3802x10⁵	6.00353x10³	21.9729x10⁶	3.86798x10⁶

SI units [kg-m-sec], λ is tip-speed ratio = RΩ/V.

Table 4. Vortical energy properties for 1.5 MW wind turbine.

Wind speed (m sec^-1)	Vortical action (mrv/2 =@_v)/molecule J.sec, x10¹⁹	Quantum number n_vor x10^-15	1-D torque mv²/mole-cule x10^-24 J	Vortical energy /molecule [(mv²)ln(n_vor), x10^-23 J	Vortical energy J/m³	Vortical wavelength x10-¹²m	Kinetic energy J/m³	Ratio Vortical/ Kinetic energy
5.0	1.2108	1.14812	1.2108	4.2812	1062.024	5.3272	15.313	69.355
10.0	2.4215	2.29615	4.8430	17.1297	4332.826	2.6627	61.250	70.737
15.0	3.6823	3.49168	10.8968	38.998	9864.433	1.7786	137.813	71.758
20.0	4.8430	4.09488	19.372	69.862	17670.951	1.1643	245.000	72.127

Radius = 1000 km; SI units (kg-m-sec); symmetry factor for action=2.

Table 5. Vortical entropic energy from infrared radiation of water condensation at the convective eyewall of a tropical cyclone. .

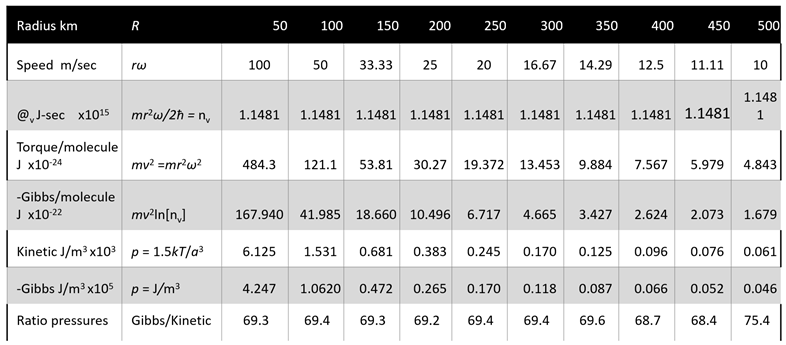
1 atm = 1.013 x 10⁵ J/m³; the integrated thermal input for 25 mm evaporation a day sustains a 500 km radius cyclone 10 km high containing 8.794743x10¹⁹ J of energy, about twice the daily input.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

New Applications of Action Mechanics to the Thermodynamics of Atmospheric Systems

Abstract

1. Introduction

2. Basic Theory and Methods

2.1. Complementary fields for virtual quanta and dynamics of material particles

2.2. The principle of least action exemplified in the Gibbs field mechanics

2.3. Mathematical basis and procedure for estimating dynamic action and quantum fields

3. Results and Discussion

3.1. Revising the Carnot cycle as a basis for a Gibbs action field

3.2. Thermodynamic stabilization with altitude for atmospheric gases by quantum fields of molecules in air

3.3. Vortical action as high level atmospheric thermodynamics in anticyclones

3.4. Estimation of power produced by wind turbines from vortical energy in anticyclones

3.5. Power in tropical cyclones from action mechanics of heat of volatilization on the ocean surface and convective condensation of water at the eyewalls

4. General Discussion

5. Conclusion

Supplementary Materials

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe