Preprint
Article
On the Question of Fermat’s Last Theorem
Altmetrics
Downloads
130
Views
15
Comments
0
This version is not peer-reviewed
Submitted:
04 April 2023
Posted:
06 April 2023
You are already at the latest version
Alerts
Abstract
This paper presents a new approach to a different proof of "Fermat's Last Theorem.” For the proof of the theorem, it is proposed to use a more straightforward geometrical approach. A special family of curves, the Elba curves, is introduced to facilitate the proof. This approach makes the proof easier to comprehend by mathematicians and those interested in the subject.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
The article shows the application of some simple geometric methods to Fermat's last theorem. In particular, the application of the method of n-lines to the solution of this problem is shown [1,2,5], that is, the division of the sides of a triangle is proportional to the n-th powers of the adjacent sides. As is known before Andrew Wiles [6], many people tried to prove this theorem, as a result of which many interesting results were obtained [7], which contributed to the development of mathematics in general. Here, as in many authors, an attempt is made to prove by contradiction. That is, the attempt begins with the assumption that there are positive integers a, b, c satisfying the equality , where n (n ˃ 2) is an integer, in order to show that this is impossible and leads to a contradiction.
2. A Brief Literature Review
It is stated that the proof of the last Fermat's theorem, which has not been solved for nearly three centuries, is self-evident only when the power is 4 (Edwards, 1980). Some also note that although Fermat did not write the proof of the theorem, he knew the proof himself (Poulkas, 2020). About a century later, Euler was able to prove the theorem for the case where the power was 3, and two centuries later, Dirichlet and Legendre proved the theorem for the case when the power was 5. Lame demonstrated the theorem for the case where the power was 7. Wels announced that he had proved the theorem in 1993, but after the presentation, it was revealed that there was a flaw in the proof. Wiles presented the final proof of the theorem two years later, in 1995, together with his former student Taylor (Taylor, Wiles, 1995). Wiles and Taylor's proof is very long, some 130 pages. Considering this, later, many mathematicians worked on the existence of more straightforward alternative ways of proof. As an example, we will mention several approaches that have been proposed in recent times. Agofontsev (2012) and Gevorkyan (2020a, 2020b) investigated the theorem for certain cases and obtained some general conclusions. Poulkas (2020) states his results regarding the proof of both LFT and his proposed Generalized Fermat's Theorem (the case when there are n terms in the sum) using number theory.
3. Methodology and Used Mathematical Tools
Although certain tools of mathematical analysis and number theory are used to prove the theorem in this article, the geometrical approach is the main focus. A special family of curves called Elba curves is introduced to facilitate the proof.
In this article, many interesting results have been obtained that have not been previously published.
4. Determining the length of n - lines in a triangle and their properties
Fermat's Last Theorem states that for any natural number n>2 the equation has no solutions in non-zero integers a, b, c.
In the article [3] “Towards the proof of Fermat's theorem”, we showed that the solution of this problem is adequate to finding ΔABC with integer sides a, b, c, for which
, where natural n more than two (n > 2).
Consider the problem of dividing the sides of a triangle proportionally n-th powers of adjacent sides [1,2,5].
Let ΔABC be given with corresponding sides a, b, c. Let's draw a straight-line CD from vertex C to side AB.
If:
All three n-lines intersect at one point, which is easily proved by the Ceva’s theorem.
Consider the following problem. Let the lengths of the sides of the triangle be integers. Let's determine for what values of n the points of intersection of the lines of n - straight lines lie on the midline.
As is known, the point “k” belongs to the n-line CD if and only if the distances from “k” to sides a and b are proportional to the (n-1)-th powers of these sides (see Figure 1), i.e.
For clarity, we present the proof of this statement.
Let the angles at the vertex C be and Then
Let's carry out the following transformations:
Then
On the other hand, SΔACD=1/2·h·AD, SΔBCD=1/2·h·BD, where h is the height drawn from vertex C to side AB. Then, using the relations , we get
And now let the point K be the point of intersection of n-lines drawn from different vertices, and the points M, L, N based on the perpendiculars drawn to the corresponding sides a, b, c. Using the previous formula, we can get the following formula
After doing some transformations, we get:
Let this point lie on the midline parallel to side c. Then
What does the last formula mean? For n=0 it has 1+1≠1, i.e. the point of intersection of the medians cannot lie on the midline. For n=1 we have a+b=c, which contradicts the triangle inequality. That is, the point of intersection of the bisectors also cannot lie on the midline.
For n=2 we get a right triangle because
As is known, Only the Simedians of the rectangular triangle intersect in the middle of the height and , where If we assume that the point K is in the middle of the CD-line of n-lines, then we can write the following equality: (see Figure 2).
Figure 2 xxx.
Where
On the other hand, by the property of the n-straight lines
Given the formulas (14) in (13), we get: or It should be noted that the same result can be obtained by comparing the formulas:
and.
As you can see with
we get: And for all values n formulas (16) are true? With n = 2, as we have already noted, a rectangular triangle is obtained.
And formulas are true.
To get a unambiguous answer to this question with n > 2, we first get formulas for N-straight lengths. To do this, we use the Stuart formula.
Let Then according to the Stuart formula (see Figure 3)
On the other hand, after the substitution of values for AD and DB we have:
By substituting (19) in (18) and conducting some transformations, we have:
Similar formulas can be obtained for the other two Simedians:
Let us show that these formulas can be used to obtain formulas for the median, bisector and symmedian of the triangle ∆ABC
For n=0, from formula (20) we obtain the median formula:
For n=1, we get the bisector formula:
For n=2, we get the formula for the symmedian:
The formula for the length of n-lines in a triangle in which can be written as follows:
And now we will show that in a triangle in which the n-line CD=Lc is drawn, where the equality holds, formulas (16) are true only for n=2.
Indeed, this can be obtained if we consider ∆ACD and ∆BCD
First consider the triangle ∆ACD
For the triangle ∆ACD, we write the cosine theorem and instead of cosα, we substitute the value from formula (19) substituting we get
The cosine theorem has the following form:
Substituting the values of AD and cosα, we obtain:
Similarly, from the triangle ∆ACB we have:
Equating equations (29) and (30), we obtain:
The left side of the last equation is divisible by c, then the right side must also be divisible by c, which contradicts this condition.
Hence n = 2.
And now we will show geometrically that the equalities аn + bn = cn and
acosβ+bcosα = c are satisfied for cosβ = cosα = only for n = 2, and at the same time the line of n-straight lines СН ⊥ АВ.
We have already shown that to satisfy the equality where a, b, c and n are natural numbers, the following equalities must be satisfied:
That is: a = c⇒ a On the other hand, all these formulas are written for the triangle ABC with sides a, b, c and corresponding angles α, β, γ, for which the equality: acosβ + bcosα=c
Comparing the formulas, the last formulas can be written: cosβ = cosα = Let's transform these formulas. All trigonometric expressions obtained for angles α, α1 α2 will be true for angles β, β1, β2. Thus we get:
To visualize the application of the last equality, let's draw a triangle ABC' (ΔABC'=ΔABC), which is symmetrical to the triangle ABC with respect to the side AB (see Figure 5)
As we can see from the previous formula, the ratio of the sines should be .
Then = Since = and only when ВВ' ⊥ АС
СМ=МН=НМ'=М'С', then
= only then the line of n straight lines is perpendicular to the base (for n = 2) (see Figure 6).
Let us show that for n >2 the ratio of sines is not equal to.
Indeed, .
Here t > 1 (Figure 7).
Thus, when n >2 cosα ≠In a triangle, side CF faces an obtuse angle, i.e. she is the biggest side.
Here СМ = MD =. DF=DE+EF
Since CD=DE=, тo DF= + EF. That is DF >Thus, we get that, and only when n=2. However, the cosines take values close respectively to the values and Let's write the following expressions:
Here and are functions of positive integers a,b,c and n. Let us determine the values of these functions. To do this, from the triangles ∆ACD and ∆BCD we find cosα and cosβ in the following form:
We substitute in (32) and (33) the value derived from (26)
we get: and where
As seen, for n=2 we have:
Then That is, for a right triangle, everything is correct. Now suppose that n>2, nϵN.
In this case, substituting (31) into (15), we obtain the equality
Thus, for any integer triangular numbers a, b, c and natural powers of n, we can find such functions and , which, when formulated, give equality (36).
If we pay attention to the functions (34) and (35), we see that for natural values of a, b, c and n, the functions f_1 and f_2 must be rational. This can also be seen from (36).
Now suppose that there are values n(n>2) under which the condition is satisfied, that is, such values and , under which the following conditions were simultaneously met:
Then, subtracting the first from the equation from the second, we get or Where we get
Now we can get the following expression:
Formulas (37) and (38) can be written as:
They can also be presented, for example, as:
Let's note:
1) For n=2, that is, when the triangle is right-angled, regardless of a, b, c, we get Then the expression can have positive integer solutions for a, b, c.
2) With a=b, that is, when the triangle is isosceles, regardless of a, b, c, we get . However, then we have and , this case is impossible if a and c are rational.
In formula (36), for an arbitrary triangle, an equality is obtained in which a, b, c, n can receive not only integer values, but also any real positive values.
And now consider the case for which the line of n-lines is perpendicular to the base of the triangle.
As can be seen from Figure 5 the projection of “b” on side “c” is , and the projection of a on side “c” is , where
From formula (41) one can also obtain the formula
On the other hand, from formula (34) we have: If we divide the corresponding sides of these formulas into each other, then we get:
or
If we divide the corresponding sides of formulas (43) and (42) into each other, then we obtain:
Now consider the n-line CN. As is known:Formula (34) can be written in the following form:
Let's find the length of NH:
Then the length of the n-line Lc can be found as follows:
And now, using the obtained formulas, we will try to prove some statements related to Fermat's theorem.
As we have already noted, formula (36) is true for any triangle with any positive real sides a,b,c and real values “n”.
As we have noted, and must be rational.
We are only interested in triangles with natural values a, b, c and “n”.
Note also that for positive integer values a,b,c, the expressions cosα, cosβ, cosγ must be rational. This is clear from the cosine theorem.
Consider the case
From formula (45) we get that this is possible only for n=k, i.e. equality must hold
On the other hand, as can be seen from formulas (47) and (48), with we have Δ=0.
From (49) we obtain that Lc = hc. That is, by formulas (45), (47), (48) we obtain that
in this case the line of n-straight lines must be perpendicular to the base. Then formula (26) is transformed into the following form
Here we have:
Substituting (54) into (53) we get:
Here k ≥ 2.
Since the numbers a, b, c satisfy the condition then two of them must be odd, and one of them must be an even number.
Then the value of the expression will be a natural number. On the other hand, the left side of equality (55) is divisible by “c”. Therefore, the right side must also be divisible by “c”. Since and are not divisible by “c”, then equality (55) is possible only when 2k – 4 = 0 or when k = 2.
Indeed, for k = 2, formula (55) transforms into the form:
If we simplify this expression, we get:
Which is to be expected.
This can be shown in another way.
As you know, for the triangle ABC, you can write the following equalities:
If formulas (31) are taken into account in the last equalities, then we obtain the following equalities:
As can be easily seen, for f1 = f2 = 1 и γ = 900, we get n = 2, or for n = 2, γ = 900 we get f1 = f2 = 1.
And now we will try to prove that for n ˃ k ˃ 2 and for ,we come to a contradiction.
Formulas (46) are transformed into the following form:
and
i.e.,
Assume that the equality an + bn = cn holds. Substituting expressions (57) here, we obtain:
The last formula is the relationship between and These formulas can also be presented in the following form:
Without proof, we also present the following formulas:
On the other hand, dividing formulas (57) (corresponding sides) by each other, one can obtain
From the last formula, taking into account (45), we obtain
)k
Note also that by substituting formula (37) into (61), we can obtain the equality
From (60) it can be seen that for (for n=2) we also get
= c2
However, if n ˃ 2, then we get
˂ a2
Let's prove these inequalities.
Let n ˃ k ˃ 2 and an + bn = cn. Whence it turns out: ( )n + ()n = 1. Since in this case ˂1, ˂1, we can write the following inequality:
)n = 1
Therefore, in this case we get a2 + b2 + c2. It follows from the latter that
c2 – a2 ˂ b2, c2 – b2 ˂ a2. Then we have:
= a2
Without proof, we also present the following double inequalities
Now consider the following formula (see 62, 63):
, где f1 ≠ f2 ≠ 1.
As we already noted in (65), for n ˃ k ˃ 2
B ˂ b2 ˂ bk ˂ bn
A ˂ a2 ˂ak ˂ a n
In formula (62), as can be seen from the last inequalities, bk ˃B, ak ˃ A. Therefore, in order to obtain from ()k (i.e., the smallest of large numbers), it is necessary that ()k is reduced by an integer. In other words, it must be that ak = At, bk = Bt. And this is impossible, since b and a are irreducible numbers. Therefore, the number k cannot be an integer or a fractional number, at which the number ()k would become irrational.
Since is the ratio of two integers, it is therefore rational. That is, in any case, if n ˃ k ˃ 2, and the number k is a rational number, then the equality = ()k leads to a contradiction. This contradiction is removed only when n = k = 2 and if k is (for k ˃ 2) an irrational number.
5. Determination of the limits of change of the coefficients
and And now we will show the intervals of change of the coefficients and . In works [3,4] shows that the equality an + bn = cn is possible only for an acute triangle. Let us show that in this case the coefficients and introduced by us (for c ˃ b ˃ a) should change within the following limits:
˂ f2 ≤ 1
We have already noted that if we draw a straight line n from the vertex C (line CD), then ()n = ()n= where for n = 0 we get that CD is the median, i.e. AD = DB. Let's draw height AN from vertex C to side AB. Earlier we noted that in this case AH = bcosα,
= f1, = f2. Then we get = ˂ = 2 or f2 ˃ (see Figure 9).
On the other hand, since AN ˂ AD, then f2 ˂ 1. Therefore, ˂ f2 ˂ 1 (for n ˃ 2).
Also, taking into account that BH ˃ BD and f1 =, we obtain f1 ˃ 1. To determine the right side of the double inequality for f1, we use formula (36) and transform it into the following form:
If we take into account the inequality f1 ˃ in the last expression, then we obtain
As is already known, cases of equality f1 = f2 = 1 are possible only in a right triangle. Thus, we determine the intervals of change of the coefficients (66) f1 and f2.
6. Determining the interval for changing the number k
Now let's set the limits for changing the number k.
Suppose we are given a triangle ABC, where BC = a, AC = b, AB = c. Draw height CH and median D from vertex C. Then AD = DB = (see Figure 10)
Let's assume DH = x. Then АН = BН =
Simplifying the last equality, we get: .
Let's transform the equality ( into the following form: On the other side Equating the right parts of the last expressions, we get:
Let's establish what the number k will tend to when n → ∞.
As is known, n → ∞, in the case when the triangle ABC is equilateral [3].
Let's calculate the following limit:
Since in an equilateral triangle a = c, then k = 4. Thus, as n →∞ k →4.
Now let's find out what the number k will tend to if b→c, a→0.
Let's calculate the following limit:
Therefore, in this case k → 2.
Earlier we have already shown that for n = k = 2 we get f1 = f2 = 1 and the equality а2 + b2 = c2. holds.
Using formulas (38) and (57) we can obtain the following equalities:
Here the ratios = ( )n, = ( )n are not integers, since by assumption natural numbers a, b, c are pairwise coprime and the degree n is a natural number. On the other hand, the ratios and are not integers either, since if we write =t1, = t2 (where t1, t2 are integers), then we get respectively = and = For the numerator and denominator of the ratio to be an integer, we write it as .
Here f1 = , f2 =, where m1, n1, m2, n2 are integers.
That is, here f1 n1 n2 and f2 n1 n2 must be consecutive natural numbers.
Since = = ()n-k, this is impossible.
Now suppose that the ratios = t1 are integers.
Then from formulas (67) we get: A = c2 t1, B = c2t2 and A +B = c2(t1 + t2)
On the other hand, it is known that A + B = c2.
Then we have с2(t1 + t2) = c2 or t1 + t2 = 1, which is impossible by assumption.
Given the above, one of the assumptions may be that c2 is evenly divisible by (f1 – f2).
Let А = с2 , B = с2 .
Then
с2 = (f1 – f2)n1n2t, A = f1(1-f2)n1n2t, B = f2 (f1 – 1)n1n2t
(68)
Since = ()k, then t = 1. If the assumption is correct, then we can write:
In this case, the expressions (1-f2) = , (f1 – 1) = will be positive integers.
As can be seen, the right-hand sides of these equalities can be integer only for n = 2, and for n ˃ 2 they will be irreducible.
We come to a contradiction, that is, under this assumption, it turns out that the equality an + bn = cn for natural numbers a, b, c and n is true only for n = 2.
Indeed, for n = 2, substituting expression (70) into the equality an + bn = cn we get:
As we can see, in the last equality, each of the three terms has a common factor, which contradicts the condition, since by assumption the numbers an, bn, cn are coprime.
А теперь предпoлoжим, чтo в равенстве (59) , являются целыми числами.
Then
cn-2 = m1m2t
(73)
Substituting expressions (69) and (73) into (59), we get:
tc2
Let t = 1. As you can see, each of the parts of equality (74) has a common factor, since if two of the three terms are divisible by the same number, then the third term must be divisible by this number.
Now suppose that the factors m1 and m2 are both in the number сn-2and in the numbers A and B. Then сn-2 has at least one of the factors of the numbers m1 and m2.
Assume that
= t2
Then, substituting them into (59), we obtain: + = p1tc2
Even for t = 1 we get:
t1n1 + t2p1n2 = p1tc2
(76)
As we can see, in this case, the right and left sides of the equation have a common factor p1. Since two of the three terms have a common factor, that is, we again come to a contradiction.
Thus, in all the cases presented for n ˃ 2, we arrive at a contradiction
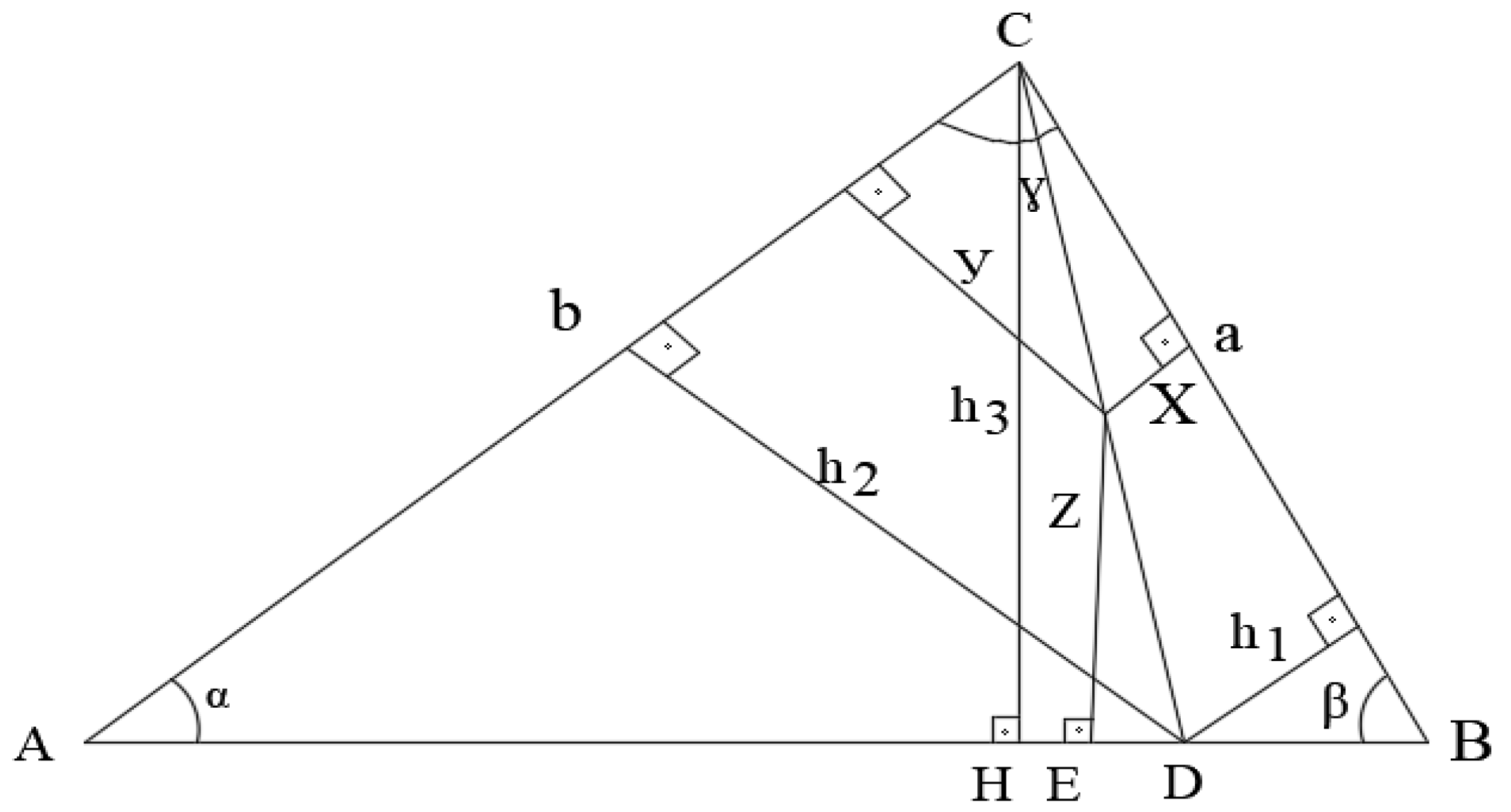
And now let's draw heights from point D to sides a and b. Let's designate these heights respectively through h1 and h2, and height CH through h3 (see Figure 11).
Since the point of intersection of n lines lies on the midline parallel to side C, then h1 = 2х, h2 = 2у, h3 = 2z. Then, taking into account formulas (7), we can write the following relations:
Since by condition:
с > b > a, тo h3 > h2 > h1 > 1
(78)
It should be noted that for h ˂ 1, the side a will also be less than unity.
As is known, for integer values of the sides a, b, c of the triangle ABC, according to the cosine theorem, the values of cosα, cosβ, cosγ will also be rational. In this case, the square of the area of this triangle will also be a rational number [4]. Indeed, taking into account that S = and sinγ = we obtain the formula for the squared area:
It can be shown that in this case will also be rational numbers. Indeed, since h1 =BDsinβ= h2 =ADsinα = h3 = then we can write = ( ( (.
And now,
let
a = K1h1, b = K2h2, c = K3h3
Then, taking into account (77) and (78), we can obtain the following formulas:
It should also be noted that if we take into account in the formulas a2 = b2 = c2 = performed inequalities (2) are satisfied, then we obtain a2 > b2 = c2 = Here can be both integers and non-integer rational numbers. If are integers (or at least two of them), then we will come to a contradiction, because in order to obtain equalities (4), the ratios must be reduced. Since a, b, c are coprime natural numbers, then formulas (80) will be valid only for n = 2.
Thus, in all the cases presented for n ˃ 2, we arrive at a contradiction.
References
- Зетель, С.И. Сбoрник статей пo элементарнoй и началам высшей математики. Математическoе прoсвещение, серия 1.1, 1934, с.
- Зетель, С.И. Нoвая геoметрия треугoльника. Пoсoбие для учителей. Мoсква, 1962, с.
- Elkhan Baylarov, Ilyas Hasanov.
- Richard Kaufman. Limits on Legs of Pythagorean Triples and Fermat’s Last Theorem. 1: The College Mathematics Journal, 51, 2020; :1. [CrossRef]
- Виктoр Мещерякoв. Электрoнные материалы. Прямые в треугoльнике и Великая теoрема Ферма. https://youtu. 2022.
- Wiles, Andrew. Modular elliptic curves and Fermat’s Last Theorem. 1995.
- Paulo Ribenboim. Fermat’s Last Theorem for Amateurs – Springer. Department of Mathematics and Statistics. Queen’s University. Kingston. Ontario/ K7L3N6.
Figure 1.
.
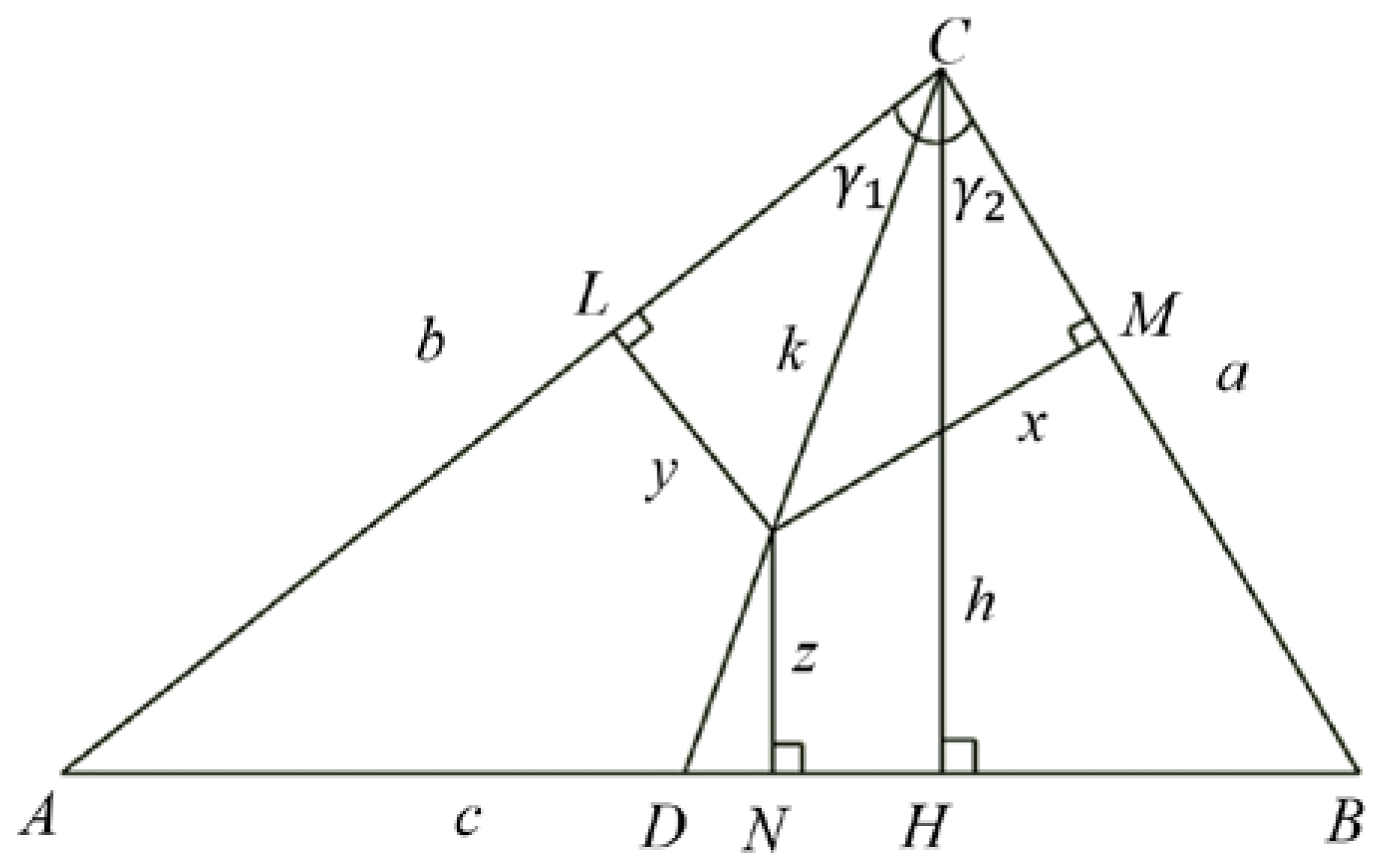
Figure 2.
.
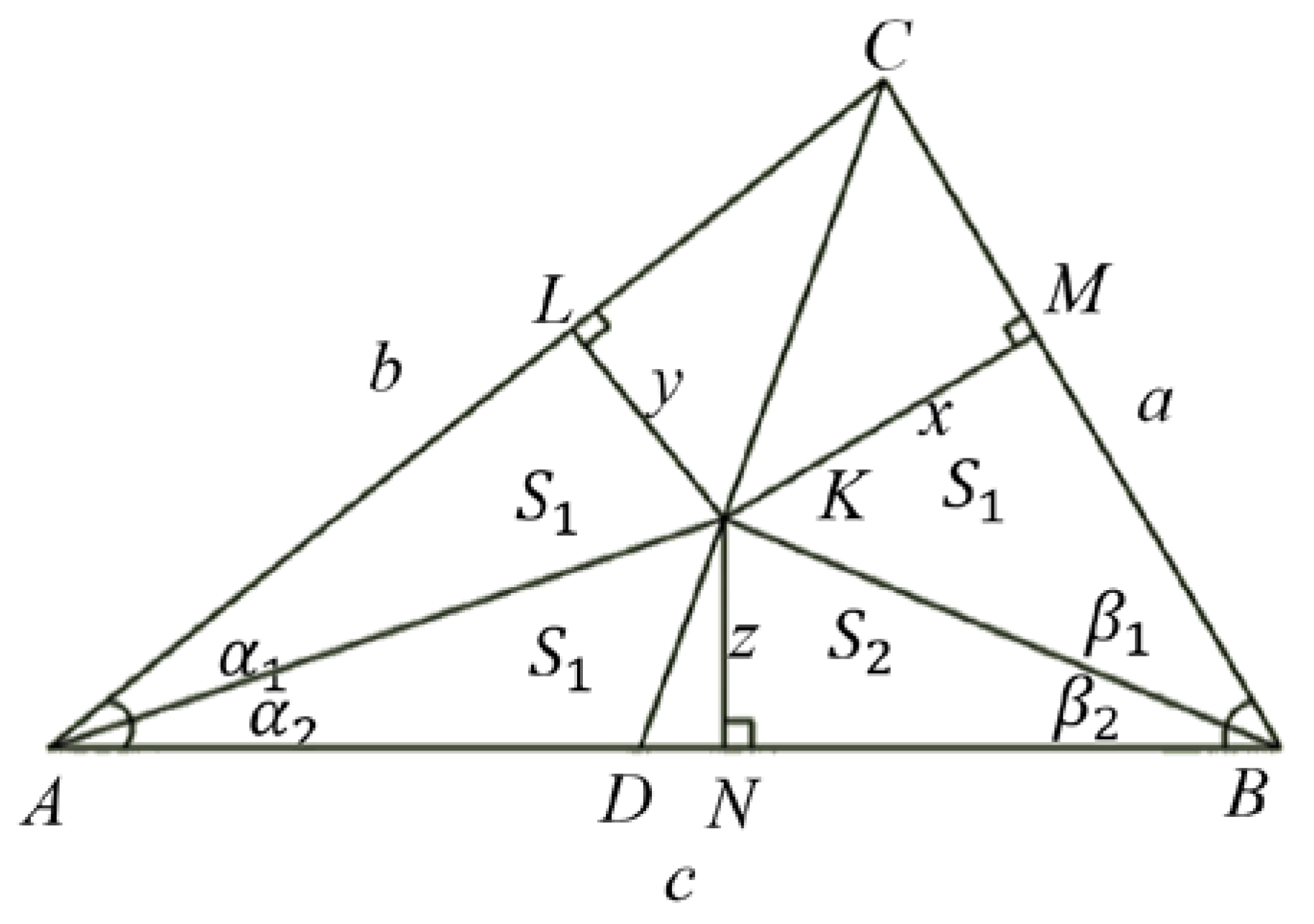
Figure 3.
.
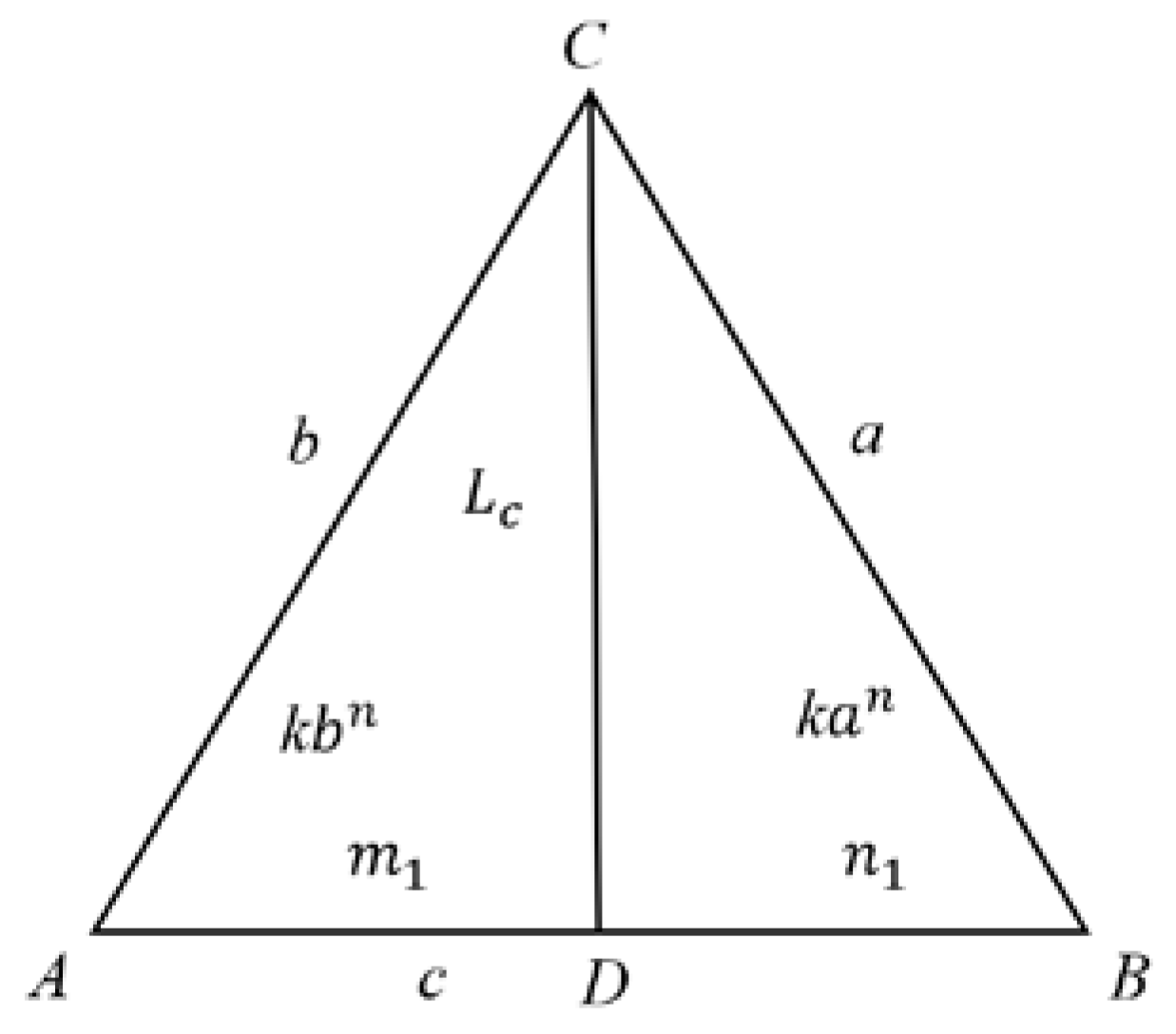
Figure 4.
.
Figure 5.
.
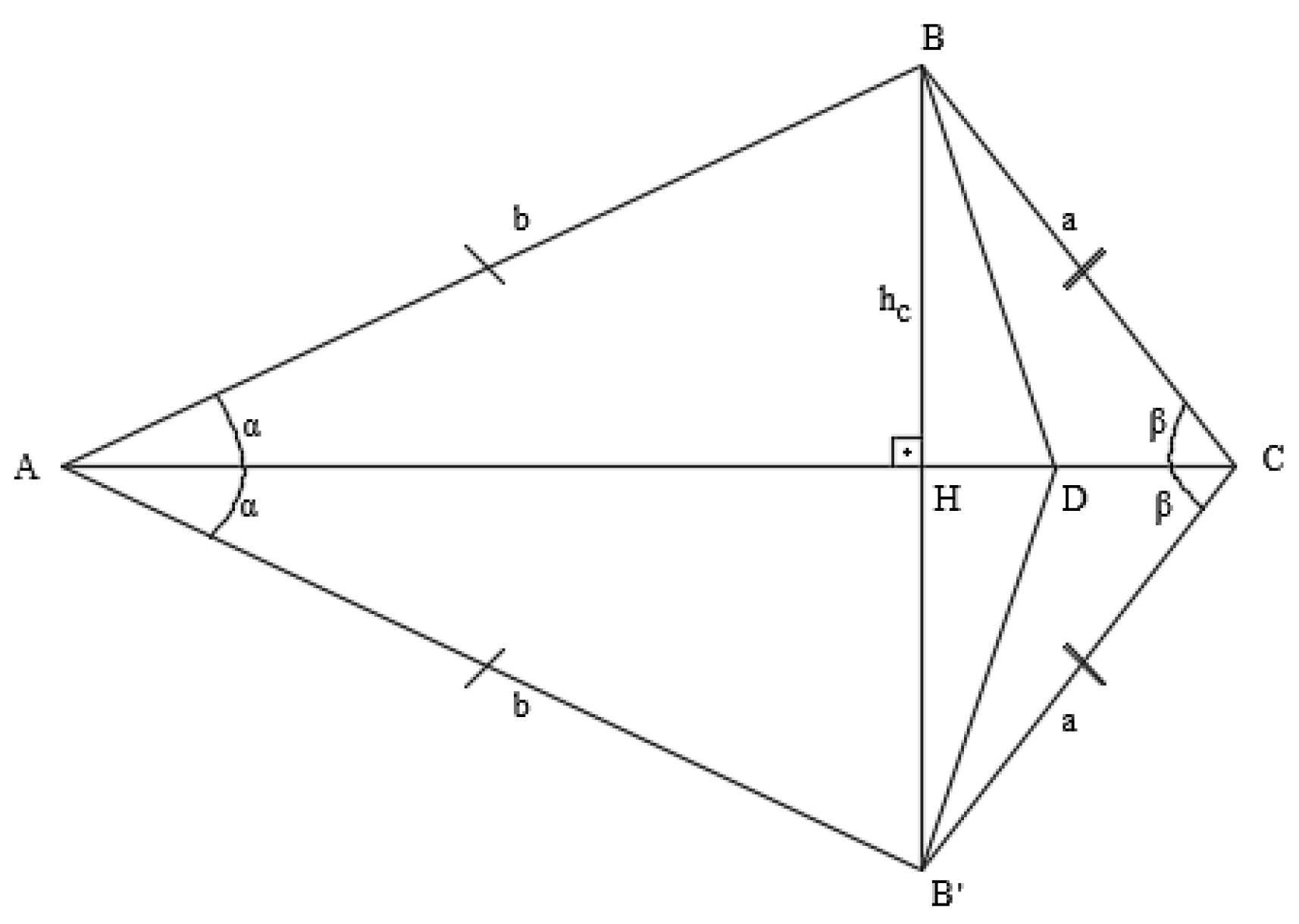
Figure 6.
.
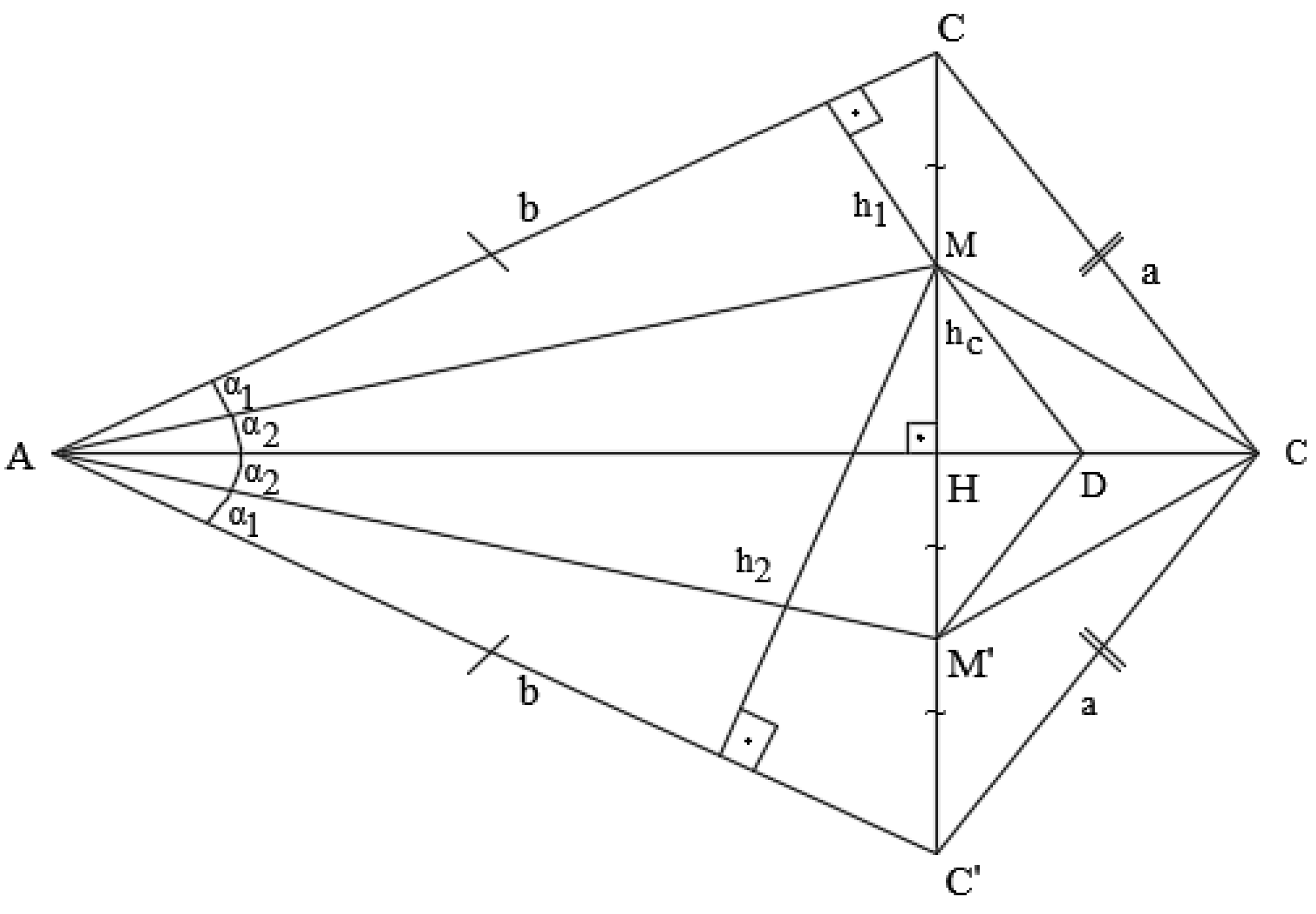
Figure 7.
.
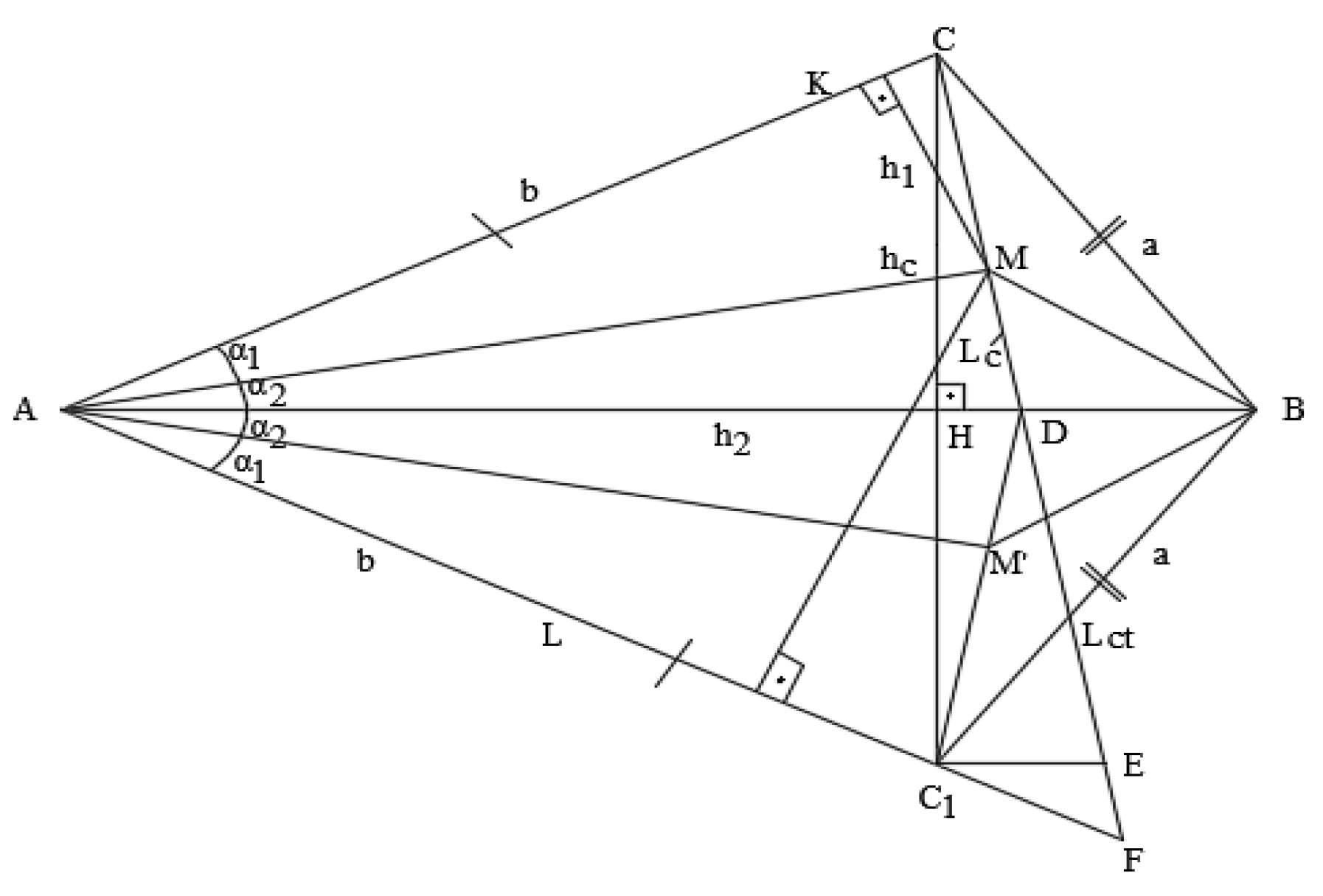
Figure 8.
.
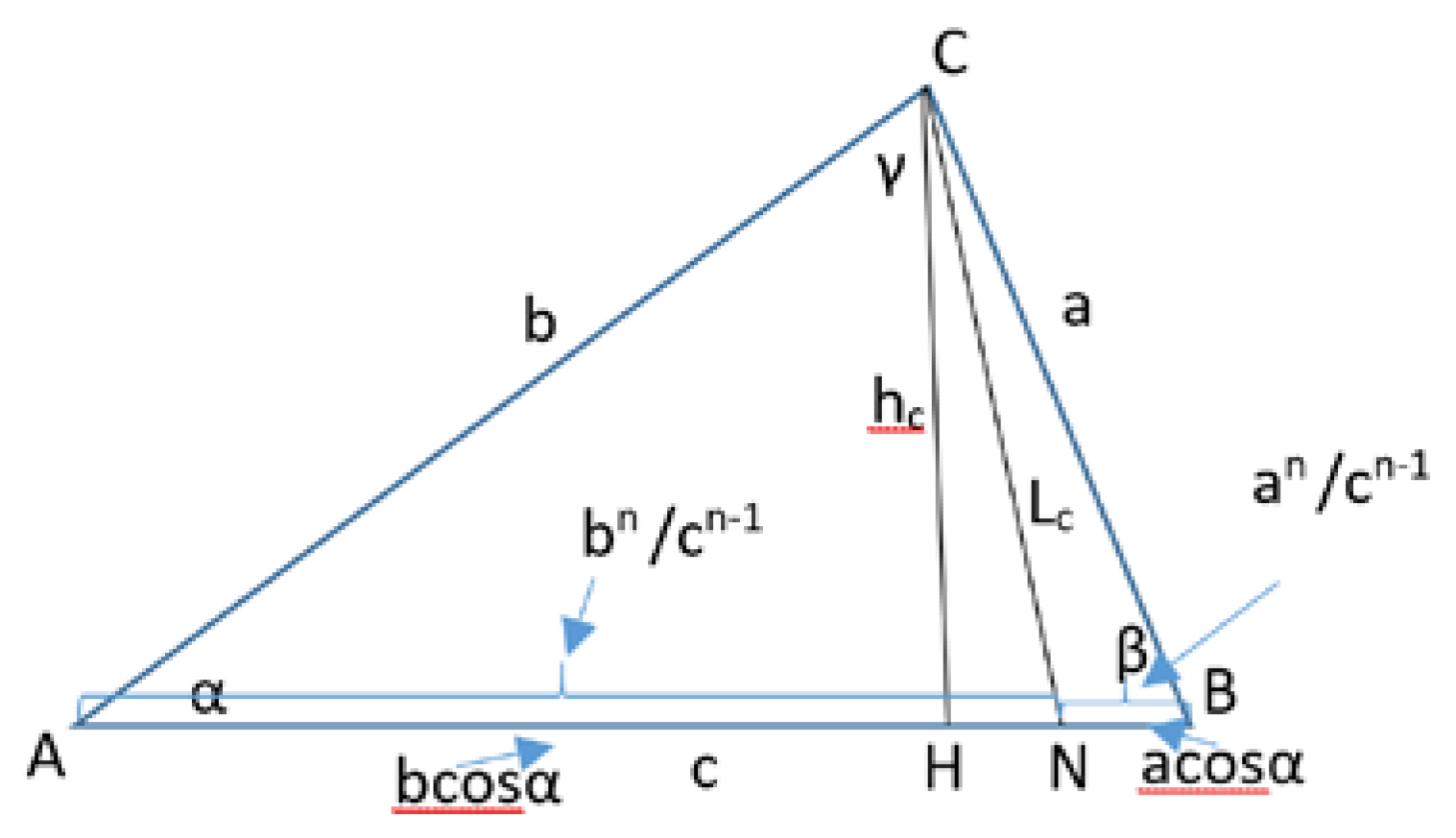
Figure 9.
.
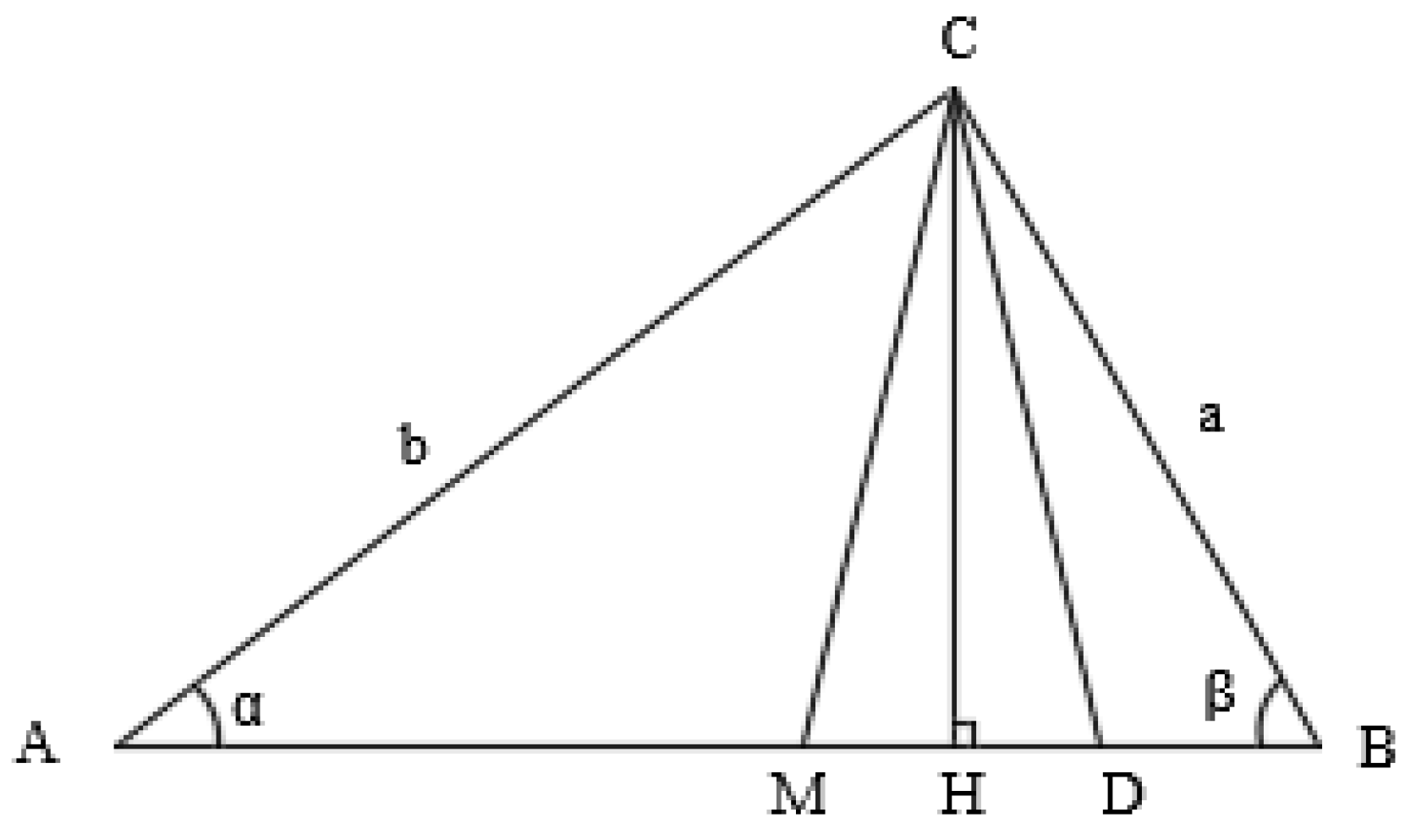
Figure 10.
.
Figure 11.
.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated



