Probabilistic Expansion Planning of Energy Storage Systems Considering the Effect of Cycle Life

Reza Ebrahimi Abyaneh; Javad Olamaei; Seyed Mostafa Abedi

doi:10.20944/preprints202304.0084.v1

Submitted:

31 March 2023

Posted:

06 April 2023

You are already at the latest version

Abstract

Energy storage systems (ESSs) are the key elements to improve the operation of power systems. On the other hand, these elements challenge the power system planners. The difficulties arise as a result of the ESSs' economic and technological features. The cycle life of ESSs is a critical aspect that influences the choices made during expansion planning processes. In this manuscript, we have focused on a new model for the expansion planning of ESSs considering the impacts of technical properties, such as the cycle life and depth of discharge. For this purpose, the proposed model consists of the hourly operation planning of ESSs in the sample days of year. A new indicator is proposed to determine the daily charging/discharging cycles of ESSs. Numerical results show the ability of the proposed model to determine the optimal technology and capacity of ESSs.

Keywords:

Cycle life

;

Depth of discharge

;

Energy storage system

;

Expansion Planning

Subject:

Engineering - Electrical and Electronic Engineering

1. Introduction

Energy storage systems (ESSs) play a significant role in distributed power systems and utility power systems [1,2]. But, the high investment cost is one of the main challenges of ESSs. As a result, expanding ESSs while taking their technical and economic aspects into account is a primary research area for power system experts [3].

In recent years, significant research was conducted on the expansion planning of the ESSs [4,5]. The main difference among these studies is how to model ESSs expansion planning problem and how to formulate the problem. In the objective function is considered to minimize the hourly social cost and maximize the penetration of wind power resources [6]. The minimizing of total system costs is considered in as the objective function [7]. But, in this manuscript, the possibility of price arbitrage and profitability resulting from the voltage and frequency control is applied in the model.

Along with the optimal expansion planning of ESSs, the wind production capacity was optimized. In the proposed model, ESS was used to reduce the need to invest in transmission systems to increase the penetration of wind generation resources [8].

A multi-objective optimization problem, which minimizes wind energy curtailment and total social cost and maximizes profit from the price arbitrage, is proposed in the ESS expansion problem [9].

A new model for expansion planning of distributed ESSs is presented in [10]. Instead of using a centralized storage system, several distributed storage systems are used in the proposed method. In the model presented in this manuscript, a three-level planning method is used to determine the location and capacity of the ESS. In the first stage, the optimal location of ESS and its power capacity is separately determined for each day of year. The second stage determines ESS's power and energy capacity at the sites selected in the previous phase. The third phase determines how to employ ESS to alleviate transmission line congestion based on the location and capacity of ESS indicated in the preceding stages. Kargarian et al. divided the ESS expansion planning problem into two different time horizons, hourly and inter-hourly [11]. In the inter-hour time horizon, the algorithm determines the optimal energy capacity of the ESS to provide the adequate ramping capability. At hourly intervals, the optimal power capacity of ESS is determined to have sufficient production capacity to supply the load.

A new model for the coordinated expansion planning of transmission systems and ESSs, taking into account transmission switching, is proposed in [12].

A three-level model for the simultaneous optimization of the transmission lines and ESSs are presented [13]. In this model, the optimal location and capacity of the ESS are determined. The centralized development of the transmission lines was carried out. The suggested model's high level optimizes the return on investment for investors. The model's intermediate level optimizes the major choices associated with ESS expansion planning. The low-level simulation models market settlement.

In the coordinated investment planning of transmission lines and ESSs is presented from the perspective of a central planner. The proposed model aims to achieve the effective and coordinated development of transmission lines and ESSs to minimize the cost of investment with significant penetration of renewable energy sources [14].

A bi-level model is presented for expansion planning of the electrical energy resources considering the ESSs [15]. The ESSs are modeled in the upper level, and Social welfare is considered in the lower level.

In a two-stage robust optimization-based model is proposed for the expansion planning of active distribution systems coupled with urban transportation networks considering ESSs. The uncertainty of renewable energy, load, and traffic demand in the proposed model are jointly considered [16].

A new stochastic model is proposed to study the expansion planning problem of ESSs in micro grids, which contain renewable resources and responsive loads. The optimization problem is prepared as two-stage stochastic programming [17].

In a mixed-integer conic programming model (MICP) and a hybrid solution approach based on classical and heuristic optimization techniques, namely mat heuristics to handle long-term distribution systems expansion planning problems is presented for sizing and allocation of dispatch able/renewable distributed generation (DG) and energy storage devices [18]. A bi-level formulation for the generation and transmission coordination problem considering the ESS expansion planning is presented in [19].

A new stochastic framework to deal with the expansion planning of large distribution networks in a smart grid context with high penetration of distributed renewable energy sources and ESSs considering the seasonal impact is proposed in [20].

In a reliability-constrained optimal ESS sizing for a micro grid is proposed [21]. The model presented for ESS expansion planning is based on cost minimization in the islanded operating mode of micro grid and profit maximization when it is operated in the grid-connected mode [22].

In pollutant emission costs are considered in the objective function of ESS expansion planning model [23].

Joint optimization of hybrid ESS and generation capacity with renewable energy resources is carried out in [24]. Optimal sizing and control strategy of the isolated grid with wind power and ESS considering the compensation costs of the curtailed wind power and load shedding is presented [25]. The proposed ESS sizing method is based on the discrete Fourier transform [26].

A simultaneous capacity optimization method for distributed generators (DGs) and ESSs considering the energy serving and annual losses costs is presented proposes a novel model for planning ESS expansions based on the dynamic investment strategy [27,28]. Presents a frequency-based strategy for expanding ESSs in the power system using the Fourier transform [29]. A new model for Optimal ESS expansion planning and load shedding to improve distribution system reliability is proposed [30].

This manuscript presents a new model for expansion planning of the ESSs. The proposed model is formulated as a probabilistic optimization problem from the perspective of system operator. The main novelty of proposed model compared to above reviewed articles is modeling the cycling properties of the ESSs in the expansion planning problem. The depth of discharge effect on the cycle life of the ESSs is formulated. In a number of articles, only the life cycle cost was examined, and exact modeling of cycle life in the expansion planning of the ESSs has not been addressed. Cycle life is defined as the maximum number of ESS charge and discharge cycles during the ESS life span.

Indeed, the novelties of presented model are as follows:

- Proposing a new indicator to determine the daily charging/discharging cycles of the ESSs.
- Modeling the cycle life in the expansion planning formulation.
- Considering the depth of discharge of ESSs in the expansion planning model.

This research is organized as follows. Section 2 introduces the proposed model for the ESS expansion planning. This section presents the formulation of the proposed model. The simulation results are described in section 3. Finally, section 4 provides the concluding remarks.

2. Model Description

2.1. ESS expansion planning

In this study, it is supposed that ESS expansion planning is carried out from the system planner's point of view. To model the limitations of charging/discharging cycles of ESSs within ESS expansion planning problem, the operation problem is solved. The proposed operation problem deals with the participation of production units and ESSs in the day-ahead market. In the presented model, in addition to determining the optimal capacity of the ESSs, the optimal technology of the ESSs will also be determined.

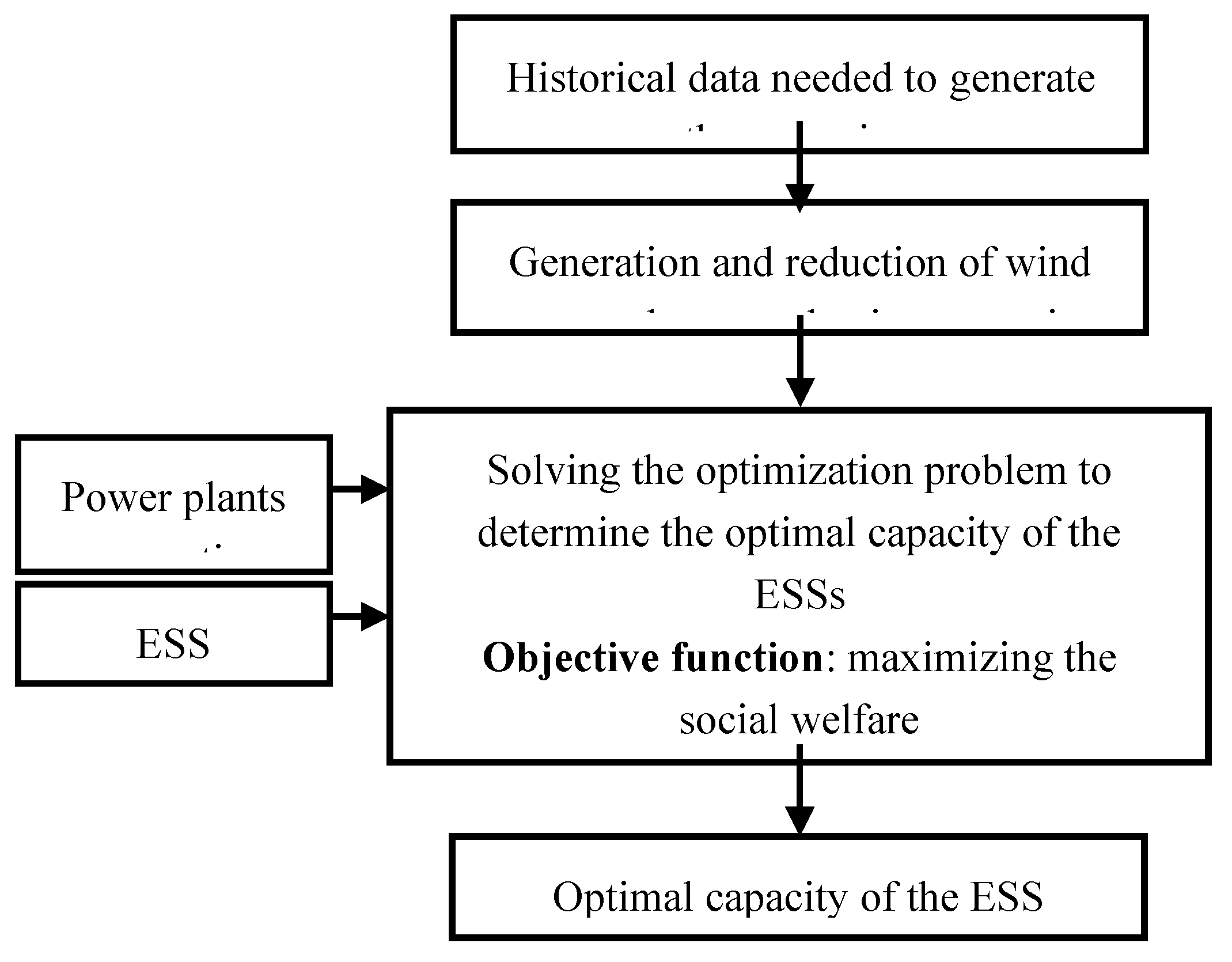
The general structure of the proposed model is shown in Figure 1. In this model, the operation planning for the hours of the annual sample days is carried out inside the expansion planning problem. System operation during this target year is therefore modeled using representative days, each of which is given a weight proportional to the probability of occurrence of a similar day. At first, the historical data of wind power plants are used to generate the probabilistic scenarios of wind power generation. After generating probabilistic scenarios, the scenarios are reduced and considered inputs in ESS expansion planning problem. The technical and economic properties of power plants and ESSs are the other inputs of the ESS expansion planning problem.

In the following, at first, the general formulation of problem without considering the limitations of charging/discharging cycles is presented. Then, the necessary relationships for modeling the cycle life of the ESSs are presented.

Figure 1. Block diagram of the proposed model.

Social welfare is defined as the difference between producers' profits and consumers' costs. In the proposed model, the price elasticity of the load is neglected. Therefore, minimization of the total operating costs of the system and investment costs of the ESSs are considered the objective function of optimization problem. The objective function of the proposed model is as follows:

\min \sum_{s = 1}^{S} λ_{s} \cdot (\begin{array}{l} \sum_{j = 1}^{N_{c}} (\overset{1}{\overset{︷}{C_{s j}^{c}}} + \overset{2}{\overset{︷}{A C_{j}^{c, O $ M}}}) + \sum_{m = 1}^{N_{w}} (\overset{3}{\overset{︷}{C_{s m}^{w}}} + \overset{4}{\overset{︷}{C_{m}^{s p i l}}} + \overset{5}{\overset{︷}{A C_{m}^{w, O $ M}}}) + \\ \sum_{n = 1}^{N_{s}} (\overset{6}{\overset{︷}{C_{n}^{s}}} + \overset{7}{\overset{︷}{C_{s n}^{s, o}}} + \overset{8}{\overset{︷}{A C_{n}^{s, O $ M}}}) + \overset{9}{\overset{︷}{\sum_{d = 1}^{D} \sum_{t = 1}^{24} L o a d_{s d t}^{c u t} \times α_{d t}^{c u t}}} \end{array})

(1)

The first and second terms refer to the traditional power plants' yearly operating and maintenance costs, respectively. The third term is used to predict the yearly running costs of wind generating installations. The fourth and fifth terms, respectively, define the yearly leakage cost and maintenance cost of wind power facilities. The sixth term is the annual cost of investing in ESSs. The annual operating cost and maintenance cost of ESSs are calculated in the seventh and eighth terms, respectively. The proposed formulation makes it possible to simultaneously determine the optimal technology and capacity of the ESSs. In fact, terms six, seven and eight terms can be calculated for different ESS technologies to determine the optimal technology. The ninth term determines the rewards paid to the flexible loads. The annual operating cost of the conventional power plants is determined using the following equation.

C_{s j}^{c} = \sum_{d = 1}^{D} \frac{365}{D} \sum_{t = 1}^{24} M C_{j}^{c} \times P_{s j d t}^{c} + S U_{j d t}^{c} + S D_{j d t}^{c} \forall s, \forall j

(2)

The annual operating cost consists of the cost of power supply and the cost of turning on and off the power plants.

The annual operating cost and spillage cost of the wind power plants are determined using (3) and (4), respectively.

C_{s m}^{w} = \sum_{d = 1}^{D} \frac{365}{D} \sum_{t = 1}^{24} M C_{m}^{w} \times P_{s m d t}^{w} \forall s, \forall m

(3)

C_{s m}^{s p i l} = \sum_{d = 1}^{D} \frac{365}{D} \sum_{t = 1}^{24} (S P_{s m d t}^{w} \times C^{w, s p i l l}) \forall s, \forall m

(4)

The investment cost and operation cost of ESSs are calculated in (5) and (6), respectively.

C_{n}^{s} = P_{n}^{s} \times A C_{n}^{p, s} + E_{n}^{s} \times A C_{n}^{e, s} + E_{n}^{s} \times A C_{n}^{r, s} \forall n

(5)

C_{s n}^{s, o} = \sum_{d = 1}^{D} \frac{365}{D} \sum_{t = 1}^{24} (P_{s n d t}^{s, c h} \times M C_{n}^{s, c h} + P_{s n d t}^{s, d i s} \times M C_{n}^{s, d i s}) \forall s, \forall n

(6)

The constraints of problem are presented below [31-32]. Minimum and maximum production of conventional power plants:

\underline{P_{j}^{c}} . I_{j d t} \leq P_{^{s j d t}}^{c} \leq \bar{P_{j}^{c}} . I_{j d t} \forall s, \forall j, \forall d, \forall t

(7)

Ramping up capability of conventional power plants:

P_{s j d t}^{c} - P_{s j d t - 1}^{c} \leq R U_{j}^{c} . I_{j d t} \forall s, \forall j, \forall d, \forall t

(8)

Ramping down capability of conventional power plants:

P_{s j d t - 1}^{c} - P_{s j d t}^{c} \leq R D_{j}^{c} . I_{j d t - 1} \forall s, \forall j, \forall d, \forall t

(9)

Startup cost of the conventional power plants:

S U_{j d t}^{c} \geq K_{j}^{c} . (I_{j d t} - I_{j d t - 1}) \forall j, \forall t, \forall d

(10)

Shut down cost of conventional power plants:

S D_{j d t}^{c} \geq J_{j}^{c} . (I_{j d t - 1} - I_{j d t}) \forall j, \forall t, \forall d

(11)

Minimum up time of conventional power plants:

\sum_{t^{'} = t}^{t + T_{j}^{o n} - 1} I_{j d t^{'}} \geq T_{j}^{o n} . (I_{j d t} - I_{j d t - 1}) \forall j, \forall t \in \{1, ..., 25 - T_{j}^{o n}\}, \forall d

(12)

Minimum down time of conventional power plants:

\sum_{t^{'} = t}^{t + T_{j}^{o f f} - 1} (1 - I_{j d t^{'}}) \geq T_{j}^{o f f} . (I_{j d t - 1} - I_{j d t}) \forall j, \forall t \in \{1, ..., 25 - T_{j}^{o f f}\}, \forall d

(13)

Dispatched production of wind power plants:

P_{s m d t}^{w, d} = P_{s m d t}^{w} - S P_{s m d t}^{w} \forall m, \forall t, \forall d, \forall s

(14)

Spillage of the wind power plants:

0 \leq S P_{s m d t}^{w} \leq P_{s m d t}^{w} \forall m, \forall t, \forall d, \forall s

(15)

Power balance of ESSs:

\sum_{t = 1}^{24} η_{_{n}}^{c h} . (P_{s n d t}^{s, c h}) = \sum_{t = 1}^{24} \frac{1}{η_{_{n}}^{d i s}} . (P_{s n d t}^{s, d i s}) \forall n, \forall s, \forall d

(16)

State of charge of ESSs:

E_{s n d t} = E_{s n d t - 1} + η_{n}^{c h} . (P_{s n d t}^{s, c h}) - \frac{1}{η_{n}^{d i s}} . (P_{s n d t}^{s, d i s}) \forall n, \forall t \in [2, 24], \forall d, \forall s

(17)

Energy limitation of ESSs:

(1 - D o D_{n}) . E_{n}^{s} \leq E_{s n d t} \leq D o D_{n}^{} . E_{n}^{s} \forall n, \forall t, \forall d, \forall s

(18)

Power limitation of ESSs:

0 \leq P_{s n d t}^{s, c h}, P_{s n d t}^{s, d i s} \leq P_{n}^{s} \forall n, \forall t, \forall d, \forall s

(19)

Power constraint for installation of ESS technologies:

P_{^{n}}^{s} \leq S C P_{n}^{\max} \forall n

(20)

Energy constraint for installation of ESS technologies:

E_{^{n}}^{s} \leq S C E_{n}^{\max} \forall n

(21)

Equality of supply and demand in energy market:

\sum_{j = 1}^{N c} P_{s j d t}^{c} + \sum_{m = 1}^{N w} (P_{s m d t}^{w} - S P_{s m d t}^{w}) + \sum_{n = 1}^{N s} P_{s n d t}^{s, d i s} = L o a d_{s d t}^{t o t a l} - L o a d_{s d t}^{c u t} + \sum_{n = 1}^{N s} P_{s n d t}^{s, c h} \forall t, \forall d, \forall s

(22)

Constraint of the flexible loads:

0 \leq L o a d_{s d t}^{c u t} \leq L o a d_{s d t}^{var} \forall t, \forall d, \forall s

(23)

10 min spinning reserve constraint of system:

\sum_{j = 1}^{N c} R_{s j d t}^{c} + \sum_{n = 1}^{N s} (R_{s n d t}^{s, c h} + R_{s n d t}^{s, d i s}) \geq S R M \forall t, \forall d, \forall s

(24)

Reserve constraint of system:

\sum_{j = 1}^{N c} \bar{P_{j}^{c}} + \sum_{m = 1}^{N w} P_{s m d t}^{w} + \sum_{n = 1}^{N s} (R_{s j d t}^{s, c h} + R_{s j d t}^{s, d i s}) - (L o a d_{s d t}^{t o t a l} - L o a d_{s d t}^{c u t}) \geq R M \forall t, \forall d, \forall s

(25)

Capability of the conventional power plants for spinning reserve provision:

0 \leq R_{s j d t}^{c} \leq 10. M S R_{j}^{c} \forall j, \forall t, \forall d, \forall s

(26)

R_{s j d t}^{c} \leq \bar{P_{j}^{c}} - P_{s j d t}^{c} \forall j, \forall t, \forall d, \forall s

(27)

Capability of the ESSs for spinning reserve provision:

R_{s n d t}^{s, d i s} + P_{s n d t}^{s, d i s} \leq η_{d i s}^{s} . E_{s n d t - 1} \forall n, \forall t, \forall d, \forall s

(28)

0 \leq R_{s n d t}^{s, d i s} \leq 10. M S R_{n}^{s} \forall n, \forall t, \forall d, \forall s

(29)

0 \leq R_{s n d t}^{s, d i s} \leq P_{n}^{s} \forall n, \forall t, \forall d, \forall s

(30)

0 \leq R_{s n d t}^{s, c h} \leq P_{s n d t}^{s, c h} \forall n, \forall t, \forall d, \forall s

(31)

2.2. Modeling the cycle life of the ESS:

One of the ESSs' technical features is their restricted number of charging/discharging cycles.

In fact, in addition to having a lifetime limit in terms of years, the ESS also has a limit on the number of charge and discharge cycles. This means that during the operation period of the ESS, even if the ESS is charged and discharged as much as the cycle life before the end of the useful life, it must be replaced.

In this manuscript, a new index is proposed to evaluate the cycle life of the ESS. In the proposed method to determine this index, the number of charge and discharge cycles is calculated for different operating scenarios every day. For this purpose, to represent the constraints of charging/discharging cycles, the cycle life of ESSs is estimated using the following equation:

N_{n s d} = \frac{\sum_{t}^{} (η_{_{n}}^{c h} \times P_{n s d t}^{c h} + \frac{1}{η_{_{n}}^{d i s}} \times P_{n s d t}^{d i s})}{2 \times E_{n}^{\max}} \forall n, \forall d, \forall s

(32)

According to the above relationship to determine the cycle life, the total energy charged and discharged in each scenario is calculated during the day. With a good approximation, the number of charge and discharge cycles can be determined by dividing the obtained energy by 2 times the energy storage capacity.

The cycle life of ESS is restricted using the following equation.

\sum_{d}^{} N_{n s d} \leq N_{n}^{\max} \forall n, \forall s

(33)

Based on the above relationship, the number of charge and discharge cycles on the days of operation of the ESS in each year should not exceed the allowed charge and discharge capacity per year.

Another important parameter affecting the performance of the ESSs is the depth of discharge, which has not usually been considered in the expansion planning studies of the ESSs. But studies show that the depth of discharge has a significant effect on the number of allowed cycles of the ESSs. So not taking this into account takes the expansion planning outputs away from what actually happens in operation. For this purpose, in this article, the effect of the depth of discharge on the lifetime of the ESS is modeled, and to model this phenomenon in the planning problem, constraints have been added to the proposed formulation.

By examining the technical characteristics of the ESSs, it can be seen that the depth of discharge of the ESSs is inversely related to the cycle life.

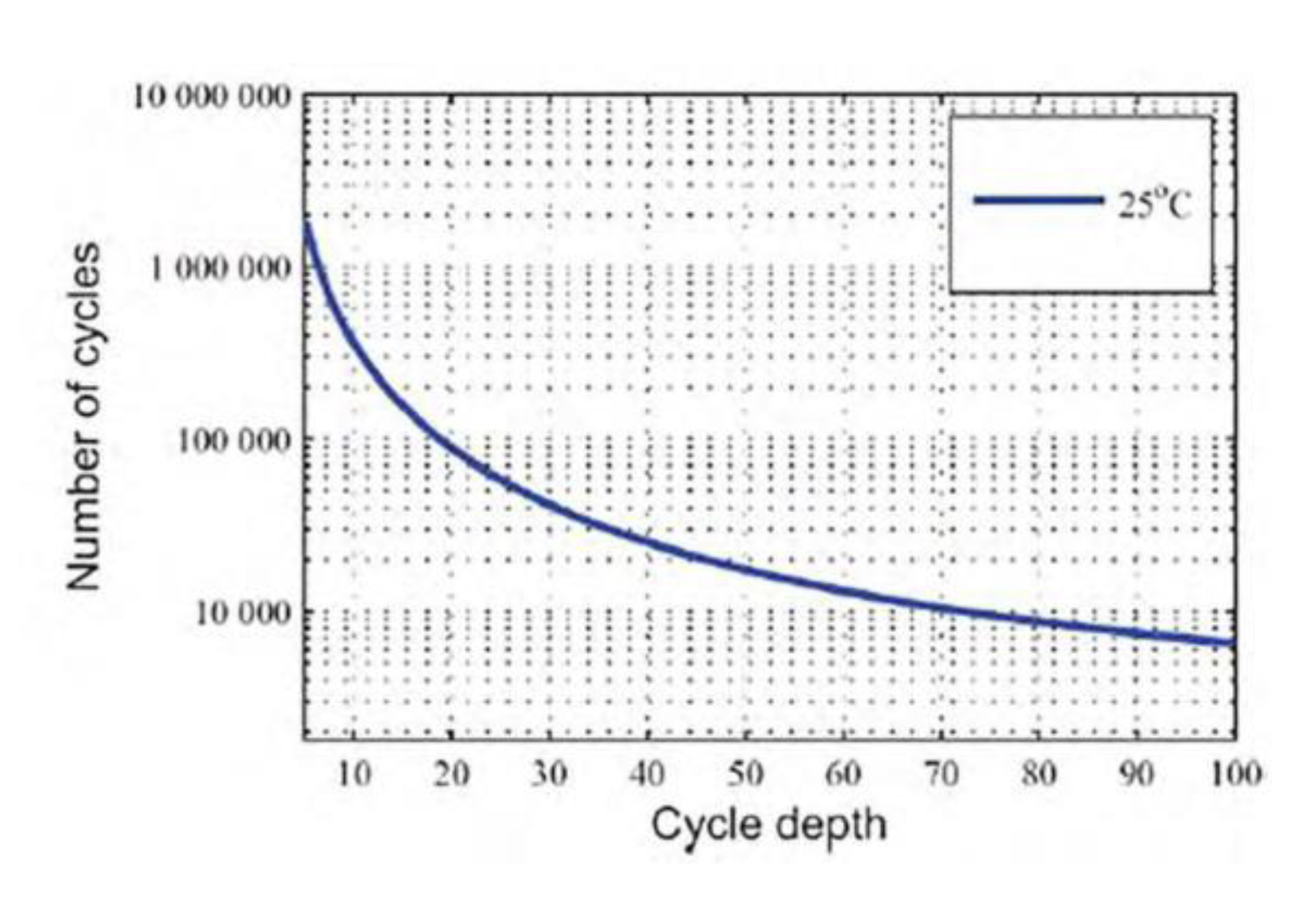
In the proposed model in this manuscript, to model the effect of depth of discharge on the cycle life, the curve of the maximum number of cycle life is modeled as the piecewise linear approximation according to Figure 2. The approximation is formulated as follows.

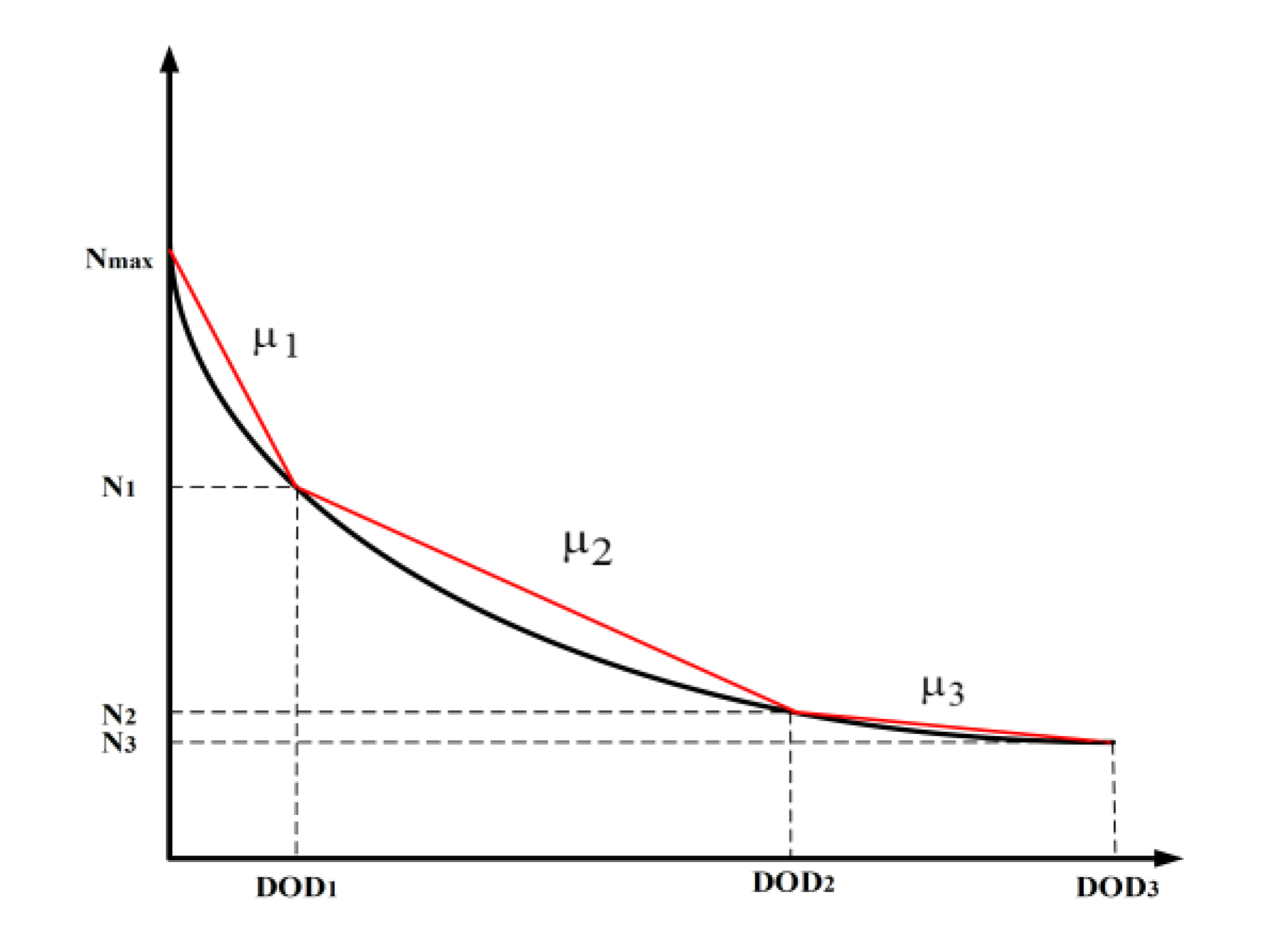
Figure 2. Piecewise linear approximation of cycle life curve of the ESSs.

N = N \max + \sum_{y = 1}^{Y} μ_{y} \times D O D^{y}

(34)

Depth of discharge is restricted as follows.

\bar{D O D^{y - 1}} \leq D O D^{y} \leq \bar{D O D^{y}}

(35)

If depth of discharge is considered as a variable, then (18) will be nonlinear. To linearize this relationship, the product of two variables,

D o D . E_{n}^{s}

, is defined as a new variable using the following equation:

D E_{n}^{s} = D o D_{n} . E_{n}^{s}

(36)

Thus (18), will be as follows:

E_{n}^{s} - D E_{n}^{s} \leq E_{s n d t} \leq D E_{n}^{s} \forall n, \forall t, \forall d, \forall s

(37)

And the following constraints are added to the formulation.

\underline{D E_{n}^{s}} \leq D E_{n}^{s} \leq \bar{D E_{n}^{s}}

(38)

\underline{D o D_{n}} \leq D o D_{n} \leq \bar{D o D_{n}}

(39)

3. Results

To illustrate the capability of the proposed model, the structure presented in Figure 3, is considered the case study. The system consists of three conventional power plants with properties displayed in Table 1. A wind power plant introduced in Table 2 is assumed in the case study. Two ESSs with properties presented in Table 3 are evaluated for allocating in the system.

In the proposed model, the sample daily demands of the year are considered the representative of each season. Demands are divided into two categories: fixed and flexible. The seasonal sample fixed demands are shown in Figure 4. The daily flexible demands are depicted in Figure 5.

In the presented method, the stochastic nature of wind power plant production is modeled by the scenario based simulation. For this purpose, the ARIMA model of the wind power plant production is determined. Then, 10000 scenarios are generated using the Monte Carlo simulation. The 10000 scenarios are then reduced to 10 scenarios using the fast forward scenario reduction technique [33]. The MATLAB software is employed to determine the ARIMA model degrees and coefficients, and scenario generation and reduction. The interruption cost for flexible demand is considered 100 $/MW, and the threshold of spinning and non-spinning reserves are defined 100 and 200 MW, respectively.

Figure 3. Structure of case study.

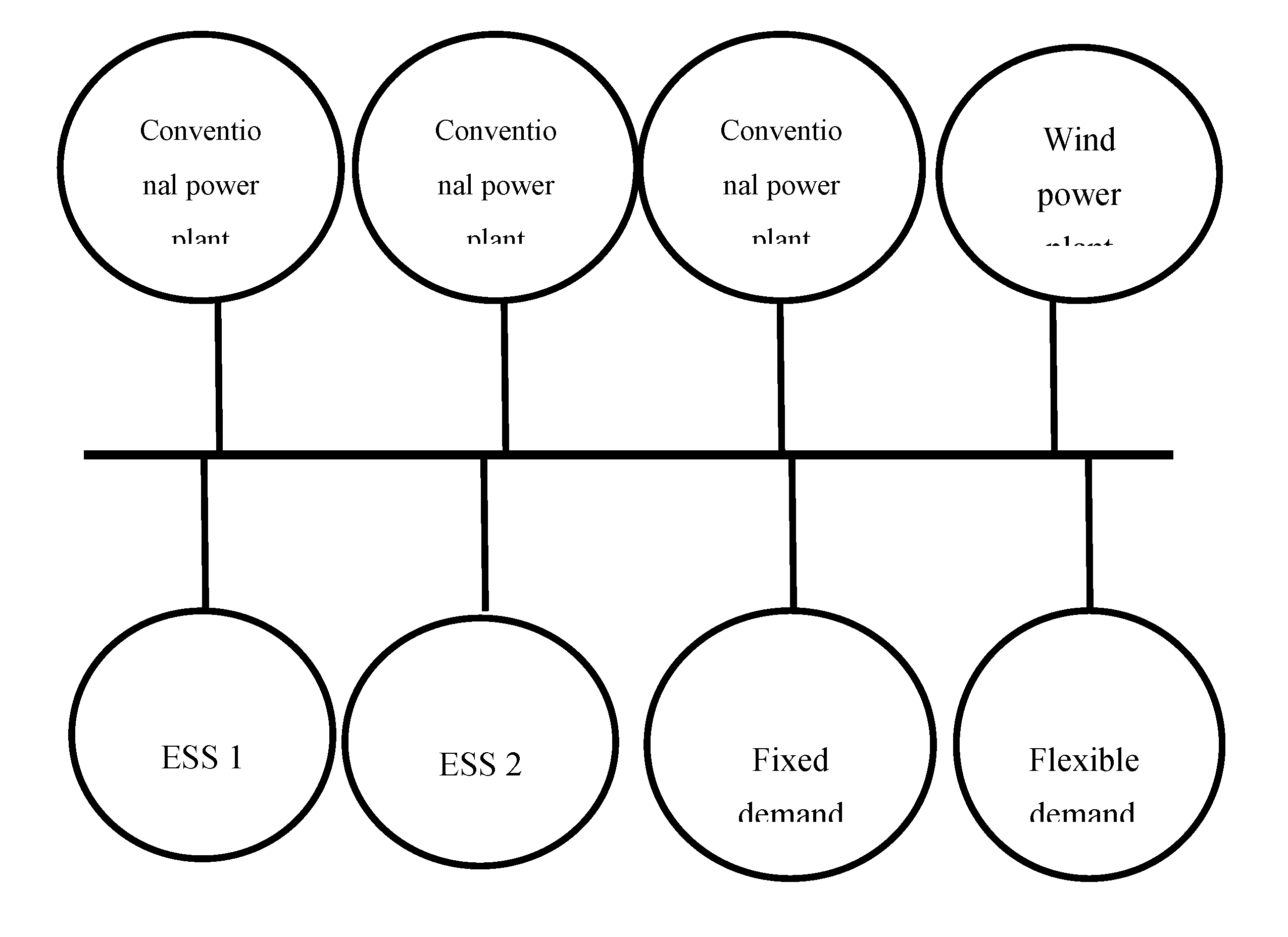
Table 1. Conventional power plants properties.

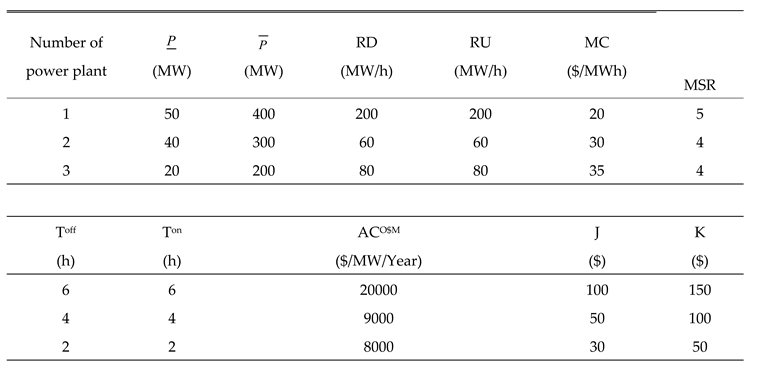
Table 2. Wind power plant properties.

Table 3. ESSs properties.

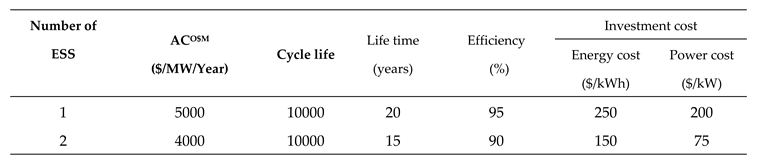
Figure 4. Daily fixed demand.

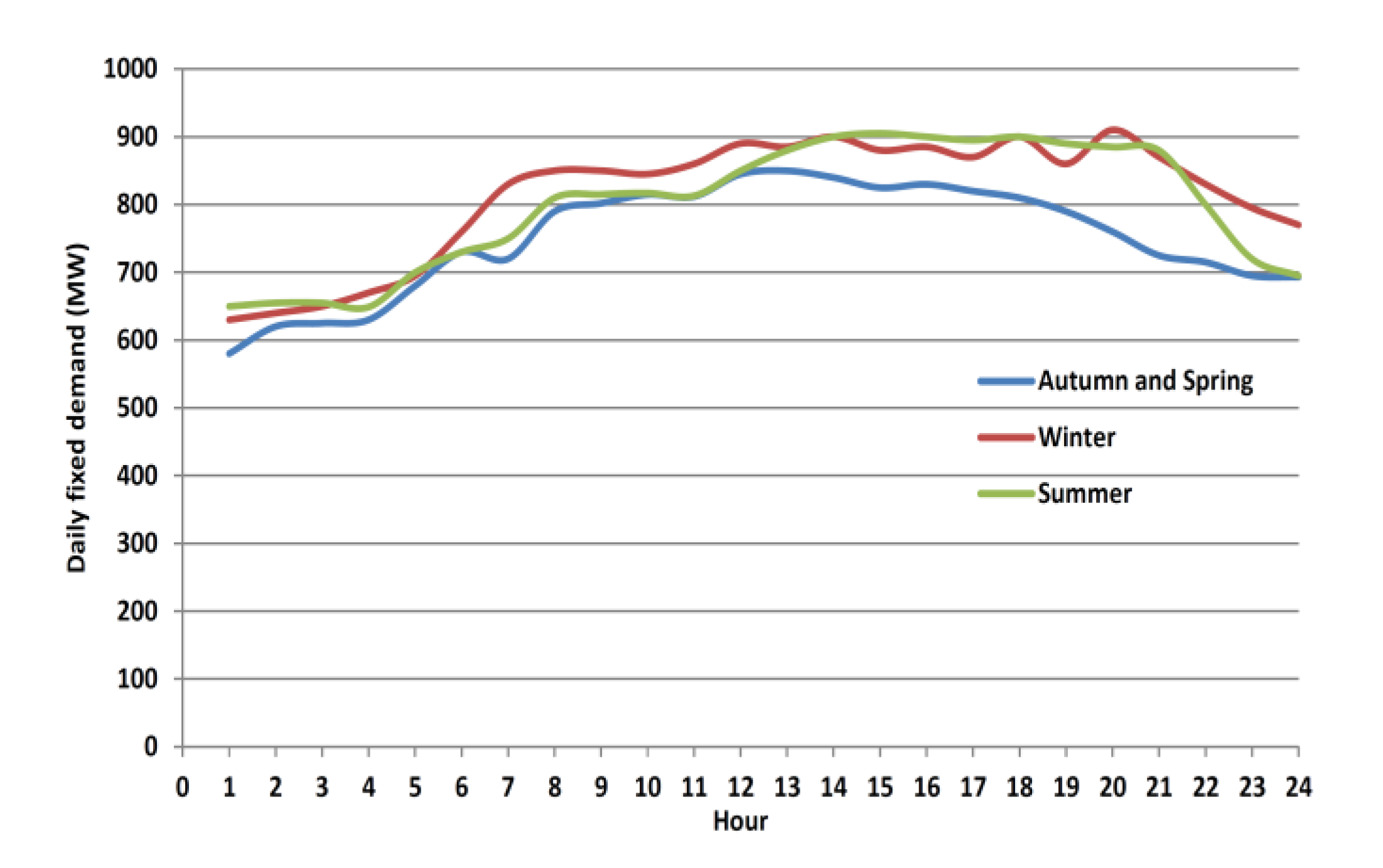
Figure 5. Daily flexible demand.

The following four simulations were performed to investigate the impacts of the ESS specifications on the expansion planning results.

Simulation 1:

- Depth of discharge is considered fixed and equal to 0.9.
- The ESSs presented in Table 3 are considered in the studies.

Simulation 2:

- Depth of discharge is considered fixed and equal to 0.9.
- The efficiency of the second ESS in Table 3 is considered equal to % 80.

Simulation 3:

- Depth of discharge is considered fixed and equal to 1.
- The efficiency of the second ESS in Table 3 is considered equal to % 80.

Simulation 4:

- Curve presented in Figure 6 is considered to model the relation between cycle life and depth of discharge.
- The ESSs presented in Table 3 are considered in the studies.

Figure 6. Cycle life curve.

Simulation 1: The results of the ESSs expansion planning for simulation 1 are presented in Table 4. In this case, only the second ESS is proposed for development due to the lower cost. The simulation results show that in this case, the demand interruption and the spillage of wind output will be zero. The number of charging/discharging cycles according to the equation defined in Equation (32) will be equal to 1.225. If the ESS is operated in all days of the year, annual cycles are about 447 cycles. Thus, during the life of this ESS (15 years), the number of required cycles will be about 6700 cycles. Therefore, there will be no challenge regarding the limitation of the charging/discharging cycles. On the other hand, using an ESS with the same specifications as the second ESS, but with fewer charging/discharging cycles, will be a good option in terms of the lower possible investment cost.

Table 4. ESS expansion planning results is simulation 1.

Simulation 2: In this case, the efficiency of the second ESS is considered to be 80%. The output of the proposed model is shown in Table 5. As can be seen, in this case, ESS expansion for both ESSs is recommended. Because the first ESS is more efficient despite the higher investment cost. The simulations reveal that in this situation, the first and second ESSs have the same number of charging/discharging cycles (1.1 and 0.9, respectively). Thus, for the first and second ESSs, the total number of charging/discharging cycles needed is 8030 and 4927 cycles, respectively.

Table 5. ESS expansion planning results is simulation 2.

Simulation 3: In this case, all assumptions are considered similar to the second simulation, but the depth of discharge is assumed to be 1. It means that the full capacity of the ESSs is used. Table 6 presents the simulation results in this case. As can be seen in this case, the capacities of ESSs are reduced. In this case, the numbers of cycles required per day for the first and second ESSs will be equal to 1.24 and 1.04, respectively. Therefore, the numbers of cycles required during the life of the first and second ESSs are equal to 9052 and 5694 cycles, respectively.

Table 6. ESS expansion planning results is simulation 3.

Simulation 4: In this case, the goal is to determine the optimal depth of discharge of the ESSs based on the equations of section 2.2. The curve presented in Figure 6, is considered as the discharge depth/number of cycles curve for ESSs. The simulation results show that in this case the proposed depth of discharge is equal to 100%. This is because in this case, even with a discharge depth of 100%, the required number of charging/discharging cycles will be less than the limit of charging/discharging cycles. This indicates the correct operation of the proposed model.

If the relation N_max= -5000*DOD+10000 is considered for modeling the discharge depth/number of cycles curve, the proposed depth of discharge will be %62.3. Because with 100% discharge depth, the maximum charging/discharging cycles will be 5000, which does not meet the required number of cycles during the ESS life.

By comparing the first and second simulations, it can be concluded that the change in ESS's efficiency has a significant effect on the composition of the developed ESSs. Comparing the second and third simulations shows that with a 10% increase in depth of discharge, the energy capacity of the first and second ESSs decreased by 10 and 22%, respectively. On the other hand, the required power capacity is slightly reduced. The results of the fourth simulation also show that optimal optimization of discharge depth can lead to more optimal decisions for ESSs development.

4. Conclusion

In this research, a model is presented for expansion planning of ESSs considering the cycle life. This model determines the optimal technology and capacity of the ESSs. Simulations were performed for different modes, and ESS expansion planning results are presented. In these studies, the impact of changing the efficiency of ESSs and the depth of discharges was studied. In each case, the number of daily charging/discharging cycles and the minimum number of charging/discharging cycles required during the life of ESSs are determined. Studies were performed for two modes of the constant discharge depth and linear modeling of the discharge depth.

The simulation results show that a reduction in the ESS efficiency reduces the energy capacity of the ESS. Efficiency significantly affects the number of daily charging/discharging cycles. The degree of impact also depends on the specifications of other ESSs. The results show that a 10% increase in the ESS depth of the discharge reduces the ESS energy capacity required by about 20%. Furthermore, the number of daily charging/discharge cycles increases by about 14%, which indicates an increase in ESS participation in energy supply.

Data Availability Statement

All data generated or analyzed during this study are included in this article.

Conflicts of Interest

The authors certify they have NO affiliations with or involvement in any organization or entity with any financial interest.

References

Wen, S.; Lan, H.; Fu, Q.; Yu, D.C.; Zhang, L. Economic Allocation for Energy Storage System Considering Wind Power Distribution. IEEE Trans. Power Syst. 2014, 30, 644–652. [Google Scholar] [CrossRef]
Oh, S.; Kong, J.; Yang, Y.; Jung, J.; Lee, C.-H. A multi-use framework of energy storage systems using reinforcement learning for both price-based and incentive-based demand response programs. Int. J. Electr. Power Energy Syst. 2023, 144. [Google Scholar] [CrossRef]
Hessami, M.A.; Bowly, D. R. Economic Feasibility and Optimization of an Energy Storage System for Portland Wind Farm (Victoria, ustralia). Appl. Energ. 2011, 88, 2755–2763. [Google Scholar] [CrossRef]
Yi, J.H.; Cherkaoui, R.; Paolone, M.; Shchetinin, D.; Knezovic, K. Expansion planning of active distribution networks achieving their dispatch ability via energy storage systems. Appl. Energ. 2022, 326, 119942. [Google Scholar] [CrossRef]
Bodong, S.; Wiseong, J.; Chengmeng, L.; Khakichi, A. Economic management and planning based on a probabilistic model in a multi-energy market in the presence of renewable energy sources with a demand-side management program. Energy 2023, 269. [Google Scholar] [CrossRef]
Ghofrani, M.; Arabali, A.; Etezadi-Amoli, M.; Fadali, M.S. A Framework for Optimal Placement of Energy Storage Units Within a Power System With High Wind Penetration. IEEE Trans. Sustain. Energy 2013, 4, 434–442. [Google Scholar] [CrossRef]
Zhang, N.; Kang, C.; Kirschen, D.S.; Xia, Q.; Xi, W.; Huang, J.; Zhang, Q. Planning Pumped Storage Capacity for Wind Power Integration. IEEE Trans. Sustain. Energy 2012, 4, 393–401. [Google Scholar] [CrossRef]
Fallahi, F.; Nick, M.; Riahy, G.H.; Hosseinian, S.H.; Doroudi, A. The value of energy storage in optimal non-firm wind capacity connection to power systems. Renew. Energy 2014, 64, 34–42. [Google Scholar] [CrossRef]
Hozouri, M.A.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. On the Use of Pumped Storage for Wind Energy Maximization in Transmission-Constrained Power Systems. IEEE Trans. Power Syst. 2015, 30, 1017–1025. [Google Scholar] [CrossRef]
Pandzic, H.; Wang, Y.; Qiu, T.; Dvorkin, Y.; Kirschen, D.S. Near-Optimal Method for Siting and Sizing of Distributed Storage in a Transmission Network. IEEE Trans. Power Syst. 2014, 30, 2288–2300. [Google Scholar] [CrossRef]
Kargarian, A.; Hug, G. Optimal sizing of energy storage systems: a combination of hourly and intra-hour time perspectives. IET Gener. Transm. Distrib. 2016, 10, 594–600. [Google Scholar] [CrossRef]
Dehghan, S.; Amjady, N. Robust Transmission and Energy Storage Expansion Planning in Wind Farm-Integrated Power Systems Considering Transmission Switching. IEEE Trans. Sustain. Energy 2016, 7, 765–774. [Google Scholar] [CrossRef]
Dvorkin, Y.; Fernandez-Blanco, R.; Wang, Y.; Xu, B.; Kirschen, D.S.; Pandzic, H.; Watson, J.-P.; Silva-Monroy, C.A. Co-Planning of Investments in Transmission and Merchant Energy Storage. IEEE Trans. Power Syst. 2017, 33, 245–256. [Google Scholar] [CrossRef]
Zhang, X.; Conejo, A.J. Coordinated Investment in Transmission and Storage Systems Representing Long- and Short-Term Uncertainty. IEEE Trans. Power Syst. 2018, 33, 7143–7151. [Google Scholar] [CrossRef]
Rafiei, S.; Mohammadi Ivatlo, A.B. Bi-level model for generation expansion planning with contract pricing of renewable energy in the presence of energy storage. IET Renew Power Generat. 2019, 13, 1544–1553. [Google Scholar] [CrossRef]
Xie, S.; Hu, Z.; Wang, J. Two-stage robust optimization for expansion planning of active distribution systems coupled with urban transportation networks. Appl. Energy 2020, 261. [Google Scholar] [CrossRef]
BiazarGhadikolaei, M.; Shahabi, M.; Barforoushi, T. Expansion planning of energy storages in microgrid under uncertainties and demand response. Int. Trans. Electr. Energy Syst. 2019, 29. [Google Scholar] [CrossRef]
Home-Ortiz, J.M.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Mantovani, J.R.S. A Mixed Integer Conic Model for Distribution Expansion Planning: Matheuristic Approach. IEEE Trans. Smart Grid 2020, 11, 3932–3943. [Google Scholar] [CrossRef]
Gonzalez-RomeroSonja, I.; Wogrin, S.; Gomes, T. Proactive transmission expansion planning with storage considerations. Energ. Strat. Revi. 2019, 24, 154–165. [Google Scholar] [CrossRef]
Gonzalez-RomeroSonja, I.; Wogrin, S.; Gomes, T. Optimal expansion planning considering storage investment and seasonal effect of demand and renewable generation. Renew. Energ. 2019, 138, 937–954. [Google Scholar]
Bahramirad, S.; Reder, W.; Khodaei, A. Reliability-constrained optimal sizing of energy storage system in a micro grid. IEEE Trans. Smart. Grid. 2012, 3, 2056–2062. [Google Scholar] [CrossRef]
Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of energy storage for micro grids. IEEE. Trans. Smart. Grid. 2012, 3, 142–151. [Google Scholar] [CrossRef]
Chen, C.; Duan, S. Optimal allocation of distributed generation and energy storage system in micro grids. IET. Renew. Power. Generat. 2014, 8, 581–589. [Google Scholar] [CrossRef]
Yang, P.; Nehorai, A. Joint Optimization of Hybrid Energy Storage and Generation Capacity With Renewable Energy. IEEE Trans. Smart Grid 2014, 5, 1566–1574. [Google Scholar] [CrossRef]
Luo, Y.; Shi, L.; Tu, G. Optimal sizing and control strategy of isolated grid with wind power and energy storage system. Energy Convers. Manag. 2014, 80, 407–415. [Google Scholar] [CrossRef]
Xiao, J.; Bai, L. Sizing of energy storage and diesel generators in an isolated micro grid using discrete Fourier transform (DFT). IEEE. Trans. Power. Sys. 2014, 5, 907–916. [Google Scholar]
Sfikas, E.E.; Katsigiannis, Y.A.; Georgilakis, P.S. Simultaneous capacity optimization of distributed generation and storage in medium voltage micro grids. Inter. J. Electric. Power. Energ. Sys. 2015, 67, 101–113. [Google Scholar] [CrossRef]
Hajipour, H.; Bozorg, M.; Fotuhi-Firuzabad, M. Stochastic capacity expansion planning of remote micro grids with wind farms and energy storage. IEEE. Trans. Power. Sys. 2015, 6, 491–498. [Google Scholar]
Liu, Y.; Du, W.; Xiao, L.; Wang, H.; Bu, S.; Cao, J. Sizing a Hybrid Energy Storage System for Maintaining Power Balance of an Isolated System With High Penetration of Wind Generation. IEEE Trans. Power Syst. 2016, 31, 3267–3275. [Google Scholar] [CrossRef]
Awad, A.S.A.; El-Fouly, T.H.M.; Salama, M.M.A. Optimal ESS Allocation and Load Shedding for Improving Distribution System Reliability. IEEE Trans. Smart Grid 2014, 5, 2339–2349. [Google Scholar] [CrossRef]
Xiong, P.; Singh, C. Optimal Planning of Storage in Power Systems Integrated With Wind Power Generation. IEEE Trans. Sustain. Energy 2016, 7, 232–240. [Google Scholar] [CrossRef]
Yang, P.; Nehorai, A. Joint Optimization of Hybrid Energy Storage and Generation Capacity With Renewable Energy. IEEE Trans. Smart Grid 2014, 5, 1566–1574. [Google Scholar] [CrossRef]
Hessami, M.A.; Bowly, D. Economic feasibility and optimization of an energy storage system for Portland Wind Farm (Victoria, Australia). 2011, Appl. Energ. 88, 2755-2763.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.