Resolution of the 3n+1 Problem Using Inequality Relation Between Indices of 2 and 3

Preprint

Article

Resolution of the 3n+1 Problem Using Inequality Relation Between Indices of 2 and 3

Altmetrics

Downloads

552

Views

609

Comments

Gaurav Goyal^*

This version is not peer-reviewed

Submitted:

06 May 2023

Posted:

09 May 2023

You are already at the latest version

Alerts

Abstract

Collatz conjecture states that an integer $n$ reduces to $1$ when certain simple operations are applied to it. Mathematically, the Collatz function is written as $f^k(n) = \frac{3^kn + C}{2^{z}}$, where $z, k, C \geq 1$. Suppose the integer $n$ violates Collatz conjecture by reappearing as $2^in$, where $i \geq 1$, then the equation modifies to $n \left(1 - \frac{3^k}{2^{z}2^i}\right) = \frac{C}{2^{z}2^i}$. The article takes an elementary approach to this problem by calculating the bounds on the values of $\frac{C}{2^{z}2^i}$ and $1 - \frac{3^k}{2^{z}2^i}$. Correspondingly, an upper limit on the integer $n$ is placed that can re-appear in the sequence. The integer $n$ lies in the $(-\infty, 5)$ range, and the limit on the number of odd steps is $k < 3$. Finally, it is shown that no integer chain exists that does not lead to 1.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Introduction

Collatz conjecture, or the

3 n + 1

problem, is a simple arithmetic function applied to positive integers. If the integer is odd, triple it and add one. It is called the odd step. If the integer is even, it is divided by two and is denoted as the even step. It is conjectured that every integer will eventually reach the number 1. Much work has been done to prove or disprove this conjecture [1,2,3,4].

The problem is easy to understand, and since it has attracted much attention from the general public and experts alike, the literature is endless. Still, the efforts made to tackle the

3 n + 1

problem can generally be categorized under the following headings:

Experimental or computational method: This method uses computational optimizations to verify Collatz conjecture by checking numbers for convergence [5,6,7]. Numbers as large as $10^{20}$ have shown no divergence from the conjecture.
Arguments based on probability: On average, the sequence of numbers tends to shrink in size so that divergence does not occur. On average, each odd number is $3 / 4$ of the previous odd integer [8].
Evaluation of stopping times: Many researchers seem to work on the $3 n + 1$ problem from this approach [9,10,11,12,13]. In essence, it is sought to prove that the Collatz conjecture yields a number smaller than the starting number.
Mathematical induction: It is perhaps the most common method to “prove" the Collatz conjecture. The literature involving this particular method seems endless [14,15].

The issue is that the Collatz conjecture is a straightforward arithmetic operation, while the methods used are not. The mismatch is created because the problem has attracted the attention of brilliant people in mathematics who are used to dealing with complex issues with equally complex tools. Therefore, an elementary analysis of the problem might be lacking.

This article takes a rudimentary approach to the Collatz conjecture and treats it as a problem of inequality between indices of 2 and 3. The inequality relation will be turned into equality using variables. The values of these variables will be investigated, and it will be shown that the Collatz conjecture does not need complex analysis.

2. Prerequisite

Consider that n is a positive odd integer, and the following Collatz function f is applied.

f (n) = \{\begin{matrix} 3 n + 1, & if n is odd \\ \frac{n}{2} & if n is even \end{matrix}

A sequence is formed by performing this operation repeatedly, taking the result at each step as the input for the next. Collatz conjecture states that, for all n,

f^{k} (n) = 1

for some non-negative integer k, where the function is applied to n exactly k times. Let the sequence of steps be:

1^st odd step, 1^st even step, ⋯, ${(k - 1)}^{t h}$ odd step, ${(k - 1)}^{t h}$ even step

The sequence ends at the odd term; an odd step is applied to obtain an even integer. This even integer is computed in terms of the function

f^{k} (n)

\begin{matrix} f^{k} (n) & = 3 \{\frac{\{3 \frac{\{3 \frac{\{\frac{3 n + 1}{2^{z_{1}}} + 1\}}{2^{z^{2}}} + 1\}}{2^{z_{3}}} + 1\}}{⋮}\} + 1 \\ f^{k} (n) & = \frac{3^{k} n + 3^{k - 1} + 3^{k - 2} 2^{z_{1}} + \dots + 3^{1} 2^{z_{1} + z_{2} + \dots + z_{k - 2}} + 2^{z_{1} + z_{2} + \dots + z_{k - 2} + z_{k - 1}}}{2^{z_{1} + z_{2} + \dots + z_{k - 2} + z_{k - 1}}} \\ f^{k} (n) & = \frac{3^{k} n + C}{2^{z}} \end{matrix}

(1)

where

z = z_{1} + z_{2} + \dots + z_{k - 2} + z_{k - 1}

and

C = 3^{k - 1} + 3^{k - 2} 2^{z_{1}} + \dots + 3^{1} 2^{z_{1} + z_{2} + \dots + z_{k - 2}} + 2^{z_{1} + z_{2} + \dots + z_{k - 2} + z_{k - 1}}

(2)

It is noted that

(z, C) > 0

3. Methodology

One of the significant results of the Collatz conjecture is that “almost all orbits of the Collatz map attain almost bounded values [9,10]." In simpler words, suppose the Collatz conjecture is valid up to the integer

n - 1

. To test if the integer n complies with the Collatz conjecture, it is enough to show that the Collatz function attains a value smaller than the integer n.

Secondly, for the integer n to repeat and form a closed chain cycle, an integer of the form

2^{i} n

must appear in the sequence where

i \geq 1

. Let

f^{k} (n) = 2^{i} n

in Eq. (1).

\begin{matrix} 2^{i} n & = \frac{3^{k} n + C}{2^{z}} \\ n (1 - \frac{3^{k}}{2^{z} 2^{i}}) & = \frac{C}{2^{z} 2^{i}} \end{matrix}

(3)

Eq. (3) tells that the maximum n that can repeat depends on the value of

1 - \frac{3^{k}}{2^{z} 2^{i}}

and the value of

\frac{C}{2^{z} 2^{i}}

Therefore, a basic strategy towards resolving the

3 n + 1

problem can be outlined as follow:

Establish the conditions that prevent the Collatz sequence from falling below the starting integer and also allow for the starting integer to re-appear.
Obtain bounds on $\frac{C}{2^{z} 2^{i}}$ .
Obtain bounds on $1 - \frac{3^{k}}{2^{z} 2^{i}}$ .

4. Conditions for an unbounded Collatz orbit & repeating integers

For an unbounded Collatz orbit, it is required that every integer in the Collatz sequence is greater than n. Therefore, the integer obtained after

{(k - 1)}^{t h}

even step obeys the following equation

\begin{matrix} f^{k - 1} (n) & > n \\ \frac{3^{k - 1} n + C}{2^{z}} & > n \\ n (1 - \frac{3^{k - 1}}{2^{z}}) & < \frac{C}{2^{z}} \end{matrix}

The above inequality is valid for only some values of

(n, C, k, z)

; therefore, it cannot be used as a general statement. However, if the value in the parenthesis of LHS is allowed to be a negative integer, then the inequality becomes true for all

(n, C)

. Hence, the necessary condition for an unbounded Collatz orbit is

\frac{3^{k - 1}}{2^{z}} > 1

(4)

Note that the indices of 3 and 2 are equivalent, i.e., the index of 3 is

k - 1

, and there are

k - 1

terms in z.

Similarly, the following relation should be true for n to be a positive integer in Eq. (3):

\frac{3^{k}}{2^{z} 2^{i}} < 1

(5)

Equation (4) and (5) are the two necessary conditions for an unbounded Collatz orbit with a repeating integer n.

5. Bounds on the value of $\frac{C}{2^{z} 2^{i}}$

5.1. Upper bound

Eq. (2) is re-written as

\begin{matrix} \frac{C}{2^{z} 2^{i}} = \underset{First term}{\underset{︸}{\frac{3^{k - 1}}{2^{z} 2^{i}}}} + \underset{Sec ond term}{\underset{︸}{\frac{3^{k - 2} 2^{z_{1}}}{2^{z} 2^{i}}}} + \dots + \underset{Last term}{\underset{︸}{\frac{2^{z}}{2^{z} 2^{i}}}} \end{matrix}

Analysis of each term starts with the Eq. (5).

First term

\begin{matrix} \frac{3^{k}}{2^{z} 2^{i}} & < 1 \\ \frac{3^{k - 1}}{2^{z} 2^{i}} & < \frac{1}{3} \end{matrix}

Second term

\begin{matrix} \frac{3^{k}}{2^{z} 2^{i}} & < 1 \\ \frac{3^{k - 2} 2^{z_{1}}}{2^{z} 2^{i}} & < \frac{2^{z_{1}}}{3^{2}} \end{matrix}

The indices of 2 and 3 on the RHS are not equivalent, i.e., the index of 3 is two while the index of 2 is

z_{1}

. Let

(k - 1) = 1

in Eq. (4) and manipulate as follow

\begin{matrix} \frac{3^{k - 1}}{2^{z}} & > 1 \\ \frac{3^{1}}{2^{z_{1}}} & > 1 \\ \frac{2^{z_{1}}}{3^{1}} & < 1 \\ \frac{2^{z_{1}}}{3^{2}} & < \frac{1}{3} \end{matrix}

Therefore, the value of the second term is

\frac{3^{k - 2} 2^{z_{1}}}{2^{z} 2^{i}} < \frac{1}{3}

Similarly, it is concluded that all terms in the expansion of

\frac{C}{2^{z} 2^{i}}

are less than

\frac{1}{3}

Last term

\begin{matrix} \frac{3^{k}}{2^{z} 2^{i}} & < 1 \\ \frac{2^{z}}{2^{z} 2^{i}} & < \frac{2^{z}}{3^{k}} \\ \frac{2^{z}}{2^{z} 2^{i}} & < \frac{1}{3} \end{matrix}

The value of the last term must be investigated further. The last term is simplified to

\frac{1}{2^{i}} < \frac{1}{3}

. A value less than

\frac{1}{3}

means

2^{i} \geq 4

i \geq 2

. In other words, starting from a positive integer n, it is impossible to obtain the integer

2 n

directly after an odd step.

Finally, there are k terms in the expansion of

\frac{C}{2^{z} 2^{i}}

and each term is less than

\frac{1}{3}

. Therefore,

\frac{C}{2^{z} 2^{i}} < \frac{k}{3}

(6)

5.2. Lower bound

Analysis of each term starts with the Eq. (4).

First term

\begin{matrix} \frac{3^{k - 1}}{2^{z}} & > 1 \\ \frac{3^{k - 1}}{2^{z}} & > \frac{1}{3} \\ \frac{3^{k - 1}}{2^{z} 2^{i}} & > \frac{1}{2^{i} 3} \end{matrix}

Second term

\begin{matrix} \frac{3^{k - 1}}{2^{z}} & > 1 \\ \frac{3^{k - 2} 2^{z_{1}}}{2^{z}} & > \frac{2^{z_{1}}}{3} \\ \frac{3^{k - 2} 2^{z_{1}}}{2^{z}} & > \frac{1}{3} \\ \frac{3^{k - 2} 2^{z_{1}}}{2^{z} 2^{i}} & > \frac{1}{2^{i} 3} \end{matrix}

Similarly, it is concluded that all terms in the expansion of

\frac{C}{2^{z} 2^{i}}

are greater than

\frac{1}{2^{i} 3}

. There are k terms in the expansion of

\frac{C}{2^{z} 2^{i}}

and each term is greater than

\frac{1}{2^{i} 3}

. Therefore,

\frac{C}{2^{z} 2^{i}} > \frac{k}{2^{i} 3}

(7)

6. Bounds on the value of $(1 - \frac{3^{k}}{2^{z} 2^{i}})$

6.1. Upper bound

Let the following inequality be valid for a repeating integer n

n (1 - \frac{3^{k}}{2^{z} 2^{i}}) > 1

Therefore, using Eq. (3) and (6)

\begin{matrix} \frac{C}{2^{z} 2^{i}} & > 1 \\ \frac{k}{3} & > 1 \\ k & > 3 \end{matrix}

The above equation does not include the known repeating cycle of

1, 4, 2, 1

for which

k = 1

. It is inferred that

n (1 - \frac{3^{k}}{2^{z} 2^{i}})

is less than 1 but greater than some real number p where

p < 1

so that the inequality

k \geq 1

is obtained. Therefore,

n (1 - \frac{3^{k}}{2^{z} 2^{i}}) < 1

(8)

6.2. Lower bound

Take the Eq. (5) and manipulate as follow:

\begin{matrix} 2^{z} 2^{i} & > 3^{k} \\ 2^{z} & > \frac{3^{k}}{2^{i}} \\ 3^{k} - 2^{z} & < 3^{k} - \frac{3^{k}}{2^{i}} \\ \frac{3^{k}}{2^{z}} - 1 & < \frac{3^{k}}{2^{z}} - \frac{3^{k}}{2^{z} 2^{i}} \\ \frac{3^{k}}{2^{z}} & < 1 + \frac{3^{k}}{2^{z}} - \frac{3^{k}}{2^{z} 2^{i}} \\ \frac{3^{k}}{2^{z} 2^{i}} & < \frac{1}{2^{i}} + \frac{3^{k}}{2^{z} 2^{i}} - \frac{3^{k}}{2^{z} 2^{i} 2^{i}} \\ 1 - \frac{3^{k}}{2^{z} 2^{i}} & > 1 - \frac{1}{2^{i}} - \frac{3^{k}}{2^{z} 2^{i}} + \frac{3^{k}}{2^{z} 2^{i} 2^{i}} \\ 1 - \frac{3^{k}}{2^{z} 2^{i}} & > - \frac{3^{k}}{2^{z} 2^{i}} \{1 - \frac{1}{2^{i}}\} + \{1 - \frac{1}{2^{i}}\} \\ 1 - \frac{3^{k}}{2^{z} 2^{i}} & > - \frac{3^{k}}{2^{z} 2^{i}} \{1 - \frac{1}{2^{i}}\} \\ 1 & > \frac{3^{k}}{2^{z} 2^{i} 2^{i}} \\ 2^{i} & > \frac{3^{k}}{2^{z} 2^{i}} \\ 1 - \frac{3^{k}}{2^{z} 2^{i}} & > 1 - 2^{i} \end{matrix}

(9)

7. Resolution to the $3 n + 1$ problem

7.1. Part 1

Substitute Eq. (9) and (6) in Eq. (3) to obtain the range of integers that repeat in the Collatz sequence.

\begin{matrix} n < \frac{k}{3} {(1 - 2^{i})}^{- 1} \end{matrix}

(10)

For all values of

(k, i)

, the integer n is a negative integer. For the lowest value of

(k, i) = (1, 1)

, the integer n belongs to the range

(- \infty, 0)

. Thus, all negative integers have a possibility of repeating. The next question regarding which negative integers do repeat is left unanswered.

7.2. Part 2

Substitute Eq. (8) and (7) in Eq. (3) to obtain

\begin{matrix} 1 & > \frac{k}{2^{i} 3} \\ k & < 2^{i} 3 \end{matrix}

Notice that k is independent of n in the above inequality.

When an integer of the form

2^{i} n

is obtained, only even steps occur until the integer n is reached; that is, the value of k does not increase or decrease after that. Therefore, the number of odd steps required to reach

2^{i - 1} n

k < 2^{i - 1} 3

, odd steps required to reach

2^{i - 2} n

k < 2^{i - 2} 3

and so on. Since k is unchanged after

2^{i} n

, the new limits placed on k do not affect the value of k. Similarly, the number of odd steps required to reach n is obtained by letting

i = 0

, i.e.,

k < 3

7.3. Value of n for $k < 3$

The value of n for

k = 1

is not calculated as it is easy to show

(n, k) = (1, 1)

. For

k = 2

, the value of n is computed as

\begin{matrix} 2^{i} n & = \frac{3^{2} n + 3 + 2^{z_{1}}}{2^{z_{1}}} \\ n & = \frac{3 + 2^{z_{1}}}{2^{z} 2^{i} - 9} \end{matrix}

z_{1}

is calculated according to Eq. (4) and is found

z_{1} = 1

. For

2^{z} 2^{i} > 9

, the value of

2^{z} 2^{i} - 9 > 1

, therefore,

\begin{matrix} n & = \frac{3 + 2}{2^{z} 2^{i} - 9} \\ n & = \frac{5}{2^{z} 2^{i} - 9} \\ n & < 5 \end{matrix}

Therefore, the integers that repeat in the Collatz sequence lie in the range

(- \infty, 0)

, or satisfy the inequality

(n, k) < (5, 3)

8. Do all positive integers reach 1?

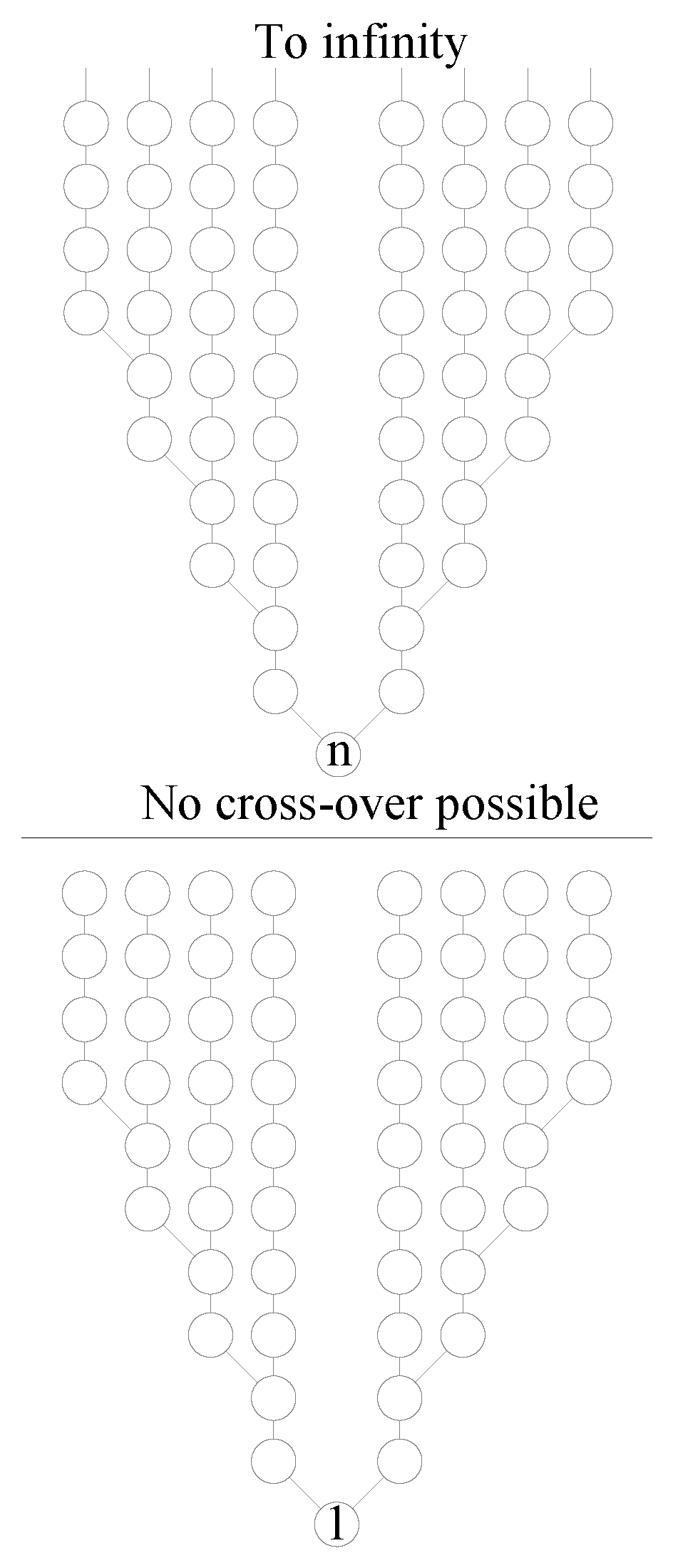
Let there exist a number chain that does not converge to 1. Since the only closed chain in the

3 n + 1

series is

1, 4, 2, 1

, this n-chain is an open chain. The n-chain converges to n from infinity and then diverges to infinity.

The n-chain contains all terms of the form

2^{i} n

where

i \geq 0

. Further, terms arising from the arithmetic function

3 n + 1

are also part of this chain. Every even integer x in the n-chain is connected to a precursor even number and a precursor odd number (iff

3 m + 1 = x

is possible for some m). Similarly, every odd integer is connected to a precursor even number. The branches that arise out of the n-chain are infinite. In short, the n-chain contains every integer greater than n up to infinity.

However, there should exist no linkage between the n-chain and the 1-chain. Because, if there were some linkage, all the integers in the n-chain would converge to 1 using the said linkage.

It is absurd, as shown in Figure 1, as this means the 1-chain ends abruptly below n. It implies that there exists no integer

2 x

in the n-chain such that

x < n

. Conversely, there exists no x in the 1-chain such that

3 x + 1 > n

It is concluded that a n-chain that does not converge to 1 is impossible.

9. Conclusion

This article re-writes the Collatz sequence in the form

n (1 - \frac{3^{k}}{2^{z} 2^{i}}) = \frac{C}{2^{z} 2^{i}}

, where

\frac{C}{2^{z} 2^{i}} = \frac{3^{k - 1}}{2^{z} 2^{i}} + \frac{3^{k - 2} 2^{z_{1}}}{2^{z} 2^{i}} + \dots + \frac{2^{z}}{2^{z} 2^{i}}

. Conditions for an unbounded Collatz orbit and repeating integers are discovered. It helps in placing bounds on the value of

(1 - \frac{3^{k}}{2^{z} 2^{i}})

and

\frac{C}{2^{z} 2^{i}}

. Correspondingly, it is found that the integers that repeat in the Collatz sequence lie in the range

(- \infty, 0)

, or

(n, k) < (5, 3)

References

Lagarias, J.C. The ultimate challenge: The 3x+ 1 problem; American Mathematical Soc., 2010.
Lagarias, J.C. The 3x+ 1 problem: An annotated bibliography (1963–1999). The ultimate challenge: the 3x 2003, 1, 267–341. [Google Scholar]
Lagarias, J.C. The 3x+ 1 problem: An annotated bibliography, II (2000-2009). arXiv preprint math/0608208.
Lagarias, J.C. The 3x+ 1 problem: An annotated bibliography. preprint 2004. [Google Scholar]
Barina, D. Convergence verification of the Collatz problem. The Journal of Supercomputing 2021, 77, 2681–2688. [Google Scholar] [CrossRef]
Rahn, A.; Sultanow, E.; Henkel, M.; Ghosh, S.; Aberkane, I.J. An algorithm for linearizing the Collatz convergence. Mathematics 2021, 9, 1898. [Google Scholar] [CrossRef]
Yolcu, E.; Aaronson, S.; Heule, M.J. An Automated Approach to the Collatz Conjecture. CADE, 2021, pp. 468–484.
Barghout, K. On the Probabilistic Proof of the Convergence of the Collatz Conjecture. Journal of Probability and Statistics 2019, 2019. [Google Scholar] [CrossRef]
Terras, R. A stopping time problem on the positive integers. Acta Arithmetica 1976, 3, 241–252. [Google Scholar] [CrossRef]
Tao, T. Almost all orbits of the Collatz map attain almost bounded values. Forum of Mathematics, Pi. Cambridge University Press, 2022, Vol. 10, p. e12.
Jiang, S.G. Collatz total stopping times with neural networks. World Scientific Research Journal 2021, 7, 296–301. [Google Scholar]
Applegate, D.; Lagarias, J. Lower bounds for the total stopping time of 3n+1 iterates. Mathematics of computation 2003, 72, 1035–1049. [Google Scholar] [CrossRef]
Chamberland, M. Averaging structure in the 3x+1 problem. Journal of Number Theory 2015, 148, 384–397. [Google Scholar] [CrossRef]
Ren, W. A new approach on proving Collatz conjecture. Journal of Mathematics 2019, 2019. [Google Scholar] [CrossRef]
Orús-Lacort, M.; Jouis, C. Analyzing the Collatz Conjecture Using the Mathematical Complete Induction Method. Mathematics 2022, 10, 1972. [Google Scholar] [CrossRef]

Figure 1. n-chain and 1-chain shown for representation purpose only; may not be factually correct.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Resolution of the 3n+1 Problem Using Inequality Relation Between Indices of 2 and 3

Abstract

1. Introduction

2. Prerequisite

3. Methodology

4. Conditions for an unbounded Collatz orbit & repeating integers

5. Bounds on the value of C 2 z 2 i

5.1. Upper bound

5.2. Lower bound

6. Bounds on the value of 1 − 3 k 2 z 2 i

6.1. Upper bound

6.2. Lower bound

7. Resolution to the 3 n + 1 problem

7.1. Part 1

7.2. Part 2

7.3. Value of n for k < 3

8. Do all positive integers reach 1?

9. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

5. Bounds on the value of $\frac{C}{2^{z} 2^{i}}$

6. Bounds on the value of $(1 - \frac{3^{k}}{2^{z} 2^{i}})$

7. Resolution to the $3 n + 1$ problem

7.3. Value of n for $k < 3$