Prerpints.org logo
Preprint
Article

The Algebraic Approach: The Double-Slit Experiment Explained

Altmetrics

Downloads

205

Views

80

Comments

0

This version is not peer-reviewed

Submitted:

06 April 2023

Posted:

07 April 2023

You are already at the latest version

Alerts
Abstract
We present a new vision on the double-slit experiment (DSE), that does not use any waves or the so-called wave-particle duality. It is based on particles, viewed as localized vibrations. Rather than being illogical, or mysterious, the approach reproduces logically the interference patterns observed externally, using the well-known ``amplification of stimulated emission'' (ASE). The conservation of particle number is not observed. Different particles can present ASE with in-phase or counter-phase behavior, making the patterns observed for electrons, other particles, even atoms. The Law of the Excluded Middle (LEM) is not broken illogically in two-states macroscopically, but broken naturally in three or more states, microscopically, using ASE. Any particle supporting ASE, in-phase or counter-phase, can enter a DSE, and provide an external interference pattern. Frequency plays a role, while amplitude is not considered. This work is important in quantum computing, possibly saving cost, time, and welcoming more participants.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

Feynman stated that the double-slit experiment (DSE) “…has in it the heart of quantum mechanics.” and applies to a wide diversity of particles, even atoms [1].
The DSE is usually understood as a demonstration that light and matter can display characteristics of both classically defined waves and particles. Based on [2], we diverge from this interpretation, which is a mixed metaphor, and consider the DSE as a LASER, where LASER means “Light Amplification by Stimulated Emission of Radiation".
We model the DSE mathematically, using rational numbers only [2]. We use the algebraic approach with different edges and updating events, that merge in an ordinary two-dimensional direct graph [3]. We view the DSE as a demonstration of QM, which we explore in various aspects in the next Sections, where the DSE shows many states at once — following the interpretation of QM by Niels Bohr [4].

2. A “One Photon DSE” Is Not Possible

Theoretically, the general state inside a one-dimensional DSE where only one slit a and slit b exist, is given by Ψ , as the one-dimensional Schrödinger equation [5]:
− ℏ 2 2 m d 2 Ψ ( x ) d x 2 = [ E − V ( x ) ] Ψ ( x ) .
with the boundary conditions Ψ ( 0 ) = Ψ ( ∞ ) = 0 . Here, Ψ is also the coherent superposition of the solutions Ψ a and Ψ b , where only slit a or slit b are open at the same time:
Ψ = 1 2 ( Ψ a + Ψ b ) .
Thus, the behavior of systems described by the Niels Bohr interpretation of QM1 is counter-intuitive according to [9] to our usual observed experience, because the coherent superposition appears to break the LEM.
According also to [9], only one photon at a time can exist in the DSE apparatus. This would visibly break the LEM, which means breaking choice and causality, and is incorrect [10]. Choice is broken because one cannot say which of the two slits the one photon can take in the experiment, and there are physically only two slits. Any attempt to determine this, would need an interaction with the particle, which would lead to decoherence, that is, loss of interference [10].
In addition to this choice problem, that remains undefined until today in the DSE, causality seems broken because one has Dirac’s well-cited intuition that "each photon then interferes only with itself”, as mentioned in [9].
These two principles have guided much of QM and the DSE to date, are used in QC, in qubits, and in research such as [9].
However, as this work shows, there is no “one photon DSE”. Both hypothesis are revealed to be certainly inconsistent and yet lots of ink has been spilled in futile attempts to resolve the QM paradox of the GSE. There is “trouble at the lab”, in physics. This includes Nobel laureate Lamb, [11], and has placed extraordinary challenges even for noted lecturers, claiming that the wave-particle duality can be proven by the DSE; that the DSE is somehow a demonstration that light and matter can display characteristics of both classically defined waves and particles, a mixed metaphor that confuses, as a succession of incongruous or ludicrous comparisons.
We herald a different future, by diverging from these two interpretations, which are both non causal. We understand [10] Dirac’s intuition in terms of an equivalence class, not as an identity, preserving causality. Interference then happens between indistinguishable photons in an equivalence class, created by ASE [6,12]. This then says that there is no “one photon DSE”. One may indeed have such low intensity as to inject only one photon in the DSE. But, even though injected with a single photon, one may have 0, 1, 2 or more photons inside, using ASE.
We claim later that this can happen also with electrons, notwithstanding Pauli’s exclusion principle, and other particles, even with atoms/molecules/plasma (objects).
In all these cases, the LEM appears to be broken, and the situation seems unavoidable. It seems broken directly by ASE. In creating three or more states by stimulated emission, stimulated absorption, and emission. Thus, it seems broken by default, by one not being able to tell after all which slit was used, without causing decoherence. There is no YES or NO answer possible, for each of the two slits, even with ASE, one could think.
We also diverge from this interpretation. The LEM is an inescapable bedrock of logical reasoning in binary logic. But any particle supporting ASE, with three or more possible logical states, thus breaking naturally the LEM, can be measured (i.e, embed) in a DSE, as a fixed interference pattern. The two-slits act as a two-state spatial filter, obeying the LEM. Thus, LEM is always obeyed externally, by physical constraint of the DSE, and one has only two possibilities to choose from.
But three or more logic level systems can exist at the same time, as asserted by Pierce, in unpublished notes, before 1910, which is the same QM principle later formulated by Niels Bohr [4], and used here.
Charles Sanders Pierce is well-known to have soundly rejected the idea that all propositions must be either True or False, as in Boolean logic, the same as Frege in semantics [13]. Pierce developed well-understood rules where the LEM is not valid, including some truth tables. A modern treatment can be seen in the results by Jones [14], and [2].
But, three or more logical states impose additional care in their application, since there is no LEM to guarantee results internally, nor a truth-reference exists, to measure success externally. This problem is well-known in land and sea navigation, spacecraft navigation, astronomy, and special relativity, and has been famously studied by Poincaré [15] before QM, in terms of uncertainty, the inverse of coherence, created by ASE. Three or more states are possible, and discontinuous functions can now be differentiated if measurable, which satisfy the mathematical concerns of this work [2].

3. Amplification by Stimulated Emission: ASE

Einstein in 1916-1917 [6,12], used Bohr’s [4] model to famously argue that, in addition to the random2 processes of absorption and emission, a third, new, and coherent process of stimulated emission must exist microscopically for physical bodies, as a result providing experimental evidence for the quantum, reproducing exactly the macroscopically studied, experimental data.
Einstein considered that each change in an electron orbit corresponds to the absorption or emission of one light quantum, and so even normal light from a candle, a lamp, or, radio wave, have a stimulated emission component. Stimulated emission provided the basis for the later invention of the laser (light amplification by stimulated emission of radiation)3.
In steady-state, the DSE is in local thermodynamic equilibrium (LTE), and the Planck statistics must be equal to the Boltzmann statistics [6], but LTE is not required in general, just for the derivation. Thus,
0 = N ˙ = − A N 1 − B ( N 1 − N 2 ) U ( ν )
where N represents the number of objects in either state (a discrete variable, in set Q), 1 or 2, N ˙ is the derivative of the discontinuous function N in respect to time, A is the Einstein coefficient for the emission4 component, B is the Einstein coefficient for stimulated emission, N 1 is the number of objects in state 1, in the lower level, N 2 is the number of objects in the state 2, in the upper level, U ( ν ) is the density of the radiation field between levels 1 and 2, corresponding to the incoming photon in sympathetic resonance, and their separation in energy is given by the Planck formula E = h ν , where h is the Planck constant, and E is the energy difference between levels 1 and 2. For simplicity we only consider two levels, and no degeneracy, but the result is the same.
Note that the intensity of the incoming photon field was not used, which is consistent with the photoelectric effect, and E = h ν , while a wave would require that the amplitude be used. Thus, the wave picture is not represented.
The ratio of the emission and the stimulated emission by the incident photon is given by A / B in Eq.(3), and is [12]:
A / B = 2 h ν 3 / c 2
in which coherence is favored at low frequencies.
Eq.(3) represents, in the second and third terms, what can be seen as a minimal collective effect, of one photon influencing the emission of another photon (see Section IV), as a necessary coherent channel that needs to exist in order to balance the first term. Stimulated emission and stimulated absorption have been extended recently, as well-known, with collective effects by other photons, such as superradiance and superabsorption, into 5 states, but with no essentially new process in the symmetries observed.
Eq.(3) represents a simplified view of the photon fields inside the DSE, with the incident photon with frequency ν , and one stage of “amplification by stimulated emission” (ASE), where the incident photon can be, as shown in Figure 1 next:
1.
removed by stimulated absorption, and thus be annihilated,
2.
copied by stimulated emission (ASE), necessarily in-phase with the incoming photon, and be, thus, interference-capable with the incoming photon, or
3.
continue, but in coherence with (2).
In Figure 1, the photons exit the DSE to the right, as three different photons, two coherent and interference-capable (cases 2 and 3), see the list above, visibly breaking the Law of the Excluded Middle (LEM) (i.e., with three states). The LEM, however, cannot be broken in two-states (i.e., only two slits physically exist). And breaking the LEM in two-states seems logically inconsistent, adding to the “counter-intuitive” lore of QM, here dismissed by using ASE to explain photon multiplication (instead of division, of trying to split the incoming photon).
An object can nonetheless create a photon by stimulated emission5 through the influence of an out-of-range photon in our model, such as by vacuum fluctuations or cosmic rays, as well-known. But the photon is produced necessarily out-of-phase, as an incoherent photon, and is not interference-capable with the incoming photon (this is shown with the color black in Figure 1, and is not caused by the incoming photon).
Interference then happens between indistinguishable photons (e.g., cases 2 and 3) in an equivalence class, created by ASE.
The DSE could still be seen as counter-intuitive, from Figure 1, viewing from the interference in two-state logic. Because it appears to break the LEM6, while one still has the LEM as the inescapable bedrock of logical reasoning in binary logic. A natural question is then satisfied, that three-or-more valued logic systems can be embedded in a two-state logical system, as the interference pattern of a DSE. The states are in different dimensions, and a continuous path in the higher dimension (tri-state) must necessarily map into a discontinuous path in the lower dimension (two-state). This happens due to a well-known theorem in topology and projection [16], that we call TR, standing for Topological Relationship.
This achieves freedom from the LEM in behavior, inside the DSE, while outside the DSE, constrained by the two-slits of the DSE, the two photons can come from either slit or from both slits, and the interference pattern can obey the LEM.
This completes our initial effort of trying to open the “black box” in the quantum state by means of the DSE, with further, better, logical analysis of the interaction process, and we use the Wolfram models of ordinary oriented graphs [3], intended to be as minimal and structureless as possible. Here, is where one can hope to find a “new hypothesis”, where one can make a wider causal sense, with the promise of bringing much higher speed, cybersecurity, and scalability to communication.
It is therefore highly desirable to understand the model of photon interaction, especially in the so-far mysterious and illogical DSE, as key to quantum computation (QC), quantum speed, and cybersecurity.

4. Particle View and Least Action: Universality

A phenomenon may be understood by two very different points of view. First, one may direct the attention towards the internal mechanics of the event. In this approach, starting from outside the attention is focused to consider the internal causes, i.e. the microsystems and their complex microexchanges, that lead to the macrobehavior. Second, one may observe the event only from the outside. In this alternative approach, the attention remains on the external aspects and the macrobehavior is understood only by its macroexchanges through the use of conservation laws and minimization principles [such as the PLA, the principle of least action]. For example, the propagation of light in a medium can be described by considering electromagnetic waves and atoms or, by considering the Fermat’s principle of least time. Both approaches can be used in order to obtain a complete picture of the phenomenon. Since the second approach is usually more concise and not concerned about the many contributing mechanisms, general trends can be easily derived without laborious calculations.
The analysis presented so far, in the three former Sections, has been along the lines of the first approach. In order to bring more insight into the DSE model proposed in this work using ASE [6], it is interesting to consider the same problem, i.e. Eq. (2) or Eq.(3), using the second approach, as universality in mathematics [2] and in physics [17,18,19]. A further advantage is to allow a direct particularization to other DSE cases, from a more general view, as done for the electron in this work.
After absorption of a photon with energy h ν , the object is in an excited state with energy surplus, where now this means also a possible dissociation energy of any breaking bond, as photodissociation. Introducing a reasonable minimization principle for the energy surplus given by "The molecule or atom will evolve in time in such a way as to dispose of the energy surplus in the least amount of time."
One may look for conditions that will enhance the production of excited atoms or excited molecules. Observing the above minimization principle is equivalent to: "The energy surplus will be preferentially used at the fastest energy channel available" as the guiding-idea to enhance the emission of energy in the DSE.
Before Einstein [6,12], a photon was considered part of a formless “fluid”, or classical wave, that can only be emitted or absorbed. Such was the philosophy at the time of Young in 1801 [20], with the DSE [9], confirmed by the well-known Maxwell equations, published by the Royal Society in 1865.
This work considers that the current description of the DSE, however, ignores the creation and annihilation of photons, the ASE, while the LASER is well-known. The existence for the ASE was calculated by Einstein about 100 years after the DSE, in 1917 [12], and occurs by wall interaction as well, therefore even in vacuum. Although it is possible to work with such low light intensities that only one photon enters the DSE apparatus at a time, because amplitude is not a concern for ASE, it is not possible to consider that the number of photons is conserved during that time, even at such low intensities. The opposite is experimentally true, more so at low frequency (see Eq.(4)), so that we expect that “the energy surplus will be preferentially used at the fastest energy channel available,” which is usually stimulated emission, with the emission of a particle, favoring ASE.
We discuss the DSE mathematically, following a model of the type Wolfram introduced [3], with a particular rule, and explain it with an algebraic approach, going from G F ( 3 p ) to G F ( 2 m ) , for a suitable m > p , where m and p are prime numbers, and GF() stands for Galois fields, here considered in a prime extension into finite integers. This is easy and fast to calculate, with modular arithmetic.
But if such a rule is found, one might then go on and ask why — out of the infinite number of possibilities — it is this particular rule, or, for example, a simple rule at all.
For example, a rule that involves more or equal to ternary edges (like our model for light, as tri-state+) cannot apply to a state with only binary edges (like qubits). Thus, any rule that cannot become simple for all cases, is less favored. And like with updating events, branches with different sequences of rules applied may reach equivalent states, and thus merge, as in stimulated emission providing an in-phase copy of the incident photon, and as we found also for electrons, discussed later, where the Pauli exclusion principle forces a “contrarian coherence".
Continuity or classical waves, are not needed [2,10] where the ontological view of the DSE becomes now, however, as ASE dictates — more indicative of a particle in all cases — and does not depend on amplitude.
This is also confirmed by the particle interpretation of the well-known photoelectric effect, which does not depend on amplitude. The energy of a particle in the case of a photon is revealed by the photoelectric effect to be equal to E = h ν , where ν is the frequency of the photon. A particle is a localized vibration, and can be a photon, an electron, a quark, or other manifestation. Wave theory, in contrast, says that the wave extends to infinity, and the intensity should be proportional to the square of the amplitude of the wave. Continuity or classical waves are, thus, less favored as a general description, for wider causal sense. But can be used in universality, as in the foregoing, for the macroscopic sense.
This leads to a discontinuity, such as three or more states transitioning to two-states, and a logical explanation under different rules (including both the absence and presence of the LEM), of all observations, separating behavior from implementation. The foregoing provides for the DSE a similar explanation for electrons, or other particles, notwithstanding the well-known Pauli exclusion principle.

5. The DSE

The foregoing creates an opening to take a “new hypothesis” here.
New Hypothesis: The DSE exemplifies a LASER.
This means that the LEM is not broken in two-states, macroscopically, but naturally in three or more possible states, microscopically [10].
Here, obeying the LEM macroscopically acts as a “Procrustean bed” [10], where binary logic, an arbitrary standard, is used to measure success externally, while completely disregarding the obvious over-simplification that results from the effort, such as three states or more, in a microscopic view, where the quantum operates more decisively. But, why bother with the quantum, when it will not matter for what is seen? Because without it, there is no ASE, and its lessons.
Figure 2 shows multiple stages of ASE for in-phase multiplication in the DSE, more likely at lower frequencies [6], due to stimulated emission prevalence, as the fastest channel to reduce the surplus energy from the incoming photon, before the object is even changed by absorption.
Stimulated emission can now be considered for coherent and secure traffic. Between the entrance and the exit of a DSE, which builds an end-to-end communication link that one cannot disturb under penalty of changing the result, one is not only capable of routing photons, but also of coding incoming photons to produce coded outgoing ones, in a coherent process, which creates the very conditions for external interference of the additional photons created in the process [10]. This reduces the influence of white noise, and is highly resilient to low power — interference is produced by frequency, not by amplitude — contrary to classical waves.
The fundamental insight [10] is that a photon exiting the apparatus can be inferred, estimated, coherently by another photon from the same or other slot, at a far away screen, and does not even have to be an exact, verbatim copy of the incoming photon.
The significant aspect [10] in QC, as the result of coherent superposition in Eq.(2), and Eq.(3), is still that the actual photon in one slit is one selected from a set of possible, like photons at the same, or the other, slit. This is achieved by coherence in Eq.(2) or Eq.(3), whereby the photon is copied in-phase inside the apparatus, using ASE, and become indistinguishable with each other, as both exit. As a consequence, the photon has the proper frequency and phase for interference, externally.
The once fuzzy concept of the “DSE” or wave-particle duality, is now proposed in a precise way as stated above, as a LASER, and using binary logic, with the LEM being strictly valid. It does not matter which slit is used for exit, the same slit, and/or the other slit, can now be used by two or more photons, and, likely, there are plenty of similar photons made available through ASE, as shown in Figure 2.
Previous work has been included, selectively, in the references given so far. However, they are necessarily inconsistent when applied to the DSE, which can be seen as a consequence of using the symmetries of a binary system for the photon, that must use the LEM and binary logic. These are insufficient — as Einstein already explained [6,12], and led to the LASER. The number of photons must not be constant inside the apparatus, breaking the LEM naturally.

6. Other Particles in the DSE

This work advances experimentally in binary logic, the observation that, the same result for the DSE has been observed for electrons, and other particles, even atoms, not just photons.
We suggest that the Pauli exclusion principle acts as a “boundary condition” restricting the very act of emission. So that, even though emission is not formed by in-phase particles, like in the case of photons, it is influenced, in a contrarian fashion, by the opposite state. These created particles are, then, particle in-phase to themselves, forming like-emitted particles. This is a process which we can also call “stimulated emission”, and include in ASE. Through the opposite state, this creates three (or more) logical processes, with two (or more) coherent with each other, in consistent behavior, not randomly occurring. The unity in the macroscopic spatial interference pattern points (again, as with photons) to a coherent process that must exist microscopically, and based on frequency, not amplitude (e.g., governed by QM). Cooperation externally, betrays cooperation internally. There must be a cause for cooperation, when viewed another way.
This allow us to separate behavior (e.g., the Pauli exclusion principle) from observed interference pattern, in ternary (or more) logic systems.
The argument, in “modus ponens”, is that, a coherent logic state, building a “coherent channel”, should exist also for electrons (and any other particle different from a boson), although seen through what has to remain a distant binary logic system. This happens in order to be able to model the DSE pattern that is seen in the binary pattern, analogous to the experimental fact that a physical state of stimulated emission must microscopically exist in the quantum communication of photons, as well-known by Einstein [6].
But this further establishes, in “modus tollens”, a physical unity between any theories for other particles, of the DSE, obeying different laws. We can use this to provide a model for QM using ASE, in-phase or in counter-phase, reducing decoherence.
The states are in different dimensions, and a continuous path in the higher dimension (tri-state) must necessarily map into a discontinuous path in the lower dimension (two-state). This happens due to a well-known theorem in topology and projection [16], that we call TR.
In QC, one can be more precise than physical QM if one makes the model, as the behavior, be more inclusive for coherence, measured microscopically, even though macroscopically one should be limited to use G F ( 2 m ) and use the LEM. Hence, QC promises to be easier to delve deeper than QM using hardware.
One feels, with the foregoing, the need to introduce more symmetries than G F ( 2 ) , or binary logic, in modeling particles by software. No longer should we be led in software, to regard particles as a formless “fluid”, or classical wave, obeying the LEM as a “Procrustean bed”.
Here, the role of an added mathematical apparatus as discussed here for Galois fields, is not to create unnecessary complications in a description of reality, but implies that there exist more adequate and representative pictures of reality where these other number fields can be used as basic elements of the mathematical description [19], in universality.
Accordingly, one moves in the macroscopic, from a classical Boolean analogy, valid for the LEM and a formless and classical “fluid” model of particles, seen in the DSE as G F ( 2 m ) , to a more complex microscopic structure, with a quantum tri-state+, where the photon (e.g., a particle) is given by an algebraic approach with ternary object symmetry, modeled by G F ( 3 n ) .

7. Photon Model: Universality

In consideration of the foregoing, a particle, as we shall consider a photon, is described by its eigenfunction, as a linear combination in the set { e − α x , x e − α x , x 2 e − α x } [2], where α is calculated variationally, in the set Q.
It is, therefore, localized, obeys the Schrödinger equation by construction [2], does not attempt to go to infinity like a sine function, but when combined with many other similar particles, can equal a sine function as close as one wants, building universality. A wave, in this concept, is a collective construct, not a primitive object like a particle. The mathematical operators curl, laplacian, and so on, are definable based on that constructed wave, and the Maxwell equations as well as classical electrodynamics can follow also.
Thus, first comes the particle in QM, then the wave is built — as a matter of scale going from microscopic to macroscopic. There is no “duality” in this model of the photon, but universality.

8. Tri-State Versus Two-State

This work advances experimentally in well-known binary logic, the observation that, for the same function, computation can be accomplished better even classically, by using three logical states, rather than one can do with binary logic. This observation can be useful here.
The two-state logic levels are given in Figure 3, offering: (1) a low-level state “0” when the lower transistor is on and the upper transistor is off; and (2) a high-level state “1” when the upper transistor is on and the lower transistor is off. The situation is analogous to the double-site experiment. There are only two options, and the LEM must be valid.
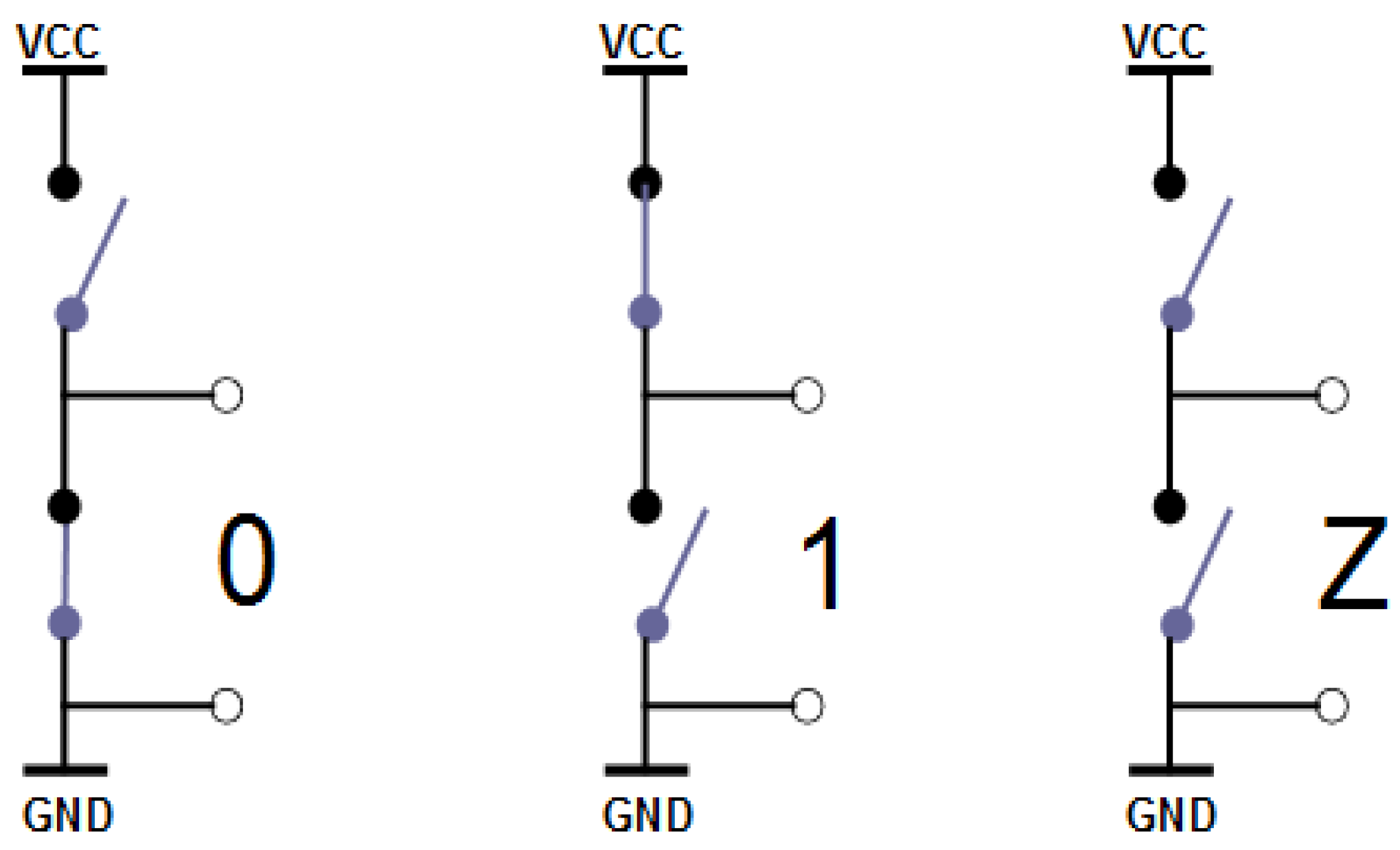
To implement three state logic, a physical case seems impossible, as in the DSE, without changing physical conditions. But in the chip set environment, a conventional tri-state buffer or gate7 can be used, even with FPGAs [21]. This can be seen in Figure 4, showing the three cases in positive logic [10].
Therefore, logic synthesis is possible, by recognizing three or more states [6], inside the apparatus, using ASE, and tri-state+ behavior, allowing implementation as two-state using the DSE, where the two-slits act as a two-state spatial filter, which produces the common interference pattern outside, in the far-field.

9. Discussion

By providing a well-known “Procrustean bed”, the DSE shuts off indeterminacy, without allowing an observer to measure it, and arrives at a apparently clean and determinate, two-state result, that applies to many different particles, even atoms.
This work’s “new hypothesis”, in trying to open the “black box” of QM, is complete in the foregoing — namely, the DSE is explained physically as a LASER. Then, any particle supporting ASE, in-phase or counter-phase, can enter a DSE, and provide the external interference pattern. No wave, nor wave division is assumed, but particle multiplication, by ASE.
This is shown in Figure 1 and Figure 2. In other words [10], the LEM is not broken by the DSE in two-states macroscopically, but naturally in three or more possible states, microscopically, using ASE.
Thus, coherence effects should be used in particle interaction, and the DSE proves it, rather than imagining a spurious wave-particle duality, which would also be a mixed metaphor. But wave-particle duality can be seen as another example of universality in physics, allowing one to use continuity, albeit continuity does not actually exist in the known universe, being a collective construct.
As another task opened by this work, multilevel logic and mathematics formulas, and software, need to be described and implemented to take full advantage of tri-state+, yet using binary, LEM computers to implement, as we already have them today. This could replace the emphasis in QC, from hardware to software, saving cost, time, and welcoming more participants.
To the current insistence on using bits and qubits, Einstein, in 1917 [6], proved that a binary signal is not enough by reproducing the law of radiation found in 1900 by Max Planck. That required a third, coherent channel to exist, invalidating qubits before their concept started. It was a historical mistake by Shannon [22], of difficult consequences until today and highlighting the importance of correct technical work, some 50 years later [2]. This now led to bits and qubits being seriously considered and spilling lots of ink on them, with reputations and careers being lost. But facts cannot be swayed by will.

Funding

This research received external funding from DCTA/ITA, DCTA/IEAv, CAPES/CNPq, CNEN, Fapesp, Network Manifold Associates, Inc. (NMA), Planalto Research, the Max-Planck Institut für Quantenoptik, the Bundesministerium fúr Forschung und Technologie, and Euratom. The author also declares no conflict of interest.

Acknowledgments

The author is indebted to Fellow of the RAS Peter Jackson, Software Engineer André Gerck, Ann Gerck Project Manager of Planalto Research, Edgardo V. Gerck doctorate student, and two anonymous reviewers. ResearchGate discussions were also used, for “live” feedback, important due to the physical isolation caused by COVID.

References

  1. Feynman RP, Leighton RB, Sands M, “The Feynman Lectures on Physics Vol. III Ch. 1: Quantum Behavior.” Caltech University; https://www.feynmanlectures.caltech.edu/III_01.html, 2011.
  2. Gerck E, “Algorithms for Quantum Computation: Derivatives of Discontinuous Functions. ” Mathematics 2023, 11, 68, available online, or Google Scholar, retrieved on Feb/27/2023, 2022. [CrossRef]
  3. Wolfram S, “A Class of Models with the Potential to Represent Fundamental Physics.” Arxiv; https://arxiv.org/ftp/arxiv/papers/2004/2004.08210.pdf, 2004.
  4. Petersen A, “The Philosophy of Niels Bohr.” Bulletin of the Atomic Scientists, Vol. 19, No. 7, 1963. [CrossRef]
  5. Schrödinger E, “Collected Papers on Wave Mechanics.” International Series of Monographs on Physics (Book 27), Clarendon Pess, 1982.
  6. Einstein A, “Zur Quantentheorie der Strahlung,” Physikalische Zeitschrift, vol. 18, pp. 121–128, Jan. 1917. [CrossRef]
  7. Grib A, Rodrigues Jr WA, “Copenhagen Interpretation. In: Nonlocality in Quantum Physics.” Springer, Boston, MA., 1999.
  8. Howard D, “Who invented the “copenhagen interpretation”? a study in mythology,” Philosophy of Science, vol. 71, no. 5, pp. 669–682, 2004. [CrossRef]
  9. Bouwmeester D, Ekert A, Zeilinger A, (Eds.), The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation. Springer Publishing Company, Incorporated, 2010. [CrossRef]
  10. Gerck, E, “On The Physical Representation Of Quantum Systems.” Computational Nanotechnology 8(3):13-18, 2021.
  11. Borenstein M, Lamb W, “Classical Laser.” Phys. Rev. A, vol.5, p. 1298, 1972.
  12. Einstein A, “Strahlungs-Emission und Absorption nach der Quantentheorie,” Deutsche Physikalische Gesellschaft, vol. 18, pp. 318–323, Jan. 1916. [CrossRef]
  13. Frege G, “Sense and Reference.” The Philosophical Review, vol. 57, no. 3, pp. 209–230, 1948.
  14. Jones DW, “Standard Ternary Logic.” http://homepage.cs.uiowa.edu/j̃ones/ternary/logic.shtml, 2016.
  15. Poincaré H, “Sur Le Probleme Des Trois Corps Et Les Equations De La Dynamique.” Acta Mathematica, Vol. 13, Online at http://www.mittag-leffler.se/sites/default/files/final_memoir.pdf, 1890.
  16. Carlson AB, “Communication Systems.” McGraw Hill Kogakusha, Ltd., 1968.
  17. Feigenbaum MJ, “Universality in complex discrete dynamics.” Los Alamos Theoretical Division Annual Report 1975-1976, 1976.
  18. Barzel B, Barabási AL, “Universality in network dynamics.” Nature Physics vol. 9, pp. 673–68, 2013. [CrossRef]
  19. Khrennikov AY, “Universality in network dynamics.” Springer Science & Business Media, Vol. 427, 2013. [CrossRef]
  20. Young T, “The 1801 Bakerian Lecture: On the theory of light and colours.” Philos. Trans. of the R. Soc. of London, 92, 12–48, 1802. [CrossRef]
  21. Actel Corporation, “Implementing Three-State and Bidirectional Buses with Multiplexers in Actel FPGAs.” Application Note AC119; https://www.microsemi.com/document-portal/doc_view/130059-threestate-bibuf-an, 1997.
  22. Shannon CE, “A mathematical theory of communication.” Bell System Technical Journal, 27, 623–656, 1948. [CrossRef]
1
Reference [6] also does not support the Copenhagen interpretation [7,8].
2
Now defined in a causal way.
3
More than 55,000 laser-related patents have been granted in the United States.
4
Also called spontaneous emission, without concern about causality.
5
Also called “spontaneous” emission, with no causality concern.
6
One cannot split the photon, but one can multiply it coherently with ASE.
7
Such as the 74LS241 octal buffer.
Preprints 70609 g001
Figure 1. Example of a photon represented in tri-state+ merging to two-states in the DSE, with one stage of “amplification by stimulated emission” (ASE).
Figure 1. Example of a photon represented in tri-state+ merging to two-states in the DSE, with one stage of “amplification by stimulated emission” (ASE).
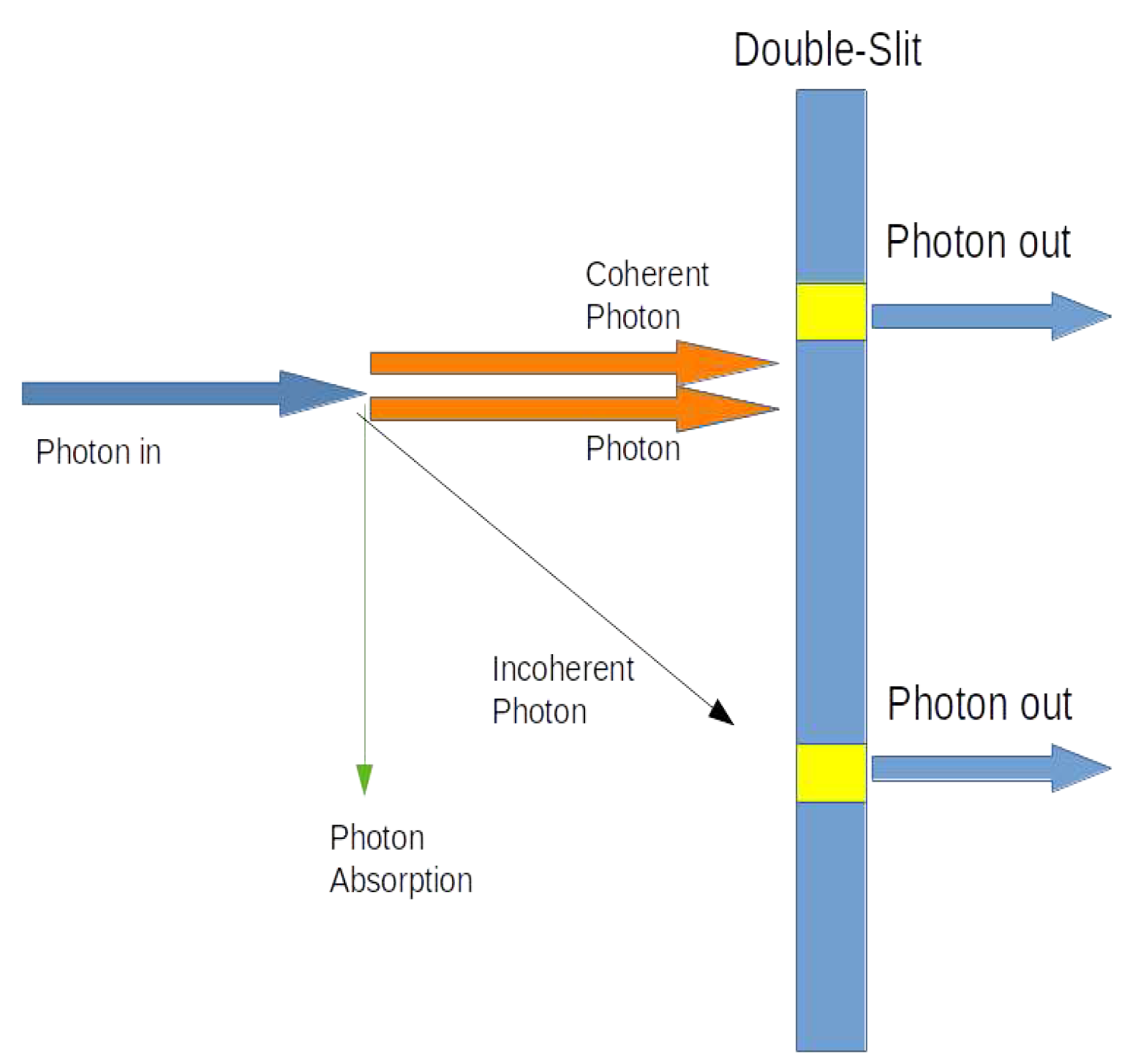
Preprints 70609 g001
Preprints 70609 g002
Figure 2. Example of a photon represented in tri-state+ merging to two-states in the DSE, with five stages of ASE in avalanche process, creating a LASER.
Figure 2. Example of a photon represented in tri-state+ merging to two-states in the DSE, with five stages of ASE in avalanche process, creating a LASER.
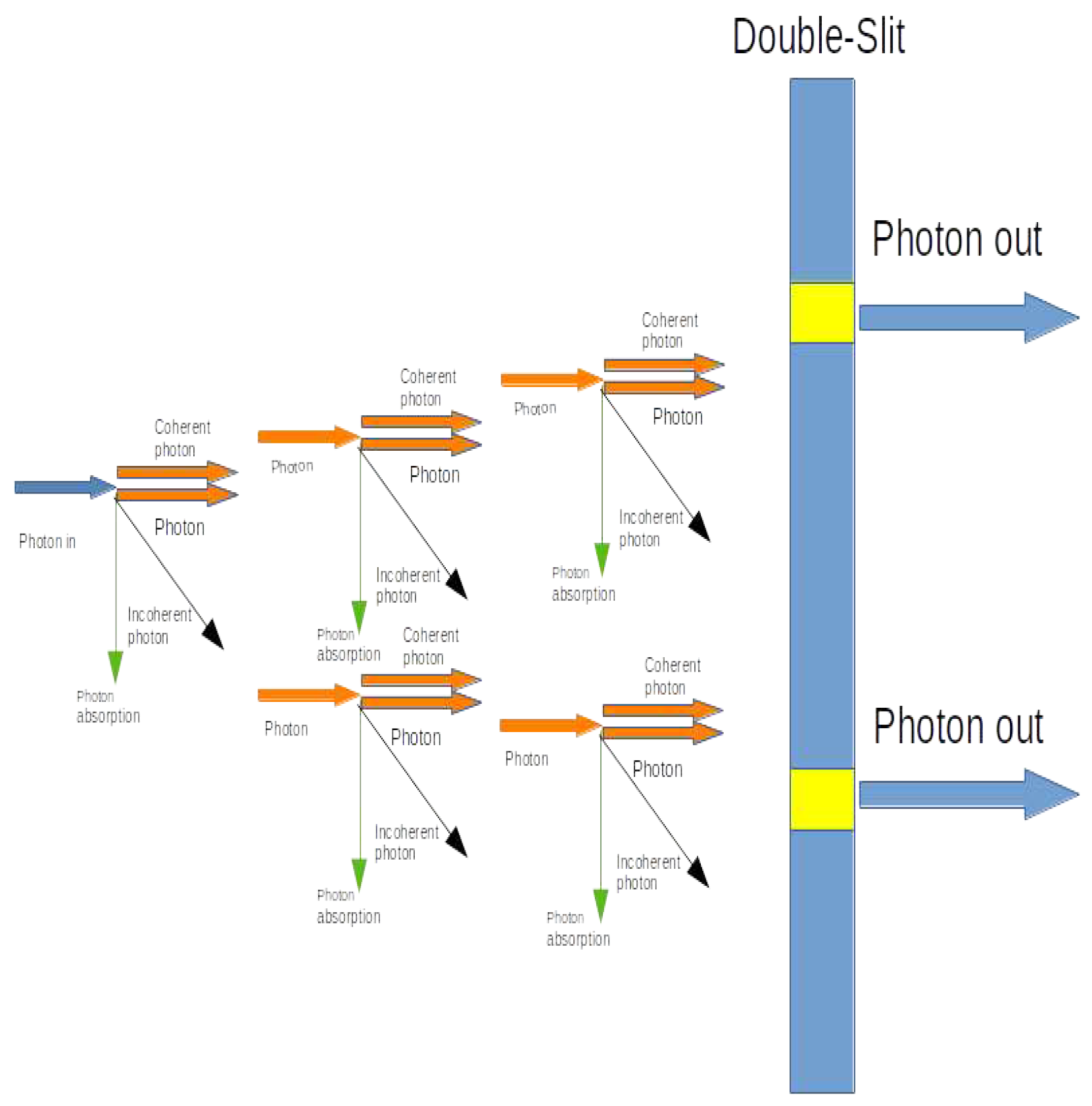
Preprints 70609 g002
Preprints 70609 g003
Figure 3. Example of two-state levels in a circuit, 0 and 1. LEM must be valid.
Figure 3. Example of two-state levels in a circuit, 0 and 1. LEM must be valid.
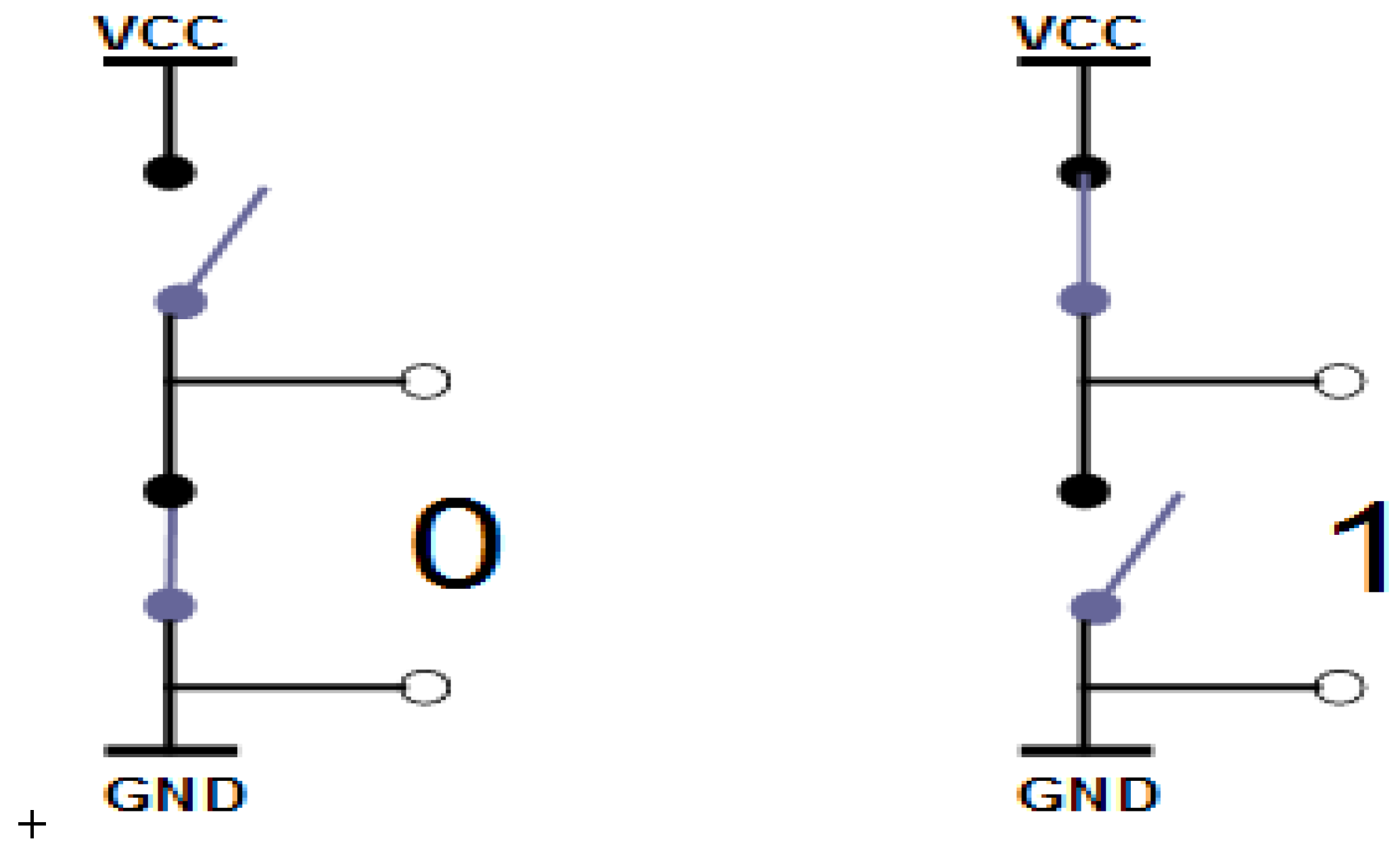
Preprints 70609 g003
Preprints 70609 g004
Figure 4. Example of three states logic: 0, 1, Z.
Figure 4. Example of three states logic: 0, 1, Z.
Preprints 70609 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated