1. Introduction
There are many cases in which one is interested in forecasting the behaviour of a chaotic system, the emblematic one is meteorology. The main obstacle is, of course, that in chaotic systems by definition a small uncertainty amplify exponentially in time [
1]. Moreover, even if one assumes to have a good computational model of a natural, chaotic system, the exact value of parameters is needed to have a faithful representation of dynamics.
Schematically, one can assume that the natural, or target system is well represented by some dynamical system, possibly with noise. One can measure some quantities on this system, but in general one is not free to choose which variable (or combination of variables) to measure nor to perform measurements at any rate.
On the other hand, if one has a good knowledge of the system under investigation, i.e., it can be modeled with good accuracy, a simulated “replica” of the system can be implemented on a computer. If moreover one has the possibility of knowing the parameters and the initial state of the original system, so to keep the replica synchronized to it (when running at the same speed), then the replica can be used to perform measurements otherwise impossible, and to get accurate forecasting (when run at larger speed).
In general, the problem of extracting the parameters of a system from a time-series of measurement on it, is called data assimilation [
2].
The problem in data assimilation is that of determining the state of the system and the parameters by minimizing an error function between data measured on the target and the respective data from the simulated system. A similar task is performed by the back-propagation techniques in machine learning [
3,
4].
The goal of this paper is that of approaching this problem from the point of view of dynamical systems [
5]. In this context the theme of synchronization is quite explored [
6], but it has to be extended in order to cover the application field of data assimilation.
The synchronization technique is particularly recommendable when the noise (in the measure and intrinsic to the system) is small, i.e., when the target system can be assumed to be well represented by a deterministic dynamics, even if this dynamics is not continuous (as in Cellular Automata [
7]).
We shall investigate here the application of synchronization methods to the classic Lorenz system [
8].
We shall start from the classic Pecora-Carrol master-slave synchronization scheme, recalled in
Section 2, in which the value of some of the state variables of the master is imposed to the corresponding variables of the slave system. This choice of coupling variables is denoted “coupling direction” in the tangent space of the system.
The synchronization threshold is connected to the value of the conditional Lyapunov exponent [
9,
10], i.e., the exponential growing rate along the difference space between master and slave, as reported in
Section 3.
This scheme will be then extended to partial synchronization, i.e., to the case in which only a portion of the value of the state variables of the master system signal is fed to the slave, as shown in
Section 4. We can thus establish the minimum fraction of signal (coupling strength) able to synchronize the two replicas, that depends on the coupling direction.
However, one cannot pretend to be able to perform measurements in continuous time, as done in the original synchronization scheme, in which the experimental reference system was a chaotic electronic circuit.
Therefore, we dealt with the problem of intermittency, i.e., performing measurements, and consequently applying the synchronization scheme, only at certain time intervals. We show that the synchronization scheme works also for intermittent measurements, provided that the coupling strength is increased, as shown in
Section 5.
In the case of systems with different parameters, the synchronization cannot be complete, and we speak of generalized synchronization. We shall show in
Section 7 that the distance among systems can be interpreted as measure of the error, and exploited to obtain the “true” value of parameters, using a simulated annealing scheme.
Finally, it may happen that the variables of the systems are not individually accessible to measurements, a situation which forbids the application of the original method. In this case one can still exploit schemes inspired by statistical mechanics, like the pruned and enriching one, simulating an ensemble of systems with different state variables and parameters, and selecting the instances with less error, cloning them with perturbations. This kind of genetic algorithms is able to approximate the actual values of parameters, as reported in
Section 8.
Conclusions are drawn in the last section.
2. Pecora-Carrol synchronization
In 1990 Louis Pecora and Thomas Carrol introduced the idea of master-slave synchronization [
9]. They studied simulated systems, like the Lorenz [
8] and Rössler [
11] ones, and also experimental electronic circuits [
12].
They considered two replicas of the same system, with same parameters. One of the replica (the master) was left evolving unperturbed. Some of state variables of the master replaced the corresponding variable of the slave system, which is therefore no more autonomous. This topic was further explored in a 2015 paper [
10].
In order to get the main idea of this master-slave (or replica) synchronization, let us consider first a one-dimensional, time-discrete dynamical system, like for instance the logistic map [
13]. It is defined by an equation of the kind
where
n labels the time interval. The usual Lyapunov exponent
is defined as
where
. Let us now introduce a replica
X such that
where
p is the coupling parameter (coupling strength).
For
the two maps are uncoupled, and since they are assumed to be chaotic, they generally take different values. For
map
X immediately synchronizes with map
x. There is a critical value
of the coupling parameter for which the synchronized state is stable, and it is related to the Lyapunov exponent
,
as can be seen by taking the linearized difference among the maps.
This scenario holds also for higher-dimensional (
K) maps, which can be written as
where
denotes the state of the system at iteration
n and has
K components. The system has now
K Lyapunov exponents, of which at least one,
, is assumed to be positive.
The synchronization procedure in this case is
where now the coupling is implemented by means of a diagonal matrix
C, with diagonal entries equal to zero or one, defining the coupling directions. In the following we shall indicate the diagonal of
C as
.
In the case in which
, i.e., all entries are mixed with the same proportion, the stability of the synchronized phase is again related to the maximum Lyapunov exponent
,
since the evolution of an infinitesimal difference among the replicas,
, is given by
where
J is the Jacobian of
F
This scheme can be extended to continuous-time systems, by replacing the entries from one system in the coupled differential equation, so
where now the Lyapunov exponents of the original system are given by the eigenvalues of the (symmetrized) time-average of Jacobian
In practice, however, the differential equation Eq. (
10) is implemented as a map, by discretizing the time, and therefore Lyapunov exponents are computed as in the previous case. Using a simple Euler scheme, we have
and
, and
In the tangent space
and the maximum Lyapunov exponent
is
The average growth of the distance
is
for time intervals such that the linearized approximation is valid.
Notice that in the continuous-time version the Jacobian and the Lyapunov exponents are defined in units of the inverse of time.
6. Generalized synchronization
What happens if the two coupled replicas evolve using different values of parameters
[
6,
14]? Even when the coupling parameters (directions and intensity) are above threshold, the distance
d remains finite. Let us indicate with
the parameters of the slave system.
We can define a parameter distance
D,
which is zero for the previous coupling schemes. We can also generalize the coupling among replicas, similar to what done for state variables, Eq.(
6), introducing a parameter coupling direction
and a strength
so that the parameters of the slave replica are
where
are the values of parameters corresponding to
, reachable according to the “direction”
.
We can notice that the distance among state variables
d decreases smoothly with
and
D only for a small interval of
D near zero. Clearly,
for
, even for
, which is what we have seen in
Section 4.
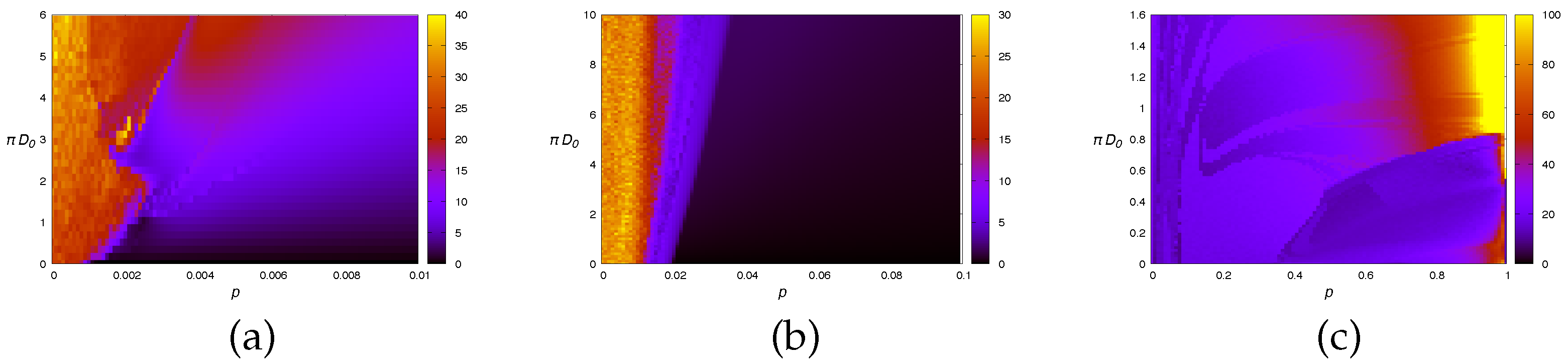
Some simulation results are presented in
Figure 4, in which the asymptotic state-variable distance
d is reported as a function of the distance between parameters
and state-variable coupling
p. The parameter coupling
always goes from 0 to 1, so the initial parameter distance
corresponds to the larger value of
D. The line
corresponds to the distance reported in
Figure 5.
Clearly, in the absence of synchronization for
(
,
Figure 5-(c)), there is no synchronization for
. In the other cases, there is a region near the synchronized phase in which
d goes smoothly to zero. Notice that in
Figure 5-(c) the larger distance
d occurs for
and large
D. This is probably due to the fact that when coupled along the
z directions, the two replicas may stay on different “leaves” of the attractor, which is almost perpendicular to
z.
Notice also that the d landscape is not smooth far from the synchronized phase. We consider this aspect in the following section.
7. Parameter estimation
We are now able to exploit the fact the the distance d goes to zero if and , thus allowing to determine the parameters of the master system by varying the parameters of the simulated replica .
However, since the convergence of
d to zero is not monotonous with
D, we relay of a simulated annealing technique [
15], that allows to overcome the presence of local minima. We introduce a fictitious temperature
, and assume that the distance
d is the analogous to an energy to be minimized.
We assume that the the synchronization time and the coupling direction C, cannot be modified at will by experimenters, being fixed by the characteristic of the measure instruments and of the actuators. We insure to be in the condition , i.e., such that if the parameter distance is null, , synchronization occurs.
The idea is the following: we simulate the coupled system for a time interval
T, measuring the state variable distance
d, after which one of the parameter
is varied by a small amount. We repeat the simulation starting from the same conditions, except the varied parameter, and compute again
d. If
d decreases the variation is accepted. It is also accepted if
d increases, with a probability
otherwise it is discarded.
The temperature
is slowly lowered (multiplying
by a factor
) every
T time interval. As shown in
Figure 5, in this way it is possible to exploit the synchronization procedure to get the value of the parameters in the master replica. In fact, for
sufficiently low, the distance
between master and slave state variables (dashed line in figure) drops to zero. For similar values of temperature (but not always the same), also the distances
between master and slave parameters drop to zero (continuous color lines). Clearly, this procedure works only for deterministic dynamical systems with little or no noise on measurement, and with very low dimensionality.
8. Pruned-enriching approach
The previous scheme cannot be always followed, since we assumed to be able to measure some of the variables of the master system and inject this value (at least intermittently) in the slave one.
However, this might be impossible, either because the state variables
are not accessible individually, or because those that are accessible do not allow the synchronization (for instance, if only the
z variable is accessible, as illustrated in
Section 4).
We can take profit of the Takens theorem [
16], that states that the essential features (among which the maximum Lyapunov exponent) of a strange attractor
can be reconstructed by intermittent observations
using the time series
as surrogate data, provided that their number is larger than the dimensionality of the attractor [
17]. Other conditions are that the observation interval
be large enough to have observations
sufficiently spaced, but not so large that the
are scattered along the attractor, making the reconstruction of the trajectory impossible. It is therefore generally convenient to take an interval
substantially larger than the minimum
, but of the same order of magnitude.
What is interesting, is that one can choose for
f an arbitrary function of the original variables, provided that their correspondence is smooth. We therefore employed a method inspired by the pruned-enriching technique [
18,
19] or genetic algorithm without cross-over [
20].
We assume that we can only measure a function of the master system, at time intervals . The master system evolves with parameters .
We simulate an ensemble composed by h replicas, each one starting from state variables () and evolving with the same equation as the master one with parameters , where . At beginning and are random quantities.
We let the ensemble evolve for a time interval
T and then we measure the distance
. We sort the replicas according with
and we replace the half with larger distances following an evolutionary law based on a cloning and perturbation scheme, as shown in
Figure 6. For a more detailed description of the procedure we can refer to Algorithms 1 and 2.
First of all we need to set the initial condition. Given a set of measures , for , we map the dynamics in an embedding space of size defined by the vectors . Then we randomly initialize the initial conditions and the initial value of the parameters of the h replicas, in a range consistent with the physical values. To create the initial embedding vectors of the replicas, we evolve the ensemble for a time .
Now we can start with the optimization problem. For a number of repetitions M, we evolve the ensemble using a time step up to time . At each further interval we update the embedding vector substituting the oldest measurement with the new one and compute the euclidean distances between the and the reference computed on the master system.
The distance is used as cost function of our optimization problem. In the Parameters updating step of Algorithm 2, we sort the elements of the set in ascending order according to and replace the second half of the set with a copy of the first half with either a random perturbation of amplitude in one of the parameters, or a random perturbation of the state variables, see Algorithm 2.
We add some check to be sure to not have inconsistent values of parameters (in our case all the need to be positive). After that we compute , the estimated parameters, as mean of the fist half of the ensemble elements.
Since in general we assume , the number of time steps in the simulated trajectories, when we restart the ensemble simulation at the initial time step, restoring initial random condition in the state space but without changing the parameters, and we recompute the initial vector evolving the ensemble member up to time .
We analyze the convergence problem for different value of . We suppose to have access at only the x component of the real system, i.e. our measurement function is simply . We evolve the system up to with time step and we measure every . We embed the system in a embedding space of dimension .
The ensemble is composed by
replicas and we repeat the procedure for
times. The final results are showed in
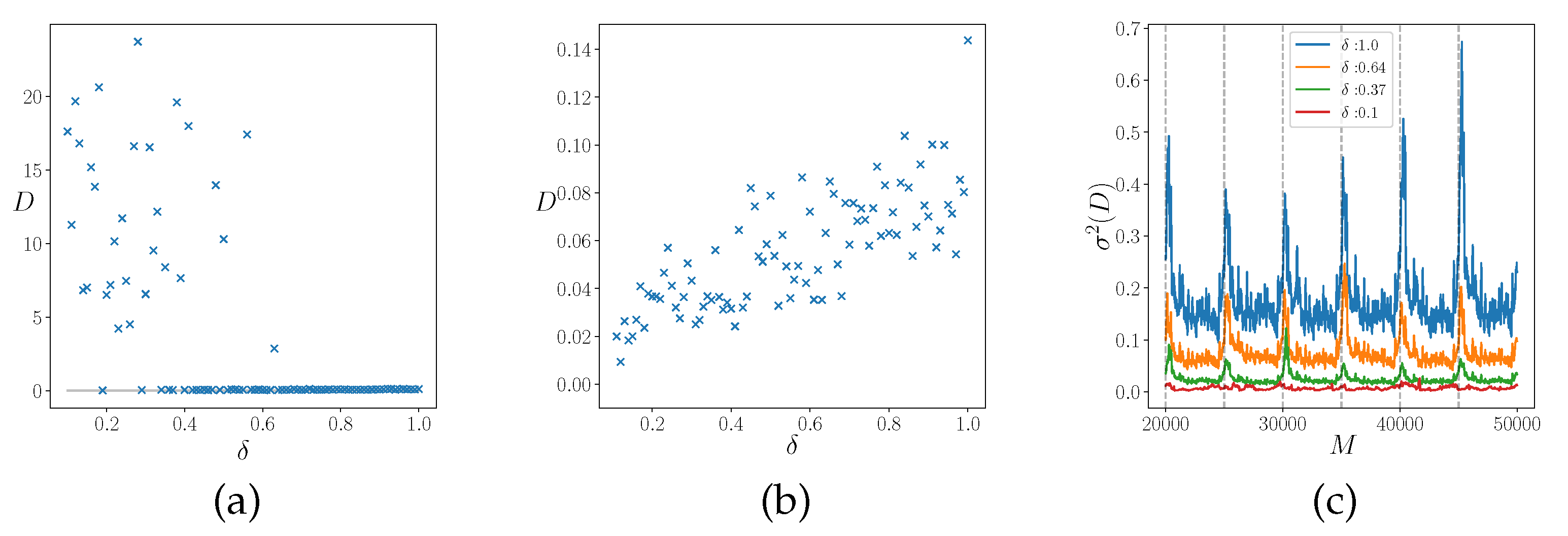
Figure 7. In
Figure 7-a we initialize the ensemble parameters randomly in the interval
and we measure the distance
D in the parameters space (Eq. (
22)) for different
. Notice that, starting from a large initial distance, larger values of
, are more effective for the convergence. The opposite phenomenon is reported in
Figure 7-b. Here we assume to approximately know the true parameter values with an error
and we test the dependence of the amplitude
in a fine tuning regime. In this case, starting from a relative small distance, smaller values of
are more effective.
In
Figure 7-c instead we show the behavior of the variance of the parameter distance
D during the optimization for different amplitude
. With a small amplitude
for the parameters updating step, the elements of the ensemble rapidly converge to the local minimum before having explored the parameter space sufficiently so, small amplitude values of
can be useful only for a fine tuning approach. Using large values of
instead is helpful to better explore the parameters landscape and allows to converge to the true values but with noisy results. These considerations suggest the use of an adaptive value of the parameter
.
Inspired from these results we modify the updating ruled introducing a variable amplitude
, where, for every ensemble members
i,
. Then, for each replica we defined an amplitude that modulates the variation step in an self-consistent manner. To test this choice we simply put
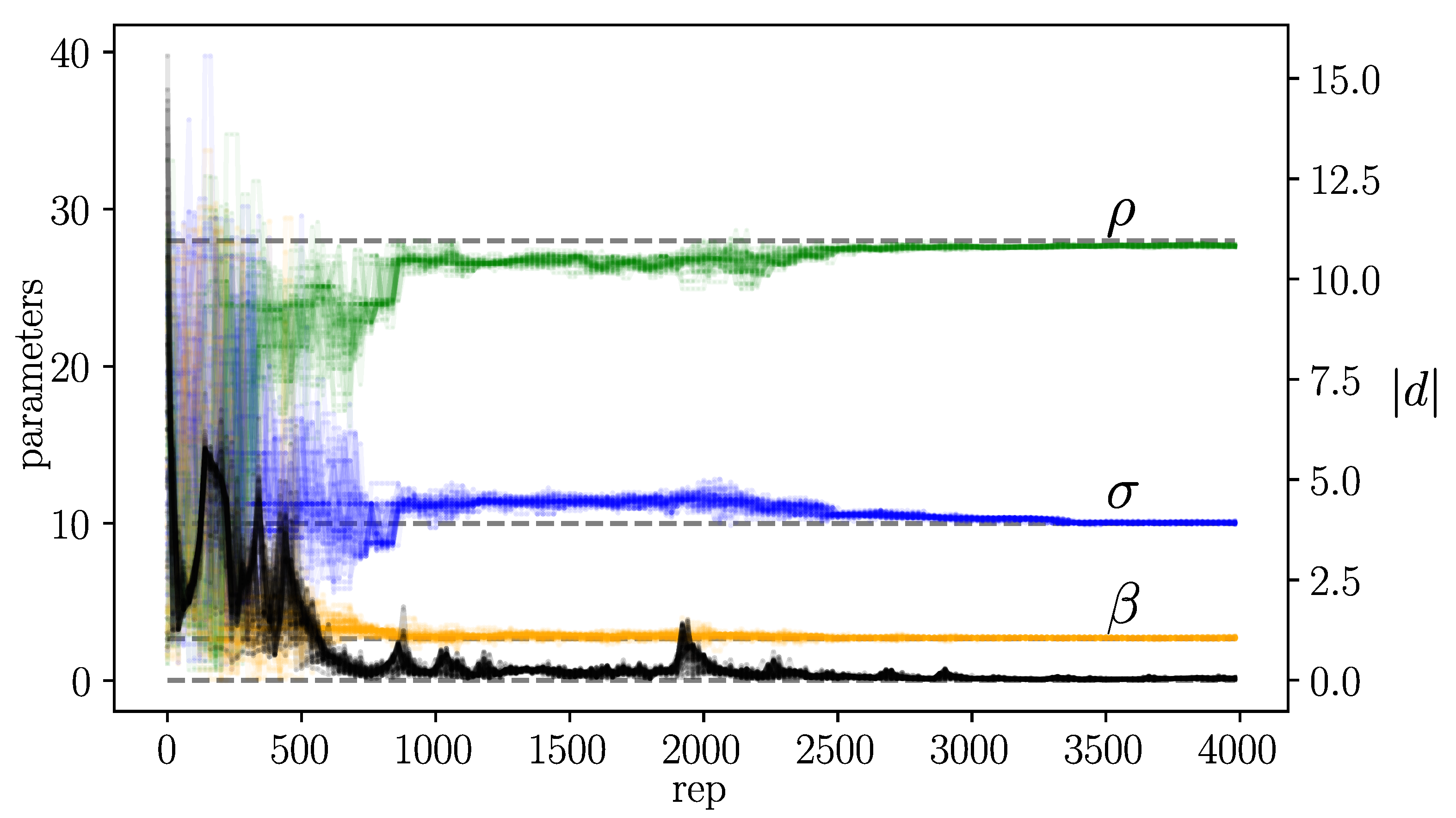
In
Figure 8 we plot the behaviour of 50 ensemble members randomly chosen in the pruned-enriching optimization problem with the amplitude factor
defined as in Eq. (
24). We suppose to be in the same situation of the last simulations, so we measure the real system only in the
direction every
. The ensemble dimension is equal to
and we choose the embedding dimension
. In this simulation we run the algorithm for
intervals. The numerical results as show in
Table 2.
|
Algorithm 1:Pruned-enriching algorithm. |
Require:
whiledo
if then
else
if then
▹ Algorithm 2
end if
end if
end while
return
|
|
Algorithm 2:Parameters updating step. |
Require:
▹ return index of d sorted in ascending order
fordo
if then
while do
end while
else
end if
end for
return
|
The pruned-enriching procedure is similar to a genetic algorithm without cross-over. In general the cross-over operation aims at combining locally-optimised solutions, and depends crucially by the coding of the solution in the “genome”. When the cost function is essentially a sum of functions of variables coded in the solution in nearby zones, the cross-over can indeed allow a jump to an almost-optimal instance. In this case we encode the parameters simply using their current values (a single genome is a vector of 3 real numbers), so there is no indication for this option to be present. It is possible however to pick parameters from “parents” instead of randomly altering them. Since the pool of tentative solutions is obtained by cloning those corresponding to the lowest distances from the master one, we expect little improvements using parameter exchange.
To add the cross-over in our procedure we modify the algorithms such that, for every element of the second half of the ensemble, we chose randomly if update the parameters as Algorithm 2 or do the cross-over step generating the new replica from two parents randomly chosen from the first half of the ensemble. Children inherit randomly two of the parameters from one parent and one from the other.
Without any a priori information about the true parameter values we randomly initialize the initial states and the parameters, so, using the cross-over operation can introduce a bias in the early stages of the optimization problem, as can be seen in
Figure 9, where we compare the estimated parameters for different repetitions using an amplitude
with (
Figure 9a) and without (
Figure 9b) cross-over at every
. As the other simulations we randomly initialize the initial states and parameter values of the ensemble, we evolve the system, after the transient time
, up to
with
and we suppose to be able to measure the
x direction with
.
The cross-over allow to make jumps in the parameters space, but in the early stage of the optimization process these jumps can cause the ensemble convergence to wrong values. On the other hand, the cross-over can reduce the variance of the ensemble estimation, so it can help in the last steps, or for fine tuning. Future work is needed to explore more in details this option.
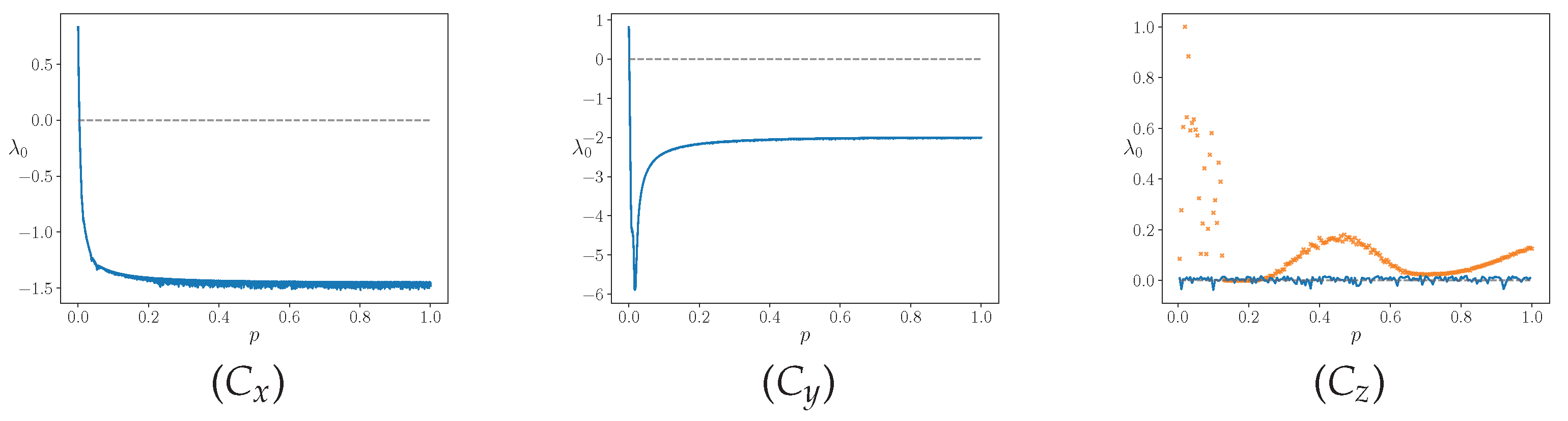
Figure 1.
Conditional Lyapunov maximal exponent for different coupling directions.
,
,
. In the last one, in orange, we also show the distance
d (normalized at it’s maximum value obtained in the simulation) between the master and slave state variables for different coupling strengths (see also
Figure 2).
Figure 1.
Conditional Lyapunov maximal exponent for different coupling directions.
,
,
. In the last one, in orange, we also show the distance
d (normalized at it’s maximum value obtained in the simulation) between the master and slave state variables for different coupling strengths (see also
Figure 2).
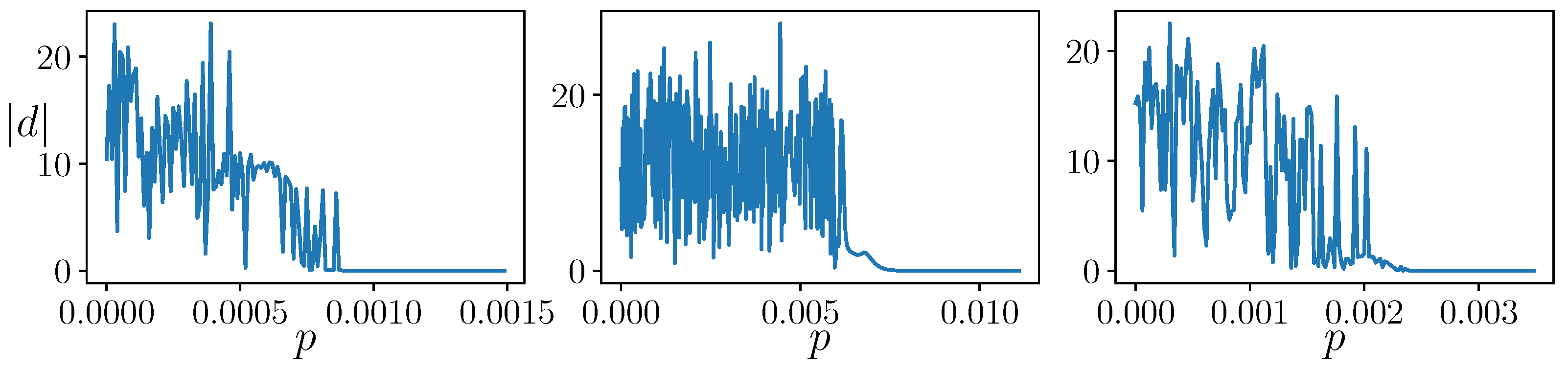
Figure 2.
Asymptotic distance d as function of the coupling strength p for different coupling directions. From the left to the right: , , .
Figure 2.
Asymptotic distance d as function of the coupling strength p for different coupling directions. From the left to the right: , , .
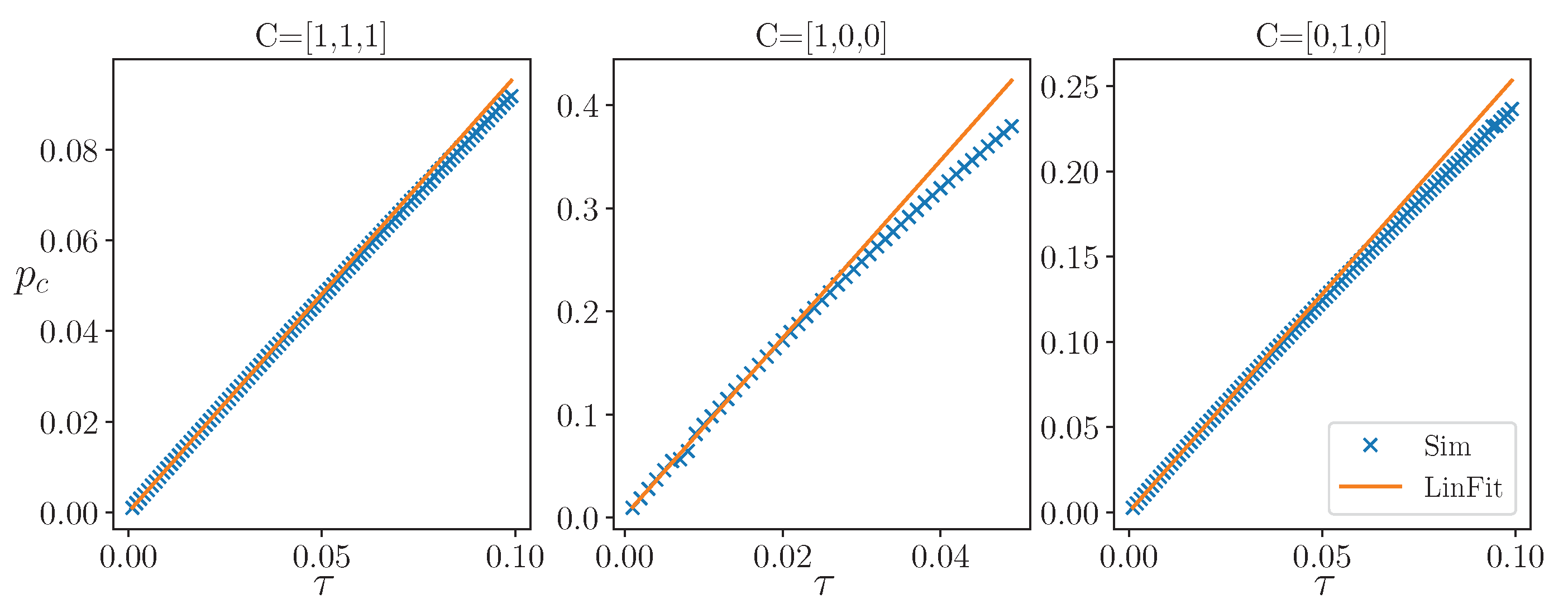
Figure 3.
The dependence of the synchronization threshold on the intermittent parameter k such that for different coupling directions and it’s linear fit obtained using the first 20 time steps. The other parameters of the simulation are: and for , for the others.
Figure 3.
The dependence of the synchronization threshold on the intermittent parameter k such that for different coupling directions and it’s linear fit obtained using the first 20 time steps. The other parameters of the simulation are: and for , for the others.
Figure 4.
Heat map of the state-variable distance
d for different values of parameter coupling
(
) and state-variable coupling
p for some state-variable coupling directions
C and parameter coupling direction
. (a)
,
; (b)
,
; (c)
,
;. The line
corresponds to
Figure 2.
Figure 4.
Heat map of the state-variable distance
d for different values of parameter coupling
(
) and state-variable coupling
p for some state-variable coupling directions
C and parameter coupling direction
. (a)
,
; (b)
,
; (c)
,
;. The line
corresponds to
Figure 2.
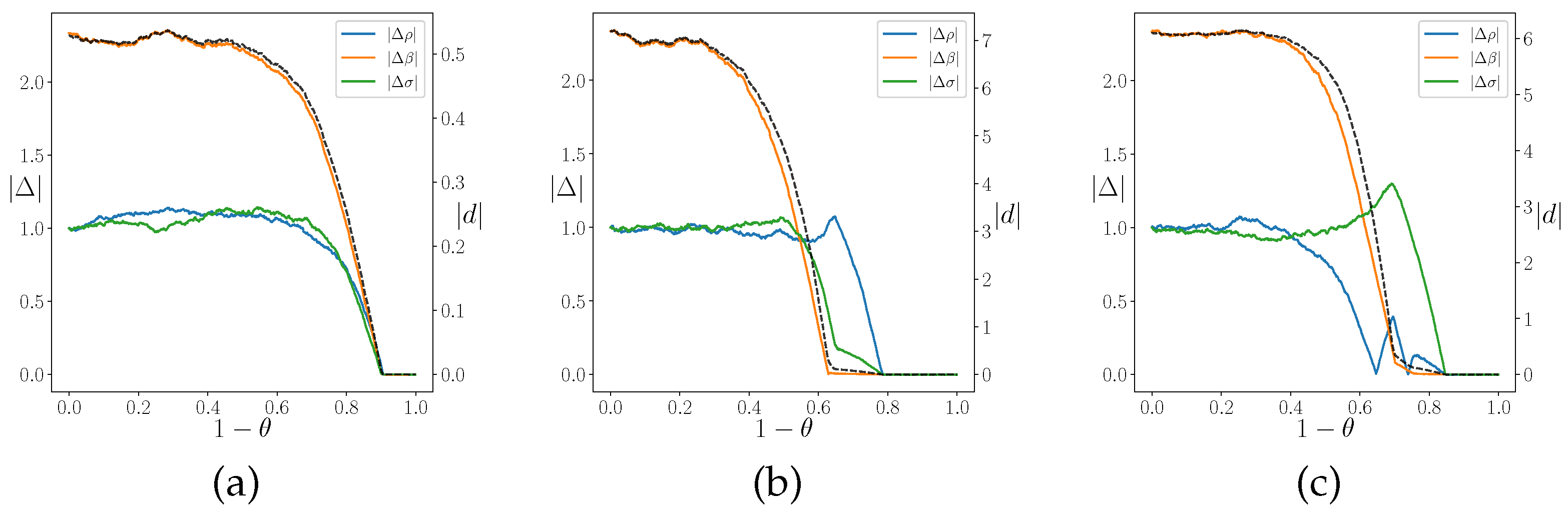
Figure 5.
The state-variable distance d (dashed line) and parameter distance (color) as a function of temperature for and different coupling directions C. (a) ; (b) ; (c) . We set , , .
Figure 5.
The state-variable distance d (dashed line) and parameter distance (color) as a function of temperature for and different coupling directions C. (a) ; (b) ; (c) . We set , , .
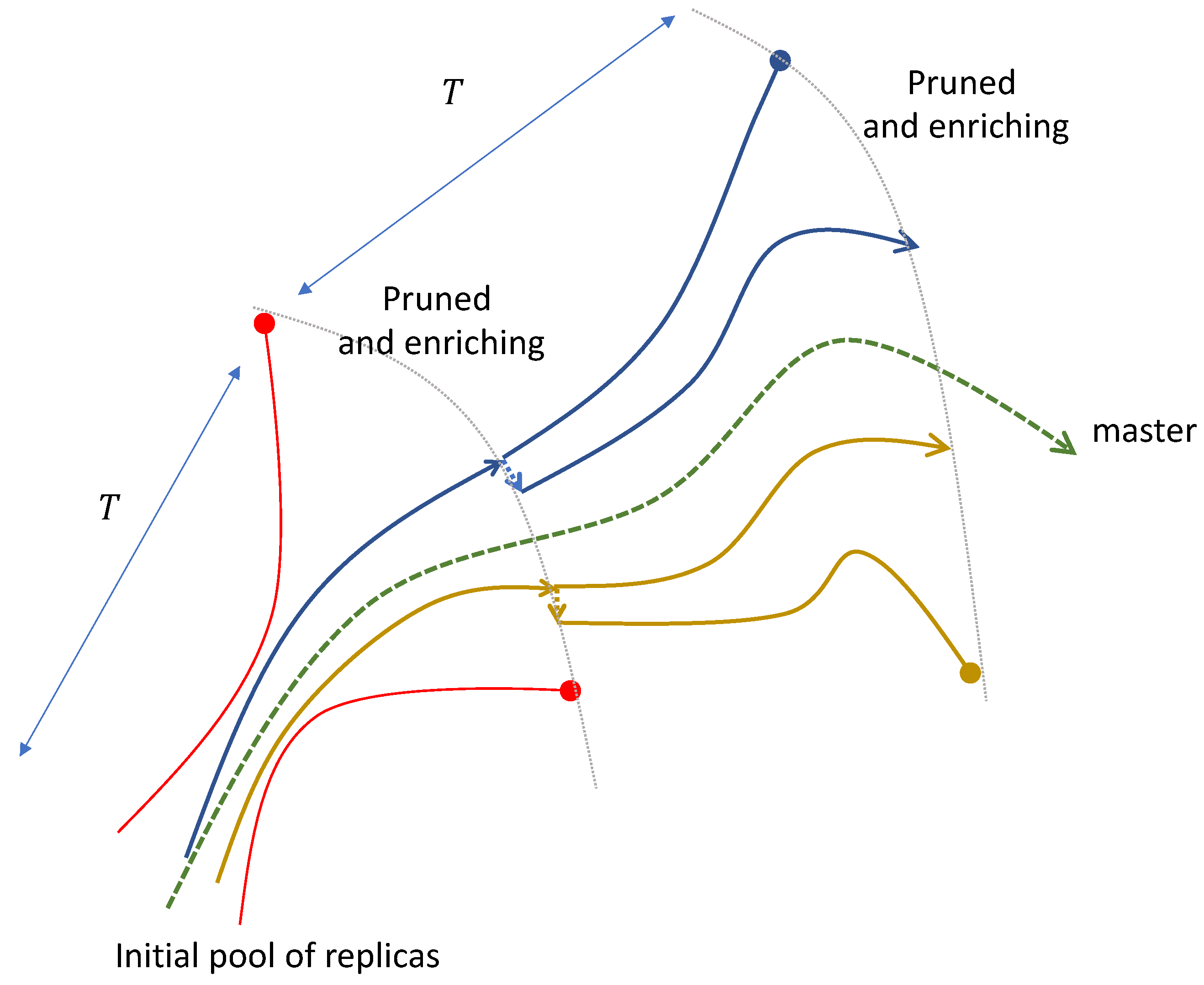
Figure 6.
The schematic of the pruned-enriching method. The variation of the duplication of the nearer replicas is either on one of the state variables or one of parameters.
Figure 6.
The schematic of the pruned-enriching method. The variation of the duplication of the nearer replicas is either on one of the state variables or one of parameters.
Figure 7.
Parameters distance D at interval M for different amplitudes with (a) randomly initialized in the interval and (b) initialized near the “true” values by adding a random noise of amplitude . (c) Variance of the distance D for different amplitudes for the last interval. The vertical lines indicate when the ensemble was restored to . The are initialized as in (a).
Figure 7.
Parameters distance D at interval M for different amplitudes with (a) randomly initialized in the interval and (b) initialized near the “true” values by adding a random noise of amplitude . (c) Variance of the distance D for different amplitudes for the last interval. The vertical lines indicate when the ensemble was restored to . The are initialized as in (a).
Figure 8.
The distance between variable (black points, right axes) and parameters (left axes) as a function of time in the pruned-enriching method for 50 randomly selected replicas of the used to estimated the parameters. We consider the situation where only measurement in coupling direction are available at every temporal steps , so we embed our time series in an embedding space of dimension .
Figure 8.
The distance between variable (black points, right axes) and parameters (left axes) as a function of time in the pruned-enriching method for 50 randomly selected replicas of the used to estimated the parameters. We consider the situation where only measurement in coupling direction are available at every temporal steps , so we embed our time series in an embedding space of dimension .
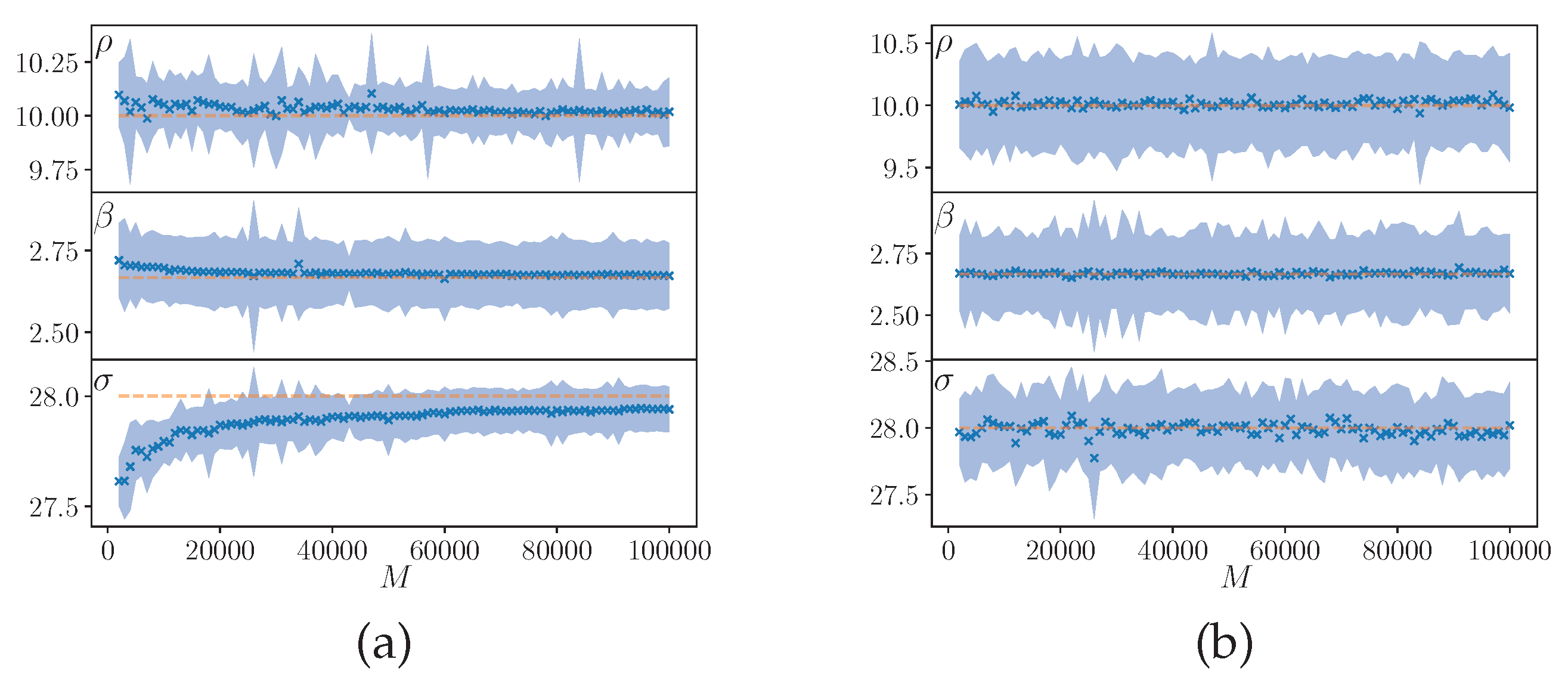
Figure 9.
Estimation (x) and standard deviation (blue area) of the parameters computed using the first half of the ensemble with (a) and without (b) cross-over. The true values are also shown (dotted orange lines).
Figure 9.
Estimation (x) and standard deviation (blue area) of the parameters computed using the first half of the ensemble with (a) and without (b) cross-over. The true values are also shown (dotted orange lines).
Table 1.
Maximum conditional Lyapunov exponent estimated using the asymptotic distance between Master and coupled Slave systems () and derived from linear fit ().
Table 1.
Maximum conditional Lyapunov exponent estimated using the asymptotic distance between Master and coupled Slave systems () and derived from linear fit ().
| |
|
|
|
|
|
|
|
|
|
|
|
Table 2.
Estimated parameters obtained using the pruned-enriching algorithm with variable. On the last column we also show the variance on the ensemble members of the estimated parameters.
Table 2.
Estimated parameters obtained using the pruned-enriching algorithm with variable. On the last column we also show the variance on the ensemble members of the estimated parameters.
| |
real |
ens. mean |
ens. variance |
|
|
|
|
|
|
|
|
|
|
|
|