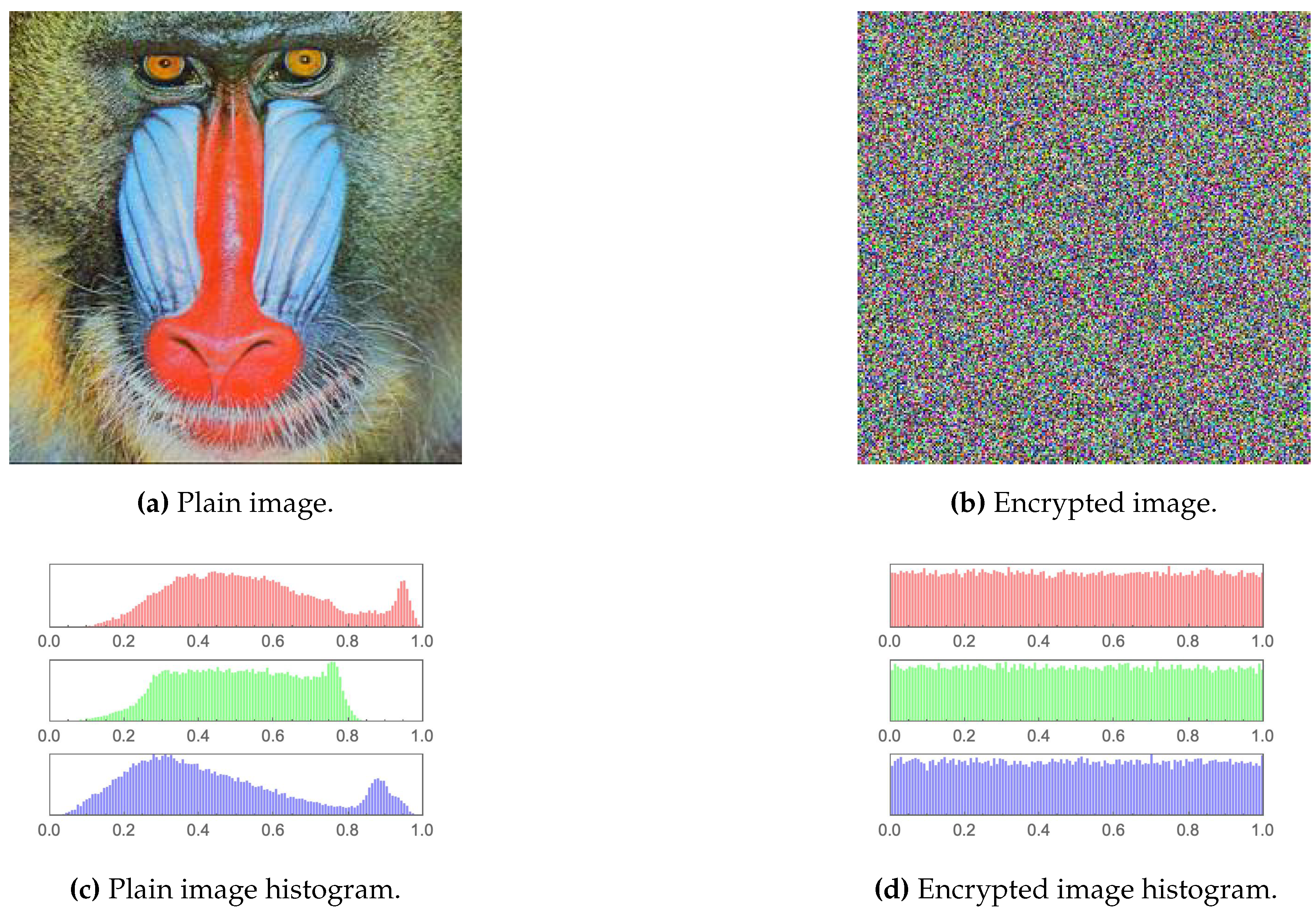
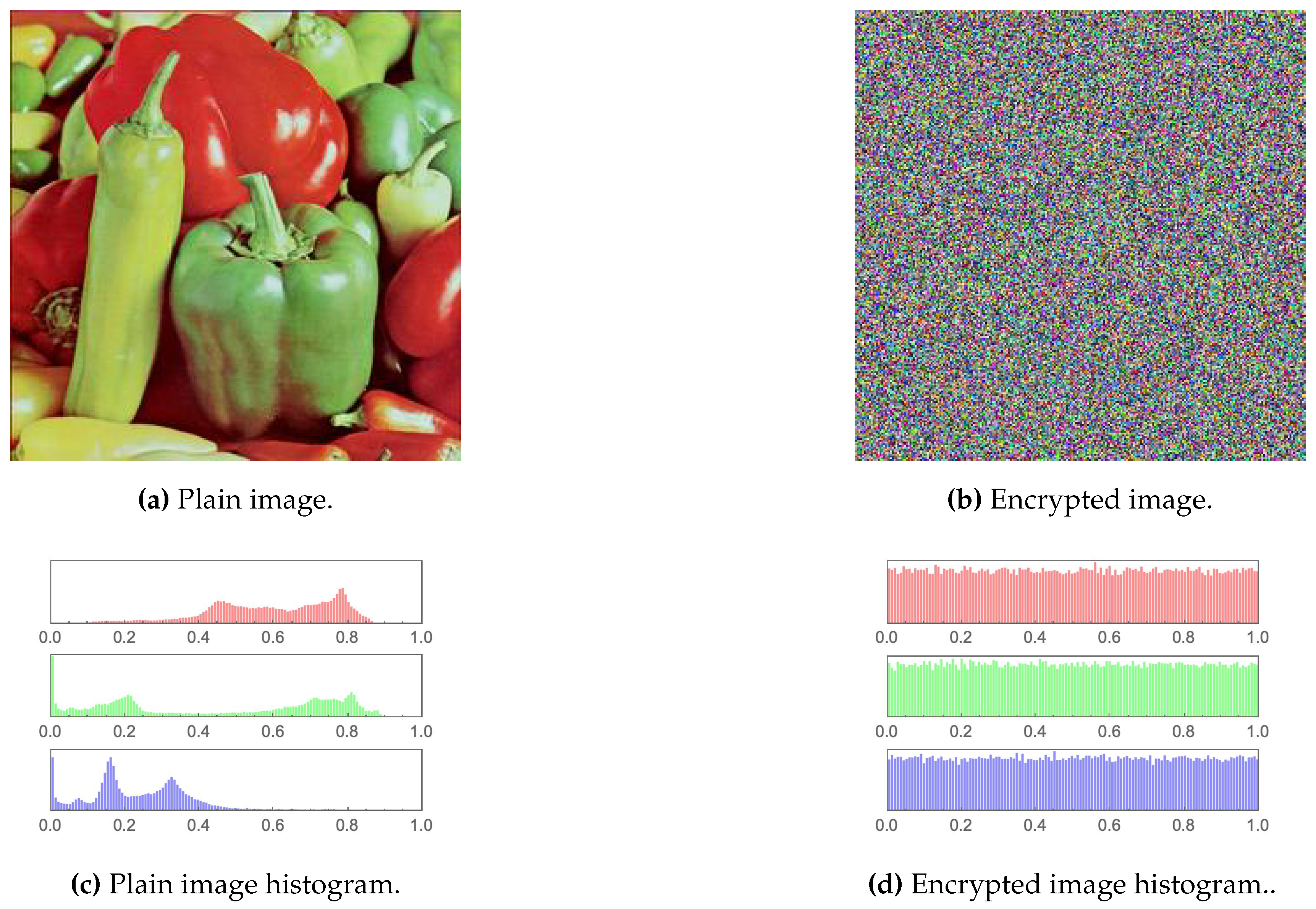
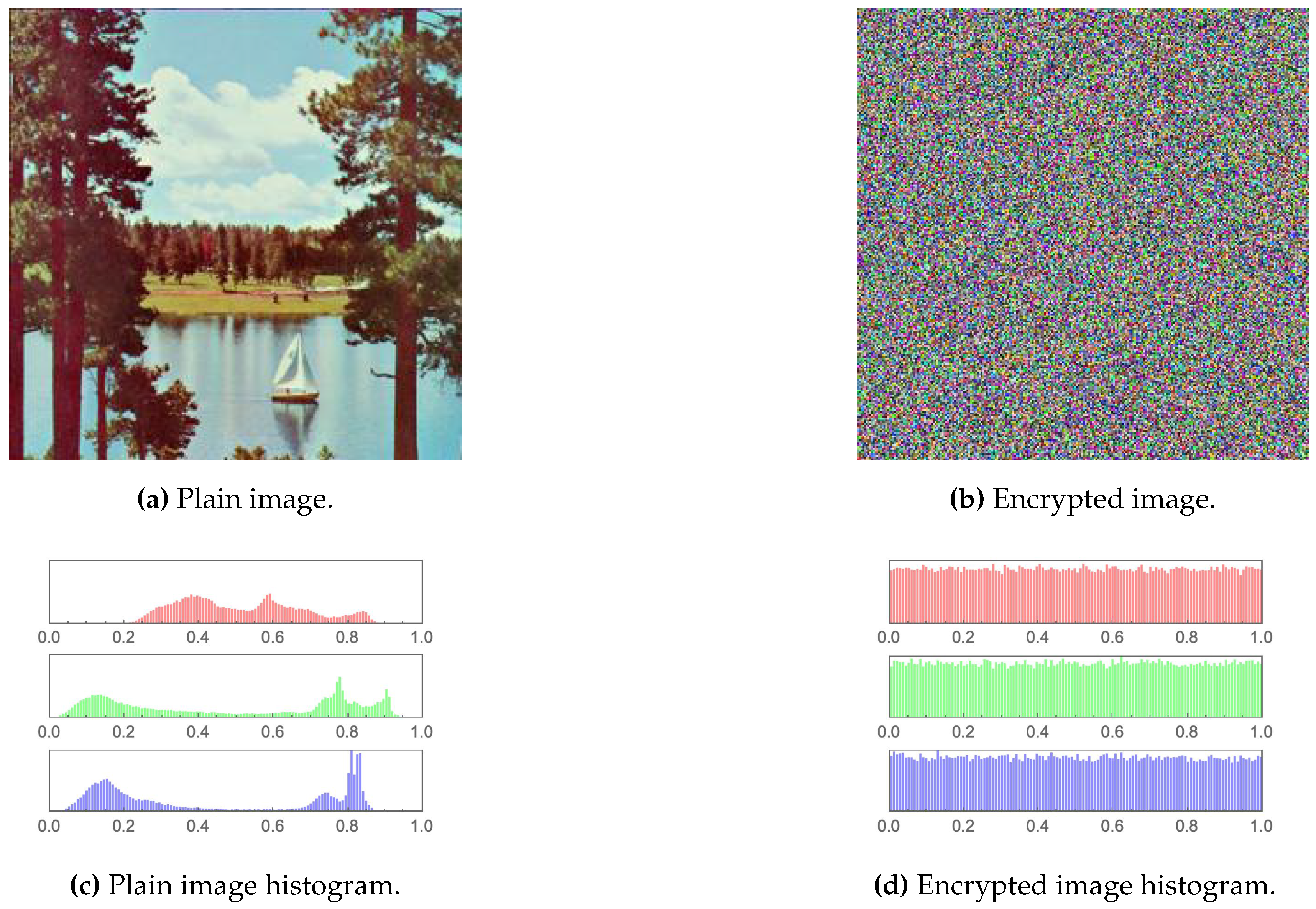
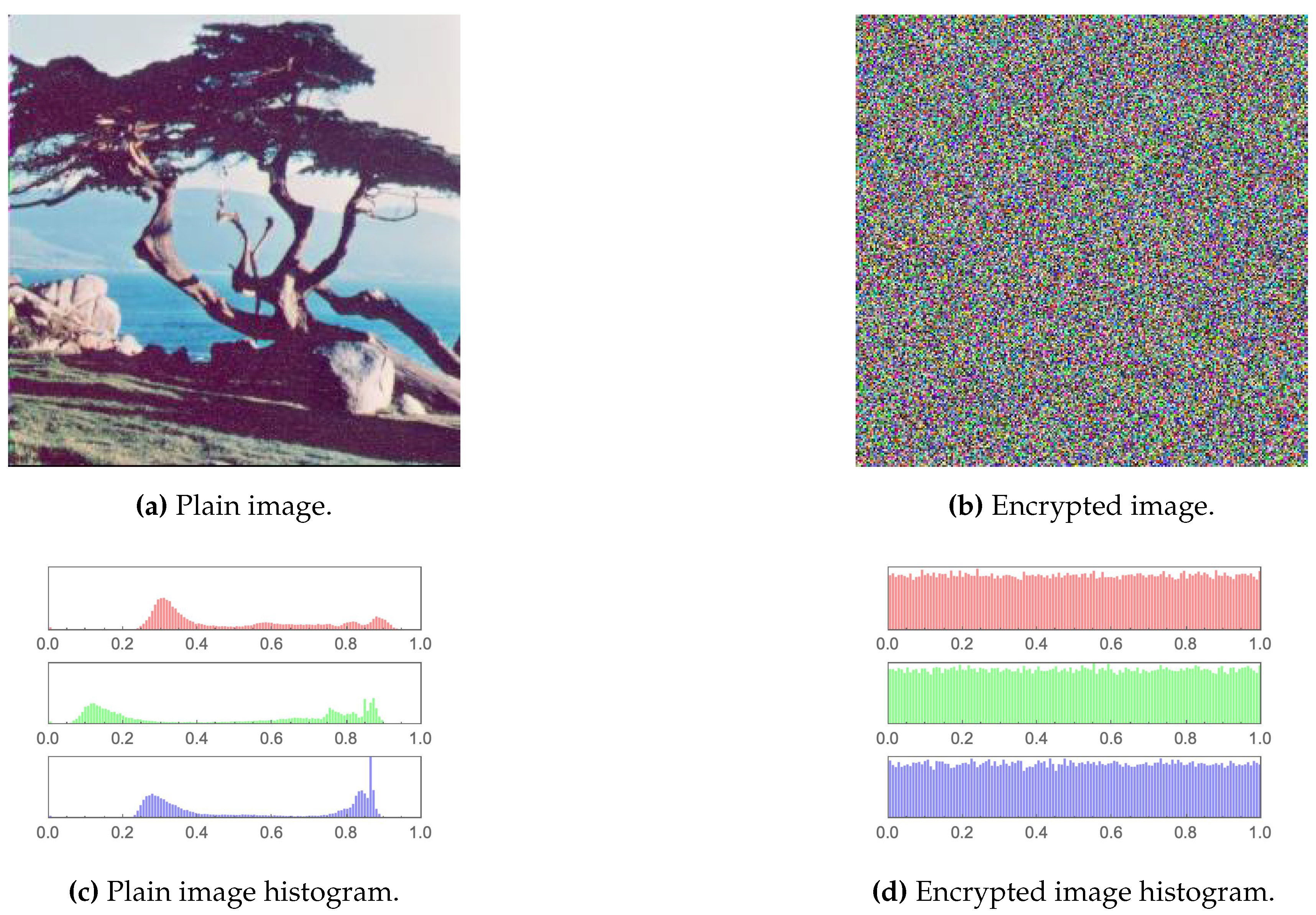
1. Introduction
With the widespread use of digital images in various fields, including healthcare, finance, and personal communication, there is a growing need to ensure their secure communication and storage. This is especially true in terms of protecting them from unauthorized access, tampering, and interception [
1,
2]. Encryption is the process of converting plaintext (unencrypted data) into ciphertext (encrypted data) using an encryption algorithm and a secret key. The encrypted data can only be decrypted and read by someone who has the correct key. Image encryption is a specific type of encryption that is designed to protect digital images, through eradicating any symmetry between a plain image and its encrypted version. The need for image encryption arises from several factors. Firstly, digital images often contain sensitive information, such as personal photos, medical images, or confidential documents. This information needs to be protected from unauthorized access or interception during transmission over the internet or storage on a device [
3]. Secondly, images can be easily tampered with, and it is often difficult to detect such tampering. Encryption can help to prevent unauthorized modifications of the image data by providing a way to verify the authenticity of the image [
4]. Thirdly, images are often stored and transmitted in large quantities, making it difficult to ensure the security of each individual image. Image encryption algorithms can help to secure large quantities of images by providing a way to efficiently and securely process their data [
5].
Recent literature shows reliance of image encryption algorithms on substitution-permutation networks (SPNs). SPNs are a popular cryptographic primitive used in symmetric key encryption algorithms. These operate by applying a series of substitution and permutation operations to plaintext blocks, producing ciphertext blocks that are difficult for an attacker to decipher without the correct key. SPNs have been widely used in image encryption research due to their ability to efficiently encrypt large amounts of data while maintaining strong security guarantees [
6,
7,
8,
9,
10]. In an image encryption algorithm, the plaintext is typically represented as a matrix of pixel values, and the SPN is applied to each pixel value individually or to a block of pixels simultaneously. One of the main advantages of using SPNs in image encryption is their ability to provide a high degree of confusion and diffusion, satisfying Shannon’s theory of secure communication [
11]. Confusion refers to the property of the encryption algorithm that makes it difficult for an attacker to relate the ciphertext to the plaintext, while diffusion refers to the property that ensures that small changes in the plaintext lead to significant changes in the ciphertext [
2].
SPNs have also been used in combination with other cryptographic techniques, such as key management and authentication, to provide a more comprehensive approach to image security [
12]. For example, some image encryption algorithms based on SPNs use secret key management techniques to ensure that the encryption key is securely distributed and protected from unauthorized access [
13]. Overall, the importance of SPNs in image encryption research lies in their ability to provide strong security guarantees while efficiently processing large amounts of data. As such, they have become a cornerstone of modern image encryption algorithms and continue to be an active area of research in the field of cryptography. In general, most recent literature on image encryption carries out confusion through the application of one or more substitution boxes (S-boxes), while diffusion is carried out through the application of an encryption key that is based on a pseudo-random number generated bit-stream, where an appropriate logical operation is utilized [
7,
8,
14,
15,
16]. The next couple of paragraphs introduce each of those steps.
Substitution boxes are an important component of many image encryption algorithms. These are used to substitute plaintext bits with ciphertext bits, and they provide a key component of the confusion step in many encryption algorithms [
7]. The importance of S-boxes in image encryption algorithms lies in their ability to provide strong security guarantees by introducing non-linear transformations into the encryption process. S-boxes help to ensure that changes to a single input bit have unpredictable and significant effects on the output, making it difficult for an attacker to analyze and reverse-engineer the encryption process. In image encryption, S-boxes are typically used in combination with permutation operations to form SPNs [
14]. As aformentioned, the SPN structure is particularly well-suited to image encryption because it provides a high degree of confusion and diffusion, which are both important properties for secure encryption. The use of S-boxes in image encryption algorithms can also help to prevent common attacks, such as differential and linear cryptanalysis, which rely on analyzing the statistical properties of the encryption process. S-boxes can help to obscure these statistical properties, making it more difficult for an attacker to break the encryption [
15].
Pseudo-random number generators (PRNGs) play an important role in image encryption algorithms. PRNGs are used to generate a sequence of random numbers that are used to encrypt the image data. These random numbers are combined with the original image data using various encryption techniques to produce encrypted image data that is difficult to decipher without the correct key [
2]. The importance of PRNGs in image encryption algorithms lies in their ability to generate a large amount of unpredictable and uniformly distributed random numbers. These random numbers are crucial for achieving the two main goals of encryption: confidentiality and integrity [
3]. Confidentiality refers to the property of the encryption algorithm that ensures that only authorized parties can access the encrypted data. Integrity refers to the property that ensures that the encrypted data has not been tampered with or modified during transmission or storage. PRNGs are designed to produce random numbers that are indistinguishable from true random numbers. However, unlike true random number generators, PRNGs are deterministic and rely on a seed value to produce the same sequence of numbers each time they are used with the same seed [
14]. The seed value is typically generated from a source of true randomness, such as atmospheric noise, mouse movements, or keyboard timings, to ensure that the resulting sequence of numbers is sufficiently unpredictable. In image encryption algorithms, PRNGs are used to produce a large sequence of random numbers that are combined with the original image data to produce encrypted data [
2]. The strength and quality of the encryption depends on the randomness and uniformity of the PRNG output. Therefore, selecting a secure and robust PRNG is essential for ensuring the security and effectiveness of the image encryption algorithm.
Chaotic functions exhibit sensitive dependence on initial conditions and cycloidal behavior, making them suitable for encryption applications [
6,
10]. There are two main types: low dimensional chaotic functions with 2-3 variables, and hyperchaotic functions with 4 or more variables. Low dimensional chaotic functions, like the Lorenz or Henon maps, have a smaller key space but simpler computational requirements, making them faster and easier to implement [
16,
17,
18]. However, their lower dimensionality means they have weaker encryption strengths. Hyperchaotic functions, on the other hand, have a much larger key space due to their extra variables, providing stronger encryption. But they also have greater complexity, requiring more computing power and being slower to compute. Each type has its advantages and disadvantages for image encryption. Low dimensional chaos is suitable for real-time encryption of streaming videos or wireless communications due to its simplicity. Hyperchaos provides very high encryption strength suitable for encrypting still images or large file transmissions. However, its added complexity may be impractical for some applications with limited resources. By tuning the parameters of a chaotic map, its dynamics can be made sufficiently random-like for encryption, yet still deterministic for decryption [
15]. Chaotic ciphers have been shown to withstand various attacks like brute-force, known-plaintext, and statistical analysis [
14]. When combined with other techniques like diffusion and confusion layers, chaos-based encryption schemes can achieve robust and versatile encryption of images and multimedia data [
19]. Chaos provides an efficient and simple means of generating the complex, nonlinear transformations needed for strong encryption.
Recent literature in the field of image encryption provides a plethora of articles that combine the use of successive applications of PRNGs and S-boxes to carry out image encryption. In many instances, chaos theory is employed to generate the PRNGs and to construct the S-boxes. In [
14], the authors numerically solve the fractional-order hyperchaotic Chen system and generate a PRNG as an encryption key from its solution. They combine its use, in a multi-layer encryption algorithm, with other keys and S-boxes based on the Mersenne Twister, OpenSSL, Rule 30 cellular automata and Intel’s math kernel library. The authors of [
7] make use of a tan variation of the Logistic map to carry out DNA coding as a first stage of encryption. Subsequent stages utilize the Lorenz chaotic system to construct an S-box, as well as the Logistic map in its original form for PRNG key generation. A a Recaman’s sequence in conjunction with the Rossler chaotic system are used to generate PRNG encryption keys in [
20]. In [
21], the authors employ chaotic functions, DNA computing, SHA-256, as well as the random movements of a chess piece, Castle, on a hypothetical chess board, to carry out image encryption. The combination of DNA coding with chaos theory is also utilized in [
22], where the authors further the image encryption abilities through SHA-2. A number of dynamical functions that exhibit chaotic behavior are utilized in [
19] to generate PRNG encryption keys, including the the linear congruential generator, the Arnold cat map, the Bernoulli map, the 2D logistic sine map and the tent map. In [
23], parameters are computed over the finite field
through the utilization of a finite field with the aim of generalizing the Logistic map and searching for an auto morphic mapping between 2 logistic maps, to carry out robust image encryption. The work of [
17] adopts a continuous chaotic system, with the aim of achieving diffusion, and an LA-semi group, with the aim of achieving confusion, for efficient image encryption. A 6D discrete hyperchaotic system is employed in [
24] to generate 6 PRNGs as encryption keys. Those are used conjunction with DNA coding, to encrypt each of the color-separated RGB channels of a color image. The authors of [
25] make use of spatio-temporal chaos of the 2D nonlinear coupled map lattices and genetic operations, to carry out low complexity image encryption. The Mandelbrot set is utilized in a color image encryption scheme proposed in [
26], where the Arnold map combined with DNA sequences enhance the attained encryption security. The authors of [
27] propose an innovative image encryption algorithm that draws on the distinctive concept of a rotor machine, in addition to the employment of a piece-wise linear chaotic map and a one time key. The Logistic map is used in combination with a dynatomic modular curve, as a form of an SPN, to perform secure image encryption in [
28]. In [
29], the authors employ a cloud model Fibonacci chaotic system and a matrix convolution operation for to implement a secure image cryptosystem. An interesting work involving the Josephus problem, and its corresponding Josephus function, is employed in [
30] in combination with a 4D hyperchaotic function. Image compression and encryption is carried out in [
31], where the Arnold map and choas theory are utilized for effective and reliable image transmission over unsecured networks.
It is clear from the literature review the abundance of techniques and algorithms that may be utilized to successfully implement a secure, robust and efficient image encryption algorithm. However, almost all of the aforementioned algorithms are only able to offer 2 out those 3 vital encryption traits. Such that the offering of higher security, through more encryption stages, is counter-acted with higher design complexity and software implementations. In some cases, efficiency is capitalized on, but security is not fully achieved, such that key spaces are rather small. In order to achieve all 3 traits of security, robustness and efficiency, this work proposes and accomplishes the following:
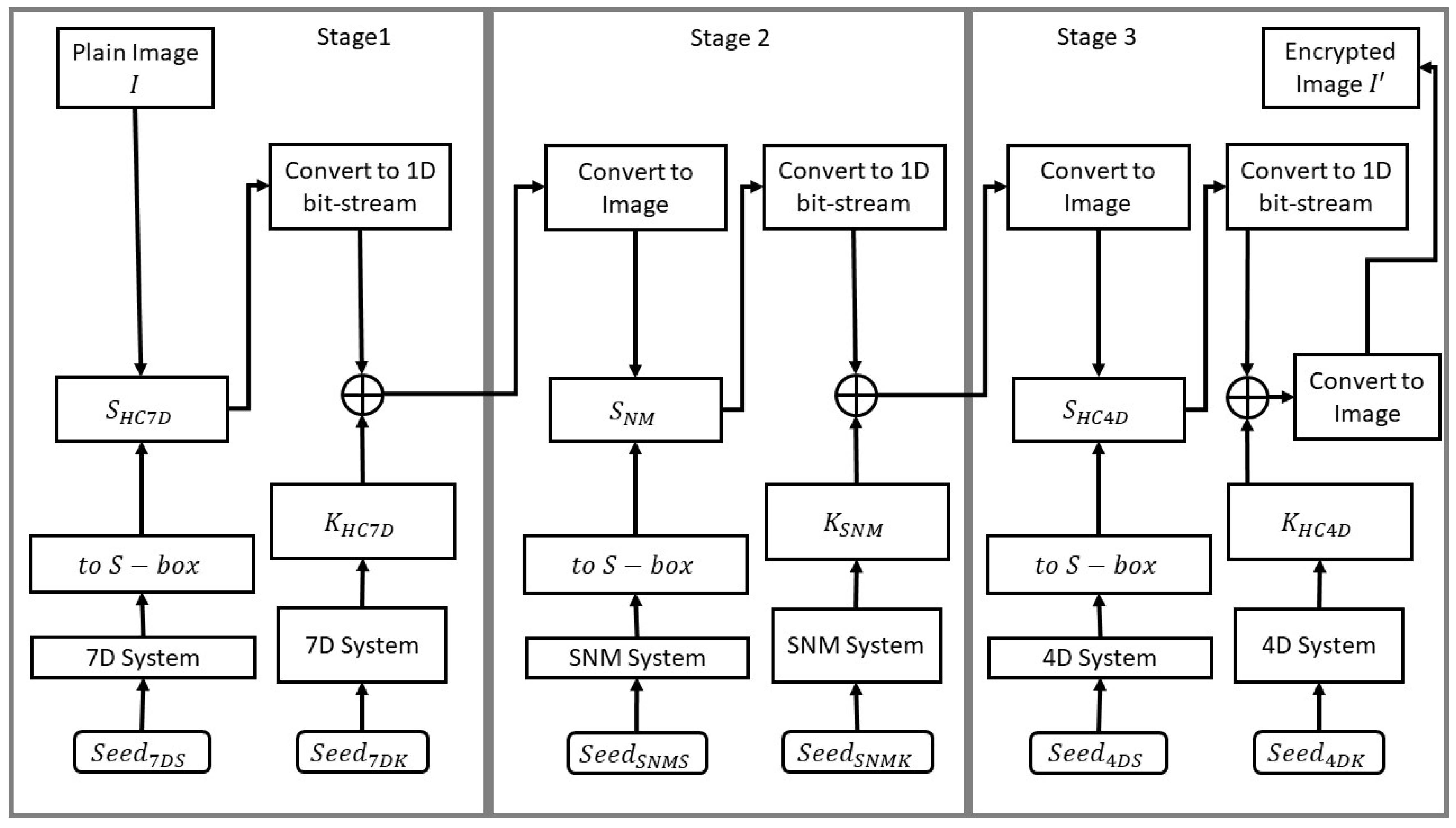
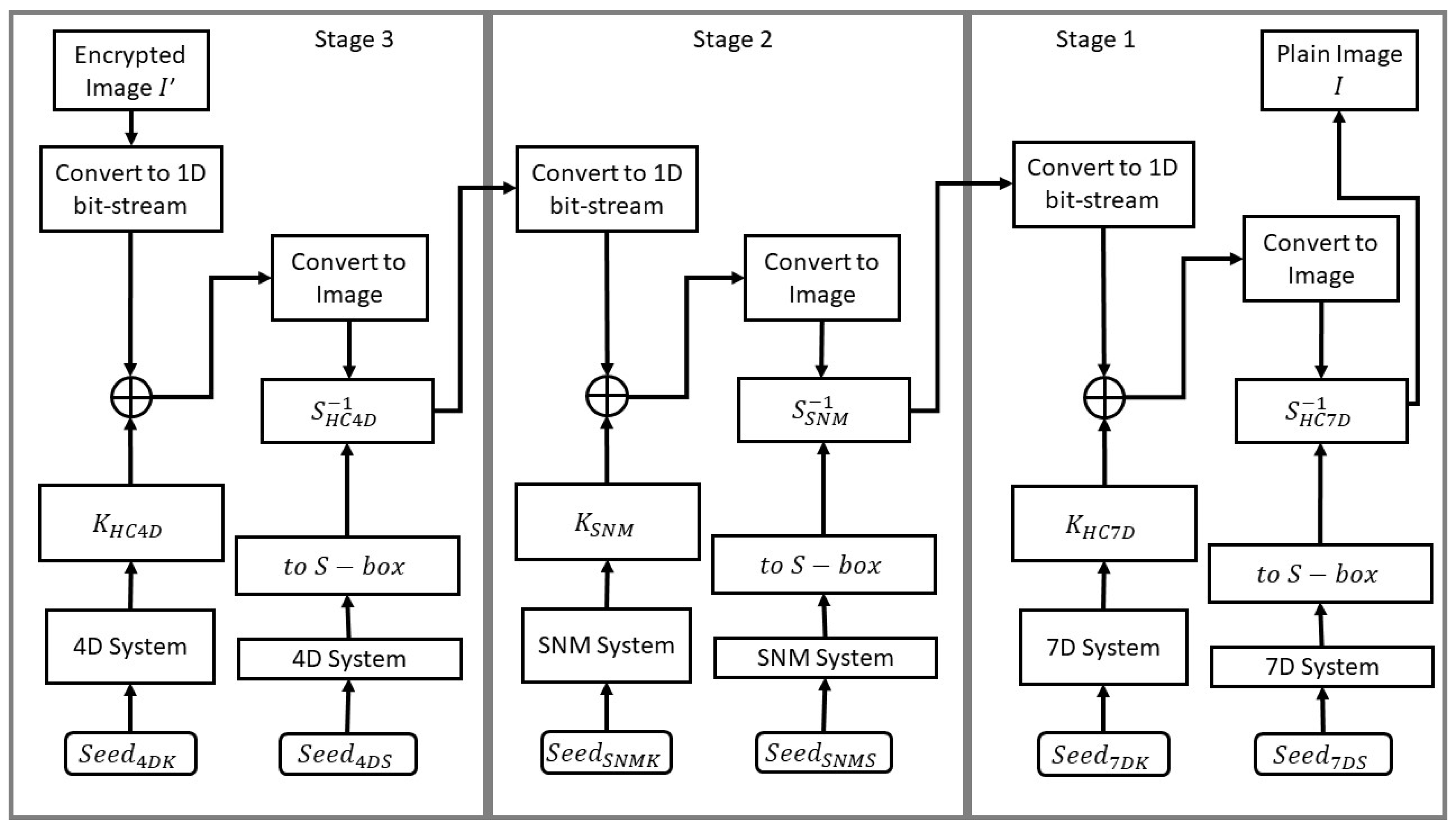
A chaos-based, 3-stage, dual-acting image encryption framework is proposed. In every stage, a novel S-box is constructed and applied. This is followed by the generation and application of the logical XOR operation between a generated PRNG key and the image bits.
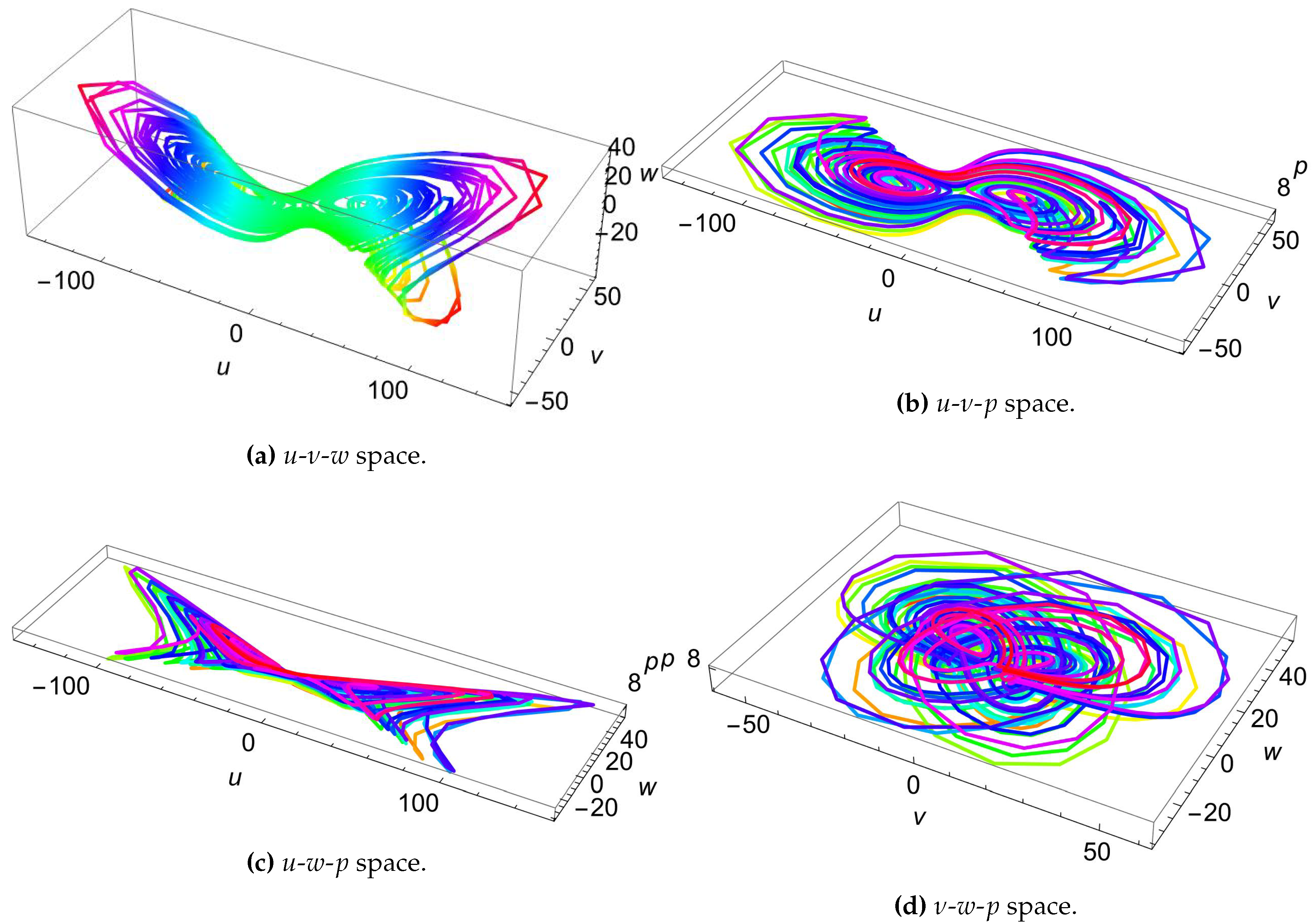
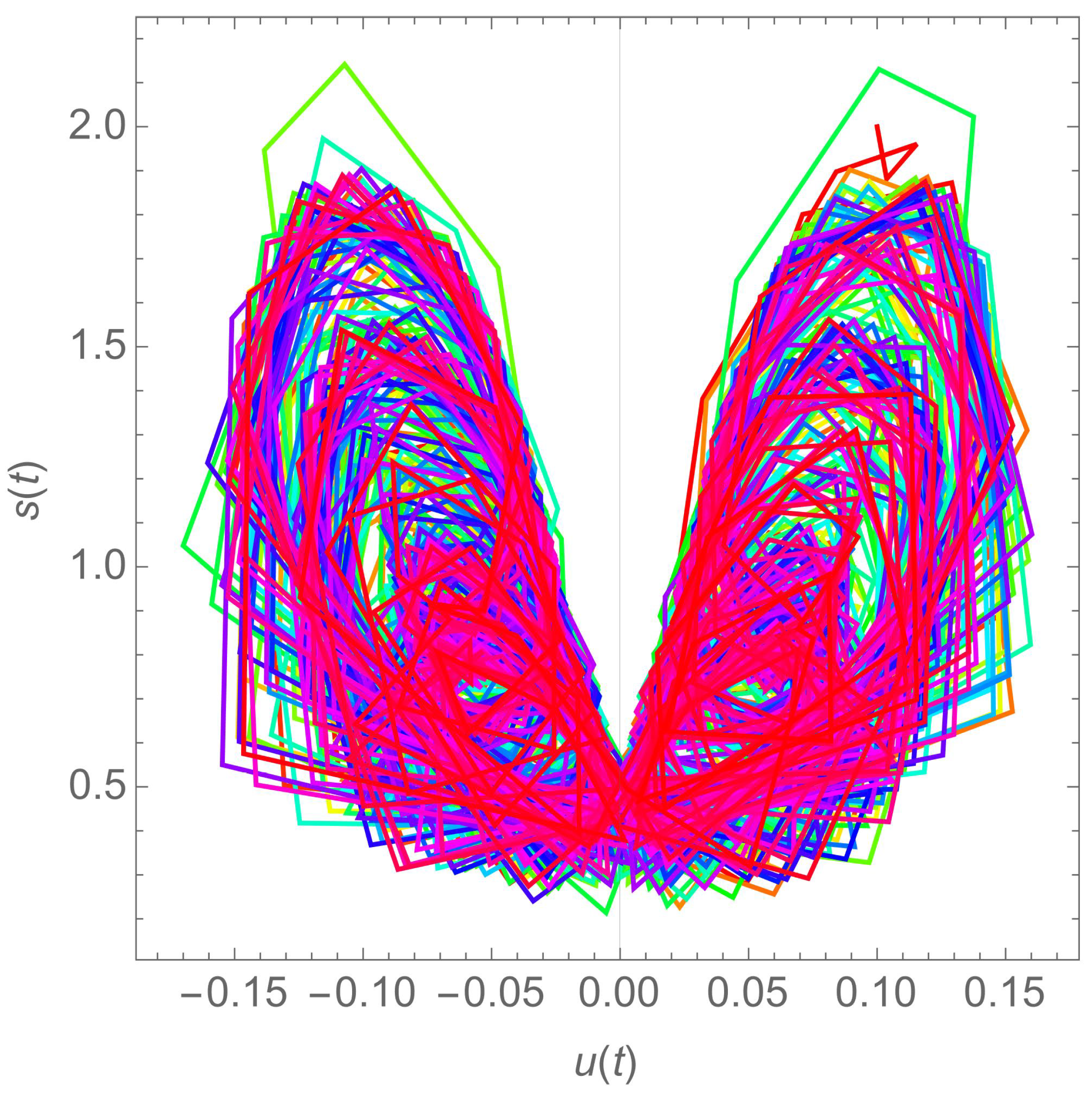
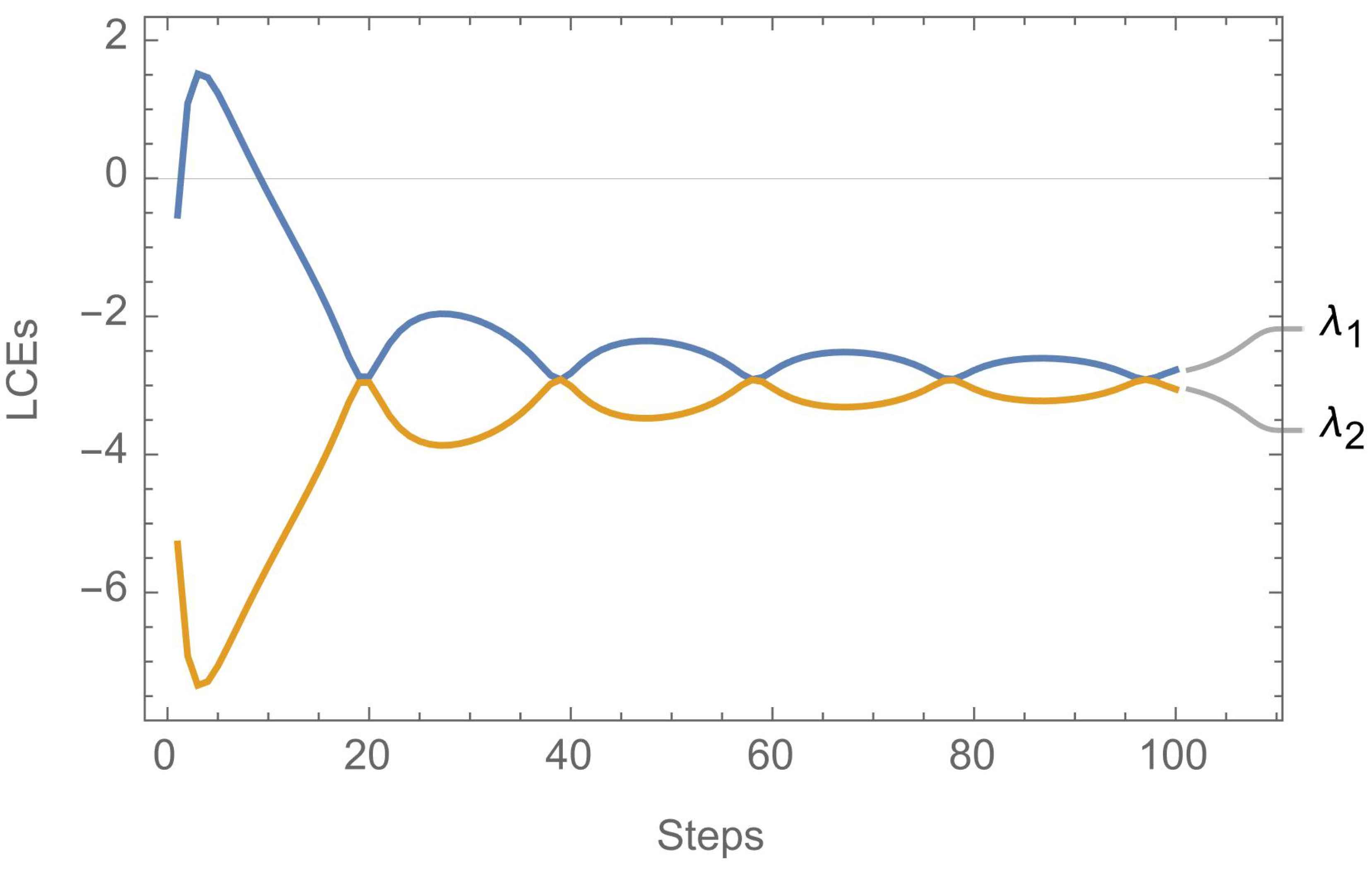
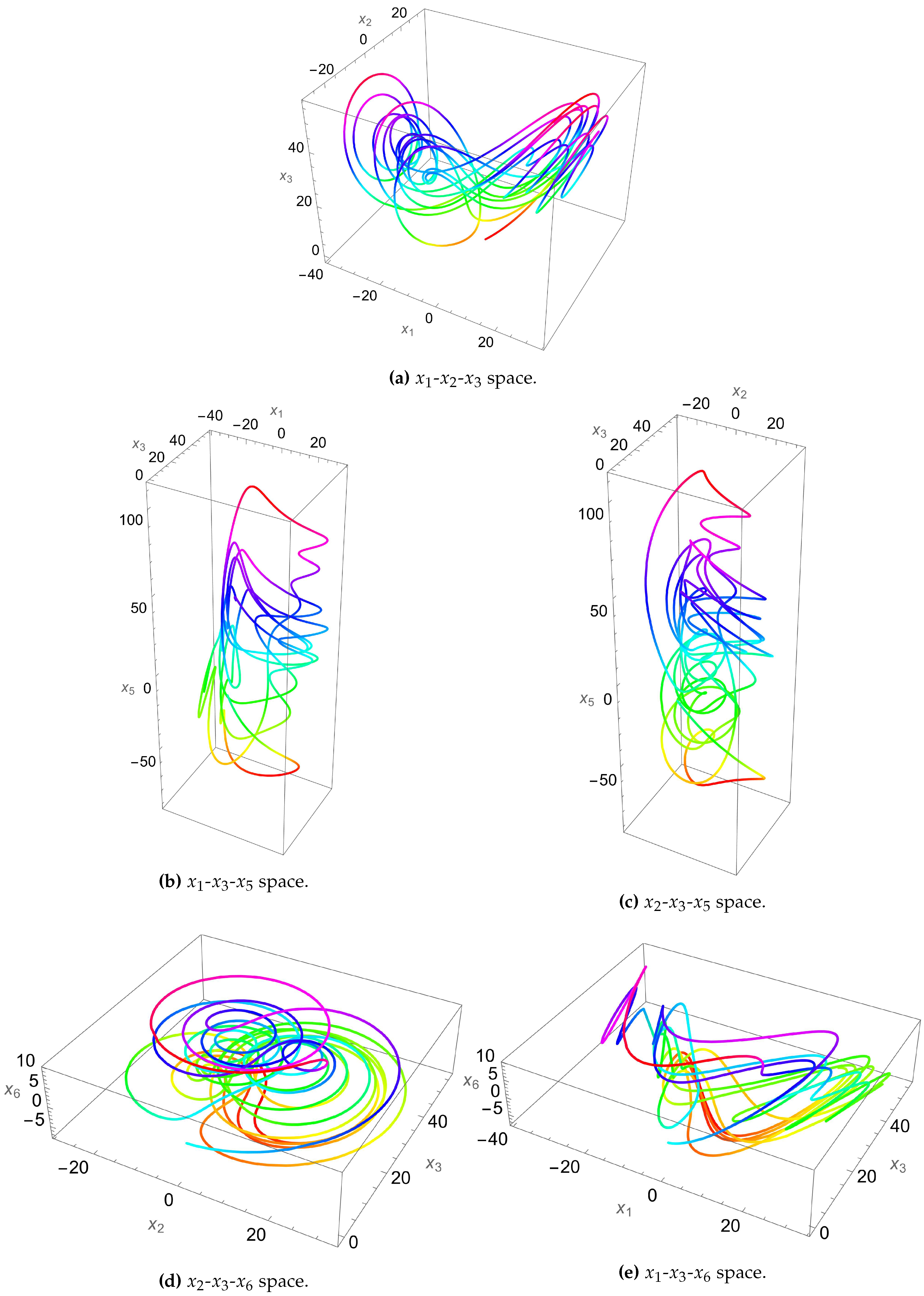
In the first stage, a 7D hyperchaotic system of differential equations is numerically solved and its solution is utilized both for PRNG key generation and S-box construction.
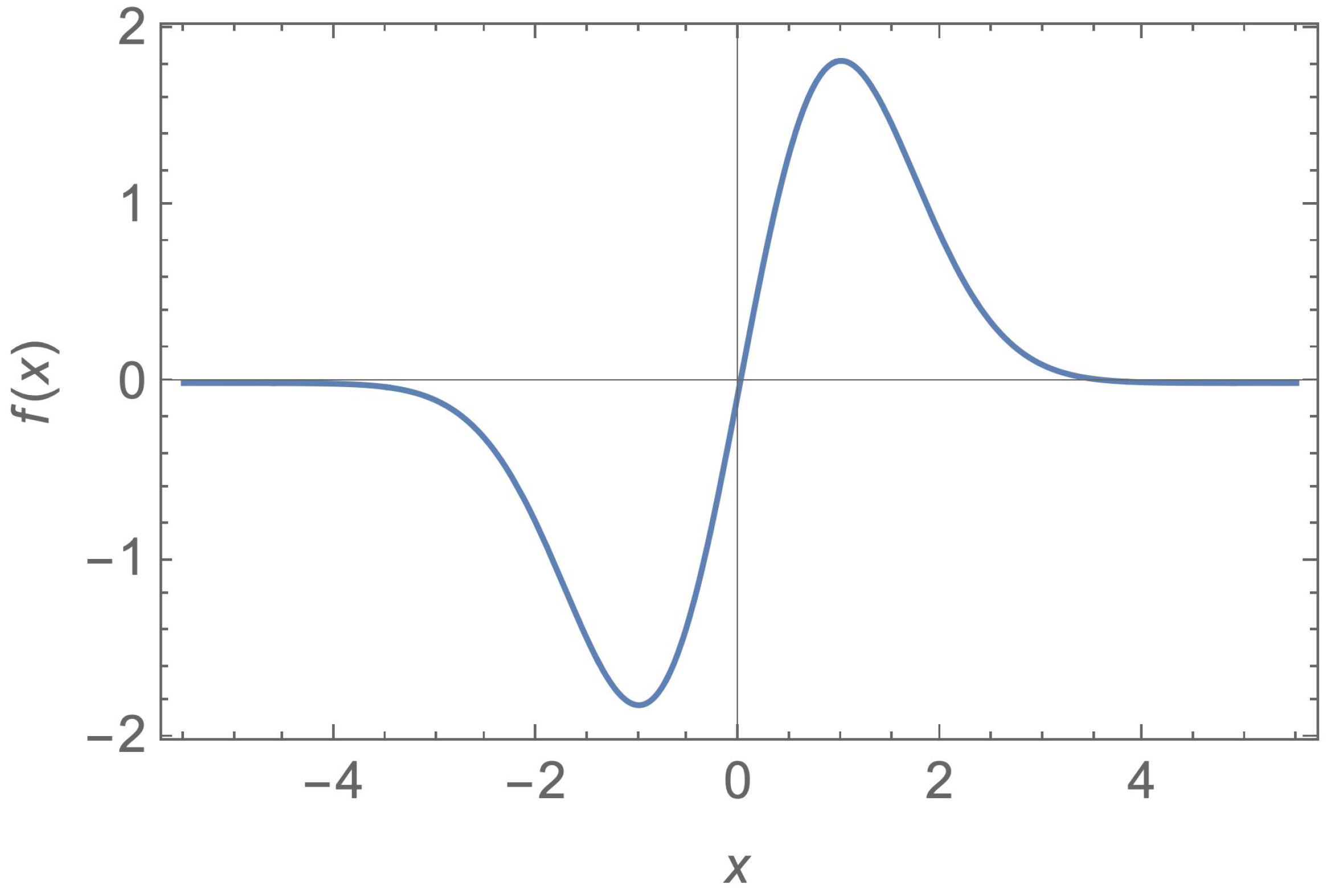
In the second stage, a single neuron model is numerically solved and its solution is utilized both for PRNG key generation and S-box construction.
In the third stage, a 4D hyperchaotic system of differential equations is numerically solved and its solution is utilized both for PRNG key generation and S-box construction.
The utilization of 3 different systems, 2 of which are hyperchaotic, as well as the selection of 3 S-boxes that satisfy certain criteria, a rather wide key space of is achieved, providing sufficient resistivity to brute-force attacks.
The software implementation of the proposed image encryption framework makes use of advanced parallel processing techniques. This allows for an average encryption rate of Mbps to be achieved.
This article is organized as follows.
Section 2 makes reference to the foundational systems of differential equations that are to be employed for PRNG key generation and outlines the adopted methodology for the construction of S-boxes.
Section 3 introduces the image encryption and decryption processes of the proposed framework.
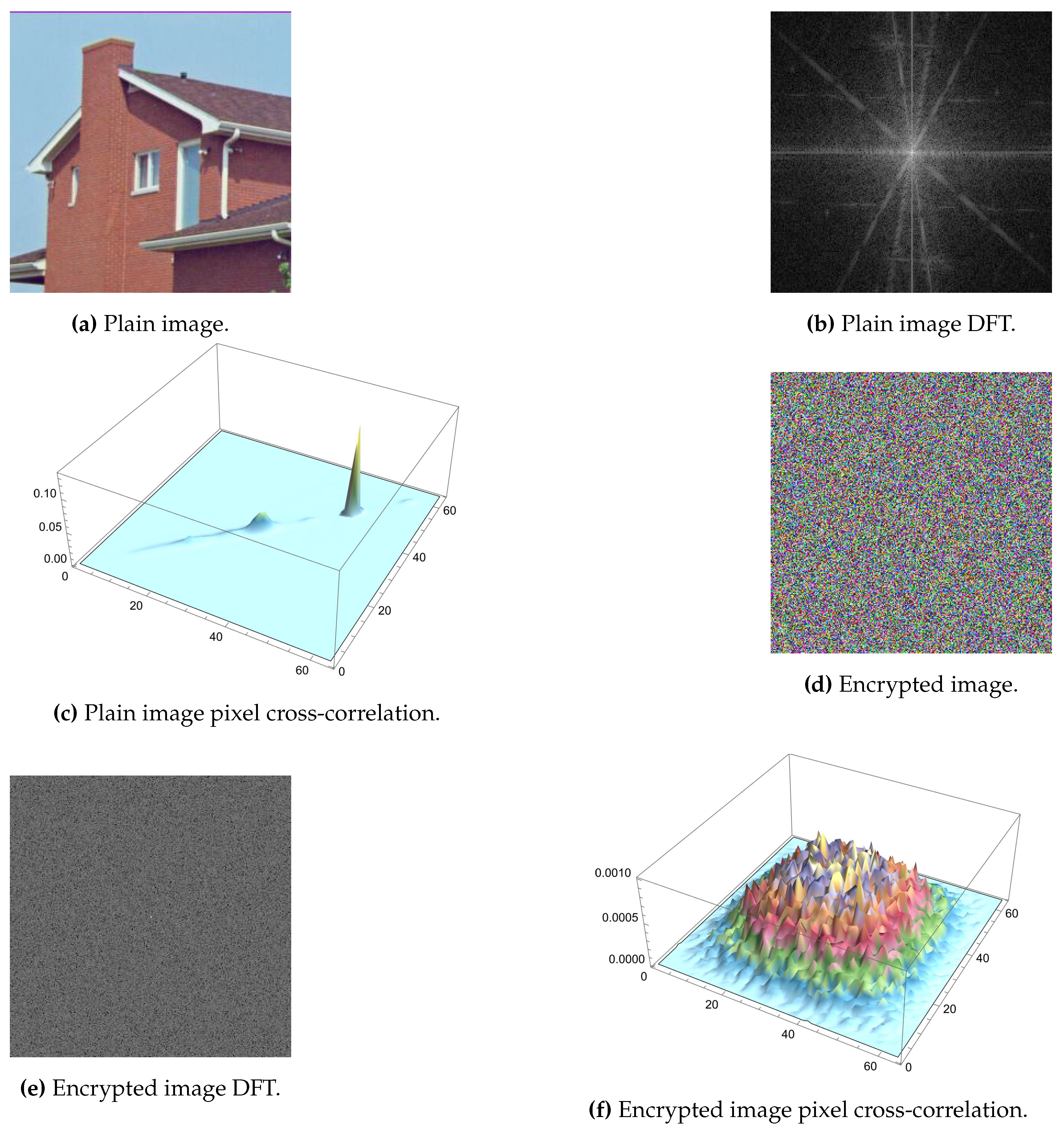
Section 4 provides the numerical results and performance evaluation of the proposed framework. A comparative study with the state-of-the-art is also carried out in this section.
Section 5 concludes this research work and provides some suggestions for possible future areas of research.