Prerpints.org logo
Preprint
Article

Three-Dimensional Cranio-Facial Landmark Detection in Series of CT Slices, Using Multi-Phased Regression Networks

Altmetrics

Downloads

167

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 April 2023

Posted:

10 April 2023

You are already at the latest version

Alerts
Abstract
Geometrical assessments of human skull have been done based on the anatomical landmarks. Automatic detection of the landmarks, if developed, will be a great help not only medically, but also anthropologically. An automated system with multi-phased deep learning networks to predict three-dimensional coordinate values of cranio-facial landmarks, was developed. From a publicly available database, computed tomography images of craniofacial area were obtained. They were digitally reconstructed into three-dimensional models. Sixteen anatomical landmarks were plotted on each of the models and coordinate values of them were recorded. Three-phased regression deep learning networks were trained respectively with 90 training datasets. For evaluation, 30 testing datasets were employed. Three-dimensional error for the first phase, testing 30 data, was 11.60 pixels in average. (1 pixel = 500 / 512 mm) For the second phase, it was significantly improved to 4.66 pixels. For the third phase, it was significantly progressed to 2.88. This was comparable to the gaps between the landmarks, plotted by two experienced practitioners. Our proposing method of multi-phased prediction, coarse detection first and narrowing down the detection area, may be a possible solution, within the physical limitation of memory and computation.
Keywords: 
Subject: Medicine and Pharmacology  -   Dentistry and Oral Surgery

1. Introduction

Measuring distances between characteristic landmarks and angles between certain planes determined by the points, is a useful approach to comprehend the shape of an object. To evaluate human skull, this approach has long been done[1,2,3,4]. For living human, direct access to the landmarks on the skull is impossible. X-ray imaging enabled to project the skull. In 1920s, Todd and Broadbent developed a device to hold human skull and mandible, which allowed for acquisition of standardized radiographs[5]. Cephalometry, first introduced by Broadbent[6] and Hofrath[7] in 1931, has been and still is one of the most helpful modalities in evaluating cranio-maxillo-facial configurations. Geometrical assessments are done based on the anatomical landmarks [8,9,10,11].
Locating anatomical landmarks demands time and expertise. Automatic detection of the landmarks will be a great help not only medically, but also anthropologically. Studies has been done to accomplish this challenge in 2-D cephalograms [12,13,14,15,16,17,18,19,20,21]. A systematic review was published[22] in 2008. Though, it was not possible to compare between methods as they used their own data, which were different from one another. Unification of image data to assess was necessary. Grand challenges were held in 2014[23] and 2015[24], in conjunction with IEEE International Symposiums on Biomedical Imaging. Cephalometric X-ray images with coordinate values of landmarks were provided by the organizers. Participants competed with their own performances on the same datasets. Top ranks were occupied by the performers used random forest method[24]. Lindner et.al[25] used the same images with a subset of coordinate values. After that, a method using convolutional neural networks was proposed[26].It outperformed previous benchmarks with the same datasets of the grand challenge. Multi-phased regression deep learning neural networks[27] with regression-voting[28] enhanced the prediction accuracy. Kim et.al utilized two stage method on larger volume datasets of their own[29]. Multi-staged convolutional neural networks were used on two dimensionally projected CBCT[30]. A study with attentive feature pyramid fusion module[31] surpassed previously published works. A systematic review for artificial intelligence in cephalometric landmark identification has been done lately[32].A new grand challenge with larger volume datasets is in session[33].
Inherently, this evaluation of the objects in two-dimensionally projected images encompasses some kinds of inaccuracy and incapability, because of the loss of some original information in three dimensions. It is rare for the cranium to be bilaterally symmetrical.
Three-dimensional cephalometric analysis was done originally with two (lateral and basilar or posteroanterior) cephalograms[34,35,36,37]. Computer assisted tomography (CT) has become popular in daily clinical practice. CT images, horizontal slices as two-dimensional pictures, are usually stored in DICOM (Digital Imaging and Communications in Medicine) formatted files. They can be digitally restructured into virtual three-dimensional objects. 3D printing can also be done. They visually help people to comprehend the bodies. Three-dimensional measurement based on the anatomical landmarks can be done on the objects. Cephalometric analysis on three-dimensional images is becoming popular[38,39,40].
In comparison with those for 2D cephalograms, reports on automatic landmark detection systems for 3D images are chronologically new and less in number[41]. Shahidi et al.[42] used an atlas based method to identify 14 landmarks on 20 cone beam computed tomography (CBCT) images in 2014. A knowledge-based method[43] was reported in 2015. Some kinds of learning based methods[44,45,46,47,48,49,50,51] have been reported. In our experience with 2D cephalograms[27,28], multi-phased deep learning system was able to predict coordinate values in high precision. It was to predict roughly in whole area of the image first, and mark down smaller area of interest in following phases. In this report, a multi-phased deep learning system to predict three-dimensional coordinate values of craniofacial landmarks in sequences of CT slices is discussed.

2. Materials and Methods

2.1. Personal computer

All procedures were done on a desk-top personal computer: CPU (Central Processing Unit): AMD Ryzen 7 2700X 3.70GHz (Advanced Micro Systems, Sunnyvale, CA, USA), memory: 64.0GB, GPU: GeForce RTX2080 8.0GB ((nVIDIA, Santa Clara, CA, USA), Windows 10 pro (Microsoft Corporations, Redmond, WA, USA). Python 3.7 (Python Software Foundation, DE USA): a programing language, was used under Anaconda 15 (FedoraProject. http://fedoraproject.org/wiki/Anaconda#Anaconda_Team_Emeritus) as an installing system, and Spyder 4.1.4 as an integrated development environment. Keras 2.31 (https://keras.io/): the deep learning library, written in Python was run on TensorFlow 1.14.0 (Google, Mountain View, CA, USA). GPU computation was employed through CUDA 10.0 (nVIDIA). For 3D reconstruction, slicer 4.11 (www.slicer.org) was used with Jupyter Notebook (https://jupyter.org/). OpenCV 3.1.0 libraries (https://docs.opencv.org/3.1.0/) were used in image processing.

2.2. Datasets

(1) CT images
From The Cancer Imaging Archive Public Access (wiki.cancerimagingarchive.net), Head-Neck-Radiomics-HN1[52], the collection of CT images from head and neck squamous cell carcinoma patients was retrieved. It consists of the folder of each patient, containing 512 x 512 pixels DICOM images (number ranged 0 to 4071 for each pixel), taken axially at 5 mm intervals in the cephalocaudal direction. The order of the images was checked and images from the top of the head to the mandible were extracted for 120 cases. The largest number of extracted images for a patient was 81. As a calibration marker, a 512-pixel length and width cross were added to the most caudal images.
(2) 3D reconstruction (STL file creation)
DICOM CT image sequence for each case was processed with 3D slicer kernel, using Jupyter notebooks. With a python script process[53], bony parts were segmented and reconstructed into 3D images and stored as STL files.
(3) Plotting anatomical landmarks
Each STL file was imported into blender (https://www.blender.org/). Spheres with 1 pixel radius were placed as the landmarks. The landmarks are listed in Table 1. and shown in Figure 1. Most of the images were from probably old patients, there were many missing teeth. Many of them were in open bite position. Therefore, landmarks on teeth were not plotted in this study. Three-dimensional coordinate values (x, y, z) of the imported STL and spheres were obtained and exported as an array of 120 cases x 16 points x 3.　Two practitioners, with 31 and 10 year-experience, respectively plotted landmarks. The coordinate values plotted by the senior was used as the ground truth.
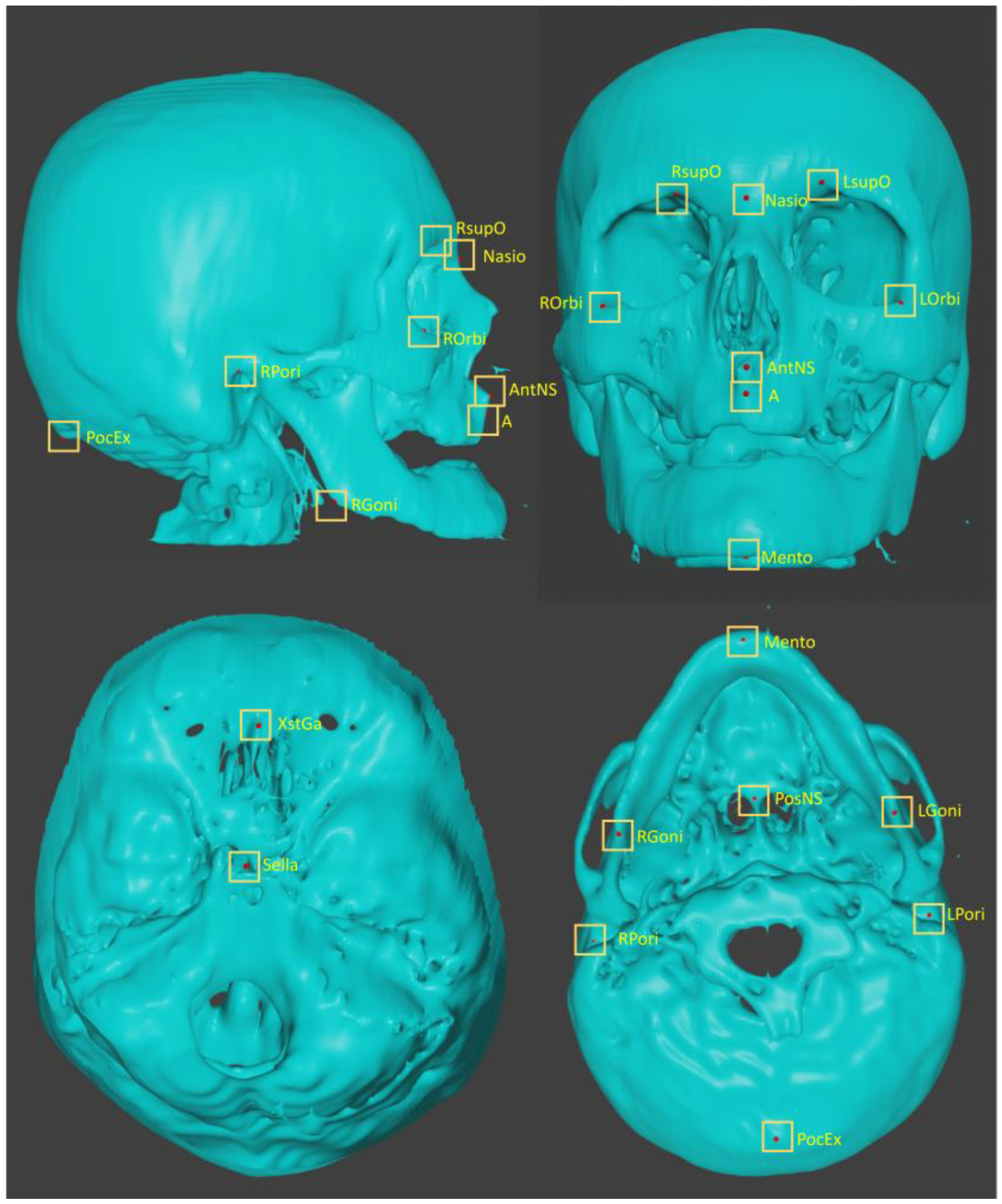
Preprints 70664 g001
Figure 1. Three dimensionally plotted landmarks.
Figure 1. Three dimensionally plotted landmarks.
Preprints 70664 g001
Table 1. Plotted landmarks.
Table 1. Plotted landmarks.
No, abbreviation description
L01 A point A
L02 AntNS Anterior Nasal Spine
L03 LGoni Left Gonion
L04 LOrbi Left inferior lateral Orbital rim
L05 LPori Left Porion
L06 LsupO Left supra Orbital incisura
L07 Mento Menton
L08 Nasio Nasion
L09 PocEx External occipital Protuberance
L10 PosNS Posterior nasal spine
L11 RGoni Right Gonion
L12 ROrbi Right inferior lateral Orbital rim
L13 RPori Right Porion
L14 RsupO Right supra Orbital incisura
L15 Sella center of Sella turcica
L16 XstaG top of crista Galli

2.3. Neural Networks and Learning Datasets

(1) 1st phase deep learning (Figure 2.)
With OpenCV, each CT image (512 x 512 pixels DICOM image) was binarized to segment bone with 1100 as threshold and compressed to 96 x 96 pixels. For each case, they were stacked up from the bottom to form a three-dimensional array of 96 x 96 x 81. As training data, 90 cases were assigned, and 30 were as testing data. A regression deep learning model, modified (only the last activation layer was changed from “softmax” to “linear”) Resnet 3d-50[54], built with 96 x 96 x 81 as input and 48 as output. It was trained for 150 epochs.
(2) 2nd phase deep learning (Figure 3.)
A 100 x 100-pixel image was cropped out from each original image with OpenCV, centered on the x and y coordinates of each landmark. Each of them were piled up from the bottom to form a 100 x 100 x 81 3D-array. For data augmentation, the images were also cropped out at shifted positions in the x and y directions and stacked in the same way to obtain the positions of feature points in each array (3240 sets in total). For each landmark, the modified Resnet 3d-50 model for regression with 100 x 100 x 81 as input and 3 as output was trained for 100 epochs.
(3) 3rd phase deep learning (Figure 4.)
A 50 x 50-pixel image was cropped out from each original image, in the same way for the 2nd phase. Stacks of 50 x 50 x 81 were obtained. For training, 3240 sets of data for each landmark were used. Modified Resnet 3d-50 with input of 50 x 50 x 81 and 3 as output was trained for 150 epochs.
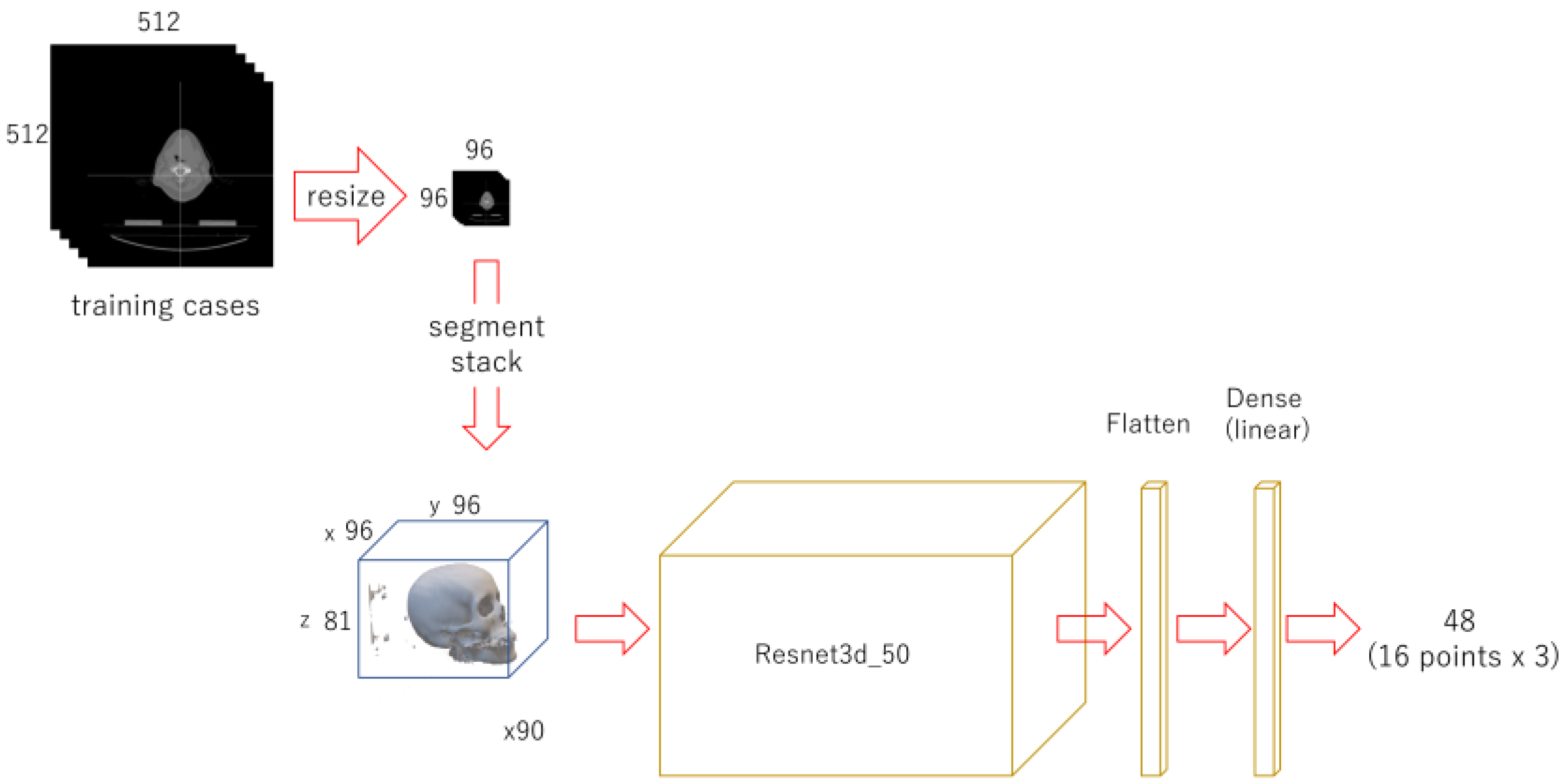
Preprints 70664 g002
Figure 2. Diagram of the 1st phase deep learning.
Figure 2. Diagram of the 1st phase deep learning.
Preprints 70664 g002
Each CT image (512 x 512 pixels) was compressed to 96 x 96 pixels and stack up. A regression deep learning model was trained with 90 cases for 150 epochs.
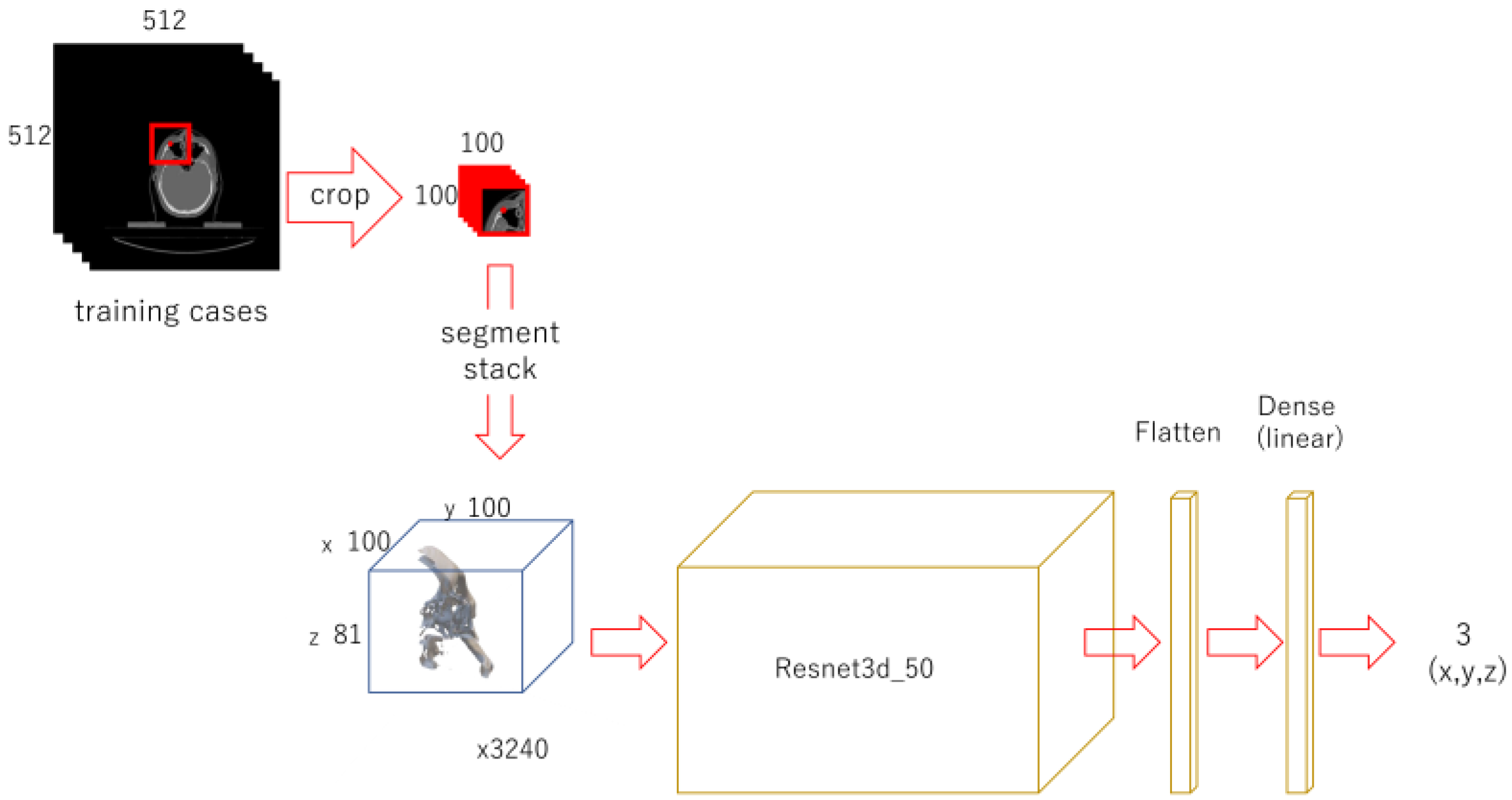
Preprints 70664 g003
Figure 3. Diagram of the 2nd phase deep learning.
Figure 3. Diagram of the 2nd phase deep learning.
Preprints 70664 g003
For each landmark, 100 x 100 pixel images were cropped out, centering the x and y coordinates of it. They were stacked up to 100 x 100 x 81 3D array. Shifted images were also cropped and piled up for data augmentation. A model was trained for each landmark.
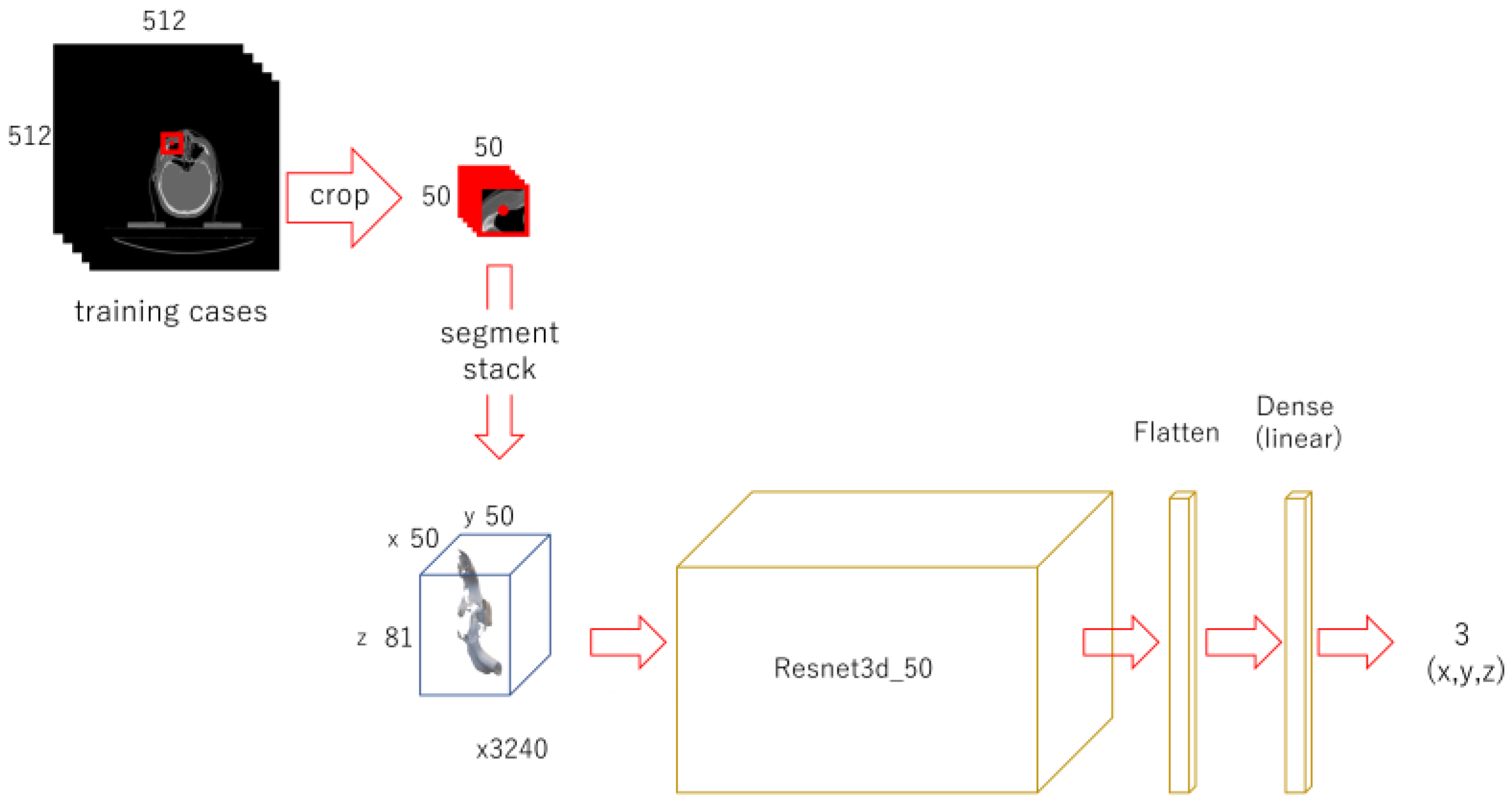
Preprints 70664 g004
Figure 4. Diagram of the 3rd phase deep learning.
Figure 4. Diagram of the 3rd phase deep learning.
Preprints 70664 g004
A 50 x 50 pixel image was cropped from the original image, centering the x and y coordinates of the landmark. Each of them was piled up to 3D array. Shifted images were also cropped and piled up. A Resnet model was trained respectively for each landmark.

2.4. Evaluation (Figure 5.)

For evaluation, 30 testing data that were not used in the training were employed.
(1) 1st phase prediction
The 96 x 96 x 81 3D-array of the 30 cases for validation was fed to the trained 1st phase model to predict the 3D coordinates of feature points.
(2) 2nd phase prediction
The 100 x 100-pixel images were cropped from the original validation images, centered on each of the 16 coordinates obtained in the 1st phase prediction, and piled up into 100 x 100 x 81 3D arrays. They were used to predict the coordinates of each feature point with the trained 2nd phase models.
(3) 3rd phase prediction
For each landmark, 50 x 50-pixel images were cropped, centered on each of the coordinates obtained in the 2nd phase prediction. They were stacked up to 50 x 50 x 81 arrays and fed to the respective 16 trained 3rd phase models.
(4) Prediction error evaluation
The distance between the predicted coordinates and the manually plotted ground truth coordinates was calculated as the absolute value in the x, y, and z directions. The square root of the sum of the squares of each was used as the 3D distance.
(5) Statistical analysis
Multiple comparisons were done using scikit-posthocs (https://scikit-posthocs.readthedocs.io/en/latest/#).
Preprints 70664 g005
Figure 5. Prediction and evaluation.
Figure 5. Prediction and evaluation.
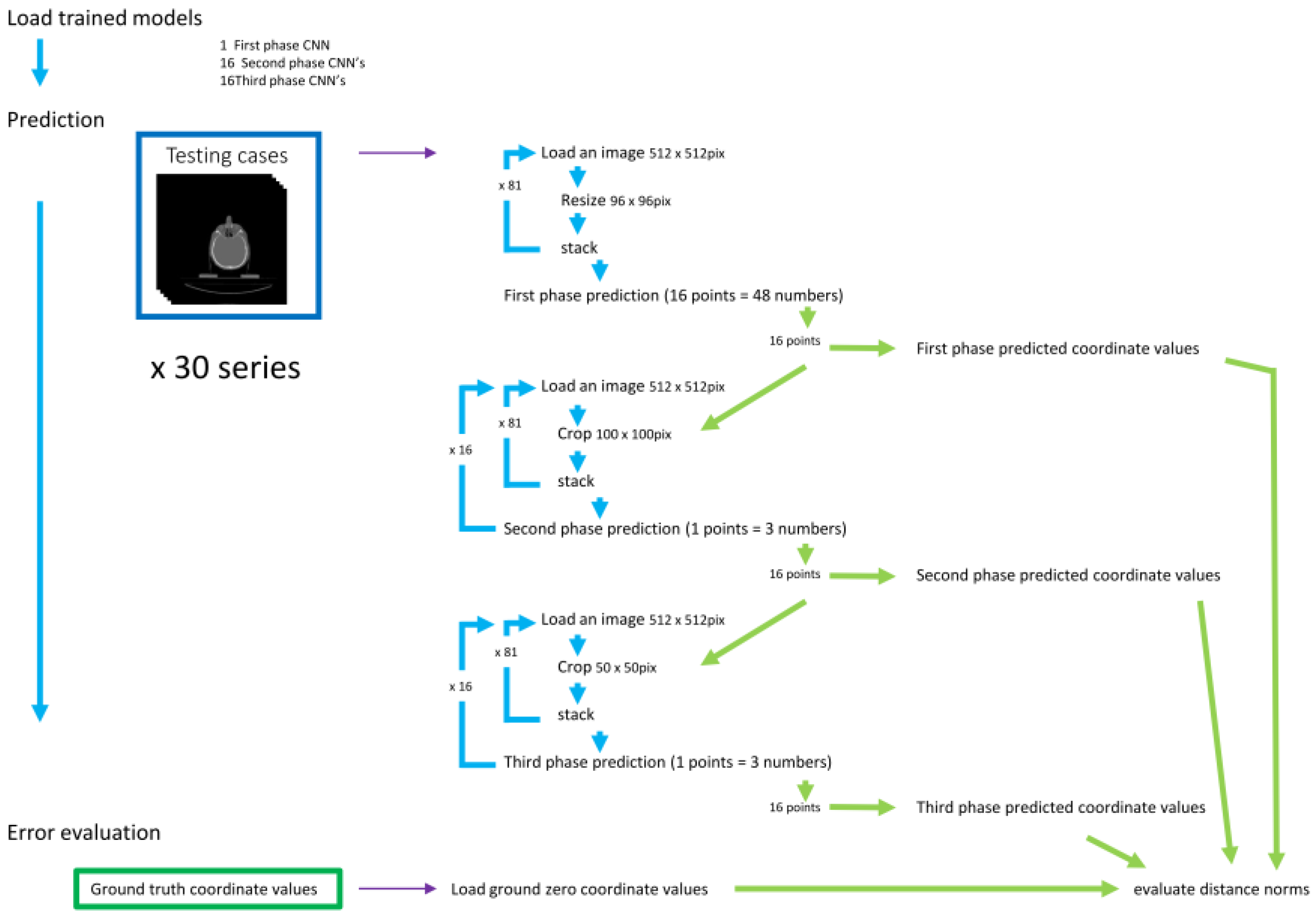
Preprints 70664 g005
Prediction of the landmark coordinate was done by 3 phases. The three-dimensional distances between the predicted and the ground truth points were evaluated.

3. Results

3.1. 1st phase prediction error

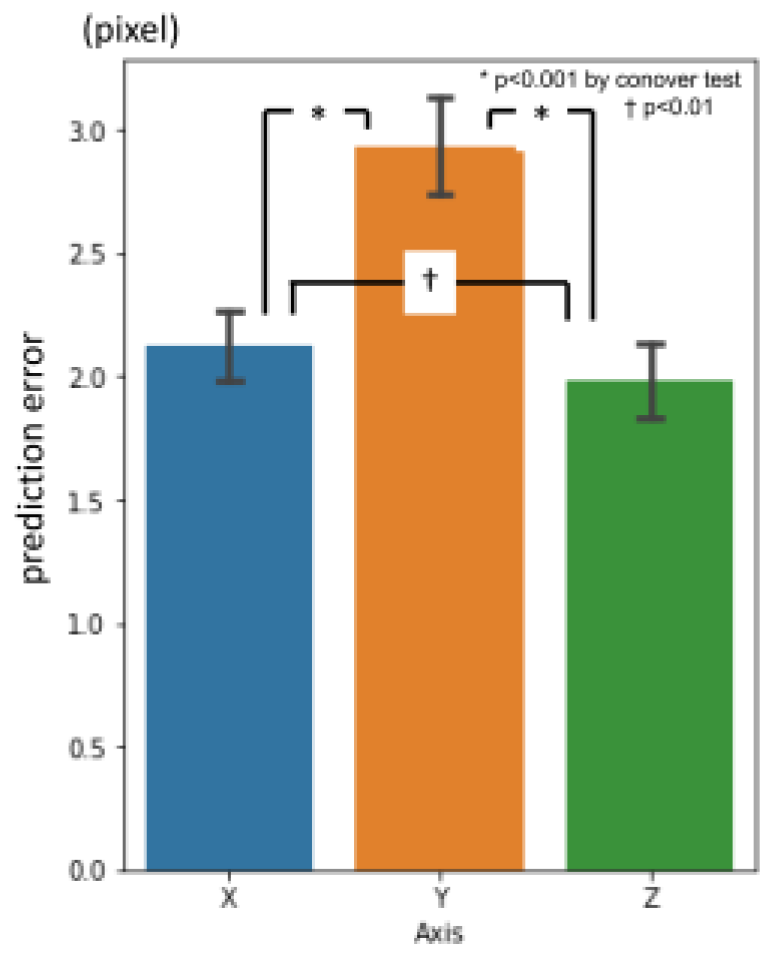
Overall average three-dimensional distance between the predicted points and the ground truth was 11.60 pixels (1 pixel = 500 / 512 mm) (Table 2.). Per landmark prediction errors are shown in Figure 6. Between axis directions, error for x-axis was significantly smaller than the others, and y-axis was the largest (Figure 7.).
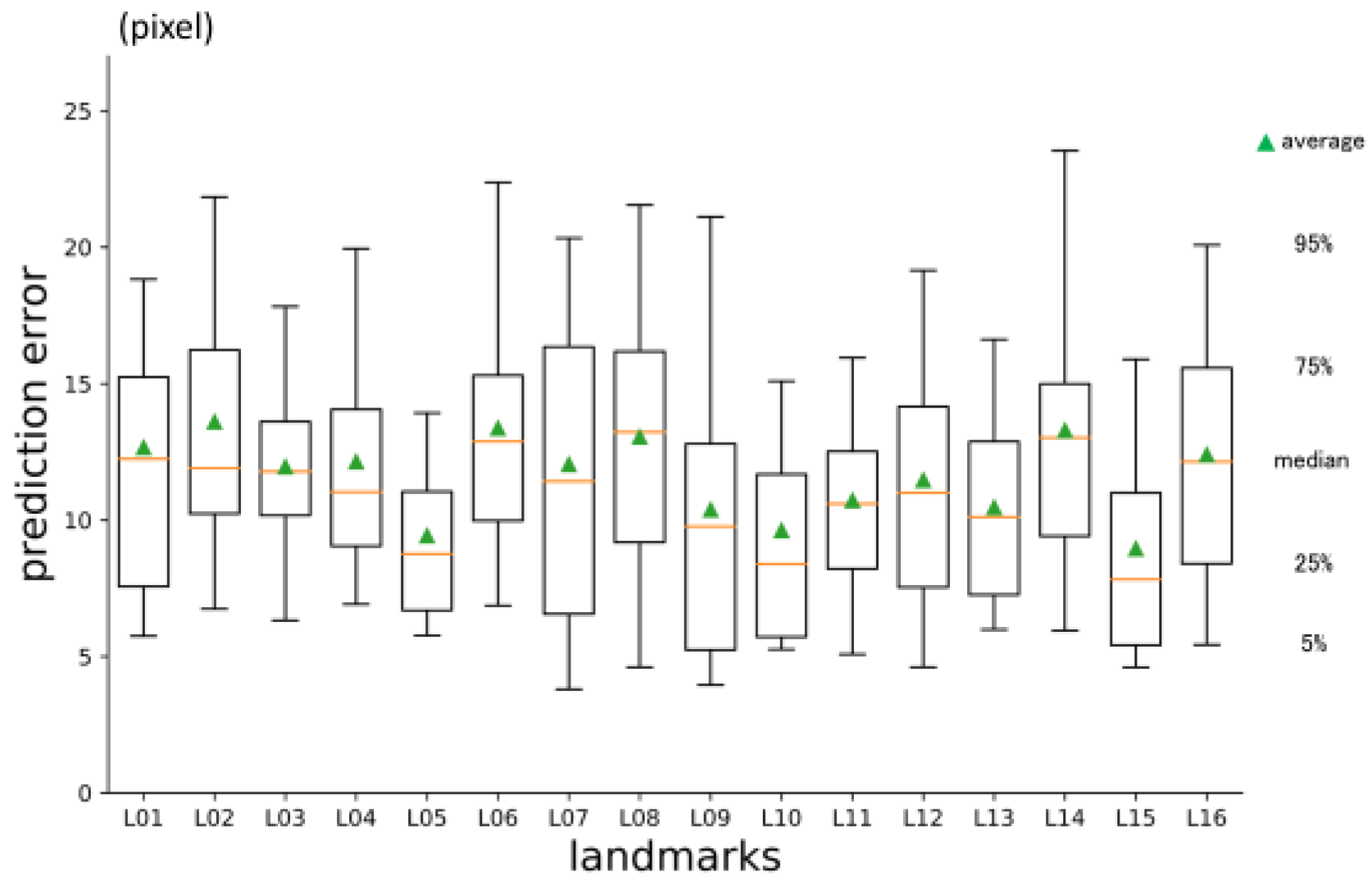
Preprints 70664 g006
Figure 6. 1st phase prediction errors per landmark (pixel = 500 / 512 mm).
Figure 6. 1st phase prediction errors per landmark (pixel = 500 / 512 mm).
Preprints 70664 g006
Preprints 70664 g007
Figure 7. 1st phase prediction errors per axis (pixel = 500 / 512 mm).
Figure 7. 1st phase prediction errors per axis (pixel = 500 / 512 mm).
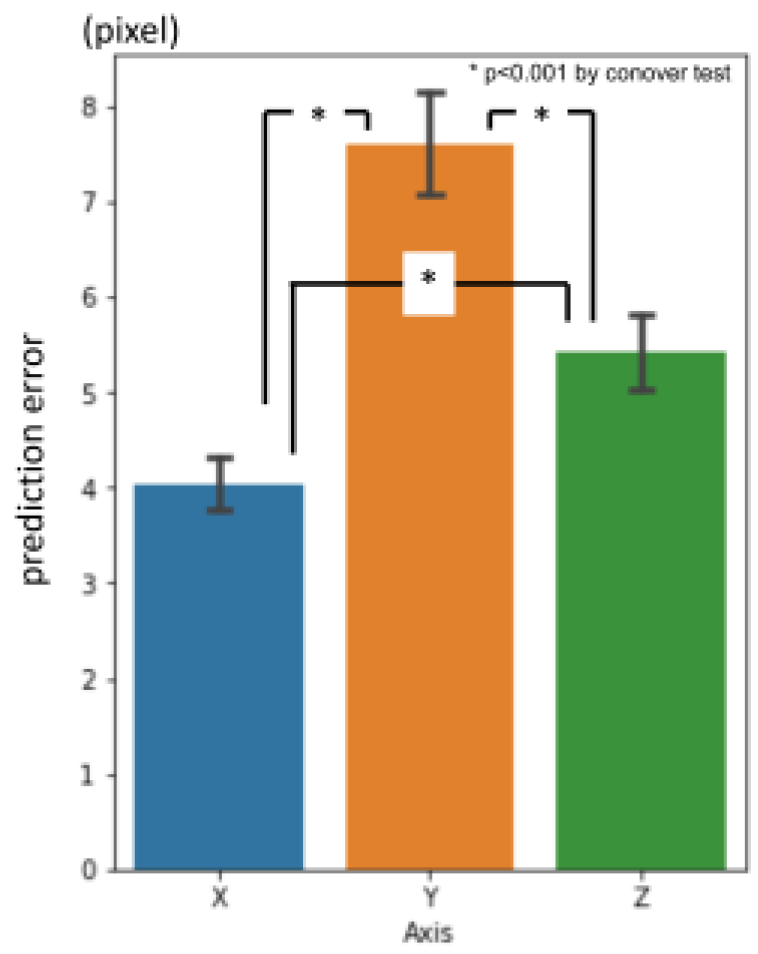
Preprints 70664 g007
Table 2. Three-dimensional prediction errors in 480 landmarks of 30 testing data. (pixel = 500 / 512 mm)　*p<0.001 by Conover test.
Table 2. Three-dimensional prediction errors in 480 landmarks of 30 testing data. (pixel = 500 / 512 mm)　*p<0.001 by Conover test.
　 　 1st phase 　 2nd phase 　 3rd phase 　 inter-observer gaps 　
average 11.6 _ * _ 4.66 _ * _ 2.88 _ N.S. _ 3.08
median 10.89 4.22 2.56 2.4
　 stdev 5.64 　 2.27 　 1.67 　 2.64 　

3.2. 2nd phase prediction error

The average prediction error in three dimensions was 4.66 pixels (Table 2.). It was significantly smaller than 1st phase prediction. Per landmark errors are shown in Figure 8. Error for y-axis direction was larger than the others. Error for z-axis was the smallest (Figure 9.).
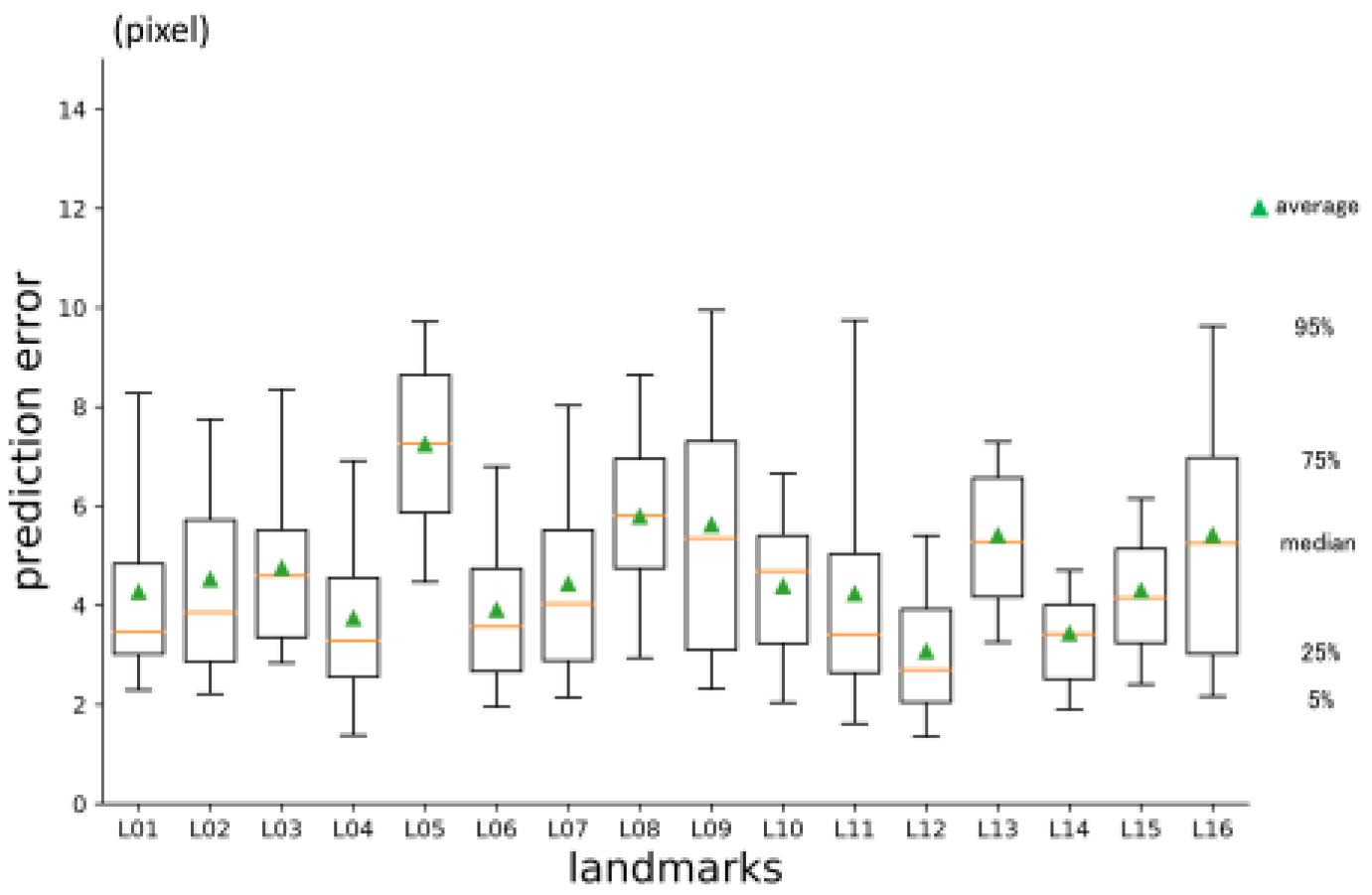
Preprints 70664 g008
Figure 8. 2nd phase prediction errors per landmark (pixel = 500 / 512 mm).
Figure 8. 2nd phase prediction errors per landmark (pixel = 500 / 512 mm).
Preprints 70664 g008
Preprints 70664 g009
Figure 9. 2nd phase prediction errors per axis (pixel = 500 / 512 mm).
Figure 9. 2nd phase prediction errors per axis (pixel = 500 / 512 mm).
Preprints 70664 g009

3.3. 3rd phase prediction error

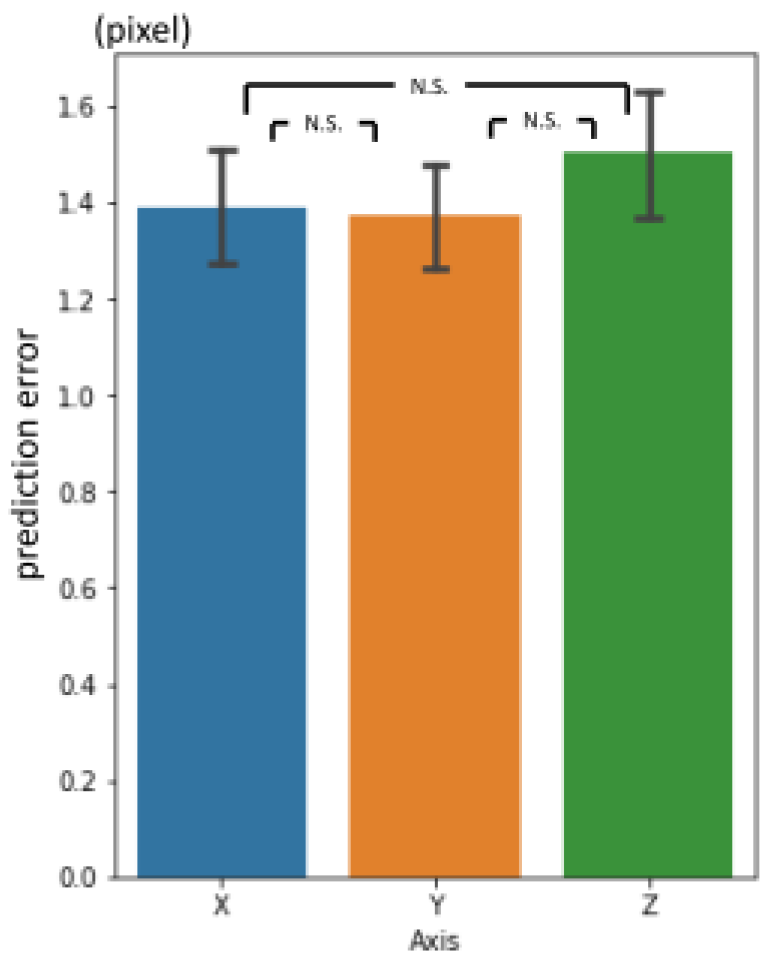
The three-dimensional prediction error was 2.88 pixels in average (Table 2.). It was significantly smaller than 2nd phase prediction. Errors per landmark are shown in Figure 10. There was no significant difference between axes (Figure 11.).
Preprints 70664 g010
Figure 10. 3rd phase prediction errors per landmark (pixel = 500 / 512 mm).
Figure 10. 3rd phase prediction errors per landmark (pixel = 500 / 512 mm).
Preprints 70664 g010
Preprints 70664 g011
Figure 11. 3rd phase prediction errors per axis (pixel = 500 / 512 mm).
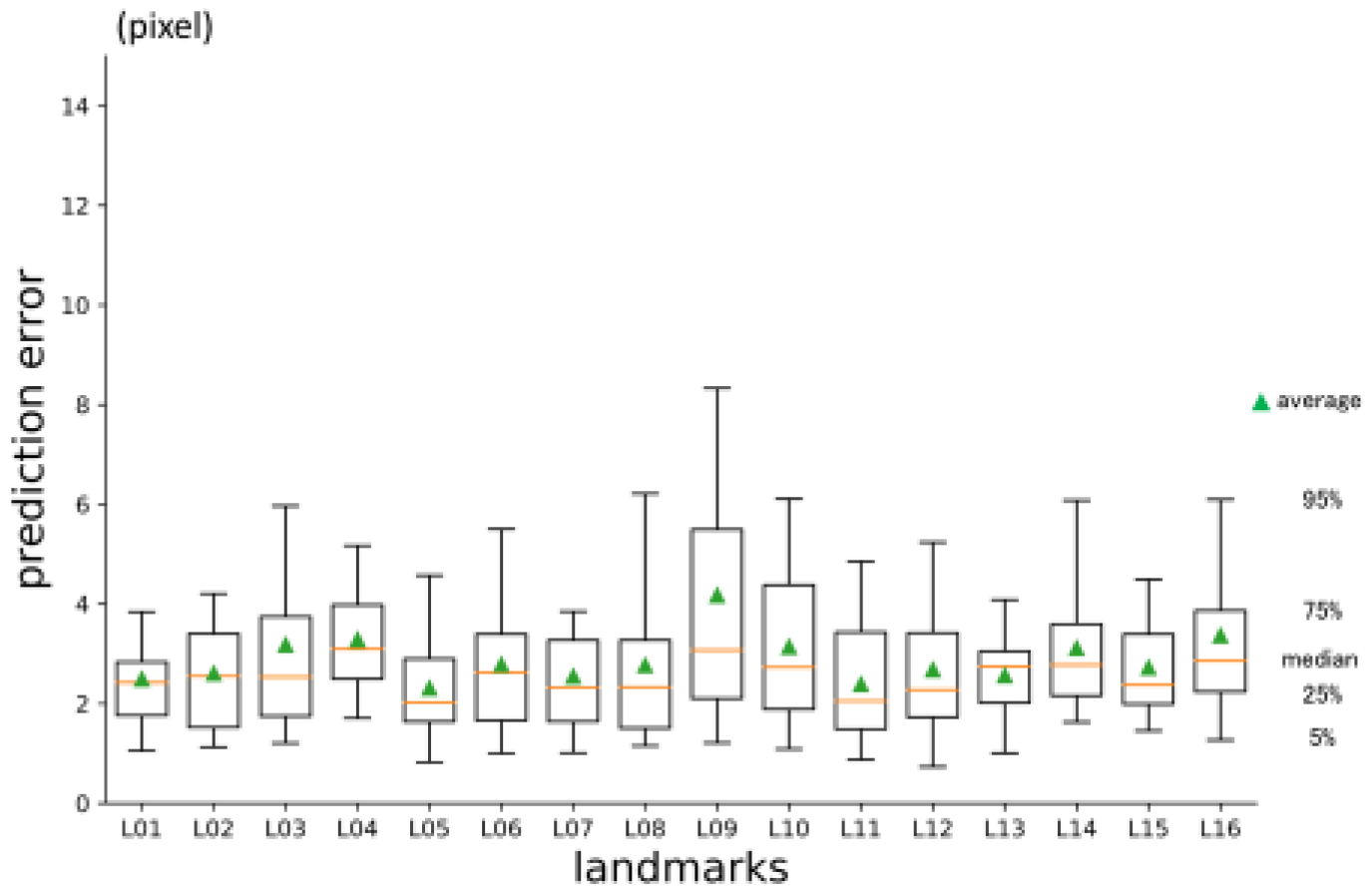
Figure 11. 3rd phase prediction errors per axis (pixel = 500 / 512 mm).
Preprints 70664 g011

3.4. Inter-phase and inter-observer plotting gap

There were significant differences between prediction errors by phases. The 3rd phase prediction error was the same level as the inter-observer plotting gaps.

4. Discussion

The history of standard cephalometry, since Broadbent[6] and Hofrath[7] first proposed. is quite long. There have been many reports on automatic landmark detection systems for cephalograms in two-dimensions. In comparison with 2D cephalograms, there are fewer reports for 3D images.
Some previous automated 3D landmark detectors in craniofacial area employed registration method[55], knowledge-based methods[43,56], atlas-based methods[42,57], random forest method[44] and so on[46,48]. Deep learning is one of the most emerging techniques in machine-learning. It is categorized as a supervised learning that to find out rules between input and output of training datasets. All we need is to prepare the datasets, and the machine will figure out the function laws between them. It is very versatile. Some attempts to utilize deep learning for automatic 3D landmark prediction have been reported[45,49,51,58,59].
The processing speed of computers and the amount of memory installed have increased at a dizzying rate. Though, the amount of computation, required to process images with deep learning is enormous. The calculation volume required to process three-dimensional piles of images, based on spatial or time axes, is incomparable to that required for two-dimensional images. One solution is to compress the images[59] and input them to deep learning, but the compression process results in the loss of detailed information. In this study, we applied the method of multi-phase deep learning, used in predicting landmarks in 2D cephalograms[27,28], to 3D craniofacial images. The concept was to emulate the way that one finds a place on the maps, when the address is provided. First, we open a map of the country. Then we try to find the state and city on a larger scale map. Then we open an even larger map to find the street and house number. Prediction errors became smaller as the phase advanced. Coarse detection was done with the first phase model and father narrowing down was done based on the prediction of the previous phase. This study was conducted on a personal computer. Within the physical limitation of memory and computation, multi-phase deep learning may be a solution to deal with large-scaled images.
There could find two reports in 3D landmark detection using fully convolutional neural networks (FCN) with high precision[49,58]. But in general, FCN is computationally expensive and slow.
Our system is logically very simple. Through all three phases, the main part of the models used were the same Resnet 3d-50 modified for regression. Though, the system consists of 33 individual networks, trained individually, to predict 16 landmarks. It cannot be denied that it is structurally complicated. There may be ways to design the system in end-to-end fashion. Again, within the calculation limit, this sequential system was practical for the authors.
In the previous studies[27,28] for 2D cephalograms, there was a database published at ISBI 2015 and prior benchmarks using it[24,26]. Authors were unable to obtain a database of feature point coordinates for craniofacial 3D-CT. The prediction accuracy could not be compared with the other published methods. Publication of unified datasets of 3D images and landmark coordinate values should be done, as grand challenges for 2D[23,24,33].
As for the current situation in Japan, it is not easy to access and build database of patient information, even for clinicians as the authors. Hence, authors constructed an original database from publicly available image sets[52]. The image sets used were from patients with head and neck tumors. Most of the images were probably from elderly patients, and there were many missing teeth.
The plotting featured points one by one took a long time. Plotting anatomical feature points in 3D requires multiple perspectives. In this study, we used five viewpoints in blender. In addition, it is often necessary to pan, zoom in and out, Bone ridges are formed by curves, not by sharp angles, so it was difficult and sometimes impossible to plot them accurately. To maintain consistency as much as possible, a series of the work was done by one person, and one feature point was plotted for all cases in succession.
The craniofacial CT data used in this study were provided at 5 mm intervals in the cranio-occipital direction. Data intensity in the z-axis was more than five times sparse than the x or y-axis. Though, to our surprise, prediction errors in the z-axis were not worse than the x or y-axis (Figure 7,9,11).
The 3rd phase prediction error revealed no significance from that of two experienced practitioners. The system performed clinician level. Ground truth coordinate values may differ from one plotter to the other. How precisely those systems should accomplish is a matter of debate. As is well known and should be taken for granted, there always exist inter-observer[60] and intra-observer errors[61,62]. It seems reasonable to set goals at the inter-expert error level.
In clinical practice, slices of less than 1 mm are commonly used to obtain detailed bone information (so-called thin slices). To apply these images in real clinical situations, such as navigation systems used in surgery, it is necessary to support these images.
CBCT, becoming popular among orthodontists and otolaryngologists, can get images with small voxels. When based on the detailed images, highly accurate estimation can be expected. Though, the computation volume will increase as the information to be processed increase. Our proposing method of multi-phased prediction, coarse detection first and narrowing down the detection area, may be a possible solution.

Author Contributions

Conceptualization, S.N.; data curation, S.N. and T.S.; formal analysis, S.N. and T.F.; funding acquisition, S.N.; investigation, S.N.; methodology, S.N.; project administration, K.K. and M.K.; resources, S.N.; software, S.N. and T.S.; validation, S.N. and T.S.; visualization, S.N. and H.I.; writing—original draft, S.N..; writing—review and editing, S.N., K.K. and M.K. All authors have read and agreed to the published version of the manuscript.

Funding

This study was partly supported by Nakatani Foundation Research grant.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The source code of this manuscript is available at https://drive.google.com/drive/folders/1RI4ZHr2l2KyIpCZpV0KSLY2YVMbX0wAU?usp=sharing. Publicly available datasets were analyzed in this study. This data can be found here: https://wiki.cancerimagingarchive.net/display/Public/Head-Neck-Radiomics-HN1[52].

Acknowledgement

A prototype (with 2-phased networks) of this study was presented in The 35th Annual Conference of the Japanese Society for Artificial Intelligence, 2021[63]. This article is a revised version of preprint: “Three-dimensional cranio-facial landmark detection in CT slices from a publicly available database, using multi-phased regression networks on a personal computer”. medRxiv 2021.03.21.21253999; doi: https://doi.org/10.1101/2021.03.21.21253999.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Finlay, L.M. Craniometry and Cephalometry: A History Prior to the Advent of Radiography. Angle Orthod. 1980, 50, 312–321.
  2. Birmingham, A.E. The Topographical Anatomy of the Mastoid Region of the Skull; with Special Reference to Operation in This Region. Br. Med. J. 1890, 2, 683-684. [CrossRef]
  3. Scott, S.R.; Lond, M.B.; Eng, F.R.C.S.; Lond, L.R.C.P. A New Method of Demonstrating the Topographical Anatomy of the Adult Human Skull. J. Anat. Physiol. 1906, 40, 171-185.
  4. Ford, E.H.R. The Growth of the Foetal Skull. J. Anat. 1956, 90, 63-72.
  5. Hans, M.G.; Martin Palomo, J.; Valiathan, M. History of Imaging in Orthodontics from Broadbent to Cone-Beam Computed Tomography. Am. J. Orthod. Dentofac. Orthop. 2015, 148, 914–921. [CrossRef]
  6. Broadbent, B.H. A New X-Ray Technique and Its Application to Orthodontia. Angle Orthod. 1931, 1, 45–66.
  7. Hofrath, H. Die Bedeutung Der Roentgenfern Der Kiefer Anomalien. Fortschr Orthod. 1931, 1, 232–248.
  8. Steiner, C.C. Cephalometrics for You and Me. Am. J. Orthod. 1953, 39, 729–755.
  9. Jacobson, A. The “Wits” Appraisal of Jaw Disharmony. Am. J. Orthod. 1975, 67, 125–138.
  10. Björk, A. Sutural Growth of the Upper Face Studied by The Implant Method. Acta Odontol Scand. 1966, 24, 109-27. [CrossRef]
  11. Doberschütz, P.H.; Schwahn, C.; Krey, K.F. Cephalometric Analyses for Cleft Patients: A Statistical Approach to Compare the Variables of Delaire’s Craniofacial Analysis to Bergen Analysis. Clin. Oral Investig. 2022, 26, 353-364. [CrossRef]
  12. Lévy-Mandel, A.D.; Venetsanopoulos, A.N.; Tsotsos, J.K. Knowledge-Based Landmarking of Cephalograms. Comput. Biomed. Res. 1986, 19, 282–309. [CrossRef]
  13. Parthasarathy, S.; Nugent, S.T.; Gregson, P.G.; Fay, D.F. Automatic Landmarking of Cephalograms. Comput. Biomed. Res. 1989, 22, 248–269. [CrossRef]
  14. Cardillo, J.; Sid-Ahmed M.A. An Image Processing System for Locating Craniofacial Landmarks. IEEE Trans. Med. Imaging 1994, 13, 275–289. [CrossRef]
  15. Forsyth, D.B.; Davis, D.N. Assessment of an Automated Cephalometric Analysis System. Eur. J. Orthod. 1996, 18, 471–478,.
  16. Giordano, D.; Leonardi, R.; Maiorana, F.; Cristaldi, G.; Distefano, M.L. Automatic Landmarking of Cephalograms by Cellular Neural Networks. In Artificial Intelligence in Medicine. AIME 2005. Lecture Notes in Computer Science; Springer, Berlin, Heidelberg: Heidelberg, 2005; pp. 333–342. [CrossRef]
  17. Yue, W.; Yin, D.; Li, C.; Wang, G.; Xu, T. Automated 2-D Cephalometric Analysis on X-Ray Images by a Model-Based Approach. IEEE Trans. Biomed. Eng. 2006, 53, 1615–1623.
  18. Rueda, S.; Alcañiz, M. An Approach for the Automatic Cephalometric Landmark Detection Using Mathematical Morphology and Active Appearance Models. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2006, 4190 LNCS, 159–166.
  19. Kafieh, R.; Sadri, S.; Mehri, A.; Raji, H. Discrimination of Bony Structures in Cephalograms for Automatic Landmark Detection. Commun. Comput. Inf. Sci. 2008, 6 CCIS, 609–620.
  20. Tanikawa, C.; Yagi, M.; Takada, K. Automated Cephalometry: System Performance Reliability Using Landmark-Dependent Criteria. Angle Orthod. 2009, 79, 1037–1046. [CrossRef]
  21. Nishimoto, S.; Sotsuka, Y.; Kawai, K.; Ishise, H.; Kakibuchi, M. Personal Computer-Based Cephalometric Landmark Detection with Deep Learning, Using Cephalograms on the Internet. J. Craniofac. Surg. 2019, 30, 91-95. [CrossRef]
  22. Leonardi, R.; Giordano, D.; Maiorana, F. Automatic Cephalometric Analysis A Systematic Review. Angle Orthod. 2008, 78, 145-51.
  23. Wang, C.W.; Huang, C.T.; Hsieh, M.C.; Li, C.H.; Chang, S.W.; Li, W.C.; Vandaele, R.; Marée, R.; Jodogne, S.; Geurts, P.; et al. Evaluation and Comparison of Anatomical Landmark Detection Methods for Cephalometric X-Ray Images: A Grand Challenge. IEEE Trans. Med. Imaging 2015, 34, 1890–1900. [CrossRef]
  24. Wang, C.W.; Huang, C.T.; Lee, J.H.; Li, C.H.; Chang, S.W.; Siao, M.J.; Lai, T.M.; Ibragimov, B.; Vrtovec, T.; Ronneberger, O.; et al. A Benchmark for Comparison of Dental Radiography Analysis Algorithms. Med. Image Anal. 2016, 31, 63–76. [CrossRef]
  25. Lindner, C.; Wang, C.-W.; Huang, C.-T.; Li, C.-H.; Chang, S.-W.; Cootes, T.F. Fully Automatic System for Accurate Localisation and Analysis of Cephalometric Landmarks in Lateral Cephalograms. Sci. Rep. 2016, 6, 33581. [CrossRef]
  26. Arik, S.Ö.; Ibragimov, B.; Xing, L. Fully Automated Quantitative Cephalometry Using Convolutional Neural Networks. J. Med. Imaging 2017, 4, 014501. [CrossRef]
  27. Nishimoto, S. Cephalometric Landmark Location with Multi-Phase Deep Learning. In Proceedings of the JSAI2020; The Japanese Society for Artificial Intelligence, 2020; pp. 2Q6GS1001-2Q6GS1001.
  28. Nishimoto, S.; Kawai, K.; Fujiwara, T.; Ishise, H.; Kakibuchi, M. Locating Cephalometric Landmarks with Multi-Phase Deep Learning. medRxiv 2020, 2020.07.12.20150433.
  29. Kim, H.; Shim, E.; Park, J.; Kim, Y.J.; Lee, U.; Kim, Y. Web-Based Fully Automated Cephalometric Analysis by Deep Learning. Comput. Methods Programs Biomed. 2020, 194, 105513. [CrossRef]
  30. Kim, M.J.; Liu, Y.; Oh, S.H.; Ahn, H.W.; Kim, S.H.; Nelson, G. Automatic Cephalometric Landmark Identification System Based on the Multi-Stage Convolutional Neural Networks with CBCT Combination Images. Sensors (Basel). 2021, 21, 1–16. [CrossRef]
  31. Chen, R.; Ma, Y.; Chen, N.; Lee, D.; Wang, W. Cephalometric Landmark Detection by AttentiveFeature Pyramid Fusion and Regression-Voting. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2019, 11766 LNCS, 873–881.
  32. Junaid, N.; Khan, N.; Ahmed, N.; Abbasi, M.S.; Das, G.; Maqsood, A.; Ahmed, A.R.; Marya, A.; Alam, M.K.; Heboyan, A. Development, Application, and Performance of Artificial Intelligence in Cephalometric Landmark Identification and Diagnosis: A Systematic Review. Healthc. 2022, 10, 2454. [CrossRef]
  33. Khalid, M.A.; Zulfiqar, K.; Bashir, U.; Shaheen, A.; Iqbal, R.; Rizwan, Z.; Rizwan, G.; Fraz, M.M. CEPHA29: Automatic Cephalometric Landmark Detection Challenge 2023. 2022, arxiv.2212.04808.
  34. Grayson, B.H.; McCarthy, J.G.; Bookstein, F. Analysis of Craniofacial Asymmetry by Multiplane Cephalometry. Am. J. Orthod. 1983, 84, 217–224. [CrossRef]
  35. Bütow, K.W.; van der Walt, P.J. The Use of Triangle Analysis for Cephalometric Analysis in Three Dimensions. J. Maxillofac. Surg. 1984, 12, 62–70.
  36. Grayson, B.; Cutting, C.; Bookstein, F.L.; Kim, H.; McCarthy, J.G. The Three-Dimensional Cephalogram: Theory, Techniques, and Clinical Application. Am. J. Orthod. Dentofac. Orthop. 1988, 94, 327–337. [CrossRef]
  37. Mori, Y.; Miyajima, T.; Minami, K.; Sakuda, M. An Accurate Three-Dimensional Cephalometric System: A Solution for the Correction of Cephalic Malpositioning. J. Orthod. 2001, 28, 143–149. [CrossRef]
  38. Matteson, S.R.; Bechtold, W.; Phillips, C.; Staab, E. V. A Method for Three-Dimensional Image Reformation for Quantitative Cephalometric Analysis. J. Oral Maxillofac. Surg. 1989, 47, 1053–1061. [CrossRef]
  39. Varghese, S.; Kailasam, V.; Padmanabhan, S.; Vikraman, B.; Chithranjan, A. Evaluation of the Accuracy of Linear Measurements on Spiral Computed Tomography-Derived Three-Dimensional Images and Its Comparison with Digital Cephalometric Radiography. Dentomaxillofac. Radiol. 2010, 39, 216–223. [CrossRef]
  40. Ghoneima, A.; Albarakati, S.; Baysal, A.; Uysal, T.; Kula, K. Measurements from Conventional, Digital and CT-Derived Cephalograms: A Comparative Study. Aust. Orthod. J. 2012, 28, 232–239. [CrossRef]
  41. Dot, G.; Rafflenbeul, F.; Arbotto, M.; Gajny, L.; Rouch, P.; Schouman, T. Accuracy and Reliability of Automatic Three-Dimensional Cephalometric Landmarking. Int. J. Oral Maxillofac. Surg. 2020, 49, 1367–1378. [CrossRef]
  42. Shahidi, S.; Bahrampour, E.; Soltanimehr, E.; Zamani, A.; Oshagh, M.; Moattari, M.; Mehdizadeh, A. The Accuracy of a Designed Software for Automated Localization of Craniofacial Landmarks on CBCT Images. BMC Med. Imaging 2014, 14, 32. [CrossRef]
  43. Gupta, A.; Kharbanda, O.P.; Sardana, V.; Balachandran, R.; Sardana, H.K. A Knowledge-Based Algorithm for Automatic Detection of Cephalometric Landmarks on CBCT Images. Int. J. Comput. Assist. Radiol. Surg. 2015, 10, 1737–1752. [CrossRef]
  44. Zhang, J.; Gao, Y.; Wang, L.; Tang, Z.; Xia, J.J.; Shen, D. Automatic Craniomaxillofacial Landmark Digitization via Segmentation-Guided Partially-Joint Regression Forest Model and Multiscale Statistical Features. IEEE Trans. Biomed. Eng. 2016, 63, 1820–1829. [CrossRef]
  45. Zhang, J.; Liu, M.; Wang, L.; Chen, S.; Yuan, P.; Li, J.; Shen, S.G.F.; Tang, Z.; Chen, K.C.; Xia, J.J.; et al. Joint Craniomaxillofacial Bone Segmentation and Landmark Digitization by Context-Guided Fully Convolutional Networks. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2017, 10434 LNCS, 720–728.
  46. De Jong, M.A.; Gül, A.; De Gijt, J.P.; Koudstaal, M.J.; Kayser, M.; Wolvius, E.B.; Böhringer, S. Automated Human Skull Landmarking with 2D Gabor Wavelets. Phys. Med. Biol. 2018, 63, 105011. [CrossRef]
  47. Montúfar, J.; Romero, M.; Scougall-Vilchis, R.J. Automatic 3-Dimensional Cephalometric Landmarking Based on Active Shape Models in Related Projections. Am. J. Orthod. Dentofac. Orthop. 2018, 153, 449–458. [CrossRef]
  48. Montúfar, J.; Romero, M.; Scougall-Vilchis, R.J. Hybrid Approach for Automatic Cephalometric Landmark Annotation on Cone-Beam Computed Tomography Volumes. Am. J. Orthod. Dentofacial Orthop. 2018, 154, 140–150. [CrossRef]
  49. O’Neil, A.Q.; Kascenas, A.; Henry, J.; Wyeth, D.; Shepherd, M.; Beveridge, E.; Clunie, L.; Sansom, C.; Šeduikytė, E.; Muir, K.; et al. Attaining Human-Level Performance with Atlas Location Autocontext for Anatomical Landmark Detection in 3D CT Data. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2018, 11131 LNCS, 470–484.
  50. Torosdagli, N.; Liberton, D.K.; Verma, P.; Sincan, M.; Lee, J.S.; Bagci, U. Deep Geodesic Learning for Segmentation and Anatomical Landmarking. IEEE Trans. Med. Imaging 2019, 38, 919–931. [CrossRef]
  51. Dot, G.; Schouman, T.; Chang, S.; Rafflenbeul, F.; Kerbrat, A.; Rouch, P.; Gajny, L. Automatic 3-Dimensional Cephalometric Landmarking via Deep Learning. J. Dent. Res. 2022, 101, 1380-1387. [CrossRef]
  52. Blake, G. Head-Neck-Radiomics-HN1 - The Cancer Imaging Archive (TCIA) Public Access - Cancer Imaging Archive Wiki Available online: https://wiki.cancerimagingarchive.net/display/Public/Head-Neck-Radiomics-HN1 (accessed on 1 February 2021).
  53. Lasso, A. Lassoan/ExtractSkin.Py Available online: https://gist.github.com/lassoan/1673b25d8e7913cbc245b4f09ed853f9 (accessed on 1 February 2021).
  54. Jihong, J. GitHub - JihongJu/Keras-Resnet3d: Implementations of ResNets for Volumetric Data, Including a Vanilla Resnet in 3D. Available online: https://github.com/JihongJu/keras-resnet3d (accessed on 1 February 2021).
  55. Mestiri, M.; Kamel, H. Reeb Graph for Automatic 3D Cephalometry. Int. J. Image Process. 2014, 8, 2014–2031.
  56. Neelapu, B.C.; Kharbanda, O.P.; Sardana, V.; Gupta, A.; Vasamsetti, S.; Balachandran, R.; Sardana, H.K. Automatic Localization of Three-Dimensional Cephalometric Landmarks on CBCT Images by Extracting Symmetry Features of the Skull. Dentomaxillofacial Radiol. 2018, 47, 20170054. [CrossRef]
  57. Codari, M.; Caffini, M.; Tartaglia, G.M.; Sforza, C.; Baselli, G. Computer-Aided Cephalometric Landmark Annotation for CBCT Data. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 113–121. [CrossRef]
  58. Torosdagli, N.; Liberton, D.K.; Verma, P.; Sincan, M.; Lee, J.S.; Bagci, U. Deep Geodesic Learning for Segmentation and Anatomical Landmarking. IEEE Trans. Med. Imaging 2019, 38, 919–931. [CrossRef]
  59. Kang, S.H.; Jeon, K.; Kim, H.-J.; Seo, J.K.; Lee, S.-H. Automatic Three-Dimensional Cephalometric Annotation System Using Three-Dimensional Convolutional Neural Networks. 2018. arXiv:1811.07889. [CrossRef]
  60. Gonçalves, F.A.; Schiavon, L.; Pereira Neto, J.S.; Nouer, D.F. Comparison of Cephalometric Measurements from Three Radiological Clinics. Braz. Oral Res. 2006, 20, 162–166. [CrossRef]
  61. Paini de Abreu, D.; Salvatore Freitas, K.M.; Nomura, S.; Pinelli Valarelli, F.; Hermont Cançado, R. Comparison among Manual and Computerized Cephalometrics Using the Softwares Dolphin Imaging and Dentofacial Planner. Dent. Oral Craniofacial Res. 2016, 2, doi:10.15761/DOCR.1000186. [CrossRef]
  62. Moon, J.H.; Hwang, H.W.; Yu, Y.; Kim, M.G.; Donatelli, R.E.; Lee, S.J. How Much Deep Learning Is Enough for Automatic Identification to Be Reliable?A Cephalometric Example. Angle Orthod. 2020, 90, 823–830.
  63. Nishimoto, S. Automatic Landmark Prediction in Craniofacial CT Images. In Proceedings of the The 35th Annual Conference of the Japanese Society for Artificial Intelligence; The Japanese Society for Artificial Intelligence, 2021; pp. 4I4GS7e04-4I4GS7e04.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated