Preprint
Article
Unraveling Soft Squeezing Transformations in Time-Variant Elastic Fields
Altmetrics
Downloads
96
Views
18
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
10 April 2023
Posted:
10 April 2023
You are already at the latest version
Alerts
Abstract
Quantum squeezing, an intriguing phenomenon that amplifies the uncertainty of one variable while diminishing that of its conjugate, may be studied as a time-dependent process, with exact solutions frequently derived from frameworks grounded in adiabatic invariants. Remarkably, we reveal that exact solutions can be ascertained in the presence of time-variant elastic forces, eschewing dependence on invariants or frozen eigenstates formalism. Delving into these solutions as an inverse problem unveils their direct connection to the design of elastic fields, responsible for inducing squeezing transformations onto canonical variables. Of particular note, the dynamic transformations under investigation belong to a class of gentle quantum operations, distinguished by their delicate manipulation of particles, thereby circumventing the abrupt energy surges commonplace in conventional control protocols.
Keywords:
Subject: Physical Sciences - Theoretical Physics
1. Introduction
In the fascinating domain of quantum mechanics, one encounters the remarkable phenomenon of squeezing, where the uncertainty tied to a canonical variable diminishes, while that of its conjugate partner swells. This delicate balance between conjugate variables emerges from the grounds of Heisenberg’s uncertainty principle, which prescribes a minimal boundary on the product of their uncertainties, granted that we confine ourselves to a realm where high-energy scales do not warrant further adjustments [1].
In light of this understanding, within the realm of quantum measurements, the uncertainty attached to a particular observable bears the responsibility for any deviations from the intended value—assuming the experimentalist refrains from inadvertently compromising the measurement through extraneous factors. Nevertheless, these imperfections can be ameliorated by attenuating the uncertainty to near-arbitrary levels, albeit at the cost of amplifying the uncertainty of the observable’s counterpart. Such an interplay transcends the familiar position and momentum duality, manifesting itself in other pairs encompassing the spin components of particles or the polarisations of light, among others.
It is precisely this versatile nature of quantum squeezing that has ignited immense interest in its exploration, with researchers drawn to its deep-seated ramifications and promising applications in diverse arenas ranging from quantum information [2] to precision measurements in quantum metrology [3,4,5,6,7] and quantum teleportation [8]. Even beyond the confines of our current understanding, efforts are being advanced to measure elusive phenomena, such as dark matter [9].
As we embark on a journey to explore quantum squeezing within the context of time-variant elastic fields, it becomes essential to embrace the Heisenberg picture of quantum mechanics. In contrast to the Schrödinger picture, which accentuates the evolution of the state vector, the Heisenberg picture proffers a complementary description, placing emphasis on the temporal progression of operators, in our case, in the presence of a time-dependent Hamiltonian. This subtle yet profound shift in perspective permits us to unravel squeezing transformations and the mechanisms that underpin them more effectively, which is the aspiration of our investigation.
Despite the abundance of theoretical frameworks that have emerged to explore the intricate facets of time-dependent problems [10,11,12,13,14,15,16,17], our approach diverges from the adiabatic invariants doctrine. In a prior groundbreaking revelation [18], Mielnik demonstrated that the time-evolution problem, characterised by quadratic Hamiltonians endowed with fluctuating elastic forces, admits exact solutions. Intriguingly, these solutions are rooted in a profound understanding of the symmetries embedded within the problem. In this work, we shall continue these solutions to inspect their role in shaping squeezing transformations, and more specifically, in fostering the kind of fields that cultivate such linear transformations.
Furthermore, as we shall show, the exact solutions are intimately entwined with the character of the elastic field. This association constitutes an aspect of an inverse problem, in which, upon obtaining an exact solution, the driving field may be meticulously designed. In a reciprocal manner, when provided with an elastic field, one can integrate the system to unveil the corresponding exact solution. This versatility inherent in the method permits us to infuse, with remarkable freedom, any driving elastic force to attain the desired outcome. Such adaptability ensures that we can manipulate the system under the influence of forces that desist from unsettling the particles to the point of dismantling their configuration.
Our work unfolds as follows. In Section 2, we introduce the class of quadratic Hamiltonians equipped with explicit time-dependency that underpin our investigation. Section 3 delves into the exact solutions to the time-dependent problem, shedding light on their constraints and implications. Section 4 and Section 5 offer succinct examples in the engineering of designing driving pulses, as well as the inventive squeezing operations that can be fashioned from them. Finally, in Section 6, we present the culminating insights of our work, exposing the limitations and unresolved problems emerged from our endeavours.
2. A Classical-Quantum Dynasty of Hamiltonians
Our investigation begins with the family of non-relativistic, quadratic Hamiltonians that are equipped with a time-dependent elastic field, denoted by . By setting the mass of the particle as for a pair of conjugate variables, q and p, the Hamiltonian assumes a simple form:
This model yields the very same equations of motion for both classical and quantum domains. In the absence of spin, each unitary evolution operator in generated by the Hamiltonian (1), is wholly determined by the corresponding canonical transformation poses [19]. Consequently, the flow generated by exhibits striking similarities in both classical and quantum regimes, inspiring further scrutiny into the quantum counterparts of classical trajectories.
Our exposition, in a sense, is devoted to this last pursuit, albeit with a focus on a family of unitary quantum operations that induce amplification () or squeezing () of canonical pairs over time. This approach is analogous to that of squeezed states, but instead of directly depicting such states, we study the dynamical operations that give rise to unitary transformations of the form and . For notable examples in this direction the reader may refer to [20,21].
Being a pragmatic thinker, the author henceforth sets ℏ to unity. With this convention in place, the time evolution of the pair is governed by the Hamiltonian (1), and follows the equations of motion given below:
where . One immediately confirms these equations of motion bear an obvious resemblance in their structure to the classical Hamilton equations: and .
Letting , we can express the system of equations (2) in a concise and advantageous form:
this notation serves a particular purpose of ours. In the Heisenberg picture, the time evolution of an observable Q, from an initial time to a given time t, can be expressed as the unitary conjugation of by the evolution operator , namely:
here, denotes the evolution matrix which is an element of the symplectic group, in our case error.
Both equations (3) and (4) provide insight into how an observable Q evolves from to t. Consequently, by differentiating (4) with respect to t and substituting into (3), we derive the evolution equation for :
since the matrix contains complete information about the system’s motion, it is possible to leverage it for various purposes, such as propagating the wave function or even expressing it in terms of the entries of , further details can be found in Section 5.
Moreover, the symplectic structure ingrained in holds the key to classifying the motion generated by (1), which has been nicely shown in [22,23]. By denoting , it becomes apparent that possesses three distinct sets of eigenvalues, computed through the formula . Each set characterises a unique class of motion:
- I
- When > 2, the eigenvalues become real, thereby causing unstable motion. This regime conduces to squeezing phenomena of canonical operators, and a, defined by the eigenvectors of .
- II
- When = 2, the eigenvalues are also real. However, unlike in regime I, these eigenvalues may lead the motion to stable regimes as well.
- III
- When < 2, the eigenvalues are complex, and the motion is (oscillatory) stable. For a periodic process of length T, will define global operators and a. This regime permits quantum operations for the confinement of particles, such as Paul traps [24].
The preeminent role of in the above classification is a natural consequence of the symplectic structure inherent in . Therefore, it is reasonable to surmise that and are intertwined to some degree. Indeed, the particular form of the pulse dictated by is ultimately responsible for the resulting class of motion. To illustrate this point, let us consider the case where is a constant value of . In this scenario, the integration of (5) is straightforward and yields . Depending on the magnitude of (and of course of ), the system demonstrates either the common oscillatory motion associated with class III, or, as nears the parametric resonance threshold, motion akin to a free particle in class II. We will delve into the relationship between and in greater detail in Section 3.
3. Time Evolution Without Adiabatic Invariants
In 2013, Mielnik [18] made a remarkable mathematical discovery regarding the system of differential equations (5). Specifically, he noted that exact solutions can be obtained for this system, presuming the elastic field is symmetric over the interval of integration. We will see these exact solutions provide us with valuable insight into the simplest cases of the evolutive problem represented by (5). As well, it is worth noting that these solutions offer an opportunity to design control operations by smoothly varying the steering fields, nearly adiabatically, without any requirement for invariant formalism [11,13]. In addition, these solutions are inherently linked to itself, allowing one to either evolve by means of an elastic pulse or design the elastic pulse required for specific purposes. The latter strategy, in particular, may have wide-ranging implications in fields such as quantum computing, quantum sensing, and metrology, where it is necessary to manipulate particles in order to achieve a desired state.
Suppose we consider a symmetric pulse with respect to the centre of the operation interval . We see that in this interval the unitary operators do satisfy , because the quadratic Hamiltonian (1) satisfies . The system described by (5) then takes the form:
using as defined in (3), we can explicitly write the former equation in terms of and the entries of :
Upon examination, we quickly observe that the diagonal elements on the left-hand side share both the same differential equation, namely . Consequently, it follows that . Now, here comes the clever part. If we insert an almost arbitrary analytical function , we can also observe from (7) that .
In turn, we shall deduce the form of based on the aforementioned information, and recalling that . Because we solve from here to finally obtain , which implies the evolution matrix has the explicit form:
With the preceding discussion, the reader may be able to anticipate the relationship that exists between and the trace of the evolution matrix. For the time-independent case, as shown in the example at the end of Section 2, this relationship becomes evident. However, in the time-dependent case, we need to provide a detailed derivation to explicitly establish this connection. Fortunately, this task is not arduous, and we shall undertake it now.
The path to unlocking the relation subtended between and lies in the differential equation for the entry in (7). Through careful examination, we uncover the expression . A rearrangement of terms and a simplification of the resulting expression brings the connection between and :
In this way, Mielnik’s discovery entails that is indeed an exact solution to the evolution problem (6), while simultaneously enabling us to tackle an inverse problem of sorts: should be known, we may infer (cf. Section 4); conversely, given , we may deduce . The interplay between these two functions therefore yields a versatile method for analysing the classes of motion regulated by (6). Yet another avenue to relate and lies in the differential equations for . By simply substituting into and performing some straightforward algebraic manipulation, (9) is once again obtained.
An interesting detail warrants our consideration. By suitably rearranging the terms of the expression in (9), we are led to a time-dependent, effective harmonic oscillator, whose frequency is given by , namely
where contains nonlinear terms that we interpret being part of an effective damping component:
these terms, and of course , shall help in explaining the class of oscillation undergoes. Is there a regime in which such non-linear terms are of no importance?
From equation (8), we can observe that whenever becomes zero at a certain point t, then at the same point must be equal to . Additionally, we notice that a time-dependent Fourier transform takes place if becomes zero at , but , then:
following the application of this matrix to a pair of conjugate variables, q and p, a transformation of the form and is obtained. In other words, this transformation swaps such two variables and rescales each one with respect to and its reciprocal. A second application of the same matrix —i.e. fixing —reverts the Fourier transform effect, restoring the variables to their original values. However, suppose now that a similar Fourier transform occurs at a different time for a function . Then the composition of two different Fourier transform matrices (or an even number of them) will lead to squeezing transformations (belonging to the class of motion I):
specifically, this results in linear transformations of the form and , wherein one variable is amplified at the expense of squeezing the other or vice versa.
3.1. What if is odd?
Squeezing phenomena have been observed to occur in intervals where is not symmetric with respect to the centre of the operation interval [25]. Therefore, upon acquiring the elastic field utilising (9), integration of equation (5) is required over an interval with a non-coinciding centre compared to that of . This analysis prompts the inquiry of whether a reformation is warranted for a spanning the entire operational interval.
This is particularly relevant if we consider the steering force to be a time-dependent, magnetic induction field, as it is crucial to note that the case where cannot even be considered. If such a condition were to hold, it would lead to imaginary forces, which are physically impossible. Upon closer examination, let us consider the Hamiltonian , where represents the vector potential—recalling we adopt the convention of setting all physical constants to unity. We shall choose a symmetric gauge in which . When we assume the magnetic induction field is oriented along the direction, we have . Thus, the identification of elucidates the requirement for to be even when the driving force originates from a magnetic field [26].
However, in the case of a scalar field, such as the electric potential used in Paul traps [24], the elastic field is directly proportional to the applied voltage on the surfaces of the trap, see Section 6. In this context, it is possible to consider the case where without impediment. We will explore this case further below. But first, to prevent any possible confusion between the distinct exact solutions for an elastic field of this type and those described in Equation (9), let us introduce some notation. We shall use the symbol * to differentiate between these solutions.
By assuming that , the Hamiltonian (1) shall satisfy , while the unitary evolution operators hold . With these premises, we may proceed to state the initial value problem (5) as:
or explicitly:
With proper attention, we notice that the diagonal elements on the left-hand side satisfy the same differential equation, up to a sign. Therefore, it follows that , and as a consequence, the matrix corresponding to a given will be traceless. This, in turn, assures that the motion will always be of class III, although the even composition of these matrices does not necessarily follow this pattern.
Furthermore, as previously discussed, we recall that is an element of , and thus its determinant is unity. From this condition, we can determine the form that the entry will take, leading us to the following expression for :
thus, we establish a relation between and the exact solution , namely:
Upon comparing equations (9) and (15) for and , we notice that they differ solely in the sign of the third term. In fact, similar to our interpretation in (10), the nonlinear terms can be viewed as constituents of an effective force that propels the time-dependent harmonic oscillator:
where
In contrast to the exact solutions presented in (9), it is necessary to carefully consider the conditions that must satisfy for the initial value problem (13). In order for these solutions to generate a corresponding well-behaved —or conversely, for any well-behaved to have a field that possesses no singularities—it is essential that does not vanish at any time t, even at those times at which becomes zero. In the event that this latter condition is met, will become a Fourier transform matrix.
However, these solutions would induce a Fourier transform at the very beginning of the interval of operation, regardless of any prior knowledge of the conjugate variable trajectories. In such scenarios, the particle would receive streams of energy significant enough to disrupt it from its original state, with a high probability of losing any control over it. Yet, since the aim of our discussion is to study quantum operations that exhibit soft transitions to a given target we shall limit our discussion to symmetric fields with respect to the centre of the interval of manipulation.
4. Shaping Elastic Fields Like a Blacksmith
According to the method we have surveyed in the previous section, the flexibility of the approach relies, in addition to the specifics, on the freedom to choose a function for designing an elastic driving field . Conversely, given a , one can imagine the corresponding , which is the exact solution to the initial value problem described by equation (5). In general, the latter presents a formidable challenge, often demanding numerical efforts, with exact solutions not invariably assuming a closed form. We shall introduce elementary arguments with the intent to streamline the solvability of equation (9), whether in its direct or inverse form.
The simplest model to consider is when we set , where is a real constant. In this case, equation (9) has an exact solution given by . This solution breaks the nonlinearities in the effective damping terms, resulting in . As a result, equation (10) is reduced to the familiar form: . Therefore, for this exact solution the evolution matrix will become a symplectic rotation matrix:
if we allow for the parameter to take values of , where n represents an integer, and restrict our considerations to the interval of operation , then the matrix in question facilitates a sequence of transitions, in intervals of length , between a Fourier transform and its inverse. Such a process is characterised by a smoothness which can be observed in the resultant sequences.
Moreover, it should be noted that setting would lead to a repulsive harmonic oscillator, with the exact solution given by . But, to what degree of validity might this solution aspire? This choice would also eliminate the nonlinearities in the effective damping terms, as becomes a linear function of . For this solution to hold, one could imagine a scenario in the context of electric potentials, where the class of operation can depend on the sign of the applied voltage. It could be stated that the system in question would possess the ability to exhibit either an attractive or repulsive behaviour depending on the steering voltage. Nevertheless, within the realm of real numbers, it appears that no single point exists at which this exact solution could culminate in a Fourier transform matrix for (8). As we commented in Section 3.1, it is not our intention to scrutinise these particular scenarios within the confines of our present discussion. Rather, we shall defer such a survey in a separate manuscript. In point of fact, in order to ensure the validity of for the purposes we seek, we must adhere to the constraints set forth in the following Lemma [18], which summarises the constraints that restrict the arbitrariness of .
Lemma 1.
Given any exhibiting symmetry with respect to the central point of the interval , the function must maintain continuity and, at a minimum, possess the quality of being three times differentiable. To ensure that both functions satisfy the necessary conditions for proper definition through equation (9), these criteria must be met:
- At any time t at which , then .
- At any time t at which , then .
- At any time t at which and , the evolution matrix represents a Fourier transform of the canonical pair at that point.
Proof.
The conditions numbered 1 and 2 are a direct consequence of equation (7), which underscores the indispensable requirement that must possess a finite value. Besides, we see from (9) that in case vanishes at a given t, we are led to , by differentiating this expression with respect to time the second condition becomes evident. The condition numbered 3 is fulfilled provided the anti-diagonal elements of induce a linear transformation that can be expressed in the form of and . □
4.1. The Inverse Problem Unveiled
The task of selecting an appropriate that satisfies Lemma 1 necessitates an empirical exploration of functions tailored to the specific control objective. In the subsequent discussion, we will narrow our focus to a particular class of functions that possess the ability to create vanishing elastic fields at both the beginning and the end of the operating interval. Hence, we allow to be expressed as
With this particular choice, the expression for the elastic field (9) becomes:
we must judiciously determine the coefficients and the frequencies , basing our search on the conditions specified in the preceding Lemma. In practice, not all of the unknown coefficients will be determined by the imposed conditions; instead, we will be required to have additional free parameters.
Let us examine the first three terms in series (19) and attempt to determine some of the coefficients. To streamline our inspection, we shall concentrate on the operational interval , with the angular frequencies established by the arbitrary choice of . According to the initial value problem in (5), at the beginning of the operation, we have and . By closely scanning, we find that attains zero at , which implies . Consequently, we have . Given these considerations, and by setting and , we derive a linear system of equations involving the coefficients , and :
as we resolve the linear system, the three coefficients will be expressed in terms of and , which are to be varied such that adopts the properties of interest. Notably, is connected to the amplitude of the scaling factor within the Fourier transformation process.
To illustrate the design of the elastic fields with utmost clarity, we have selected different values for the parameters and . As a result, the fields take shape as depicted in the plots of Figure 1, where the corresponding exact solutions are shown as well. The assortment of values we have selected for and permit the fields vanish softly at the beginning and at the end of the interval .
The pulses denoted as and persistently display positive values across the entire interval. For these pulses, the parameter adopts values of 1 and , respectively, while the parameter assumes values of and . Consider a quantum operation constructed by the consecutive combination of these two fields; the outcome at the conclusion of the operational interval would manifest as a squeezing transformation of magnitude . Contrastingly, the pulse portrayed in the figure exhibits a greater magnitude compared to its counterparts. For this particular pulse, the parameters were set as and . This suggests that the extent of the squeezing effect is intricately linked to the magnitude of the elastic field governing the quantum operation.
5. A Soft Squeezing Engine
We have previously remarked that each individual pulse depicted in Figure 1 has the attribute to yield a time-dependent Fourier transform at specific instants throughout the operational interval, particularly at the roots of . Suppose we identify the precise instances when a Fourier transform occurs for each of these elastic fields. We then construct a quantum operation using two consecutive, distinct functions, with one following immediately after the other has reached a Fourier transform, as outlined in Equation (12). However, in deviation from this portrayal, the ultimate outcome at the conclusion of the operational interval will manifest as a seamless squeezing transformation, brought forth by the driving fields in question.
In order to more effectively explain the manner in which the smooth squeezing process occurs throughout the operational time interval, we shall first examine the two fields depicted in Figure (Figure 1). At this point, the reasoning behind the deliberate simplification in our exposition, by selecting an exact solution conforming to the function in (19), ought to become apparent. Indeed, it is precisely for the three pulses studied in the preceding section that a Fourier transform arises at odd multiples of .
Envision a physical realisation in the form of a time-varying, magnetic induction field permeating a solenoid, wherein the dynamical operation commences with the pulse denoted by , succeeded immediately by the pulse , both within the operational interval . Presuming the initial conditions at to be and , the temporal progression of the squeezing effect imposed onto the canonical pair shall display a characteristic akin to that delineated in Figure 2, attaining a squeezing effect of magnitude . Even more, analogous to the process characterised in equation (12), the intrinsic machinery governing this continuous landscape shall likewise manifest as the successive employment of matrices belonging to :
which shall generate the subtle transition towards a squeezing transformation through the sequential employment of two elastic fields that smoothly vanish at the commencement and termination of their respective intervals of influence.
Both q and p shall describe semiclassical trajectories, accompanied by their corresponding uncertainty shadows—which we will discuss shortly—, as depicted in Figure 2. The instance under consideration exemplifies that the uncertainties associated with q and p undergo, respectively, amplification and squeezing at the operation’s culmination to a moderate degree—a direct ramification of the applied field’s nuanced strength. It becomes patently clear that each uncertainty belt advances in mutual correspondence with its associated trajectory, a guarantee conferred by the symplectic structure embodied in the matrices .
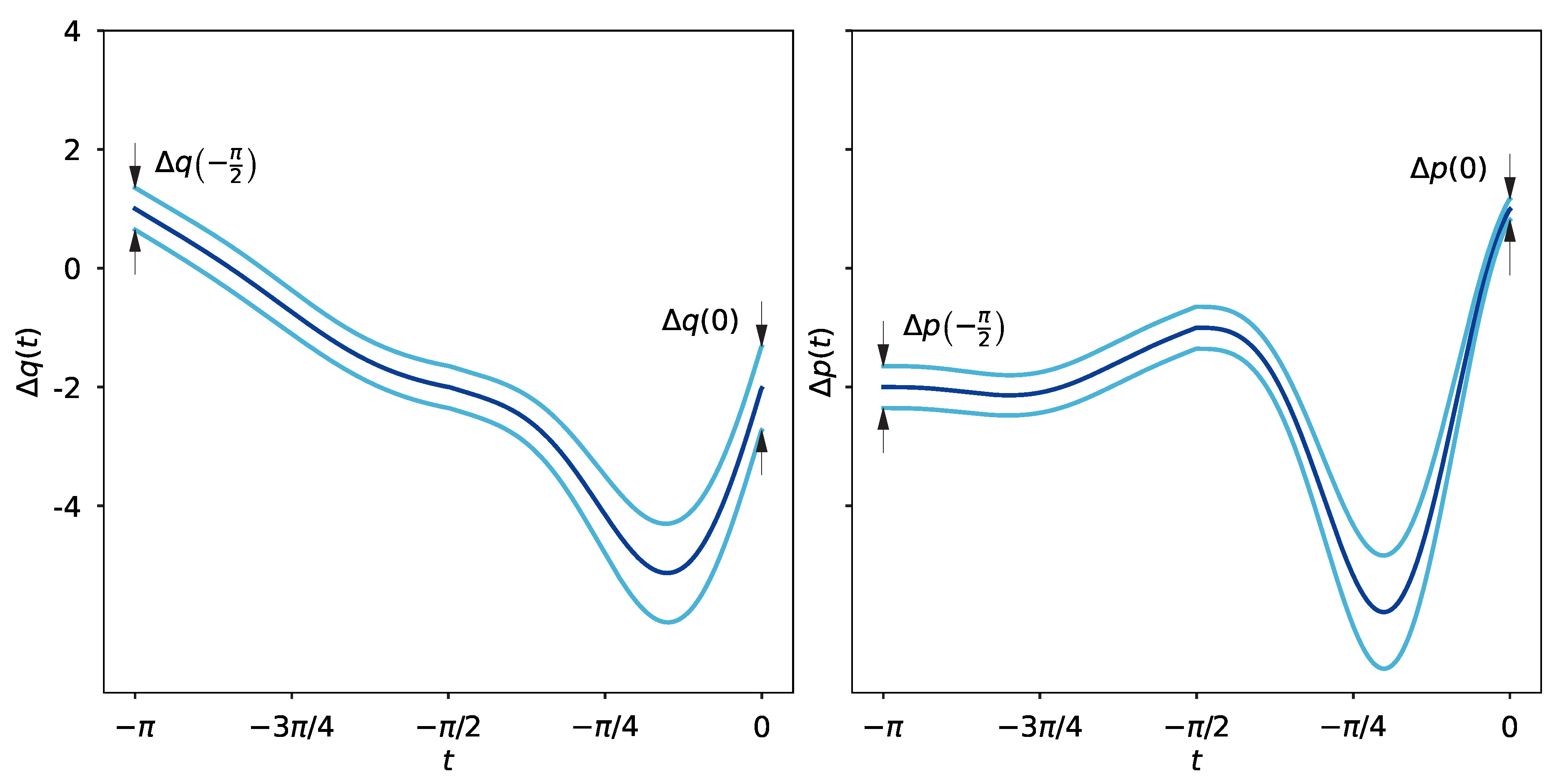
A second example, stemming from the pulses in Figure 1, merits inclusion in our discussion. We shall proceed as before, but this time our focus will be on a squeezing operation comprising pulses and . A physical realisation involving these elastic forces would necessitate the absence of a driving magnetic induction field, relying solely on the application of a time-varying electric potential, as commonly encountered in quadrupole ion traps of hyperbolic geometry. To facilitate comparison with our previous example, we shall maintain the same initial conditions and operational interval. The temporal progression of the squeezing transformation can be discerned in Figure 3, wherein the extent of the compression of uncertainty is evident, being it reduced by a factor of 2—the value the parameter assumed in order to generate pulse .
5.1. Evolving Uncertainty Shadows
The matrices facilitate not solely the evolution of the canonical pair and other observables, but that of the wave function itself. To elucidate this notion, let us consider a Gaussian wave function residing in the domain of . Presume that, in the coordinate representation, the wave function is situated at at the initial instant in the operational time:
where is the uncertainty of the variable q. To determine the value it assumes, we simply employ the customary Robertson-Schrödinger expression for the uncertainty linked to an observable , namely , where symbolises the expected value. We see that, at the inception of the operational time, the uncertainties for the canonical pair under scrutiny satisfy . Indeed, in light of the time evolution of variables q and p being dictated by the evolution matrix of form (5), it requires minimal exertion to ascertain the evolved uncertainties:
these uncertainty shadows give rise to the enveloping curves in Figure 2 and Figure 3. In addition, this phenomenon can also be construed as evidence that the matrices encapsulate every facet pertinent to the evolution of the underlying system, along with the influential role the exact solutions play in this context.
We shall probe this latter pathway concerning the wave function (22). As can be foreseen, it is far from enigmatic that the time evolution at instant t of the probability density can be expressed utilising the exact solutions . The crux of the matter principally resided in finding the uncertainties in (23); hence, it directly follows from (22) that:
we find this expression satisfactory, as it serves to underscore the significance imparted by the exact solutions in the evolved quantities. Consequently, one might inquire whether this scenario is solely restricted to Gaussian packets or can be expanded to encompass the probabilities for states beyond this special case. We maintain a steadfast conviction that the latter admits an affirmative answer, and that the evolution of other densities can be precisely characterised in terms of evolution matrices associated with time-dependent elastic fields.
Furthermore, the attributes inherent to Gaussian functions grant the ability to examine other interesting representations with relative ease. A prime example is the Wigner function. We shall initiate our brief exposition by introducing its well-known definition, taking into account the wave function in (22) at the beginning of the operational time:
the function, alas, does not find itself among the members of the Hilbert space of quantum states, and as a consequence, it lacks the property of square integrability. This peculiarity arises, in part, due to the fact that will not yield a physically meaningful quantity, and even the act of integrating it across the entirety of the phase space fails to produce a value of physical significance. However, one must not overlook the importance of this function. Apart from offering a representation of quantum states in phase space, the function in (25) serves as a tool for studying the semiclassical limit, where the Wigner function gradually approximates a classical probability distribution. Might this function, then, bear any association with the semiclassical trajectories that have been the subject of our study?
As one might anticipate, the Wigner function corresponding to our paradigm shall display a temporal dependence, adeptly assimilating the information imparted by the evolution matrices . Let us see this further. Considering the integral in (25) simplifies for the Gaussian wave function in (22), and by employing the uncertainties presented in (23), we reach a phase-space representation expressed through the exact solutions , specifically:
owing to the conditions that must fulfil as prescribed by Lemma 1, at the onset of the evolution, the conditions and shall lead both momentum and coordinate to possess the identical Gaussian width. Nevertheless, as the evolution unfolds and arrives at the Fourier points , characterised by and , we discern an expansion of magnitude in the Gaussian pulse’s width associated with the coordinates, while the momentum experiences a contraction of magnitude . In the presence of elastic forces, such behaviour can be consistently replicated throughout the execution of a gentle operation without encountering much wave packet dispersion during the control protocol. This holds true even in a class I scenario, where the motion is unbounded. In contrast, in the case of forces, akin to those deliberated in Section 3.1, the Gaussian packet’s widening will unrestrainedly spread as time evolution extends, attributable to the absence of Fourier points that allow to vanish.
6. Discussion and Perspectives
The significance of the exact solutions we have examined must not be eclipsed by the streamlined approach we employed in our work. Indeed, our endeavours have focused on time-dependent quadratic Hamiltonians characterised by elastic forces. Even with their simplicity, these elementary models boast advantages over higher-order Hamiltonians, predominantly in the design and implementation of quantum algorithms, quantum sensing procedures, and control sequence applications of micro particles [27]. In addition, setting aside the details, the capacity of this methodology to diminish uncertainty in the information domain would surpass classical approaches anchored in modified entropies [28]. Albeit, the endeavour to address the shortcomings of our approach has only just begun.
Despite the minimalist approach in our analysis, it is essential to underscore that the linear transformations resulting from successive application of elastic forces were obtained without recourse to invariants. Certainly, in Section 4 and Section 5, we have demonstrated that our scheme facilitates the construction of elastic pulses that fully vanish at both the beginning and end of the quantum operation. This contrasts with conventional methodologies where, at the start or end of the elastic operation, the constant strength of a harmonic field lingers, posing a risk of perturbing the particle by injecting sufficient energy to induce state transitions and potentially forfeiting control over it or even fomenting decoherence. In comparison, the arbitrary flexibility encompassed by Lemma 1 enables the generation of soft squeezing transformations. Thus averting the abrupt emergence of electric shocks in the form of delta pulses fetched in the Lorentz force. Yet, what is the magnitude of the physical quantities required to achieve these transitions?
Until now, our pragmatic disposition has rendered our discourse bereft of any physical dimensions. Let us shift our focus to this facet and furnish a succinct example. Picture a Paul ion trap with an internal radius whose walls are being energised by a potential . Here, symbolises the local time measured relative to the trap’s frame of reference, while t is a dimensionless quantity such that , where represents an arbitrary time scale, expressed in terms of the frequency of the fluctuating field. In the given scenario, the elastic field is ascertained as in Gaussian units. For simplicity’s sake, we shall assume that the charge e and the mass m of the particle remain constant throughout the operation, while the potential may undergo variation. Let us examine the pulse depicted in Figure 1, which reaches a peak of at every odd multiple of . Consequently, for a proton traversing within a trap of cm, whose field is oscillating at a frequency of 100Hz, a maximal potential of V would be requisite to accomplish the initial segment of the squeezing operation showcased in Figure 2 in approximately 3/200s. The delicate trajectories arise from the modest orders of magnitude characterising the operations being executed.
However, one might ponder if a distinct physical setup could jeopardise the gentle scheme. By augmenting the frequency of the oscillatory field by an order of magnitude, the voltage would inevitably have to escalate by two orders of magnitude to accomplish the same transformation, while the operational time would be diminished by an order of magnitude. Although soft operations could potentially hold true for higher orders of magnitude, our methodology does not exhibit immunity across the entire energy spectrum. This vulnerability arises due to the non-relativistic Hamiltonians present in (1), which confine our examination to a low-energy domain and impose supplementary constraints on the varieties of fields that may be taken into account.
Apart from the vast differences in scale, equally significant remain the foundational challenges that pervade our understanding. In accordance with the outlined schematic, the potential amplification of states within a two-dimensional domain may give rise to unresolved reduction problems reminiscent of the Elitzur-Vaidman model for interaction-free measurements [29]. Subsequently, the ultimate measured position, expressed as , would manifest as an observable that commutes with its initial counterpart. This, in turn, implies that an observer performing a less-than-perfect position measurement in the future might, in retrospect, acquire more precise information regarding its earlier location. The pivotal question, thus, revolves around whether the reduction of the wave packet bears an impact on the particle state from preceding moments, thereby unveiling a novel iteration of Wheeler’s enigmatic delayed choice experiment.
Author Contributions
J. Fuentes crafted the discussion and prepared the manuscript, drawing upon the foundation of prior conversations and exploratory efforts undertaken in collaboration with Professor B. Mielnik. The author has read and agreed to the published version of the manuscript.
Funding
This work was supported by grant INTER/JPND/20/14609071.
Acknowledgments
The author sincerely dedicates this manuscript to the cherished memory of Professor B. Mielnik, whose guidance inspired deep gratitude and whose absence is profoundly felt.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the writing of the manuscript, or in the decision to publish the results.
References
- Konishi, K.; Paffuti, G.; Provero, P. Minimum physical length and the generalized uncertainty principle in string theory. Physics Letters B 1990, 234, 276–284. [Google Scholar] [CrossRef]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef]
- Caves, C. Quantum-mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693–1708. [Google Scholar] [CrossRef]
- Slusher, R.E.; Hollberg, L.W.; Yurke, B.; Mertz, J.C.; Valley, J.F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 1985, 55, 2409–2412. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nature Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Gessner, M.; Smerzi, A.; Pezzé, L. Multiparameter squeezing for optimal quantum enhancements in sensor networks. Nature Communications 2020, 11, 3817. [Google Scholar] [CrossRef]
- Di Candia, R.; Minganti, F.; Petrovnin, K.V.; Paraoanu, G.S.; Felicetti, S. Critical parametric quantum sensing. npj Quantum Information 2023, 9, 23. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef]
- Shi, H.; Zhuang, Q. Ultimate precision limit of noise sensing and dark matter search. npj Quantum Information 2023, 9, 27. [Google Scholar] [CrossRef]
- Lewis, H.R. Classical and Quantum Systems with Time-Dependent Harmonic-Oscillator-Type Hamiltonians. Phys. Rev. Lett. 1967, 18, 510–512. [Google Scholar] [CrossRef]
- Lewis, H.R.; Riesenfeld, W.B. An Exact Quantum Theory of the Time-Dependent Harmonic Oscillator and of a Charged Particle in a Time-Dependent Electromagnetic Field. Journal of Mathematical Physics 1969, 10, 1458–1473. [Google Scholar] [CrossRef]
- Schuch, D. Riccati and Ermakov Equations in Time-Dependent and Time-Independent Quantum Systems. Proceedings of the Seventh International Conference Symmetry in Nonlinear Mathematical Physics 2008, 4, 043. [Google Scholar] [CrossRef]
- Berry, M. Transitionless quantum driving. Journal of Physics A: Mathematical and Theoretical 2009, 42, 365303. [Google Scholar] [CrossRef]
- Masuda, S.; Nakamura, K. Fast-forward of adiabatic dynamics in quantum mechanics. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 2010, 466, 1135–1154. [Google Scholar] [CrossRef]
- Muga, J.; Chen, X.; nez, S.I.; Lizuain, I.; Ruschhaupt, A. Transitionless quantum drivings for the harmonic oscillator. Journal of Physics B: Atomic, Molecular and Optical Physics 2010, 43, 085509. [Google Scholar] [CrossRef]
- Chen, X.; Torrontegui, E.; Muga, J. Lewis-Riesenfeld invariants and transitionless quantum driving. Phys. Rev. A 2011, 83, 062116. [Google Scholar] [CrossRef]
- Torrontegui, E.; Ibáñez, S.; Chen, X.; Ruschhaupt, A.; Guéry-Odelin, D.; Muga, J.G. Fast atomic transport without vibrational heating. Phys. Rev. A 2011, 83, 013415. [Google Scholar] [CrossRef]
- Mielnik, B. Quantum operations: technical or fundamental challenge? Journal of Physics A: Mathematical and Theoretical 2013, 46, 385301. [Google Scholar] [CrossRef]
- Combescure, M.; Robert, D. Quadratic Quantum Hamiltonians revisited, 2005, [arXiv:math-ph/math-ph/0509027].
- Baseia, B.; Mizrahi, S.S.; Moussa, M.H.Y. Generation of squeezing for a charged oscillator and for a charged particle in a time-dependent electromagnetic field. Phys. Rev. A 1992, 46, 5885–5889. [Google Scholar] [CrossRef]
- Baseia, B.; Vyas, R.; Bagnato, V.S. Particle trapping by oscillating fields: squeezing effects. Quantum Optics: Journal of the European Optical Society Part B 1993, 5, 155. [Google Scholar] [CrossRef]
- Mielnik, B.; Ramírez, A. Ion traps: some semiclassical observations. Physica Scripta 2010, 82, 055002. [Google Scholar] [CrossRef]
- Mielnik, B.; Ramírez, A. Magnetic operations: a little fuzzy mechanics? Physica Scripta 2011, 84, 045008. [Google Scholar] [CrossRef]
- Paul, W. Electromagnetic traps for charged and neutral particles. Rev. Mod. Phys. 1990, 62, 531–540. [Google Scholar] [CrossRef]
- Wolf, K.B. A Top-Down Account of Linear Canonical Transforms. Superintegrability, Exact Solvability, and Special Functions. SIGMA 2012, 8, 033. [Google Scholar]
- Fuentes, J. Quantum control operations with fuzzy evolution trajectories based on polyharmonic magnetic fields. Scientific Reports 2020, 10, 22256. [Google Scholar] [CrossRef]
- Mielnik, B. Quantum Control: discovered, repeated and reformulated ideas mark the progress. Journal of Physics: Conference Series 2014, 512, 012035. [Google Scholar] [CrossRef]
- Fuentes, J.; Obregón, O. Optimisation of information processes using non-extensive entropies without parameters. Int. J. of Information and Coding Theory 2022, 6, 35–51. [Google Scholar] [CrossRef]
- Elitzur, A.; Vaidman, L. Quantum mechanical interaction-free measurements. Foundations of Physics 1993, 23, 987–997. [Google Scholar] [CrossRef]
Figure 1.
The figure presents three distinct fields—each vanishing at both the initial and final points of the operational interval—accompanied by their respective exact solutions . In the case of the three fields, a Fourier transformation takes place at and , where attains zero. Sequentially realising the pulses designated as and within a solenoid would give rise to a quantum operation characterised by a squeezing effect with a parameter .
Figure 1.
The figure presents three distinct fields—each vanishing at both the initial and final points of the operational interval—accompanied by their respective exact solutions . In the case of the three fields, a Fourier transformation takes place at and , where attains zero. Sequentially realising the pulses designated as and within a solenoid would give rise to a quantum operation characterised by a squeezing effect with a parameter .
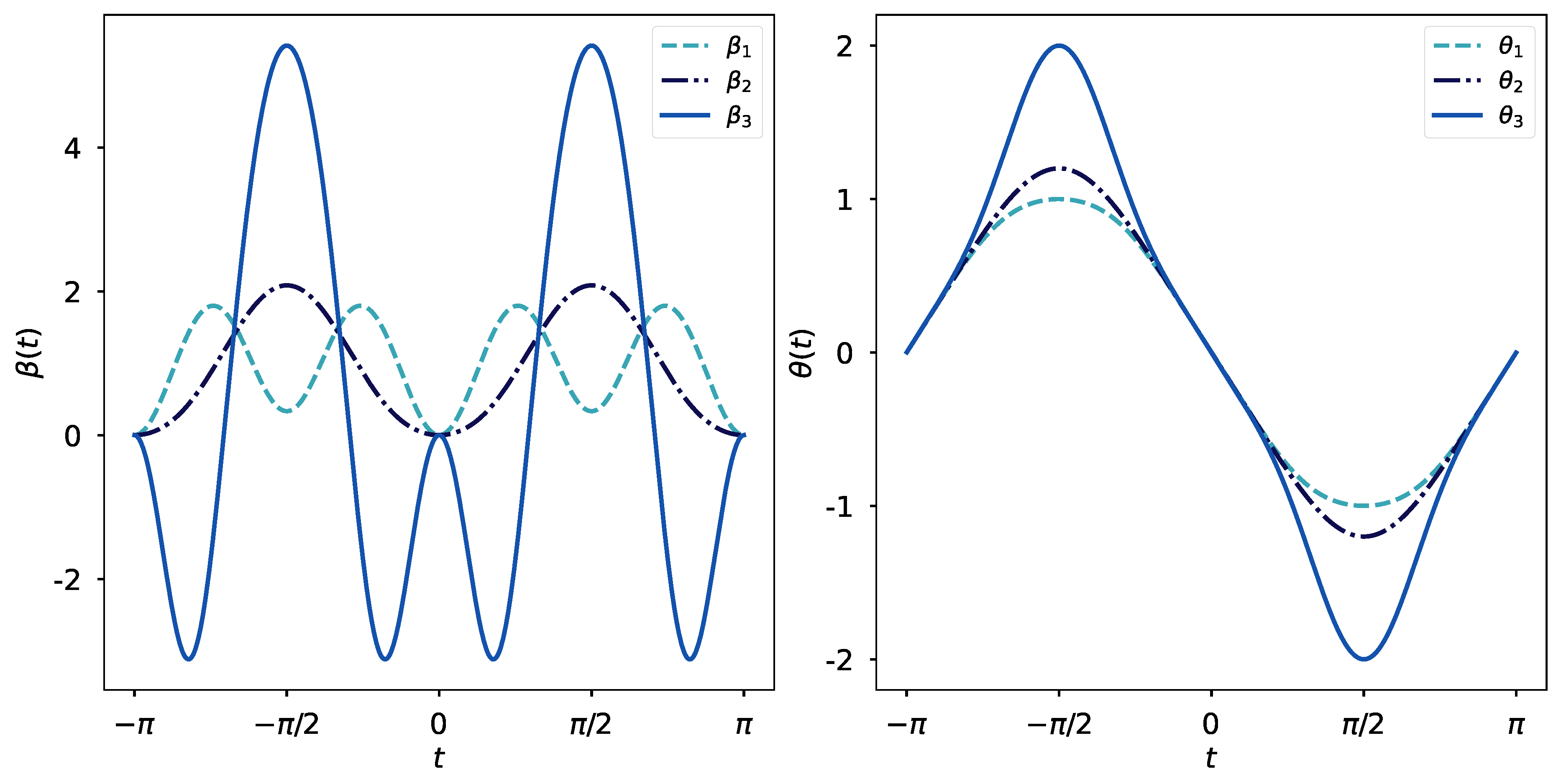
Figure 2.
Semiclassical trajectories (the curves in the centre), accompanied by their respective uncertainties (the enveloping curves), are presented for a pair of canonical variables, commencing with the initial data and . The time evolution is instigated by the amalgamation of the two fields portrayed in Figure 1 throughout the interval . In the left panel, the temporal progression of the variable q is illustrated, beginning its evolution within an uncertainty belt of width and culminating within a moderately amplified uncertainty belt of width . Contrarily, the variable p shown in the right panel, commencing its evolutionary course with an uncertainty identical to that of q, ultimately reaches its conclusion within a squeezed uncertainty belt of width .
Figure 2.
Semiclassical trajectories (the curves in the centre), accompanied by their respective uncertainties (the enveloping curves), are presented for a pair of canonical variables, commencing with the initial data and . The time evolution is instigated by the amalgamation of the two fields portrayed in Figure 1 throughout the interval . In the left panel, the temporal progression of the variable q is illustrated, beginning its evolution within an uncertainty belt of width and culminating within a moderately amplified uncertainty belt of width . Contrarily, the variable p shown in the right panel, commencing its evolutionary course with an uncertainty identical to that of q, ultimately reaches its conclusion within a squeezed uncertainty belt of width .
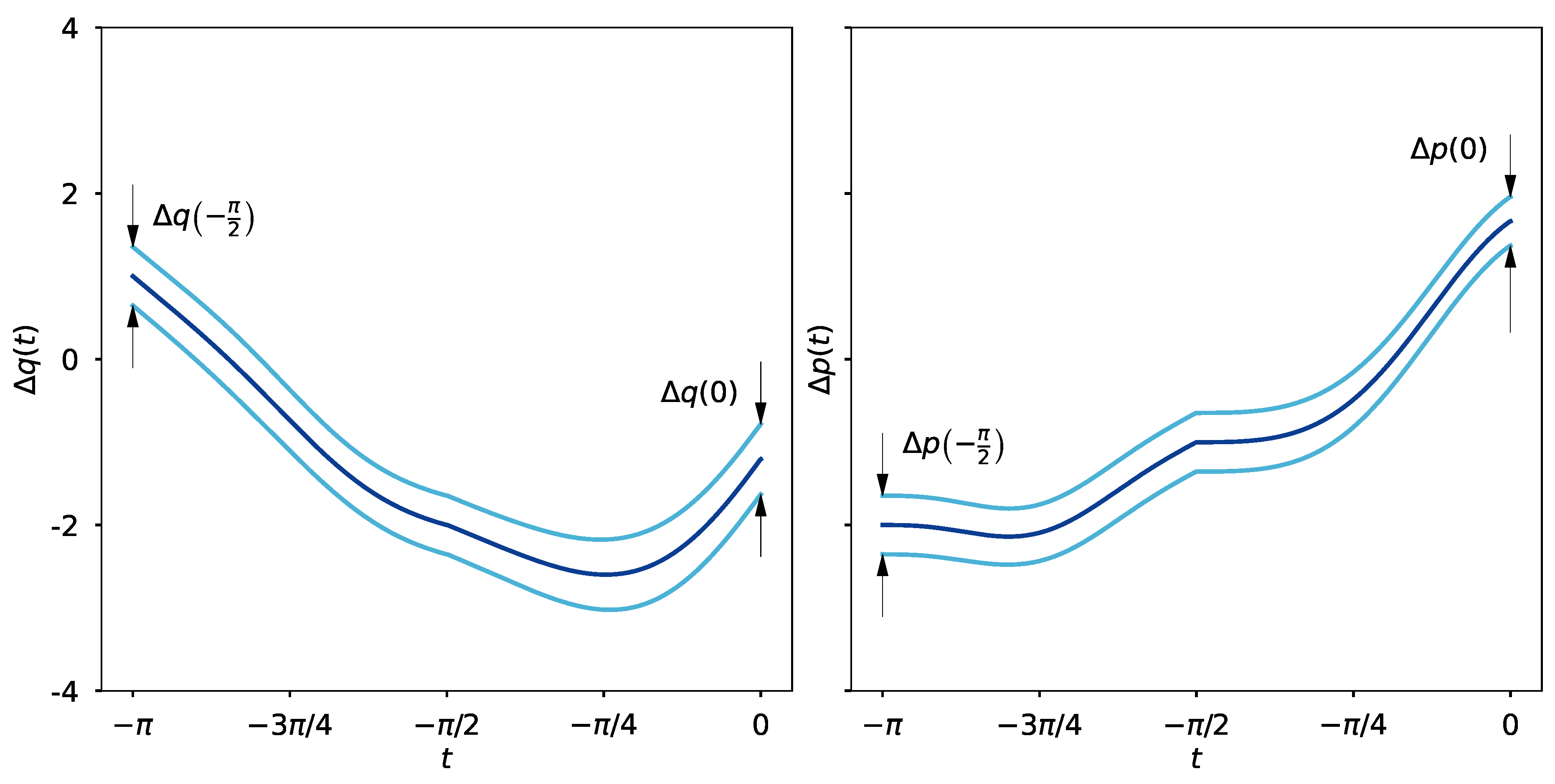
Figure 3.
The time evolution of canonical variables q and p, together with their uncertainty shadows, is brought about by a quantum operation arising from the composition of pulses and in Figure 1. Realisation of this operation could be achieved through a time-varying electric potential applied to the walls of a hyperbolic ion trap, yielding an amplification of the uncertainty tied to variable q, while simultaneously compressing the uncertainty connected to variable p. Indeed, both variables exhibit identical uncertainties at the inception of the operation. Initially, the two semiclassical trajectories are enveloped by an uncertainty band of width . Yet, upon the operation’s conclusion, the trajectories for q and p reside within uncertainty shadows of width and , respectively.
Figure 3.
The time evolution of canonical variables q and p, together with their uncertainty shadows, is brought about by a quantum operation arising from the composition of pulses and in Figure 1. Realisation of this operation could be achieved through a time-varying electric potential applied to the walls of a hyperbolic ion trap, yielding an amplification of the uncertainty tied to variable q, while simultaneously compressing the uncertainty connected to variable p. Indeed, both variables exhibit identical uncertainties at the inception of the operation. Initially, the two semiclassical trajectories are enveloped by an uncertainty band of width . Yet, upon the operation’s conclusion, the trajectories for q and p reside within uncertainty shadows of width and , respectively.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





