1. Introduction

2. System description

2.1. Workspace limitations

To illustrate the workspace limitations of CDPR, let’s assume a fully-constrained planar scheme as in Figure 1 where:

• H and W are the height and width of the frame, respectively.
• h and w are the height and width of the end-effector, respectively.
• $T_i$ for $i=1,...,4$ the tension of the cables.
• ${\tau }_i$ for $i=1,...,4$ the torques exerted by each motor.
• r the effective radius of the drums.
• $[x_e,y_e,{\delta }_e]$ the coordinates of the end-effector.

Figure 1. Conventional planar CDPR

Figure 1. Conventional planar CDPR

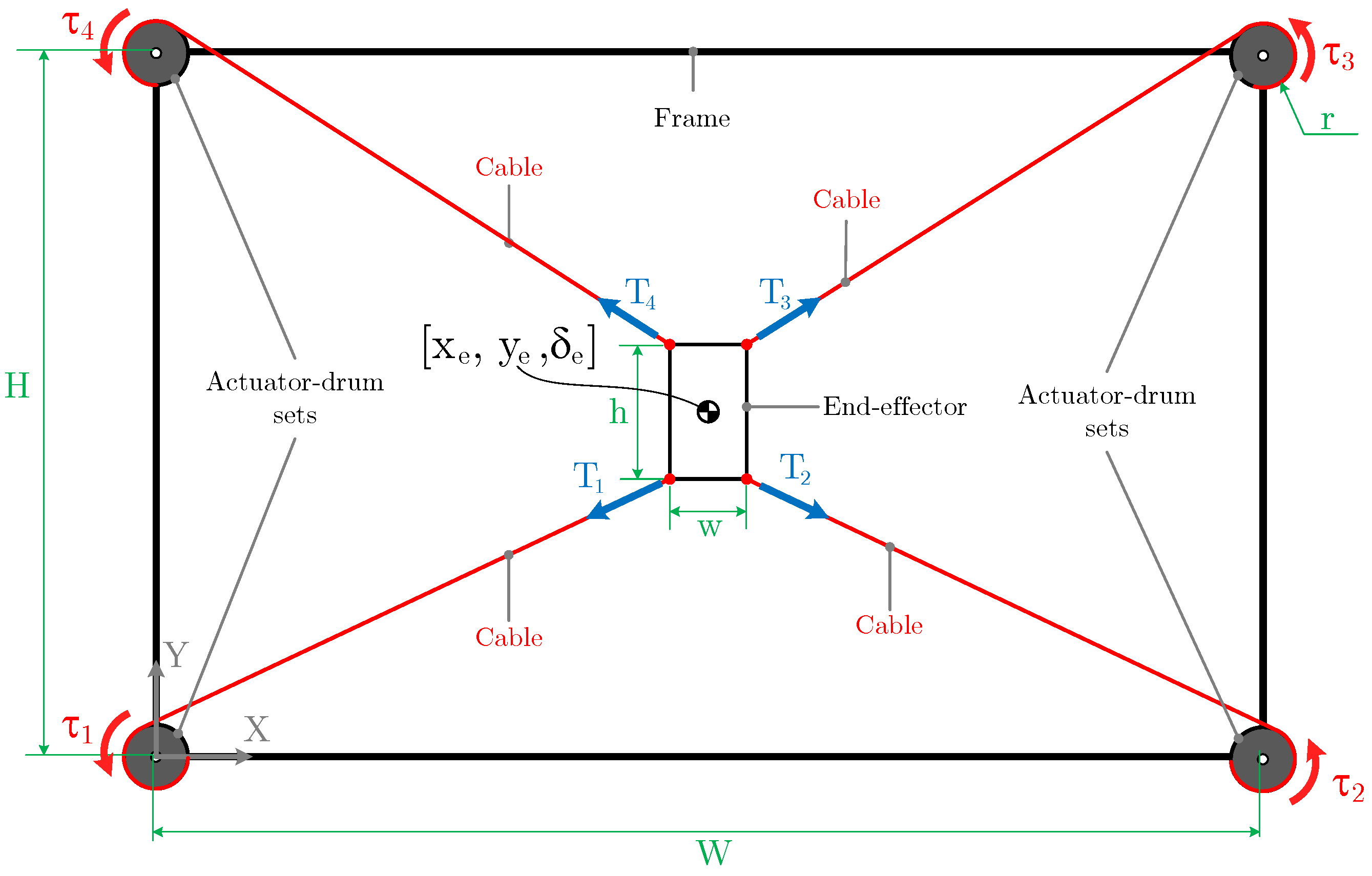
Assuming that no sagging cables are allowed (e.g. [19], the static workspace of the robot can be determined by imposing end-effector poses within the frame and checking if the force/torque equilibrium can be achieved for these poses. The main parameters affecting the workspace are the dimensional parameters of the robot (W,H, w, h and r), the end-effector mass matrix, M, and the allowable tension limit values: $T_{min}$ and $T_{max}$ [20]. The minimum tension value, $T_{min}$, must be set to avoid sagging cables and low stiffness values. The maximum tension value, $T_{max}$, is determined by the maximum holding torque of the motors and by the breaking strength of the cables [21].

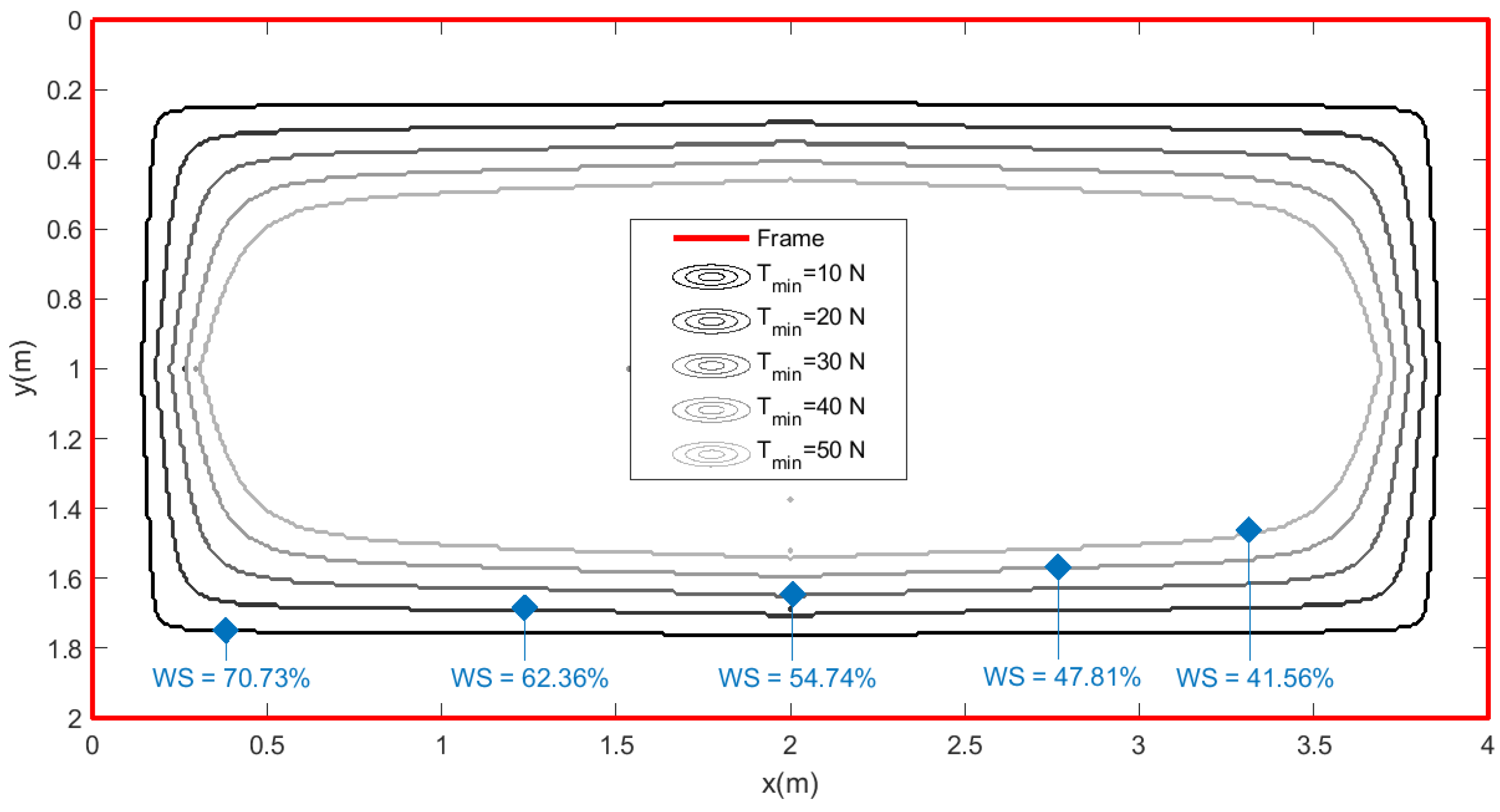
Figure 2 shows the static workspace of the robot scheme of Figure 1 with the parameters of the prototype presented in the experimental results section: $W=2.224$ m, $H=1.112$ m, $w=0.281$ m, $h=0.287$ mm, $m=2$ kg and no rotation of the end-effector $\delta =0^{\circ }$. Figure 2 illustrates that for a minimum tension value, $T_{min}=2.5$ N, the static workspace is only the 27.56% of the frame area. The static workspace is reduced when the allowed minimum tension increases and for $T_{min}=7.0$ N only the 10.53% of the frame area is accessible to the end-effector.

Figure 2. Workspace of the conventional planar CDPR

Figure 2. Workspace of the conventional planar CDPR

2.2. Novel single cable loop CDPR

As mentioned in Section 1, some of the main drawbacks of CDPR are: a) the limited workspace inside of the frame [20]; b) the lack of the robot dexterity when the end-effector is placed near the boundaries of the feasible workspace [22].

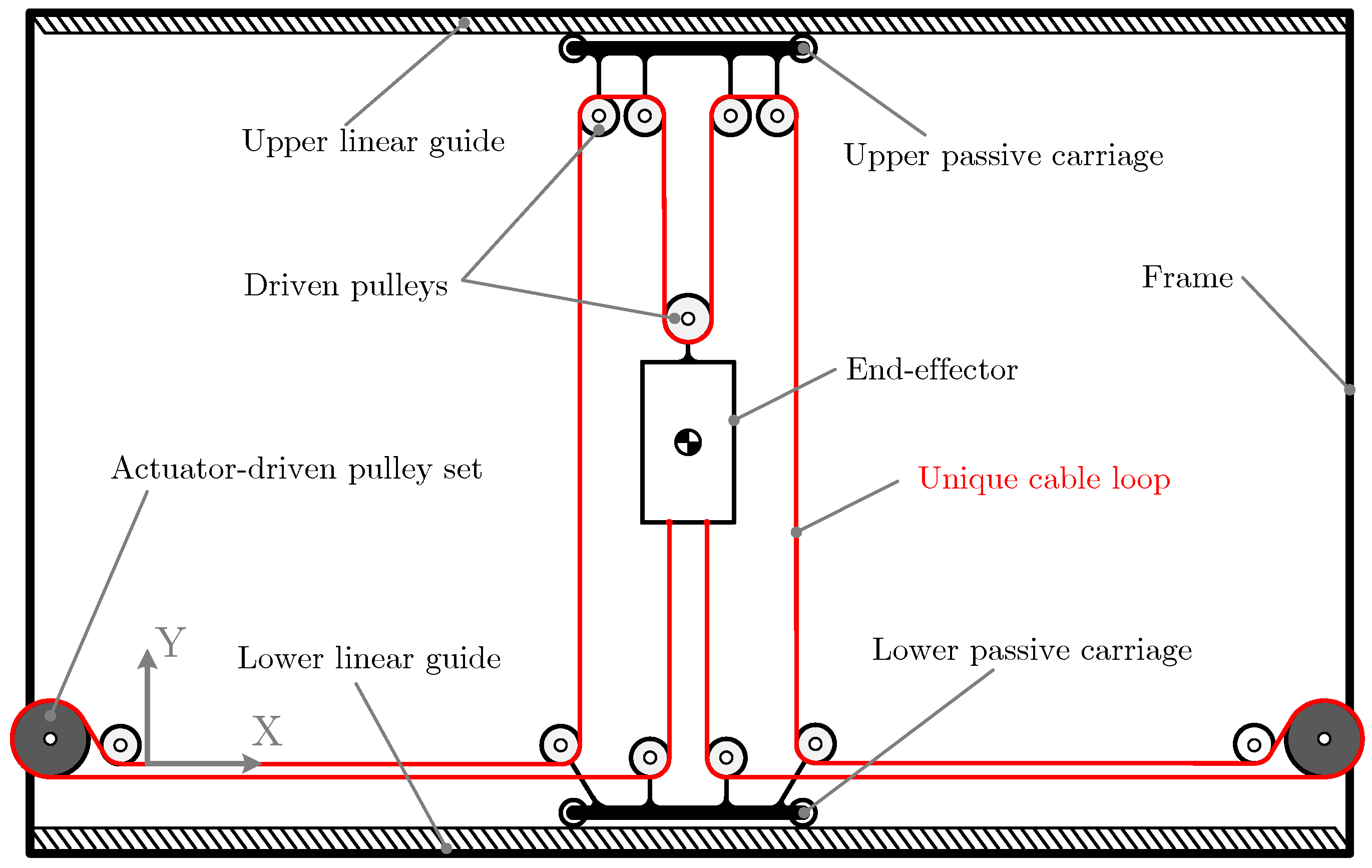
For solving these two problems, this paper proposes the single cable loop cable-driven parallel robot (sCDPR) scheme shown in Figure 3. The proposal is based on the addition of two passive carriage-linear guide sets in the upper and lower part of the frame. Through a set of driven pulleys a single cable loop can be designed and its length will remain constant for any pose of the end-effector (assuming negligible in this first step the length variation of the cable due to its elasticity). Two actuators, placed at the lower corners of the frame, provide the movement capability of the end-effector through driven pulleys.

Figure 3. Single cable loop planar CDPR proposal: sCDPR

Figure 3. Single cable loop planar CDPR proposal: sCDPR

2.3. Nomenclature

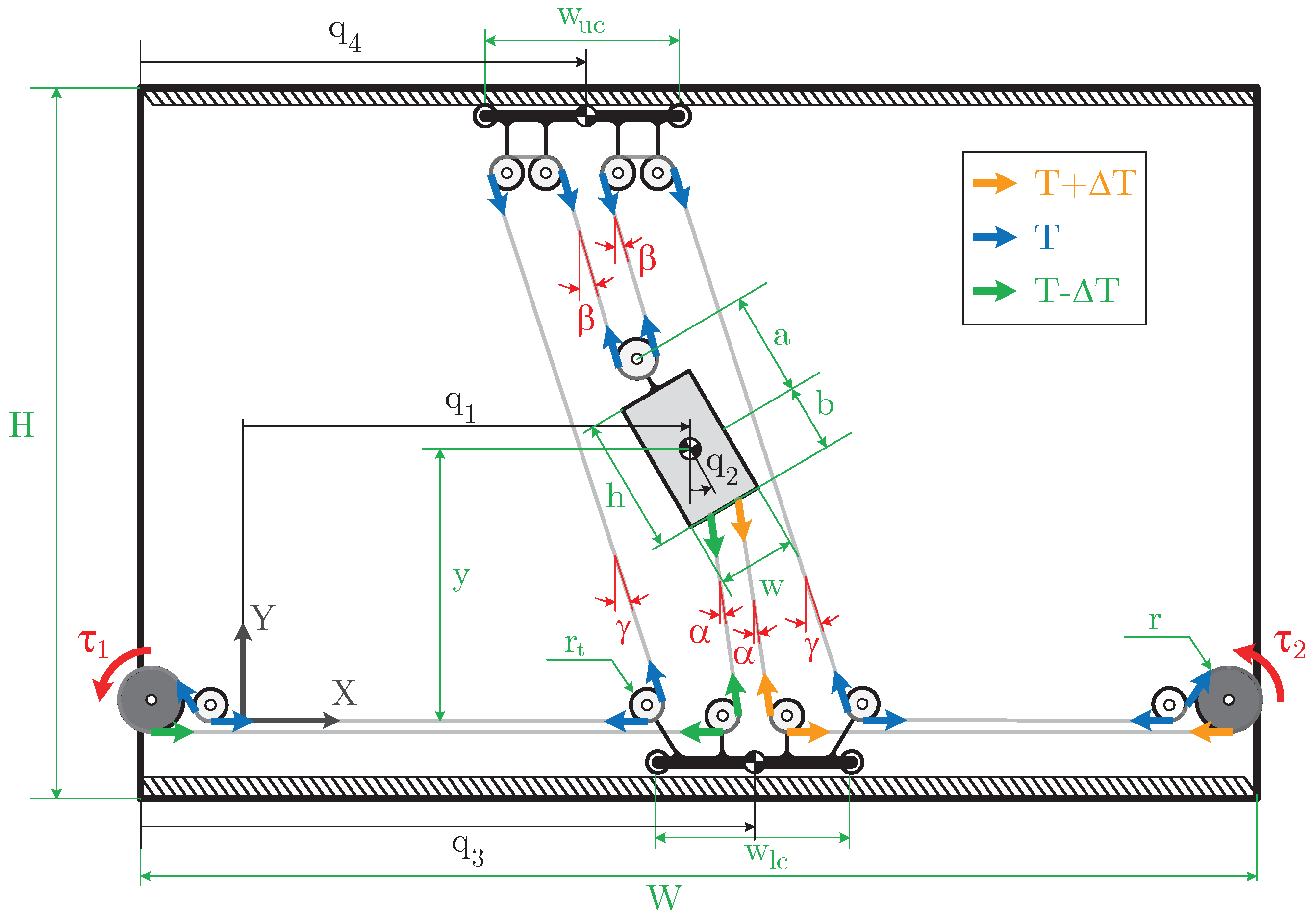
Figure 4 shows the sCDPR proposal in an arbitrary pose to present the nomenclature for the modelling of the robot

The dimensional parameters, coloured in green, are: W and H, the width and height of the frame, w and h, the width and height of the end-effector, a is the distance between the centre of mass of the end-effector and the centre of the driven pulley located at the top of the end-effector, b the distance between the centre and the bottom of the end-effector, ω_uc and ω_lc are the widths of the upper and lower passive carriages, r_t is the radius of the driver pulleys and, r the radius of the driven pulleys attached to the actuators.

The angles of the cables, in red, are α, β and γ which represent the angle with regards to Y axis of the lower inner, upper inner and outer path of the cable loop, respectively.

Being T the pretension of the cable loop, the instant tension of each path of cable loop has been noted as T, T − ΔT and T + ΔT, and depend on the actuation of the motors attached to the driven pulleys.

The generalised coordinates to develop the model are: q₁, the horizontal coordinate of the nd-effector, q₂ the angle with regards to Y axis of the end-effector, q₃ the horizontal coordinate of the lower carriage and q₄ the horizontal coordinate of the upper carriage.

Finally, the input torque of both actuators have been noted as τ₁ and τ₂.

Figure 4. Nomenclature of sCDPR

Figure 4. Nomenclature of sCDPR

2.4. Workspace gain

With this novel proposal, assuming that after a movement both carriages are almost aligned to the end-effector in the horizontal axis (see the pose of Figure 3 as example), the equilibrium of forces/torque is guaranteed and the end-effector is therefore able to reach almost all the frame area. In particular, the feasible workspace at static conditions is defined by all end-effector coordinates $[x,y]$ which satisfy:

$$\begin{array}{ccc}\frac{w_{lc}}{2}\hfill & \le x\le & \hfill W-\frac{w_{lc}}{2}\\ b\hfill & \le y\le & \hfill H-a\end{array}$$

(1)

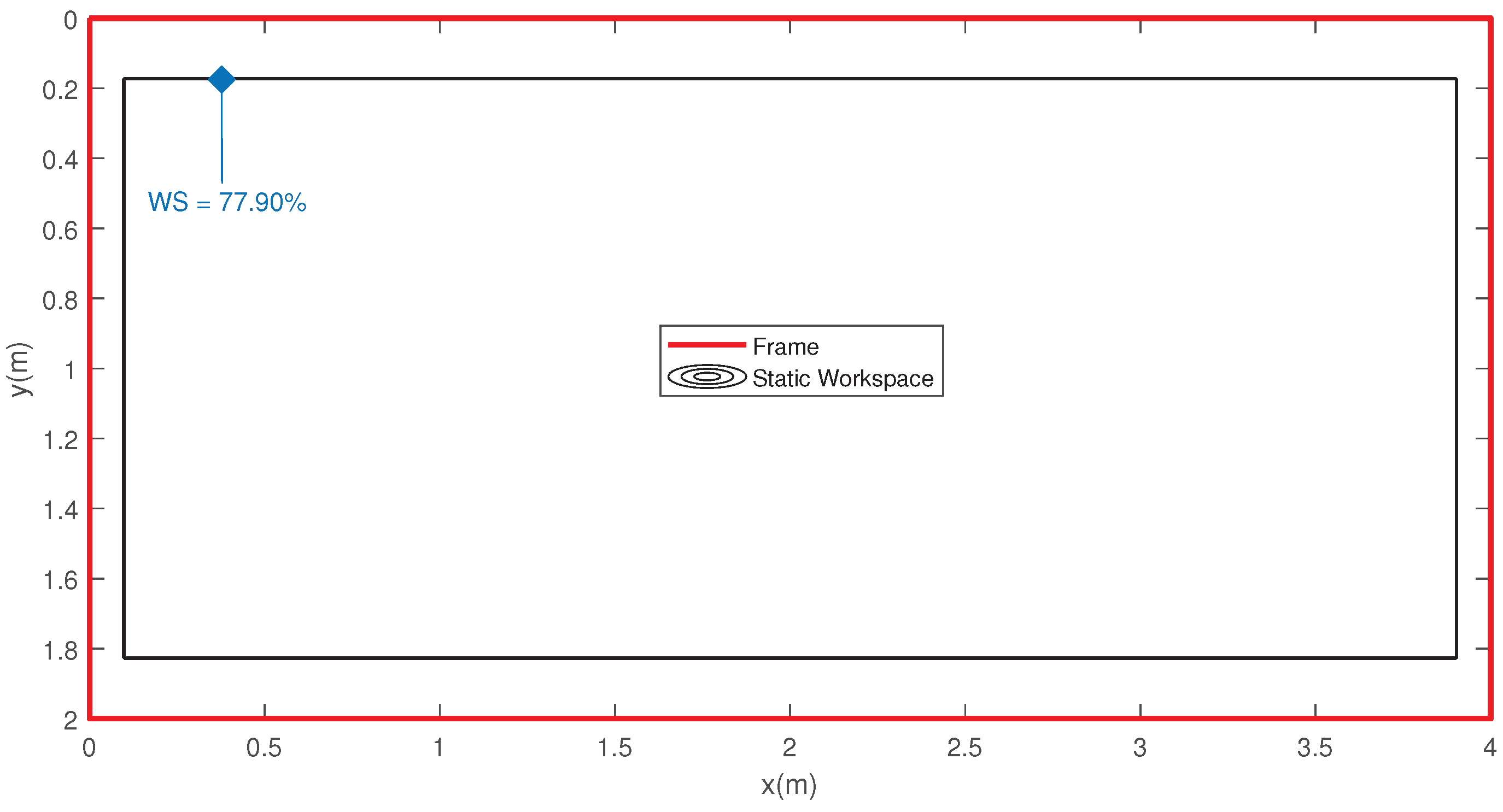
In the proposal, with a single closed loop of cable, the workspace only depends on the geometry of the frame and the end-effector (see expression (1)). Figure 5 represents the static workspace of the sCDPR proposal for the same parameters of the results regarding to the conventional scheme (see Figure 2).

Figure 5. Workspace of the sCDPR

Figure 5. Workspace of the sCDPR

3. Mathematical Model

3.2. Dynamic Model

The dynamic model has been developed under the assumption that angles $\alpha$, $\beta$ and $\gamma$ (see Figure 4) are small enough to obtain a linear equivalent model. In this way, angles of cables can be originally written as:

$$\begin{array}{ccc}\alpha & =& {tan}^{-1}\left(\frac{q_3-q_1-asin\left(q_2\right)}{y-acos\left(q_2\right)}\right)\\ \beta & =& {tan}^{-1}\left(\frac{q_1-q_4-bsin\left(q_2\right)}{H-y-bcos\left(q_2\right)}\right)\\ \gamma & =& {tan}^{-1}\left(\frac{q_3-q_4}{H}\right)\end{array}$$

(4)

The dynamics equations of the actuators and carriages have been obtained by writing their Newtonian balances due to their simplicity. For the pose detailed in Figure 4 the torque equilibrium of the motors yields:

$$\begin{array}{c}{\tau }_1+r(T-\Delta T)-rT=0\\ {\tau }_2-r(T+\Delta T)+rT=0\end{array}$$

(5)

In this sense, the instant increment of the tension of the cable loop can be written as:

$$\Delta T=\frac{{\tau }_1+{\tau }_2}{2R}$$

(6)

The horizontal equilibrium of the lower carriage force is:

$$-m_3\ddot{q_3}+\frac{1}{R}({\tau }_1+{\tau }_2)-2T\left[sin\left(\gamma \right)+sin\left(\alpha \right)\right]-2T\mu \left[cos\left(\gamma \right)\frac{\dot{q_3}}{\dot{q_3}}+cos\left(\alpha \right)\frac{\dot{q_3}}{\dot{q_3}}\right]=0$$

(7)

and the horizontal equilibrium of the upper carriage is:

$$-m_4\ddot{q_4}+2T\left[sin\left(\gamma \right)+sin\left(\beta \right)\right]-2T\mu \left[cos\left(\gamma \right)\frac{\dot{q_4}}{\dot{q_4}}+cos\left(\beta \right)\frac{\dot{q_4}}{\dot{q_4}}\right]=0$$

(8)

For obtaining the dynamic behaviour of the end-effector Lagrange formulation has been applied, being the Lagrangian, L:

$$L=\frac{1}{2}{m}_e{\left({\dot{q}}_1\right)}^2+\frac{1}{2}{I}_e{\left({\dot{q}}_2\right)}^2$$

(9)

the equations that describe the dynamics of the end-effector are:

$$\begin{array}{ccc}\hfill \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_1}\right)+\frac{\partial L}{\partial q_1}& =& Q_1\hfill \\ \hfill \frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_2}\right)+\frac{\partial L}{\partial q_2}& =& Q_2\hfill \end{array}$$

(10)

where $Q_1$ is the generalised horizontal force and $Q_2$ the generalised torque. Assuming that:

$$d{W}_t=Q_{1}d{q}_1+Q_{2}d{q}_2$$

(11)

Figure 6. End-effector scheme

Figure 6. End-effector scheme

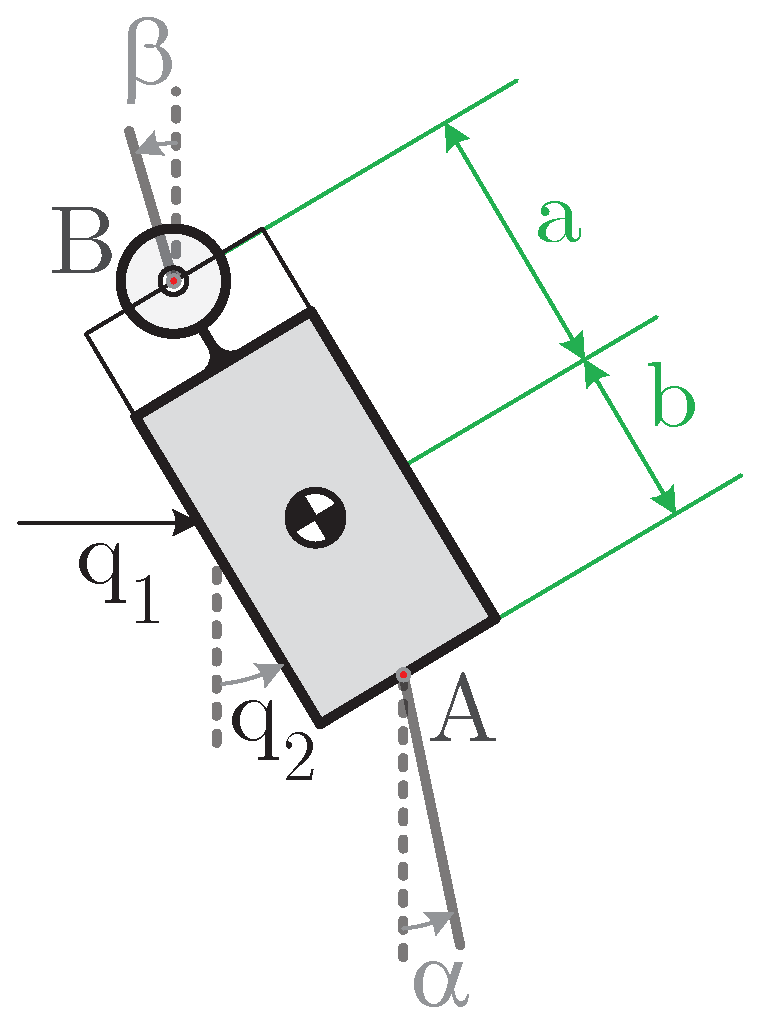being $W_t$ the total work exerted by $Q_1$ and $Q_2$. If $d{W}_t$ is determined $Q_1$ and $Q_2$ can be therefore obtained. Assuming the end-effector scheme of Figure 6 $d{W}_t$ can be determined with by computing the work exerted at points A and B as:

$$d{W}_t=d{W}_A+d{W}_B$$

(12)

being $d{W}_A={\mathbf{F}}_{A}d{\mathbf{r}}_A$ and $d{W}_B={\mathbf{F}}_{B}d{\mathbf{r}}_B$. The A and B differential position arrays can be written as:

$$\begin{array}{cccc}d{\mathbf{r}}_A& =& [d{q}_1+acos\left(q_2\right)d{q}_2,\hfill & \hfill asin\left(q_2\right)d{q}_2]\\ d{\mathbf{r}}_B& =& [d{q}_1+bcos\left(q_2\right)d{q}_2,\hfill & \hfill -bsin\left(q_2\right)d{q}_2]\end{array}$$

(13)

and the Forces applied at A and B points as:

$$\begin{array}{ccccc}{\mathbf{F}}_A& =\hfill & [& \hfill 2Tsin\left(\alpha \right),& \hfill -2Tcos\left(\alpha \right)]\\ {\mathbf{F}}_B& =\hfill & [& \hfill -2Tsin\left(\beta \right),& \hfill 2Tcos\left(\beta \right)]\end{array}$$

(14)

The differential of the total work can be easily obtaining by substituting (13) and (14) in (12):

$$\begin{array}{ccc}\hfill d{W}_t& =& 2T[sin\left(\alpha \right)+d{q}_1+asin\left(\alpha \right)cos\left(q_2\right)d{q}_2-acos\left(\alpha \right)sin\left(q_2\right)d{q}_2]+\hfill \\ \hfill & & 2T[-sin\left(\beta \right)d{q}_1+bsin\left(\beta \right)cos\left(q_2\right)d{q}_2-bcos\left(\beta \right)sin\left(q_2\right)d{q}_2]\hfill \end{array}$$

(15)

Identifying (11) with (15), $Q_1$ and $Q_2$ can be finally determined:

$$\begin{array}{c}{Q}_1=2T(sin\left(\alpha \right)-sin\left(\beta \right))\\ Q_2=2T[a(sin\left(\alpha \right)cos\left(q_2\right)-cos\left(\alpha \right)sin\left(q_2\right))+b(sin\left(\beta \right)cos\left(q_2\right)-cos\left(\beta \right)sin\left(q_2\right))]\end{array}$$

(16)

$$\begin{array}{c}{Q}_1=2T(sin\left(\alpha \right)-sin\left(\beta \right))\\ Q_2=2T(asin(\alpha -q_2)+bsin(\beta -q_2))\end{array}$$

(17)

By assuming small values of $q_2$ and that the horizontal distance between both carriages is much smaller than the vertical distance, i.e. $q_3-q_1<<Y$, $q_4-q_1<<H-Y$ and $q_3-q_4<<H$, angles in (4) can be assumed to be:

$$\begin{array}{ccc}\alpha & \approx & \frac{q_3-q_1-asin\left(q_2\right)}{y-acos\left(q_2\right)}\\ \beta & \approx & \frac{q_1-q_4-bsin\left(q_2\right)}{H-y-bcos\left(q_2\right)}\\ \gamma & \approx & \frac{q_3-q_4}{H}\end{array}$$

(18)

In this way, developing expressions (10) a linear and time invariant (LTI) dynamic model is finally achieved and expressed as:

$$\mathbf{M}\ddot{\mathbf{q}}\left(t\right)+\mathbf{K}\mathbf{q}\left(t\right)=\mathbf{w}$$

(19)

being $\mathbf{M}$, the mass/inertia matrix:

$$\mathbf{M}=\left(\begin{array}{cccc}{m}_e& 0& 0& 0\\ 0& I_e& 0& 0\\ 0& 0& m_3& 0\\ 0& 0& 0& m_4\end{array}\right)$$

(20)

$\mathbf{K}$ the stiffness matrix:

$$\mathbf{K}=\left(\begin{array}{cccc}2T\left(\frac{1}{z_2}+\frac{1}{z_1}\right)& 2T\left(\frac{a}{z_2}-\frac{b}{z_1}\right)& -\frac{2T}{z_2}& -\frac{2T}{z_1}\\ 2T\left(\frac{1}{z_2}-\frac{1}{z_1}\right)& 2T\left(\frac{a^2}{z_2}+a+\frac{b^2}{z_{1}b}+b\right)& -\frac{2Ta}{z_2}& \frac{2Tb}{z_1}\\ -\frac{2T}{z_2}& -\frac{2Ta}{z_2}& 2T\left(\frac{1}{H}+\frac{1}{z_2}\right)& -\frac{2T}{H}\\ -\frac{2T}{z_1}& \frac{2Tb}{z_1}& -\frac{2T}{H}& 2T\left(\frac{1}{H}+\frac{1}{z_1}\right)\end{array}\right)$$

(21)

with $z_1=H-Y-b$, $z_2=Y-a$ and $\mathbf{w}$ the external force array:

$$\mathbf{w}=\left(\begin{array}{c}0\\ 0\\ \frac{1}{R}({\tau }_1+{\tau }_2)-4T\mu \frac{\dot{q_3}}{\dot{q_e}}\\ -4T\mu \frac{\dot{q_4}}{\dot{q_4}}\end{array}\right)$$

(22)

Dynamic model (19) is valid as long as the small cable angles assumption is fulfilled. Simulation and experimental results will demonstrate the validity of the proposed LTI model for describing the dynamics of the sCDPR.

4. Experimental Platform Description

4.1. Robot description

The experimental platform has been designed to be mainly built by laser cutting and 3D printed parts. Figure 7 shows the designing and the final prototype, including the main functional elements.

Figure 7. Design and Prototype of the proposed sCDPR

Figure 7. Design and Prototype of the proposed sCDPR

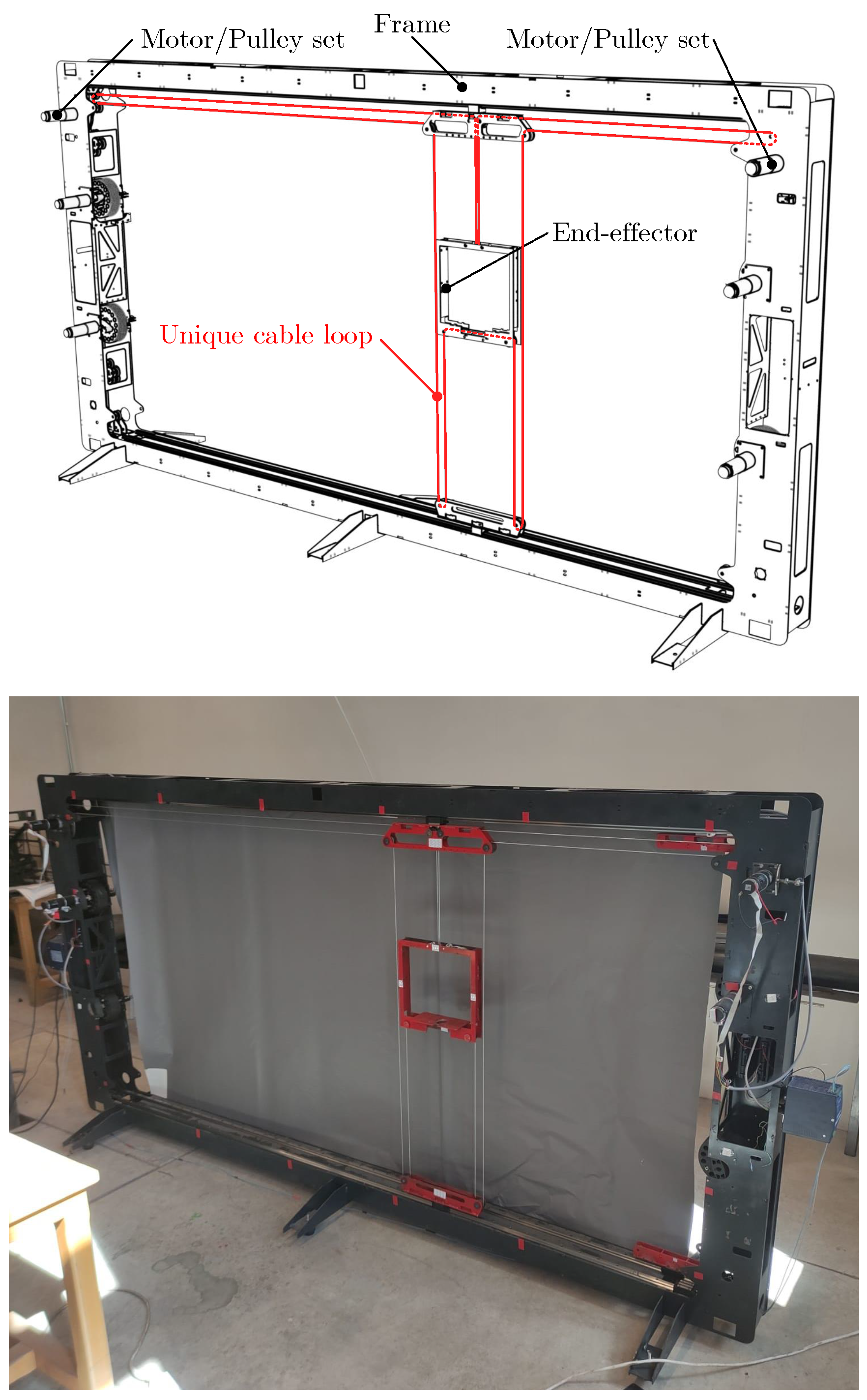
The frame and end-effector are made of 4 mm steel plates cut by laser. The pulleys have been printed with compound material and the cable is a 2 mm of diameter steel cable. The actuators are two DC motors MaxonMotor RE40, with a 26:1 gearbox. They also included 256 ppv encoders to acquire their angular position. The motors are commanded by two servoamplifiers, ESCON 70/10 which receive the control signal from the control device: a NI MyRio 1900 real-time controller. This configuration ensures a sampling frequency of 1 KHz. The cable of the closed loop is a 2 mm of diameter steel cable. Table 1 summarises the main parameters of the robot.

Table 1. Parameters of the prototype

Table 1. Parameters of the prototype

Frame
Width, W (mm)	2224
Height, H (mm)	1112
End-effector
Width, w (mm)	287
Height, h (mm)	281
Mass, $m_e$ (Kg)	2.1
Rotational Inertia, $I_e$ (Kg · m ${}^2$)	$2.5198·{10}^{-2}$
Cable
Diameter, d (mm)	2
Young’s module, E (GPa)	2.0912
Passive Carriages
Width, $w_3=w_4$ (mm)	287
Mass, $m_3=m_4$ (Kg)	1.2
Motor/Pulley sets
Rotational Inertia, J (Kg · m ${}^2$)	$1.2734·{10}^{-2}$
Viscous friction coefficient, b (Nms)	0.2
Effective radius, r (mm)	7.3

4.2. Computer vision system

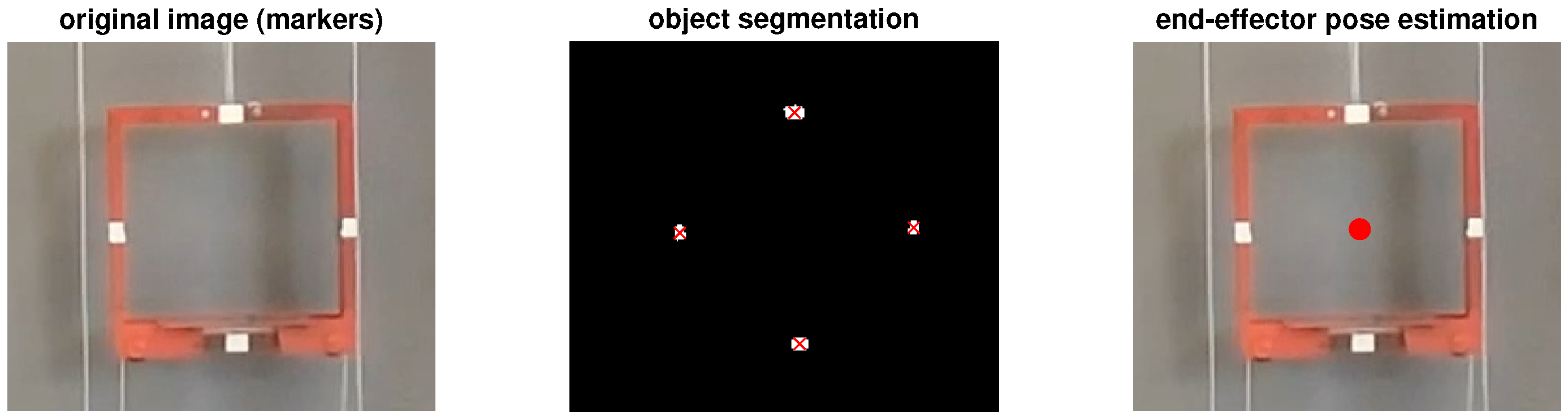
In front of the robot a vision system is placed to track some points of interest during the robot manoeuvres. Four markers have been attached to the frame, four to the end-effector and one at each passive carriage.

The camera is a 8 Megapixels 3264 × 2448 resolution with a Sony IMX179 sensor. The focal distance, brightness can be manually adjusted. After the camera calibration, the 30fps images are undistorted and the equivalence between images coordinates and world coordinates is obtained. The different points of interest are obtained by a simple colour segmentation, and the position of the end-effector and passive carriages can be therefore obtained after the experiments in an offline way.

Figure 8 represents as example a region of interest of the original image, the marker pose detection by segmentation and the end-effector position estimation.

Figure 8. Vision system for pose estimation

Figure 8. Vision system for pose estimation

5. Model identification and validation

5.1. Parameters identification

The objective of this section is to validate the dynamic model developed in Section 3.2. Dimensional parameters (see Table 1) can be directly measured but the coefficient of friction, $\mu$, shall be identified.

For this purpose, some experiments have been carried out. For a given cable loop pretension value ($T=350$ N), the voltage which control the servoamplifier has been increased in 0.1 V steps, observing the first voltage value at carriages (and end-effector) start moving. By repeating 30 times the experiment, the average value of voltage is $V_f=0.68$ V which corresponds to a motor torque of ${\tau }_f=0.8826$ Nm.

On the other hand, the dynamic model (19) has been implemented in Matlab^®/Simulink^® and both motors have been excited with ${\tau }_f=0.8826$ N. Changing the value of $\mu$, the one which minimise the error between the experimental and simulated results has been selected, $\mu =0.1723$.

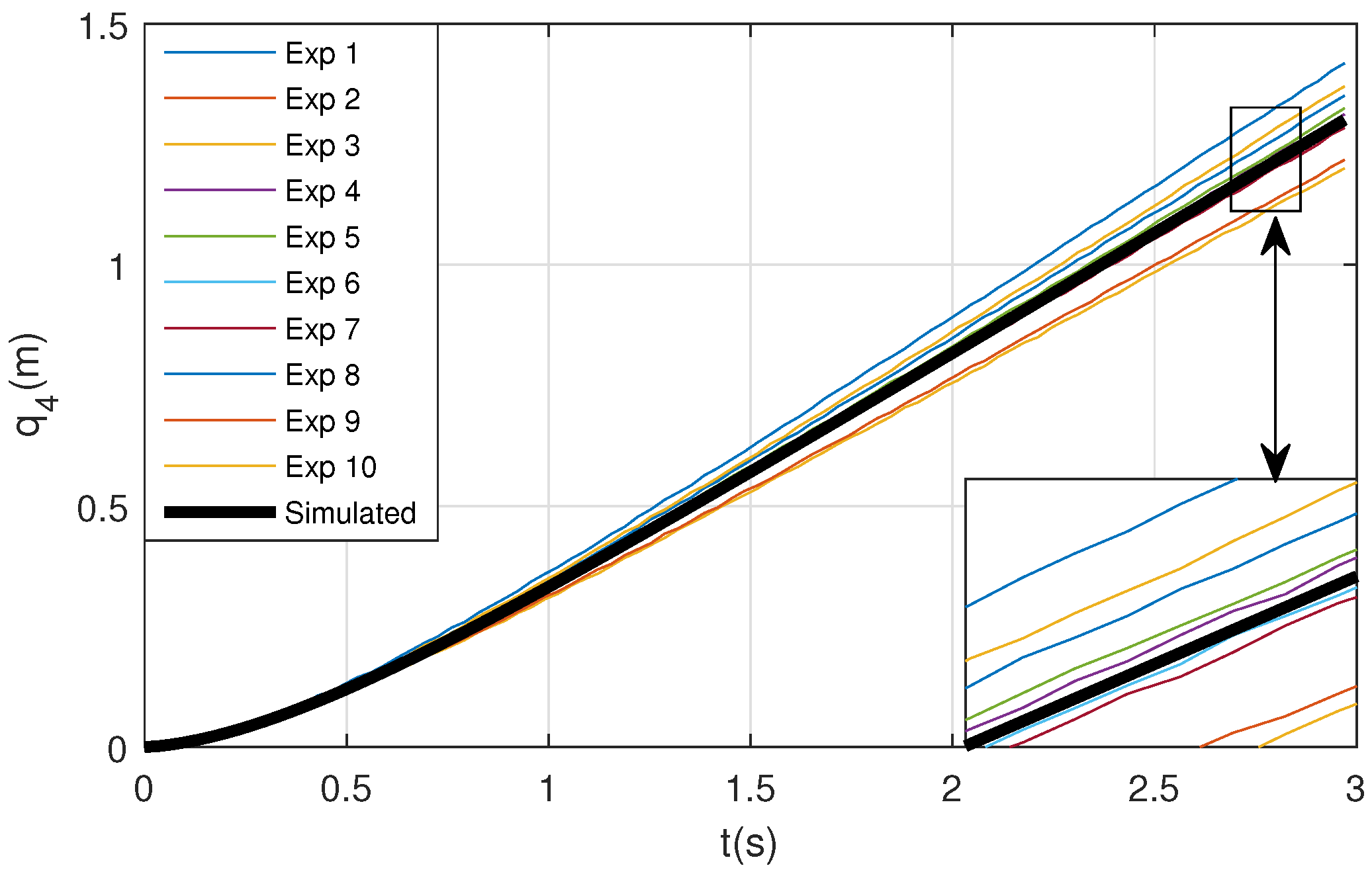
For illustrative purpose Figure 9 compares the first 10 experimental results and the simulated one after identifying $\mu$ value. The horizontal position of the upper carriage, $q_4$, initially placed at $q_4\left(0\right)=0.2$ m, is represented when $V_f$ is applied in both motors.

Figure 9. Open loop results: experiments vs. simulation ($\mu$ parameter identification)

Figure 9. Open loop results: experiments vs. simulation ($\mu$ parameter identification)

5.2. Frequency characterisation

In this Section the natural frequency of the robot will be determined to be used in further control strategies to compensate end-effector vibration during the robot manoeuvres. The cable loop pretension value, T, has a notorious influence on this natural frequency. In this way, this frequency has been determined for three values of cable pretension: a low value of 200 N, a medium value of 350 N and a high value of 500 N.

The procedure to determine the natural frequency of the end-effector is the following: For a given end-effector position, an horizontal external force is applied to it; the vision system described in Section 4.2 registers the end-effector pose; its horizontal displacement is therefore acquired, $x_e$; the continuous frequency component is removed, $x_e^0$; FFT is applied to determined the maximum frequency peak of the frequency spectrum. Figure 10 illustrates this procedure.

Figure 10. Procedure for natural frequency determination

Figure 10. Procedure for natural frequency determination

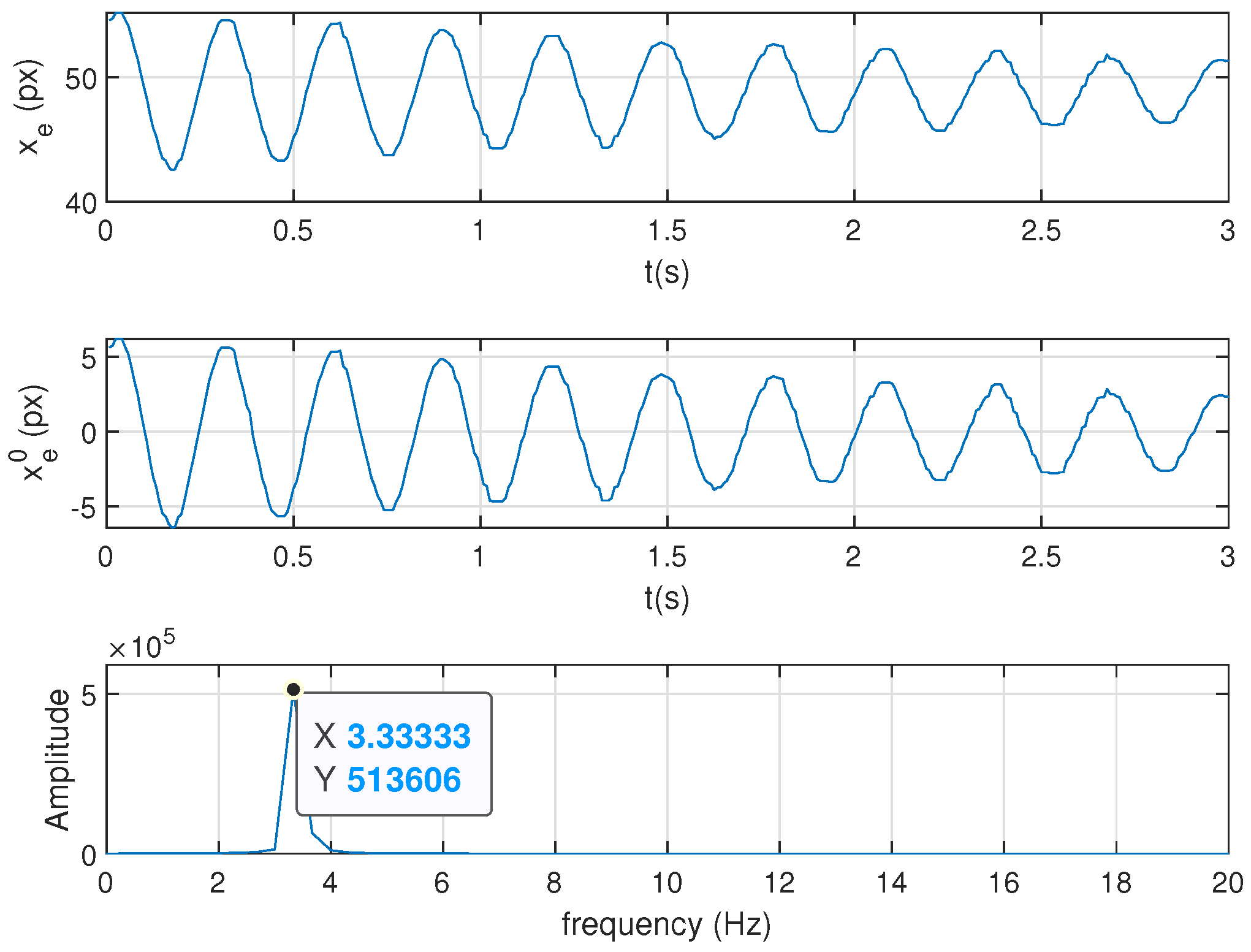
Figure 11 represents the natural frequency, $f_n\left(Hz\right)$, of the end-effector by repeating the aforementioned procedure for different positions (4 position in vertical axis and 5 in horizontal axis).

Figure 11. Natural frequency into the robot workspace

Figure 11. Natural frequency into the robot workspace

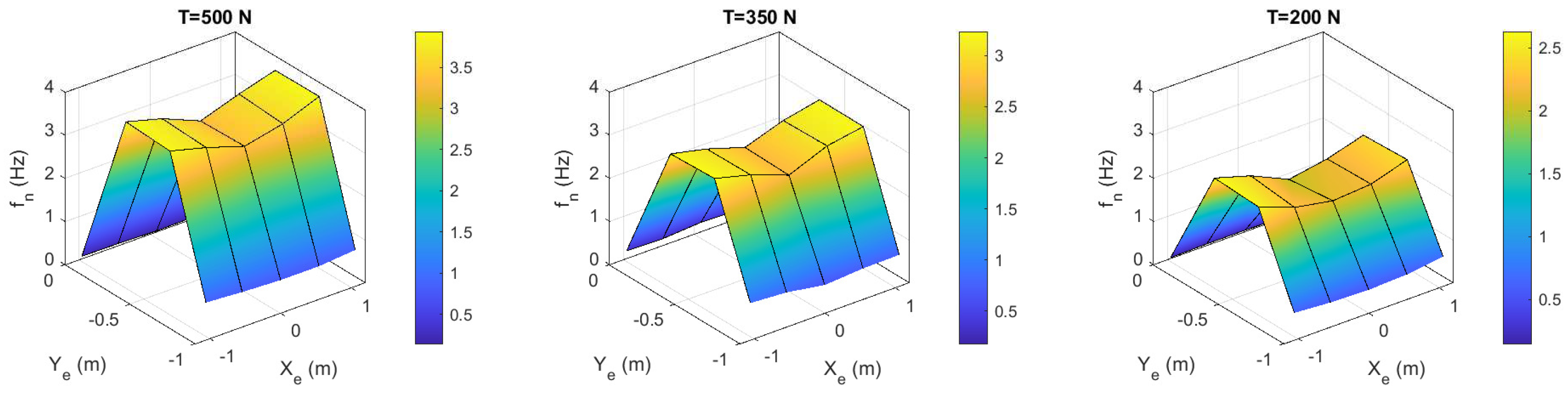
Note that natural frequency is low when the end-effector is placed near to the top or to the bottom of the frame and its grow up when vertical position is near of the centre of the frame, where it reached its maximum value. For higher values of cable loop pretension the natural frequency is about 3.9 Hz and for lower values of pretension is about 2.4 Hz.

This frequency characterisation can be used to design a control strategy to remove the non-desirable vibration of the end-effector during its manoeuvres.

5.3. Model validation

Simulated and experimental results are compared in this section for validation purposes. The experiments consist of placing the end-effector in an initial pose and applying a 1 second torque step in both motors. The experiments carried out are summarised in Table 2.

Table 2. Summary of open-loop experiments for validation

Table 2. Summary of open-loop experiments for validation

Experiment	End-effector position	Input torques
	$[x_e,y_e]$ m	$[{\tau }_1,{\tau }_2]$Nm
1	$[0.173,0.300]$	$[4.85,4.85]$
2	$[1.830,0.300]$	$[-4.78,-4.78]$
3	$[0.550,0.234]$	$[1.87,-1.87]$
4	$[0.550,0.921]$	$[-1.82,-1.82]$

For all experiments the end-effector position and the carriage positions are compared.

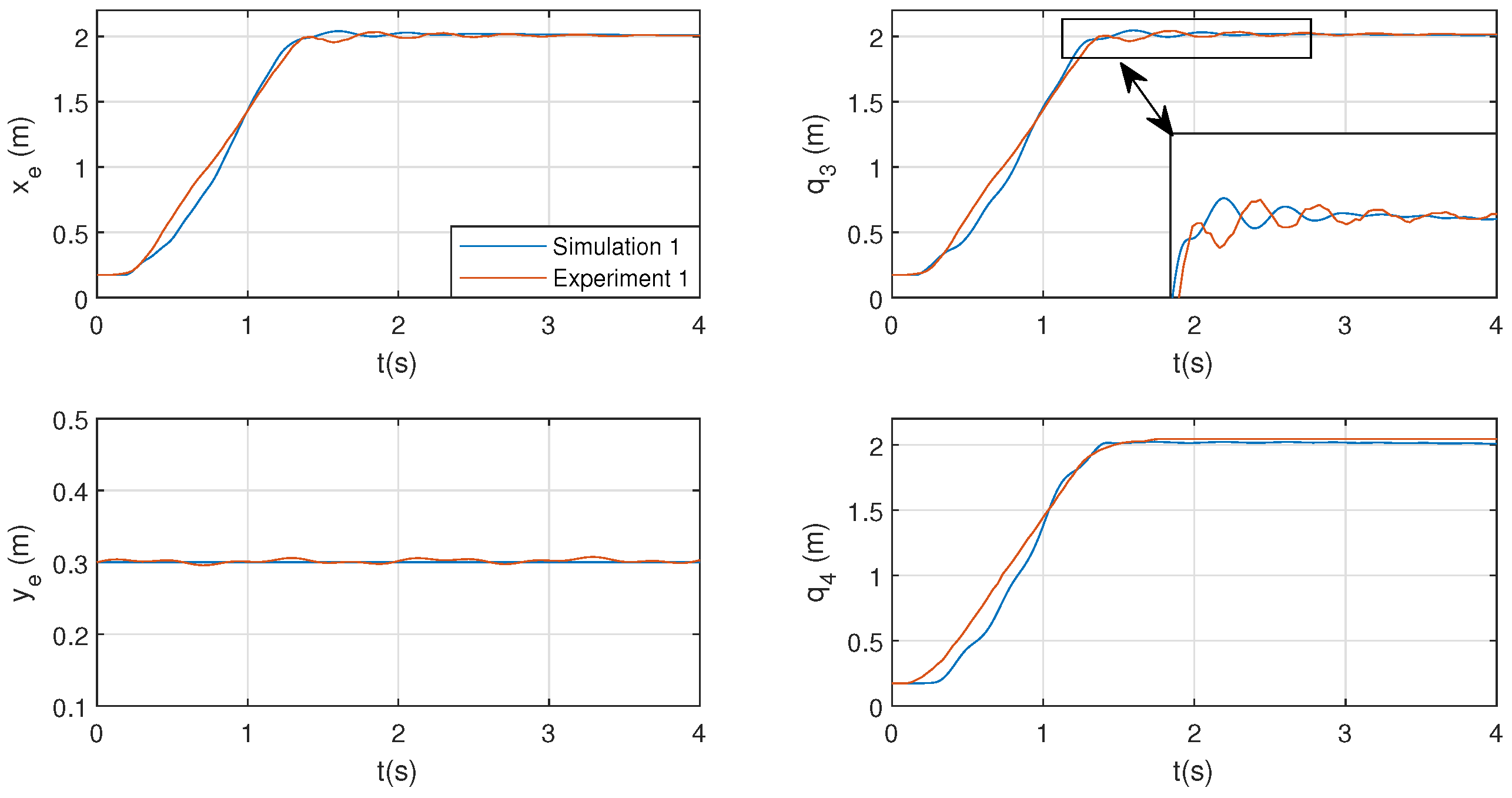
For illustrative purpose, Figure 12 shows the simulated and the experimental results of Experiment 1 in Table 2. In the link here1 an overlapped video with the simulation and experimental results can be found.

Figure 12. Identification results: experiment 1

Figure 12. Identification results: experiment 1

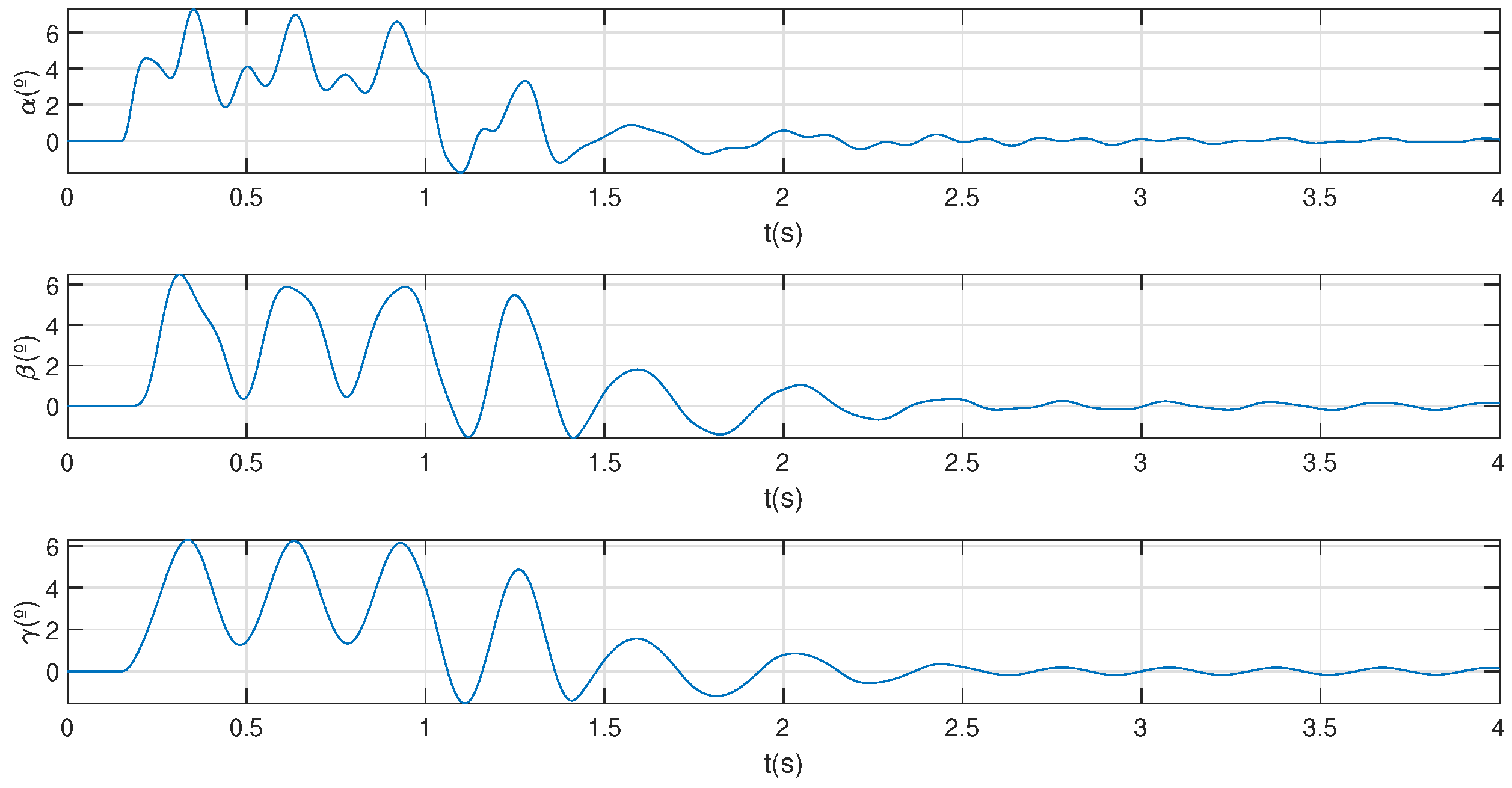
In order to validate the small angles assumption in Section 3.2, Figure 13 represents all angles of interest $\alpha$, $\beta$ and $\gamma$ of the model simulation corresponding to experiment 1. Note that during the application of the torque the cable angles reach their maximum value, but it is only about $6^{\circ }$ and the small angles assumption for dynamic model can be considered valid.

Figure 13. Cables angles in Simulation 1

Figure 13. Cables angles in Simulation 1

6. Kinematic control

6.1. Control scheme

To illustrate the workspace gain of the proposal and the controlability of the system the kinematic control shown in Figure 14 is experimentally implemented. This control scheme assumes that the dynamics of the actuators is decoupled from the sCDPR, i.e. kinematic control is applied as a first approach (e.g. [23]).

In Figure 14 ${\mathbf{Q}}_e^{*}={[x_e^{*},y_e^{*}]}^T$ is the end-effector position reference, ${\alpha }^{*}={[{\alpha }_1^{*},{\alpha }_2^{*}]}^T$ is the joint coordinates reference, $\epsilon ={[{\alpha }_1^{*}-{\alpha }_1,{\alpha }_2^{*}-{\alpha }_2]}^T$ the error signal, $\mathbf{V}={[V_1,V_2]}^T$ are the voltage control signal, $\mathit{\tau }={[{\tau }_1,{\tau }_2]}^T$ the input torque, ${\mathbf{Q}}_e={[x_e,y_e]}^T$ the end-effector pose and $\alpha ={[{\alpha }_1,{\alpha }_2]}^T$ the actual joint coordinates.

Figure 14. Kinematic control for sCDPR

Figure 14. Kinematic control for sCDPR

In this way, as control scheme is based in joint coordinates space, controller block, $\mathbf{R}$ in Figure 14 is:

$$\mathbf{R}=\left[\begin{array}{cc}{R}_1& 0\\ 0& R_2\end{array}\right]$$

(23)

where $R_1=R_2=R$ due to mechanical symmetry in the robot design.

To illustrate the controlability of the system a linear PD controller is designed for each actuator set. Its control law can be written as:

$$V_i\left(t\right)=K_p{\epsilon }_i\left(t\right)+K_d\frac{d{\epsilon }_i\left(t\right)}{dt}$$

(24)

for actuator $i=1,2$.

The prototype is actuated by means of 2 DC motor/gearbox/driver pulley sets which allow the following transfer function to be identified for the motors:

$$G\left(s\right)=\frac{\alpha \left(s\right)}{V\left(s\right)}=\frac{2169}{s(s+16.68)}$$

(25)

For the frequency requirements, gain crossover frequency, ${\omega }_c=40$ rad/s and phase margin, ${\phi }_m={60}^{\circ }$ the resulting controller is;

$$R\left(s\right)=0.6352+0.0125s$$

(26)

6.2. Position control results

Two simple manoeuvres have been experimentally tested: one horizontal and one vertical. Since the actuators model (25) is of second order, Bezier trajectories of 4^th order have been implemented to ensure smooth end-effector trajectories. Both trajectories start at the initial pose of the end-effector, execute a manoeuvre to an intermediate pose, and return to the initial pose.

Table 3 summarises the initial an final end-effector pose and the trajectory time of both controlled manoeuvres.

Table 3. Kinematic control trajectories

Table 3. Kinematic control trajectories

Trajectory	Initial pose	Intermediate pose	Final pose	Trajectory time
	$[x_e,y_e]$ m			$t_s$ (s)
Horizontal	$[0.3,0.55]$	$[1.9,0.55]$	$[0.3,0.55]$	4
Vertical	$[0.55,0.20]$	$[0.55,0.9]$	$[0.55,0.20]$	4.5

Figure 15 and Figure 16 represent the reference tracking of the horizontal and vertical trajectories of Table 3. Note that end-effector suffers some vibration during the manoeuvres in coherence with Section 5.2. The objective of this paper is to present the advantages of novel sCDPR scheme and its dynamic model. Control approach presented here will be treated in further works in order to improve the accuracy of the robot by compensating the non-desirable vibration during its movement.

Figure 15. Trajectory tracking: horizontal manoeuvre

Figure 15. Trajectory tracking: horizontal manoeuvre

Figure 16. Trajectory tracking: horizontal manoeuvre

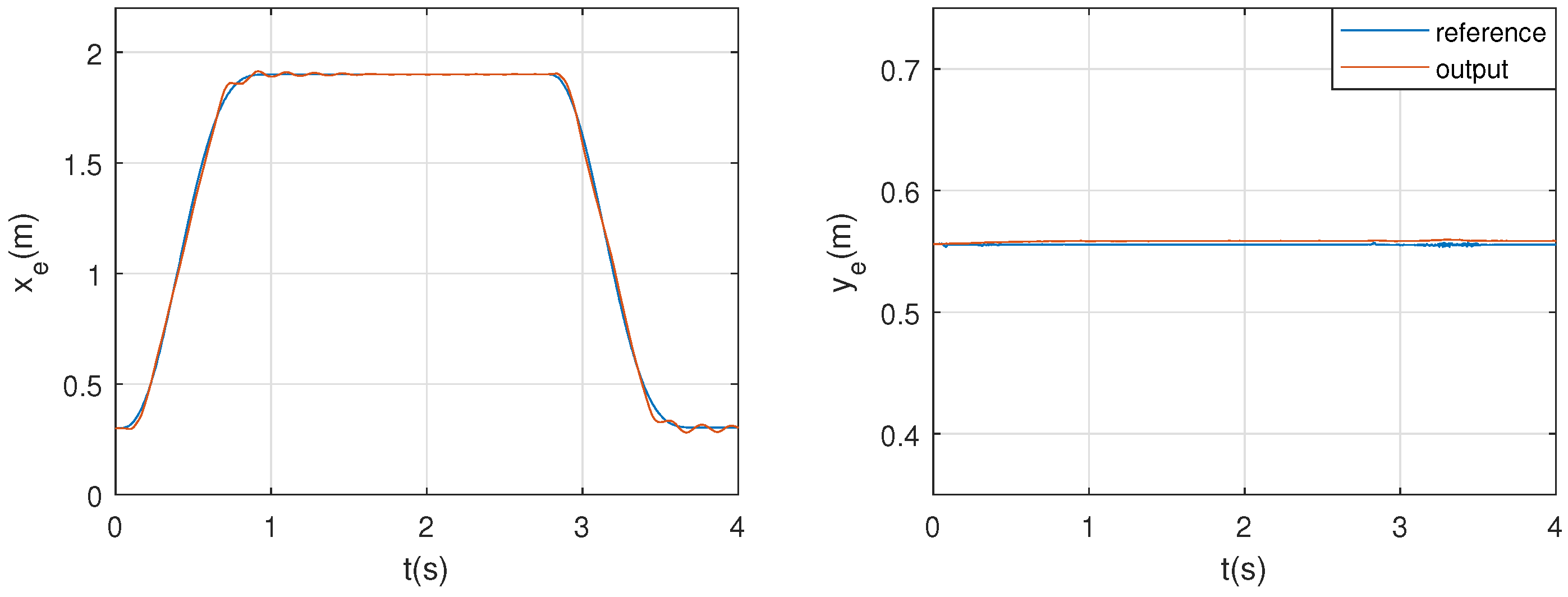
Figure 16. Trajectory tracking: horizontal manoeuvre

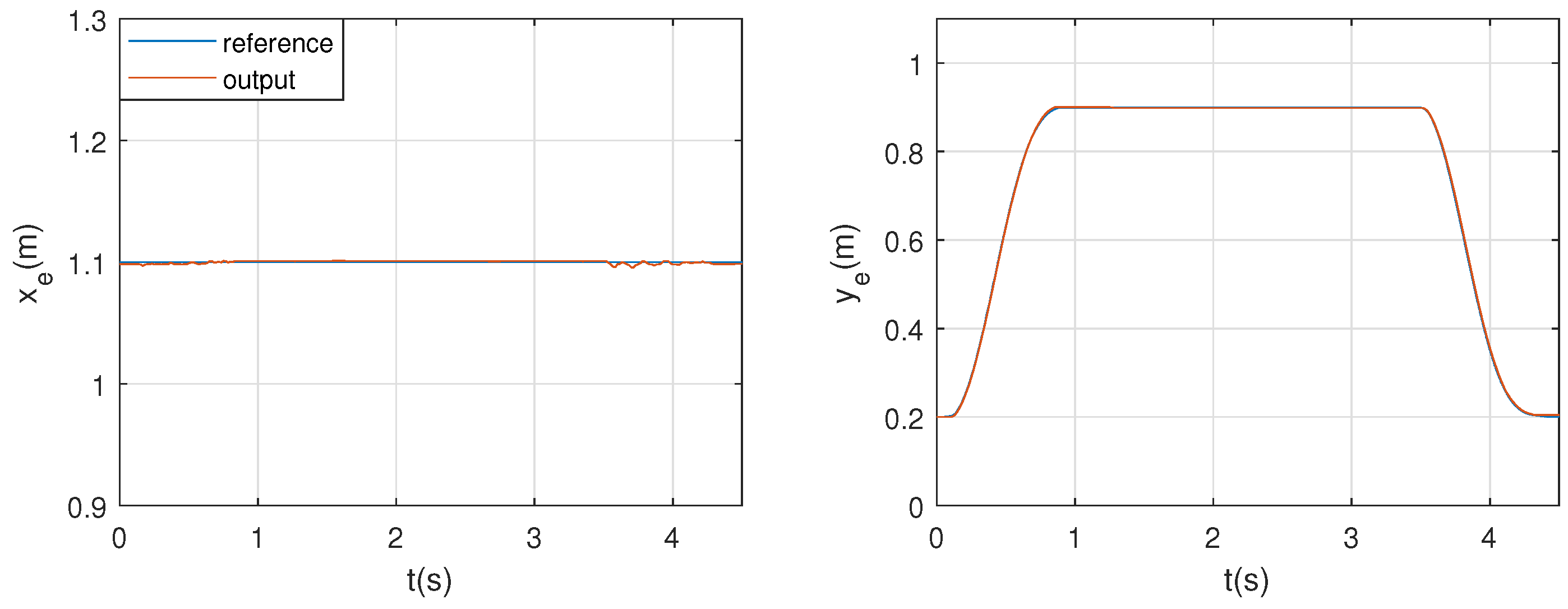
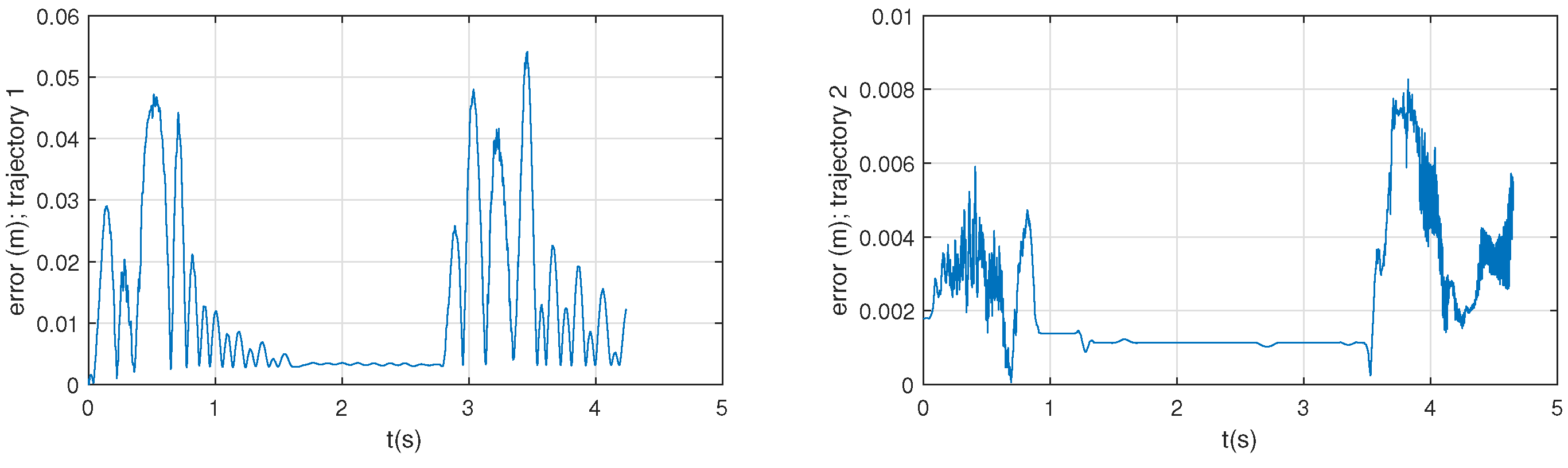
Figure 17 represents the euclidean error committed during the trajectories. Note that, although a simple kinematic control has been implemented, for horizontal manoeuvres the maximum error appears during the acceleration and deceleration phase, about 50 mm, and for the vertical about 8 mm.

Figure 17. Trajectory tracking error

Figure 17. Trajectory tracking error

7. Conclusions

Abbreviations

References

1. Gouttefarde, M.; Bruckmann, T. Cable-driven parallel robots, 2022.
2. Verhoeven, R. Analysis of the workspace of tendon based Stewart platforms. PhD thesis, Duisburg, Essen, Univ., Diss., 2004, 2006.
3. Tho, T.P.; Thinh, N.T. An Overview of Cable-Driven Parallel Robots: Workspace, Tension Distribution, and Cable Sagging. Mathematical Problems in Engineering 2022, 2022. [Google Scholar] [CrossRef]
4. Zi, B.; Duan, B.; Du, J.; Bao, H. Dynamic modeling and active control of a cable-suspended parallel robot. Mechatronics 2008, 18, 1–12. [Google Scholar] [CrossRef]
5. Pott, A. Dynamics. In Cable-Driven Parallel Robots. Springer Tracts in Advanced Robotics; Springer International Publishing: Cham, 2018; pp. 229–254. [Google Scholar]
6. Qian, S.; Zi, B.; Shang, W.W.; Xu, Q.S. A review on cable-driven parallel robots. Chinese Journal of Mechanical Engineering 2018, 31, 1–11. [Google Scholar] [CrossRef]
7. Pott, A.; Pott, A. Geometric and Static Foundations. Cable-Driven Parallel Robots: Theory and Application 2018, pp. 45–117.
8. Ming, A. Study on multiple degree-of-freedom positioning mechanism using wires (part 1). Int. J. Japan Soc. Precis. Eng. 1994, 28, 131–138. [Google Scholar]
9. Lv, W.; Tao, L.; Ji, Z. Sliding mode control of cable-driven redundancy parallel robot with 6 DOF based on cable-length sensor feedback. Mathematical Problems in Engineering 2017, 2017. [Google Scholar] [CrossRef]
10. Pott, A.; Pott, A. Workspace. Cable-Driven Parallel Robots: Theory and Application 2018, pp. 157–227.
11. Gagliardini, L.; Caro, S.; Gouttefarde, M.; Girin, A. Discrete reconfiguration planning for cable-driven parallel robots. Mechanism and Machine Theory 2016, 100, 313–337. [Google Scholar] [CrossRef]
12. Youssef, K.; Otis, M.J.D. Reconfigurable fully constrained cable driven parallel mechanism for avoiding interference between cables. Mechanism and Machine Theory 2020, 148, 103781. [Google Scholar] [CrossRef]
13. An, H.; Yuan, H.; Tang, K.; Xu, W.; Wang, X. A Novel Cable-Driven Parallel Robot With Movable Anchor Points Capable for Obstacle Environments. IEEE/ASME Transactions on Mechatronics 2022, 27, 5472–5483. [Google Scholar] [CrossRef]
14. Tan, H.; Nurahmi, L.; Pramujati, B.; Caro, S. On the reconfiguration of cable-driven parallel robots with multiple mobile cranes. 2020 5th International Conference on Robotics and Automation Engineering (ICRAE). IEEE, 2020, pp. 126–130.
15. Barbazza, L.; Oscari, F.; Minto, S.; Rosati, G. Trajectory planning of a suspended cable driven parallel robot with reconfigurable end effector. Robotics and Computer-Integrated Manufacturing 2017, 48, 1–11. [Google Scholar] [CrossRef]
16. Rodriguez-Barroso, A.; Saltaren, R.; Portilla, G.A.; Cely, J.S.; Carpio, M. Cable-driven parallel robot with reconfigurable end effector controlled with a compliant actuator. Sensors 2018, 18, 2765. [Google Scholar] [CrossRef] [PubMed]
17. Castillo-Garcia, F.J.; Rubio-Gómez, G.; Juárez, S.; Rodríguez-Rosa, D.; Bravo, E.; Ottaviano, E.; Gonzalez-Rodriguez, A. Addition of passive-carriage for increasing workspace of cable robots: automated inspection of surfaces of civil infrastructures. Smart Structures and Systems, An International Journal 2021, 27, 387–396. [Google Scholar]
18. Martin-Parra, A.; Juarez-Perez, S.; Gonzalez-Rodriguez, A.; Gonzalez-Rodriguez, A.G.; Lopez-Diaz, A.I.; Rubio-Gomez, G. A novel design for fully constrained planar Cable-Driven Parallel Robots to increase their wrench-feasible workspace. Mechanism and Machine Theory 2023, 180, 105159. [Google Scholar] [CrossRef]
19. Ottaviano, E.; Arena, A.; Gattulli, V. Geometrically exact three-dimensional modeling of cable-driven parallel manipulators for end-effector positioning. Mechanism and Machine Theory 2021, 155, 104102. [Google Scholar] [CrossRef]
20. Pott, A. Cable-Driven Parallel Robots; Vol. 1, Springer Science & Business Media, 2018.
21. Yuan, H.; Courteille, E.; Deblaise, D. Static and dynamic stiffness analyses of cable-driven parallel robots with non-negligible cable mass and elasticity. Mechanism and Machine Theory 2015, 85, 64–81. [Google Scholar] [CrossRef]
22. Abdolshah, S.; Zanotto, D.; Rosati, G.; Agrawal, S.K. Optimizing stiffness and dexterity of planar adaptive cable-driven parallel robots. Journal of Mechanisms and Robotics 2017, 9, 031004. [Google Scholar] [CrossRef]
23. Tang, J.; Zhang, Y.; Huang, F.; Li, J.; Chen, Z.; Song, W.; Zhu, S.; Gu, J. Design and kinematic control of the cable-driven hyper-redundant manipulator for potential underwater applications. Applied Sciences 2019, 9, 1142. [Google Scholar] [CrossRef]