Mutual-Inductance Computation between Coaxial Thin Conical Sheet Inductor and the Circular Loop

Preprint

Article

Mutual-Inductance Computation between Coaxial Thin Conical Sheet Inductor and the Circular Loop

Altmetrics

Downloads

143

Views

Comments

A peer-reviewed article of this preprint also exists.

Slobodan Babic^*

This version is not peer-reviewed

Submitted:

10 April 2023

Posted:

11 April 2023

You are already at the latest version

Alerts

Abstract

The paper describes a new formula for calculating the mutual inductance between a thin conical sheet inductor and a filamentary circular loop, which are coaxial. The presented formula is derived semi-analytically using the complete elliptic integrals of the first, second, and the third kind, along with the integral term which will be solved numerically. The results are validated using double and single integration methods, as well as the semi-analytical formula. The mutual inductance between a thin wall solenoid and a filamentary circular loop can be obtained using the new formula for the conical coil and circular loop. Presented formulas can be useful in various applications, such as broadband RF and wireless power transfer systems that utilize conical inductors. Overall, the paper presents a valuable contribution to the field of inductor design and can be useful in various applications involving conical inductors.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The paper discusses the challenge of computing the mutual inductance of conventional coils, which has been a topic of research since the time of Maxwell, [1]. While analytical solutions in the form of elementary functions exist for linear coils, more complex configurations, such as circular and elliptical coils require solutions in terms of elliptic integrals, Bessel and Struve functions, and hypergeometric convergent series, [2,3,4,5,6,7,8]. Numerical method and commercial software packages are also available, but there is interest in developing analytical and semi-analytical methods for more efficient computations. Reviewing the corresponding literature in the physics, electromagnetics as well as in the scientific paper in the engineering one cannot find too much the calculation of the self-inductance and the mutual inductance of the coils of the conical form. Recently in [9] the calculation of the self-inductance of thin sheet inductor is obtained in the semi-analytical form. Using the same reasoning, in this paper, a semi-analytical formula for calculating the mutual inductance between a thin conical sheet and a filamentary circular loop is given. Coils are coaxial. The new presented method is based on complete elliptical integrals of the first, second, and third kind, along with a term to be solved by numerical integration. As the special case of this new developed formula is the formula for calculating the mutual inductance between the wall solenoid and the filamentary circular loop. The calculation of the previously mentioned coils is useful for conical inductors which are of ideal form for ultra-broadband applications up to 40 GHz since the conical shapes limit effects of stray capacitances and effectively substitute a series of narrow-band inductors, creating the high impedance over a very wide bandwidth, and in wireless power transfer systems that utilize conical inductors [10,11,12,13,14,15,16,17,18,19,20]. All cases either the regular or the singular are explained with precise explications. The validation of the presented method is performed using the single and double integration as well as the semi- analytical formula. The Mathematica files with implemented formulas are available upon request.

2. Basic formulas

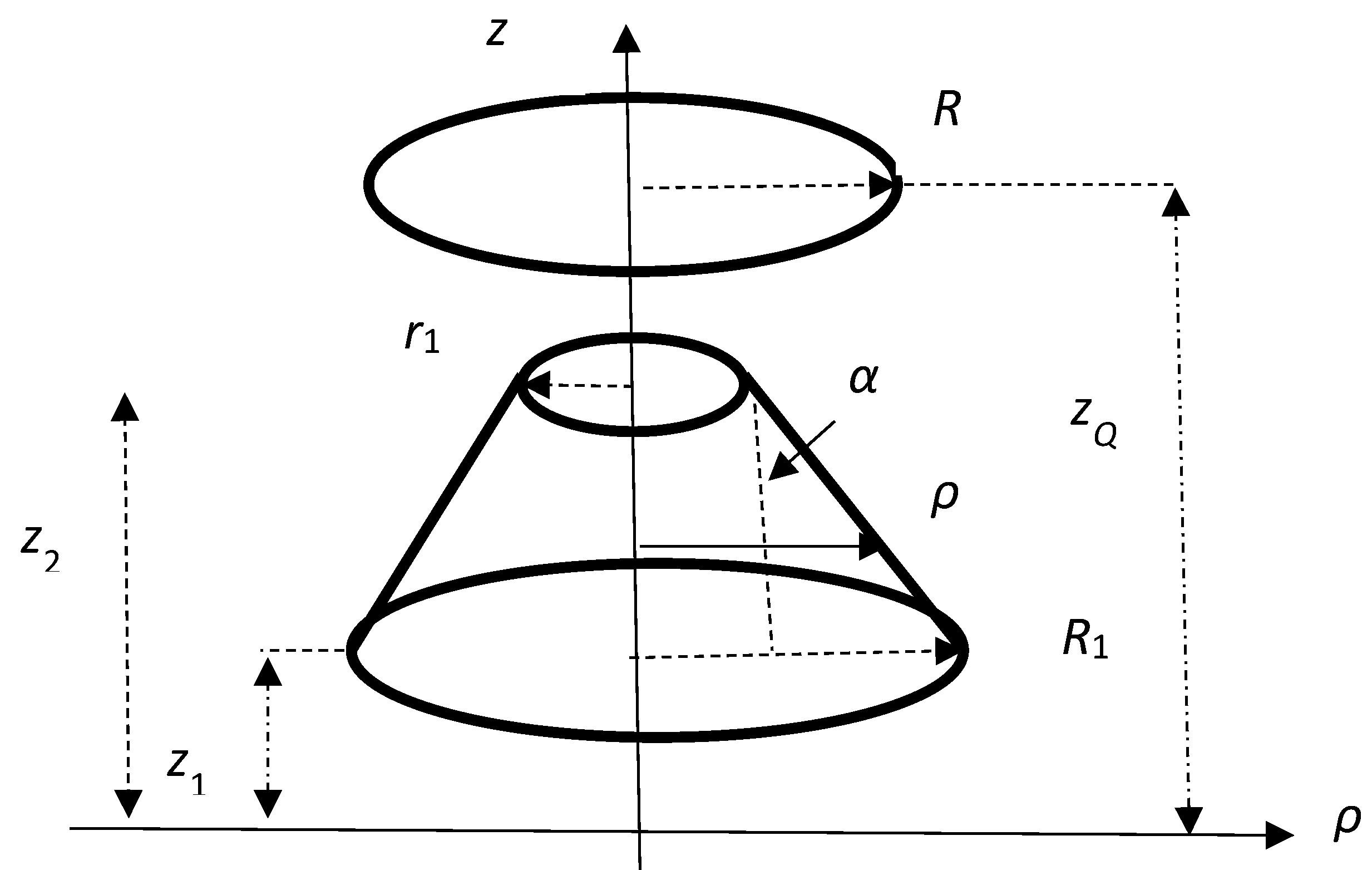
Let us consider a thin conical sheet and a circular loop as showed in Figure 1. The thin conical sheet has the radii of basis

R_{1} a n d r_{1} {(R}_{1} > r_{1})

and the axial positions

z_{1} a n d z_{2}

, with the number of sheets turns N. The circular loop has the radii R and radial position

z_{Q}

Thus, let us begin the complete analysis for the first case

{(R}_{1} > r_{1}), F i g u r e 1 .

From Figure 1. one has,

\frac{R_{1} - r_{1}}{z_{2} - z_{1}} = t a g (α) = η, R_{1} = r_{1} + η (z_{2} - z_{1}) o r r_{1} = R_{1} - η (z_{2} - z_{1})

(1)

\frac{z_{2} - z}{ρ - r_{1}} = \frac{z_{2} - z_{1}}{R_{1} - r_{1}} = \frac{1}{η}, ρ = r_{1} - η (z - z_{2}) = R_{1} - η (z - z_{1})

(2)

The mutual inductance between the thin conical sheet inductor and the circular loop can be calculated by,

= \frac{μ_{0} N}{z_{2} - z_{1}} \int_{0}^{π} \int_{z_{1}}^{z_{2}} \frac{R ρ c o s (θ)}{r_{0}} d z d θ

(3)

with

r_{0} = \sqrt{{(R_{1} - η z + η z_{1})}^{2} - 2 (R_{1} - η z + η z_{1}) R \cos (θ) + R^{2} + {(z - z_{Q})}^{2}}

(4)

Even though

R_{1} > r_{1} (η > 0)

one must use

ρ = R_{1} - η (z - z_{1}) .

By the simple verification for

R_{1} = r_{1}

(η = 0)

the thin conical sheet degenerates to the thin wall solenoid. For this case, the formula (3) begins the formula for calculating the mutual inductance between the thin wall solenoid and the circular loop, [50].

Introducing the substitution,

θ = π - 2 β

in (3) one has,

M = - \frac{2 μ_{0} N R}{z_{2} - z_{1}} \int_{0}^{π / 2} \int_{z_{1}}^{z_{2}} \frac{(R_{1} - η z + η z_{1}) c o s (2 β)}{r_{0}} d z d β

(5)

where,

r_{0} = \sqrt{{(R_{1} - η z + η z_{1})}^{2} + 2 (R_{1} - η z + η z_{1}) R \cos (2 β) + R^{2} + {(z - z_{Q})}^{2}}

Let us calculate the first integral in (5),

I_{1} = \int_{z_{1}}^{z_{2}} \frac{(R_{1} - η z + η z_{1}) d z}{r_{0}}

(6)

with

r_{0} = \frac{1}{η} \sqrt{{c_{1} t}^{2} + b_{1} t + a_{1}}

c_{1} = η^{2} + 1

b_{1} = 2 [η^{2} R \cos (2 β) - R_{1} + η (z_{Q} - z_{1})]

a_{1} = {[R_{1} - η (z_{Q} - z_{1})]}^{2} + η^{2} R^{2}

∆_{1} = 4 a_{1} c_{1} - b_{1}^{2} =

4 η^{2} \{{η^{2} R}^{2} {s i n}^{2} (2 β) - 2 R [R_{1} + η (z_{1} - z_{Q})] \cos (2 β) + {[R_{1} + η (z_{1} - z_{Q})]}^{2} + R^{2}\} = 4 η^{2} D_{10}

D_{10} = \{{η^{2} R}^{2} {s i n}^{2} (2 β) + 2 R [R_{1} - η ({z_{Q} - z}_{1})] \cos (2 β) + {[R_{1} - η ({z_{Q} - z}_{1})]}^{2} + R^{2}\}

I_{1} = \int_{r_{1}}^{R_{1}} \frac{t d t}{\sqrt{{c_{1} t}^{2} + b_{1} t + a_{1}}}

(8)

Using [21],

I_{1} = \{\frac{\sqrt{c_{1} R_{1}^{2} + b_{1} R_{1} + a_{1}}}{η^{2} + 1} - \frac{\sqrt{c_{1} r_{1}^{2} + b_{1} r_{1} + a_{1}}}{η^{2} + 1} - \frac{η^{2} R c o s (2 β) - R_{1} + η (z_{1} - z_{Q})}{{(η^{2} + 1)}^{3 / 2}} \times [A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} - A s i n h \frac{η R c o s (2 β) + η r_{1} + z_{Q} - z_{2}}{\sqrt{D_{10}}}]\}

(9)

Thus, the solution of this integral is obtained in the close form.

Now, the formula (5) can be given as follows,

M = - \frac{2 μ_{0} N R}{{(z}_{2} - z_{1}) {(η^{2} + 1)}^{3 / 2}} \int_{0}^{π / 2} V c o s (2 β) d β

(10)

where,

V = \sqrt{η^{2} + 1} [\sqrt{c_{1} R_{1}^{2} + b_{1} R_{1} + a_{1}} - \sqrt{c_{1} r_{1}^{2} + b_{1} r_{1} + a_{1}}] - [η^{2} R c o s (2 β) - R_{1} + η (z_{Q} - z_{1})] \times [A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} - A s i n h \frac{η R c o s (2 β) + η r_{1} + z_{Q} - z_{2}}{\sqrt{D_{10}}}]

(11)

Let us solve the following integrals in (10) and (11).

I_{2} = \int_{0}^{π / 2} V c o s (2 β) d β = I_{2}^{(1)} + I_{2}^{(2)} + I_{2}^{(3)} + I_{2}^{(4)}

(12)

I_{2}^{(1)} = \sqrt{η^{2} + 1} \int_{0}^{π / 2} \sqrt{c R_{1}^{2} + b R_{1} + a} c o s (2 β) d β = \sqrt{η^{2} + 1} \int_{0}^{π / 2} \sqrt{T_{1}} c o s (2 β) d β

(13)

T_{1} = c_{1} R_{1}^{2} + b_{1} R_{1} + a_{1} = η^{2} [{(R + R_{1})}^{2} + {(z_{Q} - z_{1})}^{2} - 4 R R_{1} {s i n}^{2} (β)]

I_{2}^{(1)} = \sqrt{η^{2} + 1} \sqrt{η^{2} [{(R + R_{1})}^{2} + {(z_{Q} - z_{1})}^{2}]} \int_{0}^{π / 2} ∆_{1} (1 - 2 {s i n}^{2} (β)) d β

{∆_{1} = \sqrt{1 - {k_{1}^{2} s i n}^{2} (β)}, k}_{1}^{2} = \frac{4 R R_{1}}{{(R + R_{1})}^{2} + {(z_{Q} - z_{1})}^{2}}

Using [21] one obtains,

I_{2}^{(1)} = 2 | η | \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{k_{1}} \int_{0}^{\frac{π}{2}} ∆_{1} (1 - 2 {s i n}^{2} (β)) d β = 2 | η | \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{3 k_{1}^{3}} \{(2 k_{1}^{2} - 2) K (k_{1}) + (2 - k_{1}^{2}) E (k_{1})\}

I_{2}^{(1)} = 2 |η| \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{3 k_{1}^{3}} \{(2 k_{1}^{2} - 2) K (k_{1}) + (2 - k_{1}^{2}) E (k_{1})\}

(14)

This solution is obtained in the close form where

K (k_{1}) a n d E (k_{1})

are the complete integrals of the first and second kind [21,22].

Similarly,

I_{2}^{(2)} = - \sqrt{η^{2} + 1} \int_{0}^{\frac{π}{2}} \sqrt{c r_{1}^{2} + b r_{1} + a} c o s (2 β) d β

(15)

the solution of this integral is also obtained in the close form as follows,

I_{2}^{(2)} = - 2 | η | \sqrt{η^{2} + 1} \frac{\sqrt{R r_{1}}}{3 k_{2}^{3}} \{(2 k_{2}^{2} - 2) K (k_{2}) + (2 - k_{2}^{2}) E (k_{2})\}

(16)

with

k_{2}^{2} = \frac{4 R r_{1}}{{(R + r_{1})}^{2} + {(z_{2} - z_{Q})}^{2}}

The next integral is,

I_{2}^{(3)} = - \int_{0}^{\frac{π}{2}} [η^{2} R c o s (2 β) - R_{1} + η (z_{Q} - z_{1})] \times c o s (2 β) A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} d β

(17)

I_{2}^{(3)} = - \frac{η^{2} R}{2} \int_{0}^{\frac{π}{2}} A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} d β - \frac{1}{2} \int_{0}^{\frac{π}{2}} \{η^{2} R c o s (4 β) - 2 [R_{1} - η (z_{Q} - z_{1})] c o s (2 β)\} A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} d β = - \frac{1}{2} \int_{0}^{\frac{π}{2}} \{η^{2} R c o s (4 β) - 2 [R_{1} - η (z_{Q} - z_{1})] c o s (2 β)\} A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} d β = - \frac{η^{2} R}{2} J_{10}

(18)

where,

J_{10} = \int_{0}^{\frac{π}{2}} A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} d β

(19)

This integral does not have the analytical solution so that it must be solved numerically.

The kernel function of this integral is continuous function on the interval of the integration.

Let us solve the second integral by the partial integration.

v = \int_{0}^{\frac{π}{2}} \{η^{2} R c o s (4 β) - 2 [R_{1} - η (z_{Q} - z_{1})] c o s (2 β)\} d β

v = \frac{s i n (2 β)}{2} \{η^{2} R c o s (2 β) - 2 [R_{1} - η (z_{Q} - z_{1})]\} u = A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{10}}} d u = \frac{R_{1} \sqrt{η^{2} + 1} k_{1} s i n (2 β) [c o s (2 β) + a_{22}] d β}{η \sqrt{R R_{1}} ∆ [{c o s}^{2} (2 β) - a_{11} c o s (2 β) - a_{33}]}

with

a_{11} = \frac{2 [R_{1} - η (z_{Q} - z_{1})]}{η^{2} R} a_{22} = \frac{η R^{2} + η {(z_{Q} - z_{1})}^{2} - R_{1} (z_{Q} - z_{1})}{η R R_{1}} a_{33} = \frac{{[R_{1} - η ({z_{Q} - z}_{1})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}}

Now,

I_{2}^{(3)} = - \frac{η^{2} R}{2} J_{10} - \frac{1}{2} \{u v \begin{matrix} \frac{π}{2} \\ | \\ 0 \end{matrix} - \int_{0}^{\frac{π}{2}} v d u\} = - \frac{η^{2} R}{2} J_{10} + \int_{0}^{\frac{π}{2}} \frac{{η^{2} R R}_{1} \sqrt{η^{2} + 1} k_{1} s i n (2 β) [c o s (2 β) + a_{22}] s i n (2 β) [c o s (2 β) - a_{11}] d β}{4 η \sqrt{R R_{1}} ∆ [{c o s}^{2} (2 β) - a_{11} c o s (2 β) - a_{33}]} = \frac{η^{2} R}{2} J_{10} - \frac{η \sqrt{η^{2} + 1} k_{1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \frac{[{c o s}^{2} (2 β) - 1] [c o s (2 β) - a_{11})] [c o s (2 β) + a_{22}] d β}{[{c o s}^{2} (2 β) - a_{11} c o s (2 β) - a_{33}] ∆_{1}} = \frac{η^{2} R}{2} J_{10} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \{{c o s}^{2} (2 β) + a_{22} c o s (2 β) + a_{33} - 1\} \frac{d β}{∆_{1}} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \frac{(A c o s (2 β) + B) d β}{[{c o s}^{2} (2 β) - a_{11} c o s (2 β) - a_{33}] ∆_{1}} d β

(20)

with

A = (a_{22} + a_{11}) a_{33} - a_{2}, B = a_{33}^{2} - a_{33} + a_{11} a_{22}

The expression (20) can be written as follows,

I_{2}^{(3)} = - \frac{η^{2} R}{2} J_{10} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \{{c o s}^{2} (2 β) + a_{2} c o s (2 β) - 1 + a_{3}\} \frac{d β}{∆} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \frac{(A c o s (2 β) + B) d β}{[(c o s (2 β) - p_{1}) (c o s (2 β) - p_{2})] ∆_{1}}

(21)

Let us find the solutions of the following equation,

{c o s}^{2} (2 β) - a_{11} c o s (2 β) - a_{33} = (c o s (2 β) - p_{1}) (c o s (2 β) - p_{2}) = 0

p_{1,2} = \frac{a_{11} \pm \sqrt{a_{11}^{2} + 4 a_{33}}}{2} = \frac{a_{11} \pm \sqrt{D_{1}}}{2} = \frac{[R_{1} - η (z_{Q} - z_{1})]}{η^{2} R} + \frac{\sqrt{(η^{2} + 1)}}{η^{2} R} \sqrt{T_{10}}

{D_{1} = a}_{11}^{2} + 4 a_{33} = 4 \frac{{[R_{1} - η (z_{Q} - z_{1})]}^{2}}{η^{4} R^{2}} + 4 \frac{{[R_{1} - η ({z_{Q} - z}_{1})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}}

D_{1} = \frac{4 (η^{2} + 1)}{η^{4} R^{2}} \{{[R_{1} - η (z_{Q} - z_{1})]}^{2} + η^{2} R^{2}\} = \frac{4 (η^{2} + 1)}{η^{4} R^{2}} T_{10} > 0

T_{10} = \{{[R_{1} - η (z_{Q} - z_{1})]}^{2} + η^{2} R^{2}\}

The following fraction can be obtained in the following form,

\frac{(A c o s (2 β) + B)}{[{c o s}^{2} (2 β) - a_{11} c o s (2 β) - a_{33}] ∆} = \frac{A c o s (2 β) + B}{(c o s (2 β) - p_{1}) (c o s (2 β) - p_{2})} = \frac{V_{1}}{c o s (2 β) - p_{1}} + \frac{V_{2}}{c o s (2 β) - p_{2}}

(22)

where,

V_{1} = - \frac{A p_{1} + B}{p_{2} - p_{1}}, V_{2} = - \frac{A p_{2} + B}{p_{2} - p_{1}}

The simplified form is,

I_{2}^{(3)} = - \frac{η^{2} R}{2} J_{10} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \{{c o s}^{2} (2 β) + a_{22} c o s (2 β) - 1 + a_{33}\} \frac{d β}{∆_{1}} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \frac{A c o s (2 β) + B}{(c o s (2 β) - p_{1}) (c o s (2 β) - p_{2}) ∆} = - \frac{η^{2} R}{2} J_{10} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \int_{0}^{\frac{π}{2}} \{4 {s i n}^{4} (β) - ({2 a}_{2} + 4) {s i n}^{2} (β) + a_{2} + a_{3}\} \frac{d β}{∆_{1}} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \{T_{1} \int_{0}^{\frac{π}{2}} \frac{d β}{(c o s (2 β) - p_{1}) ∆_{1}} + T_{2} \int_{0}^{\frac{π}{2}} \frac{d β}{(c o s (2 β) - p_{2}) ∆_{1}}\} = - \frac{η^{2} R}{2} J_{10} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \{4 [\frac{2 + k_{1}^{2}}{3 k_{1}^{4}} K (k_{1}) - \frac{2 + 2 k_{1}^{2}}{3 k_{1}^{4}} E (k_{1})] - \frac{(2 a_{2} + 4)}{k_{1}^{2}} [K (k_{1}) - E (k_{1})] - (a_{22} + a_{33}) K (k_{1})\} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} [\frac{V_{1}}{1 - p_{1}} Π (h_{1}, k_{1}) + \frac{V_{2}}{1 - p_{2}} Π (h_{2}, k_{1})]

(23)

with,

h_{1} = \frac{2}{1 - p_{1}}, h_{2} = \frac{2}{1 - p_{2}}

The final expression is obtained in the close form over the complete elliptic integrals of the first, second and third kind,

K (k_{1}), E (k_{1}), Π (h_{1}, k_{1}) a n d Π (h_{2}, k_{1}), [21], [22] .

Similarly,

I_{2}^{(4)} = \int_{0}^{\frac{π}{2}} [η^{2} R c o s (2 β) - R_{1} + η (z_{Q} - z_{1})] c o s (2 β) A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{2}}{\sqrt{D_{10}}} d β

(24)

can be obtained as follows,

I_{2}^{(4)} = \frac{η^{2} R}{2} J_{20} + \frac{η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{12 k_{2}^{3}} \{[3 (a_{222} + a_{333}) k_{2}^{4} - (6 a_{222} + 8) k_{2}^{2} + 8] K (k_{2}) + [(6 a_{22} 2 + 4) k_{2}^{2} - 8] E (k_{2})\} + \frac{k_{2} η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{4} [\frac{V_{3}}{1 - p_{3}} Π (h_{3}, k_{3}) + \frac{V_{4}}{1 - p_{4}} Π (h_{4}, k_{4})]

(25)

where,

k_{2}^{2} = \frac{4 R r_{1}}{{(R + r_{1})}^{2} + {(z_{Q} - z_{2})}^{2}} a_{111} = \frac{2 [r_{1} - η (z_{Q} - 2)]}{η^{2} R} a_{222} = \frac{η R^{2} + η {(z_{Q} - z_{2})}^{2} - r_{1} (z_{Q} - z_{2})}{η R r_{1}} a_{333} = \frac{{[r_{1} - η ({z_{Q} - z}_{2})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}} \frac{(C c o s (2 β) + D)}{[{c o s}^{2} (2 β) - a_{11} c o s (2 β) - a_{33}]} = \frac{C c o s (2 β) + D}{(c o s (2 β) - p_{3}) (c o s (2 β) - p_{4})} = \frac{V_{3}}{c o s (2 β) - p_{3}} + \frac{V_{4}}{c o s (2 β) - p_{4}}

(26)

C = (a_{22} + a_{11}) a_{33} - a_{22}, D = a_{33}^{2} - a_{33} + a_{11} a_{22}, p_{3,4} = \frac{a_{111} \pm \sqrt{a_{111}^{2} + 4 a_{333}}}{2} = \frac{a_{11} \pm \sqrt{D_{2}}}{2} = \frac{[r_{1} - η (z_{Q} - z_{2})]}{η^{2} R} + \frac{\sqrt{(η^{2} + 1)}}{η^{2} R} \sqrt{D_{2}} {D_{2} = a}_{111}^{2} + 4 a_{333} = 4 \frac{{[r_{1} - η (z_{Q} - z_{2})]}^{2}}{η^{4} R^{2}} + 4 \frac{{[r_{1} - η ({z_{Q} - z}_{2})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}} D_{2} = \frac{4 (η^{2} + 1)}{η^{4} R^{2}} \{{[r_{1} - η (z_{Q} - z_{2})]}^{2} + η^{2} R^{2}\} = \frac{4 (η^{2} + 1)}{η^{4} R^{2}} T_{20} > 0 T_{20} = \{{[r_{1} - η (z_{Q} - z_{2})]}^{2} + η^{2} R^{2}\} > 0 V_{3} = - \frac{C p_{3} + D}{p_{4} - p_{3}}, V_{4} = - \frac{C p_{3} + D}{p_{4} - p_{3}} J_{20} = \int_{0}^{\frac{π}{2}} A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{2}}{\sqrt{D_{10}}} d β

Finally, from (14), (16), (21) and (25) the mutual inductance between the thin conical sheet and the circular loop can be calculated in the semi-analytical form as follows,

M = - \frac{2 μ_{0} N R}{{(z}_{2} - z_{1}) {(η^{2} + 1)}^{\frac{3}{2}}} V_{0}

(27)

where,

V_{0} = - \frac{η^{2} R}{2} J_{0} - \frac{η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{12 k_{1}^{3}} \{[3 (a_{2} + a_{3}) k_{1}^{4} - (6 a_{2} + 8) k_{1}^{2} + 8] K (k_{1}) + [(6 a_{2} + 4) k_{1}^{2} - 8] E (k_{1})\} + |η| \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{12 k_{1}^{3}} \{(16 k_{1}^{2} - 16) K (k_{1}) + (16 - {8 k}_{1}^{2}) E (k_{1})\} + \frac{η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{12 k_{2}^{3}} \{[3 (a_{22} + a_{33}) k_{2}^{4} - (6 a_{22} + 8) k_{2}^{2} + 8] K (k_{2}) + [(6 a_{22} + 4) k_{2}^{2} - 8] E (k_{2})\} - |η| \sqrt{η^{2} + 1} \frac{\sqrt{R r_{1}}}{12 k_{2}^{3}} \times \{(16 k_{2}^{2} - 16) K (k_{2}) + (16 - {8 k}_{2}^{2}) E (k_{2})\} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \times [\frac{T_{1}}{1 - p_{1}} Π (h_{1}, k_{1}) + \frac{T_{2}}{1 - p_{2}} Π (h_{2}, k_{1})] + \frac{k_{2} η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{4} + [\frac{T_{3}}{1 - p_{3}} Π (h_{3}, k_{2}) + \frac{T_{4}}{1 - p_{4}} Π (h_{4}, k_{2})]

(28)

where,

k_{1}^{2} = \frac{4 R R_{1}}{{(R + R_{1})}^{2} + {(z_{Q} - z_{1})}^{2}}, k_{2}^{2} = \frac{4 R r_{1}}{{(R + r_{1})}^{2} + {(z_{Q} - z_{2})}^{2}} J_{0} = \int_{0}^{\frac{π}{2}} A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{Q} - z_{1}}{\sqrt{D_{0}}} d β - \int_{0}^{\frac{π}{2}} A s i n h \frac{η R c o s (2 β) + η r_{1} + z_{Q} - z_{2}}{\sqrt{D_{0}}} d β a_{1} = \frac{2 [R_{1} - η (z_{Q} - z_{1})]}{η^{2} R} a_{2} = \frac{η R^{2} + η {(z_{Q} - z_{1})}^{2} - R_{1} (z_{Q} - z_{1})}{η R R_{1}} a_{3} = \frac{{[R_{1} - η ({z_{Q} - z}_{1})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}} A = (a_{2} + a_{1}) a_{3} - a_{2}, B = a_{3}^{2} - a_{3} + a_{1} a_{2} p_{1,2} = \frac{a_{1} \pm \sqrt{a_{1}^{2} + 4 a_{3}}}{2}, h_{1} = \frac{2}{1 - p_{1}}, h_{2} = \frac{2}{1 - p_{2}} V_{1} = - \frac{A p_{1} + B}{p_{2} - p_{1}}, V_{2} = - \frac{A p_{2} + B}{p_{2} - p_{1}} a_{11} = \frac{2 [r_{1} - η (z_{Q} - z_{2})]}{η^{2} R} a_{22} = \frac{η R^{2} + η {(z_{Q} - z_{2})}^{2} - r_{1} (z_{Q} - z_{2})}{η R r_{1}} a_{33} = \frac{{[r_{1} - η ({z_{Q} - z}_{2})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}} C = (a_{22} + a_{11}) a_{33} - a_{22}, D = a_{33}^{2} - a_{33} + a_{11} a_{22} p_{3,4} = \frac{a_{11} \pm \sqrt{a_{11}^{2} + 4 a_{33}}}{2}, h_{3} = \frac{2}{1 - p_{3}}, h_{4} = \frac{2}{1 - p_{4}} V_{3} = - \frac{C p_{3} + D}{p_{4} - p_{3}}, V_{4} = - \frac{C p_{3} + D}{p_{4} - p_{3}} η = \frac{R_{1} - r_{1}}{z_{2} - z_{1}} > 0 b e c a u s e R_{1} > r_{1}

Thus, the general solution of equation (26) with (27) is expressed by the complete elliptic integrals K(k), E(k) and Π(h, k) as well as one term J₀ which must be solved numerically.

2.2. Singular cases

The equation (27) with (28) can be directly applied for the general cases. It is possible to have in (28) four singular cases so that one must do some corrections to overcome these problems.

2.2.1. $p_{1} = p_{3} = - 1$

From (26) one can see that case that for

p_{1} = - 1

the singular case appears and

A = B

so that,

\frac{(A c o s (2 β) + B)}{(c o s (2 β) - p_{1}) (c o s (2 β) - p_{2})} = \frac{A (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{2})} = \frac{A}{c o s (2 β) - p_{2}} = \frac{A}{1 - p_{2}} \frac{1}{1 - h_{2} {s i n}^{2} (β)}

(29)

Also, in (26) the singularity appears for

p_{3} = - 1

and

C = D

so that,

\frac{(C c o s (2 β) + D)}{(c o s (2 β) - p_{3}) (c o s (2 β) - p_{4})} = \frac{C (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{4})} = \frac{C}{c o s (2 β) - p_{4}} = \frac{C}{1 - p_{4}} \frac{1}{1 - h_{4} {s i n}^{2} (β)}

(30)

From (29) and (30), it is obvious that the complete elliptic integrals of the third kind

Π (h_{1}, k_{1})

and

Π (h_{3}, k_{3})

will vanish.

Thus, (28) begins,

V_{0} = \frac{η^{2} R}{2} J_{0} - \frac{η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{12 k_{1}^{3}} \{[3 (a_{2} + a_{3}) k_{1}^{4} - (6 a_{2} + 8) k_{1}^{2} + 8] K (k_{1}) + [(6 a_{2} + 4) k_{1}^{2} - 8] E (k_{1})\} + |η| \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{12 k_{1}^{3}} \{(16 k_{1}^{2} - 16) K (k_{1}) + (16 - {8 k}_{1}^{2}) E (k_{1})\} + \frac{η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{12 k_{2}^{3}} \{[3 (a_{22} + a_{33}) k_{2}^{4} - (6 a_{22} + 8) k_{2}^{2} + 8] K (k_{2}) + [(6 a_{22} + 4) k_{2}^{2} - 8] E (k_{2})\} - |η| \sqrt{η^{2} + 1} \frac{\sqrt{R r_{1}}}{12 k_{2}^{3}} \{(16 k_{2}^{2} - 16) K (k_{2}) + (16 - {8 k}_{2}^{2}) E (k_{2})\} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \frac{A}{1 - p_{2}} Π (h_{2}, k_{1}) + \frac{k_{2} η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{4} \frac{C}{1 - p_{4}} Π (h_{4}, k_{2})

(31)

2.2.2. $p_{1} = p_{3} = 1$

From (22) one can see that case that for

p_{1} = 1

the singular case appears and

A = - B

so that,

\frac{(A c o s (2 β) + B)}{(c o s (2 β) - p_{1}) (c o s (2 β) - p_{2})} = \frac{A (c o s (2 β) - 1)}{(c o s (2 β) - 1) (c o s (2 β) - p_{2})} = \frac{A}{c o s (2 β) - p_{2}} = \frac{A}{1 - p_{2}} \frac{1}{1 - h_{2} {s i n}^{2} (β)}

(32)

Also, in (26) the singularity appears for

p_{3} = 1

and

C = - D

so that,

\frac{(C c o s (2 β) + D)}{(c o s (2 β) - p_{3}) (c o s (2 β) - p_{4})} = \frac{C (c o s (2 β) - 1)}{(c o s (2 β) - 1) (c o s (2 β) - p_{4})} = \frac{C}{c o s (2 β) - p_{4}} = \frac{C}{1 - p_{4}} \frac{1}{1 - h_{4} {s i n}^{2} (β)}

(33)

From (32) and (33), it is obvious that the complete elliptic integrals of the third kind

Π (h_{1}, k_{1})

and

Π (h_{3}, k_{3})

will vanish.

Thus, for this case we use (31).

2.2.3. $p_{2} = p_{4} = - 1$

From (26) one can see that case that for

p_{2} = - 1

the singular case appears and

A = B

so that,

\frac{(A c o s (2 β) + B)}{(c o s (2 β) - p_{1}) (c o s (2 β) - p_{2})} = \frac{A (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{1})} = \frac{A}{c o s (2 β) - p_{1}} = \frac{A}{1 - p_{1}} \frac{1}{1 - h_{1} {s i n}^{2} (β)}

(34)

Also, in (26) the singularity appears for

p_{4} = - 1

and

C = D

so that,

\frac{(C c o s (2 β) + D)}{(c o s (2 β) - p_{3}) (c o s (2 β) - p_{4})} = \frac{C (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{3})} = \frac{C}{c o s (2 β) - p_{3}} = \frac{C}{1 - p_{3}} \frac{1}{1 - h_{3} {s i n}^{2} (β)}

(35)

From (34) and (35), it is obvious that the complete elliptic integrals of the third kind

Π (h_{2}, k_{1})

and

Π (h_{4}, k_{3})

will vanish.

Thus, (28) begins,

V_{0} = \frac{η^{2} R}{2} J_{0} - \frac{η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{12 k_{1}^{3}} \{[3 (a_{2} + a_{3}) k_{1}^{4} - (6 a_{2} + 8) k_{1}^{2} + 8] K (k_{1}) + + [(6 a_{2} + 4) k_{1}^{2} - 8] E (k_{1})\} + + |η| \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{12 k_{1}^{3}} \{(16 k_{1}^{2} - 16) K (k_{1}) + (16 - {8 k}_{1}^{2}) E (k_{1})\} + + \frac{η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{12 k_{2}^{3}} \{[3 (a_{22} + a_{33}) k_{2}^{4} - (6 a_{22} + 8) k_{2}^{2} + 8] K (k_{2}) + [(6 a_{22} + 4) k_{2}^{2} - 8] E (k_{2})\} - - |η| \sqrt{η^{2} + 1} \frac{\sqrt{R r_{1}}}{12 k_{2}^{3}} \{(16 k_{2}^{2} - 16) K (k_{2}) + (16 - {8 k}_{2}^{2}) E (k_{2})\} - - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \frac{A}{1 - p_{1}} Π (h_{1}, k_{1}) + \frac{k_{2} η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{4} \frac{C}{1 - p_{3}} Π (h_{3}, k_{2})

(36)

2.2.4. $p_{2} = p_{4} = 1$

From (26) one can see that case that for

p_{2} = 1

the singular case appears and

A = - B

so that,

\frac{(A c o s (2 β) + B)}{(c o s (2 β) - p_{1}) (c o s (2 β) - p_{2})} = \frac{A (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{1})} = \frac{A}{c o s (2 β) - p_{1}} = \frac{A}{1 - p_{1}} \frac{1}{1 - h_{1} {s i n}^{2} (β)}

(37)

Also, in (26) the singularity appears for

p_{4} = - 1

and

C = - D

so that,

\frac{(C c o s (2 β) + D)}{(c o s (2 β) - p_{3}) (c o s (2 β) - p_{4})} = \frac{C (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{3})} = \frac{C}{c o s (2 β) - p_{3}} = \frac{C}{1 - p_{3}} \frac{1}{1 - h_{3} {s i n}^{2} (β)}

(38)

From (36) and (37), it is obvious that the complete elliptic integrals of the third kind

Π (h_{2}, k_{1})

and

Π (h_{4}, k_{3})

will vanish.

Thus, for this case we use (36).

From this detailed analysis detailed all partial singular cases can be found in the previous discussed cases.

2.3. Case $r_{1} > R_{1}$

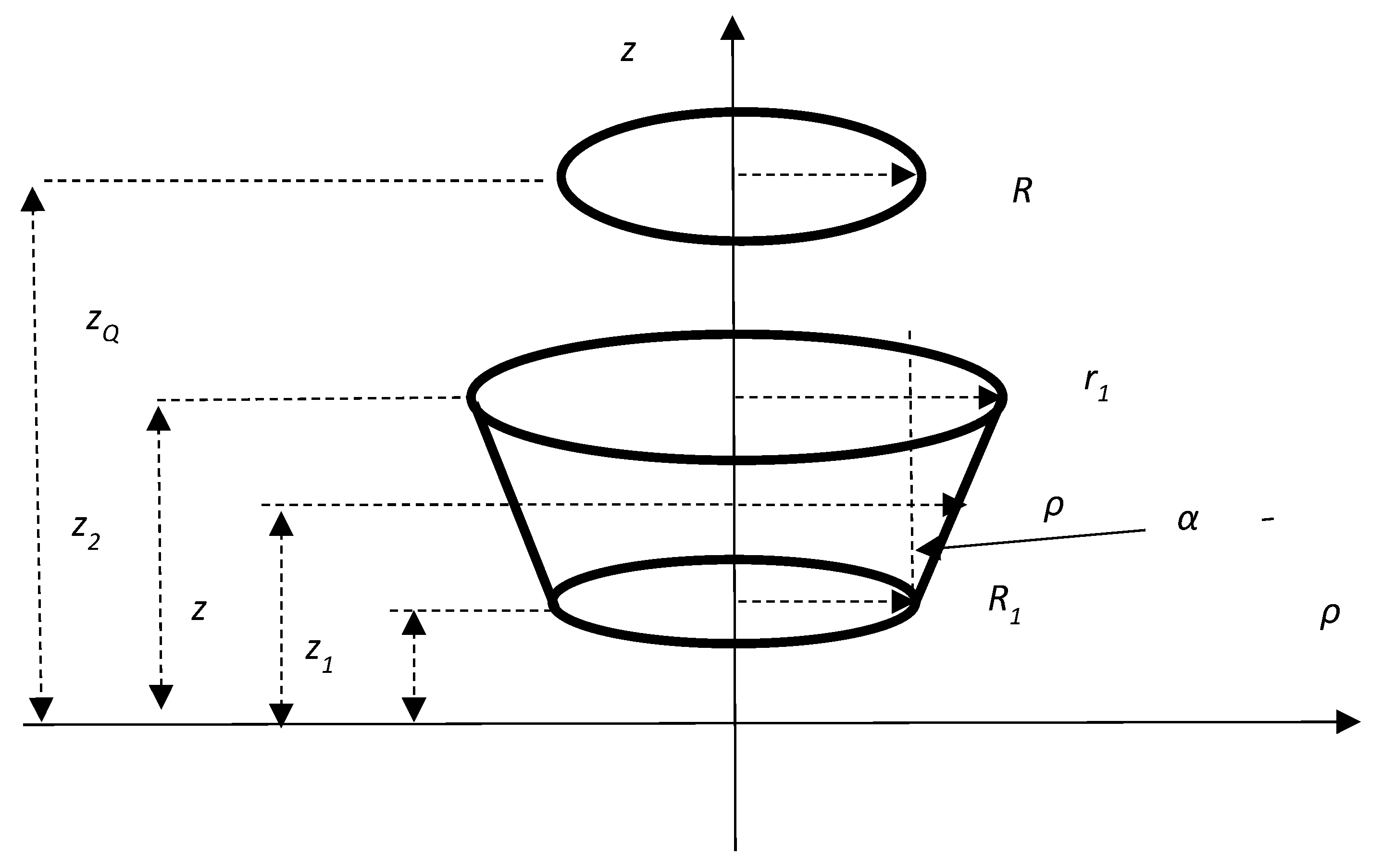
Now, let us consider a thin conical sheet and a circular loop as showed in Figure 2. The thin conical sheet has the radii of basis

R_{1} a n d r_{1} {(r}_{1} > R_{1})

and the axial positions

z_{1} a n d z_{2}

, with the number of sheets turns N. The circular loop has the radii R and radial position

z_{Q}

In this case

r_{1} > R_{1}

one can use the same reasoning as in the previous cases. This is why the final expressions for each calculation.

From Figure 2, we have,

\frac{r_{1} - R_{1}}{z_{2} - z_{1}} = t a g (α) = η, r_{1} = R_{1} + η (z_{2} - z_{1})

(39)

\frac{{z - z}_{1}}{ρ - R_{1}} = \frac{z_{2} - z_{1}}{r_{1} - R_{1}} = \frac{1}{η}, ρ = R_{1} + η (z - z_{1})

(40)

The mutual inductance can be calculated as follows,

M = \frac{μ_{0} N}{z_{2} - z_{1}} \int_{0}^{π} \int_{z_{1}}^{z_{2}} \frac{R ρ c o s (θ)}{r_{0}} d z d θ = \frac{μ_{0} N}{z_{2} - z_{1}} \int_{0}^{π} \int_{z_{1}}^{z_{2}} \frac{R (R_{1} + η z - η z_{1}) c o s (θ)}{r_{0}} d z d θ

(41)

with

r_{0} = \sqrt{{(R_{1} + η z - η z_{1})}^{2} - 2 (R_{1} + η z - η z_{1}) R \cos (θ) + R^{2} + {(z - z_{Q})}^{2}}

(42)

Introducing the substitution,

θ = π - 2 β

in (41) one has,

M = - \frac{2 μ_{0} N R}{z_{2} - z_{1}} \int_{0}^{π / 2} \int_{z_{1}}^{z_{2}} \frac{(R_{1} + η z - η z_{1}) c o s (2 β)}{r_{0}} d z d β

(43)

With

r_{0} = \sqrt{{(R_{1} + η z - η z_{1})}^{2} + 2 (R_{1} + η z - η z_{1}) R \cos (2 β) + R^{2} + {(z - z_{Q})}^{2}}

The mutual inductance can be calculated by the double integration (43). Following the procedures as in 2.1, after the first integration over the variable z, one has,

M = \frac{2 μ_{0} N R}{{(z}_{2} - z_{1}) {(η^{2} + 1)}^{3 / 2}} \int_{0}^{π / 2} V c o s (2 β) d β

(44)

where,

V = \sqrt{η^{2} + 1} [\sqrt{c_{0} R_{1}^{2} + b_{0} R_{1} + a_{0}} - \sqrt{c_{0} r_{1}^{2} + b_{0} r_{1} + a_{0}}] - [η^{2} R c o s (2 β) - R_{1} - η (z_{Q} - z_{1})] \times [A s i n h \frac{η R c o s (2 β) + η R_{1} - z_{Q} + z_{1}}{\sqrt{D_{20}}} - A s i n h \frac{η R c o s (2 β) + η r_{1} - z_{Q} + z_{2}}{\sqrt{D_{20}}}] c_{0} = η^{2} + 1 b_{0} = 2 [η^{2} R \cos (2 β) - R_{1} - η (z_{Q} - z_{1})] a_{0} = {[R_{1} + η (z_{Q} - z_{1})]}^{2} + η^{2} R^{2} ∆_{0} = 4 η^{2} D_{00} D_{10} = \{{η^{2} R}^{2} {s i n}^{2} (2 β) + 2 R [R_{1} + η ({z_{Q} - z}_{1})] \cos (2 β) + {[R_{1} + η ({z_{Q} - z}_{1})]}^{2} + R^{2}\}

(45)

Finally, using the same procedures as in 2.1 after the second integration the mutual inductance in the semi-analytical form is given as follows,

M = \frac{2 μ_{0} N R}{{(z}_{2} - z_{1}) {(η^{2} + 1)}^{3 / 2}} \int_{0}^{π / 2} V_{00} d β

(46)

The solution of the four integrals in (46),

V_{00} = V_{00}^{(1)} + V_{00}^{(2)} + V_{00}^{(3)} + V_{44}^{(4)} = - \frac{η^{2} R}{2} J_{00} - \frac{η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{12 k_{1}^{3}} \{[3 (d_{2} + d_{3}) k_{1}^{4} - (6 d_{2} + 8) k_{1}^{2} + 8] K (k_{1}) + [(6 d_{2} + 4) k_{1}^{2} - 8] E (k_{1})\} + |η| \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{12 k_{1}^{3}} \{(16 k_{1}^{2} - 16) K (k_{1}) + (16 - {8 k}_{1}^{2}) E (k_{1})\} + \frac{η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{12 k_{2}^{3}} \{[3 (d_{22} + d_{33}) k_{2}^{4} - (6 d_{22} + 8) k_{2}^{2} + 8] K (k_{2}) + [(6 d_{22} + 4) k_{2}^{2} - 8] E (k_{2})\} - |η| \sqrt{η^{2} + 1} \frac{\sqrt{R r_{1}}}{12 k_{2}^{3}} \times \{(16 k_{2}^{2} - 16) K (k_{2}) + (16 - {8 k}_{2}^{2}) E (k_{2})\} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \times [\frac{T_{11}}{1 - p_{11}} Π (h_{11}, k_{1}) + \frac{T_{22}}{1 - p_{22}} Π (h_{22}, k_{1})] + \frac{k_{2} η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{4} [\frac{T_{33}}{1 - p_{33}} Π (h_{33}, k_{2}) + \frac{T_{44}}{1 - p_{44}} Π (h_{44}, k_{2})] k_{1}^{2} = \frac{4 R R_{1}}{{(R + R_{1})}^{2} + {(z_{Q} - z_{1})}^{2}}, k_{2}^{2} = \frac{4 R r_{1}}{{(R + r_{1})}^{2} + {(z_{2} - z_{Q})}^{2}} J_{00} = \int_{0}^{\frac{π}{2}} A s i n h \frac{η R c o s (2 β) + η R_{1} + z_{1} - z_{Q}}{\sqrt{D_{00}}} d β - \int_{0}^{\frac{π}{2}} A s i n h \frac{η R c o s (2 β) + η r_{1} + z_{2} - z_{Q}}{\sqrt{D_{00}}} d β d_{1} = \frac{2 [R_{1} + η (z_{Q} - z_{1})]}{η^{2} R} d_{2} = \frac{η R^{2} + η {(z_{Q} - z_{1})}^{2} + R_{1} (z_{Q} - z_{1})}{η R R_{1}} d_{3} = \frac{{[R_{1} + η ({z_{Q} - z}_{1})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}} A_{1} = (d_{2} + d_{1}) d_{3} - d_{2}, B_{1} = d_{3}^{2} - d_{3} + d_{1} d_{2} p_{11,22} = \frac{d_{1} \pm \sqrt{d_{1}^{2} + 4 d_{3}}}{2}, h_{11} = \frac{2}{1 - p_{11}}, h_{22} = \frac{2}{1 - p_{22}} V_{11} = - \frac{A_{1} p_{11} + B_{1}}{p_{22} - p_{11}}, V_{22} = - \frac{A_{1} p_{2} + B_{1}}{p_{22} - p_{11}} d_{11} = \frac{2 [r_{1} + η (z_{Q} - z_{2})]}{η^{2} R} d_{22} = \frac{η R^{2} + η {(z_{Q} - z_{2})}^{2} + r_{1} (z_{Q} - z_{2})}{η R r_{1}} d_{33} = \frac{{[r_{1} + η ({z_{Q} - z}_{2})]}^{2} + (η^{2} + 1) R^{2}}{η^{2} R^{2}} C_{1} = (d_{22} + d_{11}) d_{33} - d_{22}, D_{1} = d_{33}^{2} - d_{33} + d_{11} d_{22} p_{33,44} = \frac{d_{11} \pm \sqrt{d_{11}^{2} + 4 d_{33}}}{2}, h_{33} = \frac{2}{1 - p_{33}}, h_{44} = \frac{2}{1 - p_{44}} V_{33} = - \frac{C_{1} p_{33} + D_{1}}{p_{44} - p_{33}}, V_{44} = - \frac{C_{1} p_{33} + D_{1}}{p_{44} - p_{34}}

(47)

Thus, the general solution of equation (46) with (47) is expressed by the complete elliptic integrals K(k), E(k) and Π(h, k) as well as one term J₀₀ which must be solved numerically.

2.4. Singular cases

It is possible to have in (47) four singular cases so that one must do some corrections to overcome these problems.

2.4.1. $p_{11} = p_{33} = - 1$

From (47) one can see that case that for

p_{11} = - 1

the singular case appears and

A_{1} = B_{1}

so that,

\frac{(A_{1} c o s (2 β) + B_{1})}{(c o s (2 β) - p_{11}) (c o s (2 β) - p_{22})} = \frac{A_{1} (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{22})} = \frac{A_{1}}{c o s (2 β) - p_{22}} = \frac{A_{1}}{1 - p_{22}} \frac{1}{1 - h_{22} {s i n}^{2} (β)}

(48)

For

p_{33} = - 1

in (47)

C_{1} = D_{1}

so that

\frac{(C_{1} c o s (2 β) + D_{1})}{(c o s (2 β) - p_{33}) (c o s (2 β) - p_{44})} = \frac{C_{1} (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{44})} = \frac{C_{1}}{c o s (2 β) - p_{44}} = \frac{C_{1}}{1 - p_{44}} \frac{1}{1 - h_{44} {s i n}^{2} (β)}

(49)

From (48) and (49), it is obvious that the complete elliptic integrals of the third kind

Π (h_{22}, k_{1})

and

Π (h_{44}, k_{3})

will vanish.

Thus, (47) begins,

V_{00} = \frac{η^{2} R}{2} J_{00} - \frac{η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{12 k_{1}^{3}} \{[3 (d_{2} + d_{3}) k_{1}^{4} - (6 d_{2} + 8) k_{1}^{2} + 8] K (k_{1}) + [(6 d_{2} + 4) k_{1}^{2} - 8] E (k_{1})\} + |η| \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{12 k_{1}^{3}} \{(16 k_{1}^{2} - 16) K (k_{1}) + (16 - {8 k}_{1}^{2}) E (k_{1})\} + \frac{η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{12 k_{2}^{3}} \{[3 (d_{22} + d_{33}) k_{2}^{4} - (6 d_{22} + 8) k_{2}^{2} + 8] K (k_{2}) + [(6 d_{22} + 4) k_{2}^{2} - 8] E (k_{2})\} - |η| \sqrt{η^{2} + 1} \frac{\sqrt{R r_{1}}}{12 k_{2}^{3}} \{(16 k_{2}^{2} - 16) K (k_{2}) + (16 - {8 k}_{2}^{2}) E (k_{2})\} - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \frac{A_{1}}{1 - p_{22}} Π (h_{22}, k_{1}) + \frac{k_{2} η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{4} \frac{C_{1}}{1 - p_{44}} Π (h_{44}, k_{2})

(50)

2.4.2. $p_{11} = p_{33} = 1$

From (47) one can see that case that for

p_{11} = 1

the singular case appears and

A_{1} = - B

so that,

\frac{(A_{1} c o s (2 β) + B_{1})}{(c o s (2 β) - p_{11}) (c o s (2 β) - p_{22})} = \frac{A_{1} (c o s (2 β) - 1)}{(c o s (2 β) - 1) (c o s (2 β) - p_{22})} = \frac{A_{1}}{c o s (2 β) - p_{22}} = \frac{A_{1}}{1 - p_{22}} \frac{1}{1 - h_{22} {s i n}^{2} (β)}

(51)

Also, in (47) the singularity appears for

p_{33} = 1

and

C_{1} = - D_{1}

so that,

\frac{(C_{1} c o s (2 β) + D_{1})}{(c o s (2 β) - p_{33}) (c o s (2 β) - p_{44})} = \frac{C_{1} (c o s (2 β) - 1)}{(c o s (2 β) - 1) (c o s (2 β) - p_{44})} = \frac{C_{1}}{c o s (2 β) - p_{44}} = \frac{C_{1}}{1 - p_{44}} \frac{1}{1 - h_{44} {s i n}^{2} (β)}

(52)

Thus, for this case we use (50).

2.4.3. $p_{22} = p_{44} = - 1$

From (47) one can see that case that for

p_{22} = - 1

the singular case appears and

A_{1} = B_{1}

so that,

\frac{(A_{1} c o s (2 β) + B_{1})}{(c o s (2 β) - p_{11}) (c o s (2 β) - p_{22})} = \frac{A_{1} (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{11})} = \frac{A_{1}}{c o s (2 β) - p_{11}} = \frac{A_{1}}{1 - p_{11}} \frac{1}{1 - h_{11} {s i n}^{2} (β)}

(53)

Also, in (47) the singularity appears for

p_{44} = - 1

and

C_{1} = D_{1}

so that,

\frac{(C_{1} c o s (2 β) + D_{1})}{(c o s (2 β) - p_{33}) (c o s (2 β) - p_{44})} = \frac{C_{1} (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{33})} = \frac{C_{1}}{c o s (2 β) - p_{33}} = \frac{C_{1}}{1 - p_{3}} \frac{1}{1 - h_{3} {s i n}^{2} (β)}

(54)

From (53) and (54), it is obvious that the complete elliptic integrals of the third kind

Π (h_{22}, k_{1})

and

Π (h_{44}, k_{3})

will vanish.

Thus, (47) begins,

V_{00} = \frac{η^{2} R}{2} J_{00} - \frac{η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{12 k_{1}^{3}} \{[3 (d_{2} + d_{3}) k_{1}^{4} - (6 d_{2} + 8) k_{1}^{2} + 8] K (k_{1}) + + [(6 d_{2} + 4) k_{1}^{2} - 8] E (k_{1})\} + + |η| \sqrt{η^{2} + 1} \frac{\sqrt{R R_{1}}}{12 k_{1}^{3}} \{(16 k_{1}^{2} - 16) K (k_{1}) + (16 - {8 k}_{1}^{2}) E (k_{1})\} + + \frac{η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{12 k_{2}^{3}} \{[3 (d_{22} + d_{33}) k_{2}^{4} - (6 d_{22} + 8) k_{2}^{2} + 8] K (k_{2}) + [(6 d_{22} + 4) k_{2}^{2} - 8] E (k_{2})\} - - |η| \sqrt{η^{2} + 1} \frac{\sqrt{R r_{1}}}{12 k_{2}^{3}} \{(16 k_{2}^{2} - 16) K (k_{2}) + (16 - {8 k}_{2}^{2}) E (k_{2})\} - - \frac{k_{1} η \sqrt{η^{2} + 1} \sqrt{R R_{1}}}{4} \frac{A_{1}}{1 - p_{11}} Π (h_{11}, k_{1}) + \frac{k_{2} η \sqrt{η^{2} + 1} \sqrt{R r_{1}}}{4} \frac{C_{1}}{1 - p_{33}} Π (h_{33}, k_{2})

(55)

2.4.4. $p_{2} = p_{4} = 1$

From (47) one can see that case that for

p_{22} = 1

the singular case appears and

A_{1} = B_{1}

so that,

\frac{(A_{1} c o s (2 β) + B_{1})}{(c o s (2 β) - p_{11}) (c o s (2 β) - p_{22})} = \frac{A_{1} (c o s (2 β) - 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{11})} = \frac{A_{1}}{c o s (2 β) - p_{11}} = \frac{A_{1}}{1 - p_{11}} \frac{1}{1 - h_{11} {s i n}^{2} (β)}

(56)

Also, in (47) the singularity appears for

p_{44} = 1

and

C_{1} = D_{1}

so that,

\frac{(C_{1} c o s (2 β) + D_{1})}{(c o s (2 β) - p_{33}) (c o s (2 β) - p_{44})} = \frac{C_{1} (c o s (2 β) + 1)}{(c o s (2 β) + 1) (c o s (2 β) - p_{33})} = \frac{C_{1}}{c o s (2 β) - p_{33}} = \frac{C_{1}}{1 - p_{3}} \frac{1}{1 - h_{3} {s i n}^{2} (β)}

(57)

From (56) and (57), it is obvious that the complete elliptic integrals of the third kind

Π (h_{22}, k_{1})

and

Π (h_{44}, k_{3})

will vanish.

Thus, for this case we use (55).

Finally, all partial singular cases can be found in the previous discussed cases.

2.5. $η = 0 (r_{1} = R_{1})$

This is the special case when the thin conical sheet degenerates to the thin wall solenoid (

r_{1} = R_{1}

). The mutual inductance between the thin wall solenoid and the circular loop is given in [7],

M = \frac{μ_{0} N}{{(z}_{2} - z_{1})} \sum_{n = 1}^{n = 2} {(- 1)}^{n - 1} Ψ_{n}

(58)

where,

Ψ_{n} = - \frac{t_{n} \sqrt{R_{1} R}}{k_{n}} [K (k_{n}) - E (k_{n})] + \frac{π}{4} s g n (t_{n}) |R_{1}^{2} - R^{2}| [1 - Λ_{0} (ε_{n}, k_{n})]

(59)

k_{n}^{2} = \frac{4 R R_{1}}{{(R + R_{1})}^{2} + t_{n}^{2}}, t_{n} = z_{n} - z_{Q}, h = \frac{4 R R_{1}}{{(R + R_{1})}^{2} + t_{n}^{2}}, ε_{n} = a r c s i n \sqrt{\frac{1 - h}{1 - k_{n}^{2}}}

Λ_{0} (ε_{n}, k_{n})

is Heuman’s Lambda function, [22].

R₁ is the radii of the thin wall solenoid,

z₁ and z₂ are the axial positions of the thin wall solenoid,

R is the radii of the circular loop,

z_Q is the axial position of the circular loop,

N is the number of turns of the thin wall solenoid.

3. Numerical validation

To verify the validity of the new presented formula for calculating the following set of examples is presented.

Example 1.

Calculate the mutual inductance between the thin conical sheet inductor and the circular loop for which R₁ = 10 m, r₁ = 2 m, z₁ = - 1 m, z₂ = 2 m, N=1000 and R = 5 m, z_Q = 0 m.

This is the case

R_{1} > r_{1} (F i g u r e 1) .

Let us begin with the basic formula (5) wherethe mutual inductance is given by the double integration.

The mutual inductance is,

M (D o u b l e) = 7.401731104798464 m H

Using the formula (10) with (11) the mutual inductance is obtained by the singleintegration.

M (S i n g l e) = 7.401731104798464 m H

Let us use the semi-analytical formula (27) with (28),

M (S e m i - a n a l y t i c a l) = 7.401731104798464 m H

Example 2.

Calculate the mutual inductance between the thin conical sheet inductor and the circular loop for which R₁ = 2 m, r₁ = 10 m, z₁ = - 1 m, z₂ = 2 m, N=1000 and R = 5 m, z_Q = 0 m.

This is the case

R_{1} < r_{1} (F i g u r e 2) .

Using the basic formula (43) for the double integration the mutual inductance is,

M (D o u b l e) = 8.607861541512988 m H

Using the formula (44) with (45) the mutual inductance is obtained by the single integration,

M (S i n g l e) = 8.607861541512988 m H

Finally, let us use the semi-analytical formula (46) with (47) the mutual inductance is,

M (S e m i - a n a l y t i c a l) = 8.607861541512988 m H

All results are in an excellent agreement.

Example 3.

Calculate the mutual inductance between the thin conical sheet inductor and the circular loop for which R₁ = 3 m, r₁ = 2 m, z₁ = 0 m, z₂ = 0.2 m, N=1000, R = 1 m, and z_Q = 0.2 m.

This is the case

R_{1} > r_{1} (F i g u r e 1) .

The basic formula for the mutual inductance is given by the double integration (5).

The mutual inductance is,

M (D o u b l e) = 0.8559140919190895 m H

Using the formula (10) with (11) the mutual inductance is obtained by the single integration.

M (S i n g l e) = 0.8559140919190892 m H

Finally, let us use the semi-analytical formula (27) with (28) for the mutual inductance which gives,

M (S e m i - a n a l y t i c a l) = 0.8559140919190874 m H

All results are in an excellent agreement. The figures that agree are bolded.

Example 4.

Calculate the mutual inductance between the thin conical sheet inductor and the circular loop for which R₁ = 2 m, r₁ = 3 m, z₁ = 0 m, z₂ = 0.2 m, N=1000 and R = 1 m, z_Q = 0.2 m.

This is the case

r_{1} > R_{1} (F i g u r e 2) .

The basic formula for the mutual inductance is given by the double integration (43) which gives,

M (D o u b l e) = 0.8529571443235432 m H

Using the formulas (44) with (45) the self-inductance is obtained by the single integration.

M (S i n g l e) = 0.8529571443235433 m H

Let us use the semi-analytical formula (46) with (47),

M (S e m i - a n a l y t i c a l) = 0.8529571443235445 m H

All results are in an excellent agreement. The figures that agree are bolded.

Example 5.

In this example one calculates the mutual inductance between the thin wall solenoid and the circular loop for which R₁ = r₁ = 2 m, z₁ = 0 m, z₂ = 0.2 m, N=1000 and R = 1 m, z_Q = 0.2 m.

In this example the thin conical sheet inductor degenerates to the thin wall solenoid (

η = 0

The exact formula for calculating the mutual inductance between the thin wall solenoid and the circular loop is given by (58) with (59) as follows, [7],

M (A n a l y t i c a l) = 1.08887170213681 m H

Using the formulas for the double and the single integration either for the case

R_{1} >

r_{1}

R_{1} < r_{1}

the mutual inductance is respectively,

M (D o u b l e) = 1.0888715096342527 m H

M (S i n g l e) = 1.0888717021367874 m H

Equations (5) and (43) for the double integration and (10) with (11) as well as (44) with (45) for the single integration are not singular for

η = 0 .

It is not case for the semi-analytical solutions (27) with (28) or (46) with (77) when they are singular or indeterminate.

However, one can take, for example, R₁ = 2.0000001 m, and r₁ = 2.0000001 m equations (28) and (47) respectively so that they give,

M (S e m i - a n a l y t i c a l) = 1.0888716126957454 m H

All figures that agree with the exact result, are bolded. Even though the results are in the particularly good agreement it is recommended to use the formula (58) with (59) for calculating the mutual inductance between the thin wall solenoid and the circular loop. This formula can be carefully obtained from (28) and (47) in the limit case when

R_{1} \to r_{1}

and vice versa.

Example 6.

Calculate the mutual inductance between the thin conical sheet inductor and the circular loop for which R₁ = 3 m, r₁ = 2 m, z₁ = 0 m, z₂ = 0.2 m, N=1000 and R = 1 m, z_Q = 0.4 m.

In this example one finds that

p_{1} = p_{3} = - 1,

so that it is the singular case 2.2.1.

Applying (31) the mutual inductance is,

M (S e m i - a n a l y t i c a l) = 0.8354647253409638 m H

Using the basic formula (5) for the double integration the mutual inductance is,

M (D o u b l e) = 0.8354647253409652 m H

Using the formula (10) with (11) the mutual inductance is obtained by the single integration.

M (S i n g l e) = 0.8354647253409652 m H

All figures, that agree, are bolded. All results are in an excellent agreement.

Example 7.

Calculate the mutual inductance between the thin conical sheet and the circular loop for which R₁ = 3 m, r₁ = 2 m, z₁ = 0 m, z₂ = 0.2 m, N=1000 and R = 1 m, z_Q = 0.8 m.

In this example one finds that

p_{1} = p_{3} = 1,

so that it is the singular case 2.2.2.

Applying (31) the mutual inductance is,

M (S e m i - a n a l y t i c a l) = 0.7397457129358785 m H

Using the basic formula (5) for the double integration the mutual inductance is,

M (D o u b l e) = 0.739745712935874 m H

Using the formula (11) the mutual inductance is obtained by the single integration.

M (S i n g l e) = 0.7397457129358738 m H

All results are in an excellent agreement. The figures that agree are bolded.

All presented results have been obtained by the Mathematica programing. One can see that they are in an excellent agreement so that the potential users can use on of the presented formulas by their preference.

4. Discussion

For the first time in the literature the new formula for calculating the mutual inductance between the thin conical sheet inductor and the filamentary loop is given. Coils are coaxial. Conical coils used in RF /Microwave and mm Wave systems have extremely ultra-wideband electrical responses and are commonly attached to transmission lines to bias microwave devices. These coils have traditionally been designed experimentally without the aid of modern 3D electromagnetic simulators due to the difficult model creation process. The calculation of the presented mutual induction is obtained in the semi-analytical form over the complete elliptical integrals of the first, second and third kind as well as one term that does not have the analytical solution and it must be solved numerically. The kernel function of this integral is continuous function on the interval of integration. All procedures of the calculation are given promptly so that the potential users can easily use them choosing the appropriate formula. The representative numerical examples are given to validate the presented method. The presented method can serve as the base to calculate the mutual inductance between more complex configurations such as the coaxial thin sheet inductor the thin wall solenoid inductor and the two coaxial thin conical inductors. It will be the future work which is the continuation of the new presented method.

Author Contributions

Conceptualization, methodology, software, validation, investigation resources, writing—original draft preparation, writing—review and editing.

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest.

References

Maxwell, J.C. A Treatise on Electricity and Magnetism, 3rd ed.; Dover Publications Inc.: New York, NY, USA, 1954; Volume 2. [Google Scholar]
Grover, F.W. Inductance Calculations; Dover: New York, NY, USA, 1964. [Google Scholar]
Snow, C. Formulas for Computing Capacitance, and Inductance; Snow, C. Formulas for Computing Ca-pacitance, and Inductance; National Bureau of Standards Circular 544: Washington, DC, USA, 1954. [Google Scholar]
Rosa, B.E. , Grover F.W. Formulas and Tables for the Calculation of Mutual and Self-Inductance, NBS Scientific Paper No.169, 3rd Edition, 16. 19 December.
P. L. Kalantarov, L. A. P. L. Kalantarov, L. A., Zeitlin, Raschet induktivnostey (Calculation of Inductances), 3rd Edition, Ener-goatomizdat, Leningrad, 1986.
Wheeler, H. A. Simple Inductance Formulas for Radio Coils, Proceedings of the Institute of Radio En-gineers, Volume: 16, Issue:10, 28. 19 October. [CrossRef]
Babic, S.; Akyel, C. Improvement in calculation of the self- and mutual inductance of thin-wall solenoids and disk coils. 2000; 36. [Google Scholar] [CrossRef]
C Akyel, S. I. Babic, K. Wu, and J. F. Mojica, Improvement in the mutual inductance calculation of thin coaxial circular coils with constant current density in air, WSEAS Transactions on Communications, Vol. 5, Issue 6, pp-970-977, Jun 2006.
Babic, S.I. SELF-INDUCTANCE COMPUTATION OF THE THIN CONICAL SHEET INDUCTOR. Prog. Electromagn. Res. B 2023, 99, 23–39. [Google Scholar] [CrossRef]
Y. Bayazitoglu and U. B. Sathuvalli, "Field gradient analysis of a conical helix", IEEE Trans. Magn., vol. 29, no. 1, pp. 88-97, Jan. 1993. [CrossRef]
T. Roberts, Electromagnetic Modeling and Application of Conical Coils, Anritsu Technical Bulletin, No. 97, 22. 20 March.
Winslow, T. Conical inductors for broadband applications. IEEE Microw. Mag. 2005, 6, 68–72. [Google Scholar] [CrossRef]
Lopez-Villegas, J.; Salas, A.; Vidal, N.; Sieiro, J. 3D-Printed Low-Pass Filter with Conical Inductors for Broadband RF Applications. 2018 48th European Microwave Conference (EuMC). LOCATION OF CONFERENCE, SpainDATE OF CONFERENCE; [CrossRef]
P. Hadadtehrani, P. P. Hadadtehrani, P. Kamalinejad, R. Molavi, Sh. Mirabbasi, On the use of conical helix inductors in wireless power transfer systems, 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), pp.1-4, 2016. [CrossRef]
J. Martinez, S. J. Martinez, S. Babic, C. Akyel, "On evaluation of inductance, dc resistance and capacitance of coaxial inductors at lof frequencies", IEEE Transactions on magnetics, Vol 50, Issue 7, 14. 20 July. [CrossRef]
Yang, H.-Y.; Li, F.-P.; Yue, J.-H.; Guo, F.-S.; Liu, X.-H.; Zhang, H. Cone-shaped source characteristics and inductance effect of transient electromagnetic method. Appl. Geophys. 2017, 14, 165–174. [Google Scholar] [CrossRef]
Jeyaraman, S.; Vanukuru, V.N.R.; Nair, D.; Chakravorty, A. Modeling of High-Q Conical Inductors and MOM Capacitors for Millimeter- Wave Applications. IEEE Trans. Electron Devices 2020, 67, 5646–5652. [Google Scholar] [CrossRef]
Patel, H.; Morales, H.; Dunleavy, L.; Goodhue, B. Conical inductor modeling using equivalent circuit technique. 2015 IEEE 16th Annual Wireless and Microwave Technology Conference (WAMICON). LOCATION OF CONFERENCE, USADATE OF CONFERENCE; pp. 1–5. [CrossRef]
Eshkoli, A.; Shapira, S.; Nemirovsky, Y. Lumped Circuit Model of Conical-Shaped Inductors for Broad-Bandwidth Applications. IEEE Trans. Ind. Electron. 2016, 63, 5087–5090. [Google Scholar] [CrossRef]
N. F. Ali Mohamed, S. S. S. N. F. Ali Mohamed, S. S. S. Al Tabouni, M. H. 2017. [Google Scholar]
I.S. Gradshteyn and I.M. Ryzhik, Table of Integrals, Series and Products", New York and London, Academic Press Inc., 1965.
Abramowitz, M.; Stegun, I.A.; Miller, D. Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables (National Bureau of Standards Applied Mathematics Series No. 55). J. Appl. Mech. 1965; 32. [Google Scholar] [CrossRef]

Figure 1. Thin conical sheet inductor and circular loop (

R_{1} > r_{1}

Figure 1. Thin conical sheet inductor and circular loop (

R_{1} > r_{1}

Figure 2. Circular loop-thin conical sheet inductor (

r_{1} > R_{1}

Figure 2. Circular loop-thin conical sheet inductor (

r_{1} > R_{1}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Mutual-Inductance Computation between Coaxial Thin Conical Sheet Inductor and the Circular Loop

Abstract

1. Introduction

2. Basic formulas

2.2. Singular cases

2.2.1. p 1 = p 3 = − 1

2.2.2. p 1 = p 3 = 1

2.2.3. p 2 = p 4 = − 1

2.2.4. p 2 = p 4 = 1

2.3. Case r 1 > R 1

2.4. Singular cases

2.4.1. p 11 = p 33 = − 1

2.4.2. p 11 = p 33 = 1

2.4.3. p 22 = p 44 = − 1

2.4.4. p 2 = p 4 = 1

2.5. η = 0 ( r 1 = R 1 )

3. Numerical validation

4. Discussion

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.2.1. $p_{1} = p_{3} = - 1$

2.2.2. $p_{1} = p_{3} = 1$

2.2.3. $p_{2} = p_{4} = - 1$

2.2.4. $p_{2} = p_{4} = 1$

2.3. Case $r_{1} > R_{1}$

2.4.1. $p_{11} = p_{33} = - 1$

2.4.2. $p_{11} = p_{33} = 1$

2.4.3. $p_{22} = p_{44} = - 1$

2.4.4. $p_{2} = p_{4} = 1$

2.5. $η = 0 (r_{1} = R_{1})$