Prerpints.org logo
Preprint
Article

Joint Flood Risks in the Grand River Watershed, Ontario Canada

Altmetrics

Downloads

137

Views

67

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 April 2023

Posted:

11 April 2023

You are already at the latest version

Alerts
Abstract
According to the World Meteorological Organization, since 2000, there has been an increase in global flood-related disasters by 134 percent as compared to the two previous decades. Efficient flood risk management strategies necessitate a holistic approach to evaluating flood vulnerabilities and risks. Catastrophic losses can occur when the peak flow values in the rivers in a basin coincide. Therefore, estimating the joint flood risks in a region is vital, especially when frequent occurrences of extreme events are experienced. This study focuses on estimating the joint flood risks due to river flow extremes in the Grand River watershed in Canada. Determining the interdependence of floods at multiple locations using state-of-the-art tools, the associated damage probabilities, and their costs will be beneficial to various stakeholders, such as the insurance industry, the disaster management sector, and most importantly, the public.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Extreme weather events such as floods, landslides, heat waves, wildfires, storms and droughts are becoming more frequent and severe. Compound extreme events refer to the interdependence of simultaneous or successive occurrences of two or more extreme events or hazard drivers that can cause severe impacts on the ecosystem. Cascading events are a type of compound events where the consecutive occurrence of events lead to major impacts [1]. Cascading events can have a significant impact on the environment, the economy, and human health and safety. To effectively manage the risks associated with compound extreme events, it is crucial to understand their interdependence and the cascading effects that can occur. By taking a holistic approach to risk assessment and management, stakeholders can develop effective strategies to mitigate the impacts of these events and protect vulnerable populations.
Floods cause disastrous impacts on humans as well as animal and aquatic life. According to the World Health Organization, floods affected more than 2 billion people worldwide in the last two decades and 80-90% of natural disasters in the last decade are from floods, droughts, and severe storms. Compound flood events and their effects are currently in the research spotlight. Traditional flood risk assessment using a univariate return period cannot incorporate the joint flood risks and might underestimate the actual risks. Joint risk estimation of cascading flood events is critical these days as more frequent and severe events are projected in the near future.
Different rivers can have varying effects on flood generation in the mainstream. When floods occur simultaneously in different rivers, it can lead to peak flow and increase the risk of flooding. To accurately assess the combination risk for hydraulic design, it's important to consider the impact of simultaneous occurrences of extreme flows in different rivers in the region. The traditional univariate frequency analysis that estimates the probability that a value of the flood characteristic will be exceeded, cannot encompass the risk of coincidence of flood risks at multiple rivers in the region. Furthermore, when the river receives significant flow from a tributary, the univariate approach does not yield reliable estimates of flood properties. In such cases, multivariate analysis that incorporates the dependence between flood variables of different rivers/tributaries is needed [2].
A bivariate model using the copula function was applied in this study to estimate the joint flood risks of two rivers in the Grand River watershed. Copula has now been widely used in varied fields where interdependence between variables plays a crucial role. For instance, copula has been successfully implemented in the analysis of extreme events such as flood and drought [3,4,5], rainfall frequency analysis [4] and other multivariate problems [6,7,8,9,10,11].
Copula functions have become increasingly important in hydrologic studies as they provide a useful tool for modeling the dependence between variables, such as river flow and rainfall, which are often correlated in hydrological systems. Copula functions are used to model the dependence structure of multivariate distributions and can be used to generate joint probability distributions, which are essential in flood risk analysis and management. Copula functions are often used to combine interrelated variables such as peak flow and flood volume and conduct analysis in a probabilistic approach. They allow assessing compound flood hazards from riverine and coastal interactions [12]. Copula-based flood frequency analysis can model the dependence structure among peak flow, volume, and duration[13]. This method could relax the limitation of traditional flood frequency analysis by selecting marginal from different families of probability distribution functions for flood characteristics[13]. It is found that copula-based flood frequency analysis performs better than conventional flood frequency analysis[13]. Xie et al. [14] assessed the joint impact of rainfall characteristics on urban floods using a coupled hydrological model based on copula.
Several studies have demonstrated the effectiveness of copula functions in flood studies [15,16,17] and found that copula-based models provided a more accurate representation of the dependence structure between the variables, which was important in accurately assessing flood risk and designing appropriate management strategies. For example, Wang et al. [18] proposed a copula simulation approach to develop a joint flood risk distribution of multi-reservoirs. They found that the copula-based approach provides valuable insights into reservoir joint risk control. Zhong et al. [19] conducted a copula-based multivariate probability analysis for flash flood risk assessment by considering the compounding effect of soil moisture and rainfall. Bačová Mitková et al. [20] focused on comparing different methods for performing frequency analysis of floods and suggested that the copula method is useful for this purpose.
Copula-based flood frequency studies have become increasingly popular in recent years as a means of modeling the dependence structure between flood characteristics of a river. These studies typically focus on the relationship between two or more flood variables, such as peak flow and volume of flow. By understanding the interdependence of these variables, researchers can gain a more accurate picture of flood risk and make better-informed decisions regarding flood management and mitigation.
The current study seeks to estimate the bivariate return period of peak flow events in two rivers in a river catchment using copulas. This involves examining the correlation between peak river flows in a catchment and using copula analysis to identify interdependence between these flows and estimate joint return periods.
The study addresses several important research questions related to peak river flows in a catchment. For example, it seeks to understand how the peak flow in multiple rivers in a catchment correlates and how copula analysis can be used to identify interdependence between these variables. The study also aims to estimate joint return periods for peak river flows and to explore how this information can be used to inform flood risk management and mitigation strategies.
By providing answers to these research questions, the study contributes to the broader field of flood risk management and provides valuable insights for policymakers, researchers, and other stakeholders. By understanding the interdependence between peak river flows and other flood variables, stakeholders can develop more effective strategies for managing flood risk, protecting communities and infrastructure, and minimizing the damage caused by floods. Ultimately, the study highlights the importance of copula analysis in flood frequency studies and underscores the need for ongoing research to further refine our understanding of flood risk and develop more effective strategies for managing this critical natural hazard.

2. Materials and Methods

2.1. Grand River Watershed

The Grand River watershed is the largest watershed in southern Ontario [21], with an area of 6800 km2. There are five major urban settlements in the area, namely Guelph, Kitchener, Waterloo, Cambridge, and Brantford. Agricultural land makes up 70% of the watershed. In this study, the Speed River and Grand River are selected as case studies. These rivers meet in the City of Cambridge and simultaneous flooding of these rivers can cause disastrous impacts in the highly populated urban settlements (Figure 1). The annual peak flows of the rivers at the meeting station (Galt) are analyzed for their interdependence structure and to estimate the bivariate return period. The annual extreme flow data has been obtained from the website of the water survey of Canada [22]. Additionally, the annual extreme flows at the two rivers, Speed and Grand at Galt, Cambridge, are analyzed to explore the probability of joint occurrence of extreme events at the two rivers.
The selected case study of the joint occurrence of flood in Two Rivers (Grand River and Speed River) is of great importance due to several reasons. Firstly, these two rivers meet at a high settlement urban area, which makes it crucial to study their joint occurrence of flood. Urbanization significantly increases the risk of flooding in urban settings [23], as is the case in the watershed selected in this study, which may lead to severe consequences, including loss of life, property damage, and environmental degradation. Therefore, studying the flood dynamics in these rivers is essential to mitigate the risk of flooding and ensure sustainable development in the region. Secondly, the frequent occurrence of floods in the area and the long history of flooding in the Grand River system highlight the urgency of the study. Floods in the region can occur in all seasons, and they have caused significant damage in the past, such as the major flood events of 1912, 1948, 1974, and 2017 [24]. Therefore, understanding the flood dynamics and predicting the flood risk accurately can help the local authorities in taking effective measures to reduce flood damage and ensure public safety. Lastly, the Grand River is the largest river in southern Ontario, which makes it a crucial water resource for the region. The river provides water for various purposes, including drinking water, irrigation, and industrial use [24]. Therefore, it is essential to study the flood dynamics in this river to ensure the sustainability of water resources in the region.

2.2. Copula in bivariate frequency analysis

To estimate a multivariate return period, joint probability analysis of the variables needs to be conducted, which would become complicated if traditional methods are employed as the marginal distributions of the variables can differ. Copulas can be efficiently used in this scenario as copulas are functions that describe the correlation structure between random variables, irrespective of their marginal distributions [25]. As per Sklar’s theorem, any multivariate joint distribution can be described in terms of univariate marginal distribution functions and a copula defining the dependence structure between the variables.
Consider two random variables, Y1 and Y2, with distribution functions F1(Y1) and F2(Y2), respectively. As per Sklar’s theorem, there always exists a copula function (C) such that,
F(Y1 = y1, Y2 = y2) = C(F1(y1), F2(y2))
where C(ul,u2) is itself a distribution function, where u1 and u2 are F1(y1) and F2(y2) respectively.
A copula can be described as a cumulative distribution function with a uniform marginal. The detailed mathematical formulations and derivations of copula can be seen in the literature [26,27,28,29].
Because of its applicability in multivariate analysis, the copula is being widely used in the financial sector and in making business decisions [30,31,32]. In the past few decades, its applicability in the field of hydrological and meteorological studies is becoming more and more popular [27,33,34].
One of the key advantages of using copula functions in flood studies is their ability to model the tail dependence of variables. The tail dependence of variables refers to the degree to which extreme values of one variable are associated with extreme values of another variable. In the context of flood studies, this means that copula functions are particularly useful for analyzing rare and extreme flood events that have the potential to cause significant damage to communities and infrastructure. Accurately modeling tail dependence is critical in accurately assessing flood risk. Traditional methods of analyzing flood risk often assume that variables are independent, which can lead to underestimating the likelihood of extreme flood events. Copula functions, on the other hand, are able to capture the complex dependencies between variables, including the tail dependence, allowing for a more accurate assessment of flood risk.
By modeling tail dependence, copula functions can provide valuable insights into the likelihood and potential impact of extreme flood events. This information can be used to inform flood risk management strategies, such as the development of flood warning systems, the construction of flood protection infrastructure, and the implementation of land-use planning and zoning policies that take into account the potential impact of floods.
Copula functions offer a powerful tool for modeling dependence of variables in flood studies. By accurately capturing the complex dependencies between flood variables, copula functions can provide valuable insights into the likelihood and potential impact of extreme flood events, helping to inform flood risk management strategies and ultimately protect communities and infrastructure from the devastating effects of floods.

2.3. Joint and conditional return period using Copula

The return period is an estimate (statistical measurement) of the interarrival time between events, such as floods or earthquakes of a certain intensity. It is often used for risk analysis and infrastructure design purposes [27].
For univariate studies, the return period (T) is the average time interval between occurrences of the event Y>y and can be described as below: [34,35,36]
T = μ P ( Y > y ) = μ 1 − F Y ( y )
Where P ( Y > y ) is the probability of exceedance, F Y ( y ) is the non-exceedance probability and μ denotes the average interarrival time between two events (or realizations of the process)

2.3.1. Joint Return Period Using Copula

In a bivariate analysis using copula, the joint /conditional probabilities and corresponding return period can be calculated using the copula distribution function. Some of such relations are given in Equations 3 to 8 below [27]:
Consider two random variables (Y1 & Y2). The copula describing the interdependence of the variables is given as C12. The joint return period for “AND” and “OR” cases and the conditional return period for different conditions can be calculated using the relations given below:
P Y 1 ≤ y 1 = F 1 y 1 = u ; P Y 2 ≤ y 2 = F 2 y 2 = v
C 12 ( u , v ) = F 12 y 1 , y 2 = P 12 Y 1 ≤ y 1 , Y 2 ≤ y 2 ;
"AND" case: Y 1 > y 1 and Y 2 > y 2
The joint return period of the "AND" (where both Y1 and Y2 are exceeded) case can be expressed as follows:
T A N D y 1 , y 2 = μ P 12 Y 1 > y 1 , Y 2 > y 2 = μ 1 − u − v + C 12 ( u , v )
"OR" case: Y 1 > y 1 or Y 2 > y 2
The joint return period of the "OR" case is simply expressed as follows:
T O R = μ 1 − P 12 Y 1 ≤ y 1 , Y 2 ≤ y 2 = μ 1 − C 12 ( u , v )

2.3.2. Conditional Return Period Using Copula

The copula can be used to determine the conditional return periods under different conditions.
Y 2 > y 2 ∣ Y 1 = y 1 ( or   Y 1 > y 1 ∣ Y 2 = y 2 ) :
The corresponding conditional return period is as follows:
T Y 2 > y 2 ∣ Y 1 = y 1 = μ 1 − C 12 ( V ≤ v ∣ U = u ) = μ 1 − ∂ C 12 ( u , v ) ∂ u U = u
Similarly, the conditional return period of
Y 1 > y 1 ∣ Y 2 = y 2 is as follows:
T Y 1 > y 1 ∣ Y 2 = y 2 = μ 1 − ∂ C 12 ( u , v ) ∂ v V = v
The detailed mathematical description of the joint probabilities and return periods using copulas can be seen in literature such as Zhang and Singh [27], Nelson [26] and Hofert et.al [28]

3. Results and Discussions

A bivariate analysis of peak river flow events in two rivers in the Grand River watershed is carried out in the study. In the bivariate analysis, the annual peak river flows at Grand River and Speed River have been analyzed and joint return periods have been estimated.

3.1. Bivariate Copula in estimating joint flood risks

The annual peak river flows from 1951 to 2021 at the Grand and Speed rivers were analyzed. The annual peak flow events at the rivers are shown in Figure 2.
The marginal probability distributions that fit each of the rivers’ peak flow data were estimated. The probability distributions such as Gumbel, Normal, Gamma, and exponential distributions were selected as possible marginal distributions for the peak flow of Speed and Grand Rivers. The parameters for the distributions were estimated using the Maximum Likelihood method and the best fit marginal distribution is selected by the Akaike information criterion [37] (with the lowest AIC value). The Speed River and Grand River data are observed to be following normal and gamma distribution, respectively.
The Speed River and Grand River flow data behaved differently in terms of probability distributions which makes it difficult to calculate joint probability distributions of the events. Copulas are hence used here, as they can be easily applied in such scenarios irrespective of the marginal distributions of individual variables. It is worth mentioning that the observed river flow data of the Speed and Grand Rivers have a Kendall correlation coefficient of 0.6, exhibiting a medium correlation between their occurrences.
The bivariate copula that fits the random variables is estimated by using the function “bicopselect” in “VineCopula” R package [38]. Before using the function, the data are preconditioned as data vectors within the range of [0, 1]. The bivariate copula is selected so that it fits the two variables (Speed and Grand Rivers data) perfectly and the selected copula is BB7 copula [39]. The observed river flow data and the simulated data by copula are given in Figure 3, showing the fitted copula can simulate the data with great accuracy. The probability distribution function (pdf) and cumulative distribution function (cdf) of the developed bivariate distribution are shown in Figure 4 and Figure 5, respectively.
The bivariate return periods of the two river flow events were also estimated using the fitted copula by applying Equations 3-8. The AND return period of the events, where the probability of both the rivers’ flow exceeding the given values, were estimated using Equation 5. The OR return period where the probability of either of the rivers’ flow conditions exceeds the given condition was estimated using Equation 6. The conditional return periods were also estimated using Equations 7 and 8. The joint return periods of Speed and Grand Rivers flow extremes are shown in Figure 6 and Figure 7. The conditional return periods of Speed and Grand Rivers flow extremes are given in Figure 8 and Figure 9. Comparing the joint return periods with the traditional univariate return periods of flow data gives a comprehensive outlook of the system. The univariate return periods have been estimated by traditional extreme value analysis using the marginal probability distributions (Equation 2) and are given in Figure 10.
By incorporating the mutual dependence of the Speed and Grand Rivers flow extremes by means of the copula, detailed information regarding the joint probability of flood risks can be obtained. The joint return period (AND) of the Speed and Grand Rivers flow extremes (Figure 6) shows the return period for the joint occurrence of both the Speed and Grand Rivers extremes. Our analysis of the copula-based approach revealed important findings regarding the dependence between the Speed and Grand Rivers flow extremes. Specifically, the conditional return period analysis of Speed River extremes given the Grand River flow (Figure 8) showed that as the Grand River flow extremes increase, the magnitude of a t-year return period event for the Speed River flow decreases until the Grand River flow was approximately near 600 m3/s. Beyond this point, the magnitude of the Speed River flow events remained constant for all return periods. Similarly, the conditional return period analysis of Grand River extremes given the Speed River flow (Figure 9) showed that as the Speed River flow extremes increase, the magnitude of a t-year return period event for the Grand River flow increases.
These results have important implications for flood risk management and planning. By incorporating the dependence structure between the two rivers using a copula-based approach, we can obtain more accurate estimates of the joint probability of flood risks. Moreover, the conditional return period analysis provides insights into how the risk of floods in one river may be affected by changes in the flow of the other river. These insights can help inform flood risk management strategies and improve our ability to plan for extreme weather events.
For a more detailed understanding, the return period for some combinations/cases of Grand and Speed River flow extremes are given in Table 1. The combinations of Grand and Speed Rivers are selected based on the basic statistics of the flow data. The mean, the 3rd Quartile, and the upper control limits (mean+1*standard deviation & mean+1.5* Standard deviation) of Speed and Grand Rivers peak flow data are used to find out the respective bivariate and univariate return periods.
Based on the observations from Table 1, it is apparent that when dealing with higher flow conditions, joint return periods should be taken into account when planning flood risk management strategies. For instance, it can be seen that while considering the joint return period for either Speed flow or Grand flow to exceed 90 and 600, respectively, in the area, it is ten years, whereas the univariate return period is 15 and 12 for Speed and Grand flow, respectively. Furthermore, it is worth noting that the 6-year return period flow of 77 and 607 in Speed and Grand rivers (while considering univariate analysis) can translate to a 9-year return period of simultaneous flow, which also needs to be considered. Therefore, the joint return period is essential in accurately assessing flood risk and planning appropriate management strategies, particularly in areas with high flow conditions.
The comparison between univariate and bivariate probabilistic analysis of extreme river flow events using copulas highlights the benefits of considering the dependencies between the extreme river flows at the two rivers. The univariate analysis focuses on modelling the marginal distribution of a single variable, here, the river flow extreme of a river. While it provides information about the likelihood of individual extreme events, it does not consider any dependencies between the extreme flow events at the two rivers. On the other hand, bivariate analysis based on copula focuses on modelling the joint distribution of two river flow extreme variables (at the Speed and Grand rivers) and considers the dependencies between variables. This leads to a more comprehensive understanding of the relationship between the two rivers’ extremes and can inform risk management and decision-making in a way that univariate analysis cannot. Bivariate analysis using copulas can provide a more accurate representation of the overall risk, as it accounts for complex dependencies, including non-linear relationships, between variables. In contrast, the univariate analysis only provides information about individual events and does not account for the interplay between variables, which can result in an underestimation of the overall risk. Bivariate analysis incorporating dependencies between variables leads to improved prediction accuracy compared to univariate analysis.

4. CONCLUSIONS

The main objective of this paper is to estimate the joint return period of river flow extremes in two rivers located in the Grand River watershed in Ontario, Canada. To achieve this goal, the study employs bivariate copula analysis, which enables the incorporation of mutual dependencies between the two events. By estimating the return period for the joint occurrence of extremes at the two rivers, the study provides valuable insights into the interdependence of the two river flows and how this interdependence influences the behavior of river flow extreme patterns. One of the key observations of the study is that the interdependence between the two river flows leads to behavioral changes in the river flow extreme pattern. The copula analysis employed in the study is able to capture the dependencies between different extreme river flow events, which traditional methods of extreme value analysis may not be able to do. The use of copulas in studying joint flood risks has several benefits, including flexibility in modeling complex relationships, separation of marginal distributions and dependence structure, better handling of extreme events, improved risk assessment, and improved prediction accuracy.
Furthermore, studying joint flood risks provides a more comprehensive understanding of the complex and interrelated risks posed by floods. This understanding can inform decision-making for effective risk management. By highlighting the importance of considering joint flood risks, the study contributes to the body of knowledge on flood risk management and provides useful insights for policymakers and other stakeholders involved in flood risk management.
In conclusion, this paper emphasizes the importance of studying joint flood risks using copula analysis. The study provides valuable insights into the interdependence between river flows and how this interdependence influences the behavior of river flow extreme patterns. The use of copulas in studying joint flood risks can provide several benefits, including improved risk assessment and prediction accuracy, and can inform decision-making for effective risk management.

References

  1. AghaKouchak, A.; Chiang, F.; Huning, L.S.; Love, C.A.; Mallakpour, I.; Mazdiyasni, O.; Moftakhari, H.; Papalexiou, S.M.; Ragno, E.; Sadegh, M. Climate Extremes and Compound Hazards in a Warming World. Annu Rev Earth Planet Sci 2020, 48, 519–548. [Google Scholar] [CrossRef]
  2. Chen, L.; Singh, V.P.; Shenglian, G.; Hao, Z.; Li, T. Flood Coincidence Risk Analysis Using Multivariate Copula Functions. J Hydrol Eng 2012, 17, 742–755. [Google Scholar] [CrossRef]
  3. Karmakar, S.; Simonovic, S.P. Bivariate Flood Frequency Analysis. Part 2: A Copula-Based Approach with Mixed Marginal Distributions. J Flood Risk Manag 2009, 2, 32–44. [Google Scholar] [CrossRef]
  4. Kao, S.; Govindaraju, R.S. A Bivariate Frequency Analysis of Extreme Rainfall with Implications for Design. Journal of Geophysical Research: Atmospheres 2007, 112, 2007JD008522. [Google Scholar] [CrossRef]
  5. Zhang, L.; Singh, V.P. Bivariate Flood Frequency Analysis Using the Copula Method. J Hydrol Eng 2006, 11, 150–164. [Google Scholar] [CrossRef]
  6. Righi, M.B.; Ceretta, P.S. Analyzing the Dependence Structure of Various Sectors in the Brazilian Market: A Pair Copula Construction Approach. Econ Model 2013, 35, 199–206. [Google Scholar] [CrossRef]
  7. Danaher, P.J.; Smith, M.S. Modeling Multivariate Distributions Using Copulas: Applications in Marketing. Marketing Science 2011, 30, 4–21. [Google Scholar] [CrossRef]
  8. Dißmann, J.; Brechmann, E.C.; Czado, C.; Kurowicka, D. Selecting and Estimating Regular Vine Copulae and Application to Financial Returns. Comput Stat Data Anal 2013, 59, 52–69. [Google Scholar] [CrossRef]
  9. Smith, M.S. Copula Modelling of Dependence in Multivariate Time Series. Int J Forecast 2015, 31, 815–833. [Google Scholar] [CrossRef]
  10. Liu, Y.R.; Li, Y.P.; Ma, Y.; Jia, Q.M.; Su, Y.Y. Development of a Bayesian-Copula-Based Frequency Analysis Method for Hydrological Risk Assessment – The Naryn River in Central Asia. J Hydrol (Amst) 2020, 580, 124349. [Google Scholar] [CrossRef]
  11. Nazeri Tahroudi, M.; Ramezani, Y.; De Michele, C.; Mirabbasi, R. Trivariate Joint Frequency Analysis of Water Resources Deficiency Signatures Using Vine Copulas. Appl Water Sci 2022, 12, 67. [Google Scholar] [CrossRef]
  12. Perz, A.; Wrzesiński, D.; Sobkowiak, L.; Stodolak, R. Copula-Based Geohazard Assessment – Case of Flood-Prone Area in Poland. J Hydrol Reg Stud 2022, 44, 101214. [Google Scholar] [CrossRef]
  13. Razmkhah, H.; Fararouie, A.; Ravari, A.R. Multivariate Flood Frequency Analysis Using Bivariate Copula Functions. Water Resources Management 2022, 36, 729–743. [Google Scholar] [CrossRef]
  14. Xie, K.; He, Y.; Kim, J.-S.; Yoon, S.-K.; Liu, J.; Chen, H.; Lee, J.H.; Zhang, X.; Xu, C.-Y. Assessment of the Joint Impact of Rainfall Characteristics on Urban Flooding and Resilience Using the Copula Method. Water Resources Management 2023, 37, 1765–1784. [Google Scholar] [CrossRef]
  15. Razmkhah, H.; Fararouie, A.; Ravari, A.R. Multivariate Flood Frequency Analysis Using Bivariate Copula Functions. Water Resources Management 2022, 36, 729–743. [Google Scholar] [CrossRef]
  16. Feng, Y.; Shi, P.; Qu, S.; Mou, S.; Chen, C.; Dong, F. Nonstationary Flood Coincidence Risk Analysis Using Time-Varying Copula Functions. Sci Rep 2020, 10, 3395. [Google Scholar] [CrossRef]
  17. Razmkhah, H.; Fararouie, A.; Ravari, A.R. Multivariate Flood Frequency Analysis Using Bivariate Copula Functions. Water Resources Management 2022, 36, 729–743. [Google Scholar] [CrossRef]
  18. Wang, S.; Wu, J.; Wang, S.; Xie, X.; Fan, Y.; Lv, L.; Huang, G. Copula-Based Multivariate Simulation Approach for Flood Risk Transfer of Multi-Reservoirs in the Weihe River, China. Water (Basel) 2022, 14, 2676. [Google Scholar] [CrossRef]
  19. Zhong, M.; Zeng, T.; Jiang, T.; Wu, H.; Chen, X.; Hong, Y. A Copula-Based Multivariate Probability Analysis for Flash Flood Risk under the Compound Effect of Soil Moisture and Rainfall. Water Resources Management 2021, 35, 83–98. [Google Scholar] [CrossRef]
  20. Bačová Mitková, V.; Halmová, D.; Pekárová, P.; Miklánek, P. The Copula Application for Analysis of the Flood Threat at the River Confluences in the Danube River Basin in Slovakia. Water (Basel) 2023, 15, 984. [Google Scholar] [CrossRef]
  21. Kaur, B.; Shrestha, N.; Daggupati, P.; Rudra, R.; Goel, P.; Shukla, R.; Allataifeh, N. Water Security Assessment of the Grand River Watershed in Southwestern Ontario, Canada. Sustainability 2019, 11, 1883. [Google Scholar] [CrossRef]
  22. Environment and natural resources Water Level and Flow (accessed on 29 March 2022).
  23. Nirupama, N.; Simonovic, S.P. Increase of Flood Risk Due to Urbanisation: A Canadian Example. Natural Hazards 2007, 40, 25–41. [Google Scholar] [CrossRef]
  24. Grand River Conservation Authority (GRCA) Our Watershed Available online:. Available online: https://www.grandriver.ca/en/our-watershed/Our-Watershed.aspx (accessed on 3 April 2022).
  25. Sklar, A. Fonctions de Repartition à n Dimensionls et Leurs Marges; Paris, 1959; pp. 229–231;
  26. Nelson, R.B. An Introduction to Copulas; Bickel, P. , Diggle, P., Fienberg, S., Gather, U., Olkin, I., Zeger, S., Eds.; 2nd ed.; Springer, 2006; ISBN 10: 0-387-28659-4.
  27. Zhang, L.; Singh, V.P. Copulas and Their Applications in Water Resources Engineering; Cambridge University Press, 2019; ISBN 9781108565103.
  28. Hofert, M.; Kojadinovic, I.; Machler, M.; Yan, J. Elements of Copula Modeling With R; Springer, 2018; ISBN 9783319896342.
  29. Chen, L.; Guo, S. Copulas and Its Application in Hydrology and Water Resources; 2019; ISBN 978-981-13-0573-3.
  30. Vaz de Melo Mendes, B.; Mendes Semeraro, M.; P. Câmara Leal, R. Pair-Copulas Modeling in Finance. Financial Markets and Portfolio Management 2010, 24, 193–213. [Google Scholar] [CrossRef]
  31. Hu, L. Dependence Patterns Across Financial Markets: A Mixed Copula Approach. Applied Financial Economics 2006, 16, 717–729. [Google Scholar] [CrossRef]
  32. Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-Copula Constructions of Multiple Dependence. Insur Math Econ 2009, 44, 182–198. [Google Scholar] [CrossRef]
  33. Bačová Mitková, V.; Halmová, D. Joint Modeling of Flood Peak Discharges, Volume and Duration: A Case Study of the Danube River in Bratislava. Journal of Hydrology and Hydromechanics 2014, 62, 186–196. [Google Scholar] [CrossRef]
  34. Gräler, B.; van den Berg, M.J.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; de Baets, B.; Verhoest, N.E.C. Multivariate Return Periods in Hydrology: A Critical and Practical Review Focusing on Synthetic Design Hydrograph Estimation. Hydrol Earth Syst Sci 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
  35. Salvadori, G.; de Michele, C. Multivariate Multiparameter Extreme Value Models and Return Periods: A Copula Approach. Water Resour Res 2010, 46, 2009WR009040. [Google Scholar] [CrossRef]
  36. Vorobevskii, I.; Kronenberg, R.; Bernhofer, C. Estimation of Joint Return Periods of Compound Precipitation-Discharge Extremes for Small Catchments. Hydrology and Earth System Sciences Discussions 2020, 1–23. [Google Scholar] [CrossRef]
  37. Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans Automat Contr 1974, 19, 716–723. [Google Scholar] [CrossRef]
  38. Nagler, T.; Schepsmeier, U.; Stoeber, J.; Brechmann, E.C.; Graeler, B.; Erhardt, T. VineCopula: Statistical Inference of Vine Copulas Available online: https://github.com/tnagler/VineCopula.
  39. Joe, H. Multivariate Models and Multivariate Dependence Concepts; Chapman and Hall/CRC, 1997; ISBN 9780367803896.
Preprints 70765 g001
Figure 1. Grand River and Speed River meeting at the City of Cambridge, Ontario, Canada.
Figure 1. Grand River and Speed River meeting at the City of Cambridge, Ontario, Canada.
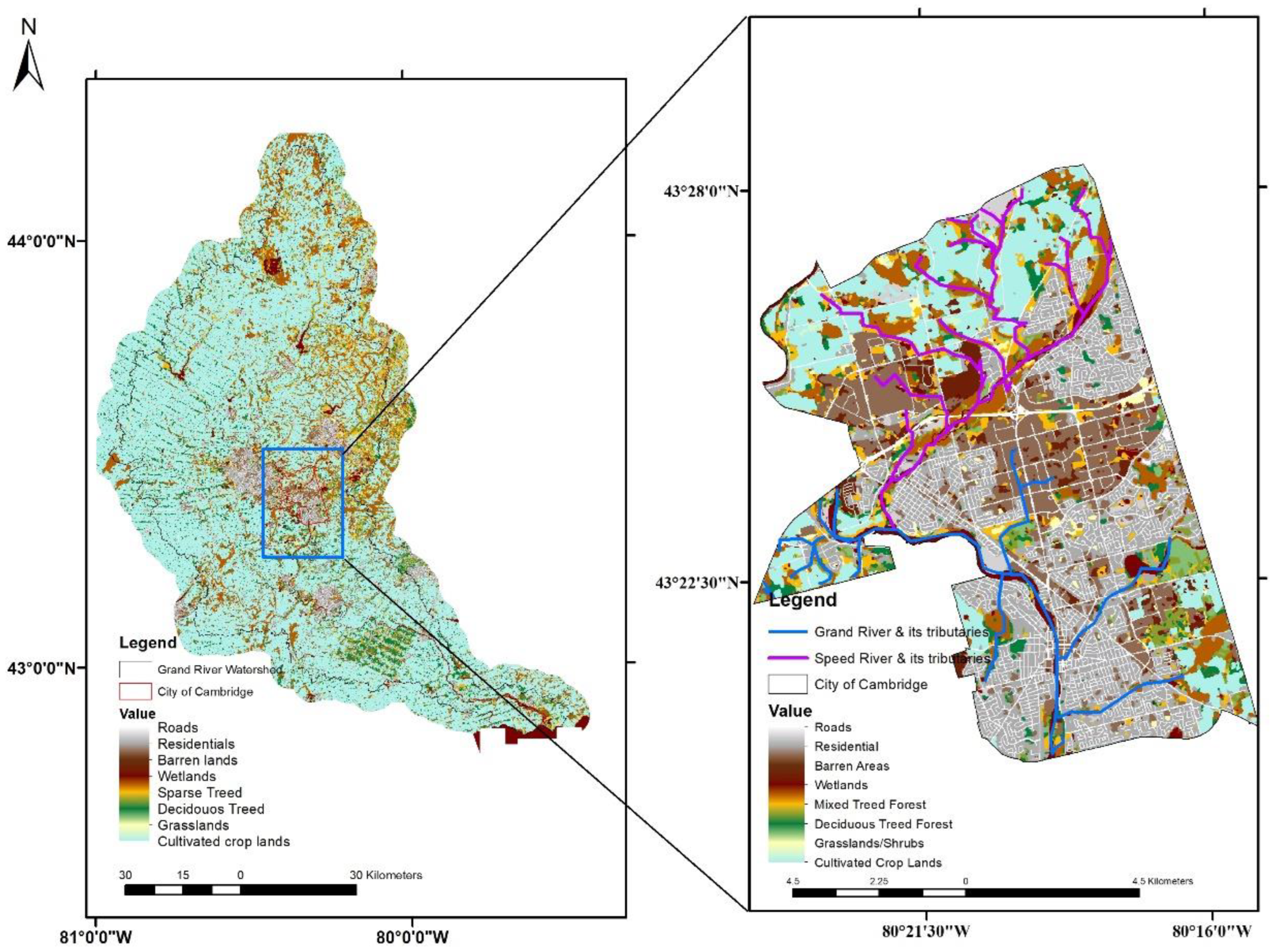
Preprints 70765 g001
Preprints 70765 g002
Figure 2. Annual peak flow events at the Speed River and Grand River in the Grand River watershed in Canada.
Figure 2. Annual peak flow events at the Speed River and Grand River in the Grand River watershed in Canada.
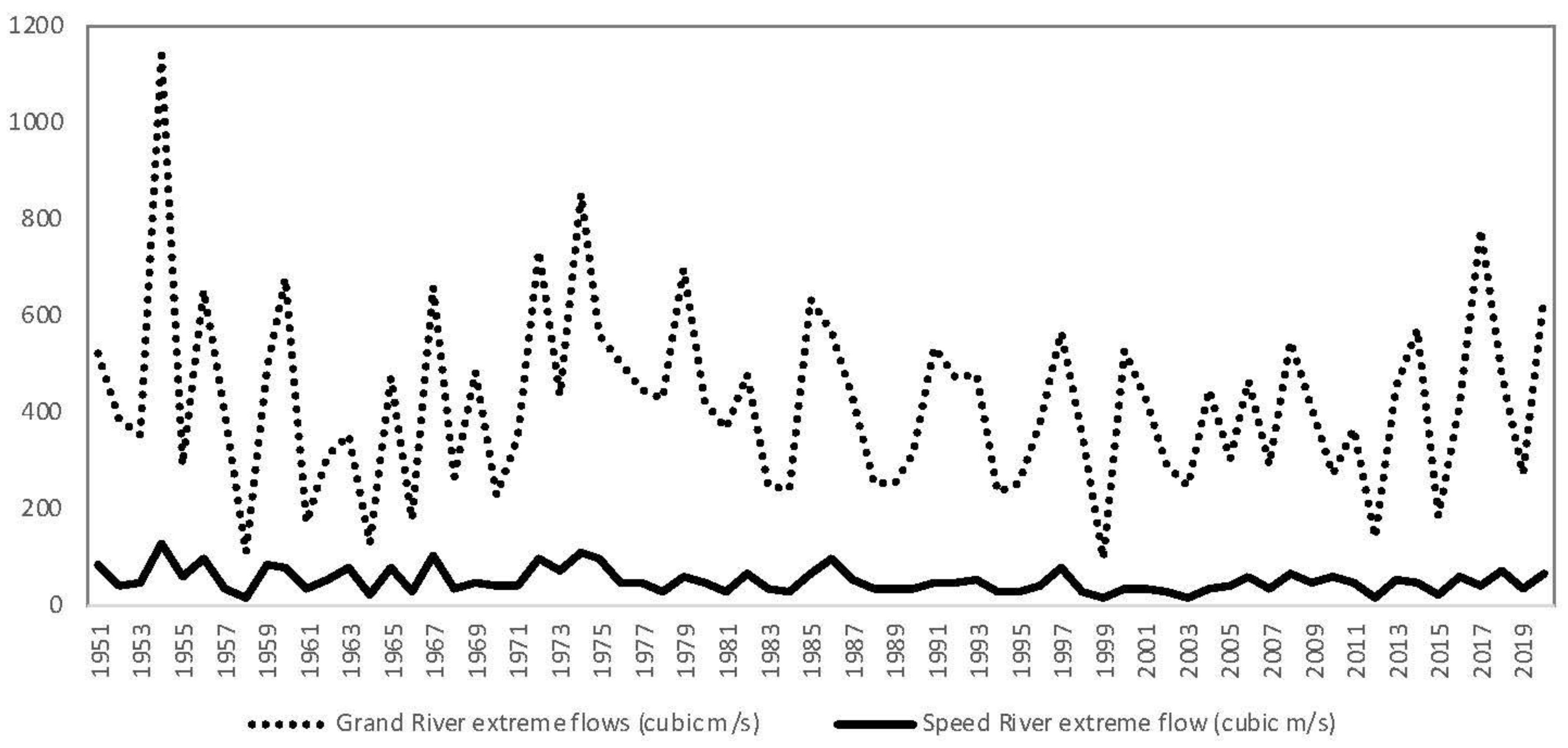
Preprints 70765 g002
Preprints 70765 g003
Figure 3. Observed river flow extremes and simulated data using bivariate copula.
Figure 3. Observed river flow extremes and simulated data using bivariate copula.
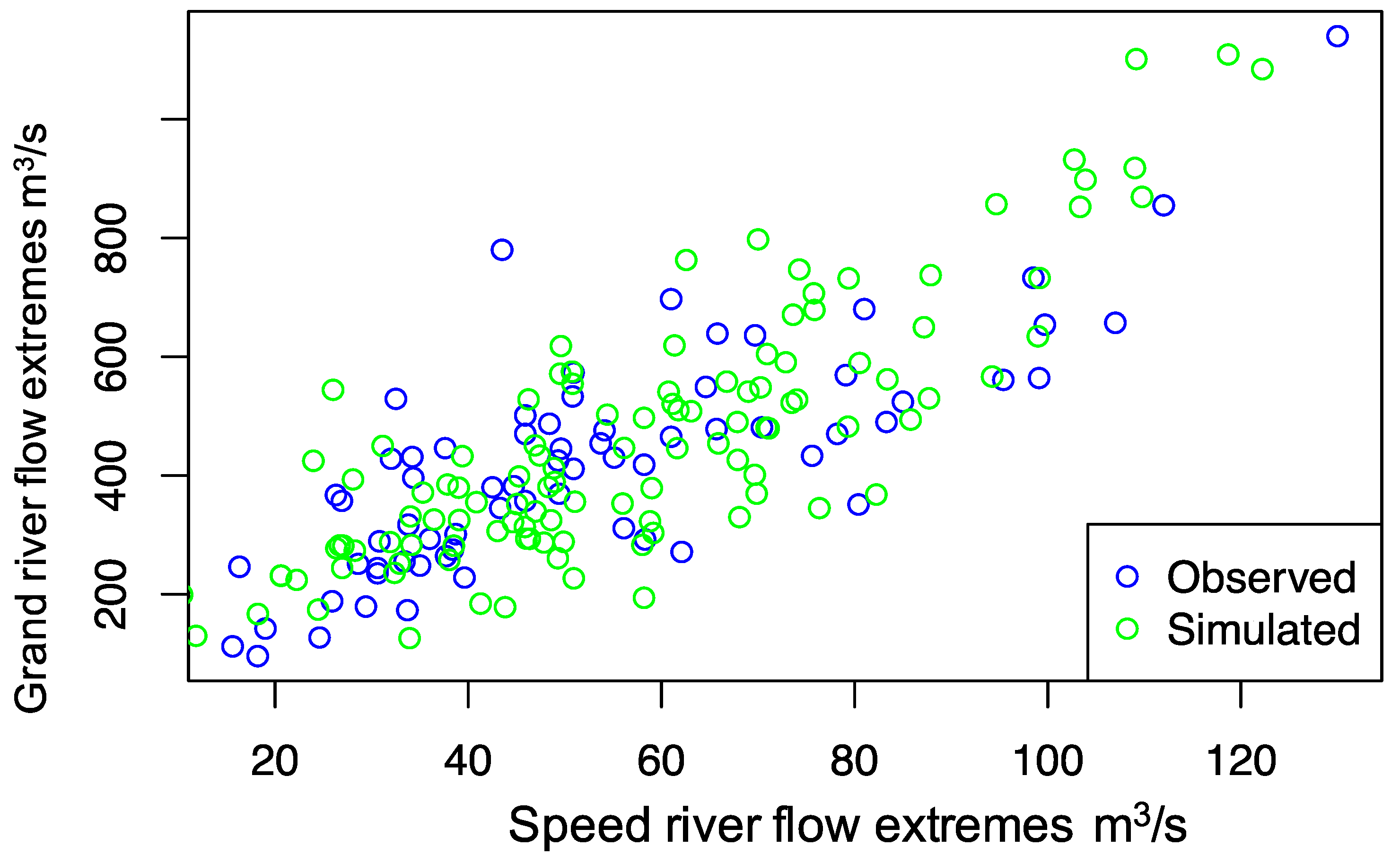
Preprints 70765 g003
Preprints 70765 g004
Figure 4. Probability distribution function (PDF) of the developed bivariate distribution (copula) of the Speed and Grand Rivers flow extremes.
Figure 4. Probability distribution function (PDF) of the developed bivariate distribution (copula) of the Speed and Grand Rivers flow extremes.
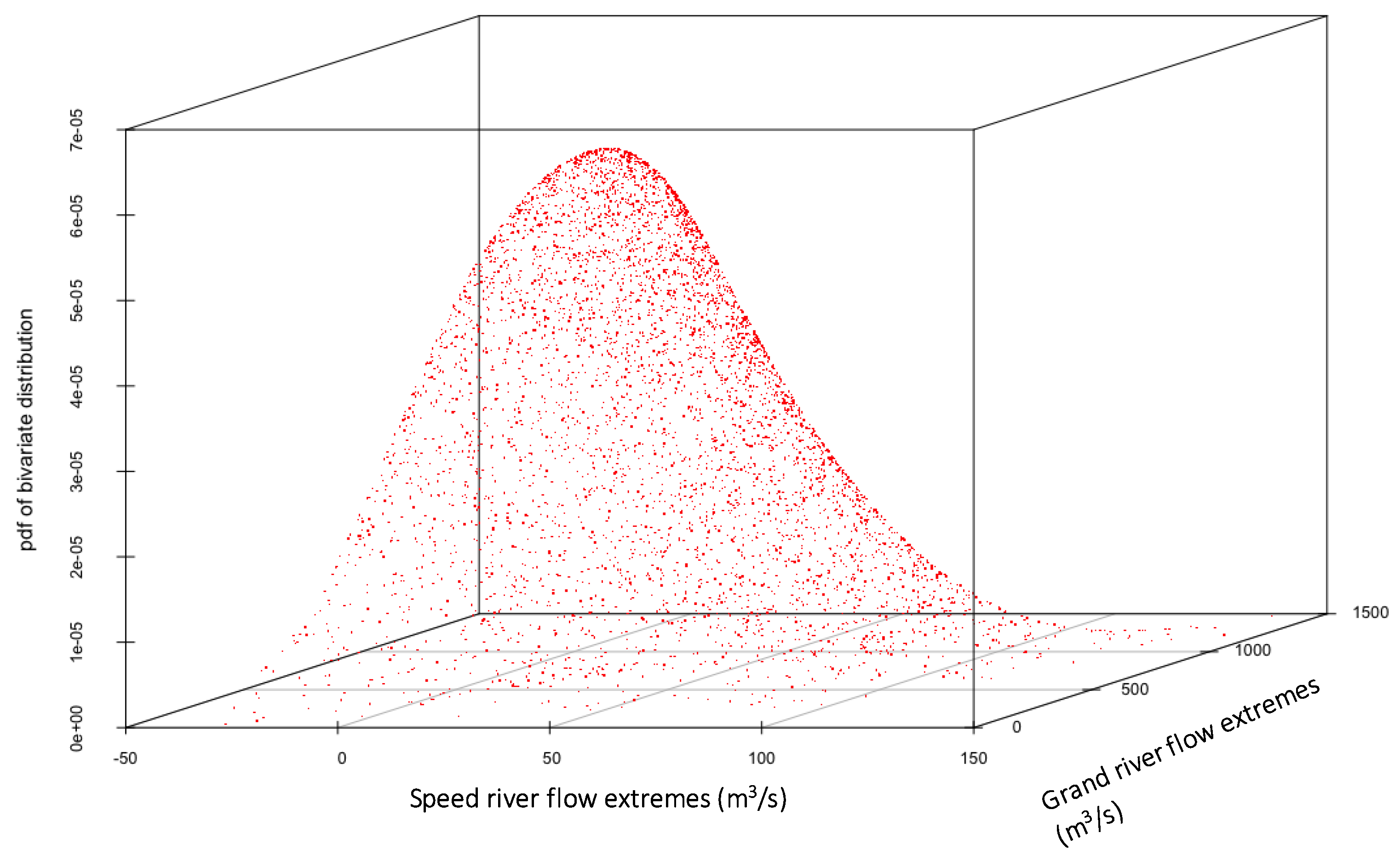
Preprints 70765 g004
Preprints 70765 g005
Figure 5. Cumulative distribution function (CDF) of the developed bivariate distribution of the Speed and Grand Rivers flow extremes.
Figure 5. Cumulative distribution function (CDF) of the developed bivariate distribution of the Speed and Grand Rivers flow extremes.
Preprints 70765 g005
Preprints 70765 g006
Figure 6. Joint return period (AND) of the Speed and Grand Rivers flow extremes.
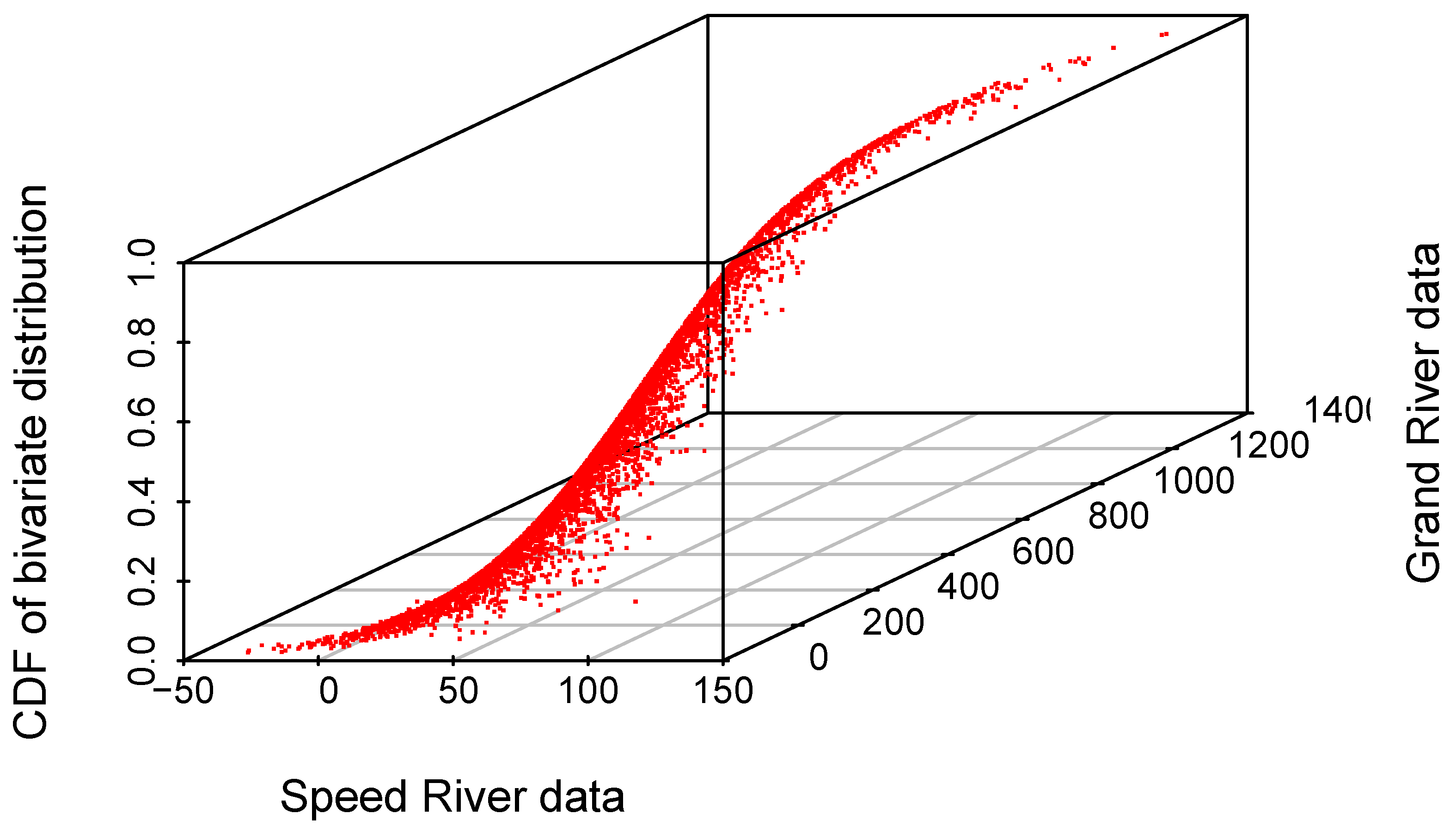
Figure 6. Joint return period (AND) of the Speed and Grand Rivers flow extremes.
Preprints 70765 g006
Preprints 70765 g007
Figure 7. Joint return period (OR) of the Speed and Grand Rivers flow extremes.
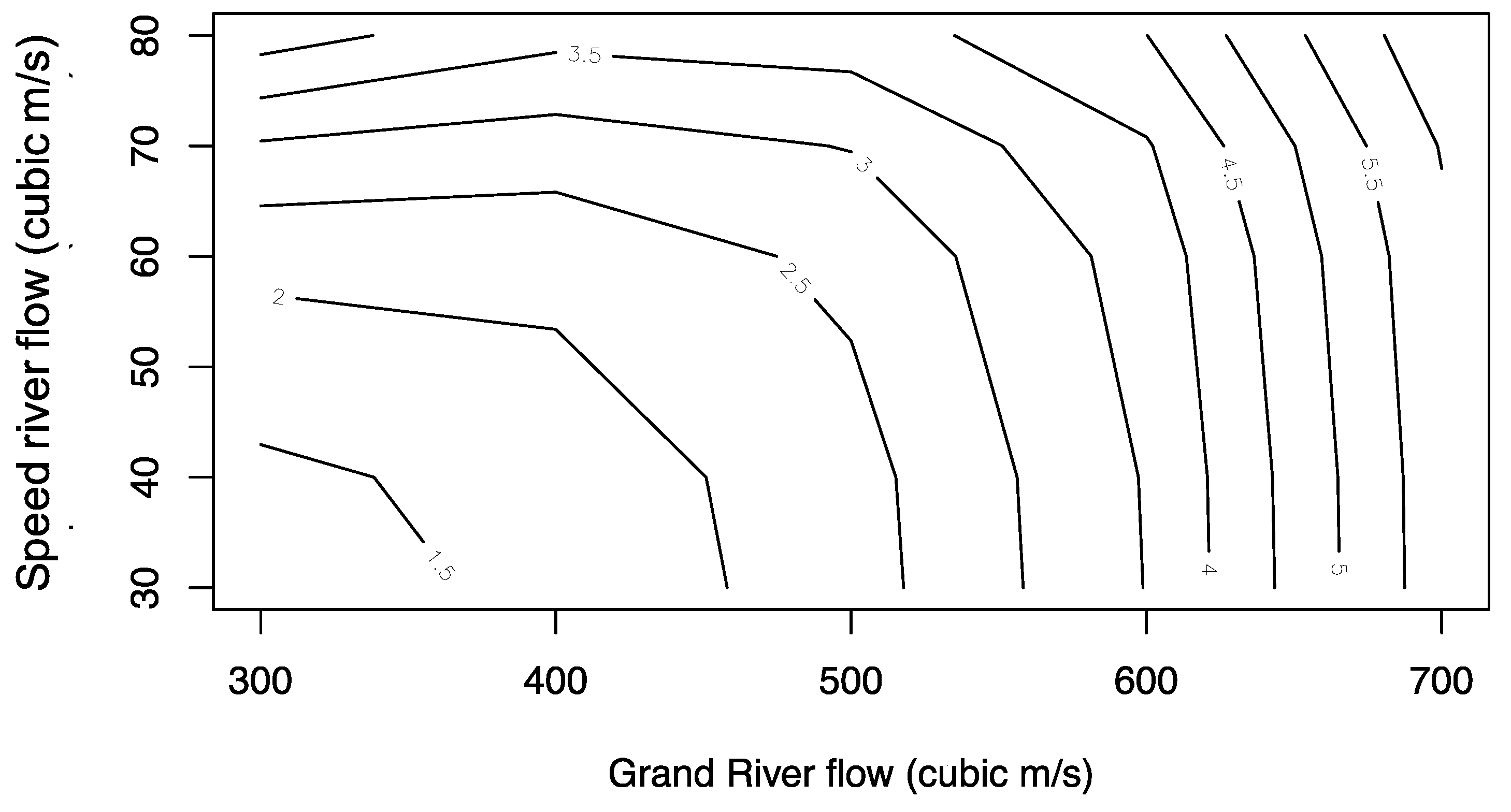
Figure 7. Joint return period (OR) of the Speed and Grand Rivers flow extremes.
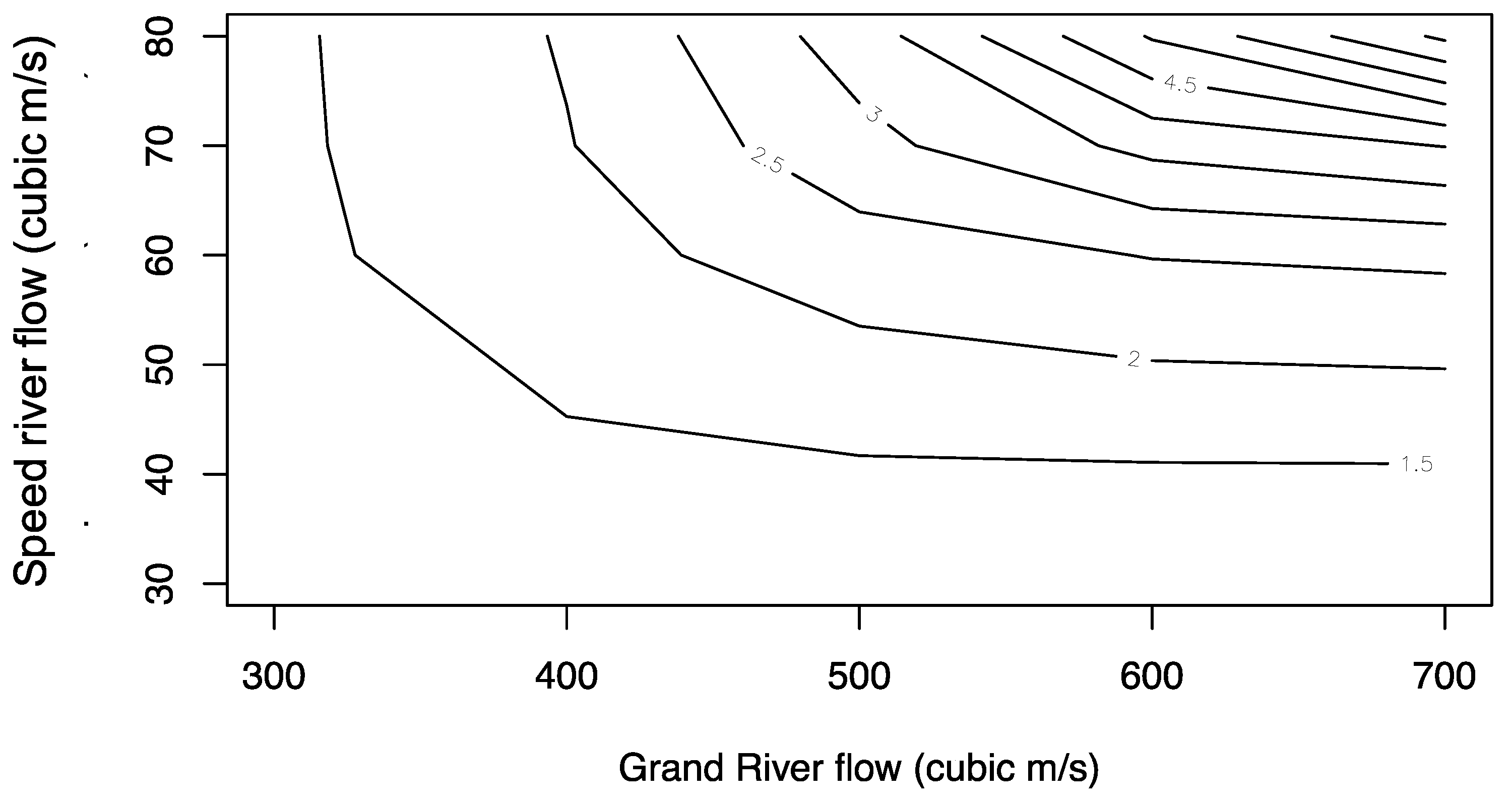
Preprints 70765 g007
Preprints 70765 g008
Figure 8. Conditional return period of Speed River flow extremes given the Grand River flows.
Figure 8. Conditional return period of Speed River flow extremes given the Grand River flows.
Preprints 70765 g008
Preprints 70765 g009
Figure 9. Conditional return period of Grand River flow extremes given the Speed River flows.
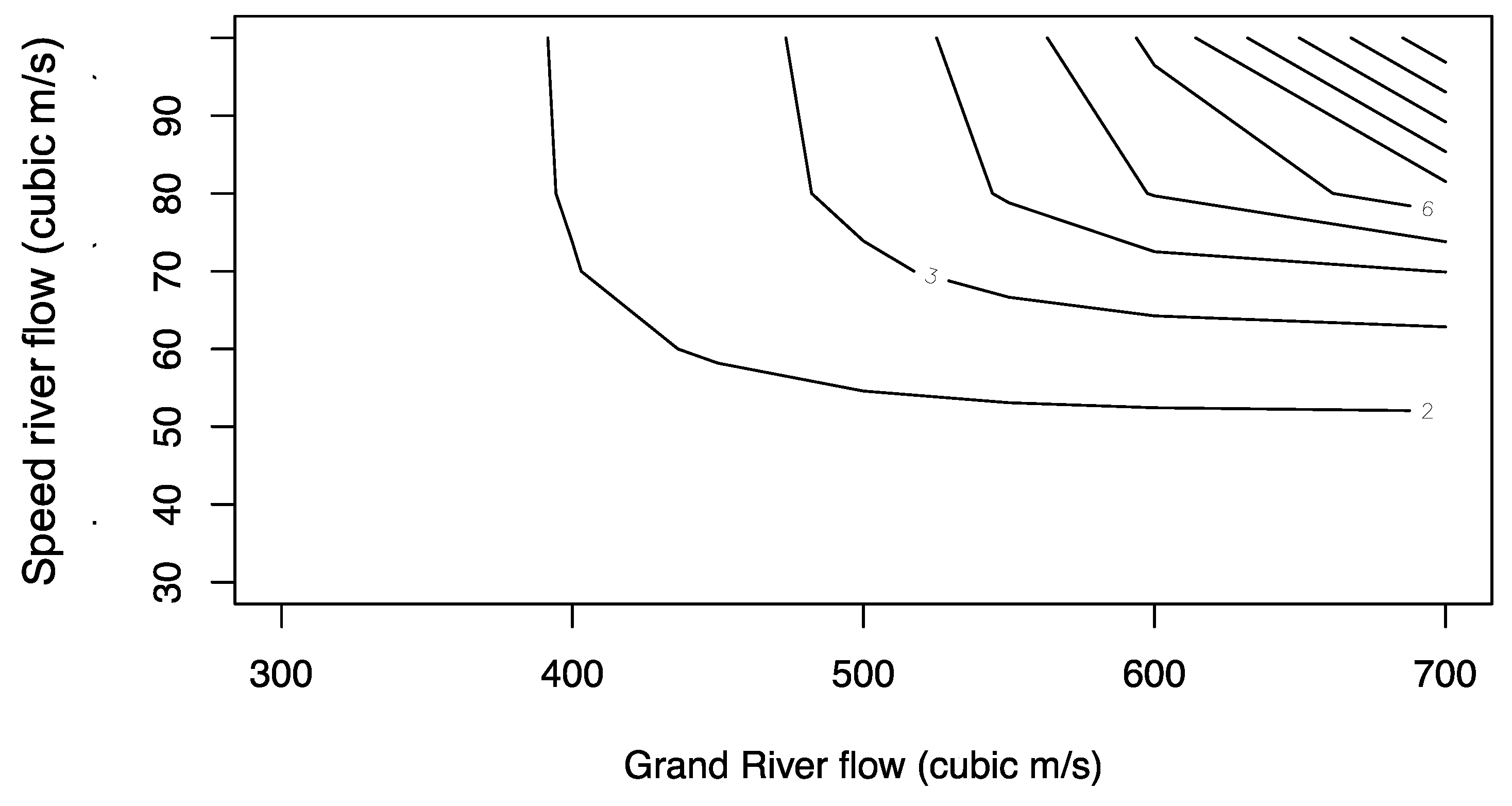
Figure 9. Conditional return period of Grand River flow extremes given the Speed River flows.
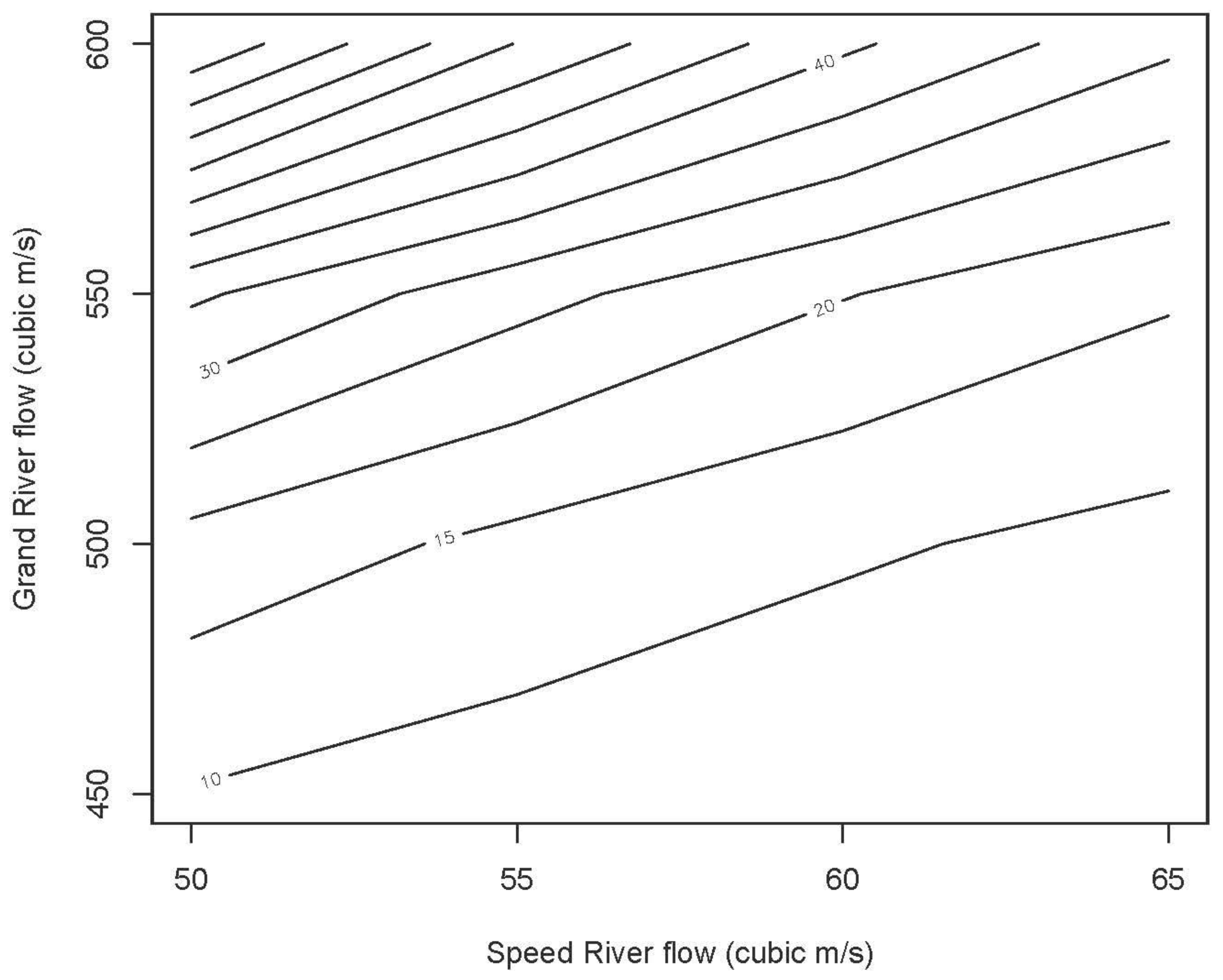
Preprints 70765 g009
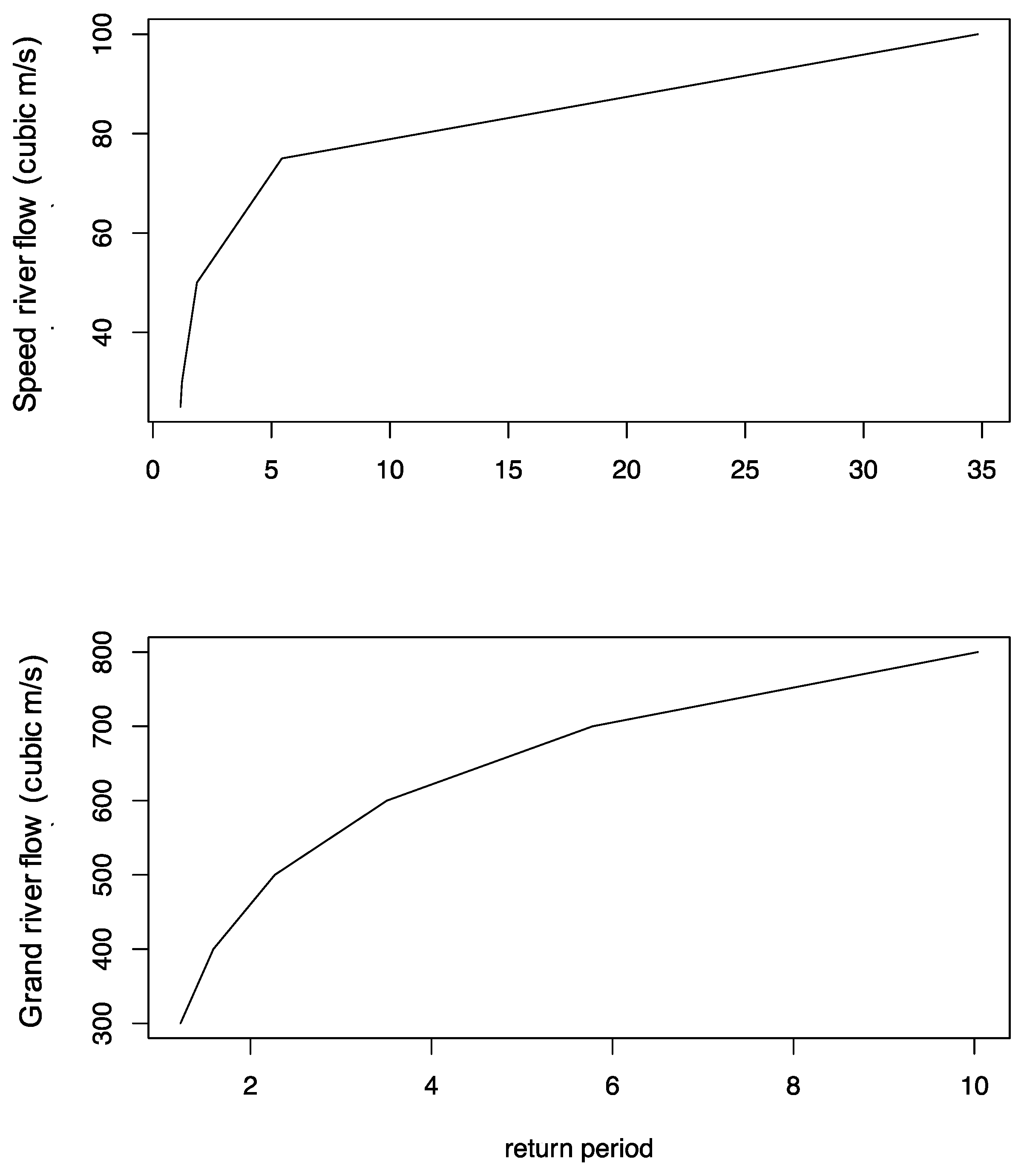
Preprints 70765 g010
Figure 10. Univariate return period of (a) Speed River flow and (b) Grand River flow.
Figure 10. Univariate return period of (a) Speed River flow and (b) Grand River flow.
Preprints 70765 g010
Table 1. Bivariate and univariate return periods of Speed and Grand Rivers flow extremes.
Table 1. Bivariate and univariate return periods of Speed and Grand Rivers flow extremes.
Speed flow (m3/s) Grand flow (m3/s) TAND TOR TS TG
52 420 2.8 1.7 2 2.2
65 518 5 2.7 3.2 3.8
77 607 9.5 4.7 6.1 6.5
90 700 20.7 10 15 12.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated