Preprint
Short Note
On the Group of Universal Gates for a Two-Qubit Quantum System
Altmetrics
Downloads
196
Views
325
Comments
0
This version is not peer-reviewed
Submitted:
10 April 2023
Posted:
11 April 2023
You are already at the latest version
Alerts
Abstract
The goal of finding a commutative group of gates from the set of unitary matrices is to simplify the process of quantum computing. If a set of gates is commutative, then we can apply the gates in any order without affecting the final outcome. This is important because quantum systems are very sensitive to errors and decoherence, and any disruption to the system can cause errors in the computation.By having a commutative group of gates, we can simplify the process of designing quantum algorithms and reduce the risk of errors. This is particularly important for solving complex computational problems that cannot be solved by classical computers.
Keywords:
Subject: Computer Science and Mathematics - Computational Mathematics
1. Introduction. Formulation of the problem
By definition, a two-qubit system is a quantum system consisting of a pair of two-level quantum elements [1]. For example, a quantum system of two spins is one. In this case, the basic quantum state of an arbitrary two-qubit system will be written uniformly as:
| 00 >, | 01 >, | 10 >, | 11 >
Based on this, the general quantum state of a two-qubit system can be written in the following form:
where λk, k = 1, 4 are the so-called complex amplitudes that satisfy the well- known normalization condition:
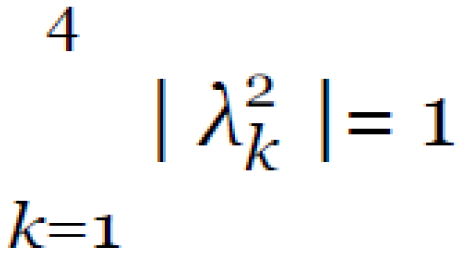
| ψ >= λ1 | 00 > +λ1 | 01 > +λ3 | 10 > +λ4 | 11 >
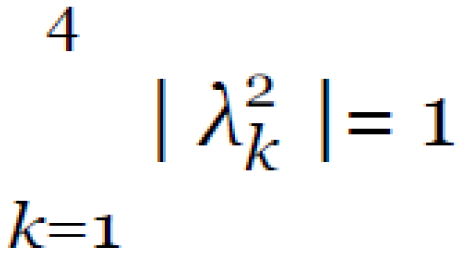
Next, let C be the complex plane. Then it is obvious that the four –vector of complex amplitudes Λ = (λ1, λ2, λ3, λ4) ∈ C4 – is an element of the four- dimensional vector (complex) space. As [2] is known, changes in the states of a quantum system are studied based on the analysis of changes in the values of the corresponding complex amplitudes –λk, k = 1, 4, over time.
Speaking differently, any change in the state of a quantum system is a conse- quence of changes in the phase space of events C4. In the language of mathemat- ics, this means that the original four-dimensional complex space C4 undergoes a linear non-degenerate transformation with the help of some unitary matrix ([2]) of the form:
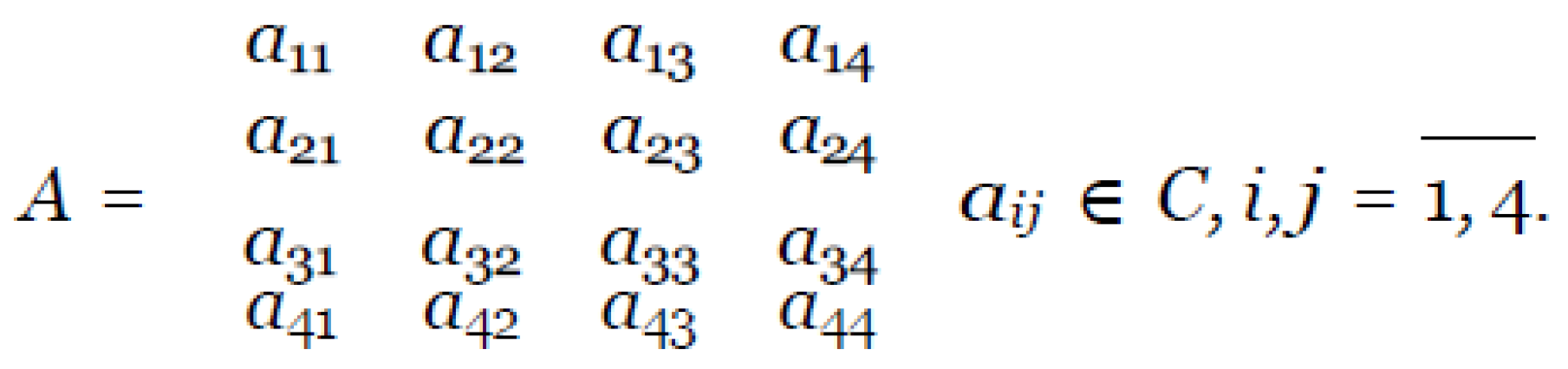
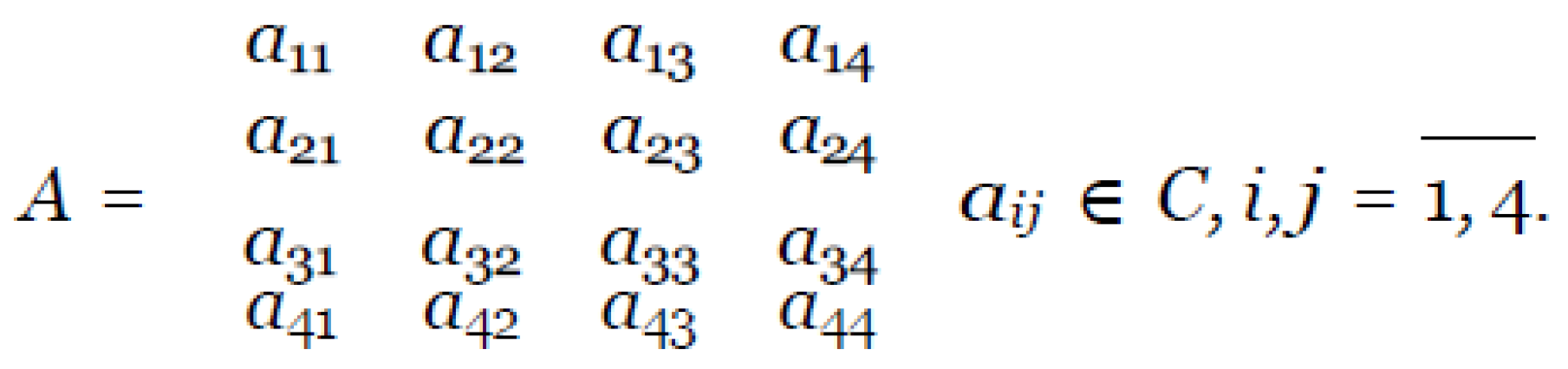
Any unitary matrix of the form (4) is called a two-qubit quantum gate. If such a gate is known, then we can say that the quantum system goes from one state Λ = (λ1, λ2, λ3, λ4) to another state Ω = (ω1, ω2, ω3, ω4) like this:
Ω = A × Λ
It is clear that the larger the set of q(6)uantum gates at our disposal, the more we know about the various states of a quantum system. A set of gates is said to be universal if any unitary transformation can be approximated with any given accuracy by a finite sequence of gates from this set. The essential problem here is that gates of the form (4) are not permutation matrices, that is, in the general case for two gates A, B we get:
A × B ̸= B × A
In this case, nothing can be said about which state of the quantum system was the previous and which was the next. Moreover, finding a gate (unitary matrix) of the form (4) in itself is still an unsolved, most difficult problem in matrix algebra. Nevertheless, in this article we pose the problem of extracting a commutative (Abelian) gate group from the entire set of unitary matrices of the form (4). If this problem is successfully solved, we will find and describe the continuum set of two-qubit quantum gates. Moreover, all valves will be per- mutable. This is a step of fundamental importance for solving applied problems of quantum informatics. We note that in what follows we will essentially rely on the mathematical methods of four-dimensional analysis, first described in the monograph [2
2. Auxiliary information. Description of the problem solving method
Let Z = (z1, z2, z3, z4), an arbitrary element of the event space C4. Then (see [2]), we can find a bijection of the following form:
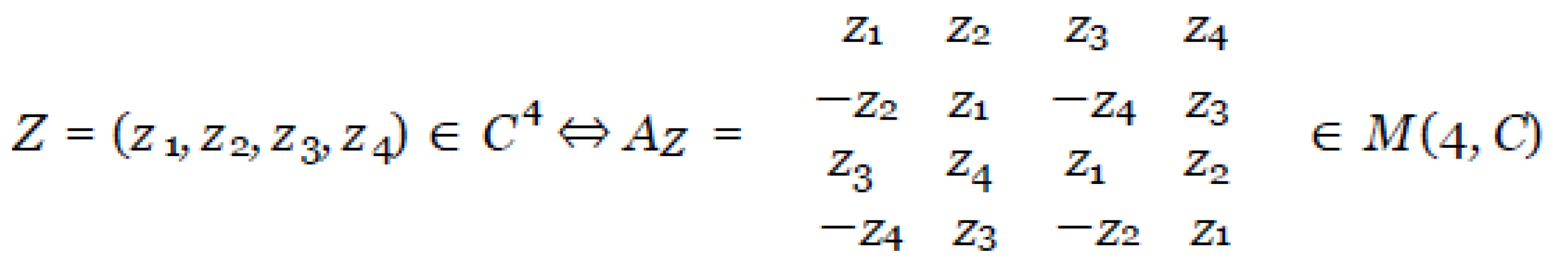
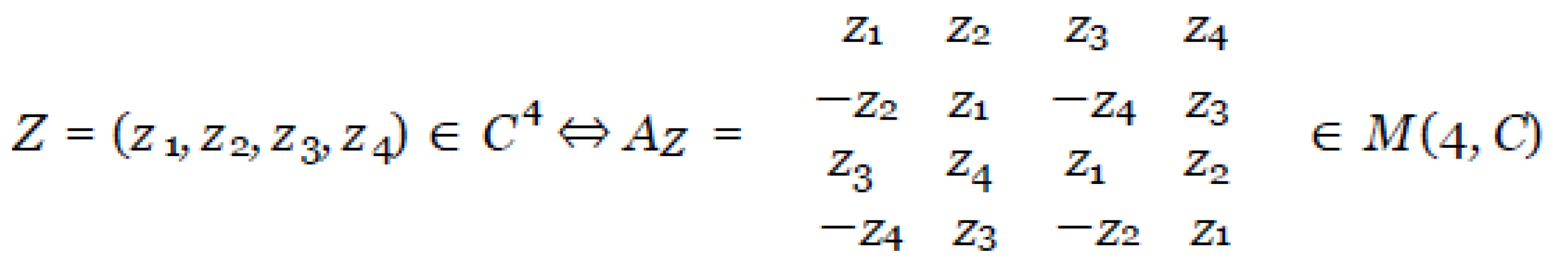
It is easy to show that the set of four-dimensional complex numbers C4 and the set of complex matrices M (4, C) are linear spaces over the field of complex num- bers. It is very important that the set M (4, C) consists entirely of permutation matrices, that is, the operation of matrix multiplication in it is commutative. This is easily verified.
Further, the key point is that there is an isomorphism between these sets, as linear spaces over the field of complex numbers. This follows automatically from the correspondence of the form:
λZ + µW ∈ C4 ⇔ AλZ+µW = λAZ + µAW ∈ M (4, C).
The presence of isomorphism shows that any movement in the space of four- dimensional complex numbers C4 corresponds to a similar movement in the matrix sets M (4, C) and vice versa. And this means that we must look for gates (unitary matrices) precisely in the class of matrices M (4, C). This is the key finding of our research. The description of a two-qubit quantum system, a priori, is given not by any matrices of the form (4), but by unitary matrices of the form AZ ∈ M (4, C) from the formula (7). The method for finding unitary (orthogonal) matrices of just this type is described in detail in the monograph [2].
3. Statement and proof of the main result
The main result of this paper can be formulated as a theorem.
Theorem 1.
There is an Abelian group of two-qubit gates with identity. In this case, any two-qubit gate (group element) has the following form:
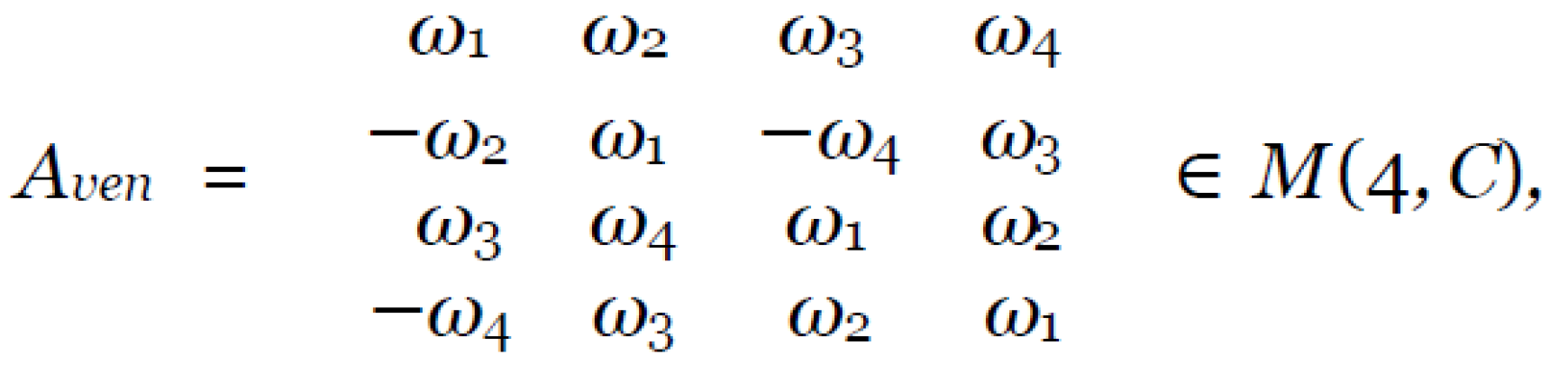
where the matrix elements are given by the formulas:
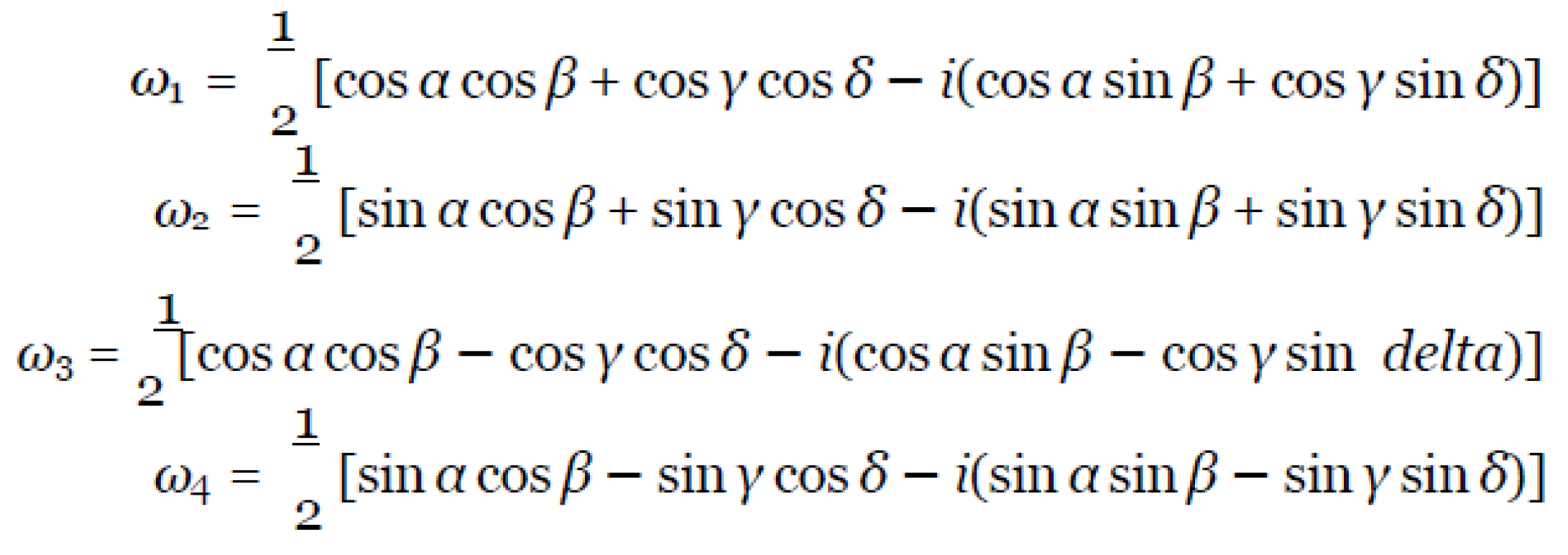
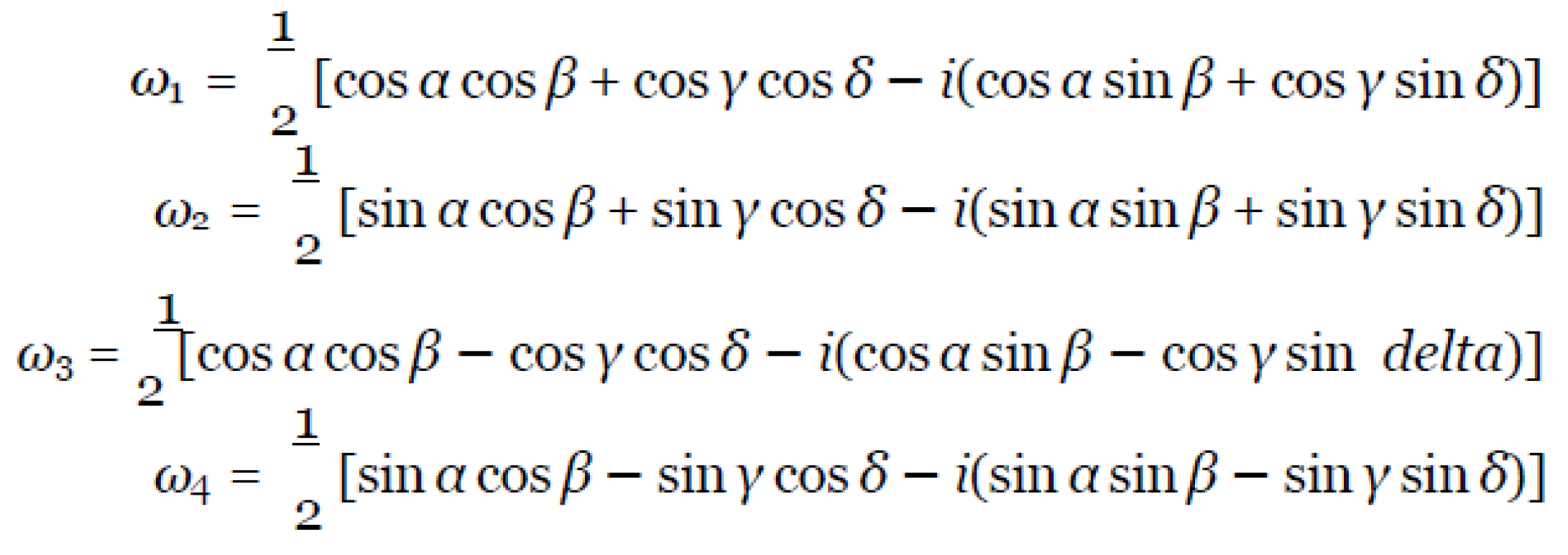
We see that the formulas (9) include four arbitrary angles α, β, γ, δ. If we take α = β = γ = δ = 0 in them, then we get an identical gate of the form:
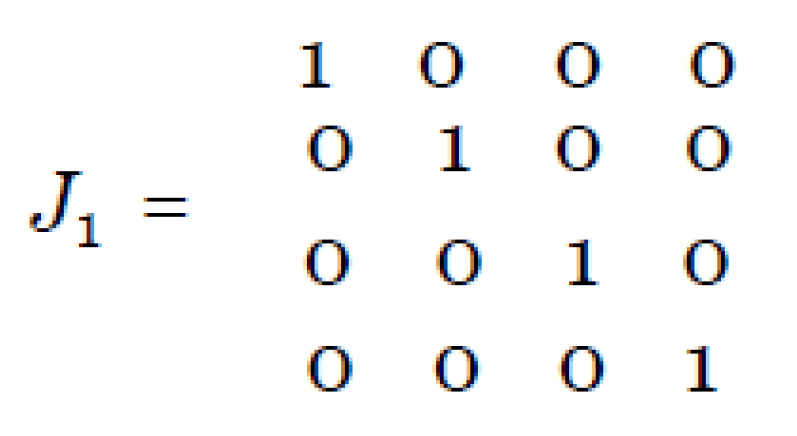
All other gates (an infinite set) are also obtained by substituting the specific values of these four, free parameters. Theorem 1 is proved simply, based on the definition of a unitary matrix. Indeed, if Aven is a unitary matrix, A∗ is a complex conjugate matrix, then by definition we have:
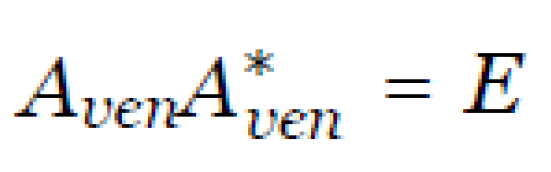 where E is the (4 × 4) identity matrix. The resulting system of nonlinear algebraic equations is solved explicitly. The general solution of this system has the form (9).
where E is the (4 × 4) identity matrix. The resulting system of nonlinear algebraic equations is solved explicitly. The general solution of this system has the form (9).
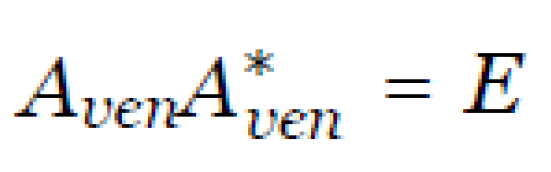
4. Discussion of the obtained results
So, using the formula (9), we found an uncountable set of all possible gates. This means that it is now possible to measure all possible states of a quantum system. For the sake of clarity, we will indicate a number of simple gates: for example, there is a shift gate
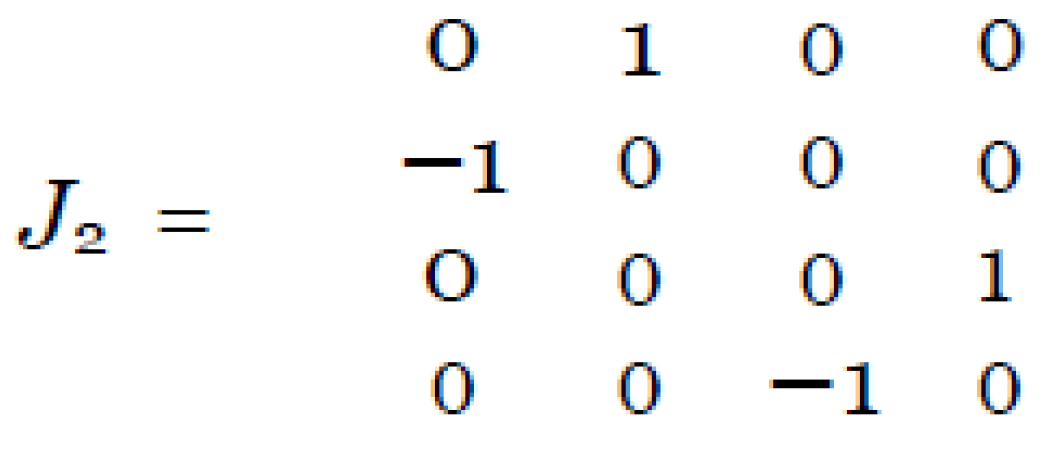
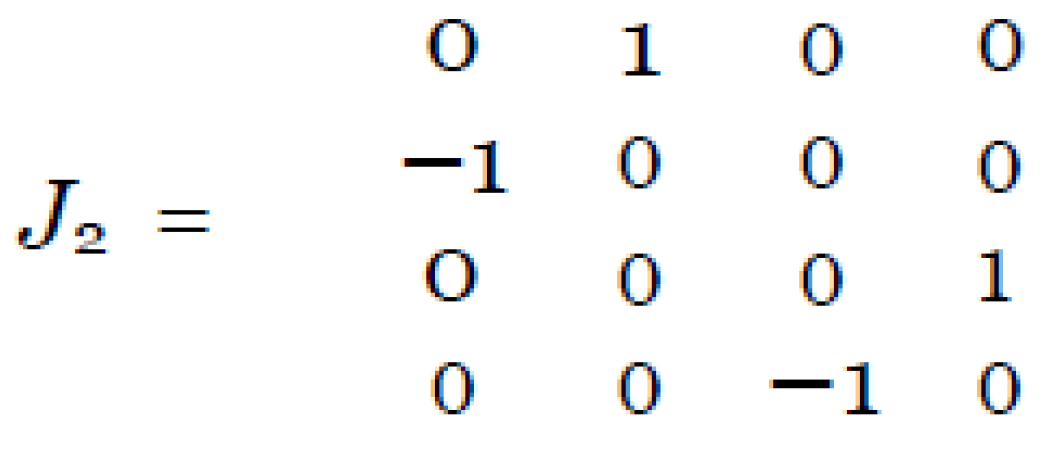
Further, it can be shown that all gates with real elements have the following form:


Similarly, all gates with purely imaginary elements have a similar form:
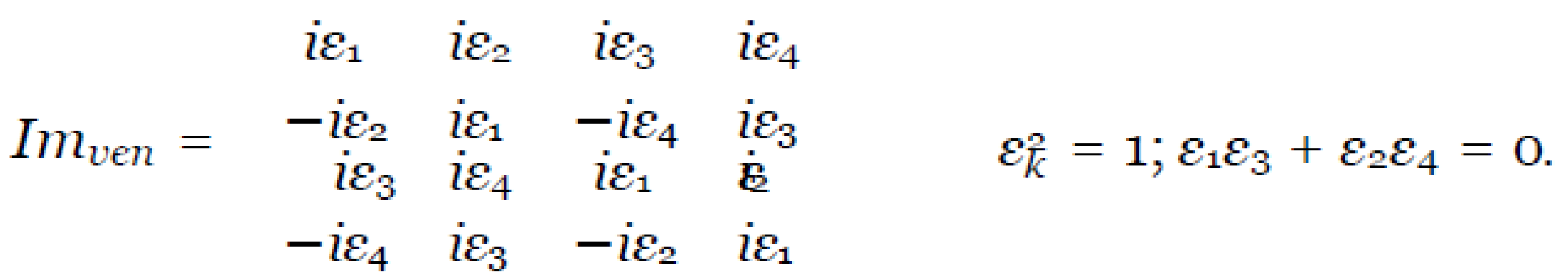
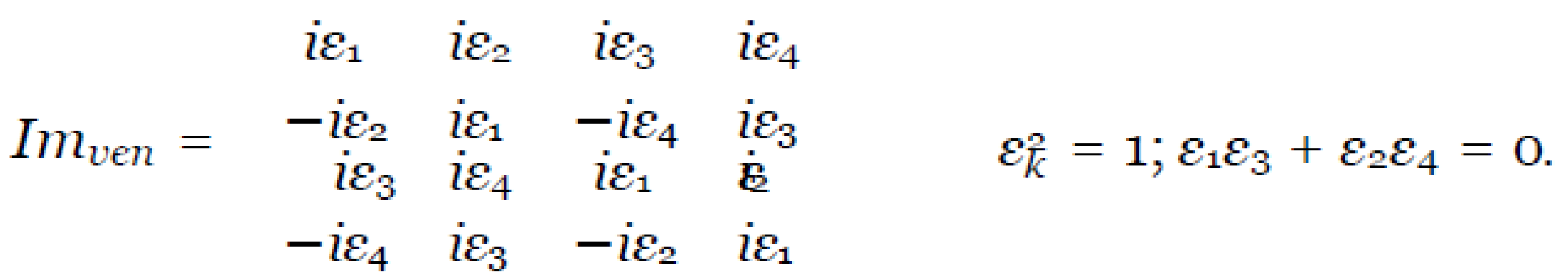
Since the set of gates form a commutative group, all possible products of these gates are also gates. Of fundamental importance is the fact that we have succeeded in describing the entire continuum set of two-qubit quantum gates, which has not been possible so far
References
- Kitaev, A. Shen, M.Vyaly Classical and quantum computing M. MC-NMO. 1999. [Google Scholar]
- M.Abenov Four-dimensional mathematics: methods and applications Al- maty From KazNU . 2019.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





