Structural Change-Point Detection for Time Series via Support Vector Regression and Self-Normalization Method

Preprint

Article

Structural Change-Point Detection for Time Series via Support Vector Regression and Self-Normalization Method

Altmetrics

Downloads

150

Views

Comments

This version is not peer-reviewed

Submitted:

10 April 2023

Posted:

11 April 2023

You are already at the latest version

Alerts

Abstract

This study considers the change-point test problem for time series based on the self-normalization ratio statistic test, which is constructed using residuals obtained from a support vector regression (SVR)-autoregressive moving average (ARMA) model. Under the null hypothesis, the series is a stationary process, and our test statistic converges to a non-degenerate distribution. Under the alternative hypothesis, there are change-points in the time series, and the self-normalization test statistic diverges to infinity. The simulations show that our proposed new test has better finite sample performance than other SVR-based tests in the literature. Finally, we illustrate its usefulness by analyzing two actual data sets.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

Change-point theory is a classical branch of statistics. In a series or process, when a statistical characteristic changes at a point in time due to systematic factors instead of chance, we define that point in time as a change-point. The generation mechanism of many actual observations can be altered by many factors such as unexpected events, which may change the statistical characteristics of one’s observed time series, i.e., containing change-points. Examining these change-points can prevent some potential risks and provide a reference basis for decision-making, which makes change-point testing an active research topic in many disciplines such as statistics and econometrics.

In general, the problem of testing parameter changes in time series models is usually called the time series structural change-point test. Since its introduction by Page[1],[2], the problem of the time series structural change-point test has attracted the attention of scholars in different fields and has been one of the important research areas in statistics. With further development, the time series structural change-point test is now widely used in different research fields. For example, the structural change-point test on epidemiological time series data[3] can find the moment of change in the transmission rate of infectious diseases during their transmission process, which is important for determining reasonable treatment and control measures. The structural change-point test on economic and financial time series data can find the existence of a subprime mortgage crisis[4] and provide feasible suggestions for macroeconomic control to stabilize the market in advance. The structural change-point test on meteorological time series data can find the existence of a subprime mortgage crisis[5]. Therefore, the study of the time series structural change-point test problem has important theoretical significance and practical significance.

In the study of the time series structural change-point test, the traditional method of time series structural change-point test[6],[7] must usually provide a consistent estimate of the long-term variance, which is used to derive the limiting distribution of the statistic[8]. However, estimating the long-term variance involves selecting redundant parameters such as the bandwidth parameter. The selection of parameters strongly affects the test effect. With the advent of the era of big data, the observed and recorded data of people continue to increase and provide a rich data source for the time series structural change-point test in terms of statistical analysis. However, the data structure becomes increasingly complex and may contain more diverse types of change points, which introduces higher requirements for the change-point test method[9],[22]. Meanwhile, the support vector regression (SVR)[23],[29] and self-normalization test method[30] can effectively avoid these problems.

In the study of time series change-point tests, the construction of the test statistic is important, and the commonly used test statistic usually carries an unknown long-term variance, which is more difficult to consistently estimate. Self-normalization is a method to turn the statistical inference problem of time series or test statistic into a pivotal quantity, where the basic idea is to use inconsistent variance estimators to absorb unknown serial correlations in the data. Self-normalization has become an important method to study the change-point test because it can avoid estimating the long-term variance. Meanwhile, the accuracy of model fitting has an important impact on improving the efficacy of the test statistic. Compared with traditional model-fitting methods, the SVR method has often been used to fit various types of time series models in recent years because it has many advantages such as the wide range of applicable models and few tuning parameters. Another important step in constructing the self-normalization test statistic is the accurate estimation of the residuals. The residuals originate from prediction errors, which makes it particularly important to correctly predict the time series. Some nonparametric forecasting methods such as SVR have a greater advantage when the time series has significant nonlinear characteristics. Because SVR has flexible use, excellent prediction accuracy, and few required tuning parameters, it can obtain a more accurate prediction error, which leads to accurate residual estimates. Thus, this paper investigates the problem of testing the structural change points of autoregressive moving average (ARMA) time series models based on SVR and self-normalization methods.

The remainder of the article is organized as follows. Section 2 introduces the model and hypothesis testing, presents our test statistics, and investigates their asymptotic properties. Section 3 presents simulation experiments and results. Section 4 introduces the example analysis. Section 5 concludes the paper and summarizes the entire paper.

2. Model and Hypothesis Testing

To implement the self-normalization test in a time series model, we considered the self-normalization test for the ARMA(p , q) model. To implement a change-point test, we constructed the self-normalization test using only the observations

y_{t}

and residuals

ε_{t}

in ARMA models. Let us consider the stationary ARMA (p , q) model:

y_{t} = \sum_{i = 1}^{p} (ϕ_{i} - y_{t - i}) + ε_{t} + \sum_{j = 1}^{q} (θ_{j} - ε_{t - j})

where

ϕ_{i}, i = 1, \dots, p; θ_{j}, j = 1, \dots, q

are real numbers, and

ε_{t}

are independent identical-distribution-mean zero random variables with covariance

σ^{2} > 0

Here, our objective is to test whether the conditional mean of

y_{t}

over past information

\sum_{i = 1}^{p} (ϕ_{i} - y_{t - i}) + \sum_{j = 1}^{q} (θ_{j} - ε_{t - j})

or the variance of the error terms

ε_{t}

experiences a change point over time

t

. Since a change occurs if the parameter vector

ϑ = {(ϕ_{1}, \dots, ϕ_{p}, θ_{1}, \dots, θ_{q}, σ^{2})}^{T}

changes, given observations

y_{1}, \dots, y_{n}

, we set up the null hypothesis and alternative hypothesis as follows:

\begin{array}{l} H_{0} : ϑ = θ, t = 1, \dots, n, \\ H_{1} : \{\begin{cases} ϑ = ϑ_{0}, t = 1, 2, \dots, [n τ], τ \in (0, 1) \\ ϑ = ϑ_{1}, ϑ_{1} \neq ϑ_{0}, t = [n τ] + 1, \dots, n \end{cases} \end{array}

Under the alternative hypothesis, we consider the situation in which

ϑ = ϑ_{0}

for

t = 1, \dots, [n τ]

for some

τ \in (0, 1)

and

ϑ = ϑ_{1}

with

ϑ_{1} \neq ϑ_{0}

for

t = [n τ] + 1, \dots, n

To test the above hypothesis, we recursively obtain the estimated value of residual

{\hat{ε}}_{t} = y_{t} - \sum_{i = 1}^{p} ({\hat{ϕ}}_{i} - y_{t - i}) + ε_{t} + \sum_{j = 1}^{q} ({\hat{θ}}_{j} - ε_{t - j})

with

y_{t} = ε_{t} = 0

for all

t \leq 0

, where

{\hat{ϕ}}_{i}

and

{\hat{θ}}_{j}

are consistent estimators of

ϕ_{i}

and

θ_{j}

. We can obtain a consistent estimate to Gaussian quasi-maximum likelihood estimates in Francq and Zakoan (2004).

Then, to test for a parameter change in

ϑ

, we constructed the self-normalization[30] test as follows. Let us denote

{\bar{ε}}_{j, k} = \frac{1}{k + j - 1} \sum_{t = j}^{k} ε_{t}, S_{t} (j, k) = \sum_{h = j}^{t} (ε_{h} - {\bar{ε}}_{j, k})

for

t = j, \dots, k, 1 \leq j < k \leq n

. For

1 \leq k \leq n

, we define

G_{n} (k) = \frac{\sqrt{n} |{\bar{ε}}_{1, k} - {\bar{ε}}_{k + 1, n}|}{n^{- 1} {\{\sum_{t = 1}^{k} S_{t}^{2} (1, k) + \sum_{t = k + 1}^{n} S_{t}^{2} (k + 1, n)\}}^{\frac{1}{2}}}

and

T_{n} = \sup_{k \in [⌊τ_{1 n}⌋, ⌊τ_{2 n}⌋]} G_{n} (k)

, where

0 < τ_{1} < τ_{2} < 1

. Here,

τ_{1}

and

τ_{2}

correspond to the trimming proportions from the left and right of the sample, respectively. Trimming is quite common in the literature on change point detection. Our test statistic resembles the sup-Wald type test statistic, which is commonly used in testing for a change point. However, we use an inconsistent normalization in the denominator to avoid consistently estimating the variance of the normalized sample mean, which is usually involved in the sup-Wald type test in the time series setting and requires a choice of tuning parameters. The self-normalization idea was used by Lobato(2001) and Shao(2010) for inference problems related to weakly dependent time series. To the best of our knowledge, its use for the inference of structural change-point detection for time series is new.

To test the above null and alternative hypotheses, we apply the following two tests proposed by Lee [29], we use

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

to express Lee's statistics, which are as follows:

{\hat{T}}_{n}^{l s} = \max_{1 \leq k \leq n} {\frac{1}{n {\hat{τ}}_{1, n}^{2}} {|\sum_{t = 1}^{k} (y_{t} - {\hat{ε}}_{t}) {\hat{ε}}_{t} - \frac{k}{n} \sum_{t = 1}^{n} (y_{t} - {\hat{ε}}_{t}) {\hat{ε}}_{t}|}^{2} + \frac{1}{n {\hat{τ}}_{2, n}^{2}} {|\sum_{t = 1}^{k} ({\hat{ε}}_{t}^{2}) - \frac{k}{n} \sum_{t = 1}^{n} (y_{t} - {\hat{ε}}_{t}^{2})|}^{2}},

{\hat{T}}_{n}^{\max} = \max_{1 \leq k \leq n} \max {\frac{1}{\sqrt{n} {\hat{τ}}_{1, n}} |\sum_{t = 1}^{k} (y_{t} - {\hat{ε}}_{t}) {\hat{ε}}_{t} - \frac{k}{n} \sum_{t = 1}^{n} (y_{t} - {\hat{ε}}_{t}) {\hat{ε}}_{t} |, \frac{1}{\sqrt{n} {\overset{\land}{τ}}_{2, n}} | \sum_{t = 1}^{k} {\hat{ε}}_{t}^{2} - \frac{k}{n} \sum_{t = 1}^{n} {\hat{ε}}_{t}^{2}|},

where

{\hat{τ}}_{1, n}^{2} = \frac{1}{n} {\sum_{t = 1}^{k} (y_{t} - {\hat{ε}}_{t})}^{2} {\hat{ε}}_{t}^{2}

{\hat{τ}}_{2, n}^{2} = \frac{1}{n} {\sum_{t = 1}^{k} {\hat{ε}}_{t}^{4} - (\frac{1}{n} \sum_{t = 1}^{n} {\hat{ε}}_{t}^{2})}^{2}

We reject

H_{0}

G_{n} (k) > 32.81446

at the nominal 0.05 level. The critical values of these two tests are obtained though Monte Carlo simulations using two-dimensional standard Brownian motion.

3. Asymptotic Property

In this section, we discuss the asymptotic properties of the above statistics. In order to derive the asymptotic distribution of statistic

T_{n} (τ)

, we begin with the following assumption and related lemmas. Here, we verified that under regularity conditions,

{\hat{G}}_{n} (k)

behaves asymptotically the same as

G_{n} (k)

under

H_{0}

as n tends to

\infty

,and thus, the limiting null distribution of

{\hat{G}}_{n} (k)

is the same as

\sup_{0 \leq s \leq 1} |B_{0} (s)|

, where

B_{0}

denotes a Brownian bridge on the unit interval because

G_{n} (k)

converges to the supremum of a Brownian bridge in distribution due to Donsker’s invariance principle.

Given an interval

v = [τ_{1}, τ_{2}]

, Riemann Integrals of the test statistic

G_{n} (τ)

are defined as follow:

J_{n} (τ) = \int_{τ_{1}}^{τ_{2}} G_{n} (τ) d τ

. When the value of

J_{n} (τ)

greater than the critical value. We reject the null hypothesis

H_{0}

and consider that there are change points in the sequence

{y_{t}}

. When

r \in [r_{1}, r_{2}], 0 \leq r_{1} < r_{2} \leq 1,

W (r; r_{1}, r_{2}) = B (r) - B (r_{1}) - B (r_{2}) - B (r_{1}) (r - r_{1}) / (r_{2} - r_{1})

The following theorem illustrates the asymptotic zero distribution of test statistics.

Theorem 2.1.

Under the null assumption of parameters

ϑ

no change, when

n \to \infty

, the limit distribution of statistics is

J_{n} (τ) \underset{D}{\Rightarrow} \int_{τ_{1}}^{τ_{2}} \frac{τ^{2} \sqrt{τ} \int_{τ}^{1} {(W (1) - W (t))}^{2} d t}{\sqrt{(1 - τ) \int_{0}^{τ} W^{2} (t) d t}} d τ .

Proof Under the null assumption of parameters

ϑ

no change, we write

k = [n τ], j = [n t]

, we consider

ϑ \neq 0

.The statistics will converge to the degenerate distribution, which is not listed here for simplicity.

When under the null hypothesis

H_{0} : ϑ = ϑ_{0}

, the following formula can be obtained by applying the continuous mapping theorem:

\begin{array}{l} G_{n} (τ) = \frac{\sqrt{[n τ] / (n - [n τ])} \sum_{j = [n τ] + 1}^{n} {(n^{- 1 / 2} \sum_{i = [n τ]}^{n} (Y_{i} - ϑ))}^{2}}{\frac{n^{2}}{{[n τ]}^{2}} \sum_{j = 1}^{[n τ]} {(n^{- 1 / 2} \sum_{i = 1}^{[n τ]} (Y_{i} - ϑ))}^{2}} \\ \Rightarrow \frac{\sqrt{τ / (1 - τ)} \int_{τ}^{1} {(W_{d} (1) - W_{d} (t))}^{2} d t}{τ^{- 2} \int_{0}^{τ} W_{d}^{2} {(t)}^{2} d t} \end{array}

Therefore, theorem 1 established by us is true.

Theorem 2.2Under the alternative assumption

H_{1}

and that the change point position is constant, when

n \to \infty,

J_{n} (τ) = O (n^{2} .)

Proof Under the alternative assumption

H_{1}

, we let

k = [n τ]

and

△_{α} \neq 0

is fixed constant, we have

S_{j} = \sum_{i = 1}^{j} Y_{i} = \sum_{i = 1}^{j} (Y_{i} - ϑ), S_{n - j + 1} = \sum_{i = 1}^{j} Y_{i} = \sum_{i = 1}^{j} (Y_{i} - △_{α}) + (n - j + 1) △_{α},

\frac{\sqrt{n} |{\bar{Y}}_{1, [n τ]} - {\bar{Y}}_{[n τ] + 1}|}{\frac{1}{n} \{\sum_{t = 1}^{[n τ]} S_{t}^{2} (1, [n τ]) + \sum_{t = [n τ] + 1}^{n} S_{t}^{2} ([n τ] + 1, n)\}} = I_{1} + I_{2} + I_{3},

I_{1} = \frac{\sqrt{([n τ] / (n - [n τ]))} \sum_{t = [n τ] + 1}^{n} {(\sum_{i = [n τ]}^{n} (Y_{i} - △_{α}))}^{2}}{\frac{n^{2}}{{[n τ]}^{2}} \sum_{j = 1}^{[n τ]} {(\sum_{i = [n τ]}^{n} (Y_{i} - △_{α}))}^{2}},

We can get

I_{1} = O_{p} (1)

from the above theorem 2.1.

\begin{array}{l} I_{2} = \frac{2 Δ_{α} \sqrt{n} \sqrt{[n τ] / (n - [n τ])} \sum_{j = [n τ] + 1}^{n} (\frac{n - [n τ] + 1}{n} (n^{- 1 / 2}) \sum_{i = [n τ]}^{n} (Y_{i} - Δ_{α}))}{\frac{n^{2}}{[n τ]} \sum_{j = 1}^{[n τ]} {(\sum_{i = 1}^{[n τ]} (Y_{i} - ϑ))}^{2},} \\ \Rightarrow \frac{2 Δ_{α} \sqrt{τ / (1 - τ)} \int_{τ}^{1} (1 - t) (W (1) - W (t)) d t}{τ^{- 2} \int_{0}^{τ} W^{2} (t) d t} O (n^{\frac{1}{2}}) \end{array}

Due to

O (n^{\frac{1}{2}}) \to \infty

, that is

I_{2} = O_{p} (n^{\frac{1}{2}})

\begin{array}{l} I_{3} = \frac{n^{2} Δ_{α}^{2} \sqrt{[n τ] / (n - [n τ])} \frac{(n - [n τ]) (n - [n τ] + 1) (2 n - 2 [n τ] + 1)}{n^{3}}}{\frac{6 n^{2}}{[n τ]} \sum_{j = 1}^{[n τ]} {(n^{- 1 / 2} \sum_{i = 1}^{[n τ]} (Y_{i} - ϑ))}^{2}} \\ \Rightarrow \frac{Δ_{α}^{2} \sqrt{τ / (1 - τ)} {(1 - τ)}^{3}}{3 τ^{- 2} \int_{0}^{τ} W^{^{2}} (t) d t} O (n^{2}) \end{array}

Due to

O (n^{2}) \to \infty

, that is

I_{3} = O_{p} (n^{2})

4. Simulation

In this section, we investigate the finite sample performance of the self-normalization test in testing the structural change points of the time series. Based on the described data generation process, data with sample sizes of 200 and 500 were generated. All results were reported based on 1000 replicate experiments. The level of each simulation test was 0.05. The empirical size and empirical power were calculated as the frequency of rejection of the no-change null hypothesis over 1000 replications. Under the alternative hypothesis, it is assumed that the change point occurs in the middle of the test sample. For SVR, we used the R package “e1071.” The simulation process is as follows.

Step 1. Generate a time series of length n with the ARMA(1,1) model.

Step 2. Estimate the model parameters of the SVR-ARMA model from a training time series sample, where an AR model is used to fit the data. Perform SVR on the first k data and the last n-k data. Establish ARMA models for the first k data and the last n-k data. Use the established models to predict the last n-k data and the first k data, and conduct cross-validation to obtain the residual.

Step 3. Conduct the self-regularization test to calculate the critical value and evaluate the size and power. To compute the size, generate a time series with no changes. To examine the power, generate a time series with a change point in the middle of the sequence.

Step 4. Iteratively repeat the above steps 1000 times and subsequently compute the empirical sizes and powers.

(1): Linear AR and ARMA Model

The following section outlines the theory of the SVR-ARMA model-based prediction methods and how to determine an optimal SVR-ARMA model and its methodology. For a given sample of training time series, we obtained the residuals of the best SVR-ARMA model by dividing it into two subsequences. A long AR model was fitted to the first subsequence to obtain the initial values of the residuals, which were used as error terms in the SVR-ARMA(p , q) model and recursively updated until the obtained residuals converged to a limit. Then, for each estimated SVR-ARMA(p, q) model, we calculated the root mean square error based on the second subsequence and selected the optimal order of the ARMA model based on the principle of minimum RMSE. The determined SVR-ARMA(p, q) model was applied to obtain the prediction errors or residuals and construct the self-normalization test. We discussed the finite sample performance of test statistics

G_{n} (k)

. We used the following data-generation process:

Model 1:

y_{t} = (ϕ \times y_{t - 1}) + ε_{t},

Model 2:

y_{t} = (ϕ \times y_{t - 1}) + ε_{t} + (θ \times ε_{t - 1}),

where

ε \sim N (0, σ^{2})

;

y_{t}

is an SVR-ARMA(p , q) process with parameter

ϑ

being 0.5, 0.7, or 2. It can be generated using the function “arima.sim” in the R package “arima.sim.” For simplicity, we fixed

(τ_{1}, τ_{2}) = (0.15, 0.85)

. We focused on the influence of the change in ϑ, i.e.,

ϕ, θ

and

σ

, on the empirical power. Under the null hypothesis, the parameters were set as follows:

\begin{array}{l} (i) ϕ = 0.3, σ^{2} = 1 \\ (i i) ϕ = 0.3, ϑ = 0, σ^{2} = 1 . \end{array}

Table 1 shows the empirical sizes and empirical power of the AR(1) model in different cases. The test statistic can well control the empirical size for different parameter values, and almost no empirical size distortion occurs. For example, at n = 200 and ϕ = 0.5, the empirical power of the SVR-based self-normalization test statistic is 0.637, while the empirical powers of

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

are 0.523 and 0.484, respectively. From Table 1, the self-normalization test has better empirical powers than

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

in most cases. This result proves the effectiveness of our proposed SVR-based self-normalization test in approximating the critical values of the statistics.

Table 2 shows the empirical size and power of the ARMA(1 , 1) model in different cases. The test statistic usually well controls the empirical size for different parameters, which proves the effectiveness of the proposed self-normalization test method based on SVR in approximating the critical value of the statistic. For example, at n = 200, ϕ = 0.3, θ = 0.7, and σ = 1, the empirical power of the SVR-based self-normalization test statistic is 0.636, while the empirical powers of

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

are 0.620 and 0.472, respectively. When the sample size increases the empirical powers of the statistics become better and closer to 1, which proves that the proposed self-normalization test method based on SVR outperforms

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

in most cases.

Table 3 summarizes the empirical size and empirical powers of the ARMA(1 , 1) model for different cases. The test statistic usually well controls the empirical size for different parameter values, which proves the effectiveness of the proposed self-normalization test method based on SVR in approximating the critical value of the statistic. For example, when n = 500, ϕ = 0.7, θ = 0.3, and µ = 2, the empirical power of the SVR-based self-normalization test statistic is 0.884, while the empirical powers of

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

are 0.838 and 0.775, respectively. Thus, the proposed SVR-based self-normalization test method outperforms

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

in most cases and is effective.

Table 4 and Table 5 summarize the empirical sizes and empirical powers of the SVR-based self-normalization test statistic for different scenarios with different parameter values at different change point locations. The changes in parameters, sample size, and location of the change points significantly impact the empirical powers of the statistic. The SVR-based self-normalization test statistic has better empirical powers than

{\hat{T}}_{n}^{l s}

and

{\hat{T}}_{n}^{\max}

under different conditions. The empirical power increases with the sample size, e.g., at n = 500, ϕ = 0.5, θ = 0.3, σ = 1, and µ = 2, the empirical powers of the SVR-based self-normalization test statistic are 0.719, 0.985, and 0.927, while the empirical powers of

{\hat{T}}_{n}^{l s}

are 0.689, 0.857, and 0.925, and those of

{\hat{T}}_{n}^{\max}

are 0.691, 0.777, and 0.870, respectively. Thus, the test powers of this chapter are higher under the alternative hypothesis in most cases. The empirical powers of the SVR-based self-normalization test are higher in the middle position than at the two end positions, which indicates that it will be easier to detect when a change point appears in the middle of the sample. This result confirms our assumption that the change point relatively occurs in the middle position.

5. Empirical Illustration

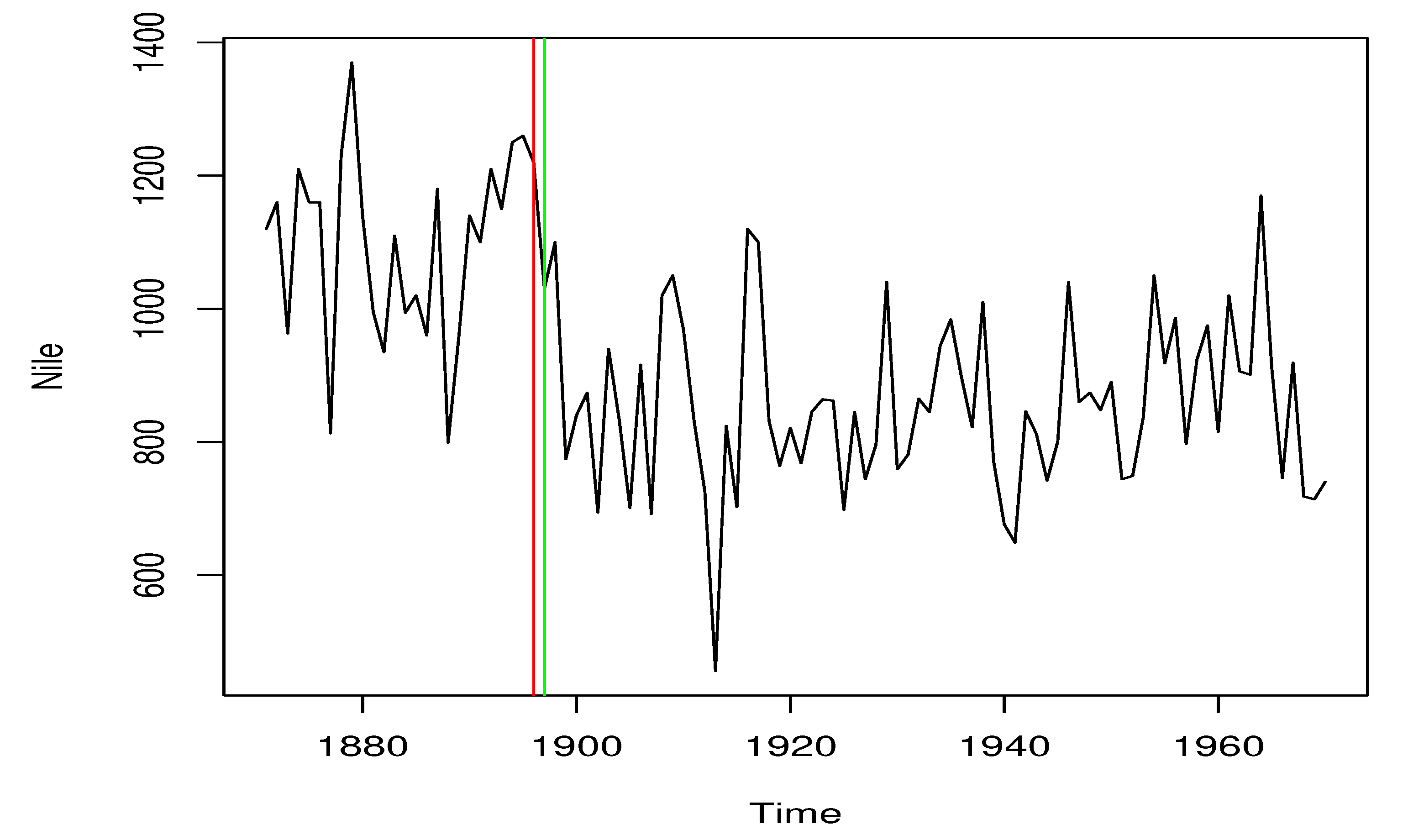
The first data set used in this section of the empirical analysis study is the annual Nile flow data from 1871 to 1970. Using the proposed self-normalization test method based on SVR, the corresponding critical value is 32.81446, and the self-normalization test statistic value is 315.5232. The statistic value is greater than the critical value, which indicates that there are change points in the time series. In Figure 1, the red vertical line indicates the self-normalization test method, and the green vertical line indicates the method in the literature. Figure 1 shows that the SVR-based self-normalization test method proposed in this paper is consistent with the results of existing literature on this data variation point test.

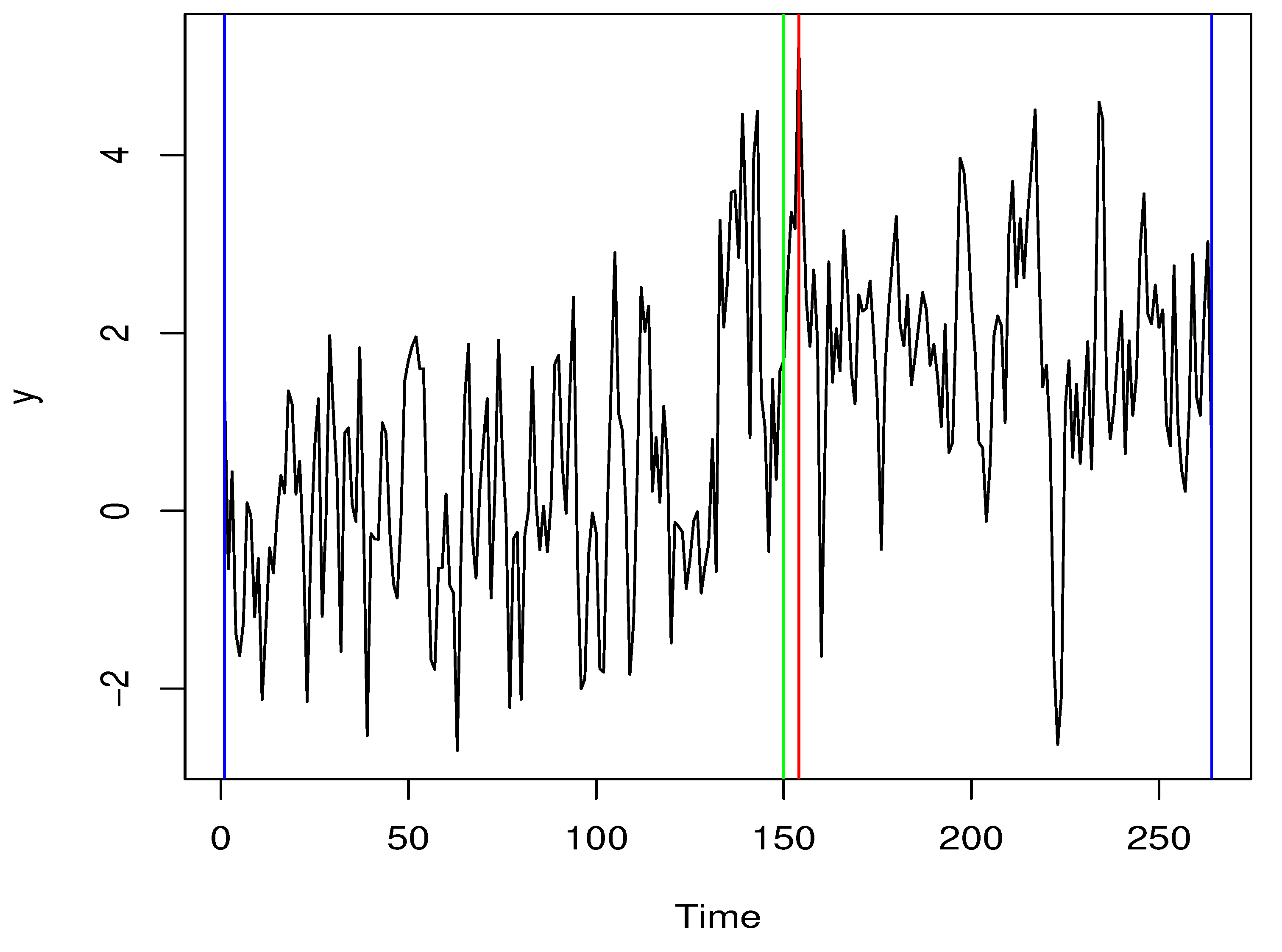
The second data set used for the example analysis in this section is the Nikkei225 index data from January 1, 2000, to December 1, 2021. The calculated critical value is 32.81446, while the self-normalization test statistic value is 70.25469. Since the statistic value is greater than the critical value, it is considered that there are change points in the time series. In Figure 2, the red vertical line indicates the change points detected by the self-normalization test method, and the green vertical line is the change points detected by the method in the literature. We find that the change points detected by the two methods are very close to each other, which indicates the effectiveness of the proposed method.

6. Conclusions

The problem of testing structural change points of time series has been an active topic in various research fields. In this paper, the structural change points of ARMA time series models are tested based on the self-normalization test statistic and SVR method. The validity of the proposed method on limited samples has been verified through theoretical analysis, numerical simulation experiments, and empirical analysis. The limiting distribution of the test statistic under the original hypothesis was derived, and its consistency under the alternative hypothesis was demonstrated. The simulation results illustrate that the SVR-based self-normalization test can control the empirical size better and achieve a good empirical power, and the SVR-based self-normalization test method is effective.

Acknowledgments

We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript. And this work was supported by the National Natural Science Foundation of China (Na.12161072), Natural Science Foundation of Qinghai Province (No.2019-ZJ-920).

References

Page, E.S. Continuous Inspection Schemes. Biometrika. 41(1922), 100-115.
Page, E.S. A test for a change in a parameter occurring at an unknown point. Biometrika. 42(1955), 523-527.
Feiyu Jiang, Zifeng Zhao, and Xiaofeng Shao. Time series analysis of COVID-19 infection curve: A change-point perspective. Journal of Econometrics. 232(2023), 1-17.
Wu-Yi Ye, Bo-Qi Miao, Yu-Chao Ma. Contagion analysis of the U.S. subprime debt crisis based on variation point detection of hazard rate function. Theory and Practice of Systems Engineering. 30(2010).
Xiongqi Huang, Zhentao Tian, Rui Qin, Xuemei Wang, Chenliang Zheng. Real-time variation point detection of meteorological data based on hybrid model adaptive LASSO method. Journal of Guangxi University for Nationalities (Natural Sciences Edition). 27(2021).
Lee, S.; Kim, C.K.; Lee, S. Hybrid CUSUM change point test for time series with time-varying volatilities based on support vector regression. Entropy. 22(2020), 578. [CrossRef]
Lee, S.; Lee, S.; Moon, M. Hybrid change point detection for time series via support vector regression and CUSUM method. Appl. Soft Comput. 89(2020), 106-101. [CrossRef]
Csörgő, M.; Horváth, L. Limit Theorems in Change-Point Analysis. John Wiley. Sons Inc., New York, 1997.
Inclán, C.; Tiao, G. Use of cumulative sums of squares for retrospective detection of changes of variance. J. Amer. Statist. Assoc. 89(1994), 913-923.
Lee, S.; Na, O.; Na, S. On the CUSUM of squares test for variance change in nonstationary and nonparametric time series models. Ann. Inst. Statist. Math. 55(2003), 467-485. [CrossRef]
Kim, S.; Cho, S.; Lee, S. On the CUSUM test for parameter changes in GARCH(1,1) models. Comm. Statist. Theory Methods. 29(2000), 445-462. [CrossRef]
Lee, S.; Tokutsu, Y.; Maekawa, K. The CUSUM test for parameter change in regression models with ARCH errors. Japan Statist. Soc. 34(2004), 173–188. [CrossRef]
Na, O.; Lee, J.; Lee, S. Change point detection in SCOMDY models. AStA Adv. Stat. Anal. 97(2013), 215–238. [CrossRef]
Lee, J.; Lee, S. Parameter change test for nonlinear time series models with GARCH type errors. J. Korean Math. Soc. 52(2015), 503-522. [CrossRef]
Gombay, E. Change detection in autoregressive time series. J. Multivariate Anal. 99(2008), 451-464. [CrossRef]
Oh, H.; Lee, S. On score vector- and residual-based CUSUM tests in ARMA-GARCH models. Stat. Methods Appl. 27(2018), 385-406. [CrossRef]
Oh, H.; Lee, S. Modified residual CUSUM test for location-scale time series models with heteroscedasticity. Ann. Inst. Statist. Math. 71(2019), 1059-1091. [CrossRef]
Lee, S. Location and scale-based CUSUM test with application to autoregressive models. 2019.
Chen, C.W.S.; Lee, S. Generalized autoregressive Poisson models for time series of counts. Comput. Statist. Data Anal. 99(2016), 51-67. [CrossRef]
Dong, M.C.; Chen, C.W.S.; Lee, S. How strong is the relationship among gold and USD exchange rates? Analytics based on structural change models. Comput. Econ. 53(2016), 343–366.
Oh, H.; Lee, S. Parameter change test for location-scale time series models with heteroscedasticity based on bootstrap. Appl. Stoch. Models Bus. 2019 Online published.
Atsalakis, G.S.; Valavanis, K.P. Surveying stock market forecasting techniques Part II: Soft computing methods, Expert Syst. Appl. 36(2009), 5932-5941. [CrossRef]
Müller, K.R.; Smola, A.J.; Rätsch, G.; Schölkopf, B. Kohlmorgen, Vapnik,J.V. Predicting time series with support vector machines, in: International Conference on Artificial Neural Networks, Springer, Berlin, Heidelberg. 1997, 999–1004.
Tay, F.E.; Cao, L. Application of support vector machines in financial time series forecasting, Omega. 29(2001), 309–317.
Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: a survey. IEEE Comput. Intell. Mag. 4(2009), 24–38. [CrossRef]
Cavalcante, R.C.; Brasileiro, R.C.; Souza, V.L.; Nobrega, J.P.; Oliveira, A.L. Computational intelligence and financial markets: A survey and future directions. Expert Syst. Appl. 55(2016), 194-211. [CrossRef]
Cao, L.J.; Tay, F.E.H. Support vector machine with adaptive parameters in financial time series forecasting. IEEE Trans. Neural Netw. 14(2003), 1506–1518. [CrossRef]
Chen, S. K.; Jeong, W.K.; Härdle, Recurrent support vector regression for a non-linear ARMA model with applications to forecasting financial returns. Comput. Statist. 30(2015), 821–843.
Lee, S.; Lee, S.; Moon, M. Hybrid change point detection for time series via support vector regression and CUSUM method. Appl. Soft Comput. 89(2020), 106-101. [CrossRef]
Xiaofeng Shao. A simple test of changes in mean in the possible presence of long-range dependence, Journal of Time Series Analysis. 32(2011), 598-606.

Figure 1. Annual volume of discharge from the Nile River at Aswan from 1871 to 1970.

Figure 2. Monthly log return data of 100 times Nikkei225 index from Jan. 1, 2000, to Dec. 1, 2021.

Table 1. Empirical sizes and powers for AR(1) model with

ϕ = 0.3, σ^{2} = 1

under the null and each alternatives.

Table 1. Empirical sizes and powers for AR(1) model with

ϕ = 0.3, σ^{2} = 1

under the null and each alternatives.

$ϕ = 0.3, σ^{2} = 1$	$n = 200, μ = 2$			$n = 500, μ = 2$
$ϕ = 0.3, σ^{2} = 1$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$
$s i z e$	0.059	0.023	0.060	0.085	0.056	0.061
$ϕ = 0.5$	0.523	0.484	0.637	0.554	0.547	0.811
$ϕ = 0.7$	0.539	0.511	0.728	0.596	0.570	0.881
$σ^{2} = 2$	0.839	0.641	0.624	0.997	0.988	0.787

Table 2. Empirical sizes and powers for the ARMA(1) model with

ϕ = 0.3, θ = 0.3, σ^{2} = 1

Table 2. Empirical sizes and powers for the ARMA(1) model with

ϕ = 0.3, θ = 0.3, σ^{2} = 1

$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	$n = 200, μ = 1$			$n = 500, μ = 1$
$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$
$s i z e$	0.062	0.025	0.061	0.086	0.053	0.054
$ϕ = 0.5$	0.426	0.303	0.496	0.874	0.801	0.899
$ϕ = 0.7$	0.642	0.524	0.688	0.947	0.921	0.952
$θ = 0.7$	0.620	0.472	0.636	0.966	0.935	0.970
$σ^{2} = 2$	0.835	0.651	0.643	0.999	0.993	0.724

Table 3. Empirical sizes and powers for the ARMA(1, 1) model with ϕ = 0.3, θ = 0.3, σ = 1, mu = 2 under the alternatives, including the null hypothesis.

$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	$n = 200, μ = 2$			$n = 500, μ = 2$
$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$
$s i z e$	0.062	0.025	0.061	0.086	0.053	0.054
$ϕ = 0.5$	0.540	0.392	0.793	0.857	0.777	0.985
$ϕ = 0.7$	0.489	0.346	0.574	0.838	0.775	0.884
$θ = 0.7$	0.673	0.545	0.825	0.974	0.940	0.989
$σ^{2} = 2$	0.899	0.701	0.724	1.000	0.994	0.963

Table 4. Empirical potential of the ARMA(1, 1) model with n = 200, ϕ = 0.3, θ = 0.3, σ = 1, and mu = 2 at different change point locations under the alternatives, including the null hypothesis.

$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	0.25			0.75
$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$
$ϕ = 0.5$	0.554	0.513	0.672	0.712	0.604	0.725
$ϕ = 0.7$	0.643	0.621	0.769	0.695	0.589	0.712
$θ = 0.7$	0.610	0.644	0.719	0.811	0.706	0.883
$σ^{2} = 2$	0.535	0.504	0.594	0.960	0.841	0.982

Table 5. Empirical potential of the ARMA(1, 1) model with n = 500, ϕ = 0.3, θ = 0.3, σ = 1, and mu = 2 at different change point locations under the alternatives, including the null hypothesis.

$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	0.25			0.75
$ϕ = 0.3, θ = 0.3, σ^{2} = 1$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$	${\hat{T}}_{n}^{l s}$	${\hat{T}}_{n}^{\max}$	$G_{n} (k)$
$ϕ = 0.5$	0.689	0.691	0.719	0.925	0.870	0.927
$ϕ = 0.7$	0.737	0.741	0.753	0.801	0.840	0.865
$θ = 0.7$	0.846	0.725	0.939	0.949	0.952	0.949
$σ^{2} = 2$	0.754	0.740	0.894	1.000	0.999	0.948

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Structural Change-Point Detection for Time Series via Support Vector Regression and Self-Normalization Method

Abstract

1. Introduction

2. Model and Hypothesis Testing

3. Asymptotic Property

4. Simulation

5. Empirical Illustration

6. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe