1. Introduction
For the studies of nuclear, atomic and chemical properties of radioactive elements, different techniques with the use of gas stopping cells are conventionally used. The primary energetic radioactive ions injected into a gas cell filled with the high-purity buffer gas (usually it is helium or argon) by passing through a thin entrance window. Due to a number of their collisions with buffer gas atoms, ions decelerate down to the gas flow velocity and thermalized. To speed up the transport of ions through big-sized gas cells, a DC gradient electric field is applied. In this case, the ion velocity is determined as a product of applied electric field in [volt cm-1] and ion mobility coefficient in [cm2 sec-1 volt-1].
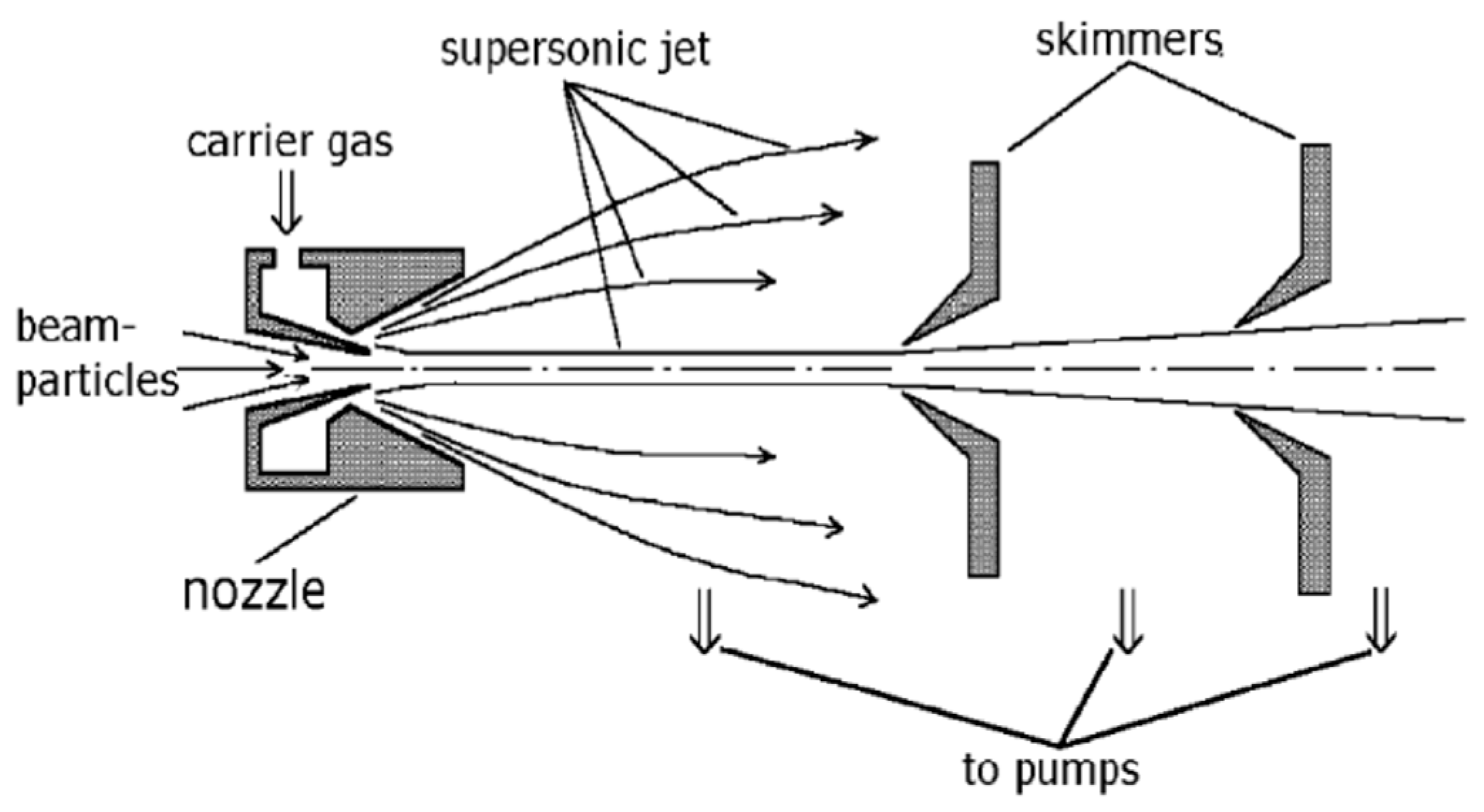
Near the extraction nozzle having the small throat diameter, ions are extracted out of the gas cell into vacuum conditions by supersonic buffer gas jet. Description of various gas cell apparatus readers can find elsewhere, for example, in [1-19] and links within them.
The extraction of the ions into high vacuum is finally performed with the use of radiofrequency quadrupoles (RFQ) [7, 8, 11 and 20–26] or radio-frequency sextupoles (SPIG) [9, 15] installed downstream for the ion beam transportation and focusing. Instead of traditional RFQ and SPIG rod-structures, a simple, compact and effective gas dynamic RF-only funnels can be used, as well. The review on the RF-only funnel technique one can find in our recent work [
27].
The other way to investigate the nuclear and atomic properties of radioactive elements extracted from the gas cell is the use of laser spectroscopy techniques. One can read about, e.g. in recent reviews [28, 29] and presentation review of Piet Van Duppen [
30].
The most attractive and promising nowadays method of laser spectroscopy for studying the properties of radioactive elements is the so-called method in-gas-jet laser resonance ionization spectroscopy that have been first proposed and experimentally tested in KU Leuven [
31]. Briefly, it consists of the following. Under applied DC electric field gradient, the thermalized in the high purity argon ions are transported through the gas cell and focused to a tip of metallic hot filament. The tip of the filament has installed on the axis of exit flow channel in front of the nozzle. After collection of ions on the filament and subsequent their thermal evaporation as neutral atoms, they are transported by only the carrier gas flow through the converging-diverging nozzle into the vacuum gas-jet chamber. Two lasers in cross beam geometry perform the high-resolution and efficient resonance excitation and ionization of the extracted into the gas-jet chamber neutral atomic beam. One laser beam (we will refer to as a Laser-1) directed along the axis in upstream the gas flow direction excites atoms of interest, and the second one (we will refer to as Laser-2) directed perpendicular to the gas jet ionizes these exited atoms. Then the ionized by the Laser-2 atoms transported as the ion beam by the carrier gas jet to the bended RFQ (e.g., S-shaped [
31], or bend 90 degrees [
32]). This curved RFQ allows for the axial laser beam injection into the gas jet and differential vacuum pumping, as well. The schematics and descriptions of various setups for the in-gas-jet laser resonance ionization spectroscopy one can find e.g. in Refs. [
29,
30,
31,
32,
33,
34,
35,
36,
37].
The article has two following goals.
The first goal - is a detailed quantitative study of the atomic beam extraction from the gas stopping cell and then its formation and cooling in the supersonic argon gas jet under the described above traditional approach to the in-gas-jet resonance ionization laser spectroscopy. As a typical representative for this study, we have chosen the experimental gas-jet apparatus [32, 33] recently created for high-resolution laser spectroscopy of the heaviest elements at the Separator for Heavy Ion reaction Products (SHIP) at GSI, Darmstadt. This project called JetRIS is under development at GSI.
The second goal - is the proposal and detailed exploration of a new double-nozzle technique for its application in-gas-jet resonance ionization laser spectroscopy.
The both goals we have reached by means of computer experiments, which were consisted in detailed gas dynamic and atom-trajectory Monte Carlo simulations, which results we present and discuss below in the next sections. The gas dynamic simulations of the buffer gas flow inside the gas cell and in the supersonic argon carrier gas jet we made have using the VARJET code. This code is based on the solution of a full system of time dependent Navier–Stokes equations and described in detail in [
39]. The results of the gas dynamic simulations (flow fields of the buffer gas velocity, density and temperature) we then used in atom-trajectory Monte Carlo simulations.
Similar computer simulations we were also making earlier for different ion beams cooling and bunching in helium buffer gas flows, and their results presented elsewhere (e.g. see [17-19, 40-48]). Note, that our calculation results (gas dynamic + Monte Carlo) for ions extracted from the gas jet into vacuum are in a good agreement with the measurements (see e.g. [43, 44]). Based on our gas dynamic calculations, setups of gas-jet internal targets [49, 50] have been created. These calculations are in a good agreement with measured parameters and structure of the supersonic gas jets, as well.
For simplicity, at comparison of two mentioned above in-gas-jet techniques, the conventional one, which is using in the project JetRIS, we will refer below to as a “GSI nozzle” and the proposed here new technique as a “double-nozzle”.
2. Results for GSI Nozzle
Schematic views of the JetRIS setup are presented in the both [
32] and [
33] articles (see
Figure 1 there).
Three different nozzles, which cross sectional profiles shown in the Figure 3 in [
33], were used at JetRIS setup in offline test measurements of neutral
164Dy atoms fluorescence induced by one-step laser excitation. All these nozzles have the same throat diameter of 1 mm, but different length and contour of diverging supersonic part. The authors of [
33] note, that these three nozzles were designed for different stagnation pressure in the gas cell (P
cell) and background pressure (P
bg) in the vacuum chamber of the gas jet expansion, we will refer to as a gas-jet chamber. The sophisticated contours of the left and right nozzles (see Figure 3 in Ref. [
33]) were designed (Ref. [
35]) and produced in KU Leuven, but due to the lack of exact information available to us about these nozzle's profiles, we could not use these two nozzles in our gas dynamic simulations. Contrary, the third nozzle, shown in the middle of Figure 3 (Ref. [
33]) and referred to as “mid-range nozzle”, has a simple conical diverging part with the length of 20 mm.
The authors of work [
33] note, "The mid-range nozzle seems to be the best overall choice, since its resolution and homogeneity are both close to the optimal values found for the other two nozzles". This is an additional reason why we chose this particular nozzle for a detailed computer study of the operation of the JetRIS setup.
The gas dynamic simulation we have performed for the argon stagnation pressure in the gas cell P
cell = 100 mbar and background pressure in the vacuum gas-jet chamber is P
bg = 6.47∙10
-3 mbar. The same pressure values were in JetRIS setup during test fluorescent measurements of neutral
164Dy atoms inside the supersonic argon jet (see Table 1 and the Figure 4 caption in [
33]).
2.1. The Exit Flow Channel
The JetRIS gas cell technical drawing shown in the left part of the Figure 5 in [
32]. The inner diameter of the gas cell DC-cage is 160 mm with the length of 164.5 mm. The total length of DC-funnel (five electrodes having gradually decreasing diameters) placed behind the DC-cage is 63.5 mm. The exit flow channel placed between the DC-funnel and the nozzle have diameter of 12 mm and a length of 34.6 mm. Due to the large diameter of DC-cage (160 mm) and only of 1 mm the nozzle throat diameter, the average velocity of the gas flow inside the DC-cage is only about 8 mm/s. That is why it is necessary to use the DC gradient field inside the cell to speed up the transport of the decelerated radioactive ions.
Early, we were making detailed (gas dynamic + Monte Carlo) simulations for different big-sized gas stopping cells [6, 17 -19]. E.g., the results of our simulations for the UNICELL project [
51], which is also under development at GSI presented in [
17]. But here we should notice, that simulations of the
164Dy ions transport through the main body of the JetRIS gas cell having inner diameter of 160 mm to the hot filament installed in-side the exit flow channel have been carefully done by the authors of [
32]. But here we should notice, that simulations of the 164Dy ions transport through the main body of the JetRIS gas cell having inner diameter of 160 mm to the hot filament installed in-side the exit flow channel have been carefully done by the authors of [
32]. Therefore, it is no much sense to repeat it, and we decided to start our gas dynamic simulation from the entrance to this exit flow channel (12 mm in diameter), where the average gas velocity in a factor of 178 higher than it is inside the DC-cage region. Notice, that the evaporated from the surface of hot filament neutral atoms are moving through the exit flow channel and then through the nozzle into the vacuum gas-jet chamber only under the effect of the gas flow. Monte Carlo atom-trajectory simulations were beginning from the filament tip, where neutral
164Dy atoms first appear in the gas flow after their evaporation. From the technical drawing shown in the left part of the Figure 5 of work [
32] we determined that the filament in the JetRIS setup has installed at about 22.5 mm distance from the nozzle.
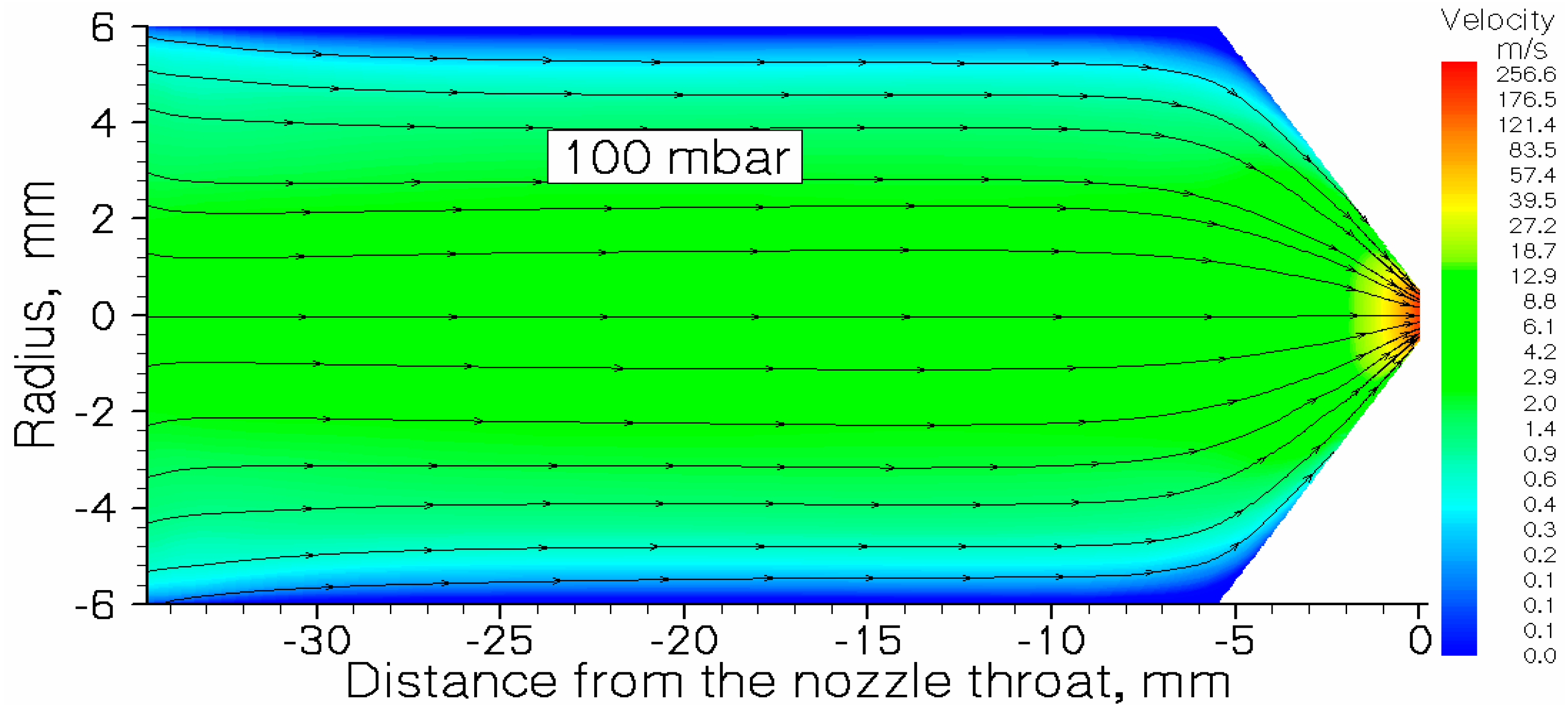
Results of the gas dynamic simulation for the gas velocity flow field inside the exit flow channel shown in
Figure 1.
The
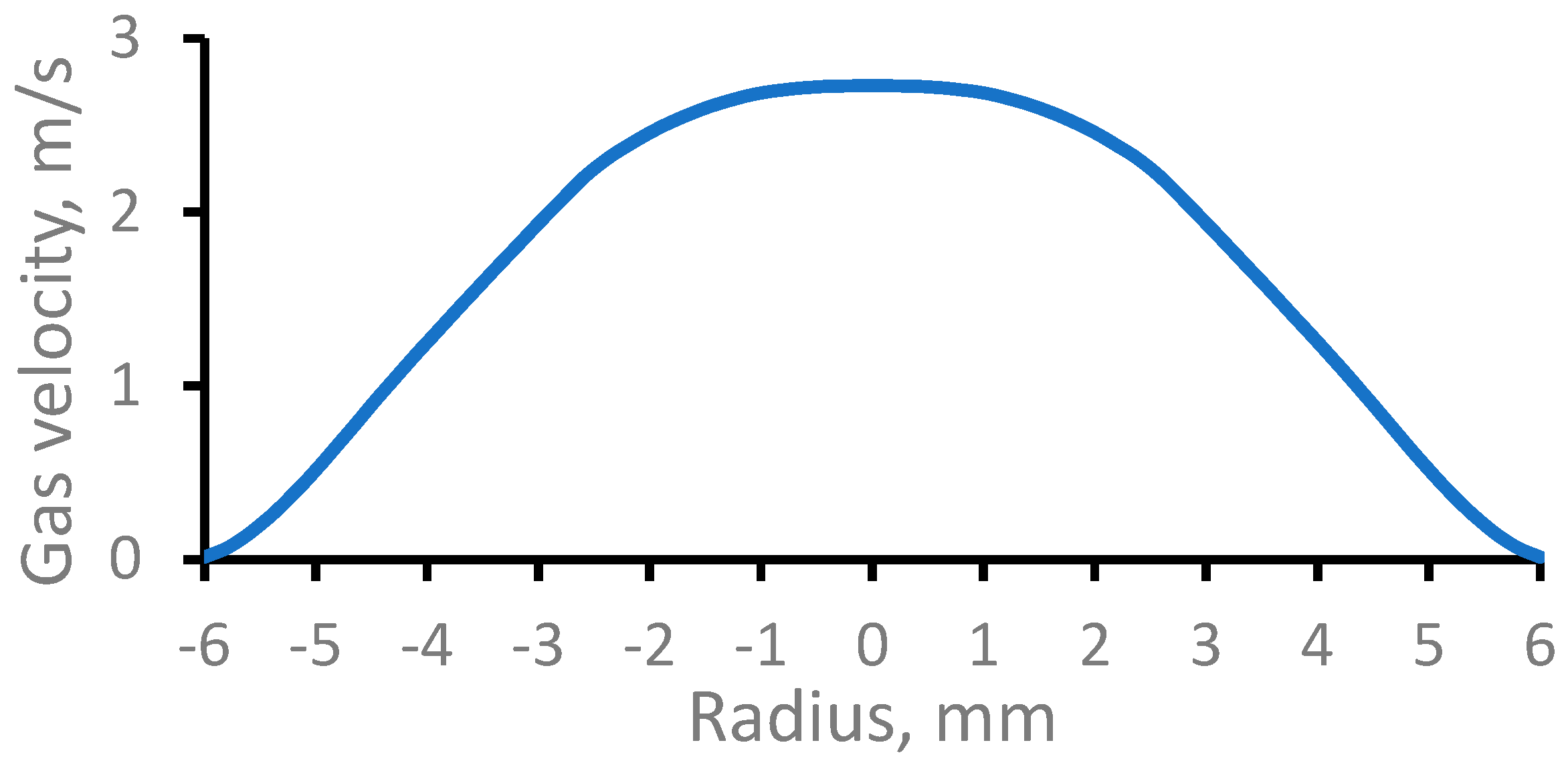
Figure 2 shows the radial gas velocity profile in the middle of this exit flow channel. The parabolic gas velocity profile, that is typical for the laminar viscous gas flow inside a tube, is clear visible. The corresponding Reynolds number is equal to 123.
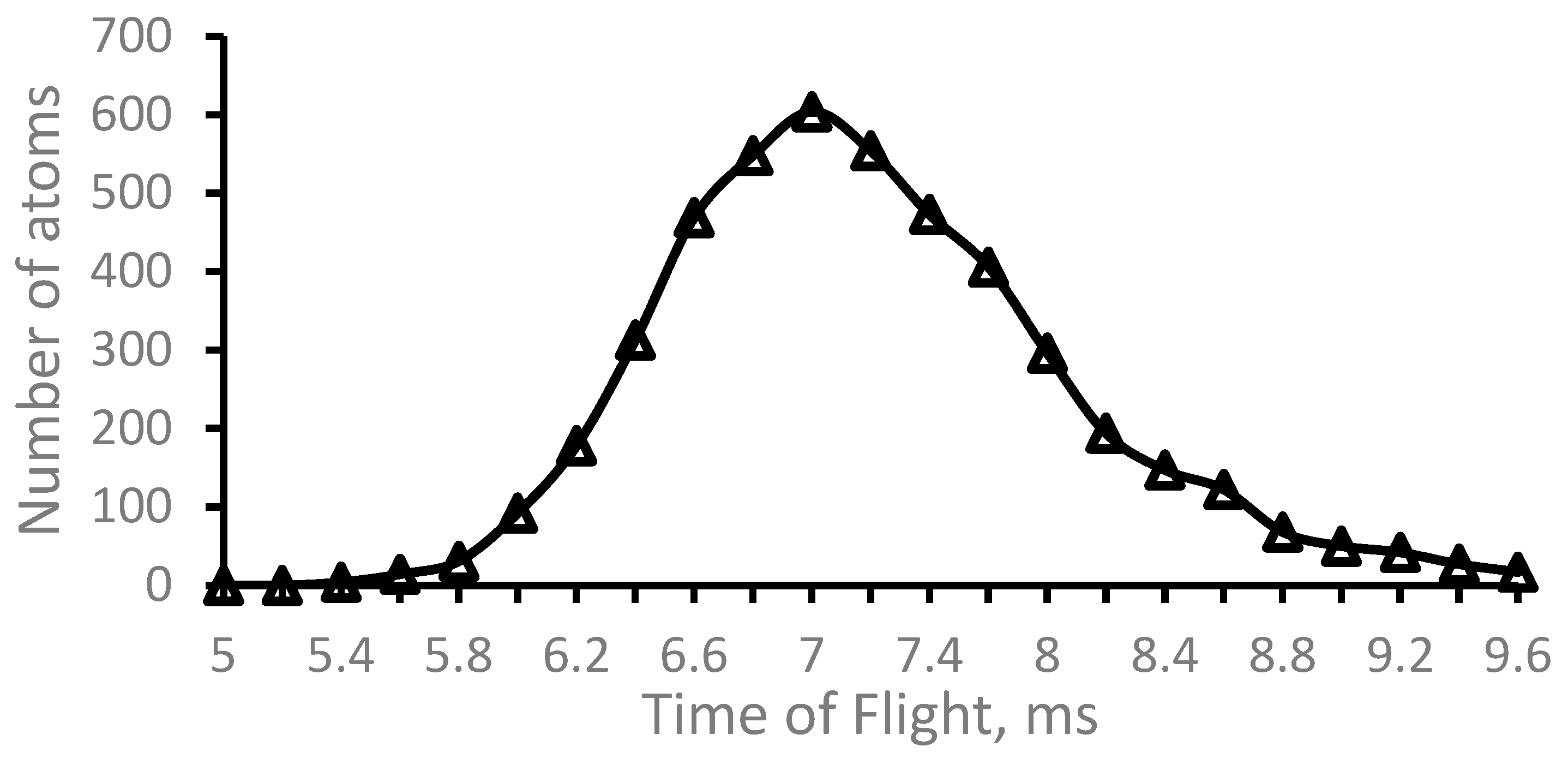
Calculation results for the time-of-flight distribution
164Dy atoms from the filament tip to the nozzle throat shown in
Figure 3. The average atoms’ extraction time is T = 7.0 ms, the time spread determined as full width at half maximum (FWHM) is ΔT = 1.4 ms. The corresponding extraction efficiency of
164Dy atoms from the exit flow channel is (94,5 ± 2.7) %.
2.2. GSI Nozzle at Gas Cell Pressure Pcell = 100 Mbar and Pbg = 6.47∙10-2 Mbar
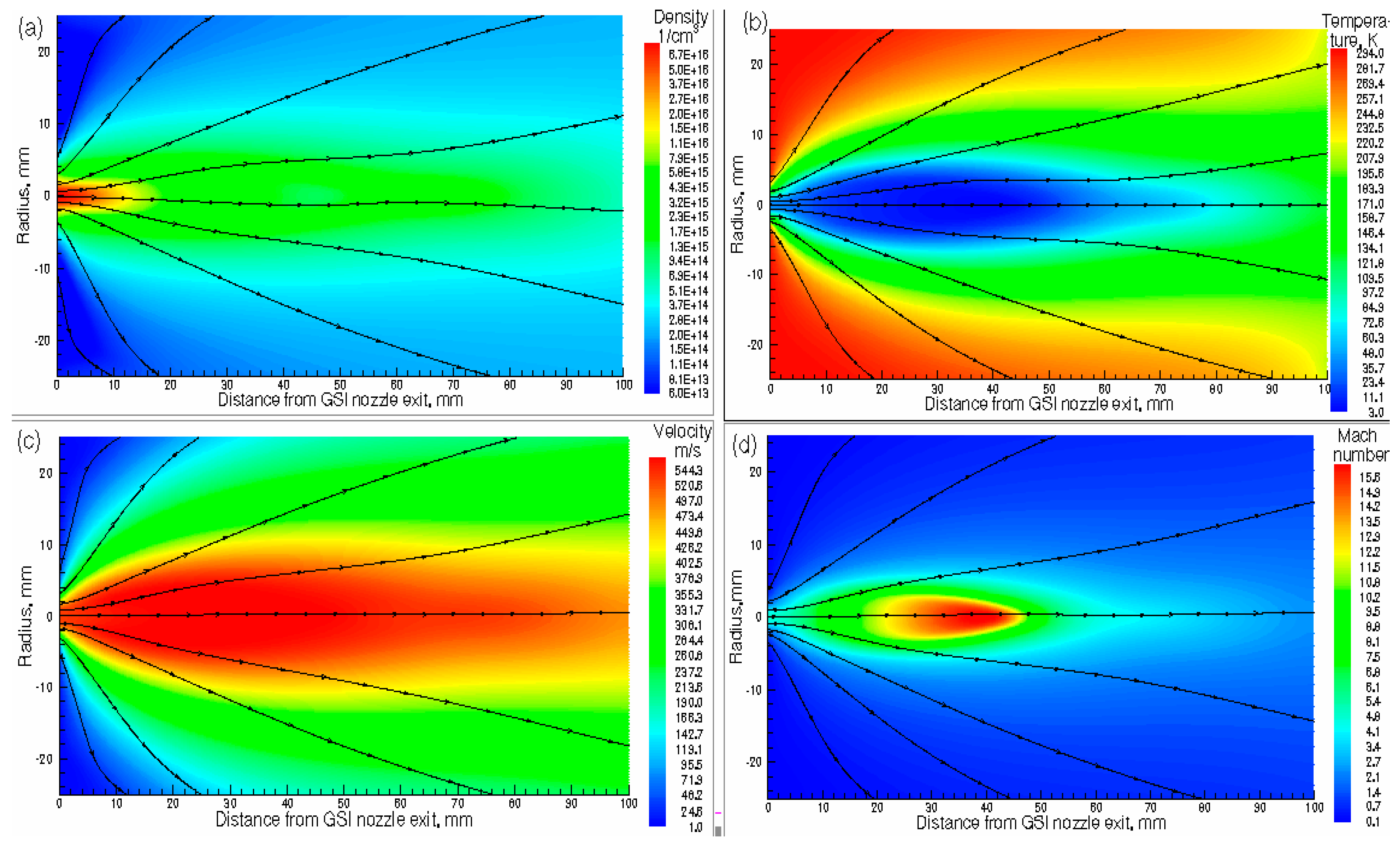
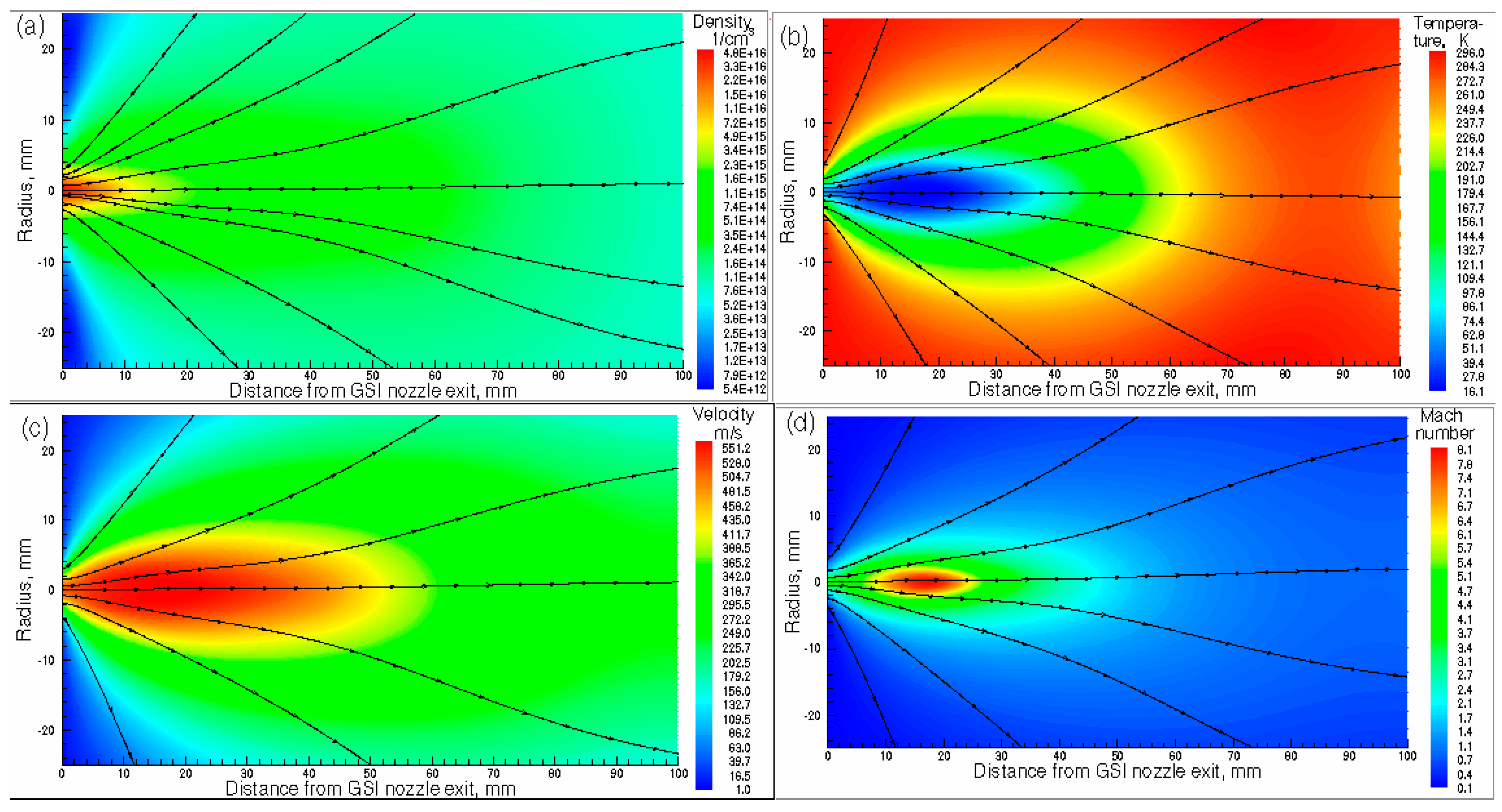
Results of the gas dynamic simulation for argon gas density, temperature, velocity and Mach number flow fields for GSI nozzle are shown in
Figure 4.
The results of gas dynamic simulation shown in
Figure 4 we have used for Monte Carlo simulations of
164Dy atomic beam. These results are presented in the next four
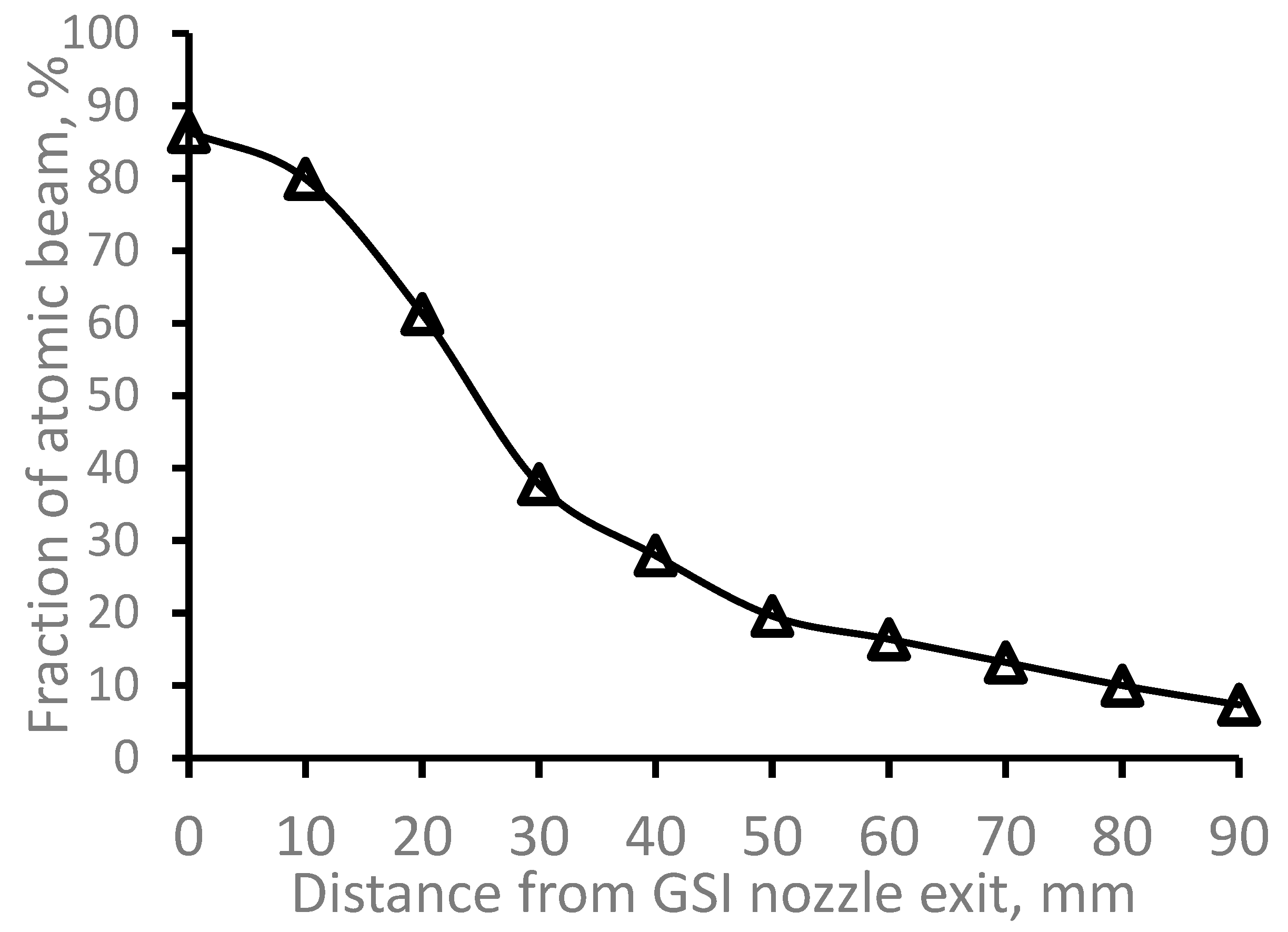
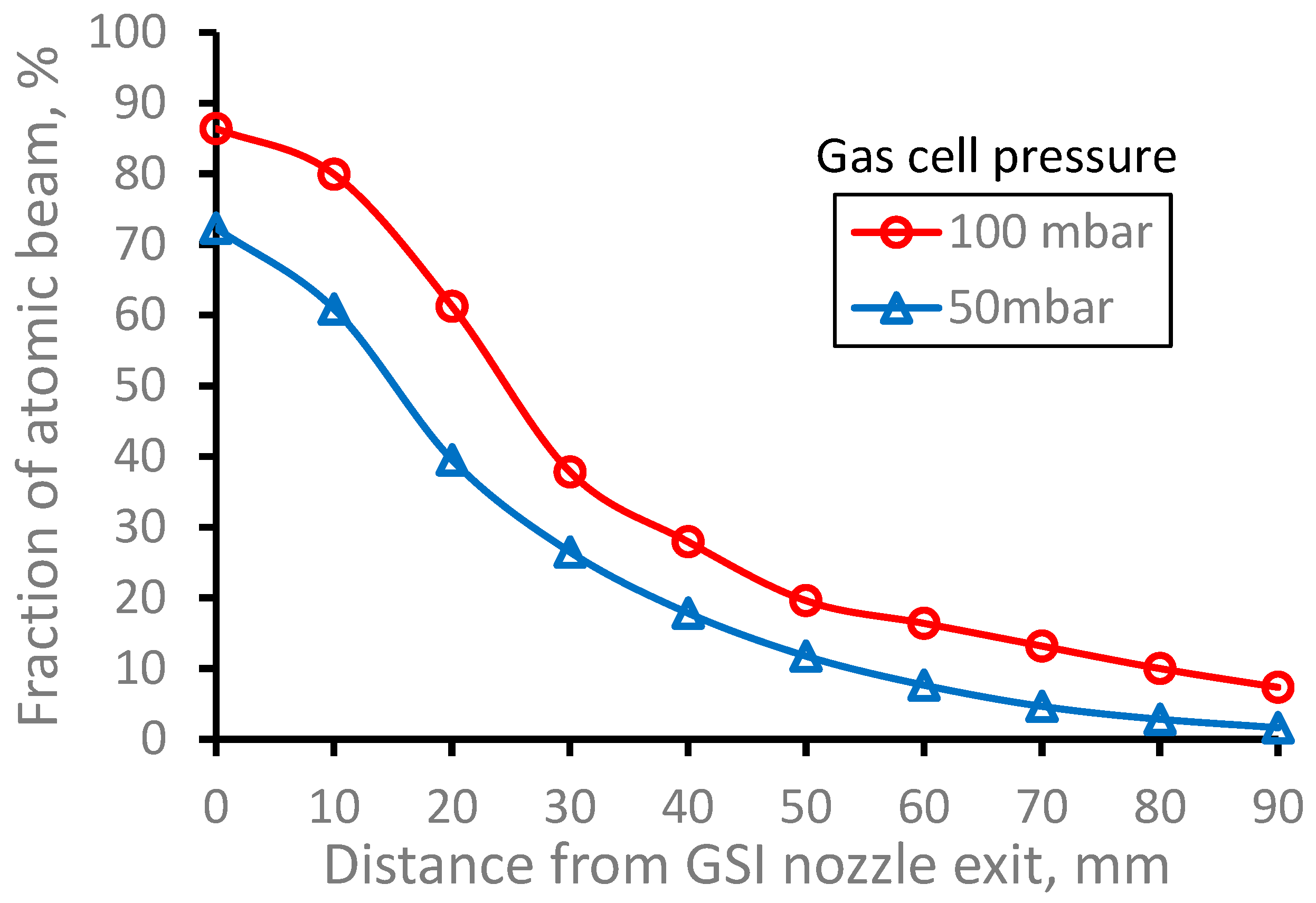
Figures. The calculated fraction of the extracted from the gas cell
164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 diameter in [
33]) as a function of distance from GSI nozzle exit, shown in
Figure 5. The decreasing of the dysprosium atomic beam fraction with the distance from GSI nozzle is simply explained by the gas jet divergence. The atomic beam diffusion losses inside GSI nozzle are equal to (15.6 ± 0.6) % and they are taken into account in the data presented in
Figure 5.
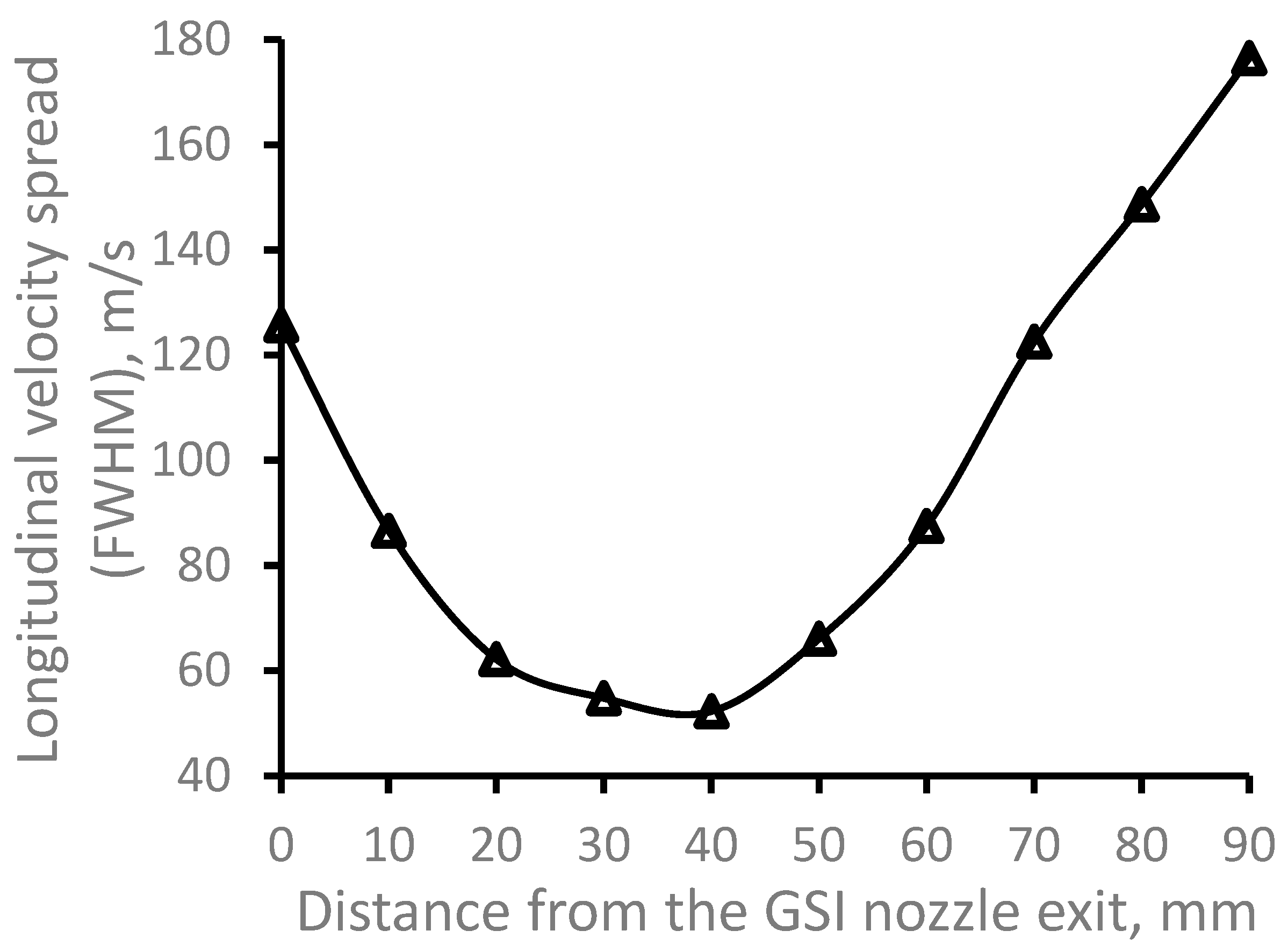
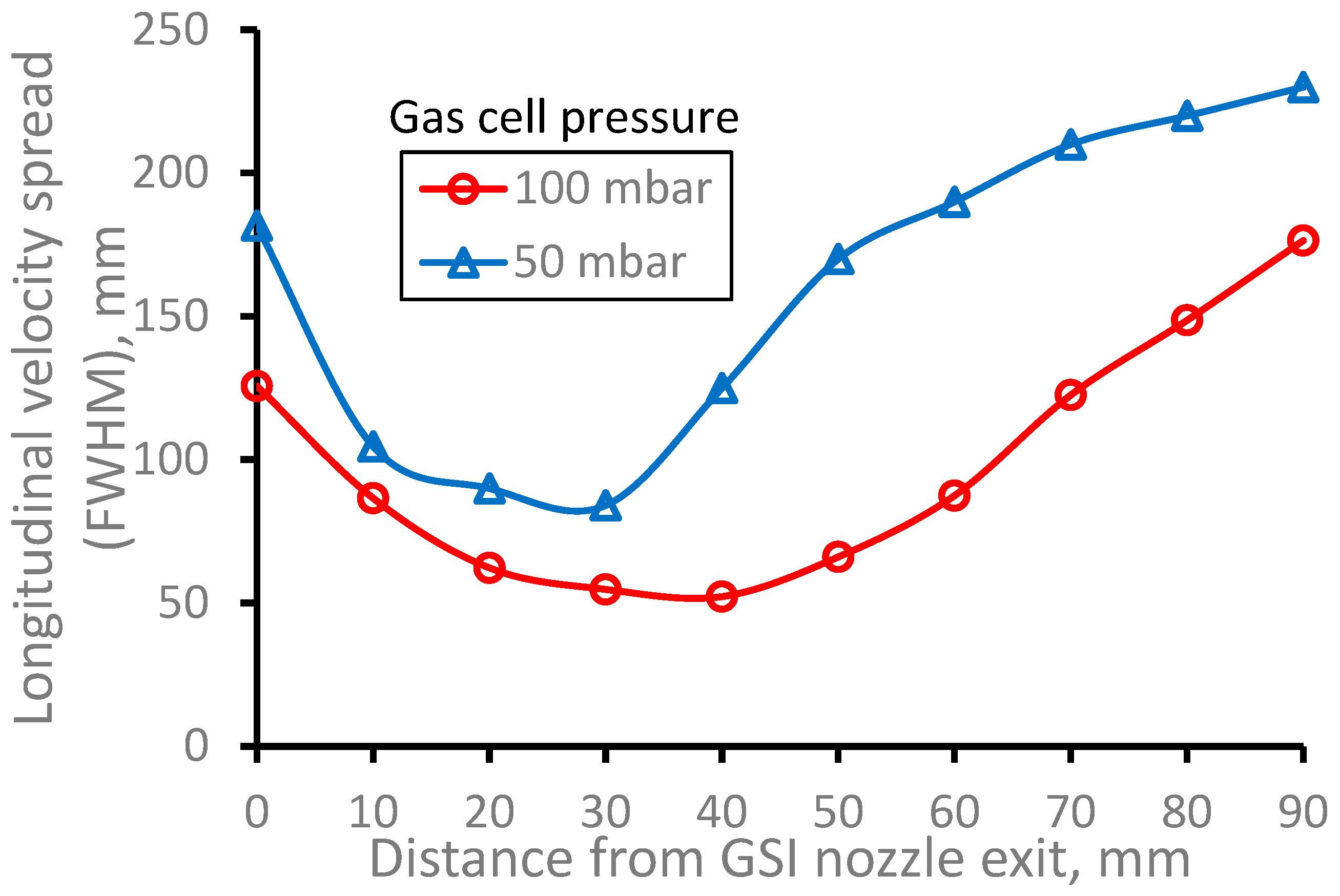
Figure 6 demonstrates how the calculated longitudinal velocity spread of dysprosium atomic beam depends on the distance from GSI nozzle. The data averaged in the radial plane over the Laser-1 beam diameter, and this makes it possible to directly and simply compare our calculations with the future experiments at JetRIS setup. Moreover, such calculations allow for getting important quantitative information on a quality of the cooled in the supersonic gas jet atomic beams.
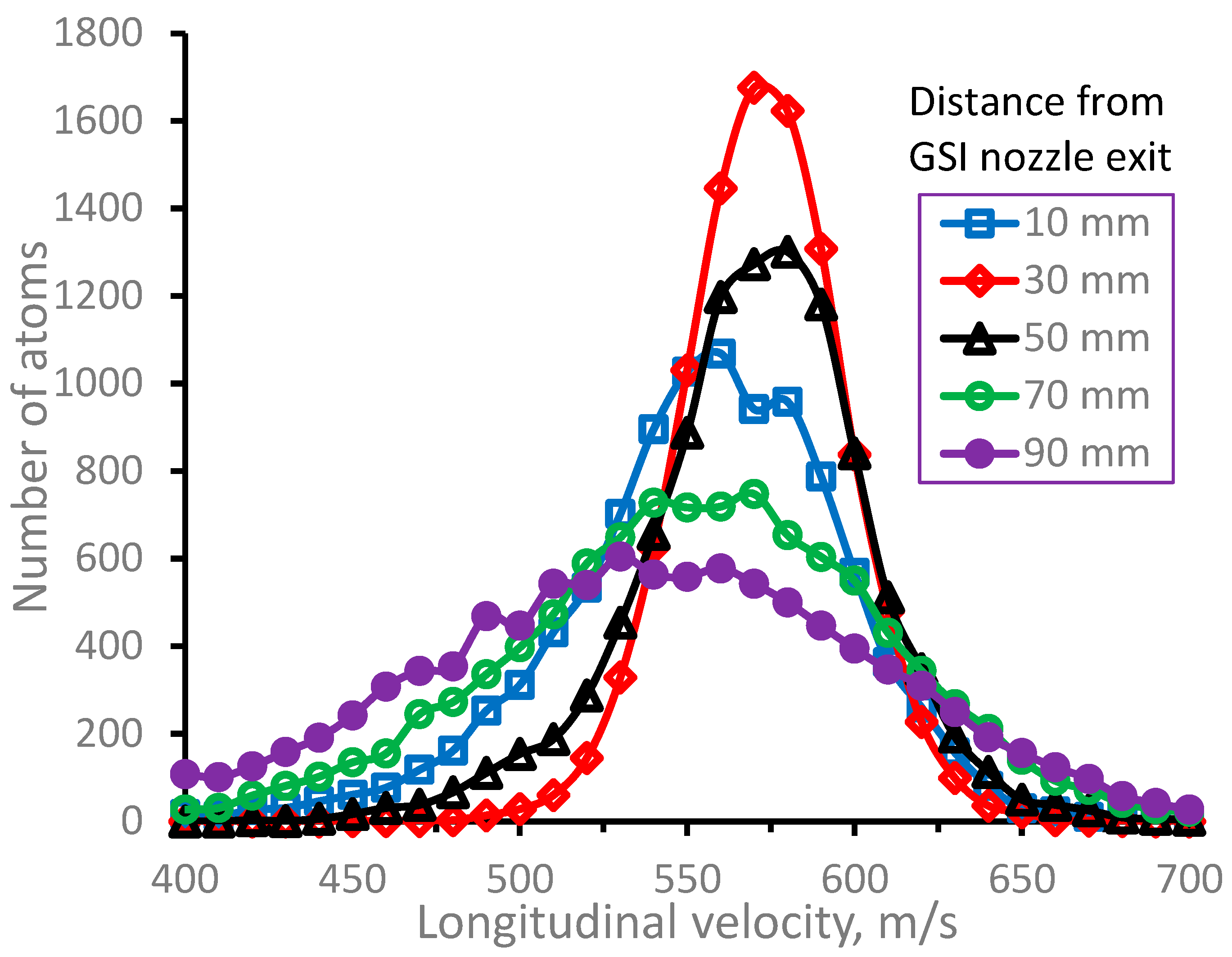
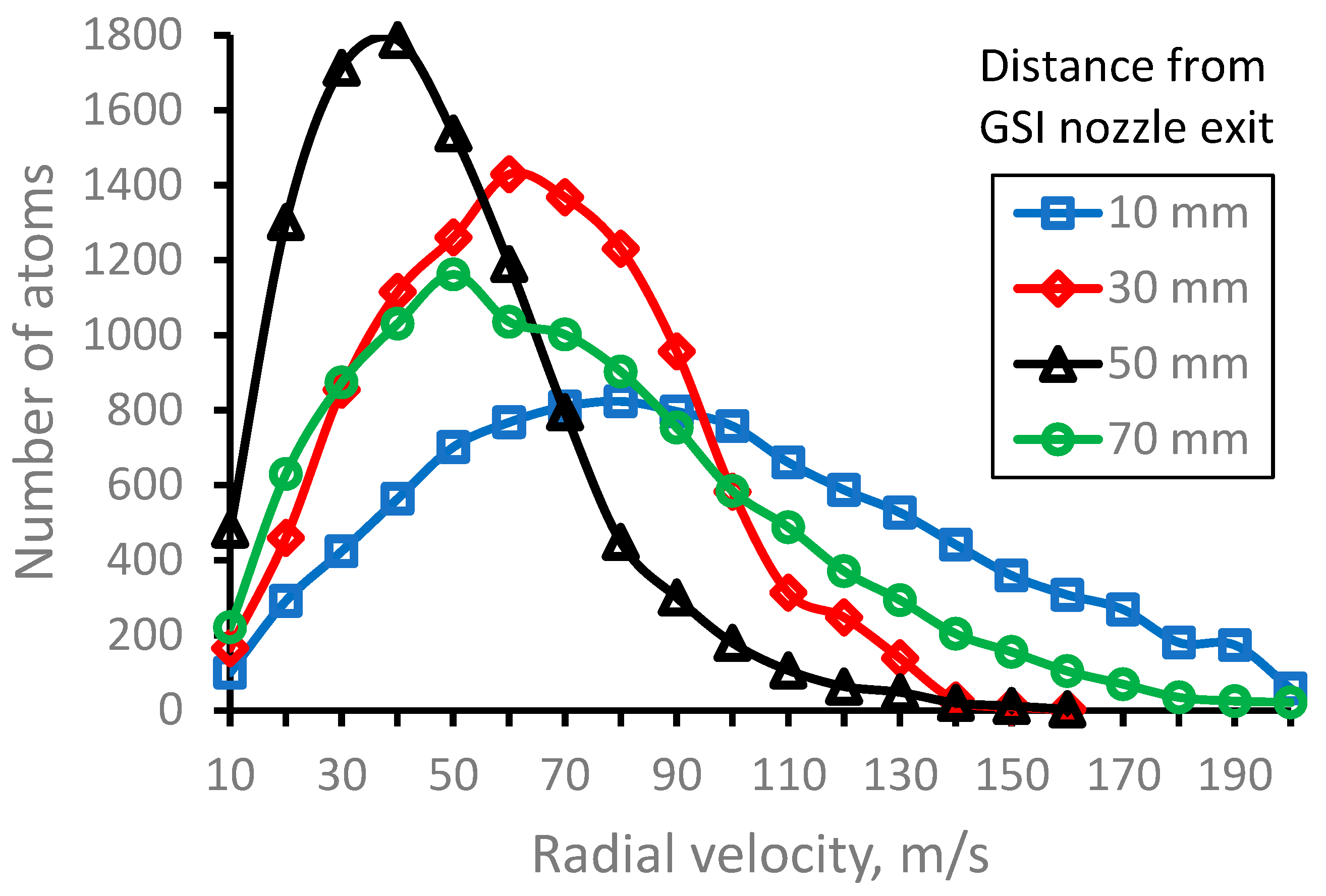
Figure 7 and
Figure 8 illustrate the distributions of longitudinal and radial
164Dy atomic beam velocity components (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from GSI nozzle.
2.3. GSI nozzle at gas cell pressure Pcell = 50 mbar and Pbg = 3.23∙10-2 mbar
To check how the supersonic gas jet structure and parameters of extracted into the jet
164Dy atomic beam will look at lower stagnation gas cell pressure, we performed calculations, which are similar to the calculations described above in the subection 2.2 for the same pumping capacity, but for the gas cell pressure of P
cell = 50 mbar. The results of the gas dynamic simulation for argon gas density, temperature, velocity and Mach number flow fields for GSI nozzle at P
cell = 50 mbar are shown in
Figure 9.
Results of the Monte Carlo simulations for the case of 50 mbar gas cell pressure shown in
Figure 10 and
Figure 11. We have included into these
Figures results of calculations presented above in the
Figure 5 and
Figure 6 for the case of P
cell = 100 mbar for comparison. Notice, that the atomic beam diffusion losses inside GSI nozzle at P
cell = 50 mbar is equal to (27.7 ± 0.8) % that is about factor 2 higher than that one at P
cell = 100 mbar.
4. Discussion and outlook.
In the section 2 of the article, we have investigated by means of detailed computer experiments the conventional nowadays technique of the so-called in-gas-jet laser resonance ionization spectroscopy. As a typical representative of this technique, we have chosen for the numerical computer analysis the setup of the JetRIS project [32, 33]. The JetRIS project is under development now at GSI, Darmstadt.
Results of gas dynamic simulation for the exit flow channel of 12 mm in diameter presented in
Figure 1 and
Figure 2. It is a laminar gas flow with Reynolds number of 123. The calculated in Monte Carlo simulation time-of-flight of evaporated 164Dy neutral atoms from the hot filament tip to the nozzle throat is (7.0 ± 1.4) ms (see
Figure 3.), the extraction efficiency is (94.5 ± 2.7) %, or in other words the atomic beam diffusion losses are equal to (5.5 ± 0.3) %. The gas dynamic + Monte Carlo simulations shows that the additional diffusion losses of the 164Dy atomic beam inside GSI nozzle at
Pcell =100 mbar are equal to (15.6 ± 0.6) %. The graphic description of the calculated argon supersonic jet (flow fields of gas density, velocity, temperature and Mach number) flowing out of GSI nozzle into the gas-jet chamber shown in
Figure 4 and
Figure 9 for the gas cell pressure of 100 mbar and 50 mbar, correspondingly. Here the strong effect of the gas viscosity of the supersonic jet structure and parameters is clear visible.
Notice that the 164Dy atomic beam diffusion losses inside GSI nozzle for P
cell = 50 mbar (27.7 ± 0.8) % are considerably higher than that one at P
cell = 100 mbar, and it looks reasonable. The production efficiency of excited by the Laser-1 dysprosium atoms in the gas jet is also less in the case of P
cell = 50 mbar (see
Figure 10). The atomic beam quality, shown in
Figure 11 as a longitudinal velocity spread, is also worse.
The section 3 of the article devoted to description and exploration of our proposal of a new double-nozzle technique. By means of gas dynamic and Monte Carlo simulations, we have shown that this new technique has many advantages over the conventional technique described in the section 2 of the article. E.g., the atomic beam diffusion losses inside the double-nozzle system are equal only to (9.5 ± 0.4) % that is in a factor 1.6 less than in the case of the use of GSI nozzle at the same gas cell pressure (P
cell = 100 mbar) and having the same nozzle throat diameter of 1.0 mm. The double nozzle method is much more efficient (see direct comparison in figures 16, 21 and 23) and it allows also obtaining better atomic beam quality (expressed in longitudinal velocity spread) for a longer downstream distance from the 2nd nozzle exit (see direct comparison in
Figure 17,
Figure 22 and
Figure 24).
The proposed double-nozzle technique can effectively work in a wide range of P
cell and Pnoz pressures. There are no needs here for the use of any butterfly valve, placed in front of the vacuum pump, as it is in [
32] to adjust the background pressure in the gas-jet chamber under changing the P
cell, or using the nozzles having different throat diameters and profiles of its diverging supersonic part. The butterfly valve allows decreasing the nominal capacity of the used vacuum pump, but it cannot increase it, when it is required.
Moreover, the same double-nozzle design, that we suggest for the use in JetRIS setup at GSI and which main parameters are listed in
Table 1, can be effectively used at different vacuum pump capacities (see for details the subsection 3.4 above).
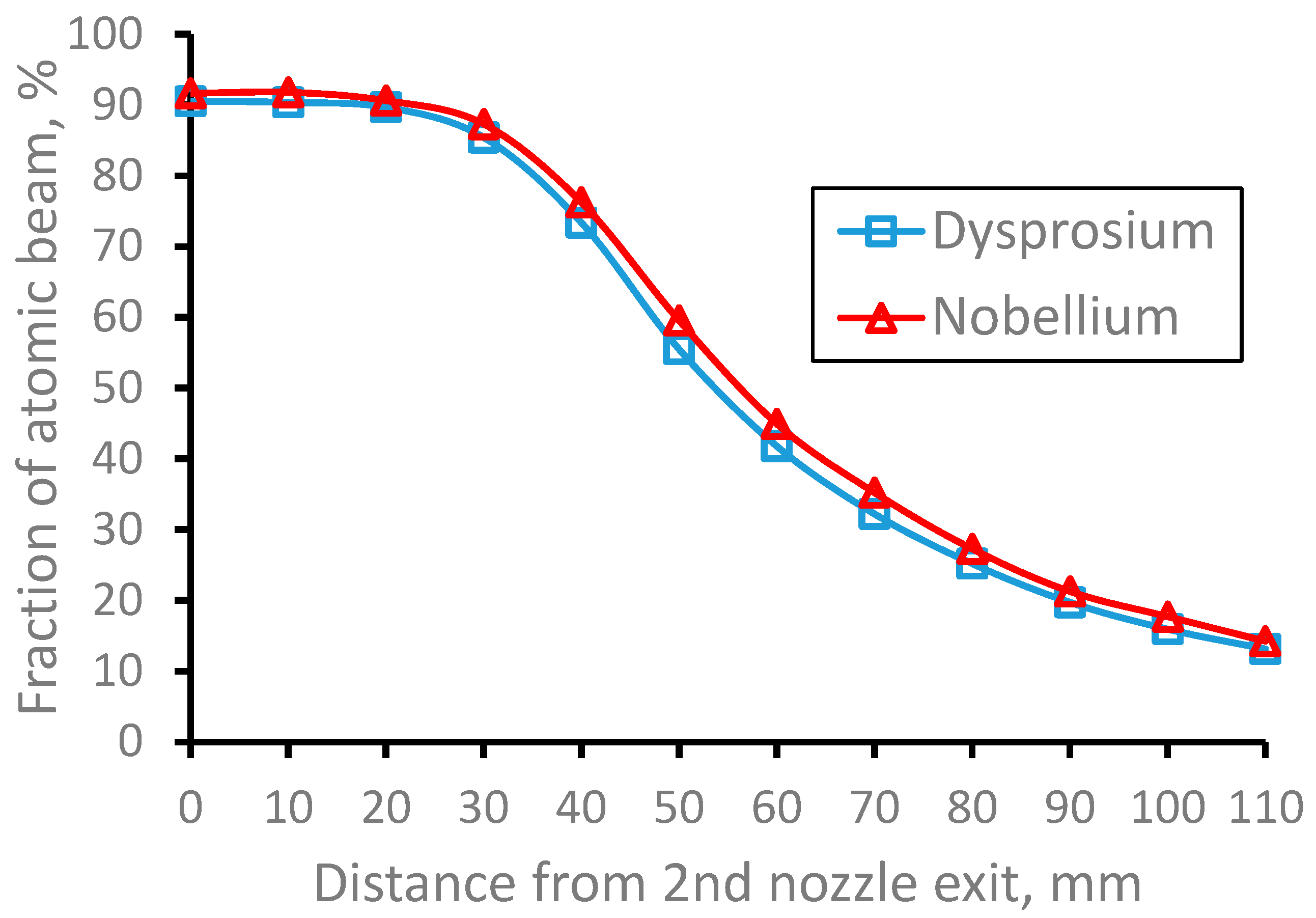
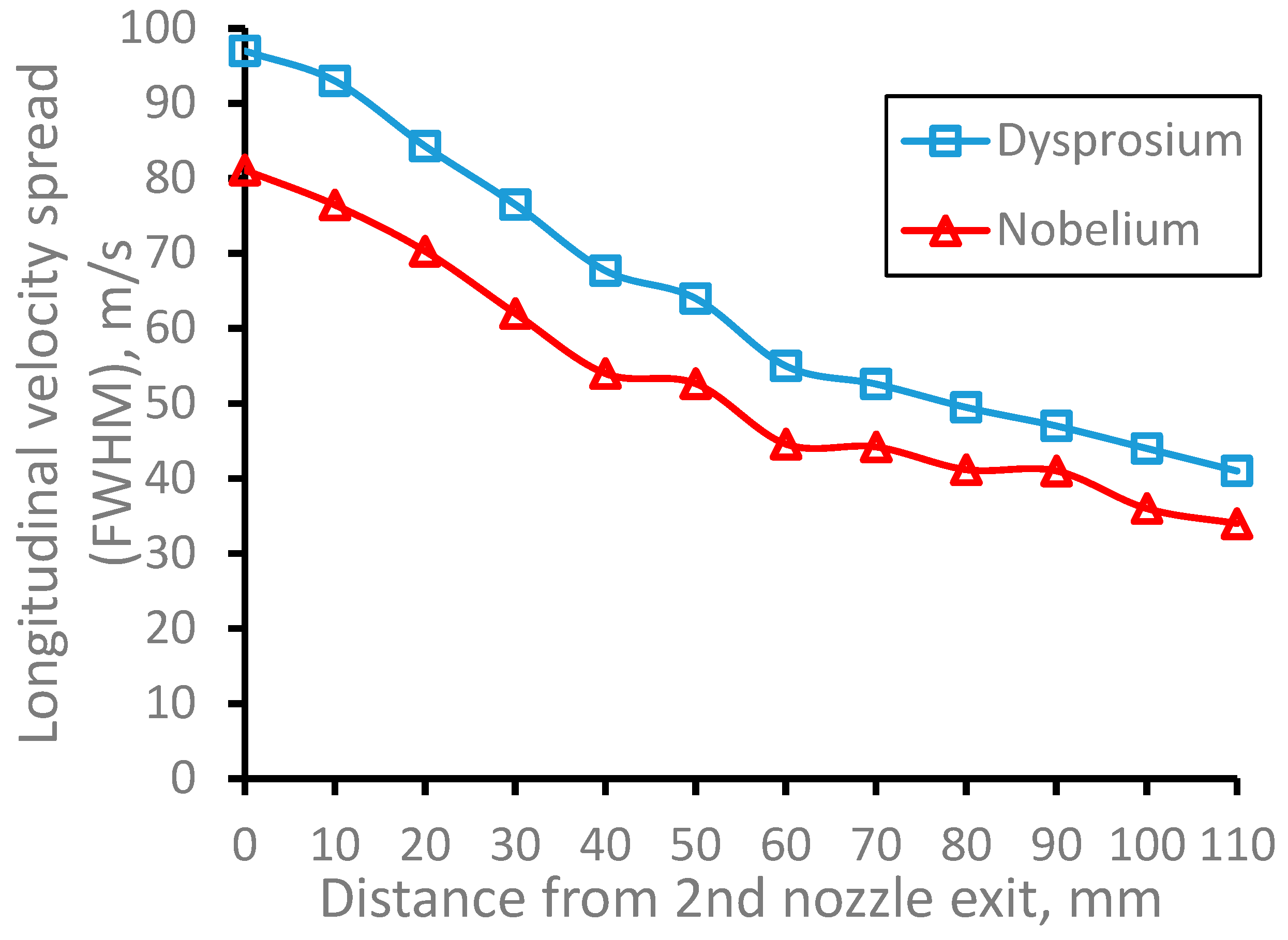
To help the authors of works [32, 33] in their preparation for the future online measurement of nobelium isotopes, we performed the Monte Carlo simulations for the 253No atomic beam in the argon supersonic jet, as well. The results of these calculations, which presented in the subsection 3.7, allow to quantitative estimate the efficiency of the JetRIS setup operation under the use in it the proposed double-nozzle technique.
To implement the proposed double-nozzle technique to the JetRIS setup, it will be enough just replace the present GSI nozzle by the double-nozzle system presented in the article.
In conclusion, we can say that the double-nozzle design, which main parameters are listed in the
Table 1, can be also used for the other similar setups or/and projects. If, e.g., operation conditions or some specific requirements to these setups/projects are very differ of that one in the JetRIS setup, and then we can make similar computer experiments to find an optimal solution for these cases upon the corresponding request.
Figure 1.
Results of the gas dynamic simulation for the argon velocity flow field inside the exit flow channel. The stagnation pressure Pcell = 100 mbar, the temperature of the channel walls Tcell = 296 K. The arrowed black lines show the gas flow direction.
Figure 1.
Results of the gas dynamic simulation for the argon velocity flow field inside the exit flow channel. The stagnation pressure Pcell = 100 mbar, the temperature of the channel walls Tcell = 296 K. The arrowed black lines show the gas flow direction.
Figure 2.
The calculated radial gas velocity profile in the middle of the exit flow channel.
Figure 2.
The calculated radial gas velocity profile in the middle of the exit flow channel.
Figure 3.
The time-of-flight of 164Dy atoms from the filament tip to the nozzle throat. Total number of calculated atoms is 5000.
Figure 3.
The time-of-flight of 164Dy atoms from the filament tip to the nozzle throat. Total number of calculated atoms is 5000.
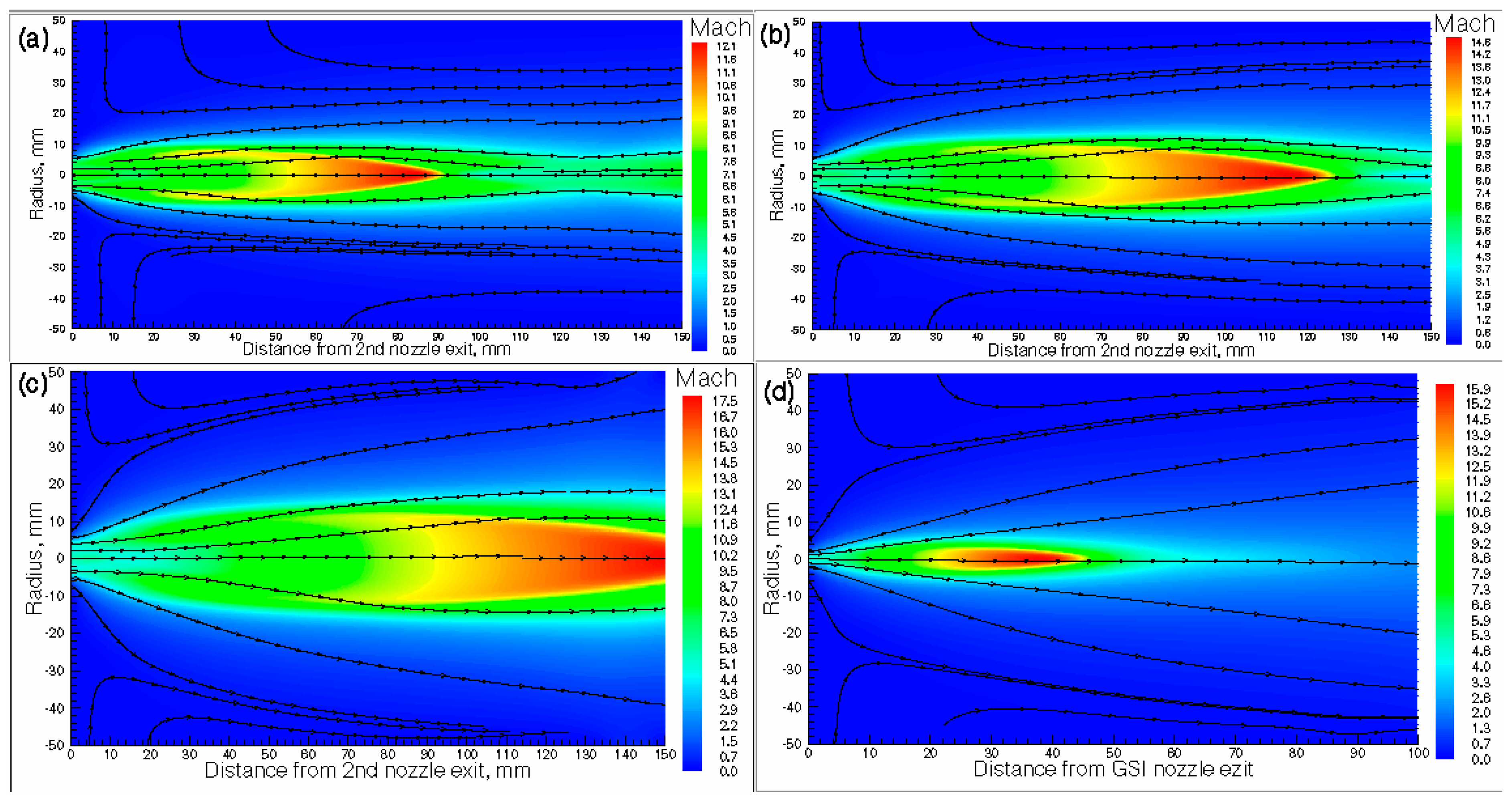
Figure 4.
Results of the gas dynamic simulation for GSI nozzle: (a) density, (b) temperature, (c) velocity and (d) Mach number flow fields. The stagnation pressure and temperature in the gas cell are Pcell = 100 mbar and Tcell = 296 K, correspondingly. Background pressure in the vacuum gas-jet chamber is Pbg = 6.47∙10-3 mbar. Black arrowed lines show the gas flow directions.
Figure 4.
Results of the gas dynamic simulation for GSI nozzle: (a) density, (b) temperature, (c) velocity and (d) Mach number flow fields. The stagnation pressure and temperature in the gas cell are Pcell = 100 mbar and Tcell = 296 K, correspondingly. Background pressure in the vacuum gas-jet chamber is Pbg = 6.47∙10-3 mbar. Black arrowed lines show the gas flow directions.
Figure 5.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 beam diameter) as a function of distance from GSI nozzle exit. Number of calculated atoms is 10000. .
Figure 5.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 beam diameter) as a function of distance from GSI nozzle exit. Number of calculated atoms is 10000. .
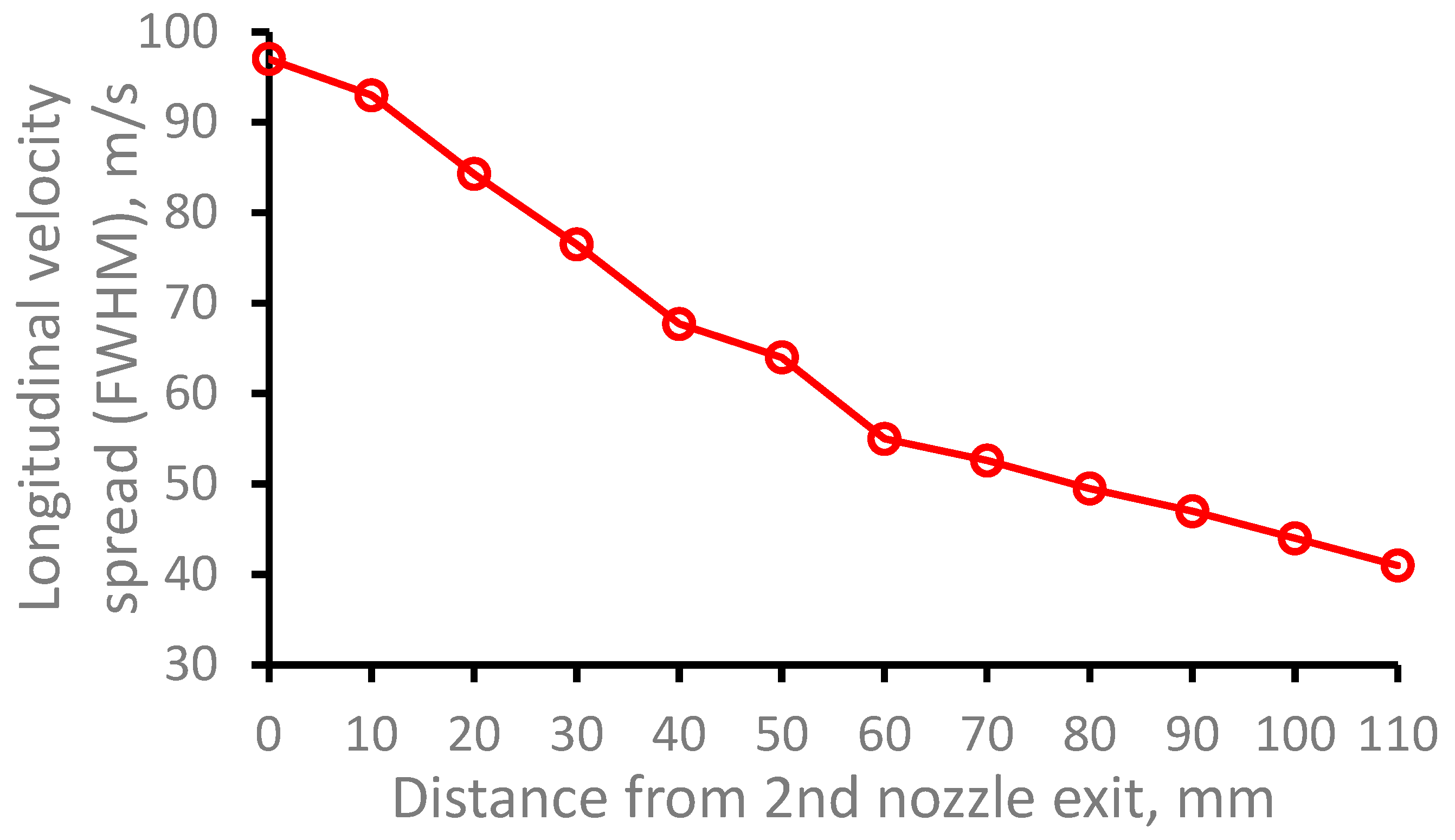
Figure 6.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) as a function of the distance from GSI nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000.
Figure 6.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) as a function of the distance from GSI nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000.
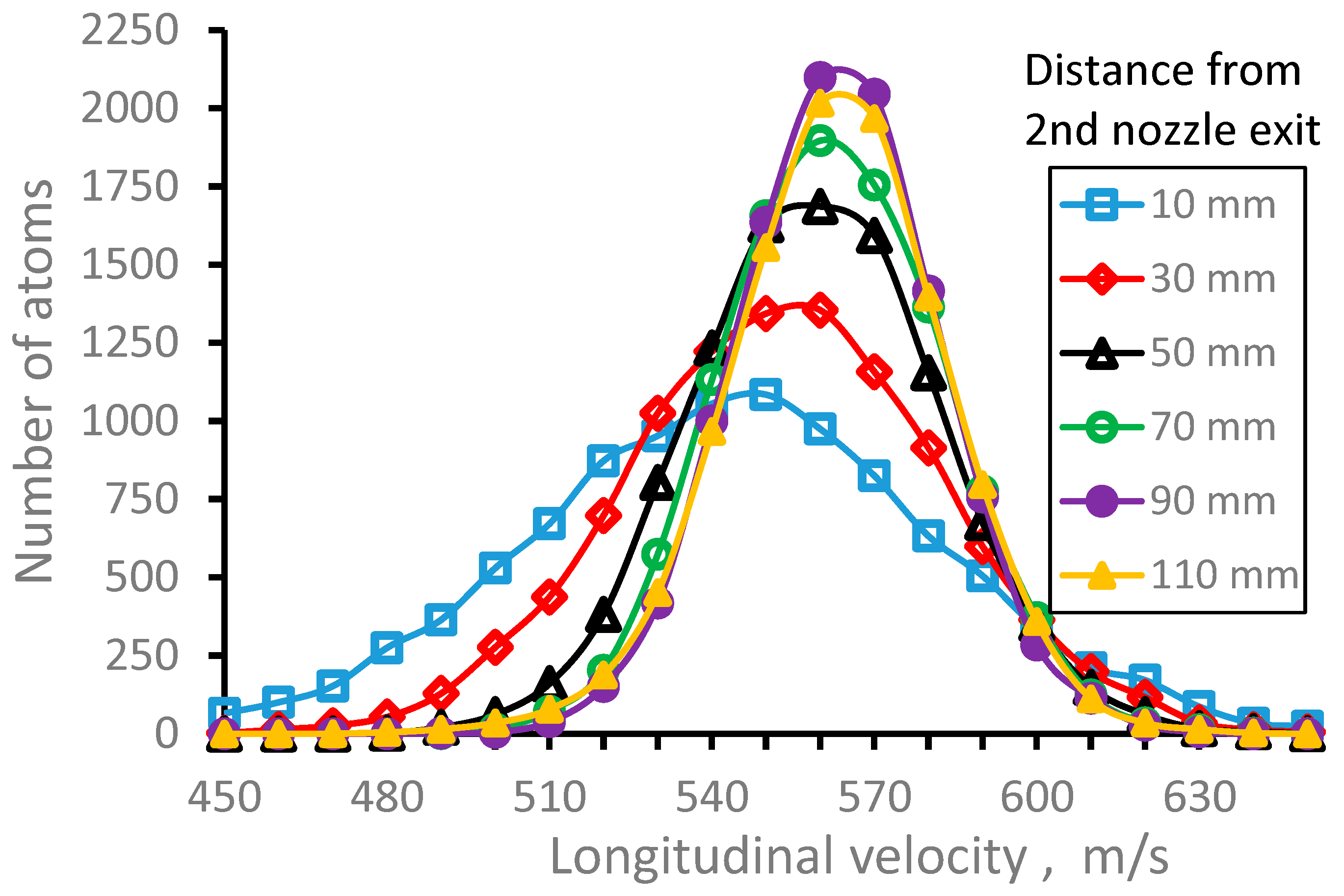
Figure 7.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from GSI nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 7.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from GSI nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
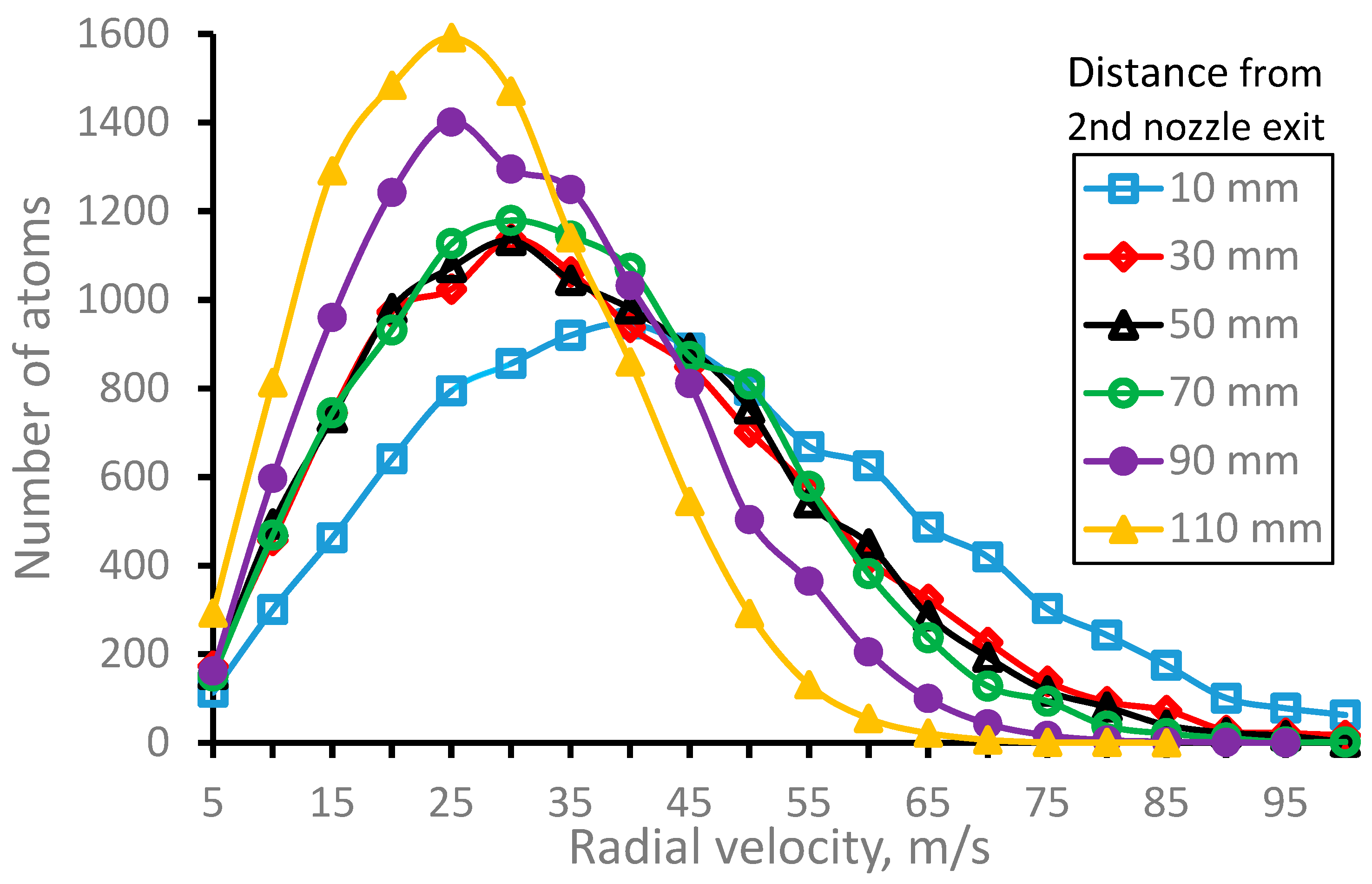
Figure 8.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam radial velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from GSI nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 8.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam radial velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from GSI nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 9.
Results of the gas dynamic simulation: (a) density, (b) temperature, (c) velocity and (d) Mach number flow fields for GSI nozzle. The stagnation pressure and temperature in the gas cell are Pcell = 50 mbar and Tcell = 296 K, correspondingly. Background pressure in the gas-jet chamber is Pbg = 3.23∙10-3 mbar. Black arrowed lines show the gas flow directions.
Figure 9.
Results of the gas dynamic simulation: (a) density, (b) temperature, (c) velocity and (d) Mach number flow fields for GSI nozzle. The stagnation pressure and temperature in the gas cell are Pcell = 50 mbar and Tcell = 296 K, correspondingly. Background pressure in the gas-jet chamber is Pbg = 3.23∙10-3 mbar. Black arrowed lines show the gas flow directions.
Figure 10.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 diameter) as a function of distance from GSI nozzle exit. Number of calculated atoms is 10000. .
Figure 10.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 diameter) as a function of distance from GSI nozzle exit. Number of calculated atoms is 10000. .
Figure 11.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) as a function of distance from GSI nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000.
Figure 11.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) as a function of distance from GSI nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000.
Figure 12.
Schematic of the method of gas dynamic cooling of low-energy molecular and ion beams. Picture from Refs. [39, 61]. See the text for details.
Figure 12.
Schematic of the method of gas dynamic cooling of low-energy molecular and ion beams. Picture from Refs. [39, 61]. See the text for details.
Figure 13.
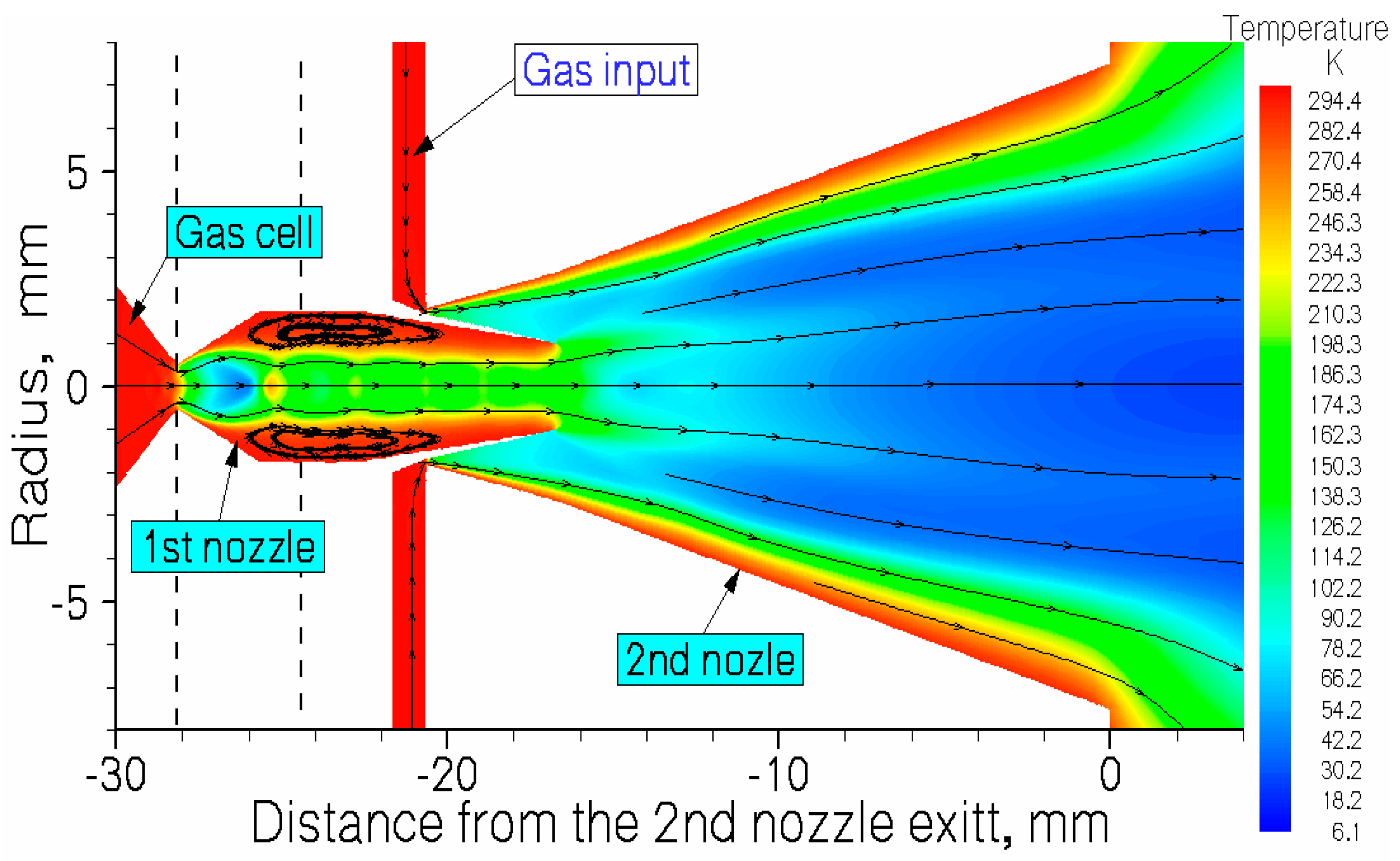
Schematic view of the double-nozzle design combined with results of the gas dynamic simulation for argon temperature flow field. The stagnation gas cell pressure Pcell = 100 mbar, gas input (stagnation) pressure Pnoz = 81 mbar, background presse in the vacuum gas-jet chamber Pbg = 2.0∙10-2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and the both nozzles is 296 K. Black arrowed lines show the gas flow directions. Two black dashed vertical lines designate a possible connection of flanges for assembling this double-nozzle device.
Figure 13.
Schematic view of the double-nozzle design combined with results of the gas dynamic simulation for argon temperature flow field. The stagnation gas cell pressure Pcell = 100 mbar, gas input (stagnation) pressure Pnoz = 81 mbar, background presse in the vacuum gas-jet chamber Pbg = 2.0∙10-2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and the both nozzles is 296 K. Black arrowed lines show the gas flow directions. Two black dashed vertical lines designate a possible connection of flanges for assembling this double-nozzle device.
Figure 14.
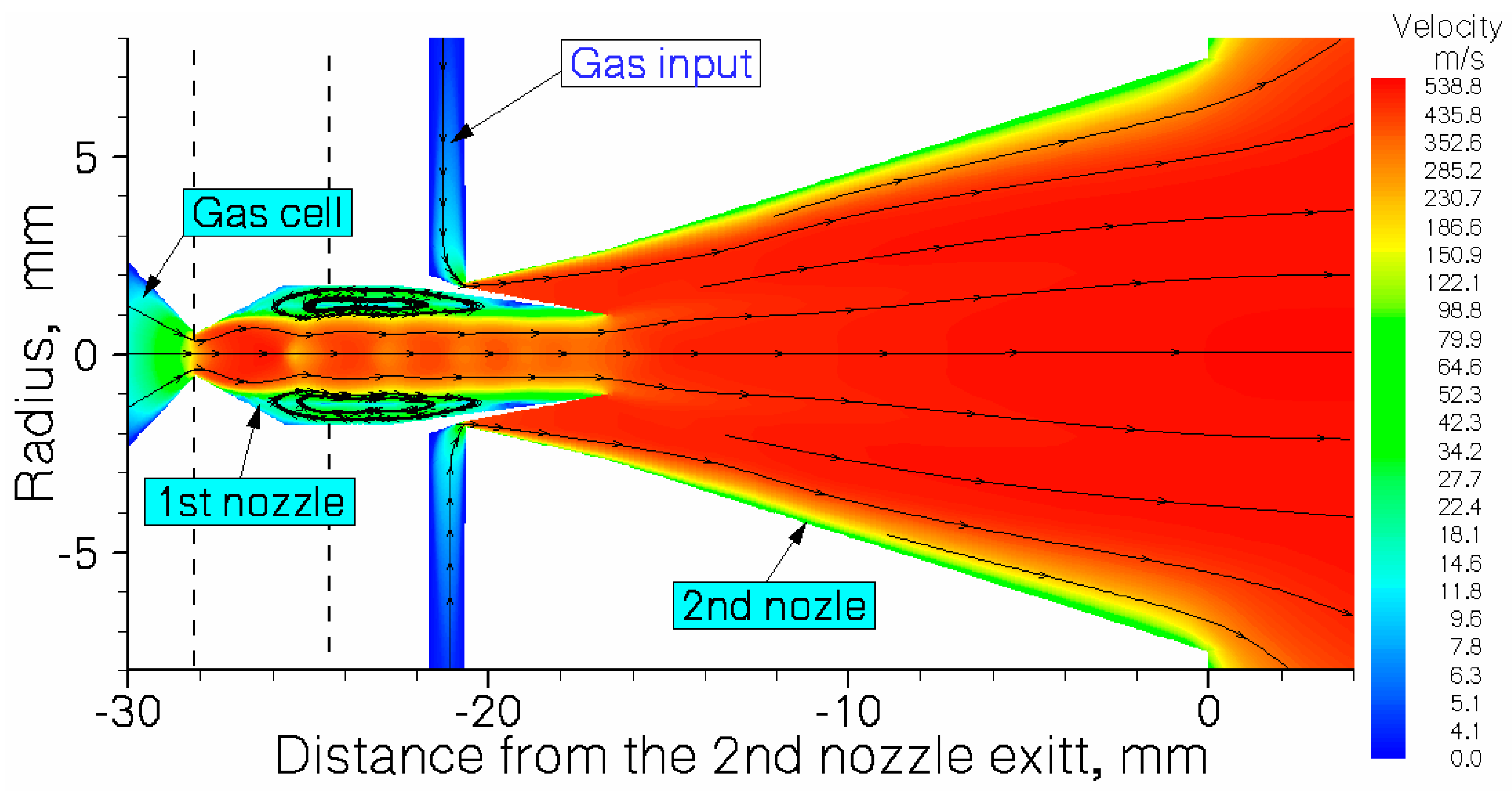
Schematic view of the double-nozzle design that shown in
Figure 10, but combined with results of the gas dynamic simulation for argon velocity flow field.
Figure 14.
Schematic view of the double-nozzle design that shown in
Figure 10, but combined with results of the gas dynamic simulation for argon velocity flow field.
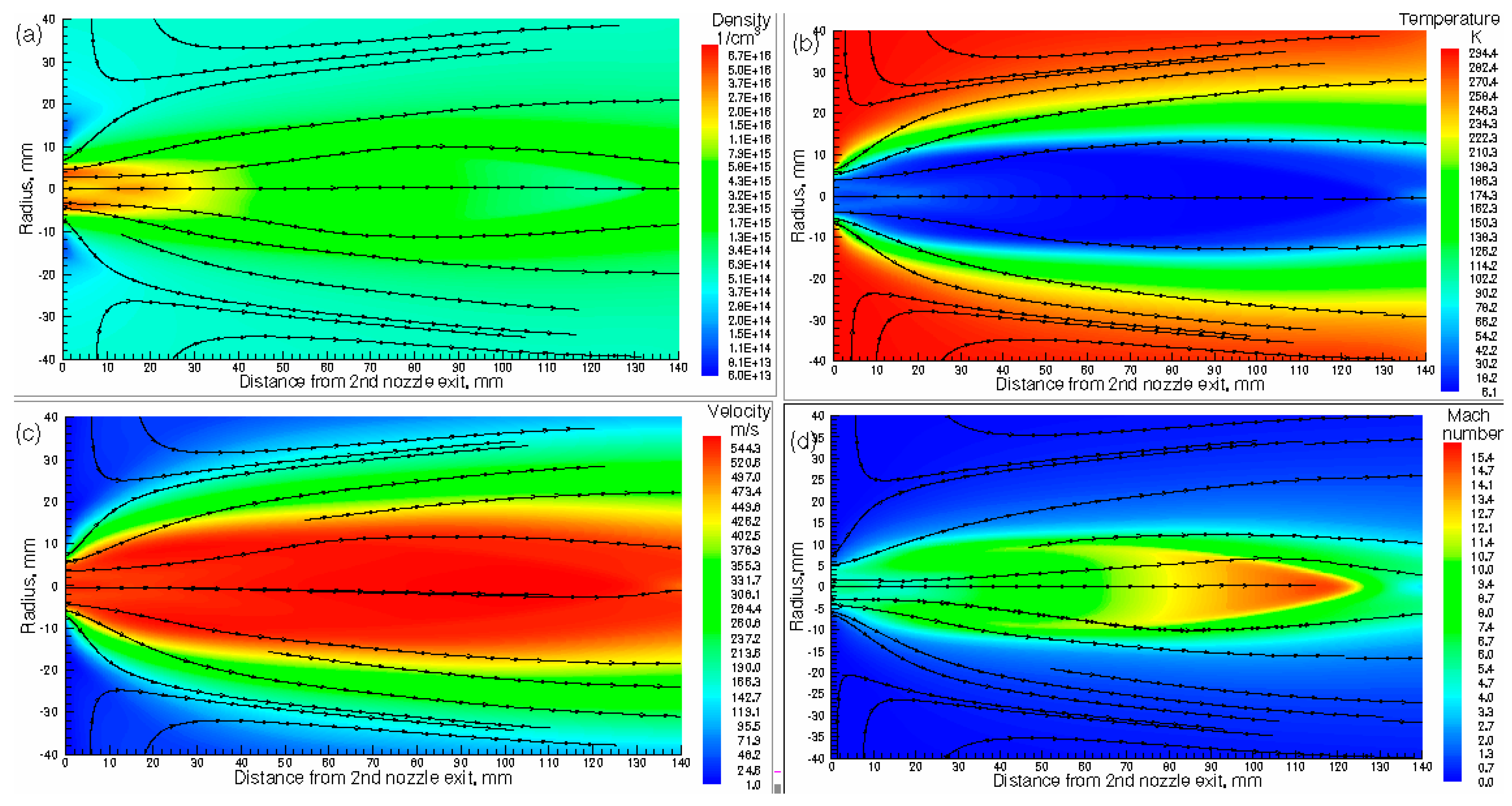
Figure 15.
Results of the gas dynamic simulation: (a) density, (b) temperature (c) velocity and (d) Mach number flow fields for the double-nozzle. The stagnation gas cell pressure Pcell = 100 mbar, gas input (stagnation) pressure Pnoz = 81 mbar, background pressure in the vacuum gas-jet chamber Pbg = 2.0∙10-2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and the both nozzles is 296 K. Black arrowed lines show the gas flow direction.
Figure 15.
Results of the gas dynamic simulation: (a) density, (b) temperature (c) velocity and (d) Mach number flow fields for the double-nozzle. The stagnation gas cell pressure Pcell = 100 mbar, gas input (stagnation) pressure Pnoz = 81 mbar, background pressure in the vacuum gas-jet chamber Pbg = 2.0∙10-2 mbar for the pumping capacity of 1300 l/s. The temperature of the gas cell and the both nozzles is 296 K. Black arrowed lines show the gas flow direction.
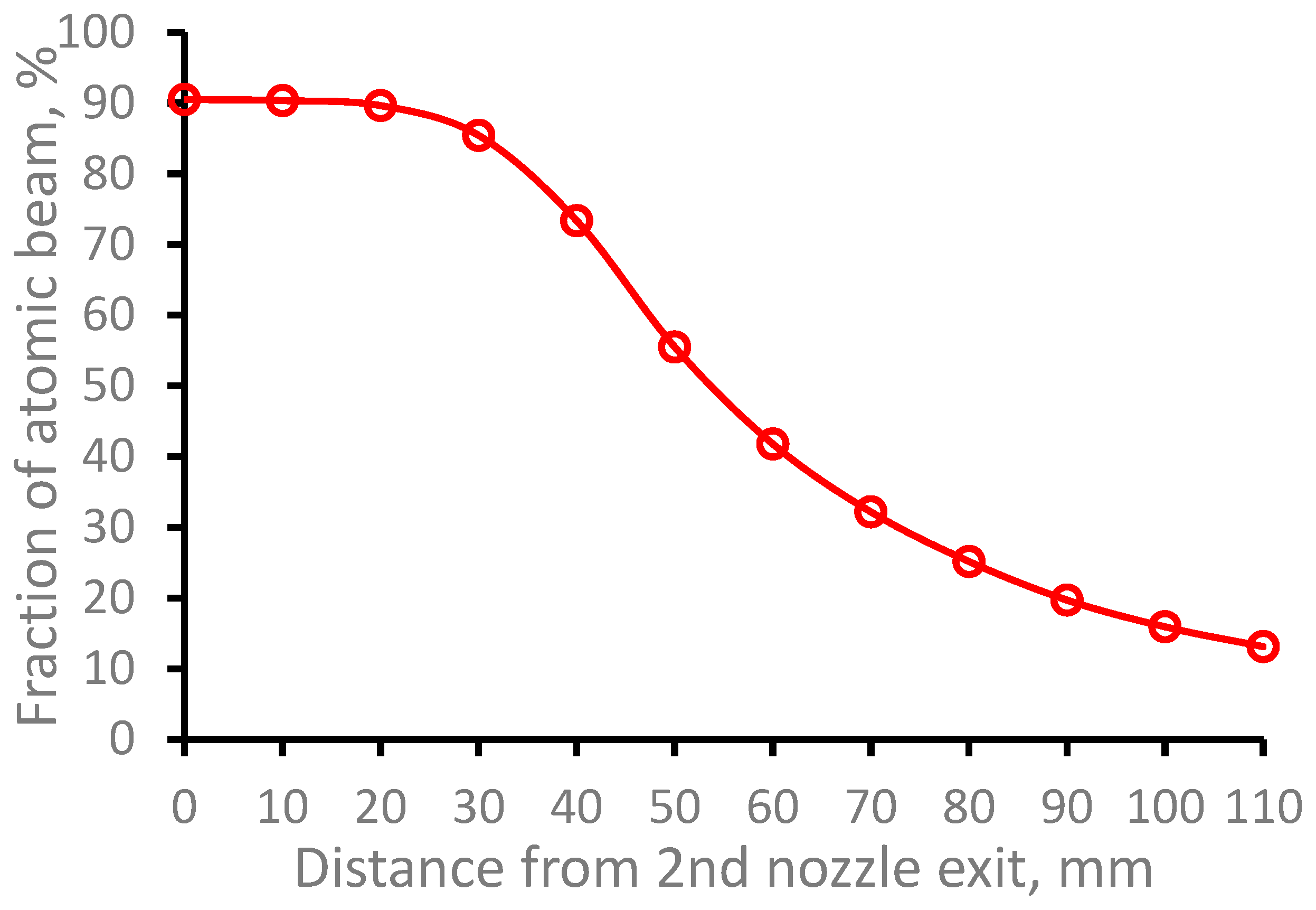
Figure 16.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the gas jet of 10 mm in diameter (it is the Laser-1 diameter) as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000. .
Figure 16.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the gas jet of 10 mm in diameter (it is the Laser-1 diameter) as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000. .
Figure 17.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000.
Figure 17.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000.
Figure 18.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from 2nd nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 18.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from 2nd nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 19.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam radial velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from 2nd nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 19.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam radial velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from 2nd nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 20.
Results of the gas dynamic simulation for Mach number flow fields for double nozzle at different pumping speeds: (a) 650 l/s, (b) 1300 l/s, (c) 2600 l/s, (d) GSI nozzle. The stagnation gas cell pressure Pcell = 100 mbar, gas input (stagnation) pressure Pnoz = 81 mbar. The temperature of the gas cell and the both nozzles is 296 K. Black arrowed lines show the gas flow direction.
Figure 20.
Results of the gas dynamic simulation for Mach number flow fields for double nozzle at different pumping speeds: (a) 650 l/s, (b) 1300 l/s, (c) 2600 l/s, (d) GSI nozzle. The stagnation gas cell pressure Pcell = 100 mbar, gas input (stagnation) pressure Pnoz = 81 mbar. The temperature of the gas cell and the both nozzles is 296 K. Black arrowed lines show the gas flow direction.
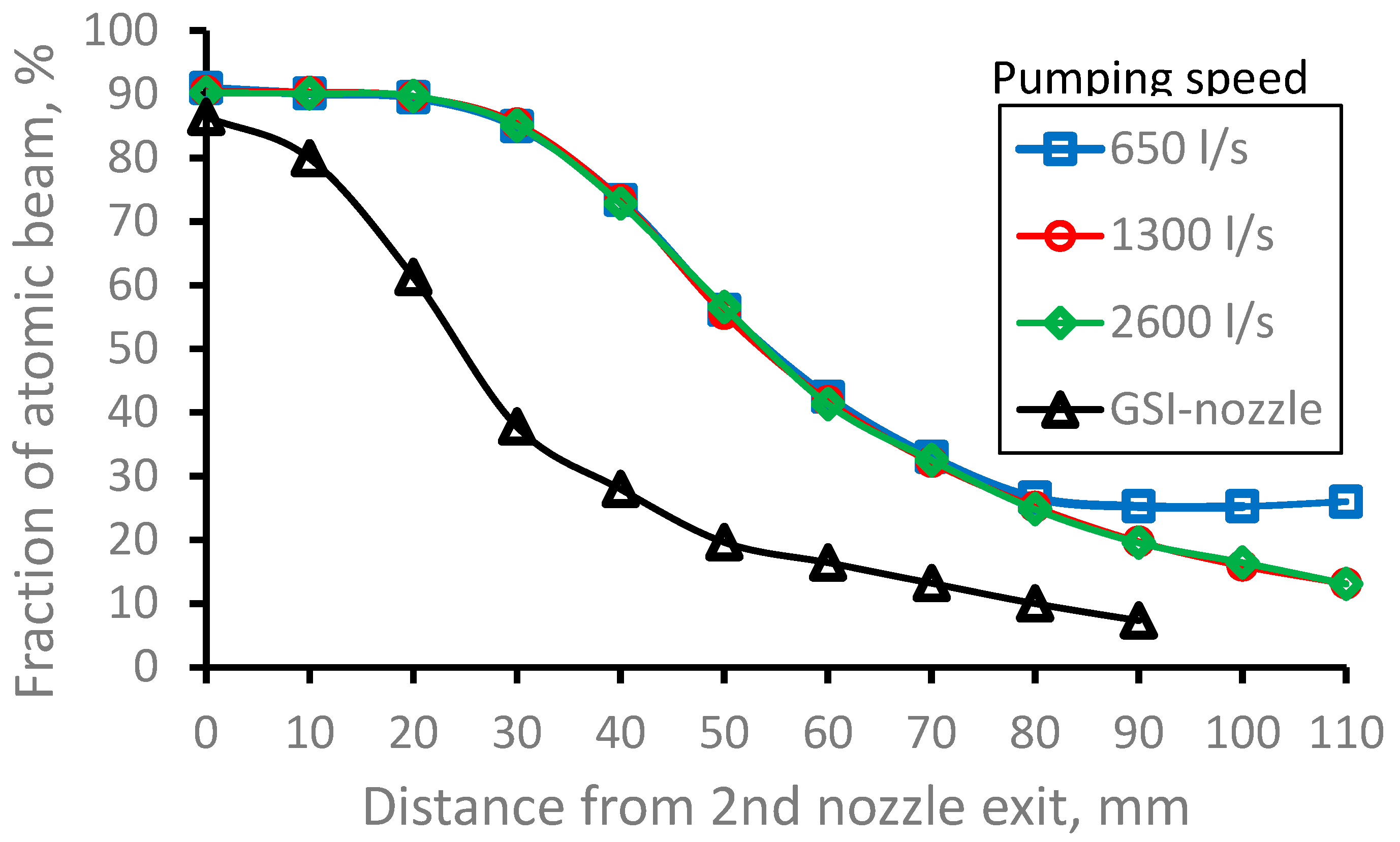
Figure 21.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the gas jet of 10 mm in diameter (it is the Laser-1 diameter) for different pumping speeds as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
Figure 21.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the gas jet of 10 mm in diameter (it is the Laser-1 diameter) for different pumping speeds as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
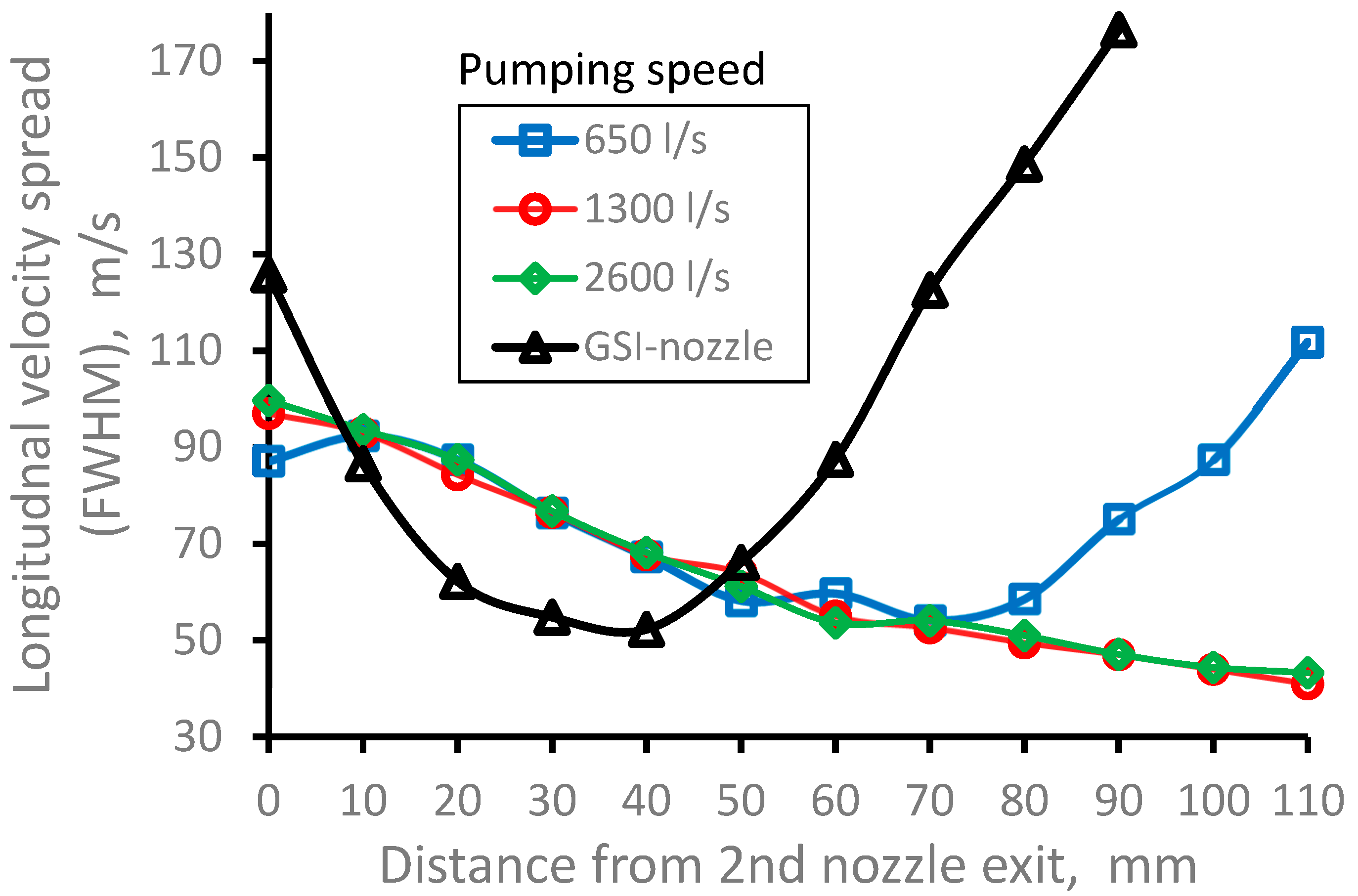
Figure 22.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different pumping speeds as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each variant.
Figure 22.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different pumping speeds as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each variant.
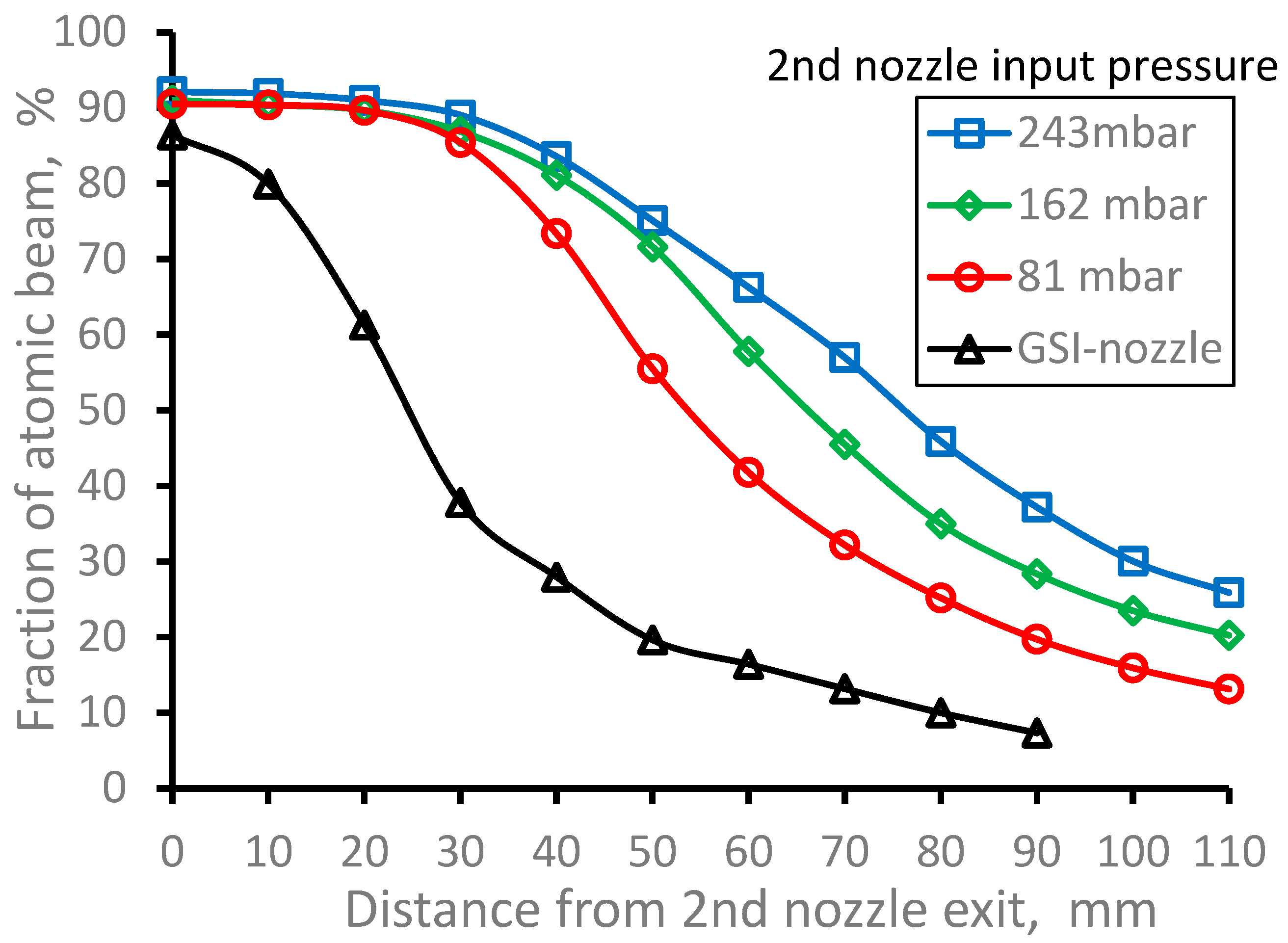
Figure 23.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 diameter) for different input pressures Pnoz as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
Figure 23.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 diameter) for different input pressures Pnoz as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
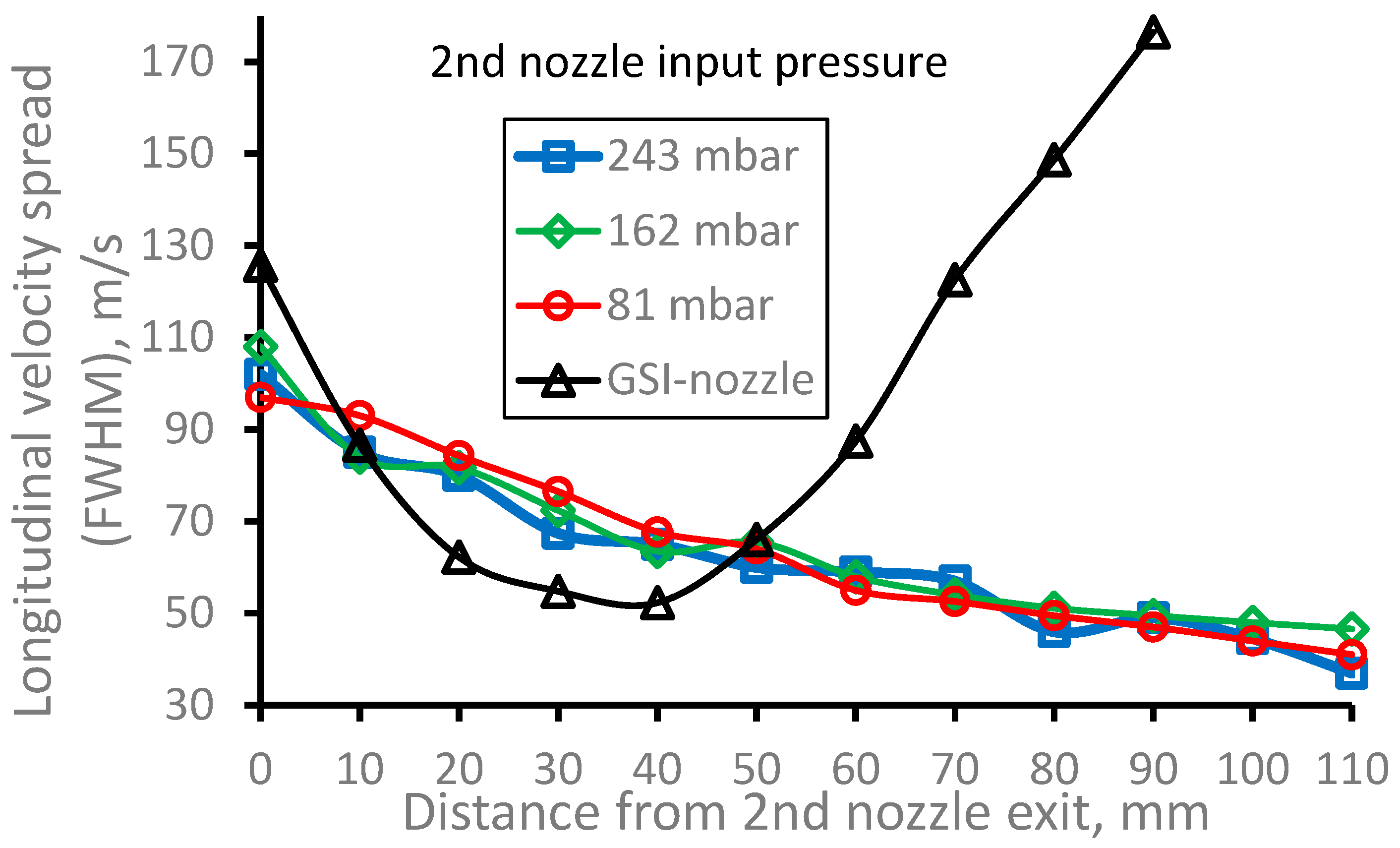
Figure 24.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different input pressures Pnoz as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each variant.
Figure 24.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different input pressures Pnoz as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each variant.
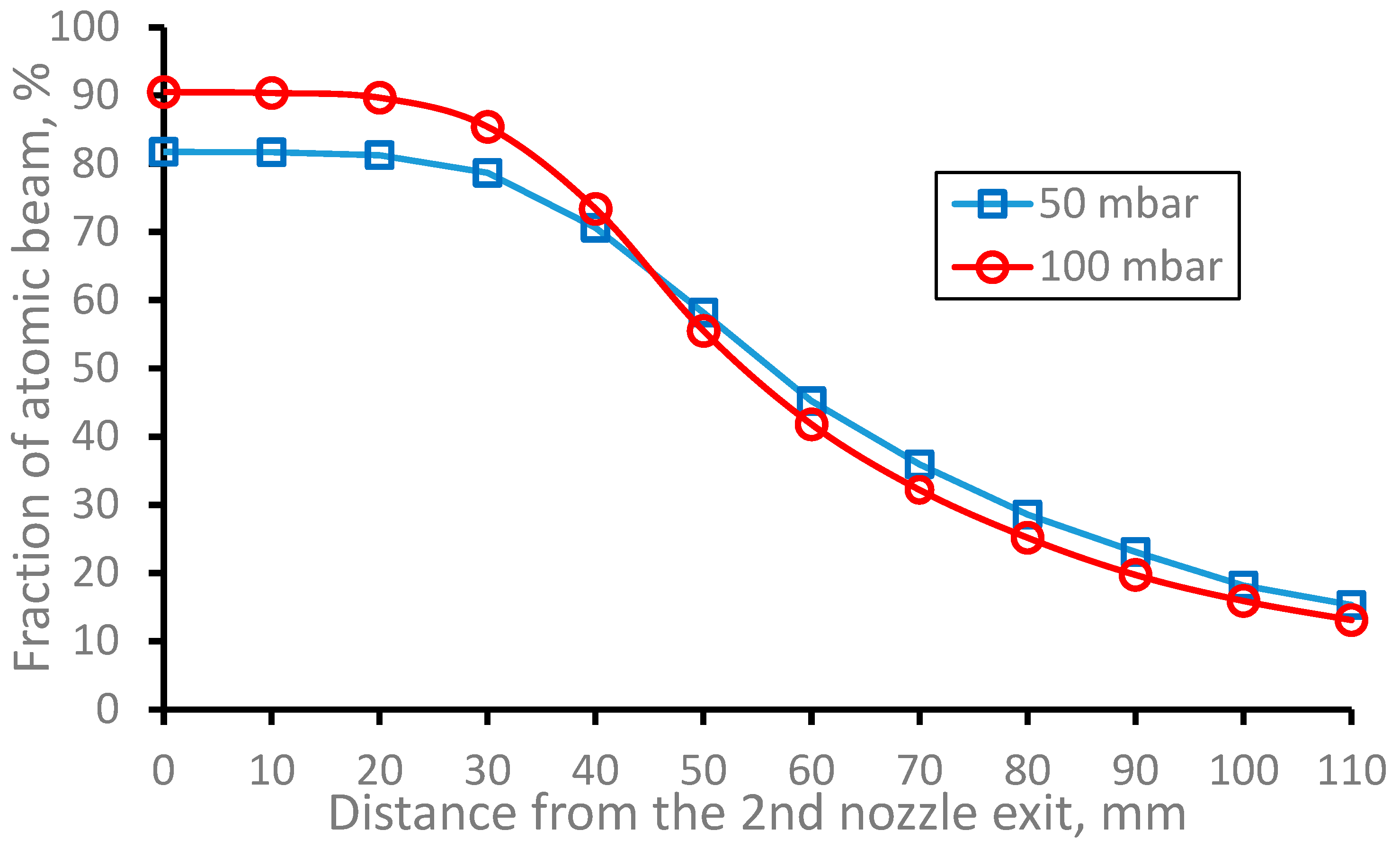
Figure 25.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 diameter) for two different gas cell pressures Pcell as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
Figure 25.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam inside the region of 10 mm in diameter (it is the Laser-1 diameter) for two different gas cell pressures Pcell as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
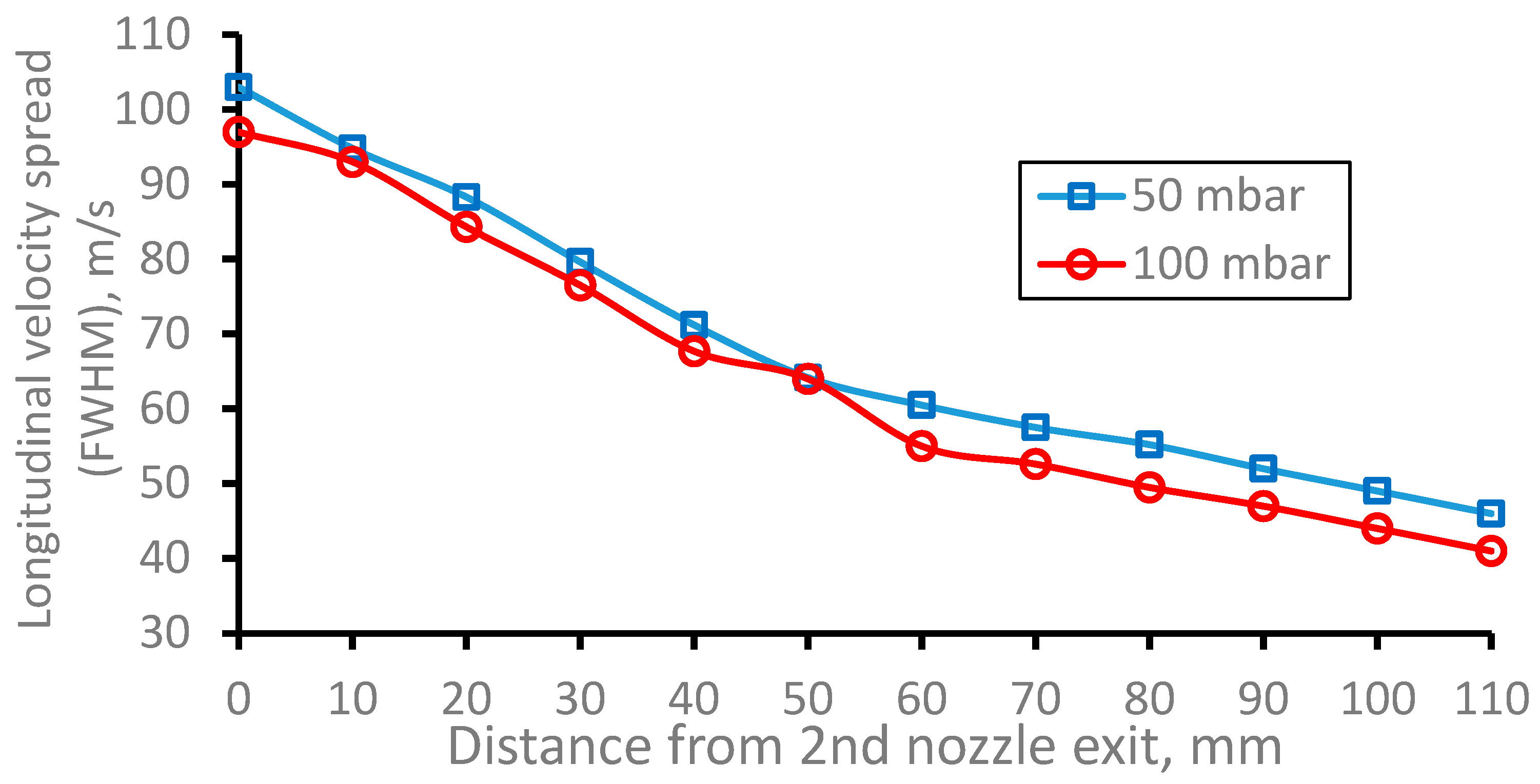
Figure 26.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different input pressures Pnoz as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each variant.
Figure 26.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different input pressures Pnoz as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each variant.
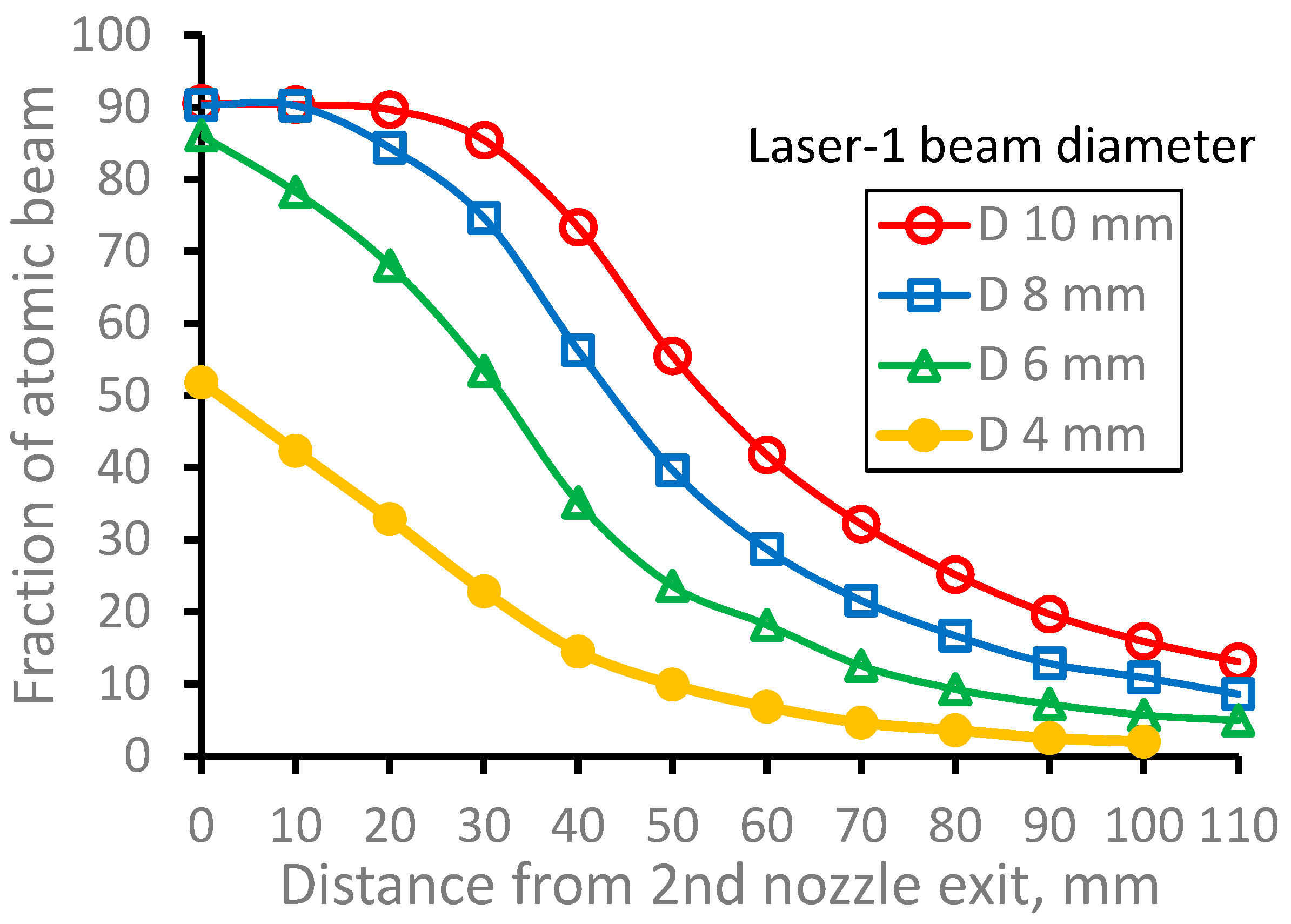
Figure 27.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam for different Laser-1 beam diameters as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
Figure 27.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 164Dy atomic beam for different Laser-1 beam diameters as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each variant. .
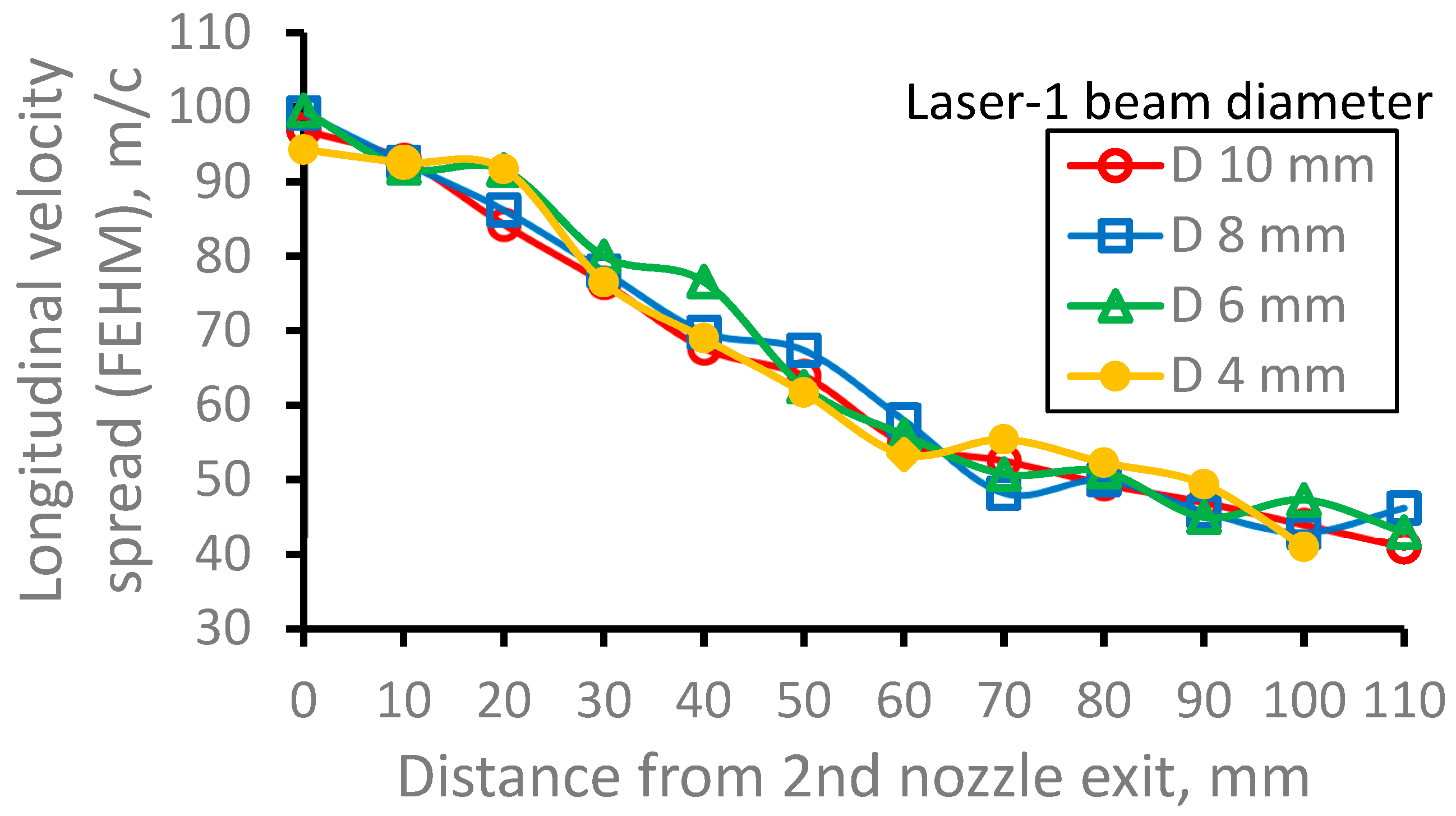
Figure 28.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different Laser-1 beam diameters as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for each Laser-1 beam diameter. Number of calculated atoms is 10000 for each variant.
Figure 28.
Results of the Monte-Carlo trajectory simulations for 164Dy atomic beam longitudinal velocity spread (FWHM) for different Laser-1 beam diameters as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for each Laser-1 beam diameter. Number of calculated atoms is 10000 for each variant.
Figure 29.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 253No atomic beam inside the gas jet of 10 mm in diameter (it is the Laser-1 diameter) for the gas cell pressure Pcell = 100 mbar, Pnoz = 81 mbar and Pbg = 2∙10-2 mbar as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each case. .
Figure 29.
Results of the Monte-Carlo trajectory simulations of the fraction of the extracted from the gas cell 253No atomic beam inside the gas jet of 10 mm in diameter (it is the Laser-1 diameter) for the gas cell pressure Pcell = 100 mbar, Pnoz = 81 mbar and Pbg = 2∙10-2 mbar as a function of distance from the 2nd nozzle exit. Number of calculated atoms is 10000 for each case. .
Figure 30.
Results of the Monte-Carlo trajectory simulations for 253No atomic beam longitudinal velocity spread (FWHM) for the gas cell pressure Pcell = 100 mbar, Pnoz = 81 mbar and Pbg =2∙10-2 mbar as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each case.
Figure 30.
Results of the Monte-Carlo trajectory simulations for 253No atomic beam longitudinal velocity spread (FWHM) for the gas cell pressure Pcell = 100 mbar, Pnoz = 81 mbar and Pbg =2∙10-2 mbar as a function of the distance from the 2nd nozzle exit. The data averaged in the radial plane for the Laser-1 beam diameter of 10 mm. Number of calculated atoms is 10000 for each case.
Figure 31.
Results of the Monte-Carlo trajectory simulations for 253No atomic beam longitudinal velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from 2nd nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Figure 31.
Results of the Monte-Carlo trajectory simulations for 253No atomic beam longitudinal velocity distributions (averaged in the radial plane for the Laser-1 beam diameter of 10 mm) for different distances from 2nd nozzle exit. Number of calculated atoms for each velocity distribution is 10000.
Table 1.
Main design parameters of the double-nozzle device.
Table 1.
Main design parameters of the double-nozzle device.
| 1st nozzle |
|
| Exit diameter |
3.5 mm |
| Throat diameter |
1.0 mm |
| Length of diverging cone |
2.5 mm |
| Connection tube between the 1st and 2nd nozzle |
|
| Tube diameter |
3.5mm |
| Tube length |
3.0 mm |
|
Inner tubein the 2nd nozzle
|
|
| Exit diameter |
2.0 mm |
| Inner entrance diameter |
3.5 mm |
| Inner total length |
6.0 mm |
| Supersonic part length |
4.0 mm |
| Out entrance diameter |
4.0 mm |
| Outer total length |
5.0 mm |
| Diverging 2nd nozzle |
|
| Throat diameter |
3.6 mm |
| Diverging cone length |
20. mm |
| Exit diameter |
15.0 mm |
| Annual gap between nozzle throat and inner tube |
0.1 mm |