Prerpints.org logo
Preprint
Article

Neural Network Technology for Cryptographic Protection of Data Transmission at UAV

Altmetrics

Downloads

230

Views

107

Comments

0

Submitted:

12 April 2023

Posted:

12 April 2023

Read the latest preprint version here

Alerts
Abstract
The neural network technology for real-time cryptographic data protection with symmetric keys (masking codes, neural network architecture and weights matrix) for unmanned aerial vehicles (UAV) onboard communication systems has been developed. It provides hardware and software implementation with high technical and operational characteristics. The development of neural network technology for real-time cryptographic data protection was performed using an integrated approach based on theoretical foundations of neural network cryptographic data protection, new algorithms and structures of neural network data encryption and decryption, modern element base with the possibility of programming for the structure, and computer-aided design of hardware and software tools. The development and implementation of the on-board system of neural network cryptographic data protection in real-time are based on the following principles: variable composition of equipment; modularity; conveyorization and spatial parallelism; specialization and adaptation of hardware and software to data encryption and decryption. The tabular-algorithmic method of calculating the scalar product has been improved, it provides fast calculation of the scalar product of input data for both fixed and floating-point by bringing to the largest common order of weights and forming tables of macro-partial products for them. Components of neural network cryptographic data encryption and decryption have been developed on the processor core supplemented by specialized scalar product calculation modules. The specialized hardware for neural network cryptographic data encryption was developed using VHDL for equipment programming in the Quartus II development environment ver. 13.1 and the appropriate libraries, and implemented on the basis of the FPGA EP3C16F484C6 Cyclone III family.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

A key problem is to guarantee cryptographic security of data transmission in the management of UAV [1,2], intelligent robots [3], microsatellites [4] and various mobile transport systems [5]. Due to the security vulnerabilities of UAVs, and illegal and malicious attacks against UAVs, especially against communication data and UAV control, solutions to prevent such attacks are needed, and one of them is to encrypt UAV’s communication data [6,7,8]. Due to limited battery capacity, Unmanned Aerial Vehicles (UAVs) must use energy-efficient data processing [9]. Solving this problem requires the development of neural network technology [10,11,12] for cryptographic data protection, which is focused on use in UAV onboard communication systems. When developing onboard cryptographic data protection systems, it is necessary to provide real-time mode, increase cryptographic resistance, and noise immunity and reduce power consumption, weight, size and cost [13,14,15,16,17,18,19,20,21,22,23]. One of the ways to meet such requirements is to use an auto-associative neural network of direct propagation, which is trained on the basis of the principal components analysis. A specific feature of such neural networks is the facility to pre-calculate weights and to apply the tabular-algorithmic method for the implementation of neuro-like elements using the basis of elementary arithmetic operations. For neural network cryptographic encryption and decryption of data, it is proposed to use symmetric keys, which include masking codes, neural network architecture and a matrix of weights [24,25].
Through the extensive use of a modern component base and the development of new VLSI methods, algorithms and structures, high technical and operational rates of on-board cryptographic data protection systems are achieved. Onboard systems for neural network cryptographic protection of data must have variable hardware for rapid changes in neural network architecture. The use of modern element base (microcontrollers, programmable logic integrated circuits FPGA) in the development of onboard and embedded systems makes it possible to reduce their weight, size and power consumption [26,27], and in the development of onboard systems of neural network cryptographic data protection provides a quick change of encryption and decryption keys.
Neural network cryptographic encryption and decryption of data in real-time is achieved through the application of parallel encryption and decryption of data, hardware implementation of neuro-like elements based on a multi-operand approach and macro-partial products tables.
Therefore, an urgent problem is to develop neural network technology for cryptographic data protection, focused on implementing in on-board systems with high technical and operational characteristics. The objective of the work is to develop the onboard neural network technology for real-time cryptographic data protection. In order to achieve this goal, the following tasks have to be solved:
development of neural network technology for cryptographic data protection;
development of the structure of the system of neural network cryptographic protection and real-time data transmission;
development of components of onboard systems of neural network cryptographic encryption-decryption of data;
implementation of the specialized hardware components of neural network cryptographic data encryption on FPGA.
This article is structured as follows. In the introduction, we have considered the problem relevancy and the main objectives of this research. Section 2 contains a brief review of the related works (the research context). The structure of neural network technology for cryptographic data protection is described in Section 3 and the main stages of neural network data encryption/decryption are considered here as well. Section 4 presents the structure of the system for neural network cryptographic data protection and transmission (stationery and UAV onboard parts) developed using an integrated approach. The components of the onboard system for neural network cryptographic data encryption and decryption are proposed in Section 5, the diagrams for the specialized hardware are given.

2. Related Works

The study of the main trends in the area of UAV onboard systems development for real-time cryptographic data protection shows that neural network methods are increasingly used for performing data encryption and decryption in such systems [28,29,30,31,32]. These publications show that the implementation of neural network methods of cryptographic data protection is performed generally by software. The critical drawback of software implementation of neural network cryptographic data protection is the difficulty of providing real-time mode and the constraints imposed on on-board systems in terms of weight, size, power consumption and cost.
The possibilities of adapting the auto-associative neural network with non-iterative learning to the tasks of cryptographic data protection are considered in [28,29,30,31,32]. The peculiarity of the functioning of such a neural network is the possibility of preliminary calculation of weights as a result of its training based on the principal components analysis (PCA). This method uses a system of eigenvectors that correspond to the eigenvalues of the covariance matrix of input data [33]. Auto-associative neural network with pre-calculated weights is used to encrypt and decrypt data. In [34] it was shown that the key to cryptographic encryption and decryption of data in neural networks is the masking codes, the architecture of the neural network and the matrix of weights.
Publications [35,36,37] are devoted to the hardware implementation of neural networks showing that they are based on neural elements. The feature of such neural elements is that the number of inputs and their bit size are determined by the neural network architecture, which is one of the characteristics of the data encryption key. The main operation of the neuroelement is the calculation of the scalar product using pre-calculated weights.
In [37,38,39] the methods for calculating the scalar product using the basis of elementary arithmetic operations—addition and shift, are considered. The peculiarity of these methods is the formation of macro-partial products, their shift, and addition to the previously accumulated amount. Hardware implementation of such methods requires significant equipment costs. The implementation of a tabular-algorithmic method for calculating the scalar product, which is reduced to the operations of reading macro-partial products, addition and shift, requires fewer equipment costs and less computation time. The disadvantage of this method is that it is focused on working with input data and weights in a fixed-point format.
Analyzing the works [31,41] it can be noted that neural network tools for cryptographic symmetric encryption and decryption of data [42] are implemented on the basis of microprocessors supplemented by hardware that implements time-consuming computational operations using FPGA [43]. High speed of neural network tools for cryptographic encryption and decryption of data is achieved through parallelization, pipeline computing processes and hardware implementation of neural elements. The disadvantage of the existing neural network tools for cryptographic data protection is the difficulty of changing the encryption and decryption key rapidly.

3. The Development of Neural Network Technology for Cryptographic Data Protection

3.1. Structure of Neural Network Technology of Cryptographic Data Protection

The development of neural network technology for cryptographic protection of data transmission is focused on hardware and software implementation with high technical and operational characteristics. It is proposed to carry out such development on the basis of an integrated approach that includes:
  • research and development of theoretical foundations of neuro-like cryptographic data protection;
  • research and development of new algorithms and structures of neuro-like encryption and decryption of data focused on modern element base;
  • modern element base with the ability to program the structure;
  • means for automated design of software and hardware.
Figure 1 shows the developed structure of neural network technology for cryptographic data protection, which is focused on hardware and software implementation.
The given neural network technology of cryptographic data protection provides encryption with symmetric keys. When implementing the symmetric cryptosystem, the encryption key and the decryption key are the same or the decryption key is easily calculated from the encryption key. The use of the tabular-algorithmic method of data encryption and decryption enables the implementation of data encryption-decryption tools with high technical and operational characteristics.

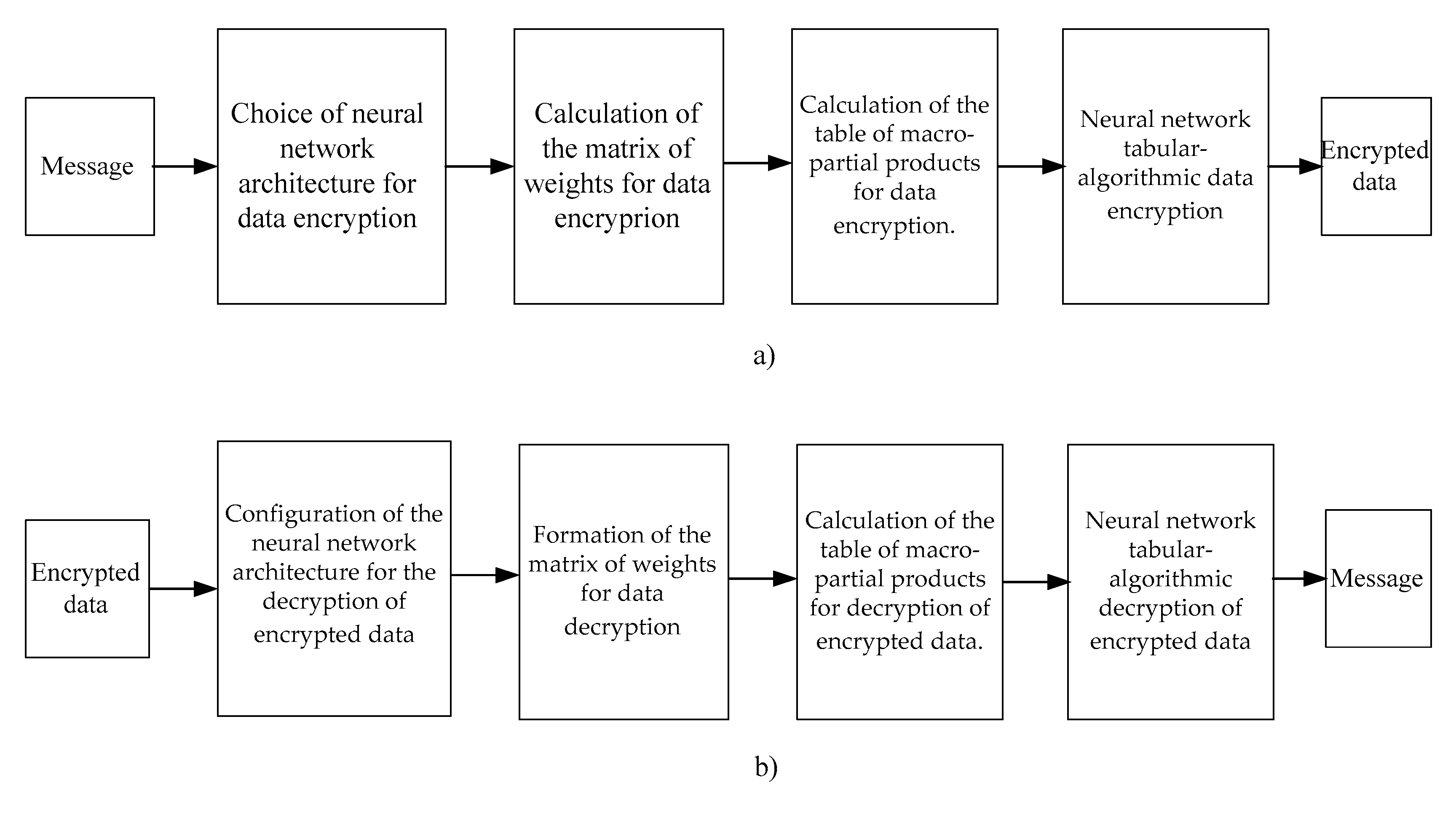
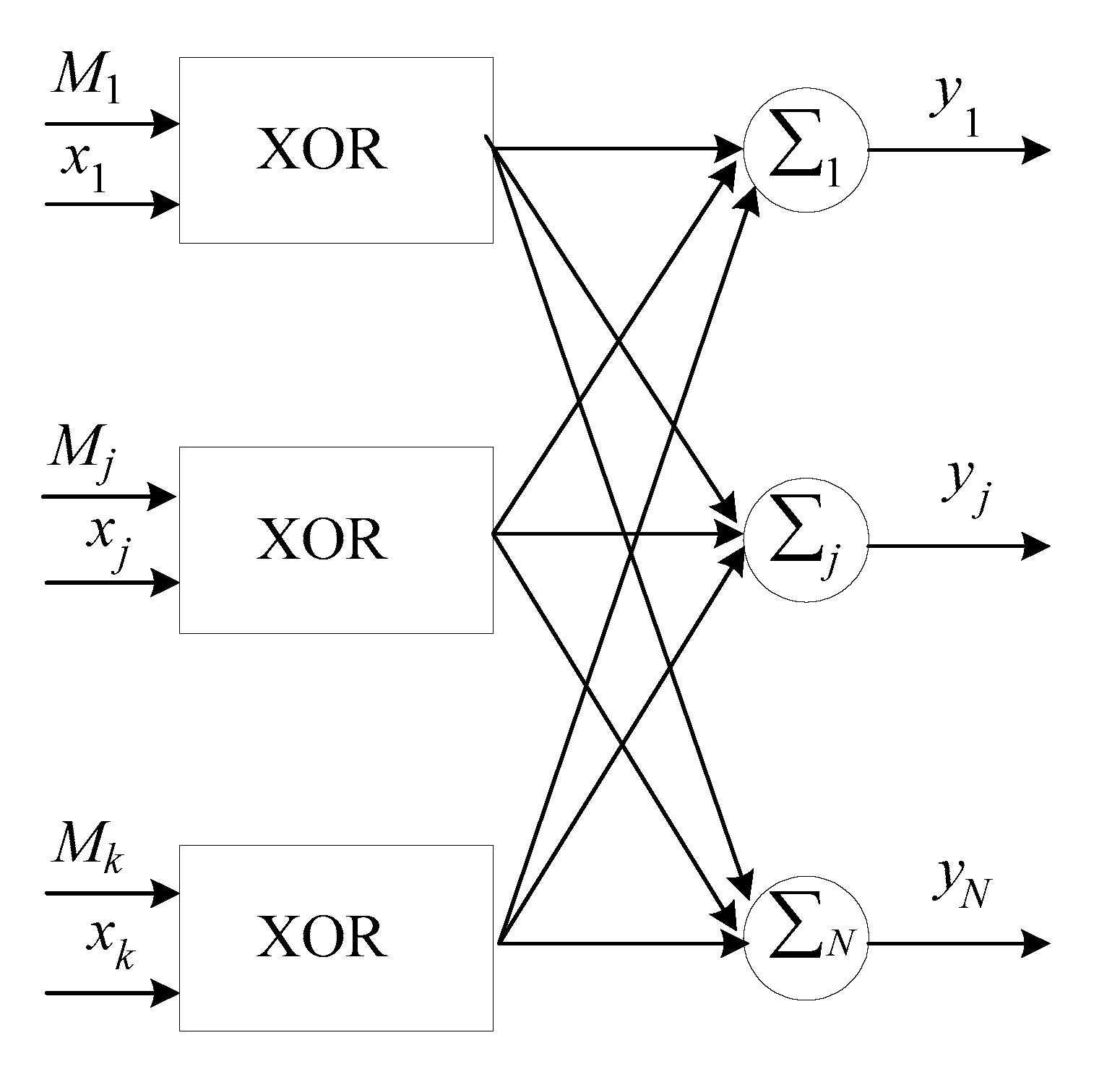
3.2. Main Stages of Neural Network Encryption

Encryption is performed over plaintext using a key, which consists of a given number of N neurons in the neural network, a matrix of weights and masking operations. Let’s consider the main stages of message encryption.
Choice of neural network architecture. The architecture of the neural network is determined by the number of neuro elements N , the number of inputs k and the bit inputs m . The number of neural elements is determined by the following formula:
N = n m ,
where n is the bit size of the message, and m —the bit size of the inputs.
The incoming messages which are encrypted can have different bit size ( n ) and different number of inputs ( k ), which is equal to the number of neuroelements N . The architecture of the neural network depends on the value of the bit size of the message n and the number of inputs k. The following variants of the neural network architecture are possible for the n = 16 bit message: m = 2 , k = 8 , N = 8 ; m = 4 , k = 4 , N = 4 ; m = 8 , k = 2 , N = 2 , and for n = 24 they are: m = 2 , k = 12 , N = 12 ; m = 3 , k = 8 , N = 8 ; m = 4 , k = 6 , N = 6 , m = 6 , k = 4 , N = 4 ; m = 8 , k = 3 , N = 3 ; m = 12 , k = 2 , N = 2 .
Calculation of the matrix of weights. For data encryption-decryption we will use an auto-associative neural network, which learns non-iteratively using the principal components analysis (PCA), which performs a linear transformation following the formula:
y ̄ = W ⋅ x ̄ .
According to formula (2), the matrix W ∈ R n * n is used to convert the input vector x ̄ ∈ R n into the output vector y ̄ ∈ R n . The transformation is performed by a system of linearly independent vectors that selects an orthonormal system of eigenvectors corresponding to the eigenvalues of the covariance matrix of the input data.
Let the input data be represented as a set of N   vectors x ̄ j   ,   j = 1 , … N   , and each of the vectors has dimension n , x ̄ j = x j 1 , x j 2 ,   . . . ,   x j n :
X = x ̄ 1 , x ̄ 2 ,   . . . ,   x ̄ N t .
The autocovariance matrix for N vectors x ̄ j can be written as:
R = X t ⋅ X ,
where each of the elements is defined by the expression:
r j l = ∑ i = 1 N x ̄ j l x ̄ i l = ∑ i = 1 N x ̄ j i − μ j x ̄ i l − μ l ,
where j ,   l = 1 ,   2 ,   … ,   n , and μ j , μ l —mathematical expectations of vectors x ̄ j , x ̄ l .
The eigenvalues of R symmetric non-negative matrix are real and positive numbers. We arrange them in descending order λ 1 > λ 2 > . . . > λ n . Similarly, we place the eigenvectors corresponding to λ i . Then the matrix W defines a linear transformation (2), where y ̄ = y 1 , y 2 ,   . . . ,   y n is a vector of the principal components of the PCA, which corresponds to the input data vector x ̄ . The number of vectors of the principal components N corresponds to the number of input data vectors x ̄ [29]. The matrix of weights used to encrypt the data is as follows:
W 11 W 12 ⋯ W 1 k W 21 W 22 ⋯ W 2 k ⋮ ⋮ ⋯ ⋮ W N 1 W N 2 ⋯ W N k .
The basic operation of the neural network used to encrypt data is the operation of calculating the scalar product. This operation should be implemented using the tabular-algorithmic method because the matrix of weights W j s , where j = 1 ,   … ,   N , s = 1 ,   … ,   k , is pre-calculated.
Calculation of the table of macro-partial products for data encryption. The specificity of the scalar product calculation operation used in data encryption is that the weights are pre-calculated (constants) and set in floating point format, and the input data X_j is in fixed point format with its fixing before the high digit of a number. The scalar product is calculated by means of the tabular-algorithmic method according to the formula:
Z = ∑ j = 1 N W j X j = ∑ i = 1 n 2 − i ∑ j = 1 N W j X j i = ∑ i = 1 n 2 − i ∑ j = 1 N P j i = ∑ i = 1 n 2 − i P M i ,
where N —number of products, X j —input data, W j — j -th weigh coefficient, n — bit size of the input data, P i j —partial product, P M i —macro-partial product, formed by adding N partial products P i j , as follows: P M i = ∑ j = 1 N P j i .
Formation of the tables of macro-partial products for floating-point weights W j = w j 2 m W j (where w j —mantissa of W j weigh coefficient, m W j —order of W j weigh coefficient) foresees the following operations to be performed:
  • defining the largest common order of weights m Wmaxc ;
  • calculation of the difference of orders for each W j weigh coefficient: Δ m W j = m Wmax с − m W j ;
  • shift the mantissa w j to the right by a difference of orders Δ m W j ;
  • calculation of P M i macro-partial product for the case when x 1 i = x 2 i = x 3 i = … = x N i = 1 ;
  • determining the number of overflow bits q in the P M i macro-partial product for the case when x 1 i = x 2 i = x 3 i = … = x N i = 1 ;
  • obtaining scalable mantissas w j h by shifting them to the right by the number of overflow bits;
  • adding to the largest common order of weight m Wmaxc the number of overflow bits q, as per formula m j = m Wmaxc + q .
The table of macro-partial products is calculated by the formula:
P M i = 0 ,     i f   x 1 i = x 2 i = x 3 i = … = x N i = 0 w 1 h ,   i f   x 1 i = 1 ,   x 2 i = x 3 i = … = x N i = 0 w 2 h ,   i f   x 1 i = 0 , x 2 i = 1 , x 3 i = … = x N i = 0 w 1 h + w 2 h ,   i f   x 1 i = 1 , x 2 i = 1 , x 3 i = … = x N i = 0 ⋮ w 2 h + … + w N h ,   i f   x 1 i = 0 , x 2 i = x 3 i = … = x N i = 1 w 1 h + w 2 h + … + w N h ,   i f   x 1 i = x 2 i = x 3 i = … = x N i = 1 ,
where x 1 i , x 2 i , x 3 i , … , x N i —address inputs of the table, w j h —mantissa of W j weigh coefficient brought to the greatest common order.
The possible combinations number of P M i macro-partial products and accordingly the table volume is determined by the formula:
Q = 2 N .
The memory volume can be reduced by dividing all N products by parts N 1 and N 2 . Separate tables of macro-partial products P N 1 M i and P N 2 M i are formed for each of these parts. Tables for P N 1 M i and P N 2 M i can be stored in separate memory blocks or a single memory block. When using two memory blocks, parts of the macro-partial products P N 1 M i and P N 2 M i are read in one clock cycle, and in one memory block—in two clock cycles. The macro-partial product P M i is the sum of two macro-partial products P N 1 M i and P N 2 M i .
Neural network tabular-algorithmic data encryption. The matrix of weights W, formed by the eigenvectors of the autocovariance matrix of the input data R, is determined during the training of the neural network. The type of auto-associative neural network used for data encryption is shown in Figure 2, where M j is the mask for the j -th input, x j is the j -th input data, XOR is the masking operation using the exclusive OR elements.
The main operation of neural network data encryption is reduced to multiplying the W matrix of weights by the input data vector x ¯ under the following formula:
y j = W 11 W 12 ⋯ W 1 k W 21 W 22 ⋯ W 2 k ⋮ ⋮ ⋯ ⋮ W N 1 W N 2 ⋯ W N k × x 1 x 2 ⋮ x k .
The multiplication of the matrix of weights W by the vector of input data x ¯ is reduced to performing N operations of calculating the scalar product:
y j = ∑ s = 1 k W j s x s
where k — number of products, s = 1 , 2 , … , k ; j = 1,2 , … , N .
The calculation of scalar products will be achieved using the tabular-algorithmic method, where the weights W j s are set in floating-point format, and the input data x s —in a fixed-point format with fixation before the highest digit. Tabular-algorithmic calculation of the mantissa of the scalar product is reduced to reading the macro-partial product P M i from the j-th table (memory) at the address corresponding to the i-th bit slice of N input data, and adding it to the before accumulated sums according to:
y M j i = 2 − 1 y M j ( i − 1 ) + P M j i ,
where y M j 0 = 0 , i = 1 , … , m , m —bit size of the input data. The number of tables of macro-partial products corresponds to N — the number of rows of the matrix (10). The result of calculating of the scalar product y j consists of the mantissa y M j and the order m j .
The time required to compute the mantissa of the scalar product (SP) is determined by the formula:
t S P = m ( t t a b l e + t r e g + t a d d ) ,
where t S P is the time of calculation of the scalar product, t t a b l e is the time of reading from the table (memory), t r e g is the time of reading (writing) from the register, t a d d is the time of adding.
Data encryption can be performed either sequentially or in parallel, depending on the speed required. In the case of sequential encryption, the encryption time is the result of the formula:
t e n c r y p t = N m ( t t a b l e + t r e g + t a d d ) ,
where t e n c r y p t —time required for encryption. The encryption time can be reduced by performing N operations of calculating the scalar product in parallel.
At the output of the neural network, we obtain N encrypted data in the following form y j = y M j 2 m j , where y M j —mantissa at the j -th output, m j —order value at the j -th output. To transmit the encrypted data for decryption, it is advisable to bring all encrypted data to the highest common order. The reduction to the greatest common order is performed in three stages:
  • define the greatest order m e n c r ;
  • for each encrypted data y j calculate the difference between the orders Δ m j = m e n c r − m j ;
  • by performing shift of the mantissa y M j to the right by the difference of orders Δ m j we obtain mantissa of the encrypted data y M j h reduced to the greatest common order.
The mantissa of the encrypted data y M j h which are reduced to the largest common order, and the largest common order m e n c r are sent for decryption.

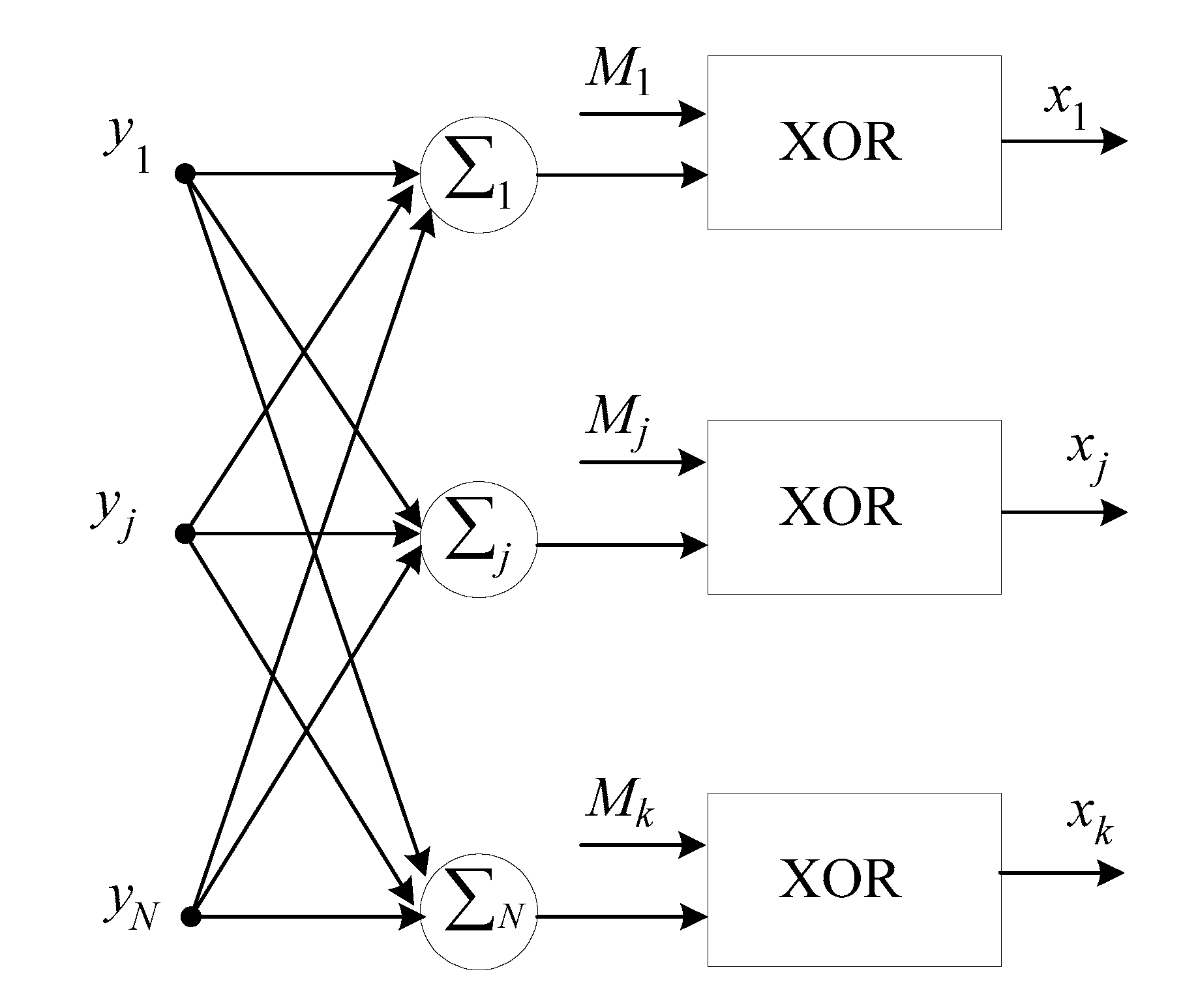
3.3. The Main Stages of Neural Network Cryptographic Data Decryption

Encrypted data in the form of mantissa y м j h , which are reduced to the largest common order m e n c r (block-floating point), come to be decrypted. Therefore, the main stages of decrypting the encrypted data are considered further.
Configuration of the neural network architecture for the decryption of encrypted data. The architecture of the neural network for the decryption of encrypted data, in terms of the number of neural elements, is the same as the architecture of the neural network used for the encryption of data. In this neural network, the number of inputs and the number of neurons corresponds to the number of the encrypted mantissa y м j h . The neural network architecture used to decrypt encrypted data is presented in Figure 3.
In the neural network for decrypting encrypted data, the bit rate of the inputs corresponds to the bit rate of the encrypted mantissa y M j h , which determines the decryption time. To reduce the decryption time, the lower bits of the mantissa may be discarded, it will not affect the recovery of the original message.
Formation of the matrix of weights. The matrix of weights for decrypting encrypted data is formed from a matrix of weights for encrypting input data by transposing it:
W 11 W 12 ⋯ W 1 k W 21 W 22 ⋯ W 2 k ⋮ ⋮ ⋯ ⋮ W N 1 W N 2 ⋯ W N k T = W 11 W 21 ⋯ W N 1 W 12 W 22 ⋯ W N 2 ⋮ ⋮ ⋯ ⋮ W 1 k W 2 k ⋯ W N k .
The basic operation for encryption of input data and decryption of encrypted data is the calculation of the scalar product, which is implemented using a tabular-algorithmic method.
Calculation of the table of macro-partial products for decryption of encrypted data. A specific feature of the scalar product calculation operation used to decrypt encrypted data is that the weights are pre-calculated (constants) and set in floating-point format, while the encrypted data y j are received in block-floating-point format. The calculation of the scalar product using the tabular-algorithmic method is performed by formula (7). Preparation and calculation of possible variants of macro-partial products is performed as in the previous case under the formula (8). The number of possible variants of macro-partial products P M i and, accordingly, the volume of the table depends on the amount of encrypted data. For each table of macro-partial products, its largest common order m P m s is computed.
Neural network tabular-algorithmic decryption of encrypted data. The main operation of neural network decryption of encrypted data is to multiply the matrix of weights W by the vector of encrypted data y ¯ by the following formula:
x s = W 11 W 21 ⋯ W N 1 W 12 W 22 ⋯ W N 2 ⋮ ⋮ ⋯ ⋮ W 1 k W 2 k ⋯ W N k × y 1 y 2 ⋮ y N .
The multiplication of the matrix of weights W T by the vector of input data y ¯ is reduced to performing N operations of scalar product calculation:
x s = ∑ j = 1 N W s j y j
where N —number of products, s = 1 , 2 , … , k ; j = 1 , 2 , … , N .
Tabular-algorithmic calculation of the mantissa of the scalar product is reduced to reading the macro-partial product P M i from the table (memory) at the address corresponding to the i-th bit-slice of k input data, and adding it to the previously accumulated sums, according to the formula:
x M s i = 2 − 1 y M s ( i − 1 ) + P M s i ,
where x s 0 = 0 , i = 1 , … , g , g —bit rate of the encrypted data. The time necessary to calculate the scalar product mantissa is defined under the formula:
t S P = g ( t t a b l e + t r e g + t a d d ) ,
where t S P —time for scalar product calculation, t t a b l e – time for reading from a table (memory), t r e g —time of reading (writing) from the register, t a d d —time for adding. The result of the calculation of x s scalar product consists of a mantissa x M s and order, which is equal to m d e c r s = m P M s + m e n c r .
At the output of the neural network (see Figure 3), we obtain k decrypted data in the following form x s = x M s 2 m d e c r s , where x M s is the mantissa at the s -th output, m d e c r s is the value of the order at the s -th output. To obtain the input data, it is necessary to shift the s -th mantissa x M s by the value of the order m d e c r s .

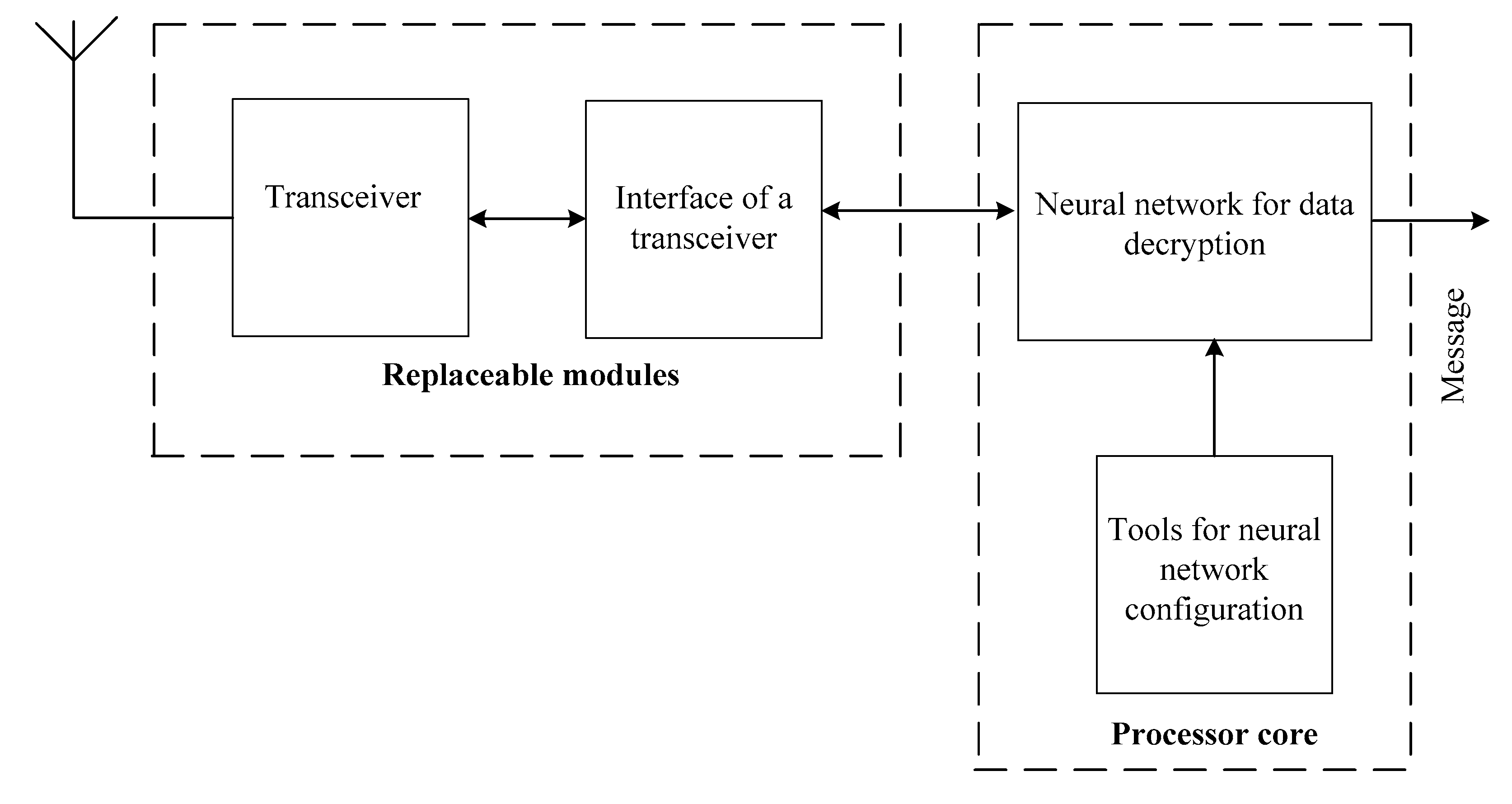
4. The Structure of the System for Neural Network Cryptographic Data Protection and Transferring in Real-Time Mode

The development of the structure of the system for neural network cryptographic data protection and transmission in real-time will be carried out using an integrated approach, which contains:
  • research and development of theoretical foundations of neural network cryptographic data encryption and decryption;
  • development of new tabular-algorithmic algorithms and structures for neural network cryptographic data encryption and decryption;
  • modern element base, development environment and computer-aided design tools.
A system for neural network cryptographic data protection in real-time was developed using the following principles:
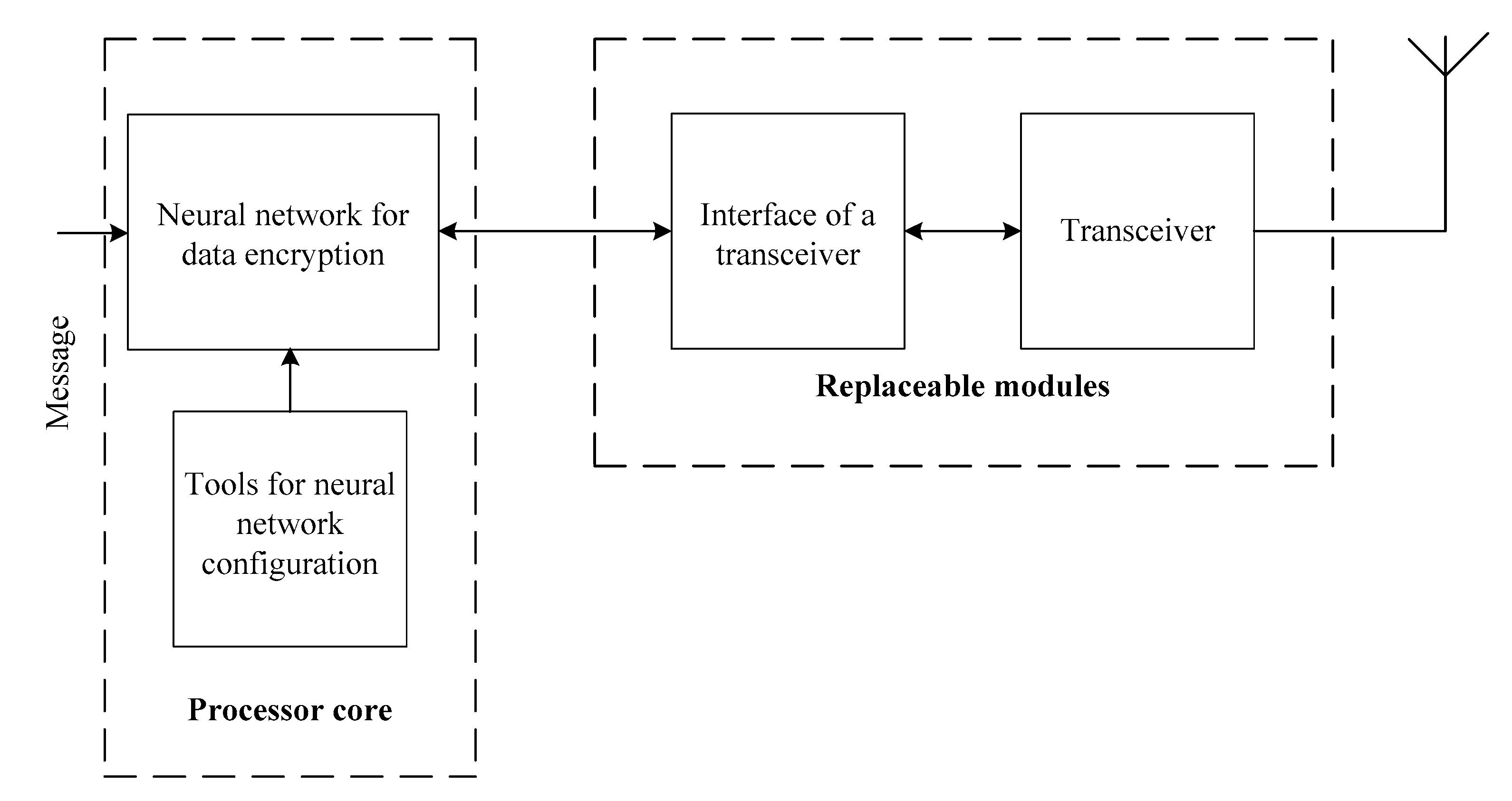
  • changeable composition of the equipment, which foresees the presence of the processor core and replaceable modules, with which the core adapts to the requirements of a particular application;
  • modularity, which involves the development of system components in the form of functionally complete devices;
  • pipeline and spatial parallelism in data encryption and decryption;
  • the openness of the software, which provides opportunities for development and improvement, maximising the use of standard drivers and software.;
  • specialising and adapting hardware and software to the structure of tabular algorithms for encrypting and decrypting data.;
  • the programmability of hardware module architecture through the use of programmable logic integrated circuits.
The system of neural network cryptographic real-time data protection and transmission consists of a stationary part, which is a remote-control centre, and an UAV onboard part. The structure of the stationary part of the system of neural network cryptographic data protection and transmission is shown in Figure 4.
The processor core of the remote-control centre is implemented on the basis of a personal computer. The transceiver is used to transmit encrypted data, it communicates with the processor core through the interface based on a microcontroller.
The UAV onboard part of the system for neural network cryptographic real-time data protection and transmission is implemented on the processor core, which is supplemented by dedicated hardware and software. The processor core of the UAV onboard part of the system is designed on a microcomputer. The structure of the onboard part of the system of neural network cryptographic data protection and receiving is depicted in Figure 5.
The effective implementation of neural network encryption-decryption and encoding-decoding algorithms in real time is achieved by combining universal and customised software and hardware. The use of modern elements (microcomputer, microcontroller, FPGA) in the development of the UAV onboard part ensures the accomplishment of the requirements for weight, dimensions and energy consumption.
The effectiveness of the system for neural network cryptographic real-time data protection and transmission is directly associated with the choice of both hardware and software implementation.

5. Development of the Components of the Onboard System for Neural Network Cryptographic Data Encryption and Decryption

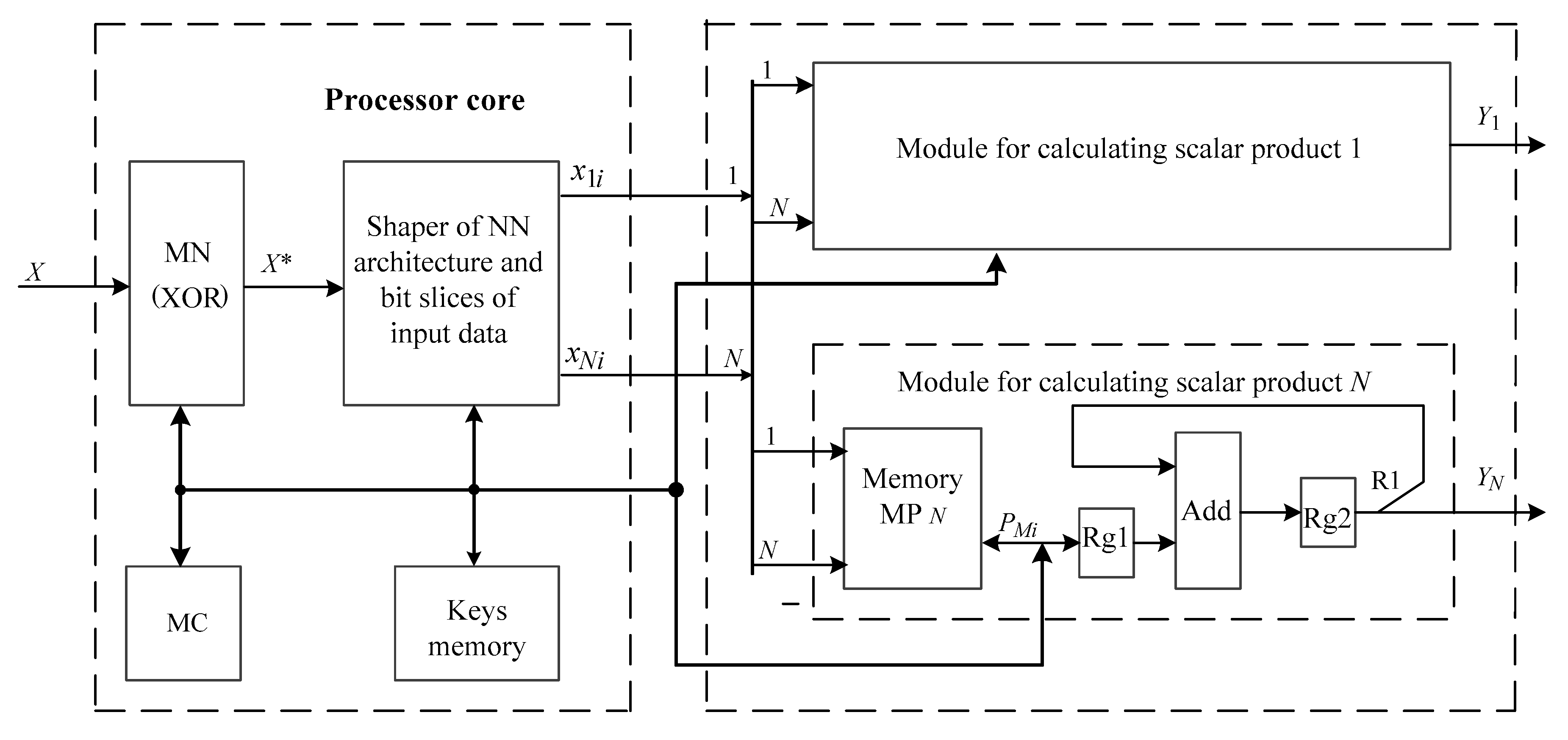
5.1. Development of the Structure of the Components for Neural Network Cryptographic Data Encryption and Decryption

In general, the problem of developing onboard systems for neural network cryptographic encryption-decryption of data can be formulated as follows:
  • to develop an algorithm for the onboard system of neural network encryption-decryption of data and present it in the form of a specified flow graph;
  • to design the structure of the onboard system for neural network data encryption-decryption with the maximum efficiency of equipment use, taking into account all the limitations and providing real-time data processing;
  • to determine the main characteristics of neural elements and carry out their synthesis;
  • to choose exchange methods, determine the necessary connections and develop algorithms for exchange between system components;
  • to determine the order of implementation in time of neural network data encryption-decryption processes and develop algorithms for their management.
Components of the onboard system of neural network cryptographic data encryption and decryption should provide the implementation of the selected neural network, the ability to change masks, calculate matrices of weights W j and tables of macro-partial products P M i for possible neural network options. To effectively implement the components of the onboard system of neural network cryptographic encryption-decryption of data, it is proposed to use hardware-software implementation of the algorithms based on a microcontroller supplemented by specialized hardware. The structure of the component of neural network cryptographic data encryption, which meets such requirements, is presented in Figure 6, where MC—microcontroller, MN—mask node, NN—neural network, MP—macro-partial product, Rg—register, Add—adder.
The developed component of neural network cryptographic data encryption has a variable composition of equipment, which is based on the core of the system and a set of modules for calculating the scalar product. The system core is constant for all applications and consists of microcontroller MC, mask node MN, keys memory and module of the shaper of the NN architecture and bit slices of input data. The scalar product calculation modules implement the basic operation of the tabular-algorithmic method of scalar product calculation under the formula:
Z i = 2 − 1 Z i − 1 + P M i ,
where Z 0 = 0 .
The number of modules for calculating the scalar product depending on the required speed is determined by the following formula:
s = N 2 v ,
where N is the number of neuro-like elements, v = 0 , … , d , d = log 2 ⁡ N . The system of neural network cryptographic data encryption reaches its highest speed when the number of computational modules of the scalar product corresponds to the number of neural elements N . To ensure real-time data encryption, it is proposed to implement the scalar product calculation modules, mask node module (MN), and module of the shaper of neural network architecture and bit slices of the input data in the form of specialized hardware.
The neural network cryptographic data encryption component works as follows. Before encrypting the data, the MC configures the neural network architecture (determines the number of neural elements N , the number of inputs k and their bit-size m ). For the selected neural network architecture matrix of weights W j and tables of P M i macro-partial products are calculated by MC, and then they are written in the memory of MP. In addition, the masks selected from the keys’ memory are stored in the MN node. The message Х to be encrypted comes to input of MN in fixed-point format, here it is masked. The masked message Х* from the output of MN comes to input of the module of the shaper of neural network architecture and bit slices, where it is divided into N groups with m bit rate and bit slices are formed x 1 i , … , x N i . It should be noted that forming of bit slices x 1 i , … , x N i begins with lower bits. The formed bit slices x 1 i , … , x N i are the addresses for reading macro-partial products P M i from the MP memory. The read macro-partial product P M i is written to the Rg1 register. The adder (Add) performs a summation of macro-partial products P M i as per formula (20). The number of cycles required to calculate the scalar product is determined by the bit-size of input m . Control of the encryption process in the onboard system of neural network cryptographic data encryption is performed by MC.
The structure of the component of neural network cryptographic decryption of the encrypted data corresponds in general to the structure of the component of neural network cryptographic encryption of data, presented in Figure 6.

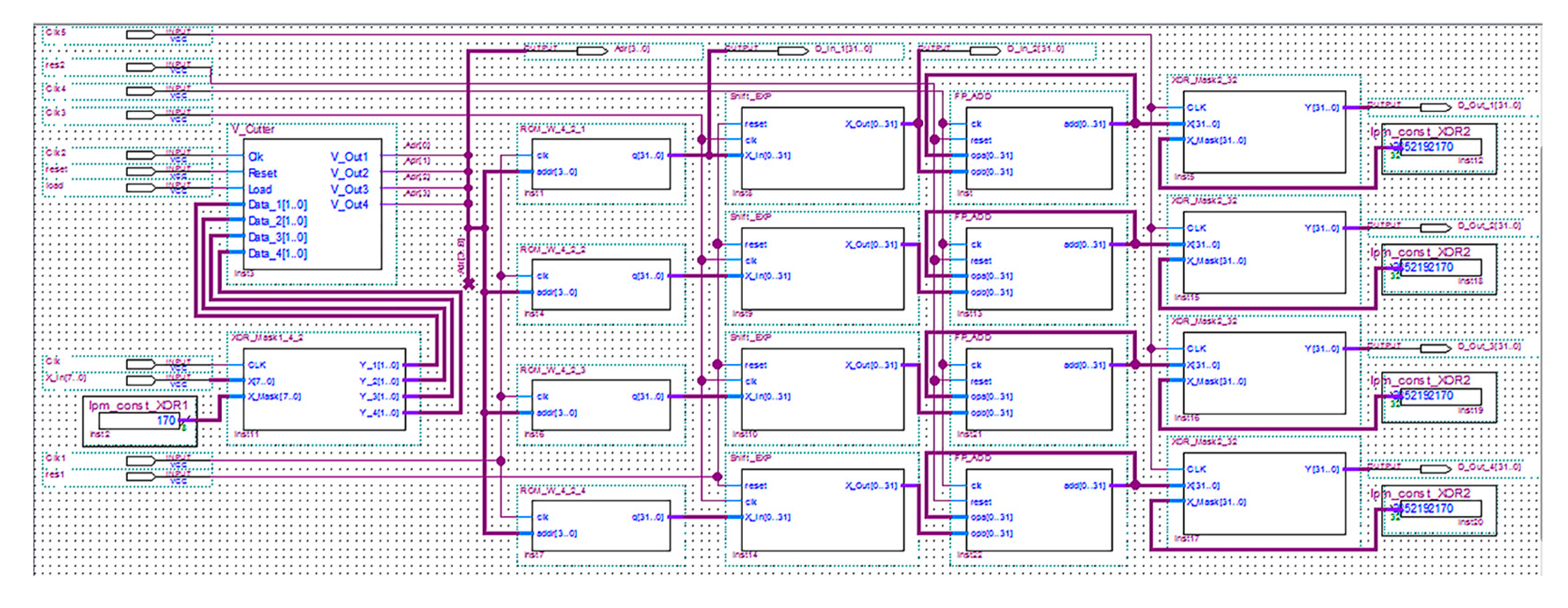
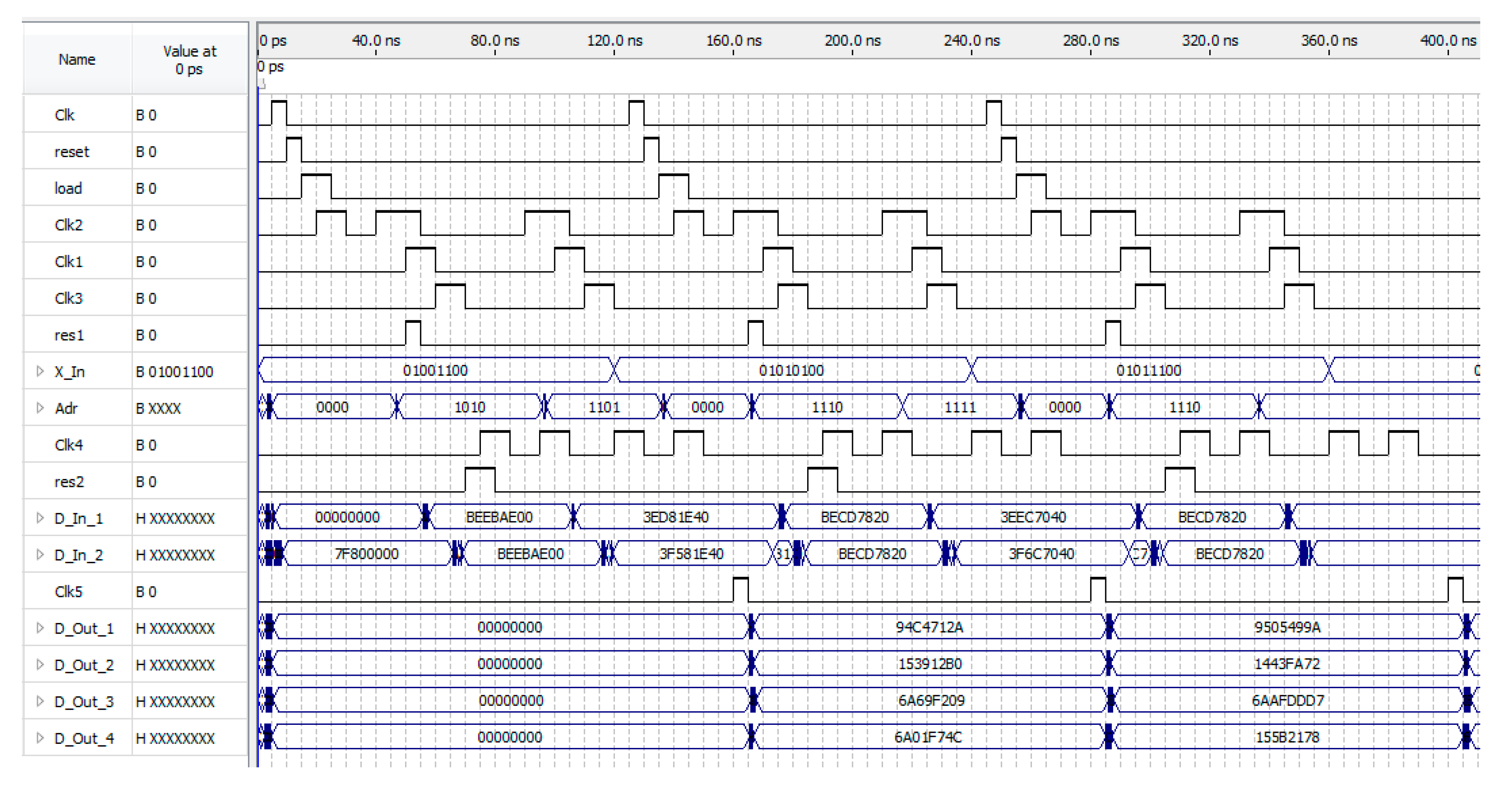
5.2. Implementation of the Specialized Hardware Components of Neural Network Cryptographic Data Encryption on FPGA

The design of specialized on-board hardware systems for neural network cryptographic data encryption was performed in the VHDL hardware programming language in the Quartus II ver. 13.1 development environment using its libraries. Nowadays, the hardware description langauges such as VHDL, VHDL-AMS, Verilog, Verilog-AMS are widely used for creating behavioral descriptions and models of digital, analog and mixed-signal devices and systems [44,45]. The Quartus II development environment supports the entire process of designing specialized hardware from user input to FPGA programming, debugging of both the chip itself and the tools as a whole.
A schematic diagram of the specialized hardware components of neural network cryptographic data encryption is shown in Figure 7. The inputs of module XOR_Mask1_4_2: X [7..0]—are the input data; Clk—input sync for input data download; X_Mask [7..0]—8-bit mask. At the output of this block N vectors with bit size m are formed. Synchronization is implemented on the leading edge of Clk pulses.
Block V_Cutter with N = 4 input vectors of bit size m = 2   consists of N registers of parallel-serial type and forms vertical bit slices. Input data: Data_1 [n-1..0],…, Data_N [n-1..0]— N   input vectors with bit size n ; Clk—pulses of synchronization of forming vertical bit slices; Reset—the signal of the initial reset in the “0” output of the registers R_Par_Ser; Load—the signal to allow data to be loaded into the R_Par_Ser registers. Outputs: V_Out1,…, V_OutN—vertical bit slice. The formation of vertical sections begins with the lower bit.
The weights of the neural network with N = 4 inputs with a bit size of m = 2 are stored in the FPGA ROM in the form of 4 tables. Each of them consists of 16 words with a bit size of 32 bits. Reading data from these tables is performed using blocks ROM_W_4_2_1,…, ROM_W_4_2_4.
Inputs of these blocks: addr [3..0]—the address of the cell of the table from which the data will be read; clk—synchronization pulses for reading data from the table. Synchronization is implemented on the leading edge of the pulses clk. Output: q [31..0]—data read from the cell with the input address.
The data read from the tables is transmitted to the input blocks Shift_EXP, which perform their multiplication by 2 j , where j = 0 , … ,   n − 1 . Upon receipt of this block of data corresponding to the zero digit, the bit counter is reset. Synchronization of this block is carried out by means of clock pulses Clk. At the output X_Out [0..31] we get the input data multiplied by 2 j .
From the output of the Shift_EXP blocks, the data are sent to one of the inputs of the adders FP_ADD. The other input of the adders is connected to their output. Adder input signals: clk—synchronization pulses; reset—signal to reset the input data opa when implementing the adder with the battery; opa [0..31], opb [0..31]—terms. On the leading edge of the first pulse clk the adders are loaded into the adder, and on the leading edge of the second pulse the received sum is displayed. Adder output: the sum add [0..31].
From the output of the adders, FP_ADD data is fed to the input of the block XOR_Mask2_32, which performs the overlay of the 32-bit mask. Inputs of the block XOR_Mask2_32: X [31..0]—encrypted output data; Clk—synchronization of input data download; X_Mask [31..0]—32-bit mask. Block output: vector Y [31..0]. Synchronization is implemented on the leading edge of Clk pulses. The encrypted data are obtained at the outputs D_Out_1, D_Out_2, D_Out_3, D_Out_4.
The timing diagram of the specialized hardware of neural network cryptographic data encryption is presented in Figure 8.
The implementation of the specialized hardware for neural network cryptographic data encryption based on the FPGA EP3C16F484C6 Cyclone III family [46] requires 3053 logic elements and 745 registers. Approximately 160 nanoseconds are required to encrypt one input vector.

6. Conclusions

The neural network technology for real-time cryptographic data protection with symmetric keys (masking codes, neural network architecture and weigh matrix) for UAV onboard communication systems has been presented in this work. It provides high cryptographic stability and hardware-software implementation with high technical and operational characteristics.
The tabular-algorithmic scalar product calculation method has been improved. It provides fast calculation of the scalar product for both fixed-point and floating-point input data. It does this by finding the largest common order of weights and building tables of macro partial products for them.
It is proposed to develop the UAV onboard system for neural network cryptographic data protection in real-time using an integrated approach based on the following principles: variable equipment composition; modularity; conveyorization and spatial parallelism; software openness; specialization and adaptation of hardware and software to data encryption and decryption keys.
Components of neural network cryptographic data encryption/decryption have been designed on the basis of the processor core supplemented by the specialized scalar product calculation modules.
The specialized hardware for neural network cryptographic data encryption was developed in the VHDL equipment programming language in the Quartus II environment and implemented using family Cyclone III FPGA EP3C16F484C6.

Author Contributions

Conceptualization, I.T. and V.T.; methodology, I.T., Y.O. and Y.L.; software, Y.L. and Y.O.; validation, Y.L., Y.O. and I.K.; formal analysis, I.T. and V.T.; investigation, A.L. and A.H.; resources, A.L. and I.K.; data curation, Y.L. and I.K.; writing—original draft preparation, I.T., I.K. and Y.O.; writing—review and editing, I.K., A.H. and A.L.; visualization, I.K. and Y.O.; supervision, V.T. and A.L.; project administration, I.T. and V.T. All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Han, B.; Qin, D.; Zheng, P.; Ma, L.; Teklu, M.B. Modeling and performance optimization of unmanned aerial vehicle channels in urban emergency management, ISPRS Int. J. Geo-Inf, 2021, 10, 478. [Google Scholar] [CrossRef]
  2. Śledź, S.; Ewertowski, M.W.; Piekarczyk, J. Applications of unmanned aerial vehicle (UAV) surveys and Structure from Motion photogrammetry in glacial and periglacial geomorphology. Geomorphology 2021, 378, 107620. [Google Scholar] [CrossRef]
  3. Zhang, C.; Zou, W.; Ma, L.; & Wang, Z.; & Wang, Z. Biologically inspired jumping robots: A comprehensive review. Robotics Auton. Syst. 2020, 124, 103362. [Google Scholar] [CrossRef]
  4. Weng, Z.; Yang, Y.; Wang, X.; Wu, L.; Hua, S.; Zhang, H.; Meng, Z. Parentage analysis in giant grouper (epinephelus lanceolatus) using microsatellite and SNP markers from genotyping-by-sequencing data. Genes 2021, 12, 1042. [Google Scholar] [CrossRef] [PubMed]
  5. Boreiko, O.; Teslyuk, V.; Zelinskyy, A.; Berezsky, O. Development of models and means of the server part of the system for passenger traffic registration of public transport in the “smart” city. EEJET 2017, 1, 40–47. [Google Scholar] [CrossRef]
  6. Kim, K.; and Kang, Y. Drone security module for UAV data encryption. In Proceedings 2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea (South), 2020, 1672-1674. [CrossRef]
  7. Samanth, S.; K V, P.; & Balachandra, M.; & Balachandra, M. Security in Internet of Drones: A Comprehensive Review. Cogent Engineering 2022, 9, 2029080. [Google Scholar] [CrossRef]
  8. Kong, P.-Y. A survey of cyberattack countermeasures for unmanned aerial vehicles. IEEE Access 2021, 9, 148244–148263. [Google Scholar] [CrossRef]
  9. Shafique, A.; Mehmood, A.; Elhadef, M.; Khan, KH. A lightweight noise-tolerant encryption scheme for secure communication: An unmanned aerial vehicle application. PLOS ONE 2022, 17, e0273661. [Google Scholar] [CrossRef]
  10. Verma, A.; and Ranga, V. Security of RPL based 6LoWPAN Networks in the Internet of Things: A Review. IEEE Sensors J. 2020, 20, 11–5690. [Google Scholar] [CrossRef]
  11. Morales-Molina, C.D.; Hernandez-Suarez, A.; Sanchez-Perez, G.; Toscano-Medina, L.K.; Perez-Meana, H.; Olivares-Mercado, J.; Portillo-Portillo, J.; Sanchez, V.; Garcia-Villalba, L.J. A Dense Neural Network Approach for Detecting Clone ID Attacks on the RPL Protocol of the IoT. Sensors 2021, 21, 3173. [Google Scholar] [CrossRef]
  12. Sohaib, O.; W. Hussain, M. Asif, M. Ahmad and M. Mazzara, A PLS-SEM neural network approach for understanding cryptocurrency adoption. IEEE Access 2020, 8, 13138–13150. [Google Scholar] [CrossRef]
  13. Holovatyy A., Łukaszewicz A., Teslyuk V., Ripak N. Development of AC Voltage Stabilizer with Microcontroller-Based Control System In Proceedings of the 2022 IEEE 17th International Conference on Computer Sciences and Information Technologies (CSIT), 2022, Institute of Electrical and Electronics Engineers, 2022, 527-530. [CrossRef]
  14. Grodzki, W. , Łukaszewicz A. Design and manufacture of unmanned aerial vehicles (UAV) wing structure using composite materials, Materialwissenschaft und Werkstofftechnik, 2015, 46, 269–278. [Google Scholar] [CrossRef]
  15. Łukaszewicz, A. CAx techniques used in UAV design process, In Proceedings of the 2020 IEEE 7th International Workshop on Metrology for AeroSpace (MetroAeroSpace), 2020, 95-98. [CrossRef]
  16. Łukaszewicz, A. , Skorulski G. In , Szczebiot R. (2018): The main aspects of training in the field of computer aided techniques (CAx) in mechanical engineering. In Proceedings of the 17th International Scientific Conference on Engineering for Rural Development, May 23-25, Jelgava, Latvia, , 865-870. 2018. [Google Scholar] [CrossRef]
  17. Łukaszewicz, A. , Miatluk K. Reverse Engineering Approach for Object with Free-Form Surfaces Using Standard Surface-Solid Parametric CAD System, Solid State Phenomena, 2009, 147-149, 706-711. [CrossRef]
  18. Miatliuk, K. Coordination method in design of forming operations of hierarchical solid objects, In Proceedings of the 2008 International Conference on Control, Automation and Systems, ICCAS 2008, pp. 2724–2727, 4694220. [CrossRef]
  19. Puchalski, R. , Giernacki W. UAV Fault Detection Methods, State-of-the-Art, Drones, 2022, 6, 330. [Google Scholar] [CrossRef]
  20. Zietkiewicz, J. , Kozierski P. , Giernacki W. Particle swarm optimisation in nonlinear model predictive control; comprehensive simulation study for two selected problems, International Journal of Control, 2021, 94, 2623–2639. [Google Scholar] [CrossRef]
  21. Kownacki, C. , Ambroziak L. Adaptation Mechanism of Asymmetrical Potential Field Improving Precision of Position Tracking in the Case of Nonholonomic UAVs, Robotica, 2019, 37, 1823–1834. [Google Scholar] [CrossRef]
  22. Kownacki, C. , Ambroziak L. , Ciężkowski M., Wolniakowski A., Romaniuk S., Bożko A., Ołdziej D. Precision Landing Tests of Tethered Multicopter and VTOL UAV on Moving Landing Pad on a Lake, Sensors 2023, 23, 2016. [Google Scholar] [CrossRef] [PubMed]
  23. Basri, E.I.; Sultan, M.T.H.; Basri, A.A.; Mustapha, F.; Ahmad, K.A. Consideration of Lamination Structural Analysis in a Multi-Layered Composite and Failure Analysis on Wing Design Application. Materials 2021, 14, 3705. [Google Scholar] [CrossRef] [PubMed]
  24. Al-Haddad, L.A. , Jaber A. A., An Intelligent Fault Diagnosis Approach for Multirotor UAVs Based on Deep Neural Network of Multi-Resolution Transform Features, Drones, 2023, 7, 82. [Google Scholar] [CrossRef]
  25. Yang, J. , Gu H. , Hu C., Zhang X., Gui G., Gacanin H. Deep Complex-Valued Convolutional Neural Network for Drone Recognition Based on RF Fingerprinting, Drones, 2022, 6, 374. [Google Scholar] [CrossRef]
  26. Holovatyy, A. , Teslyuk V., Lobur M., Sokolovskyy Y., Pobereyko S. Development of Background Radiation Monitoring System Based on Arduino Platform. International Scientific and Technical Conference on Computer Science and Information Technologies, 2018, pp. 121–124. [CrossRef]
  27. Holovatyy, A. , Teslyuk V., Lobur M., Szermer M., Maj C. Mask Layout Design of Single- and Double-Arm Electrothermal Microactuators. Perspective Technologies and Methods In MEMS Design, MEMSTECH 2016–Proceedings of 12th International Conference, 2016, pp. 28–30. [CrossRef]
  28. Volna, E.; Kotyrba, M.; Kocian, V.; & Janosek, M. ; & Janosek, M. Cryptography Based On Neural Network. In Proceedings of the 26th European Conference on Modeling and Simulation (ECMS 2012), edited by: K. G. Troitzsch, M. Moehring, U. Lotzmann. European Council for Modeling and Simulation. Koblenz, Germany, 2012, 386-391., May 29–June 1. [CrossRef]
  29. Shihab, K. A backpropagation neural network for computer network security. Journal of Computer Science 2006, 2, 710–715. [Google Scholar] [CrossRef]
  30. Sagar, V.; Kumar, K. A symmetric key cryptographic algorithm using counter propagation network (CPN). In Proceedings of the 2014 ACM International Conference on Information and Communication Technology for Competitive Strategies, November 14-16, 2014., (ICTCS’14). Udaipur Rajasthan India. [CrossRef]
  31. Arvandi, M.; Wu, S.; Sadeghian, A.; Melek, W.W.; Woungang, I. Symmetric cipher design using recurrent neural networks. In Proceedings of the IEEE International Joint Conference on Neural Networks, 2039–2046. 2006. [Google Scholar] [CrossRef]
  32. Tsmots, I.; Tsymbal, Y.; Khavalko, V.; Skorokhoda, O.; Teslyuk, T. Neural-like means for data streams encryption and decryption in real time. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP). Lviv, Ukraine, 2018, 438-443., August 21-25. [CrossRef]
  33. Scholz, M.; Fraunholz, M.; Selbig, J. Nonlinear principal component analysis: neural network models and applications. In: Gorban, A.N., Kégl, B., Wunsch, D.C., Zinovyev, A.Y. (eds) Principal Manifolds for Data Visualization and Dimension Reduction. Lecture Notes in Computational Science and Engineering, 58, 2008, Springer, Berlin, Heidelberg. [CrossRef]
  34. Rabyk, V.; Tsmots, I.; Lyubun, Z.; Skorokhoda, O. Method and Means of Symmetric Real-time Neural Network Data Encryption. In Proceedings of the 2020 IEEE 15th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT 2020), 2020, 1, 47–50. [Google Scholar] [CrossRef]
  35. Chang, A.X.M.; Martini, B.; Culurciello, E. Recurrent Neural Networks Hardware Implementation on FPGA: arXiv preprint arXiv:1511.05552. 2015. arXiv:1511.05552. 2015. [CrossRef]
  36. Nurvitadhi, E. et al. In Can FPGAs beat GPUs in accelerating next-generation deep neural networks? In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, California, USA, 2017, 5-14., February 22-24. [CrossRef]
  37. Misra, J.; Saha, I. Artificial neural networks in hardware: A survey of two decades of progress. Neurocomputing, 2010; 74, 239–255. [Google Scholar] [CrossRef]
  38. Guo, K. et al. In From model to FPGA: Software-hardware co-design for efficient neural network acceleration. In Proceedings of the 2016 IEEE Hot Chips 28 Symposium (HCS). 2016; 1–27. [Google Scholar] [CrossRef]
  39. Ovtcharov, K.; et al. Accelerating Deep Convolutional Neural Networks Using Specialized Hardware. Microsoft Research Whitepaper. 2016. Available online: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/CNN20Whitepaper.pdf (accessed on 29 April 2022).
  40. Wang, Y.; Xu, J.; Han, Y.; Li, H. and Li, X. In DeepBurning: automatic generation of FPGA-based learning accelerators for the neural network family. In Proceedings of the 53rd Annual Design Automation Conference (DAC’16). Association for Computing Machinery, New York, NY, USA, 1–6., Article 110. [CrossRef]
  41. Nurvitadhi, E.; Sheffield, D.; Sim, J.; Mishra, A.; Venkatesh, G. , and Marr, D. Accelerating Binarized Neural Networks: Comparison of FPGA, CPU, GPU, and ASIC. In Proceedings 2016 International Conference on Field-Programmable Technology (FPT), 2016, 77-84. [CrossRef]
  42. Yayik, A.; Kutlu, Y. Neural Network Based Cryptography. Neural Network Worldc, 2014, 24, 177–192. [Google Scholar] [CrossRef]
  43. Govindu, G.; Zhuo, L.; Choi, S.; and Prasanna, V. Analysis of high-performance floating-point arithmetic on FPGAs. In Proceedings of the 18th International Parallel and Distributed Processing Symposium (IPDPS 2004). 26-30 April, Santa Fe, New Mexico, USA, 149. 2004. [Google Scholar] [CrossRef]
  44. Holovatyy, A. , Teslyuk V., Lobur M. VHDL-AMS model of delta-sigma modulator for A/D converter in MEMS interface circuit. Perspective Technologies and Methods In MEMS Design, MEMSTECH 2015—Proceedings of the 11th International Conference, 2015, pp. 55–57. [CrossRef]
  45. Holovatyy, A. , Lobur M. , Teslyuk V. VHDL-AMS model of mechanical elements of MEMS tuning fork gyroscope for the schematic level of computer-aided design. Perspective Technologies and Methods In MEMS Design—Proceedings of the 4th International Conference of Young Scientists, MEMSTECH 2008, 2008, pp 138—140. [Google Scholar] [CrossRef]
  46. Electronic components database. Available online: https://www.digchip.com/datasheets/parts/datasheet/033/EP3C16F484C6.php (accessed on 29 April 2022).
Preprints 70885 g001
Figure 1. Structure of neural network technology for cryptographic data protection: a) the process of data encryption; b) the process of decrypting data.
Figure 1. Structure of neural network technology for cryptographic data protection: a) the process of data encryption; b) the process of decrypting data.
Preprints 70885 g001
Preprints 70885 g002
Figure 2. The structure of the neural network for data encryption.
Figure 2. The structure of the neural network for data encryption.
Preprints 70885 g002
Preprints 70885 g003
Figure 3. Neural network architecture for decrypting encrypted data.
Figure 3. Neural network architecture for decrypting encrypted data.
Preprints 70885 g003
Preprints 70885 g004
Figure 4. Structure of the stationary part of the system of neural network cryptographic data protection and transmission.
Figure 4. Structure of the stationary part of the system of neural network cryptographic data protection and transmission.
Preprints 70885 g004
Preprints 70885 g005
Figure 5. Structure of the UAV onboard part of the system of neural network cryptographic data protection and transmission.
Figure 5. Structure of the UAV onboard part of the system of neural network cryptographic data protection and transmission.
Preprints 70885 g005
Preprints 70885 g006
Figure 6. Structure of the component of neural network cryptographic encryption of data.
Figure 6. Structure of the component of neural network cryptographic encryption of data.
Preprints 70885 g006
Preprints 70885 g007
Figure 7. A circuit of the specialized hardware components of neural network cryptographic data encryption.
Figure 7. A circuit of the specialized hardware components of neural network cryptographic data encryption.
Preprints 70885 g007
Preprints 70885 g008
Figure 8. The timing diagram of the specialized hardware of neural network cryptographic data encryption.
Figure 8. The timing diagram of the specialized hardware of neural network cryptographic data encryption.
Preprints 70885 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated