Prerpints.org logo
Preprint
Article

Early Detection of Crop Types by Integrating Sentinel-1A and Sentinel-2 Imagery based on the CNN Model

Altmetrics

Downloads

181

Views

73

Comments

0

This version is not peer-reviewed

Submitted:

12 April 2023

Posted:

12 April 2023

You are already at the latest version

Alerts
Abstract
Early-season crop-type data are required for a variety of agricultural monitoring and decision-making applications. The early season in this study referred to the prophase and middle of a growth season. Early-season detection of crop types remains challenging because of limited discriminative features, especially for landscapes that are characterized by complex cropping patterns. In fact, different remote-sensing satellites can increase the frequency of data acquisition, which can provide more information in the early season. Moreover, optical and radar sensors have different degrees of sensitivity to crop parameters. Therefore, the integration and application of two types of multitemporal data are of great significance to improve the accuracy and timeliness of crop type detection.In deep learning (DL), convolutional neural network (CNN) and recurrent neural network (RNN) models have great potential for temporal feature extraction. Compared with RNNs, CNNs usually have fewer parameters and are more conducive to determining early-season detection dates of different crop types, which requires a lot of training because of the need to model on different dates. Nevertheless, revisit dates and temporal intervals of different satellites are usually different, resulting in different data acquisition time series; these data cannot be directly used as input for the same convolutional layer. To address this challenge, a Dual-1DCNN was bulit based on the CNN model in this study. Moreover, an incremental training method was used to attain the network on each data acquisition date and obtained the best detection date for each crop type in the early season. A case study for Hengshui City in China was conducted using time series of Sentinel-1A (S1A) and Sentinel-2 (S2). To verify this method, classical methods support vector machine (SVM) and random forest (RF) were implemented. The results demonstrated the following: (1) the Dual-1DCNN extracted discriminative features from S1A and S2 time series at the early season by producing the highest overall accuracy (OA: 87.23%); (2) for summer maize, cotton, and common yam rhizome, the Dual-1DCNN achieved F1 values of 92.39%, 87.71%, and 84.38%, respectively, at the early season (moreover, the early seasons were almost 40, 70, and 80 days before the end of the growth seasons, respectively). These findings suggested that the Dual-1DCNN is promising for the accurate and timely detection of crop types.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Crop-type mapping is an important component of agricultural monitoring and management. Early-season crop-type information are required for a variety of monitoring and decision-making applications, such as yield estimation, agricultural disaster assessment, and crop rotation, which is important for food security [1,2]. At present, there is no clear international definition for the early detection of crop types. Except for tropical or very arid regions, most crop systems have one or two growing seasons each year. According to the extant literatures [3,4,5] and the actual needs of agricultural monitoring, the early detection of crop types in this study refers to the provision of crop-type maps between the prophase and middle of a growing season.
Remote-sensing technologies have greatly improved crop-type mapping for decades at the regional to continental scale [6,7,8,9]. Multitemporal data have proved effective for crop-type mapping given that the phenological evolution of each crop produces a unique temporal profile of reflectance or the radar-backscattering coefficient [10,11]. Early detection of crop types, however, remains challenging in agricultural remote-sensing monitoring because it needs to extract distinguishable features from the limited data in the early season. Moreover, for landscapes dominated by smallholder agriculture, such as those in China, with characteristics of complex cropping patterns and a high degree of land fragmentation, the timely and accurate mapping of crop types represents an especially challenging task [12,13,14].
The launch of optical and synthetic aperture radar (SAR) remote-sensing satellites with high spatial and temporal resolutions, such as the Sentinel-1A/B (S1) and Sentinel-2A/B (S2) in the European Copernicus project [15], provides more opportunities for early crop-type detection [16]. S1 and S2 can provide SAR and optical (multispectral) images, respectively, at 10 m spatial and 5-day (S2) or 6-day (S1) temporal resolutions. The integration and application of the two types of data hold great significance for improving the accuracy of early crop-type detection. First, the wealth of crop phenology information of dense time series data (TSD) can be used to identify different crop types with the same spectrum [17,18]. Second, compared with single-source remote-sensing data, the multisource data has a higher time frequency of data acquisition, which directly improves timeliness. Third, different sensors have different degrees of sensitivity to crop parameters, and optical data can be used to estimate crop chemical components, such as chlorophyll and water [19]; additionally, SAR data are more sensitive to crop structure (e.g., height, porosity, coverage), and field conditions (e.g., field moisture content) [20]. Understanding how to effectively combine the complementary information of S1 and S2, however, remains a challenge in the field of early-season mapping.
At present, in mainstream machine learning (ML) approaches, such as the support vector machine (SVM) and random forest (RF), the sequential relationship of time series imagery is not clearly considered, which means that we might ignore some useful information during crop-type detection [21,22]. In recent years, as a breakthrough technology in ML, deep learning (DL) has shown great potential in the field of remote-sensing information extraction [23,24,25]. Among DL models, recurrent neural networks (RNNs) and convolutional neural networks (CNNs) have demonstrated unprecedented performance in the extraction of temporal features [26,27]. Long short-term memory (LSTM) and gated recurrent unit RNNs (GRU) [28] are variants of the RNN unit that solve the problem of gradient disappearance or explosion seen with an increasing time series.
In crop-type mapping, these models have been explored mainly by using single-source data, such as microwave data [21,27,29], optical data (or vegetation index) [18,22], or filling gaps of optical images by converting SAR data to normalized difference vegetation index (NDVI) using a hybrid architecture of CNN and LSTM [30]. These methods are not available for multisource data because the sequence length and time interval of different spectral bands (or polarization characteristics) of single-source time series are the same; meanwhile, the time series from different sources usually have different sequence lengths and time intervals. In addition, although Ienco et al. [31] proposed an architecture based on the GRU and CNN to boost the land cover classification task by combining S1 and S2 images, their method is not exercisable for the task of early detection of crop types. The main reason for this is that compared with CNNs, RNNs have more parameters determined by the length of the time series [32]. Different time series are usually input into architectures to find the best date, and therefore, if there are many parameters in DL architectures, the training becomes time-consuming, especially for long time series.
In a previous work [14], we evaluated CNNs, LSTM RNNs, and GRU RNNs for early crop-type classification using S1A time series data. Results confirmed that the training of CNNs used less time, and CNNs performed better for evenly distributed time series signals. In the present work, we described an architecture based on the CNN (called Dual-1DCNN) to integrate the time series data of S1A and S2, and used an incremental training method to attain the network on each data acquisition date. The aim of the Dual-1DCNN architecture is to improve the early crop-type detection by taking advantage of S1A and S2 from three levels: (1) ensuring that more information can be used in the early season; (2) complementing sensitivities of optical and radar data for different parameters; and (3) improving the timeliness of detection by having more data acquisition dates. We conducted a case study for Hengshui City, a main cropping city in North China.

2. Materials

2.1. Study Site

Hebei Province is a main cropping province located in North China. Hengshui City occupies an area of 8.12 × 103 km2 (Figure 1) and is a typical wheat–maize rotation area; its main economic crops are cotton, common yam rhizome, fruit trees, and vegetables. The growing season for winter wheat is from early October to the middle of the following June, and summer maize is planted at the end of the winter wheat season and harvested in late September. The growing seasons of cotton and common yam rhizome are from late April to the end of October and early April to the end of October, respectively. The growth periods of fruit trees generally last all year. In this study, we categorized the phenology of summer maize, cotton, and common yam rhizome into three periods: sowing, developing, and maturation. The details of these periods are shown in Figure 2.

2.2. Ground Reference Data

A field investigation in the study area was conducted in July 2019, when the main summer crops were in their reproductive period. To obtain sampling points distributed across the entire region, we designed a sampling route based on expert knowledge and recorded the main crop types and corresponding geographic coordinates on the route. A total of 1186 samples from the field survey were acquired. Afterward, 756 samples were taken by manual interpretation from the surveyed parcels on the platform Google Earth Map. Therefore, a total of 1942 sample points for five main types of local vegetation in the summer season: (1) forest, (2) summer maize, (3) cotton, (4) fruit tree, and (5) common yam rhizome were used in this study. The distribution of the number of samples per type is shown in Table 1, and the calendars are expressed in Figure 2. All geographic coordinates of samples were re-projected to WGS 84/UTM zone 50N.

2.3. Sentinel-1A/2 Data and Preprocessing

The S1A and S2 data was downloaded from the European Space Agency (ESA) Sentinels Scientific Data Hub website. The Interferometric Wide Swath (IW) Ground Range Detected (GRD) product of S1A was used in this study. This product with 10 m resolution contained both VH and VV polarizations and had a 12-day revisit time. The S2 (Level-1C) product included blue, green, red, and near-infrared 1 (NIR1) bands at 10 m; red edge (RE) 1 to 3, NIR2, and shortwave infrared 1 (SWIR1) and SWIR2 at 20 m; and three atmospheric bands (band 1, band 9, and band 10) at 60 m. For this study, the three atmospheric bands were not used because they were dedicated to atmospheric corrections and cloud screening the three atmospheric band [15]. There were 15 S1A mosaics images and 35 S2 mosaics images over Hengshui from day of year (DOY) 103 to 273 (13 April to 30 September) 2019. Note that DOY 273 was at the late season of the three crop types, and we used the data before DOY 273, which met the requirements of early crop-type detection.
We preprocessed the S1A data in the Sentinel Application Platform (SNAP) open source software version 7.0.2. The preprocessing stages included (1) radiometric calibration; (2) speckle filtering, in which case we applied the Gamma-MAP (maximum a posteriori) speckle filter with a 7 × 7 window size to all images to remove the granular noise; (3) orthorectification, for which we applied range Doppler terrain orthorectification to the images; and (4) re-projection, for which we projected the orthorectified SAR image to the Universal Transverse Mercator (UTM) coordinate system, Zone 50 North, World Geodetic System (WGS) 84.
The preprocessing stages for the S2 images were as follows:
(1)
Atmosphere calibration: We used the sen2cor plugin v2.5.5 to process reflectance images from Top-of-Atmosphere (TOA) Level 1C S2, to Bottom-of-Atmosphere (BOA) Level 2A following Sentinel-2 for Agriculture (Sen2-Agri) protocols [33] (http://www.esa-sen2agri.org/).
(2)
Masking clouds: We used Function of mask (Fmask) 4.0 [34] to mask clouds and cloud shadow (the cloud probability threshold was set to 50%). Note that compared with cloud confidence layers in the output of sen2cor, Fmask 4.0 results were more accurate in our study area.
(3)
Resampling: We resampled images of RE1, RE2, RE3, NIR2, SWIR1, and SWIR2 from step (1) and cloud masks from step (2) to 10 m.
(4)
Filling gaps: Because linear interpolation is usually appropriate for short gaps [35], we adopted the Savitzky–Golay filter to reconstruct each band value using a moving window of seven observations and a filter order of 2 [36]. Note that we used S-2A/B images observed in March and October 2019 because of missing values in early April and late September.

3. Methodology and Experiments

3.1. CNN for Multivariate

The four main types of layers in the CNN architecture are the convolutional (Conv) layer, rectified linear unit (ReLU) layer, pooling layer, and fully connected (FC) layer [37]. For classification tasks, CNNs are typically composed of various combinations of these four types followed by a softmax logistic regression layer, which acts as a classifier that produces the predictive probabilities of all the object categories in the input data [38,39]. Moreover, it is common to incorporate some other components, such as dropout and batch normalization (BN) [40], into CNN architectures to improve the generalization ability and prevent overfitting.
The one-dimensional CNN (1D CNN) is a special form of the CNN, and it employs a 1D convolution kernel to capture the temporal pattern or shape of the input series [41]. The Conv layer of 1D CNN is usually expressed as Conv1D. The convolutional operation is actually the dot products between kernels and local regions of the input. A basic 1D convolutional block always consists of a Conv1D layer followed by a ReLU layer. We expressed a multivariate time series with D0 variables of length T0 as ( x 1 , x 2 , … , x T 0 ), where x t = R D 0 denotes the t-th observations of all variables, x t d represents the value of d-th variable of xt, and 0 ≤ t ≤ T 0 . Here, all variables had the same T0 For illustrative purposes, we assumed 1× k kernels for all Conv1D layers; however, different kernel sizes also could be assigned if desired. Considering L Conv1D layers, the kernels for each Conv1D layer were parameterized by tensor W l = R D l × k × D l − 1 and biases b l ∈ R D 1 , where l ∈ ( 1 , … , L ) . For the l-th layer, the i-th component of the activation E i , t l ∈ R D 1 can be calculated by the following function:
E i , t l = Re l u b i l + ∑ k = 1 k conv1 D W i , k l , E i + k − 1 l − 1
where E l − 1 ∈ R D l − 1 × T l − 1 is from the previous layer, and Conv1D (…) is a regular 1D convolution without zero padding on the boundaries.

3.2. The Dual-1DCNN

As noted, the sequence length of the S1A time series data with a 12-day interval was 14, and the sequence length of S2 time series data with a 5-day interval was 35. The two types of time series data could not be input into a 1D CNN at the same time because their data acquisition dates were different. Therefore, the Dual-1DCNN model developed in this study integrated the time series data of S1A and S2 by building two 1D CNN modules: an S1A module, and an S2 module (Figure 3).
Both the S1A module and S2 module had three Conv1D blocks and a flattened layer. A Conv1D block contains a Conv1D layer, a BN layer, and a ReLU layer. In the S1A module, the kernel sizes of three Conv1D layers were 64, 128, and 64, and in the S2 module they were 256, 512, and 256. In each module, kernel durations of three Conv1D layers were set to 5, 4, and 3. The outputs of S1A and S2 modules were concatenated by the concatenate layer and passed to a dropout layer (the dropout rate was set 0.8) and an FC layer with 100 neurons. Finally, data were passed to a softmax classification layer with five neurons, which produced the predictive probabilities of all of the crop types in the input data.
As stated in Section 3.1, a sample can be expressed by X = x 1 , x 2 , … , x T 0 , where T0 = 35 or 14, x t ∈ R D denotes the t-th observations of all variables, and x t d represents the value of the d-th variable of xt. For all samples (1942), we first performed channel L2-norm (Equation (2)) before inputting them into the model. Note that the channel here is a band of S2 or a polarization of S1A in a data acquisition date, as follows:
∥ X ∥ 2 = x t 1 d 2 + x t 2 d 2 + … + x t 1942 d 2 1 / 2
Figure 4 shows the flow of data in each module. The input of the S1A module is a three-dimensional matrix with the shape of ( batchsize , L 1 , 2 ) ; here, batchsize is the number of input samples in a batch, L1 is the sequence length of S1A time series with a 12-day interval, and 2 indicates the two polarizations (variables) of S1A. The input shape of the S2 module is ( batchsize L 2 , 10 ; here, L2 is the sequence length of S2 time series with a 5-day interval, and 10 indicates the ten spectrum bands (variables) of S2. Note that to find the best date for early crop-type classification, L1 and L2 are variables (see details in Section 3.4). In addition, the input was a pixel-wise image for the following reasons: (1) the main objective in this study was to investigate how early in the growing season the Dual-1DCNN could achieve optimal accuracy in crop-type classification by integrating S1A and S2 time series data; and (2) it was challenging to define the optimal size of spatial regions because the agriculture parcel was usually small in the study area—parcel segmentation is a direction for our future work.
The flattened layer converted the output of Conv1D block-3 in each module into a 1D single vector. Therefore, the output shape of the S1A module is ( batchsize , L 1 × 64 , the output shape of the S2 module is batchsize , L 2 × 256 , and the output of the concatenate layer is ( batchsize L 1 × 64 + L 2 × 256 .

3.3. Evaluation

To make a comparative analysis, the Dual-1DCNN model was compared with two classical machine learning methods for crop-type mapping, including SVM and RF. The two metrics overall accuracy (OA) and F1-score (F1) were adopted. OA was used to evaluate the performance of different models for crop-type classification, and F1 was used to evaluate the best date for early-season detection of each crop type. The corresponding calculation formulas are as follows:
O A = T P + T N T P + T N + F P + F N
F 1 = 2 T P 2 T P + F P + F N
where TP, TN, FP, and FN denote numbers of pixels belonging to true positive, true negative, false positive, and false negative, respectively, in the confusion matrix.

3.4. Experimental Design

We called the DOY when S1A or S2 data was acquired in the growing season a “train date.” There were a total of 46 train dates excluding overlapping dates (Table 2). The first train date (DOY 103) was called the “start date.” From the start date to each train date, the number of times S1A or S2 data obtained was the length of the corresponding sequence (i.e., L1 or L2, respectively). The time series of dates is shown in Table 2.
Figure 5 presents an overview of our experiments. First, we randomly selected 70% and 10% of samples of each crop type to form the training set and the validation set, respectively. The remaining samples (20%) constituted the test set because the distribution of the number of samples of the different crop types was uneven. Then, we conducted incremental training—that is, starting from the start date, the model wsa trained on each train date; the input data included all of the S1A and S2 data from the start date to the train date. The following training strategies were employed:
(1)
For the Dual-1DCNN model, the number of epochs was set to 10,000 with a batch size of 128 and Adam optimizer [42]. We initially set the learning rate as 5 e − 5 and applied a global adaptation during each epoch. If the training cross-entropy error did not decrease for 100 epochs, we reduced it by 20% for the next epoch (the minimum learning rate was 1 e − 6 ). In addition, each training process was monitored through a callback function named ModelCheckpoint [43], and the model was saved when a better model of the training set was found.
(2)
For the SVM, we used the radial basis function (RBF)-based SVM (RBF-SVM), which requires two hyperparameters (i.e., penalty parameter C and kernel parameter γ) to be tuned. During the optimization process, we selected γ from 10 − 4 , 10 − 3 , … , 10 2 , and selected from 10 − 2 , 10 − 1 , … , 10 4 .
(3)
The primary parameters of the RF model were the number of predictors at each decision tree node split (max_features) and the number of decision trees (n_estimators) to run. The features in this study were all channels of each input, and therefore, we set the parameter “max_features” with the default value b (b is the number of channels) [44]. Additionally, the range of the grid search value for the “n_estimators” parameter varied from 100 to 10,000 with an interval of 100 [45].
To reduce the influence of random sample splitting bias, we performed five random splits to conduct five trainings and five corresponding tests. This allowed us to compute average performances of the five test sets. Finally, we evaluated the three types of models and attained the best date for each crop type for early-season mapping.

4. Results

4.1. Temporal Profiles of S1A and S2 Data

Figure 6 summarizes the temporal profiles of VV and VH polarizations of the five crop types. We observed the following: (1) compared with VH curves, VV curves had less overlap or intersection, which was more conducive to the identification of five crop types; (2) both VV and VH had the highest similarity for fruit tree and forest; and (3) for VH curves, common yam rhizome had a high similarity with winter wheat before DOY 130 (i.e., mid-May), whereas after DOY 190 (i.e., mid-July), it showed a similarity with fruit tree and forest.
Figure 7 summarizes the temporal profiles of ten spectrum bands of the five crop types. Each profile obtained by time series linear interpolation and Savitzky-Golay smoothing illustrated the potential for gap-filling dense time series to contribute to crop-type classification.
As observed in the figure, the curves of different crop types from visible bands (Figure 7(a)–7(c)) show obvious differences before DOY 183 (i.e., early July) and more intersections and overlaps after DOY 183, because all types were in the developing stage. The curves of RE1 were similar to the red spectrum curves, RE2 and RE3 were more similar with each other, and RE3 had the widest range of reflectivity. Furthermore, although the curves of NIR1 and NIR2 were very similar, those of SWIR1 and SWIR2 showed large differences, with the range of reflectivity of SWIR1 being larger.
Regarding different crop types, from DOY 103 to DOY 158, the visible and SWIR1/2 spectrum bands of cotton and common yam rhizome were significantly different from those of other crop types because they were in the growth phase. In addition, the RE2/3 and NIR1/2 spectrum bands of cotton were significantly enhanced during the period from DOY 218 to DOY 243 when cotton was maturing. The RE2/3 and NIR1/2 spectrum bands of fruit tree and forest showed a big difference from DOY 148 to DOY 178 but were very similar in other bands. Last, the visible, RE1, and SWIR1/2 spectrum bands of summer maize were significantly enhanced from DOY 163 to DOY 183, when summer maize was in the growth phase. In the same period, the curves of its other spectrum bands greatly overlapped with those of common yam rhizome.

4.2. Overall Assessment of Classification Accuracy

Figure 8 shows the evolution of average classification accuracies of five test sets as a function of DOY time series in Table 2 using Dual-1DCNN (red), SVM (green), and RF (blue). The OA value given for each time point was the average from five repetitions. According to our definition of early-season detection of crop types in Section 1 (i.e., the provision of crop-type maps in the prophase and middle of a growing season) and the crop calendar in Section 2.1 (Figure 2), the early seasons of maize, cotton, and common yam rhizome were DOY 166–238, DOY 91–233, and DOY 91–233, respectively. The detailed results, including the average OA and standard deviation of five test sets from DOY 103–238, are reported in Table 3.
Figure 8 shows that the accuracies of the three methods increased with the length of the time series. Moreover, the curves of Dual-1DCNN and SVM were higher than that of RF overall, and Dual-1DCNN performed best. This was an important result supporting Dual-1DCNN as an effective method for crop-type identification by integrating S1A and S2 time series data. From Table 3 we can conclude that during the early season, the highest OA of the three methods was 87.23%, which was achieved by Dual-1DCNN at DOY 226). Conversely, the highest OAs of SVM and RF were 87.02% (DOY 233) and 86.15% (DOY 238), respectively. These results confirmed that Dual-1DCNN could detect crop types in the prophase and middle of a growing season and thus provided more accurate and earlier results than SVM and RF.

4.3. Early Detection of Crop Types

The best date for early mapping is usually different for each crop type. This work used F1 to evaluate the classification accuracy of different crop types. Figure 9 shows the F1 temporal profiles of each crop type by Dual-1DCNN, SVM, and RF. The F1 value given for each time point was the average over five different random splits.
First, for winter wheat–summer maize, all three methods achieved higher accuracy than for other crop types on each date. The Dual-1DCNN, SVM, and RF attained F1 values above 90% on the prophase stage, which was when wheat–summer maize had obvious phenological differences from other crop types. Second, as analyzed in Section 4.2, before DOY 158, cotton and common yam rhizome had obvious feature differences from other crop types; therefore, their F1 increased faster in the prophase stage with all three methods. Dual-1DCNN, however, extracted distinguishable features significantly better than the other two methods, especially on cotton. Third, all three methods performed unstably on common yam rhizome. As shown in Figure 6(b) and Figure 7, the VH backscatter coefficients and reflectance values of common yam rhizome were similar more frequently to those of other crop types. This likely was due to the fact that the parcels of common yam rhizome usually were small, which resulted in more mixed-pixel samples. Finally, compared with other crop types, accuracies for forest and fruit trees were lowest for all three methods because the two types had very similar phenological characteristics.
Table 4 summarizes the maximum values of F1 for each crop type and the corresponding DOYs (i.e., early-season detection DOY) during the early season by Dual-1DCNN, SVM, and RF. Figure 10 shows the confusion matrices for the early-season detection DOYs. Overall, it was evident that Dual-1DCNN attained the highest F1 values on all three crop types. Furthermore, the early-season detection DOYs of the three crop types by Dual-1DCNN were all earlier than or the same as those obtained by SVM and RF. These results confirmed that Dual-1DCNN was effective for early-season detection of crop types.

5. Discussion

5.1. Performance of the Dual-1DCNN Algorithm

The performance of the Dual-1DCNN algorithm can be discussed from the following two points:
1. Compared with the classic SVM and RF algorithms, the Dual-1DCNN model achieved higher classification accuracy on most of the data (S1A and S2) acquisition dates, and attained higher and earlier in the early season; for early-season detection of different crop types, the Dual-1DCNN also attained higher and earlier F1 values on summer maize, cotton and common yam rhizome. As described in Section 4.1, we conducted a wide range of value training on the hyperparameters of SVM and RF on each train date, that is to say, all results on each train date were the maximum values that SVM and RF could achieve in this study. The hyperparameters (including the architecture) of Dual-1DCNN were determined based on empirical parameters [14,27,46,47,48] and the hyperparameters on each train date were the same (except for the learning rate and dropout rate). We used these two methods to train the hyperparameters of the model because the DL algorithm required a lot of computing resources, in addition, to obtain an unbiased estimation of the generalization error in the Dual-1DCNN model, we conducted five-fold cross-validation [49]. When computing resources were met, our Dual-1DCNN model showed greater potential than SVM and RF.
2. Since early-season detection of crop types required us to judge the best date for each crop type, we had to train the model many times, and the input time series data were different each time. Compared with the RNN series models, the 1D CNN model had fewer parameters, which enabled us to improve the training efficiency of the model. In addition, the input of the 1D CNN was a regular time series, that is, the time intervals of all features (i.e., spectrum or polarization) had to be the same. To address this requirement, we established the two-branch architecture, namely Dual-1DCNN in the application of S1A and S2 time series data. In addition, the Dual-1DCNN was not limited to the integration of S1A and S2. It is applicable to other different data sources, such as optical data sources (Landsat and S2) and SAR data sources (S1A and Gaofen-3). Therefore, this model can be extended to other regions, such as southern China, which is characterized by frequent rainy weather and prolonged cloud cover [50]. Note that the channels in different modules should be trained according to the number of input features.

5.2. Limitations and Future Work

Although these results proved the effectiveness and advantages of the algorithm Dual-1DCNN for early detection of crop types by integrating S1A and S2 time series data, this study had some limitations that need to be overcome.
First, the classification accuracy was closely related to the crop types and the number of samples for each crop type. In this study, two main factors reduced classification accuracies: the similar spectrum and polarization characteristics between fruit trees and forests; and the mixed pixels of common yam rhizome. Moreover, the small sample numbers of cotton and common yam rhizome affected the classification accuracy. The planting area of summer maize in the entire study area, however, was much larger than that of cotton and common yam rhizome. We tried to reduce the number of training samples of summer maize, but the accuracy of the test samples would be reduced because of the complex relationship between geographical conditions and crops, and we required a uniform sample distribution. In future mapping work, we will conduct regional training of models for small areas of crops and build transferring models for large area.
In addition, we analyzed the Dual-1DCNN algorithm on the pixel scale because our main objective was to investigate the use of new DL architecture for early-season detection of crop types by integrating S1A and S2 time series data. All of these results confirmed that our method performed better than the classical SVM and RF methods. It is challenging to identify the agricultural parcels in China, and parcel segmentation will be one of our future projects.

6. Conclusions

Early-season crop type mapping is valuable for agricultural monitoring and management and holds great significance for global food security. In the context of the continuous growth of the global population, the use of remote-sensing data with high spatial and temporal resolution to accurately, timely, and efficiently produce crop-type maps has become an important bottleneck in agricultural management. For smallholder agriculture in China, this task is even more challenging because of complex cropping patterns and a high degree of land fragmentation. To use more classification features and improve the timeliness of crop type detection, we described the Dual-1DCNN model. This algorithm offers three advantages: (1) It integrated and applied S1A and S2 time series data to detect crop types, which added phenological characteristics and spectral (or polarization) characteristics to the early-season data. (2) Compared with ML models, it explicitly considered the sequential relationship of multitemporal observations, which may be useful when dealing with time series inputs. (3) Compared with RNN models, the training of the Dual-1DCNN model was more efficient, which is important for finding the best date of different crop types.
At the early season, the Dual-1DCNN algorithm achieved an acceptable overall accuracy (87.23%). For summer maize, cotton, and common yam rhizome, Dual-1DCNN attained the highest F1 values at DOYs 233 (92.39%), 226 (87.71%), and 178 (84.38%), which were almost 40, 70, and 80 days before the end of growth seasons, respectively. Furthermore, compared with RF and SVM models, Dual-1DCNN performed better at most data acquisition dates, and thus offered significant potential in the early-season detection of crop types. Further improvements to the Dual-1DCNN model could include the use of remote-sensing data from different sources. We also could extend this model to regions in southern China.

Author Contributions

Conceptualization and methodology, H.Z.; software, H.Z and L.S.; validation, J.L. and J.R.; resources and data curation, J.L. and L.S.; writing—original draft preparation, H.Z. and J.R.; writing—review and editing, J.L. and L.S.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Supported by National Key R&D Program of China and Shandong Province, China, grant number 2021YFB3901300 and The Fundamental Research Funds for Central Non-profit Scientific Institution, grant number 1610132021021.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kolotii, A.; Kussul, N.; Shelestov, A.; Skakun, S.; Yailymov, B.; Basarab, R.; Lavreniuk, M.; Oliinyk, T.; Ostapenko, V. COMPARISON OF BIOPHYSICAL AND SATELLITE PREDICTORS FOR WHEAT YIELD FORECASTING IN UKRAINE. International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences 2015. [CrossRef]
  2. Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sensing of Environment 2015, 164, 324–333. [Google Scholar] [CrossRef]
  3. Inglada, J.; Vincent, A.; Arias, M.; Marais-Sicre, C. Improved early crop type identification by joint use of high temporal resolution SAR and optical image time series. Remote Sensing 2016, 8, 362. [Google Scholar] [CrossRef]
  4. Jiang, H.; Li, D.; Jing, W.; Xu, J.; Huang, J.; Yang, J.; Chen, S. Early season mapping of sugarcane by applying machine learning algorithms to Sentinel-1A/2 time series data: A case study in Zhanjiang City, China. Remote Sensing 2019, 11, 861. [Google Scholar] [CrossRef]
  5. Skakun, S.; Franch, B.; Vermote, E.; Roger, J.-C.; Becker-Reshef, I.; Justice, C.; Kussul, N. Early season large-area winter crop mapping using MODIS NDVI data, growing degree days information and a Gaussian mixture model. Remote Sensing of Environment 2017, 195, 244–258. [Google Scholar] [CrossRef]
  6. Homer, C.; Huang, C.; Yang, L.; Wylie, B.K.; Coan, M. Development of a 2001 national land-cover database for the United States. 2004. [CrossRef]
  7. Khan, A.; Hansen, M.C.; Potapov, P.; Stehman, S.V.; Chatta, A.A. Landsat-based wheat mapping in the heterogeneous cropping system of Punjab, Pakistan. International Journal of Remote Sensing 2016, 37, 1391–1410. [Google Scholar] [CrossRef]
  8. King, L.; Adusei, B.; Stehman, S.V.; Potapov, P.V.; Song, X.-P.; Krylov, A.; Di Bella, C.; Loveland, T.R.; Johnson, D.M.; Hansen, M.C. A multi-resolution approach to national-scale cultivated area estimation of soybean. Remote Sensing of Environment 2017, 195, 13–29. [Google Scholar] [CrossRef]
  9. Skriver, H.; Mattia, F.; Satalino, G.; Balenzano, A.; Pauwels, V.R.; Verhoest, N.E.; Davidson, M. Crop classification using short-revisit multitemporal SAR data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2011, 4, 423–431. [Google Scholar] [CrossRef]
  10. Wardlow, B.D.; Egbert, S.L.; Kastens, J.H. Analysis of time-series MODIS 250 m vegetation index data for crop classification in the US Central Great Plains. Remote sensing of environment 2007, 108, 290–310. [Google Scholar] [CrossRef]
  11. Chen, Z.; Zhou, Q.; Liu, J.; Wang, L.; Ren, J.; Huang, Q.; Deng, H.; Zhang, L.; Li, D. CHARMS-China agricultural remote sensing monitoring system. In Proceedings of the 2011 IEEE international geoscience and remote sensing symposium; 2011; pp. 3530–3533. [Google Scholar]
  12. Lebourgeois, V.; Dupuy, S.; Vintrou, É.; Ameline, M.; Butler, S.; Bégué, A. A combined random forest and OBIA classification scheme for mapping smallholder agriculture at different nomenclature levels using multisource data (simulated Sentinel-2 time series, VHRS and DEM). Remote Sensing 2017, 9, 259. [Google Scholar] [CrossRef]
  13. McCarty, J.; Neigh, C.; Carroll, M.; Wooten, M. Extracting smallholder cropped area in Tigray, Ethiopia with wall-to-wall sub-meter WorldView and moderate resolution Landsat 8 imagery. Remote Sensing of Environment 2017, 202, 142–151. [Google Scholar] [CrossRef]
  14. Zhao, H.; Chen, Z.; Jiang, H.; Jing, W.; Sun, L.; Feng, M. Evaluation of three deep learning models for early crop classification using sentinel-1A imagery time series—A case study in Zhanjiang, China. Remote Sensing 2019, 11, 2673. [Google Scholar] [CrossRef]
  15. Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote sensing of Environment 2012, 120, 25–36. [Google Scholar] [CrossRef]
  16. Dalla Mura, M.; Prasad, S.; Pacifici, F.; Gamba, P.; Chanussot, J.; Benediktsson, J.A. Challenges and opportunities of multimodality and data fusion in remote sensing. Proceedings of the IEEE 2015, 103, 1585–1601. [Google Scholar] [CrossRef]
  17. McNairn, H.; Kross, A.; Lapen, D.; Caves, R.; Shang, J. Early season monitoring of corn and soybeans with TerraSAR-X and RADARSAT-2. International Journal of Applied Earth Observation and Geoinformation 2014, 28, 252–259. [Google Scholar] [CrossRef]
  18. Cai, Y.; Guan, K.; Peng, J.; Wang, S.; Seifert, C.; Wardlow, B.; Li, Z. A high-performance and in-season classification system of field-level crop types using time-series Landsat data and a machine learning approach. Remote sensing of environment 2018, 210, 35–47. [Google Scholar] [CrossRef]
  19. Sonobe, R.; Yamaya, Y.; Tani, H.; Wang, X.; Kobayashi, N.; Mochizuki, K.-i. Crop classification from Sentinel-2-derived vegetation indices using ensemble learning. Journal of Applied Remote Sensing 2018, 12, 026019–026019. [Google Scholar] [CrossRef]
  20. Vreugdenhil, M.; Wagner, W.; Bauer-Marschallinger, B.; Pfeil, I.; Teubner, I.; Rüdiger, C.; Strauss, P. Sensitivity of Sentinel-1 backscatter to vegetation dynamics: An Austrian case study. Remote Sensing 2018, 10, 1396. [Google Scholar] [CrossRef]
  21. Ndikumana, E.; Ho Tong Minh, D.; Baghdadi, N.; Courault, D.; Hossard, L. Deep recurrent neural network for agricultural classification using multitemporal SAR Sentinel-1 for Camargue, France. Remote Sensing 2018, 10, 1217. [Google Scholar] [CrossRef]
  22. Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote sensing of environment 2019, 221, 430–443. [Google Scholar] [CrossRef]
  23. Saha, S.; Mou, L.; Qiu, C.; Zhu, X.X.; Bovolo, F.; Bruzzone, L. Unsupervised deep joint segmentation of multitemporal high-resolution images. IEEE Transactions on Geoscience and Remote Sensing 2020, 58, 8780–8792. [Google Scholar] [CrossRef]
  24. Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sensing of Environment 2020, 241, 111716. [Google Scholar] [CrossRef]
  25. Zhang, F.; Yao, X.; Tang, H.; Yin, Q.; Hu, Y.; Lei, B. Multiple mode SAR raw data simulation and parallel acceleration for Gaofen-3 mission. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2018, 11, 2115–2126. [Google Scholar] [CrossRef]
  26. Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Deep learning for time series classification: A review. Data mining and knowledge discovery 2019, 33, 917–963. [Google Scholar] [CrossRef]
  27. Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time series classification using multi-channels deep convolutional neural networks. In Proceedings of the Web-Age Information Management: 15th International Conference, WAIM 2014, Macau, China, 16-18 June 2014; Proceedings 15. pp. 298–310. [Google Scholar]
  28. Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv, arXiv:1409.1259 2014. [CrossRef]
  29. Liao, C.; Wang, J.; Xie, Q.; Baz, A.A.; Huang, X.; Shang, J.; He, Y. Synergistic use of multi-temporal RADARSAT-2 and VENµS data for crop classification based on 1D convolutional neural network. Remote Sensing 2020, 12, 832. [Google Scholar] [CrossRef]
  30. Zhao, W.; Qu, Y.; Chen, J.; Yuan, Z. Deeply synergistic optical and SAR time series for crop dynamic monitoring. Remote Sensing of Environment 2020, 247, 111952. [Google Scholar] [CrossRef]
  31. Ienco, D.; Interdonato, R.; Gaetano, R.; Minh, D.H.T. Combining Sentinel-1 and Sentinel-2 Satellite Image Time Series for land cover mapping via a multi-source deep learning architecture. ISPRS Journal of Photogrammetry and Remote Sensing 2019, 158, 11–22. [Google Scholar] [CrossRef]
  32. Sak, H.; Senior, A.W.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. 2014.
  33. Bontemps, S.; Arias, M.; Cara, C.; Dedieu, G.; Guzzonato, E.; Hagolle, O.; Inglada, J.; Matton, N.; Morin, D.; Popescu, R. Building a data set over 12 globally distributed sites to support the development of agriculture monitoring applications with Sentinel-2. Remote Sensing 2015, 7, 16062–16090. [Google Scholar] [CrossRef]
  34. Qiu, S.; Zhu, Z.; He, B. Fmask 4. 0: Improved cloud and cloud shadow detection in Landsats 4–8 and Sentinel-2 imagery. Remote Sensing of Environment 2019, 231, 111205. [Google Scholar] [CrossRef]
  35. Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations–application to MODIS LAI products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
  36. Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote sensing of Environment 2004, 91, 332–344. [Google Scholar] [CrossRef]
  37. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
  38. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Communications of the ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
  39. Zeiler, M.D.; Fergus, R. Stochastic pooling for regularization of deep convolutional neural networks. arXiv, arXiv:1301.3557 2013.
  40. Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International conference on machine learning; 2015; pp. 448–456. [Google Scholar]
  41. Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. Journal of Sensors 2015, 2015, 1–12. [Google Scholar] [CrossRef]
  42. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, arXiv:1412.6980 2014.
  43. Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM review 2021, 63, 208–228. [Google Scholar] [CrossRef]
  44. Goldstein, B.A.; Polley, E.C.; Briggs, F.B. Random forests for genetic association studies. Statistical applications in genetics and molecular biology 2011, 10. [Google Scholar] [CrossRef] [PubMed]
  45. Probst, P.; Wright, M.; Boulesteix, A. Hyperparameters and tuning strategies for random forest, WIREs Data Mining and Knowledge Discovery, 9, e1301. 2019. [CrossRef]
  46. Hatami, N.; Gavet, Y.; Debayle, J. Classification of time-series images using deep convolutional neural networks. In Proceedings of the Tenth international conference on machine vision (ICMV 2017); 2018; pp. 242–249. [Google Scholar]
  47. Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. The journal of machine learning research 2014, 15, 1929–1958. [Google Scholar]
  48. Wang, H.; Wang, Y.; Zhang, Q.; Xiang, S.; Pan, C. Gated convolutional neural network for semantic segmentation in high-resolution images. Remote Sensing 2017, 9, 446. [Google Scholar] [CrossRef]
  49. Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the Ijcai; 1995; pp. 1137–1145. [Google Scholar]
  50. Xie, L.; Zhang, H.; Li, H.; Wang, C. A unified framework for crop classification in southern China using fully polarimetric, dual polarimetric, and compact polarimetric SAR data. International Journal of Remote Sensing 2015, 36, 3798–3818. [Google Scholar] [CrossRef]
Preprints 70880 g001
Figure 1. The study area and sample distribution: (a) Hebei Province; (b) Samples in Hengshui City.
Figure 1. The study area and sample distribution: (a) Hebei Province; (b) Samples in Hengshui City.
Preprints 70880 g001
Preprints 70880 g002
Figure 2. Crop calendar of maize, cotton, and common yam rhizome in Hengshui, China. DOY, day of year.
Figure 2. Crop calendar of maize, cotton, and common yam rhizome in Hengshui, China. DOY, day of year.
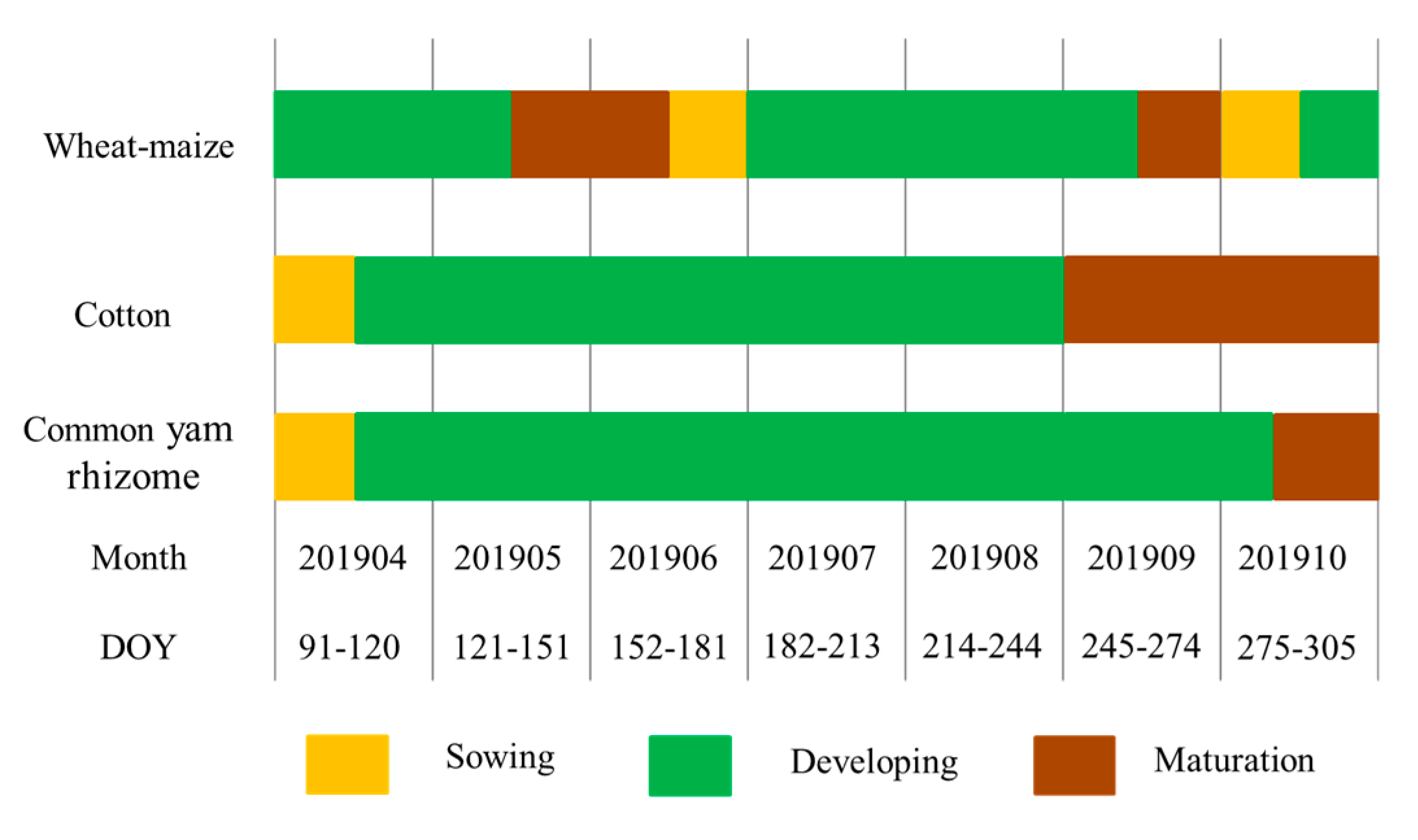
Preprints 70880 g002
Preprints 70880 g003
Figure 3. The Dual-1DCNN model.
Figure 3. The Dual-1DCNN model.
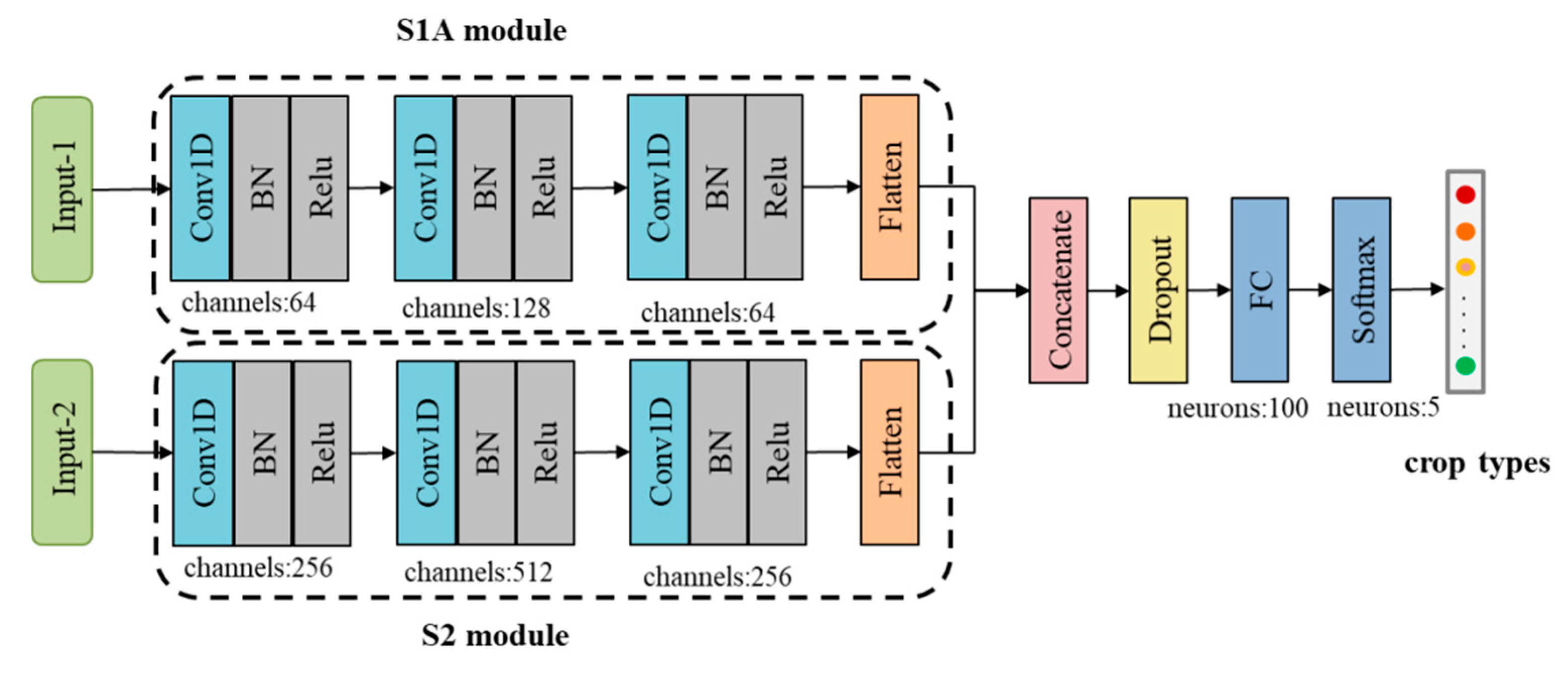
Preprints 70880 g003
Preprints 70880 g004
Figure 4. Flow of S1A time series data and S2 time series data.
Figure 4. Flow of S1A time series data and S2 time series data.
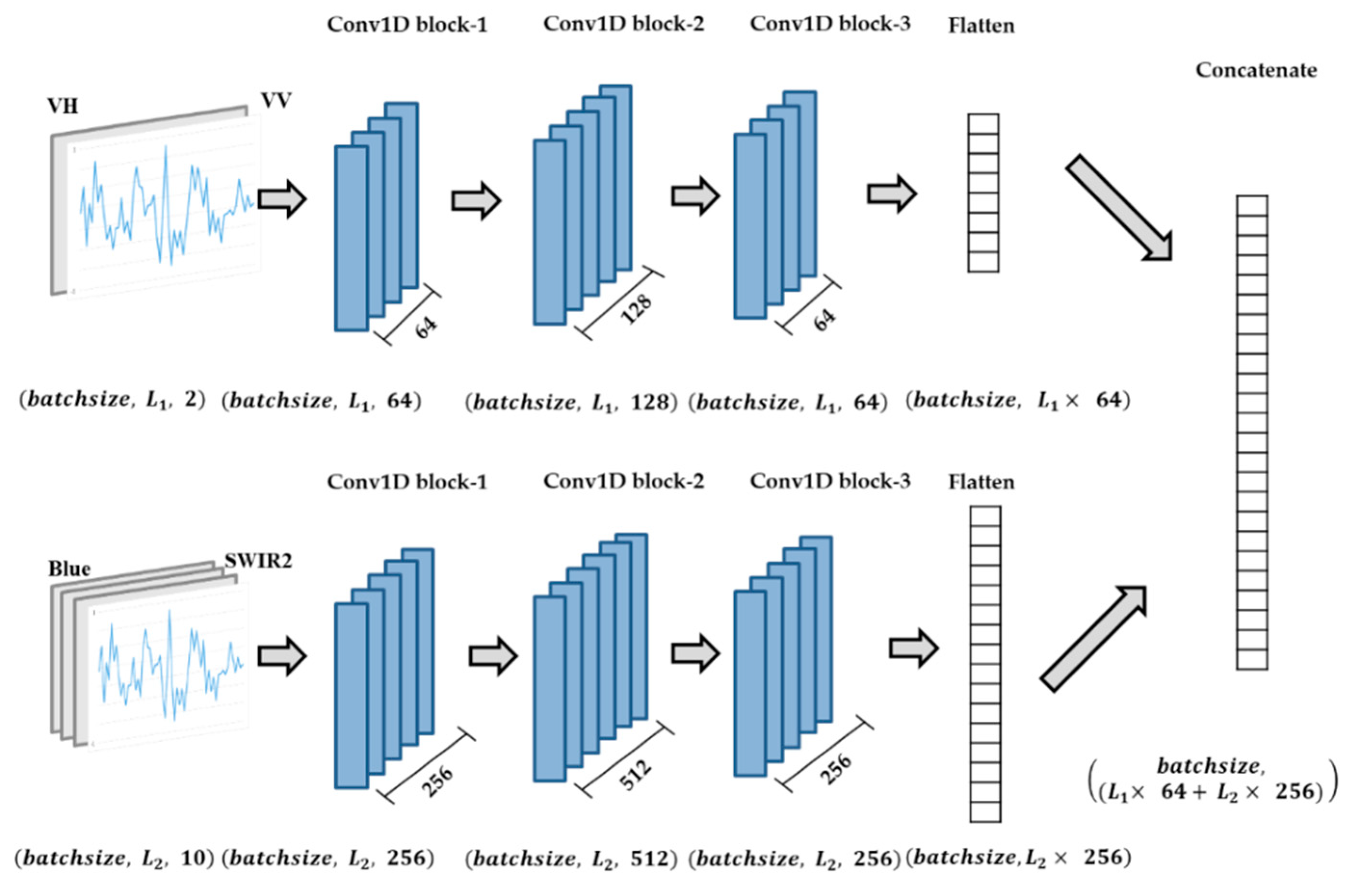
Preprints 70880 g004
Preprints 70880 g005
Figure 5. Overview of experiments. L1: the length of S1A time series imagery; L2: the length of S2 time series imagery.
Figure 5. Overview of experiments. L1: the length of S1A time series imagery; L2: the length of S2 time series imagery.
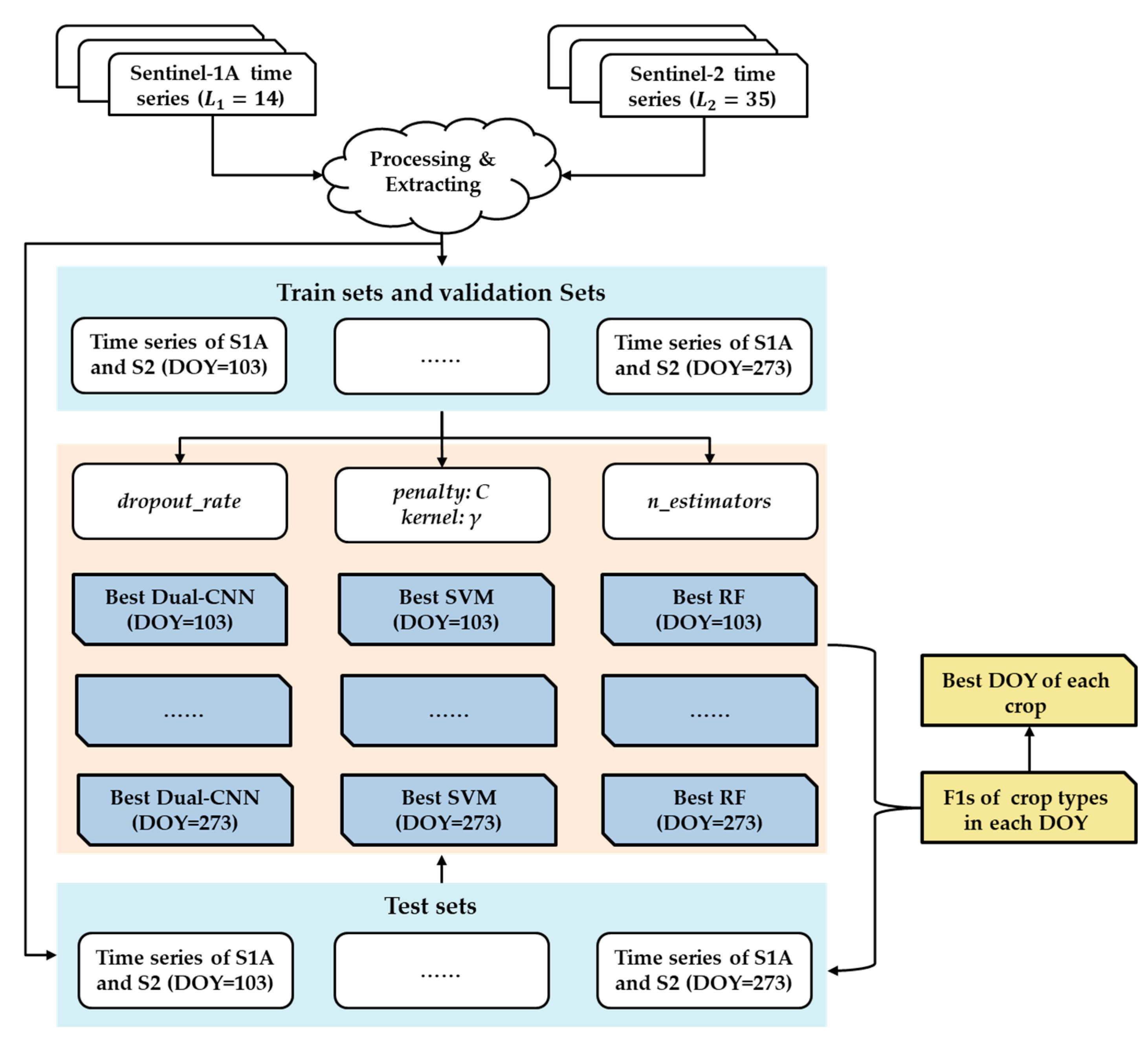
Preprints 70880 g005
Preprints 70880 g006
Figure 6. Temporal profiles of the five crop types with respect to (a) VV and (b) VH backscatter coefficients (dB).
Figure 6. Temporal profiles of the five crop types with respect to (a) VV and (b) VH backscatter coefficients (dB).
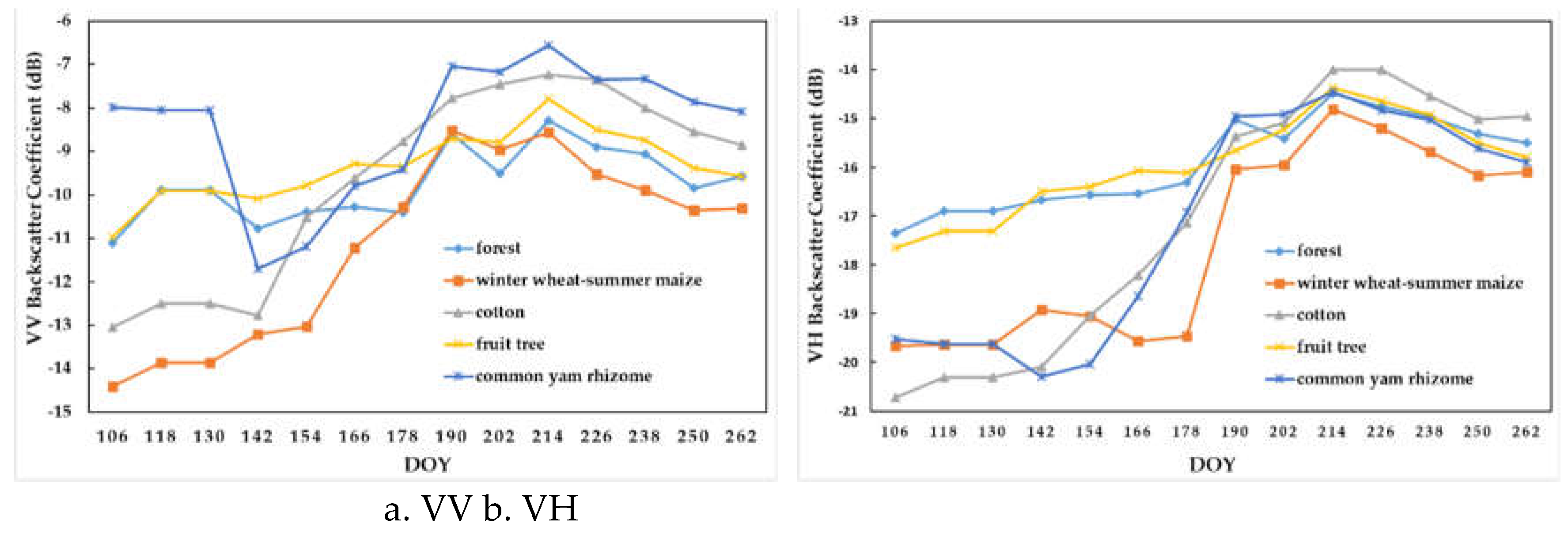
Preprints 70880 g006
Preprints 70880 g007
Figure 7. Time series profiles. RE, red edge; NIR, near-infrared; shortwave infrared, SWIR1.
Figure 7. Time series profiles. RE, red edge; NIR, near-infrared; shortwave infrared, SWIR1.
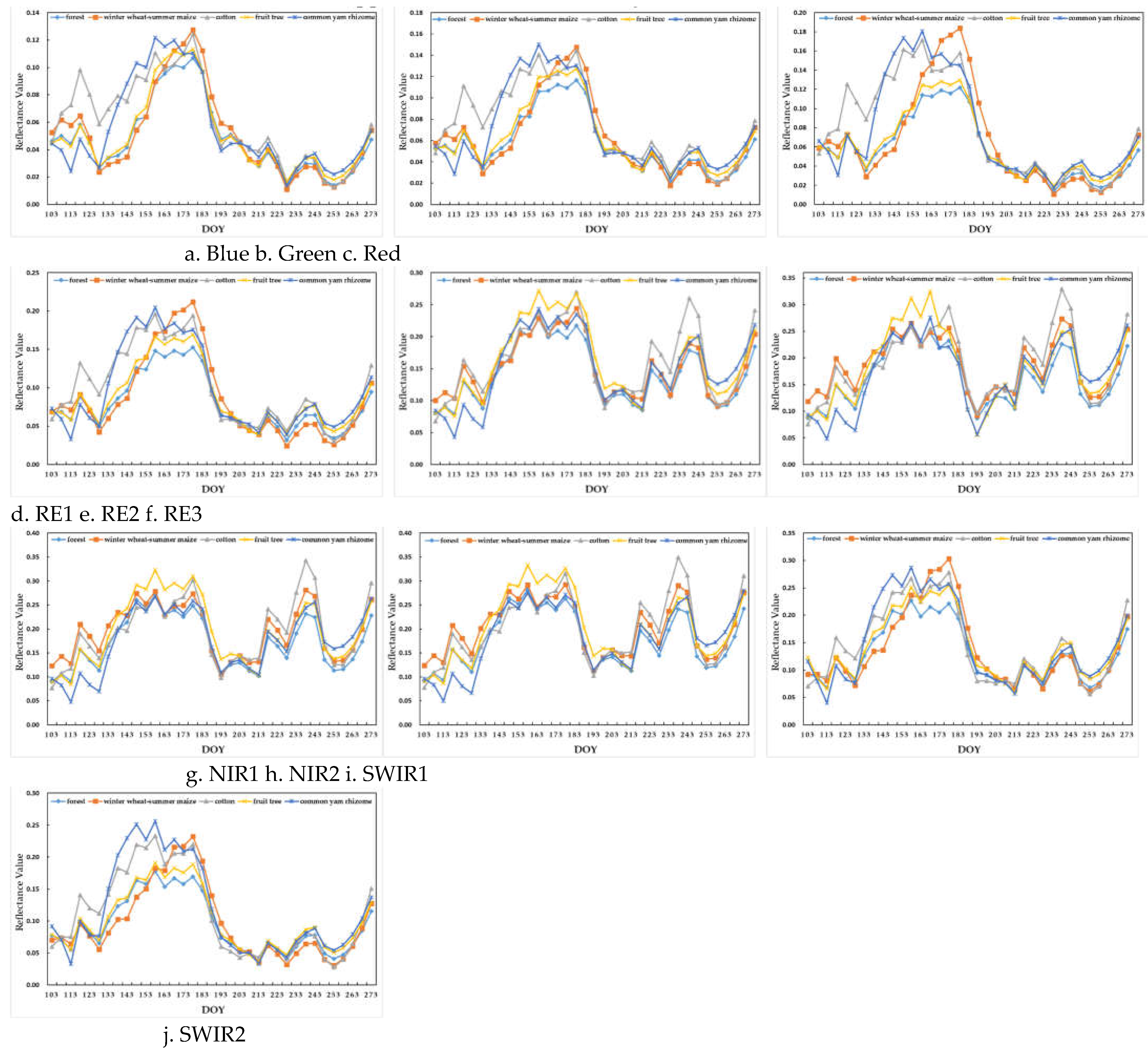
Preprints 70880 g007
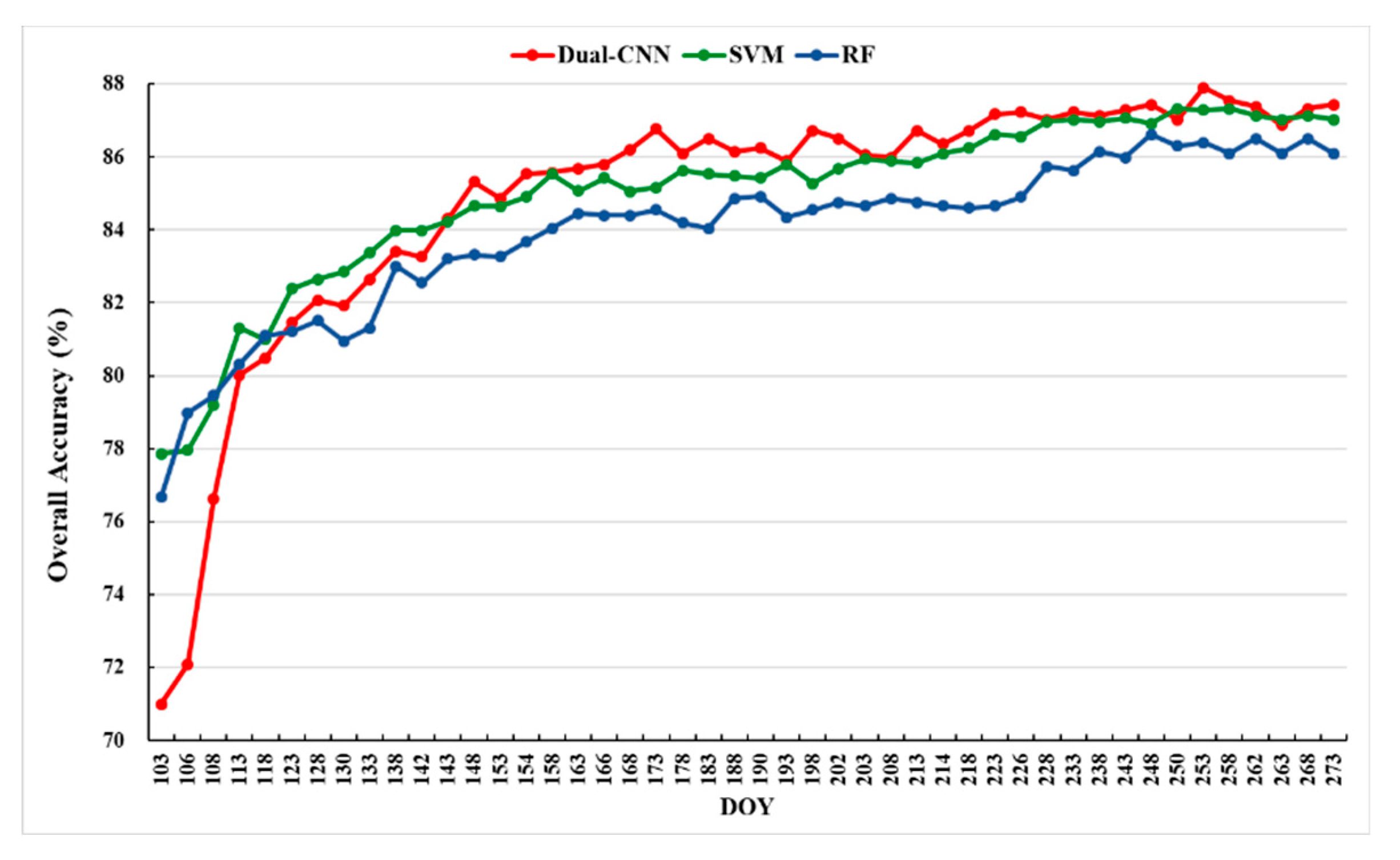
Preprints 70880 g008
Figure 8. OA profiles of the three methods (averaged over five different random splits).
Figure 8. OA profiles of the three methods (averaged over five different random splits).
Preprints 70880 g008
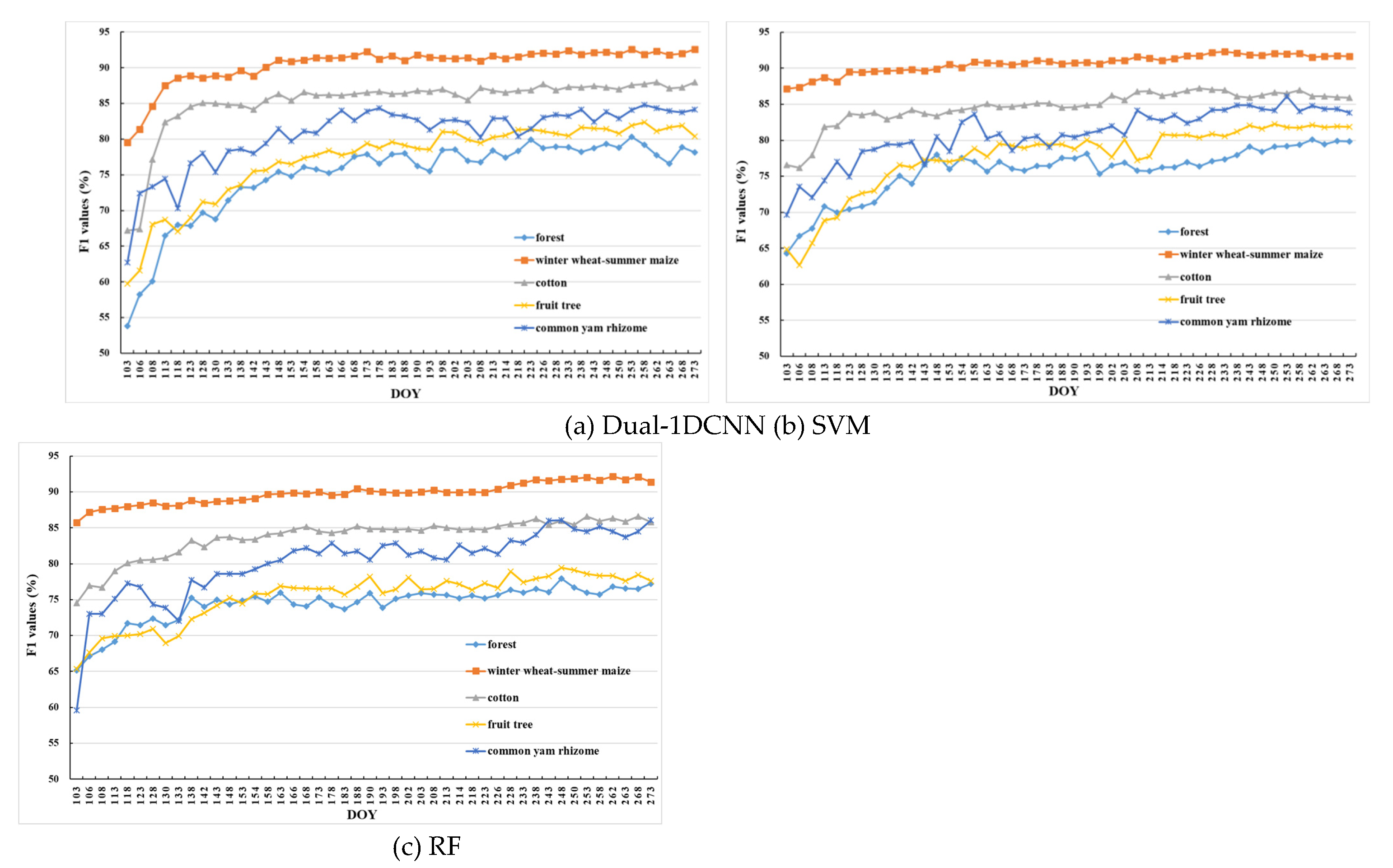
Preprints 70880 g009
Figure 9. F1 values of each crop type at every train date (the average over five different random splits).
Figure 9. F1 values of each crop type at every train date (the average over five different random splits).
Preprints 70880 g009
Preprints 70880 g010aPreprints 70880 g010b
Figure 10. Confusion matrices for early-season detection DOYs of summer maize, cotton, and common yam rhizome. Values in matrices indicate the percentage of points available in the “true label” and are the average of five test sets.
Figure 10. Confusion matrices for early-season detection DOYs of summer maize, cotton, and common yam rhizome. Values in matrices indicate the percentage of points available in the “true label” and are the average of five test sets.
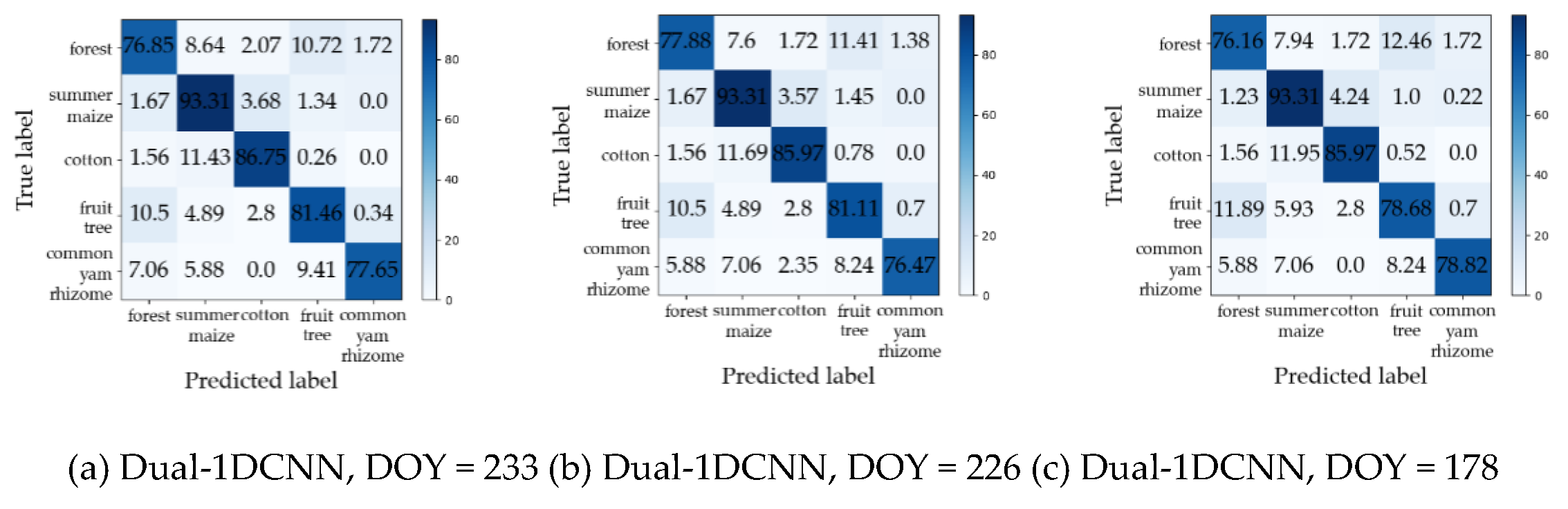
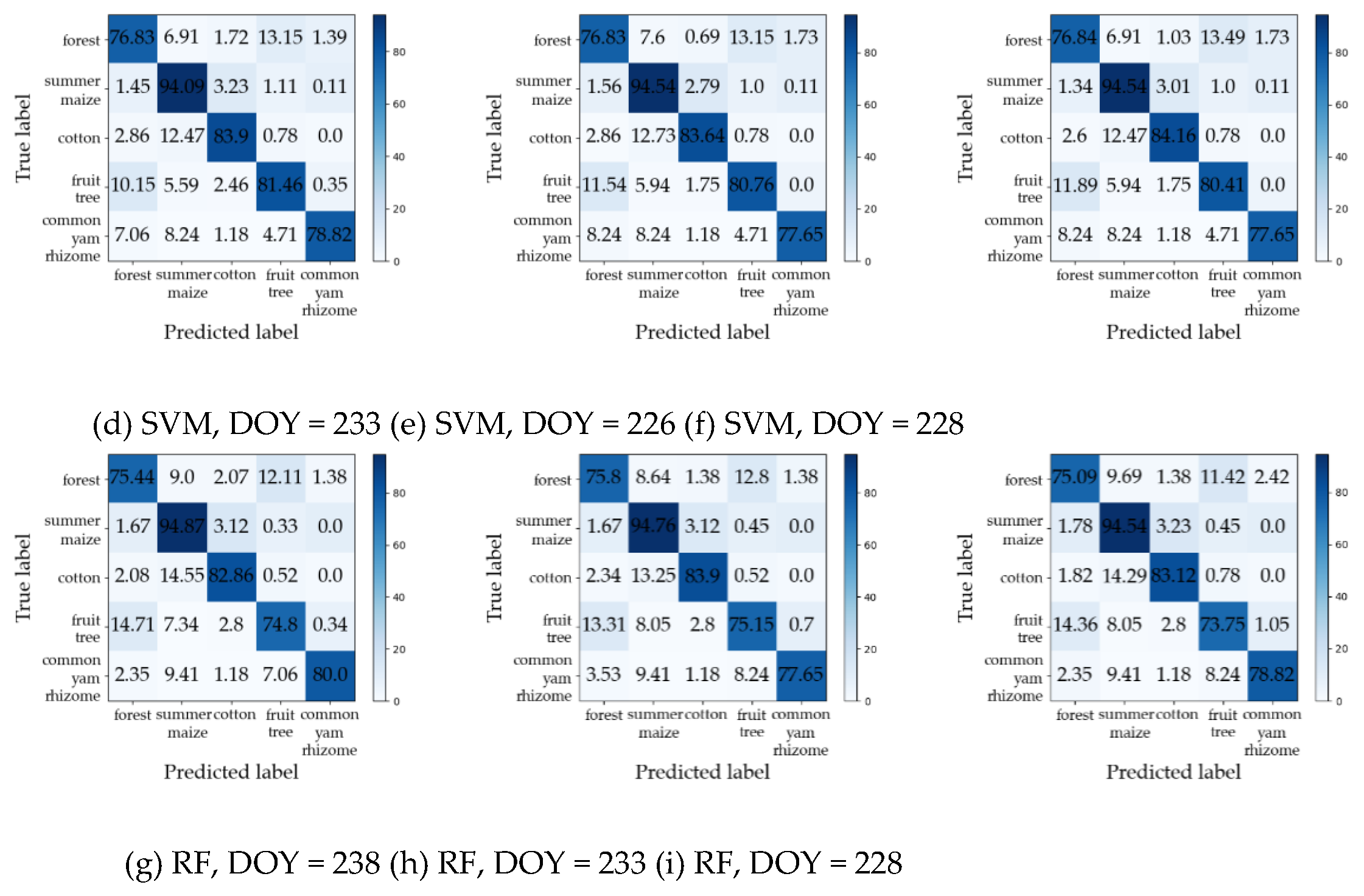
Preprints 70880 g010aPreprints 70880 g010b
Table 1. Number of samples per type.
Table 1. Number of samples per type.
Class Label 1 2 3 4 5 Total
Class type Forest Summer maize Cotton Fruit tree Common yam rhizome
Number 289 897 385 286 85 1942
Table 2. Time series of dates when we acquired S1A or S2 data. DOY: day of year in 2019; L1: the length of S1A time series imagery; L2: the length of S2 time series imagery.
Table 2. Time series of dates when we acquired S1A or S2 data. DOY: day of year in 2019; L1: the length of S1A time series imagery; L2: the length of S2 time series imagery.
DOY 103 106 108 113 118 123 128 130 133 138 142 143 148 153 154 158
L1 0 1 1 1 2 2 2 3 3 3 4 4 4 4 5 5
L2 1 1 2 3 4 5 6 6 7 8 8 9 10 11 11 12
DOY 163 166 168 173 178 183 188 190 193 198 202 203 208 213 214 218
L1 5 6 6 6 7 7 7 8 8 8 9 9 9 9 10 10
L2 13 13 14 15 16 17 18 18 19 20 20 21 22 23 23 24
DOY 223 226 228 233 238 243 248 250 253 258 262 263 268 273
L1 10 11 11 11 12 12 12 13 13 13 14 14 14 14
L2 25 25 26 27 28 29 30 30 31 32 32 33 34 35
Table 3. OA and standard deviation at every train date. OA, average over five different random splits; CNN, convolutional neural network; SVM, support vector machine; RF, random forest; DOY, day of year.
Table 3. OA and standard deviation at every train date. OA, average over five different random splits; CNN, convolutional neural network; SVM, support vector machine; RF, random forest; DOY, day of year.
DOY 103 106 108 113 118 123 128 130
Dual-CNN 71.00 ± 1.90 72.09 ± 2.3 76.63 ± 3.41 80.02 ± 3.53 80.49 ± 3.03 81.46 ± 1.41 82.08 ± 1.27 81.93 ± 1.56
SVM 77.86 ± 2.83 77.96 ± 2.75 79.2 ± 2.05 81.31 ± 2.85 81.00 ± 2.39 82.39 ± 1.94 82.65 ± 1.84 82.85 ± 1.65
RF 76.67 ± 3.21 78.99 ± 3.68 79.46 ± 3.35 80.33 ± 2.72 81.1 ± 2.72 81.21 ± 2.46 81.51 ± 2.48 80.95 ± 2.65
DOY 133 138 142 143 148 153 154 158
Dual-CNN 82.65 ± 2.03 83.42 ± 1.83 83.27 ± 1.48 84.30 ± 1.23 85.32 ± 1.77 84.86 ± 1.46 85.53 ± 1.19 85.58 ± 2.14
SVM 83.37 ± 1.84 83.99 ± 1.75 83.99 ± 1.24 84.24 ± 1.95 84.66 ± 1.58 84.65 ± 1.72 84.91 ± 1.57 85.53 ± 2.15
RF 81.31 ± 3.04 83.01 ± 2.31 82.55 ± 2.00 83.21 ± 1.74 83.32 ± 1.02 83.27 ± 1.48 83.68 ± 1.92 84.04 ± 2.13
DOY 163 166 168 173 178 183 188 190
Dual-CNN 85.69 ± 1.63 85.79 ± 1.15 86.20 ± 1.55 86.77 ± 2.15 86.10 ± 1.34 86.51 ± 1.95 86.15 ± 2.20 86.25 ± 1.49
SVM 85.07 ± 1.80 85.43 ± 2.07 85.06 ± 1.87 85.17 ± 1.82 85.63 ± 1.72 85.53 ± 1.64 85.48 ± 1.61 85.43 ± 1.82
RF 84.45 ± 2.50 84.40 ± 2.26 84.40 ± 2.38 84.55 ± 2.58 84.19 ± 2.72 84.04 ± 2.56 84.86 ± 2.87 84.92 ± 2.56
DOY 193 198 202 203 208 213 214 218
Dual-CNN 85.89 ± 2.13 86.72 ± 1.59 86.51 ± 1.64 86.05 ± 1.75 85.99 ± 0.97 86.72 ± 1.23 86.36 ± 1.39 86.72 ± 1.48
SVM 85.79 ± 2.02 85.27 ± 1.03 85.69 ± 2.19 85.94 ± 1.19 85.89 ± 1.96 85.84 ± 2.15 86.10 ± 1.54 86.25 ± 1.39
RF 84.35 ± 2.74 84.55 ± 2.81 84.76 ± 2.06 84.66 ± 3.19 84.86 ± 2.75 84.76 ± 2.30 84.66 ± 2.95 84.60 ± 2.36
DOY 223 226 228 233 238
Dual-CNN 87.18 ± 1.14 87.23 ± 1.50 87.02 ± 1.56 87.23 ± 1.44 87.13 ± 1.74
SVM 86.61 ± 1.34 86.56 ± 1.63 86.97 ± 0.69 87.02 ± 0.85 86.97 ± 1.34
RF 84.66 ± 2.36 84.91 ± 2.34 85.74 ± 1.90 85.63 ± 1.35 86.15 ± 1.35
Table 4. F1 value of each crop type at every train date (the average over five different random splits). CNN, convolutional neural network; SVM, support vector machine; RF, random forest; DOY, day of year.
Table 4. F1 value of each crop type at every train date (the average over five different random splits). CNN, convolutional neural network; SVM, support vector machine; RF, random forest; DOY, day of year.
Methods Indices Summer
Maize		 Cotton Common Yam Rhizome
Dual-1DCNN Early-season detection DOY 233 226 178
F1 value 92.39 87.71 84.38
SVM Early-season detection DOY 233 226 228
F1 value 92.33 87.20 84.19
RF Early-season detection DOY 238 233 228
F1 value 91.69 85.67 83.24
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated