Prerpints.org logo
Preprint
Brief Report

High Imperceptible Data Hiding Method for AMBTC Compressed Images Based on Combination Theory

Altmetrics

Downloads

124

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 April 2023

Posted:

14 April 2023

You are already at the latest version

Alerts
Abstract
The rapid development of digital multimedia has resulted in a massive storm of large-scale data. The data compression method reduces data size and lowers transmission costs. As a result, data-hiding research in the compression domain poses significant challenges to researchers. This paper proposes a highly imperceptible data-hiding scheme for a compressed image of Absolute Moment Block Truncation Coding (AMBTC). The combination theory is implemented to ensure the high imperceptibility of the modified compressed images. By only modifying one pixel in a block to embed secret bits, the experimental results show that the proposed method achieved high imperceptibility and high hiding capacity.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

A massive storm of large-scale data has come from the accelerated development of digital multimedia. Various applications produce images, audio, and videos daily. The security of critical data and the gigantic volume of data are the two major issues this trend has brought forth. To enhance the confidentiality of data transmission, the sender encrypt the data using conventional cryptographic techniques or imperceptibly transfer data using data-hiding techniques [1,2,3]. At the same time, the best way to minimize data size and lower transmission costs is to use a data compression technique [4]. Inevitably, data-hiding research in the compression domain presents a immense challenge to academics because it is essential to balance the hiding capacity with compressed image quality.
Data hiding defines as imperceptibly method of hiding confidential data inside other media i.e. digital image, video and audio. An image data hiding scheme categorized into three domains [5] namely spatial domain, frequency domain, and compressed domain. In order to embed confidential data, the spatial domain method is directly modifying the image pixel. It caused the low imperceptibility. On the other side, the frequency domain method hides the confidential data into transformed coefficients. Lastly, the compressed domain method manages the confidential messages in the compressed codes of digital images. Both frequency and compressed domain perform better imperceptibility than spatial domain.
In general, two metrics are used to assess the performance of a data-hiding hiding technique. The first is hiding capacity. Hiding capacity identifies as the quantity of confidential data concealed in a cover media. The second metric is imperceptibility. Imperceptibility defines as the imperceptibility defines as the level of image quality after modification. The primary issue in the data hiding research is that the higher the hiding capacity, the lower the imperceptibility.
Along with the big data age, where the volume and variety of data are abundant, compression technology is experiencing advancements. Data compression technology is efficient in data transmission. This is due to the fact that computing is simple and inexpensive. There are several widely used compression methods, including vector quantization (VQ) [6,7,8], block truncation coding (BTC) [9,10,11,12], AMBTC [13], and JPEG compression [14,15,16]. Beginning by Delp and Mitchell [9] in 1979 which proposed block truncation coding (BTC) for image compression. Then further developed in 1984 by Lema and Mitchell [13] known as absolute moment block truncation coding (AMBTC). AMBTC offers simpler computation than BTC, and performs better image quality.
Due to the benefits of the compression technique, data hiding research is evolving into compression domain data hiding. AMBTC compressed image data hiding method was done by researchers [17,18,19,20,21,22,23,24]. In 2020, Lee et al. [17] presented a reversible data hiding based on Turtle-shell for AMBTC compressed images. Their method provided lower computation complexity and achieved accepted image quality. However, the method does not achieve high hiding capacity because it cannot embed the confidential messages in the complex image.
This research proposes an innovative data hiding scheme for AMBTC compressed images based on the combination theory. Experimental findings show that our proposed scheme achieves high hiding capacity and high image quality, even in complex images.
The remainder of this work is structured as follows. Section 2 provides an overview of the related study. Our proposed data-hiding method is described in Section 3. Section 4 contains the findings of the experiments. Section 5 finally presents the conclusions.

2. Related works

2.1. Absolute Moment Block Truncation Coding (AMBTC)

In 1984, AMBTC was introduced by Lema and Mitchell [13]. The main steps of AMBTC consist of encoding and decoding procedures, and detailed explained as follows: The Encoding Procedure
Step 1. Segments the images into a collection of t × t non-overlapping blocks.
Step 2. Calculates the mean μ and standard deviation α by using (1) and (2), respectively. Assume that p i j s the value of pixel in the block’s position (i, j).
μ = 1 t × t ∑ i = 1 t ∑ j = 1 t p i , j
α = ∑ j = 1 t × t p i j 2 − μ 2 t × t
Step 3. Creates the bitmap value b m = m i j | m i j ∈ 0,1 ,   1 ≤ i , j ≤ t by using (3):
m i j = 1 ,   i f   p i j ≥ μ 0 ,   i f   p i j < μ
The Decoding Procedure
Step 1. Calculates two quantizers, i.e., high quantizer hq and low quantizer lq using (4) and (5), respectively.
h q = μ − α q t × t − q
l q = μ + α t × t − q q
Where q is the quantity of p i j which greater than or equal to the mean value μ.
Step 2. Create the reconstructed block r m = r i j | r i j ∈ h q , l q ,   1 ≤ i , j ≤ k by using (6):
r m i j = h q ,   i f   m i j = 1 l q ,   i f   m i j = 0
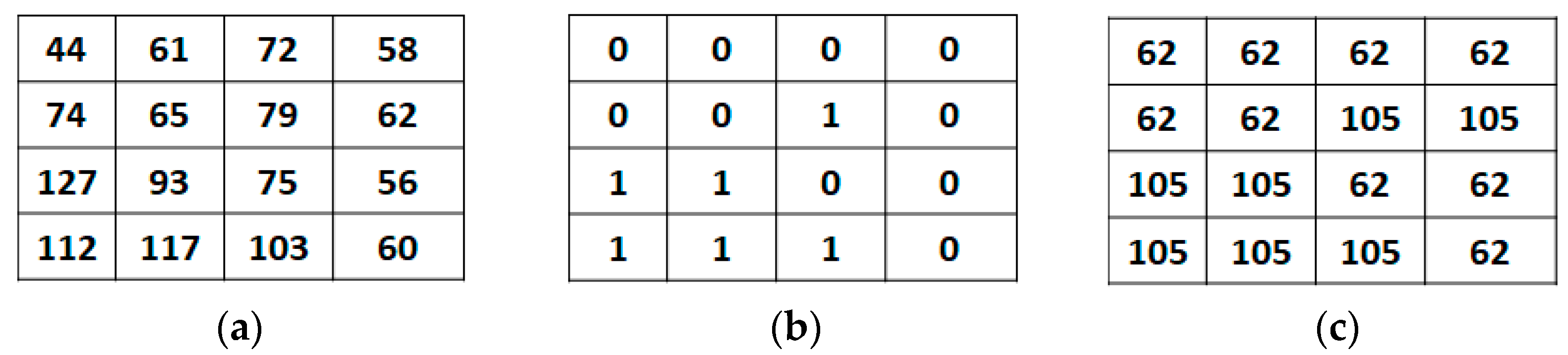
In order to provide a detailed understanding of the AMBTC compression method, we provide a numerical example as follows. Figure 1 depicts the illustration of AMBTC. First, Figure 1a depicts the original image block size of 4 × 4. Next, we computed the block means μ and standard deviation α, by using (1) and (2) respectively. In this example, the value of μ=78 and α=19. Next, we generate the bitmap in the encoding procedure using (3). The result is shown in Figure 1b. Finally, we calculate the higher and lower quantization levels, hq and lq, using (4) and (5), respectively. In this example, hq=105 and lq=62. Finally, the reconstructed image block generated in the decoding procedure using (6) is shown in Figure 1c.

2.2. The Combination Theory

Wu et al. [25] introduced a novel data-hiding method for binary images using combination theory in 2017. In their method, senders can hides more than one bit of confidential data by modifying one pixel at maximum in one block. The experimental result presented by Wu et al.’ scheme [25] increases the embedding capacity and reduces the distortion of the modified image.
The main procedure of Wu et al.’ scheme [25] is as follows:
Step 1. Calculate block maximum payload by (7):
b =   log 2 ⁡ ( u   ×   v + 1
Step 2. Develop a hidden location matrix P as described in [25].
Step 3. Produce the new computed hidden location matrix P' by P⊗Gi.
Then, using Algorithm 1, calculate the total number T(Sr, r =1, 2,..., b) of each bit of confidential data that exists in P'.
Algorithm 1 Confidential Data Calculation
FOR p = 1 : u ; q = 1 : v
  IF P’x,y hasSr
    T(Sr) = T(Sr) +1
  END
END
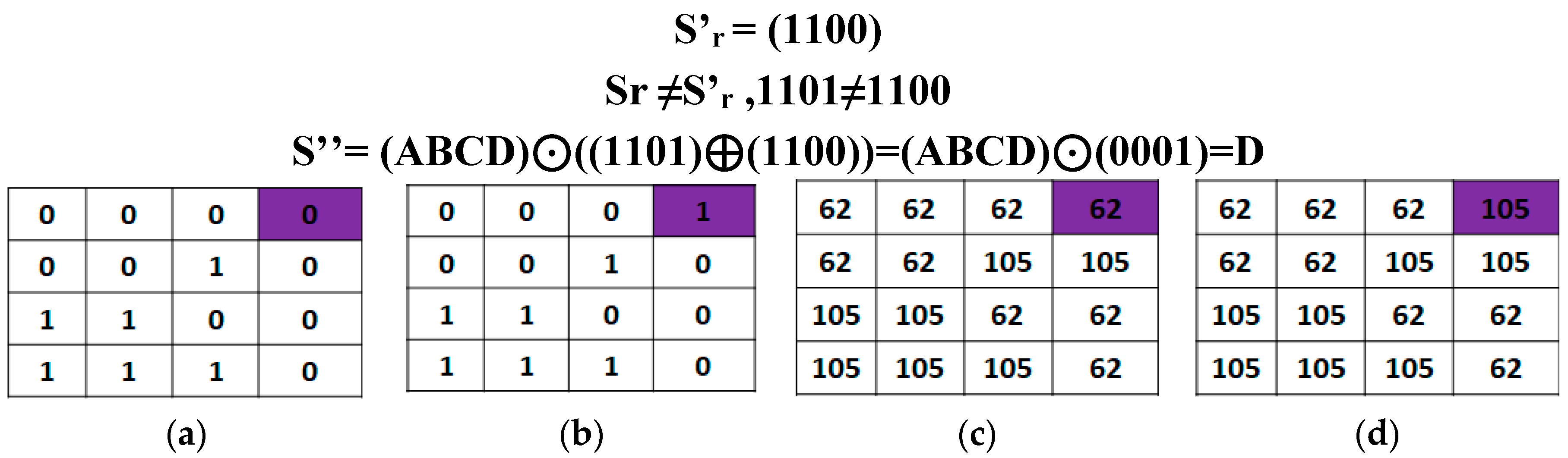
Step 4. Calculate the residual value S'r for the total amount of instances of each bit Sr by modulo as in (8)
S ′ r = T S r m o d   2 ,             w h e r e   r = 1,2 , … , b  
Step 5. Investigate the original confidential data Sr to the feature value S’r by (9) which consists of Sr such that Sr ≠S’r
S ″ = S r ⊙ ( S r ⊕ S ′ r )
Step 6. Conceal the confidential data into a block Gi by changing only one pixel of Gi according to Algorithm 2.
Algorithm 2 Confidential Data Embedding
FOR p = 1 : u ; q = 1 : v
  IF Px,y= S’’
    IF Gi (p,q) = 1
        Gi (p,q) = 0
    ELSE
        Gi (p,q) = 1
    END
  END
END

3. The Proposed Method

Inspired by Wu et al.’s scheme [25], in this paper, we propose an innovative data-hiding scheme for AMBTC image compression based on the combination theory. Figure 2 shows the flowchart of the proposed data hiding scheme, consisting of image compression and data embedding. The proposed scheme involves embedding and extracting procedures. Section 3.1 provide the embedding procedures. While, Section 3.2 present the extracting procedures.

3.1. The Embedding Procedures

In this part, we present the procedures of concealing confidential data into the compressed image using a hidden position matrix which generated by the combination theory. Our proposed embedding procedure is explained in depth as follows.
Input: an original image TI, with R width and S height, confidential data S.
Output: Compressed stego image TI’.
Given an original image TI, with R width and S height, segment into the n×n non-overlapping block image.
Step 1. Compress the original image block to obtain the bitmap value, Bm, according to Section 2.1.
Step 2. Embed the confidential data S into the bitmap Bm according to Section 2.2.
An example is given further to describe the proposed scheme for better understanding.
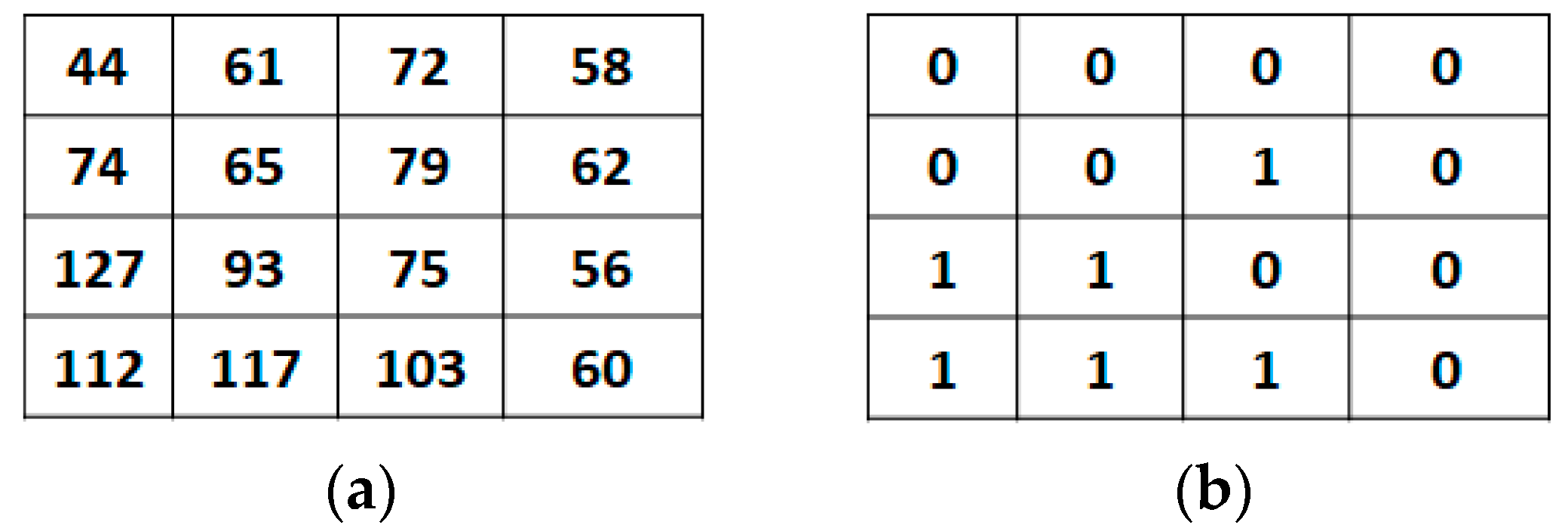
Input: Suppose we have a block size of 4×4 pixels of an image. The block consisting the original pixel values {44, 61, 72, 58, 74, 65, 79, 62, 127, 93, 75, 56, 112, 117, 103, 60}. The confidential data stream S that must be concealed is (1101)2.
Step 1. Compress the original image block by using the AMBTC method. Figure 3 is the AMBTC encoding of the given pixel value.
Step 2. Embed the confidential data bits into a bitmap by implementing the combination theory as explained in Section 2.1.
Preprints 70986 g004
Figure 4. Secret position matrix generation: (a) Bitmap; (b) Secret position matrix P; (c) New secret position matrix P’.
Figure 4. Secret position matrix generation: (a) Bitmap; (b) Secret position matrix P; (c) New secret position matrix P’.
Preprints 70986 g004
Preprints 70986 g005
Figure 5. Secret matrix calculation: (a) SUM of (A); (b) SUM of (B); (c) SUM of (C); (d) SUM of D.
Figure 5. Secret matrix calculation: (a) SUM of (A); (b) SUM of (B); (c) SUM of (C); (d) SUM of D.
Preprints 70986 g005
Preprints 70986 g006
Figure 6. Final result: (a) Original bitmap; (b) Stego bitmap; (c) Reconstructed original image; (d) Reconstructed stego image.
Figure 6. Final result: (a) Original bitmap; (b) Stego bitmap; (c) Reconstructed original image; (d) Reconstructed stego image.
Preprints 70986 g006

3.2. The Extraction Procedures

The extracting procedures are performed to retrieve confidential data. Our proposed extracting procedure is explained in depth below.
Step 1. Calculate the new matrix P ′ = P ⊙ G ′ i where p ′ x , y = P x , y × G ′ i ( x , y )   for all p=1, 2,…, u, and q=1, 2,…, v.
Step 2. Calculate the total amount of each confidential data bit T S r ,   r = 1 ,   2 , … , k in the new matrix P’ using Algorithm 3.
Algorithm 3 Confidential Data Calculation
FOR p = 1 : u ; q = 1 : v
  IF P’x,y hasSr
    T(Sr) = T(Sr) +1
  END
END
Step 3. Reassemble the confidential data bit S r = S r ∈ 0,1 ,   r = 1,2 ,   … , b , using (10).
S r = T ( S r )   m o d   2

4. Experimental Results

We performed extensive experiments to determine the efficacy of our proposed data-hiding technique. Assessment is conducted to determine hiding capacity and imperceptibility. We utilize the common test grayscale images, known as Airplane, Baboon, Barbara, Boat, Lena, and Peppers, as shown in Figure 7a,d,g,j,m,p, respectively. The entirety test images are 512×512 pixels in size. We performed a binary confidential data which produced by a pseudo-random number generator.
The hiding capacity is identifies by the number of bits. While identifies by image quality. To assess image quality, the common used parameter is the peak signal-to-noise ratio (PSNR) as defined in Equation (11).
P S N R = 10 log 10 ⁡ 255 2 M S E
The mean square error (MSE) is defined in Equation (12).
M S E = 1 N × N ∑ i = 1 N ∑ j = 1 N ( T I i j − T I ′ i j ) 2
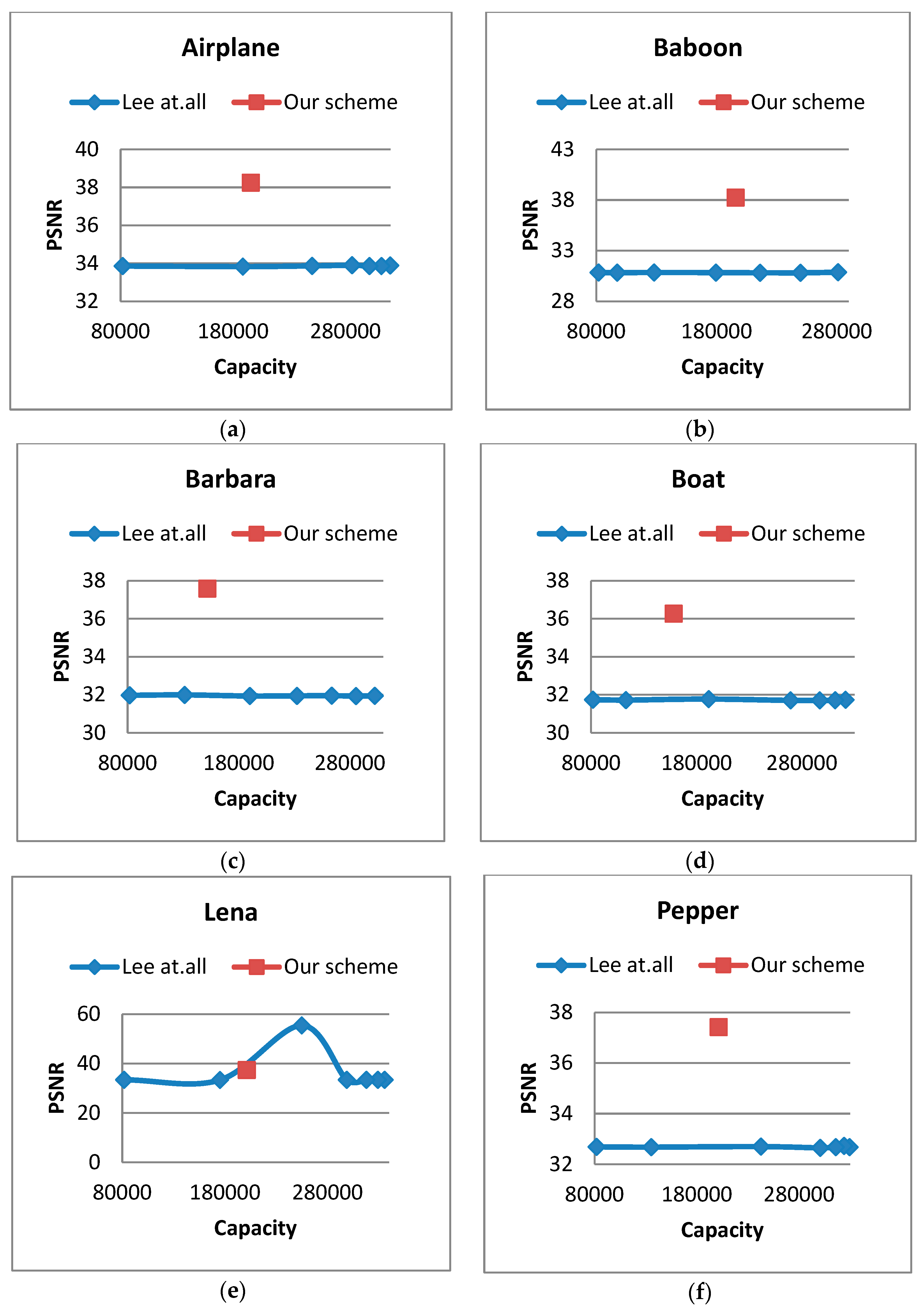
Where T I i j is the pixel in position of the i-th row and the j-th column of image T I , and T I ′ i j is the pixel in the i-th row and the j-th column image T I ′ The experimental findings are presented in Table 1, where PSNRs, MSEs, and hiding capacity are shown. According to the experimental findings, the image Lena and Pepper achieved the highest hiding capacity. Lena’s embedding capacity is 201364. Moreover, Pepper’s embedding capacity is 197632. On the other hand, in terms of image quality, the image Airplane and Baboon achieved the best image quality with less visual distortion. The airplane’s PSNR value is 38.25 dB, and Baboon’s PSNR value is 37.97 dB, respectively.
Further testing was performed by comparing our proposed method to the related method developed by Lee et al.’s scheme [17]. The performance comparison of our proposed scheme and Lee et al.’s scheme can be seen in Table 1. The scheme varied in different thresholds, i.e., TH=0, TH=5, TH=10, TH=20, TH=30, TH=40, and TH=50. It can be seen in Figure 13. Among the 6 test images, our scheme is superior in terms of image quality.
In summary, the main advantage of our proposed scheme:
  • The capacity of our scheme is between thresholds (TH 5 & TH10) of Lee et al.'s scheme [17].
  • If the picture is complex (non-smooth), the capacity of our proposed method is more excellent than Lee et al.'s scheme [17].
  • The qualification of images (PSNR) is higher than Lee et al.'s scheme [17]. Moreover, our proposed method performs satisfying image quality in complex images.
Preprints 70986 g008
Figure 8. This is a figure. The graphic of performance comparison: (a) Airplane; (b) Baboon; (c) Barbara; (d) Boat; (e) Lena; (f) Pepper.
Figure 8. This is a figure. The graphic of performance comparison: (a) Airplane; (b) Baboon; (c) Barbara; (d) Boat; (e) Lena; (f) Pepper.
Preprints 70986 g008

5. Conclusions

This paper proposed a highly imperceptible data-hiding method in AMBTC compressed images with the combination theory. Using the combination theory in the image-compressed domain, we can achieve higher embedding capacity without considering the threshold value for determining the smooth or complex image block. Further, our proposed scheme performs well with a practical and low-computation algorithm. The experimental results show that the proposed scheme achieved satisfied modified compressed image quality and high hiding capacity. Moreover, the proposed scheme performs better than Lee et al.’s scheme [17] in complex images.
For further development, our proposed scheme can be very effective and adopted appropriately in the medical image for securing electronic patient information because our proposed scheme induces invisible modification of image quality.

Author Contributions

The author's contribution to this manuscript is stated as follows: Conceptualization: Kurnia Anggriani; methodology: Kurnia Anggriani; software: Shu-Fen Chiou; validation: Nan-I Wu; formal analysis: Nan-I Wu; investigation: Shu-Fen Chiou; data curation: Shu-Fen Chiou; writing—original draft preparation: Kurnia Anggriani; writing—review and editing: Min-Shiang Hwang; project administration: Min-Shiang Hwang; funding acquisition: Min-Shiang Hwang. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by The Ministry of Science and Technology (Taiwan), grant number MOST 109-2221-E-468-011-MY3, MOST 108-2410-H-468-023, and MOST 108-2622-8-468-001-TM1. The APC was funded by The Ministry of Science and Technology (Taiwan).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. M. Alhomoud, “Image steganography in spatial domain: Current status, techniques, and trends,” Intell. Autom. Soft Comput., vol. 27, no. 1, pp. 69–88, 2021. [CrossRef]
  2. N. Min-allah et al., “Quantum Image Steganography Schemes for Data Hiding : A Survey,” Appl. Sci., vol. 12, no. 10294, 2022. [CrossRef]
  3. K. Anggriani, N. Wu, and M. Hwang, “Research on Coverless Image Steganography,” Int. J. Netw. Secur., vol. 25, no. 1, pp. 25–31, 2023. [CrossRef]
  4. Dorobant and R. Brad, “Improving Lossless Image Compression with Contextual Memory,” Appl. Sci., vol. 9, no. 2681, 2019. [CrossRef]
  5. S. Q. Saleh, “Digital Image Steganalysis : Current Methodologies and Future Challenges,” IEEE Access, vol. 10, no. August, pp. 92321–92336, 2022. [CrossRef]
  6. Y. Linde, “An Algorithm for Vector Quantizer Design,” IEEE Trans. Commun., vol. 28, no. 1, pp. 84–95, 1980. [CrossRef]
  7. K. Chiranjeevi and U. R. Jena, “Image compression based on vector quantization using cuckoo search optimization technique,” Ain Shams Eng. J., vol. 9, no. 4, pp. 1417–1431, 2018. [CrossRef]
  8. P. P. Chavan, B. S. Rani, M. Murugan, and P. Chavan, “An image compression model via adaptive vector quantization: hybrid optimization algorithm,” Imaging Sci. J., vol. 68, no. 5–8, pp. 259–277, 2020. [CrossRef]
  9. E. Robert, O. Mitchell, J. Delp, “Image Compression Using Block Truncation Coding,” IEEE Trans. Commun., vol. 27, no. 9, pp. 1335–1341, 1979.
  10. K. Somasundaram, “Efficient Block Truncation Coding,” Int. J. Comput. Sci. Eng., vol. 2, no. 6, pp. 2163–2166, 2010.
  11. E. Q. Scheme, “An Enhanced Adaptive Block Truncation Coding with,” Appl. Sci., vol. 10, no. 7340, pp. 1–15, 2019. [CrossRef]
  12. K. Sau, R. Kumar, and A. Chanda, “Image Compression based on Block Truncation Coding using Clifford Algebra,” Procedia Technol., vol. 10, pp. 699–706, 2013. [CrossRef]
  13. M. D. Lema and R. Mitchell, “Absolute Moment Block Truncation Coding and Its Application to Color Images,” IEEE Trans. Commun., vol. 32, no. 10, 1984.
  14. Perfilieva and P. Hurtik, “The F-transform preprocessing for JPEG strong compression of high-resolution images,” Inf. Sci. (Ny)., vol. 550, pp. 221–238, 2021. [CrossRef]
  15. L. Mancini, G. Kourousias, A. Velez, J. F. Barrera, K. Bredies, and M. Holler, “Developed JPEG Algorithm Applied in Image Compression Developed JPEG Compression Algorithm Applied in Image,” in 2nd International Scientific Conference of Al-Ayen University (ISCAU-2020), 2020, pp. 1–17. [CrossRef]
  16. G. Hamano and S. Imaizumi, “Effects of JPEG Compression on Vision Transformer Image Classification for Encryption-then-Compression Images,” sensors, vol. 23, no. 3400, pp. 1–19, 2023. [CrossRef]
  17. C.-F. Lee, C.-C. Chang, and G. Li, “A Data Hiding Scheme Based on Turtle-shell for AMBTC Compressed Images,” KSII Trans. Internet Inf. Syst., vol. 14, no. 6, pp. 2554–2575, 2020. [CrossRef]
  18. Kim, “Separable Reversible Data Hiding in Encrypted AMBTC Images Using Hamming Code,” Appl. Sci., vol. 12, no. 8225, 2022. [CrossRef]
  19. Kim, D. Shin, and C. Yang, “Data Hiding Method for Color AMBTC Compressed Images Using Color Difference,” Appl. Sci., vol. 11, no. 3418, 2021. [CrossRef]
  20. Kim, “Dual Reversible Data Hiding Based on AMBTC Using Hamming Code and LSB Replacement,” Electronics, vol. 11, no. 3210, 2022. [CrossRef]
  21. C. Lin, J. Lin, and C. Chang, “Reversible Data Hiding for AMBTC Compressed Images Based on Matrix and Hamming Coding,” Electronics, vol. 10, no. 281, 2021. [CrossRef]
  22. Anggriani, N. Wu, and M. Hwang, “Research on Data Hiding Schemes for AMBTC Compressed Images,” Int. J. Netw. Secur., vol. 24, no. 6, pp. 1114–1123, 2022. [CrossRef]
  23. Y. Chen, C. Chang, C. Lin, and Z. Wang, “An Adaptive Reversible Data Hiding Scheme Using AMBTC and Quantization Level Difference,” Appl. Sci., vol. 11, no. 635, 2021. [CrossRef]
  24. Anggriani, S. Chiou, N. Wu, and M. Hwang, “A High-Capacity Coverless Information Hiding Based on the Lowest and Highest Image Fragments,” Electronics, vol. 12, no. 395, 2023. [CrossRef]
  25. N. Wu and M. Hwang, “Development of a data hiding scheme based on combination theory for lowering the visual noise in binary images,” Displays, vol. 49, pp. 116–123, 2017. [CrossRef]
Preprints 70986 g001
Figure 1. An example of AMBTC Compression Images: (a) Original pixel value; (b) Bitmap; (c) Compressed pixel value.
Figure 1. An example of AMBTC Compression Images: (a) Original pixel value; (b) Bitmap; (c) Compressed pixel value.
Preprints 70986 g001
Preprints 70986 g002
Figure 2. The flowchart of the proposed scheme.
Figure 2. The flowchart of the proposed scheme.
Preprints 70986 g002
Preprints 70986 g003
Figure 3. AMBTC Encoding: (a) Original pixel value; (b) Bitmap.
Figure 3. AMBTC Encoding: (a) Original pixel value; (b) Bitmap.
Preprints 70986 g003
Preprints 70986 g007aPreprints 70986 g007b
Figure 7. This is a figure. Image Experimental Results : (a) Airplane Original Image; (b) Airplane AMBTC; (c) Airplane Stego Image; (d) Baboon Original Image; (e) Baboon AMBTC; (f) Baboon Stego Image; (g) Barbara Original Image; (h) Barbara AMBTC; (i) Barbara Stego Image; (j) Boat Original Image; (k) Boat AMBTC; (l) Boat Stego Image; (m) Lena Original Image; (n) Lena AMBTC; (o) Lena Stego Image; (p) Pepper Original Image; (q) Pepper AMBTC; (r) Pepper Stego Image.
Figure 7. This is a figure. Image Experimental Results : (a) Airplane Original Image; (b) Airplane AMBTC; (c) Airplane Stego Image; (d) Baboon Original Image; (e) Baboon AMBTC; (f) Baboon Stego Image; (g) Barbara Original Image; (h) Barbara AMBTC; (i) Barbara Stego Image; (j) Boat Original Image; (k) Boat AMBTC; (l) Boat Stego Image; (m) Lena Original Image; (n) Lena AMBTC; (o) Lena Stego Image; (p) Pepper Original Image; (q) Pepper AMBTC; (r) Pepper Stego Image.
Preprints 70986 g007aPreprints 70986 g007b
Table 1. Performance Comparison.
Table 1. Performance Comparison.
Image Metrics Lee et al Scheme [17] Proposed
TH 50 TH 40 TH 30 TH 20 TH 10 TH 5 TH 0
Airplane PSNR 33.89 33.86 33.86 33.90 33.87 33.83 33.86 38.25
MSE 26.53 26.72 26.70 26.49 26.64 26.93 26.72 9.72
Capacity 319808 311984 301424 285968 250432 188800 81920 195928
Baboon PSNR 30.87 30.82 30.82 30.84 30.85 30.83 30.85 37.97
MSE 53.17 53.80 53.86 53.60 53.41 53.76 53.41 10.36
Capacity 281136 249920 216304 179504 128112 97424 81920 104284
Barbara PSNR 31.94 31.93 31.95 31.94 31.93 31.99 31.97 37.59
MSE 41.61 41.70 41.48 41.62 41.66 41.14 41.27 11.31
Capacity 302544 285584 263808 232496 190128 131440 81920 151840
Boat PSNR 31.73 31.71 31.70 31.70 31.77 31.72 31.74 36.27
MSE 43.63 43.84 43.90 43.90 43.21 43.67 43.52 15.34
Capacity 321520 311568 297024 269280 191600 113200 81920 158440
Lena PSNR 33.43 33.43 33.40 33.422 55.47 33.38 33.42 37.42
MSE 29.51 29.50 29.66 29.56 18.43 29.80 29.58 11.76
Capacity 335680 329152 318032 298880 254976 175248 81920 201364
Pepper PSNR 32.68 32.73 32.68 32.65 32.70 32.68 32.69 35.89
MSE 35.00 34.66 35.019 35.29 34.86 35.01 34.96 16.72
Capacity 329536 324208 315904 300720 242848 135440 81920 197632
Average PSNR 32.38 32.36 32.36 32.38 32.37 32.39 32.38 37.24
MSE 38.60 38.71 38.69 38.55 38.63 38.50 38.59 12.54
Capacity 314664 301671 285226 260980 209447 140108 86993 168248
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated