A Novel Sea Horse Optimizer Based Load Frequency Controller for Two-Area Power System with PV and Thermal Units

Load Frequency Control (LFC) is essential to ensure the stability and performance of power systems. In this study, a novel optimization algorithm, the Sea Horse Optimizer (SHO) algorithm, was proposed for optimizing controller parameters in LFC problems of power system. The proposed SHO algorithm was tested on a two-area power system with photovoltaic system and reheat thermal units, under three different scenarios: a 10% load change in both area, large load disturbances, and varying solar radiation. The proposed algorithm optimizes the gain parameters of PI/PID controllers using performance metrics such as Integral of Absolute value of the Error (IAE), Integral of Square Error (ISE), Integral of Time multiplied by Square Error (ITSE), and Integral of Time multiplied by Absolute Error (ITAE). The study compared the performance of the SHO-optimized controller with other reported optimization algorithms such as Genetic Algorithm (GA), Firefly Algorithm (FA), Whale Optimization Algorithm (WOA), and Modified Whale Optimization Algorithm (MWOA). The study also evaluated the accuracy and effectiveness of the controllers using performance metrics such as Settling Time, Overshoot (M+), and Undershoot (M-). The results show that the SHO-tuned controller significantly reduces overshoot, undershoot, and settling time of the system oscillations compared to other algorithms. The study provides valuable insights into the optimization of LFC controllers and presents a significant contribution to the literature with its novel algorithm. The proposed SHO algorithm can be considered an effective alternative solution method for LFC in power systems.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Due to the expansion of industries and population growth, there has been a significant surge in the demand for electrical energy. This demand puts pressure on power systems to provide reliable and efficient electricity supply [1]. In the management of power systems, Load Frequency Control (LFC) plays a critical role in maintaining balance between the production and consumption of electricity [2]. In order to maintain the control of system frequency within a reasonable range, LFC regulates the output power of units to meet the power demands [3]. LFC is a system used to prevent frequency fluctuations in electrical systems. Frequency fluctuations caused by imbalances between electricity production and consumption can lead to unwanted consequences, such as destabilizing the energy system, causing power outages, and even risking the collapse of the entire electrical grid [4]. The importance of LFC is to bear significant importance in maintaining the stability of the energy system, preventing power outages, and even preventing the collapse of the energy system [5].

Wind and solar power which are clean energy sources are vital for meeting global energy demands. However, their fluctuating nature poses a challenge for maintaining a stable energy system as their production relies on natural conditions that can vary throughout the day and seasons. This can cause sudden surges or drops in energy supply, which destabilizes the system [6]. To address this, LFC systems must respond quickly to changes in energy demand and supply. Traditional energy sources are more easily controlled, while renewable sources require innovative solutions like energy storage systems such as batteries [7].

There has been a surge in research on various types of controllers and optimization techniques aimed at improving LFC in recent times. Several classical controllers such as, Proportional Integral (PI) and Proportional Integral Derivative (PID) have been employed in LFC regulation [8,9]. In addition, the controllers’ effectiveness was examined in [10] with regards to their ability to regulate LFC in a three-area thermal system that was merged with a solar thermal power plant. Although classical controllers are simple to implement, they require considerable effort adjusting controller’s parameters.

To address the limitations of conventional controllers, several researchers have utilized physics-based algorithms like Simulated Annealing (SA) [11], Big Bang Big Crunch (BBBC) [12], and Gravitational Search Algorithm (GSA) [13], as well as swarm-based algorithms including Artificial Bee Colony (ABC) algorithm [14], Ant Colony Optimization (ACO) [15], Cuckoo Search (CS) [16], and Particle Swarm Optimization (PSO) [17,18]. Evolutionary algorithms such as Genetic Algorithm (GA) [19], Differential Evolution (DE) [20], Firefly Algorithm (FA) [21], Flower Pollination Algorithm (FPA) [22], Whale Optimization Algorithm (WOA) [23], Water Cycle Algorithm (WCA) [24], Grasshopper Optimization Algorithm (GOA) [25], and Grey Wolf Optimizer [26] have also been employed for solving the frequency regulation problem. However, these meta-heuristic algorithms may suffer from certain limitations such as vulnerability to local minimum, gradual convergence, and longer computing times for highly-complex problems [27].

On the other hand, artificial intelligence techniques such as Fuzzy Logic (FL) [28,29,30,31] and Neural Networks (NN) [32,33] have been utilized for solving the LFC problem owing to their ability to deal with nonlinearities in the power system. However, these algorithms suffer from various disadvantages, such as the requirement of hard work to define influential signals, determining the optimal quantity of layers and neurons for a neural network can pose a significant challenge.

In this paper, we propose a novel Sea Horse Optimizer (SHO) [34] based tuning approach for PI/PID load frequency controllers in a two-area power system with PV and reheat thermal units. The proposed method aims to improve the performance of the LFC system in terms of frequency response to load changes, settling time, maximum overshoot and undershoot values. To evaluate the efficiency of the proposed SHO algorithm, comparisons were made with other optimization algorithms published in the literature, such as Genetic Algorithm (GA) [35], Firefly Algorithm (FA) [35], Whale Optimization Algorithm (WOA) [36], and Modified Whale Optimization Algorithm (MWOA) [36]. The results showed that the proposed SHO algorithm outperformed the other optimization methods. Therefore, the SHO algorithm can be considered as a potential alternative for optimizing PI/PID LFC systems.

The main contributions of this research work are as follows:

1. Development of a novel Sea Horse Optimizer algorithm for PI/PID load frequency controller tuning in a two-area power system with PV and reheat thermal units, which has not been previously proposed in the literature.

2. Application of the proposed SHO-based tuning approach to effectively optimize PI and PID controllers for LFC problem.

3. Demonstration of the effectiveness of the proposed SHO algorithm in improving the performance of the LFC system in terms of frequency response, settling time, and overshoot/undershoot values.

4. Identification of the potential of the SHO algorithm as an alternative method for optimizing PI/PID LFC systems, due to its ability to handle non-linear and complex systems more effectively, and provide better overall system performance.

The rest of this paper is organized as follows: Section 2 presents the system modeling for the two-area power system with PV and reheat thermal units. Section 3 describes the proposed Sea Horse Optimizer algorithm for tuning the PI/PID load frequency controllers. In Section 4, the optimization problem is formulated, and the proposed SHO-based tuning approach is applied to optimize the PI and PID controllers. Section 5 presents the simulation results and discussion on different conditions. Finally, Section 6 provides the conclusion part and suggests further work.

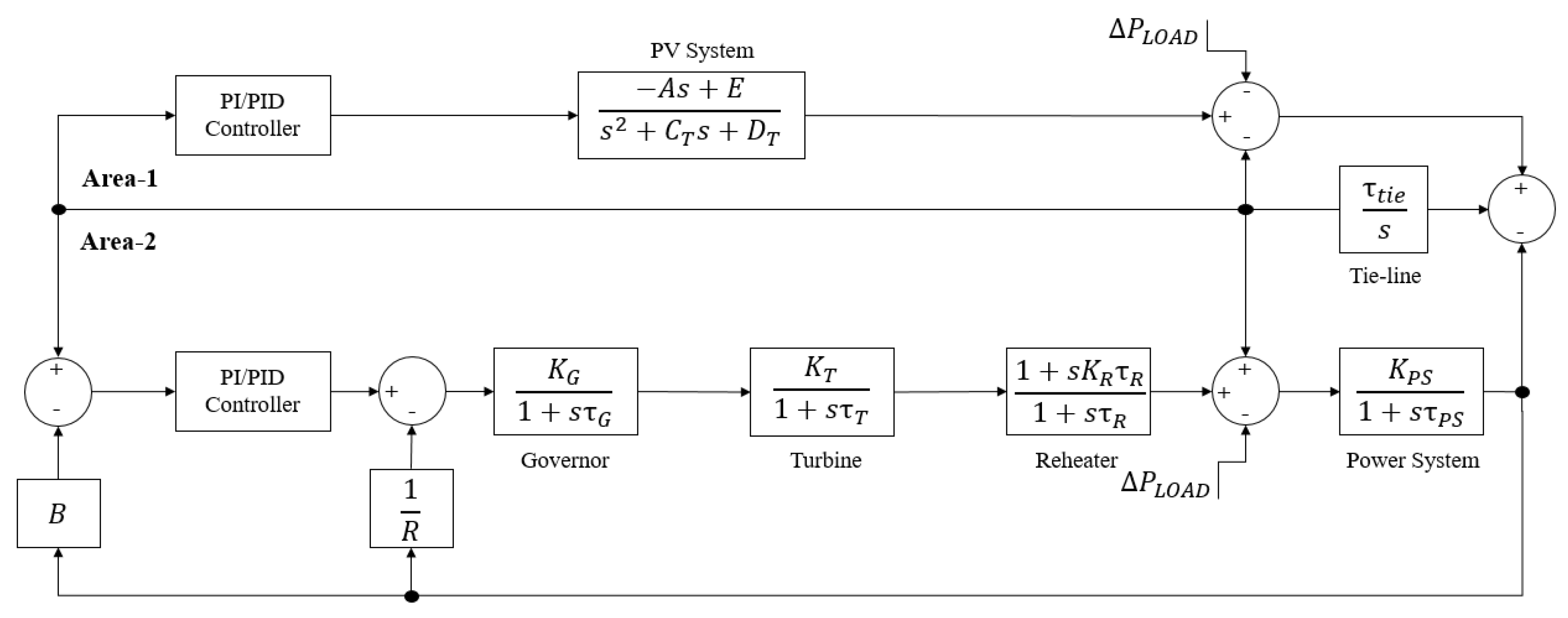
2. System Modeling

The system model is presented as a two-area test system shown in Figure 1 [35,36]. The model consists of two areas: Area 1 has a photovoltaic (PV) system with maximum power point tracking (MPPT), while Area 2 has a reheat thermal unit. The MATLAB/Simulink program was used to model the PV-thermal testing system. The components shown in Figure 1, including the PV system, Governor, Turbine, Reheater, and Power System, are modeled using their respective transfer functions. The mathematical models of these components are approximated as first-order linear transfer function models. Equation (1) to (5) represent the mathematical frameworks of the system components. The utilization of the MPPT algorithm is aimed at enhancing the effectiveness of the PV system, given that the performance of a solar panel is contingent on several factors, including solar radiation intensity and ambient temperature.

The PV system’s transfer function, which includes the photovoltaic panel, MPPT, inverter, and filter, is represented by Equation (1) [37]:

G_{P V} = \frac{- 18 s + 900}{s^{2} + 100 s + 50}

(1)

where the PV system’s transfer function is G_PV. The governor’s transfer function is given by following Equation (2).

G_{G V R} = \frac{K_{G}}{1 + s τ_{G}}

(2)

where G_GVR is the transfer function of the governor,

K_{G}

is the governor’s gain parameter,

τ_{G}

is the governor’s time constants. The turbine’s transfer function is given by following Equation (3).

G_{T R B} = \frac{K_{T}}{1 + s τ_{T}}

(3)

where the turbine’s transfer function is G_TRB,

K_{T}

is the turbine’s gain parameter, the turbine’s time constant is

τ_{T}

. The reheater’s transfer function is given by following Equation (4).

G_{R H T} = \frac{1 + s K_{R} τ_{R}}{1 + s τ_{R}}

(4)

where the reheater’s transfer function is G_RHT,

K_{R}

is the reheater’s gain parameter, the reheater’s time constant is

τ_{R}

. The power system’s transfer function is given by following Equation (5).

G_{P S} = \frac{K_{P S}}{1 + s τ_{P S}}

(5)

where the power system’s transfer function is G_PS,

K_{P S}

is the power system’s gain parameter,

τ_{P S}

is the power system’s time constants.

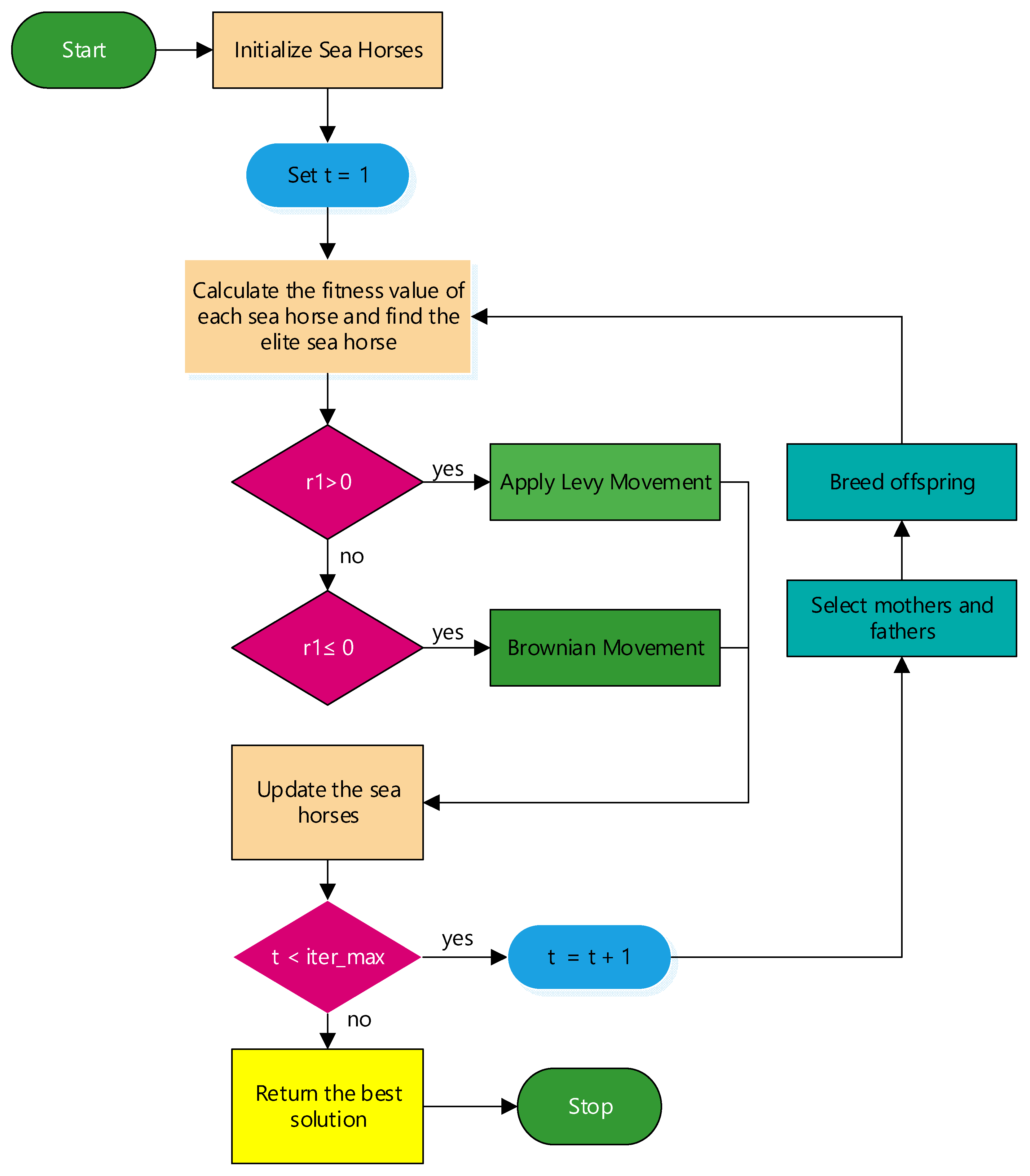
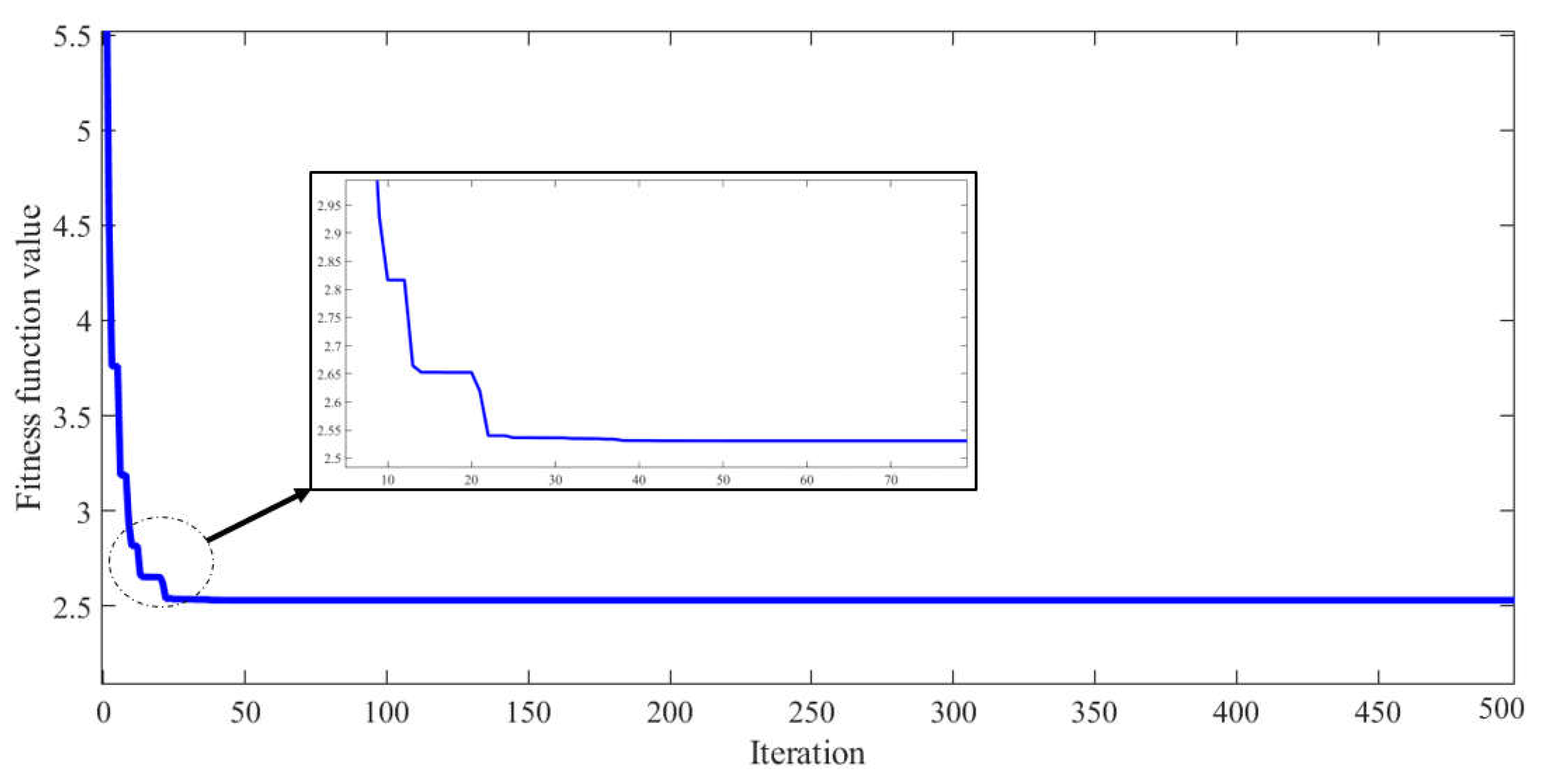
3. Sea Horse Optimizer Algorithm

A new meta-heuristic method, the Sea Horse Optimizer (SHO) algorithm, was proposed by Zhao in 2022 [34]. The SHO algorithm is an meta-heuristic algorithm based on population that imitates the social behavior of sea horses. The algorithm comprised in three main components: movement, hunting, and reproduction. To achieve a balance between exploration and exploitation capabilities of the SHO algorithm, local and global search abilities are designed for the movement and hunting behaviors, respectively, while the reproductive behavior complements them.

The SHO algorithm initializes by creating a population of candidate solutions.

S e a h o r s e s = [\begin{matrix} x_{1}^{1} & \dots & x_{1}^{d i m} \\ ⋮ & ⋱ & ⋮ \\ x_{p o p}^{1} & \dots & x_{p o p}^{d i m} \end{matrix}]

(6)

where

d i m

represents the number of dimension in the search space while

p o p

indicates the size of the population used in the SHO algorithm. Each member of the population of seahorses corresponds to a possible solution within the problem’s search space. In a minimization optimization problem, the individual with the lowest fitness value is considered as the elite individual and is denoted by

X_{e l i t e}

X_{e l i t e}

can be obtained using Equation (7).

X_{e l i t e} = a r g m i n (f (X_{i}))

(7)

where

f (.)

denotes the value of the cost function for a particular problem, which is used to evaluate the fitness of candidate solutions in the search space.

Sea horses motion behavior is composed of two states: Brownian motion and Levy flight. The brownian motion of seahorses enables better exploration in the search space, while Levy flight simulates the movement step size of seahorses, allowing them to migrate allowing them to move to different locations early on to avoid excessive local exploitation. To compute the updated position of a seahorse in iteration t, we can formulate these two scenarios as follows:

X_{n e w}^{1} (t + 1) = {\begin{matrix} X_{i} (t) + L e v y (λ) ((X_{e l i t e} (t) - X_{i} (t)) \times x \times y \times z + X_{e l i t e} (t) r_{1} > 0 \\ X_{i} (t) + r a n d * l * β_{t} * (X_{i} (t) - β_{t} * X_{e l i t e (t)} r_{1} \leq 0 \end{matrix}

(8)

where

L e v y

is defined by Lévy flight distribution function with a randomly generated parameter

λ

from the interval [0, 2]. The spiral movement component of SHO is represented by the coordinates

x, y a n d z

. The constant coefficient

l

is used to control the step size of the Lévy flight,

β_{t}

is Brownian motion’s random walk coefficient. The normal random number

r_{1}

is used to introduce stochasticity in the Brownian motion component.

The hunting behavior of seahorses can result in either success or failure. Successful hunting occurs when a seahorse catches its prey by moving faster than it, while failure means the seahorse explores the search space further. The mathematical notation representing this hunting behavior can be expressed as:

X_{n e w}^{2} (t + 1) = {\begin{matrix} α * (X_{e l i t e} - r a n d * X_{n e w}^{1} (t)) + (1 - α) * X_{e l i t e} (t) r_{2} > 0.1 \\ (1 - α) * (X_{n e w}^{1} (t) - r a n d * X_{e l i t e}) + α * X_{n e w}^{1} (t) r_{2} \leq 0.1 \end{matrix}

(9)

where, the new location of the sea horse after hunting at iteration t is denoted as

X_{n e w}^{1} (t)

r_{2}

is the randomly generater number within [0, 1],

α

is a directly decreasing parameter that adjusts seahorse-based step length during the hunting process.

The reproductive behavior of seahorses is split into male and female groups based on population fitness values, with male seahorses responsible for reproduction.

\begin{matrix} f a t h e r s = X_{s o r t}^{2} (1 : p o p / 2) \\ m o t h e r s = X_{s o r t}^{2} (p o p / 2 + 1 : p o p) \end{matrix}

(10)

where, fathers and mothers refer to the male and female populations, respectively, while

X_{s o r t}^{2}

denotes all

X_{n e w}^{2}

arranged in ascending order of their correspoding fitness values. The algorithm selects half of the best-fit individuals from the population to create a new generation of candidate solutions. The expression of the ith offspring is as follows:

X_{i}^{o f f s p r i n g} = r_{3} X_{i}^{f a t h e r} + (1 - r_{3}) X_{i}^{m o t h e r}

(11)

where

r_{3}

is the random number between [0, 1],

X_{i}^{f a t h e r}

and

X_{i}^{m o t h e r}

individuals chosen at random from the male and female populations.

The SHO algorithm is specifically designed to tackle optimization problems that involve continuous search spaces, and has demonstrated favorable outcomes in various applications. Figure 2 shows the flowchart of the proposed SHO algorithm.

The SHO algorithm provides a novel approach to solving optimization problems, and its effectiveness and efficiency make it a promising technique for various applications. This study proposes the utilization of the SHO algorithm for optimizing PI/PID controllers in the LFC problem.

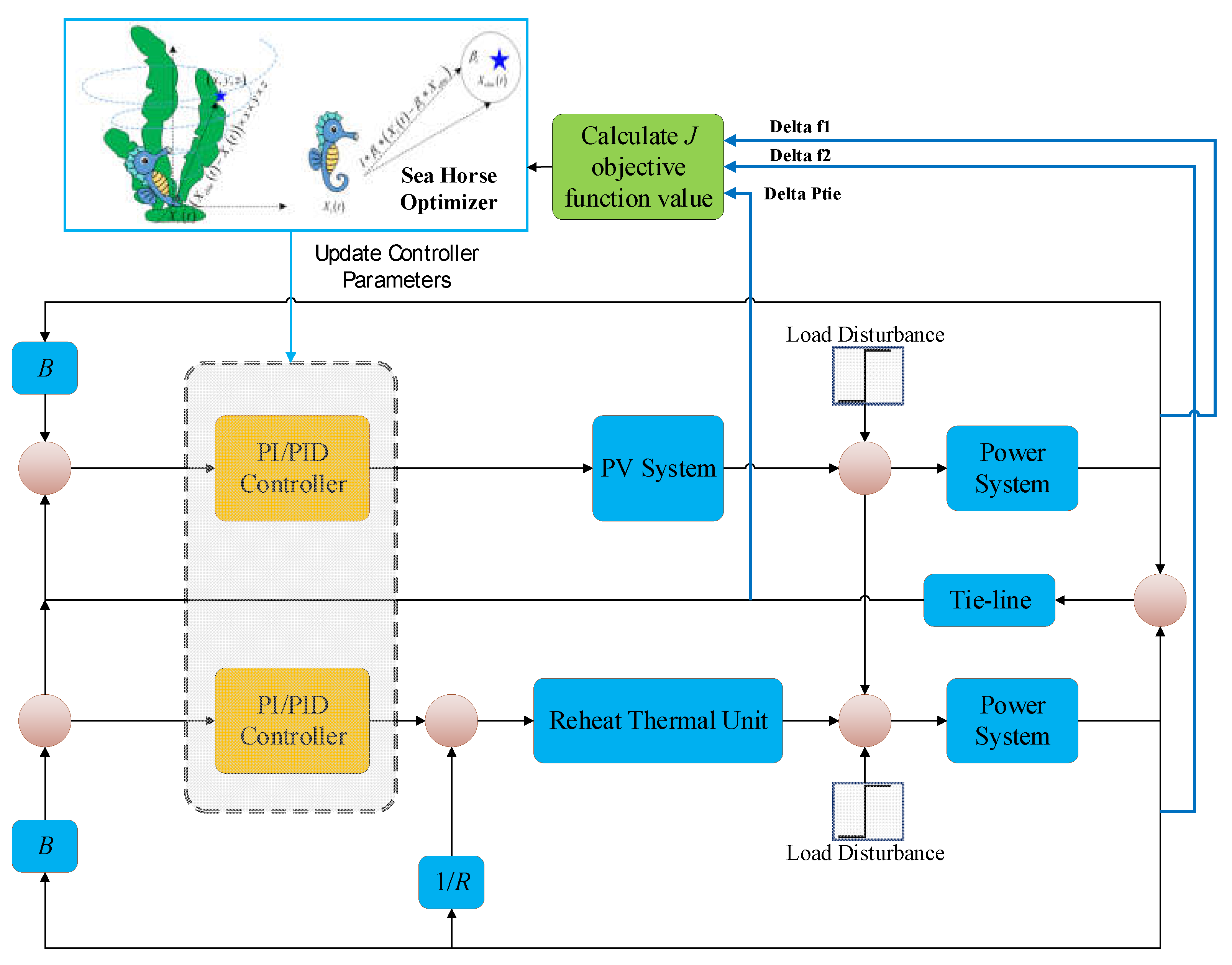
4. Sea Horse Optimization Based Load Frequency Control

When there is an mismatch between power production and demand in a power system, the system frequency may change. This frequency change leads to the formation of a signal called Area Control Error (ACE). The ACE signal is a critical input for the LFC controller, which is responsible for maintaining the equilibrium between the total system load and the total system generation. By monitoring the ACE signal, the LFC controller can adjust the power output of the generators to guarantee that the power system remains stable and reliable. Mathematically, the ACE signals for Area-1 and Area-2 can be expressed as:

A C E_{1} = B_{1} . Δ F_{1} + Δ P_{t i e}

(12)

A C E_{2} = B_{2} . Δ F_{2} + Δ P_{t i e}

(13)

where,

B_{1}

and

B_{2}

are frequency bias parameters of the both Areas 1 and 2, respectively.

Δ F_{1}

and

Δ F_{2}

are the frequency deviations for the both Areas 1 and 2, respectively.

Δ P_{t i e}

is the tie-line power variation. The LFC controller can apply various strategies to manage power generation using the ACE signal. For example, the controller can increase or decrease generator outputs based on whether the ACE signal is positive or negative, which can help to mitigate power imbalances between supply and demand in the control area. Moreover, the controller is capable of regulating generator outputs based on the rate of change of the ACE signal, which is instrumental in preserving the stability of the power system.

PI or PID controllers are control strategies that are often used to reset the ACE signal. These controllers measure the ACE signal and generate the necessary control signals to keep it close to zero.

4.1. PI Controller

The PI controller is a type of feedback control that is commonly used in LFC applications. The PI controller uses two control terms to adapt the system frequency, which are the proportional term and the integral term. The proportional term acts to stabilize the frequency quickly, while the integral term acts to eliminate the steady-state error by adjusting the control signal over time.

The transfer function of the PI controller is formulated as:

G_{P I} (s) = (K_{p} + \frac{K_{i}}{s})

(14)

where,

K_{p}

is the proportional gain and

K_{i}

is the integral gain.

4.2. PID Controller

The PID controller is a widely adopted feedback control strategy that encompasses three key elements: proportional, integral, and derivative. It serves as an extension of the PI controller and is developed to enhance the performance of the control system, particularly with regards to stability and transient response.

The transfer function of the PID controller is expressed as:

G_{P I D} (s) = (K_{p} + \frac{K_{i}}{s} + K_{d} . s)

(15)

where,

K_{p}

K_{i}

and

K_{d}

are the proportional, integral and derivative gains, respectively.

The controller gains in this study will be optimized through the proposed SHO algorithm, with the objective function being the integral of time multiply absolute error (ITAE) of the frequency deviations in both areas and tie-line power variation.

The ITAE objective function is expressed in Equation (16) and is utilized to determine the optimal controller gains, ultimately improving the power system’s performance. The ITAE is a performance metric. This criterion helps optimize the controller for fast response and stable operation. ITAE calculates the integral of multiplying the controller by the error in the ACE signal at a given time and is used to evaluate the controller performance.

J = \int_{0}^{\infty} t (| Δ f_{1} | + | Δ f_{2} | + | Δ P_{t i e} |) d t

(16)

where J is the objective function of the LFC problem. It is aimed to minimize the J.

When optimizing PID controllers, it is necessary to constrain the gain parameters

K_{p}

K_{i}

and

K_{d}

within predefined lower and upper bounds. These bounds represent variable constraints that ensure the stability and performance of the controller. Equation (17) specifies the limit ranges for the PID controller.

K_{p}^{m i n} \leq K_{p} \leq K_{p}^{m a x} K_{i}^{m i n} \leq K_{i} \leq K_{i}^{m a x} K_{d}^{m i n} \leq K_{d} \leq K_{d}^{m a x}

(17)

The proposed SHO algorithm aims to optimize the gain parameters of a PI/PID controller by utilizing the J objective function in Equation (16) and considering the vari-able constraints in Equation (17). Figure 3 illustrates how the SHO algorithm optimizes PI/PID parameters for the LFC problem. The proposed SHO algorithm was employed to the LFC problem using the test system shown in Figure 1, and the parameter values of the test model are provided in Table 1 [35,36].

Table 2 presents the parameters of the proposed SHO algorithm, while Figure 3 illustrates the block diagram of the SHO-based PI/PID controller for the LFC problem.

In the proposed SHO algorithm, the number of sea horse is set to 50, the maximum iteration number is 100, and the gain parameter range of the controller is set between -2 and 2. These parameter values were chosen to facilitate comparison with similar algorithm parameters used in other published studies, such as FA, GA, WOA, and MWOA [35,36]. The speed of a selected sea horse (u) is used when calculating a new position (v). The learning factor (l) of a selected sea horse is used when updating its position. These parameters can be adjusted to improve the effectiveness of the SHO algorithm and to reach optimal solutions faster.

5. Simulation Results and Discussion

The SHO algorithm was programmed and executed on a computer with an Intel i7 2.50 GHz processor and 16.00 GB RAM, using the MATLAB/Simulink package program. Various cases were analyzed to confirm the robustness of the proposed SHO algorithm for adjusting PI/PID controller gain parameters. In the first situation, a 10% load change was applied in both areas. The second scenario examined the effect of high load demand on system stability. The third scenario investigated the influence of solar radiation variation. Finally, to evaluate the performance of the controllers, in addition to the ITAE performance index, other performance indicators such as the IAE, the ISE and the ITSE values were compared.

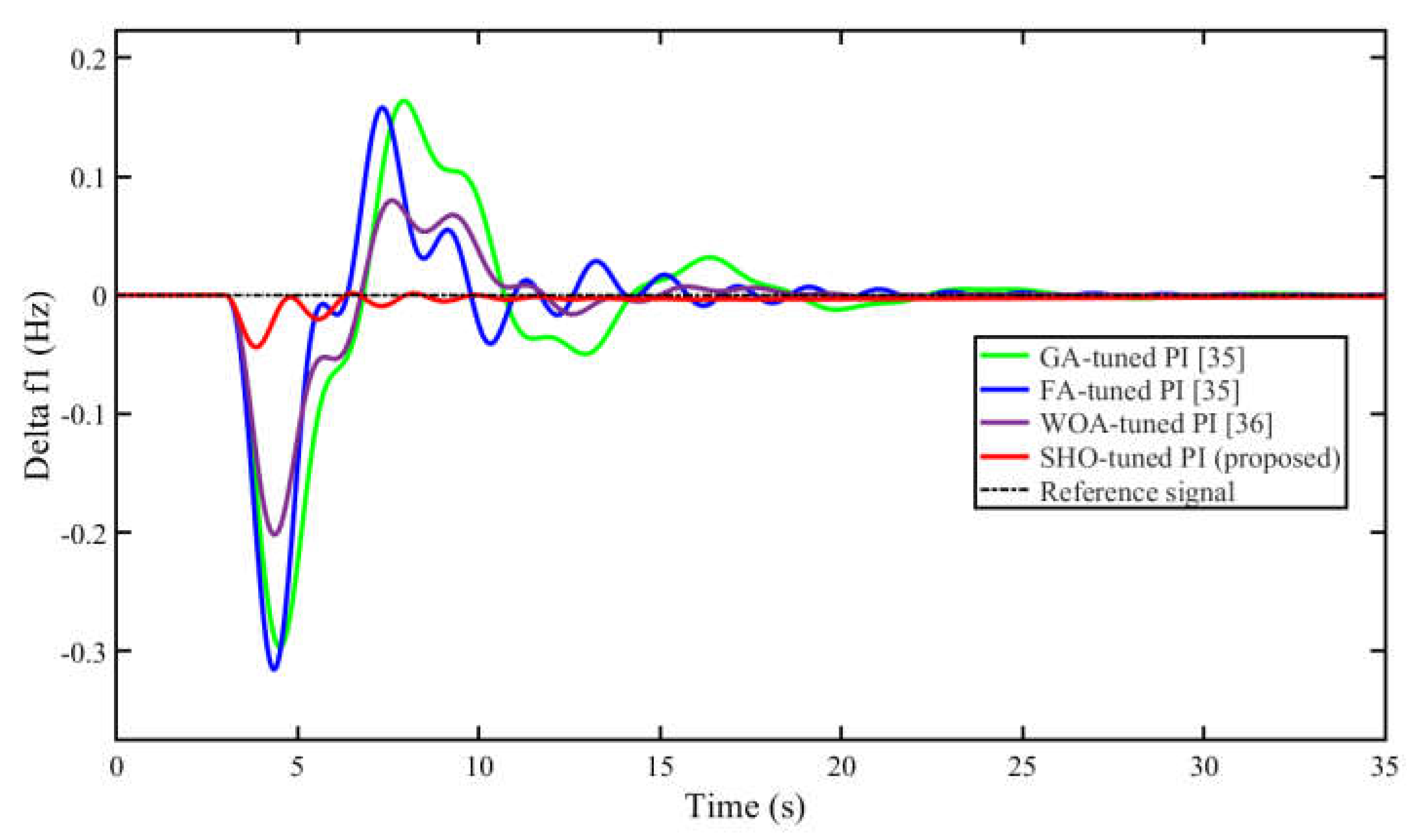
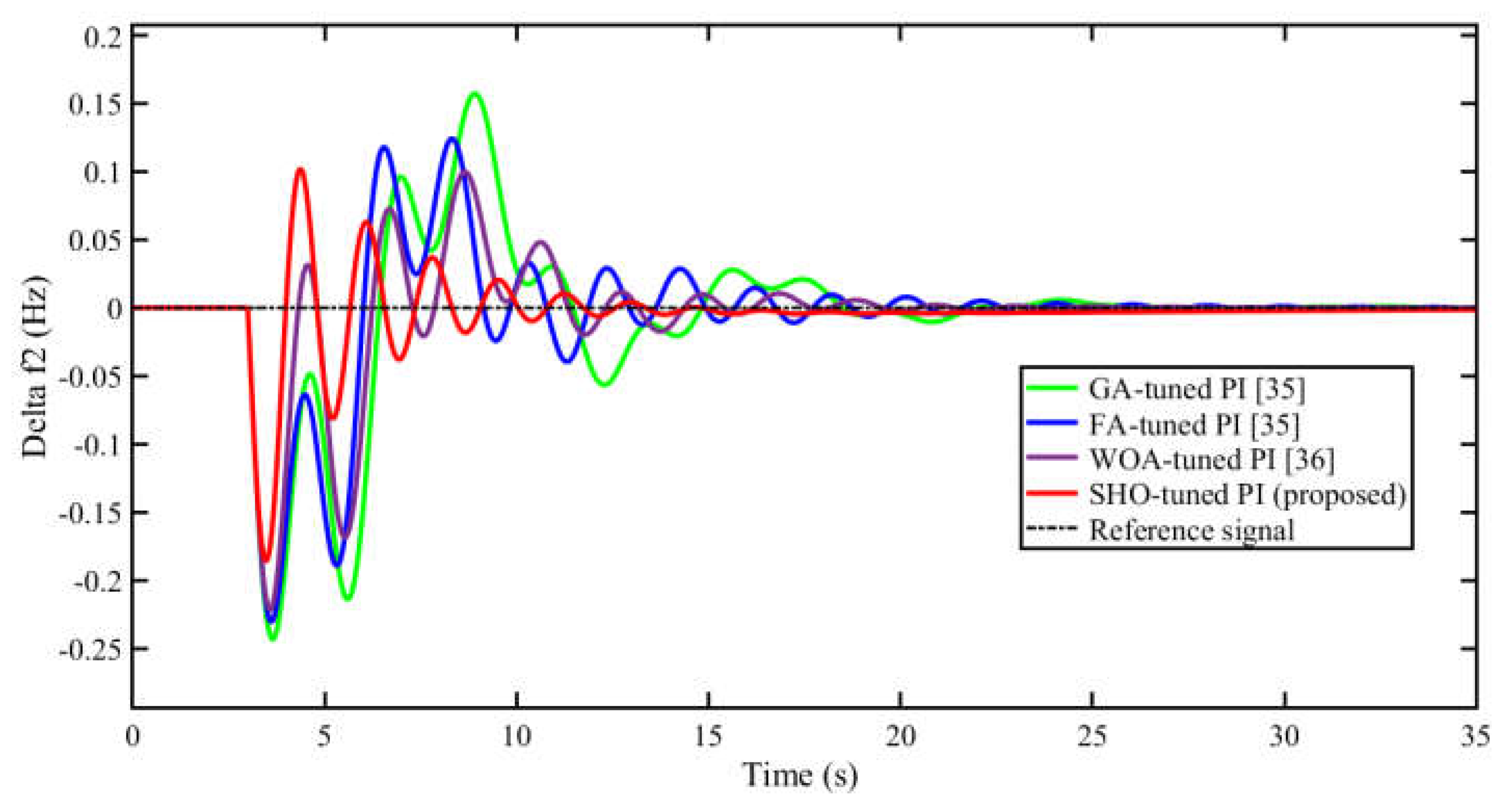
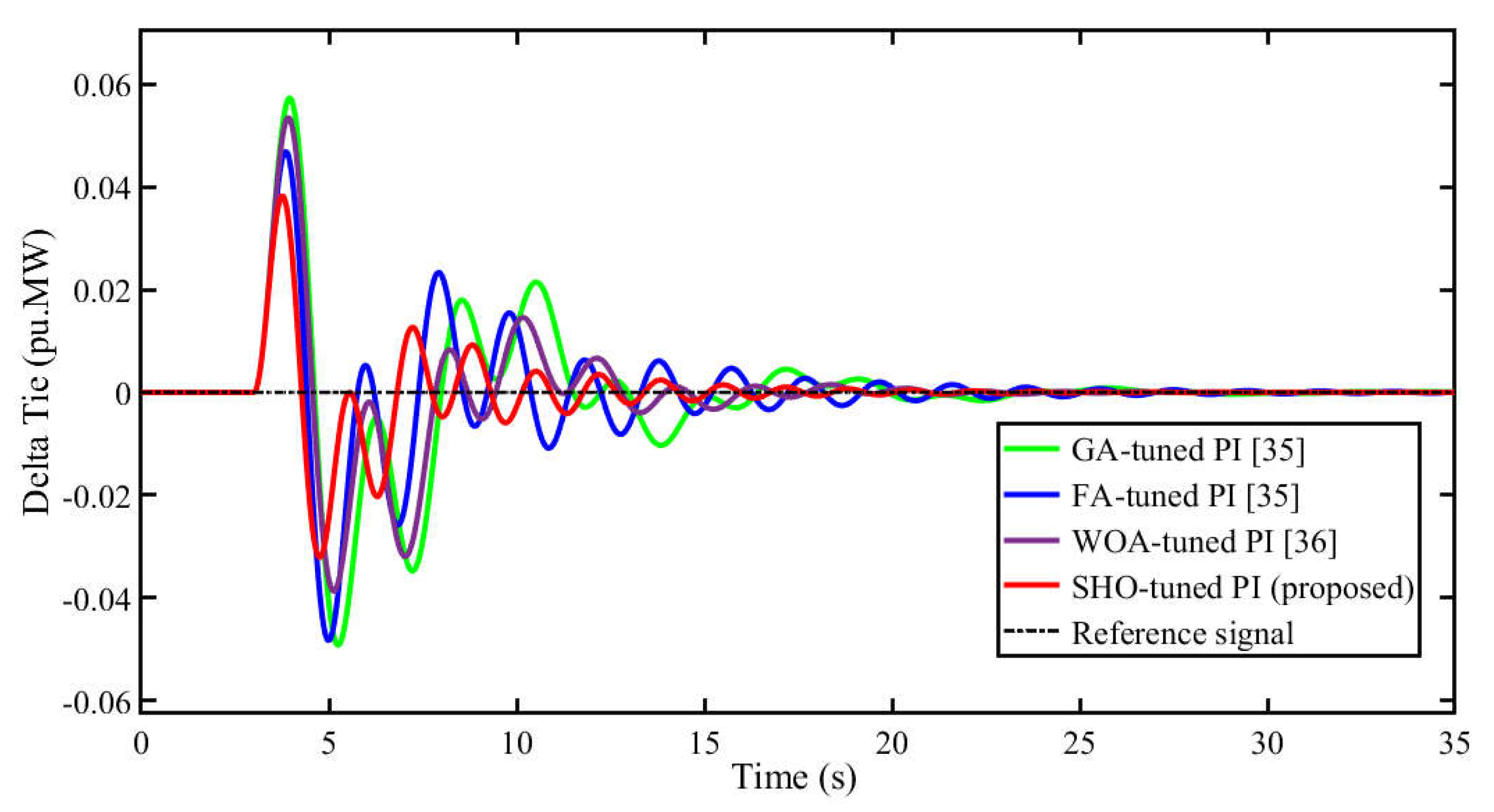
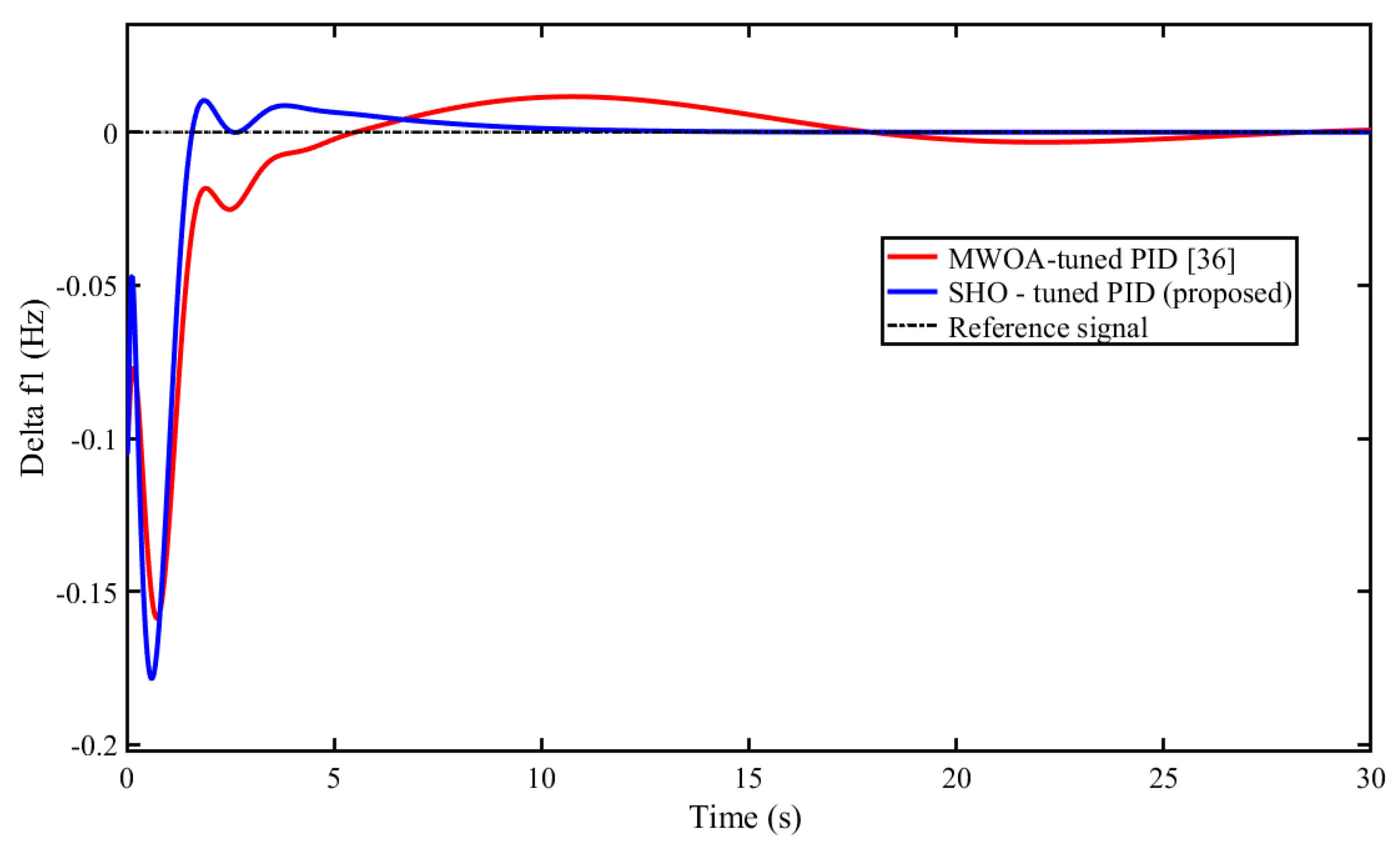
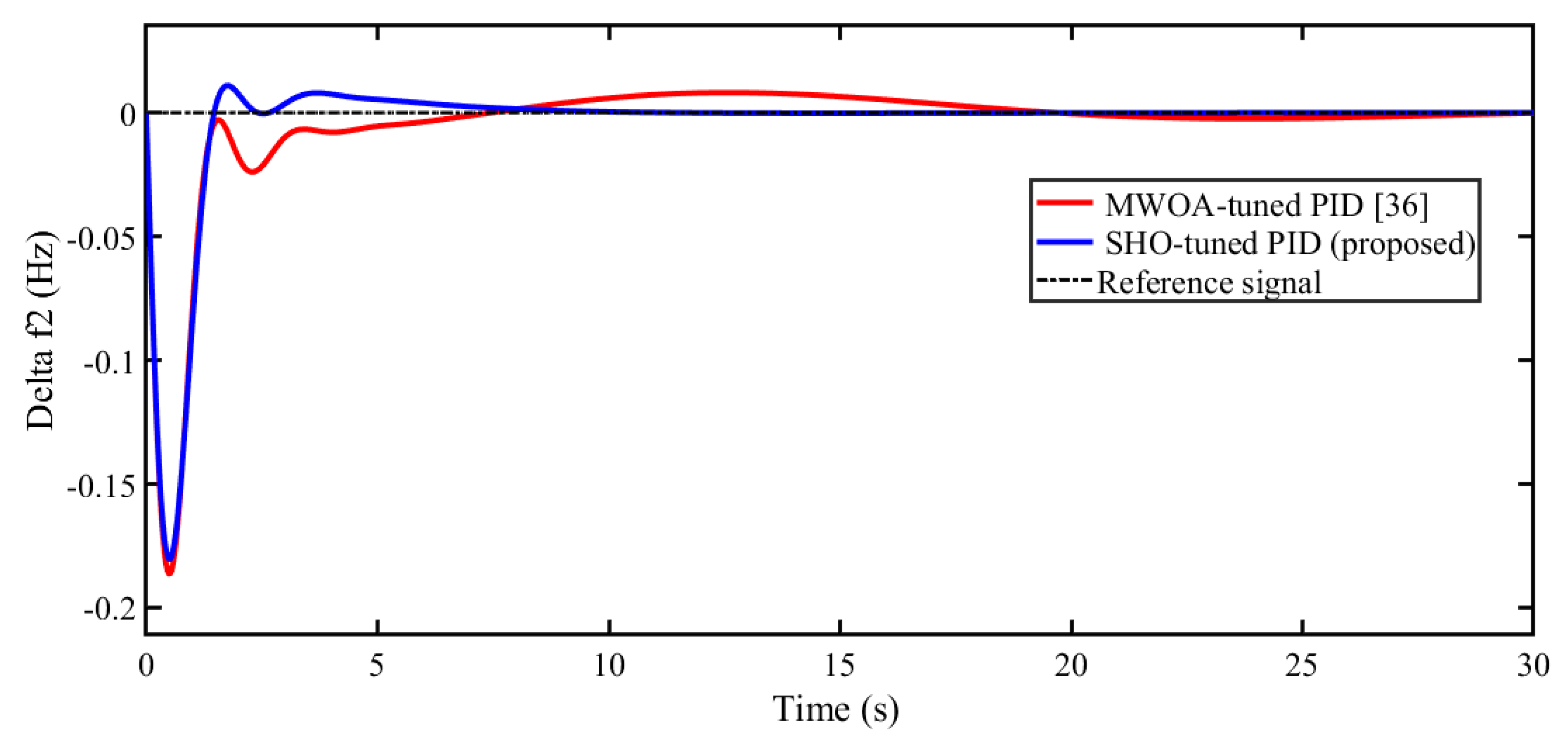
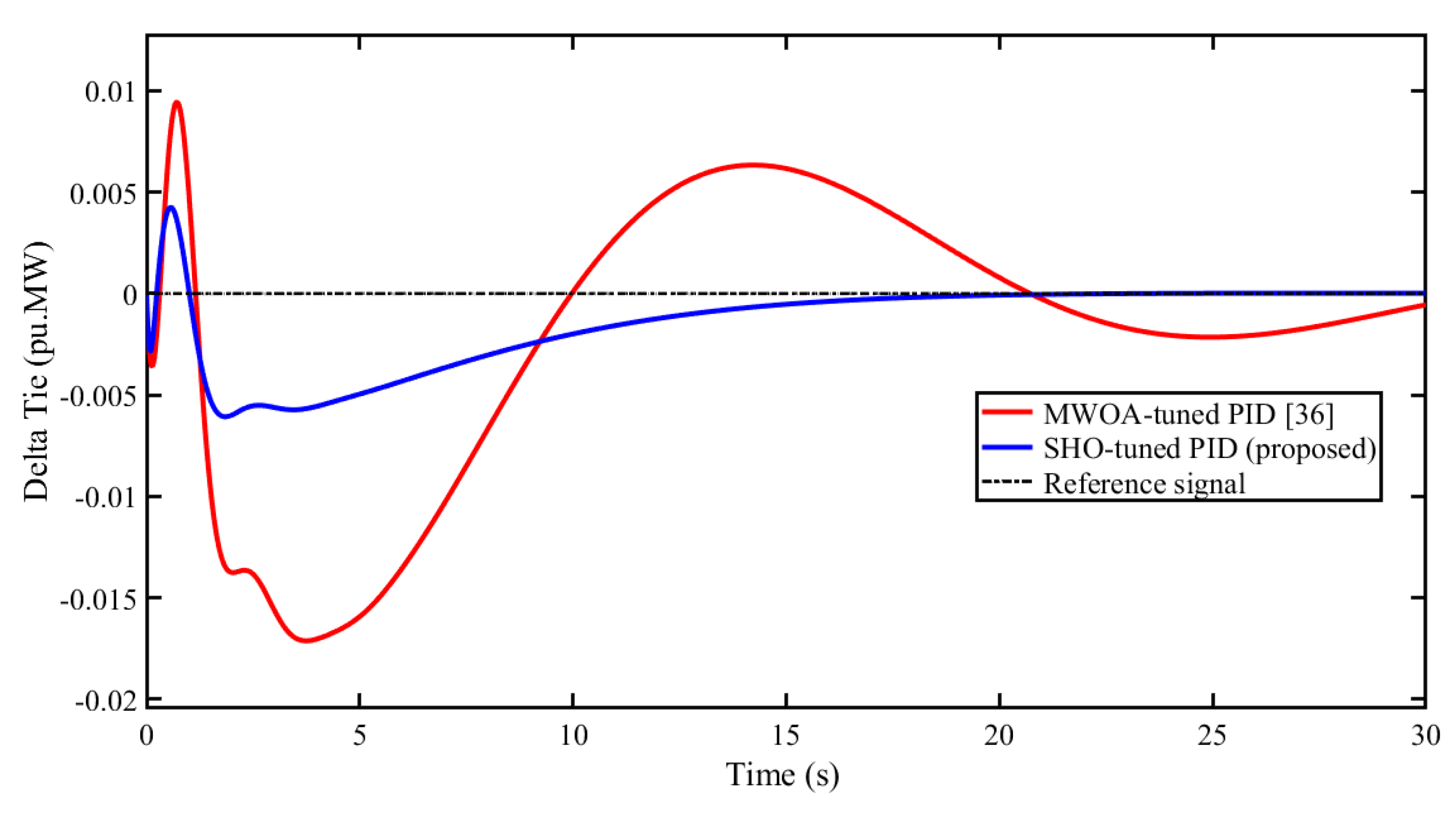
5.1. Scenario 1: Performance Comparison of Proposed SHO Optimized Controller with Other Reported Algorithms

In this scenario, a two-area system experiences a 0.1 p.u. load disturbance in both areas at the third second. The test model is regulated using GA-optimized PI [35], FA-optimized PI [35], WOA-optimized PI [36] and MWOA-optimized PID [36]. Table 3 shows the controller gains and fitness function values obtained using the SHO method.

According to Table 3, among the compared PI controllers, the SHO algorithm provides the best objective function value of 2.5308. This value represents how effectively the controller reduces the error in the ACE signal over time. Therefore, the optimal PI controller parameter values (

K_{p 1}

= -0.67012,

K_{i 1}

= -0.5371,

K_{p 2}

= -2.0000 and

K_{i 2}

= -0.8476) are obtained using the SHO algorithm. Similarly, among the compared PID controllers, the SHO algorithm provides the best objective function value of 0.8582. Therefore, the optimal PID controller parameter values (

K_{p 1}

= -0.8599,

K_{i 1}

= -0.1290,

K_{d 1} = - 1.9396, K_{p 2}

= -2.0000,

K_{i 2}

= -2.0000

, K_{d 2} = - 0.2614

) are obtained using the SHO algorithm. Moreover, these optimized values comply with the bound limits of the controller parameter values provided in Table 2, which range from -2 to 2.

Performance metrics are used to evaluate the accuracy and effectiveness of controllers for the Load Frequency Control (LFC) problem. These include the Settling Time, which measures the time it takes for the controller to bring the ACE signal close to zero. Settling time is a crucial stability. Overshoot (M+) and undershoot (M-) terms are also important metrics used to assess the performance of the controller. Maximum overshoot refers to the highest deviation from the reference frequency that occurs when the LFC controller stabilizes the system frequency. Undershoot occurs when the system frequency temporarily drops below the reference frequency due to the LFC controller reaching the reference frequency quickly. This may require a longer time for the system frequency to stabilize. Table 4 provides a comparison of the performance values for PI controllers.

Table 4 shows that the proposed SHO optimized PI controller significantly reduces overshoot, undershoot, and settling time of the system oscillations compared to the other algorithms reported. The results indicate that the system with the SHO-tuned controller demonstrates significant improvement in performance compared to GA, FA, and WOA optimized controllers. While the frequency overshoot in only second area is higher than the WOA response using the proposed SHO optimized controller, it is evident that the proposed controller has a considerable advantage in reducing undershoot and especially settling time of the responses.

Figure 4, Figure 5 and Figure 6 display the simulation results of the frequency variation in both regions and tie-line power of a power system under optimal control using an optimized PI controller. The proposed SHO algorithm uses a population size of 50 while the maximum repetition limit is set to 100. However, it needs to be shown whether the SHO algorithm is stuck at a local optimum. The convergence of the proposed SHO-based PI controller to solve LFC problem is shown in Figure 7. According to Figure 7, the convergence curve shows that the fitness function value for the problem stabilizes before reaching 100 iterations. The results presented in Table 3 indicate that the fitness function value reaches a saturation point of 2.5308, which is lower than the values obtained using GA [35], FA [35], and WOA [36].

When a PID controller is used, it is evident that the proposed SHO method yields a better objective function value of 0.8582 compared to the value of 1.5602 obtained by the MWOA [36] method. The PID controller, which has more tuning parameters, is able to respond better to frequency variations in response to load changes. Figure 8, Figure 9 and Figure 10 illustrate the frequency variations in both areas and the tie-line power in response to a 0.1 p.u. load disturbance in both areas for the proposed SHO-based PID controller and the MWOA-based PID controller [36].

The SHO-tuned PI method improves the fitness function by 79.11%, 65.38%, and 61.26% compared to GA, FA, and WOA methods, respectively. Additionally, the SHO-tuned PID method improves the fitness function by 45.02% compared to the MWOA method. These results demonstrate that the SHO method is a highly effective optimization algorithm for enhancing the performance of the PI/PID controllers in LFC applications, providing more effective and reliable control of power systems.

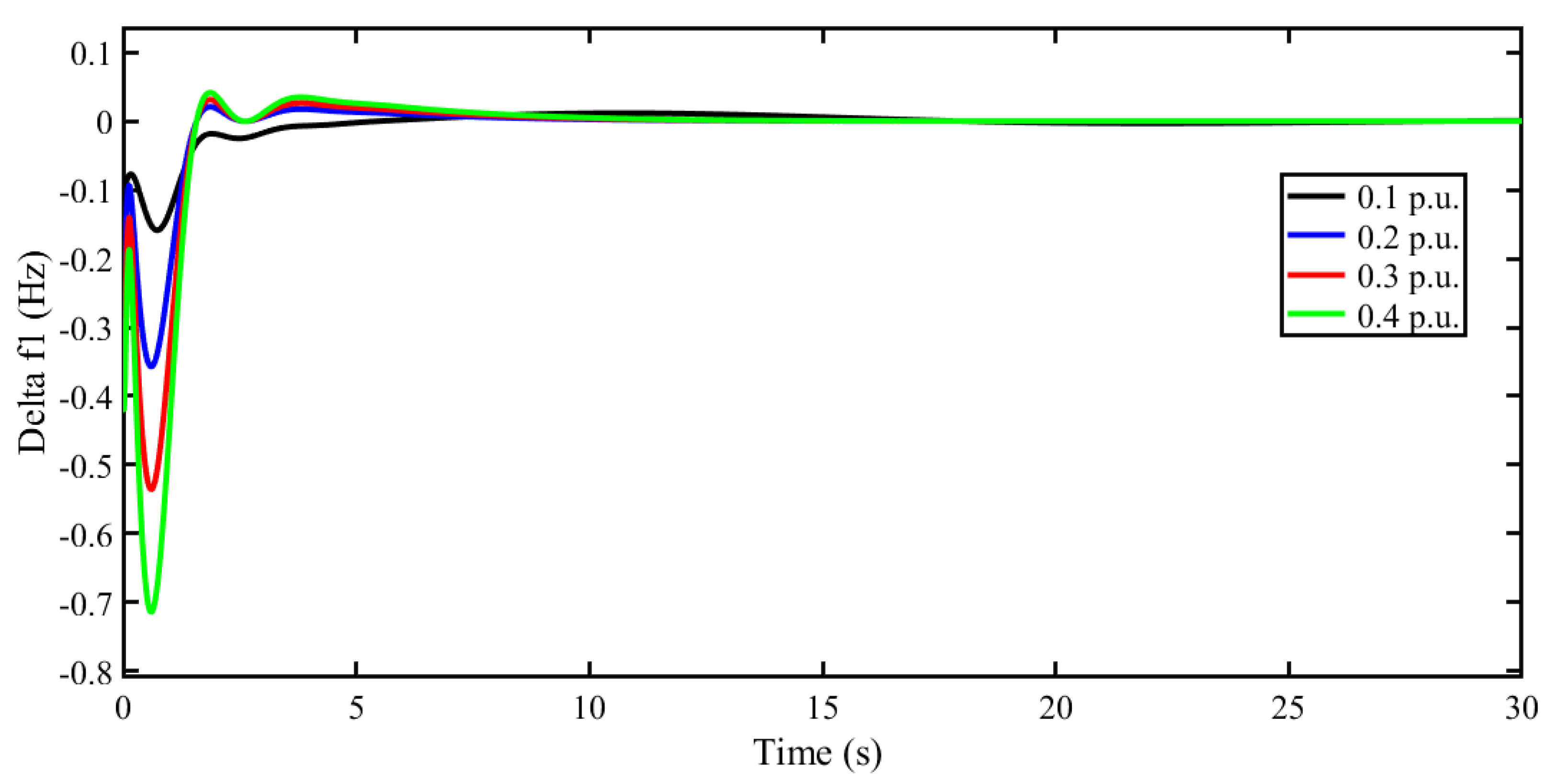
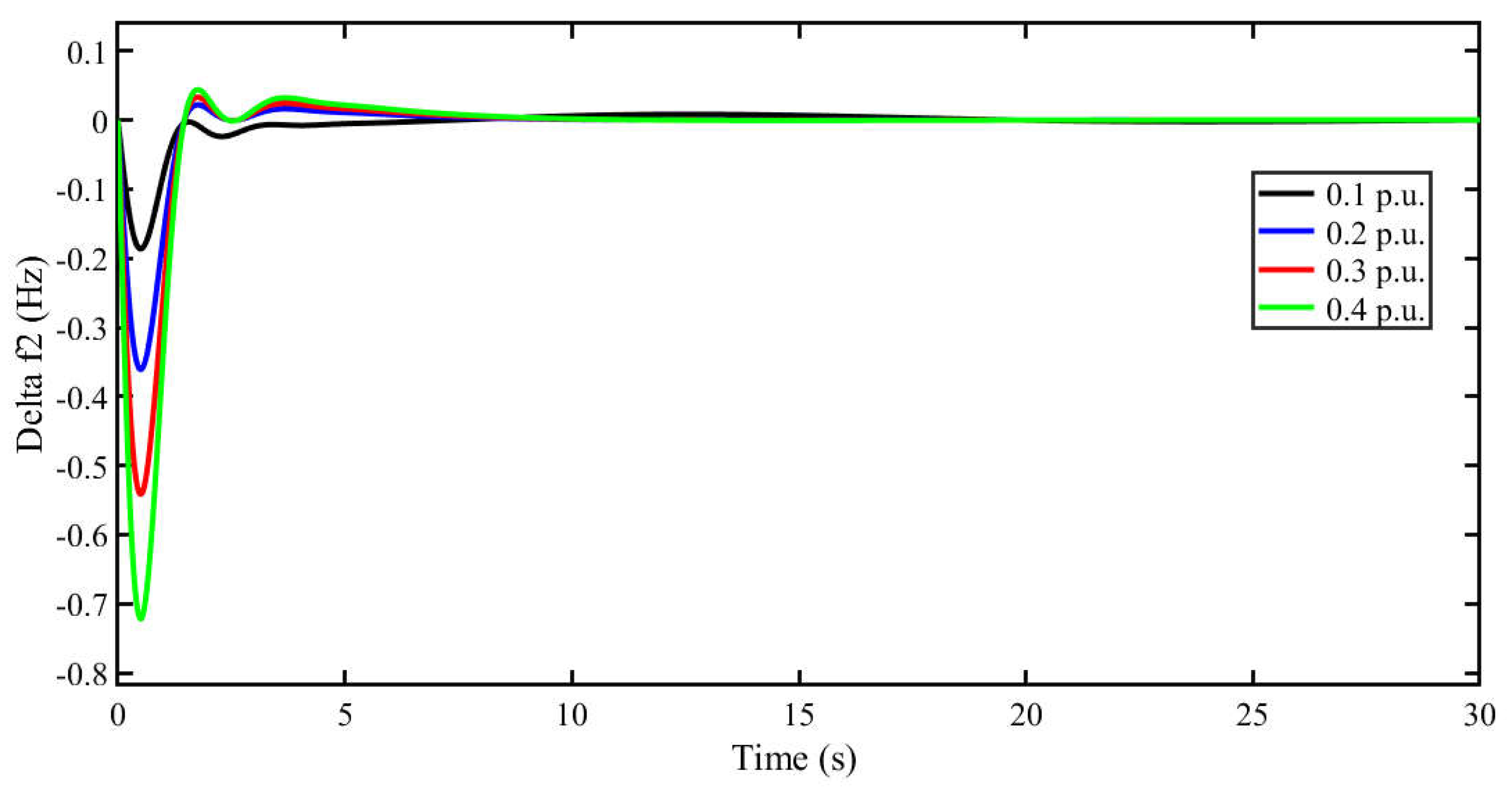
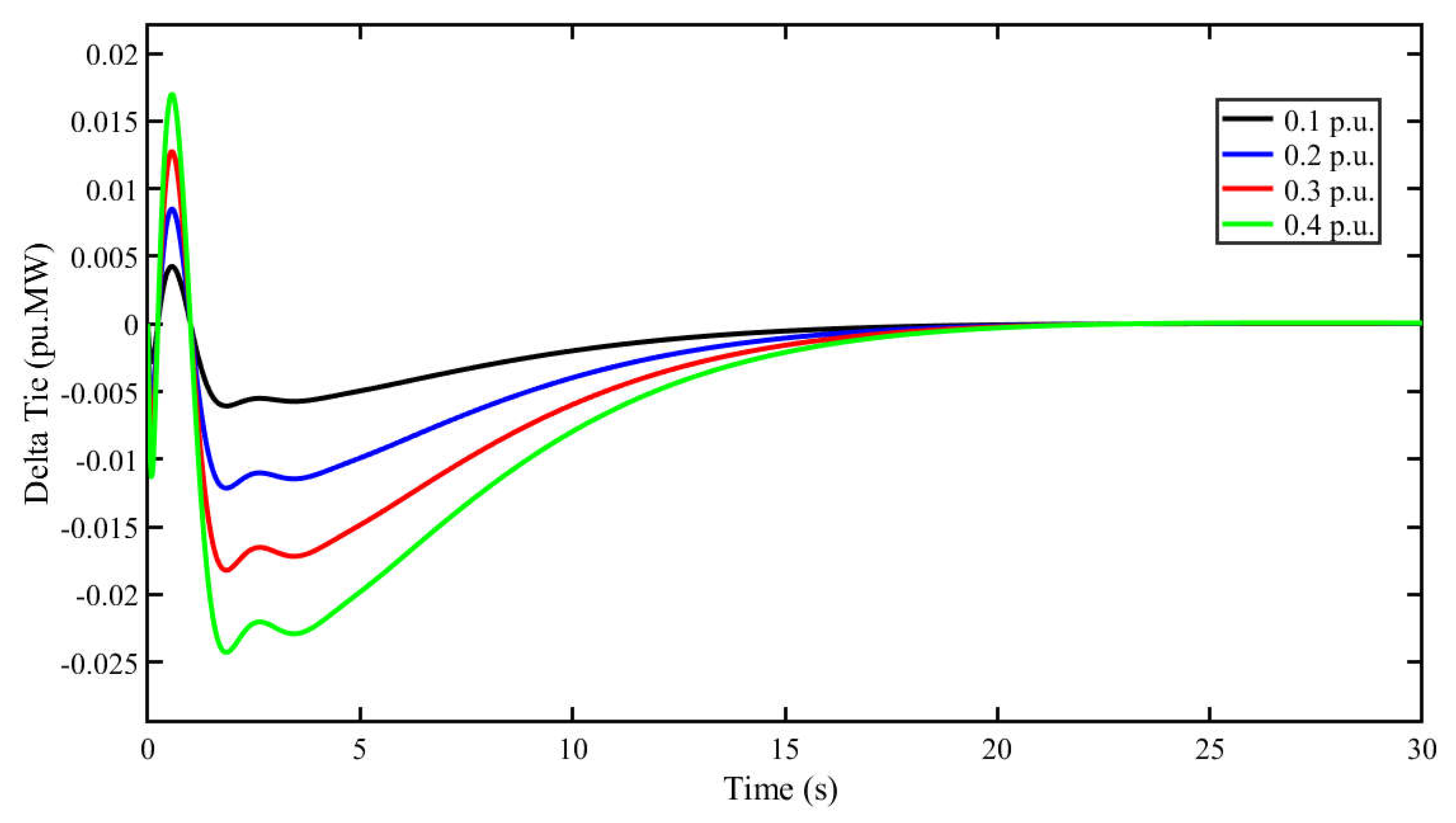
5.2. Scenario 2: Effect of High Load Demand on System Stability

In order to assess the robustness of the SHO-tuned PID controlled two-area test system, large load disturbances ranging from 0.1 p.u. to 0.4 p.u. were introduced suddenly during simulations. The results, as shown in Figure 11, Figure 12 and Figure 13, demonstrate that the proposed SHO-tuned PID controller was able to effectively mitigate the impact of these disturbances and quickly restore the system to a stable state, with minimal deviations in frequency and tie-line power. This confirms the effectiveness of the SHO optimized PID controller in maintaining system stability and reliability under challenging operating conditions. These findings have important implications for power system design and operation with renewable energy sources, where sudden load fluctuations can pose significant challenges to grid stability.

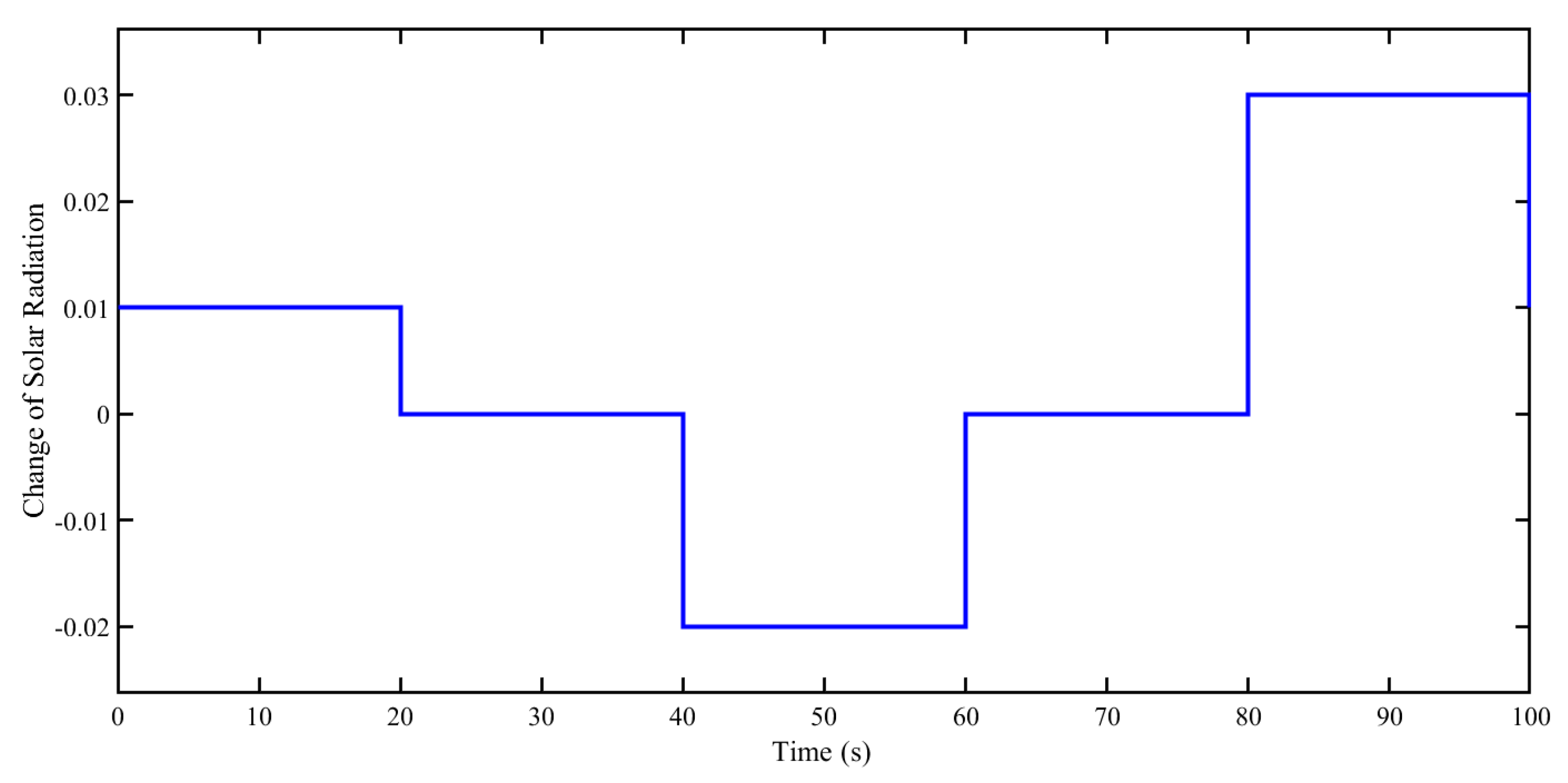
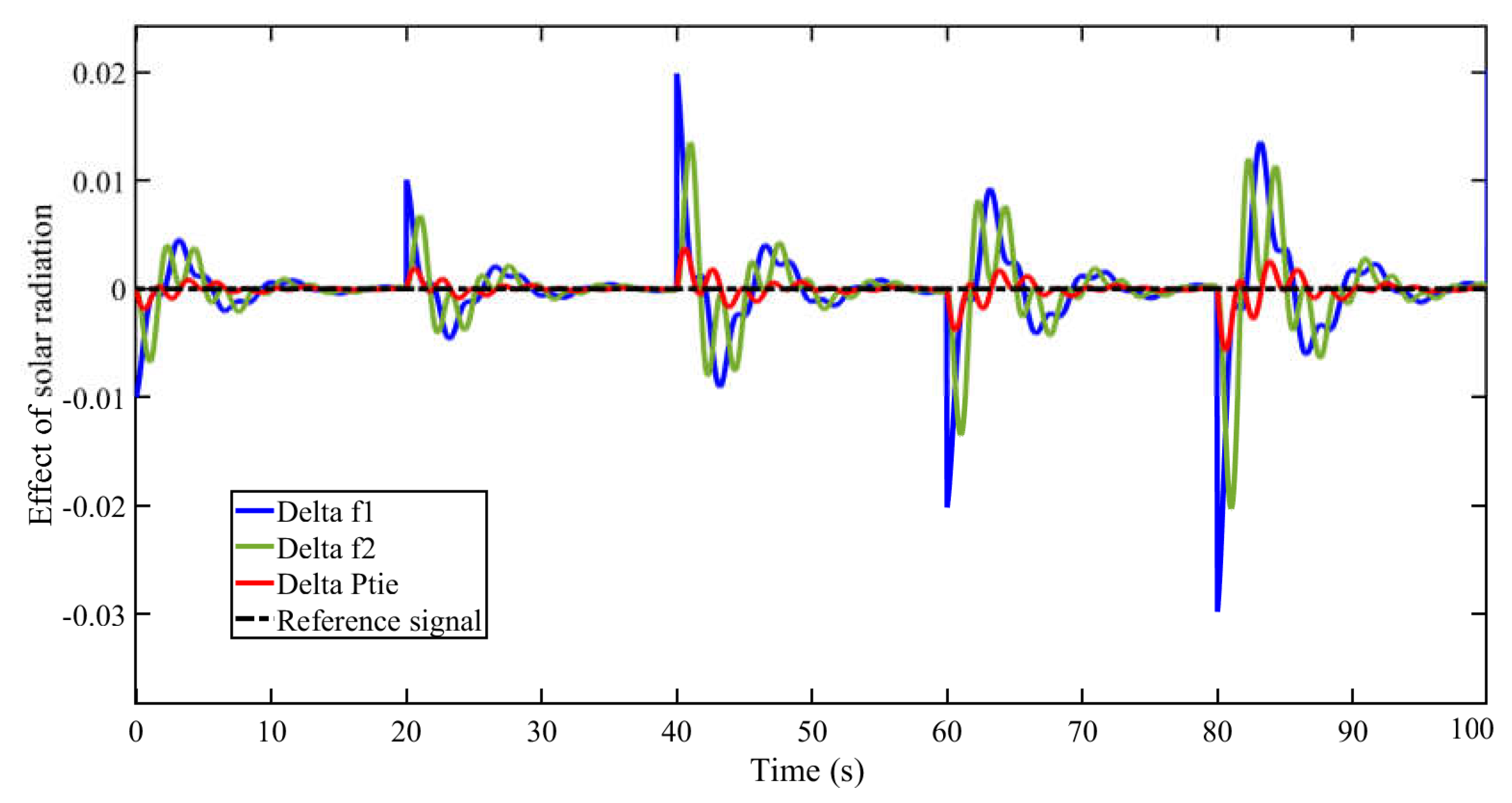
5.3. Scenario 3: Influence of Solar Radiation Variation

In this section, we performed simulations under the assumption that solar radiation would change during the time period of t=0-100 s. We present and discuss the simulation results to demonstrate the performance and robustness of the proposed SHO-based LFC method. The simulation scenario assumed the presence of random solar radiation variation in Area-1, as shown in Figure 14. To evaluate the performance of the SHO-tuned PID controllers in this particular operating condition, the system’s responses to frequency deviations ∆f₁ and ∆f₂, as well as tie-line power deviation ∆P_tie, were carefully analyzed. A graphical representation of the findings is shown in Figure 15, which provides valuable insights into the controller’s ability to regulate the system under highly dynamic and uncertain conditions.

Figure 15 clearly illustrates that the SHO-tuned PID controllers are able to effectively regulate the system despite the fluctuations in PV power generation, maintaining the frequency and power at their desired set points. The SHO optimization approach used in tuning the PID parameters ensures that the controllers can adapt to changes in the system dynamics and provide robust control, even in the presence of uncertainties such as random variations in PV power generation. Despite the disturbances caused by changes in solar radiation, the obtained results show that the proposed SHO-based controller is useful and robust in regulating the power system frequency. The study demonstrates the feasibility of using a renewable power model for power system frequency control and highlights the importance of developing robust control strategies to account for uncertainties in renewable power generation.

5.4. Performance Indices and Robustness

The performance evaluation of the designed controllers is conducted using several performance indices, including the integral of absolute error (IAE), integral of time-weighted absolute error (ITAE), integral of squared error (ISE), and integral of time-weighted squared error (ITSE). The ITAE index is given by Equation (16), while Equation (18) - (20) provide the formula for calculating the IAE, ISE, and ITSE indices. These indices provide a comprehensive measure of the controller’s performance in minimizing error over time.

I A E = \int_{0}^{\infty} (| Δ f_{1} | + | Δ f_{2} | + | Δ P_{t i e} |) d t

(18)

I S E = \int_{0}^{\infty} ({(Δ f_{1})}^{2} + {(Δ f_{2})}^{2} + {(Δ P_{t i e})}^{2}) d t

(19)

I T S E = \int_{0}^{\infty} t ({(Δ f_{1})}^{2} + {(Δ f_{2})}^{2} + {(Δ P_{t i e})}^{2}) d t

(20)

Table 5 presents corresponding performance indices of each controller.

The results indicate that the designed controllers using SHO outperform those using GA, FA, WOA, and MWOA in terms of the evaluated indices. The lower values of the per-formance indices obtained with SHO demonstrate that the time-domain characteristics of the controllers are significantly improved. Therefore, the controllers designed via SHO al-gorithm are more efficient, powerful and faster for regulating the frequency of power sys-tems in response to changes in demand.

6. Conclusions

In this study, a novel optimization algorithm, the SHO algorithm, was proposed for optimizing controller constants in LFC problems of power systems. The SHO algorithm was shown to provide better performance in comparison to other optimization algorithms such as GA, FA, WOA and MWOA. The proposed SHO algorithm was found to be robust in the face of various scenarios, including high load demand, solar radiation variation, and load changes. The proposed SHO algorithm was successfully used to optimize both PI and PID controllers in a two-area power system. The performance metrics used to evaluate the accuracy and effectiveness of controllers demonstrated that the SHO-tuned PI/PID controller significantly reduced overshoot, undershoot, and settling time of the system oscillations compared to the other algorithms reported. The simulation results indicated that the SHO-based PI/PID controller provides better performance than GA, FA, WOA and MWOA optimized controllers. Additionally, the SHO-optimized PID controller was able to respond better to frequency variations caused by load changes. The proposed SHO algorithm is robust and provides excellent performance, making it a useful tool for system control and stability analysis in the power systems. The proposed SHO algorithm could be considered as an alternative solution method for the LFC problem in power systems.

Author Contributions

Conceptualization, C.A.; methodology, software, investigation, visualization, writing—original draft preparation, S.O.; validation, methodology, software, writing—original draft preparation, M.V.; formal analysis, writing—original draft preparation, supervision, A.O.; formal analysis, writing—original draft preparation, supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Yang, S.; Huang, C.; Yu, Y.; Yue, D.; Xie, J. Load frequency control of interconnected power system via multi-agent system method. Electric Power Components and Systems 2017, 45, 839–851. [Google Scholar] [CrossRef]
Tan, W.; Xu, Z. Robust analysis and design of load frequency controller for power systems. Electric Power Systems Research 2009, 79, 846–853. [Google Scholar] [CrossRef]
Kumar, V.; Sharma, V.; Naresh, R. Leader harris hawks algorithm based optimal controller for automatic generation control in PV-hydro-wind integrated power network. Electric Power Systems Research 2023, 214, 108924. [Google Scholar] [CrossRef]
Alhelou, H.H.; Hamedani-Golshan, M.E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and opportunities of load frequency control in conventional, modern and future smart power systems: a comprehensive review. Energies 2018, 11, 2497. [Google Scholar] [CrossRef]
Mokhtar, M.; Marei, M.I.; Sameh, M.A.; Attia, M.A. An adaptive load frequency control for power systems with renewable energy sources. Energies 2022, 15, 573. [Google Scholar] [CrossRef]
Singh, A.; Sharma, V. Salp swarm algorithm-based model predictive controller for frequency regulation of solar integrated power system. Neural Computing and Applications 2019, 31, 8859–8870. [Google Scholar] [CrossRef]
Celik, E.; Ozturk, N.; Houssein, E.H. Improved load frequency control of interconnected power systems using energy storage devices and a new cost function. Neural Computing and Applications 2023, 35, 681–697. [Google Scholar] [CrossRef]
Ibrahim, M.H.; Peng, A.S.; Dani, M.N.; Khalil, A.; Law, K.H.; Yunus, S.; Rahman, M.I.; Au, T.W. A novel computation of delay margin based on grey wolf optimisation for a load frequency control of two-area-network power systems. Energies 2023, 16, 2860. [Google Scholar] [CrossRef]
Ali, T.; Malik, S.A.; Daraz, A.; Aslam, S.; Alkhalifah, T. Dandelion optimizer-based combined automatic voltage regulation and load frequency control in a multi-area, multi-source interconnected power system with nonlinearities. Energies 2022, 15, 8499. [Google Scholar] [CrossRef]
Farooq, Z.; Rahman, A.; Lone, S.A. Load frequency control of multi-source electrical power system integrated with solar-thermal and electric vehicle. International Transactions on Electrical Energy Systems 2021, 31, 12918. [Google Scholar] [CrossRef]
Chandrakala, K.V.; Balamurugan, S. Simulated annealing based optimal frequency and terminal voltage control of multi source multi area system. International Journal of Electrical Power and Energy Systems 2016, 78, 823–829. [Google Scholar] [CrossRef]
Mbuli, N.; Ngaha, W.S. A survey of big bang big crunch optimization in power systems. Renewable and Sustainable Energy Reviews 2022, 155, 111848. [Google Scholar] [CrossRef]
Sahu, R.K.; Panda, S.; Padhan, S. A novel hybrid gravitational search and pattern search algorithm for load frequency control of nonlinear power system. Applied Soft Computing 2015, 29, 310–327. [Google Scholar] [CrossRef]
Gozde, H.; Taplamacioglu, M.C.; Kocaarslan, I. Comparative performance analysis of artificial bee colony algorithm in automatic generation control for interconnected reheat thermal power system. International Journal of Electrical Power and Energy Systems 2012, 42, 167–178. [Google Scholar] [CrossRef]
Nguyen, G.N.; Jagatheesan, K.; Ashour, A.S.; Anand, B.; Dey, N. Ant colony optimization based load frequency control of multi-area interconnected thermal power system with governor dead-band nonlinearity. Smart Trends in Systems, Security and Sustainability: Proceedings of WS4 2017 2018, 1, 157–167. [Google Scholar]
Abdelaziz, A.Y.; Ali, E.S. Load frequency controller design via artificial cuckoo search algorithm. Electric Power Components and Systems 2016, 44, 90–98. [Google Scholar] [CrossRef]
Ghoshal, S.H. Optimizations of PID gains by particle swarm optimizations in fuzzy based automatic generation control. Electric Power Systems Research 2004, 72, 203–212. [Google Scholar] [CrossRef]
Abo-Elyousr, F.K.; Abdelaziz, A.Y. A novel modified robust load frequency control for mass-less inertia photovoltaics penetrations via hybrid PSO-Woa approach. Electric Power Components and Systems 2019, 47, 1744–1758. [Google Scholar] [CrossRef]
Golpira, H.; Bevrani, H. A framework for economic load frequency control design using modified multi-objective genetic algorithm. Electric Power Components and Systems 2014, 42, 788–797. [Google Scholar] [CrossRef]
Mohanty, B.; Panda, S.; Hota, P.K. Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system. International Journal of Electrical Power and Energy Systems 2014, 54, 77–85. [Google Scholar] [CrossRef]
Padhan, S.; Sahu, R.K.; Panda, S. Application of firefly algorithm for load frequency control of multi-area interconnected power system. Electric Power Components and Systems 2014, 42, 1419–1430. [Google Scholar] [CrossRef]
Jagatheesan, K.; Anand, B.; Samanta, S.; Dey, N; Santhi, V.; Ashour, A.S.; Balas, V.E. Application of flower pollination algorithm in load frequency control of multi-area interconnected power system with nonlinearity. Neural Computing and Applications 2017, 28, 475–488. [Google Scholar] [CrossRef]
Guha, D.; Roy, P.K.; Banerjee, S. Whale optimization algorithm applied to load frequency control of a mixed power system considering nonlinearities and PLL dynamics. Energy Systems 2020, 11, 699–728. [Google Scholar] [CrossRef]
Kalyan, C.N.S.; Goud, B.S.; Reddy, C.R.; Ramadan, H.S.; Bajaj, M.; Ali, Z.M. Water cycle algorithm optimized type II fuzzy controller for load frequency control of a multi-area, multi-fuel system with communication time delays. Energies 2021, 14, 5387. [Google Scholar] [CrossRef]
Jumani, T.A.; Mustafa, M.W.; Md Rasid, M.; Mirjat, N.H.; Leghari, Z.H.; Saeed, M.S. Optimal voltage and frequency control of an islanded microgrid using grasshopper optimization algorithm. Energies 2018, 11, 3191. [Google Scholar] [CrossRef]
Ibrahim, M.H.; Peng, A.S.; Dani, M.N.; Khalil, A.; Law, K.H.; Yunus, S.; Rahman, M.I.; Au, T.W. A novel computation of delay margin based on grey wolf optimisation for a load frequency control of two-area-network power systems. Energies 2023, 16, 2860. [Google Scholar] [CrossRef]
Can, O.; Ozturk, A.; Eroglu, H.; Kotb, H. A novel grey wolf optimizer based load frequency controller for renewable energy sources integrated thermal power systems. Electric Power Components and Systems 2022, 49, 1248–1259. [Google Scholar] [CrossRef]
Chaturvedi, D.K.; Umrao, R.; Malik, O.P. Adaptive polar fuzzy logic based load frequency controller. International Journal of Electrical Power and Energy Systems 2015, 66, 154–159. [Google Scholar] [CrossRef]
Cam, E. Application of fuzzy logic for load frequency control of hydroelectrical power plants. Energy Conversion and Management 2007, 48, 1281–1288. [Google Scholar] [CrossRef]
Kocaarslan, I; Cam, E. Fuzzy logic controller in interconnected electrical power systems for load-frequency control. International Journal of Electrical Power and Energy Systems 2005, 27, 542–549. [Google Scholar] [CrossRef]
Yousef, H.A.; Khalfan, A.K.; Albadi, M.H.; Hosseinzadeh, N. Load frequency control of a multi-area power system: An adaptive fuzzy logic approach. IEEE Transactions on Power Systems 2014, 29, 1822–1830. [Google Scholar] [CrossRef]
Chaturvedi, D.K.; Satsangi, P.S.; Kalra, P.K. Load frequency control: a generalized neural network approach. International Journal of Electrical Power and Energy Systems 1999, 21, 405–415. [Google Scholar] [CrossRef]
Al-Majidi, S.D.; Kh. AL-Nussairi, M.; Mohammed, A.J.; Dakhil, A.M.; Abbod, M.F.; Al-Raweshidy, H.S. Design of a load frequency controller based on an optimal neural network. Energies 2022, 15, 6223. [Google Scholar] [CrossRef]
Zhao, S.; Zhang, T.; Ma, S.; Wang, M. Sea-horse optimizer: a novel nature-inspired meta-heuristic for global optimization problems. Applied Intelligence 2022, 1, 1–28. [Google Scholar] [CrossRef]
Abd-elazim, S.M.; Ali, E.S. Load frequency controller design of a two-area system composing of PV grid and thermal generator via firefly algorithm. Neural Computing and Applications 2018, 30, 607–616. [Google Scholar] [CrossRef]
Khadanga, R.K.; Kumar, A.; Panda, S. A novel modified whale optimization algorithm for load frequency controller design of a two-area power system composing of PV grid and thermal generator. Neural Computing and Applications 2020, 32, 8205–8216. [Google Scholar] [CrossRef]
Tomy, F.T.; Prakash, R. Load frequency control of a two area hybrid system consisting of a grid connected PV system and thermal generator. International Journal of Research in Engineering and Technology 2014, 3, 573–580. [Google Scholar]

Figure 1. The two-area power system.

Figure 2. The flowchart of the proposed SHO algorithm.

Figure 3. The proposed SHO algorithm optimizing PI/PID parameters for LFC problem.

Figure 4. Frequency response of Area-1 to load changes in both regions with PI controllers.

Figure 5. Frequency response of Area-2 to load changes in both regions with PI controllers.

Figure 6. Power response in tie-line to load changes in both regions with PI controllers.

Figure 7. Converge curve of the proposed SHO algorithm for LFC problem.

Figure 8. Frequency response of Area-1 to load changes in both regions with PID controllers.

Figure 9. Frequency response of Area-2 to load changes in both regions with PID controllers.

Figure 10. Power response in tie-line to load changes in both regions with PID controllers.

Figure 11. Frequency response of Area-1 to large load disturbances.

Figure 12. Frequency response of Area-2 to large load disturbances.

Figure 13. Power response in tie-line to large load disturbances.

Figure 14. Change of solar radiation.

Figure 15. Response of LFC to change in solar radiation.

Table 1. Parameters of the test system.

$A$	PV system gain 1	18
$E$	PV system gain 2	900
$C_{T}$	PV system time constant 1	100
$D_{T}$	PV system time constant 2	50
$K_{G}$	Governor gain	1 p.u. MW
$τ_{G}$	Governor time constant	0.08 sec
$K_{T}$	Turbine gain	1 p.u. MW
$τ_{T}$	Turbine time constant	0.3 sec
$K_{r}$	Reheat gain	0.33 p.u. MW
$τ_{R}$	Reheat time constant	10 sec
$K_{P S}$	Power system gain of thermal area	120 Hz/p.u. MW
$τ_{P S}$	Power system time constant	20 sec
$R$	Regulation droop	0.4 Hz/p.u. MW
$B$	Frequency bias constant	0.8 p.u.
$τ_{t i e}$	Tie-line power coefficient	0.545

Table 2. Parameters of SHO algorithm for solving LFC problem.

Parameter	Value
Number of sea horse	50
Iteration number	100
$u$	0.05
$v$	0.05
$l$	0.05
Lower bound for [ $K_{p}$ ; $K_{i}$ ; $K_{d}$ ]	[-2; -2; -2]
Upper bound for [ $K_{p}$ ; $K_{i}$ ; $K_{d}$ ]	[2; 2; 2]

Table 3. Controller parameters for the PV-thermal power system.

Parameter	Methods
Parameter	SHO-tuned PID (proposed)	MWOA-tuned PID [36]	SHO-tuned PI (proposed)	WOA-tuned PI [36]	FA-tuned PI [35]	GA-tuned PI [35]
$K_{p 1}$	-0.8599	-0.1070	-0.67012	-0.4563	-0.8811	-0.5663
$K_{i 1}$	-0.1290	-0.0906	-0.5371	-0.2254	-0.5765	-0.4024
$K_{d 1}$	-1.9396	-0.6112	-	-	-	-
$K_{p 2}$	-2.0000	-1.8938	-2.0000	-0.8967	-0.7626	-0.5127
$K_{i 2}$	-2.0000	-1.8935	-0.8476	-0.9865	-0.8307	-0.7256
$K_{d 2}$	-0.2614	-0.2505	-	-	-	-
ITAE	0.8582	1.5602	2.5308	4.1211	7.4259	12.1244

Table 4. Specifications of dynamic responses with optimized PI controller.

Parameters		GA	FA	WOA	SHO (proposed)
∆f₁	Overshoot (M⁺)	0.1638	0.1577	0.07997	0.001733
	Undershoot (M^-)	-0.2966	-0.3154	-0.2015	-0.04374
	Settling Time (s)	26.73	26.44	26.30	12.62
∆f₂	Overshoot (M⁺)	0.1571	0.1228	0.09816	0.1012
	Undershoot (M^-)	-0.2435	-0.2295	-0.2216	-0.1807
	Settling Time (s)	23.64	23.60	25.54	15.75
∆P_tie	Overshoot (M⁺)	0.05636	0.04643	0.0534	0.03823
	Undershoot (M^-)	-0.04921	-0.04778	-0.03814	-0.03215
	Settling Time (s)	27.73	26.45	21.07	18.04

Table 5. Performance indisces values of compared algorithms.

Techniques	IAE	ITAE	ISE	ITSE
GA-tuned PI	2.3341	12.1244	0.3202	0.8618
FA-tuned PI	1.7207	7.4259	0.2907	0.4723
WOA-tuned PI	1.0566	4.1211	0.1663	0.4262
SHO-tuned PI	0.6491	2.5308	0.1021	0.26179
MWOA-tuned PID	0.5625	1.5602	0.0815	0.0601
SHO-tuned PID	0.3091	0.8582	0.0448	0.0369

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Novel Sea Horse Optimizer Based Load Frequency Controller for Two-Area Power System with PV and Thermal Units

Abstract

1. Introduction

2. System Modeling

3. Sea Horse Optimizer Algorithm

4. Sea Horse Optimization Based Load Frequency Control

4.1. PI Controller

4.2. PID Controller

5. Simulation Results and Discussion

5.1. Scenario 1: Performance Comparison of Proposed SHO Optimized Controller with Other Reported Algorithms

5.2. Scenario 2: Effect of High Load Demand on System Stability

5.3. Scenario 3: Influence of Solar Radiation Variation

5.4. Performance Indices and Robustness

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe