Prerpints.org logo
Preprint
Article

Numerical Simulation of the Lubricant-Solid Interface Using the Multigrid Method

This is a preprint, it has not been peer-reviewed.

Submitted:

14 April 2023

Posted:

17 April 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Solid asperity interactions are common and inevitable under severe loading conditions for any lubricated contact. Heavy-duty machine components (gear, bearings etc.) generally operate under Mixed Lubrication, where uneven surface features contact each other when generated fluid pressure is not enough to support the external load. The Reynolds equation is commonly used to simulate smooth lubricated contacts numerically. In rough lubricated interfaces where opposite surface asperities make contact, the Reynolds equation alone cannot accurately predict pressure using the traditional numerical simulation method. In this paper, Lubrication-Contact interface conditions (LCICs) have been implemented and extended to solve the multiple asperity contact problem using the full-multigrid approach. The developed novel algorithm has significantly accelerated the solution process and improved the accuracy and efficiency of pressure calculation for fluid-solid sub-interactions that can occur under ML regions. The Finite Difference Method (FDM) results have been compared with Computational Fluid Dynamics (CFD) simulation to validate the newly developed model. Hence, the proposed optimized solution method will provide valuable insight to researchers and industry engineers interested in simulating the ML problem where the effect of the fluid-solid interface can be captured effectively to improve reliability in the calculation of the life expectancy of the lubricated parts.
Keywords: 
  -  

1. Introduction

Lubrication of machine components is critical for the reliable and long-term performance of any mechanical system. Numerical simulation is a more cost-effective method than experimental methods for designing and investigating lubricated systems for a variety of applications. In lubrication, the hydrodynamic effect generates internal fluid pressure which maintains separation between relatively moving surfaces. The traditional Reynolds equation has been employed for calculating fluid pressure in most cases. The basis for this is founded on the fact that the film thickness is relatively smaller compared to the length of smooth and near-parallel interacting surfaces. The Reynolds equation can be applied in the situation when the opposite surfaces and their topographical features can be completely pushed away by the developed lubricating film, in full-film lubrication and Elasto Hydrodynamic Lubrication (EHL) regions. However, the majority of the lubricated machine components change the lubrication regime as the external load and speed vary. In engineering applications, rough surfaces are common (see Figure 1) which results in an inevitable effect on lubrication performance, especially when concentrated contacts operate under heavy-load and low-speed conditions known as mixed lubrication conditions. Many power and motion transition components, for example, gears, cam and followers, and bearings generally work under the Mixed region of lubrication (ML) where solid and fluid contacts coexist. Therefore, proper boundary conditions are required to numerically simulate the ML using the Reynolds equation.
In the worst circumstances of lubrication where different surface features take part to support the external load, local experimentation is nearly impossible or very expensive. Even though expensive mixed lubrication experimentation can only yield a general trend of contact performance and behaviours. In this case, simulation must be used to acquire precise information about what actually occurs at the roughness scale. The field of EHL numerical simulation has met with great success in many problems, for example, the development of efficient simulation algorithms for the precise study of film thickness and deformation calculations. The available EHL and Mixed lubrication (ML) models are based on assumptions that are not valid when roughness features (asperities) make contact resulting in an inaccurate calculation of pressure and external load-carrying capacity. In this study, a new model for predicting the pressure distribution for asperity contact has been proposed and verified using the CFD simulation.
Several studies are reported in the literature focusing on surface roughness effects on the functionality and lifespan of lubricated contact, and this topic is currently a priority for tribology industries [1,2,3,4]. A thorough assessment of the history of numerical simulation of the ML is well documented in the literature [5,6,7,8]. To numerically simulate the rough lubricated contacts stochastic and deterministic models have been used in past. Patir and Cheng [9] developed a famous stochastic average flow model for rough lubricated surfaces. Where the traditional Reynolds equation has been modified by including both pressure and shear flow factors that will be the functions of surface roughness characteristics. A separate deterministic sub-model is required for determining the flow factors, which will provide a general effect exhibited by surface roughness when using the average flow model. However, this model is unable to give specific details regarding the elevated pressure areas where roughness peaks of the opposite surface contact with each other [10,11,12,13]. Later, deterministic models had been introduced for robust design calculation where local variation in tribological parameters can be predicted. The deterministic mixed lubrication study begins with the simple irregularities in the form of a sinusoidal roughness [14] and progresses to the digital real rough surface simulation [15].
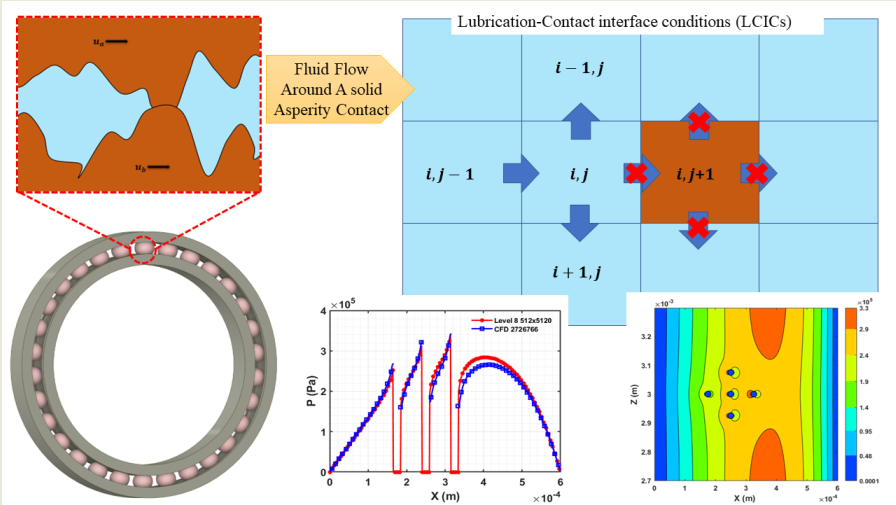
There have been various challenges to numerically simulate the mixed lubrication and asperity contact problem. The most fundamental problem is the boundary conditions (BC) which have been resolved by introducing the Lubrication-Contact interface conditions (LCICs) [11] and is applicable for the surfaces where 𝜀=dh/dL ratio is very less and velocity changes in the film thickness direction can be ignored. However, the model has limitations, since it can only be applied to a limited range of mesh sizes. In the case of multiple solid blocks, a fine mesh will be required, and this algorithm is ineffective to provide accurate solutions. Similarly, Deolalikar et al. [16] adopted the no-flow BC by treating the fluid and solid contact zone separately. Many authors have used this method to some extent [17,18]. The other problems are that we need a high degree of discretization to capture the local physical reality which will further require high computational power. The calculation of micro deformation, thermal, non-Newtonian and transient effects complicate the problem in terms of calculation time and efforts required to solve the problem.
The MG (Multigrid) technique has been an important part of numerically solving lubricated contacts for decades, ever since Lubrecht et al. [19] first used it in 1986 for their EHL solution Later Venner [20] significantly enhanced the relaxation method by utilizing the multigrid approach for isothermal EHL problems. Liu, Wang et al. [21] investigated the impact of various differential schemes on EHL calculations using the semi-system approach [22]. Various differential scheme has no effect when sufficient film thickness is achieved to keep the contacting surfaces apart. However, for ultra-thin film thickness e.g., below 10-20 nanometres the influence becomes more significant because truncation errors are large for higher-order discretization (2C) in the case of sharp gradients [21]. Whereas truncation errors are low for low-order discretization schemes (1B). Hence, the literature provides evidence that the first-order backward scheme (1B) solves the problem more accurately compared to the second-order central schemes[11,21].
This paper’s major goal is to numerically simulate the impact of asperity contact operating under ML conditions. In order to make multiple asperities the solution grid should be fine enough to capture the geometrical configuration of the gap between the contact accurately. Liu, Wang et al. have used the LCICs boundary conditions for a single block of the square and cylindrical cross-section with a mesh size of 128×128 nodes [11]. For multiple solid contacts, however, the method is limited because of computational efficiency and accuracy requirements since multiple asperities would need to be represented with a fine grid to get the local pressure distribution. The fine grid has a low residual reduction rate compared to the coarse grid, and with the increasing number of unknowns (n), the asymptotic convergence speed becomes slow [20]. In this paper for predicting the pressure distribution for multiple asperity contact, a full multigrid (FMG) method has been implemented and produced results have been verified using the CFD simulation. The shear flow term of the Reynolds equation has been solved by using the first-order backward differential scheme to improve the accuracy and it has also been demonstrated that conventionally used second-order central (2C) differential scheme cannot accurately estimate the hydrodynamic effect of asperity contact that may occur in ML conditions.

2. Modelling Approach

Conformal and nonconformal contacts have been simplified as a wedge problem with a converging gap between the two interacting surfaces. An assumption has been taken here that the inclined upper and lower surfaces are making contact through the rigid solid asperities and blocking the flow of lubricant to represent the mixed lubrication condition. This study numerically calculates the effect of solid asperities of cylindrical cross-section, blocking the lubricant flow at the interface of the converging wedge without considering deformation. Here the upper contacting wall is stationary, and the lower wall is moving with a velocity of 1m/s. Similar geometries have also been used in literature to simplify the mixed lubrication problem [11]. The Lubrication-Contact Interface Conditions (LCICs) have been adopted to ensure that no physical flow can pass through the interface [23]. Hence, a novel and advanced deterministic model has been designed to numerically simulate the converging wedge film with solid asperity contact to determine the fluid pressure using the Reynolds equation. To simplify the problem, it has been presumed that the solid pressure is larger than the pressure of the fluid film. Hence, it allows the solid asperities to make contact with the bottom surface. Therefore, the model is a simplified version of mixed lubrication without considering the solid contact pressure. To numerically simulate the problem, using the Reynolds equation the first-order backward (1B) finite difference discretization method has been utilised for the Couette Flow (CF) terms, which produced more accurate results compared to the 2nd-order central difference (2C) scheme. FDM-generated pressure has been compared with the CFD model for verifying the results. CFD uses the Navier-Strokes equations to solve the model using Finite Volume Method (FVM) [24]. To deal with cavitation during the flow simulation multiphase mixture model has been used. Where the mass transfer between the two phases is governed by the Schnerr and Sauer cavitation model [25]. When the pressure of any liquid reduces to a level below its saturation pressure (Ps = 13 Pa) then the liquid will start to convert into a vapour phase.

3. CFD Model Setup

The design module of the ANSYS software has been used to construct the 3D model of converging wedge film thickness with various shaped contacting solid asperities. It’s been presumed that the contact surfaces are smooth with no-slip boundary conditions. For greater stability, accuracy, and convergence in fluid simulation, the structured mesh has been designed using the ICEM CFD software [23,26] . The mesh sensitivity analysis has been conducted for each model. The CFD solution has been obtained using double precision, a pressure-based model where flow is considered laminar. The momentum and continuity equations have been solved by using Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithmic approach. Pressure inlet and outlet boundary conditions have been applied during the CFD simulation. The below table lists the various parameters that have been used to model the problem.
Table 1. The below table shows the parameters used in the CFD model.
Table 1. The below table shows the parameters used in the CFD model.
Parameters Value Unit
Velocity u 1 m/s
Inlet height h i 10 10-6 m
Outlet height h o 6 10-6 m
Solid Properties
Solid Elastic Modulus 210 G Pa
Solid Poisson’s ratio 0.3 -
Solid Density 7850 kg/m3
Lubricant Properties
Viscosity of the lubricant, η 0.085 Pa∙s
Kinematic viscosity, ν 100 mm3/s
Reynolds Number, Re 0.1 or less -
Oil Density ρ 850 kg/m3
Vapour density 0.0288 kg/m3
Vapour viscosity 8.97×10-6 Pa∙s

4. FDM Model

Equation 1 shows the dimensionless Reynolds equation:
∂ ∂ X ¯ ξ ∂ P ¯ ∂ X ¯ + K 2 ∂ ∂ Y ¯ ξ ∂ P ¯ ∂ Y ¯ = ∂ H ¯ ∂ X ¯
where ξ = H ¯ 3 , K = L x L Y , P ¯ = Hydrodynamic Pressure H ¯ = film thickness, X ¯ = direction of flow, Y ¯ = lateral axis to the flow direction. Here the left hand side (LHS) terms are known as the Poiseuille terms, and the right hand side (RHS) term is called the wedge term. In wedge terms, H (film thickness) can be defined analytically. Equation 2 shows the dimensionless film thickness used for the converging simple wedge geometry.
H ¯ = H 0 + 1 − X ¯
The Reynolds equation has been discretized using the 2C discretization scheme and shown in equation 3:
ξ i + 0.5 , j P ¯ i + 1 , j − ξ i + 0.5 , j + ξ i − 0.5 , j P ¯ i , j + ξ i − 0.5 , j P ¯ i − 1 , j ∆ X ¯ 2 + K 2 ξ i , j + 0.5 P ¯ i , j + 1 − ξ i , j + 0.5 + ξ i , j − 0.5 P ¯ i , j + ξ i , j − 0.5 P ¯ i , j − 1 ∆ Y ¯ 2 = H ¯ i + 1 , j − H ¯ i − 1 , j 2 ∆ X ¯
The higher-order discretization scheme (e.g., 2C) provides close to exact results for thick fluid films. Hence, both the Poiseuille terms and wedge terms have been discretized using the 2C discretization. However, for ultra-thin fluid film or where a large gradient of film thickness exists, using the 1B scheme for wedge term provides a more accurate solution than the 2C scheme, because truncation errors are significant with higher-order schemes in the case of sharp gradients [21]. Lui et al. has suggested using the 1B scheme for the RHS of the Reynolds equation [11]. Hence, following the author’s [11] recommendation, equation 1 can also be discretized as equation 4, where the Couette flow or wedge flow term has been discretized using the 1B scheme.
ξ i + 0.5 , j P ¯ i + 1 , j − ξ i + 0.5 , j P ¯ i , j − ξ i − 0.5 , j P ¯ i , j + ξ i − 0.5 , j P ¯ i − 1 , j ∆ X ¯ 2 + K 2 ξ i , j + 0.5 P ¯ i , j + 1 − ξ i , j + 0.5 P ¯ i , j − ξ i , j − 0.5 P ¯ i , j + ξ i , j − 0.5 P ¯ i , j − 1 ∆ Y ¯ 2 = H ¯ i , j − H ¯ i − 1 , j ∆ X ¯
Below, equation 5 shows the different terms of the Reynolds equation in the form of flow continuity suggested by Liu et al. [27]. Where P referred to Poiseuille Flow terms and C referred to Couette flow terms. Equation 4 can also be written by considering the right-hand side function f ( i , j ) when applying the full multigrid (FMG) approach.
Q P X i + 0.5 , j − Q P X i − 0.5 , j ∆ X ¯ + K 2 Q P Y i , j + 0.5 − Q P Y   i , j − 0.5 ∆ Y ¯ − Q c X i + 0.5 , j − Q c X i − 0.5 , j ∆ X ¯ = f i , j
The above equation 5 shows the discretized Reynolds equation in the form of flow continuity suggested by Liu et al. [11].

5. Relaxation

While solving the Reynolds equation negative pressure has been kept equals zero because the Reynolds equation is not valid in the cavitation region. The problem has been solved on a unit square domain Γ= [0,1] × [0,1]. In this paper, the model is assumed to have smooth contacting surfaces producing a converging wedge-shaped film thickness where the inclined upper wall is stationary with the moving lower surface at 1m/s velocity. The inlet height is 10μm and outlet height is 6μm, and the length of the converging wedge is 600μm. At the boundaries the pressure is assumed to be zero, and any predicted negative pressure during iteration is also considered zero. Furthermore, the residuals are only calculated for positive pressure regions hence, cavitated regions should have zero residuals. To define the interface boundary condition between the fluid and solid it has been assumed that the external load is larger than the hydrodynamic pressure generated in the lubricated contact and the fluid will flow around the solid asperity contact. On the other hand, if the fluid pressure is higher than the external load, the fluid will lift the solid asperity contact and begin flowing in without making any solid contact. Hence, to mathematically define the solid contact, we must ensure that the fluid-solid interface does not allow any physical flow to pass through it. As a result, the NO-flow restriction has been incorporated into the Reynolds equation with zero film thickness. For more information on the application of Lubrication-contact interface conditions (LCICs) readers are referred to reference [11].
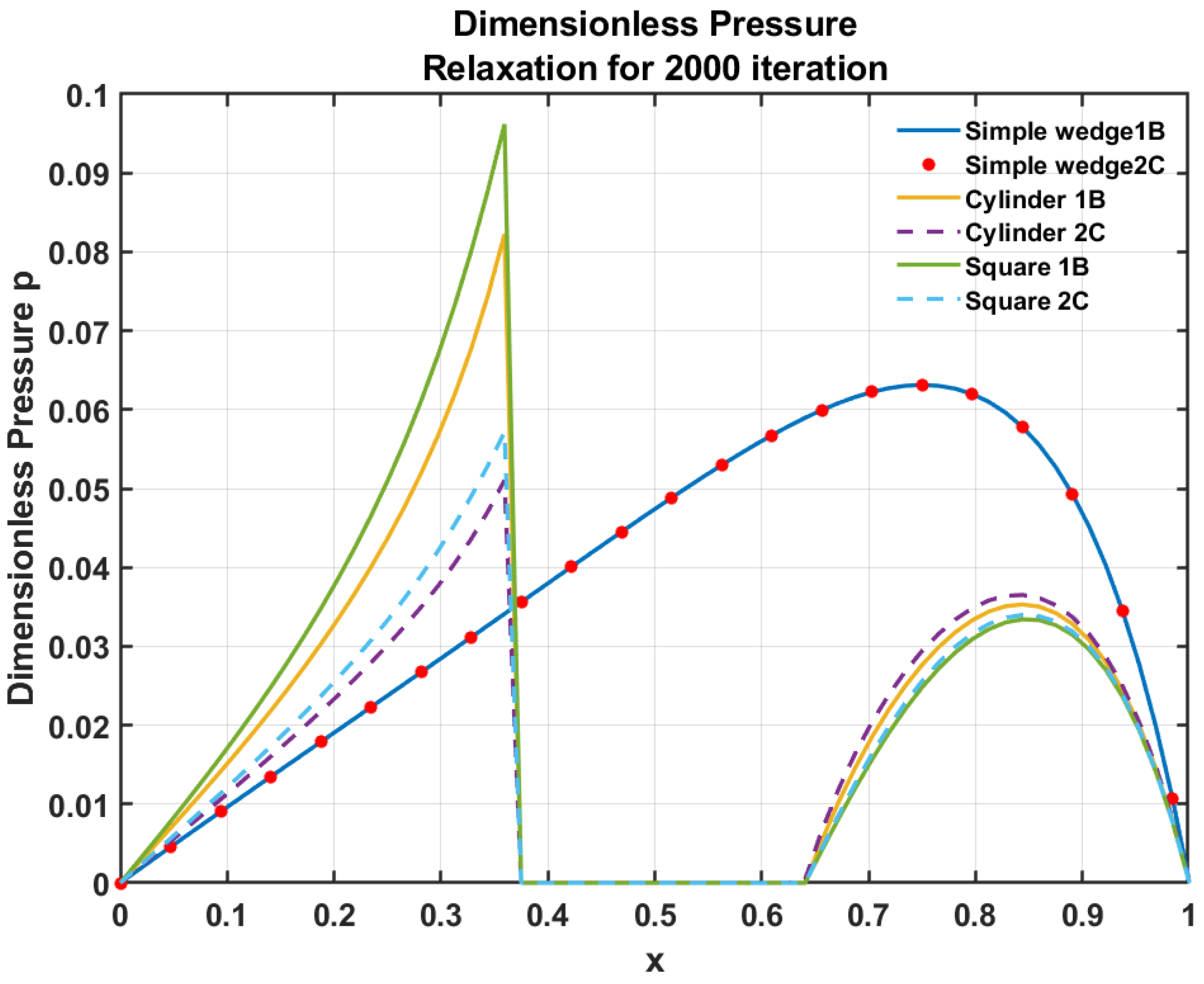
Figure 3 represents the pressure distribution calculated using the Gauss-Seidel relaxation, additionally, LCICs boundary conditions have been adopted to calculate pressure when the fluid flow is blocked by the solid obstacle of square and cylindrical cross-section [11]. The result shows that the discretization schemes (1B and 2C) do not affect pressure when the fluid film is uninterrupted. For instance, in the case of a converging simple wedge both the discretization schemes produce an equal pressure profile. However, in the case when fluid flow is blocked using 8 mm length square and 8mm diameter cylindrical asperity different discretization scheme gives different results. Figure 3 illustrates that the first-order backward scheme accurately captures the increase in pressure when the fluid hits a solid asperity. However, the second-order central scheme (2C) cannot accurately predict the pressure variation. Liu, Wang et al. have well explained why different discretization schemes give different pressure [2]. A sharp increase in the pressure is observed before the solid obstacle at which point the conversion of flowing fluid kinetic energy changes into pressure energy.
Preprints 71064 g002
Figure 2. Shows the dimensionless pressure calculated using Gauss-Seidel relaxation on a single level for 2000 iterations where K = 1, Length = 30mm, Width = 30mm, inlet height = 1mm, outlet height 0.4mm, side of square 8mm, and diameter of the circle is 8mm.
Figure 2. Shows the dimensionless pressure calculated using Gauss-Seidel relaxation on a single level for 2000 iterations where K = 1, Length = 30mm, Width = 30mm, inlet height = 1mm, outlet height 0.4mm, side of square 8mm, and diameter of the circle is 8mm.
Preprints 71064 g002
Liu, Wang et al. have solved the same geometrical problem where [11] cylindrical and square pillar blocks have been numerically simulated for many iterations to get the converged solution for a particular grid size (128×128 or 256×256). For higher grid sizes the iteration will take a long time to calculate the accurate solution. Furthermore, if multiple asperity contacts are to be simulated, a fine grid must be used. Consequently, the convergence rate will be reduced, and an accurate solution will be less likely to be obtained within a short timeframe. Therefore, A new approach is needed that can simulate the asperity contact problem efficiently, accurately and in less time. A common technique to increase the overall efficiency of the process is a multigrid method. In the next section, we have used the Full multigrid method together with LCIC’s boundary conditions around the solid object.

6. Full Multigrid Approach

The current paper employs the full multigrid (FMG) algorithm, which solves the discretized Reynolds equation starting from the coarsest grid and leading to the finest grid while interpolating the solution from the current grid to the subsequent finer grid. The main aim of the algorithm is to quickly reduce the algebraic errors below discretization errors on a given grid before actually moving to the next finer grid [20]. To get the convergence acceleration Full Multigrid methods described by Venner [20] have been used. The simulations were performed using 8 levels with 512×5120 discretization points on the finest grid. The produced results have been compared with a 3D CFD model for validation. To compare results with CFD we must make sure that the flow is laminar. It has recently been reported that in order to compare FDM with CFD for simple wedge problems, we require the wedge problem to be solved for the line contact [23].

7. Results and Discussion

Various results produced using the FDM and CFD have been shown below section. The outcomes have been examined using a pressure contour plot, which has been created on the middle plane passing through the centre of the domain. Similarly, the pressure has also been compared on the line which passes mid of the inlet and goes out mid of the outlet.

7.1. Simple Wedge Problem

The analytical equations for a 2D simple wedge problem have been described in the literature [23]. For the parameters shown in the table, a simple wedge problem has been solved using three different methods, and the produced pressure distribution (see Figure 3) demonstrates good agreement in the results. The contour plots have also been compared for the FDM and CFD methods.
Preprints 71064 g003
Figure 3. Pressure comparison for simple wedge model.
Figure 3. Pressure comparison for simple wedge model.
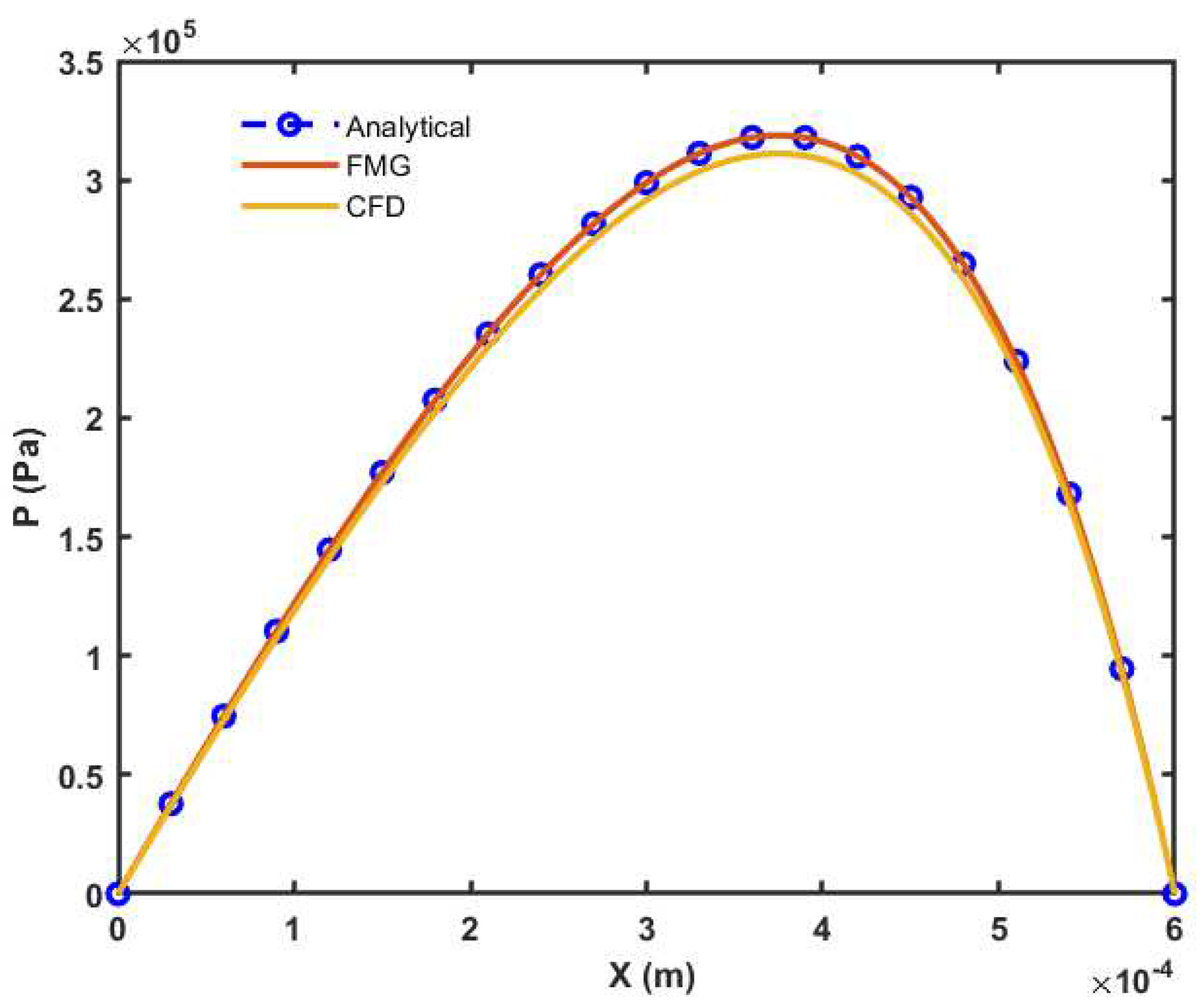
Preprints 71064 g003
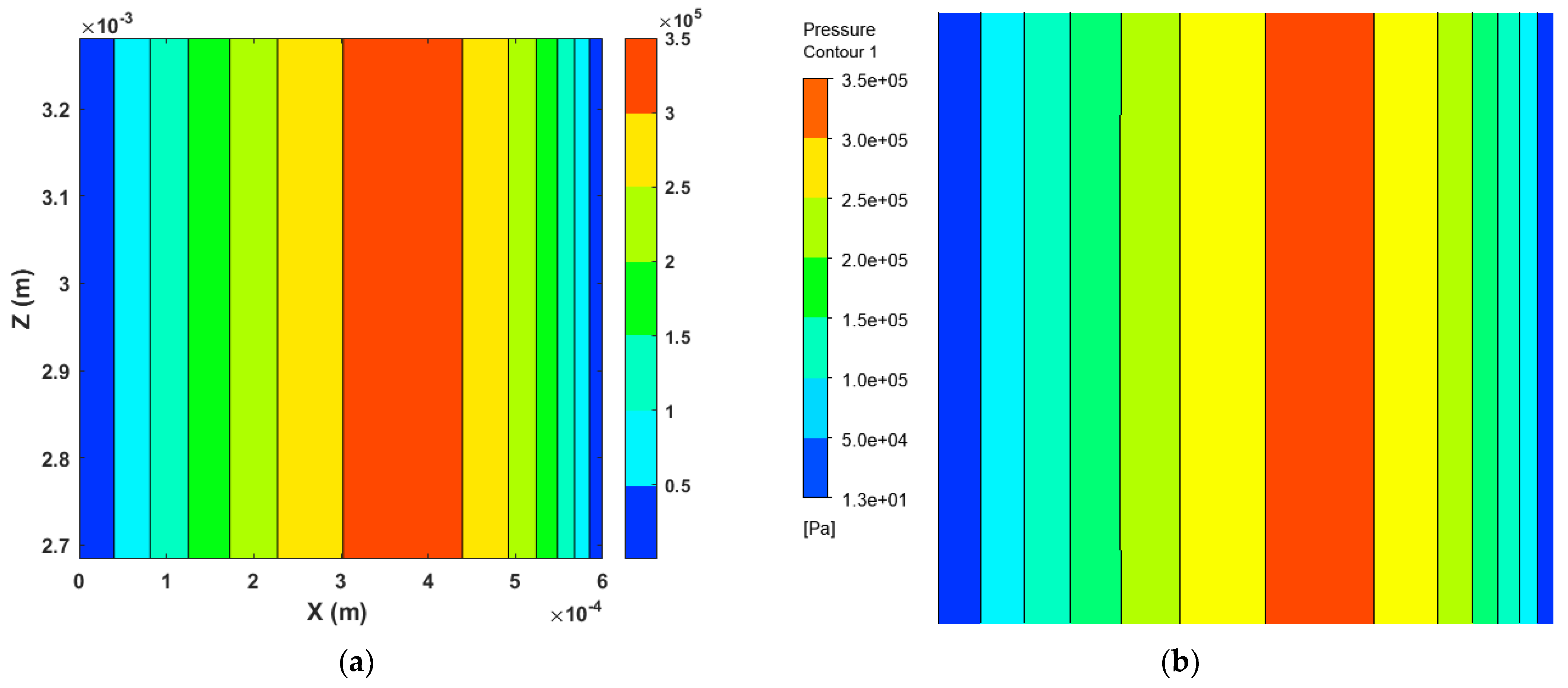
Preprints 71064 g004
Figure 4. Pressure contour plots were created using (a) FDM Method and (b) the CFD method.
Figure 4. Pressure contour plots were created using (a) FDM Method and (b) the CFD method.
Preprints 71064 g004

7.2. One Cylindrical Solid Asperity

In this section, one solid cylindrical asperity has been simulated using the Full Multigrid method. The length of the domain is 600 μ m and the width of the domain is 6000 μ m , hence, the length-to-width ratio (K) is equal to 0.1. The radius of the cylindrical asperity is 10 μ m and the position of the centre of the asperity is (250 μ m , 3000 μ m ). Below Figure 5a is showing the mesh convergence analysis which has been conducted by using the FDM. Figure 5b is showing the mesh convergence analysis which has been performed by using CFD simulation for various mesh sizes and Figure 5c represents the comparison of the pressure profile produced using FDM and CFD method using the converged mesh size. The pressure comparison on a line shows less than a 4% difference in results behind the cylindrical asperity. It is evident from the contour plots produced in Figure 6a,b that the developed algorithm, which uses the Full Multigrid method to solve fluid-solid interactions in lubrication, can calculate the correct pressure using a standard personal computer with ease.

7.3. Two Cylindrical Solid Asperity

Similar to the above section, two cylindrical asperities have been made of 10 μm radii, which are 100μm apart from each other and placed one behind the other. The two cylinders have been positioned at (200μm,3000μm) and (300μm,3000μm) respectively. The mesh sensitivity analysis for both methods has been performed and shown in Figure 7a,b. The Pressure comparison on the middle line for FDM and CFD methods shows a less than 5 % difference in Figure 7c. The pressure contour plot (see Figure 8a,b) produced using both methods give comparable results.

7.4. Three Cylindrical Solid Asperity

In this section, the three cylindrical asperities of 10μm have been simulated which are placed in a straight line and 75μm far from each other. The positions of the cylinders are (175μm, 3000μm), (250μm, 3000μm), and (325μm, 3000μm) respectively. The mesh sensitivity results produced using both methods (FDM, CFD) are acceptable (Figure 9a,b). The pressure comparison on the line passing mid of the domain shows an approximate 5% difference in results. The comparison of the pressure contour plot shown in the figure shows acceptable variation in the pressure profile (Figure 10).

7.5. Five Cylindrical Solid Asperity

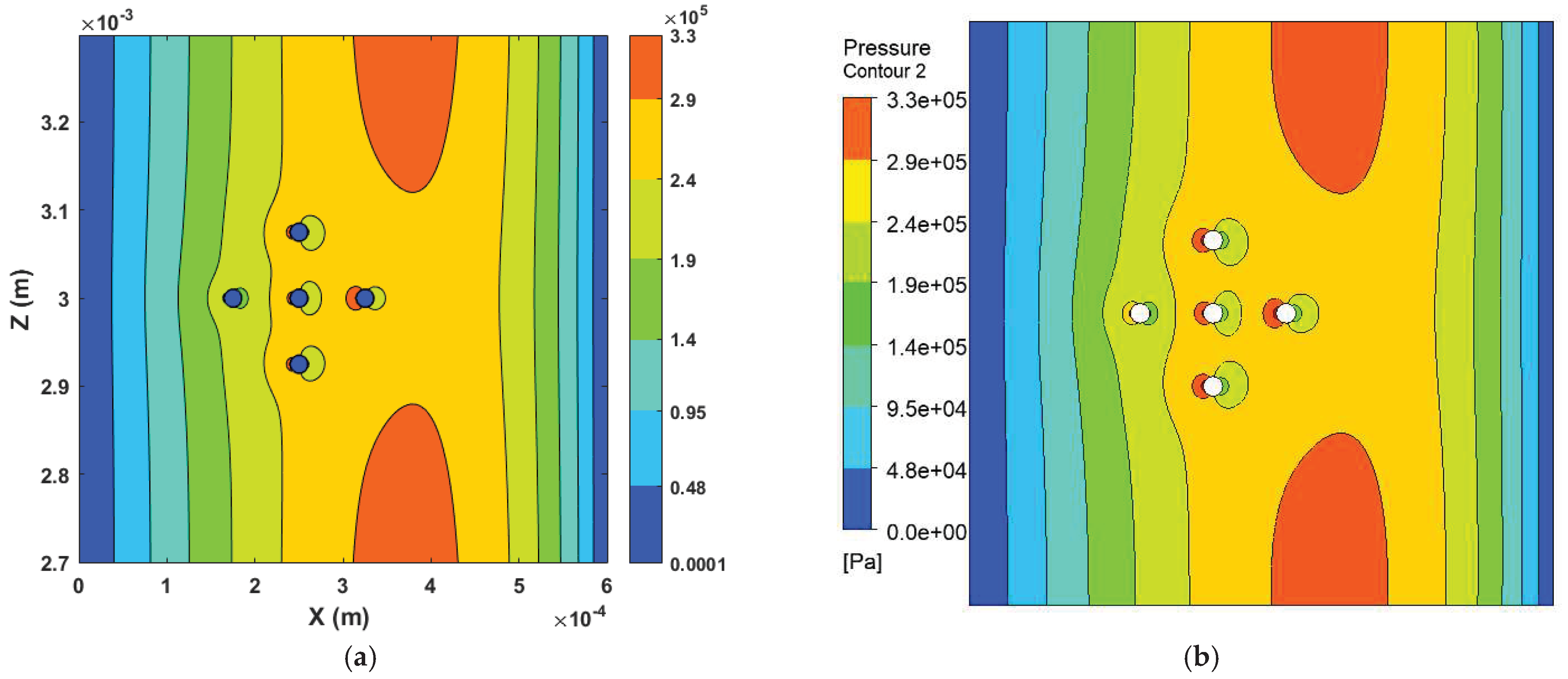
In this section, five cylindrical asperities of 10 μ m radius have been simulated which are placed 75 μ m apart from each other and have been placed as shown in the pressure contour plot in Figure 12. The middle cylinder is 250 μ m distance from the inlet. The mesh sensitivity analysis for both methods has been done by comparing the pressure with different mesh sizes and has been shown in Figure 11a,b. The pressure comparison on the mid-line shows an approximate 5% difference in results and is depicted in Figure 11c. The pressure contour plot (Figure 12) produced using the FDM and CFD matches each other except just before the solid contact. However, the areas where the difference are visible is very small and can be argued due to the difference in mesh used in both methods. In CFD the number of elements is very high compared to the FDM.

8. Conclusions

This paper presents a steady-state deterministic solid-fluid interaction model to numerically simulate the Mixed Lubricated (ML) contacts working under severe conditions. LCICs boundary conditions have been adopted for the numerical simulation of asperity contact flow problems. In this research full multigrid (FMG) algorithms have been developed for efficient and time-effective convergence of the solution with a higher degree of accuracy. This is achieved by solving the model by employing the Finite Difference Method. This analysis has been performed for circular cross-sections at the single and multiple asperity contacts. The fluid pressure distribution has been compared with the 3D CFD simulation of laminar flow under the same working conditions. In the present study, the following key findings were found:
The influence of different differential schemes has no effect on the lubricated contact where contacting surfaces are fully separated with sufficient lubricant film. In cases where solid contact that is, asperity contact considering zero film thickness, significant differences in the pressure distribution are observed when various differential schemes are applied. For example, the conventional second-order central scheme (2C) allows the artificial flow to enter and exit from the solid asperity contact and produce an inaccurate solution.
By employing the 1st Order Backward (1B) scheme in the discretization of Couette Flow terms an optimized and easy solution algorithm has been developed which gives reasonable computational efficiency on a standard personal computer to get detailed solutions around solid asperity contact. With the assistance of a multigrid algorithm, the code execution time is considerably reduced. The robustness of the model has been validated by testing with single, and multiple asperity contact of circular cross-sections. The model can be easily extended to EHL, thermal and transient calculations, where ε = d h d L ratio is smaller than or equal to 0.01, and velocity changes in the film thickness direction can be ignored.

Author Contributions

R.P.: Writing—Original Draft, Methodology, Conceptualization, Software, Formal Analysis, Visualization, and Investigation, Writing—Review and Editing; Z.A.K.: Resources, Writing—Review and Editing, Supervision, Funding Acquisition, and Project Administration; A.S.: Supervision; V.B.: Conceptualization, Formal Analysis, Validation, and Supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by SCHAEFFLER TECHNOLOGIES AG & CO. KG, GERMANY, grant number/grant ID: 12064.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy policy.

Acknowledgements

The present work is part of the project that has been funded by Schaeffler technology AG under agreement ID: 12064. The authors would like to express their gratitude to Schaeffler Technologies AG & Co. KG, Germany, for providing in-kind support for this study at Bournemouth University in the United Kingdom.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

h Film thickness ξ H ¯ 3
n Number of unknows ε dh/dL
u, u0 Velocity of the lower wall ρ Density of oil
Lx Length of the fluid domain η Dynamic viscosity of oil
Ly Transverse direction length P ¯ Dimensionless Pressure
∆ X ¯ Element size in x direction ∆ Y ¯ Element size in Y direction

References

  1. Wang, Y., et al., Understanding the Mechanism of Load-Carrying Capacity between Parallel Rough Surfaces through a Deterministic Mixed Lubrication Model, Lubricants, vol. 10 no. (or iss.) 1, pp. 12, 2022. [CrossRef]
  2. Lv, F., et al., Theoretical and experimental investigation on local turbulence effect on mixed-lubrication journal bearing during speeding up, Physics of Fluids, vol. no. (or iss.) 2022. [CrossRef]
  3. Shi, X.J., et al., Predictions of friction and flash temperature in marine gears based on a 3D line contact mixed lubrication model considering measured surface roughness, Journal of Central South University, vol. 28 no. (or iss.) 5, pp. 1570-1583, 2021. [CrossRef]
  4. Rajput, H., A. Atulkar, and R. Porwal, Optimization of the surface texture on piston ring in four-stroke IC engine, Materials Today: Proceedings, vol. 44 no. (or iss.) pp. 428-433, 2021. [CrossRef]
  5. Dobrica, M.B., M. Fillon, and P. Maspeyrot, Mixed Elastohydrodynamic Lubrication in a Partial Journal Bearing—Comparison Between Deterministic and Stochastic Models, Journal of Tribology, vol. 128 no. (or iss.) 4, pp. 778-788, 2006. [CrossRef]
  6. Spikes, H.A., Mixed lubrication — an overview, Lubrication Science, vol. 9 no. (or iss.) 3, pp. 221-253, 1997. [CrossRef]
  7. Spikes, H.A. and A.V. Olver, Mixed lubrication—Experiment and theory, Tribology Series, vol. 40 no. (or iss.) pp. 95-113, 2002. [CrossRef]
  8. Patel, R., et al., A review of mixed lubrication modelling and simulation, Tribology in Industry, vol. 44 no. (or iss.) 1, pp. 150-168, 2021. [CrossRef]
  9. Patir, N. and H.S. Cheng, An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication, Journal of Lubrication Technology, vol. 100 no. (or iss.) 1, pp. 12-17, 1978. [CrossRef]
  10. Patir, N. and H.S. Cheng, Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces, Journal of Lubrication Technology, vol. 101 no. (or iss.) 2, pp. 220-229, 1979. [CrossRef]
  11. Liu, S., et al., Lubrication–Contact Interface Conditions and Novel Mixed/Boundary Lubrication Modeling Methodology, Tribology Letters, vol. 69 no. (or iss.) 4, pp. 164, 2021. [CrossRef]
  12. Pusterhofer, M., et al., A Novel Approach for Modeling Surface Effects in Hydrodynamic Lubrication, Lubricants, vol. 6 no. (or iss.) 1, pp. 27, 2018. [CrossRef]
  13. Sahlin, F., et al., A mixed lubrication model incorporating measured surface topography. Part 1: theory of flow factors, Proceedings of the Institution of Mechanical Engineers Part J-Journal of Engineering Tribology, vol. 224 no. (or iss.) J4, pp. 335-351, 2010. [CrossRef]
  14. Burton, R.A., Effects of Two-Dimensional, Sinusoidal Roughness on the Load Support Characteristics of a Lubricant Film, Journal of Basic Engineering, vol. 85 no. (or iss.) 2, pp. 258-262, 1963. [CrossRef]
  15. Zhu, D. and Q. Jane Wang, Effect of Roughness Orientation on the Elastohydrodynamic Lubrication Film Thickness, Journal of Tribology, vol. 135 no. (or iss.) 3, 2013. [CrossRef]
  16. Deolalikar, N., F. Sadeghi, and S. Marble, Numerical Modeling of Mixed Lubrication and Flash Temperature in EHL Elliptical Contacts, Journal of Tribology, vol. 130 no. (or iss.) 1, 2008. [CrossRef]
  17. Jiang, X., et al., A Mixed Elastohydrodynamic Lubrication Model With Asperity Contact, Journal of Tribology, vol. 121 no. (or iss.) 3, pp. 481-491, 1999. [CrossRef]
  18. Zhang, S. and C. Zhang, A New Deterministic Model for Mixed Lubricated Point Contact With High Accuracy, Journal of Tribology, vol. 143 no. (or iss.) 10, 2021. [CrossRef]
  19. Lubrecht, A.A., W.E. ten Napel, and R. Bosma, Multigrid, An Alternative Method for Calculating Film Thickness and Pressure Profiles in Elastohydrodynamically Lubricated Line Contacts, Journal of Tribology, vol. 108 no. (or iss.) 4, pp. 551-556, 1986. [CrossRef]
  20. C.H. Venner, A.A.L., Multilevel Methods in Lubrication, ed. E.S. B.V. Vol. 37. 2000, The Netherlands: Elsevier. 400.
  21. Liu, Y., et al., Effects of Differential Scheme and Mesh Density on EHL Film Thickness in Point Contacts, Journal of Tribology, vol. 128 no. (or iss.) 3, pp. 641-653, 2006. [CrossRef]
  22. Wang, Y.C., et al., An Assessment of Quantitative Predictions of Deterministic Mixed Lubrication Solvers, Journal of Tribology-Transactions of the Asme, vol. 143 no. (or iss.) 1, pp. 1-42, 2021. [CrossRef]
  23. Patel, R., et al., CFD Investigation of Reynolds Flow around a Solid Obstacle, Lubricants, vol. 10 no. (or iss.) 7, pp. 150, 2022. [CrossRef]
  24. Meng, Y., et al., A review of advances in tribology in 2020–2021, Friction, vol. 10 no. (or iss.) 10, pp. 1443-1595, 2022. [CrossRef]
  25. Singh, K., et al., Fluid–Structure Interaction Modeling of Elastohydrodynamically Lubricated Line Contacts, Journal of Tribology, vol. 143 no. (or iss.) 9, 2021. [CrossRef]
  26. Hajishafiee, A., et al., A coupled finite-volume CFD solver for two-dimensional elasto-hydrodynamic lubrication problems with particular application to rolling element bearings, Tribology International, vol. 109 no. (or iss.) 1879-2464, pp. 258-273, 2016. [CrossRef]
  27. Liu, S., et al., Influences of Iteration Details on Flow Continuities of Numerical Solutions to Isothermal Elastohydrodynamic Lubrication With Micro-Cavitations, Journal of Tribology, vol. 143 no. (or iss.) 10, 2021. [CrossRef]
Preprints 71064 g001
Figure 1. Exaggerated view of roughness features representing Mixed Lubrication.
Figure 1. Exaggerated view of roughness features representing Mixed Lubrication.
Preprints 71064 g001
Preprints 71064 g005
Figure 5. Results for one cylindrical asperity (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of one cylindrical asperity. (d) Comparison of FDM (Level 8) and CFD results.
Figure 5. Results for one cylindrical asperity (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of one cylindrical asperity. (d) Comparison of FDM (Level 8) and CFD results.
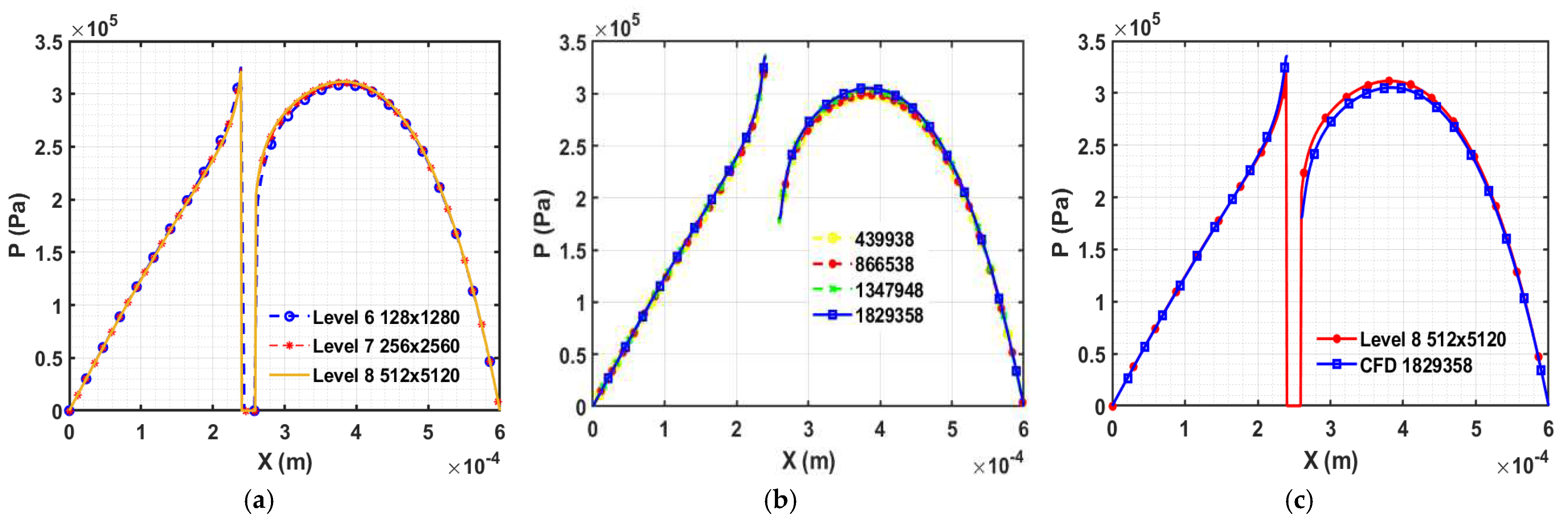
Preprints 71064 g005
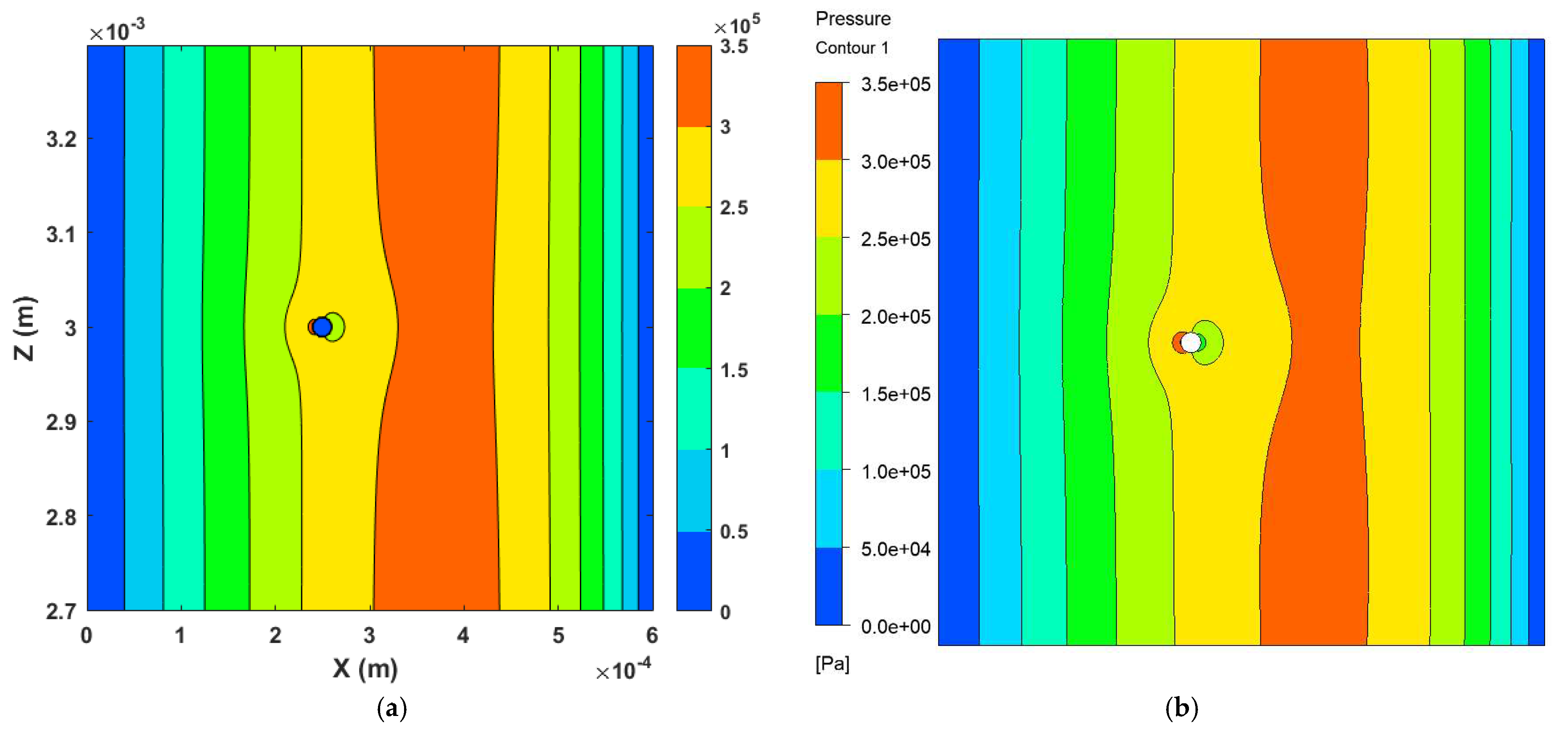
Preprints 71064 g006
Figure 6. Pressure contour plots were created using (a) the FDM method and (b) the CFD method.
Figure 6. Pressure contour plots were created using (a) the FDM method and (b) the CFD method.
Preprints 71064 g006
Preprints 71064 g007
Figure 7. Results for two cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of two cylindrical asperities. (d) Comparison of FDM (Level 8) and CFD results.
Figure 7. Results for two cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of two cylindrical asperities. (d) Comparison of FDM (Level 8) and CFD results.
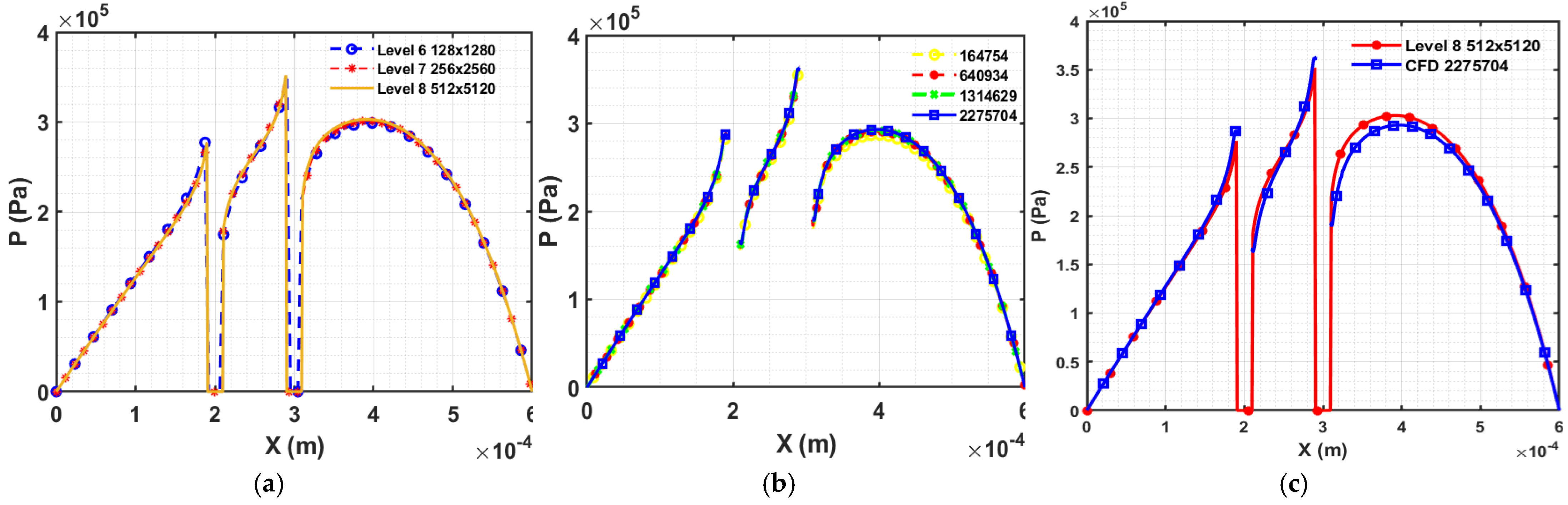
Preprints 71064 g007
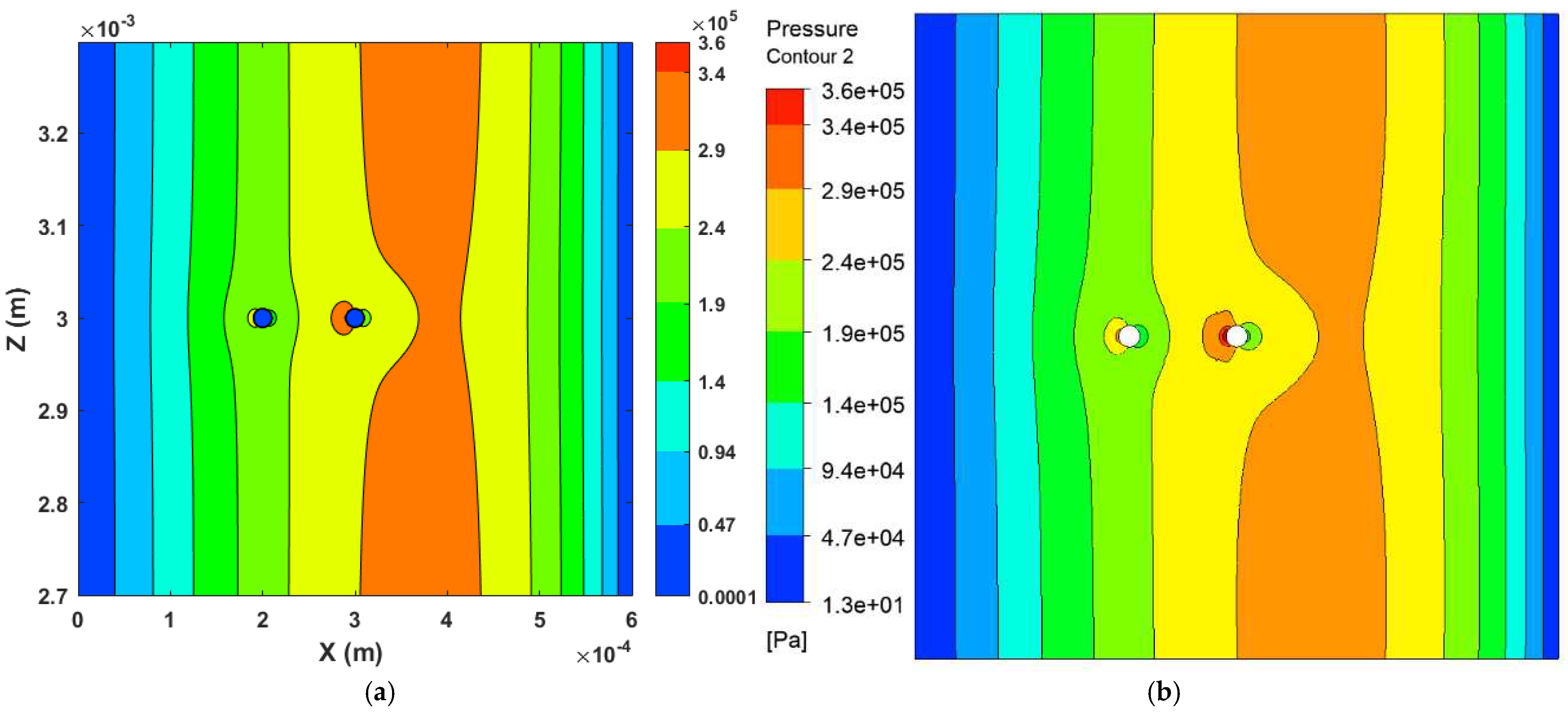
Preprints 71064 g008
Figure 8. Pressure contour plots were created using (a) FDM Method and (b) the CFD method.
Figure 8. Pressure contour plots were created using (a) FDM Method and (b) the CFD method.
Preprints 71064 g008
Preprints 71064 g009
Figure 9. Results for three cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of three cylindrical asperities (d) Comparison of FDM (Level 8) and CFD results.
Figure 9. Results for three cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of three cylindrical asperities (d) Comparison of FDM (Level 8) and CFD results.
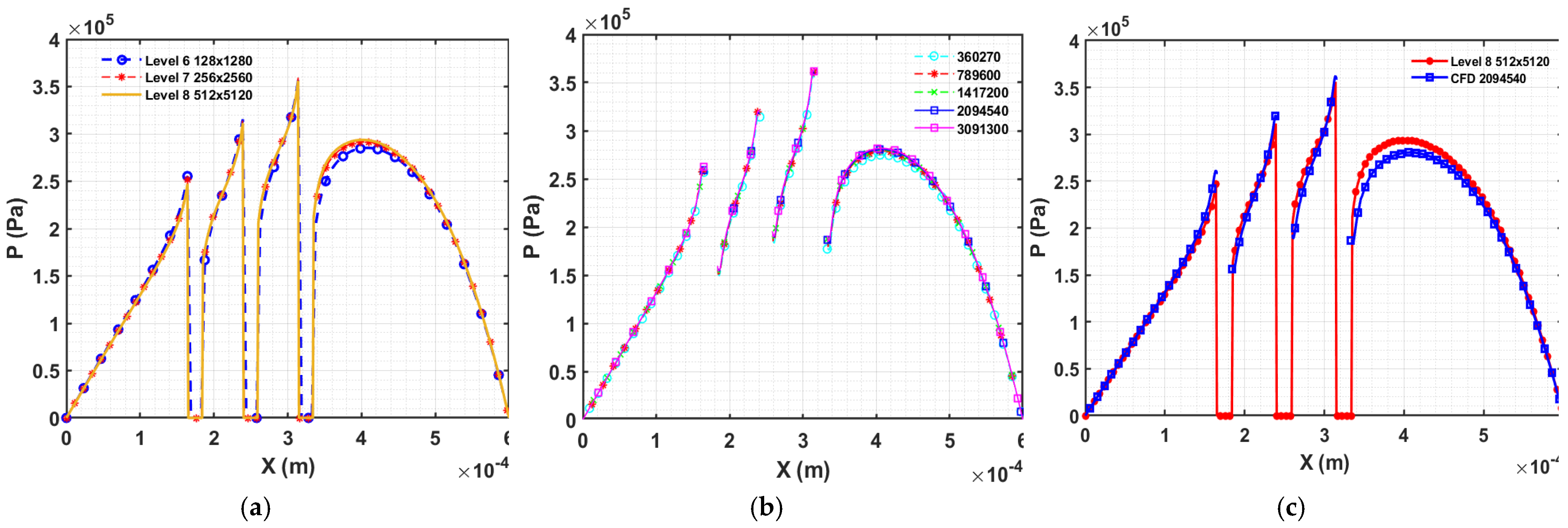
Preprints 71064 g009
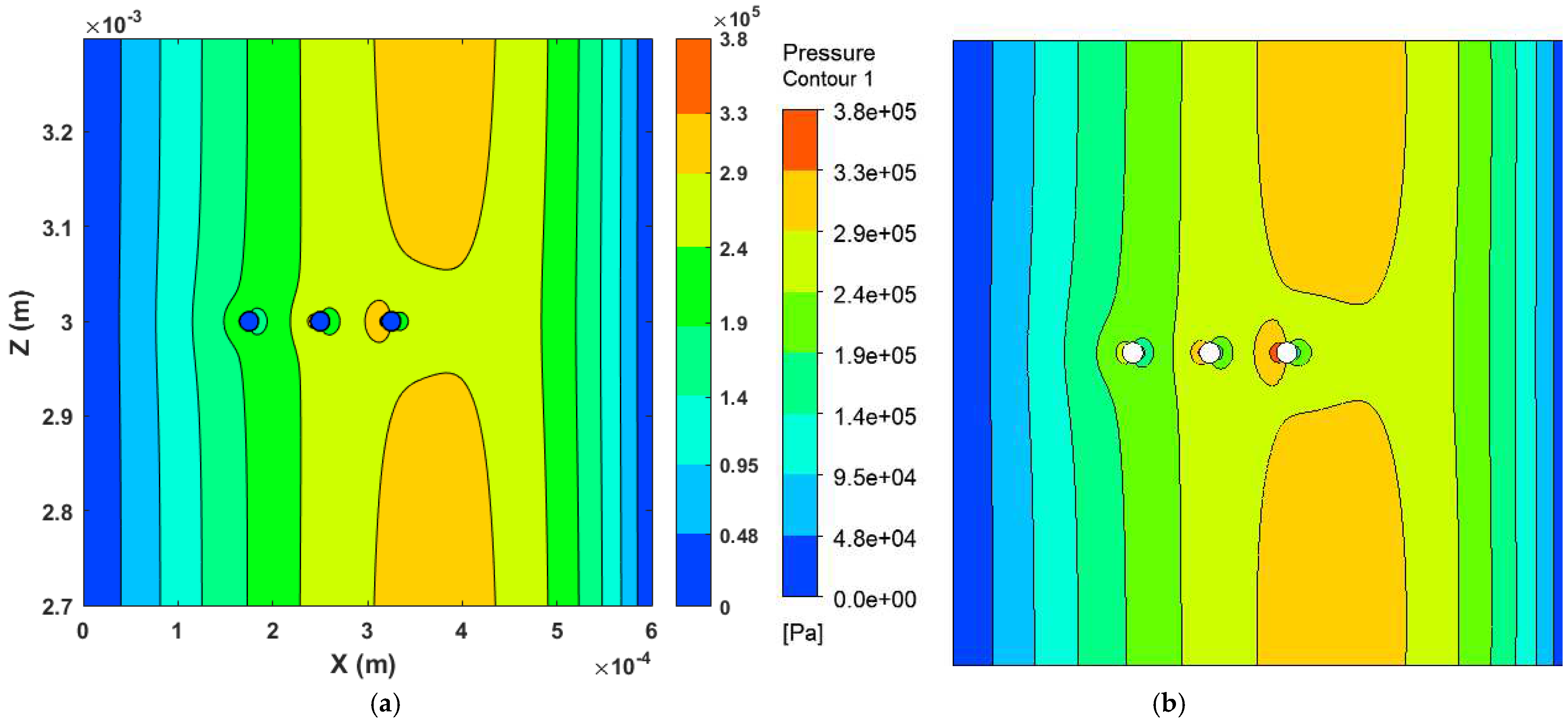
Preprints 71064 g010
Figure 10. Results for three cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of three cylindrical asperities (d) Comparison of FDM (Level 8) and CFD results.
Figure 10. Results for three cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of three cylindrical asperities (d) Comparison of FDM (Level 8) and CFD results.
Preprints 71064 g010
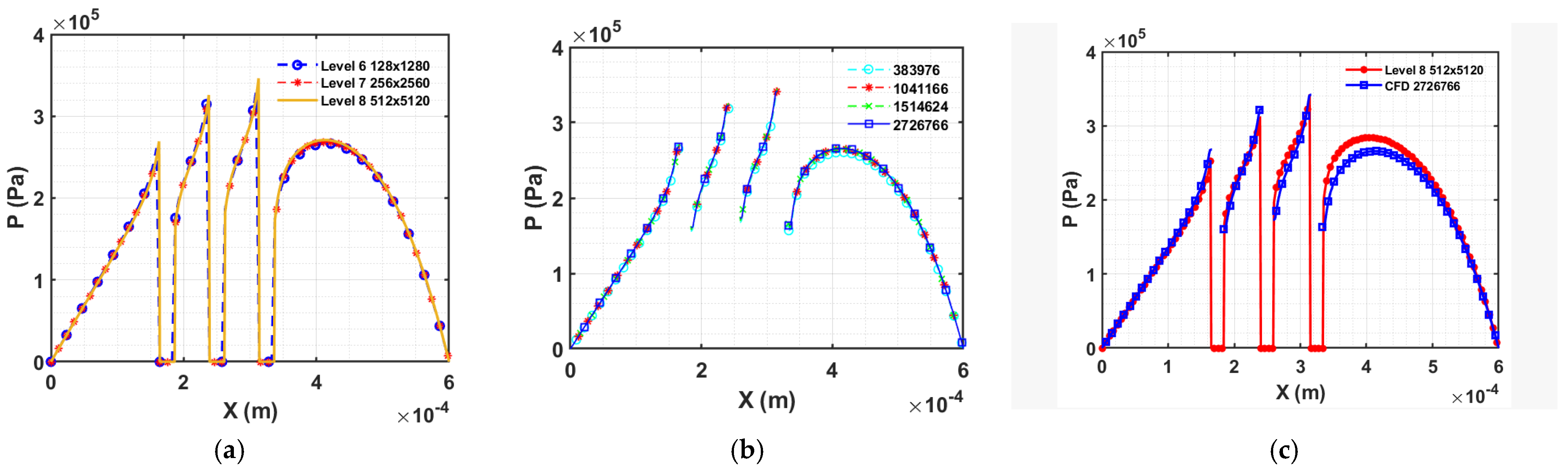
Preprints 71064 g011
Figure 11. Results for five cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of five cylindrical asperities (d) Comparison of FDM (Level 8) and CFD results.
Figure 11. Results for five cylindrical asperities (a) Mesh sensitivity analysis of FDM (K=0.1), (b) Mesh sensitivity analysis for CFD model of five cylindrical asperities (d) Comparison of FDM (Level 8) and CFD results.
Preprints 71064 g011
Preprints 71064 g012
Figure 12. Contour plot comparison has been produced using (a) the FDM and (b) the CFD Method for five cylindrical asperities contact.
Figure 12. Contour plot comparison has been produced using (a) the FDM and (b) the CFD Method for five cylindrical asperities contact.
Preprints 71064 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated