Prerpints.org logo
Preprint
Article

The Effect of Surface Oil on Ocean Wind Stress

Altmetrics

Downloads

115

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 April 2023

Posted:

17 April 2023

You are already at the latest version

Alerts
Abstract
This study provides, to our knowledge, the first detailed analysis of how surface oil modifies air-sea interaction in a two-way coupled model, i.e., the coupled-ocean-atmosphere-wave-sediment-transport (COAWST) model modified to account for oil-related changes to air-sea fluxes. This study investigates the effects of oil on surface roughness, surface wind, surface and near surface temperature differences, and boundary-layer stability, and how those conditions ultimately affect surface stress. We first conducted twin coupled modeling simulations with and without the influence of oil over the Deepwater Horizon (DWH) oil spill period (April 21 to May 5, 2010) in the Gulf of Mexico. Then we compared the results by using a modularized flux model with parameterizations selected to match those selected in the coupled model adapted to either ignore or account for different atmospheric/oceanic processes in calculating surface stress. When non-oil inputs to the bulk formula treated as unchanged by oil, the surface stress changes are always negative due to oil-related damping of surface roughness alone. However, the oil-related changes to 10-m wind speed and boundary-layer stability are found to play a dominant role in surface stress changes relative to those due to the oil-related surface roughness changes, highlighting that most of the changes in surface stress are due to the oil-related changes in wind speed and boundary-layer stability. Finally, the oil-related changes to surface stress due to the combined oil-related changes in surface roughness, surface wind, and boundary-layer stability are not large enough to have a major impact on the surface current and surface oil transport, indicating that the feedbacks from the surface oil to the surface oil movement itself are minor for forecasting the surface oil transport unless the fractional oil coverage is much larger than found in this study.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

The largest accidental marine oil spill in the history of the petroleum industry happened on April 20, 2010, in the Gulf of Mexico [1]. The Deepwater Horizon (DWH) oil platform suffered a catastrophic explosion that caused 11 deaths and injured 17 others [2]. The oil rig accident was estimated to have spilled 4.2 million barrels of oil over 87 days before the wellhead was finally capped on July 15, 2010 [3]. When oil first reaches the surface, gravity causes the oil to spread rapidly (relative to advection by currents) [4] in a layer that floats on top of the ocean, then it is transported by winds and currents. That oil slick posed an unprecedented threat to the Gulf of Mexico marine life as well as wetland and estuarine animal habitat [4,5]. Tracking the oil spill both at the surface and depth was necessary for planning mitigation efforts [6]. Trajectory forecasts using numerical models is one of important methods of tracking the spill [7,8]. Many numerical ocean circulation models from different institutions were used for trajectory forecasting such as the West Florida Shelf model [9], the Global Hybrid Coordinate Ocean Model [10], the Gulf of Mexico HYCOM (http://www.hycom.org), the South Atlantic Bight–Gulf of Mexico Model [11], the Real-Time Ocean Forecast System for the North Atlantic Ocean [12], and the Intra-Americas Sea Nowcast/Forecast System [13]. Despite some success from these modeling activities, limitations of the modeling systems called for several future improvements [14].
There are several aspects that surface oil can modify air-sea interaction (Figure 1). First, surface oil can change surface roughness by suppressing small gravity and capillary waves, leading to changes in friction velocity, ultimately contributing to a change in surface stress and surface current in the absence of other air-sea interaction process changes, as we know friction velocity is expressed as u ∗ = k v u ¯ z − u ¯ s f c l n z z o m + 1 − ψ m z , z o m , L , where where u ¯ z is the wind velocity at height z (10 m in this case); u s f c is the velocity of surface ocean current; k v is von Karman’s constant; z o m is the roughness length for momentum; ψm is a function of boundary-layer stability for momentum; and L is the Monin-Obukhov scale length.
Second, surface oil can modify sea surface temperature (SST) due to its influence on the ocean’s near-surface energy budget. Latent and sensible heat fluxes can be changed because of the changes in friction velocity and temperature. If oil slick is treated as an impermeable layer/membrane, then water vapor cannot pass through this layer, leaving only the oil-free portion of the surface available for evaporation of water, thus reducing latent heat flux and increase the SST. Third, the SST changes due to the discrepancy between oil and water can also modify the upward longwave radiative emission. The oil-related changes in SST due to the ocean energy budget can then alter the atmospheric boundary-layer stability, ultimately affecting the surface stress. None of the previous models considered how the discrepancy between water and oil in surface roughness, surface heat flux, and boundary-layer stability could modify surface stress on the ocean surface, which could impact the oil movement. Therefore, it is critically important to examine how oil modifies surface stress feedbacks, and model surface oil movement in a two-way coupled model. To quantitatively assess the involvement of how surface oil could change surface stress, one should understand how oil changes surface roughness, surface wind, and boundary-layer stability. We expected that surface stress will change because of oil-impacts on the surface roughness, surface temperature, and the atmospheric boundary-layer, and that the changed stress would modify Ekman surface currents.
This study aims to produce a more realistic physical environment for examining the impact of surface oil on surface stress and surface oil transport using a two-way coupled modeling system. The two-way coupling allows different physical processes of the atmosphere, ocean, and waves to interact with each other. To this end, a high-resolution two-way coupled ocean-atmosphere-wave-sediment-transport (COAWST) modeling system [15] for the Gulf of Mexico region was utilized over the DWH oil spill period. To our best knowledge, this is the first time a two-way coupled model was used to study the surface oil transport where oil itself modifies the coupling processes. This study was motivated by the limitations of the above-mentioned oil trajectory numerical models and by our previous study [7] which showed (assuming a water surface covered with oil) that there were likely to be substantial changes in oil transport due to oil-induced changes in SST gradient, surface roughness and surface stress.
The remainder of this paper is organized as follows. Section 2 includes the description of the models. Section 3 describes the methodology. Section 4 presents the results concerning the effect of surface oil on surface stress due to oil-related change in surface roughness, surface winds, and atmospheric boundary-layer stability separately. Section 5 discusses some caveats and section 6 summarizes the results.

2. COAWST Modeling System

2.1. Model Components

The COAWST Modeling System [15] is comprised of several components including models for the ocean, atmosphere, sea surface waves, sediment transport, and a coupler. The Model Coupling Toolkit (MCT) allows exchanges of prognostic fields between the various components shown in Figure 2.
COAWST’s ocean model is the Regional Ocean Modeling System (ROMS). ROMS is a free-surface, terrain-following numerical model that solves the three-dimensional Reynolds-averaged Navier–Stokes equations using hydrostatic and Boussinesq’s approximations [16,17]. The COAWST’s atmospheric model component is the Weather Research and Forecasting Model (WRF) [18]. It is a nonhydrostatic, quasi-compressible atmospheric model with boundary layer physics schemes and a variety of physical parameterizations of sub-grid scale processes for predicting meso- and microscales of motions. WRF incorporates various physical processes including microphysics, cumulus parameterization, longwave and shortwave radiations, surface layer, land surface, and planetary boundary layer (PBL). In most cases, there are multiple options for these parameterizations; thus, the physics options considered in our study are listed in Table 1. Model physics parameters were chosen to best support the DWH oil spill development and promote an accurate simulation. In our COAWST Modeling System, modifications of surface roughness length and surface moisture fluxes were used in the WRF module to model surface oil spill’s transport. Section 2.2 describes the modification of the surface roughness length and the modification of the surface moisture flux used in the COAWST system. The wave model is Simulating WAves Nearshore (SWAN). SWAN is a spectral wave model specifically designed for shallow water that solves the wave action balance equation in both spatial and spectral spaces [19]. SWAN simulates wind wave generation and propagation in coastal waters considering various source and sink terms including refraction, diffraction, shoaling, wave-wave interactions, and dissipation terms [15].

2.2. Parameterization Modifications

2.2.1. Surface Roughness Length

One of the physical processes that was not considered in the previously mentioned forecast models is that oil changes the surface roughness, which can affect surface stress and oil transport as suggested by an idealized study [7]. Herein, an innovative momentum roughness length parameterization is embedded in the WRF model to solve the surface water roughness and surface oil roughness. The new momentum roughness length parameterization is a modification of the Bourassa–Vincent–Wood flux model (BVW)[26,27] as applied in [7], which describes three types of surface features contributing to surface roughness: an aerodynamically smooth surface, capillary waves, and gravity waves. The surface roughness length parameterization includes a mix of roughnesses from surfaces with and without oil (tuned to the DWH spill):
z 0 m i = β s 0.11 v u ∗ i + 1 − A o i l β c , w a t e r + ε A o i l β c , o i l b σ ρ w u ∗ u ∗ · e i 2 + 1 − A o i l β g , w a t e r + ε A o i l β g , o i l a u ∗ u ∗ · e i g 2 0.5
where the β s ⁠, β c , w a t e r ⁠, β c , o i l , β g , w a t e r , β g , o i l are weights for the roughness length associated with an aerodynamically smooth surface, capillary waves, and gravity waves for water and oil, respectively [26]; v is the molecular viscosity of air; A o i l is the fractional coverage by oil; ε represents the oil damping effects on capillary waves and short gravity waves and ε is set to 0.25 for oil damping and 1 for oil-free water; b =0.019 is a dimensionless constant for capillary wave roughness length which is determined from laboratory observations [27]; σ is surface tension, which is determined by the sea surface temperature; ρ w is the water density; u ∗ is the friction velocity; a = 0.035 is Charnock's constant; and g is gravitational acceleration [26]. The roughness length is anisotropic, with unit vectors parallel e 1 and perpendicular e 2   to the mean direction of wave motions. The value of β s is determined by the relation β s = 1 − ε A o i l β g , o i l + 1 − A o i l β g , w a t e r . The roughness associated with capillary and gravity waves was modified to be a weighted average of the terms for a water surface and an oil covered surface. The new value of the weighted average terms represents an average over enough space/time for a smooth transition from an aerodynamically smooth surface to a rough surface.
For water surface, β c , w a t e r = 0 and β g , w a t e r = 0 for U e f f < U l i m . For U e f f ≥ U l i m
β c , w a t e r = tanh ⁡ 0.4 U e f f − U l i m 3
β g , w a t e r = tanh ⁡ 0.2 U e f f − U l i m 3
For oil surface, β c , o i l = 0 and β g , o i l = 0 for U e f f < U l i m . For U e f f ≥ U l i m
β c , o i l = tanh ⁡ 0.4 U e f f − U l i m 3
β g , o i l = tanh ⁡ 0.3 U e f f − U l i m 3
where U e f f = u ∗ [ ln ⁡ z z 0 + 1 + φ z , z 0 , L ] / k , ( z , z 0 , L ) is a stability-dependent modifier, k and L are von Kármán's constant and the Monin–Obukhov stability length, respectively. For a water surface U l i m = 1.0 m s − 1 , and for the Deepwater Horizon oil covered region, the value for U l i m = 7.0 m s − 1 . These value of U l i m for oil was estimated based on scatterometer observations of the surface roughness associated with the DWH spill. Using (1)-(5) is good for estimating surface roughness length because this approximation is qualitatively consistent with the wave spectra measurement of Cox and Munk [28] in the sense that both gravity waves and capillary waves are suppressed by oil and this damping is parameterized in a manner that can be easily included in the boundary-layer model. It should be pointed out that the value of U l i m is not general and will vary greatly depending on the oil conditions. Further work could be done to better estimate the values of U l i m and ε; however, it is beyond the scope of this study. Here, our goal is to show that these considerations are worthy of further analysis for modeling boundary-layers and oil spill trajectories for large oil spills.
The new surface roughness length parameterization (1) assumes that the surface is either oil free, totally covered with oil, or partial coverage of oil. For partial coverage, we modified the roughness length parameterization to include a contribution from capillary waves that are damped (0< A o i l <1), and an oil free portion (1- A o i l ) where they are not damped. In section 2.4, we will describe how we tune A o i l for much more general use in the COAWST system.

2.2.2. Surface Stress Flux and Latent and Sensible Heat Fluxes

The fluxes of stress (τ), latent heat (E), and sensible heat (H) follow.
τ = ρ u ∗ u ∗
E = ( 1 − A o i l ) ρ L v u ∗ q ∗
H = ρ C p u ∗ θ ∗
where ρ is the density of air, A o i l is the fractional coverage by oil, L v is the latent heat of vaporization, C p is the heat capacity of air. q ∗ and θ ∗ are analogous to u ∗ , however they apply to humidity and potential temperature, which are determined by
u ¯ z − u ¯ s f c = u ∗ k v ln ⁡ z z 0 m + 1 − m z , z 0 m , L
θ ¯ s f c − θ ¯ ( z ) = θ ∗ k v ln ⁡ z z 0 θ + 1 − θ z , z 0 θ , L
q ¯ s f c − q ¯ ( z ) = q ∗ k v ln ⁡ z z 0 q + 1 − q z , z 0 q , L
where the overbar indicates a mean, the boundary-layer stability terms for momentum, heat, and moisture (i.e., m , θ , q ) are calculated with an Obukhov Stability length scale [23] and u ¯ ,  θ ¯ , q ¯  at surface and height(z) are obtained from the coupled model surface datasets. The stability terms are modified by air-sea temperature differences (and to a much smaller extent humidity difference) and stress, which are two paths through which oil-modification of the surface can influence heat and momentum fluxes in addition to the air-sea difference in the bulk formulas (Eq. 9–11). These equations allow us to examine the impacts of boundary-layer stability changes related to oil, of which the change in stress directly impacts Ekman transport (wind-driven currents) of oil. Momentum roughness length parameterization considers the effects of capillary and gravity waves (Eq 1–5), while temperature, and moisture roughness length parameterizations consider the aerodynamically smooth surface only. Stability adjustment parameterization is determined by [29] for unstable conditions and by [30] for stable conditions.

2.3. Experiment Design

We conducted the twin experiments over the DWH period from April 20 to May 05, 2010. The model simulations were initialized to start 2 hours after the DWH blowout on April 20, 2010, with the model output stored every 6 hours. WRF made simulations over the Gulf of Mexico (Figure 3) where its horizontal resolution is 5km x 5km. WRF initial and boundary conditions are obtained from the 6 hourly National Centers for Environmental Prediction (NCEP), Climate Forecast System Reanalysis (CFSR) data.
The ROMS domains (2km x 2km resolution) are within the bounds of the corresponding WRF domains for stability. Since the WRF and ROMS grids are not co-located, the Spherical Coordinate Remapping Interpolation Package (SCRIP) computes interpolation weights between WRF and ROMS. ROMS is initialized with HYCOM/NCODA (Hybrid Coordinate Model/NRL Coupled Ocean Data Assimilation Data) 1/12o to reduce the spin-up time. The lower resolution in WRF will reduce the magnitude of feedbacks relative to a model with 2 km resolution in all domains. This was a necessary tradeoff given the computational requirements and the available resources and is a common practice when the modeling is focused on the ocean [31](Renault et al. 2016).
SWAN simulations are performed on the same grid as ROMS. The SWAN model was initialized from a quasi-stationary state calculated from North American Mesoscale Model (NAM) winds. The spin-up period required to generate the wind waves is typically 12 to 18 hours [32]. The boundary conditions for SWAN such as Stoke significant wave height, peak period, and average direction at the peak period, which were updated every 3 hours, are specified every 20 km (at every 10th grid point, called spec points) on the lateral open boundaries by the 10-arc minute Northern Atlantic regional grid WaveWatch 3 (WW3) model output.

2.4. Assumptions For Oil Slick Simulation

In this study, the goal of the oil simulation is to mimic the DWH blowout where oil continued to reach the surface until the oil well-head was sealed off. The version of our model does not contain the physics for oil buoyancy which could allow the oil to float from the underground well to the surface; therefore, we injected oil as a passive tracer at the surface. Using oil as a passive tracer in the model allows us to easily incorporate the surface roughness and evaporation flux equations for oil at the surface of the DWH site. A passive tracer in this scenario means that the surface water in the DWH site is acting as the surface oil. This is a common approach to modeling oil transport as a mature slick [33,34,35,36,37].
The calculation for the fractional oil coverage in the DWH area was based on the oil discharge, which is the well-head discharge rate at 9900 m3 per day, and by assuming that half of the oil reached the surface [3]. Following [4], it is assumed that the oil slick can initially be treated as distinct from water and that it spreads as a density flow on the surface. This initial expansion is very rapid (less than an hour) based on observations from natural slicks [4]. After this expansion, the initial surface slick is treated as being 50 km in diameter. We treat the oil density as crude oil (881 kgm-3) and ignore changes in this density associated with evaporation of the more volatile components of oil and weathering. Furthermore, we assume that the rate of oil reaching the surface is constant throughout our modeling period. These assumptions can be used to calculate an oil flux density added to the surface over the 50 km diameter circular area centered at the DWH site. While this is not a sophisticated plume model such as [38], it is suitable for the goals of this study. The results in this study are dependent on the effectiveness of our tuning of the oil coverage ( A o i l ).
The rate at which oil reaches the surface is determined as follows. The assumption that 50% of the oil reaches the surface, combined with a discharge rate of oil of 9900 m 3 d a y × 881 k g m 3 × 50 % = 50.46 k g s . The flux density of oil reaching the surface is determined by dividing the above flux by the area (a 50 km diameter) in which oil is added to the surface, gives a surface oil flux density of 50.46 k g s 1.96 × 10 9 m 2 = 2.57 × 10 − 8 k g m 2 s . A o i l was taken to be a linear function of the surface oil tracer concentration (SOTC) from SOTC = 0 k g m 3 and A o i l = 0, up to a SOTC value (hereafter, SOTC_crit) at and above which A o i l = 1. A crude preliminary estimate of SOTC_crit was made by running the model for 2 days with a completely passive oil tracer and taking the maximum resulting concentration to correspond to 10% oil coverage. The model was then run for 13.75 days with this preliminary SOTC_crit estimate of 2.5 × 10 − 3   k g m 3   and a fully active oil tracer, affecting the surface roughness and surface heat flux. This model run yielded reasonable maximum values of A o i l , ranging from 0.1 to 0.3 over the course of the model run. For the final tuning of the model, the ocean heat budget was adjusted by changing the value of SOTC_crit and hence A o i l until sea surface temperatures consistent with observations achieved within and around the DWH oil slick as measured by the ten channels of the Advanced Microwave Scanning Radiometer-Earth (AMSR-E) observing satellite [39]. Due to cloud frequent cover in the area of interest, it is difficult to capture/locate the oil spill boundaries through satellites (only on April 25 and 27 2010 with clear skies, which are closest to the April 20 DWH blowout). Therefore there were few pairs of temperature inside and outside of the slick and there was considerable (and difficult to quantify) uncertainty in this value. Furthermore, since the results are sensitive to the values of Aoil and SOTC_crit (section 4.3 and section 5), we recommend further study of the value of Aoil for DWH and other oil spills.

3. Methodology

3.1. Flux Model for Oil

The above twin coupled modeling experiments computed the surface stress with and without the influence of oil. These differences are due to the combined oil-related changes in surface roughness, surface wind, and atmospheric stability (including changes in air temperature and humidity). However, we still do not know which of these changes contributes most to the surface stress changes. To explore how oil-related changes in surface roughness, surface wind, and boundary-layer stability impact the change of surface stress separately, we use the coupled model output variables (i.e., SST, surface wind, surface air temperature, etc.) with and without the influence of oil as input variables in the Modularized Flux Testbed (MFT version 2021.1[27]), to calculate oil-related changes in surface stress due to each of these considerations. The MFT allows users to combine a wide range of parameterizations related to air-sea interaction and output many boundary-layer related variables such as surface stress, sensible heat, latent heat, atmospheric boundary-layer stability, and surface roughness. MFT physics parameterizations were selected to match those in the COAWST modeling system to ensure consistent surface stress calculations with the output surface stress calculations from the modeling system. The MFT code and its additional guidance can be found through https://www.coaps.fsu.edu/~bourassa/MFT_html/MFT_docs.php. Input and output variables and options are given in Appendix A.

3.2. Experimental Setup for Estimating Stress Changes Due to Oil-Related changes

In this study, we calculated the change of surface stress due to the oil-related change in momentum surface roughness, surface winds, and ABL stability using a flux model described in section 3.1. We estimated the stress changes in four cases, which are listed in Table 2.
where τ A o i l ≠ 0 is surface stress for partial oil coverage; τ A o i l = 1   is surface stress for total oil coverage; τ w a t e r   is surface stress for pure water coverage; τ A o i l ≠ 0 ;   w a t e r − r e l a t e d   w i n d   is surface stress for partial oil coverage with pure water-related surface wind; τ A o i l ≠ 0 ;   w a t e r − r e l a t e d   s t a b i l i t y is surface stress for partial oil coverage with pure water-related boundary-layer stability.
In case 1, the surface stress change was computed due to the surface roughness change only between partial oil coverage ( A o i l ≠ 0 ,   ) and pure water assuming surface wind and boundary-layer stability are the same and from the non-oil simulation output, note that Aoil was estimated in oil simulation. Case 2 is the same as case 1 except to estimate the stress change using A o i l = 1 to compute surface roughness. In case 3, the surface stress change was computed due to the surface wind change only between partial oil coverage ( A o i l ≠ 0 ) and pure water assuming surface roughness and boundary-layer stability are the same and from the non-oil simulation output. In case 4, the surface stress change was computed due to the boundary-layer stability change only between partial oil coverage and pure water assuming surface roughness and surface wind are the same and from the non-oil simulation output.

4. Results

4.1. Surface Stress Change due to Oil-induced Change in Surface Roughness

To investigate how the discrepancy in surface roughness between oil and water surface contributes to the changes in surface stress, we compare the changes in the magnitude of surface stress when roughness is the only varying factor. Wind speed and boundary-layer stability are from the model run without oil. Figure 4 shows the probability distribution function (PDF) of the changes of surface stress magnitude due to the surface roughness differences between surface oil coverage and water surface coverage obtained in case 1 (Figure 4a) and case 2 (Figure 4b) over the two weeks from 21 April 2010–5 May 2010, where case 1 is based on our estimated value of Aoil, and case 2 uses Aoil = 1. The surface stress changes were computed in oil locations only.
In case 1, surface stress decreases when oil impacts the surface roughness since surface water waves can be suppressed by partial coverage of oil slick, leading to a small surface roughness. However, the changes in surface stress magnitude only have a small dynamic range, indicating the changes in surface roughness due to the model simulated oil coverage do not significantly impact surface stress. This occurs probably because there are substantial fractions of the surface that had no layer of oil (or the layer was so thin it had little impact), despite there being plenty of oil slicks during the DWH spill period [40]. In case 2, when water surface is completely covered by oil, the changes in the magnitude of surface stress is found to be much larger than in case 1. This indicates that a water surface completely covered by oil has a much large impact on surface stress than an area with substantial gaps in oil coverage (i.e., patchy coverage). Since observations of the Deepwater Horizon spill indicated that the oil coverage was patchy [40], this simple first test reveals that proper estimation of fractional oil coverage is likely to be necessary to model the changes to air-sea interaction and surface oil motion transport.

4.2. Surface Stress Change due to Oil-induced Change in Surface Winds

Similar to section 4.1, we examined the changes in the magnitude of surface stress due to the changes in surface wind alone caused by the difference between water and oil. Both stresses are calculated with oil-free values of roughness length and boundary-layer stability. If the change in wind was due only to oil-induced changes in roughness length, then we would expect the reduced friction to increase wind speed. Figure 5 shows the PDF of the changes in the magnitude of surface stress for an oil-related 10-m wind relative to a water-related 10-m wind (case 3) over the same period as in Figure 4. The results show that the changes in surface wind due to the presence of an oil slick can increase or decrease surface stress. This happens because the surface wind speed can increase or decrease regardless of the presence of oil. It is expected because the changes of surface wind speed are not fully determined by the effect of oil alone but other dominant processes (e.g., atmospheric boundary-layer stability, changes in advection) may come into play. Figure 6 demonstrates both the increases and decreases in modeled surface speed in the oil spill region on May 4, 2010. Interestingly, the changes in surface stress magnitude due to surface wind changes appear to be larger than those due to the oil-related changes of surface roughness alone, again supporting the suggestion that factor beyond roughness length are impacting the wind speed and stress.

4.3. Surface Stress Change due to Oil-induced Change in Atmospheric Boundary-Layer Stability

Before we quantify the significance of changes in surface stress due to the oil-induced changes in boundary-layer stability, we examine the PDF of the magnitude of air-sea potential temperature differences (i.e., air potential temperature at a height of 2 m minus SST) as a function of fraction oil coverage (Aoil). Figure 7 displays such temperature differences over the 2-week period (2010-04-21 to 2010-05-05) but only for 6 pm time-steps. All 6 pm time-steps were used because thick oil appears warmer than water during the daytime due to thermal isolation from the underlying water and high absorption of solar radiation [41]. That time of day presumably associated with a greater impact on air-sea temperature difference, hence highlightling oil-induced air-sea temperature differences on the atmospheric boundary-layer stability. The results reveal that air-sea temperature differences can be positive or negative and strongly depend on the amount of oil coverage. A greater likelihood of negative air-sea temperature differences occurs over large surface oil coverages (e.g., the 0.1 < Aoil < 0.2, and Aoil > 0.2 cases in Figure 7), implying conditions that are more likely to be thermodynamically unstable. In the absence of other considerations, more stable conditions (i.e., the change in the air-sea temperature difference is positive) tend to cause the 10-m wind and stress to be smaller, while a more unstable air-sea temperature differences (i.e., the change in the air-sea temperature difference is negative) will tend to increase the 10-m wind and stress. It should be noted that the temperature changes could also attributed to the changes in oceanic and atmospheric horizontal heat advection.
Figure 8 shows the PDF of the change in the magnitude of surface stress for an oil-related atmospheric boundary-layer stability relative to a water-related ABL stability over the 2-week period (2010-04-21 to 2010-05-05) for all 6 pm time-steps as performed in case 4. These calculations used roughness length and wind speed from the model run without oil. Results reveal that a slick can increase or reduce surface stress due to oil-induced boundary-layer stability changes alone. The shape of PDF is similar to that due to oil-induced surface wind alone as shown in Figure 5. Note that the changes in surface stress magnitude due to the changes in oil-related surface wind alone (as in Figure 5) and oil-related ABL stability alone (as in Figure 8) are more likely larger than that due to the changes in oil-induced roughness alone (as in Figure 4). Interestingly, most of the change in surface stress magnitude falls near and within the zero range (i.e., the stress change is still small) as seen in Figure 5 and Figure 8, suggesting that the changes in boundary-layer stability and surface wind due to oil do not have a major impact on surface stress. These small changes in stress due to oil-induced processes are supposed to cause small changes in the currents relative to the changes in currents caused by other effects such as intrinsic ocean dynamics. As a result, the oil-induced change in stress has a minor impact on surface oil transport.

4.4. Relative Contributions to Surface Stress Changes due to Oil-induced change in Surface Roughness, Surface Wind, and Atmospheric Boundary-Layer Stability

To compare the relative contributions to surface stress changes from the oil-induced changes in surface roughness, surface wind, and boundary-layer stability, we examined the PDF of percentage changes in the above three fields contributing to the changes in surface stress over the 2-week period (Figure 9). The percentage change in surface stress that is due purely to the changes in surface roughness, the changes in surface wind, and the changes in atmospheric boundary-layer stability is defined as
P e r c = τ o i l ¯ − τ n o − o i l ¯ τ n o − o i l ¯ × 100 ,
where τ o i l ¯ is the mean surface stress output that is calculated using variables from the oil-case experiment, and τ n o − o i l ¯ is the mean surface stress output that is calculated using the same variables from the oil-case experiment except that the only varying factor (e.g., either surface roughness or surface wind, or ABL stability) is obtained from no-oil case experiment. The contribution range purely from oil-induced surface roughness changes is the smallest (-4% to -1%) with the negative sign, suggesting it always decreases stress very slightly. The contribution purely from oil-induced surface wind ranges -9% to +12%, and the contribution purely from oil-induced boundary-layer stability fall within -18% and 13%. It appears that contributions from surface wind and stability changes are more likely larger than that purely from surface roughness.
Note that the contributions from each of the three fields are not independent. For example, surface roughness due to oil can substantially affect wind speed, and both of these variables impact wind stress and the ocean surface current. Also, the presence of oil itself could affect wind speed and boundary-layer stability via the changes in air-sea temperature differences, hence could contribute to an increase in stress. The above interwoven features can be further quantitatively illustrated in Figure 10. It is seen that the changes in stress due to wind are very well correlated with the changes in surface due to boundary-layer stability (Figure 10). This is not surprising because increases in wind and SST enhance the stress. This suggests most of the changes in modeled stress are due to the changes in modeled stability coupled with the changes in the modeled wind. This indicates that the friction velocity plays a large role in the driving physics factor that is influenced by oil and thus affect air-sea interaction and currents, but also strongly suggests that oil-induced changes in SST are more important than oil-induced changes in roughness length.

5. Discussion

Oil slick affects changes in surface stress and boundary-layer stability over areas of high oil coverage and low wind speeds (< 8m/s). If wind exceeds 18 m/s, the oil is likely to be dispersed into the water column [42] and it has limited capability to dampen the ocean surface waves [43], thus forecasting an oil spill within a high wind environment is relatively easy. This study is focused on the effect of oil on stress within a low to moderate wind environment. Our results indicate the oil-induced differences in boundary-layer stability contribute to the change in surface stress for conditions typical of the DWH spill (i.e., light, and moderate winds). The boundary-layer stability is largely dependent on wind speed, SST, and surface air temperature. Our results show that the changes in air-sea temperature differences are relatively important and should be considered in future modeling.
The fraction oil coverage is shown to be important to make the changes in air-sea temperature difference, hence it modifies boundary-layer stability (stable and unstable). The drag coefficient is a crucial parameter to quantify the stress over the ocean surface, which depends on the ocean surface roughness. Figure 11 demonstrates how the five different fraction oil coverages (Aoil=0.0, 0.25, 0.50, 0.75, and1.0) influence the boundary-layer stability and surface stress (via drag coefficient) for different ranges of air-sea temperature differences and 10-m wind speed conditions. When the air potential temperature is greater than the SST (green lines), the atmosphere is considered stable, results in less surface stress. On the contrary, when the air potential temperature is less than the SST (red lines), the atmosphere is considered less stable, results in more significant surface stress. The changes in stress corresponding to a 1oC change in air-sea temperature difference are much greater for stable conditions than for unstable conditions, regardless of the fractional oil coverage. The peak of drag coefficients between 2 and 4 ms-1 is due to capillary waves (wavelength < 1.7 cm) and is reduced as the fractional oil coverage increases. The local minima in drag coefficients indicates that capillary waves and gravity waves (wavelength > 1.7 cm) make equal contribution to the roughness. The roughness due to capillary waves decreases as wind speed increases, whereas the roughness due to gravity waves increases as wind speed increases. As the amount of oil increases, the minima in drag coefficients moves to greater wind speed indicating the presence of oil is damping both capillary waves and short gravity waves. Figure 11 shows that when oil covers the ocean surface, the oil changes the drag coefficient. As the fraction of oil coverage increases, the drag coefficient decreases. The above statement explains why surface oil roughness can decrease the surface stress and surface current if the oil roughness is the only dominating factor. These figures show qualitative agreement with Figure (4b) that the amount of oil coverage can affect the wind stress and current, which affects the oil's movement. The effects of oil on changes to boundary layer processes and oil motion have not been included in oil spill models. The results in this study indicate that it could be useful to consider the effect of oil changes on the atmospheric/oceanic process, which can impact the movement of the oil, especially for large-scale oil spill situations.
The major uncertainty in our results (i.e., ignoring the weathering of oil) is the dependencies of the atmospheric/oceanic processes on the quantity of oil. Uncertainty in the parameterization of boundary-layer processes (e.g., roughness length, stability, and the impacts of stability) makes it complex to examine the effects of oil separately on surface roughness, surface wind speed, and boundary-layer stability, and how those conditions impact surface stress. Here, we used only the roughness parameterization adapted from [7] and stability impacts from WRF. A larger fraction of coverage would result in more significant changes in stress and transport of the oil, and a greater sensitivity to oil would also increase the importance of considering oil slicks with a coupled model.
Figure 12 presents a schematic diagram of the feedback mechanism of oil slick and air-sea coupling. The main dominant fact that oil slick impacted is friction velocity (see lower panel in Figure 10). The left-hand side of Figure 12 shows how oil coverage modifies roughness length and hence friction velocity, surface wind, and boundary-layer stability. All these variables depend on friction velocity; thus, makes oil and air-sea coupling more complicated. The right-hand side of Figure 12 shows how fractional oil coverage modifies the air-sea interaction through temperature differences. An oil slick can reduce the latent heat flux through inhibiting evaporation. A reduction in the latent heat flux increases the SST, which will also warm the air.

6. Summary

This study provides the first detailed analysis of how oil changes air-sea interaction in a two-way coupled model. Specifically, we focus on exploring how oil modifies surface roughness, surface wind, and boundary-layer stability and how these oil-induced changes affect surface stress separately. We choose DWH oil spill in the Gulf of Mexico over April 20 to May 5, 2010 as a simulation scenario when high wind environment is excluded. Three major conclusions were made:
(1)
Oil-related changes to surface roughness is not significant enough to cause a big impact on surface stress change;
(2)
Oil-related changes to 10-m wind speed and boundary-layer stability have a relatively greater impact than oil-related surface roughness changes upon surface stress change, though these changes are still small;
(3)
Oil-related changes to surface stress are not large enough to cause a major change in the ocean currents as compared to other effects such as intrinsic ocean dynamics, thus oil-induced changes in stress have a limited impact on the surface oil transport.
The above results are subject to the uncertainties in the amount of oil coverage and the parameterizations for boundary-layer processes. Air-sea temperature differences that affect boundary-layer stability can also be modified by atmospheric advection, which is not examined in this study. This study reveals that the consideration of oil-related temperature and oil-related surface roughness for oil trajectory forecasting is minor due to the small impact on surface stress unless the fractional oil coverage is much larger than found in this study. Thus, it could be useful to consider the effect of oil-related changes on the atmospheric/oceanic processes, which can impact the oil transport, especially for large-scale oil spill situations. Sensitivity to the fractional coverage of oil is demonstrated in several ways and could be underestimated in this modeling study. If it is greatly underestimated, the conclusions about the impact of oil on stress and currents might be changed. This study produced tools and methodology that are well suited to testing these conclusions when and if better oil coverage data are available.

Author Contributions

Conceptualization, Y.Z. and M.A.B.; methodology, Y.Z., D.B., and M.A.B.; validation, D.B., Y.Z. and M.A.B.; formal analysis, D.B.; investigation, D.B.; data curation, D.B.; writing—original draft preparation, D.B.; writing—review and editing, Y.Z. and M.A.B.; visualization, D.B.; supervision, Y.Z. and M.A.B.; project administration, Y.Z.; funding acquisition, Y.Z. and M.A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Gulf of Mexico Research Initiative (GoMRI) RFP-VI, grant number G-231820 and the U.S. National Aeronautics and Space Administration (NASA) Physical Oceanography of the Ocean Vector Winds Science Team (OVWST), subcontract number: 1639996.

Data Availability Statement

All datasets used in this study are available at https://doi.org/10.5281/zenodo.7826442, accessed on 13 April 2023.

Acknowledgments

Model simulations for this study was conducted on the HPC at the Florida State University Research Computing Center (FSU RCC) and data analysis was performed at the Center for Ocean-Atmospheric Prediction Studies (COAPS) at the FSU. We thank the COAWST modeling system for open access to their codes and their technical support. Daneisha Blair was supported by the GoMRI RFP-VI; Yangxing Zheng and Mark A. Bourassa were supported by the GoMRI RFP-VI and the U.S. NASA OVWST.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Parameterization options available within the Modularized Flux Testbed are listed in the Table below. Options can be selected independently for momentum, temperature, and moisture parameterizations. The selections used in this study have a light gray background. In the columns for stability adjustment parameterizations, the parametrization above the dashed line is for unstable conditions, and the parameterization below the dashed line is for stable conditions.
Option # Momentum Roughness Length Temperature and Moisture Roughness Length Momentum Stability Adjustment Temperature and Moisture Stability Adjustments
0 Bourassa, Vincent, and Wood ( BVW,[27]) Aerodynamically smooth surface Benoit's (1977,[50]) adaption of Dyer (1974,[29])
----------------------------------
Beljaars and Holtslag (1991,[51])		 Benoit's (1977,[50]) adaption of Dyer (1974,[29])
-----------------------------------
Beljaars and Holtslag (1991,[51])
1 [26]Bourassa (2006, [26]) Clayson, Fairall and Curry (1996,[45]) Dyer 1974,[29])
----------------------------------
Hicks (1976,[30])		 Dyer (1974,[29])
-----------------------------------
Hicks (1976,[30])
2 Taylor and Yelland (2001,[44]) with BVW capillary wave roughness Zilitinkevich et al. (2000,[46]) Benoit's (1977,[50]) adaption of Dyer (1974,[29])
----------------------------------
Hicks (1976,[30])		 Benoit's (1977,[50]) adaption of Dyer (1974,[29])
-----------------------------------
Hicks (1976,[30])
3 Taylor and Yelland (1999,[44]) Liu, Katsaros and Businger (1979, [47]) Dyer (1974, [29])
---------------------------------
Hicks (1976, [30]) with solution for lower boundary condition		 Dyer (1974, [29])
-----------------------------------
Hicks (1976, [30]) with solution for lower boundary condition
4 Zheng et. al (2013, [7]) COARE 3.0
Fairall et al. (2003,[48])
5 Aerodynamically smooth surface Griffin (2009, [49]) retuned CFC
6 Oil Spill parameterization (this study)
7 Input a value

References

  1. Xing, Q.; Li, L.; Lou, M.; Bing, L.; Zhao, R.; Li, Z. Observation of Oil Spills through Landsat Thermal Infrared Imagery: A Case of Deepwater Horizon. Aquatic Procedia 2015, 3, 151–156. [CrossRef]
  2. Klemas, V. Tracking Oil Slicks and Predicting their Trajectories Using Remote Sensors and Models: Case Studies of the Sea Princess and Deepwater Horizon Oil Spill. J. Coastal Res. 2010, 265, 789–797. [CrossRef]
  3. McNutt, M.K.; Camilli, R.; Crone, T.J.; Guthrie, G.D.; Hsieh, P.A.; Ryerson, R.B.; Savas, O.; Shaffer, F. Review of flow rate estimates of the Deepwater Horizon oil spill. Proc. Natl. Acad. Sci. 2011, 109 (50), 20260–20267. [CrossRef]
  4. Daneshgar Asl, S.; Amos, J.; Woods, P.; Garcia-Pineda, O.; MacDonald, I.R. Chronic, Anthropogenic Hydrocarbon Discharges in the Gulf of Mexico. Deep-Sea Res. II 2016, 129, 187–195. [CrossRef]
  5. Robertson, C.; Krauss, C. Gulf spill is the largest of its kind, scientists say. New York Times 2 August 2010. http://www.nytimes.com/2010/08/03/us/03spill.html?_r=0.
  6. Walsh, B. The meaning of the mess. Time Magazine 17 May 2010, 29–35.
  7. Zheng, Y.; Bourassa, M.A.; Hughes, P. Influences of sea surface temperature gradients and surface roughness changes on the motion of surface oil: A simple idealized study. J. Appl. Meteor. Climatol. 2013, 52 (7), 1561–1575. [CrossRef]
  8. Barker, C.H.; Kourafalou, V.H.; Beegle-Krause, C.J.; Bouadel, M.; Bourassa, M.A.; Buschang, S.G.; Androulidakis, Y.; Chassignet, E.P.; Dagestad, K.F.; Danmeier, D.G.; Dissanayake, A.L.; Galt, J.A.; Jacobs, G.; Marcotte, G.; Özgökmen, T.; Pinardi, N.; Schiller, R.V.; Socolofsku, S.A.; Thrift-Viveros, D.; Zelenke, B.; Zhang, A.; Zheng, Y. Progress in Operational Modeling in Support of Oil Spill Response. J. Mar. Sci. Eng. 2020, 8, 668. [CrossRef]
  9. Barth, A.; Alvera- Azcarate, A.; Weisberg, R.H. A nested model study of the Loop Current generated variability and its impact on the West Florida Shelf. J. Geophys. Res. 2008, 113, C05009. [CrossRef]
  10. Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Raraille, R.; Black, R. The HYCOM (Hybrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [CrossRef]
  11. Hyun, K.H.; He, R. Coastal upwelling in the South Atlantic Bight; A revisit of the 2003 cold event using long term observations and model hindcast solutions. J. Mar. Syst. 2010, 83, 1–13. [CrossRef]
  12. Mehra, A.; Rivin, I. A Real Time Ocean Forecast System for the North Atlantic Ocean. Terr. Atmos. Ocean. Sci. 2010, 21(1), 211–228. [CrossRef]
  13. Ko, D.S.; Martin, P.J.; Rowley, C.D.; Preller, R.H. A real-time coastal ocean prediction experiment for MREA04. J. Mar. Syst. 2008, 69, 17–28. [CrossRef]
  14. Liu, Y.; Weisberg, R.H.; Hu, G.; Zheng, L. Tracking the Deepwater Horizon oil spill: A modeling perspective. Eos Trans. Amer. Geophys. Union 2011, 92(6), 45–46. [CrossRef]
  15. Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a Coupled Ocean-Atmosphere-Wave-Sediment Transport (COAWST) Modeling System. Ocean Modelling 2010, 35 (3), 230–244. [CrossRef]
  16. Shchepetkin, A.F.; McWilliam, J.C. The regional oceanic modeling system ROMS): A split-explicit, free-surface, topography-following coordinate oceanic model. Ocean Modelling 2005, 9(4), 347–404. [CrossRef]
  17. Haidvogel, D.B.; Arango, H.; Budgell, W.P.; Cornuelle, B.D.; Curchitser, E.; Di Lorenzo, E.; Fennel, K.; Geyer, W.R.; Hermann, A.J.; Lanerolle, L.; Levin, J.; McWilliams, J.C.; Miller, A.J.; Moore, A.M.; Powell, T.M.; Shchepetkin, A.F.; Sherwood, C.R.; Signell, R.P.; Warner, J.C.; Wilkin, J. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 2007, 227, 3595–3624. [CrossRef]
  18. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 2 (No. NCAR/TN-468+STR). 2005, University Corporation for Atmospheric Research. [CrossRef]
  19. Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for castal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104 (C4), 7649–7666. [CrossRef]
  20. Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Wea. Rev. 2008, 136, 5095–5115. [CrossRef]
  21. Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14,5233–5250. [CrossRef]
  22. Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [CrossRef]
  23. Monin, A.S.; Obukhov, A.M. Basic laws of Turbulent Mixing in the Surface layer of the Atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 151, 163–187.
  24. Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. 20th Conference on weather analysis and forecasting/16th Conference on Numerical Weather Prediction, American Meteorology Society, Seattle, WA, USA, 2004.
  25. Grenier, H.; Bretherton, C.S. A moist PBL parameterization for large-scale models and its application to subtropicl cloud-toped marine boundary layers. Mon. Wea. Rev. 2001, 129, 357–377. [CrossRef]
  26. Bourassa, M.A. Satellite-based observations of surface turbulent stress during severe weather. Atmosphere-Ocean Interactions 2006, 2, 35–52.
  27. Bourassa, M.A.; Vincent, D.G.; Wood, W.L. A Flux Parameterization Including the Effects of Capillary Waves and Sea State. J. Atmos. Sci. 1999, 56 (9), 1123–1139. [CrossRef]
  28. Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter. J. Opt. Soc. Am. 1954, 44 (11), 838–850. [CrossRef]
  29. Dyer, A.J. A review of flux-profile relationships. Boundary-Layer Meteor. 1974, 7, 363–372. [CrossRef]
  30. Hicks, B.B. Wind profile relationship from the ‘Wangara’ experiment. Quar. J. R. Met. Soc. 1976, 102 (433) 535–551. [CrossRef]
  31. Renault,L.; Molemaker, M.J.; Gula, J.; Masson, S.; McWilliams, J.C. Control and stabilization of the Gulf Stream by oceanic current interaction with the atmosphere. J. Phys. Oceanogr. 2016, 46, 3439–3453. [CrossRef]
  32. Settlelmaier, J.B.; Gibbs, A.; Santos, P.; Freeman, T.; Gaer, D. Simulating waves nearshore (SWAN) modeling efforts at the national weather service (NWS) southern region (SR) coastal weather forecast Offices (WFOs). P13A.4 The 91st AMS Annual Meeting, Seattle, WA, USA, 22–28 January 2011.
  33. Maltrud, M.; Peacock, S.; Visbeck, M. On the possible long-term fate of oil released in the Deepwater Horizon incident, estimated using ensembles of dye release simulations. Environ. Res. Lett. 2010, 5, 035301. [CrossRef]
  34. Zelenke, B.; O’Connor, C.; Baker, C.; Beegel-Krause, C.J.; Eclipse, L. General NOAA Operational Modeling Environment (GNOME) Technical Documentation. U.S. Dept. of Commerce, NOAA Technical Memorandum NOS OR&R 40. Seattle, WA, USA, 2012: Emergency Response Division, NOAA, 105pp.
  35. De Dominicis, M.; Pinardi, N.; Zodiatis, G.; Lardner, R. MEDSLIK-II, a Lagrangian marine surface oil spill model for short-term forecasting – Part 1: Theory. Geosci. Model Dev. 2013, 6, 1851–1869. [CrossRef]
  36. Bourgault, D.; Cyr, F.; Dumont, D.; Carter, A. Numerical simulations of the spread of floating passive tracer released at the Old Harr prospect. Environ. Res. Lett. 2014, 9 (5), 0054001. [CrossRef]
  37. Röhrs, J.; Dagestad, K.F.; Asbjørnsen, H.; Nordam, T.; Shancke, J.; Jones, C.E.; Brekke, C. The effect of vertical mixing on the horizontal drift of oil spills. Ocean Sci. 2018, 14, 1581–1601. [CrossRef]
  38. Mariano, A.J.; Kourafalou, V.H.; Srinivasan, A.; Kang, H.; Halliwell, G.R.; Ryan, E.H.; Roffer, M. On the modeling of the 2010 Gulf of Mexico Oil Spill. Dyn. Atmos. Ocn. 2011, 52 (1–2), 322–340. [CrossRef]
  39. Wenz, F.J.; Meissner, T. AMSR-E Ocean Algorithms, Supplement 1, Vol. 051707, Remote Sensing Systems, Santa Rosa, CA, USA, 2007, pp6.
  40. Hu, C.; Feng, L.; Holmes, J.; Swayze, G.A.; Leifer, I.; Melton, C.; Garcia, O.; MacDonald, I.; Hess, M.; Muller-Karger, F.; Graettinger, G.; Green, R. Remote sensing estimation of surface oil volume during the 2010 Deepwater Horizon oil blowout in the Gulf of Mexico: Scaling up AVIRIS observations with MODIS measurements. J. Appl. Remote Sens. 2018, 12 (2), 026008. [CrossRef]
  41. Hurford, N. Review of Remote Sensing Technology. In The remote sensing of oil slicks: Proceeding of an international meeting organized by the Institute of Petroleum and held in London in May 1988. Ed. Lodge A.E.; Wiley, New York,1989, pp7.
  42. Alpers, W.; Hühnerfuss, H. The Damping of Ocean Waves by Surface Films: A New Look at an Old Problem. J. Geophys. Res. 1989, 94 (C5), 6251–6265. [CrossRef]
  43. Shen, H.; Perrie, W.; Wu, Y. Wind drag in oil spilled ocean surface and its impact on wind-drive circulation. Anthropocene Coasts 2019, 2 (1), 244–260. [CrossRef]
  44. Taylor, P.K.; Yelland, M.J. The Dependence of Sea Surface Roughness on the Height and Steepness of the Waves. J. Phys. Oceanogr. 2001, 31(2), 572–590. [CrossRef]
  45. Clayson, C.A.; Fairall, C.W.; Curry, J.A. Evaluation of turbulent fluxes at the ocean surface using surface renewal theory. J. Gophys. Res. 1996, 101, 28503–28513. [CrossRef]
  46. Zilitinkevich, S.; Calanca, P. An extended similar theory for the stably stratified atmospheric surface layer. Q. J. R. Meteor. Soc. 2000, 126, 1913–1923. [CrossRef]
  47. Liu, T.; Kassaros, K.B.; Businger, J.A. Bulk Parameterization of Air-Sea Exchanges of Heat and Water Vapor Including the Molecular Constraint at the Interface. J. Atmos. Sci. 1979, 36(9), 1722–1735. [CrossRef]
  48. Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk Parameterization of Air-Sea Fluxes: Updates and Verification for the COARE algorithm. J. Climate 2003, 16(4), 571–591. [CrossRef]
  49. Griffin, J. Characterization of Errors in Various Moisture Roughness Length Parameterizations. Thesis, Dept. of Meteorology, Florida State University, 2009. Retrieved from http://purl.flvc.org/fsu/fd/FSU_migr_etd-3958.
  50. Benoit, R. On the Integral of the Surface Layer Profile-Gradient Functions. J. Appl. Meteor., 1977, 16(8), 859–860. [CrossRef]
  51. Beljaars, A.C.M.; Holtslag, A.A.M. Flux Parameterization over Land Surfaces for Atmospheric Models. J. Appl. Meteor. Climatol. 1991, 30(3), 327 – 341. [CrossRef]
Preprints 71060 g001
Figure 1. 3D schematic diagram depicting the ocean energy budget induced by an oil slick. The oil (brown shading) absorbs some of the incoming solar radiation (yellow arrow) and becomes warmer than the surrounding water. The increase in surface oil temperature led to an increase in outgoing longwave radiation (upper-ward red arrow) and sensible heat flux (orange arrow). The smooth surface of the oil slick reduces friction velocity caused by surface winds at 10 meters above the sea surface (purple arrow). Friction velocity is proportional to the energy lost through evaporation; therefore, the surface oil reduces evaporation which in turns reduces latent heat flux (blue arrow).
Figure 1. 3D schematic diagram depicting the ocean energy budget induced by an oil slick. The oil (brown shading) absorbs some of the incoming solar radiation (yellow arrow) and becomes warmer than the surrounding water. The increase in surface oil temperature led to an increase in outgoing longwave radiation (upper-ward red arrow) and sensible heat flux (orange arrow). The smooth surface of the oil slick reduces friction velocity caused by surface winds at 10 meters above the sea surface (purple arrow). Friction velocity is proportional to the energy lost through evaporation; therefore, the surface oil reduces evaporation which in turns reduces latent heat flux (blue arrow).
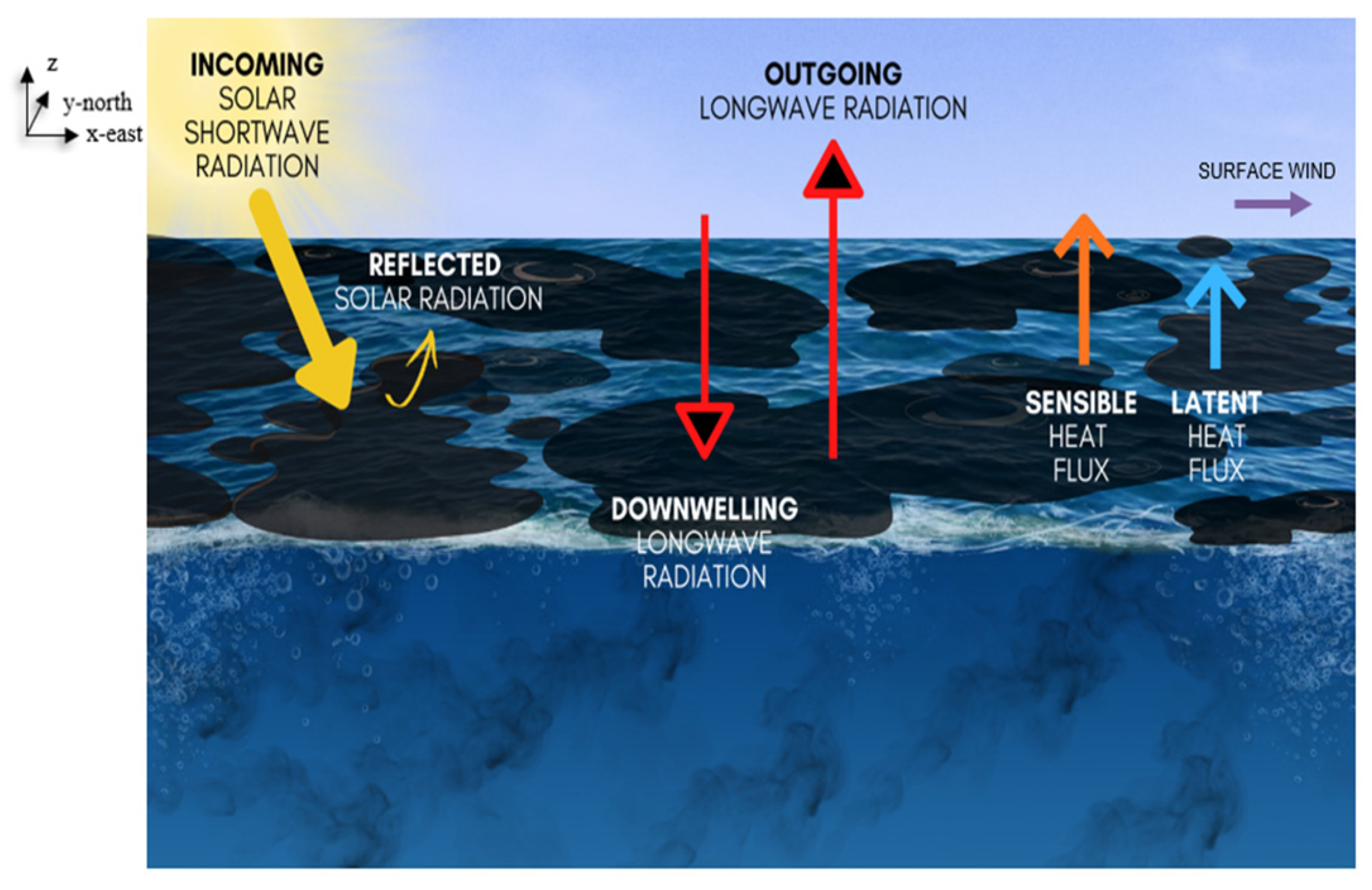
Preprints 71060 g001
Preprints 71060 g002
Figure 2. Coupled-Ocean-Atmosphere-Wave-Sediment Transport (COAWST) configuration and exchanged data fields. The COAWST coupling was modified to include the changes to physics parameterizations to support our oil spill simulation.
Figure 2. Coupled-Ocean-Atmosphere-Wave-Sediment Transport (COAWST) configuration and exchanged data fields. The COAWST coupling was modified to include the changes to physics parameterizations to support our oil spill simulation.
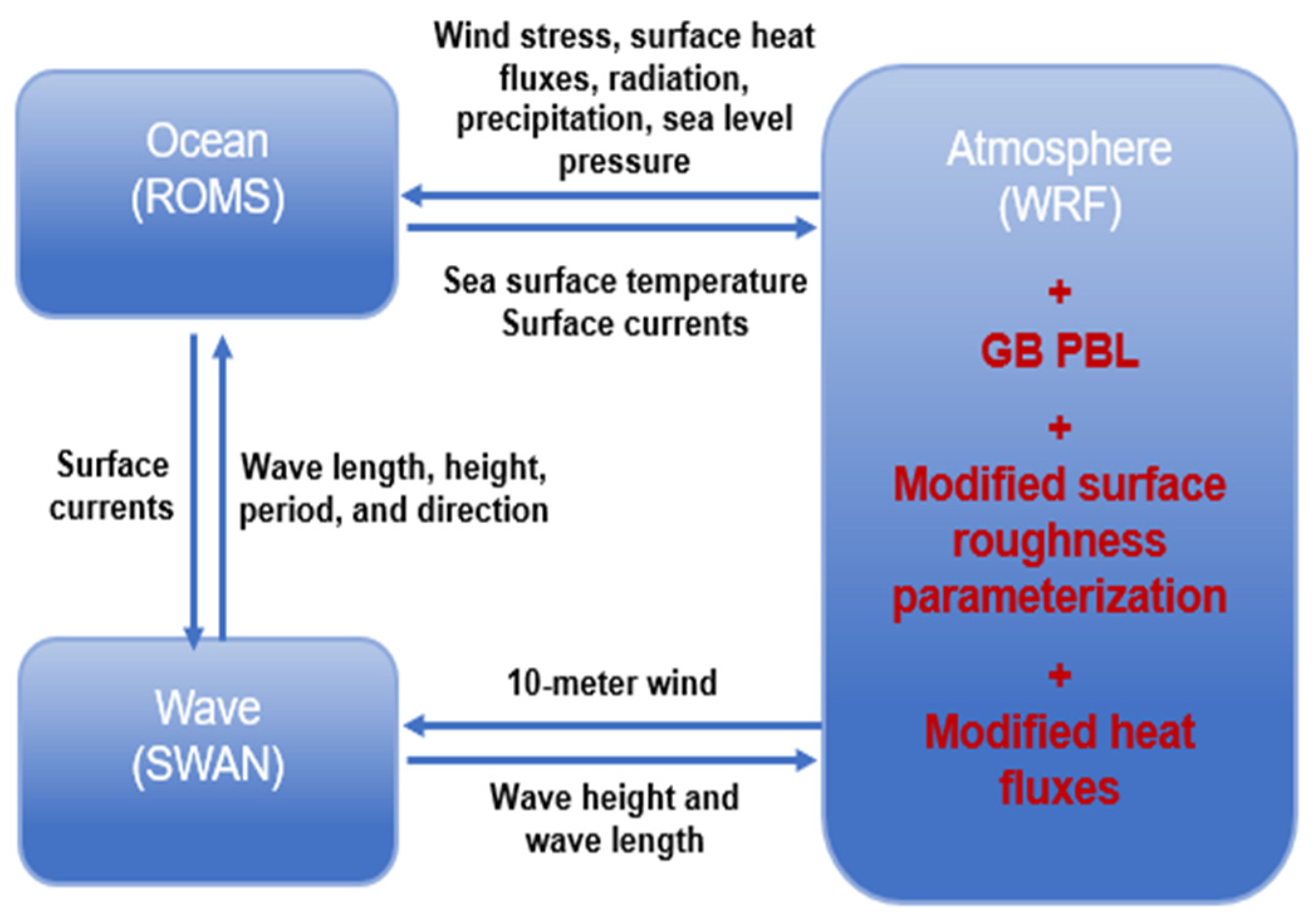
Preprints 71060 g002
Preprints 71060 g003
Figure 3. The model domains used for the COAWST simulations.
Figure 3. The model domains used for the COAWST simulations.
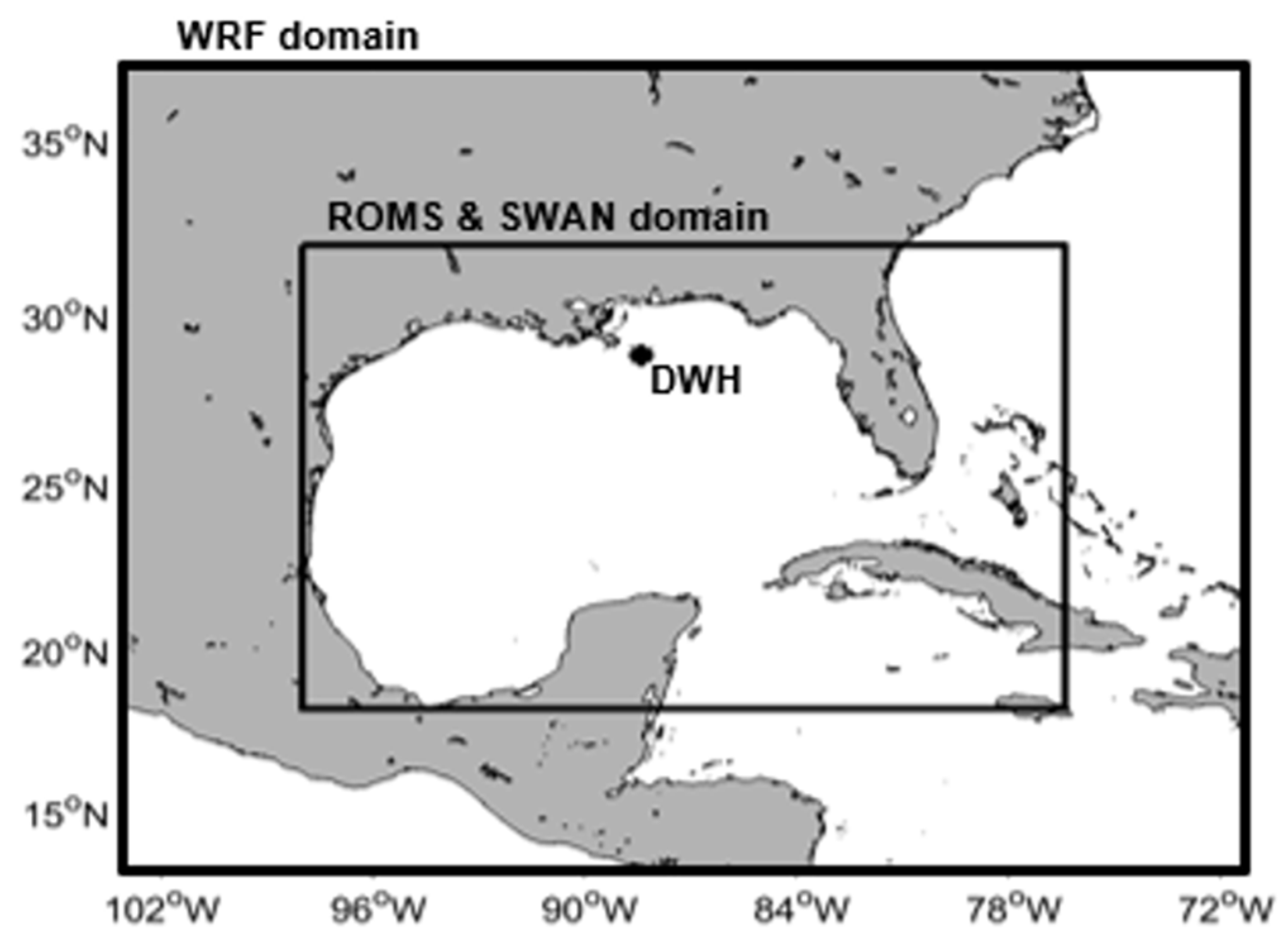
Preprints 71060 g003
Preprints 71060 g004
Figure 4. Probability distribution function of changes in surface stress (Nm-2) when roughness is the only varying factor while wind speed and boundary-layer stability are not impacted by oil over the 2-week period (21 April 2010–5 May 2010) for (a) partial oil coverage surface roughness relative to a water surface and (b) for total oil coverage surface roughness relative to a water surface. The negative changes in stress terms are from the conditions where roughness is suppressed by oil. There are no increases in stress due to oil solely impact roughness length.
Figure 4. Probability distribution function of changes in surface stress (Nm-2) when roughness is the only varying factor while wind speed and boundary-layer stability are not impacted by oil over the 2-week period (21 April 2010–5 May 2010) for (a) partial oil coverage surface roughness relative to a water surface and (b) for total oil coverage surface roughness relative to a water surface. The negative changes in stress terms are from the conditions where roughness is suppressed by oil. There are no increases in stress due to oil solely impact roughness length.
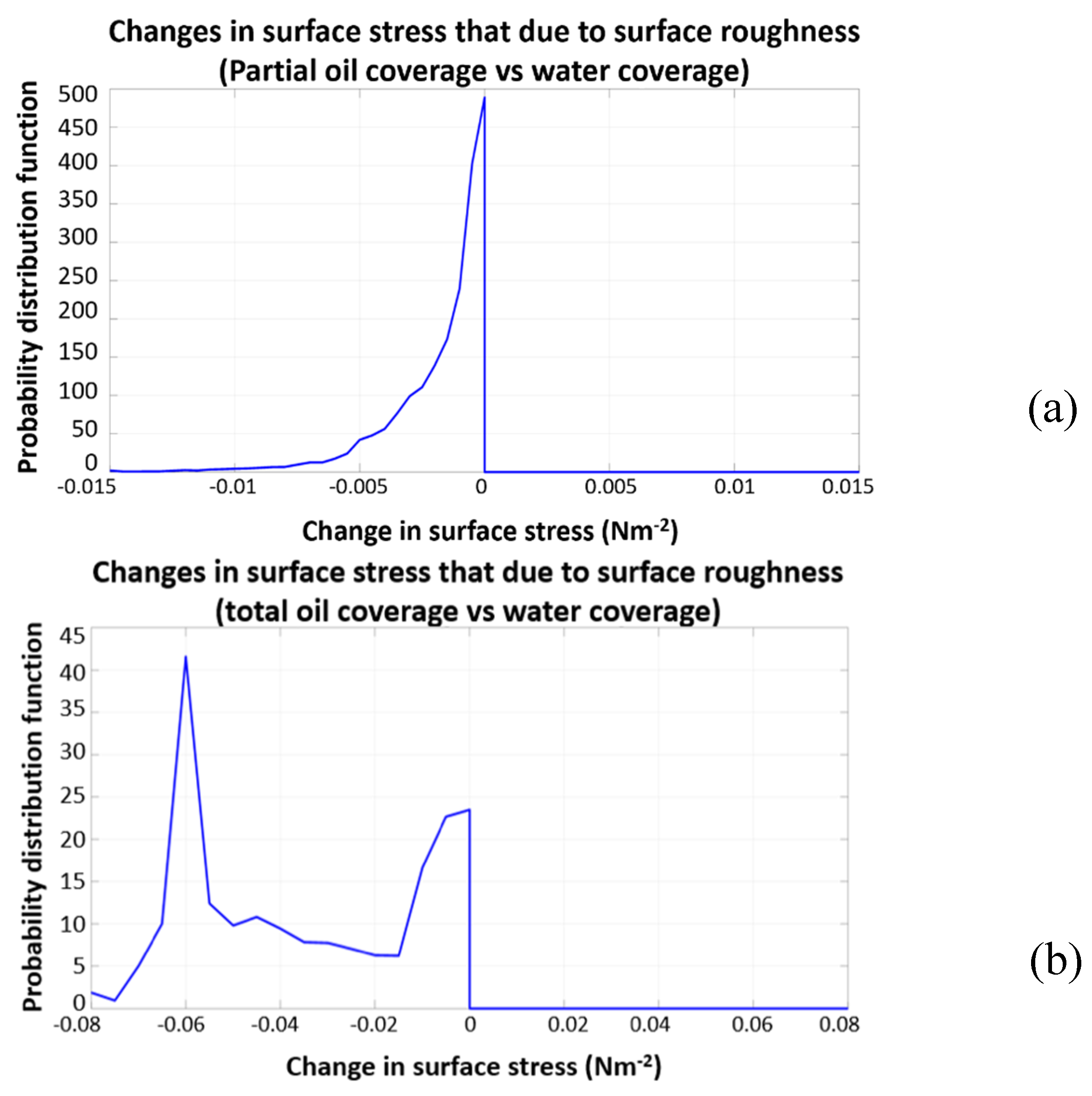
Preprints 71060 g004
Preprints 71060 g005
Figure 5. Probability distribution function of the changes in surface stress (Nm-2) for an oil-related 10 m wind relative to water-related 10 m wind when surface wind is the only varying factor over the 2-week period. On the left side of the curve, there are 34.98% of data and on the right side there are 51.92% of data above the zero line.
Figure 5. Probability distribution function of the changes in surface stress (Nm-2) for an oil-related 10 m wind relative to water-related 10 m wind when surface wind is the only varying factor over the 2-week period. On the left side of the curve, there are 34.98% of data and on the right side there are 51.92% of data above the zero line.
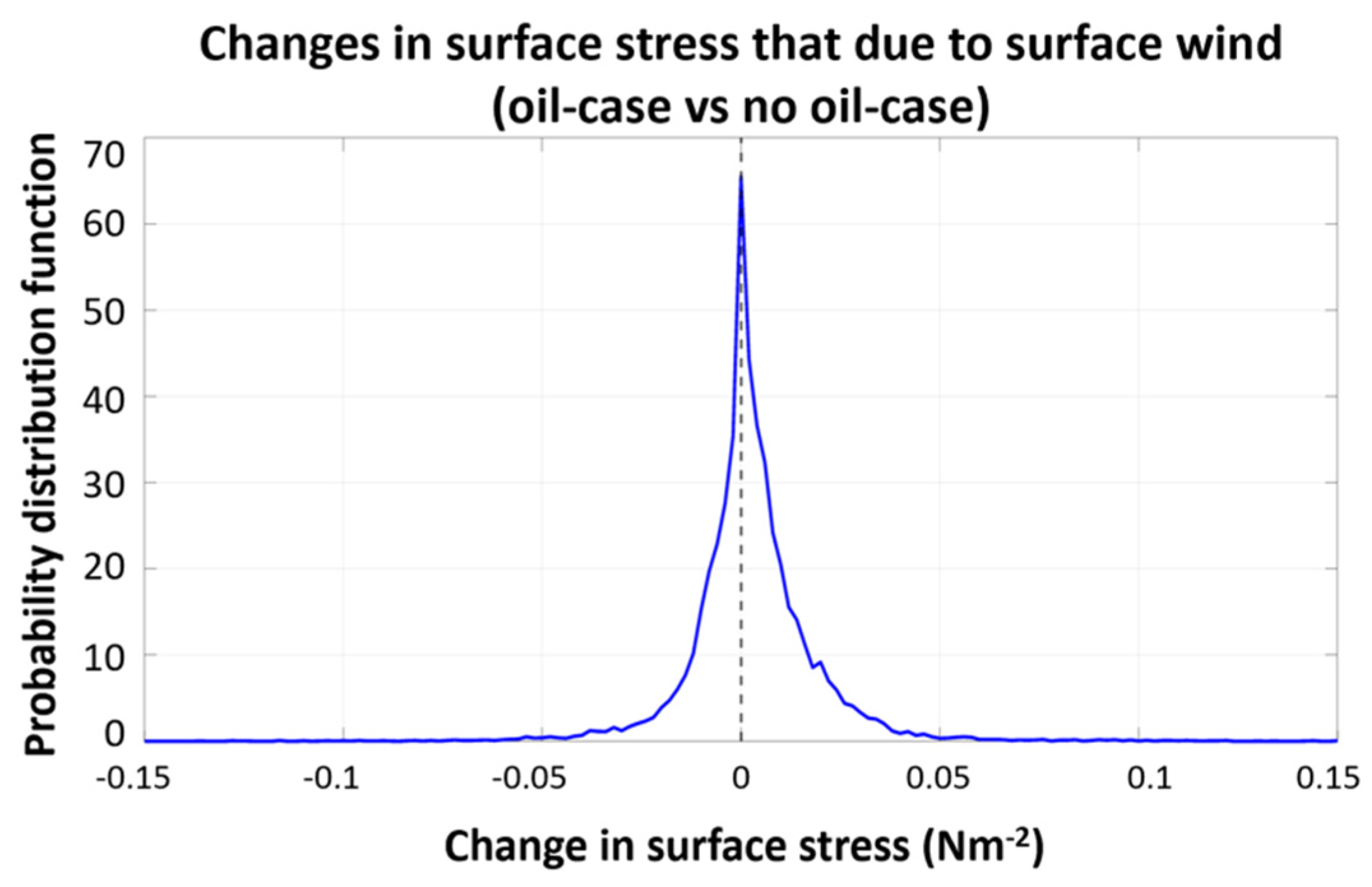
Preprints 71060 g005
Preprints 71060 g006
Figure 6. The differences in surface wind speed between the COAWST model with oil modifications relative to the COAWST model without oil modifications (shaded contours, ms-1) on May 04 at (a) 06:00, (b) 12:00, (c) 18:00, and (d) 00:00 UTC. The shaded red color indicates that the oil-case winds speeds are greater than the no oil-case wind speeds, whereas blue indicates the oil-case wind speeds are less than the no oil-case wind speeds.
Figure 6. The differences in surface wind speed between the COAWST model with oil modifications relative to the COAWST model without oil modifications (shaded contours, ms-1) on May 04 at (a) 06:00, (b) 12:00, (c) 18:00, and (d) 00:00 UTC. The shaded red color indicates that the oil-case winds speeds are greater than the no oil-case wind speeds, whereas blue indicates the oil-case wind speeds are less than the no oil-case wind speeds.
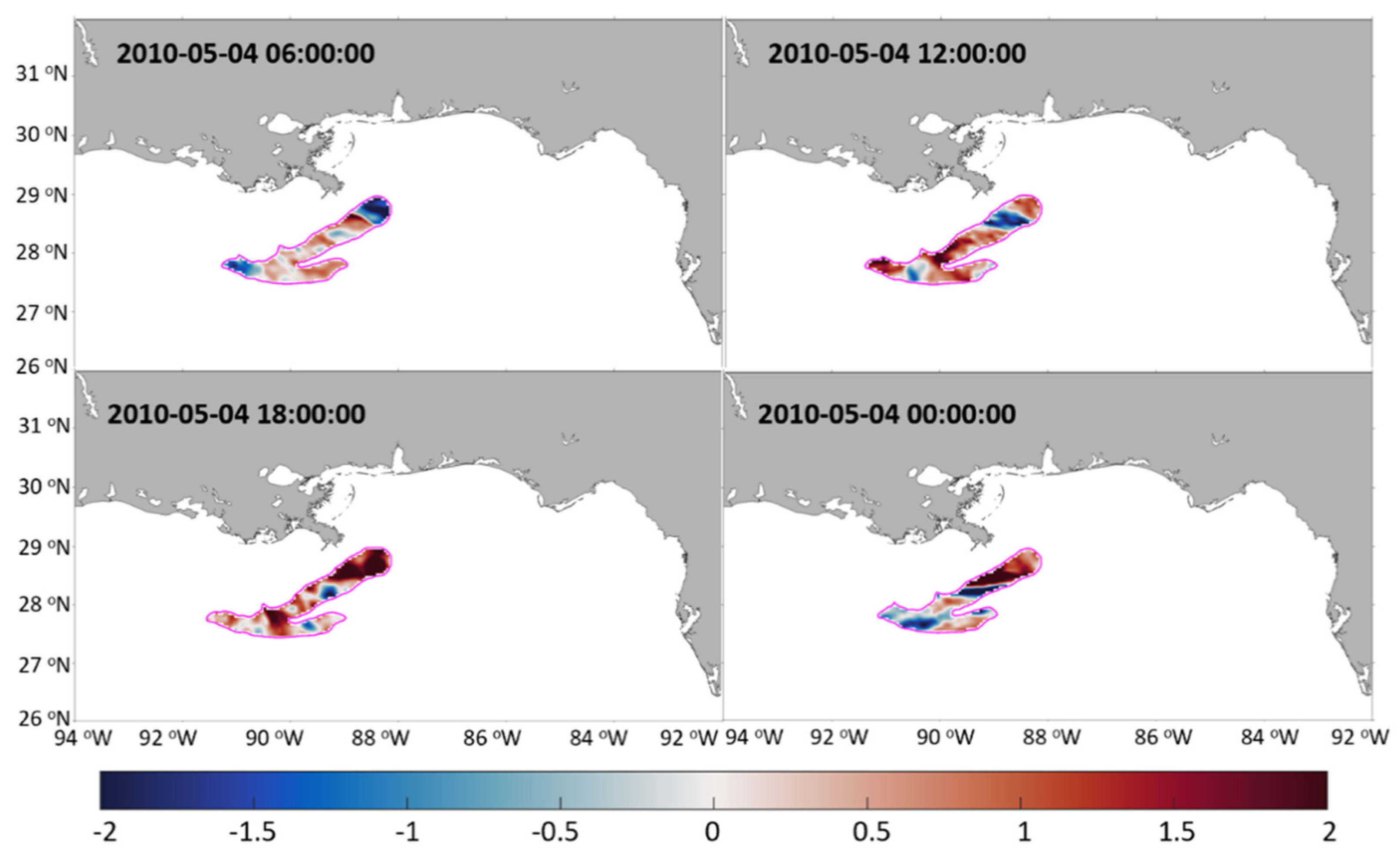
Preprints 71060 g006
Preprints 71060 g007
Figure 7. Probability distribution function of the changes in air-sea temperature differences for COAWST model with and without oil modifications over the 2-week period (2010-04-21 to 2010-05-05) only at 6 pm time-steps for different Aoil ranges.
Figure 7. Probability distribution function of the changes in air-sea temperature differences for COAWST model with and without oil modifications over the 2-week period (2010-04-21 to 2010-05-05) only at 6 pm time-steps for different Aoil ranges.
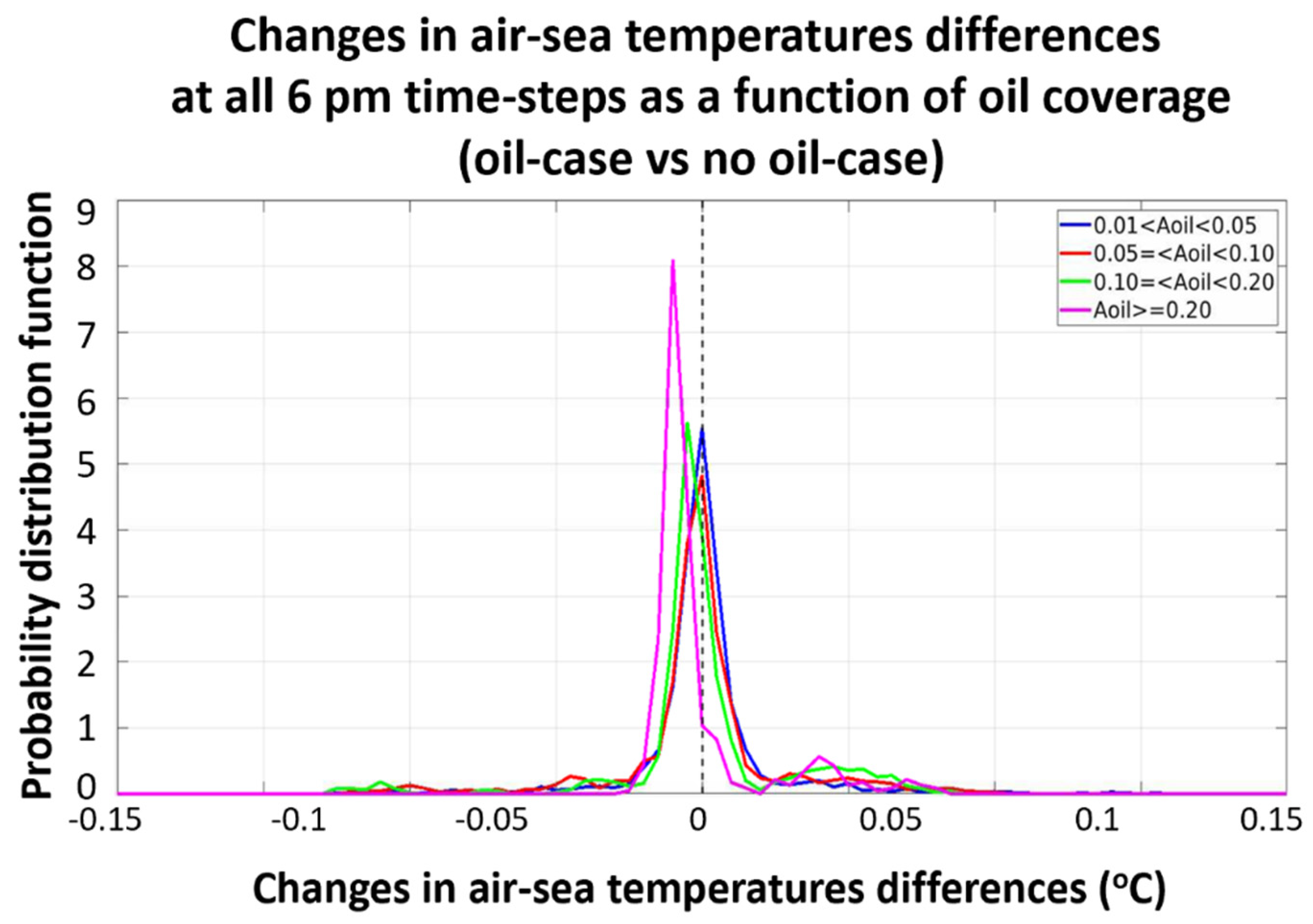
Preprints 71060 g007
Preprints 71060 g008
Figure 8. Probability distribution function of the changes in surface stress (Nm-2) for an oil-related boundary-layer stability relative to water-related boundary-layer stability when atmospheric boundary-layer stability is the only varying factor over the 2-week period.
Figure 8. Probability distribution function of the changes in surface stress (Nm-2) for an oil-related boundary-layer stability relative to water-related boundary-layer stability when atmospheric boundary-layer stability is the only varying factor over the 2-week period.
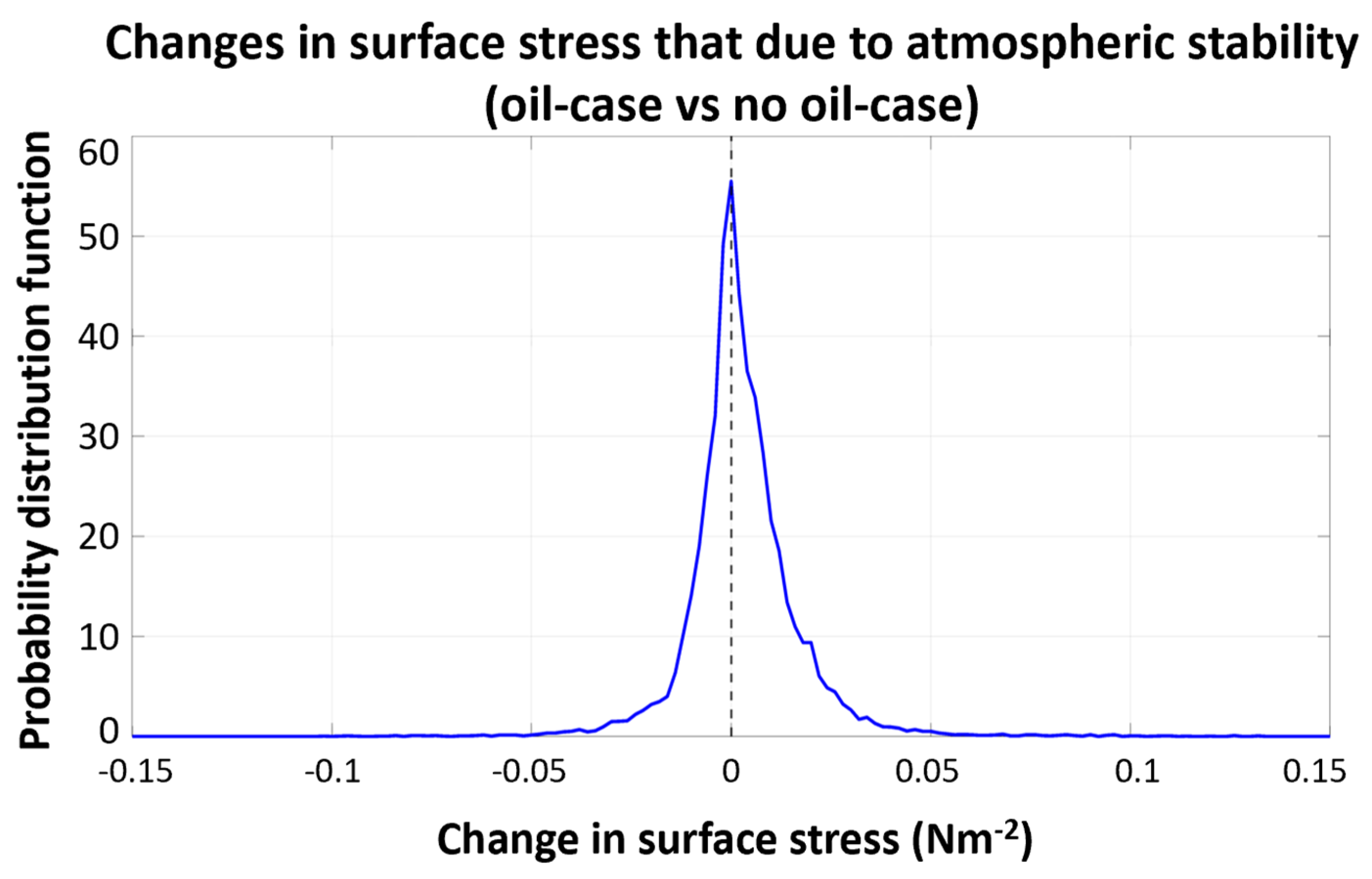
Preprints 71060 g008
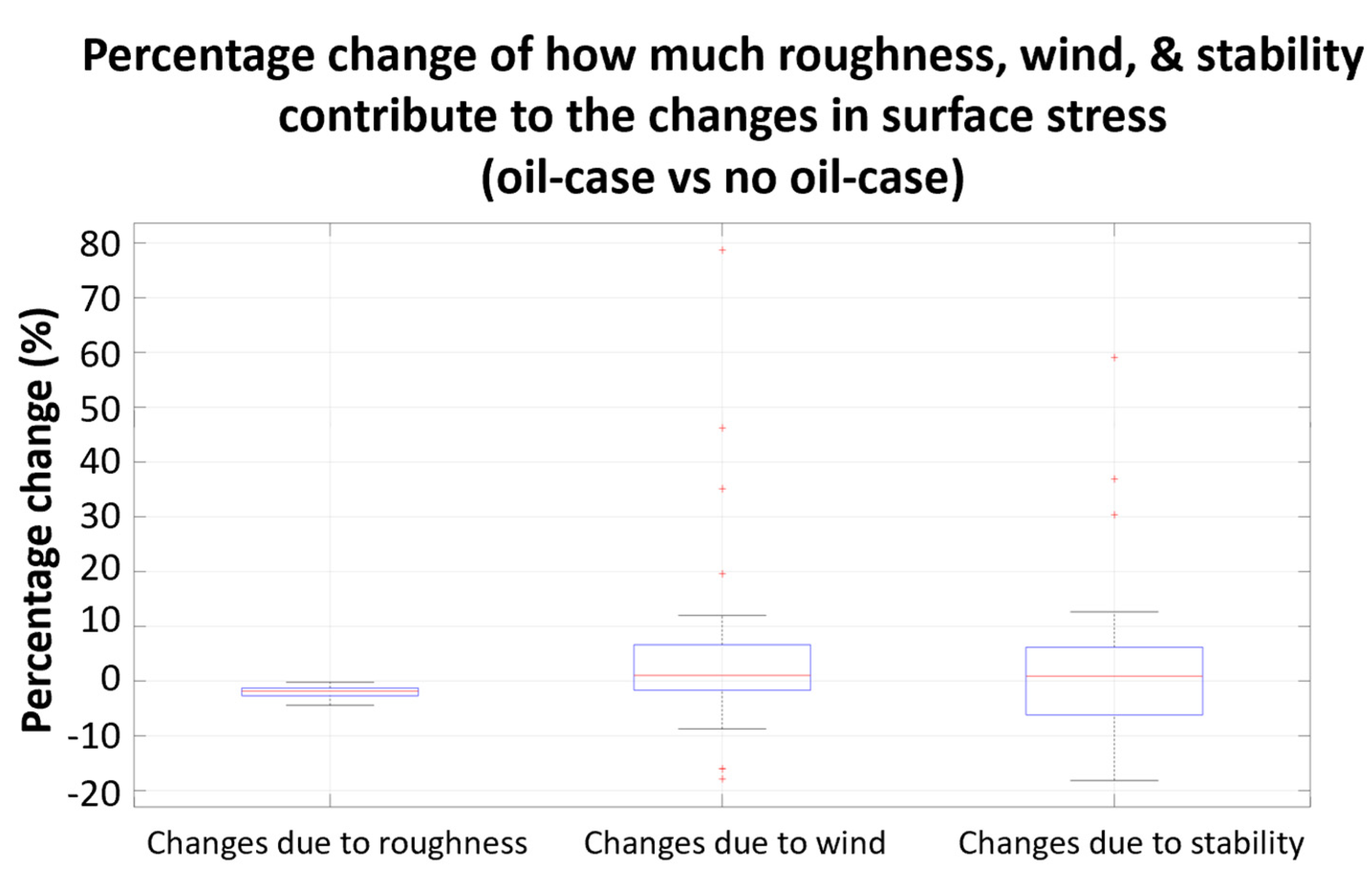
Preprints 71060 g009
Figure 9. Box plots of percentage changes representing how much changes in stress magnitude due to oil-induced changes in surface roughness only, surface wind only, and boundary-layer stability only. The length of the boxes (in blue) represents the interquartile ranges, the median is represented by the middle line (in red), and the lengths of the whiskers (in black) indicate the scatter of data away from the quartile ranges. The calculation is based on the prescribed 2-week period.
Figure 9. Box plots of percentage changes representing how much changes in stress magnitude due to oil-induced changes in surface roughness only, surface wind only, and boundary-layer stability only. The length of the boxes (in blue) represents the interquartile ranges, the median is represented by the middle line (in red), and the lengths of the whiskers (in black) indicate the scatter of data away from the quartile ranges. The calculation is based on the prescribed 2-week period.
Preprints 71060 g009
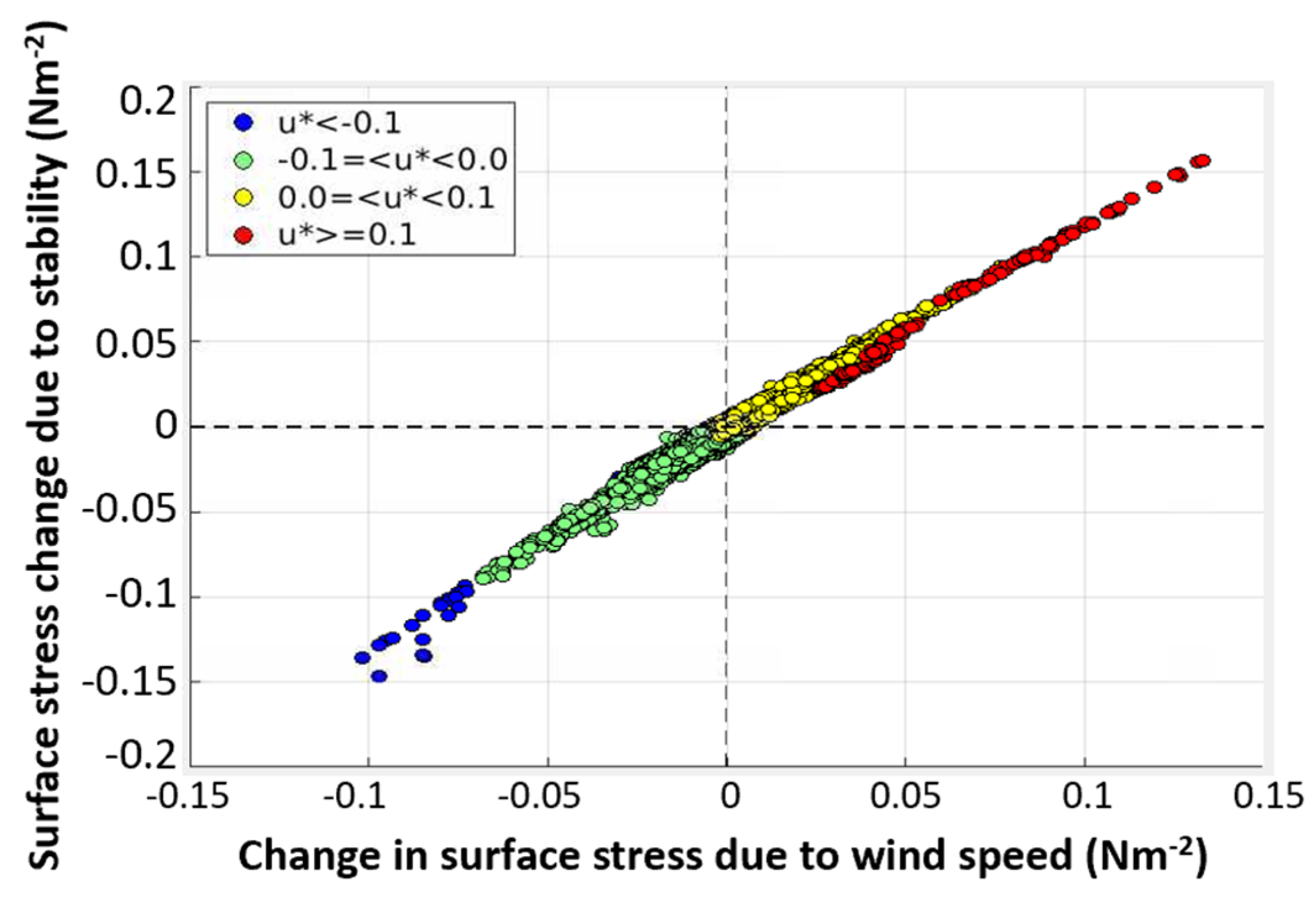
Preprints 71060 g010
Figure 10. (a) Scatterplot of changes in surface stress due to boundary-layer stability vs. changes in stress due to wind speed showing a function of friction velocity (with different colors) over the prescribed 2-week period. Unit for stress: Nm-2.
Figure 10. (a) Scatterplot of changes in surface stress due to boundary-layer stability vs. changes in stress due to wind speed showing a function of friction velocity (with different colors) over the prescribed 2-week period. Unit for stress: Nm-2.
Preprints 71060 g010
Preprints 71060 g011
Figure 11. Variations of drag coefficient for air-sea temperature differences of -40oC to +25oC and wind speeds at 10-m height for fractional oil coverage of (a) 0.0, (b) 0.25, (c) 0.50, (d) 0.75, and (e) 1.0. The red lines represent when the air temperature is less than the SST, the green lines represent when the air temperature is greater than the SST, and the black line represents when the air temperature is equal to the SST. Red lines are every 2 oC whereas green lines are every 1 oC. .
Figure 11. Variations of drag coefficient for air-sea temperature differences of -40oC to +25oC and wind speeds at 10-m height for fractional oil coverage of (a) 0.0, (b) 0.25, (c) 0.50, (d) 0.75, and (e) 1.0. The red lines represent when the air temperature is less than the SST, the green lines represent when the air temperature is greater than the SST, and the black line represents when the air temperature is equal to the SST. Red lines are every 2 oC whereas green lines are every 1 oC. .
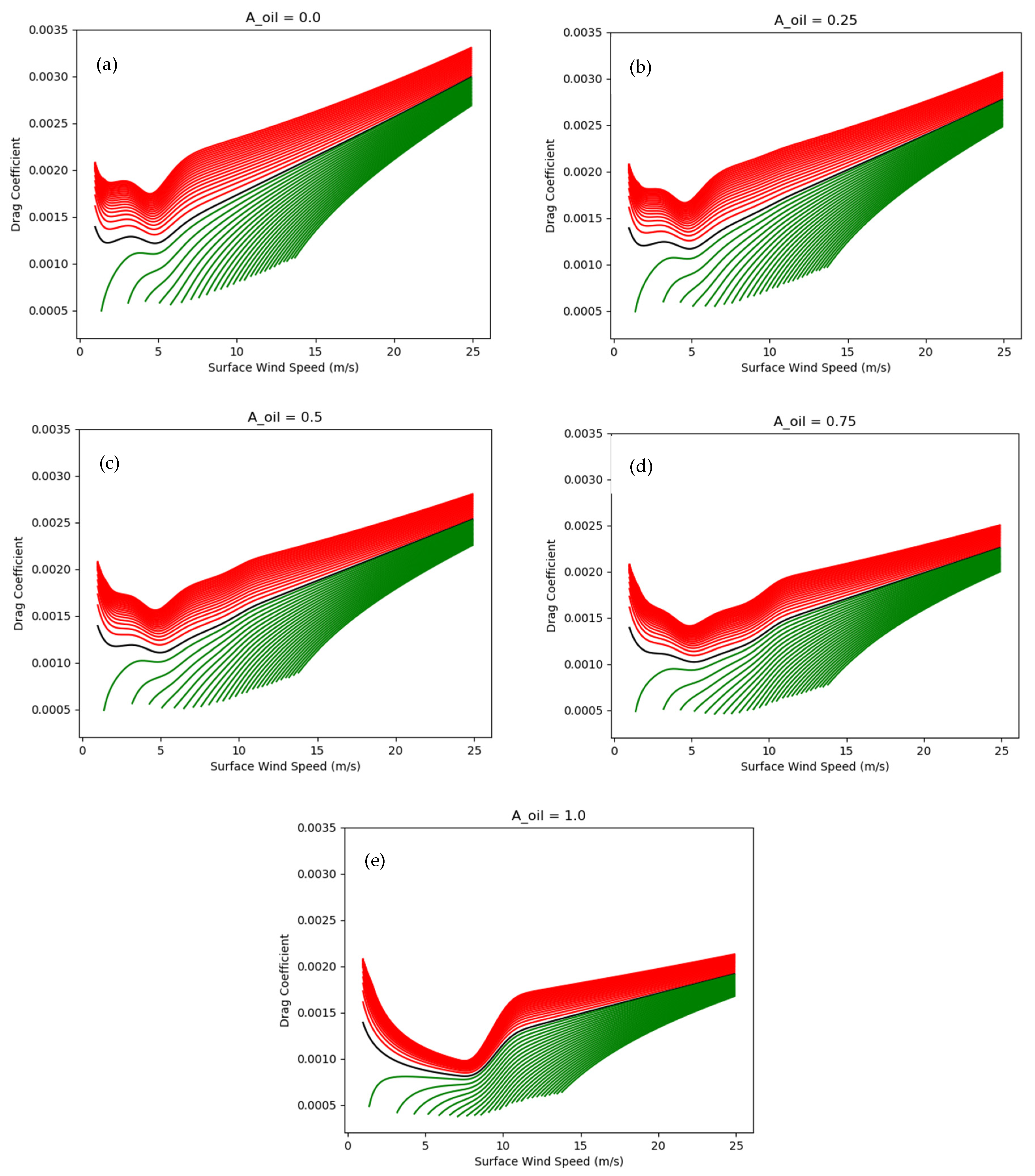
Preprints 71060 g011
Preprints 71060 g012
Figure 12. A schematic diagram of the feedback mechanism indicating how oil slick impacts air-sea coupling. The main dominant factor for the impact of oil slick is surface roughness and SST. Oil affects surface roughness which impacts the surface stress. Oil also affects SST, causing a change in air-sea temperature difference, leading to a change in boundary-layer stability, and ultimately impacts the surface stress. Oil-induced changes in friction velocity and boundary-layer stability also cause a change in surface wind which impacts surface stress.
Figure 12. A schematic diagram of the feedback mechanism indicating how oil slick impacts air-sea coupling. The main dominant factor for the impact of oil slick is surface roughness and SST. Oil affects surface roughness which impacts the surface stress. Oil also affects SST, causing a change in air-sea temperature difference, leading to a change in boundary-layer stability, and ultimately impacts the surface stress. Oil-induced changes in friction velocity and boundary-layer stability also cause a change in surface wind which impacts surface stress.
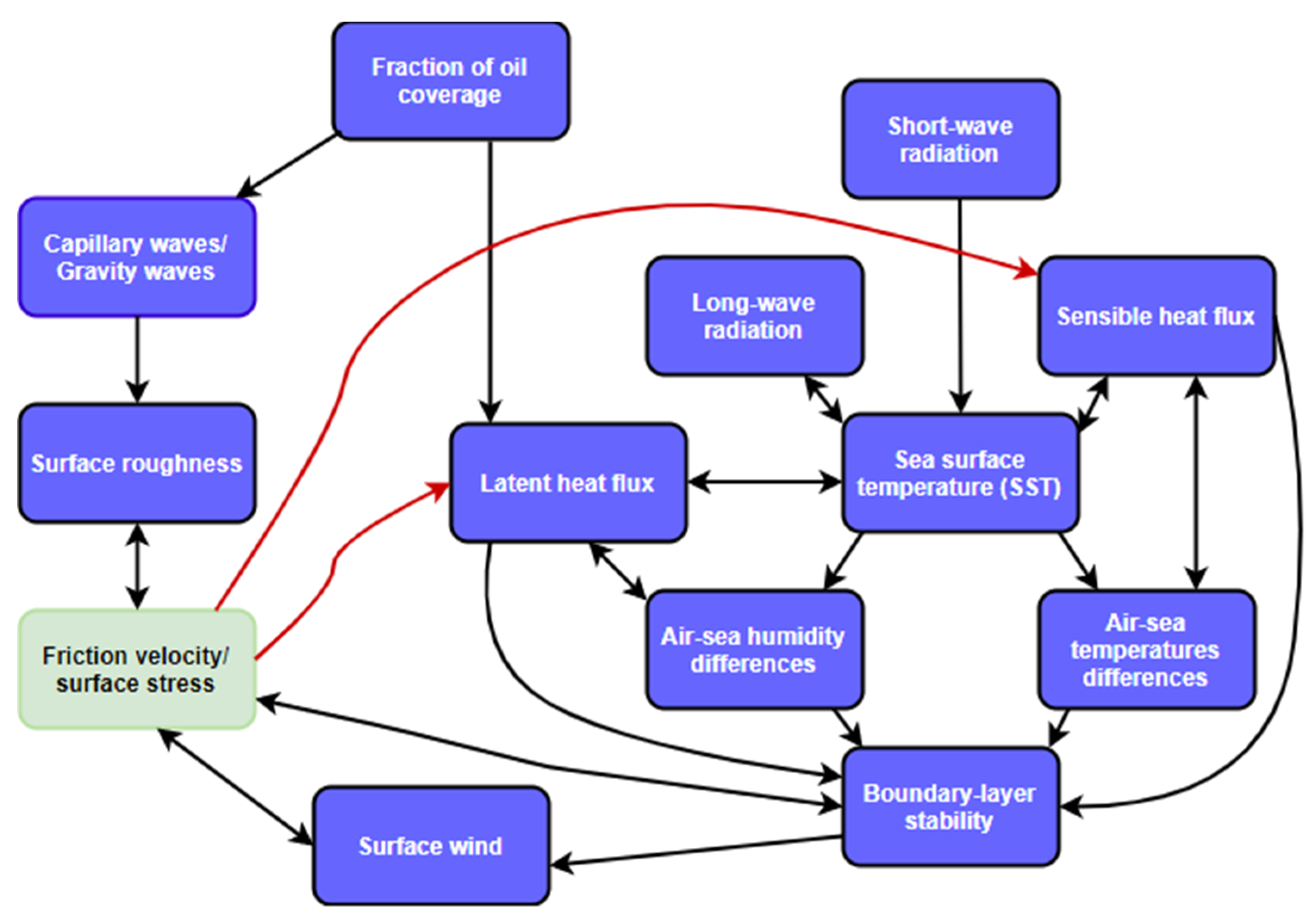
Preprints 71060 g012
Table 1. Physical parameterizations used in this study.
Table 1. Physical parameterizations used in this study.
Parameterization Physics options Reference
Microphysics Thompson graupel scheme [20]
cumulus Grell-Freitas ensemble scheme [21]
Longwave/
Shortwave radiation 		RRTMG scheme [22]
Surface layer Eta Similarity Scheme [23]
Land-surface Unified Noah Land Surface Model [24]
Planetary boundary layer GB scheme [25]
Table 2. Description of how the change of surface stress was computed due to oil-related change in surface roughness, surface wind, and boundary-layer stability, respectively.
Table 2. Description of how the change of surface stress was computed due to oil-related change in surface roughness, surface wind, and boundary-layer stability, respectively.
Cases Assumption for Oil-Related Parameters Surface stress change
Case 1: z 0 m is the only varying factor for partial oil coverage ( A o i l ≠ 0 ) τ A o i l ≠ 0 − τ A o i l = 0 ≈ w a t e r
Case 2: z 0 m is the only varying factor for total oil coverage ( A o i l = 1 ) τ A o i l = 1 − τ w a t e r
Case 3: Surface wind is the only varying factor for partial oil coverage τ A o i l ≠ 0 − τ A o i l ≠ 0 ;   w a t e r − r e l a t e d   w i n d
Case 4: ABL stability is the only varying factor for partial oil coverage τ A o i l ≠ 0 − τ A o i l ≠ 0 ;   w a t e r − r e l a t e d   s t a b i l i t y
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated