Optimization of Magnetohydrodynamic Parameters in Two- Dimensional Incompressible Fluid Flow on a Porous Channel

Preprint

Article

Optimization of Magnetohydrodynamic Parameters in Two- Dimensional Incompressible Fluid Flow on a Porous Channel

Altmetrics

Downloads

129

Views

Comments

Supplementary Material

supplementary.pdf (557.17KB )

Carolyne Onyancha^*,

Joash Kerongo,Vincent Bulinda

Carolyne Onyancha^*,

Joash Kerongo,Vincent Bulinda

This version is not peer-reviewed

This preprints belongs to the Topic

Mathematical Modeling

Submitted:

16 April 2023

Posted:

17 April 2023

You are already at the latest version

Alerts

Abstract

Optimization of Magnetohydrodynamics parameters on the velocity profile and temperature distribution of incompressible fluid flow on a porous channel was evaluated. The fluid flow was considered to be unsteady, incompressible and flowing in 2-D in porous channel. The effects of magnetic parameter, Darcy’s number and fluid pressure on velocity profiles, and the effect of variable viscosity and Eckert number on temperature distribution in incompressible fluid flow were determined. The flow was considered to be in a channel running along the x-axis on which the magnetic field exist and finally along the y-axis on the porous part of the channel. The resulting model equations were solved by Finite Difference Method (FDM) in MATLAB software. Analysis of results indicated that increasing Darcy’s number and fluid pressure leads to increase in fluid velocity profile, while increasing magnetic parameter decreases fluid velocity profile. Also, it was observed that increase in both Eckert number and fluid viscosity lead to increase in temperature distribution. Optimization in temperature was achieved by increasing the magnetic field while viscosity was optimized by increasing the length of the porous part of the channel. This study will helpful to contribute alternative equations and methodology to engineering and in factories where getting the MHD parameters optimally is the main objective, particularly on temperature, velocity and pressure.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

Nomanclature:

κ

, Permeability of porous medium;

ρ

, Density [kgm⁻³];

\cup

, Kinetic coefficient of viscosity [m²s⁻¹];

σ

, Electrical conductivity [Ω⁻¹m⁻¹];

C_{p}

, Specific heat at constant pressure [JKg⁻¹K⁻¹]; T, Temperature [K];

μ

, Coefficient of viscosity;

ϕ

, Viscous dissipation function [s⁻²]; D_H, Hydraulic diameter [m]; Q, Volumetric flow rate [m³/s]; A, The pipe's cross-sectional area [m²]; u, Mean velocity of the fluid, [m/s]; U, Characteristic velocity scale; B, Magnetic field; Ha, Hartmann number; μ, Dynamic viscosity of the fluid [Pa·s = N·s/m² = kg/(m·s)]; ν, kinematic viscosity [m²/s]; W, mass flow rate of the fluid [kg/s]; L, Characteristic length; D, Diffusion coefficient; Re, Reynolds number; Sc, Schmidt number; Pr, Prandtl number; α, Thermal diffusivity;

g_{x}

, Gravitational force on the x-axis;

g_{y}

, Gravitational force on the y-axis; R, Hall current effect.

1. Introduction

The effect of magnetohydrodynamic (MHD) fluid flow is a physical property that describes the movement of an electrically conducted fluid with the impact of externally applied magnetic effects. The electrolytes, salt water, and plasma are examples of MHD fluids. MHD fluid flow has plentiful industrial applications, for example, cooling of reactors and drug targeting. Conceptually, MHD is based upon the induction of electric current by applied magnetic field through a conducted moving fluid (Ahmad, M.; Muhammad, T.; Ahmad, I.; Aly, S., (2020).)

There is great theoretical interest in the study of Magnetohydrodynamic flow through a porous channel because it has attracted attention in applications to a variety of phenomena particularly in geophysics astrophysics. Practical interest of such studies includes applications in electromagnetic boundary cooling, lubrication and bio-physical systems. A porous material containing the fluid is considered a non-homogeneous medium but it can be considered as a homogeneous medium by taking its dynamical properties to be equal to the averages of the original non-homogeneous continuum. This way, a physical problem of the flow through a porous medium is reduced to the flow problem of a homogeneous fluid with imposed resistance (Luo C., et al., 2021).

The study of MHD fluid dynamics on a porous channel has been studied by many scholars. Anil Kumar et al., (2010) investigated an unsteady periodic flow of a viscous incompressible fluid through a porous channel in the presence of transverse magnetic field. Hady, et al., (2006) studied free convection flow along a vertical surface enclosed in electrically conducting fluid saturated porous media in the presence of internal heat generation (or absorption effect). The study focused mainly on the effect of thermal radiation and heat source on unsteady periodic flow of a viscous incompressible fluid through a porous planer channel under the influence of transverse magnetic field.

Computer based simulations are commonly used in Computational Fluid Dynamical Systems (CFDS) involving fluid flow, heat transfer and associated phenomena such as chemical reactions. Combustion in engines and gas turbines, turbo machinery and flows inside rotating passages, for example, apply this technique. (Kumar, A., et al., 2013).

The velocity at any given point in space that vary with time is considered Unsteady Flow. In reality, therefore, almost all physical flows are unsteady since in such flows the velocity varies with time. For example, the flow generated by turning off a faucet to stop the flow of water is described as non-periodic unsteady flow. The periodic injection of the air-gasoline mixture into the cylinder of an automobile engine includes such examples of flow where unsteady effects may be periodic, occurring time after time in basically the same manner. However, in many situations the unsteady character of a flow is quite random, implying that there is no repeated regular variation to the unsteadiness. This behavior is observed in turbulent flow but absent in laminar flow. Highly viscous syrup flowing smoothly onto a pancake executes a deterministic laminar flow while the irregular splashing of water from a faucet onto the sink below it represents a turbulent flow. Also, the irregular gustiness of the wind represents random turbulent flow. Generally, in an unsteady flow, the flow variables such as velocity and the thermodynamic properties at every point in space vary with respect to time. (Kumar, R., 2018).

Kumar, R. (2018) studied unsteady periodic flow of a viscous incompressible fluid through a porous planer channel with heat generation under the influence of transverse magnetic field. The governing equations were solved by perturbation techniques. Closed form solutions were obtained for the temperature and fluid velocity. The results were that the flow decelerates on the imposition of magnetic field. It was also realized that the fluid velocity decreases as the values of Reynolds number increases. Further, it was observed that fluid velocity accelerates as the radiation parameter is increased.

In this study internally generated heat and the applied magnetic field from the external were both ignored. Only the internally generated magnetic field due to the MHD parameter were considered. Danial, et al., (2018) considered a laminar viscous fluid flow being electrically conducting due to an accelerated sheet with the fluid flow through a porous medium over a porous surface. The flow was assumed to be under the effect of radiative heat source, applied magnetic field, and slip conditions.

Dimensionless numbers in fluid dynamical systems are a set of dimensionless quantities that have an important role in analyzing the behavior of fluids. Different dimensionless numbers give the relative strengths of the different phenomena of inertia, viscosity, conductive heat transport, and diffusive mass transport. Dimensionless numbers applied in this study are Darcy number, Eckert number and magnetic parameter (Li, Y.-X.; Alshbool, M.H.; Lv, Y.-P.; Khan, I.; Khan, M.R.; Issakhov, A., 2021).

This paper is organized as follows. First, the background to the study is described in Section 1. Then, the governing mathematical principles and equations are given in Section 2, model formulation and applications are presented in Section 3, results and discussion on results is provided in Section 4, summary and conclusion in Section 5, and recommendations in Section 6.

2. Background

Several potential applications arise from studying natural convection in porous channel. These applications include geophysical and engineering applications, chemical engineering in purification and filtration processes, in agricultural engineering for channel irrigation and in studying the underground water resources, and in petroleum technology to study the movement of water, oil and natural gas.

Most previous studies on Magnetohydrodynamics have focused on convective fluid, flow and heat transfer within a porous channel of flow where either the fluid is chemically reactive, viscous and electrically conductive fluid. The channels are either vertically porous, inclined angles are considered or ramped wall temperature and ramped surface concentration are put into account. In this study focus was on a two-dimensional, unsteady incompressible fluid. The effect of various variables such as viscosity, thermos-radiation, induced magnetic field, heat energy flow and temperature profiles in a free convective flow within a porous channel in two directions was considered. This study focused on an incompressible viscous fluid flow through a porous channel. The systems of governing equations were introduced in two-dimensions to optimization of MHD parameters in incompressible fluid flow in a porous channel. The equations were then discretized and solved numerically through central scheme method.

Existing literature on Magnetohydrodynamics focus on either a stationary fluid or the fluid is flowing through boundaries with radiation, stretching surfaces or vertically wavy surfaces. Some focus on the velocity moving axially. Heat transfer within a porous channel flowing in one direction in some cases were considered. In this study the effect of velocity on viscosity is considered in a two-dimensional fluid flow where the flow is considered incompressible, unsteady and flowing through a porous channel.

Ajibade, A. O. and Tafida, M. K. (2020) investigated the effect of variable thermal conductivity and variable viscosity on natural convection Couette flow. The combined effects of thermal conductivity and variable viscosity was analyzed on thermodynamics and fluid flow in a vertical channel. Perturbation method was used to solve the resulting conservation equations of energy and momentum that described the dynamics of the flow. The numerical results showed that fluid velocity and temperature decreased with increase in thermal conductivity. The theoretical analysis provided indicate that thermal conductivity and variable viscosity are important fluid properties whose incorporation into fluid flow equations affect the flow thermodynamics and fluid formation within the channel of flow.

Most previous studies have focused on convective and laminar viscous fluid flow. In most cases an electrically conducting surface or a shrinking surface has been considered. Different techniques have been used to solve the resulting problems like Homotopy analysis method, Perturbation Technique, Explicit Infinite Difference Scheme as well as Finite Element Galekin’s Approach. In this study optimization of pressure has been implemented in a two-dimensional unsteady incompressible fluid flow through a porous channel. The governing equations were then solved numerically through Central Scheme method.

3. Governing Equations and Method of Solution

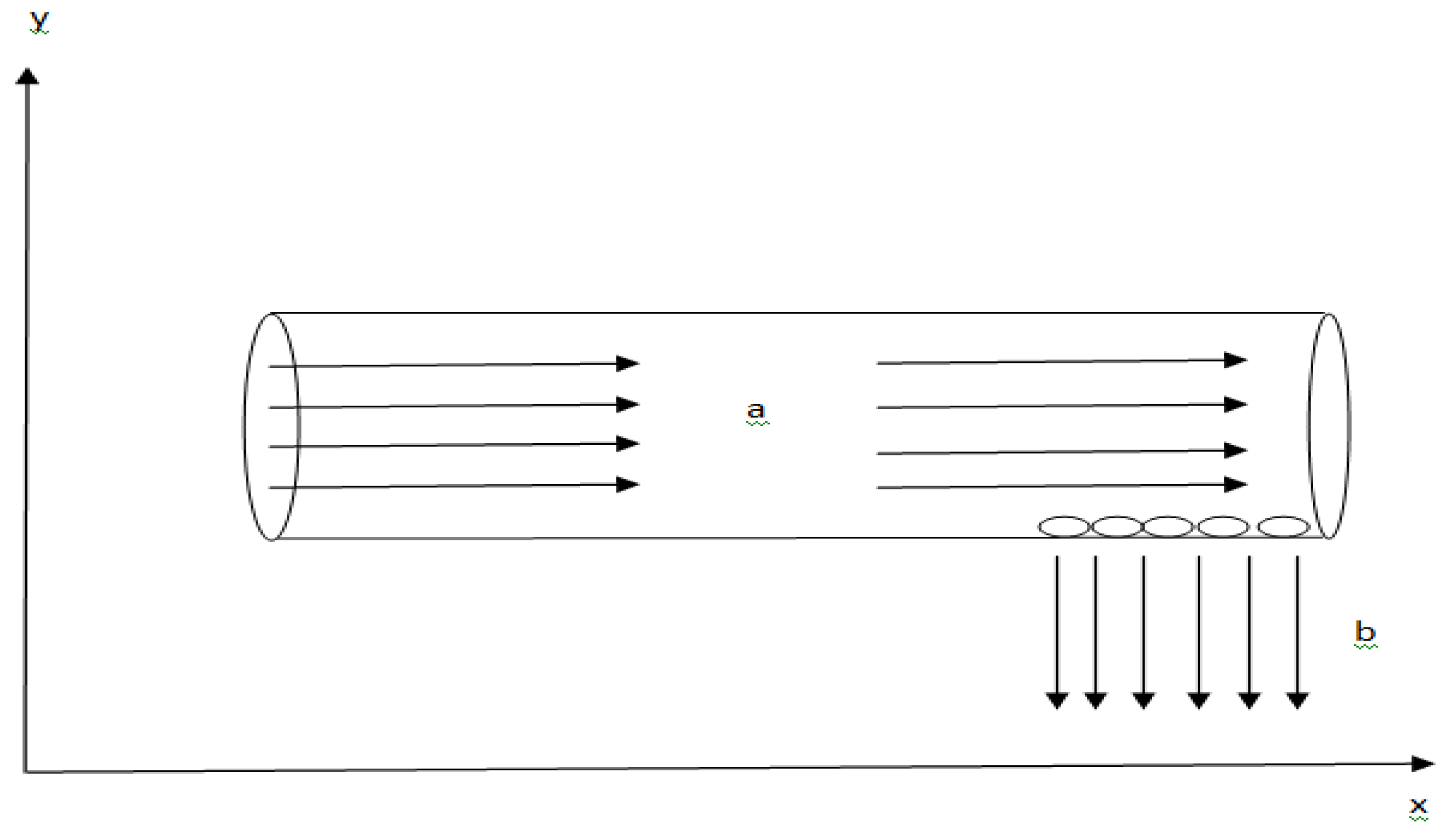
The geometry of the problem was set up as shown in Figure 3.1 and mathematical conservation equations were applied on MHD fluid flows through a channel along the x-axis (labelled, a) and along the y-axis (labelled, b) through the porous part of the channel.

The magnetic field is at the part labeled (a) in definite length where it is expected to have a difference of the pressure and the viscosity of the fluid as the flow gets through the porous part of the channel.

Figure 3.1. Geometry of the flow through the porous channel.

Dimensional analysis makes the equations more concise from the physical relationship. This process reduces the number of independent variables that defines the problem. The following non-dimensional quantities were introduced and applied on the governing equations for this study,

x = \frac{\bar{x}}{a}, y = \frac{\bar{y}}{a}, u = \frac{\bar{u}}{a}, t = \frac{\bar{t} v}{a}, p = \frac{\bar{p}}{ρ v^{2}}, θ = \frac{T - T_{ο}}{T_{1} - T_{ο}} λ = \frac{v a}{v}, D a = \frac{\bar{k} v}{v a}, M = a B_{o} \sqrt{\frac{σ}{μ}}

(3.1)

where,

t

is time,

u

is the axial velocity,

v

is the transverse velocity,

p

is the pressure,

λ

is the injection/suction parameter, Da is the Darcy number and

M

is the magnetic parameter.

3.1. Finite Difference Method

The finite difference technique involves replacing the partial derivatives occurring in the partial differential equation as well as in the boundary and initial conditions by their corresponding finite difference approximations and then solving the resulting linear algebraic system of equations by a standard iterative procedure or by using a direct method The numerical values of the dependent variable are obtained at the mesh points. Thus, finite difference approximations are obtained in algebraic form, and the solutions are presented on grid points.

Discretization of equations involves transformation of functions, continuous variables, or models into discrete forms. To investigate the predictions of PDE models, it is found necessary to numerically approximate their solutions. The approximate solution are then represented by functional values at certain discrete points.

3.2. Continuity Equation

The equation of continuity (equation of conservation of mass) is always provided based on two fundamental principles: conservation of mass of fluid, and continuity in fluid flow.

Considering an incompressible fluid (the density of the fluid is assumed to be constant), the general continuity equation in 3D is given as

\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0

(3.1)

3.3. Momentum Conservation Equations

In the momentum equation, the rate of change of momentum counters with the surface and the body forces. Surface forces are proportional to area and they result from stresses such as static pressure and viscous stresses acting on the surface of the volume element. Body forces are forces that are proportional to the volume element and act on the fluid element from external force field, such as gravitational force and centrifugal force. The forces acting on the fluid have to be specified for a particular flow configuration being considered. Classically, the equation for conservation of momentum is derived using Newton’s second law of motion. For forced convection the following momentum equation holds,

\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = - \frac{1}{ρ} \frac{\partial p}{\partial x} + μ (\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}}) - (\frac{σ B_{o}^{2}}{ρ} - \frac{ν}{K}) u

(3.2)

where

u

and

v

are the velocity components,

ρ

is the fluid density,

B_{0}

is the strength of magnetic field,

K

is the permeability.

In applications, Equation (3.2) is discretized to study the effects of magnetohydrodynamic parameters on incompressible fluid flow systems.

3.3.1. Dimensinalizing Momentum Equation

To reduce the complexity of the physical problem, first the momentum Equation (3.2) was dimensionalized by introducing Equations (3.1) into Equation (3.2), yielding

U \frac{\partial U}{\partial t} + U \frac{\partial U}{\partial x} + V \frac{\partial U}{\partial y} = - \frac{\partial P}{\partial x} + \frac{1}{λ} (\frac{\partial^{2} U}{\partial x^{2}} + \frac{\partial^{2} U}{\partial y^{2}}) - (\frac{M^{2}}{λ} + \frac{1}{D a}) U

(3.3)

where, the emerging quantities are: t is time,

U

is the axial velocity,

V

is the transverse velocity,

P

is the pressure,

λ

is the injection/suction parameter, Da is the Darcy number and

M

is the magnetic parameter.

3.3.2. Discretization of Momentum Equation

Equation (3.3) was then discretized to study the effects of pressure change

Δ P

, Darcy number Da, and magnetic parameter M on velocity profiles and temperature distribution of an incompressible fluid over a varied length of porous channel. Discretization was achieved using a central difference numerical scheme in which partial derivatives

U_{x}, U_{y}, U_{x x},

and

U_{y y}

were replaced by three-point central difference approximation by substituting these approximations into Equation (3.2), yielding

\frac{{U^{n + 1}}_{i, j} - {U^{n - 1}}_{i, j}}{2 Δ t} + U \frac{{U^{n}}_{i + 1, j} - {U^{n}}_{i - 1, j}}{2 Δ x} + V \frac{{U^{n}}_{i, j + 1} - {U^{n}}_{i, j - 1}}{2 Δ y} = - (\frac{{P^{n}}_{i + 1, j} - {P^{n}}_{i - 1, j}}{2 Δ x}) + \frac{1}{λ} (\frac{{U^{n}}_{i + 1, j} - 2 {U^{n}}_{i, j} + {U^{n}}_{i - 1, j}}{{(Δ x)}^{2}} + \frac{{U^{n}}_{i, j + 1} - 2 {U^{n}}_{i, j} + {U^{n}}_{i, j - 1}}{{(Δ y)}^{2}}) - (\frac{1}{λ} M^{2} + \frac{1}{D a}) U_{i, j}^{n}

(3.4)

The effect of Da and M on the fluid velocity profiles were investigated. Taking

Δ t = 0.01

and

Δ x = Δ y = 0.2

, in a square mesh and letting V = U = λ = 1, and multiplying by

2 Δ t

gives the central difference scheme,

- 2 {U^{n}}_{i + 1, j} + (10 + 0.2 M^{2} + \frac{0.2}{D a}) {U^{n}}_{i, j} - 3 {U^{n}}_{i - 1, j} = 2 {U^{n}}_{i, j + 1} + 3 U_{i, j - 1}^{n} + U_{i, j}^{n - 1} - U_{i, j}^{n + 1} - 0.5 P_{i + 1, j}^{n} - 0.5 P_{i - 1, j}^{n}

(3.5)

Taking i = 1, 2, …, 5 and j = 1 and n = 0 in Equation (3.5) the following systems of linear algebraic equations were formed.

i = 1, - 2 {U^{0}}_{2,1} + (10 + 0.2 M^{2} + \frac{0.2}{D a}) {U^{0}}_{1,1} - 3 {U^{0}}_{0,1} = 2 {U^{0}}_{1,2} + 3 {U^{0}}_{1,0} + {U^{- 1}}_{1,1} - {U^{1}}_{0,1} - 0.5 {P^{0}}_{2,1} - 0.5 {P^{0}}_{0,0} i = 2, - 2 {U^{0}}_{3,1} + (10 + 0.2 M^{2} + \frac{0.2}{D a}) {U^{0}}_{2,1} - 3 {U^{0}}_{1,1} = 2 {U^{0}}_{2,2} + 3 {U^{0}}_{2,0} + {U^{- 1}}_{2,1} - {U^{1}}_{1,1} - 0.5 {P^{0}}_{3,1} - 0.5 {P^{0}}_{1,0} i = 3, - 2 {U^{0}}_{4,1} + (10 + 0.2 M^{2} + \frac{0.2}{D a}) {U^{0}}_{3,1} - 3 {U^{0}}_{2,1} = 2 {U^{0}}_{3,2} + 3 {U^{0}}_{3,0} + {U^{- 1}}_{3,1} - {U^{1}}_{2,1} - 0.5 {P^{0}}_{4,1} - 0.5 {P^{0}}_{2,0} 0 i = 4, - 2 {U^{0}}_{5,1} + (10 + 0.2 M^{2} + \frac{0.2}{D a}) {U^{0}}_{4,1} - 3 {U^{0}}_{3,1} = 2 {U^{0}}_{4,2} + 3 {U^{0}}_{4,0} + {U^{- 1}}_{4,1} - {U^{1}}_{3,1} - 0.5 {P^{0}}_{5,1} - 0.5 {P^{0}}_{3,0} i = 5, - 2 {U^{0}}_{6,1} + (10 + 0.2 M^{2} + \frac{0.2}{D a}) {U^{0}}_{5,1} - 3 {U^{0}}_{4,1} = 2 {U^{0}}_{5,2} + 3 {U^{0}}_{5,0} + {U^{- 1}}_{5,1} - {U^{1}}_{4,1} - 0.5 {P^{0}}_{6,1} - 0.5 {P^{0}}_{4,0}

(3.6)

The initial conditions were set from discretization of energy equation as

U (x, y, 0) = 10, P (x, 0,0) = 0

and boundary conditions as

U (0, y, 1) = 0,

and

U (x, 0, - 1) = 0 .

Letting P(x,1,0) = ∆P and applying the set initial conditions and boundary conditions, the above algebraic Equations (3.20) were expressed in matrix form as

[\begin{matrix} (10 + 0.2 M^{2} + \frac{0.2}{D a}) & - 2 & 0 & 0 & 0 & 0 \\ - 3 & (10 + 0.2 M^{2} + \frac{0.2}{D a}) & - 2 & 0 & 0 & 0 \\ 0 & - 3 & (10 + 0.2 M^{2} + \frac{0.2}{D a}) & - 2 & 0 & 0 \\ 0 & 0 & - 3 & (10 + 0.2 M^{2} + \frac{0.2}{D a}) & - 2 & 0 \\ 0 & 0 & 0 & - 3 & (10 + 0.2 M^{2} + \frac{0.2}{D a}) & - 2 \\ 0 & 0 & 0 & 0 & - 3 & (10 + 0.2 M^{2} + \frac{0.2}{D a}) \end{matrix}] [\begin{matrix} U_{1, 1}^{0} \\ U_{2, 1}^{0} \\ U_{3, 1}^{0} \\ U_{4, 1}^{0} \\ U_{5, 1}^{0} \\ U_{6, 1}^{0} \end{matrix}] = [\begin{matrix} 0.5 Δ P + 10 \\ 0.5 Δ P + 10 \\ 0.5 Δ P + 10 \\ 0.5 Δ P + 10 \\ 0.5 Δ P + 10 \\ 0.5 Δ P + 10 \end{matrix}]

(3.7)

The solutions for varying values of

M,

Da and ∆P were obtained by solving the above matrix Equation (3.7) numerically MATLAB. The magnetic parameter

(M)

was varied between 2.0 to 4.0, while Darcy’s number (Da) was varied between 0.1 to 0.3, and fluid pressure (∆P) was varied from 1.0 KPa to 4.0 KPa The numerical results obtained for

M,

Da and ∆P were recorded in Tables 4.1, 4.2, and 4.3, spectively.

3.4. Energy Conservation Equations

It is a common practice to mathematically derive the energy equation involving dynamical systems from the first law of thermodynamics which states that the rate of energy increase in a system is equated to the work done on the system and the heat added to the system. Assuming no external heat source, the energy equation can be expressed as

ρ c_{p} \frac{\partial T}{\partial t} + ρ c_{p} u \frac{\partial T}{\partial x} + ρ c_{p} v \frac{\partial T}{\partial y} = α (\frac{\partial^{2} T}{\partial x^{2}} + \frac{\partial^{2} T}{\partial y^{2}}) + Φ

(3.8)

where, α is the thermal diffusivity and

Φ = μ \{2 [{(\frac{\partial u}{\partial x})}^{2} + {(\frac{\partial v}{\partial y})}^{2} + {(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x})}^{2}]\}

represents the dissipation function.

3.3.1. Non-Dimensinalizing Momentum Equation

To non-dimensionalize the Energy equation, Equation (3.8) below was considered,

(3.9)

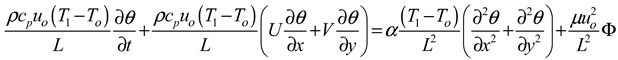
Simplifying Equation (3.9) gives

(3.10)

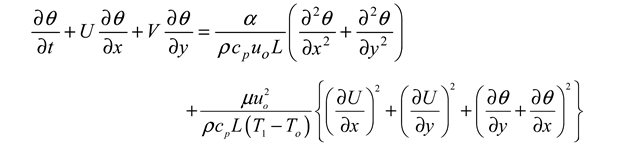
Since the flow is along the x-axis, and for low velocities viscous dissipation is negligible. Equation (3.10) becomes

(3.11)

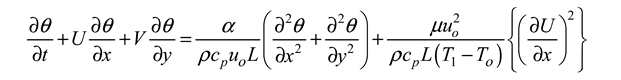
The viscosity (

δ

) of the fluid in this study was taken to be an inverse linear function of temperature and was expressed in the following form (Abdou and Zahar, 2012).

δ = \frac{1}{α (T - T_{\infty})}

(3.12)

where, α is the thermal property of the fluid and T_∞ is ambient temperature. Thus, equation (3.10) yields

\frac{μ u_{o}^{2}}{ρ c_{p} L (T_{1} - T_{ο})} = \frac{u_{o}^{2}}{ρ c_{p} L (T_{1} - T_{ο}) α (T - T_{\infty})} = (\frac{u_{o}^{2}}{ρ c_{p} (T_{1} - T_{ο})}) μ = (\frac{u_{o}^{2}}{ρ c_{p} (T_{1} - T_{ο})}) (\frac{1}{α (T - T_{\infty})})

(3.13)

Rewriting expressions in Equations (3.12):

\frac{α}{ρ c_{p} u_{ο} L} = \frac{α}{ρ c_{p} u_{ο} L} (\frac{μ}{μ}) = (\frac{α}{μ c_{p}}) (\frac{μ}{ρ u_{ο} L})

\Pr = \frac{μ c_{p}}{α}, Re = \frac{ρ u_{ο} L}{μ}, E_{c} = \frac{u_{o}^{2}}{C_{p} (T_{1} - T_{ο}) L},

and

δ = \frac{1}{α (T - T_{\infty})}

. Equation (3.10), therefore, becomes

\frac{\partial θ}{\partial t} + U \frac{\partial θ}{\partial x} + V \frac{\partial θ}{\partial y} = \frac{1}{R e P r {(\frac{\partial^{2} θ}{\partial x^{2}} + \frac{\partial^{2} θ}{\partial y^{2}})}_{c} {(\frac{\partial U}{\partial x})}^{2}}

(3.14)

3.3.1. Discretization of Energy Equation

Equation (3.14) was discretized to study the effects of Eckert number (E_c) and viscosity (δ) on temperature distribution. Using a three-central-difference numerical scheme, the partial derivatives

θ_{x}

θ_{x}

θ_{x x}

and

θ_{y y}

were replaced by three-point-central difference approximation by inserting the approximations into Equation (3.14), yielding

\frac{θ_{i j}^{n + 1} - θ_{i j}^{u}}{Δ t} + \frac{θ_{i + 1, j}^{n} - θ_{i - 1, j}^{u}}{2 Δ x} + \frac{θ_{i, j + 1}^{u} - θ_{i, j - 1}^{n}}{2 Δ y} = (\frac{1}{P r R e} () {(\frac{θ_{i + 1, j}^{u} - 2 θ_{i j}^{n} + θ_{i - 1, j}^{n}}{{(Δ x)}^{2}} + \frac{θ_{i, j + 1}^{n} - 2 θ_{i j}^{n} + θ_{i, j - 1}^{n}}{{(Δ y)}^{2}})}_{C} (\frac{{(u_{i, j + 1}^{n})}^{2} + 2 u_{i, j + 1}^{n} - u_{i, j - 1}^{n} + {(u_{i, j + 1}^{n})}^{2}}{4 {(Δ y)}^{2}}))

(3.15)

Simplifying (3.15), and letting Pr = Re = 1, the central difference scheme gives,

2 θ_{i + 1, j}^{n} - 44 θ_{i, j}^{n} - 2 θ_{i - 1, j}^{n} = 18 θ_{i, j}^{n} + 22 θ_{i, j + 1}^{n} + 10 E_{c} δ

(3.16)

Taking and i = 1, 2, 3, …, 5 and j = 1 the following systems of linear algebraic equations were formed.

i = 1, 2 θ_{2,1}^{0} - 44 θ_{1,1}^{0} - 2 θ_{0,1}^{0} = 18 θ_{1,1}^{0} + 22 θ_{1,2}^{0} + 10 E_{c} δ i = 2, 2 θ_{3,1}^{0} - 44 θ_{2,1}^{0} - 2 θ_{1,1}^{0} = 18 θ_{2,1}^{0} + 22 θ_{2,2}^{0} + 10 E_{c} δ i = 3, 2 θ_{4,1}^{0} - 44 θ_{3,1}^{0} - 2 θ_{2,1}^{0} = 18 θ_{3,1}^{0} + 22 θ_{3,2}^{0} + 10 E_{c} δ i = 4, 2 θ_{5,1}^{0} - 44 θ_{4,1}^{0} - 2 θ_{3,1}^{0} = 18 θ_{4,1}^{0} + 22 θ_{4,2}^{0} + 10 E_{c} δ i = 5, 2 θ_{6,1}^{0} - 44 θ_{5,1}^{0} - 2 θ_{4,1}^{0} = 18 θ_{5,1}^{0} + 22 θ_{5,2}^{0} + 10 E_{c} δ

(3.17)

The initial and boundary conditions obtained from discretization of energy equation were

θ_{i, 0}^{0} = θ_{0, j}^{0} = 10

and boundary conditions

θ_{i, 2}^{0} = θ_{i, 1}^{0} = 0,

respectively. Applying these conditions in the above algebraic Equations (3.17) and expressing the equations in matrix gives,

[\begin{matrix} - 44 & 2 & 0 & 0 & 0 \\ - 2 & - 44 & 2 & 0 & 0 \\ 0 & - 2 & - 44 & 2 & 0 \\ 0 & 0 & - 2 & - 44 & 2 \\ 0 & 0 & 0 & - 2 & - 44 \end{matrix}] [\begin{matrix} U_{1,1}^{0} \\ U_{2,1}^{0} \\ U_{3,1}^{0} \\ U_{4,1}^{0} \\ U_{5,1}^{0} \end{matrix}] = [\begin{matrix} 10 E_{c} δ + 20 \\ 10 E_{c} δ \\ 10 E_{c} δ \\ 10 E_{c} δ \\ 10 E_{c} δ \end{matrix}]

(3.18)

The solutions for varying values of Eckert number (E_c) and fluid viscosity (δ) were obtained by solving the above matrix Equation (3.18) in MATLAB. The numerical results obtained for varying Elkert number and fluid viscosity (δ) were recorded in Tables 4.4 and 4.5, respectively.

4. Results and Discussion

The simulation results obtained in this study focus on the effects of the Magnetic parameter M, Darcy number Da, and fluid pressure P, Eckert number E_C and viscosity

δ

, on velocity profile and temperature distribution, respectively.

4.1. Effects of Magnetic parameters on velocity profile

Equation (3.7) was solved numerically using MATLAB to obtain the results of the effects of M on velocity profile as shown in Table 4.1 below.

Table 4.1. Value of velocity profile for varying Magnetic parameters.

Magnetic parameters	Length of Porous channel
Magnetic parameters	0	1	2	3	4
M = 2	68.83728	85.55858	89.31898	88.30366	76.16492
M = 3	62.54598	76.56727	79.49516	78.66569	68.55051
M = 4	55.48979	66.722339	68.21814	68.21814	60.17463

The above results in Table 4.1 were presented in Figure 4.1 below.

Figure 4.1. Velocity profile against Length of Porous channel at varying Magnetic parameter.

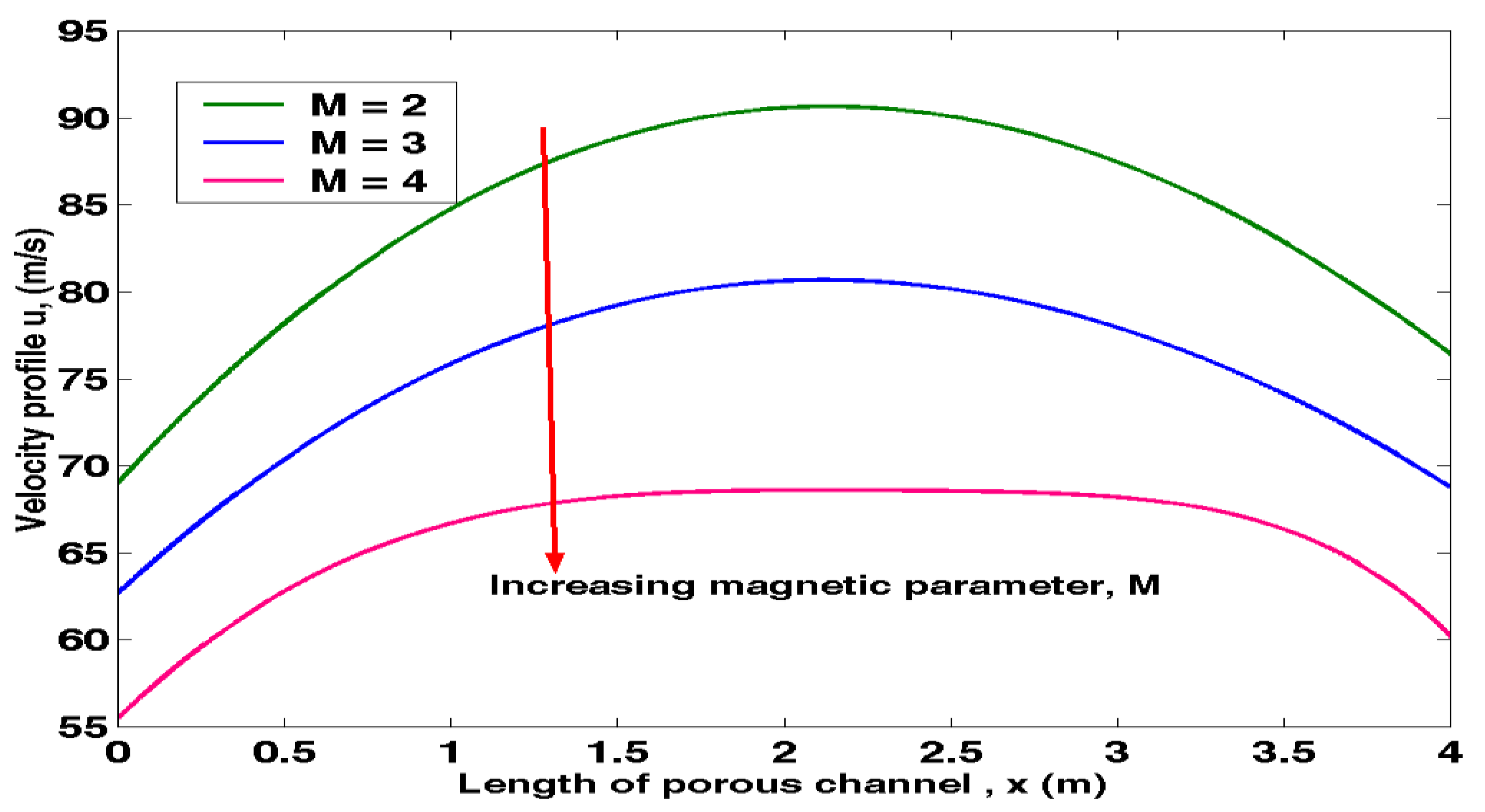
The effect of magnetic parameter can be observed from Figure 4.1. Increase in magnetic parameter leads to a decrease in the velocity profile. This is due to Lorentz force generated by the application of constant inclined magnetic field which produces resistance opposing the fluid motion thereby decreasing the flow in the channel.

4.2. Effects of Darcy numbers on velocity profile

Equation (3.7) was solved numerically in MATLAB to obtain the results of the effects of Da number on velocity profile as shown in Table 4.2 below.

Table 4.2. Value of velocity profile for varying Darcy numbers.

Darcy numbers	Length of Porous channel
Darcy numbers	0	1	2	3	4
Da = 0.1	68.83728	85.55858	89.31898	88.30366	76.16492
Da = 0.2	75.23219	97.3234	102.8954	101.5184	85.31186
Da = 0.3	84.24966	108.3732	114.6778	113.1684	95.40957

The above results in Table 4.2 were presented in Figure 4.2 below.

Figure 4.2. Graph of velocity against Length of Porous channel at varying Darcy numbers.

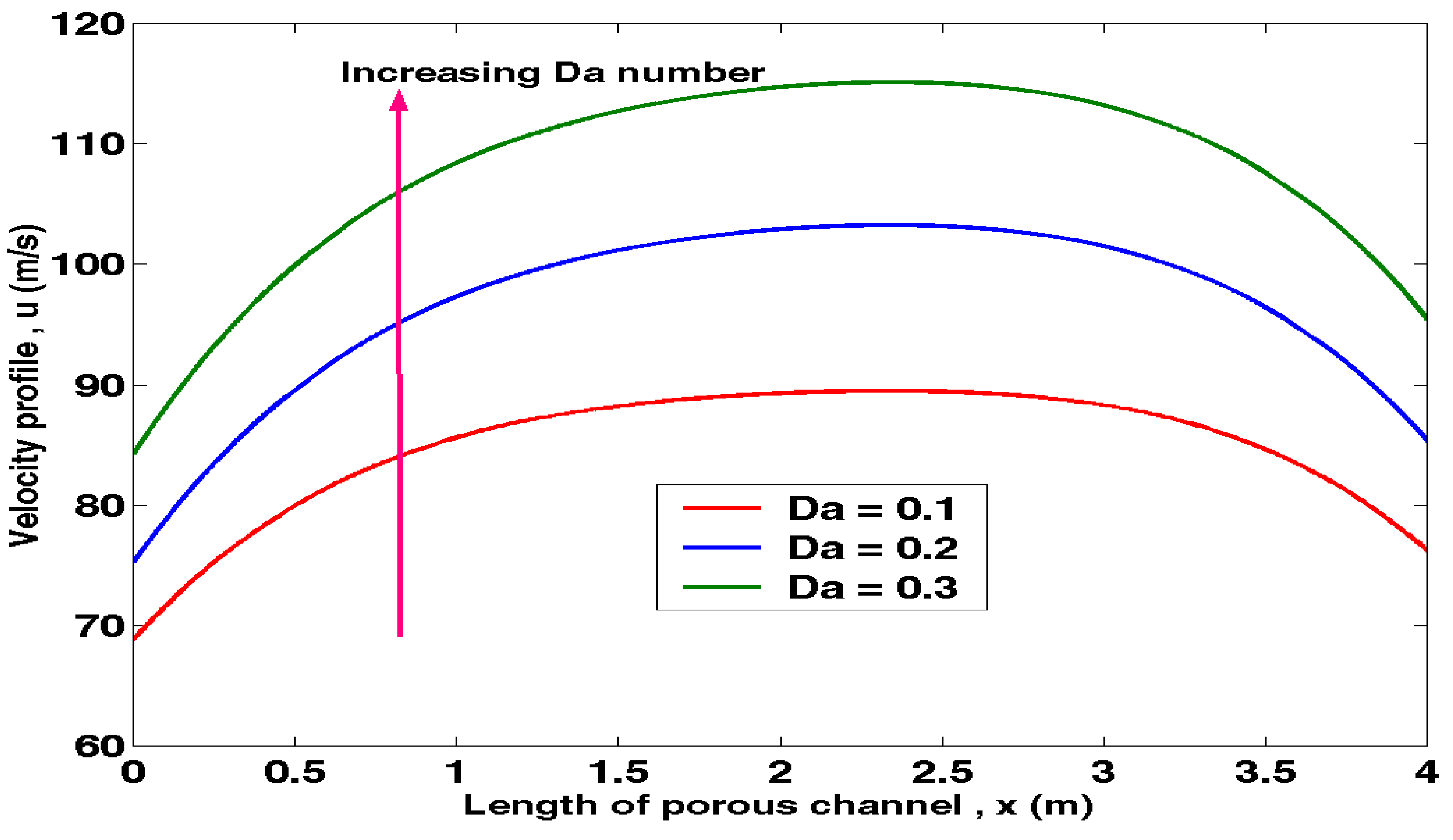
The effect of Darcy numbers can be observed from Figure 4.2. An increase in Darcy number leads to an increase in the velocity profile. Also, at initial stages the fluid velocities increase from x = 0 to x = 2 but it starts to decrease thereafter up to x = 4. It indicates that a positive increase in Darcy numbers strongly accelerates the flow. The study has important applications in nuclear heat transfer control, material processing and magnetohydrodynamic energy generators.

4.3. Effects of Pressure on velocity profile

Equation (3.7) was solved in MATLAB to obtain the results of the effects of pressure on velocity profile as shown in table 4.3 below.

Table 4.3. Value of velocity profile for varying fluid pressure.

Fluid Pressure	Length of Porous channel
Fluid Pressure	0	1	2	3	4
P = 1000	49.4465	61.45757	64.15871	63.42939	54.71001
P = 1200	59.14189	73.50807	76.73885	75.86652	65.43747
P = 1400	68.83728	85.55858	89.31898	88.30366	76.16492

The above results in Table 4.3 were presented in Figure 4.3 below.

Figure 4.3. Graph of velocity profile against Length of Porous channel at varying fluid pressure.

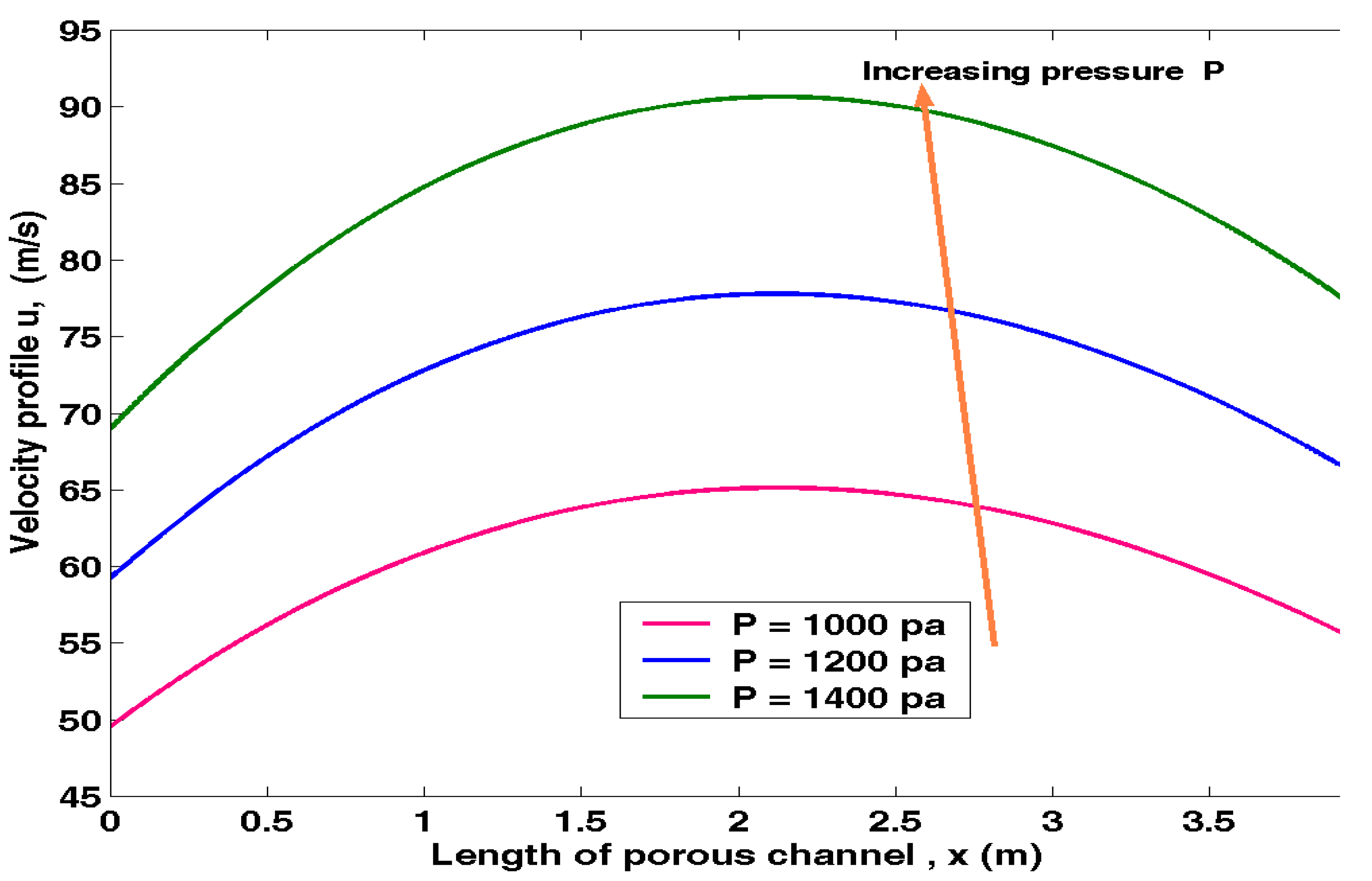
The effect of fluid pressure on fluid velocity profile can be observed from Figure 4.3. Increase in fluid pressure increases the velocity profile.

4.4. Effects of Eckert number on temperature distribution

Equation (3.18) was solved numerically in MATLAB to obtain the results of the effects of Eckert number on temperature distribution as recorded in Table 4.4 below.

Table 4.4. Value of temperature distribution for varying Eckert number.

Eckert number	Length of Porous channel
Eckert number	0	1	2	3	4
E_C = 15	1.607319	1.013841	0.8660641	0.8231372	0.7450029
E_C = 20	1.812403	1.269772	1.134412	1.092474	0.9921149
E_C = 25	2.017488	1.525702	1.402759	1.361811	1.239227

The above results in Table 4.4 were presented in Figure 4.4 below.

Figure 4.4. Temperature distribution against Length of Porous channel at varying Eckert number.

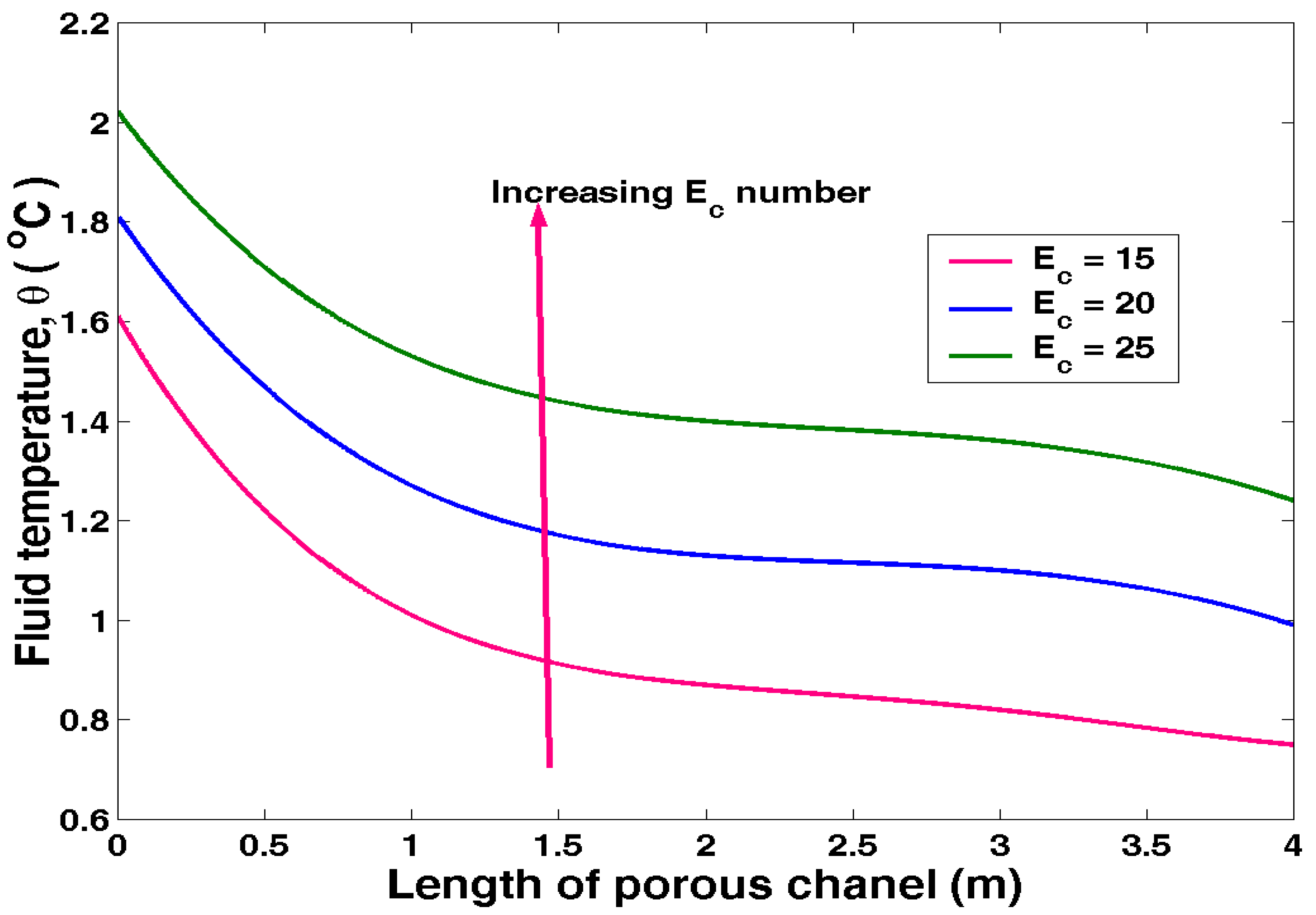
The effect of Eckert (Ec) number on fluid temperature can be observed from figure 4.4. Increase in Ec increases the temperature distribution.

4.5. Effects of Viscosity on temperature distribution

Equation (3.18) was solved numerically in MATLAB to obtain the results of the effects of viscosity on temperature distribution as shown in Table 4.5 below.

Table 4.5. Value of temperature distribution for varying viscosity.

Viscosity	Length of Porous channel
Viscosity	0	1	2	3	4
δ = 1.0	2.212403	1.269772	1.134412	1.092474	0.9921149
δ = 1.5	2.470589	1.843145	1.686362	1.634929	1.487256
δ = 2.0	2.722742	2.293498	2.207801	2.169821	1.980563

The above results in Table 4.5 were presented in Figure 4.5 below.

Figure 4.5. Temperature distribution against Length of Porous channel at varying Viscosity.

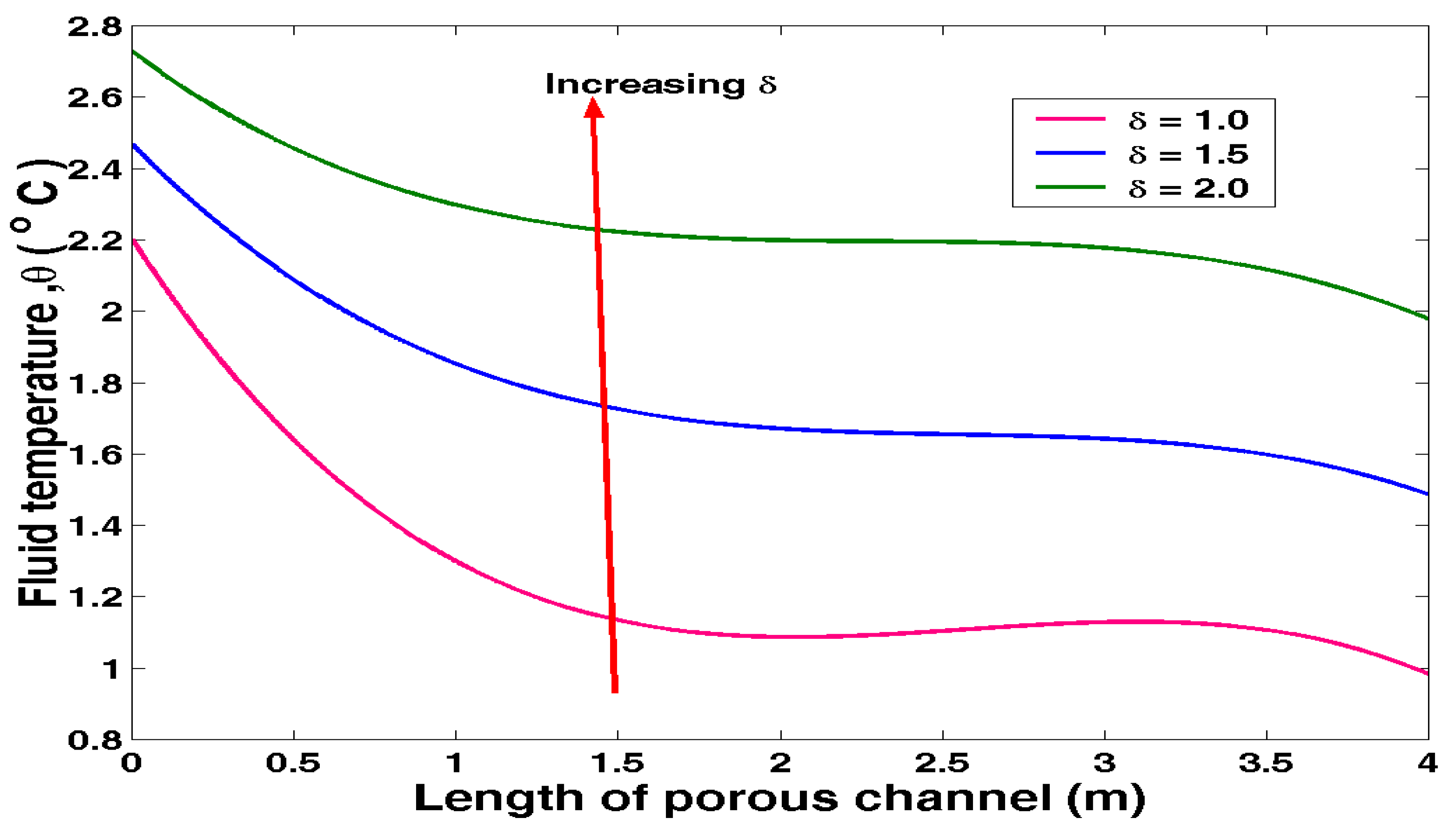
The effect of Viscosity on fluid temperature can be observed from Figure 4.5. Increase in fluid viscosity increases the temperature distribution.

5. Summary and Conclusions

The following observations and conclusions were made from the results of this study.

The flow profile increases with the greater Darcy number. A positive increase in Darcy numbers strongly accelerates the flow.
The argumentation in magnetic parameter reduces the velocity profile.
Increase in fluid pressure leads to increase in the velocity profile.
Increase in Eckert number leads to increase in the temperature distribution.
Increase in fluid viscosity leads to increases in the temperature distribution.

6. Recommendation

From this study, the following areas are recommended:

An extension of this study to the case of optimization of MHD parameters on 3-D on a porous channel with heat generation along the fluid flow.
An extension of this study to incorporate friction coefficient between flow channel and fluid surface. This will obviously affect the rate of fluid flow.

Funding

The authors of this study received no financial support for the research authorship and/or publication of this article.

Acknowledgments

The authors acknowledge Kisii University (Department of Mathematics and Actuarial Sciences) for affiliation and as well as in support of academic resources.

References

Ahmad, M.; Muhammad, T.; Ahmad, I.; Aly, S. Time-dependent 3D flow of viscoelastic nanofluid over an unsteady stretching surface. Phys. A Stat. Mech. Appl. 2020, 551, 124004. [Google Scholar] [CrossRef]
Fatunmbi, E.O.; Ogunseye, H.A.; Sibanda, P. Magnetohydrodynamic micropolar fluid flow in a porous medium with multiple slip conditions. Int. Commun. Heat Mass Transf. 2020, 115, 104577. [Google Scholar] [CrossRef]
Helmy, K.A. MHD unsteady free convection flow past a vertical porous plate. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik: Applied Mathematics and Mechanics 1998, 78, 255–270. [Google Scholar] [CrossRef]
Islam, S.; Khan, A.; Kumam, P.; Alrabaiah, H.; Shah, Z.; Khan, W.; Zubair, M.; Jawad, M. Radiative mixed convection flow of maxwell nanofluid over a stretching cylinder with joule heating and heat source/sink effects. Sci. Rep. 2020, 10, 1–18. [Google Scholar] [CrossRef] [PubMed]
Kaur, P.P.; Agrawal, S.P.; Kumar, A. Finite Difference Technique for Unsteady MHD Periodic Flow of Viscous Fluid through a Planer Channel. American Journal of Modeling and Optimization 2013, 1, 47–55. [Google Scholar]
Kim, Y.J. Unsteady MHD convective heat transfer past a semi-infinite vertical porous moving plate with variable suction. International journal of engineering science 2020, 38, 833–845. [Google Scholar] [CrossRef]
Kumar, K.A.; Sugunamma, V.; Sandeep, N. Effect of thermal radiation on MHD Casson fluid flow over an exponentiallystretching curved sheet. J. Therm. Anal. Carolim 2019, 140, 2377–2385. [Google Scholar] [CrossRef]
Li, Y.-X.; Alshbool, M.H.; Lv, Y.-P.; Khan, I.; Khan, M.R.; Issakhov, A. Heat and mass transfer in MHD Williamson nanofluid flow over an exponentially porous stretching surface. Case Stud. Therm. Eng. 2021, 26, 100975. [Google Scholar] [CrossRef]
Luo, C.; Lin, L.; Shi, J.; Liu, Z.; Cai, Z.; Guo, X.; Gao, H. Seasonal variations in the water residence time in the Bohai Sea using 3D hydrodynamic model study and the adjoint method. Ocean Dynamics 2021, 71, 157–173. [Google Scholar] [CrossRef]
Khan, A.; Kumam, W.; Khan, I.; Saeed, A.; Gul, T.; Kumam, P.; Ali, I. Chemically reactive nanofluid flow past a thin moving needle with viscous dissipation, magnetic effects and hall current 2021, 16, e0249264.
Manjunatha, S.; Kuttan, B.A.; Ramesh, G.K.; Gireesha, B.J.; Aly, E.H. 3D flow and heat transfer of micropolar fluid suspended with mixture of nanoparticles (Ag-CuO/H2O) driven by an exponentially stretching surface. Multidiscip. Modeling Mater. Struct. 2020, 16, 1691–1707. [Google Scholar] [CrossRef]
Muhammad, T.; Rafique, K.; Asma, M.; Alghamdi, M. Darcy–Forchheimer flow over an exponentially stretching curved surface with Cattaneo–Christov double diffusion. Phys. A Stat. Mech. Appl. 2020, 556, 123968. [Google Scholar] [CrossRef]
Sharma, G.C.; Jain, M.; Kumar, A. The flow between annular space surrounded by coaxial cylindrical porous medium. In Published in National Conference; Volume 556, pp. 27–30.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimization of Magnetohydrodynamic Parameters in Two- Dimensional Incompressible Fluid Flow on a Porous Channel

Abstract

1. Introduction

2. Background

3. Governing Equations and Method of Solution

3.1. Finite Difference Method

3.2. Continuity Equation

3.3. Momentum Conservation Equations

3.3.1. Dimensinalizing Momentum Equation

3.3.2. Discretization of Momentum Equation

3.4. Energy Conservation Equations

3.3.1. Non-Dimensinalizing Momentum Equation

3.3.1. Discretization of Energy Equation

4. Results and Discussion

4.1. Effects of Magnetic parameters on velocity profile

4.2. Effects of Darcy numbers on velocity profile

4.3. Effects of Pressure on velocity profile

4.4. Effects of Eckert number on temperature distribution

4.5. Effects of Viscosity on temperature distribution

5. Summary and Conclusions

6. Recommendation

Funding

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe