Self-Starting Soliton-Comb Regimes in χ(2) Microresonators

Preprint

Review

Self-Starting Soliton-Comb Regimes in χ(2) Microresonators

Altmetrics

Downloads

186

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.pdf (509.20KB )

Boris Sturman^*,Evgeni Podivilov,Segey Smirnov

This version is not peer-reviewed

Submitted:

17 April 2023

Posted:

17 April 2023

You are already at the latest version

Alerts

Abstract

Discovery of stable and broad frequency combs in monochromatically pumped high-Q optical Kerr microresonators caused by generation of temporal solitons can be regarded as one of the major breakthroughs in nonlinear optics during the last two decades. Transfer of the soliton-comb concept to χ(2) microresonators promises lowering of the pump power, new operation regimes, and entering new spectral ranges; scientifically, it is of a big challenge. Here we represent an overview of stable and accessible soliton-comb regimes in monochromatically pumped χ(2) microresonators discovered during the last several years. The main stress is made on lithium niobate based resonators. The overview pretends to be rather simple, complete, and comprehensive: It incorporates the main factors affecting the soliton-comb generation, such as the choice of the pumping scheme (pumping to the first or second harmonic), the choice of phase matching scheme (natural or artificial), the effects of temporal walk-off and dispersion coefficients, and also the influence of frequency detunings and Q-factors. Most of discovered nonlinear regimes are self-starting – they can be accessed from noise upon a not very abrupt increase of the pump power. The soliton-comb generation scenarios are not universal – they can be realized only under proper combinations of the above mentioned factors. We indicate what kind of restrictions on the experimental conditions have to be imposed to get the soliton-comb generation.

Keywords:

Subject: Physical Sciences - Optics and Photonics

1. Introduction

Generation of broad frequency combs, i.e. of a large sequences of equidistant coherent light lines, in monochromatically pumped high-Q Kerr microresonators [1,2,3,4,5] can be regarded as one of the main discoveries in nonlinear optics during the last two decades. Remarkably, the spectral positions of these lines do not generally coincide with (are not close to) the discrete resonator modes because of dispersion of the latter. This is why interpretation of the combs as a sequential parametric excitation of new resonator modes is rather fruitless. The right physical picture of the frequency comb in question is proven to be generation of a spatially narrow soliton propagating along the resonator rim with a constant velocity

v_{0}

[5]. Fourier expansion of the light field employing its periodicity over the circumference ensures equidistance of the light lines with the frequency spacing

v_{0} / R

, where R is the major resonator radius. Thus, the comb and soliton are two physical terms expressing different properties of the same nonlinear light state. Most probably, the soliton nature of broad frequency combs has no alternative.

The soliton-comb concept is nowadays generally accepted for

χ^{(3)}

resonators. It is applicable not only to glass based Kerr microresonators, but also to resonators made of

χ^{(3)}

crystals [5,6,7,8,9,10]. One can speak of the corresponding comb technology. Amount of publications on the

χ^{(3)}

combs can be estimated as

\sim 10^{2}

. Note that the dissipative solitons in question are essentially different from (and more complicated then) the so-called conservative solitons associated typically with the nonlinear Schrödinger equation [11,12]. The dissipative solitons balance not only the dispersion broadening and nonlinear compression, but also the gain owing to external pumping and internal resonator losses.

Transfer of the soliton-comb concept to the

χ^{(2)}

microresonators, possessing the lower second-order nonlinearity, promises further lowering of the pump power, entering new spectral ranges, and new attractive operation regimes, see also below. This transfer cannot be straightforward because of specific and important features inherent in the

χ^{(2)}

nonlinearity [13]. In contrast to the

χ^{(3)}

case, elementary nonlinear processes involve not four but three light quanta. These processes are the thresholdless generation of the second harmonic (or sum frequencies) and the inverse threshold process of parametric oscillation. The

χ^{(2)}

comb generation can be viewed as a cascade of these processes. Running of them requires employment of the phase matching (PM) for the first harmonic (FH) and second harmonic (SH) resonator modes. The PM conditions in

χ^{(2)}

microresonators can in turn be either natural, relevant to certain light wavelengths, or artificial, using the so-called radial poling [14,15,16,17,18], see also below.

As soon as mutually coupled FH and SH modes are distinguished, we must deal with duality of the

χ^{(2)}

solitons and combs – each of them must consist of FH and SH components, see also Figure 1. The presence of sub-combs in the FH and SH frequency ranges can definitely be regarded as a positive feature. Also, two different pumping schemes (pumping into FH or SH resonator modes) have to be envisaged. These FH and SH pumping cases are substantially different. The presence of temporal walk-off between the FH and SH modes, which can be viewed as the difference of the corresponding group velocities, is also an important feature of the

χ^{(2)}

case. The effect of the walk-off on the soliton-comb generation is generally negative – it has to be minimized when possible. Furthermore, the presence of two dispersion coefficients, relevant to the FH and SH spectral ranges, has to be taken into account. Generally, the

χ^{(2)}

case provides much more room to the search for soliton-comb regimes as compared to the

χ^{(3)}

case. Conservative solitons in

χ^{(2)}

media, that can be regarded as a basis for dissipative cavity solitons, are reviewed in [19].

Axially symmetric

χ^{(2)}

microresonators are wide spread [17,18,20,21,22,23]. Their linear properties are largely common with those of the

χ^{(3)}

resonators [17,24,25,26]. Each resonator can be characterized by a major radius R, see Figure 1. The modes (whispering gallery modes) are localized near the resonator rim; the shape of the rim can be different. Each mode can be labeled by an integer azimuth number m and, additionally, two transverse modal numbers. All modal functions are proportional to

exp (i m φ)

, where

φ

is the azimuth angle. While exact analytical solutions exist only for the spherical case, approximate methods to calculate the modal frequencies, functions, and nonlinear interactions are well developed [24,27,28,29,30,31]. This is also relevant to the methods for coupling light into and out of resonator. Owing to the presence of a coupler (tapered fiber, prism, etc.), the inverse total (loaded) quality factor

Q^{- 1}

consists of internal and coupling contributions.

The most common lithium niobate (LN) based

χ^{(2)}

resonators are discs with the major radius

R \sim 1

mm, the minor radius

r ≲ R

, and quality factors

Q = (10^{7} - 10^{8})

[17,18]. The modes can be viewed as quasi-plane waves with frequencies

ω \equiv 2 π c / λ = k_{m} c / n

, discrete wavenumbers

k_{m} = m / R

, and an effective refractive index n depended on the modal numbers, R, and r. For

R > 1

mm, n is close to the bulk index

n_{b} (λ)

; the difference

n - n_{b}

characterizes the effects of geometric dispersion. In the optical range, the azimuth number

m = 2 π n R / λ

\sim 10^{4}

. The frequency distance

δ ω = c / n R

between neighboring modes with

δ m = 1

is much larger than the line width. As LN is a uniaxial optical material, modes with ordinary (o) and extraordinary (e) polarizations have to be distinguished.

Investigations of the SH generation and parametric oscillation in

χ^{(2)}

microresonators are also known [17,18]. In LN resonators, the PM condition for the SH generation,

ω_{2 m} = 2 ω_{m}

, can be fulfilled naturally at the FH wavelength

λ_{1} ≃ 1064

nm with the use of o- and e-polarized FH and SH modes, respectively [14]. The parametric oscillation for this natural (birefringent) PM corresponds to the SH wavelength

λ_{2} = λ_{1} / 2 ≃ 532

nm. Here and later subscripts 1 and 2 refer to the FH and SH ranges respectively. Employment of the radial poling of LN resonators [15,16,17] enables one to fulfill the quasi-PM conditions at practically any wavelength on demand via a controllable breaking the axial symmetry. It is also necessary to mention that, because of very small resonator line widths, fine tuning means (like the temperature or geometric tuning) have to be used to control the linear and nonlinear phenomena [17,18,25,32].

Both

χ^{(3)}

and

χ^{(2)}

combs originate from parametric instabilities inside the resonators. This is why continuous-wave monochromatic pump is able to generate temporal solitons. The threshold pump power for the instability

P_{th}

is largely controlled by the relevant modal Q factors. Roughly speaking, in the

χ^{(3)}

and

χ^{(2)}

cases

P_{th}

is proportional to

Q^{- 2}

and

Q^{- 3}

, respectively. For

Q ≳ 10^{7}

, the

χ^{(2)}

nonlinearity is typically dominating, and

P_{th}

belongs to the

μ

W range [17,18].

Initial experimental attempts to get

χ^{(2)}

combs dealt with bulk PPLN systems [33,34,35,36] that are quite specific in physics. While some tens of comb lines were observed, neither solitons nor broad comb spectra were reported. Recently, first experimental efforts to generate the

χ^{(2)}

combs in microresonators have been made [37,38,39], no soliton-comb regimes are observed so far to the best of our knowledge. Furthermore, we can claim that this failure is in agreement with our theoretical results on the necessary conditions for realization of such regimes. Therefore, we see the main tasks of this mini-review in (i) determination of the conditions for the

χ^{(2)}

soliton-comb generation and (

i i

) in predictions of the main properties of the soliton-comb states. Also, we will indicate where and why the necessary conditions were violated in the known experiments. Lastly, we will compare our findings with the known early predictions for the

χ^{(2)}

soliton-comb states [40,41,42,43]. As far as possible, the cases considered will be applied to experimentally realizable and important situations.

A considerable part of the literature on nonlinear phenomena in microresonators, see, e.g., [4,17,20,39], extensively employs the quantum-mechanical terminology and notation deeply within the classical domain, where applicability of the classical Maxwell equations is beyond any doubt. Being well developed and attracting, the quantum-mechanical formalism looks here out of place and confusing. We claim, that it can easily be replaced by the classical Hamiltonian formalism [44,45]. Keeping all merits of the quantum formalism, it is fully adequate to the situation.

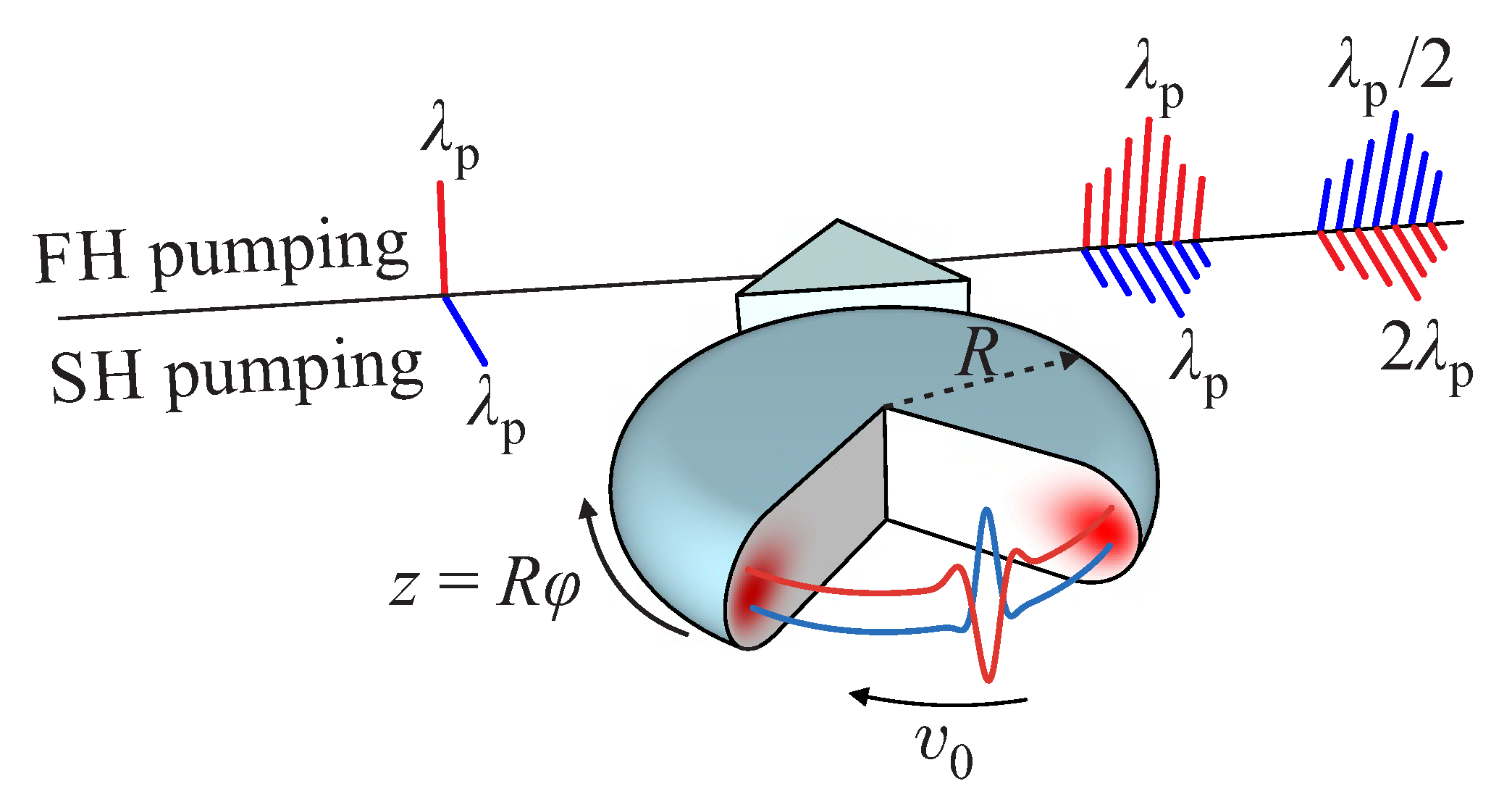
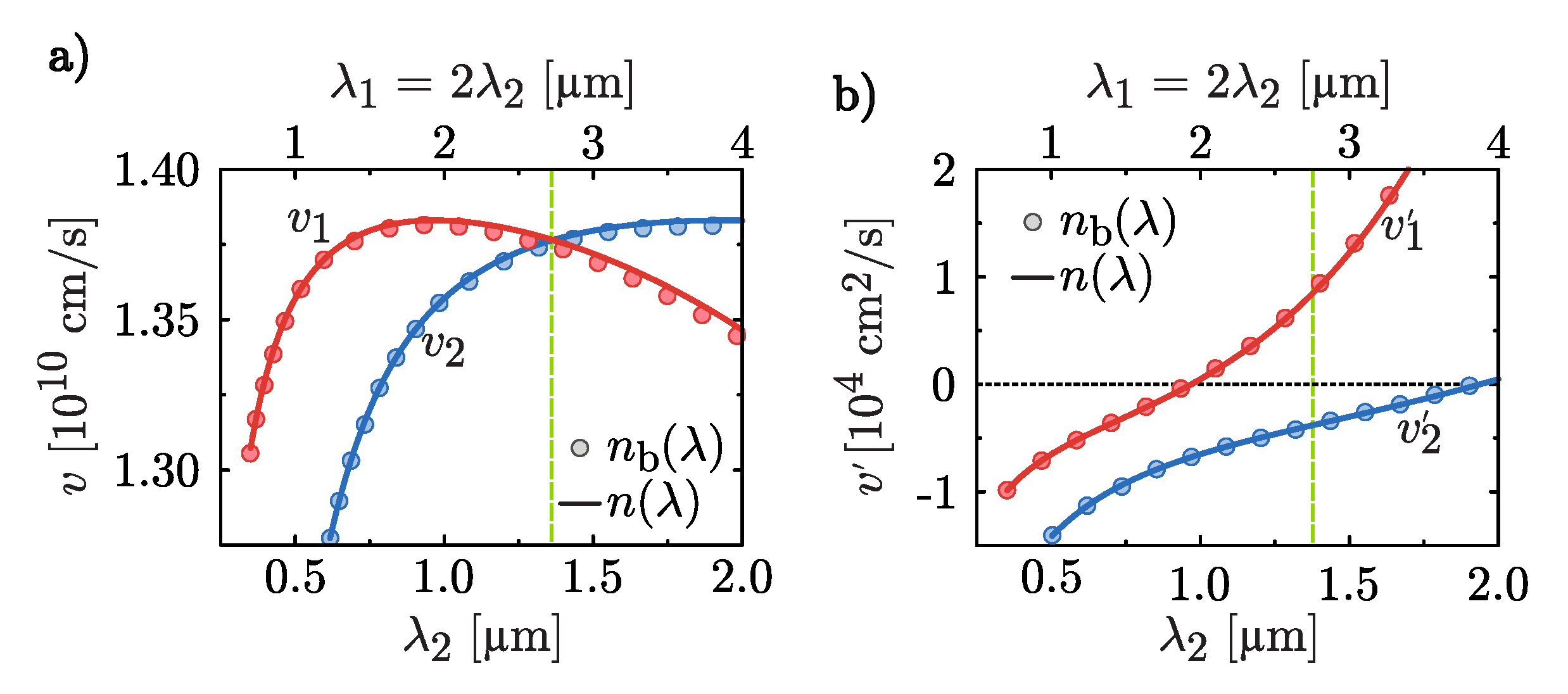
2. Basic Equations, Parameters, and Definitions

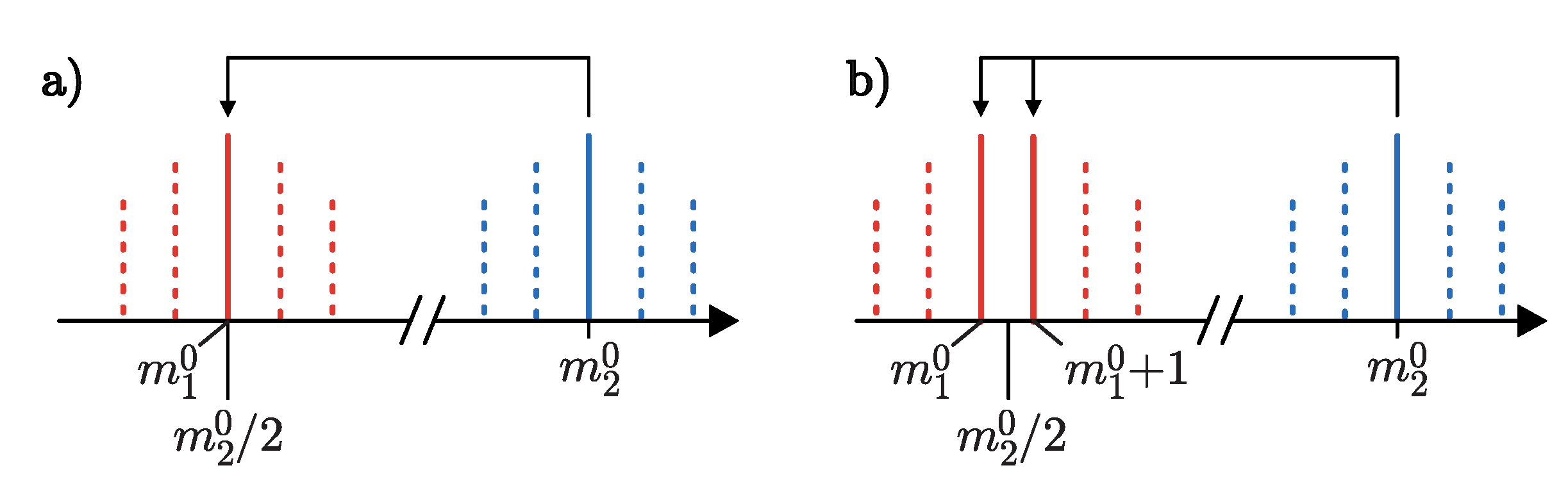
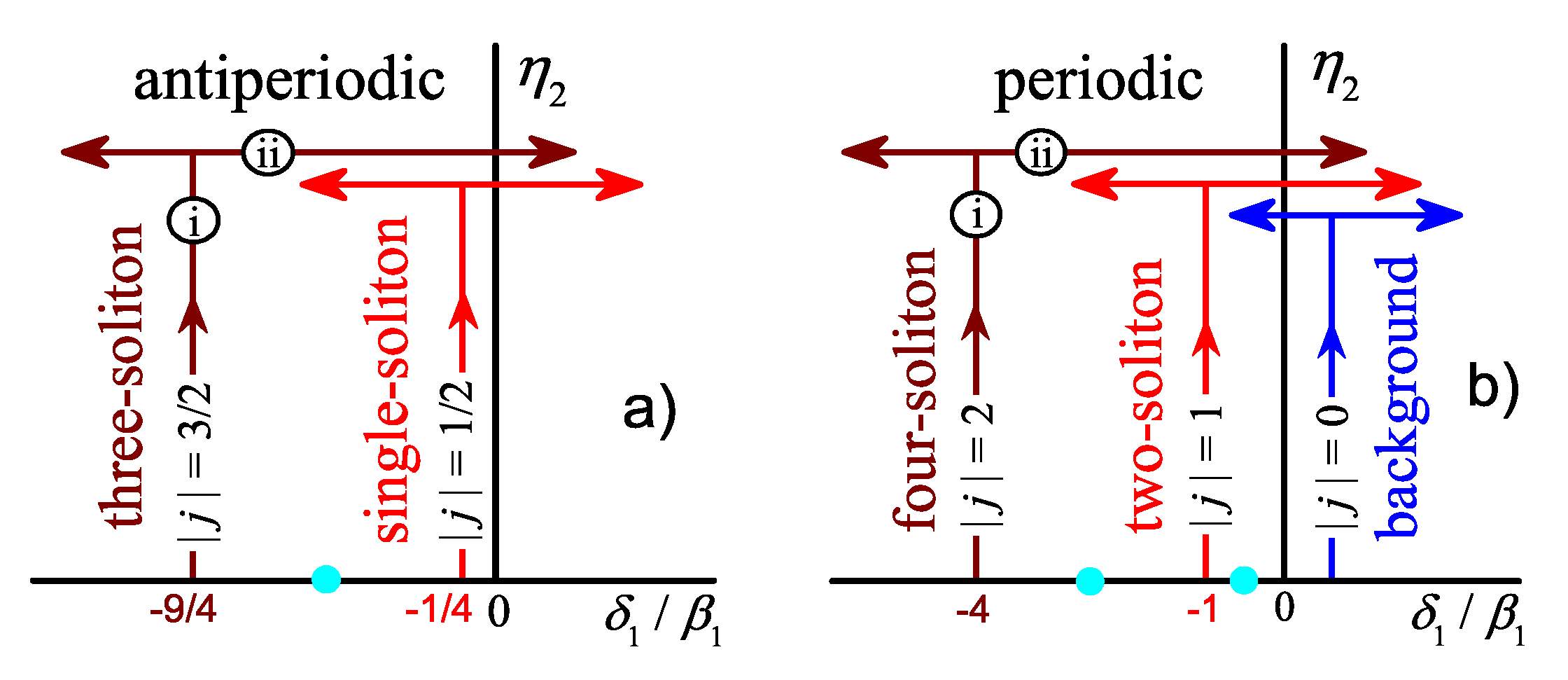
2.1. Periodic and Antiperiodic States

Let first the pump frequency

ω_{p}

be close to a modal frequency and the FH-SH phase matching be natural, i.e. the azimuth symmetry takes place. Then, two variants have to be considered, namely pumping into a FH and into a SH mode. In the FH pumping case, the PM condition

ω (2 m_{1}^{0}) ≃ 2 ω (m_{1}^{0})

can be satisfied with a high accuracy only for a single azimuth number

m_{1}^{0}

. It is implied that the frequency detunings

ω_{p} - ω (m_{1}^{0})

and

ω (2 m_{1}^{0}) - 2 ω (m_{1}^{0})

are much smaller in the values than the intermodal distance

c / n R

. The light electric field

E (φ, t)

can be represented as

E = E_{1} e^{i (m_{1}^{0} φ - ω_{p} t)} + E_{2} e^{2 i (m_{1}^{0} φ - ω_{p} t)} + c . c .,

(1)

where

E_{1} (φ, t)

and

E_{2} (φ, t)

are slowly varying (and generally vectorial) FH and SH amplitudes (envelopes). Obviously, these amplitudes are

2 π

-periodic in

φ

, and the SH azimuth number

m_{2}^{0} = 2 m_{1}^{0}

is even.

In the SH pumping case, the situation is different, as illustrated by Figure 2. The above PM condition can be fulfilled only if the azimuth number of the pumped mode

m_{2}^{0}

is even (subfigure a). If

m_{2}^{0}

is odd (subfigure b), two FH modes (with even and odd azimuth numbers) must be excited. Here, the simplest PM conditions are

ω_{m_{2}^{0}} = ω_{m_{1}^{0}} + ω_{m_{1}^{0} + 1}

m_{2}^{0} = 2 m_{1}^{0} + 1

. Let us use (regardless of parity of

m_{2}^{0}

) the ansatz

E = E_{1} e^{i (m_{2}^{0} φ - ω_{p} t) / 2} + E_{2} e^{i (m_{2}^{0} φ - ω_{p} t)} + c . c .

(2)

for the light field. Then, the first exponential factor is

2 π

periodic for even

m_{2}^{0}

and

2 π

antiperiodic for odd

m_{2}^{0}

. As the true light field

E (φ, t)

2 π

periodic, we must accept that the FH amplitude

E_{1} (φ, t)

is antiperiodic for odd

m_{2}^{0}

, i.e.

E_{1} (φ, t) = - E_{1} (φ \pm 2 π, t)

. The SH amplitude is still

2 π

periodic,

E_{2} (φ, t) = E_{2} (φ \pm 2 π, t)

. A dual FH-SH state with antiperiodic amplitude

E_{1}

and periodic amplitude

E_{2}

is named the antiperiodic state [46,47]. The antiperiodic sates (solutions) are topologically different from the conventional periodic states. No temporal evolution can make conversion between these two states.

We stress that the antiperiodic states are relevant to pumping into an odd SH mode. Otherwise, we have a periodic dual state, such that

E_{1} (φ, t) = E_{1} (φ \pm 2 π, t)

and

E_{2} (φ, t) = E_{2} (φ \pm 2 π, t)

Using above the vectorial notation, we wanted to stress the generality of the periodic and antiperiodic light states for the

χ^{(2)}

nonlinearity. While the FH and SH resonator modes can be different in polarization, one can always deal with scalar FH and SH amplitudes denoted in what follows as F and S.

2.2. Equations for the Modal Amplitudes

Now, we write down nonlinear equations for the complex modal amplitudes

F_{m_{1}}

and

S_{m_{2}}

relevant to the FH and SH frequency domains. It is assumed, as in all known theoretical studies, that the modal polarization and the transverse modal numbers stay the same within each of these domains. We start from the phase matching case relevant to an even azimuth number

m_{2}^{0} = 2 m_{1}^{0}

in the absence of radial poling (full azimuth symmetry). This takes place for the FH pumping, and is also applicable to the SH pumping into an even mode, see Figure 2a. It is useful to count the FH and SH frequencies from

ω_{1}

and

ω_{2}

. In accordance with Equations (1, 2),

ω_{1} = ω_{p}

ω_{2} = 2 ω_{p}

in the FH pumping case, while

ω_{1} = ω_{p} / 2

ω_{2} = ω_{p}

in the case of SH pumping. Furthermore, we introduce instead of

m_{1}

and

m_{2}

more convenient FH and SH modal numbers

j = m_{1} - m_{1}^{0} = 0, \pm 1, \dots

and

l = m_{2} - m_{2}^{0} = 0, \pm 1, \dots

. With these preliminaries, we have

\begin{matrix} i & {\dot{F}}_{j} - Z_{1, j} F_{j} = 2 μ \sum_{l} S_{l} F_{l - j}^{*} + i h_{1} δ_{j 0} \\ i & {\dot{S}}_{l} - Z_{2, l} S_{l} = μ \sum_{j} F_{j} F_{l - j} + i h_{2} δ_{l 0} . \end{matrix}

(3)

Here the dots indicate differentiation in time,

Z_{1, j} = ω_{j} - ω_{1} - i γ_{j}

Z_{2, l} = ω_{l} - ω_{2} - i γ_{l}

γ_{j, l} = ω_{j, l} / 2 Q_{j, l}

are modal decay rates,

μ

and

h_{1, 2}

are the nonlinear coupling coefficient and the internal pump amplitudes, and

δ_{j 0, l 0}

are Kronecker deltas. For the FH and SH pumping, we have

h_{2} = 0

and

h_{1} = 0

, respectively. The modal amplitudes

F_{j}

and

S_{l}

are defined such that

ω_{j} {| F_{j} |}^{2}

and

ω_{l} {| S_{l} |}^{2}

are the modal energies. This definition corresponds to the classical Hamiltonian formalism [44]. The dimensionless quantities

| F_{j} |^{2} / ℏ ≫ 1

and

| S_{l} |^{2} / ℏ ≫ 1

are nothing but the number of modal FH and SH light quanta in the classical limit. The presence of a factor of 2 in set (3) reflects the Hamiltonian nature of the nonlinear interaction – the total energy is conserving for

h_{1, 2} = 0

and

γ_{j, l} = 0

The coefficients

μ

and

h_{1, 2}

can be determined in a quite general manner via modeling of the modes and their coupling in and out of the resonator [29,31]:

μ ≃ \frac{d ω_{p}^{3 / 2}}{2 n^{3} R^{1 / 2} σ_{eff}^{1 / 2}}, h_{1, 2} ≃ {(\frac{P_{0}}{{\tilde{Q}}_{1, 2}})}^{1 / 2},

(4)

where d is the relevant component of the conventional susceptibility tensor,

σ_{eff}

is the effective interaction cross-section,

P_{0}

is the pump power,

{\tilde{Q}}^{- 1}

is the coupling contribution to

Q^{- 1}

, and

n ≃ n_{o} ≃ n_{e}

is a representative refraction index. Further details can be found in Sect. 1 (S1) of the Supplementary Materials.

The rate coefficients

Z_{1, j}

and

Z_{2, l}

can be expressed by the group velocities

v_{1, 2}

and dispersion coefficients

v_{1, 2}^{'}

if we use the expansion [48]

ω (k) = ω (k_{0}) + v δ k + v^{'} δ k^{2} / 2

with

δ k = k - k_{0}

near the points

k_{0} = m_{1}^{0} / R

and

m_{2}^{0} / R

\begin{matrix} Z_{1, j} & = & Δ_{1} - i γ_{1} + v_{1} j / R + v_{1}^{'} j^{2} / 2 R^{2} \\ Z_{2, l} & = & Δ_{2} - i γ_{2} + v_{2} j / R + v_{2}^{'} l^{2} / 2 R^{2} . \end{matrix}

(5)

Parameters v and

v^{'}

are expressed by the refractive index

n (λ)

v = c / (n - λ n^{'})

and

v^{'} = - c λ^{3} n^{''} / 2 π {(n - λ n^{'})}^{2}

, where the prime indicates differentiation in

λ

. Knowledge of the dependences

n_{o, e} (λ)

, with or without the geometric dispersion, enables one to calculate

v_{1, 2}

and

v_{1, 2}^{'}

as functions of

λ_{2}

and

λ_{1} = 2 λ_{2}

. Further details can be found in S2 of supplementary materials. Expressions for detunings

Δ_{1, 2}

depend on the pumping scheme. For the FH pumping,

Δ_{1} = ω_{m_{1}^{0}} - ω_{p}

and

Δ_{2} = ω_{m_{2}^{0}} - 2 ω_{p}

. In the SH pumping case,

Δ_{2} = ω_{m_{2}^{0}} - ω_{p}

and

Δ_{1} = (2 ω_{m_{1}^{0}} - ω_{p}) / 2

Consider now the remaining case of SH pumping into a mode with odd azimuth number

m_{2}^{0}

, when two FH modes with even and odd azimuth numbers enter the phase matching condition, see also Figure 2b. The SH modes can be numerated again with integer

l = m_{2} - m_{2}^{0} = 0, \pm 1, \dots

. The only way to numerate symmetrically the FH modes is to introduce semi-integer number

j = \pm 1 / 2, \pm 3 / 2, \dots

, such that

m_{1} = m_{2}^{0} / 2 + j

. The form of sets (3) and (5) remains the same, and the only difference is in the expression for detuning

Δ_{1}

Δ_{1} = (ω_{m_{1}^{0}} + ω_{m_{1}^{0} + 1} - ω_{p}) / 2

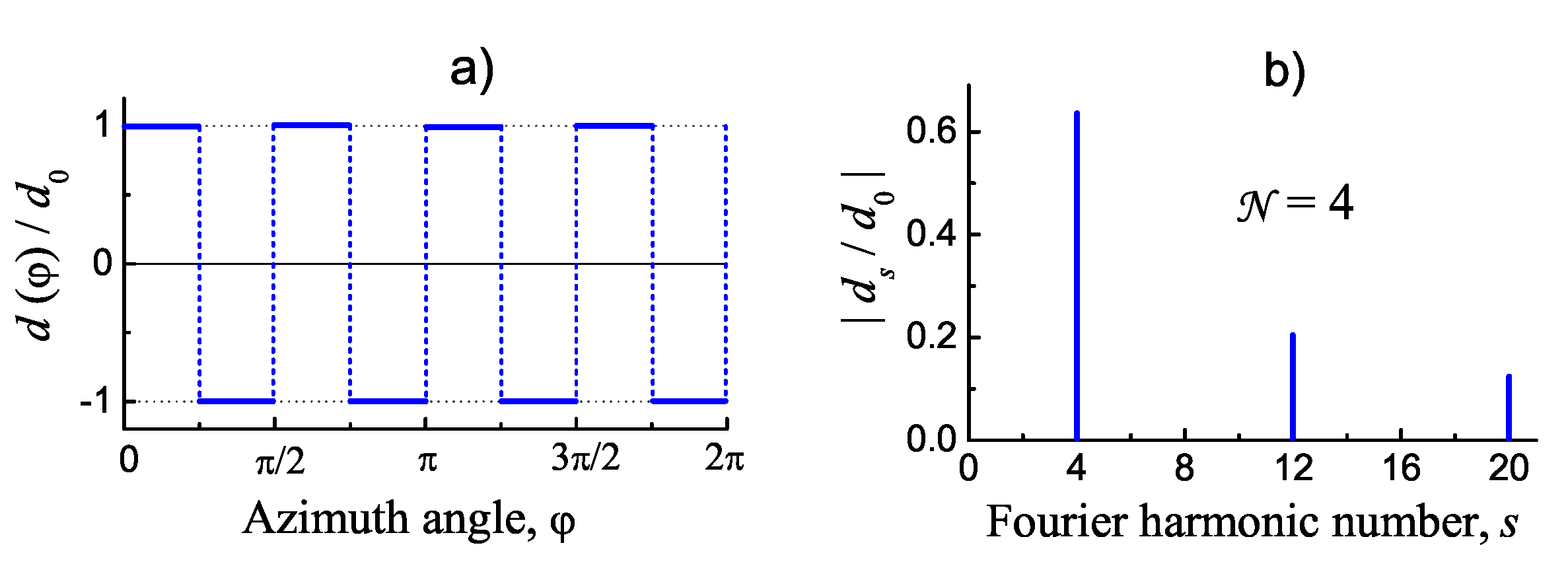
2.3. The Impact of Radial Poling

The radial poling enables one to adjust the phase matching to practically any desirable spectral point with no effect on the linear properties. In polar

χ^{(2)}

materials, like LN, the largest components of the quadratic susceptibility tensor,

d_{13}

and

d_{33}

, change sign under inversion of the spontaneous polarization. The periodic radial poling results in

φ

periodic sign changes of any of these components, as illustrated schematically by Figure 3a.

Let it be d with the absolute value

d_{0}

. The periodic sign-changing function

d (φ)

can be represented by the Fourier series

d = \sum_{s} d_{s} exp (i s φ) .

(6)

N

is the number of poling periods, the nonzero components

d_{s}

correspond to

s = 0, \pm N, \pm 2 N, \dots

. In the case of ± symmetric radial domain structure (

50 %

duty cycle ratio), which is the most suitable for quasi-phase matching, only the Fourier harmonics with odd ratios

s / N = \pm 1, \pm 3, \dots

are nonzero. For these harmonics

| d_{s} | = 2 d_{0} N / π | s |

, see also Figure 3b. The reduction factor

| d_{s} | / d_{0}

decreases with increasing

| s | / N

, but remains comparable with 1 for

| s | = N

. Typically

N ≫ 1

, and the neighboring peaks are well separated from each other.

Employment of the largest first Fourier harmonics of

d (φ)

for quasi-phase matching corresponds to the PM condition

2 ω_{m_{1}^{0}} = ω_{2 m_{1}^{0} \pm N}

for the SH generation. The sign "plus" is relevant to the most typical case of decreasing wavelength dependence of the refraction index

n (λ)

[49]. We see that the SH azimuth number

m_{2}^{0} = 2 m_{1}^{0} \pm N

is even for even alternation number

N

and odd for odd number

N

. In the second case, SH pumping leads to the excitation of periodic states. In the case of odd combination

m_{2}^{0} \mp N

, the above PM condition cannot be fulfilled. However, we can fulfill the PM condition

ω_{m_{1}^{0}} + ω_{m_{1}^{0} + 1} = ω_{2 m_{1}^{0} \pm N}

leading to the excitation of the antiperiodic states. Thus, the quasi-PM via the radial poling results in a controllable shift of the FH azimuth number

m_{1}^{0}

. Set (3) for the FH and SH amplitudes stays unchanged.

Note that microresonators made of commercial PPLN wafers [20] are not appropriate for the spectral adjustment in question. The spectrum

| d_{s} |

includes here many significant peaks

| d_{N \pm 1} |, | d_{N \pm 2} |, \dots

in addition to

| d_{N} |

leading to unwanted interference of many cascading

χ^{(2)}

processes.

The possibility to adjust the phase matching to any spectral range raises the question about specific goals and properties of the radial poling. Figure 4 shows the dependences

v_{1, 2} (λ)

and

v_{1, 2}^{'} (λ)

for e-polarized modes in a LN based resonator with

R = 1.5

mm. The effects of geometric dispersion are very weak here. Zero walk-off point corresponds to

λ_{2}^{c} ≃ 1349

nm, where the dispersion coefficients

v_{1}^{'}

and

v_{2}^{'}

are opposite in signs. Vicinity of this point, as will be shown below, is especially attractive for the soliton-comb generation. The number of periods

N

, necessary to achieve quasi-PM at this point can be estimated as 284. Further details can be found in S3 of supplementary materials.

2.4. Fundamental $z, t$ Representation

The primary set of ordinary differential Equation (3) is convenient for numerical simulations. However, many fundamental features of the soliton-comb states become more evident if we transform it to a set of partial differential equations. This can be done in terms of the FH and SH amplitudes

F (φ, t)

and

S (φ, t)

defined by the Fourier expansions

F = \sum_{j} F_{j} exp (i j φ), S = \sum_{l} S_{l} exp (i l φ) .

(7)

For integer values of

j, l

, this leads automatically to the periodic states, while for integer l and semi-integer j we arrive at a antiperiodic state.

Using Equations (3), (5), and (7) and introducing the rim coordinate

z = R φ

, one can make sure that the periodic and antiperiodic states obey the same set of nonlinear equations for any phase matching scheme [46,47]:

\begin{matrix} [ & i (\partial_{t} + v_{1} \partial_{z}) + 0.5 v_{1}^{'} \partial_{z}^{2} - Ω_{1}] F = 2 μ S F^{*} + i h_{1} \\ [ & i (\partial_{t} + v_{2} \partial_{z}) + 0.5 v_{2}^{'} \partial_{z}^{2} - Ω_{2}] S = μ F^{2} + i h_{2}, \end{matrix}

(8)

where

Ω_{1, 2} = Δ_{1, 2} - i γ_{1, 2}

. At perfect resonant pumping and phase matching, we have

Δ_{1, 2} = 0

. All parameters entering set (8) are known or controllable in experiment. For the

χ^{(2)}

solitons, set (8) plays the role similar to the role of the nonlinear Lugiato–Lefever equation for the

χ^{(3)}

soliton-comb states [4,5]. However, these two cases are fundamentally different.

Consider some important properties and useful transformations of set (8):

–: This nonlinear set admits dual steady-state solutions $F (z - v t)$ , $S (z - v t)$ circulating with a common velocity $v_{0}$ without shape changes. Solitons belong indeed to this class of solutions. Velocity $v_{0}$ has to be determined simultaneously with the shape of the envelopes.
–: Set (8) is written for a static coordinate frame. It is practical to rewrite it for a coordinate frame moving with velocity $v_{1}$ . To do this, it is sufficient to drop the term $v_{1} \partial_{z}$ in the first equation and replace $v_{2}$ by $- v_{12} = v_{2} - v_{1}$ in the second one. It is assumed from now on.
–: In a dual steady state propagating with a constant velocity $v_{0}$ , the modal amplitudes $F_{j}$ and $S_{l}$ oscillate in time as $exp (- i j v_{0} t / R)$ and $exp (- i l v_{0} t / R)$ . This elementary property is useful to control the establishment of dual steady states in numerical simulations, see Section 1.
–: Attempts to rewrite set (8) for the antiperiodic states using the replacements $F (z, t) = \tilde{F} (z, t) exp (\pm i z / 2 R)$ lead to restoration of the periodicity but also to an explicit z-dependence of the right-hand sides (non-autonomous system). This in inappropriate.

The structure of Equation (8) gives a hint about normalization of parameters relevant to the linear properties of the system. Such a normalization enables one to decrease the number of variable parameters. In what follows, we will use the following normalized detunings, walk-off, and dispersion parameters

δ_{1, 2}

α

, and

β_{1, 2}

δ_{1, 2} = \frac{Δ_{1, 2}}{γ_{1, 2}}, α = \frac{v_{12}}{γ_{2} R}, β_{1, 2} = \frac{v_{1, 2}^{'}}{2 γ_{1, 2} R^{2}} .

(9)

As a rule, the actual values of detunings are restricted by the inequalities

| δ_{1, 2} | ≲ 1

. The actual values of

α

and

β_{1, 2}

substantially depend on the group velocity difference

v_{12} = v_{1} - v_{2}

, the dispersion coefficients

v_{1, 2}^{'}

, and the decay rates

γ_{1, 2}

For LN resonators, typical values of the decay rates are

\sim 10^{7}

, such that

| β_{1, 2} | ≪ 1

. On contrary, we have typically

| α | ≫ 1

. Exception from this rule is possible in a close vicinity of zero walk-off point

λ_{2} ≃ 1349

nm. The decay rates

γ_{1}

and

γ_{2}

are typically not strongly different, such that assumption

γ_{1, 2} = γ

can be used sometimes to simplify modeling.

Generally speaking, the values of F, S, and

h_{1, 2}

also need some normalization. It is, however, different in the FH and SH pumping cases. We will provide the relevant information when necessary.

One more important property of set (8) is the presence of spatially uniform steady-state background solutions

\bar{F} \neq 0

\bar{S} \neq 0

[50]. In steady state,

F_{0} = \bar{F}

and

S_{0} = \bar{S}

. Obviously, such a dual background is possible only for the periodic states. The dual background is closely related both to the properties of solitons and to the thresholds of instabilities leading to soliton-comb formation. Omitting all derivatives in (8), one can easily come to a closed algebraic equation for

| \bar{F} |^{2}

that is, however, different for the FH and SH pumping cases. We have

| \bar{S} | = μ | \bar{F} |^{2} / | Ω_{2} |

and

| Ω_{1} | / 2 μ

for the FH and SH pumping cases, respectively. Dependence of

| \bar{F} |^{2}

on the pump amplitudes

h_{1, 2}

is presented graphically in Figure 5.

In both pumping cases, dependences

| \bar{F} |^{2} (h_{1, 2})

are controlled by the phase

Φ = arg (Ω_{1} Ω_{2})

, such that multi-valued solutions exist for sufficiently small

| Φ |

Importantly, the dual background with

\bar{F}, \bar{S} \neq 0

always exists in the FH pumping case, see Figure 5a. At the SH pumping, the situation is different. For sufficiently small values of

h_{2}

, there is a single background state, such that

\bar{F} = 0

and

| \bar{S} | = h_{2} / | Ω_{2} | \neq 0

, see Figure 5b. This difference has dramatic consequences for the dual comb-soliton states, see Section 4,Section 5,Section 6. Note also that Figure 5 gives a clear hint about normalization of the amplitudes

F, S

and pump amplitudes

h_{1, 2}

in the FH and SH pumping cases.

Lastly, we mention two limiting cases for set (8).

–: In the limit $h_{1, 2} \to 0$ , $γ_{1, 2} \to 0$ (no gain, no modal decay) we proceed to the conservative case reviewed in [19]. A number of exact soliton solutions are known here, but they are far from the subject of our study.
–: In the the dissipativeless driven limit $γ_{1, 2} \to 0$ at $Δ_{1, 2} \neq 0$ and $h_{1, 2} \neq 0$ , one can also obtain exact soliton solutions [51]. It turns out, however, that they all are unstable, i.e. cannot be realized.

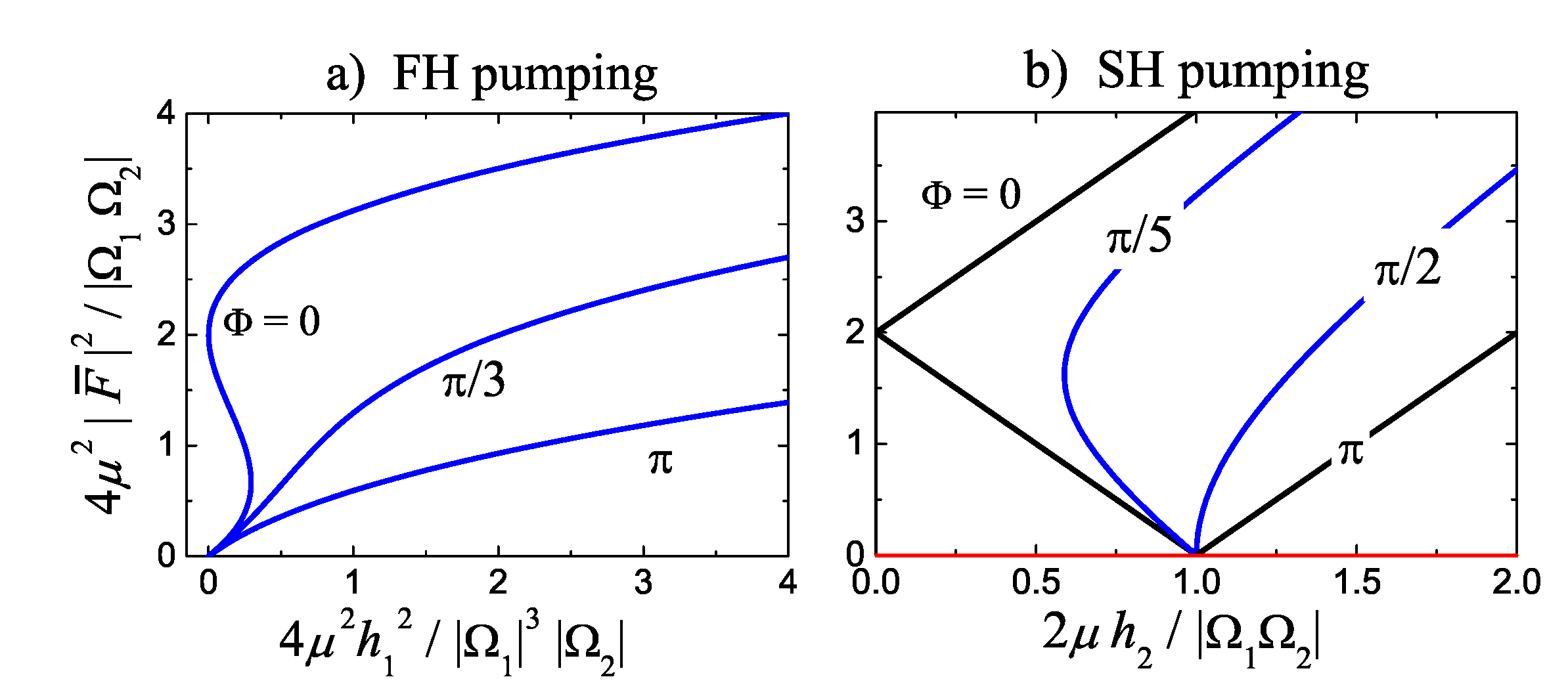
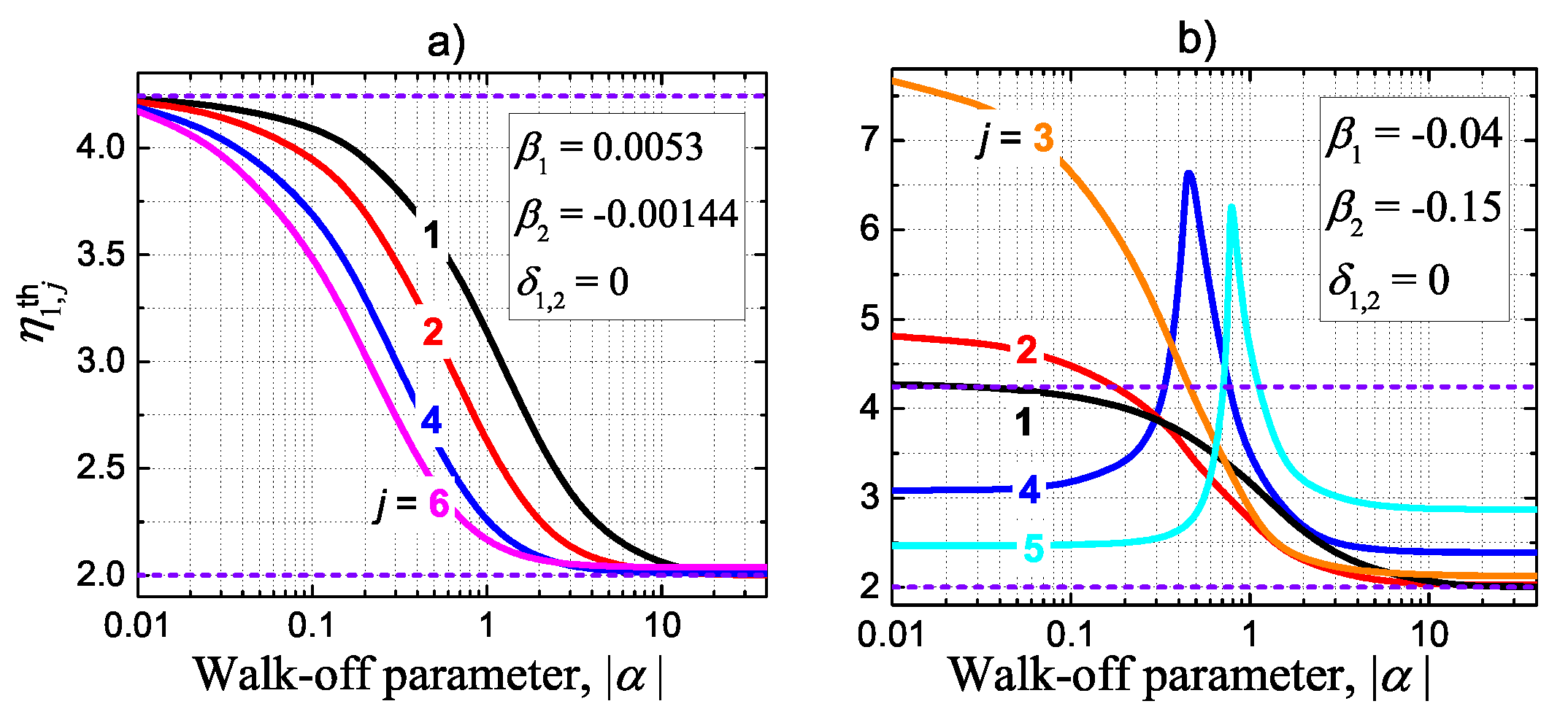
3. Instability Thresholds

As known, generation of second harmonic is thresholdless – it corresponds just to forced oscillation caused by the

χ^{(2)}

nonlinearity. This thresholdless process becomes merely more efficient in the presence of FH-SH phase matching. On contrary, excitation of FH harmonics in the presence of SH modes is always a coherent threshold process. This explains a big difference in the properties of parametric excitation for the FH and SH pumping schemes in microresonators [50].

The simplest and most efficient is the SH pumping scheme. At sufficiently small pump powers (small values of

h_{2}

h_{1} = 0

), we deal simply with the linear excitation of the pumped mode

m_{2}^{0}

. Its steady-state amplitude is

S_{0} = \bar{S} = h_{2} / (γ_{2} + i Δ_{2})

; detuning

Δ_{2}

characterizes just the distance to the linear resonance. To see the effect of

S_{0}

on the FH harmonics, we consider the first of Equation (3) with

S_{l} = S_{0} δ_{l, 0}

and

h_{1} = 0

. The quantities

F_{j}

and

F_{- j}^{*}

with an arbitrary j obey obviously two linear differential equations. Can they have a nonzero steady-state solution? Using the zero determinant solvability condition for linear algebraic equations and Equation (9) for the normalized parameters, we obtain the threshold condition in the form [46,47,50]

η_{2, j}^{th} = {[1 + {(δ_{1} + β_{1} j^{2})}^{2}]}^{1 / 2} {(1 + δ_{2}^{2})}^{1 / 2},

(10)

where

η_{2} = 2 μ h_{2} / γ_{1} γ_{2}

is the normalized pump amplitude. The same threshold equation can be obtained using a more general approach: Namely, one can set

F_{j}, F_{- j}^{*} \propto exp (- i ν t)

to determine the complex characteristic exponent

ν = ν^{'} + i ν^{''}

from an algebraic solvability condition. Then, one can make sure that

ν^{''} > 0

for

η_{2} > η_{2, j}^{th}

, while

ν^{''} < 0

for

η_{2} < η_{2, j}^{th}

. Thus, small amplitudes

F_{\pm j} (t)

decay below the threshold and grow exponentially above it. This fully justifies the use of the threshold EquatiEon (10).

Consider in some detail the threshold properties given by Equation (10). Remarkably, it includes neither the walk-off parameter

α

nor the SH dispersion coefficient

β_{2}

. The threshold equation refers to the FH pairs j and

- j

. The value of j can be integer or semi-integer depending on the type of solution in question. The thresholds are generally different for different

| j |

. However, the minimal in

δ_{1}

values of

η_{2}^{th}

are the same for all

| j |

. The value of

δ_{1}

minimizing the threshold for a pair

\pm j

δ_{1}^{(j)} = - β_{1} j^{2}

; it is substantially different for different

j^{2}

. Using this property, one can excite selectively any pair

j, - j

on demand. The absolute threshold minimum,

{[η_{2}^{th}]}_{min} = 1

can be achieved indeed at

δ_{2} = 0

, i.e. at the exactly resonant excitation of the pumped SH mode. It is clear now that parameter

η_{2}

can be expressed by the pump power as

η_{2} = {(P / P_{min}^{th})}^{1 / 2}

Now we turn to the FH pumping scheme. It is relevant not only to the comb generation issue, but also to the SH excitation. Complexity of this scheme, compared to the previous one, has fairly simple reasons. The parametric instability requires sufficiently large values of the SH amplitude

S_{0} = \bar{S}

. They can be achieved, in turn, only for sufficiently large values of the amplitude of the pumped mode

F_{0} = \bar{F} (h_{1})

. Keeping this fact in mind, we consider what happens if we admit the presence of small perturbations

δ F (φ, t)

and

δ S (φ, t)

, such that

F = \bar{F} + δ F

and

S = \bar{S} + δ S

. Substituting these expressions in Equation (8) with

h_{2} = 0

, we see that the SH perturbation

δ S

becomes linearly linked to the FH perturbation via the term

\bar{F} δ F

, which was absent earlier. As the result, we must deal with a quartet of perturbations

F_{j}

F_{- j}^{*}

S_{j}

S_{- j}^{*} \propto exp (- i ν t)

instead of the former parametric pair

F_{j}, F_{- j}^{*}

. The characteristic equation for

ν

becomes a cumbersome four-degree algebraic equation including all linear parameters

δ_{1, 2}

β_{1, 2}

, and

α

[50]. The threshold properties become complicated, they cannot be covered by simple relations similar to Equation (10).

Nevertheless, a general overview and illustrations of the threshold properties, which do not pretend to be complete, are possible. We introduce first the normalized pump amplitude

η_{1} = \sqrt{2} μ h_{1} / γ_{1} \sqrt{γ_{1} γ_{2}}

, this normalization is different from that relevant to the SH pumping. The presence of parameter

α

, ranging from 0 to very large values, in the threshold equation, raises question about the effect of walk-off. It turns out that the lowest threshold value of

η_{1}

at zero walk-off (

α = 0

) corresponds to

j = 0

, i.e. to an internal instability of the dual background [50]. For detunings

δ_{1, 2} = 0

, this value is minimal,

η_{1, 0}^{th} = 3 \sqrt{2}

. With increase of

| α |

, some quartets with

j \neq 0

become quickly the easiest to excite. However, the optimal values of

| j |

depend significantly on the dispersion coefficients. This is illustrated by Figure 6 obtained with the use of numerical methods.

SubFigure 6a is plotted for

δ_{1, 2} = 0

and representative dispersion parameters relevant to the quasi-PM in LN. Within a broad range of

| α |

, the lowest threshold corresponds to harmonics with very large values of

| j |

. SubFigure 6b corresponds to the natural PM, where the dispersion coefficients

β_{1, 2}

are negative and relatively large in the absolute values. The effect of

| α |

is strongly different here and it strongly depends on

| j |

. The reason is in competition of the walk-off and dispersion terms in the rate coefficient

Z_{2, l}

entering Equation (3) for S. Anyhow, selective excitation of modes with

| j | = 1, 2

is practically impossible. The effects of nonzero detunings

δ_{1, 2}

can also be investigated numerically. They also do not facilitate selective excitation of harmonics with small values of

| j |

With increasing

| α |

, the threshold values

η_{1, j}^{th} (α)

slowly approach 2 from above. This range is, however, not favorable for the soliton-comb generation because of a strong suppression of the side SH harmonics with

l \neq 0

, see also Section 5 and Section 6.

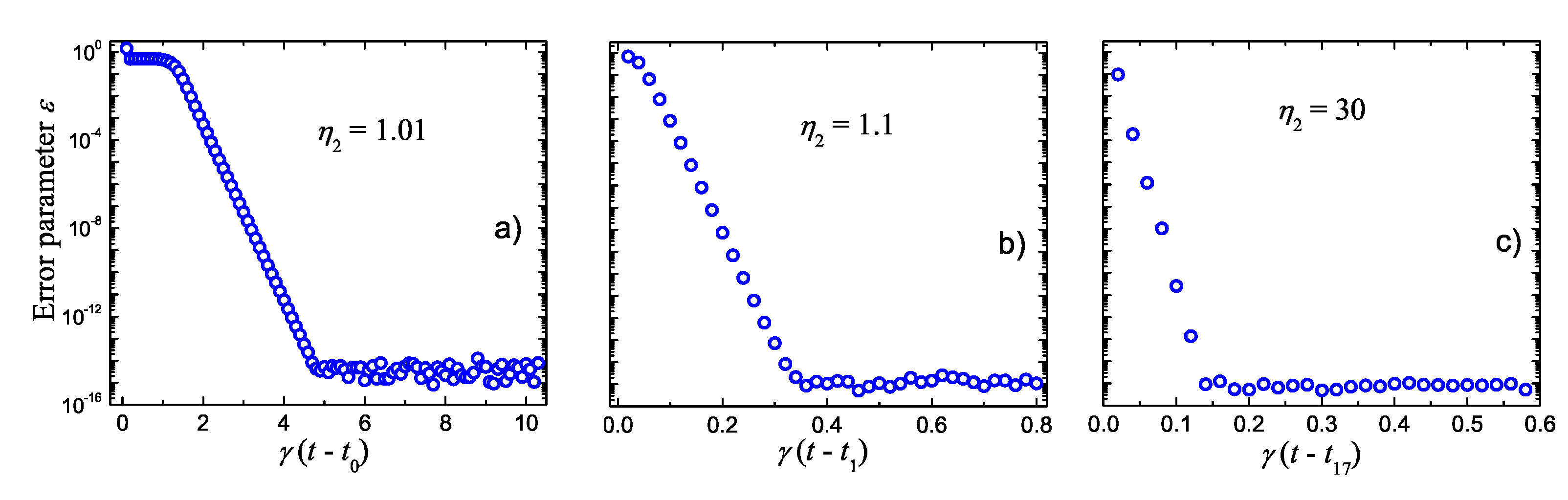
4. Numerical Methods

We simulated predominantly set (3) in the coordinate frame moving with velocity

v_{1}

using the fourth-order Runge-Kutta method. Initially, for verification purposes, we solved also set (8) of partial differential equations using the step-split Fourier method. The results were practically equivalent. The number of Fourier harmonics taken into account (and the mesh points in

φ

) ranged from 32 to 1024 within each of FH and SH frequency domains. Accuracy of the calculations was controlled by changing the time step and the number of harmonics. Different values of the variable input dimensionless parameters of the system (

η_{1, 2}, δ_{1, 2}, β_{1, 2}, α

) were used. With harmonics

F_{j} (t), S_{l} (t)

calculated, one can investigate temporal evolution of the spatial profiles

F (φ), S (φ)

and comb spectra

| F_{j} |^{2}, {| S_{l} |}^{2}

. Also, it is possible to verify establishment of steady states moving with a constant velocity and, if applicable, determine this velocity

v_{0}

Three main problems were considered numerically:

– We verified numerically the analytical results relevant to the instability thresholds. To do so, we used initial conditions with very small random complex values of

F_{j} (0)

and

S_{l} (0)

to see the initial exponential growth or decay of

| F_{j} | (t)

for different values of

η_{1, 2}

. Coincidence of the analytical and numerical results with a high accuracy was always achieved.

– We verified stability of the dual soliton solutions obtained analytically in [46,51] for the known limiting cases. As initial conditions, we used Fourier transforms of the relevant analytical expressions for

F (φ)

and

S (φ)

. Numerical analysis has shown that all the analytical solutions are unstable: Temporal evolution leads inevitably to irregular spatial profiles and comb spectra.

– We tried to generate stable steady-state soliton-comb states starting from very small random complex amplitudes

F_{j} (0)

and

S_{l} (0)

. As a rule, evolution of our nonlinear systems well above the threshold leads ultimately, after a stage of exponential growth, to highly irregular saturated behavior. For an abrupt switching the pump on, rough features of this irregular behavior depend also on the choice of initial conditions. Nevertheless, for many well defined choices of the input parameters, proper pumping scheme, and not very abrupt switching of the pump on, temporal evolution leads reliably and uniquely to multi-parametric families of comb-soliton states. Below we describe the corresponding adiabatic procedure of growing of soliton-comb states as applied (for definiteness) to the SH pumping case.

Let FH harmonics

\pm j

possess the lowest threshold. For

η_{2} < η_{2, j}^{th}

, we have then the steady state with

S_{0} \neq 0

and zero other harmonics. Switching to

η_{2}

slightly above

η_{2, j}^{th}

, we obtain a steady state including

S_{0}

and only few relatively small other essential FH and SH harmonics. After that, the steady-state harmonics are used as new initial conditions at a slightly larger value of

η_{2}

. This procedure is repeated then many times to come to a steady state well above the threshold. The number of FH and SH harmonics taken into account has to be chosen properly. The final state is insensitive to the choice of initial random amplitudes. The states achieved in this way can be qualified as self-starting steady states; their stability is doubtless. Let us stress that achievement of the soliton-comb states with the adiabatic procedure is not guaranteed. However, in many cases it takes place.

Restriction on the rise time of the pump,

τ_{p}

, necessary to achieve the steady state is found to be not very obligating. It is sufficient to fulfill the inequality

γ_{1, 2} τ_{p} ≫ 1

, which corresponds typically to

τ_{p} ≳ 1 μ

s. Note also, that soliton-comb states can be achieved often in a few steps of step-wise increase of the pump power.

Establishment of soliton-comb steady states and the corresponding velocity

v_{0}

can be quantified with a high accuracy using a correlation method. We use the fact that Fourier harmonic

A_{j} (t)

(

F_{j}

S_{j}

) known in the coordinate frame moving with velocity

v_{1}

can be recalculated in the frame moving with an arbitrary velocity

v_{*}

through multiplication by

exp [i j (v_{1} - v_{*}) t / R]

. Let us introduce the dimensionless error parameter

ε (t, τ) = \frac{\sum_{j} {| A_{j} (t) - A_{j} (t - τ) |}^{2}}{\sum_{j} (| A_{j} {(t) |}^{2} + | A_{j} (t - τ) |^{2})},

(11)

where

A_{j}

refers to a coordinate frame moving with velocity

v_{*}

, t is the calculation time and

τ

is a variable time shift. Obviously,

ε (t, τ)

turns to zero only when we deal with the steady state and, simultaneously,

v_{*} = v

. The error parameter calculated for modestly large evolution times,

γ_{1, 2} t ≳ 10^{3}

, and minimized over

v_{*}

shows extremely small values (

ε = 10^{- 14} - 10^{- 15}

) caused by the numerical noise, see also below. For smaller t, i.e., during the transient stage, it is larger by many orders of magnitude. We have thus a numerical tool to control the establishment of steady states and determine precisely velocity

v_{0}

Figure 7 shows three examples of temporal evolution of

ε (t, τ)

relevant to our adiabatic procedure applied to the antiperiodic case at

γ_{1, 2} = γ = 10^{7}

s⁻¹,

τ = 1 / γ

, and parameters

β_{1} = 0.02

β_{2} = - 0.01

α = 1

representative for a close vicinity of the zero walk-off point in LN based resonators. The harmonics in question are

F_{j}

. The normalized pump amplitude

η_{2}

takes sequentially 17 values above the threshold:

1.01

1.1

, …, and 30. SubFigure 7a,b,c exhibit evolution of

ε

after taking the first two and the last values at

t_{0}

t_{1}

, and

t_{17}

. The most general feature this evolution is always the same: It is an almost exponential decrease of

ε

from initial values of the order of 1 to extremely low values

10^{- 14} - 10^{- 15}

. Note also some quantitative details. The longest evolution, subFigure 7a, starts from modal noise. It takes about

(5 - 7) γ^{- 1}

for the harmonics to grow exponentially and reach the saturation. The corresponding evolution time can be identified with the rise time of near-threshold optical parametric oscillation. The further evolution runs, which start from regular distributions of the FH and SH harmonics achieved during the previous runs, occur substantially faster. Our choice of 17 steps of evolution to reach the state with

η = 30

is largely arbitrary. In many cases, the same final state can be achieved in a few steps.

In the next sections we will see in details the spatial and spectral properties of the dual states grown with the use of our adiabatic procedure.

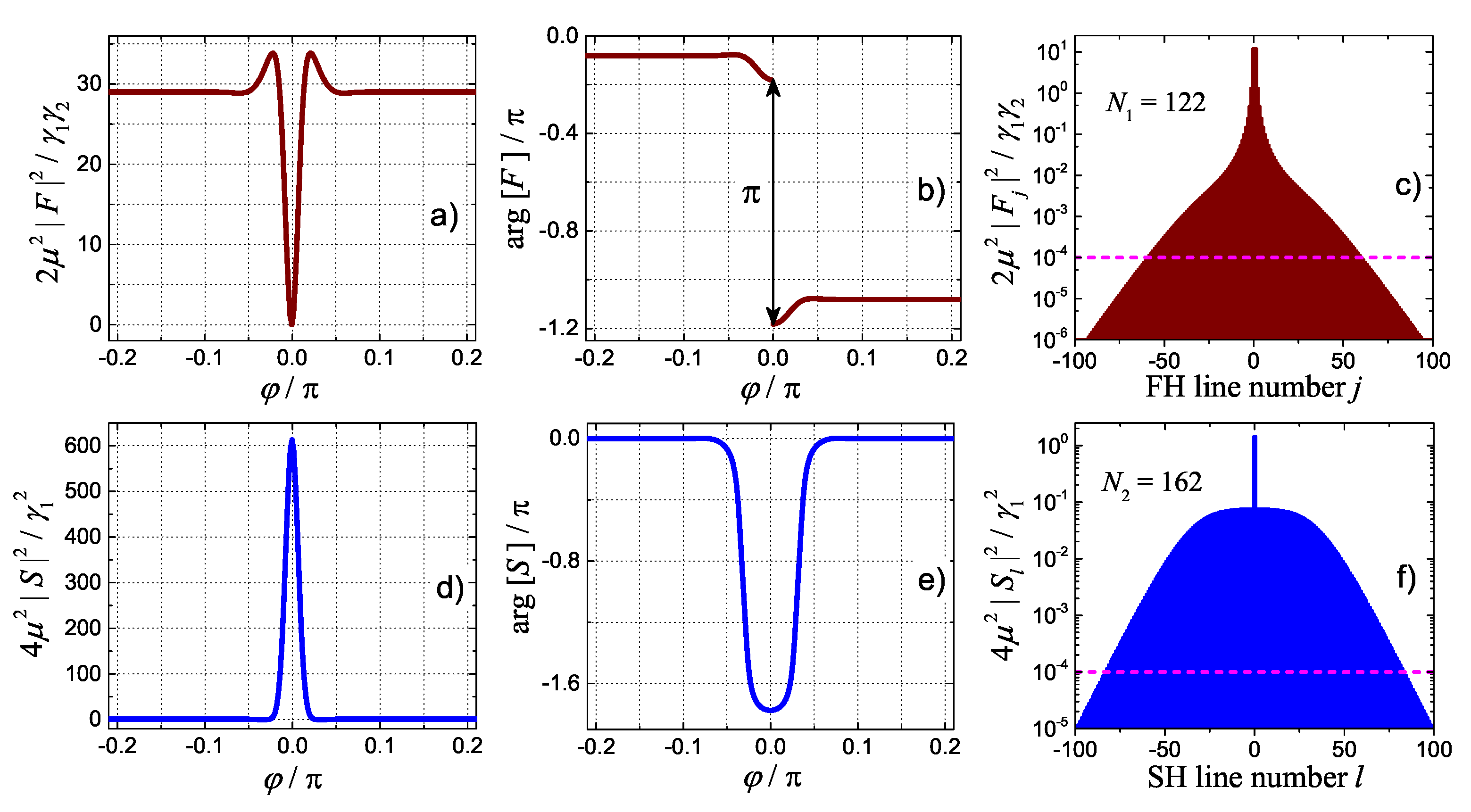
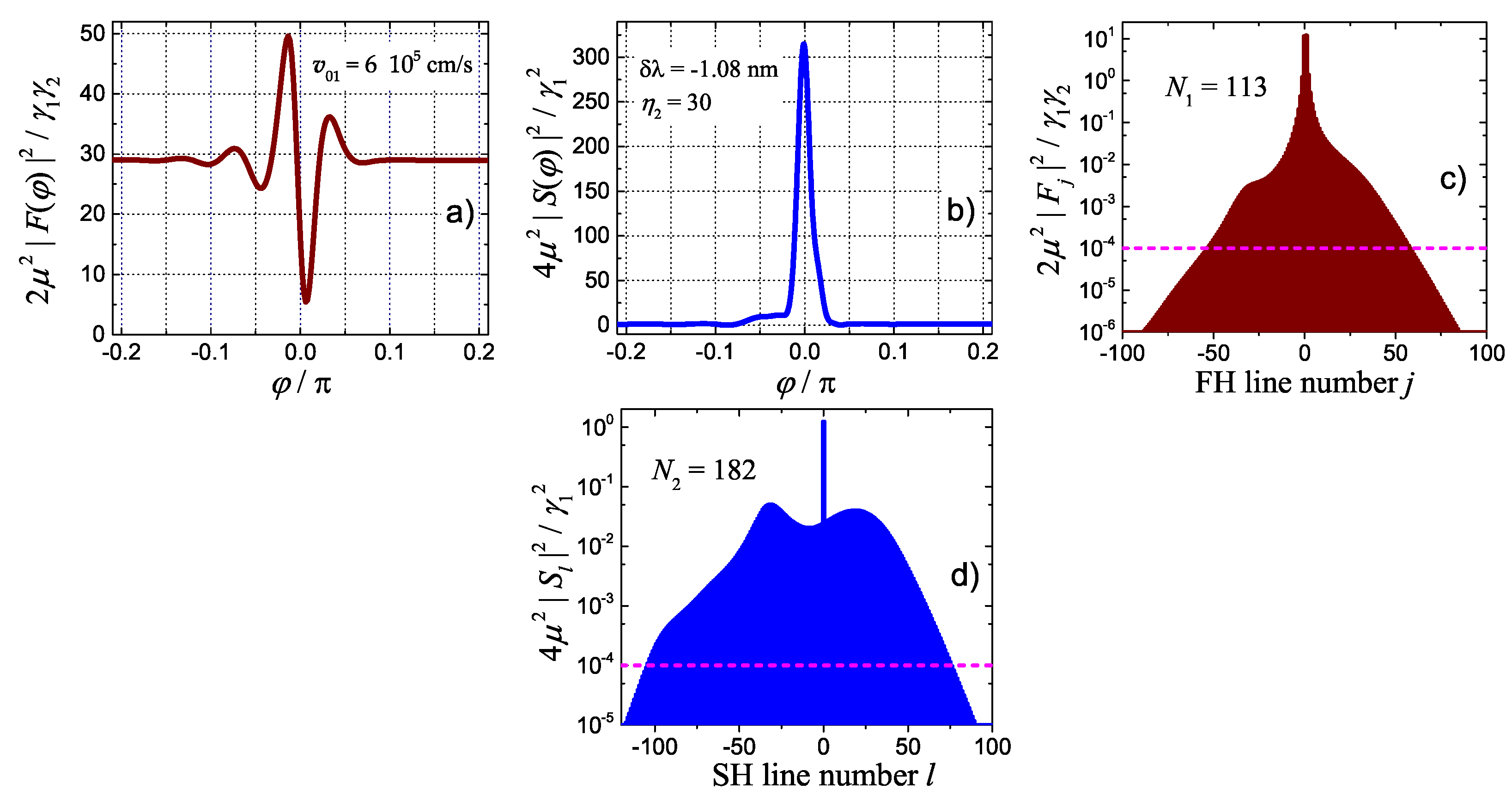
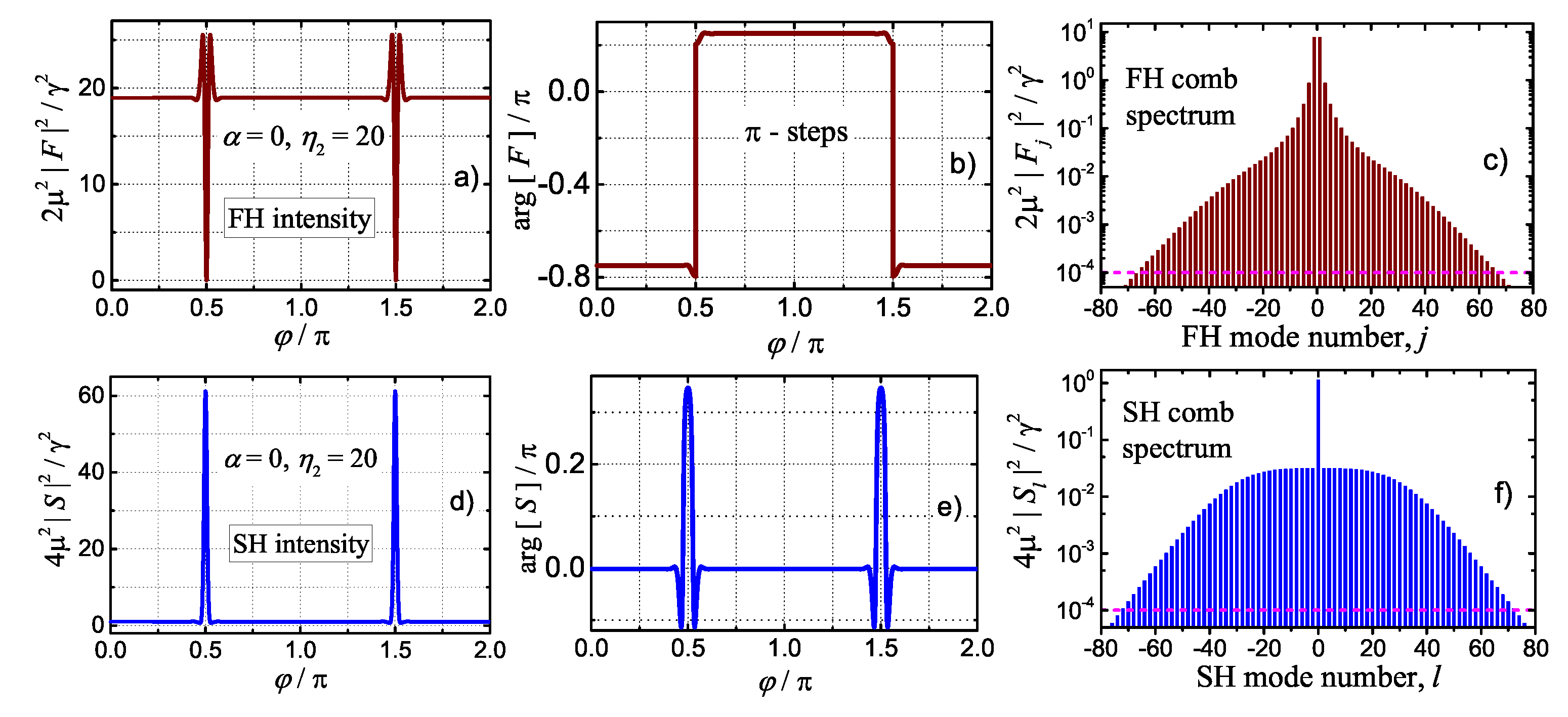
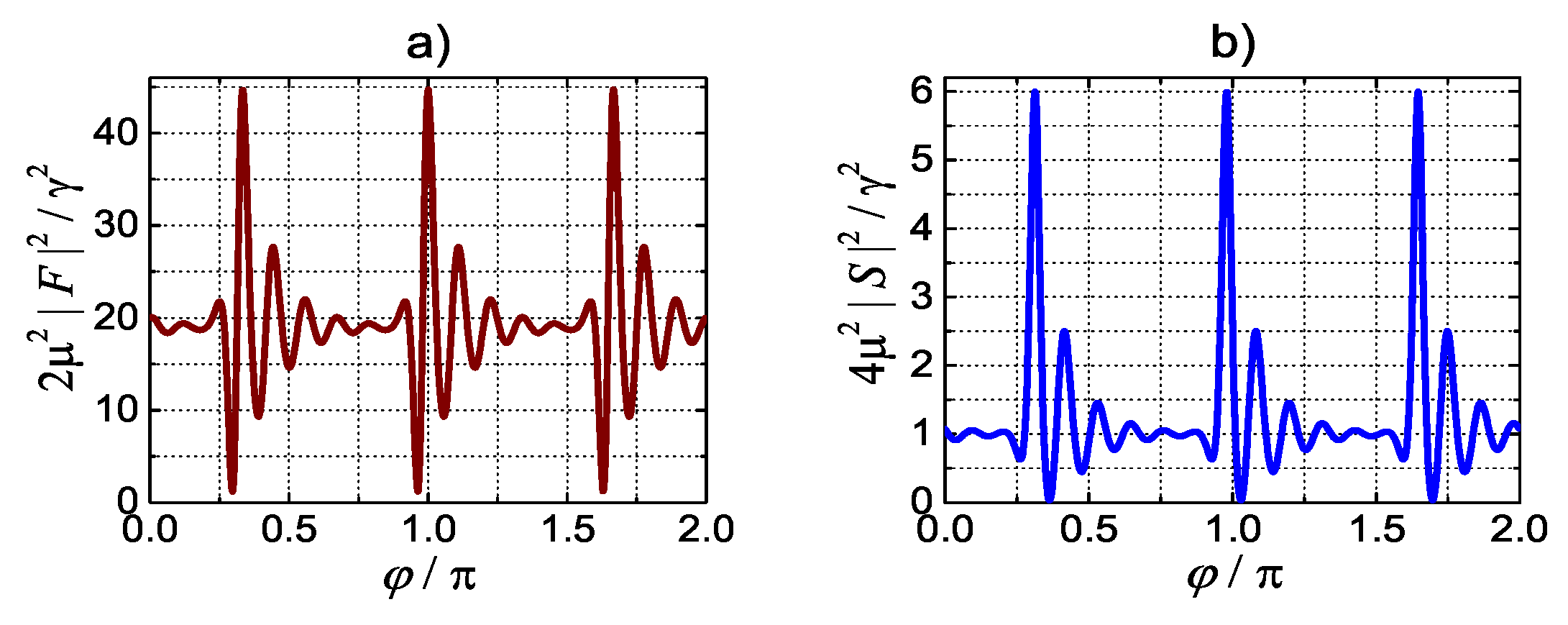
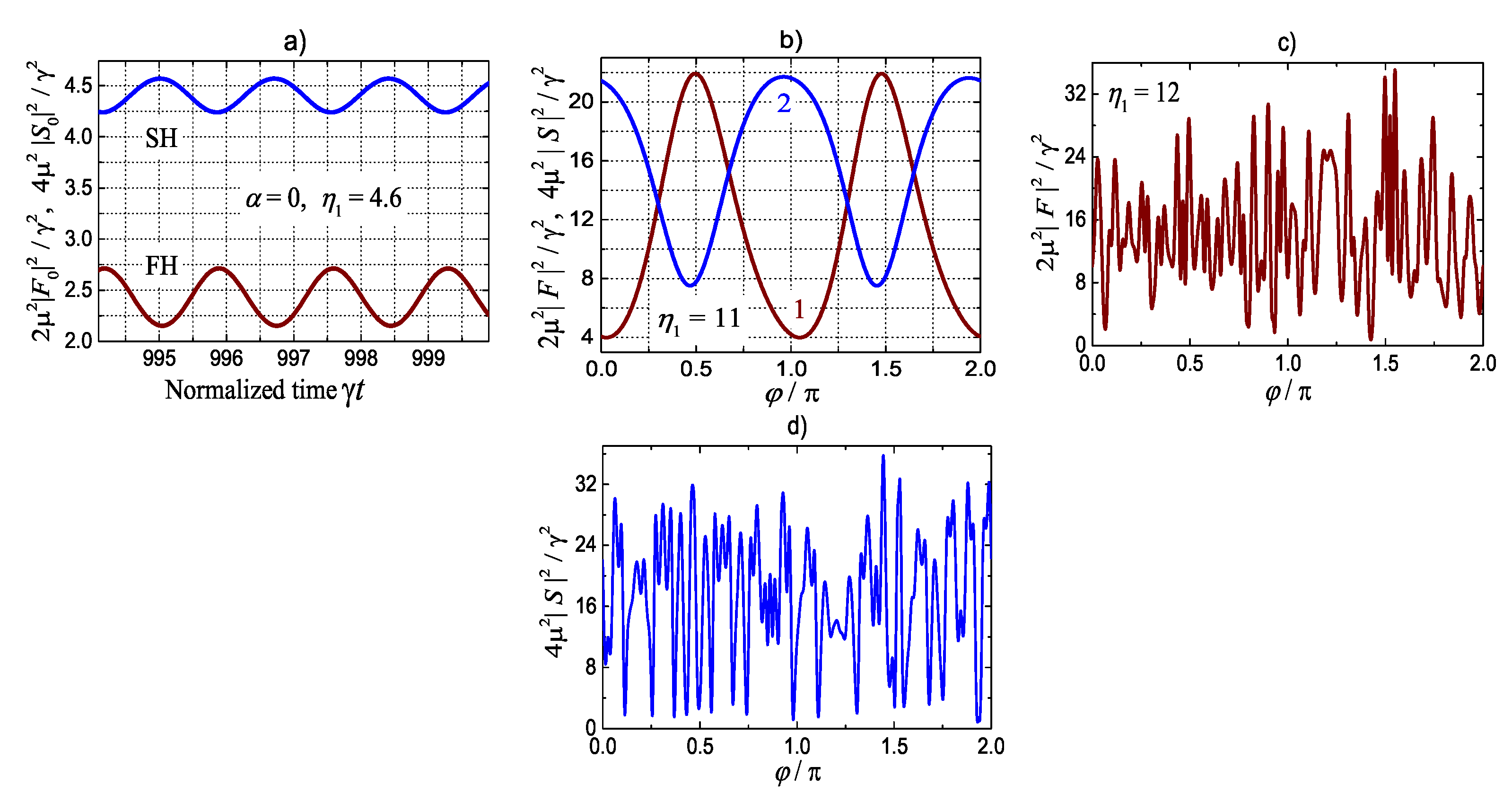
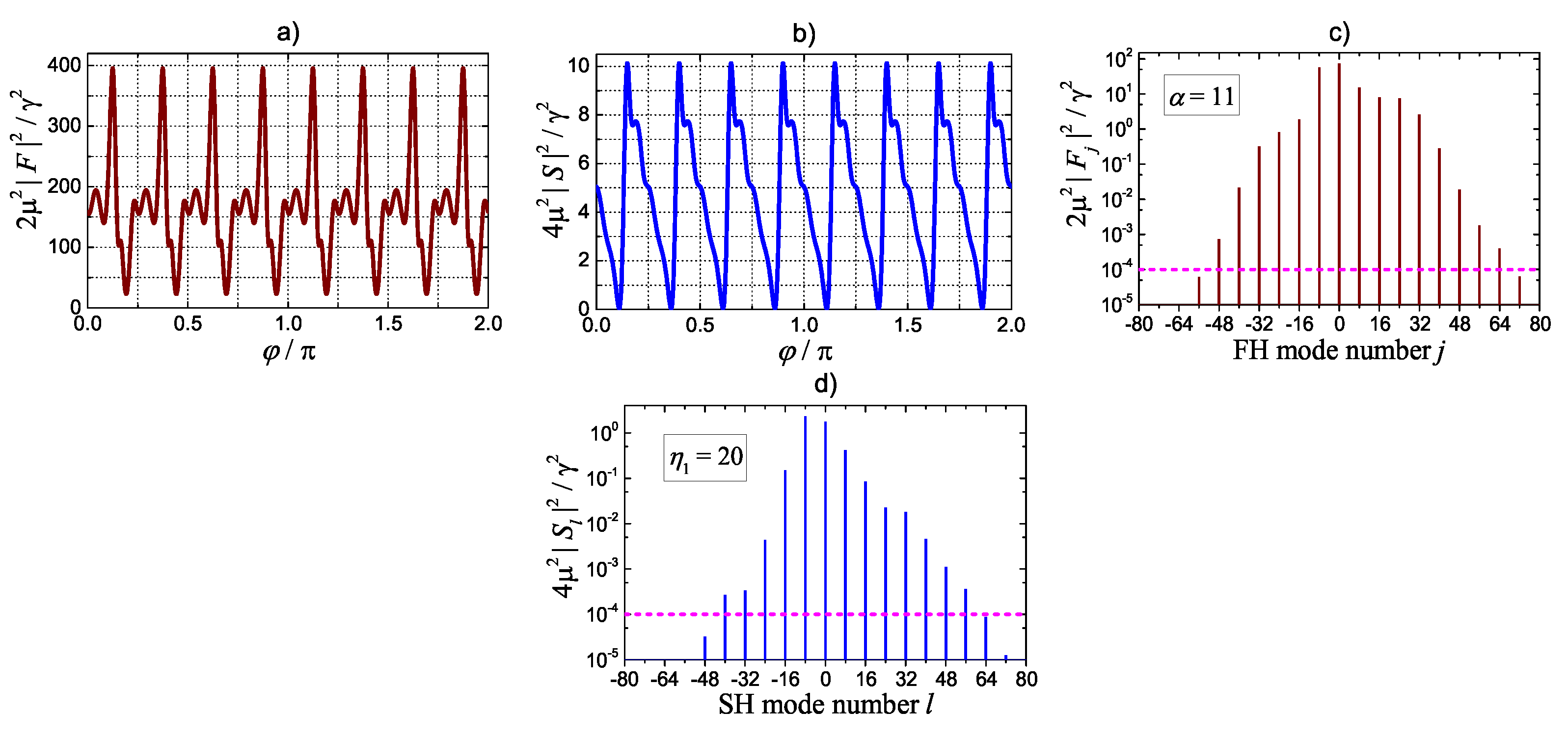
5. Soliton-Comb States for SH Pumping

Below we report the results on soliton-comb generation obtained with our adiabatic procedure in the SH pumping case for LN resonators [47,52]. The

φ

-dependences of

{| F |}^{2}

{| S |}^{2}

arg [F]

, and

arg [S]

and the spectra

| F_{j} |^{2}

and

| S_{l} |^{2}

are of our prime interest. Also, we are interested in dependences of the soliton-comb characteristics on the pump amplitude

η_{2}

, the walk-off parameter

α

, and other variable parameters of the system. Generally, the soliton position in the resonator depends on the choice of initial random amplitudes. Since the azimuth angle

φ

can be counted from any point, we can chose its zero point as convenient.

We start our report with the case of quasi-PM via the radial poling. Here, the pump wavelength

λ_{p}

can take practically any value. In particular, it can be made arbitrary close to the zero walk-off point

λ_{2}^{c} ≃ 1349

nm. This case is especially important. For sufficiently small values of

δ λ = λ_{p} - λ_{2}^{c}

, the group velocity difference is given by

v_{12} [10^{5} cm / s] ≃ - 5.9 \times δ λ [nm]

in accordance with Figure 4a. Correspondingly, for

| δ λ | ≲ 10

nm and typical values of R and

γ_{2}

the walk-off parameter

α = v_{12} / γ_{2} R

ranges from 0 to large negative and positive values, while the dispersion coefficients

β_{1, 2} (δ λ)

stay practically constant and opposite in signs,

β_{1} > 0

β_{2} < 0

5.1. Antiperiodic solutions near $λ_{2}^{c} ≃ 1349$ nm

Figure 8 corresponds to an antiperiodic steady state moving with velocity

v_{01} = v_{0} - v_{1} = 0

. It is relevant to zero walk-off (

δ λ = 0

α = 0

η_{2} = 30

, zero detunings (

δ_{1, 2} = 0

R = 1.5

mm, and decay rates

γ_{1} = 10^{7}

γ_{2} = 10^{8}

s⁻¹ (

Q_{1} ≃ 3.3 \times 10^{7}

Q_{2} ≃ 0.7 \times 10^{7}

). The total number of harmonics taken into account is 1024. SubFigure 8a,b show the central parts of the normalized FH and SH intensity profiles – far from the center the intensities stay constants. It is evident that we deal with a narrow dual dark-bright soliton. Far from the soliton core, the normalized values of

{| F (φ) |}^{2}

and

{| S (φ) |}^{2}

(

≃ 29

and 1) nicely correspond to the dual background considered in Section 2.

At the first sight, this feature is not consistent with the absence of the dual background for the antiperiodic states. The point is that the amplitude

F (φ)

tends to the opposite left and right constant values far from the center, and these values can be found from Equation (8). The facts that (i) the intensity profiles are even in

φ

and (ii) the FH intensity

{| F (φ) |}^{2}

turns exactly to zero at the soliton center are exclusively due to our zero walk-off assumption.

SubFigure 8c,d exhibit

φ

-dependences of the phases

arg [F]

and

arg [S]

. While an overall

π

change of

arg [F]

across the resonator is general for the antiperiodic states, the

π

jump at

φ = 0

is typical only for

α = 0

. More specifically, the line

Re [F] (φ), Im [F] (φ)

on the complex plane crosses the zero point at a finite angle because of the symmetry leading to an abrupt

π

jump of the phase. For

α \neq 0

, the function

arg [F] (φ)

is smooth. As concerned the SH phase

arg [S]

, it shows only smooth (but large) deviations from zero near the soliton center, see Figure 8d.

The FH and SH comb spectra are shown in subFigure 8e,f. They are symmetric in j and l and very broad. The normalizations of F and S are slightly different and specific for the SH pumping case. On the other hand, they provide the maximum values of

| F_{j} |

and

| S_{l} |

of the order of 1. The shapes of the FH and SH spectra are notably different. The central peak in Figure 8f) is due to the pump. To quantify the comb spectra, we define the number of significant FH and SH lines (

N_{1}

and

N_{2}

) whose normalized intensities are above the cut-off level

10^{- 4}

. This characteristic is conditional and rather useful; the lines of this strength are typically well above the light noise. In our case

N_{1} = 122

and

N_{2} = 161

corresponding to well developed dual combs.

With increasing

η_{2}

, the dual soliton is progressively narrowing and the comb spectra are getting broader. No deterioration of the soliton-comb states was seen up to the maximal investigated values

η_{2}^{max} \approx 10^{2}

. Despite an apparent simplicity of the soliton profiles at

α = 0

, no analytical solutions for them is known so far.

It is not difficult to estimate the numbers of light quanta

| F_{j} |^{2} / ℏ

and

| S_{l} |^{2} / ℏ

in the FH and SH modes for the data of Figure 8e,f. Using Equation (4) for

μ

and setting

σ_{eff} = 100 μ

m², we obtain that they are roughly of the order of

10^{6}

for

| j | \sim | l | \sim 1

. Thus, we are deeply within the classical range. This is valid also for the subsequent illustrations. At the same time, far tails of the comb spectra can experience quantum effects.

Next, we consider the effects of nonzero walk-off. Nonzero values of

α

influence neither the thresholds nor the outcome of the adiabatic procedure – the system still evolves to a single-soliton steady state. The most evident effects are (i) nonzero soliton velocity,

v_{01} \neq 0

, and (ii) asymmetry of the soliton profiles and the comb spectra. The larger

| α |

, the stronger is this asymmetry. This is illustrated by Figure 9. Compared to Figure 8 we have changed

δ λ

from 0 to

- 1.08

nm, this corresponds to

α ≃ 0.05

. Asymmetry of the soliton profiles and comb spectra is already evident. Furthermore, the soliton profiles acquire pronounced tails. The value of

{| F (φ) |}_{min}^{2}

is now far from zero, and

{| S (φ) |}_{max}^{2}

is about two times smaller than earlier. At the same time, the background values of the FH and SH intensities are the same, and the total number of the comb lines

N = N_{1} + N_{2}

is even slightly larger than it was at

α = 0

. Changing sign of

δ λ

results in the mirror reflection of the graphs of Figure 9 about the central vertical line and in changing sign of the soliton velocity

v_{01}

To gain new insights, we consider color maps of velocity parameter

| v_{01} | / 2 π R

and of the total comb line number

N = N_{1} + N_{2}

on the

δ λ, η_{2}

plane for a few representative combinations of the decay rates

γ_{1}

and

γ_{2}

, see Figure 10. Three first subfigures of the upper row represent the maps of

| v_{01} | / 2 π R

for the combinations

γ_{1, 2} = γ

(a1),

γ_{1} = γ

γ_{2} = 10 γ

(b1), and

γ_{1, 2} = 10 γ

(c1) with

γ = 10^{7}

s⁻¹. Subfigures a2, b2, and c2 of the lower row represent the corresponding maps of the total comb line number N. Subfigures d1 and d2 give additionally cross-sections

v_{01} (δ λ)

and

N (δ λ)

η_{2} = 20

for our combinations of

γ_{1}

and

γ_{2}

As evident from the maps, both

| v_{01} |

and N grow monotonously with increasing

η_{2}

. As concerned dependences of these parameters on

| δ λ |

(or

| α |

), they are decreasing only outside a vertical central strip, whose width depends on

γ_{1, 2}

. The decrease of

N (| δ λ |)

and

| v_{01} | (| δ λ |)

persists for

| δ λ | > 10

nm. In short, large values of the walk-off parameter,

| α | ≫ 1

are harmful for the soliton-comb generation in question.

The range of small

| δ λ |

(or

α

), illustrated in some details in the subfigures d1 and d2, is worthy of attention. The dependences

v_{01} (δ λ)

and

N (δ λ)

at large values of

η_{2}

are not always continuous. This means that small variations of

δ λ

can lead to notably different results when adiabatically increasing

η_{2}

. Continuous changes of

v_{01} (δ λ)

and

N (δ λ)

η_{2} = 20

in Figure 10 take place only for

γ_{1} = 0.1 γ_{2} = γ

. The optimum value of

| δ λ |

and the corresponding largest peak values of N take place for

γ_{1, 2} = 10 γ

. In accordance with our definition of

η_{2}

they correspond to the largest

h_{2}

(and the pump power). Anyhow, the increase of N via optimization of

δ λ

is not very large. Note lastly that the wavelength range of 20 nm relevant to Figure 10 strongly exceeds the intermodal wavelength distance of

≃ 0.08

nm, so that the indicated spectral features are not available for the standard experimental fine tuning means.

Now we turn to the effects of the frequency detunings. These effects are of two kinds. One can consider the effects of

δ_{1, 2}

on initiation of soliton-comb states via an adiabatic increase of

η_{2}

. These strong and important effects are considered in Section 5.2. Alternatively, we can vary slowly

δ_{1, 2}

upon reaching the above considered soliton states at large values of

η_{2}

. This issue, which is largely (but not only) about the area of existence of developed soliton-comb states, is considered below.

We have extended our adiabatic procedure for slow independent changes of

δ_{1}

and

δ_{2}

. In fact, two similar scanning procedures were used. Within the first one, we determined initially the soliton velocity

v_{01}

and the comb line number N by increasing and decreasing

δ_{1}

δ_{2} = 0

. After that, starting from a point

δ_{1}, 0

, we increased and decreased detuning

δ_{2}

. The achieved steady-state values of the amplitudes

F_{j}

and

S_{l}

were used as new initial conditions in each step of changing

δ_{1}

δ_{2}

. Within the second procedure, the scanning order was inverted: initially we varied

δ_{2}

δ_{1} = 0

, and after that increased and decreased

δ_{1}

starting from points

0, δ_{2}

. We have verified whether the functions

v_{01} (δ_{1}, δ_{2})

and

N (δ_{1}, δ_{2})

depend on the scanning order. Also, we have made sure that each steady state on the

δ_{1}, δ_{2}

plane is still relevant to a single-soliton antiperiodic state.

Consider first the case zero walk-off,

α = 0

. In our coordinate frame moving with velocity

v_{1}

, the positive and negative propagation directions are equivalent, such that the soliton velocity difference

v_{01} = v_{0} - v_{1}

is expected to be zero. Surprizingly, we have found that this is not always the case. Figure 11a represents color map of

| v_{01} | / 2 π R

for

δ λ = 0

γ_{1} = 10^{7}

, and

γ_{2} = 10^{8}

s⁻¹ (as in Figure 8). The uniformly dark-blue colored lower and upper parts, which are separated from the rest by two slanted borders (bifurcation lines), correspond to

v_{01} / 2 π R = 0

within an accuracy of

\sim 10^{- 9}

MHz. Between these borders we have a smooth distribution

| v_{01} | (δ_{1}, δ_{2})

whose scale is comparable with that of Figure 10. This distribution practically does not depend on the scanning order. But what is the sign of

v_{01}

? We have found that it randomly depends on fine particularities of our calculation procedure, such as the presence of very weak remnant

velocity perturbations. In essence, we have a clear example of the spontaneous symmetry breaking, when the state with a high symmetry (

v_{01} = 0

) becomes unstable against the excitation of one of two equivalent states of lower symmetry with

| v_{01} | \neq 0

. One of the most known examples of such a symmetry breaking is the ferroelectric second-order transition below the Curie temperature.

Let us now take a look at the corresponding color map of N, Figure 11b. The distribution

N (δ_{1}, δ_{2})

is rather smooth. The lower bifurcation line of Figure 11a) is barely seen here, while the upper line is pronounced. Remarkably, increase of

δ_{2}

δ_{1} \approx 0

is favorable for the comb in spite of the increasing instability threshold, see Equation (10). The characteristic scale in

δ_{1}

is here about 1, which strongly exceeds the scale

β_{1} = 0.02

relevant to the changes in

η_{2}^{th} (δ_{1})

. This assertion is general for

η_{2} ≫ 1

; it is justified by plotting maps of

N (δ_{1}, δ_{2})

for different values of

δ λ

and different combinations of

γ_{1}

and

γ_{2}

. In short, we have a vast family of single-soliton antiperiodic states continuously depending on the input parameters.

Our attempts to generate periodic soliton-comb solutions at

δ_{1, 2} = 0

failed. The reason and the possibilities to get new solutions are indicated in Section 5.2.

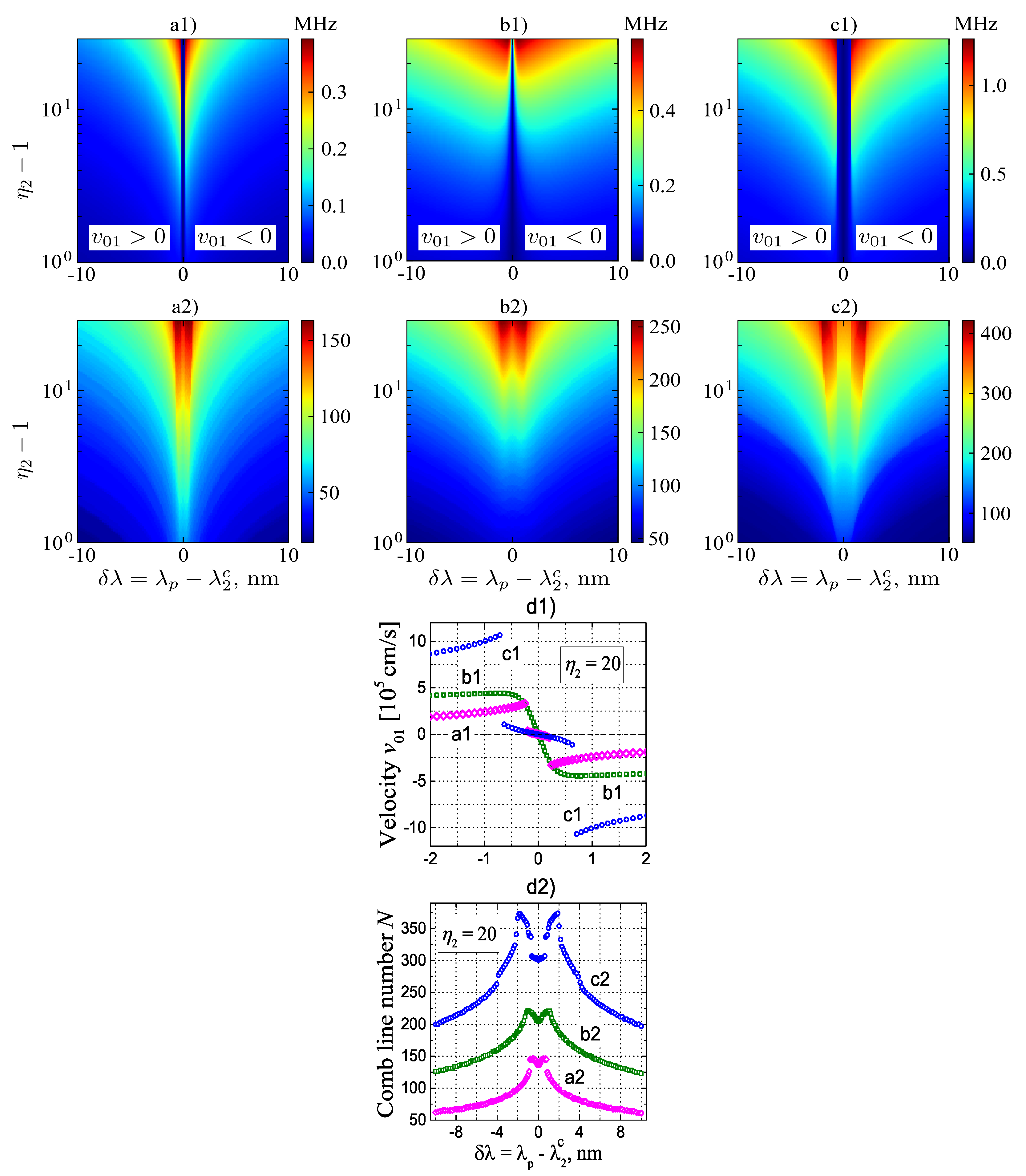
5.2. Selective Generation of Periodic and Antiperiodic Milti-Soliton States

The idea for generation of periodic and antiperiodic multi-soliton states roots in the threshold conditions of Section 3 and a simple observation. The point is that the FH profile of Figure 8 with a sharp minimum emerges with increasing

η_{2}

as a continuous (without bifurcations) development of the near-threshold profile

{| F |}^{2} \propto {sin}^{2} (φ / 2)

corresponding to the lowest threshold for FH harmonics with

j = \pm 1 / 2

. One can suggest thus that the spatial structure of developed solitons can be determined by the threshold conditions.

To develop this idea, we consider the excitation diagrams of Figure 12.

Diagrams a) and b) correspond to the antiperiodic and periodic cases. The cyan circles on the horizontal

δ_{1} / β_{1}

axis separate the regions where the lowest thresholds correspond to different values of the FH harmonic number

| j |

. Within a broad range in diagram a),

δ_{1} > - β_{1} / 2

, including the zero point, an adiabatic increase of

η_{2}

is expected to lead to single-soliton antiperiodic states. This is in line with the above considered results. For

- 9 β_{1} / 4 < δ_{1} < - β_{1} / 4

, we can expect three-soliton antiperiodic states, etc.

The periodic case, diagram b), is expected to be different. In the range

δ_{1} > - β_{1} / 2

, including the zero point, the lowest threshold corresponds to

j = 0

, i.e. to the generation of the dual background. As this background is stable, no periodic solitons are expected. However, in the range

- 5 β_{1} / 2 < δ_{1} < - β_{1} / 2

, where the lowest threshold corresponds to

| j | = 1

, two-soliton periodic state is expected. Similarly, we can hope to generate four-soliton periodic states for

δ_{1} < - 5 β_{1} / 2

. As concerned detuning

δ_{2}

, it plays a passive role by increasing non-selectively all thresholds according to Equation (10).

Now we consider the results of the corresponding numerical experiments on selective growing of multi-soliton states [53]. Figure 13 shows the periodic two-soliton state grown via adiabatic increase of

η_{2}

for

δ λ = 0

γ_{1, 2} = γ = 10^{7}

s⁻¹,

δ_{2} = 0

, and

δ_{1} = - β_{1}

. Remarkably, the phase

arg [F] (φ)

shows two opposite

π

-steps when crossing each of two narrow soliton areas. Thus, our periodic two-soliton solution consists of two equally spaced mutually repelling antiperiodic solitons. This structure emerges every time spontaneously without imposing the antiperiodic conditions. Velocity of the state is

v_{1} = v_{2}

. The FH and SH comb spectra, shown in Figure 13c,f, are symmetric and structurally similar to those of Figure 8e,f. Because of

π

-periodicity in

φ

, the comb line spacing is

2 v_{1} / R

, it is doubled compared to the single-soliton case. Correspondingly, the number of significant comb lines (above

10^{- 4}

) is about two times smaller than it would be in the single-soliton antiperiodic case at

η_{2} = 20

Changing

δ_{1}

sequentially to

δ_{1}^{(j)} = - 4 β_{1}

and

- 9 β_{1}

, which corresponds to the lowest threshold for

| j | = 2

and 3, we have grown periodic four- and six-soliton states. They all consist of pairs of the same antiperiodic solitons. The comb line spacing increases with

| j |

accordingly. Further increase of

| j |

does not lead, however, to new multi-soliton states. Temporal development tends to break such states into the former two-, four-, and six-soliton solutions. This feature is not related to insufficiently small time step and/or insufficiently large number of harmonics taken into account. Also, we mention the case

δ_{1} = 0

relevant to the lowest threshold for

j = 0

. Our adiabatic procedure leads here, as expected, to a dual background steady state

\bar{F}, \bar{S}

Generalization to the case of nonzero walk-off (

α \neq 0

) and different decay rates

γ_{1}

and

γ_{2}

is rather trivial. We still have multi-soliton periodic solutions consisting of pairs of the former antiperiodic solitons moving with velocity

v_{0} \neq v_{1, 2}

Now we switch to multi-soliton antiperiodic states relevant to semi-integer values of j, see Figure 12a. Figure 14 shows representatively the FH and SH intensity profiles for the antiperiodic three-soliton state grown for

δ_{1}^{(3 / 2)} = - 9 β_{1} / 4

and

α = - 1

. The other input parameters are the same as in Figure 13.

Each of three equally spaced solitons has a familiar structure with oscillating tails. Owing to a relatively large negative value of

α

, the tails are strongly pronounced and the spatial asymmetry is inverted as compared to Figure 9. The soliton velocity difference

v_{01} ≃ 2.2 \times 10^{5}

cm/s. Interestingly, antiperiodic five- and seven-soliton states can be easily grown for

| j | = 5 / 2

and

7 / 2

in spite of strong tail overlaps. This contrasts with multi-soliton periodic states.

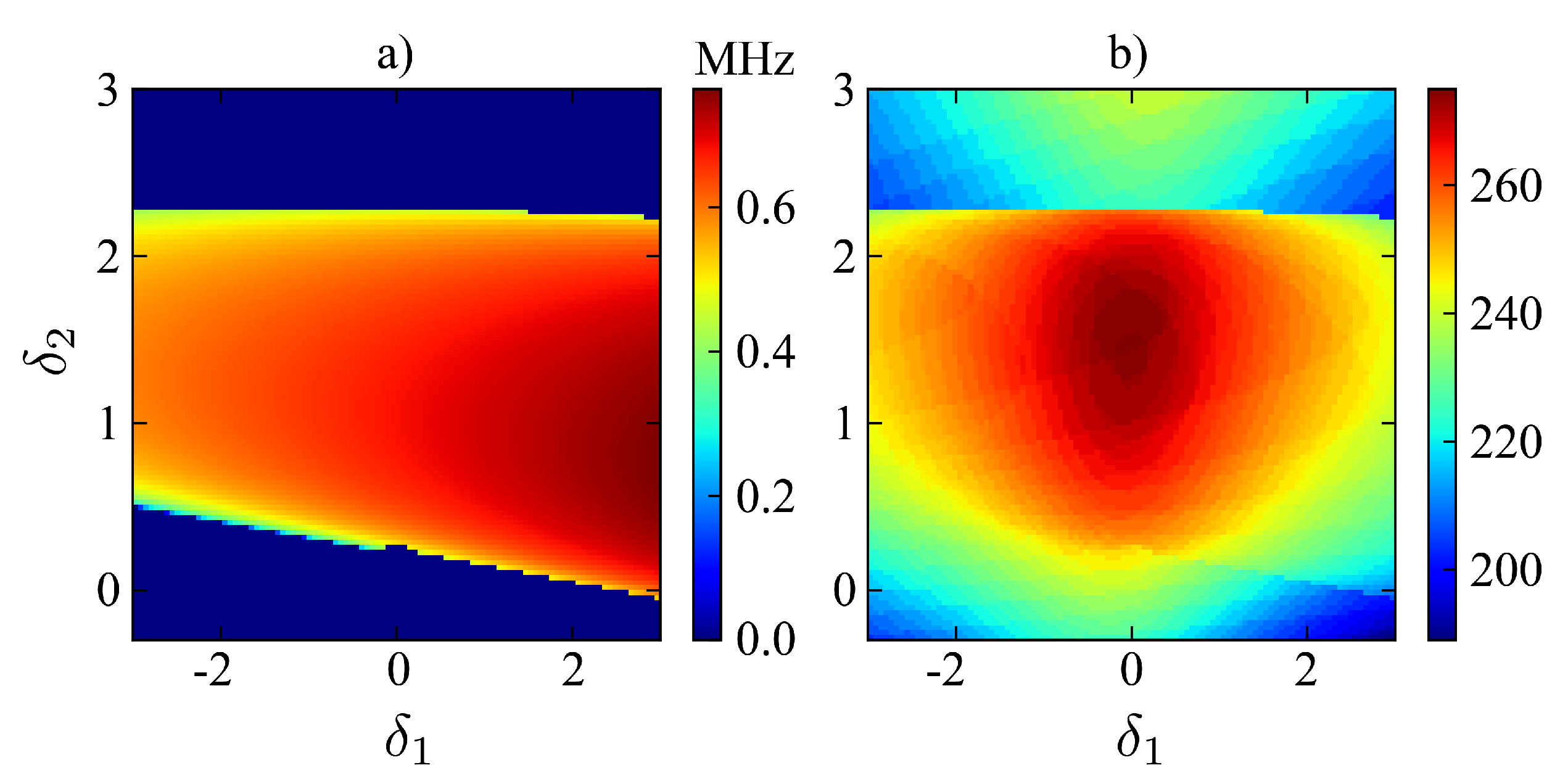
5.3. Natural PM: The Absence of Solitons

The natural phase matching, that can be realized in LN based resonators at

λ_{2} ≃ 532

nm, is of special interest. Avoiding complicated procedure of the radial poling and availability of tunable laser sources in this range make it very attractive. Furthermore, it was indicated [54] that the value of the walk-off parameter can be substantially decreased for sufficiently small microresonators (

R < 1

mm) using the effects of geometric dispersion. This implies the use of proper Sellmeier equations for

n_{o, e} (λ)

[49,55] and relations for the modal frequencies including the size corrections [29], see S2 of supplementary materials for details. It turns out, however, that the main problem with the use of natural PM for the soliton-comb generation is the dispersion issue [56]. In contrast to the above considered cases, the FH and SH dispersion parameters are both negative:

v_{1}^{'} ≃ - 0.64

and

v_{2}^{'} ≃ - 1.5

10^{4}

cm²/s.

Aiming to see the role of the signs of the dispersion parameters, we conducted first some test numerical experiments. For

γ_{1, 2} = 10^{7}

s⁻¹,

α = 0

δ_{1, 2} = 0

, the absolute values

| β_{1} | = 0.02

| β_{2} | = 0.01

and four combinations of the signs of

β_{1, 2}

, we have launched our adiabatic procedure for growing of the antiperiodic soliton states. In two cases with

β_{1} β_{2} < 0

, we got the same known single-soliton solution, see Figure 8. In two other cases with

β_{1} β_{2} > 0

we obtained no soliton states, and the comb spectra remained undeveloped. Additionally, we varied the values of input parameters

α

γ_{1, 2}

, and

δ_{1, 2}

and switched from the antiperiodic to periodic case. No soliton solutions were found as well. The sign of the product

β_{1} β_{2}

is thus crucial for the soliton formation.

6. Solutions for FH pumping

The case of FH pumping is important for experiment, because it corresponds to the conditions of SH generation, including the tuning issues. At the first sight, switching to the FH pumping case is trivial – it is sufficient to set

h_{2} = 0

and

h_{1} \neq 0

in sets (3) and (8). The normalized pump amplitude is here

η_{1} = \sqrt{2} μ h_{1} / γ_{1} \sqrt{γ_{1} γ_{2}}

, and only the periodic states are allowed. While the threshold conditions are more complicated now, they can be evaluated numerically for any set of the input parameters. With these preliminaries, we consider the most important cases [56].

We start from vicinity of the zero walk-off point

2 λ_{c} ≃ 2698

nm. The value of the walk-off parameter

α

is controlled here by the wavelength difference

δ λ = λ_{p} - 2 λ_{c}

, and the dispersion coefficients

β_{1, 2}

can be treated as constants. Setting

δ λ = 0

(

α = 0

) and

δ_{1, 2} = 0

brings us to the situation where the lowest instability threshold,

η_{1}^{th} = 3 \sqrt{2} ≃ 4.24

, corresponds to

j = 0

, i.e. to auto-oscillations of the dual background [50]. Figure 15 illustrates what happens with increasing

η_{1}

when applying our adiabatic procedure at

γ_{1, 2} = γ = 10^{7}

s⁻¹.

Close enough to the threshold we do see auto-oscillations of

| F_{0} |^{2}

and

| S_{0} |^{2}

, see Figure 15a. The oscillation amplitude and period increases and decreases with increasing

η_{1}

, respectively, while harmonics with

j, l \neq 0

remain very small. For

η_{1} ≳ 10

, these spatial harmonics become notable. Their amplitudes grow gradually, and the number of significant comb lines reaches

N \approx 10

for

η_{1} = 11

with the comb line distance

δ j = δ l = 1

. The corresponding normalized FH and SH intensity profiles are shown in Figure 15b by lines 1 and 2. Further increase of

η_{1}

results, however, in a sharp transition to an irregular spatial behavior, see subFigure 15c,d. This contrasts strongly with the case of SH pumping. Variations of the input parameters

γ_{1, 2}

and

δ_{1, 2}

do not change this unfavorable scenario.

With increase of

| α |

, the threshold values

η_{1, j}^{th}

with

j \neq 0

quickly decrease and become lower than the internal instability threshold. This is illustrated by Figure 6a relevant to our input parameters. For

α ≲ 1

, the modes with

| j | ≫ 1

possess the lowest thresholds. Application of our adiabatic procedure to the case

| α | = 1

δ_{1, 2} = 0

results, e.g., in the excitation of

π / 3

-periodic dual state (with six intensity peaks) near the threshold. With increase of

η_{1}

, it transforms via a bifurcation to a

π / 6

periodic state (at

η_{1} ≃ 6.7

). For

η_{1} ≳ 16

the system shows again an irregular spatial behavior. The number of significant comb lines N does not exceed 25 for

η_{1} ≲ 16

. Employment of nonzero detunings

δ_{1, 2}

does not help much.

For

| α | ≳ 10

, the threshold values

η_{1, j}^{th} (| α |)

approach 2 from above, and selective excitation of harmonics with

| j | = | l | = 1, 2

becomes possible. However, the thresholds for

| j | > 2

are only slightly higher. Consider representatively the case

α = 11

δ_{1} = 1 / 2

, and

δ_{2} = 0

relevant to the lowest threshold for

| j, l | = 1

. Applying the adiabatic procedure, we have a

π

-periodic dual state near the threshold. For

η_{1} \approx 7

and 18 it transforms sequentially via bifurcations to a

π / 2

- and

π / 4

-periodic states. Correspondingly, the comb line distance

δ j = δ l

increases from 2 to 4 and, lastly, to 8. Figure 16a,b show complicated steady-state

π / 4

-periodic asymmetric FH,SH intensity profiles for

η_{1}^{max} = 20

, while Figure 16c,d exhibit the corresponding comb spectra.

While the steady state found shows a regular spatial behavior, it cannot be regarded either a soliton state or a pronounced comb state.

For

| α | = 50

, the above scenario of decreasing spatial period and increasing the comb line distance with increasing

η_{1}

remains the same. At

η_{1} = 20

, we have a

π / 3

periodic dual state with a modest the comb line number

N = 20

. Suppression of SH harmonics with

l \neq 0

and asymmetry of the intensity profiles and comb spectra are strongly pronounced.

Lastly, we touch the case of natural PM at

λ_{p} ≃ 1664

nm, when small and/or modest values of

| α |

are available owing to the geometric dispersion, see S2 of supplementary materials for details. The values of the quality factors

Q_{1, 2}

are expected to be substantially larger than they are at 2698 nm [57] leading to larger absolute values of the dispersion coefficients

β_{1, 2}

. As representative values, we chose

R = 1

mm,

β_{1} = - 0.04

, and

β_{2} = - 0.15

, which corresponds to

Q_{1, 2} \approx 3 \times 10^{8}

. The relevant dependences

η_{1, j}^{th} (α)

are presented in Figure 6b. While they differ from the threshold dependences of Figure 6a, one important feature is the same: It is impossible to excite selectively the modes with

| j | = 1, 2

for

| α | ≲ 10

A large number of our numerical experiments, conducted at different values of

α

and

δ_{1, 2}

, show persistently the same scenario: Increasing

η_{1}

above the threshold leads (via bifurcations) to dual states with smaller and smaller spatial periods (larger and larger comb line spacing) and, ultimately, to an irregular spatial behavior. The larger

α

, the longer is the interval of

η_{1}

with the regular behavior. On the other hand, the number of significant comb lines N within this interval remains modest; it does not exceed 15. No signs of soliton-comb states were detected.

7. Discussion

Experimental and theoretical studies of dissipative

χ^{(2)}

soliton-comb states is a vast, perspective, and almost unexplored research area. It is strongly different from the corresponding Kerr soliton domain, which is, in turn, much broader the studies of conservative Kerr solitons. The

χ^{(2)}

nonlinearity is fundamentally different from Kerr’s one resulting in a number of specific qualitative features including duality of the nonlinear states and the necessity to employ the phase matching and to minimize the temporal walk-off. The number of important variable parameters of the system is significantly larger than it is in the Kerr case. Deficit of analytical tools forces researches to rely on numerical methods.

Combining analytical and numerical tools and approaches, we have predicted an unprecedently vast family of dual

χ^{(2)}

soliton-comb steady states. Using the term "vast", we mean a continuous dependence of the parameters of the state on all input parameters – the pump power, the modal quality factors, the frequency detunings, and the walk-off. The found states are self-starting, i.e., easily accessible via nor very abrupt switching the pump on and changing the detunings. The soliton-comb states are divided into two topological classes – periodic and antiperiodic depending on the parity of the azimuth number of the pumped SH mode. The steady state solutions can be single- and multi-soliton ones. All our soliton-comb states are dissipative, they cannot be reduced to (obtained from) the known conservative soliton solutions.

Remarkably, the predicted self-starting soliton-comb states are allowed only for the SH pumping. They require opposite signs of the FH and SH dispersion coefficients. This condition is fulfilled near the zero walk-off point

λ_{2} ≃ 1349

nm in LN based resonators. However, the phase matching at this point requires a precise radial poling. Being available, it represents a serious technical problem. For the natural phase matching in LN resonators, the necessary condition is not fulfilled, and soliton-comb states seem to be forbidden. Despite strong efforts, no soliton-comb solutions were found for the FH pumping. This contradicts initial expectations about similarity of the FH and SH pumping cases but has profound reasons behind.

Both intuitive considerations and numerical modeling indicate that substantial differences in the FH-SH group velocities

v_{12} = v_{1} - v_{2}

, which are typical of

χ^{(2)}

resonators, are unfavorable for the soliton-comb generation. Quantitatively, this means that the combination

(| v_{12} | / c) \times (λ_{2} / R) \times Q_{2}

has to be not much larger than 1. This condition is not generally fulfilled in non-structured high-Q resonators. Minimization of the walk-off parameter can be accomplished via the radial poling. Thus, there is one more physical reason to employ the radial poling for the

χ^{(2)}

comb generation.

Despite our massive failed efforts to find self-starting soliton-comb steady states for the FH pumping, we cannot claim that all sensible combinations of the input parameters (

η_{1}

α

β_{1, 2}

δ_{1, 2}

, and

γ_{1, 2}

) are exhausted. Also, we cannot claim that the initial assumption of the same transverse structure of the modes within each of FH and SH frequency domains is fully justified. This problem remains still open for both

χ^{(2)}

and

χ^{(3)}

resonators. It is likely that suppression of the excitation of unwanted transverse modes takes further efforts on the mode management.

A distinctive feature of our approach is employment of a simple classical equivalent of the Hamiltonian quantum formalism of [4,5,17] and many other papers. While quantum electrodynamics aspects of microresonators are important [17], the comb regimes belong indeed to the classical range, where the use of quantum language is redundant. As we have shown, the actual numbers of modal light quanta in the comb spectra are very large.

The effects of

χ^{(3)}

nonlinearity in

χ^{(2)}

microresonators is one more issue to consider. The possibility to neglect the

χ^{(3)}

nonlinearity is largely controlled by the modal quality factors. Let us consider for simplicity the SH pumping case. The pump power thresholds

P_{th}^{(2)}

and

P_{th}^{(3)}

for the parametric instability caused by the

χ^{(2)}

and

χ^{(3)}

nonlinearities are roughly proportional to

1 / Q^{3}

and

1 / Q^{2}

, such that for

Q_{1, 2} ≳ 10^{6}

the effects of Kerr nonlinearity are expected to be negligible. For modest quality factors,

Q ≲ 10^{5}

, which are typical for ring waveguides, the situation can be more complicated. An interplay between the

χ^{(2)}

and

χ^{(3)}

nonlinear processes becomes possible [42].

The above considered soliton-comb steady states in

χ^{(2)}

microresonators are not the first predicted ones and known in the literature. To the best of our knowledge, the other known stable dissipative soliton states [40,41,42,43] belong to the periodic ones. Furthermore, they are not self-starting, i.e., not easily accessible. The single-soliton numerical solutions of [40] are relevant to the FH pumping at the zero walk-off point. Both bright-bright and dark-dark locally stable solitons were exhibited. Similar numerical soliton solutions were found in [41,42]. Additionally, quasi-solitons at very large detunings,

| δ_{1, 2} | ≫ 1

, were predicted. Remarkably, the soliton-comb states of [40] are allowed for the same and opposite signs of the dispersion coefficients. Generation of flat-top solitons via an additional spatial modulation of the pump amplitude was found numerically in the SH pumping case for opposite signs of the dispersion coefficients [43]. A considerable amount of soliton related models was proposed for bulk parametric oscillators. They are beyond the scope of this review.

The first experimental attempts to get

χ^{(2)}

combs in high-Q LN based microresonators dealt with the FH pumping, the natural phase matching, and large walk-off [37,38]. Neither

χ^{(2)}

solitons no broad comb spectra similar to the Kerr soliton spectra, were observed. This is in agreement with our theoretical results on the necessary conditions for realization of such regimes. The authors of [39] claim for discovery of Pockels soliton microcomb in an aluminium nitride microring resonator at SH pumping. The parameters used correspond to modest quality factors

Q_{1, 2} < 10^{6}

, a large walk-off parameter

| α | ≫ 1

, and the threshold power

P_{th}^{(2)}

only slightly below

P_{th}^{(3)}

. The observed broad FH comb spectrum was practically symmetric, which is the fingerprint of the absence of dominating contribution of the

χ^{(2)}

nonlinearity. The observed and numerically modeled combs are due to the Kerr nonlinearity. The role of quadratic nonlinearity is mostly in initiation of the parametric instability. Thus, net

χ^{(2)}

soliton-comb states are still waiting for experimental discovery and exploration.

8. Conclusions

A vast family of stable soliton-comb steady states is accessible in

χ^{(2)}

microresonators via not very abrupt switching the monochromatic pump on. The necessary conditions for the soliton-comb generation are (i) pumping into a SH resonator mode and (

i i

) opposite signs of the FH and SH dispersion coefficients. Also, minimization of the group velocity (free spectral range) difference for the phase matched FH and SH modes is highly desirable. For LN based resonators, the latter can be accomplished simultaneously with (

i i

) using proper radial poling of the resonator. Pumping into FH resonator modes is not favorable for realization of the soliton-comb states. Employment of high-Q resonators (

Q > 10^{7}

) ensures low generation thresholds (within the

μ

W range) and negligibly small influence of the Kerr nonlinearity.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: Geometry of the problem; Figure S2: Wavelength dependences; Figure S3: Wavelength dependences; Figure S4: Wavelength dependences; Figure S5: Schematic of a periodically poled microresonator; Figure S6: Rim poling period.

Author Contributions

investigation, B.S. and E.P.; data curation, S.S.; writing, B.S. All authors have read and agreed to the published version of the manuscript.

Funding

The work of S. S. was funded by the Russian Science Foundation (Grant No. 17-72-30006-P).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Del’Haye, P.; Schliesser, A.; Arcizet, O.; Wilken, T.; Holzwarth, R; Kippenberg, T. J. Optical frequency comb generation from a monolithic microresonator. Nature 2007, 450, 1214–1217. [Google Scholar] [CrossRef]
Del’Haye, P.; Herr, T.; Gavartin, E.; Gorodetsky, M.L.; Holzwarth, R; Kippenberg, T. J. Octave spanning tunable frequency comb from a microresonator. Phys. Rev. Lett. 2011, 107, 063901. [Google Scholar] [CrossRef]
Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-based optical frequency combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef]
Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nature Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef]
Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, 567–572. [Google Scholar] [CrossRef]
Suh, M.G.; Vahala, K. Gigahertz-repetition-rate soliton microcombs. Optica 2018, 5, 65–66. [Google Scholar] [CrossRef]
Gaeta, A.L.; Lipson, M.; Kippenberg, T.J. Photonic-chip-based frequency combs. Nature Photonics 2019, 13, 158–169. [Google Scholar] [CrossRef]
Chang, L.; Xie, W.; et al. Shu, H.; Yang, Q; Shen, B.; Boes, A.; Peters, J.D; Jin, W.; Xiang, C.; Liu, S.; Moille, G.; Yu, S.; Wang, X.; Srinivasan, K.; Papp, S.B.; Vahala K.; Bowers, J.E.. Ultra-efficient frequency comb generation in AlGaAs-on-insulator microresonators. Nature Communications 2020, 11, 1331. [CrossRef] [PubMed]
Fujii, S.; Tanaka, S.; Ohtsuka, T.; Kogure, S.; Wada, K.; Kumazaki, H.; Tasaka, S.; Hashimoto, Y.; Kobayashi, Y.; Araki, T.; Furusawa, K.; Sekine, N.; Kawanishi, S.; Tanabe, T. Dissipative Kerr soliton microcombs for FEC-free optical communications over 100 channels. Opt. Express 2022, 30, 1351–1364. [Google Scholar] [CrossRef] [PubMed]
Fujii, S.; Wada, K.; Sugano, R.; Kumazaki, H.; Kogure, S.; Kato, Y.K.; Tanabe, T. Versatile tuning of Kerr soliton microcombs in crystalline microresonators. Communications Physics 2023, 6, 1–7. [Google Scholar] [CrossRef]
Akhmediev, N.; Ankiewicz, A. Dissipative Solitons, Lecture Notes in Physics; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nature Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
Boyd, R.W. Nonlinear Optics; Academic Press: New York, USA, 2008. [Google Scholar]
Fürst, J.U.; Strekalov, D.V.; Elser, D.; Lassen, M.; Andersen, U.L.; Marquardt, C.; Leuchs, G. Naturally phase-matched second-harmonic generation in a whispering-gallery-mode resonator. Phys. Rev. Lett. 2010, 104, 153901. [Google Scholar] [CrossRef]
Beckmann, T.; Linnenbank, H.; Steigerwald, H.; Sturman, B.; Haertle, D.; Buse, K.; Breunig, I. Highly tunable low-threshold optical parametric oscillation in radially poled whispering gallery resonators. Phys. Rev. Lett. 2011, 106, 143903. [Google Scholar] [CrossRef]
Mohageg, M.; Strekalov, D.V.; Savchenkov, A.A.; Matsko, A.B.; Ilchenko, V.S.; Maleki, L. Calligraphic poling of lithium niobate. Opt. Express 2005, 13, 3408–3419. [Google Scholar] [CrossRef]
Strekalov, D.; Marquardt, Ch.; Matsko, A.B.; Schwefel, H.G.L.; Leuchs, G. Nonlinear and quantum optics with whispering gallery resonators. J. Opt. 2016, 18, 123002. [Google Scholar] [CrossRef]
Breunig, I. Three-wave mixing in whispering gallery resonators. Laser and Photonics Reviews 2016, 10, 569–587. [Google Scholar] [CrossRef]
Buryak, A.V.; Trapani, P. Di; Skryabin, D.V.; Trillod, S. Optical solitons due to quadratic nonlinearities: from basic physics to futuristic applications. Phys. Rep. 2002, 370, 63–235. [Google Scholar] [CrossRef]
Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B.; Maleki, L. Nonlinear optics and crystalline whispering gallery mode cavities. Phys. Rev. Lett. 2004, 92, 043903–043907. [Google Scholar] [CrossRef] [PubMed]
Jia, Y.; Hanka, K.; Zawilski, K.T.; Schunemann, P.G.; Buse, K.; Breunig, I. Continuous-wave whispering-gallery optical parametric oscillator based on CdSiP₂. Opt. Express 2018, 26, 10833–10841. [Google Scholar] [CrossRef] [PubMed]
Guo, X.; Zou, C.-L.; Tang, H.X. Second-harmonic generation in aluminum nitride microrings with 2500%/W conversion efficiency. Optica 2016, 3, 1126–1131. [Google Scholar] [CrossRef]
Kuo, P.S.; Bravo-Abad, J.; Solomon, G.S. Second-harmonic generation using 4¯-quasi-phasematching in a GaAs whispering-gallery-mode microcavity. Nature Communications 2013, 5, 3109. [Google Scholar] [CrossRef] [PubMed]
Gorodetsky, M.L. High-Q Optical Microresonators; Fizmatgiz: Moscow, Russia, in Russian, 2011. [Google Scholar]
Matsko, A.B.; Ilchenko, V.S. Optical resonators with whispering-gallery modes – Part I: Basics. IEEE J. of Selected Topics in Quantum Electronics 2006, 12, 3–14. [Google Scholar] [CrossRef]
Maleki, L.; Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B. Crystalline whispering gallery mode resonators in optics and photonics. In Practical Applications of Microresonators in Optics and Photonics; Matsko, A.B., Ed.; CRC Press: Boca Raton, USA, 2019. [Google Scholar]
Gorodetsky, M.L.; Demchenko, Yu.A. Accurate analytical estimates of eigenfrequencies and dispersion in whispering-gallery spheroidal resonators. Proceedings of SPIE 2012, 8236, 823623. [Google Scholar]
Demchenko, Yu.A.; Gorodetsky, M.L. Analytical estimates of eigenfrequencies, dispersion, and field distribution in whispering gallery resonators. J. Opt. Soc. Am. B 2013, 30, 3056–3063. [Google Scholar] [CrossRef]
Breunig, I.; Sturman, B.; Sedlmeir, F.; Schwefel, H.G.L.; Buse, K. Whispering gallery modes at the rim of an axisymmetric optical resonator: Analytical versus numerical description and comparison with experiment. Opt. Express 2013, 21, 30683–30692. [Google Scholar] [CrossRef] [PubMed]
Sturman, B.; Podivilov, E.; Werner, C.S.; Breunig, I. Vectorial perturbation theory for axisymmetric whispering gallery resonators. Phys. Rev. A 2019, 99, 013810. [Google Scholar] [CrossRef]
Sturman, B.; Breunig, I. Generic description of second-order nonlinear phenomena in whispering-gallery resonators. J. Opt. Soc. Am. B 2011, 28, 2465–2471. [Google Scholar] [CrossRef]
Werner, Ch.S.; Yoshiki, W.; Herr, S.J.; Breunig, I.; Buse, K. Geometric tuning: spectroscopy using whispering-gallery resonator frequency-synthesizers. Optica 2017, 4, 1205–1208. [Google Scholar] [CrossRef]
Ricciardi, I.; Mosca, S.; Parisi, M.; Maddaloni, P.; Santamaria, L.; De Natale, P.; De Rosa, M. Frequency comb generation in quadratic nonlinear media. Phys. Rev. A 2015, 91, 063839. [Google Scholar] [CrossRef]
Leo, F.; Hansson, T.; Ricciardi, I.; De Rosa, M.; Coen, S.; Wabnitz, S.; Erkintalo, M. Walk-off-induced modulation instability, temporal pattern formation, and frequency comb generation in cavity-enhanced second-harmonic generation. Phys. Rev. Lett. 2016, 116, 033901. [Google Scholar] [CrossRef]
Mosca, S.; Ricciardi, I.; Parisi, M.; Maddaloni, P.; Santamaria, L.; De Natale, P.; De Rosa, M. Direct generation of optical frequency combs in χ⁽²⁾ nonlinear cavities. Nanophotonics 2016, 5, 316–331. [Google Scholar] [CrossRef]
Mosca, S.; Parisi, M.; Ricciardi, I.; Leo, F.; Hansson, T.; Erkintalo, M.; Maddaloni, P.; De Natale, P.; Wabnitz, S.; De Rosa, M. Modulation instability induced frequency comb generation in a continuously pumped optical parametric oscillator. Phys. Rev. Lett. 2018, 121, 093903. [Google Scholar] [CrossRef] [PubMed]
Szabados, J.; Puzyrev, D.N.; Minet, Y.; Reis, L.; Buse, K.; Villois, A.; Skryabin, D.V.; Breunig, I. Frequency comb generation via cascaded second-order nonlinearities in microresonators. Phys. Rev. Lett. 2020, 124, 203902. [Google Scholar] [CrossRef] [PubMed]
Szabados, J.; Sturman, B.; Breunig, I. Frequency comb generation threshold via second-harmonic excitation in χ⁽²⁾ optical microresonators. APL Photonics 2020, 5, 116102. [Google Scholar] [CrossRef]
Bruch, A.W.; Liu, X.; Gong, Z.; Surya, J.B.; Li, M.; Zou, C.-L.; Tang, H.X. Pockels soliton microcomb. Nature Photonics 2021, 15, 21–27. [Google Scholar] [CrossRef]
Hannson, T.; Parra-Rivas, P.; Bernard, M.; Leo, F.; Gelens, L.; Wabnitz, S. Quadratic soliton combs in doubly resonant second-harmonic generation. Opt. Lett. 2018, 43, 6033–6036. [Google Scholar] [CrossRef]
Villois, A.; Skryabin, D. Soliton and quasi-soliton frequency combs due to second harmonic generation in microresonators. Opt. Express 2019, 27, 7098–7107. [Google Scholar] [CrossRef]
Villois, A.; Kondratiev, N.; Breunig, I.; Puzyrev, D.N.; Skryabin, D.V. Frequency combs in a microring optical parametric oscillator. Opt. Lett. 2019, 44, 4443–4446. [Google Scholar] [CrossRef]
Lobanov, V.E. Two-color flat-top solitons in microresonator-based optical parametric oscillators. Phys. Rev. A 2020, 102, 013518. [Google Scholar] [CrossRef]
Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Elsevier Ltd.: Amsterdam, Netherlands, 1976. [Google Scholar]
Zakharov, V.E.; Kuznetsov, E.A. Hamiltonian formalism for nonlinear waves. Physics - Uspekhi 1997, 40, 1087–1116. [Google Scholar] [CrossRef]
Podivilov, E.; Smirnov, S.; Breunig, I.; Sturman, B. Nonlinear solutions for χ⁽²⁾ frequency combs in optical microresonators. Phys. Rev. A 2020, 101, 023815. [Google Scholar] [CrossRef]
Smirnov, S.; Sturman, B.; Podivilov, E.; Breunig, I. Walk-off controlled self-starting frequency combs in χ⁽²⁾ optical microresonators. Opt. Express 2020, 28, 18006–18017. [Google Scholar] [CrossRef]
The use of this expansion is justified, for the FH and SH spectra must be relatively narrow (|j|,|l|≪ $m_{1}^{0}$ ∼10⁴) within our envelope approximation.
Nikogosyan, D.N. Nonlinear Optical Crystals: A Complete Survey; Springer: New York, USA, 2005. [Google Scholar]
Sturman, B.; Podivilov, E.; Szabados, J.; Breunig, I. Dual backgrounds and their stability during frequency comb and second harmonic generation in χ⁽²⁾ microresonators. J. Opt. Soc. Am. B 2022, 39, 378–387. [Google Scholar] [CrossRef]
Podivilov, E.; Sturman, B.; Breunig, I. Frequency comb solutions for driven χ⁽²⁾ optical microresonators. J. Opt. Soc. Am. B 2020, 37, 3316–3324. [Google Scholar] [CrossRef]
Smirnov, S.; Andryushkov, V.; Podivilov, E.; Sturman, B.; Breunig, I. Walk-off controlled self-starting frequency combs in χ⁽²⁾ optical microresonators. Opt. Express 2021, 29, 27434–27449. [Google Scholar] [CrossRef] [PubMed]
Podivilov, E.; Smirnov, S.; Sturman, B. Adiabatic growing, multistability, and control of soliton-comb states in χ⁽²⁾ microresonators for pumping into second-harmonic modes. JETP Letters 2022, 115, 553–559. [Google Scholar] [CrossRef]
Breunig, I. , Freiburg University, Germany, Personal communication, 2020.
Umemura, N.; Matsuda, D. Thermo-optic dispersion formula for the ordinary wave in 5 mol % MgO doped LiNbO₃ and its application to temperature insensitive second-harmonic generation. Opt. Commun. 2016, 367, 167–173. [Google Scholar] [CrossRef]
Smirnov, S.; Podivilov, E.; Sturman, B. Effects of dispersion and pumping scheme on soliton-comb generation in χ⁽²⁾ microresonators. J. Opt. Soc. Am. B 2023, 40, 515–522. [Google Scholar] [CrossRef]
Leidinger, M.; Fieberg, S.; Waasem, N.; Kühnemann, F.; Buse, K.; Breunig, I. Comparative study on three highly sensitive absorption measurement techniques characterizing lithium niobate over its entire transparent spectral range. Opt. Express 2015, 23, 21690–21705. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Schematic of

χ^{(2)}

comb generation; R and

φ

are the major resonator radius and the azimuth angle. The output comb spectra are due to a dual FH-SH soliton propagating along the resonator rim with velocity

v_{0}

. The red spots indicate localization of the resonator modes near the rim.

Figure 1. Schematic of

χ^{(2)}

comb generation; R and

φ

are the major resonator radius and the azimuth angle. The output comb spectra are due to a dual FH-SH soliton propagating along the resonator rim with velocity

v_{0}

. The red spots indicate localization of the resonator modes near the rim.

Figure 2. Excitation of periodic (a) and antiperiodic (b) states for SH-pumping into even and odd resonator modes. The primary FH azimuth number

m_{1}^{0} = m_{2}^{0} / 2

is integer in (a) and semi-integer in (b). Side harmonics arise automatically in (b) above the threshold.

Figure 2. Excitation of periodic (a) and antiperiodic (b) states for SH-pumping into even and odd resonator modes. The primary FH azimuth number

m_{1}^{0} = m_{2}^{0} / 2

is integer in (a) and semi-integer in (b). Side harmonics arise automatically in (b) above the threshold.

Figure 3. (a) Illustration of the azimuth dependence of the susceptibility coefficient

d (φ)

for a perfect symmetric radial domain pattern with

N = 4

. (b) First three harmonics of the corresponding Fourier spectrum with

s = N

3 N

, and

5 N

Figure 3. (a) Illustration of the azimuth dependence of the susceptibility coefficient

d (φ)

for a perfect symmetric radial domain pattern with

N = 4

. (b) First three harmonics of the corresponding Fourier spectrum with

s = N

3 N

, and

5 N

Figure 4. Dependences

v_{1, 2} (λ)

(a) and

v_{1, 2}^{'} (λ)

(b) for an LN based resonator with

R = 1.5

mm and

R / r = 3

. The dotted and solid lines refer to the bulk index

n_{b}

and the effective index n incorporating the effects of geometric dispersion. The vertical line

λ_{2} = λ_{2}^{c} ≃ 1.349 μ

m (

λ_{1} = λ_{1}^{c} ≃ 2.698 μ

m) corresponds to zero walk-off point

v_{1} = v_{2}

Figure 4. Dependences

v_{1, 2} (λ)

(a) and

v_{1, 2}^{'} (λ)

(b) for an LN based resonator with

R = 1.5

mm and

R / r = 3

. The dotted and solid lines refer to the bulk index

n_{b}

and the effective index n incorporating the effects of geometric dispersion. The vertical line

λ_{2} = λ_{2}^{c} ≃ 1.349 μ

m (

λ_{1} = λ_{1}^{c} ≃ 2.698 μ

m) corresponds to zero walk-off point

v_{1} = v_{2}

Figure 5. Normalized dependences of

| \bar{F} |^{2}

on the pump strength parameters

h_{1, 2}

for the cases of FH (a) and SH (b) pumping. The curves are relevant to different values of the phase

Φ = arg (Ω_{1} Ω_{2})

. Zero detuning case,

Δ_{1, 2} = 0

, corresponds to

Φ = π

. The horizontal red line in (b) is related to the single background state,

\bar{F} = 0

\bar{S} = - i h_{2} / Ω_{2}

Figure 5. Normalized dependences of

| \bar{F} |^{2}

on the pump strength parameters

h_{1, 2}

for the cases of FH (a) and SH (b) pumping. The curves are relevant to different values of the phase

Φ = arg (Ω_{1} Ω_{2})

. Zero detuning case,

Δ_{1, 2} = 0

, corresponds to

Φ = π

. The horizontal red line in (b) is related to the single background state,

\bar{F} = 0

\bar{S} = - i h_{2} / Ω_{2}

Figure 6. Threshold dependences

η_{1, j}^{th} (| α |)

for FH pumping at

δ_{1, 2} = 0

. (a)

λ_{p} ≃ 2698

nm,

β_{1} = 5.3

, and

β_{2} = - 1.44

10^{- 3}

. (b)

λ_{p} ≃ 1664

nm,

β_{1} = - 4

β_{2} = - 15

10^{- 2}

. Two horizontal lines

3 \sqrt{2} ≃ 4.24

and 2 indicate the internal instability threshold and the limiting value

η_{1, j}^{th} (\infty) = 2

Figure 6. Threshold dependences

η_{1, j}^{th} (| α |)

for FH pumping at

δ_{1, 2} = 0

. (a)

λ_{p} ≃ 2698

nm,

β_{1} = 5.3

, and

β_{2} = - 1.44

10^{- 3}

. (b)

λ_{p} ≃ 1664

nm,

β_{1} = - 4

β_{2} = - 15

10^{- 2}

. Two horizontal lines

3 \sqrt{2} ≃ 4.24

and 2 indicate the internal instability threshold and the limiting value

η_{1, j}^{th} (\infty) = 2

Figure 7. Three representative evolution runs for the discrepancy parameter

ε (t, τ)

relevant to the FH harmonics

F_{j}

and

γ τ = 1

. The states under study are antiperiodic. The input dimensionless parameters are

δ_{1, 2} = 0

β_{1} = 0.02

β_{2} = - 0.01

γ = 10^{7}

s⁻¹, and

α = 1

. The time step is

0.02 γ^{- 1}

. The evolution run relevant to (a) starts at

t_{0}

from noise and ends up at

t_{1}

. The evolution runs (b,c) start from the previous steady-state values of the FH amplitudes.

Figure 7. Three representative evolution runs for the discrepancy parameter

ε (t, τ)

relevant to the FH harmonics

F_{j}

and

γ τ = 1

. The states under study are antiperiodic. The input dimensionless parameters are

δ_{1, 2} = 0

β_{1} = 0.02

β_{2} = - 0.01

γ = 10^{7}

s⁻¹, and

α = 1

. The time step is

0.02 γ^{- 1}

. The evolution run relevant to (a) starts at

t_{0}

from noise and ends up at

t_{1}

. The evolution runs (b,c) start from the previous steady-state values of the FH amplitudes.

Figure 8. Properties of the antiperiodic steady state grown adiabatically for

η_{2} = 30

R = 1.5

mm,

α = 0

δ_{1, 2} = 0

β_{1} ≃ 0.02

and

β_{2} ≃ - 0.01

; 1024 FH and SH harmonics are taken into account. The upper and lower rows refer to the FH and SH characteristics, respectively. They show the normalized intensity profiles (a and d), the phase profiles (b and e), and the comb spectra (c and f). The horizontal dashed lines indicate the cut-off level of

10^{- 4}

. The number of FH and SH comb lines above

10^{- 4}

is 122 and 162.

Figure 8. Properties of the antiperiodic steady state grown adiabatically for

η_{2} = 30

R = 1.5

mm,

α = 0

δ_{1, 2} = 0

β_{1} ≃ 0.02

and

β_{2} ≃ - 0.01

10^{- 4}

. The number of FH and SH comb lines above

10^{- 4}

is 122 and 162.

Figure 9. The effect of walk-off on the soliton-comb properties. The only difference in the input parameters as compared to Figure 8 is

δ λ = λ_{p} - λ_{2}^{c} = - 1.08

nm corresponding to the walk-off parameter

α ≃ 0.05

Figure 9. The effect of walk-off on the soliton-comb properties. The only difference in the input parameters as compared to Figure 8 is

δ λ = λ_{p} - λ_{2}^{c} = - 1.08

nm corresponding to the walk-off parameter

α ≃ 0.05

Figure 10. Subfigures a1 to c1: Color maps of velocity parameter

| v_{01} | / 2 π R

[MHz] on the

δ λ, η_{2}

plane. Subfigures a2 to c2: The same for the total comb line number

N = N_{1} + N_{2}

. The first, second, and third columns refer to

γ_{1, 2} = γ

γ_{1} = γ

;

γ_{2} = 10 γ

, and

γ_{1, 2} = 10 γ

with

γ = 10^{7}

s⁻¹. Each map is obtained by stepwise increase of

η_{2}

starting from the value of 2 and incorporates the data of

141 \times 151 = 21291

calculation variants with up to 1024 Fourier harmonics taken into account. The insets in a1 to c1 indicate the signs of

v_{01}

. Subfigures d1 and d2 give the crosssections

v_{01} (δ λ)

and

N (δ λ)

for

η = 20

relevant to the maps a1 to c1 and a2 to c2, respectively. Note different scales of

δ λ

in d1 and d2.

Figure 10. Subfigures a1 to c1: Color maps of velocity parameter

| v_{01} | / 2 π R

[MHz] on the

δ λ, η_{2}

plane. Subfigures a2 to c2: The same for the total comb line number

N = N_{1} + N_{2}

. The first, second, and third columns refer to

γ_{1, 2} = γ

γ_{1} = γ

;

γ_{2} = 10 γ

, and

γ_{1, 2} = 10 γ

with

γ = 10^{7}

s⁻¹. Each map is obtained by stepwise increase of

η_{2}

starting from the value of 2 and incorporates the data of

141 \times 151 = 21291

calculation variants with up to 1024 Fourier harmonics taken into account. The insets in a1 to c1 indicate the signs of

v_{01}

. Subfigures d1 and d2 give the crosssections

v_{01} (δ λ)

and

N (δ λ)

for

η = 20

relevant to the maps a1 to c1 and a2 to c2, respectively. Note different scales of

δ λ

in d1 and d2.

Figure 11. Dependences of

v_{01} / 2 π R

(a) and N (b) on

δ_{1}

and

δ_{2}

for

δ λ = 0

γ_{1} = 10^{7}

, and

γ_{2} = 10^{8}

s⁻¹. Each map incorporates the data of

90 \times 90 = 8100

calculation variants. Within the dark-blue colored parts in a),

v_{01} = 0

Figure 11. Dependences of

v_{01} / 2 π R

(a) and N (b) on

δ_{1}

and

δ_{2}

for

δ λ = 0

γ_{1} = 10^{7}

, and

γ_{2} = 10^{8}

s⁻¹. Each map incorporates the data of

90 \times 90 = 8100

calculation variants. Within the dark-blue colored parts in a),

v_{01} = 0

Figure 12. Diagrams of growing of antiperiodic (a) and periodic (b) multi-soliton states by (i) adiabatic increase of

η_{2}

and (ii) the subsequent slow change of

δ_{1}

. The cyan circles indicate the borders of the allowed ranges for initial values of

δ_{1} / β_{1}

. The lowest thresholds occur at

δ_{1}^{(j)} = - β_{1} j^{2}

. For

η_{2} ≳ 10

, stable states grown via the adiabatic two-step (i-ii) procedure exist in a broad range of

δ_{1} / β_{1}

exciding the shown one.

Figure 12. Diagrams of growing of antiperiodic (a) and periodic (b) multi-soliton states by (i) adiabatic increase of

η_{2}

and (ii) the subsequent slow change of

δ_{1}

. The cyan circles indicate the borders of the allowed ranges for initial values of

δ_{1} / β_{1}

. The lowest thresholds occur at

δ_{1}^{(j)} = - β_{1} j^{2}

. For

η_{2} ≳ 10

, stable states grown via the adiabatic two-step (i-ii) procedure exist in a broad range of

δ_{1} / β_{1}

exciding the shown one.

Figure 13. Periodic adiabatically grown two-soliton state for

η_{2} = 20

α = 0

δ_{1} = - β_{1}

δ_{2} = 0

, and

γ_{1, 2} = γ = 10^{7}

s⁻¹. The upper and bottom rows refer to the FH and SH characteristics, respectively. They show the normalized intensity profiles (a and d), the phase profiles (b and e), and the comb spectra (c and f).

Figure 13. Periodic adiabatically grown two-soliton state for

η_{2} = 20

α = 0

δ_{1} = - β_{1}

δ_{2} = 0

, and

γ_{1, 2} = γ = 10^{7}

Figure 14. Antiperiodic adiabatically grown three-soliton state for

α = - 1

(

δ λ ≃ 8

nm) and

δ_{1} = - 9 β_{1} / 4

. The other parameters correspond to Figure 13. Subfigures (a and b) correspond to the normalized FH and SH intensity profiles.

Figure 14. Antiperiodic adiabatically grown three-soliton state for

α = - 1

(

δ λ ≃ 8

nm) and

δ_{1} = - 9 β_{1} / 4

. The other parameters correspond to Figure 13. Subfigures (a and b) correspond to the normalized FH and SH intensity profiles.

Figure 15. FH pumping at

α = 0

and

δ_{1, 2} = 0

. a): A fragment of steady-state auto-oscillations at

η_{1} = 4.6

; the spatial harmonics with

j, l \neq 0

are negligible here. b): FH and SH intensity profiles (lines 1 and 2) at

η_{1} = 11

. c) and d): FH and SH intensity profiles at

η_{1} = 12

Figure 15. FH pumping at

α = 0

and

δ_{1, 2} = 0

. a): A fragment of steady-state auto-oscillations at

η_{1} = 4.6

; the spatial harmonics with

j, l \neq 0

are negligible here. b): FH and SH intensity profiles (lines 1 and 2) at

η_{1} = 11

. c) and d): FH and SH intensity profiles at

η_{1} = 12

Figure 16. FH pumping at 2698 nm. a) and b): Periodic FH and SH intensity profiles for

α = 11

δ_{1} = 1 / 2

δ_{2} = 0

, and

η_{1} = 20

. c) and d): The corresponding FH and SH comb spectra. The number of significant comb lines (higher than

10^{- 4}

) is

N = 28

, and the comb line distance

δ j = δ l = 8

Figure 16. FH pumping at 2698 nm. a) and b): Periodic FH and SH intensity profiles for

α = 11

δ_{1} = 1 / 2

δ_{2} = 0

, and

η_{1} = 20

. c) and d): The corresponding FH and SH comb spectra. The number of significant comb lines (higher than

10^{- 4}

) is

N = 28

, and the comb line distance

δ j = δ l = 8

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Self-Starting Soliton-Comb Regimes in χ(2) Microresonators

Abstract

1. Introduction

2. Basic Equations, Parameters, and Definitions

2.1. Periodic and Antiperiodic States

2.2. Equations for the Modal Amplitudes

2.3. The Impact of Radial Poling

2.4. Fundamental z , t Representation

3. Instability Thresholds

4. Numerical Methods

5. Soliton-Comb States for SH Pumping

5.1. Antiperiodic solutions near λ 2 c ≃ 1349 nm

5.2. Selective Generation of Periodic and Antiperiodic Milti-Soliton States

5.3. Natural PM: The Absence of Solitons

6. Solutions for FH pumping

7. Discussion

8. Conclusions

Supplementary Materials

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.4. Fundamental $z, t$ Representation

5.1. Antiperiodic solutions near $λ_{2}^{c} ≃ 1349$ nm