Prerpints.org logo
Preprint
Article

High Thermoelectric Performance of a Novel Monolayer γ-PbSnX2(X=S, Se, Te): Predicted by First-Principles

Altmetrics

Downloads

239

Views

141

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 April 2023

Posted:

17 April 2023

You are already at the latest version

Alerts
Abstract
Two-dimensional (2D) of transition metal dichalcogenides (TMDCs) are potential candidates for thermoelectric (TE) applications due to their unique structural properties. In this paper, we constructed an 2D monolayer TMDCs semiconductor γ-PbSn2(X=S, Se, Te) and first-principles calculations and Boltzmann transport theory are used to study the thermoelectric performance. We found that γ-PbSnX2 had an ultra-high carrier mobility up to 4.04×103 cm2V−1s−1 leading to a metal-like electrical conductivity. Meanwhile, γ-PbSnX2 both have high Seebeck coefficients, resulting in high power-factors, and also shows intrinsic low lattice thermal conductivity of 6-8 W/mK at room temperature. The lower lattice thermal conductivity and high power-factors resulted in excellent thermoelectric performance. The high ZT values of γ-PbSnS2 and γ-PbSnSe2 were as high as 2.65 and 2.96 at 900 K, respectively. The result suggests that the monolayer γ-PbSnX2 are better candidates for excellent thermoelectric performance.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

The world’s energy demand is increasing due to the development of science and technology. Thermoelectric modules can directly convert electricity into thermal energy for cooling and heating and can also harvest waste heat for electrical power and have thus attracted significant attention [1,2]. The performance of thermoelectric materials is usually evaluated by the dimensionless figure of merit ( Z T ), which is defined as Z T = S 2 σ T / ( κ e + κ l ) , where S is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, κ e and κ l are the electronic thermal conductivity and lattice thermal conductivity [3,4]. The higher Z T value means the better efficiency μ of thermoelectric conversion.
However, due to the Wiedemann-Franz law, there is a coupling relationship between electronic transport coefficients, which makes it a significant challenge to improve Z T and enhance thermoelectric performance[5]. To improve thermoelectric performance, many advanced methods have been proposed, which can be divided into two main categories, namely phonon engineering and electronic engineering, for optimizing phonon and electronic transport properties, respectively[6,7,8,9,10,11,12]. The phonon engineering is focused on the modulation of lattice thermal conductivity by suppress the mean free path of phonon. The electron engineering aims in the modulation of power factor and Seebeck coefficient under the optimum carrier concentration. Such as strain engineering [13,14,15,16,17,18], doping defects[19,20,21], molecular junction [4,22,23,24], superlattices[25,26,27] and heterostructure[28,29].
Two-dimensional materials are very promising candidates for thermoelectricity because of the increase in the Seebeck coefficient due to the increase in the density of states near the Fermi energy level[30,31]. In particular, single layers of transition metal dichalcogenides (TMDCs), such as MX 2 (M=Mo, W, Ti, and X=S, Se ,Te), have attracted a large attention in last decades du to their unique semiconducting characteristics[31,32,33]. Recently, a novel type of 2D TMDCs, (AX) 2 (A=Si, Ge, Sn, Pb;X=Se, Te), has been predicted theoretically from ab initio calculations[34]. Dong et al. reported that the γ -SnX (X = S, Se, or Te) has high thermoelectric performance due to the low thermal conductivity[35]. And then, Jia et al. reported that reported high thermoelectric properties due to strong anharmonic effects in monolayer (PbX) 2 (X=S, Se, Te)[36]. Thus, the γ -phase TMDCs are very promising candidates for thermoelectricity.
In this work, we constructed a series of 2D γ -phase TMDCs, i.e., γ -PbSnX 2 (X=S, Se, Te), based on γ -AX(A=Pb, Sn and X=S, Se, Te). And investigate the thermoelectric transport properties by using first-principles calculations combined with the Boltzmann transport equation. The results show that these materials have high power factors and low lattice thermal conductivity, leading to high figure of merit ( Z T ). The studies indicate that these materials are potential candidates for high temperature thermoelectric materials. thermoelectric performance.

2. Computational method

In this work, we performed first-principles simulations using the Vienna Ab initio Simulation Package ( V A S P ) software based on density functional theory (DFT) [37,38]. The generalized gradient approximation (GGA) method with the Perdew-Burke-Ernzerhof (PBE) exchange-correlation (XC) functional was employed [39]. The total energy convergence criterion of 10-8 eV, the force convergence criterion of 0.001 eV/Å, and the kinetic energy cutoff of 500 eV were used to optimize crystals [40]. A set of 15× 15 × 1 Monkhorst-Pack k-points [41] was used to sample the Brillouin zone. A 20 Å vacuum layer was set in the direction of the z-axis to avoid the interaction of periodic layers along the z-axis and the DFT-D3 method was used to correct van der Waals (VDW) interactions [42]. A hybrid functional (HSE06) was used to calculate the electronic band properties of materials. The thermoelectric transport coefficient was calculated by solving the Boltzmann transport equation with BoltzTraP-package [43]. The relaxation time was calculated by using the deformation potential theory and effective mass approximation. The 3×3×1 supercell was used to calculate the second-order and third-order force constants of the materials through the finite displacement method. The cutoff radius of the third order force constant was set as the sixth-nearest neighbors. Lattice thermal conductivity was obtained by solving the Boltzmann transport equation by ShengBTE, and the grid density of 60×60×1 k-points was used to ensure convergence[44].

3. Results

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn.

3.1. Structure and stability

The monolayer γ -PbSnX 2 (X=S, Se, Te) can be constructed from γ -AX (A=Pb, Sn and X=S, Se, Te) monolayer by replacing one layer of chalcogen Pb/Sn atoms with another layer of chalcogen Sn/Pb atoms in the middle side, showing a hexagonal lattice structure with a P 3 m 1 space group (Figure 1). The calculated lattice constants of γ -PbSnS 2 , γ -PbSnSe 2 , and γ -PbSnTe 2 are a = b = 3.96 Å, 4.11 Å, and 4.37 Å, respectively. The specific crystal structure parameters are shown in Table 1.
We verified the structure stability of monolayer γ -PbSnX 2 (X=S, Se, Te). Figure 2(a-c) shows the phonon dispersion curve of γ -PbSnX 2 . Each unit cell of the γ -PbSnX 2 monolayer has 4 atoms, with 3 acoustic and 9 optical branches. The phonon frequencies of the γ -PbSnX 2 monolayer are all positive, indicating the dynamic stability of the γ -PbSnX 2 monolayer. They all have very low phonon frequencies and lead to a decrease in their phonon frequencies as the atomic mass of sulfur group elements increases. More interestingly, an apparent coupling occurs between optical and acoustic phonon modes in γ -PbSnX 2 monolayers, which might lead to a low lattice thermal conductivity because of the anharmonic scattering. Moreover, we used ab initio molecular dynamics (AIMD) simulations to determine the stability of γ -PbSnX 2 at 900 K. The simulation results of AIMD are shown in Figure 2(d-f). The total energy is almost unchanged at a temperature of 900 K for 10 ps. These results indicate that γ -PbSnX 2 has a stable structure at 900 K.

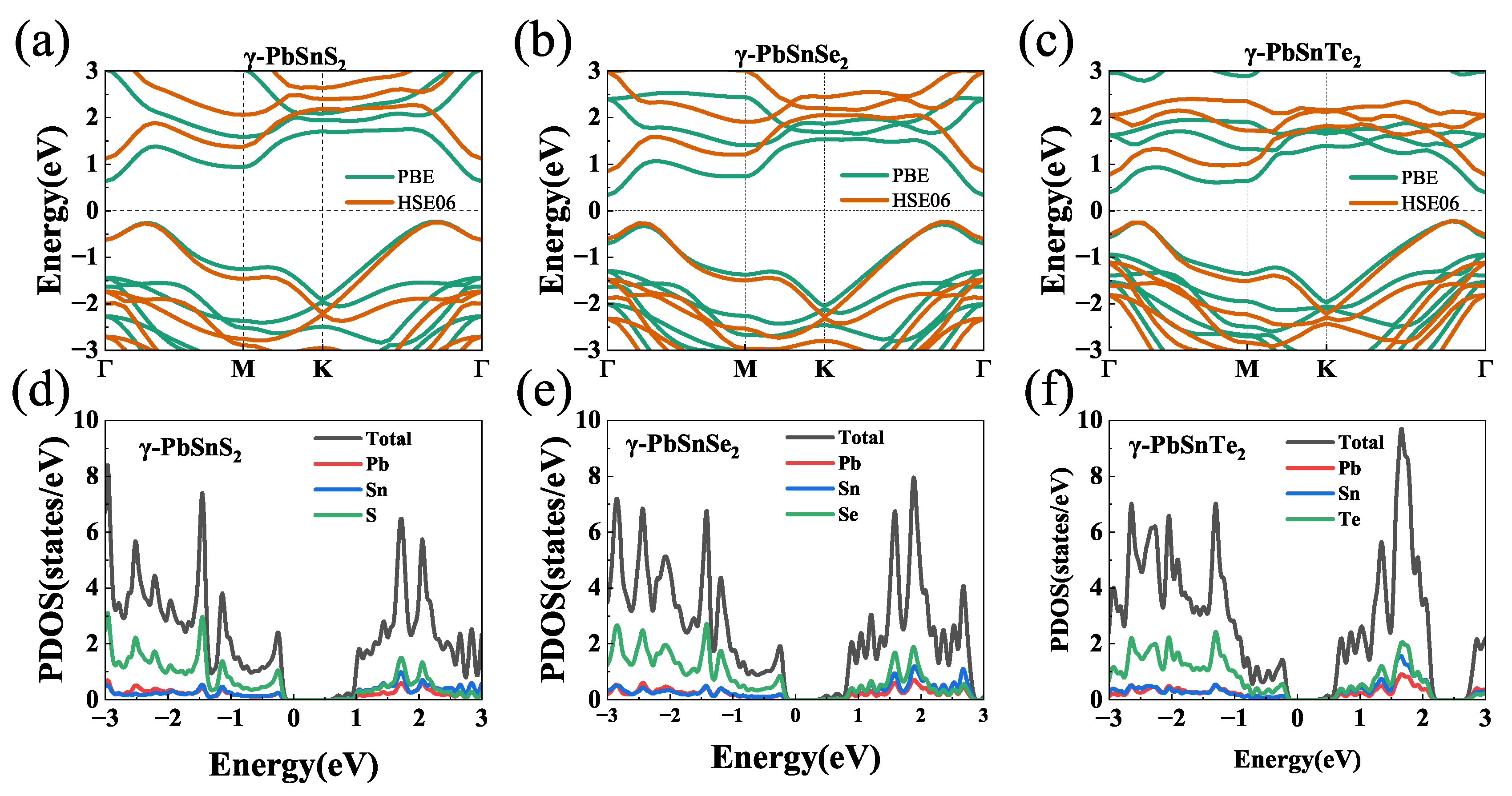
3.2. Electronic band structure

Figure 3 shows the electronic band structures of γ -PbSnX 2 (X=S, Se, Te) monolayers calculated by the PBE and HSE06 exchange-correlation functionals, respectively. The corresponding band gap values are given in Table 2. They are both indirect band gaps with conduction band minimum (CBM) at the high symmetry point Γ (0, 0, 0) and valence band maximum (VBM) between the high symmetry points Γ (0,0,0) and K (1/3, 1/3, 0). The band gap calculated by HSE06 is large than that calculated by PBE. It is noted that the PBE functional often underestimates the band gap value, while the HSE functional can give a reliable band gap value compared with experiment. The band gap of γ -PbSnS 2 , γ -PbSnSe 2 and γ -PbSnTe 2 are 0.86 (1.37) eV, 0.63 (1.08) eV and 0.61 (0.98) eV, respectively. The band gaps calculated by all the methods gradually decrease as the atomic number of the substituted chalcogenide element (S, Se, and Te) increases. Such moderate bandgaps indicate that thermoelectric properties of the γ -PbSnX 2 monolayer can be easily optimized at a reasonable doping concentration for 2D materials. Except for the band gap, there is no significant change in the type and shape of their energy bands, so we next to calculate the effective mass and carrier mobility of these materials by using the PBE generalization function. The partial density of states (PDOS) of the γ -PbSnX 2 is shown in Figure 3(d-f), with the valence bands closer to the Fermi energy level. The valence bands around the Fermi level originate from the S, Se and Te atoms, and the conduction bands are jointly contributed by Sn or Pb, S, Se and Te atoms. Figure 3(d-f) shows that γ -PbSnS 2 , γ -PbSnSe 2 and γ -PbSnTe 2 all have very sharp density of state peaks at the Fermi energy level attachment, where γ -PbSnS 2 has a higher density of state peak than γ -PbSnSe 2 and γ -PbSnTe 2 .

3.3. Carrier mobility and relaxation time

We use the BoltzTraP-package based on the semi-classical Boltzmann transport equation to estimate the electrical properties of the monolayer γ -PbSnX 2 (X=S, Se, Te). Before that, we need to calculate the relaxation time of the carriers of the material, because the result calculated by BoltzTraP-package needs to be multiplied by the relaxation time. Here, carrier mobilities and relaxation time of 2D materials are calculated using deformation potential theory[45,46,47]:
μ 2 D = e ℏ 3 C 2 D k B T | m * | 2 E 1 2
τ = ℏ 3 C 2 D k B T m * E 1 2
where μ 2 D is the carrier mobility, C 2 D is the elastic constant, m * is the effective mass, m d is the average effective mass, E 1 is the deformation potential energy, and τ is the relaxation time.
Table 3 shows the results of the electric and hole carrier mobilities calculated with the theory of deformation potential at 300 K. Among them, γ -PbSnS 2 and γ -PbSnSe 2 have ultra-high hole carrier mobility, especially, γ -PbSnS 2 has the highest hole mobility of 4.04×10 3 cm 2 V − 1 s − 1 , which is significantly higher than that of other two-dimensional semiconductors, such as MoS 2 ( 285 cm 2 V − 1 s − 1 )[48], SnS 2 ( 756 cm 2 V − 1 s − 1 )[49], SnSe 2 ( 462 cm 2 V − 1 s − 1 )[49], γ -PbX 2 ( 780 cm 2 V − 1 s − 1 ) [36] and γ -SnX 2 ( 1364 cm 2 V − 1 s − 1 )[35]. Such high carrier mobility of γ -PbSnS 2 and γ -PbSnSe 2 is due to a combination of low effective mass and deformation potential energy. The high hole carrier mobility indicates that γ -PbSnS 2 and γ -PbSnSe 2 are potential p-type semiconductors. In addition, Hung et al. showed that high carrier mobility is one of the important parameters for screening thermoelectric materials[50,51]. Such ultra-high carrier mobility indicates that γ -PbSnX 2 possesses excellent hole transport properties and thus are good thermoelectric materials.

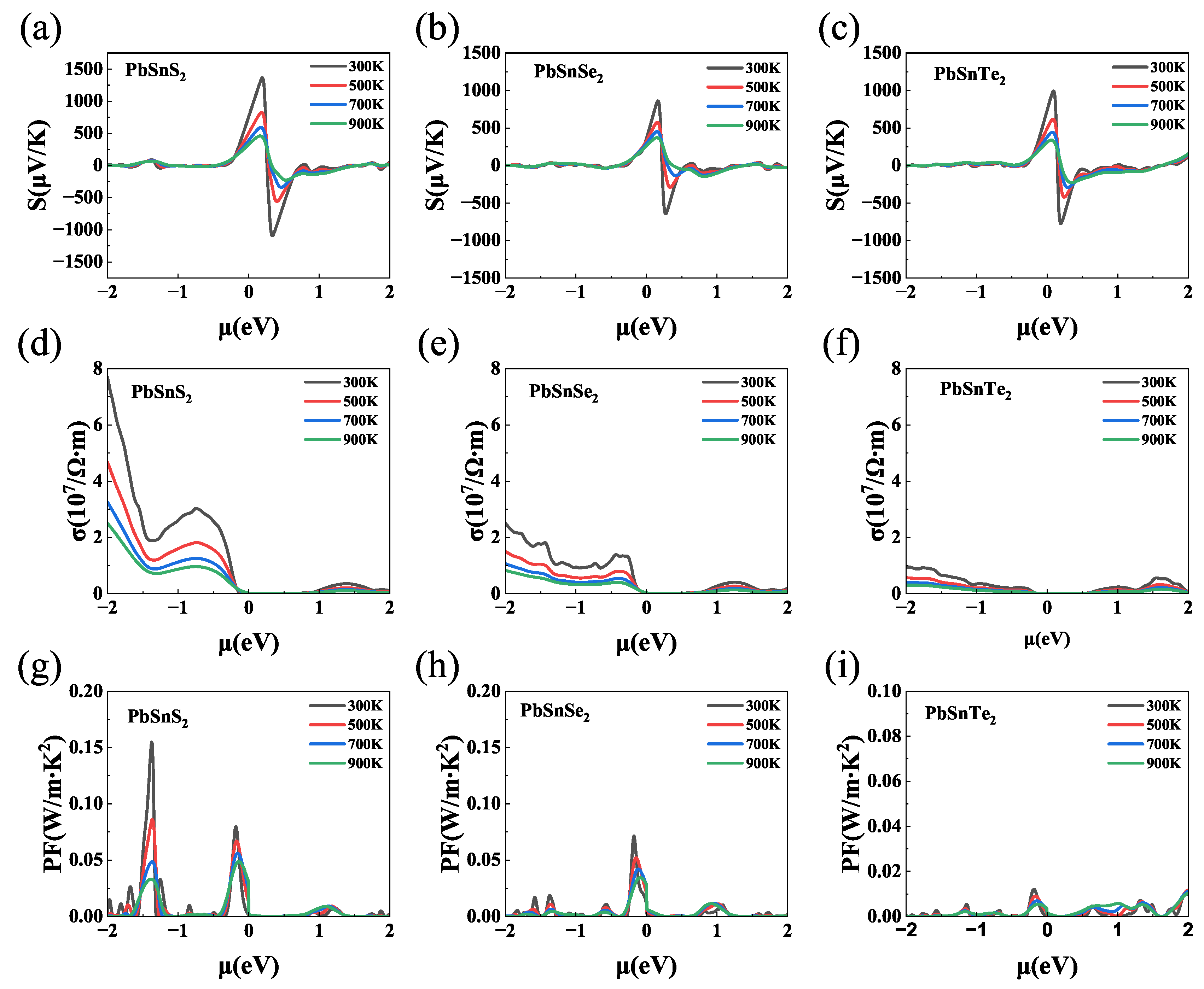
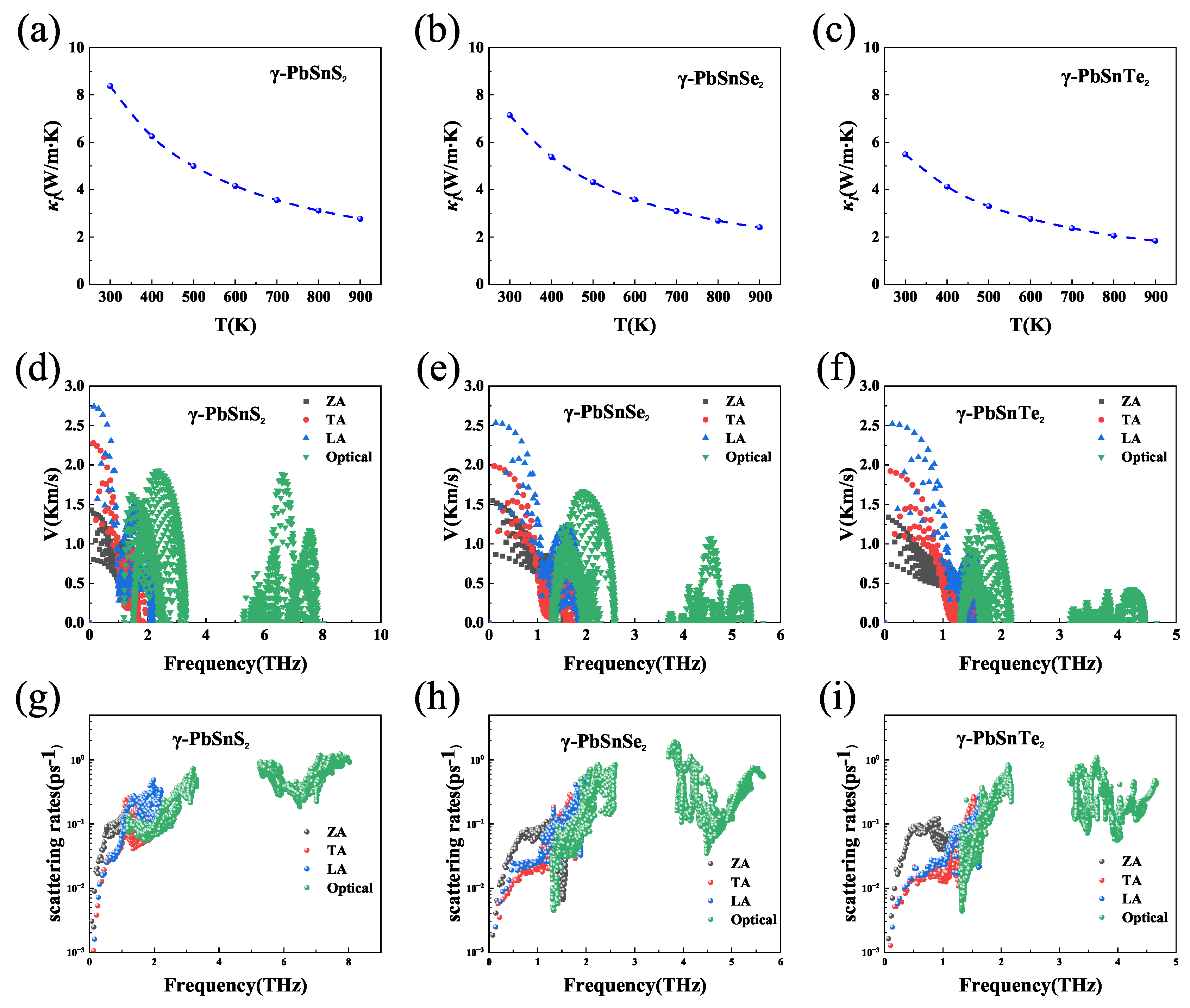
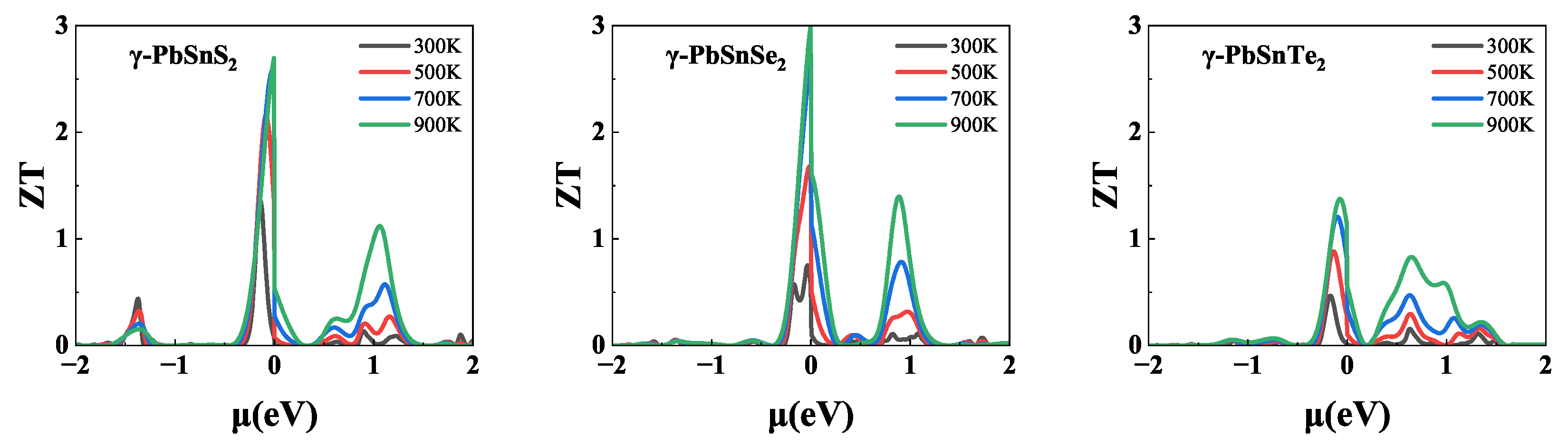
3.4. Thermoelectric properties

We investigated the thermoelectric properties of the materials in the temperature range of 300 K to 900 K. As shown in Figure 4(a-c), all three materials have a high Seebeck coefficient at 300 K. Among them, the Seebeck coefficient of γ -PbSnS 2 , γ -PbSnSe 2 and γ -PbSnTe 2 are 1400 μ V/K, 800 μ V/K and 900 μ V/K , respectively, which is much higher than that of most common 2D materials, such as SnTe (600 μ V/K) [52], MoSe 2 (427 μ V/K)[53] and WS 2 (328 μ V/K)[54]. The Seebeck coefficient of γ -PbSnS 2 is higher than γ -PbSnSe 2 and γ -PbSnTe 2 . This is because γ -PbSnS 2 has a higher density of states peak than γ -PbSnSe 2 and γ -PbSnTe 2 near the Fermi energy level (as shown in Figure 3), and the Seebeck coefficient is proportional to the density of states peak: S ∝ d ( D O S ) / d E . The high density of states peak near the Fermi energy level indicates that the material will have a higher Seebeck coefficient. Such a high Seebeck coefficient indicating that these materials may have high thermoelectric properties.
Figure 4(d-f) shows the electrical conductivities σ obtained by multiplying σ / τ by τ , where σ / τ is calculated using BoltzTraP-package and τ is the relaxation time calculated by the deformation potential theory. The electrical conductivity of γ -PbSnX 2 (X=S, Se, Te) exhibits similar behavior at different temperatures and decreases as the temperature increases. This is caused by the enhanced lattice vibrations and electron scattering at high temperature. The electric conductivity of γ -PbSnX 2 gradually decrease as the atomic number of the substituted chalcogenide element (S, Se, and Te) increases. And the value of the conductivity is related to the chemical potential. The conductivity of γ -PbSnX 2 is higher in the negative chemical potential range, which shows the characteristics of P-type semiconductors. It’s worth noting that the electrical conductivity of γ -PbSnX 2 reached the same order (10 6 -10 7 / Ω m) as that of metals due to its ultra-high carrier mobility. The high Seebeck coefficient and conductivity indicate that they have a high power-factor ( P F = S 2 σ ), which is important for thermoelectric devices. With the Seebeck coefficient and electrical conductivity, we evaluate the power factor ( P F ) of γ -PbSnX 2 (X=S, Se, Te), as show in Figure 4(g-i). All three materials have the same trend of power factor, which decreases with the increase of temperature. The γ -PbSnS 2 has the highest P F because of its highest Seebeck coefficient and electrical conductivity. And the P F values of these materials are maximum in the negative is due to their p-type properties. The P F is one of the important factors in evaluating the performance of thermoelectric materials, so a high P F predicts that the material may have high thermoelectric properties.
Materials with high thermoelectric properties require low thermal conductivity in addition to high power-factor. Figure 5 shows the phonon transport properties of γ -PbSnX 2 (X=S, Se, Te), the results show that both γ -PbSnX 2 have a very low thermal conductivity, which is about 6-8 W/mK at room temperature and the value of lattice thermal conductivity decreasing with the increasing of temperature. In order to understand the lattice thermal conductivity of the monolayer γ -PbSnX 2 , we explore the phonon-related properties such as phonon group velocity and anharmonic scattering rates. As shown in Figure 5(a-c), the three acoustic phonon branches (ZA/TA/LA) get entangled and strong coupling occurs between the optical and acoustic phonon modes, which can strengthen the phonon scattering mechanism and thus lower κ l . Figure 5(d-f) shows the phonon group velocities of γ -PbSnX 2 , and it can be seen that they are both low, and low group velocities can lead to low lattice thermal conductivity. The inverse of the phonon relaxation time in the relaxation time approximation (RTA) is equal to the total scattering rate, which is the sum of the isotopic scattering rate ( τ i 1 ), the boundary scattering rate ( τ b 1 ) and the anharmonic scattering rate ( τ a 1 ). In general, higher indicates stronger phonon-phonon scattering and lower phonon relaxation time, which is beneficial for reducing the lattice thermal conductivity. As shown in Figure 5(g-i), the γ -PbSnX 2 monolayer exhibits high phonon-phonon scattering rates (anharmonic scattering rates) and they are relatively close to each other. In addition, the value of the lattice thermal conductivity increases with the atomic number of the elements (S, Se, Te), which is mainly due to the increase of the atomic mass and the decrease of the phonon frequency. In conclusion, the strong coupling between phonons, lower phonon group velocities and higher scattering rates lead to lower lattice thermal conductivity, indicating that γ -PbSnX 2 may be suitable thermoelectric performance materials.
After all transport coefficients were obtained, the dependence of Z T on the chemical potential of γ -PbSnX 2 monolayer at different temperatures was calculated, as shown in Figure 6. All of γ -PbSnX 2 exhibited the maximum thermoelectric properties in the negative chemical potential range due to their higher hole mobility. The Z T values for all three materials showed the same trend, increasing with increasing temperature. Among them, the Z T value of γ -PbSnTe 2 is lower, reaching a maximum of only 1.4 at 900 K, which is due to its low power factor. And, γ -PbSnS 2 and γ -PbSnSe 2 reached ultra-high Z T values of 2.65 and 2.96 at 900 K due to a combination of their low lattice thermal conductivity and high power-factor. Such ultra-high Z T values of γ -PbSnX 2 are contributed to their low thermal conductivity along with their high power-factor. Such high Z T values indicates that γ -PbSnS 2 and γ -PbSnSe 2 are good performing high temperature thermoelectric materials.

4. Conclusions

In this study, we constructed a series of 2D monolayer material γ -PbSnX 2 (X = S, Se, Te) based on γ -(AX) 2 (A=Sn,Pb and X=S,Se,Te) and calculated its thermoelectric properties using Boltzmann transport theory combined with first-principles. The results show that these materials are narrow bandgap semiconductors with bandgap values of 0.98-1.37 eV by HSE06 functional. They have high hole carrier mobilities, in particular, γ -PbSnS 2 has a hole carrier mobility of 4.04×10 3 cm 2 V − 1 s − 1 . And they both have low lattice thermal conductivity and high power-factors. The ZT values of γ -PbSnS 2 , γ -PbSnSe 2 and γ -PbSnTe 2 at 900K were 2.65, 2.96 and 1.36, respectively. Such high thermoelectric performance indicates that γ -PbSnX 2 are excellent thermoelectric materials. Our theoretical study may help to discover a new stage to experimentally optimize the thermoelectric properties.

Author Contributions

Conceptualization,D.C. and D.Z.; methodology, D.C.; software, D.C. and D.Z.; validation, L.N, Z.J., T.L., R.W. and C.K.; formal analysis, X.X.; investigation, D.C. and D.Z.; resources, C.K.; data curation, D.C.; writing—original draft preparation,D.C.; writing—review and editing, C.K.; project administration, C.K.; funding acquisition, C.K. and R.W. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 11974106 and 12204163) and the Natural Science Foundation of Hunan Province of China (Grant No. 2022JJ40032). Numerical computations were performed at the National Supercomputer Center in Changsha.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
  2. Yang, L.; Chen, Z.G.; Dargusch, M.S.; Zou, J. High Performance Thermoelectric Materials: Progress and Their Applications. Advanced Energy Materials 2018, 8, 1701797. [Google Scholar] [CrossRef]
  3. Huang, H.H.; Fan, X.; Singh, D.J.; Zheng, W.T. Thermoelectric properties of monolayer GeAsSe and SnSbTe. Journal of Materials Chemistry C 2020, 8, 9763–9774. [Google Scholar] [CrossRef]
  4. Wu, D.; Cao, X.H.; Chen, S.Z.; Tang, L.M.; Feng, Y.X.; Chen, K.Q.; Zhou, W.X. Pure spin current generated in thermally driven molecular magnetic junctions: a promising mechanism for thermoelectric conversion. Journal of Materials Chemistry A 2019, 7, 19037–19044. [Google Scholar] [CrossRef]
  5. Jonson, M.; Mahan, G.D. Mott’s formula for the thermopower and the Wiedemann-Franz law. Physical Review B 1980, 21, 4223–4229. [Google Scholar] [CrossRef]
  6. Ding, Z.K.; Zeng, Y.J.; Pan, H.; Luo, N.; Zeng, J.; Tang, L.M.; Chen, K.Q. Edge states of topological acoustic phonons in graphene zigzag nanoribbons. Physical Review B 2022, 106, L121401. [Google Scholar] [CrossRef]
  7. Pan, H.; Ding, Z.K.; Zeng, B.W.; Luo, N.N.; Zeng, J.; Tang, L.M.; Chen, K.Q. Ab initio Boltzmann approach to coupled magnon-phonon thermal transport in ferromagnetic crystals. Physical Review B 2023, 107, 104303. [Google Scholar] [CrossRef]
  8. Pan, H.; Ding, Z.K.; Zeng, Y.J.; Li, Q.Q.; Tang, L.M.; Chen, K.Q. Tuning quantum heat transport in magnetic nanostructures by spin-phonon interaction. Europhysics Letters 2022, 138, 36001. [Google Scholar] [CrossRef]
  9. Pan, H.; Tang, L.M.; Chen, K.Q. Quantum mechanical modeling of magnon-phonon scattering heat transport across three-dimensional ferromagnetic/nonmagnetic interfaces. Physical Review B 2022, 105, 064401. [Google Scholar] [CrossRef]
  10. Zeng, B.; Ding, Z.K.; Pan, H.; Luo, N.; Zeng, J.; Tang, L.M.; Chen, K.Q. Strong strain-dependent phonon hydrodynamic window in bilayer graphene. Applied Physics Letters 2022, 121, 252202. [Google Scholar] [CrossRef]
  11. Zeng, Y.J.; Ding, Z.K.; Pan, H.; Feng, Y.X.; Chen, K.Q. Nonequilibrium Green’s function method for phonon heat transport in quantum system. Journal of Physics: Condensed Matter 2022, 34, 223001. [Google Scholar] [CrossRef]
  12. Zeng, Y.J.; Wu, D.; Cao, X.H.; Zhou, W.X.; Tang, L.M.; Chen, K.Q. Nanoscale Organic Thermoelectric Materials: Measurement, Theoretical Models, and Optimization Strategies. Advanced Functional Materials 2020, 30, 1903873. [Google Scholar] [CrossRef]
  13. Guo, S.D. Biaxial strain tuned thermoelectric properties in monolayer PtSe2. Journal of Materials Chemistry C 2016, 4, 9366–9374. [Google Scholar] [CrossRef]
  14. Lin, C.M.; Chen, W.C.; Chen, C.C. First-principles study of strain effect on the thermoelectric properties of LaP and LaAs. Physical Chemistry Chemical Physics 2021, 23, 18189–18196. [Google Scholar] [CrossRef] [PubMed]
  15. Miao, T.; Yu, D.; Xing, L.; Li, D.; Jiao, L.; Ma, W.; Zhang, X. Current Rectification in a Structure: ReSe2/Au Contacts on Both Sides of ReSe2. Nanoscale Research Letters 2019, 14, 1. [Google Scholar] [CrossRef] [PubMed]
  16. Wu, C.W.; Ren, X.; Xie, G.; Zhou, W.X.; Zhang, G.; Chen, K.Q. Enhanced High-Temperature Thermoelectric Performance by Strain Engineering in BiOCl. Physical Review Applied 2022, 18, 014053. [Google Scholar] [CrossRef]
  17. Wu, Y.; Chen, Z.; Nan, P.; Xiong, F.; Lin, S.; Zhang, X.; Chen, Y.; Chen, L.; Ge, B.; Pei, Y. Lattice Strain Advances Thermoelectrics. Joule 2019, 3, 1276–1288. [Google Scholar] [CrossRef]
  18. Zhou, W.X.; Wu, D.; Xie, G.; Chen, K.Q.; Zhang, G. α-Ag2S: A Ductile Thermoelectric Material with High ZT. ACS Omega 2020, 5, 5796–5804. [Google Scholar] [CrossRef]
  19. Gu, B.C.; Li, Z.; Liu, J.D.; Zhang, H.J.; Ye, B.J. Effect of vacancies on thermoelectric properties of β-CuAgSe studied by positron annihilation. Applied Physics Letters 2019, 115, 192106. [Google Scholar] [CrossRef]
  20. Han, D.; Yang, X.; Du, M.; Xin, G.; Zhang, J.; Wang, X.; Cheng, L. Improved thermoelectric properties of WS2–WSe2 phononic crystals: insights from first-principles calculations. Nanoscale 2021, 13, 7176–7192. [Google Scholar] [CrossRef]
  21. Xie, Z.X.; Chen, X.K.; Yu, X.; Deng, Y.X.; Zhang, Y.; Zhou, W.X.; Jia, P.Z. Intrinsic thermoelectric properties in biphenylene nanoribbons and effect of lattice defects. Computational Materials Science 2023, 220, 112041. [Google Scholar] [CrossRef]
  22. Cao, X.H.; Wu, D.; Feng, Y.X.; Zhou, W.X.; Tang, L.M.; Chen, K.Q. Effect of electrophilic substitution and destructive quantum interference on the thermoelectric performance in molecular devices. Journal of Physics: Condensed Matter 2019, 31, 345303. [Google Scholar] [CrossRef] [PubMed]
  23. Deng, Y.X.; Chen, S.Z.; Hong, J.; Jia, P.Z.; Zhang, Y.; Yu, X.; Chen, K.Q. Perfect spin-filtering effect in molecular junctions based on half-metallic penta-hexa-graphene nanoribbons. Journal of Physics: Condensed Matter 2022, 34, 285302. [Google Scholar] [CrossRef] [PubMed]
  24. Zeng, Y.J.; Wu, D.; Cao, X.H.; Feng, Y.X.; Tang, L.M.; Chen, K.Q. Significantly enhanced thermoelectric performance of molecular junctions by the twist angle dependent phonon interference effect. Journal of Materials Chemistry A 2020, 8, 11884–11891. [Google Scholar] [CrossRef]
  25. Gibson, Q.D.; Zhao, T.; Daniels, L.M.; Walker, H.C.; Daou, R.; Hebert, S.; Zanella, M.; Dyer, M.S.; Claridge, J.B.; Slater, B.; et al. Low thermal conductivity in a modular inorganic material with bonding anisotropy and mismatch. Science 2021, 373, 1017–1022. [Google Scholar] [CrossRef] [PubMed]
  26. Wang, J.; Cao, X.H.; Zeng, Y.J.; Luo, N.N.; Tang, L.M.; Chen, K.Q. Excellent thermoelectric properties of monolayer MoS2-MoSe2 aperiodic superlattices. Applied Surface Science 2023, 612, 155914. [Google Scholar] [CrossRef]
  27. Xie, Z.X.; Zhang, Y.; Yu, X.; Li, K.M.; Chen, Q. Ballistic thermal conductance by phonons through superlattice quantum-waveguides. Journal of Applied Physics 2014, 115, 104309. [Google Scholar] [CrossRef]
  28. Jia, P.Z.; Xie, J.P.; Chen, X.K.; Zhang, Y.; Yu, X.; Zeng, Y.J.; Xie, Z.X.; Deng, Y.X.; Zhou, W.X. Recent progress of two-dimensional heterostructures for thermoelectric applications. Journal of Physics: Condensed Matter 2023, 35, 073001. [Google Scholar] [CrossRef]
  29. Jia, P.Z.; Zeng, Y.J.; Wu, D.; Pan, H.; Cao, X.H.; Zhou, W.X.; Xie, Z.X.; Zhang, J.X.; Chen, K.Q. Excellent thermoelectric performance induced by interface effect in MoS2/MoSe2 van der Waals heterostructure. Journal of Physics: Condensed Matter 2020, 32, 055302. [Google Scholar] [CrossRef]
  30. Hicks, L.D.; Dresselhaus, M.S. Thermoelectric figure of merit of a one-dimensional conductor. Physical Review B 1993, 47, 16631–16634. [Google Scholar] [CrossRef]
  31. Shafique, A.; Shin, Y.H. Thermoelectric and phonon transport properties of two-dimensional IV–VI compounds. Scientific Reports 2017, 7, 506. [Google Scholar] [CrossRef]
  32. Gupta, R.; Kakkar, S.; Dongre, B.; Carrete, J.; Bera, C. Enhancement in the Thermoelectric Performance of SnS Monolayer by Strain Engineering. ACS Applied Energy Materials 2023, 6, 3944–3952. [Google Scholar] [CrossRef]
  33. Lu, A.Y.; Zhu, H.; Xiao, J.; Chuu, C.P.; Han, Y.; Chiu, M.H.; Cheng, C.C.; Yang, C.W.; Wei, K.H.; Yang, Y.; et al. Janus monolayers of transition metal dichalcogenides. Nature Nanotechnology 2017, 12, 744–749. [Google Scholar] [CrossRef] [PubMed]
  34. Sa, B.; Sun, Z.; Wu, B. The development of two dimensional group IV chalcogenides, blocks for van der Waals heterostructures. Nanoscale 2016, 8, 1169–1178. [Google Scholar] [CrossRef] [PubMed]
  35. Dong, B.; Wang, Z.; Hung, N.T.; Oganov, A.R.; Yang, T.; Saito, R.; Zhang, Z. New two-dimensional phase of tin chalcogenides: Candidates for high-performance thermoelectric materials. Physical Review Materials 2019, 3, 013405. [Google Scholar] [CrossRef]
  36. Jia, P.Z.; Xie, Z.X.; Deng, Y.X.; Zhang, Y.; Tang, L.M.; Zhou, W.X.; Chen, K.Q. High thermoelectric performance induced by strong anharmonic effects in monolayer (PbX)2 (X = S, Se, Te). Applied Physics Letters 2022, 121, 043901. [Google Scholar] [CrossRef]
  37. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  38. Stratmann, R.E.; Scuseria, G.E.; Frisch, M.J. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules. The Journal of Chemical Physics 1998, 109, 8218–8224. [Google Scholar] [CrossRef]
  39. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Physical Review Letters 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  40. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Physical Review B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  41. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Physical Review B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  42. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. Journal of Computational Chemistry 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
  43. Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Computer Physics Communications 2006, 175, 67–71. [Google Scholar] [CrossRef]
  44. Li, W.; Carrete, J.; A. Katcho, N.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Computer Physics Communications 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
  45. Bruzzone, S.; Fiori, G. Ab-initio simulations of deformation potentials and electron mobility in chemically modified graphene and two-dimensional hexagonal boron-nitride. Applied Physics Letters 2011, 99, 222108. [Google Scholar] [CrossRef]
  46. Fiori, G.; Iannaccone, G. Multiscale Modeling for Graphene-Based Nanoscale Transistors. Proceedings of the IEEE 2013, 101, 1653–1669. [Google Scholar] [CrossRef]
  47. Lang, H.; Zhang, S.; Liu, Z. Mobility anisotropy of two-dimensional semiconductors. Physical Review B 2016, 94, 235306. [Google Scholar] [CrossRef]
  48. Rawat, A.; Jena, N.; Dimple. ; De Sarkar, A. A comprehensive study on carrier mobility and artificial photosynthetic properties in group VI B transition metal dichalcogenide monolayers. Journal of Materials Chemistry A 2018, 6, 8693–8704. [Google Scholar] [CrossRef]
  49. Shafique, A.; Samad, A.; Shin, Y.H. Ultra low lattice thermal conductivity and high carrier mobility of monolayer SnS2 and SnSe2: a first principles study. Physical Chemistry Chemical Physics 2017, 19, 20677–20683. [Google Scholar] [CrossRef]
  50. Hung, N.T.; Hasdeo, E.H.; Nugraha, A.R.; Dresselhaus, M.S.; Saito, R. Quantum Effects in the Thermoelectric Power Factor of Low-Dimensional Semiconductors. Physical Review Letters 2016, 117, 036602. [Google Scholar] [CrossRef]
  51. Hung, N.T.; Nugraha, A.R.T.; Yang, T.; Saito, R. Confinement Effect in Thermoelectric Properties of Two–Dimensional Materials. MRS Advances 2020, 5, 469–479. [Google Scholar] [CrossRef]
  52. Li, Y.; Wu, M.N.; Ding, T.; Ma, K.; Liu, F.S.; Ao, W.Q.; Li, J.Q. Promising thermoelectric properties and anisotropic electrical and thermal transport of monolayer SnTe 2019. 114 083901. [CrossRef]
  53. Kumar, S.; Schwingenschlögl, U. Thermoelectric Response of Bulk and Monolayer MoSe2 and WSe2. Chemistry of Materials 2015, 27, 1278–1284. [Google Scholar] [CrossRef]
  54. Patel, A.; Singh, D.; Sonvane, Y.; Thakor, P.B.; Ahuja, R. High Thermoelectric Performance in Two-Dimensional Janus Monolayer Material WS-X (X = Se and Te). ACS Applied Materials & Interfaces 2020, 12, 46212–46219. [Google Scholar] [CrossRef]
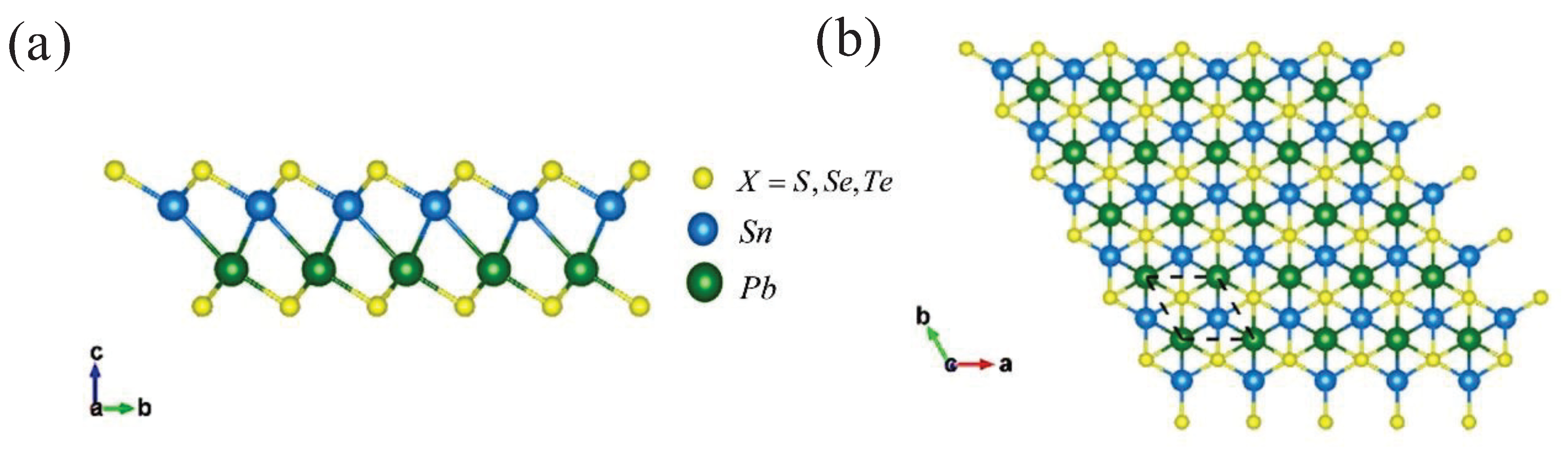
Preprints 71149 g001
Figure 1. a Side view and a top view of the optimized γ -PbSnX 2 (X=S, Se, Te) monolayer structure
Figure 1. a Side view and a top view of the optimized γ -PbSnX 2 (X=S, Se, Te) monolayer structure
Preprints 71149 g001
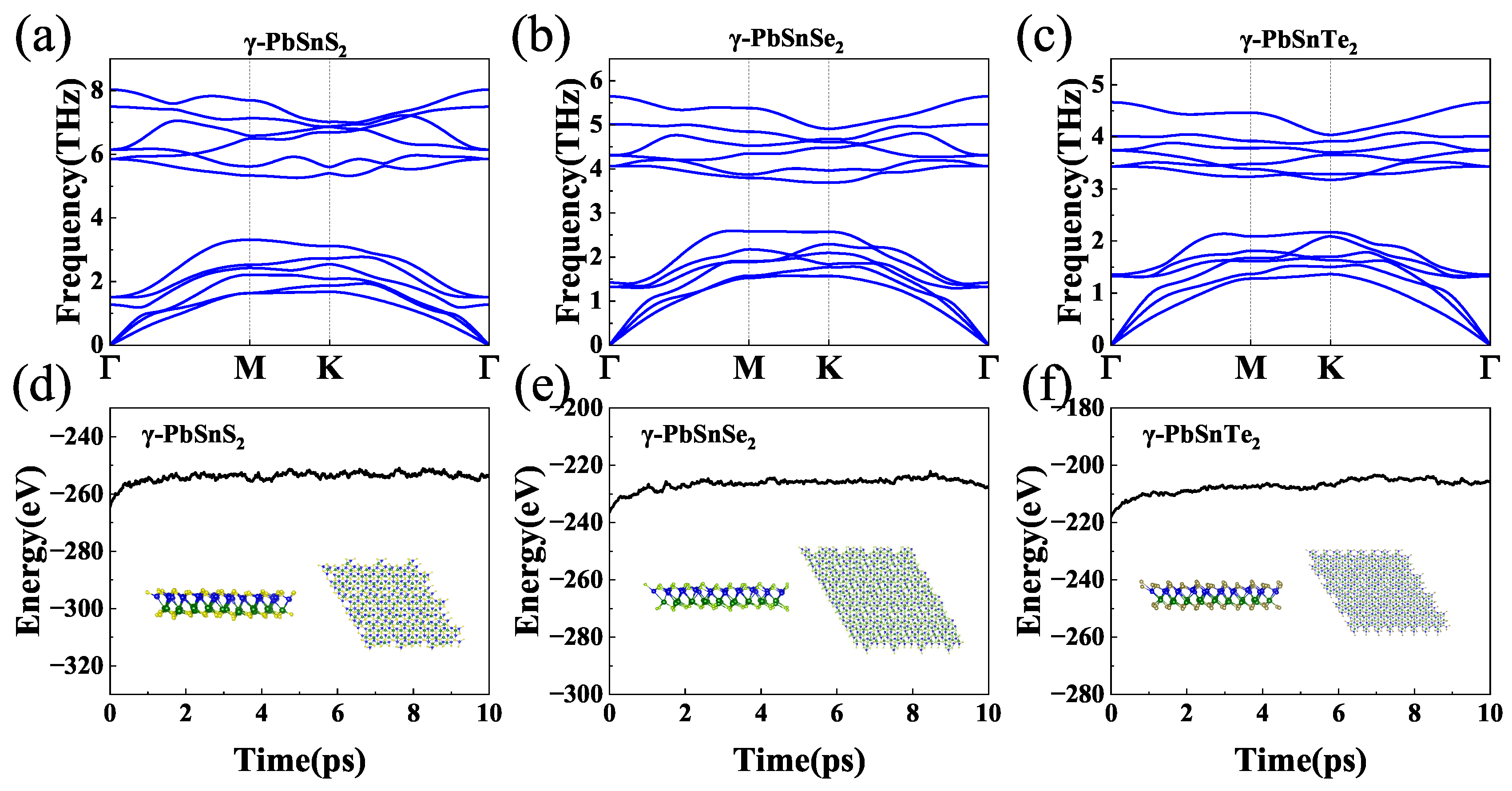
Preprints 71149 g002
Figure 2. a-c Phonon dispersions for γ -PbSnX 2 (X=S, Se, Te). d-f Total potential energy fluctuation and structures in AIMD simulations of γ -PbSnX 2 (X=S, Se, Te)
Figure 2. a-c Phonon dispersions for γ -PbSnX 2 (X=S, Se, Te). d-f Total potential energy fluctuation and structures in AIMD simulations of γ -PbSnX 2 (X=S, Se, Te)
Preprints 71149 g002
Preprints 71149 g003
Figure 3. (a-c)Band structures of γ -PbSnX 2 (X=S, Se, Te) calculated by PBE and HSE06 functionals, respectively. (d-f) Partial density of states (PDOS) of the γ -PbSnX 2 . The Fermi level was set as zero.
Figure 3. (a-c)Band structures of γ -PbSnX 2 (X=S, Se, Te) calculated by PBE and HSE06 functionals, respectively. (d-f) Partial density of states (PDOS) of the γ -PbSnX 2 . The Fermi level was set as zero.
Preprints 71149 g003
Preprints 71149 g004
Figure 4. (a-c) Seebeck coefficients, (d-f) electrical conductivity and (g-i) Power-factor ( P F ) of γ -PbSnX 2 (X=S, Se, Te).
Figure 4. (a-c) Seebeck coefficients, (d-f) electrical conductivity and (g-i) Power-factor ( P F ) of γ -PbSnX 2 (X=S, Se, Te).
Preprints 71149 g004
Preprints 71149 g005
Figure 5. (a-c) Lattice thermal conductivity at different temperatures, (d-f) phonon group velocity at 300 K and (g-i) anharmonic scattering rates at 300 K of γ -PbSnX 2 (X=S, Se, Te).
Figure 5. (a-c) Lattice thermal conductivity at different temperatures, (d-f) phonon group velocity at 300 K and (g-i) anharmonic scattering rates at 300 K of γ -PbSnX 2 (X=S, Se, Te).
Preprints 71149 g005
Preprints 71149 g006
Figure 6. (a-c) Lattice thermal conductivity at different temperatures, (d-f) phonon group velocity at 300 K and (g-i) anharmonic scattering rates at 300 K of γ -PbSnX 2 (X=S, Se, Te).
Figure 6. (a-c) Lattice thermal conductivity at different temperatures, (d-f) phonon group velocity at 300 K and (g-i) anharmonic scattering rates at 300 K of γ -PbSnX 2 (X=S, Se, Te).
Preprints 71149 g006
Table 1. Structural parameters for the γ -PbSnX 2 (X=S, Se, Te). Here a is the lattice constant, d S n − X , d P b − X and d P b − S n are the Sn-X, Pb-X and Pb-Sn bond lengths, and h is the vertical distance between the two outermost X atoms in Angstroms, as shown in Figure 1.
Table 1. Structural parameters for the γ -PbSnX 2 (X=S, Se, Te). Here a is the lattice constant, d S n − X , d P b − X and d P b − S n are the Sn-X, Pb-X and Pb-Sn bond lengths, and h is the vertical distance between the two outermost X atoms in Angstroms, as shown in Figure 1.
Material a (Å) d S n − X (Å) d P b − X (Å) d P b − S n (Å) h (Å) α = β γ
PbSnS 2 3.96 2.64 2.68 3.58 5.49 90° 120°
PbSnSe 2 4.11 2.77 2.81 3.51 5.52 90° 120°
PbSnTe 2 4.37 2.97 3.01 3.46 5.59 90° 120°
Table 2. Bandgap of γ -PbSnX 2 (X=S, Se, Te) calculated by PBE and HSE06.
Table 2. Bandgap of γ -PbSnX 2 (X=S, Se, Te) calculated by PBE and HSE06.
Material Structure Gap-type E g (PBE) E g (HSE06)
PbSnS 2 hexagonal (2D) Indirect 0.86 eV 1.37 eV
PbSnSe 2 hexagonal (2D) Indirect 0.63 eV 1.08 eV
PbSnTe 2 hexagonal (2D) Indirect 0.61 eV 0.98 eV
Table 3. Calculated effective mass ( m * ), elastic constant ( C 2 D ), deformation potential ( E 1 ), carrier mobility ( μ 2 D ) and relaxation time ( τ ) for electrons (e) and holes (h) in monolayer γ -PbSnX 2 at 300 K.
Table 3. Calculated effective mass ( m * ), elastic constant ( C 2 D ), deformation potential ( E 1 ), carrier mobility ( μ 2 D ) and relaxation time ( τ ) for electrons (e) and holes (h) in monolayer γ -PbSnX 2 at 300 K.
Material Carrier C 2 D (N/m) m * / m 0 E 1 (eV) μ 2 D (×10 3 cm 2 V − 1 s − 1 ) τ (ps)
PbSnS 2 e 39.5 0.22 4.92 0.476 0.059
h 0.50 1.02 4.04 1.14
PbSnSe 2 e 42.75 0.18 5.52 0.654 0.067
h 0.357 2.66 1.421 0.288
PbSnTe 2 e 43.55 0.23 6.52 0.256 0.033
h 0.596 4.14 0.245 0.083
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated