Prerpints.org logo
Preprint
Article

Study on the Influence of Underwater LED Illumination on Bidirectional Underwater Wireless Optical Communication

Altmetrics

Downloads

182

Views

50

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 April 2023

Posted:

17 April 2023

You are already at the latest version

Alerts
Abstract
Underwater wireless optical communication (UWOC) is acknowledged as a useful way to transmit data in ocean for short distance application. Carrying UWOC device on mobile platform is quite practical in ocean engineering, which is helpful to exploit its advantages. In application, such platform needs camera to observe surroundings and guide its action. Since the majority of ocean is always dark, active illumination is necessary to imaging. Once UWOC worked in such environment, its performance is affected by the illumination light noise. In this paper, we study the influence of underwater LED illumination on bidirectional UWOC with Monte Carlo method. We simulate forward noise from the LED illumination to the opposite receiver in the cooperative terminal, and the backscattering noise on the adjacent receiver in the same terminal. The results show that the forward noise is reduced with the increase of absorption coefficient, scattering coefficient, transmitting distance, and separated distance between receiver and the optical axis of LED. But it becomes greater with FOV of receiver. The backscattering noise is reduced with the increase of absorption coefficient and separated distance between receiver and LED. But it becomes greater with FOV and scattering coefficient, while it has little relation with transmitting distance. In order to reduce such two kind noises, besides inserting optical filter in the receivers and narrow their field, the optical axis of LED light should keep away from the receivers. The results in this paper is helpful for UWOC application.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

Underwater wireless optical communication (UWOC) is a useful way to transmit data for short distance application in ocean, thanks to its high transmission speed [1,2,3]. Recently, many researches focus on such topic, which are mainly about high communication rate [4,5,6,7] and high receiving sensitivity [8,9,10,11]. Meanwhile, several sea trials have demonstrated its potential application prospect [12,13,14,15,16,17,18,19]. From 2008 to 2014, Woods Hole Oceanographic Institution (WHOI) demonstrated the value of this technology in deep sea with up to 10Mbps speed, more than 100m distance and more than 2000m depth. In these trails, UWOC devices were usually carried on mobile platforms, such as human occupied vehicle (HOV), remote operated vehicle (ROV) and autonomous underwater vehicle (AUV). Using the same technical scheme, commercial UWOC product has been applied in ocean engineering with up to 10Mbps rate [17,18]. Also, in 2017 Japan Agency for Marine-Earth Science and Technology (JAMSTEC) demonstrated 20Mbps speed with 120m distance in dark clear water. In the system, UWOC device was carried on ROV.
These sea trials show that, a most practical application for UWOC is carrying the devices on mobile platform, which is helpful to exploit its advantages. However, while such platform works in ocean, it usually needs camera to observe surroundings and guide its action. Because the majority of ocean is always dark [20], active illumination is necessary to imaging. If UWOC worked in such environment, the illumination light affects its performance, even makes the communication unworkable. It is necessary to study the influence of light illumination on UWOC. As underwater light emitting diode (LED) is usually applied to illumination, in this work, we analyze the influence of such light on bidirectional UWOC with Monte Carlo method.
The organization of this paper is as follows: Section 2 set up a theoretical model to study light noise with Monte Carlo method. Section 3 demonstrates the simulation results. Section 4 makes a conclusion.

2. Theoretical Model

The simulation model shows in Figure 1. It has two identical terminals with transmitting distance S. Each terminal has an underwater LED and a UWOC receiver. The diameter of luminous surface for LEDs are both D. The diameter of UWOC receivers are both d. The separated distance between UWOC receiver and LED is L in each terminal. That means the interval of receivers to the center of LED illumination is L. When the LEDs and UWOC work simultaneously, because there is scattering in water, the illumination would arrive both the two receivers. For example, light from “LED 1#” in Figure 1 affects “Receiver 1#” and “Receiver 2#” simultaneously.
We simulated such influence with Monte Carlo method. This method is quite popular to study underwater optical channel [21]. It is based on the fact that light is made up of lots of photons. By tracing the photons’ path one by one and counting their characteristic, the light feature could be obtained.
For simplicity, we study the influence of light from “LED 1#” on “Receiver 1#” and “Receiver 2#”. As shown in Figure 2, supposing luminous surface of “LED 1#” is uniform and round with diameter D. We establish coordinate system with the center of “LED 1#”. Photons’ position and direction cosine are expressed as follow.
x 0 = ρ × cos α = D 2 × r a n d r × cos 360 ∘ × r a n d J y 0 = ρ × sin α = D 2 × r a n d r × sin 360 ∘ × r a n d J z 0 = 0                                    
μ x 0 = sin φ 0 sin θ 0 = sin 360 ∘ × r a n d φ × sin θ 0 μ y 0 = cos φ 0 sin θ 0 = cos 360 ∘ × r a n d φ × sin θ 0 μ z 0 = cos θ 0                              
Here (ρ, α) is the polar coordinate for photon position in the plane z=0. θ0 and φ0 are elevation angle and azimuth angle for the starting direction. randr, randJ, and randφ are random numbers, which follows uniform distribution in range of 0 and 1. Random number could be produced by computer, which will appear in several places below in the model.
The light intensity of LED is usually Lambert distribution. Its radiation intensity with elevation angle could be expressed as follow.
I ( θ 0 ) = I 0 cos θ 0
Where I(θ0) is intensity at θ0. I0 is the intensity at θ0=0. Also, it could be understood as photon probability density at θ0 is cosθ0. For an arbitrary θ0 we have the following relation.
∫ 0 θ 0 cos ξ d ξ = sin θ 0 = r a n d θ
Here randθ is random numbers. Therefore, θ0 could be expressed as follow.
θ 0 = arcsin r a n d θ
Once photon left “LED 1#”, it will transmit in water straightly until arriving at scattering particle. The free path s is
s = − 1 c ln r a n d s = − 1 a + b ln r a n d s
Here a, b, c are absorption coefficient, scattering coefficient and attenuation coefficient of water respectively. rands is random number. Then, the new position (x, y, z) for photon is
x = x 0 + μ x 0 s y = y 0 + μ y 0 s z = z 0 + μ z 0 s
Once z≤S and z≥0, photon would be absorbed or scattered in water, which is determined with the method of “Russian roulette”. That means we firstly should define a threshold WH as follow.
W H = b c
Then, we produce a random number randW from computer. If randW > WH, photon is absorbed. We stop the tracing process. Otherwise, it is scattered. The new direction (μx, μy, μz) of which is as follow.
μ x = sin θ 1 − μ z 0 2 μ x 0 μ z 0 cos φ − μ y 0 sin φ + μ x 0 cos θ μ y = sin θ 1 − μ z 0 2 μ y 0 μ z 0 cos φ + μ x 0 sin φ + μ y 0 cos θ μ z = − sin θ cos φ 1 − μ z 0 2 + μ z 0 cos θ   μ z 0 < 1                         μ x = sin θ cos φ μ y = sin θ sin φ μ x = μ z 0 cos θ   μ z 0 = 1
φ and θ are azimuth and scattering angle respectively. We suppose φ obeys uniform distribution as shown in Eq. (10), in which randφ1 is random number.
φ = 360 ∘ × r a n d φ 1
θ is determined by volume scattering function (VSF). There are several models for it, such as Petzold average particle phase function, Fournier- Forand (FF) function, Henyey- Greenstein (HG) function and its related approximations, etc.. Only HG function could give an analytical expression for scattering angle in Monte Carlo simulation. Although some literatures indicate that the function value in this model is less than the real water while scattering angle closely to zero or in the backward direction, the simulation error is acceptable in most cases. Hence, we will use HG function to generate scattering angle as shown in Eq. (11), not only for simplicity, but also because the analytical expression is useful to reduce the computing error in simulation.
cos θ = 1 2 g 1 + g 2 − 1 − g 2 1 − g + 2 g × r a n d θ 1 2
g is the asymmetry parameter that depends on the characteristics of medium, which equals to the average cosine of the scattering angle over all scattering directions. In this paper we set g=0.924, because it is considered as a good approximation for most practical situations [22]. randθ1 is random number. Then, the process of a photon’s motion in water could be described with Eqs. (1)-(11).
Once z≤0, we modify the coordinate to the plane z=0 by Eq. (12). We could use these photons to study the backscattering noise from “LED 1#” on “Receiver 1#”. If z≥S we modify the coordinate to the plane z=S by Eq. (13). We could use these photons to study the noise from “LED 1#” on “Receiver 2#”. Then, illumination from the forward light and backscattering noise on receivers are both acquired.
s ' = s 0 − z 0 z − z 0 X 1 = x 0 + μ x s ' Y 1 = y 0 + μ y s ' Z 1 = z 0 + μ z s '
s ' = s S − z 0 z − z 0 X 1 = x 0 + μ x s ' Y 1 = y 0 + μ y s ' Z 1 = z 0 + μ z s '
Light distribution from “LED 1#” is symmetrical to center usually. We set the center of “Receiver 1#” and “Receiver 2#” are at coordinates (0, L, 0) and (0, L, S) for simplicity. If photon’s coordinate (X1, Y1, Z1) satisfy Eq. (14), and its arriving angle to receiver is within the field of view (FOV), we record it and stop the tracing.
( X 1 − 0 ) 2 + ( Y 1 − L ) 2 ≤ d 2 2
Here d is the diameter of receiver. We denote the total number of tracing photons as N. If the number of photons arrived at “Receiver 2#” and “Receiver 1#” are NF and NB respectively. The relative intensity ηF and ηB are denoted as Eq. (15) and Eq. (16), which could be used to evaluate the forward noise from LED illumination to the opposite receiver and backscattering noise to the adjacent receiver.
η F = N F N
η B = N B N

3. Simulation Result

In order to study the influence of illumination noise, we set the diameter of luminous surface D is 0.1m for “LED 1#”, the diameter d of “Receiver 1#” and “Receiver 2#” is 0.1m, and the total number N of tracing photons is 109. Then, we analyze the variation of relative intensity ηB and ηF with the separated distance L from UWOC receiver to the optical axis of LED light, by setting different absorption coefficient a, scattering coefficient b, transmitting distance S and FOV of the receiver.

3.1. Analyze the Influence of Illumination Noise with Different Absorption Coefficient

We set (a, b, S, FOV) equals to (0.05m-1, 0.10m-1, 20m, 60°), (0.05m-1, 0.10m-1, 20m, 120°), (0.05m-1, 0.10m-1, 20m, 180°), (0.10m-1, 0.10m-1, 20m, 60°), (0.10m-1, 0.10m-1, 20m, 120°), (0.10m-1, 0.10m-1, 20m, 180°), (0.15m-1, 0.10m-1, 20m, 60°), (0.15m-1, 0.10m-1, 20m, 120°), and (0.15m-1, 0.10m-1, 20m, 180°) respectively. Then, we count the number of photons arriving at “Receiver 2#” and “Receiver 1#” to calculate the relative intensity ηF and ηB. The results ηF and ηB vary with L are shown in Figure 3 and Figure 4 respectively.
In Figure 3 and Figure 4, with the increase of separated distance L, the relative intensity ηF and ηb are both reduced. And the tendency of ηB is more evident. When absorption coefficient a is greater, or FOV is smaller, the relative intensity ηF and ηb would be smaller. Also, absorption coefficient has greater effect on ηF, while FOV has more influence on ηb.
Therefore, we conclude that the forward noise from LED illumination to the opposite receiver and backscattering noise to the adjacent receiver are both decreasing with absorption coefficient. And the change of forward noise is more evident. Narrowing receiver’s FOV would reduce such noises. Enlarging the separated distance between receivers and the optical axis of LED would reduce such noises too, while it is more evident to backscattering noise.

3.2. Analyze the Influence of Illumination Noise with Different Scattering Coefficient

We set (a, b, S, FOV) equals to (0.10m-1, 0.05m-1, 20m, 60°), (0.10m-1, 0.05m-1, 20m, 120°), (0.10m-1, 0.05m-1, 20m, 180°), (0.10m-1, 0.10m-1, 20m, 60°), (0.10m-1, 0.10m-1, 20m, 120°), (0.10m-1, 0.10m-1, 20m, 180°), (0.10m-1, 0.15m-1, 20m, 60°), (0.10m-1, 0.15m-1, 20m, 120°), and (0.10m-1, 0.15m-1, 20m, 180°) respectively. Then, we count the number of photons at “Receiver 2#” and “Receiver 1#” to calculate the relative intensity ηF and ηB. The results ηF and ηB vary with L are shown in Figure 5 and Figure 6 respectively.
In Figure 5, with the increase of separated distance L, the relative intensity ηF decreases. When the scattering coefficient b is greater, or the FOV is smaller, the relative intensity ηF is smaller. In Figure 6, with the increase of separated distance L, the relative intensity ηb is decreasing. And its tendency is more evident than ηF. When the scattering coefficient b and the FOV are smaller, the relative intensity ηF is smaller.
Therefore, we conclude that the forward noise from LED illumination to the opposite receiver is decreasing with scattering coefficient, while the backscattering noise to the adjacent receiver increases with it. Narrowing receiver’s FOV would reduce such noises, while the effect is more evident to backscattering noise. Enlarging the separated distance between receivers and the optical axis of LED would reduce such noises too, while it is more evident to backscattering noise.

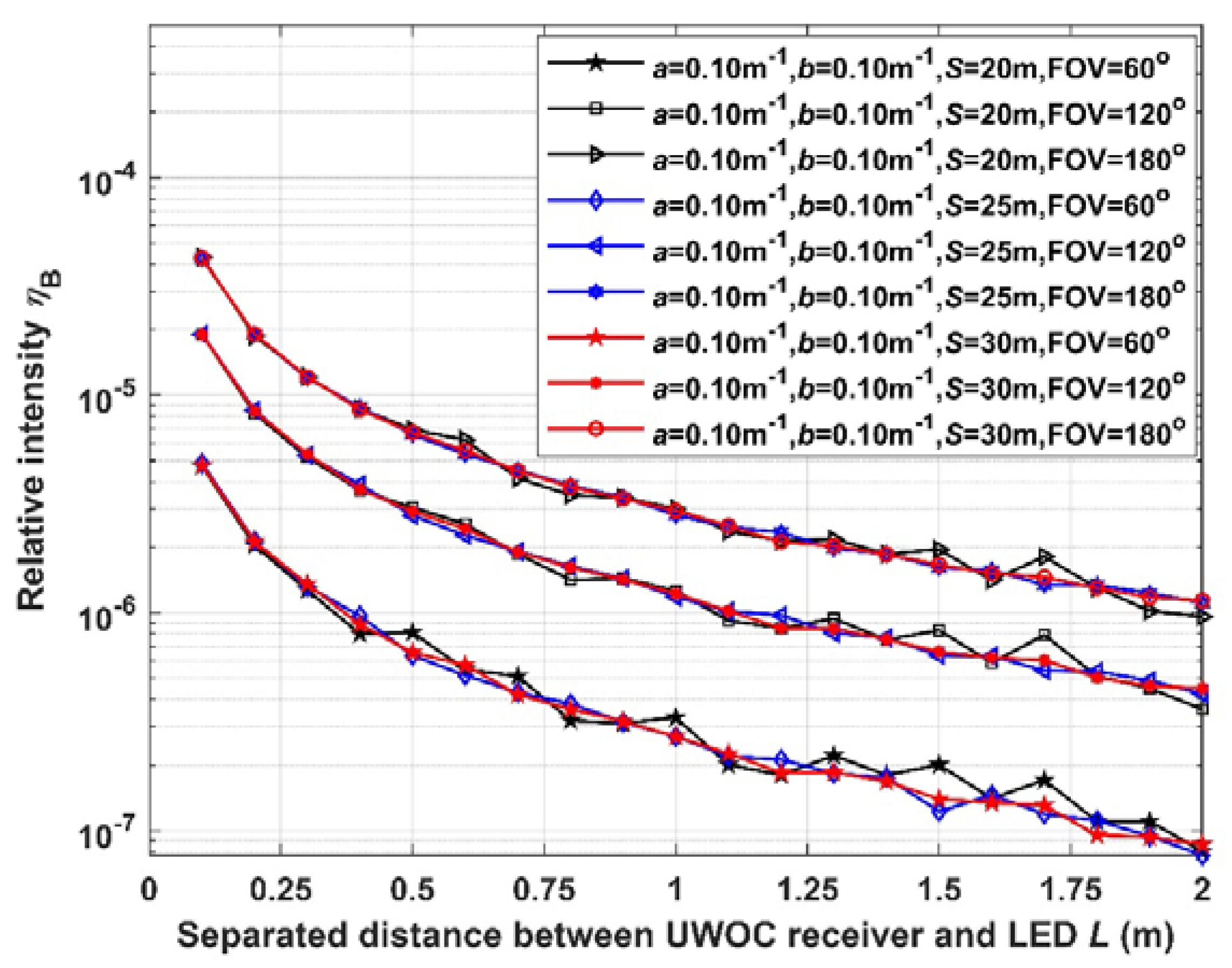
3.3. Analyze the Influence of Illumination Noise with Different Transmitting Distance

We set (a, b, S, FOV) equals to (0.10m-1, 0.10m-1, 20m, 60°), (0.10m-1, 0.10m-1, 20m, 120°), (0.10m-1, 0.10m-1, 20m, 180°), (0.10m-1, 0.10m-1, 25m, 60°), (0.10m-1, 0.10m-1, 25m, 120°), (0.10m-1, 0.10m-1, 25m, 180°), (0.10m-1, 0.10m-1, 30m, 60°), (0.10m-1, 0.10m-1, 30m, 120°), and (0.10m-1, 0.10m-1, 30m, 180°) respectively. Then, we count the number of photons at “Receiver 2#” and “Receiver 1#” to calculate the relative intensity ηF and ηB. The results ηF and ηB vary with L are shown in Figure 7 and Figure 8 respectively.
In Figure 7, with the increase of separated distance L, the relative intensity ηF decreases. When the transmitting distance S is greater, or the FOV is smaller, the relative intensity ηF is smaller. In Figure 8, with the increase of separated distance L, the relative intensity ηb is decreasing. And its tendency is more evident than ηF. When the FOV is smaller, the relative intensity ηF is smaller too. When the transmitting distance S varies, ηF nearly has no change.
Therefore, we conclude that the forward noise from LED illumination to the opposite receiver is decreasing with transmitting distance, while the backscattering noise to the adjacent nearly has no relation with it. Narrowing receiver’s FOV would reduce such noises, while the effect is more evident to backscattering noise. Enlarging the separated distance between receiver and the optical axis of LED would reduce such noises too, while it is more evident to backscattering noise.

3.4. Discussion

From the results above, it is clear that forward noise from the LED illumination affects the opposite receiver, while the backscattering noise impacts the adjacent receiver in the same terminal. With the increase of separated distance between receiver and the optical axis of LED, both the two noise decrease. And the tendency is more evident for the backscattering one. With the increase of absorption coefficient, such two noises are decrease, while the change of forward noise is more evident. With the increase of scattering coefficient, the forward noise to the opposite receiver is decreasing, while the backscattering noise to the adjacent receiver increases. With the increase of transmitting distance, the forward noise to the opposite receiver is decreasing, while the backscattering noise to the adjacent nearly has no change. With the increase of FOV, both the two noises are increasing. What needs illustration is that, when we change other simulation parameters, such results are still stand. The simulation results above could be explained theoretically.
For the opposite receiver, the forward noise is determined by the loss in the transmitting channel. When increasing the absorption coefficient, scattering coefficient, transmitting distance and the separated distance between receiver and the center of LED illumination, or narrowing the FOV of receiver, the loss becomes greater. Then, the forward noise is less.
For the adjacent receiver in the same terminal, the backscattering noise is mainly determined by the backscattering light near receiver. When the absorption coefficient enlarges, the noise light into receiver reduces a little. When the scattering coefficient enlarges, the backscattering becomes more evident and the noise is increased. When the transmitting distance increases, the backscattering has little change. When FOV reduces, or the separated distance between receiver and the center of LED increases, less light would be into receiver.
Also, from the results above, it is clear that backscattering noise from LED illumination to the adjacent receiver in the same terminal could not be neglected in application. Especially, when there are strong scattering in water.
In order to reduce such light noise from LED illumination, besides inserting optical filter in the receivers, the FOV should be smaller and the separated distance between receiver and the center of LED illumination should be longer. Such two means is more useful to the backscattering noise of the adjacent receiver.

4. Conclusions

In this paper, we study the influence of underwater LED illumination on bidirectional UWOC. Firstly, we establish a theoretical model with Monte Carlo method. Then, we simulate forward noise from the LED illumination to the opposite receiver, and the backscattering noise on the adjacent receiver in the same terminal. The results show that the forward noise is reduced with absorption coefficient, scattering coefficient, transmitting distance, separated distance between receiver and the optical axis of LED, but becomes greater with FOV of receiver. The backscattering noise is reduced with absorption coefficient and separated distance between receiver and LED, but becomes greater with FOV of receiver and scattering coefficient, while it has little relation with transmitting distance. In order to reduce such two kind noises, besides inserting optical filter in the receivers, the FOV should be smaller and the separated distance between receiver and the center of LED illumination should be longer, especially for backscattering one. The results in this paper is helpful for UWOC application. In the future, we design UWOC system with LED illumination based on them.

Author Contributions

Conceptualization, Kelin Sun, Biao Han; methodology, Kelin Sun and Jingchua Yang; investigation, Kelin Sun and Bo Li; writing-original draft preparation, Kelin Sun, Biao Han and Bin Zhang; writing review and editing, Kelin Sun and Kaibin Liu; visualization, Kelin Sun, Chen Li, and Bin Zhang; supervision, Kelin Sun. All authors have read and agreed to the published version of the manuscript

Funding

This research was funded by High level talent project of Hainan Natural Science Foundation of China, grant number 120RC676.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.

References

  1. Zhu, S.; Chen, X.; Liu, X.; Zhang, G.; Tian, P. Recent progress in and perspectives of underwater wireless optical communication. Prog. Quant. Electron. 2020, 73, 100274. [Google Scholar] [CrossRef]
  2. Kaushal, H.; Kaddoum, G. Underwater optical wireless communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
  3. Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A survey of underwater optical wireless communication. IEEE Commun. Surv. Tut. 2017, 19, 204–238. [Google Scholar] [CrossRef]
  4. Zhao, Y.; Zou, P.; Yu, W.; Chi, N. Two tributaries heterogeneous neural network based channel emulator for underwater visible light communication systems. Opt. Express 2020, 27, 22532–22541. [Google Scholar] [CrossRef] [PubMed]
  5. Hong, X.; Fei, C.; Zhang, G.; Du, J.; He, S. Discrete multitone transmission for underwater optical wireless communication system using probabilistic constellation shaping to approach channel capacity limit. Opt. Lett. 2019, 44, 558–561. [Google Scholar] [CrossRef]
  6. Chen, X.; Lyu, W.; Yu, C.; Qiu, Y.; Shao, Y.; Zhang, C.; Zhao, M.; Xu, J.; Chen, L. Diversity-reception UWOC system using solar panel array and maximum ratio combining. Opt. Express 2019, 27, 34284–34297. [Google Scholar] [CrossRef]
  7. Li, C.; Lu, H.; Huang, Y.; Huang, Q.; Xie, J.; Tsai, S. 50 Gb/s PAM4 underwater wireless optical communication systems across the water-air-water interface. Chin. Opt. Lett. 2019, 17, 100004. [Google Scholar] [CrossRef]
  8. Wang, J.; Lu, C.; Li, S.; Xu, Z. 100m/500Mbps underwater optical wireless communication using an NRZ-OOK modulated 520nm laser diode. Opt. Express 2019, 17, 12171–12181. [Google Scholar] [CrossRef]
  9. Wang, C.; Yu, H.; Zhu, Y.; Wang, T.; Ji, Y. One symbol training receiver for the SPAD-based UVLC system. Appl. Opt. 2018, 57, 5852–5858. [Google Scholar] [CrossRef] [PubMed]
  10. Yan, Q.; Li, Z.; Hong, Z.; Zhan, T.; Wang, Y. Photon-counting underwater wireless optical communication by recovering clock and data form discrete single photon pulses. IEEE Photonics J. 2019, 11, 7905815. [Google Scholar] [CrossRef]
  11. Hu, S.; Mi, L.; Zhou, T.; Chen, W. 35.88 attenuation lengths and 3.32bits/photon underwater optical wireless communication based on photon- counting receiver with 256-PPM. Opt. Express 2018, 26, 21685–21699. [Google Scholar] [CrossRef] [PubMed]
  12. Farr, N.E.; Ware, J.D.; Pontbriand, C.T.; Tivey, M.A. Demonstration of wireless data harvesting from a subsea node using a ‘ship of opportunity’. In Proceedings of the OCEANS 2013 MTS/IEEE, San Diego, USA, 23–27 September 2013. [Google Scholar]
  13. Bowen, A.D.; Jakuba, M.V.; Farr, N.E.; Ware, J.; Taylor, C.; Ibanez, D.G.; Machado, C.R.; Pontbriand, C. An un-tethered ROV for routine access and intervention in the deep sea. In Proceedings of the OCEANS 2013 MTS/IEEE, San Diego, USA, 23–27 September 2013. [Google Scholar]
  14. Pontbriand, C.; Farr, N.; Hansen, J.; Kinsey, J.C.; Pelletier, L.; Ware, J. Wireless data harvesting using the AUV sentry and WHOI optical modem. In Proceedings of the OCEANS 2015 MTS/IEEE, Washington, USA, 19–22 October 2015. [Google Scholar]
  15. Farr, N.; Bowen, A.; Ware, J.; Pontbriand, C.; Tivey, M. An integrated, underwater optical/acoustic communication system. In Proceedings of the OCEANS’10 IEEE, Sydney, Australia, 24–27 May 2010. [Google Scholar]
  16. Farr, N.; Ware, J. ; C. Pontbriand; Hammar, T.; Tivey, Sydney, Australia, 24–27 May 2010., M. Optical communication system expands CORK seafloor observatory’s bandwidth. In Proceedings of the OCEANS’10 IEEE.
  17. World’s first live video broadcast underwater uses Sonardyne’s BlueComm (2019). https://www.sonardyne.com/worlds-first-live-video-broadcast-from-underwater-uses-sonardynes-bluecomm/.
  18. Sonardyne BlueComm to stream ocean exploration missions live (2021). https://www.sonardyne.com/sonardyne-bluecomm-to-stream-ocean-exploration-missions-live/.
  19. Sawa, T.; Nishnimura, N.; Tojo, K.; Ito, Z. Practical Performance and Prospect of Underwater Optical Wireless Communication. IEICE. Trans. Fundamentals.
  20. Duntley, S. Light in the sea. J. Opt. Soc. Am. 1963, 53, 214–233. [Google Scholar] [CrossRef]
  21. Sahu, S.K.; Shanmugam, P. A theoretical study on the impact of particle scatteringinging on the channel characteristics of underwater optical communication system. Opt. Commun. 2018, 408, 3–14. [Google Scholar] [CrossRef]
  22. Gabriel, C.; Khalighi, M.; Bourennane, S.; Leon, P.; Rigaud, V. Monte-Carlo-based channel characterization for underwater optical communication systems. Opt. Commun. Netw. 2013, 5, 1–12. [Google Scholar] [CrossRef]
Preprints 71172 g001
Figure 1. Schematic diagram of simulation model.
Figure 1. Schematic diagram of simulation model.
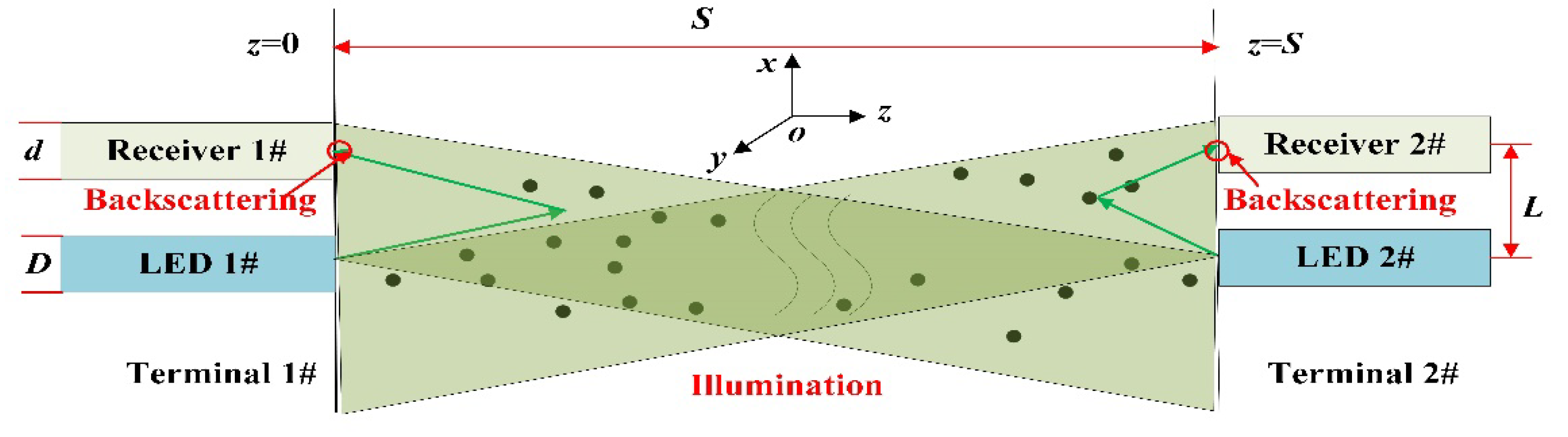
Preprints 71172 g001
Preprints 71172 g002
Figure 2. Position and direction of the initial photon.
Figure 2. Position and direction of the initial photon.
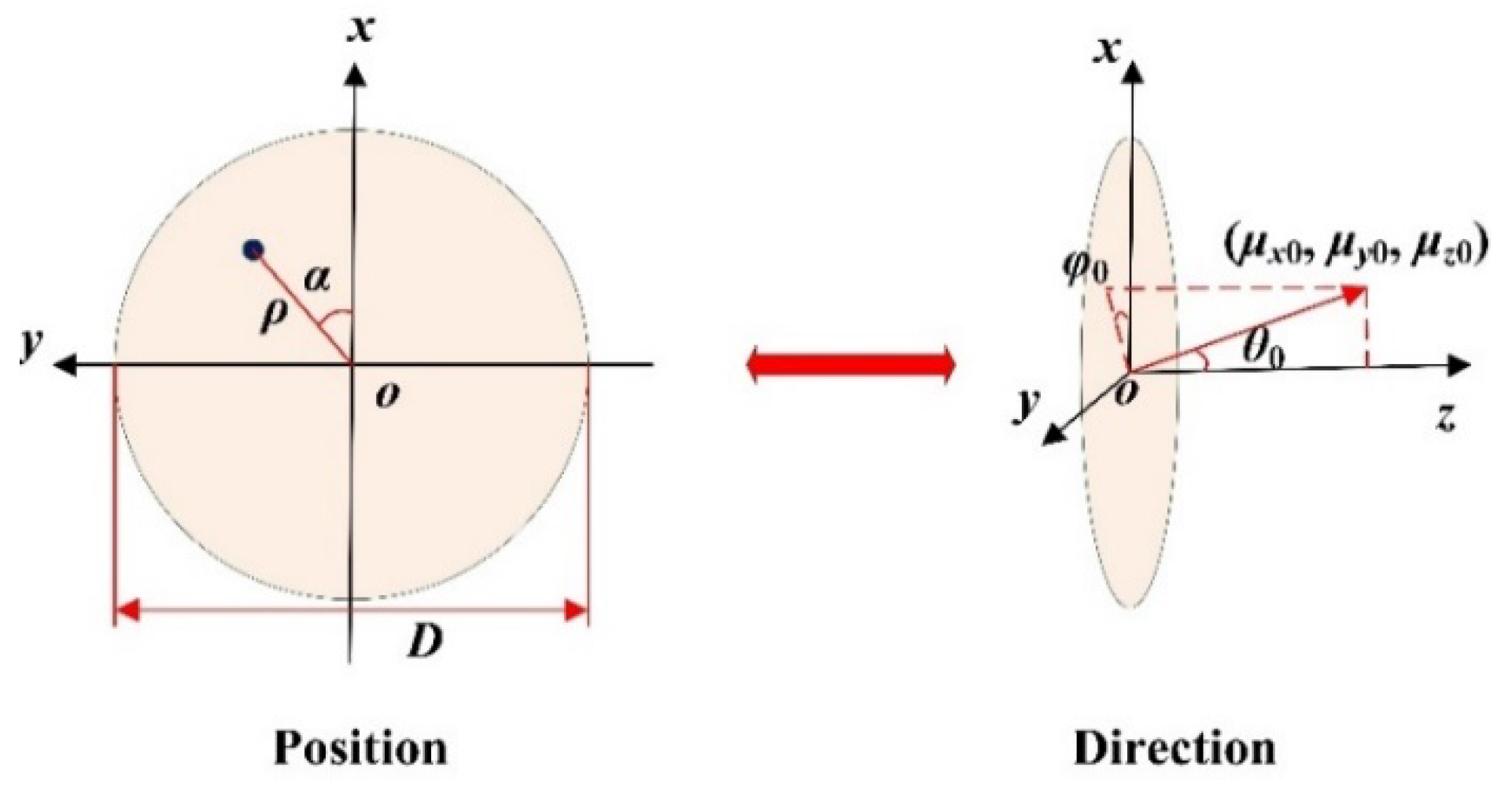
Preprints 71172 g002
Preprints 71172 g003
Figure 3. Simulation result of ηF versus L with different absorption coefficient
Figure 3. Simulation result of ηF versus L with different absorption coefficient
Preprints 71172 g003
Preprints 71172 g004
Figure 4. Simulation result of ηB versus L with different absorption coefficient
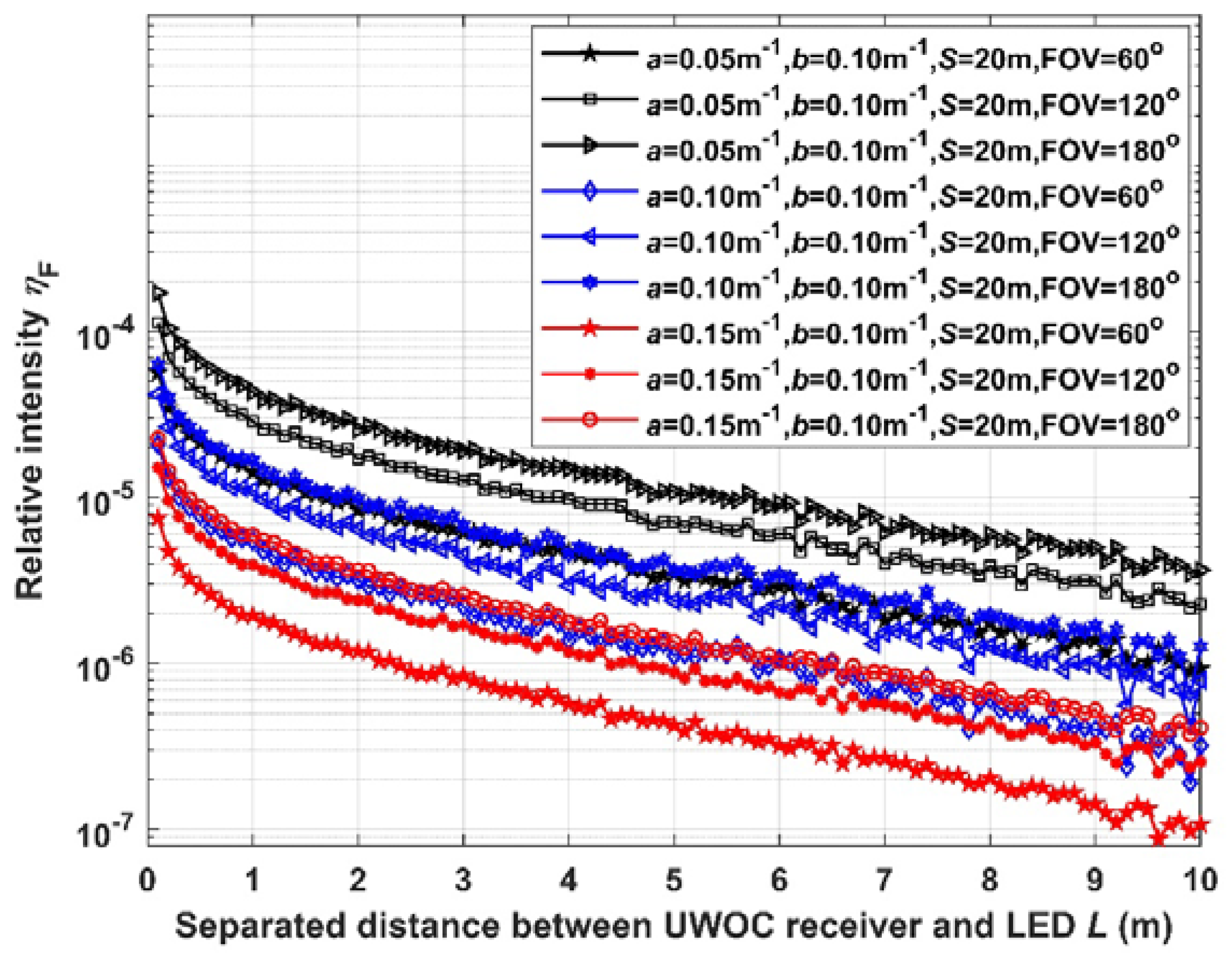
Figure 4. Simulation result of ηB versus L with different absorption coefficient
Preprints 71172 g004
Preprints 71172 g005
Figure 5. Simulation result of ηF versus L with different scattering coefficient
Figure 5. Simulation result of ηF versus L with different scattering coefficient
Preprints 71172 g005
Preprints 71172 g006
Figure 6. Simulation result of ηB versus L with different scattering coefficient
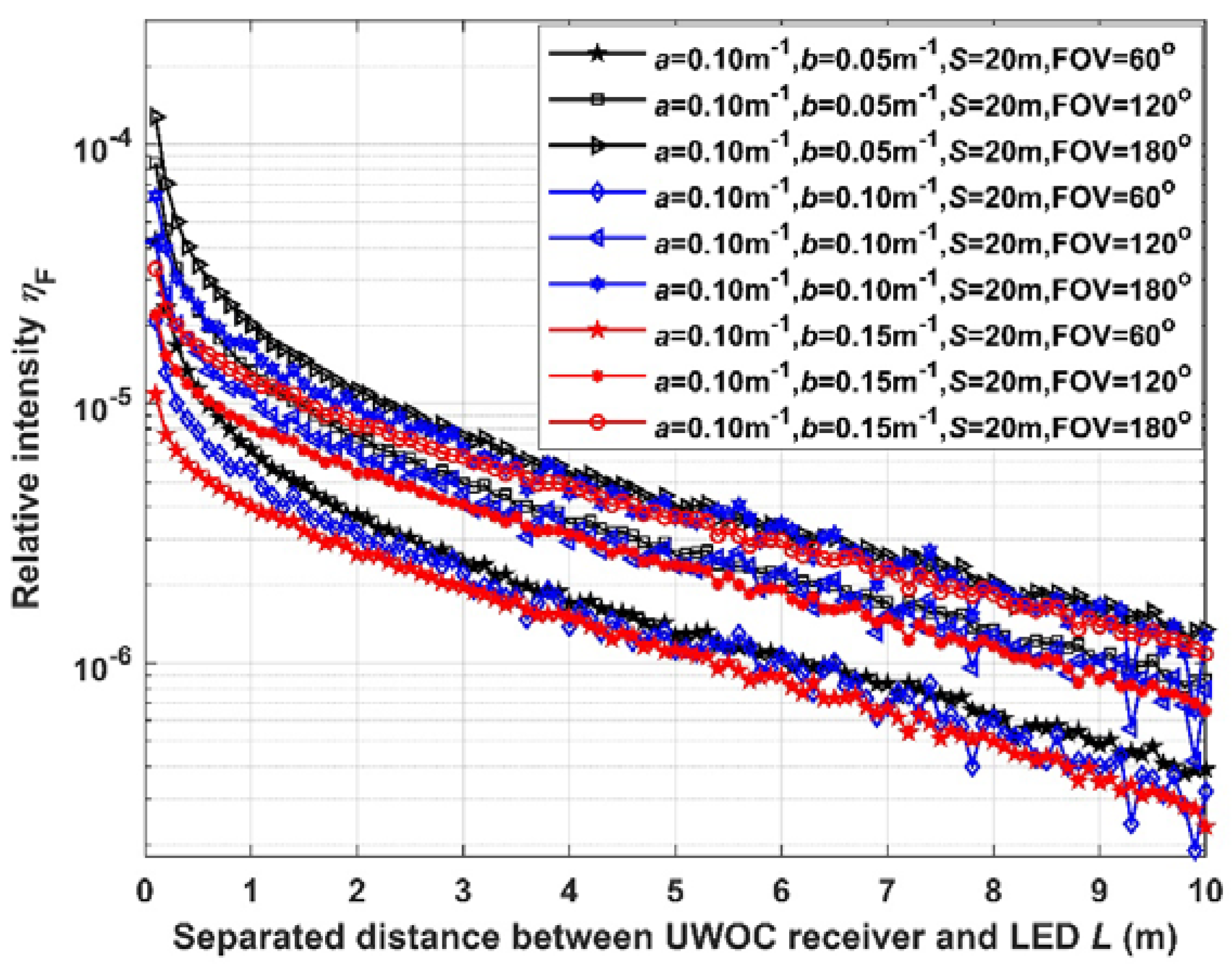
Figure 6. Simulation result of ηB versus L with different scattering coefficient
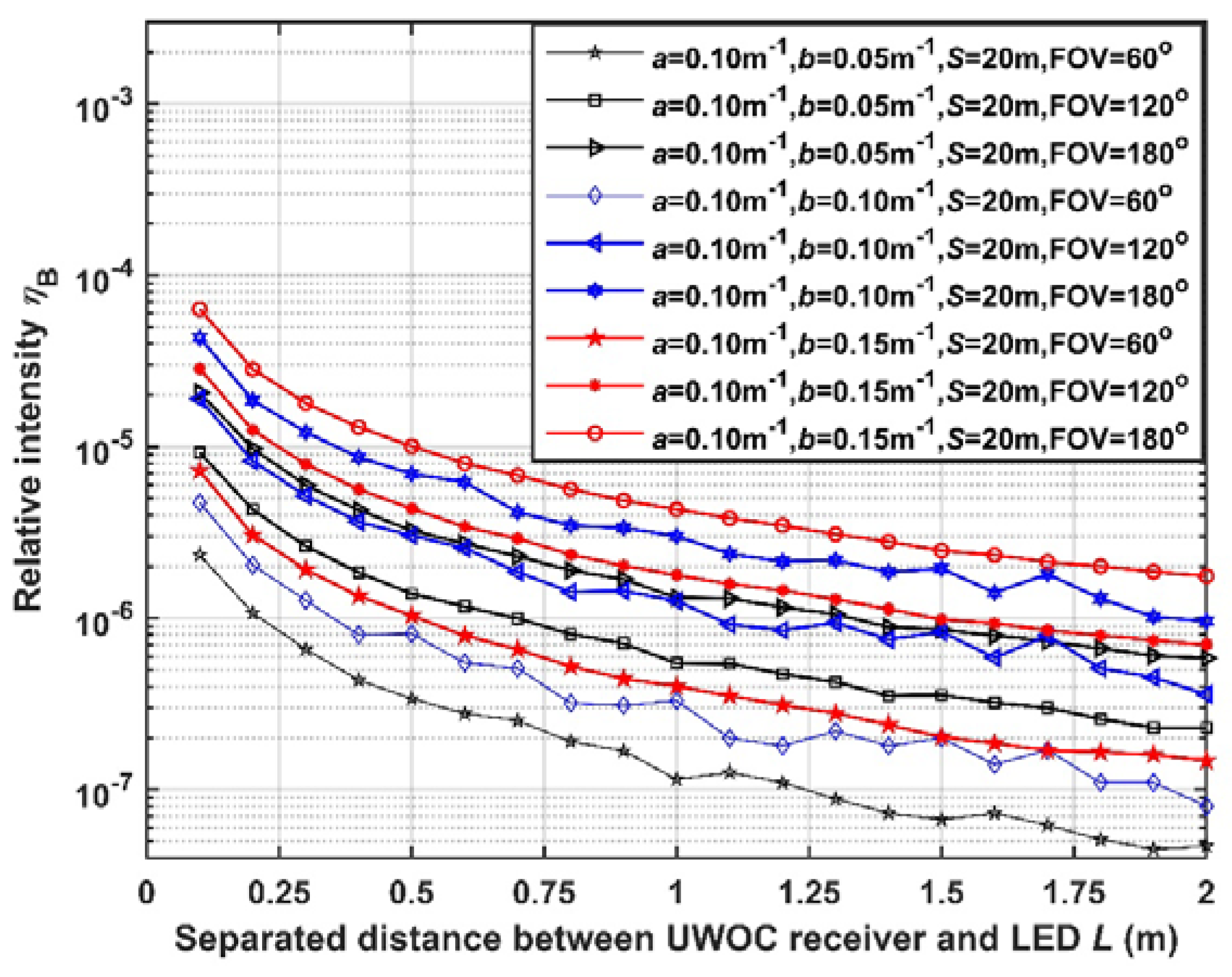
Preprints 71172 g006
Preprints 71172 g007
Figure 7. Simulation result of ηF versus L with different transmitting distance
Figure 7. Simulation result of ηF versus L with different transmitting distance
Preprints 71172 g007
Preprints 71172 g008
Figure 8. Simulation result of ηB versus L with different transmitting distance
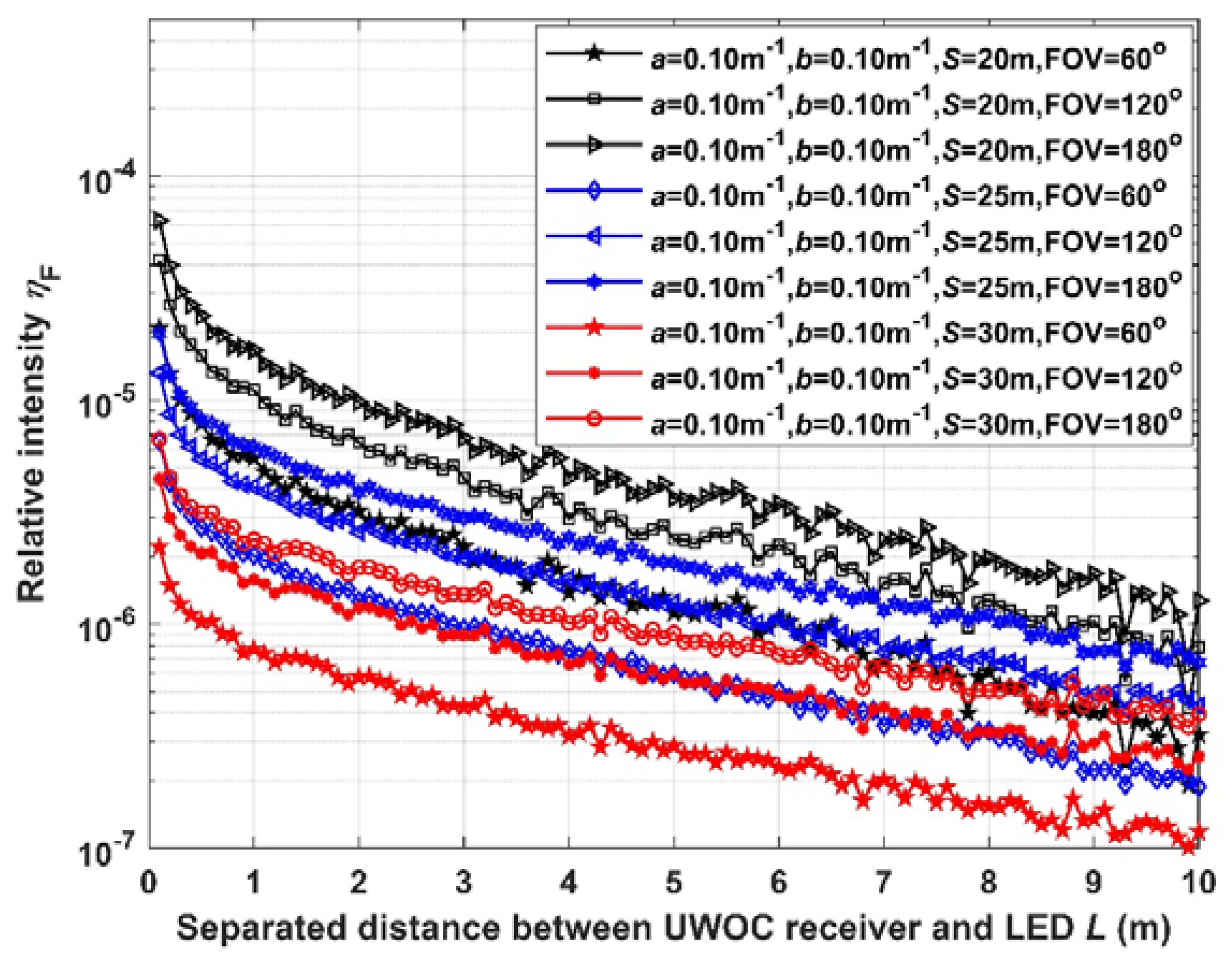
Figure 8. Simulation result of ηB versus L with different transmitting distance
Preprints 71172 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated